One Class of Ideally Secret Autonomous Symmetric Ciphering Systems Based on Wiretap Polar Codes

Preprint

Article

One Class of Ideally Secret Autonomous Symmetric Ciphering Systems Based on Wiretap Polar Codes

Altmetrics

Downloads

Views

Comments

Milan Milosavljević^*,

Jelica Radomirović,

Tomislav Unkašević

,Boško Božilović

Milan Milosavljević^*,

Jelica Radomirović,

Tomislav Unkašević

,Boško Božilović

This version is not peer-reviewed

Submitted:

10 August 2024

Posted:

13 August 2024

You are already at the latest version

Alerts

Abstract

This paper introduces a class of symmetric ciphering systems with a finite secret key, which provides ideal secrecy, autonomy in key generation and distribution, and robustness against the probabilistic structure of messages (Ideally Secret Autonomous Robust – ISAR system). The ISAR system is based on wiretap polar codes constructed over an artificial wiretap channel with a maximum secrecy capacity of 0.5. The system autonomously maintains a minimum level of key equivocation by continuously refreshing secret keys without needing additional key generation and distribution infrastructure. Thus, this class of systems generalizes Shannon's ideal and strongly ideal ciphering systems. Additionally, it can transform any stream ciphering system with a finite secret key of known length into an ISAR system without the necessity of knowing and/or changing its algorithm. Therefore, this class of system strongly supports privacy, a critical requirement for contemporary security systems. The ISAR system's reliance on wiretap polar coding for strong secrecy ensures resistance to passive attacks with known plaintext messages. Furthermore, resistance to passive attacks on generated keys follows directly from ideal secrecy and autonomy. The results presented offer an efficient methodology for synthesizing this class of systems with predetermined security margins and a complexity of the order of nlogn, where n is the block length of the applied polar code.

Keywords:

Subject: Computer Science and Mathematics - Security Systems

MSC: 94A60

1. Introduction

The notion of unconditional secrecy was introduced by Claude Shannon in [1], to describe an encryption system resistant to any passive attack on messages based on ciphertext. However, he showed in the same paper that the necessary condition for unconditional secrecy is that the secret key length must be at least as long as the message, which is impractical for most applications. To address this, various approaches have been developed to create secure ciphers with shorter keys. Shannon himself suggested so-called ideal and strongly ideal cipher systems, where an adversary is left with many equally probable decryption options, rather than a unique solution.

In this paper, we address two main questions:

Is it possible to develop a general concept for constructing ideal cipher systems with a predetermined minimum value of key equivocation, independent of the telecommunication environment, the probabilistic structure of the message, and without additional infrastructure for generating and distributing secret keys?
Is it possible to apply this solution to any existing symmetric stream ciphering system without modifying it or knowing the encryption key generation algorithm, except for the length of the applied secret key?

If feasible, such a system would possess the following properties:

Ideal secrecy - Guaranteed minimum value of key equivocation, regardless of the length of the ciphertext used by the adversary.
Autonomy - The autonomous ability to maintain a given minimum value of key equivocation by continuously refreshing keys without additional infrastructure for key generation and distribution.
Robustness - Retains guaranteed properties regardless of the probabilistic structure of the messages.

We refer to this system as the ISAR (Ideally Secure Autonomous Robust) ciphering system. This paper presents a class of ISAR systems based on wiretap polar codes.

1.1. Related Works

Since key equivocation directly depends on the entropy of messages, the first group of works on ideal ciphering systems focuses on preprocessing messages before encryption, to reduce redundancies (or equivalently to increase entropy). In this way, the minimum key equivocation available to a system attacker could be controlled. Compression and randomization techniques are standard for this approach and have a long tradition in cryptography, [1,2,3,4,5]. The homophonic coding technique, which transforms a sequence of message symbols into a uniquely decodable sequence where all symbols have the same frequency, also belongs to this approach, [2,6,7,8]. The effectiveness of this approach depends on knowledge of the probabilistic properties of messages and reliable estimates of the statistical properties of the message source being encrypted.

Another approach, not much different from the first, is entropic security, [4,9,10,11]. The main difference lies in the security metrics used as a criterion. The goal of this metric is that any function of the original message is unattainable to passive adversaries. In the limiting case, when the so-called leakage parameter is equal to zero, this criterion aligns with Shannon's definition of a perfect ciphering system. However, then all the obtained results for the length of the secret key become practically unusable or give lengths equal to the length of the messages, reducing these procedures to the Vernam cipher.

The honey cipher, introduced in [12], is similar to the concept of ideal cipher. The main goal of this approach is that an adversary is left with many highly probable hypotheses about secret keys or messages. In [13] authors combine the ideas of honey ciphers and entropic security to create, practically implementable short-key ciphering system. The dependence of the efficiency of these systems on the knowledge of the probabilistic properties of the source being encrypted is even more critical than previous approaches. This is a consequence of the very idea of the system that, in the process of brute force attacks, hypothesis messages are generated that are difficult to distinguish from the true ones. However, the future development of these systems will likely enhance understanding of the relationship between the probabilistic properties of the source and the minimum length of secret keys sufficient to prevent brute force attacks by an unbounded adversary, which brings us back to Shannon's original ideas about the meaning of non-zero equivocation values of secret keys.

The final group of methods, relevant for the construction of ideally secret systems, comes from the broad research domain of combining the methods of error correcting codes, especially wiretap codes and cryptography, [6,14,15,16,17,18,19]. In [6], a system based on wiretap codes was proposed, which proved to improve the performance of an arbitrary stream cyphering system in the regime of short messages, but whose key equivocation drops to zero for sufficiently long messages. In the paper [20], the authors integrated wiretap polar coding in encryption schemes based on learning with errors problem and showed that with appropriate refresh of secret key procedures, they achieve non-zero equivocation of keys. In paper [21], the connection between ideal secrecy and wiretap coding approach is clarified. The same authors in [22] proposed an encryption system over the MIMO wiretap channel, which for infinite lattice input alphabet guarantees perfect security, while for finite constellations guarantees ideal secrecy with high probability. In [23] authors proposed a polar coding scheme which achieves maximal secrecy capacity for a secret key of arbitrary non-zero rate, shared between transmitter and legitimate receiver. In [24] an encrypted secure polar coding scheme for general two-way wiretap channel is presented. To achieve strong security and reliability criteria, without any key pre-sharing, it is necessary to apply a complex cooperative jumming strategy.

Based on the presented analysis of the relevant published results, we can conclude the following:

Wiretap coding provides a promising environment for implementing cryptographic systems of increased security.
Works in which ideal secrecy is proven are always related to a specific ciphering system, such as in [20], or is limited to a particular physical model of the wiretap channel, as in [22] and [24].

Based on this analysis that includes all four approaches, we conclude that there is no example of an ISAR system in the available literature.

1.2. Paper Organization

Section 2 provides a basic conceptual and theoretical basis for understanding ISAR systems, particularly from the domain of wiretap channels, polar coding, privacy amplification techniques and Shannon’s notion of ideal and strongly ideal systems.

Section 3 describes the system architecture and security properties of the ISAR ciphering system. First, it is shown that the system is equivalent to a wiretap model, whose main channel is error-free, while the wiretap channel is equivalent to an embedded symmetric stream cyphering system. In Theorem 2, it is proved how wiretap coding should be constructed in order to achieve strong secrecy and reliability. Theorem 4 gives the capacity of the wiretap channel, which turns out to decrease linearly with the length of the secret key. Theorem 5 gives equivocation of secret key, while Theorem 6 gives secrecy capacity of proposed ISAR as a function of polar code length and security margins for equivocation and privacy amplification. Then it was shown that for an arbitrary cipher system to be ideal with the same lower bound of key equivocation as the ISAR system, its secret key must be

t

-times greater than that of ISAR, where

t

is proportional to message length. Thus, the superiority of the ISAR system increases with the length of the messages. The chapter concludes with a demonstration of how any symmetric stream ciphering system can be transformed into ISAR.

Section 4 provides security analysis of ISAR ciphering system, including its resistance to passive attacks both on secret keys and messages.

Section 5 summarizes the practical aspects of the implementation and application of the ISAR system in contemporary information and communication infrastructure. It is shown that the complexity of the system is

O (n \log n)

, where n is the length of the polar code. For point-to-point protection, the initial exchange of the secret key and the hash function seed is performed only once, regardless of the number of sessions or communication disruptions.

Section 6 concludes the paper with a summary of findings and suggestions for future research directions.

1.3. Notations

We define integer interval

[a, b]

as the integer set between

a

and

b

. We denote

X, Y, Z, \dots

random variables taking values in alphabets

X, Y, Z

\dots

and their realization is denoted by

x, y, z, \dots

respectively. Also, we denote a

n

size vector

X^{n} = (X_{1}, X_{2}, \dots, X_{n})

and denote

X_{a}^{b} = (X_{a}, X_{a + 1}, \dots, X_{b})

. Further, for any index set

A \subseteq [1, n]

, we define

X_{A} = {\{X_{i}\}}_{i \in A} .

H (\cdot)

denotes entropy and

I (\cdot)

denotes mutual information.

2. Preliminaries

In order to make it easier to understand the operation of the proposed system, in this section we will present basic concepts from the domain of wiretap channel model, polar coding and privacy amplification, since these three elements are its basic building blocks. In the final part of the chapter, the definition of an ideal autonomous ciphering system is given, as a kind of generalization of Shannon’s notions of ideal and strongly ideal ciphering systems, [25].

2.1. Wiretap Channel Model

The wiretap model consists of two channels

W_{m} : X \to Y

and

W_{e} : X \to Z

, the main and wiretap channels, respectively, first time introduced by Wyner [14], see Figure 1.

M

denotes the

k

-bit message that Alice wants to send to Bob. With the help of random bits, the encoder maps

M

into sequence

X

n

-bit channel symbols. This sequence is sent on the main and wiretap channels, giving the corresponding channel outputs

Y

and

Z

. On Bob's side, the decoder maps

Y

into estimate

\hat{M}

of the original message.

If the main channel is superior to the wiretap channel, we say that the wiretap channel is degraded relative to the main channel. Formally, for each wiretap channel

W_{e}

degraded with respect to the main channel

W_{m}

can be find a third channel

W_{*} : Y \to Z

, such that

W_{e}

can be represented as a cascade of channels

W_{m}

and

W_{*}

. In other words, the degraded channel always has a lower capacity compared to the main channel.

The basic purpose of wiretap coding is the design of encoders and decoders that provide for legitimate users (Alice, Bob) at the same time reliability and security when the message length

k = |M|

tends to infinity. Reliability is usually measured in terms of the probability of error in recovering the message sent by Alice at Bob's side

\lim_{k \to \infty} P r \{\hat{M} \neq M\} = 0

(1)

As a rule, security is measured in terms of mutual information between the message M and Eve's observation Z, giving the two most frequently analyzed criteria, so called week security criterion

\lim_{k \to \infty} \frac{I (M; Z)}{k} = 0

(2)

and strong security criterion

\lim_{k \to \infty} I (M; Z) = 0

(3)

As Maurer first pointed out [26,27], Eve can disclose

k^{1 - ε}, ε \in (0,1)

message bits, while (2) is still true, which is obviously unacceptable. Therefore, satisfying the strong security criterion (3) is the generally accepted gold standard of the cryptographic community. Note that there are other secrecy measures, such as advantage and semantic security, which are shown to be equivalent to the strong security criterion [15].

The largest transmission rate at which both reliability and secrecy conditions are simultaneously satisfied is commonly referred to as the secrecy capacity

C_{s}

. In case the main and wiretap channels are binary symmetric channels (BSC) and the wiretap channel is degraded with respect to the main channel,

C_{s}

was given by [28]

C_{s} = C (W_{m}) - C (W_{e}) = H (X| Z) - H (X | Y)

(4)

where the random variable

X

at the input to the channel is uniform over

X

, while

C

(

W_{m}) a n d C (W_{e})

denotes the capacities of the main and wiretap channels.

2.2. Wiretap Polar Coding

Polar codes, introduced by Erdal Arikan [29,30], are a class of error-correcting codes that achieve the capacity of binary-input symmetric memoryless (BSM) discrete channels. The key idea behind polar coding is to transform a set of

n = 2^{b}

communication channels into a set of polarized channels, where a subset of channels become nearly perfect (noiseless) and the others become completely noisy. If with

W

we denote BSM channel

〈\{0,1\}, Y, W〉

, the Bhattacharyya parameter of

W

\underset{k \to \infty}{Z (W) ≜ \sum_{y \in Y} \sqrt{W (y | 0) W (y | 1)}} = 0

(5)

Value (5) is equal to the upper bound probability of error Maximum Likelihood (ML) decoding on a single use of the channel. It is shown that

Z (W)

takes values from the interval [0,1]. Channels with small

Z (W)

values are almost noiseless, while channels with

Z (W)

values close to 1 are almost pure-noise channels [30]. The essence of wiretap polar coding is the transformation of n instances of

W_{m}

and

W_{e}

into n-input channels

W_{m}^{(i)}

and

W_{e}^{(i)}, i \in [1, n]

, which are polarized either as good or bad channels depending on their Bhattacharyya parameters

Z (W_{m}^{(i)})

and

Z (W_{e}^{(i)})

and/or symmetric capacity

C (W_{m}^{(i)}), C (W_{e}^{(i)})

. In order to achieve strong secrecy [17,18] proposed the following definition of good and bad polarized channels

P_{n} (W_{e}, δ_{n}) = \{i \in [1, n] : C (W_{e}^{(i)}) \leq δ_{n}\} δ_{n} - poor bit channels for Eve

(6)

G_{n} (W_{m}, β) = \{i \in [1, n] : Z (W_{m}^{(i)}) < 2^{- n^{β}} / n\} good for Bob

(7)

B_{n} (W_{m}, β) = \{i \in [1, n] : Z (W_{m}^{(i)}) \geq 2^{- n^{β}} / n\} bad for Bob

(8)

using security function

δ_{n}

and a parameter

β \in (0,1 / 2)

. For fixed

β

, we can define next partition of

[1, n]

R = [1, n] ∖ P_{n} (W_{e}, δ_{n}) .

(9)

A = P_{n} (W_{e}, δ_{n}) ⋂ G_{n} (W_{m}, β)

(10)

B = P_{n} (W_{e}, δ_{n}) ∖ G_{n} (W_{m}, β) .

(11)

Next, let's partition the set R into two subsets R1 and R2 (R= R1 ⋃ R2)

R 1 = R ⋂ B_{n} (W_{m}, β)

(12)

R 2 = R ⋂ G_{n} (W_{m}, β) .

(13)

This obtained subsets of polarized channels, and their meaning in terms of transmission quality in the main and wiretap channels, are shown in Table 1.

A polar wiretap encoder performs a 1-1 transformation of the original input vector

V_{1}^{n}

into an

n

-dimensional code vector

X_{1}^{n}

X_{1}^{n} = V_{1}^{n} \cdot G_{n}

(14)

where

G_{n}

is Arikan’s generator matrix, given by

G_{n} = P_{n} \cdot F^{\otimes b}

(15)

P_{n}

is the

n \times n

bit-reversal permutation matrix defined in [30], while

F^{\otimes b}

is the b-fold tensor product of

F ≜ [\begin{matrix} 1 & 0 \\ 1 & 1 \end{matrix}]

with itself. The input vector

V

has the following structure

V_{1}^{n} = [V_{R}, V_{A}, V_{B}]

(16)

The corresponding components of the input vector

V

, are set to the following values

V_{R} = e, V_{A} = M, V_{B} = 0,

(17)

where

e

is random vector, selected by Alice uniformly at random from {0, 1}. Vector of frozen bits

V_{B}

is set to 0 vector of dimension

|V_{B}| = n - |V_{B}^{C}| = n - |V_{R} \cup V_{A}|

, where

V_{B}^{C}

is the complement of

V_{B}

[1, n]

. As it was mentioned in [30], in the case of symmetric channels, any choice of frozen values is as good as other. From now on, we will assume that it is

k = |M|, m = |R|

(18)

For the described coding scheme, in [17], see Proposition 16., is proven to hold

I (M_{k}; Z_{1}^{n}) \leq |P_{n} (W_{e}, δ_{n})| δ_{n}

(19)

From here follows the conclusion that by choosing the security function

δ_{n}

, we can bound mutual information leaked to Eve, for any message distribution. Specifically, according to [17], see Theorem 17., for any security function such that

δ_{n} = o (1 / n)

(20)

described wiretap coding scheme guarantees strong security.

As for achieving reliability conditions, since it is in the general case

R 1 = R ⋂ B_{n} (W_{m}, β) \neq \emptyset

(21)

it is necessary to apply involving chaining construction [18] over multiple blocks to ensure reliability. Namely, since non frozen channels in strong security coding scheme are given by

A \cup R = G_{n} (W_{m}, β) ⋃ R 1

(22)

it is necessary to ensure reliable transmission in the channels indexed in the index set

R 1

. This is exactly what chaining construction achieves by taking a subset of indices from set

A

, i.e.,

H \subset A

such that

| H | = | R 1 |

. Random bits that are placed in

H

in the

j

-th block are used in

H

in the

(j + 1)

-th block for

j = 1, 2, 3,

…. In the first block, random bits are used that were distributed to Alice and Bob before starting communication. In this way, the SC decoder on Bob's side in each block can successfully decode the contents in the channels with indices from (22), and therefore

V_{A} = M .

Regarding the obtained secrecy capacity, the answer is provided by Theorem 1, from [17]:

Theorem 1.

For any security function

δ_{n}

, and constants

β, c_{1}, c_{2}

that satisfies condition

c_{1} 2^{{- n}^{β}} \leq δ_{n} \leq 1 - c_{2}, β \in (0,1 / 2), c_{1}, c_{2} > 0

(23)

the rate

R_{n}

of the corresponding strong-security coding scheme approaches the secrecy capacity

C_{s}

given by (4), namely

\lim_{n \to \infty} R_{n} = \underset{n \to \infty}{l i m} \frac{|A|}{n} = C (W_{m}) - C (W_{e}) = C_{s}

(24)

2.3. Privacy Amplification (PA)

Privacy amplification is a technique used in cryptography to enhance the security of a shared secret key between two parties. The primary goal is to convert a partially secure or somewhat compromised key into a highly secure key, even in the presence of an eavesdropper who may have some knowledge about the original key [19,31]. In terms of practical application, hash functions called universal families have a special role. [32].

Definition 1.

Family of

G

functions

g : A \to B

, where

A

and

B

are two final sets, is 2 – universal, or in short – universal, if it holds

\forall x_{1}, x_{2} \in A, x_{1} \neq x_{2} ⟹ P_{G} \{G (x_{1}) = G (x_{2})\} \leq \frac{1}{|B|}

(25)

where

G

is a random variable that represents a random choice of a afunction

g \in G

uniformly at random in

G

An example of a frequently used class of universal hash functions, see for example [33,34,35], is given by

H_{M} = \{h_{M} (x) = M \cdot x, x \in G F {(2)}^{k}, M \in G F {(2)}^{k \times r}\}

(26)

In applications, a random choice of a hash function from a given set is implemented using a seeded pseudorandom generator. To emphasize this fact, we explicitly introduce seed notation. Therefore, a hash function from the class

H_{M}

, is denoted as

h_{M} (x, K_{h})

(27)

where

K_{h}

denotes seed of adequate length. If

K_{h}

is available only to legitimate users, the hash functions are typically known as cryptographic hash functions.

Definition 2.

The difference between the dimensions of the domain and codomain of a given class of hash functions will be referred to as its compression rate

∆ R

Compression rate of class

H_{M}

, defined in (26) is

∆ R = r - k .

2.4. Ideal and Ideal Autonomous Cipher System

Consider a general symmetric cipher system

(X, Z, K)

, where

X

is the input plaintext,

Z

is the ciphertext, and

K

is the secret key.

According to Shannon, an ideal ciphering system is one in which the key equivocation, i.e.,

H (K| Z_{1}^{n})

remains non-zero even as the number of ciphertext symbols

n

approaches infinity, [25]. This means that the uncertainty about the key does not reduce to zero, regardless of how much ciphertext is available to an attacker. Important properties of ideal encryption systems are:

Non-zero Key Equivocation: The key remains partially unknown, no matter the length of the intercepted ciphertext.
Security over Time: The security of the system does not degrade with the amount of data encrypted and transmitted.
Practical Key Length: The key length can be shorter than the message length, unlike a one-time pad, but must be sufficient to maintain key equivocation.

A strongly ideal system has key equivocation constant at entropy of secret key, i.e

H (K| Z_{1}^{n}) = H (K) .

This implies an even higher level of security, ensuring that the key's uncertainty remains unchanged from its apriory value, regardless of the volume of ciphertext available. Key Characteristics:

Constant Key Equivocation: The amount of information about the key that remains unknown does not diminish with increasing ciphertext.
Enhanced Security: Offers superior protection against extensive ciphertext analysis, maintaining key secrecy over an indefinite amount of encrypted data.
Robust Design: Typically requires more sophisticated cryptographic techniques to ensure that key equivocation remains constant.

By distinguishing between these two concepts, Shannon's theories provide a framework for evaluating and designing cryptographic systems based on the desired level of security and practical constraints.

Starting from these founding Shannon definitions, we will define a new term - ideal autonomous ciphering system.

Definition 3.

An ideally secret autonomous robust (ISAR) ciphering system is one which can maintain minimal key equivocation at predefined value

∆_{K}

, i.e.

{H (K| Z_{1}^{n}) \geq ∆}_{K}

(27)

If several different secret keys are used during operation of one cipher system,

K_{1,} K_{2,} \dots K_{t,}

which correspond to ciphertexts

Z_{1,} Z_{2,} \dots Z_{t,}

we say that the system is ideal and autonomous if it is able to maintain a predetermined minimum value of equivocation for each of the applied keys, i.e.

H (K_{i}| Z_{i}) \geq ∆_{K}, \forall i \in [1, t]

(28)

Remark 1.

In Shannon's definition of an ideal system, it is important that the key equivocation is not reduced to zero with an unlimited increase of the available ciphertext. On the other hand, a strongly ideal cipher system requires constant maintenance of key equivocation at the entropy level of the secret key. An ideal autonomous cipher system is in a certain sense between these two extremes. It maintains the minimum value of key equivocation at a predetermined value, which in general belongs to the open interval

(0, H (K))

Remark 2.

Since

H (K| Z_{1}^{n})

is a non-increasing function of the number of observed ciphertext symbols n, the minimum in (27) is always reached at the maximum available n.

3. System Architecture and Security Properties of ISAR Cyphering System

Let the protected communication between the legitimate parties Alice and Bob take place in the successive exchange of messages

M

, which were previously divided into a series of blocks of length

k

. At their disposal is a symmetric stream cyphering system (GPSN,

K

) with short secret key

K

. As is known [1], such systems cannot provide strong security, and practical secrecy is measured by the amount of spent computer resources of the adversary (Eve) in arriving either to the message (partial system cracking) or to the secret key (total system cracking). Block

E

denotes a polar coder, which performs a 1-1 transformation of messages

M

into an

n

-dimensional codeword vector

X

, while block

E^{- 1}

performs an inverse transformation of vector

X

into message

M

. Alice and Bob have local sources of randomness (denoted by RS on Alice's side), as well as Privacy Amplification (PA) blocks, which, based on the input random string obtained in block

i - 1

, generate a shorter random string that serves as a new secret key

K (i)

for encrypting the vector

X

in block

i

. We will assume that the system uses a cryptographic hash function

h_{M} (x, K_{h})

from the class of universal hash functions (25), as well as that the seed

K_{h}

was previously exchanged between Alice and Bob. In the initial block,

K (1) = S

, i.e., the initial secret key of the given stream cipher system (GPSN,

S

Remark 3.

Additionally, we will assume that the cipher system (GPSN,

K

) is semi-injective with respect to

K

, i.e., that the knowledge of ciphers and messages uniquely determines

K

, i.e., holds

H (K | X, Z) = 0

A system conceived in this way can also be viewed as a kind of wiretap model. Legitimate users Alice and Bob are communicating over an equivalent noiseless main channel

〈M, X, W_{m}〉 = 〈\{0,1\}, \{0,1\}, I〉

, where

I

is identity matrix, see Figure 2. An eavesdropper Eve is wiretapping over an equivalent wiretap channel

〈M, Z, W_{e}〉 = 〈\{0,1\}, \{0,1\}, W_{e}〉

, where

W_{e}

is an

|M| \times |Z|

matrix

W_{e} (z| m)

being the probability of receiving

z \in Z

given that

m \in M

was sent, see Figure 4. In order to be able to apply the results presented in chapter 2, we have to prove that the equivalent wiretap channel is BSC.

Lemma 1.

Equivalent wiretap channel

〈M, Z, W_{e}〉

is a BSC.

Proof.

Equivalent wiretap channel

〈M, Z, W_{e}〉

is a BSC.

According to the proposed scheme, see Figure 4,

Z = C ⨁ X .

(29)

Since

C

is independent of

X

, (3.1) je equivalent to BSC (

σ),

where crossover probability data is

σ = P r \{C = 1\}

. □

We can now formulate the main result of this part of the work.

Theorem 2.

Let

δ_{n}

, be an arbitrary security function that satisfies condition (1). Let the index sets

A

and

R

be given by

A = P_{n} (W_{e}, δ_{n})

R = [1, n] ∖ P_{n} (W_{e}, δ_{n})

, while

e

is random vector, selected by Alice uniformly at random from {0, 1}. If in the ISAR system, the input vector is structured as follows

V_{1}^{n} = [V_{R}, V_{A}], V_{R} = e, V_{A} = M

(30)

then it satisfies both reliability and strong security criteria, precisely

P r \{M \neq \hat{M_{B}}\} = 0,

(31)

\lim_{|M| \to \infty} I (M; Z) = 0 .

(32)

Proof.

Bearing in mind that the equivalent main channel for ISAR system is noiseless, the wiretap coding scheme for strong secrecy is determined by the sets of polarized channels indices (6) – (13), which now have the following values

P_{n} (W_{e}, δ_{n}) = \{i \in [1, n] : C (W_{e}^{(i)}) \leq δ_{n}\}

(33)

G_{n} (W_{m}, β) = [1, n]

(34)

B_{n} (W_{m}, β) = \emptyset

(35)

R = [1, n] ∖ P_{n} (W_{e}, δ_{n})

(36)

A = P_{n} (W_{e}, δ_{n}) ⋂ G_{n} (W_{m}, β) = P_{n} (W_{e}, δ_{n})

(37)

B = P_{n} (W_{e}, δ_{n}) ∖ G_{n} (W_{m}, β) = P_{n} (W_{e}, δ_{n}) ∖ [1, n] = \emptyset

(38)

R 1 = R ⋂ B_{n} (W_{m}, β) = [1, n] ∖ P_{n} (W_{e}, δ_{n}) \cap \emptyset = \emptyset

(39)

R 2 = R ⋂ G_{n} (W_{m}, β) = R ⋂ [1, n] = R .

(40)

According to (39) the problematic set of indices

R 1

is an empty set, therefore it is not necessary to apply the chaining scheme. By structuring the input vector

V

according to (30), where the sets of indices

R

and

A

are given by (36) and (37) respectively, we conclude that the proposed polar coding scheme is merely an instantiation of the general polar wiretap coding scheme from section 2.2, which, under the assumptions of Theorem 2, ensures both reliability and strong secrecy. Since the main channel is noiseless, decoding on Bob's side is not performed using the SC decoder, but rather by a simple inverse operation with respect to the encoding, that is

X G_{n}^{- 1} = (V G_{n}) G_{n}^{- 1} = (V G_{n}) G_{n} = V

(41)

given that the Arikan transform matrix

G_{n}

is its own inverse over Galois field

{G F}_{2}

. Therefore, the reliability condition expressed by (31), is actually deterministically satisfied. This completes the proof. □

Theorem 3.

For any security function

δ_{n}

, and constants

β, c_{1}, c_{2}

that satisfies condition (22) the rate of the coding scheme of proposed system from Figure 2 , approaches the secrecy capacity, namely

\lim_{n \to \infty} R_{n} = \underset{n \to \infty}{l i m} \frac{|A|}{n} = 1 - C (W_{e}) .

(42)

Proof.

The proof follows directly from Theorem 1 [17], and the fact that the capacity of main channel is

C (W_{m}) = 1

. □

Remark 4.

Eve's optimal strategy is to attempt to decode the wiretapped

Z

, using the Successive Cancellation (SC) decoder, after receiving it [30]. The average block error probability at Eve’s side can be lower bounded, applying Lemma 2.9 of [36] by Korada

P_{e} (A) \geq \max_{i \in A} \frac{1}{2} (1 - \sqrt{1 - {Z (W_{n}^{i})}^{2}})

(43)

where

A

is information set. Considering that Eve does not know frozen bits on her side, the information set includes all indices, i.e.,

A = [1, n],

and the polar code applied is of rate 1, see the similar argumentation in [37]. The maximum value of

Z (W_{n}^{i})

is very close to 1, having in mind that

A

includes bad channels as well. Therefore, according to (43) it follows

P_{e} (A) \geq \frac{1}{2} - δ, δ = \frac{1}{2} \sqrt{1 - \underset{i \in A}{m a x} \{{Z (W_{n}^{i})}^{2}\}}

(44)

where

δ

is small. From this, we conclude that Eve's optimal decoding strategy of using the SC decoder results in the maximum decoding error, preventing her from obtaining both the message

M

and the purely random sequence

e

It is evident that the key properties of the proposed system depend on the capacity of the wiretap channel

C (W_{e})

. The following theorem determines the value of this quantity, depending on the length of the polar code

n

and the length of the secret key

k_{C}

Theorem 4.

The capacity of Eve’s channel in the proposed system from Figure 2 is given by

C (W_{e}) = 1 - \frac{k_{C}}{n}

(45)

where

k_{C} = |K|

is the length of the secret key of the given symmetric stream cyphering system (GPSN,

K

), while

n

is the length of the polar code.

Proof.

For a discrete memoryless symmetric channel

W_{e}

with input

X

and output

Z

, channel capacity is defined as

C (W_{e}) = \max_{p (x)} I (X; Z),

(46)

where the maximum is taken over all possible input distributions

p (x)

, [38]. Further, we have

I (X_{1}^{n}; Z_{1}^{n}) = H (X_{1}^{n}) - H (X_{1}^{n} | Z_{1}^{n}) .

(47)

The input to the wiretap channel

W_{e}

is simultaneously the input (message) to the symmetric stream ciphering system (GPSN,

K

). Message equivocation is equal to key equivocation

H (X_{1}^{n} | Z_{1}^{n}) = H (K | Z_{1}^{n})

(48)

for every semi-injective symmetric ciphering system, see Theorem 2, [39]. On the other hand, it well known that (see for example [25])

H (K| Z_{1}^{n}) = H (K) + H (X_{1}^{n}) - H (Z_{1}^{n}),

(49)

which, by substituting into (48), and then into (47) gives

I (X_{1}^{n}; Z_{1}^{n}) = H (Z_{1}^{n}) - H (K) .

(50)

One of the primary goals in the designing any cipher system is for ciphertext to appear to be totally random for as long as possible, i.e., that

H (Z_{1}^{n}) \approx n

(51)

this holds for larger values of

n

. The assumption (51) is referred to by Massey in [40] as “total randomness” assumption, and it is shown to be valid as long as

n \leq n_{u}

(52)

where

n_{u}

is the unicity distance of given cipher system, [1]. Considering (51), and the fact that

H (K) = k_{C},

since secret keys are chosen as purely random sequences, from (50) we obtain

I (X_{1}^{n}; Z_{1}^{n}) = n - k_{C}

, or normalized per bit

C (W_{e}) = \max_{p (x)} I (X; Z) = \frac{1}{n} (n - k_{C}) = 1 - \frac{k_{C}}{n},

(53)

which had to be proven. □

Remark 5.

Given Theorems 3 and 4, the secrecy capacity of the proposed system is

C_{s} = 1 - C (W_{e}) = \frac{k_{C}}{n},

(54)

from this, the fundamental impact of the secret key length is clearly evident, see Figure 5. For

k_{C} = 0

, system does not provide any security, while for

k_{C} = n

C_{s} = 1

. It means that in latter case we can choose all n bits of polar code for secure transmitting of n message bits.

In order to examine the properties of ideally secret autonomous cipher systems, we need the following theorem which provides a lower bound on the equivocation of the system’s secret keys.

Theorem 5.

The equivocation of the secret keys

K

, GPSN(

K

), when the ciphertext is known, satisfies the inequality

H (K| Z_{1}^{n}) \geq H (K) + H (V_{R}) - n,

(55)

where n is the length of the polar code,

H (K)

is the entropy of the secret key, and

V_{R} = e

is a purely random vector of dimension

|V_{R}| = | R | = |[1, n] ∖ P_{n} (W_{e}, δ_{n})|

Proof.

Generally, according to [25], for any cipher system with a secret key

K

, input

X_{1}^{n}

, and ciphertext(output)

Z_{1}^{n}

, it holds

H (K| Z_{1}^{n}) = H (K) + H (X_{1}^{n}) - H (Z_{1}^{n})

. Based on (13), the output vector

X_{1}^{n}

can be written in the form

X_{1}^{n} = V_{R} G_{R} \oplus V_{A} G_{A} = e_{1}^{n - k} G_{R} \oplus m_{1}^{k} G_{A}

(56)

where

G_{R}

and

G_{A}

are submatrices of polar code generation matrix

G,

consisting of corresponding rows in

G

The ranks of the matrices

G_{R}

and

G_{A}

are

n - k

and

k

, respectively, because the generator matrix

G

has full rank

n

. Therefore

e_{1}^{n - k} G_{R}

and

m_{1}^{k} G_{A}

can be uniquely represented by a set of basis vectors of dimensions

n - k

and

k

. These basis vectors are some of the column vectors of the matrices

G_{R}

and

G_{A}

respectively. We will denote these sets of column indices as

T_{R}

and

T_{A}

. Then there exists a one-to-one correspondence between

e_{1}^{n - k}

and

X_{T_{R}}

, and between

m_{1}^{k}

and

X_{T_{A}}

. Hence

H (V_{R} G_{R}) = H (V_{R}),

(57)

H (V_{A} G_{A}) = H (V_{A}) .

(58)

Based on the data processing properties of entropy [38] , we conclude that in the PA procedure there is a limitation,

{n C_{s} = k}_{c} \leq H (V_{R}) = n - k = n - n C_{s}

, from which it follows that the secrecy capacity in the ISAR system must be

C_{s} < \frac{1}{2} .

Thus, it holds that

H (X_{1}^{n}) = V_{R} G_{R} \oplus V_{A} G_{A} \geq m a x \{H (V_{R}), H (V_{A})\} = H (V_{R})

(59)

given the condition

C_{s} < \frac{1}{2}

and the fact that

V_{R}

is purely random vector with maximum entropy equal to

H (V_{R}) = |V_{R}| = n - k .

Since it is always true that

H (Z_{1}^{n}) \leq n,

(60)

we finally get

H (K| Z_{1}^{n}) = H (K) + H (X_{1}^{n}) - H (Z_{1}^{n}) \geq H (K) + H (V_{R}) - n

(61)

which had to be proven. □

To ensure the system possesses autonomy in generating secret keys, we must restrict the secrecy capacity, as some of the bits of the polar code need to be used for generating and distributing secret keys. Additionally, for the system to be ideal and autonomous, a further reduction in secrecy capacity is necessary to maintain the desired minimum level of key equivocation. These facts are summarized in Theorem 6 below.

Theorem 6.

The proposed system is ideal and autonomous, with secrecy capacity

C_{s} = \frac{1}{2} - \frac{1}{2 n} (∆_{K} + ∆ R),

(62)

where

∆_{K} \in (0, \frac{n}{2})

is a given minimum value of key equivocation, and

∆ R

is the compression rate of the applied class of universal hash functions.

Proof.

To prove that the proposed system is ideal, it is necessary to show that

H (K| Z) > 0

, kada

|Z| \to \infty .

Since

|Z| = |M|,

this is equivalent to the condition

H (K| Z) > 0

, as

M \to \infty .

Consider the general case where Alice sends Bob a message

M

of arbitrary length

{|M| = n}_{M}

. The message

M

will be divided into blocks of length

k = |A| = |P_{n} (W_{e}, δ_{n})| .

The total number of blocks will be

t = ⌈\frac{n_{M}}{n}⌉

, where

n

is the length of the polar code, so

M = [m_{1} |m_{2}| \dots | m_{t}] .

The last block, if it is not of length

k

, can be padded with arbitrary content. According to the proposed coding scheme that provides strong security,

n - k = |R| = n - |A| = n - |P_{n} (W_{e}, δ_{n})|

. Based on (41), in addition to the transmitted message

m_{i}

, Bob decodes without error a purely random vector

e_{i}

, of length

n - k

, which was written on the indices from the set

R

given in (36) during the encoding process on Alice's side. Thus, Alice and Bob, after decoding, possess identical random sequences

\{{e_{1}, e_{2}, \dots, e}_{t}\}

, in each of the

t

transmitted blocks of the polar code. Eve's optimal strategy is to decode her received signal at the output of the wiretap channel using the SC decoder. Eve knows the parameters of the applied polar code, such as the length

n

, and the index sets A and R, but does not know the values of the bits at those positions. This situation is equivalent to the SC decoder operating in the mode of unknown so-called frozen bits. As noted in Remark 4, Eve's error in optimal decoding is close to the maximum, so it can be said that Eve's information about the sequence

\{{e_{1}, e_{2}, \dots, e}_{t}\}

is close to zero. By applying PA to the common random sequences

\{e_{i}\}

, Alice and Bob can further reduce Eve's residual information about these sequences. In each current block, a secret key of length

k_{C}

is generated for the next block using some chosen PA algorithm

K_{i} = P A (e_{i - 1}), e_{0} = S, |K_{i}| = k_{C}, i = 1,2, \dots, t .

(63)

Given that

∆ R

is the compression rate of the class of universal hash functions applied in the PA process, it follows that

| K_{i} | = |e_{i - 1}| - ∆ R i = 1,2, \dots, t .

(64)

Considering Theorem 2 and (64), and assuming the ergodicity of the local randomness source, i.e.,

H (e_{i - 1}) = n - k

i = 1,2, \dots, t

, it can be obtained from (53)

k_{C} = n - k - ∆ R = n - n C_{s} - ∆ R, i = 1,2, \dots, t .

(65)

For the system to be ideal, it is sufficient to ensure that the right-hand side of (61) equals a predetermined minimum value of key equivocation

∆_{K} > 0

, in each block, i.e.

H (K_{i}) + H (V_{R i}) - n = ∆_{K}, i = 1,2, \dots, t .

(66)

that is

k_{C} + n - k - n = k_{C} - k = k_{C} - n C_{s} {= ∆}_{K} .

(67)

By substituting (65) into (67) it is obtained that

C_{s} = \frac{1}{2} - \frac{1}{2 n} (∆_{K} + ∆ R)

(68)

which had to be proven. □

In Figure 6 and Figure 7, the dependence of the secrecy capacity

C_{s}

on the normalized minimum value of key equivocation

\frac{∆_{K}}{n}

and the normalized compression rate

\frac{∆ R}{n}

of the hash function applied in the PA process is shown.

Note that if the security margins

∆_{K}

and

∆ R

are fixed constants, then based on Theorem 6, we conclude that

\lim_{n \to \infty} C_{s} = \frac{1}{2}

holds, which is the maximum possible value of the secret capacity of ISAR system.

The presented theoretical offer an effective methodology for synthesizing this class of systems with predetermined security margins. Table 2 outlines the algorithms for configuring the ISAR system and for enciphering/deciphering messages of arbitrary length. Based on the initial values of parameters

∆_{K}

and

∆ R

, the secrecy capacity

C_{s}

and the length of the secret key

k_{C}

are determined. If these parameters are acceptable, the synthesis of the corresponding wiretap polar code proceeds. Identifying the index sets

A = P_{n} (W_{e}, δ_{n})

and

R = [1, n] ∖ P_{n} (W_{e}, δ_{n})

, requires the polarization of the wiretap channel. For practical purposes, it is simpler to replace this channel with an equivalent

B S C ()

channel of the same capacity. Consequently, the crossover probability must satisfy the condition

= h_{b}^{- 1} (\frac{k_{C}}{n})

(69)

where

h_{b} (a) = - a \log a - (1 - a) \log 1 - a), 0 < a < 1, h_{b} (0) = h_{b} (1) = 0

(70)

is the binary entropy function, and

h_{b}^{- 1}

is its inversion. The polarization procedure under SC decoding can be performed using various methods, such as Monte-Carlo [30], Density Evolution (DE) [41,42], DE with Gaussian Approximation (GA) [43], among others. In the ISAR system, where the wiretap channel is designed by the system developer, all essential parameters for the wiretap channel are much more accessible and accurately estimated compared to a scenarios involving real wiretap channels. For instance, when determining the Bhattacharyya parameters

Z (W_{e}^{(i)})

using the Monte-Carlo method for polarization, generating an ensemble of wiretap channel output samples is manageable. This process is facilitated by the precise knowledge of the crossover probability (69), allowing for accurate assessment of the results.

Remark 6.

Let's compare the proposed ISAR system with a classic ideal cipher system that has the same minimal key equivocation value for the same length of observed ciphertext. To ensure a fair comparison, we will assume that the entropy of the input messages is identical in both systems. After encrypting blocks of messages, and assuming the blocks are independent, the ISAR system has a total equivocation of all applied keys equal to

H (K_{1}, \dots, K_{t} | Z_{1}, \dots, Z_{t}) = \sum_{i = 1}^{t} H (K_{i}| Z_{i}) = t H (K) + t H (V_{R}) - n t \geq t ∆_{k}

(71)

since the formation of each block in the polar code is independent of the previously formed blocks, a classic ideal cipher system with secret key

K_{c l a s s}

under the same conditions and for the same length of ciphertext, has an equivocation given by

H (K_{c l a s s}| Z_{1}^{n t}) = H (K_{c l a s s}) + t H (V_{R}) - n t \geq t ∆_{k} .

(72)

Equating (71) and (72) yields the condition that

H (K_{c l a s s}) = t H (K),

(73)

that is,

|K_{c l a s s}| = t |K|,

(74)

assumed that all secret keys in both systems have maximum entropy.

To ensure that a classic encryption system achieves the same lower bound on key equivocation as the ISAR system for a given ciphertext length, it would need a secret key t-times longer than the key length of the GPSN(

K

), see Figure 8. Additionally,

K_{c l a s s}

must be pre-distributed to legitimate parties. The length of this key scales linearly with the message length

|M|

, specifically with

t = ⌈\frac{|M|}{n}⌉

. In contrast, the proposed ideal autonomous system requires only a fixed-length secret key K, independent of the message length, and necessitates only an initial exchange of the key values

K_{1} = S

. Therefore, the benefits of the ISAR system become more significant as the length of the messages increases.

Remark 7.

The ISAR system can be obtained by a suitable transformation of any given stream ciphering system GPSN(

K

) with a known secret key length

| K | = k_{C}

. The procedure includes the following steps:

Based on the expression (62) for the given value of the length of the secret key $k_{C}$ , we can directly obtain the required length of the polar code, i.e.,

$n = 2 k_{C} {+ ∆}_{K} + ∆ R .$

(75)

Since the length of the polar code must be a power of 2, it is necessary to correct (75) to the value

$\tilde{n} = 2^{⌈\log_{2} n⌉} .$

(76)
The corrected value of the length of the polar code block (76) allows the eventual correction of the total security margin to the new value

${\tilde{∆}}_{K} + \tilde{∆} R = \tilde{n} - 2 k_{C}$

(77)

bearing in mind the limitation

${\tilde{∆}}_{K} \leq k_{C} .$

(78)
Since all elements for ISAR system setup are available in this step, i.e., $\tilde{n}, {\tilde{∆}}_{K}, \tilde{∆} R, δ_{\tilde{n}}$ , further operation of the system takes place according to the algorithm from Table 2.

4. Security Analysis of ISAR Ciphering System

In the following analysis, we will focus on the examination of passive attacks on the system. This implies that the attacker has access to the output of the wiretap channel and all information related to the architecture and operation of the system, except for the initial value

K_{1} = S

and the seed of the chosen hash function

K_{h} .

Based on the primary objective of the attack, we can distinguish three types: message attacks, attacks on locally generated random sequences, and attacks on the secret key.

4.1. Message Attacks

In this type of attack, Eve attempts to obtain the message

m_{i}

in each block based on the observation of the wiretap channel output

Z_{i}

According to Theorem 2, the proposed system satisfies the strong security criterion (32), which means that asymptotically, with an increase in the codeword length

n

, Eve can only acquire a negligible amount of information about the messages

m_{i}

4.2. Attacks on Locally Generated Random Sequences

In this type of attack, Eve first tries to obtain one of the random sequences

\{{e_{1}, e_{2}, \dots, e}_{t}\}

locally generated by Alice based on the observation of the wiretap channel outputs

\{Z_{1}, \dots, Z_{t}\}

. In the second step, using some obtained value

e_{i^{*}}, i^{*} \in [1, t - 1]

, Alice could potentially generate the correct secret key for the next block

i^{*} + 1

. Knowing the secret key for block

i^{*} + 1

, Eve could successfully decode all subsequent blocks, thereby obtaining all messages in the sequence

\{m_{i^{*} + 1}, m_{i^{*} + 2}, \dots, m_{t}\}

. However, this scenario is not feasible. The first step cannot be realized since, according to Remark 3.2, the average block error probability on Eve's side is close to maximal (see (44)). The second step is not possible without knowing the seed of the chosen hash function

K_{h} .

As the success of this attack depends on the success of both steps, this type of attack is practically unfeasible because the overall difficulty of the attack is equal to the product of the difficulties of both steps.

4.3. Attacks on the Secret Key GPSN( $K$ )

A far more powerful cryptanalytic attack than an attack on individual messages is an attack on the secret key of the GPSN. If Eve were to obtain the secret key

K_{i^{*}}

in block

i^{*}

where

i^{*} \in [1, t - 1]

, she would be able to access message

m_{i^{*}}

, the random sequence

e_{i^{*}}

, and consequently the secret key

K_{i^{*} + 1}

for the next block. This would allow her to repeat the same process for each subsequent block, thereby gaining access to all subsequent transmitted messages

\{m_{i^{*} + 1}, m_{i^{*} + 2}, \dots, m_{t}\}

, random sequenced

\{e_{i^{*} + 1}, e_{i^{*} + 2}, \dots, e_{t}\}

and generated secret keys

\{K_{i^{*} + 1}, K_{i^{*} + 2}, \dots, K_{t}\} .

From the system designer's perspective, it is crucial to prevent this scenario. The information-theoretic quantity that quantifies the likelihood of such an attack is the equivocation of the secret keys for a given wiretap channel output. As the ISAR system is ideally secure, its secret key equivocation, according to (66), never falls below the value

∆_{k}

, which is the security parameter in the synthesis process of ISAR. Therefore, the system designer can render this attack unsuccessful with any chosen margin of security. It is important to note that increasing the margin of security leads to a reduction in the secrecy capacity of ISAR (see Theorem 6 and Figure 7).

Example To understand the order of magnitude of the difficulty of executing this attack, let us consider a typical example of ISAR with parameters (expressed in bits)

n = 4096, ∆_{k} = 100, ∆ R = 40

. According to (62),

C_{s} = 0.4829

, and the key length is

k_{c} = n C_{s} = 1978

bits. Let’s assume that Eve’s optimal strategy for each block of the polar wiretap code reaches the lower bound of equivocation of 100 bits of the key. This means that Eve cannot resolve this uncertainty in any way. Recall that in a brute force attack examining all

2^{100}

possible keys, all decrypted messages would be equally likely and valid as potential final solutions.

The above example shows that for the polar code length n of order

2^{b}

, the key length of GPSN(

K

) is of order

2^{b - 1}

. These lengths are not common for commercial stream ciphering systems. However, this does not mean that such systems cannot be relatively easily upgraded to the required key lengths. As an example, we cite a generic model of a pseudo-random generator described in [44]. If the address and selection sequences are chosen so that they are the outputs of two multiple linear shift registers, then the lengths of the equivalent secret key of this pseudo-random generator can easily be set in ranges of order

2^{b - 1}

5. Practical Aspects

5.1. Complexity of ISAR

Computational complexity of the ISAR system includes the total complexity of polar coding and decoding, as well as the complexity of the PA block.

Polar codes are attractive in practice due to their relatively low complexity compared to other coding schemes, especially when considering the powerful error-correcting capabilities they offer. The complexity of encoding a polar code of block size n is

O (n \log n)

. This efficient complexity is due to the structured way in which the polar transform combines inputs, leveraging the recursive nature of the polar code construction, and can be performed using the Fast Fourier Transform (FFT) approach.

In general, decoding complexity depends on the applied decoding algorithm. However, in the ISAR system decoding is a deterministic procedure identical to encoding since Arikan's generator matrix is involutory. Therefore, the complexity of decoding is identical to the complexity of encoding, i.e.,

O (n \log n)

, [30].

The PA block was implemented using random binary matrices of dimension n×

k_{c}

, which have the Toeplitz structure. It is known that this class of hash functions belongs to the universal family of hash functions, see [45,46]. The Toeplitz hash functions are particularly suitable for typical values for n in polar coding (order of

2^{10} - 2^{16}

). Namely, the PA block can be efficiently implemented with a complexity of

O (n \log n)

, instead of O(

n^{2}

), in the case of hash functions in the form of random binary matrices without the Toeplitz structure.

Consequently, we can say that the complexity of the ISAR system, without taking into account the complexity of GPSN(

K

), is of the order of

O (n \log n)

, which indicates that the implementation of the proposed algorithm does not require special memory and computational resources. This makes it very attractive for practical implementation and use.

5.2. Integration of ISAR Ciphering System in Contemporary Information and Communication Infrastructure

When applying ISAR in modern information and communication infrastructure, you should keep in mind the two most important advantages of this system:

Guaranteed security margins in terms of key equivocation (ideality)
Independence of the length of the keys from the length of the messages.

The ideal position of the ISAR system is within the framework of permanent point-to-point protection of large-capacity information flows. That's when ideality and the independence of the length of the keys from the length of the messages come into play. As already mentioned, the start of communication requires the exchange of the secret key of GPSN(K) and the seed of the applied crypto hash function. It is interesting to note that disruption of protected communication or its regular termination does not require additional exchange of these values for subsequent communication. Namely, the decoded random sequences of the last block of polar code can be memorized and used to generate the initial key for subsequent communication. This raised the autonomy of the ISAR system to an even higher level.

6. Conclusions

In this paper, we introduced a class of symmetric ciphering systems termed ISAR (Ideally Secret Autonomous Robust) systems. These systems are designed to provide ideal secrecy, autonomy in key generation and distribution, and robustness to the probabilistic structure of messages. These systems address the longstanding challenge in cryptography of balancing security with practicality, particularly by eliminating the need for lengthy secret keys and additional key distribution infrastructure. By ensuring a predetermined minimum value of key equivocation and continuous key refreshing, ISAR systems provide robust security against passive attacks on both keys and messages.

Our work demonstrates that ISAR systems can be applied to any existing symmetric stream ciphering system without requiring changes to the original encryption algorithm, thus offering a versatile and efficient solution for enhancing the security of current cryptographic practices. This transformation greatly supports privacy, a critical requirement for modern security systems.

Overall, the ISAR system represents an advancement in cryptographic security, offering an efficient methodology for creating ciphering systems with predetermined security margins. Future research directions include exploring further optimizations in the ISAR architecture, extending its applicability to a broader range of cryptographic scenarios, and investigating additional techniques for enhancing its resistance to more sophisticated attack vectors. The continued development of ISAR systems holds the promise of ensuring stronger privacy and security measures in an increasingly digital world.

Author Contributions

Conceptualization, M.M.; methodology, M.M., T.U., J.R.; software, J.R.; validation, M.M., J.R., B.B.; formal analysis, M.M., J.R., T.U.; investigation, M.M., J.R.; resources, B.B.; data curation, J.R., B.B.; writing—original draft preparation, M.M., J.R.; writing—review and editing, M.M., J.R.; visualization, M.M., J.R.; supervision, M.M., B.B.; project administration, J.R.; funding acquisition, B.B. All authors have read and agreed to the published version of the manuscript.

Funding

The research is funded by the Vlatacom Institute of High Technologies under project #164 EEG_Keys.

Conflicts of Interest

The authors declare no conflict of interest.

References

Shannon, C.E. Communication Theory of Secrecy Systems*. Bell Syst. Tech. J. 1949, 28, 656–715. [CrossRef]
Gunther, C. G. A universal algorithm for homophonic coding. In Workshop on the Theory and Application of Cryptographic Techniques, Springer: Berlin, Heidelberg, 1988, pp. 405-414.
Massey, J.L. Some applications of source coding in cryptography. Eur. Trans. Telecommun. 1994, 5, 421–430. [CrossRef]
Ryabko, B. Unconditionally secure short key ciphers based on data compression and randomization. Des. Codes Cryptogr. 2023, 91, 2201–2212. [CrossRef]
Ryabko, B. Ya. A simply realizable ideal cryptographic system. Problems of Information Transmission 2000, 36, 84-89.
Oggier, F.; Mihaljevic, M.J. An Information-Theoretic Security Evaluation of a Class of Randomized Encryption Schemes. IEEE Trans. Inf. Forensics Secur. 2014, 9, 158–168. [CrossRef]
Ryabko, B.; Fionov, A. Efficient homophonic coding. IEEE Trans. Inf. Theory 1999, 45, 2083–2091. [CrossRef]
Agrikola, T.; Couteau, G.; Ishai, Y.; Jarecki, S.; Sahai, A. On pseudorandom encodings. In Theory of Cryptography Conference, Springer, Cham, 2020, pp. 639-669.
Russell, A.; Wang, H. How to fool an unbounded adversary with a short key. IEEE Trans. Inf. Theory 2006, 52, 1130–1140. [CrossRef]
Dodis, Y.; Smith, A. Entropic security and the encryption of high entropy messages. In: Theory of Cryptography Conference, Springer, Berlin, Heidelberg, 2005, pp. 556-577.
Ryabko, B. Unconditionally Secure Ciphers with a Short Key for a Source with Unknown Statistics. Entropy 2023, 25, 1406. [CrossRef]
Juels, A.; Ristenpart, T. Honey encryption: Security beyond the brute-force bound. In Advances in Cryptology-EUROCRYPT 2014, Springer, Berlin, Heidelberg, 2014, pp. 293-310.
Li, X.; Tang, Q.; Zhang, Z. Fooling an Unbounded Adversary with a Short Key, Repeatedly: The Honey Encryption Perspective. In 2nd Conference on Information-Theoretic Cryptography, Schloss Dagstuhl – Leibniz-Zentrum für Informatik, 2021, pp. 23:1-23:21.
Wyner, A.D. The wire-tap channel. Bell System Tech. J. 1975, 54, 1355–1387.
Bellare, M.; Tessaro, S.; Vardy, A. Semantic security for the wiretap channel. In International cryptology conference (CRYPTO). Springer, 2012, pp. 294–311.
Harrison, W.K.; Almeida, J.; Bloch, M.R.; McLaughlin, S.W.; Barros, J. Coding for Secrecy: An Overview of Error-Control Coding Techniques for Physical-Layer Security. IEEE Signal Process. Mag. 2013, 30, 41–50. [CrossRef]
Mahdavifar, H.; Vardy, A. Achieving the Secrecy Capacity of Wiretap Channels Using Polar Codes. IEEE Trans. Inf. Theory 2011, 57, 6428–6443. [CrossRef]
Sasoglu, E.; Vardy, A. A new polar coding scheme for strong security on wiretap channels. 2013 IEEE International Symposium on Information Theory (ISIT), Istanbul, Turkey; pp. 1117–1121.
Bloch, M.; Barros, J. Physical-layer security: From information theory to security engineering; Cambridge University Press: Cambridge, UK, 2011.
Rajagopalan, A.; Thangaraj, A.; Agrawal, S. Wiretap Polar Codes in Encryption Schemes Based on Learning with Errors Problem. 2018 IEEE International Symposium on Information Theory (ISIT), Vail, CO, USA; pp. 1146–1150.
Liu, S.; Hong, Y.; Viterbo, E. Unshared secret key cryptography: Achieving Shannon's ideal secrecy and perfect secrecy. 2014 IEEE Information Theory Workshop (ITW 2014), Hobart, TAS, Australia, 2014, 636-640.
Liu, S.; et al. Unshared Secret Key Cryptography. IEEE Transactions on Wireless Communications 2014, 13, 6670-6683.
Wang, H.; Tao, X.; Li N.; Han, Z. Polar Coding for the Wiretap Channel with Shared Key. IEEE Transactions on Information Forensics and Security 2018, 13, 1351-1360.
Zhao, Y.; Xu, S.; Chi, H. Encrypted secure polar coding scheme for general two-way wiretap channel. IET Inf. Secur. 2019, 13, 393–403. [CrossRef]
Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423.
Maurer, U.M. The strong secret key rate of discrete random triples. In Communication and Cryptography — Two Sides of One Tapestry, Blahut R.E. et al. (Eds.), Boston: Kluwer Academic, 1994; Volume 276, pp.271-285.
Maurer, U.M.; Wolf, S. Information-theoretic key agreement: From weak to strong secrecy for free. Lect. Notes Computer Science 2000, 1807, 351–368.
Leung-Yan-Cheong, S. On a special class of wire-tap channels. IEEE Trans. Inform. Theory 1977, 23, 625–627.
Arkan, E. A performance comparison of polar codes and Reed-Muller codes. IEEE Commun. Lett. 2008, 12, 447–449. [CrossRef]
Arikan, E. Channel Polarization: A Method for Constructing Capacity-Achieving Codes for Symmetric Binary-Input Memoryless Channels. IEEE Trans. Inf. Theory 2009, 55, 3051–3073. [CrossRef]
Bennett, C.; Brassard, G.; Crepeau, C.; Maurer, U. Generalized privacy amplification. IEEE Trans. Inf. Theory 1995, 41, 1915–1923. [CrossRef]
Carter, J. L.; Wegman, M. N. Universal classes of hash functions. Journal of Computer and System Sciences 1979, 18, 143–154.
Galis, M.; Milosavljević, M.; Jevremović, A.; Banjac, Z.; Makarov, A.; Radomirović, J. Secret-Key Agreement by Asynchronous EEG over Authenticated Public Channels. Entropy 2021, 23, 1327. [CrossRef]
Radomirović, J.; Milosavljević, M.; Kovačević, B.; Jovanović, M. Privacy Amplification Strategies in Sequential Secret Key Distillation Protocols Based on Machine Learning. Symmetry 2022, 14, 2028. [CrossRef]
Radomirović, J.; Milosavljević, M.; Banjac, Z.; Jovanović, M. Secret Key Distillation with Speech Input and Deep Neural Network-Controlled Privacy Amplification. Mathematics 2023, 11, 1524. [CrossRef]
Korada, S. B. Polar Codes for Channel and Source Coding, Ph.D. Thesis, Ecole Polytechnique Federale de Lausanne, Lausanne, Switzerland, 2009.
Kim, Y.-S.; Kim, J.-H.; Kim, S.-H. A Secure Information Transmission Scheme With a Secret Key Based on Polar Coding. IEEE Commun. Lett. 2014, 18, 937–940. [CrossRef]
Cover, T.M.; Thomas, J.A. Elements of Information Theory, 2nd ed., NJ: John Wiley & Sons, Hoboken, 2006.
Biondi, F.; Given-Wilson, T.; Legay, A. Attainable unconditional security for shared-key cryptosystems. Inf. Sci. 2016, 369, 80–99. [CrossRef]
Massey, J. L. Applied Digital Information Theory II, Lecture notes. Available online: https://www.isiweb.ee.ethz.ch/archive/massey_scr/ (accessed on 31 July 2024).
Tal, I.; Vardy, A. How to construct polar codes. IEEE Transactions on Information Theory 2013, 59, 6562–6582.
Mori, R.; Tanaka, T. Performance of Polar Codes with the Construction using Density Evolution. IEEE Commun. Lett. 2009, 13, 519–521. [CrossRef]
Trifonov, P. Efficient Design and Decoding of Polar Codes. IEEE Trans. Commun. 2012, 60, 3221–3227. [CrossRef]
Unkašević, T.; Banjac, Z.; Milosavljević, M. A Generic Model of the Pseudo-Random Generator Based on Permutations Suitable for Security Solutions in Computationally-Constrained Environments. Sensors 2019, 19, 5322. [CrossRef]
Tsurumaru, T.; Hayashi, M. Dual Universality of Hash Functions and Its Applications to Quantum Cryptography. IEEE Trans. Inf. Theory 2013, 59, 4700–4717. [CrossRef]
Hayashi, M.; Tsurumaru, T. More Efficient Privacy Amplification With Less Random Seeds via Dual Universal Hash Function. IEEE Trans. Inf. Theory 2016, 62, 2213–2232. [CrossRef]

Figure 1. Generic Wiretap Channel Model.

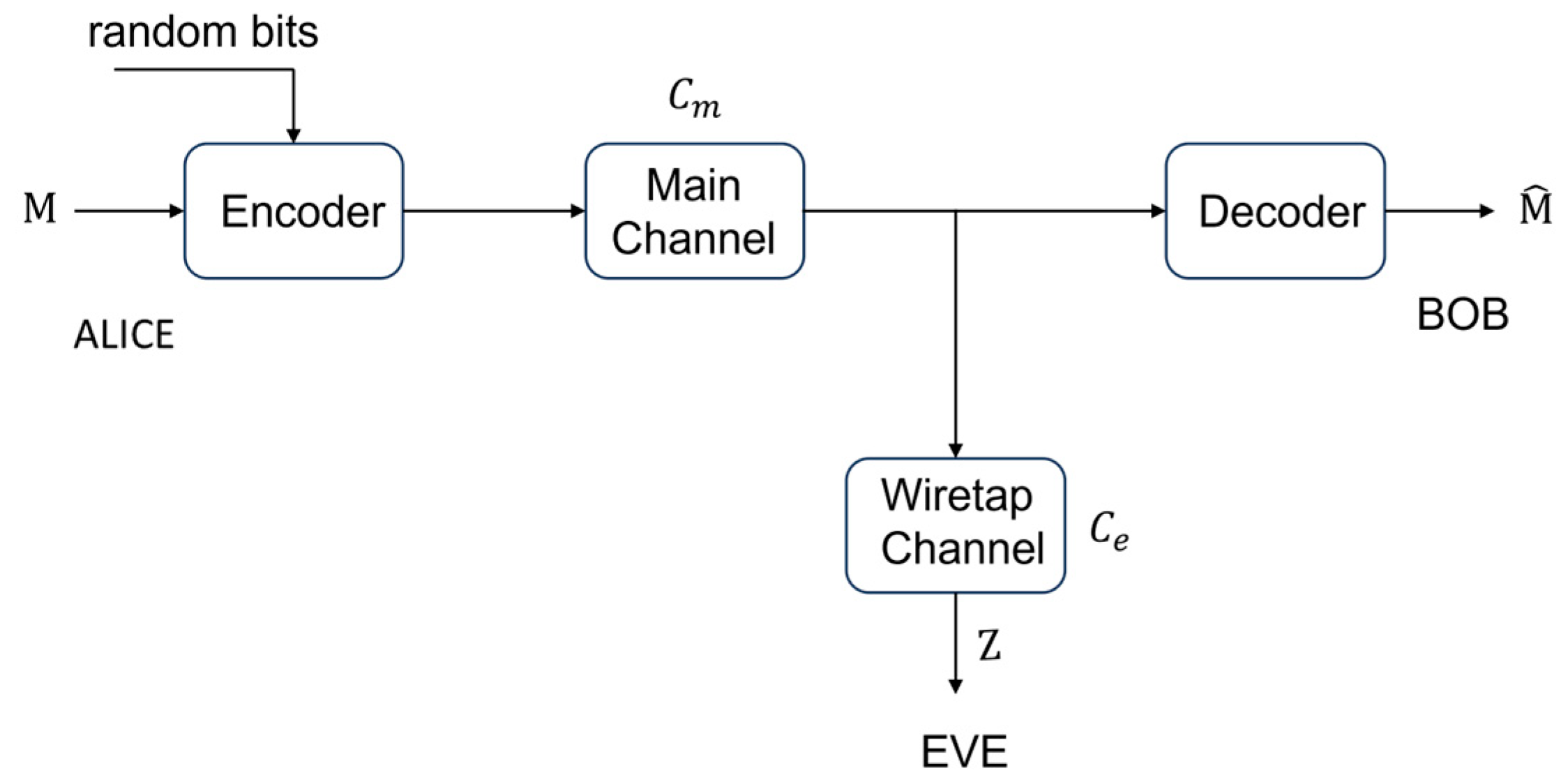
Figure 2. ISAR ciphering system for secure communication without explicit secret key exchange.

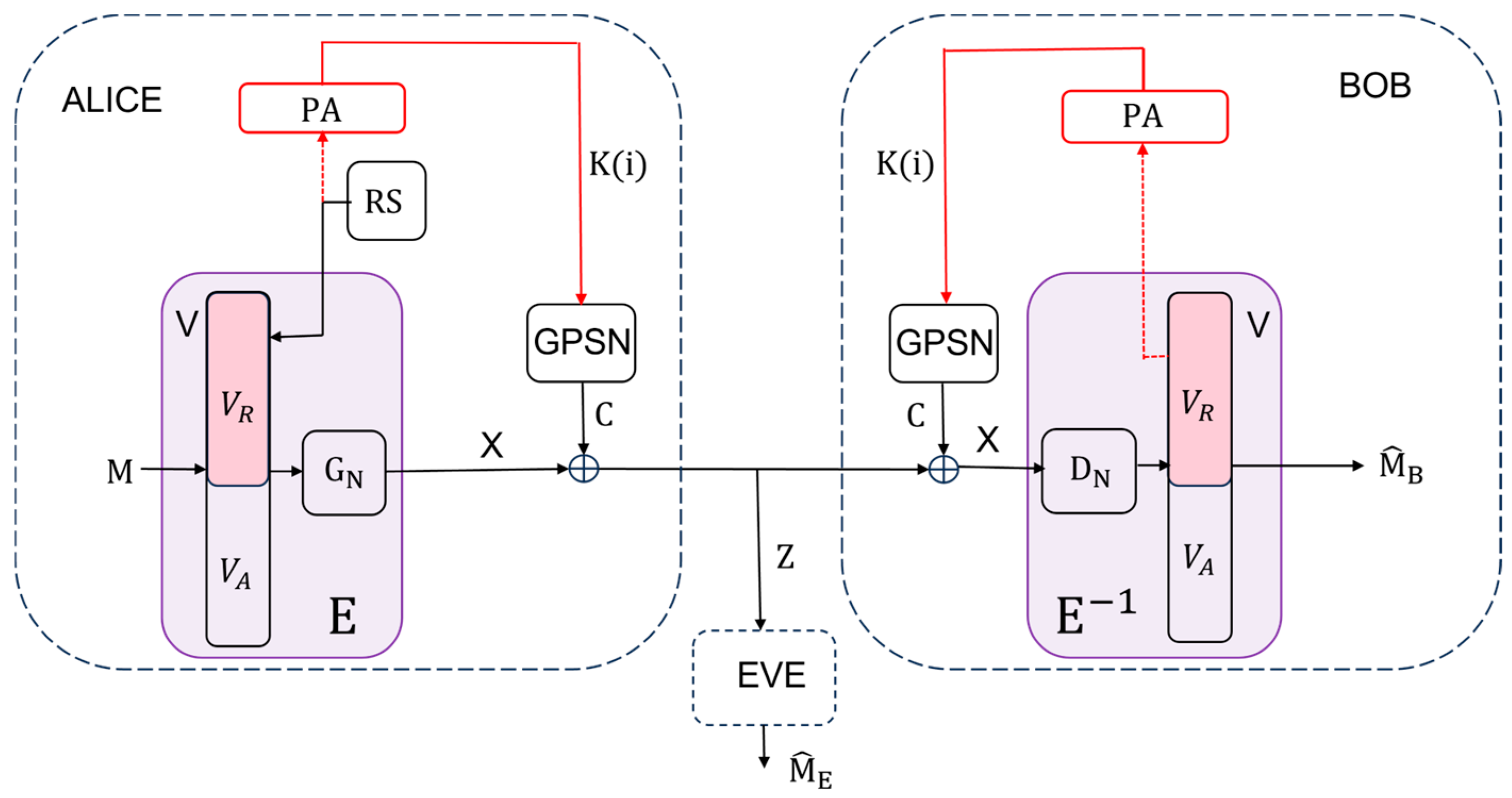
Figure 3. Equivalent main channel

Figure 4. Equivalent wiretap channel.

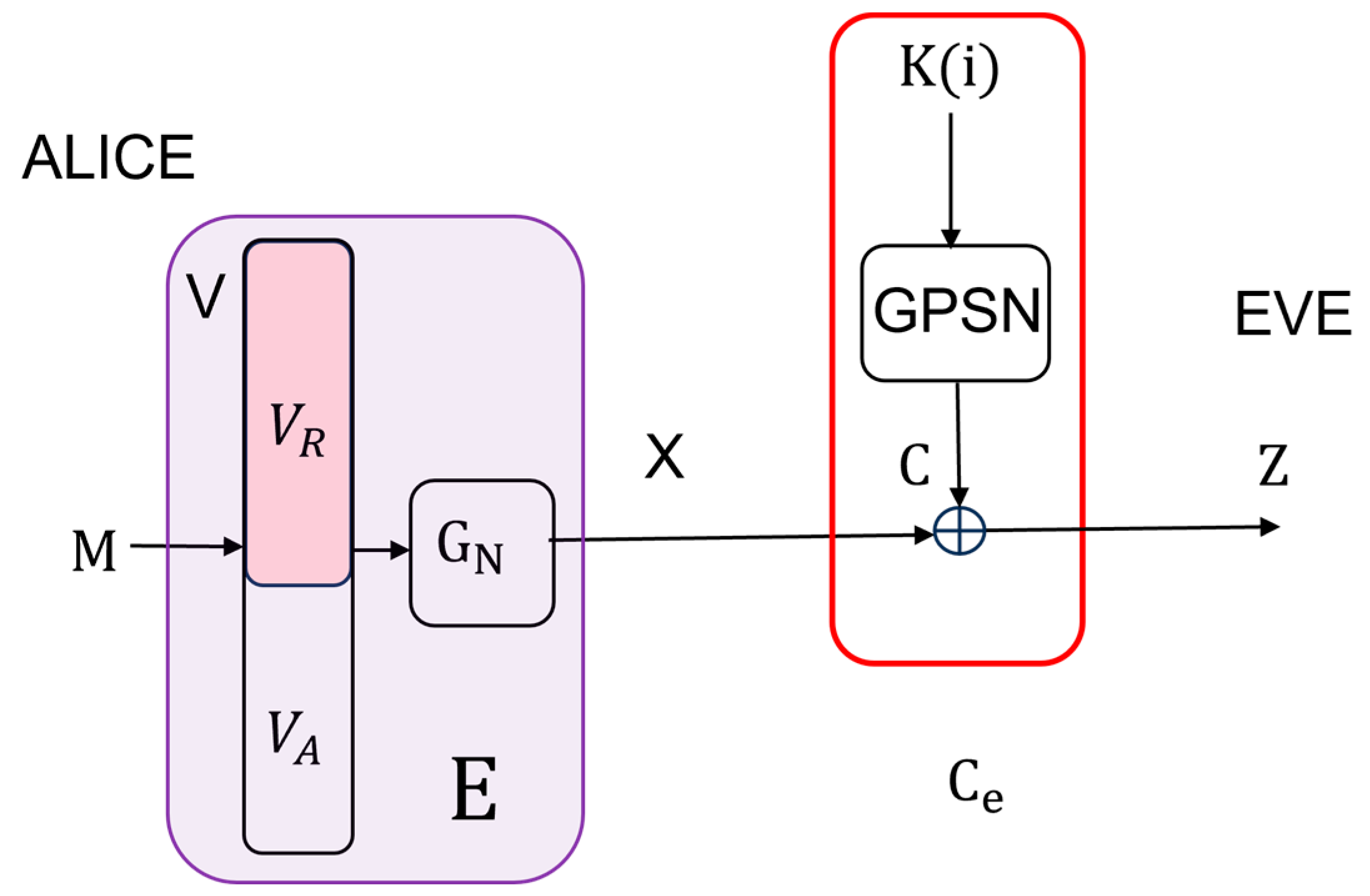
Figure 5. The linear dependence of the security capacity of the proposed system on the secret key length.

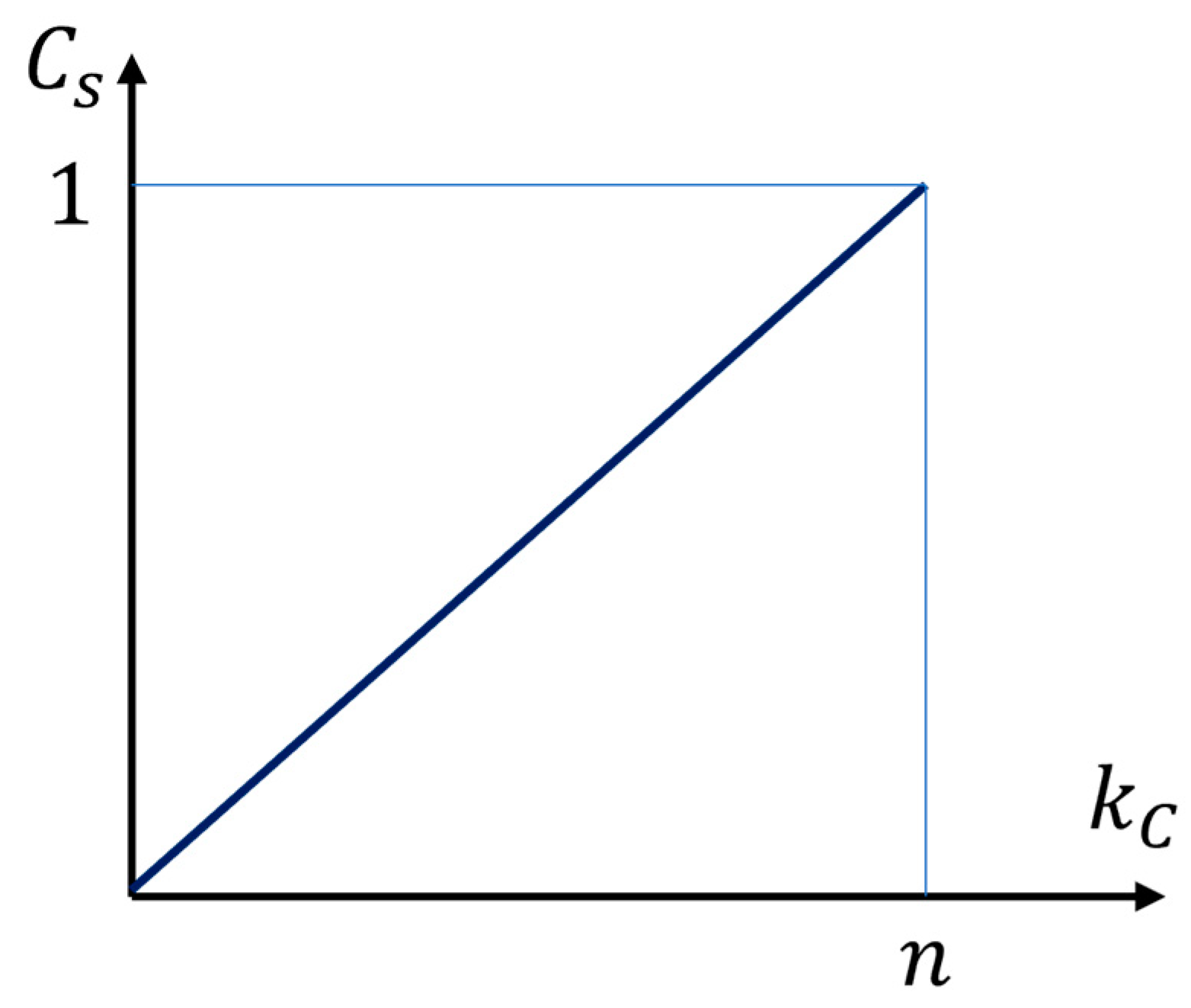
Figure 6. The dependence of the secrecy capacity

C_{s}

on the normalized compression rate

\frac{∆ R}{n}

of the hash function applied in the PA process, for different values of the normalized minimum key equivocation

\frac{∆_{K}}{n}

Figure 6. The dependence of the secrecy capacity

C_{s}

on the normalized compression rate

\frac{∆ R}{n}

of the hash function applied in the PA process, for different values of the normalized minimum key equivocation

\frac{∆_{K}}{n}

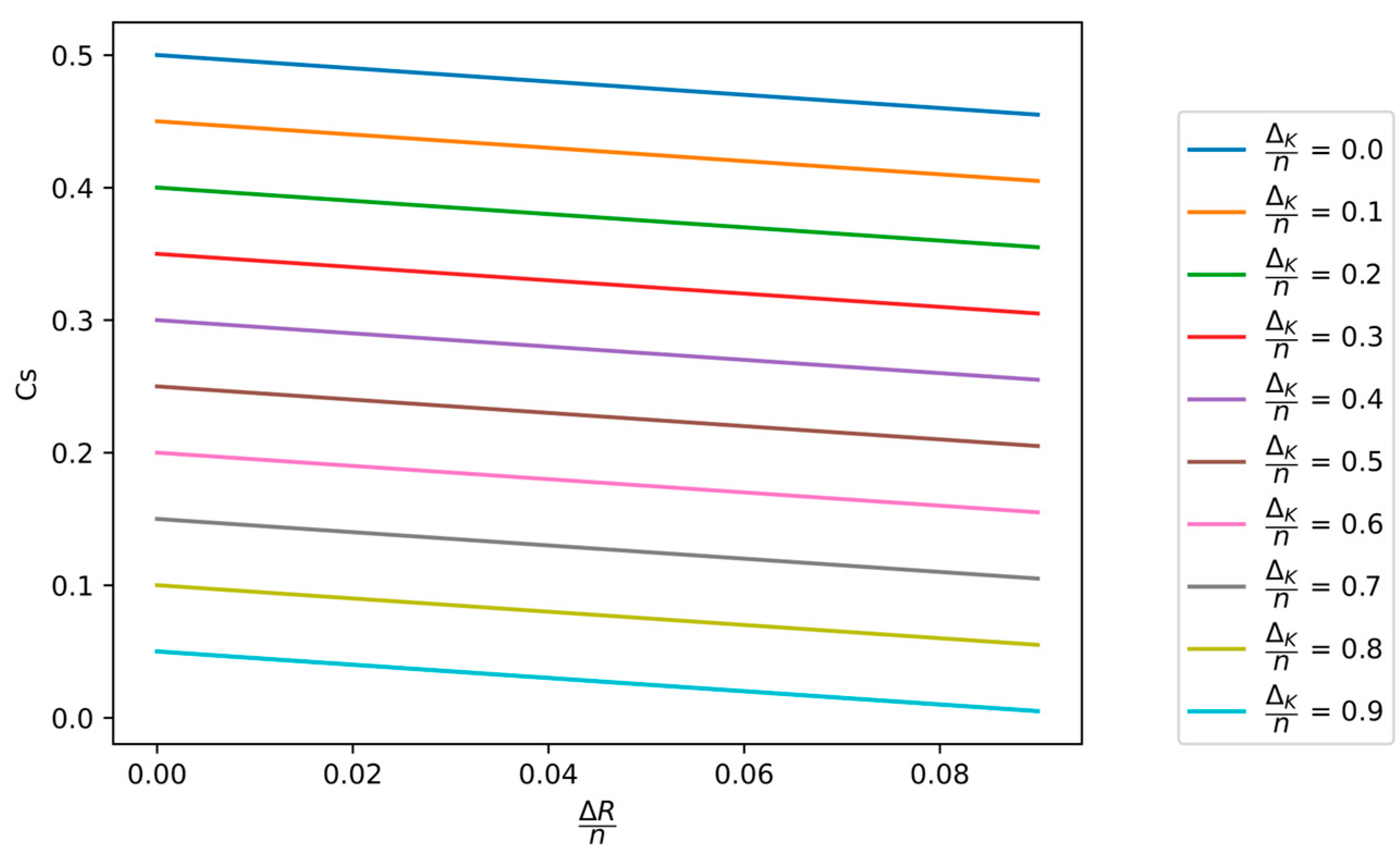
Figure 7. The dependence of the secrecy capacity

C_{s}

on the normalized minimum key equivocation

\frac{∆_{K}}{n}

, for different values of the normalized compression rate

\frac{∆ R}{n}

of the hash function applied in the PA process.

Figure 7. The dependence of the secrecy capacity

C_{s}

on the normalized minimum key equivocation

\frac{∆_{K}}{n}

, for different values of the normalized compression rate

\frac{∆ R}{n}

of the hash function applied in the PA process.

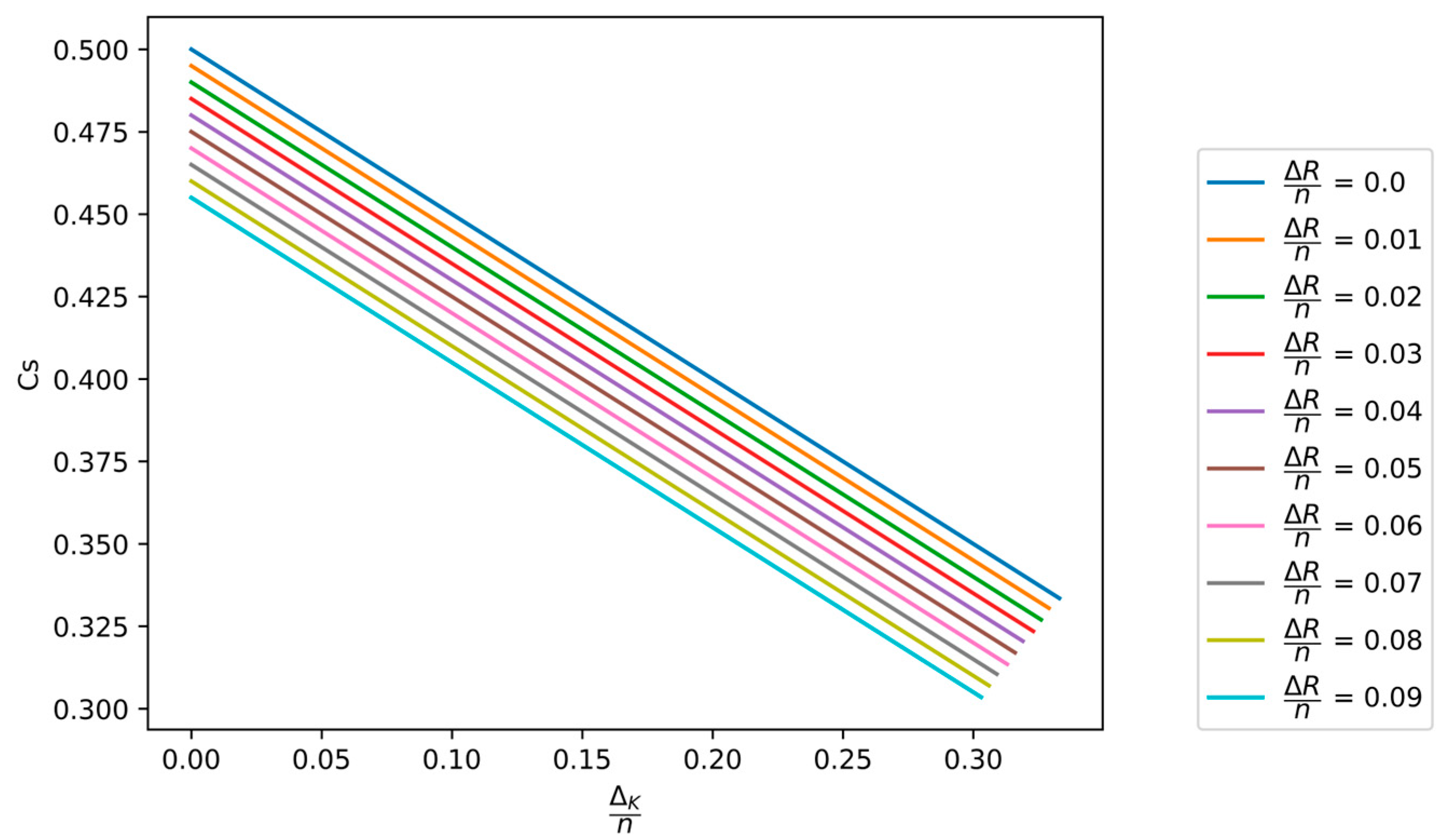
Figure 8. An example of the relationship between the key equivocation of the ISAR system (blue line) and the classic cipher system (red line) as a function of the number of encrypted blocks

t

, for a given minimum value

∆_{K}

, provided that after 4 blocks both systems have the same minimum key equivocation value. The identical slopes of both equivocations are a consequence of the same probabilistic properties of the source being encrypted. Note that in that case, the classic system must have a secret key 4 times longer than the ISAR System.

Figure 8. An example of the relationship between the key equivocation of the ISAR system (blue line) and the classic cipher system (red line) as a function of the number of encrypted blocks

t

, for a given minimum value

∆_{K}

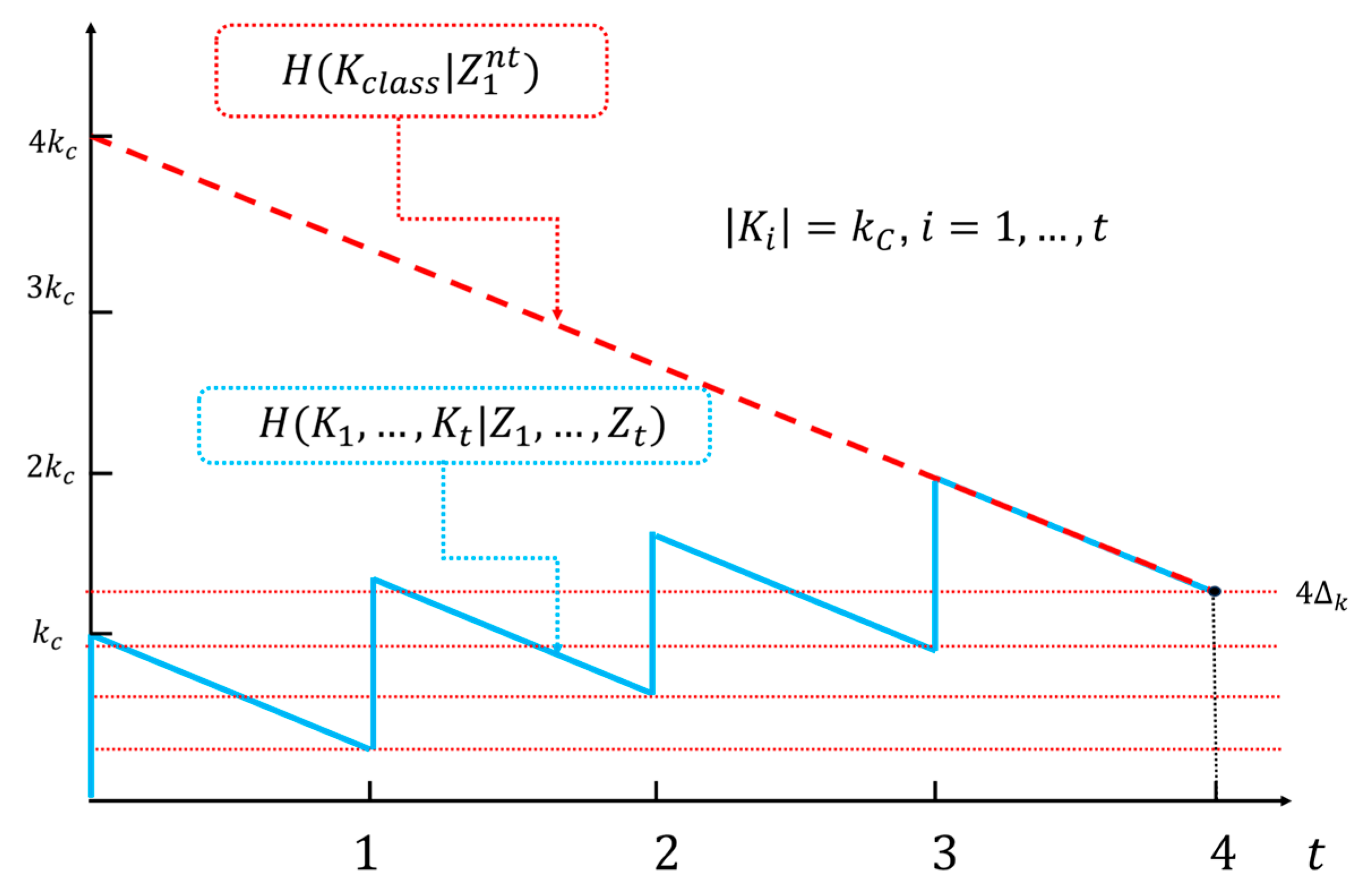
Table 1. Partition of the index of polarized channels

W_{m}^{(i)}

and

W_{e}^{(i)}, i \in [1, n]

, according to (6) – (13), which ensures strong secrecy.

Table 1. Partition of the index of polarized channels

W_{m}^{(i)}

and

W_{e}^{(i)}, i \in [1, n]

, according to (6) – (13), which ensures strong secrecy.

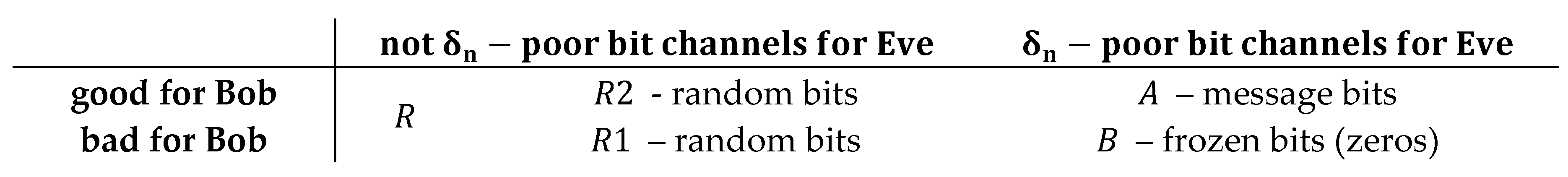
Table 2. ISAR system setup and enciphering and deciphering algorithm

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

One Class of Ideally Secret Autonomous Symmetric Ciphering Systems Based on Wiretap Polar Codes

Abstract

1. Introduction

1.1. Related Works

1.2. Paper Organization

1.3. Notations

2. Preliminaries

2.1. Wiretap Channel Model

2.2. Wiretap Polar Coding

2.3. Privacy Amplification (PA)

2.4. Ideal and Ideal Autonomous Cipher System

3. System Architecture and Security Properties of ISAR Cyphering System

4. Security Analysis of ISAR Ciphering System

4.1. Message Attacks

4.2. Attacks on Locally Generated Random Sequences

4.3. Attacks on the Secret Key GPSN( K )

5. Practical Aspects

5.1. Complexity of ISAR

5.2. Integration of ISAR Ciphering System in Contemporary Information and Communication Infrastructure

6. Conclusions

Author Contributions

Funding

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe

4.3. Attacks on the Secret Key GPSN( $K$ )