Prerpints.org logo
Preprint
Article

Physical Vulnerability and Landslide Risk Assessment in Tegucigalpa City, Honduras

Altmetrics

Downloads

84

Views

19

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

09 August 2024

Posted:

12 August 2024

You are already at the latest version

Alerts
Abstract
Tegucigalpa, the capital city of Honduras, has the highest number of landslides recorded in the country. In a previous study, landslides were found to be mainly concentrated in areas with colluvium and residual soils. The present study focused on assessing the physical vulnerability of houses and the risk linked to landslides in these types of soils. As an input for this assessment, the study generated landslide risk vulnerability functions based on empirical data. The study's findings suggest that the estimated Annual Average Losses associated with landslides in this region is USD 7.26 million. Moreover, the study developed a novel approach for the spatial and temporal estimation of landslide hazard probability, which overcomes some of the limitations identified in previous landslide risk assessment studies.
Keywords: 
Subject: Environmental and Earth Sciences  -   Geophysics and Geology

1. Introduction

Disaster risk is defined as “the potential loss of life, injury, or destroyed or damaged assets which could occur to a system, society or a community in a specific period, determined probabilistically as a function of hazard, exposure and vulnerability” [1]. This definition can be expressed quantitatively by the following expression [2,3]:
D R = ∑ H ∑ ( V E )
Where DR is disaster risk.
H is the hazard, expressed as the probability of occurrence of a hazard intensity value within a reference [2,3,4].
V is the physical vulnerability of a particular element for a given hazard. In quantitative risk analyses, it takes values between “0” (zero affectation) to “1” (total affectation) [5].
E is the value of an element exposed to a specific hazard (number of people, cost of buildings, etc.). In the case of infrastructure, the replacement value is typically utilized, which is the value of a similar good at the current market price [6].
Loss exceedance curves show the relationship between risk values, expressed as probable losses, and the likelihood that a given loss level will be surpassed in a given year [7,8,9]. The integral under the loss exceedance curve is the Average Annual Loss (AAL) [7,8,9]. The AAL is crucial for the design of cost-effective disaster risk management policies that involve various measures, such as investments in risk reduction, emergency preparedness, emergency funds, and insurance [8,9].
Slides are a type of slope movement, characterized by a displacement along one or multiple failure surfaces with a limited deformation of the soil involved. If the surface is parallel to the ground it is defined as a translational slip, and when it is cylindrical as a rotational slide. Quantitative disaster risk studies for translational and rotational landslides are particularly scarce. This is due to the difficulty in estimating movement intensity (e.g. speed) and characterizing vulnerability due to lack of data [2,3,10,11].
Landslide hazard can be characterized as (adapted from [2]):
H = ∑ P ( M i ) P ( X j | M i )
Where P(Mi) is the probability that a landslide with magnitude i occurs and P(Xj|Mi) is the probability that the landslide of magnitude i reaches a point at a distance X with an intensity j. P(Mi), the probability of the magnitude depends on the combination of spatial and temporal probabilities. Spatially, it is determined by physical conditions like the slope, type of soil, etc. Temporally, it is based on the likelihood of a triggering event happening.
The Municipality of the Central District (MCD) is the municipality in Honduras with the highest number of landslides. The city has undergone rapid expansion in recent years, resulting in the location of neighborhoods of the lowest social classes on the outskirts of the urban area. These areas are often located on high-sloped terrain, which makes them more susceptible to landslides [12]. In the MCD, single-story housing predominates, housing construction on several levels is still very scarce [12].
In the period between 1966 and 2016, the MCD concentrated 36% (237 events) of the total landslides nationwide, affecting 13.644 people, resulting in 55 casualties and the destruction of 875 homes [13]. Landslides associated with Hurricane Mitch were especially devastating. They occurred in the last days of October 1998 and caused rotational and translational landslides, such as the El Berrinche landslide. These landslides directly or indirectly affected the entire population of the city [14].
After Hurricane Mitch, several studies were carried out to characterize landslide-prone areas. A critical review of landslide studies was conducted in a previous publication [15], resulting in the development of a new inventory of translational and rotational landslides. The study found that these landslides are primarily concentrated in colluvium deposits and residual soils. The study developed a susceptibility map using a bivariate statistical method based on the presence of colluvium and residual soil land cover. Using the success curve method, the study found that this susceptibility map was more effective in explaining the spatial distribution of translational and rotational landslides than previous susceptibility maps [14}.
Although numerous studies have been conducted on inventories and susceptibility to landslides in the MCD, the city lacks access to a map identifying landslide risk [12]. This information is crucial to evaluate the significance of the issues related to these hazards and to analyze the cost-benefit of implementing measures to mitigate or manage them.
The present study aims to assess the risk of landslides in the MCD and estimate the potential economic losses associated with them.
The study area, which is shown in Figure 1, spans over 260 km2 and includes the entire MCD urban sprawl. The MCD is situated on a plateau surrounded by steep slopes, with 62% of the study area having slopes greater than 20% [12]. The region experiences rainfall mainly between May and October, with an average annual rainfall of 870 mm [16].
The study area is characterized by three main geological formations [17]: (i) the Valle de Ángeles Group, which is from the High Cretaceous period and consists of shale, sandstone, and reddish conglomerate. It is further divided into two formations, namely the Villanueva Formation and the Rio Chiquito Formation; (ii) the Padre Miguel Group, which is from the Middle Miocene period and consists of tuff and ignimbrite; and (iii) andesite and basalt most likely from the Holocene period. Deposits of quaternary alluviums and colluviums are also found atop these formations, as shown in Figure 2.

2. Materials and Methods

Landslide Hazard Estimation

Rotational and translational landslide hazard can be evaluated by analyzing landslide inventories through a statistical spatial and temporal probability model [18,19,20,21]. These models estimate the term P(Mi) of the landslide hazard equation. When the velocity of the landslide is slow or spatially well-defined, the term P(Mi) can be considered equivalent to the landslide hazard [2]. The model combines landslides' spatial and temporal probability by considering them as two separate conditional probabilities [18,19,20,21]. They apply the following formula to integrate these probabilities.
H = P t     .   P s
Where H is the landslide hazard, Pt is the temporal probability, and Ps is the spatial probability.

Spatial Probability

To characterize the spatial probability, we utilized the PISA-m program [22]. This program integrates an analytical model based on the infinite slope and treats the uncertainty of input parameters using the first-order second-moment method (FOSM). This method estimates the probability that the Safety Factor (SF) is less than 1 in each pixel. The equation used for the infinite slope is as follows [22]:
S F =   c r   +   c s   + q t   + ϒ m D + ϒ s a t − ϒ w − ϒ m H w D   c o s 2 β t a n Ø q t   + ϒ m D + ϒ s a t − ϒ m   H w D sin ⁡ β c o s β
Where SF is the safety factor, cr is the cohesive strength of tree roots (strength/area), cs is the cohesive strength of the soil (strength/area), qt is the uniform load due to the weight of vegetation (strength/area), Υm is the unit weight of wet soil (weight/volume), Υsat is the unit weight of saturated soil below the water table (weight/volume), Υw is the unit weight of water, D is the thickness of the soil above the breaking surface (length), Hw is the height of the water table above the breaking surface normalized by the thickness of the soil (dimensionless), β is the slope (degrees) and Ø is the internal friction angle (degrees).
Geotechnical parameters for the study area were determined using average values of local laboratory tests. It was assumed that these parameters followed a normal distribution, which is one of the requirements for applying the FOSM method [23]. The value of Hw was assumed to be 1, indicating the most unfavorable condition where the ground is completely saturated.
In a previous publication [24], the infinite slope model was used to characterize the SF in the study area. The results evidenced that the model tends to underestimate landslide areas in low-slope terrains. Therefore, a review of the modeling results was carried out using expert criteria to manually include potential landslide zones that were classified as stable by the model.

Temporal Probability

The temporal probability was calculated by assigning return periods to past landslide events. A landslide event was defined as one or more landslides that occurred on the same date and during the same rainy season [25]. The number of landslides that were part of these historical landslide events was obtained from the desinventar database, which was supplemented by the event-type inventory conducted by the United States Geological Service (USGS) for Hurricane Mitch [26]. Only landslide events reported in neighborhoods with colluvium and residual soil cover were considered since the temporal probability was only estimated for this cover.
For the analysis of antecedent rainfall, the daily precipitation database of the rainfall station of the National Autonomous University of Honduras (UNAH) was used, which has continuous data for the period 1980 to 2019. According to [25], episodes where the previous precipitation of 5 days was less than 20 mm were eliminated from the analysis, as the relationship with a precipitation event is considered doubtful in these cases.
The return period was obtained from the antecedent precipitation data, using the methodology proposed by [27]. Background rainfall indicators of 1, 2, 3, 5, 7, 10, 15, 30, and 60 days were selected [21,27,28,29,30] and the return period for each previous rainfall indicator was calculated, using the Gumbel probability distribution [25,27,31,32], and assigning to each event the highest return period obtained from the previous rainfall indicators [27].
The area affected by landslides in each episode was estimated using the average area of landslides from the validated inventory [33]. Since it is necessary to establish a single return period for each number of landslides, when several episodes with the same number of landslides were identified, the longest return period was considered, discarding those episodes whose return periods were not consistent with the general trend obtained.
F x = e − e − α x − μ
The Gumbel probability distribution function is as follows:
The value F(x) represents the probability that the function will take a value smaller than x. α and μ are parameters of the function, which can be calculated by different methods (i.e. Moments, Chow, least squares, maximum likelihood, and Kimball) [31,34].
Based on [31] the moment's method was selected, which uses the following equations to estimate the parameters of the probability distribution function:
α =   π σ   6
μ = x ¯ − ϒ α
Where Υ is Euler's constant (0,5772), x ¯ , is the average, and σ is the typical deviance.
The return period (T) for each antecedent rainfall indicator was obtained with the following formula:
T = 1 1 − e − e α x − μ

Integration of Spatial and Temporal Probability

To determine the probability of a landslide being triggered, an equation for integrating the probability of SF < 1 and the temporal probability was adapted [27]. The temporal probability is represented as the average likelihood of triggering a landslide in a pixel located in a high-susceptibility area and is different for each precipitation return period. This probability is assumed to be equal for all pixels within the high susceptibility area. On the other hand, the spatial probability is the likelihood of a pixel being affected by a landslide based on its location, and it was assumed to be equal to the probability of SF < 1.
F p x j l i = T a i T s F ( S F < 1 )
Where F p x j l i   is the conditional probability that pixel j will be affected by a landslide l in the precipitation event i, Tai is the number of pixels affected by landslides in the precipitation event i (based on historical data), Ts is the number of pixels susceptible to landslides, which was considered equivalent to the entire area covered by colluviums and residual soils, F(SF < 1) is the frequency that the pixel j presents an SF < 1, as the result of probabilistic modeling with the program PISA-m. The term T a i T s represents the temporary probability that a slide will be triggered (Pt) and the term F(SF <1) represents the spatial probability (Pe).

Vulnerability to Translational and Rotational Slides

The disaster risk was only evaluated for single-floor housing, as it is the most common type of housing in the MCD [12] (BID, 2015).
To assess the susceptibility of homes to translational and rotational landslides vulnerability functions were developed. Those functions determine the probability of occurrence of different levels of damage, measured as the Mean Damage Ratio (MDR), in the event of a landslide in the area. The MDR ranges from 0 to 1 and represents the proportion of the cost to replace a damaged part of the house to the total replacement cost [9].
Data from surveys conducted by the NGO GOAL between November 2010 and March 2011 were used to construct these functions. This period was characterized by an active winter season with significant landslides. Out of 1,206 surveys available, 323 were selected for being on active landslide sites. These landslides had been characterized as active in the validated inventory prepared in a previous study [15]. Specifically, the selected surveys were localized on three landslides: i) landslide in the La Ulloa and José Arturo Duarte neighborhoods, (ii) landslide in the El Edén neighborhood and (iii) landslide in the Reparto Arriba neighborhood (Figure 3).
These surveys include a field that allows a binary answer (yes / no) to the question whether the walls, floor or ceiling of the houses presented fissures. Considering these three variables there are 8 possible combinations, which correspond to "states of damage": (i) no damage, (ii) fissures in walls, (iii) fissures in the ceiling, (iv) fissures in the floor, (v) fissures in the walls + ceiling, (vi) fissures in walls + floor, (vii) fissures in floor + ceiling and (viii) fissures in walls + floor + ceiling. For each of the types of housing considered, these states of damage were correlated with the value of the MDR, establishing with expert criteria which would be the elements of the house that would have to be replaced in case a certain state of damage was reached and defined for each type of housing the cost of replacing these elements to the total value of the house.
Based on the types of housing materials identified in the surveys and the classification of neighborhoods according to their social status of [12] the MDR was estimated for the 8 states of damage for 4 types of one-story housing: (i) popular brick, (ii) precarious brick, (iii) block and (i) (v) wood. Based on the survey data, the mean and standard deviation of the MDR for each type of housing were obtained.
Vulnerability functions should consider various sources of epistemological and random uncertainty [11,35]. Among the epistemological uncertainties are those related to the simplifications made to characterize the intensity/magnitude of the movements or the models used to describe the response of the structures. Random uncertainties are related to variability: (i) associated with the intensity/magnitude of the movement and (ii) with the response of the infrastructures located on landslides.
To manage these uncertainties the damage expressed by the MDR for the condition that a landslide occurs was considered as a random variable, assuming that it follows a Beta probability density function [9,36] and using the values of the mean and standard deviation of the MDR obtained, to estimate the parameters of the Beta function, α and β. The formulas considered were the following [37]:
B   α ,   β = ∫ 0 1 x α − 1 ( 1 − x ) β − 1 d x
α = x ¯ x ¯ 1 − x ¯ / s 2 − 1
β = 1 − x ¯ x ¯ 1 − x ¯ / s 2 − 1
Where B is the Beta distribution, which takes values between 0 and 1, α and β are the parameters of the Beta distribution, x ¯ is the mean or expected value and σ is the standard deviation.

Risk Estimation

The value of homes per m2 and population in areas with colluvium and residual soils was projected for year 2020. This was done by projecting the prices per square meter of construction and the population for different MCD social categories of neighborhoods from year 2014.
The 2015 population values [12] were projected for 2020 considering the population growth rate proposed by the same study and the construction square meter values were adjusted for 2020 considering the annual depreciation. In total, 30 units of homogeneous neighborhoods were identified, corresponding to the categories of residential neighborhood (4 units), middle class (4), popular (9), and precarious (13) [12], which are located on the layer of colluvium and residual soils.
For each of the 30 units, the expected value of the economic loss conditioned on the occurrence of a landslide was estimated as:
P | l i = e ∑ N x j V x j
E L | l = ∑ i N L | l i F i
Where (P|l)i is the loss conditioned to the occurrence of a landslide d in unit i, e represents the constant exposed value of the unit in USD; Nxj is the proportion (ranging from 0 to 1) of the area of the unit that corresponds to a particular type of housing xj, where the sum of the proportions for each type of housing is equal to 1 for each unit; Vxj is the vulnerability of different housing types present in the unit, ranging from 0 to 1; Fi is the frequency of the landslide occurrence, and E is the expected value.
For each unit, a thousand (P|l)i calculations were made, using the Monte Carlo method. The Vulnerability (Vxj) is equivalent to the MDR. MDR was characterized as a random variable following a Beta-type probability density distribution function. The parameters of the Beta function for each type of housing were obtained from the surveys.
The proportion (Nxj) of different types of housing (popular brick, precarious brick, block, and wooden) was assumed to be constant for each type of neighborhood (residential, middle class, popular, and precarious). This assumption was made based on census data and expert criteria.
E[L|l] is the expected value of the losses for the unit given the occurrence of landslide l, and it is estimated as the sum of the loss values obtained in the Montecarlo modeling, multiplied by its frequency (Fi). To estimate the frequency, the values obtained from the Monte Carlo modeling were divided into 20 equal intervals and the frequency (Fi) for each interval was obtained [38].
The value of the potential loss for each pixel of the unit was estimated by applying the following equation:
( L | l )   p x j =   E L | l N p x
Where (L|l) pxj are the potential losses in pixel j given that a landslide l occurs, and Npx is the number of pixels in the unit.
The economic loss at the pixel level given a precipitation event was estimated with the following equation (adapted from [11]):
L p x j i   =   F p x j l i   ( L | l ) p x j
Where Lpxji are the losses in the pixel j given the precipitation event i, Fpxjli is the conditional probability that pixel j is affected by a landslide l in the precipitation event i, which integrates spatial and temporal probability and (L|l)pxj are the potential losses in the pixel j, given the occurrence of landslide l. This equation enables the integration of the conditional probability that a pixel will be impacted by a landslide, given a precipitation event, with the value of the economic loss conditioned on the occurrence of a landslide.
To apply this equation, the spatial probability, temporal probability, and probable losses maps were multiplied to obtain the result of the probable losses for each of the return periods considered. To facilitate the spatial analysis calculations, all the layers were rasterized into 10 x 10 m pixels.
The total value of losses L for each precipitation event i, was obtained by adding the loss values at the pixel level with the formula:
L | E v e n t i =   ∑ j = i n L p x j i
The loss values for each return period and their annual probabilities of excess were integrated through a loss exceedance curve and the area under the curve was calculated to estimate the expected annual loss for the entire study area, following the formula (adapted from [36]):
A A L =   ∑ i = n n L | E v e n t i F a E v e n t i
Where AAL is the Annual Average Loss, (L|Eventi) is the value of the Loss for the precipitation event i and Fa (Eventi) is the annual frequency of the precipitation event i.
The estimation of the AAL as the area under the excess curve was performed by applying the interval sum method [39,40].

3. Results

3.1. Spatial Probability

Figure 4 shows the results of modeling the spatial probability of SF < 1 with the PISA-m program.
Table 1 summarizes the average probability that the SF < 1 for the different types of colluviums and residual soils and the inventory of translational and rotational landslides.
The highest spatial probability value corresponds to the landslide inventory with a value of 0,44, followed by the colluvium of basalts, andesites, and rhyolites (0,42). The average probability value for all colluvium and residual soil cover is 0,37.
As a result of the review of the model with expert criteria, 14 potential landslides, classified by the model as stable, were identified. These landslides, totaling 2.861.296 m2, were manually incorporated into the spatial probability model. They represent 7% of the total area of colluviums and residual soils. It was assumed that the probability of these landslide polygons was equal to the escarpment surrounding them. (Figure 5).

3.2. Temporal Probability

52 episodes of landslides in neighborhoods located on the layer of colluviums and residual soils were identified, with 70% of the episodes characterized by 1 or 2 movements.
Based on the antecedent rainfall indicators, the return period correlated with each number of landslides was estimated. In total, values were obtained for 6 return periods. The temporal probability (Pt) of a landslide being triggered in any pixel of the colluvium and residual soil layer was estimated for each return period. See results in Table 2.

3.3. Vulnerability to Translational and Rotational Slides

Using the values of the surveys, the mean, and the standard deviation of the MDR were estimated and the parameters of the Beta function were obtained for each of the types of housing considered. The results are summarized in Table 3.

3.4. Risk Estimation

Table 4 summarizes the results of the population projected for 2020 and the economic value exposed to landslides in the study area. The projected total population for 2020 in MCD is 1.345.117 inhabitants and 328.879 households. The number of inhabitants and houses exposed to landslides represent 12% and 11,5% of the total population and housing respectively. The total value of MCD homes exposed to landslides is estimated at USD 1.255 billion, representing 4,2% of the USD 30.195 billion total housing stock replacement value for 2020.
The summary of the expected value of the economic loss conditioned to a landslide occurrence for each type of neighborhood is summarized in Table 5. As a result of the housing vulnerability (characterized by the MDR), the relationship of the expected loss with the exposed value is lower for residential neighborhoods (36%) and higher for precarious neighborhoods (51%), with the same value for residential and middle-class neighborhoods (44%).
Figure 6 shows the expected value of the economic losses at pixel level. The residential neighborhoods located north of the study area, on the slopes of El Picacho hill, show the highest probable loss value at the pixel level, ranging between 25.188 to 1.044.164 USD.
To estimate the probable loss for each return period (125, 6, 4, 2, 3, and 1 year), the spatial, temporal probability (value Pt in Table 2) and expected value of economic losses maps were multiplied. The result of the estimation of probable losses for the 125-year return period is shown in Figure 7.
The estimated total value of losses was determined for each return period. The loss exceedance curve (Figure 8) was constructed using the total value of losses and the return period expressed as annual exceedance probabilities. The AAL was calculated as the area under the loss excess curve following the interval method, which is summarized in Table 6. The value obtained for the AAL was USD 7,26 million.

4. Discussion

Validation of a probable loss estimation is complex because it represents future values and cannot be compared to historical events [33].
One option to estimate the accuracy of the results could be to compare them with the probable losses obtained for the same study area using a different method [33]. However, to date the present study is the only estimation of landslide risk made in the MCD.
A flood risk assessment was carried out in 2015 for the same study area [12]. As the estimation of flood risk is based on reliable and widely accepted methods [41,42], the comparison of the results provides a benchmark for validating the findings of the present study
The results of the flooding risk assessment were projected for 2020, obtaining an AAL of USD 6,34 million, with an exposed population of 92.531 people. The risk expressed as AAL is similar for both landslides and floods (USD 7,26 million and USD 6,34 million respectively), although it is 14,5% higher for landslides. This difference in AAL can be attributed to the higher exposed population for landslides, which is 77% greater than that of floods.
Although external validation is difficult, this comparison shows reasonable results for landslide risk estimation.

5. Conclusions

In this study, new methods were applied to estimate the hazard, vulnerability, and risk of rotational and translational landslides in the MCD while considering various sources of uncertainty.
The spatial probability was estimated using the infinite slope model, with a probabilistic analytical method. The probabilistic method was employed to manage the uncertainty associated with the input data, which can be a limitation to applying the infinite slope model. The average results of spatial probability (expressed as the probability of SF < 1) were 0,37 in colluvium and residual soil cover and 0,44 in the validated inventory of landslides and residual soils.
Based on empirical data, probabilistic vulnerability functions were developed for four types of single-floor homes: wooden, precarious brick, popular brick, and block. The average damage, expressed as a percentage of the replacement value of the dwelling, varies between 53% for precarious brick dwellings and 30% for block dwellings.
The conducted research has yielded significant insights into the spatial and temporal patterns of potential losses due to landslides in the MCD area. By integrating the likelihood of landslides, the vulnerability of residences, and exposed values, we were able to quantify and geographically illustrate the probable economic losses linked to landslides in the MCD. The estimated AAL from landslides in the region is USD 7,26 million. Furthermore, the anticipated loss associated to an event with a recurrence interval of 125 years was estimated at USD 21,3 million.
The application of the results of this work will contribute significantly to the reduction of landslide risks in the MCD by facilitating the strategic implementation of risk mitigation measures and their associated cost-benefit analysis.

Author Contributions

formal analysis; methodology; investigation; writing—original draft preparation, Gines Suarez.; writing—review and editing, María Jose Dominguez-Cuesta. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The datasets are under preparation.

Acknowledgments

The authors acknowledge the Municipal Mayor's Office of the Central District, for sharing the existing information from previous studies; the NGO GOAL for sharing the information from the surveys, and the National Autonomous University for providing the information of its rainfall station.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. UNDRR. (2017). The disaster risk reduction (DRR) glossary. https://www.undrr.org/drr-glossary/terminology. Accesed 7/27/2024.
  2. Corominas, J., Van Westen, C., Frattini, P., Cascini, L., Malet, J. P., Fotopoulou, S., Catani, F., Van Den Eeckhaut, M., Mavrouli, O., Agliardi, F., Pitilakis, K., Winter, M. G., Pastor, M., Ferlisi, S., Tofani, V., Hervás, J., & Smith, J. T. (2014). Recommendations for the quantitative analysis of landslide risk. Bulletin of Engineering Geology and the Environment, 73(2), 209–263. [CrossRef]
  3. Van Westen, C. J., Van Asch, T. W. J., & Soeters, R. (2006). Landslide hazard and risk zonation - Why is it still so difficult? Bulletin of Engineering Geology and the Environment, 65(2), 167–184. [CrossRef]
  4. Crozier, M., & Glade, T. (2005). Landslide Hazard and Risk: Issues, Concepts and Approach. In T. Glade, M. Anderson, & M. Crozier (Eds.), Landslide Hazard and Risk (1st ed., pp. 1–40). Wiley.
  5. Papathoma-Köhle, M., Kappes, M., Keiler, M., & Glade, T. (2011). Physical vulnerability assessment for alpine hazards: State of the art and future needs. In Natural Hazards (Vol. 58, Issue 2). [CrossRef]
  6. Alexander, D. (2005). Vulnerability to Landslides. In T. Glade, M. Anderson, & M. J. Crozier (Eds.), Landslide Hazard and Risk (1st ed., pp. 175–198). John Wiley & Sons Ltd. [CrossRef]
  7. Grossi, P., Kunreuther, H., & Windeler, D. (2005). An introduction to catastrophe models and insurance. In Catastrophe modeling: A new approach to managing risk (pp. 23–42). Springer US.
  8. Michel-Kerjan, E., Hochrainer-Stigler, S., Kunreuther, H., Linnerooth-Bayer, J., Mechler, R., Muir-Wood, R., Ranger, N., Vaziri, P., & Young, M. (2013). Catastrophe risk models for evaluating disaster risk reduction investments in developing countries. Risk Analysis, 33(6), 984–999. [CrossRef]
  9. Yamin, L. E., Hurtado, A. I., Barbat, A. H., & Cardona, O. D. (2014). Seismic and wind vulnerability assessment for the GAR-13 global risk assessment. International Journal of Disaster Risk Reduction, 10(PB), 452–460. [CrossRef]
  10. Galve, J. P., Cevasco, A., Brandolini, P., Piacentini, D., Azañón, J. M., Notti, D., & Soldati, M. (2016). Cost-based analysis of mitigation measures for shallow-landslide risk reduction strategies. Engineering Geology, 213, 142–157. [CrossRef]
  11. Guillard-Goncalves, C., Zêzere, J. L., Pereira, S., & Garcia, R. A. C. (2016). Assessment of physical vulnerability of buildings and analysis of landslide risk at the municipal scale: Application to the Loures municipality, Portugal. Natural Hazards and Earth System Sciences, 16(2), 311–331. [CrossRef]
  12. BID. (2015). Tegucigalpa y Comayagüela: capital sostenible, segura y abierta al público. https://issuu.com/ciudadesemergentesysostenibles/docs/plan_de_accion_-_tegucigalpa.
  13. Corporación Observatorio Sismológico del Suroccidente. (n.d.). DesInventar Database. Retrieved April 26, 2016, from https://online.desinventar.org/.
  14. Harp, E., Held, M. D., Castañeda, M. R., Mckenna, J. P., & Jibson, R. W. (2002). Landslide Hazard Map of Tegucigalpa , Honduras.
  15. Suárez, Ginés, & Domínguez-Cuesta, M. J. (2021b). Improving landslide susceptibility predictive power through colluvium mapping in Tegucigalpa, Honduras. Natural Hazards, 105(1), 47–66. [CrossRef]
  16. García-Urquía, E. (2016). Establishing rainfall frequency contour lines as thresholds for rainfall-induced landslides in Tegucigalpa, Honduras, 1980–2005. Natural Hazards, 82(3), 2107–2132. [CrossRef]
  17. Lotti. (1986). Mapa geológico del Proyecto de Aguas Subterráneas y Cerro El Chile en Tegucigalpa.
  18. Ghosh, S., Van Westen, C. J., Carranza, E. J. M., Jetten, V. G., Cardinali, M., Rossi, M., & Guzzetti, F. (2012). Generating event-based landslide maps in a data-scarce Himalayan environment for estimating temporal and magnitude probabilities. Engineering Geology, 128(February), 49–62. [CrossRef]
  19. Guzzetti, F., Reichenbach, P., Cardinali, M., Galli, M., & Ardizzone, F. (2005). Probabilistic landslide hazard assessment at the basin scale. Geomorphology, 72(1–4), 272–299. [CrossRef]
  20. Guzzetti, F., Galli, M., Reichenbach, P., Ardizzone, F., & Cardinali, M. (2006). Landslide hazard assessment in the Collazzone area, Umbria, central Italy. Natural Hazards and Earth System Science, 6(1), 115–131. [CrossRef]
  21. Jaiswal, P., Van Westen, C. J., & Jetten, V. (2010). Quantitative landslide hazard assessment along a transportation corridor in southern India. Engineering Geology, 116(3–4), 236–250. [CrossRef]
  22. Haneberg, W. C. (2007). PISA-m, Map-Based Probabilistic Infinite Slope Analysis, Version 1.0.1 User Manual (Issue March).
  23. Hidalgo, C., & Pacheco, A. (2011). Herramientas para análisis por confiabilidad en geotecnia: Aplicación Tools for reliability analysis in geotechnical engineering: Application. Revista Ingenierías Universidad de Medellín, 10(18), 79–86.
  24. Suárez, Ginés, & Domínguez-Cuesta, M. J. (2021a). Identificación de zonas susceptibles a deslizamientos en Tegucigalpa , Honduras . Limitaciones del modelo del talud. Geogaceta, 69, 51–54. https://sge.usal.es/archivos/geogacetas/geo69/Geo69_p_51_54.pdf.
  25. Valenzuela, P., Domínguez-Cuesta, M. J., Mora García, M. A., & Jiménez-Sánchez, M. (2017). A spatio-temporal landslide inventory for the NW of Spain: BAPA database. Geomorphology, 293(May), 11–23. [CrossRef]
  26. Harp, E., Castaneda, M., & Held, M. D. (2002). Landslides Triggered by Hurricane Mitch in Tegucigalpa, Honduras.
  27. Zêzere, J. L., Reis, E., Garcia, R., Oliveira, S., Rodrigues, M. L., Vieira, G., & Ferreira, A. B. (2004). Integration of spatial and temporal data for the definition of different landslide hazard scenarios in the area north of Lisbon (Portugal). Natural Hazards and Earth System Science, 4(1), 133–146. [CrossRef]
  28. Galli, M., & Guzzetti, F. (2007). Landslide vulnerability criteria: A case study from Umbria, central Italy. Environmental Management, 40(4), 649–664. [CrossRef]
  29. García-Urquía, E., & Axelsson, K. (2015). Rainfall thresholds for the occurrence of urban landslides in Tegucigalpa, Honduras: An application of the critical rainfall intensity. Geografiska Annaler, Series A: Physical Geography. [CrossRef]
  30. Tien Bui, D., Pradhan, B., Lofman, O., Revhaug, I., & Dick, Ø. B. (2013). Regional prediction of landslide hazard using probability analysis of intense rainfall in the Hoa Binh province, Vietnam. Natural Hazards, 66(2), 707–730. [CrossRef]
  31. Khan, Y. A., Lateh, H., Baten, M. A., & Kamil, A. A. (2012). Critical antecedent rainfall conditions for shallow landslides in Chittagong City of Bangladesh. Environmental Earth Sciences, 67(1), 97–106. [CrossRef]
  32. Valenzuela, P., Zêzere, J. L., Domínguez-Cuesta, M. J., & Mora García, M. A. (2019). Empirical rainfall thresholds for the triggering of landslides in Asturias (NW Spain). Landslides, 16(7), 1285–1300. [CrossRef]
  33. Bonachea, J. (2006). Desarrollo, aplicación y validación de procedimientos y modelos para la evaluación de amenazas, vulnerabilidad y riesgo debidos a procesos geomorfológicos [Universidad de Cantabria]. https://repositorio.unican.es/xmlui/handle/10902/1292.
  34. Chow, V. Te, Maidment, D., & Mays, L. (1988). Hidrologic statistics. In Applied hydrogeology (pp. 350–371). McGraw-Hill Book Co.
  35. Ciurena, R., Schroter, D., & Glade, T. (2013). Conceptual Frameworks of Vulnerability Assessments for Natural Disasters Reduction. In J. Tiefenbacher (Ed.), Approaches to Disaster Management - Examining the Implications of Hazards, Emergencies and Disasters (p. 424). IntechOpen. [CrossRef]
  36. Cardona, O. D., Ordaz, M. G., Reinoso, E., & Yamin, L. E. (2011). Enfoque integral para la evaluación probabilista del riesgo (CAPRA): iniciativa internacional para la efectividad de la gestión del riesgo de desastre. Cuarto Congreso Nacional de Ingeniería Sísmica·, 13.
  37. Forbes, C., Evans, M., Hastings, N., & Peacock, B. (2011). Beta Distribution. In Statistical Distributions (4th ed., pp. 55–62). John Wiley & Sons Ltd.
  38. Barbat, A. H., Moya, F. Y., & Canas, J. A. (1996). Damage scenarios simulation for seismic risk assessment in urban zones. Earthquake Spectra, 12(3), 371–394. [CrossRef]
  39. Jaiswal, K., Bausch, D., Rozelle, J., Holub, J., & McGowan, S. (2008). Hazus® estimated annualized earthquake losses for the United States.
  40. Reclamation, & USACE. (2019). Event Trees. In Best Practices in Dam and Levee Safety Risk Analysis (pp. 5–20). Reclamation/USACE. https://www.usbr.gov/ssle/damsafety/risk/methodology.html.
  41. Penning-Rowsell, E., Johnson, C., Tunstall, S., Tapsell, S., Morris, J., Chatterton, J., & Green, C. (2005). The Benefits of Flood and Coastal Risk Management: A Handbook of Assessment Techniques. Middlesex University Press.
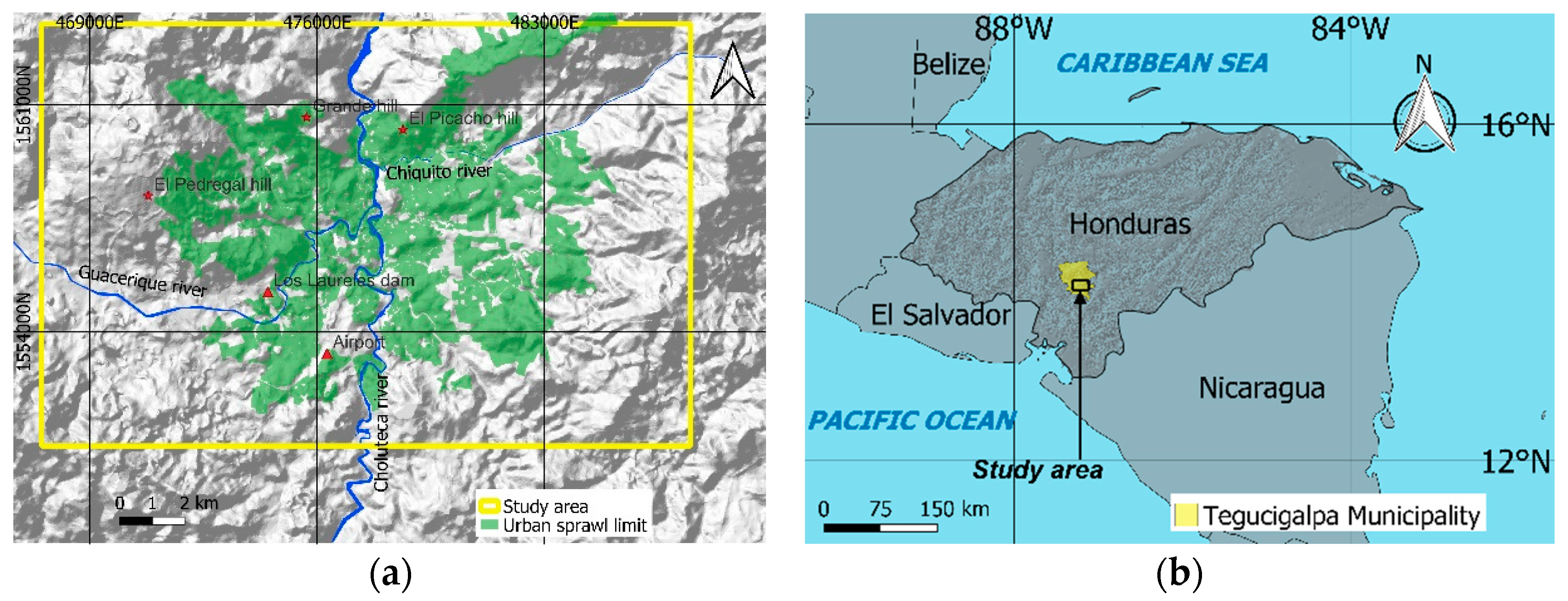
Preprints 114838 g001
Figure 1. (a) Location of the MCD; (b) Location of the study area.
Figure 1. (a) Location of the MCD; (b) Location of the study area.
Preprints 114838 g001
Preprints 114838 g002
Figure 2. Lithological map of the study area.
Figure 2. Lithological map of the study area.
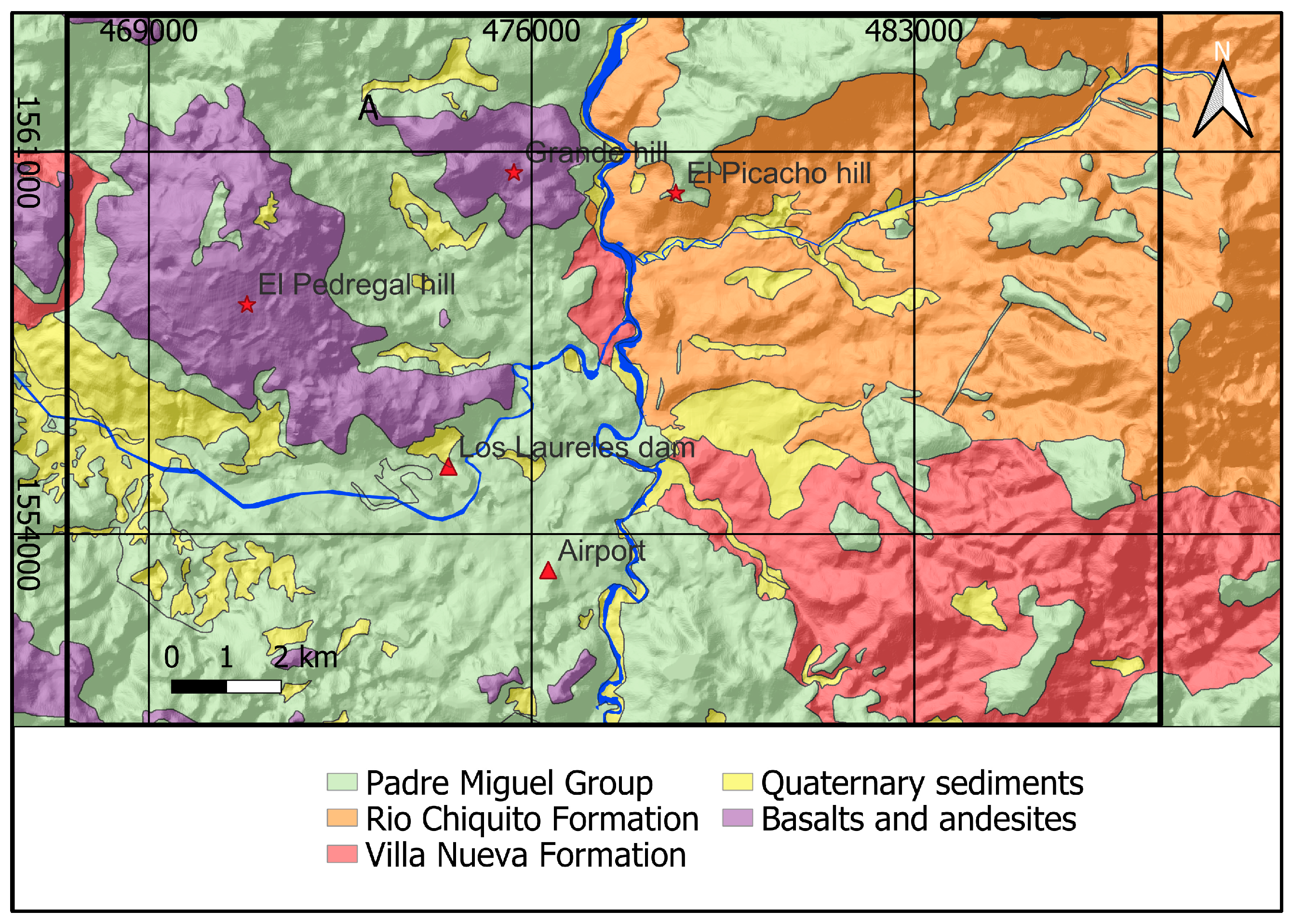
Preprints 114838 g002
Preprints 114838 g003
Figure 3. Location of landslides where housing damage surveys were collected.
Figure 3. Location of landslides where housing damage surveys were collected.
Preprints 114838 g003
Preprints 114838 g004
Figure 4. Map showing the distribution of the probability of SF <1.
Figure 4. Map showing the distribution of the probability of SF <1.
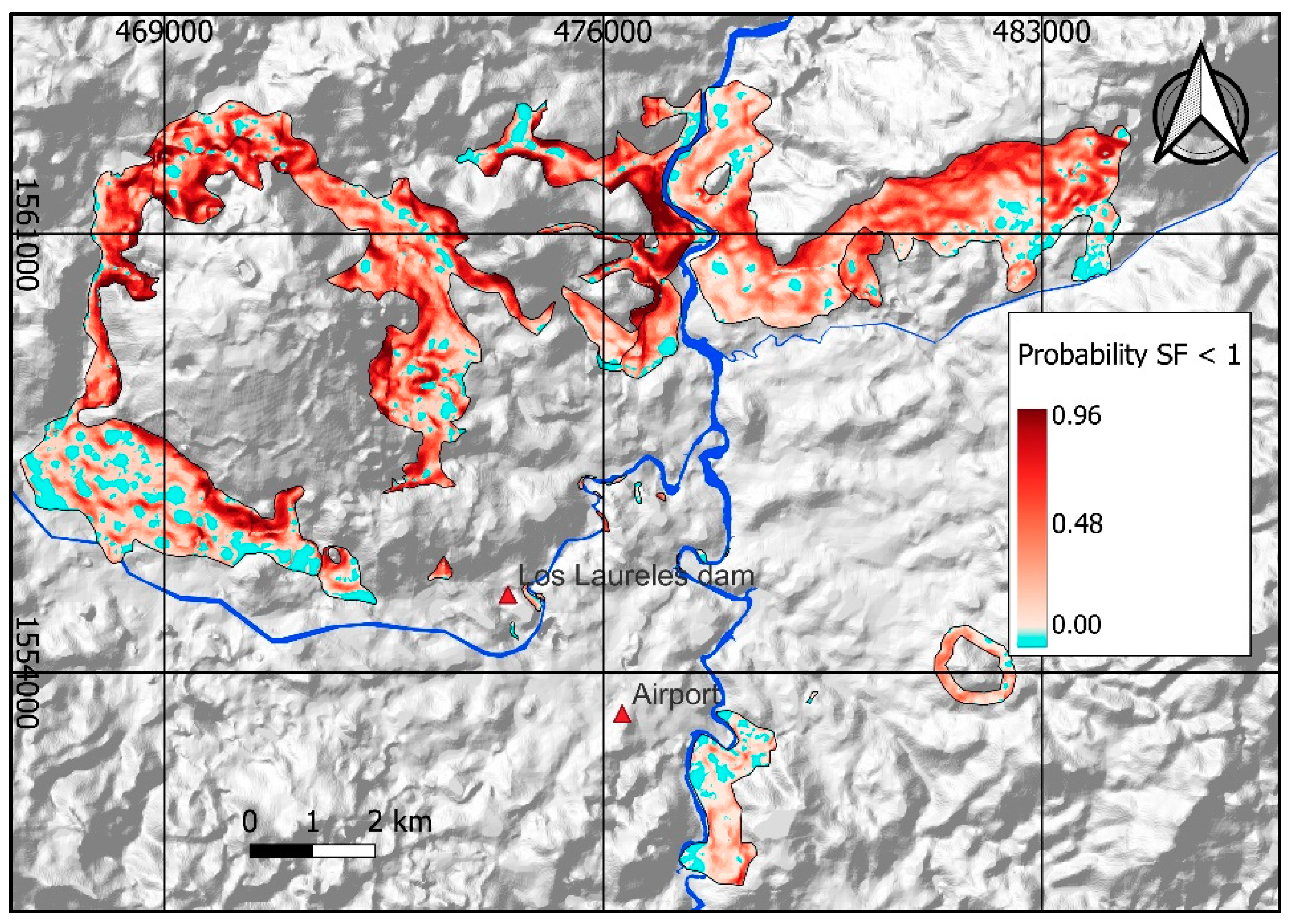
Preprints 114838 g004
Preprints 114838 g005
Figure 5. Probability of SF <1 including polygons reclassified with expert criteria.
Figure 5. Probability of SF <1 including polygons reclassified with expert criteria.
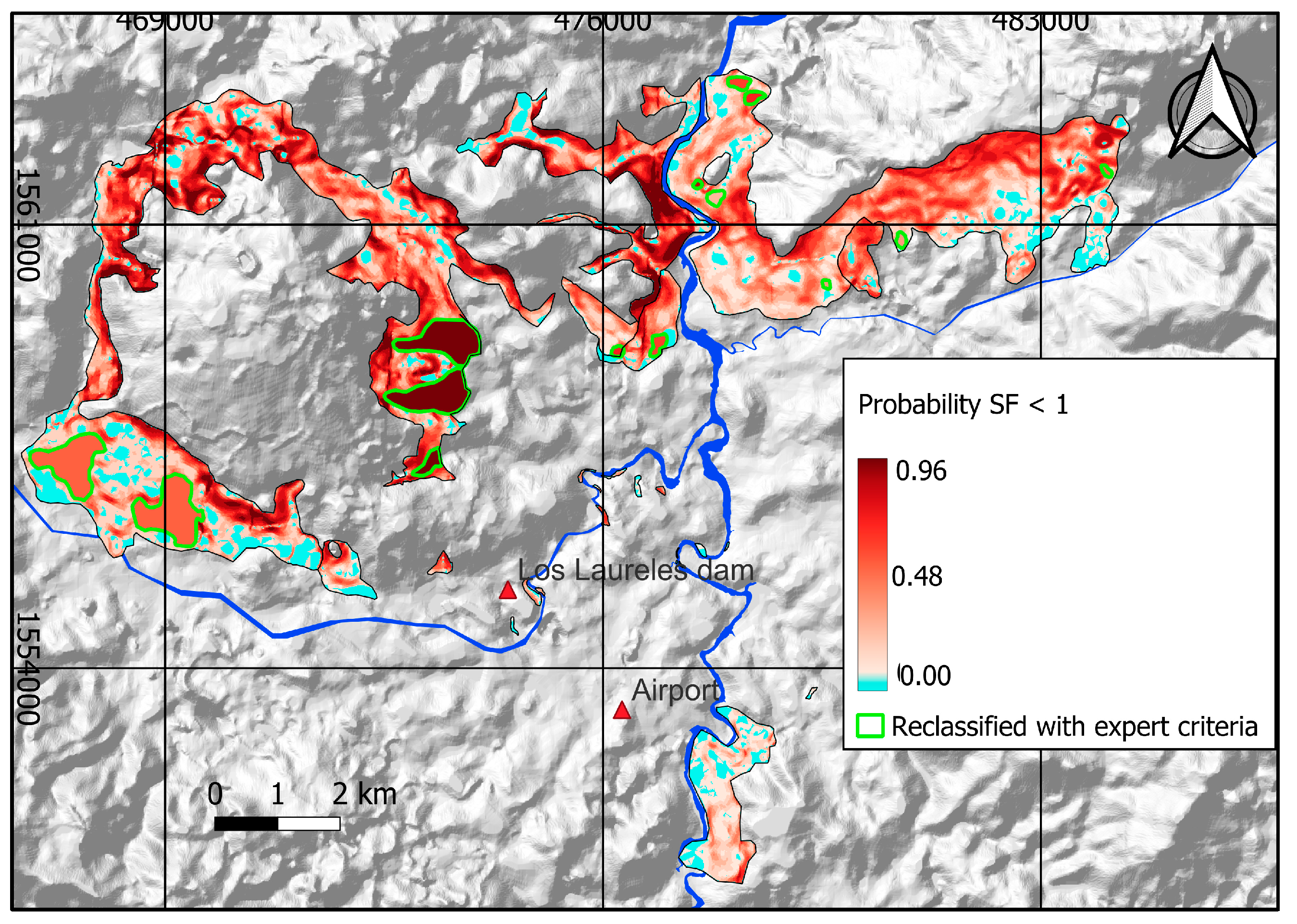
Preprints 114838 g005
Preprints 114838 g006
Figure 6. Probable USD losses due to landslide occurrence, broken down by pixel.
Figure 6. Probable USD losses due to landslide occurrence, broken down by pixel.
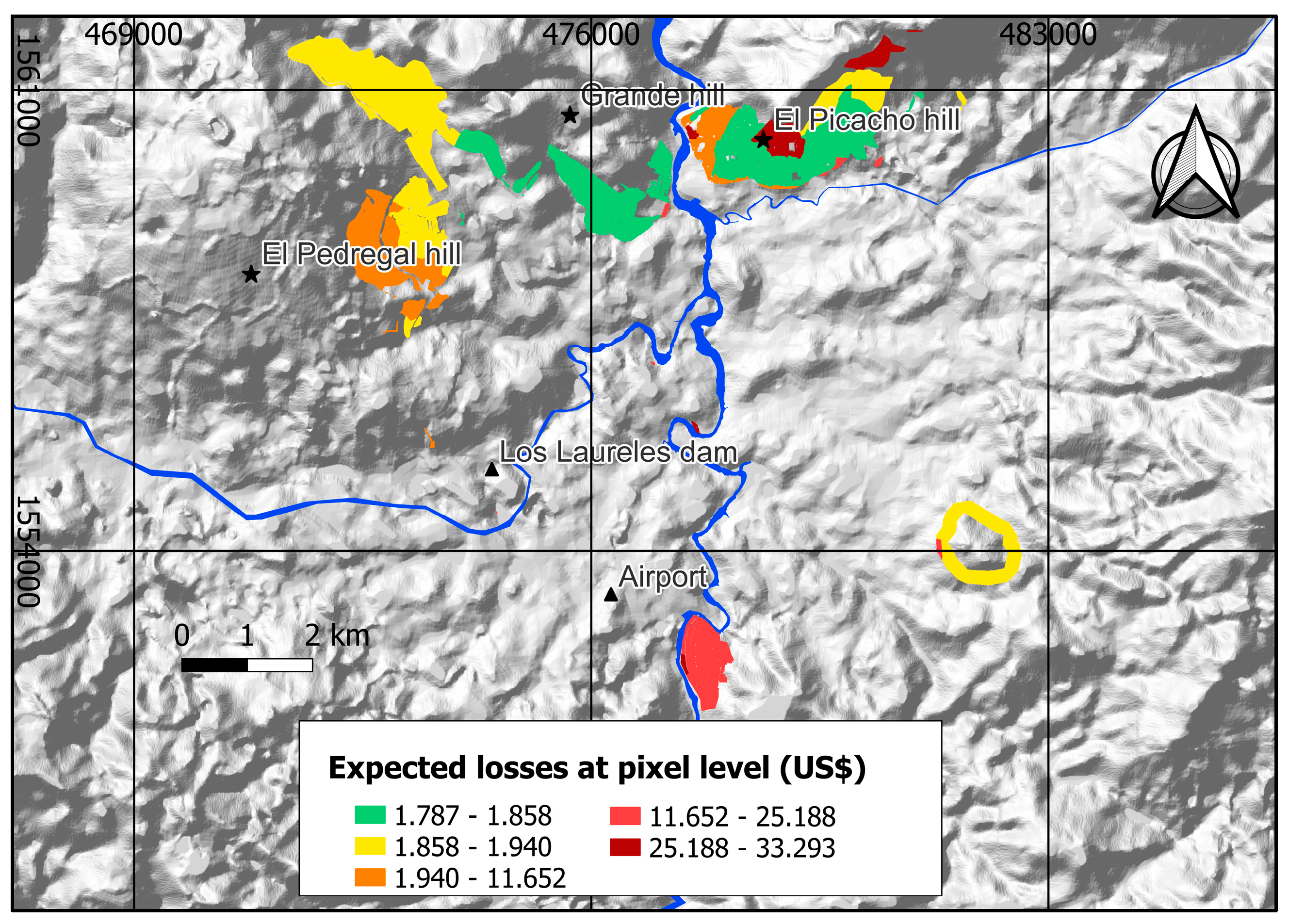
Preprints 114838 g006
Preprints 114838 g007
Figure 7. Probable loss values in USD at the pixel level, for a return period of 125 years.
Figure 7. Probable loss values in USD at the pixel level, for a return period of 125 years.
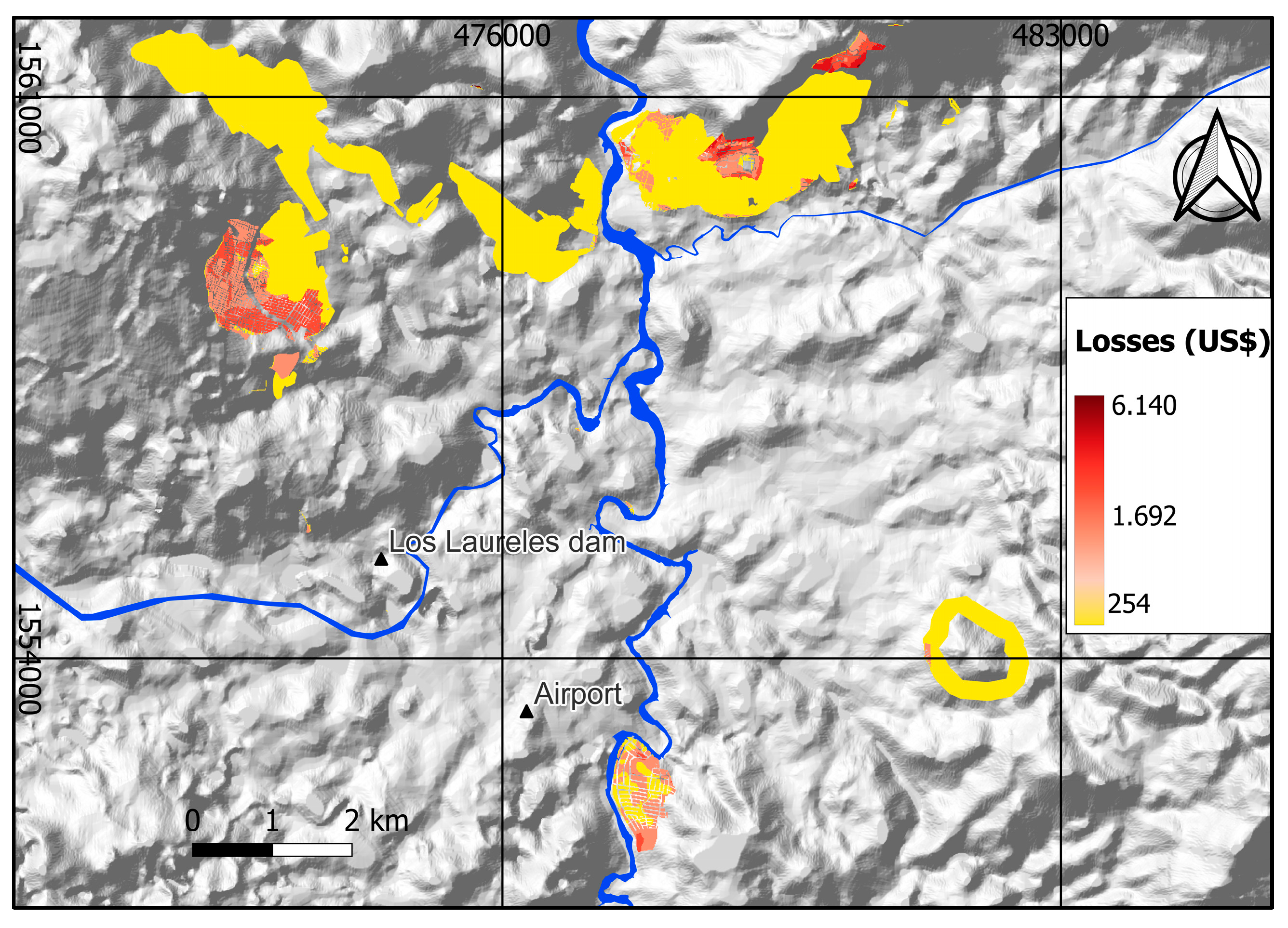
Preprints 114838 g007
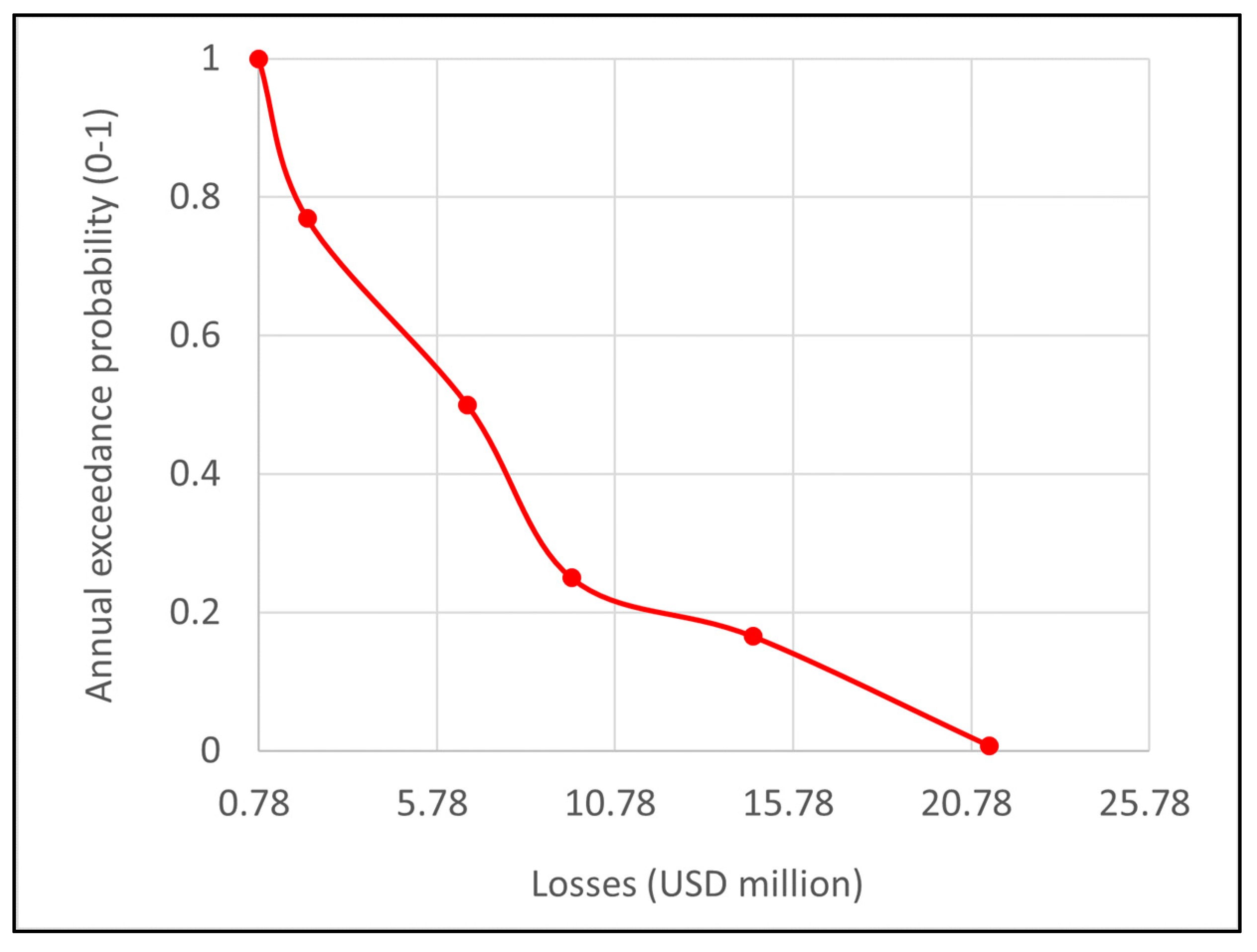
Preprints 114838 g008
Figure 8. Landslide loss exceedance curve for the study area.
Figure 8. Landslide loss exceedance curve for the study area.
Preprints 114838 g008
Table 1. Average and standard deviation of the SF < 1 probability (between 0 to 1) for the different layers.
Table 1. Average and standard deviation of the SF < 1 probability (between 0 to 1) for the different layers.
Layer X ¯ σ
Colluviums and residual soils 0,37 0,26
Validated landslide inventory 0,44 0,25
Colluvium of basalts, andesites and rhyolites 0,42 0,28
Residual soil from Valle de Ángeles group 0,4 0,23
Colluviums and residual soils 0,3 0,22
Table 2. RP: Return Period. NLS: N⁰ of Landslides, AD (pix): N⁰ of pixels of landslides. Pt: Temporal probability at the pixel level.
Table 2. RP: Return Period. NLS: N⁰ of Landslides, AD (pix): N⁰ of pixels of landslides. Pt: Temporal probability at the pixel level.
RP: (years) NLS AD (pix) (Tai) P t ( T a i T s )
125 29 42.664 0,109
6 20 29.423 0,075
4 13 19.125 0,049
2 9 13.240 0,034
1,3 3 4.413 0,011
1 1 1.471 0,004
Table 3. Average, standard deviation, and Parameters of the Beta function for each type of housing.
Table 3. Average, standard deviation, and Parameters of the Beta function for each type of housing.
Hose type X ¯ σ α β
Precarious brick housing 0,53 0,43 0,18 0,16
Wooden housing 0,47 0,38 0,35 0,40
Popular brick housing 0,42 0,34 0,46 0,63
Block housing 0,35 0,34 0,33 0,62
Table 4. Values exposed to landslides per type of neighborhood.
Table 4. Values exposed to landslides per type of neighborhood.
Neighborhood type Area (ha) Exposed houses 2020 Exposed population
2020		 Exposed population 2020
(%)		 Housing area (103 m2) m2 value (USD)1 Exposed value
(USD)1 		Exposed value (%)
Residential 43,7 1.197 3.755 2 305,8 1.246,0 381 30
Middle class 56,2 3.170 11.638 7 337,4 940,5 317 25
Popular 132,7 9.431 39.316 24 929,1 357,5 332 26
Precarious 606,6 24.072 109.566 67 4.852,9 46,3 224 18
TOTAL 839,3 37.870 164.275 100 6.425 1.255 100
1 USD values from 2020
Table 5. Average, standard deviation, and Parameters of the Beta function for each type of housing.
Table 5. Average, standard deviation, and Parameters of the Beta function for each type of housing.
Type of neighborhood E [L|l]
(MUSD)		 % EV
Residential 137 36
Middle class 139 44
Popular 146 44
Precarious 113 51
TOTAL 535 43
Table 6. The table provides a summary of the values used to estimate the average annual loss (AAL) through the interval method. LI: Lower limit. LS: Upper limit. VI: Interval value. Q: Probability.
Table 6. The table provides a summary of the values used to estimate the average annual loss (AAL) through the interval method. LI: Lower limit. LS: Upper limit. VI: Interval value. Q: Probability.
LI1 LS1 VI1 LI2 LS2 P2 AAL1
0,78 2,1 1,3 1 0,77 0,23 0,23
2,1 6,6 3,7 0,77 0,5 0,27 1,01
6,6 9,6 7,9 0,5 0,25 0,25 1,99
9,6 14,6 11,8 0,25 0,16 0,08 0,99
14,6 21,3 17,6 0,16 0,008 0,16 2,79
21,3 n/a 21,3 0,008 0 0,008 0,17
TOTAL AAL1 7,26
1 USD, 2 probability values.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated