Calculation of Some Low-Lying Electronic Excitations of Barium Monofluoride Using the Eom-CC3 Method with an Effective Core Potential Approach

Preprint

Article

Calculation of Some Low-Lying Electronic Excitations of Barium Monofluoride Using the Eom-CC3 Method with an Effective Core Potential Approach

Altmetrics

Downloads

Views

Comments

Marko Horbatsch^*

This version is not peer-reviewed

This preprints belongs to the Topic

Computational Chemistry in Metallurgy, Materials and Energy

Submitted:

09 August 2024

Posted:

12 August 2024

You are already at the latest version

Alerts

Abstract

Barium monofluoride (BaF) is a polar molecule of interest to measurements of the electron electric dipole moment [1, 2]. For this purpose efforts are under way to investigate this molecule embedded within cryogenic matrices, e.g., in solid Ne [3]. For a theoretical understanding of the electronic structure of such an embedded molecule the need arises for efficient methods which are accurate, but also can handle a number of atoms which surround the molecule. The calculation for gas-phase BaF can be reduced to involve only outer electrons by representing the inner core of Ba with a pseudopotential [4] while carrying out a non-relativistic calculation with an appropriate basis set [5]. In this work we demonstrate to which extent this can be achieved using coupled-cluster methods to deal with electron correlation. As a test case the SrF(X 2Σ+ → B 2Σ+) transition is investigated and excellent accuracy is obtained with the EOM-CC3 method. For the BaF(X 2Σ+ → A′ 2∆, X 2Σ+ → A 2Π, X 2Σ+ → B 2Σ+) transitions various coupled-cluster approaches are compared with very good agreement for EOM-CC3 with experimentally derived spectroscopic parameters except for the excitation to the A′ 2∆ state for which the excitation energy is overestimated by 200 cm−1.

Keywords:

Subject: Physical Sciences - Quantum Science and Technology

I. Introduction

The search for the electron’s electric dipole moment, as well as laser cooling with the goal of optical trapping has triggered renewed interest in polar diatomic molecules, such as barium and strontium monofluoride (BaF, SrF). On the theoretical side this interest is reflected in large-scale computational efforts: a comprehensive study of the low-lying excitations was performed using a relativistic Fock-space coupled cluster (CC) approach [6]. These calculations led to a much improved agreement with experimental data, in particular for the excitation energies

Δ T_{e}

, i.e., the differences in potential energy curves at the respective minima. Agreement was found at the level of

100 c m^{- 1}

for SrF and BaF (and larger for CaF), which represented a dramatic improvement over previous theoretical results. Subsequently, a fully relativistic treatment, including quantum electrodynamic corrections and basis set extrapolation led to an order-of-magnitude improvement for BaF [7], and agreement with experimental excitation energies

T_{e}

at the level of

10 c m^{- 1}

. The all-electron Fock-space CC method has been shown recently to account for a number of properties, such as ionization energies [8], and hyperfine constants [9].

Since all-electron calculations are computationally challenging, particularly in the relativistic frameworks, it is of interest to explore whether effective core potentials (ECP) and corresponding basis sets can be combined with high-order CC methods to reach the

100 c m^{- 1}

level precision with reduced computational effort. Our interest in this regard is the investigation of these molecules within a cryogenic matrix environment, such as argon or neon [3,10,11]. To investigate BaF in a such an environment a more economical approach is required, and this represents the motivation for this study.

The layout of the paper is as follows. We begin in Sec. Section II with a short summary of the basic equations which lead to the spectroscopic constants. In Sec. Section III we demonstrate how well the EOM-CC3 method combined with an effective core potential and appropriate basis set works for the

X^{2} Σ^{+} \to B^{2} Σ^{+}

transition in SrF, which is free of spin-orbit interactions. We then apply the EOM-CC3, EOM-CCSD and state specific

Δ - C C

methods to the low-lying excitations in BaF. We draw some conclusions in Sec. Section IV.

II. Methodology

There are a number of coupled-cluster (CC) methods to compute electronic excitations. We have recently compared some of them for magnesium monofluoride and found that the EOM-CC3 method (EOM stands for equation of motion) when combined with the the aug-cc-pVnZ basis set family can reach agreement with experimentally derived electronic excitation energies

T_{e}

[12]. The goal of the present work is to show that this methodology can work equally well for heavier systems (such as SrF or BaF) when reducing the all-electron problem to a (10+9)-electron problem by means of an effective core potential ECP [4,13]. We use the correlation consistent basis sets developed by Hill and Peterson [5].

To achieve high accuracy for electronic excitation energies of molecules the following two methods will be employed: EOM-CC3 with two basis set families, cc-pVnZ-PP and the augmented versions aug-cc-pVnZ-PP. For the former basis set family we were able to also apply the state-specific

Δ

-CC methods which were reviewed in Ref. [14,15]. These methods can be economical computationally: one generates an unrestricted Hartree-Fock (HF) Slater determinant after orbital rotation (switching highest occupied and some low unoccupied orbital) to obtain a

Δ

-SCF solution; then one follows up with a CC calculation for this state. The problem with this method is that for some large basis sets the HF calculation collapses back to the ground state. The computations in the

Δ

-CC step for the excited state usually require many more iterations than for the ground state. An interesting feature, however, is the option to treat triple excitations perturbatively. i.e., there is a

Δ

-CCSD(T) method for which there is no EOM counterpart.

One question we are interested in is how big differences are between the state-specific vs EOM methods, while using the cc-pVnZ-PP basis at the

n = 5

(5Z) level. The calculations were performed with the CCEOM package within Psi4 [16]. It allows for orbital rotations in the first irreducible representation, and we were able to carry out the necessary rotations by using different symmetries:

C_{2 v}

C_{s}

, and

C_{1}

. Our focus is on the BaF excitations from

X^{2} Σ^{+}

A^{'}^{2} Δ

A^{2} Π

, and

B^{2} Σ^{+}

states.

To obtain the spectroscopic parameters one has to calculate potential energy curves over some range of molecular separations

R_{i}

. A simpler task is to choose a fixed separation

R = R_{e}

(e.g. the

X^{2} Σ^{+}

value of

R_{e}

known from experiment), and to compute vertical excitation energies

Δ T

. The

Δ T

values overestimate the excitation energies

Δ T_{e}

which are obtained from the potential energy curves for both ground and excited states using the respective state-specific equilibrium separations

R_{e}

The potential energy curves lead to the spectroscopic parameters

ω_{e}

and

ω_{e} x_{e}

, which follow from the nuclear vibrational excitation energies in accord with [17]

E_{v} = T_{e} + ω_{e} (v + \frac{1}{2}) - ω_{e} x_{e} {(v + \frac{1}{2})}^{2} .

(1)

A practical procedure we follow is to compute data for the potential energy curves for a set of values

R_{i}

, which span the region of R-values such that one obtains a realistic energy spectrum for low-lying nuclear vibrations of the molecule, e.g.,

v = 0, 1, 2, 3

. A spline fit through the data allows to determine

R_{e}

, and the value of the minimum potential energy

T_{e}

It is convenient to fit these data to a Morse potential,

V (R) = T_{e} + D {(1 - exp [- β (R - R_{e})])}^{2} .

(2)

The two additional constants

D, β

can then be found from the fit. Here D is just a parameter (not necessarily close to the dissociation energy), as the purpose of fitting to a Morse potential is to obtain a wider range in R to accommodate the tails of the vibrational states when solving the nuclear Schrödinger equation. This procedure avoids the computation at a larger grid of values

R_{i}

. Alternatively, one can carry out direct fits of the original data to the Morse potential eq.(2) to find the four parameters.

Fitting the vibrational spectrum for

v = 0, 1, 2, 3

to eq. (1) allows one to find the parameters

ω_{e}

and

ω_{e} x_{e}

, or a more complete set including

ω_{e} y_{e}

in case one uses not a Morse potential but a more general fit of the calculated potential energy points at the given set

{R_{i}}

. For the Morse potential the values of

ω_{e}

and

ω_{e} x_{e}

are related directly to the potential parameters.

One can also deduce the parameters from the experimentally determined values of the spectroscopic constants. In atomic units one has

D = \frac{ω_{e}^{2}}{4 ω_{e} x_{e}} β = \sqrt{\frac{M}{2 D}} ω_{e},

(3)

where M is the reduced mass of the diatomic molecule.

In terms of expected accuracy for the excitation energies the goal is to be within

100 c m^{- 1}

of experimentally deduced values. Is this percent-level (or better) goal achievable? The EOM-CC3 method is claimed to be good to

40 m e V

level (

\approx 300 c m^{- 1}

) [18], in general. The reason why we can expect to do better than that for our cases is that the excitations are predominantly of single-electron type. In the case of MgF it was shown that the method when coupled with the augmented correlation consistent basis sets can deliver per mille accuracy for transition energies [12].

The results were obtained on multi-core workstations (e.g., Apple MacBook Pro with 8 cores, but during most of the computations the CPU was loaded only at the 40% level). Excited-state calculation using the EOM-CC3 method for a single root took of the order of 10-12 hours with the aug-cc-pV5Z-PP basis and about half the time for cc-pV5Z-PP.

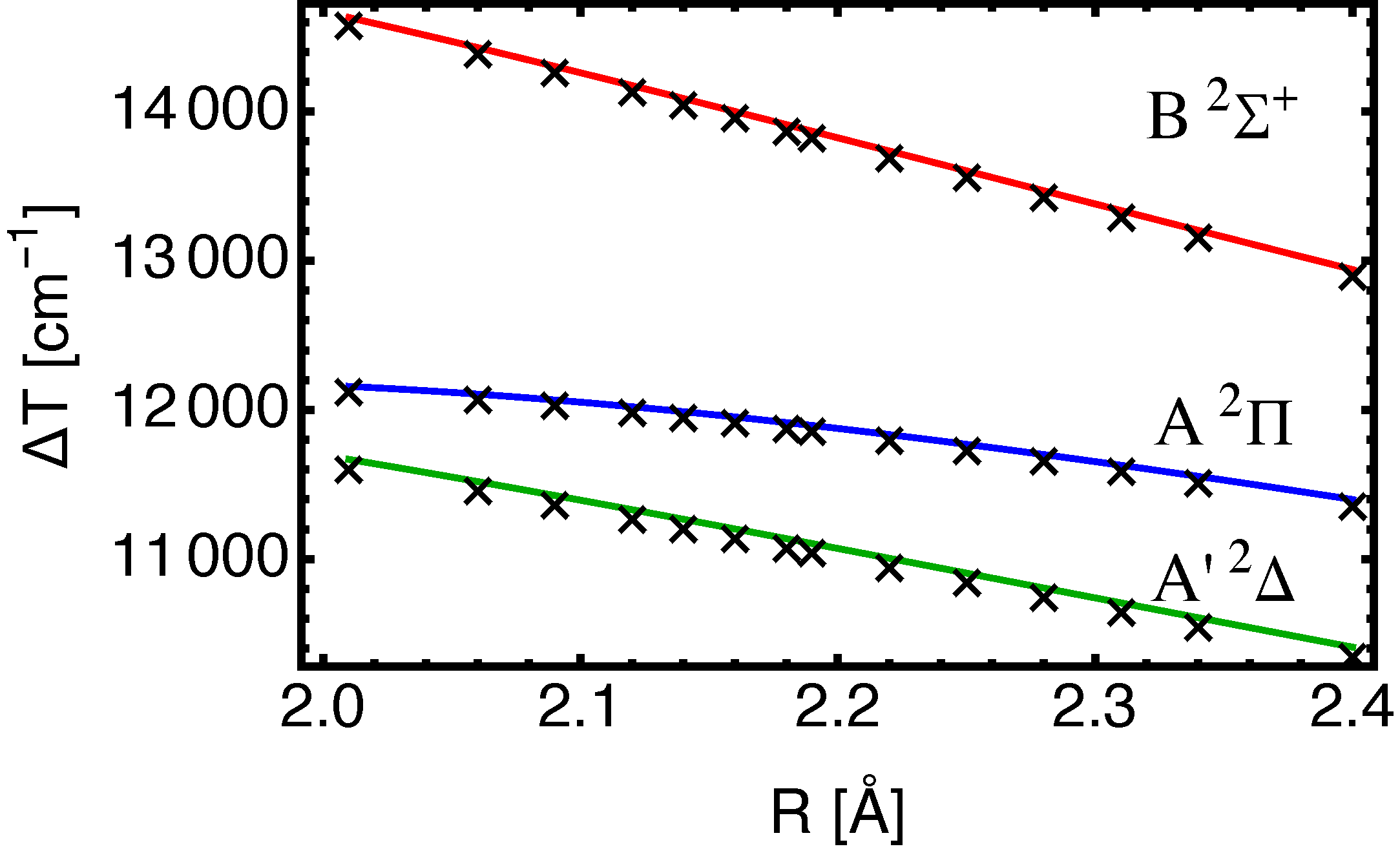
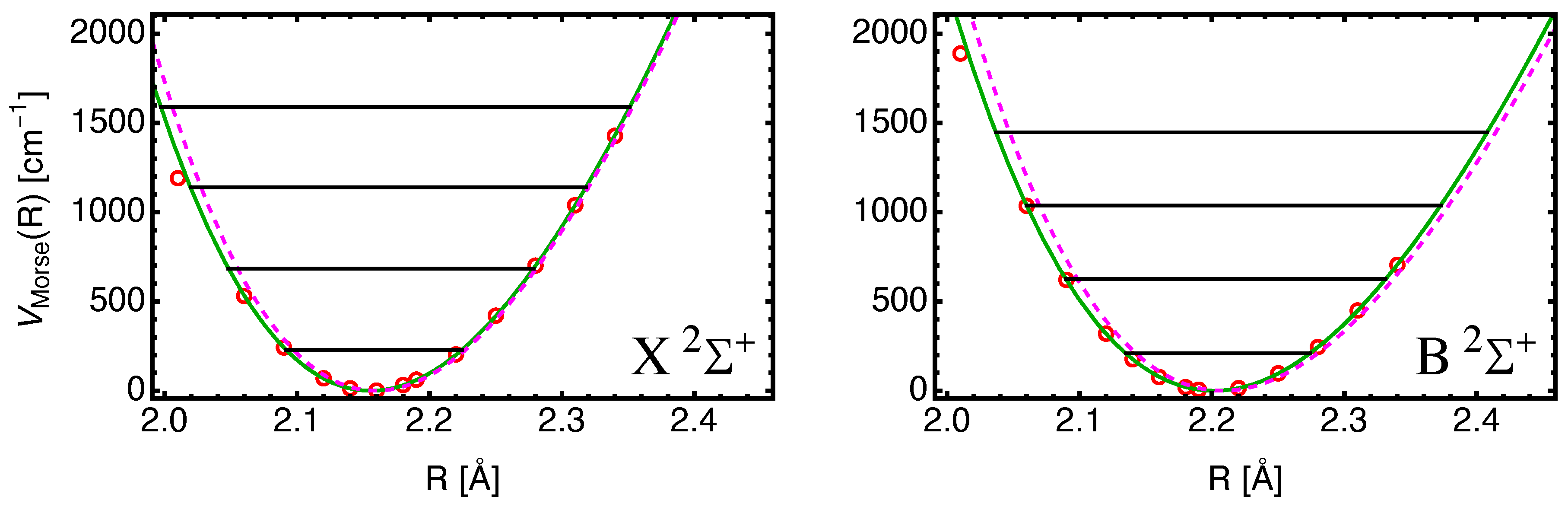
III. Results

A. SrF( $X^{2} Σ^{+} \to B^{2} Σ^{+}$ )

As a first case we look into an excitation of SrF for which the equilibrium distances of ground and excited state are very close to each other, namely

R = 2.075

and

R = 2.08

Å respectively. Vertical excitation energies are shown in Figure 1 as a function of R over a range of values that are needed to determine basic spectroscopic parameters. The variation of the excitation energies with R is large for the aug-cc-pVnZ basis with

n = 3

, i.e., TZ, but less for the QZ (

n = 4

) and 5Z (

n = 5

) calculations.

The obtained values of

R_{e}, Δ T_{e}, ω_{e}, ω_{e} x_{e}

for both states are compared in Table 1 with values derived from experiments, and with the Fock-space (FS) CC calculation of Ref. [6]. The variation of

Δ T_{e}

with the basis set quality parameter

n = 3, 4, 5

is not systematic, and the validity of extrapolation to the complete basis set limit may not be working well, and is therefore omitted.

The spectroscopic parameters

ω_{e}

and

ω_{e} x_{e}

were determined in the following way: the potential energy data for both states were obtained on a grid of 16 equidistant R values spanning

1.93 < = R < = 2.26

; these data were fitted to a local spline using the Interpolation function in Mathematica; the minimum position

R_{e}

and energy

T_{e}

was determined using FindMinimum; after subtraction of

T_{e}

the data were then fitted to either a Morse potential, or to a fourth-order polynomial including orders 2, 3 ,4 and centered on the determined value of

R_{e}

. Using the Morse and polynomial fits the Schrödinger equation for the nuclear motion was solved with NDEigensystem in Mathematica using the reduced mass for

^{88} S r^{19} F

, which is the most abundant isotope, and which was selected in experiments [19,20,21].

For the 5Z basis the present results are seen to work very well with the excitation energy

Δ T_{e}

obtained within

20 c m^{- 1}

, which is an excellent result. The focus on the excitation to the SrF(

B^{2} Σ^{+}

) state in this section is motivated by the case of BaF, for which one can argue that effective and true excitation energies may differ by over

100 c m^{- 1}

[23]. The problem of state mixing of one excited state with a vibrationally excited neighboring state becomes a problem for BaF due to the closeness of the

A^{'}^{2} Δ

and

A^{2} Π

potential energy curves. The potential energy curves for the sequence of CaF, SrF and BaF molecules are shown in Figure 1 of Ref. [6]. In contrast to BaF for SrF there should not be a problem with comparing effective experimental and theoretical parameters for the

B^{2} Σ^{+}

state.

A comment on the comparison with the calculations of Ref. [6] is perhaps in order. The scope of that work, of course, is substantially wider: the relativistic framework with an effective hamiltonian for the molecular mean-field approach is reduced to a two-component formalism (hence it is designated as the X2C-FSCC method). It includes part of the Breit interaction, and a basis set was constructed in a careful way with the doubly augmented d-aug-pVQZ relativistic basis of Dyall [25] expanded manually. This effort was required due to the treatment of the all-electron problem, and resulted in accurate spin-orbit splittings (which is not relevant for the

B^{2} Σ^{+}

state). In contrast, the present work describes relativistic effects by a pseudopotential for the inner 28 electrons of Sr (ECP28 based on multi-configuration Dirac-Fock and Breit interaction, cf. Ref. [13]), and uses a correlation-consistent basis set sequence designed for the atom [5]. Within the EOM-CC3 method this much simpler approach yields an improved excitation energy, and somewhat better values for the equilibrium distances.

B. BaF( $X^{2} Σ^{+} \to A^{'}^{2} Δ$ , $X^{2} Σ^{+} \to A^{2} Π$ , $X^{2} Σ^{+} \to B^{2} Σ^{+}$ )

In order to compare ECP based calculations which are non-relativistic in nature except for taking into account the contributions from core electrons of the heavy atom via the pseudopotential we need to look at spectroscopic results where the spin-orbit splittings are removed. A detailed analysis of BaF low-lying electronic excitations led to the discovery of the lowest excitation, namely the

A^{'}^{2} Δ

doublet [26]. The paper gives the excitation energies

Δ T_{e}

and spectroscopic parameters for the levels considered here, but experiment naturally includes the spin-orbit effect associated with

J = \frac{3}{2}, \frac{5}{2}

for

A^{'}^{2} Δ

, and

J = \frac{1}{2}, \frac{3}{2}

for

A^{2} Π

. A simple approach to obtain reference values for comparison with the present results is to average the spin-orbit splittings. These values are shown in Table 2.

In a follow-up paper [27] a detailed analysis was reported for the vibration-rotation bands

v = 0, 1, 2

, and effective constants were determined. These were derived from a model and resulted in the determination of spin-orbit coupling constants. The study was then complemented by a deperturbation approach [23], based on the notion that the excited states are predominantly 5d states. Another set of effective excitation energies was determined. The deperturbation concerns the fact that the

v = 2

vibrational excitation of the

A^{'}^{2} Δ

state becomes close to the

v = 0

A^{2} Π

state. Due to spin-orbit couplings the

B^{2} Σ^{+}

state is strongly affected, and the excitation energies

Δ T_{e}

derived from experimental data may not be exactly the quantities expected from the theoretical potential energy curves.

More complete measurements analyzing higher vibrational states are reported in Ref. [28], and the spectroscopic parameters are given in Table 2 as reference values. Recently measurements and analysis were performed not only for the most abundant isotope

^{138} B a^{19} F

, but also for

^{136} B a^{19} F

[29].

The deperturbed values of

Δ T_{e}

given in Table 3 of Ref. [23] agree with the simple averaging procedure shown in Table 2 for the

A^{'}^{2} Δ

state, are almost

20 c m^{- 1}

higher for the

A^{2} Π

state, and about

120 c m^{- 1}

lower for the

B^{2} Σ^{+}

state (

T_{Σ} = 13944.5

). This should be kept in mind when looking at the comparison with theory.

On the theoretical side we note that the relativistic FSCC method of Ref. [6] gives higher excitation energies for the properly coupled states with some overestimations at the

150 c m^{- 1}

level for

A^{'}^{2} Δ

and

A^{2} Π

. The spin-orbit splittings are obtained to reasonable accuracy. This cannot be said for the CASSCF+MRCI method with spin-orbit coupling calculated with perturbation theory [30], and our own experience while using Molpro [31] in an all-electron approach was similar in this respect.

How useful are calculated vertical excitation energies

Δ T

as approximations for

Δ T_{e}

? For the

A^{2} Π

and

A^{'}^{2} Δ

states this turns out to work, but less so for the

B^{2} Σ^{+}

state due to the variation in

Δ T (R)

as will be shown below in Figure 3. Our EOM-CC3 results for

R = 2.16

Å, with augmented basis for both Ba and F are shown in Table 2. For the excitation to the

B^{2} Σ^{+}

state the difference between

Δ T_{e}

and

Δ T

is appreciable.

Overall, the results are quite good, however with substantial room for improvement for excitation to the

A^{'}^{2} Δ

state due to the overestimation by over

200 c m^{- 1}

. For the

B^{2} Σ^{+}

state the result for

Δ T_{e}

supports the notion that theory should be compared to the value from the deperturbation analysis [23].

In order to assess the quality of the EOM-CC3 results we show in Figure 2 the calculated data with

T_{e}

subtracted for the

X^{2} Σ^{+}

and

B^{2} Σ^{+}

states. Also shown are fits to the data using the Morse potential eq. (2). The data points for

R = 2.01

Å were removed from the fit, and disagree with the Morse shape for both states. The reason for this deviation may be associated with basis set problems (superposition error) for small values of R. The dashed magenta curves are the potentials derived from the experimental parameters

R_{e}, ω_{e}, ω_{e} x_{e}

shown in Table 2 using eq. (3).

The agreement is not perfect: results from R-values to the left of the minima may be affected by the mentioned problem for the first data point, particularly in the case of the

X^{2} Σ^{+}

state. The values for

ω_{e} x_{e}

depend somewhat on the choice of data points used for the fits, and, thus, their values shown in Table 4 are, at best, estimates. The values for

R_{e}

should be accurate as stated, and those for

ω_{e}

are deemed to be accurate to 2.5 digits.

In Table 5 we present results from different CC methods and two basis set combinations for the vertical excitation energies at

R = 2.16

Å. We focus on the comparison of basis sets aug-cc-pV5Z-PP and cc-pV5Z-PP for the barium atom combined with aug-cc-pV5Z for fluorine, since the latter combination allowed us to apply state-specific CC methods in addition to the EOM approach.

We can summarize the data as follows: the best calculations are given in the second row for EOM-CC3 with augmentation on both atoms. Removing augmentation on Ba results in literally no change for the excitation to

A^{2} Π

, a small increase for the

A^{'}^{2} Δ

state, and a

45 c m^{- 1}

increase for the

B^{2} Σ^{+}

state. Interestingly, the excitation energies from the

Δ

-CC3 method are higher than the EOM-CC3 results with the same basis on the order of

40 - 50 c m^{- 1}

. The EOM-CCSD calculations yield systematically higher excitation energies, and are, thus, deemed less useful. The

Δ

-CCSD results, on the other hand are lower for the

B^{2} Σ^{+}

state. The

Δ

-CCSD(T) method gives results close to those from the

Δ

-CC3 method. In Table A1 in the Appendix the energies are given for completeness. One can observe that the actual energies for different methods disagree much more than the excitation energies.

Concerning the state-specific

Δ

-CC results for excited states, which are obtained from higher roots than the ground state, we make some following observations. The

Δ

-SCF solutions, which are required as an orbital basis to perform the CC steps are easy to find in

C_{2 v}

C_{1}

symmetry for the

A^{2} Π

and

B^{2} Σ^{+}

states, by replacing the highest occupied with nearby lowest unoccupied natural orbitals (HONO vs

L U N O + j

) with

j = 0, 1

using Psi4 terminology. For the

A^{'}^{2} Δ

state we used

C_{s}

symmetry and used the

L U N O + 4

to replace the HONO to obtain the

Δ

-SCF Slater determinant. The CCSD(T) calculation generates the CCSD energy as an intermediate result, while the

Δ

-CC3 calculations are done separately. The convergence properties of the CC correlation energy calculations were similar to ground-state calculations (on the order of 20 iterations) when working in

C_{s}

C_{2 v}

symmetry.

In Figure 3 the excitation energies from EOM-CC3 with both basis sets are shown as a function of internuclear separation. The crosses show the data with augmentation on both atoms and are calculated on a fine grid of R-values (cf. Table A1). The curves show the strong dependence of

Δ T

vs R for the excitation to

B^{2} Σ^{+}

, which is responsible for the difference between

Δ T

and

Δ T_{e}

for this state (cf. Table 2). The basis set combination which lacks augmentation on Ba gives nevertheless results of good quality, and may be preferred for more complicated situations (such as BaF within a cryogenic Ne matrix).

The

X^{2} Σ^{+}

ground-state energies for

R = 2.16

Å which are shown in the Appendix in Table A1 depend strongly on which CC method is used, and also show variation with the level of basis (aug/aug vs cc/aug for Ba/F). Nevertheless, the vertical excitation energies from the

Δ

-CC methods differ from EOM-CC3 on the

100 c m^{- 1}

scale for

Δ

-CCSD and

30 c m^{- 1}

for

Δ

-CCSD(T). Basis augmentation at Ba changes this excitation energy by

50 c m^{- 1}

At the level of full EOM-CC3 we find that only the

A^{'}^{2} Δ

state excitation energy changes noticeably (it comes out higher by about

30 c m^{- 1}

, which is on top of an

\approx 200 c m^{- 1}

overestimate). For the sake of computational economy one may recommend this approach. Neglecting the triples (CCSD over CCSD(T) or CC3) leads to

\approx 100 c m^{- 1}

differences in the excitation energies.

Figure 3. EOM-CC3 vertical excitation energies

Δ T

c m^{- 1}

as a function of R (in Å) for the electronic transitions

X^{2} Σ^{+} \to A^{'}^{2} Δ

(green),

X^{2} Σ^{+} \to A^{'}^{2} Π

(blue), and

X^{2} Σ^{+} \to B^{2} Σ^{+}

(red). The curves represent spline fits to data obtained with the basis cc-pV5Z-PP for barium and aug-cc-pV5Z for fluorine. The crosses are data points obtained with both basis sets augmented, which lowers the values for the excitation energies by up to

50 c m^{- 1}

Figure 3. EOM-CC3 vertical excitation energies

Δ T

c m^{- 1}

as a function of R (in Å) for the electronic transitions

X^{2} Σ^{+} \to A^{'}^{2} Δ

(green),

X^{2} Σ^{+} \to A^{'}^{2} Π

(blue), and

X^{2} Σ^{+} \to B^{2} Σ^{+}

50 c m^{- 1}

IV. Conclusions

EOM-CC3 calculations for electronic excitations of SrF and BaF molecules are reported on the basis of treating these molecules as 19-electron systems, while representing the inner cores of Sr and Ba with pseudopotentials, which effectively removed 28 or 46 electrons for the two heavy atoms.

For SrF only the

X^{2} Σ^{+} \to B^{2} Σ^{+}

transition was investigated. The difference between the equilibrium nuclear separations

R_{e}

for the two states is small. It was shown how the vertical excitation energy changes with separation R as a function of basis set parameter n. For the QZ and 5Z basis (aug-cc-pVnZ-PP/aug-cc-pVnZ for Ba/F) this variation is much less pronounced than for TZ. The resulting value for

Δ T_{e}

at the 5Z basis level is

20 c m^{- 1}

below the experimentally determined value, which is substantially better than other calculations. The variation of

Δ T

for fixed R as a function of basis set quality parameter n with

n = 3, 4, 5

is not systematic, and therefore the extrapolation to the complete basis set limit for

Δ T_{e}

appears to be less valid than for the ground-state energy.

For BaF calculations were carried out for excitations to three closely related states, namely

A^{'}^{2} Δ

A^{2} Π

, and

B^{2} Σ^{+}

using basis sets at the 5Z level. The

Δ T_{e}

values obtained for the

A^{'}^{2} Δ

state overestimate the experimentally derived value by over

200 c m^{- 1}

, while the results for

A^{2} Π

and for

B^{2} Σ^{+}

agree to within

30 c m^{- 1}

of the spectroscopic value obtained from a deperturbation analysis [23].

The finding of the present study for the

B^{2} Σ^{+}

excitation energy, namely that much better agreement is found with the result from a deperturbation analysis [23] than with the effective parameters derived directly from the experimental data of

v = 0, 1, 2

vibrational bands [27] is hard to reconcile with the theoretical analysis of Ref. [7], where agreement was found with the effective spectroscopic constant

Δ T_{e}

as quoted in Ref. [26].

Acknowledgments

I thank Eric Hessels, Gregory Koyanagi and Rene Fournier for many discussions. Financial support from the Natural Sciences and Engineering Research Council of Canada (NSERC) (RGPIN-2023-05072) is gratefully acknowledged.

Appendix A

Table A1. The top eight rows give energies (in Hartree) from EOM-CC3 calculations using the cc-pV5Z-PP basis set [5] for Ba and the aug-cc-pV5Z basis set for F. The scale of the correlation energy is 0.6 Hartree. The EOM-CC3 results in the bottom part of the table, and the EOM-CCSD result marked with

^{†}

, are obtained with the aug-cc-pV5Z-PP basis for Ba and the aug-cc-pV5Z basis set for F. The excitation energies from these results are represented by open circles in Figure 3. The state-specific

Δ

-CC results are obtained with the cc-pV5Z-PP basis for Ba and the aug-cc-pV5Z basis set for F, and were obtained with symmetry set to

C_{1}

^{†}

, are obtained with the aug-cc-pV5Z-PP basis for Ba and the aug-cc-pV5Z basis set for F. The excitation energies from these results are represented by open circles in Figure 3. The state-specific

Δ

-CC results are obtained with the cc-pV5Z-PP basis for Ba and the aug-cc-pV5Z basis set for F, and were obtained with symmetry set to

C_{1}

Method	R [Å]	$X^{2} Σ^{+}$	$A^{'}^{2} Δ$	$A^{2} Π$	$B^{2} Σ^{+}$
EOM-CC3	2.01	-125.27549126	-125.22232710	-125.22009727	-125.20882965
	2.06	-125.27873089	-125.22624470	-125.22357258	-125.21298780
	2.11	-125.28070218	-125.22892852	-125.22585778	-125.21592208
	2.16	-125.28116764	-125.23012756	-125.22670690	-125.21737647
	2.21	-125.28049152	-125.23019824	-125.22647458	-125.21770545
	2.26	-125.27885127	-125.22931269	-125.22532878	-125.21707479
	2.31	-125.27641989	-125.22763820	-125.22343428	-125.21565498
	2.36	-125.27334842	-125.22532102	-125.22093362	-125.21358932
EOM-CCSD	2.16	-125.25688898	-125.20589866	-125.20207560	-125.19235173
EOM-CCSD $^{†}$	2.16	-125.25729908	-125.20643000	-125.20249267	-125.19279287
$Δ$ -CCSD	2.16	-125.25688897	-125.20596253	-125.20302866	-125.19340808
$Δ$ -CCSD(T)	2.16	-125.27876575	-125.22780103	-125.22426517	-125.21485159
$Δ$ -CC3	2.16	-125.28116806	-125.23008276	-125.22652706	-125.21714501
EOM-CC3 $^{†}$	2.01	-125.27619337	-125.22314957	-125.22078430	-125.20959123
	2.06	-125.27919971	-125.22682037	-125.22403798	-125.21348092
	2.09	-125.28051516	-125.22856143	-125.22553502	-125.21536980
	2.12	-125.28130166	-125.22978244	-125.22652966	-125.21674161
	2.14	-125.28155940	-125.23033380	-125.22693976	-125.21739462
	2.16	-125.28161379	-125.23068403	-125.22715668	-125.21784780
	2.18	-125.28147360	-125.23084251	-125.22718908	-125.21810835
	2.19	-125.28133651	-125.23085492	-125.22714142	-125.21817269
	2.22	-125.28069044	-125.23065988	-125.22677682	-125.21813306
	2.25	-125.27970333	-125.23012609	-125.22608895	-125.21775394
	2.28	-125.27842499	-125.22930182	-125.22512556	-125.21708388
	2.31	-125.27688344	-125.22821412	-125.22391279	-125.21614988
	2.34	-125.27511229	-125.22689580	-125.22248262	-125.21498428
	2.40	-125.27098835	-125.22367141	-125.21907086	-125.21206175

References

P. Aggarwal, H. L. Bethlem, A. Borschevsky, M. Denis, K. Esajas, P. A. B. Haase, Y. Hao, S. Hoekstra, K. Jungmann, T. B. Meijknecht, M. C. Mooij, R. G. E. Timmermans, W. Ubachs, L. Willmann, A. Zapara, and T. N. eEDM collaboration, The European Physical Journal D 72, 197 (2018).
A. Boeschoten, V. R. Marshall, T. B. Meijknecht, A. Touwen, H. L. Bethlem, A. Borschevsky, S. Hoekstra, J. W. F. van Hofslot, K. Jungmann, M. C. Mooij, R. G. E. Timmermans, W. Ubachs, and L. Willmann (NL-eEDM Collaboration), Phys. Rev. A 110, L010801 (2024).
S. J. Li, H. D. Ramachandran, R. Anderson, and A. C. Vutha, New Journal of Physics 25, 082001 (2023).
I. S. Lim, P. Schwerdtfeger, B. Metz, and H. Stoll, The Journal of Chemical Physics 122, 104103 (2005).
J. G. Hill and K. A. Peterson, The Journal of Chemical Physics 147, 244106 (2017).
Y. Hao, L. F. PaÅ¡teka, L. Visscher, P. Aggarwal, H. L. Bethlem, A. Boeschoten, A. Borschevsky, M. Denis, K. Esajas, S. Hoekstra, K. Jungmann, V. R. Marshall, T. B. Meijknecht, M. C. Mooij, R. G. E. Timmermans, A. Touwen, W. Ubachs, L. Willmann, Y. Yin, A. Zapara, and N. eEDM Collaboration), The Journal of Chemical Physics 151, 034302 (2019).
L. V. Skripnikov, D. V. Chubukov, and V. M. Shakhova, The Journal of Chemical Physics 155, 144103 (2021).
A. A. Kyuberis, L. F. Pašteka, E. Eliav, H. A. Perrett, A. Sunaga, S. M. Udrescu, S. G. Wilkins, R. F. Garcia Ruiz, and A. Borschevsky, Phys. Rev. A 109, 022813 (2024).
M. Denis, P. A. B. Haase, M. C. Mooij, Y. Chamorro, P. Aggarwal, H. L. Bethlem, A. Boeschoten, A. Borschevsky, K. Esajas, Y. Hao, S. Hoekstra, J. W. F. van Hofslot, V. R. Marshall, T. B. Meijknecht, R. G. E. Timmermans, A. Touwen, W. Ubachs, L. Willmann, and Y. Yin (NL-eEDM Collaboration), Phys. Rev. A 105, 052811 (2022).
R. L. Lambo, G. K. Koyanagi, A. Ragyanszki, M. Horbatsch, R. Fournier, and E. A. Hessels, Molecular Physics 121, e2198044 (2023a).
R. L. Lambo, G. K. Koyanagi, M. Horbatsch, R. Fournier, and E. A. Hessels, Molecular Physics 121, e2232051 (2023b).
M. Horbatsch, Atoms 12 (2024), 10.3390/atoms12080040.
I. S. Lim, H. Stoll, and P. Schwerdtfeger, The Journal of Chemical Physics 124, 034107 (2006).
J. Lee, D. W. Small, and M. Head-Gordon, The Journal of Chemical Physics 151, 214103 (2019).
Y. Damour, A. Scemama, D. Jacquemin, F. Kossoski, and P.-F. Loos, Journal of Chemical Theory and Computation 20, 4129 (2024).
D. G. A. Smith, L. A. Burns, A. C. Simmonett, R. M. Parrish, M. C. Schieber, R. Galvelis, P. Kraus, H. Kruse, R. Di Remigio, A. Alenaizan, A. M. James, S. Lehtola, J. P. Misiewicz, M. Scheurer, R. A. Shaw, J. B. Schriber, Y. Xie, Z. L. Glick, D. A. Sirianni, J. S. OâBrien, J. M. Waldrop, A. Kumar, E. G. Hohenstein, B. P. Pritchard, B. R. Brooks, I. Schaefer, Henry F., A. Y. Sokolov, K. Patkowski, I. DePrince, A. Eugene, U. Bozkaya, R. A. King, F. A. Evangelista, J. M. Turney, T. D. Crawford, and C. D. Sherrill, The Journal of Chemical Physics 152, 184108 (2020).
P. F. Bernath, Spectra of Atoms and Molecules (4th Edition) (Oxford University Press, 2020).
P.-F. Loos, A. Scemama, A. Blondel, Y. Garniron, M. Caffarel, and D. Jacquemin, Journal of Chemical Theory and Computation 14, 4360 (2018), pMID: 29966098.
W. Ernst and J. SchrÃ¶der, Chemical Physics 78, 363 (1983).
T. C. Steimle, P. J. Domaille, and D. O. Harris, Journal of Molecular Spectroscopy 68, 134 (1977).
P. J. Domaille, T. C. Steimle, and D. O. Harris, Journal of Molecular Spectroscopy 68, 146 (1977).
R. F. Barrow and J. R. Beale, Chem. Commun. (London) , 606a (1967).
A. Bernard, C. Effantin, J. d’Incan, J. VergÃ¨s, and R. Barrow, Molecular Physics 70, 747 (1990).
G. F. de Melo and F. R. Ornellas, Journal of Quantitative Spectroscopy and Radiative Transfer 237, 106632 (2019).
K. G. Dyall, Theoretical Chemistry Accounts 135, 237 (2016).
R. Barrow, A. Bernard, C. Effantin, J. D’Incan, G. Fabre, A. El Hachimi, R. Stringat, and J. VergÃ¨s, Chemical Physics Letters 147, 535 (1988).
C. Effantin, A. Bernard, J. d’Incan, G. Wannous, J. VergÃ¨s, and R. Barrow, Molecular Physics 70, 735 (1990).
A. Bernard, C. Effantin, E. Andrianavalona, J. VergÃ¨s, and R. Barrow, Journal of Molecular Spectroscopy 152, 174 (1992).
M. Rockenhäuser, F. Kogel, E. Pultinevicius, and T. Langen, Phys. Rev. A 108, 062812 (2023).
G. J. Shuying Kang, Fangguang Kuang and J. Du, Molecular Physics 114, 810 (2016).
A. Berning, M. Schweizer, H.-J. Werner, P. J. Knowles, and P. Palmieri, Molecular Physics 98, 1823 (2000).

Figure 1. Vertical excitation energies

Δ T

c m^{- 1}

as a function of R (in Å) for the electronic transition

S r F (X^{2} Σ^{+} \to B^{2} Σ^{+})

. The blue, red, and green dots represent EOM-CC3 results obtained with the aug-cc-pVnZ-PP family with n=3, 4, 5, respectively. For

R = 2.08

Å and

n = 4, 5

the vertical excitation energies correspond to

T_{e}

according to the present work. Stars: experimental value extracted from the analysis of rotational and vibrational (

v = 0, 1, 2

) excitations [20]; the symbol location indicates the values of

R_{e}

for both states. Other theoretical values for

T_{e}

: squares are theCAS-SCF/MRCI values (Ref. [24]); diamonds: X2C-FSCC (Ref. [6])

Figure 1. Vertical excitation energies

Δ T

c m^{- 1}

as a function of R (in Å) for the electronic transition

S r F (X^{2} Σ^{+} \to B^{2} Σ^{+})

. The blue, red, and green dots represent EOM-CC3 results obtained with the aug-cc-pVnZ-PP family with n=3, 4, 5, respectively. For

R = 2.08

Å and

n = 4, 5

the vertical excitation energies correspond to

T_{e}

according to the present work. Stars: experimental value extracted from the analysis of rotational and vibrational (

v = 0, 1, 2

) excitations [20]; the symbol location indicates the values of

R_{e}

for both states. Other theoretical values for

T_{e}

: squares are theCAS-SCF/MRCI values (Ref. [24]); diamonds: X2C-FSCC (Ref. [6])

Figure 2. Morse potentials derived from the calculated data points (red circles) are shown as solid green curves for the states BaF(

X^{2} Σ^{+}

) on the left, and BaF(

B^{2} Σ^{+}

) on the right. The magenta dashed curves show experimentally determined Morse potentials using eq. 3 and values from Ref. [28]. The black vertical lines indicate the calculated vibrational energy levels for

v = 0, 1, 2, 3

. The data points are for the aug-cc-pV5Z-PP/aug-cc-PV5Z basis set combination. The fits omitted the data points for

R = 2.01

Å, (cf. text).

Figure 2. Morse potentials derived from the calculated data points (red circles) are shown as solid green curves for the states BaF(

X^{2} Σ^{+}

) on the left, and BaF(

B^{2} Σ^{+}

v = 0, 1, 2, 3

. The data points are for the aug-cc-pV5Z-PP/aug-cc-PV5Z basis set combination. The fits omitted the data points for

R = 2.01

Å, (cf. text).

Table 1. Spectroscopic data for the

X^{2} Σ^{+}

and

B^{2} Σ^{+}

states of

^{88} S r^{19} F

. The values of

R_{e}

are given in Å, while all energies are given in

c m^{- 1}

. Data extracted from the present EOM-CC3 calculations using the aug-cc-pVnZ-PP basis sets [5] with effective core potential ECP28MDF [13] for Sr and aug-cc-pVnZ for F are shown for

n = 3, 4, 5

Table 1. Spectroscopic data for the

X^{2} Σ^{+}

and

B^{2} Σ^{+}

states of

^{88} S r^{19} F

. The values of

R_{e}

are given in Å, while all energies are given in

c m^{- 1}

. Data extracted from the present EOM-CC3 calculations using the aug-cc-pVnZ-PP basis sets [5] with effective core potential ECP28MDF [13] for Sr and aug-cc-pVnZ for F are shown for

n = 3, 4, 5

	$X^{2} Σ^{+}$			$B^{2} Σ^{+}$
	$R_{e}$	$ω_{e}$	$ω_{e} x_{e}$	$R_{e}$	$ω_{e}$	$ω_{e} x_{e}$	$Δ T_{e}$
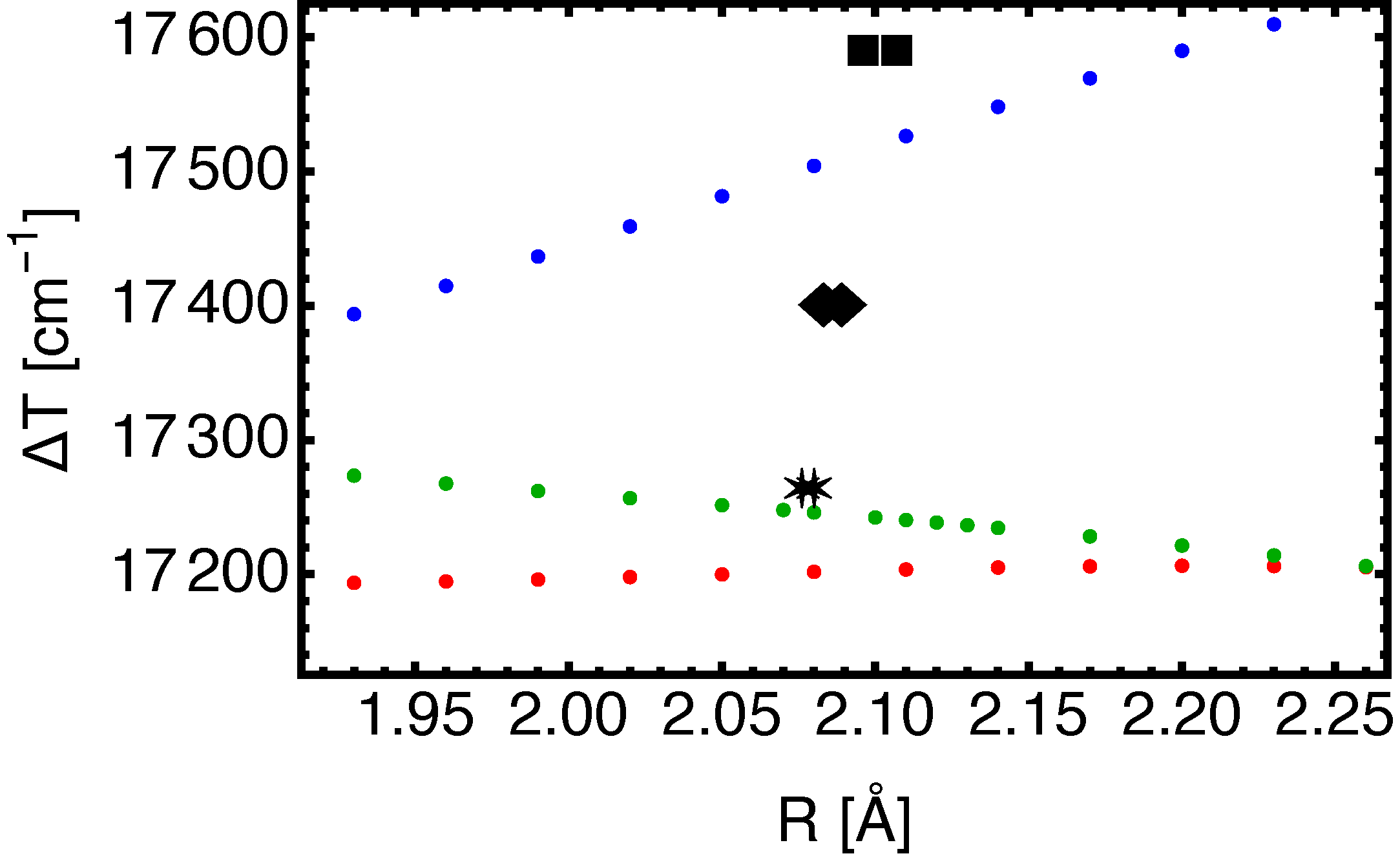
Expt [20,22]	2.076	501	2.27	2.080	496	2.34	17 264
X2C-FSCC [6]	2.083	500	2.45	2.089	492	2.16	17 405
EOM-CC3(5Z)	2.079	495	2.1	2.081	493	2.1	17 246
EOM-CC3(4Z)	2.075	507	2.2	2.074	507	2.3	17 202
EOM-CC3(3Z)	2.099	510	2.3	2.093	516	2.4	17 516

Table 2. Experimentally derived effective spectroscopic parameters for the low-lying electronic states of BaF. The values in columns 2 to 5 are taken from Table III in Ref. [28] (with the least certain digits truncated), while the values of

R_{e}

are taken from Table III in Ref. [6]. All energies are given in

c m^{- 1}

R_{e}

are taken from Table III in Ref. [6]. All energies are given in

c m^{- 1}

State	$Δ T_{e}$	$ω_{e}$	$ω_{e} x_{e}$	$10^{2} ω_{e} y_{e}$	$R_{e}$ [Å]
$X^{2} Σ^{+}$	0	469.416	1.837	0.33	2.1593
$A^{'}^{2} Δ$	10 940.3	437.4	1.83		-
$A^{2} Π$	11 962.2	437.9	1.85		2.183
$B^{2} Σ^{+}$	14 062.5	424.8	1.85	0.39	2.208

Table 3. The present EOM-CC3 results for

Δ T

(

R = 2.16

Å ) and

Δ T_{e}

, using the aug-cc-pV5Z-PP basis set [5] with effective core potential ECP46MDF [13] for Ba and aug-cc-pV5Z basis for F, are shown in columns 2 and 3. The deperturbation results of Ref. [23] are given in column 4 to complement the data given in Table 2. Note that the deperturbed

T_{e}

value for the

B^{2} Σ^{+}

state is lower by about

120 c m^{- 1}

compared to the effective value given in Ref. [27].

Table 3. The present EOM-CC3 results for

Δ T

(

R = 2.16

Å ) and

Δ T_{e}

T_{e}

value for the

B^{2} Σ^{+}

state is lower by about

120 c m^{- 1}

compared to the effective value given in Ref. [27].

State	$Δ T$	$Δ T_{e}$	Ref. [23]
$A^{'}^{2} Δ$	11 178	11 168	10 938.9
$A^{2} Π$	11 952	11 947	11 979.6
$B^{2} Σ^{+}$	13 995	13 927	13 944.5

Table 4. Spectroscopic parameters as obtained from EOM-CC3 calculations using the cc-pV5Z-PP basis set [5] for Ba and the aug-cc-pV5Z basis set for F are shown in the upper rows, while aug-cc-pV5Z-PP/aug-cc-pV5Z basis set results are shown in the lower rows for each state.

State	$R_{e}$	$ω_{e}$	$ω_{e} x_{e}$
$X^{2} Σ^{+}$	2.153	456	1.6
aug/aug:	2.155	459	1.5
$A^{'}^{2} Δ$	2.189	427	1.4
aug/aug:	2.188	430	1.7
$A^{2} Π$	2.173	428	1.4
aug/aug:	2.174	432	1.7
$B^{2} Σ^{+}$	2.201	417	1.3
aug/aug:	2.202	419	1.6

Table 5. Vertical excitation energies (in

c m^{- 1}

) from the

X^{2} Σ^{+}

ground state at

R = 2.16

Å, as calculated with different methods and two basis sets. The results for the augmented basis sets on both Ba and F are marked with

^{†}

Table 5. Vertical excitation energies (in

c m^{- 1}

) from the

X^{2} Σ^{+}

ground state at

R = 2.16

Å, as calculated with different methods and two basis sets. The results for the augmented basis sets on both Ba and F are marked with

^{†}

Method	$A^{'}^{2} Δ$	$A^{2} Π$	$B^{2} Σ^{+}$
EOM-CC3	11 202	11 953	14 000
EOM-CC3 $^{†}$	11 178	11 952	13 955
$Δ$ -CC3	11 212	11 992	14 051
EOM-CCSD	11 191	12 030	14 164
EOM-CCSD $^{†}$	11 164	12 029	14 157
$Δ$ -CCSD	11 177	11 821	13 932
$Δ$ -CCSD(T)	11 185	11 961	14 027

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Calculation of Some Low-Lying Electronic Excitations of Barium Monofluoride Using the Eom-CC3 Method with an Effective Core Potential Approach

Abstract

I. Introduction

II. Methodology

III. Results

A. SrF( X 2 Σ + → B 2 Σ + )

B. BaF( X 2 Σ + → A ′ 2 Δ , X 2 Σ + → A 2 Π , X 2 Σ + → B 2 Σ + )

IV. Conclusions

Acknowledgments

Appendix A

References

MDPI Initiatives

Important Links

Subscribe

A. SrF( $X^{2} Σ^{+} \to B^{2} Σ^{+}$ )

B. BaF( $X^{2} Σ^{+} \to A^{'}^{2} Δ$ , $X^{2} Σ^{+} \to A^{2} Π$ , $X^{2} Σ^{+} \to B^{2} Σ^{+}$ )