Economic dynamics has a solid theoretical foundation, so before delving into its specific dynamic aspects, it is necessary to first introduce the theoretical preparations, which include the following three parts.
First, Scientific Observation Theory. Economic dynamics, as an economic theory, belongs to the social sciences. However, its theoretical framework extensively applies conceptualization and modeling methods from theoretical physics. What is the scientific basis for this basic theoretical research approach? What is the basis for its scientific methodology? These questions are crucial for understanding economic dynamics. Economics, psychology, and physics are all essentially empirical sciences, but their directions of scientific observation differ. Physics conducts outward observations of the physical world, psychology conducts inward observations of the mental world, while economics conducts backward observations of history and forward observations of the future. We will introduce the orthogonal principle of scientific observation for this purpose. Scientific observation is limited by the means of observation, which led Dirac to introduce the concept of observational interference. The level of interference in observation varies, and the mathematical methods used to characterize observation also differ accordingly. For this, we introduce the diagonal rule of scientific observation.
Second, Economic Rationality Theory. Economics cannot exist without its theory of rationality. This section first introduces the decision theory framework, followed by the introduction of three types of economic rationality theories: economic rationality, bounded rationality, and ordinary rationality. In market dynamics, economic rationality is the global gauge potential, while bounded rationality is the local gauge potential. Ordinary rationality is composed of eight principles and shares three fundamental properties with the Higgs field in the Standard Model of particle physics. The latter serves as the physical model for the former. In the Standard Model, the Higgs field interacts with gauge particles, causing spontaneous symmetry breaking, which generates mass terms in the Lagrangian, known as the Higgs mechanism. In economic dynamics, the corresponding ordinary rationality mechanism is responsible for the consequences of market behavior and other economic activities, which is the economic dynamics version of spontaneous symmetry breaking. The technical details of the Higgs mechanism and the ordinary rationality mechanism will be elaborated in subsequent articles.
Third, Monetary Theory of Capitals. Distinction is made between the currency nature and the money nature of money. Economic dynamics uses the language of gauge field theory to describe its symmetry requirements. Gauge field theory is a part of quantum field theory, which is formed by integrating quantum mechanics and special relativity. Therefore, to understand economic dynamics, one must first grasp its quantization methods and the handling of special relativity. Its quantization methods will be introduced later in the market dynamics section. To meet its requirements for special relativity, we first discuss what monetary money nature is and demonstrate that it satisfies the conditions of being light-like and having a spin of 1, treating monetary money nature as an invariant. Next, within the framework of special relativity, we describe the global cone model of absolute market prices and the local momentum cone model of individual proper prices.
3.1. Scientific Observation Theory
We first introduce the orthogonal principle and the diagonal rule of cross-scientific observation. Economic dynamics involves economics, psychology, and physics, all of which are essentially empirical sciences. The theories of empirical sciences are and can only be hypothetical, called scientific hypotheses, because scientists can only observe samples, not the entire population. Scientific hypotheses need experimental support, so they cannot do without scientific observation. In this sense, the mother tongue of empirical sciences is statistics, and its methodology is inductive. This section introduces the directionality, orthogonal principle, and diagonal rule of scientific observation. We will see how these three empirical sciences are interconnected through different mathematical paths.
3.1.1. Directionality of Observation and Orthogonal Principle
In physics, the observer, as the subject of observation, observes the external physical world. Here, the term "external" suggests a sense of directionality inherent in scientific observation. Abstractly conceptualizing this, it is called outward observation. In psychology and cognitive science, the observer observes the internal mental world, called inward observation. In economics, empirical research relies on data. Data provided in the public domain come from statistical analyses of past economic phenomena. Data collected in laboratories come from statistical analyses after experiments. In short, various data reflect observations of history, called backward observation. It is well known that economists are never satisfied with speaking only about history; there is an impulse in economics to predict the future. Extending the observational telescope into the future is called forward observation.
Faced with these directional observations, further conceptualization establishes the concept of "directionality" in scientific observation. We see that observations in different empirical disciplines have different directions, but these various types of scientific observations finally converge under the concept of directionality. The significance of this convergence lies in the first task of orthogonalizing these different scientific observation directions. In mathematical language, this is called trivialization.
Orthogonalization can be characterized by a function: generally speaking, pairwise directions, if the same, are 1; if different, are 0. Obviously, pairwise perpendicular directions are a special case of orthogonalization. The formula for this is as follows:
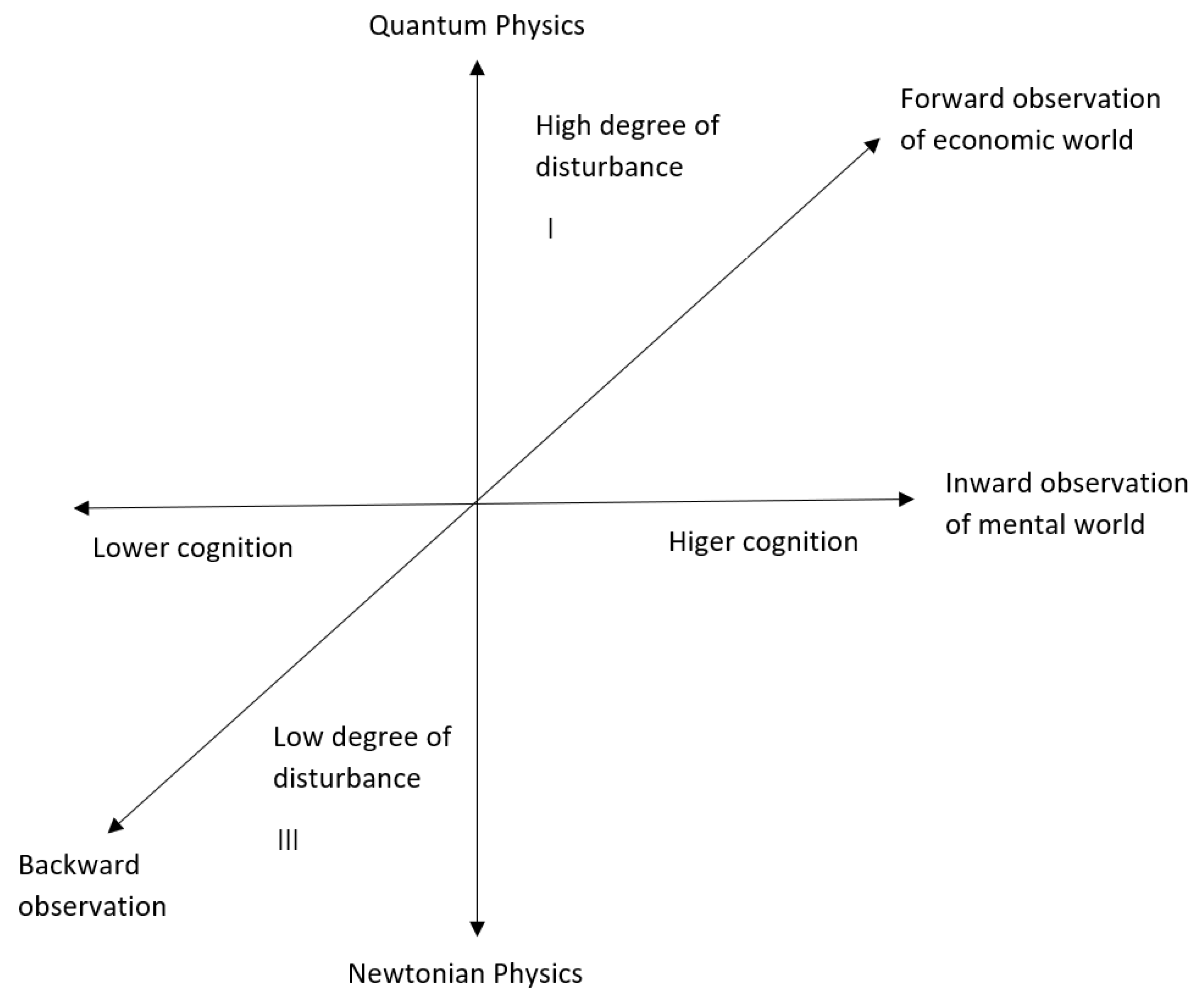
Now, use a bit of imagination. First, draw a horizontal axis to represent the mental world. Next, draw a vertical axis to represent the physical world. Then, draw a diagonal axis from the lower left through the origin to the upper right to represent the economic world. In this way, a three-dimensional framework is constructed. This is called the orthogonal principle of the directionality of scientific observation. If a metric, such as positive and negative values, is embedded in this three-dimensional framework, it becomes a space.
3.1.2. Observation Disturbance Degree and the Diagonal Rule
Please observe the orthogonal framework in
Figure 2 below. The top of the vertical physical axis is labeled quantum mechanics, and the bottom passing through the origin is labeled Newtonian mechanics. On the right end of the horizontal mental axis is labeled higher cognition, while the left end is labeled lower cognition. Additionally, on the diagonal economic axis passing through the origin, the top right end is labeled forward observation, and the bottom left end is labeled backward observation.
As shown in
Figure 2, quantum mechanics, higher cognition, and economic forward observation are concentrated in the first quadrant, while Newtonian mechanics, lower cognition, and economic backward observation are concentrated in the third quadrant. The first and third quadrants are diagonally opposite, which is called the "Diagonal Rule." This rule has two meanings.
First, in the first quadrant, quantum mechanics and quantum field theory lead to the modeling of higher cognition and economic forward observation, which is appropriate. In the third quadrant, Newtonian classical mechanics leads to the modeling of lower cognition and economic backward observation, which is also appropriate. In the second quadrant, if quantum mechanics leads to the modeling of lower cognition and economic backward observation, it is considered excessive modeling. In the fourth quadrant, if Newtonian mechanics leads to higher cognition and economic forward observation, it is considered insufficient modeling.
Second, the first quadrant can be regarded as the high disturbance zone for observation, while the third quadrant can be regarded as the low disturbance zone for observation. Here, the concept of "observation disturbance" is introduced by Dirac: the higher the degree of disturbance in observation, the smaller the world we can observe. In Newtonian mechanics, the disturbance is low, so Newtonian mechanics is the study of the macroscopic world. In quantum mechanics, the disturbance is high, so quantum mechanics is the study of the microscopic world. The study bridging the two is called "mesoscopic physics." Some say that in observations of the macroscopic world, such as cosmology, quantum physics is also used, which refers to the study of microscopic phenomena within the classical macroscopic world.
What is observation disturbance? In simple terms, it is the limitation of experimental methods and observational tools. We know that every science has its boundaries. According to Popper's philosophy of science, having boundaries allows for falsifiability, and falsifiability is what makes something scientific. A theory without boundaries is considered religious because it lacks falsifiability. The boundary of an empirical science largely depends on the limitations of its experimental methods and observational tools. You can improve experimental methods and enhance observational tools, but this only shifts the boundary rather than removing it. This reality, converted by physicist Dirac into the concept of observation disturbance, is truly an insightful contribution. Disturbance is not an endogenous concept of a physical system but a meta-concept about a physical system. The establishment of meta-concepts is one of the signs of a mature basic theory.
3.1.3. Low Disturbance Zone
We need to explain why quantum mechanics, higher cognition, and economic forward observation are in the high disturbance zone, while Newtonian mechanics, lower cognition, and economic backward observation are in the low disturbance zone.
The characteristic of Newtonian mechanics is that the phenomena it observes are directly observable. Newton, sitting under an apple tree, was able to observe the apple falling and its trajectory. This may seem trivial, but it is a fortunate combination of the human eye’s ability, the apple’s size, and the falling speed. The empirical foundation of Newtonian mechanics is direct observability. The reason why the human eye can observe the apple falling is that the apple is relatively large and moves slowly, which can be described as "large/slow" physics. Regardless of how observational tools advance, even with high-energy accelerators and radio telescopes, they are still extensions of the human eye. Scientists are human and are the subjects of observation.
The "low" in low-level cognition should not be misunderstood as implying a lower rank; rather, it refers to a lower level of disturbance, comparable to the "low" in low-energy physics. Lower cognition, developed from traditional psychophysics, studies perception, attention, perception, auditory, visual, and human-computer interaction, among other subfields. For example, in certain computerized visual experiments, different points of varying colors, shapes, sizes, and positions are sequentially displayed on a screen. Subjects make judgment responses based on prior understanding of the experimental instructions by clicking different buttons. This type of experimental task is called a "click task." The reaction time for each specific click task is usually measured in microseconds. The judgment content for each specific click task is relatively simple. In such simple and quick mental activities, the chance of data noise is very small, meaning the disturbance in observation is low. Generally, psychological experiments are conducted within 40-60 minutes to obtain optimal mental performance. Within such a 60-minutes period, thousands of click tasks can be completed. With such a high task density, behavioral performance can be approximately connected into a learning curve. This learning curve is similar in nature to the trajectory curve of a falling apple. Such experiments can be called observations of "simple/fast" psychological processes.
In economics, backward observation, also known as empirical research in economics, belongs to this category. Empirical research relies on data. Whether the data is collected from the public domain or obtained from the laboratory, if the data is valid, it indicates that the events have already occurred. Thus, data reflects observations of past events, i.e., historical observations. When presenting these data, it is usually done in charts or curves. These curves are similar in function to the apple falling curve and the learning curves of lower cognition. Backward observations of history are considered low disturbance observations compared to forward observations of the future. While backward observations of economic events may still face various disturbances, these are considered "process disturbances" that can theoretically be ignored in the present context.
3.1.4. High Disturbance Zone
Quantum mechanics is in the high disturbance zone. The basic particles and their motion states observed in quantum mechanics experiments are often difficult to observe directly, such as massless bosons and "confined" fermion quarks. Additionally, basic particles move at or near the speed of light and can be very small (down to just residual energy), leading to unavoidable high disturbance in observations. Such physical observations can be called "small/fast" observations.
Heisenberg's uncertainty principle is the best explanation of high disturbance. The uncertainty principle, also known as the principle of indeterminacy, states that the more precisely the position of a particle is known, the less precisely its momentum can be known, and vice versa. In other words, both are uncertain quantities. Similarly, energy and time are also a pair of uncertain quantities that satisfy the uncertainty principle. Observing two uncertain quantities is sensitive to the order of observation; the results differ depending on which is observed first, and the difference is not zero, which is called the "non-commutation rule." Establishing a certain non-commutation relationship in a field means realizing quantization in this sense [
18]
.
In quantum mechanics and quantum field theory, because dynamical analysis is a sourced analysis considering various particle load states, particles have internal spaces. This internal space is rotational, thus called dynamic phase space; its rotational angular momentum is called spin, which is an intrinsic property of particles, which has no comparison of not the classical Newtonian mechanics. The intrinsic properties of particles are difficult to observe directly. To establish the local symmetry of different particle states, a type of gauge particle called gauge field is introduced to balance phase changes in the phase space. At the same time, a type of differential operation called "covariant derivative" is introduced to balance the rate of phase change. These are not directly observable and are fundamental reasons for the high disturbance in quantum physical observations.
In a certain sense, higher cognition is the language of economics. Its research scope is broad but includes three main subfields: reasoning, decision-making, and game theory. Each of these three subfields has its standard theory, namely logic, decision theory, and game theory. In other words, every specific observational task used in experiments has a "standard" rational answer. Various misconceptions, biases, and irrational answers are relative to the standard rational answer. For example, in reasoning experiments, after presenting a set of premises, either a valid or invalid conclusion is given for the subject to make a "yes/no" judgment. This type of experimental task is called an "evaluation task." Unlike the priming click tasks used in lower cognition experiments, higher cognition experiments generally use verbal tasks [
18,
19].
In higher cognition experiments, observation disturbance comes from several aspects. First, because subjects need to read and understand a verbal task, the response time is significantly longer, measured in minutes/seconds, with microseconds being negligible. During this relatively long period, process noise, such as attention dispersion, significantly increases. Second, within the 40-60 minutes experimental time, the time spent on each task increases significantly, reducing the number of tasks. In other words, limited observation results cannot form an approximate learning curve. Third and most importantly, the solution to a language reasoning task should have a mental expression and process predicted by the theoretical model, called the "task structure." Compared to lower cognition, the task structure in higher cognition observation is much more complex, termed "complex/slow" mental tasks. The objective data we can directly observe are accuracy or error rates and time spent. However, we cannot directly observe the mental processes through complex task structures. In other words, we can observe whether subjects got it right or wrong, but it is difficult to observe how they did it. This is the main source of high disturbance.
Economists are always driven by the impulse for forward observation. Theoretically, economics textbooks tell us not to consider sunk costs and to let the past be the past. Economics emphasizes efficiency, defined by marginal utility, which describes the benefit of investing one more unit of resource. Here, "one more unit" implies future tense or at least general present tense, not past tense. Observing future economic phenomena drastically increases uncertainty, which is a general source of high disturbance in forward observations. This is easy to understand, and specific market observations require deeper analysis.
3.1.5. Two Mathematical Paths
The previous subsections explained what constitutes low and high disturbance zones and their significance in distinguishing different mathematical paths. We know that a science is only truly developed when it can successfully apply mathematics. Penrose said in
The Road to Reality, "Calculus is absolutely fundamental to understanding theoretical physics. [
20] In a field, the use of calculus is a prerequisite for applying more advanced mathematics. This is natural in the low disturbance zone; Newton and Leibniz were indeed the inventors of calculus. In the low disturbance zone, Newtonian mechanics’ apple falling curve, lower cognition’s learning curve, and backward economic data curves can all be approximately represented as smooth curves, i.e., continuous functions that are differentiable almost everywhere.
However, in the high disturbance zone, the path to calculus is "twisty and long." Von Neumann pointed out in his book [
21] that experimental observations in quantum mechanics can be reduced to a kind of "Yes/No" measurement. Penrose also elaborates on this idea in details. In short, in a quantum experimentation, the particle detector is referred to as the "Yes gate." When the particle source excites a particle and the detector receives it, it is said that the particle has entered the Yes gate. If the detector does not receive the particle, rather than saying the particle was not excited, it is said that the excited particle has entered the "No gate." This description differs from classical mechanics and is counterintuitive, but it is a key feature of quantum mechanics. Similarly, in high-level cognitive experiments, answering correctly is equivalent to entering the Yes gate; answering incorrectly is equivalent to entering the No gate. In economic forecasting, a correct prediction means entering the Yes gate, while an incorrect prediction means entering the No gate. Regardless of whether one enters the Yes or No gate, the economist has made certain effort. Such "Yes/No" type observations are mathematically represented by the Dirac δ-function,
This function consists of two formulas. The first formula states that if an excited particle enters the Yes gate (the detector, the correct answer, or the predicted future event), the function value is infinite; if the excited particle enters the No gate (not detected, the question is answered incorrectly, or the prediction is wrong), the function value is zero. The second formula is the indefinite integral of the first formula, and its value equals a constant. Here, the second formula tells us that regardless of whether the particle enters the Yes gate or the No gate, the particle has been excited. In philosophical terms, the first formula of the Dirac function can be considered its epistemological support, while the second formula represents its ontological commitment. The Dirac function almost perfectly characterizes "Yes/No" type observations, but it is not a mathematically well-defined function.
It was not until later that the theory of distributions in mathematics was developed. In this theory, starting from the second formula of the original Dirac function (the integral formula) to make an ontological commitment, and using the first formula as the integrand, called the test function, to provide the epistemological path, requiring that this test function must have at least one "support point." This support point is the excited particle detected by the original quantum observation detector, a correctly solved question in high-level cognition, or a future economic event predicted by economic forecasting. By following this path, the high-interference region can finally legally and properly apply calculus, laying a solid foundation for introducing more advanced mathematical tools.
There is a popular game called "20 Questions," also known as the mind-reading game. One player thinks of something, such as an apple. The other player can ask up to 20 "Yes/No" questions, such as Is it a tool? Is it food? Is it meat? Is it grain? And so on, gradually approaching the correct answer. The renowned theoretical physicist John Wheeler once wrote that quantum mechanical observation is akin to playing the "20 Questions" game with nature. Similarly, observation in higher cognition is like playing the "20 Questions" game with the mental world, and economic forecasting is like playing the same game with future economic events. Wheeler’s statement captures the essence of microscopic scientific observations.
3.2. Economic Rationality Theories
Rationality theory is the lens of economics; discussing economics inevitably involves discussing rationality theory. Rationality theory is not a general discussion but specifically refers to principled theories. In economics, rationality theory is generally defined within the framework of decision theory and is discussed in the language of decision theory. There are three types of rationality theory in economics: economic rationality, bounded rationality, and ordinary rationality, which will be briefly introduced below.
Economic rationality in traditional economics is merely a concept with unclear definitions, making it difficult to model. The bounded rationality prevalent in contemporary behavioral economics is more focused on empirical research and lacks a thorough theoretical model framework. In economic dynamics, the framework of gauge field theory is used: economic rationality represents the global gauge potential of market dynamics, bounded rationality represents local gauge potential, while ordinary rationality is modeled by the Higgs field.
3.2.1. Decision Theoretic Framework
In past textbooks, the structure of decision theoretic language was not very clear. Here, borrowing from the formal language structure of logic, the classical decision theory framework can be divided into three standard components: syntactic structure, semantics, and system meta-properties [
22].
First, let's discuss the syntax of decision theory. The syntax of decision theory is a three-layer structure: The first layer is a set of choices, or more plainly, a set of options; the second layer is a set of possible outcomes for each choice; the third layer characterizes each outcome with exactly two properties: its desirability and its likelihood. That's it. Solving a decision problem requires establishing a strict full order preference across all choices. Preference is a binary relation where, given any two choices, the decision-maker must prefer one to another, with no option preferring not-to-prefer, i.e., not choose. Preferences must be well-ordered and satisfy properties like transitivity, which is why contemporary decision theory is also known as axiomatic decision theory.
If someone says they have a decision problem, they must express it using the decision theory structure described above. Otherwise, they have not yet formulated a decision problem. To formulate a decision theoretic syntactic structure, five words, and only five words, are used: choices, outcomes, desirability, feasibility, and preference. This is called the lexicon or vocabulary. This distinction between syntax and semantics is one of the benefits of the formal approach. Differentiating between syntax and semantics is not only a theoretical advancement but also aligns with cognitive routines.
Next, the semantics of decision theory. What is the meaning of the syntactic structure mentioned earlier? It cannot be explained using our everyday accumulated common sense; it must be strictly defined in terms of decision theory, which is called semantics or model theory. The syntactic structure is defined from the top down, while semantics must be explained from the bottom up.
First, at the bottom layer of the syntactic structure are two concepts: desirability and likelihood. In decision theory, especially within the context of economics, desirability has only one interpretation: its monetary value. Regardless of any desire, it is expressed in terms of monetary value. Some may find this demeaning, thinking that linking desires to money only would reduce human values to mere materialism. They might argue that their love for their country is priceless, their affection for family is spontaneous, and their faith is unconditional. Decision theory, however, states that you are a good person with emotions and sentiments, but it has never heard you say that you "decide" to love your country, decide to love your family, or decide what to believe. Love and faith belong to ethics and religion, not to decision theory. This is also why ordinary people generally dislike making decisions; decisions have costs, known as opportunity costs in economics.
Desirability and feasibility are interrelated. If you want to buy a space shuttle, become a billionaire, or have anything you want, how likely is that? Generally, in decision theory, feasibility refers to whether it is possible, and possibilities range from high to low. The magnitude of likelihood can often be explained using probabilities. However, caution is needed when using probabilistic language, as likelihood here refers to a specific given outcome. In standard probability theory, a single independent event has no probability; however, subjective probability theory in psychology does offer related concepts. Furthermore, a choice can produce several outcomes; how can you determine the probability of a specific outcome? Decision theory states that for each possible outcome of a choice, the decision-maker will determine a strategy, which means assigning weights to each outcome, forming a weight distribution. If this option is chosen by the decision-maker, it becomes a reality with a probability of 1. Thus, when the decision-maker's strategy forms a probability distribution, all probabilities must sum up to 1, known as normalization. With a normalized probability distribution, each possible outcome can be assigned a corresponding probability. In decision theory, the meaning of feasibility is the allocation probability after normalization.
Second, moving one layer up from the bottom, we define the decision theoretic meaning of an outcome as the product of its desirability value and its feasibility probability, known as "utility." Thus, the semantics of decision theory is called utility semantics. The product of desirability and probability is the simplest form of the utility function. Utility functions can be quite complex; for example, Jeffrey's referential decision theory involves conditional probabilities.
The concept of utility is clearly very subjective because value functions and weighting strategies vary from person to person. Samuelson disliked utility. In his 1938 paper [
3] introducing the concept of "revealed preference," he stripped away the last vestige of psychology from utility. Consequently, modern advanced microeconomics textbooks, although starting with consumer theory, dedicate one chapter to classical preferences based on utility functions and another chapter to Samuelson's revealed preferences.
Samuelson argued that revealing preferences was intended to make economics a true science, focusing solely on observable consumer behavior rather than subjective consumer psychology. This research paradigm led mainstream economic models of the 20th century to develop within the Newtonian mechanics framework. It missed the significant advances in theoretical physics since the early 20th century and did not benefit from the remarkable improvements in cognitive psychology experimental methods since the 1950s. Yang (2013) used Kripke's possible world semantics from modal logic to analyze revealed preferences, showing that revealed preferences are essentially a form of modal preference, which is weaker than, but not stronger than, explicit statement type preference, highlighting a logical foundation issue in current economics.
Third, returning to the top layer of the decision structure, we have a set of choices. The decision theory meaning of each choice is called its mathematical expectation. A choice can lead to several outcomes, and the mathematical expectation of this choice is the sum of the utilities of all these outcomes. Thus, the preference between two choices can be determined by comparing their mathematical expectation values.
Note that the concepts of desirability value, likelihood probability, outcome utility, and choice expectation discussed above are all numerical, and their linear combinations are still numerical. Therefore, utility semantics is a numerical model. The reason decision theory semantics uses numerical models is because we are familiar with these numerical domains and understand concepts like greater than, less than, or equal to. In contrast, desirability, likelihood, outcomes, choices, and preferences are new concepts we are not as familiar with. Using familiar things to systematically explain unfamiliar concepts is the rationale behind modeling.
With the syntactic structure and its utility semantics in decision theory, we require an overall match between the two, with the intensity being exactly equal. This is a type of systemic symmetry, also known as a meta-property. The standard meta-property of decision theory requires: for any given two choices, preference for one over the other if and only if the mathematical expectation of the first is greater than that of the second. This is called the representation theorem. The representation theorem in contemporary axiomatic decision theory must be proven, as the "greater than" relationship in the model and the preference relationship in the syntax must satisfy the same conditions and properties, such as transitivity.
Regarding the representation theorem, four additional points can be added. First, "any given two choices" indicates that the representation theorem provides a global symmetry within the system. Second, "any two choices" implies that preference is a binary relation; it can only be discussed in terms of pairs of choices. Thus, decision theory's rationality is discrete, not continuous. Third, the structure of the representation theorem is borrowed from logic, representing a decision theoretic version of logical completeness and consistency, and is a standard requirement in contemporary formal sciences. Finally, the representation theorem directly introduces the concept of irrationality. Nobel laureate Amartya Sen believes that preferring one choice over another, while the mathematical expectation of the preferred choice is not greater than that of the other, is called the correspondence irrationality. Conversely, if the mathematical expectation of a choice is greater than that of another, but the decision-maker prefers the latter, it is called the reflection irrationality.
Additionally, it should be emphasized that the decision theory framework described above is classical decision theory, where preference refers only to mental states, termed "knowing." A decision-maker can change their mind without cost. Contemporary decision theory emphasizes "doing," establishing preference relations based on possible action functions. Each possible action is a function with variables called states, and each state is a description of the environment. Descriptions can vary in detail; even a single differing detail constitutes a different description. Decision making involves choosing an action within a given state. Savage is generally considered the founder of contemporary decision theory; he proposed a classic decision theory puzzle known as the "Small-Grand World" problem, solved by the present author (2006) [
23].
3.2.2. Economic Rationality
Economic rationality is one of the foundational concepts in economics (e.g., mainstream economics, traditional economics, or neoclassical economics, etc.). Economic rationality has an anthropomorphized (personified) term called the economic rational man. Note that "man" is singular, which will refer to the global level in gauge structure. It will play a crucial role in solving the puzzle of "economic rationality" later.
There are various interpretations of economic rationality. For example, one view is that economic rationality seeks to maximize efficiency, while another view is that the economic rational man instinctively seeks to maximize his own benefits, and so on. Logic and epistemology tell us that the generation of knowledge involves a cognitive process that moves from ideas, to primary concepts, then to advanced notions, and finally to definitions. The current academic understanding of economic rationality might not score high. In the decision theory framework, we define economic rationality (or economic rational man) as meeting four conditions [
24]: full knowledge, full capacity, full scale, and full logic, briefly described as follows.
Condition 1: Full Knowledge. In a decision structure, there can be numerous choices, each choice can lead to many outcomes, and each outcome has its own desirability and feasibility. All this information is describable, resulting in a vast amount of knowledge. Regardless of how massive the information is, the economic rational man knows all of it. This is a purely syntactic requirement.
Condition 2: Full Capacity. The utility function of a decision problem can be quite complex, and the computational demands can be substantial. However, regardless of the computational complexity required by the utility semantics, the economic rational man has the complete ability to perform the calculations. This is a purely semantic requirement.
Condition 3: Full Scale. The economic rational man ensures that the utility function is a one-to-one correspondence mapping between choices and their mathematical expectations. Thus, the economic rational man can establish a strict full order among the set of choices. This is a requirement by the representation theorem.
Condition 4: Full Logic. Psychology of decision making tells us that people are sensitive to the way choices are presented, known as the framing effect [
25]. For instance, if a doctor tells a patient's family that there is a 40% chance of surgery failure, the family may not react well. They would prefer to hear that there is a 60% chance of success, even though both statements are logically equivalent. Full logic requires that the economic rational man is never influenced by the framing effect and makes judgments about logically equivalent choices without differentiation; in other words, being indifference to any logically equivalent contents.
It is not hard to imagine that a market participant who meets all four requirements of the economic rational man will eventually amass all market wealth. A test question is: How many economic rational men are there in the market? Clearly, if there are two or more economic rational men competing, it will lead to an economic rationality paradox. Alternatively, if there is only one economic rational man, this individual will eventually capture all the market wealth, which is evidently not a realistic scenario for any particular market participant.
Note that economic rationality is one of the theoretical cornerstones of economics, and it must have its reason for existence. So, who is this economic rational man? There is only one answer: economic rationality is an abstraction of the characteristics of the market, and the economic rational man is an anthropomorphic portrayal of the market. Here’s why, explained according to the aforementioned conditions:
First, the ideal modern perfectly competitive market requires maximum information and transparency, and the market itself is the container of all market information. The market is "all-knowing."
Second, the market has a pricing function. We say that the market creates wealth because its pricing function can minimize transaction costs to the greatest extent. What does it mean for a product to enter the market? It means that the product obtains a price in the market. The market can be ever-changing; no matter how complex it is, it always performs the function of generating prices for goods. This is what makes the market a market; in terms of pricing, the market is "all-capable."
Third, Modern markets, such as financial markets, are artificially designed markets; their greatest secret is the pricing function. Why do so many physics and mathematics PhDs go to Wall Street? They don't go to become traders; they go to conduct research, trying to crack the pricing function. The market generates a unique price for a good, making it possible to compare prices pairwise. Thus, ideally, the market is "totally ordered."
Fourth, Regulation in Perfectly Competitive Markets. A perfectly competitive market, especially an artificially designed one, particularly a financial market, cannot exist without regulation. Do you remember the emphasis on the importance of market regulation by governments worldwide after the 2008 global financial crisis? The role of regulation is to prevent false information from misleading the market, to disallow substandard goods from being passed off as good, and to prevent information from being hidden. Regulation must prevent the market itself from experiencing the description effect; ideal regulation ensures the market's "full logic."
When all four conditions are met, the economic rational man turns out to be an anthropomorphized depiction of the market, rather than a depiction of any actual market participant. This is the “Da Vinci Code” of economic rationality. Once this code is deciphered, it opens up at least the following four theoretical avenues:
Avenue One: The term "economic rational man" is singular in English, specifically referring to the market. The concept of bounded rationality, which will be discussed in the next section, specifically depicts market participants as managers, also known as businessmen, traders, entrepreneurs, investors, financiers, etc. The English term is "businessmen," which is plural. The theoretical significance of this singular vs. plural opposition, i.e., "man vs. men," is considerable. Generally, in a social science field, if a theory is well-developed, its core concept is often anthropomorphized as the singular "man"; whereas its practice or application, involving multiple practitioners, is naturally depicted by the plural "men."
Avenue Two: In the gauge field theory models of market dynamics, there are two levels to distinguish: "global" and "local." The distinction between economic rational man and bounded rational businessmen is crucial for distinguishing these two levels, with "man" representing the global level and "men" representing the local level. In field theory models, at the global level, the phase of the wave function is an arbitrary constant, depicting the overall market change. At the local level, the phase of the wave function is a function of participants, representing a form of local symmetry. logically,The economic rationality implies the "inclusion" relationship between sets, and the bounded rationality implies the "belonging" relationship between the elements and a set. The indistinguishability between the two would commit to the well-known Russell Paradox.
Avenue three: We say that the economically rational person is a personified portrayal of the perfect competitive market, although it is reasonable, but it feels that the words are not fully explained; It is inevitable to ask ourselves, are economic rationality and the market really the same thing? The answer is, not really. In the gauge field theory model, there are two levels, namely, the global and the local. Local. At each level, there is another distinction between the "gauge potential" and the "gauge field strength". In our gauge field theory model of market dynamics [
9], economic rationality is the global gauge potential, and the real market is the global gauge field strength.
Avenue four: Economic rationality implies the global symmetry of the market. T. D. Lee [
12] said that in physics, non-observability implies a certain symmetry. This has two meanings. One level means that if a phenomenon cannot be observed by any observer, it constitutes a symmetry among all observers. On the other hand, if a certain type of phenomenon is beyond the boundaries of our means of observation, then such phenomena are symmetrical, because they are not observable anyway. Economic rationality, as the overall characteristic of the market, cannot be characterized by any realistic market participant. Nor are the four conditions of the economically rational man that can be met by any specific market participant. This is called "unreachable" and is the economic market version of "non-observability". The fact that the economic rational man is inaccessible to all particular real market participants indicates a global symmetry
The global symmetry of the market is important because it ensures the stability and sustainable development of the market, making the market a conservation system. Imagine, In the financial market, if an investor has inside information, does illegal operations in the bureau, manipulates the market, treats the market as a backyard, and always makes money from other people's pockets, then he would become a shadow economic rational person. Over time, other market participants have only one way to go, and that is to exit the market, and the market becomes unsustainable. Non-observability implies symmetry, and symmetry implies conservation, which is the connotation of a very profound and well-known theorem in mathematical physics, which is called Noether's theorem.
3.2.3. Bounded Rationality
The Nobel Prize in Economics often favors traditional mainstream economists, but it has been awarded three times to behavioral economists: Simon (1978), Kahneman et al. (2002), and Thaler (2017). Bounded rationality is the flagship concept of behavioral economics; it is referred to as a flagship concept rather than a theory because behavioral economics research is primarily empirical, with literature mainly consisting of experimental reports, and its basic theory is relatively weak.
The concept of bounded rationality was first proposed by Herbert Simon [
26]. During World War II, the U.S. defense industry rapidly expanded, and government agencies grew large. Simon, then a doctoral student, began studying decision-making processes in large corporations and institutions. He discovered that these large organizations had a "multi-layered structure," where top-level managers had the most information and faced the most significant decision problems, while managers at lower levels had progressively less information and faced smaller decision problems. This is the original meaning of "bounded." Simon was one of the founders of cognitive science and also won the Turing Award in computer science, but he received the Nobel Prize in Economics for pioneering the study of "bounded rationality."
Bounded rationality was initially intended to describe what is known as the real-world manager," also termed businessmen (plural). Later, the term also broadly referred to entrepreneurs or businesspeople. Within the framework of decision theory, the focus is on the first layer of choices for economic rationality, while businessmen focus more on the second layer, which involves the consequences generated by each choice. This reflects a more realistic aspect of businessmen.
From a semantic perspective, managers are not only realistic but also wise. Managers understand that there is no free lunch, and one cannot take all the advantages. They know that achieving something requires a cost, with both gains and losses, and it is important to complete the transaction as fairly as possible. This represents a form of practical rationality. The key concept in managerial semantics is the "threshold." Managers weigh the pros and cons and then set a threshold; if all consequences generated by a choice exceed the set threshold, they prefer that choice. If the resulting preferred choice is not unique, they may increase the threshold until a unique preferred choice is obtained, thereby solving the decision problem.
Daniel Kahneman, a psychologist and economist at Princeton University, won the Nobel Prize in Economics in 2002. His award lecture was titled "Advances Under the Umbrella of Bounded Rationality." Kahneman and his collaborators conducted extensive empirical research and reported numerous experimental results in behavioral economics and decision psychology in several books. I once described this type of research as discovering one psychological phenomenon after another, naming various psychological effects, with the implication that theoretical progress is slow and modeling is weak.
Kahneman and his collaborators made roughly four theoretical contributions. The first was the introduction of "prospect theory" in decision psychology, which has three main points: (1) People tend to overestimate very small probabilities and underestimate very large probabilities, known as the S-curve effect; (2) People tend to reframe decision problems, known as the editing effect; (3) People are sensitive to the way decision problems are presented, known as the framing effect. The second theoretical contribution was the development of a set of subjective probability theories, published in
Psychological Review (1996) [
27]. The third theoretical contribution was the belief that basic cognitive patterns are innate, which has sparked much controversy. The fourth contribution was the proposal of a dual-process theory of problem-solving, with details available in Kahneman's post-Nobel book,
Thinking, Fast and Slow [
28].
As mentioned in another work [
29], in our model of market dynamics within gauge field theory, economic rationality and the real market constitute the global gauge potential and gauge field strength, while bounded rationality and businessmen constitute the local gauge potential and local gauge field strength. This forms a bilayer bipolar four-cell base map in the gauge field theoretic model. To reiterate, at the global level, the dynamic phase of the wave function is an arbitrary constant, representing global changes. At the local level, the dynamic phase of the wave function is a function, with the independent variable representing individual differences.
This is similar to a standard educational test, such as the GRE, where the test creator can design different test items, representing the constant in the global level wave function. Which set of questions is used is unrelated to the test-taker. The test creator, such as ETS, represents the global gauge potential, and the specific set of test items represents the global gauge field strength. Once the test paper is given to the test-takers and the exam begins, the dynamic phase of wave function becomes a function at the local level, with values varying from person to person. The test-taker's potential becomes the local gauge potential, and their performance during the exam represents the local gauge field strength.
3.2.3. Ordinary Rationality
Ordinary rationality theory was proposed and developed by Yang (2021) [
30] and is an important part of economic dynamics, with its ordinary rationality mechanism being modeled by the Higgs mechanism in theoretical physics. The Higgs particle is called the "God’s particle," and the market version of ordinary rationality views ordinary people as the gods of the market.
The concept of ordinary man is central to Western legal philosophy because of the jury system in Western judicial systems, a reflection of Western legal traditions. "Ordinary people" is a difficult concept to define and has sparked countless academic debates in Western philosophy. In judicial practice, the concept is even more sensitive because one fundamental principle of the jury system is that it must consist only of ordinary people. You cannot exclude a citizen from being a jury member for reasons such as race, age, gender, or wealth, but you can exclude them for the reason that "they are not ordinary people." For example, someone with cognitive impairments or someone who is a member of an elite academic society might be excluded. A friend was once disqualified from jury duty for this reason. In high-profile cases, such as the O.J. Simpson trial, the presence or absence of a particular demographic in the jury could influence the verdict, so both legal teams try to influence the selection of jury members.
In economic dynamics, ordinary rationality (people) is defined by eight principles, summarized as follows:
Principle 1: High Selectivity, also known as the picky principle. Ordinary people have limited incomes, such as salaried workers, and must live within their means. They carefully consider what to buy, how much to buy, where to buy, and at what price. When a young person goes shopping with mother and sees her compare prices and be meticulous, that is an example of ordinary rationality. The young person may find the process annoying because they do not yet understand the value of money. Selection is a social instinct, a survival instinct, and an advanced evolution of maternal nurturing instincts, which is a form of great rationality.
Principle 2: Subjective Certainty. This concept was first introduced by Wittgenstein. Wittgenstein, a prominent 20th-century philosopher known for his work in language philosophy and analytical philosophy, believed that social communication could be seen as a language game, with speakers conveying meaning and listeners interpreting it, often ambiguously. He argued that it is difficult to find a set of rules to define such language games due to pervasive uncertainty. Hence, Wittgenstein's philosophy is often associated with the skepticism. He studied a great deal of uncertainty. Later, his students edited and published a small book titled,
On Certainties [
9]. In this book, Wittgenstein emphasized that doubting everything is not a form of doubt; you can only doubt what you have previously believed. He argued that while the world is full of uncertainties, people develop a significant amount of "subjective certainty" through their life experiences. For example, when crossing the street, there is always a possibility of an accident, but based on past experiences, you should cross the street. This is a form of ordinary rationality—otherwise, how would you go about your life? If you were constantly anxious and paralyzed by uncertainty, you wouldn’t be able to do anything. This is what is meant by subjective certainty.
Decision making means taking an action. For ordinary people, daily life often consists of habitual actions doing what needs to be done according to routines, such as brushing teeth, washing face, eating, going to work, buying groceries, receiving salary, being happy, expressing emotions, greeting people, taking the subway, buying tickets, etc. These are habitual routine actions rather than "taking" actions. Ordinary people prefer to avoid making decisions as much as possible because decision-making involves costs. They do not like having someone constantly pressuring them to take actions, as it can be stressful and annoying. The principle of subjective certainty is also known as the "daily life principle."
An ordinary person knows how to live daily life and has established many routine pathways, which is a fundamental aspect of social life and the basis of human civilization—this is the most basic form of rationality. These fundamental aspects have been overlooked by economics for too long. The most common phenomena occurring in our own lives and surroundings are often the ones most easily ignored by theories—hence the saying "the darkest place is under the light."
Principle 3: Taking Null Actions. When people have to make decisions, the most common decision is to take a "null action." For example, a customer walks into a store, sees an interesting item, checks the price, and thinks, "I will consider it." Just as they are about to leave, a salesperson asks if they need help, and they respond, "I will come back tomorrow." This decision to "think about it and come back" is a common type of null action decision. Similarly, if there is an election for student council president at school and you have two friends running—one who supported you during an illness and another who helped you during difficult times—you might feel conflicted and decide to send a message saying you are too sick to vote, avoiding the decision. This is also a type of null action decision, motivated by avoiding higher opportunity costs.
Note that daily life and null decisions are not the same, but they are difficult to distinguish in practice. For instance, if someone takes their child out on a hot summer day and pretends to shop just to enjoy air conditioning in a mall before leaving, that’s one scenario. In another case, a customer may initially intend to shop but decides to leave because the prices are too high. From an observational perspective, these scenarios are generally difficult to distinguish. This is similar to the "equivalence principle" in general relativity, applied to the market.
Principle 4: Sunk costs. It is said that to gauge an undergraduate's understanding of economics, one should assess their grasp of the concept of "sunk costs." Sunk costs are costs that have already been incurred and cannot be recovered. For example, if you bought a stock for $10 and it has dropped to $8, the $2 loss is a sunk cost. Economists advise ignoring sunk costs. The core technique of neoclassical economics is "marginal analysis," which examines the additional benefit from an extra unit of scarce resources, termed marginal benefit. The ratio of marginal benefit to marginal cost is called efficiency. Here, "additional unit" refers to future or present conditions, not past ones, thus not related to sunk costs.
However, who can completely ignore past events? History is part of your life. For instance, if you bought stocks without informing your family and now face a loss, how do you explain it at home? Another example is if you are in a relationship and your partner wants to break up, causing you emotional distress. Friends and family may advise you to move on, but you still dwell on past investments of time, emotion, and money. These are sunk costs. Considering sunk costs is not shameful; it is a natural rationality of ordinary people, reflecting respect for oneself.
Principle 5: Hesitation. People often experience hesitation in life. For instance, if you receive admission offers from Harvard and Princeton with full scholarships, you may hesitate over which to accept, weighing various factors. Seeking opinions from family, friends, and classmates is a form of showcasing. It is a natural rationality to want to maximize the benefit of being accepted by top universities and to delay making decisions to enjoy the recognition. This is ordinary rationality.
Similarly, when shopping, if the price of an item feels a bit high, you might hesitate, deciding to wait until next month to purchase if you are short on funds. This reflects ordinary people's responsibility towards themselves and their families, indicating maturity. Hesitation is a form of rationality, especially ordinary rationality.
Principle 6: Better Life. People want to make their lives better, which seems like a given and requires no further discussion. However, it is an important principle. Macroeconomics has two implicit assumptions: first, that the economy will rise in the long run; second, that it rises cyclically. Correspondingly, microeconomics also assumes that people want their lives to improve, not the opposite. The desire for a better life is a baseline of ordinary rationality; indifference to life quality is not economics.
Principle 7: Face. Ordinary people care about face, also known as dignity or self-esteem, which is a common trait across cultures and history. Having face is an expression of great rationality. If people lacked self-esteem and dignity, society would be chaotic, and human civilization would be in jeopardy.
Principle 8: Emotions. In daily life, emotions are reflections of human nature. Shouldn’t one be happy about good things, sad about misfortunes, or angry about injustices? Feeling emotions is not only a basic form of rationality but also the very healthy rationality.
These eight principles summarize ordinary rationality. This is only a conceptualization of ordinary rationality, and theoretical development is only halfway done. Many social science theories stop here, or add some empirical research and statistical analysis, and consider their work complete. This explains why many new economic theories have not challenged the mainstream status of neoclassical economics. The mainstream status of neoclassical economics is due to its mature core analytical techniques (such as marginal analysis) and model frameworks (e.g., Newtonian mechanics), which other emerging economic schools have not yet reached. Economic dynamics break through this limitation. To find a model applicable to ordinary rationality, one must summarize the overall properties of its eight principles. There are three key properties, summarized as follows:
Property 1: The state of ordinary rationality is a state of minimum energy. Newtonian mechanics considers particles as solid points; in economic market analysis under Newtonian mechanics, the internal mental world of market participants is not considered, and ordinary people are treated as a vacuum state, an empty state in the Newtonian sense. Quantum mechanics posits that vacuum is not empty but contains energy and is in a state of minimum energy, known as vacuum with a non-zero expectation value. In the framework of quantum field theory, economic dynamics considers market participants as ordinary people with internal mental worlds and acknowledges individual differences.
Routine, exercise and health, interpersonal communication, adapting to the environment—what doesn’t require energy? Hence, vacuum is not truly empty. On the other hand, ordinary people lead a stable life without constant upheavals, naturally maintaining a state of minimum energy. Ordinary people do have moments of great ambition, bravery, or extraordinary achievements, but these are states of excitement and beyond the scope of this discussion.
Property 2: Ordinary rationality (people) is an inertial system with zero spin. Ordinary people go about their lives day after day, year after year, forming an inertial system, just as the vacuum is an inertial system in quantum field theory. T. D. Lee [
12] once said that an inertial system has zero spin and breaks all symmetries. For details on this, see Yang [
30], Ordinary Rationality and the Higgs Mechanism.
Property 3: Ordinary rationality (people) is a "degenerate state." This is a remarkable observation, as it fits the description so precisely that it is hard to imagine otherwise. In physics, a particle in a degenerate state is one where the state of the particle cannot be isolated and observed alone; observing this particle state will also involve observing other related particle states. Such a particle is said to be "confined." In quantum chromodynamics, quarks are confined.
In reality, whether one is a worker, farmer, various types of office worker, entrepreneur, financier, professor, scientist, civil servant, or a member of royalty, each shares the common aspect of ordinary people while also having unique characteristics. This is the degenerate state. Ordinary rationality is difficult to observe in isolation; in physical terms, it is not a characteristic state, and the observation results can only be a spectrum. In other words, ordinary rationality serves as a base, with additional elements like color, lines, and backgrounds painting the diverse human conditions. Ordinary rationality is not something easily grasped, but it is omnipresent.
These three fundamental properties correspond to the three basic properties of the Higgs field in theoretical physics: the minimum energy vacuum state, the inertial system, and the degenerate state. Therefore, the Higgs field is a model of ordinary rationality. What is the Higgs field? A common analogy is that the Higgs field is like a swimming pool. When you’re on the shore wearing several layers of clothing, you don’t feel much. But if you jump into the pool with those clothes on, you will feel the weight of the clothing. This illustrates the role of the Higgs field, just as it illustrates the role of ordinary rationality.
The Standard Model of particle physics consists of three basic structures: the single-charge quantum electrodynamics, the isospin weak force model, and the three-charge quantum chromodynamics. These correspond to the physical models of market dynamics, externality dynamics, and sub-economic dynamics in economic dynamics, respectively, and share the corresponding mathematical symmetry groups. This forms the core of economic dynamics, using the Standard Model as its physical model. However, the Standard Model has a critical flaw.
Modern particle physics is described using quantum field theory, with gauge field theory becoming the standard language of the model. When Yang Chen-Ning and Robert Mills initially introduced gauge field theory in particle physics, it did not attract immediate attention from the physics community. This is because the Lagrangian formulas used to describe particle states in their dynamical analysis did not include mass terms. In other words, all the fundamental particles defined in the Standard Model using gauge field theory are massless, reflecting a gauge symmetry. This obviously does not match experimental results. In economic terms, masslessness equates to having no consequences. In other words, the various charges discussed in economic dynamics, such as market charges, impulsive color charges, and externality gauge fields, cannot account for market or economic consequences, meaning there is no baseline for predictive mechanisms. This is also an issue with other economic theories.
Later, British physicist Peter Higgs and others proposed a solution, introducing the Higgs field to interact with gauge particles, allowing them to acquire mass and spontaneously breaking gauge symmetry. This mechanism is known as the "Higgs mechanism."。Some physicists began referring to the Higgs particle as the "God particle," which, over time, was further shortened to simply "the particle." Ordinary rationality is the social science version of the Higgs field. In social and economic life, ordinary people perform the role of the Higgs mechanism. Ordinary rationality is the ground state (grand state), while other forms, such as bounded rationality, are excited states. Understanding the baseline of universally shared ordinary rationality helps in assessing the difficulty of other rational efforts, which reflects the "magnitude of quality" in social life. In economic life, the actual effectiveness of various economic policies, regardless of how much they are promoted, depends on how well they are accepted by ordinary people. When a new product is launched in the market, regardless of the advertising efforts, its sales depend on the degree of acceptance by ordinary people. The saying "the customer is always right" means that ordinary people are the true arbiters of the market. We will detail the modeling specifics of the Higgs mechanism and the corresponding ordinary rationality mechanism in future articles.
3.3. Theory of the Monetary Nature of Currency
Economic dynamics uses gauge field theory as a modeling method, which is a part of quantum field theory, integrated from quantum mechanics and special relativity. The quantum aspects of economic dynamics will be introduced in the market dynamics section; here we mainly discuss the special relativity model of money. This work was initially presented in Yang (2013) [
31] (Modern Principles of Economic Mechanics, Chapters 3 to 5), and has since been further developed by the author. This section describes its methodology, photon-like money nature, light-cone and money cones, and poverty-cones and wealth-cones.
3.3.1. Methodology
A scientific theory must have its boundaries, as it needs to possess falsifiability according to Popper's philosophy of science. A theory without boundaries is termed theology. Therefore, when establishing a new theoretical model, you need to know not only what you intend to say but also what you do not intend to say. The following points are not addressed in this paper.
Firstly, money has dual characteristics: its monetary nature and its money nature, as well as its currency nature. This introduces three research paths in monetary studies. The monetary nature refers to the content typically covered in general economics textbooks, which is highly specialized but less understood. The money nature involves the social cognition and behavioral mechanisms of money, falling under monetary psychology and behavioral finance. This content seems to be somewhat common knowledge; however, its scientific level is quite low due to a lack of conceptualization and modeling. The currency nature studies the systemic overall properties of the relationship between monetary nature and money nature, generally referred to as meta-theory. This paper is limited to discussing the money nature.
Secondly, this paper does not discuss political finance. This topic concerns the national nature of money, known as sovereign money. Sovereign money is issued by national central banks, and sovereign countries depend on a healthy sovereign currency, with its strength rooted in its currency reserves and trustworthiness. Hayek, in the Denationalization of Money [
32], advocates for currency free markets and the privatization of currency issuance, which illustrates, in the contrary, that contemporary money is nationalized. This paper does not cover this aspect.
Furthermore, this paper does not delve into the philosophy of money. The leading figure in the philosophy of money is Georg Simmel, whose classic, Philosophy of Money [
33], has several Chinese translations. Simmel summarized four types of excellent qualities of money's monetary nature into twelve points. For instance, everyone spends money and everyone receives money. Money is never short of energy; when people want money, they infuse their own energy into it. Money is never short of wisdom; when people budget with money, they infuse their own wisdom into it. Money has a limited capacity for abstraction, continuously evolving invisible abilities, and dream-like imaginative capacities, among others. Finally, money evolves into a unitary system that fits human cognitive channels, where people easily make mistakes in other calculations, but not generally in money calculations. This paper borrows three themes from Simmel: money is not a commodity but the relationship between commodities; money is not functional; money itself represents function; and money is the logic of the market.
Of course, not discussing something does not mean never discussing it. Cognitive science and psychology have many overlaps, but the former emphasizes interdisciplinary conceptualization and modeling, including computational models or mathematical physics models. Where the model leads, the theory follows; where the model is limited, the theory remains unspoken. Modeling is like the currency of theory; the more money, the more speech. If the content phenomenon exceeds the modeling level, it is called insufficient modeling; conversely, it is called excessive modeling. The requirement is for conceptualization to be "just right." This is a principle of contemporary formal philosophy. Some may be puzzled as to why emphasis is placed on conceptualization and modeling in fundamental theoretical research. Conceptualization is progress in cognitive level to avoid simple repetition. Modeling is the evolution of knowledge accumulation to avoid piecemeal progress.
3.3.2. Photon-like Money Nature
Economic dynamics and cognitive dynamics both use the particle physics standard model and the Higgs mechanism as their models. Economic dynamics, with its content trimming meeting the "just right" conceptualization requirement, means its models not only share gauge symmetry groups with the standard model but also sometimes share notation. The language of the standard model is quantum field theory, which integrates quantum mechanics and special relativity. When referring to the money nature as "money particles" depicted by photons, money particles must satisfy two types of photon-like conditions, which are the requirements of quantum mechanics and special relativity, respectively, which are briefly described as follows.
The first condition is quantum mechanics. Money particles have a spin of 1. Spin is an intrinsic property assigned to particles by quantum mechanics, which has no counterpart in Newtonian classical mechanics. Classical mechanics views particles as solid points, whereas quantum mechanics considers particles to have internal space. Just as classical economics does not address the internal mental world of market participants, assuming that under the law of large numbers, different individuals' mental states are averaged out, and it suffices to consider their market behavior as point-like behavior. Economic dynamics, however, commits ontologically and epistemologically to the mental world of individual participants and their internal space. In quantum mechanics, particles have rotational internal space; with rotation comes angular momentum, and spin is the unit measure of this angular momentum.
However, the concept of angular momentum is not intuitive in economics and the mental world. Over a decade ago, I was somewhat confused about this and consulted Mr. Zhengxing Wang from Peking University. Mr. Wang explained that intuitively, you can imagine several directions of rotation in the particle’s internal space. Material particles, such as fermions, generally have two fundamental directions of rotation, such as the spin-up and spin-down of an electron, which are two base states. Other spin directions can be seen as superpositions of these two base states. The number of base states equals the spin quantum number, for example, the electron’s spin is 1/2. Mediators, such as bosons like photons, have only one spin direction, which is the direction of their longitudinal wavefront, hence their spin is 1.
This can be understood as follows: Economic goods, including commodities and services, have two directions or spin base states: yes or no. If a person is hungry and you give him a bowl of rice, he says yes and eat it. After finishing the first bowl, if you give him another bowl, he again says yes and eat it. After finishing the second bowl, if you give him a third bowl, he might say that he is full and cannot eat more. That is, a bowl of rice has two spin directions: being eaten or not being eaten, so its spin is 1/2. Money, however, is different. If you give someone one hundred dollars, he says thank you and accept it. If you give him a thousand dollars, he accepts it again and ask for a check. If you give him ten thousand dollars or more, they still accept it and say a transfer is more convenient. In other words, "money particles" have only one spin direction, which equals one, so its spin is 1.
Note that when applying the concept from physics to social sciences, the voice form used in physics should be converted to passive voice. For example, the spin in physics should be translated to "being spun" in economic dynamics. Saying a bowl of rice or money is spun might seem conceptually awkward, but using people as examples makes it easier to understand. For instance, if someone is job hunting, they have the commodity attributes of the job market. If this person receives a job interview opportunity and is told the results will be announced in two weeks, these two weeks are hard to endure. Today, they might think their interview performance was appropriate, considering their advantages, and feel they will be hired. Tomorrow, they might think about something inappropriate they said during the interview, reflecting on their weaknesses, and feel they might not be hired. This anxiety is the state of being spun.
The second condition is special relativity. Special relativity is based on the invariance of the speed of light, which provides a constant. Each observer is an inertial system with different inertial velocities, but through the Lorentz transformation, all observers see the speed of light as the same, which gives symmetry corresponding to the light speed invariance.
Firstly, the non-functionality of money particles allows them to operate at the fastest speed in the economic world, just as photons operate at the fastest speed in the material world, partly because of the photon's masslessness. According to Einstein's mass-energy equation, particles with mass require enormous (almost impossible) energy to approach the speed of light.
Since childhood, people have learned about the purchasing power of money. Wanting to buy a piece of candy requires asking for coins from an adult. In college, saving money for tuition or buying a used car makes people understand money’s saving function. After starting work, having some spare money, people learn about the investment function of money. These are the potential functional uses of money, which are its functionalities. However, during a conversation, if a familiar friend suddenly asks what you really want, and you reply, "I just want to make more money," the friend fully understands you without needing to specify the exact functions of money.
In the economic world, similar to the masslessness of photons, only money particles can reach this state of self-sufficient non-functionality, and it can be handled with the concept of de-functionalization. No other economic goods can be compared to this, so money operates the fastest. Here, "money speed" is not related to the transaction and market circulation speed of money, which pertains to the currency nature.
Moreover, money particles have finite speed. This is because the money nature is constrained by the currency nature, mainly the national nature of money. The national and sovereign nature of money restricts the issuance amount and exchange rate. Common sense tells us that money is finite. Ordinary rationality tells ordinary people that income is limited. Therefore, people understand that the speed of spending money must be limited. Holding this idea, money speed is thus limited.
Additionally, money speed is conserved. Simmel, in Philosophy of Money [
32], stated that money is not functionally objective; money itself is the function, and this function as a meta-economic property is stable. Money is not a commodity; money is the relationship between commodities, and this "relationality" is stable. Money is not the market but the logic of the market; markets can change, but the logic of the market is constant. This is an economic philosophical argument.
As mentioned above, money particles in the economic world are the fastest, finite, conserved, and have a spin of 1, which defines their photon-like nature. The degree of photon-like nature can vary, just as individual differences in the demand for money can vary, which can be achieved through Lorentz transformations to reach symmetry. The key point is that photon-like nature requires consistency in the conceptualization of money nature. Of course, some may say they dislike money and prefer a simple life, which is a respectable religious sentiment, but unfortunately, it is not economics.
In the social sciences, to apply special relativity, one must first find an invariant with photon-like properties. In the cognitive world, it is language; in the political world, it is power; in the sub-economic or sub-cognitive world, it is consciousness, and so on. Thus, photons, money particles, language, power, and consciousness constitute the fivefold photon-like state. If money is the light in economic life, the similar can be said to language, power, and consciousness, people will understand what you mean. This is the power of conceptualization. The next step is to explore how to model this.
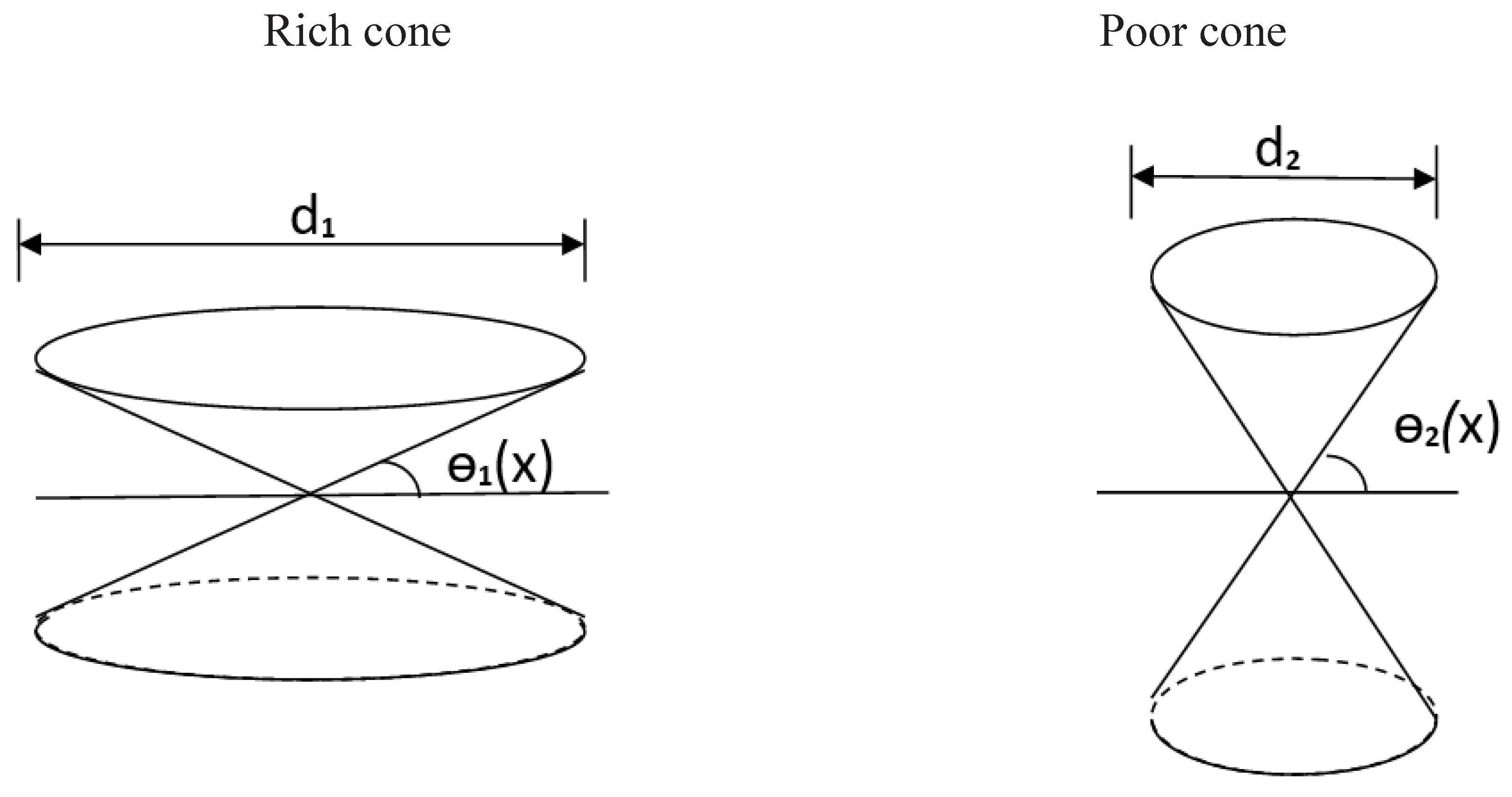
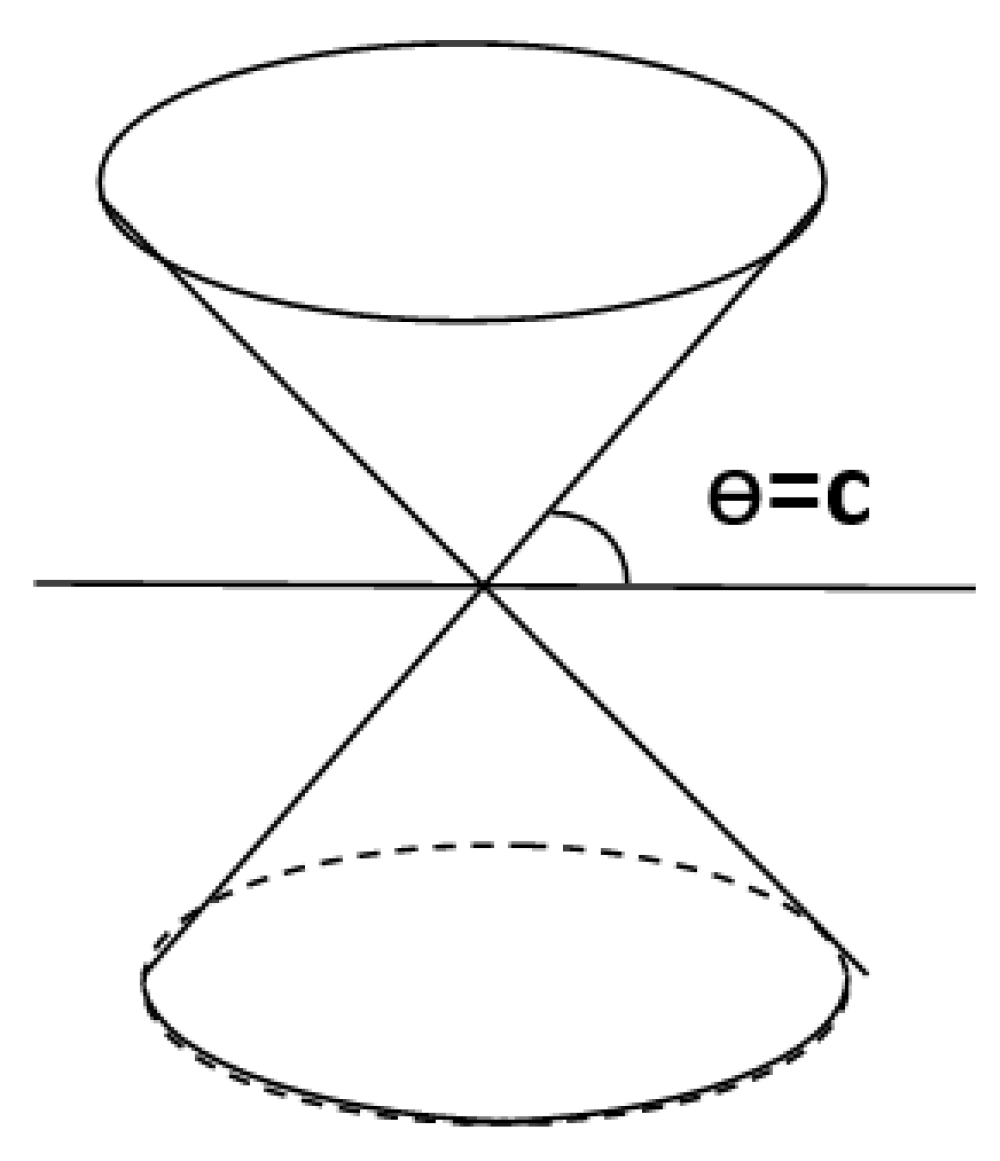
3.3.3. Light Cone and Money Cone
Conceptualization and modeling are closely related but differ in style. Developing a new foundational theory requires a substantial understanding of phenomena within the field as well as models outside the field. Conceptualization, also known as conceptual processing, involves revisiting phenomena within the domain after anchoring external models and re-conceptualizing existing theories. Abstract trimming must be appropriate. This is actually the most challenging phase in basic theoretical research. Modeling, also known as model embedding, involves seamless integration based on conceptualization, with technical craftsmanship being crucial. This is the most meticulous phase in fundamental theoretical research. Experience in interdisciplinary research often suggests that the most central aspects across different fields are usually the most communicable. Therefore, whether in conceptualization or modeling, focusing on the core often leads to significantly more efficient results.
Special relativity operates in four-dimensional Minkowski spacetime. We are accustomed to thinking in three-dimensional Euclidean space from elementary school, where a point is defined by three variables and the distance between two points is the square root of the sum of three squared terms. Speed, including the speed of light, is calculated as distance divided by time, and so on. These concepts change in four-dimensional spacetime and need to be redefined. Here are several newly introduced necessary concepts:
The first concept to be reintroduced is "metric," denoted as . The metric is the most fundamental algebraic structure in algebraic space. In three-dimensional space, it is positive, = (+, +, +). In the four-dimensional spacetime, the metric is one positive and three negatives,
or equivalently one negative and three positives, depending on the convention.
Second, a new time dimension is introduced, often multiplied by the speed of light, called the energy dimension. A point in four-dimensional spacetime is called an event.
Third, the concept of velocity is replaced by "composite velocity." In four-dimensional spacetime, the concept of velocity no longer applies, but "composite velocity" is introduced. The corresponding symmetry now states that all objects (including light) have the same composite velocity in four-dimensional spacetime. However, light has the least composite velocity along the time axis and the most in the three spatial dimensions. This aligns with the notion that light is the fastest in three-dimensional space. The idea of this conceptual shift is quite fascinating.
Fourth, and particularly crucial, is the concept of an event's "interval," defined as follows:
The interval is defined by a linear combination of four terms. The first term is the speed of light squared multiplied by the time increment squared, with a positive sign, representing the energy term. In the context of economics, the speed of light is replaced by the speed of money, and the energy term represents budget or purchasing power. The other three terms are the squares of the spatial increments, each with a negative sign. In the context of economics, these spatial terms represent consumption.
With these concepts in place, we can introduce the well-known light cone, which is analogous to the money cone model. For a given light source, since light travels fastest, it is reasonable to initially assume it travels in a straight line. From the light source, one can imagine various directions of scattering forming a downward cone. Similarly, scattering in upward directions from the same light source forms an upward cone. The intersection of these upward and downward cones at the source defines the light cone. Replacing the light source with a money source yields the money cone model (
Figure 3).
An event can be located on the surface of the light cone, inside it, or outside it. The light cone model provides a significant characterization in economics. Events on the surface of the money cone have an interval of zero, referred to as a "null event" in Chinese. In an economic context, this means that purchasing power and consumption exactly balance each other, often described as being "living paycheck to paycheck." Events inside the money cone have an interval greater than zero and are called "quasi-temporal events," indicating that purchasing power exceeds consumption and there is a surplus, meaning there is no shortage of money. Events outside the money cone are called "quasi-empty" events, with an interval less than zero, signifying that actual consumption exceeds purchasing power, which is referred to as excessive consumption.
In physics, the light cone model introduces worldlines passing from the lower cone through the light source to the upper cone to characterize historical causality. In the context of economics, for example, during the 2007 global financial crisis, the U.S. Congress passed a $700 billion bailout package, which serves as a source of money emission. Not all past economic activities are responsible for this money source's creation; only those events related to causing the subprime mortgage crisis are considered internal time-like events of the lower money cone. Similarly, not all industry companies or individuals benefit from the special appropriations by Congress; most are space-like events. Only those who benefit from the special appropriations are considered time-like events and enter the upper cone.
3.3.4. Proper Cost Value: Poor Cone vs. Rich Cone
In the previous section, it was reasonably assumed that light travels in a straight line, but this is not absolute. When we discussed the generalized relativity model of welfare economics in another paper, we introduced the concept of economic gravity. When considering both Einstein's special relativity and general relativity, under significant gravitational influence, light rays can become polarized, and the light cone itself can deform. For example, during severe global pandemics, the economic gravity as negative curvature has a significant impact, and the monetary nature may lower its noble stance. At such times, while the money cone may maintain its internal topological structure, it may need to bend and twist to adapt to the curvature and winding of the worldlines. These models are illustrated with diagrams in Penrose (2005), The Road to Reality [
20]. The model of the poor cone and rich cone can be found in Yang Y. (2013), Modern Principles of Economic Mechanics [
31]
.
If readers find the previous descriptions somewhat distant from personal real-life experiences, this section will place personal real-life experiences within the framework of special relativity. A concept in special relativity, seemingly divinely inspired and particularly suited for psychology and economics, especially economic dynamics, is "proper time." A common example involves a pair of twin sisters, each carrying a clock. Suppose one sister travels through space on a spaceship while the other remains on Earth. The time related to the spaceship's speed is called absolute time. The principle states that due to the fast speed of the spaceship, the clock with the sister on it runs slower relative to Earth; conversely, the clock with the sister on Earth runs faster. Thus, when the sister returns to Earth, she is still young, while the other sister has aged. This clock time is called proper time. Proper time is inversely related to speed. Proper time is evidently individual-specific, so when representing proper time with a symbol, it should have a subscript, denoted as , indicating that proper time is a variable that can vary for each individual. Thus, proper time can reflect individual differences. In economics, decisions are always individual actions. Decision-making involves the mind, and the mental world can only be embodied in individual lives. To discuss "group decision-making," one must explain the mechanism by which decisions by each individual lead to what is termed group decision-making. Understanding this principle allows for discussion of behavioral economics.
The market price of a good or service is called the absolute price, meaning it does not vary by individual or clock. However, each consumer has an intrinsic psychological price, called the "proper value," denoted as , which refers to proper time. For example, two classmates go shopping at a mall on the weekend and look for a place to have lunch when they are hungry. They see a high-end restaurant with a buffet priced at 60 dollars per person. One classmate, coming from a financially well-off family, considers 60 dollars for a buffet to be inexpensive. The other classmate, from a poor background, finds 60 dollars for lunch too expensive. Thus, the absolute price of 60 dollars is considered cheap by one consumer and too expensive by another, reflecting that different individual consumers have different intrinsic values for the same absolute price.
The light cone and money cone introduced in the previous section are static cones. By dividing each of the four terms in the linear combination used to define the event interval by proper time or intrinsic value, we obtain the concept of momentum. Accordingly, a momentum cone can be drawn. Since intrinsic value varies from person to person, the momentum cone also varies accordingly. Now, let's transform the static cone described in the previous section into a momentum cone. First, draw a horizontal line passing through the cone's apex (i.e., the top and bottom cone vertices) or slice a horizontal equatorial plane. This creates an angle between the horizontal line (or equatorial plane) and the cone's surface. Momentum varies with intrinsic value, so the shape of the momentum cone varies with momentum. Thus, is a variable that differs from person to person and is denoted as ; for different individual consumers, the higher the proper value , the larger , which is a proportional relationship.
Next, consider the upper part of the money cone (and similarly for the lower cone). The width of the opening, denoted as , is called the consumption impulse. The width of the upper cone's opening , is inversely proportional to , meaning that consumption impulse is inversely proportional to the proper cost value. In other words, the higher an individual's proper cost value, the smaller the corresponding consumption impulse, and vice versa. Simply put, if you think something is more expensive, the impulse to buy it is smaller, which conforms to the common sense.
From a geometric perspective, for an individual consumer, the poorer the person, the higher the proper value , the larger the angle of the momentum money cone, and the smaller the consumption impulse , resulting in a narrower opening of the upper cone. In this case, the momentum money cone becomes thinner and is referred to as the poor cone (see the right cone below). Conversely, the wealthier the person, the lower the proper cost value , the smaller the angle , the wider the opening of the upper cone, and the larger the consumption impulse , resulting in a flatter momentum money cone, known as the rich cone (see the left cone below).
Figure 4.
Rich cone and poor cone.
Figure 4.
Rich cone and poor cone.
Poverty and wealth are always relative; everyone is lacking compared to those above and has more compared to those below. Thus, the individualized intrinsic cone can reflect general individual differences.