Prerpints.org logo
Preprint
Review

Securing the Internet of Things (IoT) in the Quantum Era: Challenges and Future Directions for Quantum-Resistant Cryptography

Altmetrics

Downloads

119

Views

55

Comments

0

This version is not peer-reviewed

Submitted:

11 August 2024

Posted:

12 August 2024

You are already at the latest version

Alerts
Abstract
Internet of thing (IoT) has been used in different aspect of life as industry, and daily life. Aligned with IoT, Quantum computers have been generated with high features that can accomplish complicated tasks with high speed. IoT and Quantum computers don’t match in resources and due to this collaboration between the two terms, it was found there are many challenges with quantum computers brought some security concerns. This paper will examine all challenges and future direction that face the use of IoT through using different quantum cryptograph methods. The first part on the paper discussed the vulnerabilities of existing cryptographic methods like RSA and ECC. these two methods were used as basic level for IoT security protocols. These cryptographic algorithms could be easily attacked by quantum computers so to ensure that IoT devices are secure must develop quantum resistant cryptographic algorithms. Next this paper will examine the challenges in implementing quantum resistant cryptographic algorithm in any IoT device through quantum resistant cryptographic algorithms such as lattice-based cryptography, code-based cryptography, multivariate cryptography, and hash-based signatures. Then, the paper discussed the future direction of securing IoT in quantum computing. In conclusion, securing IoT devices in quantum presents many challenges that require to be addressed where quantum resistant algorithms can be a solution that mitigate threats.
Keywords: 
Subject: Computer Science and Mathematics  -   Security Systems

1. Introduction

The deployment of Internet of things (IoT) brought many security concerns. As the world is moving toward quantum technology, quantum computers have powerful resources such as super computational power. Due to these resources, the security of IoT is facing unexpected threats. This paper discussed all challenges and future direction of IoT in the quantum era using the application of quantum- resistant cryptograph.
The security of IoT in the past deponed on using different security protocols and cryptographic algorithms like RSA (Rivest-Shamir-Adleman) and ECC (Elliptic Curve Cryptography) but these things were vulnerable and can easily get attacked by the quantum computers (Kuwakado, H,2010). To avoid all of these security issues, it is required to develop quantum– resistant cryptography to ensure the long – term of securing IoT systems (Umana, V.G , 2011).
To start with, the resources which are used by IoT technologies are limited. The resources can be power, memory, and other energy requirements. Where quantum computers resources are extremely much better. Here was the problem between the collaboration between IoT and quantum computers. To keep all IoT devices secure, the implementation of quantum- resistant cryptograph on IoT devices must match with these resources otherwise there will be different challenges and it will introduce the difficulties on updating and maintaining cryptographic algorithms across the IoT ecosystem (Umana, V.G , 2011).
There are different approaches that have been proposed to achieve quantum-resistant security in IoT like lattice-based cryptography, code-based cryptography, multivariate cryptography, and hash-based signatures. Each approach has some advantages and limitations and suitability for IoT system (Abd El-Aziz, R. M, 2022).
The future of securing IoT systems in quantum computers will need many things to be establish such as post-quantum key exchange protocols and the advance implementation of post-quantum cryptography. In conclusion, the security of IoT systems faced many challenges when the world started using quantum computers (Beullens, W ,2021).
In this research, I will make the following main contributions:
  • Provide a comparative study of the pre-quantum and post-quantum IoT security architectures.
  • Analyze the Challenges and Future Directions of Post – quantum cryptograph on IoT.

2. Overview of the Technology Principles

2.1. Cryptographic Fundamental

Cryptographic is an old method used to ensure the security of information. This method is used to ensure the message will be secure while transferred between the sender and receiver. It has been under two processes which are encryption and decryption (Bernstein, D. J., & Lange, T. (2017)). The following figure illustrates how the message will be transferred.
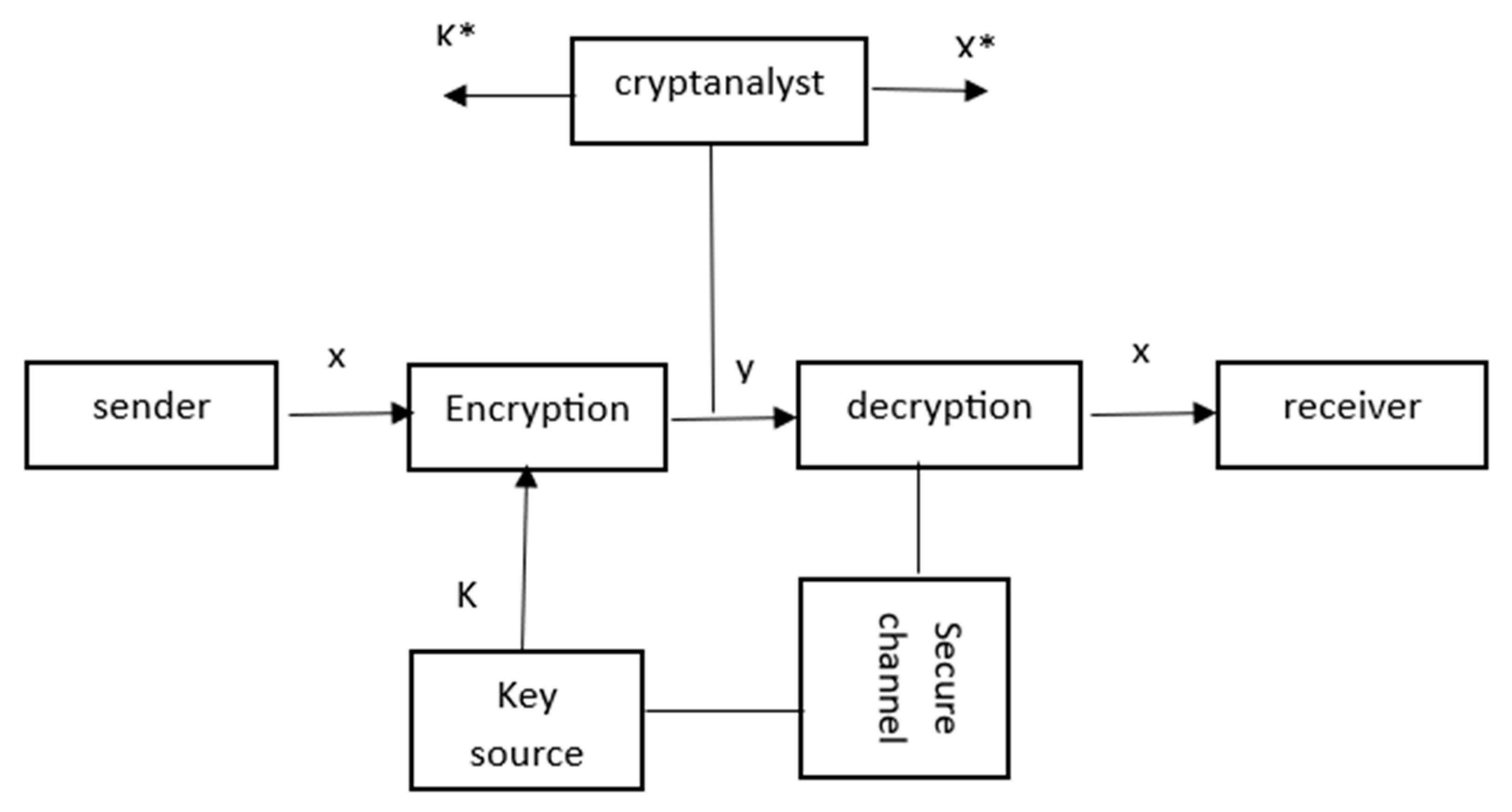
Preprints 114925 g001
Figure 1. Cryptographic method.
Figure 1. Cryptographic method.
Preprints 114925 g001

2.2. Pre – Postquantum Cryptographic Methods

There are some pre post cryptographic methods like RSA and ECC, which are commonly used as the basic level for IoT security protocols. But these methods have some vulnerabilities that can be exploited by various attacks (Rahman, M., & Jahankhani, H. (2021)).
RSA cryptography:
A cryptosystem, or collection of cryptographic algorithms used for particular security services or purposes, is built on the RSA algorithm (Rivest-Shamir-Adleman), which enables public key encryption and is frequently used to secure sensitive data, especially when it is sent over an insecure network like the internet.
The RSA method of working relied on generating a number by multiplying two sufficiently large numbers together but factorizing that number back into the original prime numbers is extremely difficult. The public and private key are created with two numbers, one of which is a product of two large prime numbers. Both use the same two prime numbers to compute their value. RSA keys tend to be 1024 or 2048 bits in length, making them extremely difficult to factorize, though 1024 bit keys are believed to break soon.
For RSA vulnerabilities can be as follows:
  • Integer Factorization: RSA relied on mathematical calculation. It relied on the difficulty of factoring large composite numbers into their prime factors. But due to the advancements in factorization algorithms, such as the General Number Field Sieve (GNFS), have reduced the security of RSA (May, A. (2003)). The emergence of quantum computers with the powerful process which contained algorithm which known by with Shor's algorithm broke RSA, as it could efficiently factor large numbers.
  • Low Key Generation: all the methods used public key which can be generated to different key. If the random number generator used to generate RSA keys is flawed or the entropy source is weak, it can lead to the generation of weak keys that are susceptible to attacks like brute force or factorization (May, A. (2003)).
  • Side-Channel Attacks: RSA implementations can be vulnerable to side-channel attacks, such as timing attacks, power analysis (May, A. (2003)). These attacks exploit information leaked during the execution of the algorithm to recover the private key.
ECC cryptography:
Data encryption using elliptic curve cryptography (ECC), a method dependent on keys. For the purposes of decrypting and encrypting online traffic, ECC focuses on pairs of public and private keys. In relation to the Rivest-Shamir-Adleman (RSA) cryptographic algorithm, ECC is widely discussed. RSA uses prime factorization to accomplish one-way encryption for items like emails, data, and software.
For ECC vulnerabilities as follows:
  • Elliptic Curve Discrete Logarithm Problem (ECDLP): ECC relied on the hardness of solving the ECDLP, which involves finding the scalar value 'd' given a point on an elliptic curve and the result of multiplying that point by 'd'. If a sufficiently powerful quantum computer is developed, it could potentially solve the ECDLP and break ECC-based cryptographic systems (Rahnama, B., Sari, A., & Ghafour, M. Y. (2016)).
  • Choice of Curve Parameters: ECC required careful selection of curve parameters. If the parameters are poorly chosen or generated with insufficient randomness, it can weaken the security of ECC and make it vulnerable to attacks (Rahnama, B., Sari, A., & Ghafour, M. Y. (2016)).
  • Implementation Flaws: Vulnerabilities in the implementation of ECC algorithms or protocols can lead to security flaws (Gabsi, S., Beroulle, V., Kieffer, Y., Dao, H. M., Kortli, Y., & Hamdi, B. (2021)). These vulnerabilities can be exploited by attackers to recover private keys or launch attacks, such as invalid curve attacks or point compression attacks.

2.3. Post – Quantum Cryptography Fundamental:

Post-Quantum Cryptography (PQC), also known as quantum-resistant cryptography or quantum-safe cryptography, refers to a new class of cryptographic algorithms designed to be secure against attacks from quantum computers. As quantum computing technology advances, it is expected that quantum computers will be able to efficiently break certain classical cryptographic algorithms that are widely used today (Ahn, J., Kwon, H. Y., Ahn, B., Park, K., Kim, T., Lee, M. K., ... & Chung, J. (2022).
Post-quantum cryptographic algorithms are designed to resist attacks from quantum computers. These algorithms are based on entirely different mathematical problems that are believed to be hard for quantum computers to solve (Ahn, J., Kwon, H. Y., Ahn, B., Park, K., Kim, T., Lee, M. K., ... & Chung, J. (2022).).
The goal of post-quantum cryptography is to ensure that sensitive data, communications, and other cryptographic processes remain secure even in the presence of powerful quantum computers (Alagic, G., Alperin-Sheriff, J., Apon, D., Cooper, D., Dang, Q., Kelsey, J., ... & Smith-Tone, D. (2020)). Researchers are actively working on developing, analyzing, and standardizing post-quantum cryptographic algorithms to prepare for the eventual deployment of quantum-resistant security solutions(Alagic, G., Alperin-Sheriff, J., Apon, D., Cooper, D., Dang, Q., Kelsey, J., ... & Smith-Tone, D. (2020)).
The transition to post-quantum cryptography is expected to be gradual and is an essential step in securing our digital infrastructure in the quantum era. All of post-quantum cryptography depend on quantum key distribution. Post-Quantum Key Distribution (PQKD) is a method of securely distributing encryption keys that is designed to be resistant against attacks from quantum computers. It addresses the potential threat that quantum computers pose to conventional key distribution schemes, such as those based on public-key cryptography (Yavuz, A. A., Nouma, S. E., Hoang, T., Earl, D., & Packard, S. (2022, December)).
In traditional key distribution systems, cryptographic keys are often exchanged using public-key algorithms, where a public key is shared openly, and a private key is kept secret. However, quantum computers could factor large numbers efficiently and solve certain mathematical problems underlying these conventional schemes, rendering them vulnerable to attacks (Rahnama, B., Sari, A., & Ghafour, M. Y. (2016)). Post-quantum key distribution, also known as quantum-safe key exchange, relies on different mathematical principles that are considered secure even in the presence of quantum computers. Two prominent examples of PQKD are:
  • Quantum Key Distribution (QKD): QKD is a quantum cryptographic protocol that enables two parties, often referred to as Alice and Bob, to exchange a shared secret key over an insecure communication channel, while detecting any potential eavesdropping attempts (Yavuz, A. A., Nouma, S. E., Hoang, T., Earl, D., & Packard, S. (2022, December). Examples of QKD protocols include BB84 (Bennett and Brassard 1984) and E91 (Ekert 1991).
  • New Hope: New Hope is a post-quantum key exchange algorithm based on lattice-based cryptography. It is designed to provide security against both classical and quantum adversaries. New Hope is considered a candidate for use in Transport Layer Security (TLS) to secure internet communications Yavuz, A. A., Earl, D., Packard, S., & Nouma, S. E. (2022, June)
The main advantage of post-quantum key distribution schemes is that they provide a future-proof solution for securely exchanging encryption keys, even in a world where quantum computers become powerful enough to break classical cryptographic systems. By incorporating PQKD into existing communication protocols and security frameworks, organizations can enhance the long-term security of their sensitive data and communications.
In addition to that , there are Common approaches in post-quantum cryptography include:
 ●
Code-based Cryptography:
Code Based Cryptography introduced by McEliece in 1978 which relied on hardness of decoding random linear codes. Due to this concept, the code-based cryptograph provided high level of security against quantum attacks but with the implantation of IoT devices faced challenges due to the overhead and key size (Aguilar-Melchor, C., & Fúster-Sabater, A. (2017).) This method used public key that depends on the hardness of decoding which contains error correcting codes. This method depends on another method which is McEliece cryptosystem (Cayrel, P.L, 2014). It used specified code known as Goppa code which is used for encryption and decryption where the security will be so difficult to be attack(Sendrier, N ,2017).
 ●
Lattice-based Cryptography:
It is a form of post-quantum cryptography that depended on the hardness of certain mathematical problems related to lattices. It is classified as an alternative to traditional public-key cryptosystems such as RSA and ECC, as it is believed to be resistant to attacks by quantum computers (Chen, M. ,2020). This method offers various cryptographic primitives like encryption, digital signatures, and key exchange protocols.
 ●
Hash-based Cryptography:
It is known as hash-based digital signatures or one-time signatures, are a form of digital signature scheme that is based on cryptographic hash functions. This method relied on the properties of hash functions, such as collision resistance, to provide security (Ducas, L, 2021). Hash-based signatures have the advantage of being resistant to attacks by quantum computers, making them a potential candidate for post-quantum cryptography. However, they typically have larger signature sizes and may have limitations in terms of the number of signatures that can be produced with a given key pair. Hash based signatures are built upon collision resistance of hash function and have been proven to be secure against quantum attacks but with IoT devices require significant computational resources (Buchmann, J., Dahmen, E., Göpfert, F., & Leander, G. (2017).
 ●
Multivariate Polynomial-based Cryptography:
It is a form of public-key cryptography that is based on the difficulty of solving multivariate polynomial equations over finite fields. It is income how utilize mathematics concept which is algebraic structures and equations to construct cryptographic algorithms (Chen, M. ,2020). The advantages of using this method are in terms of smaller key sizes and faster computations compared to traditional cryptographic algorithms (Chi, D.P ,2015). However, it is vulnerable to attacks based on algebraic techniques.
Based on the features of post quantum cryptograph methods, there are some differences and similarities. The following Table 1 shows these differences and similarities.

2.4. Post – Quantum Cryptography Challenges:

There are different security challenges posed by the quantum computer and the cryptograph algorithm in securing the internet of things (IoT). Based on these methods, the challenges were different from one method to another method.
For the Code-Based Cryptography the challenges are as follows:
1. Key size: it required large key sizes to ensure security, which can be challenging in resource constrained IoT devices with limited computational power and memory (Sendrier, N. ,2017).
2. Decoding Complexity: The decoding process in code-based cryptography can be computationally expensive, making it unsuitable for low-power IoT devices (Sendrier, N. ,2017).
3. Post-Quantum Transition: While code-based cryptography is believed to be resistant to attacks by quantum computers, it may still face challenges in terms of transitioning from traditional cryptographic algorithms to code-based schemes (Sendrier, N,2017).
For the Lattice-Based Cryptography the challenges are as follows:
1. Key Sizes and Efficiency: it requires larger key sizes compared to other traditional cryptographic schemes (Lei, D., He, D., Peng, C., Luo, M., Liu, Z., & Huang, X. (2023). This can result on challenges in terms of storage, transmission, and computational efficiency, especially in resource-constrained environments.
2. Parameter Selection: Selecting parameters that are too weak can make the scheme vulnerable to attacks, while selecting parameters that are too large can result in inefficient computations (Aikata, A., Basso, A., Cassiers, G., Mert, A. C., & Roy, S. S. (2023).
3. Cryptanalysis Advances: The field of lattice-based cryptography is still relatively new compared to other well-established cryptographic schemes (Lei, D., He, D., Peng, C., Luo, M., Liu, Z., & Huang, X. (2023)). As a result, new cryptanalytic techniques and advancements could potentially uncover vulnerabilities in existing lattice-based schemes, necessitating constant evaluation and updates.
For the Hash-Based Signatures Cryptography the challenges are as follows:
  • Signature Size and Efficiency: Hash-based signatures typically have larger signature sizes compared to other signature schemes (Srivastava, V., Baksi, A., & Debnath, S. K. (2023).). This can result in increased bandwidth and storage requirements, making them less practical in some scenarios.
  • Collision Resistance: Hash functions used in hash-based signatures must be collision-resistant to prevent attackers from finding two different inputs that produce the same hash value (Srivastava, V., Baksi, A., & Debnath, S. K. (2023).).The security of hash-based signatures depends on the strength of the underlying hash function.
  • Post-Quantum Security: As quantum computers advance, many traditional cryptographic schemes, including hash-based signatures, are at risk of being broken. The development of post-quantum secure hash-based signature schemes is an active area of research to address these concerns (Kichna, A., & Farchane, A. 2023).
For the Multivariate Cryptography the challenges are as follows:
  • Key Size and Signature Size: it requires larger key and signature sizes compared to other cryptographic algorithms. This can have implications for storage, transmission, and computational efficiency (Dey, J., & Dutta, R. 2023). Progress in Multivariate Cryptography:).
  • Key Generation and Distribution: generating and distributing keys in multivariate cryptography can be computationally expensive and time-consuming, particularly for large systems (Dey, J., & Dutta, R. 2023).
  • Security margins: it relies on the difficulty of solving large systems of polynomial equations. Ensuring an appropriate security margin against attacks is challenging, as advancements in algebraic and computational techniques could reduce the security level of these schemes.

2.5. Post – Quantum Cryptography Future Directions:

As quantum computers continue to advance, traditional cryptographic schemes may become vulnerable to quantum attacks and with the use of post quantum cryptographic still there are some challenges. Most of recent research emphasis on the intersect of quantum cryptography with Internet of Things (IoT) devices presents unique challenges due to resource constraints and limited computational capabilities of these devices and the future direction of using this post quantum.
Code based cryptograph future direction:
  • Efficient Implementations: Future research should focus on developing efficient implementations of code-based cryptography specifically tailored for IoT devices, considering their resource limitations (Akter, M. S. (2023).
  • Lightweight Code-Based Schemes: Exploring lightweight code-based cryptographic schemes that offer a good balance between security and computational efficiency would be beneficial for IoT applications.
Preprints 114925 i001
Lattice-Based Cryptography future direction:
  • Optimization Techniques: Research should focus on developing optimization techniques to reduce the computational and memory requirements of lattice-based cryptography, making it more feasible for IoT devices (Aikata, A., Basso, A., Cassiers, G., Mert, A. C., & Roy, S. S. (2023).
  • Standardization Efforts: Collaborative efforts towards standardization and the development of efficient lattice-based cryptographic algorithms suitable for IoT environments are needed to facilitate adoption.
Preprints 114925 i002
Hash-Based Signatures future direction:
  • Signature Size Reduction: Research efforts should focus on developing techniques to reduce the signature size of hash-based schemes without compromising their security (Kichna, A., & Farchane, A. (2023, May).
  • Scalable Signature Schemes: Exploring scalable hash-based signature schemes that can support many signatures with a given key pair would be beneficial for IoT deployments (Akter, M. S. 2023).
Preprints 114925 i003
Multivariate Cryptography future direction:
  • Hybrid Schemes: Hybrid cryptosystems, which combine multiple cryptographic techniques, are often used to leverage the strengths of different algorithms. Researchers may explore hybrid approaches that integrate MPBC with other post-quantum or traditional cryptographic primitives.
  • Implementation and Standardization: If MPBC becomes widely adopted, there will be a need for standardized implementations and libraries to ensure interoperability and ease of integration into various software systems and devices(Dey, J., & Dutta, R. (2023). Progress in Multivariate Cryptography:)
  • Formal Verification: With the increasing complexity of cryptographic algorithms, formal verification techniques may be employed to rigorously prove the correctness and security properties of MPBC schemes.
Preprints 114925 i004
In general, the challenges and future directions for quantum cryptography in IoT required the need for efficient implementations, resource optimization, standardization efforts, and addressing the constraints of IoT devices such as limited computational power, memory, and bandwidth. Continued research and collaboration are essential to overcome these challenges and enable secure and practical quantum cryptography solutions for IoT.

Conclusions

This work has extensively reviewed the emerging technologies over QC with IoT technology. More importantly, several potential quantum cryptography algorithms have been identified and discussed. Furthermore, this study provides the recent challenges of using quantum cryptography algorithms align with IoT -inspired future network and future directions.

References

  1. Aguilar-Melchor, C., & Fúster-Sabater, A. (2017). Resource-constrained devices and code-based cryptography: The McEliece cryptosystem on 8-bit AVR CPUs. International Journal of Information Security, 16(3), 315-330.
  2. Ahn, J., Kwon, H. Y., Ahn, B., Park, K., Kim, T., Lee, M. K., ... & Chung, J. (2022). Toward quantum secured distributed energy resources: Adoption of post-quantum cryptography (pqc) and quantum key distribution (qkd). Energies, 15(3), 714.‏ . [CrossRef]
  3. Aikata, A., Basso, A., Cassiers, G., Mert, A. C., & Roy, S. S. (2023). Kavach: Lightweight masking techniques for polynomial arithmetic in lattice-based cryptography. IACR Transactions on Cryptographic Hardware and Embedded Systems, 366-390.‏. [CrossRef]
  4. Akter, M. S. (2023). Quantum Cryptography for Enhanced Network Security: A Comprehensive Survey of Research, Developments, and Future Directions. arXiv preprint arXiv:2306.09248.‏ . [CrossRef]
  5. Alagic, G., Alperin-Sheriff, J., Apon, D., Cooper, D., Dang, Q., Kelsey, J., ... & Smith-Tone, D. (2020). Status report on the second round of the NIST post-quantum cryptography standardization process. US Department of Commerce, NIST, 2.‏.
  6. Beullens, W.; D’Anvers, J.; Hülsing, A.; Lange, T.; Panny, L.; de S. Guilhem, C.; Smart, N.P. Post-Quantum Cryptography: Current State and Quantum Mitigation; Technical Report; European Union Agency for Cybersecurity: Athens, Greece, 2021. 21.
  7. Buchmann, J., Dahmen, E., Göpfert, F., & Leander, G. (2017). Practical signatures for resource-constrained devices—Hash-based signatures, lattice-based signatures, and their integration. In International Conference on Cryptology and Network Security (pp. 126-145). Springer.
  8. Cayrel, P.L.; ElYousfi, M.; Hoffmann, G.; Meziani, M.; Niebuhr, R. Recent Progress in Code-Based Cryptography. In International Conference on Information Security and Assurance; Springer: Berlin/Heidelberg, Germany, 2014; pp. 21–32. 26.
  9. Chen, M.; Ding, J.; Kannwischer, M.; Patarin, J.; Petzoldt, A.; Schmidt, D.; Yang, B. Rainbow Signature. Available online: https://www.pqcrainbow.org/ (accessed on 27 August 2020). https://www-polsys.lip6.fr/Links/NIST/GeMSS.html (accessed on 8 December 2020).
  10. Chi, D.P.; Choi, J.W.; Kim, J.S.; Kim, T. Lattice Based Cryptography for Beginners. Available online: https://eprint.iacr.org/2015 /938 (accessed on 20 November 2020).
  11. Dey, J., & Dutta, R. (2023). Progress in Multivariate Cryptography: Systematic Review, Challenges, and Research Directions. ACM Computing Surveys, 55(12), 1-34.‏ . [CrossRef]
  12. Gabsi, S., Beroulle, V., Kieffer, Y., Dao, H. M., Kortli, Y., & Hamdi, B. (2021). Survey: Vulnerability analysis of low-cost ECC-based RFID protocols against wireless and side-channel attacks. Sensors, 21(17), 5824.‏ . [CrossRef]
  13. Kichna, A., & Farchane, A. (2023, May). Secure and Efficient Code-Based Cryptography for Multi-Party Computation and Digital Signatures. In Computer Sciences & Mathematics Forum (Vol. 6, No. 1, p. 1). MDPI.‏ . [CrossRef]
  14. Kuwakado, H.; Morii, M. Quantum distinguisher between the 3-round Feistel cipher and the random permutation. In Proceedings of the IEEE International Symposium on Information Theory, Austin, TX, USA, 12–18 June 2010; pp. 2682–2685. 5. [CrossRef]
  15. Lei, D., He, D., Peng, C., Luo, M., Liu, Z., & Huang, X. (2023). Faster Implementation of Ideal Lattice-based Cryptography Using AVX512. ACM Transactions on Embedded Computing Systems.‏ . [CrossRef]
  16. May, A. (2003). New RSA vulnerabilities using lattice reduction methods (Doctoral dissertation, University of Paderborn).‏.
  17. Rahman, M., & Jahankhani, H. (2021). Security vulnerabilities in existing security mechanisms for iomt and potential solutions for mitigating cyber-attacks. Information security technologies for controlling pandemics, 307-334.‏ . [CrossRef]
  18. Rahnama, B., Sari, A., & Ghafour, M. Y. (2016). Countering RSA vulnerabilities and its replacement by ECC: elliptic curve cryptographic scheme for key generation. In Network security attacks and countermeasures (pp. 270-312). IGI Global.‏.
  19. Sendrier, N. (2017). Code-based cryptography: State of the art and perspectives. IEEE Security & Privacy, 15(4), 44-50.‏. [CrossRef]
  20. Sendrier, N. Code-Based Cryptography: State of the Art and Perspectives. IEEE Secur. Priv. 2017, 15, 44–50. 27. Ding, J.; Petzoldt, A. Current state of multivariate cryptography. IEEE Secur. Priv. 2017, 15, 28–36. 28.
  21. Srivastava, V., Baksi, A., & Debnath, S. K. (2023). An Overview of Hash Based Signatures. Cryptology ePrint Archive.‏.
  22. Umana, V.G. Post Quantum Cryptography. Ph.D. Thesis, Technical University of Denmark, Lyngby, Denmark, 2011. 20.
  23. Yavuz, A. A., Earl, D., Packard, S., & Nouma, S. E. (2022, June). Hybrid low-cost quantum-safe key distribution. In Quantum 2.0 (pp. QTu4C-5). Optica Publishing Group.‏.
  24. Yavuz, A. A., Nouma, S. E., Hoang, T., Earl, D., & Packard, S. (2022, December). Distributed Cyber-infrastructures and Artificial Intelligence in Hybrid Post-Quantum Era. In 2022 IEEE 4th International Conference on Trust, Privacy and Security in Intelligent Systems, and Applications (TPS-ISA) (pp. 29-38). IEEE.‏. [CrossRef]
Table 1. Post-Quantum cryptography.
Table 1. Post-Quantum cryptography.
Code _ based cryptography Lattice-Based Cryptography Multivariate Cryptography Hash-Based Signatures
Differences
Underlying Mathematical Foundations It relies on error-correcting codes It relies on lattice problems It relies on multivariate polynomial equations They rely on cryptographic hash functions
Security Assumptions It is based on different assumptions. It assumes the hardness of decoding error-correcting It assumes the hardness of lattice problems It assumes the hardness of solving multivariate polynomial equations They rely on the properties of cryptographic hash functions.
Post-Quantum Security It is designed to resist attacks by quantum computers. It is designed to resist attacks by quantum computers. is not considered a post-quantum scheme, as it is vulnerable to certain algebraic attacks. It is designed to resist attacks by quantum computers.
Similarities
Public-Key Cryptography They are a form of public key. They involve the use of public and private key pairs for encryption and decryption, digital signatures, and other cryptographic operations
Post-Quantum Candidates They are alternatives to traditional public-key cryptosystems that may be vulnerable to attacks by quantum computers
Resistance to Quantum Attacks They are designed to provide security even in the presence of quantum computers. Their aims to resist attacks by leveraging mathematical problems that are believed to be hard even for quantum computers.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated