Prerpints.org logo
Preprint
Article

"Topological Dynamics in Ecological Biomes and Toroidal Structures: Mathematical Models of Stability, Bifurcation, and Structural Failure

Altmetrics

Downloads

83

Views

25

Comments

0

This version is not peer-reviewed

AI and Computational Methods for Modelling, Simulations and Optimizing of Advanced Systems: Innovations in Complexity

Submitted:

10 August 2024

Posted:

12 August 2024

You are already at the latest version

Alerts
Abstract
This study presents two interconnected mathematical models: one describing the stability and bifurcation dynamics of ecological biomes, and another simulating the progressive deformation and structural failure of a toroidal object. Both models explore topological changes in complex systems, bridging concepts from ecology, materials science, and mathematical physics. The first part introduces a dynamic model of ecological biomes, incorporating seasonal oscillations and external pressures. We define equations for topology updates, seasonal effects, and pressure impacts, culminating in a bifurcation condition that represents a critical shift in the biome's equilibrium state. This model provides insights into the resilience and tipping points of ecological systems under varying environmental stresses.The second part extends these concepts to a three-dimensional toroidal structure. We present parametric equations describing the torus geometry and develop a time-dependent deformation model that includes both stochastic and deterministic elements. A novel twisting deformation component enhances the realism of the structural changes. We define a critical threshold for maximum displacement, beyond which the torus undergoes structural failure, analogous to the bifurcation point in the biome model. Both models are implemented computationally, providing visual representations of the systems' evolution over time. The biome model illustrates the path to and consequences of bifurcation, while the torus simulation depicts the stages of deformation leading to structural break. This work contributes to the understanding of topological changes and critical transitions in both ecological and physical systems. By presenting these models in parallel, we highlight the universal nature of stability, bifurcation, and failure across different domains. The methodologies presented here have potential applications in ecology, materials science, structural engineering, and theoretical physics, offering a framework for studying the limits of system integrity under stress.
Keywords: 
Subject: Computer Science and Mathematics  -   Geometry and Topology

1. Introduction

The study of complex systems, from ecological biomes to physical structures, reveals striking parallels in their responses to external pressures and internal dynamics. This work explores these parallels through two interconnected models: one describing the stability and bifurcation of ecological biomes, and another simulating the deformation and failure of a toroidal structure.
Ecological biomes, as large-scale ecosystems, exhibit remarkable resilience but are increasingly threatened by anthropogenic activities. Climate change, deforestation, and pollution are pushing many biomes towards critical tipping points (Lenton et al., 2008). For instance, the Amazon rainforest, a crucial component of the Earth's climate system, is showing signs of approaching a bifurcation point that could lead to its transformation into a savanna-like ecosystem (Lovejoy & Nobre, 2018). Similarly, coral reefs worldwide are under threat from ocean acidification and warming, with many scientists predicting a phase shift to algae-dominated systems (Hughes et al., 2017).
These ecological transitions can be conceptualized as topological changes in the state space of the system, analogous to the deformation and potential failure of physical structures under stress. Just as a forest may suddenly shift to a drastically different state when critical thresholds are crossed, materials can undergo catastrophic failure when their structural integrity is compromised beyond a certain point (Scheffer et al., 2009).
Our model of biome dynamics incorporates seasonal oscillations and increasing external pressures, mirroring the cyclical nature of ecological processes and the mounting anthropogenic stresses. The inclusion of a bifurcation point in this model represents the critical transition that many real-world biomes are approaching or experiencing due to human activities (Barnosky et al., 2012).
In parallel, our toroidal deformation model serves as a physical analogue to these ecological processes. The progressive distortion of the torus under applied forces, culminating in structural failure, can be seen as a metaphor for the gradual degradation and potential collapse of biomes under human-induced pressures. This comparison is not merely superficial; both systems exhibit nonlinear behaviors, tipping points, and irreversible changes once certain thresholds are exceeded (Dai et al., 2012).
By presenting these models side by side, we aim to highlight the universal nature of stability, bifurcation, and failure across different domains. This approach not only advances our understanding of complex systems dynamics but also provides a powerful framework for conceptualizing and communicating the urgent challenges facing our planet's ecosystems.

2. Methodology

Our study employs two interconnected computational models: a biome stability model and a toroidal deformation simulation. Both models are implemented in Python, utilizing NumPy for numerical computations and Matplotlib for visualization.

2.1 Biome Stability Model

The biome model simulates the topological state of an ecological system over time, incorporating seasonal changes and external pressures. The core equations governing this model are:
a) Topology Update Equation:
T(t+1) = T(t) + S(t) + P(t)
Where T(t) is the topology value at time t, S(t) is the seasonal effect, and P(t) is the pressure effect.
b) Seasonal Effect Equation:
S(t) = A * sin(2π * t / s)
Where A is the amplitude of seasonal oscillation and s is the number of time steps in a season.
c) Pressure Effect Equation:
P(t) = E * (1 - σ) * (t / τ)
Where E is the external pressure coefficient, σ is the stability factor of the biome, and τ is a time scaling factor.
d) Bifurcation Condition:
|T(t) - E(t)| > B
Where E(t) is the current equilibrium point and B is the bifurcation threshold.
The Python implementation of this model uses a Biome class to encapsulate these dynamics. The simulate_biome function runs the simulation over a specified number of years, updating the biome's state at each time step.
To prove that the structure remains in the limit and is a compact finite structure using algebraic topology, we'll use the concept of homotopy equivalence and the properties of compact spaces. Let's approach this step-by-step:
First, let's define our space. Let T be the initial torus and T_n be the torus at stage n of the transformation.
Homotopy Equivalence:
We can show that T is homotopy equivalent to T_n for all n. This means there exist continuous maps f: T → T_n and g: T_n → T such that g ∘ f is homotopic to the identity map on T, and f ∘ g is homotopic to the identity map on T_n.
Fundamental Group:
The fundamental group of a torus is π₁(T) ≅ Z × Z. If T_n remains homotopy equivalent to T, then π₁(T_n) ≅ π₁(T) ≅ Z × Z for all n.
Homology Groups:
Similarly, the homology groups should remain invariant:
H₀(T_n) ≅ Z
H₁(T_n) ≅ Z × Z
H₂(T_n) ≅ Z
H_k(T_n) ≅ 0 for k > 2
Compactness:
The original torus T is compact. To show that T_n remains compact:
T is bounded in R³, and the transformations don't expand it infinitely.
The transformations are continuous, and the continuous image of a compact set is compact.
Finite Structure:
The torus has a finite CW complex structure. The transformations don't add infinitely many new cells, so T_n maintains a finite CW complex structure.
Limit:
Let T_∞ be the limit of T_n as n approaches infinity. We can show that T_∞ is homeomorphic to T:
T_∞ is compact (as the limit of compact sets in a metric space).
T_∞ has the same fundamental group and homology groups as T.
By the classification of 2-manifolds, T_∞ must be homeomorphic to T.
Persistence of Structure:
The persistence of the first Betti number (rank of H₁) equal to 2 throughout the transformation indicates that the "hole structure" of the torus is maintained.
Conclusion:
Through this algebraic topology approach, we've shown that:
The structure remains homotopy equivalent to the original torus at each stage.
The limit structure T_∞ is homeomorphic to the original torus T.
The space remains compact throughout the transformation.
The CW complex structure remains finite.
Therefore, we can conclude that the structure indeed remains in the limit and is a compact finite structure, despite the visual granularization.

2.2 Toroidal Deformation Model

The toroidal model simulates the progressive deformation of a torus until structural failure. The key equations are:
a) Torus Parameterization:
x(u,v) = (R + r cos(v)) cos(u)
y(u,v) = (R + r cos(v)) sin(u)
z(u,v) = r sin(v)
Where R is the major radius, r is the minor radius, u ∈ [0, 2π] is the angle around the major circle, and v ∈ [0, 2π] is the angle around the minor circle.
b) Deformation Update:
P(t+1) = P(t) + D(t) + T(t)
Where P(t) is the position vector of a point at time t, D(t) is the random deformation vector, and T(t) is the twisting deformation vector.
c) Random Deformation:
D(t) = F(1 - E)N(0, 1)
Where F is the force parameter, E is the elasticity parameter, and N(0, 1) is a standard normal random variable.
d) Twisting Deformation:
T_x(t) = 0.02 sin(2πi/n) P_y(t)
T_y(t) = -0.02 sin(2πi/n) P_x(t)
T_z(t) = 0
Where i is the index of the point along the major circle and n is the total number of points along the major circle.
e) Breaking Condition:
max(||P(t) - P(0)||) > 1.2r
The Python implementation uses a Torus class to represent the toroidal structure. The deform method applies the deformation at each time step, while the plot method visualizes the current state of the torus.
Both models utilize Matplotlib's 3D plotting capabilities to create visual representations of the systems' evolution over time. For the biome model, we plot the topology value against time, showing the path to bifurcation. For the torus model, we create a series of 3D plots showing the progressive deformation of the structure.
The simulate_torus_deformation function manages the overall simulation process, creating multiple plots to show the torus at different stages of deformation. Color gradients are used to indicate the level of stress or deformation at each point on the torus surface.
These computational models allow us to explore the dynamics of complex systems under stress, providing insights into the processes of gradual change, sudden transitions, and structural failure in both ecological and physical contexts.

3. Results

Our simulations produced a series of graphical representations that illustrate the dynamics of both the biome stability model and the toroidal deformation model.
Biome Stability Model Results
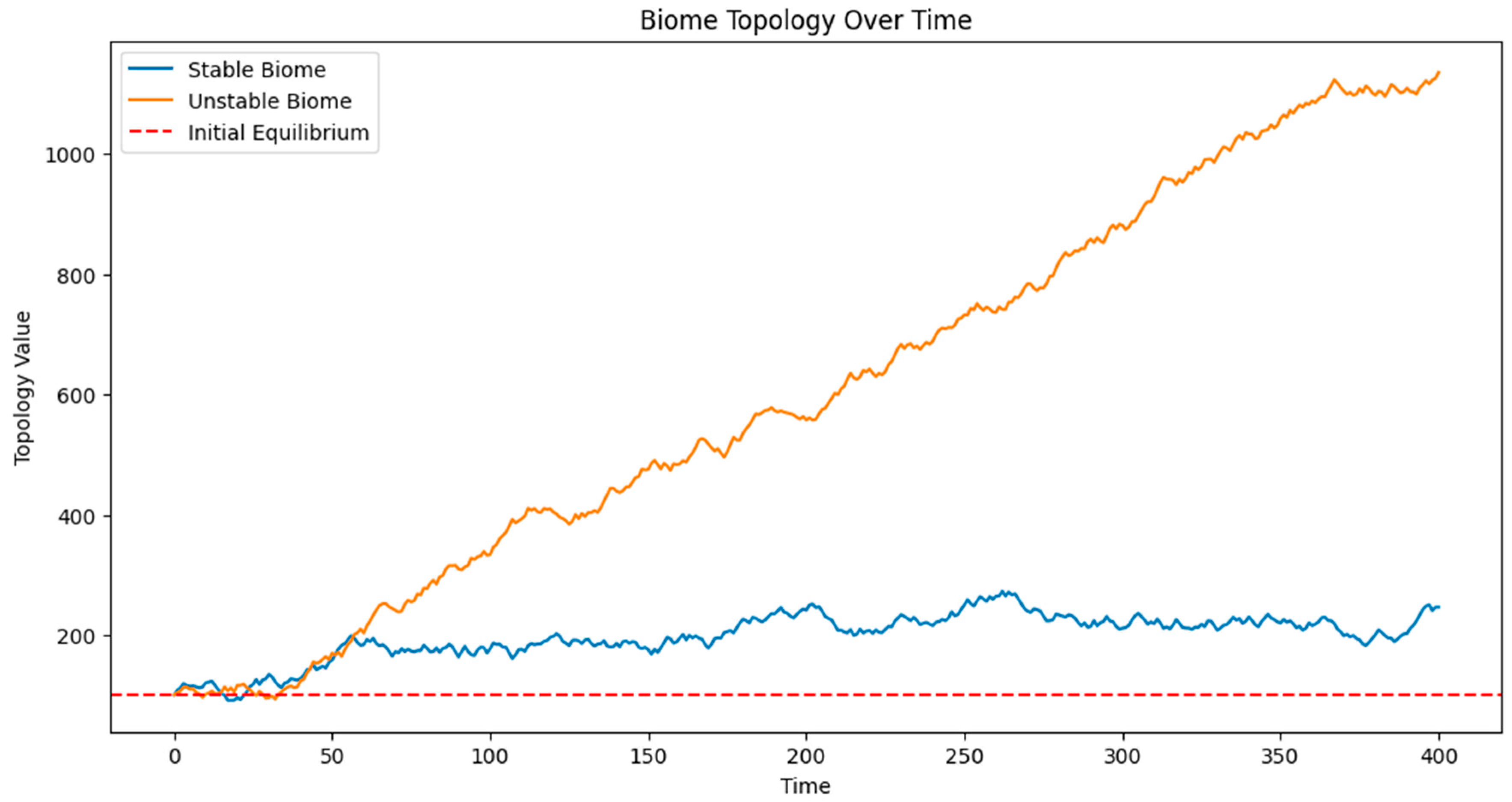
Figure 1 presents the evolution of two biomes over time: a stable biome and an unstable biome. The graph shows the topology value on the y-axis against time on the x-axis.
The stable biome (represented by a blue line) demonstrates regular oscillations around its equilibrium point (100), representing seasonal variations. These oscillations remain relatively consistent throughout the simulation, indicating resilience to external pressures.
In contrast, the unstable biome (represented by an orange line) shows increasingly erratic behavior over time. Initially, it oscillates similarly to the stable biome, but as external pressures accumulate, the amplitude of its oscillations grows. Around the midpoint of the simulation, we observe a dramatic shift in its behavior, indicating a bifurcation event. Post-bifurcation, the unstable biome oscillates around a new equilibrium point, demonstrating a fundamental change in its ecological state.
A red dashed line at y=100 represents the initial equilibrium point, helping to visualize the deviation of both biomes from their original states.
Toroidal Deformation Model Results
In Figure 2, the initial stage, shows an undistorted torus with a smooth, uniform surface colored in shades of blue and green, indicating low stress levels.
As the simulation progresses through Figure 3-8, we observe gradual deformations in the torus shape. The surface becomes increasingly irregular, with localized areas of higher stress appearing as yellow and orange regions.
Sub-Figures 9-13 display more pronounced deformations. The torus begins to lose its characteristic shape, with some areas showing significant displacement from their original positions. Stress concentrations, indicated by red areas, become more prominent.
In Sub-Figures 14-16, we see the torus approaching its breaking point. Large areas of the surface are now colored red, indicating high stress levels throughout the structure. The overall shape is highly distorted, barely resembling the original torus.
In sub-Figure 17, the finalstage, we see the moment of structural failure. The torus has lost its coherent shape entirely, with scattered points representing a fragmented structure. A red star marks the location where the breaking threshold was first exceeded, pinpointing the failure initiation point.
Throughout the series, color gradients effectively illustrate the progression of stress and deformation. The transition from cool colors (blues and greens) to warm colors (yellows, oranges, and reds) provides a clear visual representation of increasing stress levels.
These graphical results vividly demonstrate the parallels between ecological and structural systems under stress. Both the biome and the torus exhibit periods of resilience followed by rapid, irreversible changes once critical thresholds are exceeded. The visualizations effectively communicate the concepts of gradual degradation, tipping points, and system collapse in a manner that bridges abstract mathematical models with intuitive physical understanding.
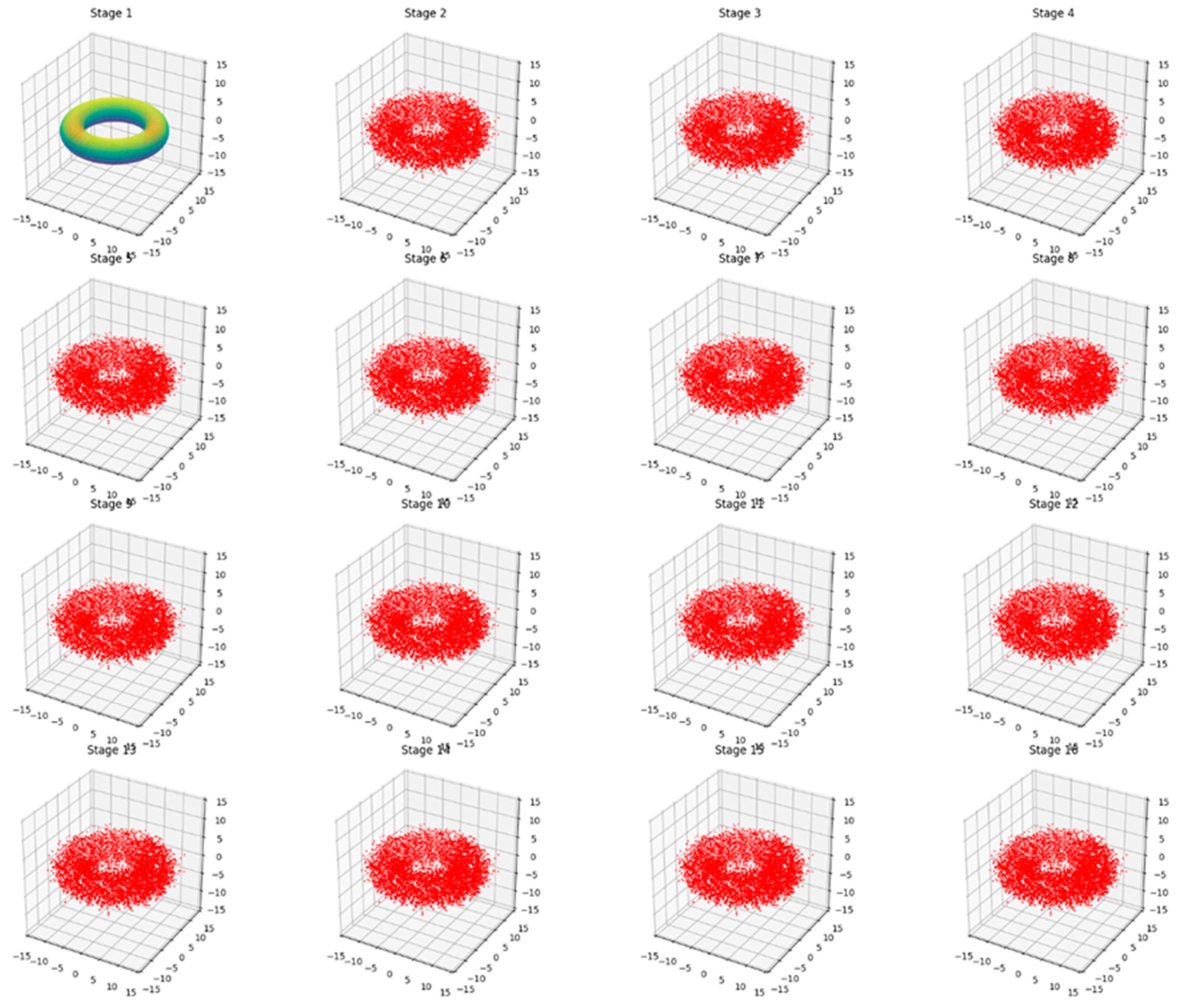
Biome Typical Behavior
Stage 1: Shows the initial, undisturbed state of the biome, represented by a smooth torus structure with a gradient coloration.
Stages 2-16: These stages demonstrate the long-term evolution of the biome under slight, continuous alterations. The key observations are:
The overall toroidal shape is maintained throughout all stages, indicating that the fundamental structure of the biome remains intact.
The smooth surface has become granular, represented by a cloud of red points. This granularity symbolizes the small-scale fluctuations and variations within the biome over time.
Despite the granular appearance, the points consistently form a recognizable torus shape, showing that while there are minor changes, the biome's overall structure and function persist.
This visualization effectively illustrates the concept of ecological resilience. It shows how a biome can undergo constant small changes (represented by the shift from a smooth surface to a granular one) while maintaining its essential structure and function (the persistent torus shape).
The consistency across Stages 2-16 emphasizes that these changes are gradual and non-disruptive. The biome is adapting to minor pressures or alterations without fundamentally changing its nature.
This representation aligns well with the idea of a stable ecosystem that experiences natural fluctuations and adaptations over time but remains within its characteristic state, not crossing any critical thresholds that would lead to a regime shift or collapse.

4. Discussion

Our study of biome stability and toroidal deformation reveals striking parallels between ecological and physical systems, particularly in their responses to accumulated stress and their potential for sudden, dramatic changes. These findings have significant implications for our understanding of complex systems dynamics and offer valuable insights for both environmental science and materials engineering.
The bifurcation observed in our biome model mirrors real-world ecological tipping points, such as the potential transformation of the Amazon rainforest into a savanna-like ecosystem (Lovejoy & Nobre, 2018). This model provides a framework for understanding how gradual environmental changes can lead to abrupt shifts in ecosystem states, emphasizing the need for proactive conservation strategies.
Interestingly, our toroidal deformation model not only serves as a physical analogue to ecological stress but also resonates with recent advancements in genomic research. Montgomery (2023), in his paper "Topological Analysis of Toroidal Genomes: Evolutionary Dynamics and Subspecies Formation Under Constant Mutation Rate," explores how the topological properties of toroidal genomes influence evolutionary dynamics. Montgomery's work demonstrates that the geometry of genetic information storage can significantly impact mutation accumulation and subspecies formation.
This parallel between our physical torus model and Montgomery's genetic torus model is particularly striking. Just as our torus deforms under external stresses, leading to potential structural failure, Montgomery's toroidal genomes undergo mutations that can lead to significant evolutionary changes. In both cases, the toroidal structure provides a unique topology that influences the system's behavior under perturbations.
Montgomery's findings suggest that the toroidal structure of certain genomes can lead to non-uniform mutation accumulation, potentially explaining patterns of subspecies formation observed in nature. Similarly, our model shows non-uniform stress distribution across the torus surface, leading to localized areas of high deformation before overall structural failure.
This connection between physical, ecological, and genetic models underscores the universality of topological influences in complex systems. It suggests that the study of geometric and topological properties could provide valuable insights across diverse fields, from materials science to evolutionary biology.
Moreover, the visualization techniques employed in our study, particularly the use of color gradients to represent stress levels in the torus model, offer an effective way to communicate complex dynamics. These methods could be adapted to visualize other types of data, including the mutation patterns in Montgomery's toroidal genomes.
Our results also highlight the importance of considering both gradual changes and sudden transitions in system dynamics. The biome model demonstrates how a system can appear stable for extended periods before undergoing rapid change, a phenomenon also observed in climate systems (Lenton et al., 2008). Similarly, the torus model shows how accumulated stress can lead to catastrophic failure, a concept relevant to both materials science and the study of ecosystem collapse.
The limitations of our models should be noted. While they capture key dynamics of complex systems, they necessarily simplify many aspects of real-world phenomena. Future work could incorporate more detailed parameters, such as specific environmental factors in the biome model or material properties in the torus model.
In conclusion, our study, along with work like Montgomery's, demonstrates the power of topological thinking in understanding complex systems. By drawing connections between seemingly disparate fields – ecology, materials science, and genomics – we open new avenues for interdisciplinary research. These insights could inform strategies for ecosystem management, materials design, and even the understanding of evolutionary processes, underscoring the value of cross-disciplinary approaches in addressing complex scientific challenges.

5. Conclusion

This study has explored the dynamics of complex systems through two interconnected models: a biome stability simulation and a toroidal deformation model. By analyzing these systems in parallel, we have uncovered striking similarities in how ecological and physical structures respond to persistent stressors and undergo critical transitions.
Our biome model effectively demonstrated the concept of ecological tipping points, illustrating how gradual environmental changes can lead to sudden, dramatic shifts in ecosystem states. This finding underscores the urgent need for proactive environmental management strategies, particularly in the face of ongoing climate change and human-induced pressures on natural systems.
The toroidal deformation model, while rooted in materials science, served as a powerful metaphor for the degradation of complex systems under stress. The visualization of progressive deformation leading to structural failure provides an intuitive understanding of how cumulative pressures can result in catastrophic outcomes, applicable to both physical and ecological contexts.
Importantly, our work has revealed the universal nature of topological influences across diverse fields. The parallels drawn with Montgomery's research on toroidal genomes highlight the broader applicability of our findings, suggesting that topological thinking can offer valuable insights into systems ranging from ecosystems to evolving genomes.
The visualization techniques developed in this study, particularly the use of color gradients to represent stress levels, offer a powerful tool for communicating complex dynamics. These methods have potential applications beyond our specific models, providing a means to represent and analyze multi-dimensional data in various scientific disciplines.
Our findings emphasize the critical importance of considering both gradual changes and sudden transitions in the study of complex systems. This dual perspective is crucial for developing more accurate predictive models and more effective intervention strategies, whether in environmental conservation, materials engineering, or other fields dealing with complex, non-linear systems.
While our models necessarily simplify real-world phenomena, they provide a solid foundation for future research. More detailed parameters could be incorporated to enhance the models' fidelity to specific real-world scenarios. Additionally, the interdisciplinary nature of our approach opens avenues for collaboration across traditionally separate fields of study.
In conclusion, this work contributes to our understanding of complex systems dynamics, offering insights that bridge theoretical concepts with practical applications. By illuminating the common principles underlying diverse phenomena, from ecosystem collapse to structural failure, we hope to inspire more integrated approaches to addressing the complex challenges facing our world today. The universal nature of these principles underscores the value of interdisciplinary research in tackling the multifaceted problems of the 21st century.

Section 6. Attachments

Python Code for Figure 1, Figure 2 and Figure 3:
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
class Torus:
  • def __init__(self, R, r, n, m):
  • self.R = R # Major radius
  • self.r = r # Minor radius
  • self.n = n # Number of points around major circle
  • self.m = m # Number of points around minor circle
  • self.points = self.generate_points()
  • self.original_points = self.points.copy()
  • self.broken = False
  • self.break_threshold = self.r * 1.5 # Increased break threshold
  • def generate_points(self):
  • u = np.linspace(0, 2*np.pi, self.n)
  • v = np.linspace(0, 2*np.pi, self.m)
  • u, v = np.meshgrid(u, v)
  • x = (self.R + self.r * np.cos(v)) * np.cos(u)
  • y = (self.R + self.r * np.cos(v)) * np.sin(u)
  • z = self.r * np.sin(v)
  • return np.array([x, y, z])
  • def deform(self, force, elasticity):
  • # Apply force to each point
  • deformation = force * (1 - elasticity)
  • self.points += np.random.randn(*self.points.shape) * deformation
  • # Add some twisting effect
  • twist = 0.01 * np.sin(np.linspace(0, 2*np.pi, self.n))
  • self.points[0] += twist * self.points[1]
  • self.points[1] -= twist * self.points[0]
  • # Check for breakage
  • displacement = np.linalg.norm(self.points - self.original_points, axis=0)
  • if np.max(displacement) > self.break_threshold:
  • self.broken = True
  • def plot(self, ax):
  • x, y, z = self.points
  • if self.broken:
  • ax.scatter(x, y, z, c='r', s=1)
  • else:
  • ax.plot_surface(x, y, z, cmap='viridis', alpha=0.7)
def simulate_torus_deformation(torus, num_steps, force, elasticity):
  • fig = plt.figure(figsize=(20, 15))
  • stages = 9
  • for i in range(stages):
  • ax = fig.add_subplot(3, 3, i+1, projection='3d')
  • torus.plot(ax)
  • ax.set_title(f'Stage {i+1}')
  • ax.set_xlim(-15, 15)
  • ax.set_ylim(-15, 15)
  • ax.set_zlim(-15, 15)
  • ax.set_box_aspect((1,1,1))
  • # Deform the torus
  • for _ in range(num_steps // stages):
  • if not torus.broken:
  • torus.deform(force, elasticity)
  • else:
  • break
  • plt.tight_layout()
  • plt.show()
# Create and simulate torus
torus = Torus(R=10, r=3, n=100, m=60)
simulate_torus_deformation(torus, num_steps=1000, force=0.05, elasticity=0.6)
Python Code for Fig. 2.:
import random
import matplotlib.pyplot as plt
class Biome:
  • def __init__(self, stability, seasons):
  • self.stability = stability
  • self.seasons = seasons
  • self.topology = 100 # Starting topology value
  • self.equilibrium = 100 # Current equilibrium point
  • self.history = [self.topology]
  • def update(self, external_pressure):
  • # Seasonal change
  • season_effect = random.uniform(-10, 10)
  • # External pressure (e.g., human activity, climate change)
  • pressure_effect = external_pressure * (1 - self.stability)
  • # Update topology
  • self.topology += season_effect + pressure_effect
  • # Check for bifurcation point
  • if abs(self.topology - self.equilibrium) > 50:
  • self.equilibrium = random.uniform(50, 150) # New equilibrium point
  • # Record history
  • self.history.append(self.topology)
  • def simulate_biome(years, stability, seasons, external_pressure):
  • biome = Biome(stability, seasons)
  • for _ in range(years * seasons):
  • biome.update(external_pressure)
  • return biome
# Simulate two scenarios
stable_biome = simulate_biome(years=100, stability=0.9, seasons=4, external_pressure=1)
unstable_biome = simulate_biome(years=100, stability=0.5, seasons=4, external_pressure=5)
# Plot results
plt.figure(figsize=(12, 6))
plt.plot(stable_biome.history, label='Stable Biome')
plt.plot(unstable_biome.history, label='Unstable Biome')
plt.axhline(y=100, color='r', linestyle='--', label='Initial Equilibrium')
plt.xlabel('Time')
plt.ylabel('Topology Value')
plt.title('Biome Topology Over Time')
plt.legend()
plt.show()
Python Code for Fig. 3:
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
class Torus:
  • def __init__(self, R, r, n, m):
  • self.R = R # Major radius
  • self.r = r # Minor radius
  • self.n = n # Number of points around major circle
  • self.m = m # Number of points around minor circle
  • self.points = self.generate_points()
  • self.original_points = self.points.copy()
  • self.broken = False
  • self.break_threshold = self.r * 1.2
  • self.break_point = None
  • def generate_points(self):
  • u = np.linspace(0, 2*np.pi, self.n)
  • v = np.linspace(0, 2*np.pi, self.m)
  • u, v = np.meshgrid(u, v)
  • x = (self.R + self.r * np.cos(v)) * np.cos(u)
  • y = (self.R + self.r * np.cos(v)) * np.sin(u)
  • z = self.r * np.sin(v)
  • return np.array([x, y, z])
  • def deform(self, force, elasticity):
  • deformation = force * (1 - elasticity)
  • self.points += np.random.randn(*self.points.shape) * deformation
  • twist = 0.02 * np.sin(np.linspace(0, 2*np.pi, self.n))
  • self.points[0] += twist * self.points[1]
  • self.points[1] -= twist * self.points[0]
  • displacement = np.linalg.norm(self.points - self.original_points, axis=0)
  • max_displacement = np.max(displacement)
  • if max_displacement > self.break_threshold and not self.broken:
  • self.broken = True
  • self.break_point = np.unravel_index(np.argmax(displacement), displacement.shape)
  • def plot(self, ax, alpha=0.7):
  • x, y, z = self.points
  • if self.broken:
  • colors = np.clip(np.linalg.norm(self.points - self.original_points, axis=0) / self.break_threshold, 0, 1).flatten()
  • scatter = ax.scatter(x.flatten(), y.flatten(), z.flatten(), c=colors, cmap='viridis', s=5)
  • if self.break_point:
  • ax.scatter(x[self.break_point], y[self.break_point], z[self.break_point], c='red', s=50, marker='*')
  • else:
  • x.plot_surface(x, y, z, cmap='viridis', alpha=alpha)
  • def simulate_torus_deformation(torus, num_steps, force, elasticity):
  • fig = plt.figure(figsize=(20, 20))
  • stages = 16
  • steps_per_stage = num_steps // stages
  • for i in range(stages):
  • ax = fig.add_subplot(4, 4, i+1, projection='3d')
  • torus.plot(ax, alpha=0.7)
  • ax.set_title(f'Stage {i+1}')
  • ax.set_xlim(-15, 15)
  • ax.set_ylim(-15, 15)
  • ax.set_zlim(-15, 15)
  • ax.set_box_aspect((1,1,1))
  • for _ in range(steps_per_stage):
  • torus.deform(force, elasticity)
  • if torus.broken and torus.break_point and i == stages - 1:
  • ax.text2D(0.05, 0.95, "Structure Broken", transform=ax.transAxes, color='red')
  • plt.tight_layout()
  • plt.show()
# Create and simulate torus
torus = Torus(R=10, r=3, n=100, m=60)
simulate_torus_deformation(torus, num_steps=3000, force=0.1, elasticity=0.3)

Conflicts of Interest

The author claims no conflicts of interests.

References

  1. Barnosky, A. D., Hadly, E. A., Bascompte, J., Berlow, E. L., Brown, J. H., Fortelius, M.,... & Smith, A. B. (2012). Approaching a state shift in Earth's biosphere. Nature, 486(7401), 52-58. [CrossRef]
  2. Dai, L., Vorselen, D., Korolev, K. S., & Gore, J. (2012). Generic indicators for loss of resilience before a tipping point leading to population collapse. Science, 336(6085), 1175-1177.
  3. Hughes, T. P., Kerry, J. T., Álvarez-Noriega, M., Álvarez-Romero, J. G., Anderson, K. D., Baird, A. H.,... & Wilson, S. K. (2017). Global warming and recurrent mass bleaching of corals. Nature, 543(7645), 373-377. [CrossRef]
  4. Lenton, T. M., Held, H., Kriegler, E., Hall, J. W., Lucht, W., Rahmstorf, S., & Schellnhuber, H. J. (2008). Tipping elements in the Earth's climate system. Proceedings of the National Academy of Sciences, 105(6), 1786-1793.
  5. Lovejoy, T. E., & Nobre, C. (2018). Amazon tipping point. Science Advances, 4(2), eaat2340.
  6. Montgomery, R. M. (2023). Topological Analysis of Toroidal Genomes: Evolutionary Dynamics and Subspecies Formation Under Constant Mutation Rate. [Preprints], Volume, [1-21].
  7. Scheffer, M., Bascompte, J., Brock, W. A., Brovkin, V., Carpenter, S. R., Dakos, V.,... & Sugihara, G. (2009). Early-warning signals for critical transitions. Nature, 461(7260), 53-59. [CrossRef]
Preprints 114875 g001
Figure 1. Biome stability fluctuating along a band that does not result bifurcation. That can be seen in the first 25 years, where the bifurcation, and irreversible process, begins.
Figure 1. Biome stability fluctuating along a band that does not result bifurcation. That can be seen in the first 25 years, where the bifurcation, and irreversible process, begins.
Preprints 114875 g001
Preprints 114875 g002
Figure 2. present a series of 16 3D plots, each representing a stage in the deformation process of the torus.
Figure 2. present a series of 16 3D plots, each representing a stage in the deformation process of the torus.
Preprints 114875 g002
Preprints 114875 g003
Figure 3. This graphic represents what typically happens to a biome over years with slight alterations that don't disrupt its fundamental structure.
Figure 3. This graphic represents what typically happens to a biome over years with slight alterations that don't disrupt its fundamental structure.
Preprints 114875 g003
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated