Submitted:
11 August 2024
Posted:
13 August 2024
You are already at the latest version
Abstract
Keywords:
1. Introduction
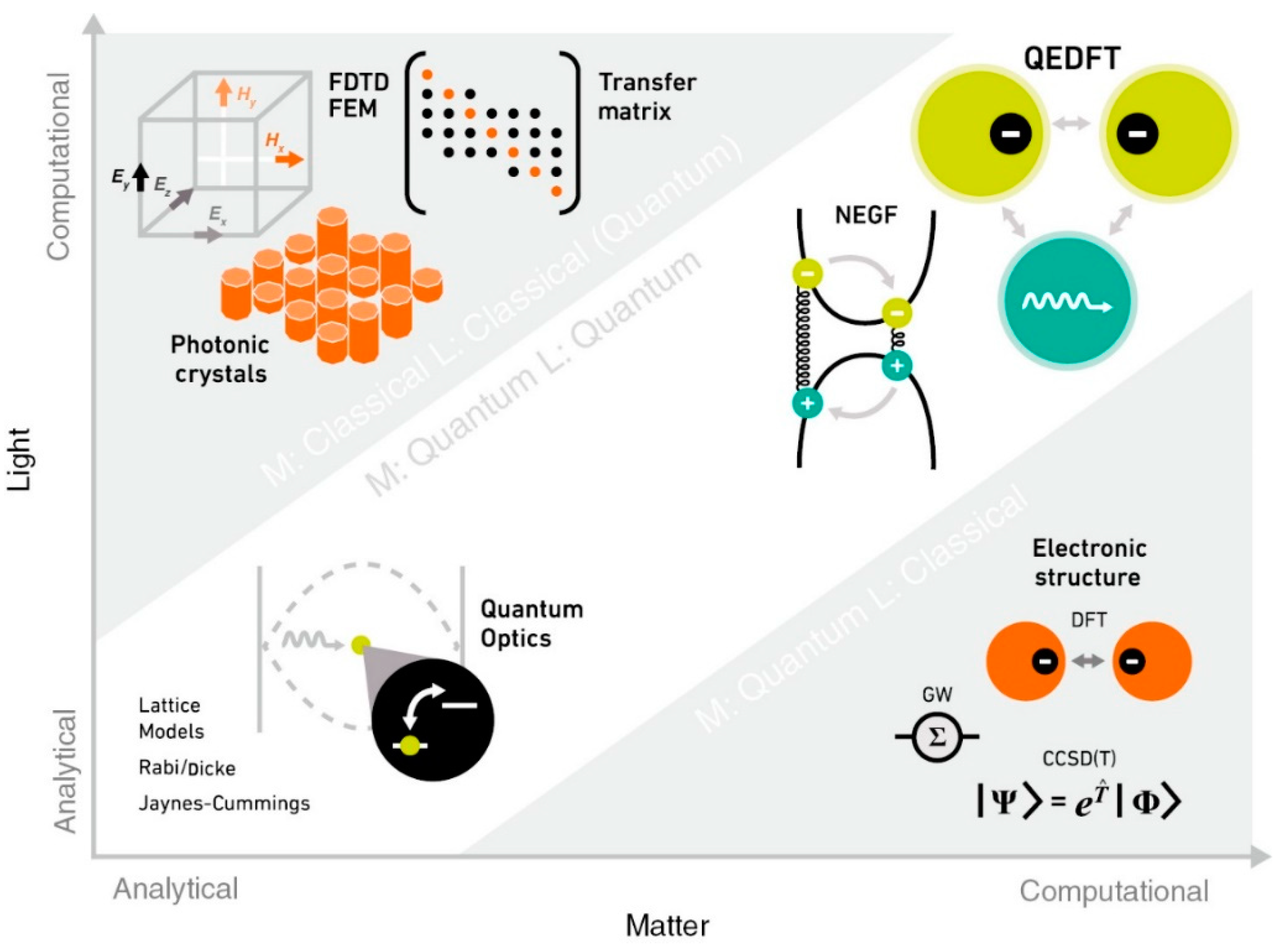
2. Fundamentals of Strong Light–Matter Coupling
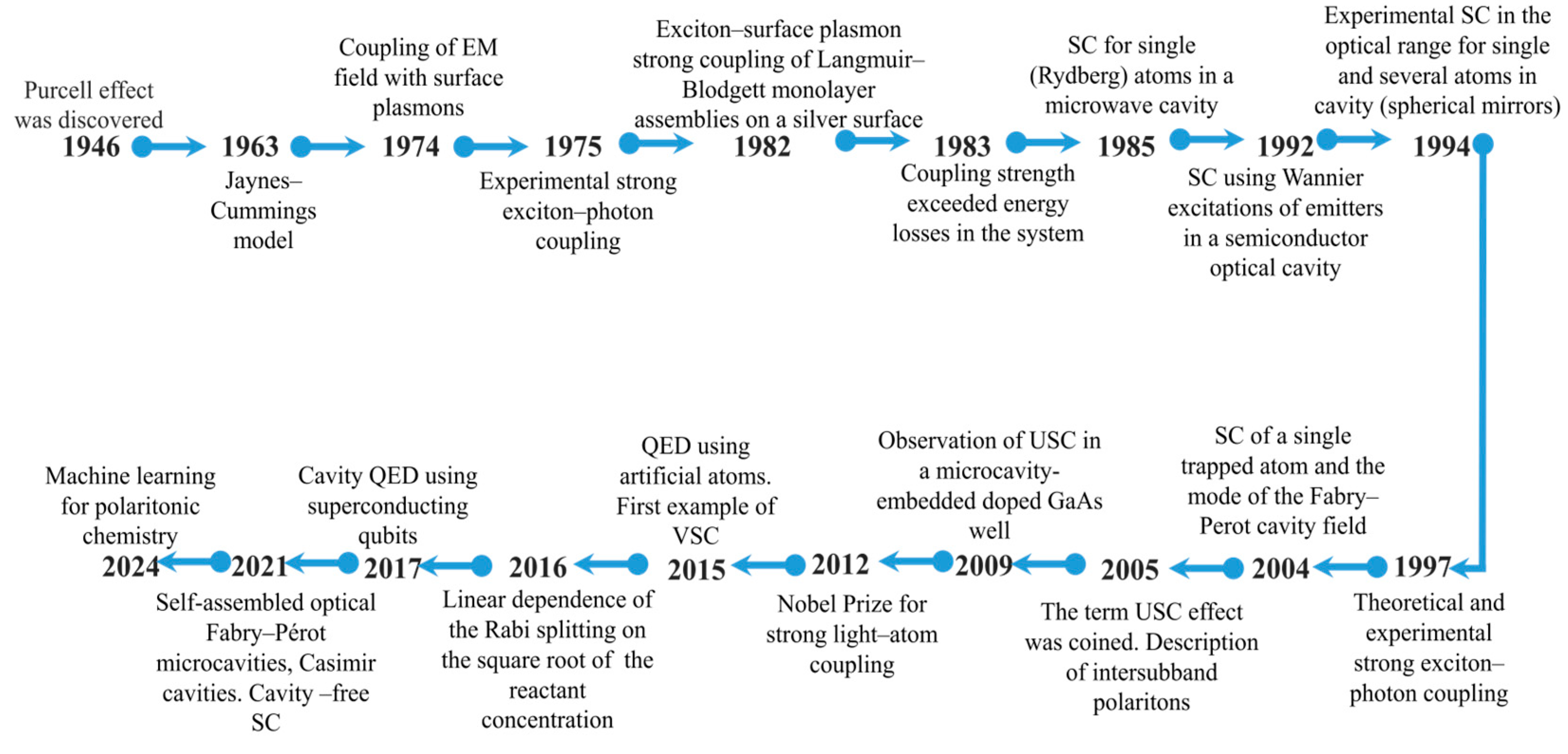
2.1. Light–Matter Coupling Regimes
2.2. Optical Characteristics
2.3. Classical Approach
2.4. Quantum Approach
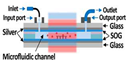
3. Methods and Techniques for Obtaining Strong Light–Matter Coupling in Micro- and Nanofluidic Systems
4. Configurations Combining Strong Light–Matter Coupling with Micro- and Nanofluidics
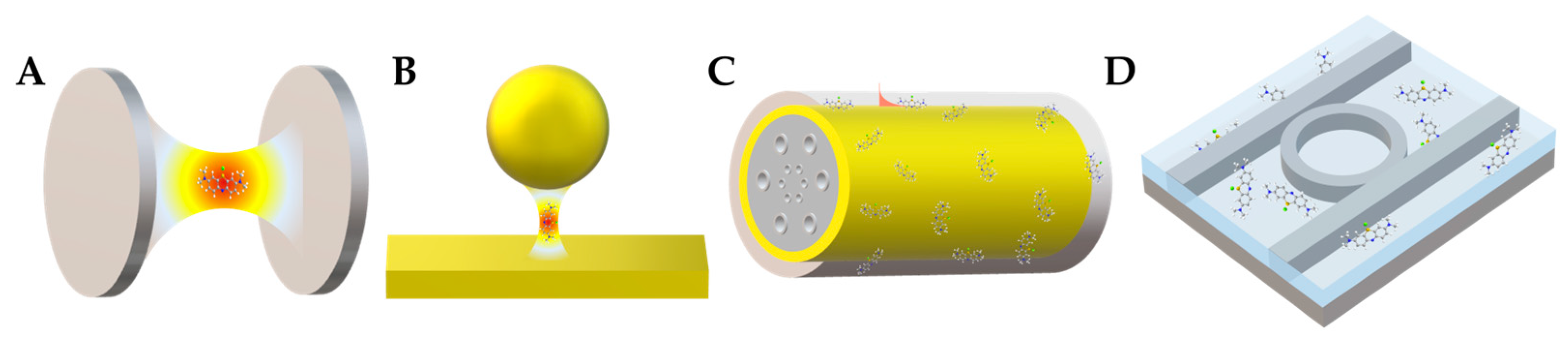
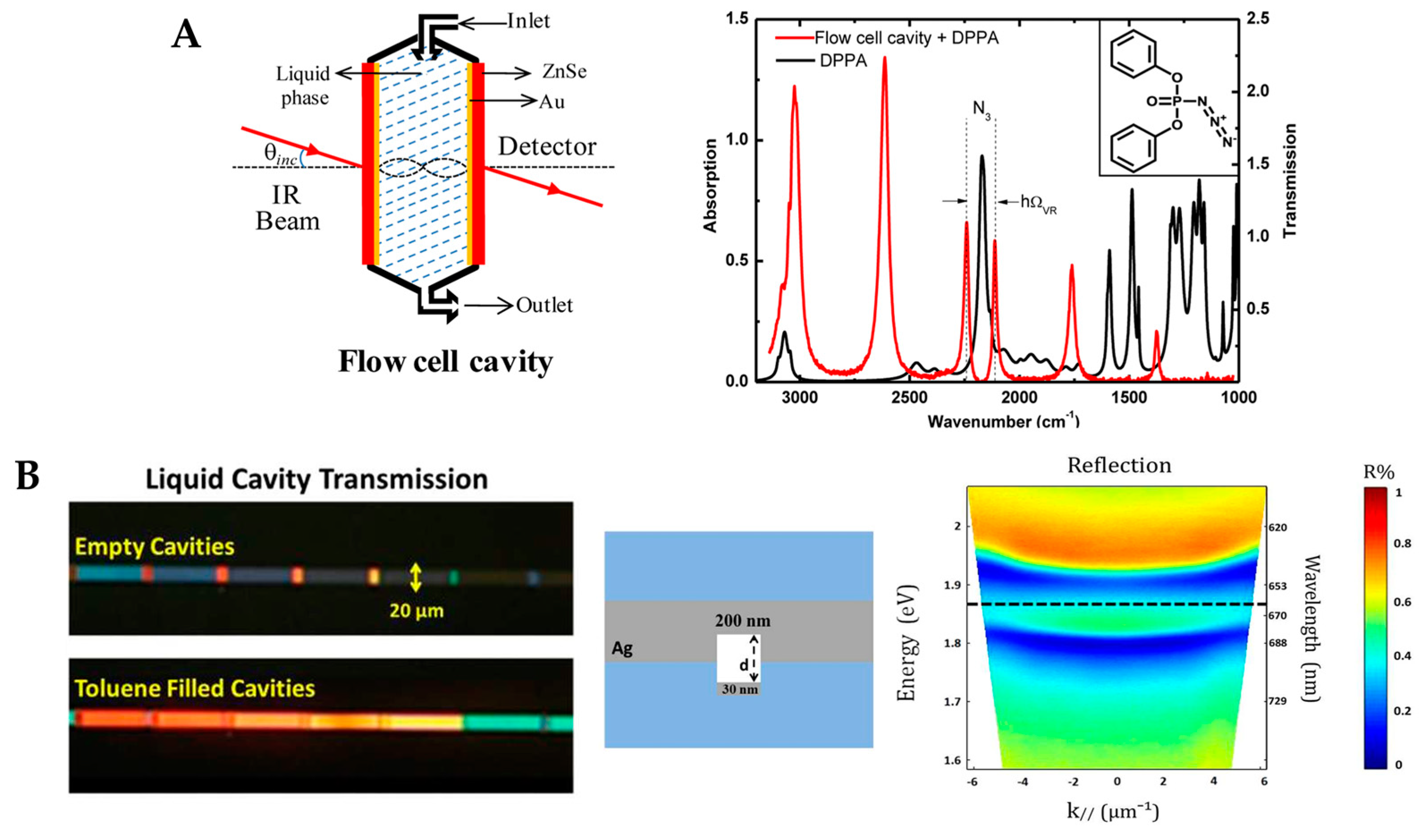
4.1. Fabry–Pérot Microcavity
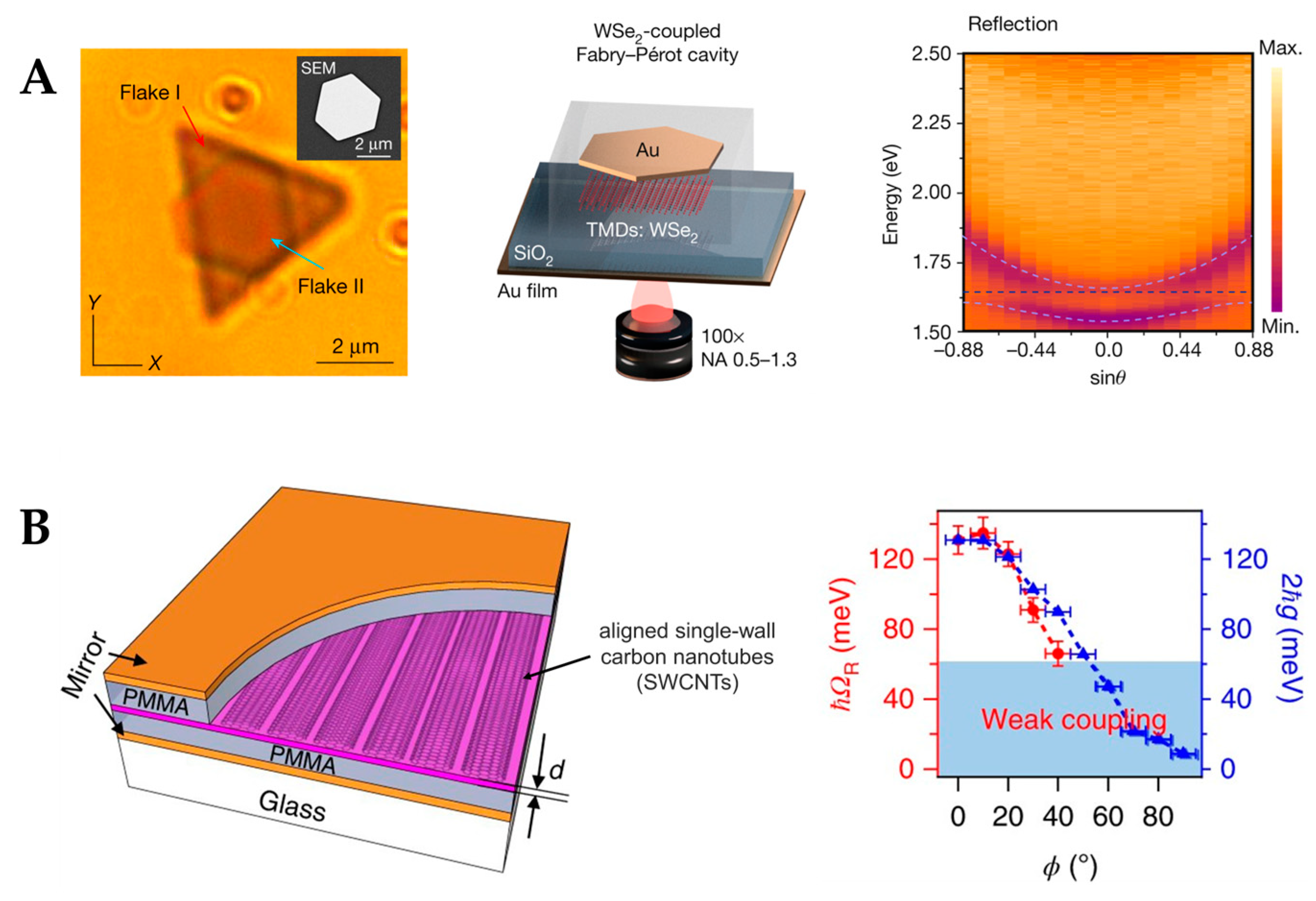
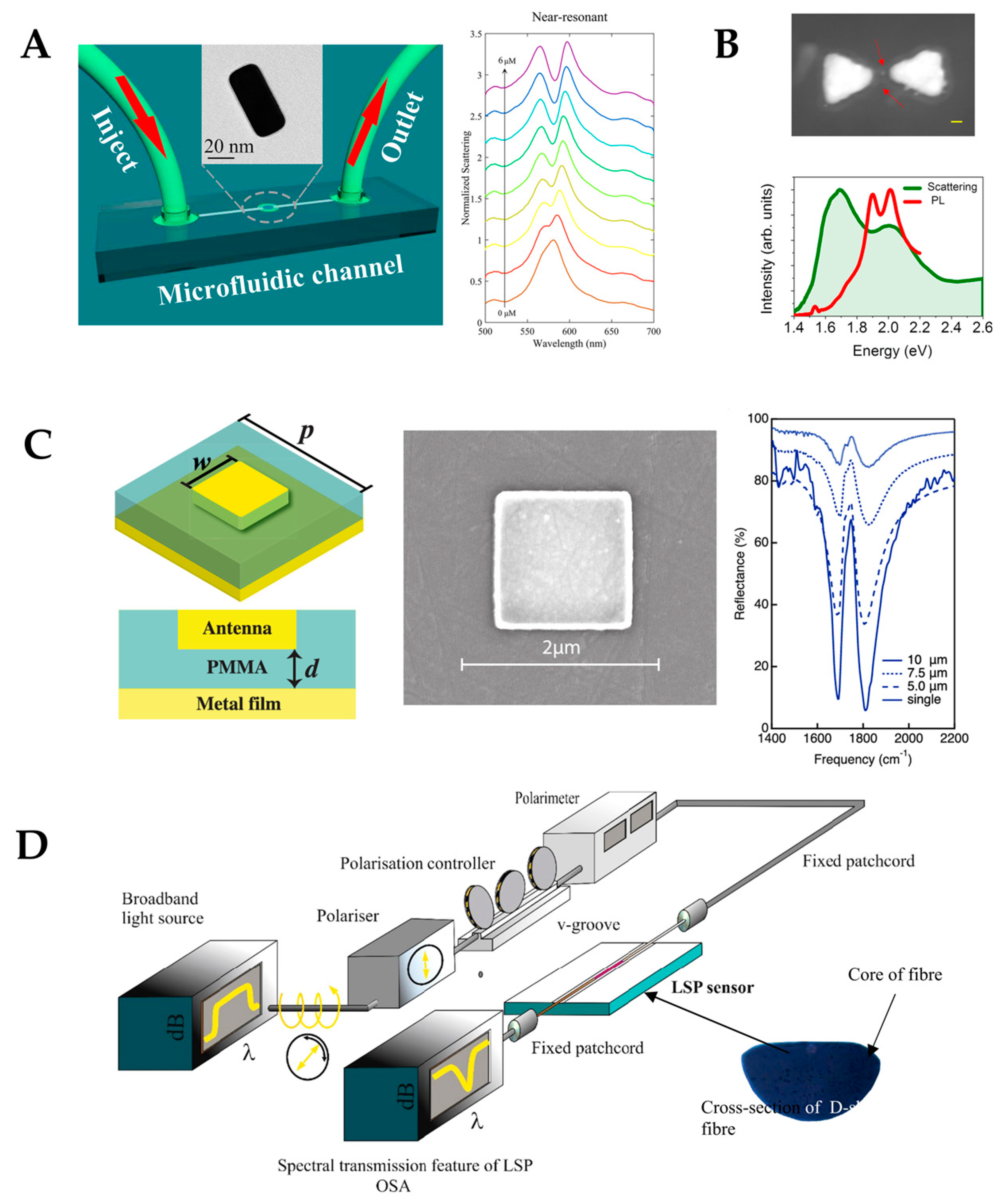
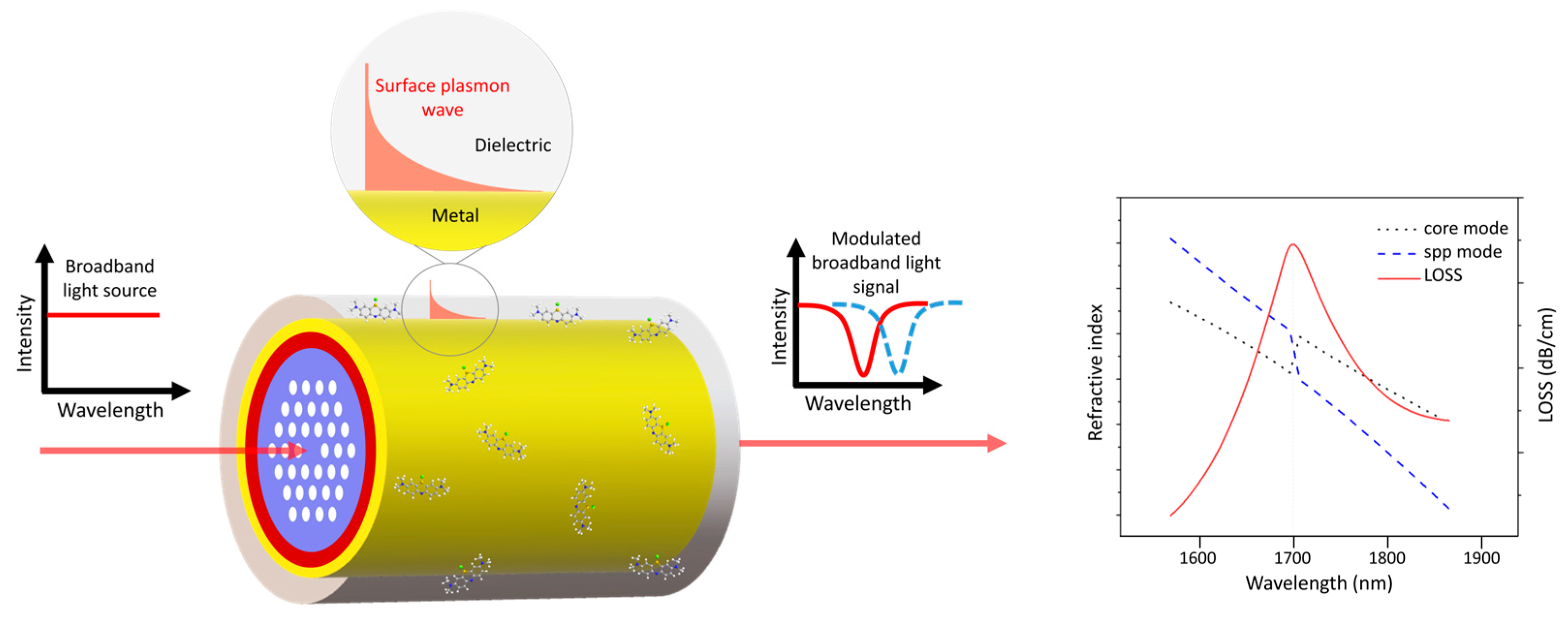
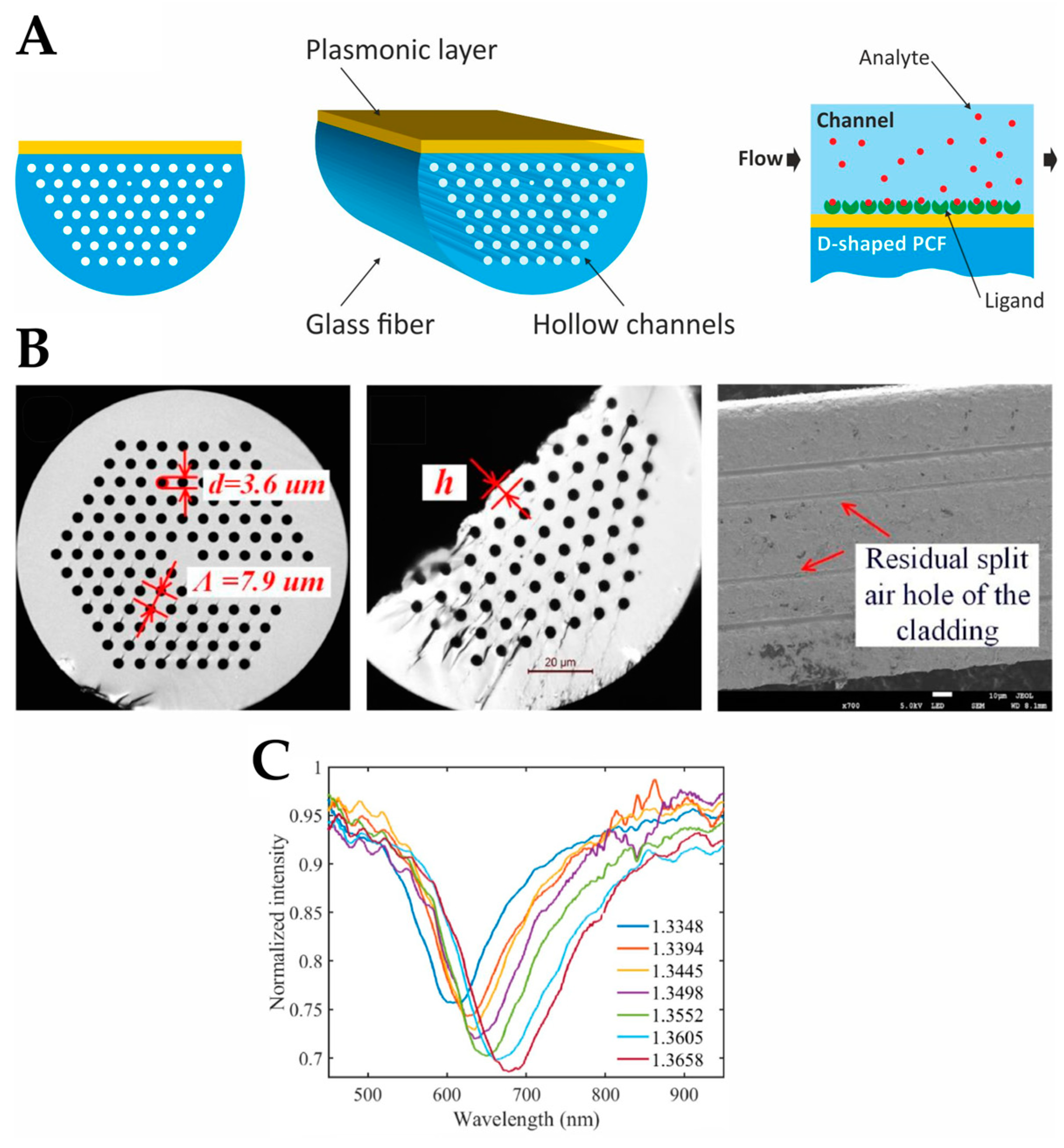
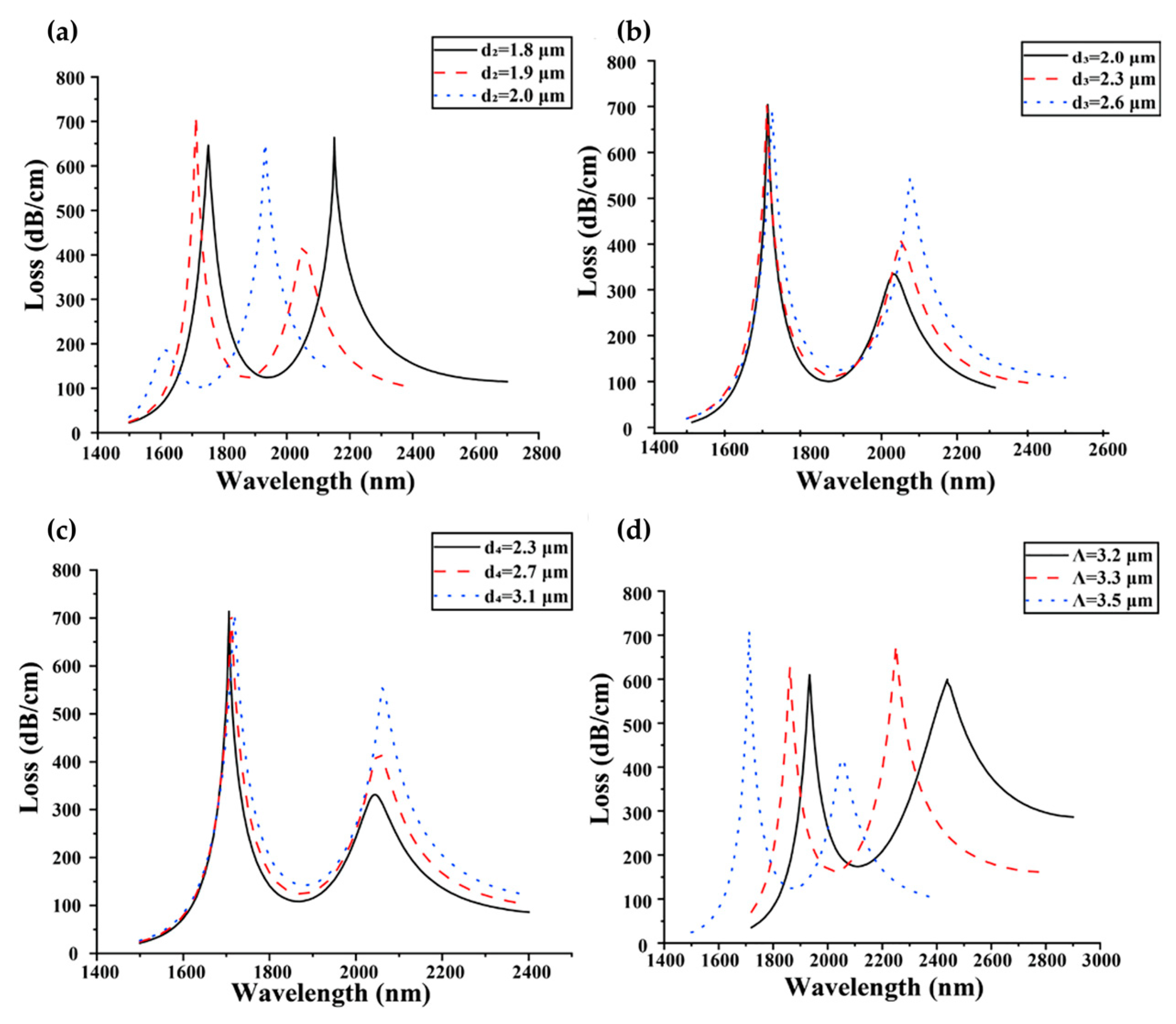
4.2. Photonic-Crystal Fiber Plasmonic Sensor
4.3. Plasmonic Nanocavity
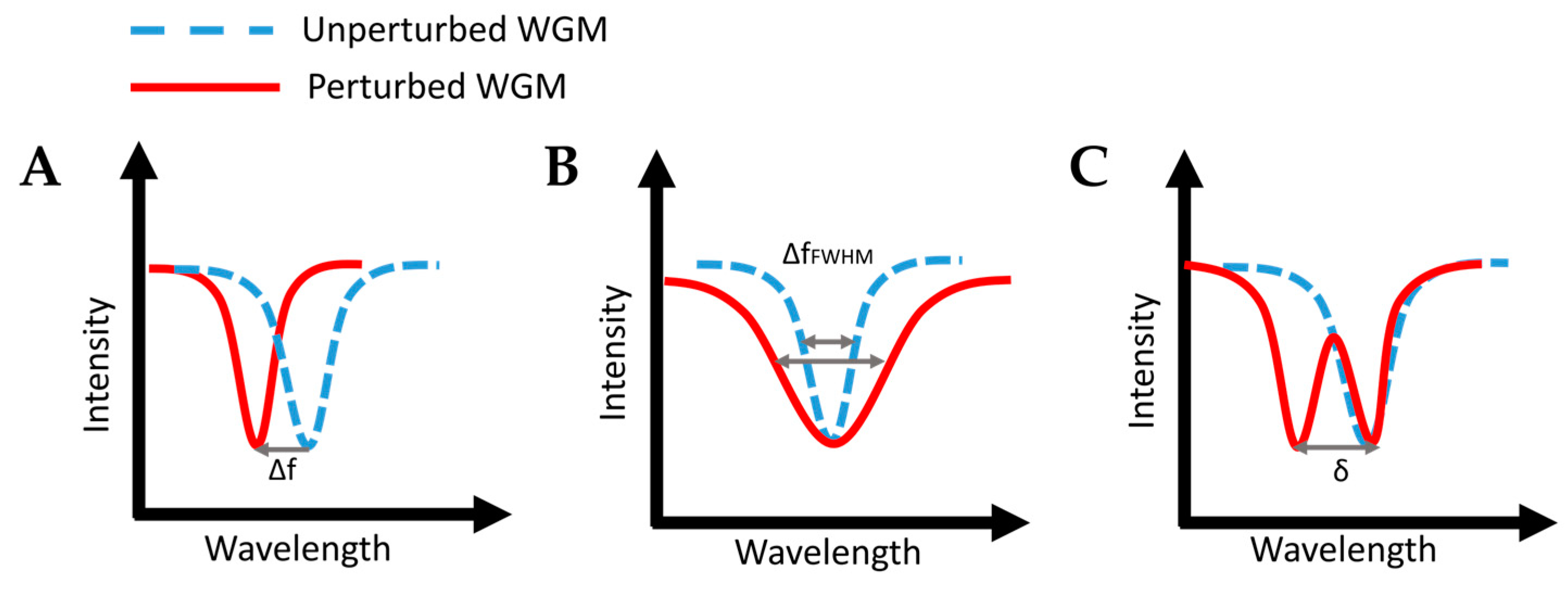
4.4. Whispering-Gallery Mode Microcavity
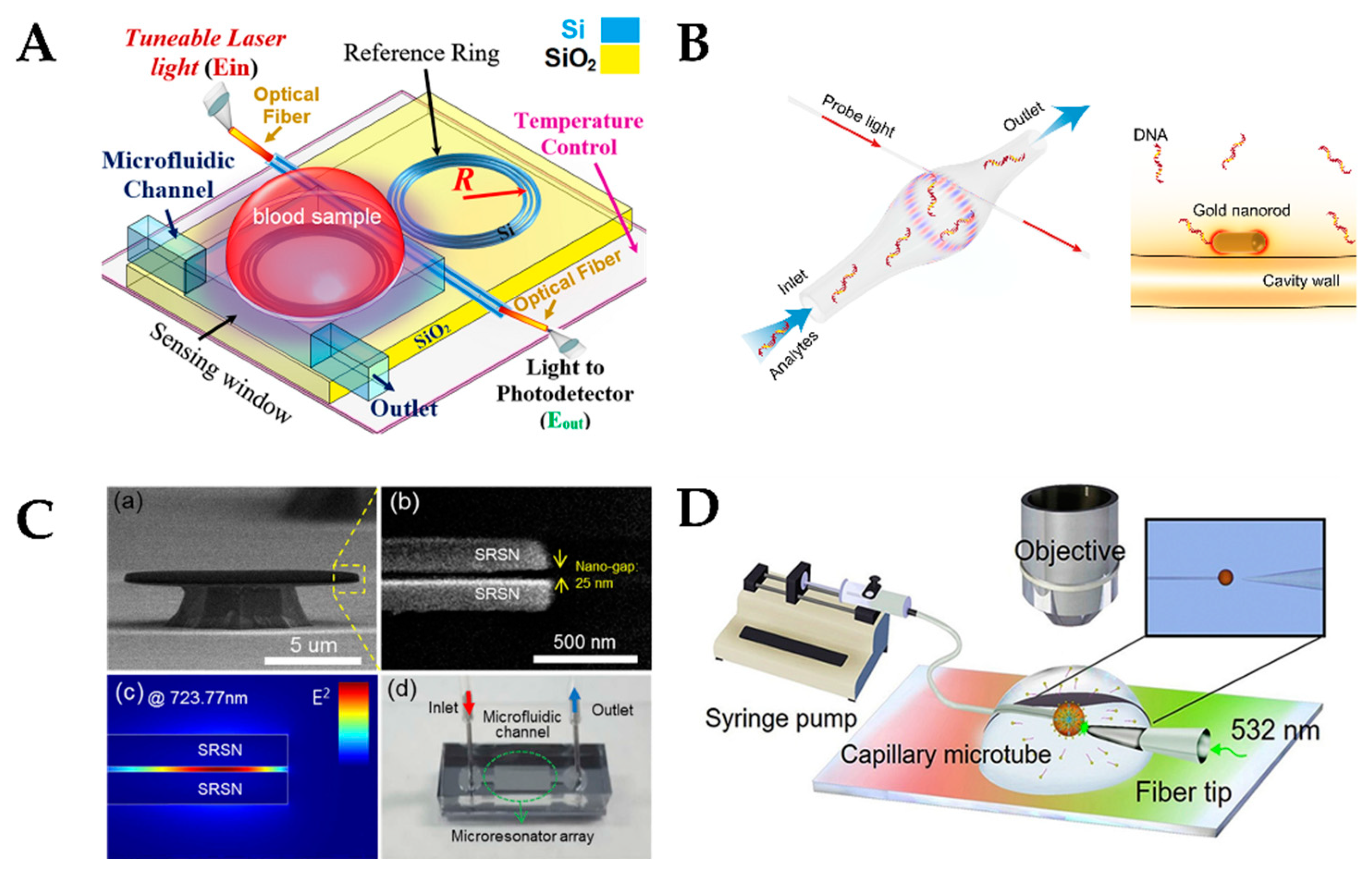
5. Potential Applications of Strong Light–Matter Coupling in Micro- and Nanofluidics
6. Future Prospects and Concluding Remarks
| Configuration | Scheme | Principle of operation | Sensing | Sample studied | Performance | Limitations | Ref. | |
|---|---|---|---|---|---|---|---|---|
| Photonic crystal fiber (PCF) plasmonic sensor |  |
Guided light confined in a periodic dielectric structure and enhanced by plasmonic effects | Label-free | - | D-shaped PCF biosensor based on a plasmonic layer with a resolution of 9.53×10−6 RIU and a maximum sensitivity of 10,493 nm/RIU | Difficult to fabricate; Poor attachment of the bio-analyte to the sensor surface and a large distance between the core and the plasmonic layer; Mostly simulations |
[224] | |
| Fabry–Pérot (F–P) microcavity | 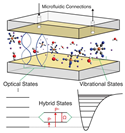 |
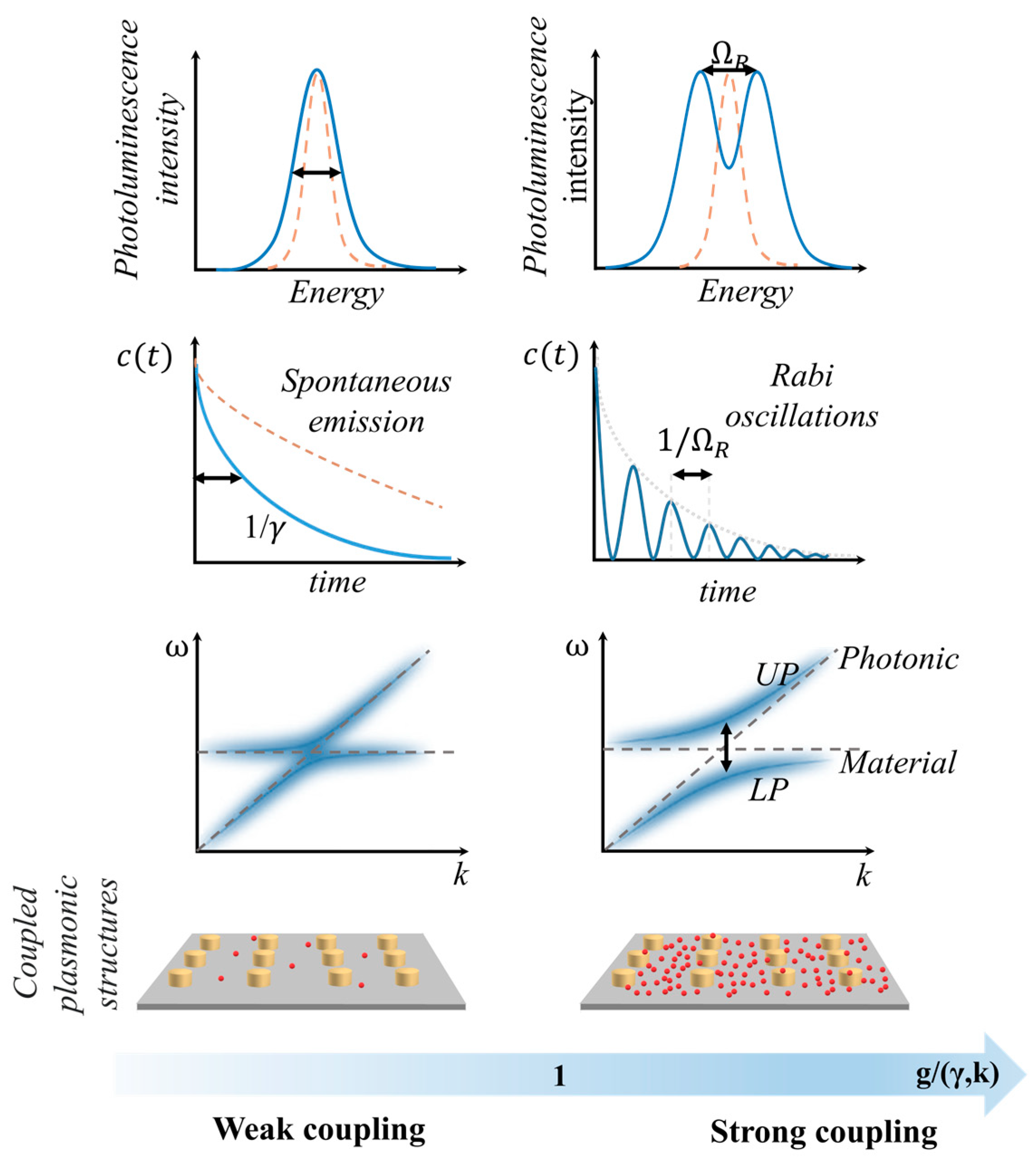
* | Multiple reflections between two parallel mirrors | Label | K4[Fe(CN)6] solutions at concentrations within the water solubility range of the compound | 15 mM with a Rabi splitting of ~20 cm–1 | Large mode volumes | [82] |
 |
** | Streptavidin and human C-reactive protein (CRP) | 1.35 nM for streptavidin,377 pM for CRP | [83] | ||||
| Plasmon cavity | 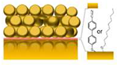 |
† | Localized surface plasmons confined in metal nanostructures | Label | Poly-γ-D-glutamic acid (PGA) | 100 pg/mL | Low quality factors | [225] |
| Molecular glue cucurbit[5]uril | Coupling strength g ~ 100 cm−1 | [226] | ||||||
| Whispering-gallery-mode (WGM) microring resonator | 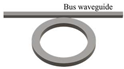 |
Total internal reflection at a curved surface leading to a circumnavigational path | Label-free | Carcinoembryonic antigen, a pancreatic cancer biomarker | 2.5 ng/mL | The fabrication and design are neither simple nor straightforward | [163] | |
| Whispering-gallery-mode (WGM) microbubble resonator |  |
‡ | Label-free | GR-5 DNAzyme | 15 fM; dynamic detection range from 0.1 to 100 pM | [227] | ||
| D-biotins | 0.41 pM | [228] | ||||||
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Purcell, E.M.; Torrey, H.C.; Pound, R.V. Resonance Absorption by Nuclear Magnetic Moments in a Solid. Phys. Rev. 1946, 69, 37–38. [Google Scholar] [CrossRef]
- Degen, C.L.; Reinhard, F.; Cappellaro, P. Quantum Sensing. Rev. Mod. Phys. 2017, 89, 035002. [Google Scholar] [CrossRef]
- Wendin, G. Quantum Information Processing with Superconducting Circuits: A Review. Rep. Prog. Phys. 2017, 80, 106001. [Google Scholar] [CrossRef]
- Jaynes, E.T.; Cummings, F.W. Comparison of Quantum and Semiclassical Radiation Theories with Application to the Beam Maser. Proc. IEEE 1963, 51, 89–109. [Google Scholar] [CrossRef]
- Agranovich, V.M.; Malshukov, A.G. Surface Polariton Spectra If the Resonance with the Transition Layer Vibrations Exist. Optics Communications 1974, 11, 169–171. [Google Scholar] [CrossRef]
- Yakovlev, V.A.; Nazin, V.G.; Zhizhin, G.N. The Surface Polariton Splitting Due to Thin Surface Film LO Vibrations. Optics Communications 1975, 15, 293–295. [Google Scholar] [CrossRef]
- Pockrand, I.; Brillante, A.; Möbius, D. Exciton–Surface Plasmon Coupling: An Experimental Investigation. The Journal of Chemical Physics 1982, 77, 6289–6295. [Google Scholar] [CrossRef]
- Kaluzny, Y.; Goy, P.; Gross, M.; Raimond, J.M.; Haroche, S. Observation of Self-Induced Rabi Oscillations in Two-Level Atoms Excited Inside a Resonant Cavity: The Ringing Regime of Superradiance. Phys. Rev. Lett. 1983, 51, 1175–1178. [Google Scholar] [CrossRef]
- Meschede, D.; Walther, H.; Müller, G. One-Atom Maser. Phys. Rev. Lett. 1985, 54, 551–554. [Google Scholar] [CrossRef]
- Weisbuch, C.; Nishioka, M.; Ishikawa, A.; Arakawa, Y. Observation of the Coupled Exciton-Photon Mode Splitting in a Semiconductor Quantum Microcavity. Phys. Rev. Lett. 1992, 69, 3314–3317. [Google Scholar] [CrossRef] [PubMed]
- Thompson, R.J.; Rempe, G.; Kimble, H.J. Observation of Normal-Mode Splitting for an Atom in an Optical Cavity. Phys. Rev. Lett. 1992, 68, 1132–1135. [Google Scholar] [CrossRef] [PubMed]
- Rempe, G.; Thompson, R.J.; Kimble, H.J. Cavity Quantum Electrodynamics with Strong Coupling in the Optical Domain. Phys. Scr. 1994, T51, 67–77. [Google Scholar] [CrossRef]
- Agranovich, V.; Benisty, H.; Weisbuch, C. Organic and Inorganic Quantum Wells in a Microcavity: Frenkel-Wannier-Mott Excitons Hybridization and Energy Transformation. Solid State Communications 1997, 102, 631–636. [Google Scholar] [CrossRef]
- Lidzey, D.G.; Bradley, D.D.C.; Skolnick, M.S.; Virgili, T.; Walker, S.; Whittaker, D.M. Strong Exciton–Photon Coupling in an Organic Semiconductor Microcavity. Nature 1998, 395, 53–55. [Google Scholar] [CrossRef]
- Boca, A.; Miller, R.; Birnbaum, K.M.; Boozer, A.D.; McKeever, J.; Kimble, H.J. Observation of the Vacuum Rabi Spectrum for One Trapped Atom. Phys. Rev. Lett. 2004, 93, 233603. [Google Scholar] [CrossRef] [PubMed]
- Ciuti, C.; Bastard, G.; Carusotto, I. Quantum Vacuum Properties of the Intersubband Cavity Polariton Field. Phys. Rev. B 2005, 72, 115303. [Google Scholar] [CrossRef]
- Anappara, A.A.; De Liberato, S.; Tredicucci, A.; Ciuti, C.; Biasiol, G.; Sorba, L.; Beltram, F. Signatures of the Ultrastrong Light-Matter Coupling Regime. Phys. Rev. B 2009, 79, 201303. [Google Scholar] [CrossRef]
- Lodahl, P.; Mahmoodian, S.; Stobbe, S. Interfacing Single Photons and Single Quantum Dots with Photonic Nanostructures. Rev. Mod. Phys. 2015, 87, 347–400. [Google Scholar] [CrossRef]
- Shalabney, A.; George, J.; Hutchison, J.; Pupillo, G.; Genet, C.; Ebbesen, T.W. Coherent Coupling of Molecular Resonators with a Microcavity Mode. Nat Commun 2015, 6, 5981. [Google Scholar] [CrossRef]
- George, J.; Shalabney, A.; Hutchison, J.A.; Genet, C.; Ebbesen, T.W. Liquid-Phase Vibrational Strong Coupling. J. Phys. Chem. Lett. 2015, 6, 1027–1031. [Google Scholar] [CrossRef]
- Thomas, A.; George, J.; Shalabney, A.; Dryzhakov, M.; Varma, S.J.; Moran, J.; Chervy, T.; Zhong, X.; Devaux, E.; Genet, C.; et al. Ground-State Chemical Reactivity under Vibrational Coupling to the Vacuum Electromagnetic Field. Angewandte Chemie 2016, 128, 11634–11638. [Google Scholar] [CrossRef]
- Gu, X.; Kockum, A.F.; Miranowicz, A.; Liu, Y.; Nori, F. Microwave Photonics with Superconducting Quantum Circuits. Physics Reports 2017, 718–719, 1–102. [Google Scholar] [CrossRef]
- Munkhbat, B.; Canales, A.; Küçüköz, B.; Baranov, D.G.; Shegai, T.O. Tunable Self-Assembled Casimir Microcavities and Polaritons. Nature 2021, 597, 214–219. [Google Scholar] [CrossRef] [PubMed]
- Canales, A.; Baranov, D.G.; Antosiewicz, T.J.; Shegai, T. Abundance of Cavity-Free Polaritonic States in Resonant Materials and Nanostructures. The Journal of Chemical Physics 2021, 154, 024701. [Google Scholar] [CrossRef] [PubMed]
- Schäfer, C.; Fojt, J.; Lindgren, E.; Erhart, P. Machine Learning for Polaritonic Chemistry: Accessing Chemical Kinetics. J. Am. Chem. Soc. 2024, 146, 5402–5413. [Google Scholar] [CrossRef] [PubMed]
- Fedutik, Y.; Temnov, V.V.; Schöps, O.; Woggon, U.; Artemyev, M.V. Exciton-Plasmon-Photon Conversion in Plasmonic Nanostructures. Phys. Rev. Lett. 2007, 99, 136802. [Google Scholar] [CrossRef] [PubMed]
- Liu, D.; Xue, C. Plasmonic Coupling Architectures for Enhanced Photocatalysis. Advanced Materials 2021, 33, 2005738. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Zeng, S.; Humbert, G.; Ho, H. Microfluidic Whispering Gallery Mode Optical Sensors for Biological Applications. Laser & Photonics Reviews 2020, 14, 2000135. [Google Scholar] [CrossRef]
- Gubin, A.I.; Barannik, A.A.; Cherpak, N.T.; Protsenko, I.A.; Pud, S.; Offenhausser, A.; Vitusevich, S.A. Whispering-Gallery-Mode Resonator Technique With Microfluidic Channel for Permittivity Measurement of Liquids. IEEE Trans. Microwave Theory Techn. 2015, 63, 2003–2009. [Google Scholar] [CrossRef]
- Zhao, X.; Guo, Z.; Zhou, Y.; Guo, J.; Liu, Z.; Li, Y.; Luo, M.; Wu, X. Optical Whispering-Gallery-Mode Microbubble Sensors. Micromachines 2022, 13, 592. [Google Scholar] [CrossRef]
- Luo, W.; Li, X.; Meng, J.; Wang, Y.; Hong, X. Surface Plasmon Resonance Sensor Based on Side-Polished D-Shaped Photonic Crystal Fiber With Split Cladding Air Holes. IEEE Trans. Instrum. Meas. 2021, 70, 1–11. [Google Scholar] [CrossRef]
- Purcell, E.M. Spontaneous Emission Probabilities at Radio Frequencies. In Confined Electrons and Photons; Burstein, E., Weisbuch, C., Eds.; NATO ASI Series; Springer US: Boston, MA, 1995; Vol. 340, pp. 839–839. ISBN 978-1-4613-5807-7. [Google Scholar]
- Kelly, K.L.; Coronado, E.; Zhao, L.L.; Schatz, G.C. The Optical Properties of Metal Nanoparticles: The Influence of Size, Shape, and Dielectric Environment. J. Phys. Chem. B 2003, 107, 668–677. [Google Scholar] [CrossRef]
- Nagarajan, K.; Thomas, A.; Ebbesen, T.W. Chemistry under Vibrational Strong Coupling. J. Am. Chem. Soc. 2021, 143, 16877–16889. [Google Scholar] [CrossRef] [PubMed]
- Tavis, M.; Cummings, F.W. Exact Solution for an $N$-Molecule---Radiation-Field Hamiltonian. Phys. Rev. 1968, 170, 379–384. [Google Scholar] [CrossRef]
- Tavis, M.; Cummings, F.W. Exact Solution for an N -Molecule—Radiation-Field Hamiltonian. Phys. Rev. 1968, 170, 379–384. [Google Scholar] [CrossRef]
- Bisht, A.; Cuadra, J.; Wersäll, M.; Canales, A.; Antosiewicz, T.J.; Shegai, T. Collective Strong Light-Matter Coupling in Hierarchical Microcavity-Plasmon-Exciton Systems. Nano Lett. 2019, 19, 189–196. [Google Scholar] [CrossRef] [PubMed]
- Yadav, R.K.; Bourgeois, M.R.; Cherqui, C.; Juarez, X.G.; Wang, W.; Odom, T.W.; Schatz, G.C.; Basu, J.K. Room Temperature Weak-to-Strong Coupling and the Emergence of Collective Emission from Quantum Dots Coupled to Plasmonic Arrays. ACS Nano 2020, 14, 7347–7357. [Google Scholar] [CrossRef] [PubMed]
- Hertzog, M.; Wang, M.; Mony, J.; Börjesson, K. Strong Light–Matter Interactions: A New Direction within Chemistry. Chem. Soc. Rev. 2019, 48, 937–961. [Google Scholar] [CrossRef] [PubMed]
- Haugland, T.S.; Schäfer, C.; Ronca, E.; Rubio, A.; Koch, H. Intermolecular Interactions in Optical Cavities: An Ab Initio QED Study. The Journal of Chemical Physics 2021, 154, 094113. [Google Scholar] [CrossRef]
- Orgiu, E.; George, J.; Hutchison, J.A.; Devaux, E.; Dayen, J.F.; Doudin, B.; Stellacci, F.; Genet, C.; Schachenmayer, J.; Genes, C.; et al. Conductivity in Organic Semiconductors Hybridized with the Vacuum Field. Nature Mater 2015, 14, 1123–1129. [Google Scholar] [CrossRef]
- Zeng, H.; Pérez-Sánchez, J.B.; Eckdahl, C.T.; Liu, P.; Chang, W.J.; Weiss, E.A.; Kalow, J.A.; Yuen-Zhou, J.; Stern, N.P. Control of Photoswitching Kinetics with Strong Light–Matter Coupling in a Cavity. J. Am. Chem. Soc. 2023, 145, 19655–19661. [Google Scholar] [CrossRef] [PubMed]
- Sau, A.; Nagarajan, K.; Patrahau, B.; Lethuillier-Karl, L.; Vergauwe, R.M.A.; Thomas, A.; Moran, J.; Genet, C.; Ebbesen, T.W. Modifying Woodward–Hoffmann Stereoselectivity Under Vibrational Strong Coupling. Angew Chem Int Ed 2021, 60, 5712–5717. [Google Scholar] [CrossRef] [PubMed]
- Lather, J.; George, J. Improving Enzyme Catalytic Efficiency by Co-Operative Vibrational Strong Coupling of Water. J. Phys. Chem. Lett. 2021, 12, 379–384. [Google Scholar] [CrossRef] [PubMed]
- Lather, J.; Bhatt, P.; Thomas, A.; Ebbesen, T.W.; George, J. Cavity Catalysis by Cooperative Vibrational Strong Coupling of Reactant and Solvent Molecules. Angew Chem Int Ed 2019, 58, 10635–10638. [Google Scholar] [CrossRef] [PubMed]
- Lather, J.; Thabassum, A.N.K.; Singh, J.; George, J. Cavity Catalysis: Modifying Linear Free-Energy Relationship under Cooperative Vibrational Strong Coupling. Chem. Sci. 2022, 13, 195–202. [Google Scholar] [CrossRef] [PubMed]
- Vahala, K.J. Optical Microcavities. Nature 2003, 424, 839–846. [Google Scholar] [CrossRef] [PubMed]
- Boroditsky, M.; Coccioli, R.; Yablonovitch, E.; Rahmat-Samii, Y.; Kim, K.W. Smallest Possible Electromagnetic Mode Volume in a Dielectric Cavity. IEE Proceedings - Optoelectronics 1998, 145, 391–397. [Google Scholar] [CrossRef]
- Hugall, J.T.; Singh, A.; Van Hulst, N.F. Plasmonic Cavity Coupling. ACS Photonics 2018, 5, 43–53. [Google Scholar] [CrossRef]
- Liu, W.; Tang, S.-J.; Xiao, Y.-F. Nonlinear Optical Microcavities Towards Single-Molecule Sensing. In Single Molecule Sensing Beyond Fluorescence; Bowen, W., Vollmer, F., Gordon, R., Eds.; Springer International Publishing: Cham, 2022; pp. 97–123. ISBN 978-3-030-90338-1. [Google Scholar]
- Huang, Y.; Wu, F.; Yu, L. Rabi Oscillation Study of Strong Coupling in a Plasmonic Nanocavity. New J. Phys. 2020, 22, 063053. [Google Scholar] [CrossRef]
- Liang, K.; Guo, J.; Wu, F.; Huang, Y.; Yu, L. Dynamic Control of Quantum Emitters Strongly Coupled to the Isolated Plasmon Cavity by the Microfluidic Device. J. Phys. Chem. C 2021, 125, 17303–17310. [Google Scholar] [CrossRef]
- Patra, A.; Caligiuri, V.; Krahne, R.; De Luca, A. Strong Light–Matter Interaction and Spontaneous Emission Reshaping via Pseudo-Cavity Modes. Advanced Optical Materials 2021, 9, 2101076. [Google Scholar] [CrossRef]
- Cao, J.; De Liberato, S.; Kavokin, A.V. Strong Light–Matter Coupling in Microcavities Characterised by Rabi-Splittings Comparable to the Bragg Stop-Band Widths. New J. Phys. 2021, 23, 113015. [Google Scholar] [CrossRef]
- Ruggenthaler, M.; Flick, J.; Pellegrini, C.; Appel, H.; Tokatly, I.V.; Rubio, A. Quantum-Electrodynamical Density-Functional Theory: Bridging Quantum Optics and Electronic-Structure Theory. Phys. Rev. A 2014, 90, 012508. [Google Scholar] [CrossRef]
- Haugland, T.S.; Ronca, E.; Kjønstad, E.F.; Rubio, A.; Koch, H. Coupled Cluster Theory for Molecular Polaritons: Changing Ground and Excited States. Phys. Rev. X 2020, 10, 041043. [Google Scholar] [CrossRef]
- Sidler, D.; Schäfer, C.; Ruggenthaler, M.; Rubio, A. Polaritonic Chemistry: Collective Strong Coupling Implies Strong Local Modification of Chemical Properties. J. Phys. Chem. Lett. 2021, 12, 508–516. [Google Scholar] [CrossRef] [PubMed]
- DePrince, A.E. Cavity-Modulated Ionization Potentials and Electron Affinities from Quantum Electrodynamics Coupled-Cluster Theory. The Journal of Chemical Physics 2021, 154, 094112. [Google Scholar] [CrossRef] [PubMed]
- Latini, S.; Shin, D.; Sato, S.A.; Schäfer, C.; De Giovannini, U.; Hübener, H.; Rubio, A. The Ferroelectric Photo Ground State of SrTiO 3 : Cavity Materials Engineering. Proc. Natl. Acad. Sci. U.S.A. 2021, 118, e2105618118. [Google Scholar] [CrossRef]
- Flick, J.; Rivera, N.; Narang, P. Strong Light-Matter Coupling in Quantum Chemistry and Quantum Photonics. Nanophotonics 2018, 7, 1479–1501. [Google Scholar] [CrossRef]
- Kang, T.; Bahk, Y.-M.; Kim, D.-S. Terahertz Quantum Plasmonics at Nanoscales and Angstrom Scales. Nanophotonics 2020, 9, 435–451. [Google Scholar] [CrossRef]
- Marlow, E.; Murphy, A.; Pollard, R. Investigating Electromagnetic Field Enhancements from Gold Nanostructured Arrays for Plasmon Enhanced Fluorescence. In Proceedings of the Plasmonics: Design, Materials, Fabrication, Characterization, and Applications XVII; Tanaka, T., Tsai, D.P., Eds.; SPIE: San Diego, United States, 9 September 2019; p. 54. [Google Scholar]
- Rabi, I.I. On the Process of Space Quantization. Phys. Rev. 1936, 49, 324–328. [Google Scholar] [CrossRef]
- Brune, M.; Schmidt-Kaler, F.; Maali, A.; Dreyer, J.; Hagley, E.; Raimond, J.M.; Haroche, S. Quantum Rabi Oscillation: A Direct Test of Field Quantization in a Cavity. Phys. Rev. Lett. 1996, 76, 1800–1803. [Google Scholar] [CrossRef]
- Galego, J.; Climent, C.; Garcia-Vidal, F.J.; Feist, J. Cavity Casimir-Polder Forces and Their Effects in Ground-State Chemical Reactivity. Phys. Rev. X 2019, 9, 021057. [Google Scholar] [CrossRef]
- Herrera, F. Photochemistry with Quantum Optics from a Non-Adiabatic Quantum Trajectory Perspective. Chem 2020, 6, 7–9. [Google Scholar] [CrossRef]
- Vurgaftman, I.; Simpkins, B.S.; Dunkelberger, A.D.; Owrutsky, J.C. Negligible Effect of Vibrational Polaritons on Chemical Reaction Rates via the Density of States Pathway. J. Phys. Chem. Lett. 2020, 11, 3557–3562. [Google Scholar] [CrossRef]
- Prakash, S.; Yeom, J. Nanofluidics and Microfluidics: Systems and Applications; William Andrew, 2014; ISBN 978-1-4377-4470-5. [Google Scholar]
- Gale, B.K.; Jafek, A.R.; Lambert, C.J.; Goenner, B.L.; Moghimifam, H.; Nze, U.C.; Kamarapu, S.K. A Review of Current Methods in Microfluidic Device Fabrication and Future Commercialization Prospects. Inventions 2018, 3, 60. [Google Scholar] [CrossRef]
- Xie, Y.; Dai, L.; Yang, Y. Microfluidic Technology and Its Application in the Point-of-Care Testing Field. Biosensors and Bioelectronics: X 2022, 10, 100109. [Google Scholar] [CrossRef]
- Zhu, J.M.; Shi, Y.; Zhu, X.Q.; Yang, Y.; Jiang, F.H.; Sun, C.J.; Zhao, W.H.; Han, X.T. Optofluidic Marine Phosphate Detection with Enhanced Absorption Using a Fabry–Pérot Resonator. Lab Chip 2017, 17, 4025–4030. [Google Scholar] [CrossRef]
- Xia, Y.; Whitesides, G.M. SOFT LITHOGRAPHY. Annu. Rev. Mater. Sci. 1998, 28, 153–184. [Google Scholar] [CrossRef]
- Morikawa, K.; Kazoe, Y.; Takagi, Y.; Tsuyama, Y.; Pihosh, Y.; Tsukahara, T.; Kitamori, T. Advanced Top-Down Fabrication for a Fused Silica Nanofluidic Device. Micromachines 2020, 11, 995. [Google Scholar] [CrossRef] [PubMed]
- Do, T.C.; Bui, H.; Nguyen, T.V.; Nguyen, T.A.; Nguyen, T.H.; Pham, V.H. A Microcavity Based on a Porous Silicon Multilayer. Adv. Nat. Sci: Nanosci. Nanotechnol. 2011, 2, 035001. [Google Scholar] [CrossRef]
- Panagopoulos, C.N.; Markaki, A.; Hontzopoulos, E. Excimer Laser Treatment of Copper-Coated Mild Steel. Journal of Materials Science 1997, 32, 1425–1430. [Google Scholar] [CrossRef]
- Han, P.; Tsai, C.-M.; Lee, H.-B. The Proposed Necessary and Sufficient Condition for Spectral Switches with Concave Reflectance of Aluminum Metal. Advances in Mechanical Engineering 2017, 9, 168781401774406. [Google Scholar] [CrossRef]
- Ung, T.; Liz-Marzán, L.M.; Mulvaney, P. Gold Nanoparticle Thin Films. Colloids and Surfaces A: Physicochemical and Engineering Aspects 2002, 202, 119–126. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, L.; Zhang, D.; Krasavin, A.V.; Zheng, J.; Pan, C.; He, E.; Wang, Z.; Zhong, S.; Li, Z.; et al. Effect of Mirror Quality on Optical Response of Nanoparticle-on-Mirror Plasmonic Nanocavities. Advanced Optical Materials 2023, 11, 2201914. [Google Scholar] [CrossRef]
- Hayashi, S.; Ishigaki, Y.; Fujii, M. Plasmonic Effects on Strong Exciton-Photon Coupling in Metal-Insulator-Metal Microcavities. Phys. Rev. B 2012, 86, 045408. [Google Scholar] [CrossRef]
- Dovzhenko, D.; Mochalov, K.; Vaskan, I.; Kryukova, I.; Rakovich, Y.; Nabiev, I. Polariton-Assisted Splitting of Broadband Emission Spectra of Strongly Coupled Organic Dye Excitons in Tunable Optical Microcavity. Opt. Express 2019, 27, 4077. [Google Scholar] [CrossRef] [PubMed]
- Bahsoun, H.; Chervy, T.; Thomas, A.; Börjesson, K.; Hertzog, M.; George, J.; Devaux, E.; Genet, C.; Hutchison, J.A.; Ebbesen, T.W. Electronic Light–Matter Strong Coupling in Nanofluidic Fabry–Pérot Cavities. ACS Photonics 2018, 5, 225–232. [Google Scholar] [CrossRef]
- Casey, S.R.; Sparks, J.R. Vibrational Strong Coupling of Organometallic Complexes. J. Phys. Chem. C 2016, 120, 28138–28143. [Google Scholar] [CrossRef]
- Rho, D.; Kim, S. Demonstration of a Label-Free and Low-Cost Optical Cavity-Based Biosensor Using Streptavidin and C-Reactive Protein. Biosensors 2020, 11, 4. [Google Scholar] [CrossRef]
- Schmidt, F.; Callegari, A.; Daddi-Moussa-Ider, A.; Munkhbat, B.; Verre, R.; Shegai, T.; Käll, M.; Löwen, H.; Gambassi, A.; Volpe, G. Tunable Critical Casimir Forces Counteract Casimir–Lifshitz Attraction. Nat. Phys. 2022. [Google Scholar] [CrossRef]
- Gao, W.; Li, X.; Bamba, M.; Kono, J. Continuous Transition between Weak and Ultrastrong Coupling through Exceptional Points in Carbon Nanotube Microcavity Exciton–Polaritons. Nature Photon 2018, 12, 362–367. [Google Scholar] [CrossRef]
- Forn-Díaz, P.; Lamata, L.; Rico, E.; Kono, J.; Solano, E. Ultrastrong Coupling Regimes of Light-Matter Interaction. Rev. Mod. Phys. 2019, 91, 025005. [Google Scholar] [CrossRef]
- Frisk Kockum, A.; Miranowicz, A.; De Liberato, S.; Savasta, S.; Nori, F. Ultrastrong Coupling between Light and Matter. Nat Rev Phys 2019, 1, 19–40. [Google Scholar] [CrossRef]
- Le Boité, A. Theoretical Methods for Ultrastrong Light–Matter Interactions. Adv Quantum Tech 2020, 3, 1900140. [Google Scholar] [CrossRef]
- Liu, Q.; Chen, J.; Hou, S.; Lei, J. Investigation into Micro-Polishing Photonic Crystal Fibers for Surface Plasmon Resonance Sensing. Crystals 2022, 12, 1106. [Google Scholar] [CrossRef]
- Chaudhary, V.S.; Kumar, D.; Pandey, B.P.; Kumar, S. Advances in Photonic Crystal Fiber-Based Sensor for Detection of Physical and Biochemical Parameters—A Review. IEEE Sensors J. 2023, 23, 1012–1023. [Google Scholar] [CrossRef]
- Dash, J.N.; Jha, R. SPR Biosensor Based on Polymer PCF Coated With Conducting Metal Oxide. IEEE Photon. Technol. Lett. 2014, 26, 595–598. [Google Scholar] [CrossRef]
- Caucheteur, C.; Guo, T.; Albert, J. Review of Plasmonic Fiber Optic Biochemical Sensors: Improving the Limit of Detection. Anal Bioanal Chem 2015, 407, 3883–3897. [Google Scholar] [CrossRef] [PubMed]
- Rifat, A.A.; Ahmed, R.; Yetisen, A.K.; Butt, H.; Sabouri, A.; Mahdiraji, G.A.; Yun, S.H.; Adikan, F.R.M. Photonic Crystal Fiber Based Plasmonic Sensors. Sensors and Actuators B: Chemical 2017, 243, 311–325. [Google Scholar] [CrossRef]
- Cao, S.; Shao, Y.; Wang, Y.; Wu, T.; Zhang, L.; Huang, Y.; Zhang, F.; Liao, C.; He, J.; Wang, Y. Highly Sensitive Surface Plasmon Resonance Biosensor Based on a Low-Index Polymer Optical Fiber. Opt. Express 2018, 26, 3988. [Google Scholar] [CrossRef]
- Lu, J.; Li, Y.; Han, Y.; Liu, Y.; Gao, J. D-Shaped Photonic Crystal Fiber Plasmonic Refractive Index Sensor Based on Gold Grating. Appl. Opt. 2018, 57, 5268. [Google Scholar] [CrossRef] [PubMed]
- Quero, G.; Zito, G.; Managò, S.; Galeotti, F.; Pisco, M.; De Luca, A.; Cusano, A. Nanosphere Lithography on Fiber: Towards Engineered Lab-On-Fiber SERS Optrodes. Sensors 2018, 18, 680. [Google Scholar] [CrossRef] [PubMed]
- Aćimović, S.S.; Ortega, M.A.; Sanz, V.; Berthelot, J.; Garcia-Cordero, J.L.; Renger, J.; Maerkl, S.J.; Kreuzer, M.P.; Quidant, R. LSPR Chip for Parallel, Rapid, and Sensitive Detection of Cancer Markers in Serum. Nano Lett. 2014, 14, 2636–2641. [Google Scholar] [CrossRef] [PubMed]
- Xu, D.; Xiong, X.; Wu, L.; Ren, X.-F.; Png, C.E.; Guo, G.-C.; Gong, Q.; Xiao, Y.-F. Quantum Plasmonics: New Opportunity in Fundamental and Applied Photonics. Adv. Opt. Photon. 2018, 10, 703. [Google Scholar] [CrossRef]
- Xu, Y.; Xiong, M.; Yan, H. A Portable Optical Fiber Biosensor for the Detection of Zearalenone Based on the Localized Surface Plasmon Resonance. Sensors and Actuators B: Chemical 2021, 336, 129752. [Google Scholar] [CrossRef]
- Wei, T.; Ren, P.; Huang, L.; Ouyang, Z.; Wang, Z.; Kong, X.; Li, T.; Yin, Y.; Wu, Y.; He, Q. Simultaneous Detection of Aflatoxin B1, Ochratoxin A, Zearalenone and Deoxynivalenol in Corn and Wheat Using Surface Plasmon Resonance. Food Chemistry 2019, 300, 125176. [Google Scholar] [CrossRef] [PubMed]
- Calatayud-Sanchez, A.; Ortega-Gomez, A.; Barroso, J.; Zubia, J.; Benito-Lopez, F.; Villatoro, J.; Basabe-Desmonts, L. A Method for the Controllable Fabrication of Optical Fiber-Based Localized Surface Plasmon Resonance Sensors. Sci Rep 2022, 12, 9566. [Google Scholar] [CrossRef]
- Bastús, N.G.; Comenge, J.; Puntes, V. Kinetically Controlled Seeded Growth Synthesis of Citrate-Stabilized Gold Nanoparticles of up to 200 Nm: Size Focusing versus Ostwald Ripening. Langmuir 2011, 27, 11098–11105. [Google Scholar] [CrossRef]
- Khalek, Md.A.; Chakma, S.; Ahmed, K.; Paul, B.K.; Vigneswaran, D.; Zakaria, R. Materials Effect in Sensing Performance Based on Surface Plasmon Resonance Using Photonic Crystal Fiber. Plasmonics 2019, 14, 861–867. [Google Scholar] [CrossRef]
- Luan, N.; Zhao, L.; Lian, Y.; Lou, S. A High Refractive Index Plasmonic Sensor Based on D-Shaped Photonic Crystal Fiber With Laterally Accessible Hollow-Core. IEEE Photonics J. 2018, 10, 1–7. [Google Scholar] [CrossRef]
- Lee, H.W.; Schmidt, M.A.; Tyagi, H.K.; Sempere, L.P.; Russell, P.St.J. Polarization-Dependent Coupling to Plasmon Modes on Submicron Gold Wire in Photonic Crystal Fiber. Applied Physics Letters 2008, 93, 111102. [Google Scholar] [CrossRef]
- Lee, H.W.; Schmidt, M.A.; Russell, R.F.; Joly, N.Y.; Tyagi, H.K.; Uebel, P.; Russell, P.St.J. Pressure-Assisted Melt-Filling and Optical Characterization of Au Nano-Wires in Microstructured Fibers. Opt. Express 2011, 19, 12180. [Google Scholar] [CrossRef] [PubMed]
- Russell, P. Photonic Crystal Fibers. Science 2003, 299, 358–362. [Google Scholar] [CrossRef] [PubMed]
- Ashok, N.; Shin, W. Effective D-Shape Fiber with Air Hole Assistant Design for Birefringence Analysis. Optik 2018, 162, 27–34. [Google Scholar] [CrossRef]
- Boehm, J.; François, A.; Ebendorff-Heidepriem, H.; Monro, T.M. Chemical Deposition of Silver for the Fabrication of Surface Plasmon Microstructured Optical Fibre Sensors. Plasmonics 2011, 6, 133–136. [Google Scholar] [CrossRef]
- Srivastava, R.; Prajapati, Y.K.; Pal, S.; Kumar, S. Micro-Channel Plasmon Sensor Based on a D-Shaped Photonic Crystal Fiber for Malaria Diagnosis With Improved Performance. IEEE Sensors J. 2022, 22, 14834–14841. [Google Scholar] [CrossRef]
- Luo, W.; Li, X.; Abbasi, S.A.; Zhu, S.; Ho, H.-P.; Yuan, W. Analysis of the D-Shaped PCF-Based SPR Sensor Using Resonance Electron Relaxation and Fourier Domain Method. Optics and Lasers in Engineering 2023, 166, 107588. [Google Scholar] [CrossRef]
- Ma, Y.; Liu, F.; Ren, Q.; Zhang, H.; Zhang, A. Dual-Band Highly-Sensitive SPR Photonic Crystal Fiber Sensor Based on Birefringence Analysis. Optics Communications 2023, 532, 129253. [Google Scholar] [CrossRef]
- Islam, N.; Faizul Huq Arif, Md.; Abu Yousuf, M.; Asaduzzaman, S. Highly Sensitive Open Channel Based PCF-SPR Sensor for Analyte Refractive Index Sensing. Results in Physics 2023, 46, 106266. [Google Scholar] [CrossRef]
- Mawa Nijhum, J.; Ahmed, T.; Hossain, Md.A.; Atai, J.; Hai, N.H. Microchannel-Embedded D-Shaped Photonic Crystal Fiber-Based Highly Sensitive Plasmonic Biosensor. Applied Sciences 2022, 12, 4122. [Google Scholar] [CrossRef]
- Chen, N.; Chang, M.; Lu, X.; Zhou, J.; Zhang, X. Photonic Crystal Fiber Plasmonic Sensor Based on Dual Optofluidic Channel. Sensors 2019, 19, 5150. [Google Scholar] [CrossRef]
- Sharif, V.; Pakarzadeh, H. High-Performance Surface Plasmon Resonance Fiber Sensor Based on Cylindrical Vector Modes. Sci Rep 2023, 13, 4563. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Yuan, J.; Qu, Y.; Qiu, S.; Mei, C.; Zhou, X.; Yan, B.; Wu, Q.; Wang, K.; Sang, X.; et al. A Novel Surface Plasmon Resonance-Based Photonic Crystal Fiber Refractive Index Sensor with an Ultra-Wide Detection Range. Optik 2022, 259, 168977. [Google Scholar] [CrossRef]
- Aruna Gandhi, M.S.; Senthilnathan, K.; Babu, P.R.; Li, Q. Visible to near Infrared Highly Sensitive Microbiosensor Based on Surface Plasmon Polariton with External Sensing Approach. Results in Physics 2019, 15, 102590. [Google Scholar] [CrossRef]
- Liu, J.; Jalali, M.; Mahshid, S.; Wachsmann-Hogiu, S. Are Plasmonic Optical Biosensors Ready for Use in Point-of-Need Applications? Analyst 2020, 145, 364–384. [Google Scholar] [CrossRef] [PubMed]
- Huang, C.-B.; Huang, J.-S. Integrated Plasmonics Nanocircuits. In Plasmonic Materials and Metastructures; Elsevier, 2024; pp. 245–283. ISBN 978-0-323-85379-8. [Google Scholar]
- Mondal, M.; Semenov, A.; Ochoa, M.A.; Nitzan, A. Strong Coupling in Infrared Plasmonic Cavities. J. Phys. Chem. Lett. 2022, 13, 9673–9678. [Google Scholar] [CrossRef]
- Rastogi, R.; Dogbe Foli, E.A.; Vincent, R.; Adam, P.-M.; Krishnamoorthy, S. Engineering Electromagnetic Hot-Spots in Nanoparticle Cluster Arrays on Reflective Substrates for Highly Sensitive Detection of (Bio)Molecular Analytes. ACS Appl. Mater. Interfaces 2021, 13, 32653–32661. [Google Scholar] [CrossRef] [PubMed]
- Fan, M.; Andrade, G.F.S.; Brolo, A.G. A Review on the Fabrication of Substrates for Surface Enhanced Raman Spectroscopy and Their Applications in Analytical Chemistry. Analytica Chimica Acta 2011, 693, 7–25. [Google Scholar] [CrossRef]
- Russell, K.J.; Liu, T.-L.; Cui, S.; Hu, E.L. Large Spontaneous Emission Enhancement in Plasmonic Nanocavities. Nature Photon 2012, 6, 459–462. [Google Scholar] [CrossRef]
- Wertz, E.; Isaacoff, B.P.; Flynn, J.D.; Biteen, J.S. Single-Molecule Super-Resolution Microscopy Reveals How Light Couples to a Plasmonic Nanoantenna on the Nanometer Scale. Nano Lett. 2015, 15, 2662–2670. [Google Scholar] [CrossRef]
- Allsop, T.D.P.; Neal, R.; Wang, C.; Nagel, D.A.; Hine, A.V.; Culverhouse, P.; Ania Castañón, J.D.; Webb, D.J.; Scarano, S.; Minunni, M. An Ultra-Sensitive Aptasensor on Optical Fibre for the Direct Detection of Bisphenol A. Biosensors and Bioelectronics 2019, 135, 102–110. [Google Scholar] [CrossRef]
- Di Martino, G.; Turek, V.A.; Lombardi, A.; Szabó, I.; De Nijs, B.; Kuhn, A.; Rosta, E.; Baumberg, J.J. Tracking Nanoelectrochemistry Using Individual Plasmonic Nanocavities. Nano Lett. 2017, 17, 4840–4845. [Google Scholar] [CrossRef]
- Katzen, J.M.; Tserkezis, C.; Cai, Q.; Li, L.H.; Kim, J.M.; Lee, G.; Yi, G.-R.; Hendren, W.R.; Santos, E.J.G.; Bowman, R.M.; et al. Strong Coupling of Carbon Quantum Dots in Plasmonic Nanocavities. ACS Appl. Mater. Interfaces 2020, 12, 19866–19873. [Google Scholar] [CrossRef] [PubMed]
- Bitton, O.; Haran, G. Plasmonic Cavities and Individual Quantum Emitters in the Strong Coupling Limit. Acc. Chem. Res. 2022, 55, 1659–1668. [Google Scholar] [CrossRef]
- Gupta, S.N.; Bitton, O.; Neuman, T.; Esteban, R.; Chuntonov, L.; Aizpurua, J.; Haran, G. Complex Plasmon-Exciton Dynamics Revealed through Quantum Dot Light Emission in a Nanocavity. Nat Commun 2021, 12, 1310. [Google Scholar] [CrossRef] [PubMed]
- Lin, Q.-Y.; Li, Z.; Brown, K.A.; O’Brien, M.N.; Ross, M.B.; Zhou, Y.; Butun, S.; Chen, P.-C.; Schatz, G.C.; Dravid, V.P.; et al. Strong Coupling between Plasmonic Gap Modes and Photonic Lattice Modes in DNA-Assembled Gold Nanocube Arrays. Nano Lett. 2015, 15, 4699–4703. [Google Scholar] [CrossRef] [PubMed]
- Le, T.H.H.; Tanaka, T. Plasmonics–Nanofluidics Hydrid Metamaterial: An Ultrasensitive Platform for Infrared Absorption Spectroscopy and Quantitative Measurement of Molecules. ACS Nano 2017, 11, 9780–9788. [Google Scholar] [CrossRef]
- Dayal, G.; Morichika, I.; Ashihara, S. Vibrational Strong Coupling in Subwavelength Nanogap Patch Antenna at the Single Resonator Level. J. Phys. Chem. Lett. 2021, 12, 3171–3175. [Google Scholar] [CrossRef]
- Yankovich, A.B.; Munkhbat, B.; Baranov, D.G.; Cuadra, J.; Olsén, E.; Lourenço-Martins, H.; Tizei, L.H.G.; Kociak, M.; Olsson, E.; Shegai, T. Visualizing Spatial Variations of Plasmon–Exciton Polaritons at the Nanoscale Using Electron Microscopy. Nano Lett. 2019, 19, 8171–8181. [Google Scholar] [CrossRef]
- Kleemann, M.-E.; Chikkaraddy, R.; Alexeev, E.M.; Kos, D.; Carnegie, C.; Deacon, W.; De Pury, A.C.; Große, C.; De Nijs, B.; Mertens, J.; et al. Strong-Coupling of WSe2 in Ultra-Compact Plasmonic Nanocavities at Room Temperature. Nat Commun 2017, 8, 1296. [Google Scholar] [CrossRef]
- Del Real Mata, C.; Siavash Moakhar, R.; Hosseini, I.I.; Jalali, M.; Mahshid, S. A Nanostructured Microfluidic Device for Plasmon-Assisted Electrochemical Detection of Hydrogen Peroxide Released from Cancer Cells. Nanoscale 2021, 13, 14316–14329. [Google Scholar] [CrossRef] [PubMed]
- Chikkaraddy, R.; De Nijs, B.; Benz, F.; Barrow, S.J.; Scherman, O.A.; Rosta, E.; Demetriadou, A.; Fox, P.; Hess, O.; Baumberg, J.J. Single-Molecule Strong Coupling at Room Temperature in Plasmonic Nanocavities. Nature 2016, 535, 127–130. [Google Scholar] [CrossRef] [PubMed]
- Ahmadivand, A. Tunneling Plasmonics: Vacuum Rabi Oscillations in Carbon Nanotube Mediated Electromigrated Nanojunctions. J. Phys. Chem. C 2021, 125, 782–791. [Google Scholar] [CrossRef]
- Park, M.K.; Kee, J.S.; Quah, J.Y.; Netto, V.; Song, J.; Fang, Q.; La Fosse, E.M.; Lo, G.-Q. Label-Free Aptamer Sensor Based on Silicon Microring Resonators. Sensors and Actuators B: Chemical 2013, 176, 552–559. [Google Scholar] [CrossRef]
- Yu, D.; Humar, M.; Meserve, K.; Bailey, R.C.; Chormaic, S.N.; Vollmer, F. Whispering-Gallery-Mode Sensors for Biological and Physical Sensing. Nat Rev Methods Primers 2021, 1, 83. [Google Scholar] [CrossRef]
- Zhu, J.; Ozdemir, S.K.; Xiao, Y.-F.; Li, L.; He, L.; Chen, D.-R.; Yang, L. On-Chip Single Nanoparticle Detection and Sizing by Mode Splitting in an Ultrahigh-Q Microresonator. Nature Photon 2010, 4, 46–49. [Google Scholar] [CrossRef]
- Jiang, X.; Qavi, A.J.; Huang, S.H.; Yang, L. Whispering-Gallery Sensors. Matter 2020, 3, 371–392. [Google Scholar] [CrossRef] [PubMed]
- Cai, L.; Pan, J.; Zhao, Y.; Wang, J.; Xiao, S. Whispering Gallery Mode Optical Microresonators: Structures and Sensing Applications. Physica Status Solidi (a) 2020, 217, 1900825. [Google Scholar] [CrossRef]
- Ashadi Md Johari, M.; Hafiz Bin Jali, M.; Helmi Bin Mohd Yusof, H.; Rafis Bin Abdul Rahim, H.; Binti Ahmad, A.; Imran Mustafa Abdul Khudus, M.; Wadi Harun, S. Polyvinyl Alcohol Coating Microbottle Resonator on Whispering Gallery Modes for Ethanol Liquid Sensor. Optics & Laser Technology 2021, 143, 107379. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, M.; Zhu, N.; Han, B.; Liu, Y. Optical Fiber Hydrogen Sensor Based on Self-Assembled PDMS/Pd-WO3 Microbottle Resonator. Sensors and Actuators B: Chemical 2023, 375, 132866. [Google Scholar] [CrossRef]
- Mehta, S.; Nayak, B. N.; Singh, M. Engineering Porous Silicon-Based Plasmonic Microdisk Resonator for Highly Sensitive Methanol Sensing. IEEE Sensors J. 2024, 24, 12304–12311. [Google Scholar] [CrossRef]
- Guo, Z.; Qin, Y.; Chen, P.; Hu, J.; Zhou, Y.; Zhao, X.; Liu, Z.; Fei, Y.; Jiang, X.; Wu, X. Hyperboloid-Drum Microdisk Laser Biosensors for Ultrasensitive Detection of Human IgG. Small 2020, 16, 2000239. [Google Scholar] [CrossRef] [PubMed]
- Vollmer, F.; Arnold, S.; Keng, D. Single Virus Detection from the Reactive Shift of a Whispering-Gallery Mode. Proc. Natl. Acad. Sci. U.S.A. 2008, 105, 20701–20704. [Google Scholar] [CrossRef] [PubMed]
- Brice, I.; Grundsteins, K.; Draguns, K.; Atvars, A.; Alnis, J. Whispering Gallery Mode Resonator Temperature Compensation and Refractive Index Sensing in Glucose Droplets. Sensors 2021, 21, 7184. [Google Scholar] [CrossRef] [PubMed]
- Ozgur, E.; Roberts, K.E.; Ozgur, E.O.; Gin, A.N.; Bankhead, J.R.; Wang, Z.; Su, J. Ultrasensitive Detection of Human Chorionic Gonadotropin Using Frequency Locked Microtoroid Optical Resonators. Anal. Chem. 2019, 91, 11872–11878. [Google Scholar] [CrossRef]
- Wang, Z.; Mallik, A.K.; Wei, F.; Wang, Z.; Rout, A.; Wu, Q.; Semenova, Y. Enhancing the Thermo-Optic Tuning Performance of Whispering Gallery Modes in a Microcapillary Resonator Filled with Nematic Liquid Crystal. Optics Communications 2023, 537, 129442. [Google Scholar] [CrossRef]
- Wan, H.; Chen, J.; Wan, C.; Zhou, Q.; Wang, J.; Zhang, Z. Optofluidic Microcapillary Biosensor for Label-Free, Low Glucose Concentration Detection. Biomed. Opt. Express 2019, 10, 3929. [Google Scholar] [CrossRef]
- Schuler, S.; Muench, J.E.; Ruocco, A.; Balci, O.; Thourhout, D.V.; Sorianello, V.; Romagnoli, M.; Watanabe, K.; Taniguchi, T.; Goykhman, I.; et al. High-Responsivity Graphene Photodetectors Integrated on Silicon Microring Resonators. Nat Commun 2021, 12, 3733. [Google Scholar] [CrossRef]
- Bahadoran, M.; Seyfari, A.K.; Sanati, P.; Chua, L.S. Label Free Identification of the Different Status of Anemia Disease Using Optimized Double-Slot Cascaded Microring Resonator. Sci Rep 2022, 12, 5548. [Google Scholar] [CrossRef]
- Vollmer, F.; Braun, D.; Libchaber, A.; Khoshsima, M.; Teraoka, I.; Arnold, S. Protein Detection by Optical Shift of a Resonant Microcavity. Applied Physics Letters 2002, 80, 4057–4059. [Google Scholar] [CrossRef]
- Shao, L.; Jiang, X.; Yu, X.; Li, B.; Clements, W.R.; Vollmer, F.; Wang, W.; Xiao, Y.; Gong, Q. Detection of Single Nanoparticles and Lentiviruses Using Microcavity Resonance Broadening. Advanced Materials 2013, 25, 5616–5620. [Google Scholar] [CrossRef] [PubMed]
- Zhu, N.; Shi, B.; Guo, Y.; Han, B.; Zhang, Y. Polydimethylsiloxane Self-Assembled Whispering Gallery Mode Microbottle Resonator for Ethanol Sensing. Optical Materials 2020, 107, 110024. [Google Scholar] [CrossRef]
- Ghulinyan, M.; Navarro-Urrios, D.; Pitanti, A.; Lui, A.; Pucker, G.; Pavesi, L. Whispering-Gallery Modes and Light Emission from a Si-Nanocrystal-Based Single Microdisk Resonator. Opt. Express 2008, 16, 13218. [Google Scholar] [CrossRef] [PubMed]
- Lin, S.; Schonbrun, E.; Crozier, K. Optical Manipulation with Planar Silicon Microring Resonators. Nano Lett. 2010, 10, 2408–2411. [Google Scholar] [CrossRef] [PubMed]
- Liao, J.; Qavi, A.; Dong, R.; Yang, L. Packaging of Optofluidic Microbubble Resonator Sensors. In Proceedings of the Chemical, Biological, Radiological, Nuclear, and Explosives (CBRNE) Sensing XX; Guicheteau, J.A., Howle, C.R., Eds.; SPIE: Baltimore, United States, 17 May 2019; p. 46. [Google Scholar]
- Arnold, S.; Keng, D.; Shopova, S.I.; Holler, S.; Zurawsky, W.; Vollmer, F. Whispering Gallery Mode Carousel – a Photonic Mechanism for Enhanced Nanoparticle Detection in Biosensing. Opt. Express 2009, 17, 6230. [Google Scholar] [CrossRef] [PubMed]
- Riesen, N.; Peterkovic, Z.Q.; Guan, B.; François, A.; Lancaster, D.G.; Priest, C. Caged-Sphere Optofluidic Sensors: Whispering Gallery Resonators in Wicking Microfluidics. Sensors 2022, 22, 4135. [Google Scholar] [CrossRef] [PubMed]
- Bailey, R.C.; Washburn, A.L.; Qavi, A.J.; Iqbal, M.; Gleeson, M.; Tybor, F.; Gunn, L.C. A Robust Silicon Photonic Platform for Multiparameter Biological Analysis. In Proceedings of the Silicon Photonics IV; SPIE, 17 February 2009; Vol. 7220, pp. 147–152. [Google Scholar]
- Chen, Y.; Yin, Y.; Ma, L.; Schmidt, O.G. Recent Progress on Optoplasmonic Whispering-Gallery-Mode Microcavities. Advanced Optical Materials 2021, 9, 2100143. [Google Scholar] [CrossRef]
- Kang, T.Y.; Lee, W.; Ahn, H.; Shin, D.-M.; Kim, C.-S.; Oh, J.-W.; Kim, D.; Kim, K. Plasmon-Coupled Whispering Gallery Modes on Nanodisk Arrays for Signal Enhancements. Sci Rep 2017, 7, 11737. [Google Scholar] [CrossRef] [PubMed]
- Willets, K.A.; Van Duyne, R.P. Localized Surface Plasmon Resonance Spectroscopy and Sensing. Annu. Rev. Phys. Chem. 2007, 58, 267–297. [Google Scholar] [CrossRef]
- Yu, X.-C.; Tang, S.-J.; Liu, W.; Xu, Y.; Gong, Q.; Chen, Y.-L.; Xiao, Y.-F. Single-Molecule Optofluidic Microsensor with Interface Whispering Gallery Modes. Proc. Natl. Acad. Sci. U.S.A. 2022, 119, e2108678119. [Google Scholar] [CrossRef]
- Qavi, A.J.; Bailey, R.C. Multiplexed Detection and Label-Free Quantitation of MicroRNAs Using Arrays of Silicon Photonic Microring Resonators. Angew Chem Int Ed 2010, 49, 4608–4611. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Sanchez, M.M.; Yin, Y.; Herzer, R.; Ma, L.; Schmidt, O.G. Silicon-Based Integrated Label-Free Optofluidic Biosensors: Latest Advances and Roadmap. Adv Materials Technologies 2020, 5, 1901138. [Google Scholar] [CrossRef]
- Kim, Y.; Lee, H. On-Chip Label-Free Biosensing Based on Active Whispering Gallery Mode Resonators Pumped by a Light-Emitting Diode. Opt. Express 2019, 27, 34405. [Google Scholar] [CrossRef] [PubMed]
- Duan, R.; Hao, X.; Li, Y.; Li, H. Detection of Acetylcholinesterase and Its Inhibitors by Liquid Crystal Biosensor Based on Whispering Gallery Mode. Sensors and Actuators B: Chemical 2020, 308, 127672. [Google Scholar] [CrossRef]
- Mudumba, S.; De Alba, S.; Romero, R.; Cherwien, C.; Wu, A.; Wang, J.; Gleeson, M.A.; Iqbal, M.; Burlingame, R.W. Photonic Ring Resonance Is a Versatile Platform for Performing Multiplex Immunoassays in Real Time. Journal of Immunological Methods 2017, 448, 34–43. [Google Scholar] [CrossRef] [PubMed]
- Soni, V.; Chang, C.-W.; Xu, X.; Wang, C.; Yan, H.; D Agati, M.; Tu, L.-W.; Chen, Q.Y.; Tian, H.; Chen, R.T. Portable Automatic Microring Resonator System Using a Subwavelength Grating Metamaterial Waveguide for High-Sensitivity Real-Time Optical-Biosensing Applications. IEEE Trans. Biomed. Eng. 2021, 68, 1894–1902. [Google Scholar] [CrossRef] [PubMed]
- Meserve, K.; Qavi, A.J.; Aman, M.J.; Vu, H.; Zeitlin, L.; Dye, J.M.; Froude, J.W.; Leung, D.W.; Yang, L.; Holtsberg, F.W.; et al. Detection of Biomarkers for Filoviral Infection with a Silicon Photonic Resonator Platform. STAR Protocols 2022, 3, 101719. [Google Scholar] [CrossRef]
- Balac, S. WGMode : A Matlab Toolbox for Whispering Gallery Modes Volume Computation in Spherical Optical Micro-Resonators. Computer Physics Communications 2019, 243, 121–134. [Google Scholar] [CrossRef]
- Khani, S.; Hayati, M. An Ultra-High Sensitive Plasmonic Refractive Index Sensor Using an Elliptical Resonator and MIM Waveguide. Superlattices and Microstructures 2021, 156, 106970. [Google Scholar] [CrossRef]
- Butt, M.A.; Khonina, S.N.; Kazanskiy, N.L. Highly Sensitive Refractive Index Sensor Based on Hybrid Plasmonic Waveguide Microring Resonator. Waves in Random and Complex Media 2020, 30, 292–299. [Google Scholar] [CrossRef]
- Yu, D.; Vollmer, F. Microscale Whispering-Gallery-Mode Light Sources with Lattice-Confined Atoms. Sci Rep 2021, 11, 13899. [Google Scholar] [CrossRef] [PubMed]
- Shen, H.; Zhao, C.Y. On-Chip Fluid Information Detection Based on Micro-Ring Optical Frequency Comb Technology and Machine Learning 2024.
- Jacobson, L.D.; Bochevarov, A.D.; Watson, M.A.; Hughes, T.F.; Rinaldo, D.; Ehrlich, S.; Steinbrecher, T.B.; Vaitheeswaran, S.; Philipp, D.M.; Halls, M.D.; et al. Automated Transition State Search and Its Application to Diverse Types of Organic Reactions. J. Chem. Theory Comput. 2017, 13, 5780–5797. [Google Scholar] [CrossRef]
- Behler, J. Perspective: Machine Learning Potentials for Atomistic Simulations. The Journal of Chemical Physics 2016, 145, 170901. [Google Scholar] [CrossRef] [PubMed]
- Munkhbat, B.; Wersäll, M.; Baranov, D.G.; Antosiewicz, T.J.; Shegai, T. Suppression of Photo-Oxidation of Organic Chromophores by Strong Coupling to Plasmonic Nanoantennas. Sci. Adv. 2018, 4, eaas9552. [Google Scholar] [CrossRef] [PubMed]
- Hutchison, J.A.; Schwartz, T.; Genet, C.; Devaux, E.; Ebbesen, T.W. Modifying Chemical Landscapes by Coupling to Vacuum Fields. Angew Chem Int Ed 2012, 51, 1592–1596. [Google Scholar] [CrossRef] [PubMed]
- George, J.; Wang, S.; Chervy, T.; Canaguier-Durand, A.; Schaeffer, G.; Lehn, J.-M.; Hutchison, J.A.; Genet, C.; Ebbesen, T.W. Ultra-Strong Coupling of Molecular Materials: Spectroscopy and Dynamics. Faraday Discuss. 2015, 178, 281–294. [Google Scholar] [CrossRef]
- George, J.; Chervy, T.; Shalabney, A.; Devaux, E.; Hiura, H.; Genet, C.; Ebbesen, T.W. Multiple Rabi Splittings under Ultrastrong Vibrational Coupling. Phys. Rev. Lett. 2016, 117, 153601. [Google Scholar] [CrossRef]
- Hirai, K.; Takeda, R.; Hutchison, J.A.; Uji-i, H. Modulation of Prins Cyclization by Vibrational Strong Coupling. Angew Chem Int Ed 2020, 59, 5332–5335. [Google Scholar] [CrossRef]
- Ahn, W.; Triana, J.F.; Recabal, F.; Herrera, F.; Simpkins, B.S. Modification of Ground-State Chemical Reactivity via Light–Matter Coherence in Infrared Cavities. Science 2023, 380, 1165–1168. [Google Scholar] [CrossRef]
- Kadyan, A.; Shaji, A.; George, J. Boosting Self-Interaction of Molecular Vibrations under Ultrastrong Coupling Condition. J. Phys. Chem. Lett. 2021, 12, 4313–4318. [Google Scholar] [CrossRef]
- Lidzey, D.G.; Bradley, D.D.C.; Virgili, T.; Armitage, A.; Skolnick, M.S.; Walker, S. Room Temperature Polariton Emission from Strongly Coupled Organic Semiconductor Microcavities. Phys. Rev. Lett. 1999, 82, 3316–3319. [Google Scholar] [CrossRef]
- Holmes, R.J.; Forrest, S.R. Strong Exciton-Photon Coupling and Exciton Hybridization in a Thermally Evaporated Polycrystalline Film of an Organic Small Molecule. Phys. Rev. Lett. 2004, 93, 186404. [Google Scholar] [CrossRef] [PubMed]
- Kéna-Cohen, S.; Davanço, M.; Forrest, S.R. Strong Exciton-Photon Coupling in an Organic Single Crystal Microcavity. Phys. Rev. Lett. 2008, 101, 116401. [Google Scholar] [CrossRef] [PubMed]
- Tropf, L.; Dietrich, C.P.; Herbst, S.; Kanibolotsky, A.L.; Skabara, P.J.; Würthner, F.; Samuel, I.D.W.; Gather, M.C.; Höfling, S. Influence of Optical Material Properties on Strong Coupling in Organic Semiconductor Based Microcavities. Applied Physics Letters 2017, 110, 153302. [Google Scholar] [CrossRef]
- Graf, A.; Tropf, L.; Zakharko, Y.; Zaumseil, J.; Gather, M.C. Near-Infrared Exciton-Polaritons in Strongly Coupled Single-Walled Carbon Nanotube Microcavities. Nat Commun 2016, 7, 13078. [Google Scholar] [CrossRef] [PubMed]
- Dietrich, C.P.; Steude, A.; Schubert, M.; Ohmer, J.; Fischer, U.; Höfling, S.; Gather, M.C. Strong Coupling in Fully Tunable Microcavities Filled with Biologically Produced Fluorescent Proteins. Advanced Optical Materials 2017, 5, 1600659. [Google Scholar] [CrossRef]
- Coles, D.M.; Yang, Y.; Wang, Y.; Grant, R.T.; Taylor, R.A.; Saikin, S.K.; Aspuru-Guzik, A.; Lidzey, D.G.; Tang, J.K.-H.; Smith, J.M. Strong Coupling between Chlorosomes of Photosynthetic Bacteria and a Confined Optical Cavity Mode. Nat Commun 2014, 5, 5561. [Google Scholar] [CrossRef] [PubMed]
- He, Z.; Li, F.; Zuo, P.; Xu, C.; He, W.; He, J.; Zhou, Y.; Zhang, Q.; Chen, K.; Huang, H.; et al. Strong Coupling in a Hybrid System of Silver Nanoparticles and J-Aggregates at Room Temperature. J. Phys. Chem. C 2022, 126, 17141–17151. [Google Scholar] [CrossRef]
- Krivenkov, V.; Samokhvalov, P.; Nabiev, I.; Rakovich, Y.P. pH-Sensing Platform Based on Light–Matter Coupling in Colloidal Complexes of Silver Nanoplates and J-Aggregates. J. Phys. Chem. C 2021, 125, 1972–1979. [Google Scholar] [CrossRef]
- Melnikau, D.; Samokhvalov, P.; Sánchez-Iglesias, A.; Grzelczak, M.; Nabiev, I.; Rakovich, Y.P. Strong Coupling Effects in a Plexciton System of Gold Nanostars and J-Aggregates. Journal of Luminescence 2022, 242, 118557. [Google Scholar] [CrossRef]
- Schäfer, C.; Hultmark, S.; Yang, Y.; Müller, C.; Börjesson, K. Room Temperature Dye Glasses: A Guideline Toward the Fabrication of Amorphous Dye Films with Monomeric Absorption and Emission. Chem. Mater. 2022, 34, 9294–9302. [Google Scholar] [CrossRef]
- Tang, J.; Zhang, J.; Lv, Y.; Wang, H.; Xu, F.F.; Zhang, C.; Sun, L.; Yao, J.; Zhao, Y.S. Room Temperature Exciton–Polariton Bose–Einstein Condensation in Organic Single-Crystal Microribbon Cavities. Nat Commun 2021, 12, 3265. [Google Scholar] [CrossRef]
- Ren, J.; Liao, Q.; Huang, H.; Li, Y.; Gao, T.; Ma, X.; Schumacher, S.; Yao, J.; Bai, S.; Fu, H. Efficient Bosonic Condensation of Exciton Polaritons in an H-Aggregate Organic Single-Crystal Microcavity. Nano Lett. 2020, 20, 7550–7557. [Google Scholar] [CrossRef]
- Mischok, A.; Lüttgens, J.; Berger, F.; Hillebrandt, S.; Tenopala-Carmona, F.; Kwon, S.; Murawski, C.; Siegmund, B.; Zaumseil, J.; Gather, M.C. Spectroscopic Near-Infrared Photodetectors Enabled by Strong Light–Matter Coupling in (6,5) Single-Walled Carbon Nanotubes. The Journal of Chemical Physics 2020, 153, 201104. [Google Scholar] [CrossRef] [PubMed]
- Shahnazaryan, V.A.; Saroka, V.A.; Shelykh, I.A.; Barnes, W.L.; Portnoi, M.E. Strong Light–Matter Coupling in Carbon Nanotubes as a Route to Exciton Brightening. ACS Photonics 2019, 6, 904–914. [Google Scholar] [CrossRef]
- Lasave, L.C.; Urteaga, R.; Koropecki, R.R.; Gonzalez, V.D.; Arce, R.D. Real-Time Study of Protein Adsorption Kinetics in Porous Silicon. Colloids and Surfaces B: Biointerfaces 2013, 111, 354–359. [Google Scholar] [CrossRef] [PubMed]
- Liang, L.; Zheng, P.; Zhang, C.; Barman, I. A Programmable DNA-Silicification-Based Nanocavity for Single-Molecule Plasmonic Sensing. Advanced Materials 2021, 33, 2005133. [Google Scholar] [CrossRef] [PubMed]
- Allison, G.; Sana, A.K.; Ogawa, Y.; Kato, H.; Ueno, K.; Misawa, H.; Hayashi, K.; Suzuki, H. A Fabry-Pérot Cavity Coupled Surface Plasmon Photodiode for Electrical Biomolecular Sensing. Nat Commun 2021, 12, 6483. [Google Scholar] [CrossRef] [PubMed]
- Thomas, P.A.; Menghrajani, K.S.; Barnes, W.L. All-Optical Control of Phase Singularities Using Strong Light-Matter Coupling. Nat Commun 2022, 13, 1809. [Google Scholar] [CrossRef]
- Wang, Y.; Zeng, S.; Crunteanu, A.; Xie, Z.; Humbert, G.; Ma, L.; Wei, Y.; Brunel, A.; Bessette, B.; Orlianges, J.-C.; et al. Targeted Sub-Attomole Cancer Biomarker Detection Based on Phase Singularity 2D Nanomaterial-Enhanced Plasmonic Biosensor. Nano-Micro Lett. 2021, 13, 96. [Google Scholar] [CrossRef]
- Sreekanth, K.V.; Sreejith, S.; Han, S.; Mishra, A.; Chen, X.; Sun, H.; Lim, C.T.; Singh, R. Biosensing with the Singular Phase of an Ultrathin Metal-Dielectric Nanophotonic Cavity. Nat Commun 2018, 9, 369. [Google Scholar] [CrossRef] [PubMed]
- Ermolaev, G.; Voronin, K.; Baranov, D.G.; Kravets, V.; Tselikov, G.; Stebunov, Y.; Yakubovsky, D.; Novikov, S.; Vyshnevyy, A.; Mazitov, A.; et al. Topological Phase Singularities in Atomically Thin High-Refractive-Index Materials. Nat Commun 2022, 13, 2049. [Google Scholar] [CrossRef] [PubMed]
- Wu, F.; Thomas, P.A.; Kravets, V.G.; Arola, H.O.; Soikkeli, M.; Iljin, K.; Kim, G.; Kim, M.; Shin, H.S.; Andreeva, D.V.; et al. Layered Material Platform for Surface Plasmon Resonance Biosensing. Sci Rep 2019, 9, 20286. [Google Scholar] [CrossRef] [PubMed]
- Jain, S.; Choudhary, K.; Kumar, S. Photonic Crystal Fiber-Based SPR Sensor for Broad Range of Refractive Index Sensing Applications. Optical Fiber Technology 2022, 73, 103030. [Google Scholar] [CrossRef]
- Chaudhary, V.S.; Kumar, D.; Mishra, G.P.; Sharma, S.; Kumar, S. Plasmonic Biosensor With Gold and Titanium Dioxide Immobilized on Photonic Crystal Fiber for Blood Composition Detection. IEEE Sensors J. 2022, 22, 8474–8481. [Google Scholar] [CrossRef]
- Wang, W.; Zhang, J.; Ye, P.; Liu, W.; Mao, W.; Shi, Z.; Cui, Q.; Wang, M.; Zhu, G.; Xu, C. Protein Aggregation Monitoring in Microdisk Optofluidic Sensor through Microcavity Enhanced Raman Scattering. Colloids and Surfaces A: Physicochemical and Engineering Aspects 2023, 679, 132561. [Google Scholar] [CrossRef]
- Vázquez-Guardado, A.; Smith, A.; Wilson, W.; Ortega, J.; Perez, J.M.; Chanda, D. Hybrid Cavity-Coupled Plasmonic Biosensors for Low Concentration, Label-Free and Selective Biomolecular Detection. Opt. Express 2016, 24, 25785. [Google Scholar] [CrossRef] [PubMed]
- Vázquez-Guardado, A.; Mehta, F.; Jimenez, B.; Biswas, A.; Ray, K.; Baksh, A.; Lee, S.; Saraf, N.; Seal, S.; Chanda, D. DNA-Modified Plasmonic Sensor for the Direct Detection of Virus Biomarkers from the Blood. Nano Lett. 2021, 21, 7505–7511. [Google Scholar] [CrossRef] [PubMed]
- Anderson, M.; O’Brien, E.; Grayek, E.; Hermansen, J.; Hunt, H. The Detection of Helicobacter Hepaticus Using Whispering-Gallery Mode Microcavity Optical Sensors. Biosensors 2015, 5, 562–576. [Google Scholar] [CrossRef]
- Wilson, K.A.; Finch, C.A.; Anderson, P.; Vollmer, F.; Hickman, J.J. Whispering Gallery Mode Biosensor Quantification of Fibronectin Adsorption Kinetics onto Alkylsilane Monolayers and Interpretation of Resultant Cellular Response. Biomaterials 2012, 33, 225–236. [Google Scholar] [CrossRef]
- Frustaci, S.; Vollmer, F. Whispering-Gallery Mode (WGM) Sensors: Review of Established and WGM-Based Techniques to Study Protein Conformational Dynamics. Current Opinion in Chemical Biology 2019, 51, 66–73. [Google Scholar] [CrossRef] [PubMed]
- Granizo, E.; Knysh, A.; Sokolov, P.; Samokhvalov, P.; Nabiev, I. Polaritonic Photocatalysis and Polariton-Driven Control of Energy Relaxation Pathways in a Tunable Microcavity. Phys. Atom. Nuclei 2023, 86, 2454–2458. [Google Scholar] [CrossRef]
- Thomas, P.A.; Menghrajani, K.S.; Barnes, W.L. Cavity-Free Ultrastrong Light-Matter Coupling. J. Phys. Chem. Lett. 2021, 12, 6914–6918. [Google Scholar] [CrossRef] [PubMed]
- Kaeek, M.; Damari, R.; Roth, M.; Fleischer, S.; Schwartz, T. Strong Coupling in a Self-Coupled Terahertz Photonic Crystal. ACS Photonics 2021, 8, 1881–1888. [Google Scholar] [CrossRef]
- Munkhbat, B.; Baranov, D.G.; Stührenberg, M.; Wersäll, M.; Bisht, A.; Shegai, T. Self-Hybridized Exciton-Polaritons in Multilayers of Transition Metal Dichalcogenides for Efficient Light Absorption. ACS Photonics 2019, 6, 139–147. [Google Scholar] [CrossRef]
- An, G.; Hao, X.; Li, S.; Yan, X.; Zhang, X. D-Shaped Photonic Crystal Fiber Refractive Index Sensor Based on Surface Plasmon Resonance. Appl. Opt. 2017, 56, 6988. [Google Scholar] [CrossRef] [PubMed]
- Gao, R.; Ko, J.; Cha, K.; Ho Jeon, J.; Rhie, G.; Choi, J.; deMello, A.J.; Choo, J. Fast and Sensitive Detection of an Anthrax Biomarker Using SERS-Based Solenoid Microfluidic Sensor. Biosensors and Bioelectronics 2015, 72, 230–236. [Google Scholar] [CrossRef] [PubMed]
- Arul, R.; Grys, D.-B.; Chikkaraddy, R.; Mueller, N.S.; Xomalis, A.; Miele, E.; Euser, T.G.; Baumberg, J.J. Giant Mid-IR Resonant Coupling to Molecular Vibrations in Sub-Nm Gaps of Plasmonic Multilayer Metafilms. Light Sci Appl 2022, 11, 281. [Google Scholar] [CrossRef] [PubMed]
- Fu, L.; Lu, Q.; Liu, X.; Chen, X.; Wu, X.; Xie, S. Combining Whispering Gallery Mode Optofluidic Microbubble Resonator Sensor with GR-5 DNAzyme for Ultra-Sensitive Lead Ion Detection. Talanta 2020, 213, 120815. [Google Scholar] [CrossRef]
- Li, Z.; Zhu, C.; Guo, Z.; Wang, B.; Wu, X.; Fei, Y. Highly Sensitive Label-Free Detection of Small Molecules with an Optofluidic Microbubble Resonator. Micromachines 2018, 9, 274. [Google Scholar] [CrossRef]
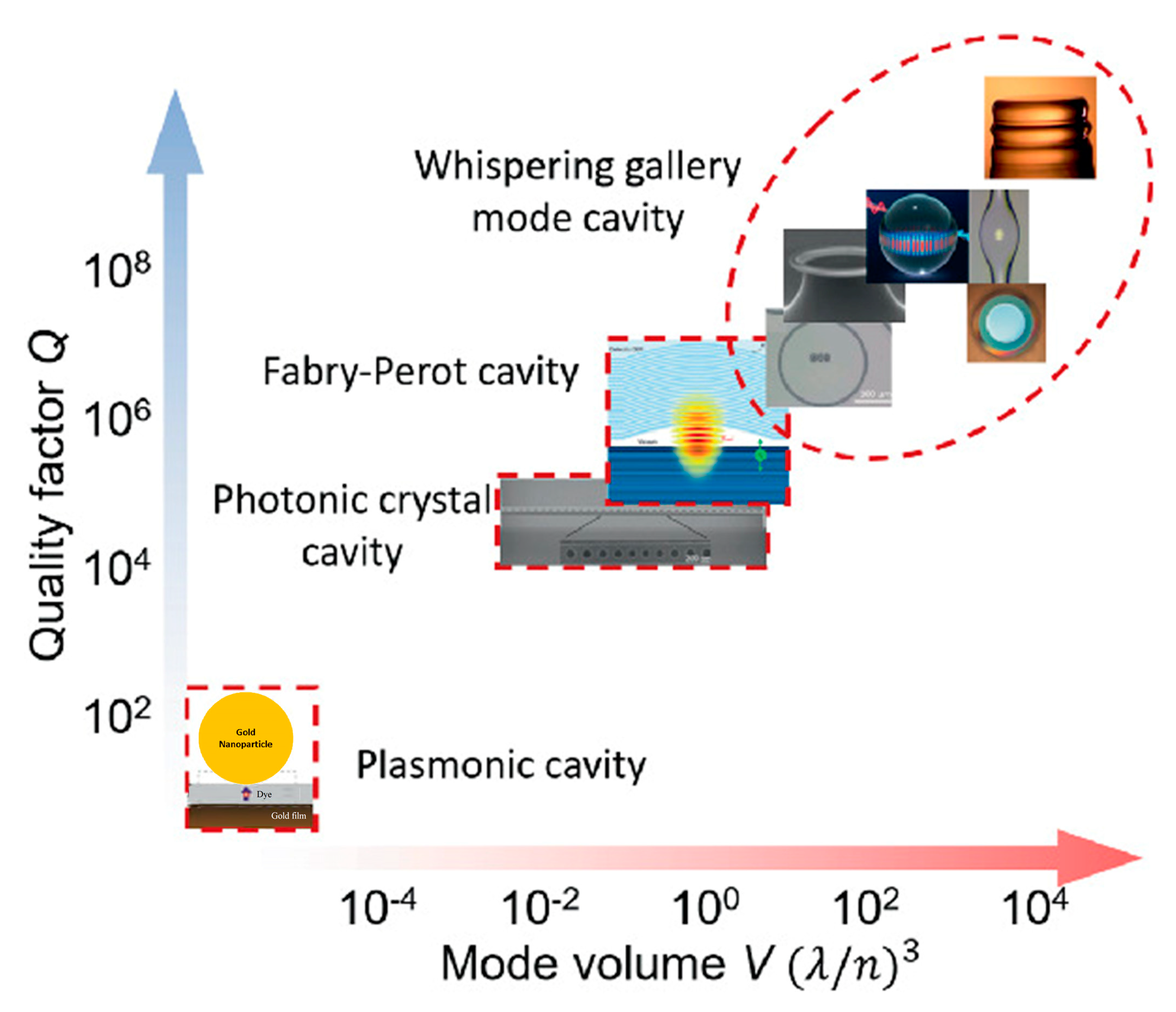

| Whispering-gallery mode microcavity | Scheme | Fabrication method | Ref. | |
|---|---|---|---|---|
| Microsphere | 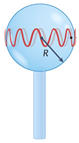 |
* | Heating of an optical fiber tip with CO2 laser, arc discharge, H2 flame | [140] |
| Microbubble | 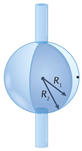 |
* | Local heating of a capillary with CO2 laser, arc discharge, H2 flame, while applying internal aerostatic pressure to inflate the SiO2 | [140] |
| Microbottle | 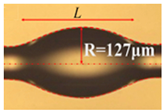 |
** | - Heating and stretching two regions into thinner ones. - Heating and softening an optical fiber and squeezing it along the axis to build up material in the pinched region |
[157] |
| Microdisks |  |
† | Lithographically forming disks by wet and dry chemical etching | [158] |
| Microrings |  |
‡ | Photolithography and etching, without laser reflow or other high-temperature process | [159] |
| Microtoroid |  |
* | Photolithography to form the disk, etching with HF for thermal oxide layer. CO2 laser to melt the silica at the edge | [140] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





