Version 1
: Received: 5 August 2024 / Approved: 13 August 2024 / Online: 14 August 2024 (03:05:04 CEST)
How to cite:
Xie, M.; Wang, Q.-W.; Zhang, Y. The BiCG Algorithm for Solving the Minimal Frobenius Norm Solution of Generalized Sylvester Tensor Equation over the Quaternions. Preprints2024, 2024080929. https://doi.org/10.20944/preprints202408.0929.v1
Xie, M.; Wang, Q.-W.; Zhang, Y. The BiCG Algorithm for Solving the Minimal Frobenius Norm Solution of Generalized Sylvester Tensor Equation over the Quaternions. Preprints 2024, 2024080929. https://doi.org/10.20944/preprints202408.0929.v1
Xie, M.; Wang, Q.-W.; Zhang, Y. The BiCG Algorithm for Solving the Minimal Frobenius Norm Solution of Generalized Sylvester Tensor Equation over the Quaternions. Preprints2024, 2024080929. https://doi.org/10.20944/preprints202408.0929.v1
APA Style
Xie, M., Wang, Q. W., & Zhang, Y. (2024). The BiCG Algorithm for Solving the Minimal Frobenius Norm Solution of Generalized Sylvester Tensor Equation over the Quaternions. Preprints. https://doi.org/10.20944/preprints202408.0929.v1
Chicago/Turabian Style
Xie, M., Qing-Wen Wang and Yang Zhang. 2024 "The BiCG Algorithm for Solving the Minimal Frobenius Norm Solution of Generalized Sylvester Tensor Equation over the Quaternions" Preprints. https://doi.org/10.20944/preprints202408.0929.v1
Abstract
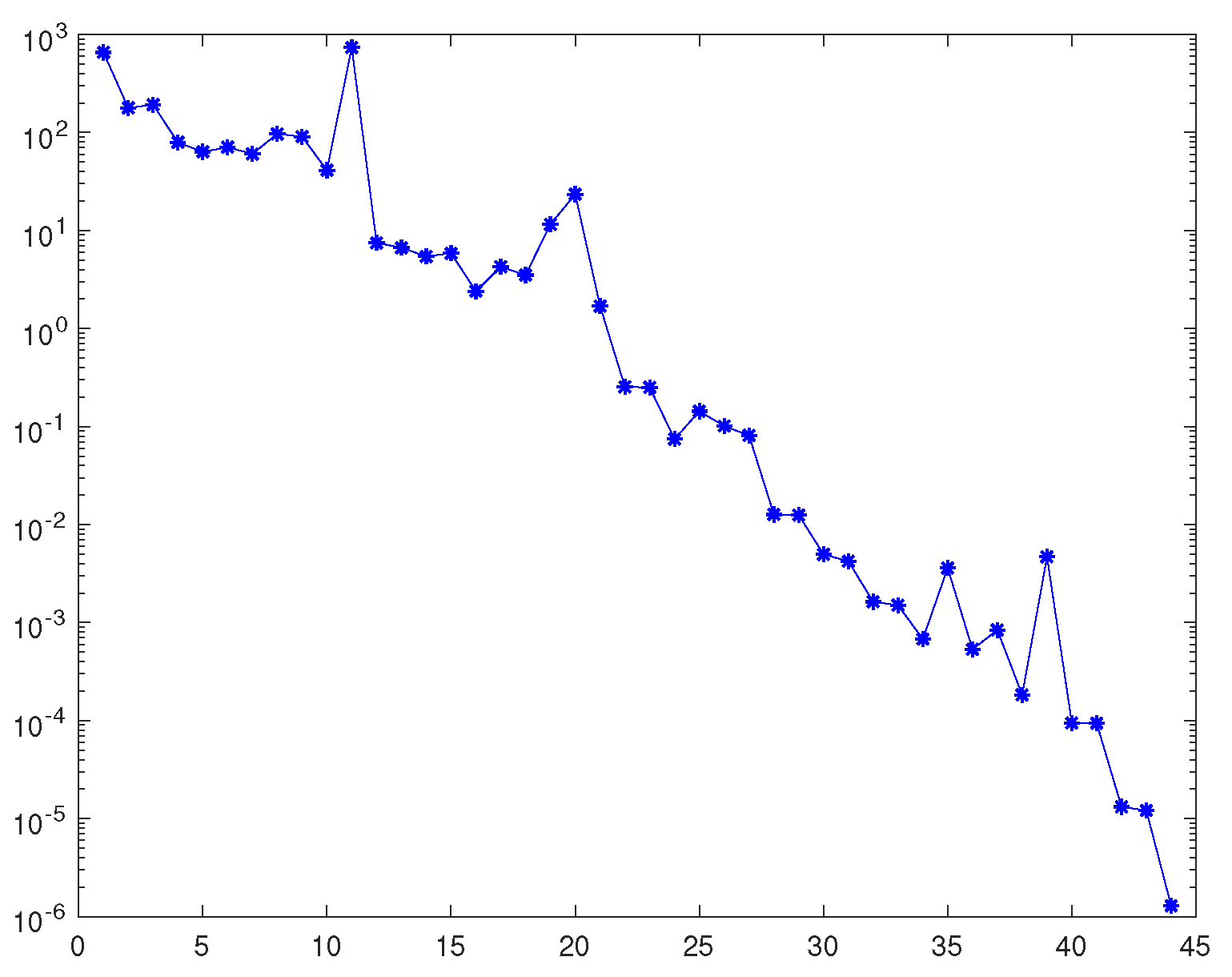
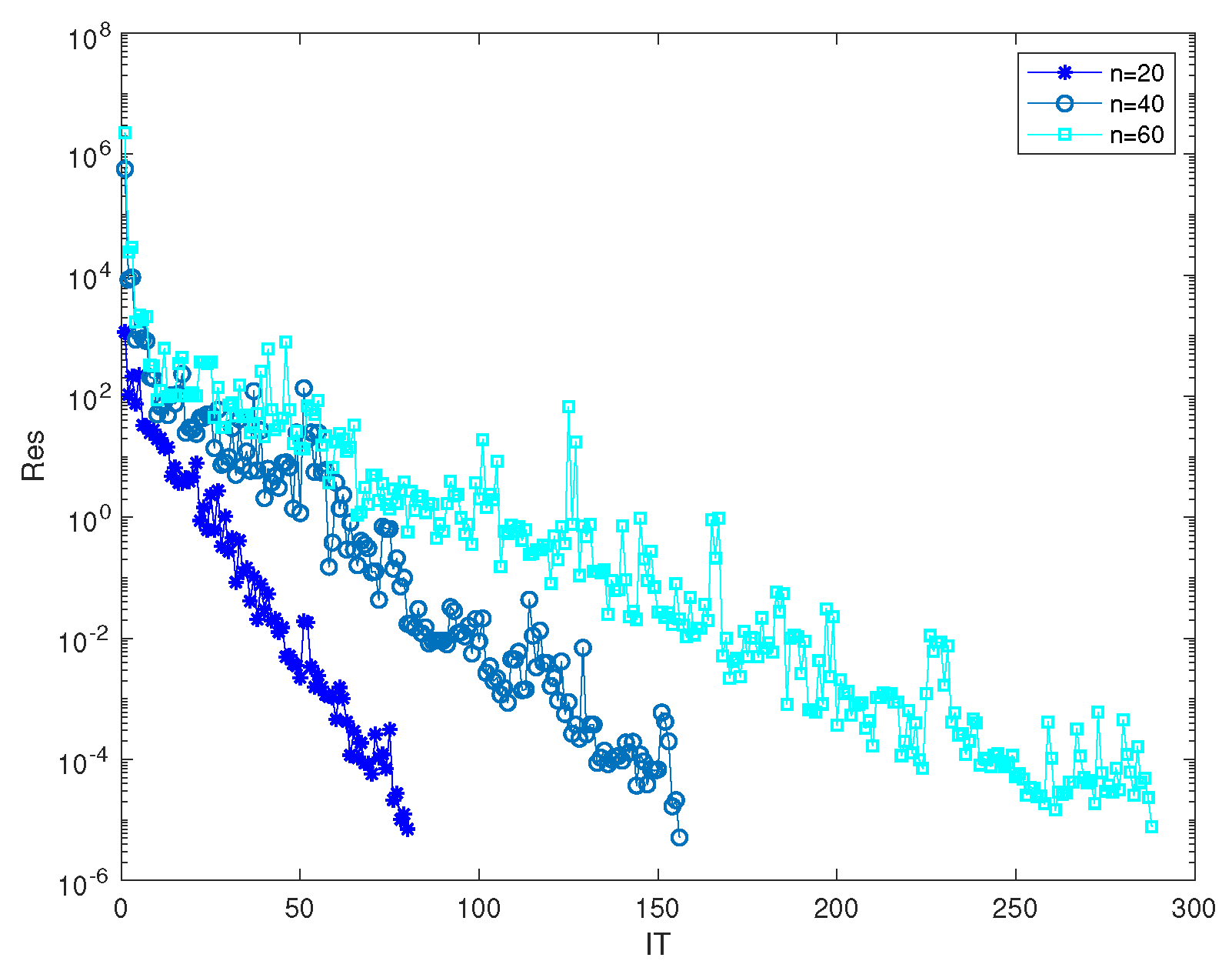
In this paper, we develop an effective iterative algorithm to solve a generalized Sylvester tensor equation over quaternions which includes several well-studied matrix/tensor equations as special cases. We discuss the convergence of this algorithm within a finite number of iterations, assuming negligible round-off errors for any initial tensor. Moreover, we demonstrate the unique minimal Frobenius norm solution achievable by selecting specific types of initial tensors. Additionally, numerical examples are presented to illustrate the practicality and validity of our proposed algorithm. These examples include demonstrating the algorithm’s effectiveness in addressing three-dimensional microscopic heat transport and color video restoration problems.
Keywords
Quaternion tensor; Sylvester tensor equation; Iterative algorithm; Color video restoration
Subject
Physical Sciences, Mathematical Physics
Copyright:
This is an open access article distributed under the Creative Commons Attribution License which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
