Preprint
Article
Classification Scheme for the Three-Points Dubins Problem
Altmetrics
Downloads
92
Views
23
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
12 August 2024
Posted:
13 August 2024
You are already at the latest version
Alerts
Abstract
This paper proposes an optimal path type classification scheme for the three-point Dubins problem. It allows to directly extract the shortest path type from a Dubins set, evaluating only the relative initial and final configurations with the via point position using a suitable partition of the Cartesian plane. Two alternative approaches are proposed to address the problem: an analytical approach and a heuristic one. The latter was revealed to be much faster from a computational point of view. The proposed classification logic makes the path planning for the three-point Dubins problem much more effective and suitable for real-time applications. Numerical examples are provided to show the efficiency of the proposed strategy.
Keywords:
Subject: Engineering - Control and Systems Engineering
1. Introduction
The technological advances of the last years opened up astonishing possibilities for research. From virtual reality to artificial intelligence and self-driving cars, the promise of a tomorrow’s world where such technologies permeate into human society is exciting, and it drives the research in these fields with a renewed and powerful thrust. Among the most fascinating topics, the goal of designing mobile devices that autonomously are able to safely handle human mobility is advancing every day to reality.
In this latter scenario, and other similar ones, a central theme is the autonomy of a device in decision-making, ensuring that robots are able to find feasible paths in various environments, avoiding obstacles and minimizing travel time or energy consumption. For this reason, the challenging problem of safe and autonomous navigation surged as a central topic in robotics and autonomous systems. Overall, path planning is a foundational aspect of robotic vehicle that impacts the performance, safety, and effectiveness of robotic systems across a wide range of applications [1]. One key aspect of path planning is to produce feasible reference paths for the robot, namely paths that are compliant with the robot kinematics, so that it is able to track them without jumps or errors. A fundamental kinematic model that has been extensively explored in path planning applications is the `Dubins vehicles’ [2]. Basically, it refers to a point moving in the plane with constant forward speed and bounded curvature, while Dubins path refers to the shortest path between two poses of a Dubins vehicle [2]. It is well suited to represent the movement of vehicles that do not require hard braking, slowdown or stop; common examples are airplanes or marine crafts. For these reasons, since the milestone contribution by Dubins [3], the Dubins vehicle has been constantly studied over the years, as witnessed by the works in [4,5,6,7]. In these works, Dubins paths are obtained through necessary optimality conditions derived by exploiting the theoretical framework based on the Pontryagin’s Maximum Principle. However, this approach results in solutions that are computationally demanding and not readily applicable for real-time applications. A significant contribution to overcome this issue is the work in [8], where the computational complexity is reduced by selecting the optimal path type based only on the initial and final pose (namely, position and orientation) in the Cartesian plane. Other research lines emerged over the years are related to the generalizations of the Dubins problem through N points, as the Dubins Traveling Salesman Problem (DTSP) [9,10,11,12].
Several contributions on this subject [13] showed that when the order of via-points is fixed, the solution of the DTSP can be decomposed at each step in sub-problems known as three-Point Dubins Problem, namely the path planning problem for a Dubins vehicle with an intermediate via point [14,15,16].
The three points Dubins problem leads to efficient navigation solutions in different application domains including air, ground and marine environments. In the field of Unmanned Aerial Vehicles (UAVs), solving the 3PDP is essential for optimizing flight paths when navigating through constrained environments or for executing complex missions. This can be particularly important in surveillance, reconnaissance, and delivery operations [17]. Even drones used in precision agriculture often need to navigate around specific via points. In [18], for example, a variation of a Traveling Salesman Problem (TSP) solver, that is an extension of the 3PDP, is proposed to investigate optimal trajectories in order to visit a specific number of plants that require intervention. Aircraft, especially those with limited maneuverability, may encounter the 3PDP during specific flight scenarios [19], such as air-to-air refueling or navigating around airspace restrictions. Efficient path planning is crucial for ensuring safe and precise movements in these situations.
In scenarios where search and rescue missions involve aerial or ground vehicles with Dubins motion constraints, solving the 3PDP with fast algorithms can be a key tool for safe and length-optimal reference path generation. Indeed, these applications often require real-time path planning to reach a target location with an intermediate point, optimizing the trajectory for quick and effective response [20]. Moreover, Dubins vehicles, such as autonomous cars and ground robots, encounter the 3PDP when planning paths that involve navigating around obstacles or following specific via point. Solving this problem is vital for ensuring safe and efficient transportation in urban environments or other constrained spaces [21,22]. In automated warehouses, multiple robots may need to navigate through narrow aisles and around obstacles while efficiently reaching intermediate points for picking or restocking purposes. Solving the 3PDP is relevant basis for optimizing the movement of robotic vehicles in such environments [23].
Also Autonomous underwater vehicles (AUVs) face challenges in path planning, especially when they need to travel from one point to another with an intermediate via point. The 3PDP and its extension Multiple Traveling Sales Person (MTSP) solution can be applied to optimize their trajectories and conserve energy during underwater missions [24].
Summarizing, the significance of solving the Three Points Dubins Problem lies in its potential to enhance the performance, safety, and efficiency of various autonomous systems operating in diverse real-world applications. This has motivated recent researches on developing increasingly faster and more efficient methods to address the 3PDP [13,14,25]. The solution proposed in [13] is based on inversive geometry. Two methods are presented, an “Approximate Method” that, while computationally efficient, provides an approximate optimal heading at the via-point, and an “Iterative Method” that recursively converges to the exact heading by iterative corrections, thus achieving greater accuracy at the cost of increased computational resources. A significant contribution is found in the work of [14], which utilizes the Pontryagin principle and optimality criteria. This research offers a solution encompassing all possible cases. The method requires solving polynomial equations, ensuring an accurate/exact solution by construction. A promising solution has been proposed recently in [25], it is based on novel methodologies related to optimal properties of conic sections. The solution can be computed either graphically, or analytically, utilizing the matrix description of conic sections. It provides solutions with an adequate level of accuracy as well as a reduced computational effort. Overall, any existing approach for the 3PDP, despite its peculiar methodology, selects the minimum length path through an exhaustive search among all possible path type combinations. This is detrimental for the run time and it is a significant drawback for these methodologies when dealing with the applications described above. The main goal of this paper is to remove this bottleneck, thus extending the classification rules from [8] to the 3PDP. This would allow for the direct determination of the optimal path type based on the initial and final poses and the intermediate via point only. As a result, the results of this paper can be applied in conjunction with any algorithm, to get solutions in real-time applications.
2. Problem Formulation
In the following, we introduce the logical framework of the problem, and we briefly summarize some classical results that are the basis of our analysis, together with the notation that we adopt along the paper.
2.1. Notation and Preliminary Results
Consider a vehicle whose motion is described by:
where is a bound on the maximal curvature. A feasible path is a curve in the plane that is viable for the Dubins vehicle, namely a curve satisfying (1), whose maximum curvature along the path is bounded by .
The state vector q is the pose or configuration of the vehicle, where is the position of the vehicle in the Euclidean plane, and its orientation (see Figure 1a); the control u sets the angular speed, within the range defined by the bound . Associated to each configuration, we draw two circles of radius each lying on one side of the position P (denoted, resp., for the left circle and for the right circle, and their centers and ), each corresponding to the sharpest turn.
Given an initial configuration and a final configuration , without loss of generality (as in [8]), it is possible to set and , with d the Euclidean distance between them, as depicted in Figure 1b.
Consider two such circles , with (namely, “initial" or “final”) and (i.e., “right” or “left”), it is possible to identify four different common tangent lines, i.e., two cross tangents and two external ones (see e.g., Figure 2). We denote all possible common tangent lines between an initial and a final circle as , with , , and (where c and e stand for “cross” and “external”, + and − for “superior” and “inferior”).
Consider a line r in the Cartesian plane described by all the points satisfying , (see Figure 3); r divides the Cartesian plane into two half-planes. A point is in the upper half-plane if and it is shortly denoted by . The point P is said to be in the lower half-plane if , denoted in the following by .
Finally, each directed line with unit vector divides the Cartesian plane into two half-planes; the one on its right is shortly denoted as , and the other on its left denoted as . If points to the right, then coincides with the upper half-plane.
2.2. Preliminary Results
One fundamental topic within this framework is the shortest path Problem, that consists in finding the shortest curve among the viable ones connecting an initial configuration to a final configuration for a Dubins’ car. This problem was firstly introduced and solved by L.E. Dubins [3] by showing that an optimal path is constructed by combining at most three segments, which can be either a straight line (denoted as S) or a circular arc of maximum curvature (denoted as C).
A circular path C can have a right or left turning direction, and in the following it is denoted resp. by R or L. As a consequence, the minimum length path can be found by direct search among six possible combinations given by the , , , , , cases, or part of them. If the distance between the initial and final points is sufficiently large, more than , paths are never optimal and the analysis can be restricted to the occurrence of paths. Moreover paths are incovenient in practice since small variations on the terminal configurations produce large variations of solutions, namely the recalculation of a reference path may produce a completely different reference path, with possible serious drawbacks on a mission execution.
For these reasons, in this paper we propose an algorithm that seeks the solution type of the optimal-length Dubins Path restricted to a search among the four combinations , , , . When is far more than both from and , the path type solution is optimal, in general for most of the practical applications such path type is the most reasonable choice.
The Three-Point Dubins Problem (3PDP) is as follows. For any assigned triple (, , ), namely the initial configuration , the final configuration and a pre-assigned via point far from and more than , find the shortest curve of (1) connecting , and , with tangent direction at and at , among all the curves in the plane with curvature bounded by .
According to the Bellman’s principle for optimality, the solution of the optimal path for a Dubins vehicle between three consecutive configurations can be obtained by concatenating two optimal Dubins paths:
- the path between the initial configuration and the via point configuration with length denoted as , and
- the path between the via point configuration and the final configuration with length denoted as .
In this paper, we deduce the classification rules for selecting the type of the optimal path for those points of the plane far from and more than , so that each of the elementary optimal Dubins path must be of type , so the solution is made of three elementary motions: left or right turn both along a circle of radius , straight line motion, and left or right turn both along a circle of radius . In the following we denote as t, p and q the length of its basic elements referring to resp. the initial turn, the straight line segment and the final turn and we add the subscript 1 or 2 to refer resp. to the path between to and from to , see Figure 4.
We can therefore state that the optimal-length path through three consecutive points satisfying the long distance hypothesis is the concatenation of two Dubins paths of type , hence the solution of the 3PDP must be of a type . If such hypothesis is not satisfied, however, one may use a sub-optimal solution of type, thus a-priori avoiding curves (which can be optimal, but notwithstanding unconveninent).
An important result, conjectured in [15], and then proved in [26] and [13], is related to the optimality conditions for a shortest path of type :
Lemma 1.
Given , in a shortest path of type CSC-CSC the line segment between and the center of the circle associated with the optimal heading bisects the angle between the line segment and .
Denote by and the vectors parallel to the initial and final line segments of the path , ( and in Figure 4 and Figure 5), and with the vector connecting the center of the circle associated with the optimal heading at the via point . Define as the vector parallel to the optimal heading at the via point, hence, orthogonal to , by construction, as shown in Figure 5.
Denoting by v the vector bisecting the angle between and , the optimality condition of Lemma 1can be equivalently rewritten as:
Moreover, since two arcs incident to the via point must have the same turning direction, it holds:
Corollary 1.
The optimal solution of the 3PDP when is far more than from both and must be of a type in , , , , , , , , where any circular arc may possibly be of zero length.
As a consequence, the optimal-length path through three consecutive points can be found by direct search among the eight possible combinations in .
2.3. A Classification Approach for Fast Solution
In this paper, we propose a classification based on a partition of the Cartesian plane which allows to drastically reduce the number of potential path types.
Indeed, in order to solve the 3PDP, one should calculate the lengths of all path type in , and then select the shortest one of the computed paths. This requires to compute the optimal orientation angle at the via point (not specified a priori) for each path type, given by the following length optimality criterion:
The problem addressed in this paper can be formulated as follows.
Problem 1.
Given the 3PDP, find a simple logical procedure to select the optimal path type among the combinations given in without any explicit length computation.
Inspired by the classification rules derived in [8], in this paper we extend this strategy to the 3PDP, namely given a 3PDP problem, find a simple logical procedure to select the optimal path type among those in without any explicit length computation.
3. Classification Rules
Our goal is to build a partition of the Cartesian plane as the one illustrated in Figure 6, which represents a partition for the classification of a 3PDP with distance between the initial and final point, and initial and final orientation, and on quadrant I. Recurring to this partition, given any via point , it is possible to immediately deduce the optimal path type by simply identifying the region to which it belongs to. Consider the via point in Figure 6, it lies on the region classified as . Indeed, computing the optimal path type with the conventional methods available in literature, the resulting path reported in Figure 6 is actually a path type.
In general, to build a complete path type classification, we need to select the optimal turning directions in the three points of interest, i.e., the curvature at the initial point , the curvature at the final point , and the curvature at the via point .
3.1. Curvature at the Initial Point
As a first step, draw a straight line starting from with orientation , and denote it as , as in Figure 6. A first simple intuitive idea that we explode is that, if the via point is on the left of , then the first turning direction is necessarily on the left, while if is on the right with respect to , then the optimal path turn is on the right (see Figure 7).
However, a deeper insight on this point shows that there are some points close to which do not follow the above logic, and the reason is subtle. Without loss of generality, consider the example reported in Figure 8 where the via point is on the right, near to . In such a case the optimal path type has the first turn on the left instead of on the right.
It is possible to clarify the reason for this phenomenon, which is the following. The orientation at requires a right turn, so if the initial turning point ( in Figure 8) is on the opposite side of with respect to , then the initial turn is on the left.
In order to correctly identify and manage this phenomenon, two different approaches can be adopted: an analytical approach and a heuristic one.
3.1.1. Analytical Approach
As an illustrative example, we still consider a case with and on quadrant I as in Figure 8.
The analytical approach exploits the optimal condition, Eq. (2)).Following this approach, the main goal is to derive the exact boundary, denoted as in the following, between paths that differs for curvature at the initial point, i.e., and for the example under investigation. Analytically, the boundary of the two regions and is defined by those points for which and paths have the same lengths, i.e.,:
From a geometrical point of view, given that the second elementary Dubins paths between the via point and the final configuration are the same ( type of length ), the two types of paths and have the same lengths when the length of the straight line segment associated to the first elementary Dubins path is the same,
For the path, the segment is given by the common external tangent between the circles and ; while for the path, the segment is given by the common cross tangent between the circles Frontier between and (see tangents in the Figure 9). As a consequence, the optimality condition in eq. (4) is:
This happens when the circle is tangent to the line , in this case the point . As a consequence, the first arc has zero length (i.e., ) and the two paths collapse in a path of type . Refer to Figure 9 for a clear geometric representation of the optimality condition.
In order to actually find the locus of via points that correspond to such an optimal path type, the optimality condition given by the Lemma 1 for the path should be verified, that is:
where
and R is the standard rotation matrix. We also recall that in the intersection domain the first arc vanishes, i.e., , the direction of coincides with the initial orientation and the first elementary Dubins path reduces to a type path (see Figure 10).
As a result, the centers lie on the line , namely a line parallel to and distant on its right, so that the optimal right via point circle is a circle passing through the via point and tangent to the line . The versor identifies the direction of the cross tangent of the circles and . Hence, the points of the curve can be obtained by adding at each center , the versor (i.e., the versor in the direction of ) multiplied by .
Summarizing, from an analytical point of view, we have one equation (6) with two variables and . We can solve it by taking one variable as a parameter. The analytical result is a curve that admits as asymptote the line (see Figure 11).
Figure 11a and Figure 11b show the curve , i.e., the frontier between the regions and for and on quadrant I, for different values of the maximum turning radius: and , respectively. At this point, we can formulate the classification rules for identifying the curvature at the initial point as given in Algorithm 1.
| Algorithm 1 Initial Curvature - Analytical approach |
|
It is worth noting that the derivation of the exact curve could be demanding from a computational point of view (it requires solving nonlinear equations), so when the available computational load is limited, it could be preferable to resort to an heuristic approach - which is simpler, more efficient and practical - as detailed below.
3.1.2. Heuristic Approach
A heuristic solution to determine the initial curvature for points close to is still based on the fact that the boundary is associated to paths having (hence, the first arc of zero length for the example under investigation). As a result, the maximum distance between the point on the frontier and the line is . It is obtained by imposing that the optimal circle at the via point is tangent to the line , or equivalently, for the example under investigation, the first arc of zero length, i.e., . This allows to consider a region, between and the line (being a line parallel to on its right and distant ) where the investigation should consider two types of potentially optimal paths (either starting with L turn, or R turn). This region is highlighted in grey in Figure 11a. A practical way to manage the points in this region is to test both possibilities, which is simpler and less demanding.
The above result is still valid for on quadrant II, whereas symmetric considerations hold for on quadrants III and IV. In the latter cases, the region that requires to test both possibilities is the area between and the line , namely a line parallel to on its left and distant (see Figure 12).
The resulting classification rules for identifying the curvature at the initial point are summarized in Algorithm 2. The output of the algorithm is the turning direction at the initial point: "R" for a right turning, "L" for a left turning, and "C" for a generic curvature on the left or on the right (that is when both should be tested). It is worth noticing that in the boundary between the quadrants - and - (i.e., ) a more conservative region has been considered, that is the union of the candidate regions associated to both cases.
| Algorithm 2 Initial Curvature - Heuristic approach |
|
3.2. Curvature at the Final Point
Similar considerations hold for the optimal turning direction at the final point. Draw the line passing through with orientation . If the via point is on the left of then the last turning direction is on the left, while if is on its right the optimal path type is associated to a right last turn. An example is illustrated in Figure 13.
Also in this case, if the via point lies in the neighborhood of , an analogous phenomenon to the one described in Section 3.1 happens.
Consider Figure 14a where the via point is near to and on its left. In such a case the optimal path type has the last turn on the right (instead of on the left). Again, it is possible to manage this phenomenon adopting an analytical approach or an heuristic one.
3.2.1. Analytical Approach
As an illustrative example, we still take a case with and on quadrant I as shown in Figure 6. We can resort to an analytical approach, similar to the one presented in the previous section, to derive the exact frontier that differs for curvature at the final point, e.g., and for the example at hand. This partition domain is given by the via points where the two types of paths have the same length. Similarly to the case of initial turning direction, such a condition is satisfied when the turning operation at have its ending point on the line , i.e., so that the two paths collapse in a path of type , and the last arc has zero length (i.e., ). In order to actually find the locus of via points corresponding to such an optimal path type, the optimality condition given by the Lemma 1 for the path is:
where
Again, in the intersection domain the last arc vanishes, i.e., , so that the direction of coincides with the final orientation . As a result, the centers lie on the line , namely a line parallel to on its left and distant , so that the optimal left via point circle will be a circle passing through the via point and tangent to the line .
Therefore, from an analytical point of view, Eq. (11) with the two variables and provides the solution. The analytical result is a curve that admits as asymptote the line . The classification rules for identifying the curvature at the final point are given in Algorithm 3.
| Algorithm 3 Final Curvature - Analytical approach |
|
3.2.2. Heuristic Approach
The heuristic solution to determine the final curvature for points close to is based on the fact that the boundary is associated to paths having the point (hence, the last arc of zero length for the example under investigation). As a consequence, the maximum distance between the point on the frontier and the line is . Again, it is possible to consider a region between and the line parallel to on its left and distant , so that a way to manage the points in this region is to test both possibilities. This region is highlighted in grey in Figure 14a. Outside this region the curvature can be immediately obtained following a simple classification rule.
This result is valid for , whereas when the final orientation symmetric considerations holds, so the line parallel to on its right should be considered, as shown in Figure 14b. The resulting classification rules for identifying the curvature at the final point are summarized in Algorithm 4.
| Algorithm 4 Final Curvature - Heuristic approach |
|
3.3. Curvature at the via Point
In this subsection, we complete the classification scheme with the identification of the turning direction at the via point. We consider separately the cases of paths with “zero” and “non-zero” curvature at the via point.
3.3.1. Paths with Zero Curvature at the via Point
We start with the consideration that paths with zero curvature at the via point are all and only those having the via point on the length-optimal Dubins path between and (see for example the light blue line in Figure 15). We denote such an oriented segment (starting from the initial optimal circle and ending to the final optimal circle) as from now on (its orientation is defined as positive from to ). The importance of the segment is that all the via-points on the left of () are associated to paths with right turning direction at the via point (hence of type ), and those on the right () are paths with left turning direction at , i.e., paths.
In order to derive the conditions to identify paths with zero curvature at the via point, we start from the property of the Three-Point Dubins Path provided in Lemma 1, see Figure 5.
According to Lemma 1, for a shortest path of type , the bisector between and is collinear with (see Figure 5) and consequently orthogonal to , leading to the optimality condition .
The condition of zero curvature at the via point is verified when the bisector is the null vector, i.e., , that is when
In this condition, and lie on the common tangent between the circles associated to the optimal initial and final turn.
3.3.2. Paths with Non-Zero Curvature at the via Point
As for paths with a non-zero curvature at the via point, it is possible to derive a condition useful to identify regions that differ only for the curvature at the via point. Indeed, the boundary of these regions is made of all points for which the two types of path have the same length. In order to exploit such idea, consider again the example of partition of the Cartesian plane in Figure 16.
Note that there are distinct areas where the optimal path type has different curvature at the via point. It is useful to define an appropriate notation to separate these areas:
- Region 1: boundary denoted as
- Region 0: boundary denoted as
- Region 2: boundary denoted as
In the following, we derive the exact frontier between paths with different curvatures at the via point as follows either recurring to an analytical or and to the heuristic one.
3.3.3. Derivation of the Boundary between Domains with Different Curvatures at the via Point
Consider the boundary first. A clear representation of this case is illustrated in Figure 17 where and are on quadrant I.
The and path types associated to the via point in Figure 17 have the same length, they differ only for the curvature at the via point. The optimal direction associated to the path type and associated to the path type have opposite direction, so that
Therefore, they are both orthogonal to the vector , having denoted with the vector connecting the center of the circle associated with the optimal heading and the via point .
In order to analytically derive the partition boundary between and path types, the first condition to be verified is that the two types of path should have the same length, so:
that results in the following equation:
From the optimality condition (Lemma 1) for the and paths, the following condition must be verified:
where the superscripts R and L denote that the versors or refer to the path with right and left curvature at the via point, respectively. This leads to a system of three equations (17-19) with four variables ():
The analytical result, obtained solving the above system of equations, is a curve quite close to the common tangent (superior cross tangent) between the circles associated to the optimal initial and final turn as shown in Figure 18.
The classification rule for identifying the curvature at the via point related to the considered boundary is given in Algorithm 5.
| Algorithm 5 Via Point Curvature - Analytical approach - Example in Figure 17 - Region 1 |
|
Alternatively, following an heuristic approach, the solution can be sought considering an approximation of this boundary given by . The resulting classification rules are summarized in Algorithm 6.
| Algorithm 6 Via Point Curvature - Heuristic approach - Example in Figure 17 - Region 1 |
|
More generally, by following the described approach to derive each boundary, one can verify that each boundary can be approximated by an appropriate common tangent line.
For the sake of completeness, the complete scenario that occurs when and are on quadrant I (see for example Figure 19) resorting to an heuristic approach (i.e., to a proper approximation of each boundary) is summarized in Algorithms 7 and 8.
| Algorithm 7 Via Point Curvature - Heuristic approach - - Region 1 |
|
| Algorithm 8 Via Point Curvature - Heuristic approach - - Region 2 |
|
For the sake of brevity, the general schema that occurs for heading at initial and final points within any of the four quadrants is not detailed here. However, any case can be derived following analogously the detailed case afforded so far.
4. An Illustrative Example
In this section we provide a simple example to illustrate how the proposed classification rules work, demonstrating the functionality of the proposed algorithms. Let consider the following initial and final configurations , , a maximal curvature , and the via point (see Figure 19).
The optimal path type have the form "", thus we need to identify the Curvature at the initial point, at the final point, and at the via point. We can rely to the heuristic approach - more practical with respect to the analytical counterpart. Applying Algorithm 2 since and , we immediately deduce that . Similarly, Applying Algorithm 4 since and , we immediately deduce that . With reference to the curvature at the via point, since the initial and final configurations are both in the first quadrant, and the via point is on Region 2 we can apply the Algorithm 8. This allow us to deduce that . Thus, we can directly deduce the optimal path type without making any calculation.
Following a conventional approach the optimal solution should have been found by searching among the eight candidate paths: using any of the existing methods in the literature, such as those presented in references [13,14,25]. By applying one of these methods, the lengths of the eight candidate paths should have been calculated and compared to determine the optimal path.
5. Conclusions
In this paper, we afforded the shortest path type classification between an initial and a final configuration passing through an intermediate via point for a Dubins vehicle. The proposed methodology allows to select the optimal path type without any calculation, so that it is well fit to be used in real-time applications. The proposed strategy is described through the explanation of a simple worked example. Future research includes the extension of the approach to a time-varying and multi-robot scenario, as well as the use of the algorithm in practice.
References
- Lin, S.; Liu, A.; Wang, J.; Kong, X. A Review of Path-Planning Approaches for Multiple Mobile Robots. Machines 2022, 10. [Google Scholar] [CrossRef]
- LaValle, S.M. Planning Algorithms; Cambridge University Press: USA, 2006. [Google Scholar]
- Dubins, L.E. On curves of minimal length with a constraint on average curvature, and with prescribed initial and terminal positions and tangents. American Journal of mathematics 1957, 79, 497–516. [Google Scholar] [CrossRef]
- Boissonnat, J.D.; Cérézo, A.; Leblond, J. Shortest paths of bounded curvature in the plane. Journal of Intelligent and Robotic Systems 1994, 11, 5–20. [Google Scholar] [CrossRef]
- Bicchi, A.; Pallottino, L. On Optimal Cooperative Conflict Resolution for Air Traffic Management Systems. IEEE Transactions on Intelligent Transportation Systems 2000, 1, 221–231. [Google Scholar] [CrossRef]
- Savla, K.; Frazzoli, E.; Bullo, F. Traveling salesperson problems for the Dubins vehicle. IEEE Transactions on Automatic Control 2008, 53, 1378–1391. [Google Scholar] [CrossRef]
- Meyer, Y.; Isaiah, P.; Shima, T. On Dubins paths to intercept a moving target. Automatica 2015, 53, 256–263. [Google Scholar] [CrossRef]
- Shkel, A.M.; Lumelsky, V. Classification of the Dubins set. Robotics and Autonomous Systems 2001, 34, 179–202. [Google Scholar] [CrossRef]
- Berdyshev, Y. Berdyshev, Y. Time-optimal control of a nonlinear system in the problem of visiting a group of points. Cybernetics and Systems Analysis 1991, 27, 949–952. [Google Scholar] [CrossRef]
- Berdyshev, Y. A problem of the sequential approach to a group of moving points by a third-order non-linear control system. Journal of Applied Mathematics and Mechanics 2002, 66, 709–718. [Google Scholar] [CrossRef]
- Kaya, C. Markov-Dubins interpolating curves. Computational Optimization and Applications 2019, 73, 647–677. [Google Scholar] [CrossRef]
- Frego, M.; Bevilacqua, P.; Saccon, E.; Palopoli, L.; Fontanelli, D. An iterative dynamic programming approach to the multipoint markov-dubins problem. IEEE Robotics and Automation Letters 2020, 5, 2483–2490. [Google Scholar] [CrossRef]
- Sadeghi, A.; Smith, S.L. On efficient computation of shortest dubins paths through three consecutive points. Decision and Control (CDC), 2016 IEEE 55th Conference on. IEEE, 2016, pp. 6010–6015.
- Chen, Z.; Shima, T. Shortest Dubins paths through three points. Automatica 2019, 105, 368–375. [Google Scholar] [CrossRef]
- Parlangeli, G.; Ostuni, L.; Mancarella, L.; Indiveri, G. A motion planning algorithm for smooth paths of bounded curvature and curvature derivative. Mediterranean Conference on Control and Automation(MED); IEEE,, 2009; pp. 73–78.
- Parlangeli, G.; Indiveri, G. Dubins inspired 2D smooth paths with bounded curvature and curvature derivative. IFAC Proceedings Volumes 2010, 43, 252–257. [Google Scholar] [CrossRef]
- Hota, S.; Ghose, D. Optimal trajectory planning for unmanned aerial vehicles in three-dimensional space. Journal of aircraft 2014, 51, 681–688. [Google Scholar] [CrossRef]
- Becce, L.; Bloise, N.; Guglieri, G. Optimal path planning for autonomous spraying uas framework in precision agriculture. 2021 International Conference on Unmanned Aircraft Systems (ICUAS). IEEE, 2021, pp. 698–707.
- Hansen, K.D.; La Cour-Harbo, A. Waypoint planning with Dubins curves using genetic algorithms. 2016 European Control Conference (ECC). IEEE, 2016, pp. 2240–2246.
- Zhu, M.; Zhang, X.; Luo, H.; Wang, G.; Zhang, B. Optimization Dubins path of multiple UAVs for post-earthquake rapid-assessment. Applied Sciences 2020, 10, 1388. [Google Scholar] [CrossRef]
- Du, X.; Li, X.; Liu, D.; Dai, B. Path planning for autonomous vehicles in complicated environments. 2016 IEEE International Conference on Vehicular Electronics and Safety (ICVES). IEEE, 2016, pp. 1–7.
- Bayar, G. Reference path generation and obstacle avoidance for autonomous vehicles based on waypoints, dubins curves and virtual force field method. International Journal of Applied Mathematics Electronics and Computers 2017, 5, 1–6. [Google Scholar] [CrossRef]
- Sharma, K.; Doriya, R. Coordination of multi-robot path planning for warehouse application using smart approach for identifying destinations. Intelligent Service Robotics 2021, 14, 313–325. [Google Scholar] [CrossRef]
- Cai, W.; Zhang, M.; Zheng, Y.R. Task assignment and path planning for multiple autonomous underwater vehicles using 3D dubins curves. Sensors 2017, 17, 1607. [Google Scholar] [CrossRef] [PubMed]
- Parlangeli, G.; De Palma, D.; Attanasi, R. A novel approach for 3PDP and real-time via point path planning of Dubinsâ vehicles in marine applications. Control Engineering Practice 2024, 144, 105814. [Google Scholar] [CrossRef]
- Goaoc, X.; Kim, H.S.; Lazard, S. Bounded-curvature shortest paths through a sequence of points using convex optimization. SIAM Journal on Computing, Society for Industrial and Applied Mathematics 2013, 42, 662–684. [Google Scholar] [CrossRef]
Figure 1.
a) Graphic interpretation of the left and right centres for an initial configuration . b) Initial and final configurations.
Figure 1.
a) Graphic interpretation of the left and right centres for an initial configuration . b) Initial and final configurations.
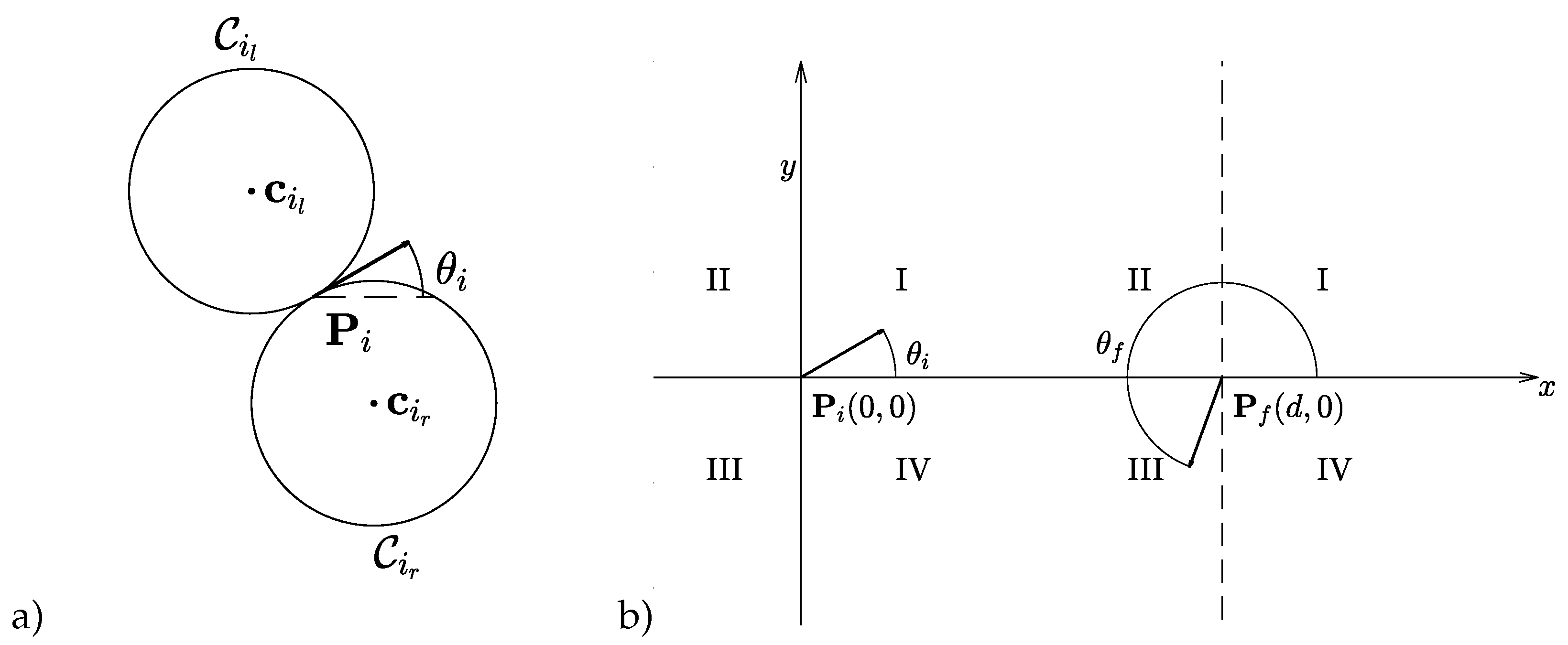
Figure 2.
Representation of the common tangents between the circles and : superior cross tangent, inferior cross tangent, superior external tangent, and inferior external tangent.
Figure 2.
Representation of the common tangents between the circles and : superior cross tangent, inferior cross tangent, superior external tangent, and inferior external tangent.
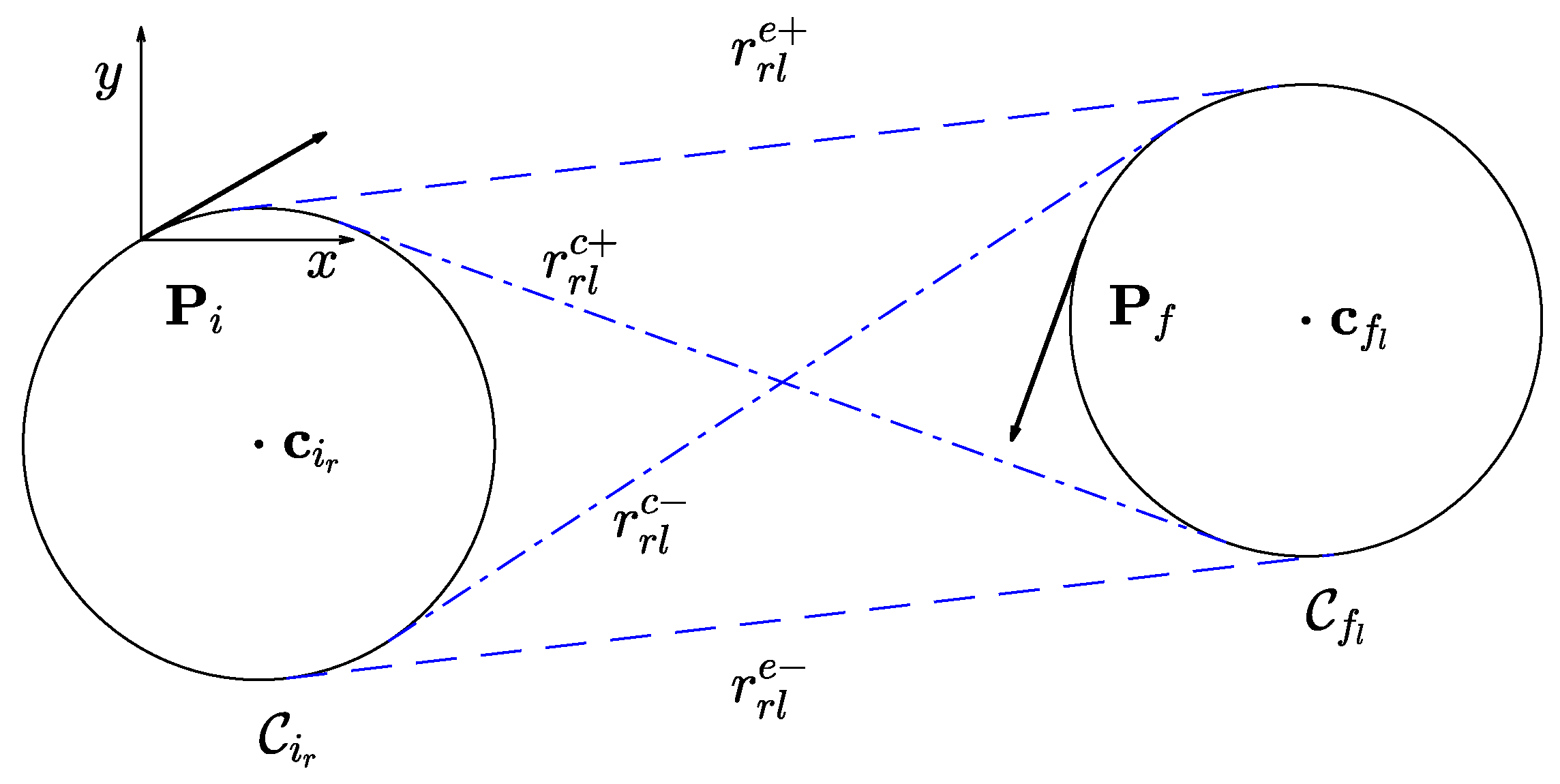
Figure 3.
Notation used for identifying the position of a point with respect to a line r and an oriented line (curve) .
Figure 3.
Notation used for identifying the position of a point with respect to a line r and an oriented line (curve) .
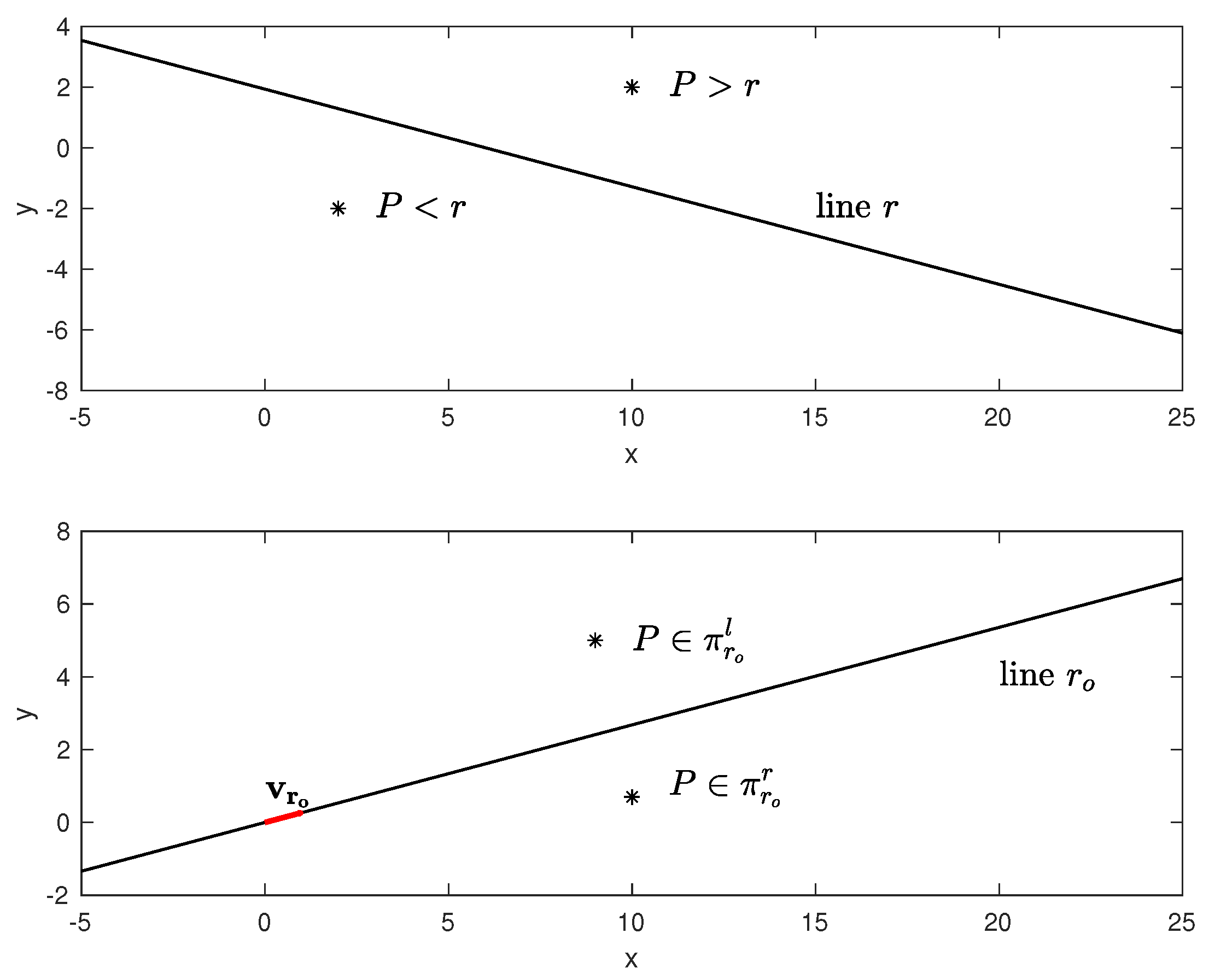
Figure 4.
A sketch of path.
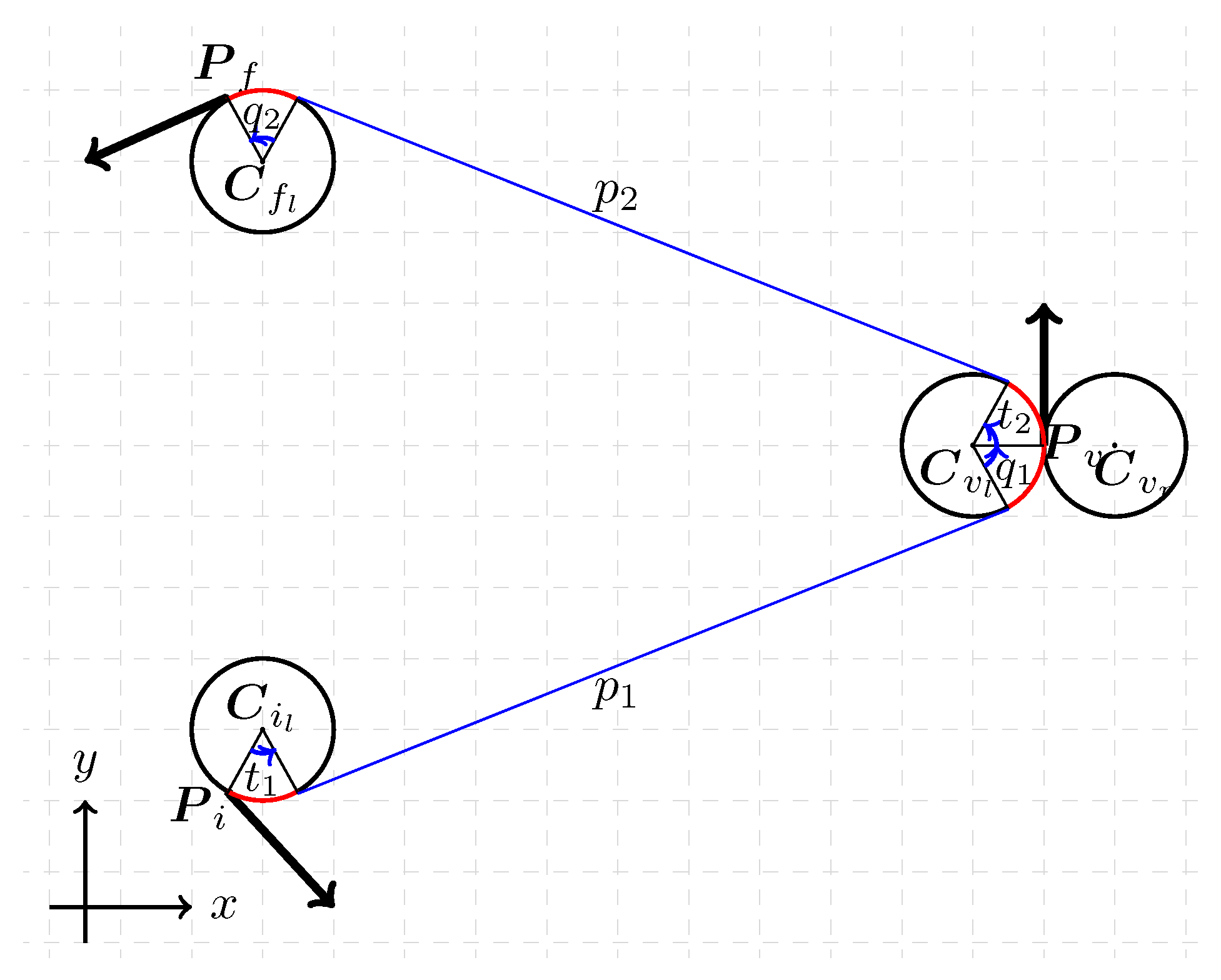
Figure 5.
The vectors , , , and for a path.
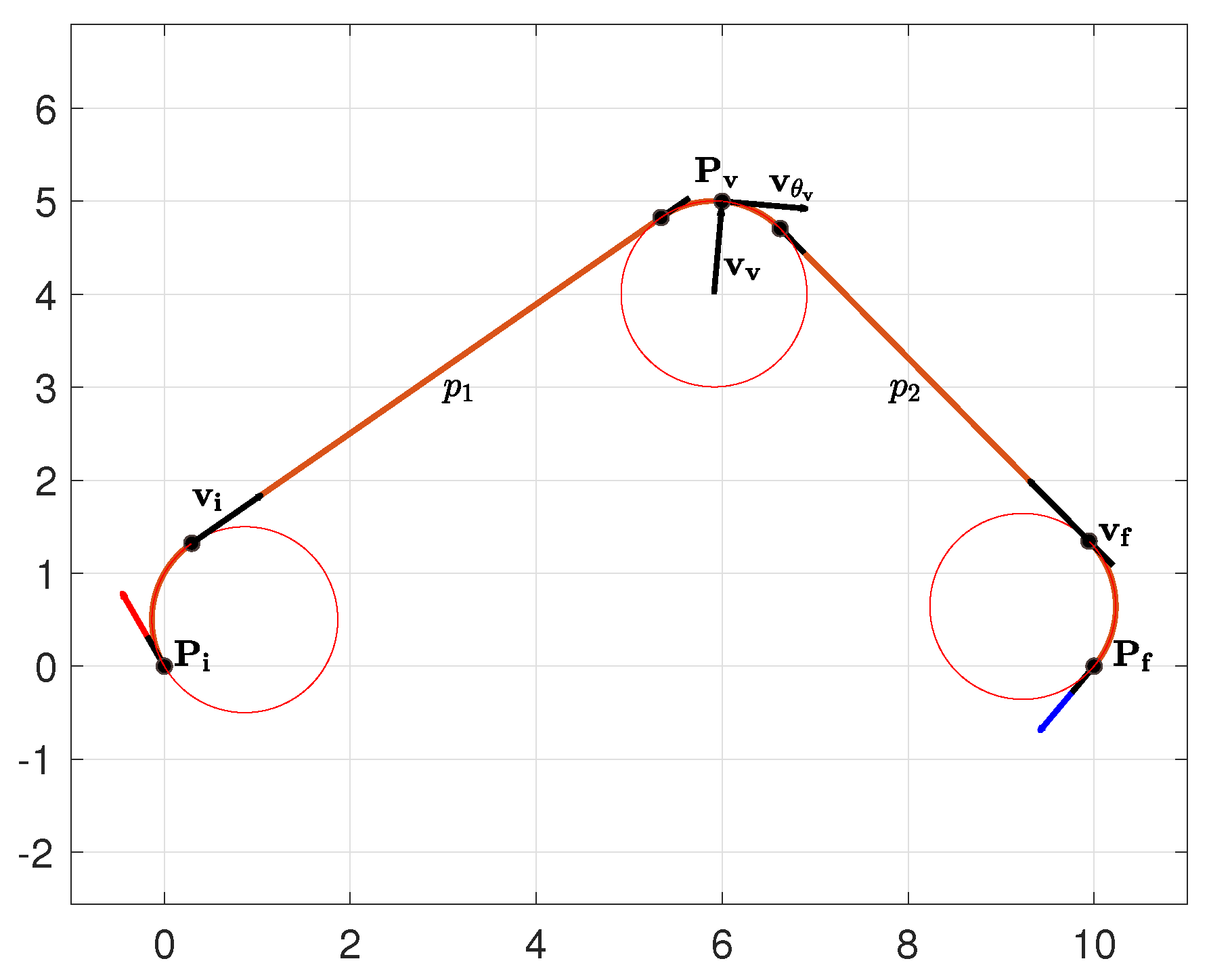
Figure 6.
Classification of paths with and on quadrant I: example of partition
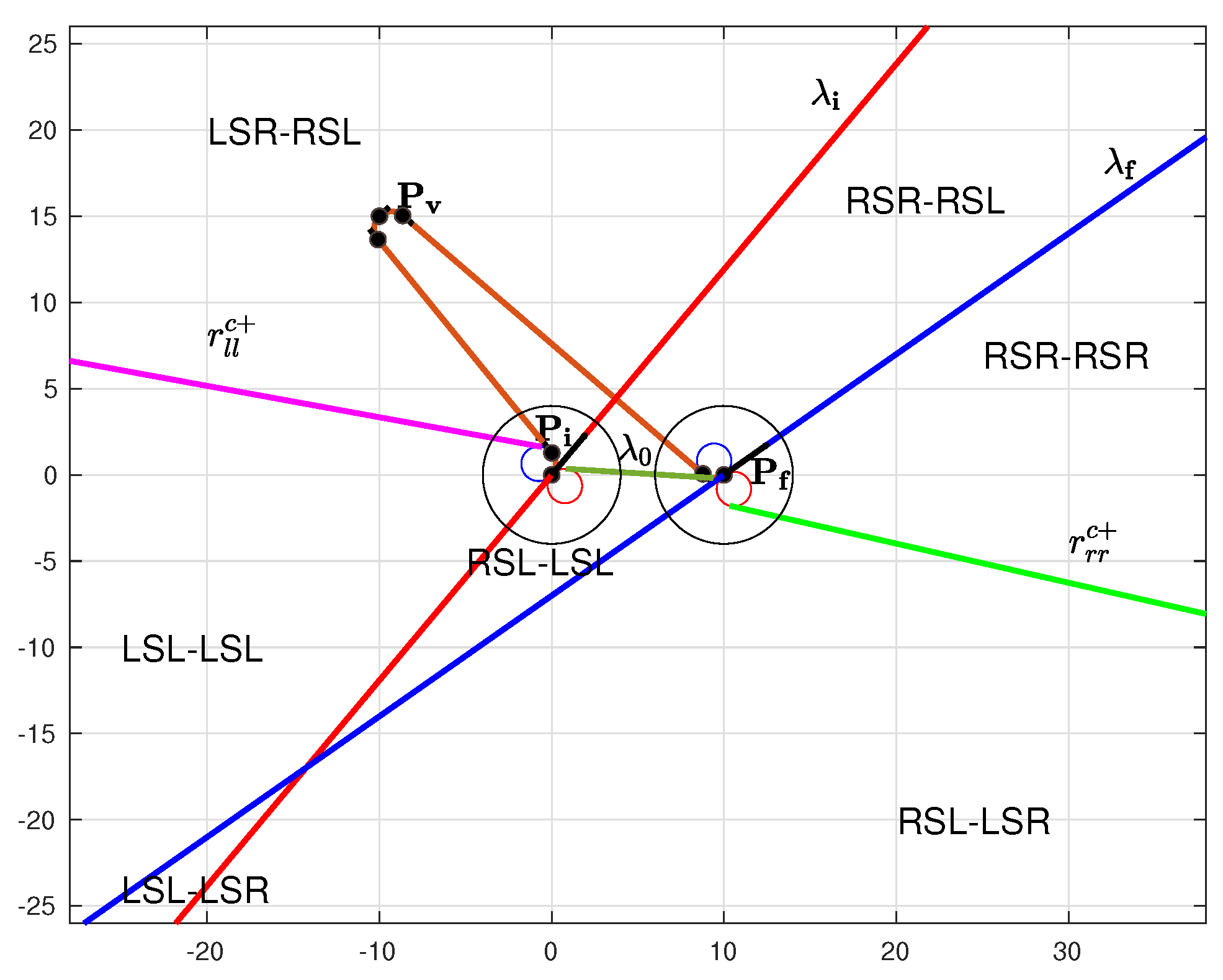
Figure 7.
Optimal paths with on the right and on the left of the straight line .
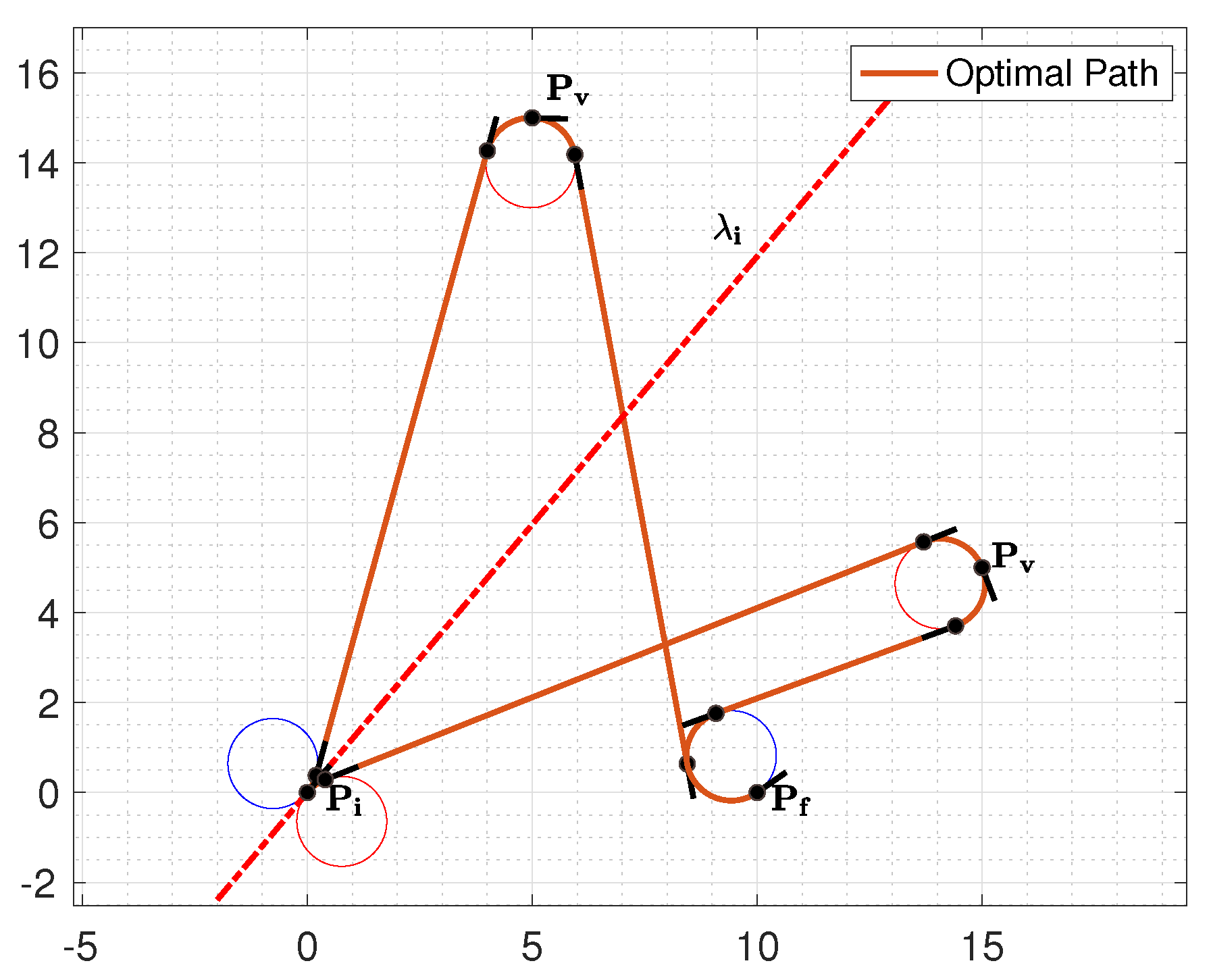
Figure 8.
Example with is on the right of and first turn on the left.
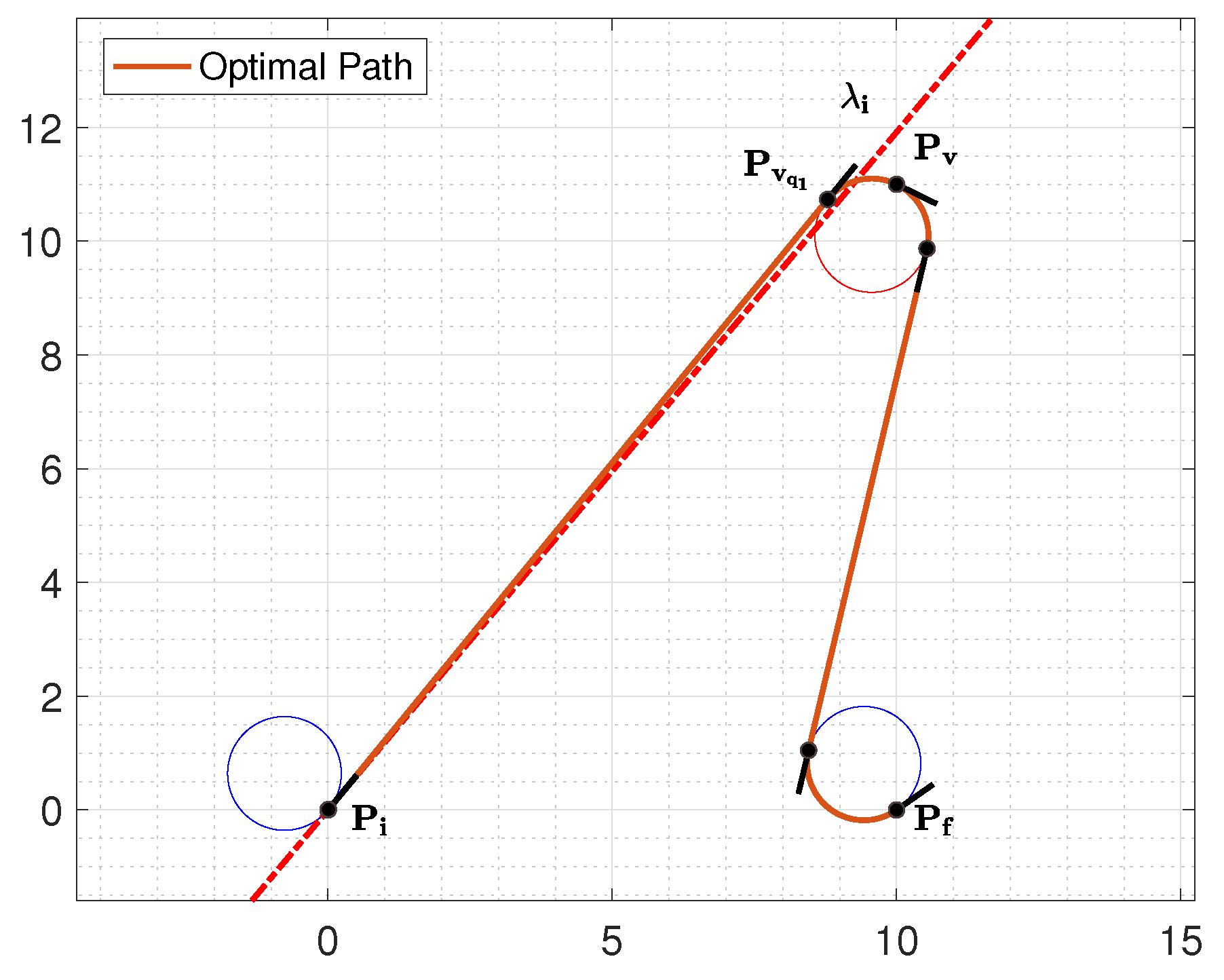
Figure 9.
Geometric representation of the optimality condition in (5).
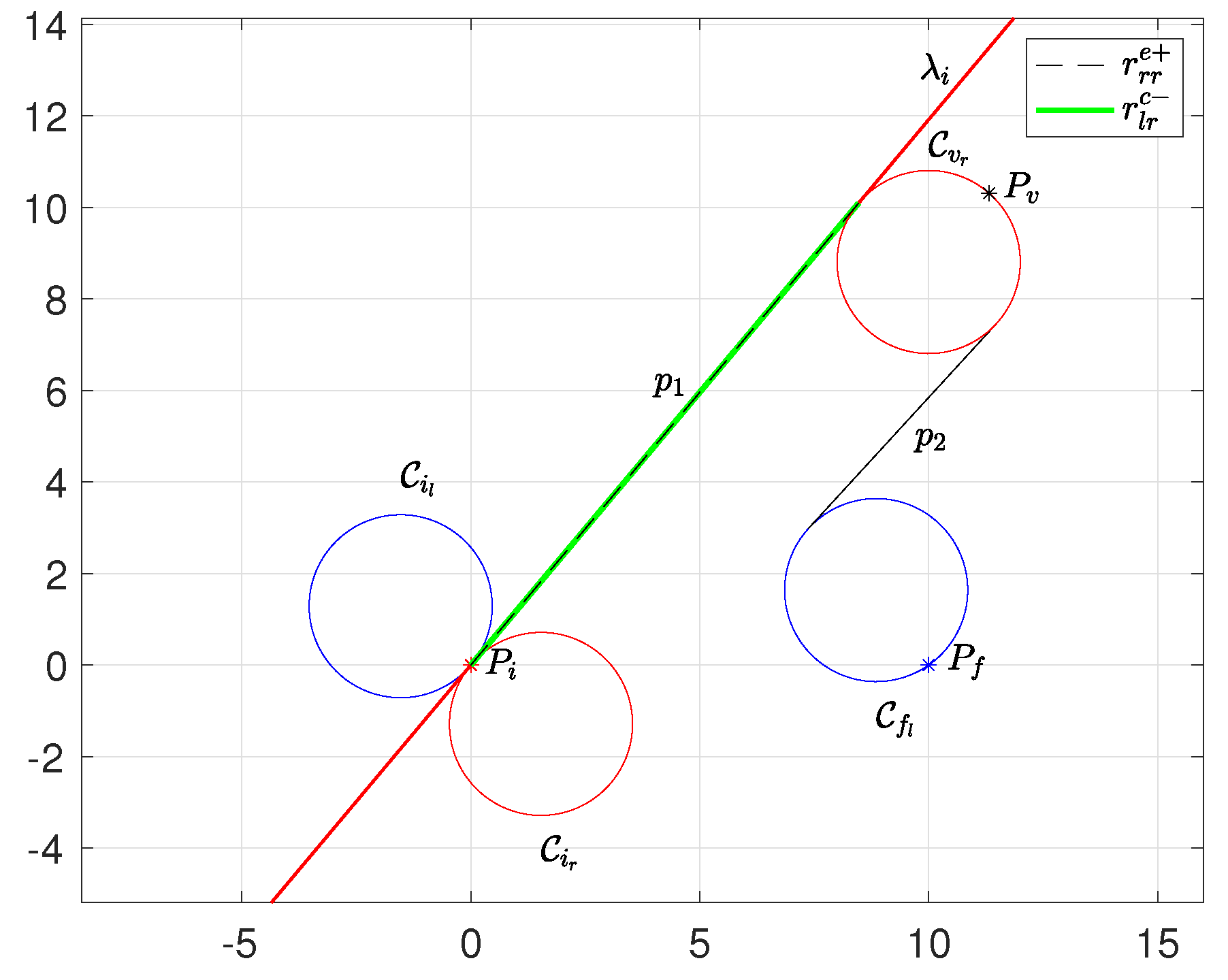
Figure 10.
Optimal path ().
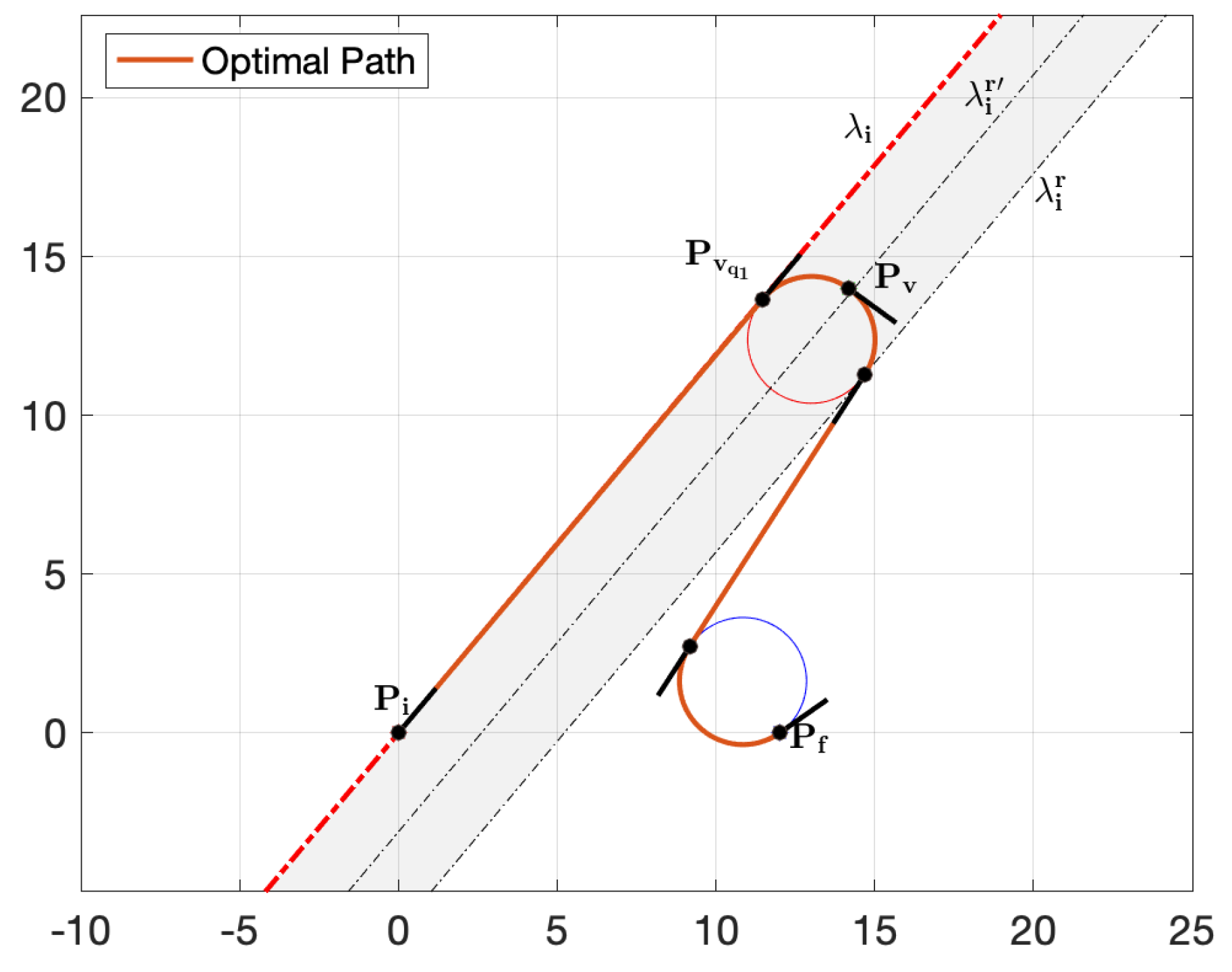
Figure 11.
Frontier between and for and on quadrant I: a) radius of the limiting circles , b) radius of the limiting circles .
Figure 11.
Frontier between and for and on quadrant I: a) radius of the limiting circles , b) radius of the limiting circles .
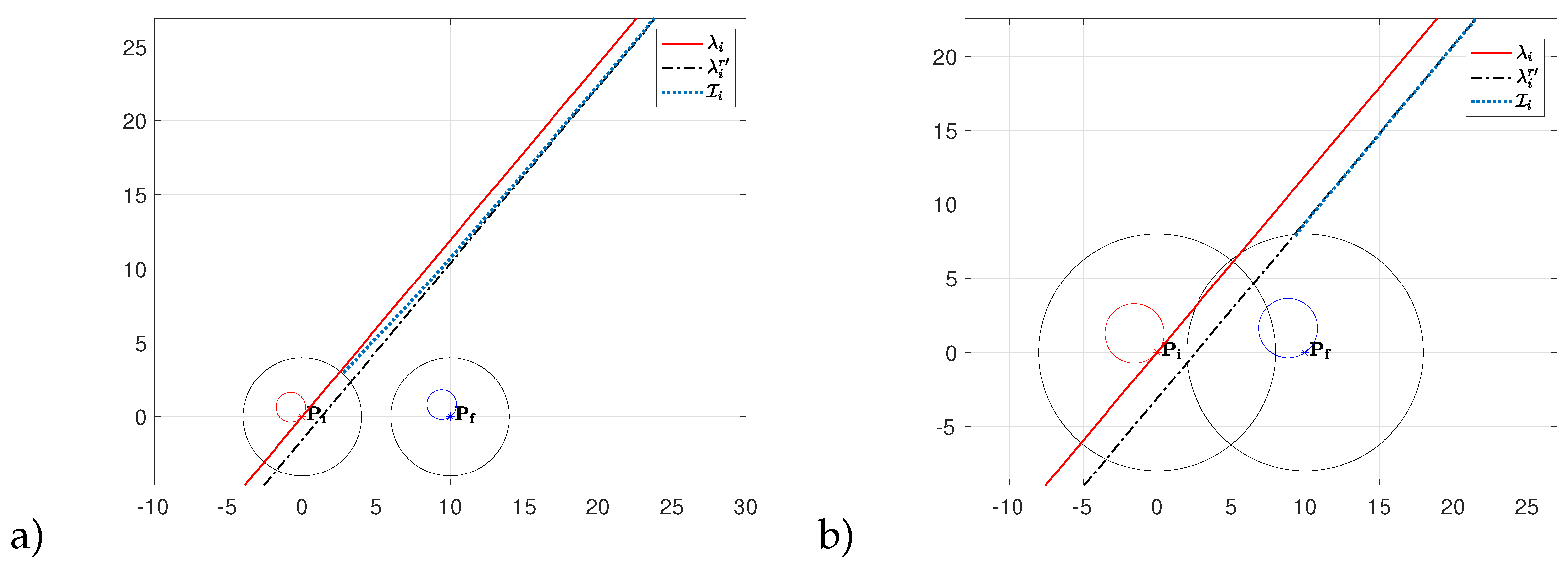
Figure 12.
Example of optimal path with on quadrant III where is on the left of but the optimal initial turn is right.
Figure 12.
Example of optimal path with on quadrant III where is on the left of but the optimal initial turn is right.
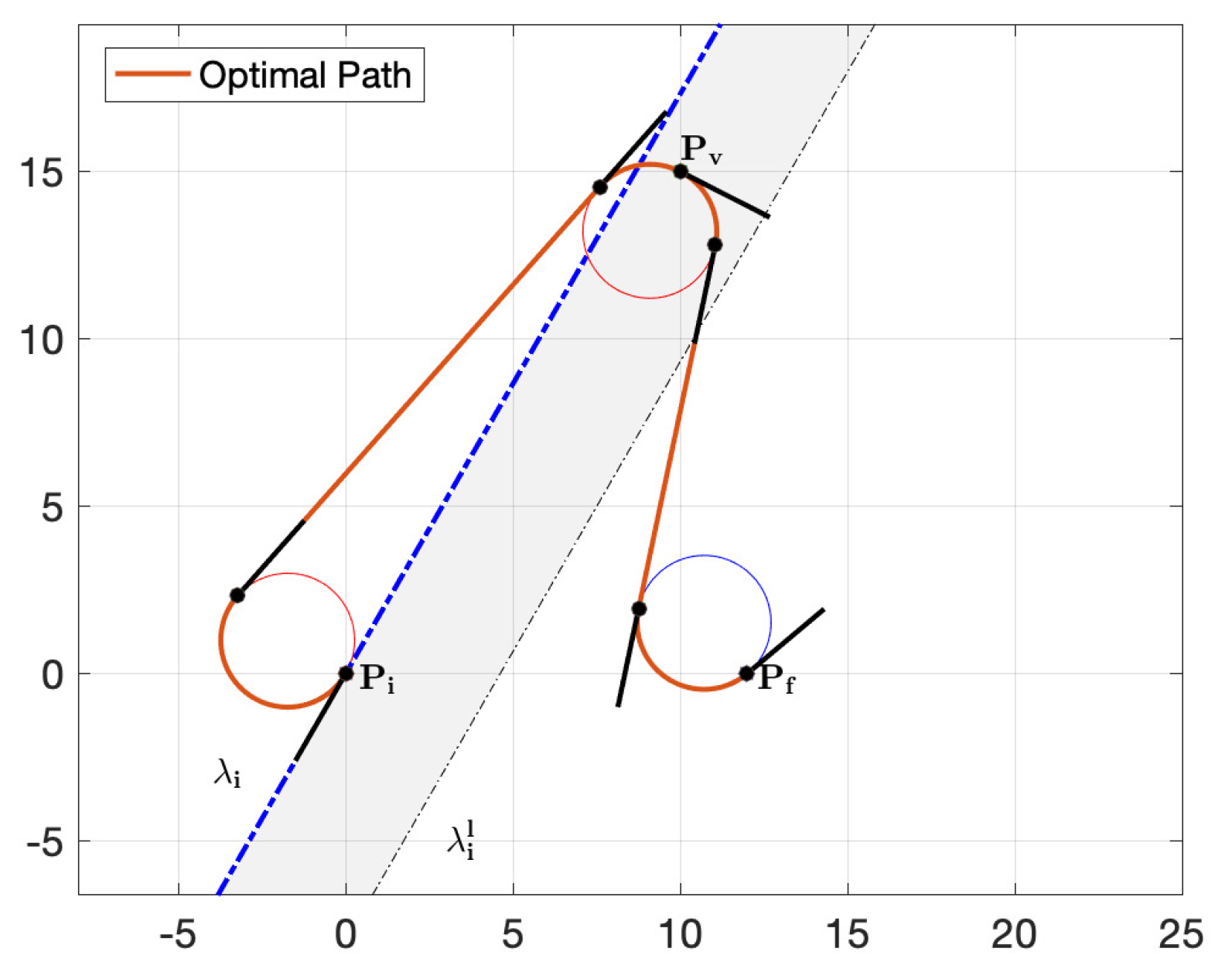
Figure 13.
Example of optimal paths where is on the right and on the left of the straight line .
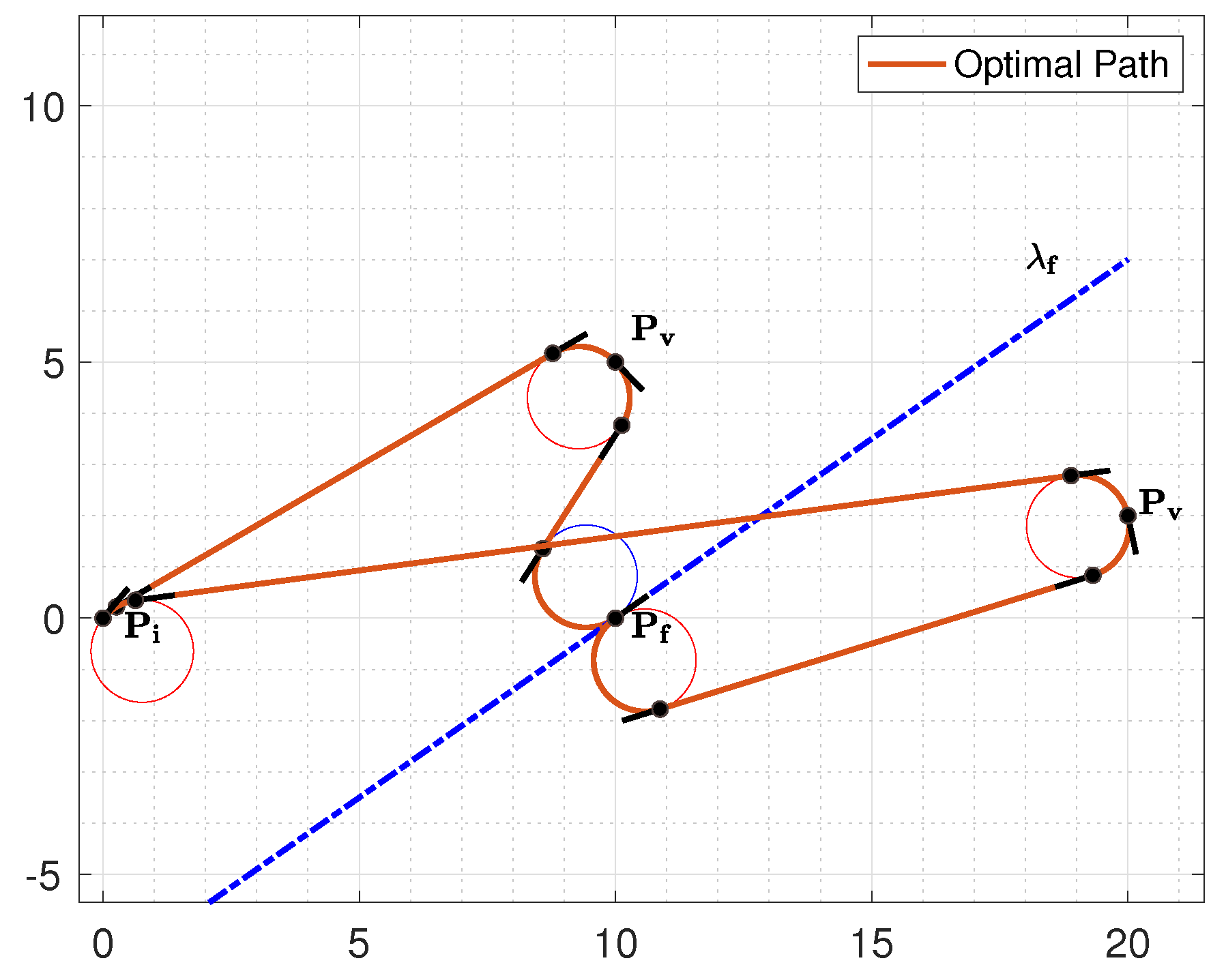
Figure 14.
a) Example of situation with on quadrant I b) Example of situation with on quadrant IV
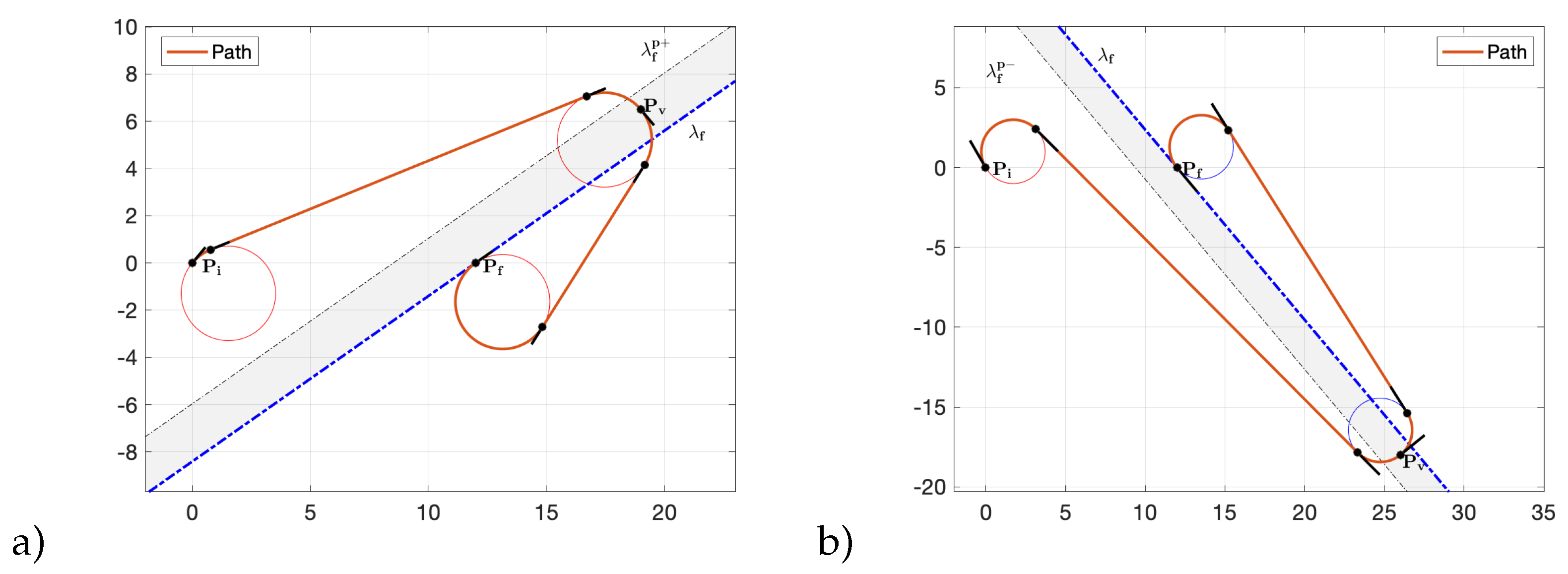
Figure 15.
The vectors and for a path with zero curvature at the via point.
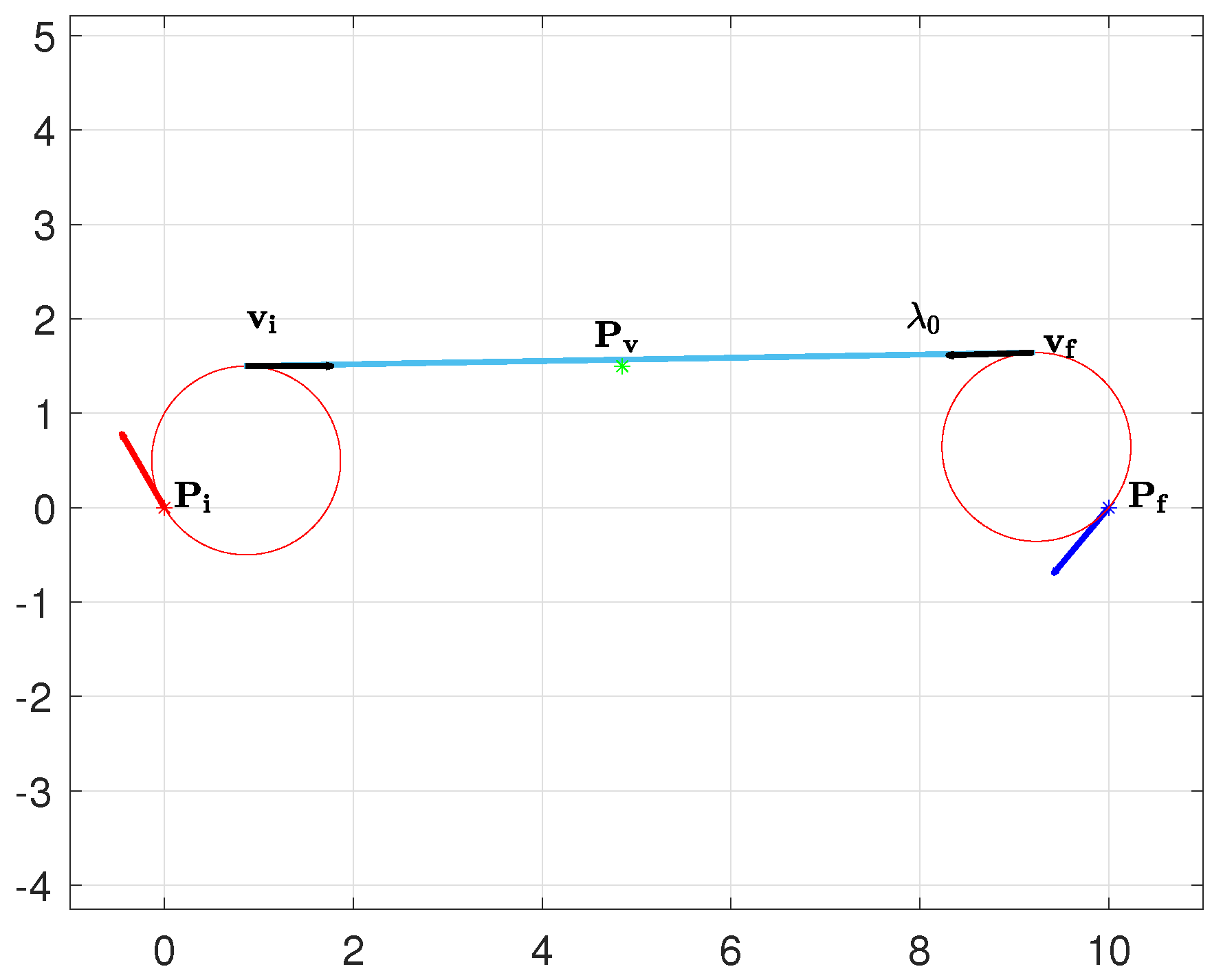
Figure 16.
Example of plane partitioning for classification. Three different regions are highlighted in the Cartesian plane.
Figure 16.
Example of plane partitioning for classification. Three different regions are highlighted in the Cartesian plane.
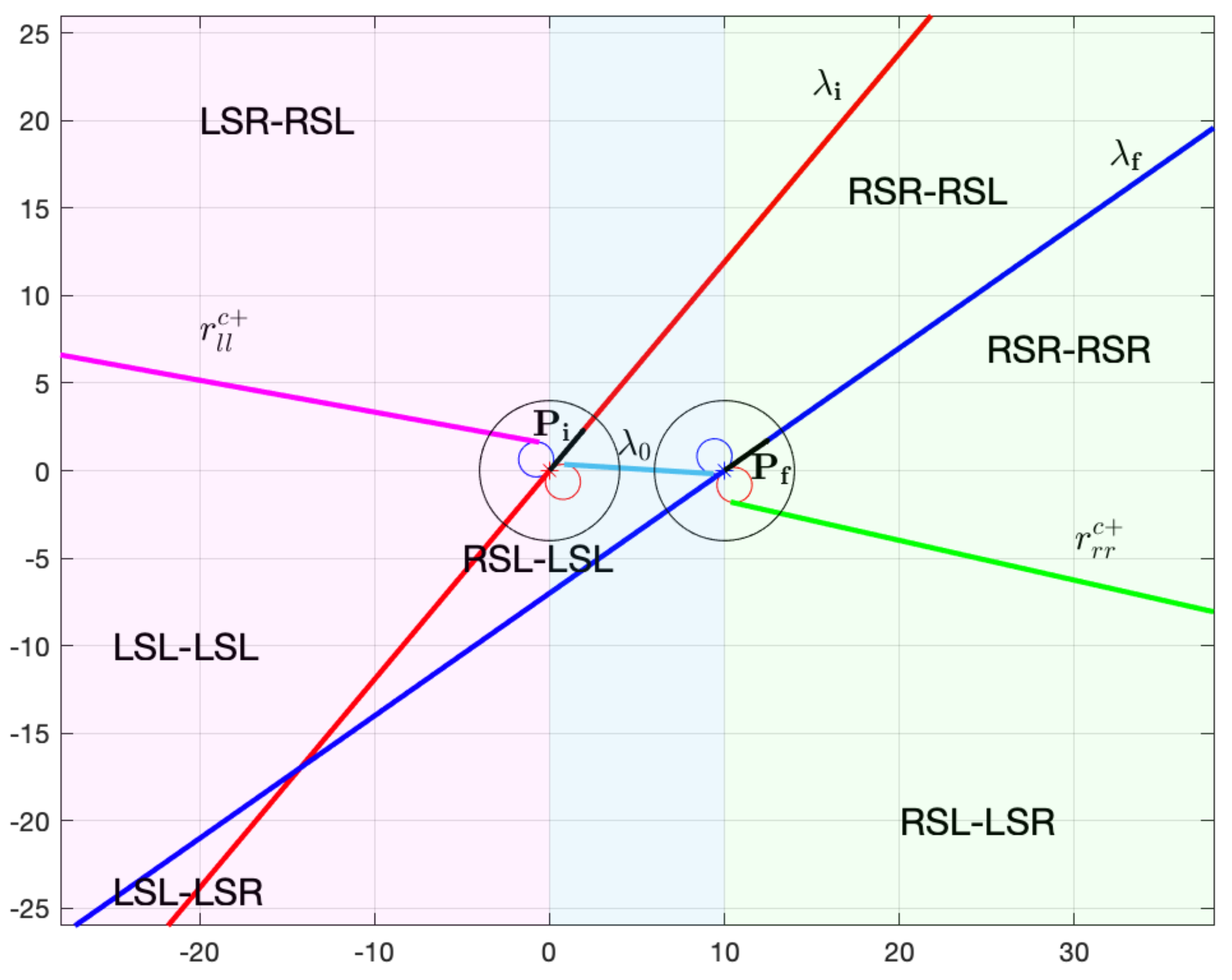
Figure 17.
Example of paths with equal length for a case with and on quadrant I, and on : a) path type, b) path type.
Figure 17.
Example of paths with equal length for a case with and on quadrant I, and on : a) path type, b) path type.
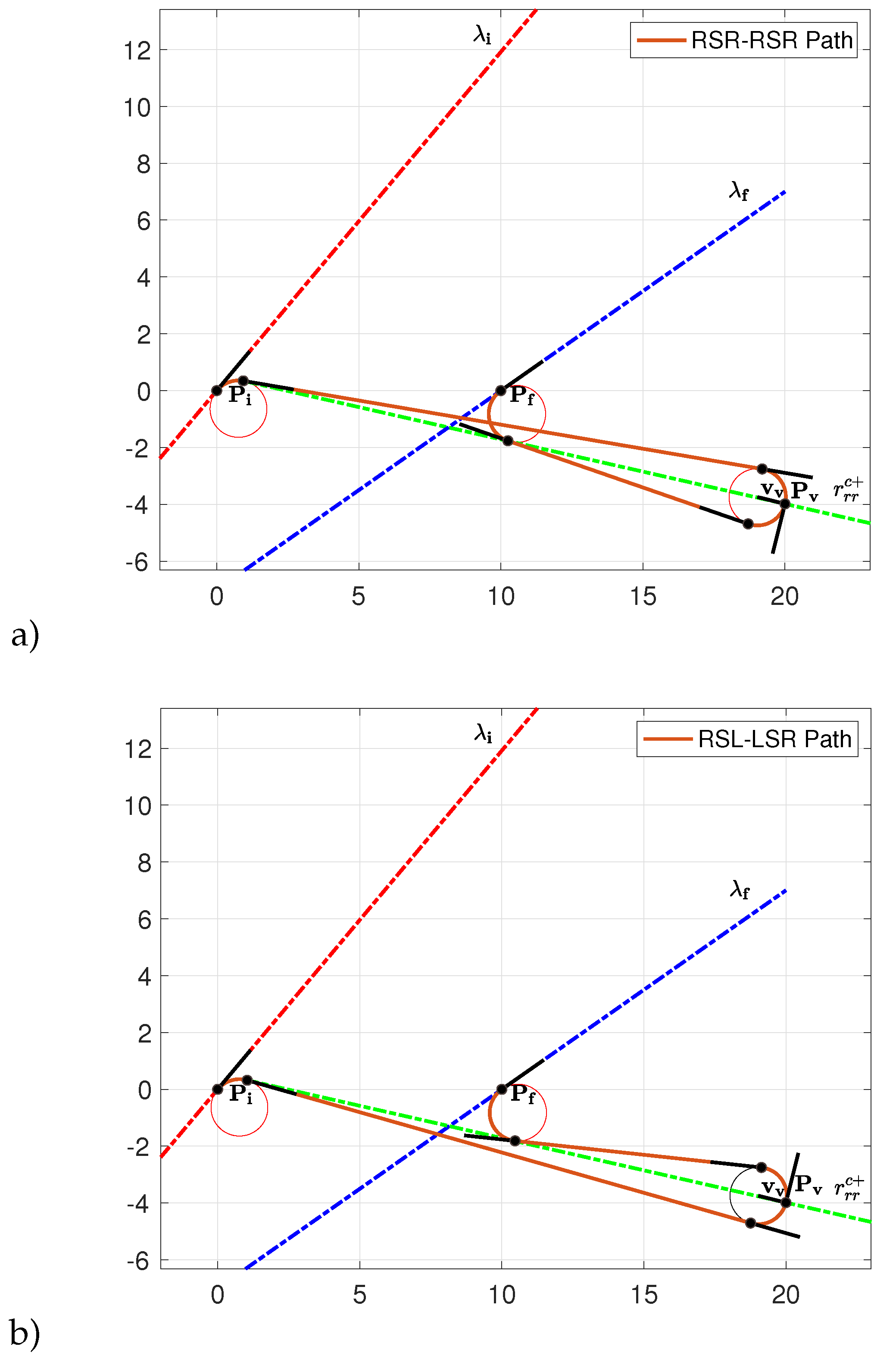
Figure 18.
Curve : frontier between and path types computed numerically exploiting eq. (16) and eq. (17).
Figure 18.
Curve : frontier between and path types computed numerically exploiting eq. (16) and eq. (17).
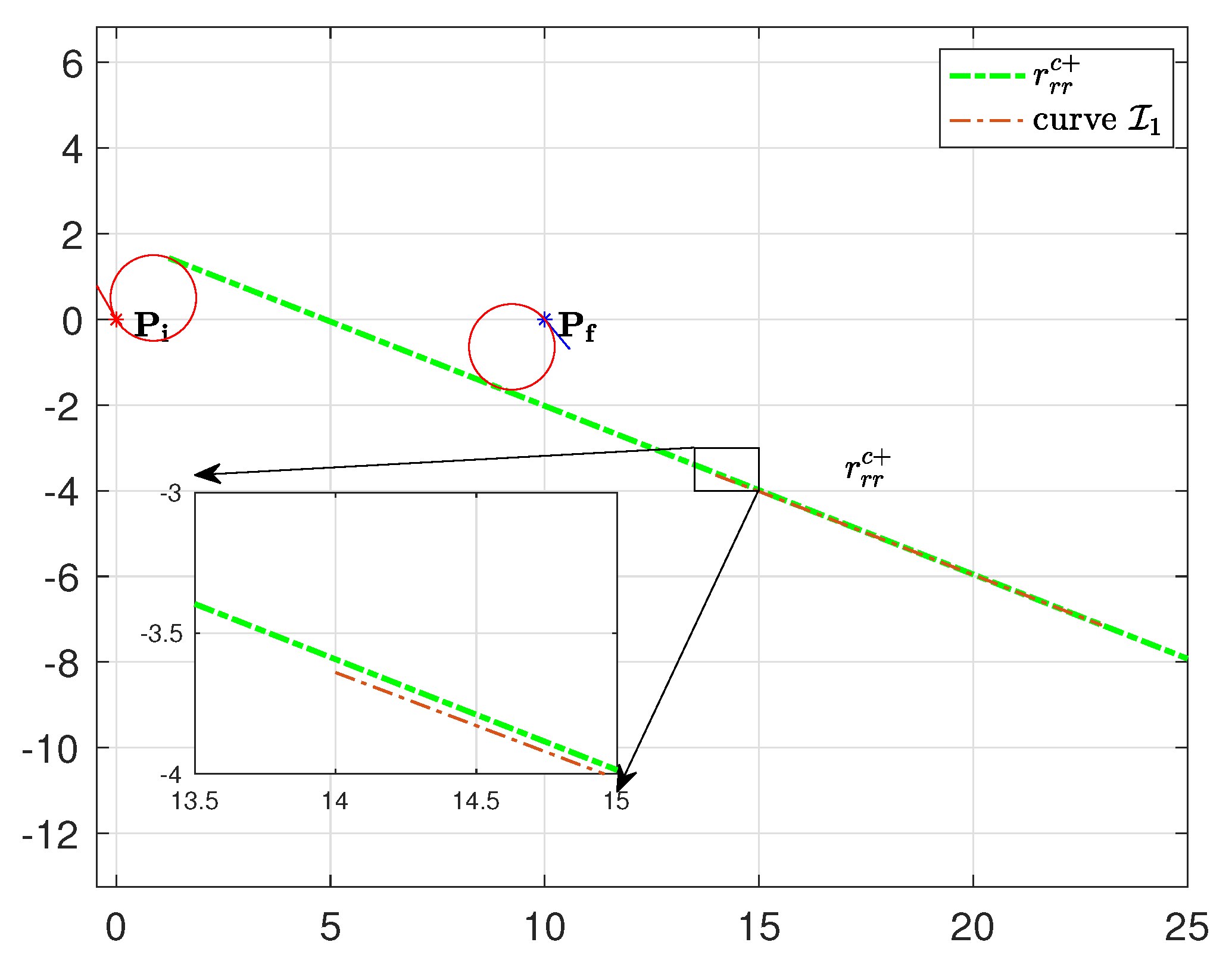
Figure 19.
Illustrative Example: and
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated





