Prerpints.org logo
Preprint
Article

Spectral-Based Fault Diagnosis Methodology for Industrial Shot Blast Machinery Leveraging XGBoost and Feature Importance

This version is not peer-reviewed.

Submitted:

13 August 2024

Posted:

13 August 2024

You are already at the latest version

A peer-reviewed article of this preprint also exists.

Abstract
The optimal functionality and dependability of mechanical systems are important for the sustained productivity and operational reliability of industrial machinery which has direct impact on it’s longevity and profitability. Therefore, failure of a mechanical system or any of it component would be detrimental to production continuity and availability. Consequently,this study proposes a robust diagnostic framework for analyzing the blade conditions of shot blast industrial machinery. The framework involves analyzing the spectral characteristics of the vibration signals generated by Industrial Shot Blast. Additionally, a peak detection algorithms is introduced to identify and extract the unique features present in the peak magnitudes of each signal spectrum. A feature importance algorithm is then deployed as the feature selection tool, and these selected features are fed into 10 machine learning classifier, with Extreme gradient boosting (XGB) as the core classifier. Results show that the XGB classifier achieved the best accuracy of 98.05%, with a cost-efficient computational cost of 0.83 seconds. Other global assessment metrics were also implemented in the study to further validate the model.
Keywords: 
Subject: 
Engineering  -   Safety, Risk, Reliability and Quality

1. Introduction

Over the years, research studies and development with respect to Prognostics and Health Management has significantly shown an impressive spark in intensity across industries and academia, cutting across various disciplines namely, physics, mathematics, computer science, Engineering and so on. PHM which in simple terms implies a computational framework that involves a balanced integration of information, physical knowledge, and in-debt information pertaining the performance, operation, and maintenance of systems, components and also structures [1,2].
Since the onset of Industry 4.0, which introduced Artificial Intelligence, the interaction between humans and machines has positively evolved. This transformation involves the integration of human intelligence with the Internet of Things (IoT), Cyber-Physical Systems, and Machine Learning. These advancements enhance efficiency and productivity, fostering seamless collaboration between humans and intelligent systems [2,3,4,5]. The synergy between AI, IoT, and machine learning has led to smarter, more responsive technologies, revolutionizing industries and improving overall human-machine interactions. Consequently, researchers have employed these advanced methodologies—AI, ML, and Deep Learning (DL)—to explore and extend the useful life of industrial machinery [6,7]. These advanced methodologies achieve this by exploiting the unique features inherent in the generated data signals, such as vibration signals, thermal signals, current signals, and acoustic signals, via sensors. These signals are utilized by these advanced technologies, either individually or collectively, for pattern recognition, aiding in prognostics, classification, prediction, diagnostics, and more. This is often termed a data-driven approach in research studies, and in most cases, its optimal performance is heavily reliant on the quality and quantity of the generated dataset and, most importantly, the signal processing tools and quality of features extracted, especially in ML fault diagnostics and isolation (FDI) scenarios [8,9].
Over the decades, Fourier analysis has been one of the renowned techniques for analyzing current signals and vibration signals owing to it implementation simplicity and also its unique ability of decomposing a given signal into its constituent sinusoidal components [10,11]. In FDI instances, the Fourier transform has been successfully implemented in developing robust and efficient platforms and models. Nevertheless, its setbacks, which include computational speed limitations while handling large datasets and also its tendency to provide an average view of the frequency spectrum. This implies that it does not bear additional information as to how the different frequency components change over time [11,12].
Fast Fourier transform (FFT), with its fast computational speed, and short-Fourier transform (STFT), with its unique ability of transforming a signal into its frequency and time domains, addresses the drawback of the FT. Fourier analysis compatibility with vibration signals is highlighted in this review study [11,12,13,14]. In addition, the performance of a ML-based model is highly dependent on the nature of the features fed to the machine learning classifier. Feature extraction and selection technique are known to help extract and select useful feature, which optimize the performance an MLC model [15].
Although DL-based algorithms are often considered more power than traditional ML-based model, due to computation strength and versatility, especially in instances of complex and large datasets; traditional MLCs are often preferred in instances of small or medium-sized and where computational cost efficiency is paramount. Furthermore, a traditional MLC like Extreme gradient boosting (XGB) provide high efficiency in terms of accuracy and efficient computational cost requirements, which is often a challenge with most MLC models [16].

2. Motivation and Literature Review

The importance of PHM has grown over the years as researchers have devised numerous model to enhance productivity and lifespan of industrial machinery. In this study, an FDI model is implemented for fault classification in the blades of a Shot-blast machine. A Shot-blast machine is an industrial machine used for polishing, cleaning, strengthen metallic surfaces using fine particles called shot-balls. Its working mechanism, which is shown in Figure 1, involves forcibly thrusting of abrasive materials (shot-ball) by its blades in a rotary motion against a given surface at a very high velocity.
Failures encountered in shot-blast machinery cuts across wheel bearing failure, blade failure, mechanical failure, motor failure, belt failure, worn out parts due the abrasiveness of the shot-balls, incorrect angling by the blade thereby there directing the shot-balls to the wrong spots, dust accumulation leading to wear and tear, and other failures due to human error [17]. According to this study [18], the most commonly encountered failure is blade failure due to the abrasive nature of the shot-balls and the high shooting velocity. Blade failure is often cause by four major failure which include:
  • Fine shots: The abrasive nature of the shot-ball will wear the blades over time, which one of the major causes of blade failure.
  • Sand presence: Sand particles will wear a blade faster that the fine shot-balls, causing irregularities on the blades. These sand particles often travel by the edge of the blade, wearing them down and causing the shot-balls to drop from one blade to another, other hence causing irregularities.
  • Presence of chips and flakes: The presence of chips and flakes just like sands, will wear the the blade faster. Most times, the flakes and chip are added to the fine shot-balls via torn sieve from air separators.
  • Cast defect: This is a manufacturing issue that often leads to the quick deterioration of the blade, causing it to wear off faster than usual.
The presence of these failures often leads to downtime, loss of revenue and increased power consumption. Hence, there is a need for an FDI framework to ensure that these faults are mitigated or detected early. For an efficient FDI, it is important that all the necessary techniques required for the desired outcome to be adequately deployed. FFT has been deployed in various studies due its compatibility with vibration signals. In literature, numerous instances have been discussed where FFT has been successfully implemented in fault diagnosis across diverse scenarios. For instance, in [19], the study presented a simple diagnostic model using FFT as the signal processing technique. In their methodology, vibration signals from the bearing of an induction motor are processed with FFT to reveal intrinsic features about the fault bearing signals, which are then fed to a random forest classifier algorithm to classify the various fault types involved in the study. synergy of vibration signals and FFT for fault diagnosis was also demonstrated in this study [20]. The authors exploited the underlying frequencies in the vibration signal of a bearing for fault detection and analysis. They conducted an on-line bearing vibration defect analysis using an enhanced FFT algorithm. However, they concluded that to achieved, more sophisticated signal analytical tool were need. This was also highlighted in this study by Altobi et. al. [21], where they implemented a model for fault classification for five centrifugal pump operating conditions using a frequency-domain analysis. They deployed an FFT algorithm to identify faults generated from stationary and non-stationary centrifugal pump vibration signals. In their findings, they emphasized the need to improve or argument the FFT with other methods, especially in the case of non-stationary signal.
The drawbacks of FFT such as spectral leakage, interpretation complexity, noise sensitivity, and poor performance with non-stationary signals, have led to its optimal performance in an MLC model often depending on its combination or replacement by more robust signal processing techniques such as Hilbert transform (HT), STFT, wavelet-transform (WT), and so on [22,23,24,25]. For instance, in this study [26], the authors considered the pitfalls of the FFT and Incorporated FFT and least square method in their model to achieve the desired output. Another technique that can be used to bypass the low performance of FFT with complex datasets involves data fusion. Although vibration signal are compatible with FFT, the difficulty encountered with vibration signals often lies with their interference with Gaussian noise, thereby, affecting the original signal. Consequently, researchers often introduce techniques to generate a wider range of exploring the characteristics of a system by fusing multi-signals together for ease of analysis. In this study [27], Fang et.al., implemented a multi-mode signal technique for fault diagnosis in a rolling bearing. Their framework involved the fusion of vibration and acoustic signals, which they labeled vibro-acoustic signal, to achieve their goal. Furthermore, to make the different signal complement each, the first deployed a pre-processing techniques as highlighted in their investigation and then processed the signal with FFT, which further enhanced the signal for FDI. According to their investigation, their model recorded an accuracy of 99.98%, which validated approach.
Furthermore, research study overtime has highlighted the importance of feature extraction and selection. A model could have a robust signal processing tool and yet fail to achieve a set goal if the feature extraction and feature selection methodologies implemented are not efficient enough. Many feature extraction and feature selection tools have been discussed and utilized in models to enhance their accuracy and interpretability, especially when combined with signal processing techniques, as they retain meaningful characteristics that often represent the relevant underlying traits required for an effective diagnosis [24,25]. This was demonstrated in this study [28], the author deployed a simple feature extraction technique that, according to their findings, aided in optimizing their model. In their methodology, they applied FFT to the raw signal vibration signals of an induction motor as the signal processing tool to excite the frequency components of the signals as well as their amplitudes. They then divided the frequency spectrum obtained from the FFT into frequency segments, and the energy coefficients of each segment are calculated as the sum of the FFT amplitudes. These coefficients were deployed as the features, which they trained using a machine learning algorithm. The efficiency of their model was validated, achieving a 99.7% model precision. Another study [29], also highlighted the importance of feature extraction and selection in the VSA using time and frequency domain features in diagnosing defects in various rolling bearing components. In their analysis, the deployed a time and frequency statistical feature extraction methods and further integrated the Fisher Score (FS) and the Genetic algorithm (GA) as a their feature selection methodology, which achieved remarkable accuracies when fed to the Support Vector classifier.
Generally, an MLC model is incomplete without a machine-learning classifier. Every ML-classifier algorithm has its strong points and pitfalls. However, in terms of performance, some tree algorithms and boosting algorithms stand out from other classifiers. XGB, being an enhanced version of Gradient Boosting algorithm, offers high performance at a very efficient computational cost. Shukla, Kankar, and Pachori in their study [30], compared various autonomous methods for condition monitoring using ensemble learning and machine learning methods for fault classification in bearings. They evaluated the performances of decision tree (DT), Support vector machine (SVM), XGB. Their result revealed that the XGB outperformed the other classifiers, validating its unique performance capability even in instances of small datasets. Additionally, another performance analysis was conducted in this study [31], focusing on the exploitation of ensemble learning methods, which are know to be a high-performing machine learning algorithm. The authors compared the accuracy performances of random forest (RF), AdaBoost, and XGB. Their experiment demonstrated that the scalable XGB outperformed other models and also showed an improved predictive accuracy compared to the original PFA algorithm.
Overall, these case studies have shown the uniqueness of FFT despite its pitfalls and further highlighted the importance of infusing feature enhancement techniques in a diagnostic model. The core motivation for this lies in this study [10], the authors concatenated the peak extracts from the FFT, power spectral density, and high auto-correlation features for their diagnostic model using current signals from various operating conditions of an induction motor. Their model achieved an accuracy of 79.25%, which did not meet expectations.
In a drive to represent a robust framework that would mitigate some of the setbacks that deter the accuracy of vibration analytical models that embrace FFT as the signal processing tool, this study makes the following contributions:
  • A proposed framework for fault VSA-based diagnosis on the blade of a shot-blast machine using peak detection approach. The proposed peak detection approach served as a discriminative feature extraction technique which exploited the amplitude of that raw signal’s FFT.
  • An implementation of a robust and efficient feature selection techniques–feature importance method which the selected the most relevant feature for an adequate fDI .
  • An extensive comparison and analysis of various MLC algorithm including XGB which was the core classifier algorithm.
  • A computational cost evaluation of the MLC algorithm to ensure that the the model presents an efficient yet computational inexpensive model.
The remaining sections are structured in this manner: Section 3 talks about the theoretical background of the core backbone of the study, Section 4 discusses the experimental model and the model’s technicality, Section 5 presents the experimental setup and the visualizations, Section 6 discusses the results of the study and future works, and Section 7 concludes the study.

3. Theoretical Background

3.1. Vibration Signal Analysis

VSA is one of the most popular methods for fault detection in mechanical systems, owing to the nature of vibration signals, which contain rich spectral content of mechanical systems, especially in faulty states. VSA exploits these generated signals to extract and analyze their characteristics. In fault detection, these signal characteristics often contain the signal unique signatures, which are harnessed in VSA to utilized their individual discriminative features to develop an FDI model. These signatures inherent in vibration signals differ significantly between healthy and faulty states, as faulty signals tend to generate fault harmonics that become more visible when signal processing tools are deployed. However, vibration signals are often laced with noise, typically Gaussian noise and white noise, the can envelop the original signal. FFT, DFT, STFT, HT, Discrete wavelet transform (DWT), Continous wavelet transform (CWT), etc. have been deployed in various studies reveal the spectral constituents signal of mechanical systems in VSA, aiding in the development of robust diagnostic models [23,24,32,33,34]. Amongst these, Fourier analysis has been one of the most widely used techniques, with DFT and FFT have serving as the bedrocks for many advanced signals processing tools [10], as they segments by signals by representing them through their constituent sinusoidal components. However, the inherent pitfall of FFT, such as its sensitivity to noise, limited time-frequency resolution, and the assumption of signal stationarity, etc., led to the introduction and utilization of STFT. STFT provides time-frequency components of signals, addressing some of the limitations with FFT, as documented in research studies [12].
On the other hand, wavelet transform is also a powerful tool that has been employed in research studies with great efficiency, as it analyzes signals at different scales and resolutions using wavelet-series. Unlike FT, WT dissects signals into square integrable wavelets, providing the signal’s transient time and frequency characteristics [32,33,34]. However, its complexity in implementation, especially in selecting an appropriate mother wavelet remains a concern [34]. These challenges with traditional signal processing tool often inspire the development of new methods, as research aims to present alternatives that offer a variety of choice. For instance, HT, Hilbert Huang transform, variation mode decomposition etc. have been developed to address most of these issues,particularly noise sensitivity [23,35,36].
Generally, the VSA implementation depends on the nature of data, the choice of signal processing tool, and the adaptability of classifier algorithms to the discriminative features, especially in the context of a diagnostic model.

3.2. Extreme Gradient Boosting (XGB)

The extreme gradient boosting (XGB) employs the gradient boosting machine (GBM) structure, which is a subset of an ensemble learning technique [37]. It represents a unique class of Gradient boosting algorithm that can be effectively applied to both classification and regression modelling. Generally, GBM classifier or regressors models are known for their high efficiency and often outperform most machine learning algorithms, as documented in numerous studies [30,31]. XGB, however, introduces several structural improvements to address the limitations and errors found in traditional ensemble learning methods such as GBM and AdaBoost [30,31,37]. One of the core drawbacks of most ensemble learning classifier, expensive computational demands, makes the XGB a unique model as it presents a relative faster model [37]. The influence of XGB algorithm has be widely recognized and reported in studies such machine learning data mining challenges, as it has been commonly employed amongst kaggle’s competitors as well as data scientist in this particular field [31,38].
To dig deeper into the structural architecture of boosting algorithm for an in-depth understanding; assume that a given set: D = x i , y i : i = 1 , … , m , x i ∈ R n , y i ∈ R , with m pairs and n features. Subsequently, y ^ i can be defined as the prediction value of the given model and is shown in Equation 1[31]:
y ^ i = ∑ K = 1 k f k ( x i ) , f k ∈ k
Where f k ( x i ) represent the predicted valued generated by the K t h tree of the i t h sample. At every given iteration of the gradient boosting, the residuals are tuned to correct the errors on the initial predictors so as to optimize the loss function. The introduction of the XGB enhances the function by minimizing the objective function as shown below:
O b j = ∑ i = 1 n l y ^ i , y i + ∑ k = 1 K Ω f k
With
Ω f k = γ T + 1 2 λ ω 2
Where l represents the loss function which is a measure of the difference between y ^ i the predicted value and the target value y i . Ω stands for the regularization term which in this context is a factor utilized to measure of tree f k complexity, γ and λ present the degrees of regularization. ω and T stands for the the vector and numbers of leaves assigned to each tree respectively.
To obtain the value of f k ) that minimizes the loss function, there is need for optimization. To easily accommodation of different loss functions, the second order derivation of Equation 2 is determined as shown below [30,31]:
O b j ( t ) ≃ ∑ i = 1 n l y i , y ^ i ( t − 1 ) + g i f i x i + 1 2 h i f t x i 2 + Ω f t
Where h i and g i are the first and second order gradient statistics on the loss function:
h i = ∂ y ^ ( t − 1 ) 2 I y i , y ^ i ( t − 1 ) , g i = ∂ y ^ ( t − 1 ) I y i , y ^ i ( t − 1 )
Removing the constant terms to expand Ω , an approximated version of the equation is obtained and is shown in Equation 5 below [31]:
O b j ( t ) = ∑ i = 1 n g i f i x i + 1 2 h i f t x i 2 + γ T + 1 2 λ ∑ j = 1 T ω j 2 = ∑ j = 1 T ∑ i ∈ l j g i ω j + 1 2 ∑ i ∈ l j h i + λ ω j 2 + γ T
Th instance of leaf j is denoted in the equation by l j = { | q ( x i ) = j } . For a given fixed tree structure p, its optimal weight value of each leaf j can be calculated thus: w j * = − G j 2 H j + λ . Substituting the w j * into the the objective function–Equation 5, a simplified optimal objective value of the objective function is generated as shown in Equation 6:
O b j * = 1 2 ∑ j = 1 T G J 2 H j + λ + λ T
where G j and H j are ∑ i ∈ i j g i and ∑ i ∈ i j h i respectively.
In reality, it is quite unattainable to illustrate all the functionality of all the leaf in the tree structure p. A greed algorithm from a single leaf and iteratively add branches to the tree is implemented instead. The decision to further add a split to a given tree is implemented by the function below:
G = 1 2 ∑ i ∈ l L g i 2 ∑ i ∈ l L h i + λ + ∑ i ∈ I R g i 2 ∑ i ∈ I R h i + λ + ∑ i ∈ I l g i 2 ∑ i ∈ l l h i + λ − γ
I R and I L represents instance sets of the right and the left nodes after the spliting.

4. Experimental Model

The proposed diagnostic flowchart, illustrated in Figure 2, highlights the critical importance of subjecting signals (in our case vibration signals) to unique signal processing techniques to facilitate the development of any robust diagnostic model. This model primarily consist of four (4) stages. The first step involves the data collection stage which entails gathering raw vibration data signals from the shotblast industrial machine, encompassing both healthy and fault datasets. The second stage involves the implementation of signal processing techniques, where the collected signals are subjected to spectral transformations which aims at unveiling their detailed components. This transformation enhances the interpretability of the signals by the diagnostic algorithms. Subsequently, in the feature extraction and selection stage, useful characteristics are extracted from the signals, serving as the operating conditions features. The model employs a robust feature extraction technique to ensure optimal feature representation of the each class.
This optimizes the computation cost of the model’s training processing; a feature importance methodology is implemented as the feature selecting tool for the most important feature and reduces the extracted features to 20 features. The final stage involves the feature training phase for fault detection, various machine learning classifiers are introduced to train the features of each of the machine’s operating conditions, this enables the model to distinguish and/or classify the fault and health signals accurately. To validate the efficiency of our model, we introduce performance assessment metrics that ensure high precision and accuracy in predictions.
This multi-stage approach as show in Figure 3 ensures that the diagnostic model is not only robust but also capable of delivering reliable and precise fault detection model, thus enhancing the overall efficacy of the diagnostic process. Due the nature of our dataset being a vibration data, the spectral transform of the signals are determined using the FFT and also to further enhance the data signals for more comprehension, the FFT of the signals are also subjected to the PSD whose major advantage is to enhance the amplitude of the signal frequencies especially the higher frequencies. These output are concatenated and a peak detection algorithm is implemented to serve as the feature extraction technique. The mechanism of the core constituents of the techniques implemented in our study are broken-down thus:

4.1. The Spectral Peak Detection Technique for Feature Characteristics Extraction

Vibration signal analysis has long been a dependable methodology for condition monitoring in PHM. In the case of a shot blast machine blade vibration signals, owing to its nature of operation, the signals are assumed to be composed of varying periodic signals which is a reflection of its operational changes. Despite their complexity and non-stationary characteristics, which often don’t conform to the regular sine and cosine wave functions, these signals can still be effectively analyzed using the FFT technique. By leveraging on the varying magnitudes of alternating spectral peaks observed in the FFT of raw signals under different operating conditions, we utilized these spectral peaks and their corresponding frequencies as distinctive features for our fault diagnostics framework.
Mathematically, given that the raw one- dimension vibration signal from the shot blast industrial machine is given S ( x ) = { x 1 , x 2 , ⋯ , x N } , then the FFT of the this signal S ( x ) denoted by X k can be derived using Equation 7:
X k = ∑ n = 0 N − 1 x n e − j 2 π N k n
Where x n is the n-th sample of the vibration signal, N is the total number of of the signal samples, k is the index of the frequency ranging from 0 to N − 1 , X k is the frequency domain output.
To achieve peak detection extraction, the magnitude spectrum, which represents the strength of the frequency components present in the FFT signal, is first derived. Equation 8 illustrates the mathematical procedure of the magnitude spectrum derivation:
| X k | = error ( X k ) 2 + error ( X k ) 2
Where R e ( X k ) and I m ( X k ) are the real and imaginary components of the Fourier coefficient X k .
Hence, the peak detection algorithm, which identifies frequency components in the magnitude spectrum possessing the highest amplitude, is implemented to signify the dominant frequencies signal in the given signal. The mathematical representation for a peak at an index K p is shown as follows:
| X k p | > X k p − 1 and X k p > X k p + 1
Practically, to filter insignificant peaks and noise, conditions like thresholds are implemented.

4.2. Feature Selection Technique

The importance of feature selection cannot be overstretched owing to its indispensable role in a diagnostic setup; if a wrong feature selection technique is implemented, the performance of a model can be greatly altered. The XGBoost library provides an option that computes feature importance based on different metrics. The feature importance technique is a tree-based algorithm model which is a type of the Embedding feature selection method; however, the default method used by the XGBoost for feature importance is Weight also know as Frequency whose principle involves counting the times a given feature is utilized in splitting the data across all trees in a model. Other methods used by the XGBoost includes Gain and Cover; the Gain method uses the average gain of a feature across all trees in a given model which is often considered the most accurate, the Cover method uses the average coverage of data points affected and/or impacted whenever a feature is used to make a decision. XGBoost utilizes the F-score to measure a feature’s performance across all trees in the feature selection process. In this study, the feature selection is setup using Frequency method which was more suitable for our dataset. Mathematically, for a given feature f the feature importance I using the he frequency methodology can be computed using Equation 10:
I f = ∑ t ∈ T 1 v ( t ) = f
T is the set of all nodes in all trees.
v ( t ) is the feature used at a node t.
1 v ( t ) = f is an indicator function which shows 1 when feature j is used at node t, and 0 otherwise.

4.3. Model Performance Evaluation Criteria

Model evaluation is a perquisite in setting up a model to ensure its efficacy. Architecturally, machine learning models vary and differ in structure, making their performance unique across different datasets in diagnostic scenarios at a given instance. Therefore, these standards ensure that the performance of a machine learning algorithm is thoroughly assessed and verified, regardless of its performance compared across other previous similar models.
The core purpose of the global standard metrics is to ensure that the most suitable machine learning algorithm is selected for a given model to consummate its robustness. Some of these global metrics employed in this study include accuracy ( A c ), precision ( P r ), F1-score, sensitivity ( S n ), specificity ( S p ) and false alarm rate ( F A R ). Mathematically, these global standards can be defined as shown in Equations 11-16:
A c = T P T P + F P + T N + F N
P r = T P T P + F P
F 1 - Score = 2 * Sensitivity * Precision Precision + sensitivity
S n = T P T P + F N
S p = T N T N + F P
FAR = F P F P + T N = 1 − S p
where T P , F P , T N , and F N represents true positive, false positive, true negative and false negative respectively. In the context of classification, TP indicates the correctly predicted classes by a model at a given instance. FP stands for the number of instance a model predicts a class positive while it is actually negative; this is also know as false alarm. When a model correctly predicts a class as negative, it is known as TN. FN indicates the instances where a model incorrectly predicts a class to be negative. Additionally, other evaluation metrics are also introduced to ensure that the models are thoroughly evaluated to give the desire output Such metrics include computational cost, complexity, and the confusion matrix. The prowess of the confusion matrix lies in the ability to showcase the individual performance in classification algorithms. It summarizes the outputs of a given model’s prediction, providing a detailed breakdown of TP, FP, TN, and FN. It aids in giving and in-depth analysis of the performance of a classification model, for both binary and multi-class classification issues.

5. Experimental Setup and Visualization

This study proposes a peak detection vibration analysis diagnostic framework, which was setup in a company called TSR located in Gumi-si, South Korea. The headquarters is located in Gumi, Gyeongsangbuk-do, South Korea, with mass production also taking place at the TSR Mexico Plant. TSR is an automobile parts manufacturing company that satisfied the needs of the global automobile market through world class product development continuous technology development. The setup was carried out out on the Shot-blast industrial machine at TSR. Due to the size of the machine and the fact that it is an industrial machine and not a prototype, all safety precautions were observed. An accelerometer was attached at the most appropriate position using a Vibrometer.
Figure 4 shows the machine setup and sensor placement at the STR industrial complex. As shown, the major components of the Shot-blast machine include the belt, motor and the Shot-balls. The rotary motion of the shot-blast blades is provided by the induction motor which is transferred to the blade via the belt. Figure 5 illustrates the functionality (input and output) of the Shot-blast machine; Figure 5a shows the condition of a cylinder before undergoing the shot-blasting process while Figure 5b shows the cylinder after it has undergoes a shot-blasting process.
Due to the inherent complexities of Shot-blast machine’s operation and the experiment being conducted using a running industrial machinery,an extensive long-range monitoring process of the Shot-blast machine was conducted to observe potential failure occurrences. The major fault observed during this period was the Shot-blast blade deterioration, which is one of its most frequently occurring faults. Figure 6 shows a visual representation of the healthy blades and the deteriorated blades as involved in the experiment providing a comprehensive perceptions into the observed and monitored healthy and deteriorated states of the Shot-blast blades. Table 1 details the operational conditions involved in the study.
The operational functionality of the Shot-blast which primary centered on the removal of scales, rust, and debris from a products by rotating and shooting fine tiny metallic and non-metallic particles, known as shots or grits. The operational specifications of the Shot-blast blades are predominantly determined by the dimensions and types of motor, pulley and belt powering the Shot-blades. In the study, the Shot-blast blade operated at an approximate speed of 2000 RPM, propelling the shot-balls at a high velocity ranging from 60 to 100 meters per second (m/s). This substantial high blasting velocity often results to the deterioration of the shot-blades, transitioning from HSBB-1 to DSBB-2.

5.1. Signal Processing for Feature Engineering

Vibration Data were collected from the Shot-blast industrial machine at just two operating conditions; HSBB-1, DSBB-1. Figure 7a,b show the visual representation of the vibration signals as collected from the Shot-blast industrial machine at both operating conditions, with blue representing the HSBB-1, and red representing the DSBB-2.
The visualization clearly reveals the dissimilarity between the operating conditions of both signals generated from the Shot-blast machine. Analytically, the signal the signals appears similar at the onset; However, significant differences in spikes and amplitudes emerges as the number of data samples increases. The data collection scheme employed in the experiment involved collecting and extensive dataset over a prolonged period. The data collection was halted after a blade maintenance was conducted, the collected data signals are visualized to observed their variations over time. This process enables the extraction of fault data signals from the entire dataset, highlighting the core differences in operating conditions and labeled. Next, the signals were subjected to an FFT signal processing for feature extraction using the technique discussed in Section 4 and shown in Figure 7c nad Figure 7b. As highlighted in the previous section, a peak detection approach was implement for feature extraction. Through engineered mathematical procedures, thirty (30) feature were generated from the peak frequencies and standardized. These efficiently characterize both operational conditions and serve as their unique and distinguishing attributes. Figure 8 represents the FFTs and their corresponding peak detection initialization for feature extraction.
Furthermore, a feature importance technique is implemented for feature selection, which is vital in removing redundant features and also maintaining a healthy computational cost, especially in cases where the data is extensive. Figure 9 outlines the procedures involved in implementing the feature selection technique. Firstly, a correlation plot of the features is presented to determine the most suitable feature selection technique for our model. The correlation plot of all 30 features, a shown in Figure 9a, the feature showed no correlation, which suggests that a correlation-filter feature selection approach is not appropriate in this instance. Consequently, a more suitable and robust ’feature importance’ technique is adopted in this study.
Secondly, the feature importance scores are determined, Figure 9b illustrates the visualization of each feature’s performance of the 30 features. The F-score displays the individual performance of each feature across all XGBoost tree during the feature selection process. The final step, which heavily relies on the expertise and experimentation of the researcher, involves selecting features that deemed less importance based on their F-scores. In our approach, we implemented a benchmark F-score of 275 for feature selection. Using this yardstick, we retained 11 features eliminated 19 features. Figure 9c,d shows the 11 selected features and their correlation plots, respectively.

5.2. Feature Evaluation

Theoretically, the performance of a traditional machine learning mazodel is heavily dependent on discriminative strength of their training features. In our study, the implementation of the Spearman correlation filter for discriminative feature selection was not feasible because the extracted features were already highly discriminative, as illustrated in Figure 9a. Over the years, various techniques have been employed in selecting discriminative features, which are crucial for a successful diagnostic model. These techniques include the filter method, wrapper method, embedded method, and more. Due to the inherently discriminative nature of our features, methods like the correlation filter-based method were ruled out. Figure 9a shows the Spearman’s correlation heatmap of the 30 peak features extracted from the Shot-blast machine signal, which were mostly uncorrelated with a mean correlation score of the features below zero. This indicates that the features are not correlated and can be efficiently employed for a diagnostic model. However, our study aimed to present a cost efficient model. Therefore, we focused on reducing the number of features by removing redundant ones while retaining the important features using their feature importance scores as a means of selection. Figure 9d shows the visualization of the correlation heatmap of 11 selected features, Confirming that they are discriminative enough for our diagnostic modeling.

5.3. Machine-Learning Algorithm Based Diagnosis

Practically, the success of a traditional machine-learning classifier for a diagnostic diagnostics model is heavily reliant on the success of the feature extraction and selection techniques in a given model. Furthermore, the architectural structure and learning technique of an ML-model also plays a vital role in the performance of a given model; hence the need for employed a wide range of ML-classifier to ascertain their performance, ensuring that the best ML-classifier that is most suitable for a model is affixed to the model. Accordingly, in our study, we deployed 10 popular and robust ML-classifier in our feature training and classification for fault diagnosis. Table 2 presents the summary of the individual parameters of the ML-classifiers deployed in our modeling. which were selected based on their hyper-parameter tuning performance.
For optimal efficiency of the ML-classifiers, adequate parameter optimization is deployed to ensure that the desire and best results are achieved for most efficiency. As earlier highlighted, the computation cost of the model were also deployed as a means of ML-classifier validation and assessment along side other other global performance metrics. Table 3 and Figure 10 shows the break down of the individual performance of the ML-model using the evaluation metrics deployed in our study.
Generally, the performance of a model an ML-classifier is often pinned to its accuracy score most especially the test accuracy which is so because it shows the ability of the model to perform as deemed. In addition to the accuracy scores, the precision, recall, F1-score, and specificity of these model were determine for thorough evaluation. Out of the 10 models, 7 performed perfectly well with regards to their test score. Of all, the XGB had the best accuracy with GBC coming next with less that 0.1 % difference, SGD and linear had the lowest test accuracy scores of 51.50% and 51.58% respectively which indicates that the model didn’t adequate adapted to the feature of efficiency.
Given that the accuracies of most models are relatively high and fairly similar, it becomes necessary to evaluate their performances using other metrics. The precision score, defined as the ratio of true positives to the total predicted positives, indicates that the GBC has the highest score at 98.3906%, followed closely by the XGB model at 98.2730%, with a difference of less than 0.02%. In contrast, the recall metric, which measures the ratio of true positives to the total actual positives, reveals that the Linear SVM, despite its overall poor performance, achieved a perfect score of 100%. This indicates that the Linear SVM correctly predicted the positive class more accurately than any other model. Furthermore, evaluations of the F1-score, which is the harmonic mean of precision and recall, and specificity, which is the ratio of true negatives to total actual negatives, show that XGB scored the highest F1-score at 98.1101%, while GBC achieved the highest specificity at 98.3075% respectively. Overall, the XGB and GBC models significantly outperformed the other models across all global evaluation metrics. This highlights the importance of employing additional evaluation criteria to comprehensively assess and select the optimal ML classifier algorithm for our model.
The two best performing ML-classifier algorithms, XGB and GBC, as shown in Table 4, took 0.83 seconds and 188 seconds, respectively, to achieve their results. The cost efficiency of the XGB can be attributed to its advanced techniques, which include tree pruning, regularization, and parallelization, making it an optimized version of GBC. In contrast, GBC involves training multiple tree sequentially, which often makes it computationally expensive. Technically, linear-SVM is expected to be computationally less expensive than RBF-SVM. However, this is not the case in this study, RBF-SVM took 96.22 seconds, while linear SVM took 477.22 seconds. This discrepancy can be attributed to factors such as data size, data complexity, and inefficiencies of the parameters implemented. Overall, the classifier model are computationally fair, except for Linear-SVM and RF, which exhibited high computational costs of 477.55 and 276.73 seconds, respectively, in their execution processes. Although NBC displayed the lowest computational cost, its poor accuracy limits it from being our ideal classifier model. The high computational of RF can be attributed to its ensemble nature and the complexity of training many trees. Therefore, this assessment indicates that the XGB is the best ML-classifier algorithm for our model, as it provided the best accuracy with minimal computational expense.
Upon examining the confusion matrix, we conducted a final assessment by evaluating each algorithm’s performance on each class using confusion matrix visualization. This revealed the exact predictions and mis predictions of each class, i.e., operating conditions, by each ML classifier algorithm. Figure 11 shows the confusion matrix resulting from a 5-fold cross-validation of each algorithm based on the test data. Surprisingly, the Linear SVM returned the highest true positives (TP); however, it also returned the highest false positives (FP) while having zero predictions in both true negative (TN) and false negative (FN) instances. This suggests that the Linear SVM classifier predicted all features to be of one class, which resulted in a 100% recall. This means that its specificity and false alarm rate are 0% and 100%, respectively. The Stochastic Gradient Descent (SGD) classifier returned the highest FN, while GBC and XGB returned the highest TN. Focusing on the best-performing classifier algorithms, XGB and GBC, XGB returned a higher TP with 5918 samples (97.9477%) compared to GBC’s 5869 samples (97.1367%), a difference of 0.811%, which corresponds to their recall difference. Conversely, GBC returned a slightly higher TN with 5576 samples (98.3075%) compared to XGB’s 5568 samples (98.1664%), a difference of 0.1411%, which corresponds to their specificity difference.
Analytically, it is clear that the slightly higher accuracy of XGB over GBC lies in its higher prediction of the positive class.

6. Discussion and Future Works

Shot-blast machines are indispensable in various industries, especially in construction, aerospace, ship construction, manufacturing, re-cycling, re-furbishing, and automobile sectors, where high-quality finishing is required for optimal product performance and durability. This highlights the importance of a robust diagnostic framework to minimize breakdowns and advert unnecessary downtime. This study aimed to develop a computationally cost effective and highly efficient diagnostic model to ensure adequate condition monitoring of the shot-blast blades. Overall, the study’s goals were achieved, with the XGB achieving a test accuracy of 98.0536% at a computation cost of just 0.83 seconds. This performance validates the efficiency of the XGB as a diagnostic tool and also validates our model. XGB’s prowess is attributed to its advanced architecture and optimization techniques, including tree pruning, regularization, and parallel processing, making it one of the most powerful machine learning algorithms, particularly for complex datasets.
XGB’s ability to handle complex data efficiently, incorporate regularization to prevent overfitting, and parallel computational execution significantly enhances its execution speed and accuracy. Additionally, XGB’s flexibility in handling various data types and support for custom objective functions further solidifies its robustness and adaptability. The model’s success in this study further demonstrates XGB’s suitability and adaptions in real-time Condition monitoring, in this case shot-blast blades., ensuring continual and reliable operating conditions in critical industrial applications. However, being an ML- algorithm, it success is highly dependent on the dicriminative rate of the input features deployed for diagnosis. In the study, the combination of a peak detection feature extract and a feature importance feature selection approach presented features that enable the XGB give the desired output.
For future work, there is potential to test our model on different industrial machinery to ensure its robustness and adaptability to various data types. The current study conducted a diagnostic assessment using only two classes, which may not suffice for multi-class scenarios. Therefore, further studies should explore different stages of blade degradation to verify the model’s classification efficiency. However, the nature of the industrial shot-blast machine might limit data generation across various shot-blast blade degradation stages. Thus, while our initial results are promising, expanding the model’s application and testing it under more complex conditions is crucial for validating its effectiveness in diverse settings.

7. Conclusion

This project presented a peak detection-based approach for high discriminative feature extraction, focusing on the FFT peak coordinates from the vibration signal of shot blast industrial machinery to extract 30 discriminative features. A feature selection technique using feature importance was implemented to select the 11 most important features using the XGBoost library. These highly discriminative features are fed to 10 ML-based classifiers, and their classification accuracies were summarized in the study.
An extensive comparison of ML-based diagnostic classifier models was conducted, providing a generalization blueprint for shot blast blade fault diagnosis. The results demonstrated that XGBoost exhibited high speed and accuracy, achieving the best test accuracy of 98.0536% with a computational cost of 0.83 seconds, which was the second lowest. The model with the lowest computational cost was Naive Bayes at 0.09 seconds; however, its accuracy was one of the poorest, making it inadequate for adaptation as our model’s classifier. Gradient Boosting Classifier (GBC) displayed a very good accuracy of 97.7036%, but its computational cost was very high, making it unsuitable for the goal of the study, which aimed for a cost-efficient model.
Overall, the study highlights the effectiveness of XGBoost as a robust and efficient model for fault diagnosis in shot blast machinery, balancing high accuracy and reasonable computational cost.

Author Contributions

Conceptualization, J.-H.L. and C.N.O.; methodology, C.N.O.; software, J.-H.L. and C.N.O.; formal analysis, C.N.O.; investigation, J.-H.L. C.N.O. and B.C.N.; resources, J.-H.L., C.N.O., B.C.N. and J.-W.H.; data curation, J.-H.L.; writing—original draft, J.-H.L. and C.N.O.; writing—review and editing, C.N.O.; visualization, J.-H.L. and C.N.O.; supervision, B.C.N. and J.-W.H; project administration, J.-W.H.; funding acquisition, J.-W.H. All authors have read and agreed to the published version of the manuscript.

Funding

This research was supported by the MSIT (Ministry of Science and ICT), Korea, under the Innovative Human Resource Development for Local Intellectualization support program (IITP-2023-2020-0-01612) supervised by the IITP (Institute for Information and communications Technology Planning and Evaluation).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The data presented in this study are available upon request from the corresponding author. The data are not publicly available due to laboratory regulations.

Conflicts of Interest

All authors declare no conflict of interest.

References

  1. Hu, Y.; Miao, X.; Si, Y.; Pan, E.; Zio, E. Prognostics and health management: A review from the perspectives of design, development and decision. Reliability Engineering & System Safety 2022, 217, 108063. [Google Scholar] [CrossRef]
  2. Lee, J.-H.; Okwuosa, C.N.; Hur, J.-W. Extruder Machine Gear Fault Detection Using Autoencoder LSTM via Sensor Fusion Approach. Inventions 2023, 8, 140. [Google Scholar] [CrossRef]
  3. Kumar, S.; Tiwari, P.; Zymbler, M. Internet of Things is a revolutionary approach for future technology enhancement: A review. J. Big Data 2019, 6, 111. [Google Scholar] [CrossRef]
  4. Zhou, I.; Makhdoom, I.; Shariati, N.; Raza, M.A.; Keshavarz, R.; Lipman, J.; Abolhasan, M.; Jamalipour, A. Internet of Things 2.0: Concepts, Applications, and Future Directions. IEEE Access 2021, 9, 70961–71012. [Google Scholar] [CrossRef]
  5. Do, J.S.; Kareem, A.B.; Hur, J.-W. LSTM-Autoencoder for Vibration Anomaly Detection in Vertical Carousel Storage and Retrieval System (VCSRS). Sensors 2023, 23, 1009. [Google Scholar] [CrossRef]
  6. Lei, Y.; Yang, B.; Jiang, X.; Jia, F.; Li, N.; Nandi, A.K. Applications of machine learning to machine fault diagnosis: A review and roadmap. Mechanical Systems and Signal Processing 2020, 138, 106587. [Google Scholar] [CrossRef]
  7. Zhao, R.; Yan, R.; Chen, Z.; Mao, K.; Wang, P.; Gao, R.X. Deep learning and its applications to machine health monitoring. Mechanical Systems and Signal Processing 2019, 115, 213–237. [Google Scholar] [CrossRef]
  8. Wang, Z.; Zhao, W.; Du, W.; LI, N.; Wang, J. Data-driven fault diagnosis method based on the conversion of erosion operation signals into images and convolutional neural network. Process Safety and Environmental Protection 2021, 591–601. [Google Scholar] [CrossRef]
  9. Yang, H.; Meng, C. Data-Driven Feature Extraction for Analog Circuit Fault Diagnosis Using 1-D Convolutional Neural Network. IEEE Access 2020, 08, 18305–18315. [Google Scholar] [CrossRef]
  10. Okwuosa, C.N.; Akpudo, U.E.; Hur, J.-W. A Cost-Efficient MCSA-Based Fault Diagnostic Framework for SCIM at Low-Load Conditions. Algorithms 2022, 15, 212. [Google Scholar] [CrossRef]
  11. Sejdić, E.; Djurović, I.; Stanković, L. Fractional Fourier transform as a signal processing tool: An overview of recent developments. Signal Processing 2011, 91, 1351–1369. [Google Scholar] [CrossRef]
  12. Akan, A.; Cura, O. K. Time–frequency signal processing: Today and future. Digital Signal Processing 2021, 119, 103216. [Google Scholar] [CrossRef]
  13. Boudinar, A.H.; Aimer, A.F.; Khodja, M.E.A.; Benouzza, N. Induction Motor’s Bearing Fault Diagnosis Using an Improved Short Time Fourier Transform. In Lecture Notes in Electrical Engineering; Springer: Cham, Switzerland, 2019; pp. 411–426. [Google Scholar] [CrossRef]
  14. Yoo, Y.J. Fault Detection of Induction Motor Using Fast Fourier Transform with Feature Selection via Principal Component Analysis. Int. J. Precis. Eng. Manuf. 2019, 20, 1543–1552. [Google Scholar] [CrossRef]
  15. Theng, D.; Bhoyar, K.K. Feature selection techniques for machine learning: a survey of more than two decades of research. Knowl Inf Syst. 2024, 66, 1575–1637. [Google Scholar] [CrossRef]
  16. Li, K.; Yao, S.; Zhang, Z.; Cao, B.; Wilson, C.M.; Kalos, D.; Kuan, P. F.; Zhu, R.; Wang, X. Efficient gradient boosting for prognostic biomarker discovery. Bioinformatics 2022, 38, 1631–1638. [Google Scholar] [CrossRef] [PubMed]
  17. Wrona, R.; Zyzak, P.; Zioikowskia, E.; Brzezinskia, M. Methodology of Testing Shot Blasting Machines in Industrial Conditions. ARCHIVES of FOUNDRY ENGINEERING 2012, 12, 1897–3310. [Google Scholar] [CrossRef]
  18. Pandurang, K.A.; Varpe, R.S. Factors. In National Conference on Emerging Trends in Engineering & Technology (NCETET-2023); 2023. [Google Scholar]
  19. Sikder, N.; Bhakta, A.; Al Nahid, A.; Islam, M.M.M. Fault Diagnosis of Motor Bearing Using Ensemble Learning Algorithm with FFT-based Preprocessing. 2019 International Conference on Robotics,Electrical and Signal Processing Techniques (ICREST), Dhaka, Bangladesh; 2019; pp. 564–569. [Google Scholar] [CrossRef]
  20. Lin, H.-C.; Ye, Y.-C.; Huang, B.-J.; Su, J.-L. Bearing vibration detection and analysis using enhanced fast Fourier transform algorithm. Advances in Mechanical Engineering. 2016, 8, https. [Google Scholar] [CrossRef]
  21. ALTobi, M.A.S.; Bevan, G.; Wallace, P.; Harrison, D.; Ramachandran, K.P. Centrifugal Pump Condition Monitoring and Diagnosis Using Frequency Domain Analysis. Advances in Condition Monitoring of Machinery in Non-Stationary Operations. CMMNO 2018. Applied Condition Monitoring 2018, 15, 1631–1638. [Google Scholar] [CrossRef]
  22. Okwuosa, C.N.; Hur, J.-w. A Filter-Based Feature-Engineering-Assisted SVC Fault Classification for SCIM at Minor-Load Conditions. Energies 2022, 15, 7597. [Google Scholar] [CrossRef]
  23. Okwuosa, C.N.; Hur, J.-w. An Intelligent Hybrid Feature Selection Approach for SCIM Inter-Turn Fault Classification at Minor Load Conditions Using Supervised Learning. IEEE Access 2023, 11, 89907–89920. [Google Scholar] [CrossRef]
  24. Lee, J.-H.; Okwuosa, C.N.; Hur, J.-W. Extruder Machine Gear Fault Detection Using Autoencoder LSTM via Sensor Fusion Approach. Inventions 2023, 8, 140. [Google Scholar] [CrossRef]
  25. Domingo, D.; Kareem, A.B.; Okwuosa, C.N.; Custodio, P.M.; Hur, J.-W. Transformer Core Fault Diagnosis via Current Signal Analysis with Pearson Correlation Feature Selection. Electronics 2024, 13, 926. [Google Scholar] [CrossRef]
  26. Wang, Y.; Zheng, L.; Gao, Y.; Li, S. Vibration Signal Extraction Based on FFT and Least Square Method. IEEE Access 2020, 8, 224092–224107. [Google Scholar] [CrossRef]
  27. Fang, X.; Zheng, J.; Jiang, B. A rolling bearing fault diagnosis method based on vibro-acoustic data fusion and fast Fourier transform (FFT). Int J Data Sci Anal 2024. [Google Scholar] [CrossRef]
  28. Duc Nguyen, V.; Zwanenburg, E.; Limmer, S.; Luijben, W.; Back, T.; Olhofer, M. A Combination of Fourier Transform and Machine Learning for Fault Detection and Diagnosis of Induction Motors. 2021 8th International Conference on Dependable Systems and Their Applications (DSA), Yinchuan, China; https, 2021; pp. 344–35. [Google Scholar] [CrossRef]
  29. Kumar, R.; Anand, R.S. Bearing fault diagnosis using multiple feature selection algorithms with SVM. Prog Artif Intell 2024, 13, 119–133. [Google Scholar] [CrossRef]
  30. Shukla, R.; Kankar, P.K.; Pachori, R.B. Automated bearing fault classification based on discrete wavelet transform method. Life Cycle Reliab Saf Eng 2021, 10, 99–111. [Google Scholar] [CrossRef]
  31. Asselman, A.; Khaldi, M.; Aammou, S. Enhancing the prediction of student performance based on the machine learning XGBoost algorithm. Interactive Learning Environments 2021, 31, 3360–3379. [Google Scholar] [CrossRef]
  32. Yuan, W. Study on Noise Elimination of Mechanical Vibration Signal Based on Improved Wavelet. In Proceedings of the 12th International Conference on Measuring Technology and Mechatronics Automation (ICMTMA), Phuket, Thailand, 28–29 February 2020; pp. 141–143. [Google Scholar] [CrossRef]
  33. Chen, X.; Yang, Y.; Cui, Z.; Shen, J. Wavelet Denoising for the Vibration Signals of Wind Turbines Based on Variational Mode Decomposition and Multiscale Permutation Entropy. IEEE Access 2020, 8, 40347–40356. [Google Scholar] [CrossRef]
  34. Akpudo, U.E.; Hur, J.-W. An Automated Sensor Fusion Approach for the RUL Prediction of Electromagnetic Pumps. IEEE Sens. J. 2021, 9, 38920–38933. [Google Scholar] [CrossRef]
  35. Chaitanya, B.K.; Yadav, A.; Pazoki, M.; Abdelaziz, A.Y. Chapter 8—A comprehensive review of islanding detection methods. In Uncertainties in Modern Power Systems; Academic Press: Cambridge, MA, USA, 2021; pp. 1664–1674. [Google Scholar] [CrossRef]
  36. Chen, X.; Yang, Y.; Cui, Z.; Shen, J. Wavelet Denoising for the Vibration Signals of Wind Turbines Based on Variational Mode Decomposition and Multiscale Permutation Entropy. IEEE Access 2020, 8, 40347–40347. [Google Scholar] [CrossRef]
  37. Demir, S.; Sahin, E.K. An investigation of feature selection methods for soil liquefaction prediction based on tree-based ensemble algorithms using AdaBoost, gradient boosting, and XGBoost. Neural Comput & Applic. 2023, 35, 3173–3190. [Google Scholar] [CrossRef]
  38. Zhang, D.; Gong, Y. The Comparison of LightGBM and XGBoost Coupling Factor Analysis and Prediagnosis of Acute Liver Failure. IEEE Access 2020, 8, 220990–221003. [Google Scholar] [CrossRef]
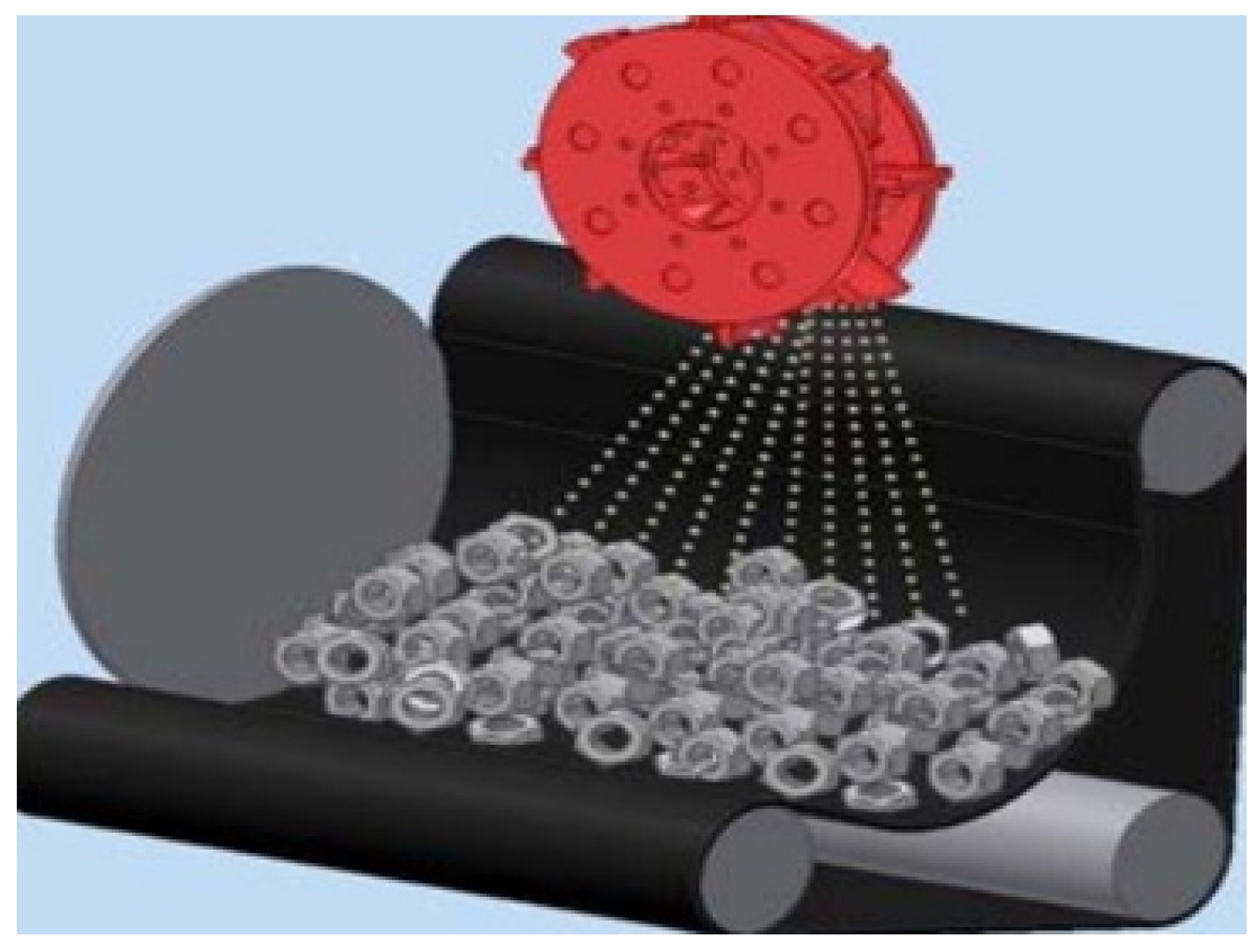
Preprints 115095 g001
Figure 1. Detailed Diagnostic Model.
Figure 1. Detailed Diagnostic Model.
Preprints 115095 g001
Preprints 115095 g002
Figure 2. The proposed diagnostic Flowchart.
Figure 2. The proposed diagnostic Flowchart.
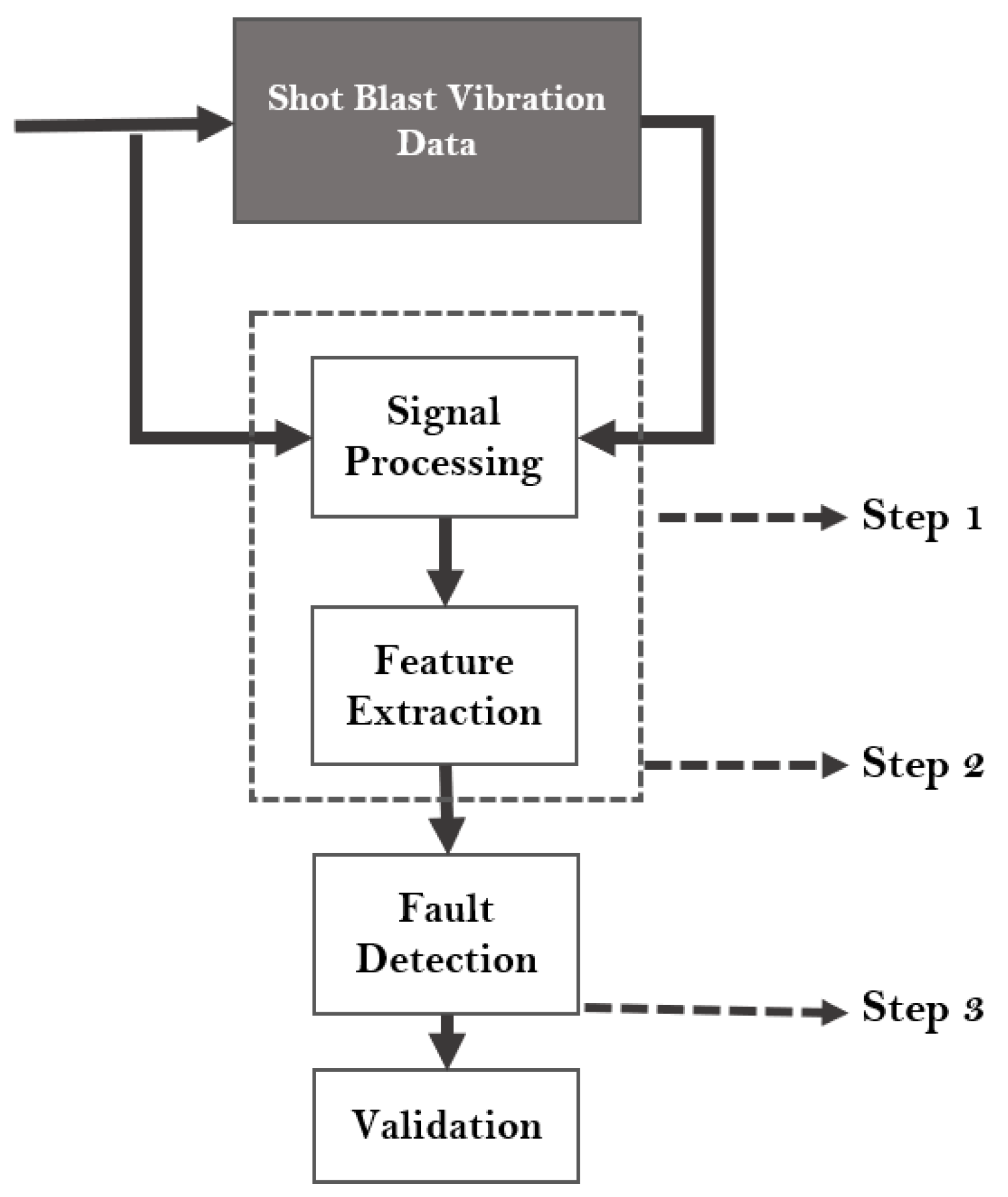
Preprints 115095 g002
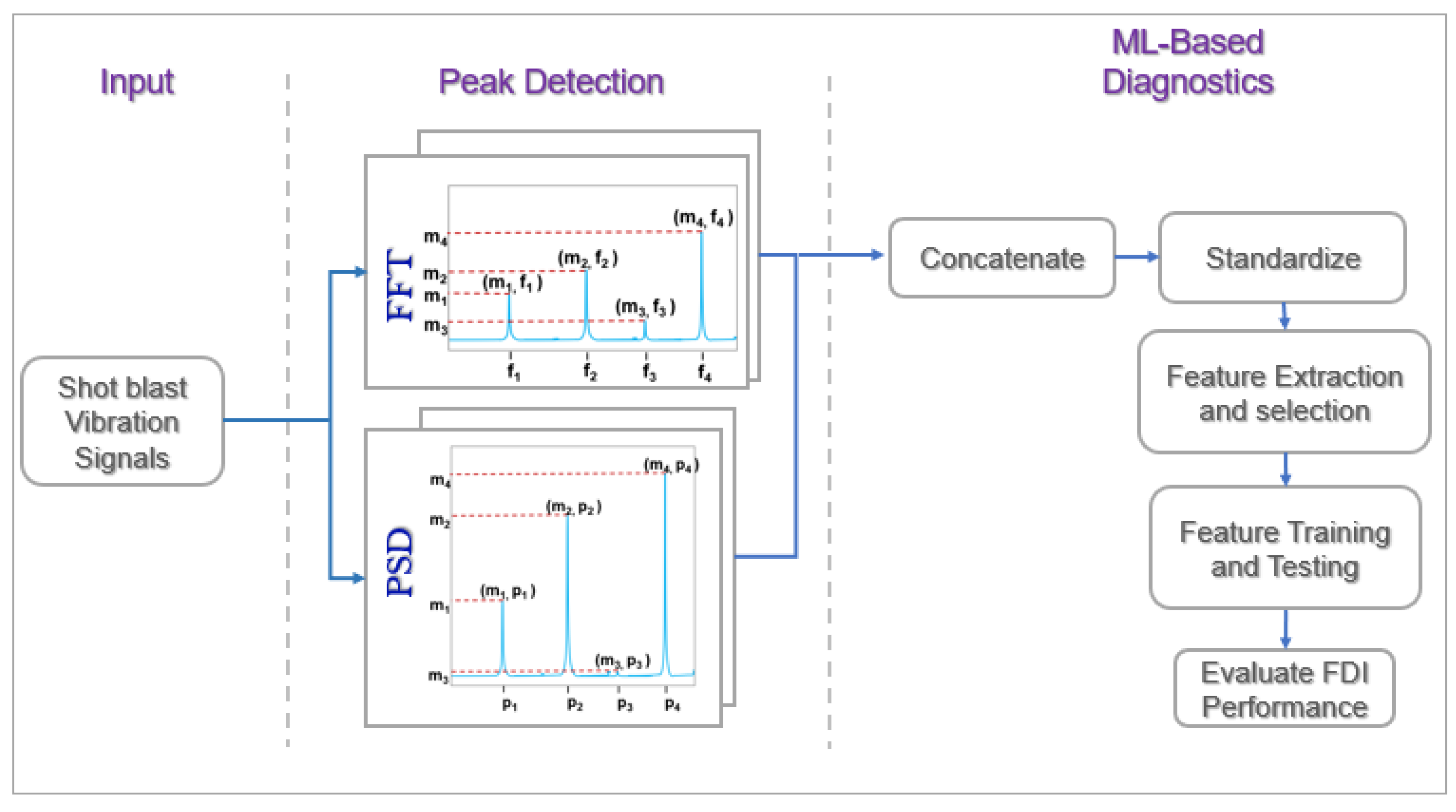
Preprints 115095 g003
Figure 3. Detailed Diagnostic Model.
Figure 3. Detailed Diagnostic Model.
Preprints 115095 g003
Preprints 115095 g004
Figure 4. Data Collection Setup.
Figure 4. Data Collection Setup.
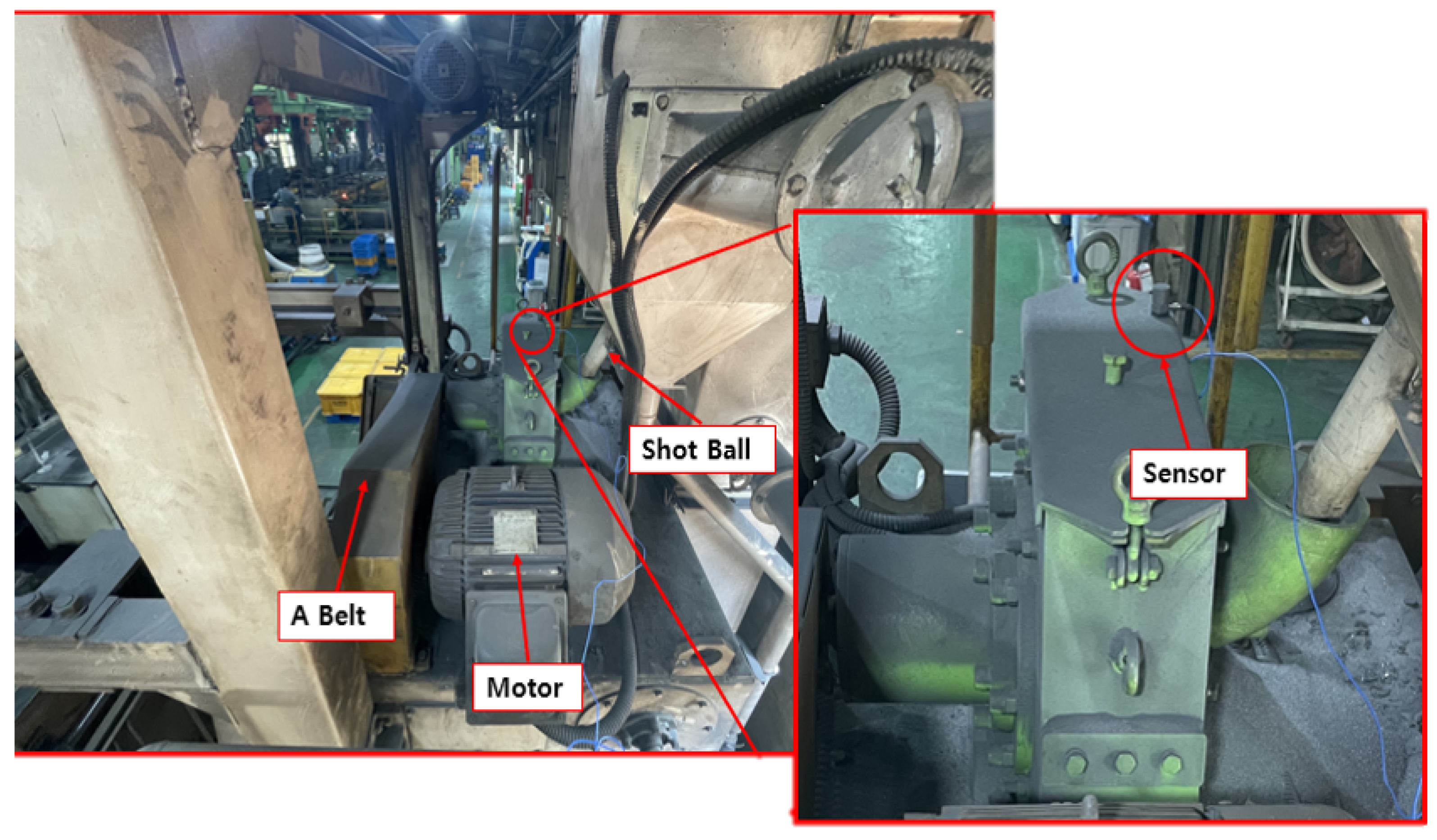
Preprints 115095 g004
Preprints 115095 g005
Figure 5. Shot-blast Product Finishing: (a) Raw Input, (b) Finished Product.
Figure 5. Shot-blast Product Finishing: (a) Raw Input, (b) Finished Product.
Preprints 115095 g005
Preprints 115095 g006
Figure 6. Blade Conditions: (a) Healthy Blade, (b) Faulty Blade.
Figure 6. Blade Conditions: (a) Healthy Blade, (b) Faulty Blade.
Preprints 115095 g006
Preprints 115095 g007
Figure 7. Current signals collected from the Shot-blast Machine: (a) Raw Healthy Signal, (b) Raw Faulty Signal, (c) FFT of the Healthy Signal, (d) FFT of the Faulty Signal.
Figure 7. Current signals collected from the Shot-blast Machine: (a) Raw Healthy Signal, (b) Raw Faulty Signal, (c) FFT of the Healthy Signal, (d) FFT of the Faulty Signal.
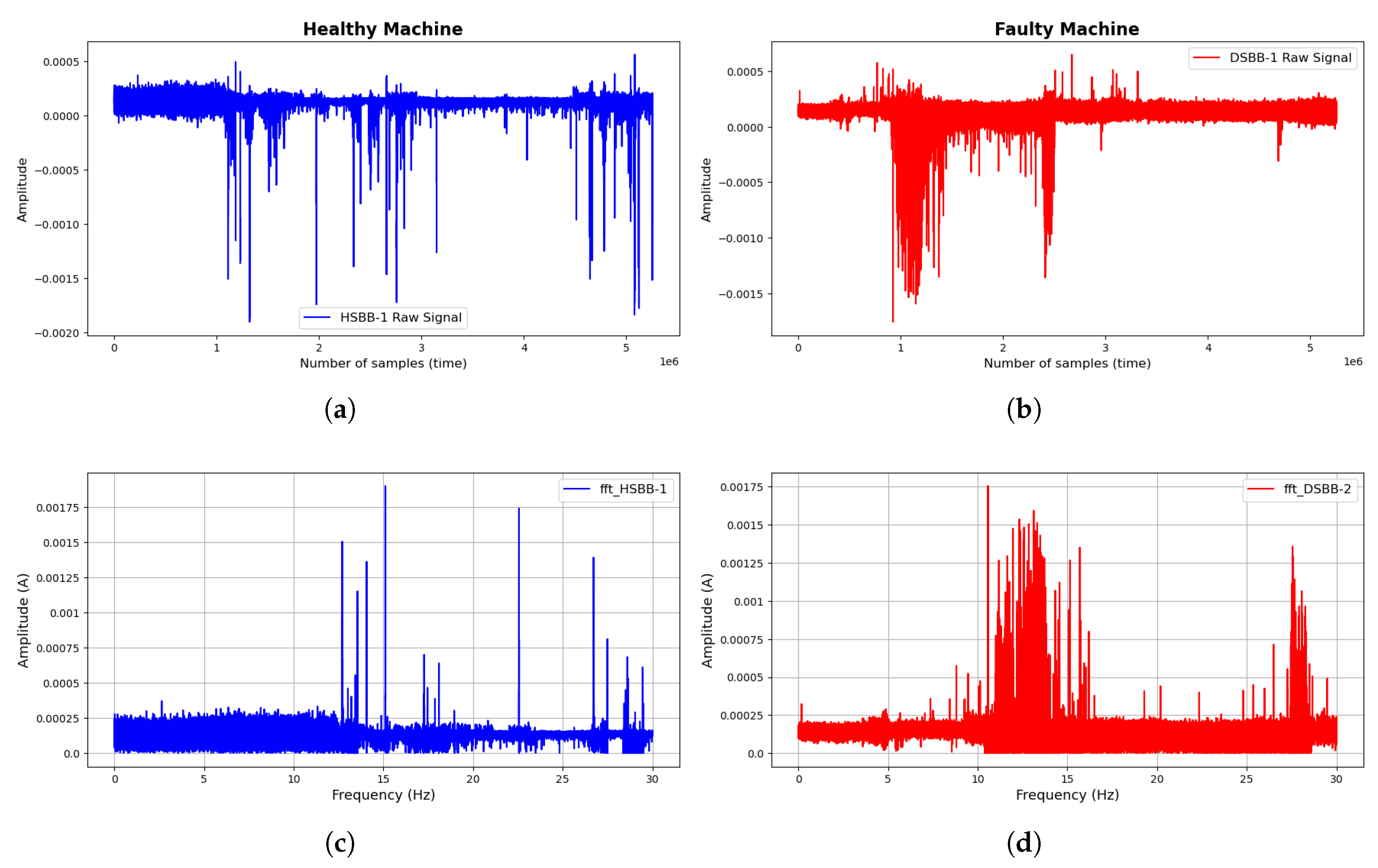
Preprints 115095 g007
Preprints 115095 g008
Figure 8. Peak Detection Feature Extraction: (a) Peak Detection Extract from Healthy Signal’s FFT, (b) Peak Detection Extract from Faulty Signal’s FFT.
Figure 8. Peak Detection Feature Extraction: (a) Peak Detection Extract from Healthy Signal’s FFT, (b) Peak Detection Extract from Faulty Signal’s FFT.
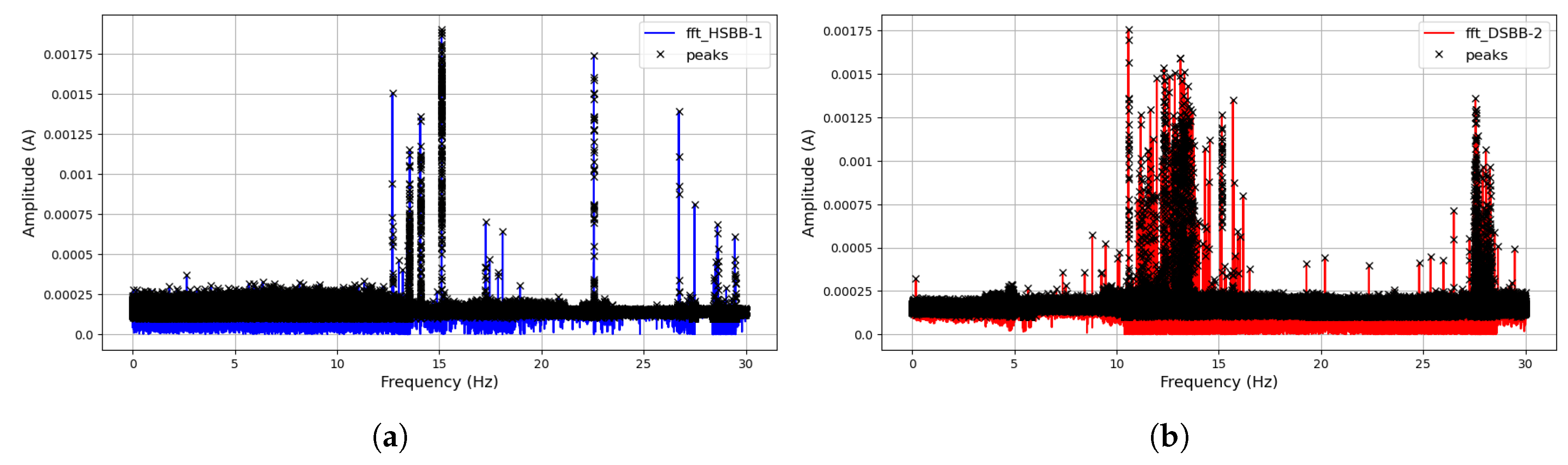
Preprints 115095 g008
Preprints 115095 g009
Figure 9. Signal Processing: (a) Correlation Plot of all Extracted Features, (b) Feature Importance Plot of all Extracted Features (c) Selected Feature Plot, (d) Correlation Plot of the Selected Features.
Figure 9. Signal Processing: (a) Correlation Plot of all Extracted Features, (b) Feature Importance Plot of all Extracted Features (c) Selected Feature Plot, (d) Correlation Plot of the Selected Features.
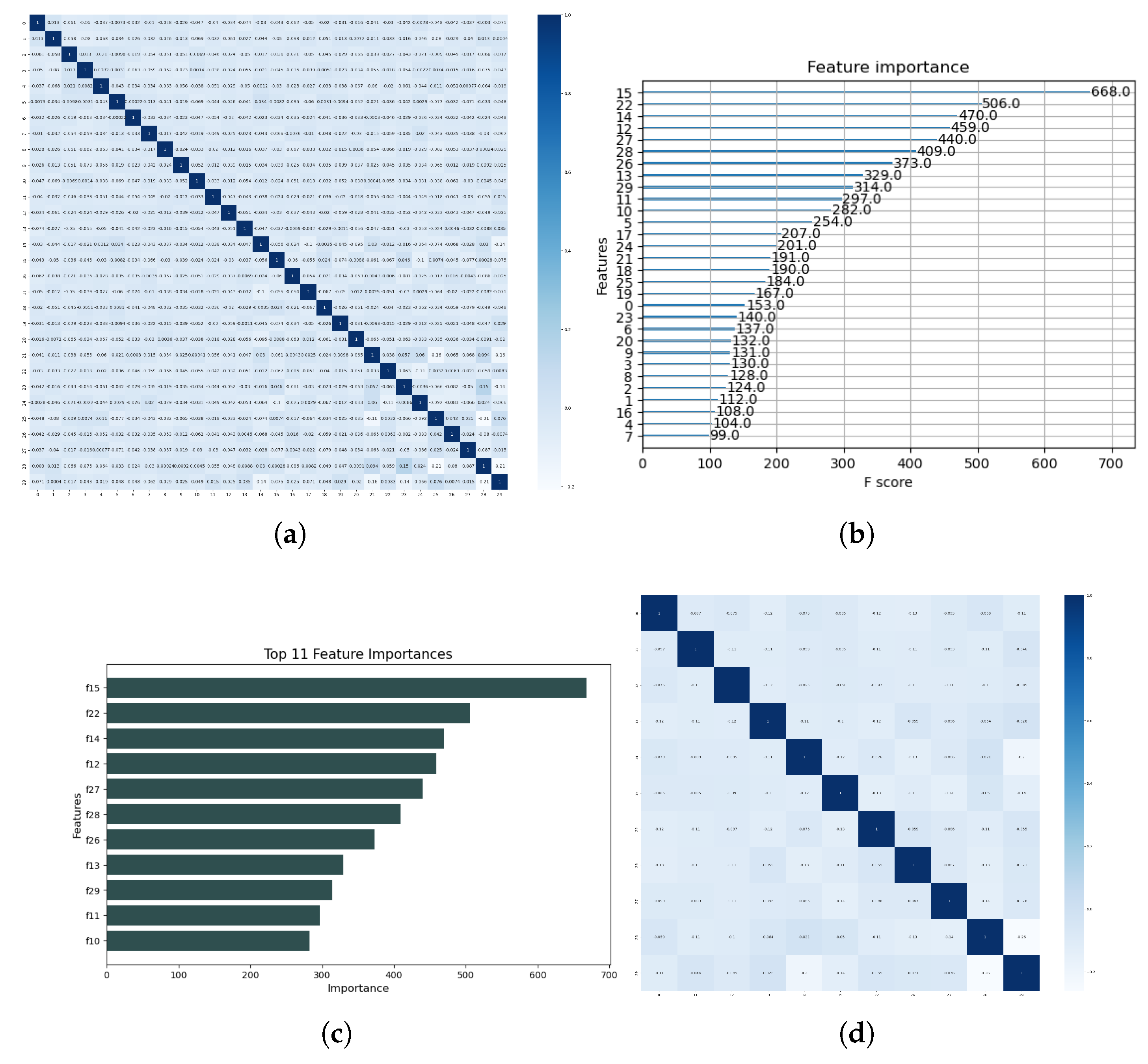
Preprints 115095 g009
Preprints 115095 g010
Figure 10. Performance Metrics Plot of all ML-Classifier Models.
Figure 10. Performance Metrics Plot of all ML-Classifier Models.
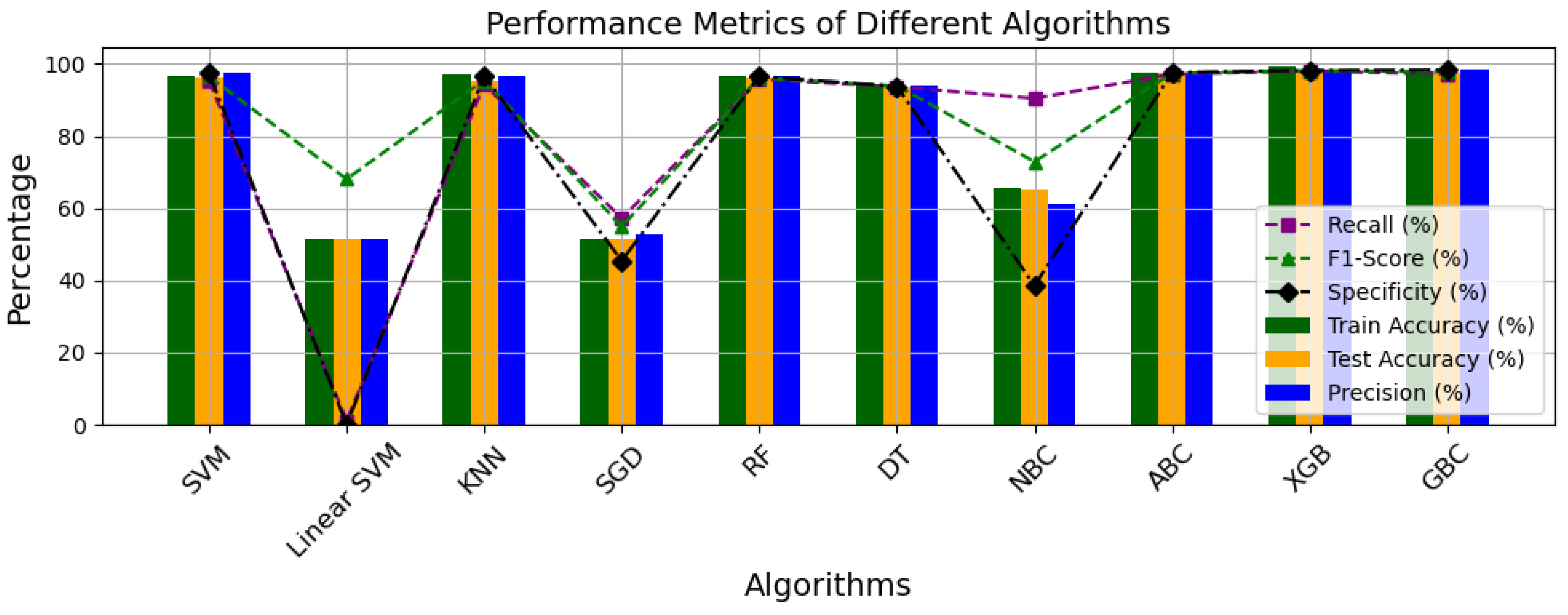
Preprints 115095 g010
Preprints 115095 g011aPreprints 115095 g011b
Figure 11. Test Data Confussion Matrix of all ML-Classifier Algorithms: (a) RBF SVM, (b) Linear SVM, (c) KNN, (d) SGD, (e) RF, (f) DT, (g) NBC, (h) ABC, (i) XGB, (j) GBC.
Figure 11. Test Data Confussion Matrix of all ML-Classifier Algorithms: (a) RBF SVM, (b) Linear SVM, (c) KNN, (d) SGD, (e) RF, (f) DT, (g) NBC, (h) ABC, (i) XGB, (j) GBC.
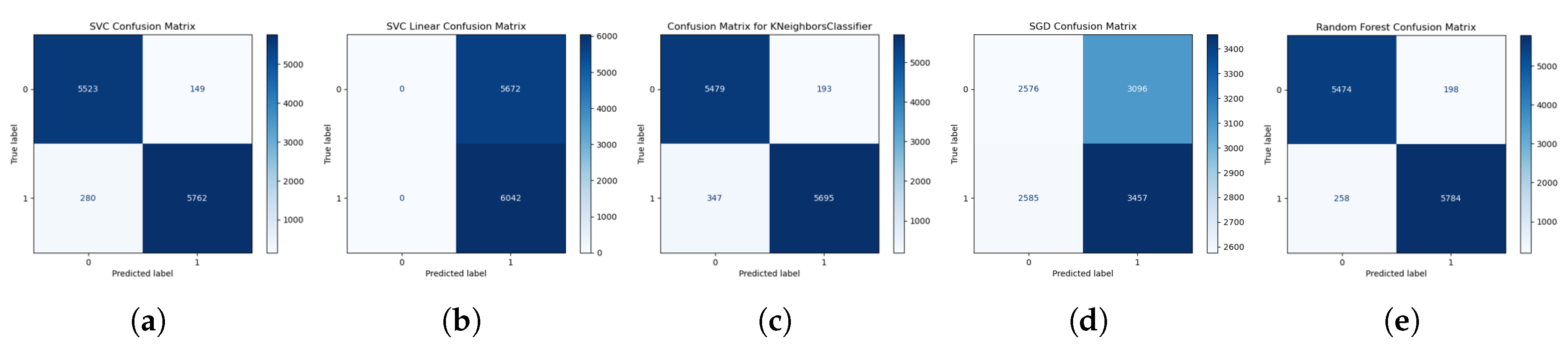
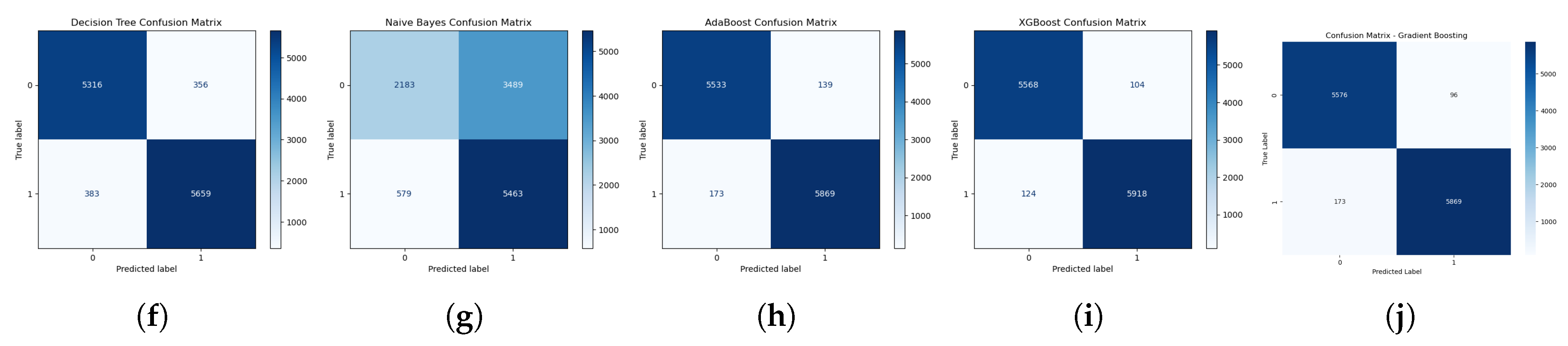
Preprints 115095 g011aPreprints 115095 g011b
Table 1. Operating conditions used in the study.
Table 1. Operating conditions used in the study.
Label Operating Conditions Description
HSBB-1 Healthy Shot-blast blade The normal state of the Shot-blast blades in operation.
DSBB-2 Deteriorated Shot-blast blade The state when the blades are worn out during operation.
Table 2. Classifiers and their respective architecture.
Table 2. Classifiers and their respective architecture.
Algorithm Parameter Value
Gaussian SVM kernel RBF
Linear SVM kernel linear
k-nearest neighbor (KNN) k 5
Stochastic Gradient Descent (SGD) kernel RBF
Random forest (RF) n estimators 120
Decision tree (DT) Criterion, Max depth entropy, 7
Naive Bayes classifier (NBC) Gaussian Default
Adaptive boosting classifier (ABC) n estimators, learning rate Default
Extreme Gradient Boosting Classifier (XGB) — Default
Gradient boosting classifier (GBC) n estimators Default
Table 3. Classifiers and their respective Performance Matrix Results.
Table 3. Classifiers and their respective Performance Matrix Results.
Algorithm Train Accuracy(%) Test Accuracy(%) Precision (%) Recall (%) F1-Score (%) Specificity (%)
SVM 96.4634 96.3377 97.4792 95.3658 96.4109 97.3731
Linear SVM 51.5823 51.5793 51.5793 100.0000 68.0559 0.0000
KNN 96.9600 95.3901 96.7221 94.2569 95.4736 96.5957
SGD 51.5012 51.5025 52.7545 57.2162 54.8948 45.4161
RF 96.6524 96.0304 96.5448 95.7299 96.1356 96.5092
DT 94.3201 93.6828 94.0951 93.6279 93.8610 93.7236
NBC 65.2428 65.2723 61.0255 90.4171 72.8691 38.4873
ABC 97.4200 97.3365 97.6864 97.1367 97.4108 97.5494
XGB 99.4810 98.0536 98.2730 97.9477 98.1101 98.1664
GBC 97.9631 97.7036 98.3906 97.1367 97.7596 98.3075
Table 4. Computational costs of training and testing process.
Table 4. Computational costs of training and testing process.
Classifier SVM–RBF SVM-Lin k NN SGD RF DT NBC ABC XGB GBC
Cost (Secs) 96.22 477.55 3.50 0.90 276.73 4.16 0.09 34.50 0.83 188.00
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Alerts
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2025 MDPI (Basel, Switzerland) unless otherwise stated