Prerpints.org logo
Preprint
Article

Research on Short‐Term Forecasting Model of Global Atmospheric Temperature and Wind in the Near Space Based on Deep Learning

Altmetrics

Downloads

92

Views

27

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

13 August 2024

Posted:

13 August 2024

You are already at the latest version

Alerts
Abstract
Developing short-term forecasting model for global atmospheric temperature and wind in the near space is crucial for understanding atmospheric dynamics and supporting human activities in this region. While numerical models have been extensively developed, deep learning techniques have recently shown promise in improving atmospheric forecasting accuracy. In this study, convolutional long short-term memory (ConvLSTM) and convolutional gated recurrent unit (ConvGRU) neural networks were applied to build for short-term global-scale forecasting model of atmospheric temperature and wind in the `near space based on the MERRA-2 reanalysis dataset from 2010-2022. The model results showed that the ConvGRU model outperforms the ConvLSTM model in the short-term forecast results. The ConvGRU model achieved a root mean square error in the first three hours of approximately 1.8 K for temperature predictions, and errors of 4.2 m/s and 3.8 m/s for eastward and northward wind predictions, respectively.
Keywords: 
Subject: Environmental and Earth Sciences  -   Atmospheric Science and Meteorology

1. Introduction

Establishing reliable short-term froecasting model can enhance humanity's understanding of near-space atmosphere and provide support for human activities [1]. Near-space, characterized by its thin atmosphere, experiences significant temperature and wind variations. These strong fluctuations not only affect the environmental adaptability of high-speed aircraft but also influence the aircrafts' flight trajectories and attitude control, posing a threat to the safety of high-speed vehicles [2]. Reliable forecasting of atmospheric temperature and winds in the near-space will facilitate pre-flight assessments, in-flight trajectory predictions, and post-mission environmental evaluations for aircraft [2], thereby safeguarding human activities in near-space. Moreover, as a transition zone from the lower to the upper atmosphere, forecasting atmospheric temperature and winds in the near-space will aid in understanding the interaction mechanisms between these atmospheric layers and the characteristics of atmospheric circulation changes [1,3].
The forecast range for the near-space environment is positioned between meteorological forecasting and space weather forecasting, primarily utilizing two methods: numerical and statistical forecasting. Numerical forecasting attempts to establish global prediction models to achieve forecasting outcomes, whereas statistical forecasting relies predominantly on regional near-space environmental detection data, employing statistical analysis models for regional forecasts. In the domain of numerical forecasting, years of development have led to the maturation of models such as the HWM series wind field model [4], the NRLMSISE-00 empirical model [5], WACCM-X 2.0 [6], and the U.S. Navy's global numerical forecasting model NOGAPS-ALPHA (NOGAPS-Advanced Level Physics and High Altitude) [7]. These models can forecast atmospheric temperature and wind fields from the ground to near-space altitudes on a global scale. However, numerical models are influenced by calculable models, initial fields, boundary conditions, and parameterization schemes, which introduce errors. Consequently, forecast data from numerical models often exhibit systematic biases compared to actual observations [8]. In terms of statistical forecasting, Jason A. Roney and colleagues studied the wind field at an altitude range of 18-30 km in the near-space to ensure the safe operation of high-altitude aircraft. They established a statistical forecasting model based on observation data from Akon, OH, USA, and White Sands, NM, USA [9]. Liu Tao and others explored the AR (Autoregressive) model based on continuous detection data from single stations in near-space [10]. In recent years, with the rapid development of computer science and artificial intelligence, statistical methods for environmental forecasting based on deep learning have gradually been applied to the meteorological forecasting field [11]. Weather prediction models trained using deep learning methods, such as WF-UNet [12], ClimaX [13], GraphCast [14], and Pangu-Weather [15], have improved the real-time accuracy of weather predictions. Notably, the Pangu model's accuracy in predicting extreme weather has surpassed that of NWP methods for the first time [15]. Inspired by the integration of weather forecasting and artificial intelligence, deep learning methods have also been extended to the near-space environment forecasting field. Biao Chen and others constructed LSTM and BiLSTM deep learning networks to develop a near-space short-term (48h) atmospheric temperature forecasting model by applying deep learning to ERA-5 dataset single-point temperature values at 20-50 km altitude from 1991 to 2000 [16]. The model's forecast accuracy in December reached 0.4371 K (RMSE).
In the exploration of near-space environment forecasts discussed above, the approach of employing statistical routes for environmental forecasting has been based on either single-site or small regional spatial scales, lacking exploration into global-scale near-space environment forecasts. This paper selects the recently applied ConvLSTM [17] and ConvGRU [9] neural learning networks in the meteorological forecast domain to explore a short-term global-scale near-space environment forecast model based on these networks. To our knowledge, no team has yet modeled the MERRA-2 reanalysis dataset using convolutional neural networks to perform short-term global-scale forecasts of the near-space environment.
Chapter One primarily discusses the significance of short-term forecasts in the near-space atmospheric temperature and wind. Motivated by the current popularity of utilizing deep learning for atmospheric forecasting, this chapter proposes the idea of applying deep learning techniques to global-scale, short-term forecasts in the near-space. Chapter Two details the dataset used in this study along with the deep learning methods tailored for it, and describes the deep learning neural network that was developed. Chapter Three presents the main forecasting results, analyzing the trained model's temporal scale prediction accuracy, detailed comparisons between two models, prediction accuracy across different altitudes, and accuracy along latitudinal variations. Chapter Four provides a summary.

2. Data Sources and Preprocessing

2.1. Data Source

MERRA-2 is NASA's latest generation of high spatial and temporal resolution global atmospheric reanalysis data. The advantages of MERRA-2 include: it utilizes real-time atmospheric temperature data acquired by the Microwave Limb Sensor (MLS) on the MODIS Aura satellite. The improved calibration coefficients provided by MLS data have achieved better atmospheric correction results in polar regions [18]. Numerous studies indicate that the temperature and wind field data from MERRA-2 are highly accurate and reliable.
Our study employs the MERRA-2 temperature and wind field products, which offer a spatial resolution of 1.9x2.5 degrees and a temporal resolution of three hours, referred to as 3-hourly MERRA2. These products are structured over 72 isobaric surfaces. The data can be accessed at: https://rda.ucar.edu/datasets/ds313.3/dataaccess/#. For this study, data from the years 2010 to 2020 were selected for training, data from 2021 for cross-validation, and data from 2022 for testing.
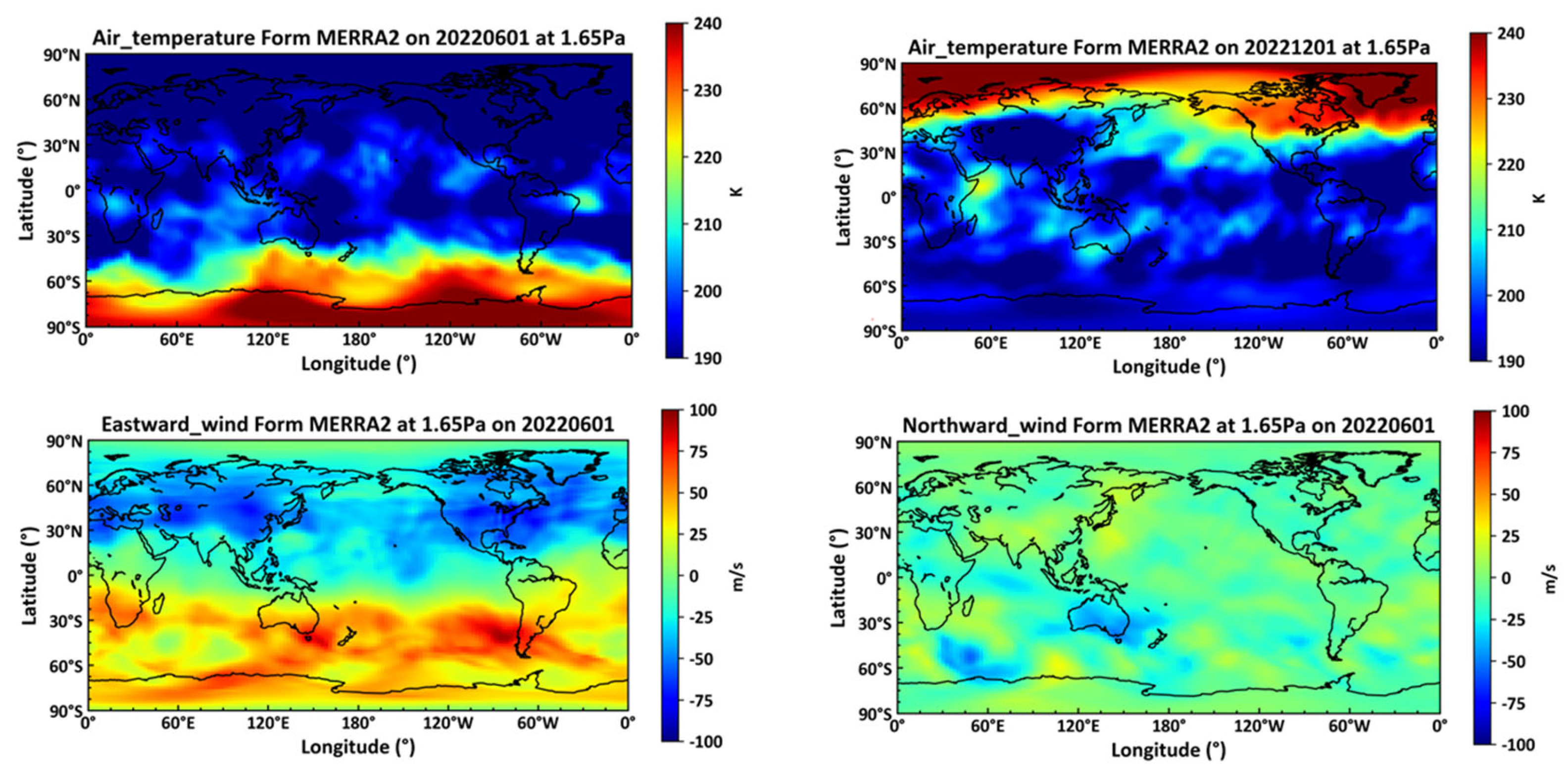
Figure 1 displays temperature profiles and horizontal winds at a height of 1.65 Pa from the MERRA2 reanalysis dataset, captured between 9 AM and 12 PM.

2.2. Data Preprocessing

In utilizing recurrent neural networks for predictive modeling, data normalization is typically a crucial step to ensure the stability of both model training and performance.
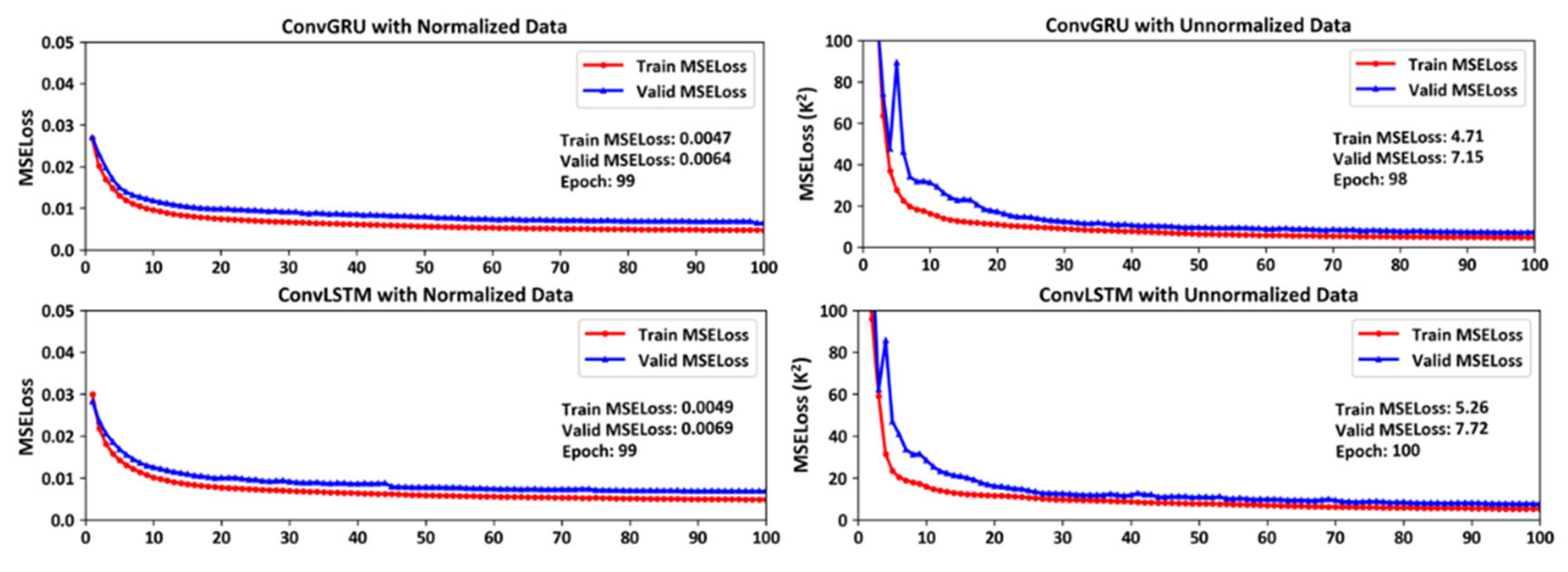
Our study conducts training modeling on standardized and non-standardized temperature data for a period of 10 years across 72 isobaric surface levels, and performs cross-validation with one year of data. It is observed that standardized data allows for quicker convergence during training, and prevents sudden spikes in validation MSELoss in Figure 2. In the process of deep learning training, occurrences of sudden spikes in MSELoss can lead to non-convergence of the model.
The purpose of standardization is to transform data into a standard normal distribution with a mean of zero and a standard deviation of one. This aids in accelerating model convergence and enhancing model performance. Our study, all data from a single time step (one day) is treated as a collection, from which the mean and standard deviation are computed.
Our study computes the mean and standard deviation for the data collected in a single time step (1 day), treating it as a unified dataset. Each data point is standardized by subtracting the mean of the dataset and then dividing by its standard deviation:
x n o r m a l i z e d = x − μ σ
Here, x represents the original input data, μ denotes the mean of the data set, and σ signifies the standard deviation of the data set.
The output data is standardized using the same formula, employing the mean and standard deviation of the input data set.

3. Methodology

In the domain of spatiotemporal sequence forecasting, Long Short-Term Memory (LSTM) and Gated Recurrent Unit (GRU) network represent significant advances within the realm of Recurrent Neural Networks (RNNs). Extensions such as ConvLSTM and ConvGRU have enhanced these traditional models by replacing the fully connected operations in standard RNN units with convolutional operations, thereby enabling the network to process spatiotemporal data more effectively. Shi et al. were the pioneers in employing the ConvLSTM architecture to address the challenge of rainfall forecasting. They constructed an end-to-end trainable model for short-term precipitation forecasting and empirically demonstrated that ConvLSTM outperforms traditional LSTM in capturing spatiotemporal relationships [17]. Kim et al. developed a model using ConvLSTM to predict rainfall amounts from weather radar data. Their experimental findings indicated that a two-layer ConvLSTM model reduced the Root Mean Square Error (RMSE) by 23.0% compared to linear regression [19]. Given the substantial number of parameters in ConvLSTM, which poses a barrier to training, Shi et al. further proposed the ConvGRU model to address this issue. Experimental results showed that it performs better and is easier to train.
Our study targets the spatiotemporal resolution of the MERRA2 dataset and constructs two deep learning networks, ConvLSTM and ConGRU. Below are the construction methods for both networks.

3.1. Design of Neural Networks

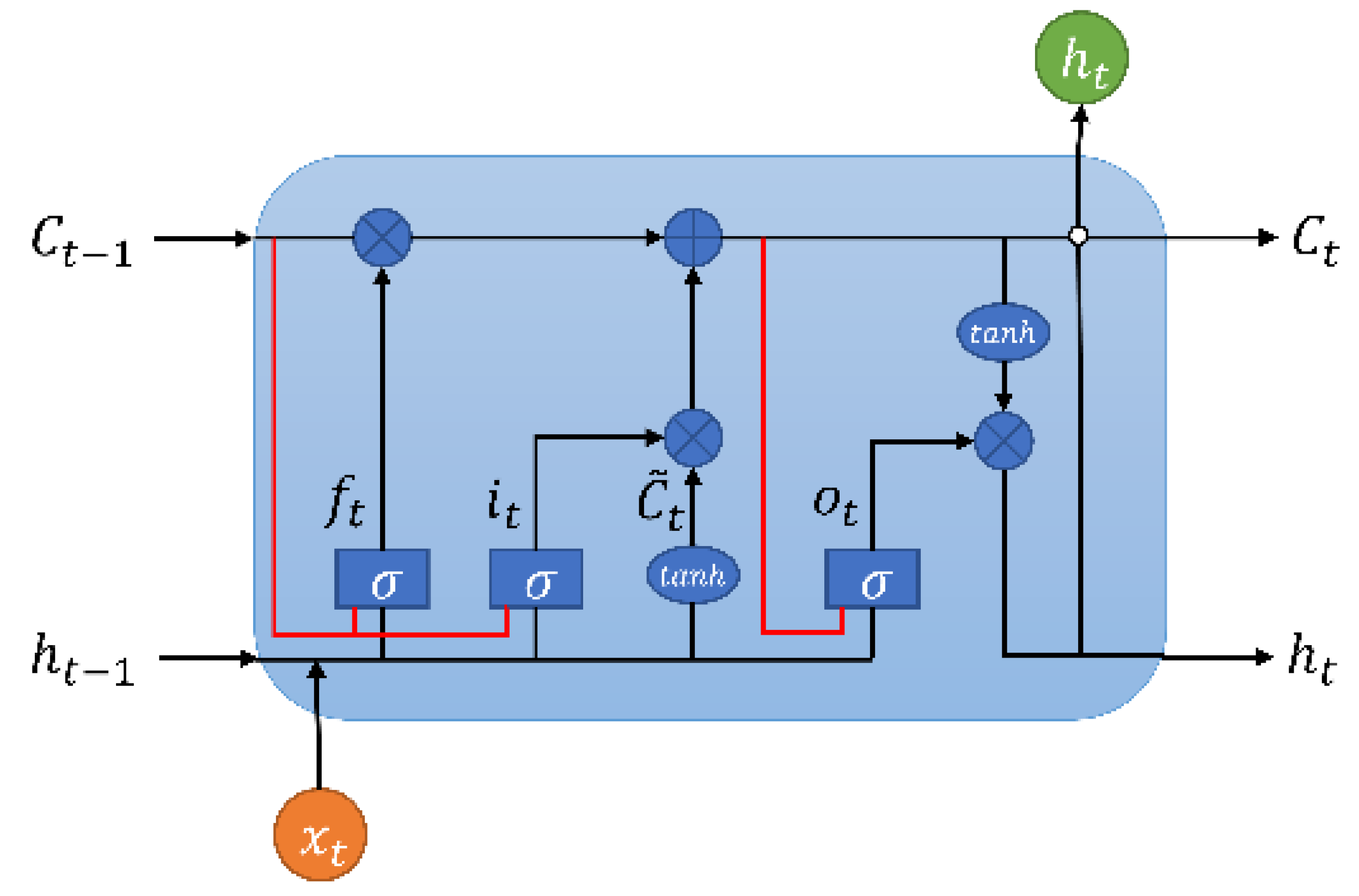
3.1.1. ConvLSTM

In the ConvLSTM network, all input states { X 1 , … , X t } , memory states { C 1 , … , C t } , hidden states { H 1 , … , H t } , and various gating signals i t ,     f t ,     g t ,     o t are manifested as three-dimensional tensors R P × M × N . Here, the first dimension represents the number of channels for the input data transformed into image data or the channels of hidden state features. The latter two dimensions represent the rows M and columns N of the hidden states in spatial scale, which can be envisioned as vectors of length P standing on a spatial grid with an area of M × N. The structure of the ConvLSTM unit is illustrated in Figure 3.
Without considering the errors between the actual state and observed values, the specific computations for a ConvLSTM unit are as follows:
f t = σ W x f ∗ x t + W h f ∗ h t − 1 + W c f ∘ C t − 1 + b f
i t = σ W x i ∗ x t + W h i ∗ h t − 1 + W c i ∘ C t − 1 + b i
C t ˜ = tanh W x c ∗ x t + W h c ∗ h t − 1 + b c
o t = σ W x o ∗ x t + W h o ∗ h t − 1 + W c o ∘ C t + b o
C t = f t ∘ C t − 1 + i t ∘ C t ˜
h t = o t ∘ tanh C t
Here, ∘ represents the Hadamard operation (element-wise multiplication of matrices), and σ denotes the activation function. At time t , f t represents the result of the computation after the information passes through the forget gate, i t represents the result after passing through the input gate, C t ˜ represents the cell state input at time t, o t represents the outcome after passing through the output gate, C t is the cell state at time t, and h t represents the output of the LSTM network at time t. In ConvLSTM, the connections between various gates and the input involve convolution operations, as do the interactions between states.
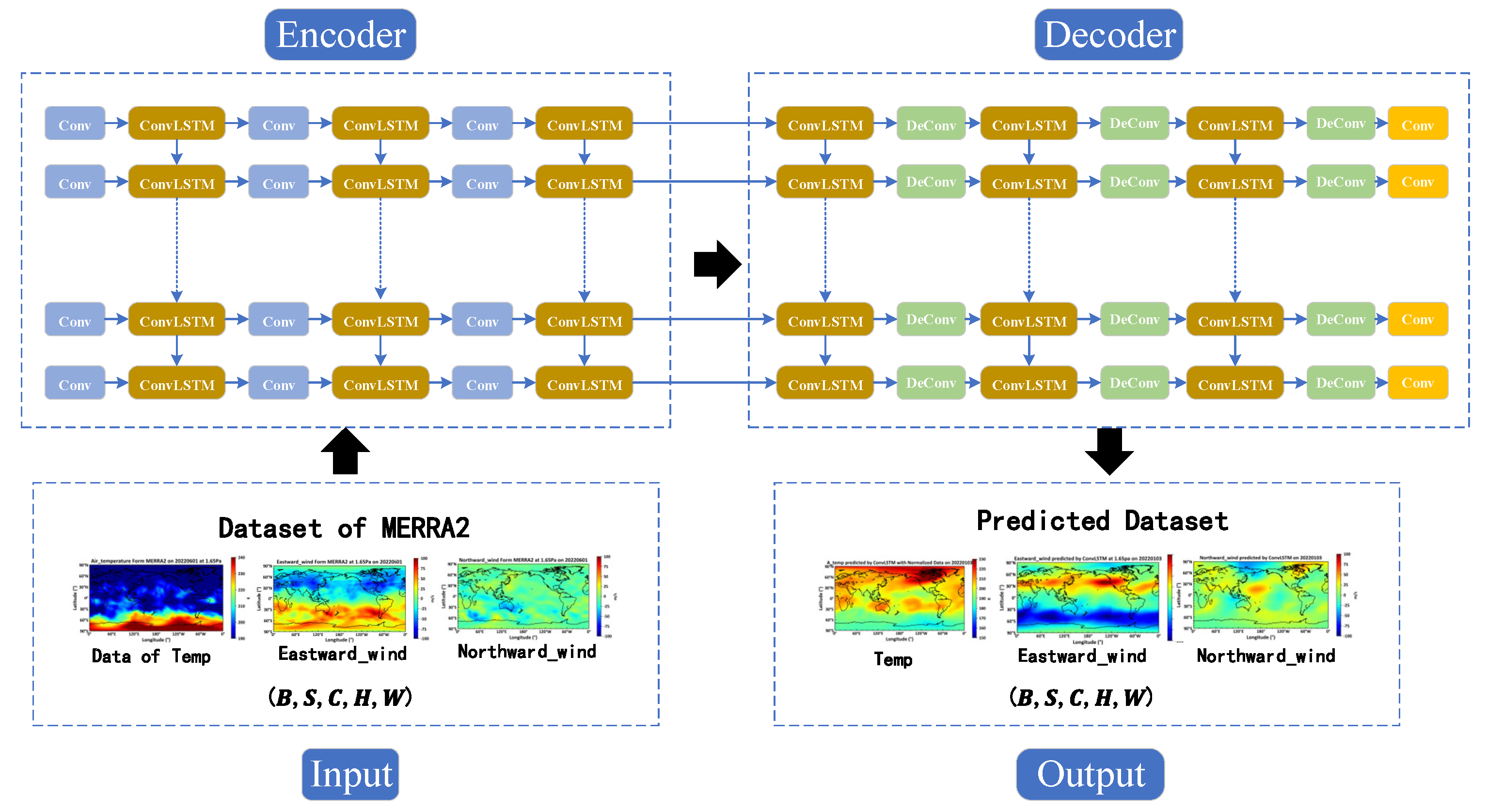
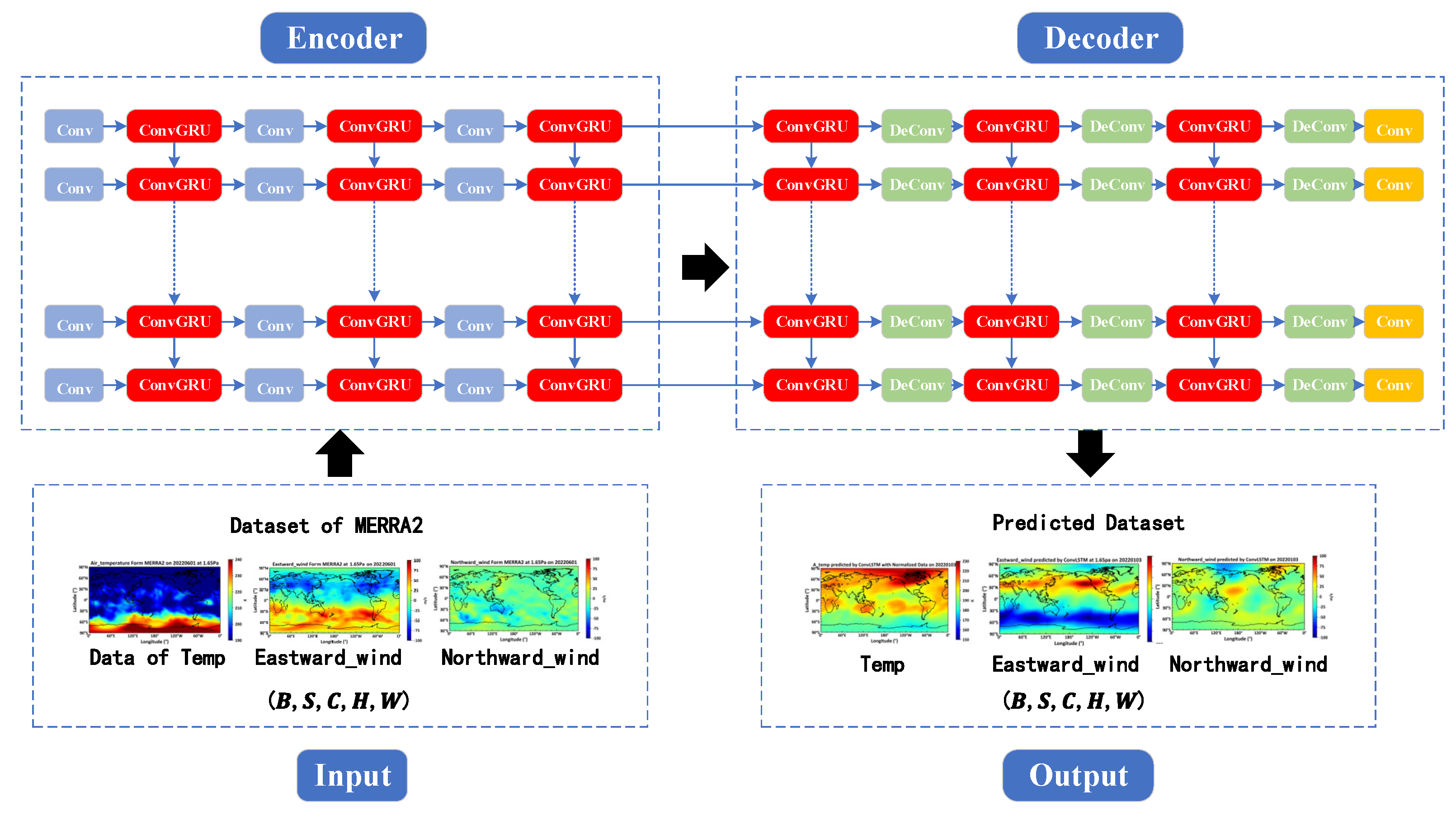
The workflow diagram for the near-space environment forecast model based on ConvLSTM is shown below in Figure 4.
The forecast model consists of four parts: the input layer, the encoder, the decoder, and the output layer. A detailed description of the structure of these four parts is provided below.
1.
The input layer: The matrix dimension of the input layer is denoted as (B, S, C, H, W), where B represents the batch size, indicating the number of samples processed concurrently in a single training iteration; S stands for sequence length, denoting the temporal length of a sample; C refers to the number of channels, indicating the quantity of channels in the data; H is the height, representing the vertical dimension of the data; and W is the width, denoting the horizontal extent of the data.
2.
The encoder is comprised of Convolutional Layers (Conv) and Convolutional LSTM (ConLSTM) units:
a)
Conv is one of the commonly used layers in deep learning models, primarily utilized for extracting features from input data. Each convolutional layer is represented by an ordered dictionary, which contains the parameters required for the convolution operation. These parameters include: Input channel number, which specifies the number of channels in the input data; Output channel number, which determines the number of convolutional kernels and consequently the depth of the output feature map; Kernel size, which specifies the dimensions of the convolutional kernel; Stride, which determines the step length of the convolutional kernel as it slides over the input data, affecting the size of the output feature map; Padding, which involves adding zeros to the edges of the input data to control the size of the output feature map.
b)
The ConLSTM unit, a specialized type of Recurrent Neural Network, integrates convolutional operations with the LSTM architecture. Each ConLSTM unit consists of a set of convolutional kernels and gating units (forget gate, input gate, and output gate), designed to capture spatio-temporal dependencies in sequential data. Within the encoder, the ConLSTM units receive feature representations from convolutional layers and utilize the convolutional kernels to slide along the sequence dimension, effectively capturing the spatio-temporal information of the input sequence.
3.
The decoder consists of Deconvolutional Layers (DeConv), Convolutional LSTM (ConLSTM), and Feature Mapping Recovery (Conv) processes: Deconvolutional layers are a primary component of the decoding layer, tasked with transforming the abstract representations from the encoded data back into the original data space.
a)
The deconvolution process is the inverse of the convolution process, gradually restoring the resolution from a lower resolution feature map to that of the original input. Each deconvolution layer contains a set of parameters, including the number of input channels, output channels, kernel size, stride, and padding.
b)
Within the decoder, Convolutional LSTM units are also employed to handle spatio-temporal sequence data, progressively restoring the original data space.
c)
The final phase of the decoding layer includes a feature mapping recovery step, which systematically transforms the abstract representations back to the form of the original data through convolution operations.
4.
The output layer: The matrix dimension of the output layer is identical to that of the input layer.

3.1.2. Conger

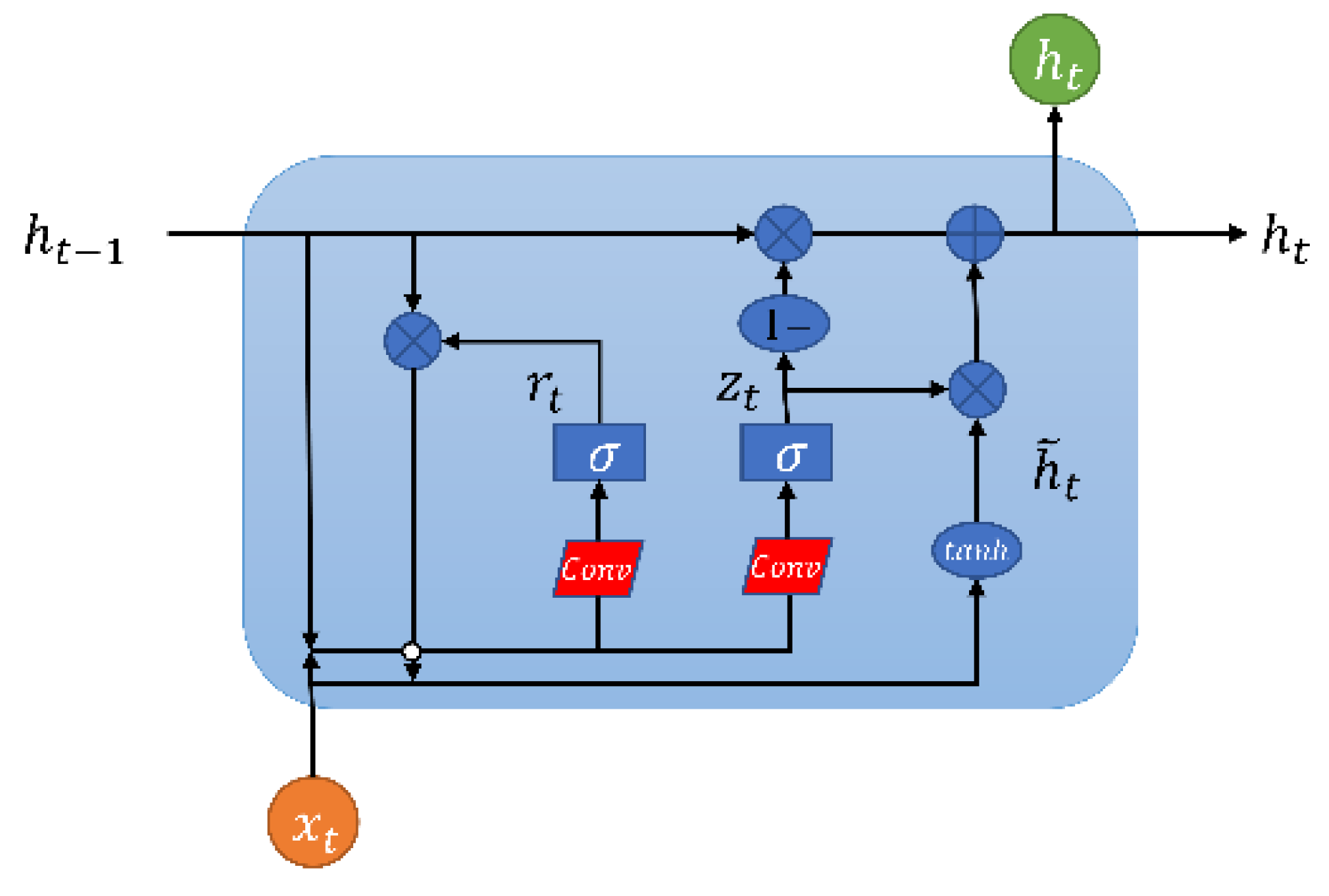
The ConvGRU network represents a structural simplification over the ConvLSTM network. Besides retaining the capability to address long-term dependencies, the ConvGRU network features a simpler architecture, fewer parameters, and enhanced operational speed. The structure of the ConvGRU unit is illustrated in Figure 5 below.
Unlike the three gate structures of the ConvLSTM network, the ConvGRU network comprises only two gates: the update gate and the reset gate. These mechanisms facilitate the memory and filtering of information. The update gate determines the degree to which information from the previous time step is retained, with values ranging from 0 to 1. A value closer to 0 indicates a greater disposition towards discarding information from the previous moment, causing the ConvGRU cell to diminish this information; conversely, a value closer to 1 suggests a tendency to preserve information from the previous time step. The function of the reset gate is to filter information from the previous time step. A reset gate value nearing 0 signifies that more of the previous moment's information is discarded; on the other hand, a higher value indicates greater retention of information. Thus, the update gate enables the retention of more useful information during the model's iterative computations, while the reset gate assists in blocking irrelevant information. Together, these gates collaborate to enhance the GRU network's performance in sequential prediction tasks. The mathematical expression for the ConvGRU network is as follows:
r t = σ W x r ∗ x t + W h r ∗ h t − 1 + b r
z t = σ W x z ∗ x t + W h z ∗ h t − 1 + b z
h t ˜ = tanh W x h ∗ x t + W h h ∗ h t − 1 ∘ r t + b h
h t = 1 − z t ∘ h t − 1 + z t ∘ h t ˜
In this context, ∘ represents the Hadamard operation (element-wise multiplication of matrices), and σ denotes the activation function. Here, r t is the reset gate, z t is the update gate, h t ˜ is the candidate output at time t, and h t is the actual output at time t.
In our study, to investigate the differences in the capabilities of ConvLSTM and ConvGRU for processing spatiotemporal sequence data, the network structures and parameter settings of the proximate spatial environment forecasting models based on both are made identical. The network structure of the model based on ConvGRU also consists of four parts, with the only modification being the replacement of the ConvLSTM unit with a ConvGRU unit. The specific design is illustrated in Figure 6.

3.2. Neural Network Parameter Configuration

This study demonstrates the feasibility of near-space atmospheric short-term forecasting on a global scale based on deep learning by training on MERRA2 data from 2011 to 2020, cross-validating with 2021 data, and testing with 2022 data, while comparing the merits of two algorithms through corresponding analyses.
Table 1 below details the span and amount of data used in the training, validation, and test sets for forecasting the near-space atmosphere. The dataset spans 3653 days from 2011 to 2020 for training, 365 days in 2021 for validation, and 365 days in 2022 for testing, with a data ratio of approximately 10:1:1. The data includes temperature, eastward wind, and northward wind at eight daily intervals.
After preprocessing the data, it is necessary to configure the various parameters of the deep learning neural network constructed using ConvLSTM units. The parameters of the neural network built for this study are presented in the following Table 2.
As previously described, the parameter settings for the deep learning neural network built using ConvGRU units are as shown in the following Table 3.

4. Discussion

This paper constructs neural networks with ConvLSTM and ConvGRU units to train on ten years of MERRA2 data for temperature, eastward wind, and northward wind, and to cross-validate with one year of data over 100 iterations. The following eight models were developed, allowing for short-term forecasts of temperature, eastward wind, and northward wind for eight time periods of the subsequent day, based on the previous day's data from the MERRA2 dataset.
Spatially, the input consists of global-scale temperature, eastward wind, and northward wind data (for an example, see 2022.06.02) covering 72 isobaric surfaces, aiming to predict the corresponding values of temperature, eastward wind, and northward wind for the next day in the same spatial domain (for an example, see 2022.06.03). Temporally, the input includes data from eight-time intervals of the previous day (specifically at 00:00, 03:00, 06:00, 09:00, 12:00, 15:00, 18:00, and 21:00 on 2022.06.02), with the output providing forecasts for the same time intervals on the following day (at 00:00, 03:00, 06:00, 09:00, 12:00, 15:00, 18:00, and 21:00 on 2022.06.03). By analyzing the discrepancies between the forecasted environmental values and the actual measurements, the usability of the method and the strengths and weaknesses of the model are assessed.

4.1. Predictive Accuracy

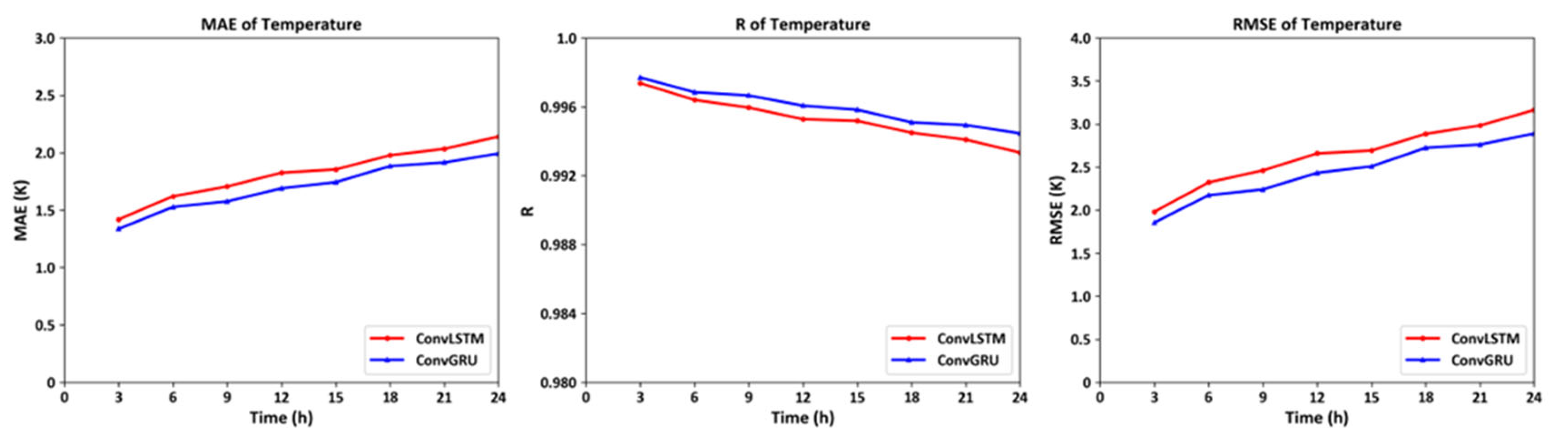
In terms of timing, the input data covers eight-time segments per day, exemplified by the intervals at 03:00, 06:00, 09:00, 12:00, 15:00, 18:00, 21:00, and 24:00 on January 2, 2022. The output consists of predicted values for the corresponding eight-time segments on the following day, January 3, 2022, at the same times. By calculating the Mean Absolute Error (MAE), correlation coefficient (R), and Root Mean Square Error (RMSE) for these eight time points against actual data (from MERRA2), it was observed that both models demonstrated a trend of decreasing predictive accuracy with increasing time span. Moreover, the model trained using ConvGRU units performed better than that using ConvLSTM units. This finding aligns with the conclusions drawn by Shi et al. in their study, which indicated superior performance of ConvGRU [17].
Preprints 115098 g007
Figure 7. The MAE, R and RMSE Curve of temperature on 72 isobaric surfaces on global scales at eight time periods on January 3, 2022.
Figure 7. The MAE, R and RMSE Curve of temperature on 72 isobaric surfaces on global scales at eight time periods on January 3, 2022.
Preprints 115098 g007
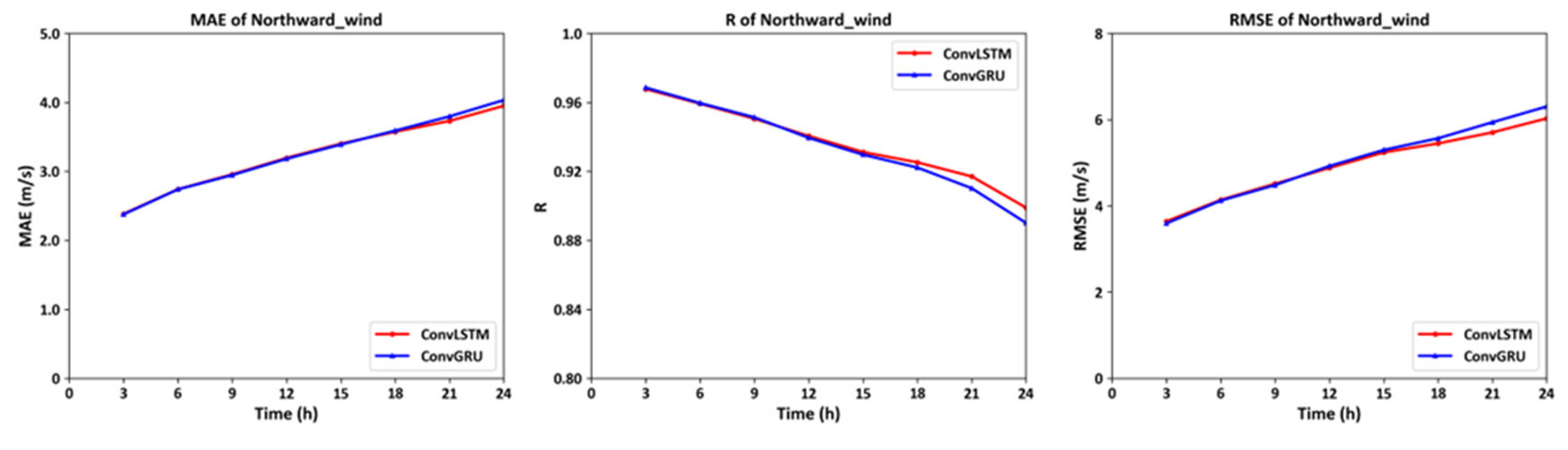
Preprints 115098 g008
Figure 8. The MAE, R and RMSE Curve of northward wind on 72 isobaric surfaces on global scales at eight time periods on January 3, 2022.
Figure 8. The MAE, R and RMSE Curve of northward wind on 72 isobaric surfaces on global scales at eight time periods on January 3, 2022.
Preprints 115098 g008
Preprints 115098 g009
Figure 9. The MAE, R and RMSE Curve of eastward wind on 72 isobaric surfaces on global scales at eight time periods on January 3, 2022.
Figure 9. The MAE, R and RMSE Curve of eastward wind on 72 isobaric surfaces on global scales at eight time periods on January 3, 2022.
Preprints 115098 g009
The model trained to use the previous day's temperature values predicts the root mean square error (RMSE) for temperature values at various altitudes in the first three hours of the next day to be approximately 1.8K. The RMSE for the predicted eastward and northward wind values compared to the actual measurements also displays notable accuracy, with values of 4.2 m/s and 3.8 m/s respectively. Moreover, as time progresses, the neural network built with ConvGRU units demonstrates superior performance over the one constructed with ConvLSTM units. Although the former has a simpler structure, it captures long-term temporal information more effectively. This not only supports the reliability of the developed model but also offers guidance for future long-term predictions of near-space atmospheric elements.

4.2. Models Comparison

To refine the study of the accuracy in short-term forecasting for temperature, eastward wind, and northward wind, as well as the differences between the two models, we employed the trained models to predict the near-space atmospheric factors on June 3, 2022.

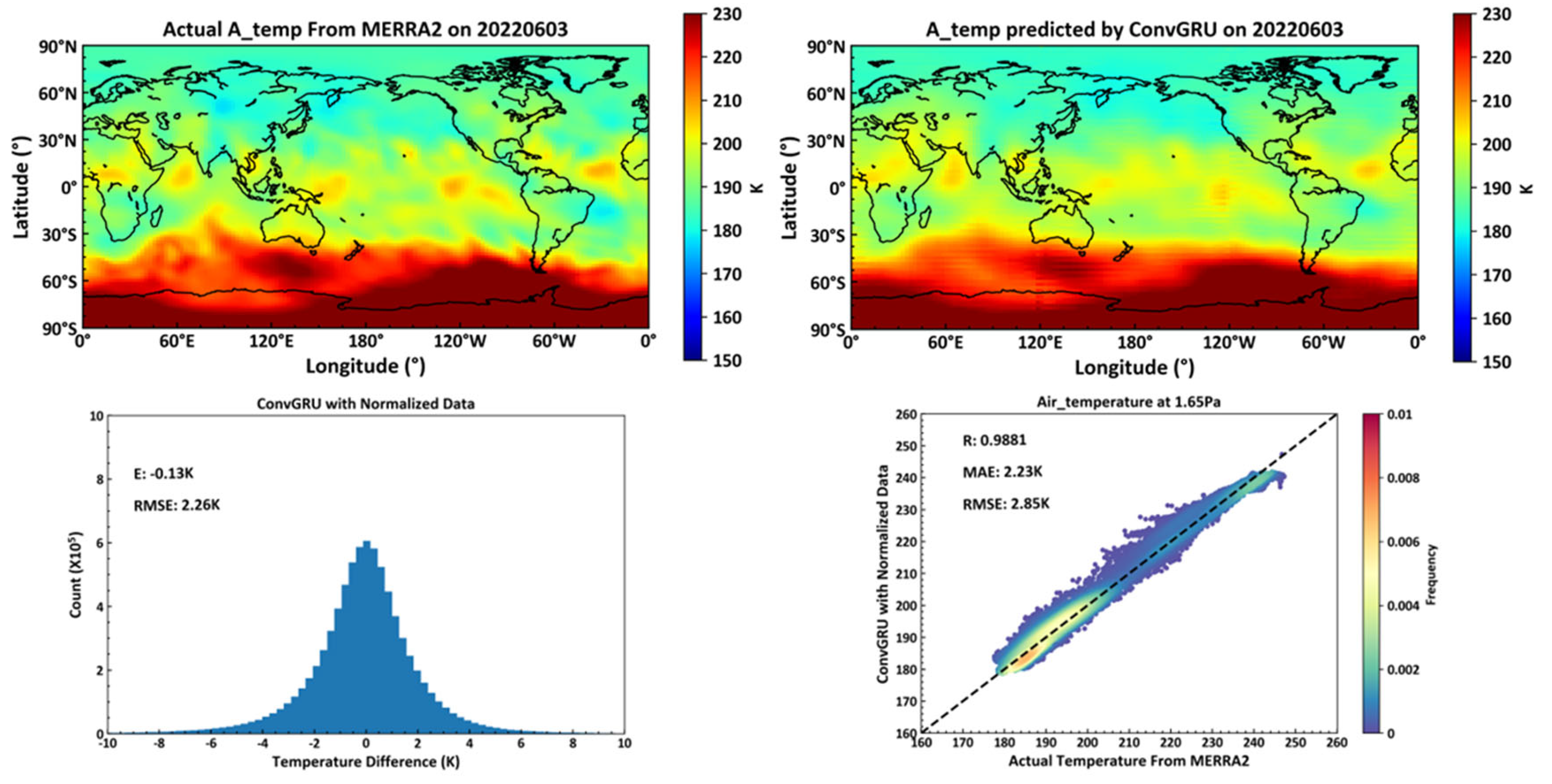
4.2.1. Temperature

A random experiment on temperature forecasting was conducted on June 3, 2022, across 72 global isobaric surfaces, revealing a root mean square error of all temperature values at 2.31K, indicating high precision [20] Temperature profiles demonstrate that short-term temperature forecasts not only predict major trends accurately but also yield good results for sudden temperature increases on a smaller scale. At a higher altitude (on the 1.65pa isobaric surface, approximately 70 km above sea level), the correlation coefficient between predicted and actual temperature values reaches 98.49%. This finding is significantly meaningful for short-term temperature forecasts in near space and for exploring the physical mechanisms related to temperature variations in this region.
As illustrated in Figure 10, the upper left shows the actual temperature data on June 3, 2022, at the 1.65pa isobaric surface height from the MERRA2 dataset. The upper right displays the temperature data for the same date and isobaric height, predicted by a model trained using a deep learning neural network based on the ConvLSTM unit, utilizing the MERRA2 data from June 2, 2022. The lower left indicates the average and root mean square errors between the actual temperatures across all 72 isobaric surfaces globally on June 3, 2022, and those predicted by the ConvLSTM-based model. Lastly, the lower right presents the correlation coefficient, average error, and root mean square error between the actual and predicted temperature values at the 1.65pa isobaric surface height.
As illustrated in Figure 11, the upper left shows the actual temperature data on June 3, 2022, at the 1.65pa isobaric surface height from the MERRA2 dataset. The upper right displays the temperature data for the same date and isobaric height, predicted by a model trained using a deep learning neural network based on the ConvGRU unit, utilizing the MERRA2 data from June 2, 2022. The lower left indicates the average and root mean square errors between the actual temperatures across all 72 isobaric surfaces globally on June 3, 2022, and those predicted by the ConvGRU-based model. Lastly, the lower right presents the correlation coefficient, average error, and root mean square error between the actual and predicted temperature values at the 1.65pa isobaric surface height.
A deep learning network model constructed using ConGRU units across 72 isobaric surfaces on a global scale predicted temperature data with a root mean square error (RMSE) of 2.26K. This performance surpasses that of models built with ConvLSTM units. However, at the 1.65pa isobaric surface, the RMSE of the predicted temperature relative to the actual temperature was 2.85K, which represents a 13.6% improvement over the 3.3K RMSE observed in models constructed with ConvLSTM units.

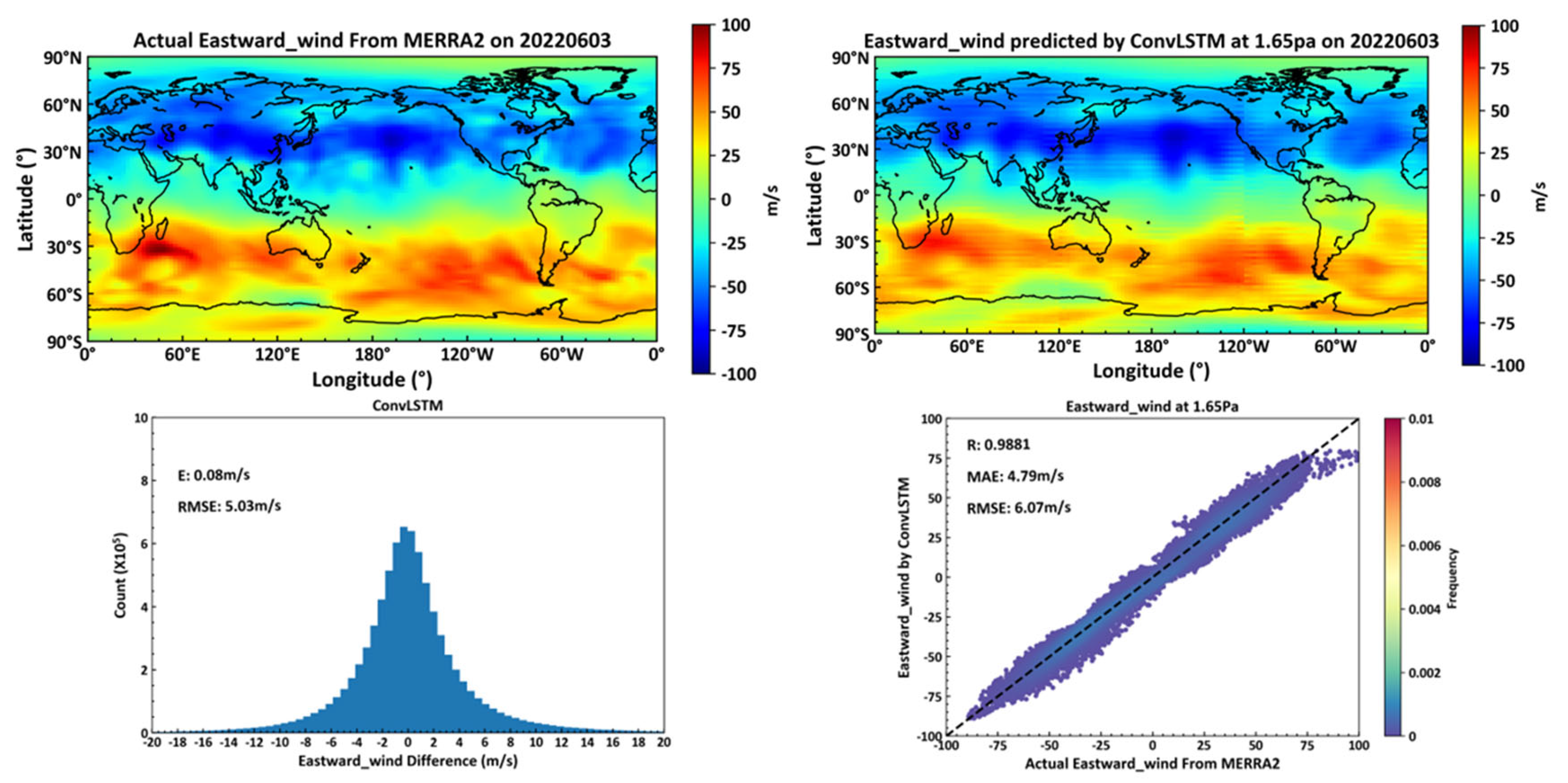
4.2.2. Eastward Wind

The model trained using a neural network built with ConvLSTM units demonstrates favorable outcomes in predicting the eastward wind over 72 isobaric surfaces on a global scale, with a root mean square error (RMSE) of 5.03 m/s for near-space zonal wind forecasts over a 24-hour period. Moreover, at the 1.65 pa isobaric surface (approximately 70 km altitude), the RMSE for eastward wind is 6.07 m/s, which shows an improvement over ground-based meteor radar observations (which measure wind fields between altitudes of 70 km and 110 km) as documented in the literature. Additionally, upon evaluating actual numerical values of eastward winds across multiple isobaric surfaces, it has been observed that near the equator, the values of eastward winds are typically around 0 m/s. This results in a degradation of performance metrics such as correlation coefficient, mean error, and RMSE for eastward wind forecasts in equatorial regions.
As illustrated in Figure 12, the top left panel displays actual eastward wind data from the MERRA2 dataset on June 3, 2022, at the 1.65pa isobaric level. The top right panel shows temperature data predicted by a deep learning neural network, constructed using ConvLSTM as the basic unit, based on MERRA2 dataset data from June 2, 2022. The bottom left panel presents the global scale average error and root mean square error (RMSE) between actual eastward winds and predicted temperatures by the ConvLSTM model across all 72 isobaric levels for June 3, 2022. The bottom right panel shows the correlation coefficient, average error, and RMSE between actual and predicted eastward wind values at the 1.65pa level.
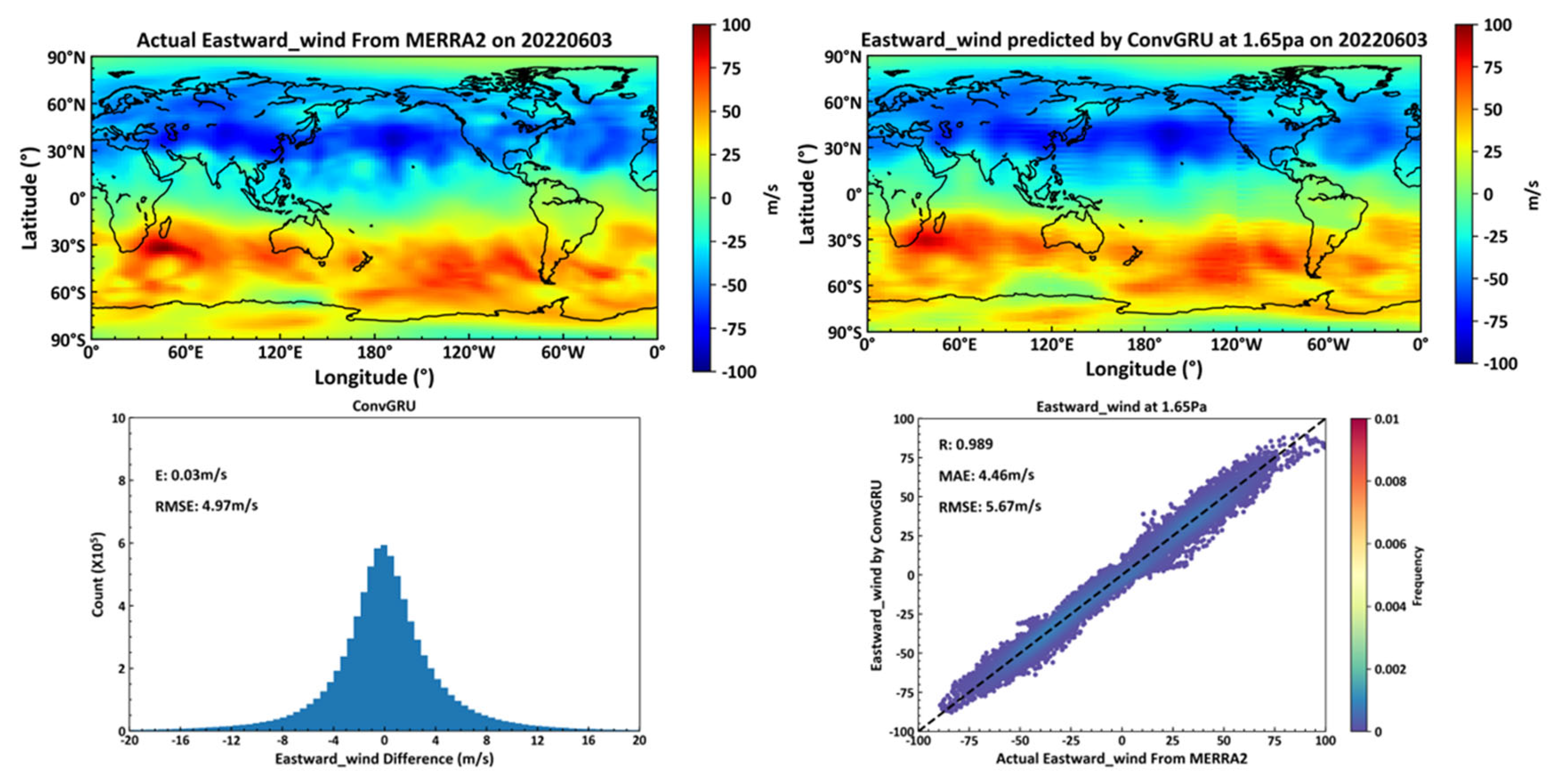
Figure 13 depicts, in the top left, actual eastward wind data from the MERRA2 dataset on June 3, 2022, at the 1.65pa isobaric height. The top right features data predicted by a deep learning neural network built with ConvGRU as the foundational element, using data from June 2, 2022, from the MERRA2 dataset. The bottom left details the average error and RMSE for actual versus predicted eastward winds across all 72 isobaric levels globally on June 3, 2022, by the ConvGRU model. The bottom right provides the correlation coefficient, average error, and RMSE for actual and predicted eastward winds at the 1.65pa level.
A neural network constructed using ConvGRU units and trained on data predicts eastward winds across 72 global isobaric levels more effectively than those constructed with ConvLSTM units. For global scale predictions within a single day across 72 levels, the predicted RMSE is 4.97 m/s, while at the 1.65pa level, it achieves an RMSE of 5.67 m/s, representing a 6.6% improvement over the ConvLSTM model.

4.2.3. Northward Wind

The model trained using ConvLSTM neural network cells demonstrates commendable performance in predicting northward winds at 72 isobaric surfaces globally, with a root mean square error (RMSE) of 4.25 m/s for near-space zonal winds prediction over one day. The zonal wind RMSE at the 1.65pa isobaric level (approximately 70km altitude) is 5.35 m/s, which is superior to ground-based meteor radar observations (70km-110km altitude) of northward winds, as cited in the literature.
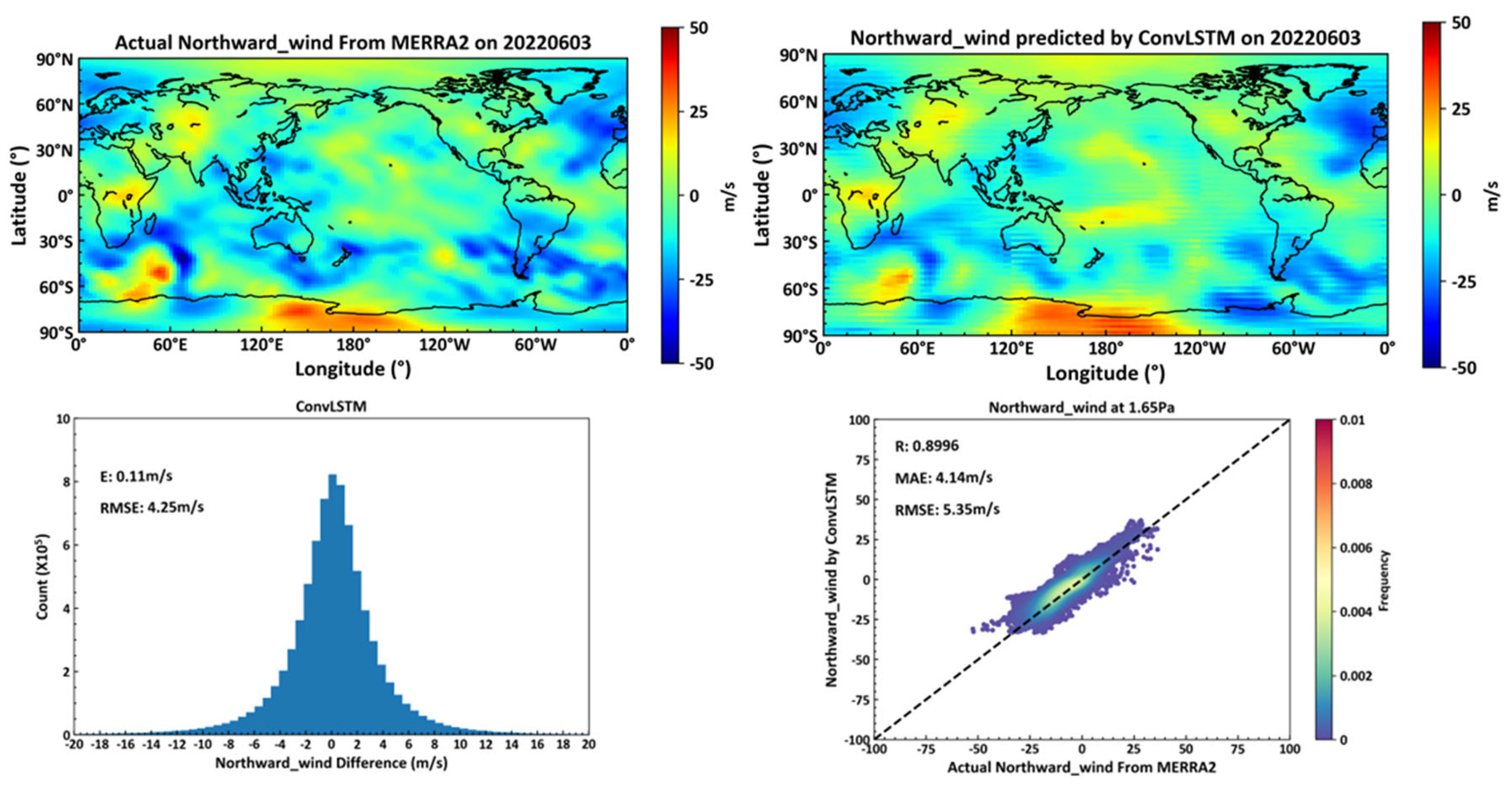
As shown in Figure 14, the top left panel displays actual northward wind data on June 3, 2022, at the 1.65pa isobaric height from the MERRA2 dataset. The top right panel presents northward wind predictions at the same height for June 3, 2022, based on the previous day's MERRA2 data, generated by a deep learning neural network constructed with ConvLSTM cells. The bottom left illustrates the average and root mean square errors between actual and predicted northward winds across all 72 isobaric surfaces globally on June 3, 2022. The bottom right details the correlation coefficient, mean error, and RMSE for northward winds at the 1.65pa height.
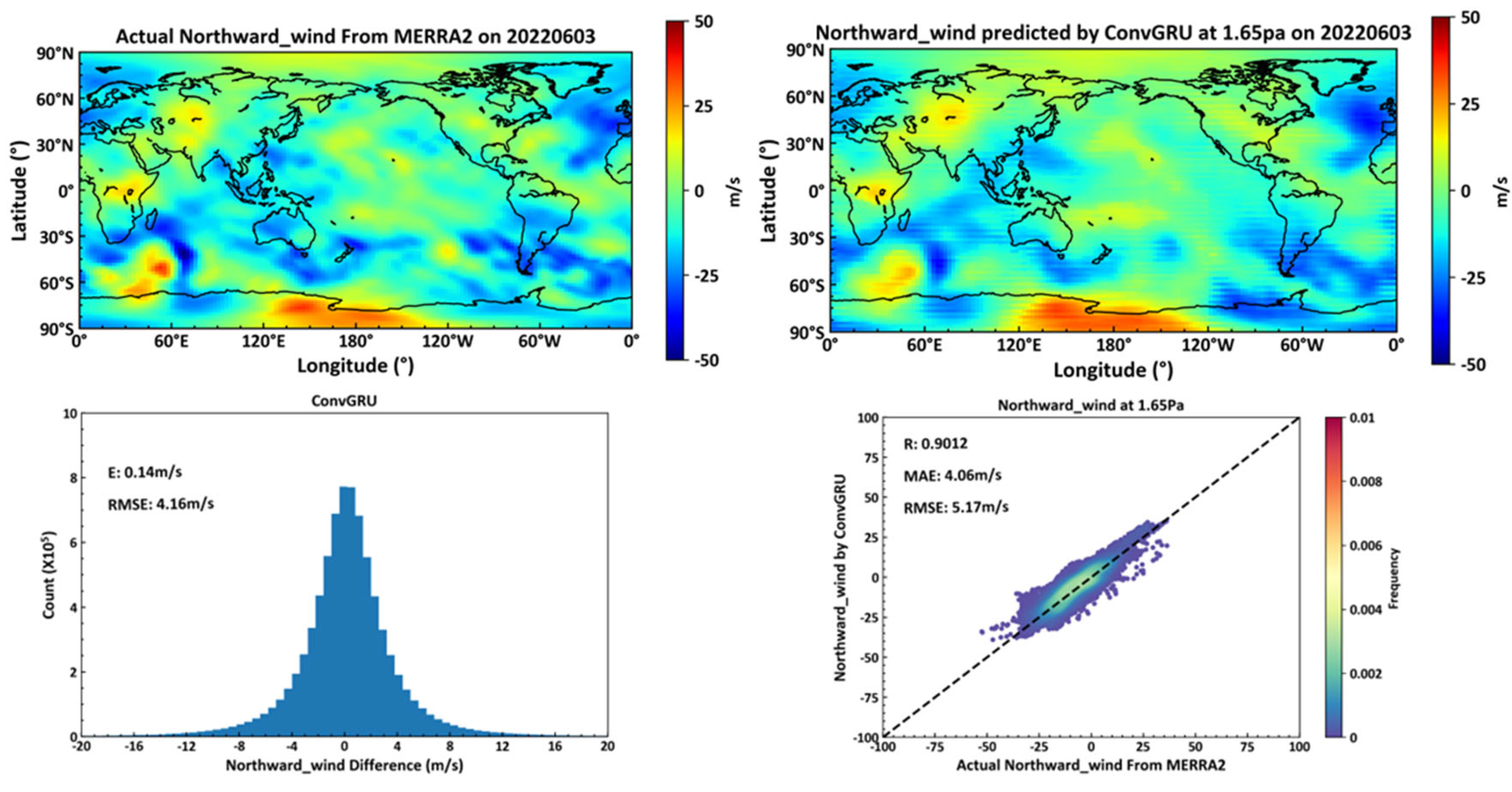
Figure 15 depicts, in the top left, actual northward wind data from the MERRA2 dataset on June 3, 2022, at the 1.65pa isobaric height. The top right shows northward wind predictions for the same day and height, generated by a deep learning neural network constructed with ConvGRU cells, based on data from June 2, 2022. The bottom left displays average and RMSE errors for the actual versus predicted northward winds at all 72 global isobaric surfaces on June 3, 2022. The bottom right shows the correlation coefficient, average error, and RMSE for northward winds at the 1.65pa height.
The neural network constructed with ConvGRU cells, compared to that with ConvLSTM cells, demonstrates superior forecasting accuracy in predicting northward winds across 72 global isobaric surfaces, with a global RMSE of 4.16 m/s and 5.17 m/s at the 1.65pa height, marking an 8.8% improvement over the ConvLSTM model.
In summary, both neural networks constructed with ConvGRU and ConvLSTM cells exhibit strong performance in short-term forecasts of environmental elements such as near-space temperature, zonal winds, and northward winds. Both are capable of effectively predicting the next day's environmental conditions; however, the ConvGRU approach proves to be more effective than the ConvLSTM model.

4.2.4. Performance at different isobaric surface

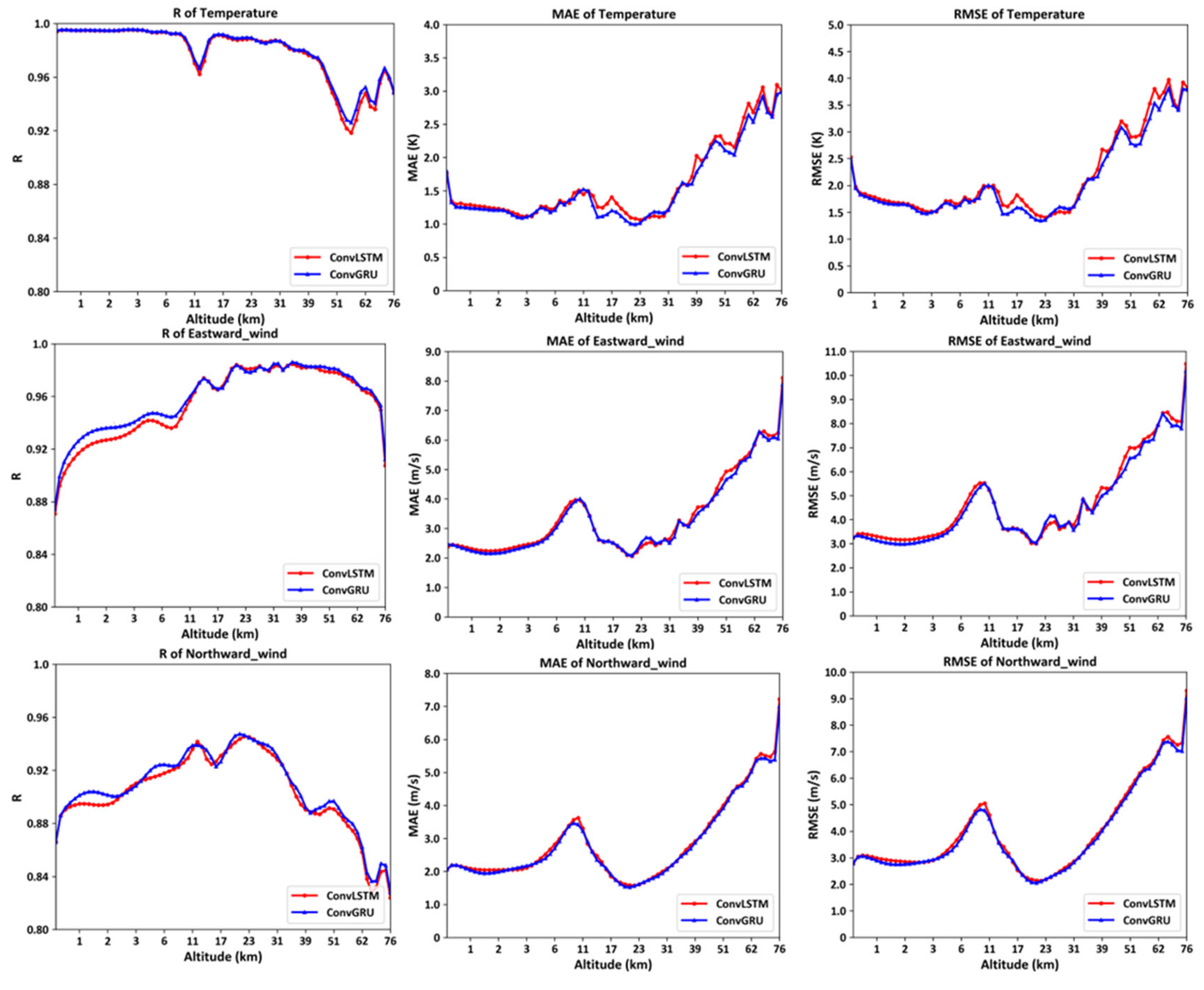
By statistically analyzing the correlation coefficients, mean errors, and root mean square errors between the predicted and actual values at different 72 isobaric surfaces for the entire year of 2022 and at various latitudes and longitudes, the following Figure 16 is obtained.
As illustrated in Figure 16, the left column shows the correlation coefficient curves of temperature, eastward wind, and northward wind at 72 isobaric surfaces, the middle column depicts the mean error curves of temperature, eastward wind, and northward wind at 72 isobaric surfaces, and the right column presents the root mean square error curves of temperature, eastward wind, and northward wind at 72 isobaric surfaces. The following conclusions can be drawn: The models trained through deep learning using ConvGRU and ConvLSTM effectively predict environmental variables at various altitudes, though the prediction accuracy generally decreases to varying degrees as the altitude increases, which is related to the higher reliability of MERRA2 dataset at lower altitudes. Furthermore, at altitudes around 10 km and 52 km, corresponding to the interface between the troposphere and stratosphere, and the interface between the stratosphere and mesosphere, respectively, complex atmospheric changes, dynamical-thermodynamic features, and intrinsic mechanisms exist, leading to varying degrees of degradation in the prediction accuracy of temperature, eastward wind, and northward wind.

4.2.5. Performance at different latitudes

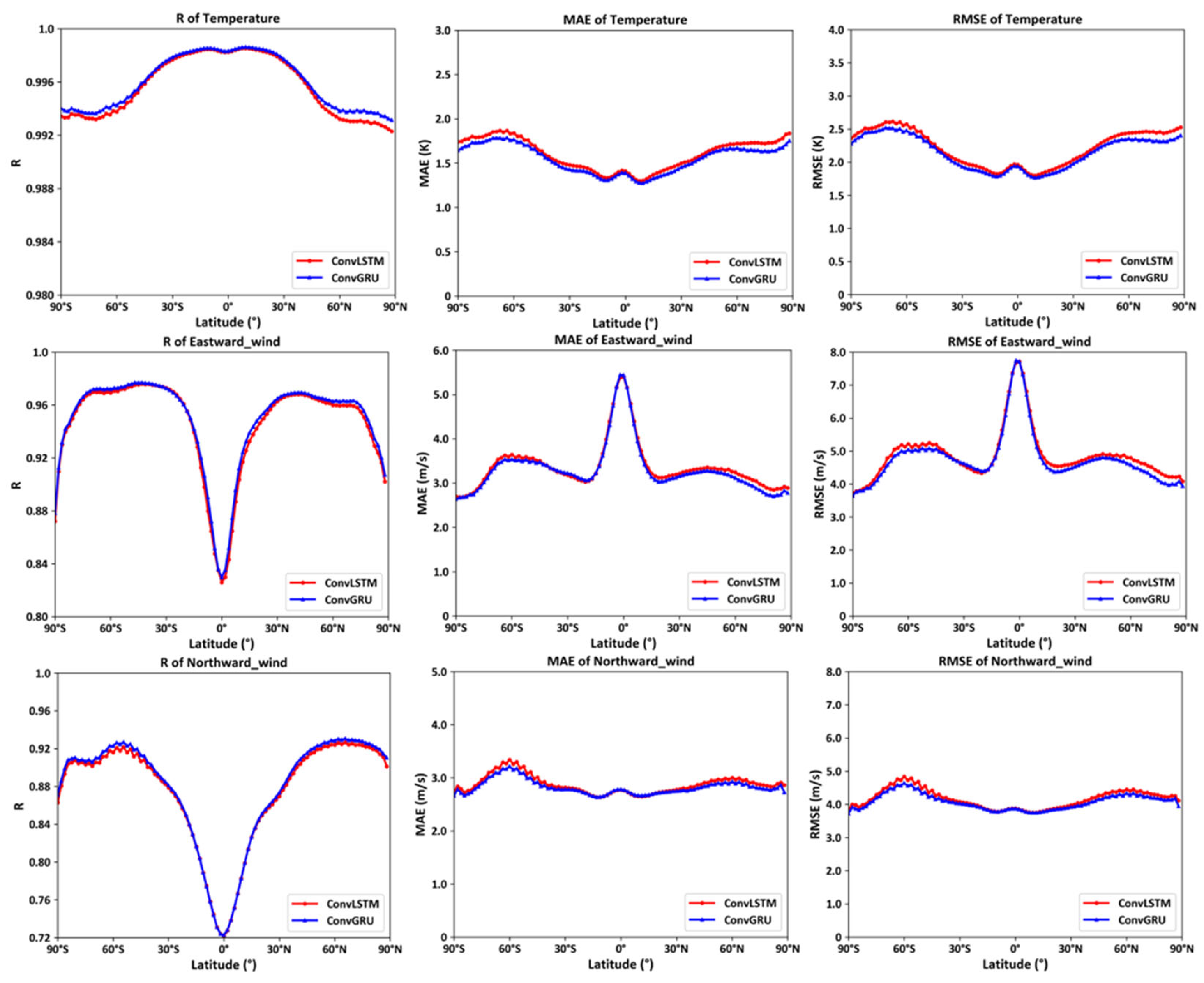
By statistically analyzing the correlation coefficients, mean errors, and root mean square errors between the predicted and actual values at different 96 latitudes for the entire year of 2022 and at various altitudes and longitudes, the following curve plots are obtained.
As depicted in Figure 17, the left column shows the correlation coefficient curves of temperature, eastward wind, and northward wind at 96 latitudes, the middle column displays the mean error curves of temperature, eastward wind, and northward wind at 96 latitudes, and the right column illustrates the root mean square error curves of temperature, eastward wind, and northward wind at 96 latitudes. The following conclusions can be drawn: The models trained through deep learning using ConvGRU and ConvLSTM effectively predict environmental variables at various latitudes, with ConvGRU performing slightly better. Near the polar regions, the prediction results of both models do not exhibit a significant decline, as the MERRA2 dataset utilizes the real-time atmospheric temperature values obtained from the Microwave Limb Sensor (MLS) on the MODIS Aura satellite, which provides improved calibration coefficients for better atmospheric correction in polar regions [20]. This corroborates the conclusion that the MERRA2 dataset has relatively high reliability in polar regions. However, when predicting eastward wind, a considerable decrease in the correlation coefficient is observed near the equatorial regions, accompanied by an increase in mean error and root mean square error, which is related to the fact that the eastward wind values are essentially zero near the equator, as mentioned earlier.

5. Conclusions

In this study, we constructed neural networks based on ConvLSTM and ConvGRU units to perform deep learning on a ten-year dataset from MERRA2, obtaining a global-scale short-term forecasting model (daily forecast) for the near-space atmosphere. The model's effectiveness was validated through testing on the 2022 dataset, demonstrating that deep learning is a promising approach for near-space atmospheric forecasting. Additionally, through model comparison and spatiotemporal analysis, the following conclusions were drawn:
  • When predicting for eight different times in a day, as the time span increases, the model's prediction accuracy tends to decrease, and the ConvGRU model outperforms the ConvLSTM model in forecasting results.
  • In a comparison experiment using randomly selected data from June 2, 2022, to predict the environmental parameters for June 3, 2022, the ConvGRU model performed better than the ConvLSTM model in forecasting temperature, eastward wind, and northward wind, with smaller root-mean-square errors (RMSEs). Specifically, at the 1.65 Pa pressure level, the ConvGRU model showed a significant improvement in prediction accuracy over the ConvLSTM model, with a 13.6% improvement in temperature, a 6.6% improvement in eastward wind, and an 8.8% improvement in northward wind.
  • By evaluating the correlation coefficients, mean errors, and root-mean-square errors between the predicted and actual values across different pressure levels (72 levels in total) for the entire year of 2022 and various latitudes and longitudes, it was found that the models' forecasting capability decreases with increasing altitude. Furthermore, both models exhibited significant decreases in forecasting accuracy for temperature, eastward wind, and northward wind at the interfaces between the Troposphere and Stratosphere, and between the Stratosphere and Mesosphere, which is related to the complex atmospheric changes at these interfaces.
  • By evaluating the correlation coefficients, mean errors, and root-mean-square errors between the predicted and actual values across different latitudes (96 latitudes in total) for the entire year of 2022 and various altitudes and longitudes, it was found that the models' prediction accuracy in the polar regions was not significantly lower than other latitudes, indicating that the MERRA2 dataset has relatively high reliability in the polar regions.
The reliability of the MERRA2 dataset is not sufficiently high at higher altitudes, and environmental data for the near-space region above 70 km is missing. Therefore, it is worth considering using the output results of the trained model as the initial field for the WACCM numerical model, and utilizing the WACCM numerical model to forecast environmental parameters above 70 km in altitude.

Author Contributions

Conceptualization, X.S., C.Z., J.F. and Y.L.; methodology, X.S., Y.Z. and C.Z.; investigation, J.F., T.X., Z.D. and Z.C.; validation, Z.C.; formal analysis, X.S. and Y.L.; resources, T.L. and Z.Z.; visualization, H.Y. and T.L.; funding acquisition, Y.L. and T.X. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the National Natural Science Foundation of China (NSFC grant No. 42204161), the Hubei Natural Science Foundation (grant No. 2023AFB200, 2022CFB651).

Data Availability Statement

The use of MERRA-2 data was provided by NASA (NASA's latest generation of high spatial and temporal resolution global atmospheric reanalysis data, https://rda.ucar.edu/datasets/ds313.3/dataaccess/#, accessed on 20 December 2023).

Conflicts of Interest

The authors declare that they have no conflict of interest.

References

  1. Chen, H. An overview of the space-based observations for upper atmospheric research[J]. Advances in Earth Science, 2009, 24, 229. [Google Scholar]
  2. Tomme, E.B.; Phil, D. The paradigm shift to effects-based space: Near-space as a combat space effects enabler[M]. Airpower Research Institute, College of Aerospace Doctrine, Research and Education, Air University, 2005.
  3. Goncharenko, L.P.; Chau, J.L.; Liu, H.L. , et al. Unexpected connections between the stratosphere and ionosphere[J]. Geophysical Research Letters, 2010, 37, 10. [Google Scholar]
  4. Drob, D.P.; Emmert, J.T.; Meriwether, J.W. , et al. An update to the Horizontal Wind Model (HWM): The quiet time thermosphere[J]. Earth and Space Science, 2015, 2, 301–319. [Google Scholar]
  5. Picone, J.M.; Hedin, A.E.; Drob, D.P. , et al. NRLMSISE-00 empirical model of the atmosphere: Statistical comparisons and scientific issues[J]. Journal of Geophysical Research: Space Physics, 2002, 107, SIA 15–1. [Google Scholar]
  6. Liu, H.L.; Bardeen, C.G.; Foster, B.T. , et al. Development and validation of the whole atmosphere community climate model with thermosphere and ionosphere extension (WACCM-X 2.0)[J]. Journal of Advances in Modeling Earth Systems, 2018, 10, 381–402. [Google Scholar]
  7. Allen, D.R.; Eckermann, S.D.; Coy, L., et al. Stratospheric Forecasting with NOGAPS-ALPHA[J]. 2004.
  8. Greenberg, D.A.; Dupont, F.; Lyard, F.H. , et al. Resolution issues in numerical models of oceanic and coastal circulation[J]. Continental Shelf Research, 2007, 27, 1317–1343. [Google Scholar]
  9. Roney, J.A. Statistical wind analysis for near-space applications[J]. Journal of Atmospheric and Solar-Terrestrial Physics, 2007, 69, 1485–1501. [Google Scholar] [CrossRef]
  10. Liu, T. Research on statistical forecasting method of atmospheric wind field in adjacent space [D]. Beijing: National Space Science Center of Chinese Academy of Sciences, 2017.
  11. Bi, K.; Xie, L.; Zhang, H. , et al. Accurate medium-range global weather forecasting with 3D neural networks[J]. Nature, 2023, 619, 533–538. [Google Scholar] [PubMed]
  12. Kaparakis, C.; Mehrkanoon, S. Wf-unet: Weather fusion unet for precipitation nowcasting[J]. arXiv:2302.04102, 2023.
  13. Nguyen, T.; Brandstetter, J.; Kapoor, A., et al. Climax: A foundation model for weather and climate[J]. arXiv:2301.10343, 2023.
  14. Lam, R.; Sanchez-Gonzalez, A.; Willson, M.; et al. GraphCast: Learning skillful medium-range global weather forecasting[J]. arXiv:2212.12794, 2022.
  15. Bi, K.; Xie, L.; Zhang, H., et al. Pangu-weather: A 3d high-resolution model for fast and accurate global weather forecast[J]. arXiv:2211.02556, 2022.
  16. Chen, B.; Sheng, Z.; Cui, F. Refined short-term forecasting atmospheric temperature profiles in the stratosphere based on operators learning of neural networks[J]. Earth and Space Science, 2024, 11, e2024EA003509. [Google Scholar] [CrossRef]
  17. Shi, X.; Chen, Z.; Wang, H., et al. Convolutional LSTM network: A machine learning approach for precipitation nowcasting[J]. Advances in neural information processing systems, 2015, 28.
  18. Palmer, T.N.; Shutts, G.J.; Hagedorn, R.; et al. Representing model uncertainty in weather and climate prediction[J]. Annu. Rev. Earth Planet. Sci., 2005, 33, 163–193. [Google Scholar] [CrossRef]
  19. Kim, S.; Hong, S.; Joh, M.; Song, S.K. Deeprain: Convlstm network for precipitation prediction using multichannel radar data. arXiv arXiv:1711.02316, 2017.
  20. Gelaro, R.; McCarty, W.; Suárez, M.J. , et al. The modern-era retrospective analysis for research and applications, version 2 (MERRA-2)[J]. Journal of climate, 2017, 30, 5419–5454. [Google Scholar]
Preprints 115098 g001
Figure 1. The results from the MERRA2 reanalysis dataset at a height of 1.65 Pa on June 1, 2022. (top left: temperature at 9:00 on June 1, 2022; top right: temperature at 9:00 on December 1, 2022; bottom left: eastward wind at 9:00 on December 1, 2022; bottom right: northward wind at 9:00 on December 1, 2022).
Figure 1. The results from the MERRA2 reanalysis dataset at a height of 1.65 Pa on June 1, 2022. (top left: temperature at 9:00 on June 1, 2022; top right: temperature at 9:00 on December 1, 2022; bottom left: eastward wind at 9:00 on December 1, 2022; bottom right: northward wind at 9:00 on December 1, 2022).
Preprints 115098 g001
Preprints 115098 g002
Figure 2. The MSE Loss curves during the training of ConvGRU and ConvLSTM.
Figure 2. The MSE Loss curves during the training of ConvGRU and ConvLSTM.
Preprints 115098 g002
Preprints 115098 g003
Figure 3. The structure of the ConvLSTM unit.
Figure 3. The structure of the ConvLSTM unit.
Preprints 115098 g003
Preprints 115098 g004
Figure 4. The workflow diagram of the ConvLSTM model.
Figure 4. The workflow diagram of the ConvLSTM model.
Preprints 115098 g004
Preprints 115098 g005
Figure 5. The structure of the ConvGRU unit.
Figure 5. The structure of the ConvGRU unit.
Preprints 115098 g005
Preprints 115098 g006
Figure 6. The workflow diagram of the ConvGRU model.
Figure 6. The workflow diagram of the ConvGRU model.
Preprints 115098 g006
Preprints 115098 g010
Figure 10. Predicted Temperature by ConvLSTM.
Figure 10. Predicted Temperature by ConvLSTM.
Preprints 115098 g010
Preprints 115098 g011
Figure 11. Predicted Temperature by ConvGRU.
Figure 11. Predicted Temperature by ConvGRU.
Preprints 115098 g011
Preprints 115098 g012
Figure 12. Predicted Eastward by ConvLSTM.
Figure 12. Predicted Eastward by ConvLSTM.
Preprints 115098 g012
Preprints 115098 g013
Figure 13. Predicted Eastward by ConvGRU.
Figure 13. Predicted Eastward by ConvGRU.
Preprints 115098 g013
Preprints 115098 g014
Figure 14. Predicted Northward by ConvLSTM.
Figure 14. Predicted Northward by ConvLSTM.
Preprints 115098 g014
Preprints 115098 g015
Figure 15. Predicted Northward by ConvGRU.
Figure 15. Predicted Northward by ConvGRU.
Preprints 115098 g015
Preprints 115098 g016
Figure 16. Model performance at different 72 isobaric surfaces.
Figure 16. Model performance at different 72 isobaric surfaces.
Preprints 115098 g016
Preprints 115098 g017
Figure 17. Model performance at different 96 latitudes surfaces.
Figure 17. Model performance at different 96 latitudes surfaces.
Preprints 115098 g017
Table 1. Dataset details.
Table 1. Dataset details.
Dataset Type Date Year Amount of data
Training set 2011-2012 3653*8*144*96*72*3
Validation set
Test set		 2021 365*8*144*96*72*3
2022 365*8*144*96*72*3
Table 2. The configuration of ConvLSTM.
Table 2. The configuration of ConvLSTM.
Block Module Channel Number Kernel size Stride Padding
Input Output
Encoder Stage1(Sequential) 72 16 (3, 3) (1, 1) (1, 1)
RNN1(ConvLSTM) 80 256 (5, 5) (1, 1) (2, 2)
Stage2(Sequential) 64 64 (3, 3) (2, 2) (1, 1)
RNN2(ConvLSTM) 160 384 (5, 5) (1, 1) (2, 2)
Stage3(Sequential) 96 96 (3, 3) (2, 2) (1, 1)
RNN3(ConvLSTM) 192 384 (5, 5) (1, 1) (2, 2)
Decoder RNN3(ConvLSTM) 192 384 (5, 5) (1, 1) (2, 2)
Stage3(Sequential) 96 96 (4, 4) (2, 2) (1, 1)
RNN2(ConvLSTM) 192 384 (5, 5) (1, 1) (2, 2)
Stage2(Sequential) 96 96 (4, 4) (2, 2) (1, 1)
RNN1(ConvLSTM) 160 256 (5, 5) (1, 1) (2, 2)
Stage1(Sequential) 64 16 (3, 3) (1, 1) (1, 1)
Stage0(Conv) 16 72 (3, 3) (1, 1) (0, 0)
Table 3. The configuration of ConvGRU.
Table 3. The configuration of ConvGRU.
Block Module Channel Number Kernel size Stride Padding
Input Output
Encoder Stage1(Sequential) 72 16 (3, 3) (1, 1) (1, 1)
RNN1(ConvGRU) 80 256 (5, 5) (1, 1) (2, 2)
Stage2(Sequential) 64 64 (3, 3) (2, 2) (1, 1)
RNN2(ConvGRU) 160 384 (5, 5) (1, 1) (2, 2)
Stage3(Sequential) 96 96 (3, 3) (2, 2) (1, 1)
RNN3(ConvGRU) 192 384 (5, 5) (1, 1) (2, 2)
Decoder RNN3(ConvGRU) 192 384 (5, 5) (1, 1) (2, 2)
Stage3(Sequential) 96 96 (4, 4) (2, 2) (1, 1)
RNN2(ConvGRU) 192 384 (5, 5) (1, 1) (2, 2)
Stage2(Sequential) 96 96 (4, 4) (2, 2) (1, 1)
RNN1(ConvGRU) 160 256 (5, 5) (1, 1) (2, 2)
Stage1(Sequential) 64 16 (3, 3) (1, 1) (1, 1)
Stage0(Conv) 16 72 (3, 3) (1, 1) (0, 0)
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated