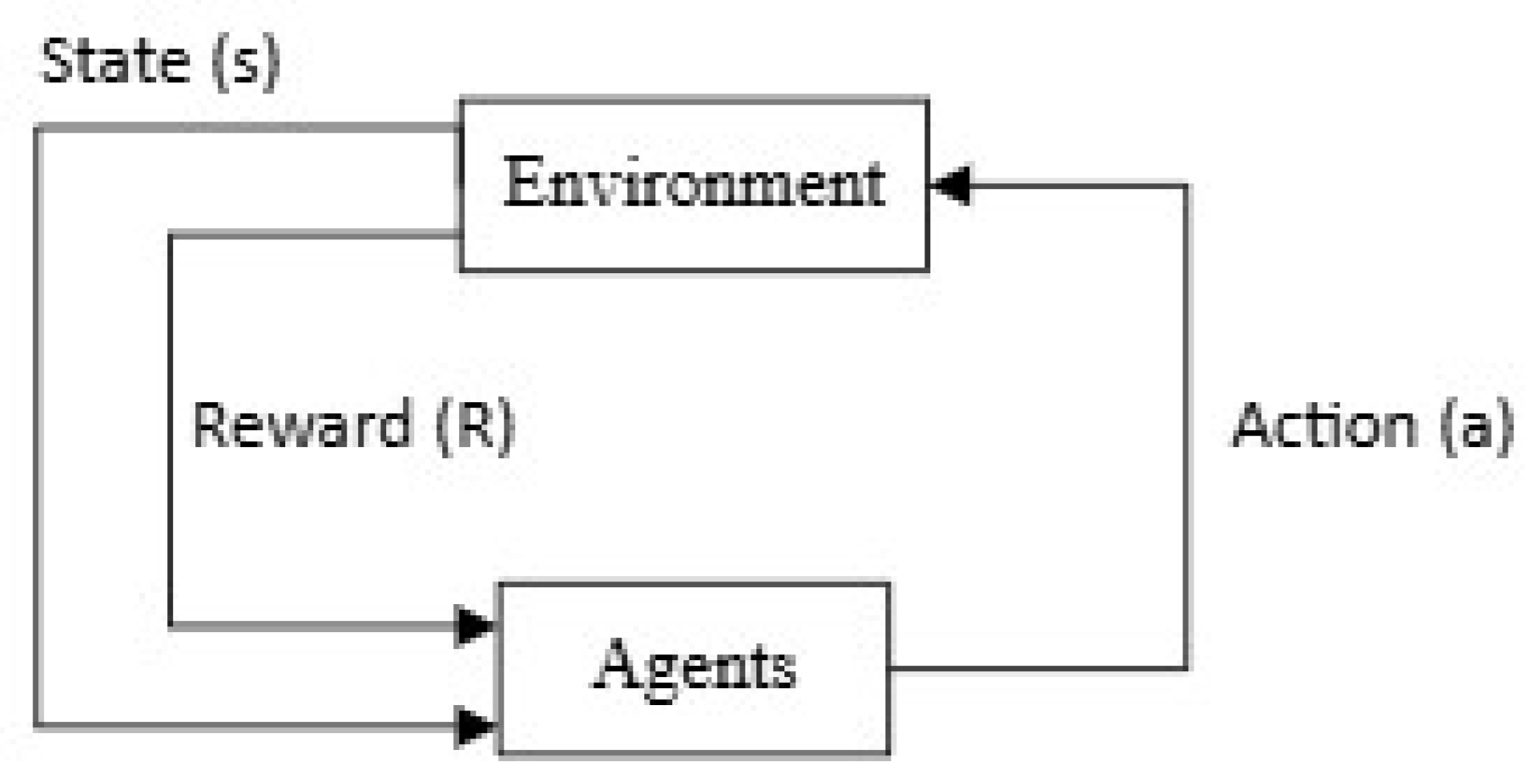
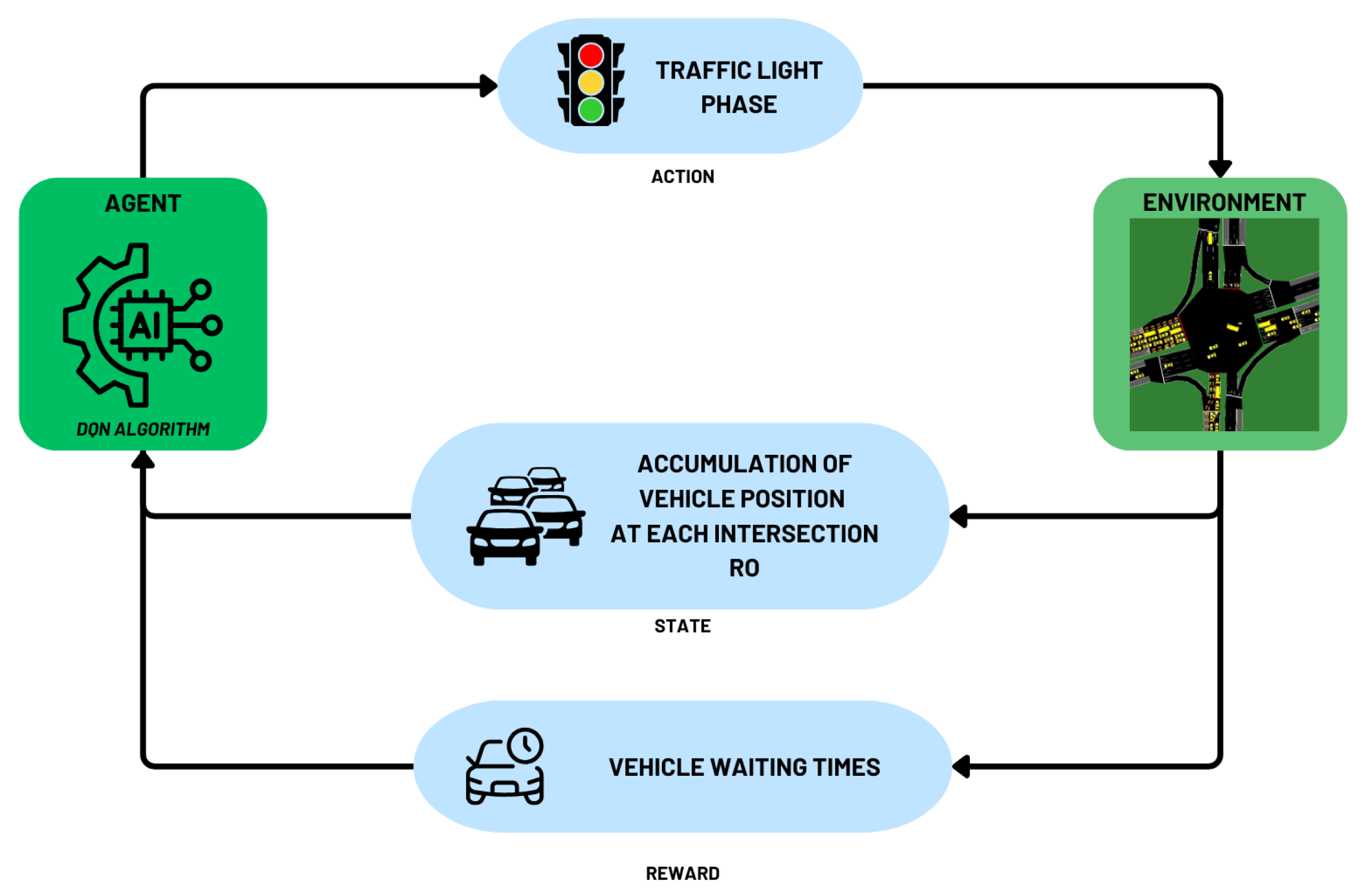
5.1. Experiments Result
There are ten parameters used in this study to collect data, with each parameter representing a different condition and type of data:
QL-Reg-Current
QL-Reg-No RL
QL-Reg-With RL
QL-ML-No RL
QL-ML-With RL
WT-Reg-Current
WT-Reg-No RL
WT-Reg-With RL
WT-ML-No RL
WT-ML-With RL
The explanation of each subparameter of these parameters is provided in
Table 8.
During the testing process, ten parameters previously explained were used. These parameters were analyzed to observe the impact of implementing two-wheeled vehicle lanes and the DQN algorithm compared to previous conditions. The analysis not only examined changes from the current state to the final state but also compared the current conditions with conditions after adding two-wheeled vehicle lanes without the DQN algorithm. Additionally, comparisons were made between two-wheeled vehicle lanes without DQN and with DQN, as well as the current conditions with those incorporating both two-wheeled vehicle lanes and RL as shown on
Figure 15.
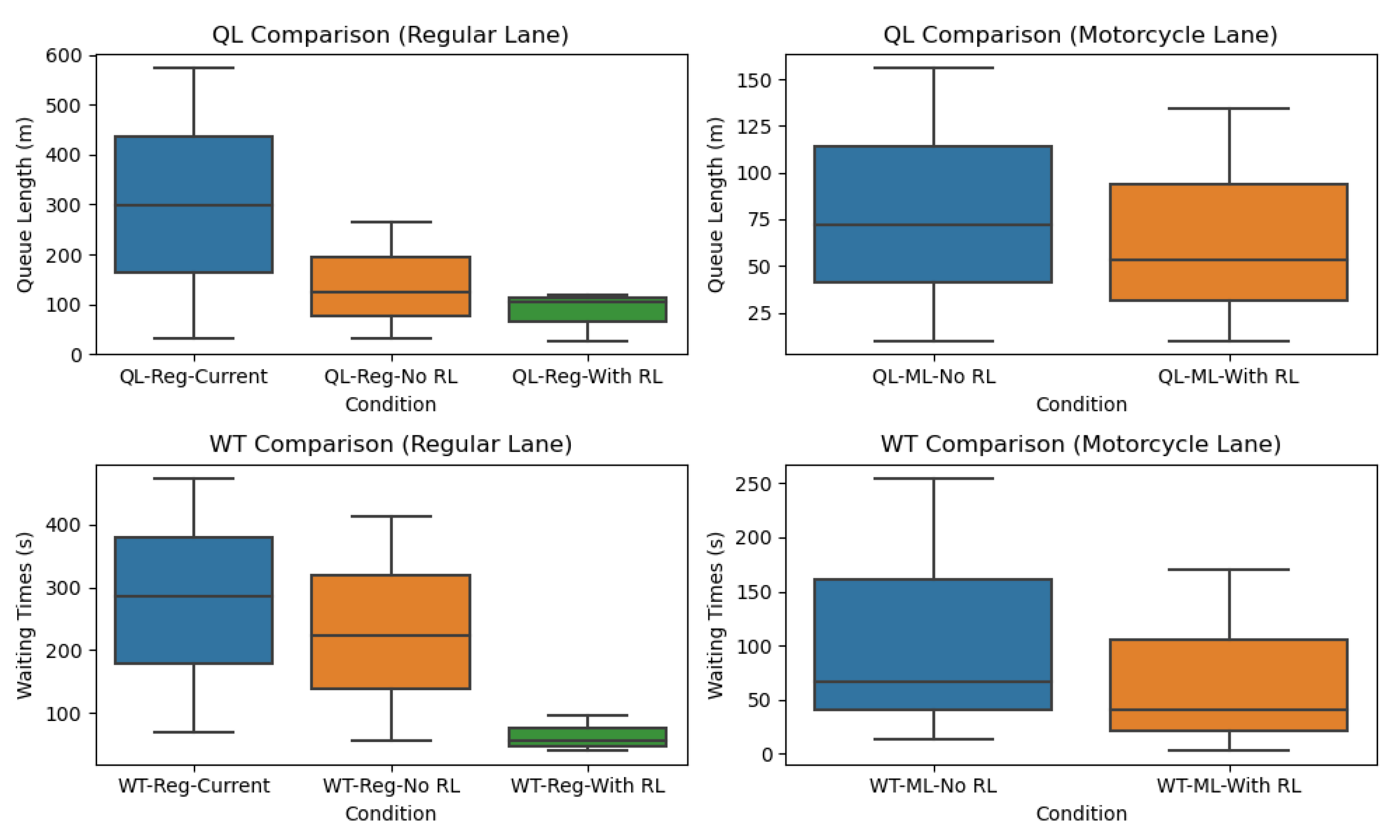
The box plots in
Figure 15 provide a detailed comparative analysis of Queue Length (QL) and Waiting Times (WT) across two different lane types: Regular Lane and two-wheeled vehicle lane, under varying conditions. These plots enable a deeper understanding of the traffic dynamics and the effect of reinforcement learning (RL) control on traffic management.
The first subplot (QL-Comparison in Regular Lane) focuses on the queue lengths in regular lanes under three specific conditions. The data indicates that the highest queue lengths are observed under current conditions, labeled as QL-Reg-Current, with an average queue length of 297.9m, a minimum of 30m, and a maximum of 574m. Comparatively, when reinforcement learning control is not applied, marked as QL-Reg-No RL, there is a noticeable decrease in queue lengths to an average of 124.9m, with a minimum of 30m and a maximum of 264m. This scenario depicts the traffic situation where traditional traffic management techniques are employed, excluding advanced RL methods. The shortest queue lengths are achieved with RL control using Deep Q-Network (DQN), designated as QL-Reg-With RL, with an average of 104.58m, a minimum of 27m, and a maximum of 119.4m. This condition demonstrates the effectiveness of RL in optimizing traffic flow and reducing congestion significantly in regular lanes. The RL approach leads to an average queue length reduction of 193.32m compared to the current conditions and 20.32m compared to the traditional methods.
The second subplot (QL-Comparison in two-wheeled vehicle lane) presents the comparison of queue lengths in two-wheeled vehicle lanes under two conditions. Without the application of RL control, referred to as QL-ML-No RL, longer queue lengths are evident, with an average of 72m, a minimum of 10m, and a maximum of 156m. This situation reflects the conventional traffic management approach that does not utilize advanced RL techniques. In contrast, when RL control using DQN is implemented, indicated as QL-ML-With RL, there is a substantial reduction in queue lengths to an average of 53m, a minimum of 10m, and a maximum of 134m. This outcome showcases the capacity of RL to efficiently manage motorcycle traffic, thereby minimizing delays and enhancing the overall traffic flow. The RL approach results in an average queue length reduction of 19m.
The third subplot (WT-Comparison in Regular Lane) focuses on waiting times in regular lanes under three different conditions. The current waiting times, marked as WT-Reg-Current, are the longest, with an average waiting time of 284.85 seconds, a minimum of 70 seconds, and a maximum of 474.3 seconds, highlighting the inefficiencies in the existing traffic management system. When RL control is not applied, represented by WT-Reg-No RL, the waiting times decrease to an average of 223.4 seconds, with a minimum of 55 seconds and a maximum of 414 seconds, showing some improvement over the current conditions but still lacking the efficiency of RL methods. The shortest waiting times are recorded under RL control using DQN, labeled as WT-Reg-With RL, with an average of 55.6 seconds, a minimum of 40 seconds, and a maximum of 95 seconds. This scenario underscores the superior performance of RL in reducing waiting times, thereby improving the overall traffic efficiency in regular lanes. The RL approach leads to an average waiting time reduction of 229.25 seconds compared to the current conditions and 167.8 seconds compared to the traditional methods.
The fourth subplot (WT-Comparison in two-wheeled vehicle lane) compares the waiting times in two-wheeled vehicle lanes under two conditions. Longer waiting times are observed without RL control, indicated as WT-ML-No RL, with an average of 66.62 seconds, a minimum of 14 seconds, and a maximum of 255 seconds. This scenario reflects the limitations of traditional traffic management systems in handling motorcycle traffic efficiently. Conversely, the implementation of RL control using DQN, marked as WT-ML-With RL, results in decreased waiting times to an average of 40 seconds, a minimum of 3 seconds, and a maximum of 170 seconds. This demonstrates the effectiveness of RL in optimizing the flow of motorcycle traffic, significantly reducing delays. The RL approach results in an average waiting time reduction of 26.62 seconds.
These detailed numerical reductions highlight the impact of RL in managing traffic more effectively compared to current and traditional traffic management systems.
Overall, the application of reinforcement learning control using DQN proves to be highly effective in reducing both queue lengths and waiting times in both regular and two-wheeled vehicle lanes. The analysis reveals that the current conditions in regular lanes exhibit the highest queue lengths and waiting times compared to other conditions, emphasizing the need for advanced traffic management solutions. In two-wheeled vehicle lanes, RL control shows a marked improvement in managing traffic flow, highlighting its potential in enhancing traffic efficiency.
The box plots provide a summary of the overall QL and WT at all intersection approaches. These plots, lower boundary represents the minimum values (min), the upper boundary denotes the maximum values (max), and the body of the box plot illustrates the average values (mean). This detailed analysis offers a comprehensive understanding of traffic conditions and highlights the significant improvements achieved through the application of reinforcement learning control.
Figure 15 clearly demonstrates the substantial impact of reinforcement learning control on enhancing traffic flow efficiency.
The percentage change is calculated using the following formula:
where:
By using Equation (
8), the summarized results can be effectively presented in the form of a table as follows:
5.2. Discussion
The experiment results demonstrate a significant reduction in both queue lengths and waiting times under conditions where Reinforcement Learning (RL) is applied, specifically using the Deep Q-Network (DQN) algorithm, in both regular and two-wheeled vehicle lanes. These findings can be explained scientifically through several key mechanisms.
The DQN algorithm is designed to learn optimal traffic signal control strategies by continuously interacting with the traffic environment. It employs a reward-based system to maximize traffic flow and minimize congestion. By leveraging this approach, DQN dynamically adjusts traffic signal timings to respond to real-time traffic conditions, leading to more efficient traffic management. This improvement is achieved through state-action mapping, where DQN maps current traffic conditions to traffic signal adjustments via a neural network. This allows the model to predict the most effective actions to take, significantly reducing the average queue length in regular lanes from 297.9m to 104.58m, a decrease of 64.89%. Additionally, the introduction of exclusive two-wheeled vehicle lanes segregates motorcycles from regular lanes, reducing overall congestion in both lane types. RL further optimizes the flow within these exclusive two-wheeled vehicle lanes, decreasing average queue lengths from 72m to 53m, a reduction of 26.39%.
Regarding waiting times, the DQN algorithm optimizes the duration of green, yellow, and red lights based on real-time traffic data. This dynamic adjustment minimizes waiting times by reducing idle periods at intersections, leading to a substantial decrease in average waiting times in regular lanes from 284.85 seconds to 55.6 seconds, an 80.49% reduction. Unlike static traffic control systems, RL adapts in real-time to changing traffic patterns. This continuous learning process ensures that traffic signals are always set to the most efficient timings, accommodating fluctuations in traffic volumes and patterns. This adaptability results in a reduction of average waiting times in two-wheeled vehicle lanes from 66.62 seconds to 40 seconds, a 39.96% decrease. The advantage of RL over traditional methods lies in its ability to improve through experience. By interacting with the traffic environment, the DQN algorithm learns from previous actions and outcomes, refining its strategy over time to achieve better results, leading to more efficient traffic signal control and reduced congestion.
The DQN algorithm utilizes a neural network to approximate the optimal policy for traffic signal control, relying on a reward function that penalizes long queues and waiting times while rewarding smoother traffic flow. By continuously updating its policy based on observed state-action-reward transitions, the DQN algorithm improves its decision-making process, resulting in more effective traffic management. Additionally, the separation of two-wheeled vehicle lanes allows for more specialized control strategies tailored to the specific dynamics of motorcycle traffic, further enhancing the overall efficiency of the traffic system. The ability of RL to adapt to real-time traffic conditions and learn from historical data makes it a powerful tool for modern traffic management systems, significantly outperforming traditional static methods.
Overall, the implementation of RL using DQN demonstrates a marked improvement in traffic efficiency, as evidenced by the significant reductions in queue lengths and waiting times. This scientific approach underscores the potential of advanced machine learning algorithms in optimizing urban traffic management.
Despite the promising results, this study has several limitations that need to be addressed. First, the simulations were conducted in a controlled environment, which may not fully capture the complexities and variabilities of real-world traffic conditions. Factors such as unexpected events, weather conditions, and human driver behaviors were not included in the model, which could affect the performance of RL algorithms in practice.
Additionally, the study focused primarily on queue lengths and waiting times as performance metrics. Other important factors such as fuel consumption, emissions, and overall travel time were not considered. Future research should incorporate these variables to provide a more comprehensive evaluation of the benefits of RL-based traffic signal control.
Moreover, the implementation of RL in real-world traffic systems requires significant investments in infrastructure, including the installation of advanced sensors and communication networks. The feasibility and cost-effectiveness of such implementations need to be thoroughly investigated.