Magnetostrophic Flow and Electromagnetic Columns in Magneto-Fluid Dynamics

Preprint

Article

Magnetostrophic Flow and Electromagnetic Columns in Magneto-Fluid Dynamics

Altmetrics

Downloads

118

Views

Comments

A peer-reviewed article of this preprint also exists.

Peter Vadasz^*

This version is not peer-reviewed

Submitted:

15 September 2024

Posted:

16 September 2024

You are already at the latest version

Alerts

Abstract

An analogy between magneto-fluid dynamics (MFD/MHD) and geostrophic flow in a rotating frame of reference including the existence of electromagnetic columns identical to Taylor-Proudman columns is identified and demonstrated theoretically. The latter occurs in the limit of large values of a dimensionless group representing the magnetic field number. Such conditions are shown to be easily satisfied in reality. Consequently, the electromagnetic fluid flow subject to these conditions is two dimensional and the streamlines are being shown to be identical to the pressure lines in complete analogy to rotating geostrophic flows. An experimental setup is suggested to confirm the theoretical results experimentally.

Keywords:

Subject: Physical Sciences - Fluids and Plasmas Physics

1. Introduction

Flow of electric charges within or with a fluid or alternatively freely moving in free space is being analyzed as part of magneto-fluid dynamics (MFD). The latter appears also under the acronym MHD (magneto-hydrodynamics) although inaccurately linked to water (hydro) flow due to historical reasons. It applies to plasmas, liquid metals as well as beams of charges moving in free space. The present paper deals with the theoretical demonstration of two linked MFD effects that are being shown to be analogous to fluid flow in a rotating frame of reference. The flow of fluids in a rotating frame of reference has been studied extensively and has applications in geophysics, astrophysics, as well as in engineering. The specific effects related to rotating flows are predominantly a result of centripetal and Coriolis accelerations (Greenspan [1]) as well as possibly centrifugal buoyancy Vadasz [2]. The Coriolis effect and the resulting vortex formations have been identified theoretically as well as experimentally. Amar et al. [3] demonstrated the latter numerically as well as analytically and compared their results with experimental data. They focused on the separation between geostrophic flow and Ekman and Stewartson boundary layers. Asymptotic analyses of rotating flows identify Taylor-Proudman columns and two-dimensional flow at the leading order and Ekman as well as Stewartson boundary layers for higher order corrections [1], results that were confirmed numerically as well as experimentally (Subbotin et al. [4], and Burmann and Noir [5]). The explanation of the appearance of von Karman vortex streets around invisible bluff bodies as captured by satellite images over certain islands in the Atlantic and Pacific Oceans was provided by Vadasz [6] in terms of Taylor-Proudman columns. Sarkar et al. [7] investigated the effect of a magnetic field on Taylor-Proudman columns in a rotating electrically conducting fluid (MFD). They concluded that the “application of a magnetic field” “suppresses the Taylor column” in certain circumstances. In an electrically conducting fluid the balance between the Coriolis acceleration and the Lorentz force is the mechanism that controls the Taylor-Proudman column. Extensive research results on the problem of natural convection due to centrifugal buoyancy in rotating porous media were presented by Vadasz [8,9,10,11,12,13] and by Vadasz and Govender [14]. Vadasz [8] focused on the centrifugal buoyancy in a porous layer distant from the axis of rotation, Vadasz [9] analyzed the Coriolis effect on a rotating porous layer heated from below via linear as well as weak nonlinear methods. Other investigations of centrifugal buoyancy in rotating porous media were performed by Saravanan and Vigneshwaran [15] and Kang et al. [16].

The effect of the magnetic field on the flow of conducting fluids has been studied extensively, e.g., identifying the law of isorotation (Allen et al. [17]). An analogy between the Taylor-Proudman theorem for rotating fluids and the law of isorotation for MFD might evolve as a consequence of the present paper’s derivations.

The analogy between the Coriolis and Lorentz forces is not new, e.g., the analogy between the gyrocompass and the magnetic compass was demonstrated by Opat [18]. In the present paper it is demonstrated also for fluids rather than compasses.

The next section describes the analogy between rotating and magnetic (MFD) flows followed by the theoretical demonstration on how electromagnetic columns are being created when a flowing fluid carrying electric charges is exposed to an externally imposed magnetic field. The consequent two-dimensional magnetostrophic flow then emerges. The final section presents the fact that the conditions required for the electromagnetic columns and magnetostrophic flow to emerge are well satisfied in reality and should then be observable in lab experiments.

2. Analogy between Magneto-Fluid Dynamics (MFD/MHD) and Rotating Flows

The equations governing the isothermal compressible flow in a rotating frame of reference are the continuity and momentum equations presented in the form

\frac{\partial ρ}{\partial t} + \nabla \cdot (ρ V) = 0

(1)

ρ [\frac{\partial V}{\partial t} + (V \cdot \nabla) V + 2 ω \times V + ω \times (ω \times X)] = - \nabla p + ρ g + μ \nabla^{2} V

(2)

where

V (t, x) = u {\hat{e}}_{x} + v {\hat{e}}_{y} + w {\hat{e}}_{z}

is the velocity vector,

{\hat{e}}_{x}, {\hat{e}}_{y}

and

{\hat{e}}_{z}

are unit vectors in the

x, y

, and

z

directions, respectively,

ω

is the constant angular velocity of rotation,

is pressure,

μ

is the dynamic viscosity, and

X = x {\hat{e}}_{x} + y {\hat{e}}_{y} + z {\hat{e}}_{z}

is the position vector. By assuming the fluid to be barotropic and using a linear relationship between pressure and density (this assumption applies to isothermal conditions for an ideal gas, and approximately also for isentropic conditions of the latter, and for liquids) in the form

p = p_{o} + v_{o}^{2} (ρ - ρ_{o})

(3)

where

v_{o}^{2} = {(\partial p / \partial ρ)}_{T}

v_{o}^{2} = {(\partial p / \partial ρ)}_{s}

. Moving the Coriolis and centripetal terms to the right-hand side of the equation, and dividing Equation (2) by

ρ

it yields

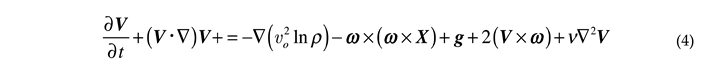
where

ν = μ / ρ

is the kinematic viscosity. The centripetal acceleration term

ω \times (ω \times X)

has a potential and can be therefore moved under the gradient term in the form

\frac{\partial V}{\partial t} + (V \cdot \nabla) V + = - \nabla [v_{o}^{2} \ln ρ + \frac{1}{2} (ω \times X) \cdot (ω \times X)] + g + 2 (V \times ω) + ν \nabla^{2} V

(5)

It becomes appealing now to define a generalized reduced pressure term (a specific kinetic energy) in the form

p_{r} = v_{o}^{2} \ln ρ + \frac{1}{2} (ω \times X) \cdot (ω \times X)

(6)

Substituting (6) into (5) leads to

\frac{\partial V}{\partial t} + (V \cdot \nabla) V + = - \nabla p_{r} + g + 2 (V \times ω) + ν \nabla^{2} V

(7)

The momentum equation for an MFD fluid, i.e., a fluid that carries electric charges (even when as a whole it is neutrally charged) includes the electric and magnetic fields via the Lorentz force, and when neglecting the gravitational field, the latter being much weaker than the electromagnetic fields can be presented in the form

ρ [\frac{\partial V}{\partial t} + (V \cdot \nabla) V] = - \nabla p + ρ_{q} E + ρ_{q} (V \times B_{i}) + μ \nabla^{2} V

(8)

where

E (t, x, y, z)

is the electric field due to the distributed charges in the fluid,

V

is the velocity of the charges, and

ρ_{q} (V \times B_{f})

is the induced magnetic field that results from the electric current due to the moving charges. When the fluid is exposed to an external magnetic field then an additional term in the form

ρ_{q} (V \times B_{f})

is to be added in Equation (8). Substituting Equation (3) into Equation (8), dividing Equation (8) by

ρ

, and using the definition of the generalized reduced pressure (6) for the case without rotation (i.e.,

) produces

\frac{\partial V}{\partial t} + (V \cdot \nabla) V = - \nabla p_{r} + s_{q} β_{q}^{- 1} E + s_{q} β_{q}^{- 1} (V \times B_{i}) + ν \nabla^{2} V

(9)

where

β_{q} = ρ / | ρ_{q} |

is assumed to be constant and equal to the ratio between the total mass of the electric charges to the total electric charge, i.e.,

β_{q} = ρ / | ρ_{q} | = m_{q} / | q |

, and

s_{q} = {\begin{cases} 1 \forall ρ_{q} > 0 \\ - 1 \forall ρ_{q} < 0 \end{cases}

(10)

is the electric charge sign function. Comparing Equation (9) for the magnetic-fluid dynamics flow to Equation (7) for non-magnetic fluid dynamics in a rotating frame of reference one observes the analogy where the gravitational field term

g

was replaced by the electric field term

s_{q} β_{q}^{- 1} E

, and the Coriolis acceleration term

2 (V \times ω)

was replaced by the magnetic term

s_{q} β_{q}^{- 1} (V \times B_{i})

. Consequently it is plausible to anticipate that the magnetic field term

B_{i} / β_{q}

in MFD has an identical effect as the angular velocity of rotation term

2 ω

in the Coriolis acceleration of the rotating flow. Note that even the units of

B_{i} / β_{q}

are

[T C / k g] = [s^{- 1}]

identical to the units of

ω

. Since the analogy between MFD flow and rotating flows was established by this comparison, one can therefore anticipate similar effects in MFD flow as in the corresponding Coriolis effects for rotating flow.

A similar analogy applies if the fluid is exposed to an externally imposed magnetic field. Then Equation (9) takes the form

\frac{\partial V}{\partial t} + (V \cdot \nabla) V = - \nabla p_{r} + s_{q} β_{q}^{- 1} E + s_{q} β_{q}^{- 1} (V \times B_{i}) + s_{q} β_{q}^{- 1} (V \times B_{f}) + ν \nabla^{2} V

(11)

where

B_{f} = B_{f} {\hat{e}}_{f}

is the imposed magnetic field, which is constant, i.e.,

B_{f} = const .

, and

{\hat{e}}_{f}

is a unit vector in the direction of the imposed magnetic field.

3. Emerging Electromagnetic Columns in an Electrically Charged Fluid Flowing Subject to an Imposed Magnetic Field

When the fluid is incompressible, or when the fluid can be assumed to be weakly compressible (i.e., the density does not change but only when in a body force term in the momentum equation) the continuity Equation (1) transforms into

\nabla \cdot V = 0

(12)

By considering the flow subject to an imposed magnetic field, then Equation (11) is to be solved together with Maxwell equations presented in the form

Coulomb law in field form

\nabla \cdot E = \frac{1}{ε_{o}} ρ_{q}

(13)

where

ε_{o}

is the permittivity of vacuum.

Ampere law

c_{o}^{2} \nabla \times B_{i} = \frac{1}{ε_{o}} ρ_{q} V + \frac{\partial E}{\partial t}

(14)

where

c_{o}^{2} = 1 / ε_{o} μ_{o}

is the speed of light in vacuum, and

μ_{o}

is the permeability of free space.

Faraday law of induction

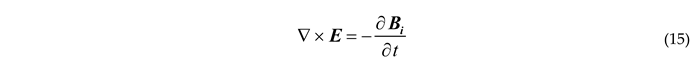
Gauss law for the magnetic field

\nabla \cdot B_{i} = 0

(16)

Note that

B_{f}

does not appear in Equations (14)–(16) because it is constant and therefore its derivatives vanish.

Converting the equations into a dimensionless form requires the introduction of scales or characteristic values. The only requirement from such scales is that they are non-zero constants. Selecting

l_{c}

ρ_{c}

, ,

v_{c}

q_{c} > 0

, and

m

as the length, mass density, charge density, velocity, electric charge, and mass scales, respectively, one can introduce the following additional scales in terms of the latter

t_{c} = l_{c} / v_{c}

Δ p_{c} = ρ_{c} v_{c}^{2}

E_{c} = q_{c} / ε_{o} l_{c}^{2}

B_{i c} = μ_{o} q_{c}^{2} / {(m ε_{o} l_{c}^{5})}^{1 / 2}

B_{f c} = | B_{f} | = B_{f}

. One can also relate the mass density scale to the mass scale, i.e.,

ρ_{c} = m / l_{c}^{3}

and the charge density scale to the charge scale, i.e.,

ρ_{q c} = q_{c} / l_{c}^{3}

. By using these scales the following dimensionless variables are being defined as follows

x_{*} = x / l_{c}

t_{*} = t v_{c} / l_{c}

ρ_{q *} = ρ_{q} / ρ_{q c}

v_{*} = v / v_{c}

p_{*} = p / ρ_{c} v_{c}^{2}

E_{*} = E ε_{o} l_{c}^{2} / q_{c}

B_{i *} = B_{i} {(m ε_{o} l_{c}^{5})}^{1 / 2} / μ_{o} q_{c}^{2}

B_{f *} = {\hat{e}}_{f}

. Substituting these dimensionless variables into Equations (11) and (12) transforms the latter into the following dimensionless form

\nabla_{*} \cdot V_{*} = 0

(17)

\frac{\partial V_{*}}{\partial t_{*}} + (V_{*} \cdot \nabla_{*}) V_{*} = - \frac{1}{M a^{2}} \nabla_{*} p_{r *} + \frac{s_{q}}{M_{E}} E_{*} + \frac{s_{q}}{M_{i}^{2}} (V_{*} \times B_{i *}) + s_{q} M_{B} (V_{*} \times {\hat{e}}_{f}) + \frac{1}{R e} \nabla_{*}^{2} V_{*}

(18)

where the following dimensionless groups emerged

the Mach number

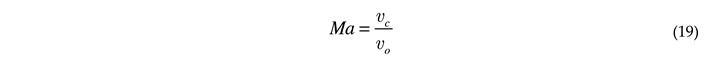
the electric field number

M_{E} = \frac{β_{q} l_{c} v_{c}^{2} ε_{o}}{q_{c}}

(20)

the induced magnetic field number

M_{i}^{2} = \frac{β_{q} v_{c} {(m ε_{o} l_{c}^{3})}^{1 / 2}}{μ_{o} q_{c}^{2}}

(21)

the imposed magnetic field number

M_{B} = \frac{B_{f} l_{c}}{β_{q} v_{c}}

(22)

the Reynolds number

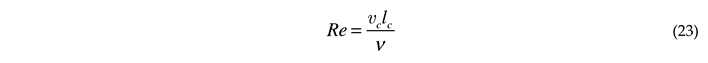
Dividing Equation (18) by

M_{B}

produces (after dropping the symbol * as now all variables are dimensionless)

R o_{M} \frac{\partial V}{\partial t} + R o_{M} (V \cdot \nabla) V = - \nabla {\tilde{p}}_{r} + \frac{s_{q}}{M_{B} M_{E}} E + \frac{s_{q}}{M_{B} M_{i}^{2}} (V \times B_{i}) + s_{q} (V \times {\hat{e}}_{f}) + E k_{M} \nabla^{2} V

(24)

where a rescaled pressure was introduced in the form

{\tilde{p}}_{r} = p_{r} / M_{B} M a^{2}

and where new dimensionless groups emerged as follows

the magnetic Rossby number

R o_{M} = M_{B}^{- 1} = \frac{l_{c}}{(B_{f} / β_{q}) v_{c}}

(25)

the magnetic Ekman number

E k_{M} = M_{B}^{- 1} R e^{- 1} = \frac{ν}{(B_{f} / β_{q}) l_{c}^{2}}

(26)

Assuming steady state, and

M_{B} > > 1

which implies

R o_{M} < < 1

. Then if also

R e = O (1)

(or

R e > > 1

) which implies

E k < < 1

, and if

M_{E} = O (1)

(or

M_{E} > > 1

), and if also

M_{i}^{2} = O (1)

(or

M_{i}^{2} > > 1

) then neglecting the terms in Equation (24) corresponding to the small coefficients leads to

{\hat{e}}_{f} \times V = - \nabla (s_{q} {\tilde{p}}_{r})

(27)

since

s_{q} = 1 / s_{q}

by definition presented in Equation (10). Selecting the coordinates axes in a such a way that the direction of the imposed magnetic field

B_{f}

is aligned with the negative direction of the

z

-axis, i.e.,

{\hat{e}}_{f} = - {\hat{e}}_{z}

transforms (27) into

{\hat{e}}_{z} \times V = \nabla (s_{q} {\tilde{p}}_{r})

(28)

Taking the curl (

\nabla \times

) of Equation (28) produces

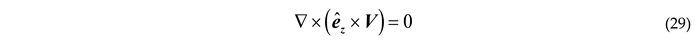
However, by using Equation (17) and evaluating the curl in (29) leads to

\nabla \times ({\hat{e}}_{z} \times V) = - ({\hat{e}}_{z} \cdot \nabla) V = 0

(30)

Evaluating the dot product yields

({\hat{e}}_{z} \cdot \nabla) V = \frac{\partial V}{\partial z} = 0

(31)

Equation (31) is the electromagnetic equivalent to the Taylor-Proudman theorem from rotating flows. It implies in particular that

and since

w = 0

z = 0

due to impermeability boundary conditions it means that

w = 0

for all values of

z

. This indicates that a flow over an object aligned with the imposed magnetic field as presented in Figure 1 is impossible because it introduces a vertical component of velocity,

w \neq 0

, and consequently is violating Equation (31). The conclusion is that the flow will adjust around the object as presented in Figure 2a.

However, this flow pattern is also independent of z because Equation (31) implies

\frac{\partial V}{\partial z} = 0 \Rightarrow \frac{\partial u}{\partial z} = \frac{\partial v}{\partial z} = \frac{\partial w}{\partial z} = 0

(32)

and consequently the flow pattern extends over the whole height creating a fluid column above the object which behaves like a solid body, as presented in Figure 2b.

4. Magnetostrophic Flow

The lack of a vertical component of velocity leads to two-dimensional flow and then it becomes appealing to introduce a stream function that causes the continuity Equation (17) to be identically satisfied, i.e.,

u = - \frac{\partial ψ}{\partial y}; v = \frac{\partial ψ}{\partial x}; w = 0

(33)

Substituting (33) in Equation (28) after performing the vector product on its left-hand side produces

\nabla_{H} ψ = \nabla_{H} (s_{q} {\tilde{p}}_{r})

(34)

where

\nabla_{H} = \partial / \partial x {\hat{e}}_{x} + \partial / \partial y {\hat{e}}_{y}

is the horizontal gradient operator.

As both the generalized reduced pressure,

{\tilde{p}}_{r}

, and the stream function,

ψ

, can be related to an arbitrary reference value, the conclusion from (34) is that the stream function and the generalized reduced pressure are the same in the limit of small magnetic Ekman and Rossby numbers. This type of magnetostrophic flow (in analogy to the geostrophic type in rotating flows) means thar isobars represent streamlines at the leading order for

E k_{M} < < 1

and

R o_{M} < < 1

, i.e., for

M_{B} > > 1

5. Parameter Estimation and Suggested Experimental Setup

In this section an evaluation of the conditions for electromagnetic columns and magnetostrophic flow to exist are tested via parameter estimation and a suggested experimental setup is proposed. The objective is in establishing the criteria for the theoretical results to be detectable in practice. The main condition for the emergence of electromagnetic columns and magnetostrophic flow was derived as

M_{B} > > 1 \Rightarrow \frac{v_{c}}{(B_{f} / β_{q}) l_{c}} < < 1 \Rightarrow \frac{B_{f}}{β_{q}} > > \frac{v_{c}}{l_{c}}

(35)

For the flow of free charges one can estimate the value of

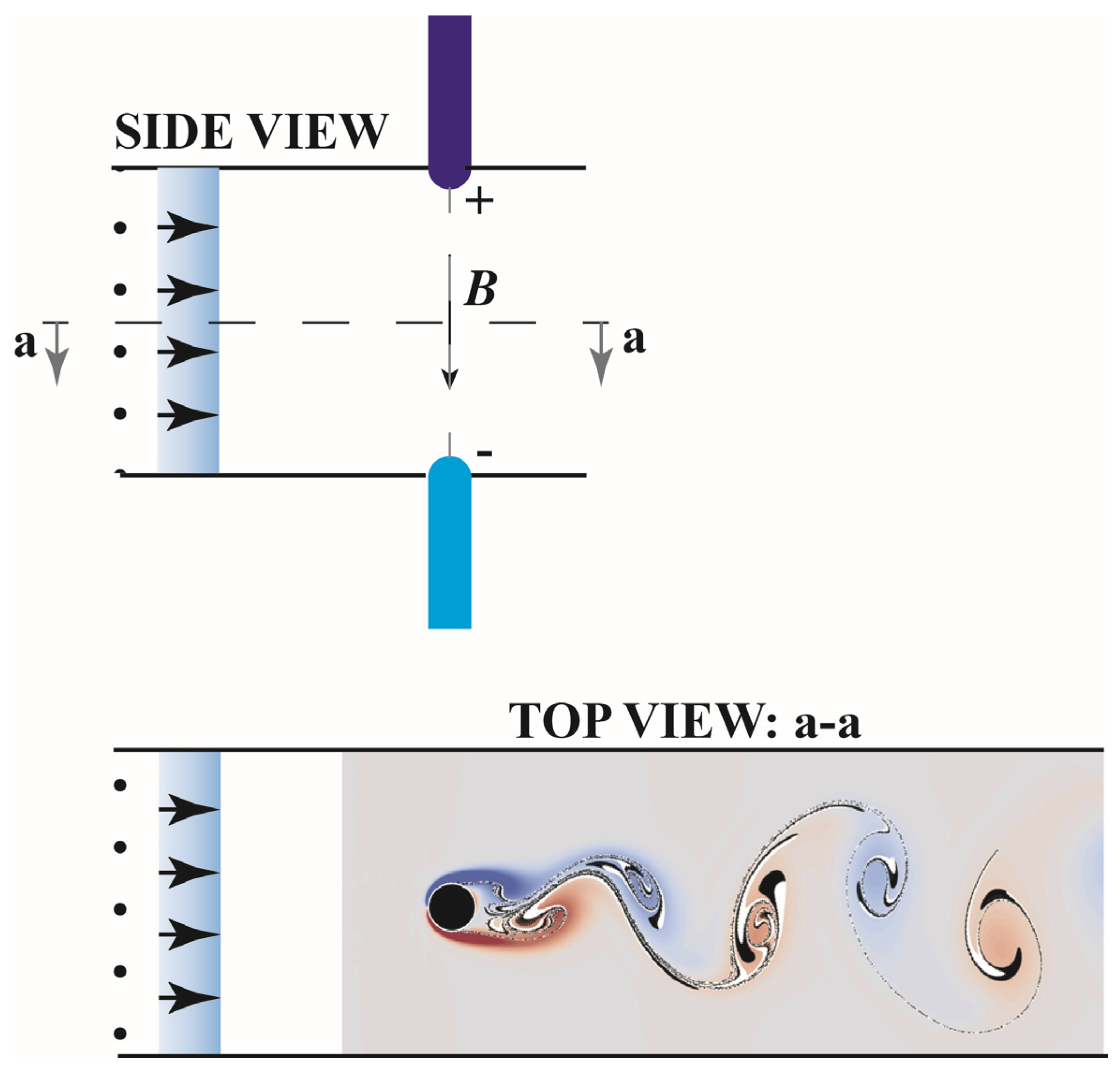
as the ratio between the mass of the elementary charge (the electron) and the absolute value of its electrical charge. For flow of charges via fluids one has to account for the mass of the fluid too when evaluating the mass, however for rarified gases the former estimation still applies as an approximation. Then for an imposed magnetic field of

B_{f} = 1 [T]

the ratio and condition (35) implies

(v_{c} / l_{c}) < < 1.75 \cdot 10^{11} [s^{- 1}]

. This means that for length scales of

v_{c} < < 1.75 \cdot 10^{8} [m / s]

v_{c} < < 1.75 \cdot 10^{8} [m / s]

, and

l_{c} = 10^{- 3} [m]

, the condition that the average fluid velocity should satisfy is

v_{c} < < 1.75 \cdot 10^{11} [m / s]

v_{c} < < 1.75 \cdot 10^{9} [m / s]

, and

v_{c} < < 1.75 \cdot 10^{8} [m / s]

, respectively. The first two values exceed the speed of light in vacuum. These conditions are easily satisfied in any realistic experimental setups. Even if the value of

β_{q}

turns out to be much larger even by a few orders of magnitude it should not be difficult to satisfy this condition, which on extreme cases will require stronger magnetic fields. Estimates for the secondary conditions, i.e.,

R e = O (1)

(or

R e > > 1

M_{E} = O (1)

(or

M_{E} > > 1

), (or

M_{i}^{2} > > 1

) indicate that they can also be satisfied in reality. For example, for plasmas large velocities are required such that for length scales of

v_{c} < < 1.75 \cdot 10^{8} [m / s]

v_{c} < < 1.75 \cdot 10^{8} [m / s]

, and

l_{c} = 10^{- 3} [m]

, the condition that the average fluid velocity should satisfy when combined with the condition for

M_{B} > > 1

1.75 \cdot 10^{11} [m / s] > > v_{c} > > 1.2 \cdot 10^{3} [m / s]

1.75 \cdot 10^{9} [m / s] > > v_{c} > > 1.2 \cdot 10^{5} [m / s]

, and

1.75 \cdot 10^{8} [m / s] > > v_{c} > > 1.2 \cdot 10^{6} [m / s]

, respectively. For liquid metals the conditions are much less constrained as

1.75 \cdot 10^{11} [m / s] > > v_{c} > > 10^{- 7} [m / s]

1.75 \cdot 10^{9} [m / s] > > v_{c} > > 10^{- 7} [m / s]

, and

1.75 \cdot 10^{8} [m / s] > > v_{c} > > 10^{- 4} [m / s]

. Therefore experiments to confirm the emergence of electromagnetic columns and magnetostrophic flow are being suggested and planned by using the constraints evaluated in this section and an experimental setup as described in Figure 1 and Figure 2. Using earth magnets for creating the imposed magnetic field is also quite practical given the estimated parameters values.

6. Conclusions

The theoretical derivation identifying an analogy between magneto-fluid dynamics (MFD/MHD) and geostrophic flow in a rotating frame of reference was presented. The latter includes the existence of electromagnetic columns identical to Taylor-Proudman columns. The emergence of these columns is conditional upon very small magnetic Rossby numbers or alternatively very large values of its reciprocal, the electromagnetic number. This condition was shown to be possible to satisfy in reality.

As a result, the electromagnetic fluid flow is two dimensional and the streamlines are being shown to be identical to the pressure lines in complete analogy to rotating geostrophic flows. A possible setup is suggested to confirm the theoretical results experimentally in Figures 1, 2, and in detail in Figure 3. Using earth magnets for creating the imposed magnetic field is also quite practical given the estimated parameters values. An imposed magnetic field is anticipated to be affecting a stream of beams of charges or MFD type fluids that is flowing through. A specific type of detection via a tracer, PIV, or optical methods such as interferometry or similar can be used for the detection of the flow of charges. When magnetostrophic flow and magnetic virtual columns are detected, it raises the possibility of the creation of von-Kármán vortex streets as presented in Figure 3 on the “top view”. This is similar to the creation of von-Kármán vortex streets in the wake of Taylor-Proudman columns in rotating flows as captured by satellite images and presented theoretically by Vadasz [6].

References

H.P. Greenspan, Theory of Rotating Fluids, Cambridge University Press, (1968).
Vadasz, P. Centrifugal buoyancy in a rotating fluid layer next to and distant from the rotation axis. Phys. Fluids 2021, 33, 034123. [Google Scholar] [CrossRef]
Amar, S.D.; Rashkovan, A.; Ziskind, G. Analysis of a stable bathtub vortex in a rotating container. Phys. Fluids 2023, 35. [Google Scholar] [CrossRef]
Subbotin, S.; Shmakova, N.; Kozlov, V.; Ermanyuk, E. Nonlinear regimes of inertial wave attractors generated by a precessing lid: Zonal flows and Rossby waves. Phys. Fluids 2023, 35. [Google Scholar] [CrossRef]
Burmann, F.; Noir, J. Effects of bottom topography on the spin-up in a cylinder. [CrossRef]
P. Vadasz, “von Kármán vortex streets around invisible bluff bodies”, Physics of Fluids, Vol. 35 (9), pp. 096604 (1-5), (2023). [CrossRef]
Sarkar, S.; Sahoo, B.; Sekhar, T.V.S. Influence of magnetic field in the control of Taylor column phenomenon in the translation of a sphere in a rotating fluid. Phys. Fluids 2021, 33, 073606. [Google Scholar] [CrossRef]
Vadasz, P. Stability of free convection in a rotating porous layer distant from the axis of rotation. Transp. Porous Media 1996, 23, 153–173. [Google Scholar] [CrossRef]
Vadasz, P. Coriolis effect on gravity-driven convection in a rotating porous layer heated from below. J. Fluid Mech. 1998, 376, 351–375. [Google Scholar] [CrossRef]
P. Vadasz, “Fluid Flow and Thermal Convection in Rotating Porous Media”, Handbook of Porous Media, Marcel Dekker, New York, pp. 395-439, (2000).
P. Vadasz, Fluid Flow and Heat Transfer in Rotating Porous Media, Springer (Springer Briefs in applied Science and Engineering), ISBN: 978-3-319-20055-2 (Print), 978-3-319-20056-9 (Online), (2016).
P. Vadasz, “Natural Convection in Rotating Flows”, Handbook of Thermal Science and Engineering, F. A. Kulacki (ed.), Chapter 11, Springer International Publishing AG, pp. 691-758, (2018).
Vadasz, P. Instability and Convection in Rotating Porous Media: A Review. Fluids 2019, 4, 147. [Google Scholar] [CrossRef]
Vadasz, P.; Govender, S. Stability and stationary convection induced by gravity and centrifugal forces in a rotating porous layer distant from the axis of rotation. Int. J. Eng. Sci. 2001, 39, 715–732. [Google Scholar] [CrossRef]
S. Saravanan and S. Vigneshwaran “Centrifugal filtration convection in bidisperse media”, Physics of Fluids, Vol. 32 (8), pp. 084109 (1-8), (2020).
Kang, J.; Chen, X.; Fu, C.; Tan, W. Centrifugally driven thermal convection in a rotating porous cylindrical annulus. Phys. Fluids 2013, 25, 044104. [Google Scholar] [CrossRef]
E Allen, J.; Auer, P.L.; Endean, V.G. On the law of isorotation and laboratory experiments. Plasma Phys. 1976, 18, 143–154. [Google Scholar] [CrossRef]
Opat, G.I. Coriolis and magnetic forces: The gyrocompass and magnetic compass as analogs. Am. J. Phys. 1990, 58, 1173–1176. [Google Scholar] [CrossRef]

Figure 1. An impossible type of flow above a small object aligned with the magnetic field.

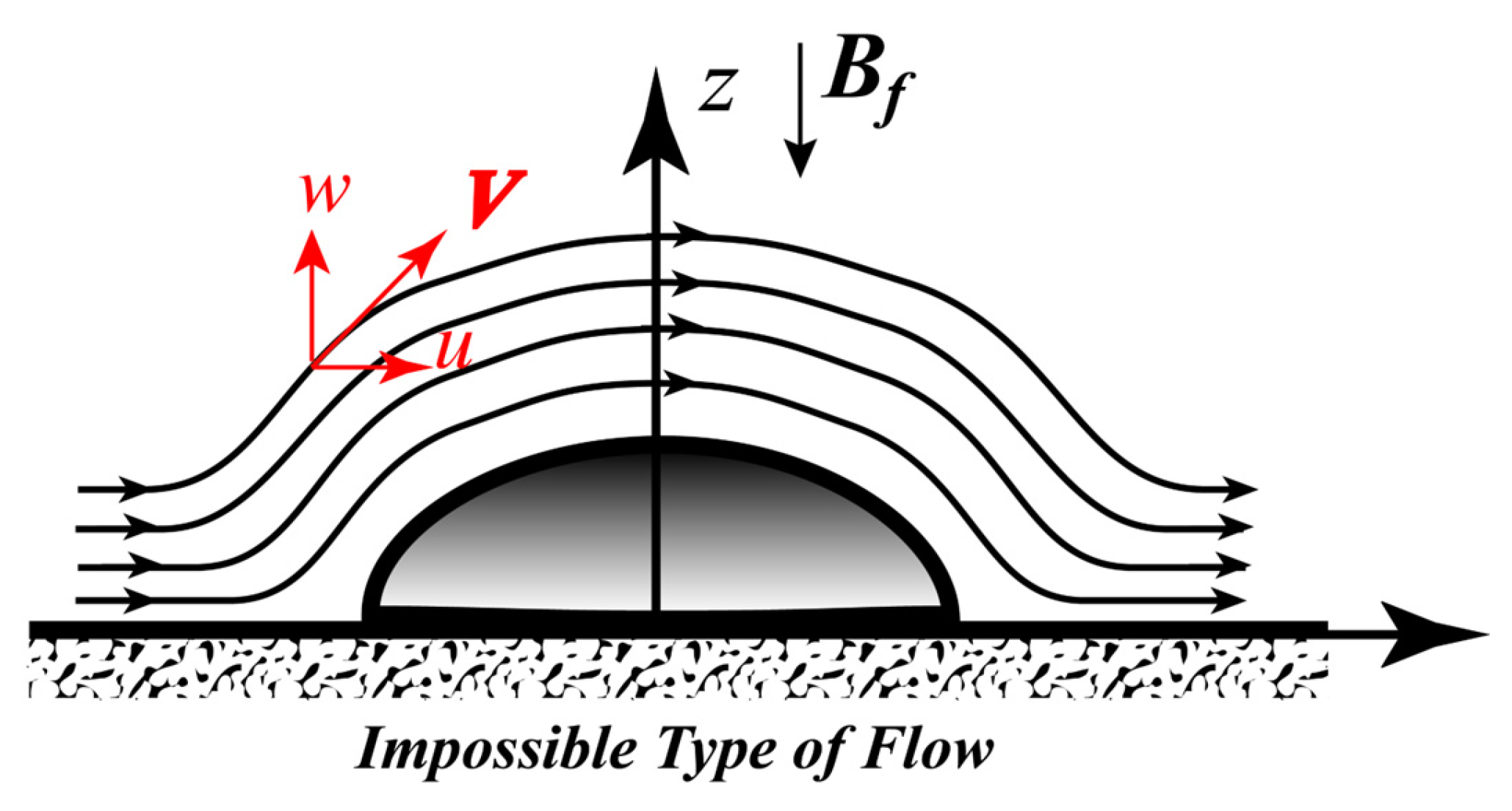
Figure 2. (a) The flow will adjust around the object (b) The flow pattern extends over the whole height creating a fluid column above the object, which behaves like a solid body.

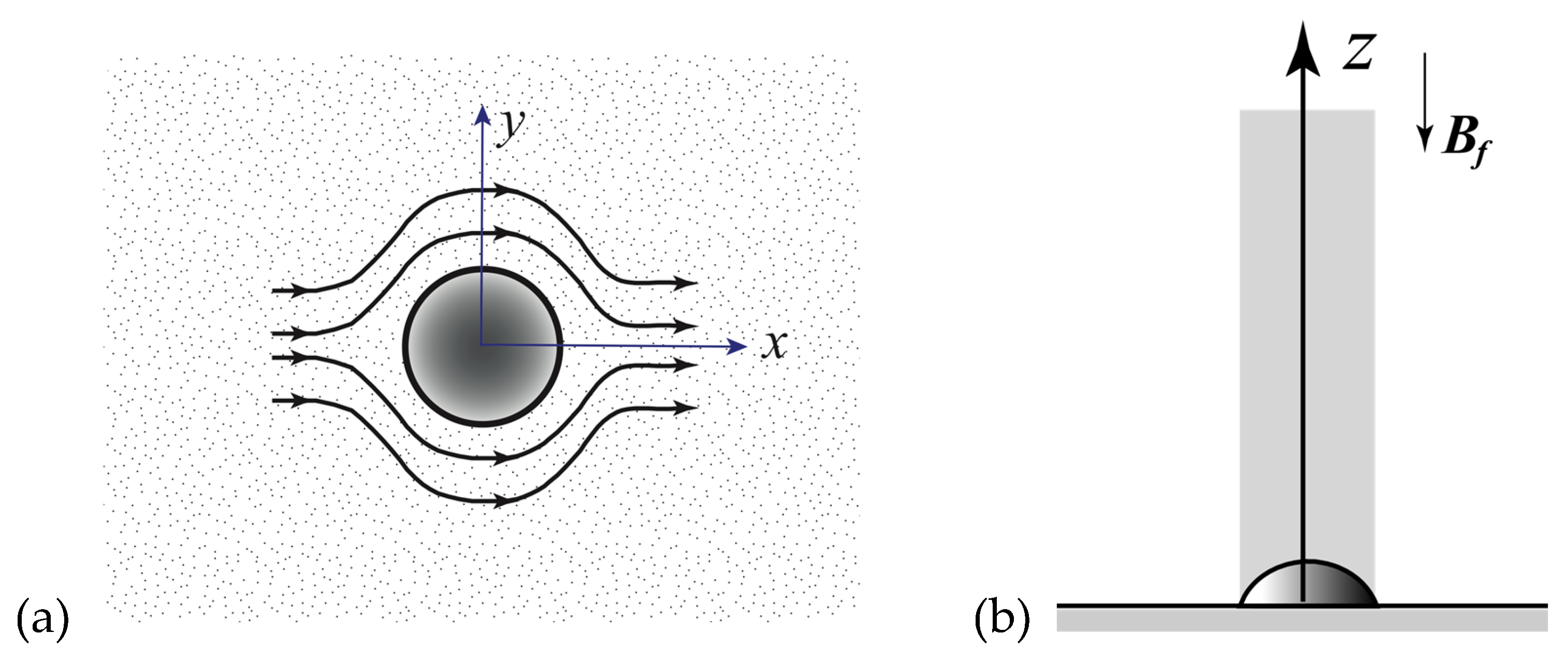
Figure 3. Proposed experimental set-up: An imposed magnetic field affecting a stream of beams of charges or MFD type fluids. (the top view von-Kármán vortex street courtesy: Andrew Yeckel, PhD https://andrewyeckel.com).

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Magnetostrophic Flow and Electromagnetic Columns in Magneto-Fluid Dynamics

Abstract

1. Introduction

2. Analogy between Magneto-Fluid Dynamics (MFD/MHD) and Rotating Flows

3. Emerging Electromagnetic Columns in an Electrically Charged Fluid Flowing Subject to an Imposed Magnetic Field

4. Magnetostrophic Flow

5. Parameter Estimation and Suggested Experimental Setup

6. Conclusions

References

MDPI Initiatives

Important Links

Subscribe