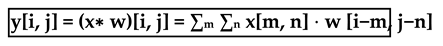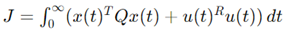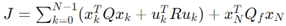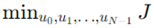Role of Artificial Intelligence in Autonomous Vehicles

1. Introduction

Autonomous vehicles represent a transformative leap in the realm of transportation, promising safer, more efficient, and increasingly intelligent mobility solutions. As technological advancements in Artificial Intelligence (AI) continue to evolve, their integration into autonomous vehicles has become pivotal. This paper provides a comprehensive exploration of AI techniques in autonomous driving systems, focusing on perception, decision-making, and control strategies.

Recent literature underscores the critical role of AI in enhancing the capabilities of autonomous vehicles. Chen et al. (2020) discuss the application of AI techniques within intelligent transportation systems, highlighting their profound impact on the development of autonomous vehicles' perception systems. Similarly, Badue et al. (2021) provide a detailed survey of AI algorithms employed in self-driving cars, emphasizing their diverse applications and technological implications.

Deep learning, a subset of AI, has emerged as a cornerstone in the advancement of autonomous driving technology. Grigorescu et al. (2020) survey deep learning techniques specifically tailored for autonomous vehicles, outlining their efficacy in perception tasks such as object detection and recognition. Moreover, planning and decision-making algorithms play a crucial role in navigating complex environments. Schwarting et al. (2018) review state-of-the-art planning strategies, underscoring the role of AI-driven approaches in enabling safe and efficient decision-making processes for autonomous vehicles.

Early seminal works, such as Thrun's (2010) exploration of robotic cars, laid the groundwork for integrating AI into autonomous vehicle development, highlighting the transformative potential of AI in realizing autonomous driving capabilities. Liu et al. (2019) provide a comprehensive survey on the broader application of AI in autonomous driving, discussing various methodologies and their impact on vehicle autonomy and safety.

Motion planning remains another critical aspect in the realization of fully automated driving systems. Gonzalez et al. (2016) review motion planning techniques, emphasizing AI-driven methods that optimize trajectory plan

The block diagram presented in Figure 1 illustrates the essential components and flow of information in an autonomous vehicle system. It is divided into two main sections: Sensors and Control. These sections are interconnected through the Perception and Planning modules, which are crucial for the autonomous functioning of the vehicle.

1.1. Sensors:

• Camera: Captures visual information from the vehicle's surroundings, aiding in object detection and recognition.
• Radar: Uses radio waves to detect the distance, speed, and movement of objects, providing crucial data for obstacle avoidance.
• Lidar: Employs laser beams to create high-resolution 3D maps of the environment, essential for accurate distance measurement and object detection.
• Ultrasonic: Utilized for short-range detection, often in parking scenarios, to identify nearby obstacles.
• GPS: Provides global positioning data, enabling the vehicle to determine its precise location and navigate routes.
• IMU (Inertial Measurement Unit): Measures the vehicle's acceleration and rotational rates, helping in understanding the vehicle's motion and orientation.
• The data from these sensors feed into the Perception module.

1.2. Perception:

The perception module processes the raw data from the sensors to generate a comprehensive understanding of the vehicle's environment. This includes identifying objects, understanding their positions, predicting their movements, and creating a real-time map of the surroundings. This processed information is then passed to the Planning module.

1.3. Planning:

The planning module uses the information from the perception module to make decisions about the vehicle's movements. This includes path planning, trajectory optimization, and maneuver decisions to ensure safe and efficient navigation. The planning module considers the current environment, destination, and any obstacles to generate a plan that the vehicle should follow.

1.4. Control:

• Brake: Controls the braking system to slow down or stop the vehicle as needed.
• Engine: Manages the power output of the engine to control the vehicle's speed and acceleration.
• Speed: Adjusts the speed of the vehicle according to the planned trajectory and current road conditions.

Acceleration: Regulates the acceleration to achieve smooth and efficient motion.

• Steering Wheel: Adjusts the direction of the vehicle based on the planned path.
• The control module executes the plan created by the planning module, translating the high-level decisions into specific commands for the vehicle’s mechanical systems.

This paper consolidates these perspectives to provide a holistic understanding of how AI technologies are shaping the future of autonomous vehicles. By synthesizing current research and insights, this study aims to contribute to the ongoing discourse on AI's role in advancing autonomous driving technology. focusing on key components such as perception, decision-making, and control mechanisms. Perception forms the foundation of AV functionality, allowing these vehicles to interpret and understand their surroundings accurately.

Advanced perception algorithms enable AVs to identify objects, pedestrians, and road conditions, crucial for safe navigation. Additionally, environmental inference techniques empower AVs to make sense of complex and dynamic surroundings, ensuring robust performance in diverse driving scenarios.

In the realm of decision-making, AI plays a central role in orchestrating intelligent behaviors and responses. Utilizing neural networks and reinforcement learning algorithms, AVs can analyze vast amounts of data in real-time, enabling them to make optimal decisions regarding navigation, route planning, and interaction with other road users. Moreover, optimization techniques facilitate precise decision-making under uncertainty, enhancing overall safety and efficiency.

Control mechanisms form the final layer of AV operation, translating high-level decisions into precise actions. Predictive modeling and precision-guided control techniques enable AVs to execute maneuvers with accuracy and reliability, ensuring smooth and safe navigation through complex environments.

However, the journey towards widespread adoption of AVs is not devoid of challenges. Regulatory frameworks must evolve to address the unique legal and ethical considerations posed by autonomous technologies. Technical hurdles, such as ensuring robustness in diverse environmental conditions and achieving seamless integration with existing infrastructure, also warrant careful attention.

Despite these challenges, the prospects for AV technology are promising. Breakthroughs in AI capabilities, coupled with adaptive regulatory regimes and societal acceptance, hold the potential to unlock new frontiers in transportation. By navigating through these challenges and capitalizing on emerging opportunities, AVs have the potential to redefine the future of mobility, ushering in an era of safer, more accessible, and sustainable transportation.

2. AI in Autonomous Vehicles

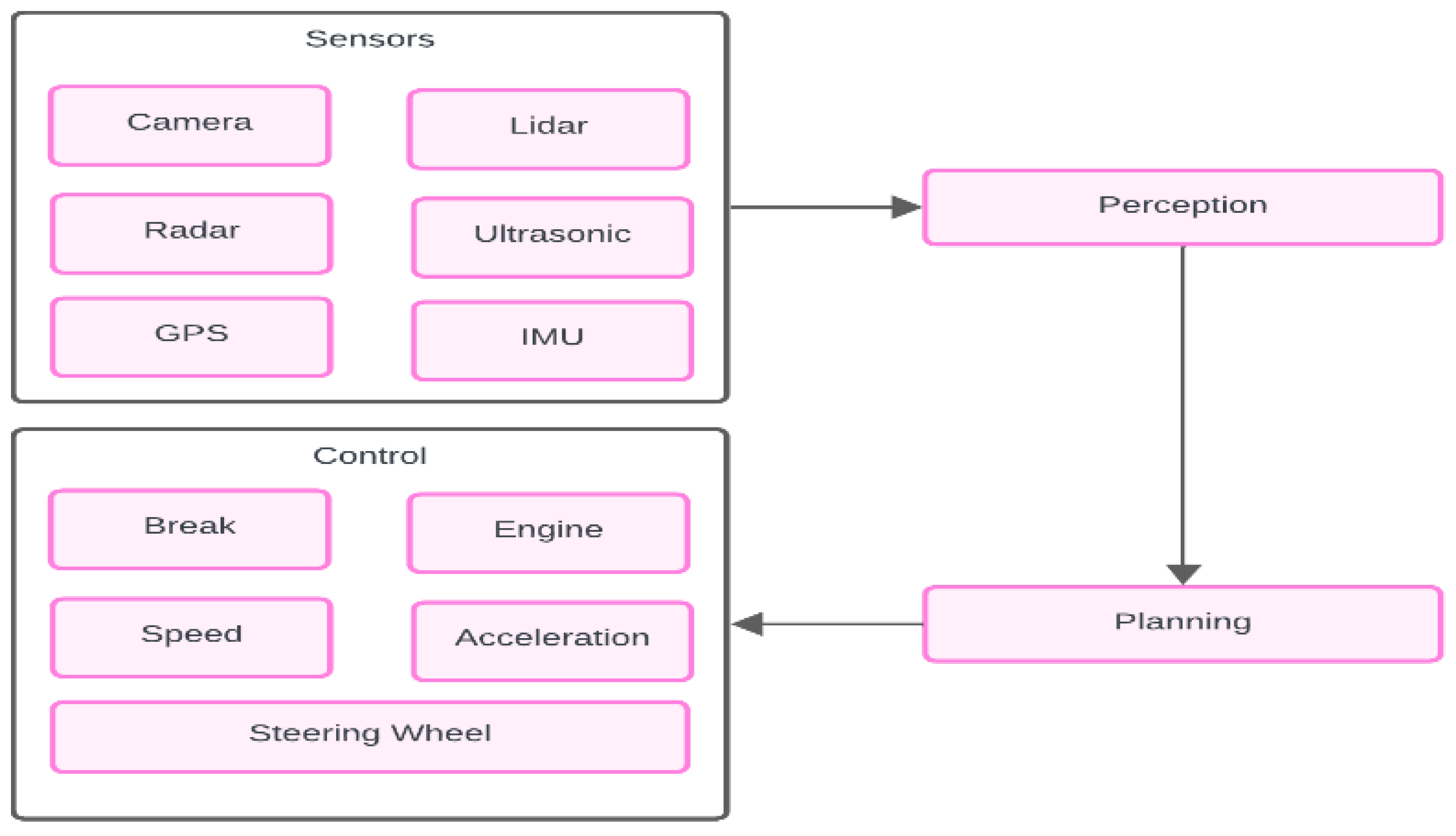
The block diagram titled "AI in Autonomous Vehicles" shown in Figure 2 provides a high-level overview of the key components and processes involved in the application of Artificial Intelligence (AI) within autonomous vehicles. It breaks down the AI system into three primary modules: Perception, Decision Making, and Actuation, each with its respective sub-components. Autonomous vehicles (AVs) rely on a complex interplay of various artificial intelligence (AI) components to perceive their environment, make decisions, and execute actions. Some of the key AI components of autonomous vehicles include:

Perception Systems: AVs use sensors such as cameras, LiDAR (Light Detection and Ranging), radar, and ultrasonic sensors to perceive their surroundings. AI algorithms process data from these sensors to identify objects, detect lane markings, recognize traffic signs, and assess road conditions.

Machine Learning Algorithms: AVs employ machine learning algorithms, including deep learning techniques such as convolutional neural networks (CNNs) and recurrent neural networks (RNNs), to analyze sensor data and extract meaningful information. These algorithms enable AVs to classify objects, predict their movements, and understand complex spatial relationships.

Localization and Mapping: AI-powered localization and mapping systems, often referred to as SLAM (Simultaneous Localization and Mapping), allow AVs to accurately determine their position and create detailed maps of their environment in real-time. These systems fuse sensor data with prior maps to localize the vehicle within its surroundings and update maps as the vehicle navigates.

Decision-Making Algorithms: AVs use decision-making algorithms to plan routes, navigate through traffic, and make decisions in complex driving scenarios. These algorithms consider various factors such as traffic laws, road conditions, nearby vehicles' behavior, and the vehicle's destination to determine the optimal course of action.

Control Systems: AI-based control systems translate high-level decisions into precise control commands to steer the vehicle, accelerate, and brake safely. These systems incorporate predictive modeling, trajectory planning, and feedback control mechanisms to ensure smooth and stable vehicle operation.

Sensor Fusion: AVs integrate data from multiple sensors using sensor fusion techniques to create a comprehensive and accurate representation of their surroundings. Sensor fusion algorithms combine information from cameras, LiDAR, radar,

And other sensors to enhance perception and decision-making capabilities and mitigate sensor limitations.

Behavior Prediction: AI algorithms predict the future behavior of surrounding vehicles, pedestrians, and other objects to anticipate potential hazards and plan proactive responses. By analyzing historical data and real-time sensor observations, AVs can anticipate possible trajectories and adjust their behavior accordingly to avoid collisions and ensure safe navigation.

These AI components collaborate seamlessly to allow autonomous vehicles to navigate safely and efficiently through various environments, setting the stage for a future where autonomous transportation becomes a reality. Let's explore each AI component in greater detail.

2.1. Perception Systems

Perception systems in autonomous vehicles (AVs) play a critical role in enabling the vehicle to understand and interpret its surroundings accurately. These systems utilize a variety of sensors, including cameras, LiDAR (Light Detection and Ranging), radar, and ultrasonic sensors, to collect data about the environment. The data from these sensors is then processed by advanced artificial intelligence (AI) algorithms to identify objects, detect obstacles, recognize road signs and markings, and assess the overall driving conditions. Let's delve deeper into the components and functioning of perception systems in autonomous vehicles:

2.1.1. Sensor Types

Cameras: Cameras capture visual information from the surroundings, providing high-resolution images that can be used for object detection, lane detection, traffic sign recognition, and pedestrian detection.

LiDAR: LiDAR sensors emit laser pulses and measure the time it takes for the pulses to bounce back from surrounding objects. This data is used to create detailed 3D maps of the environment, enabling precise localization, object detection, and obstacle avoidance.

Radar: Radar sensors use radio waves to detect the distance, speed, and direction of objects in the vehicle's vicinity. Radar is particularly useful in adverse weather conditions or low visibility scenarios where other sensors may be less effective.

Ultrasonic Sensors: Ultrasonic sensors emit high-frequency sound waves and measure the time it takes for the waves to reflect back from nearby objects. These sensors are often used for short-range obstacle detection and parking assistance.

Data Fusion:

Perception systems in AVs typically employ a technique called sensor fusion, where data from multiple sensors are combined to create a comprehensive and accurate representation of the environment. Sensor fusion helps mitigate the limitations of individual sensors and enhances the overall reliability of perception.

2.1.2. Object Detection and Classification:

AI algorithms analyze the sensor data to detect and classify various objects in the environment, such as vehicles, pedestrians, cyclists, and road signs. Object detection algorithms use techniques like convolutional neural networks (CNNs) to identify objects based on their visual features.

Semantic Segmentation:

Semantic segmentation is a technique used to partition images into meaningful segments, such as road, sidewalk, buildings, and vehicles. This information is crucial for understanding the layout of the environment and planning safe navigation paths.

Depth Estimation:

Depth estimation algorithms utilize stereo vision or LiDAR data to estimate the distance to objects in the scene. This information helps the vehicle accurately perceive the spatial relationships between objects and navigate safely.

Environmental Understanding:

Perception systems enable the vehicle to understand various aspects of the environment, including road geometry, traffic flow, road signs, traffic lights, and pedestrian behavior. This understanding is essential for making informed decisions and executing appropriate driving maneuvers.

Overall, perception systems serve as the eyes and ears of autonomous vehicles, providing them with the necessary information to navigate complex environments safely and efficiently. Continuous advancements in sensor technology and AI algorithms are driving improvements in perception capabilities, bringing us closer to the realization of fully autonomous transportation.

2.2. Machine Learning Algorithms:

Recent advancements in artificial intelligence (AI) have significantly impacted various industries, including the automotive sector. Smith and Johnson (2020) explored the effects of AI on autonomous vehicles, highlighting the potential for improved safety and efficiency. Additionally, Chen, Hu, Peng, Tang, and Wu (2020) provide a comprehensive review of autonomous vehicles within intelligent transportation systems, discussing the AI techniques used for perception, decision-making, and control.

Machine learning algorithms play a crucial role in autonomous vehicles (AVs) by enabling them to analyze sensor data, make decisions, and adapt to changing environments. These algorithms utilize mathematical models and statistical techniques to learn patterns and relationships from data, allowing AVs to perceive their surroundings, predict future events, and navigate safely. Here, I'll explain some key machine learning algorithms used in autonomous vehicles along with relevant concepts and equations:

2.2.1. OpenCV and Python in AI Automotive:

OpenCV Overview:

• OpenCV is a powerful open-source computer vision library designed for real-time image processing and computer vision tasks.
• It provides a wide range of functions and algorithms for tasks such as image/video capture, image manipulation, object detection and tracking, feature extraction, and more.
• OpenCV is written in C++, but it has Python bindings, making it accessible and widely used in Python-based projects.

Python's Role in AI Automotive with OpenCV:

• Python serves as a versatile programming language for developing AI algorithms, including those used in autonomous vehicles.
• Its ease of use, extensive libraries, and readability make it a preferred choice for prototyping, testing, and implementing algorithms.
• Python integrates seamlessly with OpenCV, allowing developers to leverage OpenCV's functionalities within Python scripts for automotive AI tasks.

Image Processing and Computer Vision in Autonomous Vehicles:

• Autonomous vehicles heavily rely on image processing and computer vision for environment perception.
• OpenCV, combined with Python, enables developers to perform a range of tasks critical for autonomous driving:
• Object Detection: Detecting and recognizing objects such as vehicles, pedestrians, cyclists, and obstacles in real-time video streams using techniques like Haar cascades or deep learning-based models (e.g., YOLO, SSD).
• Lane Detection: Identifying lane markings and boundaries to facilitate lane-keeping and autonomous navigation.
• Traffic Sign Recognition: Recognizing and interpreting traffic signs and signals for compliance and decision-making.
• Pedestrian Detection: Detecting and tracking pedestrians to ensure safe interactions in urban environments.
• Feature Extraction: Extracting relevant features from images or video frames for scene analysis and understanding.

Algorithm Implementation with OpenCV and Python:

• Developers can implement algorithms using OpenCV's functions and methods within Python scripts.
• For example, object detection can be achieved by using pre-trained models (e.g., Haar cascades or deep learning models) provided by OpenCV or custom-trained models integrated with OpenCV's deep learning module.
• Lane detection algorithms can utilize techniques like edge detection (e.g., Canny edge detector) and Hough transforms for line detection, which are readily available in OpenCV's library.
• Python's flexibility allows for algorithmic customization, parameter tuning, and integration with other AI frameworks or modules.

Integration into Autonomous Systems:

• The results obtained from OpenCV and Python algorithms are integrated into the broader autonomous vehicle system.
• These algorithms contribute to the perception module of autonomous systems, providing crucial inputs for decision-making and control.
• For instance, object detection outputs inform collision avoidance strategies, lane detection results guide autonomous steering, and traffic sign recognition influences navigation decisions.

2.2.2. Convolutional Neural Networks (CNNs):

CNNs are a type of deep learning algorithm commonly used for visual perception tasks in AVs, such as object detection, lane detection, and traffic sign recognition.

The core building blocks of CNNs are convolutional layers, which apply convolution operations to input images to extract features. Mathematically, a convolution operation can be represented as:

Equation [1]

where

x is the input image,

w is the convolution kernel, and

y is the output feature map.

Let's dive deeper into the equation for the convolution operation in convolutional neural networks (CNNs):

y[i, j] = (x∗ w)[i, j] = ∑_m​∑_n​ x[m, n] ⋅ w[i−m, j−n]

Components of the Equation

Output Feature Map Value (y[i,j]): y[i,j] represents the value at the position (i,j) in the output feature map after the convolution operation.

Input Image (x): x is the input image or input feature map to which the convolution operation is applied.

Convolution Kernel/Filter (w): w is the convolution kernel, also known as the filter, which slides over the input image to compute the output feature map.

Convolution Operation (x∗w): The convolution of the input image x with the kernel w is denoted as x∗w.

Indices and Iterations

Output Spatial Dimensions (i,j): i and j are indices that iterate over the spatial dimensions (height and width) of the output feature map. They determine the position in the output feature map where the value is being calculated.

Kernel Spatial Dimensions (m,n): m and n are indices that iterate over the spatial dimensions of the convolution kernel (filter). They determine which elements of the input image and the kernel are being multiplied and summed.

Detailed Explanation of the Convolution Operation

The convolution operation involves sliding the kernel www over the input image x and computing the sum of the element-wise product of the overlapping regions. Here's a step-by-step explanation:

Kernel Alignment: For a given position (i,j) in the output feature map, align the kernel www with the input image x such that the center of the kernel is positioned at (i,j).

Element-wise Multiplication and Summation: Multiply each element of the kernel w with the corresponding element of the input image x that overlaps with it. This is done for all elements within the kernel's window.

Summing the Products:Sum all the resulting products to obtain a single value, which becomes the value of the output feature map at position (i,j).

Mathematical Representation

For a specific position (i,j) in the output feature map:

∑_m​∑_n​ x[m, n] ⋅ w[i−m, j−n]

This equation can be interpreted as follows:

Sum Over m and n:Sum the contributions from all elements within the kernel.

Element-wise Multiplication:For each element (m,n) in the kernel, multiply x[m, n] (the input image value at position (m,n)) by w[i - m, j - n] (the kernel value corresponding to the shifted position (i−m,j−n).

Convolution Example

Let's consider a simple example to illustrate the convolution operation:

Input Image (x):$\left[\begin{array}{ccc}1& 2& 3\\ 4& 5& 6\\ 7& 8& 9\end{array}\right]$

Kernel (w): $\left[\begin{array}{cc}1& 0\\ 0& -1\end{array}\right]$

Output Feature Map (y): The output feature map y is computed by sliding the kernel www over the input image x and performing the element-wise multiplication and summation:

y[0,0]=(1⋅1)+(2⋅0)+(4⋅0)+(5⋅−1)=1−5=−4

y[0,1]=(2⋅1)+(3⋅0)+(5⋅0)+(6⋅−1)=2−6=−4

y[1,0]=(4⋅1)+(5⋅0)+(7⋅0)+(8⋅−1)=4−8=−4

y[1,1]=(5⋅1)+(6⋅0)+(8⋅0)+(9⋅−1)=5−9=−4

Thus, the output feature map y is:$\left[\begin{array}{cc}-4& -4\\ -4& -4\end{array}\right]$Here's a step-by-step explanation of how the convolution operation works:

• Positioning the Kernel:

At each position (i,j) in the output feature map, the kernel w is overlaid onto the corresponding region of the input image x.

• Element-wise Multiplication:

For each position (i,j), the elements of the input image x that overlap with the kernel w are multiplied element-wise with the corresponding elements of the kernel.

• Summation:

The products obtained from the element-wise multiplication are summed up. The double summation over m and n represents the sliding of the kernel across the entire input image, computing the weighted sum of pixel values within the kernel's receptive field at each position (i,j).

• Output Assignment:

The resulting sum is assigned to the corresponding position.

(i, j) in the output feature map y.

The convolution operation captures spatial relationships within the input image, enabling the network to extract features such as edges, textures, and patterns. By learning appropriate values for the convolution kernel during the training process, CNNs can automatically discover hierarchical representations of the input data, facilitating tasks such as object detection, image classification, and semantic segmentation.

CNNs also include pooling layers to reduce spatial dimensions and fully connected layers for classification tasks.

In addition to the few rules-of-thumb outlined above, it is also important to acknowledge a few ’tricks’ about generalised CNN training techniques. The authors suggest a read of https://www.geeksforgeeks.org/how-do-convolutional-neural-networks-cnns-work/#

2.2.3. Recurrent Neural Networks (RNNs):

RNNs are another type of deep learning algorithm that can capture temporal dependencies in sequential data, making them suitable for tasks such as trajectory prediction and natural language processing.

The key feature of RNNs is their ability to maintain a hidden state that captures information from previous time steps. Mathematically, the hidden state h_t ​of an RNN at time step t is computed as:

Equation [2]

ℎ  = f(W_hh h_t−1 +W_xh x_t +b_h)

where:

h_t​: Hidden state at time step t.

f: Activation function (e.g., tanh, ReLU, sigmoid).

W_hh​: Weight matrix for the hidden state (recurrent weights).

W_xh​: Weight matrix for the input to hidden state (input weights).

b_h​: Bias vector.

x_t​: Input at time step t.

Components in Detail

Hidden State hth_tht​:

This is a vector that stores information about what the network has seen so far in the sequence.

At each time step ttt, hth_tht​ is updated based on the previous hidden state h_t−1​ and the current input x_t​.

Activation Function fff:

The activation function introduces non-linearity into the network, enabling it to learn complex patterns.

Common activation functions include tanh (hyperbolic tangent) and ReLU (Rectified Linear Unit).

Weight Matrices W_hh​ and W_xh​:

WhhW_{hh}Whh​: This matrix contains weights for the connections between the hidden states across time steps. It defines how the previous hidden state ht−1h_{t-1}ht−1​ influences the current hidden state hth_tht​.

WxhW_{xh}Wxh​: This matrix contains weights for the connections between the current input xtx_txt​ and the current hidden state hth_tht​. It defines how the current input influences the hidden state.

Bias Vector b_h:

This is a vector added to the hidden state computation to allow the model to learn an offset. It helps in shifting the activation function to better fit the data.

Input x_t​:

This is the current input at time step t. In tasks like natural language processing, x_t could be a word or a character.

Detailed Computation

At each time step ttt:

Previous Hidden State Contribution:

Multiply the previous hidden state h_t−1​ by the weight matrix Whh​: W_hhh_t−1​.

This captures the influence of the past hidden state on the current hidden state.

Current Input Contribution:

Multiply the current input x_t by the weight matrix W_xh​: W_xhxt​.

This captures the influence of the current input on the current hidden state.

Summing and Adding Bias:

Add the results from the previous hidden state contribution and the current input contribution.

Add the bias vector b_h_h_b​ to this sum: W_hhh_t−1+W_xhx_t+b_h.

Applying Activation Function:

Apply the activation function f to the summed result to get the new hidden state h_t​: h_t=f(W_hhh_t−1+W_xhx_t+ _.).

Example

Let's consider an example with a simple RNN.

Suppose the activation function f is the tanh function.

Assume we have the following values:

Previous hidden state h_t−1=[0.5,−0.3]

Current input xt=[1.0,0.5]

Weight matrices

W_xh ​= $\left[\begin{array}{cc}0.2& 0.4\\ 0.3& 0.1\end{array}\right]$ and W_xh​ = $\left[\begin{array}{cc}0.5& 0.6\\ 0.7& 0.8\end{array}\right]$

Bias vector b_h=[0.1,0.2]

Compute the contribution from the previous hidden state:

W_hh​h_t−1 = $\left[\begin{array}{cc}0.5& 0.6\\ 0.7& 0.8\end{array}\right]$ $\left[\begin{array}{c}0.5\\ -0.3\end{array}\right]$ = $\left[\begin{array}{c}0.2.0.5+0.4.-0.3\\ 0.3.0.5+0.1.-0.3\end{array}\right]$ = $\left[\begin{array}{c}0.1\\ 0.12\end{array}\right]$

Compute the contribution from the current input:

W_xhx_t = $\left[\begin{array}{cc}0.5& 0.6\\ 0.7& 0.8\end{array}\right]$ $\left[\begin{array}{c}1.0\\ 0.5\end{array}\right]$ = $\left[\begin{array}{c}0.5.1.0+0.6.0.5\\ 0.7.1.0+0.8.0.5\end{array}\right]$ = $\left[\begin{array}{c}0.8\\ 1.1\end{array}\right]$

Sum the contributions and add the bias:

W_hhh_t−1+W_xhx_t+b_{h =} $\left[\begin{array}{c}0.1\\ 0.12\end{array}\right]$ + $\left[\begin{array}{c}0.8\\ 1.1\end{array}\right]$ + $\left[\begin{array}{c}0.1\\ 0.2\end{array}\right]$ = $\left[\begin{array}{c}1.0\\ 1.42\end{array}\right]$

Apply the activation function (tanh in this case):

h_t​ = tanh ( $\left[\begin{array}{c}1.0\\ 1.42\end{array}\right]$ ) ≈ $\left[\begin{array}{c}0.76\\ 0.89\end{array}\right]$

So, the new hidden state hth_tht​ at time step ttt is approximately [0.76,0.89]

2.2.4. Decision Trees and Random Forests:

Decision trees are a type of supervised learning algorithm used for classification and regression tasks. In the context of AVs, decision trees can be used for tasks such as obstacle detection and trajectory planning.

Random forests are an ensemble learning method that combines multiple decision trees to improve performance and robustness. They work by training multiple decision trees on different subsets of the data and averaging their predictions.

The decision rule at each node of a decision tree is determined by optimizing a splitting criterion such as Gini impurity or information gain.

2.2.5. Deep Reinforcement Learning:

Deep reinforcement learning (DRL) is a combination of deep learning and reinforcement learning techniques used to train agents to make sequential decisions in environments with long-term rewards. In the context of AVs, DRL can be used to train agents to navigate complex traffic scenarios, learn driving policies, and optimize driving behaviors.

The agent learns to interact with the environment by taking actions a_t based on observations o_t and receiving rewards r_t. The goal is to learn a policy π (a_t ∣o_t) that maximizes the cumulative reward over time.

These are just a few examples of machine learning algorithms used in autonomous vehicles. The choice of algorithm depends on the specific task and the characteristics of the data. Continuous research and advancements in machine learning are driving improvements in autonomous vehicle technology, bringing us closer to the realization of fully autonomous transportation.

2.3. Localization and Mapping:

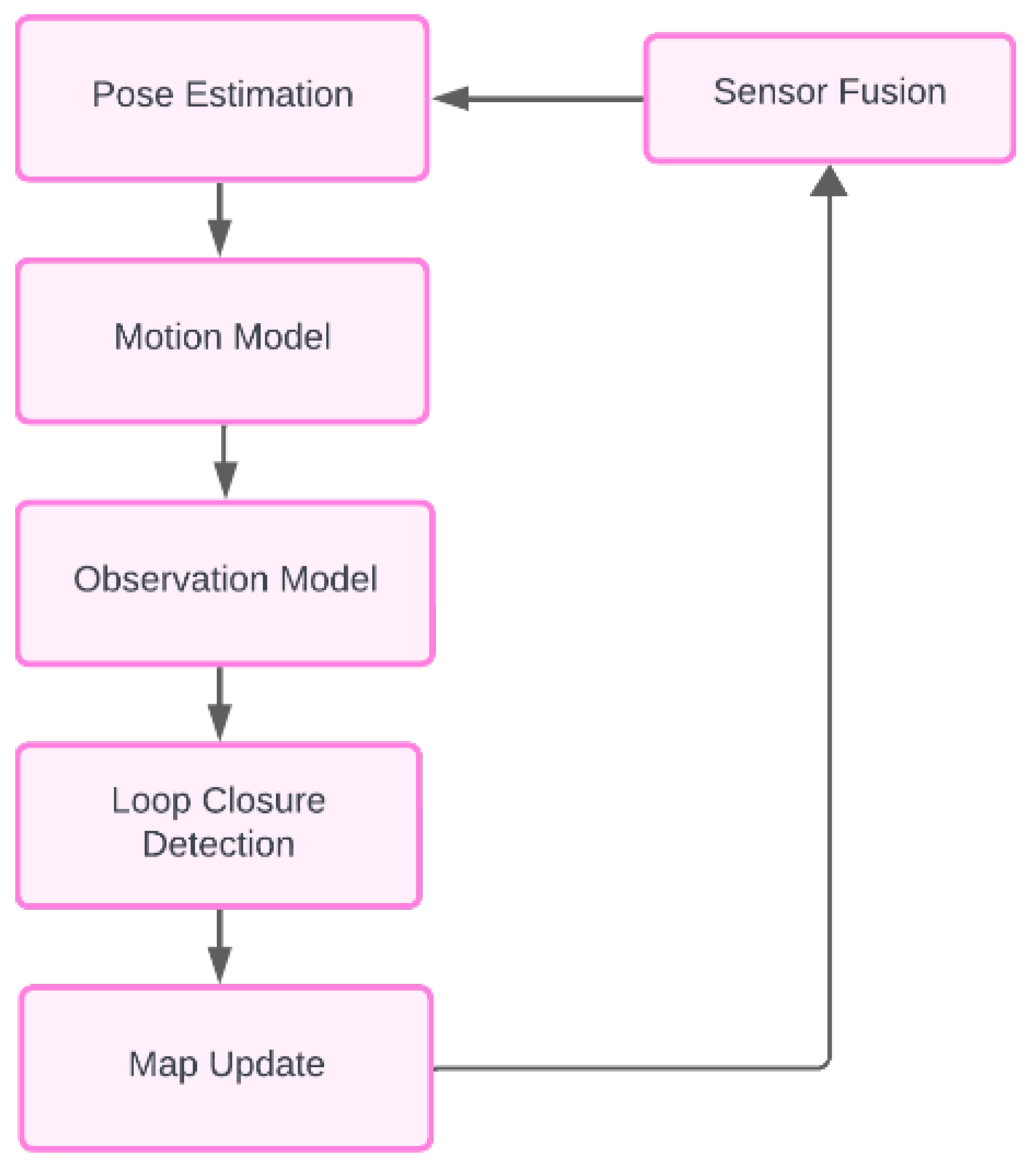
Simultaneous Localization and Mapping (SLAM) is a fundamental problem in robotics, particularly in the context of autonomous vehicles. It involves the estimation of a vehicle's trajectory (i.e., localization) and the creation of a map of its environment simultaneously. SLAM algorithms enable autonomous vehicles to navigate and localize themselves in unknown environments without prior knowledge of their surroundings.

Figure 3. Localization and Mapping Block Diagram.

Figure 3. Localization and Mapping Block Diagram.

2.3.1. SLAM Algorithm Overview:

SLAM algorithms typically consist of two main components: the localization module and the mapping module.

Localization Module: The localization module estimates the vehicle's pose (position and orientation) relative to a global coordinate system. This is achieved by integrating sensor measurements, such as odometry (motion) data and observations from onboard sensors (e.g., GPS, IMU, wheel encoders), using techniques like Kalman filters, particle filters (Monte Carlo localization), or graph-based optimization methods (e.g., pose graph optimization).

Mapping Module: The mapping module constructs a detailed map of the environment based on sensor observations. It utilizes sensor data, such as laser scans from LiDAR sensors or visual features from cameras, to create a geometric or probabilistic representation of the surroundings. Common mapping techniques include occupancy grid mapping, feature-based mapping, and probabilistic methods like grid-based or graph-based SLAM.

Key Components of SLAM:

Feature Extraction: SLAM algorithms often rely on feature extraction techniques to identify distinctive landmarks or keypoints in sensor data. These features are used to match observations across different time steps and constrain the vehicle's motion and map estimation.

Data Association: Data association involves associating sensor measurements with features in the environment or landmarks in the map. This is crucial for maintaining correspondences between observations and map elements, especially in the presence of noise, occlusions, and dynamic objects.

Loop Closure Detection: Loop closure detection is the process of identifying previously visited locations and closing loops in the trajectory to improve localization accuracy and map consistency. This is typically done by comparing current sensor data with past observations and detecting similarities or repeating patterns.

2.3.2. Equations and Formulations:

The SLAM process is essential for autonomous navigation, enabling a robot to build a map of its environment while simultaneously determining its location within that map. The SLAM framework typically consists of the following interconnected components:

Pose Estimation

Pose estimation is the process of determining the robot's current position and orientation. This is often achieved using probabilistic methods such as the Kalman Filter or Particle Filter.

Motion Model: SLAM algorithms often incorporate a motion model to predict the vehicle's pose based on control inputs (e.g., velocity commands) and previous pose estimates. Common motion models include odometry-based models (e.g., odometry error models) and dynamic models (e.g., vehicle dynamics equations).

Kalman Filter: The state estimation $\widehat{x}$_k∣k at time step k is updated using:

Equation [3]

$${\widehat{x}}_{k\mid k} \mathrm{}={\widehat{x}}_{k\mid k-1}\mathrm{}+K_k(z_k\mathrm{}-H{\widehat{x}}_{k\mid k-1\mathrm{})}$$

where $K_k$ is the Kalman gain, $z_k$ is the measurement, and H is the observation model matrix.

Sensor Fusion

Sensor fusion combines data from multiple sensors to provide a more accurate estimate of the robot's state.

Extended Kalman Filter (EKF): For prediction,

Equation [4]

$${\widehat{x}}_{k\mid k-1} \mathrm{}={f(\widehat{x}}_{k-1\mid k-1}\mathrm{},u_{k })$$

where $f$ is the state transition model and $u_k$ is the control input.

The covariance prediction is:

Equation [5]

$$P_{k\mid k-1} \mathrm{}={F_k\mathrm{P}}_{k-1\mid k-1}\mathrm{}{F}_K^T+Q_K$$

where $F_k$​ is the Jacobian of $f$ with respect to the state, and $Q_K$ is the process noise covariance.

Motion Model

The motion model describes how the robot's state evolves over time.

Equation [6]

$$x_{k+1}\mathrm{}=x_k\mathrm{}+\Delta t\cdot v_k\mathrm{}\mathrm{c}\mathrm{o}\mathrm{s}\left({\theta }_k\mathrm{}\right)$$

$$y_{k+1}\mathrm{}=y_k\mathrm{}+\Delta t\cdot v_k\mathrm{}\mathrm{s}\mathrm{i}\mathrm{n}\left({\theta }_k\mathrm{}\right)$$

$${\theta }_{k+1}\mathrm{}={\theta }_k\mathrm{}+\Delta t\cdot {\omega }_k$$

where $v_k$​ is the linear velocity and ${\omega }_k$ is the angular velocity.

Observation Model

The observation model relates the robot's state to the sensor measurements.

For a range-bearing sensor model:

Equation [7]

$$zk\mathrm{}=\left[{\displaystyle \frac{rk}{\varphi k}}\mathrm{}\mathrm{}\mathrm{}\right]=\left[{\displaystyle \frac{{(x_l\mathrm{}-x_k\mathrm{})}^2+{(y_l\mathrm{}-y_k\mathrm{})}^2}{\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{t}\mathrm{a}\mathrm{n}\left(\frac{y_l\mathrm{}-y_k}{xl\mathrm{}-xk}\mathrm{}\mathrm{}\mathrm{}\right)-\theta k\mathrm{}\mathrm{}]}}\mathrm{}\right]$$

where $(xl,y_l)$is the landmark position

Reference: The first source, Introduction to Robotics and Perception, offers a foundational understanding of how a robot's state evolves over time using linear and angular velocities. It explains the mathematical relationship between these velocities and the robot's motion, making it essential for grasping basic motion models​ (RoboticsBook)​. The second reference, Probabilistic Models for Robot Motion, delves into the complexities of real-world robot motion, accounting for uncertainties and noise. This resource provides a probabilistic approach, enhancing the robustness of motion models by incorporating random errors into the control inputs​ (Wolfram Demonstrations Project)​. The third paper, Mobile Robot Motion Control Using a Combination of Fuzzy Logic Method and Kinematic Model, presents an innovative approach by combining fuzzy logic with traditional kinematic models, offering practical insights and simulation results that demonstrate the effectiveness of this hybrid method in controlling robot motion​ (ar5iv)​. Lastly, Calculating Wheel Velocities for a Differential Drive Robot is a practical tutorial that breaks down the conversion of linear and angular velocities into wheel velocities for differential drive robots. This step-by-step guide is invaluable for understanding the implementation of motion models in real-world scenarios, providing detailed calculations and examples​ (Automatic Addison)​.

These references collectively cover theoretical foundations, probabilistic considerations, hybrid control methods, and practical implementations, offering a comprehensive overview of robot motion modeling.

Loop Closure Detection

Loop closure detection identifies when the robot has returned to a previously visited location, enhancing map accuracy.

Mathematically, this is expressed as:

Equation [8]

$$d(pi\mathrm{},pj\mathrm{})\le ϵ$$

where $d(pi\mathrm{},pj\mathrm{})$ is the distance between two poses $pi$ and $pj$ ​, and $ϵ$ is a threshold.

Reference:

Loop closure detection is a critical component in enhancing the accuracy of SLAM systems by identifying when a robot returns to a previously visited location. This process involves comparing the current pose of the robot with past poses to detect overlaps, thereby correcting accumulated drift in the map. Techniques like those discussed by Lowry et al. (2015) highlight the evolution from feature-based methods, such as SIFT and SURF, to advanced deep learning models for visual place recognition. Similarly, Mur-Artal and Tardós (2017) demonstrate the practical application of loop closure in their ORB-SLAM2 system, utilizing ORB features for robust and real-time SLAM across various camera types. These advancements underscore the importance of loop closure detection in maintaining accurate and reliable maps in diverse environments.

Map Update

The map update step incorporates new sensor data into the existing map.

For grid-based maps, the occupancy probabilities of grid cells are updated using

Equation [9]

$$P\left(m_i\mathrm{}\right|{ z}_{1:t}\mathrm{},x_{1:t\mathrm{}})={[1+{\displaystyle \frac{1-P\left(m_{i\mathrm{}}\right)}{P\left(m_{i\mathrm{}}\mathrm{}\right)}}{\displaystyle \frac{1}{P(z_{1:t}\mathrm{}\mid m_i\mathrm{},x_{1:t\mathrm{}})}}\mathrm{}]}^{-1}$$

where $P\left(m_{i\mathrm{}}\mathrm{}\right)$is the prior probability of cell $i$ being occupied, and $P(z_{1:t}\mathrm{}\mid m_i\mathrm{},x_{1:t\mathrm{}})$ is the likelihood of the observations given the map.

Observation Model: The observation model describes how sensor measurements are generated based on the vehicle's pose and the characteristics of the environment. This can involve geometric transformations (e.g., perspective projection for cameras) and sensor-specific error models (e.g., Gaussian noise for range measurements).

SLAM Implementation and Challenges:

Implementing SLAM algorithms in real-world scenarios involves addressing various challenges, such as sensor noise, calibration errors, computational complexity, and handling dynamic environments. Researchers continue to develop advanced SLAM techniques, including visual SLAM, semantic SLAM, and multi-robot SLAM, to overcome these challenges and improve the robustness and scalability of autonomous navigation systems.

By integrating AI-powered SLAM algorithms, autonomous vehicles can accurately localize themselves and create detailed maps of their environment in real-time, enabling safe and efficient navigation in diverse and dynamic surroundings.

2.4. Decision-Making Algorithms:

Decision-making algorithms play a crucial role in autonomous vehicles (AVs) by enabling them to navigate through complex environments, adhere to traffic laws, and make safe driving decisions. Here's a detailed explanation of decision-making algorithms used in AVs, along with technical terms, equations, and algorithms:

Route Planning:

Pathfinding Algorithms: AVs utilize pathfinding algorithms such as Dijkstra's algorithm, A* algorithm, or variations like A* with heuristic functions (e.g., A* with Euclidean distance heuristic) to find the shortest or optimal route from the vehicle's current position to its destination.

Graph Representation: The environment is represented as a graph, where nodes represent locations (e.g., intersections, waypoints) and edges represent possible transitions between locations (e.g., road segments, lanes). Pathfinding algorithms search this graph to find the optimal route while considering factors like road connectivity, traffic flow, and travel time.

Traffic Navigation:

Traffic Prediction: AVs use predictive modeling techniques, such as time-series analysis, recurrent neural networks (RNNs), or Long Short-Term Memory (LSTM) networks, to forecast traffic conditions and anticipate congestion or traffic patterns along the planned route.

Dynamic Path Adjustment: AVs continuously monitor traffic conditions and adjust their routes dynamically based on real-time traffic updates, congestion levels, and alternative route options. This ensures efficient and adaptive navigation in dynamic traffic environments.

2.4.1. Behavior Prediction

Predictive Modeling: AVs employ machine learning algorithms, such as recurrent neural networks (RNNs), convolutional neural networks (CNNs), or Long Short-Term Memory (LSTM) networks, to predict the future behavior of nearby vehicles, pedestrians, and other objects in the environment.

Trajectory Forecasting: By analyzing historical data and real-time sensor observations, AVs predict the trajectories of surrounding vehicles and pedestrians, considering factors like speed, acceleration, lane changes, and interaction patterns. Predictive models enable AVs to anticipate potential collision risks and plan proactive responses to ensure safe navigation.

2.4.2. Decision-Making Algorithms

Rule-Based Systems: AVs adhere to traffic laws and regulations using rule-based decision-making systems. These systems encode traffic rules, right-of-way principles, and safety guidelines into logical rules or decision trees, enabling the vehicle to make lawful and safe driving decisions.

Reinforcement Learning: Some AVs employ reinforcement learning algorithms, such as deep Q-learning or policy gradient methods, to learn driving policies and decision-making strategies through trial-and-error interactions with the environment. Reinforcement learning enables AVs to learn optimal driving behaviors and adapt to diverse driving scenarios.

Markov Decision Processes (MDPs): AV decision-making can be modeled as an MDP, where the vehicle's actions (e.g., acceleration, steering) influence future states and rewards. Solving the MDP using techniques like value iteration or policy iteration yields an optimal policy for decision-making in uncertain environments.

Safety Considerations:

Safety Constraints: Decision-making algorithms incorporate safety constraints and risk assessment criteria to prioritize safety-critical actions and avoid hazardous situations. Safety constraints may include maintaining safe distances from other vehicles, obeying traffic signals, and avoiding aggressive maneuvers.

Equations and Algorithms:

A Algorithm*: The A* algorithm is an informed search algorithm used for pathfinding in graphs or grids. It uses a heuristic function to estimate the cost of reaching the goal from each node and efficiently explores the most promising paths.

xl

Q-Learning: Q-learning is a model-free reinforcement learning algorithm used for learning optimal policies in Markov decision processes. It iteratively updates a Q-value function that represents the expected cumulative reward for taking a particular action in a given state.

By integrating advanced decision-making algorithms, autonomous vehicles can navigate safely and efficiently in complex and dynamic traffic environments, considering factors like traffic laws, road conditions, nearby vehicles' behavior, and the vehicle's destination to determine the optimal course of action.

The above section says how to prepare a subsection. Just copy and paste the subsection, whenever you need it. The numbers will be automatically changes when you add new subsection. Once you paste it, change the subsection heading as per your requirement.

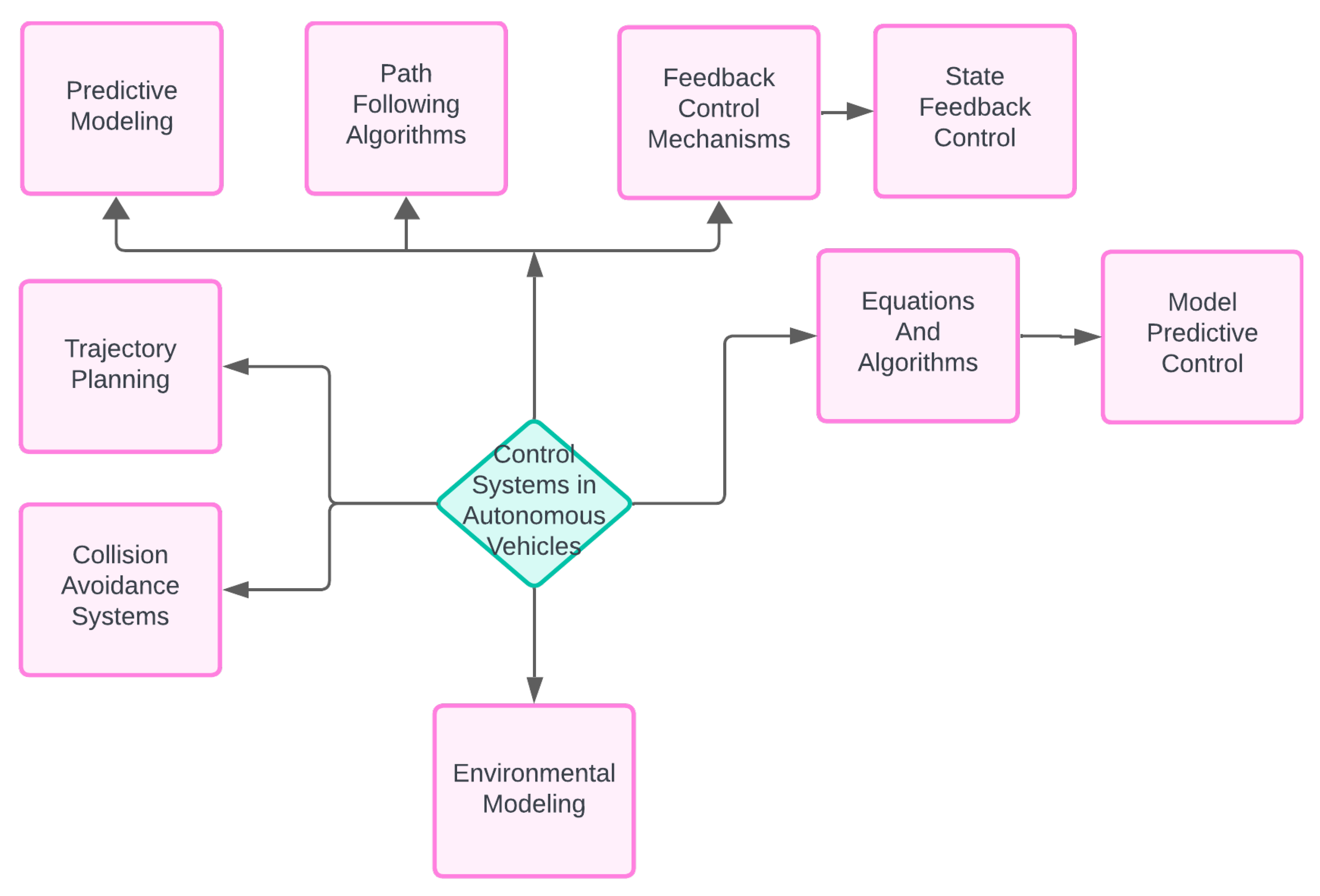
2.5. Control Systems:

Control systems in autonomous vehicles (AVs) play a critical role in translating high-level decisions into precise control commands to steer the vehicle, accelerate, and brake safely. Here's a detailed explanation of control systems used in AVs, along with technical terms, equations, and algorithms:

Figure 4. Block Diagram of Control System.

Figure 4. Block Diagram of Control System.

Predictive Modeling:

Vehicle Dynamics Modeling: Control systems incorporate predictive models of the vehicle's dynamics, including its motion, acceleration, and braking characteristics. These models capture the relationship between control inputs (e.g., steering angle, throttle position, brake pressure) and vehicle state variables (e.g., position, velocity, orientation) to predict the vehicle's future behavior.

Environmental Modeling:

Control systems also model environmental factors such as road conditions, friction coefficients, and obstacle locations. Predictive models of the environment enable AVs to anticipate changes in the driving environment and adapt their control strategies accordingly.

Trajectory Planning:

Optimal Control Theory: Trajectory planning algorithms utilize optimal control theory to generate smooth and collision-free trajectories for the vehicle. Optimal control algorithms, such as Linear Quadratic Regulator (LQR), Model Predictive Control (MPC), or Dynamic Programming, optimize a cost function representing desired performance criteria (e.g., minimum time, minimum energy) subject to system dynamics and constraints.

Path Following Algorithms:

Path following algorithms ensure that the vehicle follows a predefined path or reference trajectory accurately. These algorithms adjust control inputs (e.g., steering angle, throttle, brake) based on feedback from sensors to minimize tracking errors and maintain desired trajectory following performance.

Feedback Control Mechanisms:

Proportional-Integral-Derivative (PID) Control: PID control is a classic feedback control mechanism widely used in AVs to regulate vehicle motion and maintain desired performance. It adjusts control inputs based on the error between desired and actual states (e.g., position, velocity) and integrates proportional, integral, and derivative terms to achieve stable and responsive control behavior.

State Feedback Control:

State feedback control techniques, such as Linear Quadratic Regulator (LQR) or State Feedback MPC, directly manipulate control inputs based on feedback of the vehicle's state variables. These techniques design control laws to stabilize the vehicle and achieve desired performance objectives while considering system dynamics and constraints.

2.5.1. Safety Considerations

Safety Constraints:

Control systems incorporate safety constraints and limits to ensure safe vehicle operation. Safety constraints may include maximum steering angles, maximum acceleration and deceleration rates, minimum safe distances from obstacles, and adherence to traffic laws and regulations.

Collision Avoidance Systems: Control systems integrate collision avoidance algorithms to detect and respond to potential collision threats in real-time. These algorithms use sensor data (e.g., LiDAR, radar, cameras) to detect obstacles, predict collision risks, and execute evasive maneuvers (e.g., steering, braking) to avoid collisions.

2.5.2. Equations and Algorithms

Linear Quadratic Regulator (LQR):

Linear Quadratic Regulator (LQR): LQR is a control design technique used to design optimal feedback control laws for linear dynamical systems. It minimizes a quadratic cost function representing the deviation from desired states while considering control effort and system dynamics.

LQR Problem Formulation: Given a linear time-invariant system described by the state-space equations:

Equation [10]

x˙(t) = Ax(t) + Bu(t)

where:

• x(t)) is the state vector.
• u(t) is the control input.
• A is the state matrix.
• B is the input matrix.

The LQR problem aims to find the control input u(t) that minimizes the following quadratic cost function:

Equation [11]

where:

• Q is a positive semi-definite state weighting matrix.
• R is a positive definite control weighting matrix.

LQR Optimal Control Law: The optimal control law for LQR is given by:

u(t) = −Kx(t)

where K is the feedback gain matrix calculated as:

K = R⁻¹B^TP

P is the solution to the continuous-time algebraic Riccati equation (CARE):

Equation [12]

A^TP + PA − PBR⁻¹B^TP+Q = 0

Reference: The Linear Quadratic Regulator (LQR) is a pivotal control design technique in optimal control theory, aimed at minimizing a quadratic cost function that balances state deviation and control effort. The LQR formulation involves linear time-invariant systems, and the optimal control law is derived by solving the continuous-time algebraic Riccati equation. Key resources, such as Anderson and Moore's "Optimal Control: Linear Quadratic Methods" and Stanford University's lecture notes on time-varying LQR, provide a comprehensive understanding of the theoretical foundations, practical implementations, and extensions of LQR to more complex, time-varying systems. These references highlight the importance and applicability of LQR in designing robust and efficient control systems​ (Underactuated Robotics)​​ (GitHub)​​ (Stanford University)​.

Model Predictive Control (MPC): MPC is a control strategy that solves a finite-horizon optimal control problem at each time step using a predictive model of the system. It generates control inputs by optimizing a cost function over a finite prediction horizon while satisfying system dynamics and constraints.

By integrating advanced control systems, autonomous vehicles can translate high-level decisions into precise control commands, ensuring smooth and stable vehicle operation while adhering to safety constraints and environmental conditions.

MPC Problem Formulation:

Given a discrete-time linear system described by:

x_k+1 = Ax_k + Bu_k

The MPC problem at each time step involves minimizing the following cost function over a finite prediction horizon N:

Equation [13]

where:

• Q is a positive semi-definite state weighting matrix.
• R is a positive definite control weighting matrix.
• Q_f​ is the terminal state weighting matrix.
• x_k​ is the state vector at time step k.
• u_k​ is the control input at time step k.

MPC Optimization:

At each time step, solve the optimization problem:

subject to:

• System dynamics: x_k+1 = Ax_k+Bu_k
• Control input constraints: u_min ≤ uk ≤ u_max
• State constraints: x_min ≤ xk ≤ x_{max ​}

The first control input u0u_0u0​ from the optimal sequence {u0,u1,…,uN−1 is applied to the system, and the optimization is repeated at the next time step with updated state information.

Reference: The Model Predictive Control (MPC) problem formulation for discrete-time linear systems involves minimizing a quadratic cost function over a finite prediction horizon. Qin and Badgwell (2003) provide an extensive survey of industrial applications of MPC, highlighting its practical relevance and implementation challenges in various industries. They emphasize the importance of choosing appropriate weighting matrices Q and R to balance state deviations and control efforts. Additionally, Mayne et al. (2000) delve into the theoretical underpinnings of MPC, discussing stability and optimality conditions that ensure the effectiveness of the control strategy. Their work forms a cornerstone for understanding how MPC can be applied to maintain system constraints while optimizing performance.

These references provide a comprehensive view of both the theoretical and practical aspects of MPC, demonstrating its robustness and versatility in handling complex control problems in industrial settings.

2.6. Sensor Fusion:

Sensor fusion is a critical aspect of autonomous vehicles (AVs), enabling them to integrate data from multiple sensors to create a comprehensive and accurate representation of their surroundings. Here's a detailed explanation of sensor fusion techniques used in AVs, along with technical terms, equations, and algorithms:

2.6.1. Sensor Types and Characteristics

Cameras: Cameras provide visual information about the environment, including color images, depth information, and object detection. They have high spatial resolution but are susceptible to lighting conditions, occlusions, and changes in viewpoint.

LiDAR (Light Detection and Ranging): LiDAR sensors emit laser pulses to measure distances to objects and create detailed 3D point clouds of the surroundings. LiDAR offers accurate depth information and is robust to lighting conditions but has limited range and resolution.

Radar (Radio Detection and Ranging): Radar sensors use radio waves to detect objects and measure their range, velocity, and angle relative to the vehicle. Radar provides long-range detection and is robust to weather conditions but has lower spatial resolution than LiDAR.

IMU (Inertial Measurement Unit): IMU sensors measure the vehicle's acceleration and angular velocity to estimate its motion and orientation. IMUs provide high-frequency data but suffer from drift and noise over time.

GPS (Global Positioning System): GPS receivers provide global positioning information to localize the vehicle's position on Earth's surface. GPS offers wide-area coverage but has limited accuracy and reliability in urban environments or under dense foliage.

2.6.2. Sensor Fusion Techniques

Kalman Filters: Kalman filters are recursive estimation algorithms used for sensor fusion to combine measurements from multiple sensors while accounting for their noise characteristics. Kalman filters maintain a state estimate and covariance matrix that represents the vehicle's position, velocity, and orientation, incorporating new sensor measurements to update the state estimate iteratively.

Extended Kalman Filters (EKF): EKF extends the Kalman filter to handle nonlinear systems and measurements by linearizing the system dynamics and measurement equations around the current estimate. EKF is commonly used in sensor fusion for nonlinear sensors such as GPS and IMU.

Unscented Kalman Filters (UKF): UKF is an alternative to EKF that approximates the nonlinear transformation using a set of sigma points sampled from the Gaussian distribution. UKF achieves better accuracy than EKF for highly nonlinear systems and is used in sensor fusion for LiDAR, radar, and camera data.

Particle Filters: Particle filters are probabilistic Bayesian inference algorithms used for non-Gaussian and nonlinear estimation problems. Particle filters represent the posterior distribution using a set of weighted particles, where each particle represents a possible state hypothesis. Particle filters are well-suited for sensor fusion in complex and dynamic environments.

Equations and Algorithms:

State Space Representation: Sensor fusion algorithms typically model the system state using a state vector x that represents the vehicle's position, velocity, orientation, and other relevant variables. The state space representation includes dynamic equations that describe how the state evolves over time and observation equations that relate sensor measurements to the state variables.

Bayesian Estimation: Sensor fusion algorithms compute the posterior distribution p(x∣z), where x is the state vector and z is the sensor measurement vector, using Bayes' theorem. Bayes' theorem updates the prior distribution p(x) based on new sensor measurements p(z∣x), yielding the posterior distribution p(x∣z) that represents the updated state estimate.

Sensor Model: Sensor fusion algorithms incorporate sensor models that describe the relationship between sensor measurements and the true state of the environment. Sensor models include measurement equations that map the state variables to sensor measurements, as well as error models that characterize sensor noise, biases, and uncertainties.

By integrating advanced sensor fusion techniques, autonomous vehicles can create a comprehensive and accurate representation of their surroundings, enhancing perception and decision-making capabilities while mitigating sensor limitations and uncertainties.

2.7. Behavior Prediction:

Behavior prediction is a crucial aspect of autonomous vehicles (AVs) that involves predicting the future trajectories and actions of surrounding vehicles, pedestrians, and other objects in the environment. Here's a detailed explanation of behavior prediction techniques used in AVs, along with technical terms, equations, and algorithms:

Predictive Modeling:

Trajectory Forecasting: Trajectory forecasting algorithms predict the future positions and trajectories of surrounding objects based on historical data and real-time sensor observations. These algorithms analyze past motion patterns, velocity profiles, and interaction behaviors to anticipate future trajectories and potential collision risks.

Probabilistic Models: Behavior prediction often employs probabilistic models, such as Bayesian networks, Hidden Markov Models (HMMs), Recurrent Neural Networks (RNNs), or Long Short-Term Memory (LSTM) networks, to represent the uncertainty associated with future predictions. Probabilistic models capture the stochastic nature of human behavior and environmental dynamics, allowing AVs to make informed decisions under uncertainty.

Sensor Data Fusion:

Sensor Fusion: Behavior prediction integrates data from multiple sensors, including cameras, LiDAR, radar, and IMUs, to capture different aspects of the environment and improve prediction accuracy. Sensor fusion techniques combine information from diverse sensor modalities while considering their complementary strengths and weaknesses.

Feature Extraction: Behavior prediction algorithms extract relevant features from sensor data, such as object positions, velocities, accelerations, and trajectories, to represent the state of surrounding objects. Feature extraction may involve techniques like object detection, tracking, motion estimation, and semantic segmentation.

Machine Learning Algorithms:

Recurrent Neural Networks (RNNs): RNNs are a class of neural networks capable of processing sequential data and capturing temporal dependencies. In behavior prediction, RNNs analyze historical motion sequences of surrounding objects to learn patterns and dynamics, enabling them to forecast future trajectories and actions.

Long Short-Term Memory (LSTM) Networks: LSTM networks are a specialized type of RNNs designed to overcome the vanishing gradient problem and capture long-term dependencies in sequential data. LSTM networks are well-suited for behavior prediction tasks that require modeling complex temporal dynamics and capturing subtle changes in behavior over time.

Conditional Variational Autoencoders (CVAEs): CVAEs are generative models that learn a latent representation of input data conditioned on some context information. In behavior prediction, CVAEs encode contextual information about the environment and past observations to generate diverse and realistic future trajectories for surrounding objects.

Safety Considerations:

Uncertainty Estimation: Behavior prediction algorithms quantify the uncertainty associated with future predictions and incorporate it into decision-making processes. Uncertainty estimation enables AVs to assess the reliability of predictions and adjust their behavior accordingly to mitigate potential risks and ensure safety.

Risk Assessment: Behavior prediction algorithms assess the potential collision risks associated with predicted trajectories and actions of surrounding objects. Risk assessment considers factors such as object dynamics, interaction patterns, traffic rules, and environmental conditions to identify high-risk scenarios and prioritize safety-critical actions.

Equations and Algorithms:

Recurrent Neural Network Equations: The equations governing RNNs, including the forward pass equations (e.g., hidden state update, output computation) and the backward pass equations (e.g., gradient computation, parameter updates), describe how RNNs process sequential data and learn temporal dependencies.

Bayesian Inference Equations: Bayesian inference equations, such as Bayes' theorem and the posterior distribution update equations, formalize the probabilistic reasoning process used in behavior prediction to update beliefs about future trajectories based on observed data and prior knowledge.

By integrating advanced behavior prediction techniques, autonomous vehicles can anticipate potential hazards, forecast future trajectories of surrounding objects, and plan proactive responses to ensure safe and efficient navigation in complex and dynamic environments.