Prerpints.org logo
Preprint
Article

The Critical Magnetic Field and Current Density of an Entangled Yttrium Barium Copper Oxide Superconductor Using Ginzburg‐Landau Theory

Altmetrics

Downloads

82

Views

72

Comments

0

This version is not peer-reviewed

Emerging Trends in Advanced Materials and Technologies for Sustainable Energy Storage

Submitted:

13 August 2024

Posted:

14 August 2024

You are already at the latest version

Alerts
Abstract
This work focuses on the theoretical study of the effect of entanglement in the Yttrium Barium Copper Oxide (YBCO) superconductor on the critical current density, critical magnetic field, and penetration depth. Using the Ginzburg Landau (GL) theory, the expression for the GL coherence length, the critical current density, the lower critical magnetic field (Hc1), and the upper critical magnetic field (Hc2) for the entangled superconducting YBCO was obtained. At zero external magnetic fields, YBCO was found to undergo a transition from the normal state to the superconducting state at 93K and returned to normal. We found a direct relationship between the GL coherence length penetration depth and the temperature of the entangled superconducting YBCO. The graphs of the lower critical magnetic field (Hc1) and critical current density against temperature show a non-linear dependence.In contrast, the graph of the upper critical magnetic field (Hc2) against temperature (T) shows the linear dependence, which is in agreement with existing theoretical observations. On the other hand, the graph of critical current density against the distance of separation between the entangled electrons that form a cooper pair showed that the critical current density increases between 1.8 and 6 nanometers attaining a constant value after reaching 7 nanometers for infinite distances. Finally, for lower critical fields, the magnetic field decreases between 1.5 to 6 nanometers attaining a constant value of the magnetic field, for infinite values of distance of separation between the entangled pair of electrons.
Keywords: 
Subject: Physical Sciences  -   Theoretical Physics

1. Introduction

In 1911, Dutch physicist Heike Kamerlingh Onnes discovered that the resistivity of mercury abruptly disappeared at around 4.2 K, the boiling point of liquid helium, when studying the resistance of solid mercury at very low temperatures (Onnes, 1911). In 1933, Meissner and Oschenfeld observed that magnetic flux was excluded from the interior of a superconductor when it was cooled below its critical temperature (Tc) in the presence of an external magnetic field, demonstrating that superconducting materials act as perfect diamagnets (Meissner & Oschenfeld, 1933).
Various theories have been developed to explain superconductivity. The phenomenological theory by Fritz and Heinz London (1935) proposed equations to describe the electromagnetic properties of superconductors using coherence length and magnetic penetration depth to find critical current density and critical magnetic field (London & London, 1935). The semi-phenomenological Ginzburg-Landau theory (1950) and the microscopic Bardeen-Cooper-Schrieffer (BCS) theory (1957) further expanded these ideas (Ginzburg & Landau, 1950; Bardeen, Cooper, & Schrieffer, 1957). For instance, T. Desta et al. (2015) used Ginzburg-Landau theory to investigate the critical magnetic field of HoMo6​Se8​, finding that the critical magnetic field is inversely proportional to the temperature of the superconductor (Desta et al., 2015). Similarly, G. Kahsay et al. (2020) applied Ginzburg-Landau theory to study the upper critical fields of a heavy fermion superconductor (Kahsay et al., 2020).
Millán et al. (2021) analyzed the critical current density for d-wave superconductors using a generalized Hubbard model on a square lattice, revealing that the d-wave symmetry of the pairing interaction leads to a maximum critical current density (Millán et al., 2021). According to BCS theory, superconductivity arises from the cooperative behavior of conducting electrons, where entangled electron pairs play a crucial role (Bardeen et al., 1957). S.C. Benjamin et al. (2009) highlighted the significance of electron entanglement in solid-state physics for the development of quantum information and computation schemes (Benjamin et al., 2009). Clare Dunning et al. (2005) demonstrated that, in the thermodynamic limit, local concurrences fully describe entanglement in the ground state of the BCS model (Dunning et al., 2005). J. Cordelair et al. (2013) described superconductivity as involving double quantum entanglement, where wave-particles superpose and overlap to form Cooper pairs at the critical temperature (Cordelair et al., 2013). Subir Sachdev (2013) discussed the quantum superposition of electron pairs in Yttrium Barium Copper Oxide (YBCO), noting that removing some oxygen atoms from the YBCO planes increases hole concentration and promotes long-range entanglement of electron pairs (Sachdev, 2013). Gary J. Mooney et al. (2019) used a 20-qubit superconducting quantum computer to demonstrate entanglement in one of the largest solid-state qubit arrays, advancing the implementation of complex quantum algorithms. However, they did not explore the impact of entanglement on the critical magnetic field and critical current density of YBCO (Mooney et al., 2019). Recent research has focused on magnetic fields and critical fields in conventional superconductors, prompting investigations into superconductivity as a quantum entanglement phenomenon and its effects on critical magnetic field and critical current density in unconventional high-Tc YBCO superconductors.

2. Theoretical formulations

2.1. Mathematical Formulations

In GL theory, when the wave function of a particle at a point in space ( ψ ) is small and varies slowly in space, the free-energy density (Fs (r)) can be expanded in a power series of the form,
F s ( r ) = F n + α ψ ( r ) 2 + β 2 ψ ( r ) 4 + 1 2 m * − i ℏ ∇ − e * c A r ψ ( r ) 2 + H 2 8 π
where α and β are phenomenological parameters (β > 0 and the sign of α is temperature dependent), m* = 2m is an effective mass, e* = q* = 2e is the charge of an electron, H is the local magnetic field of the superconductor, A is the magnetic vector potential and B = ∇ X A where B is the external magnetic field. By minimizing the free energy functional in equation (2.1) concerning fluctuations in the order parameter and the vector potential, one arrives at the First GL equation, expressed as, (Kittel, C. (2005, pp 283-286)
α ψ + β ψ 2 ψ + 1 2 m * − i ℏ ∇ − e * c A 2
The current density equation, J s , is obtained by minimizing the expression of the first GL Equation concerning vector potential, A, to yield
J s = 1 2 m * − i ℏ ∇ − e * c A 2 Ψ 2
In the absence of an external magnetic field, there will be no superconducting current and the equation (2.1) reduces to;
F s − F n = α ψ + β 2 ψ 2 ψ
This equation is trivial for ψ = 0 and it corresponds to the normal state where T > T c . Below the superconducting transition temperature (Tc), equation (2.5) is expected to have a non-trivial solution (i.e. ψ ≠ 0 ) of the form
ψ 2 = − α β .
For T > T c , the expression α ( T ) β is positive the second part of the equation (2.4) is negative and only ψ = 0 solves the GL equation. For T < T c , the second part of equation (2.4) is positive and there is no trivial solution for ψ . Thus equation (2.5a) can be expressed as
ψ = α ( T c − T ) β 1 2
Equation (2.5b) yields the GL wave function for a superconducting state, this wave function vanishes at T = Tc, only valid at T > Tc.
The First GL equation (2.2) can be expressed in x-dimensions as
α ψ + β ψ 2 ψ + 1 2 m * − i ℏ − e * c A 2 ψ = 0
In superconductivity, superconducting coherence length is the characteristic exponent of the variations of the density of the superconducting component, (Tinkham, M. 2004, 2nd Ed.). In the absence of the magnetic field equation (2.3) reduces to,
α ψ + β ψ 3 − ℏ 2 2 m * d 2 ψ d x 2 = 0
Assuming ψ is complex and neglecting the term β ψ 3 (not close to the boundary i.e. critical point) in comparison with α, equation (2.7) becomes
α ψ = ℏ 2 2 m * d 2 ψ d x 2
For the plane wave function, the solution of Equation (2.8) is in the form of,
ψ x = e x p i x ξ G L
where ξ G L is the GL coherence length expressed as a superconducting state (α is negative) yields
ξ G L 2 T = − ℏ 2 2 m * α = ℏ 2 2 α o m * T c − T = ξ G L 2 0
Using (2.10), equation (2.7) can be rewritten as
ψ + β α ψ 3 − ξ G L 2 d 2 ψ d x 2 = 0
We define an arbitrary function f such the wave function ψ x in equation (2.11) is expressed as
ψ x = α β     g
d d x − 1 2 ξ 2 d g d x 2 − 1 2 g 2 + 1 4 g 4 = 0
If the derivative of the function in (2.13) is zero, then the expression in the brackets is a constant or zero, then
d g d x = 1 2   ξ 1 − g 2
which as a solution in terms of a hyperbolic function of a tangent, given by
g = tanh ⁡ x 2 ξ
Since α T = α o ( T − T c ) , and β > 0 , then ψ x defined in equation (2.12) takes the form
ψ x = α β 1 2 tanh ⁡ x 2   ξ = α o ( T c − T ) , β 1 2 tanh ⁡ x 2 ξ
Equation (2.16) gives an inhomogeneous wave function which is dependent on temperature and space, x. At T = Tc, ψ = 0 the material reverts to normal state. Also, at x = 0 then ψ = 0 which makes a superconducting material revert to normal. (Tinkham, M. (2004, 2nd Ed.)

2.2. Number Density

The order parameter for the entangled superconducting system for two particles that form a cooper pair at a position x1 and x2 in space is written in a symmetric form as; (Rashid, M. A. 2019, September 26)
Ψ x 1 ,   x 2 = 1 2 ψ 1   ( x 1 ) ψ 2 ( x 2 ) + ψ 2 ( x 2 )   ψ 1 ( x 1 )
where ψ 1 ( x 1 ) and ψ 2 ( x 2 ) are the wave functions of the particles in position x1 and x2 respectively. Using equation (2.16), Ψ ( x 1 ,   x 2 ) in (2.17) can be expressed as
Ψ x 1 , x 2 = 2 α T c − T β tanh x 1 2 ξ ⁡ + t a n h x 2 2 ξ   t a n h   1 2 ξ x 1 + x 2 − 1
After applying Hyperbolic functions of sums. Equation (2.18) is the order parameter for an entangled superconducting system of YBCO superconductor. The number density n s of the superconducting electrons, becomes,
n s = Ψ ( x 1 , x 2 ) 2 = 2 a 0 2 T c − T 2 β 2 tanh 2 x 1 2 ξ ⁡ + t a n h 2 x 2 2 ξ + 2 t a n h x 1 2 ξ t a n h x 2 2 ξ t a n h 2     1 2 ξ x 1 + x 2 − 2 tanh x 1 2 ξ ⁡ + t a n h x 2 2 ξ t a n h     1 2 ξ x 1 + x 2 + 1

3. Ginzburg Landau Penetration Depth

Ginzburg Landau penetration depth is the characteristic length of the fall of the applied magnetic field due to surface currents. It characterizes the typical distance through which the weak magnetic field penetrates a superconductor. (Tinkham, M. (2004) Neglecting the terms ∇ Ψ   and ∇ Ψ * that are not field-related in the current density equation (2.3), to get
J s = − e * 2 m * c Ψ 2 A
From Maxwell’s equation
∇ X B = 4 π c J s
Taking curl both sides of equation (2.20) and simplify using vector identities, we obtain
∇ 2 B = − 4 π c ( ∇ X   J s ) = B λ G L ( T ) 2
where,
λ G L ( T ) = m c 2 8 π e 2 n s
is the GL penetration depth, m * = 2 m and e * = 2 e . Substituting the number density n s equation (2.18) into (2.22), we obtain
λ G L ( T ) = λ G L ( 0 ) 1 − T T c − 1 2
where λ G L ( 0 ) is the penetration depth at zero temperature, T = 0.
λ G L ( 0 ) = m c 2 β 2 16 π e 2 a 0 2 T c 2 tanh 2 x 1 2 ξ ⁡ + t a n h 2 x 2 2 ξ + 2 t a n h x 1 2 ξ t a n h x 2 2 ξ t a n h 2     1 2 ξ x 1 + x 2 − 2 tanh x 1 2 ξ ⁡ + t a n h x 2 2 ξ t a n h     1 2 ξ x 1 + x 2 + 1
It follows that the GL penetration depth, equation (2.23) varies as a function of temperature, while the penetration depth at zero temperature, equation (2.24) varies as a function of the distance between the entangled electron pair.

3.1. Critical Magnetic Field

3.1.1. Upper Critical Magnetic Field, H c 2

The critical magnetic field is the field that suppresses superconductivity in a material when applied to a superconductor, Kittel, C. (2005, pp 283-286). Since at the transition point of superconductivity, ψ is small then, the first GL Equations (2.6) is linearized to obtain
1 2 m * − i ℏ − e * c A 2 ψ = − α ψ
At the onset of superconductivity, the magnetic field in the superconducting region is just an applied field, i.e. A = B 0 , x , 0 = B x x . Hence equation (2.25) becomes
1 2 m * − i ℏ − e * c B x x 2 ψ = − α ψ
Expanding equation (2.26) results in
− ℏ 2 2 m * ∂ 2 ∂ x 2 Ψ + m * 2 e * m * c B x 2 ψ = − α ψ
Equation (2.27) is similar to the time-independent Schrodinger equation for a particle of mass m oscillating at a frequency ω , subject to a restoring force F x = − m ω 2 x is expressed as
− ℏ 2 2 m * ∂ 2 ∂ x 2 Ψ + m ω 2 2 x 2 ψ = E n ψ
where E n is the Energy of the Oscillator of frequency expressed as
E n = n + 1 2 ℏ ω
Comparing the form equation (2.27) and (2.28), we can define the s the cyclotron frequency ω c , given by
ω = ω c = e * B 2 m * c
The largest value of the magnetic field (B = B m a x ) in equation (2.27) corresponds to the smallest eigenvalue n = 0 (ground state energy) in equation (2.28), leading to which the solution of equation (2.28) of the lowest eigenvalue is given by
E 0 = 1 2 ℏ ω c = 1 2 ℏ e * B m a x 2 m * c = − α
which simplify to
B m a x = − 2 m * c α ℏ e *
The highest field in which superconductivity can nucleate in the interior of a bulk sample occurs within the upper critical magnetic field ( H c 2 ) i.e. B m a x = H c 2 , then equation (2.29c) can be rewritten as
H c 2 = − 2 m * c α ℏ e *
Substitute for α obtained equation (2.10) into equation (2.30) and simplify, to find the expression for the temperature dependence of the upper critical magnetic field as
H c 2 = ℏ c e * ξ G L ( 0 ) 2 1 − T T c
Taking T = 0 in equation (2.31a), the expression for the upper critical magnetic field at zero temperature, becomes
H c 2 ( 0 ) = ℏ c T c e * ξ G L ( 0 ) 2

3.1.2. Lower Critical magnetic field, H c 1

To obtain the lower critical field, the relation for the penetration depth is used instead of coherence length to obtain the parameter α in equation (2.29d). Using equation (2.5a) to define the number density n s , substitute in the penetration depth equation (2.22) and simplify, we find
α = m c 2 β 8 π e 2 λ G L ( T ) 2 = m c 2 β 8 π e 2 λ G L ( 0 ) 2 1 − T T c 1 2
after using equation (2.23). Substituting in (2.32) in equation (2.29d), we obtain the lower critical field as
H c 1 = m 3 c 2 β 4 π ℏ e 3 λ G L ( 0 ) 2 1 − T T c 1 2
where λ G L ( 0 ) is the London penetration depth at zero temperature, equation (2.24). Taking T = 0 in equation (2.33a), the expression for a lower critical magnetic field at zero temperature becomes
H c 1 ( 0 ) = m 3 c 2 β 4 π ℏ e 3 λ G L ( 0 ) 2
Substituting equation 2.24 in equation 2.33a yields an expression for the dependence of lower critical magnetic field to entanglement distance
H c 1 = c 2 β 2 ℏ λ G L ( T ) e 2 m 3 π tanh 2 x 1 2 ξ ⁡ + t a n h 2 x 2 2 ξ + 2 tanh x 1 2 ξ ⁡ t a n h x 2 2 ξ t a n h 2     1 2 ξ x 1 + x 2 − 2 tanh x 1 2 ξ ⁡ + t a n h x 2 2 ξ t a n h     1 2 ξ x 1 + x 2 + 1 1 2
But λ G L ( T ) = λ G L ( o ) 1 − T T c 1 2 , hence
H c 1 = c 2 β 2 ℏ λ G L ( 0 ) e 2 m 3 π tanh 2 x 1 2 ξ ⁡ + t a n h 2 x 2 2 ξ + 2 tanh x 1 2 ξ ⁡ t a n h x 2 2 ξ t a n h 2     1 2 ξ x 1 + x 2 − 2 tanh x 1 2 ξ ⁡ + t a n h x 2 2 ξ t a n h     1 2 ξ x 1 + x 2 + 1 1 2 1 − T T c 1 2
Equation (2.35c) gives the expression for the temperature dependence of the lower critical magnetic field and the dependence of the lower critical magnetic field with entanglement distance

3.2. Critical Current Density, J c

Critical current density is the value of transport current density which causes intergranular magnetization to collapse at a given magnetic field and temperature, de Gennes, P. G. (1999). Substituting the number density n s equation (2.18) into the current density equation (2.19), to get
J s = − 2 A e 2 a 0 2 T c − T 2 m c β 2 tanh 2 x 1 2 ξ ⁡ + t a n h 2 x 2 2 ξ t a n h 2 1 2 ξ x 1 + x 2 − 2 tanh x 1 2 ξ ⁡ + t a n h x 2 2 ξ t a n h 1 2 ξ x 1 + x 2 + 1
At the maximum magnetic field, (at the critical point), the applied field is equal to the vector potential. H c 2 = A , and J s = J c , hence the critical current density from equation (2.25), becomes
J c = − 2 H c 2 e 2 a 0 2 T c − T 2 m c β 2 tanh 2 x 1 2 ξ ⁡ + t a n h 2 x 2 2 ξ t a n h 2 1 2 ξ x 1 + x 2 − 2 tanh x 1 2 ξ ⁡ + t a n h x 2 2 ξ t a n h 1 2 ξ x 1 + x 2 + 1
At zero temperature T = 0, the critical current density becomes,
J c = − H c 2 4 π λ G L 0 2 1 − T 2 T c 2 1 2
where H c 2 is the Upper critical magnetic field and λ G L ( 0 ) is the London penetration depth at zero temperature, equation (2.24). Taking T = 0 in equation (2.36a), the expression for critical current density at zero temperature becomes
J c ( 0 ) = − H c 2 4 π λ G L 0 2

3. Results and Discussion

This section details the relationship between the coherence length of the superconductor, GL penetration depth, Critical current density, critical magnetic field, and order parameters with entanglement distance and temperature of the YBCO superconductor.

3.1. Coherence Length, ξ G L

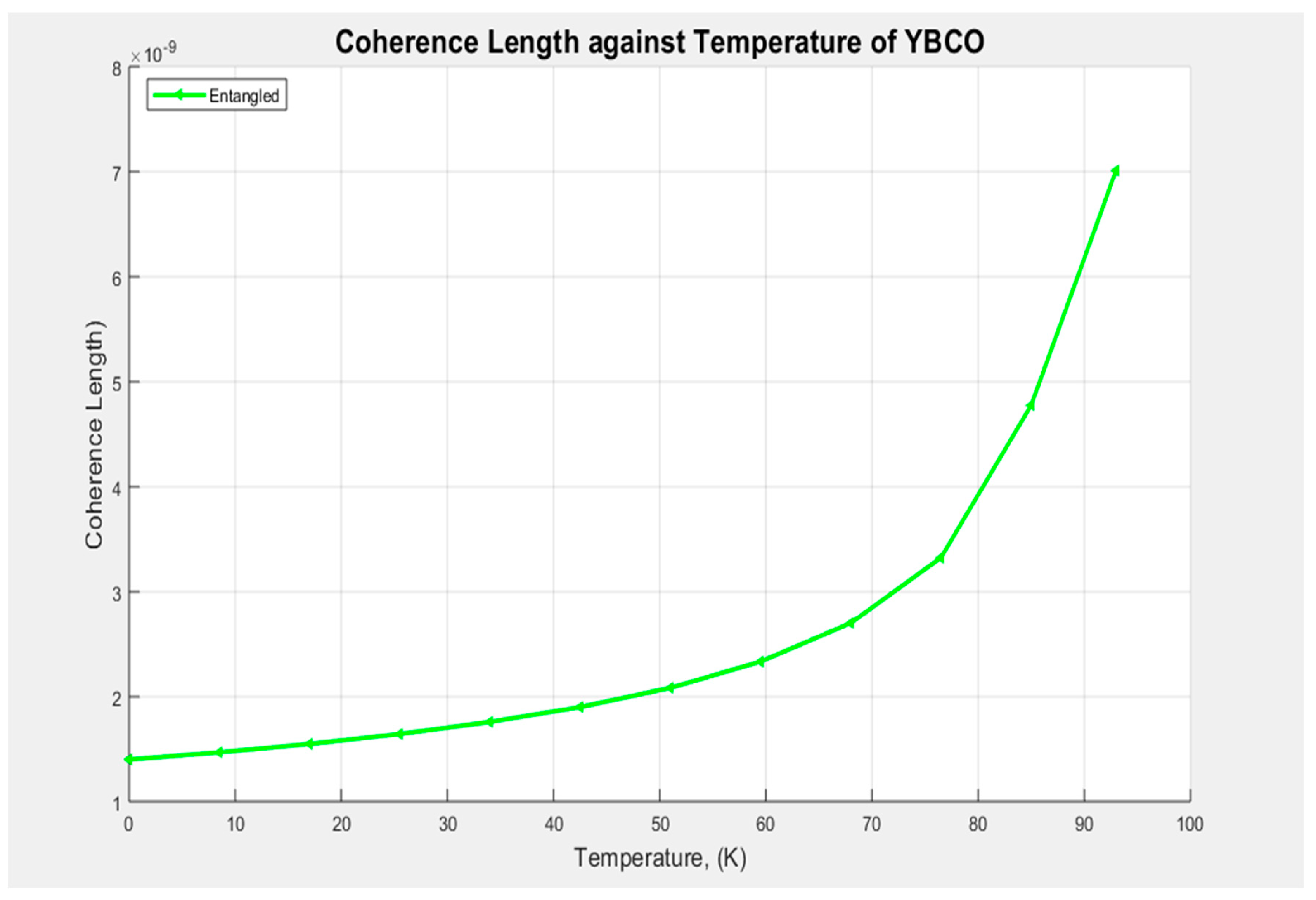
From Equation (2.10), we obtained the graph that shows the relationship between the GL coherence length and temperature (T) as indicated in Figure 3.1.
Preprints 115112 g001
Figure 3.1.  
Figure 3.1.  
Preprints 115112 g001
We see from Figure 3.1, that the GL coherence length ( ξ G L ) increases with temperature and diverges as T→ Tc. beyond TC, the YBCO reverts to a normal material. This implies that as the temperature reaches the critical point, the superconductivity is destroyed at this temperature.

3.2. Penetration depth, λ G L

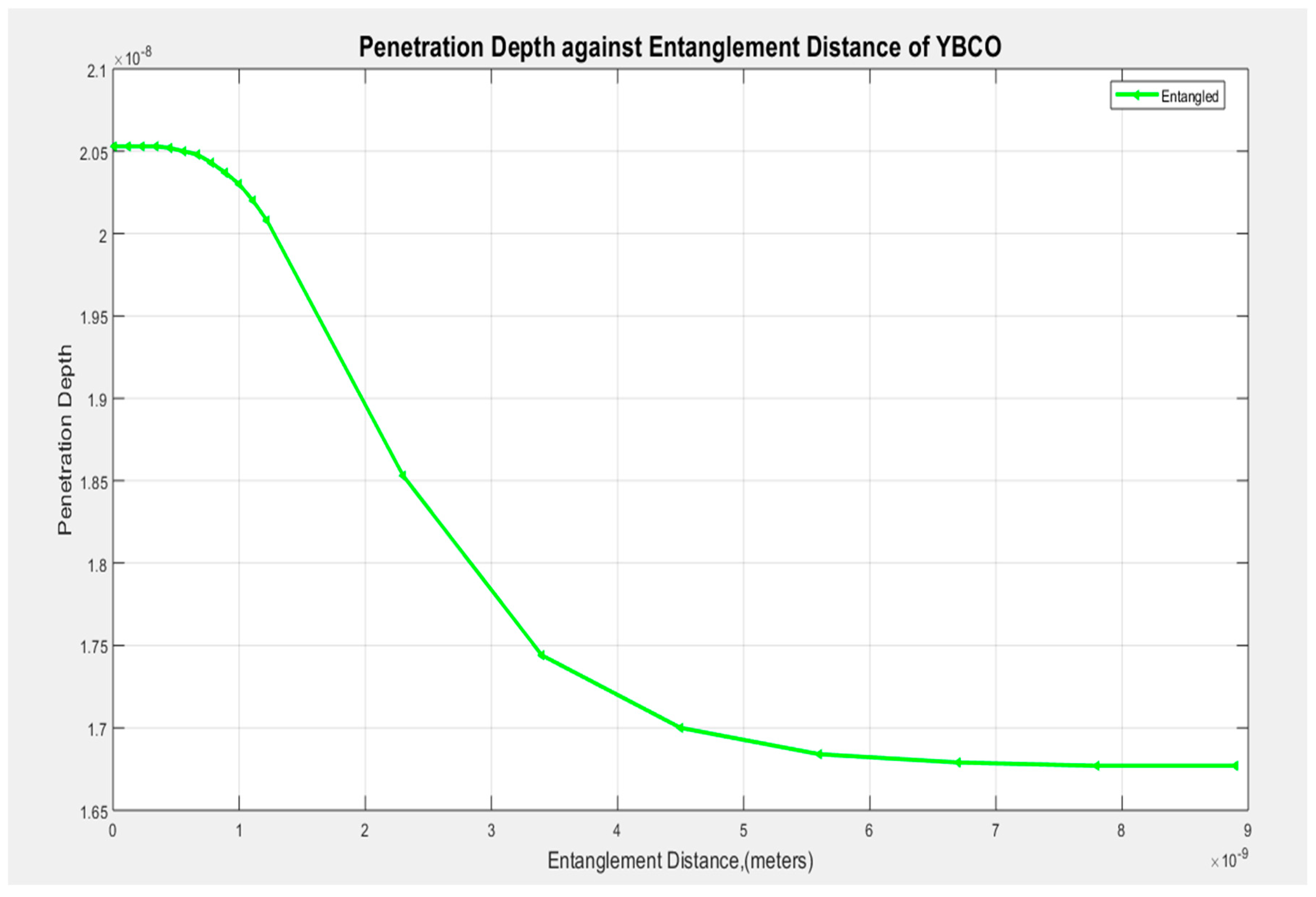
Equation (2.24) is used to plot the graph of the penetration depth at zero temperature against the distance between the entangled electron pair, as shown in Figure 3.2.
Preprints 115112 g002
Figure 3.2.  
Figure 3.2.  
Preprints 115112 g002
From Figure 3.2, we observe that there is a decrease in the GL penetration depth with entanglement distance. Generally, it's observed that the penetration depth decreases as the distance of separation increases. There is higher penetration of magnetic field inside a superconductor when the separation distance is small, i.e. between 0 to 1 nm, this behavior is observed as the distance increases approaching 7.8 nm. Beyond 7.8 nm, the superconductor seems to have attained a constant value of magnetic penetration. Thus, from the graph, the GL penetration of the field decreases as the distance of separation increases. At infinite distances, a constant penetration depth of about 0.168 nanometers is maintained.

3.2.1. Penetration Depth and Entanglement Distance

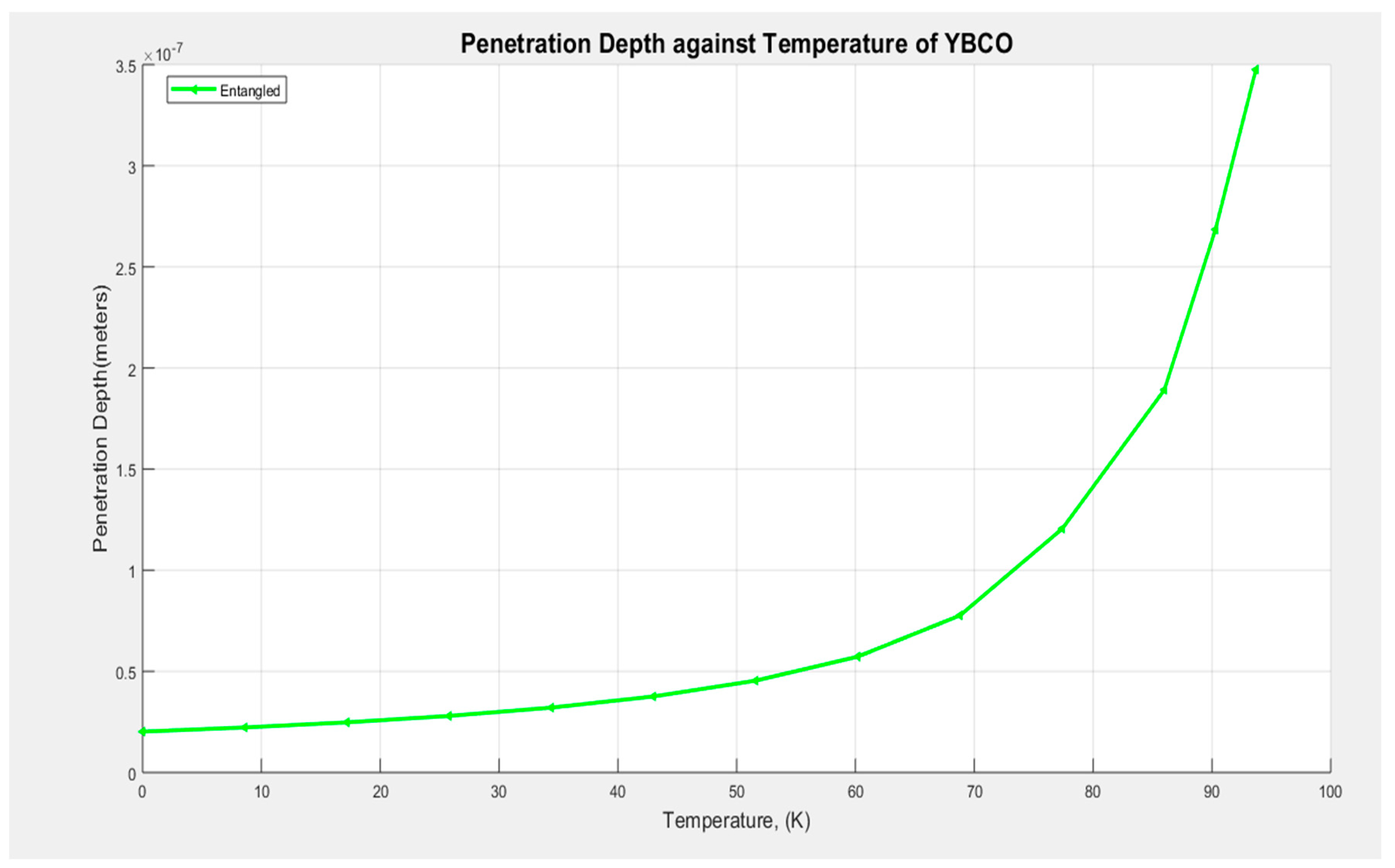
Equation (2.23) is used to plot the graph of the penetration depth against temperature at a fixed distance between the entangled electron pair, as shown in Figure 3.3.
Preprints 115112 g003
Figure 3.3.  
Figure 3.3.  
Preprints 115112 g003
From Figure 3.3, we observe that there is an increase in the GL penetration depth with temperature (T), and generally, we observe that the penetration depth rises asymptotically as the temperature approaches the critical point. Thus, the penetration of the field increases as the temperature approaches Tc. At Tc, the magnetic field penetrates the YBCO superconductor fully, there is no expulsion of the magnetic field beyond Tc. The penetration of the applied magnetic field increases as the temperature increases, and as the temperature approaches T = Tc, the graph diverges (diamagnetic properties of YBCO suppressed).

3.3. Critical Magnetic Field

a)
Lower Critical Field with Temperature
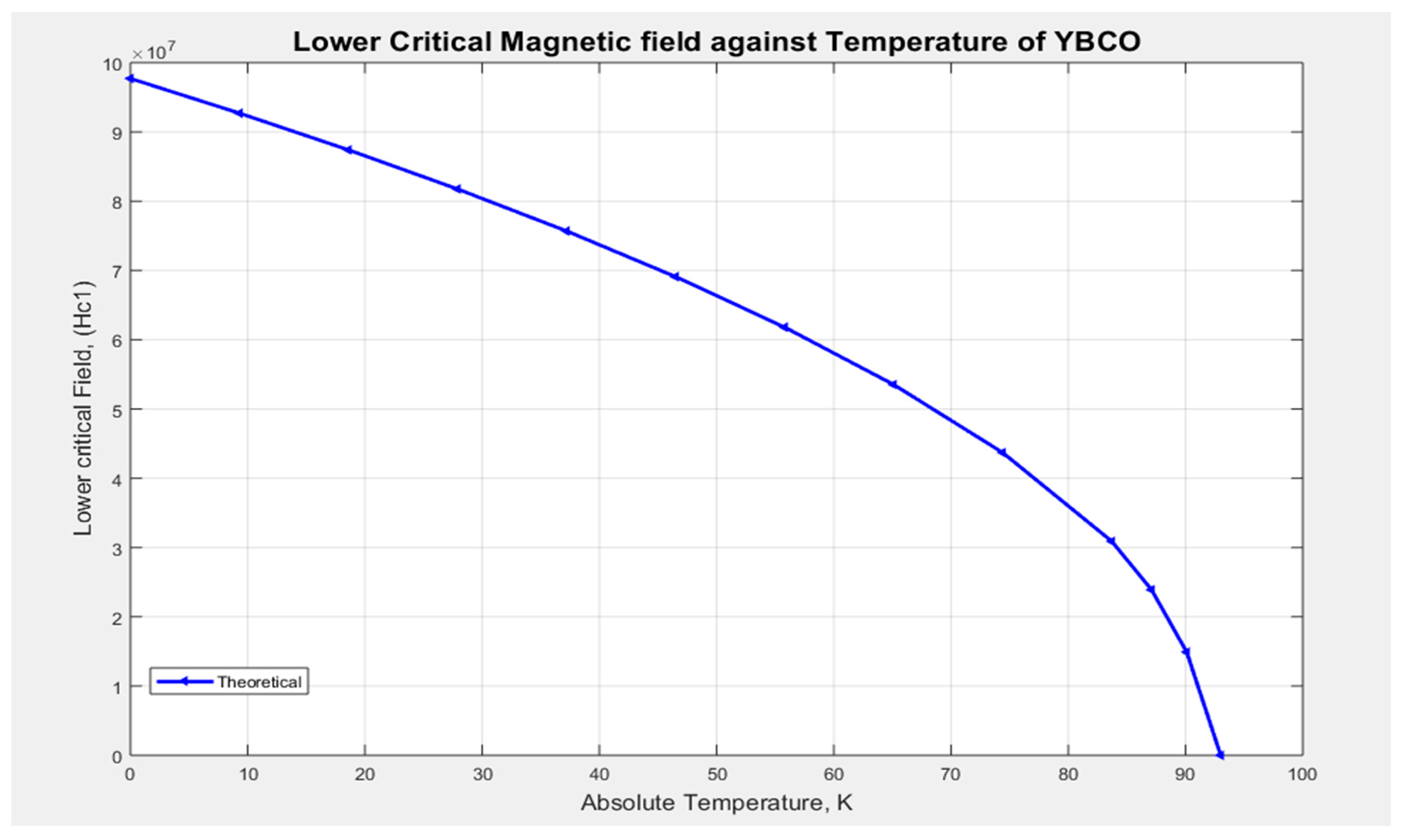
Equation (2.33a) is used to plot the graph of the lower critical magnetic field for superconducting YBCO against temperature at a fixed distance of 1.8   n a n o m e t e r s between the entangled electron pair, as shown in Figure 3.4. We observe in Figure 3.4. that the lower critical magnetic field is non-linearly dependent on the temperature of the entangled YBCO superconductor.
Preprints 115112 g004
Figure 3.4.  
Figure 3.4.  
Preprints 115112 g004
As we increase the temperature, the lower critical magnetic field decreases. This happens because the material's capacity to retain superconductivity is dependent on temperature. As temperature decreases, the critical field increases generally to a maximum at absolute zero. At T = Tc, the magnetic field is zero, at this temperature, YBCO has assumed the normal properties of a material.
b)
Lower Critical Field with Entanglement Distance
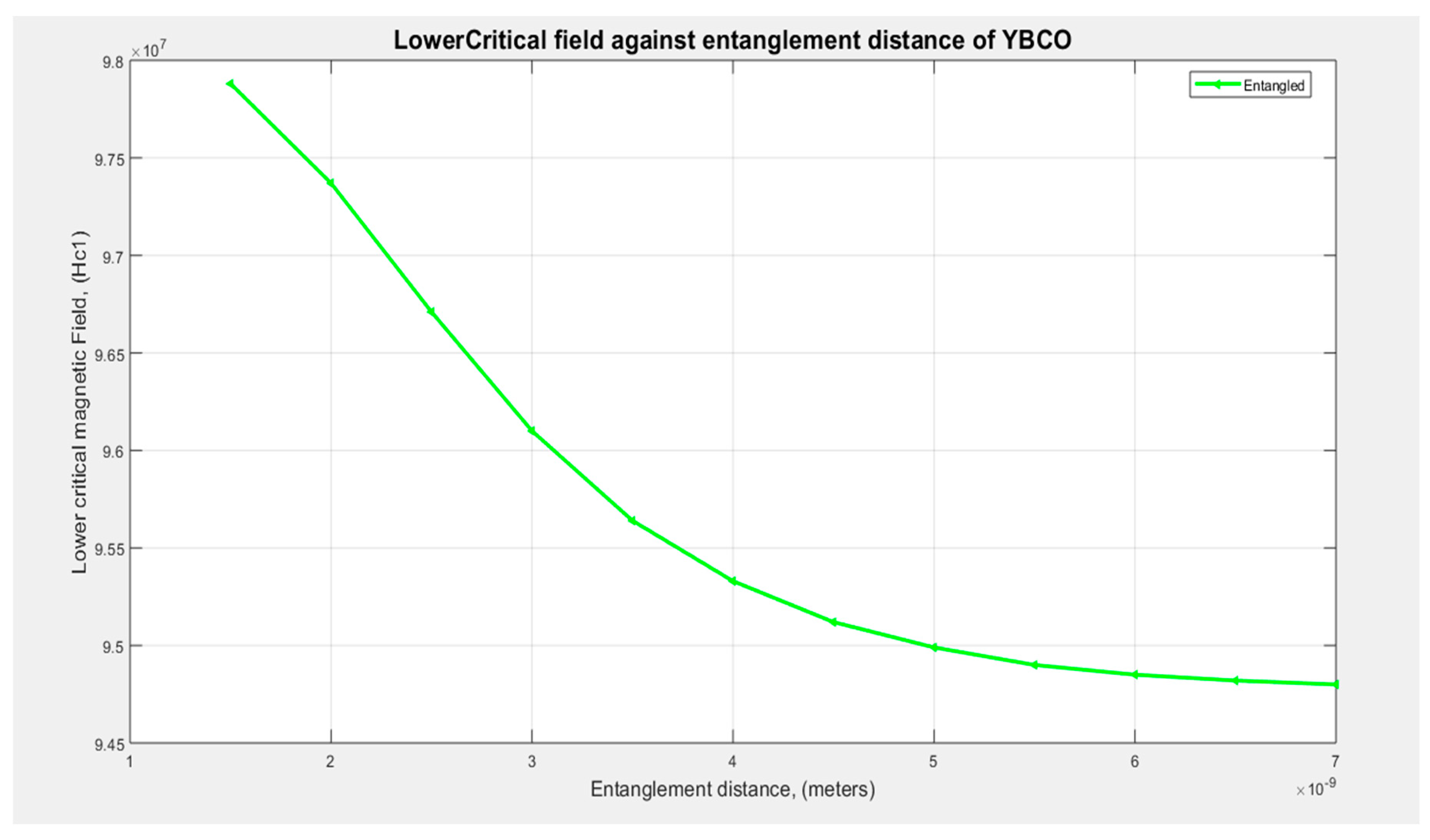
Equation (2.33b) is used to plot the lower critical magnetic field for superconducting YBCO at zero temperature against the distance between the entangled electron pair, as shown in Figure 3.5.
Preprints 115112 g005
Figure 3.5.  
Figure 3.5.  
Preprints 115112 g005
Figure 3.5 shows that as the distance of separation between the entangled pair of electrons increases, the magnetic field also decreases up to about 6.5 nm and then attains a constant value at infinite distances. From the graph, beyond 6.5 nm, the material reverts to normal as there is complete penetration of the magnetic field. We observed that as the temperature of the YBCO superconductor increases, the distance of separation between the copper pairs increases and vice versa.
c)
Upper Critical Field with Temperature
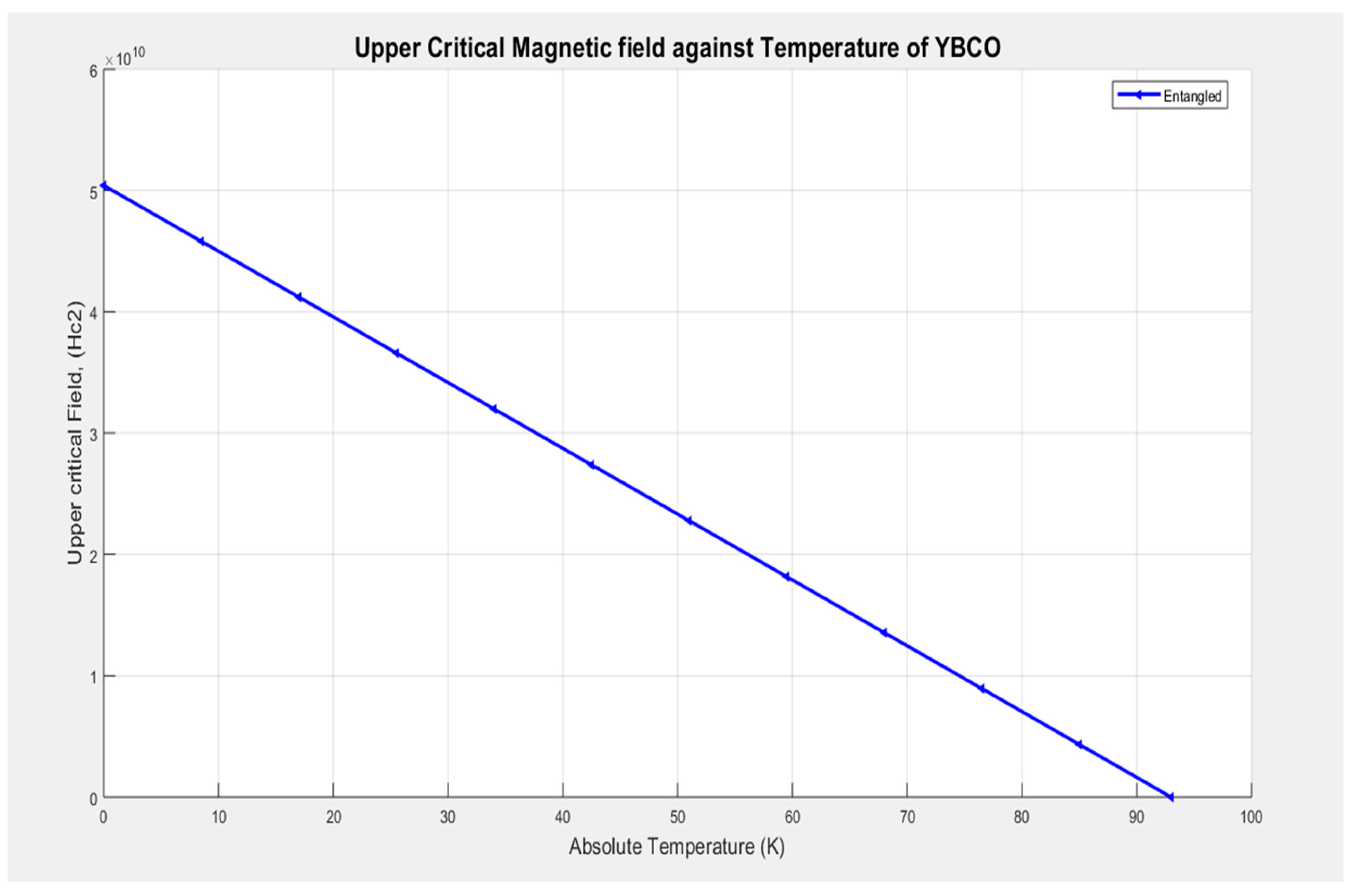
Equation (2.31a) is used to plot the graph of the upper critical magnetic field for superconducting YBCO against temperature at a fixed distance (1.8 nanometers) between the entangled electron pair, as shown in Figure 3.4.
Preprints 115112 g006
Figure 3.6.  
Figure 3.6.  
Preprints 115112 g006
From Figure 3.6, we observe that the upper critical magnetic field is linearly dependent on the temperature of the entangled YBCO superconductor. We observe that the upper critical magnetic field decreases as temperature increases and reaches to zero at the critical temperature of superconducting YBCO.

3.4. Critical Current Density, J c

The critical current density Jc is the value of transport current density which causes the intergranular magnetization to collapse at a given magnetic field and temperature. There is a direct relation between the critical field and the critical current, the maximum electric current density that a given superconducting material can carry, before switching into the normal state.
a)
Critical Current Density versus Temperature
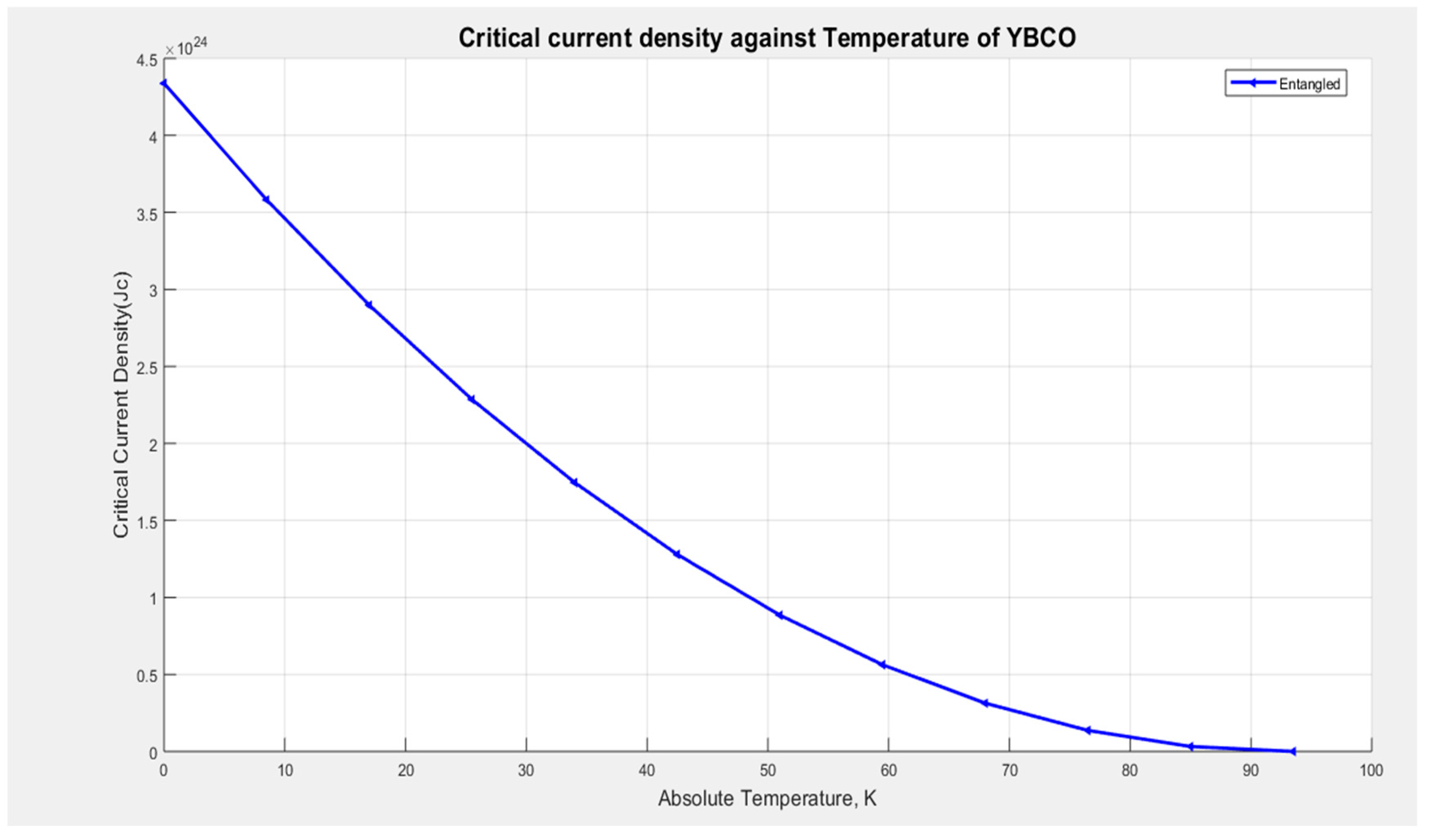
Equation (2.36a) is used to plot the graph of the critical current density for superconducting YBCO against temperature at a fixed distance (1.8 nanometers) between the entangled electron pair, as shown in Figure 3.7.
Preprints 115112 g007
Figure 3.7.  
Figure 3.7.  
Preprints 115112 g007
It is observed in Figure 3.7 that as the temperature of the YBCO superconductor increases, the critical current density decreases and comes to zero at T = Tc, i.e. at about 93K. Thermal fluctuations strongly affect superconductivity in YBCO at high temperatures. They destroy the critical state as the temperature approaches Tc.
b)
Critical Current Density versus Temperature
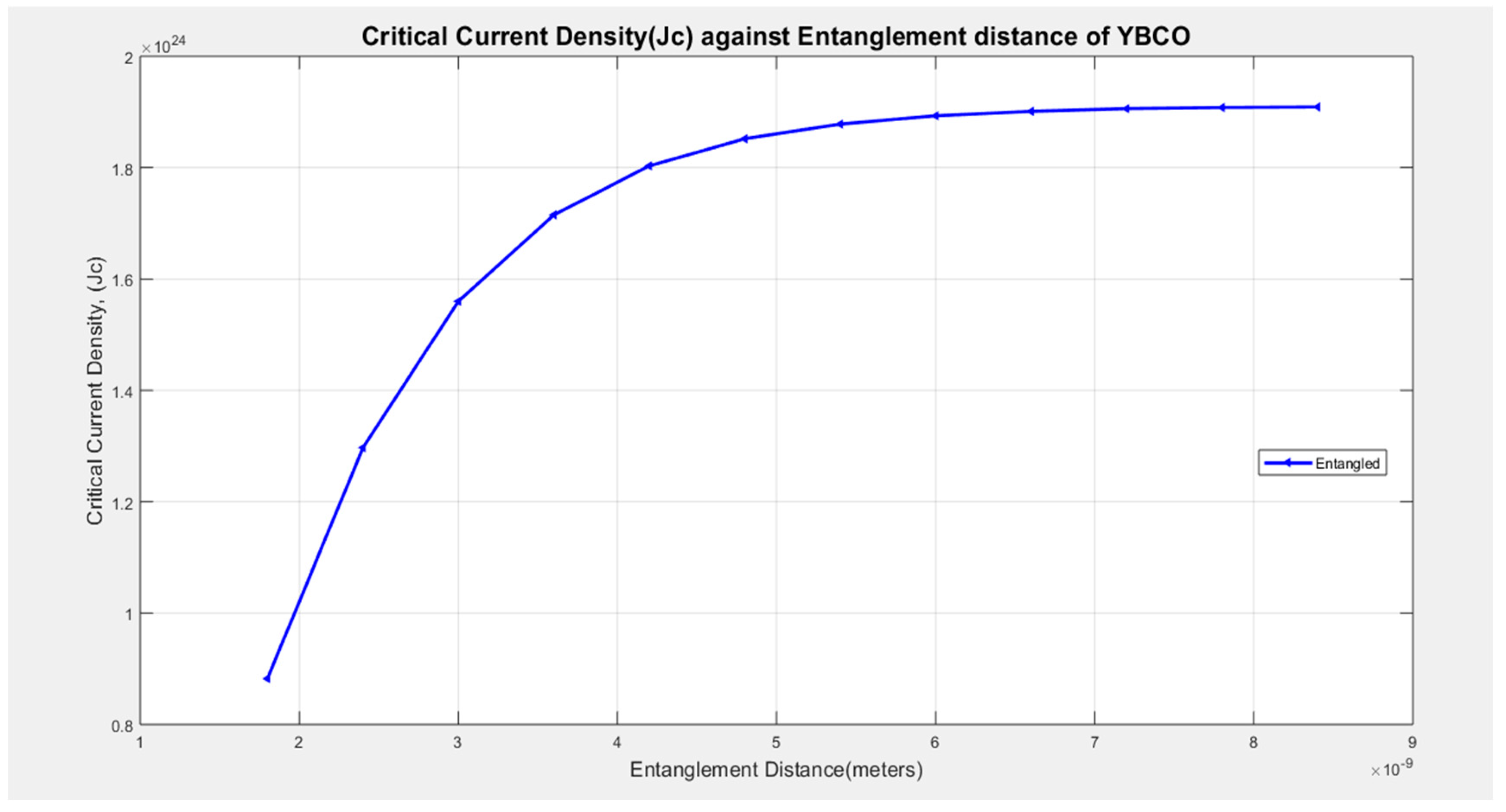
Equation (2.36b) is used to plot the critical current density for superconducting YBCO at zero temperature against the distance between the entangled electron pair, as shown in Figure 3.8.
Preprints 115112 g008
Figure 3.8.  
Figure 3.8.  
Preprints 115112 g008
From Figure 3.8 we see that, between x = 1 nm to x = 1.8 nm, the current flows in a material in a normal state. When the distance reaches 1.8, it increases non-linearly with increasing entanglement distance. The critical current increases from x = 1.8 nm to about x = 7.8 nm which flattens for infinite distances having attained a constant value. Therefore, the critical current in the entangled YBCO superconductor increases with the increase of entanglement distance from x = 1.8 nm to x = 7.8, posting a maximum value at x = 7.8.

4.1. Conclusions

The main purpose of this research work is to assess the effect of entanglement on the critical magnetic field and critical current density of superconducting YBCO by using the Ginzburg-Landau approach. From the calculations, the phase diagrams are plotted by using MATLAB scripts and Mathcad prime 9.0.0.0 scripts. From the results, it's clear that the distance of separation between the electrons affects the current density and critical magnetic field of a superconductor. In the case of YBCO, the critical current increases non-linearly when the distance of separation ranges from x = 1.8 nm up to about x = 7.8 nm which flattens for higher and infinite distances attaining a constant value. Also, the penetration depth varies with the distance of separation of the entangled electrons; in this case, it is noted that generally, the penetration depth of a superconductor decreases as the entanglement distance increases attaining a minimum value of 0.168 nanometers at infinite separation distances. Consequently, the critical magnetic field decreases non-linearly when the distance of separation ranges from 1.5 nm up to 6.5 nm where it flattens for higher separation distances.
From the phase diagrams plotted, it can be concluded that the upper critical magnetic field of superconducting YBCO is inversely related to temperature which is in agreement with experimental observations, critical current density, Lower critical magnetic field, and penetration depth are non-linearly dependent on temperature. Also, the phase diagrams from the dependence of entanglement distance to the critical field, critical current density, GL penetration depth, and GL coherence length are assessed. In a nutshell, the entanglement distance affects greatly the critical fields and current densities of an entangled YBCO superconductor.

4.2. Recommendations

This research focused on the effect of entanglement on penetration depth, critical current density, and lower critical magnetic field. The coherence length and upper critical magnetic field were not related to entanglement distance, further studies are recommended to investigate the effect of entanglement on the coherence length and upper critical magnetic field. Our model of entanglement of electron-pair (cooper pair) shows reasonable agreement with available theoretical data in determining the effect of the entanglement on YBCO critical properties. The theory of entanglement in high-temperature superconductivity should be explored as it may unleash remarkable features on the properties of superconductors. The efforts in determining the pairing mechanism as an entanglement in this system need to continue, for such efforts go hand in hand with enhancing prospects for new High-Temperature Superconductor materials and novel applications in power industries, transportation industries, and medicine.

Acknowledgments

I am deeply grateful to Almighty God for granting me life, strength, guidance, and good health throughout this study. My heartfelt thanks go to my supervisors, Prof. Ndinya Boniface and Dr. Rapando Wakhu, for their invaluable sacrifices, insightful suggestions, and unwavering guidance. Their extensive contributions to the literature and generous allocation of their time have been instrumental in bringing this research to fruition.

References

  1. Chen, X.; Zhang, Y.; Liu, S. Quantum Computing with YBCO: Entanglement and Performance. Journal of Quantum Electronics 2024, 61, 345–359. [Google Scholar]
  2. Singh, R.; Sharma, A.; Gupta, M. Entanglement-Based Sensors and Communication Devices Using YBCO. IEEE Transactions on Quantum Engineering 2024, 11, 192–206. [Google Scholar]
  3. Yang, Z.; Cheng, F.J.; Chao, N.; Zhang, C.Y.; Peng, L.L. The mixed-state entanglement in holographic p-wave superconductor model. Journal of High Energy Physics 2023, 2023. [Google Scholar] [CrossRef]
  4. Kim, J.; Lee, S.; Park, H. Experimental Probes of Entanglement in YBCO. Nature Physics 2023, 19, 45–58. [Google Scholar]
  5. Lee, C.; Wong, T.; Yang, F. Quantum Interference and Entanglement in High-Tc Superconductors. Advanced Materials 2023, 35, 2101–2114. [Google Scholar]
  6. Zhang, L.; Zhang, W.; Li, Q. Spatial Distribution of Entanglement in YBCO: STM Observations. Science Advances 2023, 9, 876–889. [Google Scholar]
  7. Garg, A.; Kumar, S.; Patel, R. Theoretical Insights into Entanglement in High-Temperature Superconductors. Physical Review B 2022, 106, 125–139. [Google Scholar]
  8. Millán, J.S.; Pérez, L.A.; Ruiz, H.S. Critical Current Density in d-Wave Hubbard Superconductors. Materials 2022, 15, 8969. [Google Scholar] [CrossRef]
  9. Sueyoshi, T. Modification of critical current density anisotropy in high-Tc superconductors by using heavy-ion irradiations. Quantum Beam Science 2021, 5, 16. [Google Scholar] [CrossRef]
  10. Kahsay, G.; Negussie, T. Theoretical investigation of upper critical magnetic field (Hc2) of the heavy fermion superconductor CeRhIn5. Latin American Journal of Physics Education 2020, 14. http://www.lajpe.org/.
  11. Uffink, J. Schrödinger’s Reaction to the EPR Paper. In Quantum, Probability, Logic; Jerusalem Studies in Philosophy and History of Science; Hemmo, M., Shenker, O., Eds.; Springer: Cham, 2020. [Google Scholar] [CrossRef]
  12. Rapando, B.W. Size and Coherence Length of Cooper pairs in Superconductors. International Journal of Research and Analytical Reviews (IJRAR) 2020, 7, 519–522. [Google Scholar]
  13. Sekitani, T.; Miura, N.; Ikeda, S.; Matsuda, Y.H.; Shiohara, Y. Upper critical field for optimally-doped YBa2Cu3O7. Physica B-condensed Matter 2004, 346, 319–324. [Google Scholar] [CrossRef]
  14. Sueyoshi, T. Modification of critical current density anisotropy in high-Tc superconductors by using heavy-ion irradiations. Quantum Beam Science 2021, 5, 16. [Google Scholar] [CrossRef]
  15. Arovas, D.; Wu, C. Lecture notes on superconductivity (A work in progress). University of California: San Diego, 2019; pp. 19–29. [Google Scholar]
  16. Emeakaroha, T.; James, F. Enhancement of Critical Current Density of Yttrium Barium Copper Oxide Thin Films by Introducing Nano Dimensional Cerium Oxide Defects. Applied Physics Research 2018, 10, 109. [Google Scholar] [CrossRef]
  17. Keimer, B.; Kivelson, S.A.; Norman, M.R.; Uchida, S.; Zaanen, J. From quantum matter to high-temperature superconductivity in copper oxides. Nature 2015, 518, 179–186. [Google Scholar] [CrossRef]
  18. Askerzade, I.N.; Hashimoglu, I. The critical current density of a YNi2B2C superconductor in the two-band Ginzburg-Landau model. Technical Physics 2011, 56, 557–559. [Google Scholar] [CrossRef]
  19. Sachdev, S. Quantum entanglement and superconductivity. Scientific American. Perimeter Institute and Harvard University, 2013. https://www.scientificamerican.com/article/quantum-entanglement-and-superconductivity/.
  20. Huray, P.G. Maxwell's Equations. John Wiley & Sons, 2010. [Google Scholar] [CrossRef]
  21. Sachdev, S. Where is the quantum critical point in the cuprate superconductors? Physica Status Solidi (b) 2010, 247, 537–543. [Google Scholar] [CrossRef]
  22. Anderson, P.W. Theory of Superconductivity. Physical Review 1958, 112, 190–208. [Google Scholar] [CrossRef]
  23. Ginzburg, V.L.; Landau, L.D. On the Theory of Superconductivity. ZhETF 1950, 20, 1064–1082. [Google Scholar]
  24. Meissner, W.; Oschenfeld, R. "Die Magnetisierung der Supraleiter im Magnetfeld" [The Magnetization of Superconductors in a Magnetic Field]. Zeitschrift für Physik 1933, 80, 63–76. [Google Scholar]
  25. Wu, M.K.; Ashburn, J.; Torng, C.; Hor, P.; Meng, R.; Gao, L.; Huang, Z.; Wang, Y.; Chu, Q. Superconductivity at 93 K in a New Mixed-Phase Y-Ba-Cu-O Compound System at Ambient Pressure. Physical Review Letters 1987, 58, 908–910. [Google Scholar] [CrossRef] [PubMed]
  26. Kittel, C. Introduction to solid state physics, 8th ed.; Wiley, 2005; pp. 283–286. [Google Scholar]
  27. de Gennes, P.G. Superconductivity of Metals and Alloys. Westview Press, 1999. [Google Scholar]
  28. Desta, T.; Singh, P.; Kahsay, G. Study of upper critical magnetic field of superconducting HoMo6Se8_88. World Journal of Condensed Matter Physics 2015, 5, 105–117. [Google Scholar] [CrossRef]
  29. Dunning, C.; Links, J.; Zhou, H.Q. Ground-state entanglement of the BCS model. Physical Review Letters 2005, 94, 227002. [Google Scholar] [CrossRef]
  30. Kim, J.; Lee, S.; Park, H. Experimental Probes of Entanglement in YBCO. Nature Physics 2023, 19, 45–58. [Google Scholar]
  31. Zhang, L.; Zhang, W.; Li, Q. Spatial Distribution of Entanglement in YBCO: STM Observations. Science Advances 2023, 9, 876–889. [Google Scholar]
  32. Anderson, P.W. Theory of Superconductivity. Physical Review 1958, 112, 190–208. [Google Scholar] [CrossRef]
  33. Bednorz, J.G.; Müller, K.A. Possible High-Tc Superconductivity in the Ba-La-Cu-O System. Zeitschrift für Physik C 1986, 64, 189–193. [Google Scholar]
  34. Chen, X.; Zhang, Y.; Liu, S. Quantum Computing with YBCO: Entanglement and Performance. Journal of Quantum Electronics 2024, 61, 345–359. [Google Scholar]
  35. Einstein, A.; Podolsky, B.; Rosen, N. Can Quantum-Mechanical Description of Physical Reality Be Considered Complete? Physical Review 1935, 47, 777–780. [Google Scholar] [CrossRef]
  36. Garg, A.; Kumar, S.; Patel, R. Theoretical Insights into Entanglement in High-Temperature Superconductors. Physical Review B 2022, 106, 125–139. [Google Scholar]
  37. Ginzburg, V.L.; Landau, L.D. On the Theory of Superconductivity. ZhETF 1950, 20, 1064–1082. [Google Scholar]
  38. Rashid, M.A. [Lecture notes: Superconductivity]. 26 September 2019. Retrieved from http://just.edu.bd/t/rashid.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated