Preprint
Article
Calibration for Improving the Medium‐Range Soil Forecast over Central Tibet: Effects of Objective Metrics’ Diversity
Altmetrics
Downloads
83
Views
33
Comments
0
A peer-reviewed article of this preprint also exists.
supplementary.pdf (2.66MB )
This version is not peer-reviewed
Submitted:
14 August 2024
Posted:
14 August 2024
You are already at the latest version
Alerts
Abstract
The high spatial complexities of soil temperature modelling over semiarid land have challenged the calibration—predication framework, whose composited objective lacks comprehensive evaluation. Therefore, this study, based on the Noah land surface model and its full parameter table, utilizes two global searching algorithms and eight kinds of objective with dimensional—varied metrics, combined with dense site soil moisture and temperature observations of central Tibet, to explore different metrics’ performances on the spatial heterogeneity and uncertainty of regional land surface parameters, calibration efficiency and effectiveness, as well as spatiotemporal complexities in surface forecasting. Results have shown that metrics’ diversity has shown greater influence on the calibration—predication framework than the global searching algorithms themselves. Besides being significantly better than other metrics, the enhanced multi objective metric (EMO) and the enhanced Kling-Gupta efficiency (EKGE) have their own advantages and disadvantages in simulations and parameters respectively. Especially, EMO that composited with four metrics as correlated coefficient, root mean square error, mean absolute error, and Nash–Sutcliffe efficiency, has shown relatively balanced performance in surface forecasting when compared to EKGE. In general, the calibration—predication framework that benefited from EMO could greatly reduce the spatial complexities in soil temperature modelling of the semiarid land.
Keywords:
Subject: Engineering - Other
1. Introduction
Soil moisture (SM) and soil temperature (ST) are crucial variables modulating land-atmosphere fluxes [1,2,3,4]. However, due to the complexity of ST modelling over semi-arid regions, the ST simulations directly produced by land surface model (LSM) exhibit spatiotemporal deficiencies, posing challenges in their regional weather and climate applications [5,6]. Research efforts in improving ST simulations have suggested that the manually corrected high-sensitivity land parameters could benefit the greater scale ST modeling physics [7,8], and the auto-calibrated LSM’s parameter table could benefit the joint SM-ST modeling configuration [9]. Given the great challenges in solving the highly non-linearity in joint SM-ST modeling, e.g., the high-dimensional land parameters and nonlinear physics, the composited objectives evaluating the distance between simulations and observations is proposed to enhance calibration performance (e.g., Kling-Gupta efficiency) [10], whose various internal multi-metrics’ credits need more endeavor to meet with a robust real-world application [11,12]. Therefore, evaluating the effects of the objective metrics’ diversity on calibration performance in solving the spatial complexities of surface simulations is of great significance for improving ST modeling and forecasting over semiarid land.
The LSM parameters optimization or identification has been evolving for decades with the regional application of auto-calibration techniques, primarily achieved by utilizing global search algorithms (GSA, e.g., particle swarm optimization and shuffled complex evolution; PSO [13,14,15,16,17,18] and SCE [19,20,21,22]) to seek optima against specific model objective. As LSM parameter number usually decreases GSA’ efficiency and effectiveness, especially in high-dimensional cases, early research advocated for dimensionality reduction through generalized land parameter sensitivity analysis, such as focusing on reducing insensitive parameters for specific objectives, based on land surface parameter categorization (e.g., soil, vegetation, general, and initial types) to enhance calibration optima [23,24,25]. Moreover, given the intensifying diversity of land surface model applications (e.g., runoff, fluxes), globally applicable land surface parameter estimation has garnered great attention [26,27,28,29], but this has been challenged by the largely varied sensitivities of the distinguished LSM parameters in arid and semi-arid land (ASAL) [30,31].
The well-known Noah LSM though has been widely employed in finer numerical studies [32], but faces increasingly prominent issues related to the representativeness of parameters in complex ASAL applications, such as varying sensitivities of vegetation and general parameters to thermal flux respectively [25,33,34]. This poses continuous challenges for refined land surface applications in Tibet, a region with diverse climatic zones, e.g., LSM parameter diverse advantages in different regions of a similar surface [18,28,29]. Despite the establishment of a refined SM-ST observation network under a semiarid climate over central east Tibet (i.e., northwest Naqu) [35], which features grassland as the primary land cover and clay as the dominant soil texture, more comprehensive calibration objective against the LSM parameter uncertainties reduction and surface enhancement is still required for the robust ST modeling [9,36,37,38].
In fact, with the development of land remote sensing, given the diversity of GSA’ strategies and application objectives (such as SM, ST, runoff, and fluxes), the objective metric designs of auto-calibration have greatly developed to enhance LSM modelling performances. For instance, LSM calibration using multi-source remote sensing data, the multi-objective design concentrates on the comprehensive inversion characteristics of remote sensing SM and/or ST observations are essential [39,40,41]. Similarly, in calibrating applications aimed at improving the spatial accuracy of surface state predictions, a multi-objective design that considers horizontal variations [42,43,44,45] and/or vertical stratification [46,47,48,49,50,51,52,53,54,55,56,57,58,59] of states and observations is crucial. Generally, the multi-objective metrics can, to a certain extent, address the issues of observational data fusion and multi-state complex error measurement in specific calibration applications, emphasizing the enhanced role of spatial dimensions of single or multiple land surface state errors as holistic objectives.
Moreover, as the inherent scale uncertainties of land surface state (e.g., the distance between simulation and observation could fall into the non-Euclidean space) lead to challenges in assessing and ranking LSM’ performances in high-dimensional searching space, the holistic objectives with differentiated metrics have been widely developed to simplify and enhance the calibration [50,51,52]. And they can be primarily categorized into flexible (e.g., Pareto front [53,54,55,56], and dominated Pareto [57,58,59]) and deterministic approaches. The Pareto front adjusts the cumulative distribution of metrics based on external algorithm storage and aims at general LSM modelling with globally applicable parameters, which can be an expensive evaluator that independent from GSA. While within the GSA’s evaluator, the dominated Pareto compares relationships among metrics and the deterministic approach combines various metrics, and then aims at determining the optimally combined solution of various simulations.
However, though metrics offer the deterministic reference for estimating diversity of model performances, research indicates that the application of computational methods employed by these metrics often exhibits blindness against same datasets. For instance, integrated metrics such as Nash–Sutcliffe efficiency and Kling–Gupta efficiency can be utilized for algorithm comparison, yet for actual model evaluation, direct metrics are still necessary to indicate [60,61,62,63]. The optimal applicability of direct metrics like root mean square error and mean absolute error in describing data is premised on their distributions conforming to normal and Laplacian distributions, respectively [64,65]. Furthermore, correlated coefficient (CC) is susceptible to the monotonicity and nonlinearity of two types of data [66,67]. Consequently, the performance of these metrics, when combined across different dimensions, often necessitates a comprehensive evaluation of their calibration suitability tailored to varied spatiotemporal requirements of LSM simulations [68,69].
Overall, due to the high short-term surface simulation biases and the high dimensionality of parameter space of Noah LSM, there is a lack of comparisons for the multi-objective metric methods targeted at SM-ST joint calibration to validate their ability in reducing spatial complexities of regional land simulations over ASAL. Therefore, to fill this gap, this study, based on the Noah LSM and its full parameter table, utilizes the PSO/SCE method and various SM-ST objective metrics, combined with intensive regional soil site observations, to explore the impacts of metric objective differences on the spatial heterogeneity and uncertainty of regional land surface parameters, calibration efficiency and effectiveness, as well as temporal and spatial errors in surface forecasting. And suggestions are provided for the regional ST modeling configuration, aiming to improve medium-range ST forecasting of semi-arid regions.
2. Methods
2.1. Calibration Schemes
2.1.1. Evolution Algorithms
Group and individual social behaviors are incorporated into the core PSO algorithm process [13,14,15,16,17,18]. The algorithm first randomly selects the scaled (or normalized) parameters () to generate the initial population including the individual position and the speed of position change, i.e., , and further obtain the local and global optimal position ( and ) through evaluating and sorting, where the superscript represents the time slice (Figure 1). Then proceed with following steps repeatedly till the stop criteria is met. Comparing individuals’ current and previous evaluation values to obtain the current local optima (); then sorting local optima to find the current global optima (); each particle’s speed and position are updated using and respectively, where and equal to 0.5 and 0.15, and equal to 0.5 and 0.15, equal to 0.9, , , and equal to 2.0, 2.0, and 10-7 [9]. Note that except , all the other parameters that can affect the generality of PSO were vaguely related to the dimension of the parameter space.
Community and induvial social behaviors are incorporated into the core SCE algorithm process [19,20,21,22]. The algorithm first randomly selects the scaled (or normalized) parameters () to generate the initial population, then further obtain initial local and global optima ( and ) through evaluating and sorting with marked orders. Then proceed with following steps repeatedly till the stop criteria is met. Evaluating and marking the individuals to reorganize the original population into communities (each community has points) ; through complex competitive evaluation (CCE) of each point where the triangular probability distribution , to determine the previous generation, and the new individuals from each community are mixed to form a new population; then reorder the individuals to form new communities and obtain the current local and global optima ( and ) (Figure 1). Also, and equal to 2 and , while the outer cycling number (), the internal and external iteration number of CCE ( and ) equal to , , and , respectively. Note that except and , all five parameters that can affect the generality of SCE were only related to the dimension of the parameter space.
Note that is scaled with equation as for both PSO and SCE. The totals individual number () of SCE and total particle number () of PSO both equal to . And for both SCE and PSO, the GSA stops when the evaluation contour () is greater than 105 Noah runs [9]. The equitable population size and stop criteria intend to reduce that the objective metrics’ impact could be affected by the algorithms themselves and ensure the relatively equitable investigation.
2.2.2. Optional Evaluator
The evaluator of the above-mentioned GSA algorithms used in our study is shown in Figure 2, which includes a fixed physical constraint and an optional objective function. The physical constraint formula () represents the soil moisture of the first two surface soil layers ( and ) only varies between the wilting point () and the soil moisture where transpiration stress begins () [9,24,39].
Under this constraint (), the unscaled parameters will drive the target model to run simulation once for evaluation based on the corresponding objective value, which can be selected based on the objective type (), and is a constant that varies between 1 and 8. Note that once is determined, the predefined corresponding objective metric or function () that measures the distances between simulation () and observation () is also determined at the very beginning.
2.2. Composited Metrics
For calibration schemes based on GSA, the parameter simulation problem in LSM is addressed by searching for the optimal parameters and/or simulations that minimizes or maximums the objective function (). Especially, has been extended into multi-dimensions, i.e., layers () and variables , to meet the multiple dimensional SM and ST objectives, and eight different metrics are investigated during present study (Table 1).
This study mainly examines fixed metrics composed of fundamental measures such as linear correlation coefficient () [66], Kling-Gupta efficiency () [10], absolute error () [65], Nash-Sutcliffe efficiency () [63], and root mean square error () [64] across different dimensions. Specifically, correlation coefficients (CCS), enhanced Kling-Gupta efficiencies (EKGE), mean absolute errors (MAES), Nash-Sutcliffe efficiencies (NSES), and root mean square errors (RMSES) represent the average of , , , , and across both the variable and layer dimensions. Additionally, the enhanced multiple objectives (EMO) integrate the average values of the measure that combines , , , and in the variable and layer dimensions.
Furthermore, since the surface variations of the topsoil layer could often determine the sublayer’s variations according to infiltration [32], therefore, the dimensional target of the upper layer is assumed to be the dominated Pareto solution, and the top layer’s objective that is larger (or smaller) than sublayers’ is taken as the current optimally maximum (or minimum) solution [57—59]. Consequently, the Pareto-dominant KGE (PKGE) and the Pareto-dominant multi objectives (PMO) indicates the dominated top layer’s value of EKGE and EMO respectively.
All the above-mentioned multi-objective metrics’ variable and layer dimensional number are 2 (e.g., SM and ST) and 4 respectively. CCS varies in [-1, 1]. EKGE and NSES both vary in (-∞, 1], EMO, MAES, and RMSES all vary in [0, +∞). PKGE varies in (-∞, 1], and PMO varies in [0, +∞). Therefore, the value of the metric determines the performance of the evaluator, and the direction of the metric determines the direction of the search, that is, continuously approaching the optimal value of the metric (i.e. the final ideal termination condition) towards the calibrated optimal solution.
2.3. Performance Evaluation
2.3.1. Parameter
During this study, parameter heterogeneity was defined as variations or sensitivities of land parameters across sites. Due to the immense dimensionality of parameter—site sensitivities, parameter relative sensitivities based on the two predefined limits of the parameter space are suggested, e.g., if more (fewer) sites met (failed to meet) a parameter's limit compared to others, indicating sites' relative sensitivity to that parameter within the limit's confidence [9,24]. Since the parameter relative sensitivities (or heterogeneity) are usually large while their homogeneity could be small (and thus be easily observed), here to qualify this and simplify metrics’ diversity investigation, we further propose the parameter numbers with low site sensitivities as homogeneity (H). Consequently, low H (>0) of this study indicates high heterogeneity of one metric quantitatively. Note that when all and no sites cross the parameter’s limits, H equals 0 and respectively.
The parameter’ spatial uncertainty is defined as the land parameter range and outlier against the sites, e.g., one parameter’s inter quartile range (IQR, >0), smaller parameter ranges and outlier numbers indicated fewer uncertainties and fewer unaccountable factors respectively [9]. Especially, to simplify different metrics’ effects on parameter uncertainty, the whole parameter space’s uncertainty is defined as the inter quartile range of all the IQR ensembles of different parameters (or IQRD) in the parameter space. Consequently, the IQRD’s inter quartile range and outlier indicate the quantitative parameter—uncertainties among metrics.
Especially, compared to SCE, the parameter number with less parameter uncertainties (PNL, >0) and the outlier number reduction of parameter uncertainties (ONR) in PSO are summarized in this study to qualify the justice that if the metrics’ parameter uncertainty is affected by GSA itself or not. As the heterogeneity and uncertainty differences of different metrics could account for the metric-informed method’s performance in solving parameter spatial complexities during SM-ST calibration, thereby, the metric with less parameter uncertainties and heterogeneity could meet the preferable LSM configuration demand in surface forecasting.
2.3.2. Objective
As the population position of on generation, e.g., the best (Pb) or medium (Pm, if non solution is met) locations that known as fitness against the number of LSM runs (or the convergence speed), could indicate the method’s performance in calibration efficiency, therefore, the better fitness values (e.g., larger EKGE values or smaller EMO values) with fewer LSM runs indicate more efficiency, where the success rate exploring evolution abilities is usually put alongside with.
Moreover, as the optimal objectives (e.g., the final EKGE or EMO values) could indicate method’s performance in calibration effectiveness, the larger or smaller optimal objectives that depend on the direction of predefined metrics indicate more effectiveness. Furthermore, since the kernel density distribution of optimal values across different sites demonstrates their spatial enrichment characteristics, the variation in enrichment between different algorithms (such as PSO or SCE) to a certain extent reflects their capacity to address the spatial disparity in SM-ST simulation.
2.3.3. Simulation
To simplify the spatial complexity among regional datasets, linear fitting between the observations (OBS) and simulations (SIM) for all sites is conducted [68]. The linear fitting’s slope (s) demonstrates the sensitivity of SIM to OBS, while its coefficient of determination (r2) or the goodness of fit demonstrates if the sensitivity or linear model is robust or not. Moreover, under the assumption of the normal distribution of the errors between SIM and OBS () of all sites, Gaussian fit of that are resampled with 100 bins 100 is conducted to generate at most two signals determining the main distribution characteristic., e.g., the amplitude (or frequency, f) and center (c) [69]. Here the compound feature of f and c that is closer to the normal distribution indicates the better performance or more consistent with the assumption.
The method’s performance in optimal simulation and forecast is qualified using the spatial differences and similarities of surface conditions among different datasets, e.g., ST and SM simulations or reanalysis, and observations, by the following equation:
where and represent the time and the site, respectively, and represent for the total number of stations. And smaller and/or high indicate better performance.
Meanwhile, the Taylor diagram [60,61,62,63] that could assemble the comprehensive statistics (i.e., standard deviation, root-mean-square difference, and correlation) in a temporal sequence between SIM and OBS was also created for comparison with the method’s skills. Usually, a smaller distance away from the reference location (OBS) indicated more skills. Note that the SIM datasets (30 min) were linearly interpolated into 3 h for a broad comparison with the land reanalysis.
In addition, aside from the uncertainties and heterogeneous requirements in surface prediction parameters (manifested as variations in calibration performance), addressing the precision demands inherent to surface prediction (evidenced by differences in calibration robustness), this study employs indicators such as KGE increment, reduction, and increment to clarify the performance of various SM-ST objectives in the parameter—simulation and/or calibration—prediction frameworks, aiming to explore the target metrics for both the optimal configuration of LSM and the maximum benefits of surface predictions.
3. Experiments
3.1. Model and Data
The Unified Noah LSM is created to better predict the effects of land surface processes on regional weather, climate, and hydrology. It is intended to comprehend the intricate biophysical, hydrological, and biogeochemical interactions between the land surface and the atmosphere at micro- and mesoscales (Figure 3A) [32]. The simple driver Noah LSM (version 3.4.1, https://ral.ucar.edu/model/unified-noah-lsm, accessed on 31 July 2024) has been recently extended into the muti-point applications over central Tibet [9].
The SM-ST observations that are firstly derived from the highest altitude soil moisture network in the world (Figure 3B, whose elevations are above 4470 m), which is constructed by the Institute of Tibetan Plateau Research, Chinese Academy of Sciences (ITPCAS) with four soil depths (i.e., 0–5, 10, 20, and 40 cm) [35], and are further assembled into the multi-site (i.e., 12) observations of the local warm season (i.e., covering from 1 April to 31 July 2014) over northwest Naqu city that has a typical semiarid climate by using simple quality control based time continuity correction (detailed described in Ref [9]). Also, the global land data assimilation system (GLDAS) [70] grid soil reanalysis data with resolutions of 3 h/0.25°is collected for broader comparison with the surface simulations during this study.
The gridded meteorological surface datasets that merging a variety of data sources are firstly developed by ITPCAS, with a 3 h interval (3 h) and a resolution of 0.1° × 0.1°, were produced by [71], and are further reassembled into the multi-site LSM forcing dataset by using the inverse distance-weighted quadratic spline interpolation method to drive the Noah LSM.
According to the observational soil and surface characteristics, the multi-site Noah LSM is configured with a 4-layer depth and 30-min runtime step, and the soil and vegetation types are mainly silt and grassland, while the slop type is assumed to be flat (e.g., 1). And the forcing time step (3 h) and screen height (10 m for winds and 2 m for temperature) for the LSM are the same as the input forcing data [9].
3.2. Experimental Description
Three month long warm-up run (covering the period from April 1 to July 1 of 2014) of the multi-site LSM, that initialized with the unobserved default parameters (i.e., the “General”, “Vegetation”, “Soil”, and partial “Initial” types) [32] and partially observational “Initial” parameters (i.e. SMC1-4 and STC1-4), is firstly conducted to obtain the default multi-site parameter tables including spatially distinguished “Initial” parameters for the following experimental runs [9]. Based on this, one-month long run ranged from July 1 to July 31 (or the control run briefed as CTR hereafter) is conducted as the referenced surface conditions resulted from the default LSM parameter table configuration.
The multi-objective metrics varied calibration runs that ranged from July 1 to July 15 are conducted to obtain the calibrated multi-site LSM models with metrics informed parameter tables and further investigate the metrics’ impact on calibration’s abilities in solving the spatial complexities of Noah LSM. Then the abovementioned various objective informed LSM models run from July 15 to July 31 to obtain the hopefully improved surface forecasts and further investigate metrics’ impact on surface forecast.
Therefore, the difference between CTR and calibration could account for the calibration performance, and the difference among different calibration runs could account for the metric’s impact on the calibration. Meanwhile, the difference between CTR and calibrated forecast runs could account for the calibrated models’ performances, and the difference among different calibrated forecast runs should account for the metric’s impact on surface forecast. Note that all objective metrics within both PSO and SCE algorithms are conducted to explore if the potentially improved surface forecast could be highly affected by the calibration algorithms themselves or not.
4. Results
4.1. Case Perspective
As land surface models utilize parameters and forcing inputs to prepare land surface forecasts, the issues of surface simulation and local application in typical semi-arid regions (i.e., rapidly applying calibrated parameters to surface forecasts) are exemplified here. To this end, a review of the spatiotemporal characteristics of the default forcing, initial parameters, and their overall simulation status across different periods, including control, simulation calibration, and forecast verification, is conducted to clarify the fundamental manifestations of the issues involved in this study.
4.1.1. Model Configure
The site averaged 3-h meteorological forcing values against time during the study period are shown in Figure 4 a~d. During July 2014, the diurnal variation in temperature () mostly ranged between 5 and 15 °C, with an extremely dry atmosphere whose relative humidity () values were mostly below 1%. The relatively low wind speed () generally varied between 0 and 6 m s–1, and the wind direction () was mostly dominated by southern flow (between 180° and 270°) from July 1 to July 10 and from July 16 to July 21, respectively, but the opposite in other periods. The incoming shortwave radiation () exhibited strong diurnal variation between 0 and 600 W m–2, and the incoming longwave radiation (L) varied between 250 and 350 W m–2. The pressure () was generally around 586 hPa and the maximum hourly precipitation () was about 5 mm h-1 on July 10.
The initial land parameters of all the sites (or default parameters) that needs calibration has shown great variety for the “Initial” types (Figure 4 e), and this is especially pronounced for the moisture-related parameters, i.e., the SMC and the SH2O. This should attribute to the differences in pre-experiment 3-month simulation of different sites. Furthermore, due to the lack of direct observations for other types of land surface parameters, they are configured using statistical data from optimization experiments based on limited benchmarks from the previous study (serving only as reference inputs for control experiments, consistent with conventional numerical model configurations) [9]. Therefore, in numerical operations, parameter variations among different stations mainly exist in the initial types. Consideration of multi-site calibration can account for the differences among stations with unobserved parameters under existing observational constraints, namely, the spatial heterogeneity and uncertainty of the parameter space. Consequently, the spatial heterogeneity of parameters (i.e., the sensitivity of commonly used parameters to different stations or the number of intersections of the same parameters at different stations in the parameter space) and the characteristics of uncertainty (such as the inter quartile range and outlier features of parameters at different stations) in relation to the differences in various optimization objectives are the key areas of focus for further investigation in this study.
4.1.2. Forecast Problem
The CTR simulations and observation datasets (OBS) for the surface layer are compared in Figure 4 e~f. For the whole experimental period, the linear fit for the surface soil moisture () exhibited a small increasing slope (about 0.21) with weak consistency, and the surface soil temperature () had a larger decreasing slope (about –0.45) with strong differences. Moreover, the linear fits of for the calibration and forecast periods were 0.22 and 0.15 respectively, and the linear fits of for calibration and forecast periods were -0.48 and -0.4 respectively. This indicates that the surface conditions of the forecast period were slightly better than those for calibration period. Generally, fits better than .
In addition, the Gaussian fits of the errors between observation and simulation () for whole experimental period had a sharp and narrow distribution, which was centered around 0.15 with a frequency of around 800, while the distributions of the calibration and forecast periods had centered around 0.16 and 0.13 , with the frequency of around 500 and 300 respectively. This indicates were mostly underestimated for all periods and this is more pronounced at the calibration period. Nevertheless, the of for different periods had shown bimodal distributions (Figure 4i), whose centers were located around -4 and 9 K (whole period), -5 and 9 K (calibration period), and -4 and 8 K (forecast period) respectively. This indicates were both under- and over-estimated, and the later were more pronounced. Generally, and were both underestimated.
In general, though in CTR exhibited better consistency with OBS than , the overall surface simulation underestimation of Noah LSM could be great for regional surface forecast applications. Note that either the ITPCAS forcing data sets or the improved heat-sensitive parameter Z0h (also known as CZIL) to improve with the Noah LSM over a surface near our study area [7], and the non-negligible biased and the spatially diversed parameter space in CTR indicated a more effective calibration in present study. Since multi-objective calibration can reduce these spatiotemporal errors through parameter identification to improve subsequent forecasts [9], the next focus is on how different target metrics affect the performance of calibration and forecasting.
4.2. Effects on Calibration
4.2.1. Optimal Parameters
Due to the significant spatial heterogeneity exhibited by most optimal parameters in PSO and SCE, this study conducted a statistical analysis of spatially homogeneous (or heterogeneous) parameters based on parameter type classifications (see Figure S1-1, briefed in Table 2). For the "Vegetation" type, except for the SCE scenario considering CCS, the number of homogeneity parameters in other scenarios is zero, indicating heterogeneity. Regarding the "Soil" type, the counts (Hp, Hs) of homogeneity parameters for PSO and SCE calibration schemes based on EKGE, EMO, MAES, and RMSES metrics are (1, 3), (2, 2), (1, 1), and (2, 1), respectively. For the "General" type, the (l1, l2) based on CCS, EKGE, EMO, MAES, and RMSES metrics are (1, A), (2, 2), (2, 2), (1, 1), and (1, 1), respectively. For the "Initial" type, the (l1, l2) based on EKGE, EMO, and MAES metrics are (4, 2), (3, 2), and (2, 1), respectively. Evidently, among all pairs, the spatial homogeneity of optimal parameters for all "Vegetation" types in PSO and SCE is relatively minimal, suggesting the strongest heterogeneity. Conversely, "Soil" and "General" types exhibit minimal spatial heterogeneity, while "Initial" types fall in the middle. Notably, QTZ and SBETA parameters consistently demonstrate homogeneity, below the parameter space threshold (0.03), across PSO and SCE schemes based on EKGE, EMO, MAES, and RMSES metrics.
Regarding the counts of homogeneity parameters in PSO and SCE schemes, when considering the disparities among metrics, we observe the following: for CCS, the counts are 1 and 40, respectively; for EKGE, both schemes yield 7; for EMO, the counts are 7 and 6; for MAES, 4 and 3; for NSES, 2 and none; both PKGE and PMO register none; and for RMSES, the counts are 5 and 2. Evidently, there exist substantial variations in the homogeneity or heterogeneity of parameters among calibration schemes based on different metrics. Notably, CCS exhibits the lowest parameter heterogeneity, followed by EKGE, then EMO, and subsequently MAES and RMSES. NSES displays relatively poor parameter heterogeneity, whereas PKGE and PMO manifest the highest degree of parameter heterogeneity.
In addition, the inter quartile ranges (IQR) of various parameters and the entire parameter space of PSO and SCE contributed by different metrics are shown in Figure 5. For PSO, the maximum IQR, which has about 4.8 of the parameter SNP in the “Vegetation” type, had the largest uncertainties, while the EMO made the largest contribution. However, the IQR, which is about 1.2 of the SBETA parameter in the “General” type, behaves oppositely, while EKGE, EMO and RMSES make the smallest contributions (Figure 5a). For SCE, the maximum IQR around 1.82 of the CZIL parameter in the “General” type has the largest uncertainties, while EMO has the largest contribution. Nevertheless, the IQR that is around 0.61 of the parameter CSOIL in the “General” type behaves conversely, while EKGE, EMO and RMSES make the smallest contributions (Figure 5b). In general, PSOs have achieved higher IQRs than SCEs on most metrics. And PSO and SCE achieved the lowest uncertainties of the parameters SBETA and CSOIL in the “General” type.
The Inter quartile Range (IQR) distribution of the global optimal parameter space for the PSO schemes across various metrics exhibits a broader and more scattered range compared to that of the SCE (Figure 5c). For PSO, the median sizes of the IQR distributions (IQRD) within the global optimal parameter space, ranked from highest to lowest, are PKGE > PMO > NSES > CCS > EMO > EKGE > RMSES > MAES. In contrast, for SCE, the order is PMO > PKGE > EKGE > EMO > MAES > RMSES > CCS. Furthermore, for PSO, the number of outliers in the IQRD is highest for EKGE with 3, followed by EMO and CCS with 2, while the rest of the metrics have 0 outliers. For SCE, EKGE and RMSES share the highest number of outliers at 2, followed by EKGE and MAES with 1 outlier each, and the rest are 0 (Figure 5d). In summary, significant differences exist in the IQRD of the global optimal parameter spaces across different metrics, with SCE exhibiting smaller IQRD but relatively more outliers. Notably, EKGE and EMO exhibit relatively large numbers of outliers in both PSO and SCE.
Furthermore, the PSO’s parameter spatial IQRs are compared with SCE in different types in Table 3, e.g., the parameter number with less uncertainties (PNL) and the outlier number reduction of parameters’ uncertainties (ONR) in PSO when compared to SCE. For the "Vegetation" type, all metrics are null except for the PNL value of EKGE, which is 2, while the ONR of all metrics is non-positive. For the "Soil" type, the PNL values are positive for all metrics except for CCS, NSES, and PKGE, which are null. The ONR values are positive for EKGE, EMO, PMO, and RMSES, while negative for the rest. Regarding the "General" type, all metrics exhibit positive PNL values except for NSES, PKGE, and PMO, whose PNL values are null. The ONR values are positive for EKGE, EMO, MAES, and RMSES, and negative for the others. In the "Initial" type, only EKGE and EMO have positive PNL values, with the rest being null. The ONR values are positive for all metrics except for CCS, PKGE, and PMO, which are non-positive. In summary, summing the PNL values across types, EKGE has the highest total (8), followed by EMO and RMSES (7), then MAES (5), with PMO and CCS having the lowest totals (1). PKGE has no PNL value. For the ONR values, EMO has the highest total (9), followed by EKGE (3), then RMSES (3), while PMO has the lowest (2). The rest of the metrics have negative ONR values.
In summary, for the SM-ST calibration of the same metric, SCE consistently achieves lower parameter uncertainty than PSO, albeit at the cost of relatively higher spatial heterogeneity. Specifically, in terms of parameter uncertainty, MAES in PSO and CCS in SCE exhibit the smallest metrics. As for parameter spatial heterogeneity, EKGE and EMO in PSO yield the smallest metrics, while SCE solely displays the smallest EKGE.
4.2.2. Effectiveness and Efficiency
Figure 6 shows the different metrics’ fitness (i.e., the best position of one population, Pb) curves of calibration, the median convergency position, and the median converged Noah run numbers of PSO () and SCE () for all sites. For CCS, both PSO and SCE had both sharply increased before 3,000 Noah runs, and both converged to 1 but at around 79,475 and 66,663 runs respectively. For EKGE, PSO and SCE have both sharply increased before 10,000 Noah runs but converge to 0.56 at 99,017 runs and 0.53 at 90,731 runs respectively. For EMO, PSO and SCE both decrease to 1 before 8,000 Noah runs but converge to 1 at 99,297 runs and 1.08 at 82,709 runs respectively. For MAES, PSO and SCE both quickly decrease to the range of 0.7-1.1 before 10,000 Noah runs but converge to 0.79 at 99,765 runs and 0.81 at 94,795 runs respectively. For NSES, PSO and SCE have both instantly reaching 1 at 187 runs, indicating the most rapid convergence among all metrics. However, for PKGE and PMO, since volatile finesses (e.g., who vary within and respectively) are found for all sites in each generation, nonstrict solutions can be observed. For RMSES, PSO and SCE both sharply decrease to 1 before 5,000 Noah runs but converge to 0.97 at 99,391 runs and 0.98 at 94,029 runs respectively.
Generally, except PKGE and PMO, other metrics of PSO have achieved better effectiveness as indicated their better fitness values, but with relatively worse efficiency as indicated their larger converged runs compared to those of SCE. The non solution performance for the metric PKGE and PMO of both PSO and SCE have indicated their requirements of more Noah runs in achieving convergence, or the potential failure of the Paetro dominated logic (i.e., that surface improvement likely improve the subsurface). For MAES, NSES, and RMSES, fitness curve of site C4 is found to be notably biased from (or worse than) that of other sites. Nevertheless, for all the metrics’ convergences, MAES has the largest range, and this could indicate the divergent convergence domain.
Figure 7 presents the success rate curves for calibration across various metrics. For CCS, PSO experiences a decline from 70% to 20% during the first 10,000 Noah runs, followed by a gradual decrease to near zero. In the case of EKGE, PSO initially shows a decline from 80% within the first 5,000 Noah runs, subsequently exhibiting two distinct patterns: fluctuations around 40% and 20%, respectively. For EMO, PSO drops from 80% to nearly 0% within the initial 25,000 Noah runs, with some stations subsequently exhibiting strong fluctuations between 0% and 80%. MAES follows a similar trend, with PSO declining from 80% to near 0% within the first 15,000 Noah runs, and subsequent intense fluctuations between 0% and 80% at certain stations. For NSES, PSO gradually decreases from 80% to 20% within the first 35,000 Noah runs and remains stable thereafter. PKGE and PMO exhibit similar behavior, with PSO slowly declining from 80% to 20% within the first 20,000 Noah runs and fluctuating slightly around 20% thereafter. SCE's performance in PKGE resembles that of CCS. In contrast, RMSES displays a fluctuating decline from 80% to 0% within the initial 20,000 Noah runs for PSO, followed by drastic fluctuations between 20% and 80%. However, SCE consistently demonstrates a rapid initial decrease from 80% to 20% across nearly all metrics, maintaining this level thereafter.
For all metrics, the search domain of SCE exhibits a consistent pattern, characterized by an L-shaped thin linear region. In contrast, PSO's search domain displays significant fluctuations and notable variations across different metrics (e.g., EKGE, EMO, MAES, RMSES), albeit with an overall larger area than SCE. This suggests that for most metrics, PSO demonstrates stronger evolutionary capabilities compared to SCE, which primarily contributes to PSO's slightly slower convergence rate compared to SCE.
Figure 8 presents the statistical performance of the optimal objectives across all stations for various metrics. For CCS, both PSO and SCE exhibit a concentrated distribution near 1, with PSO displaying a tighter clustering and an outlier at 0.973. In the case of EKGE, PSO and SCE concentrate around 0.58 and 0.53, respectively, with PSO showing a more focused distribution and an outlier at 0.34. For EMO, PSO and SCE are centered near 1 and 1.1, respectively, with PSO displaying a relatively dispersed distribution and an outlier at 1.5. MAES values for PSO and SCE are centered around 0.79 and 0.81, respectively, demonstrating similar distributions. For NSES, PKGE, and PMO, both PSO and SCE have concentrated distributions near 1, with NSES exhibiting a more tightly clustered distribution compared to the other two metrics. Finally, for RMSES, PSO and SCE are centered around 0.9 and 1.1, respectively, with SCE displaying a more focused distribution, and both having outliers at around 2.4.
It is evident that for the optimal solutions of PKGE and PMO, both PSO and SCE yield values of 1, indicating the absence of optimal solutions or the need for more time to locate them. In contrast, numerical optimal solutions were achieved for other metrics. Furthermore, while PSO consistently outperformed SCE in attaining better optimal solutions across almost all metrics, significant variations were observed in the enrichment levels of optimal solutions between PSO and SCE under different metrics. For instance, PSO surpassed SCE in CCS and EKGE, whereas SCE surpassed PSO in EMO, MAES, and RMSES. Notably, PSO and SCE exhibited similar performance in NSES. This underscores the disparate spatial variability characteristics of optimal solutions influenced by distinct metrics (whereby the enrichment levels of optimal solutions at different sites reflect the extent of spatial variability). Additionally, notable outliers were identified in PSO's performance within CCS, EKGE, and EMO metrics, while both PSO and SCE exhibited outliers in the RMSES metric. This indicates that for RMSES, unquantifiable factors within the spatial variability of optimal solutions are more pronounced, whereas for other metrics, PSO's performance relative to SCE is more significantly influenced.
In summary, apart from PKGE and PMO, for other metrics, PSO typically exhibits better optimal solutions, i.e., enhanced effectiveness, compared to SCE, albeit at the cost of relatively lower efficiency. Notably, for CCS, EKGE, and RMSES, the optimal solutions obtained by PSO demonstrate higher kernel densities than those by SCE. Conversely, for EMO and MAES, the performance trend is reversed.
4.2.3. Optimal Simulation
Figure S2-1 presents linear fitting (s, r²) between simulations and observations of and under varying metrics. For , PSO s (in descending order) are EMO, EKGE, RMSES, MAES, PMO, NSES, CCS, PKGE, with r² values also descending from EMO to PKGE. In contrast, SCE slope (s) are EMO, PMO, EKGE, MAES, PKGE, NSES, RMSES, CCS, with r² following a similar but slightly different descending order. For 's linear fitting (Figure S2-1-2), PSO s are EKGE, EMO, MAES, RMSES, CCS, NSES, PKGE, PMO, while r² values show a distinct ordering: PMO, followed closely by EMO/PKGE, then MAES/RMSES/NSES, EKGE, and finally CCS. SCE fitting for exhibits a different ordering for s (EKGE, EMO, CCS, RMSES, MAES, NSES, PMO, PKGE) and r² values (PKGE, PMO, NSES, EKGE, EMO, RMSES, with CCS and MAES closely grouped).
Generally, for , except for NSES, PKGE, and PMO metrics, both PSO and SCE exhibit negative s values, while the rest are positive (Table 4). This indicates that most linear relationships between calibrated simulations and observations are positively correlated, which aligns with the improvement objectives of this study. Specifically, for EMO and EKGE, the s values of PSO (SCE) in the calibration of and are 0.96 (0.83) and 0.18 (0.23), respectively, showcasing the optimal calibration performance (Figure 9). Furthermore, it is noteworthy that for , the highest r² value of 0.11 is comparable to the lowest r² value observed in (PKGE), implicitly suggesting a greater challenge in modeling .
The Gaussian fitting, i.e., center (frequency) as c(f) with units of (1), of for in Figure S2-2-1 reveals: CTR’s are widely distributed, peaking at ~0.15 (f=297). CCS, PSO, SCE errors span widely around -0.04, 0.11 (f≈350, 295). EKGE's PSO, SCE errors narrowly center at 0 (f≈1276, 608). EMO's PSO, SCE errors narrowly peak at 0, 0.01 (f≈1178, 700). MAES's PSO, SCE errors widen slightly at 0.01, 0.02 (f≈344, 416). NSES's PSO, SCE errors are wide at 0.05 (f≈274, 230). PKGE's PSO, SCE errors widely center at 0.08, 0.11 (f≈322, 325). PMO's PSO, SCE errors narrowly peak at 0.02, 0.03 (f≈480, 444). RMSES's PSO, SCE errors narrowly center at -0.02, 0 (f≈426, 296). Moreover, The Gaussian fitting, i.e., center (frequency) as c (f) with units of K (1), of OBS-SIM for (Figure S2-2-2) shows: CTR errors have a wide bimodal dist. centered at ~7.1, -3.8 (f≈192, 134). CCS, PSO, SCE errors widely center at ~2.3, 1.1 (f≈216, 167). EKGE's PSO, SCE errors widely center at ~1.3, 2.5 (f≈200, 203). EMO's PSO, SCE errors center at ~0.85, 1.23 (f≈170, 207). MAES's PSO, SCE errors center at ~-0.06, 0.88 (f≈200, 230). NSES's PSO, SCE errors widely center at ~5.86, 5.03 (f≈169, 213). PKGE's PSO, SCE errors widely center at ~4.91, 5.01 (f≈237, 152). PMO's PSO, SCE errors widely center at ~6.1, 5.19 (f≈300, 224). RMSES's PSO, SCE errors center at ~0.16, 1.29 (f≈200, 206).
In summary, for of , EKGE's performance in both PSO and SCE is closest to a normal distribution, whereas for that of , MAES exhibits the closest resemblance to normality (Figure 10), with EKGE performing relatively poorly (Table 5). This underscores the significant influence of metric discrepancies on calibration simulation errors, contingent upon distinct calibration objectives. Furthermore, excessively wide peaks with low frequencies in unimodal distributions (e.g., CCS, NSES, PKGE, and PMO) indicate the dispersed fitting distribution, potentially necessitating the multimodal (e.g., more than two peaks) fitting. Conversely, bimodal distributions characterized by narrower peaks may call for a single-peak fitting centered around the modes.
Figure 11a depicts temporal () variations for . CTR's is generally largest, 0.15 (decreasing during July 5th and 10th rainfalls), with a slight upward trend. For CCS, PSO's 0.15 increases slightly, while SCE's fluctuates around 0.07. EKGE and EMO show PSO(SCE) RMSEs of 0.01(0.03) and 0.01(0.02), respectively, both trending downward. MAES's PSO/SCE 0.04, both declining. NSES's around 0.07, up trending. PKGE's PSO(SCE) 0.12(0.1), up trending. PMO's PSO decreases from 0.1 to 0.05, SCE's 0.07, slightly down. RMSES's PSO(SCE) 0.04(0.05), both declining. Moreover, Figure 11b illustrates the overall RMSES distribution for . Median ranking from highest to lowest for PSO: CCS (0.13) > PKGE (0.12) > NSES (0.08) > PMO (0.07) > RMSES (0.039) > MAES (0.038) > EMO (0.018) > EKGE (0.017); for SCE: PKGE (0.1) > CCS (0.09) > NSES (0.085) > PMO (0.065) > RMSES (0.056) > MAES (0.039) > EKGE (0.03) > EMO (0.02). Notably, EKGE and EMO exhibit the lowest median for PSO and SCE, respectively, whereas CCS and PKGE have the highest.
Figure 11c depicts temporal variations in spatial correlation coefficients () for simulations. CTR's significantly drops Jul 5-6 (0.5 to -0.6), fluctuating at ~0.2 otherwise. CCS: PSO's stable at -0.5, SCE increases Jul 5 (-0.4 to 0.5), fluctuating -0.2. EKGE: PSO 1, SCE 0.8. EMO: Both are ~1. MAES: PSO increases (0.2 to 1), SCE initially declines (0.4 to 0), then ~0.2. NSES: PSO ~0.7, drops post-Jul 10 to ~0.5; SCE ~0.2. PKGE: PSO ~0.45, sharp drop Jul 5 to ~-0.4; SCE -0.4 to unspecified, sharp drop, ~-0.3. PMO: PSO 0.6, sharp drop Jul 6 to -0.5, rises to 0.2; SCE 0.8, drops to 0, rises to 0.4. RMSES: PSO increases (0.5 to 0.8), stabilizes ~0.8 post-Jul 4; SCE ~0.45, declines Jul 4-6, rises to ~0.26. EMO and EKGE consistently outperform MAES for PSO and SCE in , with other metrics displaying varied trends. Moreover, Figure 11d illustrates the overall distribution for . Median ranking from highest to lowest for PSO: EMO > EKGE > MAES > RMSES > NSES > PMO > PKGE > CCS; for SCE: EKGE > EMO > MAES > PMO > PKGE > NSES > RMSES > CCS. Notably, EMO and EKGE exhibit the highest median for PSO and SCE, respectively, whereas CCS have the lowest.
For , CTR's shows a marked diurnal variation, averaging 8K fluctuations (Figure S2-3-1). Due to overlapping diurnal error ranges, its performance complexity surpasses . Notably, NSES, PKGE, PMO peak >14K (CTR's max), indicating inferiority (Figure 11e). Conversely, MAES and RMSES peak at 8K, surpassing CTR. EKGE and EMO, excluding initial days, also peak near 8K, outperforming CTR. Median (K) ranking from highest to lowest yields the following order for PSO: PMO (7.5) > PKGE (6) > NSES (5.8) > CCS (4) > EKGE (3.5) > MAES (2.8) > RMSES (2.5) > EMO (2.48); and for SCE: PKGE (6.1) > PMO (5.8) > NSES (5.6) > CCS (3.6) > EKGE (3.3) > MAES (2.9) > RMSES (2.7) > EMO (2.5) (Figure 11f). In both PSO and SCE, EMO exhibits the lowest median , whereas PMO and PKGE respectively possess the highest.
Furthermore, for , CTR's varies from -0.5 to 0.7, showing distinct diurnal patterns (Figure 11g). Overlapping diurnal error ranges complicate performance compared to (Figure S2-3-2). CCS and EKGE's max < 0.7 (CTR's max), indicating inferiority. NSE, PKGE, PMO max rival CTR, but min > -0.5, outperforming CTR. EMO, MAES, RMSE max ~0.8, exceeding CTR. Hence, for , performance ranks EMO, MAES, RMSE best, followed by NSE, PKGE, PMO; CCS, EKGE perform bad. Moreover, Figure 11h illustrates the overall distribution for . Median ranking from highest to lowest for PSO: EMO > MAES > RMSES > NSES > PMO > PKGE > EKGE > CCS; for SCE: EMO > RMSES > CCS > EKGE > MAES > PKGE > PMO > NSES. Notably, EMO exhibit the highest median for both PSO and SCE, whereas CCS and NSES have the lowest.
In summary, for , EKGE and EMO exhibit the lowest median and the highest median for PSO and SCE, respectively, whereas CCS and PKGE have the highest for PSO and SCE, respectively, and CCS have the lowest for both. For , in both PSO and SCE, EMO exhibits the lowest median , whereas PMO and PKGE respectively possess the highest; EMO exhibit the highest median for both PSO and SCE, whereas CCS and NSES have the lowest. Generally, EKGE and EMO have the best and performances of for PSO and SCE respectively, while EMO has the best and performances of for both.
4.3. Effects on Forecast
4.3.1. Linear and Gaussian Fitting
Figure S3-1 illustrates disparities in linear fitting (s, r2) between SIM and OBS for and across metrics. For 's linear fit (Figure S3-1-1), PSO s (descending): EKGE > EMO > MAES > RMSES > NSES > PMO > CCS > PKGE; r² order matches. For SCE, s: EMO > EKGE > PMO > MAES > NSES > RMSES > CCS > PKGE; r² differs: EKGE > EMO > MAES > PMO > NSES > PKGE > RMSES > CCS. For 's fit (Figure S3-1-2), PSO s: MAES > RMSES > EMO ≥ EKGE/CCS > NSES > PKGE > PMO; r²: PMO > PKGE > EMO > RMSES ≥ MAES/NSES > EKGE > CCS. SCE's s: MAES/CCS > RMSES > EMO/EKGE > NSES > PMO > PKGE; r²: PKGE > RMSES/PMO > MAES/EMO > NSES > CCS/EKGE.
Generally, in addition to NSES, PKGE, PMO in , and PKGE in , both PSO and SCE exhibit positive s values (Table 6). This indicates that most linear relationships between validation forecasts and observations are positively correlated, which aligns with the improvement objectives of this study. Specifically, for EKGE and MAES, the s values of PSO (SCE) in the validation of and are 0.98 (0.84) and 0.14 (0.15), respectively, showcasing the best forecast performance (Figure 12). Furthermore, it is noteworthy that for , the highest r² value of 0.1 is much smaller than the highest r² value observed in (EKGE), implicitly suggesting a greater challenge in forecasting .
The Gaussian fitting (c (f)) of for (Figure S3-2-1) reveal: CTR centered at 0.19 (f=272); CCS, PSO, SCE at 0.15, 0.07 (f=189, 225); EKGE, PSO, SCE narrowly at 0 (f=383, 363); EMO, PSO, SCE at 0 (f=416, 359); MAES, PSO, SCE at -0.01, 0 (f=359, 284); NSES, PSO, SCE at 0.06, 0.05 (f=343, 322); PKGE, PSO bimodal at 0.13, 0.04 (f=234, 220), SCE bimodal at 0.16, 0.06 (f=199, 365); PMO, PSO, SCE widely at 0.01, 0.04 (f=367, 323); RMSES, PSO, SCE at -0.02, 0.01 (f=293, 326). Similarly, for (Figure S3-2-2): CTR bimodal at 7.28, -3.57 (f=211, 160); CCS, PSO, SCE widely at 3.2, -0.38 (f=187, 181); EKGE, PSO, SCE at -0.09, 3.39 (f=143, 189); EMO, PSO, SCE at -1.41, -0.98 (f=175, 148); MAES, PSO, SCE at 0.49, 0.29 (f=181, 206); NSES, PSO, SCE widely at 5.81, 4.56 (f=204, 210); PKGE, PSO, SCE widely at 4.9, 5.7 (f=214, 217); PMO, PSO, SCE widely at 6.17, 5.47 (f=221, 187); RMSES, PSO, SCE at 0.55, 0.32 (f=194, 198).
Generally, for of , EMO’s and EKGE's performances in both PSO and SCE are closest to the normal distribution, whereas for that of , EKGE in PSO and MAES in SCE exhibit the closest resemblance to normality (Figure 13), with EKGE performing relatively poorly (Table 7). This underscores the significant influence of metric discrepancies on forecast errors. Furthermore, excessively wide peaks with low frequencies in unimodal distributions (e.g., CCS, NSES, PKGE, and PMO) indicate the dispersed fitting distribution, potentially necessitating the multimodal (more than two peaks) fitting.
4.3.2. Spatial Difference and Similarity
Figure 14a depicts the temporal () variations for . CTR's is largest (~0.15), fluctuating with a dip on Jul 24. CCS's PSO RMSES ranges around 0.13, trending up, while SCE's remains stable at 0.1. EKGE’s and EMO's PSO/SCE (~0.02 / 0.01) and (~0.02), both trends slightly up. MAES's are ~0.04. NSES's hover at 0.07, declining slightly. PKGE's is ~0.12. PMO's decline from ~0.07 to 0.05. RMSES's PSO/SCE are ~0.04/0.06. Furthermore, Figure 14b illustrates the overall distribution for . Median ranking from highest to lowest for PSO, CCS(0.12) > PKGE(0.11) > NSES(0.07) > PMO(0.05) > MAES(0.04) > RMSES(0.036) > EMO(0.028) > EKGE(0.02); for SCE, PKGE(0.11) > CCS(0.1) > NSES(0.07) > RMSES(0.052) > PMO(0.05) > MAES(0.04) > EMO(0.02) > EKGE(0.019). Notably, EKGE has the lowest median for both PSO and SCE, whereas CCS and PKGE have the highest, respectively.
Figure 14c shows temporal variations for . CTR's significantly drops from July 20th to 21st (0.1 to -0.7), stable at ~0.2 otherwise. PSO and SCE in CCS hover around -0.3. EKGE's PSO remains ~0.8, SCE jitters ~0.3. EMO's ~1 for both methods. MAES's PSO ~0.8, declining gradually; SCE's drops from 0.4 to 0 (July 5th), rises slightly to ~0.2. NSES's PSO starts at 0.7, dropping to ~0.5 post-July 10th; SCE jitters ~0.2. PKGE's PSO CCS ~0.45, sharply drops to ~-0.4 post-July 5th; SCE initially jitters ~-0.4, spikes, then jitters ~-0.3. PMO's PSO CCS starts ~0.6, sharply drops to ~-0.5 (July 6th), rises to ~0.2; SCE similar, starts ~0.8, drops to 0, rises to ~0.4. RMSES's PSO jitters, rises (0.5 to 0.8), stabilizing ~0.8 post-July 4th; SCE starts ~0.45, drops to ~0 (July 4th-6th), rises, fluctuating ~0.26. For 's , PSO and SCE consistently rank EMO > EKGE > MAES; others exhibit unstable/inferior performance. Figure 14d depicts the overall distribution for . Ranking metrics by the median , from highest to lowest for PSO: EKGE > EMO > MAES > RMSES > NSES > PMO > PKGE > CCS; for SCE: EKGE > EMO > MAES > PMO > NSES > RMSES > PKGE > CCS. Notably, EKGE has the highest median for both PSO and SCE, while CCS and PKGE have the lowest, respectively.
Figure 14e displays temporal variations for . CTR's exhibits pronounced diurnal fluctuations 10K. Metric performances are intricate due to overlapping diurnal error amplitudes (Figure S3-3-1). NSES, PKGE, PMO peak > 15K (CTR's max), indicating inferior performance. EMO, MAES, RMSES max < 7K, superior to CTR. CCS, EKGE extreme 8K (except July 1-2), also outperform CTR. For , hierarchically show EMO, MAES, RMSES best, followed by CCS, EKGE, with NSES, PKGE, PMO worst. Moreover, Figure 14f shows the distribution for , ranked by median . For PSO: PMO (7.5) > PKGE (6.9) > NSES (6.6) > CCS (4) > EKGE (3) > RMSES (2.9) > MAES (2.7) > EMO (2); for SCE: PKGE (7) > PMO (6.8) > NSES (6.4) > CCS (3.8) > EKGE (3.3) > MAES (2.7) > RMSES (2.5) > EMO (2.3). EMO has the lowest median for both methods, whereas PMO and PKGE have the highest for PSO and SCE, respectively.
Figure 14g presents temporal variations for , with CTR's displaying strong diurnal fluctuations between -0.7 and 0.7. Overlapping diurnal error amplitudes complicate performance compared to (Figure S3-3-2). Notably, EMO, MAES, RMSE metrics exceed CTR's extremes, demonstrating superior performance. Moreover, Figure 14h depicts the overall CCS distribution for . Ranking metrics by the median CCS, from highest to lowest for PSO: EMO > RMSES > MAES > NSES > PMO > PKGE > CCS > EKGE; for SCE: RMSES > CCS > EMO > MAES > EKGE > NSES > PKGE > PMO. Notably, EMO and RMSES has the highest median for PSO and SCE, respectively, while CCS and PMO have the lowest, respectively.
In summary, for , EKGE has the lowest median and the highest median for both PSO and SCE, whereas CCS and PKGE behave oppositely, respectively. For ST05cm, EMO has the lowest median for both methods, whereas PMO and PKGE have the highest for PSO and SCE, respectively; EMO and RMSES has the highest median for PSO and SCE, respectively, while CCS and PMO have the lowest, respectively. Generally, EKGE have the best and performances of for both PSO and SCE, while EMO and RMSES has the best and performances of for PSO and SCE, respectively.
4.3.3. Surface States Intercomparison
Figure 15 presents Taylor Diagram plots of calibrated and CTR simulations of during the forecast period, compared with observations and/or GLDAS data, across various metrics. For the comparison of simulations with observations (Figure 15a), CTR exhibits a root mean square difference () greater than 0.02 , surpassing other simulated metrics and GLDAS. However, the correlation coefficient () between CTR and observations is above 0.5, outperforming other simulations and GLDAS except for EKGE and EMO metrics. Additionally, CTR's standard deviation () reaches approximately 0.03 , significantly higher than that of other simulated metrics and GLDAS. Thus, EKGE and EMO metrics, when applied in PSO and/or SCE, effectively improve the simulation of . In the comparison of with observations (Figure 15b), CTR, GLDAS, and multiple simulations demonstrate no skill. Nevertheless, like , simulations using EKGE and EMO metrics consistently yield the lowest and , as well as the highest among all evaluated metrics.
Furthermore, for the comparison of sensible heat flux (HFX) with GLDAS (Figure 15c), CTR displays higher and lower than other simulated metrics, albeit with a relatively low . This suggests that while most other metrics' HFX simulations outperform CTR in terms of and , their STD values are relatively increased, with EKGE and EMO ranking top two in both PSO and SCE for . In contrast, for the comparison of latent heat flux (LH) with GLDAS (Figure 15d), CTR exhibits lower RMSD and higher than other simulated metrics, but with a relatively high . Notably, CTR's LH simulation surpasses other metrics in both and . Specifically, EKGE and EMO rank top two for both and in both PSO and SCE, which is a notable contrast to the findings for HFX.
In summary, compared with observations, the and simulations of EKGE and EMO exhibit higher Taylor diagram skill (TDS) in both PSO and SCE, significantly outperforming CTR. In contrast, when compared with GLDAS reanalysis, the TDS of HFX simulations for all metrics in both PSO and SCE are superior to CTR, whereas the performance of LH simulations is the opposite. Evidently, the enhancement of surface SM and ST simulations often yields more divergent surface flux simulation results, indicating the high complexity of modeling surface states and fluxes in arid regions.
4.4. Configure and Benefit
Figure 16 compares the parameter ranges of the "best metric’s simulations" between PSO and SCE, alongside the KGE values of various metrics for surface soil moisture simulations against observations. It is observable that in PSO, the optimal parameter range of EMO is larger than that of EKGE, whereas the opposite holds true for SCE, where EMO's optimal parameter range is smaller than EKGE's (Figure 16A). The KGE values of from optimal simulations of different metrics indicate that in PSO, EKGE achieves the highest KGE value, whereas in SCE, EMO attains the peak (Figure 16a). For , however, EKGE's optimal simulation yields the highest KGE value in both PSO and SCE (Figure 16b). In terms of forecasted , EKGE consistently produces the highest KGE values in both PSO and SCE. Conversely, for , CCS achieves the highest KGE values in both PSO and SCE, with EKGE following closely.
Figure 17 illustrates the changes in reductions and increases of the simulations for various metrics and CTR during the calibration and validation periods. For , during the calibration period, most metrics, except CCS, exhibit a reduction in compared to CTR, with EMO and EKGE showing the most significant improvements (Figure 17a), which is also reflected in their highest (Figure 17e). During the validation period, EKGE and EMO stand out among the metrics, excluding CCS and PKGE, in terms of reduction (Figure 17b), again accompanied by the highest (Figure 17e). For , during the calibration period, reductions relative to CTR are observed for most metrics except PKGE, PMO, and NSES, with MAES, RMSES, and EMO demonstrating the most pronounced improvements (Figure 17c), which also correspond to the highest (Figure 17g). Similarly, during the validation period, reductions are observed for most metrics except PKGE, PMO, and NSES, with MAES, RMSES, and EMO continuing to show the most significant improvements (Figure 17d), accompanied by the highest (Figure 17h).
In summary, the parameter uncertainty range of EMO is slightly smaller than that of EKGE in both PSO and SCE, but the two metrics exhibit a trade-off in terms of reduction and increase during the forecast and calibration periods for and . Specifically, EKGE shows the greatest reduction for both calibration and forecast periods of , and the largest increase during the forecast period of . Notably, EMO demonstrates the largest reduction and increase for both forecast and calibration of , while EKGE performs poorest. This is notably different from the clear advantage of EKGE observed in our previous studies [9], which can be attributed to the use of four layers in all objective metrics in this study. This suggests that the EKGE metric with different vertical dimensions (number of layers) can significantly impact the improvement capability of forecasts. Additionally, the failure of PKGE and PMO during the forecast and calibration of (e.g., even inferior to CTR) indicates the ineffectiveness of using surface-layer-dominated Pareto objectives and highlights the limitations of adjusting subsurface simulations through improvements in surface simulations within Noah LSM.
5. Discussion
Though a comparative analysis of eight kinds of the introduced multi-objective calibration has effectively portrayed the multifaceted impacts of metric differences on the joint SM—ST calibration under the month—long calibration—prediction framework, offering insights for ST modeling and prediction in semi-arid regions, this study is nevertheless subject to limitations: 1) the imperfect datasets such as the unavailability of the site scale forcing data [35,71], which may lay certain spatial effects on the simulations; 2) the absence of solutions for calibration schemes based on the dominant Pareto metrics (e.g., PKGE and PMO) (Figure 6), which might indicate a need for extended search time or fewer physical constraints.
Significant heterogeneities in optimal parameters are observed across different objective metrics (Figure S1-1 and Table 2), while within the same metric, the heterogeneities are relatively closer across different algorithms (e.g., PSO and SCE), indicating that the parameter heterogeneities are largely determined by the choice of metrics rather than the algorithms themselves. Furthermore, for all metrics, the uncertainty of optimal parameters associated with PSO is higher than that of SCE (Figure 5), consistent with our previous findings [9]. Additionally, the "Vegetation" type exhibits a general pattern of null values (e.g., NA) in PNL and non-positive values in ONR compared to other types (Table 3), suggesting higher relative uncertainty and more unexplainable factors within the "Vegetation" type parameters. In particular, the EKGE metric comprehensively performs best in reducing spatial heterogeneities and uncertainties in LSM parameters compared to other metrics.
Moreover, significant disparities exist in the fitness curves of identical algorithms with different metrics, whereas the differences are relatively minor in the fitness curves of distinct algorithms with the same metric (Figure 6), indicating that metric variations exert a more profound influence on the convergence efficiency of calibration than the algorithm itself. Notably, the rapid convergence observed in CCS and NSES, as well as the non-convergence in PKGE and PMO, likely signify the presence of locality and sub-optimality in the numerical solutions [50]. Furthermore, substantial variations in success rates across different metrics are evident in PSO, whereas minimal changes are observed in SCE (Figure 7), suggesting that the evolutionary capability of the PSO algorithm is constrained by metric differences. Analogous to convergence efficiency, the degree of enrichment in numerical solutions also exhibits greater disparities between identical algorithms with different metrics than between distinct algorithms with the same metric (Figure 8), highlighting that metric variations have a more profound impact on the validity of numerical solutions compared to the algorithm itself.
There are considerable discrepancies among different metrics in addressing the spatial complexity of land surface modeling (e.g., fitting, errors, and similarities of land surface states during calibration and forecasting), and they are sensitive to algorithmic variations (Section 4.3). Specifically, the EKGE metric and the EMO metric exhibit the best overall performance for and , respectively (Figure 9-14). However, the EKGE metric's performance for is inferior to our previous study [9], which can be attributed to the consideration of subsurface soil in the SM-ST target dimension, also demonstrating significant vertical variability in regional land surface modeling targets [36,49]. Although the EMO metric is not the overall best for , its relatively balanced performance with no notable weaknesses can mitigate this issue to some extent (Figure 16-17).
Overall, the selection of calibration objectives must be carefully considered due to the profound impact of metric differences on the spatial heterogeneity of parameters in calibration, the efficiency and effectiveness of calibration, and the spatial complexity of surface conditions. Especially, the establishment of an automated soil observation network at regional stations, with the entire SM—ST sates serving as the joint calibration objective, can enhance operational land surface applications. Considering the less restrictive nature of EMO that combine multiple metrics in various applications, the benefits are relatively more robust. Future research should strengthen the regional application of EMO to improve the representation of surface characteristics in regional weather and climate numerical forecasting.
6. Conclusions
The surface conditions are crucial for both regional hydrology and weather. Using ITPCAS dataset from April 1 to July 31, 2014, the present study investigates the performance of various multi-objective metrics that combined with the multi-parameter tables as varied criteria of GSA on enhancing the Noah LSM calibration and forecasting. Comprehensive comparisons are conducted among these enhancements such as the optimal land parameters, objectives, and simulations, and the objective-informed forecasts that brought by these different metrics, to identify the effect of metric’s diversity on SM-ST calibration and surface forecast. Results have shown that:
The case study presented herein can be succinctly characterized as a configuration-forecasting problem. Initially, in terms of model configuration, the forcing manifestations encompass locally elevated surface temperatures (>5°C), low relative humidity (<1%), feeble wind speeds (<5m s-1), a shift in wind direction from south to north, low atmospheric pressure (586hPa), and minor hourly rainfall intensities (<5mm h-1). Subsequently, within the default model parameter configuration, significant spatial disparities emerge in the parameter space due to the static parameters being set as the globally optimal defaults, while the initial parameters are derived from forecasts spanning the preceding three months. The surface forecasting challenge manifests in the form of consistent simulations but poor simulations. Considering the variations in default model parameters across the calibration and validation (or forecast) periods, these periods are analyzed separately. Specifically, during the calibration and forecasting periods, the slope (s) and goodness of fit (r²) for the simulations under the default parameter configuration are 0.22/0.14 and 0.15/0.05, respectively, with Gaussian fits of their errors exhibiting positive skew distributions centered at 0.16 and 0.13 m³.m-³. In contrast, the s/r² values for the ST05cm simulations are -0.48/0.17 and -0.4/0.15, with their errors displaying broader bi-modal distributions.
Firstly, for the optimal parameters of SM-ST calibration of the same metric, SCE consistently achieves lower parameter uncertainty than PSO, albeit at the cost of relatively higher spatial heterogeneity; specifically, in terms of parameter uncertainty, MAES in PSO and CCS in SCE exhibit the smallest; as for parameter spatial heterogeneity, EKGE and EMO in PSO yield the smallest, while EKGE in SCE displays smallest. Moreover, apart from PKGE and PMO, for other metrics, PSO typically exhibits better optimal solutions, i.e., enhanced effectiveness, compared to SCE, albeit at the cost of relatively lower efficiency; notably, for CCS, EKGE, and RMSES, the optimal solutions obtained by PSO demonstrate higher kernel densities than those by SCE; conversely, for EMO and MAES, the performance trend is reversed. Furthermore, EMO’s and EKGE’s PSO (SCE) calibration of and with the maximum upward slope as 0.96 (0.83) and 0.18 (0.23), respectively, showcase the optimal linear fitting (Figure 9); for of , EMO’s and EKGE's performances in both PSO and SCE are closest to the normal distribution, whereas for that of , EKGE in PSO and MAES in SCE exhibit the closest resemblance to normality (Figure 13); EKGE and EMO have the best and performances of for PSO and SCE respectively, while EMO has the best and performances of for both.
EKGE’s and MAES’s PSO (SCE) and forecasts with the maximum upward slope as 0.98 (0.84) and 0.14 (0.15), respectively, showcase the best linear fitting (Figure 12). For of , EMO’s and EKGE's performances in both PSO and SCE are closest to the normal distribution, whereas for that of , EKGE (in PSO) and MAES (in SCE) exhibit the closest resemblance to normality (Figure 13). EKGE have the best and performances of for both PSO and SCE, while EMO and RMSES has the best and performances of for PSO and SCE, respectively. Furthermore, compared with observations, the and simulations of EKGE and EMO exhibit higher Taylor diagram skill (TDS) in both PSO and SCE, significantly outperforming CTR. In contrast, when compared with GLDAS reanalysis, the TDS of HFX simulations for all metrics in both PSO and SCE are superior to CTR, whereas the performance of LH simulations is the opposite.
The parameter uncertainty range of EMO is slightly smaller than that of EKGE in both PSO and SCE, but the two metrics exhibit a trade-off in terms of reduction and increase during the forecast and calibration periods for and . However, due to the failure of vertical dimension expansion, EKGE performs poor in simulation improvement. Evently, EMO showcases the greatest benefit in surface forecast improvement among all metrics and with the hopeful low parameter uncertainties, which shows the most promising application performance.
Specifically, in the SM-ST calibration of Noah LSM, for optimal parameters, MAES (in PSO) and CCS (in SCE) exhibit the lowest levels of uncertainty; EKGE/EMO (in PSO) and EKGE (in SCE) yield the smallest spatial heterogeneity, while other metrics demonstrate nearly irregular or non-discriminatory patterns. For optimal solutions, apart from Pareto dominance-based metrics (e.g., PKGE and PMO), other metrics do not alter the generality of GSA algorithms (such as effectiveness and convergence domain). Notably, although CCS and NSES can accelerate GSA convergence, their impacts on model calibration and prediction remain highly uncertain or even negative. Furthermore, regarding optimal modeling performance for calibration and forecast compared to observations, substantial variations exist among different metrics, among them, EMO and EKGE yield the best modeling abilities, while EKGE and MAES exhibit the best modeling abilities, respectively. In terms of observation-simulation error fitting, EMO and EKGE in both perform optimally, while EKGE (in PSO) and MAES (in SCE) in demonstrate the best performance. For optimal spatial error and similarity performance in calibration and forecast periods, EKGE’s performs best, while EMO’s excels.
Overall, the metrics, apart from their impact on GSA itself (e.g., convergence), could significantly influence the performances (including parameters, numerical solutions, and simulations) in SM-ST calibration and prediction. Furthermore, the vertical dimensionality of the objective metrics in this study notably affects the modeling of , indicating that the improvement of surface states through metrics based on subsurface soil conditions is not absolute. Additionally, since the optimal performance of different metrics in individual or joint modeling of and is not entirely consistent, the selection criteria for metrics in GSA applications are not unique. Specifically, EMO outperforms others in calibrating and predicting the surface layer states. These findings could enhance our understanding of the spatial complexity of parameters and simulations in surface forecasting in semi-arid regions, thereby facilitating the improvement of regional surface forecasting.
Supplementary Materials
The following supporting information can be downloaded at the website of this paper posted on Preprints.org, Figure S1: title; Table S1: title; Video S1: title.
Author Contributions
Conceptualization, methodology, validation, and formal analysis, Y.G. (Yakai Guo); investigation, resources, and data curation, Y.G. (Yakai Guo), C.S., G.N., and Y.G. (Yong Gao); writing—original draft preparation, Y.G. (Yakai Guo) and C.S.; writing—review and editing, Y.G. (Yakai Guo), C.S., G.N., and Y.G. (Yong Gao); visualization, G.N.; supervision, Y.G. and B.Y.; project administration, Y.G. and B.Y.; funding acquisition, B.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Henan Provincial Natural Science Foundation Project (grant numbers: 242300421367, 222300420468), the China Meteorological Administration Meteorological Development and Planning Institute Special Research Project (grant number: JCXM2024014), and the Open Project of KLME CIC-FEMD NUIST (grant number: KLME201906).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Acknowledgments
We would like to express our gratitude to the Henan Meteorological Bureau, the China Meteorological Administration Meteorological Observation Centre, and the China Meteorological Administration Meteorological Development and Planning Institute for their support in carrying out this study. We would like to give our many thanks to those who made efforts to advance this work, and the fellow travelers encountered along the way.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Min, J.; Guo, Y.; Wang, G. Impacts of Soil Moisture on Typical Frontal Rainstorm in Yangtze River Basin. Atmo., 2016, 7. [CrossRef]
- Li, K.; Zhang, J.; Wu, L.; Yang, K.; Li, S. The role of soil temperature feedbacks for summer air temperature variability under climate change over East Asia. Earth's Future, 2022, 10, e2021EF002377.
- García-García, A.; Cuesta-Valero, F.J.; Miralles, D.G.; Mahecha, M.D.; Quaas, J.; Reichstein, M.; Zscheischler, J.; Peng, J. Soil heat extremes can outpace air temperature extremes. Nat. Clim. Chang., 2023, 13,1237–1241.
- Guo, Y.; Shao, C.; Su, A. Investigation of Land-Atmosphere Coupling during the Extreme Rainstorm of 20 July 2021 over Central East China. Atmos., 2023, 14. [CrossRef]
- Gao, Y.; Li, K.; Chen, F.; Jiang, Y.; Lu, C. Assessing and improving Noah-MP land model simulations for the central Tibetan Plateau. Journal of Geophysical Research: Atmospheres 2015, 120, 9258-9278. [CrossRef]
- Li, C.; Lu, H.; Yang, K.; Han, M.; Wright, J.; Chen, Y.; Yu, L.; Xu, S.; Huang, X.; Gong, W. The Evaluation of SMAP Enhanced Soil Moisture Products Using High-Resolution Model Simulations and In-Situ Observations on the Tibetan Plateau. Remote Sensing 2018, 10. [CrossRef]
- Chen, Y.; Yang, K.; He, J.; Qin, J.; Shi, J.; Du, J.; He, Q. Improving land surface temperature modeling for dry land of China. J. Geophys. Res. Atmos., 2011, 116(D20104).
- He, Q.; Lu, H.; Yang, K.; Zhao, L.; Zou, M. Improving Land Surface Temperature Simulation of NOAH-MP on the Tibetan Plateau. In Proceedings of the 2021 IEEE International Geoscience and Remote Sensing Symposium IGARSS, 2021; pp. 6217-6220.
- Guo, Y.; Yuan, B.; Su, A.; Shao, C.; Gao, Y. Calibration for Improving the Medium-Range Soil Temperature Forecast of a Semiarid Region over Tibet: A Case Study. Atmos., 2024, 15. [CrossRef]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the mean squared error and NSE performance criteria,Implications for improving hydrological modelling. J. Hydro., 2009, 377(1-2), 80-91.
- Kumar, S.; Kolassa, J.; Reichle, R.; Crow, W.; Lannoy, G.; Rosnay, P.; MacBean, N.; Girotto, M.; Fox, A.; Quaife, T. et al. An agenda for land data assimilation priorities, Realizing the promise of terrestrial water, energy,and vegetation observations from space. J. Adv. Model Earth Sys., 2022, 14, c2022MS003259.
- Ma, Y.M.; Yao, T.D.; Zhong, L.; Wang, B.B.; Xu, X.D.; Hu, Z.Y.; Ma, W.Q.; Sun, F.L.; Han, C.B.; Li, M.S.; et al. Comprehensive study of energy and water exchange over the Tibetan Plateau: A review and perspective: From GAME/Tibet and CAMP/Tibet to TORP, TPEORP, and TPEITORP. Earth-Sci. Rev. 2023, 237, 104312.
- Clerc, M.K., J.. The particle swarm - explosion, stability, and convergence in a multidimensional complex space. IEEE Transactions on Evolutionary Computation 2002, 6, 58-73. [CrossRef]
- Kennedy, J. Bare bones particle swarms. In Proceedings of the Proceedings of the 2003 IEEE Swarm Intelligence Symposium. SIS'03 (Cat. No.03EX706), Indianapolis, IN, USA, 2003; pp. 80-87.
- Shami, T.M.; El-Saleh, A.A.; Alswaitti, M.; Al-Tashi, Q.; Summakieh, M.A.; Mirjalili, S. Particle Swarm Optimization: A Comprehensive Survey. IEEE Access 2022, 10, 10031-10061. [CrossRef]
- Ketabchi, H.; Ataie-Ashtiani, B. Evolutionary algorithms for the optimal management of coastal groundwater: A comparative study toward future challenges. Journal of Hydrology 2015, 520, 193-213. [CrossRef]
- Deng, Y.; Yang, Q.; Zuo, H.; Li, W. Land Surface Model and Particle Swarm Optimization Algorithm Based on the Model-Optimization Method for Improving Soil Moisture Simulation in a Semi-Arid Region. Plos One 2016, 11. [CrossRef]
- Yang, Q.; Ling, C.; Du, B.; Wang, L.; Yang Y. Application of the particle swarm optimization in the land surface model parameters calibration. Plateau Meteorology 2017, 36(4), 1060-1071. (In Chinese). [CrossRef]
- Duan, Q.; S., Soroosh; Gupta, Vuai. Effective and Efcient Global Optimizationfor Conceptual Rainfall-Runoff Models. Water Resources Research 1992, 28, 1015-1031.
- Duan, Q.S., Soroosh; Gupta, Vuai. Optimal use of the SCE-UA global optimization method forcalibrating watershed models. Journal of Hydrology 1994, 158, 265-284.
- Jeon, J.-H.; Park, C.-G.; Engel, B. Comparison of Performance between Genetic Algorithm and SCE-UA for Calibration of SCS-CN Surface Runoff Simulation. Water 2014, 6, 3433-3456. [CrossRef]
- Naeini, M.A., B. ; Gupta, H.V; Duan, Q.; Sorooshiana, S. Three decades of the Shufed Complex Evolution(SCE-UA)optimization algorithm: Review andapplications. Scientia lranica, Transaclions A: Civil Engineering 2019, 26, 2015-2031. [CrossRef]
- Liu, Y.Q.; Gupta, H.V.; Sorooshian, S.; , L.A.; Shuttleworth, W.J. Exploring parameter sensitivities of the land surface using a locally coupled land-atmosphere model. J Geophys Res-Atmos 2004, 109, doi:Artn D2110110.1029/2004jd004730. [CrossRef]
- Bastidas, L.A.; Hogue, T.S.; Sorooshian, S.; Gupta, H.V.; Shuttleworth, W.J. Parameter sensitivity analysis for different complexity land surface models using multicriteria methods. J Geophys Res-Atmos 2006, 111, doi:Artn D2010110.1029/2005jd006377. [CrossRef]
- Peng, F.; Sun, G.D. Identifying Sensitive Model Parameter Combinations for Uncertainties in Land Surface Process Simulations over the Tibetan Plateau. Water 2019, 11, doi:ARTN 172410.3390/w11081724. [CrossRef]
- Gudmundsson, L.; Cuntz, M. Soil Parameter Model Intercomparison Project (SP-MIP): Assessing theinfluence of soil parameters on the variability of Land Surface Models; GEWEX–SoilWat workshop, Leipzig, German, 28–30 June 2016; pp. 1–6. Available online: https://www.gewexevents.org/wp-content/uploads/GLASS2017_SP-MIP_Protocol.pdf (accessed on 30 April 2024).
- Chaney, N.W.; Herman, J.D.; Ek, M.B.; Wood, E.F. Deriving global parameter estimates for the Noah land surface model using FLUXNET and machine learning. J. Geophys. Res. Atmos. 2016, 121, 13218–13235.
- Zeng, Y.; Anne, V.; Or, D.; Cuntz, M.; Gudmundsson, L.; Weihermueller, L.; Kollet, S.; Vanderborght, J.; Vereecken, H. GEWEX-ISMC SoilWat Project:Taking Stock and Looking Ahead; GEWEX GLASS meeting, USA, 23-25 November, 2020; GEWEX QUARTERLY II 2021, 31(2), 4-9; pp. 4–9. Available online: https://gewex.org/gewex-content/files_mf/1633983474Q22021.pdf (accessed on 30 April 2024).
- Stephens, G.; Polcher, J.; Zeng, X.B.; van Oevelen, P.; Poveda, G.; Bosilovich, M.; Ahn, M.H.; Balsamo, G.; Duan, Q.Y.; Hegerl, G.; et al. The First 30 Years of GEWEX. Bull. Amer. Meteor. Soc. 2023, 104, E126–E157.
- Zhao, X.; Liu C.; Tong, B.; Li, Y.; Wang, L.; Ma, Y.; Gao, Z. Study on Surface Process Parameters and Soil Thermal Parameters at Shiquanhe in the Western Qinghai-Xizang Plateau. Plateau Meteorol. 2021, 40, 711–723. (In Chinese).
- Sun, S.; Chen, B.; Che, T.; Zhang, H.; Chen, J.; Che, M.; Lin, X.; Guo, L. Simulating the Qinghai—Tibetan Plateau seasonal frozen soil moisture and improving model’s parameters—A case study in the upper reaches of Heihe River. Plateau Meteorol. 2017, 36, 643–656. (In Chinese).
- Chen, F.; Dudhia, J. Coupling an advanced land-surface/hydrology model with the Penn State/NCAR MM5 modeling system. Part I, Model implementation and sensitivity, Mon. Weather. Rev. 2001, 129, 569–585.
- Hogue, T.S.; Bastidas, L.A.; Gupta, H.V.; Sorooshian, S. Evaluating model performance and parameter behavior for varying levels of land surface model complexity. Water Resour. Res. 2006, 42, W08430.
- Rosero, E.; Yang, Z.L.; Gulden, L.E.; Niu, G.Y.; Gochis, D.J. Evaluating Enhanced Hydrological Representations in Noah LSM over Transition Zones: Implications for Model Development. J Hydrometeorol 2009, 10, 600-622. [CrossRef]
- Yang, K.; Qin, J.; Zhao, L.; Chen, Y.; Tang, W.; Han, M.; Lazhu; Chen, Z.; Lv, N.; Ding, B.; et al. A multi-scale soil moisture and freeze-thaw monitoring network on the third pole. Bull. Amer. Meteor. Soc. 2013, 94, 1907–1916.
- Yang, K.; Chen, Y.Y.; Qin, J. Some practical notes on the land surface modeling in the Tibetan Plateau. Hydrol. Earth Sys. Sci. 2009, 13, 687–701.
- Coon, E.T.; David Moulton, J.; Painter, S.L. Managing complexity in simulations of land surface and near-surface processes. Environmental Modelling & Software 2016, 78, 134-149. [CrossRef]
- Fisher, R.A.; Koven, C.D. Perspectives on the Future of Land Surface Models and the Challenges of Representing Complex Terrestrial Systems. Journal of Advances in Modeling Earth Systems 2020, 12. [CrossRef]
- Crow, W.T.; Wood, E.F.; Pan, M. Multiobjective calibration of land surface model evapotranspiration predictions using streamflow observations and spaceborne surface radiometric temperature retrievals. J Geophys Res-Atmos 2003, 108, doi:Artn 472510.1029/2002jd003292. [CrossRef]
- Coudert, B.; Ottle, C.; Boudevillain, B.; Demarty, J.; Guillevic, P. Contribution of thermal infrared remote sensing data in multiobjective calibration of a dual-source SVAT model. J Hydrometeorol 2006, 7, 404-420. [CrossRef]
- Khaki, M. Land Surface Model Calibration Using Satellite Remote Sensing Data. Sensors 2023, 23. [CrossRef]
- Dembélé, M.; Hrachowitz, M.; Savenije, H.H.G.; Mariéthoz, G.; Schaefli, B. Improving the Predictive Skill of a Distributed Hydrological Model by Calibration on Spatial Patterns with Multiple Satellite Data Sets. Water Resources Research 2020, 56, doi:ARTN e2019WR02608510.1029/2019WR026085. [CrossRef]
- Zhou, J.; Wu, Z.; Crow, W.T.; Dong, J.; He, H. Improving Spatial Patterns Prior to Land Surface Data Assimilation via Model Calibration Using SMAP Surface Soil Moisture Data. Water Resources Research 2020, 56. [CrossRef]
- Abhervé, R.; Roques, C.; Gauvain, A.; Longuevergne, L.; Louaisil, S.; Aquilina, L.; de Dreuzy, J.-R. Calibration of groundwater seepage against the spatial distribution of the stream network to assess catchment-scale hydraulic properties. Hydrol Earth Syst Sc 2023, 27, 3221-3239. [CrossRef]
- Adeyeri, O.E.; Folorunsho, A.H.; Ayegbusi, K.I.; Bobde, V.; Adeliyi, T.E.; Ndehedehe, C.E.; Akinsanola, A.A. Land surface dynamics and meteorological forcings modulate land surface temperature characteristics. Sustainable Cities and Society 2024, 101. [CrossRef]
- Cunha, A.P.M.A.; Alvalá, R.C.S.; Sampaio, G.; Shimizu, M.H.; Costa, M.H. Calibration and Validation of the Integrated Biosphere Simulator (IBIS) for a Brazilian Semiarid Region. J Appl Meteorol Clim 2013, 52, 2753-2770. [CrossRef]
- Burke, E.J.; Shuttleworth, W.J.; Houser, P.R. Impact of horizontal and vertical heterogeneities on retrievals using multiangle microwave brightness temperature data. Ieee T Geosci Remote 2004, 42, 1495-1501. [CrossRef]
- Hagedorn, B. Hydrograph separation through multi objective optimization: Revealing the importance of a temporally and spatially constrained baseflow solute source. Journal of Hydrology 2020, 590, doi:ARTN 12534910.1016/j.jhydrol.2020.125349. [CrossRef]
- Kuban, M.; Parajka, J.; Tong, R.; Pfeil, I.; Vreugdenhil, M.; Sleziak, P.; Adam, B.; Szolgay, J.; Kohnová, S.; Hlavcová, K. Incorporating Advanced Scatterometer Surface and Root Zone Soil Moisture Products into the Calibration of a Conceptual Semi-Distributed Hydrological Model. Water 2021, 13, doi:ARTN 336610.3390/w13233366. [CrossRef]
- Zitzler, E.; Thiele, L.; Laumanns, M.; Fonseca, C.M.; da Fonseca, V.G. Performance assessment of multiobjective optimizers: an analysis and review. IEEE Transactions on Evolutionary Computation 2003, 7, 117-132. [CrossRef]
- Coello, C.A.C.L., G. B. ; Veldhuizen, D. A. V. . Evolutionary Algorithms for Solving Multi-Objective Problems Second Edition; Springer: New York, USA, 2007; pp. XXI, 800.
- Loridan, T.; Grimmond, C.S.B.; Grossman-Clarke, S.; Chen, F.; Tewari, M.; Manning, K.; Martilli, A.; Kusaka, H.; Best, M. Trade-offs and responsiveness of the single-layer urban canopy parametrization in WRF: An offline evaluation using the MOSCEM optimization algorithm and field observations. Quarterly Journal of the Royal Meteorological Society 2010, 136, 997-1019. [CrossRef]
- Yapo, P.; Gupta, H.; Sorooshian, S. Multi-objective global optimization for hydrologic models. Journal of Hydrology 1998, 204, 83-97.
- Vrugt, J.A.; Gupta, H.V.; Bastidas, L.A.; Bouten, W.; Sorooshian, S. Effective and efficient algorithm for multiobjective optimization of hydrologic models. Water Resources Research 2003, 39. [CrossRef]
- Fenicia, F.; Savenije, H.H.G.; Matgen, P.; Pfister, L. A comparison of alternative multiobjective calibration strategies for hydrological modeling. Water Resources Research 2007, 43, doi:Artn W0343410.1029/2006wr005098. [CrossRef]
- Deng, L.; Guo, S.; Yin, J.; Zeng, Y.; Chen, K. Multi-objective optimization of water resources allocation in Han River basin (China) integrating efficiency, equity and sustainability. Scientific Reports 2022, 12. [CrossRef]
- Dumedah, G.; Berg, A.A.; Wineberg, M. An Integrated Framework for a Joint Assimilation of Brightness Temperature and Soil Moisture Using the Nondominated Sorting Genetic Algorithm II. J Hydrometeorol 2011, 12, 1596-1609. [CrossRef]
- Li, M.; Yang, S.; Liu, X. Pareto or Non-Pareto: Bi-Criterion Evolution in Multiobjective Optimization. IEEE Transactions on Evolutionary Computation 2016, 20, 645-665. [CrossRef]
- Liu, Y.; Zhu, N.; Li, K.; Li, M.; Zheng, J.; Li, K. An angle dominance criterion for evolutionary many-objective optimization. Information Sciences 2020, 509, 376-399. [CrossRef]
- Pool, S.; Vis, M.; Seibert, J. Evaluating model performance: towards a non-parametric variant of the Kling-Gupta efficiency. Hydrological Sciences Journal 2018, 63, 1941-1953. [CrossRef]
- Knoben, W.J.M.; Freer, J.E.; Woods, R.A. Technical note: Inherent benchmark or not? Comparing Nash–Sutcliffe and Kling–Gupta efficiency scores. Hydrol Earth Syst Sc 2019, 23, 4323-4331. [CrossRef]
- Vrugt, J.A.; de Oliveira, D.Y. Confidence intervals of the Kling-Gupta efficiency. Journal of Hydrology 2022, 612. [CrossRef]
- Mathevet, T.; Le Moine, N.; Andréassian, V.; Gupta, H.; Oudin, L. Multi-objective assessment of hydrological model performances using Nash–Sutcliffe and Kling–Gupta efficiencies on a worldwide large sample of watersheds. Comptes Rendus. Géoscience 2023, 355, 1-25. [CrossRef]
- Chai, T.; Draxler, R.R. Root mean square error (RMSE) or mean absolute error (MAE)? – Arguments against avoiding RMSE in the literature. Geoscientific Model Development 2014, 7, 1247-1250. [CrossRef]
- Hodson, T.O. Root-mean-square error (RMSE) or mean absolute error (MAE): when to use them or not. Geoscientific Model Development 2022, 15, 5481-5487. [CrossRef]
- Armstrong, R.A. Should Pearson's correlation coefficient be avoided? Ophthalmic and Physiological Optics 2019, 39, 316-327. [CrossRef]
- Schober, P.; Boer, C.; Schwarte, L.A. Correlation Coefficients: Appropriate Use and Interpretation. Anesthesia & Analgesia 2018, 126, 1763-1768. [CrossRef]
- Cheng, C.L.; Shalabh; Garg, G. Coefficient of determination for multiple measurement error models. Journal of Multivariate Analysis 2014, 126, 137-152. [CrossRef]
- Contessi, D.; Recati, A.; Rizzi, M. Phase diagram detection via Gaussian fitting of number probability distribution. Physical Review B 2023, 107, L121403. [CrossRef]
- Rodell, M.; Houser, P.R.; Jambor, U.; Gottschalck, J.; Mitchell, K.; Meng, C.; Arsenault, K.; Cosgrove, B.; Radakovich, J.; Bosilovich, M.; et al. The Global Land Data Assimilation System. Bull. Amer. Meteor. Soc. 2004, 85, 381–394.
- Yang, K.; He, J.; Tang, W.; Lu, H.; Qin, J.; Chen, Y.; Li, X. China Meteorological Forcing Dataset (1979–2018). TPDC. 2019. https://data.tpdc.ac.cn/en/data/8028b944-daaa-4511-8769-965612652c49 (accessed on 30 August 2024).
Figure 1.
The pseudo code of the algorithms used in this study.

Figure 2.
The pseudo code of the evaluator used in this study.

Figure 3.
(A) Noah LSM description. (B) Soil observation network, (a) Tibet and soil observation network location (boxes), (b) site locations (filled dots) in the soil observation network, with three types of observation networks (rectangular boxes), roads (white line), and sites (red dots), (c) soil sampling sites (filled dots) in the study area (bold black dots were our study sites).
Figure 3.
(A) Noah LSM description. (B) Soil observation network, (a) Tibet and soil observation network location (boxes), (b) site locations (filled dots) in the soil observation network, with three types of observation networks (rectangular boxes), roads (white line), and sites (red dots), (c) soil sampling sites (filled dots) in the study area (bold black dots were our study sites).
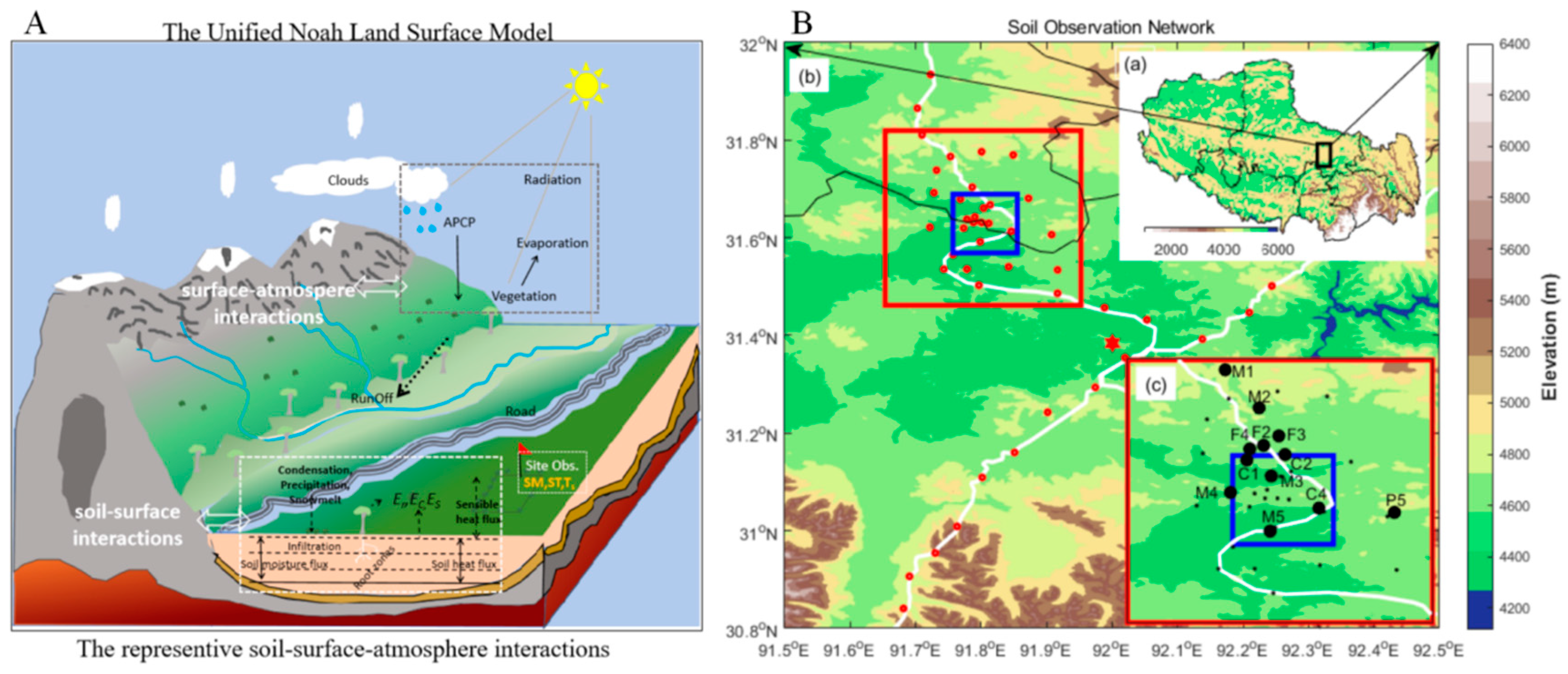
Figure 4.
The case overview in CTR experiment. (a)~(d) The meteorological forcing, which were derived from Ref [9]. (e) The threshold normalized default parameters of different sites (colored) for calibration. (f)~(g) The linear and Gaussian fits of the errors between observation and simulation () for of different periods (colored, the whole study period was in black, while the calibration and validation periods were in red and blue respectively). (h)~(i) were the same as (f)~(g), but for .
Figure 4.
The case overview in CTR experiment. (a)~(d) The meteorological forcing, which were derived from Ref [9]. (e) The threshold normalized default parameters of different sites (colored) for calibration. (f)~(g) The linear and Gaussian fits of the errors between observation and simulation () for of different periods (colored, the whole study period was in black, while the calibration and validation periods were in red and blue respectively). (h)~(i) were the same as (f)~(g), but for .
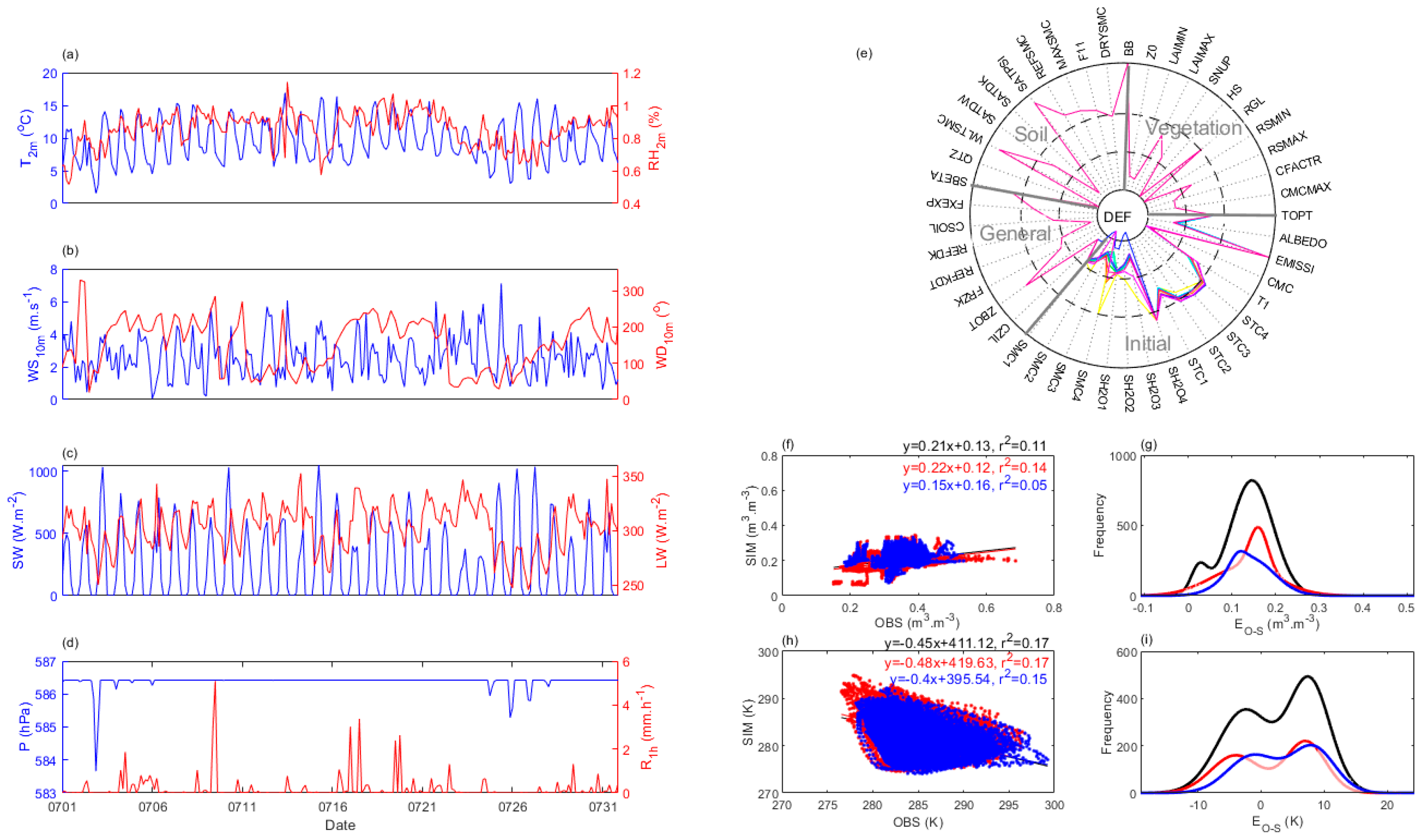
Figure 5.
The different metrics’ parameter spatial uncertainties. (a) The stacked inter quartile ranges (IQR, colored) of different optimal parameters for PSO. (b) is the same as (a), but for SCE. (c) The boxplot of the IQR ensembles (or the IQR distributions; IQRD) of the optimal parameter space for various metrics, and their outlier numbers (d).
Figure 5.
The different metrics’ parameter spatial uncertainties. (a) The stacked inter quartile ranges (IQR, colored) of different optimal parameters for PSO. (b) is the same as (a), but for SCE. (c) The boxplot of the IQR ensembles (or the IQR distributions; IQRD) of the optimal parameter space for various metrics, and their outlier numbers (d).
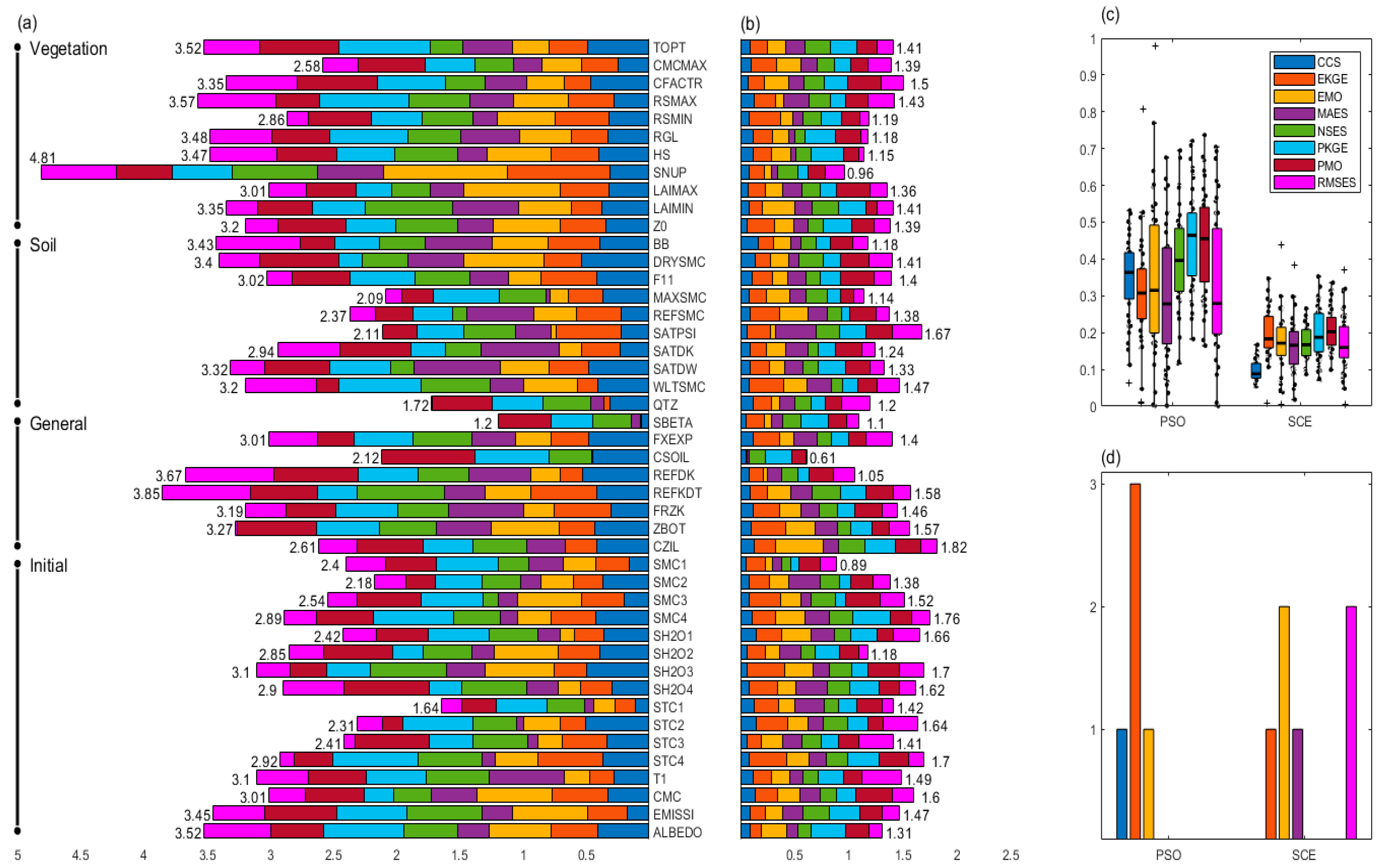
Figure 6.
The different metrics’ impact on calibration effectiveness and efficiency. Fitness curves of different sites (colored) against Noah runs for PSO (solid) and SCE (dashed). Except PKGE and PMO whose fitness were Pm, others were Pb.
Figure 6.
The different metrics’ impact on calibration effectiveness and efficiency. Fitness curves of different sites (colored) against Noah runs for PSO (solid) and SCE (dashed). Except PKGE and PMO whose fitness were Pm, others were Pb.
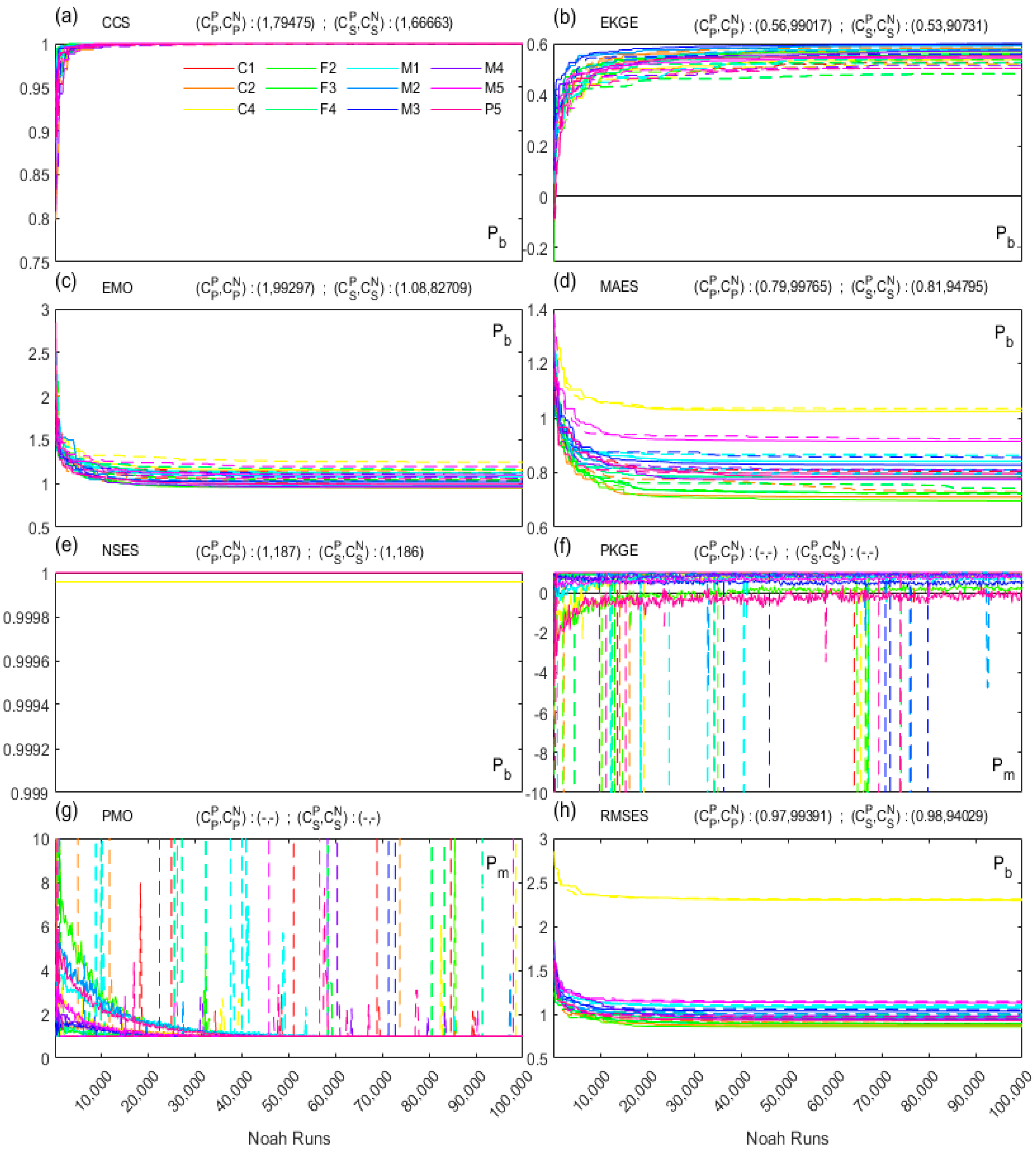
Figure 7.
Success rate curves of different sites (colored) against Noah runs for PSO (top) and SCE (bottom).
Figure 7.
Success rate curves of different sites (colored) against Noah runs for PSO (top) and SCE (bottom).
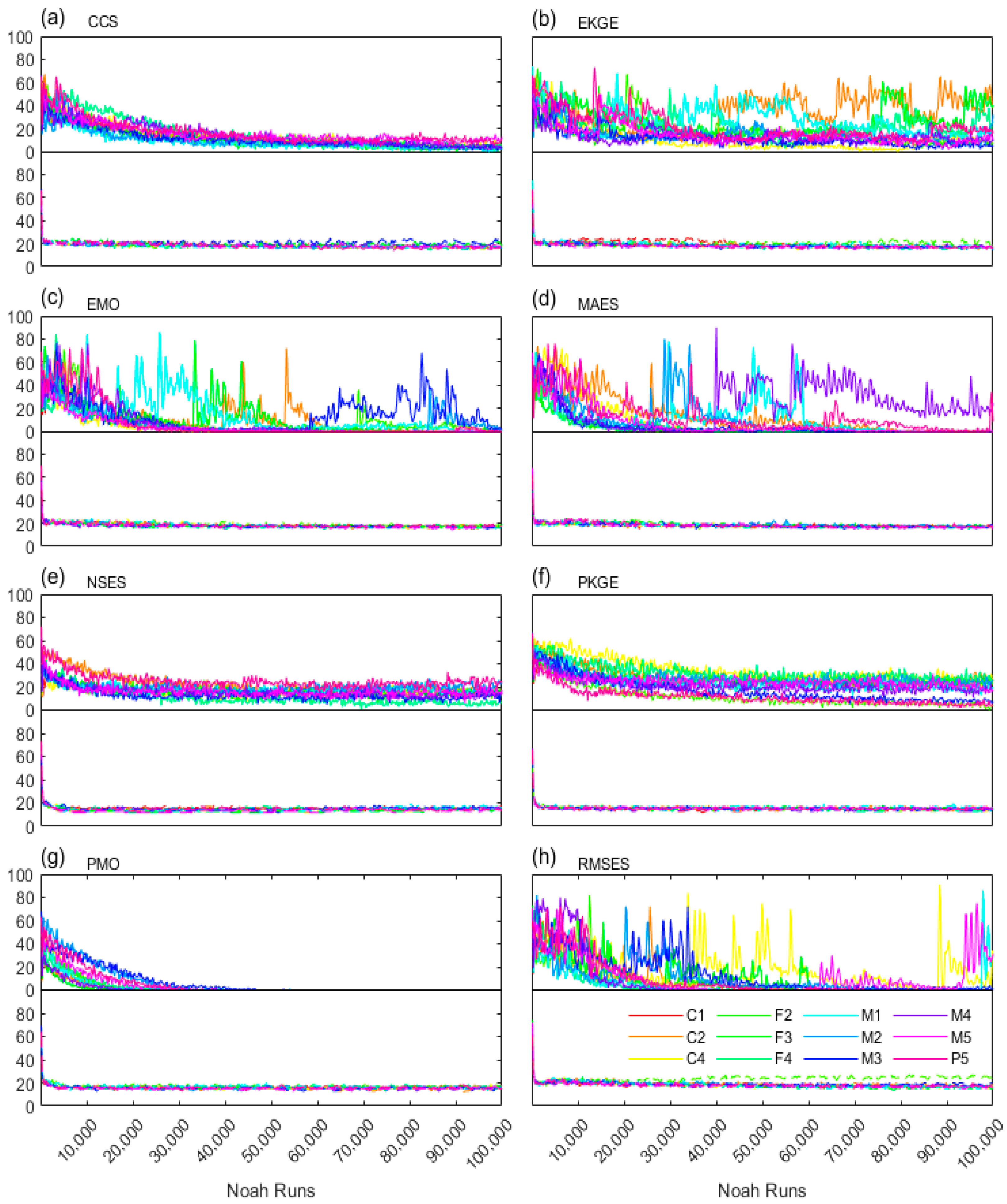
Figure 8.
The different metrics’ impact on optimal objective uncertainties against sites for PSO and SCE.
Figure 8.
The different metrics’ impact on optimal objective uncertainties against sites for PSO and SCE.
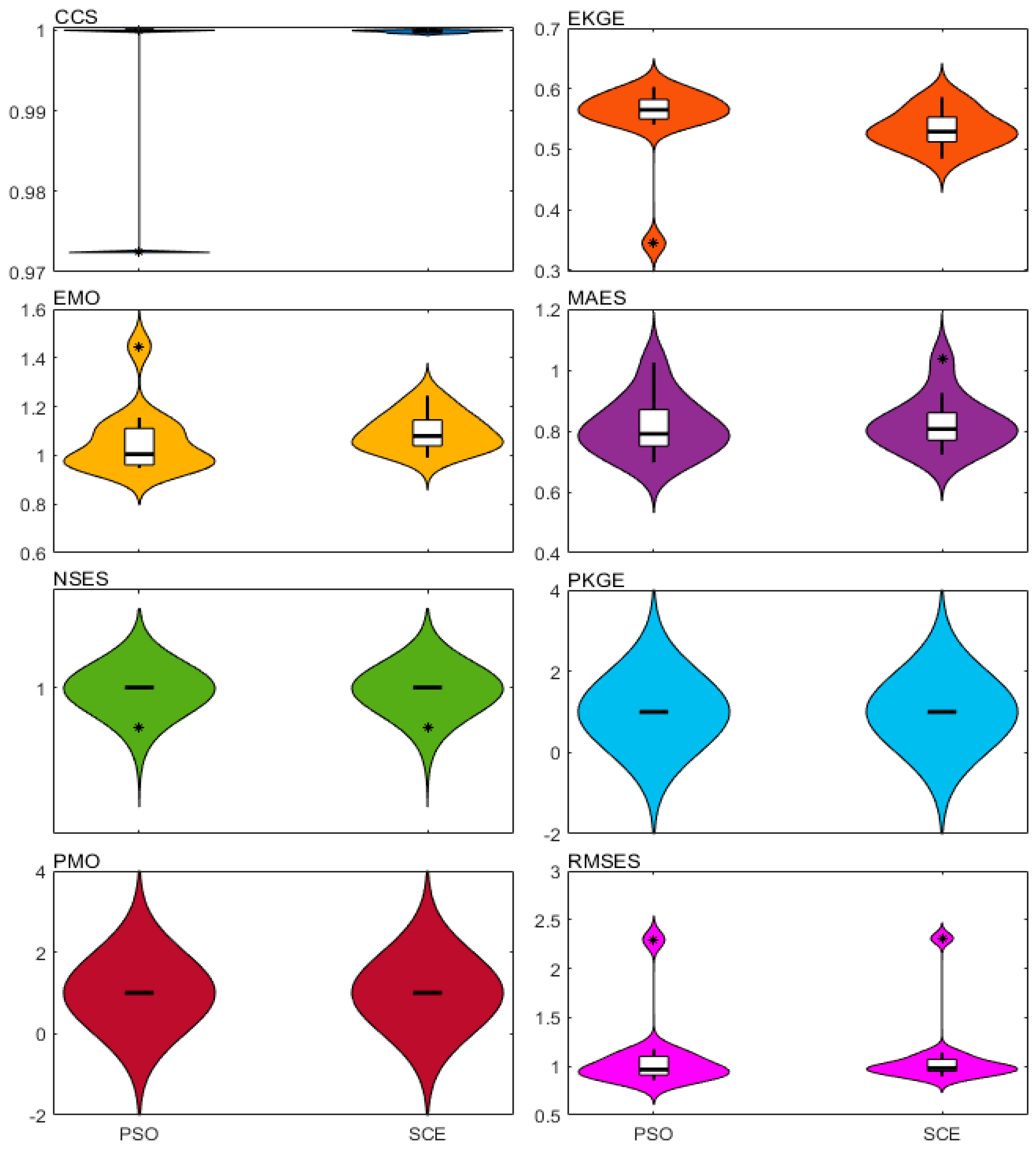
Figure 9.
Different metrics’ best linear fits against sites for (a) and (b) during the calibration period. CRT, PSO and SCE are plotted in black, red and blue respectively.
Figure 9.
Different metrics’ best linear fits against sites for (a) and (b) during the calibration period. CRT, PSO and SCE are plotted in black, red and blue respectively.
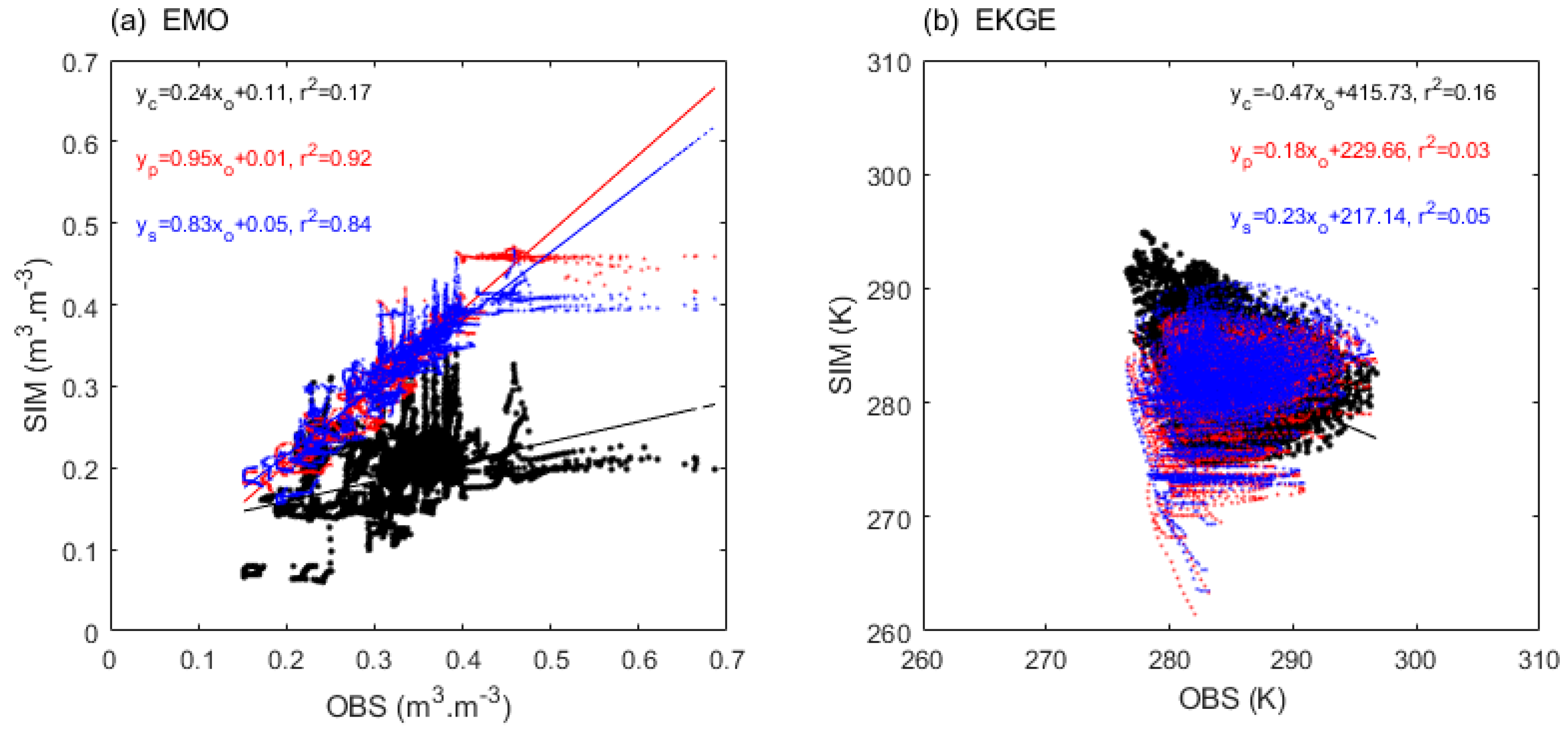
Figure 10.
Different metrics’ best Gaussian fits of against sites for (a) and (b) during the calibration period. CRT, PSO and SCE are plotted in black, red and blue respectively. Also, the two typically characterized “amplitude [peak position, peak width]” in Gaussian fitting are displayed together. Note that two amplitudes with one same peak could be summed to one amplitude.
Figure 10.
Different metrics’ best Gaussian fits of against sites for (a) and (b) during the calibration period. CRT, PSO and SCE are plotted in black, red and blue respectively. Also, the two typically characterized “amplitude [peak position, peak width]” in Gaussian fitting are displayed together. Note that two amplitudes with one same peak could be summed to one amplitude.
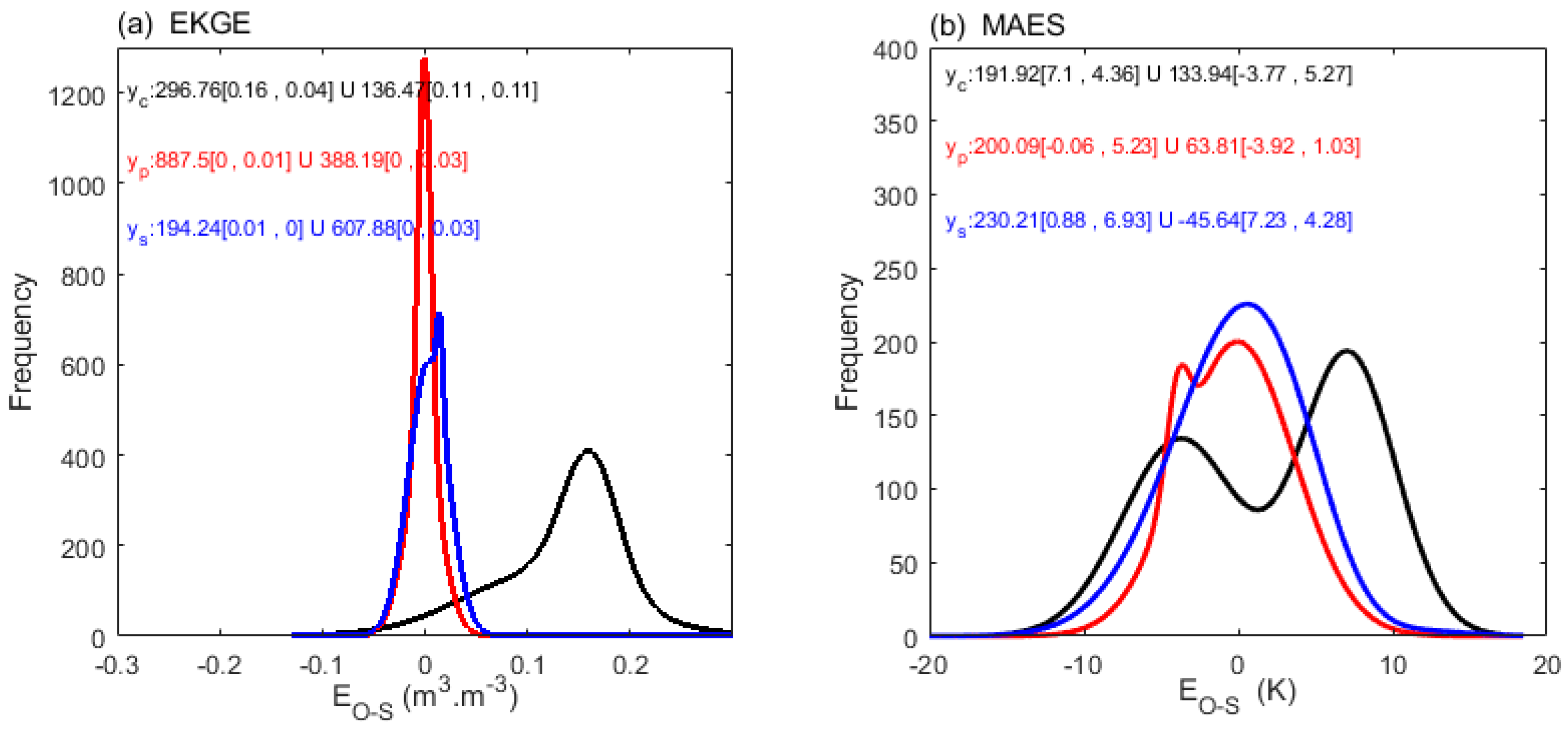
Figure 11.
The different metrics’ impact on the optimal surface simulation. (a) The temporally varied and (b) the boxplot of spatial errors (RMSES) for . (c)~(d) are the same as (a)~(b) but showing the spatial correlation coefficients (CCS) for . (e)~(h) are the same as (a)~(d), but for , note that only the best metric performance is shown in (e) and (g) to avoid overlaps.
Figure 11.
The different metrics’ impact on the optimal surface simulation. (a) The temporally varied and (b) the boxplot of spatial errors (RMSES) for . (c)~(d) are the same as (a)~(b) but showing the spatial correlation coefficients (CCS) for . (e)~(h) are the same as (a)~(d), but for , note that only the best metric performance is shown in (e) and (g) to avoid overlaps.
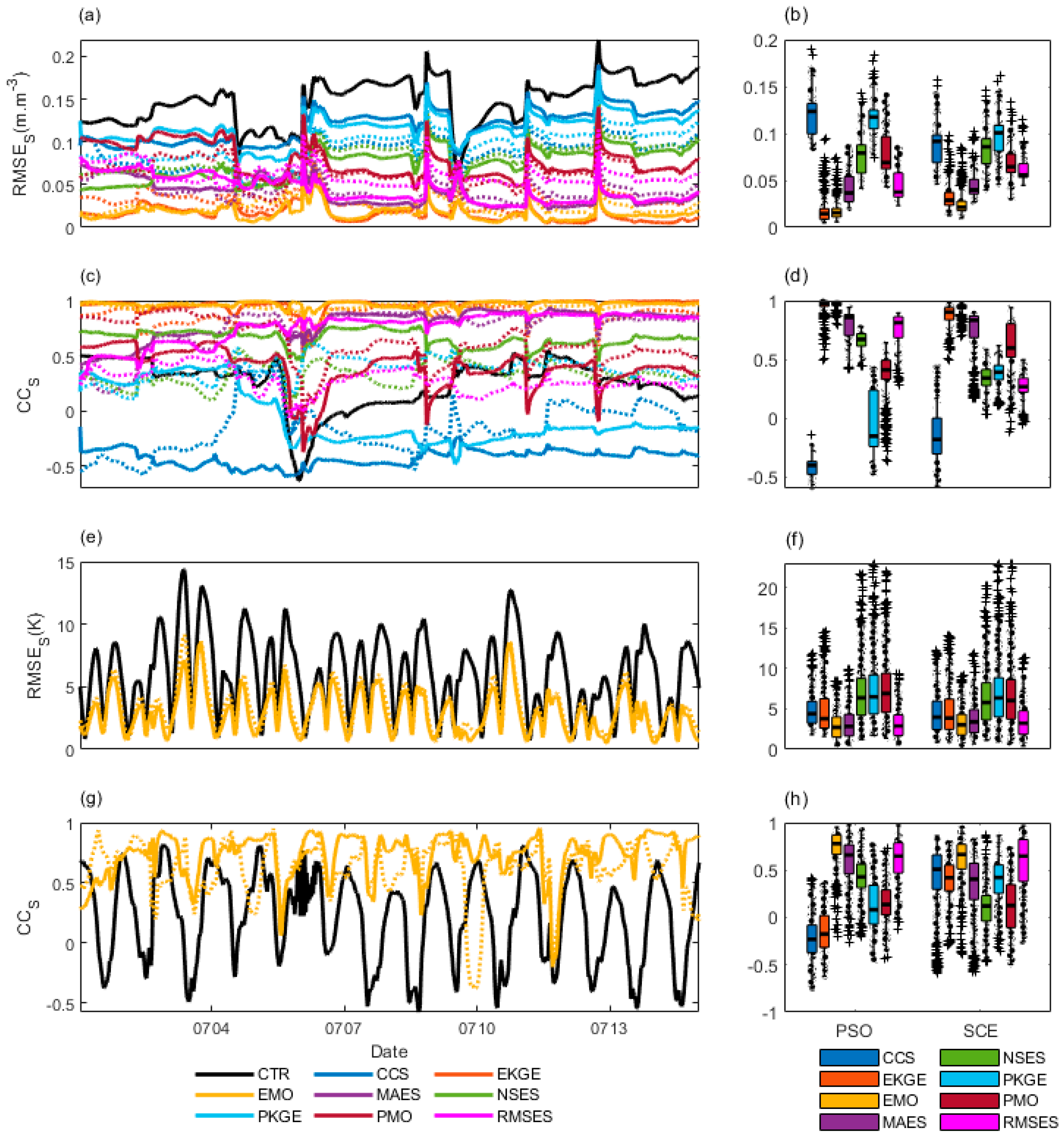
Figure 12.
Different metrics’ best linear fits against sites for (a) and (b) during the forecast period. CRT, PSO and SCE are plotted in black, red and blue respectively.
Figure 12.
Different metrics’ best linear fits against sites for (a) and (b) during the forecast period. CRT, PSO and SCE are plotted in black, red and blue respectively.
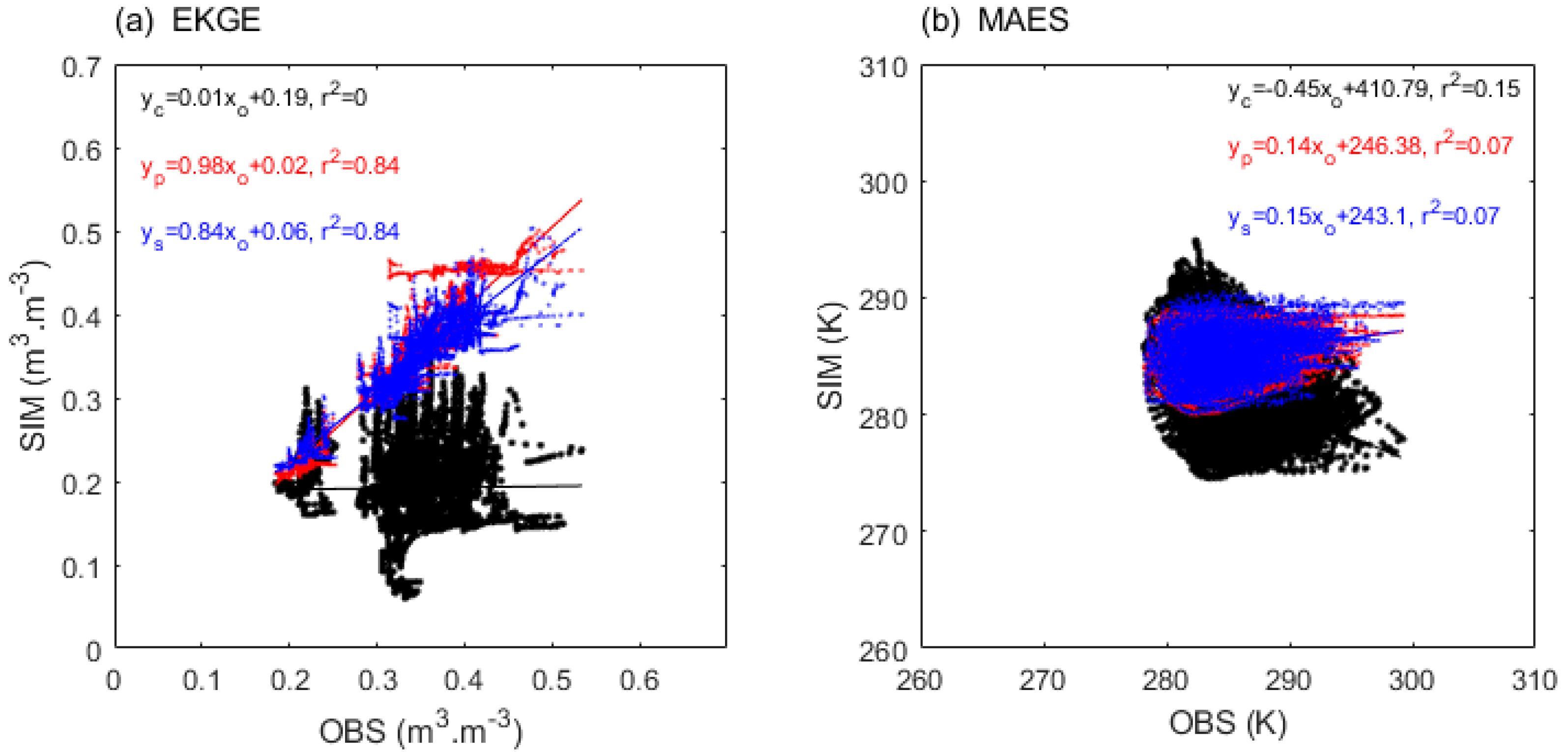
Figure 13.
Different metrics’ best Gaussian fits of against sites for (a) and (b) during the calibration period. CRT, PSO and SCE are plotted in black, red and blue respectively. Also, the two typically characterized “amplitude [peak position, peak width]” in Gaussian fitting are displayed together. Note that two amplitudes with one same peak could be summed to one amplitude.
Figure 13.
Different metrics’ best Gaussian fits of against sites for (a) and (b) during the calibration period. CRT, PSO and SCE are plotted in black, red and blue respectively. Also, the two typically characterized “amplitude [peak position, peak width]” in Gaussian fitting are displayed together. Note that two amplitudes with one same peak could be summed to one amplitude.

Figure 14.
The different metrics’ impact on the optimal surface simulation. (a) The temporally varied and (b) the boxplot of spatial errors () for . (c)~(d) are the same as (a)~(b) but showing the spatial correlation coefficients () for . (e)~(h) are the same as (a)~(d), but for , note that only the best metric performance is shown in (e) and (g) to avoid overlaps.
Figure 14.
The different metrics’ impact on the optimal surface simulation. (a) The temporally varied and (b) the boxplot of spatial errors () for . (c)~(d) are the same as (a)~(b) but showing the spatial correlation coefficients () for . (e)~(h) are the same as (a)~(d), but for , note that only the best metric performance is shown in (e) and (g) to avoid overlaps.
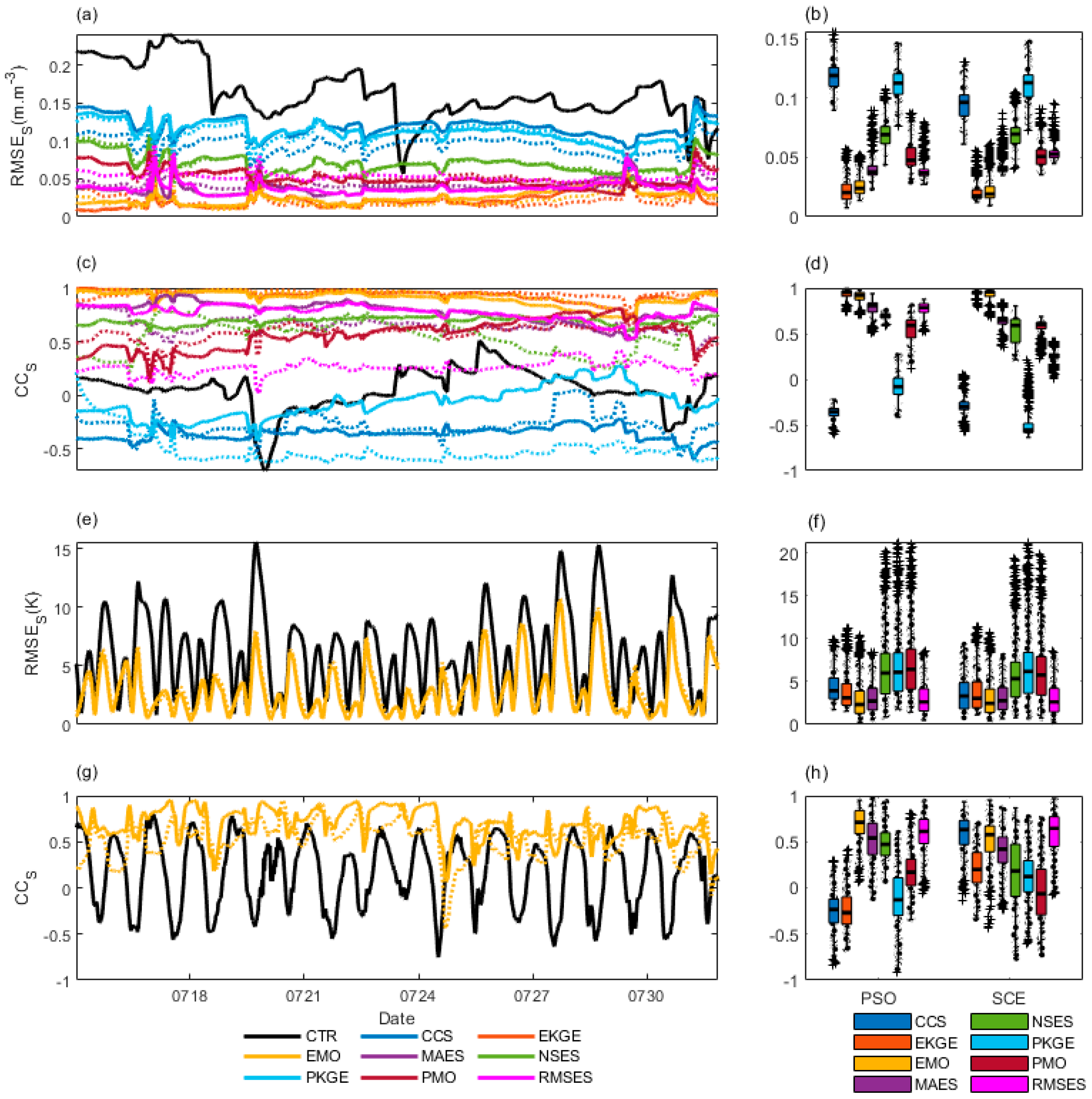
Figure 15.
The different metrics’ impact on surface forecast. (a) and (b) The Taylor diagram against observations for and respectively, and the CTR and GLDAS are shown in cross and asterisk markers, while PSO and SCE are shown in circles and triangles respectively. (c) and (d) The Taylor diagram against GLDAS for HFX and LH respectively, and the CTR are shown in cross markers.
Figure 15.
The different metrics’ impact on surface forecast. (a) and (b) The Taylor diagram against observations for and respectively, and the CTR and GLDAS are shown in cross and asterisk markers, while PSO and SCE are shown in circles and triangles respectively. (c) and (d) The Taylor diagram against GLDAS for HFX and LH respectively, and the CTR are shown in cross markers.
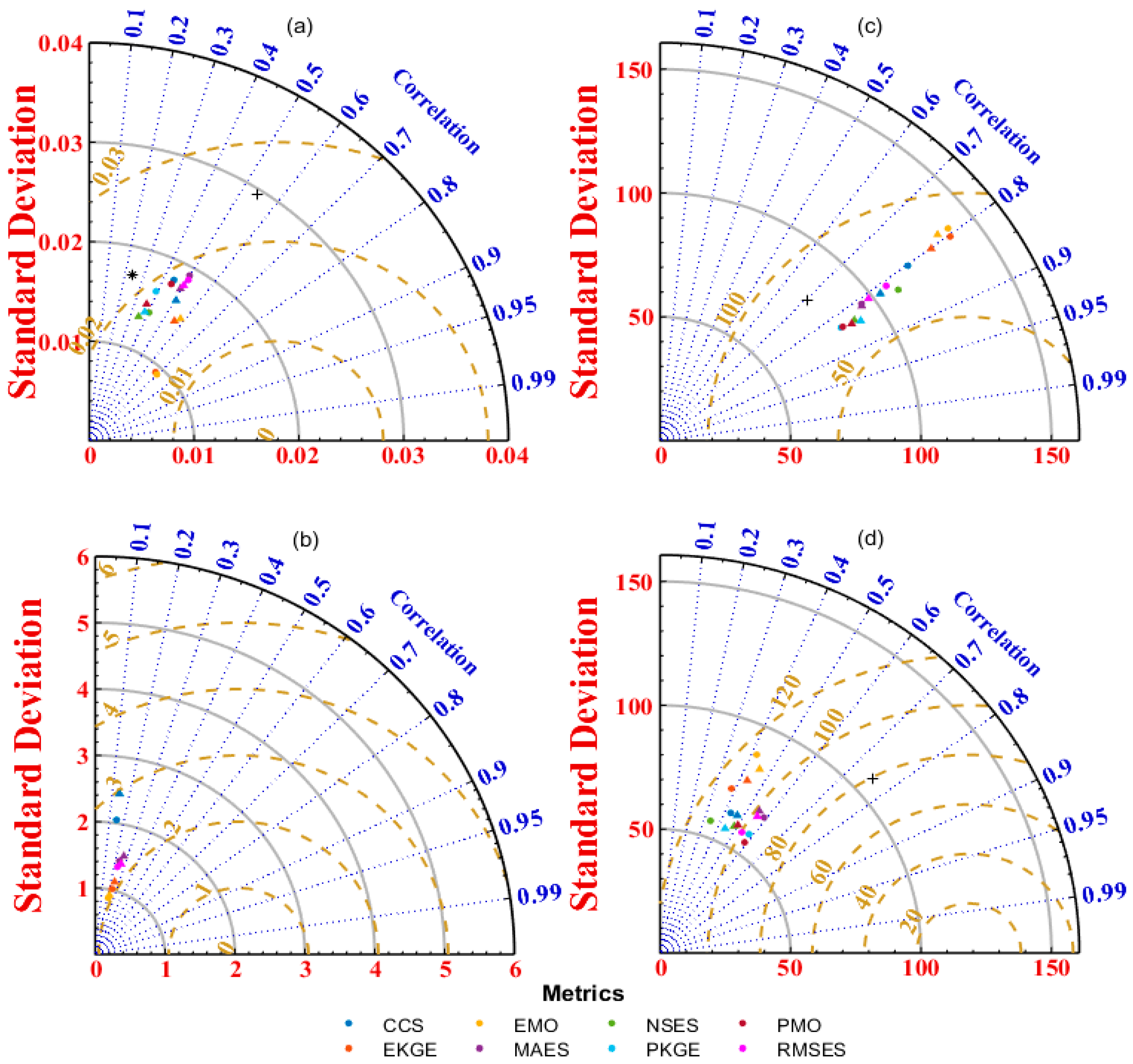
Figure 16.
The best LSM parameters’ configuration (A), and the different metrics’ impact on the KGE indicators of surface simulation (B) in PSO and SCE. Among B, (a) and (b) represent the KGEs of the calibration and forecast periods respectively for , while (c) and (d) are the same as (a) and (b), but for .
Figure 16.
The best LSM parameters’ configuration (A), and the different metrics’ impact on the KGE indicators of surface simulation (B) in PSO and SCE. Among B, (a) and (b) represent the KGEs of the calibration and forecast periods respectively for , while (c) and (d) are the same as (a) and (b), but for .

Figure 17.
The different metrics’ impact on the LSM’s spatial difference reduction and similarity increment. (a) Time varied reduction (PSO, solid; SCE, dotted) compared to CTR (left) and the box-plotted reduction during the calibration period for , (b) is same to (a), but for the validation period. (c) and (d) are the same as (a) and (b), but for . (e)~(h) are the same to (a)~(d), but for the increments when compared to CTR.
Figure 17.
The different metrics’ impact on the LSM’s spatial difference reduction and similarity increment. (a) Time varied reduction (PSO, solid; SCE, dotted) compared to CTR (left) and the box-plotted reduction during the calibration period for , (b) is same to (a), but for the validation period. (c) and (d) are the same as (a) and (b), but for . (e)~(h) are the same to (a)~(d), but for the increments when compared to CTR.
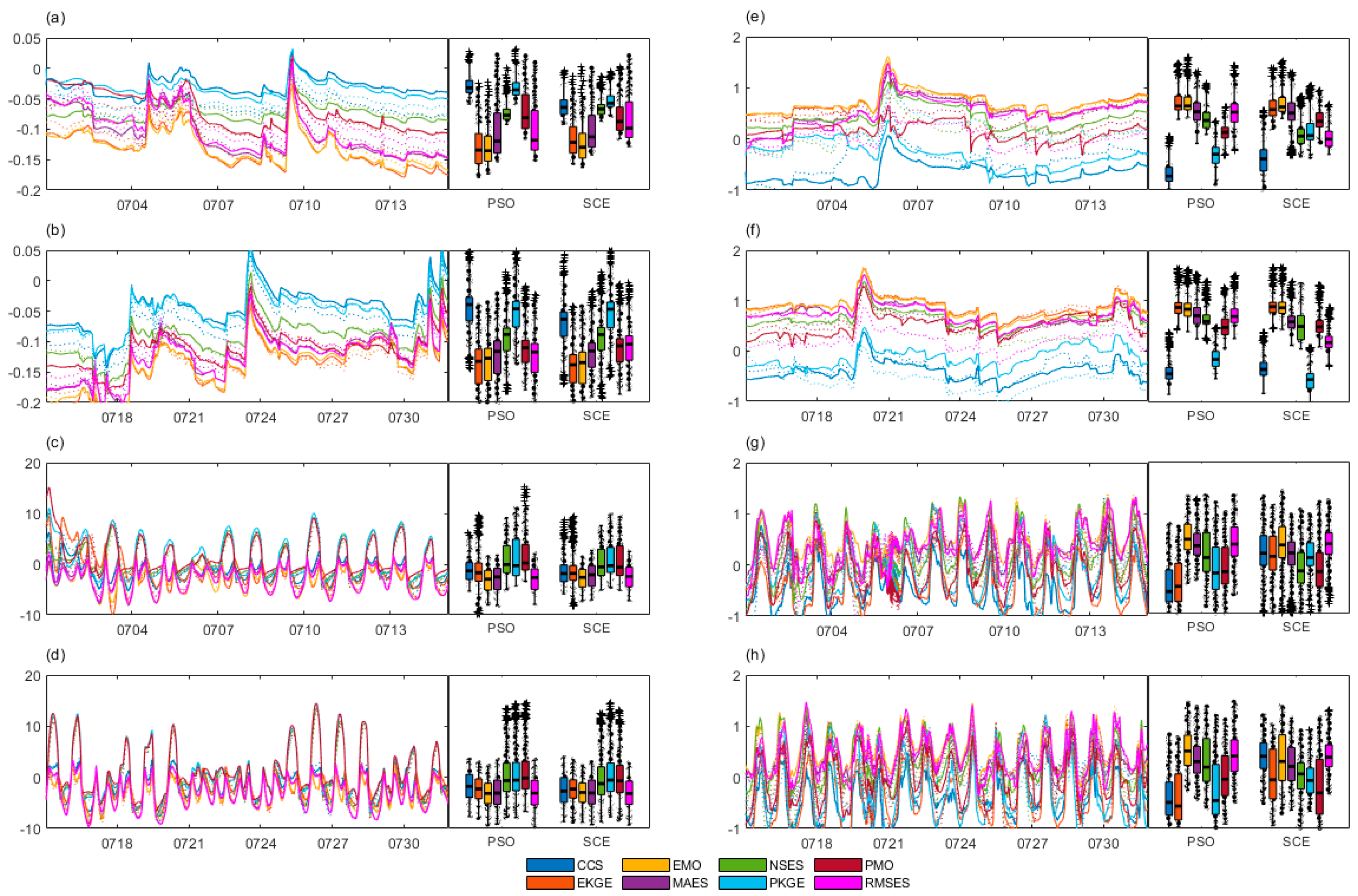
Table 1.
Description of the objective metrics used in this study.
| Metric | Reference Formula* | Direction, Optima | |
|---|---|---|---|
| CCS | Correlation coefficients | ||
| EKGE | Enhanced Kling-Gupta efficiency |
|
|
| EMO | Enhanced multiple objectives | ||
| MAES | Mean absolute errors | ||
| NSES | Nash Sutcliffe efficiencies | ||
| PKGE | Pareto dominant KGE |
|
|
| PMO | Pareto dominant MO |
|
|
| RMSES | Root mean square errors |
*Note that the superscripts and are the variable and layer indexes, respectively, and and are the total numbers of variables and layers. and represent for the simulation and observation respectively. For EKGE, the factors , and indicate the vectored objective statistics such as correlation coefficient, mean value, and standard deviation respectively. For EMO, PKGE and PMO, the lower cases (e.g., , , , and ) represent for only one-dimensional objectives. The superiority and inferiority relationship between different objectives in Pareto optimality is determined using non dominated sorting method, e.g., the top layer dimensional objective is assumed to be the dominated Pareto solution.
Table 2.
Parameter spatial homogeneity for all metrics.
| Metrics | Vegetation (Hp, Hs) * | Soil (Hp, Hs) | General (Hp, Hs) | Initial (Hp, Hs) |
|---|---|---|---|---|
| CCS | 0, | 0, | 1, | 0, 1 |
| EKGE | 0, 0 | 1, 3 | 2, 2 | 4, 2 |
| EMO | 0, 0 | 2, 2 | 2, 2 | 3, 2 |
| MAES | 0, 0 | 1, 1 | 1, 1 | 2, 1 |
| NSES | 0, 0 | 0, 0 | 0, 0 | 2, 0 |
| PKGE | 0, 0 | 0, 0 | 0, 0 | 0, 0 |
| PMO | 0,0 | 0, 0 | 0, 0 | 0, 0 |
| RMSES | 0, 0 | 2, 1 | 1, 1 | 2, 0 |
*Note that Hp and Hs represent for the parameter numbers with low site sensitivities (or homogeneity) of PSO and SCE, respectively.
Table 3.
Parameter spatial uncertainties comparison for all metrics.
| Metrics | Vegetation (PNL, ONR) * |
Soil (PNL, ONR) * |
General (PNL, ONR) * |
Initial (PNL, ONR) * |
|---|---|---|---|---|
| CCS | NA, -2 | NA, -1 | 1, -2 | NA, -1 |
| EKGE | 2, -1 | 2, 2 | 2, 1 | 2, 1 |
| EMO | NA, -1 | 3, 3 | 3, 2 | 1, 5 |
| MAES | NA, -5 | 2, -1 | 3, 0 | NA, 2 |
| NSES | NA, -5 | NA, -1 | NA, -2 | NA, 2 |
| PKGE | NA, -1 | NA, -2 | NA, -2 | NA, -4 |
| PMO | NA, 0 | 1, 3 | NA, -1 | NA, 0 |
| RMSES | NA, -3 | 4, 4 | 3, 1 | NA, 1 |
*Note that PNL represents for the parameter number with less uncertainties in PSO compared to SCE, where NA represents for none. While ONR represents for the outlier number reduction of parameters’ uncertainties in PSO compared to SCE.
Table 4.
Linear fits between SIM and OBS against sites for all metrics.
| Metrics | PSO SM (s, r2) * | SCE SM (s, r2) | PSO ST (s, r2) | SCE ST (s, r2) |
|---|---|---|---|---|
| CCS | 0.29, 0.11 | 0.03, 0.01 | 0, 0 | 0.1, 0.01 |
| EKGE | 0.91, 0.9 | 0.73, 0.75 | 0.18, 0.03 | 0.23, 0.05 |
| EMO | 0.96, 0.92 | 0.83, 0.84 | 0.14, 0.1 | 0.11, 0.04 |
| MAES | 0.76, 0.6 | 0.44, 0.55 | 0.13, 0.05 | 0.06, 0.01 |
| NSES | 0.57, 0.39 | 0.25, 0.2 | -0.41, 0.05 | -0.44, 0.08 |
| PKGE | 0.19, 0.04 | 0.26, 0.11 | -0.57, 0.1 | -0.56, 0.11 |
| PMO | 0.68, 0.31 | 0.74, 0.48 | -0.63, 0.11 | -0.51, 0.09 |
| RMSES | 0.77, 0.57 | 0.16, 0.13 | 0.12, 0.05 | 0.09, 0.02 |
*Note that s and r2 represent for the slope and determination coefficient, respectively. Bold numbers indicate the best performance among all metrics, while italics indicate a negative slope.
Table 5.
Gaussian fits of OBS-SIM against sites for all metrics.
| Metrics | PSO SM (f, c) * | SCE SM (f, c) | PSO ST (f, c) | SCE ST (f, c) |
|---|---|---|---|---|
| CCS | 350, -0.04 | 295, 0.11 | 216, 2.13 | 167, 1.07 |
| EKGE | 1276, 0 | 608, 0 | 142, 4.37 | 204, 2.48 |
| EMO | 1178, 0 | 386, 0.01 | 170, 0.85 | 206, 1.23 |
| MAES | 344, 0.01 | 416, 0.02 | 200, -0.06 | 230, 0.88 |
| NSES | 274, 0.05 | 230, 0.05 | 169, 5.86 | 213, 5.03 |
| PKGE | 322, 0.08 | 325, 0.11 | 237, 4.91 | 152, 5.01 |
| PMO | 480, 0.02 | 444, 0.03 | 300, 6.10 | 224, 5.19 |
| RMSES | 426, -0.02 | 296, 0 | 200, 0.16 | 206, 1.29 |
*Note that f and c represent for the maximum amplitude (i.e. frequency) and its center (i.e. location), respectively. Bold numbers indicate the best performance among all metrics.
Table 6.
Linear fits between surface SIM and OBS against sites for all metrics.
| Metrics | PSO SM (s, r2) * | SCE SM (s, r2) | PSO ST (s, r2) | SCE ST (s, r2) |
|---|---|---|---|---|
| CCS | -0.32, 0.08 | -0.07, 0.02 | 0.04, 0 | 0.15, 0.04 |
| EKGE | 0.98, 0.84 | 0.84, 0.84 | 0.04, 0.01 | 0.1, 0.04 |
| EMO | 0.96, 0.78 | 0.86, 0.82 | 0.09, 0.08 | 0.1, 0.07 |
| MAES | 0.83, 0.58 | 0.42, 0.37 | 0.14, 0.07 | 0.15, 0.07 |
| NSES | 0.75, 0.45 | 0.31, 0.27 | -0.45, 0.07 | -0.33, 0.05 |
| PKGE | -0.04, 0 | -0.21, 0.14 | -0.53, 0.1 | -0.54, 0.1 |
| PMO | 0.52, 0.30 | 0.46, 0.31 | -0.58, 0.11 | -0.46, 0.09 |
| RMSES | 0.77, 0.56 | 0.16, 0.08 | 0.13, 0.08 | 0.14, 0.09 |
*Note that s and r2 represent for the slope and determination coefficient, respectively. Bold numbers indicate the best performance among all metrics, while italics indicate a negative slope.
Table 7.
Gaussian fits of OBS-SIM against sites for all metrics.
| Metrics | PSO SM (f, c) * | SCE SM (f, c) | PSO ST (f, c) | SCE ST (f, c) |
|---|---|---|---|---|
| CCS | 189, 0.15 | 225, 0.07 | 187, 3.2 | 181, -0.38 |
| EKGE | 383, 0 | 363, 0 | 143, -0.09 | 189, 3.39 |
| EMO | 416, 0 | 359, 0 | 175, -1.41 | 148, -0.98 |
| MAES | 359, -0.01 | 284, 0 | 181, 0.49 | 206, 0.29 |
| NSES | 343, 0.06 | 322, 0.05 | 204, 5.81 | 210, 4.56 |
| PKGE | 234, 0.13 | 365, 0.06 | 214, 4.9 | 217, 5.69 |
| PMO | 367, 0.01 | 323, 0.04 | 221, 6.17 | 187, 5.47 |
| RMSES | 293, -0.02 | 326, 0.01 | 194, 0.55 | 198, 0.32 |
*Note that f and c represent for the maximum amplitude (i.e. frequency) and its center (i.e. location), respectively. Bold numbers indicate the best performance among all metrics.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated






