Submitted:
14 August 2024
Posted:
15 August 2024
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Results and discussion
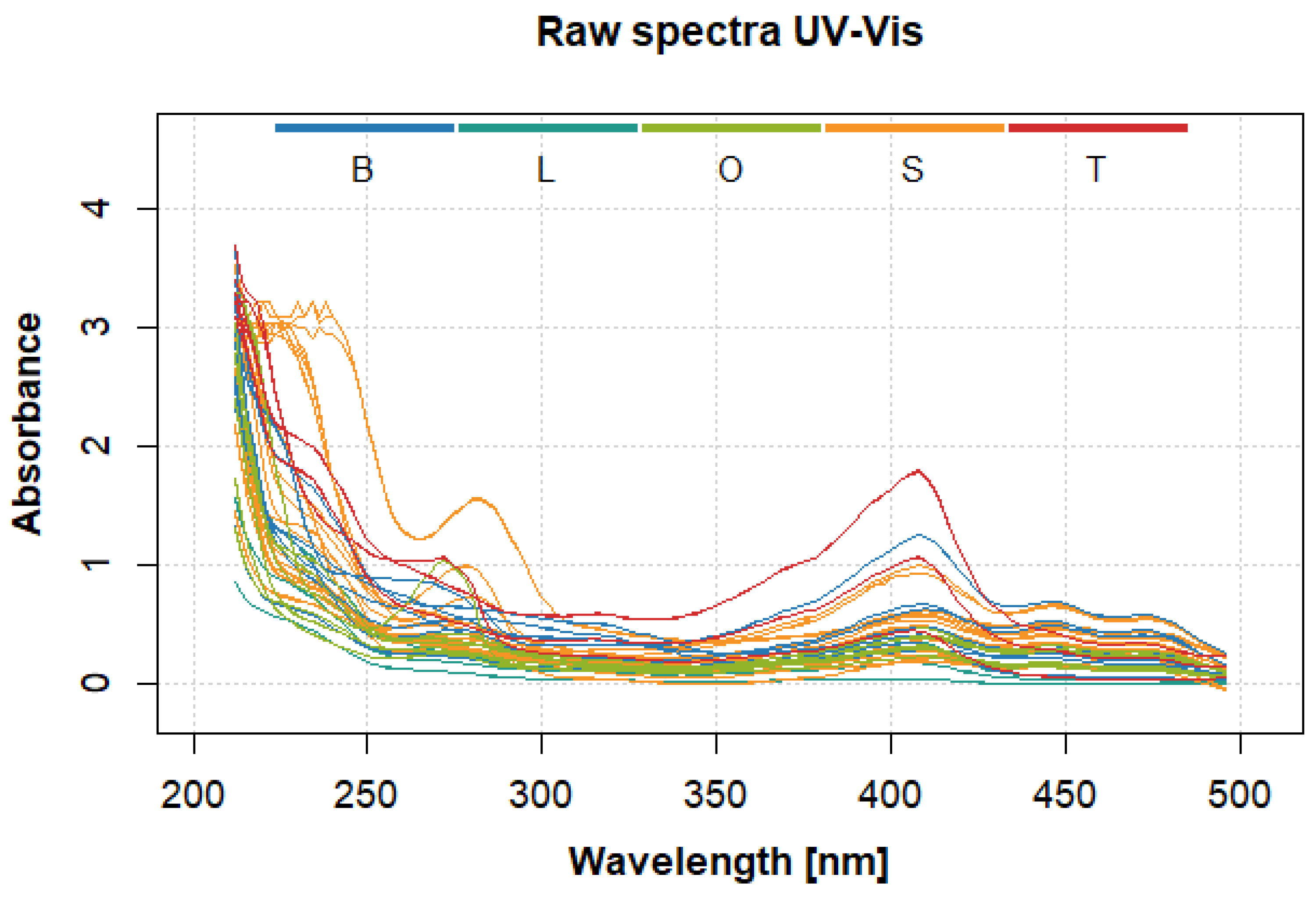
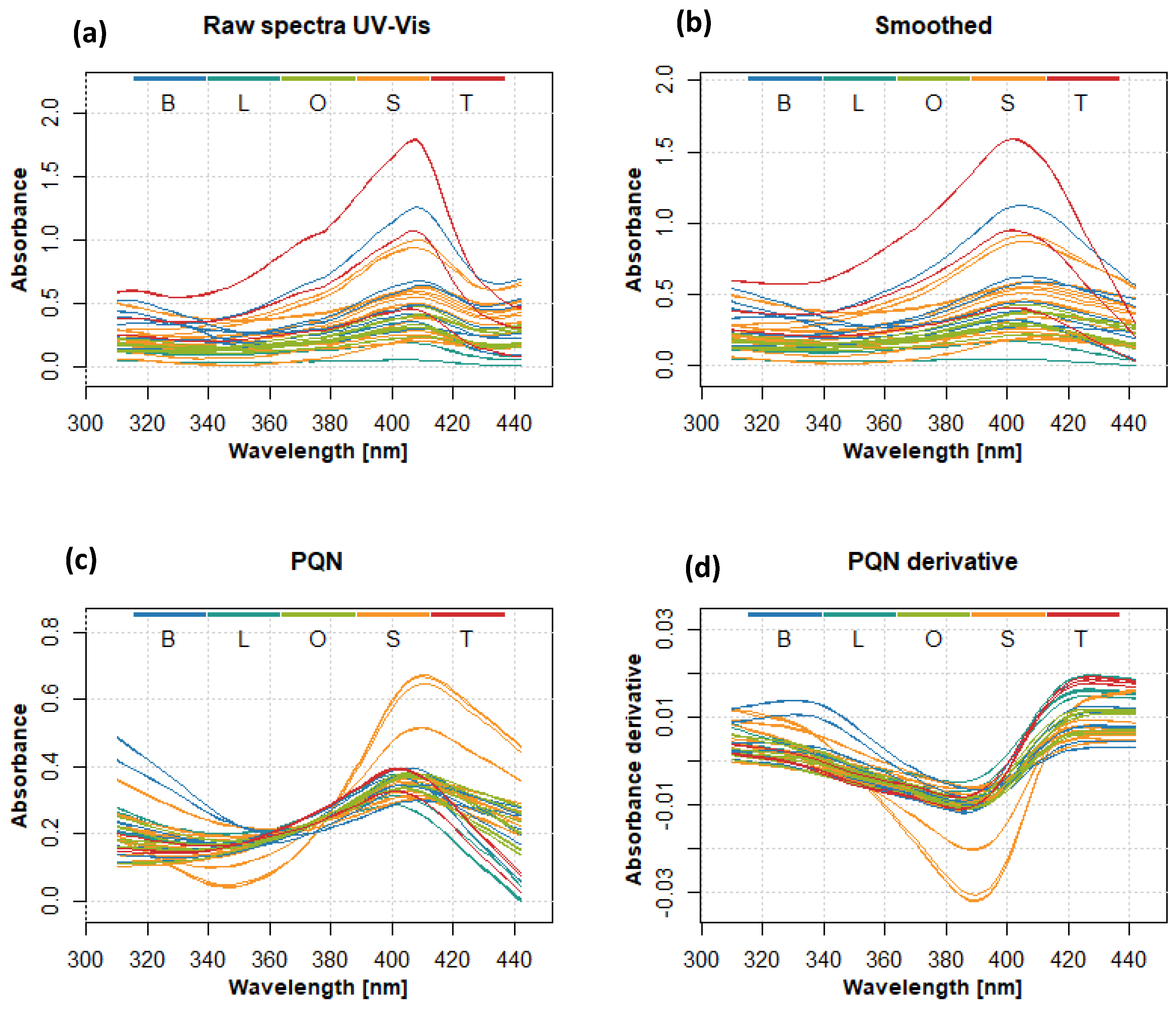
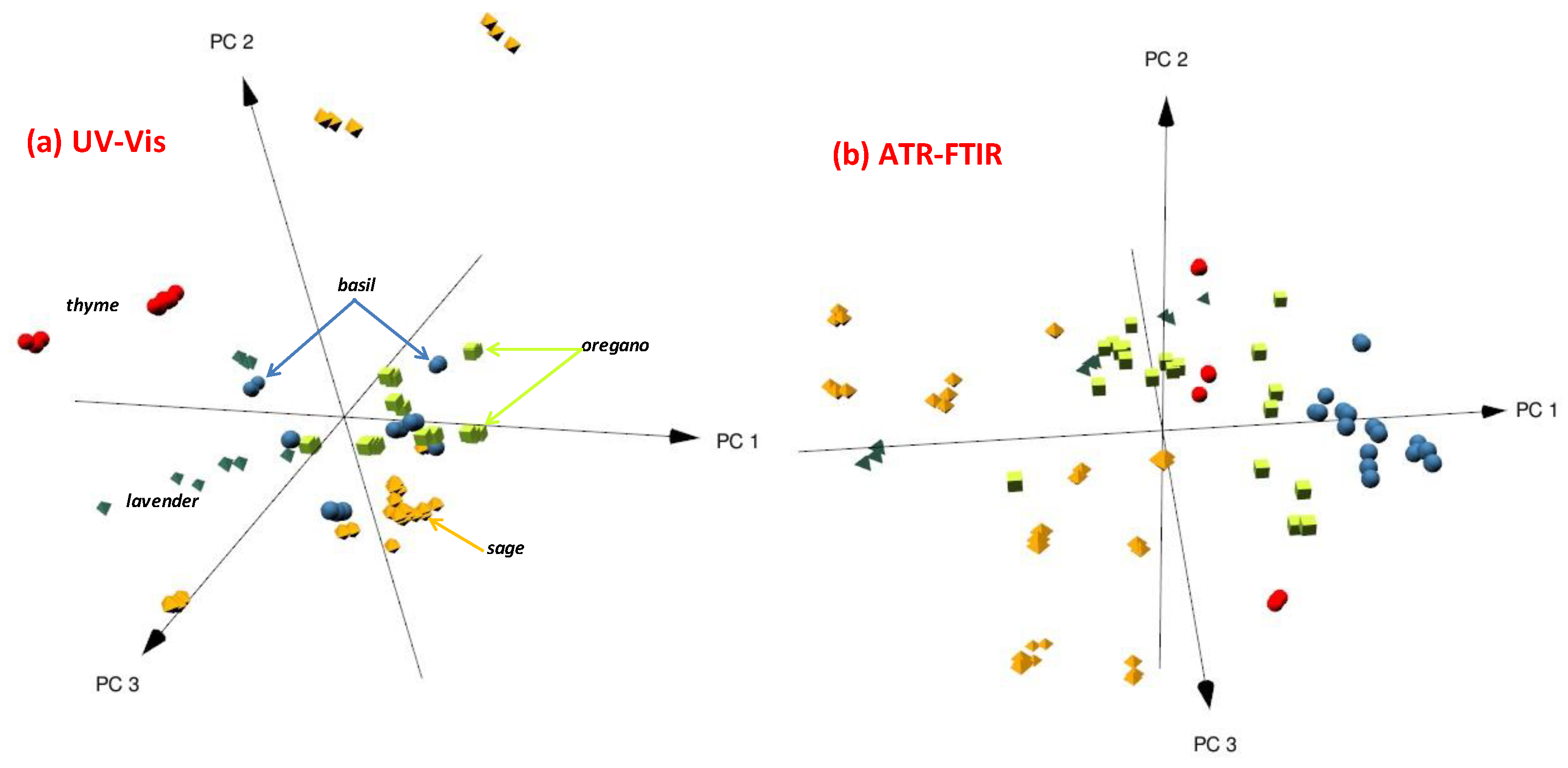
2.1. UV-Vis Spectra Analysis
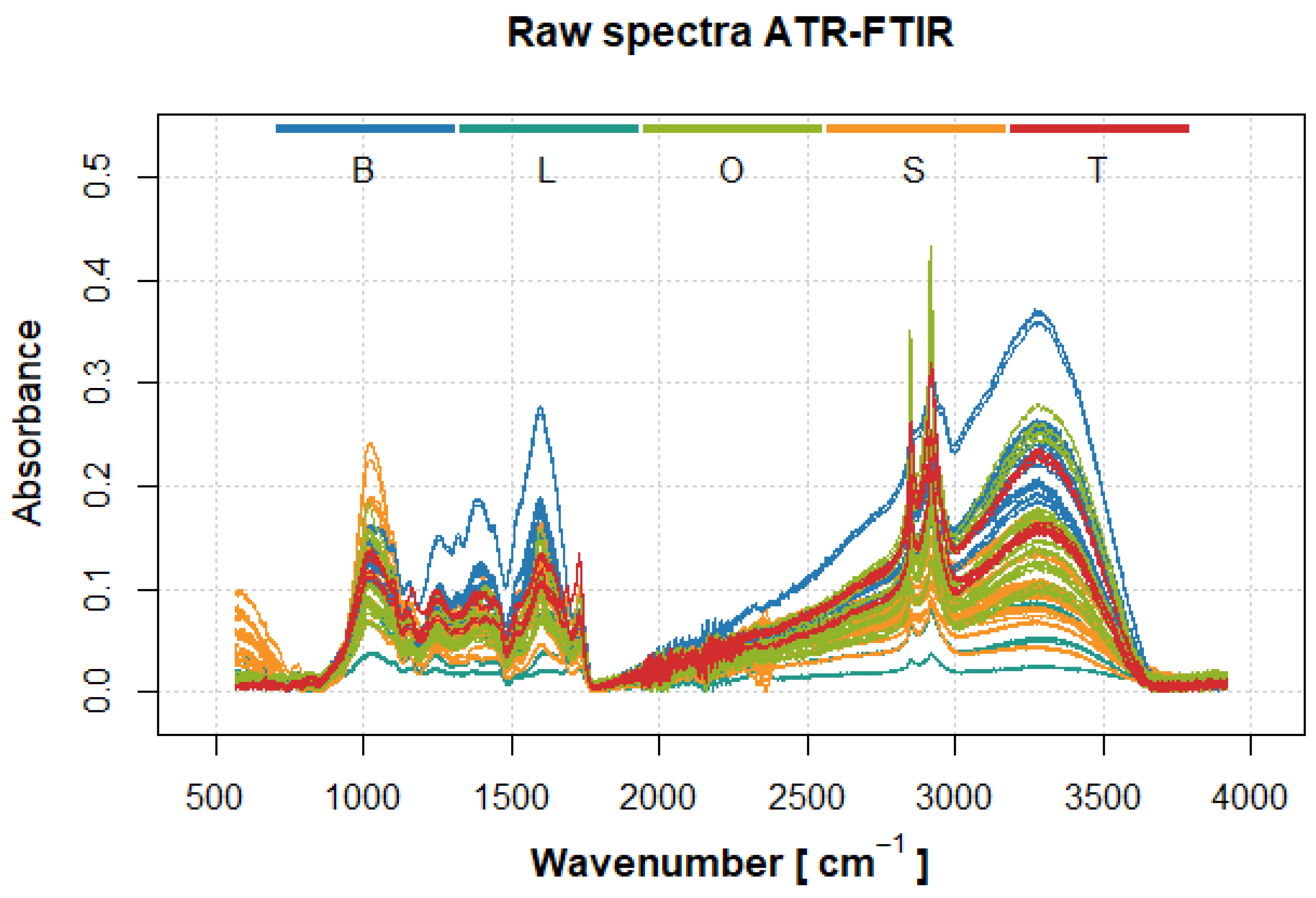
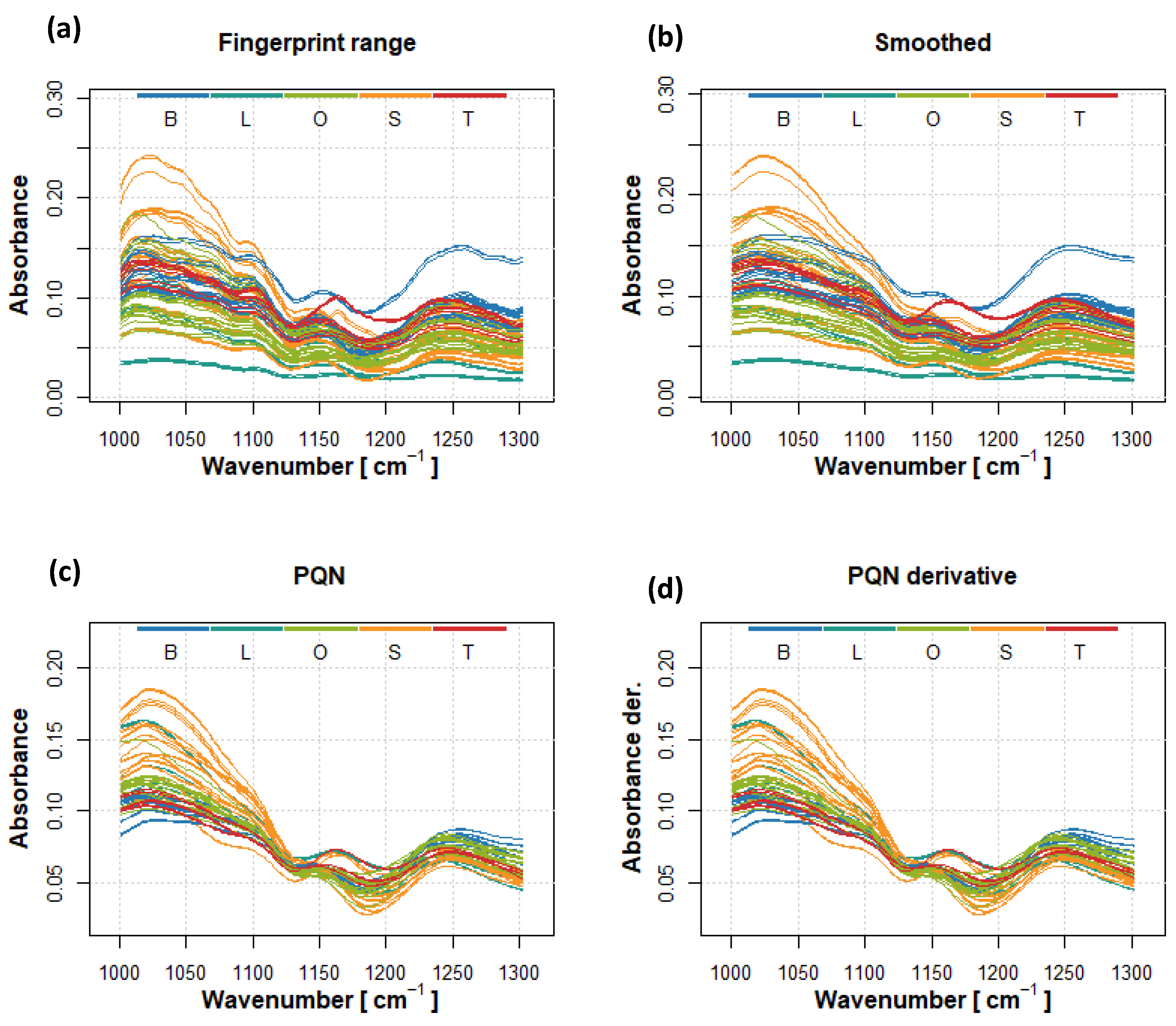
2.2. FTIR-ATR Spectra Analysis
2.3. Multivariate Statistical Analysis and Classification
2.3.1. Principal Components Analysis
2.3.2. Discriminant Analysis Methodology
2.3.3. Objectives
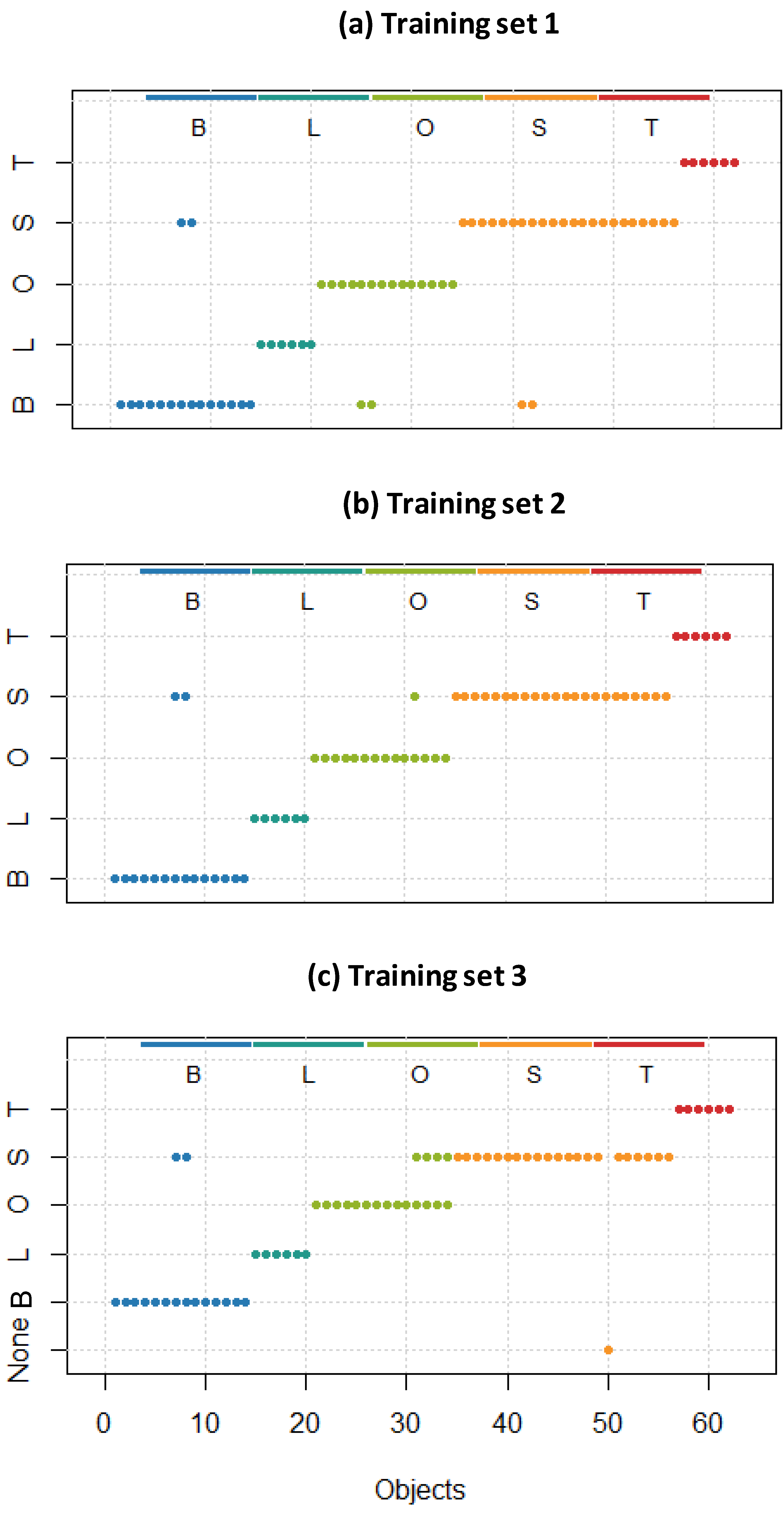
2.3.4. UV-Vis Discriminant Analysis
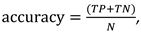 where F(P,N) means False Positives (Negatives), T(P,N) True Positives (Negatives). To compare the performance of different discrimination methodologies on the same dataset and to assess their robustness and sensitivity to class boundaries, various k coefficients, ranging from 0.3 to 0.8, are applied. The k coefficient refers to the proportion of data allocated to the training and test sets. For example, a k value of 0.3 means that 30% of the dataset is used for training, while the remaining 70% is for testing. This process allows for the evaluation of how each method handles varying levels of class separation or overlap, as represented by the different k values. By analyzing the resulting classification accuracies, one can determine which methods are more consistent or exhibit superior discrimination under various conditions. This comparison is crucial for selecting the most suitable methodology for specific datasets, especially when class separability varies. The results from applying the techniques described above on the UV dataset with different k values are summarized in Table 1. Due to the identical structure of the sample set, this table accurately illustrates the comparative efficacy of the various methodologies.
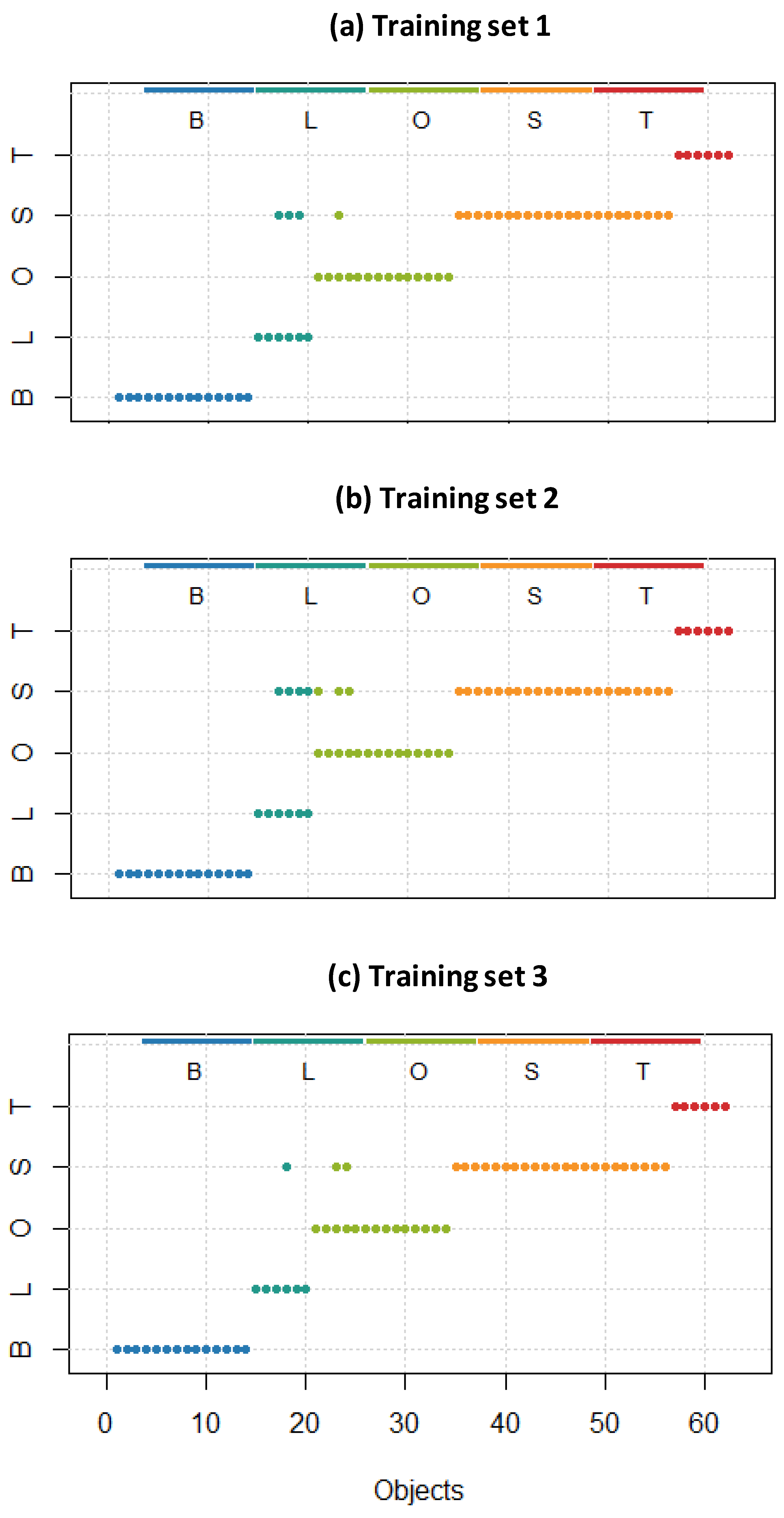
where F(P,N) means False Positives (Negatives), T(P,N) True Positives (Negatives). To compare the performance of different discrimination methodologies on the same dataset and to assess their robustness and sensitivity to class boundaries, various k coefficients, ranging from 0.3 to 0.8, are applied. The k coefficient refers to the proportion of data allocated to the training and test sets. For example, a k value of 0.3 means that 30% of the dataset is used for training, while the remaining 70% is for testing. This process allows for the evaluation of how each method handles varying levels of class separation or overlap, as represented by the different k values. By analyzing the resulting classification accuracies, one can determine which methods are more consistent or exhibit superior discrimination under various conditions. This comparison is crucial for selecting the most suitable methodology for specific datasets, especially when class separability varies. The results from applying the techniques described above on the UV dataset with different k values are summarized in Table 1. Due to the identical structure of the sample set, this table accurately illustrates the comparative efficacy of the various methodologies.2.3.4. ATR-FTIR Discriminant Analysis
3. Discussion
4. Materials and Methods
4.1. Samples
4.2. Statistical Analysis
4.3. UV-VIS Spectra Measurement
4.4. FTIR-ATR Spectra Measurement
5. Conclusions
Supplementary Materials
Author Contributions
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Galvin-King, P.; Haughey, S.A.; Elliott, C.T. Herb and spice fraud; the drivers, challenges and detection. Food Control 2018, 88, 85–97. [Google Scholar] [CrossRef]
- Wielogorska, E.; Chevallier, O.; Black, C.; Galvin-King, P.; Delêtre, M.; Kelleher, C.T.; Haughey, S.A.; Elliott, C.T. Development of a comprehensive analytical platform for the detection and quantitation of food fraud using a biomarker approach. The oregano adulteration case study. Food Chemistry 2018, 239, 32–39. [Google Scholar] [CrossRef]
- Kucharska-Ambrożej, K.; Karpinska, J. The application of spectroscopic techniques in combination with chemometrics for detection adulteration of some herbs and spices. Microchemical Journal 2020, 153, 104278. [Google Scholar] [CrossRef]
- Kucharska-Ambrożej, K.; Martyna, A.; Karpińska, J.; Kiełtyka-Dadasiewicz, A.; Kubat-Sikorska, A. Quality control of mint species based on UV-VIS and FTIR spectral data supported by chemometric tools. Food Control 2021, 129, 108228. [Google Scholar] [CrossRef]
- Gudi, G.; Krähmer, A.; Krüger, H.; Schulz, H. Attenuated total reflectance–Fourier transform infrared spectroscopy on intact dried leaves of sage (Salvia officinalis L.): accelerated chemotaxonomic discrimination and analysis of essential oil composition. Journal of agricultural and food chemistry 2015, 63, 8743–8750. [Google Scholar] [CrossRef]
- Javaid, M.; Haleem, A.; Singh, R.P.; Suman, R.; Gonzalez, E.S. Understanding the adoption of Industry 4.0 technologies in improving environmental sustainability. Sustainable Operations and Computers 2022, 3, 203–217. [Google Scholar] [CrossRef]
- Ingrid, M.E.; Dana, O.; Bastiaan, J.V. Current challenges in the detection and analysis of falsified medicines. Journal of Pharmaceutical and Biomedical Analysis 2021, 197, 113948. [Google Scholar]
- Gan, F.; Ye, R. New approach on similarity analysis of chromatographic fingerprint of herbal medicine. Journal of Chromatography A 2006, 1104, 100–105. [Google Scholar] [CrossRef]
- Li, Y.; Shen, Y.; Yao, C.-l.; Guo, D.-a. Quality assessment of herbal medicines based on chemical fingerprints combined with chemometrics approach: A review. Journal of Pharmaceutical and Biomedical Analysis 2020, 185, 113215. [Google Scholar] [CrossRef] [PubMed]
- Bahadur, S.; Taj, S.; Ahmad, M.; Zafar, M.; Gul, S.; Shuaib, M.; Butt, M.A.; Hanif, U.; Nizamani, M.M.; Hussain, F.; et al. Authentication of the therapeutic Lamiaceae taxa by using pollen traits observed under scanning electron microscopy. Microscopy Research and Technique 2022, 85, 2026–2044. [Google Scholar] [CrossRef]
- Black, C.; Haughey, S.A.; Chevallier, O.P.; Galvin-King, P.; Elliott, C.T. A comprehensive strategy to detect the fraudulent adulteration of herbs: The oregano approach. Food Chemistry 2016, 210, 551–557. [Google Scholar] [CrossRef]
- Figuérédo, G.; Cabassu, P.; Chalchat, J.-C.; Pasquier, B. Studies of Mediterranean oregano populations. VIII—Chemical composition of essential oils of oreganos of various origins. Flavour and Fragrance Journal 2006, 21, 134–139. [Google Scholar] [CrossRef]
- Gad, H.A.; El-Ahmady, S.H.; Abou-Shoer, M.I.; Al-Azizi, M.M. A Modern Approach to the Authentication and Quality Assessment of Thyme Using UV Spectroscopy and Chemometric Analysis. Phytochemical Analysis 2013, 24, 520–526. [Google Scholar] [CrossRef] [PubMed]
- Dankowska, A.; Majsnerowicz, A.; Kowalewski, W.; Włodarska, K. The application of visible and near-infrared spectroscopy combined with chemometrics in classification of dried herbs. Sustainability 2022, 14, 6416. [Google Scholar] [CrossRef]
- Fan, Y.; Bai, X.; Chen, H.; Yang, X.; Yang, J.; She, Y.; Fu, H. A novel simultaneous quantitative method for differential volatile components in herbs based on combined near-infrared and mid-infrared spectroscopy. Food Chemistry 2023, 407, 135096. [Google Scholar] [CrossRef]
- Elfiky, A.M.; Shawky, E.; Khattab, A.R.; Ibrahim, R.S. Integration of NIR spectroscopy and chemometrics for authentication and quantitation of adulteration in sweet marjoram (Origanum majorana L.). Microchemical Journal 2022, 183, 108125. [Google Scholar] [CrossRef]
- McVey, C.; McGrath, T.F.; Haughey, S.A.; Elliott, C.T. A rapid food chain approach for authenticity screening: The development, validation and transferability of a chemometric model using two handheld near infrared spectroscopy (NIRS) devices. Talanta 2021, 222, 121533. [Google Scholar] [CrossRef] [PubMed]
- Abdulkarem, A.H.A.K.H.; Lebnane, H.A.H.M.I. Chemotaxonomy and spectral analysis (GC/MS and FT-IR) of essential oil composition of two Ocimum basilicum L. varieties and their morphological characterization. Jordan Journal of Chemistry (JJC) 2017, 12, 147–160. [Google Scholar]
- Al-Asmari, A.K.; Athar, M.T.; Al-Faraidy, A.A.; Almuhaiza, M.S. Chemical composition of essential oil of Thymus vulgaris collected from Saudi Arabian market. Asian Pacific Journal of Tropical Biomedicine 2017, 7, 147–150. [Google Scholar] [CrossRef]
- Casale, M.; Oliveri, P.; Casolino, C.; Sinelli, N.; Zunin, P.; Armanino, C.; Forina, M.; Lanteri, S. Characterisation of PDO olive oil Chianti Classico by non-selective (UV–visible, NIR and MIR spectroscopy) and selective (fatty acid composition) analytical techniques. Analytica chimica acta 2012, 712, 56–63. [Google Scholar] [CrossRef]
- Rohaeti, E.; Rafi, M.; Syafitri, U.D.; Heryanto, R. Fourier transform infrared spectroscopy combined with chemometrics for discrimination of Curcuma longa, Curcuma xanthorrhiza and Zingiber cassumunar. Spectrochimica acta. Part A, Molecular and biomolecular spectroscopy 2015, 137, 1244–1249. [Google Scholar] [CrossRef] [PubMed]
- Ying, C.; Jinfang, H.; Yeap, Z.; Xue, Z.; Shuisheng, W.; Ng, C.; Yam, M. Rapid authentication and identification of different types of A. roxburghii by Tri-step FT-IR spectroscopy. Spectrochimica Acta Part A: Molecular and Biomolecular Spectroscopy 2018, 199. [Google Scholar]
- Beale, D.J.; Morrison, P.D.; Karpe, A.V.; Dunn, M.S. Chemometric Analysis of Lavender Essential Oils Using Targeted and Untargeted GC-MS Acquired Data for the Rapid Identification and Characterization of Oil Quality. Molecules 2017, 22, 1339. [Google Scholar] [CrossRef] [PubMed]
- Economou, G.; Tarantilis, P.; Panagopoulos, G.; Kotoulas, V.; Polysiou, M.; Karamanos, A. Variability in essential oil content and composition of Origanum hirtum L., Origanum onites L., Coridothymus capitatus (L.) and Satureja thymbra L. populations from the Greek island Ikaria. Industrial Crops and Products 2011, 33. [Google Scholar] [CrossRef]
- Ercioglu, E.; Velioglu, H.M.; Boyaci, I.H. Determination of terpenoid contents of aromatic plants using NIRS. Talanta 2018, 178, 716–721. [Google Scholar] [CrossRef] [PubMed]
- Govindaraghavan, S.; Sucher, N.J. Quality assessment of medicinal herbs and their extracts: Criteria and prerequisites for consistent safety and efficacy of herbal medicines. Epilepsy Behav 2015, 52, 363–371. [Google Scholar] [CrossRef] [PubMed]
- Joshi, A.; Prakash, O.; Pant, A.K.; Kumar, R.; Szczepaniak, L.; Kucharska-Ambrożej, K. Methyl eugenol, 1, 8-cineole and nerolidol rich essential oils with their biological activities from three melaleuca species growing in Tarai region of North India. Brazilian Archives of Biology and Technology 2022, 64. [Google Scholar] [CrossRef]
- Lee, S.-J.; Umano, K.; Shibamoto, T.; Lee, K.-G. Identification of volatile components in basil (Ocimum basilicum L.) and thyme leaves (Thymus vulgaris L.) and their antioxidant properties. Food chemistry 2005, 91, 131–137. [Google Scholar] [CrossRef]
- Nezhadali, A.; Nabavi, M.; Rajabian, M.; Akbarpour, M.; Pourali, P.; Amini, F. Chemical variation of leaf essential oil at different stages of plant growth and in vitro antibacterial activity of Thymus vulgaris Lamiaceae, from Iran. Beni-Suef University Journal of Basic and Applied Sciences 2014, 3, 87–92. [Google Scholar] [CrossRef]
- Sánchez, A.M.; Carmona, M.; Zalacain, A.; Carot, J.M.; Jabaloyes, J.M.; Alonso, G.L. Rapid Determination of Crocetin Esters and Picrocrocin from Saffron Spice (Crocus sativus L.) Using UV–Visible Spectrophotometry for Quality Control. Journal of Agricultural and Food Chemistry 2008, 56, 3167–3175. [Google Scholar] [CrossRef]
- Suhandy, D.; Yulia, M. Peaberry coffee discrimination using UV-visible spectroscopy combined with SIMCA and PLS-DA. International Journal of Food Properties 2017, 20, S331–S339. [Google Scholar] [CrossRef]
- Coelho de Oliveira, H.; Elias da Cunha Filho, J.C.; Rocha, J.C.; Fernández Núñez, E.G. Rapid monitoring of beer-quality attributes based on UV-Vis spectral data. International Journal of Food Properties 2017, 20, 1686–1699. [Google Scholar] [CrossRef]
- Pages-Rebull, J.; Pérez-Ràfols, C.; Serrano, N.; del Valle, M.; Díaz-Cruz, J.M. Classification and authentication of spices and aromatic herbs by means of HPLC-UV and chemometrics. Food Bioscience 2023, 52, 102401. [Google Scholar] [CrossRef]
- Rafi, M.; Jannah, R.; Heryanto, R.; Kautsar, A.; Septaningsih, D.A. UV-Vis spectroscopy and chemometrics as a tool for identification and discrimination of four Curcuma species. International Food Research Journal 2018, 25, 643–648. [Google Scholar]
- Bunghez, F.; Socaciu, C.; Zagrean, F.; Pop, R.; Ranga, F.; Florina, R. Characterisation of an aromatic plant-based formula using UV-Vis Spectroscopy, LC-ESI(+)QTOF-MS and HPLCDAD analysis. Bulletin of University of Agricultural Sciences and Veterinary Medicine Cluj-Napoca: Food Science and Technology 2013, 70. [Google Scholar]
- Bevilacqua, M.; Bucci, R.; Magrì, A.D.; Magrì, A.L.; Marini, F. Tracing the origin of extra virgin olive oils by infrared spectroscopy and chemometrics: A case study. Analytica Chimica Acta 2012, 717, 39–51. [Google Scholar] [CrossRef] [PubMed]
- Vasas, M.; Tang, F.; Hatzakis, E. Application of NMR and Chemometrics for the Profiling and Classification of Ale and Lager American Craft Beer. Foods 2021, 10, 807. [Google Scholar] [CrossRef]
- Zeaiter, M.; Roger, J.-M.; Bellon-Maurel, V. Robustness of models developed by multivariate calibration. Part II: The influence of pre-processing methods. TrAC Trends in Analytical Chemistry 2005, 24, 437–445. [Google Scholar] [CrossRef]
- Dieterle, F.; Ross, A.; Schlotterbeck, G.; Senn, H. Probabilistic Quotient Normalization as Robust Method to Account for Dilution of Complex Biological Mixtures. Application in 1H NMR Metabonomics. Analytical Chemistry 2006, 78, 4281–4290. [Google Scholar] [CrossRef]
- Correia, G.D.S.; Takis, P.G.; Sands, C.J.; Kowalka, A.M.; Tan, T.; Turtle, L.; Ho, A.; Semple, M.G.; Openshaw, P.J.M.; Baillie, J.K.; et al. 1H NMR Signals from Urine Excreted Protein Are a Source of Bias in Probabilistic Quotient Normalization. Analytical Chemistry 2022, 94, 6919–6923. [Google Scholar] [CrossRef]
- Sommer, A.A.; Arega, F.B.; Vodovotz, Y. Assessment of Fish Oil Oxidation Using Low-Field Proton Nuclear Magnetic Resonance Spectroscopy. ACS Food Science & Technology 2023, 3, 1476–1483. [Google Scholar]
- Luypaert, J.; Heuerding, S.; Vander Heyden, Y.; Massart, D. The effect of preprocessing methods in reducing interfering variability from near-infrared measurements of creams. Journal of pharmaceutical and biomedical analysis 2004, 36, 495–503. [Google Scholar] [CrossRef] [PubMed]
- Wold, S. , Sjöström,M in: BR Kowalski (Ed. ). Chemometrics: Theory and Application, Am. In Proceedings of the Chem. Sot. Symp. Ser; 1977. [Google Scholar]
- Vitale, R.; Cocchi, M.; Biancolillo, A.; Ruckebusch, C.; Marini, F. Class modelling by Soft Independent Modelling of Class Analogy: why, when, how? A tutorial. Analytica Chimica Acta 2023, 1270, 341304. [Google Scholar] [CrossRef]
- Avohou, T.H.; Sacré, P.-Y.; Hamla, S.; Lebrun, P.; Hubert, P.; Ziemons, É. Optimizing the soft independent modeling of class analogy (SIMCA) using statistical prediction regions. Analytica Chimica Acta 2022, 1229, 340339. [Google Scholar] [CrossRef]
- Lee, L.C.; Liong, C.-Y.; Jemain, A.A. Partial least squares-discriminant analysis (PLS-DA) for classification of high-dimensional (HD) data: a review of contemporary practice strategies and knowledge gaps. Analyst 2018, 143, 3526–3539. [Google Scholar] [CrossRef] [PubMed]
- Xu, Y.; Zomer, S.; Brereton, R.G. Support Vector Machines: A Recent Method for Classification in Chemometrics. Critical Reviews in Analytical Chemistry 2006, 36, 177–188. [Google Scholar] [CrossRef]
- FISHER, R.A. THE USE OF MULTIPLE MEASUREMENTS IN TAXONOMIC PROBLEMS. Annals of Eugenics 1936, 7, 179–188. [Google Scholar] [CrossRef]
- Wang, P.; Fan, E.; Wang, P. Comparative analysis of image classification algorithms based on traditional machine learning and deep learning. Pattern Recognition Letters 2021, 141, 61–67. [Google Scholar] [CrossRef]
- Pérez-Ràfols, C.; Serrano, N.; Díaz-Cruz, J.M. Authentication of soothing herbs by UV–vis spectroscopic and chromatographic data fusion strategy. Chemometrics and Intelligent Laboratory Systems 2023, 235, 104783. [Google Scholar] [CrossRef]
- Fahmi, Z.; Mudasir, M.; Rohman, A. Attenuated Total Reflectance-FTIR Spectra Combined with Multivariate Calibration and Discrimination Analysis for Analysis of Patchouli Oil Adulteration. Indonesian Journal of Chemistry 2019, 20, 1–8. [Google Scholar] [CrossRef]
- Oliveira, M.M.; Cruz-Tirado, J.; Barbin, D.F. Nontargeted analytical methods as a powerful tool for the authentication of spices and herbs: A review. Comprehensive Reviews in Food Science and Food Safety 2019, 18, 670–689. [Google Scholar] [CrossRef] [PubMed]
- McGoverin, C.M.; September, D.J.; Geladi, P.; Manley, M. Near infrared and mid-infrared spectroscopy for the quantification of adulterants in ground black pepper. Journal of Near Infrared Spectroscopy 2012, 20, 521–528. [Google Scholar] [CrossRef]
- Pasquini, C. Near infrared spectroscopy: A mature analytical technique with new perspectives–A review. Analytica chimica acta 2018, 1026, 8–36. [Google Scholar] [CrossRef] [PubMed]
- Petrakis, E.A.; Polissiou, M.G. Assessing saffron (Crocus sativus L.) adulteration with plant-derived adulterants by diffuse reflectance infrared Fourier transform spectroscopy coupled with chemometrics. Talanta 2017, 162, 558–566. [Google Scholar] [CrossRef] [PubMed]
- Shah, P.P.; Mello, P. A review of medicinal uses and pharmacological effects of Mentha piperita. 2004.
- Dankowska, A.; Kowalewski, W. Tea types classification with data fusion of UV–Vis, synchronous fluorescence and NIR spectroscopies and chemometric analysis. Spectrochimica Acta Part A: Molecular and Biomolecular Spectroscopy 2019, 211, 195–202. [Google Scholar] [CrossRef] [PubMed]
- Wenables, W.N.; Ripley, B.D. Modern Applied Statistics with S, Fourth edition. Springer, New York. ISBN 0-387-95457-0. 2002.
- Meyer, D.; Dymitriadou, E.; Hornik, K.; Weingssel, A.; leisch, F.; Chang, C.-C.; Lin, C.-C. e1071: Misc Functions of the Department of Statistics, Probability Theory Group (Formerly: E1071), TU Wien. R package version 1.7-14 1999.
- Bergmeir, C.; Benítez, J.M. Neural Networks in R Using the Stuttgart Neural Network Simulator: RSNNS. Journal of Statistical Software 2012, 46, 1–26. [Google Scholar] [CrossRef]
- Liaw, A.; Wiener, M. Classification and Regression by randomForest. R News 2002, 2, 18–22. [Google Scholar]
| Accuracy with k= | |||||||
| Method | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | |
| SIMCA | 0.83 | 0.83 | 0.84 | 0.87 | 0.95 | 1.00 | |
| LDA | 0.77 | 0.88 | 0.79 | 0.77 | 0.93 | 1.00 | |
| PLS/DA | 0.51 | 0.54 | 0.59 | 0.63 | 0.66 | 0.71 | |
| SVM | 0.68 | 0.71 | 0.74 | 0.68 | 0.75 | 0.88` | |
| MLP | 0.61 | 0.67 | 0.66 | 0.72 | 0.84 | 0.97 | |
| RF | 0.64 | 0.68 | 0.79 | 0.79 | 0.88 | 1.00 | |
| Accuracy with k= | |||||||
| Method | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | |
| SIMCA | 0.83 | 0.87 | 0.93 | 0.92 | 0.94 | 1.00 | |
| LDA | 0.67 | 0.77 | 0.79 | 0.81 | 0.82 | 0.86 | |
| PLS/DA | 0.49 | 0.59 | 0.66 | 0.77 | 0.77 | 0.81 | |
| SVM | 0.52 | 0.67 | 0.72 | 0.81 | 0.75 | 0.95 | |
| MLP | 0.58 | 0.61 | 0.69 | 0.77 | 0.86 | 0.92 | |
| RF | 0.67 | 0.69 | 0.81 | 0.92 | 0.86 | 0.95 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).





