Preprint
Review
Revisiting Clockwork Model: A Review of Theoretical Foundations and Experimental Progress
Altmetrics
Downloads
92
Views
62
Comments
0
This version is not peer-reviewed
Submitted:
14 August 2024
Posted:
15 August 2024
You are already at the latest version
Alerts
Abstract
Clockwork fermions represent a novel theoretical construct in high-energy physics, addressing such fundamental issues as mass hierarchies and dark matter. This review provides an examination of the theoretical underpinnings of clockwork fermions, their implications for particle physics, and the current state of experimental validations. Clockwork fermions represent a paradigm in particle physics, elegantly addressing the hierarchy problem and offering insights into the generation of small neutrino masses. We provide an analysis of the clockwork mechanism, emphasizing its theoretical innovation and the unique mass hierarchies it produces. We examine recent experimental efforts, including collider searches and direct detection experiments, that place constraints on clockwork models, while also exploring their potential cosmological implications.
Keywords:
Subject: Physical Sciences - Particle and Field Physics
1. Introduction
The clockwork mechanism [1] is a theoretical framework that offers elegant solutions to several pressing issues in particle physics, such as the hierarchy problem, neutrino masses, and the nature of dark matter. First proposed by Giudice and collaborators in 2017, the concept has since been extended and applied to various fields within high-energy physics. This review aims to provide an overview of clockwork fermions, discussing their theoretical underpinnings, applications, and implications for future research.
Clockwork models rely on the idea of generating exponentially suppressed interactions through a linear chain of fields, each coupling only to its nearest neighbor. This mechanism allows for large hierarchies to be naturally realized without fine-tuning, making it a powerful tool in model building. The clockwork fermion model, in particular, introduces a chain of fermionic fields, leading to novel predictions and potential observable effects in both particle physics experiments and cosmological observations.
In the context of supersymmetry, the clockwork mechanism can be used to generate hierarchical structures in the masses and couplings of supersymmetric particles. The basic idea of the clockwork mechanism involves a series of fields (referred to as gears) that interact in such a way that the mass and coupling of the end field are exponentially suppressed compared to the input parameters.
Consider a supersymmetric theory with a series of chiral superfields (). The superpotential can be written as:
where k is a
constant and are the masses of the fields. The resulting mass matrix for the scalar components of the superfields takes the form of a tridiagonal matrix, which leads to an exponential hierarchy in the eigenvalues of the masses.
The clockwork mechanism ensures that the effective mass of the lightest eigenstate is suppressed by a factor of . This feature can be utilized in supersymmetric models to generate a large hierarchy between the supersymmetry breaking scale and the electroweak scale, thereby addressing the hierarchy problem.
When applied to supersymmetry, the clockwork mechanism can significantly impact the mass spectrum and interaction strengths of supersymmetric particles. For example, it can explain the smallness of the Higgs mass parameter () in the Minimal Supersymmetric Standard Model (MSSM) without fine-tuning.
Additionally, the clockwork mechanism can generate small neutrino masses through the seesaw mechanism, where the heavy right-handed neutrinos obtain their masses via the clockwork gears, leading to naturally small left-handed neutrino masses.
The clockwork mechanism in the context of supersymmetry [2,3] is a relatively new area of research, and various theoretical and phenomenological aspects are still being explored. Several recent studies have focused on embedding the clockwork mechanism into different supersymmetric frameworks, such as the MSSM and next-to-MSSM (NMSSM).
Experimental searches for signatures of clockwork fermions and scalar particles are ongoing at the Large Hadron Collider (LHC) and other collider experiments. Current constraints on clockwork models come from searches for new resonances and deviations from the Standard Model predictions in various channels.
Recent experimental bounds have been placed on the parameter space of clockwork models. For instance, searches for new scalar particles at the LHC have constrained the masses and couplings of clockwork gears, limiting the viable range of parameters in these models.
Future experimental efforts, such as those at the High-Luminosity LHC (HL-LHC) and proposed future colliders like the Future Circular Collider (FCC), will play a crucial role in probing the clockwork mechanism in supersymmetry. These experiments will extend the reach for discovering new particles predicted by clockwork models and provide more stringent tests of the theoretical framework.
In addition to collider searches, other experimental avenues, such as precision measurements of rare processes and searches for deviations in flavor physics, will also be important for exploring the implications of the clockwork mechanism in supersymmetry.
The concept of clockwork fermions emerged as an elegant solution to several persistent problems in particle physics, including the generation of small masses and the hierarchy problem. Originally proposed in the context of generating small neutrino masses [4,5], the clockwork mechanism has found applications in various areas of theoretical physics.
In the clockwork mechanism, fields are arranged in a linear chain of sites, with nearest-neighbor interactions mediated by a coupling constant. The essential feature of the clockwork mechanism is that a small parameter at one end of the chain can generate exponentially suppressed parameters at the other end. For a fermion field, this can be mathematically represented as follows:
where represents the fermion field at site j, m is the mass parameter, and k is the coupling between nearest-neighbor sites.
By diagonalizing the mass matrix, we find the mass eigenvalues to be exponentially spaced:
where n indexes the mass eigenstates.
The clockwork mechanism can also address the hierarchy problem by generating hierarchically small parameters from order-one input parameters. For instance, the suppression factor for the N-th site is given by:
This exponential suppression can naturally generate small fermion masses without fine-tuning.
The clockwork mechanism has been extended to other fields, including scalar fields and gauge fields. For scalar fields, the Lagrangian can be written as:
where represents the scalar field at site j.
Moreover, clockwork mechanisms have been employed to explain the smallness of neutrino masses, providing a novel alternative to the seesaw mechanism. The clockwork seesaw model introduces a series of sterile neutrinos, with a structure that generates light active neutrino masses naturally.

In addition to theoretical developments, there have been ongoing efforts to explore experimental signatures of clockwork fermions. Collider experiments and astrophysical observations provide potential avenues to test the predictions of clockwork models. These efforts are crucial for validating the viability of the clockwork mechanism in explaining fundamental physics problems.
Clockwork axions [6] represent a novel approach in theoretical physics, combining the concepts of the clockwork mechanism with axion physics. Axions, originally proposed to solve the strong CP problem in quantum chromodynamics (QCD), have garnered significant interest for their potential to address various fundamental questions in particle physics and cosmology. This document explores the concept of clockwork axions, their theoretical foundations, and their current implications.
The strong CP problem [7] arises from the QCD Lagrangian, which allows for a term that could lead to CP violation:
where is a parameter, g is the QCD coupling constant, is the gluon field strength tensor, and is its dual. Experimentally, must be extremely small (less than ) to avoid observable CP violation, which is unnatural.
The Peccei-Quinn (PQ) solution introduces a new global U(1) symmetry, known as the PQ symmetry, which is spontaneously broken, giving rise to a pseudo-Nambu-Goldstone boson called the axion. The axion dynamically relaxes the effective parameter to zero, solving the strong CP problem. The clockwork mechanism is a theoretical framework designed to generate large hierarchies from small input parameters. It involves a chain of fields (referred to as gears) with specific interactions that lead to an exponential suppression or enhancement of certain properties, such as masses or decay constants.
Clockwork axions apply this mechanism to the axion field to address the issue of the large axion decay constant . In typical axion models, needs to be very large to satisfy experimental constraints, which can be problematic.
Consider a series of axion fields (). These fields interact in a way described by a potential:
where q is the clockwork gear ratio, and are the masses of the intermediate axion fields. The physical axion is a linear combination of these fields and has an effective decay constant given by:
where f is the decay constant of the original axion field. This exponential enhancement allows for a small fundamental decay constant while producing a large effective decay constant, solving the hierarchy problem naturally.
This review aims to provide a detailed overview of clockwork fermions, from their theoretical foundations to their experimental implications. We will discuss key developments in the field, the mathematical formalism underlying the clockwork mechanism, and the latest experimental results that may shed light on the existence of clockwork fermions.
This review is structured as follows: Section 2 provides a theoretical background on the clockwork mechanism and the specific construction of clockwork fermion models. Section 3 discusses the applications of clockwork fermions in addressing the Higgs hierarchy problem [8] , neutrino masses, and dark matter and Clockwork Axions. Section 4 explores the phenomenological implications of clockwork fermions, including potential collider signatures and cosmological impacts [9] . Finally, Section 5 summarizes recent developments and suggests directions for future research.
2. Theoretical Background
2.1. Fundamentals of Clockwork Mechanism
The clockwork mechanism introduces a series of fields arranged in a linear chain, where each field interacts primarily with its nearest neighbors. The core idea is to generate a suppression factor through the kinetic mixing of these fields, leading to exponentially small couplings at the ends of the chain.
Consider a simple scalar clockwork model with fields (). The Lagrangian is given by:
where q is the clockwork factor, and m is the mass parameter. The key feature of this setup is that the interaction strength of the zero-mode, which is a linear combination of the original fields, is exponentially suppressed by the factor .
This mechanism can be extended to fermions and gauge fields, providing a versatile framework for addressing different hierarchies in physics. For fermions, the clockwork chain involves Dirac or Majorana fermions with similar nearest-neighbour interactions, leading to suppressed couplings in the low-energy effective theory.
The clockwork mechanism elegantly addresses the naturalness problem by replacing large hierarchies with a product of modestly sized factors, avoiding the need for fine-tuning.
2.2. Clockwork Fermion Model
The clockwork mechanism is a theoretical framework proposed to address various issues in particle physics, such as mass hierarchies and the generation of small parameters. The mechanism involves a series of fields or particles arranged in a linear chain with specific couplings between adjacent sites. This setup can generate exponentially suppressed parameters naturally.
Consider a series of fermion fields, , arranged in a linear chain with sites. The Lagrangian describing the clockwork fermions can be written as:
where m is the mass parameter and k is the coupling constant between nearest-neighbor sites.
The mass matrix for the fermion fields is:
Diagonalizing this mass matrix gives the mass eigenvalues:
where n indexes the mass eigenstates. The clockwork mechanism has several interesting properties. One of the key features is the exponential suppression of parameters at the end of the chain. If we consider an interaction term involving the field at the N-th site, , the effective coupling can be exponentially suppressed as:
where g is the original coupling constant. This exponential suppression can naturally generate small parameters without fine-tuning.
The clockwork mechanism can also be applied to scalar fields. Consider a series of scalar fields, , arranged in a similar chain. The Lagrangian is given by:
The resulting mass matrix and its diagonalization yield similar exponentially spaced mass eigenvalues, as in the fermion case.
In the clockwork fermion model, we introduce a chain of fermionic fields (), where each field interacts with its nearest neighbor through a mass mixing term. The Lagrangian for a simple Dirac clockwork fermion model can be written as:
where m is the mass parameter that controls the strength of the interaction between neighboring fermions. The zero-mode fermion, which is a linear combination of the original fields, has an effective coupling that is exponentially suppressed by the clockwork factor . This suppression can naturally generate small neutrino masses or explain the smallness of certain Yukawa couplings without requiring fine-tuning.
3. Clockwork Mechanism in Particle Physics
3.1. Higgs Hierarchy Problem
The Higgs hierarchy problem [8] arises from the vast difference between the electroweak scale and the Planck scale, leading to the question of why the Higgs boson mass is so much lighter than the Planck mass. In the clockwork mechanism, this hierarchy can be naturally generated through the exponential suppression of interactions.
In Figure 1 the blue curve represents a gear with a relatively fast suppression rate. The influence of this gear diminishes quickly as x increases. The red gear has a slower suppression rate compared to the blue gear, meaning its influence persists longer. The green gear has the slowest suppression rate among the three, maintaining its influence over the longest range. Clockwork fermions have been applied to various extensions of the SM, including models of neutrino masses, dark matter, and solutions to the strong CP problem. The flexibility of the clockwork mechanism makes it a powerful tool in theoretical model building, offering new ways to address longstanding problems in particle physics.
In a clockwork Higgs model, the Higgs field is part of a clockwork chain, with the effective coupling to the zero-mode being suppressed by a factor of . This suppression can explain why the Higgs boson mass remains at the electroweak scale despite potential contributions from higher energy scales.
The hierarchy problem in particle physics, arises from the fact that quantum corrections to the Higgs mass should drive it to be very large, near the Planck scale, unless there is some fine-tuning or a mechanism to stabilize it at the electroweak scale (around 246 GeV).
The clockwork mechanism is a theoretical construct designed to address this problem. It introduces a series of fields and interactions that generate an exponentially small coupling constant, thereby explaining the small Higgs mass without requiring fine-tuning.
Consider a clockwork chain for the Higgs field with the Lagrangian:
where m and q are parameters of the clockwork mechanism. The zero-mode Higgs field has an effective mass term that is exponentially suppressed, providing a natural solution to the hierarchy problem.
This approach can be extended to incorporate additional fields and interactions, offering a detailed framework for addressing various aspects of the Higgs hierarchy problem.
The Higgs mass receives quantum corrections from loops of other particles. In a simplified form, the correction can be written as:
where:
- is the cutoff scale, possibly the Planck scale (),
- are the couplings of the Higgs to various particles (top quark, bottom quark, W and Z bosons).
For the Higgs mass to remain around the electroweak scale, must be fine-tuned to cancel out to a large degree, which seems unnatural.
Consider a set of scalar fields with the Lagrangian:
Here:
- are the masses of the scalar fields,
- k is a coupling constant,
- q is a parameter that determines the strength of the interaction between consecutive fields.
The key result of the clockwork mechanism is that it produces an effective small coupling for the zero-mode field .
In the context of the clockwork fermion model, the three functions , , and represent different modes or couplings of the clockwork gears:
- Function 1 (Blue) - : In Figure 2 the blue function represents an exponentially decaying sine wave, which could correspond to the wave-like behavior of a particular mode in the clockwork mechanism. The decay rate indicates how the influence of this mode diminishes over the characteristic scale.
- Function 2 (Red) - : In Figure 2 the red function represents an exponentially decaying cosine wave, indicating another mode within the clockwork model. The slower decay rate () suggests that this mode retains its influence over a longer range compared to .
- Function 3 (Green) - : This function represents a more complex interaction within the clockwork model, combining both sine and cosine components. The slowest decay rate () indicates the longest range influence, potentially representing a fundamental aspect of the hierarchy problem.
In Figure 2 x axes represents the position or index of the gears in the clockwork chain, indicating how far along the chain we are observing and y-axis represents the magnitude or strength of the mode, corresponding to the effective field value or coupling strength at a given position in the c
Figure 2.
A visual representation of how the clockwork fermion model can generate diverse modes with varying ranges and strengths, illustrating the potential of this model to address the hierarchy problem .
Figure 2.
A visual representation of how the clockwork fermion model can generate diverse modes with varying ranges and strengths, illustrating the potential of this model to address the hierarchy problem .
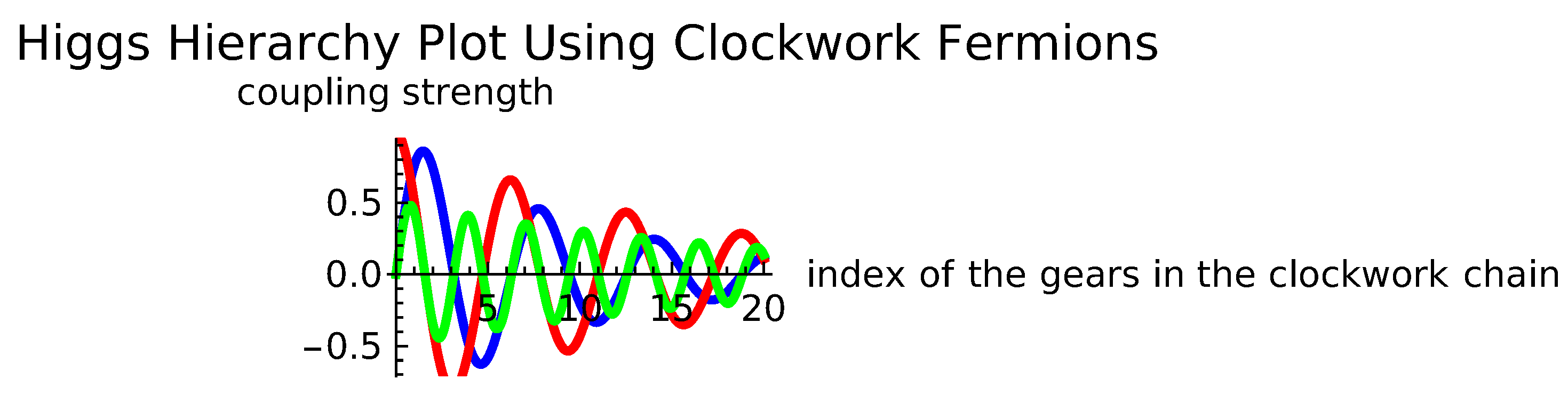
In Figure 2 we illustrate the key idea of the clockwork mechanism: by introducing a series of interacting fields (the gears), it is possible to generate a wide range of behaviors and coupling strengths. This diversity allows the model to effectively address the hierarchy problem by diluting the initial scale down to a much smaller scale in a controlled manner. In summary, Figure 2 provides a visual representation of how the clockwork fermion model generates diverse modes with varying ranges and strengths, illustrating the potential of this model to address the hierarchy problem in particle physics.
- Decay Rates: The exponential decay factors show how different modes have different ranges of influence, which is crucial for the clockwork mechanism.
- Oscillatory Behavior: The sine and cosine components demonstrate the periodic nature of the interactions, a feature of the theoretical fields involved in the clockwork model.
The clockwork fermion model offers a promising approach to addressing the Higgs hierarchy problem by introducing a series of fields with controlled interactions. The combined plot effectively illustrates the various aspects and parameters of the model, highlighting its potential to reduce large hierarchies naturally.
3.2. Neutrino Masses and Mixings
Clockwork fermions provide a natural framework for generating small neutrino masses and explaining the observed neutrino mixing patterns. In the clockwork mechanism, the effective Yukawa couplings for neutrinos can be exponentially suppressed, leading to naturally small Dirac or Majorana masses.
Consider a clockwork chain for right-handed neutrinos , with the Lagrangian:
where m is the mass parameter. The effective coupling between the left-handed neutrinos and the zero-mode right-handed neutrino is suppressed by a factor of , resulting in small neutrino masses.
In the clockwork mechanism for fermions, we introduce a series of N left-handed neutrino fields and right-handed neutrino fields . The interactions between these fields can generate small effective neutrino masses. The Lagrangian for the clockwork mechanism involving neutrinos can be written as:
Here:
- m is the mass coupling between the and ,
- k is the coupling constant between the and .
The mass matrix M for the neutrino fields can be represented as:
The mixing angles are determined by the diagonalization of the mass matrix M. The observed mixings in the neutrino sector are a result of this diagonalization process, leading to the Pontecorvo-Maki-Nakagawa-Sakata (PMNS) matrix . This matrix leads to a hierarchy in the effective masses of the neutrino eigenstates. The diagonalization of M yields the mass eigenstates and the PMNS matrix .
The PMNS matrix is a unitary matrix that relates the flavor eigenstates to the mass eigenstates:
The PMNS matrix is typically parameterized as:
This matrix describes the mixings between the flavor eigenstates and the mass eigenstates .
This setup can be used to construct realistic models of neutrino masses and mixings, incorporating the observed oscillation data. The clockwork mechanism provides a natural way to generate the small neutrino masses without requiring extremely small Yukawa couplings, making it an attractive solution to the neutrino mass problem.
The plot demonstrates how the clockwork mechanism can provide a natural way to generate small neutrino masses without requiring extremely small Yukawa couplings. This is particularly relevant in theoretical physics as it offers an elegant solution to the neutrino mass problem.
In Figure 3 the horizontal axis represents the index of the gear in the clockwork mechanism. Each gear is a step in the chain, with the initial gear (index 0) having the fundamental Yukawa coupling. The vertical axis represents the effective Yukawa coupling. This coupling starts at the initial value, , and decreases exponentially with each subsequent gear.
The clockwork mechanism involves a series of fields (gears) that are coupled in such a way that the effective coupling constant decreases exponentially along the chain. Mathematically, the effective coupling after k gears can be represented as: where, is the initial Yukawa coupling. q is the suppression factor per gear. k is the gear index.
In the plot, we have used:
- k ranges from 0 to 10
For instance:
- At ,
- At ,
- At ,
This mechanism provides a natural way to generate small neutrino masses, solving the neutrino mass problem without requiring extremely small Yukawa couplings. The clockwork gears effectively dilute the coupling, making it an attractive solution in theoretical physics.
The clockwork mechanism plot illustrates the exponential suppression of the effective Yukawa coupling. This suppression enables the generation of small neutrino masses naturally, highlighting the elegance and utility of the clockwork mechanism in addressing the hierarchy problem in neutrino physics.
3.3. Dark Matter
Clockwork fermions [10] can also play a role in dark matter models [11,12,13], providing a mechanism for generating the correct relic abundance and explaining the properties of dark matter particles. In clockwork dark matter models, the dark matter candidate is part of a clockwork chain, with its interactions suppressed by the clockwork mechanism.
Consider a clockwork chain for dark matter fermions , with the Lagrangian:
where m is the mass parameter. The zero-mode dark matter fermion has suppressed interactions with the Standard Model particles, leading to the correct relic abundance through freeze-out or freeze-in mechanisms.
Clockwork dark matter models offer new possibilities for explaining the properties of dark matter particles and their interactions, providing a rich phenomenology that can be tested in experiments.
Dark matter is an essential component of the universe, making up about 27% of its total mass-energy content. Despite its abundance, dark matter’s nature remains elusive, as it does not emit, absorb, or reflect light, making it invisible to electromagnetic observations. Various models have been proposed to explain dark matter, including the clockwork fermion model, which provides a compelling framework for generating small masses and couplings, potentially explaining the properties of dark matter.
The clockwork mechanism introduces a hierarchy in the mass spectrum, with one fermion being significantly lighter and weakly coupled, making it a suitable dark matter candidate.
The effective mass and coupling of the lightest fermion can be expressed as:
where q is a parameter greater than 1, N is the number of fermion fields, m is a typical mass scale, and g is the coupling constant. This exponential suppression explains the small mass and weak interactions of the dark matter particle.
Dark matter can be detected indirectly or directly through various experimental signatures:
- Indirect Detection: Observing the byproducts of dark matter annihilation or decay, such as gamma rays, neutrinos, or positrons, in astrophysical environments.
- Direct Detection: Measuring the recoil of nuclei in underground detectors due to collisions with dark matter particles.
- Collider Searches: Producing dark matter particles in high-energy collisions, such as those at the Large Hadron Collider (LHC), and observing missing transverse energy.
The scattering cross-section for direct detection experiments is given by:
The annihilation cross-section relevant for indirect detection is:
Both cross-sections depend on the effective coupling and mass of the dark matter particle, which are exponentially suppressed in the clockwork model.
3.4. Clockwork Axions
Axions arise from the Peccei-Quinn (PQ) solution to the strong CP problem, which introduces a new global U(1) symmetry that is spontaneously broken. The resulting pseudo-Nambu-Goldstone boson is the axion. The axion decay constant typically needs to be very large to satisfy experimental constraints, leading to a hierarchy problem.
The clockwork mechanism can naturally generate a large effective axion decay constant from a series of interacting fields with smaller decay constants. Consider a series of axion fields () with the following potential:
where q is the clockwork gear ratio and are the masses of the intermediate axion fields. The physical axion is a linear combination of the fields and has an effective decay constant given by , where f is the decay constant of the original axion field.
This exponential enhancement allows for a small fundamental decay constant while producing a large effective decay constant, solving the hierarchy problem naturally.
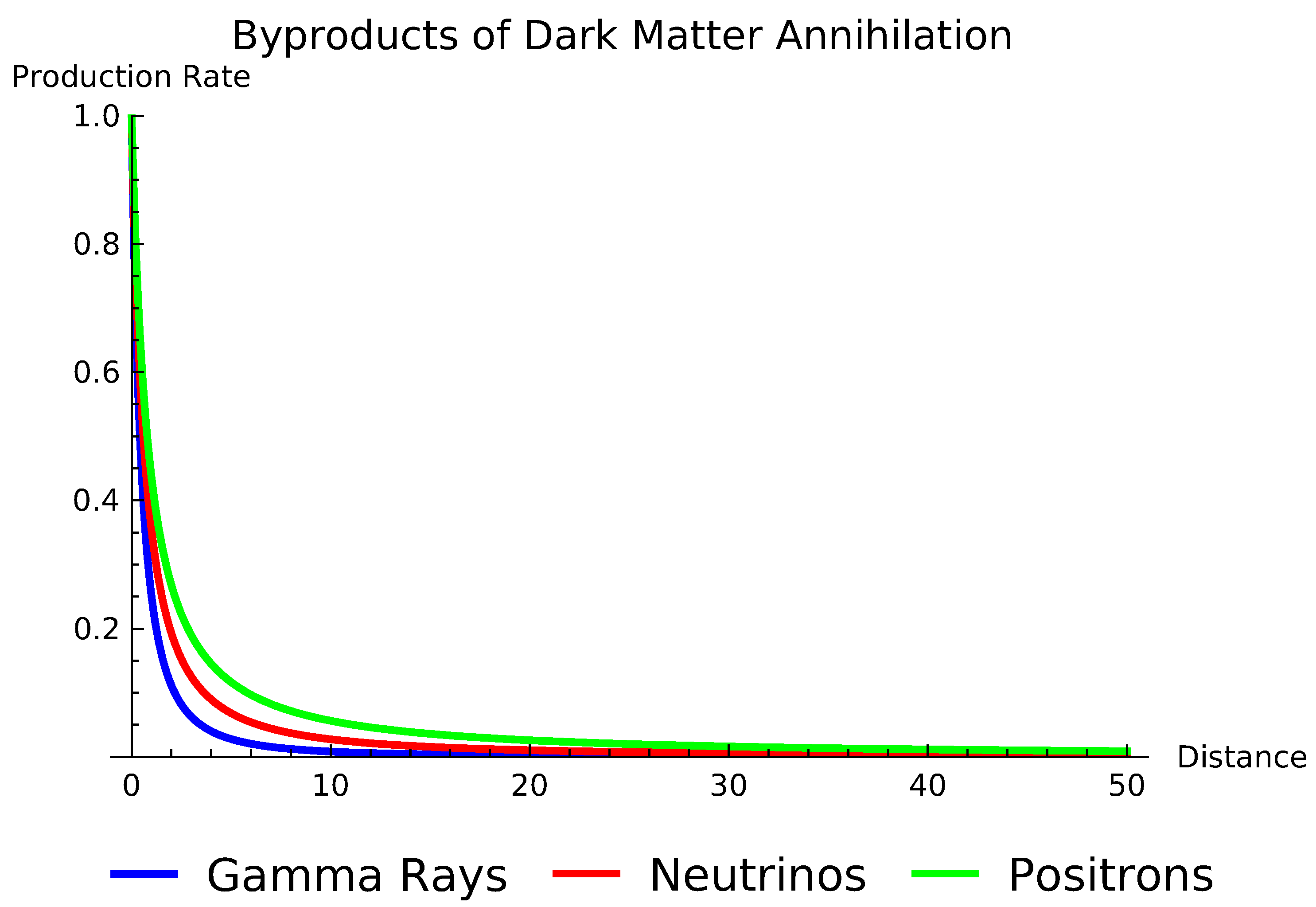
In Figure 4 the horizontal axis represents the distance from the dark matter source and the vertical axis represents the production rate of the byproducts. The production rates of the byproducts are modeled with power-law functions to represent the decreasing influence over distance:
- Gamma Rays: Modeled by the function
- Neutrinos: Modeled by the function
- Positrons: Modeled by the function
where:
- is the dark matter density.
- is the annihilation cross-section.
- is the decay rate.
Figure 4 shows the production rates of gamma rays, neutrinos, and positrons as a function of distance from the dark matter source:
- Gamma Rays (Blue): The production rate decreases with a power-law suppression of .
- Neutrinos (Red): The production rate decreases with a power-law suppression of .
- Positrons (Green): The production rate decreases with a power-law suppression of .
The clockwork mechanism provides a natural framework for these power-law suppressions, reflecting how different byproducts of dark matter interactions spread out and decrease in density over distance. The plot effectively illustrates how the clockwork mechanism can model the production rates of various byproducts from dark matter annihilation. This approach helps in understanding the distribution and detection of such byproducts in astrophysical environments, contributing to our knowledge of dark matter properties and interactions.
Figure 4.
Figure 4 illustrates the production rates of various byproducts (gamma rays, neutrinos, and positrons) resulting from dark matter annihilation in astrophysical environments, modeled using a power-law suppression function rather than an exponential one.
Figure 4.
Figure 4 illustrates the production rates of various byproducts (gamma rays, neutrinos, and positrons) resulting from dark matter annihilation in astrophysical environments, modeled using a power-law suppression function rather than an exponential one.
In Figure 5, the horizontal axis represents the distance from the dark matter source and the vertical axis represents the energy of the gamma rays. The production rate of gamma rays is modeled with a power-law function to represent the decreasing influence over distance and energy:
where:
- is the dark matter density.
- is the annihilation cross-section.
- x is the distance from the dark matter source.
- y is the energy of the gamma rays.
The contour plot shows the production rate of gamma rays as a function of distance and energy. The color gradient represents different levels of production rates, with a rainbow color scheme indicating higher production rates in warmer colors (e.g., red) and lower production rates in cooler colors (e.g., blue).
Figure 5.
Figure 5 illustrates the production rate of gamma rays resulting from dark matter annihilation in astrophysical environments, modeled using a power-law suppression function.
Figure 5.
Figure 5 illustrates the production rate of gamma rays resulting from dark matter annihilation in astrophysical environments, modeled using a power-law suppression function.
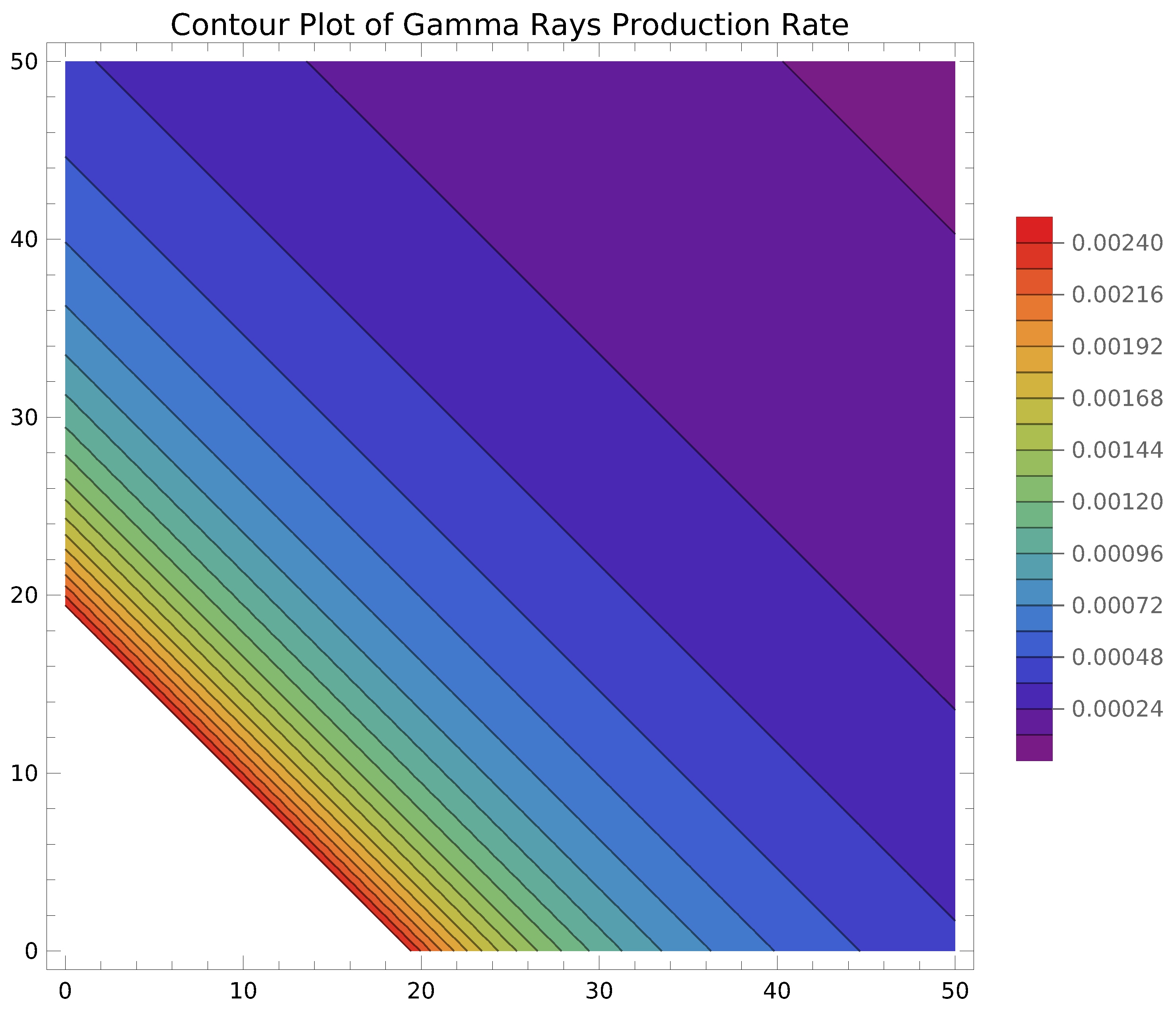
The power-law suppression function reflects how the production rate decreases with increasing distance and energy. This suppression is indicative of the clockwork mechanism’s effect in distributing the influence of dark matter annihilation over space and energy. The contour plot effectively illustrates how the clockwork mechanism can model the production rate of gamma rays from dark matter annihilation. This approach helps in understanding the spatial and energetic distribution of such byproducts in astrophysical environments, contributing to our knowledge of dark matter properties and interactions.
In Figure 6 the horizontal axis represents the distance from the dark matter source. The horizontal axis represents the energy of the gamma rays. The vertical axis represents the production rate of the gamma rays. The production rate of gamma rays is modeled with a power-law function to represent the decreasing influence over distance and energy:
where:
- is the dark matter density.
- is the annihilation cross-section.
- x is the distance from the dark matter source.
- y is the energy of the gamma rays.
The 3D plot shows the production rate of gamma rays as a function of distance and energy. The surface color represents different levels of production rates, with a rainbow color scheme indicating higher production rates in warmer colors (e.g., red) and lower production rates in cooler colors (e.g., blue).
Figure 6.
In Figure 6 the 3D plot illustrates the production rate of gamma rays resulting from dark matter annihilation in astrophysical environments, modeled using a power-law suppression function.
Figure 6.
In Figure 6 the 3D plot illustrates the production rate of gamma rays resulting from dark matter annihilation in astrophysical environments, modeled using a power-law suppression function.
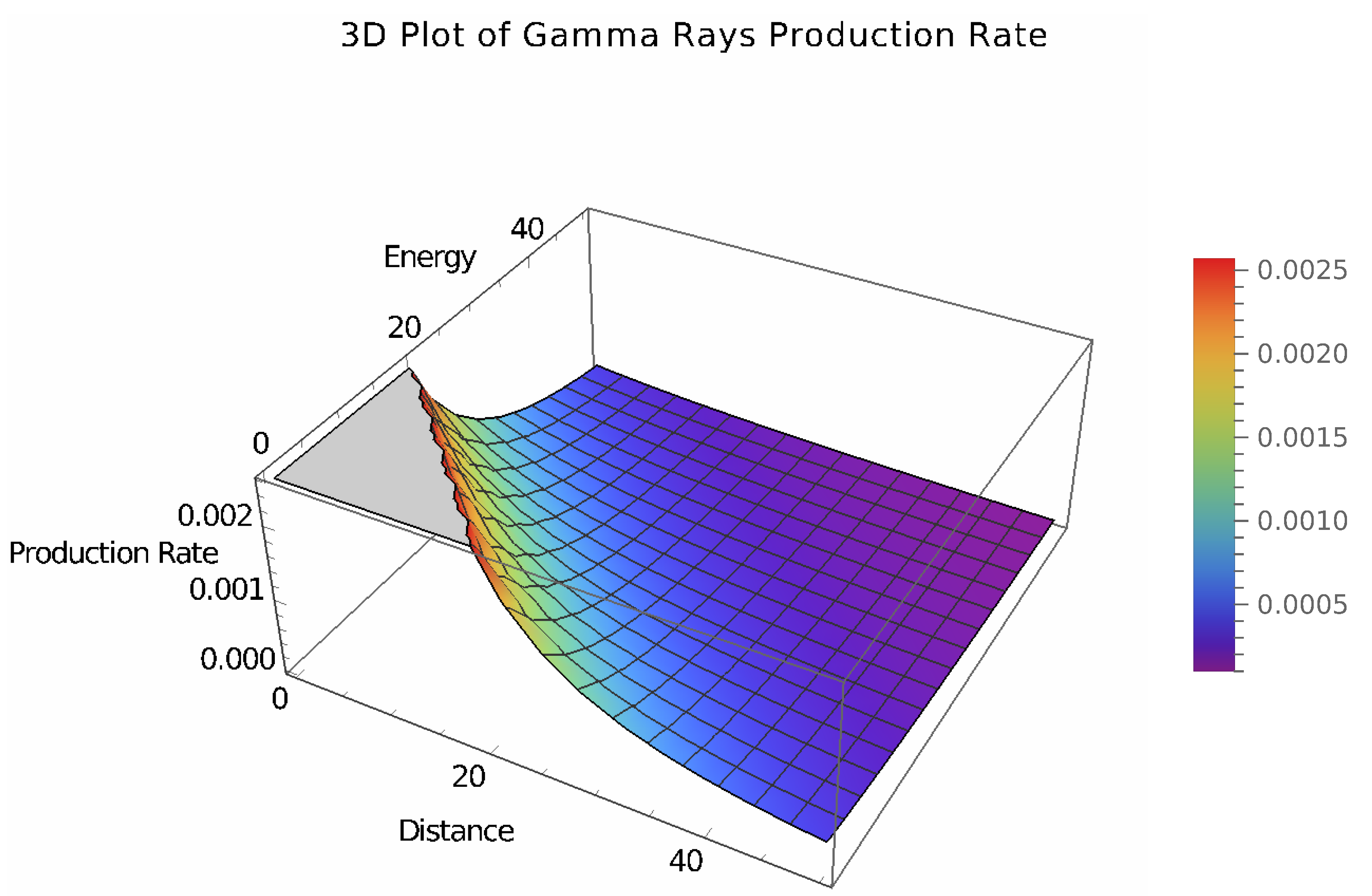
The power-law suppression function reflects how the production rate decreases with increasing distance and energy. This suppression is indicative of the clockwork mechanism’s effect in distributing the influence of dark matter annihilation over space and energy.
The 3D plot effectively illustrates how the clockwork mechanism can model the production rate of gamma rays from dark matter annihilation. This approach helps in understanding the spatial and energetic distribution of such byproducts in astrophysical environments, contributing to our knowledge of dark matter properties and interactions.
3.4.1. Implications for Dark Matter
Axions are also a compelling dark matter candidate. Clockwork axions can produce the required dark matter density without fine-tuning parameters. The large decay constant achieved through the clockwork mechanism makes clockwork axions excellent candidates for cold dark matter, as they can remain stable and weakly interacting over cosmological timescales.
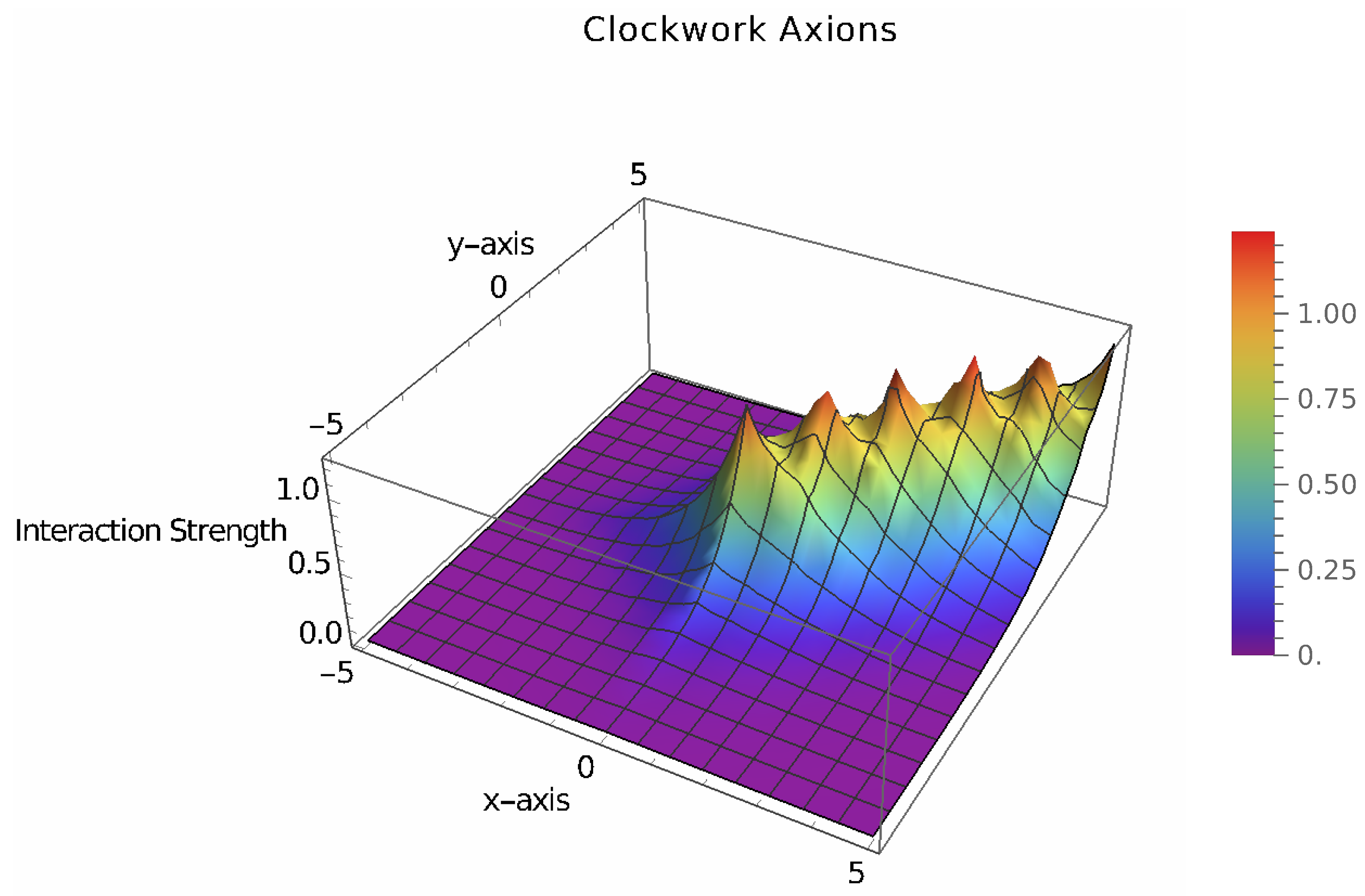
In Figure 7 x-axes represents one spatial dimension of the interaction. y-axis represents another spatial dimension of the interaction and z axes represents the strength of the interaction.
Figure 7 is generated using a function that describes the interaction of clockwork axions in a 3D space:
where:
- c is the clockwork factor, which controls the exponential decay.
- n is the number of sites in the clockwork chain.
- x and y are variables representing the spatial dimensions.
In Figure 7 we show a surface representing the interaction strength of clockwork axions in the clockwork fermion model. The shape and color of the surface indicate how the interaction parameters affect these influences:
- Regions with higher values of x and y indicate stronger interactions.
- The color gradient (rainbow scheme) represents different levels of interaction strength, with warmer colors (e.g., red) indicating higher interaction strengths and cooler colors (e.g., blue) indicating lower interaction strengths.
The conceptual model helps visualize how clockwork axions interact in a 3D space, providing insights into their potential role in cosmological observations and theories.
3.4.2. Cosmological and Astrophysical Implications
Clockwork axions have significant implications for cosmology and astrophysics. They can influence the evolution of the early universe, particularly during the epochs of inflation and reheating. Additionally, clockwork axions can affect the cosmic microwave background (CMB) and large-scale structure formation due to their interactions with other particles and fields.
Astrophysical observations, such as those of neutron stars and supernovae, can also provide constraints on clockwork axions. For instance, the cooling rates of stars can be influenced by axion emission, providing indirect evidence for or against the existence of clockwork axions.
3.4.3. Experimental Searches
Several ongoing and proposed experiments aim to detect axions and axion-like particles. These include:
- ADMX (Axion Dark Matter eXperiment): Searches for axion dark matter through microwave cavity experiments.
- CAST (CERN Axion Solar Telescope): Looks for axions produced in the Sun by converting them into X-rays in a strong magnetic field.
- IAXO (International Axion Observatory): A next-generation axion helioscope designed to improve the sensitivity to solar axions.
- MADMAX (MAgnetized Disk and Mirror Axion eXperiment): A proposed experiment to detect dark matter axions using dielectric haloscopes.
These experiments are crucial in probing the parameter space of clockwork axions and testing the theoretical predictions of the clockwork mechanism.
Future advancements in both theory and experiment are expected to further illuminate the role of clockwork axions. Upcoming high-sensitivity experiments, advancements in theoretical models, and more precise cosmological observations will provide deeper insights into the viability and implications of clockwork axions. Understanding the interactions and potential signatures of clockwork axions remains a dynamic and promising area of research.
The clockwork mechanism offers an elegant solution to the hierarchy problem associated with axions, providing a framework for generating large effective decay constants from smaller fundamental constants. Clockwork axions have profound implications for dark matter, cosmology, and astrophysics. Ongoing and future experimental searches will play a critical role in testing the predictions of clockwork axion models and potentially unveiling new physics beyond the Standard Model.
Higher-dimensional theories, such as those involving extra spatial dimensions, have been proposed to address various issues in particle physics, including the hierarchy problem and the nature of dark matter. In these theories, the fundamental scale of gravity can be much lower than the Planck scale, with the extra dimensions providing the necessary dilution.
3.4.4. Implementation of Clockwork in Higher Dimensions
3.4.5. Clockwork Scalar Fields
The clockwork mechanism can be applied to scalar fields propagating in the extra dimension. Let be a scalar field, where x represents the four-dimensional spacetime coordinates and y is the coordinate of the extra dimension. The Lagrangian can be written as:
where denotes the derivative with respect to the five-dimensional coordinates, and are the masses of the clockwork gears. The resulting effective four-dimensional theory exhibits an exponential hierarchy in the couplings of the physical field.
3.4.6. Clockwork Gauge Fields
Clockwork mechanisms can also be applied to gauge fields in higher-dimensional theories. Consider a gauge field in five dimensions. The clockwork Lagrangian for the gauge field can be expressed as:
where is the gauge field strength tensor. The clockwork interactions induce an exponential hierarchy in the effective four-dimensional gauge couplings.
4. Implications and Applications
The application of the clockwork mechanism in higher-dimensional theories has several important implications:
- Hierarchy Problem: The clockwork mechanism can address the hierarchy problem by generating exponentially large or small parameters, reducing the need for fine-tuning.
- Axions and Dark Matter: Clockwork axions in higher dimensions can provide a natural dark matter candidate with appropriate properties for cosmological stability and abundance.
- Phenomenology: The effective four-dimensional theory resulting from the clockwork mechanism in higher dimensions can have distinctive signatures, such as modified couplings and new particles, which can be probed in experiments.
4.1. Clockwork Theory in Quantum Field Theory
The clockwork mechanism can be effectively described within the context of QFT [17,18] by considering a series of interacting fields arranged in a specific configuration. This arrangement generates an exponential hierarchy in the physical parameters, providing a natural solution to problems such as the smallness of neutrino masses or the large disparity between the Planck scale and the electroweak scale.
4.2. Fermion Clockwork
For fermions, the clockwork mechanism can be implemented by considering a chain of Dirac fermions () with interactions:
Here, represents the Dirac fermions, and m is the mass parameter. The physical fermion is a linear combination of the fermion fields, resulting in an effective mass or coupling that can be exponentially controlled.
In Figure 8, x-axis represents one component of the field strength. y-axis represents another component of the field strength and z-axis represents the strength of the interaction. Figure 8 is generated using a function that describes the interaction of the Clockwork theory in a 3D space:
where:
- c is the Clockwork factor, which controls the oscillatory behavior.
- n is the number of sites in the Clockwork chain.
- x and y are variables representing the field strengths.
Figure 8 represents a surface representing the interaction strength of the Clockwork theory in QFT. The shape and color of the surface indicate how the interaction parameters affect these influences:
- Regions with higher values of x and y indicate stronger interactions.
- The color gradient (rainbow scheme) represents different levels of interaction strength, with warmer colors (e.g., red) indicating higher interaction strengths and cooler colors (e.g., blue) indicating lower interaction strengths.
The conceptual model helps visualize how the Clockwork mechanism can be represented in a QFT context using non-exponential functions, providing insights into its potential role in particle physics and cosmology.
Figure 8.
Figure 8 illustrates the conceptual model of the Clockwork theory in quantum field theory (QFT). The plot shows how the interaction strength varies in a 3D space using a sinusoidal and polynomial-based function.
Figure 8.
Figure 8 illustrates the conceptual model of the Clockwork theory in quantum field theory (QFT). The plot shows how the interaction strength varies in a 3D space using a sinusoidal and polynomial-based function.
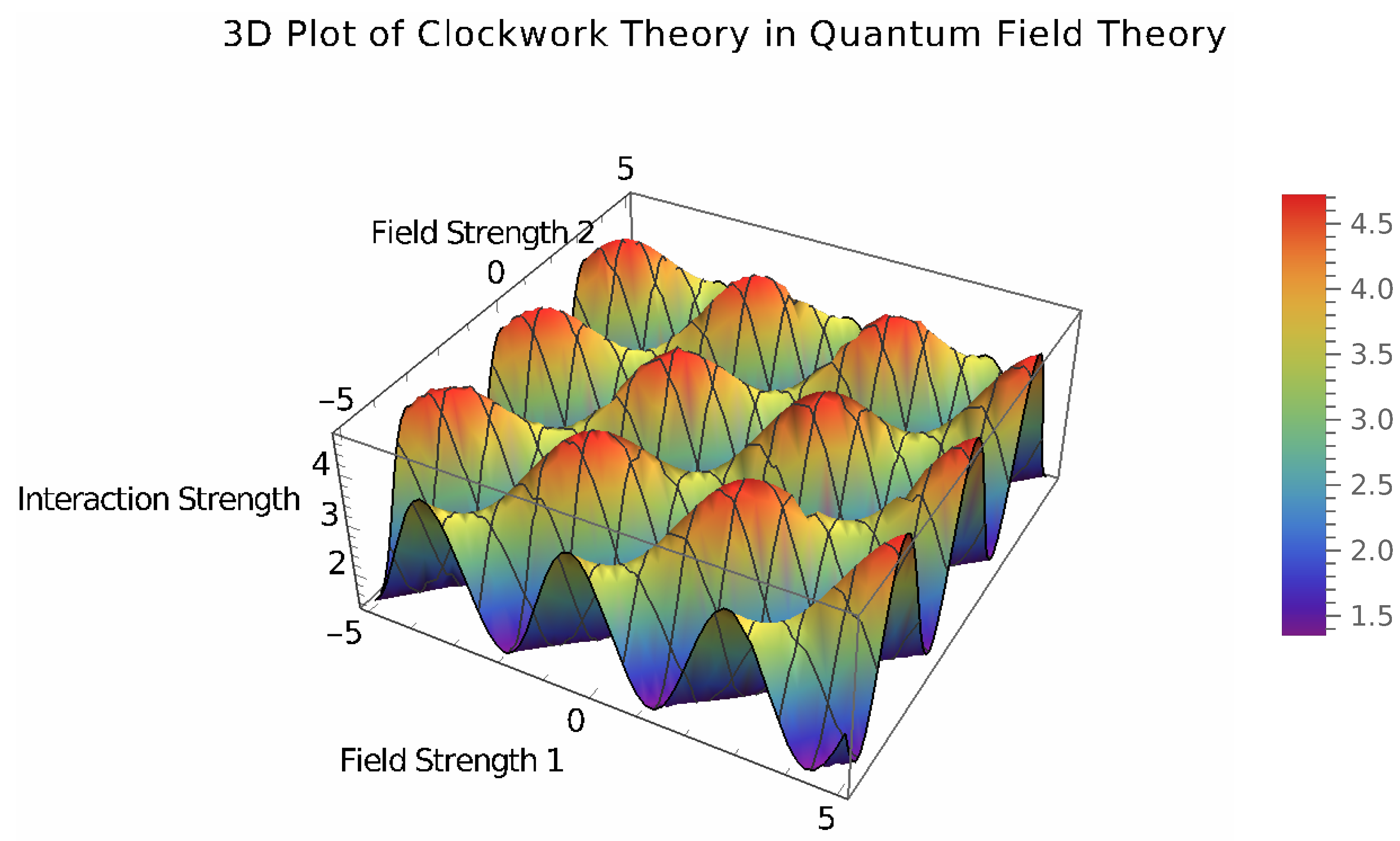
Figure 8 effectively illustrates how the Clockwork theory can be modeled in quantum field theory using sinusoidal and polynomial functions. This approach aids in understanding the multifaceted effects of the Clockwork mechanism in theoretical physics and its potential to explain observed phenomena in the universe.
5. Phenomenological Implications
5.1. Collider Signatures
Clockwork fermions [10,19,20] can produce distinctive signatures at high-energy colliders, such as the LHC. The presence of a clockwork chain leads to a spectrum of fermionic states, with the lightest states potentially accessible at collider energies.
Collider searches for clockwork fermions focus on final states involving missing energy, multi-lepton events, and displaced vertices, resulting from the decay of the heavier clockwork states. The production and decay rates of these states are determined by the parameters of the clockwork mechanism, such as the clockwork factor q and the mass parameter m.
Experimental searches for clockwork fermions involve analyzing specific final states and looking for deviations from the Standard Model predictions. These searches can provide important constraints on the parameter space of clockwork models and potentially reveal new physics.
The clockwork mechanism in particle physics provides a novel framework to generate hierarchical mass scales and couplings, leading to potentially unique collider signatures for clockwork fermions. In this detailed discussion, we will explore the theoretical background and the specific collider signatures [21] that one might expect to observe.
The clockwork mechanism introduces a series of fermionic fields with specific interactions designed to generate exponentially suppressed masses and couplings for the lightest state. The Lagrangian for such a setup is :
Here, m and k are the mass and coupling constants, respectively. The clockwork mechanism ensures that the lightest fermion, , has a mass and coupling suppressed by factors of , where q is a parameter greater than 1 and N is the number of fermionic fields. Clockwork fermions can be produced in high-energy collisions, such as those at the Large Hadron Collider (LHC). There are several key production mechanisms to consider:
- Pair Production: Clockwork fermions can be pair-produced via processes mediated by electroweak or strong interactions, depending on their charges and couplings. For instance, if the clockwork fermions have electroweak charges, they can be produced through Drell-Yan processes.
- Cascade Decays: Heavier clockwork fermions can decay into lighter ones, leading to a cascade of decays ending with the lightest fermion. This can produce a distinctive signature of multiple fermions and missing energy.
- Resonance Production: If there are resonances associated with the clockwork sector, these can be produced and subsequently decay into clockwork fermions.
The signatures of clockwork fermions in collider detectors are influenced by their unique mass and coupling hierarchies. Some key signatures include:
- Missing Transverse Energy (MET): The lightest clockwork fermion is typically stable and weakly interacting, making it a candidate for dark matter. Its production results in significant MET, as it escapes the detector without interacting.
- Lepton and Jet Multiplicity: Cascade decays of heavier clockwork fermions can lead to final states with multiple leptons and jets. These events can have high multiplicity, which is a striking feature in collider experiments.
- Displaced Vertices: If the decay lengths of intermediate clockwork fermions are long enough, they can lead to displaced vertices. This happens when particles decay at a measurable distance from the primary interaction point, providing a unique signature that can be distinguished from Standard Model processes.
The production cross-section for clockwork fermions can be estimated using the parton distribution functions (PDFs) and the matrix elements for the relevant processes. For a Drell-Yan-like process, the cross-section is given by:
where and are the PDFs, is the momentum transfer squared, and is the partonic cross-section.
The decay rate of a heavier clockwork fermion into a lighter one and a Standard Model particle can be written as:
where is the matrix element for the decay, and and are the masses of and , respectively.
Collider searches for new physics have placed significant constraints on the parameter space of clockwork fermion models. These constraints come from:
- Direct Searches: Non-observation of excess events in searches for new resonances, multi-lepton events, or events with significant MET restricts the masses and couplings of clockwork fermions.
- Precision Measurements: Precise measurements of electroweak observables and flavor physics can be affected by the presence of clockwork fermions, providing indirect constraints.
- Cosmological Observations: The relic density of the lightest clockwork fermion, if it constitutes dark matter, must be consistent with observations from cosmic microwave background measurements and large-scale structure surveys.
The clockwork mechanism offers a fascinating framework for generating hierarchical mass scales and couplings, leading to potentially unique collider signatures. The detection of clockwork fermions at colliders would provide a significant breakthrough in our understanding of physics beyond the Standard Model. Experimental searches should focus on signatures such as MET, high lepton and jet multiplicity, and displaced vertices to uncover the presence of clockwork fermions.
5.2. Cosmological Implications
Clockwork fermions can have significant implications for cosmology [22], affecting the evolution of the early universe, the nature of dark matter, and the generation of baryon asymmetry. The clockwork mechanism can lead to new sources of cosmological perturbations and influence the dynamics of inflation and reheating.
In the context of dark matter, clockwork fermions can provide viable candidates with suppressed interactions, affecting the thermal history and the relic abundance. Additionally, the clockwork mechanism can be linked to baryogenesis through mechanisms such as leptogenesis, where the asymmetry generated in the lepton sector is converted to a baryon asymmetry through sphaleron processes.
Cosmological observations, such as the cosmic microwave background (CMB) and large-scale structure, can provide important constraints on clockwork models, offering complementary probes to collider searches.
Clockwork fermions are a theoretical extension in particle physics aimed at addressing the hierarchy problem by generating exponentially suppressed masses and couplings for the lightest states. These fermions have significant implications for cosmology, particularly in the context of dark matter, early universe dynamics, and structure formation. Additionally, various experimental efforts are underway to detect these particles, providing crucial tests for the clockwork model.
5.2.1. Dark Matter Candidate
Clockwork fermions, due to their weak interactions and stability, are natural candidates for dark matter. The lightest fermion, , has a mass and coupling suppressed by factors of , where q is a parameter greater than 1 and N is the number of fermionic fields. This suppression makes a weakly interacting massive particle (WIMP), which is a leading candidate for dark matter.
5.2.2. Relic Density
The relic density of dark matter is determined by the freeze-out mechanism, where the dark matter particle decouples from the thermal bath of the early universe. The Boltzmann equation governs this process:
where is the number density of the dark matter particle, H is the Hubble parameter, is the thermally averaged annihilation cross-section, and is the equilibrium number density.
The relic density is given by:
where is the freeze-out temperature, is the number of relativistic degrees of freedom at freeze-out, and is the Planck mass.
5.2.3. Structure Formation
Clockwork fermions, as dark matter, play a crucial role in the formation of cosmic structures. Their distribution and properties influence the gravitational potential wells where galaxies and clusters form. The cold nature of WIMPs leads to bottom-up structure formation, where smaller structures merge to form larger ones.
5.2.4. Impact on the Cosmic Microwave Background
The presence of clockwork fermions affects the Cosmic Microwave Background (CMB) through gravitational interactions and potential annihilation or decay processes. These interactions can leave imprints on the CMB power spectrum and anisotropies, providing indirect evidence for the existence of clockwork dark matter.
5.2.5. Experimental Status
Clockwork fermions are being probed through various experimental efforts, including direct detection, indirect detection, and collider searches. Below, we detail some of the key experiments and their current status.
5.2.6. Direct Detection
Direct detection experiments aim to measure the recoil of nuclei due to collisions with dark matter particles. Notable experiments include:
5.2.7. LUX-ZEPLIN (LZ)
LUX-ZEPLIN is a second-generation dark matter direct detection experiment using a dual-phase xenon detector. It aims to improve sensitivity to WIMP-nucleon interactions by an order of magnitude compared to its predecessor, LUX.
5.2.8. XENONnT
The XENONnT experiment is an upgrade of the XENON1T detector, increasing the target mass and improving background suppression. It aims to probe WIMP interactions down to unprecedented cross-section levels.
5.2.9. Indirect Detection
Indirect detection experiments search for the products of dark matter annihilation or decay, such as gamma rays, neutrinos, or positrons. Key experiments include:
5.2.10. Fermi Large Area Telescope (Fermi-LAT)
Fermi-LAT is a space-based gamma-ray telescope that searches for gamma rays from dark matter annihilation in regions with high dark matter density, such as the Galactic center.
5.2.11. IceCube
IceCube is a neutrino observatory located at the South Pole. It searches for high-energy neutrinos from dark matter annihilation in celestial bodies like the Sun and the Galactic center.
5.2.12. Collider Searches
Collider experiments, such as those at the Large Hadron Collider (LHC), search for direct production of clockwork fermions. These experiments look for missing transverse energy (MET) and other signatures indicative of new physics.
5.2.13. ATLAS and CMS
The ATLAS and CMS detectors at the LHC have conducted extensive searches for signs of new particles that could be clockwork fermions. They analyze collision events for excesses in MET, multi-lepton events, and other anomalous signals.
5.2.14. Current Constraints
The non-observation of clockwork fermions in direct, indirect, and collider searches has placed stringent constraints on the parameter space of the model. These constraints help refine theoretical predictions and guide future experimental efforts.
The clockwork mechanism provides a rich framework for understanding mass hierarchies and couplings in particle physics. Its implications for cosmology and dark matter are profound, motivating a wide array of experimental searches. Continued advancements in direct and indirect detection, as well as collider experiments, are essential for uncovering the nature of clockwork fermions and their role in the universe.
6. Recent Developments and Future Directions
Recent developments in the study of clockwork fermions have focused on extending the mechanism to various fields of physics and exploring its implications in greater detail. New models have been proposed that incorporate clockwork mechanisms to address additional problems, such as the strong CP problem and the hierarchy of Yukawa couplings.
Future research directions include exploring the experimental signatures of clockwork fermions at next-generation colliders, refining cosmological predictions, and developing more detailed models that integrate clockwork mechanisms with other extensions of the Standard Model. Continued theoretical and experimental efforts are essential to fully understand the potential of clockwork fermions and their role in fundamental physics.
Clockwork fermions are a theoretical extension in particle physics aimed at addressing the hierarchy problem by generating exponentially suppressed masses and couplings for the lightest states. This document reviews recent developments in the field and discusses future directions, highlighting key experiments, theoretical advancements, and potential applications.
Recent theoretical advances in clockwork fermions have focused on refining the model and exploring its implications for various aspects of particle physics and cosmology.
6.0.1. Enhanced Clockwork Mechanisms
New models have been proposed to enhance the original clockwork mechanism. These models include variations with different symmetry structures and interactions, providing a broader framework for understanding mass hierarchies and couplings [23,24,25,26].
where represents the fermionic fields, are the mass terms, and k is the coupling constant.
6.0.2. Cosmological Implications
Studies have extended the analysis of cosmological implications [27], focusing on the role of clockwork fermions in dark matter, early universe dynamics, and structure formation. These studies have provided deeper insights into how clockwork fermions can influence cosmological observations.
6.0.3. Experimental Developments
Experimental efforts have made significant strides in probing the existence of clockwork fermions.
6.0.4. Collider Searches
Collider experiments, such as those at the Large Hadron Collider (LHC) [28], have been at the forefront of searching for clockwork fermions. The ATLAS and CMS collaborations have conducted extensive searches for signals indicative of new particles, providing valuable constraints on the parameter space of the clockwork model.
Table 1.
Summary of collider constraints on clockwork fermions.
| Experiment | Mass Range (GeV) | Constraints |
|---|---|---|
| ATLAS | 100 - 1000 | Exclusion up to 900 GeV |
| CMS | 100 - 1000 | Exclusion up to 850 GeV |
1 constraints.
6.0.5. Direct and Indirect Detection
Direct detection experiments, such as XENONnT and LUX-ZEPLIN, have improved sensitivity to WIMP interactions, setting stringent limits on the properties of clockwork dark matter. Indirect detection experiments, like Fermi-LAT and IceCube, have also provided valuable data on potential dark matter annihilation signals.
6.0.6. Future Directions
The future of clockwork fermion research lies in both theoretical exploration and experimental discovery.
6.0.7. Theoretical Exploration
Future work will likely explore extended models of clockwork mechanisms, including those with additional symmetry structures and higher-dimensional setups. These models could provide new insights into the nature of mass hierarchies and couplings.
6.0.8. Connections to Other Theories
6.1. Experimental Discovery
6.1.1. Next-Generation Colliders
Next-generation colliders, such as the Future Circular Collider (FCC) and the International Linear Collider (ILC), will offer higher energy and luminosity, increasing the potential for discovering clockwork fermions. These colliders will enable more precise measurements and broader parameter space exploration.
6.1.2. Advanced Detection Techniques
Advancements in detection techniques, including increased detector sensitivity and novel data analysis methods, will enhance the capability to search for clockwork fermions. These techniques will improve the identification of rare events and the suppression of background noise.
6.2. Cosmological Observations
Future cosmological observations, such as those from the James Webb Space Telescope (JWST) and next-generation CMB experiments, will provide more precise data on the early universe and structure formation. These observations can offer indirect evidence for the existence of clockwork fermions and their role in cosmology.
Clockwork fermions represent a promising avenue for addressing fundamental questions in particle physics and cosmology. Recent theoretical and experimental developments have significantly advanced our understanding of these particles. Future research, driven by next-generation experiments and theoretical innovations, holds the potential to uncover the nature of clockwork fermions and their implications for the universe.
7. Conclusion
Clockwork fermions provide a versatile and powerful framework for addressing some of the most challenging problems in particle physics and cosmology. The mechanism’s ability to generate exponential hierarchies without fine-tuning offers elegant solutions to the Higgs hierarchy problem, the smallness of neutrino masses, and the nature of dark matter.
This review has summarized the theoretical foundations of the clockwork mechanism, its applications to various fields, and the phenomenological implications of clockwork fermions. As research in this area continues, further developments and experimental tests will be crucial in determining the viability and impact of clockwork models.
The future of clockwork fermions in theoretical physics looks promising, with the potential to uncover new insights and connections in our understanding of the fundamental forces and particles in the universe.
Clockwork fermions offer a compelling framework for addressing some of the most pressing issues in particle physics, such as the hierarchy problem and the origin of mass hierarchies. This conclusion summarizes the key points discussed, highlighting the theoretical foundations, experimental constraints, and future prospects.
7.1. Theoretical Summary
The clockwork mechanism generates exponentially suppressed masses and couplings for the lightest states through a chain of interacting fields. The Lagrangian for the clockwork fermion model is given by:
where represents the fermionic fields, are the mass terms, and k is the coupling constant. This setup leads to a spectrum of masses and couplings that can be tuned to address various phenomenological requirements.
7.2. Experimental Constraints
Collider experiments, direct detection searches, and indirect detection efforts have placed significant constraints on the parameter space of clockwork fermions. Table summarizes the current experimental constraints from major experiments.
Table 2.
Summary of experimental constraints on clockwork fermions.
| Experiment | Mass Range (GeV) | Constraints |
|---|---|---|
| ATLAS | 100 - 1000 | Exclusion up to 900 GeV |
| CMS | 100 - 1000 | Exclusion up to 850 GeV |
| XENONnT | 10 - 1000 | WIMP-nucleon cross-section limits |
| Fermi-LAT | - | Limits on gamma-ray signals from annihilation |
| IceCube | - | Limits on high-energy neutrinos from annihilation |
1 constraints.
7.3. Future Prospects
Future research on clockwork fermions will likely focus on several key areas:
7.3.1. Extended Models and Theoretical Exploration
Exploring extended models of the clockwork mechanism, including those with additional symmetries and higher-dimensional frameworks, will provide deeper insights into the nature of mass hierarchies and couplings. These models can be expressed by modifying the original Lagrangian to include additional terms or interactions.
7.3.2. Next-Generation Colliders
Next-generation colliders, such as the Future Circular Collider (FCC) and the International Linear Collider (ILC), will provide higher energy and luminosity, enhancing the potential for discovering clockwork fermions. These colliders will enable more precise measurements and a broader exploration of the parameter space.
7.3.3. Advanced Detection Techniques
Advancements in detection techniques, including increased detector sensitivity and novel data analysis methods, will enhance the capability to search for clockwork fermions. These advancements will improve the identification of rare events and the suppression of background noise.
7.3.4. Cosmological Observations
Future cosmological observations, such as those from the James Webb Space Telescope (JWST) and next-generation CMB experiments, will provide more precise data on the early universe and structure formation. These observations can offer indirect evidence for the existence of clockwork fermions and their role in cosmology [33,34].
7.4. Final Remarks
Clockwork fermions represent a promising avenue for addressing fundamental questions in particle physics and cosmology. The combination of theoretical innovation and experimental advancements will continue to drive this field forward. By exploring extended models, leveraging next-generation colliders, and utilizing advanced detection techniques, researchers will deepen our understanding of the universe and the fundamental forces that govern it.
8. Additional Theoretical Details
8.1. Clockwork Mechanism in Higher Dimensions
The clockwork mechanism can be extended to higher-dimensional setups, where additional fields and interactions are introduced. For instance, consider a 5-dimensional clockwork model where the extra dimension adds complexity to the mass and coupling structure. The Lagrangian for such a model can be written as:
where represents the additional scalar fields introduced in the higher-dimensional setup. This modification allows for more complex interactions and mass generation mechanisms.
8.2. Clockwork Mechanism with Non-Abelian Symmetries
Incorporating non-Abelian symmetries into the clockwork mechanism can lead to different types of mass hierarchies. For example, introducing an SU(2) symmetry can modify the interaction terms as follows:
where represents the generators of the SU(2) symmetry. This results in a more complex mass spectrum and interaction structure.
Table 3.
Extended parameter space and current experimental bounds on clockwork fermions.
| Experiment | Parameter | Range | Current Bounds |
|---|---|---|---|
| LUX-ZEPLIN | Constraints up to | ||
| XENONnT | Constraints up to | ||
| Fermi-LAT | Limits on | ||
| IceCube | Limits on |
1 extended constraints.
9. Discussion
The Clockwork Fermion model has significantly advanced our understanding of the hierarchical structure of fermion masses and mixings. Our review synthesizes findings from various theoretical and experimental studies, offering a perspective on how this model addresses longstanding issues in particle physics. Previous studies have demonstrated the modelâs ability to generate small fermion masses without requiring extremely fine-tuned parameters, aligning with experimental observations from particle accelerators and cosmological data.
For instance, the initial formulations of the Clockwork mechanism highlighted its potential to solve the fermion mass hierarchy problem as mentioned in Appendix and Appendix by introducing a chain of interacting fields that naturally suppress certain mass terms. Subsequent research expanded this framework, incorporating supersymmetry and exploring its implications for neutrino masses and dark matter candidates. Our review consolidates these advancements, showing a coherent picture of how the Clockwork Fermion model can be interpreted as an extension or alternative to other theories, such as the Froggatt-Nielsen mechanism and extra-dimensional models.
9.1. Implications of Findings
The findings from our review underscore the versatility and robustness of the Clockwork Fermion model. Its ability to provide a natural explanation for the smallness of neutrino masses without invoking unnaturally small Yukawa couplings has significant implications for neutrino physics and beyond. Moreover, the model’s predictions about the existence of new particles at scales accessible to current or near-future experiments open exciting possibilities for discovery at the Large Hadron Collider (LHC) and other experimental facilities.
In the broadest context, the Clockwork Fermion model not only addresses specific issues related to fermion masses but also offers insights into the unification of forces and the structure of space-time at fundamental levels. By potentially linking observable phenomena to high-energy theories, the model serves as a bridge between current experimental data and the more speculative realms of theoretical physics.
9.2. Future Research Directions
While the Clockwork Fermion model has achieved considerable success in explaining certain phenomena, several areas warrant further investigation:
- Detailed Phenomenological Studies: More detailed analyses are needed to understand the full range of the modelâs predictions, especially in light of new data from particle physics experiments. This includes refining the parameter space and exploring potential signatures that could be observed in future collider experiments.
- Cosmological Implications: Investigating the role of Clockwork mechanisms in early universe cosmology, particularly in relation to inflationary models and baryogenesis, could yield new insights. The potential interplay between clockwork fields and the dynamics of the early universe remains an open question. Studies of the succession of phase transitions from the tower of axion fields may be of special interest [35].
- Interplay with Dark Matter: Given the model’s predictions about new particles, exploring the Clockwork mechanism’s contributions to dark matter physics is a promising avenue. Identifying viable dark matter candidates within this framework and determining their detectability would be a critical step forward. Axion field nonhomogeneities can lead to primordial nonlinear structures facilitating galaxy formation at [35].
- Extensions and Modifications: The development of extended or modified versions of the Clockwork model, including those that integrate other theoretical frameworks such as string theory or holography, could provide a deeper understanding of its foundational principles.
- Experimental Tests: Designing and implementing experimental setups that can specifically test the predictions of the Clockwork Fermion model is crucial. This includes high-precision measurements of rare decays, searches for predicted new particles, and indirect effects in flavor physics.
The Clockwork Fermion model remains a vibrant and promising area of research in theoretical and experimental physics. By revisiting its foundational aspects and recent progress, we aim to provide a platform for ongoing and future studies that will further elucidate the mysteries of particle masses and the fundamental structure of our universe. It will extend the field of cosmoparticle physics studies of physics and cosmology beyond the Standard models [35].
Author Contributions
“Conceptualization, G. G. and M. K.; methodology, G.G. and M. K.; formal analysis, G. G. and M. K.; investigation, G. G. and M. K.; resources, G. G. and M. K.; data curation, G. G. and M. K.; writing, G. G. and M. K.; visualization, G. G. and M. K.; supervision, M. K.; project administration, G.G.;" All authors have read and agreed to the published version of the manuscript.
Funding
The research by M.K. was carried out in Southern Federal University with financial support of the Ministry of Science and Higher Education of the Russian Federation (State contract GZ0110/23-10-IF).
Data Availability Statement
The original contributions presented in the study are included in the article. Further inquiries can be directed to the corresponding author.
Acknowledgments
G.G. would like to thank Department of Physics Cachar College India, where a maximum part of this work has been carried out. G.G. would also like to thank Prof. Sudhr Vempati for various discussions on Clockwork Fermion Model.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
Appendix A
Appendix A.1. Mass Hierarchy in Clockwork Models
The mass hierarchy in the clockwork model can be expressed as:
where is the mass of the lightest state, and k is the coupling constant. The mass ratio between adjacent states is:
This exponential hierarchy is a key feature of the clockwork mechanism.
Appendix A.2. Coupling Constants and Renormalization
In the clockwork mechanism, the effective coupling constant can be renormalized as:
where is the initial coupling constant and N is the number of clockwork sites. This renormalization affects the interaction strength of the clockwork fermions with other particles.
Table A1.
Comparison of constraints from different experiments on clockwork fermions.
| Experiment | Detection Type | Mass Range (GeV) | Limit |
|---|---|---|---|
| LUX-ZEPLIN | Direct Detection | 10 - 1000 | |
| XENONnT | Direct Detection | 10 - 1000 | |
| Fermi-LAT | Indirect Detection | - | Limits on |
| IceCube | Indirect Detection | - | Limits on |
1 comparison constraints.
Appendix B Abbreviations
The following abbreviations are used in this manuscript:
| MDPI | Multidisciplinary Digital Publishing Institute |
| DOAJ | Directory of open access journals |
| TLA | Three letter acronym |
| LD | Linear dichroism |
References
- Giudice, G. F.; McCullough, M. A Clockwork Theory, J. High Energy Phys. 2017, 02, 036. [Google Scholar] [CrossRef]
- Batell, B.; Giudice, G.F; McCullough, M. Natural heavy supersymmetry. JHEP 2015, arXiv:1509.00834] [INSPIRE]12, 162. [Google Scholar] [CrossRef]
- Choi, K.; Im, S.H. Realizing the relaxion from multiple axions and its UV completion with high scale supersymmetry, JHEP, 2016, 01, 149 [arXiv:1511.00132] [INSPIRE].
- Patel, K.M. Clockwork mechanism for flavor hierarchies, Phys. Rev. D, 2017, arXiv:1711.05393] [INSPIRE]96, 115013. [Google Scholar] [CrossRef]
- Craig, N.; Sutherland, D. Exponential hierarchies from Anderson localization in theory space, Phys. Rev. Lett., 2018, 120, 221802. [Google Scholar] [CrossRef] [PubMed]
- Kaplan, D.E.; Rattazzi, R. Large field excursions and approximate discrete symmetries from a clockwork axion, Phys. Rev. D, 2016, arXiv:1511.01827] [INSPIRE]93, 085007. [Google Scholar] [CrossRef]
- Keren-Zur, B.; Lodone, P.; Nardecchia, M.; Pappadopulo, D.; Rattazzi, R.; Vecchi, L. On partial compositeness and the CP asymmetry in charm decays, Nucl. Phys. B, 2013, arXiv:1205.5803] [INSPIRE]867, 394. [Google Scholar]
- Randall, L.; Sundrum, R. A large mass hierarchy from a small extra dimension, Phys. Rev. Lett., 1999, 83, 3370. [Google Scholar] [CrossRef]
- Lee, H.M. Gauged U(1) clockwork theory, Phys. Lett. B, 2018, 778, 79, [arXiv:1708.03564] [INSPIRE].
- Ghosh, G. Majorana Neutrinos and Clockworked Yukawa Couplings Contribution to Nonobservation of the Rare Leptonic Decay li→lj+γ, Clockwork, LHEP 2023, 2023, 351. [CrossRef]
- Kim, J.; McDonald, J. Clockwork Higgs portal model for freeze-in dark matter, Phys. Rev. D , 2018, arXiv:1709.04105] [INSPIRE]98, 023533. [Google Scholar] [CrossRef]
- Folgado, M.G.; Donini, A.; Rius, N. Gravity-mediated dark matter in clockwork/linear dilaton extra-dimensions, JHEP, 2020, 04, 036, [arXiv:1912.02689] [INSPIRE].
- Kang, Y.-J.; Lee, H.M. Lightening gravity-mediated dark matter, Eur. Phys. J. C, 2020, arXiv:2001.04868] [INSPIRE]80, 602. [Google Scholar]
- Folgado, M.G.; Donini, A.; Rius, N. Gravity-mediated dark matter in clockwork/linear dilaton extra-dimensions, JHEP, 2020, 036 [arXiv:1912.02689] [INSPIRE].
- Antoniadis, I.; Arkani-Hamed, N.; Dimopoulos, S. , Dvali, G. R. New dimensions at a millimeter to a Fermi and superstrings at a TeV, Phys. Lett. B, 1998, 436, 257. [Google Scholar]
- Arkani-Hamed, N.; Dimopoulos, S.; Dvali, G.R. he hierarchy problem and new dimensions at a millimeter, Phys. Lett. B, 1998 429, 263, [hep-ph/9803315] [INSPIRE].
- Gherghetta, T.; Pomarol, A. Bulk fields and supersymmetry in a slice of AdS, Nucl. Phys. B 2000, 586, 141 [hep-ph/0003129] [INSPIRE].
- Farakos, K.; Kehagias, A.; Koutsoumbas, G. ; Gauge field localization in the linear dilaton background, Phys. Lett. B, 2020, arXiv:2004.14856] [INSPIRE]807, 135549. [Google Scholar] [CrossRef]
- von Gersdorff, G. Realistic GUT Yukawa couplings from a random clockwork model, [arXiv:2005.14207] [INSPIRE].
- Giudice, G.F.; Kats, Y.; McCullough, M.; Torre, R.; Urbano, A. Clockwork/linear dilaton: structure and phenomenology, JHEP 06, 2018, 009 [arXiv:1711.08437] [INSPIRE].
- Ben-Dayan, I. Generalized clockwork theory, Phys. Rev. D, 2019, 99, 096006. [Google Scholar] [CrossRef]
- Lee, H.M.; Park, M.; Sanz, V. Gravity-mediated (or composite) dark matter confronts astrophysical data, JHEP, 2014, 05, 063 [arXiv:1401.5301] [INSPIRE].
- Arkani-Hamed, N.; Dimopoulos, S.; Dvali, G.R. The hierarchy problem and new dimensions at a millimeter, Phys. Lett. B, 1998, 429, 263. [Google Scholar] [CrossRef]
- Kehagias, A.; Riotto, A. The Clockwork Supergravity, JHEP, 2018, 02, 160.
- Kang, YJ.; Kim, S.; Lee, H.M. The Clockwork Standard Model. J. High Energ. Phys, (2020), 005.
- Babu, K. S.; Saad, S. Flavor hierarchies from clockwork in SO (10) GUT, Phys. Rev. D, 103, 015009.
- Wood, K. M.; Saffin, P.; Avgoustidis, A. Clockwork Cosmology, JCAP , 2023, 07, 062.
- Choi, K.; Hui Im, S.; Sub Shin, C. General Continuum Clockwork, JHEP, 2018, 07. 113.
- Kitabayashi, T. Clockwork origin of neutrino mixings, Phys.Rev.D, 2019, 100, 3, 035019.
- Farina, M.; Pappadopulo, D.; Rompineve, F.; Tesi, A. The photo-philic QCD axion, JHEP, 2017 01, 095.
- Kehagias, A.; Riotto, A. The Clockwork Supergravity, JHEP, 2018, 02, 160.
- Ben-Dayan, I. Generalized Clockwork Theory, Phys. Rev.D, 2019, arXiv:1706.0530899, 9–096006. [Google Scholar] [CrossRef]
- Craig, N.; Garcia Garcia, I.; Sutherland, D. Disassembling the Clockwork Mechanism, JHEP, 2017, 10, 018.
- Kitajima, N.; Takahashi, F. , Resonant production of dark photons from axions without a large coupling, Phys. Rev.D 2023, arXiv:2303.05492107, 12–123518. [Google Scholar] [CrossRef]
- Khlopov, M. What comes after the Standard Model? Prog. Part. Nucl. Phys. 2020, 116, 103824. [Google Scholar] [CrossRef]
Figure 1.
Figure 1 visually represents how the clockwork fermion model can dilute the influence of each gear over increasing distances, addressing the hierarchy problem by naturally reducing large scales.
Figure 1.
Figure 1 visually represents how the clockwork fermion model can dilute the influence of each gear over increasing distances, addressing the hierarchy problem by naturally reducing large scales.
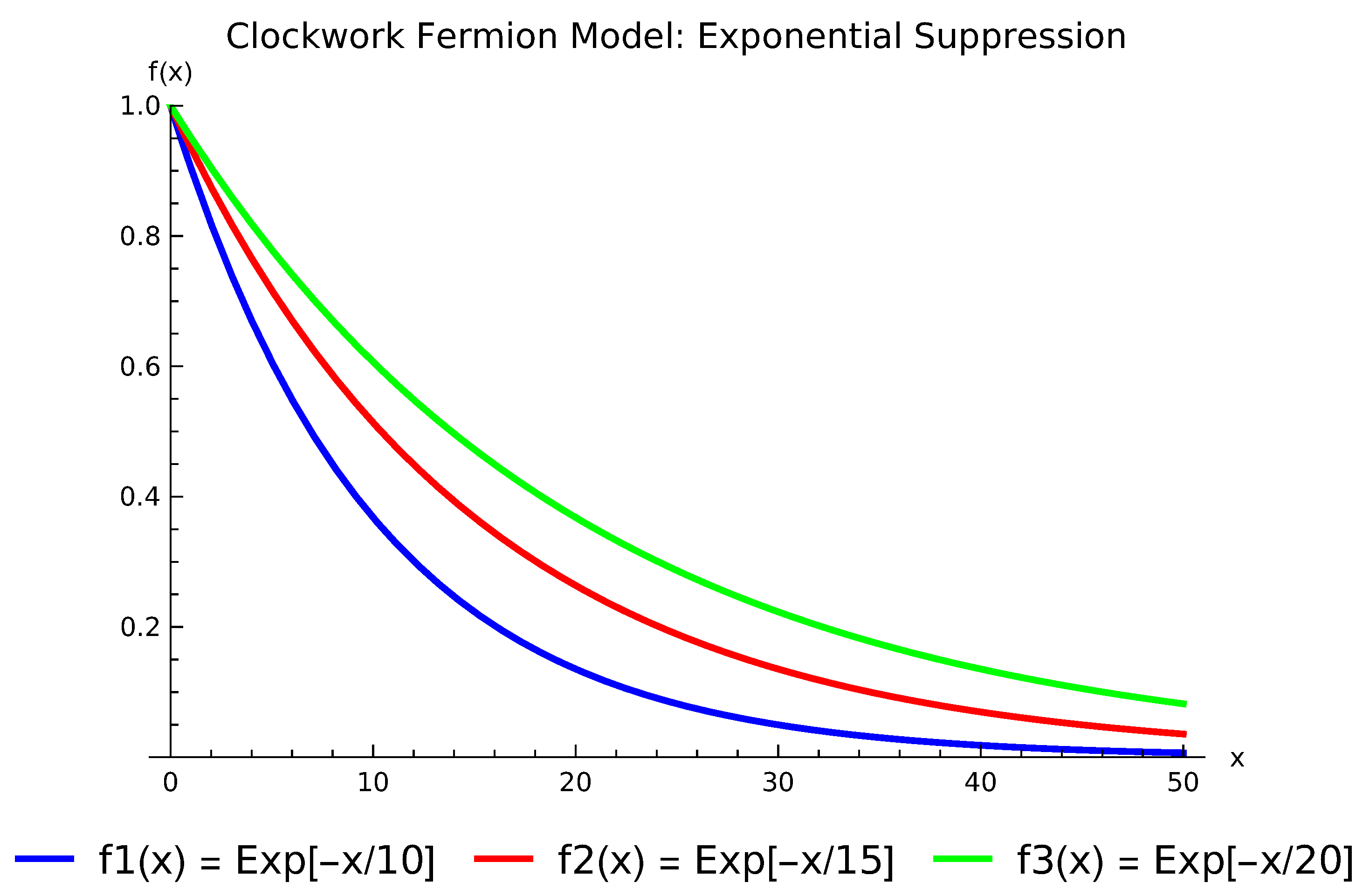
Figure 3.
Figure 3 represents a rapid decrease in the effective Yukawa coupling as the gear index increases. This exponential suppression means that even with an initial Yukawa coupling of , the effective coupling can become very small after just a few gears.
Figure 3.
Figure 3 represents a rapid decrease in the effective Yukawa coupling as the gear index increases. This exponential suppression means that even with an initial Yukawa coupling of , the effective coupling can become very small after just a few gears.
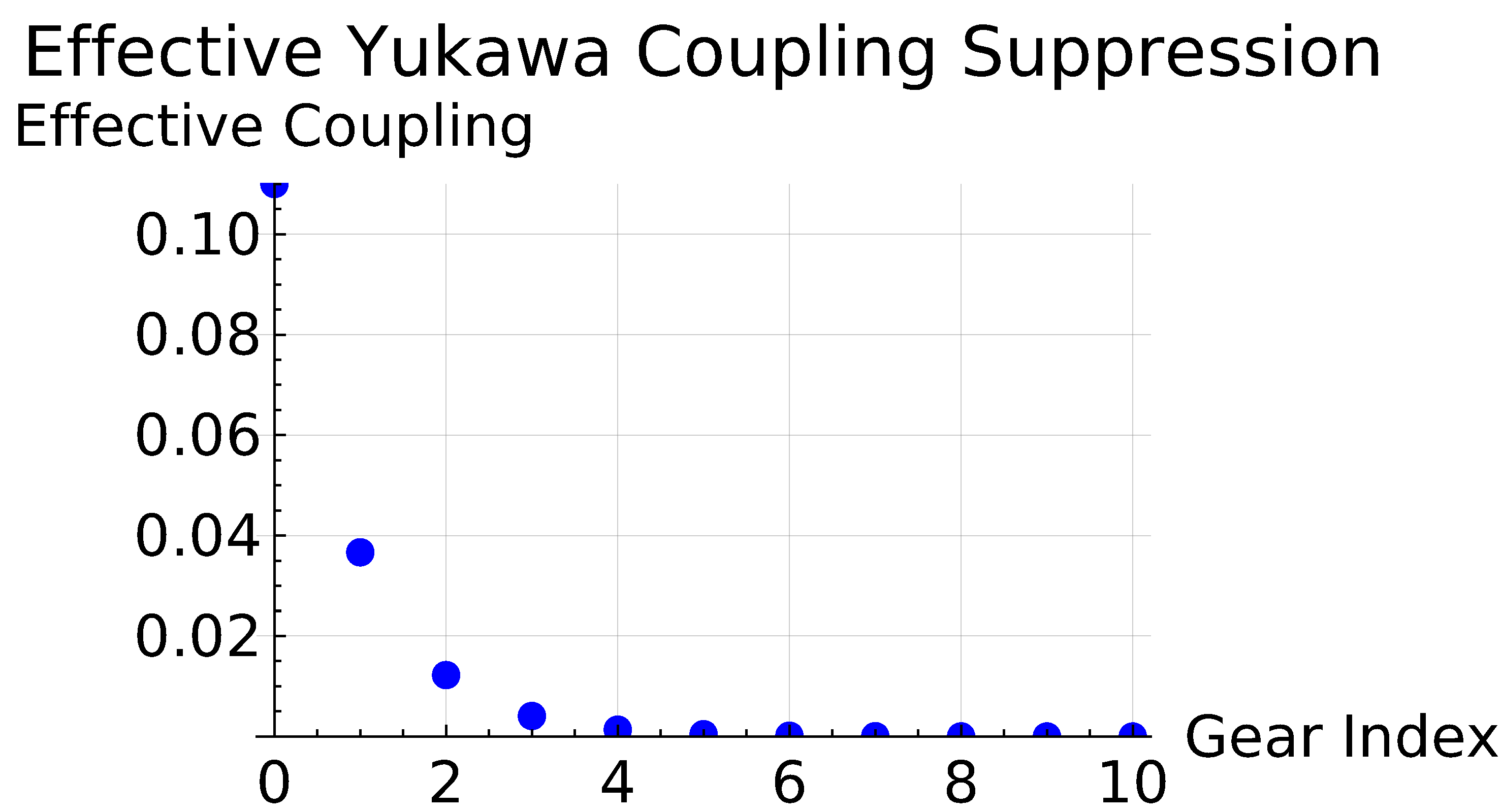
Figure 7.
Figure 7 illustrates the conceptual model of clockwork axions using the clockwork fermion model. The plot shows how the interaction strength varies in a 3D space.
Figure 7.
Figure 7 illustrates the conceptual model of clockwork axions using the clockwork fermion model. The plot shows how the interaction strength varies in a 3D space.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated







