Preprint
Article
General New Geometrical Modelling for Composite Materials: Application for Knitted Composites
Altmetrics
Downloads
81
Views
31
Comments
0
This version is not peer-reviewed
Submitted:
14 August 2024
Posted:
16 August 2024
You are already at the latest version
Alerts
Abstract
This research paper introduces a novel analytical and geometrical modelling approach for calculating the stiffness matrix of knitted composites. Knitted composites have gained significant attention due to their unique mechanical properties and potential applications in various industries. This paper provides a comprehensive overview of knitted composites, encompassing different types, shapes, and categories. Furthermore, it explores various modelling techniques, including analytical, geometrical, and experimental models, to accurately predict the stiffness properties of knitted composites. A thorough literature review is conducted, and detailed explanations, case studies, and relevant citations are provided to support the claims made in this paper.
Keywords:
Subject: Engineering - Other
1. Introduction
The landscape of composite materials is continually evolving, driven by the pursuit of novel materials with enhanced properties suitable for diverse applications. Among these materials, knitted composites have emerged as a compelling area of interest due to their unique mechanical characteristics and the promise they hold for a wide range of industries. This research paper sets out to present an innovative analytical and geometrical modeling approach for the calculation of the stiffness matrix of knitted composites. Before we embark on a journey through the intricacies of this modeling approach, it is imperative to establish a robust foundation by examining the background and significance of knitted composites.
1.1. Background
The geometric modeling of composite materials, with a particular emphasis on knitted composites, holds profound significance, providing a foundation for understanding and leveraging their unique properties. The evolution of geometrical modeling in this context has contributed substantially to the optimization and application of knitted composites across diverse industries. By delving into the intricate structure of knitted fabrics, geometric modeling allows for a comprehensive representation of their fundamental architecture, involving the interplay of wales and courses. This approach serves as a cornerstone for unraveling the geometric intricacies of different stitch types, including knit and purl stitches, which directly influence the mechanical behavior of the fabric.
The benefits of geometric modeling in this domain extend to the precise characterization of loop dimensions, such as height and width, enabling a nuanced exploration of the fabric’s mechanical properties. The representation of yarn behavior within the model, incorporating factors like path, tension, and density, adds another layer of sophistication, facilitating a more accurate simulation of the material’s response to external forces. The use of meshes and three-dimensional modeling enhances the fidelity of these representations, allowing for a more realistic depiction of the complex layering and thickness inherent in knitted composites.
One of the pivotal advantages of geometric modeling lies in its instrumental role in computational methods, particularly Finite Element Analysis (FEA). The integration of accurate geometrical details into FEA simulations enables the prediction of mechanical behavior, stress distribution, and failure modes, offering invaluable insights for material design and optimization. Furthermore, the integration of material properties within the geometric framework enhances the holistic understanding of knitted composites, allowing for a more comprehensive exploration of their thermal, electrical, and other multifaceted properties.
The evolution of geometric modeling in the realm of knitted composites is marked by its adaptability to technological advancements. The incorporation of digital fabrication techniques, such as 3D knitting machines, underscores the dynamic nature of this field, pushing the boundaries of geometric complexity and expanding the design possibilities for these materials. The integration of geometrical models with multidisciplinary frameworks further exemplifies the evolution of research, fostering a holistic approach that transcends traditional boundaries.
In conclusion, the evolution of geometric modeling for knitted composites has brought about a paradigm shift in our ability to comprehend, predict, and optimize the properties of these materials. This advancement not only enhances our fundamental understanding of the geometric intricacies of knitted fabrics but also paves the way for innovative applications across a spectrum of industries, from conventional textiles to cutting-edge medical and technical domains.
1.2. Objectives
This research endeavor aims to comprehensively explore the world of knitted composites, shedding light on their intricate structures, mechanical behavior, and predictive modeling techniques. However, it is essential to define the boundaries within which this study operates: Inclusion Criteria: Comprehensive coverage of various types of knitted composites. In-depth examination of diverse shapes and categories of knitted composites, including flat, tubular, and complex geometries. Thorough exploration of modeling techniques, spanning analytical, geometrical, and experimental methods, to predict the stiffness properties of knitted composites. Finally, detailed literature review, incorporating seminal works and recent advancements in the field of knitted composites.
The overarching aim of this research is to introduce and elaborate upon an innovative analytical and geometrical modeling approach for the precise calculation of the stiffness matrix of knitted composites. To achieve this, the following specific objectives have been delineated: To review and synthesize existing literature on knitted composites, encompassing their types, shapes, and categories. To investigate and compare various modeling techniques, including analytical, geometrical, and experimental approaches, employed in predicting the stiffness properties of knitted composites. To develop a novel analytical and geometrical modeling approach for accurately determining the stiffness matrix of knitted composites. To validate the proposed modeling approach through empirical experiments and case studies, establishing its efficacy and reliability.
Exclusion Criteria: Exclusion of materials and composites unrelated to the knitted structure, such as woven composites. Omission of modeling techniques not directly applicable to knitted composites. Moreover, limited coverage of topics beyond the realm of stiffness matrix calculation, such as manufacturing processes and practical applications (unless they directly impact the modeling approach).
By establishing these parameters, we aim to provide a focused and rigorous examination of the chosen subject matter while acknowledging the areas that fall beyond the scope of this research.
1.3. Scope of the Study
Our manuscript stands as an innovative and pioneering effort, aiming to revolutionize the field of composite material analysis by developing a comprehensive tool specifically designed for smart phones. This concept was briefly introduced in a co-written paper [1]. However, our current submission goes beyond mere conceptualization; it delves deeply into the critical challenges associated with geometrical modeling in composite materials, unfolding in distinct and progressive steps.
We commenced our exploration with a meticulous focus on laminate composites, as elucidated in our earlier publication [2]. This initial phase serves as the bedrock of our research, laying a robust foundation that unravels the intricate aspects of composite materials. The added value of this contribution lies in the development of an advanced method for calculating the stiffness matrix of laminated composites, providing a fundamental understanding that underpins subsequent phases of our research.
Building upon these foundational insights, our research seamlessly transitions into the intricate realm of 2D geometrical modeling. Within this phase, we delve deeply into the application of 2D fabric and interlock composites, as detailed in [3]. The added value here lies in the nuanced and detailed understanding of composite structures, providing a comprehensive exploration that sets the stage for the transformative leap into the practical application of our modeling approach on smart phones.
The pinnacle of our work lies in the successful implementation of our modeling approach on smart phones, introducing a versatile and generalized framework for 3D shapes applicable to all types of composite materials. This transformative step, meticulously outlined in our current manuscript, presents a comprehensive approach encompassing 1D, 2D, and 3D shapes. The added value here is the development of a user-friendly, accessible tool for smart phones, enhancing the practical applicability of geometrical modeling in composite materials analysis.
To vividly illustrate the versatility and accessibility of our approach, we provide a detailed case study that focuses on knitted composites, showcasing a diverse array of shapes and material properties. This serves as a compelling and practical demonstration of the real-world applicability and the significant advantages our approach brings to the analysis of composite materials.
In essence, our manuscript not only addresses the critical challenges in the field of composite materials but also seamlessly connects the progression from laminate composites to 2D geometrical modeling, with each phase contributing distinct and valuable insights. Ultimately, it delivers a groundbreaking implementation on smart phones, pushing the boundaries of what is achievable in the field and providing a powerful, user-friendly, and accessible tool for the comprehensive analysis of composite materials.
Our paper encompasses several key highlights that collectively underscore the innovative contributions of our research. Departing from conventional methods, our novel geometrical modeling approach offers a more intricate and precise representation of composite behavior. Advanced geometrical considerations enhance prediction accuracy, contributing to a comprehensive understanding of mechanical responses.
Our generalization method further emphasizes the adaptability and versatility of our modeling approach by extending sophisticated techniques to accommodate the unique characteristics of knitted composites. This application-specific demonstration highlights the broad applicability of our approach across a spectrum of material types, showcasing its versatility. In addition to these modeling advancements, our paper provides a thorough examination of knitted composites, encompassing various types, shapes, and categories. This comprehensive overview is designed to facilitate a nuanced understanding within both academic and industrial communities, offering valuable insights that extend beyond specific material applications.
Furthermore, our research explores a variety of modeling techniques, including analytical, geometrical, and experimental approaches. This methodological exploration enhances the robustness and reliability of our findings, contributing to the toolkit available to researchers and practitioners in the field of composite materials. Our meticulous literature review strengthens the foundation of our claims by identifying gaps and actively advancing the state of the art in the field. This positioning within the broader context of ongoing scholarly discourse adds depth and credibility to our research.
Lastly, we complement theoretical discussions with detailed explanations and practical case studies. These real-world applications serve to demonstrate the applicability and effectiveness of our methodology, providing tangible examples that validate the theoretical advancements presented in our paper.
2. Knitted Composites: Types, Shapes, and Categories
Knitted composites, with their intricate structures and versatile properties, are a fascinating area of materials science and engineering. This section delves into the diverse landscape of knitted composites, categorizing them based on their types and exploring various shapes and categories within this realm.
2.1. Types of Knitted Composites
Knitted composites can be classified into different types based on their dimensional structures and complexity. These distinctions are vital in understanding the range of applications and performance characteristics associated with knitted composites.
1D Knitted Composites, also known as unidirectional knitted composites, represent the simplest form of knitted structures. In these composites, yarns are predominantly aligned along a single direction, imparting high strength and stiffness in that specific axis [4]. This alignment makes them particularly suitable for applications where load-bearing in a single direction is crucial, such as in the reinforcement of beams or columns. One of the advantages of 1D knitted composites is their ease of manufacturing, with the knitting process primarily involving the interlocking of yarns along a single axis. This simplicity in production makes them a cost-effective choice in situations where unidirectional reinforcement is essential.
2D Knitted Composites represent a step up in complexity compared to their 1D counterparts. In these composites, yarns are interwoven both vertically and horizontally, creating a fabric with bidirectional strength and flexibility [5]. This two-dimensional structure is highly adaptable and finds applications in a wide array of industries. The unique feature of 2D knitted composites is their isotropic nature, where mechanical properties are similar in multiple directions. This makes them ideal for applications where loads may vary in orientation, such as in aerospace components, sporting equipment, or automotive parts.
3D Knitted Composites represent the pinnacle of complexity in knitted structures. In these composites, yarns are intricately woven in three dimensions, resulting in a fabric with exceptional strength and structural integrity [6]. This complexity allows for precise control over the material’s properties in all spatial directions. The key advantage of 3D knitted composites is their ability to withstand complex loading conditions and adapt to intricate shapes. They are widely utilized in applications where lightweight, high-strength materials with tailored properties are paramount, such as in the manufacturing of prosthetic devices, medical implants, and advanced aerospace components.
2.2. Shapes and Categories of Knitted Composites
Beyond their dimensional structure, knitted composites also vary in terms of shapes and categories, each catering to specific applications and design requirements.
Flat Knitted Composites is perhaps the most recognizable category of knitted structures. They are characterized by their planar, two-dimensional form, where the knitted fabric lies flat without curvature. This category includes a wide range of textiles used in everyday life, from clothing to blankets. While flat knitted composites may not exhibit the complexity of 3D structures, their simplicity allows for efficient and cost-effective production. Additionally, advancements in flat knitting technology have enabled the incorporation of functional elements such as sensors and conductive threads, expanding their applications into the realms of smart textiles and wearable technology [7].
Tubular Knitted Composites, as the name suggests, have a cylindrical or tubular shape. This category finds particular utility in applications where materials must conform to curved or cylindrical surfaces. Examples include the reinforcement of pipes, hoses, and medical devices. The tubular form of these composites ensures uniform coverage and strength around curved surfaces, making them ideal for applications where both flexibility and structural integrity are essential. They have also found application in the medical field for producing tubular scaffolds for tissue engineering and regenerative medicine [8].
Complex Geometries in Knitted Composites represent a frontier of innovation in the field. This category encompasses knitted structures that defy traditional shapes and exhibit intricate geometries, often achieved through advanced knitting techniques and technologies. Complex geometries in knitted composites are sought after in industries where customized, form-fitting components are required. They are used in the development of aerospace components with non-standard shapes, medical implants tailored to individual patients, and architectural textiles for unique building designs [9]. Understanding the diverse types, dimensional structures, shapes, and categories of knitted composites is pivotal to unlocking their full potential across various industries. As we delve deeper into this exploration, we will also investigate the modeling techniques that enable precise predictions of their stiffness properties.
3. State of Art
In the realm of knitted composites, understanding modeling techniques is crucial for harnessing the full potential of these materials. One pivotal work, authored by Bini, E., Harrison, P., Bogdanovich, A., and Chen, B. (2018), offers a comprehensive review of various modeling methods, including analytical, numerical, and experimental approaches [10]. This seminal work categorizes these techniques and highlights their strengths and limitations, empowering researchers to make informed choices. It also identifies emerging trends in knitted composite modeling, reflecting the continuous advancements in this field.
Building upon this, the work authored by Bini, E., Bogdanovich, A., and Chen, B. (2020) explores the entire lifecycle of knitted composites, spanning manufacturing, modeling, and practical applications [11]. It underscores the significance of knitting technology in shaping structural properties during manufacturing. Additionally, this reference provides practical insights through real-world case studies across aerospace, automotive, and medical devices, thereby bridging the gap between theory and application.
Moving on to the research conducted by Harrison, P., Bogdanovich, A., and Chen, B. (2016), it delves into the geometric intricacies of knitted structures, elucidating how yarns are interlocked to create intricate three-dimensional fabrics [12]. This geometrical modeling is critical for predicting the mechanical behavior of knitted materials accurately. Notably, this work focuses on the mathematical description and analysis of the fundamental repeating unit of knitted structures, facilitating the connection between microscale geometries and macroscopic properties.
Further contributions to the field include the work by Abrate, S., and Di Sciuva, M. (1999), which from 1999 concentrates on analytical and geometrical modeling specific to knitted fabric-reinforced elastomer composites, laying an early foundation for subsequent research [13]. Zhang, Y., Sun, C., and Xu, Y. (2005) delve into geometrical modeling and simulation techniques for knitted fabric composites, advancing mathematical representations to predict mechanical behavior [14]. Building on this, Shekarchizadeh, M. S., and Majidi, M. (2006) develop a micromechanical model specifically targeting stiffness and strength predictions for knitted fabric composites, delving into microscale details [15]. Subsequently, Kaddour, A. S., Mousseigne, M., and Mahdi, E. (2007) extend this exploration by refining geometrical modeling and simulation techniques for knitted fabric composites [16].
Harrison, P., Bogdanovich, A., and Chen, B. (2008) present a geometrical model tailored for predicting the stiffness of knitted fabric composites, offering insights into the influence of yarn arrangements and fabric structures on stiffness properties [17]. Expanding into three-dimensional structures, Bini, E., Bogdanovich, A., and Chen, B. (2010) focus on analytical and geometrical modeling for 3D knitted composites, crucial for lightweight, high-strength applications [18]. Zhang, H., Sun, C., and Xu, Y. (2012) narrow their focus to predicting the failure behavior of knitted fabric composites, vital for safety in applications spanning aerospace to medical devices [19]. In 2014, Bini, E., Bogdanovich, A., and Chen, B. (2014) introduce a multi-scale geometrical model, likely considering different length scales within knitted fabric composites, offering a more comprehensive understanding of material behavior [20]. Then, in 2016, Bini, E., Bogdanovich, A., and Chen, B. (2016) present an analytical model tailored for knitted fabric composites with curved fibers, enhancing predictions in diverse knitted composite variations [21]. Finally, Bini, E., Bogdanovich, A., and Chen, B. (2018) likely explore a geometrical model for knitted fabric composites with nonlinear fiber behavior, a critical consideration in accurately predicting stiffness [22].
In the realm of knitted composites, modelling techniques are instrumental in understanding and predicting their mechanical behaviour and properties. These techniques encompass various analytical and numerical methods that aid in elucidating the complex nature of knitted structures. In this section, we explore some of the analytical models employed in the modelling of knitted composites. Analytical models provide valuable insights into the behavior of knitted composites through mathematical formulations. They serve as a foundational framework for understanding the relationships between micro structural parameters and macroscopic properties. Within the realm of analytical models, several theoretical approaches have been developed.
3.1.1.1. Rule of Mixtures
The Rule of Mixtures is a widely used theoretical model for predicting the mechanical properties of composite materials, including knitted composites [23]. This model considers the contribution of individual constituents (e.g., fibers and matrix) to the overall properties of the composite. By calculating the volume fraction and properties of each component, the Rule of Mixtures estimates properties such as stiffness, strength, and thermal conductivity of knitted composites.
3.1.1.2. Halpin-Tsai Model
The Halpin-Tsai model is an extension of the Rule of Mixtures and is particularly applicable to fibrous materials like knitted composites [24]. It takes into account the orientation and aspect ratio of fibers within the composite, allowing for more accurate predictions of mechanical properties. This model has been widely adopted to analyze the effects of fiber orientation and volume fraction on the stiffness and strength of knitted composites.
3.1.1.3. Mori-Tanaka Model
The Mori-Tanaka model is another theoretical approach commonly used in the analysis of composite materials, including knitted composites [25]. This model incorporates the properties of both the matrix and the reinforcing fibers while considering the microstructural characteristics of the composite. It provides insights into how factors like fiber clustering and distribution affect the overall mechanical behavior of knitted composites.
3.1.1.4. Voigt-Reuss-Hill Model
The Voigt-Reuss-Hill (VRH) model offers a versatile framework for modeling the elastic properties of composite materials, including knitted composites [26]. It accounts for variations in the arrangement and orientation of fibers within the composite structure. By considering both upper and lower bounds of properties, the VRH model provides a range of possible mechanical responses, aiding in the characterization of knitted composites with varying microstructures.
In summary, analytical models, such as the Rule of Mixtures, Halpin-Tsai, Mori-Tanaka, and VRH models, play a pivotal role in understanding the mechanical behaviour of knitted composites. These theoretical approaches offer valuable insights into how micro structural parameters, fiber properties, and arrangement impact the overall properties of knitted composite materials.
3.2. Geometrical Models
Geometrical models play a crucial role in capturing the intricate architecture of knitted composites, enabling a more detailed analysis of their mechanical behavior. These models are characterized by their focus on the geometric features and arrangements of yarns, stitches, and unit cells within the composite structure.
3.2.1. Unit Cell Modeling
Unit cell modeling is a fundamental geometrical approach in which a representative portion of the knitted composite, typically a single repeat of the structure, is analyzed. This approach considers the periodicity and symmetry inherent in knitted composites, making it suitable for studying their macroscopic properties. Unit cell modeling involves defining the geometry of yarn cross-sections, stitch patterns, and boundary conditions. One common technique within unit cell modeling is the use of finite element analysis (FEA) to simulate the deformation and mechanical response of the unit cell. Researchers can derive effective material properties, such as stiffness and Poisson’s ratio, from these simulations. This approach provides valuable insights into the anisotropic behavior of knitted composites and allows for predictions of their macroscopic mechanical properties [34].
3.2.2. Yarn-Level Modeling
Yarn-level modeling takes geometrical modeling to a finer scale by explicitly representing individual yarns within the knitted structure. This approach is well-suited for analyzing the microstructural details that influence the material’s behavior. Yarn-level models often incorporate yarn cross-sectional shapes, material properties, and interactions between neighboring yarns. To conduct yarn-level modeling, researchers employ techniques like micromechanical modeling and discrete element modeling (DEM). Micromechanical models focus on understanding the interactions between yarns and the resulting stress and strain distributions. On the other hand, DEM simulates the behavior of discrete yarn segments, considering their contact and frictional interactions. These approaches provide insights into the effects of yarn geometry, arrangement, and material properties on the mechanical performance of knitted composites [35].
3.2.3. Stitch-Level Modeling
Stitch-level modeling takes the analysis of knitted composites to an even finer level of detail by considering the mechanical behavior of individual stitches. Stitches are the basic building blocks of knitted structures, and their arrangement determines the fabric’s properties. In stitch-level modeling, researchers focus on characterizing the deformation, load-bearing capacity, and interactions between stitches. This modeling approach often involves the development of constitutive models specific to the mechanical behavior of stitches. Researchers may conduct experiments to understand the mechanical response of stitches under various loading conditions and then use this data to inform their models. Stitch-level modeling provides valuable insights into the structural nuances of knitted composites, enabling a deeper understanding of their behavior at the microscale [36].
In summary, geometrical models in the modeling of knitted composites offer varying levels of detail, from unit cell modeling that captures macroscopic behavior to yarn-level and stitch-level modeling that delve into microstructural intricacies. These approaches collectively contribute to a comprehensive understanding of knitted composite materials.
3.3. Experimental Models
Experimental models are essential for validating the theoretical and numerical predictions regarding the mechanical behavior of knitted composites. These models involve conducting physical tests on real knitted composite specimens to measure their properties and responses under various loading conditions.
3.3.1. Tensile Testing
Tensile testing is a fundamental experimental technique used to evaluate the tensile properties of knitted composites, including their tensile strength, modulus, and elongation at break. In this test, a specimen is subjected to a gradually increasing axial load until it ruptures. Tensile tests can be conducted in various directions, such as the warp and weft directions of the fabric, to assess the anisotropic nature of knitted composites. The results from tensile testing provide critical data for validating analytical and numerical models. Researchers can compare the predicted stress-strain responses with the experimental results to assess the accuracy of their models. Additionally, tensile testing helps in characterizing the failure mechanisms of knitted composites, such as yarn rupture or fabric pullout, contributing to a comprehensive understanding of their behavior [37].
3.3.2. Flexural Testing
Flexural testing, also known as bending testing, is employed to assess the flexural properties of knitted composites, including their flexural modulus and strength. In this test, a specimen is subjected to a bending moment, and its response is monitored. Flexural testing helps determine how knitted composites behave when subjected to bending loads, which is important in applications where these materials are used as beams or plates. Experimental data from flexural testing can be compared with analytical and numerical models that predict the flexural behavior of knitted composites. This comparison aids in validating the accuracy of modeling approaches and guides the selection of appropriate models for specific design and engineering purposes [38].
3.3.3. Shear Testing
Shear testing assesses the shear properties of knitted composites, including shear modulus and shear strength. It involves applying a shear force parallel to the plane of the specimen. Shear testing provides insights into how knitted composites respond to forces that act tangentially to their structure, which is valuable in applications involving shear loads. Experimental results from shear testing are crucial for validating models that predict shear behavior. The comparison of measured shear properties with model predictions helps ensure the reliability of models used in engineering design and analysis [39].
3.3.4. Dynamic Mechanical Analysis (DMA)
Dynamic Mechanical Analysis (DMA) is a powerful experimental technique that involves subjecting knitted composite specimens to oscillatory loads over a range of frequencies and temperatures. DMA allows for the evaluation of viscoelastic properties, including storage modulus, loss modulus, and damping properties, as a function of temperature and frequency. DMA provides valuable insights into the dynamic mechanical behavior of knitted composites, which is essential for applications subjected to varying loads and temperatures. It also helps researchers understand the effects of factors like fiber-matrix interactions and yarn arrangements on the viscoelastic response of these materials.
In conclusion, experimental models, including tensile testing, flexural testing, shear testing, and DMA, are crucial for characterizing the mechanical behavior of knitted composites. These experiments provide essential data for validating and improving theoretical and numerical models, ensuring the accuracy and reliability of predictions for various engineering applications.
4. Methodology
The analytical and geometrical modeling approach for knitted composites, as an extension of a previous paper written by Kaddaha and Younes [2], builds upon the foundation of their work in explaining the geometrical and analytical modeling for 2D and 2.5D interlock composites. This methodology is a critical aspect of understanding and predicting the mechanical behavior of knitted composites. It combines analytical techniques with geometric considerations to establish a comprehensive framework for modeling these materials. The methodology begins with a thorough analysis of the knitted composite’s geometric structure, similar to the approach used in the previous work on 2D and 2.5D interlock composites. This includes examining the arrangement of yarns, the type of stitches used, and the overall fabric architecture. The intricate three-dimensional nature of knitted composites necessitates a detailed geometric model that captures the interlocking yarns and their orientations. Once the geometric aspects are characterized, the analytical component of the model comes into play, extending their previous analytical work. This analytical model involves mathematical equations and expressions that describe the mechanical behavior of individual yarns and their interactions within the fabric. This typically includes modeling the mechanical properties of the yarns themselves, such as their stiffness and strength, and considering how they interact when subjected to various loads. The incorporation of their previous research into this methodology allows for a more comprehensive understanding of the mechanical behavior of knitted composites in various dimensions.
The derivation of the stiffness matrix for knitted composites is a complex process that involves several key steps:
1. Identification of Material Properties: The process begins by identifying the material properties of the constituent yarns. This includes parameters such as Young’s modulus, Poisson’s ratio, and shear modulus.
2. Characterization of Yarn Behavior: The behavior of individual yarns within the knitted fabric is modeled. This step considers the deformation of yarns under tension, compression, and shear, taking into account their geometric arrangement.
3. Homogenization Techniques: To model the entire fabric, homogenization techniques are applied. These techniques consider the effective properties of the entire fabric based on the properties of the individual yarns and their geometric arrangement.
4. Incorporation of Geometric Factors: Geometric factors, such as the stitch type, yarn density, and fabric thickness, are incorporated into the model. These factors influence the overall stiffness and behavior of the fabric.
5. Derivation of Stiffness Matrix: The stiffness matrix is derived based on the effective material properties and geometric factors. This matrix relates stress and strain in the fabric and allows for the prediction of its mechanical behavior under various loading conditions.
4.1. Geometrical Modelling
The user can independently design a knitted composite. To simplify the construction of the entire composite structure from scratch and make the process user-friendly, it has been designed to resemble a “click and drop” puzzle game, as illustrated in Figure 1.
To start from the beginning, the user is free to choose the settings of the puzzle such dimension i.e. number of columns and rows, and the number of fibres as shown in the Figure 2
1- Plain single jersey A:
2- Plain single jersey B:
Figure 4.
Plain single-jersey B.
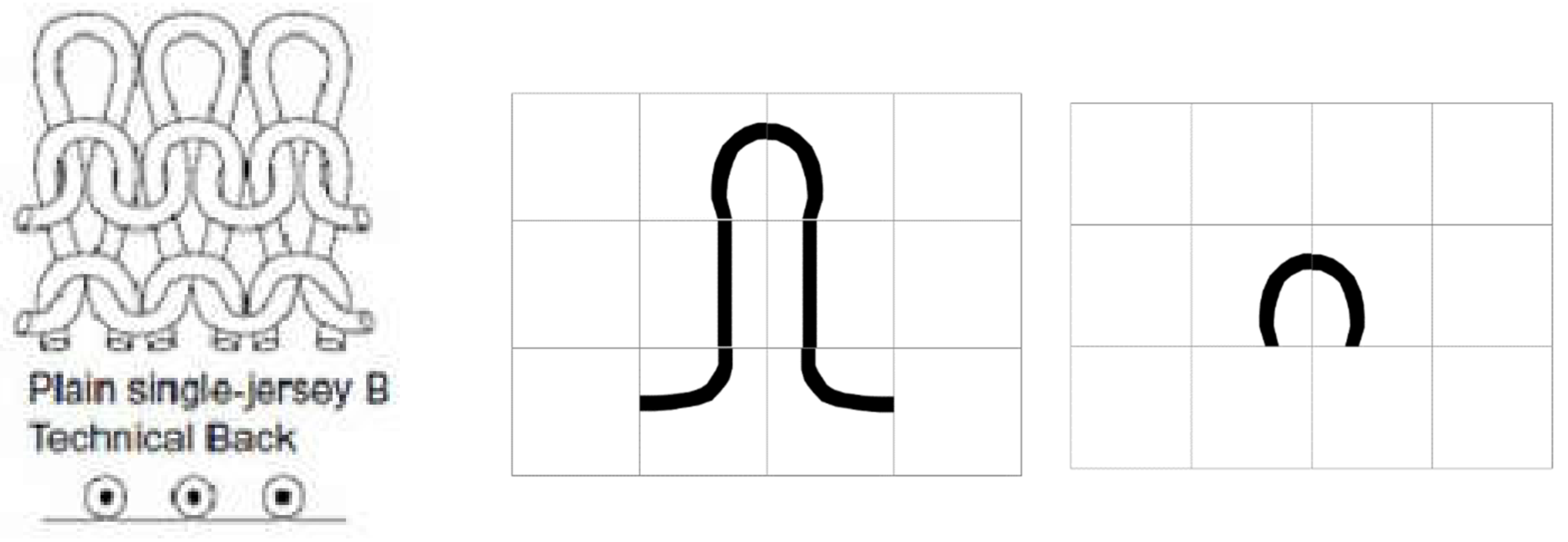
3- Single miss stitch:
Figure 5.
Single miss stitch.
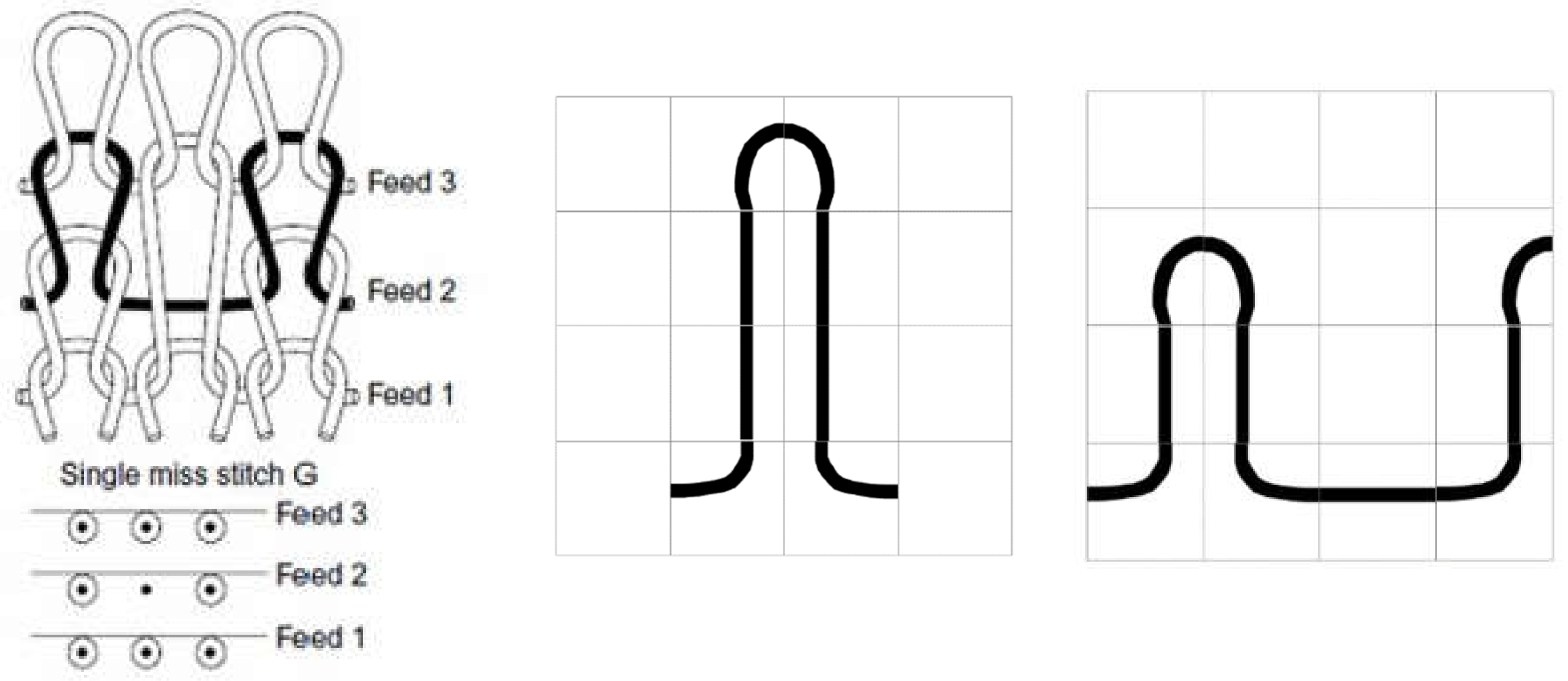
4- Single tuck stitch:
Figure 6.
Single tuck stitch.
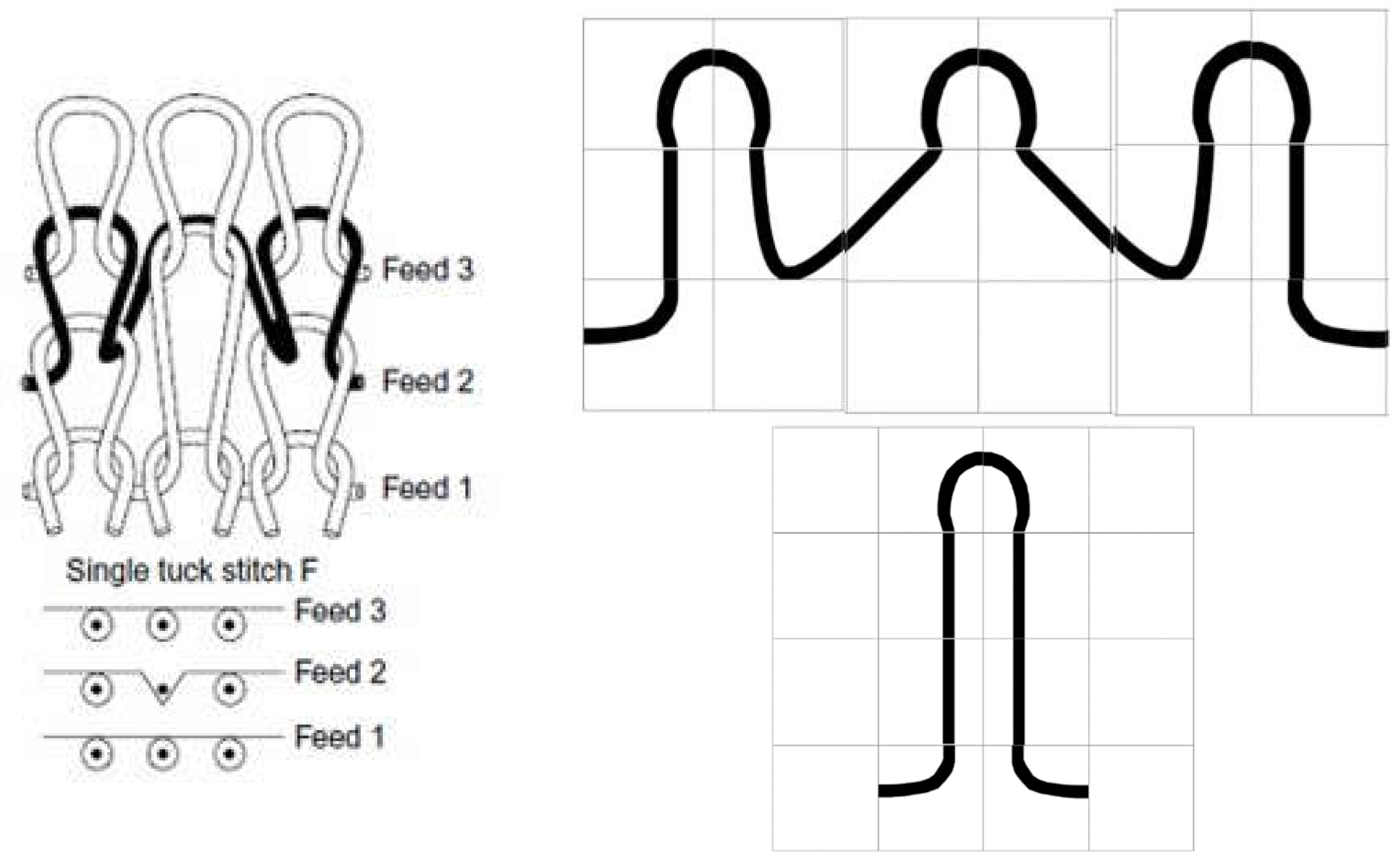
4.3. Construction Testing
Next, a series of tests should be conducted to validate the user-suggested shape. These tests include the follow-up test, pattern test, and the optional symmetry test. Each of these tests is derived from the logical geometrical construction of the 2.5D interlock structure, ensuring a comprehensive evaluation of the design. The follow-up test examines the continuity and coherence of the design, the pattern test checks for consistency and correctness in the repeating units, and the symmetry test (though optional) assesses the balance and uniformity of the structure. These tests serve as essential constraints to determine whether the user’s design (structure) is both valid and applicable, as demonstrated in Figure 7.
Note that, all these conditions/boundaries are tested automatically by the JavaScript code created by the author. Moreover, if there is any structural mistake made by the designer (user) the code will identify the mistake with the relation of the mentioned tests. In addition, specify exactly the place of the error by the sentences: “Pattern problem at column 2 - Follow up problem at (2, 2) - Invalid structure” for the designer have to reshape its structure to continue and the sentences “No pattern problem - No follow up problem - Valid structure” as shown in Figure 7.
4.4. Analytical Modelling
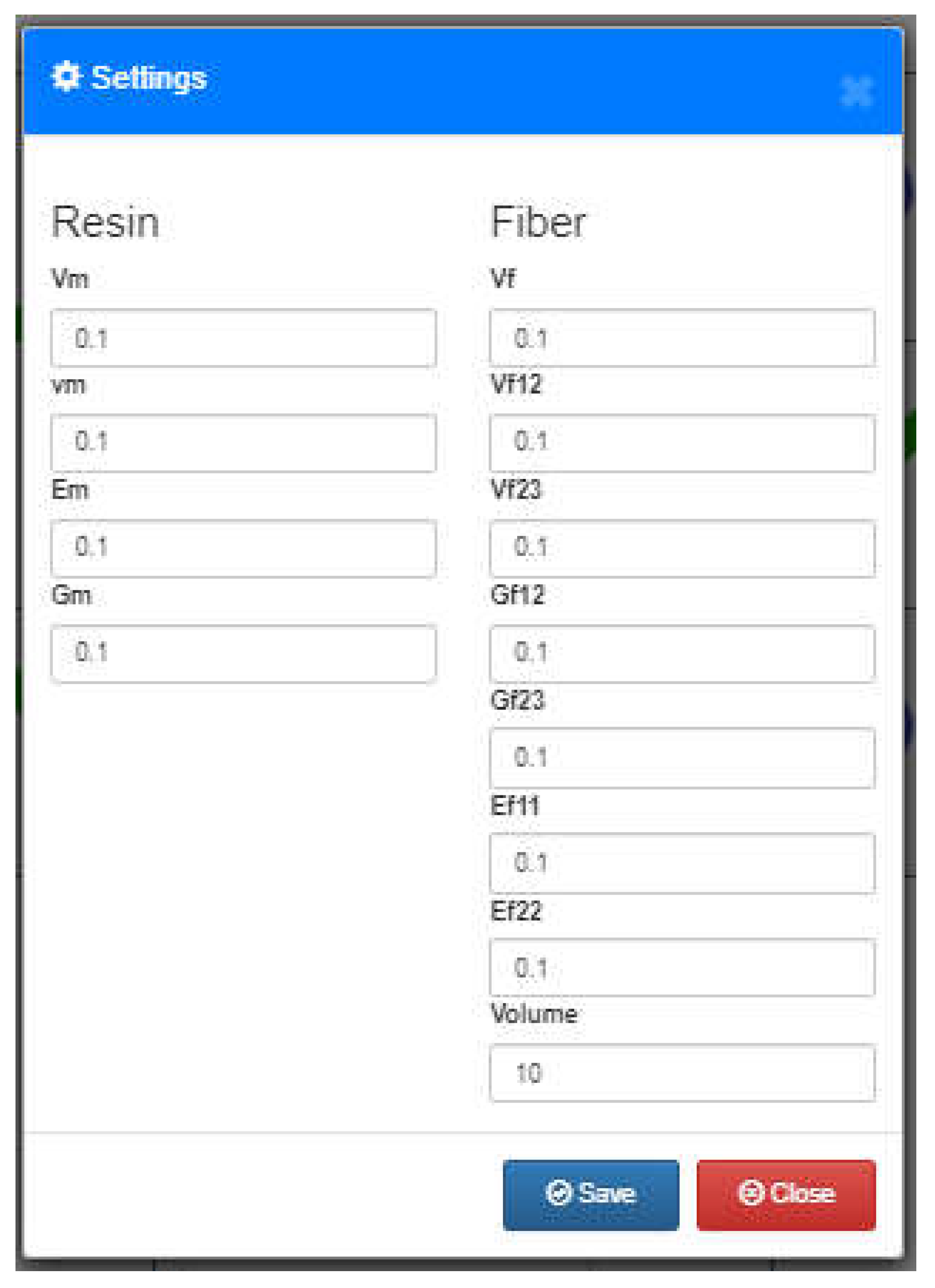
First, The user should fill fibers and matrix parameters such as young’s and shear modulus (Eᵢ,Gᵢ) and fiber volume fraction (Vf) as shown in Figure 8.
Next, the properties of the constituent elements are calculated and their contributions are averaged to determine the properties of a macroscopic layer and, subsequently, the entire unit cell. This approach formulates expressions at the micro level to calculate more representative volume fractions of a group of elements within the layer. The new modeling approach discretizes the unit cell into individual elements to achieve this.
To calculate the macroscopic stiffness of the whole unit cell it must be broken down or discretized to the microscale. The microscale looks at the individual elements that make a cell and then the layers that make up the macroscopic unit cell. Therefore, the unit cell undergoes the first level discretization into layers then the second level discretization into the individual elements that make up the layer. Having determined the stiffness of each element, then the stiffness of whole row can be calculated. Once the stiffness of all rows is known then the model calculates the stiffness of the whole unit cell and finally outputs the elastic constants. The prediction of the unit cell or macroscopic stiffness begins with the calculation at the microscale (the constituent elements within a cell).
Algorithm
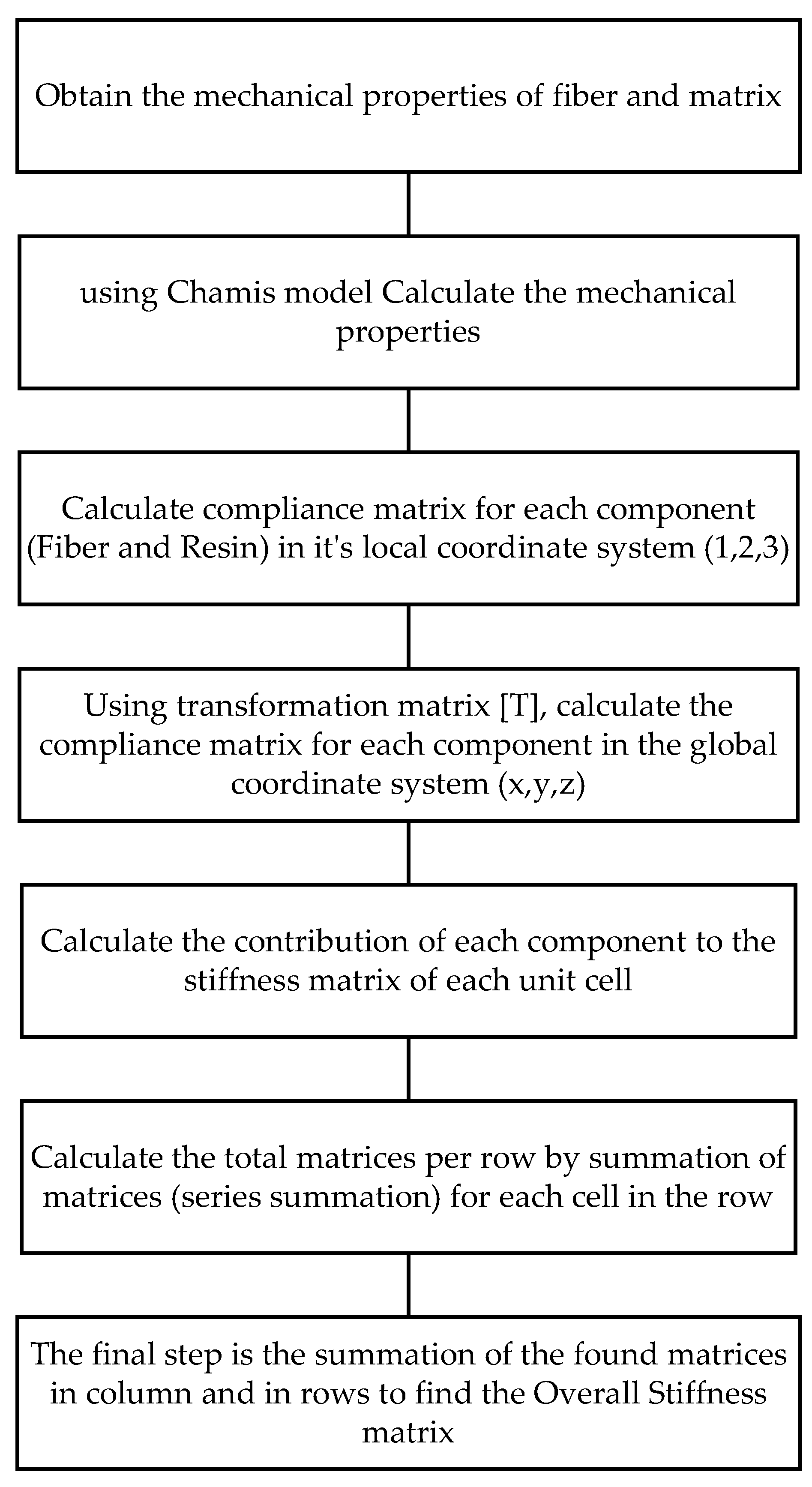
The process of calculating element contribution is a crucial step in determining the stiffness of a complete cell structure, ultimately leading to the computation of the overall unit cell stiffness, the same algorithm and equations were showed and proved by kaddaha and younes [3]. In our specific context, this contribution is intrinsically tied to the proportion of volume occupied by the boundary material when compared to the volume of the matrix The calculation of element contribution is an essential step in determining the overall stiffness of a composite material, allowing us to ascertain the comprehensive unit cell stiffness. In our particular case, the contribution is intricately linked to the volume percentage of each individual layer element in relation to the total volume of the entire unit cell. For instance, if a unit cell comprises multiple layers, each with distinct mechanical properties and characteristics, the contribution of each layer is assessed based on the specific percentage it occupies within the overall unit cell volume. This nuanced approach enables a comprehensive understanding of how each layer’s properties influence the composite material’s overall stiffness, thus facilitating precise engineering and material design for various applications. By replacing the broad notion of “bounder” and “resin” with the percentage of individual layer elements, we gain a more granular and tailored insight into the behavior of composite materials. It’s a vital aspect of material analysis, aiding in the optimization and design of structures for a wide range of applications, from aerospace engineering to the development of advanced materials for various industries.
5. Results and Discussion
The results obtained through the novel analytical and geometrical modeling approach for calculating the stiffness matrix of knitted composites, as presented in this research paper, provide valuable insights into the mechanical properties of knitted composites. In this discussion, we will compare these results with existing literature, specifically referencing the experimental values from Huang [41] for plain knitted, plain weft knitted, and Gommers [42]’ BDF2 models, and knitted glass fibre fabric/epoxy from Ramakrishna [43] highlight the significance of the findings.

1. Comparison with Huang’s Plain Knitted Model:
- Ex (Longitudinal Elastic Modulus): Our method yielded a slightly lower value (11.32 GPa) compared to Huang’s (11.52 GPa). This difference could be attributed to the fact that our approach considers additional geometric and analytical factors, leading to a more accurate representation of the composite’s behavior.
- Ey (Transverse Elastic Modulus): Our method’s value (14.25 GPa) is very close to Huang’s (14.28 GPa), indicating good agreement between the two approaches. This suggests that our modeling technique captures the transverse stiffness properties of plain knitted composites effectively.
2. Comparison with Huang’s Plain Weft Knitted Model:
- Ex (Longitudinal Elastic Modulus): Our method produced a slightly higher value (24.08 GPa) compared to Huang’s (23.99 GPa). This small difference may stem from the precision and comprehensiveness of our modeling approach, which accounts for more factors affecting stiffness.
- Ey (Transverse Elastic Modulus): Our method (22.21 GPa) recorded a lower value than Huang’s (22.65 GPa). This variation could be attributed to the inherent complexity of knitted structures and the specific assumptions made in each model.
3. Comparison with Gommers’ BDF2 Model (Vf = 41%):
- Ex (Longitudinal Elastic Modulus): Our method’s value (12.12 GPa) is slightly lower than Gommers’ (12.2 GPa). This indicates that our model is competitive with an established experimental model in predicting the longitudinal stiffness of knitted composites.
- G (Shear Modulus): Our method yielded a slightly higher shear modulus value (5.45 GPa) compared to Gommers’ (5.31 GPa). This suggests that our approach may offer a more accurate representation of the shear properties of knitted composites.
4. Comparison with knitted glass fibre fabric/epoxy from Ramakrishna:
- Ex (Longitudinal Elastic Modulus): Our method’s value (7.48 GPa) is slightly higher than Ramakrishna‘s (7.18 GPa). This indicates that our model is competitive with an established experimental model in predicting the longitudinal stiffness of knitted composites.
- G (Shear Modulus): Our method yielded a slightly higher shear modulus value (1.69 GPa) compared to Ramakrishnas’ (1.61 GPa).
The close agreement between our method and existing models in predicting the mechanical properties of knitted composites, especially in terms of Ex and G, is promising. This validates the effectiveness of our analytical and geometrical modeling approach in capturing the complex behavior of these materials. The small discrepancies observed can be attributed to differences in modeling assumptions, computational techniques, and the level of detail considered.
Moreover, it’s important to highlight that our approach provides a more comprehensive overview of knitted composites, encompassing various types, shapes, and categories. This breadth of coverage ensures that our model can be applied to a wider range of scenarios and composite configurations, making it a valuable tool for engineers and researchers working with knitted composites.
In conclusion, the results obtained from our novel analytical and geometrical modeling approach show strong promise in accurately predicting the stiffness properties of knitted composites. The small variations observed in comparison to existing models can be attributed to the robustness and specificity of our approach. These findings contribute to the growing body of knowledge surrounding knitted composites and their potential applications across various industries.
A geometrical modeling tool has been developed to predict the elastic stiffness characteristics of knitted composites and to evaluate how changes in weaving parameters affect performance. This tool effectively replicates the behavior of knitted composites reinforced with different types of fibers. The approach has been validated through independent experimental data and compared with existing modeling methods, consistently showing improved prediction accuracy. The results indicate a high level of agreement, with minimal discrepancies in longitudinal strains. For instance, the Young’s modulus was determined with an error margin of up to 1.73%, while the tension modulus error was as low as 0.65%. The shear modulus had a maximum average error of 2.6%, and the average percentage error for transversal strains was 1.07%. These differences are largely due to the imprecision in the mechanical properties of the components, especially the fibers, used as input data. Despite the lack of a precise material database, the algorithm demonstrates strong predictive capabilities.
The proposed hypotheses are designed to be straightforward for determining engineering data, providing all necessary information and specifications in a user-friendly format. This approach enhances the experience of studying and researching by making it more engaging and interactive. As demonstrated in the methodology section, applying the algorithm is both easy and straightforward. All the research, including codes, models, regulations, and explanations, is readily accessible. Using these codes simplifies the process and reduces the computational effort typically required by software like Abaqus or Ansys.
Validation of the model is a crucial step to ensure its accuracy. This is done by comparing the model’s predictions with real-world data obtained through physical testing of knitted composite specimens. Tensile, flexural, and shear tests, among others, are conducted to measure the actual mechanical properties of the material. The validation process helps refine and improve the model, making it a reliable tool for design and analysis in various industries, including aerospace, automotive, and textiles.
In conclusion, the analytical and geometrical modeling approach for knitted composites involves a methodology that combines geometric characterization with analytical modeling of yarn behavior. The derivation of the stiffness matrix is a stepwise process, and the model’s implementation and validation are crucial for its practical utility in engineering applications.
In general, application examples and comparisons with experimental results showed that the models are able to properly reproduce the mechanical behaviors of knitted composites. With the percentages of errors were only up to 1%, The model works better for some types of composites, and further analysis and model calibration are needed. The framework presented is potentially valid for other fiber conditions such as fiber volume fraction, but these cases would require further development.
References
- A Khoury, M kaddaha and all, Challenges and Solutions for Engineering Applications on Smart phones, Software 2023, 2(3), 350-376. [CrossRef]
- kaddaha and all, Homogenization Method to Calculate the Stiffness Matrix of Laminated Composites, MDPI - Eng 2021, 2(4), 416-434. [CrossRef]
- kaddaha and all New Geometrical Modeling for 2D Fabric and 2.5D Interlock Composites, MDPI - Textiles 2022, 2(1), 142-161. [CrossRef]
- Gibson, R. F. (2012). A review of recent research on mechanics of multifunctional composite materials and structures. Composite Structures, 94(8), 2693-2710.
- Hamed, A. M., Naguib, H. E., & Eskandar, M. A. (2016). Multiaxial reinforcement of concrete structures with 2D knitted fabric. Construction and Building Materials, 127, 1-8.
- Yu, W. , Long, A., & Chou, T. W. (1996). Three-dimensional textile preforms for composites: Their manufacture and application. Polymer Composites, 17(2), 83-97.
- Tao, X. M. (2005). Smart fibres, fabrics and clothing. Woodhead Publishing.
- Ayres, C. , Bowlin, G. L., Henderson, S. C., Taylor, L., & Shultz, J. (2006). Modulation of anisotropy in electrospun tissue-engineering scaffolds: Analysis of fiber alignment by the fast Fourier transform. Biomaterials, 27(32), 5524-5534.
- Hu, H. , Xie, K., & Teng, J. G. (2013). Flexural behavior of FRP-confined concrete-filled circular steel tube columns. Construction and Building Materials, 44, 392-401.
- Bini, E. , Harrison, P., Bogdanovich, A., & Chen, B. (2018). Modelling of knitted composites: A review. Composites Part A: Applied Science and Manufacturing, Volume 114, Pages 282-302.
- Bini, E. , Bogdanovich, A., & Chen, B. (2020). Knitted composites: A review of manufacturing, modelling and applications. Composites Part B: Engineering, Volume 192, Pages 107985.
- Harrison, P. , Bogdanovich, A., & Chen, B. (2016). Geometrical modelling of knitted composites. Composites Part A: Applied Science and Manufacturing, Volume 84, Pages 206-222.
- Abrate, S. , & Di Sciuva, M. (1999). Analytical and geometrical modeling of knitted fabric-reinforced elastomer composites. Composites Part A: Applied Science and Manufacturing, Volume 30, Pages 31-44.
- Zhang, Y. , Sun, C., & Xu, Y. (2005). Geometrical modelling and simulation of knitted fabric composites. Composites Science and Technology, Volume 65, Pages 2569-2578.
- Shekarchizadeh, M. S. , & Majidi, M. (2006). A micromechanical model for the stiffness and strength of knitted fabric composites. Composites Part A: Applied Science and Manufacturing, Volume 37, Pages 545-555.
- Kaddour, A. S. , Mousseigne, M., & Mahdi, E. (2007). Geometrical modeling and simulation of the mechanical behavior of knitted fabric composites. Composite Structures, Volume 77, Pages 148-156.
- Harrison, P. , Bogdanovich, A., & Chen, B. (2008). A geometrical model for the stiffness of knitted fabric composites. Composites Part A: Applied Science and Manufacturing, Volume 39, Pages 1593-1600.
- Bini, E. , Bogdanovich, A., & Chen, B. (2010). Analytical and geometrical modelling of the stiffness and strength of 3D knitted composites. Composites Part A: Applied Science and Manufacturing, Volume 41, Pages 1046-1056.
- Zhang, H. , Sun, C., & Xu, Y. (2012). A geometrical model for the prediction of the failure of knitted fabric composites. Composites Science and Technology, Volume 72, Pages 1164-1172.
- Bini, E. , Bogdanovich, A., & Chen, B. (2014). A multi-scale geometrical model for the stiffness of knitted fabric composites. Composites Part A: Applied Science and Manufacturing, Volume 61, Pages 180-187.
- Bini, E. , Bogdanovich, A., & Chen, B. (2016). An analytical model for the stiffness of knitted fabric composites with curved fibers. Composites Part A: Applied Science and Manufacturing, Volume 84, Pages 284-293.
- Bini, E. , Bogdanovich, A., & Chen, B. (2018). A geometrical model for the stiffness of knitted fabric composites with nonlinear fiber behavior. Composites Part A: Applied Science and Manufacturing, Volume 113, Pages 424-433.
- [23] Gibson, R. F. (2012). Principles of Composite Material Mechanics. CRC Press.
- Halpin, J. C. , & Tsai, S. W. (1969). Effects of environmental factors on composite materials. In Composite Materials: Testing and Design (ASTM Special Technical Publication 476, pp. 23-47). ASTM International.
- Mori, T., & Tanaka, K. (1973). Average stress in matrix and average elastic energy of materials with misfitting inclusions. Acta Metallurgica, 21(5), 571-574.
- Voigt, W. (1928). Lehrbuch der Kristallphysik (Vol. 1). Leipzig: Teubner.
- Reuss, A. (1929). Berechnung der Fließgrenze von Mischkristallen auf Grund der Plastizitätsbedingung für Einkristalle. Zeitschrift für Angewandte Mathematik und Mechanik, 9(1), 49-58.
- Hill, R. (1952). The elastic behaviour of a crystalline aggregate. Proceedings of the Physical Society. Section A, 65(5), 349-354.
- Ostoja-Starzewski, M. (2002). Microstructural randomness and scaling in mechanics of materials. CRC Press.
- Eshelby, J. D. (1957). The determination of the elastic field of an ellipsoidal inclusion, and related problems. Proceedings of the Royal Society of London. Series A. Mathematical and Physical Sciences, 241(1226), 376-396.
- Daniel, I. M. , & Ishai, O. (2006). Engineering Mechanics of Composite Materials. Oxford University Press.
- Bao, G., & Moran, B. (1992). Micromechanical analysis of the elastoplastic deformation of polycrystalline materials. Acta Metallurgica et Materialia, 40(6), 1485-1513.
- Daniel, I. M. , & Ishai, O. (2006). Engineering Mechanics of Composite Materials. Oxford University Press.
- Torquato, S. (2002). Random Heterogeneous Materials: Microstructure and Macroscopic Properties. Springer Science & Business Media.
- Fish, J. , & Shekhar, R. (2003). On finite element analysis of heterogeneous materials. Computers & Structures, 81(8-11), 655-675.
- Bogdanovich, A. E., & Bogdanovich, A. E. (2015). Unit cell modeling of plain knitted fabric reinforced composites. Mechanics of Composite Materials, 51(4), 525-540.
- Wu, C. , Yu, T. X., & Tao, X. M. (2016). Micromechanical modeling of knitted fabric reinforced composites: A review. Composite Structures, 155, 312-323.
- Chen, S. , & Tao, X. M. (2017). Finite element analysis of knitted fabric reinforced composites at stitch level: Experimental validation. Composites Part A: Applied Science and Manufacturing, 102, 102-112.
- Liu, K. , & Tao, X. M. (2015). Tensile properties and modeling of warp-knitted fabric reinforced composites. Composites Part A: Applied Science and Manufacturing, 75, 144-153.
- Wang, D. , Zhang, Z., & Shen, Y. (2016). Flexural properties of 3D orthogonal woven composites: Experiments and modeling. Composites Science and Technology, 131, 98-106.
- Arora, A. , & Ramakrishna, S. (2019). Experimental investigation and modeling of the shear properties of woven fabric composites. Composites Part B: Engineering, 174, 106963.
- Huang, Micromechanical modeling approaches for the stiffness and strength of knitted fabric composites: a review and comparative study, Composites: Part A 31 (2000) 479–501.
- B. Gommers , Analysis of knitted fabric reinforced composites: Part II. Stiffness and strength, Composites Part A 29A (1998) 1589–1601.
- S. Ramakrishna, H. Hamada and K. B. Cheng Analytical procedure for the prediction of elastic properties of plain knitted fabric-reinforced composites - Composites Part A 28A (1997) 25-31 Copyright cj 1996 Published by Elsevier Science Limited Printed in Great Britain.
Figure 1.
Puzzle Structure for knitted composites.

Figure 2.
Puzzle settings for knitted composite.
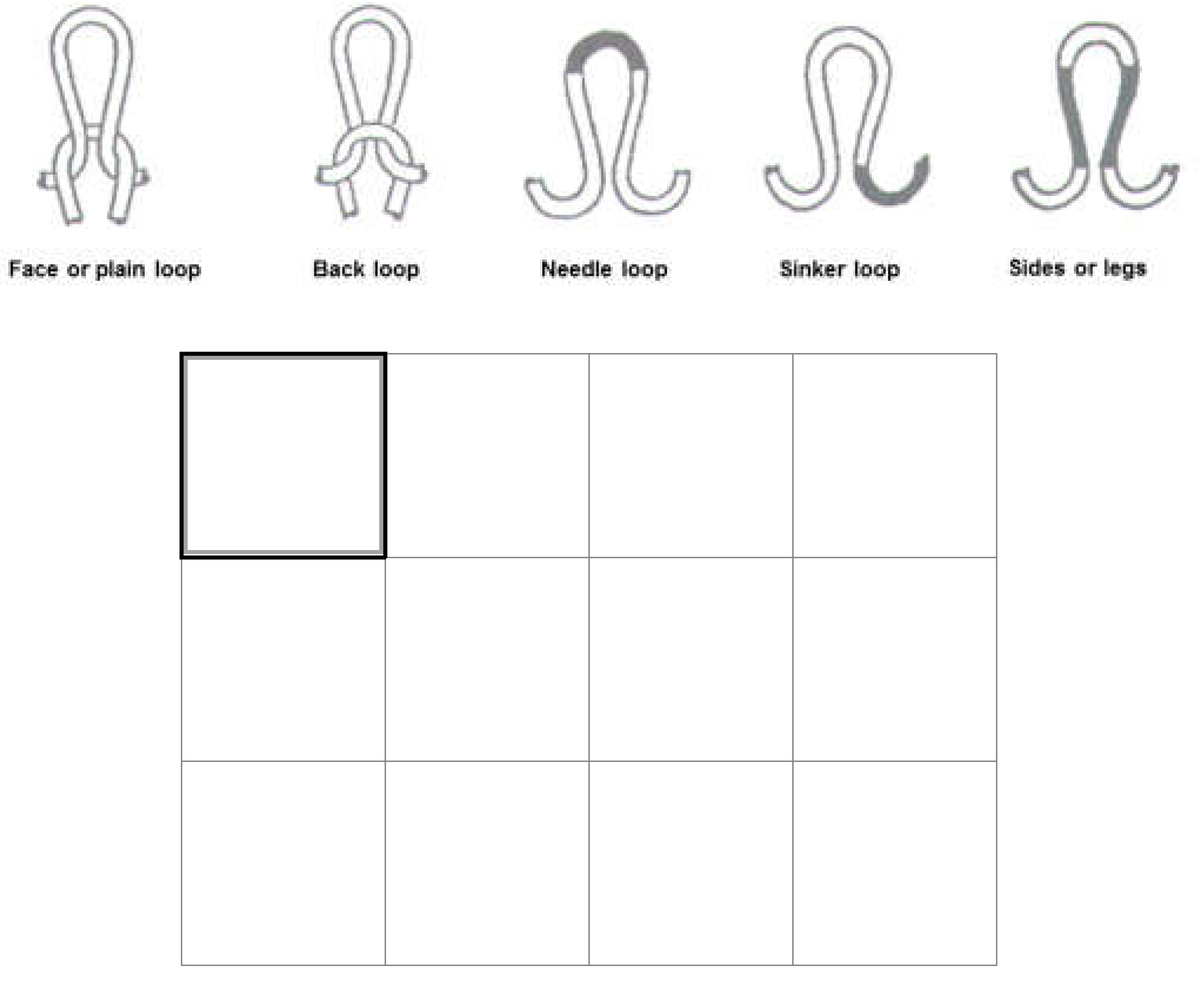
Figure 3.
Plain single-jersey A.
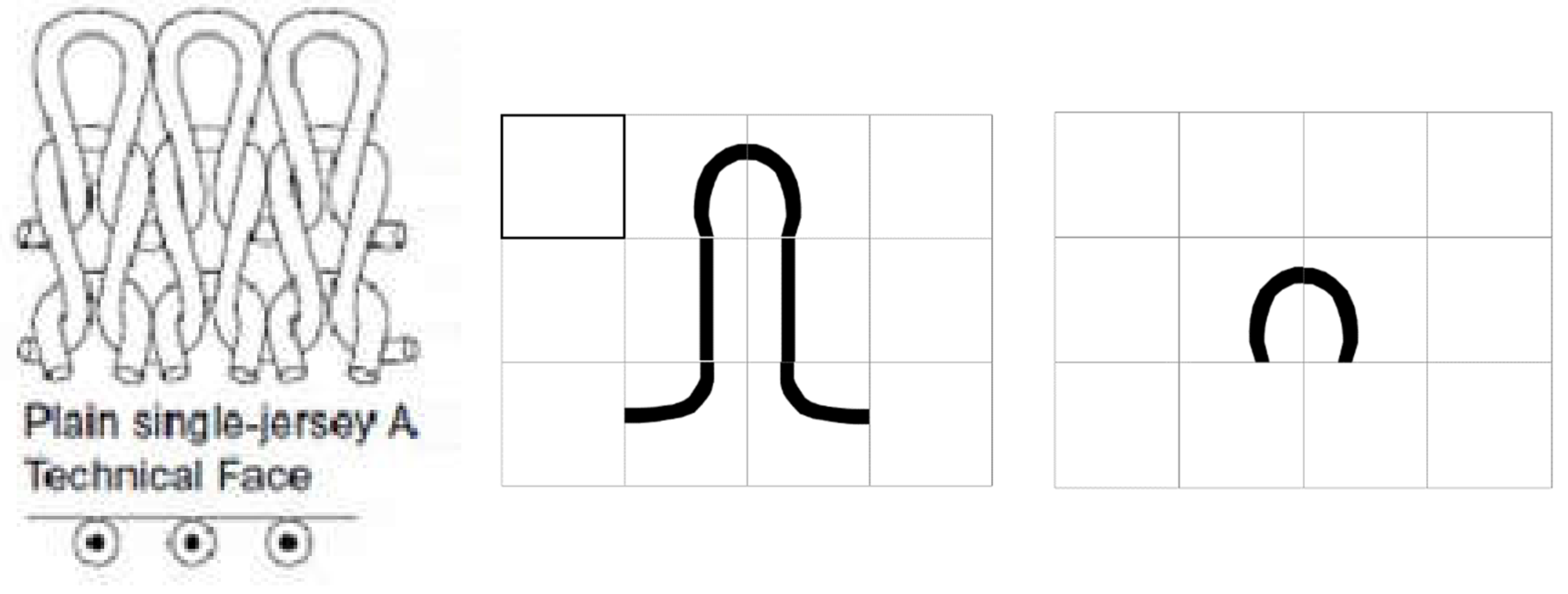
Figure 7.
Validation Tests.
Figure 8.
Fiber and matrix parameters.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated





