An Exploration of Ideals and Filters In Triangle Algebras

In the study of algebraic structures related to logical systems, Ideals and filters have different meanings and they are algebraic notions related to logical provable formulas. Unlike the classical Boolean lattice theory, ideals and filters are not dual notions in residuated lattices. An interesting subclass of residuated lattices is the class of triangle algebras, which is an equational representation of interval-valued residuated lattices that provides an algebraic framework for using closed intervals as truth values in fuzzy logic. The main aim of this article is to introduce and study the concept of ideals in triangle algebras and investigate the connection between ideals and filters. We first point out that the construction procedure for the filter generated by a subset of a triangle algebra established by Zahiri et al. is incorrect, and we proceed to give an alternative characterization.

Keywords:

Subject: Computer Science and Mathematics - Mathematics

MSC: (2020) 03G10; 06B10; 06B75; 03B52

Introduction

Ideal theory is a very effective tool for studying various algebraic and logical systems. Indeed, the notion of ideal has been introduced in many algebraic structures, including

lattices: here, ideals are examples of convex sublattices, and many conditions on elements and ideals of lattices amount to weakened forms of distributivity [3];
rings: the set of all ideals of a ring is a common example of a residuated lattice, and ideals are in a one-to-one correspondence with congruence relations. Furthermore, the kernel of any homomorphism is an ideal and reciprocally any ideal is the kernel of a homomorphism. Moreover, the set of all ideals of a ring was used to study some subclasses of the variety of rings; these researches aimed to investigate properties of some subclasses of rings whose residuated lattices of ideals belong to a specific subvariety of residuated lattices (see [1,4]. for example, Belluce et al.[1] studied those rings whose semiring of ideals, under ideal sum and ideal product, can be equipped with the structure of a Heyting algebra.
residuated lattices: ideals have crystallized researchers’ attention in MV-algebras [6,7], whereas in general residuated lattices it is filters (shown to be equivalent to deductive systems) that focus researchers’ attention. In MV-algebras, filters and ideals are dual notions (see [10]), but this is no longer the case in the general framework of residuated lattices (see [20]). Some authors have claimed that the notion of ideals is missing in BL-algebras; to fill this gap, Lele and Nganou [6] introduced the notions of ideal, prime ideal and Boolean ideal in BL-algebras and derived some of their characterizations. They used their notion of ideal to characterize BL-algebras.

It is well known in literature that in general, there are more filters than ideals in a residuated lattice (see [7,13,14]). Liu et al. [7] studied ideals and established links with filters in residuated lattices. Furthermore, Tchoua et al. [14] have introduced the notion of N-involutive filters by using the set of complement elements, and they have proved that in a residuated lattice the class of N-involutive filters is isomorphic to the lattice of all ideals. Therefore, in residuated lattices an N-involutive filter is a dual notion of the notion of ideal.

On the other hand, to represent imperfect information without paying too much in terms of computational complexity and to nicely accommodate and combine the facets of vagueness and uncertainty, closed intervals of [0,1] stand out as a particularly appealing and promising choice. Interval-valued fuzzy set theory is an increasingly popular extension of fuzzy set theory where traditional [0,1]-valued truth degrees are replaced by closed intervals of [0,1] that approximate the partially unknown exact degrees. For example, it is quite impossible to measure the crowdness of the roads of the network for a particular time duration as a single value, because, the crowdness in a duration is not fixed, it varies time to time. So, more convenient technique to grade the crowdness is an interval not a point (see application in [9]). Triangle algebras introduced by Van Gasse et al. [15,16,17] as an equational representation of interval-valued residuated lattices (IVRL) provide an algebraic framework for using closed intervals as truth values in fuzzy logic. The same authors introduced and studied the notion of filter in triangle algebras [18] and used it to prove chain completeness, and later the standard completeness [16] of interval-valued fuzzy logics based on triangle algebras. Many other results on triangle algebras have been obtained by various authors, such as Zahiri et al. [21,22,23] and Zhang(2023) et al. [26].

The above discussion motivates us to introduce and investigate the notion of ideal in the framework of triangle algebras. Moreover, this paper delves into the exploration of the link between ideals and filters in triangle algebras. In the context of residuated lattices, filters and ideals have been linked using different operators by Liu [7] on the one hand, and Tchoua Yinga et al. [13] on the other hand. Here, we prove that these operators are equal in residuated lattices. However, in triangle algebras the situation is more complex: although filters are changed into ideals by these operators, as in the case of residuated lattices, the image of an ideal is not always a filter. Therefore, we introduce a new linking operator in the case of triangle algebras.

The paper is organized as follows: In Section 2, we first recall some preliminaries on residuated lattices and triangle algebras. In Section 3, we introduce the notion of ideal in triangle algebras and investigate some of its characterizations. Furthermore, we establish the link between ideals and filters and the link between ideals and congruences. Next, we argue that the existing constructive characterization of the filter generated by a subset of a triangle algebra proposed in [22] by Zahiri et al. is incorrect. For this reason, we introduce and prove a new characterization of the filter generated by a subset in triangle algebras. The section ends with an investigation of the structure of the set of all ideals of a triangle algebra. Finally, in Section 4 we conclude and point out directions for further research.

1. Preliminaries

In this section, we review the basic definitions and results on residuated lattices [2,5,7,18,19], and triangle algebras [16,17,18] that will be used in the sequel.

1.1. Residuated Lattices

A bounded commutative residuated lattice is an algebraic structure

(L, \land, \lor, ⊙, \to, 0, 1)

of type

(2, 2, 2, 2, 0, 0)

satisfying the following conditions:

(RL1): $(L, \land, \lor, 0, 1)$ is a bounded lattice;
(RL2): $(L, ⊙, 1)$ is a commutative monoid;
(RL3): for every $x, y, z \in L$ , $x ⩽ y \to z \Leftrightarrow x ⊙ y ⩽ z$ , where ⩽ is the lattice order induced by the lattice operations ∧ and ∨.

Unless otherwise specified, we denote a residuated lattice

(L, \land, \lor, ⊙, \to, 0, 1)

by L. For all

x \in L

, we define

x^{*} : = x \to 0

x^{* *} : = {(x^{*})}^{*}

x ⊘ y : = x^{*} \to y

x \oplus y : = {(x^{*} ⊙ y^{*})}^{*}

x^{0} : = 1

and

x^{n} = x^{n - 1} ⊙ x

, for

n \geq 1

In any bounded commutative residuated lattice L, we have the following rules of calculus (for detailed proofs, see [2,7,10,12,19]):

(r₁): $x ⩽ y \Leftrightarrow x \to y = 1$ ;
(r₂): $x ⊙ y ⩽ x, y$ ;
(r₃): $x ⊙ (x \to y) ⩽ y$ ;
(r₄): $x ⩽ y \Rightarrow x ⊙ z ⩽ y ⊙ z$ ;
(r₅): $x ⩽ y \Rightarrow \{\begin{matrix} y \to z ⩽ x \to z \\ z \to x ⩽ z \to y \end{matrix}$ ;
(r₆): $x ⩽ y \Rightarrow y^{*} ⩽ x^{*}$ ;
(r₇): $x ⩽ x^{* *}$ and $x ⩽ y \Rightarrow x^{* *} ⩽ y^{* *}$ ;
(r₈): $x^{*} = x^{* * *}$ ;
(r₉): $x^{* *} ⊙ y^{* *} ⩽ {(x ⊙ y)}^{* *}$ ;
(r₁₀): $(x \to y) ⊙ (y \to z) ⩽ x \to z$ ;
(r₁₁): $x \to y ⩽ (x \land z) \to (y \land z)$ ;
(r₁₂): $x \to y ⩽ (x ⊙ z) \to (y ⊙ z)$ ;
(r₁₃): $x \to y ⩽ (x \lor z) \to (y \lor z)$ ;
(r₁₄): $x \to y ⩽ y^{*} \to x^{*}$ ;
(r₁₅): ${(x \lor y)}^{*} = x^{*} \land y^{*}$ ;
(r₁₆): $x^{*} \lor y^{*} ⩽ {(x \land y)}^{*}$ ;
(r₁₇): $x^{* *} \land y^{* *} = {(x^{* *} \land y^{* *})}^{* *}$ ;
(r₁₈): $(x \lor y) ⊙ (x \lor z) ⩽ x ⊙ (y \lor z)$ ;
(r₁₉): ${(x ⊙ y)}^{*} = x \to y^{*} = y \to x^{*} = x^{* *} \to y^{*} = y^{* *} \to x^{*}$ .

Filters and ideals play an important role in the connection between algebras and formal logic, and they have been intensively studied from an algebraic point of view.

A filter of L is any non-empty subset F of L satisfying:

(F1): $(\forall x, y \in L) ((x ⩽ y$ and $x \in F) \Rightarrow y \in F)$ ;
(F2): $(\forall x, y \in L) ((x \in F$ and $y \in F) \Rightarrow x ⊙ y \in F$ ).

Let us now consider the following formulas: for I a subset of L,

(I1): $(\forall x, y \in L) ((x ⩽ y$ and $y \in I) \Rightarrow x \in I)$ ;
(I’1): $0 \in I$ ;
(I2): $(\forall x, y \in L) ((x \in I$ and $y \in I) \Rightarrow x ⊘ y \in I)$ ;
(I3): $(\forall x, y \in L) ((x \in I$ and $y \in I) \Rightarrow x \oplus y \in I)$ ;
(I4): $(\forall x, y \in L) ((x \in I$ and $x^{*} ⊙ y \in I) \Rightarrow y \in I$ );
(I5): $(\forall x, y \in L) ((x \in I$ and ${(x^{*} \to y^{*})}^{*} \in I) \Rightarrow y \in I$ );
(I6): $(\forall x \in L) (x \in I \Leftrightarrow x^{* *} \in I)$ .

An ideal of L is a non-empty subset I of L that satisfies (I1) and (I2).

Some alternative characterizations of the notion of ideal in residuated lattices are given in the literature. Particularly, in [5], it is proved that a subset I of L is an ideal of L if and only if (I1) and (I3) are satisfied. In [7], it is proved that a subset I of L is an ideal of L if and only if (I’1) and (I4) are satisfied, if and only if (I’1) and (I5) are satisfied. For any ideal I of L, (I6) is always satisfied.

1.2. Triangle Algebras

Van Gasse et al. [15,16,17,18] introduced triangle algebras as a variety of residuated lattices equipped with approximation operators and with an angular point u different from 0 and 1.

A triangle algebra is an algebraic structure

A = (A, \land, \lor, ⊙, \to, ν, μ, 0, u, 1)

of type (2,2,2,2,1,1,0,0,0) such that

(A, \land, \lor, ⊙, \to, 0, 1)

is a bounded commutative residuated lattice, and in which the following conditions hold: for all

x, y \in A

(T1) $ν x ⩽ x$	(T’1) $x ⩽ μ x$ ;
(T2) $ν x ⩽ ν ν x$ ;	(T’2) $μ μ x ⩽ μ x$ ;
(T3) $ν (x \land y) = ν x \land ν y$ ;	(T’3) $μ (x \land y) = μ x \land μ y$ ;
(T4) $ν (x \lor y) = ν x \lor ν y$ ;	(T’4) $μ (x \lor y) = μ x \lor μ y$ ;
(T5) $ν u = 0$ ;	(T’5) $μ u = 1$ ;
(T6) $ν μ x = μ x$ ;	(T’6) $μ ν x = ν x$ ;
(T7) $ν (x \to y) ⩽ ν x \to ν y$ ;
(T8) $ν (x \leftrightarrow y) ⊙ μ (x \leftrightarrow y) ⩽ x \leftrightarrow y$ ;
(T9) $ν x \to ν y ⩽ ν (ν x \to ν y)$ .

Where,

x \leftrightarrow y : = (x \to y) \land (y \to x)

. Hereafter, we denote by

A

a triangle algebra

(A, \land, \lor, ⊙, \to, ν, μ, 0, u, 1)

, unless otherwise specified.

The following is a simple example of a triangle algebra, which we will use in the sequel.

Example 1.

Let

A_{0} = {0, u, 1}

, such that

0 < u < 1

and the operators

ν, μ, ⊙

, and → are defined by Table 1; then

A_{0} = (A_{0}, \land, \lor, ⊙, \to, ν, μ, 0, u, 1)

is a triangle algebra (see [22]).

In general, there is a way to construct a triangle algebra from a residuated lattice by means of the triangularization process; for details, we refer to [16]. In any triangle algebra

A

, we have the following rules of calculus (see [15,16,17,18]): for all

x, y \in A

(p₁): $ν (x \to y) = (ν x \to ν y) \land (μ x \to μ y)$ ;
(p₂): $μ (x \to y) = (μ x \to (μ (u ⊙ u) \to μ y)) \land (ν x \to μ y)$ ;
(p₃): $ν (x ⊙ y) = ν x ⊙ ν y$ ;
(p₄): $μ (x ⊙ y) = (ν x ⊙ μ y) \lor (μ x ⊙ ν y) \lor (μ x ⊙ μ y ⊙ μ (u ⊙ u))$ ;
(p₅): $ν 1 = 1$ , $μ 0 = 0$ , $ν 0 = 0$ and $μ 1 = 1$ ;
(p₆): $ν ν x = ν x$ , $μ μ x = μ x$ , and $ν (ν x \to ν y) = ν x \to ν y$ ;
(p₇): $ν ({(ν x)}^{*}) = {(ν x)}^{*}$ , $μ ({(μ x)}^{*}) = {(μ x)}^{*}$ ;
(p₈): $μ ({(ν x)}^{*}) = {(ν x)}^{*}$ , $ν ({(μ x)}^{*}) = {(μ x)}^{*}$ ;
(p₉): ${(μ x)}^{*} = ν (x^{*})$ .

The notion of filter in triangle algebras has been introduced in [18]: a filter of

A

is any non-empty subset F of A such that for all

x, y \in A

(F1): $(x ⩽ y$ and $x \in F) \Rightarrow y \in F$ ;
(F2): $(x \in F$ and $y \in F) \Rightarrow x ⊙ y \in F$ ;
(FT): $x \in F \Rightarrow ν x \in F$ .

Observe that a filter of a triangle algebra is also a filter of the underlying residuated lattice. We denote by

F (A)

the set of all filters of

A

2. Ideals in Triangle Algebras

In MV-algebras, filters and ideals are dual notions, but this is not necessarily the case in general residuated lattices (see [6,7,13,20]). The authors in [7,13] have studied ideals and established a link with filters in residuated lattices by using different operators. In this section, we start by introducing the notion of ideal in the framework of triangle algebras. To establish the link between filters and ideals, we first prove that the operators used by [7] and [13] in residuated lattices are equal. Then, we prove that applying this operator to an ideal does not yield a filter in triangle algebras. Hence, we set up a new operator to link ideals to filters in the case of triangle algebras. We end by investigating the link between ideals and congruences, and some characterizations of the ideal generated by a given subset.

2.1. Definition and Characterizations of the Notion of Ideal

Since we want an ideal of a triangle algebra to be an ideal of the underlying residuated lattice, and taking into account the approximation operators

ν

and

μ

, we propose the following definition.

Definition 1.

An ideal of

A

is any non-empty subset I of A satisfying, for all

x, y \in A

(I1): $(x ⩽ y$ and $y \in I) \Rightarrow x \in I$ ;
(I2): $(x \in I$ and $y \in I) \Rightarrow x ⊘ y \in I$ ;
(IT): $x \in I \Rightarrow μ x \in I$ .

We denote by

I (A)

the set of all ideals of

A

The following lemma will be helpful in the sequel.

Lemma 1.

The following properties hold in any triangle algebra

A

, for all

x, y \in A

1.: $μ (x^{*}) ⩽ {(ν x)}^{*}$ and ${(μ x)}^{*} ⩽ μ (x^{*})$ ;
2.: $μ (ν x \oplus ν y) = ν x \oplus ν y$ and $μ (μ x \oplus μ y) = μ x \oplus μ y$ ;
3.: $μ (x \oplus y) ⩽ μ x \oplus μ y$ and $μ (x ⊘ y) ⩽ μ x ⊘ μ y$ (triangle inequalities).

Proof.

1.: Since $ν x ⩽ x$ (T1), we have $x^{*} ⩽ {(ν x)}^{*}$ $(r_{6})$ , thus $μ (x^{*}) ⩽ μ ({(ν x)}^{*}) = {(ν x)}^{*}$ ((T’3) and $(p_{8})$ ).

Since $x ⩽ μ x$ , we have ${(μ x)}^{*} ⩽ x^{*} ⩽ μ (x^{*})$ by ( $T^{'} 1$ and $(r_{6})$ ).
2.: $\begin{matrix} μ ((ν x) \oplus (ν y)) & = μ ({({(ν x)}^{*} ⊙ {(ν y)}^{*})}^{*}) \\ ⩽ {(ν ({(ν x)}^{*} ⊙ {(ν y)}^{*}))}^{*} (a c c o r d i n g t o 1 . a b o v e) \\ = {(ν ({(ν x)}^{*}) ⊙ ν ({(ν y)}^{*}))}^{*}, (p_{3}) \\ = {({(ν x)}^{*} ⊙ {(ν y)}^{*})}^{*}, (p_{7}) \\ = (ν x) \oplus (ν y) \\ ⩽ μ ((ν x) \oplus (ν y)), (T^{'} 1) \end{matrix}$

Hence, we have $μ ((ν x) \oplus (ν y)) = (ν x) \oplus (ν y)$ .

By replacing x and y in the above by $μ x$ and $μ y$ , respectively, and using $ν μ x = μ x$ and $ν μ y = μ y$ , we have $μ (μ x \oplus μ y) = μ x \oplus μ y$ .
3.: Since $x ⩽ μ x$ and $y ⩽ μ y$ $(T_{1}^{'})$ , we have $x \oplus y ⩽ μ (x) \oplus μ (y)$ . Therefore, $μ (x \oplus y) ⩽ μ (μ (x) \oplus μ (y)) = μ (x) \oplus μ (y)$ .

Furthermore,

$\begin{matrix} μ (x ⊘ y) & = μ (x^{*} \to y) \\ ⩽ ν (x^{*}) \to μ y, (p_{2}) \\ ⩽ {(μ x)}^{*} \to μ y, (p_{9}) \\ = μ x ⊘ μ y \end{matrix}$

□

The following propositions are some characterizations of the notion of ideal in the case of triangle algebras. Some proofs are omitted, since in any residuated lattice we have the following equivalences [2]:

((I1) + (I2)) ⇔ ((I1) + (I3)) ⇔ ((I’1) + (I4)) ⇔ ((I’1) + (I5)).

Proposition 1.

A non-empty subset I of A is an ideal of

A

iff for all

x, y \in A

(I1): $(x ⩽ y$ and $y \in I) \Rightarrow x \in I$ ;
(I3): $(x \in I$ and $y \in I) \Rightarrow x \oplus y \in I$ ;
(IT): $x \in I \Rightarrow μ x \in I$ .

Proposition 2.

A non-empty subset I of A is an ideal of

A

iff for all

x, y \in A

(I’1): $0 \in I$ ;
(I4): $(x \in I$ and $x^{*} ⊙ y \in I) \Rightarrow y \in I$ ;
(IT): $x \in I \Rightarrow μ x \in I$ .

Proposition 3.

A non-empty subset I of A is an ideal of

A

iff for all

x, y \in A

(I’1): $0 \in I$ ;
(I5): $(x \in I$ and ${(x^{*} \to y^{*})}^{*} \in I) \Rightarrow y \in I$ ;
(IT): $x \in I \Rightarrow μ x \in I$ .

The following result will be useful in some proofs.

Proposition 4.

Let I be an ideal of

A

and

x \in A

, then the following conditions are equivalent:

(N₁): $x \in I$ ;
(N₂): $μ x \in I$ ;
(N₃): $x^{* *} \in I$ ;
(N₄): ${(μ x)}^{* *} \in I$ ;
(N₅): ${(ν x^{*})}^{*} \in I$ .

Proof.

From (I6), we have

(N_{1}) \Leftrightarrow (N_{3})

, i.e,

x \in I \Leftrightarrow x^{* *} \in I

From (I1), (IT) and (T’1), we have

(N_{1}) \Leftrightarrow (N_{2})

, i.e,

x \in I & \Leftrightarrow & μ x \in I

From (I6), we have

(N_{2}) \Leftrightarrow (N_{4})

, i.e,

μ x \in I \Leftrightarrow {(μ x)}^{* *} \in I

Since

x ⩽ μ x

(T_{1}^{'})

, we have

{(μ x)}^{*} ⩽ x^{*}

(r_{6})

. Hence,

{(μ x)}^{*} = ν ({(μ x)}^{*}) ⩽ ν (x^{*})

(p_{8}, T 3)

, which implies

{(ν (x^{*}))}^{*} ⩽ {(μ x)}^{* *}

(a)

Since

ν (x^{*}) ⩽ x^{*}

, we have

x^{* *} ⩽ {(ν (x^{*}))}^{*}

(b)

From (a) and (I1), we have

(N_{4}) \Rightarrow (N_{5})

, i.e,

{(μ x)}^{* *} \in I \Rightarrow {(ν (x^{*}))}^{*} \in I

From (b) and (I1), we have

(N_{5}) \Rightarrow (N_{3})

, i.e,

{(ν (x^{*}))}^{*} \in I \Rightarrow x^{* *} \in I

Thus,

(N_{1}) \Leftrightarrow (N_{2}) \Leftrightarrow (N_{3}) \Leftrightarrow (N_{4}) \Leftrightarrow (N_{5})

. □

2.2. Pseudo-Duality

In the case of residuated lattices, in [7] and [13], the authors studied how to obtain a filter from an ideal, and vice versa, an ideal from a filter.

Let us first recall the procedure followed in [7]. Given F a filter and I an ideal of L, we obtain that

F_{*} : = {x \in L; \exists y \in F, x^{* *} ⩽ y^{*}}

is an ideal and

I_{*} : = {x \in L; \exists y \in I, y^{*} ⩽ x^{* *}}

is a filter of L. One can also prove that

I_{* *} = I

F \subseteq F_{* *}

and

F_{*} = F_{* * *}

In [13], for F and I a filter and an ideal of L respectively, it was shown that

N (I) : = {x \in L; x^{*} \in I}

is a filter and

N (F) : = {x \in L; x^{*} \in F}

is an ideal of L. This induces the following properties:

N (N (I)) = I

F \subseteq N (N (F))

and

N (N (N (F))) = N (F)

When a filter F satisfies

N (N (F)) = F

, it is said to be an N-involutive filter.

In the following, we prove that for the pseudo-duality in residuated lattices the operators proposed by [7] and [13] are equal.

First, to simplify the proofs, we will use the following characterization of

F_{*}

Proposition 5.

Let F be a filter of a residuated lattice L. Then,

F_{*} = {x \in

; \exists y \in F, x ⩽ y^{*}}

Proof.

Let $z \in F_{*}$ , then there exists $a \in F$ such that $z^{* *} ⩽ a^{*}$ . Since $z ⩽ z^{* *}$ , we have $z ⩽ a^{*}$ . Hence $z \in {x \in$ L $; \exists y \in F, x ⩽ y^{*}}$ .
Let $x \in L$ such that there exists $y \in F$ , $x ⩽ y^{*}$ , then $x^{* *} ⩽ y^{* * *} = y^{*}$ . Hence $x \in F_{*}$ .

□

Proposition 6.

Let F be a filter and I an ideal of a residuated lattice L, then

(i): $N (I) = I_{*}$ ;
(ii): $N (F) = F_{*}$ .

Proof.

(i): Let $x \in N (I)$ , then $x^{*} \in I$ . Putting $a = x^{*}$ , we have $a^{*} ⩽ x^{* *}$ , $x \in I_{*}$ .

Reciprocally, let $x \in I_{*}$ , then there exists $a \in I$ such that $a^{*} ⩽ x^{* *}$ , which implies $x^{*} ⩽ a^{* *}$ . Since $a \in I$ , we have $a^{* *} \in I$ , by (I6), thus $x^{*} \in I$ , by (I1), i.e., $x \in N (I)$ .
(ii): Let $x \in N (F)$ , then $x^{*} \in F$ . Since $x ⩽ x^{* *}$ , we have $x \in F_{*}$ , with $a = x^{*}$ .

Reciprocally, let $x \in F_{*}$ , then there exists $a \in F$ such that $x ⩽ a^{*}$ , which implies $a^{* *} ⩽ x^{*}$ . Since $a ⩽ a^{* *} ⩽ x^{*}$ , we have $x^{*} \in F$ , i.e., $x \in N (F)$ .

□

Let us now, in the case of triangle algebras, consider the pseudo-duality between filters and ideals. We first show that the image of an ideal by the above operator in the case of triangle algebras is not always a filter.

Example 2.

Let us consider the triangle algebra

A_{0}

of Example 1.

I = {0}

is an ideal of

A_{0}

, but

N (I) = {u, 1}

is not a filter of

A_{0}

. Indeed,

u \in N (I)

, but

ν u = 0 \notin N (I)

, so

(F T)

is not true.

Hence, in the following we introduce a new operator for the pseudo-duality in the case of triangle algebras.

Proposition 7.

Let I be an ideal of

A

. Then

T (I) : = {x \in A; \exists a \in I, a^{*} ⩽ {(ν x)}^{* *}}

is a filter of

A

Proof.

We have to show that

T (I)

is a filter of

A

For (F1),: let $x, y \in A$ such that $x \in T (I)$ and $x ⩽ y$ , we have to show that $y \in T (I)$ .

It holds that $x ⩽ y$ implies $ν x ⩽ ν y$ , thus ${(ν x)}^{* *} ⩽ {(ν y)}^{* *}$ . Since $x \in T (I)$ , there exists $a \in I$ such that $a^{*} ⩽ {(ν x)}^{* *}$ , so by transitivity, $a^{*} ⩽ {(ν y)}^{* *}$ , thus $y \in T (I)$ .
For (F2),: let $x, y \in T (I)$ , we have to show that $x ⊙ y \in T (I)$ .

Since $x \in T (I)$ , there exists $a \in I$ such that $a^{*} ⩽ {(ν x)}^{* *}$ .

Since $y \in T (I)$ , there exists $b \in I$ such that $b^{*} ⩽ {(ν y)}^{* *}$ . Then, by $(r_{4})$ , $a^{*} ⊙ b^{*} ⩽ {(ν x)}^{* *} ⊙ {(ν y)}^{* *}$ , thus ${(a^{*} ⊙ b^{*})}^{* *} ⩽ {({(ν x)}^{* *} ⊙ {(ν y)}^{* *})}^{* *}$ , i.e., ${(a \oplus b)}^{*} ⩽ {({(ν x)}^{* *} ⊙ {(ν y)}^{* *})}^{* *}$ .

Since $a, b \in I$ and I is an ideal, $a \oplus b \in I,$ and we have by $(r_{9})$ ${(ν x)}^{* *} ⊙ {(ν y)}^{* *} ⩽ {((ν x) ⊙ (ν y))}^{* *}$ , we obtain

$\begin{matrix} {({(ν x)}^{* *} ⊙ {(ν y)}^{* *})}^{* *} & ⩽ {({((ν x) ⊙ (ν x))}^{* *})}^{* *}, (r_{9}) \\ = {((ν x) ⊙ (ν x))}^{* *}, (r_{8}) \\ = {(ν (x ⊙ y))}^{* *}, (p_{3}) \end{matrix}$

It follows that ${(a \oplus b)}^{*} ⩽ {(ν (x ⊙ y))}^{* *}$ , thus $x ⊙ y \in T (I)$ .
For (FT),: let $x \in T (I)$ . We have to show that $ν x \in T (I)$ . Since $x \in T (I)$ , there exists $a \in I$ such that $a^{*} ⩽ {(ν x)}^{* *}$ . Since $ν ν x = ν x$ , $(p_{6})$ we have $a^{*} ⩽ {(ν ν x)}^{* *}$ , thus $ν x \in T (I) .$

□

The following is a characterization of the above operator.

Proposition 8.

Let I be an ideal of

A

, then

T (I) = {x \in A; {(ν x)}^{*} \in I}

Proof.

Let $z \in A$ such that ${(ν z)}^{*} \in I$ . Since ${({(ν z)}^{*})}^{*} ⩽ {(ν z)}^{* *}$ , we have $z \in {x \in A; \exists a \in I, a^{*} ⩽ {(ν x)}^{* *}} = T (I)$ , for $a = {(ν z)}^{*}$ .
Let $x \in T (I)$ . Hence, there exists $a \in I$ such that $a^{*} ⩽ {(ν x)}^{* *}$ , which implies ${(ν x)}^{*} ⩽ a^{* *}$ . Since $a \in I$ , by (I6), $a^{* *} \in I$ , so ${(ν x)}^{*} \in I$ , by (I1).

□

According to the relation between

μ

and

ν

, we introduce the following operator for filters of triangle algebras.

Proposition 9.

Let F be a filter of

A

, then

T (F) : = {x \in A; {(μ x)}^{*} \in F}

is an ideal of

A

Proof.

For (I1),: let $x, y \in A$ such that $x ⩽ y$ and $y \in T (F)$ . We have that ${(μ y)}^{*} \in F$ and $x ⩽ y$ imply ${(μ y)}^{*} ⩽ {(μ x)}^{*}$ . Hence, ${(μ x)}^{*} \in F$ , because F is a filter. Thus $x \in T (F)$ .
For (I3),: let $x, y \in T (F)$ . Then, ${(μ x)}^{*} \in F$ and ${(μ y)}^{*} \in F$ . Hence, ${(μ x)}^{*} ⊙ {(μ y)}^{*} \in F$ . Furthermore,

$\begin{matrix} {(μ x)}^{*} ⊙ {(μ x)}^{*} & ⩽ {({(μ x)}^{*} ⊙ {(μ y)}^{*})}^{* *}, (r_{7}) \\ = {({({(μ x)}^{*} ⊙ {(μ y)}^{*})}^{*})}^{*} \\ = {(μ x \oplus μ y)}^{*} \end{matrix}$

Therefore, ${(μ x \oplus μ y)}^{*} \in F$ . From the triangle inequality $μ (x \oplus y) ⩽ μ x \oplus μ y$ , we have ${(μ x \oplus μ y)}^{*} ⩽ {(μ (x \oplus y))}^{*}$ . Hence, ${(μ (x \oplus y))}^{*} \in F$ . Thus, $x \oplus y \in T (F)$ .
For (IT),: it holds because $μ μ x = μ x$ .

□

In the following, we prove that the above operator is equal to the one define, in the case of residuated lattices, on filters, and some characterizations are given.

Proposition 10.

Let F be a filter of

A

, then

T (F) = {x \in A; \exists a \in F, μ x ⩽ a^{*}} = {x \in A; \exists a \in F, x ⩽ {(ν a)}^{*}} = N (F)

Proof.

Let $z \in T (F)$ , we have to find $a \in F$ such that $μ z ⩽ a^{*}$ .

Since $z \in T (F)$ , we have ${(μ z)}^{*} \in F$ . Because $μ z ⩽ {(μ z)}^{* *}$ , we have $z \in {x \in A; \exists a \in F, μ x ⩽ a^{*}}$ , with $a = {(μ z)}^{*}$ .
Let $z \in {x \in A; \exists a \in F, μ x ⩽ a^{*}}$ . We have to find $b \in F$ such that $z ⩽ {(ν b)}^{*}$ . Since $z \in {x \in A; \exists a \in F, μ x ⩽ a^{*}}$ , there exists $a \in F$ such that $μ z ⩽ a^{*}$ . Hence, $a^{* *} ⩽ {(μ z)}^{*}$ . Because $a ⩽ a^{* *}$ , we have $a^{* *} \in F$ , which implies ${(μ z)}^{*} \in F$ , by (F1). Since ${(ν ({(μ z)}^{*}))}^{*} = {(μ z)}^{* *}$ $(p_{8})$ and $z ⩽ μ z ⩽ {(μ z)}^{* *}$ $(T^{'} 1)$ , we have $z ⩽ {(ν ({(μ z)}^{*}))}^{*}$ . Thus, $z \in {x \in A; \exists b \in F, x ⩽ {(ν b)}^{*}}$ , with $b = {(μ z)}^{*}$ .
Let us prove that ${x \in A; \exists a \in F, x ⩽ {(ν a)}^{*}} \subseteq T (F)$ . Let $z \in {x \in A; \exists a \in F, x ⩽ {(ν a)}^{*}}$ . Then, there exists $a \in F$ such that $z ⩽ {(ν a)}^{*}$ . Therefore, $μ z ⩽ μ ({(ν a)}^{*}) = {(ν a)}^{*}$ $(T^{'} 3, p_{8})$ . Hence, ${(ν a)}^{* *} ⩽ {(μ z)}^{*}$ . Because $a \in F$ , we have $ν a \in F$ , by (FT). Since $ν a ⩽ {(ν a)}^{* *}$ , we have ${(ν a)}^{* *} \in F$ , and then ${(μ z)}^{*} \in F$ , by (F1). Thus, $z \in T (F)$ .

Next, we have to prove that

T (F) = N (F)

Let $x \in N (F)$ , then $x^{*} \in F$ , which implies by (FT) $ν (x^{*}) \in F$ . Since $ν (x^{*}) = {(μ x)}^{*}$ $(p_{9})$ , we have ${(μ x)}^{*} \in F$ . Thus $x \in T (F)$ .
Let $x \in T (F)$ , then ${(μ x)}^{*} \in F$ , i.e., $ν (x^{*}) \in F$ , by $(p_{9})$ . Since $ν (x^{*}) ⩽ x^{*}$ , we have $x^{*} \in F$ , by $(F 1)$ . Thus $x \in N (F)$ .

□

Proposition 11.

Let I be an ideal and F a filter of

A

. Then,

(1): $T (T (I)) = I$ ;
(2): $x \in T (T (F)) \Leftrightarrow {(ν x)}^{* *} \in F$ ;
(3): $F \subseteq T (T (F))$ ;
(4): $T (T (T (F))) = T (F)$ .

Proof.

(1): $\begin{matrix} x \in T (T (I)) & \Leftrightarrow {(μ x)}^{*} \in T (I) \\ \Leftrightarrow {(ν ({(μ x)}^{*}))}^{*} \in I \\ \Leftrightarrow {(μ x)}^{* *} \in I, (p_{8}) \\ \Leftrightarrow x \in I, (P r o p o s i t i o n 4) \end{matrix}$
(2): Let $x \in A$ .

$\begin{matrix} x \in T (T (F)) & \Leftrightarrow {(ν x)}^{*} \in T (F) \\ \Leftrightarrow {(μ {(ν x)}^{*})}^{*} \in F \\ \Leftrightarrow {(ν x)}^{* *} \in F, (by p_{9}) \end{matrix}$
(3): Let $x \in F$ . Then, $ν x \in F$ , and since $ν x ⩽ {(ν x)}^{* *}$ , we have ${(ν x)}^{* *} \in F$ , which implies $x \in T (T (F))$ . Thus $F \subseteq T (T (F))$ .
(4): Since $T (F)$ is an ideal, then $T (T (T (F))) = T (F)$ , by Proposition 11 (1).

□

We have in the following example an illustration of the previous Propositions; it also highlighted that in Proposition 11 (3), we do not always have an equality.

Example 3.

Let

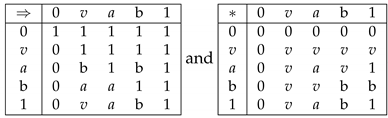
A = {[0, 0]; [0, v]; [0, a]; [0, b]; [0, 1]; [v, v]; [v, a]; [v, b]; [v, 1]; [a, a]; [a, 1]; [b, b]; [b, 1]; [1, 1]}

. We define

* and \Rightarrow

by the Table 2;

\forall x, y, z, t \in A, [x, y] ⊙ [z, t] = [x * z, y * t], and

[x, y] \to [z, t] = [(x \Rightarrow z) \land (y \Rightarrow t), (y \Rightarrow t)]

μ [x, y] = [y, y]

ν [x, y] = [x, x]

. Then,

A = (A, \land, \lor, ⊙, \to, ν, μ, [0, 0], [0, 1], [1, 1])

is a triangle algebra [24] whose lattice is given by Figure 1 .

Let

F = {[a, a], [a, 1], [1, 1]}

G = {[v, v], [v, a], [v, b], [v, 1], [a, a], [b, b], [a, 1], [b, 1], [1, 1]}

, and

I = {[0, 0]}

then:

i): $F and G$ are filters and I is an ideal;
ii): $T (F) = I$ , $T (T (F)) = T (I) = G$ , $T (T (I)) = T (G) = I$ , $T (T (T (F))) = T (F)$ , and $I = T (T (I))$ . We have $F \subset T (T (F))$ , but $[v, v] \in T (T (F))$ and $[v, v] \notin F$ , so $F ⊊ T (T (F))$ .

Guided by the above observations, for pseudo-duality in triangle algebras, we will use the operator T, i.e., for any ideal I and filter F of

A

\begin{matrix} T (I) & = & {x \in A; {(ν x)}^{*} \in I} \\ T (F) & = & {x \in A; {(μ x)}^{*} \in F} . \end{matrix}

2.3. Ideals and Congruences

Let us now investigate the link between ideals and congruences. In particular, we will explain how to build a congruence from an ideal and vice versa.

Definition 2.

A congruence relation on

A

is an equivalence relation which is compatible with all operations on

A

Lemma 2.

Let

A = (A, \land, \lor, ⊙, \to, ν, μ, 0, u, 1)

be a triangle algebra, θ be an equivalence of

A

and

α \in {\land, \lor, ⊙, \to}

If for all

x, y, z \in A

x θ y \Rightarrow (x α z) θ (y α z)

and

(z α x) θ (z α y)

, then, for all

x, y, z, t \in A

, (

x θ y

and

z θ t) \Rightarrow (x α z) θ (y α t)

Proof.

let assume

x θ y \Rightarrow (x α z) θ (y α z)

,for all

x, y, z \in A

. Let

α \in {\land, \lor, ⊙, \to}

a, b, c, d \in A

such that

a θ b

and

c θ d

; we have to show that

(a α c) θ (b α d)

Since

a θ b

, then,

(a α c) θ (b α c)

, and

(c α a) θ (c α b)

. Also, since

c θ d

, then

(c α b) θ (d α b)

and

(b α c) θ (b α d)

. Furthermore

\{\begin{matrix} (a α c) θ (b α c) \\ (b α c) θ (b α d) \end{matrix}

which implies

(a α c) θ (b α d)

. Likely,

\{\begin{matrix} (c α a) θ (c α b) \\ (c α b) θ (d α b) \end{matrix}

which implies

(c α a) θ (d α b)

□

The following proposition shows that any ideal of a triangle algebra induces a congruence relation.

Proposition 12.

Let I be an ideal of

A

. Then, the binary relation

\sim_{I}

defined by

x \sim_{I} {y \Leftrightarrow ((ν (x \to y))}^{*} \in I

and

{(ν (y \to x))}^{*} \in I)

, for all

x, y \in A

, is a congruence on

A

Proof.

$\sim_{I}$ is an equivalence relation.

Reflexivity:

let $x \in A$ , we have ${(ν (x \to x))}^{*} = {(ν 1)}^{*} = 0 \in I .$

Symmetry:

$\sim_{I}$ is symmetric by definition.

Transitivity:

let $x, y, z \in A$ such that $x \sim_{I} y$ and $y \sim_{I} z$ , we have to show that $x \sim_{I} z$ .

Since $x \sim_{I} y$ , we have ${(ν (x \to y))}^{*} \in I$ and ${(ν (y \to x))}^{*} \in I$ ;

since $y \sim_{I} z$ , we have ${(ν (y \to z))}^{*} \in I$ and ${(ν (z \to y))}^{*} \in I$ ;

since $(z \to y) ⊙ (y \to x) ⩽ (z \to x)$ $(r_{10})$ , then by (T3) and $(p_{3})$ , $ν (z \to y) ⊙ ν (y \to x) ⩽ ν (z \to x),$ by residuation $ν (z \to y) ⩽ ν (y \to x) \to ν (z \to x)$ . Furthermore, $ν (y \to x) \to ν (z \to x) ⩽ {(ν (z \to x))}^{*} \to {(ν (y \to x))}^{*}$ $(r_{14})$ , then by transitivity $ν (z \to y) ⩽ {(ν (z \to x))}^{*} \to {(ν (y \to x))}^{*}$ . Hence, ${({(ν (z \to x))}^{*} \to {(ν (y \to x))}^{*})}^{*} ⩽ {(ν (z \to y))}^{*}$ . Since ${(ν (z \to y))}^{*} \in I$ , we have ${({(ν (z \to x))}^{*} \to {(ν (y \to x))}^{*})}^{*} \in I .$

Since ${(ν (z \to x))}^{*} \to {(ν (y \to x))}^{*} ⩽ {(ν (y \to x))}^{* *} \to {(ν (z \to x))}^{* *}$ $(r_{14})$ , we have ${({(ν (y \to x))}^{* *} \to {(ν (z \to x))}^{* *})}^{*} ⩽ {({(ν (z \to x))}^{*} \to {(ν (y \to x))}^{*})}^{*}$ ; then, ${({(ν (y \to x))}^{* *} \to {(ν (z \to x))}^{* *})}^{*} \in I$ . Furthermore, ${(ν (y \to x))}^{* *} \to {(ν (z \to x))}^{* *})^{*} \in I$ and ${(ν (y \to x))}^{*} \in I$ , which implies ${(ν (z \to x))}^{*} \in I$ , by Proposition 3.

Likewise, we can show that ${(ν (x \to z))}^{*} \in I$ .
$\sim_{I}$ is compatible with the operations of $A$

Let $x, y, z \in A$ , such that $x \sim_{I} y$ , that is ${(ν (x \to y))}^{*} \in I$ and ${(ν (y \to x))}^{*} \in I$ .

1.

We have to show that $(x \land z) \sim_{I} (y \land z)$ .

We have $x \to y ⩽ (x \land z) \to (y \land z)$ $(r_{11})$ , then $ν (x \to y) ⩽ ν ((x \land z) \to (y \land z))$ , since $ν$ is increasing. Consequently, ${(ν ((x \land z) \to (y \land z)))}^{*} ⩽ {(ν (x \to y))}^{*}$ . Hence, ${(ν ((x \land z) \to (y \land z)))}^{*} \in I$ , since ${(ν (x \to y))}^{*} \in I$ . Likewise, we show that ${(ν ((y \land z) \to (x \land z)))}^{*} \in I$ . Thus $(x \land z) \sim_{I} (y \land z)$ .

2.

We have to show that $(x \lor z) \sim_{I} (y \lor z)$ .

We have $x \to y ⩽ (x \lor z) \to (y \lor z)$ by $(r_{13})$ , then $ν (x \to y) ⩽ ν ((x \lor z) \to (y \lor z))$ . Consequently ${(ν ((x \lor z) \to (y \lor z)))}^{*} ⩽ {(ν (x \to y))}^{*}$ . Hence, ${(ν ((x \lor z) \to (y \lor z)))}^{*} \in I$ , since ${(ν (x \to y))}^{*} \in I$ . Likewise, we show that ${(ν ((y \lor z) \to (x \lor z)))}^{*} \in I$ . Thus $(x \lor z) \sim_{I} (y \lor z)$ .

3.

We have to show that $(x ⊙ z) \sim_{I} (y ⊙ z)$ .

We have $x \to y ⩽ (x ⊙ z) \to (y ⊙ z)$ by $(r_{12})$ , then $ν (x \to y) ⩽ ν ((x ⊙ z) \to (y ⊙ z))$ . Hence, ${(ν ((x ⊙ z) \to (y ⊙ z)))}^{*} ⩽ {(ν (x \to y))}^{*}$ , then ${(ν ((x ⊙ z) \to (y ⊙ z)))}^{*} \in I$ , since ${(ν (x \to y))}^{*} \in I$ . Likewise, we show that ${(ν ((y ⊙ z) \to (x ⊙ z)))}^{*} \in I$ . Thus $(x ⊙ z) \sim_{I} (y ⊙ z)$ .

4.

We have to show that $(x \to z) \sim_{I} (y \to z)$ .

We have $x \to y ⩽ (y \to z) \to (x \to z)$ by $(r_{10})$ and residuation. Hence, $ν (x \to y) ⩽ ν ((y \to z) \to (x \to z))$ , then ${(ν ((y \to z) \to (x \to z)))}^{*} ⩽ {(ν (x \to y))}^{*} .$ Therefore ${(ν ((y \to z) \to (x \to z)))}^{*} \in I$ , since ${(ν (x \to y))}^{*} \in I$ . Likewise, we show that ${(ν ((x \to z) \to (y \to z)))}^{*} \in I$ . Thus $(x \to z) \sim_{I} (y \to z)$ .

5.

We have to show that $z \to x \sim_{I} z \to y$ .

We have $y \to x ⩽ (z \to y) \to (z \to x)$ by $(r_{10})$ and residuation. Hence, $ν (y \to x) ⩽ ν ((z \to y) \to (z \to x))$ , then ${(ν ((z \to y) \to (z \to x)))}^{*} ⩽ {(ν (y \to x))}^{*} .$ It follows ${(ν ((z \to y) \to (z \to x)))}^{*} \in I$ , since ${(ν (y \to x))}^{*} \in I$ . Likewise, we show that ${(ν ((z \to x) \to (z \to y)))}^{*} \in I$ . Thus $(z \to x) \sim_{I} (z \to y)$ .

6.

We have to show that $ν x \sim_{I} ν y$ .

We have $ν (x \to y) ⩽ ν x \to ν y$ by (T7). Then ${(ν x \to ν y)}^{*} ⩽ {(ν (x \to y))}^{*}$ , hence ${(ν x \to ν y)}^{*} \in I$ . We have ${(ν (ν x \to ν y))}^{*} \in I$ , since $ν (ν x \to ν y) = ν x \to ν y$ , $(p_{6})$ . Likewise, we show that ${(ν (ν y \to ν x))}^{*} \in I$ . Thus $ν x \sim_{I} ν y$ .

7.

We have to show that $μ x \sim_{I} μ y$ .

We have $ν (x \to y) ⩽ μ x \to μ y$ by $(p_{1})$ . Therefore, $ν (x \to y) = ν ν (x \to y) ⩽ ν (μ x \to μ y)$ by $(p_{6}, T 3)$ . Hence, ${(ν (μ x \to μ y))}^{*} ⩽ {(ν (x \to y))}^{*}$ , and ${(ν (μ x \to μ y))}^{*} \in I$ .Likewise, we show that ${(ν (μ y \to μ x))}^{*} \in I$ . Thus $μ x \sim_{I} μ y$ .

□

For any ideal I of

A

, the

\sim_{I}

-class of any

x \in A

is denoted by

{[x]}_{\sim_{I}}

and the set of all

\sim_{I}

-class is denoted by

A / I

The following proposition establishes a one-to-one correspondence between the set

I (A)

of ideals and the set

C o n (A)

of congruences of

A

Proposition 13.

Let I be an ideal of

A

, then

I = {[0]}_{\sim_{I}}

Proof.

Let $x \in I$ , then ${(ν (x \to 0))}^{*} = {(ν x^{*})}^{*} \in I$ , by Proposition 4.

Moreover, ${(ν (0 \to x))}^{*} = {(ν 1)}^{*} = 1^{*} = 0 \in I$ . Hence, $x \sim_{I} 0$ , and consequently $x \in {[0]}_{\sim_{I}}$ .
Since I is an ideal, it holds that $0 \in I$ .

Let $x \in {[0]}_{\sim_{I}}$ , then ${(ν x^{*})}^{*} \in I$ , which implies $x \in I$ , by Proposition 4.

□

The following result proves that any congruence relation on a triangle algebra induces an ideal.

Proposition 14.

For any congruence ∼ of

A

{[0]}_{\sim}

is an ideal.

Proof.

For (I1),: let $x, y \in A$ such that $x ⩽ y$ and $y \in {[0]}_{\sim}$ . Since $y \in {[0]}_{\sim}$ , then $y \sim 0$ , which implies $(x \land y) \sim (x \land 0)$ , because ∼ is a congruence. Therefore, $x \sim 0$ , because $0 ⩽ x ⩽ y$ . Hence, $x \in {[0]}_{\sim}$ .
For (I3),: let $x, y \in {[0]}_{\sim}$ . Since $x \in {[0]}_{\sim}$ , then $x \sim 0$ . Consequently, $x^{*} \sim 0^{*} = 1$ . Similarly, $y^{*} \sim 1$ . Hence, $(x^{*} ⊙ y^{*}) \sim (1 ⊙ 1) = 1$ , therefore ${(x^{*} ⊙ y^{*})}^{*} \sim 1^{*} = 0$ , i.e., $x \oplus y \sim 0$ . Thus $x \oplus y \in {[0]}_{\sim}$ .
For (IT),: let $x \in {[0]}_{\sim}$ . Since $x \in {[0]}_{\sim}$ , then $x \sim 0$ thus $μ x \sim μ 0 = 0$ , which implies $μ x \in {[0]}_{\sim}$ .

Hence

{[0]}_{\sim}

is an ideal. □

Given a congruence relation ∼ on

A

, it is not clear whether

\sim_{{[0]}_{\sim}} = \sim

holds. This remains an open question.

As a consequence of Proposition 12, the following result establishes that the quotient of a triangle algebra by a congruence induced by an ideal is a triangle algebra.

Proposition 15.

Let I be an ideal of

A

, then

A / I = (A / I, \land, \lor, ⊙, \to, ν, μ, I,

{[u]}_{\sim_{I}}, {[1]}_{\sim_{I}})

is a triangle algebra, where for all

x, y \in A

θ ({[x]}_{\sim_{I}}) = {[θ (x)]}_{\sim_{I}}, \forall θ \in {ν, μ}

and

{[x]}_{\sim_{I}} α {[y]}_{\sim_{I}} = {[x α y]}_{\sim_{I}}, \forall α \in {\land, \lor, \to, ⊙}

Proof.

This is a direct consequence of the fact that

\sim_{I}

is a congruence. □

Definition 3.

[25]

A homomorphism between

A = (A, \lor, \land, *, \to, ν, μ, 0, u, 1)

and

B = (B, ⊔, ⊓, ⊙, \Rightarrow, \bar{ν}, \bar{μ}, 0, \bar{u}, 1)

two triangle algebras is any mapping

f : A \to B

, that satisfies for all a,

b \in A

f (a \lor b) = f (a) ⊔ f (b)

f (a \land b) = f (a) ⊓ f (b)

f (a * b) = f (a) ⊙ f (b)

f (a \to b) = f (a) \Rightarrow f (b)

f (ν a) = \bar{ν} (f (a))

f (μ a) = \bar{μ} (f (a))

; the kernel of f, denoted by

k e r (f)

, is define by

k e r (f) : = {x \in A; f (x) = 0}

The following establish that the kernel of any homomorphism is an ideal.

Proposition 16.

Let

A, B

be two triangle algebras and

f : A \to B

a homomorphism, then

K e r (f)

is an ideal of

A

Proof.

1.: Let $x, y \in A$ , such that $x ⩽ y$ and $y \in K e r (f)$ .

Since $x ⩽ y$ , we have $x \land y = x$ . Hence, $f (x \land y) = f (x)$ . Because f is a homomorphism, we have $f (x) \land f (y) = f (x)$ . Then $f (x) ⩽ f (y)$ .

Since $y \in K e r (f)$ , we have $f (y) = 0$ . Therefore, $f (x) = 0$ . Hence, $x \in K e r (f)$ .
2.: Let $x, y \in K e r (f)$ . Then $f (x) = 0$ and $f (y) = 0$ . Furthermore, because f is a homomorphism, we have $f (x \oplus y) = f (x) \oplus f (y) = 0$ . Thus, $x \oplus y \in K e r (f)$ .
3.: Let $x \in K e r (f)$ . We have $f (μ x) = μ (f (x)) = μ (0) = 0$ . Therefore, $μ x \in K e r (f)$ .

Thus,

K e r (f)

is an ideal of

A

. □

The following proposition establishes that any ideal is the kernel of a homomorphism of triangle algebras.

Proposition 17.

Let I be an ideal of a triangle algebra

A

, then there exists a homomorphism f of triangle algebras such that

I = K e r (f)

Proof.

Let us consider

\begin{matrix} π : & A & ⟶ & A / I \\ x & ⟼ & {[x]}_{\sim_{I}} \end{matrix}

π

is a homomorphism between the triangle algebras

A

and

A / I

. Let

x \in K e r (π)

, then

π (x) = I = {[0]}_{\sim_{I}}

, i.e.,

ν (x \to 0) * = {(ν x^{*})}^{*} \in I

. Hence, by Proposition 4,

x \in I

. □

2.4. Ideals Generated by a Subset

Before we dive into the case of ideals, let us first highlight that we have identified an inaccuracy in the characterization of the filter generated by a subset of a triangle algebra as proposed in [22]. Here, we provide an example to counter the arguments in the proof given in ([22], Proposition 4.2). Subsequently, we provide some accurate characterizations of the filter generated by a subset of a triangle algebra. Furthermore, we describe the ideal induced by a subset of a triangle algebra.

Recall that for any subset X of a triangle algebra

A

, the filter generated by X which we will denote

[X)

is the smallest filter of

L

containing X.

In ([22], Proposition 4.2) they mentioned that for any subset S of a triangle algebra

A

[S) = {x \in L ∣ \exists (n, x_{i}) \in N^{*} \times S, ν x \geq x_{1} ⊙ x_{2} ⊙ \dots ⊙ x_{n}, \forall i \in {1, 2, \dots, n}}

, which we claim is not accurate, as we can see in Example 4 below.

Example 4.

Let us consider the triangle algebra

A_{0}

of Example 1. In the following two cases, we have

[S) \neq {x \in A; s_{1} ⊙ s_{2} ⊙ \dots ⊙ s_{n} ⩽ ν x, n \in N, i \in 1; n, s_{i} \in S}

1.: For $S = {u, 1}$ , S is a filter of the residuated lattice $(A_{0}, \land, \lor, ⊙, \to, 0, 1)$ , but S is not a filter of the triangle algebra $A_{0}$ (see Example 2). Using the fact that $[S)$ is the smallest filter of $A$ containing S, we have $[S) = A_{0}$ ; however, using the characterization above given in [22], we have $0 \notin {x \in A_{0}; s_{1} ⊙ s_{2} ⊙ \dots ⊙ s_{n} ⩽ ν x, n \in N, i \in 1; n, s_{i} \in S}$ . Hence, $[S) \neq {x \in A_{0}; s_{1} ⊙ s_{2} ⊙ \dots ⊙ s_{n} ⩽ ν x, n \in N, i \in 〚 1; n 〛, s_{i} \in S}$ .
2.: For $S = {u}$ . Since $u ⊙ u = u$ , we have $u^{n} = u$ , $\forall n \in N^{*}$ . Therefore, $\forall n \in N^{*}$ , ${\underset{︸}{u ⊙ \dots ⊙ u}}_{n - t i m e s} = u > 0 = ν u$ . Hence, $u \notin {x \in A; s_{1} ⊙ s_{2} ⊙ \dots ⊙ s_{n} ⩽ ν x, n \in N, i \in 〚 1; n 〛, s_{i} \in S}$ . Thus $S \neg \subseteq {x \in A; s_{1} ⊙ s_{2} ⊙ \dots ⊙ s_{n} ⩽ ν x, n \in N, i \in 〚 1; n 〛, s_{i} \in S}$ .

To mend this problem, we introduce the following characterization of the filter induced by a subset of a triangle algebra.

Proposition 18.

Let S be a non-empty subset of A. Then,

[S) = {x \in A; ν s_{1} ⊙ ν s_{2} ⊙ \dots ⊙ ν s_{n} ⩽ x, n \in N, i \in 〚 1; n 〛, s_{i} \in S} .

Proof.

Let

B = {x \in A; ν s_{1} ⊙ ν s_{2} ⊙ \dots ⊙ ν s_{n} ⩽ x, n \in N, i \in 〚 1; n 〛, s_{i} \in S}

. We will show that

B = [S)

First, we show that B is a filter.

For (F1),

let $x, y \in A$ such that $x ⩽ y$ and $x \in B$ . Therefore, there exists $n \in N$ , $s_{1}, \dots, s_{n} \in S$ such that $ν s_{1} ⊙ ν s_{2} ⊙ \dots ⊙ ν s_{n} ⩽ x$ . Since $x ⩽ y$ , then $ν s_{1} ⊙ ν s_{2} ⊙ \dots ⊙ ν s_{n} ⩽ y$ . Thus $y \in B$ .

For (F2),

let $x, y \in B$ . Then, there exists $n \in N$ , $s_{i} \in S, i \in 〚 1; n 〛$ such that $ν s_{1} ⊙ ν s_{2} ⊙ \dots ⊙ ν s_{n} ⩽ x$ and there exists $m \in N$ , $t_{i} \in S, i \in 〚 1; m 〛$ such that $ν t_{1} ⊙ ν t_{2} ⊙ \dots ⊙ ν t_{m} ⩽ y$ . By $(r_{4})$ , we have $ν s_{1} ⊙ ν s_{2} ⊙ \dots ⊙ ν s_{n} ⊙ ν t_{1} ⊙ ν t_{2} ⊙ \dots ⊙ ν t_{m} ⩽ x ⊙ y$ . Thus $x ⊙ y \in B$ .

For (FT),

let $x \in B$ . Therefore, there exists $n \in N$ , $s_{i} \in S, i \in 〚 1; n 〛$ such that $ν s_{1} ⊙ ν s_{2} ⊙ \dots ⊙ ν s_{n} ⩽ x$ . Hence, by (T3), we have $ν (ν s_{1} ⊙ ν s_{2} ⊙ \dots ⊙ ν s_{n}) ⩽ ν x$ which implies, by $(p_{6})$ and $(p_{3})$ : $ν s_{1} ⊙ ν s_{2} ⊙ \dots ⊙ ν s_{n} ⩽ ν x$ . Thus $ν x \in B$ .
Next, we show that $S \subseteq B$ .

Let $s \in S$ . Since $ν s ⩽ s$ $(T 1)$ , we have $s \in B$ .
Let F be a filter of $A$ containing S. Let $x \in B$ , then there exists $n \in N$ , $s_{i} \in S, i \in 〚 1; n 〛$ , such that $ν s_{1} ⊙ ν s_{2} ⊙ \dots ⊙ ν s_{n} ⩽ x$ . Let $i \in 〚 1; n 〛$ , then $s_{i} \in S \subseteq F$ , thus $s_{i} \in F$ , so by (FT) $ν s_{i} \in F$ . Because this is true for all $i \in 〚 1; n 〛$ , we have, by (F2): $ν s_{1} ⊙ ν s_{2} ⊙ \dots ⊙ ν s_{n} \in F$ . Since $ν s_{1} ⊙ ν s_{2} ⊙ \dots ⊙ ν s_{n} ⩽ x$ , we have, by (F1): $x \in F$ .

Concluding,

B = [S)

. □

Below is another characterization of the filter induced by a subset of a triangle algebra.

Proposition 19.

Let S be a non-empty subset of A.

Then

[S) = {x \in A; ν s_{1} ⊙ ν s_{2} ⊙ \dots ⊙ ν s_{n} ⩽ ν x, n \in N, i \in 〚 1; n 〛, s_{i} \in S}

Proof.

Let $a \in [S)$ , then (FT), $ν a \in [S)$ , so $a \in {x \in A; ν s_{1} ⊙ ν s_{2} ⊙ \dots ⊙ ν s_{n} ⩽ ν x, n \in N, i \in 〚 1; n 〛, s_{i} \in S}$ .
Let $a \in {x \in A; ν s_{1} ⊙ ν s_{2} ⊙ \dots ⊙ ν s_{n} ⩽ ν x, n \in N, i \in 〚 1; n 〛, s_{i} \in S}$ , then there exists $n \in N$ , $s_{i} \in S, i \in 〚 1; n 〛$ , such that $ν s_{1} ⊙ ν s_{2} ⊙ \dots ⊙ ν s_{n} ⩽ ν a$ . Since $ν a ⩽ a$ (by (F1)), it holds that $a \in [S)$ .

□

We recall that, for any subset S of a triangle algebra

A

, the ideal generated by S is the smallest ideal of

A

containing S, it is denoted by

(S]

. Next, we introduce a characterization of the ideal induced by a non-empty subset of a triangle algebra.

Proposition 20.

Let S be a non-empty subset of a triangle algebra

A

. We have

(S] = {x \in A; x ⩽ μ s_{1} \oplus μ s_{2} \oplus \dots \oplus μ s_{n}, n \in N, i \in 〚 1; n 〛, s_{i} \in S}

Proof.

Let

I = {x \in A; x ⩽ μ s_{1} \oplus μ s_{2} \oplus \dots \oplus μ s_{n}, n \in N, i \in 〚 1; n 〛, s_{i} \in S}

We first show that I is an ideal.

For (I1),

this is obvious.

For (I3),

let $x, y \in I$ . Therefore, $x ⩽ μ s_{1} \oplus μ s_{2} \oplus \dots \oplus μ s_{n}$ , with $n \in N, i \in 〚 1; n 〛, s_{i} \in S$ , and $y ⩽ μ t_{1} \oplus μ t_{2} \oplus \dots \oplus μ t_{m}$ , with $m \in N, i \in 〚 1; m 〛, t_{i} \in S$ . Hence, $x \oplus y ⩽ μ s_{1} \oplus μ s_{2} \oplus \dots \oplus μ s_{n} \oplus μ t_{1} \oplus μ t_{2} \oplus \dots \oplus μ t_{m}$ . Thus $x \oplus y \in I$ .

For (IT),

let $x \in I$ . Then, we have $x ⩽ μ s_{1} \oplus μ s_{2} \oplus \dots \oplus μ s_{n}$ , with $n \in N, i \in 〚 1; n 〛, s_{i} \in S$ . Hence,

$\begin{matrix} μ x & ⩽ μ (μ s_{1} \oplus μ s_{2} \oplus \dots \oplus μ s_{n}) \\ ⩽ μ s_{1} \oplus μ s_{2} \oplus \dots \oplus μ s_{n}, (L e m m a (3), p_{6}) \end{matrix}$

Thus $μ x \in I$ .
Let $s \in S$ . Since $s ⩽ μ s$ , (T’1), we have $s \in I$ . Thus $S \subseteq I$ .
Let J be an ideal of $A$ containing S. Let $x \in I$ , we have $x ⩽ μ s_{1} \oplus μ s_{2} \oplus \dots \oplus μ s_{n}$ , with $n \in N, i \in 〚 1; n 〛, s_{i} \in S$ . Let $i \in 〚 1; n 〛$ , then $s_{i} \in S \subseteq J$ . Because J is an ideal of $A$ , $μ s_{i} \in J$ (IT), for all $i \in 〚 1; n 〛$ . Hence, by (I3), $μ s_{1} \oplus μ s_{2} \oplus \dots \oplus μ s_{n} \in J$ and by (I1), $x \in J$ . Thus $I \subseteq J$ .

In conclusion,

(S] = I

. □

Any ideal generated by

{a}

will be denoted by

(a]

and will be called principal ideal.

Let us now explore the algebraic structure of

I (A)

, the set of ideals of

A

. One can observe that, if I and J are two ideals of

A

, then

I \cap J

is an ideal of

A

In what follows, we establish that the set of ideals of

A

is a Heyting algebra.

Proposition 21.

(I (A), \land, \lor, {0}, A)

is a complete lattice, with

I \land J = I \cap J

I \lor J = (I \cup J]

, for all

I, J \in I (A)

Proof.

Let

I, J, K \in I (A)

;

Idempotence:: $I \land I = I \cap I = I$ ; $I \lor I = (I \cup I] = (I] = I$
Symmetry:: $I \land J = I \cap J = J \cap I = J \land I$ ; $I \lor J = (I \cup J] = (J \cup I] = J \lor I$
Associativity:: $I \land (J \land K) = I \cap (J \cap K) = (I \cap J) \cap K$ . Moreover,

Since $J \subseteq I \cup J \subseteq I \lor J \subseteq (I \lor J) \lor K$ , and $K \subseteq (I \lor J) \lor K$ , we have $J \cup K \subseteq (I \lor J) \lor K$ , thus $(J \cup K] \subseteq (I \lor J) \lor K$ , i.e., $J \lor K \subseteq (I \lor J) \lor K$ . Moreover, $I \subseteq (I \lor J) \lor K$ , thus $I \cup (J \lor K) \subseteq (I \lor J) \lor K$ , consequently, $(I \cup (J \lor K)] \subseteq (I \lor J) \lor K$ , i.e., $I \lor (J \lor K) \subseteq (I \lor J) \lor K$ .

We show likewise $(I \lor J) \lor K \subseteq I \lor (J \lor K)$ , therefore, $I \lor (J \lor K) = (I \lor J) \lor K$ .
Absorption laws:: $I \land (I \lor J) = I \cap (I \lor J) = I$ ; $I \lor (I \land J) = (I \cup (I \land J)] = (I] = I$ .
Bounds:: Let ${I_{i}}_{i \in Γ}$ a be non-empty family of elements of $I (A)$ . For this family the infimum is given by $\underset{i \in Γ}{⋀} I_{i} : = ⋂_{i \in Γ} I_{i}$ and the supremum $\underset{i \in Γ}{⋁} I_{i} : = (⋃_{i \in Γ} I_{i}]$ .

□

Proposition 22.

(I (A), \land, \lor, \to, {0})

is a Heyting algebra, where

J \to K : = {a \in A; J \land (a] \subseteq K}

, for all

J, K \in I (A)

Proof.

Let us show first that $(I (A), \land, \lor, \land, \to, {0}, A)$ is a residuated lattice.

For RL1,

$(I (A), \land, \lor, 0, A)$ is a bounded lattice.

For RL2,

$(I (A), \land, A) = (I (A), \cap, A)$ is a commutative ordered monoid.

For RL3,

let $I, J, K \in I (A)$ . We will prove that $I \land J \subseteq K \Leftrightarrow I \subseteq J \to K$ .

*

Assume that $I \land J \subseteq K$ and let $a \in I$ .

Let $x \in J \land (a]$ , then $x \in J$ and $x \in (a] \subseteq I$ . Hence, $x \in I \land J \subseteq K$ . Therefore, $J \land (a] \subseteq K$ , i.e., $a \in J \to K$ . Thus $I \subseteq J \to K$ .

*

Assume that $I \subseteq J \to K$ .

Let $x \in I \land J$ , then $x \in I$ and $x \in J$ . Then $x \in J \to K$ , since $x \in I \subseteq J \to K$ . Hence, $x \in J \land (x] \subseteq K$ . Thus $I \land J \subseteq K$ .
Since $(I (A), \land, \lor, \land, \to, 0, A)$ is a residuated lattice and the product and the conjunction coincide, it holds that $(I (A), \land, \lor, \to, {0})$ is a Heyting algebra.

□

3. Conclusion and Future Work

In this paper, we aimed to introduce and examine the notion of ideals within triangle algebras. We delved into the relations between ideals and filters, as well as the correlations between ideals and congruences. Notably, we have rectified an existing error in the filter construction procedure proposed by Zahiri et al. [22]; as a result, we give an alternative characterization of the filter generated by a subset of a triangle algebra, and this leads to offer a more accurate framework for understanding the relationship between ideals and filters. Particularly, we have proved that the operators given by Liu et al.[7] and Tchoua et al. [13] in the case of residuated lattices are equal, moreover we have proved that in the case of triangle algebras, this operator changes filters to an ideals but the converse is not true. Furthermore, we used the characterization of the ideal generated by a subset to prove that the set of all ideals of a triangle algebra is a Heyting algebra.

In our future work, we plan to study how to use the notion of ideal to develop a logic that formally characterizes antitologies in triangle algebras; moreover, we plan to look about solving equations in algebraic structures as done by [8,11].

Author Contributions

Conceptualization and methodology: Blaise Blériot Koguep Njionou; writing—original draft preparation, Euclide Noumen; writing—review and editing, All authors.

Funding

This research received no external funding.

Acknowledgments

The authors thank the academic editor for his valuable comments and suggestions and the anonymous referees for their remarks which helped them to improve the presentation of the paper.

Conflicts of Interest

The authors declare no conflicts of interest.

References

Belluce, L. P.; Di Nola, A. Commutative rings whose ideals form an MV-algebra. Mathematical Logic Quarterly 2009, 55, 468–486. [Google Scholar] [CrossRef]
Buşneag, D.; Piciu, D.; Dina, A. M. Ideals in residuated lattices. Carpanthian Journal of Mathematics 2021, 37, 53–63. [Google Scholar] [CrossRef]
Gratzer, G. Lattice Theory: First Concepts and Distributive Lattices; Dover Books on Mathematics Series, 2009.
Heubo-Kwegna O., A.; Lele, C.; Ndjeya, S.; Nganou, J. B. BL-rings. Logic Journal of the IGPL, 2018, 26, 290–299. [Google Scholar] [CrossRef]
Holdon, L. C. On ideals in De Morgan residuated lattices. Kybernetika, 2018, 54, 443–475. [Google Scholar]
Lele, C.; Nganou, J. B. MV-algebras derived from ideals in BL-algebras. Fuzzy Sets and Systems 2013, 218, 103–113. [Google Scholar] [CrossRef]
Liu, Y.; Qin, Y.; Qin, X.; Xu, Y. Ideals and fuzzy ideals on residuated lattices. International Journal of Machine Learning and Cybernetic, 2017, 8, 239–253. [Google Scholar] [CrossRef]
Oner, T.; Senturk, I.; Oner, G. An Independent Set of Axioms of MV-Algebras and Solutions to the Set-Theoretical Yang-Baxter Equation. Axioms 2017, 6. [Google Scholar] [CrossRef]
Pal, A.; Pal, M. Some Results on Interval-Valued Fuzzy Matrices. Advances in Intelligent Systems Research, In Proceedings of the 1st International Conference on E-Business Intelligence (ICEBI 2010), Atlantis Press 2010, 554–559.
Piciu, D. Algebras of fuzzy logic. University of Craiova, Editura Universitaria, 2007.
Senturk, I. , Oner, T., Borumand S. A. Theoretical Solutions for the Yang-Baxter Equation in Triangle Algebras. Discussiones Mathematicae-General Algebra and Applications 2024, 44, 15–42. [Google Scholar]
Tallee, K. A. G.; Koguep, N. B. B.; Lele, C.; StrÃ¼ngmann, L. Relative annihilator in bounded commutative residuated lattices. Indian Journal of Pure and Applied Mathematics 2023, 54, 359–374. [Google Scholar] [CrossRef]
Tchoua, Y. F.; Koguep N., B. B ; Temgoua A. E. R. ; Lele, C. n-fold boolean, implicative and integral ideals on bounded commutative residuated lattices. New mathematics and natural computation 2019, 15, 427–445. [Google Scholar] [CrossRef]
Tchoua, Y.F.; Koguep, N.B.B.; Lele, C.; Temgoua, A.E.R. Ideals and N-Involutive filters on residuated lattices, (submitted).
Van Gasse, B.; Cornelis, C.; Deschrijver, G.; Kerre, E. E. Triangle Algebras: Towards an Axiomatization of Interval-Valued Residuated Lattices. In Lecture Notes in Computer Science, Proceedings of the 5th International Conference on Rough Sets and Current Trends in Computing (RSCTC 2006); 2006; pp. 117–126. [Google Scholar]
Van Gasse, B.; Deschrijver, G.; Cornelis, C.; Kerre, E. E. Triangle algebras :a formal logic approach to interval-valued residuated lattices. Fuzzy Sets and Systems 2008, 159, 1042–1060. [Google Scholar] [CrossRef]
Van Gasse, B.; Deschrijver, G.; Cornelis, C.; Kerre, E. E. The pseudo-linear semantics of interval-valued fuzzy logics. Information Sciences 2009, 179, 717–728. [Google Scholar] [CrossRef]
Van Gasse, B.; Deschrijver, G.; Cornelis, C.; Kerre, E. E. Filters in residuated lattice and triangle algebras. Information Sciences 2010, 180, 3006–3020. [Google Scholar] [CrossRef]
Ward, M.; Dilworth, R. Residuated lattices. Transactions of the American Mathematical Society 1939, 45, 335–354. [Google Scholar] [CrossRef]
Yongwei, Y. , Xiaolong, X. On characterizations of BL-algebras via implicative ideals. Italian Journal of Pure and Applied Mathematics 2017, 37, 493–506. [Google Scholar]
Zahiri, S. , Saeid, A.B., Eslami, E. On maximal filters in triangle algebras. Journal of Intelligent and Fuzzy Systems: Applications in Engineering and Technology 2016, 30, 1181–1193. [Google Scholar] [CrossRef]
Zahiri, S. , Borumand, S. A., Eslami, E. A new approach to filters in triangle algebras. Mathematics, Publications de l’Institut Mathématique (Belgrade) 2017, 101, 267–283. [Google Scholar] [CrossRef]
Zahiri, S. , Borumand, S. A., Eslami, E. An Investigation on the Co-annihilators in Triangle Algebras. Iranian Journal of Fuzzy Systems 2018, 15, 91–102. [Google Scholar]
Zahiri, S. , Borumand, S. A., Kerman An Investigation On THE n-Fold IVRL-Filters In Triangle Algebras. Mathematica Bohemica, 2020, 1, 75–91. [Google Scholar] [CrossRef]
Zahiri, S. , Borumand, S. A., Turunen, E. On local triangle algebras. Fuzzy Sets and Systems 2021, 418, 126–138. [Google Scholar] [CrossRef]
Zhang, X. , Liang, R. Interval-Valued General Residuated Lattice-Ordered Groupoids and Expanded Triangle Algebras. Axioms 2022, 12. [Google Scholar] [CrossRef]

Figure 1. Lattice of Example 3.

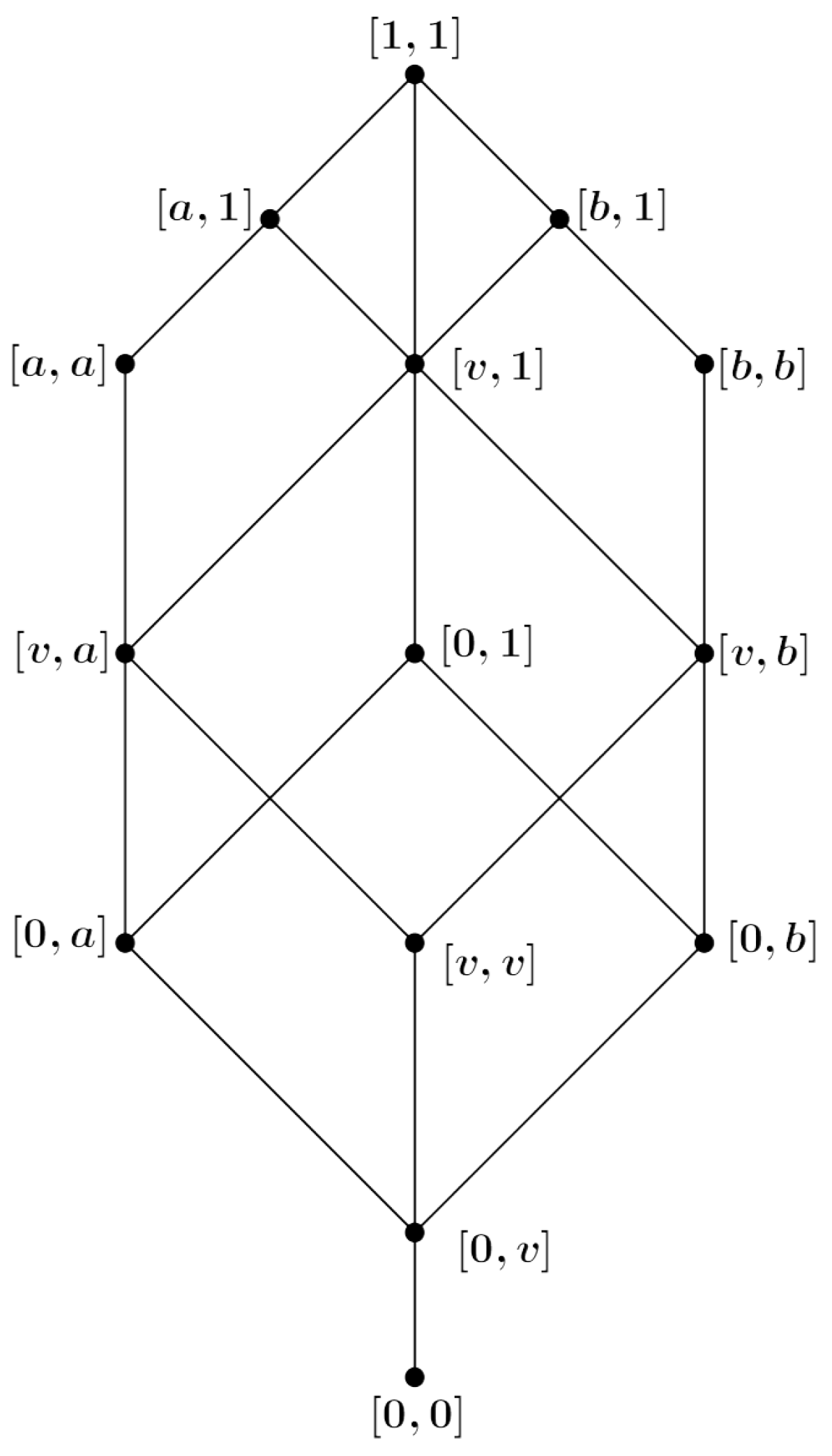
Table 1. Tables of

ν

μ

, ⊙ and →.

Table 1. Tables of

ν

μ

, ⊙ and →.

Table 2. Tables of ⇒ and *.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

An Exploration of Ideals and Filters In Triangle Algebras

Abstract

Introduction

1. Preliminaries

1.1. Residuated Lattices

1.2. Triangle Algebras

2. Ideals in Triangle Algebras

2.1. Definition and Characterizations of the Notion of Ideal

2.2. Pseudo-Duality

2.3. Ideals and Congruences

2.4. Ideals Generated by a Subset

3. Conclusion and Future Work

Author Contributions

Funding

Acknowledgments

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe