Evaluating Kolmogorov–Arnold Networks for Scientific Discovery: A Simple Yet Effective Approach

Preprint

Article

Evaluating Kolmogorov–Arnold Networks for Scientific Discovery: A Simple Yet Effective Approach

Altmetrics

Downloads

151

Views

Comments

Josh Sun^*

This version is not peer-reviewed

Submitted:

14 August 2024

Posted:

19 August 2024

You are already at the latest version

Alerts

Abstract

Kolmogorov–Arnold Network (KAN) is an emerging interpretable neural network compared to fully black-box MLPs. Recently, emerging works focus on comprehensive and fair comparisons between KAN and MLP in various tasks. However, these works didn't focus on the strongest advantage of KAN: generating symbolic outputs. The ability of KAN to provide scientific insights or even discover new science is under-examined. In this work, we propose several novel metrics to measure how well a KAN performs on symbolic function fitting: R^2-Mean, weighted R^2-complexity loss, and ranking metrics. We also propose a metric to determine mathematical complexity of a target function and evaluate KAN with several functions of different mathematical complexity. Additionally, we also tried inputs with different ranges to find the effect of normalization.

Keywords:

Subject: Computer Science and Mathematics - Artificial Intelligence and Machine Learning

1. Introduction

Kolmogorov–Arnold Network (KAN) [1] is a new neural network architecture based on the Kolmogorov-Arnold representation theorem [4]. This theorem states that any multivariate continuous function can be expressed as a finite sum of continuous functions of one variable. KAN utilizes this principle through learnable activation functions rather than fixed activation functions which is typical in traditional Multi-Layer Perceptron (MLP) [5]. This unique feature enhances KAN’s ability to discover symbolic representations of complex functions, making it particularly valuable for tasks in data fitting and scientific discovery.

The primary advantage of KAN over MLP is interpretability. While MLPs act as black boxes with fixed nonlinear activation functions, KAN’s learnable activation functions provide a clear pathway to deriving symbolic functions from the learned model. This transparency is crucial for scientific applications where understanding the underlying relationships is as important as prediction accuracy. The process of generating symbolic outputs in KAN involves training with sparsification, pruning, assigning symbolic functions (automatically or manually), and fine-tuning affine parameters.

Recently, there’re emerging works focusing on comprehensive and fair comparison between KAN and MLP in differential equations [2], symbolic function fitting [3], image classification [3], and text classification tasks [3]. However, these works didn’t focus on KAN’s strongest advantage: generating symbolic outputs. The ability of KAN to provide scientific insights or even discover new science is under-examined.

To better evaluate the performance of a KAN symbolic output, we first look at individual function evaluation, using

R^{2}

or RMSE to describe how close the learned function is to the target symbolic function in a given range. We adapt a simple strategy to extend that to compound functions by taking the average of all

R^{2}

values for learnable functions on each node, called

R^{2}

-Mean. We also tried weighted

R^{2}

-complexity loss defined in [1], by leveraging the complexity of a candidate symbolic function and it’s

R^{2}

score. However, the symbolic tree of learnable functions is ordered, but the function itself is unordered. For example, if the ground truth function is

y = exp (sin (x_{1}) + cos (x_{2})) + \sqrt{{(x_{1})}^{2} + x_{2}}

, then another solution,

y = \sqrt{{(x_{1})}^{2} + x_{2}} + exp (sin (x_{1}) + cos (x_{2}))

, is also correct. These two are the same function but correspond to two different symbolic trees, which means we need to search to find the best metric given a symbolic tree and its reference function. Here, we simply perform an exhaustive search. We also test with weighted

R^{2}

-complexity loss [1], leveraging the complexity of a function and its fitting accuracy.

We also hope the ground truth function for each node can be ranked high, providing useful scientific insights when combined with domain knowledge. Therefore, we use ranking metrics to compute the average rank of all ground truth functions. To rank a function, we apply

R^{2}

-Mean or weighted

R^{2}

-complexity loss.

2. Reproduction

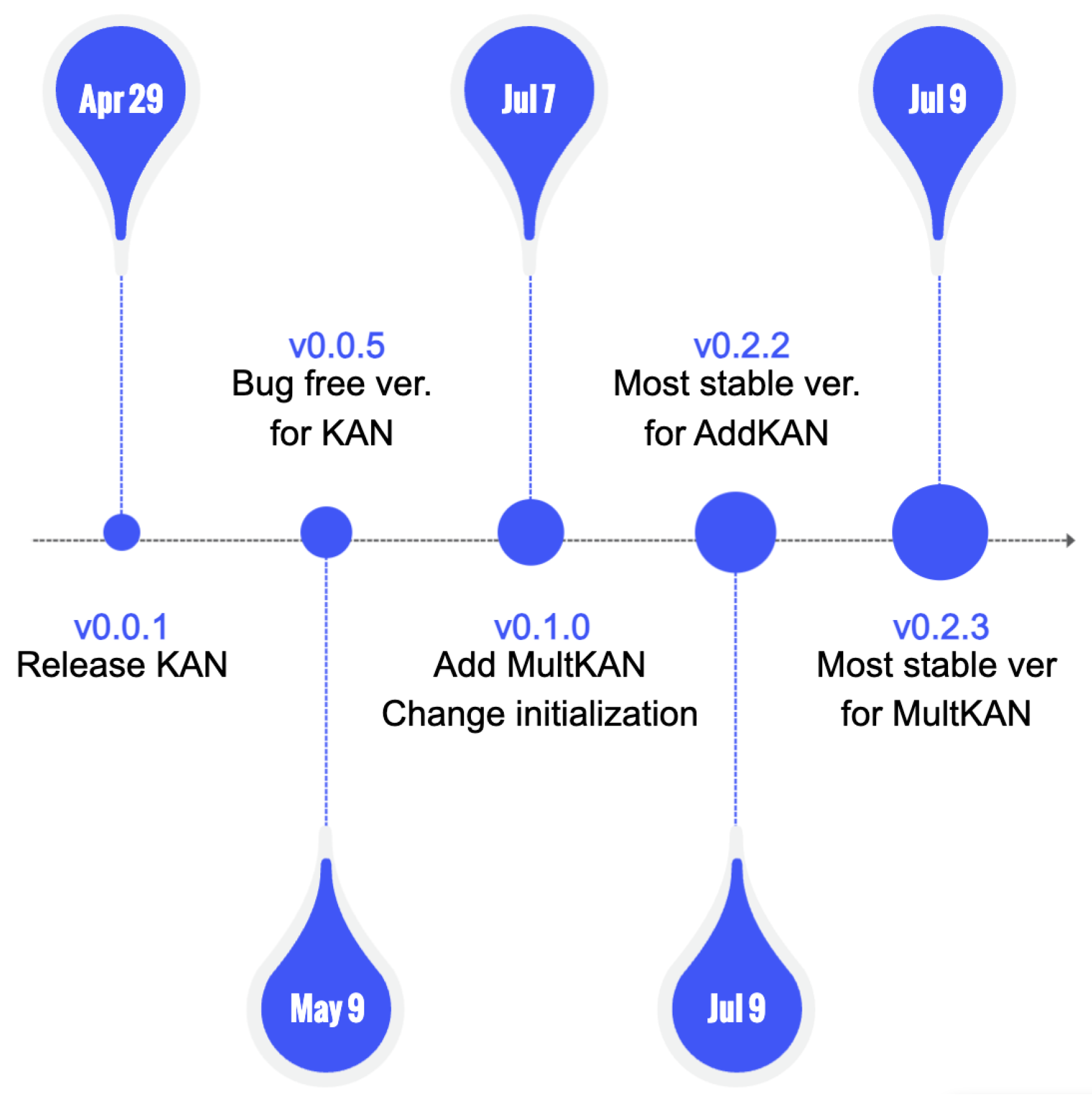
The KAN has not been officially published yet, and the GitHub repository has frequent updates (selected release version in Figure 1). To ensure accurate reproduction, it’s essential to review different releases and stick to one.

v0.0.1: This was the initial release of the KAN model, laying the groundwork with core functionalities.
v0.0.5: Recognized as the most stable early version of KAN, addressing several early-stage bugs and performance issues.
v0.1.0 and v0.2.0: These versions introduced significant improvements. One major change was in the model’s initialization process. Additionally, the method model.learn() was replaced with model.fit(), and support for multiplication was added. Originally, KAN handled multiplication by decomposition, e.g., $x y = \frac{{(x + y)}^{2} - {(x - y)}^{2}}{4}$ . The introduction of a direct multiplication operator enhanced performance but introduced bugs in the addition operator.
v0.2.2: Currently, this is the most stable version regarding the addition operator. This version is used in this paper.
v0.2.3: The latest version, which still has unresolved bugs related to the addition operator.

Due to instability in training with the multiplication operator, this paper does not explore its impact on KAN’s symbolic output.

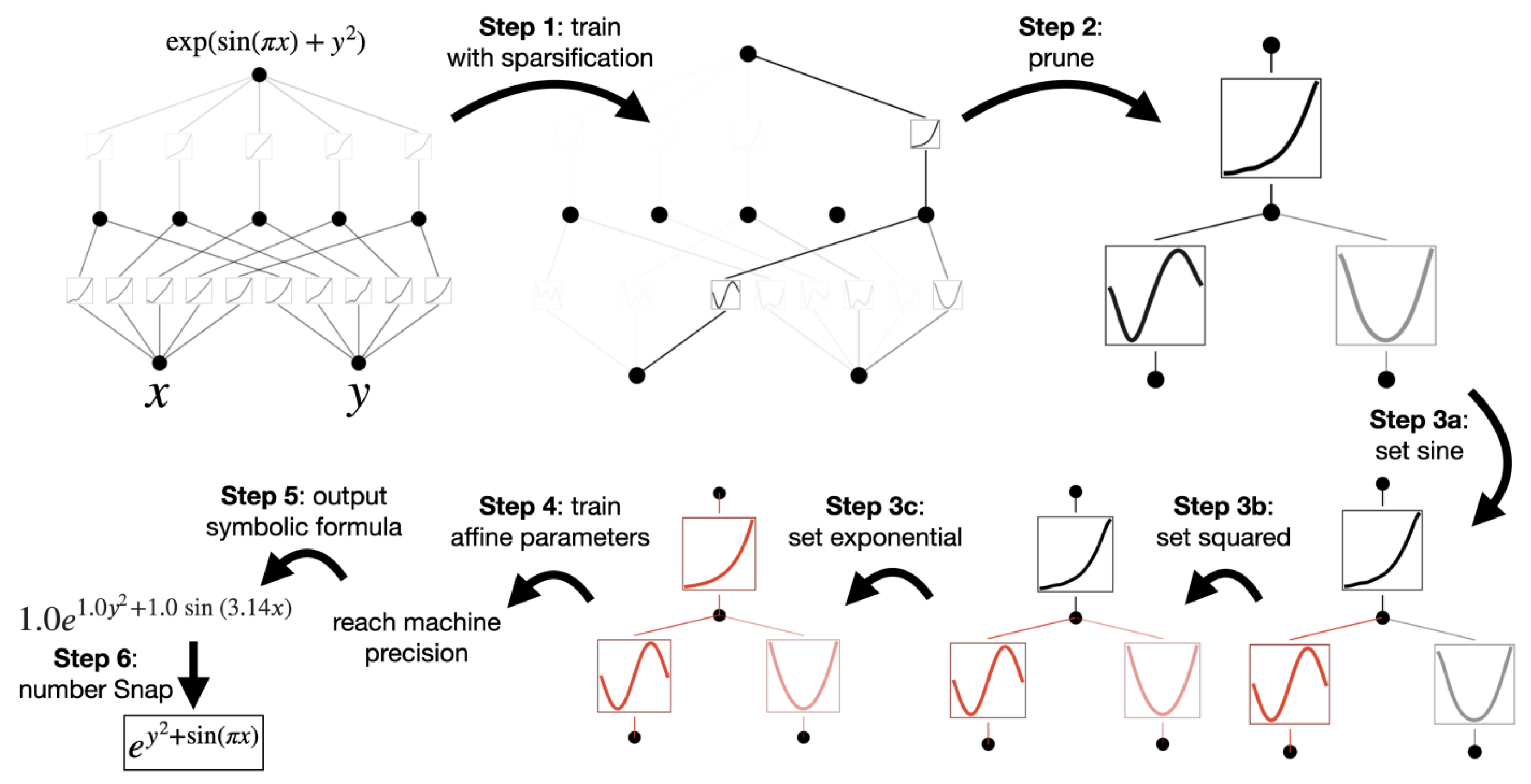
3. KAN Preliminary

KANs utilize activation functions on the edges (weights) instead of fixed functions on the nodes. These activation functions are learnable and can be represented as splines, allowing the network to approximate complex functions accurately. Kolmogorov-Arnold Networks (KANs) provide a method to convert learned neural network functions into interpretable symbolic expressions. This process leverages learnable activation functions and involves several key steps (Figure 2).

3.1. Steps to Generate Symbolic Output

Training with Sparsification Start with a fully connected KAN, such as a [2, 5, 1] structure. During training, sparsification regularization is applied to prune unnecessary neurons, resulting in a sparse and more interpretable network.

Pruning Automatically prune the network to remove all but the essential neurons. For example, the pruning might reduce the network to a [2, 1, 1] structure.

Setting Symbolic Functions Inspect the pruned network to hypothesize the symbolic forms of the remaining activation functions. Use the function fix_symbolic(l, i, j, f) to set the activation functions to specific symbolic forms, e.g., fix_symbolic(0, 0, 0, ’sin’). If unsure about the symbolic forms, employ the suggest_symbolic function, which proposes potential symbolic candidates for the activation functions.

Further Training After assigning symbolic forms to the activation functions, continue training to adjust the affine parameters (shifts and scalings) to match the symbolic expressions accurately. Continue training until the loss drops to machine precision, indicating the symbolic expressions have been correctly identified.

Outputting the Symbolic Formula Once training is complete, use the sympy library to compute the symbolic formula of the output node. This process will yield a symbolic expression that represents the function learned by the KAN. For instance, a user might obtain a formula like

1.0 e^{1.0 y^{2}} + 1.0 sin (3.14 x)

, closely matching the true symbolic function.

4. Metrics

4.1. Performance Metrics

To evaluate the performance of Kolmogorov–Arnold Networks (KAN) in generating symbolic outputs, we utilize several metrics. These metrics help us assess how well the learned functions approximate the target symbolic functions, taking into account various aspects of accuracy and complexity. Below, we describe the primary metrics used in our evaluation.

$R^{2}$ Score For individual functions, the most common metric is

R^{2}

score, also known as the coefficient of determination, measuring the proportion of variance in the target variable that is predictable from the features. It is defined as:

R^{2} = 1 - \frac{\sum_{i = 1}^{n} {(y_{i} - {\hat{y}}_{i})}^{2}}{\sum_{i = 1}^{n} {(y_{i} - \bar{y})}^{2}}

where

y_{i}

is the true value,

{\hat{y}}_{i}

is the predicted value, and

\bar{y}

is the mean of the true values. An

R^{2}

score close to 1 indicates a high level of approximation.

Weighted $R^{2}$ -Complexity Loss In most cases, several candidate symbolic function can all have very high

R^{2}

-score, e.g.,

R^{2} > 0.999

. It’s very likely that some functions with a higher

R^{2}

-score is actually over-fitting. Therefore, it’s important to assign a complexity number for every candidate function and leveraging that. The weighted

R^{2}

-complexity loss [1] incorporates both the complexity of the symbolic function and its fitting accuracy. It is defined as:

Weighted Loss = α \cdot Complexity + (1 - α) \cdot {log}_{2} (1 - R^{2})

where

α

is a weighting factor and complexity refers to the computational complexity of the symbolic function. This metric balances the trade-off between simplicity and accuracy of the learned symbolic functions. The complexity of symbolic functions are given in Table 1. Usually we take

α = 0.8

So far, we know the metric for evaluating how close each individual learned function is given a corresponding symbolic function. But the symbolic output of KAN is a special tree structure, and ground truth functions are usually compound functions. To address this issue, we use

R^{2}

-Mean.

$R^{2}$ -Mean

R^{2} - Mean = \frac{1}{m} \sum_{j = 1}^{m} R_{j}

where

R_{j}^{2}

represents the

R^{2}

score for the j-th node, and m is the total number of nodes. This metric helps in evaluating how well the learned symbolic functions fit the data across different nodes.

Exhaustive Search for Metric Selection To determine the most suitable metric for evaluating the symbolic tree, we perform an exhaustive search. This involves evaluating all possible permutations of the symbolic tree and comparing them against the reference function to find the optimal metric. The pseudo-code for this search is as follows:

for each possible permutation of compound function f:

for each individual function f_{j} in f:

find corresponding learnable function node f_{j}^{learned}

compute R^2 for (f_j, f_j^{learned})

compute R^2-Mean

end for

select best R^2-Mean.

This approach ensures that we consider all potential metrics and select the one that best aligns with the reference function, leading to more accurate and meaningful evaluations of KAN’s performance.

Ranking Metrics Ranking metrics, such as rank@1 and rank@5, are crucial for evaluating the performance of information retrieval models. These metrics measure the effectiveness of a system by determining how often the relevant item appears within the top-k positions of the ranked list returned by the system. For instance, rank@1 checks if the desired item is the first result, while rank@5 evaluates whether it appears within the top five results. In this task, if the ground truth function ranks high, it means it’s capturing the correct pattern.

4.2. Mathematical Complexity

To evaluate KAN with different functions, it’s important to assess the complexity of each function. The mathematical complexity of a compound function can be defined recursively. For a function

f (x)

expressed as

f (x) = ϕ (g_{1} (x), g_{2} (x), \dots, g_{n} (x))

, where

ϕ

represents an operation or function applied to

g_{1} (x), g_{2} (x), \dots, g_{n} (x)

, the complexity is computed as:

Complexity (f (x)) = Complexity (ϕ) \cdot \sum_{i = 1}^{n} Complexity (g_{i} (x))

Base Case For individual symbolic functions, use the complexity values provided in Table 1.

5. Results

5.1. Simple Functions

We evaluated 18 simple functions with all of them having a depth of 3. We initialized KAN with shape [2, 1, 1] which actually matches the nodes corresponding to the functions. For other KAN hyper-parameters, we use default settings. The inputs are within range [0.01, 1]. The results are shown in Table 2.

KAN is not good at complex functions Using mathematical complexity, we can still classify these 18 functions "comparably complex" (Cplx

> 9

) and "comparably simple" (Cplx

\leq 9

). The performance of KAN is notably better on simpler functions, achieving 100% rank@5 on 8 out of 9 samples. For comparably complex functions (Cplx > 9), KAN struggles, achieving 100% rank@5 on only 5 out of 9 samples. This trend indicates that as the complexity of the function increases, KAN’s ability to fit and rank the correct symbolic expressions diminishes. Notably, functions such as tan(cos

x_{1}

x_{2}^{3}

) with a complexity of 15 were particularly challenging for KAN, showing lower

R^{2}

and rank metrics, likely due to the increased nonlinearity and complexity.

Analysis of $\frac{1}{(expression)}$ -type Functions. Function:

\frac{1}{cos (x 1) + x 2}

and

\frac{1}{{(cos (x 1) + x 2)}^{2}}

. These functions have a complexity close to or slightly above the threshold of 9, which KAN generally handles well. The results suggest that KAN can accurately fit inverse functions when the expression inside the inverse is not overly complex.

Comparison with Non-Inverse Functions In comparison with non-inverse functions of similar complexity, KAN’s performance on inverse functions is relatively robust. For instance,

\frac{1}{cos (x 1) + x 2}

with Cplx 8 performs just as well as simpler non-inverse functions like

exp (cos (x 1) + x 2)

. This suggests that the inclusion of an inverse operation does not inherently introduce significant difficulty, provided the complexity of the expression inside the inverse remains manageable.

Complexity within the Inverse Functions In addition to the general performance on simple functions, it is important to consider the class of functions of the form

\frac{1}{(expression)}

. As seen in other complex functions, increasing the complexity within the inverse, such as adding nested or compounded operations, can reduce KAN’s performance. This trend indicates that while KAN is robust in handling moderate-complexity inverse functions, it may face difficulties as the complexity inside the inverse grows, which is an important consideration for future improvements.

5.2. Analysis of Input Range

KAN limits its input to be with range [-1, 1] and in some scenarios, for example, dealing with log or sqrt, it has to be in (0, 1]. However, in real worlds, most variables doesn’t hold this assumption, and in most cases have a large range. Table 3 provides a detailed comparison of the KAN model’s performance across various input ranges for specific functions. The table reveals how the input range can significantly impact the model’s ability to fit and rank the correct symbolic expressions.

Impact of Expanding Input Range on Performance Function:

\exp (cos (x_{1}) + x_{2})

. For smaller input ranges like

[0.01, 1]

and

[0.01, 2]

, KAN performs exceptionally well, achieving near-perfect

R^{2}

values and 100% rank@5 across all metrics. As the input range increases, the performance gradually deteriorates. For instance, at

[0.01, 10]

, the

R^{2}

value drops to 0.9352, and the rank@5 metric also declines, reflecting a reduced accuracy in ranking the correct expressions. When the input range expands to

[0.01, 100]

, the model fails completely, indicating that the model is unable to fit the data at all within this extensive range.

Impact of Input Range on Inverse Function For

\exp (cos (x_{1}) + \frac{1}{x_{2}})

, when it’s within the smaller range

[0.5, 1]

, KAN achieves a high

R^{2}

value of 0.9990, but the rank@1 metric is only 66.6%, indicating some difficulty in ranking the top expression. As the range expands to

[0.1, 1]

, performance drops significantly, with

R^{2}

reducing to 0.9772, and the rank@1 and rank@3 metrics falling to 0%. For the range

[0.01, 1]

, the model again fails entirely. The model is vulnerabe in handling inverse functions over larger domains.

Effectiveness of Data Preprocessing Techniques For

\exp (cos (x_{1}) + x_{2})

with input range

[0.01, 10]

, applying MinMax scaling improves the

R^{2}

value from 0.9352 to 0.9584, and significantly boosts the rank@3 and rank@5 metrics to 100%. For the inverse function

\exp (cos (x_{1}) + \frac{1}{x_{2}})

, applying MinMax scaling and shifting the input range to

[0.1, 1]

recovers some performance, improving

R^{2}

to 0.9469 and rank@5 to 66.6%. If we already know the inverse pattern and put that step to be part of pre-processing, we can improve

R^{2}

to 0.9949.

5.3. Complex Functions

Table 4 presents the results of KAN’s performance on various complex functions, all with a complexity (Cplx) score of 14. These functions involve combinations of logarithmic, square root, and inverse operations layered with exponential and trigonometric functions. The function log(exp

x_{1}

x_{2}^{2}

) + exp(

x_{1}

+ cos

x_{2}

) achieves the highest

R^{2}

score (0.9656) and better ranking metrics compared to others. This indicates that KAN can handle the combination of logarithmic and exponential functions reasonably well, even when combined with trigonometric elements like cosine. For the inverse function 1/(exp

x_{1}

x_{2}^{2}

) + exp(

x_{1}

+ cos

x_{2}

), the

R^{2}

score drops to 0.9049, with a significant decline in ranking metrics (R@1 = 0). This indicates that KAN struggles to identify the correct expression when inverse operations are introduced, leading to poorer performance in ranking the top correct expressions. When the inverse function is squared, the performance further degrades to an

R^{2}

score of 0.8499. However, interestingly, the ranking metrics show some improvement at R@3 and R@5, suggesting that while the model finds it difficult to fit the exact expression, it may still capture the broader structure of the function.

6. Conclusion

We introduce several new metrics to evaluate how well a KAN performs in symbolic function fitting:

R^{2}

-Mean, weighted

R^{2}

-complexity loss, and ranking metrics. By analyzing mathematical complexity, we find that KAN performs well on simple functions but its performance drops with more complex functions, especially inverse functions. For inputs with ranges outside [-1, 1], normalization is important. Otherwise, KAN may not find the true pattern.

References

Liu, Z.; Wang, Y.; Vaidya, S.; Ruehle, F.; Halverson, J.; Soljačić, M.; Hou, T.Y.; Tegmark, M. Kan: Kolmogorov-arnold networks. arXiv 2024, arXiv:2404.19756. [Google Scholar] [CrossRef]
Shukla, K.; Toscano, J.D.; Wang, Z.; Zou, Z.; Karniadakis, G.E. A comprehensive and fair comparison between mlp and kan representations for differential equations and operator networks. arXiv 2024, arXiv:2406.02917. [Google Scholar] [CrossRef]
Yu, R.; Yu, W.; Wang, X. Kan or mlp: A fairer comparison. arXiv 2024, arXiv:2407.16674. [Google Scholar] [CrossRef]
Kolmogorov, A. N. On the representation of continuous functions of many variables by superposition of continuous functions of one variable and addition. In Akademii Nauk; Russian Academy of Sciences, 1957; vol. 114, pp. 953–956. [Google Scholar]
Hornik, K.; Stinchcombe, M.; White, H. Multilayer feedforward networks are universal approximators. Neural networks 1989, 2, 359–366. [Google Scholar] [CrossRef]

Figure 1. An image of KAN release history.

Figure 2. An example of how to do symbolic regression with KAN. From [1].

Table 1. Complexity of symbolic functions given by [1].

Symbolic Function	Complexity	Symbolic Function	Complexity
x	1	$1 / x$	1
$x^{2}$	2	$1 / x^{2}$	2
$x^{3}$	3	$1 / x^{3}$	3
$x^{4}$	4	$1 / x^{4}$	4
$x^{5}$	5	$1 / x^{5}$	5
$\sqrt{x}$	3	$1 / \sqrt{x}$	3
$exp x$	2	$log x$	2
$\| x \|$	3	$s g n (x)$	3
$sin x$	2	$cos x$	2
$tan x$	3	$tanh x$	3
$arcsin x$	4	$arccos x$	4
$arctan x$	4	$arctanh x$	4
0	0	$g a u s s i a n$	3

Table 2. Results on simple functions. Cplx corresponds to Mathematical Complexity in Section 4.2. We use

R^{2}

and weighted

R^{2}

-Complexity loss as metrics, and compute average and ranking metrics.

Table 2. Results on simple functions. Cplx corresponds to Mathematical Complexity in Section 4.2. We use

R^{2}

and weighted

R^{2}

-Complexity loss as metrics, and compute average and ranking metrics.

Func	Cplx	Metric: $R^{2}$				Metric: $R^{2}$ -Complexity loss
Func	Cplx	-Avg	R@1	R@3	R@5	-Avg	R@1	R@3	R@5
exp(cocs $x_{1}$ + $x_{2}$ )	6	0.9998	100	100	100	-1.49	100	100	100
exp(cos $x_{1}$ + $x_{2}^{2}$ )	8	0.9999	100	100	100	-1.63	100	100	100
exp(cos $x_{1}$ + $x_{2}^{3}$ )	10	0.9998	100	100	100	-0.75	100	100	100
cos(cos $x_{1}$ + $x_{2}^{3}$ )	10	0.9999	100	100	100	-1.43	100	100	100
log(cos $x_{1}$ + $x_{2}^{3}$ )	10	0.9999	100	100	100	-1.43	100	100	100
sqrt(cos $x_{1}$ + $x_{2}^{3}$ )	10	0.9999	100	100	100	1.17	66.6	100	100
tan(cos $x_{1}$ + $x_{2}^{3}$ )	15	0.7499	0	33.3	33.3	1.44	0	33.3	33.3
1/(cos $x_{1}$ + $x_{2}$ )	6	0.9999	100	100	100	-1.69	100	100	100
1/(cos $x_{1}$ + $x_{2}$ )²	6	0.9995	100	100	100	-0.96	66.6	100	100
1/(cos $x_{1}$ + $x_{2}^{2}$ )	8	0.9997	100	100	100	-1.13	100	100	100
1/(cos $x_{1}$ + $x_{2}^{2}$ )²	8	0.9988	33.3	100	100	-0.46	33.3	100	100
1/(cos $x_{1}$ + $x_{2}^{3}$ )	10	0.9999	100	100	100	-1.03	66.6	100	100
1/(cos $x_{1}$ + $x_{2}^{3}$ )²	10	0.9982	33.3	33.3	66.6	-0.14	33.3	66.6	66.6
1/(cos $x_{1}$ + $x_{2}$ )³	9	0.9992	33.3	66.6	100	-0.49	33.3	66.6	100
1/(cos $x_{1}$ + $x_{2}^{2}$ )³	12	0.9987	0	66.6	100	-0.11	0	66.6	100
1/(cos $x_{1}$ + $x_{2}^{3}$ )³	15	0.9968	0	0	66.6	0.25	0	0	66.6
1/(cos $x_{1}$ + $x_{2}$ )	6	0.9977	0	33.3	100	-0.37	0	33.3	100
1/(cos $x_{1}$ + $x_{2}^{2}$ )²	8	0.9896	0	66.6	66.6	-0.12	0	66.6	66.6
1/(cos $x_{1}$ + $x_{2}^{3}$ )³	15	0.9968	0	0	66.6	0.25	0	0	66.6

Table 3. Impact of input range on performance.

Func	Input Range	Metric: $R^{2}$
Func	Input Range	-Avg	R@1	R@3	R@5
exp(cocs $x_{1}$ + $x_{2}$ )	[0.01, 1]	0.9999	100	100	100
exp(cocs $x_{1}$ + $x_{2}$ )	[0.01, 2]	0.9998	100	100	100
exp(cocs $x_{1}$ + $x_{2}$ )	[0.01, 5]	0.9974	66.6	100	100
exp(cocs $x_{1}$ + $x_{2}$ )	[0.01, 10]	0.9352	33.3	66.6	66.6
exp(cocs $x_{1}$ + $x_{2}$ )	[0.01, 100]	nan
exp(cocs $x_{1}$ + $x_{2}$ )	[0.01, 10] + minmax	0.9584	33.3	100	100
exp(cocs $x_{1}$ + $1 / x_{2}$ )	[0.5, 1]	0.9990	66.6	66.6	66.6
exp(cocs $x_{1}$ + $1 / x_{2}$ )	[0.1, 1]	0.9772	0	0	66.6
exp(cocs $x_{1}$ + $1 / x_{2}$ )	[0.01, 1]	nan
exp(cocs $x_{1}$ + $1 / x_{2}$ )	[0.1, 1] + minmax	0.6833	33.3	33.3	100
exp(cocs $x_{1}$ + $1 / x_{2}$ )	[0.1, 1] + minmax + shifted	0.9469	33.3	33.3	66.6
exp(cocs $x_{1}$ + $x_{3}$ ) ( $x_{3} = 1 / x_{2}$ )	[0.1, 1]	0.9949	33.3	33.3	66.6

Table 4. Results on complex functions.

Func	Cplx	Metric: $R^{2}$
Func	Cplx	-Avg	R@1	R@3	R@5
log(exp $x_{1}$ + $x_{2}^{2}$ ) + exp( $x_{1}$ + cos $x_{2}$ )	14	0.9656	16.7	50	66.6
sqrt(exp $x_{1}$ + $x_{2}^{2}$ ) + exp( $x_{1}$ + cos $x_{2}$ )	14	0.9653	16.7	33.3	66.6
1/(exp $x_{1}$ + $x_{2}^{2}$ ) + exp( $x_{1}$ + cos $x_{2}$ )	14	0.9049	0	16.7	50
1/(exp $x_{1}$ + $x_{2}^{2}$ )² + exp( $x_{1}$ + cos $x_{2}$ )	14	0.8499	16.7	66.6	66.6

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Evaluating Kolmogorov–Arnold Networks for Scientific Discovery: A Simple Yet Effective Approach

Abstract

1. Introduction

2. Reproduction

3. KAN Preliminary

3.1. Steps to Generate Symbolic Output

4. Metrics

4.1. Performance Metrics

4.2. Mathematical Complexity

5. Results

5.1. Simple Functions

5.2. Analysis of Input Range

5.3. Complex Functions

6. Conclusion

References

MDPI Initiatives

Important Links

Subscribe