Prerpints.org logo
Preprint
Article

Assessment of Rapid Antigen Diagnostic Tests at Mass Events: Identifying Optimal Floor Plan Configurations for Enhanced Efficiency

Altmetrics

Downloads

111

Views

45

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Preprints on COVID-19 and SARS-CoV-2

Submitted:

15 August 2024

Posted:

16 August 2024

You are already at the latest version

Alerts
Abstract
Introduction: The COVID-19 pandemic highlighted the necessity for rapid, efficient testing at large-scale events. Developing rapid and efficient testing methods was critical, especially for events with a high risk of virus spread. The queueing theory offers a powerful tool to manage the flow of people through testing centers. This study uses the M/M/c model to examine how different floor plan configurations impact the efficiency of RADT testing centers. Aim of the study: This research applies queueing theory to optimize the Rapid Antigen Diagnostic Test (RADT) processes at mass gatherings. The study uses the M/M/c queueing model to evaluate the dynamics of RADT centers configured in U-shaped and straight-line layouts. The primary goal is to assess the feasibility of using RADTs efficiently at events and mass gathering entrances, aiming to enhance throughput and minimize wait times. Methodology: The study involved 500 healthy participants, managed by medical staff across a U-shaped and a straight floor plans. Agile management techniques were employed to enhance operational efficiency. The process stages included queue number issuance, registration, sample collection, sample mixing, and results dissemination. Results: Both floor plans enabled the completion of RADT screening in approximately 2 minutes per participant. The U-shaped layout slightly outperformed the straight-line setup in efficiency, demonstrating its effectiveness in optimizing the testing process. Conclusion: This study confirms the feasibility of implementing Rapid Antigen Diagnostic Test (RADT) processes at mass gatherings. It was found that the U-shaped floor plan configuration is particularly effective, indicating its potential suitability for future mass testing scenarios.
Keywords: 
Subject: Public Health and Healthcare  -   Health Policy and Services

1. Introduction:

Diagnostics and screening have been vital in responding to the COVID-19 pandemic; rapid and efficient testing methodologies were necessary for quick screening, particularly at large-scale events [1]. Rapid Antigen Diagnostic Tests (RADTs) for COVID-19 are designed to detect the presence of viral proteins (antigens) expressed by the SARS-CoV-2 virus in samples typically taken from a person’s nasal cavity using swabs [2]. RADTs can provide results quickly, often within 15 to 30 minutes, which makes them especially useful in settings requiring fast decision-making, such as airports, and mass gatherings [3]. RADTs are designed to detect specific antigens associated with the SARS-CoV-2 virus through a methodical process that begins with sample collection and ends with the display of results [4]. The procedure initiates with the collection of a nasopharyngeal swab, which involves obtaining respiratory epithelial cells from the posterior nasopharynx, where viral load is typically concentrated in infected individuals [5].
Following collection, the swab is immersed in a specialized reagent solution that serves multiple functions: it lyses viral particles to release their components, stabilizes viral proteins, and enhances the detectability of viral antigens [6].
The prepared sample is then applied to a test strip embedded with a nitrocellulose membrane pre-coated with antibodies that are specific to the SARS-CoV-2 antigens [6]. As the sample migrates along the strip by capillary action, any viral antigens present will bind to these immobilized antibodies [6].
The accuracy of RADTs for SARS-CoV-2 is quantitatively evaluated through two principal metrics: sensitivity and specificity [7]. Sensitivity, defined as the test’s ability to identify infected individuals (true positive rate) correctly, exhibits considerable variability among RADTs, with values ranging from approximately 50% to above 90% [7]. This range depends on several critical factors: the temporal proximity to symptom onset, which correlates with peak viral shedding, the viral load present in the collected specimen, and the precision of the sample collection technique employed [7].
Specificity, which measures the test’s ability to identify uninfected individuals (true negative rate) correctly, typically maintains a higher consistency across various RADT platforms, often exceeding 95% [7]. This high level of specificity indicates a low incidence of false positives, where the test erroneously suggests the presence of SARS-CoV-2 [8]. The robust specificity of RADTs underscores their utility in minimizing the likelihood of unnecessary quarantine or additional diagnostic procedures for individuals wrongly identified as infected [8].
A study by the University of Illinois at Urbana-Champaign (UIUC) encapsulates the importance of efficient testing infrastructure [9]. In the UIUC’s study, a discrete event simulation model was utilized to optimize the design of saliva-based COVID-19 testing stations [9]. This model was crucial in determining the optimal number of machines and operators required, as well as their efficient allocation at various workstations, based on daily testing volumes and resource availability [9].
A study conducted by Conor G. McAloon and colleagues, is instrumental in shaping the strategic deployment of RADTs at large-scale public events [2]. This research provides crucial insights into how RADTs can effectively screen attendees for SARS-CoV-2 infection, offering a practical solution for enhancing public health safety during mass gatherings [2]. The Conor G. McAloon et. al. study assessed the potential prevalence of infectious individuals under varying epidemiological scenarios by employing a simulation approach [2]. The findings reveal the conditions under which RADTs yield the most value, demonstrating their ability to significantly reduce the risk of virus transmission among large groups [2].
Our study is driven by employing the principles of queueing theory-based approach. [10]. By applying an analytical approach to queue dynamics, this study aims to substantially reduce waiting times, thereby accelerating the testing process and bolstering public health and safety during mass gatherings. Queueing theory, investigates into the interactions between the customers and those providing services (servers) [11]. The daily experience of waiting in line plays a critical role in managing the flow of customers, especially when resources are limited [11]. Queuing theory offers actionable insights by focusing on essential variables: the average number of customers in the system (L), the arrival rate (λ), and the time spent in the system (W) [12]. Central to this theory is Little’s Law, which facilitates the estimation of crucial metrics like waiting times and queue lengths from minimal input data [13].
Within the context of RADTs the M/M/c queueing model, a model that accounts for Poisson-distributed arrivals and exponentially distributed service times, with ‘c’ representing the number of service channels or testing stations [12], is of particular relevance. It intricately incorporates the complexities of multiple servers and setup times, allowing for detailed calculations of arrival rates, service rates, and the requisite number of servers to optimize system efficiency [14].
We designed a proposed U-shaped and straight-line floor plans to streamline operations, supported by systematic data collection and analytical assessment of different testing scenarios. Furthermore, advanced analytics and computational models have shown significant potential in predicting outcomes across various medical fields [15]. In this study, we developed a Python algorithm to rigorously test and validate the principles of queueing theory within the context of RADTs.

2. Method:

The research was designed to assess the processing speed of the RADTs in a large-scale setting. We chose the widely available Abbott Panbio COVID-19 RADTs (Abbott Laboratories, Chicago, Illinois, USA) [16] for this analysis. The aim was to determine how different floor plan arrangements could enhance the flow and expedite the processing of the test kits among a diverse group of event attendees.
The study involved 500 healthy participants aged between 17 and 55, including 250 females, with a mean age of 32 ± 8.4 years. Five staff from medical backgrounds operated on each stage. All individuals gave their informed consent before participating in the study. The choice of the sample size for this study was guided by the need to ensure robust statistical power and representation while balancing the practicalities of managing a large-scale testing event.
Notably, the participants were introduced at various flow rates throughout the day of the experiment, which provided a dynamic range of scenarios to simulate real-world conditions at mass events better.
The study was conducted in a controlled test center environment organized into two-floor plans. The first configuration adopted a U-shaped layout, whereas the second was designed in a straight-line format. Each configuration was segmented into five crucial stages as it is illustrated in Figure 1
Figure 2 depict the floor plans, emphasizing the strategic placement of the entrance kiosks, waiting areas, sample mixing zones, result kiosks, and exits, all contributing to a well-ordered and efficient testing process. All simulations and floor design were designed on software Autodesk Revit (Autodesk Revit, Autodesk, Newton, Massachusetts, USA) [17]
Upon entering the testing center, each subject was given a number sticker, promoting a sequential progression through the designated testing stages and enhancing procedural methods. Data collection was carefully managed using a shared Google Sheet (Google LLC, Menlo Park, California, United States) [18], where the study’s data collectors recorded timestamps for each stage for every participant, ensuring synchronized timekeeping and precise data collection. Participants were guided to specific seats for sample collection, followed by the immediate processing of samples in the adjacent mixing area to reduce wait times and streamline the process; after processing, results were relayed to the participants at a designated result kiosk; depending on these outcomes, participants were either directed to leave the center or provided additional instructions.
Data acquisition was thorough, capturing detailed records on arrival rates, service times, and the setup duration for each layout. Appropriate queuing models, specifically M/M/c, were implemented to assess system efficiency under various conditions, considering setup times.
Agile management techniques were employed, particularly in the distribution of tasks among the testing team. Each team member was responsible for a specific portion of the testing process, allowing for concentrated expertise and rapid execution of tasks.
In addition, Python algorithms (Python, Python Software Foundation, Wilmington, Delaware, USA) [19] were developed to test and validate the principles of queueing theory within the framework of RADTs.

3. Results

Statistical analysis employing a t-test revealed no statistical significant differences in the time spent at each stage between the two-floor plans, indicating a p-value > 0.05.
Furthermore, the mean completion time for the entire screening process was approximately 2 minutes for both layouts. Stages 4 (sample mixing) and 5 (result dissemination) were the most time-intensive, with sample mixing times ranging from 29 to 31 seconds and result stages varying from 46 to 62 seconds.
However, the average completion time for the U-shaped layout demonstrated a slight advantage over the straight-line configuration, with average completion times of 114 seconds compared to 122 seconds, respectively. Furthermore, for the U-shaped layout and the straight-line layout confidence intervals for the mean time spent at each stage were illustrated in Table 1. While the differences in time taken at each stage of the testing process between floor plans 1 and 2 were not substantial, the U-shaped layout demonstrated a slight edge in overall efficiency.
The detailed box plot visualizations in Figure 3 and Figure 4 provide insights into the time dynamics at each stage.
For floor plan 1, as depicted in Figure 3, the initial Number Collecting stage is characterized by its swiftness, with a median time of around 7 seconds and a tight interquartile range (IQR) from approximately 5 to 12 seconds, indicating consistent and rapid processing. The Registration stage follows, with a median of about 21 seconds and an IQR from 18 to 30 seconds, displaying stability without significant outliers. In the Sample Collection stage, although the median time remains efficient at around 20 seconds, the IQR widens substantially from 14 to 43 seconds, suggesting variable delays likely due to differing sample complexities. The Sample Mixing stage then shows further variability, with a median time of 29 seconds and an even broader IQR from 11 to 73 seconds, highlighting pronounced inconsistencies and procedural challenges. Finally, the Results stage exhibits the most significant fluctuation, with a median time of 45 seconds and an IQR from 38 to 63 seconds, plus outliers indicating sporadic delays, which could impact overall throughput.
Switching to floor plan 2 in Figure 4, the Number Collecting stage slightly improves with a median time of 6 seconds and an IQR from 4 to 14 seconds, though outliers above the upper whisker hint at occasional procedural hiccups. The Registration stage shows a slight decrease in median time to 18 seconds with a narrower IQR from 12 to 27 seconds, suggesting a more streamlined process without outliers. However, in the Sample Collection stage, while the median time drops to about 15 seconds, the presence of outliers above the upper whisker within an IQR of 10 to 29 seconds indicates occasional delays. The Sample Mixing stage continues to be a bottleneck with a median time near 29 seconds and an IQR stretching from 15 to 53 seconds, underscored by several outliers pointing to significant procedural variability. Lastly, although slower with a median time of 63 seconds, the Results stage shows a moderate IQR from 39 to 95 seconds but no outliers, reflecting inherent variability without extreme deviations.
This comparative analysis of the two floor plans underscores the potential for improvement that different spatial arrangements and procedural workflows can bring to the operational efficiency at each stage of the RADTs screening process. Figure 5 provide an analysis of the relationship between the number of lanes needed, the arrival rate of visitors and available processing time, each considering different parameters like the available processing time and number of target visitors. for instance, an arrival rate of 4 visitors per minute necessitates nine lanes if there is a 2 hours available processing time. As shown in the Figure 5 as more time becomes available, the number of lanes required and the arrival rate decrease. This shows a sharp decline in resource needs as more time allows for more efficient processing—fewer lanes are necessary to handle the same number of visitors over an extended period.
As the arrival rate (λ) is defined as the number of visitors arriving per unit of time, in our study the average was around ten visitors per minute. The service rate (μ), which represents the capacity of each testing lane to process visitors, is set based on the time it takes for each visitor to complete the screening process since the whole test duration from the average of both layouts was around two minutes per visitor, which gives a service rate of around 0.5 visitors per minute per lane.
Traffic intensity (ρ) is then calculated using the formula:
ρ = λ ( c × μ )             Equation 1   [ 20 ]
where c represents the number of lanes or servers available.
The formula measures the system’s workload, quantifying the fraction of time servers are expected to be busy.
When ρ<1, it indicates that the system has enough capacity to handle the incoming rate without queues growing indefinitely over time.
When ρ=1, it suggests that the system is at full capacity, and this is a critical threshold where any increase in arrival rate or decrease in service rate could lead to queues growing without bounds.
When ρ>1, the system is overloaded, and queues will continue to grow.
To avoid excessive queuing and ensure efficiency, the number of lanes needed (c) is determined by the equation
c = λ μ             Equation 2   [ 13 ]
For the given arrival rate of 10 visitors per minute and a service rate of 0.5, approximately 20 lanes are required to handle the demand effectively. Furthermore, the average waiting time in the queue (Wq) for an M/M/c queue where the arrival rate is less than the service capacity (λ<cμ) is estimated by the Pollaczek–Khinchine formula:
W q = ( ρ 2 ) ( μ × ( 1 − ρ ) )             Equation 3   [ 14 ]
This mathematical framework supports the design and operational strategies needed to manage the testing process efficiently at the event.
In more complex models where arrival rates (λ) and service rates (μ) are stochastic (randomly varying), it would be possible to use advanced queuing theory models like M/G/1 or G/M/1, which involve probabilistic frameworks and can result in non-linear relationships [20].
Consider a case where service efficiency decreases as more lanes are added due to coordination overhead or resource sharing. The equation will be:
c n e w = λ μ − α c o l d               Equation 4   [ 20 ]
where α represents the rate of efficiency loss per additional lane. This equation is no longer linear and requires solving for c in terms of λ and μ considering α.
Furthermore, differential equations can be used if the system has more varying factors to model the testing process, providing a dynamic framework for understanding how individuals move through the system and allowing for precise calculation of the number of testing lanes required to manage the flow efficiently. Two equations for unprocessed individuals describe the system as the following:
d u d t = a − λ U             Equation 5   [ 21 ]
U(t) represents the number of individuals at a time ‘t’ who have entered the testing center but have yet to be tested. The term ‘a’ stands for the rate of new arrivals at the testing center, and ‘λ’ is the effective processing rate, which indicates how quickly individuals are moved from waiting to being tested. For processed individuals as the following
d p d t = λ U − μ P                 Equation 6   [ 21 ]
Equation 6 models the rate of change of processed individuals. In this context, ‘P(t)’ denotes the number of individuals at time ‘t’ who have completed the testing process. The term ‘λU’ here describes the transition rate of individuals from untested to tested, which depends on both the effective processing rate ‘λ’ and the current number of untested individuals ‘U(t).’ The term ‘μP’ potentially includes post-test processing rates, such as the time required to deliver results to individuals or to prepare individuals for exit from the testing facility.
The processing rate λ, a key parameter in our model, is directly proportional to the number of operational lanes. This relationship is given by λ=0.5×c, where each lane contributes 0.5 tests per minute to the processing capability. To ensure the system remains efficient and does not become overwhelmed, the condition where U(t) would indefinitely increase λ and must at least match the arrival rate a is crucial. Thus, setting λ≥a and knowing λ=0.5×c informs us that c≥2a. This means the number of lanes c must be double the peak arrival rate to maintain a balance where the testing capacity efficiently meets or exceeds demand.
For practical application, if the peak arrival rate a is, for example, ten visitors per minute, the calculation c≥2×10 determines that at least 20 lanes are necessary. This calculation ensures that 20 lanes are the minimum required to process up to 10 visitors per minute without forming a backlog. This approach is crucial for managing large-scale testing facilities effectively, particularly in scenarios like airports or event entrances where timely processing is critical.

4. Discussion:

The t-test results indicated no significant differences in the processing times between the two floor plans (p > 0.05), suggesting that the different spatial configurations did not impact the efficiency of individual process stages significantly. However, a granular look into the data revealed that these two setups’ overall flow and operational logistics influenced the cumulative testing time, although slightly.
Both floor plans achieved an approximate mean completion time of 2 minutes for the entire screening process. Notably, stages 4 (Sample Mixing) and 5 (Results Dissemination) consistently required more time across both setups, with observed variations likely influenced by manual handling and processing inherent to these stages. Despite similar median times, the U-shaped layout demonstrated a marginally faster average completion time (114 seconds) compared to the straight-line setup (122 seconds). This slight advantage is attributed to the U-shaped design facilitating better movement and less crowding, enhancing overall flow efficiency.
The 95% confidence intervals for the mean times at each stage were generally narrower in the U-shaped layout, indicating less variability and greater consistency in processing times compared to the straight-line configuration.
The arrival rate (λ), averaged about ten visitors per minute. In contrast, the service rate (μ), determined based on the average duration it took for each visitor to complete the screening process—approximately two minutes per visitor, yielding a service rate of 0.5 visitors per minute per lane.
Regarding the number of lanes, we assessed the system’s capacity to manage incoming visitor rates without excessive queuing. To ensure efficiency and avoid excessive wait times, the model suggested that approximately 9 lanes are necessary to handle the given arrival rate effectively. This was derived from the equation c = λ / μ, tailored to maintain an efficient flow within the testing facility.
For advanced models alike M/G/1 or G/M/1 for non-linear relationships, these models accommodate scenarios where the efficiency decreases as more lanes are added due to coordination overhead or resource sharing, illustrated by the modified equation cnew = λ / (μ – α cold), where α represents the rate of efficiency loss per additional lane.
Future studies could build upon this research by exploring additional variables that may affect the efficiency of RDATs testing centers, such as staffing levels, participant compliance, and the use of automated systems to reduce manual handling times.

5. Conclusion:

This study has successfully validated the feasibility of employing RADTs in large-scale public settings. Our findings highlight that meticulous management of queue dynamics—particularly the correlation between the number of testing lanes and the arrival rates of individuals—is crucial for optimizing the efficiency of the testing process. Notably, the U-shaped floor plan configuration demonstrated a notable advantage in overall process efficiency compared to the straight-line layout, underscoring the significant impact that spatial arrangements can have on the effectiveness of testing procedures at mass events.
Through a detailed analysis of these dynamics, our research not only substantiates the practicality of utilizing RADTs in scenarios necessitating swift decision-making but also informs the strategic allocation of resources to maximize testing throughput. These insights are essential for effectively designing and implementing health safety protocols at large-scale gatherings, ensuring rapid and efficient screening processes.

References

  1. R. W. Peeling, D. L. Heymann, Y.-Y. Teo and P. J. Garcia, “Diagnostics for COVID-19: moving from pandemic response to control,” The Lancet (British edition), vol. 399, no. 10326, 2022. [CrossRef]
  2. C. G. McAloon, D. Dahly, C. Walsh, P. Wall, B. Smyth, S. J. More and C. Teljeur, “Potential Application of SARS-CoV-2 Rapid Antigen Diagnostic Tests for the Detection of Infectious Individuals Attending Mass Gatherings – A Simulation Study,” Frontiers in Epidemiology, vol. 2, 2022. [CrossRef]
  3. R. W. Peeling, P. L. Olliaro, D. I. Boeras and N. Fongwen, “Scaling up COVID-19 rapid antigen tests: promises and challenges,” The Lancet infectious diseases, vol. 21, no. 9, 2021. [CrossRef]
  4. C. Wertenauer, G. Brenner Michael, A. Dressel, C. Pfeifer, U. Hauser, E. Wieland, C. Mayer, C. Mutschmann, M. Roskos, H.-J. Wertenauer, A. P. Moissl, S. Lorkowski and W. März, “Diagnostic Performance of Rapid Antigen Testing for SARS-CoV-2: The COVid-19 AntiGen (COVAG) study,” Frontiers in medicine, vol. 9, 3/2022. [CrossRef]
  5. S. Pondaven-Letourmy, F. Alvin, Y. Boumghit and F. Simon, “How to perform a nasopharyngeal swab in adults and children in the COVID-19 era,” European annals of otorhinolaryngology, head and neck diseases, vol. 137, no. 4, 9/ 2020. [CrossRef]
  6. O. Filchakova, D. Dossym, A. Ilyas, T. Kuanysheva, A. Abdizhamil and R. Bukasov, “Review of COVID-19 testing and diagnostic methods,” Talanta (Oxford), vol. 244, 07/ 2022. [CrossRef]
  7. J.-W. Xie, Y. He, Y.-W. Zheng, M. Wang, Y. Lin and L.-R. Lin, “Diagnostic accuracy of rapid antigen test for SARS-CoV-2: A systematic review and meta-analysis of 166,943 suspected COVID-19 patients,” Microbiological research, vol. 265, 12/2022. [CrossRef]
  8. J. P. Skittrall, M. Wilson, A. A. Smielewska, S. Parmar, M. D. Fortune, D. Sparkes, M. D. Curran, H. Zhang and H. Jalal, “Specificity and positive predictive value of SARS-CoV-2 nucleic acid amplification testing in a low-prevalence setting,” Clinical microbiology and infection, vol. 27, no. 3, 03/2021. [CrossRef]
  9. M. Saidani, H. Kim and J. Kim, “Designing optimal COVID-19 testing stations locally: A discrete event simulation model applied on a university campus,” PloS one,, vol. 16, no. 6, 06/2021. [CrossRef]
  10. R. Kumar, Modeling and Simulation Concepts, India : Laxmi Publications Private Limited, 12/2020.
  11. L. V. Green, Patient Flow: Reducing Delay in Healthcare Delivery, New York : Springer , 2006.
  12. J. S. Smith and D. T. Sturrock, Simio and Simulation: Modeling, Analysis, Applications, Sewickley, Pennsylvania.: Simio LLC, 2021.
  13. J. D. Little and S. C. Graves, Building Intuition: Insights from Basic Operations Management Models and Principles, Massachusetts: Springer , 2008.
  14. J. F. Shortle, J. M. Thompson, D. Gross and C. M. Harris, Fundamentals of Queueing Theory, 4th ed., Hoboken, NJ, USA: Wiley, 2018.
  15. A. Turki and E. Raml, “Enhancing Pediatric Adnexal Torsion Diagnosis: Prediction Method Utilizing Machine Learning Techniques,” Children (Basel), vol. 10, no. 10, 09/2023. [CrossRef]
  16. Abbott, “COVID-19 Ag Rapid Test Device,” 2021. [Online]. Available: https://dam.abbott.com/en-gb/panbio/120007883-v1-Panbio-COVID-19-Ag-Nasal-AsymptomaticSe.pdf. [Accessed 05 2024].
  17. “Autodesk Revit: BIM software to design and make anything,” Autodesk , [Online]. Available: https://www.autodesk.com/products/revit/overview?term=1-YEAR&tab=subscription. [Accessed May 2024].
  18. “Google Sheet,” Google LLC, [Online]. Available: https://docs.google.com/spreadsheets/u/0/?usp=sheets_ald. [Accessed May 2025].
  19. Python, [Online]. Available: https://www.python.org/psf-landing/. [Accessed May 2024].
  20. I. I. Gerontidis and V. V. Kalashnikov, Mathematical Methods in Queuing Theory., vol. 44, 1995. [CrossRef]
  21. A. M. Haghighi and D. Mishev, Difference and Differential Equations with Applications in Queueing Theory, John Wiley & Sons, Inc, 2013.
  22. J. L. Wiler, E. Bolandifar, R. T. Griffey, R. F. Poirier and T. Olsen, An emergency department patient flow model based on queueing theory principles, vol. 20, 2013. [CrossRef]
  23. D. S. Mouliou, The Deceptive COVID-19: Lessons from Common Molecular Diagnostics and a Novel Plan for the Prevention of the Next Pandemic, vol. 11, 2023. [CrossRef]
  24. N. Health, “Public Health – NSW COVID-19 Response,” April 2023. [Online]. Available: https://www.health.nsw.gov.au/Infectious/covid-19/evidence-hub/Publications/phr-report.pdf. [Accessed May 2024].
  25. “Overview of Testing for SARS-CoV-2, the virus that causes COVID-19,” CDC, March 2024. [Online]. Available: https://www.cdc.gov/coronavirus/2019-ncov/hcp/testing-overview.html. [Accessed May 2024].
  26. N. Castelletti and e. al, “The interplay of viral loads, clinical presentation, and serological responses in SARS-CoV-2 – Results from a prospective cohort of outpatient COVID-19 cases,” Virology , vol. 569, 2022.
  27. M. Alqahtani, A. Abdulrahman, F. Mustafa, A. I. Alawadhi, B. Alalawi and S. I. Mallah, “Evaluation of Rapid Antigen Tests Using Nasal Samples to Diagnose SARS-CoV-2 in Symptomatic Patients,” Frontiers in public health, vol. 9, 2022.
  28. K. A. Walsh, N. Broderick, S. Ahern, C. G. Fawsitt, K. M. O’Brien, M. Carrigan, P. Harrington, M. O’Neill, S. M. Smith, S. Spillane, C. Teljeur and M. Ryan, “Effectiveness of rapid antigen testing for screening of asymptomatic individuals to limit the transmission of SARS-CoV-2: A rapid review,” Reviews in medical virology, vol. 32, no. 5, 9/2022.
  29. A. Khan, Y. Alsofayan, A. Alahmari, J. Alowais, A. Algwizani, H. Alserehi, A. Assiri and H. Jokhdar, “COVID-19 in Saudi Arabia: the national health response,” Eastern Mediterranean health journal, vol. 27, no. 11, 12/2021. [CrossRef]
Preprints 115341 g001
Figure 1. Test Five Stages.
Figure 1. Test Five Stages.
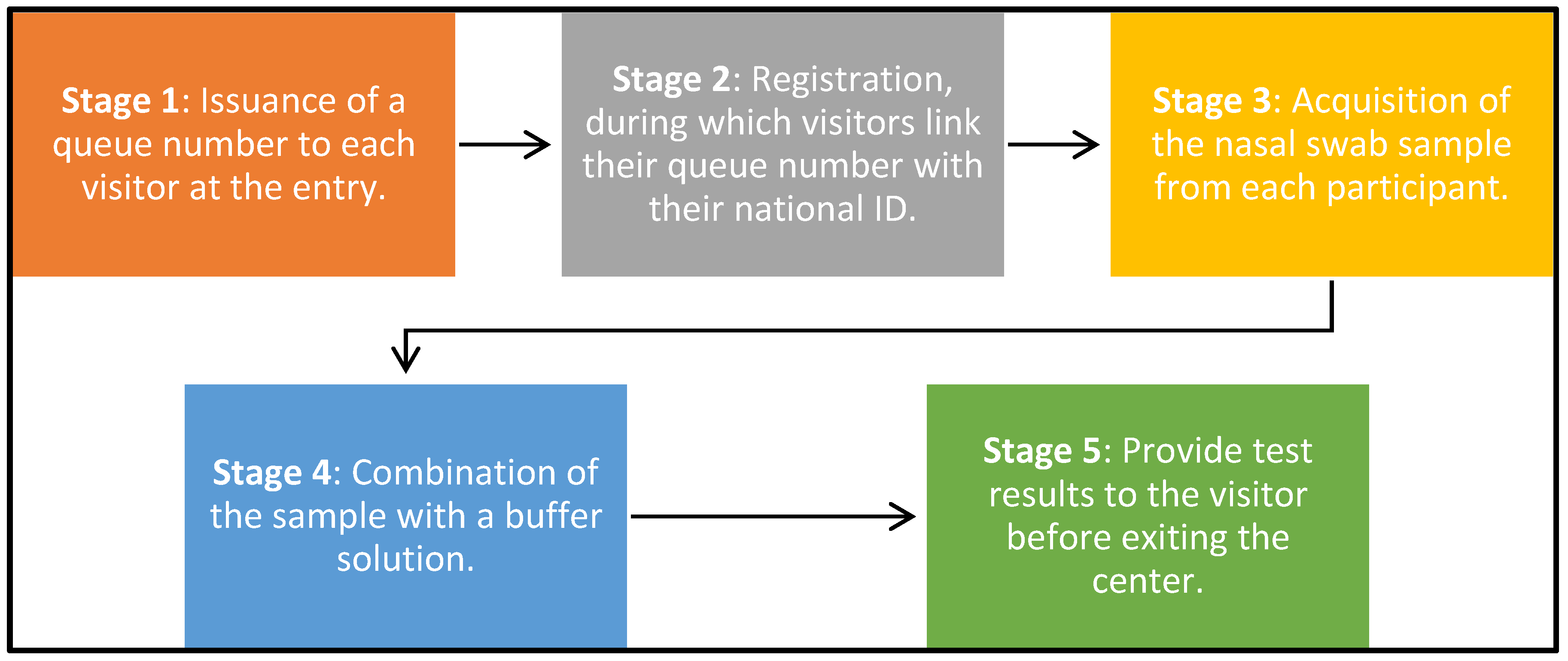
Preprints 115341 g001
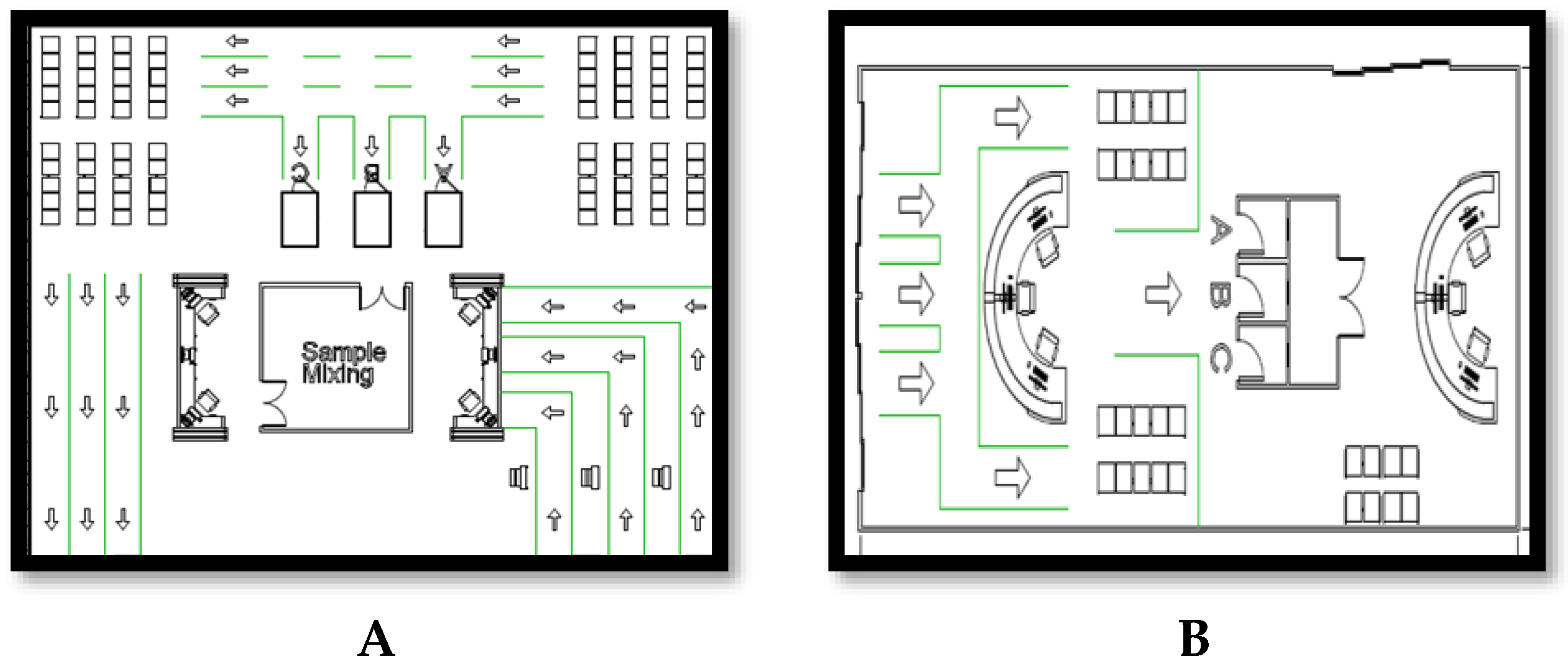
Preprints 115341 g002
Figure 2. A: Floor Plan 1(U-Shape), B: Floor Plan 2 (Straight-Line).
Figure 2. A: Floor Plan 1(U-Shape), B: Floor Plan 2 (Straight-Line).
Preprints 115341 g002
Preprints 115341 g003
Figure 3. Box Plot for Time Spent Across the Stages in Floor Plan 1 (U-Shape).
Figure 3. Box Plot for Time Spent Across the Stages in Floor Plan 1 (U-Shape).
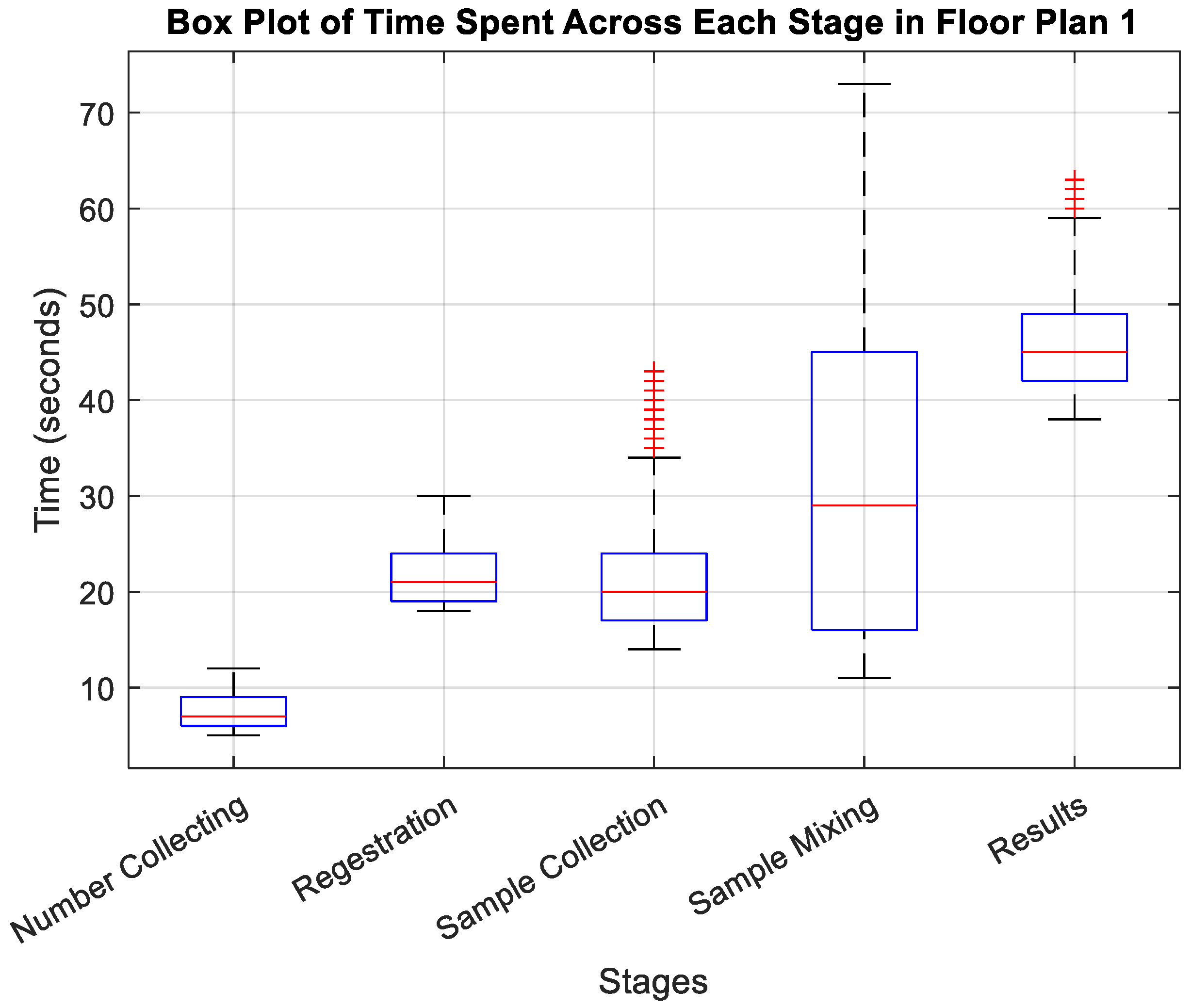
Preprints 115341 g003
Preprints 115341 g004
Figure 4. Box Plot for Time Spent Across the Stages in Floor Plan 2 (Straight-Line).
Figure 4. Box Plot for Time Spent Across the Stages in Floor Plan 2 (Straight-Line).
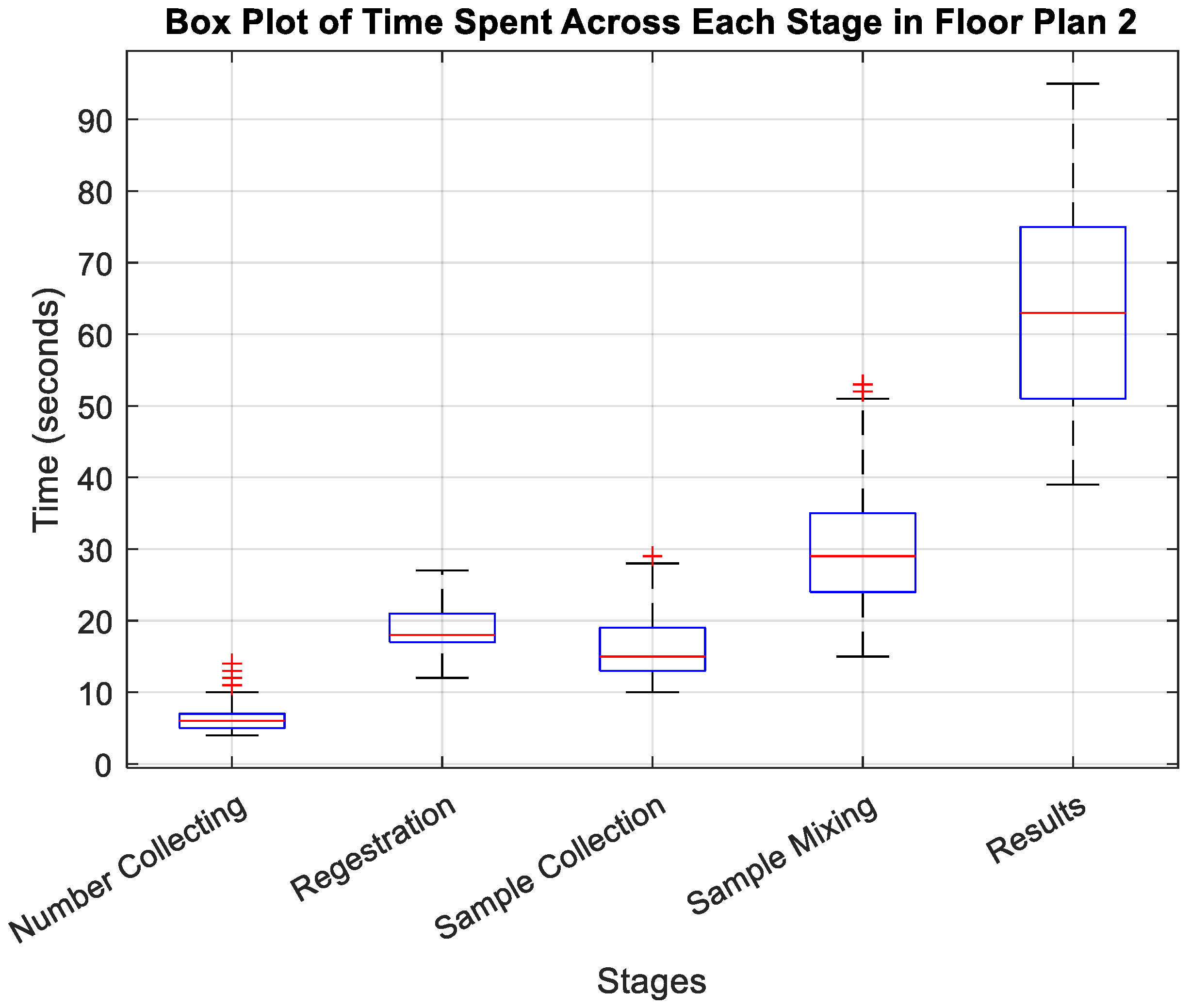
Preprints 115341 g004
Preprints 115341 g005
Figure 5. Relationship between number of lanes needed and arrival rate for dynamic available time processing.
Figure 5. Relationship between number of lanes needed and arrival rate for dynamic available time processing.
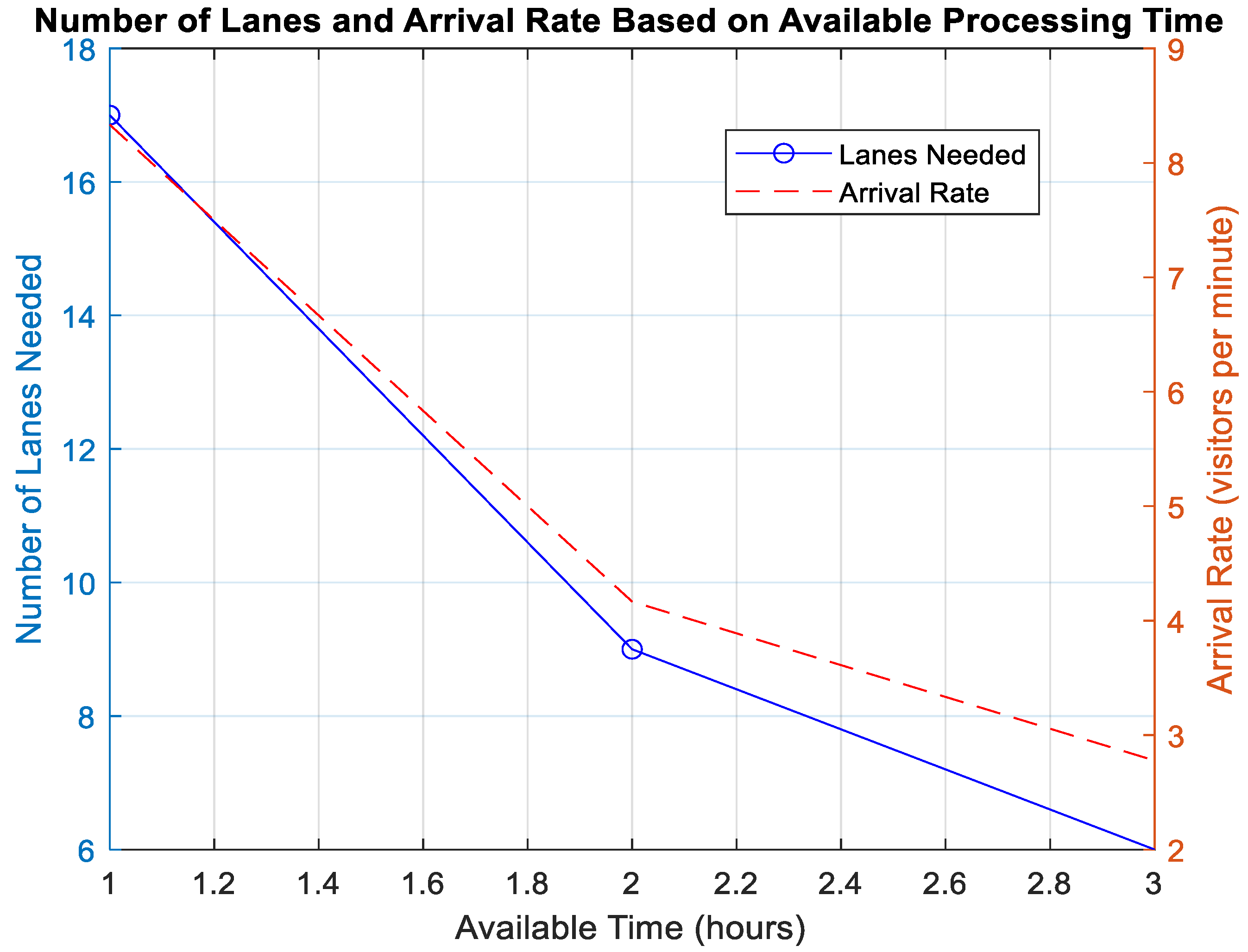
Preprints 115341 g005
Table 1. U-shape and straight-line floor plans stages statistics.
Table 1. U-shape and straight-line floor plans stages statistics.
Stage Process U-Shape Stright-Line
Mean Time (second) Standard Deviation
(second)		 95%
CI
(second)		 Mean Time (second) Standard Deviation
(second)		 95%
CI
(second)
Stage 1 Que Number Collecting 7.8 2.0 7.62 to 7.98 6.8 2.2 6.61 to 6.99
Stage 2 Registration 21.9 3.3 21.61 to 22.19 18.6 3.1 18.33 to 18.87
Stage 3 Sample Collection 21.1 5.4 20.63 to 21.57 16.5 4.6 16.10 to 16.90
Stage 4 Sample Mixing 31.4 15.7 30.02 to 32.78 29.8 8.4 29.06 to 30.54
Stage 5 Result 46.1 5.1 45.65 to 46.55 62.6 14.8 61.30 to 63.90
Average Total Time 114.2 seconds 122.7 seconds
Total Time Standard Deviation 17.8 Seconds 17.6 Seconds
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated