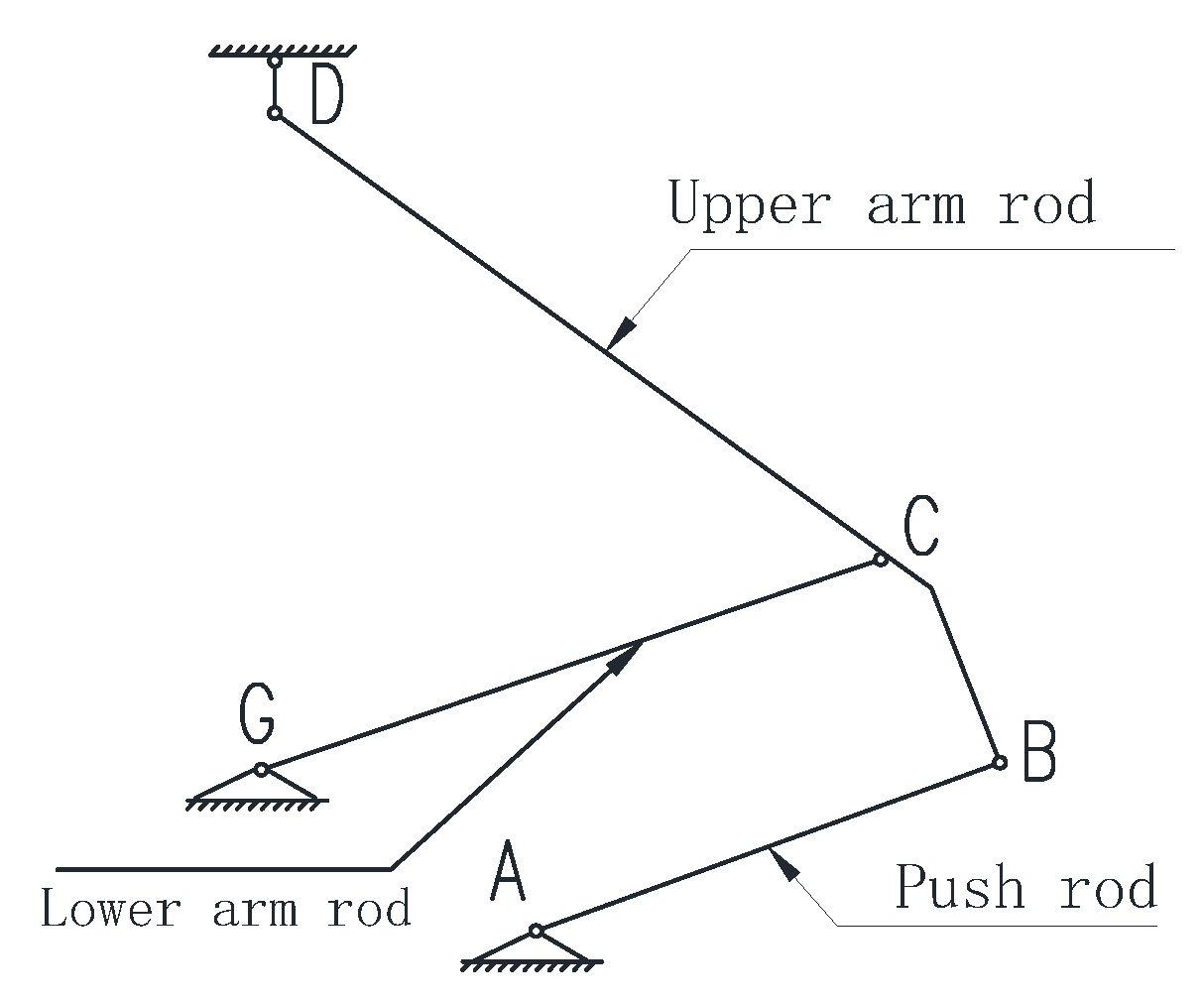
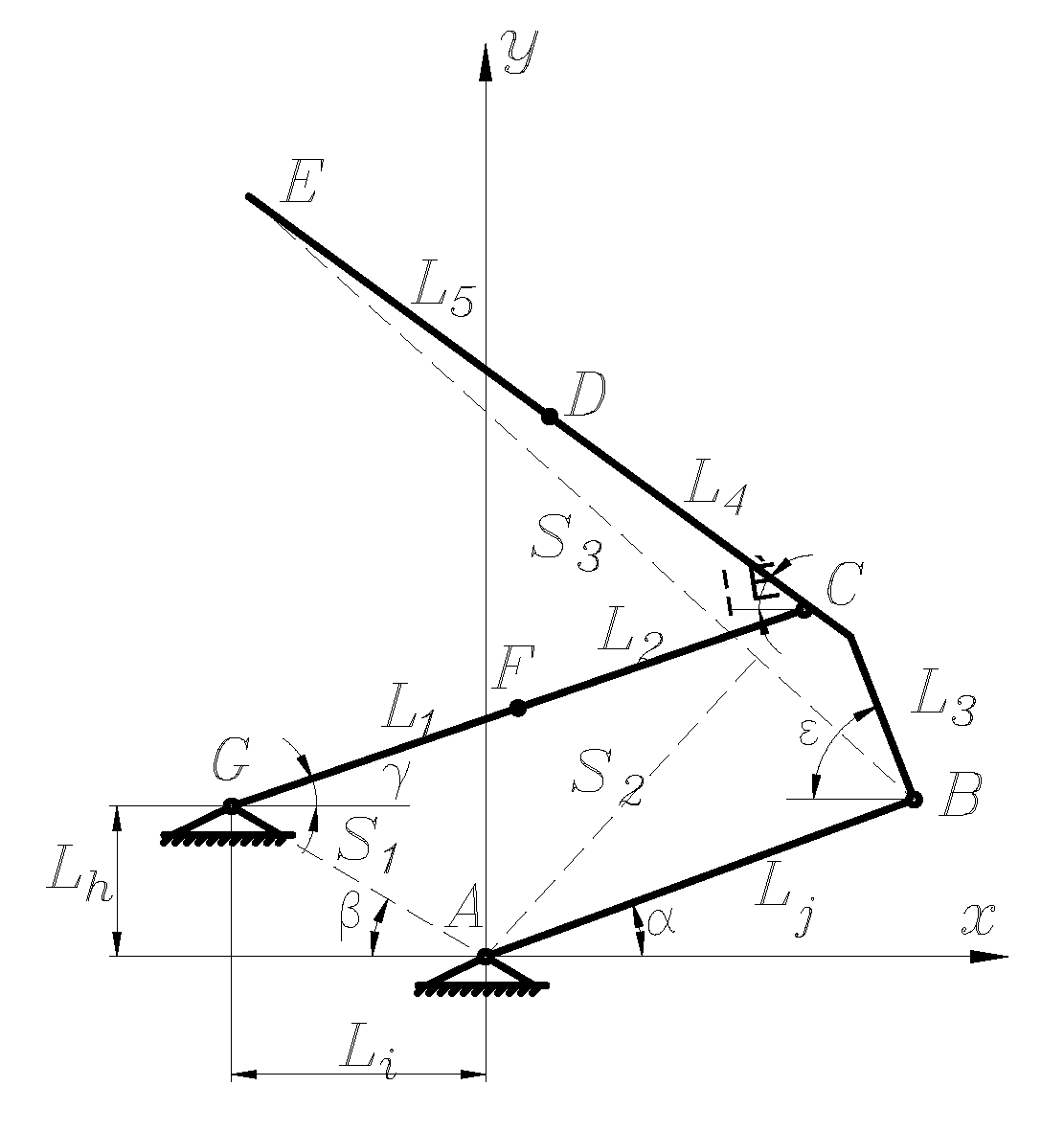
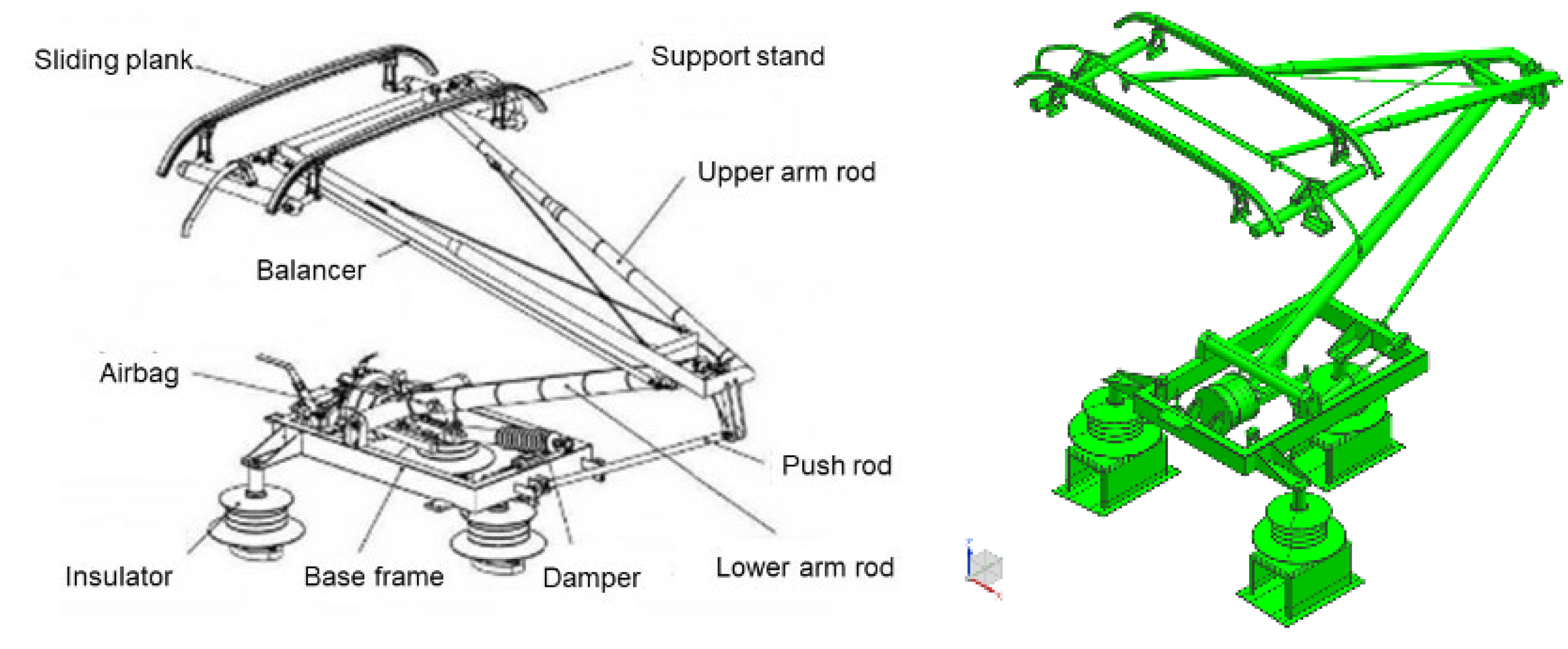
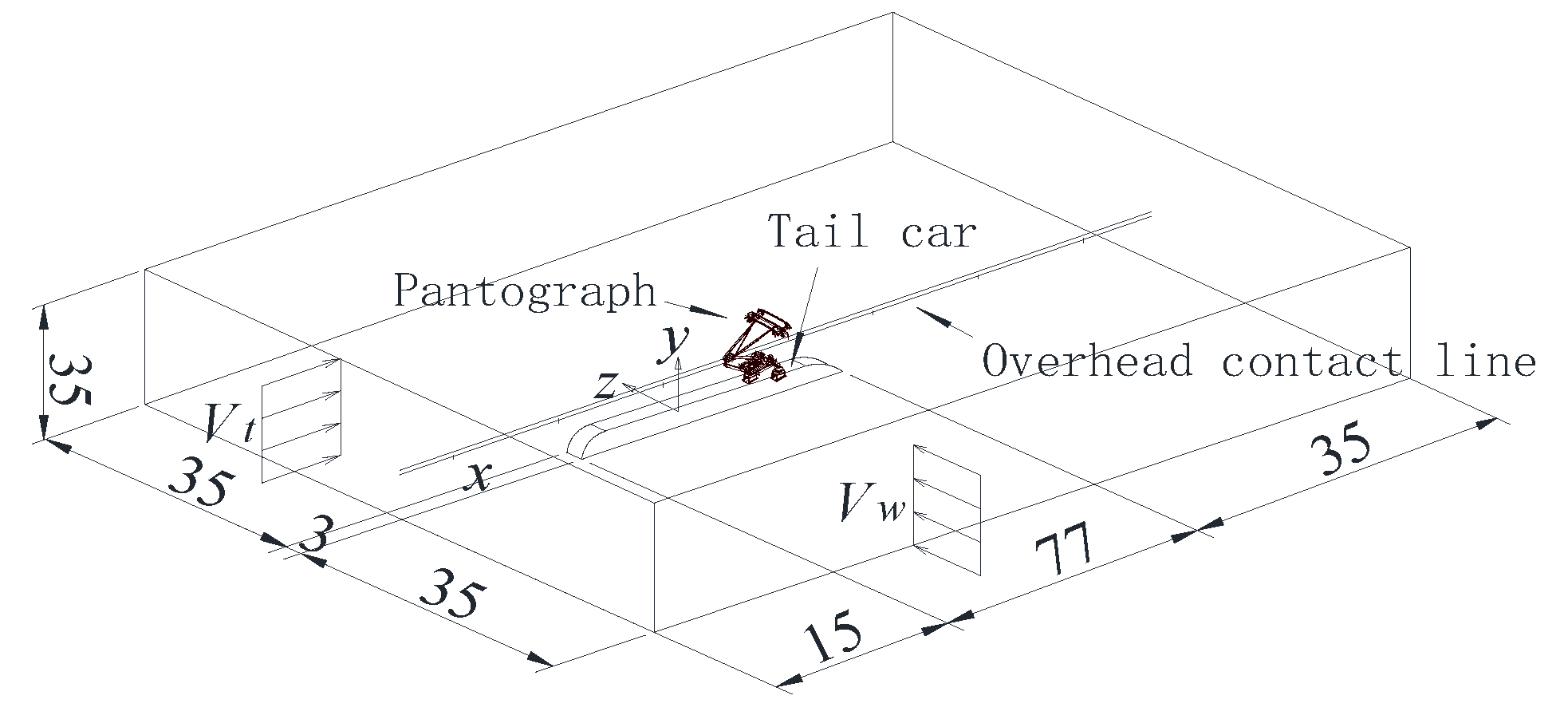
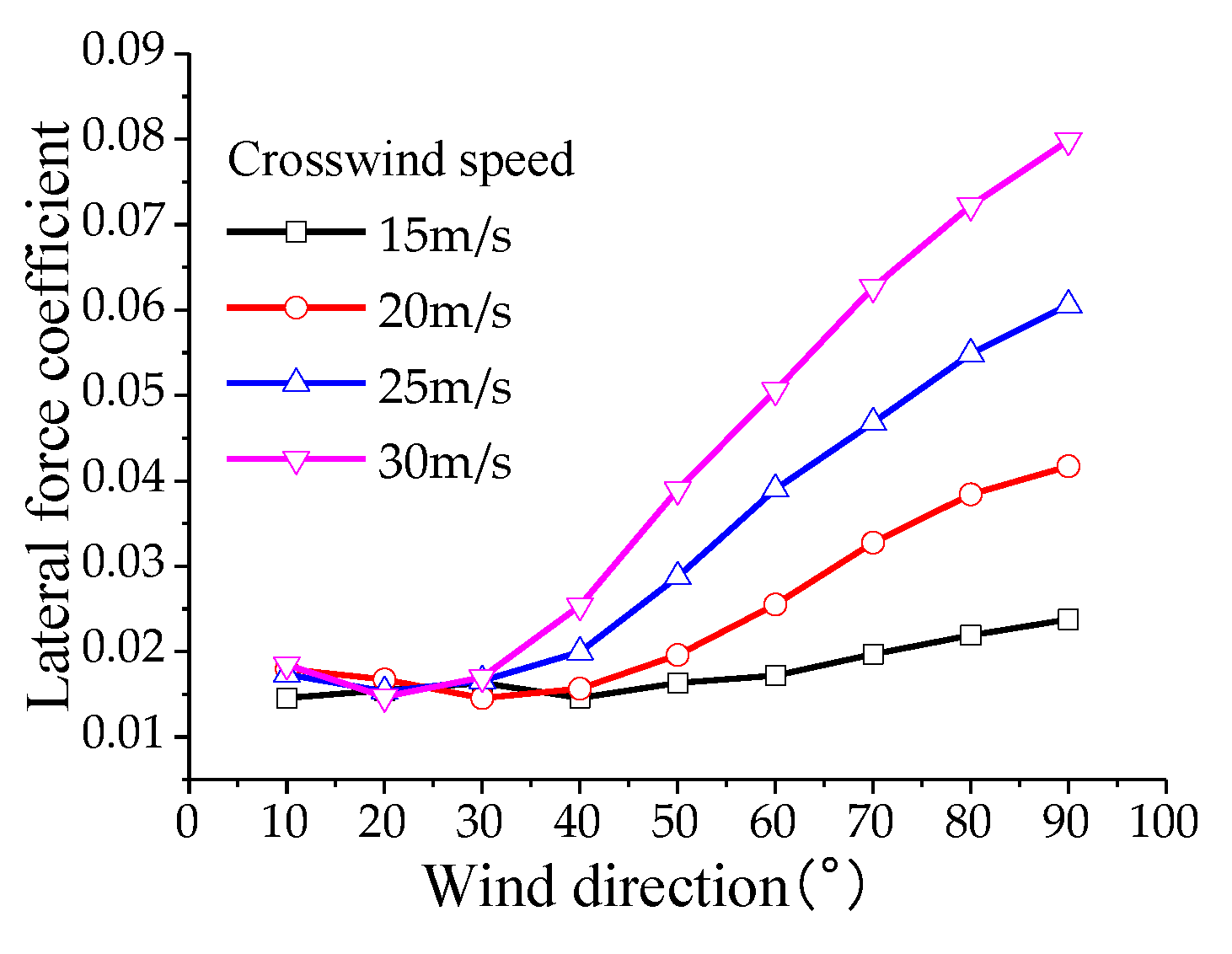
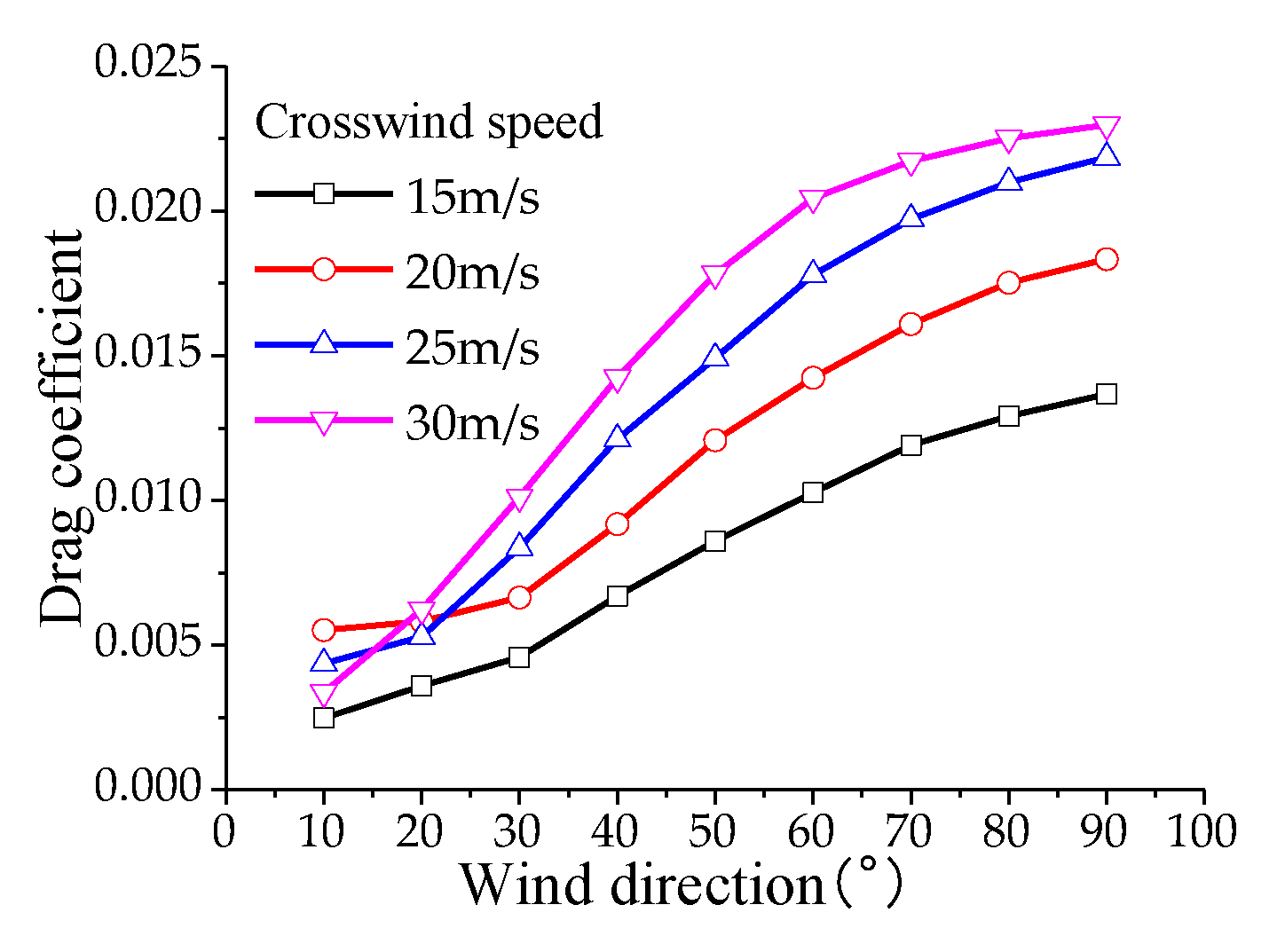
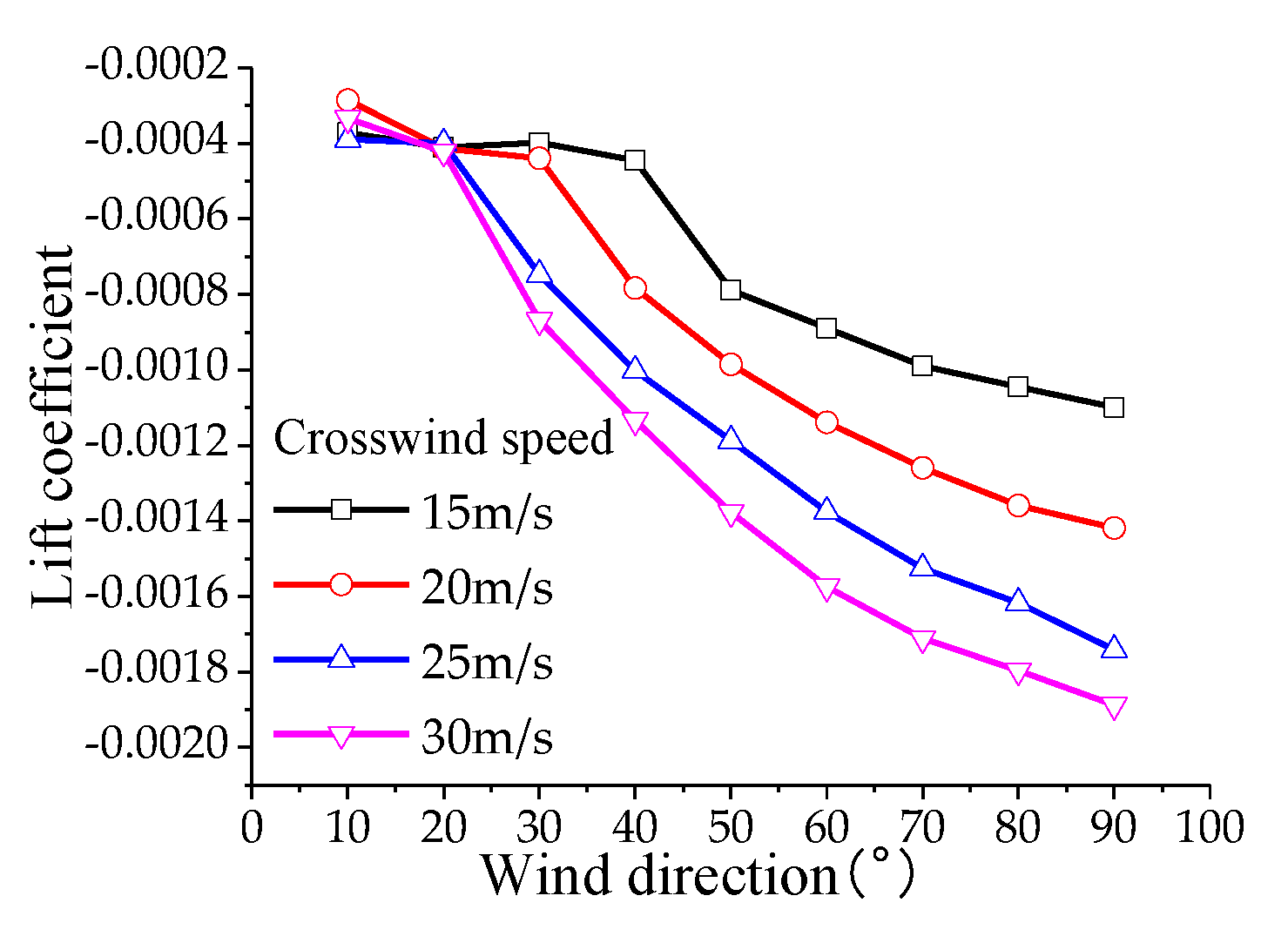
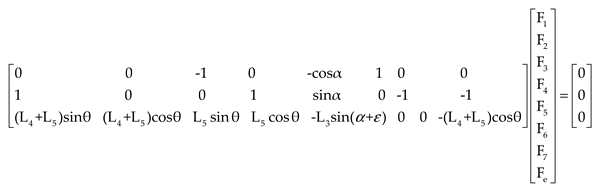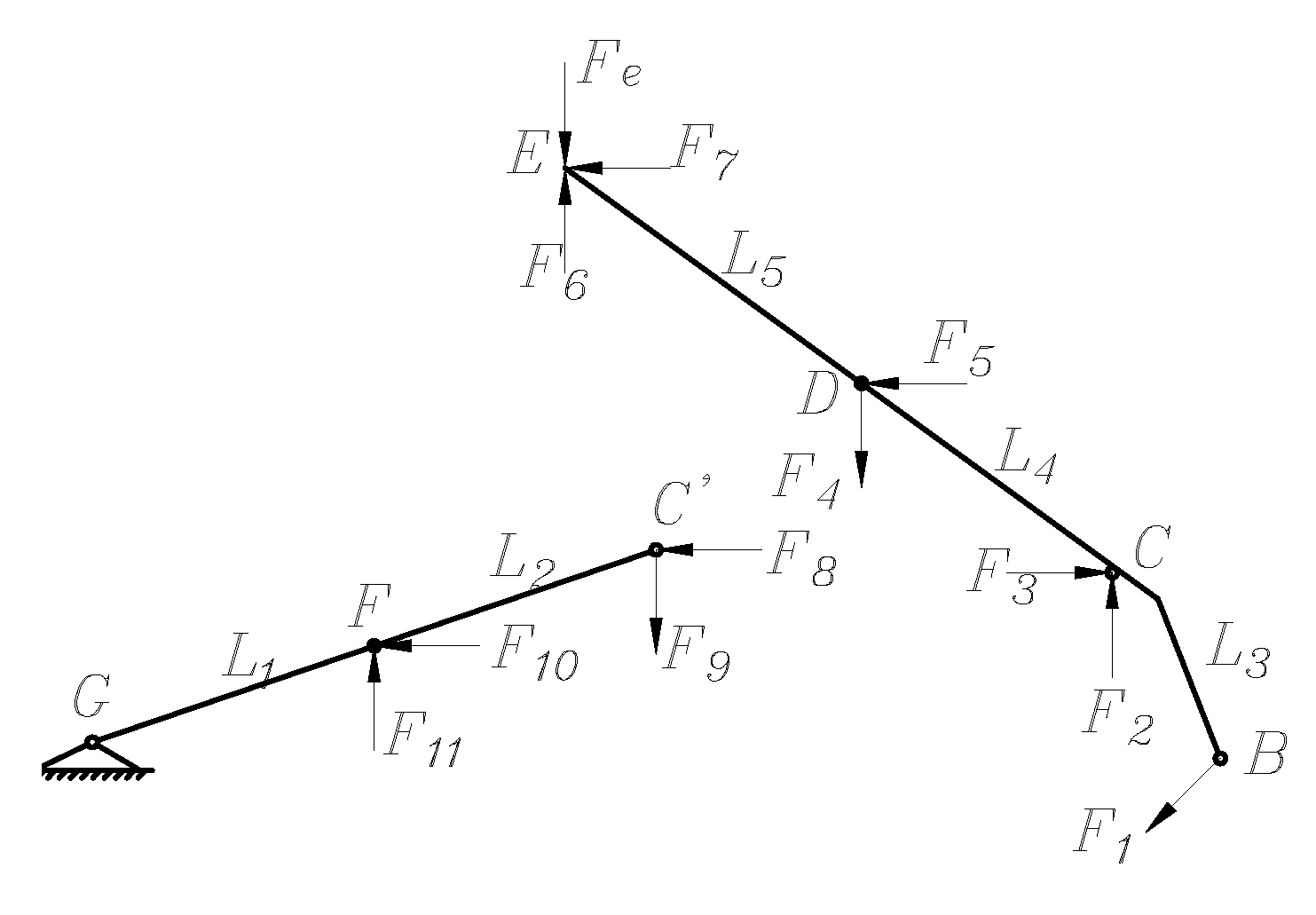Research on the Uplift Characteristics of Pantographs of High-Speed Trains Under Crosswind Conditions

Preprint

Article

Research on the Uplift Characteristics of Pantographs of High-Speed Trains Under Crosswind Conditions

Altmetrics

Downloads

120

Views

Comments

A peer-reviewed article of this preprint also exists.

Meng Zhao,

Yaning Duan,Xingbo Lan,

Zile Jia^*

Meng Zhao,

Yaning Duan,Xingbo Lan,

Zile Jia^*

This version is not peer-reviewed

Submitted:

15 August 2024

Posted:

19 August 2024

You are already at the latest version

Alerts

Abstract

Through the geometric relationships and force analysis of the main components of the panto-graph on high-speed trains, coefficients of aerodynamic forces and lift transmission between the pantograph and main components under crosswind conditions were derived. Based on the aer-odynamic forces acting on the pantograph at different crosswind speeds, wind angles, and oper-ating speeds, the aerodynamic lift of the pantograph and main components was ultimately de-termined. The results indicate that the aerodynamic lift of the pantograph is mainly distributed on the bow structure, with the aerodynamic lift of the upper frame all being negative values, while the absolute value of the aerodynamic lift of the lower arm rod is the smallest. The oper-ating speed of the pantograph and the wind angle of the crosswind have a significant impact on the aerodynamic lift of the main components, while the impact of the crosswind speed is rela-tively small. At the same operating speed of the pantograph, the lower the corresponding crosswind speed, the smaller the aerodynamic lift of the pantograph. The aerodynamic lift of the pantograph tends to decrease gradually with the increase of crosswind speed, and the impact of crosswind speed decreases gradually with the increase of pantograph operating speed. A com-prehensive relationship formula between the aerodynamic lift of the pantograph and the oper-ating speed, crosswind speed, and wind angle is obtained, and the empirical formula for the contact force of the bow net and train operating speed is modified. The research results are of great significance and value for the study and application of lift forces on pantographs under crosswind conditions.

Keywords:

Subject: Engineering - Transportation Science and Technology

1. Introduction

The good quality of current collection by the pantograph is an important factor in ensuring the stable operation of high-speed trains. Research on the uplift characteristics of pantographs under crosswind conditions has been advanced through significant contributions from scientists worldwide. Initial studies, such as those by Brandani, V. [1] laid the groundwork by identifying the increased uplift forces caused by crosswinds, leading to further investigations using wind tunnel models by Sanquer, Stéphane et al [2]. European researchers have since focused on integrating aerodynamic analyses with overall train stability and control, contributing to the development of robust pantograph designs that maintain reliable contact with the catenary under varying wind conditions [3]. Meanwhile, American scientists have emphasized advanced CFD modeling and experimental studies, which have deepened the understanding of complex airflow patterns and dynamic responses of pantographs [4]. These global efforts have collectively improved the safety and efficiency of high-speed rail systems, although challenges remain, particularly in addressing extreme crosswind conditions as train speeds continue to rise. This study seeks to build on these global contributions by offering a comprehensive analysis of pantograph uplift under crosswind conditions, aiming to enhance the overall understanding and mitigation strategies.

The contact force of the bow net includes two parts: static lift force and aerodynamic lift force generated by the pantograph, collectively referred to as the dynamic contact force of the bow net. The static lift force is generally around 70N, typically not exceeding 90N [5,6,7]. During high-speed operation, the contact pressure between the bow net and the pantograph is the sum of the static lift force and the aerodynamic lift force generated by the pantograph, known as the dynamic contact force of the bow net. During the sliding contact between the pantograph and the contact line, if the dynamic contact force is too small, the contact resistance increases, leading to phenomena such as pantograph lifting and arcing during operation [8]. Conversely, if the contact pressure is too high, local grooves may be formed on the sliding block, resulting in serious accidents such as contact wire bouncing and pantograph scraping. Therefore, it is necessary to ensure reasonable aerodynamic lift force for the pantograph during operation, which requires the pantograph itself to have good aerodynamic characteristics [9,10,11]. A large amount of research has been conducted based on the dynamics of the bow net, but there is relatively little research on the impact of aerodynamic forces on the contact force of the bow net, especially without considering the change in aerodynamic effects of the pantograph under crosswind conditions [12,13,14,15]. Furthermore, as the train speed increases, the impact of aerodynamic forces cannot be ignored. Combined with the effect of crosswind, the law of aerodynamic lift force of the pantograph also changes. Therefore, further in-depth analysis is needed.

When the pantograph operates at high speed, the average value

p_{v}

of the experimental bow net contact force can be obtained through

p_{v} = p_{1} + p_{2} = 0.00097 V^{2} + 70

, where the static contact force

p_{2}

of the bow net is 70N, as shown in Figure 1, and

p_{1}

represents the aerodynamic lift force of the pantograph [16]. Under the influence of crosswind, the aerodynamic load of the pantograph changes with the speed of the train, wind speed, and wind angle, resulting in a change in aerodynamic lift force. Therefore, it is not appropriate to simply use the train speed as the criterion for determining the aerodynamic lift force. Consequently, an in-depth study of the aerodynamic lift force of the pantograph under crosswind conditions is necessary. In this paper, by establishing a model of the aerodynamic lift force of the pantograph under crosswind conditions and combining it with numerical simulation methods of aerodynamic forces acting on the pantograph, the lift force of the pantograph and its main components are analyzed. The results have certain engineering practical value.

2. Pantograph Aerodynamic Lift Calculation Model

The pantograph prototype consists of components such as the sliding block, bracket, balance lever, upper arm rod, hinge seat, lower arm rod, push rod, and base frame, all considered rigid bodies. In the analysis of pantograph lift force, the main components of the pantograph are selected, and the geometric model of the pantograph is simplified. It can be observed from the physical model that the pantograph structure is complex, and it is feasible to describe its motion and mechanical analysis using an equivalent two-dimensional framework in practice. For clarity, here the pantograph sliding block and bracket are referred to as the bow head. Components with relatively small aerodynamic forces, such as the balance lever, are neglected, resulting in the final geometric model of the pantograph used for lift force calculation, as shown in Figure 2.

The aerodynamic lift generated by the pantograph during high-speed operation is the combined effect of aerodynamic drag, lift, lateral force, and aerodynamic moments on each component. It results in a vertical force at the bow head, which is equivalent to the top end of the upper arm rod. Neglecting the deformation of the bow head spring under the aerodynamic action of the pantograph, the bow head can only undergo vertical motion. Therefore, a vertical constraint is applied at the top end of the upper arm rod to calculate the vertical constraint reaction forces generated by each component of the pantograph under aerodynamic forces, thereby obtaining the aerodynamic lift of the pantograph.

3. Methods for Calculating the Aerodynamic Lift of the Pantograph

The method adopted in this paper for calculating the aerodynamic lift of the pantograph begins with a rational simplification and force analysis of the pantograph on high-speed trains, deriving the conversion relationship between the aerodynamic forces and lift forces of the main components of the pantograph. Based on the analysis of the aerodynamic characteristics of the pantograph, the aerodynamic forces acting on each component are determined. These aerodynamic forces are then applied to the lift force calculation model, establishing the mechanical equilibrium equations of the model, and ultimately solving for the aerodynamic lift of the pantograph and its main components. The geometric model of the pantograph used in this paper is consistent with that in references, and similar simplifications have been applied. Initially, the case without crosswind is considered, and a comparison with the calculated values from references shows good agreement. The calculated values in these references also exhibit good consistency with experimental values, as depicted in Figure 3. Therefore, adopting the calculation method from these references for determining the aerodynamic lift of the pantograph in this paper is reliable and accurate.

3.1. Geometric Relationships and Force Analysis of Pantograph Components

To analyze the transfer coefficients of the resistance and lift of each component of the pantograph into aerodynamic lift, the aerodynamic forces are equivalent to a point where the aerodynamic moment is zero. Figure 4 illustrates the geometric relationships of the pantograph components during operation [17]. In the figure, L₁, L₂, L₃, L₄, L₅, S₁, S₂, and S₃ represent the distances of segments GF, FC, CB, CD, DE, AG, AC, and BE, respectively. α, β, γ, ε, and θ represent the angles between the lines of the push rod, hinge A, line connecting points G and F, lower arm rod, and segments BC and CE of the upper arm rod with the x-axis. Points D and F represent the points on the upper and lower arm rods where the aerodynamic moment is zero.

According to design requirements, the pantograph bow head moves vertically. Neglecting the deformation caused by the aerodynamic lift force on the spring, only vertical displacement occurs at the pantograph bow head and the top of the upper arm rod. After applying a vertical constraint at the top end of the upper arm rod, the vertical constraint reaction forces generated by each component of the pantograph under aerodynamic forces can be calculated, thereby obtaining the aerodynamic lift of the pantograph, which is equal in magnitude but opposite in direction to this force. Figure 5 illustrates the force analysis of the upper arm rod and lower arm rod. In the figure, Fe represents the vertical constraint reaction force; F₇, F₅, and F₁₀ are the resistances acting on the bow head, upper arm rod, and lower arm rod, respectively; F₆, F₄, and F₁₁ are the lifts acting on the bow head, upper arm rod, and lower arm rod, respectively; F₂ and F₃ represent the forces exerted by the lower arm rod on the upper arm rod at the hinge C; F₈ and F₉ represent the forces exerted by the upper arm rod on the lower arm rod at the hinge C'; and F₁ represents the internal force of the push rod.

3.2. Calculation of Transfer Coefficients

Based on the geometric relationships and force analysis of the pantograph components described above, the force balance equation for the lower arm rod and the moment balance equation for point G in the Cartesian coordinate system are established, as shown in Equation (1). Similarly, the force balance equation for the upper arm rod and the moment balance equation for point C in the Cartesian coordinate system are established, as shown in Equation (2). From the force analysis of the upper and lower arm rods, it is known that F₂ equals F₉ and F₃ equals F₈. The segments L₄ and L₅ of the upper arm rod are denoted as L₄₅, while the segments L₁ and L₂ of the lower arm rod are denoted as L₁₂. By solving the above two equations simultaneously, the vertical constraint force Fe can be obtained, as shown in Equation (3).

The angles α, β, γ, ε, and θ are determined based on the geometric relationships of the pantograph components, while L₁ and L₄ are obtained based on the equivalent points with zero aerodynamic moment. As indicated by the equations above, once the aerodynamic force equivalent positions and angles of the pantograph components are determined, the transfer coefficients for converting the aerodynamic drag and lift into aerodynamic lift force can be obtained. The effect of crosswind is considered in the form of resultant force. A positive transfer coefficient indicates that the force increases the aerodynamic lift force, while a negative transfer coefficient indicates that the force reduces the aerodynamic lift force. The transfer coefficient reflects the efficiency of converting the aerodynamic force of the pantograph into aerodynamic lift force. Once the transfer coefficients are determined, the aerodynamic lift forces of the pantograph and its main components can be calculated.

[{(L}_{1} {+ L}_{2}) \sin γ {- (L}_{1} {+ L}_{2}) \cos γ L_{2} \sin γ L_{2} \cos γ] [\begin{array}{l} F_{8} \\ F_{9} \\ F_{10} \\ F_{11} \end{array}] = 0

(1)

(2)

[\begin{matrix} \frac{a}{m} & 1 & \frac{b}{m} & \frac{c}{m} & \frac{d}{n} & \frac{e}{n} \end{matrix}] [\begin{matrix} F_{7} \\ F_{6} \\ F_{5} \\ F_{4} \\ F_{10} \\ F_{11} \end{matrix}] = F_{e}

(3)

a = \sin γ \sin (α + ε) L_{3} - \sin θ \sin (α - γ) L_{45}

b = \sin γ \sin (α + ε) L_{3} - \sin θ \sin (α - γ) L_{2}

c = - \sin θ \sin (α - γ) L_{2} - \sin γ \sin (α + ε) L_{3}

d = \sin γ \sin (α + ε) L_{1} L_{3}

e = \cos γ \sin (α + ε) L_{1} L_{3}

m = \cos θ \sin (α - γ) L_{45} + \cos γ \sin (α + ε) L_{3}

n = [\cos θ \sin (α - γ) L_{45} + \cos γ \sin (α + ε) L_{3}] L_{12}

3.3. Pantograph Aerodynamics Model

The pantograph consists of components such as the sliding block, sliding block bracket (bow head), upper arm rod, balance lever, lower arm rod, push rod (pull rod), base frame, damper, support insulators, airbags, etc. In numerical simulation calculations, the aerodynamic characteristics and flow field characteristics of the main components of the pantograph are focused on. Therefore, the pantograph is appropriately simplified, as shown in Figure 6.

A model of the electric train set, including the pantograph, train, and overhead contact system, was built to scale at a 1:1 ratio. Considering that the pantograph is mainly affected by the wall area on the top of the train, a train model with three carriages was used, with the bogie part simplified, and the pantograph was positioned in the middle of the train. The lengths of the front, middle, and rear cars are 25.7m, 25m, and 25.7m respectively, with a width of 3m, and the contact line is 6.0m above the ground. The dimensions of the computational domain are: length × width × height = 267m × 192m × 34m, as shown in Figure 7.

It is specified that the pantograph moves along the

+ x

direction in the computational domain, indicating that the main airflow moves along the

- x

direction, with

- V_{t}

specified as the main airflow velocity. The crosswind moves along the

+ z

direction, with

V_{w}

specified as the crosswind velocity, and

θ

representing the angle between the crosswind and the main airflow direction, specified as the crosswind angle. This is illustrated in Figure 8.

The computational domain grid uses the Trim grid, and the surfaces of the pantograph and the train body are treated using the wall function method. To ensure smooth connection between the boundary grid and the main flow area, the boundary grid thickness is set to 6.8mm, and the boundary layer grid is divided into 6 layers, with the first layer grid near the wall set at a distance of 0.2mm from the wall. Regions with significant changes in flow field, such as the pantograph, train surface, and wake, are refined. The total number of grids is 13.97 million, ensuring the accuracy of the calculation, as shown in Figure 9.

3.4. Numerical Simulation Method

The Detached Eddy Simulation (DES) method combines the advantages of Reynolds-Averaged Navier-Stokes (RANS) and Large Eddy Simulation (LES). In this study, the DES simulation method is employed, with the SST turbulence model selected. The SST model is based on the assumption of shear stress transport (SST) and combines the characteristics of the k-ε and k-ω turbulence models through a blending function[18]. The numerical simulation results are compared and analyzed against the experimental results of a 1:8 scaled model of high-speed train aerodynamic performance conducted in the 8m x 6m wind tunnel at the China Aerodynamics Research and Development Center. The aim is to validate the accuracy of the numerical simulation method. The results show that the error between the numerical simulation and model experiments is within a reasonable range, demonstrating the feasibility of analyzing the aerodynamic loads on high-speed train pantographs using numerical simulation.

4. Aerodynamic Lift of the Pantograph

4.1. Aerodynamic Loads on the Pantograph

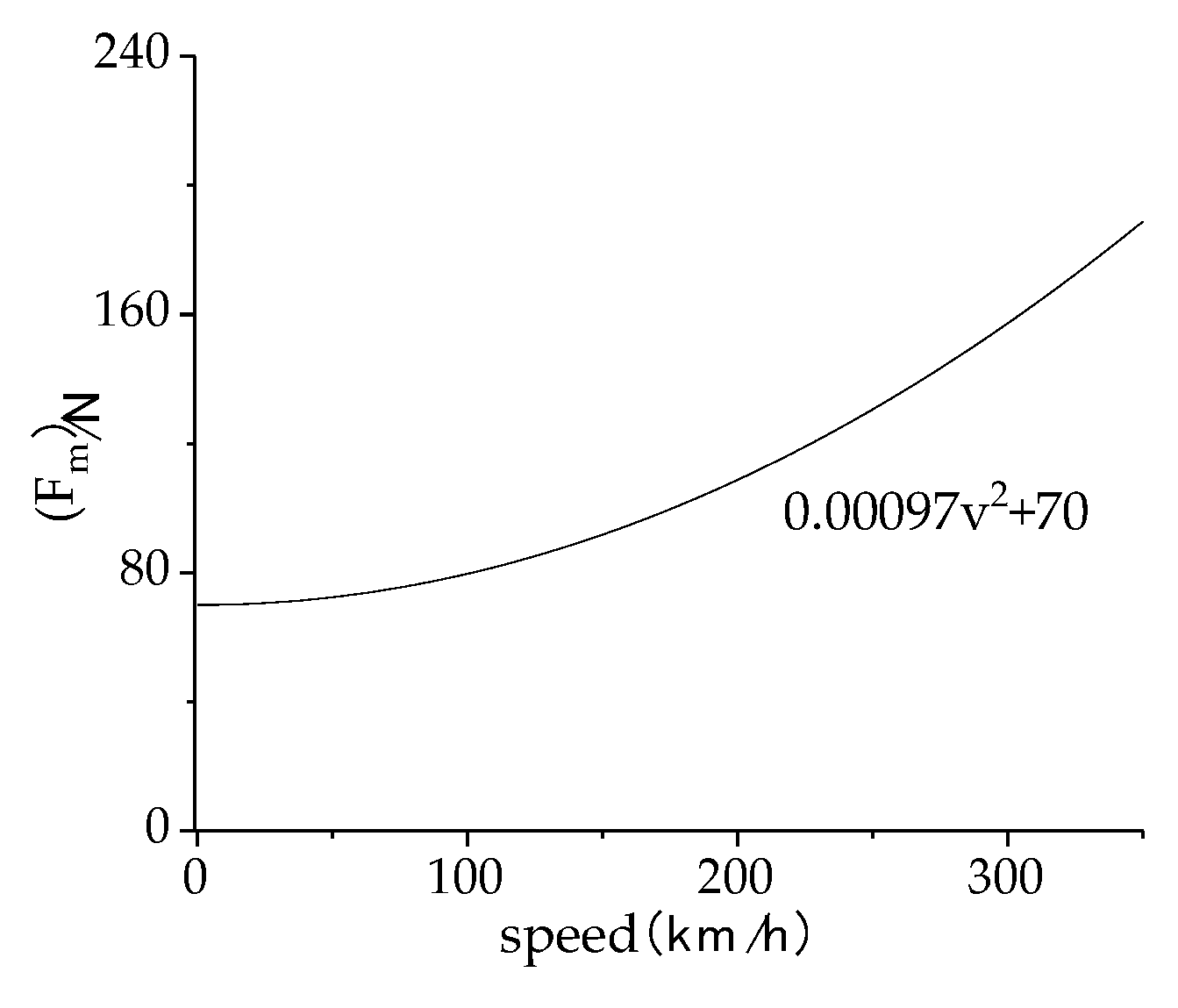
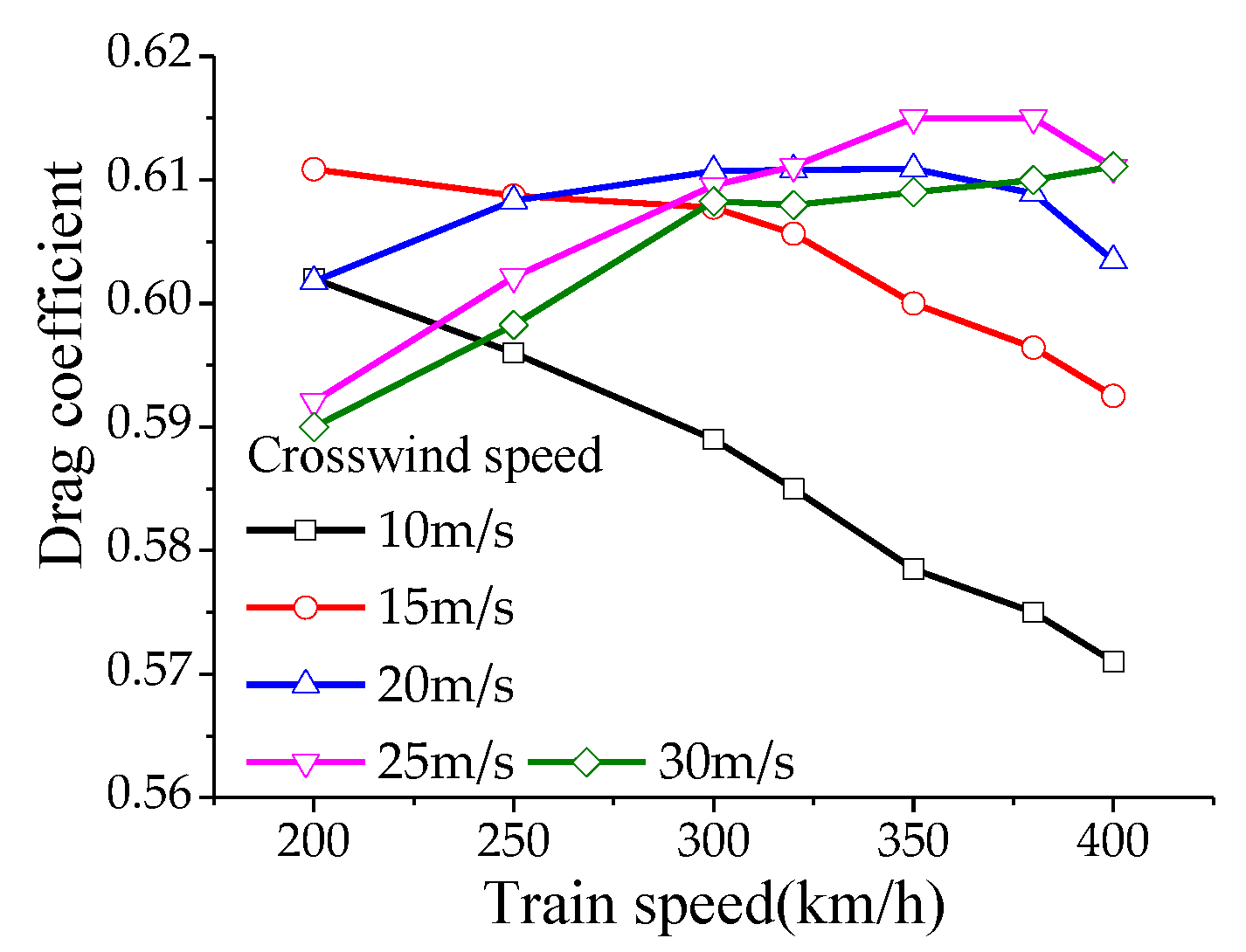
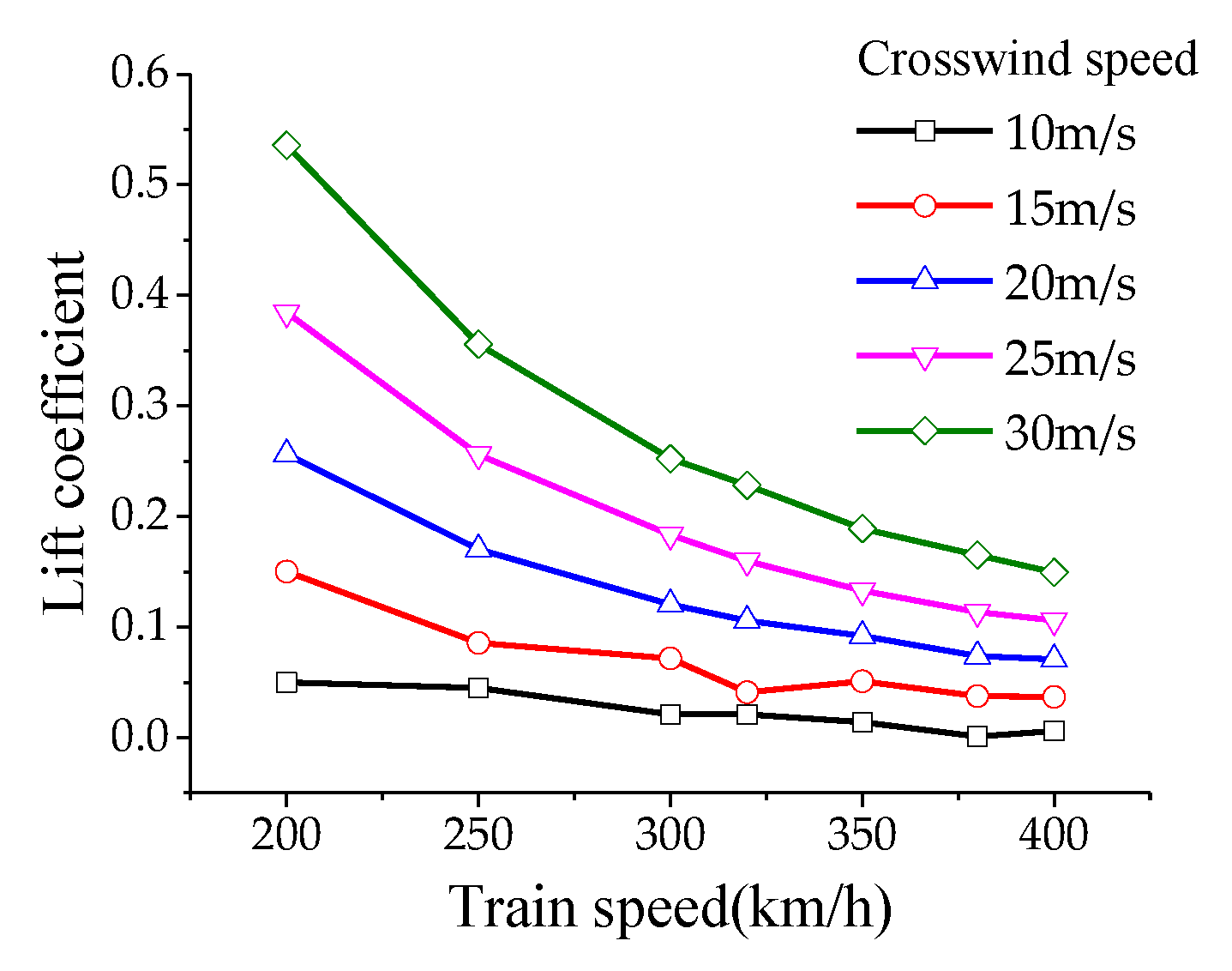
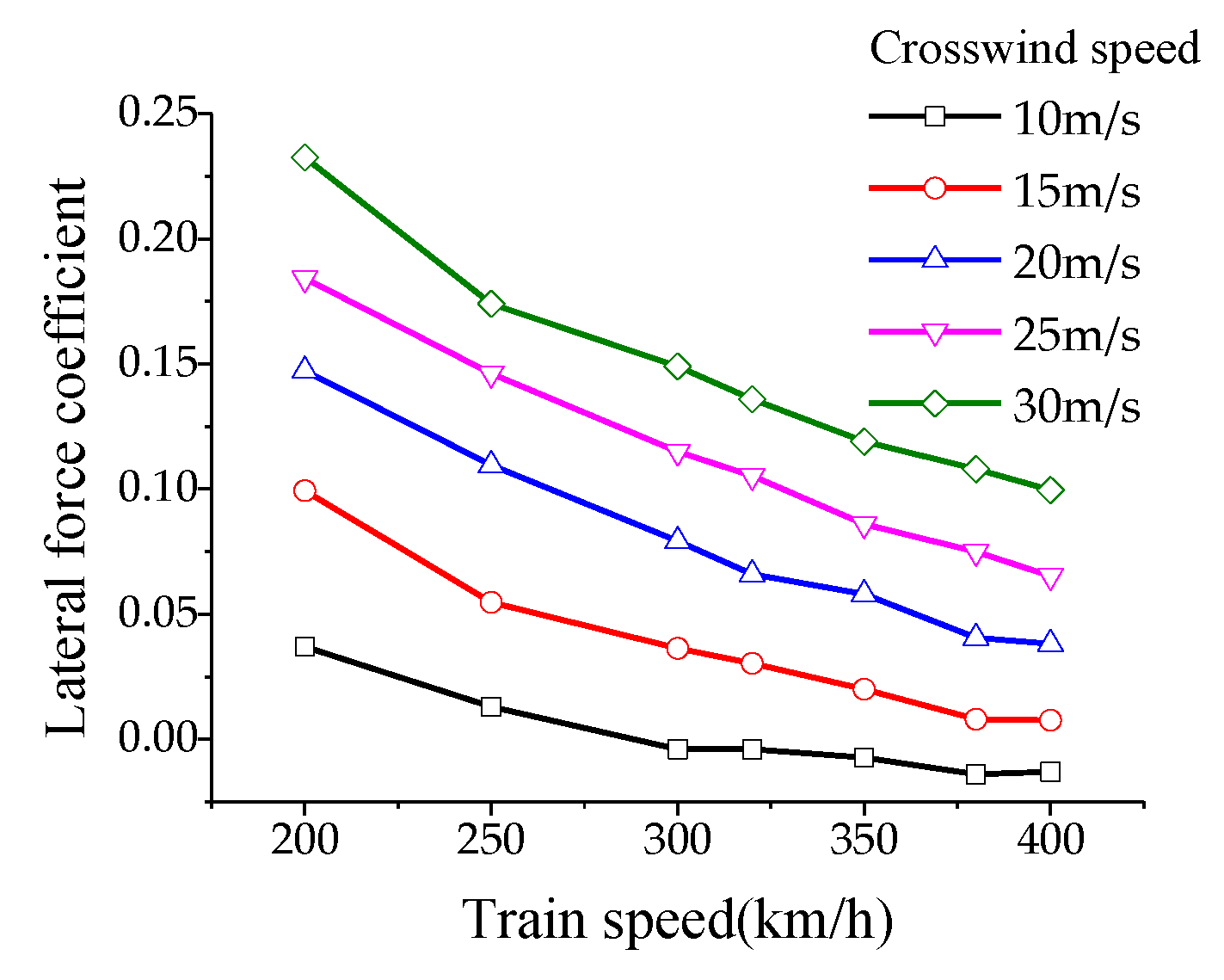
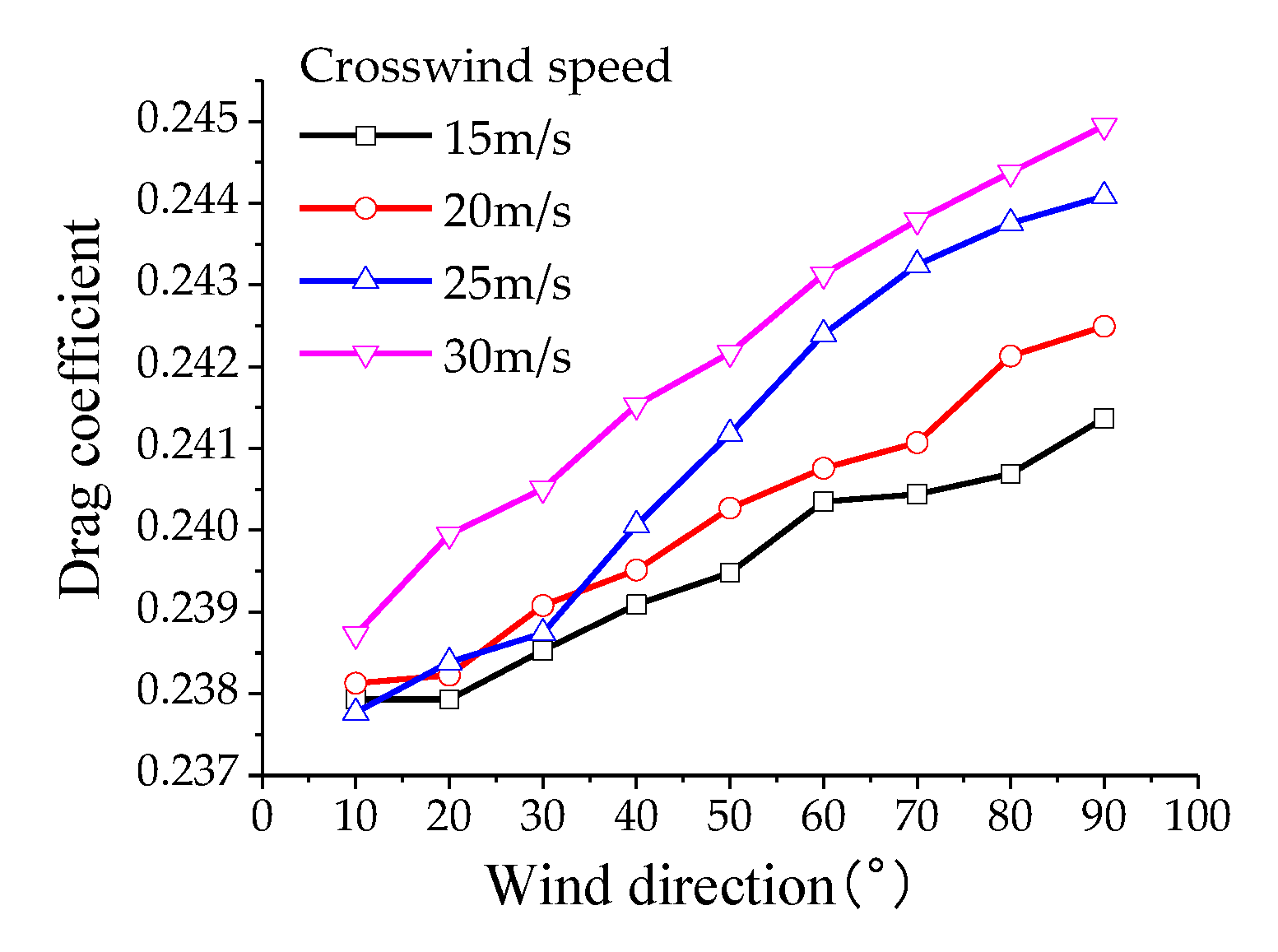
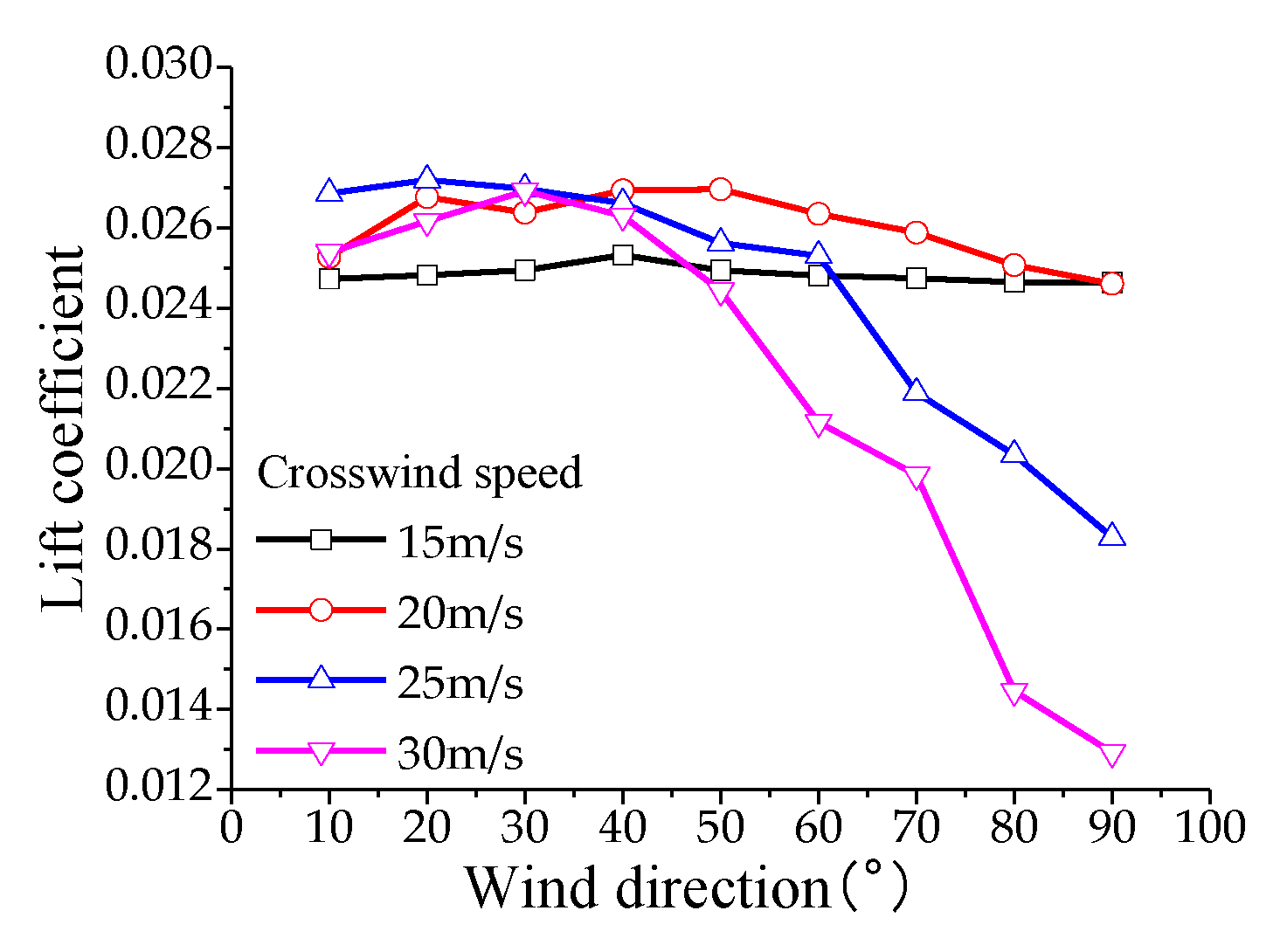
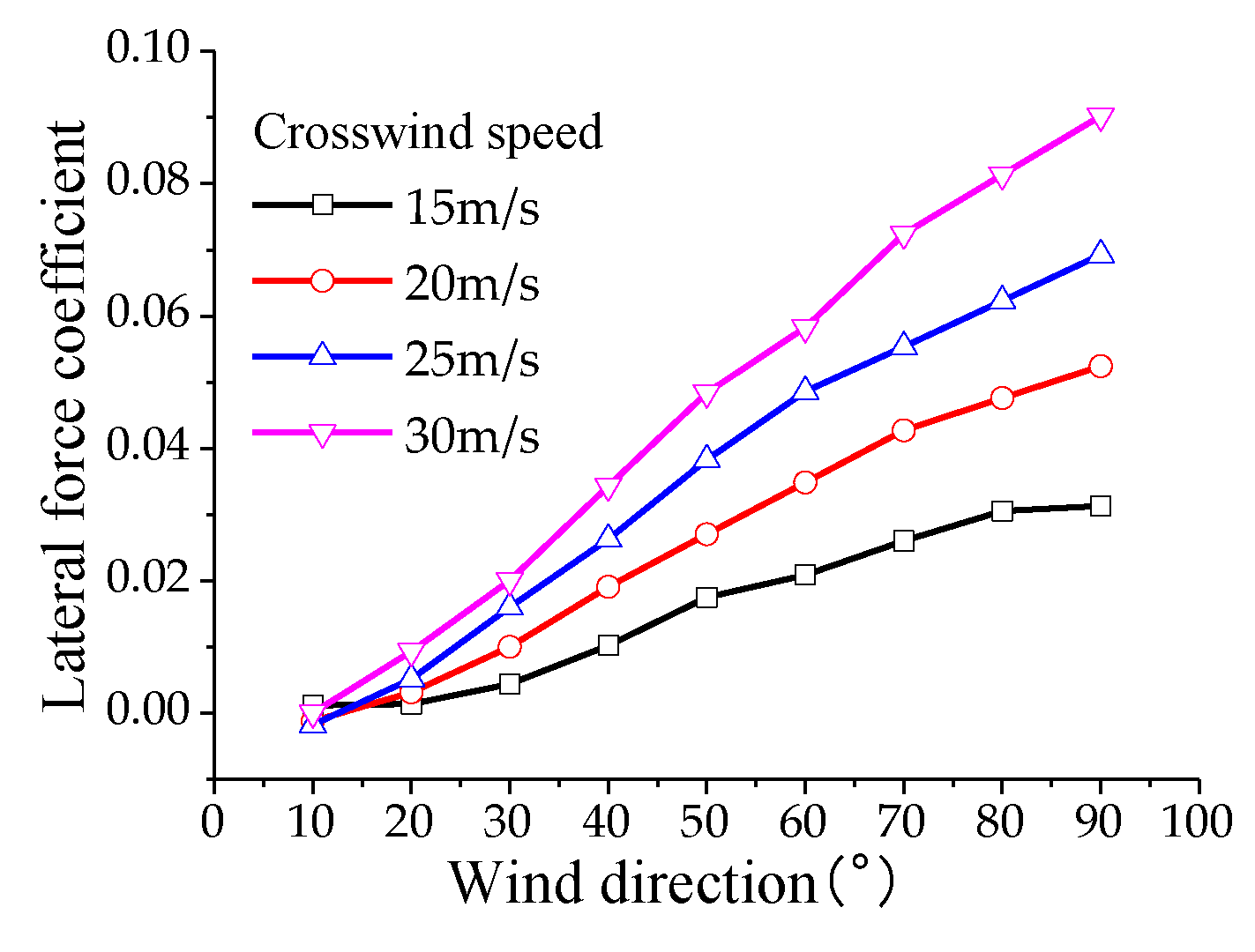
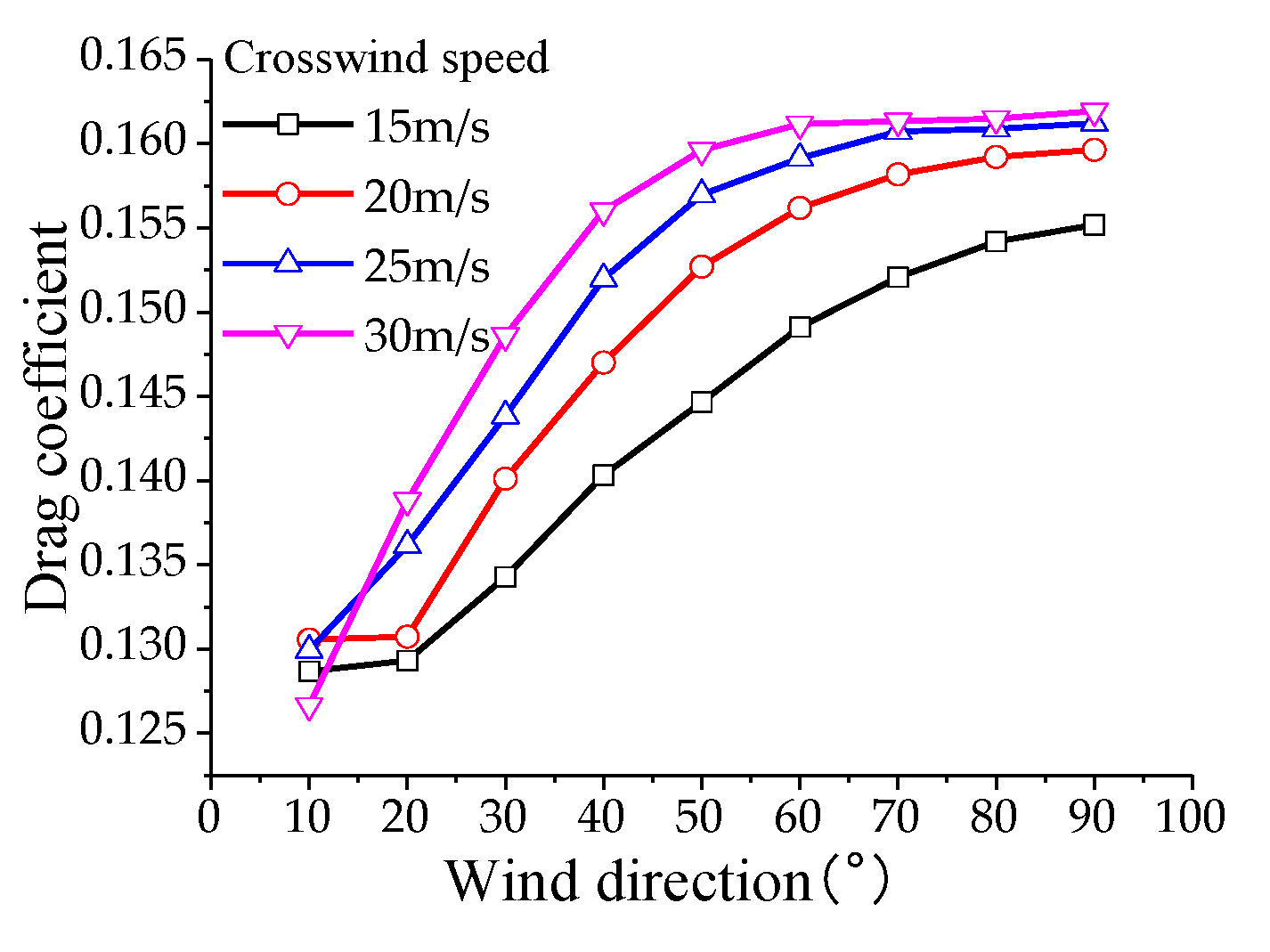
To analyze the aerodynamic lift experienced by the pantograph, the calculation conditions for aerodynamic loads on the pantograph are as follows: the operating speed of the high-speed train ranges from 200 km/h to 400 km/h (in increments of 50 km/h), with crosswind speeds of 10, 15, 20, 25, and 30 m/s, and crosswind angles ranging from 10° to 90° (in increments of 10°). According to the results of numerical simulations: Under the influence of crosswind, the drag coefficient of the pantograph varies non-monotonically with increasing train speed, reaching its maximum value at a speed of 350 m/s and then decreasing. The lift and lateral force coefficients decrease monotonically with increasing train speed. The drag coefficient of the pantograph varies non-monotonically with increasing crosswind speed, reaching its maximum value at a crosswind speed of 25 m/s and then decreasing. The lift and lateral force coefficients increase monotonically with increasing crosswind speed. The drag, lift, and lateral force coefficients increase monotonically with increasing crosswind angle, with the maximum drag coefficient occurring at a crosswind speed of 30 m/s and a crosswind angle of 90°, as shown in Figure 11, Figure 12 and Figure 13.

Based on the numerical simulation, a comprehensive relationship equation for the aerodynamic forces and moment coefficients of the pantograph with respect to the train speed, crosswind speed, and wind direction angle is proposed. Taking the aerodynamic drag of the pantograph as an example, the aerodynamic drag F_x is related to the pantograph's operating speed (i.e., train speed)

V_{t}

_, crosswind speed

V_{w}

, air density

ρ

, dynamic viscosity coefficient

μ

, characteristic size of the pantograph

h

, and surface roughness of the pantograph

k_{s}

, and can be expressed by the following equation:

f (F_{x}, V_{t}, V_{w}, θ, ρ, μ, h, k_{s}) = 0

(4)

Base on

R e = V_{t} ρ h / μ

,Therefore:

\frac{F_{x}}{V_{t}^{2} ρ h^{2}} = f (\frac{V_{w}}{V_{t}}, \frac{1}{R e}, \frac{k_{s}}{h}, θ)

(5)

The drag coefficient of the pantograph is given by:

C_{x} = F_{x} / V^{2} ρ h^{2} S_{x}

Where

V^{2} = V_{t}^{2} + V_{w}^{2} + 2 V_{t} V_{w} \cos θ

thus can derive:

C_{x} = F_{x} / V^{2} ρ h^{2} S_{x}, V^{2} = V_{t}^{2} + V_{w}^{2} + 2 V_{t} V_{w} \cos θ

(6)

Therefore

C_{x} = \frac{1}{1 + {(\frac{V_{w}}{V_{t}})}^{2} + 2 (\frac{V_{w}}{V_{t}}) \cos θ} f (\frac{V_{w}}{V_{t}}, \frac{1}{R e}, \frac{k_{s}}{h}, θ)

(7)

Since the geometric dimensions of the pantograph remain constant, and

k_{s} / h

is a constant, the drag coefficient of the pantograph is only related to

V_{w} / V_{t}

and

θ

. Expressing

θ

in the form of

c o s θ

, where

V_{t}

and

V_{w}

represent the train speed and crosswind speed, respectively, and their ratio is dimensionless, defined as the wind speed to train speed ratio

λ_{w t}

，

λ_{w t} = V_{w} / V_{t}

. Thus, we have:

C_{x} = \frac{1}{1 + {(λ_{w t})}^{2} + 2 (λ_{w t}) \cos θ} f (λ_{w t}, \cos θ)

(8)

From the above equation, it is evident that the drag coefficient of the pantograph is only related to the wind speed to train speed ratio

λ_{w t}

and the cosine of the crosswind angle cosθ. Based on the variation patterns of the aerodynamic force and moment coefficients of the pantograph, a functional form

f (λ_{w t}, \cos θ)

can be obtained, thus providing the specific expression of the drag coefficient. By fitting the data, the values of the coefficients in the equation can be determined, leading to the final comprehensive relationship between the drag coefficient and the train speed, crosswind speed, and wind direction angle.

Let

f (λ_{w t}, \cos θ) = a λ_{w t}^{b} (1 + m λ_{w t}^{c} {|\cos θ|}^{n})

, substituting it into Equation (7), we can obtain the specific expression of the drag coefficient:

C_{x} = \frac{1}{1 + {(λ_{w t})}^{2} + 2 (λ_{w t}) \cos θ} f (λ_{w t}, \cos θ)

(8)

From the above equation, it is evident that the drag coefficient of the pantograph is only related to the wind speed to train speed ratio

λ_{w t}

and the cosine of the crosswind angle cosθ. Based on the variation patterns of the aerodynamic force and moment coefficients of the pantograph, a functional form

f (λ_{w t}, \cos θ)

Let

f (λ_{w t}, \cos θ) = a λ_{w t}^{b} (1 + m λ_{w t}^{c} {|\cos θ|}^{n})

, substituting it into equation (7), we can obtain the specific expression of the drag coefficient:

C_{x} = \frac{a λ_{w t}^{b} (1 + m λ_{w t}^{c} {|\cos θ|}^{n})}{1 + λ_{w t}^{2} + 2 λ_{w t} \cos θ}

(9)

In the above equation, a, b, c, mm, and n are undetermined coefficients, which are solved through data fitting to obtain

a = 0.779

b = 0.128

c = 1.267

m = 1.951

, and

n = 0.683

, thereby obtaining the drag coefficient.

C_{x} = \frac{0.779 {λ_{w t}}^{0.128} (1 + 1.951 {λ_{w t}}^{1.267} {|\cos θ|}^{0.683})}{1 + {λ_{w t}}^{2} + 2 λ_{w t} \cos θ}

(10)

When the wind direction angle θ=90°, the drag coefficient is

C_{x} = 0.779 λ_{w t}^{0.128} / (1 + λ_{w t}^{2})

; when the wind direction angle θ=0°, the drag coefficient is

C_{x} = (0.779 λ_{w t}^{0.128} + 1.519 λ_{w t}^{1.395}) / (1 + 2 λ_{w t} + λ_{w t}^{2})

. The above equation considers the special conditions when the wind direction is 0° and 90°. For situations without crosswind (

ν_{w} = 0

), separate treatment is required. Similarly, the comprehensive relationship equations for the lift coefficient, lateral force coefficient, and aerodynamic coefficient with respect to vehicle speed, crosswind speed, and wind direction angle can be obtained.

Lift coefficient:

C_{y} = \frac{2.653 λ_{w t}^{2.171} (1 - 3.063 λ_{w t}^{1.170} | \cos θ |^{1.506})}{1 + λ_{w t}^{2} + 2 λ_{w t} \cos θ}

(11)

Sideways force coefficient:

C_{z} = \frac{- 0.087 + 0.975 λ_{w t} - 1.59 {λ_{w t}}^{2} + 2.097 {λ_{w t}}^{3} + 0.388 \cos θ - 0.600 \cos^{2} θ + 0.166 \cos^{3} θ}{1 + {λ_{w t}}^{2} + 2 λ_{w t} \cos θ}

(12)

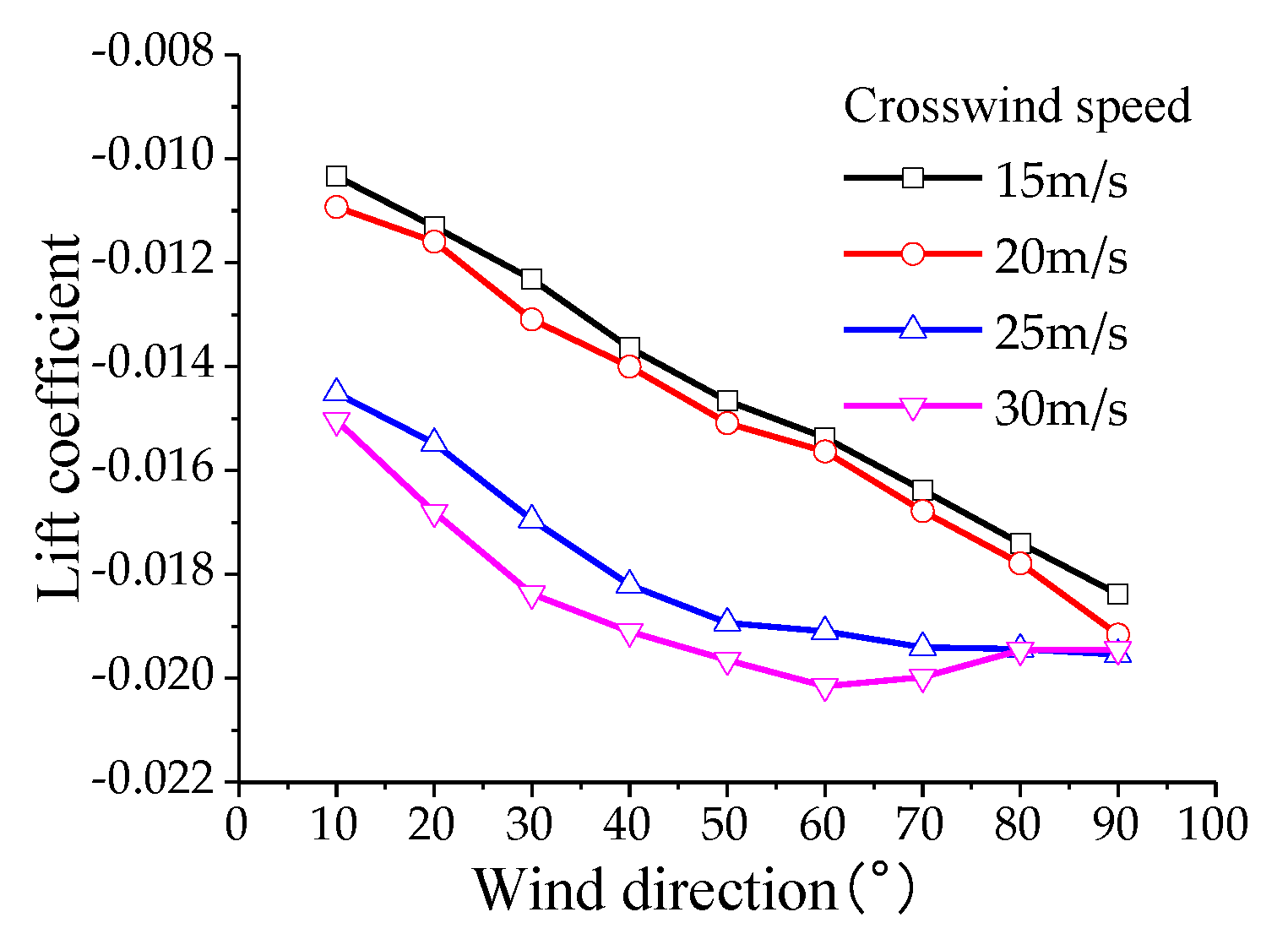
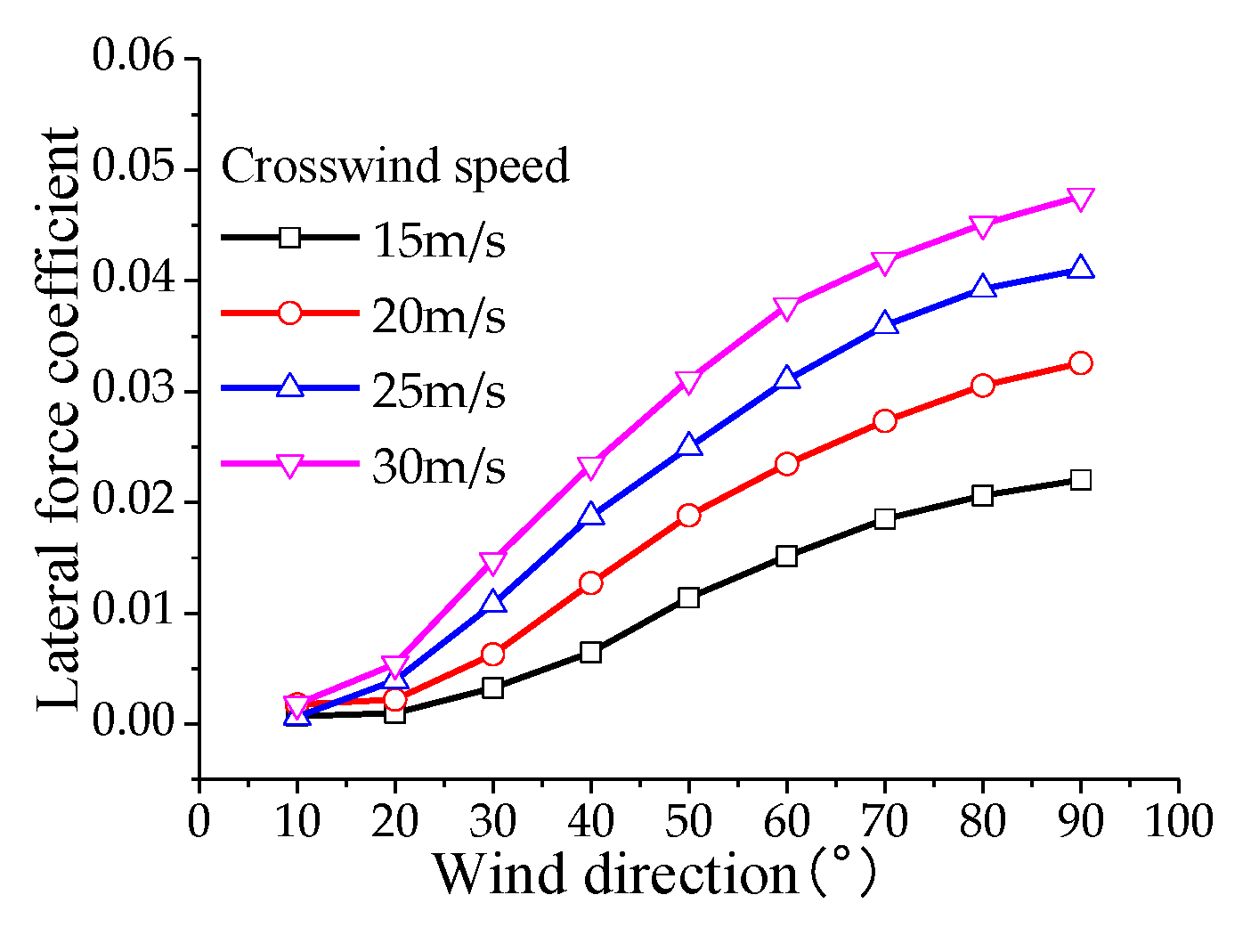
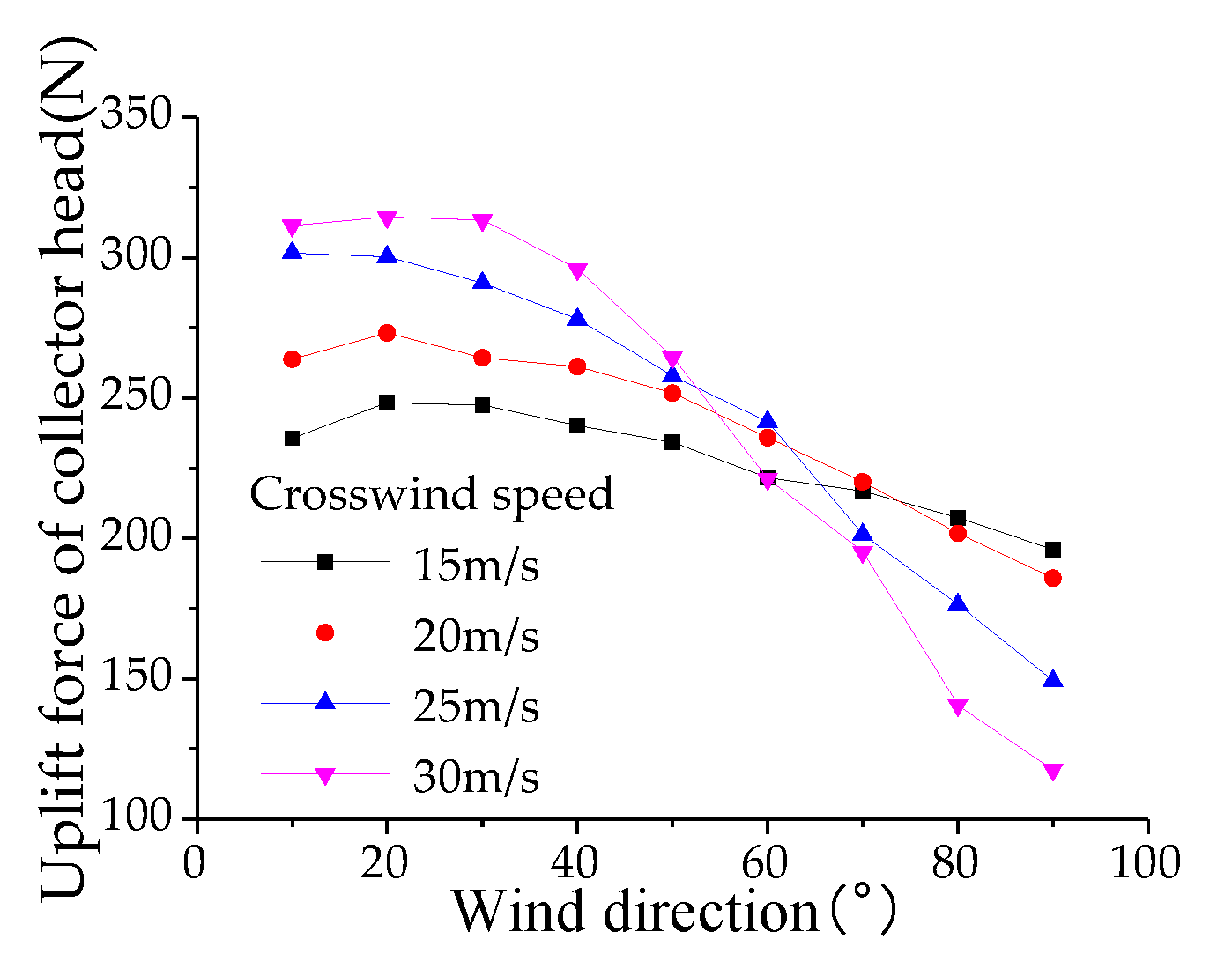
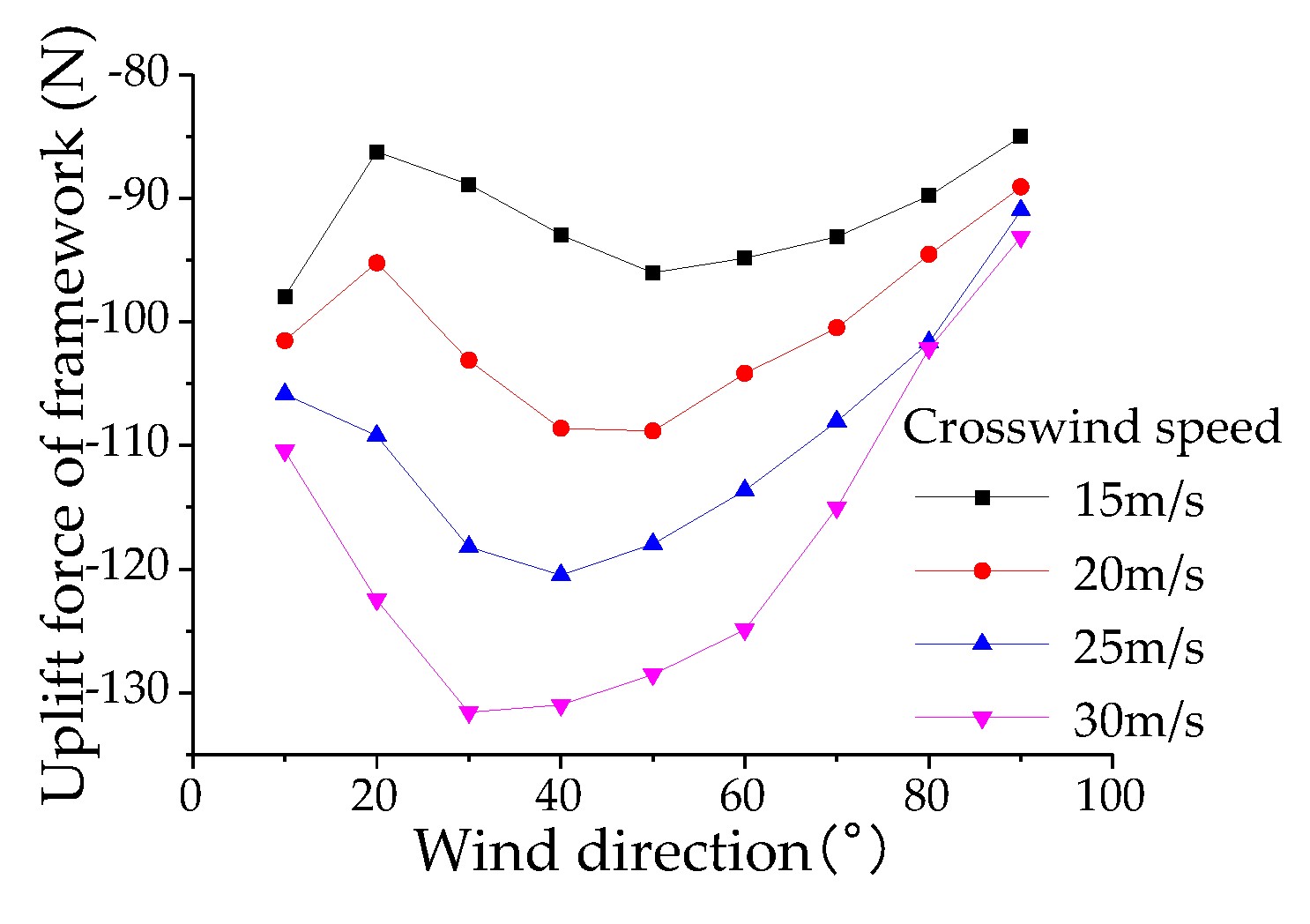
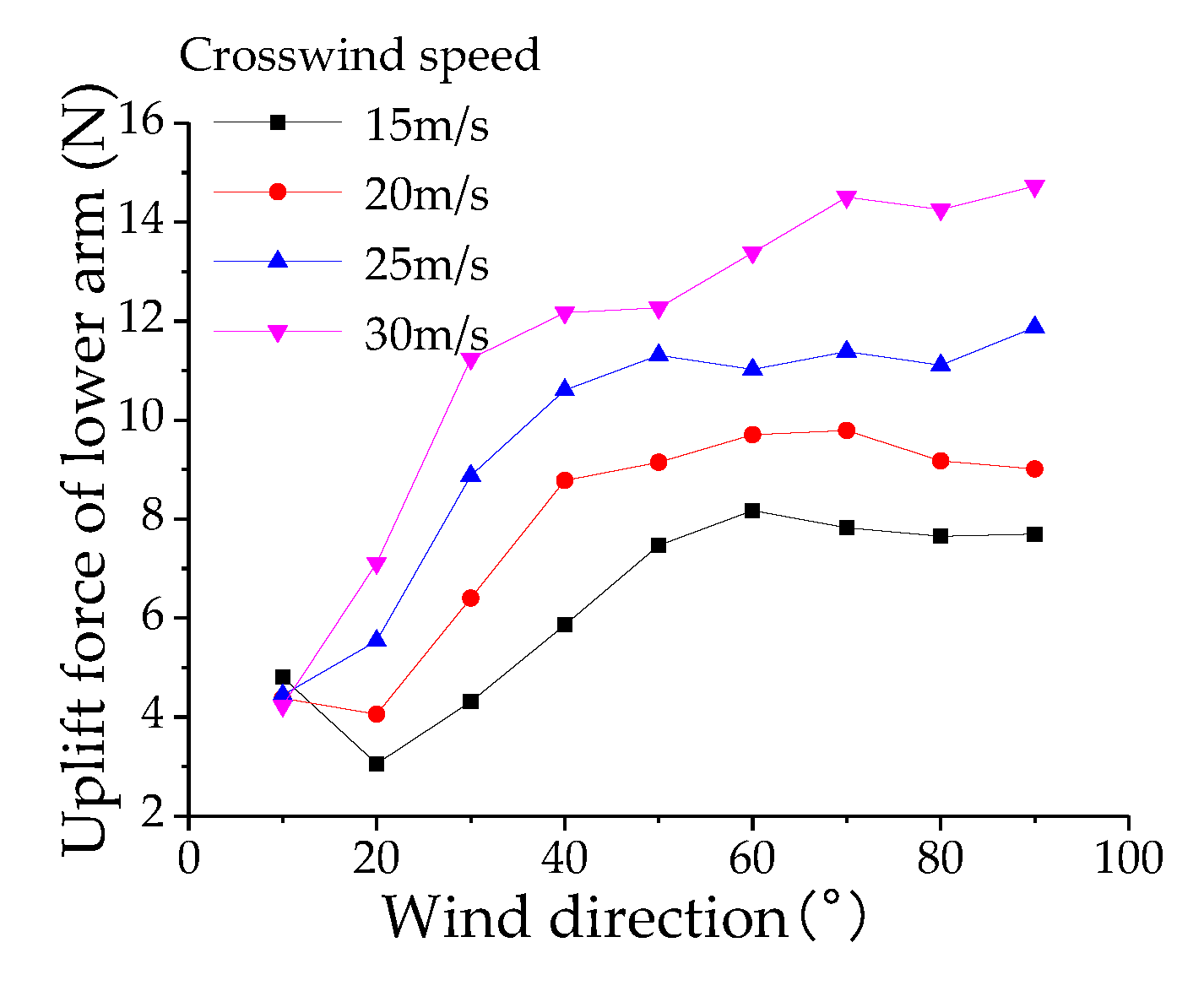
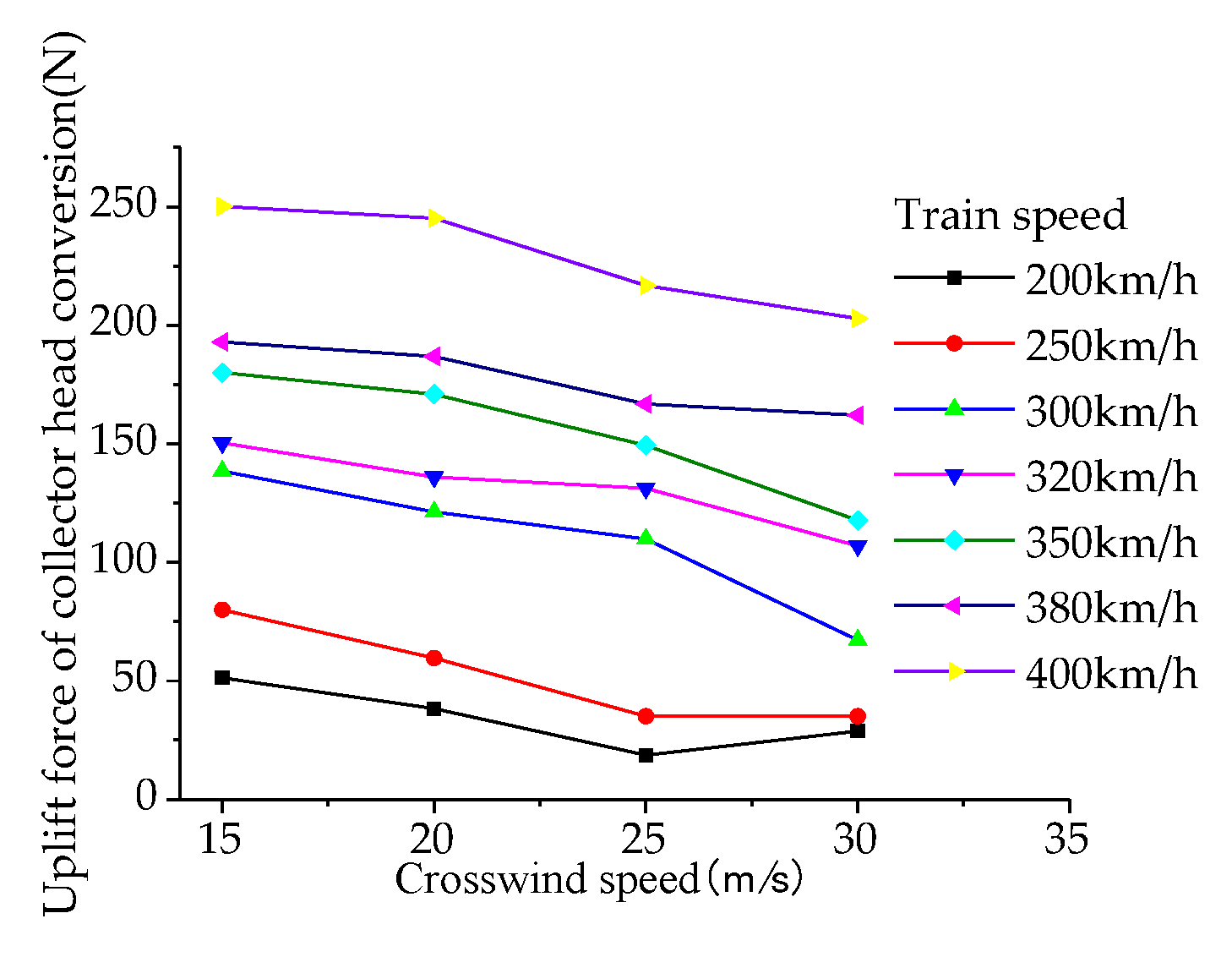
To analyze the aerodynamic lift forces acting on the components of the high-speed train pantograph, aerodynamic loads for the head, upper framework, and lower arm were obtained through numerical simulations. 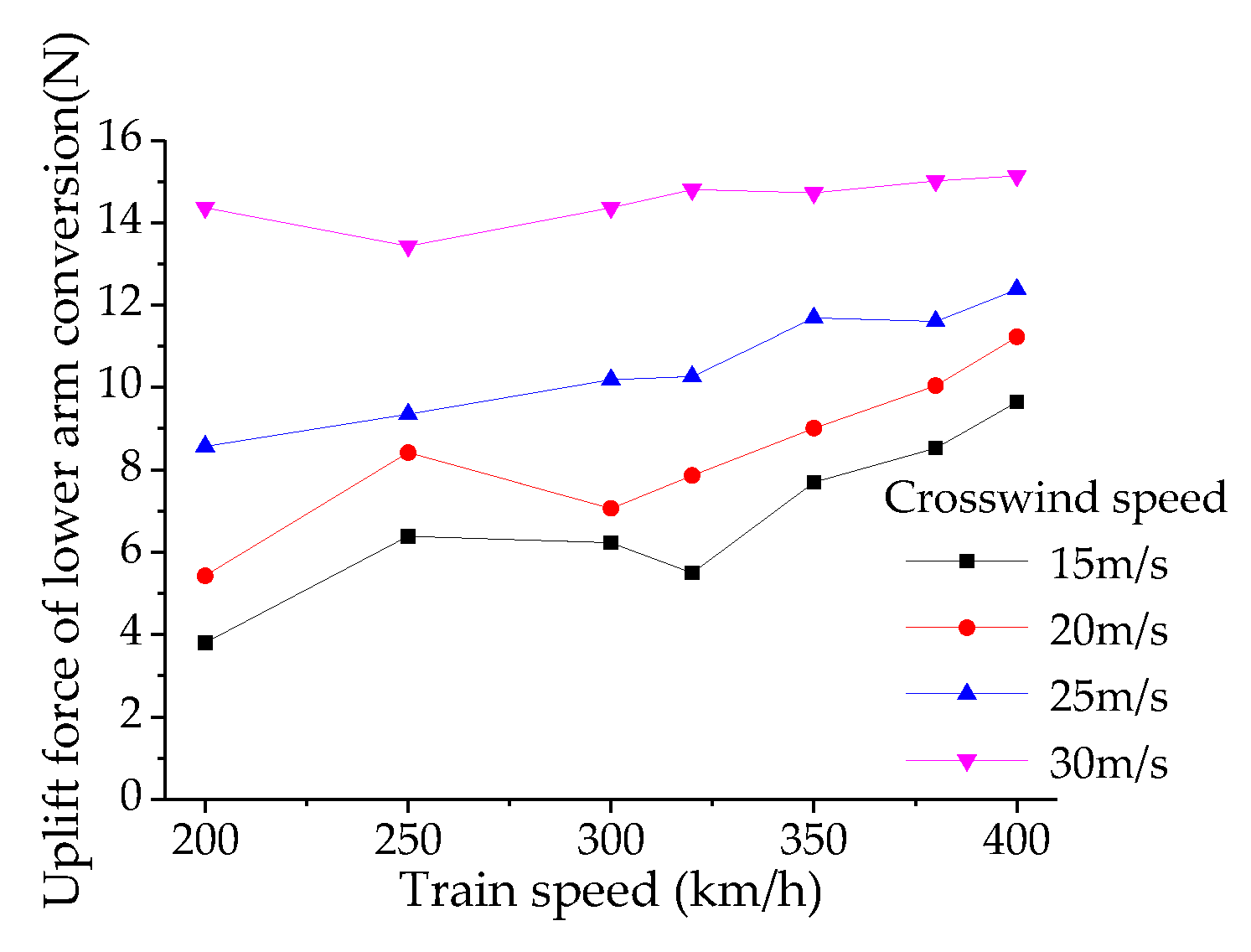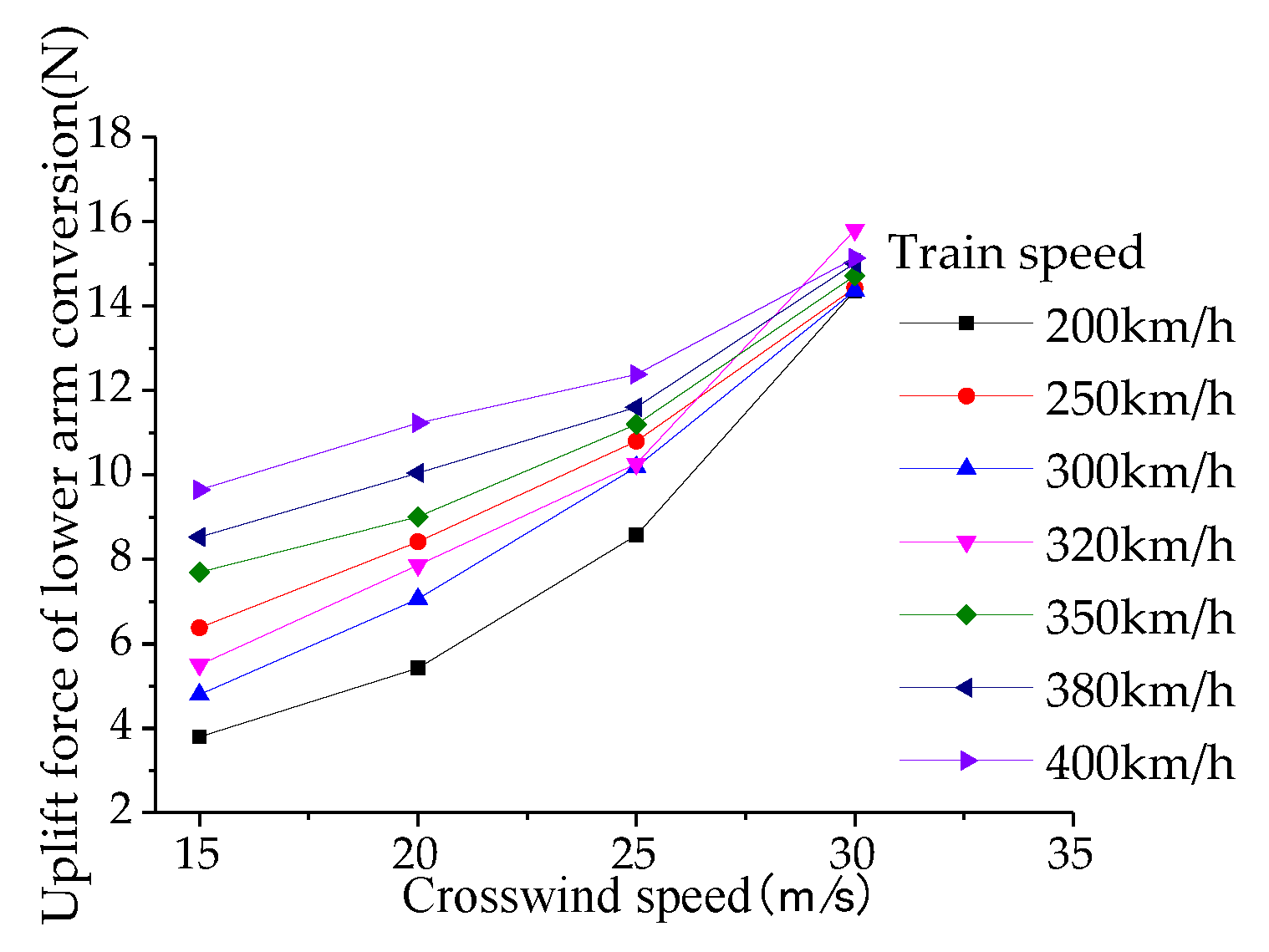The variation patterns of aerodynamic loads for the head are shown in Figure 14, Figure 15 and Figure 16, for the upper framework in Figure 17, Figure 18 and Figure 19 and for the lower arm in Figure 20, Figure 21 and Figure 22 Under the influence of crosswinds, with increasing wind speed and wind direction angle, the resistance, lateral force coefficients, overturning moment, and lateral moment coefficients of the head, upper framework, and lower arm exhibit consistent trends with those of the pantograph, but with values lower than those experienced by the pantograph under corresponding crosswind speeds and angles. Among these components, the head exhibits the highest resistance coefficient, indicating a clear direction for reducing drag on a per-component basis. Compared to the pantograph, the lift coefficient patterns for the head, upper framework, and lower arm show significant changes. Therefore, in the design and optimization process of the pantograph, special attention should be paid to the lift forces acting on the head, upper framework, and lower arm to prevent excessive aerodynamic lift from causing catenary accidents and excessive pitching moments from enhancing longitudinal section vibrations of the pantograph, thereby affecting the stability of current collection from the overhead lines.

4.2. Aerodynamic Lift of the Main Components of the Pantograph

Analysis of the aerodynamic lift of the main components of the pantograph reveals the variation of aerodynamic lift with the operating speed, crosswind speed, and wind direction angle of the pantograph. Figure 14, Figure 15, Figure 16, Figure 17, Figure 18, Figure 19, Figure 20, Figure 21 and Figure 22 depict the variation of aerodynamic lift of the bow collector, upper frame, and lower arm with the wind direction angle, where the operating speed of the pantograph is 97.22 m/s and the wind direction angle ranges from 10° to 90°. 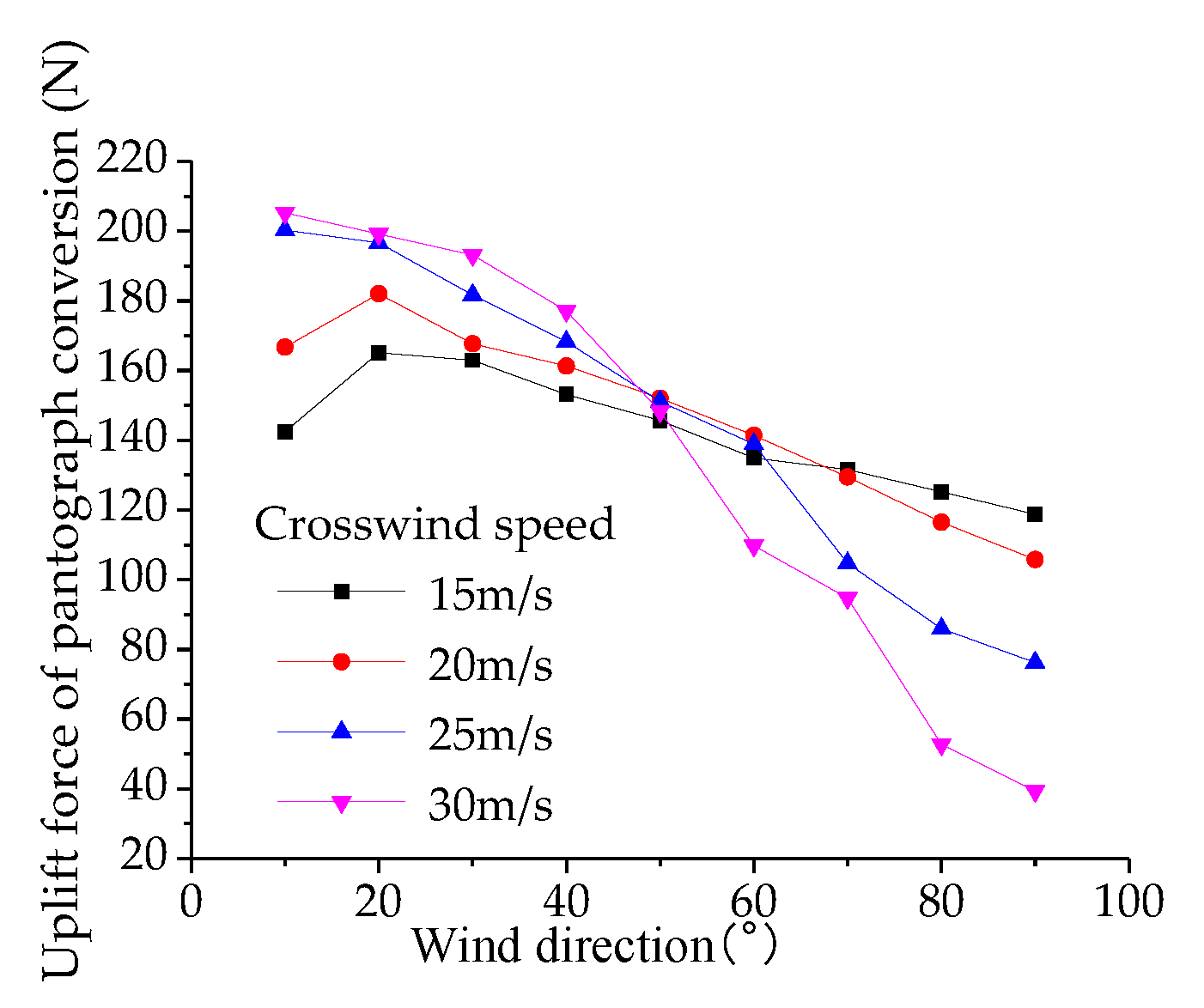Figure 23 illustrates the variation of aerodynamic lift of the bow collector with the vehicle speed and crosswind speed at a wind direction angle of 90°. The aerodynamic lift of the bow collector gradually decreases with an increase in the wind direction angle. When the wind direction angle reaches 60° and the crosswind speed is 30 m/s, the aerodynamic lift of the bow collector sharply decreases and becomes lower than that for crosswind speeds of 15, 20, and 25 m/s. This indicates that the conditions of maximum crosswind speed and wind direction angle do not necessarily result in the maximum aerodynamic lift.

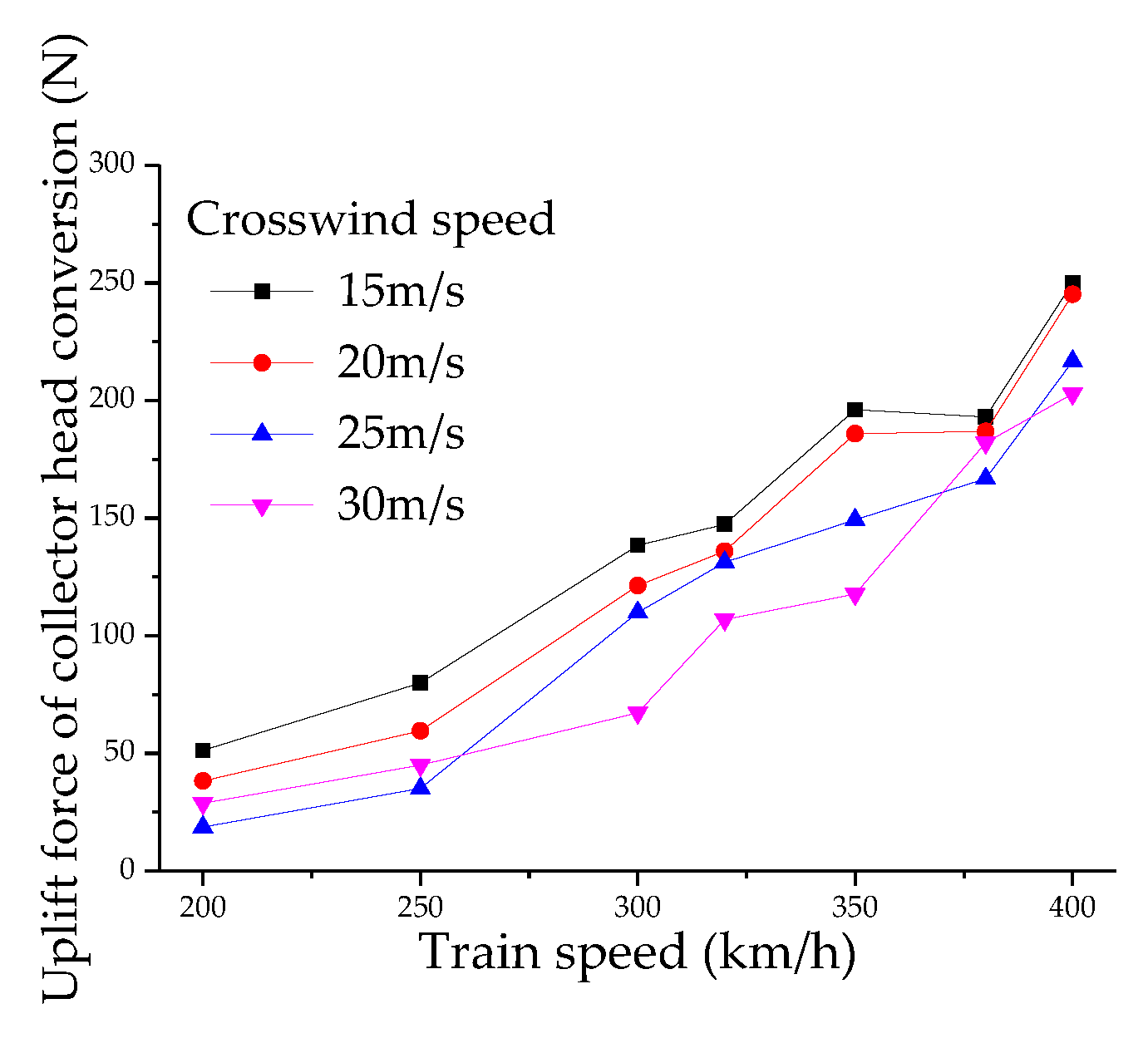
Figure 24, Figure 25 and Figure 26 illustrate the variation of aerodynamic lift of the bow collector, upper frame, and lower arm with the operating speed of the pantograph. The operating speed ranges from 200 km/h to 400 km/h, crosswind speeds range from 15 m/s to 30 m/s, and the wind direction angle is 90°. The aerodynamic lift of the bow collector increases with the operating speed of the pantograph. Under conditions where the wind direction angle is 90°, the aerodynamic lift of the bow collector reaches its maximum value when the pantograph operating speed is 400 km/h at crosswind speeds of 15 m/s and 20 m/s. The aerodynamic lift of the upper frame decreases linearly with an increase in the operating speed of the pantograph, with little influence from the crosswind speed. As the crosswind speed increases, the influence of the operating speed of the pantograph on the aerodynamic lift of the lower arm gradually decreases, highlighting the importance of considering the aerodynamic lift of the bow collector.

Figure 27, Figure 28 and Figure 29 show the variation of aerodynamic lift of the bow collector, upper frame, and lower arm with the operating speed of the pantograph, where the operating speed ranges from 200 km/h to 400 km/h, the crosswind speed ranges from 15 m/s to 30 m/s, and the wind direction angle is 90°. The aerodynamic lift of the bow collector increases with the operating speed of the pantograph, reaching its maximum value when the pantograph operating speed is 400 km/h at crosswind speeds of 15 m/s and 20 m/s in conditions where the wind direction angle is 90°. The aerodynamic lift of the upper frame decreases linearly with an increase in the operating speed of the pantograph, with little influence from the crosswind speed. As the crosswind speed increases, the influence of the operating speed of the pantograph on the aerodynamic lift of the lower arm gradually decreases, highlighting the importance of considering the aerodynamic lift of the bow collector.

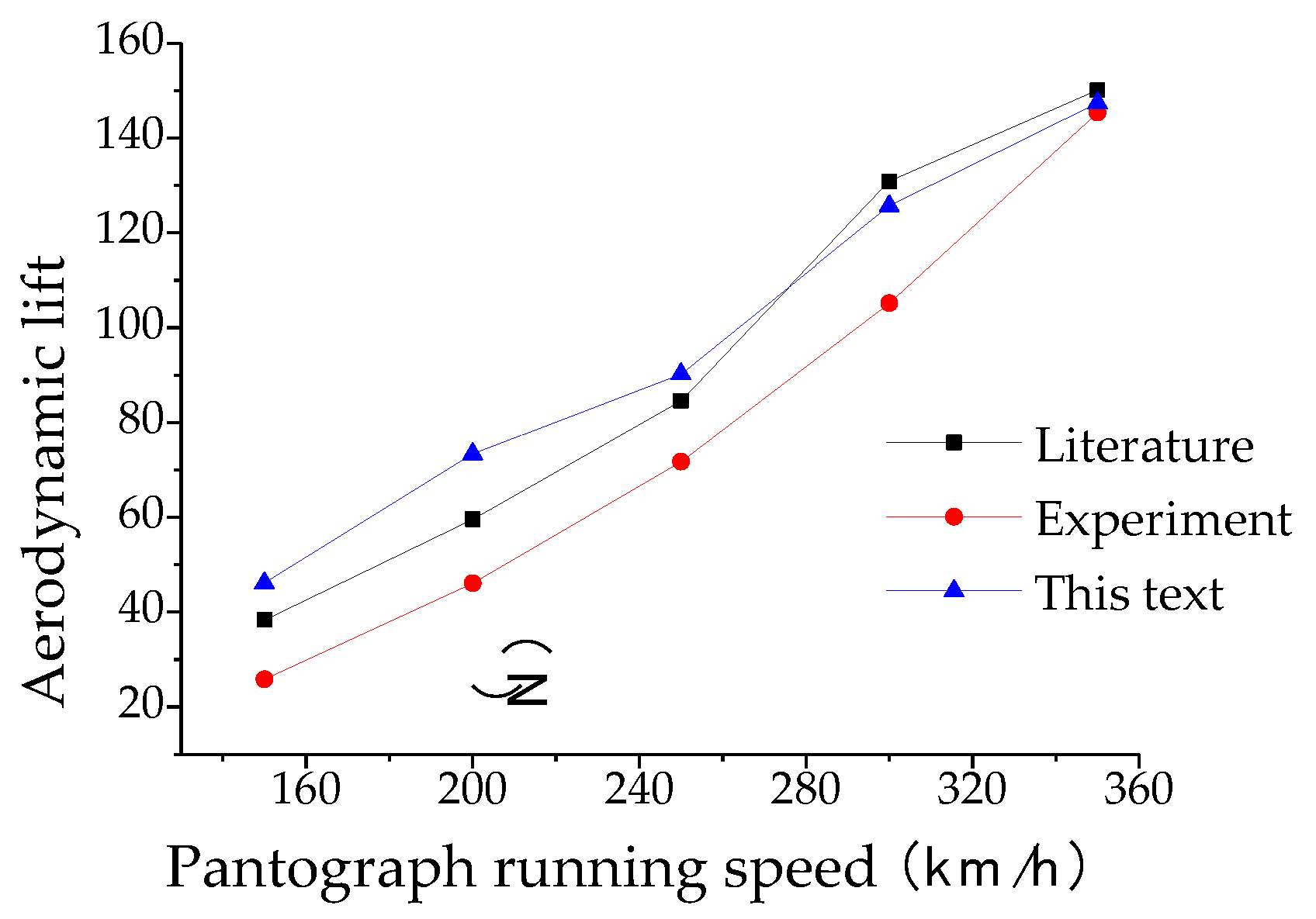
From the analysis of the aerodynamic lift of the main components of the pantograph, it can be observed that the aerodynamic lift of the bow collector head is the largest, while the absolute value of the aerodynamic lift of the lower arm is the smallest. Additionally, the aerodynamic lift of the upper arm is consistently negative, which conforms to the flow characteristics of the pantograph's collector head, upper arm, and lower arm in the unsteady external flow field. The running speed of the pantograph significantly affects the collector head and upper frame, while the crosswind speed has a greater impact on the lower arm and minimal effect on the aerodynamic lift of the upper frame. The combined influence of the running speed and crosswind speed, with a certain yaw angle (or crosswind direction angle), acts on the main components of the pantograph, determining the variation of aerodynamic forces and torques based on the flow characteristics of each component, thereby determining the distribution of aerodynamic lift.

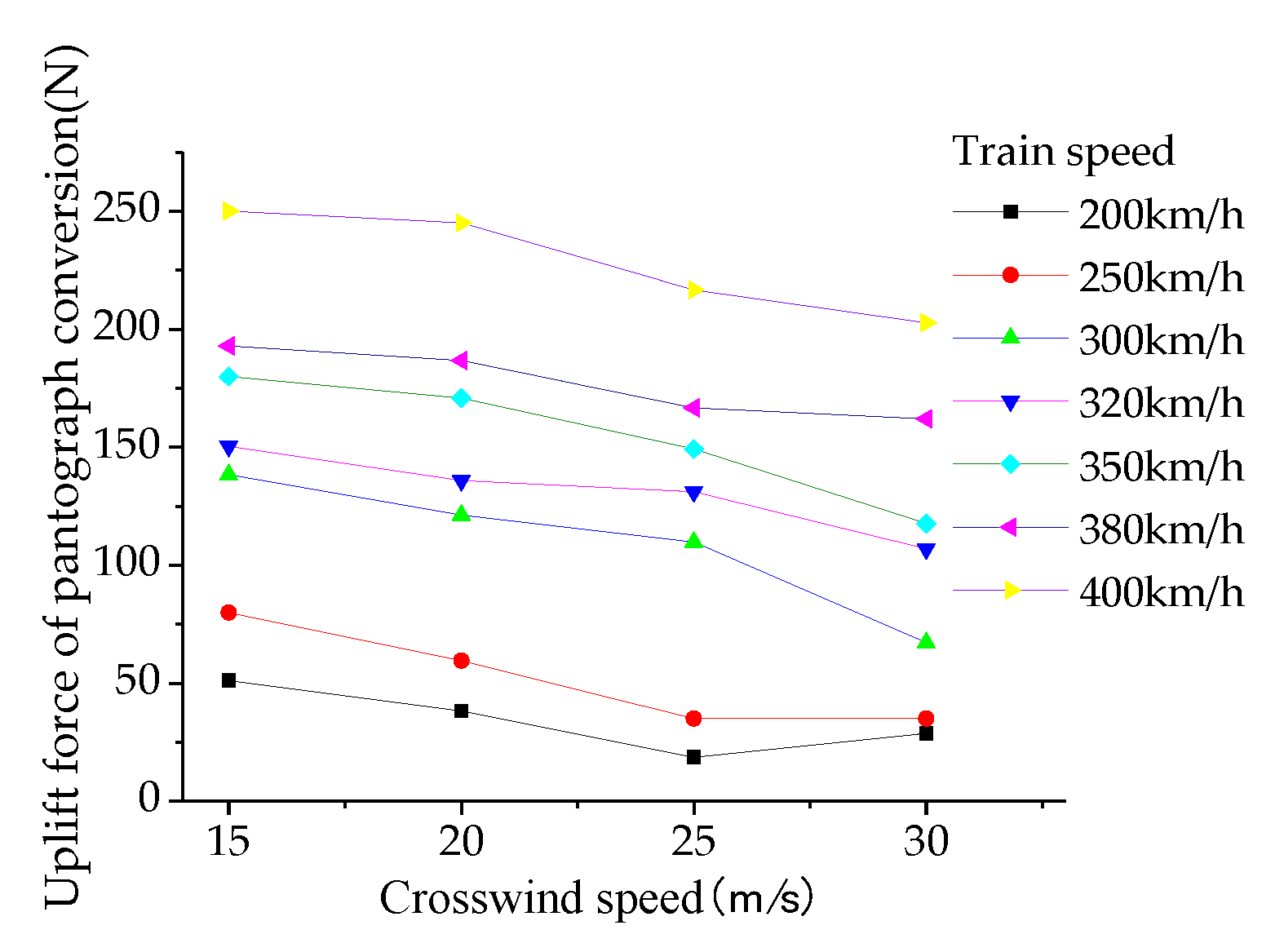
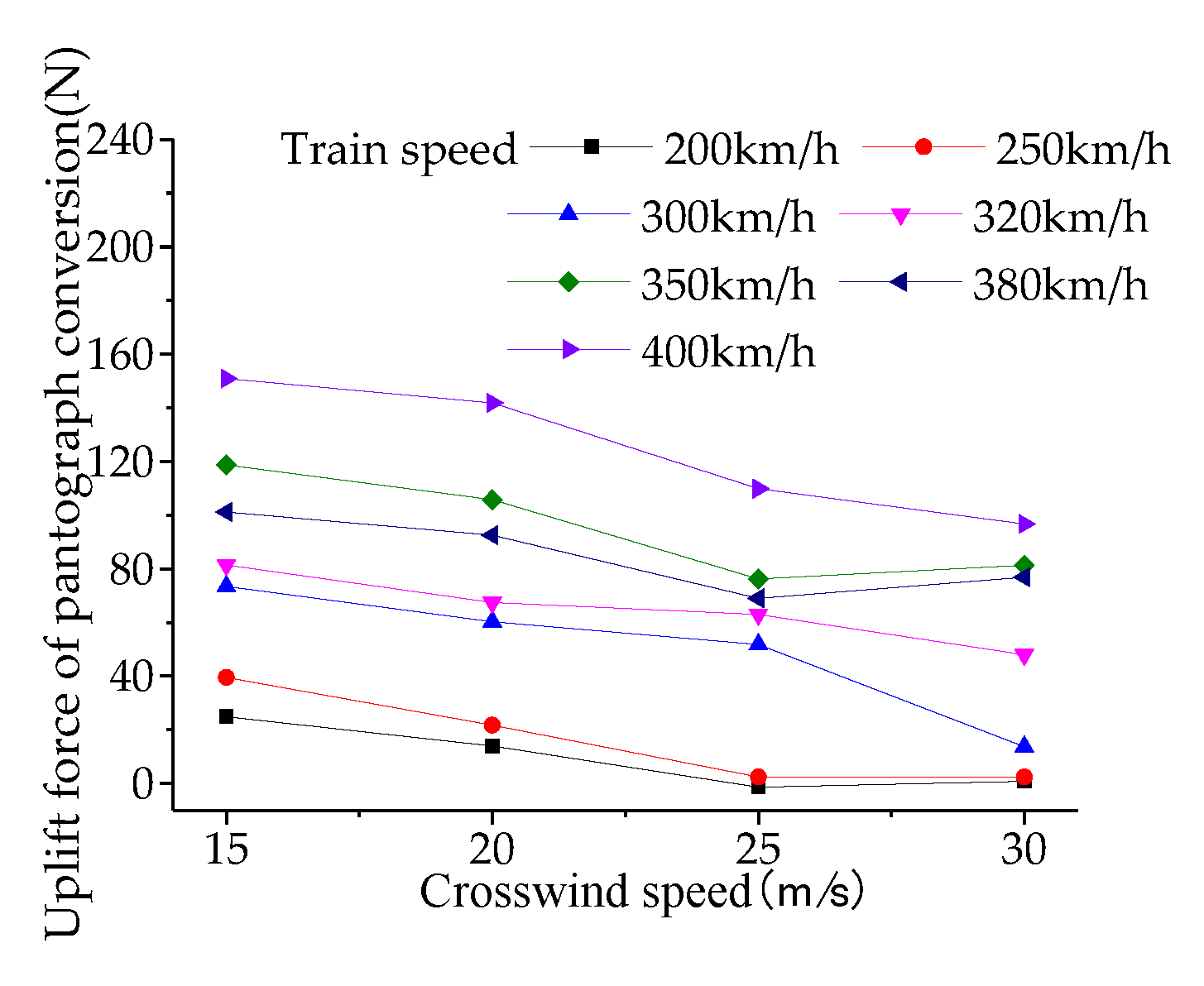
4.3. Analysis of Pantograph Aerodynamic Lift

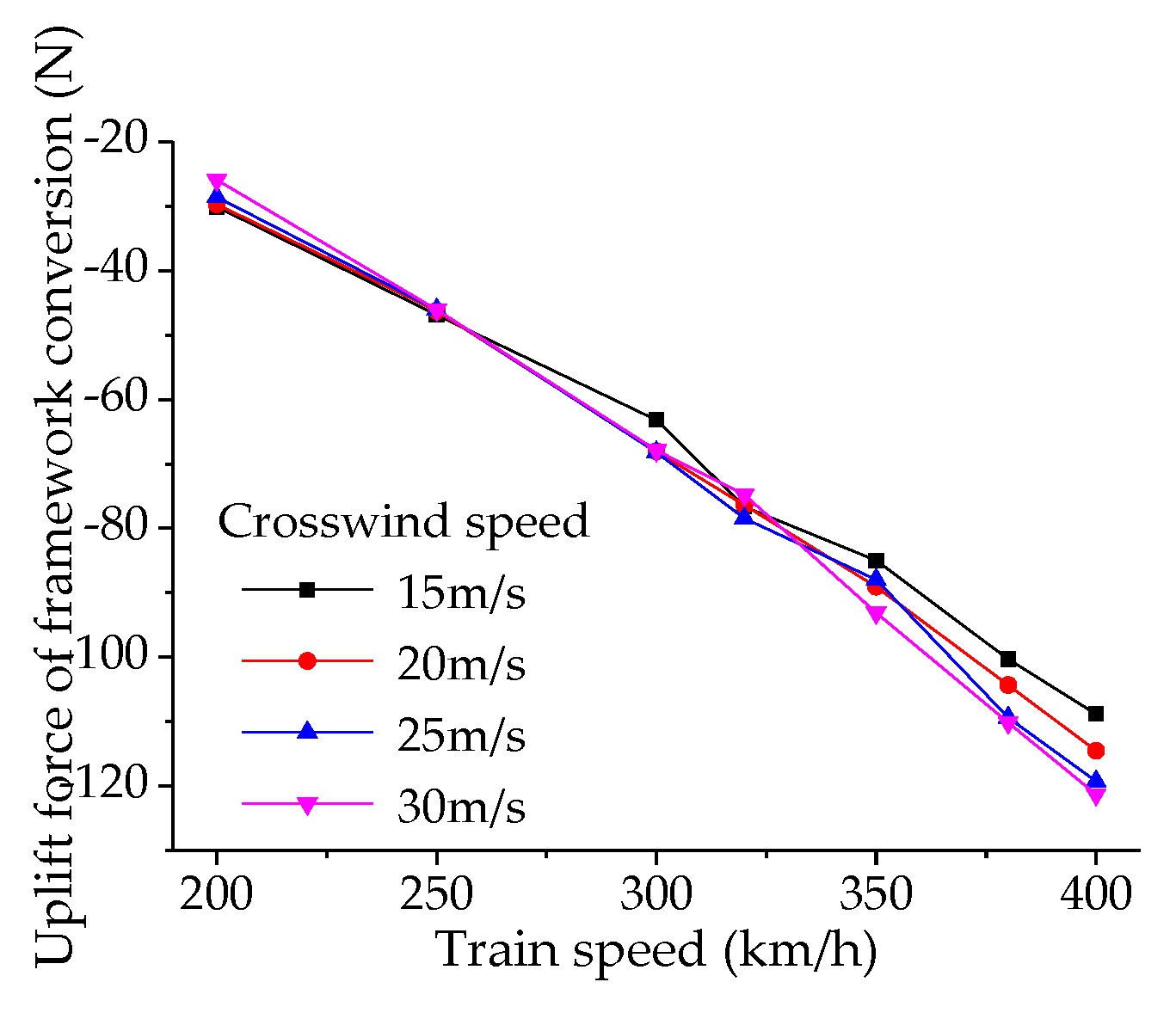
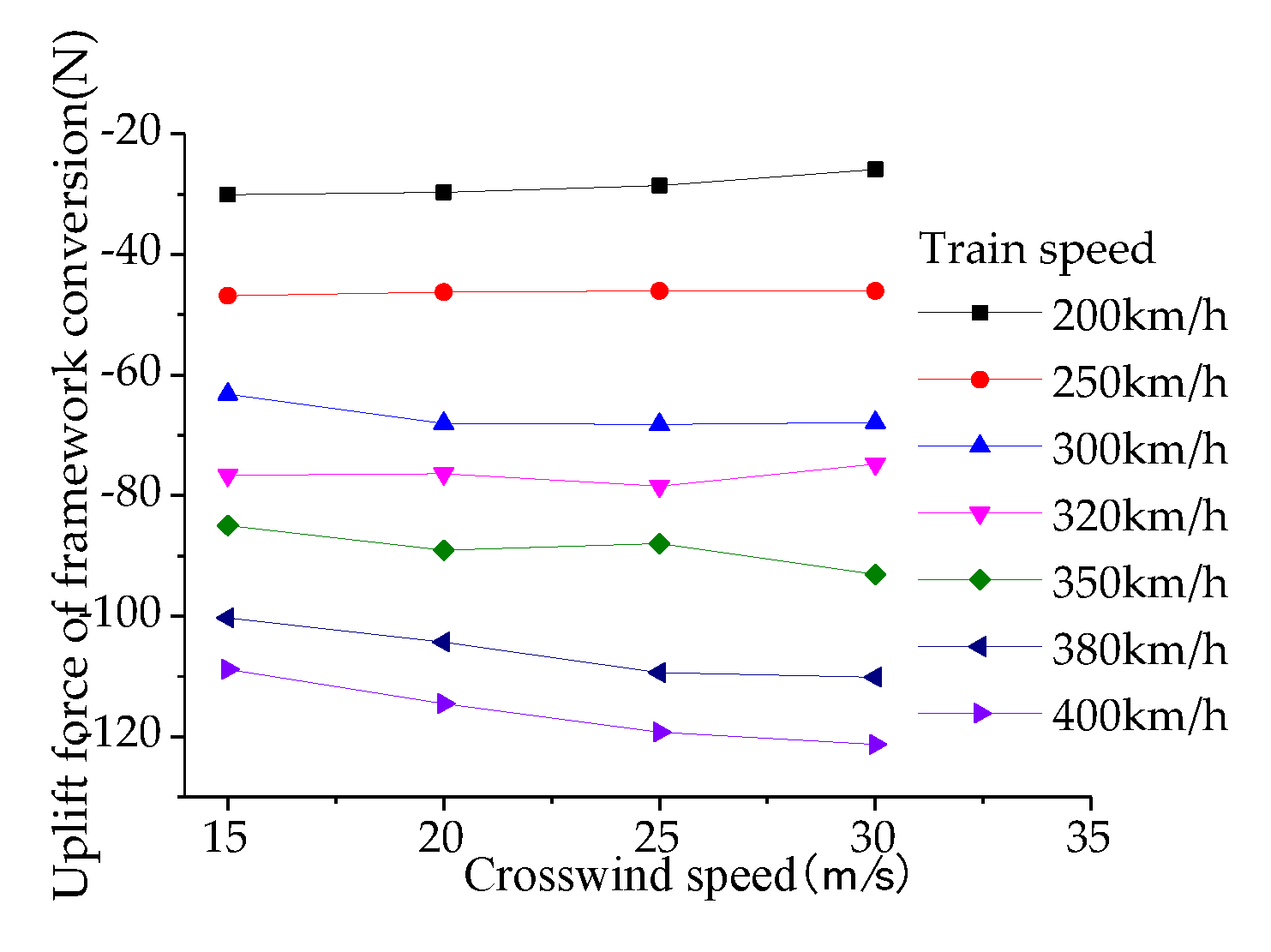
The pantograph, composed of various components, forms a structurally complex three-dimensional geometry. Under aerodynamic forces, each component of the pantograph generates vertical constraint forces, known as the pantograph aerodynamic lift. Figure 30, Figure 31 and Figure 32 illustrate the variation of pantograph aerodynamic lift with wind direction, train operating speed, and crosswind speed, with wind direction ranging from 10° to 90°, train speed (vehicle speed) from 200 km/h to 400 km/h, and crosswind speed from 15 m/s to 30 m/s. When the train speed is 350 km/h, the pantograph aerodynamic lift decreases with increasing wind direction angle. Within the range of wind direction angles from 10° to 50°, there is a rapid decrease in lift when the wind direction angle reaches 50° under a crosswind speed of 30 m/s. The slopes of the curves increase with increasing crosswind speed, and the variation pattern of pantograph lift changes significantly when the wind direction angle reaches 50°. The minimum aerodynamic lift occurs in the condition with a wind direction angle of 90° and a crosswind speed of 30 m/s (Figure 32). The aerodynamic lift of the pantograph generally increases with the train speed. In conditions with crosswind speeds of 15 m/s, 20 m/s, and 25 m/s, there is a significant inflection point in pantograph aerodynamic lift when the train speed reaches 380 km/h, while this phenomenon is not observed in conditions with a crosswind speed of 30 m/s (Figure 34).

The aerodynamic uplift force of the pantograph gradually decreases with the increase of crosswind speed. In operating conditions where the pantograph speeds are 200, 250, 300, 320, 350, 380, and 400 km/h, the aerodynamic uplift force of the pantograph decreases by 96.7%, 93.9%, 81.4%, 41.1%, 31.5%, 24.0%, and 35.9%, respectively, with the increase of crosswind speed. It can be observed that as the pantograph operating speed increases, the influence of crosswind speed gradually decreases.

5. Comprehensive Analysis of Pantograph Uplift Force

In order to comprehensively analyze the factors affecting the aerodynamic lifting force of the pantograph, we derive a comprehensive relationship between the lifting force, train speed, crosswind speed, and wind direction angle based on the calculated values obtained in this chapter. Here, we define the ratio of crosswind speed

V_{w}

to train speed

V_{t}

as the wind speed to velocity ratio

λ_{w t}

, and represent the influence of wind direction angle

θ

using

\cos θ

. Through a data-fitting process, we obtain the functional form of the comprehensive formula for aerodynamic lifting force, train speed, wind speed, and wind direction angle. Thus, we ultimately derive the comprehensive relationship between the pantograph aerodynamic lifting force

F_{e}

and the wind speed to velocity ratio

λ_{w t}

, as well as the wind direction angle

θ

F_{e} = 20.216 \times λ_{w t}^{0.787} (1 + 22.151 λ_{w t}^{- 1.660} {|\cos θ|}^{0.933})

(13)

Without considering the effect of crosswind, the relative air density

p_{v}

can be obtained through

p_{v} = 0.00097 V^{2} + 70

Taking into account the influence of train speed, crosswind speed, and wind direction angle, the aerodynamic uplift force of the pantograph is no longer a simple quadratic function of the cosine of the wind speed-to-vehicle speed ratio cosθ. Therefore, using the above formula to calculate the contact force of the pantograph is inaccurate. Empirical calculations suggest that by considering the vector sum of train speed and crosswind speed (

V = \vec{V_{t}} + \vec{V_{w}} = \sqrt{V_{t}^{2} + V_{w}^{2} + 2 V_{t} V_{w} \cos θ}

), the calculated values using this formula have errors within 10% when the train speed is 350 km/h and crosswind speed is within 20 m/s. However, when the crosswind speed increases to 25 m/s and 30 m/s, the formula deviates from the real situation. In the calculation of the aerodynamic uplift force of the pantograph, the transmission coefficient is determined by establishing the balance equation based on the geometric relationship of each component of the pantograph and force analysis. Since aerodynamic forces include the influence of crosswind, under the effect of crosswind, the uplift force of the pantograph should be determined by the following equation.

F_{m} = F_{e} + 70 = 20.216 \times λ_{w t}^{0.787} (1 + 22.151 λ_{w t}^{- 1.660} {|\cos θ|}^{0.933}) + 70

(14)

6. Conclusions

(1) The aerodynamic uplift force of the pantograph is primarily distributed on the pantograph head structure, where the aerodynamic uplift forces on the upper framework are all negative, while the absolute values of the aerodynamic uplift forces on the lower arm rods are the smallest. The aerodynamic uplift force on the pantograph head gradually decreases with increasing wind direction angle. Within the range of wind directions from 10° to 50°, under the same crosswind angle, the aerodynamic uplift force on the pantograph head increases with increasing crosswind speed. However, when the wind direction angle reaches 60° and the crosswind speed is 30 m/s, the aerodynamic uplift force on the pantograph head sharply decreases. Additionally, the aerodynamic uplift force of the pantograph gradually increases with increasing pantograph operating speed or crosswind speed.

(2) The operating speed of the pantograph and the wind direction angle have a significant impact on the aerodynamic uplift force of the main components, while the crosswind speed has a relatively minor effect on both the pantograph and main component's aerodynamic uplift forces. When the wind direction angle is small or the pantograph operating speed is high, the aerodynamic uplift force reaches higher values, increasing the likelihood of pantograph catenary contact and even bow scraping accidents. Conversely, in conditions with high crosswind speeds and low pantograph operating speeds, the pantograph is prone to experiencing insufficient aerodynamic uplift force, leading to arcing and disconnection phenomena.

(3) Through a comprehensive analysis of the factors influencing the aerodynamic uplift force of the pantograph, a relationship formula is derived that considers the aerodynamic uplift force of the pantograph in relation to the pantograph operating speed

V_{t}

, crosswind speed

V_{w}

, and wind direction angle

θ

. Furthermore, adjustments are made to empirical formulas relating to pantograph contact force and train operating speed.

7. Discussion

Extensive research has been conducted both domestically and internationally on the aerodynamic characteristics and behavior of pantographs under various conditions, establishing a robust foundation for comparative analysis with the results of the present study. Xiao, C [19] identified that the aerodynamic lift acting on the pantograph is predominantly concentrated on the head structure. Building upon this finding, the current research investigates the variation of aerodynamic lift as a function of crosswind angles, providing critical insights for the design and operational safety of high-speed trains. Li, X [20] demonstrated that operating speed and wind angle significantly influence the aerodynamic lift on the primary components of the pantograph. This study extends their work by deriving a comprehensive formula that correlates aerodynamic lift with variables such as operating speed, crosswind speed, and wind angle. Additionally, Abbas-Bayoumi [21] employed both empirical and numerical methods to predict key aspects of aerodynamic behavior. Building on their methodology, the present study formulates a relationship between pantograph aerodynamic lift, pantograph operating speed

V_{t}

, crosswind speed

V_{w}

, and wind angle

θ

, while optimizing the empirical formula for pantograph contact force and train operating speed. Through a comparative analysis of these key findings with existing literature, this research not only affirms the consistency of the results but also underscores significant advancements and contributions in the field.

Author Contributions

Conceptualization, M.Z.; formal analysis, Y.D. and Z.J.; data curation, Z.J.; investigation, X.L.; project administration, M.Z.; resources, Z.J.; software, Y.D.; supervision, X.L.; validation, M.Z.; writing—original draft, M.Z.; writing—review and editing, Y.D. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by Inner Mongolia Autonomous Region Natural Science Fund, grant number 2023LHMS01010; Basic scientific research business fee project for directly affiliated universities in Inner Mongolia Autonomous Region JY20240056

Institutional Review Board Statement

Not applicable

Informed Consent Statement

Not applicable

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Conflicts of Interest

The authors declare no conflicts of interest.

References

Brandani, V.; Galeotti, G.; Toni, P. A FEM method combined with modal analysis for evaluating the dynamical performance of a pantograph. Advances in Engineering Software 1992, 14, 171–177. [Google Scholar]
Sanquer, S.; Barré, C.; de Virel, M. D.; Cléon, L.-M. Effect of cross winds on high-speed trains: Development of a new experimental methodology. Journal of Wind Engineering and Industrial Aerodynamics 2004, 92, 535–545. [Google Scholar]
Carnevale, M.; Facchinetti, A.; Rocchi, D. Procedure to assess the role of railway pantograph components in generating the aerodynamic uplift. Journal of Wind Engineering and Industrial Aerodynamics 2017, 160, 16–29. [Google Scholar]
Arsene, S.; Sebesan, I.; Popa, G. The Influence of Wind on the Pantograph Placed on the Railway Electric Vehicles Bodywork. Procedia - Social and Behavioral Sciences 2015, 186, 1087–1094. [Google Scholar]
Wang, X.; Liu, T.; Xia, Y.; Gao, H.; Huo, X.; Xu, B.; Chen, Z. Effect of railway cutting depths on running safety and pantograph–catenary interaction of trains under crosswind. Journal of Wind Engineering and Industrial Aerodynamics 2024, 245, 105659. [Google Scholar]
Yang, K.; Liu, Y.; Li, X.; Bai, Z.; Wan, Y.; Xiao, Y.; Li, J. A high-accuracy single-frame 3D reconstruction method with color speckle projection for pantograph sliders. Measurement 2024, 237, 115192. [Google Scholar]
Zhao, Y.-y.; Yang, Z.-g.; Li, Q.-l.; Xia, C. Analysis of the near-field and far-field sound pressure generated by high-speed trains pantograph system. Applied Acoustics 2020, 169, 107506. [Google Scholar]
Araya Reyes, C. E.; Brambilla, E.; Tomasini, G. Evaluation of the Aerodynamic Effect of a Smooth Rounded Roof on Crosswind Stability of a Train by Wind Tunnel Tests. Applied Sciences 2023, 13. [Google Scholar]
Brambilla, E.; Carnevale, M.; Facchinetti, A.; Rocchi, D. Influence of train roof boundary layer on the pantograph aerodynamic uplift: A proposal for a simplified evaluation method. Journal of Wind Engineering and Industrial Aerodynamics 2022, 231, 105212. [Google Scholar]
Huang, G.; Wu, G.; Yang, Z.; Chen, X.; Wei, W. Development of surrogate models for evaluating energy transfer quality of high-speed railway pantograph-catenary system using physics-based model and machine learning. Applied Energy 2023, 333, 120608. [Google Scholar]
Kan, X.; Li, Y.; Li, T.; Zhang, J. Aerodynamic Analysis and Optimization of Pantograph Streamline Fairing for High-Speed Trains. Fluid Dynamics and Materials Processing 2024, 20, 1075–1091. [Google Scholar]
Li, T.; Qin, D.; Zhou, N.; Zhang, J.; Zhang, W. Numerical study on the aerodynamic and acoustic scale effects for high-speed train body and pantograph. Applied Acoustics 2022, 196, 108886. [Google Scholar]
Li, X.; Zhou, D.; Jia, L.; Yang, M. Numerical study of the influence of dome shape on the unsteady aerodynamic performance of a high-speed train's pantograph subjected to crosswind. Journal of Traffic and Transportation Engineering (English Edition) 2023, 10, 13–30. [Google Scholar]
Liu, H.; Zhou, S.; Chen, R.; Li, Z.; Zhang, S.; Zhao, Y. Numerical Study on the Aeroacoustic Performance of Different Diversion Strategies in the Pantograph Area of High-Speed Trains at 400 km/h. Applied Sciences 2022, 12. [Google Scholar]
Liu, Z.; Wang, H.; Chen, H.; Wang, X.; Song, Y.; Han, Z. Active pantograph in high-speed railway: Review, challenges, and applications. Control Engineering Practice 2023, 141, 105692. [Google Scholar]
Xiao, C.; Yang, M.; Tan, C.; Lu, Z. Effects of platform sinking height on the unsteady aerodynamic performance of high-speed train pantograph. Journal of Wind Engineering and Industrial Aerodynamics 2020, 204. [Google Scholar]
Li, X. F.; Zhou, D.; Jia, L. R.; Yang, M. Z. Effects of yaw angle on the unsteady aerodynamic performance of the pantograph of a high-speed train under crosswind. Journal of Wind Engineering and Industrial Aerodynamics 2018, 182, 49–60. [Google Scholar]
Zhang, Q.; Cai, X.; Wang, T.; Zhang, Y.; Wang, C. Aerodynamic performance and dynamic response of high-speed trains passing by each other on cable-stayed bridge under crosswind. Journal of Wind Engineering and Industrial Aerodynamics 2024, 247, 105701. [Google Scholar]
Xiao, C.; Yang, M.; Tan, C.; Lu, Z. Effects of platform sinking height on the unsteady aerodynamic performance of high-speed train pantograph. Journal of Wind Engineering and Industrial Aerodynamics 2020, 204, 104284. [Google Scholar]
Li, X.; Zhou, D.; Jia, L.; Yang, M. Effects of yaw angle on the unsteady aerodynamic performance of the pantograph of a high-speed train under crosswind. Journal of Wind Engineering and Industrial Aerodynamics 2018, 182, 49–60. [Google Scholar]
Abbas-Bayoumi, A.; Becker, K. An industrial view on numerical simulation for aircraft aerodynamic design. Journal of Mathematics in Industry 2011, (1), 10. [Google Scholar]

Figure 1. Dynamic contact force of the bow net.

Figure 2. Pantograph geometry model.

Figure 3. Comparative analysis of pantograph aerodynamic lift.

Figure 4. Geometric Relationships of Various Components of the Pantograph.

Figure 5. Force analysis of the upper arm rod and lower arm rod of the pantograph.

Figure 6. Composition of the pantograph and simplified model.

Figure 7. Dimensions of the computational domain.

Figure 8. Definition of wind angle.

Figure 9. Division of pantograph and computational domain grids.

Figure 10. Wind tunnel experiment.

Figure 11. Variation Curve of Drag Coefficient.

Figure 12. The life coefficient Variation Curve of Lift Coefficient.

Figure 13. Variation Curve of Lateral Force Coefficient.

Figure 14. Curve of variation in bow head drag coefficient.

Figure 15. Curve of variation in bow head lift coefficient.

Figure 16. Curve of variation in bow head lateral force coefficient.

Figure 17. Curve of variation in upper frame drag coefficient.

Figure 18. Curve of variation in upper frame lift coefficient.

Figure 19. Curve of variation in upper frame lateral force coefficient.

Figure 20. Curve of variation in lower arm rod drag coefficient.

Figure 21. Curve of variation in lower arm rod Lift coefficient.

Figure 22. Curve of variation in lower arm rod lateral force coefficient.

Figure 23. Aerodynamic lift of the bow section.

Figure 24. Aerodynamic lift of the upper framework.

Figure 25. Aerodynamic lift of the lower arm rod.

Figure 26. Aerodynamic lift of the bowhead.

Figure 27. Aerodynamic lift of the upper frame.

Figure 28. Aerodynamic lift of the lower arm rod.

Figure 29. Lift force of the bowhead.

Figure 30. Lift force of the upper frame.

Figure 31. Lift force of the lower arm rod.

Figure 32. Pantograph lift force.

Figure 33. Pantograph lift force (vehicle speed).

Figure 34. Pantograph lift force (crosswind).

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Research on the Uplift Characteristics of Pantographs of High-Speed Trains Under Crosswind Conditions

Abstract

1. Introduction

2. Pantograph Aerodynamic Lift Calculation Model

3. Methods for Calculating the Aerodynamic Lift of the Pantograph

3.1. Geometric Relationships and Force Analysis of Pantograph Components

3.2. Calculation of Transfer Coefficients

3.3. Pantograph Aerodynamics Model

3.4. Numerical Simulation Method

4. Aerodynamic Lift of the Pantograph

4.1. Aerodynamic Loads on the Pantograph

4.2. Aerodynamic Lift of the Main Components of the Pantograph

4.3. Analysis of Pantograph Aerodynamic Lift

5. Comprehensive Analysis of Pantograph Uplift Force

6. Conclusions

7. Discussion

Author Contributions

Funding

Institutional Review Board Statement

Informed Consent Statement

Data Availability Statement

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe