Prerpints.org logo
Preprint
Article

Application of ALRW‐DDPG Algorithm on Offshore Oil‐Gas‐Water Separation Control

Altmetrics

Downloads

80

Views

32

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

16 August 2024

Posted:

16 August 2024

You are already at the latest version

Alerts
Abstract
With the offshore oil-gas fields entering decline phase, high-efficiency separation of oil-gas-water mixtures becomes a significant challenge. As essential equipment for separation, the three-phase separators play a key role in Offshore Oil-Gas production. However, level control is critical in the operation of three-phase gravity separators on offshore facilities, as it directly affects the efficacy and safety of the separation process. This paper introduces an advanced deep deterministic policy gradient with adaptive learning rate weights (ALRW-DDPG) control algorithm, which improves the convergence and stability of the conventional DDPG algorithm. An adaptive learning rate weight function is meticulously designed, and an ALRW-DDPG algorithm network is constructed for simulating three-phase separator liquid level control. The effectiveness of the ALRW-DDPG algorithm is subsequently validated through simulation experiments. The results show that the ALRW-DDPG algorithm achieves a 15.38% improvement in convergence rate compared to the traditional DDPG algorithm, and the control error is significantly smaller than that of PID and DDPG algorithms.
Keywords: 
Subject: Engineering  -   Energy and Fuel Technology

1. Introduction

With the continuous development of offshore oil-gas fields, many oil-gas fields in South China Sea enter the high water cut stage and the water fraction in the produced fluid increases significantly [1].The produced fluid is commonly a heterogeneous mixture of crude oil, natural gas, water, and solids, which must be processed through oil and gas treatment facilities before it can be stored or transported [2]. As essential equipment for separation, the three-phase separators play a key role in this process. The fluid produced from the wellhead can be separated into natural gas, crude oil and wastewater with the separators. During this process, the level of the separator is an important parameter that determines the effectiveness and quality of the separation. An excessively high level can alter the separation space for oil and water phases, reducing the dehydration rate and efficiency of the separator [3].
Currently, the liquid level in separators is commonly controlled using Proportional-Integral-Derivative (PID) control methods on offshore platforms [4,5]. However, conventional PID control strategies unable to adaptively change model parameters, leading to dramatic level fluctuations in the separator, which may trigger alarms or even production shutdowns. Therefore, operators have to adjust the control parameters frequently to adapt to the randomly changing conditions during oil-gas production. Nevertheless, the absence of personnel on unmanned platforms, coupled with the delays in remote control operations and the disparity in operational experience, results in poor stability of the separator liquid level control [6].
In order to enhance the stability of the separator liquid level control, numerous advanced control strategies have been employed to deal with the random disturbances and condition changes in the production process. Among these strategies, the reinforcement learning (RL) algorithm has been effectively utilized to resolve complex nonlinear control challenges.

1.1. Related Work

In the domain of liquid level control for three-phase separators, there are several related research works in the literature [7,8,9,10]. Song et al. employed the HYSYS software to construct a model of the production process for an offshore platform and a PID liquid level control model for the three-phase separator. By simulating the process of oil-gas treatment, they completed a sensitivity analysis of PID control parameters and provided recommended parameter values for PID liquid level controllers. However, these recommended values are only applicable to specific operational conditions, and the PID parameters cannot adjust automatically to adapt to changed scenarios [11]. Ma et al. utilized the K-Spice software to establish a dynamic model of the three-phase separator’s operational process. Through simulation calculations, he obtained the changes in the separator’s liquid level when there was a failure in the oil phase outlet level control valve, thus correcting the value of the three-phase separator’s liquid level. Nevertheless, this research only analyzed broken conditions and did not consider the flow fluctuation in pipelines during normal production [12]. Fan et al. developed a mathematical model that relates the dewatering efficiency of the separator to the height of the oil-water interface. By employing the genetic algorithm, she derived the optimal oil-water interface height, yet did not provide a specific engineering implementation method [13]. Feng Wu established a mathematical model for the optimal oil-water interface height in the separator, utilizing the genetic algorithm within MATLAB to determine the best separation height for the oil-water interface under different conditions of produced fluid. He also realized control of the liquid level through the interaction between WinCC and MATLAB. However, the control model based on the genetic algorithm is highly dependent on the breadth of the training dataset [14]. Petar et al. introduced a model-based robust H∞ control solution that manages the entire de-oiling system and found that the robust H∞ control significantly enhanced the performance of the de-oiling process. Nevertheless, the H∞ control solution requires an accurate mathematical model, which is difficult in many practical engineering problems [15].
In response to the limitations of existing control methods, deep reinforcement learning (DRL) has emerged as a promising alternative. DRL does not require complex models and has exhibited strong adaptability to numerous operational conditions [16]. Consequently, the DDPG (Deep Deterministic Policy Gradient) algorithm, as a renowned DRL method, has been successfully employed in recent years to address decision-making problems involving continuous action space [17,18,19,20]. In [21], a novel self-adapted Advantage-Weighted Actor-Critic algorithm was proposed and evaluated in both simulated and real-world building environments. Mai et al. implemented a deep deterministic policy gradient in satellite communications to adjust congestion rates [22]. Chang et al. utilized the DDPG and Recurrent Deterministic Policy Gradient (RDPG) algorithms, in conjunction with Convolutional Neural Networks (CNNs), to achieve autonomous driving control for self-driving cars [23].
Although the DDPG algorithm exhibits superior control accuracy compared to the conventional algorithms, the estimation of hyperparameters during DDPG training presents a substantial challenge. These hyperparameters, such as learning rate, critically influence the learning process and time, which is of importance for real-time online control systems. To address the instability and slow convergence speed of the conventional DDPG algorithm in complex and uncertain environments, an improved DDPG algorithm is proposed in this paper.

1.2. Main Contributions

Addressing the challenges of overshoot and instability commonly associated with traditional level control techniques in three-phase separators, ALRW-DDPG algorithm is proposed in this paper. This algorithm introduces an adaptive learning rate weighting strategy to optimize learning rate, thereby improving the convergence rate of the DDPG algorithm and ultimately leading to a more efficient control response speed and stability. This model incorporates an environment vector to elucidate the influence of slug flow and flow oscillations. A reward function is proposed to expedite convergence, and a DDPG online learning network is developed. The accuracy of control using the deep reinforcement learning model is confirmed through simulations using the physical parameters of the Century FPSO (Floating Production Storage and Offloading).
The main contributions of this research are summarized in the following key points:
  • Based on the physical parameters of the three-phase separator on the Century platform and the principles of fluid dynamics, a mathematical model is developed, taking into account variables such as inlet flow rate, pressure difference, cross-sectional dimensions, and valve opening. This model serves as the environmental model and is suitable to construct the ALRW-DDPG algorithm network.
  • An improved method for the traditional DDPG algorithm using the adaptive learning rate weight is proposed, enhancing the convergence speed and stability of the control algorithm. Additionally, the adaptive learning rate weight function is meticulously designed to dynamically adjust the learning rate.
  • The ALRW-DDPG algorithm network for three-phase separator liquid level control is constructed. An environmental state vector is created, incorporating the current level height, level deviation, integral of the height error, derivative of the height error, inlet flow rate, and valve pressure differential. This state vector characterizes the liquid level fluctuations resulting from slug flow. An error reward function is designed to reduce the rate of change of the reward value as the target value is approached, thereby mitigating liquid level fluctuations.
  • A comparative analysis is conducted to evaluate the differences in convergence speed and control error between the PID, traditional DDPG control methods, and the proposed ALRW-DDPG control algorithm, and which confirms the effectiveness of the ALRW-DDPG control algorithm, demonstrating its ability to enhance the stability of liquid level control in the three-phase separator.

2. Methods

2.1. The Principle and Model of Three-Phase Separator

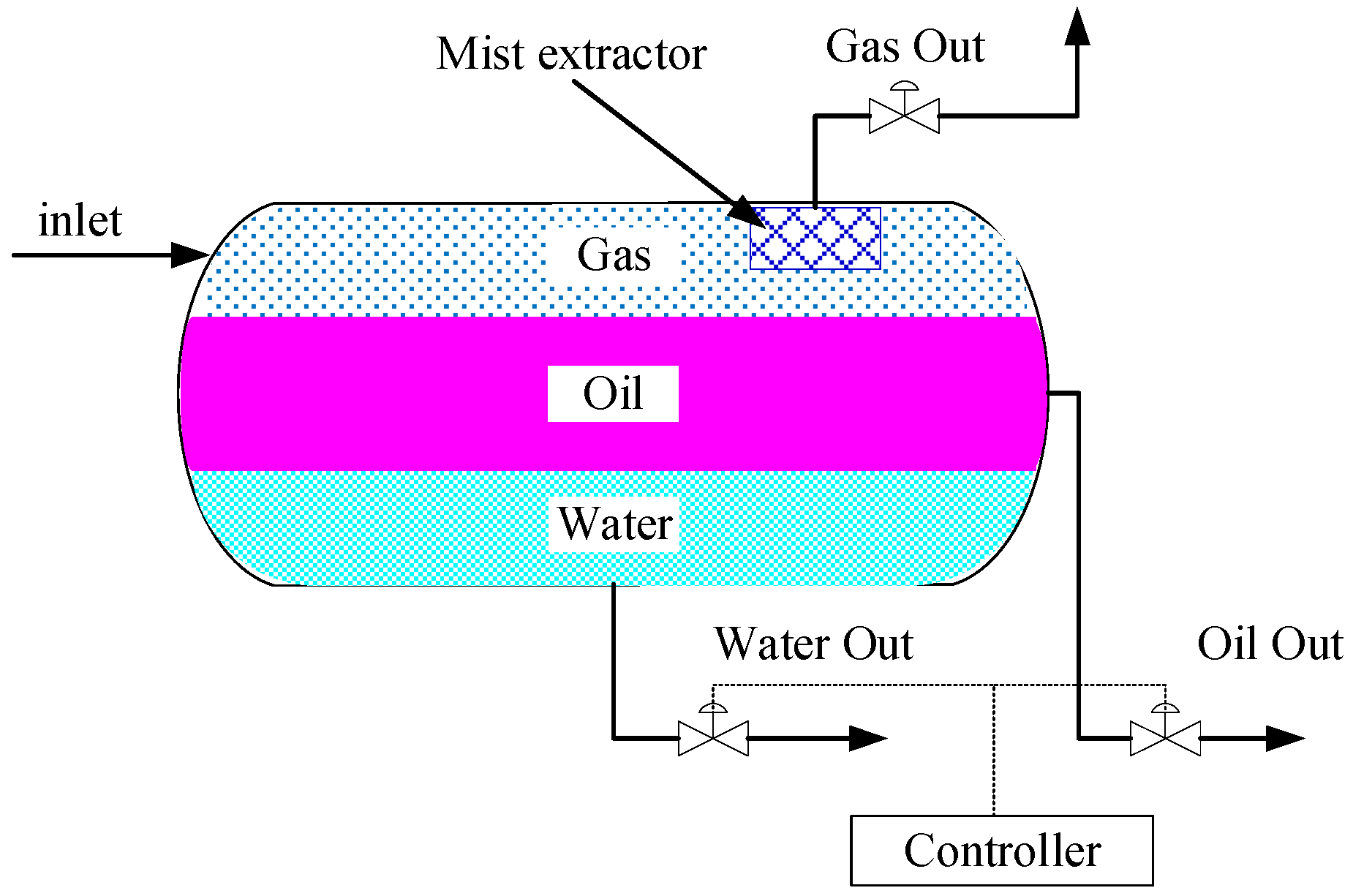
Three-phase separators are designed to separate an oil-gas-water mixture. The gas phase is extracted at the inlet via a mist extractor and subsequently evacuated through the gas phase outlet. Simultaneously, owing to disparities in density and viscosity, gravitational forces facilitate the separation of oil and water within the mixture, with the oil rising and the water sinking, thereby forming distinct oil and water layers. Subsequently, the separated components pass through the oil-gas-water control valves and proceed to the next processing stage [14]. To achieve optimal oil-water separation, the control system uses level meters to monitor the liquid level in the oil chamber and compares it to a predetermined value. Based on the difference, the control system calculates the required adjustments to the oil and water regulating valve openings, thereby controlling the liquid level. The operational mechanism of the three-phase separator is illustrated in Figure 1.
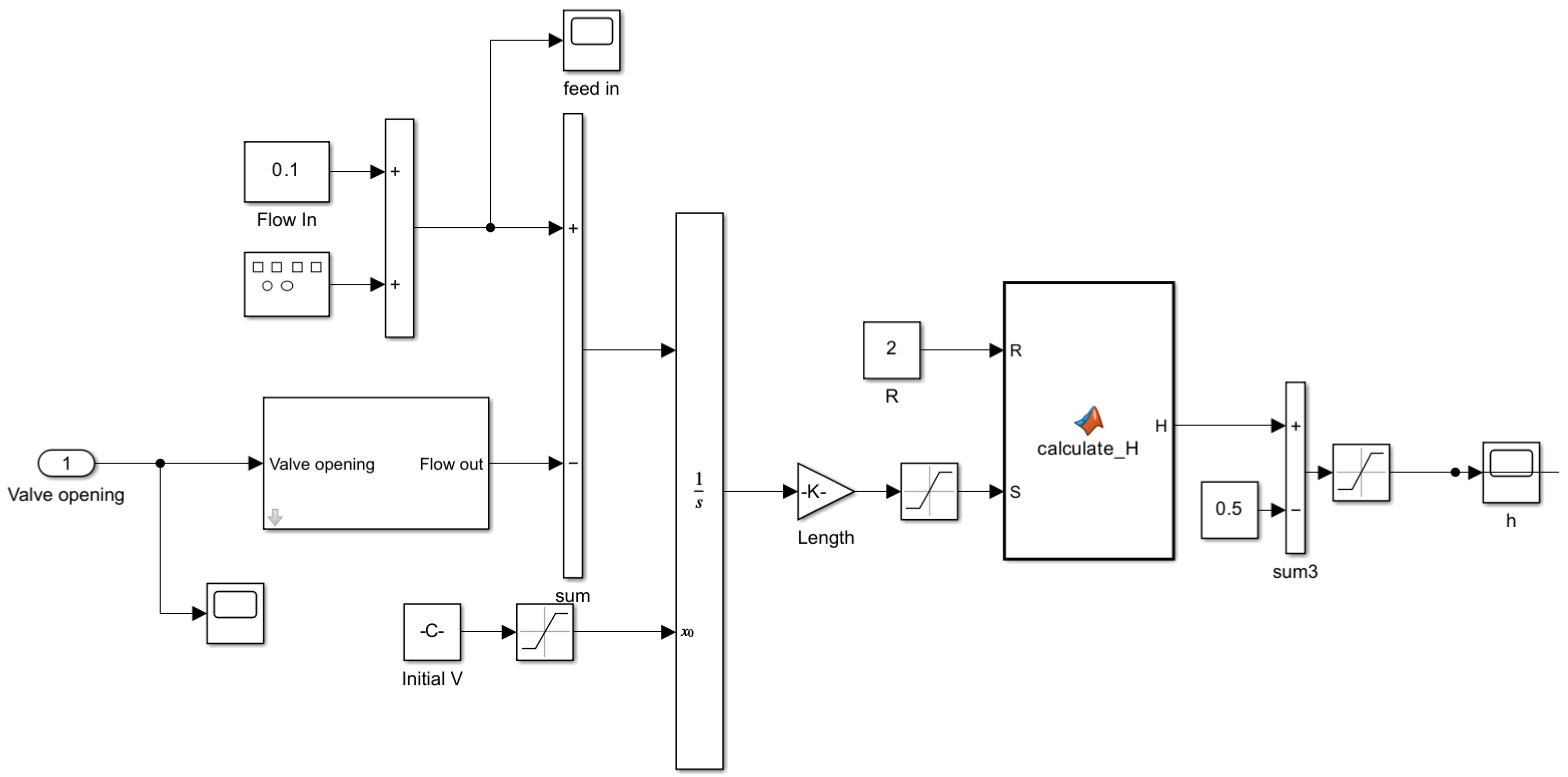
According to the analysis of the working principle of the three-phase separator, this paper establishes a SIMULINK model for the three-phase separator onboard the Century FPSO. Equation (1) represents the calculation formula for the outlet flow rate of the valve [24].
Q = x K v Δ P S G
where x is the valve opening, K v is the valve flow coefficient, Δ P is the pressure difference across the valve, and SG is the specific gravity of the medium and the value is 0.8.
The flow coefficient for the oil phase outlet valve can be calculated using Equations (2) and (3):
C v o i l = C v w a t e r D o i l 2 D w a t e r 2
1 K v = 0.865 C v
where D is the valve diameter, K v and C v are the flow coefficients in different units of measurement, with K v in m3/h and C v in GPM.
The relationship between the liquid level and the cross-sectional area within the three-phase separator is given by Equation (4):
S = a r c c o s ( l r ) r 2 − l ( r 2 − l 2 )
where S is the cross-sectional area of the three-phase separator, r is the radius of the separator, and l is the difference between the radius and the liquid level height.
Using the inlet flow rate, outlet flow rate, and the calculation formula for the liquid level height of the three-phase separator, the mathematical model of the liquid level in the three-phase separator is established as shown in Figure 2.

2.2. DDPG Algorithm

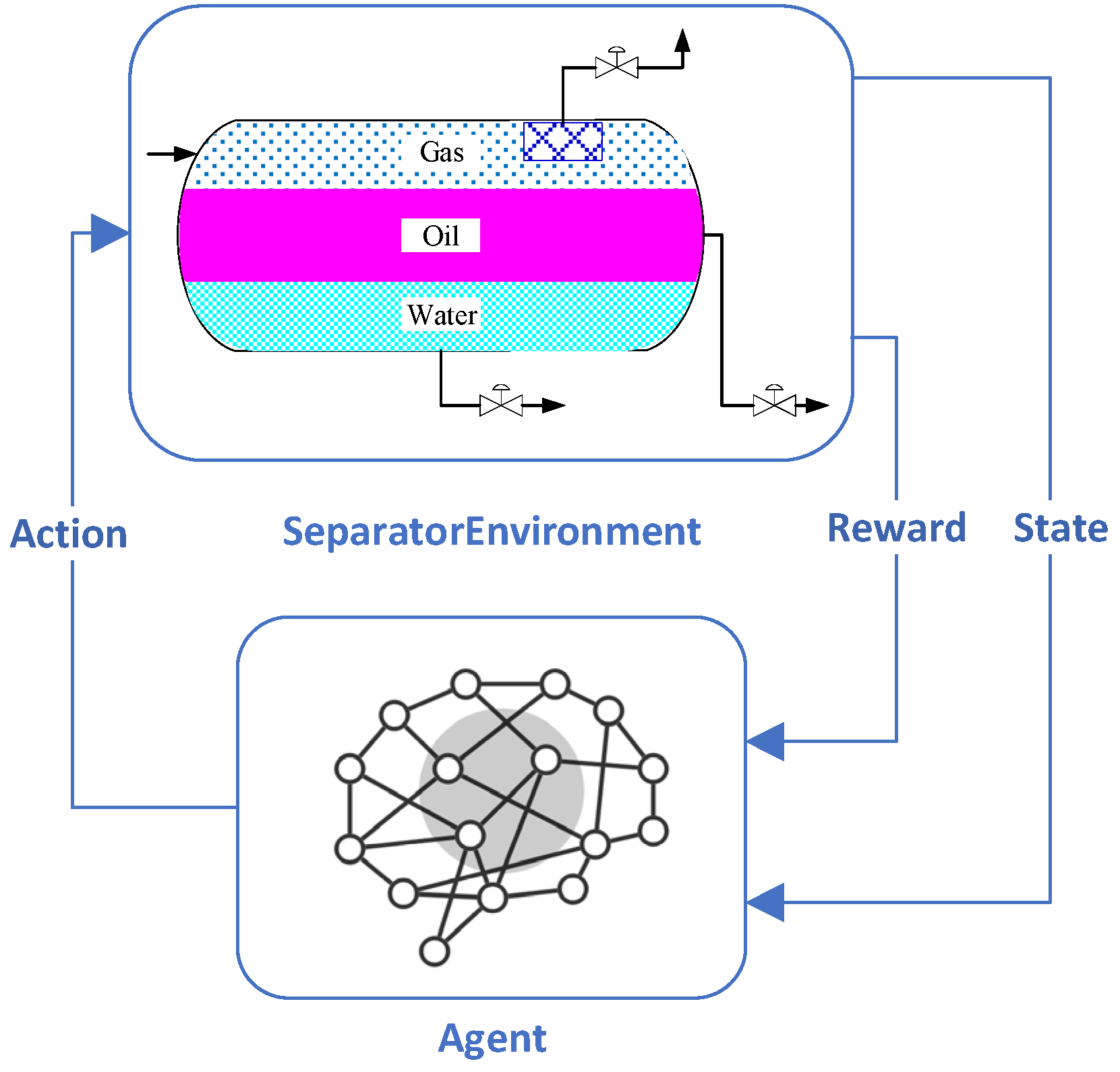
Compared to the traditional PID control algorithm, deep reinforcement learning(DRL) integrates deep learning and reinforcement learning, making it suitable for higher-dimensional and more complex environments [25,26]. The deep reinforcement learning framework primarily consists of five key elements: agent, environment, state, action, and reward [27,28]. The agent selects an action based on the current environment state and adjusts its action strategy according to the reward obtained from the executed action. The agent is trained through continuous interaction with the environment, thereby making optimal decisions [29,30]. A diagram illustrating the structure of deep reinforcement learning is provided in Figure 3.
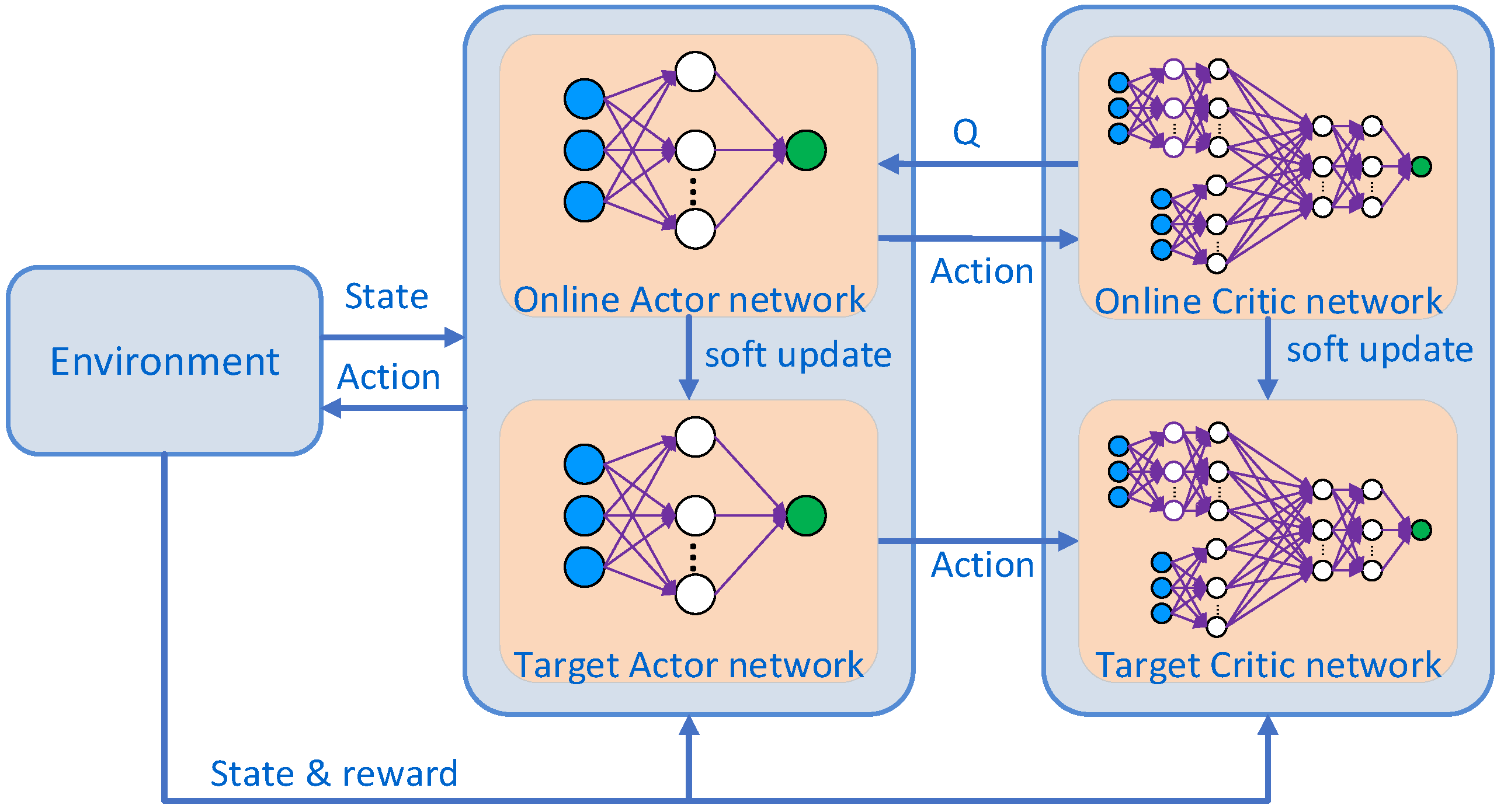
The DDPG algorithm represents an evolution in deep reinforcement learning, drawing inspiration from the Deep Q-Networks (DQN) algorithm. It adapts the DQN framework for use in a multi-dimensional continuous action space by fusing it with the Deterministic Policy Gradient (DPG) method. The DDPG algorithm is anchored in the actor-critic (AC) framework, inheriting the DQN’s approach of utilizing neural networks to approximate value functions and the DPG’s strategy for policy iteration. It enhances the convergence rate of the algorithm by adopting the experience replay mechanism from DQN and strategically sampling to reduce correlations between data points [31]. The core of the DDPG algorithm lies in the construction and continual update of the action network and the evaluation network. The DDPG architecture comprises four deep neural networks: the critic network, the actor network, the target critic network, and the target actor network. A graphical depiction of the DDPG algorithm network structure is provided in Figure 4.
Critic Network Update: The critic network estimates the Q-value of an action based on the reward generated by the actor’s action and the subsequent state. It calculates the Temporal Difference (TD) error, as shown in Equation (5).
δ = r + γ Q ω ′ ′ ( s t + 1 , a t + 1 ) − Q ω ( s t , a t )  
where Q ω ( s t , a t ) is the Q-value estimated by the critic network, Q ω ′ ′ ( s t + 1 , a t + 1 ) is the Q-value estimated by the target critic network, and γ is the discount factor.
The critic network updates its parameters by minimizing the loss function L ( ω ) , which is expressed as in Equation (6):
L ( ω ) = 1 N ∑ i δ i 2
Here, N represents the size of the sample batch.
The update equation for the critic network parameters is given by Equation (7):
w ← w + α ∇ w L ( w )
where α is the learning rate of the critic network, and ∇ w L ( w ) is the gradient of the loss function.
Actor Network Update: The actor network updates its parameters by maximizing the expected return, as shown in Equation (8):
θ ← θ + β ∇ θ log π θ ( s t , a t ) δ
where β is the learning rate of the actor network, π θ ( s t , a t ) is the action policy of the actor network, and θ is the network parameters.
Soft Update: The target network, as a slowly updated copy of the original actor and critic networks, provides a stable learning target, reducing training instability and helping the algorithm avoid overfitting, thus smoothing the learning process. After the actor and critic networks are updated, a soft update of the target network is updated with the formula given by equation (9):
w ′ ← τ w + 1 − τ w ′ θ ′ ← τ θ + 1 − τ θ ′

2.3. Design of the ALRW-DDPG

DDPG algorithms are capable of promoting effective information iteration and self-improvement, thereby achieving favorable performance, making them suitable for continuous control systems. However, traditional DDPG algorithms often suffer from slow convergence and poor stability, and are difficult to achieve real-time online control of the separator’s level in the face of uncertain and changing flow rates [32]. To address these limitations, We propose a deep deterministic policy gradient with adaptive learning rate weights (ALRW-DDPG) control strategy.
DDPG algorithms can benefit from employing varying learning rates during the training process to mitigate fluctuations in reward values and hasten convergence. However, traditional algorithms lack the capability to dynamically adjust the learning rate. To overcome this limitation, we have devised a method that modulates the learning rate in real-time based on the reward values. This method advocates for a higher learning rate during periods of low reward values, enabling swift strategic adjustments to enhance performance. Conversely, a lower learning rate is adopted during high-reward phases, ensuring training stability and preventing fluctuation that may arise from excessive iteration steps.
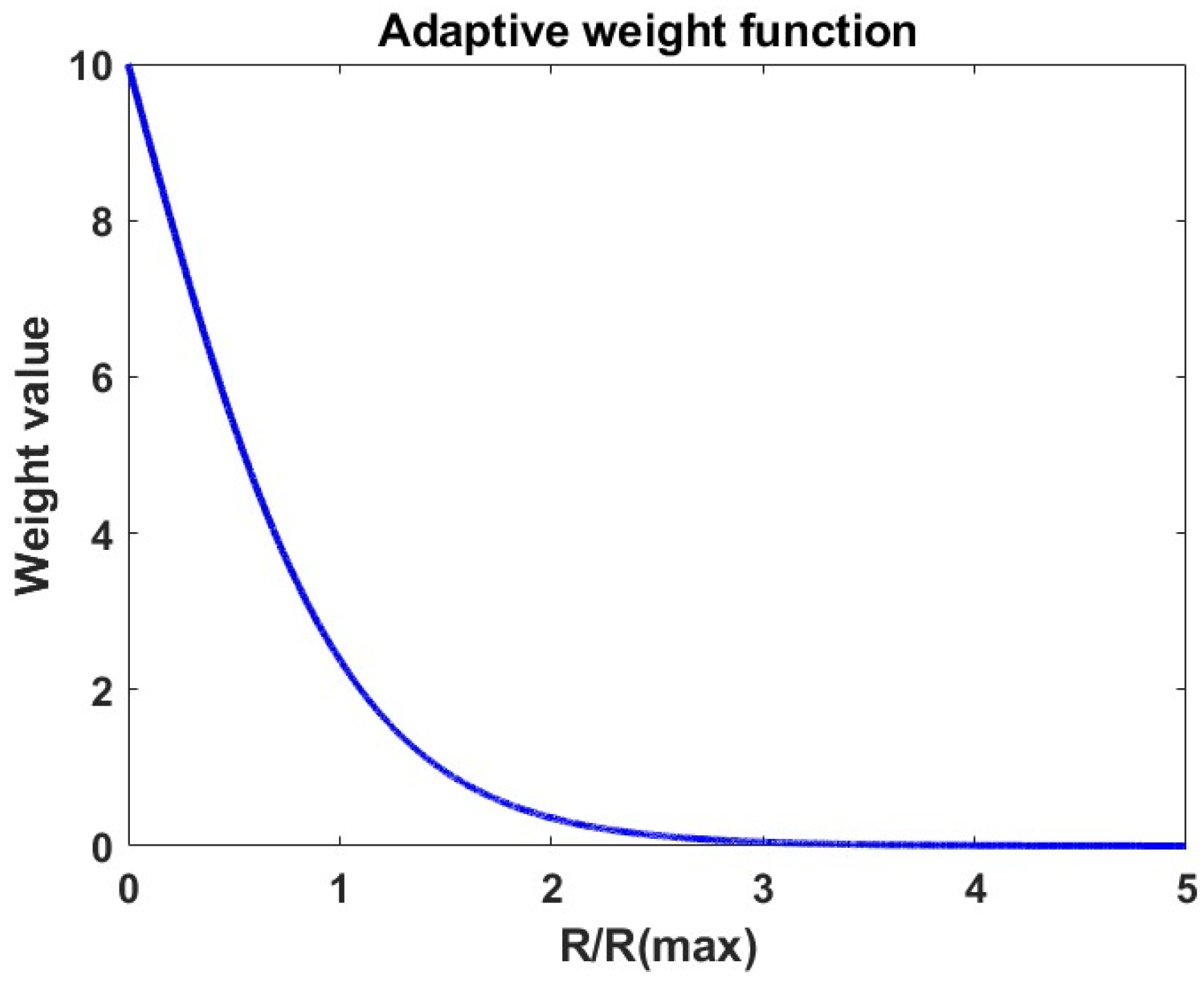
The adaptive learning rate weight is calculated based on the difference between the current reward value and the maximum and minimum reward values. The calculation of the adaptive learning rate weights, proposed in this study, is detailed in Equation (10) and visually represented in Figure 5.
c = 10 − 10 e − R R max − e R R max e − R R max + e R R max
where, R is the difference between the reward value for each episode and the minimum reward value, while R max is the difference between the maximum reward value and the minimum reward value for each episode. The weight c for each episode is determined using Equation (10). Subsequently, the learning rates of both the actor and critic networks are adjusted in accordance with Equation (11).
α = c α ′ β = c β ′
where, α is the set value for the learning rate of the critic network, and β is the set value for the learning rate of the actor network.
In order to explore more effective optimization strategies under complex operating conditions, An Ornstein-Uhlenbeck (OU) noise is introduced into the output valve opening degree. This method enhances the DDPG algorithm’s capability to explore a broader action space, mitigating the risk of convergence to a local optimum. Furthermore, it achieving a balance between exploration and cooperation for the actor and critic networks. The modified calculation formula for the optimized valve opening degree is shown in Equation (12):
a = n o i s y a t + N
where a t is the valve opening degree with the ranging from 0 to 1.The expression for the OU noise N is given by Equation (13):
N = α ( μ − a t ) T s + σ T s
where, α is a mean regression parameter, μ is the mean, σ is the standard deviation, and T s is the sampling time.
The Algorithm 1 demonstrates detailed steps of the ALRW-DDPG algorithm for the three-phase separator level control.
Algorithm 1. Pseudocode of ALRW-DDPG
1. Initialization of DDPG Params: Actor θ, Critic ω, θ ′ ← θ , ω ′ ← ω , initialize replay buffer
2. for episode =1 to M do
3.  Initialize the state s 1 randomly
4.  for t =1 to T do
5.    Determine a t using policy network and exploration
6.    Apply action a t compute system reward r ( s t , a t ) and determine next state s t + 1
7.    Save transitions ( s t , a t , r t , s t + 1 ) in replay buffer R
8.    if t > m do
9.        Sample a batch ( s i , a i , r i , s i + 1 ) from replay buffer R
10.      Calculate TD error δ
11.      Minimize the loss function to update the critic network parameter:
                   w ← w + α ∇ w L ( w )
12.      Update the critic network parameter using the policy gradient:
                   θ ← θ + β ∇ θ J ( θ )
13.      Update the target networks parameter:
                   w ′ ← τ w + 1 − τ w ′ θ ′ ← τ θ + 1 − τ θ ′
14.    end if
15.  end for
16.  Updates the actor network and critic network learning rate
                   α = c α ′ β = c β ′
17: end for

3. Simulation and Result Analysis

3.1. Separator and Parameters

The simulation model for the three-phase separator is developed in accordance with the configuration of the separator onboard the Century FPSO, as illustrated in Figure 6. Table 1 lists the key parameters associated with this separator.

3.2. Simulation Model of Slug Flow

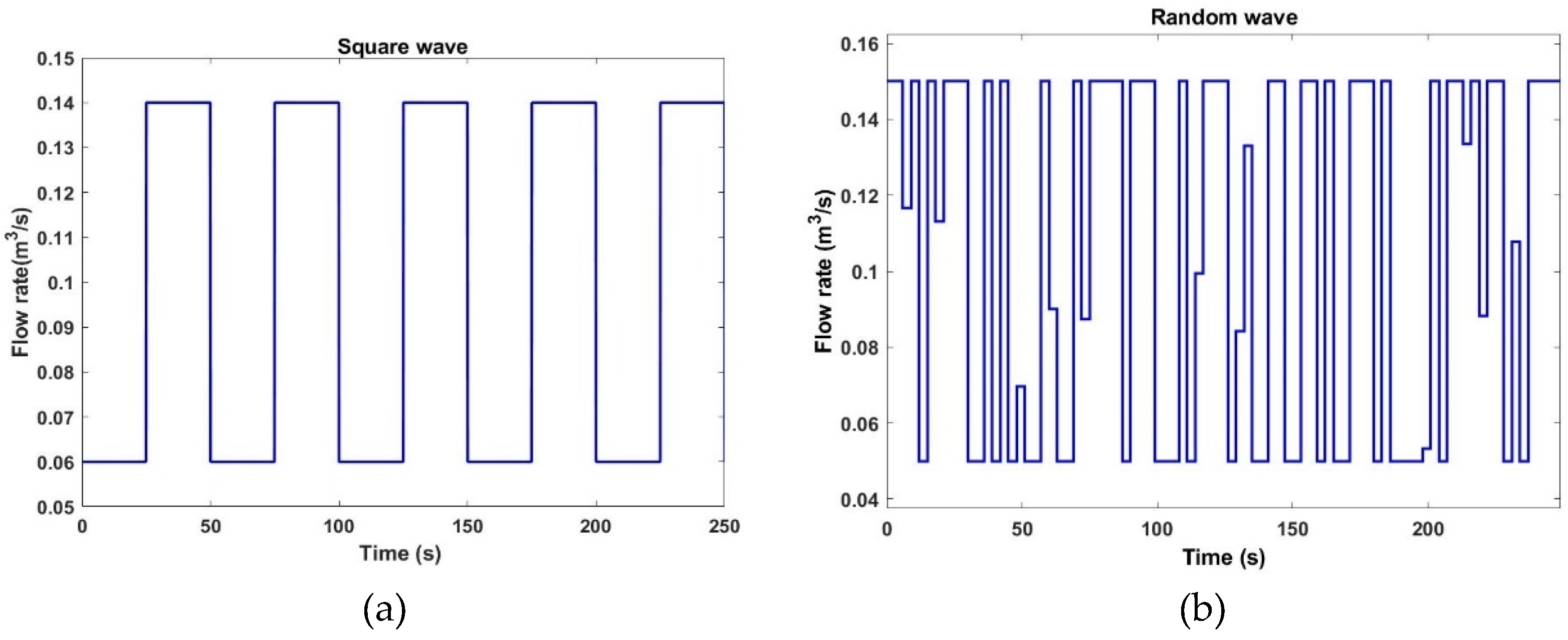
To accurately simulate the effects of slugging, we have incorporated a disturbance signal to represent flow fluctuations at the inlet, based on the characteristic flow patterns of slugging. Considering the inherent randomness of slug flow, square wave and random wave have been selected to represent the changes in inlet flow rate. The resultant variations in the inlet flow rate are visually presented in Figure 7.

3.3. State Vector and Reward Function

3.3.1. State Vector

The environment state vector of the three-phase separator level control model in the ALRW-DDPG algorithm play a pivotal role in information exchange between the environment and the agent. The state vector is composed of the current level height (h), the level deviation (u), the integral of the height error ( ∫ u d u ), derivative of the height error( d u ), the inlet flow rate( f i n ), and the valve pressure differential( Δ P ), denoted as s ( t ) = ( h , u , ∫ u d t , d u , f i n , Δ P ) . In this state vector, u is the control target, with the aim of minimizing its value to approach zero. The magnitude of Δ P is primarily determined by the pressure in the gas chamber and fluctuates in response to the quantity of gas separated from the mixture. To ensure the accuracy of the simulation, we statistically analyzed one week’s pressure data from the Century FPSO’s separator, revealing that the pressure differential across the valve can be regarded as a random signal conforming to a Gaussian distribution. Consequently, Δ P is set as a random variable following a Gaussian distribution with a mean of 101.6 kPa and a variance of 79.32.

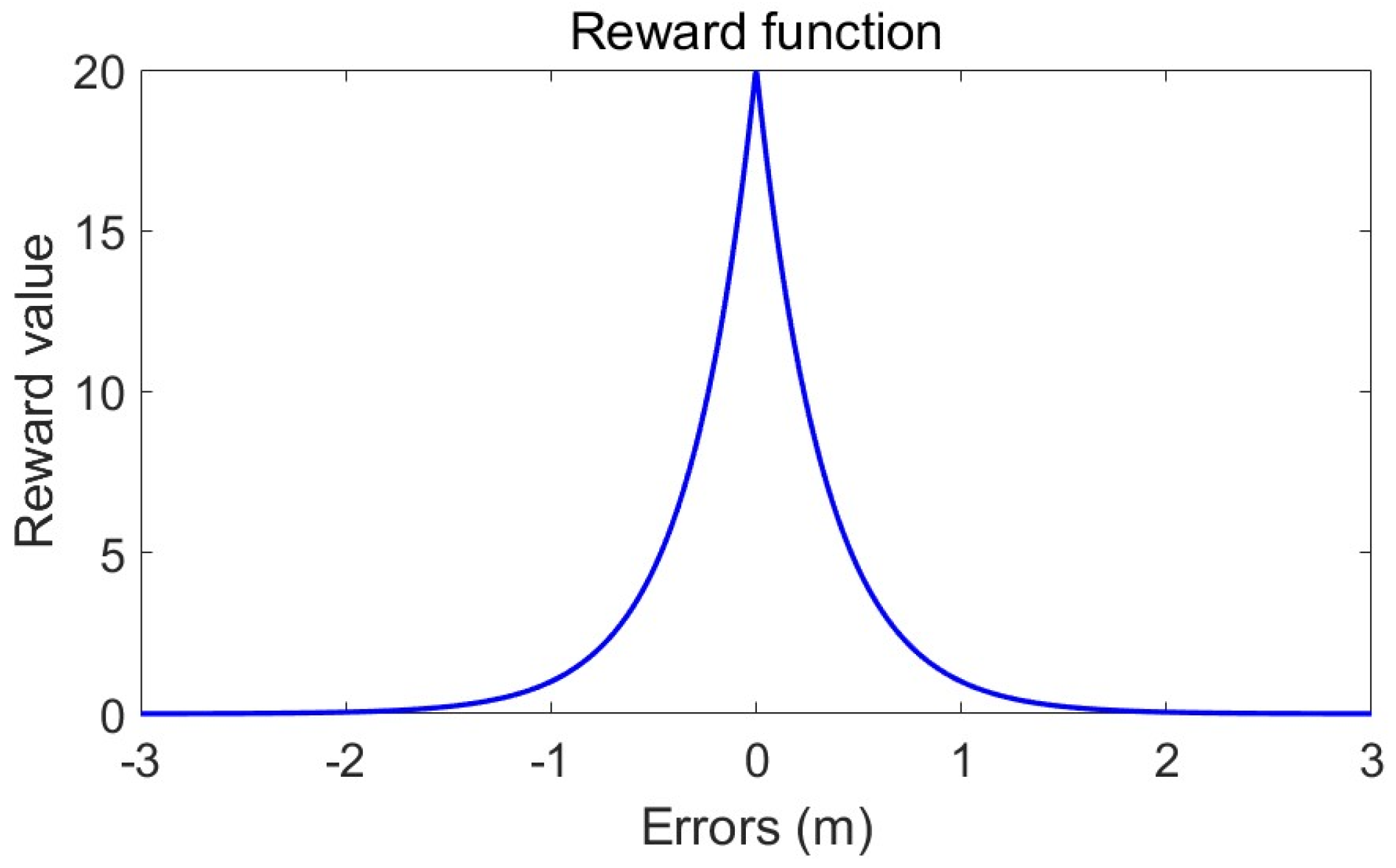
3.3.2. Design of the Reward Function

The reward function is important for the DDPG algorithm, which provides a critical feedback mechanism to evaluate the effectiveness of the agent’s actions. A well-crafted reward function can significantly enhance learning efficiency, enabling the agent to swiftly adopt the desired behavior and minimize fluctuations, especially in the presence of external disturbances such as slug flow. To ensure a stable control process, it is preferable for the rate of change in valve opening to decrease as the liquid level approaches the target value, thereby reducing the amplitude of level oscillations. Consequently, the reward function with the liquid level difference as the dependent variable is formulated by drawing inspiration from the exponential function. Hence, the reward function is expressed as Equation (14), and its graphical representation is illustrated in Figure 8.
r ( t ) = e − 3 ( u − 1 )

3.4. ALRW-DDPG Simulation Network

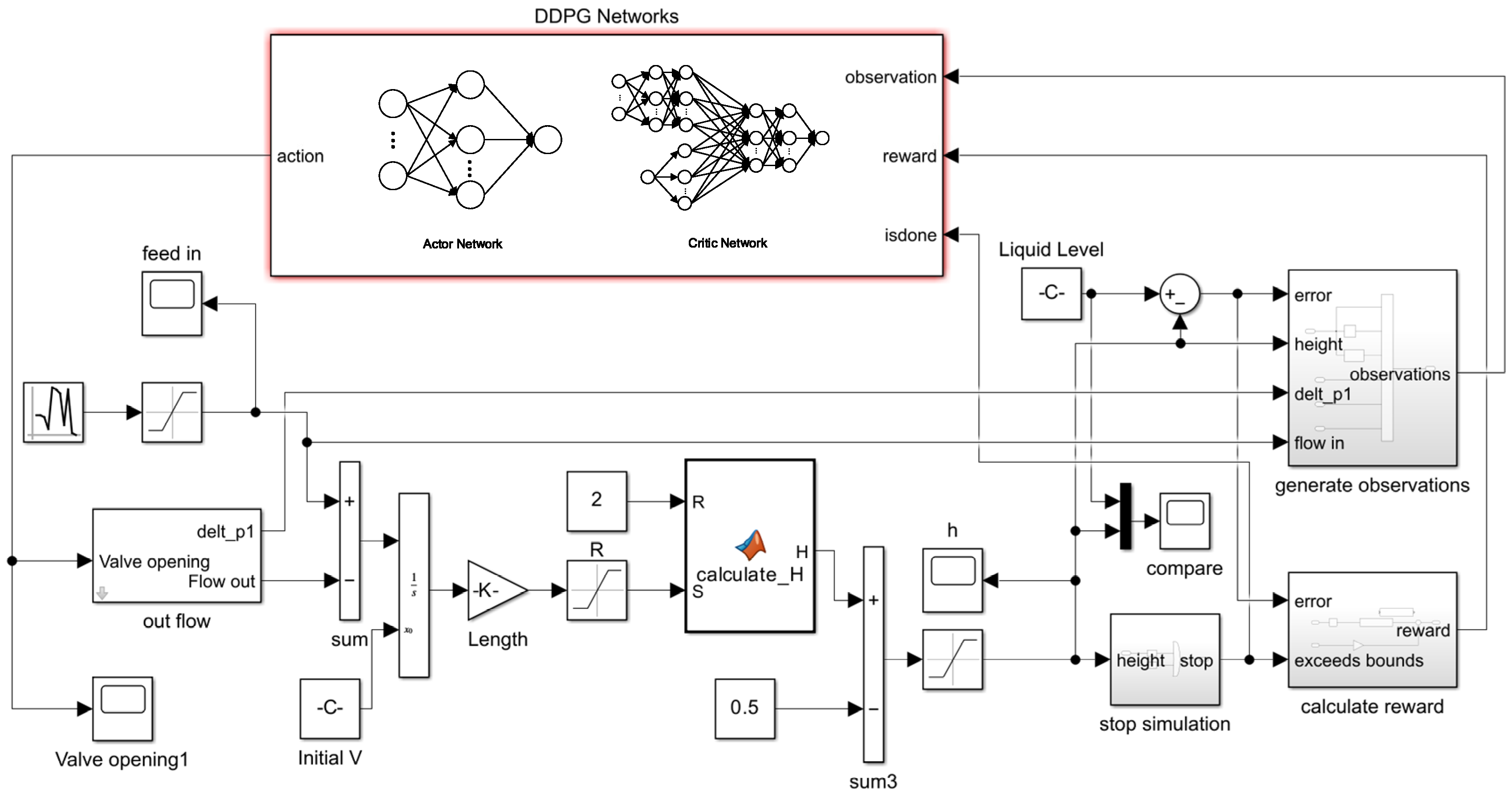
A schematic of the ALRW-DDPG simulation network is shown as Figure 9, which illustrates the three-phase separator level control system. In this diagram, the lower section represents the three-phase separator model. This model functions as the environmental object within the reinforcement learning algorithm, providing interactive feedback parameters to the ALRW-DDPG network. The upper section, labeled “DDPG Networks,” represents the ALRW-DDPG algorithm model. Within this model, the actor network learns the policy function and outputs the agent’s action, taking the environmental state vector s ( t ) as a input and outputting a valve opening value a ( t ) . The actor network architecture comprises a hidden layer with 50 neurons. The critic network evaluates the quality of the actor network’s actions by the action-value function and updates parameters of the actor network. The critic network structure includes two input streams: Action and State. The action stream consists of one hidden layer with an input of valve opening. The state stream incorporates two hidden layers with an input of the environmental state vector. After concatenating the action and state paths and passing them through two hidden layers, the network outputs an evaluation of the actor network’s performance. Both hidden layers of the critic network contain 50 neurons.

3.5. Simulation and Analysis

In this section, a comparative analysis of the simulation results from the ALRW-DDPG algorithm and other control strategies is conducted under identical conditions.

3.5.1. Simulation Conditions

A simulation validation of the three-phase separator level control is performed within the SIMULINK environment. In order to comparatively validate the efficacy of the ALRW-DDPG algorithm against other control algorithms, simulations are conducted utilizing the same simulation parameters as illustrated in Table 2.
To ascertain the efficacy of the training process, the initial and target level heights for the three-phase separator are randomly assigned at the commencement of each simulation iteration. This ensures a uniform starting point for each training session and mitigates the potential for correlation among the training samples.
In the actual production process, the level height of the three-phase separator is maintained within a range of 1000 mm to 2800 mm. The resultant parameter is the degree of opening for the export valves, which ranges from 0 to 1. In this context, a value of 0 denotes complete closure of the valve, while a value of 1 indicates full openness.

3.5.2. Comparison between DDPG and ALRW-DDPG

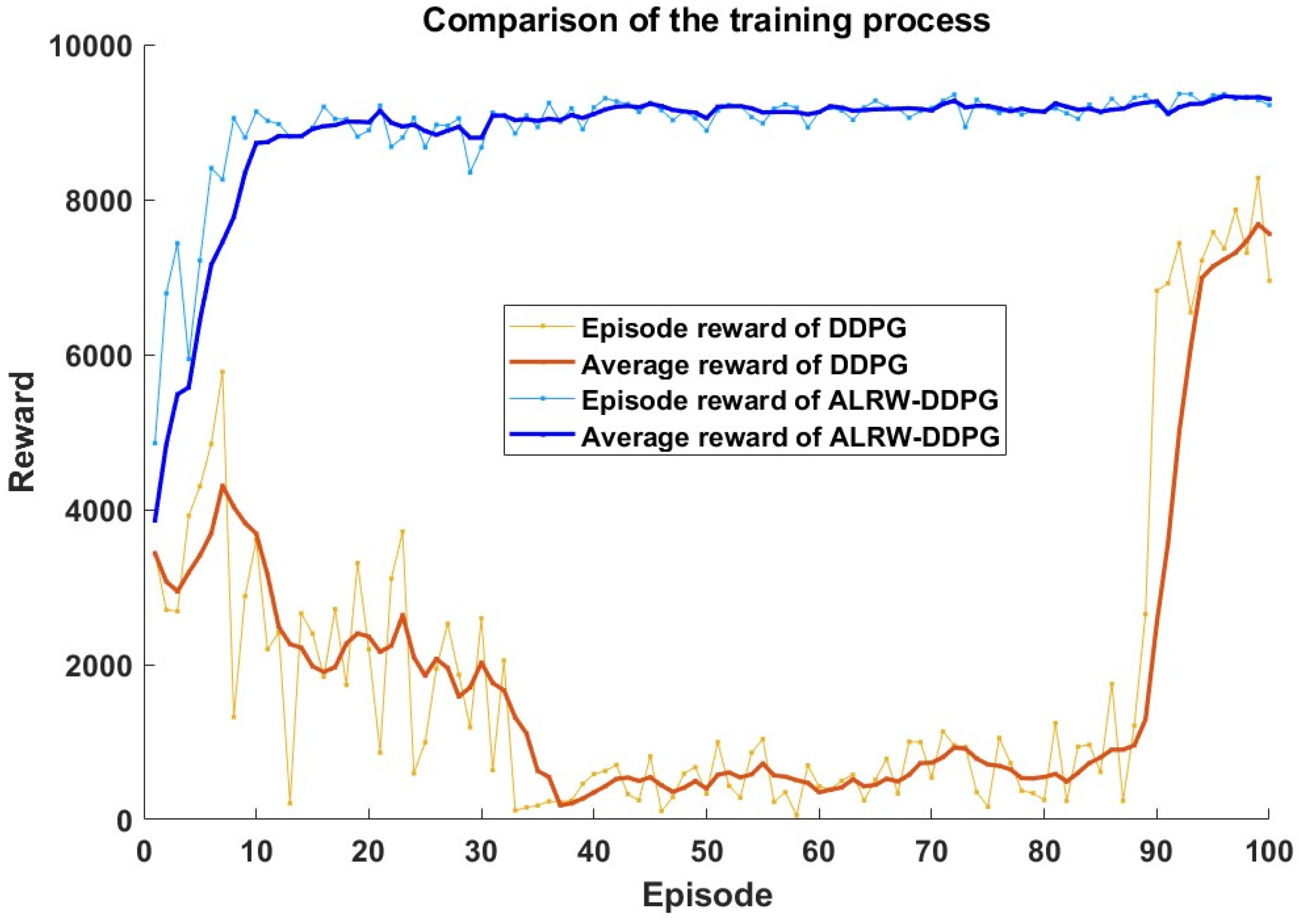
To assess the efficacy of the improved algorithm, this paper compares the DDPG algorithm and the ALRW-DDPG algorithm in terms of learning reward values. Figure 10 illustrates the evolution of the average episode reward of the DDPG and ALRW-DDPG algorithms. The average reward value of the ALRW-DDPG algorithm achieves 9000 at the 100th episode, while the average reward value of DDPG is only 7800. Notably, the training speed of the ALRW-DDPG algorithm is enhanced by 15.38%.

3.5.3. Comparative Analysis of Liquid Level Control Algorithms

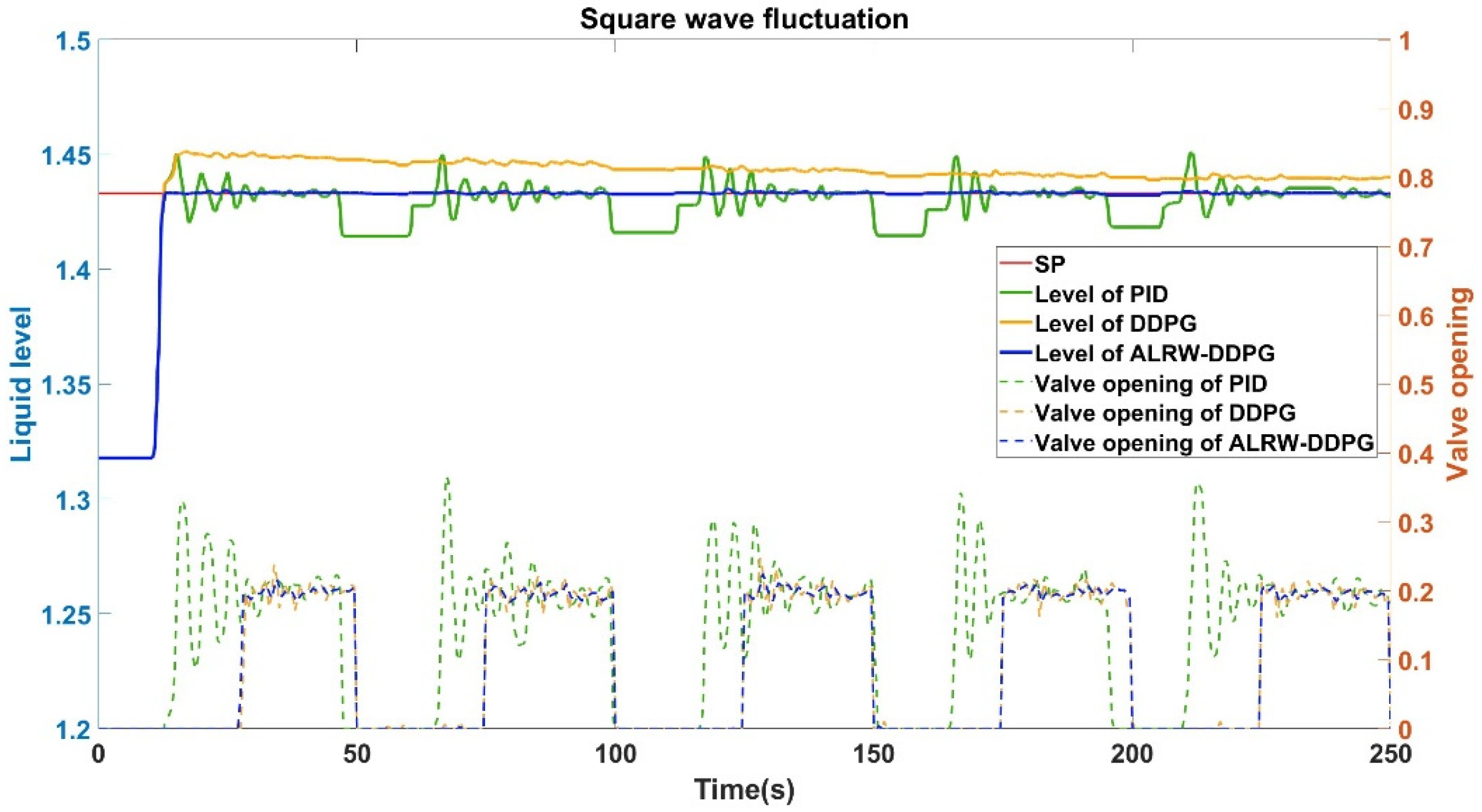
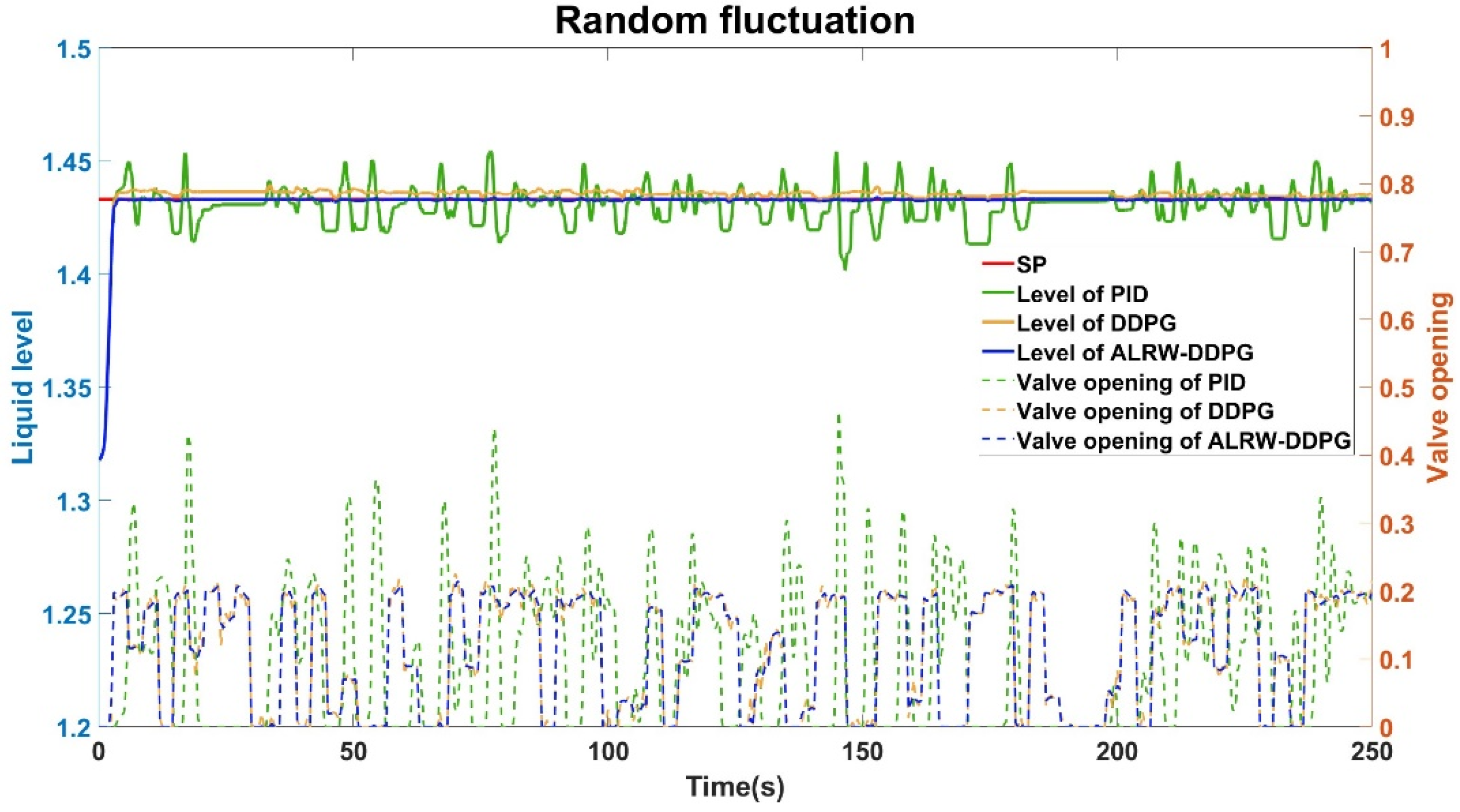
The simulation results show that the ALRW-DDPG algorithm is of a distinct advantage against other control strategies in terms of convergence and stability in liquid level control simulations. The response of the liquid level and the controlled valve opening to square wave and random wave disturbances in the inlet flow rate is depicted in Figure 11 and Figure 12, respectively.
As shown in Figure 11, when the flow rate fluctuates with a square wave disturbance at a predetermined liquid level of 1.433 meters, the PID control method exhibits a fluctuation range of 0.04 meters, corresponding to a fluctuation rate of 2.8%. Simultaneously, the DDPG control algorithm has an obvious overshoot, exceeding the set liquid level value about 0.02 meters, and failing to achieve the set level within the simulation period. In stark contrast, the ALRW-DDPG control algorithm achieves the set level within 12.7 seconds, with a significantly reduced fluctuation range of merely 0.001 meters, and the fluctuation rate is only 0.07%.
Figure 12 depicts a scenario where the flow rate undergoes random fluctuations with a set liquid level of 1.433 meters. Under PID control, the liquid level fluctuates within a range of 0.05 meters, indicating a fluctuation rate of 3.48%. Meanwhile, the DDPG algorithm always has an error of 0.006 meters and the deviation ratio is 0.7%. Conversely, the ALRW-DDPG algorithm reaches the set level within 3.09 seconds, with a minimal fluctuation range of 0.001 meters, corresponding to an insignificant fluctuation rate of 0.07%.
Furthermore, it is noteworthy that throughout the 250-second simulation period, the PID and conventional DDPG control method continuously adjusts without achieving a stable state. In contrast, the ALRW-DDPG control algorithm rapidly attains stability after a sufficient learning period.

4. Conclusions

To address the challenge of substantial fluctuations in the level control of three-phase separators, particularly under the influence such as slug flow, this study proposes a novel ALRW-DDPG algorithm based on the conventional Deep Deterministic Policy Gradient algorithm with an adaptive leaning rate weight. In this study, we construct an ALRW-DDPG algorithm network in consideration of the physical characteristics of the separator. Furthermore, the environment state vector and reward function are meticulously designed to improve the performance of convergence and stability. To align with actual conditions, we conduct a statistical analysis of one week’s pressure data from the Century FPSO’s separator and use square wave and random wave to represent the changes of the flow rate. The effectiveness of the proposed optimization control method is validated through simulation experiments. The results demonstrate that the ALRW-DDPG control algorithm achieves a 15.38% enhancement in convergence rate over the traditional DDPG algorithm. When subjected to square wave disturbances, the control error of the ALRW-DDPG algorithm is only 2.5% and 5% of that of the PID and conventional DDPG algorithms, respectively. Similarly, under random disturbances, the control error of the ALRW-DDPG algorithm is only 2% and 16.7% of the PID and traditional DDPG algorithm, respectively. Consequently, the ALRW-DDPG control algorithm demonstrates superior accuracy and effectively minimizes liquid level fluctuations.

Author Contributions

Conceptualization, He.X. and Liu.B.; methodology, He.X. and Pang.H; validation, Chen Y.; investigation, Chen Y.; resources, He.X. and Liu.B.; writing—original draft preparation, He.X. and Pang.H; writing—review and editing, Liu.B.and Chen Y.; project administration, He.X.; funding acquisition, Pang.H All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by Open Fund Project of State Key Laboratory of Offshore Oil and Gas Exploitation, grant number CCL2023RCPS0165RQN, and the National Key Research and Development Program of China, grant number 2021YFB3401405-1.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Chen, X.; Zheng, J.; Jiang, J.;Peng, H.; Luo, Y.; Zhang, L. Numerical Simulation and Experimental Study of a Multistage Multiphase Separation System. Separations 2022, 9, 405. [CrossRef]
  2. Bai, Y.; Zhang, R. Application of oil gas water three-phase separator in Oilfield. Chem. Manage. 2020, 12, pp.215–216.
  3. Guo, S.;Wu, J.; Yu, Y.; Dong, L. Research progress of oil gas water three-phase separator. Pet. Mach. 2016, 44, pp.104–108.
  4. Flores-Bungacho, F.; Guerrero, J.; Llanos, J.; Ortiz-Villalba, D.; Navas, A.; Velasco, P. Development and Application of a Virtual Reality Biphasic Separator as a Learning System for Industrial Process Control. Electronics 2022, 11, pp.636-657. [CrossRef]
  5. Fadaei, M.; Ameri, M.J.; Rafiei, Y.; Asghari, M.; Ghasemi, M. Experimental Design and Manufacturing of a Smart Control System for Horizontal Separator Based on PID Controller and Integrated Production Model. Journal of Petroleum Exploration and Production Technology 2024, 6, pp.525-547. [CrossRef]
  6. John Pretlove, Steve Royston. Towards Autonomous Operations, the Offshore Technology Conference, Houston, TX, USA, 1– 4 May, 2023.
  7. Li, Y.; Kamotani, Y. Control-Volume Study of Flow Field in a Two-Phase Cyclonic Separator in Microgravity. Theoretical and Computational Fluid Dynamics. 2023, 37, pp.105–127. [CrossRef]
  8. Sayda, A.F.; Taylor, J.H. Modeling and Control of Three-Phase Gravity Separators in Oil Production Facilities. In Proceedings of the 2007 American Control Conference, Marriott Marquis Hotel at Times Square, New York City, USA, 2007, 6, 11–13.
  9. Charlton, J.S.; Lees, R.P. The Future of Three Phase Separator Control. In Proceedings of the SPE Asia Pacific Oil and Gas Conference and Exhibition, Melbourne, Australia, 8–10, 10, 2002.
  10. Li, Z.; Li, Y.; Wei, G. Optimization of Control Loops and Operating Parameters for Three-Phase Separators Used in Oilfield Central Processing Facilities. Fluid Dynamics & Materials Processing, 2023, 19, 3. [CrossRef]
  11. SONG S., LIU X., CHEN H. The influence of PID control parameters on the production process of gravity three-phase separator. Petroleum Science Bulletin 2023, 8,pp. 179-192.
  12. MA C; HUANG Z.;LIU X.Analysis and optimization of liquid level setting for three-phase separators based on K-Spice software.China Offshore Oil and Gas, 2021, 33, pp.172-178.
  13. Fan, X. Research on Oil-Water Treatment Control of Three-Phase Separator Based on Dynamic Mathematical Model and GA Algorithm. Automation and Instrumentation, 2024, 4, 220-224.
  14. Wu, F.; Huang, K.; Li, H.; Huang, C. Analysis and Research on the Automatic Control Systems of Oil–Water Baffles in Horizontal Three-Phase Separators. Processes 2022, 10, 1102–1111. [CrossRef]
  15. Durdevic, P.; Yang, Z. Application of H∞ Robust Control on a Scaled Offshore Oil and Gas De-Oiling Facility. Energies 2018, 11, 287. [CrossRef]
  16. Yao, J.; Ge, Z. Path-Tracking Control Strategy of Unmanned Vehicle Based on DDPG Algorithm. Sensors 2022, 22, 7881. [CrossRef]
  17. Duguleana, M.; Mogan, G. Neural networks based reinforcement learning for mobile robots obstacle avoidance. Expert Systems with Applications.2016, 62, 104–115. [CrossRef]
  18. Zhao, J.; Wang, P.; Li, B.; Bai, C. A DDPG-Based USV Path-Planning Algorithm. Applied Sciences. 2023, 13, 10567. [CrossRef]
  19. Yang, J.; Peng, W.; Sun, C. A Learning Control Method of Automated Vehicle Platoon at Straight Path with DDPG-Based PID. Electronics 2021, 10, 2580. [CrossRef]
  20. Pokhrel, S.R.; Kua, J.; Satish, D.; Ozer, S.; Howe, J.; Walid, A. DDPG-MPCC: An Experience Driven Multipath Performance Oriented Congestion Control. Future Internet 2024, 16, 37. [CrossRef]
  21. apaioannou, I.; Dimara, A.; Korkas, C.; Michailidis, I.; Papaioannou, A.; Anagnostopoulos, C.-N.; Kosmatopoulos, E.; Krinidis, S.; Tzovaras, D. An Applied Framework for Smarter Buildings Exploiting a Self-Adapted Advantage Weighted Actor-Critic. Energies 2024, 17, 616. [CrossRef]
  22. Mai, T.; Yao, H.; Jing, Y.; Xu, X.; Wang, X.; Ji, Z. Self-learning Congestion Control of MPTCP in Satellites Communications. In Proceedings of the 2019 15th International Wireless Communications & Mobile Computing Conference (IWCMC), Tangier, Morocco, 24–28 June 2019; pp. 775–780.
  23. Chang, C.-C.; Tsai, J.; Lin, J.-H.; Ooi, Y.-M. Autonomous Driving Control Using the DDPG and RDPG Algorithms. Applied Sciences. 2021, 11, 10659. [CrossRef]
  24. Song Yanyong, SU Mingxu, Wang Zian. Research on the Measurement Principle and Method of Valve Flow Coefficient. Automatic Instrumentation, 2022, 43, 28-32.
  25. Faria, R.d.R.; Capron,B.D.O.; Secchi, A.R.; de Souza, M.B.,Jr. Where Reinforcement Learning Meets Process Control: Review and Guidelines. Processes 2022, 10, 2311.
  26. Lu, Z.; Yan, Y. Temperature Control of Fuel Cell Based on PEI-DDPG. Energies 2024, 17, 1728. [CrossRef]
  27. DENG Luke, LYU Dongpo. PID parameter tuning of remotely operated vehicle control attitude based on genetic algorithm. Manufacturing Automation, 2023, 45, 177-179, 206.
  28. ZENG Xiongfei. The PID control algorithm based on particle swarm optimization optimized BP neural network. Electronic Design Engineering, 2022, 30, 69-73, 78.
  29. Grondman I, Busoniu L, Lopes G A D, Babuska R. A Survey of Actor-Critic Reinforcement Learning: Standard and Natural Policy Gradients. IEEE Transactions on Systems, Man, and Cybernetics, Part C: Applications and Reviews, 2012, 42, 1291-1307. [CrossRef]
  30. Chung, J.; Han, D.; Kim, J.; Kim, C.K. Machine Learning Based Path Management for Mobile Devices Over MPTCP. In Proceedings of the 2017 IEEE International Conference on Big Data and Smart Computing (BigComp), Jeju, Republic of Korea, 13–16 February 2017; pp. 206–209.
  31. Ebrahim H. S.; Said J. A.; Hitham S. A.; Safwan M. A.; Alawi A.; Mohammed G. R.; Suliman M. F. Deep deterministic policy gradient algorithm: A systematic review. Heliyon 2024, 10, e30697.
  32. Li, H.; Kang, J.; Li, C. Energy Management Strategy Based on Reinforcement Learning and Frequency Decoupling for Fuel Cell Hybrid Powertrain. Energies 2024, 17, 1929. [CrossRef]
Preprints 115425 g001
Figure 1. Three phase horizontal separator schematic.
Figure 1. Three phase horizontal separator schematic.
Preprints 115425 g001
Preprints 115425 g002
Figure 2. Mathematical model of the liquid level in the Three-Phase Separator.
Figure 2. Mathematical model of the liquid level in the Three-Phase Separator.
Preprints 115425 g002
Preprints 115425 g003
Figure 3. The DRL algorithm architechure.
Figure 3. The DRL algorithm architechure.
Preprints 115425 g003
Preprints 115425 g004
Figure 4. DDPG network structure.
Figure 4. DDPG network structure.
Preprints 115425 g004
Preprints 115425 g005
Figure 5. The adaptive learning rate weight function.
Figure 5. The adaptive learning rate weight function.
Preprints 115425 g005
Preprints 115425 g006
Figure 6. Separator on the Century FPSO.
Figure 6. Separator on the Century FPSO.
Preprints 115425 g006
Preprints 115425 g007
Figure 7. Variations in inlet flow rate under different disturbances. (a) Square wave flow disturbance; (b) Random flow disturbance.
Figure 7. Variations in inlet flow rate under different disturbances. (a) Square wave flow disturbance; (b) Random flow disturbance.
Preprints 115425 g007
Preprints 115425 g008
Figure 8. Reward function.
Figure 8. Reward function.
Preprints 115425 g008
Preprints 115425 g009
Figure 9. ALRW-DDPG simulation network.
Figure 9. ALRW-DDPG simulation network.
Preprints 115425 g009
Preprints 115425 g010
Figure 10. Comparison of training result graphs.
Figure 10. Comparison of training result graphs.
Preprints 115425 g010
Preprints 115425 g011
Figure 11. The performance of liquid level control response to square wave disturbance.
Figure 11. The performance of liquid level control response to square wave disturbance.
Preprints 115425 g011
Preprints 115425 g012
Figure 12. The performance of liquid level control response to random wave disturbance.
Figure 12. The performance of liquid level control response to random wave disturbance.
Preprints 115425 g012
Table 1. The parameters of Centry FPSO.
Table 1. The parameters of Centry FPSO.
Parameters Value
Separator Length 4 m
Separator Inner Diameter 16.5 m
Pressure 350 kPa
Pressure 50~70 °C
Processing Capacity (oil) 293 m3/h
Water Phase Export Valve Size 8 in
Water Phase Valve Flow Coefficient Cv 180.807 GPM
Oil Phase Export Valve Size 10 in
Table 2. Simulation parameters.
Table 2. Simulation parameters.
Parameters Value
Initial learning rate for Critic network 0.001
Initial learning rate for Actor network 0.0001
Sampling time (s) 0.5s
Smooth factor 0.001
Discount factor 0.99
Noise mean value 0
Noise regression parameter 0.15
Initial value of noise standard deviation 0.3
Number of iterations 500
Experience pool playback training batches 64
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated