Prerpints.org logo
Preprint
Article

Exploring the Role of Global Value Chain Position in Economic Models for Bankruptcy Forecasting

Altmetrics

Downloads

83

Views

41

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

16 August 2024

Posted:

16 August 2024

You are already at the latest version

Alerts
Abstract
This study addresses a gap in the literature by conducting a comparative analysis of statistical and artificial intelligence techniques for predicting bankruptcy in small and medium-sized enterprises (SMEs). Using a comprehensive database of 7,104 Belgian SMEs, our findings demonstrate that intelligent techniques offer superior predictive accuracy for bankruptcy. Notably, our results indicate that a firm's position in the global value chain significantly affects prediction accuracy, with lower performance for firms operating upstream in the production process. This suggests that bankruptcy risk may spread upward along the value chain. This insight is particularly valuable for practitioners, as it highlights the importance of focusing on specific performance factors based on the type of firms they manage, advise, or collaborate with.
Keywords: 
Subject: Business, Economics and Management  -   Economics

1. Introduction

When a firm goes bankrupt, it triggers a ripple effect that significantly impacts a broad spectrum of stakeholders, including customers, creditors, suppliers, and most acutely, the firm’s employees (Weitzel and Jonsson, 1989; Refait, 2000; Daubie and Meskens, 2001). Despite the critical nature of this issue, the financial literature has largely overlooked the topic of bankruptcy over the past seventy years. Yet, the consequences of bankruptcy can be profound, not only at the macroeconomic level—where it can affect overall societal well-being—but also at the microeconomic level, where it can devastate the partners and other associated entities of the affected firm (Charest et al., 1990; Ooghe and Balcaen, 2002).
The exploration of bankruptcy as a financial phenomenon began with Fitzpatrick's pioneering work in 1932. Since then, researchers have developed a variety of models aimed at predicting bankruptcy, typically by analyzing financial ratios (Beaver, 1966; Argenti, 1976; Ohlson, 1980; Altman, 1984; Morris, 1997; Guilhot, 2000; Daubie and Meskens, 2001; Ooghe and De Prijcker, 2008; Xu and Zhang, 2009, Ogachi et al., 2020; Charalambous et al., 2021; Kitowski et al., 2022). These models, however, have predominantly focused on large firms. Small and medium-sized enterprises (SMEs), despite being a vital part of the global economy, have received comparatively little attention in the context of bankruptcy prediction (Peel and Peel, 1987; Storey et al., 1987; Keasey and Watson, 1991; Altman and Sabato, 2007; Ciampi and Gordini, 2008; Van Caillie and Crutzen, 2009; Zoricak et al., 2020; Papik and Papikova, 2023).
The literature's emphasis on larger firms can be attributed to the diverse nature of SMEs and the unique characteristics that differentiate them from their larger counterparts. SMEs are often more agile, able to quickly adapt to changes and find creative, ad hoc solutions during uncertain times due to the highly personalized nature of their management structures (Ciampi and Gordini, 2008). However, this same agility comes with significant challenges. SMEs must manage vast amounts of information, make numerous critical decisions, and handle a wide array of skills, all within a typically lean organizational structure (Ciampi and Gordini, 2008). Moreover, SMEs are often at a disadvantage due to their smaller size, higher turnover, and elevated failure rates (Peacock, 2004). The centralization of authority in a single manager and the heavy reliance on external factors, such as clients, suppliers, and financial providers, further exacerbate their vulnerabilities (Julien, 1997; Van Caillie, 2000). Financially, SMEs often struggle with inadequate structures, relying heavily on short-term credit while facing difficulties in securing medium- to long-term financing (Ciampi and Gordini, 2008). Consequently, traditional financial ratios, which are typically effective for large firms, are less applicable to SMEs, leading to a need for tailored bankruptcy prediction models (Ciampi and Gordini, 2009).
Recent efforts have aimed to address this gap by developing bankruptcy prediction models specifically designed for SMEs. However, there remains a significant gap in the literature, particularly concerning (i) the comparative performance of different variable selection processes and (ii) the potential influence of a firm’s position within the Global Value Chain (GVC) on bankruptcy prediction. While existing studies, such as those by Chava and Jarrow (2004), suggest that sectoral affiliation can influence global bankruptcy prediction models, these studies often overlook the impact of specific key variables within the SME category. Furthermore, emerging research indicates that a firm's position in the GVC could significantly influence its risk of bankruptcy. For example, upstream firms, such as manufacturers, may be more vulnerable to the decisions and failures of downstream firms, such as retailers, due to potential contagion effects (Fujiwara, 2008; Zhongsheng et al., 2011; Delli Gatti et al., 2009). These findings suggest that upstream firms might be more affected by external events rather than their financial ratios, further complicating bankruptcy prediction in this context.
This study seeks to contribute to the literature in several key ways. First, we focus specifically on SMEs and compare the predictive power of two broad categories of data selection methods: statistical techniques, including backward and forward procedures, and artificial intelligence techniques, such as the machine learning lasso algorithm and the ensemble method known as Classification and Regression Trees (CART) analysis. By comparing the outcomes of these different variable selection methods, we aim to rank the predictive models according to their effectiveness, providing insights that have not been previously explored in the context of SMEs. Second, we examine the role of a firm's position in the GVC in influencing bankruptcy prediction, particularly how this position may affect the selection of key variables. This analysis allows us to highlight the specific influence of the industrial sector on the choice of the most effective variable selection algorithm.
By integrating these dimensions, our study not only fills a gap in the current literature but also provides practical insights for stakeholders involved in managing, advising, or working with SMEs. Understanding the nuances of bankruptcy prediction in SMEs, particularly in relation to their position in the GVC, can help improve risk assessment and management strategies, ultimately contributing to the stability and resilience of this crucial segment of the economy.
The paper is organized as follows: Section 2 provides a comprehensive overview of the current literature on bankruptcy prediction, particularly in the context of SMEs. Section 3 reviews the variable selection methods and data used in our study. Section 4 presents the empirical results, offering a detailed comparison of the different variable selection techniques. Finally, Section 5 discusses the implications of our findings, providing a concluding analysis that highlights the practical and theoretical contributions of our work.

2. Materials and Methods

2.1. Data

The empirical data for this study are collected from the Bureau Van Dijk database (hereafter, BVD), namely Belfirst (i.e., Financial Reports and Statistics on Belgian and Luxembourg Companies) which gathers detailed information over 32,000 Belgian firms and 4,000 firms established in Luxembourg. We first select a balanced sample of Belgian SMEs covering the period 2002-2012. After removing firms with missing or inappropriate variables (such as negative net sales for example), the number of firms registered as bankrupt is 3,552. Then, the same number of non-failing firms is also included in the sample, leading the total balanced sample to 7,104 Belgian SMEs.

2.2. Variables

2.2.1. Bankruptcy Indicator

In order to build our prediction model, a bankruptcy indicator is needed as a dummy variable that equals 1 if the firm has experienced corporate bankruptcy over the investigated period, 0 otherwise. For the set of explanatory variables, and following Shumway (2001), we extract a time-varying panel dataset where each firm-year observation in our sample is treated as a separate observation. The final dataset therefore contains all the predictor variables used in this study and the binary response variable indicating the firm’s bankruptcy status. This panel data structure allows us to consider all the information of the firms as a potential predictor of the future bankruptcy and should provide consistent and accurate out-of-sample prediction (Mai et al., 2019).

2.2.2. Predictors

Using firms’ balance sheets and income statements, we calculate 50 financial ratios commonly used in the literature when predicting corporate bankruptcy (Beaver, 1966; Altman, 1968; Ohlson, 1980; Dimitras et al., 1996; Dimitras et al., 1999; Balcaen and Ooghe, 2006; Agarwal and Taffler, 2008; Amendola et al., 2011; Jackson and Wood, 2013; Wang et al., 2014; Altman and Branch, 2015; Kim et al., 2016, Veganzones and Séverin, 2018). Among these, several variables possess the same numerator or denominator, so we check for multicollinearity and remove all variables with a variance inflation factor (VIF) greater than 10 (O’Brien, 2007). This leads to an initial sample of 30 financial ratios, which are reported in Table 1. Still, and since including all 30 financial ratios would lead to a very high-dimensional feature space, reducing the model’s predictive power (Veganzones and Séverin, 2018), we perform variable selection processes allowing us to robustly reduce the predictors to a subset of the most relevant financial ratios.

2.3. Variables Selection Methods

The variable selection method used may influence the performance of prediction models (Veganzones and Séverin, 2018; du Jardin et al., 2019). Therefore, we implement four different selection techniques in order to select the best predictors among those listed above. These techniques can be gathered in two main categories: statistical techniques, with the backward and forward procedures; and artificial intelligence based techniques, with the machine learning lasso and the ensemble classification and regression trees (CART) procedures.

2.3.1. Statistical Techniques

Backward Procedure. Backward selection consists in starting with all potential predictors, testing the deletion of each potential predictor using a chosen model fit criterion, deleting the potential predictor (if any) whose loss gives the most statistically insignificant alteration of the model fit, and repeating this process until no further potential predictors can be deleted without a statistically significant loss of fit. It is thus an iterative search procedure that identifies which independent variables, previously thought to be of some importance, have the strongest predictive power of the dependent variable (Cultrera and Brédart, 2016). Several criteria can be used to select the predictors during the backward selection. We use a p-value threshold of .05 as a criterion to exclude the weakest predictors from the model at each step. Once variables have been dropped, they cannot reenter the equation. Accordingly, the software automatically drops one by one variables with the highest p-value until only those that are significant at the .05 level are remaining.
Forward Procedure. The forward procedure, on the other hand, starts from the null model, and step by step, chooses the best model with one additional predictor. At each step, the predictor satisfying the entry criterion is added to the model (Tsai, 2009). More precisely, the selection method sequentially includes variables based on the F-stat until adding more variables is not able to improve the model, with the final model including only significant predictors (Miller, 2002). In order to select our predictors during the process, we followed the Tsai’s (2009) criteria, i.e. a variable is included in the model if the F stat is less than .05 and removed from the model if the F stat is more than .10 (Bauweraerts, 2016).

2.3.2. Artificial Intelligence Techniques

Machine Learning Lasso Procedure. There is a cost to including lots of regressors, and we can reduce the objective function by throwing out those that contribute little to the model’s fit. Clearly, fitting a model with a higher polynomial degree is useful only if it significantly reduces the error compared to a simpler model. Penalized logistic regression imposes a penalty to the logistic model for having too many variables, leading to selection variables processes to be even more crucial. This model, also known as regularization, shrinks the coefficients of the less contributive variables toward zero (James et al., 2013; Kassambara, 2018). As consequence, the variance of the model is reduced. The mostly used penalized regression methods are the ridge regression and the Lasso regression (Tibshirani, 1996; Park and Casella, 2008), with the later having the advantage of involving in the final model only a subset of the predictors, which in turn improves the model interpretability by eliminating irrelevant variables not associated with the response variable, reducing overfitting (James et al., 2013; Fonti and Belitser, 2017). Controlling the trade-off between error and complexity of the model, the Lasso procedure penalizes the model by setting the coefficients for some variables to zero. It provides a coefficients matrix which is a continuous linear function of a tuning parameter λ that controls the strength of the penalty and is computed through cross-validation process. As λ increases, variables are settled to zero and are removed from the model. The only need is to settle the penalty level, i.e. the λ. Several ways of selecting λ are available, and follow the information criteria approach developed by Chen and Chen (2008) who introduce the Extended BIC (Bayesian Information Criterion) computation, imposing an additional penalty on the number of parameters.
Ensemble Classification and Regression Trees (CART) Procedure. Classification and regression tree is a recursive algorithm in data mining which explores the structure of a dataset and develops visualised decision rules for predicting a categorical variable, i.e. classification tree, and a continuous variable, i.e. regression tree (Brezigar-Masten and Masten, 2012; Singh et al., 2015; Choubin et al., 2018). One advantage in relying on CART compared to other artificial intelligence methods is that it provides easily understandable decision rules (Li et al., 2010). Classification trees use a binary tree to recursively partition the predictor space into subsets. The terminal nodes of the tree correspond to the distinct regions of the partition, and the partition is determined by splitting rules associated with each of the internal nodes. By moving from the root node through to the terminal node of the tree, each observation is then assigned to a unique terminal node. CART analysis is nonparametric and can detect complex relationships between dependent variable and explanatory variables (Brezigar-Masten and Masten, 2012). Therefore, CART analysis is particularly suited for discovering nonlinear structures and variables interactions in datasets with a large number of potential explanatory variables.

2.4. The Position in the GVC

In order to take into account the potential influence of the position of the firm in the GVC, we isolate from the dataset the group of firms we may define as upstream, i.e. those being part of the following industrial sectors (NACE Rev 2): Agriculture, forestry and fishing (NACE A), Mining and Quarrying (NACE B), Manufacturing (NACE C), Electricity, gas, steam and air conditioning supply (NACE D) and Water supply (NACE E), representing a balanced subsample of 882 firms (441 firms registered as bankrupt and 441 non-failing firms).

2.5. The Logistic Model and Misclassification Evaluation

Since our dependent variable, i.e. bankruptcy, is a dichotomous variable, trying to estimate the relation through a linear regression may lead to estimations qualified as aberrant and biased, that is to say a dependant variable exceeding the limits of 0 and 1. We then use as estimation techniques a logistic regression model, fitted to binomial variables. This model is particularly used in the majority of studies focusing on the occurrence of the bankruptcy phenomenon (Ohlson, 1980; Premachandra et al., 2009). A logistic regression ties a link between a dependant variable that takes two different values: 1 if the firm is bankrupt and 0 if it is healthy, and k other explanatory variables. These variables can be quantitative or qualitative. The first step is to identify that our response variable is binary, and then defined as:
y i = 1 0   i f t h e   i t h   f i r m   i s   b a n k r u p t o t h e r w i s e
y i can be seen as a realization of the random variable that takes the value one or zero with the probability P i and 1 − P i , respectively, and with the distribution of Y i known as a Bernoulli distribution. This distribution can be written for y i = 0.1 1as:
P r Y i = y i = P i y i 1 − P i 1 − y i
1 Note that in the case where y i = 1 we obtain Pi, and if yi = 0, we obtain 1 − Pi
Then, the probability to go bankrupt, P i , depends on observed covariates X i . Given that ordinary least squares techniques do not ensure that the predicted value of the dependent variable will be in the correct range between zero and one unless complex restrictions are settled, we need as a second step to transform the probability in order to remove these range restrictions. To do so, we first compute the odds as the ratio of favourable to unfavourable cases, that is:
o d d s i = P i 1 − P i
Secondly, we transform the odds into logarithms, which gives the logit such as:
l o g i t   P i = l o g P i 1 − P i
This leads to the fact that if the probability to go bankrupt goes down to zero, the odds approaches zero and the logit approaches − ∞. Conversely, if the probability to go bankrupt approaches one, the odds approaches + ∞ and the logit approaches + ∞ also.
The logistic regression model therefore assumes a linear function of the predictors, with a vector of covariates and the related coefficients, such as:
l o g i t   P i = x i β
From that point, coefficients may be interpreted as in linear models, but we may be careful that the left-hand-side is a logit rather than a mean as it is in ordinary least squares for example. Practically, each represents the change in the logit of the probability associated to a one unit change in the given predictor. In turn, we are only able to know, through the observation of the regression coefficients, the direction and the significance of the relation between the dependent variable and the independent variables but not the magnitude of this variation. And so, a positive coefficient will show that the independent variable increases the probability that yi takes the value 1 but we have no information about the way the magnitude of this probability increase. To know this, we compute the marginal effects:
∂ E y i | x i ∂ x i k = ∂ P y i = 1 x i ∂ x i k = e x i ' β 1 + e x i ' β 2 β k
The marginal effects measure the impact of a change in the variable xi on the probability for the dependent variable y i to take the value of 1. In other words, the marginal effects of a regressor represents how much the (conditional) probability of the outcome variable changes when we change the value of a regressor by one unit, all other regressors remaining constant at given values.
In order to evaluate the prediction capacity of variables selected through the aforementioned procedures, we select four evaluation metrics: sensitivity, specificity, overall classification and area under the receiver operating characteristic (ROC) curve (AUC). Classification metrics are computed with a 10-fold cross-validation method that has been repeated 50 times, representing an average performance of 500 individual testing subsets. This out-of-sample prediction is also in line with the current BASEL III recommendations for default model validation purpose (Mai et al., 2019). We therefore randomly separate the dataset by selecting 70% of the data as the training set and the remaining 30% as the testing set, which is common in previous researches (du Jardin, 2016; Cultrera and Brédart, 2016; Cultrera and Vermeylen, 2018, among others).
Sensitivity and specificity metrics focus on evaluating a type of firm sensitivity for failed firms and specificity for non-failed firms, such as (Veganzones and Séverin, 2018):
S e n s i t i v i t y = C l a s s B a n k r u p t C l a s s B a n k r u p t + M i s s C l a s s B a n k r u p t    
S p e c i f i c i t y = C l a s s N o n _ B a n k r u p t C l a s s N o n _ B a n k r u p t + M i s s C l a s s N o n _ B a n k r u p t    
where Sensitivity represents the percentage of bankrupt firms correctly classified, Specificity is the percentage of non-bankrupt firms correctly classified, ClassBankrupt represents bankrupt firms correctly classified, MissClassBankrupt represents bankrupt firms misclassified; ClassNon_Bankrupt represents non-bankrupt firms correctly classified, and MissClassNon_Bankrupt represents non-bankrupt firms misclassified.
Classical models of classification usually compute sensitivity and specificity metrics on the bases of an average risk score (cutoff) of 0.5. This article also improves the accuracy evaluation through computing the best cutoff points that fit the data, by providing graphs of sensitivity versus risk score and specificity versus risk score. This allows us to compute sensitivity and specificity statistics with respect to the more precise cutoff points.
Then, we compute the AUC metric, allowing us to evaluate overall performance. AUC provides a graphical representation of the trade-off between a failed firm that have been correctly classified and a failed firm that have been incorrectly classified. For a classifier, the ROC curve measures how well a model discriminates between bankrupt and non-bankrupt firms and needs to be graphically as far to the top left corner as possible, where its value will be close to 1. A value of 0.5 means a random model with no predictive ability. At the extreme, a value of 1 means perfect discrimination (Chava and Jarrow, 2004). Current literature on bankruptcy prediction referring to ROC analysis shows a ROC statistic ranging between 0.7392 (Zmijewski, 1984) and 0.9113 (Shumway, 2001), with the pioneer Altman’s model (1968) standing in the middle with a ROC area of 0.8662.

3. Results

3.1. Variable Selection

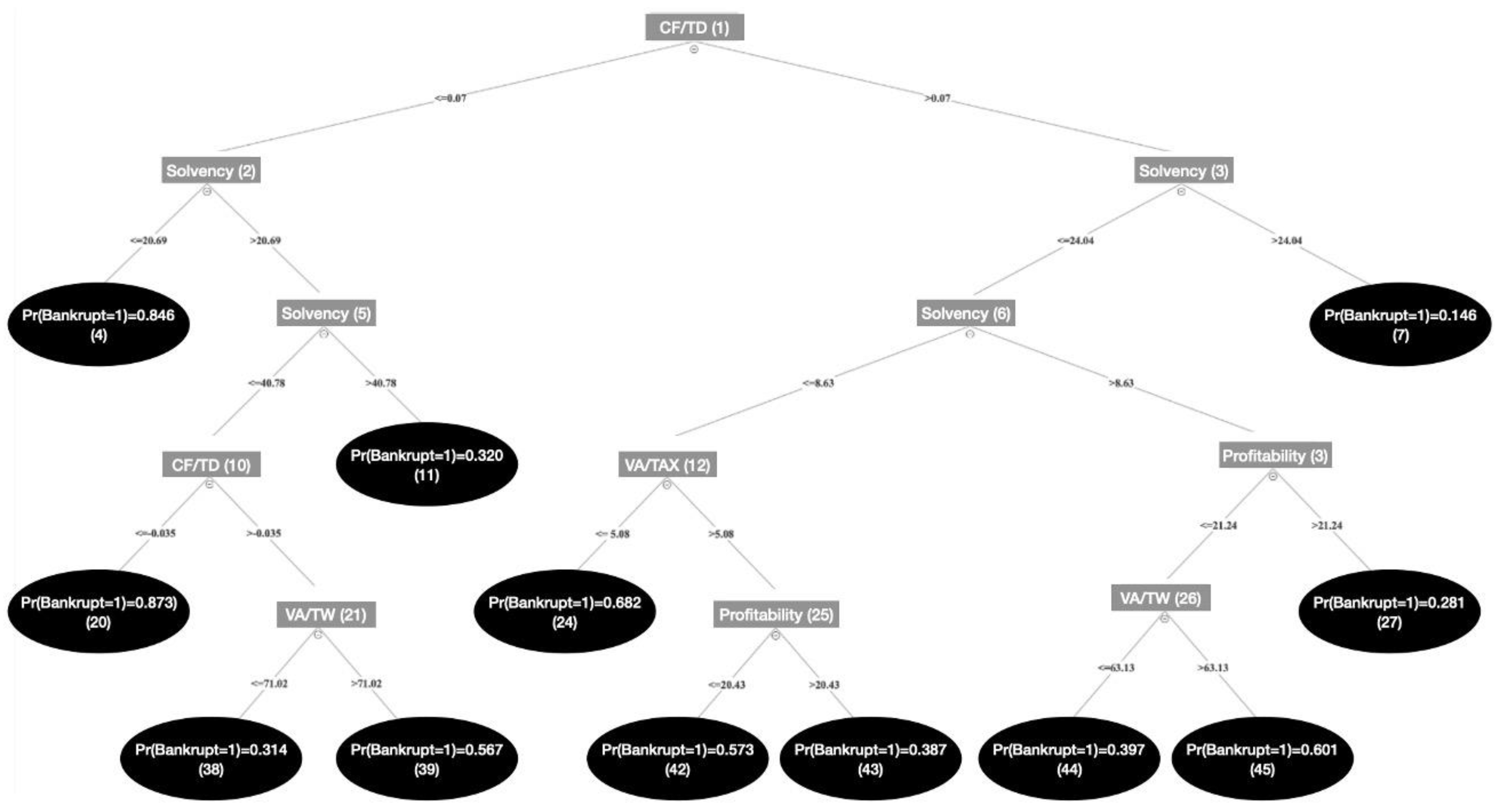
Applying the aforementioned variable selections procedures allows us to select a short list of accurate predictors among the initial set of 30. The Table 2 gathers the information extracted from each selection procedure. Focussing on CART procedure (see Figure 1) and following Cho et al. (2010), the variables identified enter as key variables into our bankruptcy prediction model (Model 1 as denoted in the fourth column of Table 2). But, this estimation strategy does not take advantage of the information given by the classification tree as nonlinearities in the relation between each predictor selected and the probability of bankruptcy are highlighted in each node. A way to capture this information is to create a set of dummy variables taking the value 1 if the values of the variable that defines a branch fall into the region above the CART threshold and zero otherwise. All dummy variables are therefore implemented in the prediction Model 2 of the Table 2.

3.2. The Position in the GVC

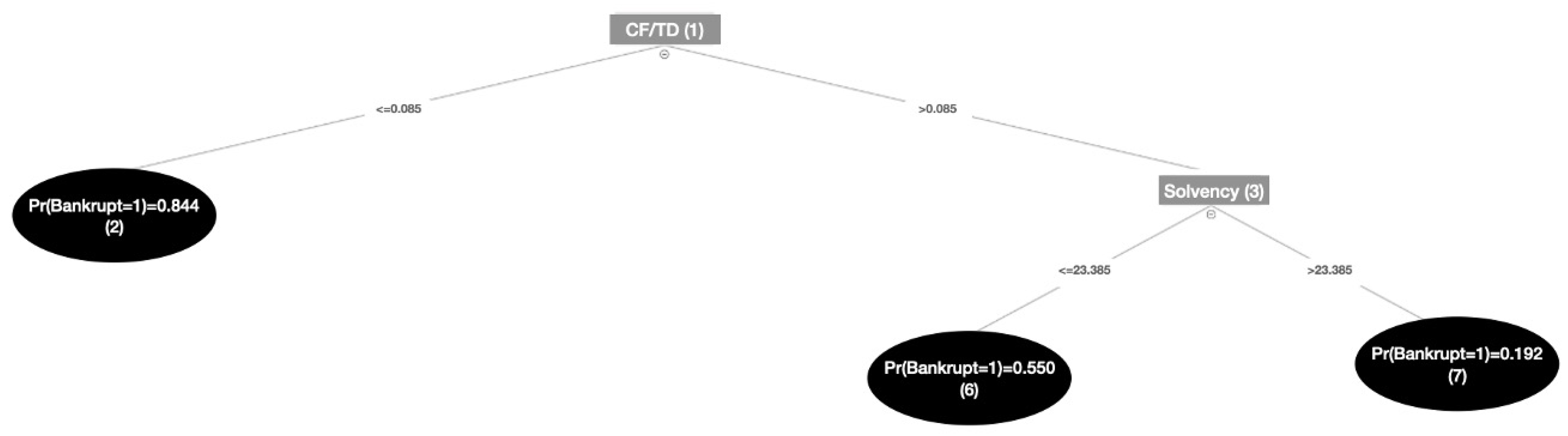
Applying In a second step, we reimplement the estimation strategy according to whether the firm belongs to an industrial sector located upstream in the GVC. The four variables selection techniques have therefore been run on the subsample of 882 firms, leading to the subsets of predictors presented in Table 3 and Figure 2. Globally, the predictors selected are the same as for the whole sample of firms, though the selection processes seem to be more restrictive.

3.3. Accuracy and Misclassification Evaluation

Table 4 presents the four evaluation metrics (sensitivity, specificity, overall classification and area under the receiver operating characteristic-ROC curve-AUC) obtained by running the logit model on each variable selection procedures, which allow us to compare performance associated with each variable selection process. First, and in order to be more accurate in the evaluations, we compute the cutoff points to be implemented in classification analysis (fifth row). Then, ROC areas are all significant and imply models with a concrete predicting ability (ROC statistic ranging between 0.7021 and 0.8662 according to the selection method used, fourth row of Table 4). Evaluation metrics also show that, on the whole, prediction performance increases when intelligence selection techniques (both Lasso and CART models) are implemented rather than statistical techniques (third row). Within the intelligence techniques, and regarding sensitivity analysis presented in first row, which represents the major statistic since it represents the capability of our model to recognize bankrupt firms, results clearly show that the CART selection procedure (Model 2) outperforms other selection methods. It therefore seems that CART selection procedure better fit the specific characteristics of Belgian SMEs, generating discrimination rules that correspond to the data.
In a second step, we measure the influence of the position of the firm in the GVC on the prediction capacity of our models. As mentioned before, this allows us to test whether financial ratios may be as good predictors of bankruptcy for upstream firms as for the overall sample. The results presented in Table 5 first show that ROC areas (fourth row) still confirm the predicting power of our models (ROC statistic ranging between 0.7248 and 0.8521 depending on the selection method used). Then, sensitivity (first row) is sharply decreasing, suggesting that the position in the GVC may have an effect on the capability for financial ratios to predict bankruptcy. Therefore, for such firms, there seems to exist some noise in the forecasting strategy, providing support to the presence of other variables affecting bankruptcy for these upstream firms such as contagion effect that could be more pronounced in such upstream industrial sectors (Fujiwara, 2008; Delli Gatti et al., 2009; Zhongsheng et al., 2011).

4. Discussion and Conclusion

The current literature on bankruptcy prediction has predominantly concentrated on models designed for larger firms, with limited attention given to those tailored for smaller, country-specific contexts (Crutzen and Van Caillie, 2007, 2010). In recent years, only a few studies have laid the groundwork for investigating bankruptcy prediction specifically for SMEs (Altman and Sabato, 2007; Ciampi and Gordini, 2008, 2009; Yazdanfar, 2011; Cultrera and Brédart, 2016; Zoricak et al., 2020; Papik and Papikova, 2023). In Belgium, the growing number of SMEs, along with the country's unique political landscape, regional institutional differences, and the uncertainties in the current economic environment, highlight the need to conduct more in-depth analyses focused on bankruptcy prediction for Belgian SMEs.
However, most studies trying to predict corporate bankruptcy mainly focus on robust and sometimes innovative prediction methods to enhance the models’ performance, without sufficiently considering other model elements, such as an upwind variables selection. Therefore, the added-value of this paper has wide-ranging implications for managers in the improvement of bankruptcy prediction models.
As we show, variables selection method can have significant influences on the performance of the model. That is, this paper shows that intelligence techniques outperforms more classical statistics ones in terms of predictive accuracy. More precisely, it seems that decision trees such as CART are the most efficient and are therefore not employed as much as they deserve in bankruptcy prediction perspective. Also, we show that specific variables related to the position of the firm within the production process may disrupt debates. That is, variables selection processes presented in this research are found to be less extensively efficient regarding financial-oriented variables for bankruptcy prediction of firms located upstream in the production process, such as it is for their downstream counterparts. Therefore, for such upstream firms, there seems to exist some other influences, i.e. some noise, in the forecasting strategy. This provides support to other variables affecting bankruptcy for these firms such as contagion effects that could be more pronounced in upstream industrial sectors (Fujiwara, 2008; Delli Gatti et al., 2009; Zhongsheng et al., 2011). At the end of the day, we hope this research will lead other researchers to pay more attention to this element in their efforts to develop more accurate models as well.
Beside the contributions of this study to the academic literature on variables selection strategies and bankruptcy prediction models, investors and managers may rely on such a new mode of information technology deployment in their evaluation and anticipation of their firms’ bankruptcy risks. This research may also offer inputs to financial institutions in their evaluation of the risk profiles of SMEs, since such variables selection models may help them to better identify firms with a higher risk of failure in their lending decisions.

Author Contributions

All authors contributed equally to the conceptualization, methodology, software, validation, formal analysis, investigation, resources, data curation, original draft preparation, review and editing, visualization, supervision, project administration. All authors also have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

The research data for this article was sourced from the Bureau Van Dijk Belfirst database.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Agarwal, V., & Taffler, R. 2008. Comparing the Performance of Market-based and Accounting based Bankruptcy Prediction Models. Journal of Banking and Finance, 32, 1541–1551. [CrossRef]
  2. Altman, E.I. 1968. Financial ratios, discriminant analysis and the prediction of corporate bankruptcy. The Journal of Finance, 23, 589–609. [CrossRef]
  3. Altman, E.I. 1984. The success of business failure prediction models: an international survey. Journal of Banking and Finance, 8, 171-198. [CrossRef]
  4. Altman, E.I., & Sabato, G. 2007. Modelling Credit Risk for SMEs: Evidence from the U.S. Market. Abacus, 43, 332-357. [CrossRef]
  5. Altman, E.I., & Branch, B. 2015. The Bankruptcy System's Chapter 22 Recidivism Problem: How Serious is It. The Financial Review, 50, 1–26. [CrossRef]
  6. Amendola, A., Restaino, M., & Sensini, L. 2011. Variable Selection in Default Risk Models. The Journal of Risk Model Validation, 5, 3–19. [CrossRef]
  7. Argenti, J. 1976. Corporate Collapse: the causes and symptoms. Ed. Holsted Press McGraw-Hill.
  8. Aziz, A., Emanuel, D.C., & Lawson, G.H. 1988. Bankruptcy Prediction: an Investigation of Cash Flow Based Models. Journal of Management Studies, 25, 419-437. [CrossRef]
  9. Balcaen, S., & Ooghe, H. 2006. 35 years of studies on business failure: an overview of the classic statistical methodologies and their related problems. The British Accounting Review, 38, 63–93. [CrossRef]
  10. Bauweraerts, J. 2016. Predicting Bankruptcy in Private Firms: Towards a Stepwise Regression Procedure. International Journal of Financial Research, 7, 147-153. [CrossRef]
  11. Bauweraerts, J., & Cultrera, L. 2017. Exploring Corporate Bankruptcy in Belgian Private Firms. International Journal of Economics and Finance, 40, 108-114. [CrossRef]
  12. Beaver, W.H. 1966. Financial ratios as predictors of failure. Journal of Accounting Research, 4, 71–111. [CrossRef]
  13. Bell, T. 1997. Neural nets or the logit model: a comparison of each model’s ability to predict commercial bank failures. International Journal of Intelligent Systems in Accounting, Finance and Management, 6, 249-264. [CrossRef]
  14. Brezigar-Masten, A. & Masten, I. 2012. CART-based selection of bankruptcy predictors for the logit model. Expert Systems with Applications, 39, 10153-10159. [CrossRef]
  15. Charalambous, C. , Martzoukos, S. H., & Taoushianis, Z. 2021. Estimating corporate bankruptcy forecasting models by maximizing discriminatory power. Review of Quantitative Finance and Accounting, 58, 297-328. [CrossRef]
  16. Charest, G., Lusztig, P., & Schwab, B. 1990. Gestion financière. Editions du renouveau pédagogique.
  17. Chava, S. & Jarrow, R.A. 2004. Bankruptcy Prediction with Industry Effects. Review of Finance, 8, 537-569. [CrossRef]
  18. Chen, J. & Chen, Z. 2008. Extended Bayesian information criteria for model selection with large model spaces. Biometrika, 95, 759-771. [CrossRef]
  19. Choubin, B., Darabi, H., Rahmati, O., Sajedi-Hosseini, F. & Klove, B. 2018. River suspended sediment modelling using the CART model: A comparative study of machine learning techniques. Science of The Total Environment, 615, 272-281. [CrossRef]
  20. Ciampi, F., & Gordini, N. 2008 (June). Using Economic-Financial Ratios for Small Enterprise Default Prediction Modeling: an Empirical Analysis. Oxford Business and Economics Conference Proceedings, Oxford, UK.
  21. Ciampi, F., & Gordini, N. 2009. Default Prediction Modeling for Small Enterprises: evidence from Small Manufacturing Firms in Northern and Central Italy. Oxford Journal, 8, 13-32.
  22. Cormier, D., Magnan, M., and Morard, B. 1995. The Auditor’s Consideration of the Going Concern Assumption: a Diagnostic Model. Journal of Accounting, Auditing and Finance, 10, 201-221. [CrossRef]
  23. Crutzen, N. & Van Caillie, D. 2007. The prevention of business failure: a state of the art. HEC Working Paper.
  24. Crutzen, N. & Van Caillie, D. 2010. Towards a Taxonomy of Explanatory Failure Patterns for Small Firms: A Quantitative Research. Review of Business and Economics, 55, 438-463.
  25. Cultrera, L. , & Brédart, X. 2016. Bankruptcy prediction: the case of Belgian SMEs,” Review of Accounting and Finance, 15, 101-119. [CrossRef]
  26. Cultrera, L. , & Vermeylen, G. 2018. Prédire la faillite des PME belges? Une modélisation statistique. In Galanti, S. (Eds.), Risques financiers. Mesures et conséquences. Presses Universitaires de Rennes.
  27. Dambolena, I.G., & Khoury, S. 1980. Ratio Stability and Corporate failure. Journal of Finance, 35, 1017-1026. [CrossRef]
  28. Daubie, M., & Meskens, N. 2001. Bankruptcy Prediction: Literature Survey of the Last Ten Years. Belgian Journal of Operations Research, Statistics and Computer Science, 41, 43-58.
  29. Delli Gatti, D. , Gallegati, M., Greenwald, B.C., Russo, A. & Stiglitz, J.E. 2009. Business fluctuations and bankruptcy avalanches in an evolving network economy. Journal of Economic Interaction and Coordination, 4, 195–212. [CrossRef]
  30. Dimitras, A.I. , Zanakis, S.H., & Zopounidis, C. 1996. A survey of business failures with an emphasis on failure prediction methods and industrial applications. European Journal of Operational Research, 90, 487–513. [CrossRef]
  31. Dimitras, A.I. , Slowinski, R., Susmaga, R. & Zopounidis, C. 1999. Business failure prediction using rough sets. European Journal of Operational Research, 114, 263–280. [CrossRef]
  32. du Jardin, P. 2015. Bankruptcy prediction using terminal failure processes. European Journal of Operational Research, 242, 286–303. [CrossRef]
  33. du Jardin, P. 2016. A two-stage classification technique for bankruptcy prediction. European Journal of Operational Research, 254, 236–252. [CrossRef]
  34. du Jardin, P. , Veganzones, D., & Séverin, E. 2019. Forecasting corporate bankruptcy using accrual-based models. Computational Economics, 54, 7–43. [CrossRef]
  35. Fitzpatrick, P. 1932. A comparison of ratios of successful industrial enterprises with those of failed firms. Certified Public Accountant, 2, 598–605.
  36. Fonti, V. , & Belitser, E. 2017. Feature selection using lasso. VU Amsterdam Research Paper in Business Analytics.
  37. Fujiwara, Y. 2008. Chain of Firms’ bankruptcy: A macroscopic study of link effect in a production network. Advances in Complex Systems, 11, 703–717. [CrossRef]
  38. Guilhot, B. 2000. Défaillance d’entreprise: Soixante-dix ans d’analyses théoriques et empiriques. Revue Française de Gestion, 26, 52–67.
  39. Hwang, R-C., Cheng, K.F. & Lee, J.C. 2007. A semiparametric method for predicting bankruptcy. Journal of Forecasting, 26, 317–342. [CrossRef]
  40. Jackson, R.H.G. , & Wood, A. 2013. The Performance of Insolvency Prediction and Credit Risk Models in the U.K: A Comparative Study. The British Accounting Review, 45, 183–202. [CrossRef]
  41. James, G., Witten, D., Hastie, T., & Tibshirani, R. 2013. An introduction to statistical learning. Ed. Springer.
  42. Julien, P.A. 1997. Les PME: bilan et perspectives. Economica Publishing.
  43. Kassambara, A. 2018. Machine Learning Essentials – Practical Guide in R. Ed. CreateSpace Independent.
  44. Keasey, K. , & Watson, R. 1987. Non-Financial Symptoms and the Prediction of Small Company Failure: A Test of Argenti’s Hypotheses. Journal of Business Finance & Accounting, 14, 335–354. [CrossRef]
  45. Kim, M. J. , & Kang, D. K. 2010. Ensemble with neural networks for bankruptcy. Expert Systems with Applications, 37, 3373–3379. [CrossRef]
  46. Kim, H.J. , Jo, N.O., & Shin, K.S. 2016. Optimization of cluster-based evolutionary undersampling for the artificial neural networks in corporate bankruptcy prediction. Expert Systems with Applications, 59, 226–234. [CrossRef]
  47. Kitowski, J.; Kowal-Pawul, A. & Lichota, W. 2022. Identifying Symptoms of Bankruptcy Risk Based on Bankruptcy Prediction Models—A Case Study of Poland. Sustainability, 14, 1–18. [CrossRef]
  48. Laitinen, E.K. 1991. Financial ratios and different failure processes. Journal of Business, Finance and Accounting, 18, 649–673. [CrossRef]
  49. Li, H. , Sun, J & Wu, J. 2010. Predicting business failure using classification and regression tree: An empirical comparison with popular classical statistical methods and top classification mining methods. Expert Systems with Applications, 37, 5895–5904. [CrossRef]
  50. Mai, F. , Tian, S., Lee, C. & Ma, L. 2019. Deep learning models for bankruptcy prediction using textual disclosures. European Journal of Operational Research, 274, 743–758. [CrossRef]
  51. Marco, L. 1989. La montée des faillites en France. Ed. L’Harmattan.
  52. McKee, T.E. & Greenstein, M. 2000. Predicting bankruptcy using recursive partitioning and a realistically proportioned data set. Journal of Forecasting, 19, 219–230. [CrossRef]
  53. Miller, A. 2002. Subset Selectin in Regression. Ed. Chapman & Hall/CRC.
  54. Morris, R. 1997. Early Warning Indicators of Corporate Failure: A critical review of previous research and further empirical evidence. Ashgate Publishing Limited.
  55. Mossman, C. , Bell, G., Swartz, L., & Turtle, H. 1998. An empirical comparison of bankruptcy models. Financial Review, 33, 35–54. [CrossRef]
  56. Nam, C.W. , Kim, T.S., Park, N.J. & Lee, H.K. 2008. Bankruptcy prediction using a discrete-time duration model incorporating temporal and macroeconomic dependencies. Journal of Forecasting, 27, 493–506. [CrossRef]
  57. O’Brien, R. 2007. A Caution Regarding Rules of Thumb for Variance Inflation Factors. Quality & Quantity, 41, 673–690. [CrossRef]
  58. Ogachi, D. , Ndege, R., Gaturu, P. and Zoltan, Z. 2020. Corporate Bankruptcy Prediction Model, a Special Focus on Listed Companies in Kenya. Journal of Risk and Financial Management, 13, 1–14. [CrossRef]
  59. Ohlson, J.A. 1980. Financial ratios and the probabilistic prediction of bankruptcy. Journal of Accounting Research, 18, 109–131. [CrossRef]
  60. Ooghe, H. , & Balcaen, S. 2002. Are failure prediction models transferable from one country to another? An empirical study using Belgian Financial Statements. Vlerick Leuven Gent Management School Working Paper, 132, 1–64.
  61. Ooghe, H. , Spaenjers, C., & Vandermoere, P. 2005. Business failure prediction: simple-intuitive models versus statistical models. IUP Journal of Business Strategy, 6, 7–44.
  62. Ooghe, H. , & De Prijcker, S. 2008. Failure processes and causes of company bankruptcy: a typology. Management Decision, 46, 223–242. [CrossRef]
  63. Papik, M. & Papikova, L. 2023. Impacts of crisis on SME bankruptcy prediction models’ performance. Expert Systems with Applications. 214, 119072. [CrossRef]
  64. Park, T. & Casella, G. 2008. The Bayesian Lasso. Journal of the American Statistical Association, 103, 681–686. [CrossRef]
  65. Peacock, R.W 2004. Understanding small business: practice, theory and research. Adelaide: Scarman Publishing.
  66. Peel, M.J. , & Peel, D.A. 1987. Some Further Empirical Evidence on Predicting Private Company Failure. Accounting and Business Research, 18, 57–66. [CrossRef]
  67. Platt, H. , & Platt, M. 1990. Development of a class of stable predictive variables: the case of bankruptcy prediction. Journal of Business Finance and Accounting, 17, 31–51. [CrossRef]
  68. Premachandra, I.M. , Bhabra, G.S., & Sueyoshi, T. 2009. DEA as a tool for bankruptcy assessment: a comparative study with logistic regression technique. European Journal of Operational Research, 193, 412–424. [CrossRef]
  69. Press, J. , & Wilson, S. 1978. Choosing between logistic regression and discriminant analysis. Journal of the American Statistical Association, 73, 699–705. [CrossRef]
  70. Refait, C. 2000. Estimation du risque de défaut par une modélisation stochastique du bilan: application à des firmes industrielles françaises. Finance, 21, 103–129.
  71. Shumway, T. 2001. Forecasting bankruptcy more accurately: A simple hazard model. The Journal of Business, 74, 101–124. [CrossRef]
  72. Singh, S. , Doyle Corner, P., & Pavlovich, K. 2015. Failed, not finished: A narrative approach to understanding venture failure stigmatization. Journal of Business Venturing, 30, 150–166. [CrossRef]
  73. Storey, D., Keasey, K., Watson, R., & Wynarczyk, P. 1987. The performance of small firms: profits, jobs and failures. Ed. Routldege.
  74. Sung, T.K. , Chang, N, & Lee, G. 1999. Dynamics of Modeling in Data Mining: Interpretive Approach to Bankruptcy Prediction. Journal of Management Information Systems, 16, 63–85. [CrossRef]
  75. Tibshirani, R. 1996. Regression Shrinkage and Selection via the Lasso. Journal of the Royal Statistical Society. Series B, 58, 267–288.
  76. Tsai, C.F. 2009. Feature selection in bankruptcy prediction. Knowledge-Based Systems, 22, 120–127. [CrossRef]
  77. Van Caillie, D. 2000 (October). La détection des signaux financiers annonciateurs de faillite en contexte PME: une approche méthodologique spécifique. 5th International French speaking Conference on SME, Lille, France.
  78. Van Caillie, D., & Dighaye, A. 2002 (June). La recherche en matière de faillite d’entreprise: un état de sa situation et de ses perspectives d’avenir. 11th International Conference on Strategic Management, Paris (France), June 5-7.
  79. Veganzones, D. , & Séverin, E. 2018. “An investigation of bankruptcy prediction in imbalances datasets,” Decision Support Systems, 112, 111-124. [CrossRef]
  80. Wang, G. , Ma, J., & Yang, S. 2014. An improved boosting based on feature selection for corporate bankruptcy prediction. Expert Systems with Applications, 41, 2353–2361. [CrossRef]
  81. Weitzel, W. , & Jonsson, E. 1989. Decline in Organizations: A literature Integration and Extension. Administrative Sciences Quarterly, 34, 91–109. [CrossRef]
  82. Wilcox, J.W. 1973. A Prediction of Business Using Accounting Data. Journal of Accounting Research, 11, 163–179.
  83. Xu, M. , & Zhang, C. 2009. Bankruptcy prediction: the case of Japanese listed companies. Revieww of Accounting Studies, 14, 534–558. [CrossRef]
  84. Yang, Z.R. , Platt, M.B., & Platt, H.D. 1999. Probabilistic Neural Networks in Bankruptcy Prediction. Journal of Business Research, 44, 67–74. [CrossRef]
  85. Yazdanfar, D. 2011. Predicting bankruptcy among SMEs, Evidence from Swedish firm-level data. International Journal of Entrepreneurship and Small Business, 14, 551–564. [CrossRef]
  86. Zhongsheng, H. , Yanhong, S. & Xiaoyan,.X 2011. Operational causes of bankruptcy propagation in supply chain. Decision Support Systems, 51, 671–681. [CrossRef]
  87. Zmijewski, M. 1984. Methodological Issues Related to the Estimation of Financial Distress Prediction Models. Journal of Accounting Research, 22, 59–82. [CrossRef]
  88. Zoricak, M. , Gnip, P., Drotar, P. & Gazda, V. 2020. Bankruptcy prediction for small- and medium-sized companies using severely imbalanced datasets. Economic Modelling, 84, 165-176. [CrossRef]
Preprints 115446 g001
Figure 1. Classification Tree – Overall sample.
Figure 1. Classification Tree – Overall sample.
Preprints 115446 g001
Preprints 115446 g002
Figure 2. Classification Tree – Upstream firms.
Figure 2. Classification Tree – Upstream firms.
Preprints 115446 g002
Table 1. List of Potential Corporate Bankruptcy Predictors.
Table 1. List of Potential Corporate Bankruptcy Predictors.
Variable Abbreviation
Firm age Firm age
Log of total employees Firm size
Shareholder equity/Total assets Solvency
EBIT/Total assets Profitability
Current ratio Current
Accruals/Total assets Accruals
Value added/Total workers VA/TW
Acid test Acid
Log of sales LnS
Number of days of client credit ClientDays
Number of days of supplier credit SupplierDays
Long term debts/Total assets LTD/TA
Gross sales margin GSM
Net sales margin NSM
Net income/Sales NI/S
Net income/Total assets NI/TA
Cash-flow/Equity CF/E
Cash-flow/Total debts CF/TD
Net Working Capital/Sales NWC/S
Net Working Capital/Total assets NWC/TA
Long term debts/Equity LTD/E
Total debts/Total assets TD/TA
Cash-flow/Total debts CF/TD
Net income/Current debts NI/CD
EBITDA/Total debts EBITDA/TD
Cash-flow/Current assets CF/CA
Net income/Total debts NI/TD
Net income/Current assets NI/CA
Current debts/Sales CD/S
Tax expense/Total assets Tax/TA
Table 2. Key predictors selected by each selection procedure – Overall sample.
Table 2. Key predictors selected by each selection procedure – Overall sample.
Backward Forward Lasso CART
(Model 1)		 CART
(Model 2)*
Profitability Profitability Profitability Profitability Profitability_D1
Solvency Solvency Solvency Solvency Profitability_D2
Current Current Current VA/TW Solvency_D1
VA/TW VA/TW VA/TW VA/TAX Solvency_D2
Firm size Firm Size CF/TD CF/TD Solvency_D3
Firm age Accruals ClientDays Solvency_D4
NWC/TA SupplierDays VA/TAX_D
LTD/TA VA/TW_D1
VA/TW_D2
CF/TD_D1
CF/TD_D2
* With the corresponding thresholds used: Profitability_D1 =1 if Profitability ≤ 21.24; 0 otherwise; Profitability_D2 =1 if Profitability ≤ 20.43; 0 otherwise; Solvency_D1 = 1 if Solvency ≤ 20.69; 0 otherwise; Solvency_D2 = 1 if Solvency ≤ 24.04; 0 otherwise; Solvency_D3 = 1 if Solvency ≤ 40.78; 0 otherwise; Solvency_D4 = 1 if Solvency ≤ 8.63; 0 otherwise; VA/Tax_D = 1 if VA/Tax ≤ 5.08; 0 otherwise; VA/TW_D1 = 1 if VA/TW ≤ 71.02; 0 otherwise; VA/TW_D2 = 1 if VA/TW ≤ 63.13; 0 otherwise; CF/TD_D1 = 1 if CF/TD ≤ 0.07; 0 otherwise; CF/TD_D2 = 1 if CF/TD ≤ -0.035; 0 otherwise.
Table 3. Key predictors selected by each selection procedure – Upstream firms.
Table 3. Key predictors selected by each selection procedure – Upstream firms.
Backward Forward Lasso CART
(Model 1)		 CART
(Model 2)*
Profitability Profitability Profitability CF/TD CF/TD_D
Solvency Solvency Solvency Solvency Solvency_D
Current Current Current
VA/TW VA/TW VA/TW
Firm size CF/TD
Firm size
* With the corresponding thresholds used: CF/TD_D = 1 if CF/TD ≤ 0.085; 0 otherwise; Solvency_D = 1 if Solvency ≤ 23.38 ; 0 otherwise.
Table 4. Accuracy evaluation rates achieved with prediction model – Overall sample.
Table 4. Accuracy evaluation rates achieved with prediction model – Overall sample.
Backward Forward Lasso CART
(Model 1)		 CART
(Model 2)*
Sensitivity 49.45 % 62.48 % 75.37 % 78.56 % 84.28 %
Specificity 94.67 % 89.86 % 78.38 % 80.24 % 77.72 %
Correctly classified 74.79 % 74.96 % 76.76 % 79.22 % 80.70 %
ROC 0.8489
Preprints 115446 i001 		0.7021
Preprints 115446 i002 		0.8425
Preprints 115446 i003 		0.8365
Preprints 115446 i004 		0.8662
Preprints 115446 i005
Cutoff 0.60
Preprints 115446 i006 		0.60
Preprints 115446 i007 		0.60
Preprints 115446 i008 		0.60
Preprints 115446 i009 		0.625
Preprints 115446 i010
Table 5. Accuracy evaluation rates achieved with prediction model – Upstream sample.
Table 5. Accuracy evaluation rates achieved with prediction model – Upstream sample.
Backward Forward Lasso CART
(Model 1)		 CART
(Model 2)*
Sensitivity 42.42% 55.88 % 47.37 % 66.10 % 69.84 %
Specificity 79.19% 71.03 % 96.15 % 83.22 % 62.22 %
Correctly classified 65.81 % 67.38 % 75.56 % 73.75 % 66.67 %
ROC 0.7391
Preprints 115446 i011 		0.7248
Preprints 115446 i012 		0.8473
Preprints 115446 i013 		0.8521
Preprints 115446 i014 		0.7278
Preprints 115446 i015
Cutoff 0.65
Preprints 115446 i016 		0.65
Preprints 115446 i017 		0.75
Preprints 115446 i018 		0.625
Preprints 115446 i019 		0.75
Preprints 115446 i020
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated