1. Problem

2. Massive black holes’ cores and event horizons size

Massive Black Hole Definition:

A massive black hole is a black hole with a single core resulting from a supernova event.

Reminder: “The Universe cannot compress Energy indefinitely because there is no infinite Energy anywhere in the Universe (not even the possibility of infinite Energy density at a point). This restriction leads us to conclude that a state of Matter with a maximum density MUST exist.

I name this state of maximum Matter density “Dachus” (derived from the Hebrew word for compressed.) I use the term “Dachus density” to denote this maximal density” [1].

I denote Dachus density by ${\rho }_D\approx 1.5744283·{10}^{161}\left[Kg{m}^{-3}\right]$ [1]

Reminder: “Continual compression of Matter within a black hole ultimately compresses its Matter until it reaches Dachus density within a non-zero volume in the center of the black hole. As the Matter inside the black hole compresses to its maximum degree, it reaches a state where any further compression only contributes to the expansion of the black hole’s core size, which maintains its Dachus state.

Remark: The concept of a black hole without a singularity challenges the calculations of esteemed physicists who predict singularities at the core of black holes. However, it is essential to note that these calculations, which suggest the existence of singularities as a mathematical necessity, did not account for the possibility of an upper limit to matter density. Consequently, the conclusion that geodesics inside a black hole inevitably converge at a singularity is invalid” [1].

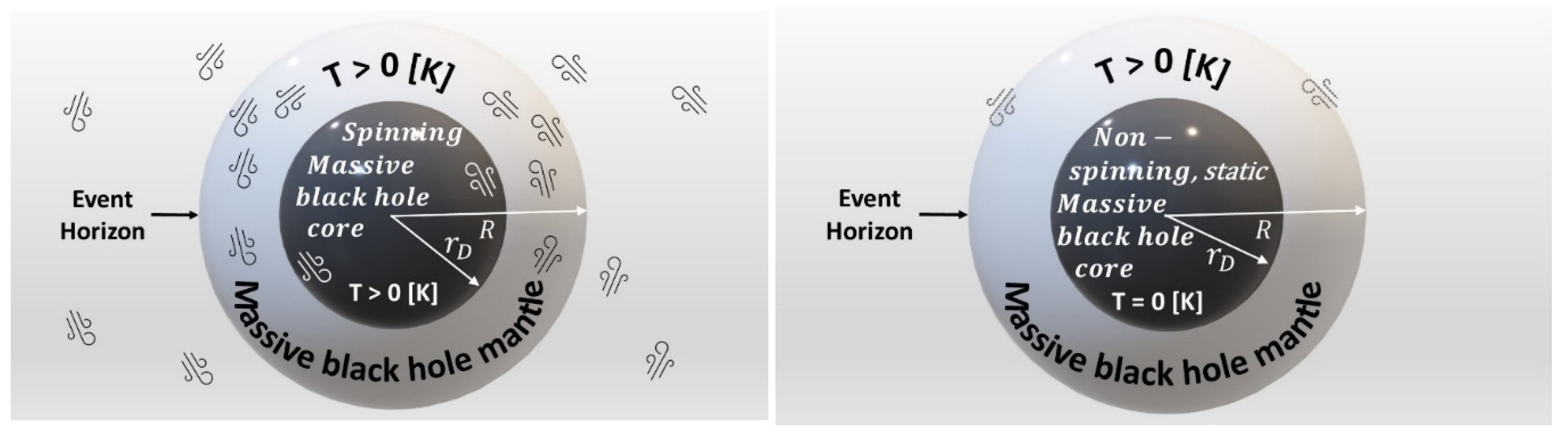
All massive black holes have a core at Dachus density: ${\mathsf{\rho }}_D|0<r\le r_D$.In this context, $r_D$ represents the distance from the center of the black hole to the radius where the maximal possible density begins to decrease.

During the supernova contraction phase, the gravitational attraction force is so big that it overcomes the tremendous deflecting centrifugal force of the elementary particles and creates a massive black hole with a small core at its center in Dachus density. In this core, all Energy compresses to the Dachus state, and the elementary particles lose their identity as elementary particles; they stop spinning because, in the Dachus state, there is no room for movement (the constituents of the black hole’s core do not move in relation to each other), and all that remains of them are their charges. After creating the massive black hole, the mighty gravitational attraction forces keep bending the space-time curvature around the core, causing any Energy near the core to join the core and then compressing it up to the Dachus density. (This is how a massive black hole’s core grows.)

Aside: Are there circumstances in which a black hole’s core shrinks?

Discussion: There are two possibilities: When anti-Matter encounters its corresponding Matter at the core’s rim, they annihilate each other, and some of the Matter charges may spread outside the core because of the kinetic Energy discharged—emanating from the incoming anti-Matter Universe part. On very rare occasions, a surge of very intense uncertainty-related Energy hits the core’s rim, and if it is intense enough, it tears away some charges from the core’s rim. Both these occurrences can reduce the core size. Note: These two occurrences describe what can happen at the black hole’s core rim. However, the same occurrences can also happen between the core and the black hole’s border or at the border of the black hole. If these events occur at the black hole’s rim, the size of the black hole will decrease.

Most massive black holes’ cores rotate relativistically fast, maintaining some of their pre-supernovae star’s angular momentum, which had maintained the angular momentum of the revolving dust cloud that precedes them.

Short-range forces (of quarkic (aka color) and weak charges) do not affect massive black holes at their borders because their charge’s diminishing points (range) are less than the massive black holes’ event horizons. Negative and positive electric charges appear in equal quantities and negate each other, so they do not influence the event horizon of the massive black hole.

Therefore, I will use the Kerr equation for the event horizons: $R^2-{\displaystyle \frac{2MGR}{c^2}}+a^2=0$, where R is the massive black hole radius.

The calculations presented here assume a spherical shape for the black hole’s core. I have not considered the slight flattening of the core at its poles near the spin axis, which occurs when the black hole spins at a very high rate, forming a slightly oblated spheroid.

How big are the cores and horizons of spinning Massive black holes?

To answer, I will use two examples. The first black hole, Cygnus X-1, is a massive black hole in Cygnus’s constellation. It has 21.2 ± 2.2 Solar Masses [3]. The second black hole is a supermassive black hole in the center of the Milky Way galaxy—Sagittarius A* with $4.154\mp 0.014·{10}^6$ solar Masses [4].

I will calculate the Dachus core radius using ${r_D=\left({\displaystyle \frac{3M_{Blackhole}}{4\pi {\rho }_D}}\right)}^{{\displaystyle \frac{1}{3}}}$.

$r_D$ is extremely small (it can be more than 48 orders of magnitude smaller than the Massive black hole event horizon radius in the case of Cygnus X-1—see table below.) When calculating the event horizon radius and its volume, I can assume that (almost) all the black hole Mass resides in its core. Thus, I can treat the Mass of a Massive black hole as a point Mass in the following angular momentum calculations. Assuming the black hole rotates very relativistically $J=Mv{R}_{Blackhole},a={\displaystyle \frac{J}{MC}}={\displaystyle \frac{v}{c}}{R}_{Blackhole}$ [5], Remark: The observed Mass $M$ already includes the relativistic effects.

Observations show that for Cygnus X-1: $dimensionlessa\approx 0.967\left(3\sigma \right)$ [6].

Observations show that for Sagittarius A*: $dimensionlessa\approx 0.90\pm 0.06$ [7].

Equation (1) Event horizon radius for a rotating massive black hole

$$R_{Blackhole}={\displaystyle \frac{2MG}{c^2+v^2}}|v<c$$

(1)

where “v” is the linear velocity at the equator of the spinning black hole. $R$ is the boundary of the black hole.

We know very little about the Energy density distribution between the Dachus core and the rest of the massive black hole enveloping the core, except that most of the Massive black hole Energy is in the core. I name the volume between the black hole’s core and rim: the “Black Hole Mantle.” The black hole mantle must revolve very fast due to the relativistically fast rotating Dachus core that drags the Energy encompassing it. As we look further from the core, the revolving Energy speed inside the massive black hole decreases—but not too much, as seen in the two examples I presented in which the revolution speed of the entire black hole is very large.

Table 1. Sizes comparison for Dachus core versus the entire black hole event horizon for highly relativistically rotating massive black holes.

Table 1. Sizes comparison for Dachus core versus the entire black hole event horizon for highly relativistically rotating massive black holes.

Star	Solar Masses	$\mathrm{Dachus}\mathrm{core}{r}_D$
		Radius [m]			Volume [m3]
Cygnus X-1	$21.2\pm 2.2$	$3.998·{10}^{-44}$	$2.6769·{10}^{-130}$
Sagittarius A*	$4.154\pm 0.014·{10}^6$	$2.322·{10}^{-42}$	$5.2452·{10}^{-125}$
Star		$\mathrm{Event}\mathrm{horizon}R$
		Radius [Km]		Volume [Km3]
Cygnus X-1		$32.3$	$1.42·{10}^5$
Sagittarius A*		$\mathrm{6,776,393}$	$1.30·{10}^{21}$

The massive black hole’s core is a speck inside its total size. Cygnus X-1’s Dachus core volume is approximately $2·{10}^{144}$ times smaller than its event horizon volume, and Sagittarius A*‘s Dachus core volume is approximately $4·{10}^{155}$ times smaller than its event horizon volume.

3. A Method to Determine Whether Massive Black Holes Have Internal Structure

3.1. 0[K]?

Temperature is a measure of the movement of particles and their subatomic constituents.

What happens if there is no particle movement?

To answer, I need to define a new limit:

Minimal Temperature Limit Definition:The minimal temperature limit is the “Absolute Zero Temperature,” designated 0[K]. It occurs in the total absence of kinetic Energy.

Kinetic Energy Definition

Kinetic Energy is Energy without charges that always change.

There can never be a neighborhood in space-time with zero temperature if it contains kinetic Energy. If a neighborhood contains only the rest Energy (the corresponding Energy for the rest Mass,) it means that this Energy does not move. Therefore, it must have the lowest temperature limit: the absolute zero temperature of 0[K].

At absolute zero (0[K]), Matter and its subatomic particles are theoretically at a standstill—they have no kinetic Energy, which seems impossible with the existence of uncertainty-related Energy [9].

Question: Is there a place in space-time where the temperature is 0[K]?

Discussion: The Matter within a black hole’s core is always at the Dachus state. It remains motionless when comparing subparts of the core to other subparts of the core. Any movement within the core’s subparts would indicate additional space for compression—which is impossible in this Dachus state.

Reminder: “We must remember that the Universal physical limits (we listed,) the speed of light, and the maximal Matter density cannot be circumnavigated—they hold at every possible physical phenomenon. Therefore, no amount of Energy will make Matter move at the speed of light or higher, and no amount of Energy will squeeze Matter and Energy further than the Dachus density” [1].

Therefore, any uncertainty-related Energy appearing within the core is swiftly deflected outside the core without changing the Dachus state.

Note: If the core as a whole spins, it has rotational Energy, and therefore, its temperature is greater than 0[K].

If a Massive black hole exists and it does move, notably does not spin, then and only then is its core at a standstill. In this state, none of its composing components move in relation to each other or collectively; therefore, it has a temperature of 0[K].

This rarely happens. It happens if the Massive black hole originated from a molecular cloud without any trigger that causes the molecular cloud to spin. Then, after the Massive black hole creation, its core does not spin and, therefore, does not drag the mantle of the black hole. However, the Massive black hole attracts some Energy from outside the black hole, causing movement in the mantle and, therefore, increasing the mantle temperature above 0[K]. In time, this mantle movement may cause core movement, which will raise the core temperature above 0[K]

Usually, the Massive black hole spins; therefore, its core has rotational Energy and a temperature higher than the absolute zero. The core of these Massive black holes rotates fast, dragging the rest of the black hole (the black hole mantle) into a swift rotational movement with currents. As such, the temperature inside the black hole’s mantle is higher than absolute zero.

Figure 1. Temperatures within spinning and non-spinning, and static massive black holes. Figure components are not on the same scale

Figure 1. Temperatures within spinning and non-spinning, and static massive black holes. Figure components are not on the same scale

4. Conclusions

References

1. Elementary particles and their interaction with space-time curvature. Lavi, Eran Magshim. s.l. 2024. [CrossRef]
2. Black hole mergers in compact star clusters and massive black hole formation beyond the mass gap. Francesco P R. s.l. : Royal Astronomical Society Monthly notices, 2022. [CrossRef]
3. Cygnus X-1 contains a 21-solar mass black hole. Miller-Jones, James C.A. s.l. : Astro physics HE. [CrossRef]
4. A geometric distance measurement to the Galactic center black hole with 0.3% uncertainty. Abuter, R. s.l. : Astronmoy & Astrophysics, 2019, Vol. 625. [CrossRef]
5. David L. Wiltshire, Matt Visser, Susan M. Scott. The Kerr Spacetime: Rotating Black Holes in General Relativity. s.l. : Cambridge University Press, 2009.
6. Confirming the spin parameter of the black hole in Cygnus X-1 using the Insight-HXMT. Zhao, Xue-Shan. s.l. : Journal of High Energy Astrophysics, 2020, Vol. 27. [CrossRef]
7. New black hole spin values for Sagittarius A∗ obtained with the outflow method. Daly, Ruth A. s.l. : Royal astronomical society, 2023. [CrossRef]
8. On the Dependence of the Relativistic Angular Momentum of a Uniform Ball on the Radius and Angular Velocity of Rotation. F., Sergey G. s.l. : International Frontier Science Letters, Vol. 15.
9. New Methods for Approaching Absolute Zero. Lounasmaa, O. V. 6, s.l. : Scientific American, 2019, Vol. 221.