Prerpints.org logo
Preprint
Article

A Lightweight Model Enhancing Facial Expression Recognition with Spatial Bias and Cosine‐Harmony Loss

Altmetrics

Downloads

133

Views

125

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

17 August 2024

Posted:

19 August 2024

You are already at the latest version

Alerts
Abstract
This paper proposes a novel facial expression recognition network called the Lightweight Facial Network with Spatial Bias (LFNSB). The LFNSB model balances model complexity and recognition accuracy. It has two key components: a lightweight feature extraction network (LFN) and a Spatial Bias (SB) module for aggregating global information. The LFN introduces combined channel operations and depthwise convolution techniques, effectively reducing the number of parameters while enhancing feature representation capability. The Spatial Bias module enables the model to focus on local facial features while also capturing the dependencies between different facial regions. Additionally, a novel loss function called Cosine-Harmony Loss is designed. This function optimizes the relative positions of feature vectors in high-dimensional space, resulting in better feature separation and clustering. Experimental results on the AffectNet and RAF-DB datasets show that the proposed LFNSB model performs excellently in facial expression recognition tasks. It achieves high recognition accuracy while significantly reducing the number of parameters, thus substantially lowering model complexity.
Keywords: 
Subject: Computer Science and Mathematics  -   Artificial Intelligence and Machine Learning

1. Introduction

Facial expression recognition (FER) is an active research area with broad applications in interpersonal communication, education, medical rehabilitation, and safe driving [1]. Researchers have explored various frameworks and models for FER [2]. However, a key issue with existing FER techniques is their high model complexity, leading to significant computational resource requirements and large storage demands [3]. To address these issues, Ref. [4] proposed a facial expression recognition model based on MobileFaceNets called MFN. This model employs multi-level feature extraction and a complex network architecture to effectively capture expression information in images, achieving high recognition accuracy. Nevertheless, the network still has high computational complexity and remains unfriendly to resource-constrained mobile devices. Therefore, this paper further optimizes MFN and designs a more computationally efficient network called Lightweight Facial Network (LFN). LFN removes some large convolution kernels [5] and combines convolution operations with batch normalization into a single step, reducing computational complexity while maintaining good feature extraction capabilities. Additionally, the Spatial Bias (SB) module [6] is introduced into the LFN architecture to address LFN’s shortcomings in capturing dependencies between different facial regions while maintaining computational efficiency.
Another key challenge in the field of FER is that different expressions may have similar facial features, making it relatively complex to distinguish between different expression categories [7]. Increasing the distance between class centers can prevent overlap between classes and enhance the distinction between different categories. In the field of facial recognition, many loss functions have emerged to address these issues, such as ArcFace [8]and CosFace [9]. However, they only focus on the direction of feature vectors. Other loss functions, such as Center Loss, only consider the spatial distance of feature vectors. This paper proposes a new loss function called Cosine-Harmony Loss. This loss function uses an adjusted cosine distance to measure the similarity between feature vectors and class centers, considering both the direction and distance of the vectors. Using Cosine-Harmony Loss in LFN results in samples from the same class being more tightly clustered in the feature space, while samples from different classes are more widely separated. This leads to enhanced recognition performance of the model.
The contributions of our research can be summarized as follows:
(1)
This paper introduces a lightweight and efficient LFNSB model that utilizes a deep convolutional neural network to capture both detailed and global features of facial images while maintaining high computational efficiency.
(2)
This paper introduces a new loss function called Cosine-Harmony Loss. It utilizes adjusted cosine distance to optimize the computation of class centers, balancing intra-class compactness and inter-class separation.
(3)
Experimental results show that the proposed LFNSB method achieves an accuracy of 63.12% on AffectNet-8, 66.57% on AffectNet-7, and 91.07% on RAF-DB.

2. Materials and Methods

This section begins by providing a comprehensive overview of the related works about three key aspects of FER: backbone architectures, attention mechanisms, and loss functions used in facial recognition research. Building upon this foundation, this paper then shifts the focus to the method used to address the FER problem.

2.1. Related work

2.1.1. FER

Facial expression recognition (FER) has seen significant advancements recently, particularly within computer vision and artificial intelligence, and is now widely applied in areas such as education, healthcare, and safe driving [1,2,3]. Existing networks, such as VGG [10], ResNet [11], and Inception [12], utilize deep network architectures with multi-level feature extraction to effectively capture facial expression information from images. However, these existing technologies typically require substantial computational resources and storage space [13]. To address these issues, Ref. [4] proposed an improved facial expression recognition network based on MobileFaceNets [14], called MFN. MFN incorporates MixConv operations from [15], which naturally mix multiple kernel sizes within a single convolution. This allows for better capture and expression of the diversity and complexity of features. Additionally, a coordinate attention mechanism [16] is introduced in each bottleneck to better capture the dependencies between different facial regions. Although MFN achieves high recognition accuracy, its computational complexity remains high, making it less suitable for resource-constrained environments. This paper further improves upon MFN, resulting in a network called LFN, which balances recognition accuracy with computational complexity

2.1.2. Attention Mechanism

Attention mechanisms are implemented to enhance the model’s expressive power by emphasizing key areas or features in an image, thereby effectively capturing subtle changes and important features in expressions. In existing FER research, common attention mechanisms include spatial attention, channel attention, and local-global attention. Spatial attention mechanisms enhance the detection of subtle changes and important features in facial expressions by focusing on and highlighting localized areas related to emotions, such as the eyes and mouth [17]. However, this mechanism may be insufficient when processing global context, as focusing solely on local features might lead to the neglect of important overall features. Channel attention mechanisms reflect the interdependencies between different feature channels, which helps to better understand and capture semantic information in expressions. By enhancing important feature channels and suppressing irrelevant channels, the model can improve the accuracy of expression recognition [18]. However, using channel attention mechanisms alone also has limitations, as they cannot fully utilize spatial information. To overcome the above issues, some studies combine spatial and channel attention mechanisms, enabling the model to deeply understand expression details and improve the classification accuracy of emotional states [16]. Although these attention mechanisms significantly enhance FER accuracy, they often come with high computational complexity and a large number of parameters. To address these issues, a module known as Spatial Bias, as introduced in [6], is incorporated into LFN. Unlike traditional attention mechanisms, The SB module is both lightweight and fast, adding a small amount of spatial bias to the convolutional feature maps through simple convolution operations, thereby effectively learning global knowledge. This module captures global features while preserving local information by reducing the spatial dimensions of the feature maps and compressing the number of channels. It can better establish connections among different facial regions, such as the mouth, eyes, nose, etc.

2.1.3. Loss Function

In recent years, various improved loss functions have emerged in the domain of facial recognition and expression recognition, aiming to enhance the discriminative power of facial features. Examples include Center Loss [19], Separate Loss [20]. These improved loss functions share a common goal: to maximize inter-class variance and minimize intra-class variance. The Center Loss proposed in [21] enhances feature discriminability by reducing intra-class variation. However, it only focuses on intra-class compactness, neglecting inter-class sparsity, which limits its effectiveness in distinguishing different classes. To address the limitations of center loss, [22] proposes Affinity Loss. This loss function calculates the Euclidean distance between each sample and its class center. Additionally, it enlarges the inter-class boundaries by using the standard deviation among class centers, effectively preventing class overlap. Furthermore, Angular Softmax Loss, which uses angles as distance measures, was introduced in [23]. Subsequent improvements to angular loss functions have also been proposed [24]. Building on these methods, this paper proposes a new Cosine-Harmony Loss that optimizes cosine distance to harmonize feature clustering and class separation, effectively integrating both angular information and distance metrics.

1.2. Method

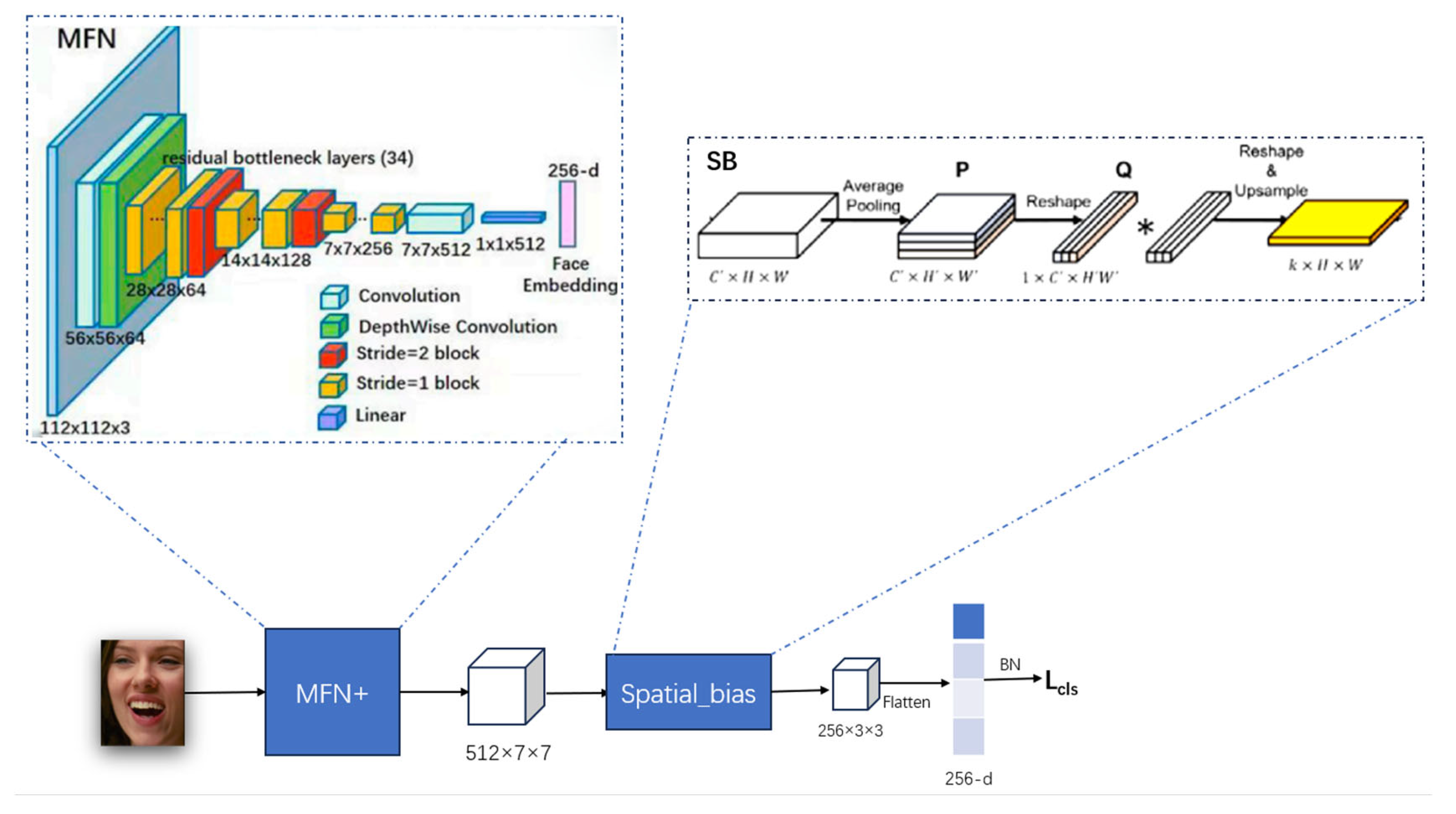
The architectural overview of the LFNSB is depicted in Figure 1, comprising two main components: the LFN and the SB. Initially, facial images are fed into the LFN, which produces basic feature maps as outputs. Subsequently, these feature maps are input into the SB to capture more detailed global features of facial expressions. Eventually, after flattening and passing through a fully connected layer, LFNSB outputs predictions for the num_class categories.

2.2.1. LFN

The LFN architecture optimizes feature extraction capabilities through a hierarchical design and modular construction. It consists of the following components:
Residual Bottleneck: Capture complex features and facilitate information flow.
Non-Residual Blocks: Enhance the model’s representation capability.
Conv2d_BN: Simplify computation processes and improve inference efficiency.
RepVGGDW: Reduce computational complexity and parameter count while maintaining robust feature extraction capabilities.
The integration of these components in the LFN architecture enables efficient facial feature extraction, leveraging the strengths of each module to optimize feature extraction and representation.

Improved Face Expression Recognition Network LFN Based on MFN

MFN is a face expression recognition architecture based on MobileFaceNet, utilizing the lightweight network MobileFaceNet [14] as its foundation. It employs a combination of two primary building blocks: residual bottlenecks and non-residual blocks. The residual bottleneck block was designed to capture complex features. The block leverages residual connections to mitigate the degradation problem. The improved baseline presented in this paper is called LFN, as shown in Table 1. The first two layers’ Conv_blocks are replaced with Conv2d_BN, and the final Conv_block is replaced with RepVGGDW. The original MFN network depth is retained, with large kernel sizes of 5 and 7 removed in the shallow layers and only a few large kernel sizes used in the deeper layers.

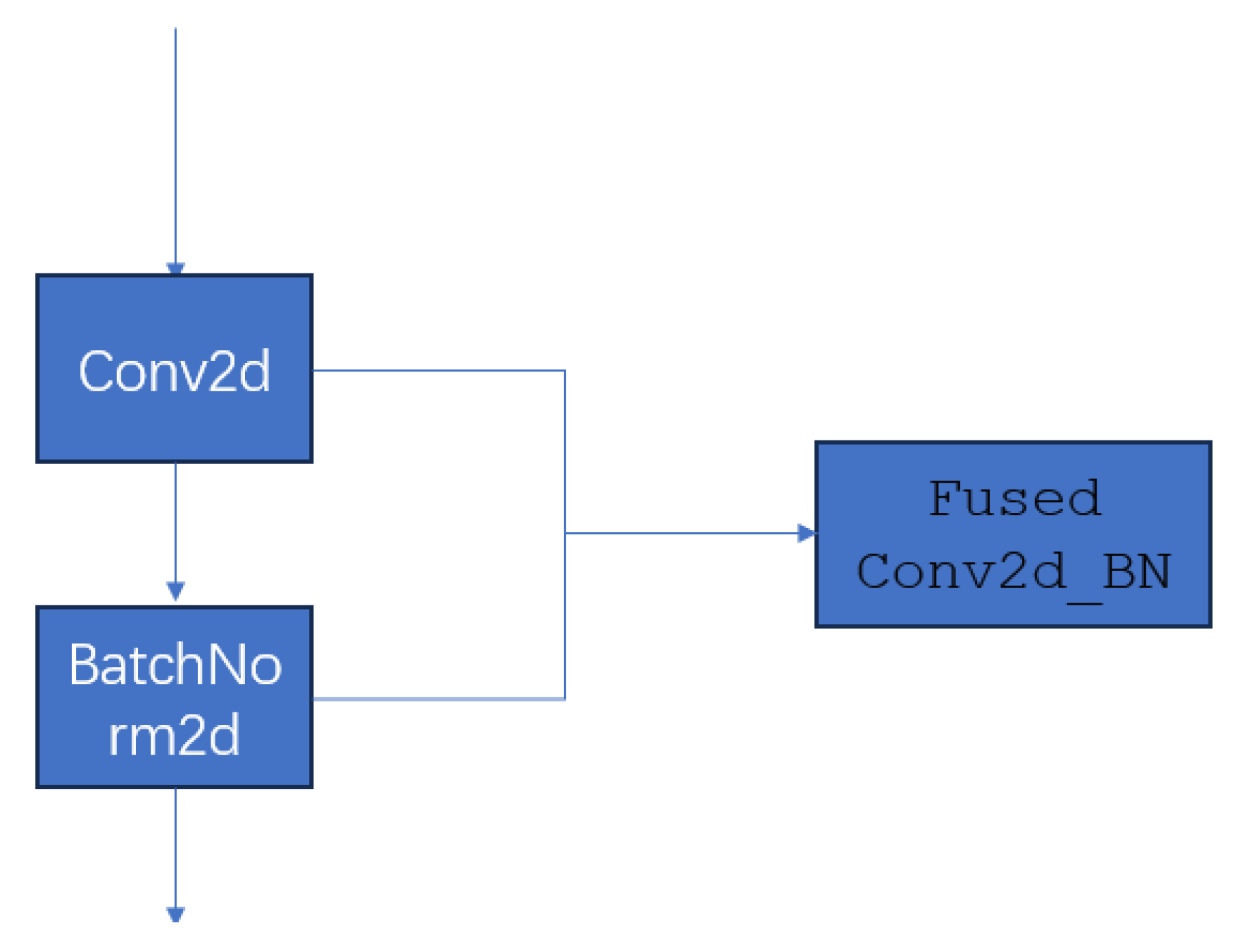
2.2.1.2. Conv2d_BN

Convolutional layers have limitations in expressing complex features, which can lead to performance degradation when handling intricate expression recognition tasks. To maintain high feature extraction capability while keeping low computational complexity, we introduced the Conv2d_BN module [13]. Conv2d_BN performs only two operations: convolution and batch normalization. As shown in Figure 2, after fusion, the parameters of the batch normalization operation are directly integrated into the convolutional layer. This improves inference efficiency. The fused weight formula is:
ω ’ = ω γ r u n n i n g _ v a r
where ω is the weight of the original convolutional layer, γ is the weight of the batch normalization layer, r u n n i n g _ v a r is the running variance of the batch normalization layer, and ϵ is a small constant for numerical stability. By multiplying the original convolutional weight ω by γ, we account for the scaling effect of the batch normalization layer. This ensures that the input data processing in the fused convolutional layer still reflects the adjustment of the data distribution made by the batch normalization layer, thereby maintaining consistency and stability in the output. The fused bias formula is:
b ’ = β − r u n n i n _ m e a n ∗ γ r u n n i n g _ v a r + ϵ
where β is the bias of the batch normalization layer, and r u n n i n _ m e a n is the running mean of the batch normalization layer. The bias term   b ’ needs to subtract the effect of the running mean adjusted by γ from the original bias β to maintain the overall translation effect.

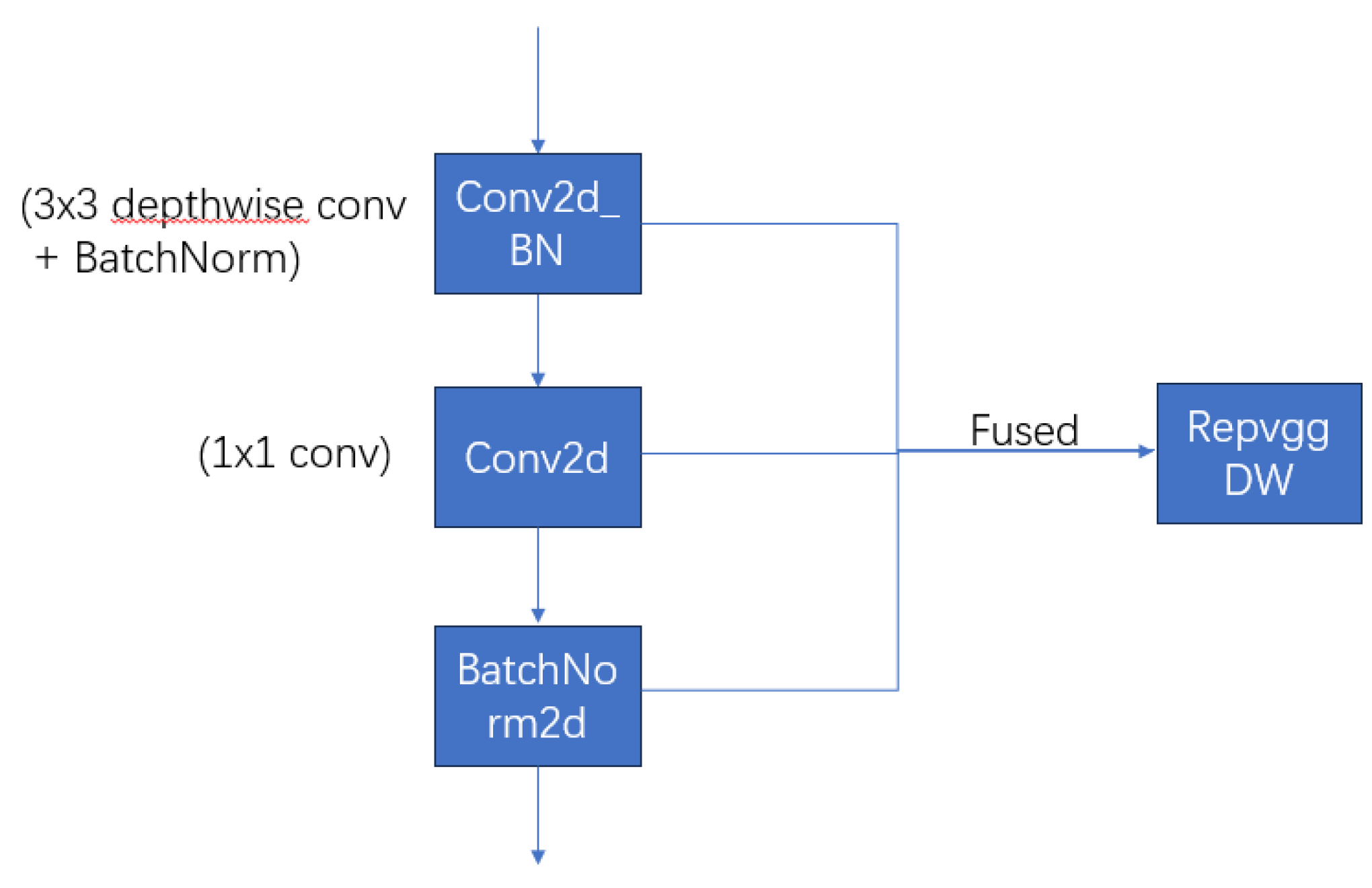
2.2.1.2. RepVGGDW

When models become deeper, they may encounter issues such as gradient vanishing or explosion, which complicates training. Additionally, deeper networks require more computational resources, increasing training time and computational cost. Replacing the final `Conv_block` layer with the `RepVGGDW` module can help address these issues [13]. The `RepVGGDW` module consists of the previously described `Conv2d_BN` (3x3 depthwise convolution), a 1x1 convolution (`Conv2d`), and a batch normalization layer (`BatchNorm2d`). As illustrated in Figure 3, this module uses fusion technology. The fusion process integrates the weights and biases of the depthwise and pointwise convolutions with the batch normalization parameters, achieving parameter reduction and decreased complexity while maintaining effective feature extraction capabilities. Importantly, the `RepVGGDW` module forms a residual connection by adding the input `x` to the result of the convolution and batch normalization, facilitating gradient flow and preventing issues with gradient diminishing or exploding in deep networks. Additionally, the `RepVGGDW` module does not alter the number of output channels, preserving the 256-channel output, which makes integration into existing facial expression recognition models more convenient and efficient. Experimental validation shows that this replacement improves both recognition accuracy and inference efficiency, demonstrating the effectiveness of the `RepVGGDW` module in optimizing deep network structures and enhancing model performance.

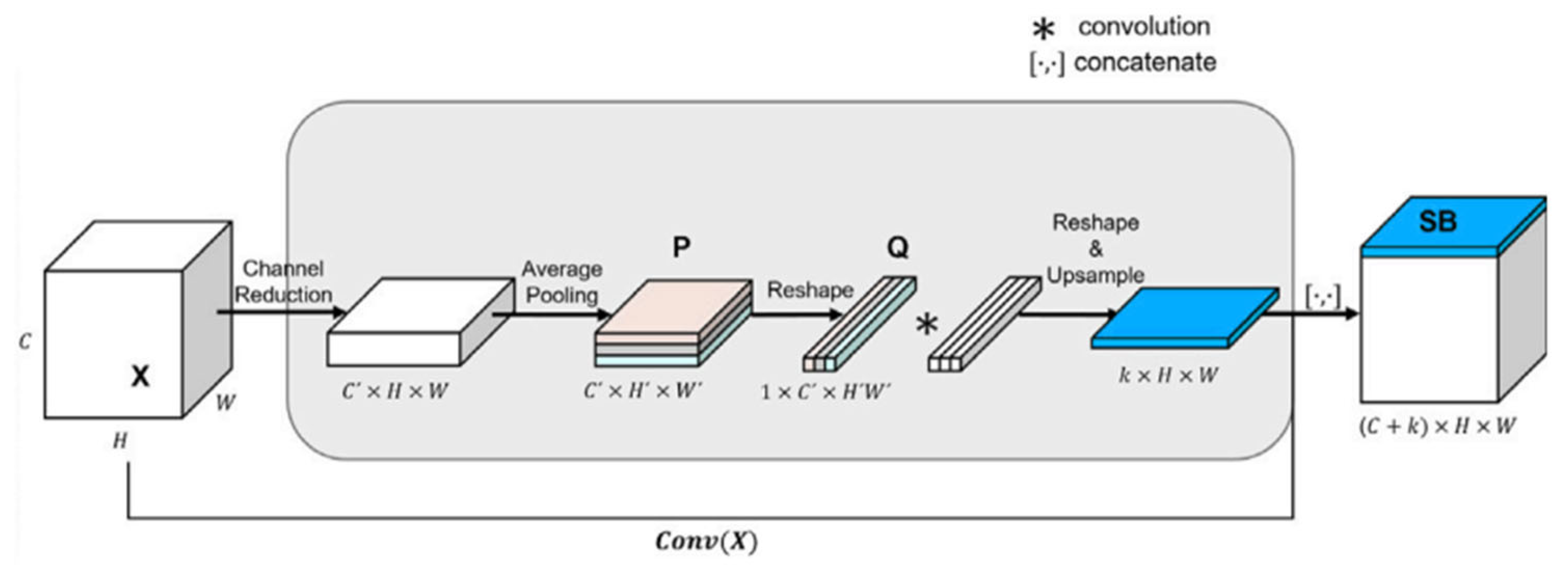
1.2.1. Spatial Bias

To ensure that the model can capture the dependencies between different regions of the face while maintaining computational efficiency, we introduce the Spatial Bias (SB) module. The channel and spatial size of the feature map are reduced through the 1×1 convolution and average pooling operations. Its workflow is illustrated in Figure 4 and operates as follows:
  • Input Feature Map Compression: The input feature map is first compressed through a 1×1 convolution, resulting in a feature map with fewer channels. Then, an adaptive average pooling layer is used to spatially compress the feature map, producing a smaller feature map.
  • Feature Map Flattening: The feature map for each channel is flattened into a one-dimensional vector, resulting in a transformed feature map.
  • Global Knowledge Aggregation: A 1D convolution is applied to the flattened feature map to encode global knowledge, capturing global dependencies and generating the spatial bias map.
  • Upsampling and Concatenation: The spatial bias map is upsampled to the same size as the original convolutional feature map using bilinear interpolation, and then concatenated with the convolutional feature map along the channel dimension.
In this way, the Spatial Bias module enables the network to learn both local and global information, improving feature representation and enhancing the overall effectiveness of the model.

1.2.1. Cosine-Harmony Loss

In FER, features can vary significantly among different samples within the same class, while features across different classes may exhibit high levels of similarity. This paper introduces a new loss function called Cosine-Harmony Loss to address this issue. This loss function enhances the discriminative power of feature vectors by using an adjusted cosine distance, thereby improving both direction and distance aspects.
In face recognition, cosine distance is commonly used to compute the similarity between two facial images. The conventional cosine distance is defined as follows:
c o s i n e _ d i s t a n c e ( x , c ) = 1 - x · c | x | · | c |
Here, x represents the input feature vector, and c   denotes the class center. This method focuses on the directional difference of the vectors but ignores the magnitude. To address this, adjusted cosine distance is introduced, subtracting the mean from each vector to mitigate the impact of different feature distributions:
a d j u s t e d _ c o s i n e _ d i s t a n c e ( x , c ) = 1 − ( x − m e a n x ) · ( c − m e a n c ) x − m e a n x | c − m e a n c |
The adjusted cosine distance considers both the direction and magnitude of the vectors, crucial in feature clustering and enhancing discriminative power.
Cosine-Harmony Loss utilizes adjusted cosine distance to calculate distances between feature vectors and class centers within the same class (intra-class distance) and between different classes (inter-class distance). Using a mask to differentiate intra-class and inter-class distances, the intra-class distance is:
i n t r a _ c l a s s _ d i s t a n c e = 1 N ∑ i = 1 N d i s t ( x i , c y i )
where N  is the number of samples, x i  is the feature vector of the i-th sample, and c y i is its corresponding class center. The inter-class distance is calculated by dividing the sum of distances by the number of classes minus one, to measure the dispersion of features between different classes. It is defined as follows:
i n t e r _ c l a s s _ d i s t a n c e = 1 N ( C − 1 ) ∑ i = 1 N ∑ j ≠ y i d i s t ( x i , c j )
where C is the number of classes.
Additionally, we use intra-class variance to measure the variation of feature vectors within each class.
c l a s s _ v a r i a n c e = 1 N ∑ i = 1 N ( x i − μ ) 2
Where μ   is the mean vector of all feature vectors. Furthermore, we incorporate a weight parameter ∝ to flexibly balance intra-class variance and inter-class distance contributions in the loss function. The final loss function balances intra-class distance, inter-class distance, and class variance, computed as:
l o s s = ∝ i n t r a _ c l a s s _ d i s t a n c e c l a s s _ v a r i a n c e ( ) + ( 1 - ∝ )   i n t e r _ c l a s s _ d i s t a n c e
The proposed Cosine-Harmony Loss function demonstrates significant effectiveness in enhancing the discriminative power of feature vectors. It employs an adjusted cosine distance that considers feature vectors’ direction and magnitude. By minimizing intra-class distance and maximizing inter-class distance, Cosine-Harmony Loss more effectively clusters features, thereby improving model performance in tasks such as FER.

3. Results

In this section, we provide a detailed description of our experimental evaluation results. We demonstrate the superiority of the proposed method on two widely used benchmark datasets. The experimental evaluation began with a series of ablation experiments, analyzing the individual contributions of each component within LFNSB. This allowed us to assess the significance of each component in enhancing the overall performance of LFNSB. Subsequently, we conducted comparative analyses with other state-of-the-art networks.

3.1. Datasets

AffectNet [25]: AffectNet is a comprehensive database of facial expressions collected from the internet, designed to facilitate research in automated facial expression recognition and affective computing. It consists of over 1 million facial images gathered using 1250 emotion-related keywords across six languages. Approximately 440,000 of these images were manually annotated for seven discrete facial expressions (categorical model) and the intensity of valence and arousal (dimensional model). AffectNet is notably the largest dataset of its kind, enabling studies in both emotion models.
RAF-DB [26]: RAF-DB (Real-world Affective Faces Database) is a large-scale dataset specifically designed to advance research in facial expression recognition. It includes 29,672 images with strong diversity, covering various factors such as age, gender, and ethnicity. The dataset features diverse conditions including lighting variations, head poses, and occlusions (such as glasses or facial hair).To facilitate effective model training and evaluation, RAF-DB is logically partitioned into training and test sets, with the training set being five times larger than the test set.

3.2. Implementation Details

During the preprocessing stage, we utilized the RetinaFace model to detect facial regions in the AffectNet and RAF-DB datasets, identifying five key points: both eyes, the nose, and both corners of the mouth. All images were resized to 112×112 pixels. We employed several data augmentation techniques to mitigate overfitting, including random horizontal flipping, random rotations and cropping, color normalization, and random pixel erasure. These augmentation strategies enhanced the robustness and generalization capability of the LFNSB model during training.
To ensure a fair comparison with other backbone architectures, the MFN backbone was pre-trained on the Ms-Celeb-1M dataset [27]. All experiments were conducted using the PyTorch 1.8.0+ framework on a server equipped with an NVIDIA TESLA P40 GPU. Our code is open-sourced at https://github.com/1chenchen22/LFNSB.
Training for all tasks used a consistent batch size of 256 over 40 epochs. During training, we applied various optimization strategies to adjust model parameters. Specifically, for the AffectNet-7 and AffectNet-8 datasets, we started with an initial learning rate of 0.0001. On the RAF-DB dataset, we adjusted the learning rate to 0.01. These parameter selections were aimed at optimizing the model effectively to achieve better training efficiency and performance.

3.3. Ablation Studies

To validate the effectiveness of each component in the LFNSB model, this section conducted ablation experiments across multiple datasets, demonstrating the generalization capability of the proposed LFNSB model and the effectiveness of its components.

3.3.1. Effectiveness of the Cosine-Harmony Loss

To evaluate the effectiveness of LFNSB, this section conducted multiple comparative experiments on the RAF-DB dataset. Table 2 presents the performance of the original MFN and the improved LFNSB. LFNSB achieved an accuracy of 91.07% on RAF-DB. Despite its slightly higher computational complexity than MobileFaceNet, LFNSB reduces complexity relative to MFN, with parameters decreasing by 30.8% and FLOPs reducing by 27.1%. This demonstrates that LFNSB strikes a balance between model complexity and recognition accuracy. It provides a lightweight and efficient foundational model for future facial expression recognition tasks.

3.3.2. Effectiveness of the Cosine-Harmony Loss

To validate the effectiveness of the Cosine-Harmony Loss in facial expression recognition tasks, we conducted a series of ablation experiments focusing on assessing the impact of this loss function on model performance. As shown in Table 3, using only the cross-entropy loss function in the proposed LFN backbone resulted in accuracy rates of 89.57% and 64.26% on the RAF-DB and AffectNet-7 datasets, respectively. Upon integrating the newly proposed Cosine-Harmony Loss function, the accuracy rates improved by 0.65% and 1.19%, respectively, further confirming its effectiveness.
To determine the optimal alpha value for the Cosine-Harmony Loss function and validate its reliability, we conducted multiple experiments, setting the epochs to 40. We tested different alpha values, including 0.1, 0.2, 0.3, 0.4, and 0.5. In each experiment, we evaluated the model’s performance on the validation set, primarily using validation accuracy and loss value as evaluation metrics.
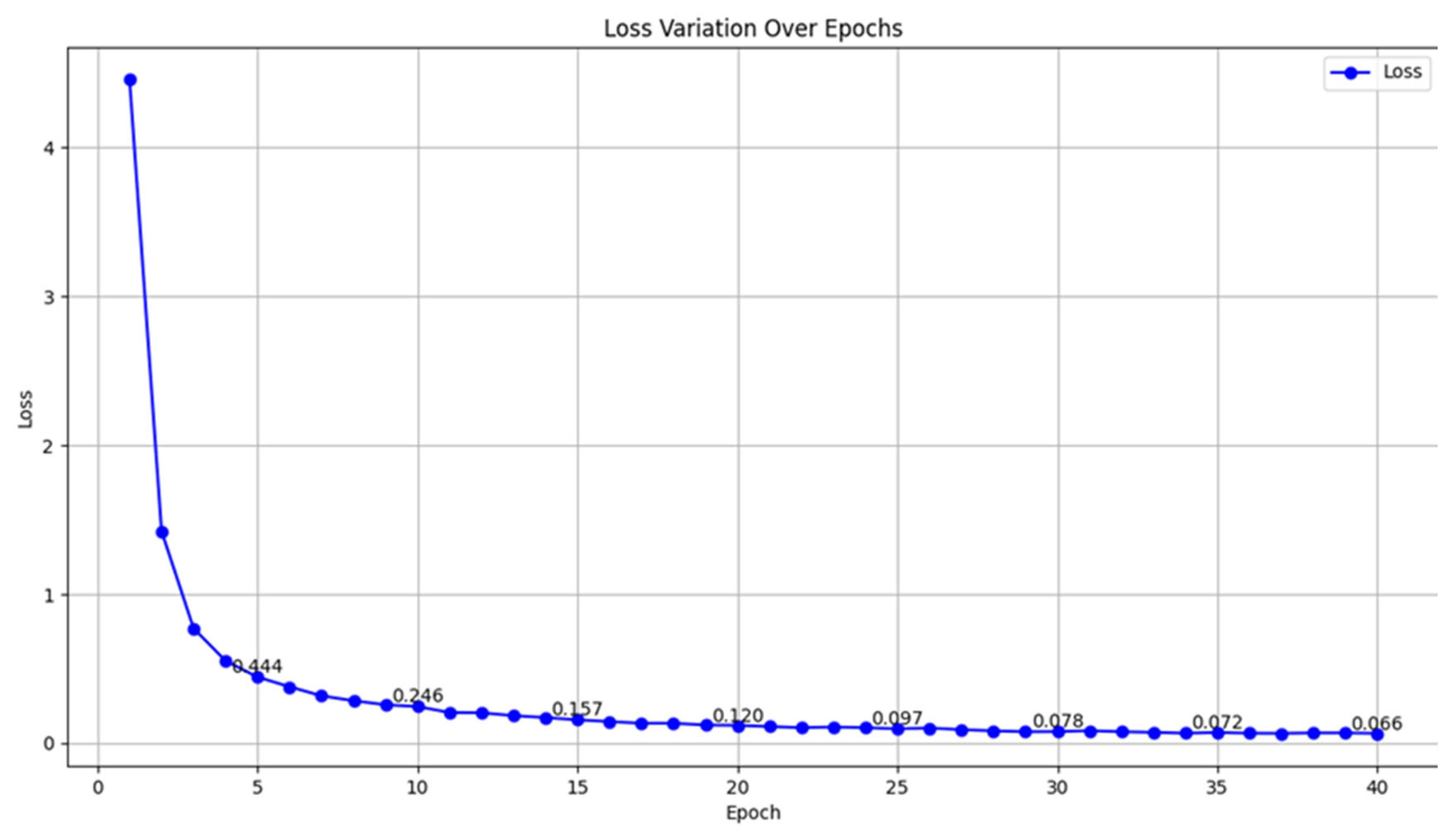
From Table 4, it can be seen that when the alpha value is 0.1, the validation accuracy reaches 90.22%, and the loss value decreases to 0.066, indicating the best model performance. This may be because the inter-class distance is more critical for facial expression recognition tasks, whereas focusing too much on the intra-class distance could lead to overfitting or excessive compression of the feature space. Therefore, we chose an alpha value of 0.1 as the final parameter for the Cosine-Harmony Loss function. Additionally, we plotted the loss curve for alpha = 0.1, as shown in Figure 1. The figure shows a significant decrease in the loss value with the increase in training epochs, indicating good convergence of the model under this setting.
Preprints 115488 g005
Figure 5. Loss Curve with α=0.1 Over Epochs.
Figure 5. Loss Curve with α=0.1 Over Epochs.
Preprints 115488 g005

3.3.3. Effectiveness of the LFNSB

To further validate the contribution of the Spatial Bias module, we integrated it into the LFN backbone and utilized the Cosine-Harmony Loss function as proposed, forming the LFNSB model. Experiments were conducted on the RAF-DB and AffectNet-7 datasets. The results, shown in Table 5, indicate performance improvements of 0.85% and 1.117% on RAF-DB and AffectNet-7, respectively. The effect is more pronounced on the larger AffectNet dataset. The Spatial Bias module enhances the model’s ability to capture complex expression features by effectively integrating global information, leading to improved accuracy.
These ablation experiments confirm the effectiveness and reliability of both the LFN and the Spatial Bias module. Overall, the LFNSB model maintains a good balance between parameter count and computational complexity, providing new insights and directions for future research in related fields.

3.4. Quantitative Performance Comparisons

This section presents a quantitative performance comparison of the LFNSB model with other existing models on the AffectNet and RAF-DB datasets, as shown in Table 6, Table 7 and Table 8. The results indicate that the proposed LFNSB model achieves higher recognition accuracy than the average of existing models. Specifically, the LFNSB model reached an accuracy of 66.57% on AffectNet-7, 63.12% on AffectNet-8, and 91.07% on RAF-DB. These results demonstrate the potential of the LFNSB model in facial expression recognition tasks.

3.5. K-Fold Cross-Validation

To comprehensively evaluate the effectiveness and reliability of LFNSB, we conducted K-fold cross-validation on the RAF-DB and AffectNet-7 datasets, as shown in Table 9. In this process, the dataset is randomly divided into k mutually exclusive subsets of equal size. The model is then trained using k-1 of these subsets, while the remaining subset is used for testing. This procedure is repeated for each subset, and the results are collected to compute the average accuracy. This validation method ensures that all data points are used for both training and testing, effectively reducing the risk of overfitting.
The results in Table 9 show that LFNSB achieved an average accuracy of 90.635% on the RAF-DB dataset and 65.72% on the AffectNet-7 dataset. These results indicate that the model maintains consistently high performance, further validating the reliability and robustness of the LFNSB model in facial expression recognition tasks.

3.6. Confusion Matrix

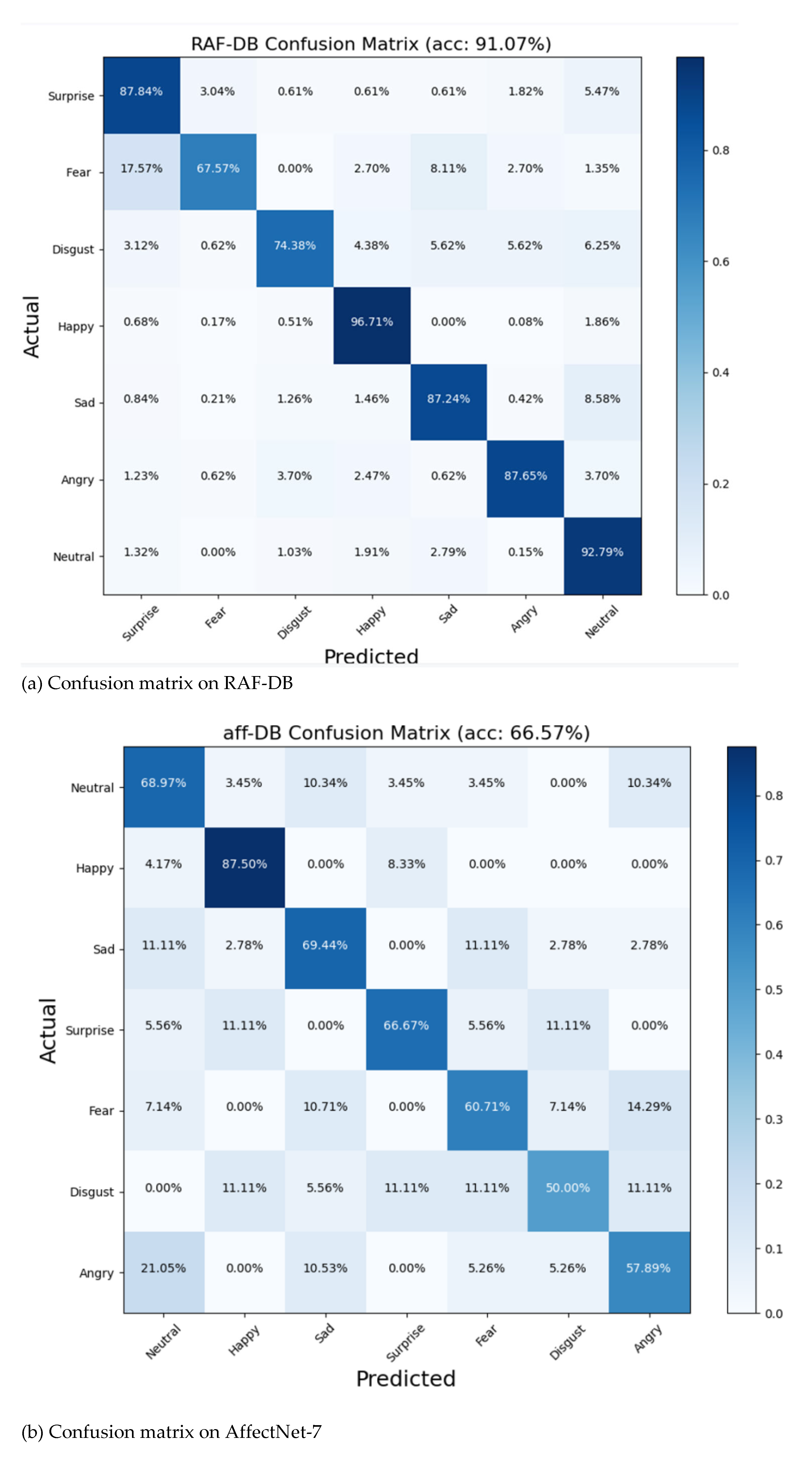
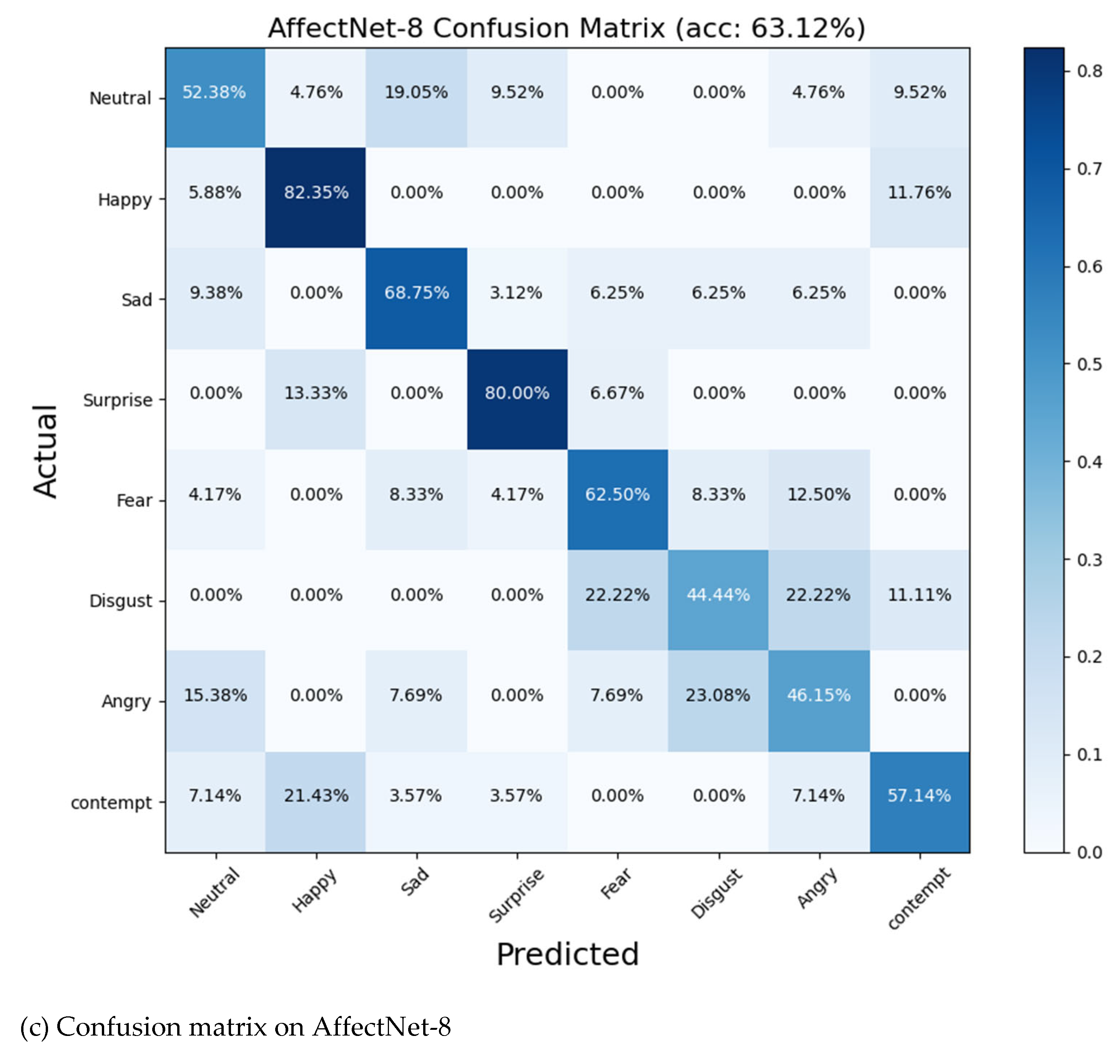
In classification tasks, a confusion matrix is commonly used to evaluate a classification model’s performance across different categories, providing a comprehensive understanding of the model’s effectiveness. This section presents the confusion matrices for the LFNSB model tested on three datasets, as shown in Figure 6a-c. From these confusion matrices, it can be observed that the "happy" category consistently exhibits the highest recognition rates across all three datasets, likely because it is the most prevalent category in each dataset.
Figure 6b,c reveal that categories such as "disgust," "angry," and "contempt" perform poorly in the AffectNet dataset. This underperformance is due to the small number of samples for these categories, which are only in the thousands, compared to other categories with tens of thousands of samples. Additionally, the data quality for these categories is lower, with noticeable noise interference. Furthermore, the AffectNet dataset suffers from class imbalance, which may impact the recognition accuracy of various categories.
To address issues related to dataset imbalance and data quality, future research will explore methods such as label distribution learning and correction, as suggested in [10,17], to mitigate these problems.
From Figure 6a, it can be observed that the recognition accuracy for the Disgust and Fear expressions in the RAF-DB dataset is relatively low, at 74.38% and 67.57%, respectively. Further analysis reveals that Fear is often misclassified as Surprise or Angry, which may be due to the similarities in certain features among these expressions. Additionally, Disgust is frequently misclassified as Sad, indicating that the model has difficulty distinguishing between these two categories. To improve the model’s performance, we plan to implement further dual-view data augmentation for the Fear and Disgust categories in the future to increase the sample size and diversity.

4. Conclusions

Facial expression recognition (FER) technology has broad application prospects, but the high complexity of existing FER models limits their use in mobile devices with constrained computational performance and storage space. To address this issue, this paper proposes a new model called LFNSB. The model introduces Conv2d_BN modules, RepVGGDW modules, and Spatial Bias modules. These additions effectively reduce the computational complexity of the model, enhance feature extraction capabilities, and focus on the global features of facial expressions. The proposed Cosine-Harmony Loss aims to optimize class centers, improving feature clustering and model generalization. This allows the LFNSB model to achieve high recognition accuracy with fewer parameters. Experimental results on the AffectNet and RAF-DB datasets verify the effectiveness of the proposed method. The findings of this paper provide a reference for further design of lightweight FER models and promote the further application and development of FER technology.

Author Contributions

Conceptualization, Xuefeng Chen and Liangyu Huang; methodology, Xuefeng Chen and Liangyu Huang; software, Xuefeng Chen; validation, Xuefeng Chen; formal analysis, Xuefeng Chen; investigation, Xuefeng Chen; resources, Xuefeng Chen; data curation, Xuefeng Chen; writing—original draft preparation, Xuefeng Chen; writing—review and editing, Xuefeng Chen and Liangyu Huang; visualization, Xuefeng Chen; supervision, Liangyu Huang; project administration, Xuefeng Chen; funding acquisition, Liangyu Huang. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by the General Program of the Natural Science Foundation of Guangxi (No. 2023GXNSFAA026347), the Central Government Guidance Funds for Local Scientific and Technological Development, China (No. Guike ZY22096024), and the University-Industry Collaborative Education Program of Ministry of Education, China (No. 230702496270001).

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors on request.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Banerjee, R., De, S., & Dey, S. (2023). A survey on various deep learning algorithms for an efficient facial expression recognition system. International Journal of Image and Graphics, 23(03), 2240005. [CrossRef]
  2. Sajjad, M., Ullah, F. U. M., Ullah, M., Christodoulou, G., Cheikh, F. A., Hijji, M.,... & Rodrigues, J. J. (2023). A comprehensive survey on deep facial expression recognition: challenges, applications, and future guidelines. Alexandria Engineering Journal, 68, 817-840. [CrossRef]
  3. Adyapady, R. R., & Annappa, B. (2023). A comprehensive review of facial expression recognition techniques. Multimedia Systems, 29(1), 73-103. [CrossRef]
  4. Zhang S, Zhang Y, Zhang Y, et al. A dual-direction attention mixed feature network for facial expression recognition. Electronics, 2023, 12(17): 3595.
  5. Tan, M.; Le, Q.V. Mixconv: Mixed depthwise convolutional kernels. In Proceedings of the 30th British Machine Vision Conference 2019, Cardiff, UK, 9–12 September 2019. [Google Scholar]
  6. Go, J., & Ryu, J. (2024). Spatial bias for attention-free non-local neural networks. Expert Systems with Applications, 238, 122053. [CrossRef]
  7. Deep Facial Expression Recognition: A Survey.
  8. Deng, J., Guo, J., Xue, N., & Zafeiriou, S. (2019). Arcface: Additive angular margin loss for deep face recognition. In Proceedings of the IEEE/CVF conference on computer vision and pattern recognition (pp. 4690-4699).
  9. Wang, H., Wang, Y., Zhou, Z., Ji, X., Gong, D., Zhou, J., ... & Liu, W. (2018). Cosface: Large margin cosine loss for deep face recognition. In Proceedings of the IEEE conference on computer vision and pattern recognition (pp. 5265-5274).
  10. Simonyan, K.; Zisserman, A. Very Deep Convolutional Networks for Large-Scale Image Recognition. In Proceedings of the International Conference on Learning Representations (ICLR), San Diego, CA, USA, 7–9 May 2015; pp. 1–14. [Google Scholar]
  11. He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
  12. Altaher, A., Salekshahrezaee, Z., Abdollah Zadeh, A., Rafieipour, H., & Altaher, A. (2020). Using multi-inception CNN for face emotion recognition. Journal of Bioengineering Research, 3(1), 1-12.
  13. Wang A, Chen H, Lin Z, et al. Repvit: Revisiting mobile cnn from vit perspective[C]//Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. 2024: 15909-15920.
  14. Chen, S., Liu, Y., Gao, X., & Han, Z. (2018). Mobilefacenets: Efficient cnns for accurate real-time face verification on mobile devices. In Biometric Recognition: 13th Chinese Conference, CCBR 2018, Urumqi, China, August 11-12, 2018, Proceedings 13 (pp. 428-438). Springer International Publishing.
  15. Tan, M.; Le, Q.V. Mixconv: Mixed depthwise convolutional kernels. In Proceedings of the 30th British Machine Vision Conference 2019, Cardiff, UK, 9–12 September 2019. [Google Scholar]
  16. Hou, Q.; Zhou, D.; Feng, J. Coordinate Attention for Efficient Mobile Network Design. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 19–25 June 2021; pp. 13713–13722. [Google Scholar]
  17. Q. You, H. Jin, and J. Luo, Visual sentiment analysis by attending on local image regions,in Proc. AAAI Conf. Artif. Intell., 2017, pp. 231–237. [CrossRef]
  18. S. Zhao, Z. Jia, H. Chen, L. Li, G. Ding, and K. Keutzer, PDANet: Polarity-consistent deep attention network for fine-grained visual emotion regression, in Proc. 27th ACM Int. Conf. Multimedia, Oct. 2019, pp. 192–201.
  19. Farzaneh, A.H., Qi, X.: Facial expression recognition in the wild via deep attentive center loss. In: Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, pp 2402–2411 (2021).
  20. Li, Y., Lu, Y., Li, J., & Lu, G. (2019, October). Separate loss for basic and compound facial expression recognition in the wild. In Asian conference on machine learning (pp. 897-911). PMLR.
  21. Yandong Wen, Kaipeng Zhang, Zhifeng Li, and Yu Qiao. A discriminative feature learning approach for deep face recognition. In European conference on computer vision, pages 499–515. Springer, 2016. [CrossRef]
  22. Wen, Z.; Lin, W.; Wang, T.; Xu, G. Distract your attention: Multi-head cross attention network for facial expression recognition. Biomimetics 2023, 8, 199. [Google Scholar] [CrossRef] [PubMed]
  23. Weiyang Liu, Yandong Wen, Zhiding Yu, Ming Li, Bhiksha Raj, and Le Song. Sphereface: Deep hypersphere embedding for face recognition. In Proceedings of the IEEE conference on computer vision and pattern recognition, pages 212–220, 2017.
  24. Yu Liu, Hongyang Li, and Xiaogang Wang. Learning deep features via congenerous cosine loss for person recognition. arXiv preprint. arXiv:1702.06890, 2017.
  25. Abhinav Dhall, Roland Goecke, Simon Lucey, and Tom Gedeon. Collecting large, richly annotated facial expression databases from movies. IEEE multimedia, 19(03):34–41, 2012.
  26. Shan Li and Weihong Deng. Reliable crowdsourcing and deep locality-preserving learning for unconstrained facial expression recognition. IEEE Transactions on Image Processing, 28(1):356–370, 2018. [CrossRef]
  27. Guo, Y.; Zhang, L.; Hu, Y.; He, X.; Gao, J. Ms-celeb-1m: A dataset and benchmark for large-scale face recognition. In Proceedings of the European Conference on Computer Vision, Amsterdam, The Netherlands, 11–14 October 2016; pp. 87–102. [Google Scholar]
  28. Kai Wang, Xiaojiang Peng, Jianfei Yang, Debin Meng, and Yu Qiao. Region attention networks for pose and occlusion robust facial expression recognition. IEEE Transactions on Image Processing, 29:4057–4069, 2020. [CrossRef]
  29. Kai Wang, Xiaojiang Peng, Jianfei Yang, Shijian Lu, and Yu Qiao. Suppressing uncertainties for large-scale facial expression recognition. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pages 6897–6906, 2020.
  30. Farzaneh, A.H.; Qi, X. Facial expression recognition in the wild via deep attentive center loss. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, Virtual, 5–9 January 2021; pp. 2402–2411. [Google Scholar]
  31. Xue F, Wang Q, Tan Z, et al. Vision transformer with attentive pooling for robust facial expression recognition[J]. IEEE Transactions on Affective Computing, 2022, 14(4): 3244-3256.
  32. Thanh-Hung Vo, Guee-Sang Lee, Hyung-Jeong Yang, and Soo-Hyung Kim. Pyramid with super resolution for in-the-wild facial expression recognition. IEEE Access, 8:131988–132001, 2020. [CrossRef]
  33. Savchenko A V, Savchenko L V, Makarov I. Classifying emotions and engagement in online learning based on a single facial expression recognition neural network[J]. IEEE Transactions on Affective Computing, 2022, 13(4): 2132-2143.
  34. Wagner N, Mätzler F, Vossberg S R, et al. CAGE: Circumplex Affect Guided Expression Inference[C]//Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. 2024: 4683-4692.
  35. Li, H.; Sui, M.; Zhao, F.; Zha, Z.; Wu, F. Mvt: Mask vision transformer for facial expression recognition in the wild. arXiv 2021, arXiv:2106.04520. [Google Scholar]
  36. Zhao Z, Liu Q, Wang S. Learning deep global multi-scale and local attention features for facial expression recognition in the wild[J]. IEEE Transactions on Image Processing, 2021, 30: 6544-6556.
  37. Yuedong Chen, Jianfeng Wang, Shikai Chen, Zhongchao Shi, and Jianfei Cai. Facial motion prior networks for facial expression recognition. In 2019 IEEE Visual Communications and Image Processing (VCIP), pages 1–4. IEEE, 2019.
  38. Xiaojun Qi Farzaneh, Amir Hossein. Discriminant distribution-agnostic loss for facial expression recognition in the wild. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops, pages 406–407, 2020.
  39. Zhang, W.; Ji, X.; Chen, K.; Ding, Y.; Fan, C. Learning a Facial Expression Embedding Disentangled from Identity. In Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 19–25 June 2021; pp. 6755–6764. [Google Scholar]
Preprints 115488 g001
Figure 1. The architecture of LFNSB is shown in Figure 2 and consists of two main components: LFN and SB. First, facial images are input into the LFN, which processes the images and extracts basic facial feature maps. Subsequently, these feature maps are processed by the Spatial Bias module, which accentuates the global features related to facial expressions. Additionally, the LFN module utilizes a novel loss function we proposed, the Cosine-Harmony Loss, to improve the discriminative power of the feature vectors. Finally, the enhanced features are combined and passed through a fully connected layer to predict the expression categories of the images.
Figure 1. The architecture of LFNSB is shown in Figure 2 and consists of two main components: LFN and SB. First, facial images are input into the LFN, which processes the images and extracts basic facial feature maps. Subsequently, these feature maps are processed by the Spatial Bias module, which accentuates the global features related to facial expressions. Additionally, the LFN module utilizes a novel loss function we proposed, the Cosine-Harmony Loss, to improve the discriminative power of the feature vectors. Finally, the enhanced features are combined and passed through a fully connected layer to predict the expression categories of the images.
Preprints 115488 g001
Preprints 115488 g002
Figure 2. The fuse method of Conv2d_BN is used to merge the convolutional and batch normalization layers, reducing the number of parameters and potentially enhancing computational efficiency.
Figure 2. The fuse method of Conv2d_BN is used to merge the convolutional and batch normalization layers, reducing the number of parameters and potentially enhancing computational efficiency.
Preprints 115488 g002
Preprints 115488 g003
Figure 3. The RepVGGDW module optimizes computational efficiency and reduces parameter count by integrating 3x3 depthwise convolution, 1x1 convolution, and batch normalization while maintaining effective feature extraction capabilities.
Figure 3. The RepVGGDW module optimizes computational efficiency and reduces parameter count by integrating 3x3 depthwise convolution, 1x1 convolution, and batch normalization while maintaining effective feature extraction capabilities.
Preprints 115488 g003
Preprints 115488 g004
Figure 4. illustrates the Spatial Bias module, which reduces the feature map size through 1×1 convolution and pooling, followed by aggregating spatial information using 1D convolution.
Figure 4. illustrates the Spatial Bias module, which reduces the feature map size through 1×1 convolution and pooling, followed by aggregating spatial information using 1D convolution.
Preprints 115488 g004
Preprints 115488 g006aPreprints 115488 g006b
Figure 6. The confusion matrix of the LFNSB tested on different datasets. (a) RAF-DB (b) AffectNet-7; (c) AffectNet-8;
Figure 6. The confusion matrix of the LFNSB tested on different datasets. (a) RAF-DB (b) AffectNet-7; (c) AffectNet-8;
Preprints 115488 g006aPreprints 115488 g006b
Table 1. The proposed LFN architecture. For the table, n refers to the number of repetitions, c refers to output channels, t refers to the expansion factor, and s refers to the stride
Table 1. The proposed LFN architecture. For the table, n refers to the number of repetitions, c refers to output channels, t refers to the expansion factor, and s refers to the stride
Input Operator t c n s
112 × 112 ×3 Conv2d_BN - 64 1 2
56 × 56 × 64 depthwiseConv2d_BN - 64 1 1
56 × 56 × 64 bottleneck (MixConv 3 × 3, 5 × 5) 2 64 1 2
28 × 28 × 64 bottleneck (MixConv 3 × 3) 2 128 9 1
28 × 28 × 128 bottleneck (MixConv 3 × 3, 5 × 5) 4 128 1 2
14 × 14 × 128 bottleneck (MixConv 3 × 3) 2 128 16 1
14 × 14 × 128 bottleneck (MixConv 3 × 3, 5 × 5, 7 × 7) 8 256 1 2
7 × 7 × 256 bottleneck (MixConv 3 × 3, 5 × 5) 2 256 6 1
7 × 7 × 256 RepvggDW - 256 1 1
7 × 7 × 256 linear GDConv7 × 7 - 256 1 1
1 × 1 × 256 Linear - 256 1 1
Table 2. Evaluation (%) of the LFNSB and other networks on RAF-DB.
Table 2. Evaluation (%) of the LFNSB and other networks on RAF-DB.
Methods Accuracy (%) Params Flops
MobileFaceNet 87.52 1.148M 230.34M
MFN 90.32 3.973M 550.74M
LFNSB（ours） 91.07 2.676M 397.35M
Table 3. Ablation studies for the loss function in the LFN.
Table 3. Ablation studies for the loss function in the LFN.
Methods RAF-DB AffectNet-7
CrossEntropyLoss 89.57 64.26
CrossEntropyLoss+CosineHarmony Loss 90.22 65.45
Table 4. The impact of different α values in the loss function on model performance.
Table 4. The impact of different α values in the loss function on model performance.
α Accuracy Loss
0.1 90.22% 0.066
0.2 90.12% 0.083
0.3 89.96% 0.137
0.4 90.03% 0.096
0.5 89.86% 0.161
Table 5. Evaluation (%) of the LFN and the LFNSB on RAF-DB and AffectNet-7.
Table 5. Evaluation (%) of the LFN and the LFNSB on RAF-DB and AffectNet-7.
LFN LFNSB RAF-DB AffectNet-7
√ - 90.22 65.45
√ √ 91.07 66.57
Table 6. Performance comparison on the RAF-DB dataset.
Table 6. Performance comparison on the RAF-DB dataset.
Methods Accuracy (%)
Separate-Loss [20] 86.38
RAN [28] 86.90
SCN [29] 87.03
DACL [30] 87.78
APViT [31] 91.98
DDAMFN [4] 91.34
DAN [22] 89.70
LFNSB（ours） 91.07
Table 7. Performance comparison for AffectNet-8.
Table 7. Performance comparison for AffectNet-8.
Methods Accuracy (%)
PSR [32] 60.68
Multi-task EfficientNet-B0 [33] 61.32
DAN [22] 62.09
CAGE [34] 62.3
MViT [35] 61.40
MA-Net [36] 60.29
DDAMFN [4] 64.25
LFNSB（ours） 63.12
Table 8. Performance comparison for AffectNet-7.
Table 8. Performance comparison for AffectNet-7.
Methods Accuracy (%)
Separate-Loss [20] 58.89
FMPN [37] 61.25
DDA-Loss [38] 62.34
DLN [39] 63.7
CAGE [34] 67.62
DAN [22] 65.69
DDAMFN [4] 67.03
LFNSB（ours） 66.57
Table 9. The results of K-fold cross-validation.
Table 9. The results of K-fold cross-validation.
Fold Fold 1 Fold 2 Fold 3 Fold 4 Fold 5 Fold 6 Fold 7 Fold 8 Fold 9 Fold 10 Average
RAF-DB 90.48 90.22 90.61 90.35 90.48 90.12 91.07 90.65 90.32 90.16 90.34
Afectnet-7 65.71 66.57 66.11 64.69 65.65 65.45 65.61 65.25 65.12 66.03 65.72
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated