A Distributed Algorithm for Reaching Average Consensus in Unbalanced Tree Networks

Preprint

Article

A Distributed Algorithm for Reaching Average Consensus in Unbalanced Tree Networks

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

Gianfranco Parlangeli^*

This version is not peer-reviewed

Submitted:

16 August 2024

Posted:

19 August 2024

You are already at the latest version

Alerts

Abstract

In this paper, a distributed algorithm for reaching average consensus is proposed for multi-agent systems with tree communication graph, when the edge weight distribution is unbalanced. First, the problem is introduced as a key topic of core algorithms for several modern scenarios. Then, the relative solution is proposed as a finite-time algorithm, which can be included in any application as a preliminary setup routine, and it is well-suited to be integrated with other adaptive setup routines, thus making the proposed solution useful in several practical applications. A special focus is devoted to the integration of the proposed method with a recent Laplacian eigenvalue allocation algorithm, and the implementation of the overall approach in a wireless sensor network framework. Finally, a worked example is provided, showing the significance of this approach for reaching a more precise average consensus in uncertain scenarios.

Keywords:

Subject: Engineering - Control and Systems Engineering

1. Introduction

In the last decades, research on the collective behavior of a team of agents through iterative local interactions has been intense, due to the significance of applications in a wide range of fields, from computer science to social networks, from complex technological networks (e.g. electric smart grid), to biological ecosystems [1]. In each framework, a fundamental property to reach agreement among all agents through local interactions is the consensus condition, which happens when all agents recursively update a local variable using local information to asymptotically get a common value for all participants [2].

One special yet fundamental consensus condition regards the value of such agreement as a function of the initial conditions of all nodes, and, in particular, the average of all initial conditions of the agents is known in the literature as the average consensus [3,4]. This special condition is adopted in a large number of applications of distributed estimation, WSN algorithms, robotics, and many more [5].

Average consensus is the natural equilibrium condition for a multi-agent system whenever the communication graph is undirected and unweighted, or more in general, whenever it is weight-balanced, and this special condition allows solving several basic goals in a distributed fashion [1].

Unfortunately, one fundamental limitation when dealing with classical average consensus through the use of undirected communication graphs with the traditional symmetric edge weight assignment is a limited convergence rate, which significantly decreases when the number of participants grows [5]. This condition has the drawback of a large time span for convergence, and in turn, this makes consensus not even possible in practice when the unavoidable presence of communication delays, computation errors or agents’ faults over a large time span are accounted for [6].

However, the practical significance of this condition for the large number of the applications referenced above pushed the scientific community to a significant effort to derive sophisticated algorithms for general unbalanced graphs, as, for example, through the use of additional state variables [7], dedicated atomic transactions between pairs of neighbors [8], a chain of two integrators that are coupled with a distributed estimator [9] average tracking with incomplete measurement through a distributed averaging filter and a decentralized tracking controller [10], and recently considering also signed networks [11].

In the last few years, advances have been made in adopting the strategy of assigning asymmetric weights to neighbors’ edges [12]. Indeed, it was found that a proper choice of asymmetric weights can significantly improve the convergence rate, even over the symmetric optimal design [13], and it makes the convergence rate independent of the size of the graph with asymmetric weights, which is in striking contrast with the fundamental limitations of symmetric weights [1]. On the other hand, the choice of asymmetric weights makes the network converge to a different function of the nodes instead of the average of the initial conditions.

In general, there are several scenarios where edge weight asymmetry should be taken into account, other than a design choice. Indeed, empirical research clearly shows that real-world networks usually have a large heterogeneity in the intensity or capacity of the connections (and hence the weights of the links) [14]. These asymmetries are related to defects and uncertainties in the network, and they result in an inaccurate and biased consensus condition (namely, the asymptotic values of network nodes are only roughly close to each other). The technique proposed in this paper can be useful in these scenarios, as it would produce a much more precise consensus condition.

The approach proposed in this paper can be combined with an asymmetric design of the edge weights as in [15] to achieve the ambitious goal of average consensus with prescribed dynamics. Analogous techniques have been adopted to achieve prescribed-time consensus [16]. The opportunity of setting the Laplacian eigenvalues through an appropriate choice of edge weights has also a beneficial effect on security; indeed most of the algorithms designed to monitor network evolution to exclude the presence of edge faults [17] or malicious nodes [18] require the knowledge of eigenstructure of the network It is worth noting that malicious attacks can destabilize the entire system when there is access of at least one of its eigenvalues [19].

The theoretical backbone of the proposed approach is the distributed estimation of the Perron vector, which allows for a scaling of the initial conditions to reach average consensus, thus combining the beneficial effects of asymmetric edge weight assignment with the large practical applications of average consensus problems. It is worth remarking that the use of Perron vector to achieve a more precise average estimation is discussed in [20]. The results developed in this paper are inspired by [21], as described in detail in Section 3.

The paper is organized as follows. After a brief description of the notation hereafter, in Section 2 some motivating examples of the research pursued in this paper are described, and hence two facets of the problem are stated. In Section 3, the main theoretical results are provided for two graph topologies, namely path graphs and star graphs, which are prodromal for the inductive general solution, whose theoretical backbone is given in Section 4. These results are then exploited in Section 5, where the iterative algorithm is deduced through a worked example. A final simulation is provided in Section 6, where the application of the results to an uncertain WSN network, computing the average value of an environmental quantity, shows the effectiveness of the proposed results to achieve a more precise consensus value.

Notation

Here we briefly describe the notation adopted along the paper. We denote by

N

R

R_{\geq 0}

R_{+}

the set of natural, real numbers and non-negative real numbers, and positive real numbers. We denote by

0_{d}

d \in N

, the d-dimensional vectors with components equal to 0 and by

1_{d}

those vectors whose components are all 1.

0_{d_{1} \times d 2_{2}}

d_{1}, d_{2} \in N

, is the

d_{1} \times d_{2}

matrix made by all zero entries. Vector

e_{i}

denotes the i-th canonical vector, e.g.

e_{1} = {[\begin{matrix} 1 & 0 & . . . & 0 \end{matrix}]}^{⊤}

. Vectors are denoted in bold letters. For a vector

v \in R^{d}

we denote

v_{i}

the ith component of

v

so that

v = {[v_{1} . . . v_{d}]}^{⊤}

. The spectral radius of A is the maximum modulus of its eigenvalues, namely

ρ_{A} = {max}_{i \in {1, \dots n}} {| λ_{i} | where λ_{i} \in Λ_{A}} .

A nonnegative (positive) matrix

A \in R^{n \times n}

satisfies

{[A]}_{i j} \geq 0

(

{[A]}_{i j} > 0

). A permutation matrix P is a matrix obtained by permuting the rows of the

n \times n

identity matrix. A nonnegative matrix

A \in R^{n \times n}

is reducible if there exist a permutation matrix P such that the matrix

P A P^{⊤}

is in block triangular form, i.e.:

P A P^{⊤} = [\begin{matrix} B_{11} & B_{12} \\ 0 & B_{22} \end{matrix}] .

where

B_{11}

B_{22}

are square matrices. An irreducible matrix is a matrix that is not reducible. A nonnegative matrix

A \in R^{n \times n}

is primitive if there exist a positive integer m such that

A^{m} > 0

A graph

G = (V, E)

is made of a vertex set

V = {1, 2, . . ., n}

and an edge set

E \subset V \times V

. It is undirected if

(j, i) \in E

if and only if

(i, j) \in E

. The neighbors set of a node

i \in V

is defined as

N_{i} = {j \in V | (i, j) \in E}

. A path connecting vertex

j_{1}

with

j_{k + 1}

is a subset of nodes connected by graph edges

{j_{ℓ} such that (j_{ℓ}, j_{ℓ + 1}) \in E}_{|_{ℓ \in [1, k]}}

. An undirected graph

G

is connected if there is a path connecting i and j for every pair of vertices

i, j \in V

such that

i \neq j

An undirected graph

T

with no cycles is called a tree if it is connected, otherwise it is called forest. For a vertex w of a tree

T

T_{w}

denotes the forest obtained from

T

by deleting w, and it is made of

| N_{w} |

trees. For any v neighbor of w,

v \in N_{w}

T_{v}

denotes the subtree of

T_{w}

having v as a vertex. The center (or Jordan center) of a graph is the set of all vertices

u \in V

where the greatest distance

d (u, v)

to other vertices

v \in V

is minimal. Equivalently, it is the set of vertices with eccentricity equal to the graph’s radius. Every tree has a center consisting of one vertex or two adjacent vertices. The center is the middle vertex or middle two vertices in every longest path.

For a graph

G = (V, E)

, the adjacency matrix

A \in R^{n \times n}

is the matrix

{[A]}_{i j} = 1

(i, j) \in E

and

{[A]}_{i j} = 0

(i, j) \notin E

, the weighted adjacency matrix as

{[A_{w}]}_{i j} = α_{i j}

with

α_{i j} > 0

(i, j) \in E

and

{[A_{w}]}_{i j} = 0

(i, j) \notin E

. The weighted Laplacian matrix is built upon the rule

{[L_{w}]}_{i j} = - {[A_{w}]}_{i j}

i \neq j

{[L_{w}]}_{i i} = \sum_{j = 1, i \neq j}^{n} {[A_{w}]}_{i j}

. By construction,

L_{w} 1 = 0

, i.e. the Laplacian is a zero-row sum matrix. In the following, given a graph

G

L_{w} (G)

denotes the set of all

n \times n

zero row-sum

G

-structured square matrices. There are connections between the properties of nonnegative matrices and their related graphs explaining their zero-nonzero pattern, as the following result shows [1]:

Lemma 1.1.

A matrix

A \in R^{n \times n}

is irreducible if and only if its relative graph

G_{A}

encoding its zero-nonzero pattern is strongly connected.

2. Motivating Examples

In this Section, we introduce the abstract mathematical framework of our problem, namely average consensus for a multi-agent system running distributed iterative algorithm to accomplish a global task, which is usually in terms of network coordination or synchronization. After that, several applications in modern fields adopting the described framework are reported.

2.1. Multi-Agent Systems Running Consensus Algorithms

Here, we introduce the mathematical framework of multi-agent systems running consensus algorithm [1,2].

This setting is made of a set of N nodes, each holding a variable

x_{i} (t)

i \in {1, \dots, N}

updated as

{\dot{x}}_{i} (t) = u_{i} (t)

where

u_{i} (t)

is set by each node i to update its value. Some nodes of the team can communicate between themselves, and two neighbor nodes i, j are able to exchange their values. In this setting, each node i assigns as input

u_{i} (t) = \sum_{j \in N_{i}} k_{i j} (x_{j} (t) - x_{i} (t))

where

k_{i j}

are set by node i. The resulting evolution of the team can be effectively computed using the aggregate vector

x \in R^{N}

chosen as

{[x]}_{i} (t) = x_{i} (t)

and updating as

\dot{x} (t) = - L_{κ} x (t)

, which gives rise to the Laplacian flow [1]:

\begin{matrix} x (t) & = Φ (t) x (0), \\ Φ (t) & = e^{- L_{κ} t} = \sum_{i = 0}^{\infty} \frac{{(- L_{κ})}^{i} t^{i}}{i!}, \end{matrix}

(1)

for a

L_{κ}

in the set

L_{w}

. Network evolution is dictated by the spectrum of

L_{κ}

[22]. It is worth mentioning that the design of asymmetric gains was recently proposed [13,23,24] as a key feature to improve the convergence rate, and it was recently explored also in [25,26,27].

Other multi-agent processes are better described by discrete updates of a local quantity, namely

x (t + 1) = (I - γ L_{κ}) x (t)

, where

γ \in R_{+}

is called coupling factor and it should be chosen sufficiently small to keep the system stable [1], and analogously in this case one gets the following global evolution:

\begin{matrix} x (t) & = Φ (t) x (0), \\ Φ (t) & = {(I - γ L_{κ})}^{t} \end{matrix}

(2)

Both in case of of (1) and (2), matrix

Φ (t)

shows some interesting properties inherited from the properties of

L_{κ}

that

L_{κ} 1 = 0

w_{L}^{⊤} L_{κ} = 0^{⊤}

, namely [1]:

\begin{matrix} Φ 1 = 1, w_{L_{k}}^{⊤} Φ = w_{L_{k}}^{⊤}, \\ Φ (t) is positive if G is strongly connected, \end{matrix}

(3)

Moreover, even if the eigenvalues of matrix

Φ (t)

are related to those of

L_{k}

according to

λ_{Φ} = e^{{- λ_{L}}_{k} t}

for systems (1) and

λ_{Φ} = {(1 - γ {λ_{L}}_{k})}^{t}

when dealing with (2), eigenvectors of (1) and (2) do coincide.

By direct consequence of (3), system (1) and (2) are called consensus networks, namely for every choice of the initial conditions

x_{i} (0), i = 1, 2, \dots, N,

there exists

α \in R

such that:

lim_{t \to + \infty} x_{i} (t) = α, \forall i \in {1, \dots, N},

(4)

or, equivalently,

{lim}_{t \to + \infty} x (t) = α 1_{N}, \exists α \in R

. The constant

α

is called the consensus value (or collective decision) [2] for system (1), corresponding to the given initial conditions. The consensus value is a key tool in many applications, indeed it encapsulates a global information, equal to:

α = \frac{w_{L}^{⊤} x (0)}{w_{L}^{⊤} 1_{N}} .

(5)

where

w_{L}

is a left eigenvector of

Φ (t)

associated to the unitary eigenvalue and satisfying the normal condition

w_{L}^{⊤} 1 = 1

[28]. In a wide number of applications, it holds

w_{L} = \frac{1}{N} 1

and Equation (5) simplifies to the average of the initial conditions of the whole network, i.e.:

α = \sum_{i = 1}^{N} \frac{x_{i} (0)}{N}

(6)

and we refer to this condition as average consensus.

Average consensus became a very popular and significant tool in many applications as for example sensor fusion and data aggregation, distributed optimization and machine learning, collective motion, vehicle coordination, and more [1]. However, one main issue of multi-agent systems running standard consensus protocols is a low convergence rate, which is related to the algebraic connectivity of graph

G

and it is often a key limiting feature of the original consensus protocol [1].

The fundamental mathematical background for our analysis is the renowned Perron-Frobenius Theorem [1]:

Theorem 2.1

(PerronâFrobenius). Let

A \in R^{n \times n}

be an irreducible nonnegative matrix. Then:

A has a positive eigenvalue equal to $ρ (A)$ , and it is a simple eigenvalue of A.
The left and right eigenvectors relative to the eigenvalue $ρ (A)$ are positive.

It is worth remarking that, for any nonnegative matrix

A \in R^{n \times n}

ρ (A)

is an eigenvalue of A and the right and left eigenvectors of

λ = ρ (A)

can be selected non-negative. If A is additionally irreducible, then the multiplicity of

λ = ρ (A)

is one and the relative left and right eigenvector are strictly positive and uniquely determined (up to a scalar factor).

In general, the positive left and right eigenvectors relative to the eigenvalue

ρ (A)

are called left and right Perron vectors. However, considering Equation (3), vector

1

is always a right eigenvector of

Φ

so that in the following, we refer to the left eigenvector of

1 = ρ (A)

as the Perron vector of

Φ

(e.g. vector

w_{L_{κ}}

in Equation (3)).

In the following of the paper, for a given Laplacian matrix

L_{w}

related to a connected graph

G

, we denote by

w_{L}

its left eigenvector corresponding to

λ = 0

. If matrix

L_{w}

is the generator of a dynamical flow

x (t) = e^{- L_{w}} x (0)

, then

w_{L}

is the Perron vector of the positive matrix

e^{- L_{w}}

, and with a little abuse of notation we refer to

w_{L}

as the Perron vector of

L_{w}

The importance of the Perron vector in such applications is that it explains how the final distribution is [29], so it allows to detect aggregrations, clusters, or, conversely, the weight of each node influence on the asymptotic consensus value.

In the following, we provide some recent technological applications where the above framework has been exploited to design decentralized average consensus algorithms.

2.2. Some Examples of Modern Applications

The above setting is the abstract representation of several technological modern applications, where average consensus is the key methodology for distributed algorithm architectures, as described in the following.

In [5], the authors survey the scientific literature on distributed estimation and control applications using linear consensus algorithms. In the paper, there are interesting examples on how some classical estimation and control problems can be rephrased as the average value of some suitable quantities, thus allowing for being efficiently computed in a distributed fashion through average consensus algorithms.

Average consensus is the key strategy for sharing global information through local interactions. In the field of wireless sensor networks, clock synchronization is a fundamental problem and it can be efficiently solved through consensus [30]. In [31] the same synchronization problem is solved through average consensus in IoT applications. Within the above application scenarions, average consensus is adopted also for achieving the estimation of an environmental quantity [8].

In the field of Electric grid, Smart Power Grids and Renewable energies, average consensus-based algorithms are widely adopted for the following fundamental issues: (1) generators synchronization[32] (2) economic dispatch [33] (3) clock synchronization [34].

Finally, several tasks of great value in the area of robotic networks can be accomplished through the exploitment of average consensus. Among the others, it is worth mentioning the rendez-vous and, conversely, the deployment of a team of robots, which is fundamental for surveillance and, in general, for coverage purposes. Also attaining and keeping a formation can be executed through properly designed average consensus protocols, without recurring to a supervisory device [35]

2.3. Problem Statement

Inspired by the applications discussed in the previous Paragraph, we are now ready to state the Problem that we afford in the following of this paper.

Problem Statement 1. Given a weighted Laplacian matrix

L_{κ} \in L

of a tree graph

T

, compute the (left) Perron vector of the positive matrix

Φ (t)

, either in case of (1) or (2).

However, in view of the motivations discussed above and considering the applications described so far, Problem Statement 1 can be rephrased in a more application-oriented enginnering fashion, as follows.

Problem Statement 2. Given a weighted tree graph

T = (V, E)

and a multi-agent system (either (1) or (2)) running consensus algorithm so that each node asymptotically reaches the value

α

as in (4) with

α

equal to (5), compute a set of scaling factors

ζ_{i}

i = 1, \dots, N

such that the state vector

χ (t)

defined as

{(χ (t))}_{i} = \frac{{(x (t))}_{i}}{ζ_{i}}

converges to

χ (t) \overset{t \to \infty}{\to} α 1

with

α = \sum_{i = 1}^{N} \frac{x (0)}{N}

, thus solving the average consensus problem for the original problem.

The above two problems are indeed two facets of the same argument, the first being closer to a mathematical fashion while the second in an engineering style. It is worth noting that Statement 2 can be also effectively encapsulated into the Problem Statement of [15], which is related to the Laplacian eigenvalue allocation by a proper asymmetric edge weights assignment, so that the two problems can be integrated each other as follows:

Problem Statement 2-bis. Given a tree graph

T = (V, E)

, and one node ℓ triggering the distributed algorithm in [36] to allocate the Laplace spectrum and grounded Laplacian to, resp.,

λ_{i}

and

μ_{i} \in R

(satisfying

0 < μ_{1} < λ_{2} < . . . < μ_{n - 1} < λ_{n}

), compute a set of scaling factors

ζ_{i}

i = 1, \dots, N

such that the state vector

χ (t)

defined as

{(χ (t))}_{i} = \frac{{(x (t))}_{i}}{ζ_{i}}

converges to

χ (t) \overset{t \to \infty}{\to} α 1

with

α = \sum_{i = 1}^{N} \frac{x (0)}{N}

, thus solving the average consensus problem with prescribed dynamics adopting the asymmetric weight distribution.

Remark.

The connection and equivalence of the different Problem Statements stated above is clearly established by considering Equation (5) and (6). Namely, the asymptotic value of

χ (t)

χ (t) \overset{t \to \infty}{\to} α 1

with

α = \sum_{i = 1}^{N} \frac{w^{⊤} χ (0)}{w^{⊤} 1}

, so that, considering that

{(χ (0))}_{i} = \frac{{(x (0))}_{i}}{ζ_{i}}

and imposing:

\frac{w_{1}}{w^{⊤} 1} χ_{1} (0) + \frac{w_{2}}{w^{⊤} 1} χ_{2} (0) + \dots = \frac{1}{N} x_{1} (0) + \frac{1}{N} x_{2} (0) + \dots

(7)

one has that the system evolution seeks average consensus for any set of initial conditions

x_{i} (0)

if the scaling factors

ζ_{i}

are set equal to

ζ_{i} = N \frac{w_{i}}{1^{⊤} w} .

(8)

Remark.

Even if it is not explicitly stated in the above Problem Statement, a further feature of the proposed Algorithm is that it can be implemented distributedly, namely each component of the scaling vector can be computed through the use of local data.

3. Problem Solution

We start by seeking the solution of some special topologies, namely path graphs and star graphs, which constitute the topology of the most peripherical branches of any tree, as well as widely adopted graph topologies in general [1]. We further extend the solution to a generic n tree graphs.

In the case of path and star graph, we are able to provide the full characterization of the Perron vector by exploiting some recent mathematical results concerning structured matrix manipulation and inversion.

On the other hand, the general solution for tree graphs is inductive, and it can be implemented through an iterative algorithm.

3.1. Solution for Path Graphs

The Laplacian matrix of Path Graphs is a special case of tridiagonal matrix, so the theoretical background of the construction of the solution is based on [37] adapted to our special structure of matrices. The following statement is proved in [37], and it is our main mathematical tool to get the explicit solution of Path Graph.

Proposition 3.1

([37]). Consider the tridiagonal matrix:

L = [\begin{matrix} a_{1} & b_{1} & 0 & \dots \\ c_{1} & a_{2} & b_{2} \\ ⋱ & b_{n - 1} \\ \dots & 0 & c_{n - 1} & a_{n} \end{matrix}]

(9)

and assume that L is nonsigular. Build the two sequences:

\begin{matrix} θ_{i} = a_{i} θ_{i - 1} - b_{i - 1} c_{i - 1} θ_{i - 2}, for i = 2, . . ., n, \\ with initial conditions θ_{0} = 1 and θ_{1} = a_{1} \end{matrix}

(10)

and

\begin{matrix} φ_{i} = a_{i} φ_{i + 1} - b_{i} c_{i} φ_{i + 2}, for i = n - 1, . . ., 1, \\ with initial conditions φ_{n + 1} = 1 and φ_{n} = a_{n}, \end{matrix}

(11)

then the inverse of matrix L can be computed using the following formula:

{[L^{- 1}]}_{i j} = \{\begin{matrix} [l] & {(- 1)}^{i + j} b_{i} \dots b_{j - 1} θ_{i - 1} φ_{j + 1} / θ_{n}, if i < j, \\ θ_{i - 1} φ_{j + 1} / θ_{n}, if i = j, \\ {(- 1)}^{i + j} c_{j} \dots c_{i - 1} θ_{j - 1} φ_{i + 1} / θ_{n}, if i > j \end{matrix},

(12)

It is possible to exploit the above result for the computation of the Perron vector in the case of path graphs, as follows.

Proposition 3.2.

Let

α_{i, j} \in R_{+}

, and consider the Laplacian matrix:

L_{w} = [\begin{matrix} α_{(1, 2} & - α_{1, 2} & \dots \\ - α_{2, 1} & a_{2, 2} \\ ⋱ & - α_{(n - 1), n} \\ \dots & 0 & - α_{n, (n - 1)} & α_{n, (n - 1)} \end{matrix}]

(13)

with diagonal entries

a_{i, i} = α_{i, (i - 1)} + α_{i, (i + 1)}

for

i = 2, \dots, n

. The corresponding (left) Perron vector is equal to:

w_{L} = κ [\begin{matrix} 1 & \frac{α_{12}}{α_{21}} & \frac{α_{23} α_{12}}{α_{32} α_{21}} & \dots & \prod_{j = 2}^{i} \frac{α_{(j - 1), j}}{α_{j, (j - 1)}} & \dots \end{matrix}] κ \in R - {0} .

(14)

Proof.

The proof is conducted by direct inspection on the relation

w^{⊤} L_{w}

with

L_{w}

as in (13) for a nonzero

w \in R^{n}

. Consider the partition of

L_{w}

as follows:

L_{w} = [\begin{matrix} α_{12} w i d t h & L_{1 *} \\ L_{* 1} w i d t h & L_{1} \end{matrix}]

(15)

with

L_{1 *} = [\begin{matrix} - α_{12} & 0 & \dots & 0 \end{matrix}]

L_{* 1} = {[\begin{matrix} - α_{21} & 0 & \dots & 0 \end{matrix}]}^{⊤}

and

L_{1} = [\begin{matrix} α_{2, 1} + α_{23} & - α_{2, 3} & 0 & \dots \\ - α_{3, 2} & a_{3, 3} \\ 0 & ⋱ & - α_{(n - 1), n} \\ \dots & 0 & - α_{n, (n - 1)} & α_{n, (n - 1)} \end{matrix}],

(16)

so that, taking

w = [\begin{matrix} w_{1} & \tilde{w_{1}} \end{matrix}]

with

w_{1} \in R

\tilde{w_{1}} \in R^{n - 1}

, one has:

w^{⊤} L_{w} = 0 \Rightarrow \{\begin{matrix} w_{1} α_{12} + {\tilde{w_{1}}}^{⊤} L_{* 1} = 0 \\ w_{1} L_{1 *} + {\tilde{w_{1}}}^{⊤} L_{1} = 0 \end{matrix};

(17)

from the second relation it is possible to parametrize

w

as:

w^{⊤} = κ [\begin{matrix} 1 & L_{* 1} L_{1}^{- 1} \end{matrix}] with κ \in R - {0} .

(18)

Considering that

L_{1 *} = - α_{12} e_{1}^{⊤}

, it is possible to find an explicit expression for (18) by computing the first row of

L_{1}^{- 1}

through (12) to get:

L_{* 1} L_{1}^{- 1} = (- α_{12}) [\begin{matrix} - \frac{1}{α_{21}} & - \frac{α_{23}}{α_{21} α_{32}} & \dots & - \frac{α_{23} \dots α_{(n - 1), n}}{α_{21} α_{32} \dots α_{n, (n - 1)}} \end{matrix}]

(19)

so that, putting together (18) with (19), Equation (14) follows. □

3.2. Solution for Star Graphs

The explicit parametric structure of the Perron vector can be easily computed by direct inspection in the case of star graphs. Indeed,

Proposition 3.3.

Let

G

be a star graph having n rays, and suppose that the central node is selected as first node. Let

L_{w}

be its corresponding Laplacian matrix for any choice of edge weights, so that:

L_{w} = [\begin{matrix} a_{11} & - α_{12} & \dots & - α_{1 n} \\ - α_{21} & α_{21} & 0 & \dots \\ ⋮ & 0 & ⋱ \\ - α_{n 1} & 0 & \dots & α_{n 1} \end{matrix}]

(20)

where

a_{11} = \sum_{j = 2}^{n} α_{1 j} .

(21)

Then, the corresponding Perron vector is equal to:

w_{L} = κ [\begin{matrix} 1 & \frac{α_{12}}{α_{21}} & \frac{α_{13}}{α_{31}} & \dots & \frac{α_{j, (j + 1)}}{α_{(j + 1), j}} & \dots \end{matrix}] κ \in R - {0} .

(22)

Proof.

The proof is conducted by direct inspection on the relation

w^{⊤} L_{w}

, with

L_{w}

as in (20) for a nonzero

w \in R^{n}

. Consider the partition of

L_{w}

as::

L_{w} = [\begin{matrix} a_{11} w i d t h & L_{1 *} \\ L_{* 1} w i d t h & L_{1} \end{matrix}]

(23)

with

L_{1 *} = [\begin{matrix} - α_{12} & - α_{13} & \dots & - α_{1 n} \end{matrix}]

L_{* 1} = {[\begin{matrix} - α_{21} & - α_{31} & \dots & - α_{n 1} \end{matrix}]}^{⊤}

and

L_{1} = [\begin{matrix} α_{2, 1} & 0 & 0 & \dots \\ α_{3, 1} & 0 \\ 0 & ⋱ & 0 \\ \dots & 0 & 0 & α_{n, 1} \end{matrix}] = diag ({α_{j, 1}}_{| j = 2, . ., n}),

(24)

so that, taking

w = [\begin{matrix} w_{1} & \tilde{w_{1}} \end{matrix}]

with

w_{1} \in R

\tilde{w_{1}} \in R^{n - 1}

, it is possible to analogously parametrize

w

as:

w^{⊤} = κ [\begin{matrix} 1 & - L_{* 1} L_{1}^{- 1} \end{matrix}] with κ \in R - {0} .

(25)

and considering (16) and (25), one has:

L_{* 1} L_{1}^{- 1} = [\begin{matrix} - \frac{α_{12}}{α_{21}} & - \frac{α_{13}}{α_{31}} & \dots & - \frac{α_{1 n}}{α_{n 1}} \end{matrix}] .

(26)

Putting together Equation (26) with Equation (25), Equation (22) follows. □

4. A Recursive General Solution Tree Graphs

In this Section, we derive a solution for a general tree graph

T

. The structure of the solution in such case is not in a closed form as for path and star graphs, but it is based on an inductive process over

N

, so that the resulting algorithmic solution is recursive. The proposed approach is inspired by the subdivision of the computation of the Perron vector into smaller problems of [21], and it perfectly fits the eigenvalue allocation algorithm in [15], so it can be integrated into the final algorithmic solutiono, thus solving the ambitious problem of eigenvalue allocation for average consensus problems.

Proposition 4.1.

Consider a tree graph

T

L_{w}

its corresponding Laplacian, and let

ℓ = | N_{1} |

T_{j}

j = 1, \dots, ℓ

represent the subtrees of

T

after remotion of node 1, each made of

ℓ_{j} = | T_{j} |

nodes,

j = 1, \dots, ℓ

and finally

L_{w}^{j} \in R^{ℓ_{j} \times ℓ_{j}}

the submatrix of

L_{w}

being the Laplacian of

T_{j}

If we denote by

w = [\begin{matrix} w_{1} & {\tilde{w}}_{1} & \dots & {\tilde{w}}_{ℓ} \end{matrix}]

a Perron vector for

T

, where

w_{1} \in R

and each

{\tilde{w}}_{j} \in R^{ℓ_{j}}

then it holds that:

Each ${\tilde{w}}_{j}$ is a Perron vector for each $L_{w}^{j}$ .
The first component of each ${\tilde{w}}_{j}$ satisfies:

${({\tilde{w}}_{i})}_{1} = w_{1} \frac{α_{1 i}}{α_{i 1}} .$

(27)

Proof.

Let

N_{1} = {i_{1}, . ., i_{ℓ}}

, so that a convenient labeling allows to write the Laplacian matrix without loss of generality as:

L_{w} = [\begin{matrix} a_{11} & w i d t h & \begin{matrix} - α_{1 i_{1}} & 0 & \dots \end{matrix} & w i d t h & \dots & w i d t h & \begin{matrix} - α_{1 i_{ℓ}} & 0 & \dots \end{matrix} \\ \begin{matrix} - α_{i_{1} 1} \\ 0 \\ ⋮ \end{matrix} & w i d t h & {\bar{L}}_{i_{1}} & w i d t h & \dots & w i d t h & 0_{i_{1} \times i_{ℓ}} \\ ⋮ & w i d t h & ⋮ & w i d t h & w i d t h & ⋮ \\ \begin{matrix} - α_{i_{ℓ} 1} \\ 0 \\ ⋮ \end{matrix} & w i d t h & 0_{i_{ℓ} \times i_{1}} & w i d t h & \dots & w i d t h & {\bar{L}}_{i_{ℓ}} \end{matrix}]

(28)

where

{\bar{L}}_{i} = L_{T_{i}} + α_{i_{i} 1} e_{1} e_{1}^{⊤}

with

L_{T_{i}}

being the weighted Laplacian of

T_{i}

, and

a_{11} = \sum_{k = 1}^{ℓ} α_{1 i_{k}}

. Now take a vector

w

partitioned conformably to the Laplacian (28), so that

w = [\begin{matrix} w_{1} & {\tilde{w}}_{1} & \dots & {\tilde{w}}_{ℓ} \end{matrix}]

with dimension of each

{\tilde{w}}_{i}

according to those of the related subtree

T

and detailed in the above statement. By direct inspection of the relation

w^{⊤} L_{w} = 0_{n}^{⊤}

one gets:

\begin{matrix} \sum_{k = 1}^{ℓ} α_{1 i_{k}} w_{1} - \sum_{k = 1}^{ℓ} {({\tilde{w}}_{k})}_{1} = 0 \\ w_{1} [\begin{matrix} α_{1 i} & 0 & \dots & 0 \end{matrix}] + {\tilde{w}}_{1}^{⊤} {\bar{L}}_{1} = 0_{ℓ_{1}}^{⊤} \\ w_{1} [\begin{matrix} α_{2 i} & 0 & \dots & 0 \end{matrix}] + {\tilde{w}}_{2}^{⊤} {\bar{L}}_{2} = 0_{ℓ_{2}}^{⊤} \\ ⋮ \end{matrix}

(29)

and considering that

{\tilde{w}}_{1}^{⊤} {\bar{L}}_{i} = {\tilde{w}}_{1}^{⊤} (L_{T_{i}} + α_{i_{i} 1} e_{1} e_{1}^{⊤}) = {\tilde{w}}_{1}^{⊤} L_{T_{i}} + α_{i_{i} 1} {({\tilde{w}}_{i})}_{1} e_{1}^{⊤}

, Equation (29) can be rewritten as:

\begin{matrix} \sum_{k = 1}^{ℓ} α_{1 i_{k}} w_{1} - \sum_{k = 1}^{ℓ} {({\tilde{w}}_{k})}_{1} = 0, \\ [\begin{matrix} w_{1} α_{1 i} + α_{i_{i} 1} {({\tilde{w}}_{1})}_{1} & 0 & \dots & 0 \end{matrix}] + {\tilde{w}}_{1}^{⊤} L_{T_{1}} = 0_{ℓ_{1}}^{⊤}, \\ [\begin{matrix} w_{1} α_{2 i} + α_{i_{i} 2} {({\tilde{w}}_{2})}_{1} & 0 & \dots & 0 \end{matrix}] + {\tilde{w}}_{2}^{⊤} L_{T_{2}} = 0_{ℓ_{2}}^{⊤}, \\ ⋮ \end{matrix}

(30)

so that, assuming that each

{\tilde{w}}_{i}

satisfies

{\tilde{w}}_{i}^{⊤} L_{T_{i}} = 0^{⊤}

, one has:

\begin{matrix} \sum_{k = 1}^{ℓ} α_{1 i_{k}} w_{1} - \sum_{k = 1}^{ℓ} {({\tilde{w}}_{k})}_{1} = 0, \\ w_{1} α_{1 i} + α_{i_{i} 1} {({\tilde{w}}_{1})}_{1} = 0 \\ w_{2} α_{2 i} + α_{i_{i} 1} {({\tilde{w}}_{2})}_{1} = 0 \\ ⋮ \end{matrix}

(31)

and hence the statement follows. □

The previous result provides the main tools for setting an algorithm which solves Problem 1 iteratively, though some Remarks are needed to fully describe the proposed approach. In the next Section we exploit the results gained in this Section and we deduce an algorithm for the solution of Problem 1 and 2, thus achieving our main goal for this paper.

5. A Distributed Algorithm for the General Solution

The results of Section 4 are useful to establish an interative procedure for the distributed computation of the Perron vector. In the following, we solve Problem 1 for a worked example, which is taken from the Simulation Results of [36]. Then we provide the general algorithm, based on the experience gained through the example.

5.1. An Illustrative Example

Consider the weighted tree graph in Figure 1, and Node 1 be the reference node for the algorithm execution. Considering the notation adopted in this paper, which is reported in Fig. Figure 1 (b), we take a vector

w \in R^{9}

partitioned as:

w^{⊤} = [\begin{matrix} w_{1} & {\tilde{w}}_{2} & {\tilde{w}}_{4}^{⊤} & {\tilde{w}}_{7}^{⊤} \end{matrix}]

(32)

where

{\tilde{w}}_{2}^{⊤} L_{T_{2}} = 0^{⊤} {\tilde{w}}_{4}^{⊤} L_{T_{4}} = 0^{⊤} {\tilde{w}}_{7}^{⊤} L_{T_{7}} = 0^{⊤}

(33)

and the first component of each subvector must satisfy:

{({\tilde{w}}_{2})}_{1} = w_{1} \frac{α_{12}}{α_{21}} {({\tilde{w}}_{4})}_{1} = w_{1} \frac{α_{14}}{α_{41}} {({\tilde{w}}_{7})}_{1} = w_{1} \frac{α_{17}}{α_{71}}

(34)

Consider now that each subtree has the topology of either a path or a star graph, so that we can recur to the results of Section 3.1 and Section 3.2. Specifically,

T_{2}

is either a path of two nodes or equiv. a star with one ray,

T_{4}

is a path made of 3 nodes and finally

T_{7}

is a three-node two-ray star, thus:

{\tilde{w}}_{2} = [\begin{matrix} κ_{1} & κ_{1} \frac{α_{23}}{α_{32}} \end{matrix}] {\tilde{w}}_{4} = [\begin{matrix} κ_{2} & κ_{2} \frac{α_{45}}{α_{54}} & κ_{2} \frac{α_{45} α_{56}}{α_{54} α_{65}} \end{matrix}] {\tilde{w}}_{7} = [\begin{matrix} κ_{3} & κ_{3} \frac{α_{78}}{α_{87}} & κ_{3} \frac{α_{79}}{α_{97}} \end{matrix}] .

(35)

Combining (35) with (33), one has that the structure of

w

is as follows:

w^{⊤} = [\begin{matrix} w_{1} & w_{1} \frac{α_{12}}{α_{21}} & w_{1} \frac{α_{12}}{α_{23}} \frac{α_{21}}{α_{32}} & w_{1} \frac{α_{14}}{α_{41}} & w_{1} \frac{α_{14}}{α_{41}} \frac{α_{45}}{α_{54}} & w_{1} \frac{α_{14}}{α_{41}} \frac{α_{45} α_{56}}{α_{54} α_{65}} & w_{1} \frac{α_{17}}{α_{71}} & w_{1} \frac{α_{17}}{α_{71}} \frac{α_{78}}{α_{87}} & w_{1} \frac{α_{17}}{α_{71}} \frac{α_{79}}{α_{97}} \end{matrix}]

(36)

for a nonzero

w_{1} \in R

. We now seek the value of

w_{1}

to match the normal condition

w^{⊤} 1_{N} = 1

, which leads to:

1 = w_{1} [1 + \frac{α_{12}}{α_{21}} \underset{c_{T_{2}}}{\underset{︸}{(1 + \frac{α_{23}}{α_{32}})}} + \frac{α_{14}}{α_{41}} \underset{c_{T_{4}}}{\underset{︸}{(1 + \frac{α_{45}}{α_{54}} + \frac{α_{45} α_{56}}{α_{54} α_{65}})}} + \frac{α_{17}}{α_{71}} \underset{c_{T_{7}}}{\underset{︸}{(1 + \frac{α_{78}}{α_{87}} + \frac{α_{79}}{α_{97}})}}]

(37)

so that (36) together with

w_{1} = {(1 + \frac{α_{12}}{α_{21}} c_{T_{2}} + \frac{α_{14}}{α_{41}} c_{T_{4}} + \frac{α_{17}}{α_{71}} c_{T_{7}})}^{- 1}

(38)

solves Problem 1. It is worth noting here, in view of Problem 2 and a distributed implementation of the proposed approach, that coefficients

c_{T_{i}}

are analogous coefficients related to each subtree, and indeed we can write

w_{1} = c_{T}^{- 1} where c_{T} = 1 + \frac{α_{12}}{α_{21}} c_{T_{2}} + \frac{α_{14}}{α_{41}} c_{T_{4}} + \frac{α_{17}}{α_{71}} c_{T_{7}},

(39)

and each

c_{T_{i}}

can be analogously be computed referring to the subgraphs of each

T_{i}

, thus opening the path for a distributed implementation for its computation. Coefficients

{c_{T}}_{7}

are reminiscent of the normalizing terms in [21] called coupling factors, and in the following if this paper we use the same name.

5.2. Algorithm Description

Starting from the experience gained from the example, we now generalize the iterative algorithm to retrieve the value of the scaling factors that allow for reaching average consensus, as stated in Problem Statement 2.

Considering the solution computed in the example, and in particular Equation (37), (38), (39), it is straight to see that a first stage of the computation of the coupling factors should flow from the peripherical nodes to the inner ones. Indeed, each coupling factor

c_{T_{i}}

can be determined only following this order, since

c_{T_{i}} = 1

for leaf nodes while it is unknown in advance for the other nodes.

The first stage of the algorithm is as follows. Each leaf node starts the computation with

c_{ℓ} = 1

, and sends it to its (only) neighbor v. At each time instant, each node

v \in V

should run the following algorithm:

if v has received less than $| N_{v} | - 1$ coefficients $c_{w}$ from its neighbors, node v must stay idle.
if v has received $| N_{v} | - 1$ coefficients $c_{w}$ from its neighbors, node v must compute

$c_{v} = 1 + \sum_{w \in N_{v}} \frac{α_{v w}}{α_{w v}} c_{w},$

(40)

and send it to the remaining neighbor.

The above computation is active until there is at least one node executing the second line, and it is easy to see that there exists an instant when a node, that we call it c in the following, receives all the coefficients

c_{v}

from each one of its neighbors. When this condition happens, then node c triggers the second stage of the algorithm, as follows:

makes the computation as in Equation (39), namely:

$w_{c} = (1 + \sum_{v \in N_{c}} \frac{α_{c v}}{α_{v c}} {c_{T}}_{v})^{- 1}),$

(41)

thus computing the component of the Perron vector corresponding to its own location $w_{c}$ .
sends the result back to its neighbors v (but ℓ), $v \in N_{c} - {ℓ}$ .
According to (8), node c sets its own scaling factor $ζ_{c}$ equal to $ζ_{c} = N w_{c}$ .

Then, this latter procedure propagates from node c back to the leaf nodes. At this stage, when any node, say node j, receives

w_{ℓ}

from one of its neighbors ℓ, then:

computes $w_{j} = \frac{α_{ℓ j}}{α_{j ℓ}} w_{ℓ}$ , namely the component of the Perron vector corresponding to its own location according to the structure of Equation (36),
sends the result back to its neighbors v, $v \in N_{j}$ ,
According to (8), node j sets its scaling factor $ζ_{j}$ equal to $ζ_{j} = N w_{j}$ .

The above procedure prosecutes until there are more peripherical neighbor nodes, thus ending when it reaches the leaf nodes.

The above procedure allows to compute the scaling factors for average consensus in a distributed fashion. A final issue of the above procedure is the time instant when the leaf node should start running stage one. There are several possible strategies according to the specific setting, described in the foillowing. However, it is not an issue for the algorithm execution, but only for an estimation in advance of the time needed for execution.

If all the leaf nodes start synchronously at time

\bar{t}

, then the algorithm lasts until

\bar{t} + 2 R

, where R is the radius of the graph, In this case, the ending node is the center of the tree. However, if the leaves are not synchronized and each node has its own starting time, then the algorithm still have a finite execution with a correct solution, though it cannot be computed in advancethe execution time nor the location of the last node(s) running the algorithm.

Finally, there are scenarios where one leader node is present and it can trigger the algorithm. In this latter case, our reference scenario is the Laplacian allocation algorithm in [15], where weights are set in a distributed fashion, starting from the leader node to leaf nodes. However, several different frameworks are possible, also adopting a virtual leader. In this latter setting, where a leader triggers the algorithm, the total algorithm time execution is equal to

e + 2 R

, where e represents the eccentricity of the leader within the network graph.

6. Simulation Results

In this Section, we show the results of the proposed approach in the consensus network described by the graph in Figure 2, where a parameter

ε

denotes an uncertainty term and it is a variation of the edge value with respect to the nominal one equal to 1.

Our reference scenario for this simulation is the WSN Implementation of the Average Consensus Algorithm as described in [38] Figure 3 , where the architecture of a wireless sensor node is sketched, allowing the scaling of the initial measurements in the preliminary initialization step (Stage I and II).

We assume to have a set of 9 sensor nodes connected as depicted in Figure 2, each holding a measured quantity, the initial values are set equal to

x 0 = [\begin{matrix} 33 & - 12 & - 12 & 4 & - 17 & 6 & 48 & 2 & - 10] \end{matrix}]

with average value equal to

\sum_{i = 1}^{9} x_{i} (0) / 9 = 4.667

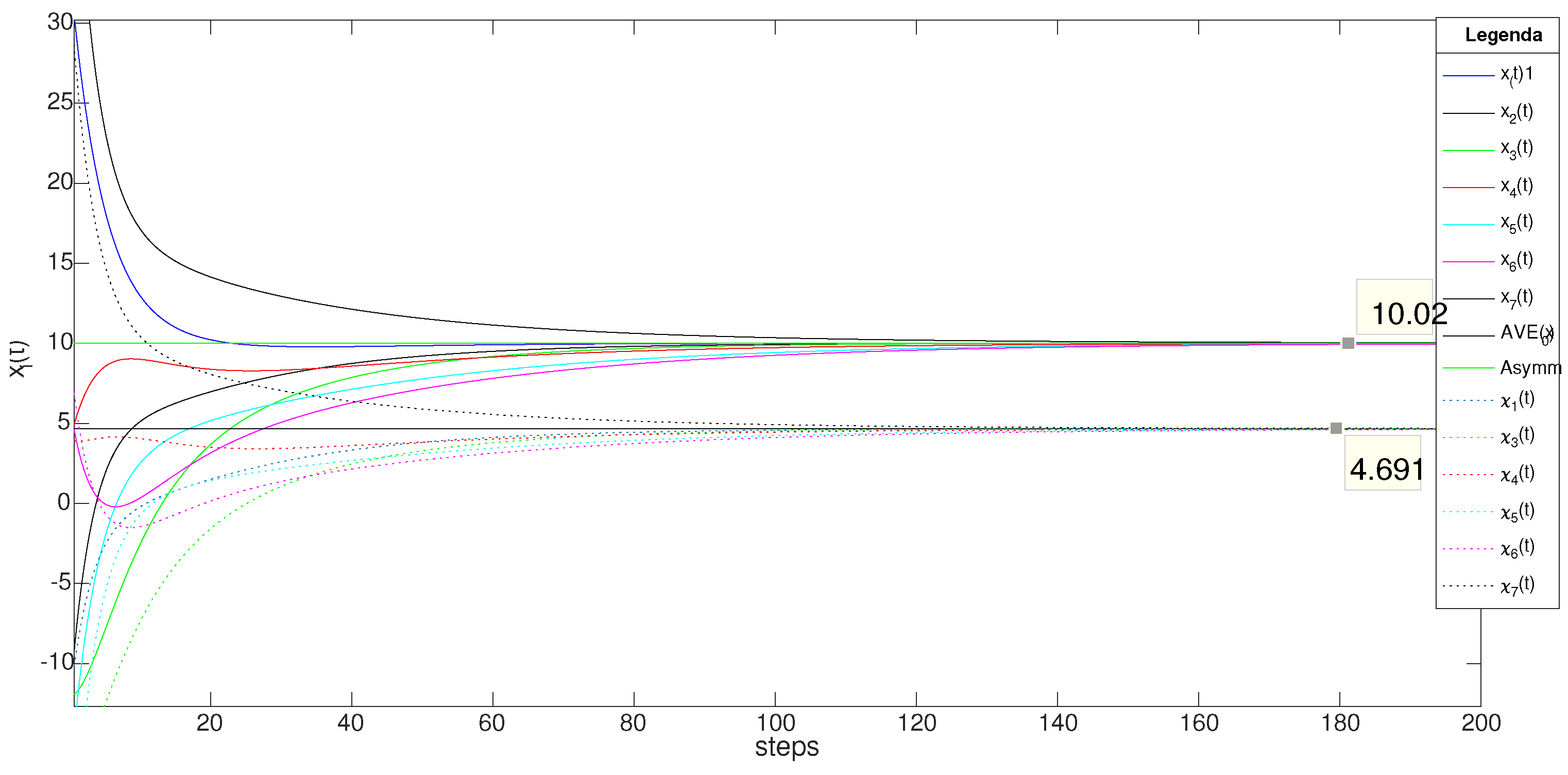
The first simulation shows the results of the evolution of the system when the uncertainty parameter

ε = 0.05

. The evolution of the system is shown in Figure 3, solid lines.

A first notable point is the magnitude of the drift of the consensus value from the initial average value. Indeed, in such a case, the consensus value turns to

5.9

, which is

26, 4 %

away from the nominal average value, even if the variation was only of magnitude

5 %

The above phenomenon is even more evident for values of

ε = 0.2

. Indeed, in such case the asymptotic value is equal to

10.02

, so that it is more than

100 %

far from the nominal one, and it is useless even as a rough estimation of the average value.

The reason for this phenomenon is related to the variation of the Perron vector. Even if each component has limited variation, the overall weighted sum results so far from the average. The Perron vector is equal to

w = {[\begin{matrix} 1.5 & 1 & 0.7 & 1 & 0.7 & 0.7 & 1.5 & 1 & 1] \end{matrix}]}^{'}

so that a suitable rescaling of the initial values according to Equation (8) provides:

χ (0) = {[\begin{matrix} 2 & - 12 & - 18 & 4 & - 25.5 & 9 & 32 & 2 & - 10] \end{matrix}]}^{'}

which restores the original consensus value to the average of

x_{(} 0)

(dashed lines).

7. Conclusions

In this paper, a distributed algorithm is derived for the computation of suitable scaling factors which allow reaching average consensus in unbalanced tree networks. The general algorithm is iterative and based on local data, and it is appropriate to be run as a preliminary routine. Simulation results show that the proposed algorithm can be effectively integrated with other set-up routines, and it gathers beneficial effects on the precision of the computed average value. Further research is oriented in different directions, e.g. the extension of the proposed approach to more general and time-varying graphs, considering more general dynamics of a single agent allowing for vehicle and mobile robot network applications, and testing the algorithm in experimental stages of WSN applications.

References

Bullo, F. Lectures on Network Systems, 1 ed.; 2022.
Olfati-Saber, R.; Fax, A.J.; Murray, R. Consensus and Cooperation in Networked Multi-Agent Systems. Proceedings of the IEEE 2007, 95, 215–233. [Google Scholar] [CrossRef]
Rezaee, H.; Abdollahi, F. Average consensus over high-order multiagent systems. IEEE Transactions on Automatic Control 2015, 60, 3047–3052. [Google Scholar] [CrossRef]
Kia, S.S.; Van Scoy, B.; Cortes, J.; Freeman, R.A.; Lynch, K.M.; Martinez, S. Tutorial on dynamic average consensus: The problem, its applications, and the algorithms. IEEE Control Systems Magazine 2019, 39, 40–72. [Google Scholar] [CrossRef]
Garin, F.; Schenato, L. A survey on distributed estimation and control applications using linear consensus algorithms. In Networked control systems; Springer, 2010; pp. 75–107.
Patterson, S.; Bamieh, B.; El Abbadi, A. Convergence rates of distributed average consensus with stochastic link failures. IEEE Transactions on Automatic Control 2010, 55, 880–892. [Google Scholar] [CrossRef]
Cai, K.; Ishii, H. Average consensus on general digraphs. In Proceedings of the 2011 50th IEEE Conference on Decision and Control and European Control Conference. IEEE; 2011; pp. 1956–1961. [Google Scholar]
Guyeux, C.; Haddad, M.; Hakem, M.; Lagacherie, M. Efficient distributed average consensus in wireless sensor networks. Computer Communications 2020, 150, 115–121. [Google Scholar] [CrossRef]
Sun, S.; Chen, F.; Ren, W. Distributed average tracking in weight-unbalanced directed networks. IEEE Transactions on Automatic Control 2020, 66, 4436–4443. [Google Scholar] [CrossRef]
Sen, A.; Sahoo, S.R.; Kothari, M. Distributed average tracking with incomplete measurement under a weight-unbalanced digraph. IEEE Transactions on Automatic Control 2022, 67, 6025–6037. [Google Scholar] [CrossRef]
Du, M.; Meng, D.; Wu, Z.G. Distributed averaging problems over directed signed networks. IEEE Transactions on Control of Network Systems 2021, 8, 1442–1453. [Google Scholar] [CrossRef]
Shafi, S.Y.; Arcak, M.; El Ghaoui, L. Graph weight allocation to meet Laplacian spectral constraints. IEEE Transactions on Automatic Control 2011, 57, 1872–1877. [Google Scholar] [CrossRef]
Hao, H.; Barooah, P. Improving convergence rate of distributed consensus through asymmetric weights. In Proceedings of the 2012 American Control Conference (ACC). IEEE; 2012; pp. 787–792. [Google Scholar]
Gao, L.; Zhao, J.; Di, Z.; Wang, D. Asymmetry between odd and even node weight in complex networks. Physica A: Statistical Mechanics and its Applications 2007, 376, 687–691. [Google Scholar] [CrossRef]
Parlangeli, G. Laplacian Eigenvalue Allocation Through Asymmetric Weights in Acyclic Leader-Follower Networks. IEEE Access 2023, 11, 126409–126419. [Google Scholar] [CrossRef]
Parlangeli, G. Prescribed-time average consensus through data-driven leader motion. IEEE Access 2024. [Google Scholar] [CrossRef]
Valcher, M.E.; Parlangeli, G. On the effects of communication failures in a multi-agent consensus network. In Proceedings of the 2019 23rd International Conference on System Theory, Control and Computing (ICSTCC). IEEE; 2019; pp. 709–720. [Google Scholar]
Parlangeli, G. A Supervisory Algorithm Against Intermittent and Temporary Faults in Consensus-Based Networks. IEEE Access 2020, 8, 98775–98786. [Google Scholar] [CrossRef]
Dibaji, S.M.; Pirani, M.; Flamholz, D.B.; Annaswamy, A.M.; Johansson, K.H.; Chakrabortty, A. A systems and control perspective of CPS security. Annual reviews in control 2019, 47, 394–411. [Google Scholar] [CrossRef]
Kenyeres, M.; Kenyeres, J. Average Consensus with Perron Matrix for Alleviating Inaccurate Sensor Readings Caused by Gaussian Noise in Wireless Sensor Networks. In Proceedings of the Software Engineering and Algorithms: Proceedings of 10th Computer Science On-line Conference 2021, Vol.; pp. 12021391–405.
Meyer, C.D. Uncoupling the Perron eigenvector problem. Linear Algebra and its applications 1989, 114, 69–94. [Google Scholar] [CrossRef]
Liu, Z.; Guo, L. Synchronization of multi-agent systems without connectivity assumptions. Automatica 2009, 45, 2744–2753. [Google Scholar] [CrossRef]
Sardellitti, S.; Giona, M.; Barbarossa, S. Fast distributed average consensus algorithms based on advection-diffusion processes. IEEE Transactions on Signal Processing 2009, 58, 826–842. [Google Scholar] [CrossRef]
Chen, Y.; Tron, R.; Terzis, A.; Vidal, R. Corrective consensus with asymmetric wireless links. In Proceedings of the 2011 50th IEEE Conference on Decision and Control and European Control Conference. IEEE; 2011; pp. 6660–6665. [Google Scholar]
Song, Z.; Taylor, D. Asymmetric Coupling Optimizes Interconnected Consensus Systems. arXiv preprint arXiv:2106.13127, arXiv:2106.13127 2021.
Parlangeli, G.; Valcher, M.E. Leader-controlled protocols to accelerate convergence in consensus networks. IEEE Transactions on Automatic Control 2018, 63, 3191–3205. [Google Scholar] [CrossRef]
Parlangeli, G.; Valcher, M.E. Accelerating consensus in high-order leader-follower networks. IEEE Control Systems Letters 2018, 2, 381–386. [Google Scholar] [CrossRef]
Mirzaev, I.; Gunawardena, J. Laplacian dynamics on general graphs. Bulletin of mathematical biology 2013, 75, 2118–2149. [Google Scholar] [CrossRef] [PubMed]
Dietzenbacher, E. Aggregation in multisector models: using the Perron vector. Economic Systems Research 1992, 4, 3–24. [Google Scholar] [CrossRef]
Schenato, L.; Fiorentin, F. Average TimeSynch: A consensus-based protocol for clock synchronization in wireless sensor networks. Automatica 2011, 47, 1878–1886. [Google Scholar] [CrossRef]
Shi, F.; Yang, S.X.; Mukherjee, M.; Jiang, H.; da Costa, D.B.; Wong, W.K. Parameter-sharing-based average-consensus time synchronization in IoT networks. IEEE Internet of Things Journal 2022, 10, 8215–8227. [Google Scholar] [CrossRef]
Wu, J.; Li, X. Collective synchronization of Kuramoto-oscillator networks. IEEE Circuits and Systems Magazine 2020, 20, 46–67. [Google Scholar] [CrossRef]
Duan, Y.; He, X.; Zhao, Y. Distributed algorithm based on consensus control strategy for dynamic economic dispatch problem. International Journal of Electrical Power & Energy Systems 2021, 129, 106833. [Google Scholar]
Macii, D.; Rinaldi, S. Time synchronization for smart grids applications: Requirements and uncertainty issues. IEEE Instrumentation & Measurement Magazine 2022, 25, 11–18. [Google Scholar]
Bullo, F.; Cortés, J.; Martínez, S. Distributed Control of Robotic Networks; Princeton University Press, 2009. Applied Mathematics Series.
Parlangeli, G. A distributed algorithm for the assignment of the Laplacian spectrum for path graphs. Mathematics 2023, 11, 2359. [Google Scholar] [CrossRef]
Usmani, R.A. Inversion of a tridiagonal Jacobi matrix. Linear Algebra and its Applications 1994, 212, 413–414. [Google Scholar] [CrossRef]
Kenyeres, J.; Kenyeres, M.; Rupp, M.; Farkas, P. WSN implementation of the average consensus algorithm. In Proceedings of the 17th European Wireless 2011-Sustainable Wireless Technologies. VDE; 2011; pp. 1–8. [Google Scholar]

Figure 1. Worked Example from [36] : (a) Unbalanced tree graph (b) Subdivision of the graph according to the notation.

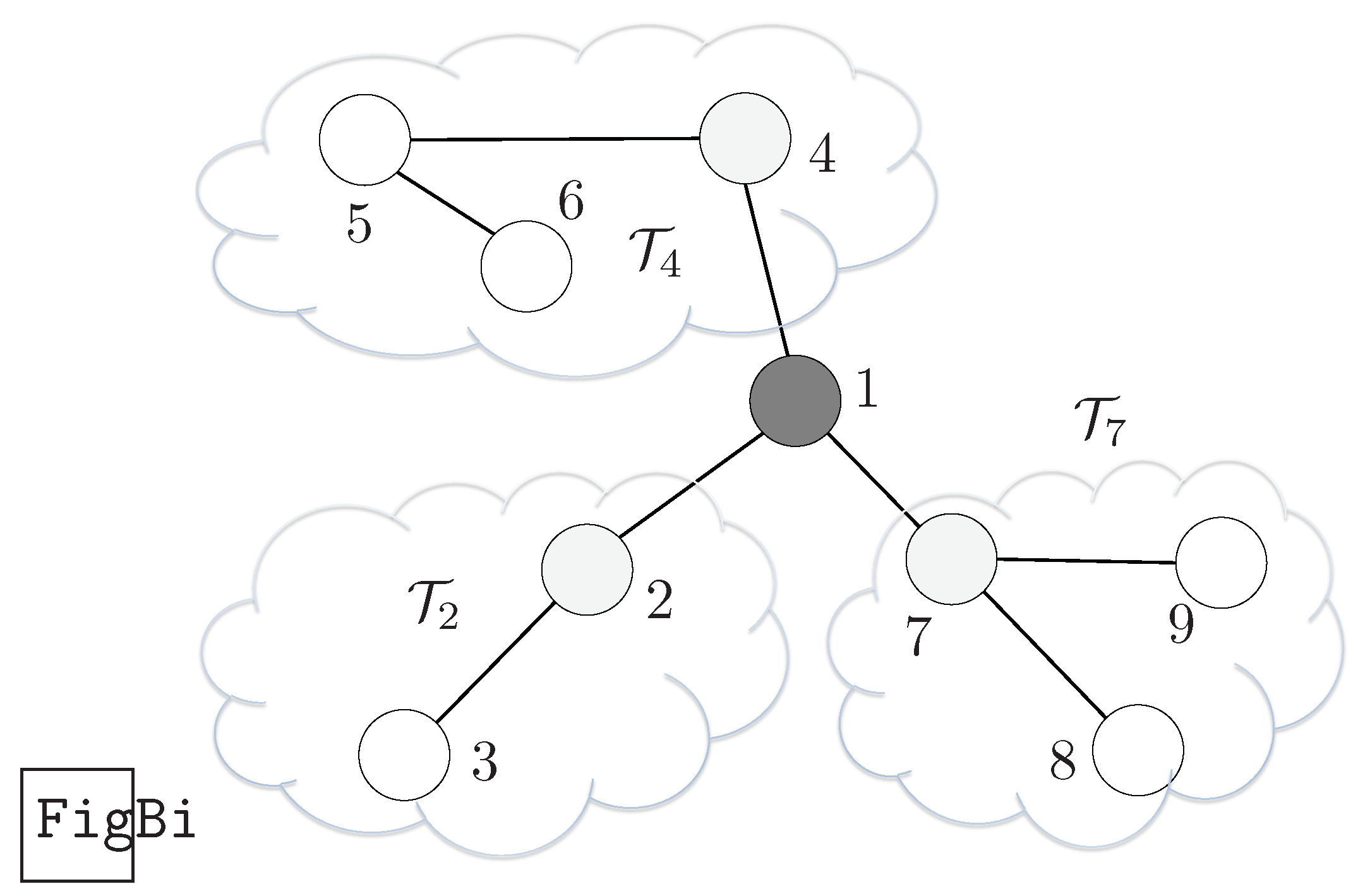
Figure 2. Simulation results: perturbed consensus network topology adopted in the simulations.

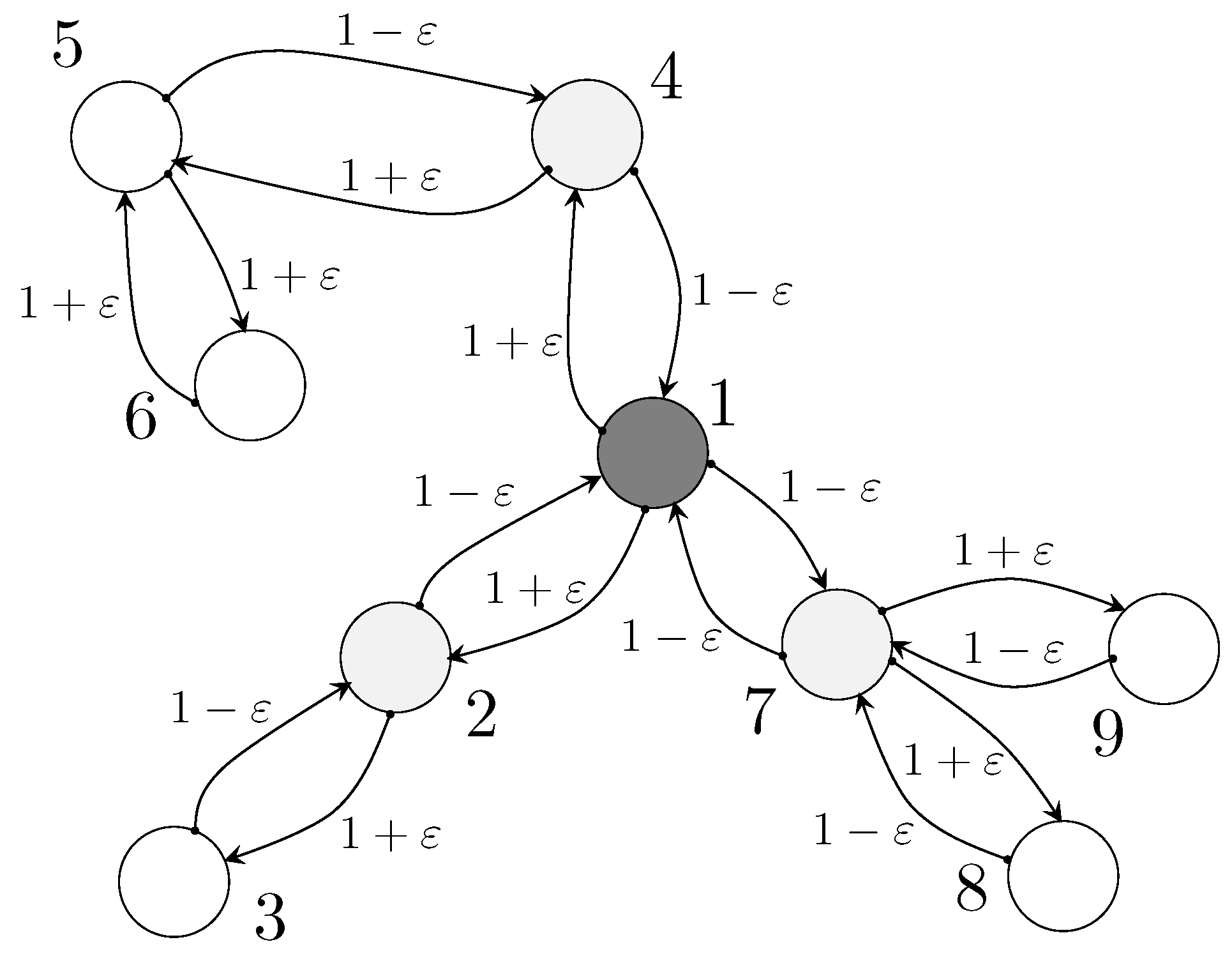
Figure 3. Simulation results: perturbed consensus network. Case

ε = 0.05

. Solid lines plots show uncompensated trajectories, dashed lines show the evolution with scaled initial conditions.

Figure 3. Simulation results: perturbed consensus network. Case

ε = 0.05

. Solid lines plots show uncompensated trajectories, dashed lines show the evolution with scaled initial conditions.

Figure 4. Simulation results: perturbed consensus network. Case

ε = 0.2

. Solid lines plots show uncompensated trajectories, dashed lines show the evolution with scaled initial conditions.

Figure 4. Simulation results: perturbed consensus network. Case

ε = 0.2

. Solid lines plots show uncompensated trajectories, dashed lines show the evolution with scaled initial conditions.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

A Distributed Algorithm for Reaching Average Consensus in Unbalanced Tree Networks

Abstract

1. Introduction

Notation

2. Motivating Examples

2.1. Multi-Agent Systems Running Consensus Algorithms

2.2. Some Examples of Modern Applications

2.3. Problem Statement

3. Problem Solution

3.1. Solution for Path Graphs

3.2. Solution for Star Graphs

4. A Recursive General Solution Tree Graphs

5. A Distributed Algorithm for the General Solution

5.1. An Illustrative Example

5.2. Algorithm Description

6. Simulation Results

7. Conclusions

References

MDPI Initiatives

Important Links

Subscribe