Preprint
Article
Evaluating Feature Impact Prior to Phylogenetic Analysis Using Machine Learning Techniques
This version is not peer-reviewed.
Submitted:
16 August 2024
Posted:
20 August 2024
You are already at the latest version
A peer-reviewed article of this preprint also exists.
Abstract
The purpose of this paper is to describe a feature selection algorithm and its application to enhance the accuracy of the reconstruction of phylogenetic trees by improving the efficiency of tree construction. Applying machine learning models for Arabic and Aramaic scripts such as Deep Neural Networks (DNN), Support Vector Machines (SVM) and Random Forests (RF) each model was used to compare the phylogenies. The methodology was utilized with a dataset containing Arabic and Aramaic scripts, demonstrating its relevance in a range of phylogenetic analyses. Results emphasize the essential role of feature selection by DNNs is outperforming other models in terms of Area Under the Curve (AUC) and Equal Error Rate (EER) across various datasets and fold sizes. Additionally, SVM and RF models show important understandings, advantages and limits of each approach within the context of phylogenetic analysis. This method not only simplifies the tree structures but also enhances their Consistency Index. Therefore offering a robust framework for evolutionary studies. The findings highlight the applications of machine learning in phylogenetics suggesting a path toward accurate and efficient evolutionary analyses and adding a deeper understanding of evolutionary relationships.
Keywords:
Subject:
Computer Science and Mathematics - Artificial Intelligence and Machine Learning1. Introduction
The study of the evolutionary history and relationships among or within groups called phylogenetics. Traditionally phylogenetic inference has relied on models like Maximum Likelihood (ML) and Bayesian inference. While effective these methods need substantial computational power specially with the increasing size of data. Lately the integrating between Machine Learning and phylogenetic analysis has shown promise in addressing these challenges thus enhancing the efficiency and accuracy of phylogenetic tree construction and tree inference.
In phylogenetic analysis features are categorized either as homology or homoplasy. Homology refers to traits received from the common ancestor on other hand homoplasy one describes traits that develop independently, often due to convergent or parallel evolution. Distinguishing between these features is essential for accurate phylogenetic reconstruction. Homologous features indicate shared lineage, whereas homoplasies can obscure these connections if not properly identified. By accurately differentiating these features, researchers can improve the precision of phylogenetic analyses and gain deeper insights into evolutionary history.
Our dataset consists of binary data (0’s and 1’s) forming an matrix, where represents taxa, and represents features. We are particularly interested in exploring n-dimensional aspects, such as finding the best phylogenetic tree using the maximum parsimony criteria.
The principal objective of our research is to improve the accuracy and efficiency of phylogenetic tree reconstruction by optimizing feature selection with the help of machine learning models, including Deep Neural Networks (DNN), Support Vector Machines (SVM), and Random Forests (RF). By identifying the most informative features prior to the phylogenetic analysis, we aim to simplify the tree structure and enhance its consistency.
To achieve our research objectives, we propose the following steps
- Perform maximum parsimony to extract the phylogenetic tree [1]
- Identify all branches and their ancestral values
- Determine the amount of change for each feature
- Develop a model to predict feature quality before phylogenetic analysis
1.1. Identify Subgroups and Their Quality
Our research focuses on creating and utilizing a feature selection algorithm to enhance phylogenetic tree reconstruction. Feature selection is inherently challenging, particularly when identifying subgroups of features with a high Consistency Index (CI), which significantly impacts the efficacy of phylogenetic analysis. Our goal is to address these challenges and demonstrate the robustness of our methodology.
In recent experiments, we highlighted the complexities involved in feature selection. While identifying the most parsimonious tree is crucial, understanding the variability and computational complexity of feature selection is equally important. To explore these challenges, we randomly selected subgroups of features and used the PAUP* program to perform a Branch and Bound search. We recorded search times, feature counts, and CI values, as shown in Figure 1.
In Figure 1.A shows the relationship between the number of elements in a subset and the subset size. As the subset size decreases, the number of possible combinations increases exponentially
On the other hand, Figure 1.B presents a scatter plot of the time taken for the Branch and Bound search relative to the number of features in each subset. The color coded Consistency Index (CI) values illustrate the variability in the data.
Finally, Figure 1.C offers a 3D plot depicting the relationship between the Consistency Index (CI), the number of features, and the processing time, highlighting the challenge of finding subgroups that balance computational feasibility with high CI values.
These figures collectively underscore the delicate balance required in feature selection for phylogenetic analysis, emphasizing the combinatorial explosion and the variability in search times and CI values as key challenges. This analysis demonstrates the importance of developing robust feature selection methods to improve the accuracy and efficiency of phylogenetic studies.
1.2. Leveraging Machine Learning for Phylogenetic Analysis of Historical Scripts
Systematics has expanded beyond biology into the field of scriptinformatics, which applies evolutionary modeling and computer science to understand the historical evolution of scripts. Scripts are treated similarly to living organisms, enabling a systematic study of their development and cultural dissemination [2,3,4,5,6,7,8,9].
Advances in computational methods, particularly in feature selection and machine learning, have significantly enhanced the accuracy of phylogenetic inference. The complexity of high dimensional data in phylogenetics necessitates advanced algorithms to select informative features thereby improving model effectiveness and deepening evolutionary understanding [3,4,5,7,8,9].
Despite these advancements, constructing phylogenetic trees especially calculating Maximum Parsimony scores remains time consuming and costly. Traditional methods often struggle with large, complex datasets creating bottlenecks in evolutionary biology research. Additionally, identifying informative features from large datasets is challenging, as it frequently requires reconstructing trees to evaluate different feature subsets, making the process increasingly impractical as data sizes grow [10].
Neural network approaches, as demonstrated in previous studies, offer a groundbreaking solution by directly predicting tree lengths from datasets, thereby avoiding exhaustive phylogenetic analysis. This method significantly reduces computational time, eliminating the need for repeated tree construction and scoring, thus streamlining phylogenetic studies [2,4].
Although neural network methods simplify feature selection and allow quick assessment of feature impacts on predicted tree lengths, their full potential for handling complex evolutionary scenarios such as feature duplication, loss, and introgression in large-scale phylogenetic analyses remains to be fully explored. These scenarios introduce significant heterogeneity into datasets, which our application aims to address [11].
In scriptinformatics, scripts are analyzed as pattern systems representing symbolic communication through their symbols, syntax, and layout rules. These systems are defined by binary features that indicate the presence (1) or absence (0) of specific traits, enabling the study of scripts’ evolutionary development. This approach highlights the importance of pattern systems, like Morse code and historical scripts, in the evolution of writing [4]. A notable example is a review paper that discusses the use of taxonomy in graph neural networks, citing 327 relevant studies to demonstrate the extensive research in this field [12].
The field of scriptinformatics leverages computational advancements to study the evolution of scripts, viewing them as pattern systems defined by symbols, syntax, and layout rules. This method allows for the examination of the properties and evolutionary paths of scripts, providing a framework to understand the dynamic relationship between writing systems and the societies that develop them [3,4,5,7,8,9].
Given these developments, our research focuses on the evolutionary analysis of historical scripts using optimized feature selection techniques to reconstruct phylogenetic trees of various script variants. We study Arabic, Aramaic, and Middle Iranian scripts to uncover their evolutionary relationships and contribute to the broader field of scriptinformatics. The dataset used in this study is publicly accessible, promoting transparency and encouraging further research in this growing field [3,4,5,7,8,9].
Beyond its contributions to scriptinformatics, our research offers practical applications in archaeology. This method has the long-term potential to gradually unravel script evolution, bringing us closer to deciphering previously undeciphered inscriptions found by archaeologists.
This research explores the evolution of Arabic, Aramaic, and Middle Iranian scripts by analyzing them as distinct pattern systems to reconstruct their phylogenetic trees. We utilize publicly accessible datasets from GitHub [13]. By uncovering deep evolutionary connections, this study significantly advances the field of scriptinformatics, offering new insights into the historical development of these scripts.
This article is structured as follows: the Background section introduces the use of artificial neural networks in phylogenetic reconstruction; the Methods section describes our approach; the Experimental Results section presents our findings; the Discussion section interprets the results and their implications; and the Conclusions section summarizes the outcomes and suggests future research directions.
2. Background
Phylogenetics, essential to molecular biology and evolutionary studies, uses phylogenetic trees to represent evolutionary relationships, emphasizing the need for accurate visualization of ancestries and diversification. Traditional methods, such as multiple sequence alignment (MSA) and tree construction algorithms, often struggle with large datasets and biases arising from evolutionary differences. These challenges underscore the need for innovative approaches to effectively manage the complexity and scale of genomic data [14,15].
Reconstructing phylogenetic trees and analyzing evolutionary relationships have long been fundamental tasks in evolutionary biology. Traditionally, methods like Maximum Parsimony and Maximum Likelihood (ML) have been widely used [1] However, recent advancements in machine learning (ML) have opened new avenues for enhancing the accuracy and efficiency of phylogenetic analyses [11,15]. This literature review examines the evolution of these methodologies, focusing on the integration of ML techniques and their potential benefits.
2.1. Established Phylogenetic Methods
The application of machine learning in phylogenetics has gained significant traction in recent years, with several innovative approaches being explored.
Maximum Parsimony [1] aims to find the tree topology that requires the fewest evolutionary changes. While this method is straightforward and often effective, it can suffer from issues such as long branch attraction, which may lead to incorrect tree topology under certain conditions [16]. In contrast, Maximum Likelihood (ML) methods are statistically robust, as they evaluate the likelihood of a tree based on a specific model of sequence evolution. However, ML methods are computationally intensive and may not be feasible for large datasets [17].
Heuristic Tree Searches traditional methods for phylogenetic tree reconstruction use heuristic searches to manage the computational complexity of evaluating many possible trees. Machine learning has been employed to enhance these heuristic strategies. For instance, Azouri et al. (2021) developed a machine learning algorithm that predicts neighbouring trees that increase likelihood without computing their likelihood, thereby reducing the search space and computational burden [18].
Cherry Picking and Network Construction: A machine learning model introduced by Bernardini et al. [19] assists in constructing phylogenetic networks using cherry-picking heuristics, ensuring that all input trees are included in the resulting network. This method is particularly useful for large datasets, demonstrating the practical application of machine learning in managing complex evolutionary scenarios.
Neural Networks for Phylogenetic Inference: Zou et al. [20] proposed using deep residual neural networks to infer phylogenetic trees. This method avoids the need for explicit evolutionary models, enabling the neural networks to effectively handle complex substitution heterogeneities. Their results demonstrated improved performance over traditional methods, especially in scenarios involving extensive evolutionary variation.
DendroNet Approach: Layne et al. [21] employed supervised learning to create models that incorporate phylogenetic relationships among training data, thereby enhancing the robustness and generalization of the models in evolutionary studies.
PhyloGAN: Smith and Hahn [22] applied Generative Adversarial Networks (GANs) to phylogenetics by developing PhyloGAN, which infers phylogenetic trees by generating and distinguishing between real and synthetic data. This method shows promise for handling the large model spaces inherent in phylogenetic inference.
ModelTeller: This machine learning-based approach, introduced by Abadi et al. [23], selects the most accurate nucleotide substitution model for phylogenetic reconstruction. It optimizes branch-length estimation, providing more precise tree constructions compared to traditional statistical methods.
Reinforcement Learning: Lipták and Kiss [24] investigated the use of reinforcement learning for constructing unrooted phylogenetic trees, demonstrating the potential of this approach to improve the efficiency and accuracy of tree construction tasks
2.2. Machine Learning in Phylogenetics
The advent of neural network applications has offered promising solutions to the challenges in phylogenetics, with machine learning (ML), particularly deep learning, transforming tree topology inference, branch length estimation, and model selection [11,15]. Despite their potential, applying supervised ML in phylogenetics presents challenges, such as generating realistic training data and adapting to high-dimensional, heterogeneous biological data [11].
Kalyaanamoorthy et al. introduced ModelFinder, a tool that enhances the accuracy of phylogenetic estimates by incorporating a model of rate heterogeneity across sites. This model selection approach significantly improves the precision of phylogenetic trees, demonstrating the potential of machine learning in model-based phylogenetics [25].
Recent studies have explored the use of deep learning (DL) for phylogenetic inference. For example, one study [15] demonstrated the application of deep neural networks (DNN) to predict branch lengths in phylogenetic trees, showing superior performance in challenging parameter spaces. Another study introduced Fusang, a DL-based framework for phylogenetic tree inference, which achieved performance comparable to ML-based tools and offered potential for optimization through customized training datasets [26].
Support Vector Machines (SVMs) have been used to infer phylogenetic relationships by optimizing the hyperplane that separates different evolutionary states. These models are robust in handling high-dimensional data and have shown promise in various classification tasks [18].
Random Forest (RF) algorithms, which build an ensemble of decision trees, have also been applied to phylogenetic inference. Their ability to handle large datasets and provide feature importance metrics makes them valuable for identifying key evolutionary traits [19]. Additionally, combining machine learning with heuristic methods to construct phylogenetic networks has efficiently integrated multiple phylogenetic trees into a single network, showcasing the practical application of machine learning in managing complex evolutionary datasets
2.3. Challenges and Future Directions
While machine learning offers significant benefits for phylogenetic analyses, several challenges persist. Common issues include overfitting, model interpretability, and the substantial need for large training datasets. A recent study [11] discussed these barriers and suggested that careful network designs and data encodings could help machine learning achieve its full potential in phylogenetics.
Tang et al. [27] introduced a neural network model that outperforms traditional methods under long-branch attraction (LBA) conditions. By accounting for tree isomorphisms, this model reduces memory usage and can seamlessly extend to larger trees, addressing a critical issue in phylogenetic inference.
The addition of machine learning techniques in phylogenetics represents a significant progression in the field. These approaches enhance model selection (Tree) improve inference accuracy (Tree construction) and offer scalable solutions for large datasets delivering powerful tools for evolutionary biologists.
3. Methods
This research seeks to enhance the precision and efficiency of phylogenetic tree reconstruction by contrasting diverse machine learning models. Specifically, we evaluate how well these approaches predict the impact of each feature in a phylogenetic tree before analysis. Accurate predictions can streamline tree construction, reduce computational demands, and improve the reliability of phylogenetic trees.
We use three machine learning algorithms: Deep Neural Networks (DNN), Support Vector Machines (SVM), and Random Forest (RF). We also test three data preprocessing methods to find the most effective combination of model and technique for this task.
Phylogenetic tree construction depends on the number of taxa involved. The number of rooted, bifurcating trees can be calculated using the formula in [28] can be seen in (1).
3.1. Data Representation
As shown in Figure 2 we tread different approaches to test the effect of data preprocessing of the model overall. In the first case, we enter the binary data it self with out any modification to classifier as in DS1. The binary features assign to this (): Each feature is represented as either 0 (absence) or 1 (presence) for each taxon. Labels assigned (): The amount of change each feature contributes to the phylogenetic tree.
3.1.1. DS1 Direct Use of Binary Dataset
The original binary dataset is directly fed into the classifiers. Advantage: Simple and straightforward approach. Disadvantage: The input size varies with the number of taxa, which can be problematic for classifier models when training on datasets of different sizes. The dataset, comprising binary genetic sequences from a diverse array of taxa, is sourced from a publicly available GitHub repository [13].
3.1.2. DS2 Feature Extraction from DS1
In our study, we extract features from binary datasets DS1 to analyzed. The DS1 is composed of binary sequences of features, where each sequence corresponds to a taxon, and each position in the sequence represents a specific phylogenetic feature. The following notations are used in the feature extraction process and each formula is shown on Table 1.
Statistical features are essential for understanding the overall distribution and tendencies within a dataset. These features include total counts, densities, and measures of central tendency and dispersion for both ’1’s and ’0’s within each feature in As shown in equations these statistical calculations are fundamental in preparing the dataset for subsequent machine learning tasks.
Positional features capture the specific locations of certain values within a, which can be critical for identifying patterns and anomalies. These features include the positions of the first occurrences of ’1’s and ’0’s as in Equation (2) and for last occurrences of ’1’s and ’0’s as in Equation (3).
These positional metrics help in understanding the spatial distribution of features across the , which can be especially useful in sequence analysis. As illustrated, these features provide valuable context that complements the statistical measures.
Entropy-based features quantify the randomness or unpredictability within a dataset, providing a measure of its complexity. Shannon entropy () is calculated for each features in , where higher entropy values indicate greater unpredictability. This measure considers the probabilities of observing ’1’s and ’0’s.
Entropy is particularly useful for identifying homogeneity or variability within the data, making it a key feature for classification tasks. As illustrated in Equation(4), entropy captures the inherent uncertainty in the dataset, thus informing model development and evaluation.
3.1.3. DS3 Normalization DS2
Normalize the extracted features (DS2) using Min-Max Normalization to scale the values between -1 and 1. Each feature is normalized using the Formula (5). Where and are the minimum and maximum values of the feature across all taxa.
If the minimum and maximum are equal, the normalized feature value is set to zero. Advantage of DS3 ensures that all features contribute equally to the analysis, preventing any feature from dominating due to scale differences.
3.2. Cross-Validation and Data Transformation
To validate model robustness, cross-validation is performed. The dataset is split into training and testing sets for each separated test in DS1, DS2 and DS3. Training Features Dataset used to train the machine learning models. Testing Features Dataset used to evaluate the performance of the trained models. We applied k-fold cross-validation for model assessment. This approach not only allowed for a comprehensive assessment of the models predictive capability but also ensured that each data subset was utilized for both training and validation. In this research we set k=2,3 and 4 to see the effect of different size of training and testing on each model.
We focus on the features that cause the least amount of change in the phylogenetic tree. Specifically, we select only the features in bin 1 as in Figure 3, which cause only one change where δ is the threshold as in Equation (6).
3.3. Classification Phase
Three classifiers are employed to analyze the impact of features on the phylogenetic tree the Deep Neural Networks (DNN), Support Vector Machines (SVM) and Random Forest (RF). The hyperparameters setup are demonstrated in the below Table 3.
3.3.1. Deep Neural Networks (DNN)
The model is trained on the training dataset, optimizing the weights to minimize the loss function. We carefully explored various neural network topologies and parameter settings to optimize model performance and prevent overfitting, a critical concern in machine learning applications. Specifically, our methodology included iterative adjustments to the network architecture and thorough tuning of the learning rate and performance (MSE) parameters and different activation function as in Table 3.
After obtaining the raw output probabilities from the DNN, a thresholding mechanism is applied to convert these probabilities into binary classifications. This adjustment is done as in Equation (7) where is the output of DNN model.
This adjustment ensures that the classifier output is in binary form, making it easier to evaluate the classification accuracy.
3.3.2. Support Vector Machine (SVM)
3.3.3. Random Forest (RF)
An ensemble of decision trees is trained on various subsets of the training dataset. The performance of the Random Forest model is evaluated on the testing dataset also.
3.4. Experimental Setup
Our experimental analyses were performed by PAUP* version 4.0a (build 168) for Unix/Linux. The server featured an Intel® Xeon® CPU E5-2640 v2 @ 2.00GHz with a dual-socket configuration hosting 24 CPU cores. This setup, optimized for Intel® 64 architecture and compiled with GNU C compiler (gcc) version 4.4.7, supports SSE vectorization and SSSE3 instructions, along with multithreading capabilities via Pthreads. Parallel to the PAUP* runs, our method, referred to as ANN4P, was deployed. This approach, coded in MATLAB R2023b, employed the same machine’s computational prowess to conduct neural network estimations.
4. Experimental Results
The performance of the proposed models DS1 (), DS2 () and DS3 (). The evaluation is presented in terms of Acc means Accuracy, FAR, FRR, AUC and EER
In this study, we analyzed the impact of feature selection on the phylogenetic tree reconstruction using Maximum Parsimony criteria. Our findings are summarized through a series of figures and a table that highlight the distribution of feature changes, the resulting phylogenetic trees, and the consistency index (CI) across different thresholds of feature selection.
The histogram of Figure 3 illustrates of features based on the number of changes they induce. The histogram shows that the majority of features cause only one change, with a decreasing number of features causing higher amounts of changes. This distribution is crucial as it underscores the direct relation for reducing the complexity of the phylogenetic tree by focusing on the most impactful features.
The data in Table 4 highlights the trade-off between the number of features and the phylogenetic tree’s consistency and length. Selecting features that cause fewer changes not only simplifies the tree but also enhances its consistency, as indicated by higher Consistency Index (CI) values.
By focusing on features that cause minimal changes, we produced a phylogenetic tree that is both shorter and more consistent. Specifically, selecting only those features that induce one change results in a cladogram with a tree length equal to the number of features which equal to 32 and a perfect CI of 1.0. This approach significantly improves the efficiency and accuracy of phylogenetic analysis, as evidenced by the simplified tree structure and higher CI values.
In Figure 4 two phylogenetic trees are obtained using a Maximum Parsimony search. Figure 4.A includes all 97 features, resulting in a tree length of 229 and a Consistency Index (CI) of 0.424. In contrast, Figure 4.B features a subset of features that cause only one change, significantly simplifying the tree structure. This tree has a length equal to the number of features is 32 and achieves a perfect CI of 1.0. This comparison clearly demonstrates that selecting features causing minimal changes leads to a more parsimonious and consistent phylogenetic tree.
Moreover, shows the number of features selected at different δ (threshold) values, along with their corresponding tree lengths and CI values. As δ decreases in (6) fewer features are selected, resulting in shorter tree lengths and higher CI values, which suggest better consistency in the phylogenetic trees.
The table also includes the Optimal tree and Time Sec columns. The Optimal tree column indicates the number of optimal trees found after performing a Branch and Bound search, all having similar maximum parsimony scores. Generally, fewer optimal trees are found as δ decreases, reflecting more stable feature selection. The Time Sec column shows that computation time drops significantly with lower δ values, from 369.3 seconds at δ = 6 to nearly 0 seconds at , highlighting the efficiency gained through feature reduction.
Given that Deep Neural Networks (DNN), Support Vector Machines (SVM), and Random Forests (RF) are nondeterministic algorithms, we performed each test 50 times to ensure the stability and reliability of our results. By averaging the outcomes over these multiple runs, we mitigated the effects of random variation and provided a robust assessment of each model’s performance. This approach ensures that the results presented in the subsequent figures accurately reflect the true performance characteristics of the models across different datasets and folds.
In order to show the effect of different models and sizes for training and testing we use the ROC curve and EER for different k-fold sizes as demonstrated on Figure 5 to show the tests of k=4 folds, Figure 6 for k=3 and in case of k=2 is shown in Figure 7.
In case of k-4 folds=4, Figure 5 illustrates the ROC curves for the three different machine learning models Deep Neural Network (DNN), Support Vector Machine (SVM), and Random Forest (RF) across four folds (k=4) for each of the three datasets (DS1, DS2, and DS3). Each row in the figure corresponds to a different fold (Fold 1 to Fold 4), and each column corresponds to a different dataset. The ROC curves for each model are plotted, with the Area Under the Curve (AUC) values annotated for comparative performance analysis. Additionally, the Equal Error Rate (EER) locations are marked on each curve.
In Figure 5 the SVM model demonstrated superior performance for in Fold 1 with an AUC of 0.98, while all models showed similar performance for with DNN slightly outperforming others for . In Fold 2, SVM again outperformed the others for and with DNN leading for . In Fold 3, DNN achieved the highest AUC for performed similarly well for , and both DNN and SVM showed equal AUC for . Finally, in Fold 4 SVM maintained the highest AUC for while DNN outperformed for and . These results highlight the robustness and variable effectiveness of each model across different datasets and folds, underscoring the importance of selecting a model suited to the specific dataset.
Additionally, Figure 6 presents the ROC curves for the DNN, SVM, and RF models across three folds (k=3) for each of the three datasets (, , and ). All row relates to a different fold and each column to a different dataset. The ROC curves are plotted with AUC values marked for comparison and EER locations are marked on each curve for reference.
Fold 1 Figure 6 the DNN outperformed other models for with on other hand SVM had the highest AUC for equal to 0.95 and RF led for with . In Fold 2, SVM and RF performed similarly well for , both achieving an AUC of 0.85. DNN topped for with an while RF maintained the lead for with . In Fold 3, DNN proven the best performance comes using with SVM intended for with and RF persisted to perform effectively for with .
Moreover, Figure 7 describes the ROC for DNN, SVM, and RF models across two folds to each of the three datasets we have , , and . Each row relates to a different fold and each column to different dataset. The ROC curves are plotted alongside AUC values and EER locations are marked on each curve.
Figure 7 particularly Fold 1 the DNN shown the highest performance for with whereas SVM displayed better performance in with . For RF held the greatest AUC value . In Fold 2 DNN to with and SVM showed a high performance for with . RF continued to perform best for with . These results indicate the varying strengths of each model across different datasets and folds highlighting the importance of selecting the most suitable model based on dataset characteristics to achieve ideal performance.
Table 5 presents the average accuracy (Acc), FRR and FAR for the DNN, SVM and RF models across different folds to datasets , , and . This thorough comparison shows the values of each metric demonstrating the efficiency of each model.
Given the non-deterministic characteristics of DNN, SVM, and RF algorithms, there is a possibility of generating slightly different results for each execution using the same data and parameters in our case , , and . To counteract this variability, we carried out 50 iterations of every test and determined. The average results AUC and EER across different fold sizes for the datasets Table 6 presents these.
The outcomes in Table 6 show that DNN delivers strong performance across different datasets and fold sizes, with AUC values spanning from to and EER values between and . Notably DNN reached the highest AUC of for both and at , highlighting it exceptional predictive ability.
SVM also shown robust performance for and with AUC and at . However, its performance on was somewhat decreased with AUC between , and and EER values from to .
RF displayed more variable performance with AUC ranging from to across datasets. Although RF variability it kept relatively low EER values particularly in where it achieved an AUC of 0.91 and an EER of 0.17 at k=4.
In summary tho all models shown effective performance DNN appeared as overall due to its high AUC values and low EER around all datasets and folds. SVM also performed well, particularly for and , while RF proved reliable though slightly more variable, performance.
Lastly, Figure 8 illustrates the number of epochs required for the DNN training across different folds and datasets (, , ) for k=2, k=3, and k=4. Each bar represents the number of epochs needed to achieve the final model performance for each fold within the respective k-fold cross-validation setup.
The results indicate that the number of epochs varies significantly across different datasets and folds. For k=2, required the highest number of epochs in both folds, indicating that this dataset posed more complexity for the DNN model to learn effectively. In contrast, required fewer epochs, suggesting it was easier for the model to converge.
When k=3, the variability in the number of epochs increased, particularly for , which again required the most training epochs across all folds, highlighting its complexity. also showed a substantial increase in epochs needed for Fold 2, suggesting variability in the training process.
For k=4, continued to demand a high number of epochs, with Fold 1 showing the maximum epochs among all the datasets and folds. , however, showed more consistency across folds, indicating a more stable training process for this dataset under the k=4 setup.
The analysis shows that consistently required more training epochs across all k values, reflecting its higher complexity and the model’s need for more iterations to learn effectively. generally required fewer epochs, suggesting it was less complex and easier for the DNN to train. This variability in training epochs across datasets and folds underscores the importance of considering dataset complexity and ensuring adequate training to achieve optimal model performance.
5. Discussion
This research examined the influence of feature selection on the reconstruction of phylogenetic trees through machine learning algorithms. The results highlight the essential importance of proficient feature selection in improving both the accuracy and reliability of phylogenetic studies. We applied DNN, SVM and RF to the binary dataset and preprocessed datasets (, and ) assessing and comparing their performance across different fold sizes.
An important observation pertains to the utilization of binary dataset which offers simplicity to easier implementation and faster processing times. However, its general limitation is the different number of input size to machine learning algorithms which restricts its application on different datasets that hold different sizes.
In contrast, using preprocessed features or normalized one leads to additional complexity due to preprocessing steps. However, these offer the flexibility of maintaining a fixed input size letting machine learning models to be applied across datasets of varying sizes. This adaptability is crucial for generalizing models to a broader range of phylogenetic analyses and ensuring robust performance across different scenarios.
Our results indicate that DNN consistently performed well across all datasets and folds, achieving the highest AUC values and maintaining low EER values, particularly for and . This suggests that DNN effectively captures complex patterns within the data, making it a reliable choice.
SVM also demonstrated strong performance, particularly for and , where it achieved high AUC values. However, its slightly lower performance on . This aligns with the known strengths of SVMs, which perform well with well-defined boundaries but may struggle with more complex or noisy data.
RF exhibited more variable performance, with AUC values ranging from 0.82 to 0.91 across the datasets. Although this variability RF maintained relatively low EER values, particularly for . RF’s ability to handle large datasets makes it valuable for identifying key evolutionary traits, even though overall performance was less compared to DNN and SVM.
Our study also highlights the importance of considering dataset complexity consistently required more training epochs in case of DNN across all k values showing its higher complexity and the need for more iterations to achieve effective learning. This highlights the necessity of adequate training to optimize model performance.
Finally, using cross-validation provided a comprehensive assessment of each model’s predictive capability. Because DNN, SVM, and RF are nondeterministic algorithms, each run with the same data and settings can yield slightly different results. To account for this variability we ran each test 50 times and averaged the outcomes. This approach Reduced the effects of random variation and ensured the stability and reliability of our results, providing a more accurate evaluation of each model’s performance.
6. Conclusions
This research introduces a feature selection method aimed at improving phylogenetic reconstructions using machine learning methods such as DNN, SVM and RF. Our results show that DNN consistently outperformed other models in AUC and EER demonstrating strong performance across various preprocessed datasets and folds. SVM and RF also achieved well nonetheless with some range.
These machine learning techniques significantly enhances the accuracy and efficiency of phylogenetic analyses offering powerful tools for evolutionary studies. This approach not only simplifies tree structure but also improves CI. This enabling deeper insights into evolutionary relationships.
Future research should focus on integrating these models to further improve the robustness of phylogenetic inference. Additionally, exploring the application of these techniques to more complex evolutionary scenarios, such as feature duplication, loss, and introgression, could provide even greater insights into evolutionary processes.
Author Contributions
Conceptualization, Osama Salman and Gábor Hosszú; Data curation, Osama Salman and Gábor Hosszú; Formal analysis, Osama Salman; Funding acquisition, Osama Salman and Gábor Hosszú; Investigation, Osama Salman and Gábor Hosszú; Methodology, Osama Salman; Project administration, Osama Salman and Gábor Hosszú; Resources, Osama Salman and Gábor Hosszú; Software, Osama Salman; Supervision, Osama Salman and Gábor Hosszú; Validation, Osama Salman; Visualization, Osama Salman; Writing – original draft, Osama Salman and Gábor Hosszú; Writing – review & editing, Osama Salman and Gábor Hosszú. All authors have read and agreed to the published version of the manuscript.
Data Availability Statement
The applied datasets can be found on GitHub [13].
Acknowledgments
The authors extend their sincere appreciation to their colleague Péter Pálovics from the Department of Electron Devices, Budapest University of Technology and Economics, for his invaluable assistance in configuring the server that played a critical role in our research. Additionally, we wish to express our gratitude to the Stipendium Hungaricum scholarship programme for its vital support. The scholarship programme has been instrumental in facilitating our research endeavors, contributing substantially to our academic development and the successful realization of our project.
Conflicts of Interest
The authors declare that they have no competing interests.
References
- Semple, C., and Steel, M., "Phylogenetics," Oxford University Press on Demand, 2003.
- Salman, O.A., and Hosszú, G., "Cladistic Analysis of the Evolution of Some Aramaic and Arabic Script Varieties," Int. J. Appl. Evol. Comput. (IJAEC), vol. 12, no. 4, pp. 18-38, 2021. [CrossRef]
- Salman, O.A., and Hosszú, G., "Enhanced Phylogenetic Inference through Optimized Feature Selection and Computational Efficiency Analysis," Acta Polytechnica Hungarica, under review, 2024.
- Salman, O.A., Hosszú, G., and Kovács, F., "A new feature selection algorithm for evolutionary analysis of Aramaic and Arabic script variants," Int. J. Intell. Eng. Informatics, vol. 10, no. 4, pp. 313-331, 2022. [CrossRef]
- Salman, O.A., and Hosszú, G., "Optimised feature dimension reduction method and its impact on the search for optimal trees," in Book Optimised Feature Dimension Reduction Method and its Impact on the Search for Optimal Trees, BME Dept. Control Eng. Inform. Technol., 2023.
- Salman, O.A., and Hosszú, G., "A Phenetic Approach to Selected Variants of Arabic and Aramaic Scripts," Int. J. Data Anal., vol. 3, no. 1, pp. 1-23, 2022. [CrossRef]
- Salman, O.A., and Hosszú, G., "Phylogenetic Inference Using Advanced Feature Selection," in Book Phylogenetic Inference Using Advanced Feature Selection, IEEE, 2023, pp. 000173-000178.
- Salman, O.A., and Hosszú, G., "Phylogenetic modelling scripts for identifying script versions," in Book Phylogenetic Modelling Scripts for Identifying Script Versions, 2023.
- Salman, O.A., and Hosszú, G., "Using distance-based methods to calculate optimal and suboptimal parsimony trees," in Book Using Distance-Based Methods to Calculate Optimal and Suboptimal Parsimony Trees, BME Dept. Control Eng. Inform. Technol., 2024.
- Wu, C.H., Chen, H.-L., and Chen, S.-C., "Gene classification artificial neural system," Int. J. Artif. Intell. Tools, vol. 4, no. 4, pp. 501-510, 1995.
- Mo, Y.K., Hahn, M., and Smith, M.L., "Applications of Machine Learning in Phylogenetics," 2023. [CrossRef]
- Zhou, Y. , Zheng, H., Huang, X., Hao, S., Li, D., and Zhao, J., "Graph neural networks: Taxonomy, advances, and trends," ACM Trans. Intell. Syst. Technol. (TIST), vol. 13, no. 1, pp. 1-54, 2022.
- Available online: https://github.com/OsamaAliSalman/Extended_Arabic-Aramaic-DataSet.git (accessed on 2 August 2024).
- Halgaswaththa, T., Atukorale, A.S., Jayawardena, M., and Weerasena, J., "Neural network based phylogenetic analysis," in Book Neural Network Based Phylogenetic Analysis, IEEE, 2012, pp. 155-160.
- Suvorov, A., and Schrider, D.R., "Reliable estimation of tree branch lengths using deep neural networks," bioRxiv, 2022, pp. 2022.2011.2007.515518. [CrossRef]
- Philippe, H., Zhou, Y., Brinkmann, H., Rodrigue, N., and Delsuc, F., "Heterotachy and long-branch attraction in phylogenetics," BMC Evol. Biol., vol. 5, pp. 1-8, 2005. [CrossRef]
- Sullivan, J., and Swofford, D.L., "Should we use model-based methods for phylogenetic inference when we know that assumptions about among-site rate variation and nucleotide substitution pattern are violated?" Syst. Biol., vol. 50, no. 5, pp. 723-729, 2001.
- Azouri, D., Abadi, S., Mansour, Y., Mayrose, I., and Pupko, T., "Harnessing machine learning to boost heuristic strategies for phylogenetic-tree search," 2020.
- Bernardini, G., van Iersel, L., Julien, E., and Stougie, L., "Constructing phylogenetic networks via cherry picking and machine learning," Algorithms Mol. Biol., vol. 18, no. 1, pp. 13, 2023. [CrossRef]
- Zou, Z., Zhang, H., Guan, Y., and Zhang, J., "Deep residual neural networks resolve quartet molecular phylogenies," Mol. Biol. Evol., vol. 37, no. 5, pp. 1495-1507, 2020. [CrossRef]
- Layne, E., Dort, E.N., Hamelin, R., Li, Y., and Blanchette, M., "Supervised learning on phylogenetically distributed data," Bioinformatics, vol. 36, Supplement_2, pp. i895-i902, 2020. [CrossRef]
- Smith, M.L., and Hahn, M.W., "Phylogenetic inference using generative adversarial networks," Bioinformatics, vol. 39, no. 9, pp. btad543, 2023. [CrossRef]
- Abadi, S., Avram, O., Rosset, S., Pupko, T., and Mayrose, I., "ModelTeller: model selection for optimal phylogenetic reconstruction using machine learning," Mol. Biol. Evol., vol. 37, no. 11, pp. 3338-3352, 2020. [CrossRef]
- LIPTÁK, P., and Attila, K., "Constructing unrooted phylogenetic trees with reinforcement learning," Studia Univ. Babeș-Bolyai Inform., pp. 37-53, 2021.
- Kalyaanamoorthy, S., Minh, B.Q., Wong, T.K., Von Haeseler, A., and Jermiin, L.S., "ModelFinder: fast model selection for accurate phylogenetic estimates," Nat. Methods, vol. 14, no. 6, pp. 587-589, 2017. [CrossRef]
- Wang, Z., Sun, J., Gao, Y., Xue, Y., Zhang, Y., Li, K., Zhang, W., Zhang, C., Zu, J., and Zhang, L., "Fusang: a framework for phylogenetic tree inference via deep learning," Nucleic Acids Res., vol. 51, no. 20, pp. 10909-10923, 2023. [CrossRef]
- Tang, X., Zepeda-Nuñez, L., Yang, S., Zhao, Z., and Solís-Lemus, C., "Novel symmetry-preserving neural network model for phylogenetic inference," Bioinformatics Advances, vol. 4, no. 1, pp. vbae022, 2024. [CrossRef]
- Felsenstein, J., "Inferring phylogenies," Sinauer Associates, 2004.
Figure 1.
Average processing time Vs CI to Randomly selected features of different dataset sizes.
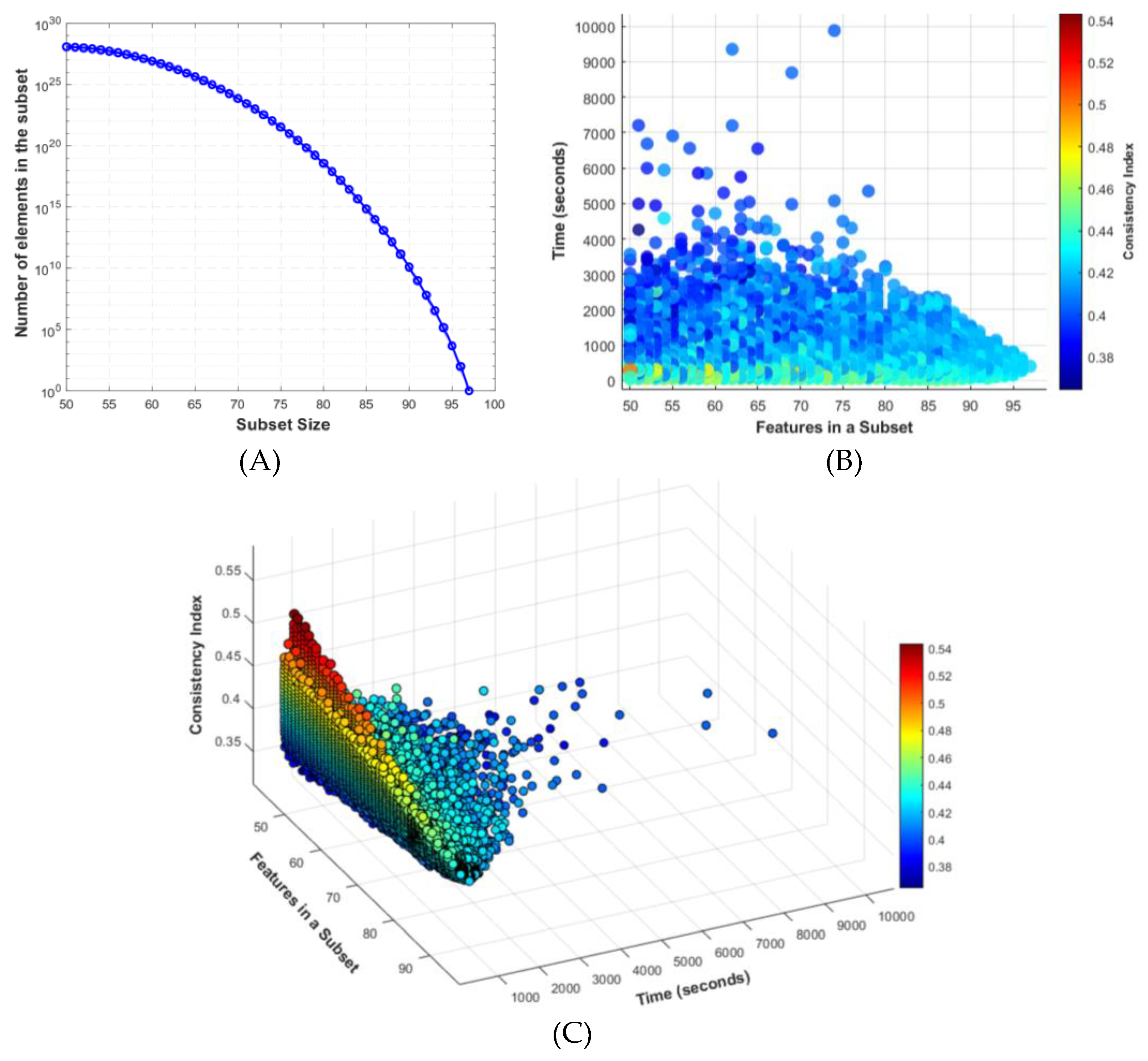
Figure 2.
Flowchart of the phylogenetic analysis using advanced machine learning algorithms.
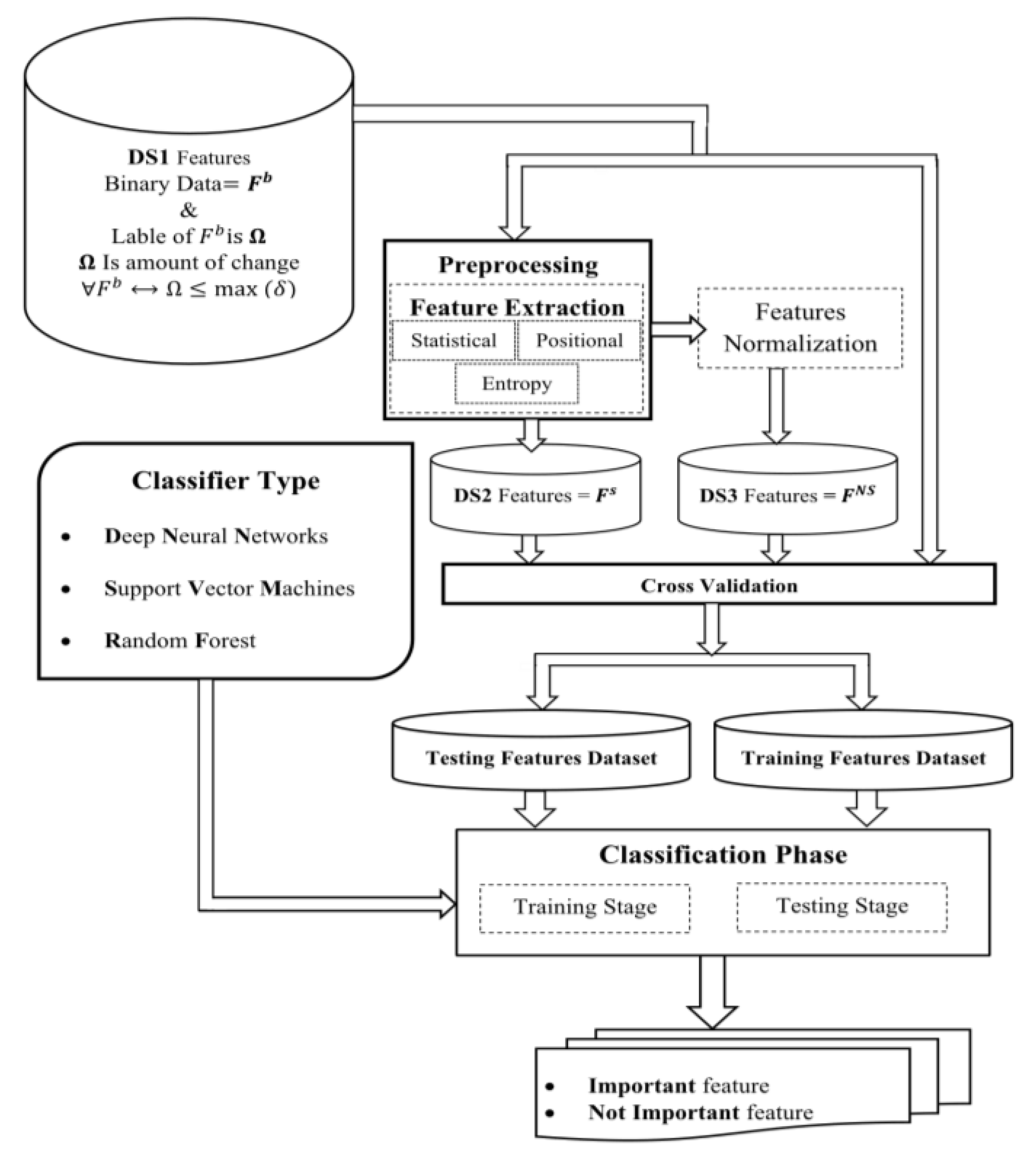
Figure 3.
Histogram of features that hold a similar number of changes.
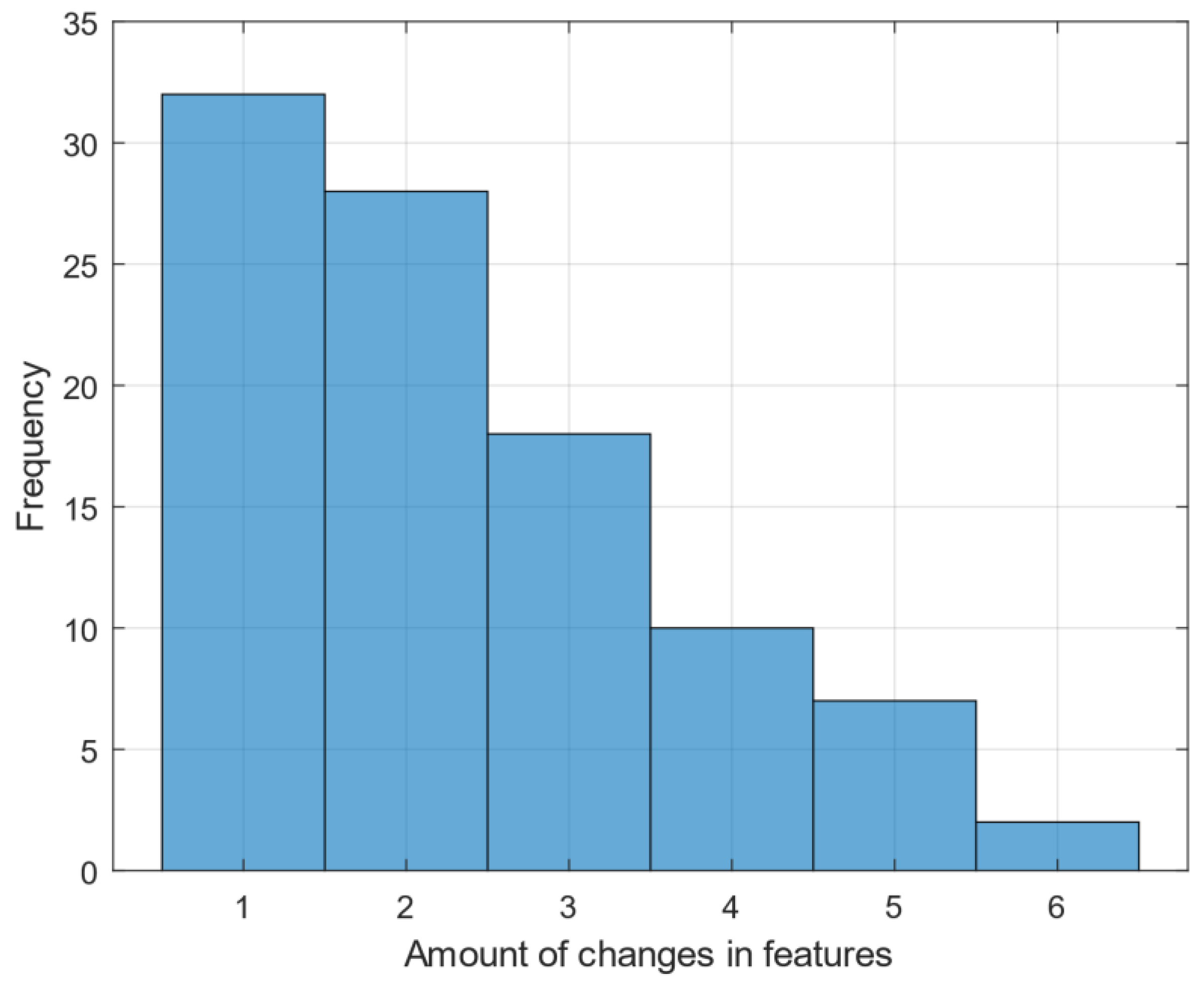
Figure 4.
Phylogenetic trees after doing Maximum Parsimony search for including all features as in (A), on other hand on subset of features as in (B).
Figure 4.
Phylogenetic trees after doing Maximum Parsimony search for including all features as in (A), on other hand on subset of features as in (B).
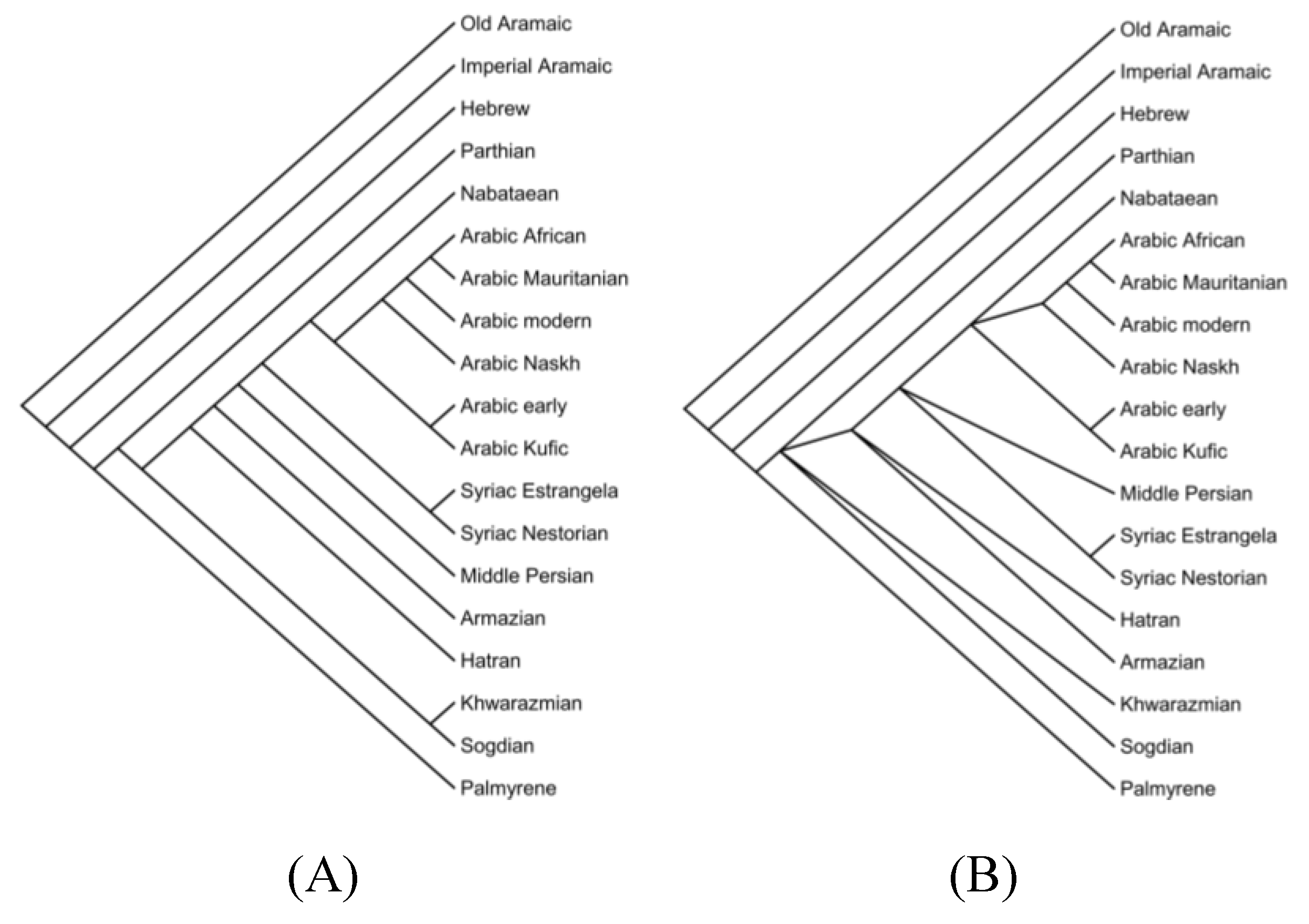
Figure 5.
ROC Curves of DNN, SVM, and RF Models Across 4 Folds for , and .
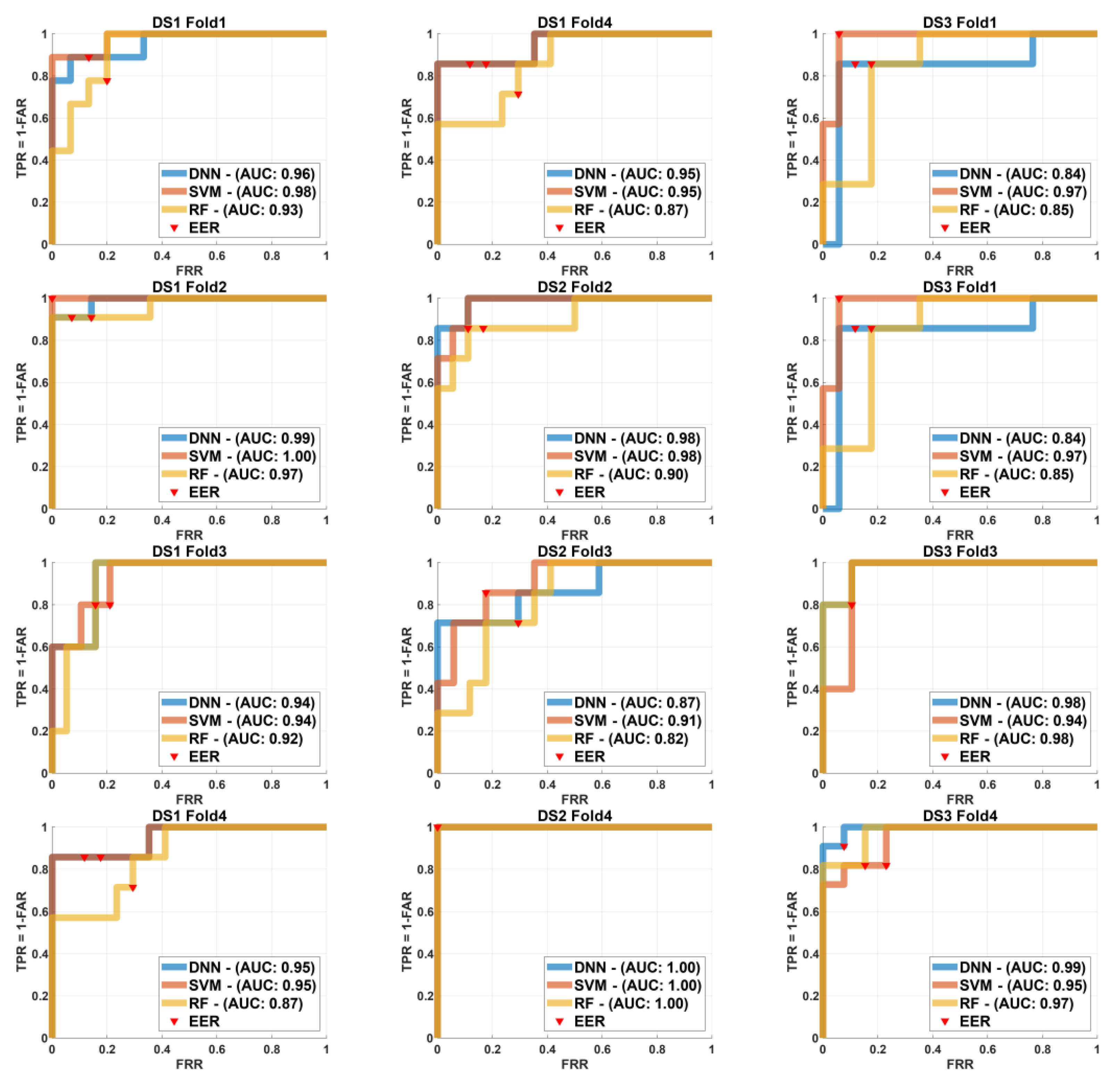
Figure 6.
ROC Curves of DNN, SVM, and RF Models Across 3 Folds for , and .
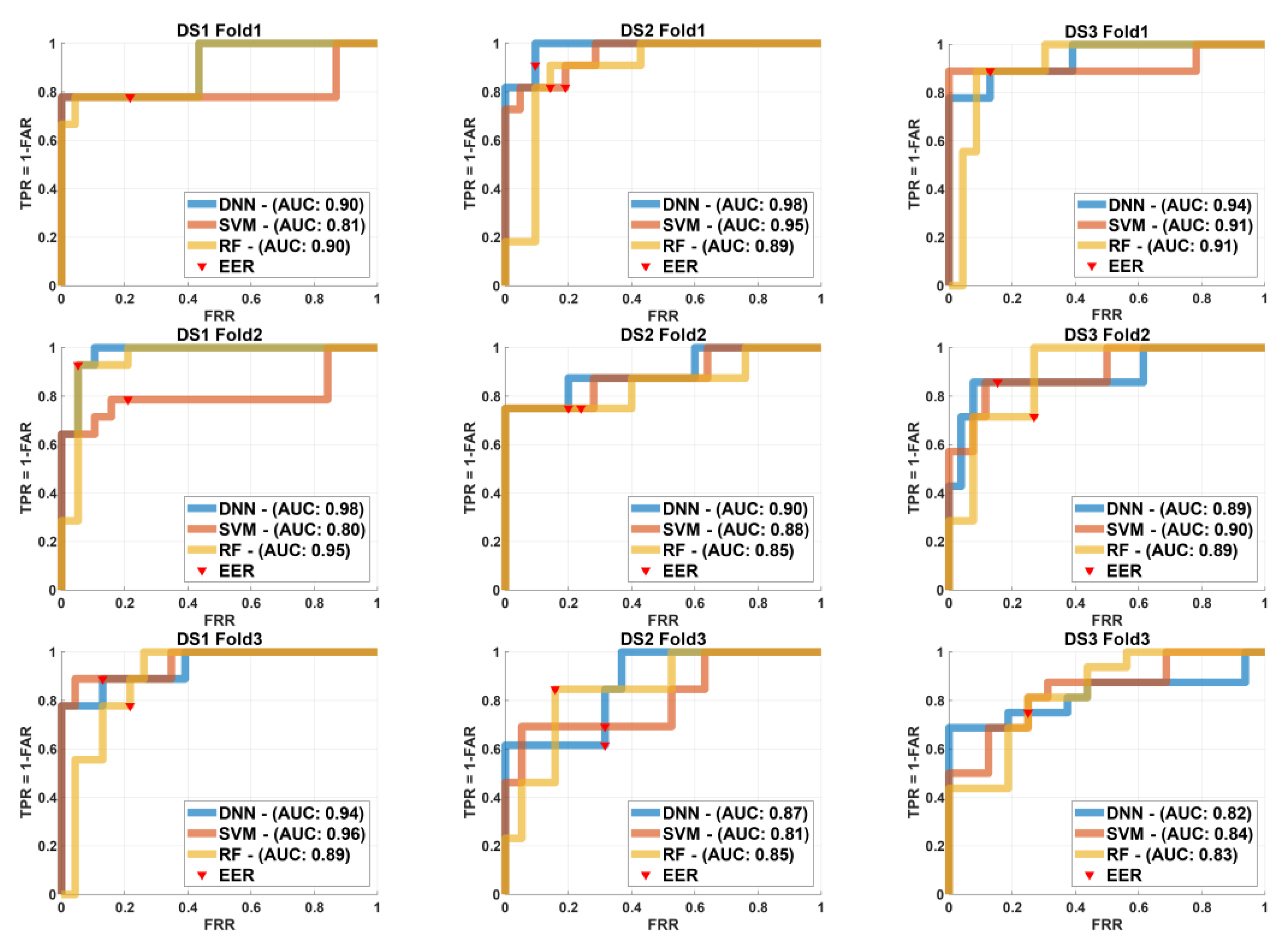
Figure 7.
ROC Curves of DNN, SVM, and RF Models Across 2 Folds for , and .
Figure 8.
Training Epochs Required for DNN Across Different Folds and Datasets , , and with k=2, k=3, and k=4.
Figure 8.
Training Epochs Required for DNN Across Different Folds and Datasets , , and with k=2, k=3, and k=4.
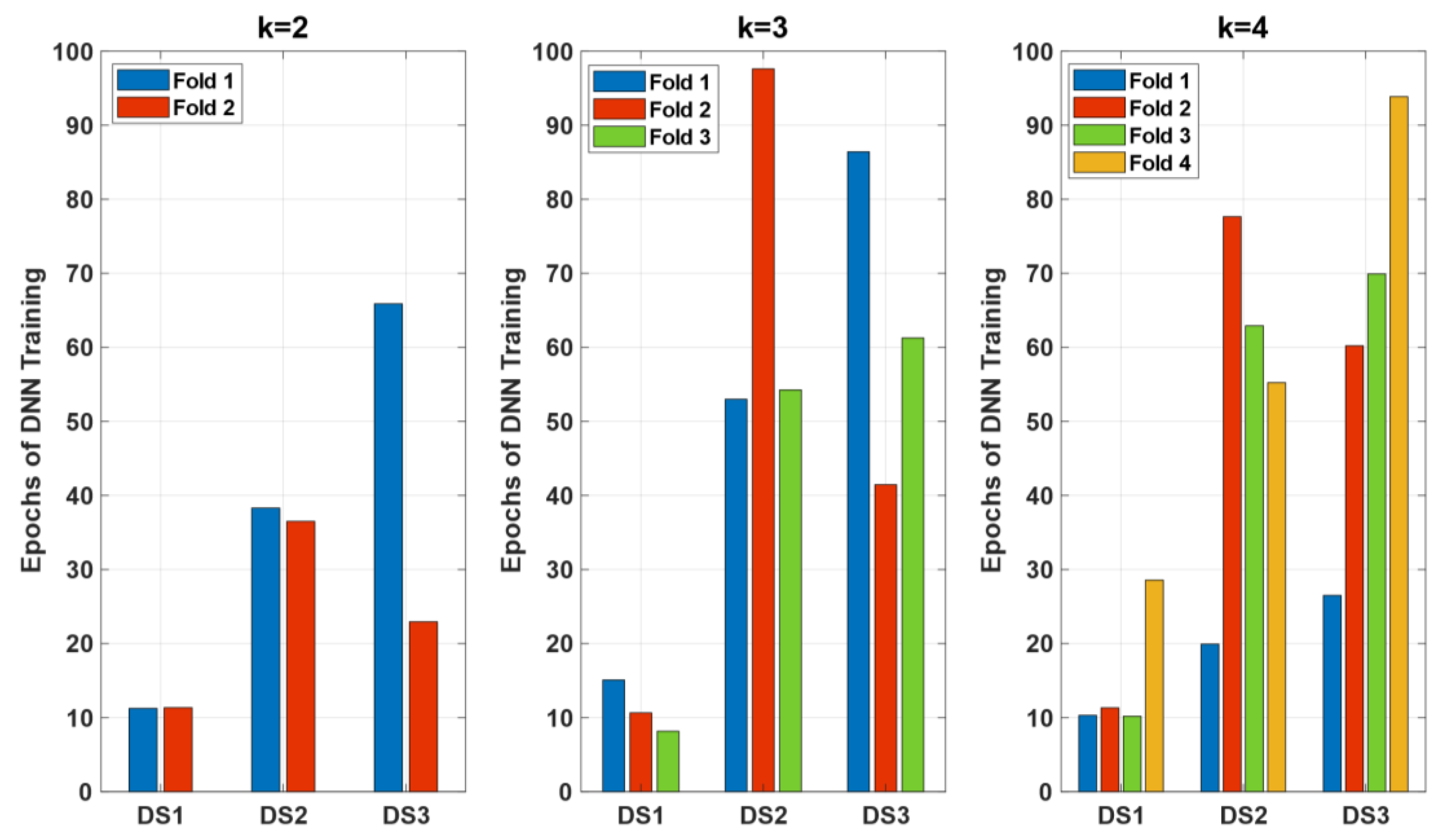
Table 1.
Mathematical Notations for Feature extraction DS2.
| Notation | Description |
|---|---|
| The total number of Taxa in DS1. | |
| The total number of features in DS1. | |
| The value at the feature position for Taxa in or DS1 | |
| The Shannon entropy for the features in DS1, a measure of randomness in the features. | |
| The feature value for the taxa in DS2 before normalization. | |
| The normalization of and save it in DS3. | |
| A small constant added to probabilities to avoid undefined log calculations during entropy computation. | |
| A value could be either 0 or 1 to make a selection of running the equation if it will run for 0’s or 1’s |
Table 2.
Statistical Features of DS1 .
| Equation | Description |
|---|---|
| Total count of 0’s/ 1’s in feature of DS1. | |
| The density of 0’s/ 1’s for the feature in , where the total count of K’s | |
| The mean position of ’s in for feature | |
| Median position of ’s in | |
| Variance of positions of ’s in |
Table 3.
Hyperparameters for each Model.
| DNN | Three hidden layer there sizes are: [15 | 8 | 4] Mean Squared Error: 0.001 Learning Rate: 0.001 Actvation function to hidden layers (tansig) Actvation function for output node is (logsig) |
| SVM | Kernel Function: Radial Basis Function (RBF) Box Constraint: 30 Kernel Scale: 10 |
| RF | Number of Trees: 300 Max Number of Splits: 50 Number of Variables to Sample: All Minimum Leaf Size: 5 |
Table 4.
Amount of bins selected according to equation (6).
| No. Features | Tree Length | Optimal tree | CI | Time Sec | |
|---|---|---|---|---|---|
| 6 | 97 | 229 | 2 | 0.424 | 369.3 |
| 5 | 95 | 217 | 3 | 0.438 | 184.7 |
| 4 | 88 | 181 | 2 | 0.486 | 28.8 |
| 3 | 78 | 140 | 3 | 0.557 | 1.33 |
| 2 | 60 | 86 | 2 | 0.698 | 0.03 |
| 1 | 32 | 32 | 1 | 1 | 0.005 |
Table 5.
Average Accuracy, False Rejection Rate, and False Acceptance Rate of Different Models Across Various Folds for , , and .
Table 5.
Average Accuracy, False Rejection Rate, and False Acceptance Rate of Different Models Across Various Folds for , , and .
| Fold | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Acc | FRR | FAR | Acc | FRR | FAR | Acc | FRR | FAR | ||
| DNN | 2 | 81.12 | 0.09 | 0.32 | 79.74 | 0.08 | 0.35 | 84.26 | 0.1 | 0.24 |
| 3 | 80.45 | 0.09 | 0.3 | 85.07 | 0.1 | 0.21 | 83.9 | 0.13 | 0.25 | |
| 4 | 83.66 | 0.06 | 0.31 | 90.3 | 0.05 | 0.18 | 86.37 | 0.09 | 0.22 | |
| SVM | 2 | 88.71 | 0.13 | 0 | 88.56 | 0.1 | 0.14 | 83.19 | 0.17 | 0.13 |
| 3 | 87.65 | 0.15 | 0 | 83.23 | 0.13 | 0.22 | 79.56 | 0.2 | 0.11 | |
| 4 | 92.75 | 0.09 | 0 | 86.43 | 0.11 | 0.17 | 84.61 | 0.13 | 0.17 | |
| RF | 2 | 82.65 | 0.11 | 0.27 | 82.26 | 0.08 | 0.31 | 85.66 | 0.08 | 0.24 |
| 3 | 78.64 | 0.13 | 0.25 | 82.4 | 0.1 | 0.29 | 77.01 | 0.18 | 0.33 | |
| 4 | 81.8 | 0.14 | 0.28 | 82.79 | 0.09 | 0.29 | 84.16 | 0.12 | 0.19 | |
Table 6.
Average AUC and EER of Different Models Across Various Folds for , , and .
| Fold | |||||||
|---|---|---|---|---|---|---|---|
| AUC | EER | AUC | EER | AUC | EER | ||
| DNN | 2 | 0.92 | 0.19 | 0.87 | 0.16 | 0.94 | 0.13 |
| 3 | 0.94 | 0.13 | 0.91 | 0.2 | 0.88 | 0.17 | |
| 4 | 0.95 | 0.13 | 0.95 | 0.12 | 0.9 | 0.15 | |
| SVM | 2 | 0.81 | 0.25 | 0.9 | 0.16 | 0.92 | 0.16 |
| 3 | 0.85 | 0.18 | 0.88 | 0.24 | 0.88 | 0.17 | |
| 4 | 0.96 | 0.11 | 0.95 | 0.09 | 0.91 | 0.17 | |
| RF | 2 | 0.91 | 0.21 | 0.82 | 0.15 | 0.93 | 0.15 |
| 3 | 0.91 | 0.16 | 0.86 | 0.18 | 0.87 | 0.21 | |
| 4 | 0.91 | 0.19 | 0.91 | 0.13 | 0.91 | 0.17 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Alerts
MDPI Initiatives
Important Links
© 2025 MDPI (Basel, Switzerland) unless otherwise stated





