Prerpints.org logo
Preprint
Article

From Play to Understanding: LLMs in Logic and Spatial Reasoning Coloring Activities for Children

Altmetrics

Downloads

158

Views

145

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

19 August 2024

Posted:

19 August 2024

You are already at the latest version

Alerts
Abstract
Visual thinking leverages spatial mechanisms in animals for navigation and reasoning. Therefore, given the challenge of abstract mathematics and logic, spatial reasoning-based teaching strategies can be highly effective. Our previous research verified that innovative box and ball coloring activities help teach elementary school students complex notions like quantifiers, logical connectors, and dynamic systems. However, given the richness of the activities, correction is slow, error-prone, and demands high attention and cognitive load from the teacher. Moreover, feedback to the teacher should be immediate. Thus, we propose to provide the teacher with real-time help with LLMs. We explored various prompting techniques with and without context Zero shot, Few shot, Chain of Thought, Visualization of Thought, Self Consistency, logicLM and Emotional to test GPT-4o’s visual, logical, and correction capabilities. We obtained that Visualization of Thought and Self Consistency techniques enabled GPT-4o to correctly evaluate 90% of logical-spatial problems that we tested. Additionally, we propose a novel prompt combining some of these techniques that achieved 100% accuracy on a testing sample, excelling in spatial problems and enhancing logical reasoning.
Keywords: 
Subject: Computer Science and Mathematics  -   Artificial Intelligence and Machine Learning

1. Introduction

Visual reasoning is fundamental in both animals and humans. Animals rely on spatial reasoning for navigation, hunting, and survival, using mental maps and visual cues to move through their environment. In humans, these skills are used not only for physical orientation but also for problem-solving and learning. Visual expressions like diagrams and gestures utilize space to convey meanings and improve information processing and decision-making. Drawing aids in comprehending complex ideas, making abstract concepts more tangible and understandable [7,8,9].
For example, the Programme for International Student Assessment (PISA) research measures creative thinking in 15-year-olds, which is defined as the ability to produce original and diverse ideas, as well as to evaluate and improve on the ideas of others. This is critical because, in the future, societies will increasingly rely on innovation and knowledge creation to address the issues they face [10]. One of the assessment domains that PISA 2024 measures is visual expression, which is situated in the ability to generate creative ideas. This further reinforces the importance of applying visual teaching methodologies to children, thus developing their mathematical abilities and creative thinking in problem-solving.
To address this educational challenge, Gamification has emerged as an effective strategy for teaching complex mathematical concepts. Moreover, the inclusion of universal and existential quantifiers in elementary school children can be posed as attractive spatial reasoning coloring games and activities. A recent study explored how playful activities, such as coloring boxes and balls, can enhance the understanding of logical and spatial notions in children from first to sixth grade [1]. These activities are currently being implemented and are designed for children to promote computational, mathematical, and STEM thinking, encouraging the development of computational thinking through natural language, which is foundational for using generative AI and reasoning for programming [11,12]. Through games and interactive activities, children can internalize mathematical and logical concepts more effectively, developing skills that will be fundamental in their future education.
These coloring exercises present millions of possible correct solutions, yet the probability of randomly achieving a correct result is extremely low (less than 0.1%). Unlike multiple-choice activities, these exercises are challenging and time-consuming for teachers to correct, requiring significant cognitive effort. Teachers utilize these exercises in two primary ways: during the session, they select samples of students’ work for real-time class analysis, necessitating immediate teacher assistance multiple times throughout the session. On the other hand, teachers must correct all the exercises after class, which, while not as time-sensitive, involves a substantial volume of work, demanding considerable time and support. The complexity, novelty, and abundance of possible solutions in these coloring activities could place a significant cognitive load on teachers. The sheer number of options and the need to evaluate nuanced responses can be overwhelming, potentially leading to suboptimal teaching practices [13]. To ensure that teachers can fully leverage the potential of these activities, it is crucial to provide them with real-time support [14]. This support can help alleviate their cognitive load, enabling them to focus on facilitating student learning and providing meaningful feedback.
Fortunately, contemporary Large Language Models (LLMs) like Generative Pre-trained Transformer (GPT) are demonstrating substantial potential in general and spatial reasoning (for example, GPT-4o could be indistinguishable from a human [15]). GPT-4o also has potential in the educational domain, particularly in automating correction and providing immediate, detailed feedback, thereby enhancing the efficacy of the educational process. This capability has evolved significantly over time. Previous iterations, such as GPT 3.5, exhibited limitations in identifying errors within incoherent responses [16], showing no significant improvement over traditional machine learning methods. Currently, empirical evidence supports the educational applications of the latest GPT versions [17,18], including their role in assisting educators [19] and in the correction and creation of exercises involving computational thinking [20,21].
In this study, we examined the visual, logical, and correction abilities of the GPT-4o model using different stimulus techniques. The coloring balls and boxes exercises teach two essential types of reasoning in computational thinking: logical reasoning and spatial reasoning. On one side, the basic use of mathematical quantifiers is applied to reinforce logical aspects, while spatial aspects use coloring dependencies between boxes and balls. These problems require LLMs not only to understand the content of the task but also to apply critical reasoning to provide a correct solution.
Given the slow pace of manual correction in traditional educational settings, we propose leveraging LLMs to provide immediate and accurate feedback on box and ball coloring activities. This study aims to explore the feasibility of using LLMs as correction and feedback tools in educational gamification and to assess the visual, logical, and correction capabilities of GPT-4o across different prompting techniques. Specifically, we address three key research questions:
  • To what extent can GPT-4o accurately assess and correct coloring activities completed by elementary school students, given instructions involving multiple logical quantifiers and spatial relationships?
  • What are the visual, logical, and correction capabilities of GPT-4o, and what type of prompts are most effective for obtaining accurate and detailed GPT-4o corrections when assessing coloring activities involving logical quantifiers and spatial relationships?
  • Can GPT-4o be effectively utilized as a teaching assistant to provide immediate feedback for class discussions on these exercises?

2. Related Work

The state of the art in logic problem solving clearly concludes that quite specific and elaborate techniques are needed to address this type of problem. Some techniques such as Chain of Thought prompting with problem specification [22], giving feedback to the machine on incorrect answers [23], use of agents [5], fine-tuning [24], etc.[25,26] have been shown to improve the accuracy of GPT answers to mathematical and verbal logic problems. For example, in [5], a framework that integrates LLMs with symbolic solvers to improve logical problem-solving is introduced. This method involves translating natural language problems into symbolic formulations, which are then processed by deterministic symbolic solvers. The study highlights the need for detailed and sequential instructions, such as the "Chain of Thought" technique, to guide models through complex reasoning processes and ensure each step is methodically and accurately addressed. It is noted that to achieve good improvements in logic formulations, sophisticated prompting techniques are crucial for tackling complex logical problems.
Moreover, LLMs are susceptible to changes in opinion, which can affect the reliability of their logical responses, as shown in [28]. They use techniques like "Chain of Thought" to mitigate these effects and improve consistency. The susceptibility to opinion changes highlights the need for robust prompting techniques that can guide models through precise and consistent logical reasoning.
Recent studies have explored the visual capabilities of LLMs and compared them to human reasoning to address spatial problems. Despite limitations in comprehension and processing in 2D and 3D GPT-4o tasks [29], techniques such as Visualization of thought have been shown to be especially effective, surpassing even pioneering techniques such as Chain of Thought [2], in improving LLM performance on spatial problems [3]. In this method, clear visual cues should be provided, and answers should be segmented into meaningful parts, adding the instruction to visualize the current state of the solution. 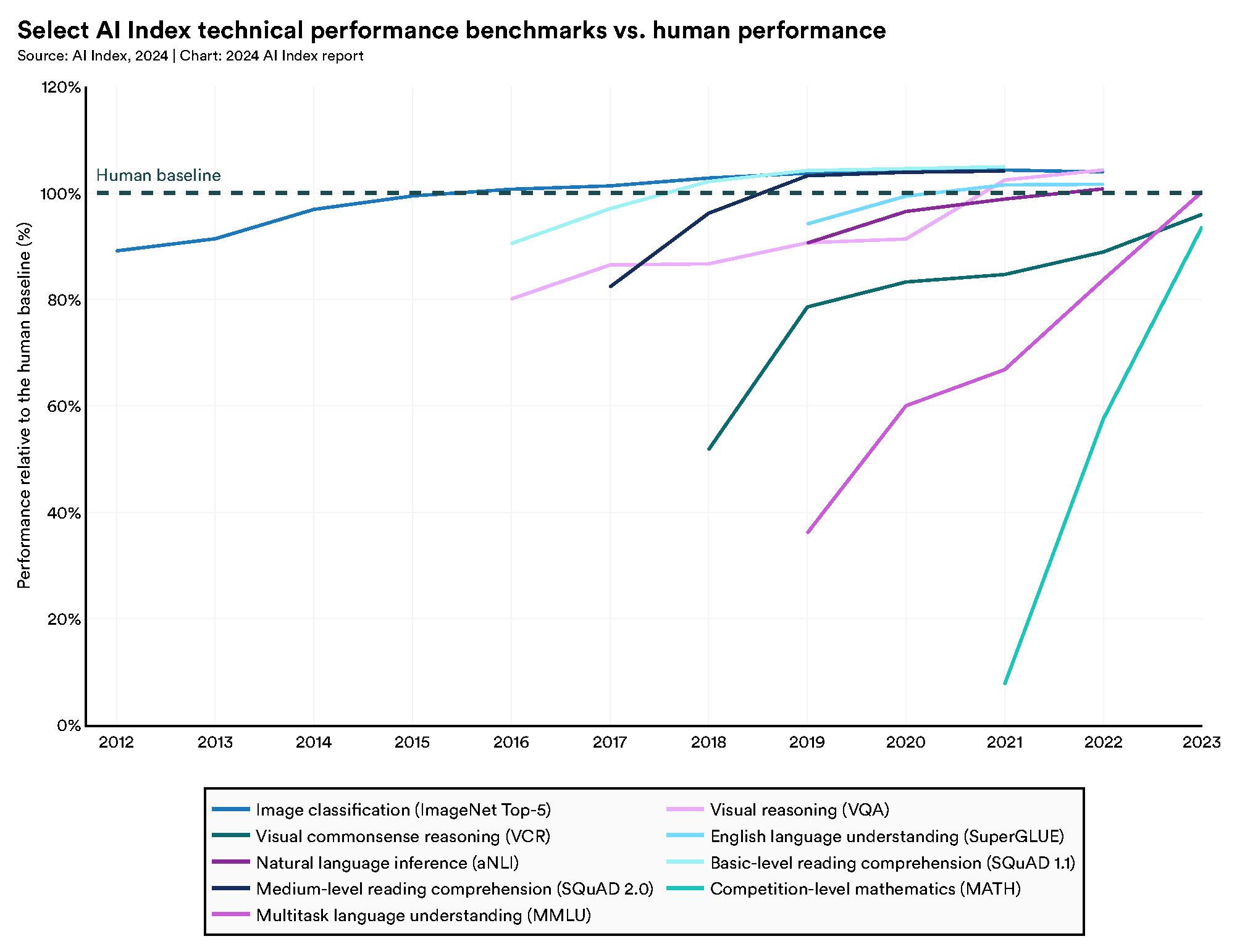According to the Stanford AI report [30], AI has now outperformed human performance on several benchmark tests and, in particular, visual reasoning, as shown in Figure 1, further reinforcing the visual potential of LLMs.
In addition, visual guidance techniques improve LLMs’ understanding of images, allowing them to compare more closely with human reasoning. Techniques such as image segmentation or image representations using code [31,32] allow for increased accuracy and consistency in GPT-4o spatial reasoning.
Moreover, the probabilistic nature of LLMs can introduce variability in the generated responses. To address this, we propose using techniques like Self Consistency [4], where multiple responses are generated for the same prompt, and the most recurrent result is selected. It has been shown that this technique helps reduce uncertainty and improve the reliability of the corrections provided by LLMs. Generating several solutions and selecting the most common one can ensure greater consistency and accuracy in evaluating complex problems.

3. Methodology

3.1. Box and Ball Coloring Activities

The box and ball coloring exercises consist of several problems designed to teach mathematical quantifiers, spatial reasoning, and dynamical systems through visual and interactive methods. Each exercise includes a primary instruction and an illustration featuring boxes containing balls that must be colored according to the given instruction. These exercises aim to teach mathematical logic in a visual way by means of existence and universality quantifiers, as well as in spatial relationships between objects. Figure 2 provides examples of these activities.
Figure 3 shows the blank worksheet to be filled out by each student to pose a similar kind of problem to a classmate.
In total, the instructions used in this work are five and given by:
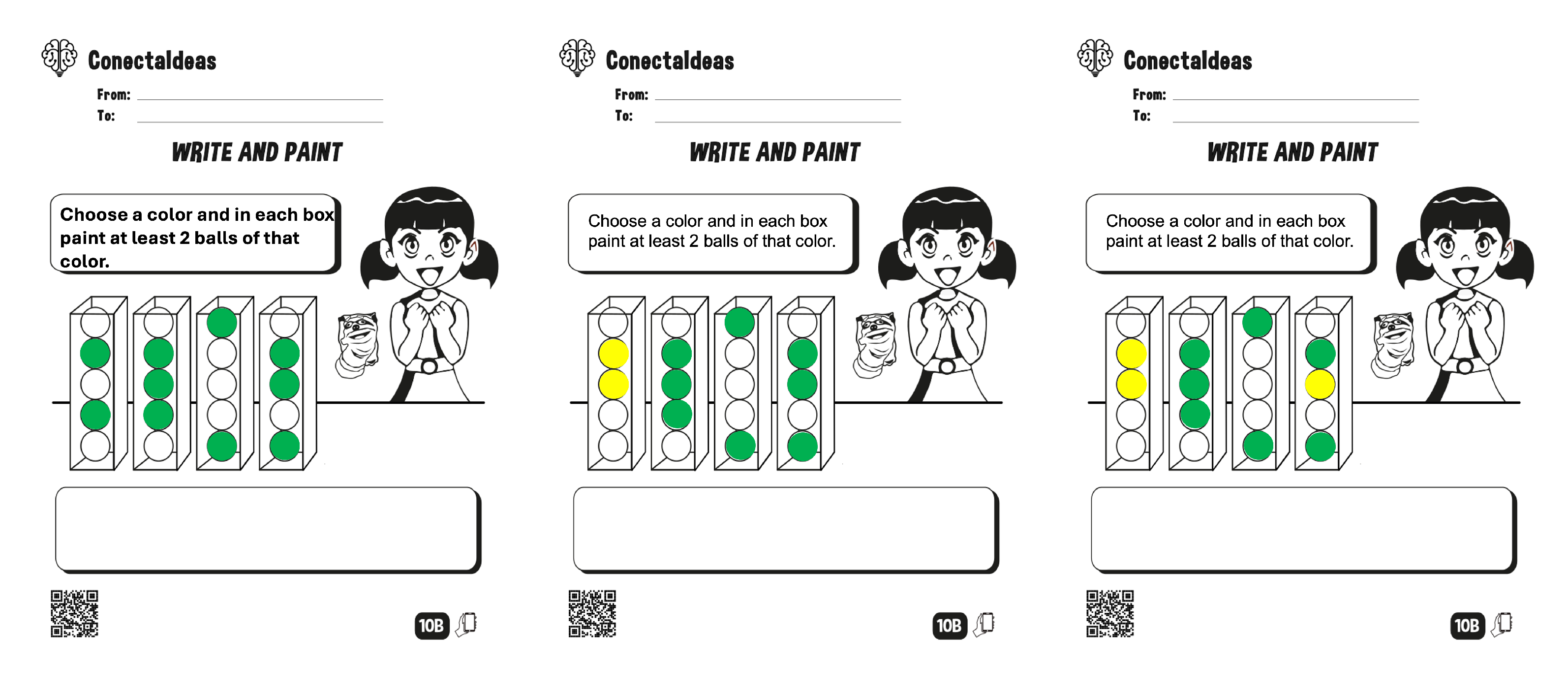
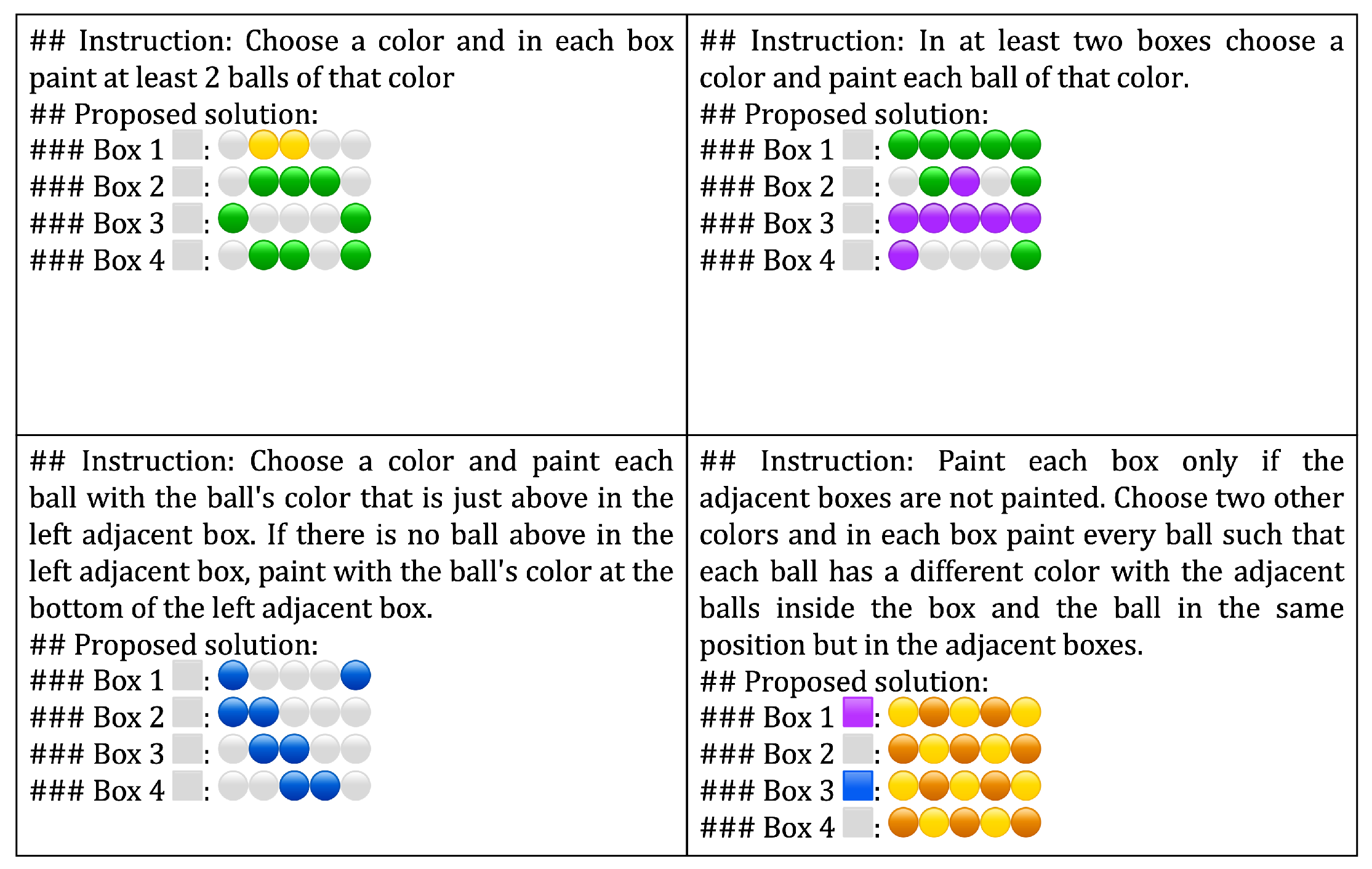
  • Choose a color and in each box paint at least 2 balls of that color.
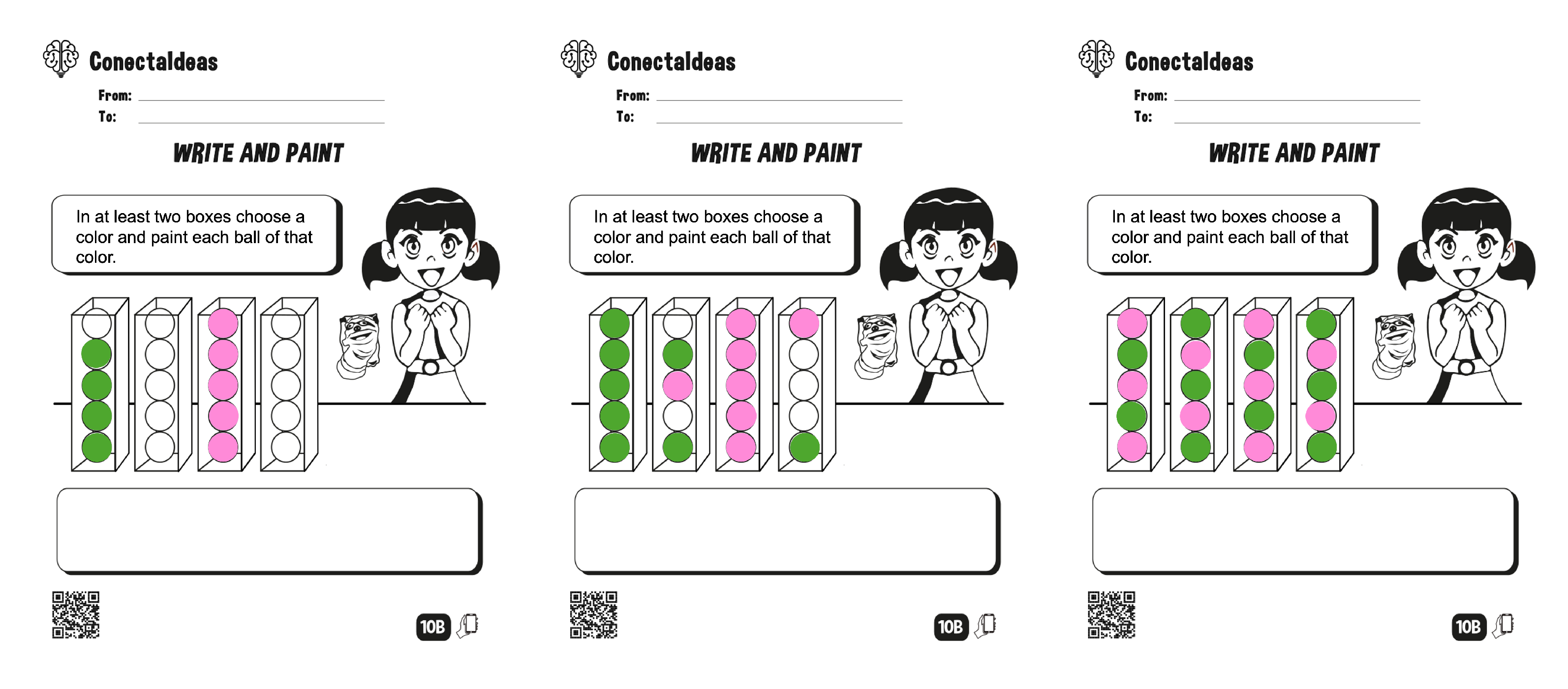
  • In each box choose a color and paint at least 2 balls of that color.
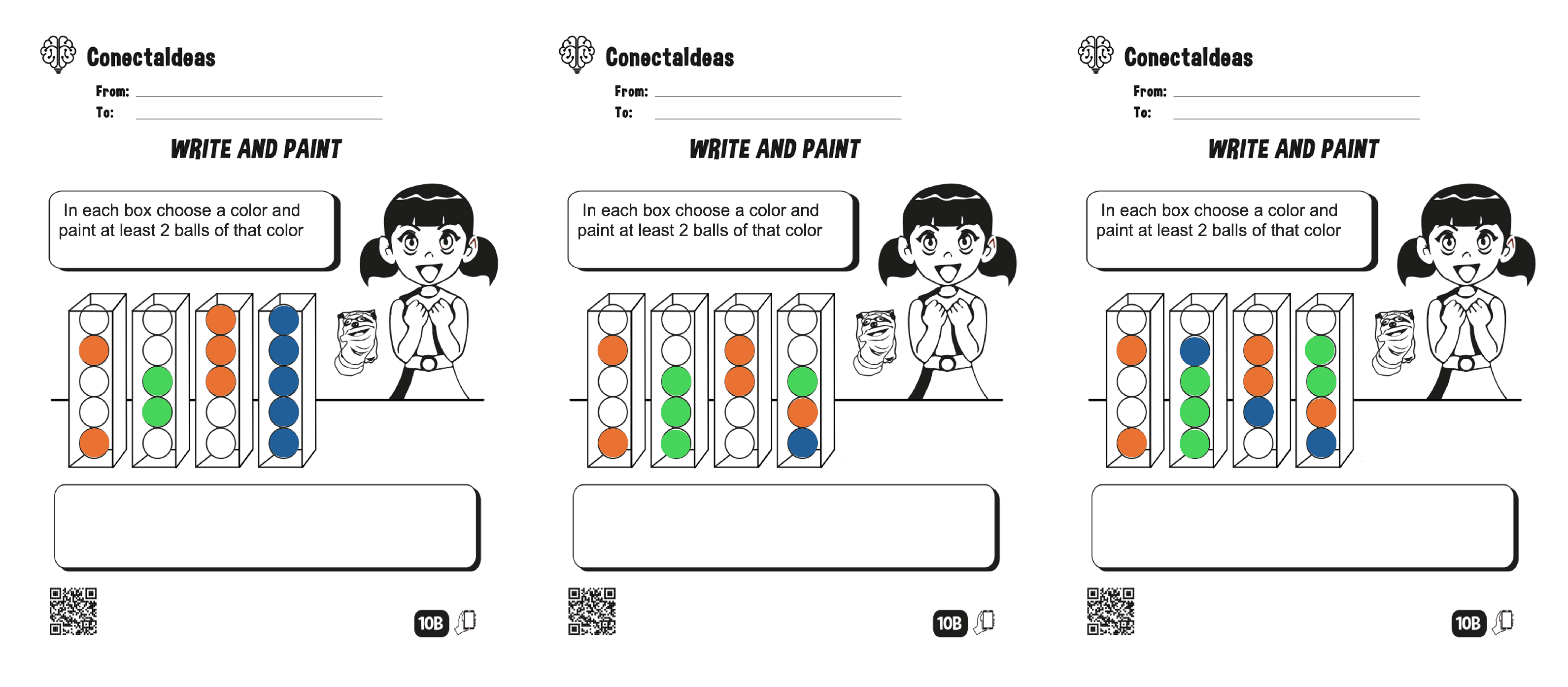
  • In at least two boxes choose a color and paint each ball of that color.
  • Paint each box only if the adjacent boxes are not painted. Choose two other colors and in each box paint every ball such that each ball has a different color with the adjacent balls inside the box and the ball in the same position but in the adjacent boxes.
  • Choose a color and paint each ball with the ball’s color that is just above in the left adjacent box. If there is no ball above in the left adjacent box, paint with the ball’s color at the bottom of the left adjacent box.
Table 1 shows every instruction with its quantifiers and explanation.
Existential and universal quantifiers are essential for understanding and using mathematical propositional logic. The order of these quantifiers is critical, as it significantly affects the proposition’s meaning.
For example, let us consider the definition of a function’s convergence to a point when the input is very large, essentially infinite. This dictates the following: “For any small error, there exists an instant in the inputs such that from that instant, the function is at a distance less than the error from the point”. Here we can identify the universal quantifier “for all” and the existence quantifier “exists”, as well as other mathematical indicators, both of spatial and numeric nature, such as “distance”, “less than” or “small error”. Note that if we change the order of the quantifiers in the definition, we obtain something like: “There exists an instant in the inputs for any small error, such that from that instant, the function is at a distance less than the error from the point”. This essentially states that from an instant, the function is constant and equal to the point, a definition that is completely different from the first one.
On the other hand, instruction 5 describes a spatial process that mirrors the typical behavior of dynamic systems. Think of the boxes with their corresponding colored balls as a time series of interconnected states. The rule for coloring each ball based on its neighbor represents a transition function, determining how the system moves from one state to the next. An initial random coloring of the balls of the leftmost box serves as the system’s initial condition, and the subsequent colorings propagating to the right result from repeatedly applying the transition function. These exercises give students specific instructions corresponding to fundamental logical and mathematical statements, transforming abstract concepts into engaging activities.
Visual statements involve coloring balls and boxes based on their positions in the drawing, emphasizing the dependency between colors and spatial arrangements. These exercises not only teach elementary school children the existence and universality of colors but also require children to color a ball or box based on the painting status of other balls or boxes. Some of these exercises introduce algorithmic structures dependent on initial states or dynamical systems, concepts present in computational problems, ordinary differential equations, and also chaotic systems, in which case, the final solution to the problem is highly dependent on the initial state (e.g., the three-body problem [33]).
These exercises also introduce other logical conditionals such as “if”, “only if” and “and” in order to add conditionality between boxes and balls. It is more than clear the importance of these conditions in algorithmic developments is a fundamental part of computational thinking. In mathematical terms, they are recurrent when it is required to demonstrate equivalence or implication of definitions with each other. An example can be the implication “if a function is derivable at all points, then it is continuous at all points”. Here, the implication is in one direction since it is false that a continuous function is always derivable. It also indicates that a necessary condition for a function to be derivable is to be continuous because if a function is not continuous, it cannot be derivable.
In the case of boxes and balls it is similar. Spatial dependence would give instructions such as that a ball should be painted only if other balls or boxes are painted. That is, a necessary condition for such a ball to be painted is that other balls are already painted. Therefore, the reasoning at the moment of painting should be, “If I want to paint the balls according to the instructions, then such balls and boxes must be painted”. However, if these other balls are colored, it does not mean they are painted following the previous instruction. We can note the logical similarity of this last expression with the example of continuity and derivability presented previously.
This type of visual reasoning is also useful in mathematics in discovering patterns that allow us to deduce and demonstrate mathematical relationships through coloring and positioning numbers. Chapter 2 of [34] mentions several examples of mathematical results that can be deduced from patterns in natural numbers, such as the classification of odd and even numbers by grouping integers in two columns or equivalence classes for more columns and the multiplication table that appears by positioning the above-mentioned columns in a table, where their diagonal also corresponds to square numbers.
We can notice that the instructions in Table 1 have many possible solutions. Unlike the typical multiple choice questions present in the vast majority of assessments, where the answer is one and only one and has a fixed probability of being solved randomly, these visual exercises can be solved in many ways and only limited by the number of colors the child possesses. In addition, the probability of painting randomly and getting a correct answer is very low. Consider, for example, a simple pencil box containing six colors. For this set of colors, the probabilities of randomly solving each of the instructions are given in Table 2.
From Table 2, it is observed that all the probabilities of success are less than 1%, so it is totally unfeasible to rely on randomness to solve these exercises. This effectively compels students to adhere strictly to the given instructions. We also note that these probabilities can be even lower if we consider boxes with a larger number of colored pencils e.g., 12 or 24.
It is also noteworthy to consider that the probability of success decreases as more constraints are added to the problem, reducing the set of favorable solutions. From this, given that Instruction 4 has the most constraints, we infer that its probability of success when guessed randomly is the lowest among all the probabilities listed in the table, which is why we bound it to the smallest calculated probability.
The vast number of possible answers for each instruction poses a significant challenge for teachers, as correcting these exercises is tedious and time-consuming. Each response must be meticulously checked to ensure compliance with the given instructions. This process is prone to serious errors, especially if the teacher lacks a strong grasp of mathematical logic or does not take special care during correction.

3.2. Prompting Techniques

Given the high complexity of correcting these exercises, we proposed delegating this task to a Large Language Model (LLM). At present, ChatGPT features GPT-4V (GPT-4 Vision), which possesses the capability to analyze images provided in prompts. We will leverage this functionality by directly delivering exercises completed by children, given in Figure 2, accompanied by prompts designed to enhance visual analysis, data interpretation, and element counting, such as giving the role "You are an expert in counting colored and uncolored balls and boxes in an image". Unfortunately, this feature of GPT presents problems in counting elements when they are not easy to interpret or are hidden by other objects [35]. In this case, the worksheets present several distracting elements for GPT, including the fact that the boxes are hidden from the balls. Therefore, trying other ways of entering the problem in the prompts is also necessary.
Two ways of writing the problems and various prompting techniques were employed to accurately classify student responses. These techniques included Zero-Shot, Few-Shot, Chain of Thought, Visualization of Thought, Self-Consistency, and code generation. A prompt inspired by LogicLM was also utilized, along with context augmentation in simple prompts and a final prompt that combined several of the aforementioned techniques.
The problems were introduced into the prompt in two distinct ways, depending on whether the technique required visual aids, as illustrated in Figure 4. Each setup of boxes and balls was paired with the corresponding instruction.

3.2.1. Zero-Shot, Few-Shot, and Chain of Thought

Zero-Shot and Few-Shot are relatively straightforward prompting techniques. In Zero-Shot prompting, concise instruction is provided without additional context or examples. For this study, the Zero-Shot approach involved directly presenting the problem as in Figure 4 left, followed by the query: “Is the solution correct or incorrect?". Few-Shot prompting, in contrast, involved providing the model with several labeled examples of correct and incorrect solutions, formatted similarly to Figure 4 left, before posing the same question as in the Zero-Shot prompt.
While both Zero-Shot and Few-Shot techniques are simple and easy to implement, they often result in hallucinations or misclassifications, where the model incorrectly assesses the correctness of a solution [36]. These limitations highlight the need for more advanced techniques such as Chain of Thought. In this technique, the model is guided through a step-by-step reasoning process, either by giving concrete examples of developments as we would like it to reason or by adding the instruction “Think step-by-step”. CofT has been shown to potentially reduce hallucinations in answers and obtain better response labeling performance [2]. In this work, the CofT-like prompts contain concrete but general examples for every given problem, along with a step-by-step explanation of how they should be solved. These examples are in Figure 5.
Another way to decrease hallucinations is to provide a prior context with problem information [37] and indications in the prompt so that the LLM knows in advance the type of problem to deal with and reasons in such a way that it can correctly classify the problems. The context is added at the beginning of each prompt in Zero-Shot, Few-Shot, and Chain of Thought techniques and corresponds to the following phrase:
“Consider the following problem: You will have four boxes arranged from left to right and each box has five balls inside arranged from top to bottom. Each box and each ball can be colored or uncolored. There will be an instruction and a solution that consists of colored and uncolored boxes and balls.
  • Your job is to verify if the proposed solution satisfies the instruction the verbatim.
  • Consider that there could be many possible solutions to the instruction.
  • Conclude only at the end of your answer.”
For the Chain of Thought, we added the following extra indication: "Analyze the instruction in detail before concluding" to add an extra reasoning step.

3.2.2. Visualization of Thought

While CofT decreases hallucinations in the LLM, this prompt is too specific, as the machine is given too many clues as to how it should reason when one of the main objectives is to observe its logical and spatial reasoning ability. We recall that the exercises were divided into logical and spatial exercises, and the presented prompts do not explicitly address both topics. For spatial exercises, Visualization of Thought is expected to perform better. The prompt consists of the same context used in Chain of Thought, a proposed solution introduced with emojis as in Figure 4 and followed by the question "Is the solution correct or incorrect? Visualize the state after each reasoning step". That is, the VofT technique is combined with Zero-Shot in how the instruction is performed and combined with a context according to the technique. This prompt gives No hints or specifications on how to reason.

3.2.3. Logic Prompting and Self-Consistency

Inspired by LogicLM, we propose another type of prompt to approach logic exercises. In LogicLM, several agents are used, and a specific one is in charge of translating the problem and writing it with symbolic mathematics. Our prompt adds an extra hint to the Zero-Shot technique at the end of the prompt: “Write the instruction using math quantifiers and then solve the problem”. This prompt emulates the intermediate step of LogicLM since we only have one agent. This prompt is expected to increase performance in exercises with quantifiers.
This ensures that the machine first translates the instruction into mathematical language and then verifies whether the proposed solution is correct or incorrect. With this prompt, the machine is expected to perform better for quantifiers and logic reasoning than visual statements.
A detail that has not been discussed in the previous prompts is the effect that the probabilistic nature of the generative models may have on the obtained answers. In order to mitigate these effects, Self-Consistency adapted for single-agent use is used. The original technique also consists of several agents, where one is in charge of receiving prompts and giving several answers with several thought paths. At the same time, another one takes all these answers and chooses the final value that is most repeated, ignoring the thought paths. The adaptation consists of generating several answers to the same prompt from the conversation with the LLM. The user is responsible for counting the repeated answers, thus concluding a final answer.
In this case, the prompt combines CofT with VofT but with general examples for all problems instead of particular examples for each one. The prompt starts with the context given in VofT, followed by two problems with instructions and proposed solutions written with emojis that are different from the other problems and with step-by-step instructions on how to solve each one. Figure 5 shows the two examples and their step-by-step input. At the end of the prompt, the instruction and proposed solution to be classified are entered with emojis, as in VofT, and the same question is asked in Zero-Shot. A total of five responses to the same prompt are generated per problem, and the most repeated label is chosen.
In order to have more variety of techniques and to test the logical reasoning of the LLMs, computer code generation prompts are tested, which, as a priori, should have good accuracy on the logical problems. The prompt is similar to the one used in Zero-Shot, with the addition of the indication “Generate a Python code to check whether the solution is correct or incorrect” at the end.

3.2.4. Emotional Prompting

The last tested prompt was inspired by the indications used in prompts in [38] for documentation search. It corresponds to a combination of VofT with Self-Consistency and a list of indications for the LLM to reason accordingly. The indications are the same as used in Visualization of Thought but adding the following:
  • “Write the instruction using math quantifiers and then solve the problem”, which implements the use of logic;
  • "Be careful to identify colors. It is different if a color is applied for all the balls in all boxes or each box has its own color for all its balls", preventing errors when interchanging quantifier positions;
  • “Visualize each logical step”, which implements the visualization of the steps;
  • "If the proposed solution is incorrect, don’t propose a correct solution", which prevents unnecessarily long responses, and
  • "Unless the instruction says otherwise, you have to check all balls in all boxes whether or not the boxes are painted or not", which prevents errors by not considering uncolored boxes.
The main motivation for this prompt is twofold: to solve common errors that occurred with the other techniques and to give the machine fewer examples so that it can reason for itself. In [38], an emotional prompt is used to prevent the virtual assistant from using certain computer language to write mathematical symbols. Instead, it is instructed to use the logical-mathematical language of quantifiers. In our case, the machine could deliver wrong answers by trying to give a final answer before reasoning, even if we tell it not to. That is why we tried two ways for this prompting: one where the machine is asked to conclude only after reasoning out the problem and another by adding emotional prompting with the indication "Conclude only at the end of your answer. If you conclude the correctness of the proposed solution before, an innocent kitty will die." In [6], it is evidenced that the use of emotional prompting improves the response of LLMs.
The proposed solution in this prompt is entered with emojis similar to VofT, and a total of five answers are generated, with the user in charge of choosing the most repeated one.

3.3. Experiments and Analysis

We used ChatGPT integrated with GPT-4o to correct the problems in this study. It was decided to use ChatGPT instead of OpenAI API because of its ease of use and ease of entering problems. In addition, teachers who choose to correct using an LLM are more likely to do so with ChatGPT than through an API. However, we do not discard the use of API in the future to create a correction app for this type of exercise.
For instructions 1, 2, 3, and 5, three solutions were considered, and for instruction 4, two were considered. These solutions are correct or incorrect depending on the instruction. They are all different from each other to give more variety and are different from the examples given in some prompting techniques. We consider the problems in Figure 2 and others in Figure 6. In total, we tested 14 different problems, and each problem is listed as x . 1 , x . 2 or x . 3 , where x corresponds to the instruction used. The indices 1, 2, and 3 do not represent anything specific; they are just an internal order for each instruction.
For the Zero-Shot, Few-Shot, Chain of Thought, and Visualization of Thought techniques, the prompts were entered into ChatGPT as a single prompt, and the first response generated was recorded. That is because, as if it were a human assistant, if ChatGPT is required to function as a virtual correction assistant that delivers immediate feedback to the teacher, the first answer it produces must necessarily be taken. Particular attention was given to the reasoning process used to arrive at the answer, as there are instances where the model may reach the correct conclusion through flawed reasoning, leading to false positives.
For prompts utilizing the Self-Consistency approach, the first five responses were generated, and the most repeated answer was selected, with intermediate reasoning disregarded due to the nature of the technique. This total choice of answers was merely made due to the machine’s limitations, which limit the number of answers it can give daily. In addition, generating several answers in ChatGPT for each problem takes time and human effort.
The results were classified with a score of 1 if ChatGPT provided the correct answer and demonstrated sound reasoning. A score of 0 was assigned if the model either produced an incorrect answer or arrived at a correct answer through faulty reasoning. This scoring system does not apply to the Self-Consistency prompts, where reasoning is inherently not evaluated. In the Results section, we provide detailed explanations of the 0 scores for each technique, highlighting instances of false positives.
Given our goal of using ChatGPT as an automatic teacher assistant to help teachers discuss with their students, solve the exercises, and offer detailed explanations, we also analyzed common ChatGPT errors in the reasoning process leading to the final answer. These errors were examined step by step to identify their origins, which ranged from logical and visual misunderstandings to instances of hallucination by the model. These findings will be elaborated on in the Results section.

4. Results

4.1. Performance in Correcting Coloring Activities

When directly entering the image into ChatGPT with a suitable prompt, it generally fails to count the colored balls in each box, although it does manage to determine the total number of boxes. Figure 7 shows an example of ChatGPT’s response.
Then, the need to write the problems in the same prompt and not rely on direct image input is justified since GPT’s ability to count balls and painted boxes in an image is unreliable.
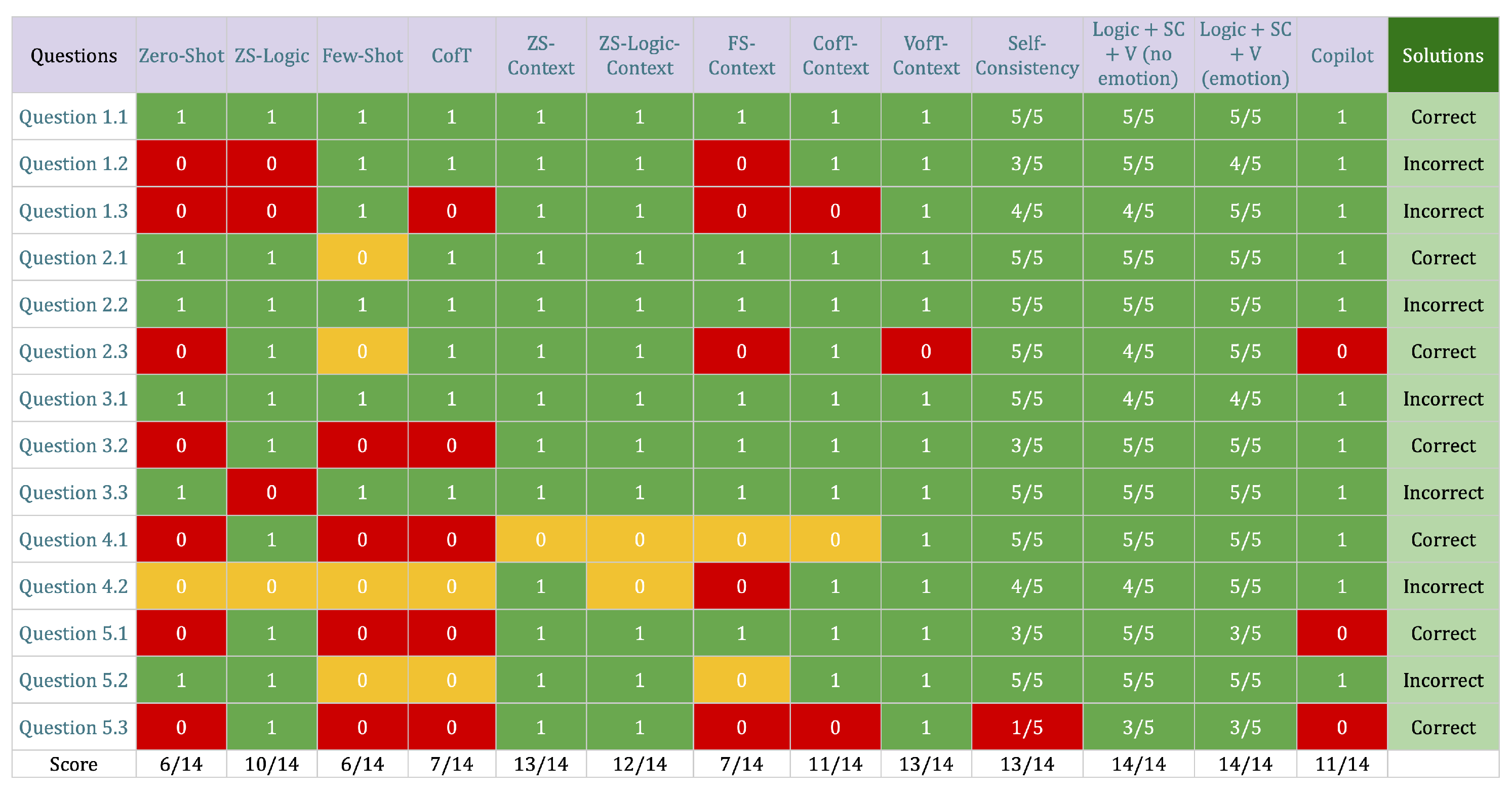
Regarding the prompting techniques used, the results are summarized in Figure 8. The columns represent each prompting technique employed, while the rows correspond to the problems to be corrected. The "Solutions" column indicates whether the solution proposed in each problem is correct or incorrect according to its instruction. The bottom row indicates the total score obtained, which corresponds to the sum of the ones and zeros of each column divided by the total number of problems, except for Self-Consistency and Logic-SC-V, where the score corresponds to the sum of green cells divided by the total number of questions.
The performance of GPT-4o was notably poor when using the Zero-Shot, Few-Shot, and Chain of Thought techniques. Specifically, both Zero-Shot and Few-Shot achieved a correction accuracy of only 43%. Chain of Thought performed slightly better, with a 50% success rate, excelling in simpler tasks, such as problem 1.1 or 2.2, but struggling significantly with problems in sections 4 and 5, which require more advanced visual reasoning.
However, the performance improved considerably when these same techniques were applied with prior context. The Zero-Shot technique saw the most dramatic improvement, reaching an accuracy of 93%, with errors only occurring in the visual reasoning tasks of instruction 4. In contrast, the Few-Shot technique showed only a slight improvement, correcting one additional problem compared to its counterpart without context. The Chain of Thought method also benefited from added context, increasing its success rate to 79%. Despite this overall improvement, it continued to exhibit reasoning errors, particularly in question 4.1, which heavily relied on spatial reasoning.
For the Zero-Shot with logic technique, there was a noticeable improvement over the classic Zero-Shot, although challenges remained, particularly in problems requiring logical development, such as questions 1.2 and 1.3. When context was added, a similar pattern to the other techniques emerged, with performance improving from 10 out of 14 correct answers without context to 12 out of 14 with context. The technique still faltered on questions 4.1 and 4.2, where spatial reasoning was crucial, reinforcing the need for prompts specifically designed for spatial visualization tasks.
Code-like answers generated using Copilot achieved a commendable accuracy rate of 79%, showing strong performance, especially in problems involving quantifiers. However, Copilot struggled with tasks like problems 5.1 and 5.3, which required visual reasoning and the identification of patterns influenced by initial conditions, characteristic of dynamical systems. These challenges likely contributed to its lower performance in these areas, highlighting a limitation in handling tasks that extend beyond traditional coding logic into more complex, visually dependent reasoning.
The Visualization of Thought technique enabled GPT-4o to achieve a 93% accuracy rate across all tasks, only failing to correctly address problem 2.3, where the primary focus was on mathematical logic involving quantifiers. This significant improvement compared to the other techniques clearly demonstrates the effectiveness of Visualization of Thought in enhancing GPT’s performance on tasks that require advanced visual reasoning.
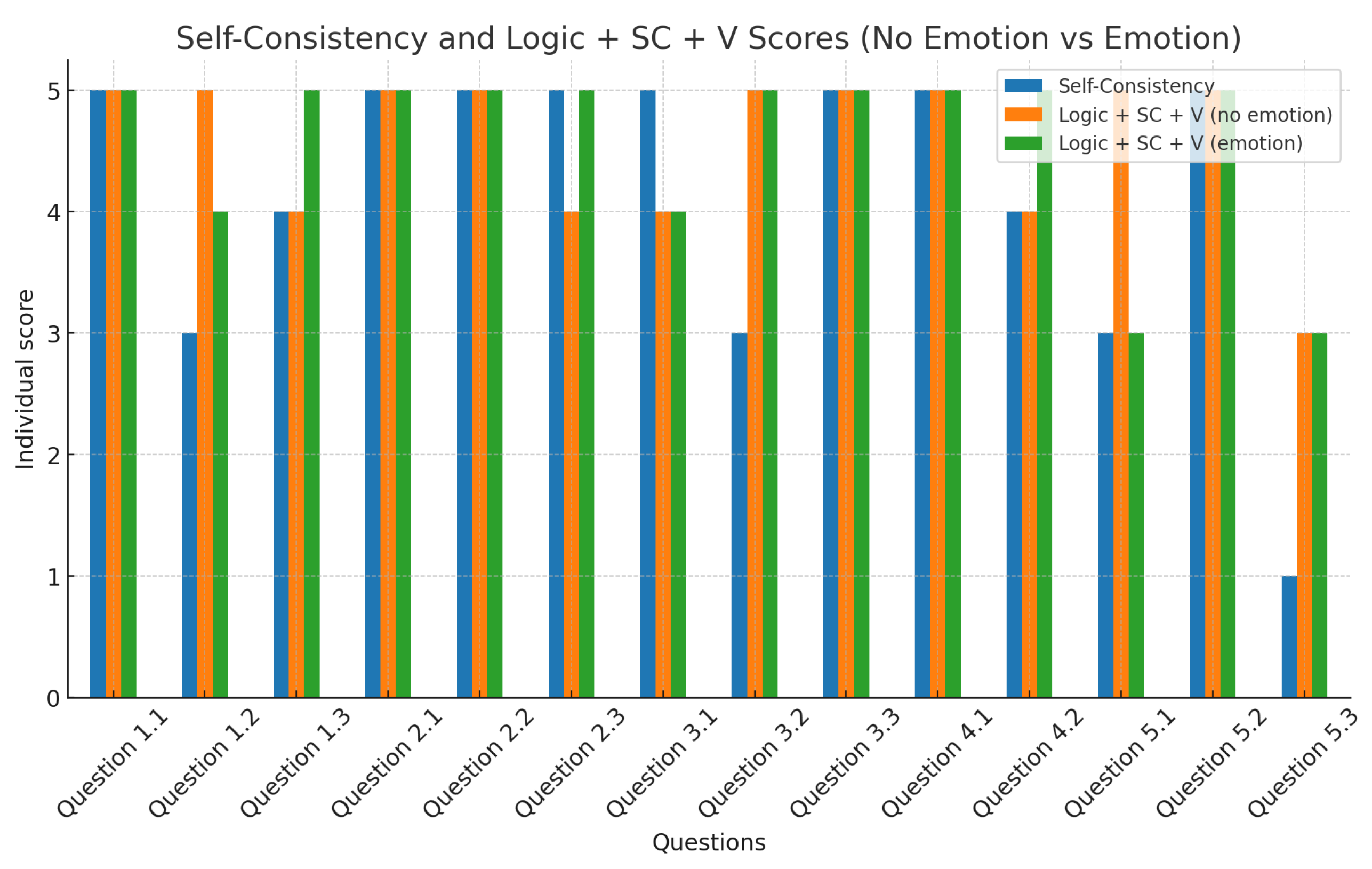
Prompts using Self-Consistency achieved outstanding performance among the various techniques tested. Self-consistency alone correctly solved 13 out of 14 problems, only failing on problem 5.3. Considering the total number of responses generated for each question, Self-Consistency accurately corrected 58 out of 70 cases, reflecting a performance rate of 83%
In addition, our new prompt, which combines different techniques from this study, achieved an accuracy of 100% in providing correct answers for all problems independent of adding an emotional prompt. Considering the total number of generated answers, both versions of the prompt achieved ChatGPT reaching the correct answer in 64 out of 70 cases, or performance of approximately 91%, but with correctness in different questions. Taking the total number of responses shows the robustness and consistency of the techniques used for these prompts, but no major differences between adding emotion and not adding emotion. In Figure 9, we compare the individual results obtained by Self-Consistency and our prompt with and without emotion.

4.2. Common Errors

In this section, we present the most common reasoning errors returned by ChatGPT. These errors were generally observed in prompts without context and/or without examples. We classify them as logic and spatial errors, as well as other errors that we found interesting to discuss.

4.2.1. Logic Errors

As previously discussed, the order of quantifiers is crucial in formulating logical statements. For instance, in instruction 1, the initial color choice is universal across all boxes, meaning the coloring condition must be applied using only that color. This contrasts with instruction 2, where the color is chosen separately for each box. Errors related to this distinction appeared frequently across various techniques, particularly in problems associated with instruction 1. Figure 10 illustrates a miscorrection in problem 1.3, where the solution was incorrectly marked as correct because one color was applied to each box.
Fortunately, adding appropriate context often mitigates this issue. However, to ensure it never occurs, it is advisable to explicitly specify the difference in the order of quantifiers within the prompt, as done in our prompt.
Another type of logical error, more prone to machine hallucinations, involves reaching false conclusions when there is sufficient evidence to conclude the opposite. For example, in Problem 2.3 using Zero-Shot without context, the analysis of the fourth box states, "Two balls are painted green, but the colors are split across green, orange, and blue, with no color having at least two balls." Here, the model correctly identifies two green balls but incorrectly concludes that there are at least two balls with no color.
A similar hallucination occurs in Problem 3.2 using Few-Shot with context. The model responds, "Box 1 has all balls painted green. Box 3 has all balls painted pink. However, the colors green and pink are not applied consistently across two or more boxes in a way that every ball in those boxes is painted the same color." Despite having sufficient evidence to conclude that two or more boxes have all their balls painted one color, the model still arrives at the wrong conclusion. This error persisted even with prior context and solved examples, suggesting that these alone may not be sufficient to eliminate hallucinations.

4.2.2. Spatial Errors

We define "spatial errors" as reasoning mistakes where ChatGPT fails to correctly interpret the positions of elements, leading to erroneous comparisons between objects. A common issue arises in problems related to instruction 4, where the model incorrectly compares the colors of balls in non-adjacent positions or boxes. In these instances, ChatGPT often arrives at the correct conclusions but through flawed reasoning. For example, in problem 4.1 using Chain of Thought with context, the model returned: "Box 1: Colors alternate between yellow and orange, with no two adjacent balls having the same color: Condition satisfied. Box 3: Colors alternate between yellow and orange, with no two adjacent balls having the same color: Condition satisfied," omitting the analysis of boxes 2 and 4, which, as a reminder, were both uncolored.
Another example occurs in the same problem using Chain of Thought without context: "In Box 1, balls are alternating between yellow and orange. In Box 3, balls are alternating between yellow and orange, but since Box 1 has the same pattern and both are painted, the balls in the same position in Box 1 and Box 3 share the same color (which violates the rule)." Here, the machine draws an incorrect conclusion by comparing two non-adjacent boxes, mistakenly assuming that only the colored boxes should be compared. Fortunately, the Visualization of Thought technique addresses this issue by preventing ChatGPT from comparing non-adjacent boxes, thereby improving the accuracy of its spatial reasoning.
In problems related to instruction 5, the machine often either confuses the colors of previous balls or misinterprets the instruction by assuming that if the previous ball is uncolored, it should take the ball’s color at the bottom of the previous box. For instance, in problem 5.3 using Chain of Thought with context, the machine concluded: "Box 2 (uncolored): ... ball 3 (uncolored): This should take the color of ball 3 from Box 1, which is uncolored. The color should then be taken from the bottom ball in Box 1, which is blue. Therefore, ball 3 should be blue, but it is uncolored, so this is incorrect." These types of errors are resolved through the use of Visualization of Thought or with our prompt.

4.2.3. Other

A recurring error observed when entering several prompts without context or specific instructions was early conclusion. In these instances, ChatGPT prematurely provides an answer on whether the solution is correct or incorrect before fully analyzing the problem. In many cases, the model later revises its initial answer, sometimes correcting it. When this happens, even if the final answer is correct, we classify it as a reasoning error. A clear example of this is shown in Figure 11. To mitigate this issue, our prompt includes the instruction both with and without emotion to ensure that the machine reaches a conclusion only after thoroughly reasoning through the problem.

5. Discussion

In addressing the research questions, the results of this study offer valuable insights but also highlight areas where further refinement and exploration are necessary.
First, regarding the extent to which GPT-4o can accurately assess and correct coloring activities involving logical quantifiers and spatial relationships, the findings demonstrate that while GPT-4o shows promise, its performance varies significantly depending on the prompting techniques used. The effectiveness of GPT-4o in accurately evaluating these activities is clearly dependent on how prompts are structured and the use of specific techniques, such as Visualization of Thought and Self-Consistency. These techniques, when applied, lead to a substantial increase in accuracy, with Visualization of Thought and Self-Consistency achieving 93%. However, there remain notable limitations in GPT-4o’s handling of complex spatial and logical tasks, particularly when techniques like Zero-Shot, Few-Shot, and Chain of Thought are employed without additional context. The performance is especially poor in tasks that require nuanced spatial reasoning and the correct application of logical quantifiers. The study reveals that in order to fulfill this first research question effectively, the reliance on simple prompting techniques without context is insufficient, and the model still requires structured, guided prompts to ensure accuracy.
The second research question, which explored the visual, logical, and correction capabilities of GPT-4o and the most effective prompts, finds a more conclusive answer. The study demonstrates that GPT-4o, particularly when guided by advanced techniques such as Visualization of Thought and Self-Consistency, can handle a wide range of logical and spatial tasks with commendable success. These results suggest that GPT-4o’s correction capabilities are highly dependent on the structure of the prompts, as shown by the 100% accuracy achieved with a combination of multiple techniques. Moreover, the inclusion of logic-enhanced prompts provides notable improvements over simpler prompting methods, although further development is needed to ensure that these techniques generalize well across different types of problems. For example, while logic-enhanced prompts address many logical errors, some spatial reasoning tasks remain challenging, particularly those involving the comparison of non-adjacent elements or complex dynamical systems. Hence, while the study successfully identifies several effective prompting strategies, further refinement is needed to enhance GPT-4o’s consistency across all problem types.
Using GPT-4o as a correction tool that classifies whether students’ answers are correct or incorrect is feasible when an appropriate context is provided, and a majority voting approach like Self-Consistency is employed. This approach ensures that, despite the varying reasoning paths the model might take, the majority of responses converge on the correct conclusion, thereby enhancing the robustness of the corrections.
However, it is still premature to conclude that ChatGPT can fully incorporate these elements when it comes to providing immediate reasoning feedback to teachers. While GPT-4o performs well in simpler tasks where the logical order of quantifiers is not critical—such as in problems 1.1 and 2.1—it struggles with more complex reasoning. This limitation is particularly evident in problems 4.1 and 4.2, where the model often fails to reason as expected, with visual techniques dominating its responses in these cases.
The third research question, regarding GPT-4o’s potential as a teaching assistant capable of providing immediate feedback, also sees mixed results. While GPT-4o shows the potential to support teachers by automating correction processes and offering immediate feedback, its inconsistencies in handling more complex tasks—especially those requiring spatial reasoning or careful application of logical quantifiers—suggest that it is not yet fully reliable for this role without careful prompt design and oversight. The errors identified in the common reasoning and spatial mistakes section indicate that without advanced prompting techniques, GPT-4o could introduce more confusion or errors in classroom discussions rather than providing the necessary clarity and support. Therefore, while GPT-4o offers significant potential as an educational tool, its use as a teaching assistant should be approached with caution, especially in tasks involving complex reasoning. More robust prompt engineering and possibly additional training for educators on how to effectively leverage these techniques may be required before widespread implementation in classrooms can occur.

5.1. Limitations

Despite these advances, there are several limitations and areas for improvement that could strengthen the study and further enhance the robustness of the results. One of the main limitations is the lack of a larger and more diverse sample of problems to correct. A broader and more varied dataset would enhance the reliability of the results and allow for a more comprehensive assessment of the LLM’s ability to correct coloring problems. Importantly, increasing variety should not simply involve adding more problems with similar instructions but should also incorporate problems with different logical structures that can be executed as coloring activities [11,12]. For example, introducing recursion by embedding boxes within boxes that satisfy additional conditions could add valuable complexity to the tasks.
Another challenge stems from using ChatGPT’s interface for entering prompts rather than utilizing APIs. While ChatGPT provides a user-friendly and widely accessible interface, it introduces inefficiencies for techniques like Self-Consistency, where obtaining responses can be a lengthy and tedious process due to the need for manual user intervention. This manual process also increases the risk of human error in data collection. Furthermore, the probabilistic nature of LLMs as generative models complicates reaching a precise conclusion for each problem. Although Self-Consistency can help mitigate this issue, it inherently lacks access to the underlying logical reasoning, making it insufficient for providing complete feedback. To overcome these limitations, more advanced prompting techniques, such as Multi-Agent or Self-Refine methods, should be explored, as they could potentially enhance performance in these exercises.
A significant limitation identified in this study is ChatGPT’s inability to accurately identify boxes and balls from images of the solved problems. This necessitates an additional step of manually rewriting the problems into the prompt, which increases the time and effort required for the task. This step not only adds to the cognitive load on researchers and educators but also introduces the potential for errors during transcription.
Additionally, while the study introduces a novel prompt that achieves 100% accuracy on the testing sample, it remains to be seen whether this performance holds across larger and more diverse datasets, as well as whether these majority response patterns are preserved at higher numbers of responses generated i.e., whether in prompts with Self-Consistency, the correctness ratio is preserved if more than five responses are considered, which were the ones we used in total in this study. Future research should evaluate the prompt on a wider array of problems, including those that incorporate more intricate logical structures, varied spatial configurations, and even scenarios that involve ambiguous or incomplete information. Such testing would help determine the scalability of the proposed techniques and their practical utility in real-world classroom settings.
Moreover, one of the key areas that remain underexplored is the model’s capacity to generalize to different types of logical or spatial tasks beyond those specifically tested in this study. The findings suggest that GPT-4o’s effectiveness is highly task-dependent, and it is unclear how well these prompting techniques would transfer to other domains of mathematics, logic, or visual reasoning. Expanding the study to include a broader variety of tasks, perhaps incorporating more complex dynamical systems or multi-step reasoning processes, could provide a more comprehensive understanding of GPT-4o’s capabilities and limitations.

5.2. Future Work

There are several areas that require further improvement and exploration, which should be addressed in future work. To make the application of this research feasible in a classroom setting, the development of more advanced techniques to provide immediate and reliable feedback is essential. This would likely involve transitioning to the use of APIs to develop specialized software tailored specifically for educational purposes. Such software would streamline the process, enabling real-time, accurate corrections and feedback, thereby enhancing the practicality and effectiveness of using LLMs in education.
Moreover, the current study focuses solely on the correction of coloring activities based on given instructions, but these tasks often require a more comprehensive assessment. Typically, students are also asked to explain their reasoning in a designated space below their solution (as illustrated in Figure 3). This explanation is crucial, as it reveals the student’s understanding and the logical processes behind their choices. At present, the study does not address the evaluation of these written explanations. However, future research should aim to integrate LLMs into this aspect of the assessment as well. By analyzing the correctness of the student’s explanation in relation to the instruction and solution and by assessing whether the explanation demonstrates an advanced logical approach, LLMs could provide valuable feedback on both the accuracy and depth of the student’s reasoning.
This capability would be particularly significant, as it would indicate that the student is not only following instructions but is also capable of applying deep mathematical concepts in their reasoning. Identifying and nurturing this ability is a key goal in education. Therefore, the development of prompting techniques that enable LLMs to detect and evaluate the application of advanced logical reasoning in student explanations would represent a major advancement in the use of AI in education. Such advancements could lead to more personalized and effective teaching strategies, ultimately helping students to develop stronger critical thinking and problem-solving skills.
While GPT-4o and its variants show great promise, the cognitive load on teachers remains a concern. The need for careful prompt crafting and oversight could potentially offset the benefits of automated correction, especially in high-stakes educational environments where accuracy is critical. Developing user-friendly interfaces or tools that help teachers more easily implement these advanced techniques could mitigate this issue and make AI systems like GPT-4o more accessible and practical for everyday classroom use.

6. Conclusions

The coloring activities presented in this study pose a significant challenge to traditional assessment methods. Unlike multiple-choice questions with a finite set of correct answers, these activities admit a vast array of correct solutions. This combinatorial nature of the problem creates a substantial cognitive load for teachers, who must carefully evaluate each student’s work to identify correct and incorrect elements. The risk of human error is high due to the volume and complexity of the tasks. Moreover, it is not feasible to provide the teacher with a list of correct solutions as in the multiple-choice case.
To address this challenge, we propose using AI, specifically GPT-4o, to assist teachers in the assessment process. By providing real-time feedback and explanations, GPT-4o can significantly reduce the teacher’s cognitive load and improve the accuracy of assessments. Our initial findings suggest that GPT-4o can effectively identify and correct errors in student work, particularly when using prompts that encourage detailed explanations. GPT4 can provide valuable support to the teacher, not only by assessing each student´s coloring but also by providing an explanation of why it is correct or incorrect.
However, it is essential to acknowledge that GPT-4o is still under development and may not be perfect in all cases. While the model has shown promising results, further testing with newer versions of GPT is necessary to refine its capabilities and address potential shortcomings, as well as to continue to explore ways and prompting techniques that will fully exploit ChatGPT’s capabilities. By continuously improving the AI tool and integrating it into classroom practice, we can create a powerful and supportive environment for teachers.
Ultimately, the goal is to develop AI-powered assessment tools that can not only identify errors but also provide meaningful feedback that helps teachers assess students’ work and help them explain to their students their mistakes. Thus, improve their students´ problem-solving skills. Combining teachers’ expertise with AI technology, we can create a more efficient and effective learning experience for all.
In conclusion, this study partially successfully addresses the research questions, highlighting both the potential and limitations of using the GPT-4o as a tool for assessing logical and spatial reasoning tasks in educational settings. Advanced guidance techniques demonstrate clear efficacy in improving accuracy, but areas remain to be explored and refined, particularly in ensuring consistent performance on a variety of problem types and reducing the cognitive load on educators. Future studies should continue to build on these results, expanding the scope of testing and refining methodologies to better integrate AI-based tools into educational practice.

Author Contributions

Conceptualization, R.A.; methodology, S.T. and R.A.; software, S.T.; validation, S.T. and R.A.; formal analysis, S.T. and R.A.; investigation, S.T. and R.A.; resources, R.A.; data curation, S.T. and R.A..; writing—original draft preparation, S.T.; writing—review and editing, S.T. and R.A.; visualization, S.T. and R.A.; supervision, R.A.; project administration, R.A.; funding acquisition, R.A.

Funding

This research was funded by ANID/PIA/ Basal Funds for Centers of Excellence FB0003.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Data including results and prompts can be found in https://drive.google.com/drive/folders/16qaNhPesgYnTymIXaSelZQtQeDAwn_YC?usp=sharing

Acknowledgments

Support from ANID/ PIA/ Basal Funds for Centers of Excellence FB0003 is gratefully acknowledged.

Conflicts of Interest

The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.

Appendix A. Tested Problems

Figure A1, Figure A2, Figure A3, Figure A4 and Figure A5 show all the problems used in this work.
Preprints 115591 g0a1
Figure A1. Problems for instruction 1.
Figure A1. Problems for instruction 1.
Preprints 115591 g0a1
Preprints 115591 g0a2
Figure A2. Problems for instruction 2.
Figure A2. Problems for instruction 2.
Preprints 115591 g0a2
Preprints 115591 g0a3
Figure A3. Problems for instruction 3.
Figure A3. Problems for instruction 3.
Preprints 115591 g0a3
Preprints 115591 g0a4
Figure A4. Problems for instruction 4. We omit the complete instruction in the images because it is too long.
Figure A4. Problems for instruction 4. We omit the complete instruction in the images because it is too long.
Preprints 115591 g0a4
Preprints 115591 g0a5
Figure A5. Problems for instruction 5. We omit the complete instruction in the images because it is too long.
Figure A5. Problems for instruction 5. We omit the complete instruction in the images because it is too long.
Preprints 115591 g0a5

References

  1. Araya, R. Gamification Strategies to Teach Algorithmic Thinking to First Graders. Advances in Human Factors in Training, Education, and Learning Sciences; Z., T.; Salman, K.W.N.; Ahram., Eds. Springer International Publishing, 2021, pp. 133–141.
  2. Wei, J.; Wang, X.; Schuurmans, D.; Bosma, M.; Ichter, B.; Xia, F.; Chi, E.; Le, Q.; Zhou, D. Chain-of-Thought Prompting Elicits Reasoning in Large Language Models. 2023; arXiv:cs.CL/2201.11903. [Google Scholar]
  3. Wu, W.; Mao, S.; Zhang, Y.; Xia, Y.; Dong, L.; Cui, L.; Wei, F. Mind’s Eye of LLMs: Visualization-of-Thought Elicits Spatial Reasoning in Large Language Models. 2024; arXiv:cs.CL/2404.03622. [Google Scholar]
  4. Wang, X.; Wei, J.; Schuurmans, D.; Le, Q.; Chi, E.; Narang, S.; Chowdhery, A.; Zhou, D. Self-Consistency Improves Chain of Thought Reasoning in Language Models. 2023; arXiv:cs.CL/2203.11171. [Google Scholar]
  5. Pan, L.; Albalak, A.; Wang, X.; Wang, W.Y. Logic-LM: Empowering Large Language Models with Symbolic Solvers for Faithful Logical Reasoning. 2023; arXiv:cs.CL/2305.12295. [Google Scholar]
  6. Li, C.; Wang, J.; Zhang, Y.; Zhu, K.; Hou, W.; Lian, J.; Luo, F.; Yang, Q.; Xie, X. Large Language Models Understand and Can be Enhanced by Emotional Stimuli. 2023; arXiv:cs.CL/2307.11760. [Google Scholar]
  7. Tversky, B. Visualizing thought. Topics in Cognitive Science 2011, 3, 499–535. [Google Scholar] [CrossRef] [PubMed]
  8. Franconeri, S.L.; Padilla, L.M.; Shah, P.; Zacks, J.M.; Hullman, J. The Science of Visual Data Communication: What Works. Psychological Science in the Public Interest 2021, 22, 110–161. [Google Scholar] [CrossRef] [PubMed]
  9. Fan, J.E.; Bainbridge, W.A.; Chamberlain, R.; Wammes, J.D. Drawing as a versatile cognitive tool, 2023. [CrossRef]
  10. OECD. New PISA results on creative thinking, 2024.
  11. Somsaman, K.; Isoda, M.; Araya, R., Eds. Guidebook for Unplugged Computational Thinking; SEAMEO STEM-ED, 2024; pp. 1–9.
  12. Araya, R.; Isoda, M. Unplugged Computational Thinking with Colouring Books. Journal of Southeast Asian Education, 2023; 72–91. [Google Scholar]
  13. Feldon, D. Cognitive Load and Classroom Teaching: The Double-Edged Sword of Automaticity. Educational Psychologist 2007, 42, 123–137. [Google Scholar] [CrossRef]
  14. Ravi, P.; Broski, A.; Stump, G.; Abelson, H.; Klopfer, E.; Breazeal, C. UNDERSTANDING TEACHER PERSPECTIVES AND EXPERIENCES AFTER DEPLOYMENT OF AI LITERACY CURRICULUM IN MIDDLE-SCHOOL CLASSROOMS. ICERI2023 Proceedings. IATED, 2023, ICERI2023. [CrossRef]
  15. Jones, C.R.; Bergen, B.K. People cannot distinguish GPT-4 from a human in a Turing test. ArXiv, 2024; abs/2405.08007. [Google Scholar]
  16. Urrutia, F.; Araya, R. Who’s the Best Detective? LLMs vs. MLs in Detecting Incoherent Fourth Grade Math Answers.
  17. Yan, L.; Sha, L.; Zhao, L.; Li, Y.; Martinez-Maldonado, R.; Chen, G.; Li, X.; Jin, Y.; Gašević, D. Practical and ethical challenges of large language models in education: A systematic scoping review, 2024. [CrossRef]
  18. Anderson, N.; McGowan, A.; Galway, L.; Hanna, P.; Collins, M.; Cutting, D. Implementing Generative AI and Large Language Models in Education. ISAS 2023 - 7th International Symposium on Innovative Approaches in Smart Technologies, Proceedings. Institute of Electrical and Electronics Engineers Inc., 2023. [CrossRef]
  19. Jeon, J.; Lee, S. Large language models in education: A focus on the complementary relationship between human teachers and ChatGPT. Education and Information Technologies 2023, 28, 15873–15892. [Google Scholar] [CrossRef]
  20. Pinto, G.; Cardoso-Pereira, I.; Ribeiro, D.M.; Lucena, D.; de Souza, A.; Gama, K. Large Language Models for Education: Grading Open-Ended Questions Using ChatGPT. 2023; arXiv:cs.SE/2307.16696. [Google Scholar]
  21. Rahman, M.M.; Watanobe, Y. ChatGPT for Education and Research: Opportunities, Threats, and Strategies. Applied Sciences (Switzerland) 2023, 13. [Google Scholar] [CrossRef]
  22. Wang, K.D.; Burkholder, E.; Wieman, C.; Salehi, S.; Haber, N. Examining the potential and pitfalls of ChatGPT in science and engineering problem-solving. Frontiers in Education 2023, 8. [Google Scholar] [CrossRef]
  23. Orrù, G.; Piarulli, A.; Conversano, C.; Gemignani, A. Human-like problem-solving abilities in large language models using ChatGPT. Frontiers in Artificial Intelligence 2023, 6. [Google Scholar] [CrossRef]
  24. Plevris, V.; Papazafeiropoulos, G.; Rios, A.J. Chatbots Put to the Test in Math and Logic Problems: A Comparison and Assessment of ChatGPT-3.5, ChatGPT-4, and Google Bard. AI (Switzerland) 2023, 4, 949–969. [Google Scholar] [CrossRef]
  25. Drori, I.; Zhang, S.; Shuttleworth, R.; Tang, L.; Lu, A.; Ke, E.; Liu, K.; Chen, L.; Tran, S.; Cheng, N.; Wang, R.; Singh, N.; Patti, T.L.; Lynch, J.; Shporer, A.; Verma, N.; Wu, E.; Strang, G. A neural network solves, explains, and generates university math problems by program synthesis and few-shot learning at human level. Proceedings of the National Academy of Sciences 2022, 119. [Google Scholar] [CrossRef] [PubMed]
  26. Collins, K.M.; Jiang, A.Q.; Frieder, S.; Wong, L.; Zilka, M.; Bhatt, U.; Lukasiewicz, T.; Wu, Y.; Tenenbaum, J.B.; Hart, W.; Gowers, T.; Li, W.; Weller, A.; Jamnik, M. Evaluating Language Models for Mathematics through Interactions. 2023; arXiv:cs.LG/2306.01694. [Google Scholar]
  27. Verma, A.; Mukherjee, K.; Potts, C.; Kreiss, E.; Fan, J.E. Evaluating human and machine understanding of data visualizations.
  28. Wang, B.; Yue, X.; Sun, H. Can ChatGPT Defend its Belief in Truth? Evaluating LLM Reasoning via Debate. 2023; arXiv:cs.CL/2305.13160. [Google Scholar]
  29. Yan, H.; Hu, X.; Wan, X.; Huang, C.; Zou, K.; Xu, S. Inherent limitations of LLMs regarding spatial information. 2023; arXiv:cs.CL/2312.03042. [Google Scholar]
  30. Maslej, N.; Fattorini, L.; Perrault, R.; Parli, V.; Reuel, A.; Brynjolfsson, E.; Etchemendy, J.; Ligett, K.; Lyons, T.; Manyika, J.; Niebles, J.C.; Shoham, Y.; Wald, R.; Clark, J. The AI Index 2024 Annual Report, 2024.
  31. Singh, K.; Khanna, M.; Biswas, A.; Moturi, P. ; Shivam. VISUAL PROMPTING METHODS FOR GPT-4V BASED ZERO-SHOT GRAPHIC LAYOUT DESIGN GENERATION. The Second Tiny Papers Track at ICLR 2024, 2024.
  32. Sharma, P.; Shaham, T.R.; Baradad, M.; Fu, S.; Rodriguez-Munoz, A.; Duggal, S.; Isola, P.; Torralba, A. A Vision Check-up for Language Models. 2024; arXiv:cs.CV/2401.01862. [Google Scholar]
  33. Musielak, Z.E.; Quarles, B. The three-body problem. Reports on Progress in Physics 2014, 77, 065901. [Google Scholar] [CrossRef] [PubMed]
  34. Guy, J.H.C.R.K. The Book of Numbers. The Crimean Karaim Bible 2019. [Google Scholar]
  35. Yang, Z.; Li, L.; Lin, K.; Wang, J.; Lin, C.C.; Liu, Z.; Wang, L. The Dawn of LMMs: Preliminary Explorations with GPT-4V(ision). 2023; arXiv:cs.CV/2309.17421. [Google Scholar]
  36. Huang, L.; Yu, W.; Ma, W.; Zhong, W.; Feng, Z.; Wang, H.; Chen, Q.; Peng, W.; Feng, X.; Qin, B.; Liu, T. A Survey on Hallucination in Large Language Models: Principles, Taxonomy, Challenges, and Open Questions. 2023; arXiv:cs.CL/2311.05232. [Google Scholar]
  37. DAIR.AI. Prompt Engineering Guide: Elements of a Prompt, 2024. https://www.promptingguide.ai/introduction/elements [Accessed: 2024-08-17].
  38. Photonics, M.Q.; Group, A. ChatTutor. https://github.com/ChatTutor/chattutor.git, 2023.
Preprints 115591 g001
Figure 1. Plot obtained from [30]. We can observe the growth in the visual reasoning index, surpassing the human baseline in recent years.
Figure 1. Plot obtained from [30]. We can observe the growth in the visual reasoning index, surpassing the human baseline in recent years.
Preprints 115591 g001
Preprints 115591 g002
Figure 2. Examples of the completed exercises by students with their instruction. Note that, from left to right, the first two are correct, whether the third is incorrect. In the blank box below, the student must explain in his or her own words how he or she solved the coloring problem.
Figure 2. Examples of the completed exercises by students with their instruction. Note that, from left to right, the first two are correct, whether the third is incorrect. In the blank box below, the student must explain in his or her own words how he or she solved the coloring problem.
Preprints 115591 g002
Preprints 115591 g003
Figure 3. Corresponding blank worksheet where each student has to write instructions to pose a problem to a peer.
Figure 3. Corresponding blank worksheet where each student has to write instructions to pose a problem to a peer.
Preprints 115591 g003
Preprints 115591 g004
Figure 4. Ways in which the boxes and balls were introduced in the prompts. On the left, the colors were given in parentheses, while on the right, colored emojis were used to give a visual aid for VofT and Self-Consistency.
Figure 4. Ways in which the boxes and balls were introduced in the prompts. On the left, the colors were given in parentheses, while on the right, colored emojis were used to give a visual aid for VofT and Self-Consistency.
Preprints 115591 g004
Preprints 115591 g005
Figure 5. Examples used in Self-Consistency and Chain of Thought prompts. For Chain of Thought, the emojis are replaced with text, as in Figure 4
Figure 5. Examples used in Self-Consistency and Chain of Thought prompts. For Chain of Thought, the emojis are replaced with text, as in Figure 4
Preprints 115591 g005
Preprints 115591 g006
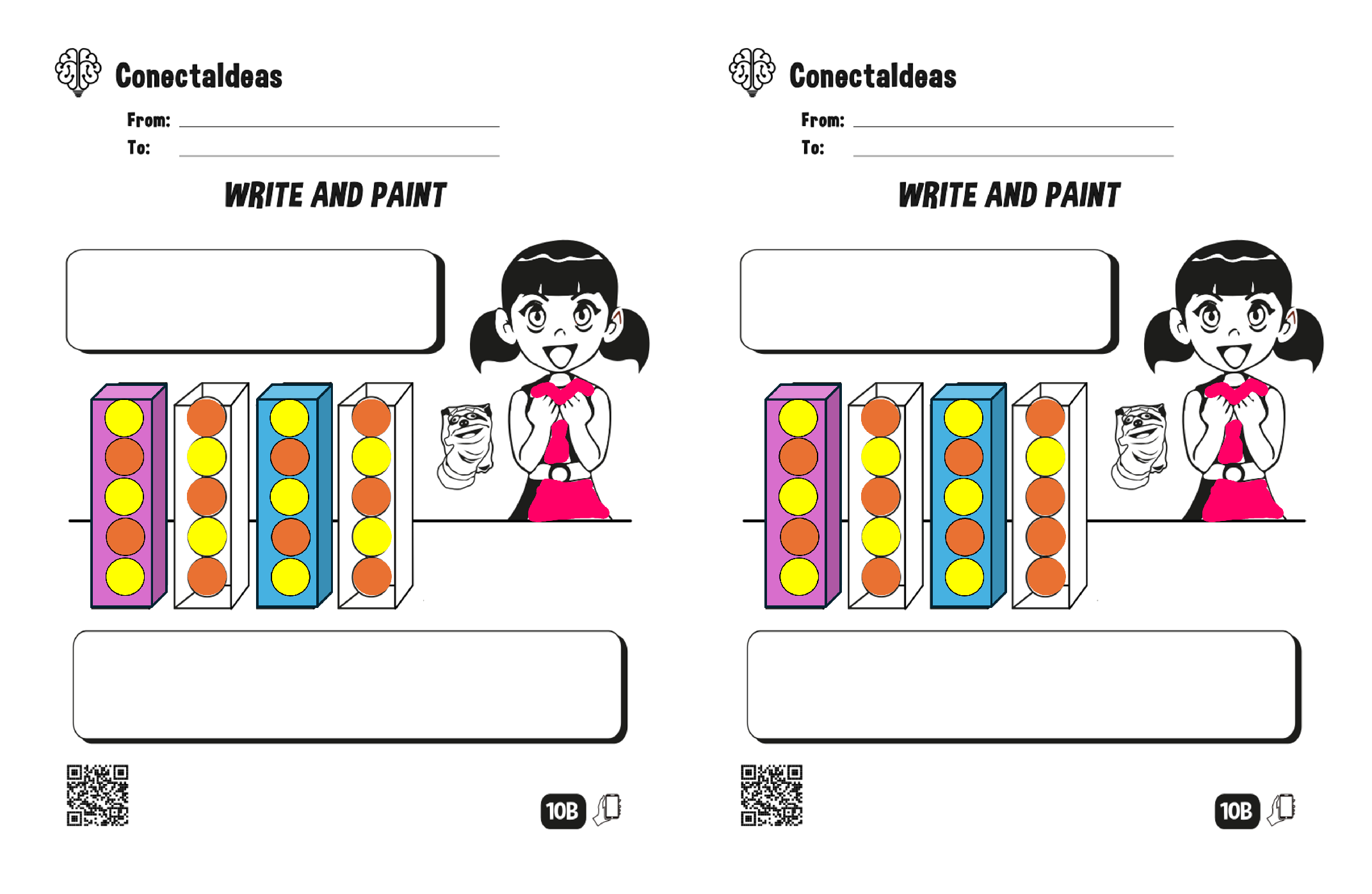
Figure 6. Some other problems tested in this work. The remaining are listed in Appendix A.
Figure 6. Some other problems tested in this work. The remaining are listed in Appendix A.
Preprints 115591 g006
Preprints 115591 g007
Figure 7. Example for instruction 1.1 by directly entering the image in Figure 2 with the proposed solution solved by a child.
Figure 7. Example for instruction 1.1 by directly entering the image in Figure 2 with the proposed solution solved by a child.
Preprints 115591 g007
Preprints 115591 g008
Figure 8. Results obtained for each technique in each problem. Cells in green indicate correct answers with correct reasoning, in yellow correct answers with incorrect reasoning, and in red incorrect answers. ZS stands for Zero-Shot, FS stands for Few-Shot, CofT stands for Chain of Thought, VofT stands for Visualization of Thought, and SC and V stand for Self-Consistency and Visualization, respectively.
Figure 8. Results obtained for each technique in each problem. Cells in green indicate correct answers with correct reasoning, in yellow correct answers with incorrect reasoning, and in red incorrect answers. ZS stands for Zero-Shot, FS stands for Few-Shot, CofT stands for Chain of Thought, VofT stands for Visualization of Thought, and SC and V stand for Self-Consistency and Visualization, respectively.
Preprints 115591 g008
Preprints 115591 g009
Figure 9. Individual scores for Self-Consistency and the two versions of our prompt. The vertical axis shows the number of correct answers given a total of 5 generated answers.
Figure 9. Individual scores for Self-Consistency and the two versions of our prompt. The vertical axis shows the number of correct answers given a total of 5 generated answers.
Preprints 115591 g009
Preprints 115591 g010
Figure 10. Error in correcting problem 1.3 while using Zero-Shot with logic but no context. The machine interprets the instruction as "For every box, there exists a color" when in fact, it is "There exists a color for every box".
Figure 10. Error in correcting problem 1.3 while using Zero-Shot with logic but no context. The machine interprets the instruction as "For every box, there exists a color" when in fact, it is "There exists a color for every box".
Preprints 115591 g010
Preprints 115591 g011
Figure 11. Early conclusion error in correcting problem 1.2 while using Zero-Shot without context. ChatGPT initially concludes that the solution is incorrect (which is accurate), but then reverses its decision, incorrectly stating that the solution is correct.
Figure 11. Early conclusion error in correcting problem 1.2 while using Zero-Shot without context. ChatGPT initially concludes that the solution is incorrect (which is accurate), but then reverses its decision, incorrectly stating that the solution is correct.
Preprints 115591 g011
Table 1. Problems with their quantifiers. This nomenclature is not common for a wide range of people.
Table 1. Problems with their quantifiers. This nomenclature is not common for a wide range of people.
Quantifiers Explanation
1. ∃ C color ∀ B box: | { b ∈ B : c o l o r ( b ) = C } | ≥ 2 The color C is applied for all the boxes.
2. ∀ B box ∃ C color: | { b ∈ B : c o l o r ( b ) = C } | ≥ 2 Each box has its own color to apply.
3. ∃ B i , B j boxes: ∃ C color ∀ b ∈ B i , B j , c o l o r ( b ) = C In two or more boxes a color is chosen and applied for every ball.
4*. ∀ i : ( C c o l o r , color(Bi) = C C, C c o l o r s , color(Bi-1) = C, color(Bi+1) = C ) (bjiBi, color(bji) color(bj+1i) color(bji) color(bji+1)) A box must be painted if the left and right boxes are not. Each ball has a different color than the ball below and the ball in the right box.
5*. ∀ i , j , ∀ b j i ∈ B i : (j1 color(bji) = color(bj-1i-1)) (color(b1i) =color(b5i-1)) A ball is painted with the color of the top-left ball or the bottom ball in the left box, if the ball to be painted is the first one.
* For simplicity, the notation does not include boundary cases in the indices.
Table 2. Probability of random hit on each instruction.
Table 2. Probability of random hit on each instruction.
Instruction Probability
1.- Choose a color and in each box paint at least 2 balls of that color. ≈ 0.025 %
2.- In each box choose a color and paint at least 2 balls of that color. ≈ 0.29 %
3.- In at least two boxes choose a color and paint each ball of that color. ≈ 0.0000000000000003 %
4.- Paint each box only if the adjacent boxes are not painted. Choose two other colors and in each box paint every ball such that each ball has a different color with the adjacent balls inside the box and the ball in the same position but in the adjacent boxes. ≤ 0.0000000000000003 %
5.- Choose a color and paint each ball with the ball’s color that is just above in the left adjacent box. If there is no ball above in the left adjacent box, paint with the ball’s color at the bottom of the left adjacent box. ≈ 0.000000000002 %
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated