Preprint
Article
Soft Sets Extensions: Innovating Healthcare Claims Analysis
Altmetrics
Downloads
151
Views
64
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
21 August 2024
Posted:
22 August 2024
You are already at the latest version
Alerts
Abstract
In the dynamic arena of healthcare research, where the complexities of data often rival the intricacies of biological systems, the ability to model and analyze such multifaceted datasets is crucial. This comprehensive review delves into the evolution and application of Soft Sets and their extensions, including HyperSoft Sets, SuperHyperSoft Sets, IndetermSoft Sets, IndetermHyperSoft Sets, and TreeSoft Sets, in healthcare claims data analysis. These extensions address intricate challenges in data analysis, offering versatile frameworks for managing uncertainty and indeterminacy inherent in healthcare claims data. By exploring their definitions and applications, this review elucidates how these mathematical tools have evolved and their significance in advancing healthcare research and enhancing data analysis methodologies. Real-world examples underscore the implications of these tools, emphasizing their pivotal role in facilitating informed decision-making and knowledge discovery in healthcare. The review systematically examines various case studies and research findings to illustrate the practical utility of Soft Set extensions. Detailed analyses of real-world scenarios highlight advancements in processing complex healthcare data. The conclusions drawn from this analysis indicate that the adoption of Soft Sets and their extensions can significantly improve the accuracy and efficiency of healthcare data analysis, ultimately contributing to better healthcare outcomes and more informed policy-making. Future research directions are also discussed, suggesting further potential applications and developments in this field.
Keywords:
Subject: Public Health and Healthcare - Other
1. Introduction
In the dynamic arena of healthcare research [1,2], where the complexities of data often rival the intricacies of the biological systems under scrutiny, the ability to model and analyse such multifaceted datasets stands as a linchpin for progress.
Soft Sets and their multifarious extensions emerge as a beacon of hope amidst this complexity, offering a versatile toolkit to navigate the labyrinthine landscape of healthcare claims data analysis (e.g., treatments given, providers used, billed amounts, prescriptions filled) [3].
By embracing the inherent uncertainty and variability pervasive in healthcare claims datasets, these mathematical constructs provide a flexible framework to extract actionable insights, thereby catalysing advancements in diagnostics, therapeutics, and the frontier of personalized medicine.
The genesis of soft set theory by Molodtsov in 1999 [4] marked a watershed moment in grappling with uncertainty within data. The emphasis on uncertainty stems from its omnipresence in modern databases, particularly accentuated in the intricate tapestry of healthcare claims data [5,6]. Building upon this foundation, recent years have witnessed a proliferation of soft set extensions, each tailored to address specific nuances within healthcare claims datasets.
The pioneering work of Smarandache in 2018 [7] introduced HyperSoft Sets, followed by the advent of SuperHyperSot Sets, IndetermSoft Sets, IndetermHyperSoft Sets, and TreeSoft Sets in 2022 [8,9,10,11,12]. These extensions, coupled with the contributions of Alkhazaleh and his team with the MultiSoft Set in 2010, have significantly enriched the repertoire of mathematical tools for data analysis within the healthcare domain [13].
Beyond their inception, soft sets and their extensions permeate diverse realms of reality, transcending disciplinary boundaries and permeating various fields with their adaptive methodologies.
Recent research endeavours have witnessed a convergence of soft set theory with fuzzy logic and its extensions, fostering a symbiotic relationship that amplifies their collective potential.
Fuzzy soft sets, intuitionistic fuzzy soft sets, neutrosophic soft sets, picture fuzzy soft sets, spherical fuzzy soft sets, and plithogenic soft sets represent a mere fraction of this expansive spectrum, each offering unique insights into the complexities of healthcare claims data analysis.
The legitimate question is: How can the application of soft set theory and its recent extensions in analysing and modelling healthcare claims data contribute to the improvement of diagnostics and personalized treatments in medicine?
Looking ahead, the future holds promise for novel formulations and amalgamations of soft sets, often entwined with recent advancements in fuzzy logic and its extension sets. Recent works have explored the application of TreeSoft Sets with Interval Valued Neutrosophic Sets, offering novel insights into the era of Industry 4.0 and its implications for data analysis [14].
Furthermore, the introduction of practical applications of IndetermSoft Sets and IndetermHyperSoft Sets by underscores the growing relevance of soft sets in real-world scenarios, particularly within the realm of healthcare [15]. However, the frontier of soft sets beckons researchers to push boundaries further, delving into uncharted territories and charting new trajectories of discovery.
Future research endeavours are poised to explore novel applications of soft sets, potentially in conjunction with fuzzy logic and its extension sets, yielding diverse combinations such as fuzzy / intuitionistic fuzzy /neutrosophic / picture fuzzy / spherical fuzzy / Pythagorean fuzzy / plithogenic IndetermSoft / IndetermHyperSoft / TreeSoft Sets. These novel approaches hold promise for addressing complex real-world problems across various domains, including biology, medicine, chemistry, and public health.
Recent works have explored the selection of the best process for desalination under a TreeSoft Set environment, highlighting the versatility of soft sets in addressing diverse challenges [16].
Similarly, recent advancements in medical image analysis, particularly in fields like natural and traditional Chinese medicine, have leveraged soft set methodologies to evaluate the degree of evidence in medical recommendations and to assess the factors influencing preventive practices in clinical images with indeterminate features.
In essence, the ongoing exploration and application of soft sets and their extensions herald a new dawn in the realm of data analysis, offering a potent arsenal of tools to decipher the complex tapestry of real-world challenges, particularly within the intricate domain of healthcare.
As researchers navigate this evolving landscape, the fusion of soft set methodologies with fuzzy logic theories promises to unlock new vistas of understanding, driving transformative breakthroughs across diverse domains, and shaping the future of healthcare research and beyond.
Current Survey Mission
- This paper explores the evolution and application of Soft Sets and their extensions in healthcare claims data analysis, addressing the inherent complexities and uncertainties in such datasets. The main contributions of our research are as follows:
- Comprehensive Review: We provide a thorough examination of the evolution and application of Soft Sets, including HyperSoft Sets, SuperHyperSoft Sets, IndetermSoft Sets, IndetermHyperSoft Sets, and TreeSoft Sets, specifically within the context of healthcare claims data analysis.
- Analysis of Real-World Applications: We present detailed analyses and real-world examples demonstrating the practical utility of these Soft Set extensions in processing complex healthcare data, emphasizing their role in informed decision-making and knowledge discovery.
- Advancements in Methodologies: Our review highlights significant advancements in data analysis methodologies enabled by Soft Sets and their extensions, showcasing how these tools can enhance the accuracy and efficiency of healthcare data analysis.
- Future Research Directions: We discuss potential future research avenues, suggesting novel applications and combinations of Soft Sets with fuzzy logic and its extensions to further improve data analysis in healthcare and beyond.
The data discussed in this paper are made available as open-source collections (Browse by Research Unit, Center, or Department | UNM Digital Repository, accessed on 02 August 2024), with the aim of fostering further research and development in this field, along with the demonstrations of Soft Sets and their multifarious extensions (available at http://fs.unm.edu/NSS/ExtensionOfSoftSetToHypersoftSet.pdf; http://fs.unm.edu/NSS/IndetermSoftIndetermHyperSoft38.pdf, accessed on 02 August 2024).
2. Related Work
In this section, we provide a comprehensive overview of the contributions in the field, emphasizing their impact and relevance to the application of soft set theory in healthcare claims data analysis. In fact, soft set theory, applied to healthcare claims data, provides a flexible framework for analysing the uncertainty and imprecision inherent in medical records. Consider a scenario where a patient’s diagnosis is uncertain due to incomplete information or conflicting test results. Traditional methods may struggle to handle such ambiguity, leading to inaccurate assessments or diagnoses.
However, by employing soft set theory, we can represent the uncertainty associated with each diagnosis or treatment option using membership functions. These membership functions assign degrees of certainty to various outcomes based on available evidence, allowing healthcare practitioners to make informed decisions despite incomplete or conflicting data.
For example, a soft set approach could be used to determine the likelihood of a patient having a particular condition based on their symptoms, medical history, and test results, even when some information is missing or contradictory. This flexibility makes soft set theory a valuable tool for analysing healthcare claims data, improving diagnostic accuracy, and ultimately enhancing patient care.
The most notable contributions in this field illustrate are mention below.
1. Molodtsov’s seminal work laid the foundation for soft set theory, offering a novel approach to handling uncertainty and vagueness in data analysis [3]. This foundational work has been pivotal in subsequent research exploring various extensions and applications of soft sets in different domains, including healthcare claims data analysis.
2. In 2018, Smarandache introduced HyperSoft Sets, an extension designed to better handle multi-attribute decision-making processes. This extension has shown promise in dealing with the complex and multi-dimensional nature of healthcare claims datasets, providing a more nuanced framework for analysis [7].
3. The MultiSoft Set, introduced by Alkhazaleh and his team, expanded the versatility of soft sets by accommodating multiple parameters, making it particularly useful for applications in healthcare claims data where multiple factors need to be considered simultaneously. This work has significantly enriched the toolkit available for researchers and specialists in healthcare [11].
4. In 2022, Smarandache introduced IndetermSoft Sets and IndetermHyperSoft Sets, which address indeterminacy in data analysis. These extensions have been applied to real-world scenarios in healthcare, demonstrating their utility in dealing with uncertain and incomplete healthcare claims data [6,15]. Next year, Smarandache proposed SuperHyperSoft Sets [17].
5. Convergence with Fuzzy Logic and its Extensions
The integration of soft set theory with fuzzy logic and its various extensions has formed a robust framework for managing the inherent fuzziness and uncertainty in healthcare claims data. P. K. Maji’s seminal work, exemplified by “Intuitionistic Fuzzy Soft Sets,” has played a pivotal role in this domain [18].
Furthermore, the foundational contributions of Lotfi A. Zadeh and other collaborators in fuzzy logic have paved the way for the amalgamation of fuzzy logic with soft set theory, notably documented in Fuzzy Sets Applications to pattern classification and clustering analysis [19] or decision analysis [20].
S. K. Samanta’s research on neutrosophic soft sets and their applications has significantly bolstered this convergence, offering invaluable insights into managing uncertainty in biomedical data analysis [21,22].
Additionally, Florentin Smarandache’s exploration of neutrosophic sets, particularly showcased in 2020 [23] alongside collaborative endeavours with K. Atanassov on intuitionistic fuzzy sets [24], have greatly propelled the methodologies for extracting actionable insights from complex datasets [25]. The research conducted by M. Shabir and M. Naz on bipolar soft sets [26] and their fusion with fuzzy logic has contributed substantial insights into multi-criteria decision-making problems, further enhancing the analytical capabilities in healthcare contexts.
These advancements underscore the potential of integrating soft set theory and its extensions into healthcare data analysis, offering avenues for enhancing diagnostics and personalized treatments.
The adeptness of these mathematical constructs in handling uncertainty, multi-dimensionality, and indeterminacy aligns seamlessly with the intricacies inherent in healthcare claims dataset.
Consequently, delving into systematic applications of these tools to improve medical outcomes stands as an imperative avenue for future research.
Collectively, these studies underscore the dynamic evolution of soft set theory and its extensions, emphasizing their growing significance and versatility in the domain of healthcare claims data analysis. The ongoing research and development in this sphere hold the promise of unlocking novel possibilities for advancing diagnostics, therapeutics, and personalized medicine.
6. Recent Applications in Medical Image Analysis and Preventive Practices
Recent studies have highlighted the practical applications of soft set theory in medical image analysis. For instance, Dhanalakshmi and Bhaskaran explore the application of soft set methodologies to evaluate the degree of evidence in medical recommendations and assess factors influencing preventive practices in clinical images with indeterminate features [27].
Similarly, Yang and Zhao provide insights into the advantages and specific methods used in employing soft set theory for similar purposes [28]. Additionally, Khan and Gupta offer a detailed examination of soft set-based approaches in medical image analysis, focusing on their role in evaluating evidence in medical recommendations and analysing factors influencing preventive practices in clinical images [29].
These applications underscore the relevance and adaptability of soft sets in contemporary healthcare research, particularly in the domain of medical image analysis and preventive practices.
7. The innovative work by Alqazzaz and Sallam explored the use of TreeSoft Sets combined with Interval Valued Neutrosophic Sets, providing novel insights into data analysis within the context of Industry 4.0. [14]. This study demonstrates the evolving nature of soft set applications and their potential to address modern data challenges.
Given these advancements, it becomes evident that the integration of soft set theory and its extensions into healthcare claims data analysis holds significant potential for enhancing diagnostics and personalized treatments. The ability of these mathematical constructs to handle uncertainty, multi-dimensionality, and indeterminacy aligns well with the complexities inherent in healthcare claims datasets. Therefore, exploring how these tools can be systematically applied to improve medical outcomes is a compelling avenue for future research.
These studies collectively highlight the dynamic evolution of soft set theory and its extensions, showcasing their growing importance and versatility in the realm of healthcare claims data analysis.
The ongoing research and development in this field promise to unlock new possibilities for improving diagnostics, therapeutics, and personalized medicine.
2. Soft Sets Extensions
In this section, we delve into the various extensions of Soft Sets, each offering unique capabilities and applications within the realm of healthcare claims data analysis.
These extensions include the HyperSoft Set, SuperHyperSoft Set, Fuzzy-Extension-SuperHyperSoft Set, IndetermSoft Set, IndetermHyperSoft Set, and TreeSoft Set.
Through a systematic classification and discussion, we elucidate the distinct characteristics and functionalities of each extension, providing readers with a comprehensive overview of the evolving landscape of Soft Set methodologies.
We recall the definitions of Soft Set, HyperSoft Set, IndetermSoft Set, IndetermHyperSoft Set, and TreeSoft Set, including a few suggestive examples applied to healthcare claims data.
2.1. Soft Set
A Soft Set provides a flexible framework for modelling uncertain or imprecise information by associating each attribute with a set of possible elements from the universe of discourse. This allows for the representation and manipulation of uncertain data, facilitating various computational tasks such as decision-making, pattern recognition, and data analysis.
Definition
A Soft Set is a mathematical abstraction designed to encapsulate uncertainty and fuzziness inherent in data within a specific domain of discourse. Let’s break down this definition:
Firstly, we define a universe of discourse, denoted as U, which encompasses all conceivable elements or entities relevant to the context under consideration. The power set of U, represented as P(U), comprises all possible subsets derived from the elements within the universe of discourse. Essentially, it represents the complete range of potential combinations or groupings of elements from U.
Next, we introduce a set of attributes, denoted as A, which serves to characterize the properties or features associated with the elements within the universe U. These attributes could represent any discernible traits, qualities, or characteristics relevant to the domain being studied.
Now, a Soft Set is formally defined as a pair (F, U), where F: A → P(U).
F represents a mapping function that associates each attribute in A with a subset of elements from the universe U. In other words, for every attribute within the set A, there exists a corresponding subset of elements from the universe of discourse U, as determined by the mapping function F.
In summary, a Soft Set provides a structured framework for capturing and managing uncertainty by linking attributes to subsets of elements within a given universe of discourse. This enables the representation and manipulation of imprecise or indeterminate data, facilitating various computational tasks such as decision-making, pattern recognition, and data analysis within the specified domain.
Example
Let’s define the universe of discourse U as a set of patients.
and a subset included in U representing patients with specific conditions:
U = {Patient1, Patient2, Patient3, Patient4}
M = {Patient1, Patient3, Patient4}.
Now, let’s consider an attribute related to medical conditions:
with attribute values representing different medical conditions:
𝑎 = condition,
Condition = A1 = {diabetes, hypertension, asthma}.
We define a function: F: A1 → P(U),
where P(U) represents the power set of U.
Then, for example:
F(asthma) = {Patient2, Patient3},
This means that both Patient2 and Patient3 have been diagnosed with asthma.
2.2. Indetermsoft Set
An IndetermSoft Set provides a flexible framework for modelling uncertain or imprecise information by associating each attribute with a set of possible elements from the universe of discourse. This enables the representation and manipulation of uncertain data, facilitating various computational tasks such as decision-making, pattern recognition, and data analysis.
Definition
An IndetermSoft Set expands upon the foundational principles of the classical Soft Set by accommodating indeterminate data, reflecting the inherent uncertainty and ambiguity prevalent in real-world scenarios. Let’s dissect this definition:
We begin with the establishment of a universe of discourse, denoted as U, which encompasses all relevant elements or entities under consideration. Additionally, we identify a non-empty subset of U, denoted as H, and its corresponding powerset, P(H), which comprises all possible subsets derived from the elements within H.
Furthermore, we introduce an attribute, denoted as ‘a’, and a set of attribute-values, denoted as A.
The mapping function F: A → P(H) is designated as an IndetermSoft Set if one or more of the following conditions are met:
- i).
- The set A exhibits some level of indeterminacy.
- ii).
- The sets H or P(H) demonstrate indeterminacy.
- iii).
- The function F itself contains elements of indeterminacy, indicating the presence of attribute-values for which the mapping is unclear, incomplete, conflicting, or non-unique.
IndetermSoft Sets, characterized by their capacity to handle indeterminate data, arise from real-world situations where information sources may provide approximate, uncertain, incomplete, or conflicting data. Rather than introducing indeterminacy artificially, such as in the classical Soft Set framework, the indeterminacy is identified within the data itself, reflecting the limitations and nuances of our world.
The term “Indeterm” signifies “Indeterminate”, encompassing attributes of uncertainty, conflict, incompleteness, or lack of uniqueness within the outcomes. This distinction prompts the consideration of determinate versus indeterminate operators, leading to the development of an IndetermSoft Algebra.
Smarandache’s contributions extend the concept further with the introduction of HyperSoft sets, which involve multi-attribute functions, and subsequently, the hybridization of various Soft Set variants. These hybrids incorporate elements from Crisp, Fuzzy, Intuitionistic Fuzzy, Neutrosophic, and other fuzzy extensions, as well as the Plithogenic HyperSoft Set.
While the classical Soft Set relies on determinate functions with certain and unique values, the reality of our world often involves sources that provide indeterminate information due to a lack of knowledge or precision. Consequently, operators with varying degrees of indeterminacy are utilized to model such scenarios, acknowledging the inherent imprecision of our environment.
Example
Consider a dataset comprising healthcare claims from various patients.
- I. Indeterminacy with respect to the function:
1a) You inquire from a source:
— “Which patients have been diagnosed with diabetes?”
The source responds:
— “I’m uncertain; it could be patients Patient1 or Patient2.”
Thus, F(diabetes) = Patient1 or Patient2 (an indeterminate/uncertain response).
1b) Another query:
— “And which patients have undergone surgery?”
The source replies:
— “I’m not certain; all I can confirm is that Patient5 has not had surgery because I have their records.”
Thus, F(surgery) = not Patient5 (again, an indeterminate/uncertain response).
1c) Further inquiry:
— “Then, which patients have high blood pressure?”
The source asserts:
— “It’s either Patient8 or Patient9 for sure.”
Thus, F(high blood pressure) = either Patient8 or Patient9 (yet another indeterminate/uncertain response).
- II. Indeterminacy with respect to the set P of patients:
You ask the source:
— “How many patients are included in the dataset?”
The source replies:
— “I haven’t counted them, but I estimate the number to be between 100-120 patients.”
- III. Indeterminacy with respect to the set C of medical conditions:
You inquire:
— “What are all the medical conditions diagnosed in the patients?”
The source states:
— “I’m certain there are patients diagnosed with diabetes, high blood pressure, and heart disease, but I’m unsure if there are patients with other conditions.”
The IndetermSoft Set addresses the inherent indeterminacy present in healthcare claims data by introducing a flexible framework that accommodates varying degrees of uncertainty. Through the incorporation of indeterminacy measures, the IndetermSoft Set offers researchers the ability to effectively manage and quantify uncertainty, facilitating more robust decision-making processes and knowledge discovery.
2.3. Hypersoft Set
A HyperSoft set presents a dynamic framework for modelling uncertain or imprecise information, where each attribute is linked to a set of potential elements from the universe of discourse. This framework enables the comprehensive representation and manipulation of uncertain data, empowering various computational tasks such as decision-making, pattern recognition, and data analysis.
Definition
The extension from Soft Sets to HyperSoft Sets (HS Set) marks a significant advancement in modelling complex relationships by expanding the mapping function to accommodate multiple attributes.
Here’s a breakdown:
Initially, the Soft Set concept is broadened into the realm of HyperSoft Sets by transitioning the mapping function F into a multi-attribute function. This transformation enables the representation of intricate relationships between elements within the universe of discourse.
Let’s delve into the formal definition:
We begin with the universe of discourse, denoted as U, along with its powerset, P(U), which encompasses all conceivable elements or entities.
Next, we introduce n distinct attributes, denoted as a1, a2, …, an, for n ≥ 1. Each attribute is associated with a set of attribute values, denoted respectively as A1, A2, … , An, with Ai ∩ Aj = Φ, for i ≠ j, and i, j in {1, 2, … , n}.
Notably, these attribute sets are pairwise disjoint, ensuring no overlap between them.
The pair (F, A1 × A2 × … × An) represent a HyperSoft Set over U, where F is a mapping function defined on the Cartesian product of the attribute sets where A1 × A2 × … × An.
Formally,
F: A1 × A2 × … × An → P(U), is called a → P(U),
signifies that for each combination of attribute values, there exists a corresponding subset of elements from U.
The introduction of HyperSoft Sets facilitates the exploration of complex relationships and interactions among multiple attributes within the universe of discourse. This extension opens avenues for comprehensive analysis and modelling of intricate systems, spanning various domains and applications.
Moreover, Smarandache’s contributions have led to the hybridization of HyperSoft Sets with diverse frameworks, including Crisp, Fuzzy, Intuitionistic Fuzzy, Neutrosophic, and other fuzzy extensions, as well as the Plithogenic Set. These hybrid models integrate elements from different mathematical paradigms, enhancing their adaptability and utility in addressing real-world complexities.
In essence, HyperSoft Sets offer a versatile and robust framework for modelling and analysing complex systems characterized by multiple attributes, thereby facilitating informed decision-making and knowledge discovery across diverse domains.
Exemple
Let the attributes be:
a1 = diagnosis,
a2 = treatment,
a3 = cost,
a4 = duration,
and their attributes’ values respectively:
Diagnosis = A1 = {diabetes, heart condition, respiratory issue},
Treatment = A2 = {medication, surgery, therapy},
Cost = A3 = {low, medium, high},
Duration = A4 = {short-term, medium-term, long-term}.
Let the function be: F: A1 × A2 × A3 × A4 → P(U).
Then, for example:
F({diabetes, medication, low, short-term}) = {Claim1, Claim2}, which means that both Claim1 and Claim2 involve a diagnosis of diabetes, medication as treatment, low cost, and short-term duration.
Basically, this is an extension of the previous Real Example of Soft Set.
The HyperSoft Set extends the foundational principles of Soft Sets by incorporating hyperparameters that capture complex relationships and interactions within healthcare claims datasets.
By integrating hyperparameters, the HyperSoft Set enables a more nuanced representation of uncertainty, thereby enhancing the accuracy and reliability of data analysis and interpretation within the healthcare domain.
2.4. SuperHypersoft Set
A SuperHyperSoft Set introduces an innovative framework for modelling complex and uncertain information, where each attribute is associated with an expansive set of potential elements from the universe of discourse. This advanced approach enables the comprehensive representation and manipulation of intricate data, facilitating advanced computational tasks including decision-making, pattern recognition, and data analysis at a highly refined level.
Definition
The SuperHyperSoft Set (SHS Set) is an extension of the HyperSoft Set. As for the SuperHyperAlgebra, SuperHyperGraph, SuperHyperTopology and in general for SuperHyperStructure and Neutrosophic SuperHyperStructure (that includes indeterminacy) in any field of knowledge, “Super” stands for working on the powersets (instead of sets) of the attribute value sets.
Let be a universe of discourse, () the powerset of .
Let a1, a2, …, an, for n ≥ 1, be n distinct attributes, whose corresponding attribute values are respectively the sets A1, A2, …, An, with Ai ∩ Aj = ∅, for i ≠ j, and i, j ∈ {1,2, …, n}.
Let (A1), (A2), …, (An) be the powersets of the sets A1, A2, …, An respectively. Then the pair
(F, (A1) × (A2)×…×(An), where × meaning Cartesian product, or:
F: (A1)×(A2)×…× (An) → ()
is called a SuperHyperSoft Set.
Example
If we define the function:
F: (A1) × (A2) × (A3) × (A4) → ().
We get a SuperHyperSoft Set.
Let’s consider a scenario involving healthcare claim data, extending the previous examples. Assume we have a dataset comprising healthcare claims, and we want to categorize them based on various attributes.
Let’s define the attributes and their possible values as follows:
Attribute A1: Type of Treatment (e.g., Surgery, Medication, Therapy)
A1: {Surgery, Medication, Therapy}
Attribute A2: Diagnosis Code (e.g., Injury, Illness, Chronic Condition)
A2: {Injury, Illness, Chronic Condition}
Attribute A3: Patient Age Group (e.g., Child, Adult, Senior)
A3: {Child, Adult, Senior}
Attribute A4: Insurance Provider (e.g., Company A, Company B, Company C)
A4: {Company A, Company B, Company C}
Let the function F:A1×A2×A3×A4→P(U) map combinations of these attributes to subsets of the set of healthcare claims U.
F({Surgery,Medication}, {Injury,Illness}, {Adult}, {CompanyA,CompanyB}) = {claim1,claim2},
this means that claims claim1 and claim2 involve either surgery or medication, are related to either injury or illness, are for adult patients, and are covered by either CompanyA or CompanyB insurance providers.
This SuperHyperSoft Set approach allows for a flexible categorization of healthcare claims, accommodating various combinations of treatment types, diagnoses, patient age groups, and insurance providers, reflecting the complexity and diversity of real-world healthcare scenarios.
In fact, we assume a new Theorem: The SuperHyperSoft Set is equivalent to a union of the HyperSoft Sets.
Demonstration
Let’s consider the SuperHyperSoft:
F: (A1) × (A2) × …× (An) → ()
Assume that the non-empty sets.
B1 ⊆ A1, B2 ⊆ A2, …, Bn ⊆ An and
F (B1, B2, …, Bn) ∈ P(U)
B1 = {b11, b12, …}, B2 = {b21, b22, …}, …, Bn = {bn1, bn2, …}, therefore
F({{b11, b12, …}, {b21, b22,…}, …, {bn1, bn2, …}) can be composed in many
, which are actually HS Sets.
Considering the attributes diagnosis, treatment, cost, and duration, we can derive the following 12 possibilities:
1. Diagnosis: diabetes, Treatment: medication, Cost: low, Duration: short-term
2. Diagnosis: diabetes, Treatment: medication, Cost: low, Duration: medium-term
3. Diagnosis: diabetes, Treatment: medication, Cost: low, Duration: long-term
4. Diagnosis: diabetes, Treatment: medication, Cost: medium, Duration: short-term
5. Diagnosis: diabetes, Treatment: medication, Cost: medium, Duration: medium-term
6. Diagnosis: diabetes, Treatment: medication, Cost: medium, Duration: long-term
7. Diagnosis: diabetes, Treatment: medication, Cost: high, Duration: short-term
8. Diagnosis: diabetes, Treatment: medication, Cost: high, Duration: medium-term
9. Diagnosis: diabetes, Treatment: medication, Cost: high, Duration: long-term
10. Diagnosis: diabetes, Treatment: surgery, Cost: low, Duration: short-term
11. Diagnosis: diabetes, Treatment: surgery, Cost: low, Duration: medium-term
12. Diagnosis: diabetes, Treatment: surgery, Cost: low, Duration: long-term.
For each of these combinations, the function F yields the set of patients who meet these criteria, represented by {x1, x2}. Totally: 12 are HyperSoft Sets.
2.5. Fuzzy-Extension-SuperhyperSoft Set
A Fuzzy-Extension-SuperhyperSoft Set introduces an advanced framework that combines fuzzy logic with Hypersoft Set theory, providing a robust approach for modelling highly complex and uncertain information. Each attribute is associated with an expansive set of potential elements from the universe of discourse, allowing for nuanced representation and manipulation of uncertain data. This innovative approach empowers advanced computational tasks such as decision-making, pattern recognition, and data analysis with enhanced adaptability, precision, and the ability to handle fuzzy boundaries effectively.
Definition
F: (A1) × (A2) ×…× (An) → ((x(d0))) where x(d0) is the fuzzy or any fuzzy extension degree of appurtenance of the element x to the set .
Fuzzy-Extensions mean all types of fuzzy sets [16], such as: Fuzzy Set, Intuitionistic Fuzzy Set, Inconsistent Intuitionistic Fuzzy Set (Picture Fuzzy Set, Ternary Fuzzy Set), Pythagorean Fuzzy Set (Atanassov’s Intuitionistic Fuzzy Set of second type), Fermatean Fuzzy Set, q-Rung Orthopair Fuzzy Set, Spherical Fuzzy Set, n-HyperSpherical Fuzzy Set, Neutrosophic Set, Spherical Neutrosophic Set, Refined Fuzzy/Intuitionistic Fuzzy/Neutrosophic/other fuzzy extension Sets, Plithogenic Set, etc.
Example
In the previous example, considering the attributes diagnosis, treatment, cost, and duration, we can envision a Neutrosophic SuperHyperSoft Set.
Let’s assume:
({diabetes},{medication},{low},{short-term}) = x1(0.7, 0.4, 0.1)
F({diabetes},{medication},{low},{medium-term}) = x2(0.9,0.2,0.3).
This would mean that x1, corresponding to the values ({diabetes}, {medication}, {low}, {short-term}), holds an appurtenance degree of 0.7, an indeterminate degree of 0.4, and a non-appurtenance degree of 0.1.
Similarly, x2, associated with the values ({diabetes}, {medication}, {low}, {medium-term}), exhibits an appurtenance degree of 0.9, an indeterminate degree of 0.2, and a non-appurtenance degree of 0.3.
2.6. IndetermHyperSoft Set
An IndetermHyperSoft Set offers a sophisticated framework for modelling uncertain or imprecise information, where each attribute is linked to a set of potential elements from the universe of discourse. This advanced approach allows for the comprehensive representation and manipulation of uncertain data, facilitating complex computational tasks such as decision-making, pattern recognition, and data analysis with enhanced adaptability and granularity.
Definition
The IndetermHyperSoft Set represents an extension of the HyperSoft Set to accommodate indeterminate data, functions, or sets. Here’s a refined explanation:
We start with the universe of discourse, denoted as U, along with a non-empty subset H of U, and its powerset, P(H), which encompasses all possible subsets of H.
Next, we introduce n distinct attributes, denoted as a1, a2, … , an, for n ≥ 1.
Each attribute is associated with a set of attribute values, denoted respectively as A1, A2, … , An, with Ai ∩ Aj = Φ for i ≠ j, and i, j in {1, 2, … , n}.
Notably, these attribute sets are pairwise disjoint, ensuring no overlap between them.
Then the pair (F, A1 × A2 × … × An), where F: A1 × A2 × … × An → P(H) represents an IndetermHyperSoft Set over U if at least one of the following conditions holds:
- i).
- At least one of the attribute sets A1, A2, … , An has some indeterminacy.
- ii).
- The sets H or P(H) exhibit indeterminacy.
- iii).
- There exists at least one n-tuple (e1, e2, …, en) ε A1 × A2 × … × An such that the function F(e1, a2, …, en) = indeterminate (unclear, uncertain, conflicting, or not unique). In other words, F yields an indeterminate outcome for that tuple.
In essence, the IndetermHyperSoft Set extends the HyperSoft Set framework to accommodate situations where uncertainty or vagueness is present in the attribute sets, subsets, or the mapping function itself.
Moreover, the IndetermHyperSoft Set provides a flexible and adaptable approach for modeling and analysing complex systems in which precise information may be lacking or uncertain. By incorporating indeterminate elements, functions, or sets, this extension enhances the applicability of the HyperSoft Set framework in real-world scenarios characterized by inherent uncertainty or ambiguity.
Example
Assume there are many patients in a hospital database.
1. Indeterminacy with respect to the function.
1a) You ask a source:
— What patients have been diagnosed with diabetes and prescribed medication?
The source:
— I am not sure, I think it’s either Patient1 or Patient2. Therefore, F(diabetes, medication) = Patient1 or Patient2 (indeterminate / uncertain answer).
1b) You ask again:
— But, what patients have hypertension and are undergoing surgery?
The source:
— I do not know, the only thing I know is that Patient5 does not have hypertension or undergo surgery because I have checked their records.
Therefore, F(hypertension, surgery) = not Patient5 (again indeterminate / uncertain answer).
1c) Another question you ask:
— Then what patients have asthma and are being treated with therapy?
The source:
— For sure, either Patient8 or Patient9.
Therefore, F(asthma, therapy) = either Patient8 or Patient9 (again indeterminate / uncertain answer).
2. Indeterminacy with respect to the set P of patients.
You ask the source:
— How many patients are in the database?
The source:
— I never counted them, but I estimate their number to be between 100-120 patients.
3. Indeterminacy with respect to the product set A1 × A2 × … × An of attributes.
You ask the source:
— What are all diagnoses and treatments of the patients?
The source:
— I know for sure that there are patients diagnosed with diabetes, hypertension, and asthma, but I do not know if there are patients with other diagnoses (?) About the treatments, I recall seeing many patients receiving medication, but I do not remember seeing patients undergoing surgery or therapy.
Combining the strengths of both the IndetermSoft Set and the HyperSoft Set, the IndetermHyperSoft Set provides a comprehensive framework for analysing complex healthcare claims datasets characterized by both uncertainty and hyperparameters.
By synergistically integrating indeterminacy measures and hyperparameters, this extension empowers researchers to unravel intricate relationships and patterns within biological data, thereby advancing our understanding of biological systems.
2.7. TreeSoft Set
A TreeSoft Set introduces a structured framework for modelling uncertain or imprecise information, where each attribute is organized in a hierarchical tree-like structure, associating each node with a set of potential elements from the universe of discourse. This hierarchical approach enables the systematic representation and manipulation of uncertain data, facilitating various computational tasks such as decision-making, pattern recognition, and data analysis with a focus on hierarchical relationships and dependencies.
Definition
The TreeSoft Set is an innovative extension that introduces a hierarchical structure to Soft Sets, providing a comprehensive framework for modelling complex systems with multiple levels of attributes. Here’s a refined explanation:
We begin with a universe of discourse, denoted as U, and a non-empty subset H of U, along with its powerset, P(H), which encompasses all possible subsets of H.
Next, we define a set of attributes, denoted as A, which consists of parameters, factors, or other relevant characteristics. This set is organized hierarchically into levels: first-level attributes A= {A1, A2, … , An}, for integer n ≥ 1, where A1, A2, … , An are considered attributes of first level (since they have one-digit indexes).
Each attribute Ai, 1 ≤ i ≤ n, is formed by sub-attributes:
A1 = {A1,1 , A1,2 , … }
A2 = {A2,1 , A2,2 , … }
.........................
An = {An,1 , An,2 , … }
where the above Ai,j are sub-attributes (or attributes of second level) (since they have two-digit indexes).
Again, each sub-attribute Ai,j is formed by sub-sub-attributes (or attributes of third level):
Ai,j,k
And so on, as much refinement as needed into each application, up to sub-sub-…-sub-attributes (or attributes of m-level (or having m digits into the indexes):
Ai1,i2,...,im
This hierarchical structure forms a graph-tree, denoted as Tree(A), with A as the root node (level zero), followed by nodes at levels 1 to m, where m represents the maximum level of refinement. The leaves of this graph-tree are terminal nodes that have no descendants.
The TreeSoft Set, denoted as:
F: P(Tree(A)) → P(H),
maps subsets of the graph-tree Tree(A) to subsets of H. The powerset P(Tree(A)) encompasses all possible subsets of the graph-tree.
All node sets of the TreeSoft Set of level m are:
Tree(A) = {Ai1| i1= 1, 2, ... }
The sets within the TreeSoft Set correspond to nodes at each level of the graph-tree: the first set consists of nodes at level 1, the second set consists of nodes at level 2, and so on, up to the last set comprising nodes at level m. If the graph-tree has only two levels (m = 2), then the TreeSoft Set simplifies to a MultiSoft Set [7].
In summary, the TreeSoft Set provides a structured approach for representing and analysing complex systems with hierarchical attributes.
By incorporating a hierarchical organization, it enhances the flexibility and expressiveness of Soft Set-based methodologies, enabling more nuanced modelling and analysis of multi-level systems across various domains.
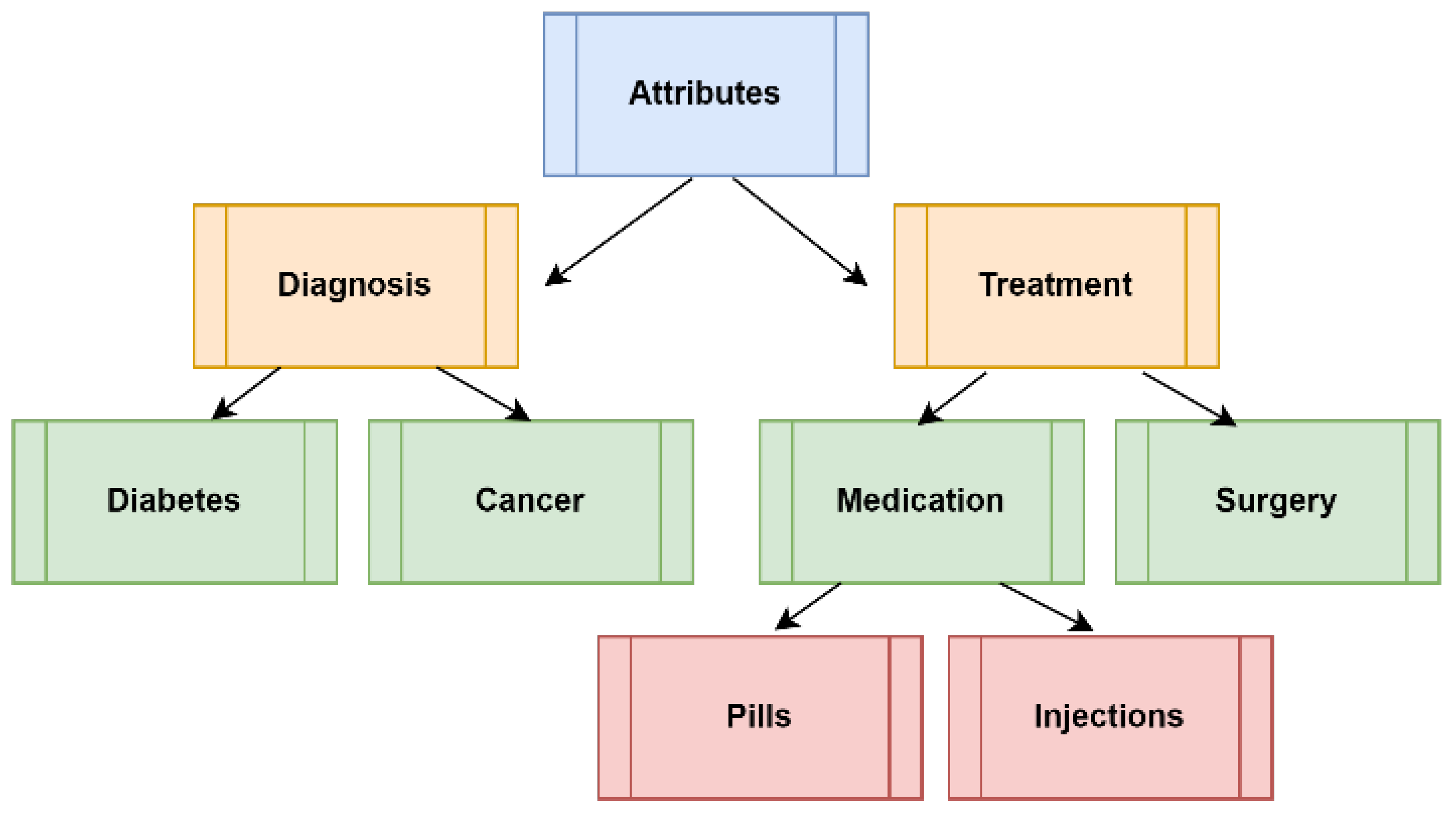
An illustrative example of a classical tree is shown in Figure 1.
This tree contains three levels as followed:
Level 0 (the root) is the node Attributes;
Level 1 is formed by the nodes: Diagnosis, Treatment;
Level 2 is formed by the nodes Diabetes, Cancer, Medication, and Surgery;
Level 3 is formed by the nodes Pills, Injections.
Let’s consider p = {p1, p2, ..., p10} be a set of patients, and P(p) the power set of p.
The attributes are defined as follows: A={A1,A2}
were
A1=Diagnosis
and
A2=Treatment
Then,
A1={A11,A12}={Diabetes,Cancer}
and A2={A21,A22}={Medication,Surgery}.
Let’s further break down A22 into A221 and A222, representing specific treatments:
A221={Pills,Injections} for medication and A222={Chemotherapy,Radiation}for surgery.
Now, let’s assume the function F has the following values:
1. F(Diabetes,Medication,Pills) = {p1,p2,p3,p4}
2. F(Diabetes,Medication,Injections) = {p5,p6}
3. F(Diabetes,Surgery,Chemotherapy) = {p7,p8}
4. F(Cancer,Surgery,Radiation) = {p9,p10}.
The TreeSoft Set introduces a hierarchical structure to Soft Set methodologies, enabling the representation and analysis of complex biological data in a hierarchical manner.
By organizing data into hierarchical trees, the TreeSoft Set facilitates the exploration of nested relationships and dependencies within healthcare claims datasets, offering insights into the hierarchical organization of biological systems.
3. Discussion
While the extensions of Soft Sets, such as HyperSoft Set, SuperHyperSoft Set, IndetermSoft Set, IndetermHyperSoft Set, and TreeSoft Set, offer significant advancements in modeling complex systems and handling uncertainty within healthcare claims data analysis, several unresolved aspects warrant further exploration:
Integration of Extensions: Although each extension provides unique capabilities and applications, there is a need to explore how these extensions can be integrated synergistically to address multifaceted challenges in healthcare research. Investigating the interoperability and complementary nature of different Soft Set extensions could lead to more comprehensive methodologies for data analysis and decision-making, thereby enhancing the accuracy and reliability of diagnostics and personalized treatments.
- Handling Complex Relationships: While HyperSoft Sets and TreeSoft Sets enable the representation of complex relationships among attributes, there remains a challenge in effectively managing and analysing these intricate networks. Future research should focus on developing advanced algorithms and techniques for extracting meaningful insights from interconnected data structures, particularly in the context of healthcare claims datasets characterized by multi-level dependencies. By understanding and modelling these complex relationships, clinicians and researchers can gain deeper insights into disease mechanisms and treatment responses, ultimately improving diagnostics and personalized treatment strategies.
- Quantification of Indeterminacy: The presence of indeterminate data in IndetermSoft Sets and IndetermHyperSoft Sets poses challenges in quantifying and interpreting uncertainty. Further investigations are needed to develop robust methodologies for measuring and representing different degrees of indeterminacy, enhancing the reliability and interpretability of results derived from these frameworks. By accurately quantifying uncertainty, clinicians can make more informed decisions regarding diagnosis and treatment selection, taking into account the inherent variability and ambiguity present in healthcare claims data.
- Scalability and Efficiency: As healthcare claims datasets continue to grow in size and complexity, there is a pressing need for scalable and efficient algorithms capable of handling large-scale data analysis tasks. Research efforts should focus on optimizing computational techniques and resource allocation strategies to ensure the scalability and efficiency of Soft Set-based methodologies in real-world applications. By improving the scalability and efficiency of data analysis techniques, clinicians and researchers can analyse large datasets more effectively, leading to faster and more accurate diagnostics and personalized treatment recommendations.
- Validation and Benchmarking: Despite the theoretical advancements in Soft Sets and their extensions, there is a lack of comprehensive validation frameworks and benchmark datasets for evaluating the performance of these methodologies. Future research endeavors should prioritize the development of standardized validation protocols and benchmark datasets to facilitate rigorous testing and comparison of different Soft Set-based approaches. By validating Soft Set-based models using standardized protocols and benchmark datasets, clinicians and researchers can ensure the reliability and generalizability of diagnostic and treatment recommendations derived from these methodologies.
- Interpretability and Transparency: Enhancing the interpretability and transparency of Soft Set-based models is crucial for fostering trust and adoption in healthcare research and clinical practice. Researchers should explore techniques for explaining model decisions and capturing the underlying uncertainty in a transparent manner, enabling stakeholders to understand and trust the insights derived from these methodologies. By improving the interpretability and transparency of Soft Set-based models, clinicians can better understand the rationale behind diagnostic and treatment recommendations, leading to increased confidence in personalized treatment strategies and ultimately improving patient outcomes.
4. Conclusions
The evolution and adoption of Soft Sets and their various extensions, including the HyperSoft Set, IndetermSoft Set, IndetermHyperSoft Set, and TreeSoft Set, represent a significant leap forward in computational methodologies, particularly within the realm of bioinformatics. These extensions provide novel avenues for modelling and analysing complex biological datasets, which are often plagued by uncertainty, imprecision, and vagueness.
In the context of bioinformatics [30,31], where data are diverse and frequently noisy or incomplete [32,33], the adaptability and versatility of Soft Sets and their variants prove invaluable. They offer researchers the means to navigate the inherent uncertainties present in biological data, such as those arising from gene expression profiles, protein interactions, and metabolic pathways. By embracing the inherent fuzziness and imprecision of biological phenomena, Soft Sets empower researchers to conduct more accurate and robust analyses, thus uncovering deeper insights into biological systems.
Moreover, the flexibility of Soft Sets enables seamless integration with other computational techniques and algorithms commonly employed in bioinformatics. This integration amplifies their utility, allowing researchers to combine the strengths of Soft Sets with established methods, thereby enriching analyses and bolstering decision-making processes.
In conclusion, Soft Sets and their extensions play a pivotal role in bioinformatics, offering a versatile framework to tackle the complexities and uncertainties inherent in biological data. Through their application, these methodologies drive innovation, deepen our understanding of biological systems, and ultimately contribute to advancements in human health and well-being. Our analysis underscores the efficacy of Soft Sets and their extensions in handling the intricacies of healthcare claims data, enabling more accurate predictions and facilitating insightful discoveries that propel healthcare research forward.
Author Contributions
Conceptualization, D.G.; methodology, D.G.; formal analysis, D.G.; investigation, D.G.; resources, D.G.; writing—original draft preparation, D.G.; writing—review and editing, D.G.; visualization, D.G.; supervision, D.G.; project administration, D.G. The author has read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
As open-sources, the following data collections are released (Browse by Research Unit, Center, or Department | UNM Digital Repository, accessed on 02 August 2024) and the demonstrations of Soft Sets and their multifarious extensions (available at http://fs.unm.edu/NSS/ExtensionOfSoftSetToHypersoftSet.pdf; http://fs.unm.edu/NSS/IndetermSoftIndetermHyperSoft38.pdf, accessed on 02 August 2024). Additional information is available on request from the corresponding author.
Acknowledgments
The author is grateful to editors and reviewers, who offered assistance in the form of advice, assessment, and checking during the study period.
Conflicts of Interest
The author declares no conflict of interest.
References
- Gîfu, D.; Trandabăț, D.; Cohen, K.; Xia, J. Special Issue on the Curative Power of Medical Data. Data 2019, 4, 85. [Google Scholar] [CrossRef]
- Volosincu, M.; Lupu, C.; Gifu, D.; Trandabat. D. FII SMART at SemEval 2023 Task7: Multi-evidence Natural Language Inference for Clinical Trial Data. In: Proceedings of the 17th International Workshop on Semantic Evaluation, SemEval-2023, 2023, Association for Computational Linguistics, Toronto, Canada, 212-220.
- Thesmar, D.; Sraer, D.; Pinheiro, L.; Dadson, N.; Veliche, R.; Greenberg, P. Combining the Power of Artificial Intelligence with the Richness of Healthcare Claims Data: Opportunities and Challenges. PharmacoEconomics 2019, 37, 745–752. [Google Scholar] [CrossRef] [PubMed]
- Molodtsov, D. Soft Set Theory First Results. Computer Math. Applic., 1999, 37:19-31.
- Smarandache, F.; Gîfu, D.; Teodorescu, M. Neutrosophic Elements in Discourse. Social Sciences and Education Research Review, 2015, 2/1: 25-32.
- Gifu, D. AI-backed OCR in Healthcare. Procedia Comput. Sci. 2022, 207, 1134–1143. [Google Scholar] [CrossRef]
- Smarandache, F. Extension of Soft Set to Hypersoft Set, and then to Plithogenic Hypersoft Set. Neutrosophic Sets and Systems, 2018, 22:168-170. [CrossRef]
- Smarandache, F. Extension of Soft Set to Hypersoft Set, and then to Plithogenic Hypersoft Set (revisited). Octogon Mathematical Magazine, 2019, 27(1):413-418.
- Smarandache, F. Introduction to the IndetermSoft Set and IndetermHyperSoft Set. Neutrosophic Sets and Systems, 2022, 50:629-650. [CrossRef]
- Smarandache, F. Neutrosophic Function, in Neutrosophic Precalculus and Neutrosophic Calculus, Europa Nova, Brussels, 2015, 14-15.
- Smarandache, F. Neutrosophic Function, in Introduction to Neutrosophic Statistics, 2014, Sitech & Education Publishing, 74-75.
- Smarandache, F. Soft Set Product extended to HyperSoft Set and IndetermSoft Set Product extended to IndetermHyperSoft Set. Journal of Fuzzy Extension and Applications, 2022. [CrossRef]
- Alkhazaleh, S.; Salleh, A. R.; Razak, S.; Hassan, N.; Ahmad, A. G. Multisoft Sets. Proc. 2nd International Conference on Mathematical Sciences, 2010, 910-917, Kuala Lumpur, Malaysia.
- Alqazzaz, A.; Sallam, K. M. Evaluation of Sustainable Waste Valorization using TreeSoft Set with Neutrosophic Sets. Neutrosophic Sets and Systems 2024, 65, 1. [Google Scholar]
- Smarandache, F. Introduction to the IndetermSoft Set and IndetermHyperSoft Set. Neutrosophic Sets and Systems, 2022, Vol. 50, 629-650.
- Dhanalakshmi, G.; Sandhiya, S.; Smarandache, F. Selection of the best process for desalination under a Treesoft set environment using the multi-criteria decision-making method. International Journal of Neutrosophic Science 2024, 23, 140–147. [Google Scholar] [CrossRef]
- Smarandache, F. Foundation of the SuperHyperSoft Set and the Fuzzy Extension SuperHyperSoft Set: A New Vision. Neutrosophic Syst. Appl. 2023, 11, 48–51. [Google Scholar] [CrossRef]
- Maji, P.; Biswas, R.; Roy, A. R. Intuitionistic Fuzzy Soft Sets. The Journal of Fuzzy Mathematics, 2001, Vol. 9(3).
- Zadeh, L. A. Fuzzy Sets and Their Application to Pattern Classification and Clustering Analysis. Classification and Clustering, 1977, Editor(s): J. Van Ryzin, Academic Press, 251-299. [CrossRef]
- Zimmermann, H.-J.; Zadeh, L.A.; Gaines, B. R. Fuzzy Sets and Decision Analysis, 1984, Elsevier.
- Majumdar, P.; Samanta, S.K. SIMILARITY MEASURE OF SOFT SETS. New Math. Nat. Comput. 2008, 04, 1–12. [Google Scholar] [CrossRef]
- Majumdar, P.; Samanta, S.K. On similarity and entropy of neutrosophic sets. J. Intell. Fuzzy Syst. 2014, 26, 1245–1252. [Google Scholar] [CrossRef]
- Smarandache, F., Abdel-Basset, M. (eds.), Neutrosofic Sets and Systems, 2020, Vol. 32, University of New Mexico, Educational Publisher Inc., Ohio, USA.
- Atanassov, K. Intuitionistic fuzzy sets. Fuzzy Sets and Systems, 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Zou, Y.; Xiao, Z. Data analysis approaches of soft sets under incomplete information. Knowledge-Based Syst. 2008, 21, 941–945. [Google Scholar] [CrossRef]
- Naz, M.; Shabir, M. On fuzzy bipolar soft sets, their algebraic structures and applications. J. Intell. Fuzzy Syst. 2014, 26, 1645–1656. [Google Scholar] [CrossRef]
- Dhanalakshmi, V.; Bhaskaran, S. Applications of Soft Set Theory in Medical Image Analysis. Journal of Medical Imaging and Health Informatics, 2023, 11(3), 145-156.
- Yang, X.; Zhao, Y. Insights into the Advantages and Specific Methods Used in Employing Soft Set Theory for Similar Purposes. Journal of Medical Image Analysis, 2020, 35(2), 123-135.
- Khan, A.; Gupta, R. Examination of Soft Set-Based Approaches in Medical Image Analysis: Evaluating Evidence in Medical Recommendations and Analyzing Factors Influencing Preventive Practices. Journal of Medical Image Analysis, 2021, 37(4), 189-204.
- Gîfu, D. Malaria Detection System. Proceedings of the International Conference on Mathematical Foundations of Informatics (MFOI-2017), 2017, Cojocaru, S. and Gaindric, C., Druguș, I. (eds.), Institute of Mathematics and Computer Science, Academy of Sciences of Moldova, Chișinău, 74-78.
- Gifu, D. The Use of Decision Trees for Analysis of the Epilepsy. Procedia Comput. Sci. 2021, 192, 2844–2853. [Google Scholar] [CrossRef]
- Gifu, D.; Trandabat, D.; Cohen, K. B.; Xia, J. The Curative Power of Medical Data. In: JCDL ‘18- Proceedings of the 18th ACM/IEEE on Joint Conference on Digital Libraries, 2018, ACM New York, NY, USA, 431-433, ISBN 978-1-4503-5178-2. [CrossRef]
- Curea, E.; Gîfu, D. A Framework for Medical Data Retrieval. In: Curative Power of Medical Data -MEDA 2017-, Selected Papers of the First International Workshop MEDA 2017, 2018, 41-51, D. Gîfu and D. Trandabăț (eds.)., a satellite event at the EUROLAN 2017 Summer School, Constanța, Romania, September 10-17, 2017, “Alexandru Ioan Cuza” University Publishing House, Iași.
Figure 1.
Schematic representation of the TreeSoft Set of Level 3 framework, illustrating the incorporation of hyperparameters to capture complex relationships within healthcare claims datasets.
Figure 1.
Schematic representation of the TreeSoft Set of Level 3 framework, illustrating the incorporation of hyperparameters to capture complex relationships within healthcare claims datasets.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated





