The Extremal Trees for Logarithmic VDB Topological Indices

Preprint

Article

The Extremal Trees for Logarithmic VDB Topological Indices

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

19 August 2024

Posted:

20 August 2024

You are already at the latest version

Alerts

Abstract

Vertex-degree-based (VDB) topological indices have been applied in QSPR/QSAR. As an important category, the general logarithmic VDB topological index $T_{lnf}(G)$, is defined as the summation of $ln{f(d(u),d(v))}$, where the summation over all $uv\in E(G)$. In this paper, we give the sufficient conditions for that (1) the path $P_{n}$ is the only tree with the minimal $T_{lnf}$; (2) the star $S_n$ is the only tree with the maximal and the minimal $T_{lnf}$, respectively. As applications, the minimal and maximal trees of some logarithmic VDB indices are determined.

Keywords:

Subject: Computer Science and Mathematics - Applied Mathematics

MSC: 05C05; 05C09; 05C92

1. Introduction

Topological indices (or graphical indices, or chemical indices) have an important role in studying the structures and properties of a molecular compound. Related studies have shown that topological indices are closely related to physico-chemical properties or biological activity [1,2]. Vertex-degree-based (VDB shortly) topological indices, as an important type of topological index, have long been considered and applied in QSPR/QSAR research [3,4]. Due to its importance in the field of chemistry, a large number of mathematical and chemical literature for the extremal values and extremal graphs have been published, and they are often considered and verified to have some excellent chemical properties. For relevant research, see [5,6,7].

Throughout the whole paper, all graphs we considered are simple, undirected and connected. Let G is a graph of order n, the vertex set and edge set are

V (G)

and

E (G)

, respectively. We use

d_{G} (u)

, or shortly by

d (u)

to represent the degree of vertex v. A vertex v is said to be pendant if

d (v) = 1

. If the edge

u v \in E (G)

, then the two vertices u and v in G are said to be adjacent. The vertex set adjacent to v is known as its neighbors, which denoted by

N_{G} (v)

N (v)

. If

u v \notin E (G)

, the graph

G + u v

represents the resulting graph by adding the edge

u v

from G. Meanwhile, we use

G - u v

represents the resulting graph by deleting the edge

u v

in G for the edge

u v \in E (G)

. We use

S_{n}

P_{n}

, and

T_{n}

to denote the star, the path, and the set of trees with order of n, respectively. Denote

S_{r, n - r}

to represent the double star with the degrees of two centers being r and

n - r

, where

2 \leq r \leq ⌊ \frac{n}{2} ⌋

A general VDB (vertex-degree-based) index of a connected graph G is defined as

T_{f} = T_{f} (G) = \sum_{u v \in E (G)} f (d (u), d (v)),

where

f (x, y) = f (y, x)

is a real symmetric function for

x \geq 1

and

y \geq 1

. To learn more about the relevant results, readers can refer to [8,9,10]. Especially, Gutman in [8] collected some important and well-studied VDB topological indices.

In 2019, the exponential of

T_{f}

, was first introduced in [11] by Rada, is defined as

T_{e^{f}} = T_{e^{f}} (G) = \sum_{u v \in E (G)} e^{f (d (u), d (v))} = \sum_{u v \in E (G)} β (d (u), d (v)),

where

β (x, y) = e^{f (x, y)}

. The notation

T_{e^{f}}

is known as an exponential VDB topological index, or abbreviated as exponential VDB index.

The sdudy of VDB topological index has attracted increasing attention, especially, to find the extremal values of

T_{f}

T_{e^{f}}

for some special types of graphs. The authors in [12] provides a general way to obtain whether the star

S_{n}

or the path

P_{n}

are extremal trees of the VDB topological index. Also, if

f (x, y)

is concave upwards and increasing relative to the variable x, the maximum trees of

T_{f}

were determined in [13]. Gao in [14] provided some conditions for the function

f (x, y)

. If

f (x, y)

satisfies some conditions, then the necessary and sufficient conditions for a chemical tree to be a maximal

T_{f}

are attained. Very recently, the authors [15] gave sufficient conditions for

P_{n}

is the only tree with the smallest

T_{e^{f}}

, the sufficient conditions for

S_{n}

S_{⌊ \frac{n - 2}{2} ⌋, ⌈ \frac{n - 2}{2} ⌉}

is the only tree with the largest

T_{e^{f}}

. For research on

T_{f}

T_{e^{f}}

, readers can refer to [16,17,18].

Inspired by [11], we introduce a new VDB topological indices, the logarithmic topological index, it is defined as

T_{l n f} = T_{l n f} (G) = \sum_{u v \in E (G)} l n f (d (u), d (v)) = \sum_{u v \in E (G)} γ (d (u), d (v)),

where

γ (x, y) = l n f (x, y)

, and

f (x, y) = f (y, x)

is a real symmetric function for

x \geq 1

and

y \geq 1

. As a VDB topological indices corresponding to exponential of

T_{f}

, the study for logarithmic of

T_{l n f}

is of great significance.

In this paper, we mainly studied the extremal trees for logarithmic VDB topological indices. In section 3, we give the sufficient conditions for that the path

P_{n}

is the only tree with the minimal

T_{l n f}

. In section 4, we obtain the sufficient conditions for that the star

S_{n}

is the only tree with the maximal and minimal

T_{l n f}

. In addition, as applications, the minimal and maximal trees of some logarithmic VDB indices are determined in section 5.

2. Preliminaries

In the remainder of the paper, assume that

γ (x, y) = l n f (x, y)

, and

f (x, y) = f (y, x)

is the real symmetric function, where

x \geq 1

and

y \geq 1

. In this section, we give the some lemmas firstly.

Lemma 1.

\frac{\partial f}{\partial x} > 0

, then

γ (x, y)

is strictly increasing on

x \geq 1

Proof.

Since

\frac{\partial γ}{\partial x} = {(l n f (x, y))}_{x}^{'} = \frac{f_{x}^{'} (x, y)}{f (x, y)}

, thus

γ (x, y)

is strictly increasing on

x \geq 1

under the condition

\frac{\partial f}{\partial x} > 0

. □

Lemma 2.

Let

γ (x, y) = l n f (x, y)

, where

f (x, y) > 0

for

x, y \geq 1

. For any positive integer

r \geq 1

, if

f (x_{1}, y_{1}) \cdot f (x_{2}, y_{2}) \dots f (x_{r}, y_{r}) \geq f (x_{1}^{'}, y_{1}^{'}) \cdot f (x_{2}^{'}, y_{2}^{'}) \dots f (x_{r}^{'}, y_{r}^{'})

, then

γ (x_{1}, y_{1}) + γ (x_{2}, y_{2}) + \dots + γ (x_{r}, y_{r}) \geq γ (x_{1}^{'}, y_{1}^{'}) + γ (x_{2}^{'}, y_{2}^{'}) + \dots + γ (x_{r}^{'}, y_{r}^{'}) .

Proof.

Since

γ (x, y) = l n f (x, y)

, according to the condition of lemma, we have

\begin{matrix} γ (x_{1}, y_{1}) + γ (x_{2}, y_{2}) + \dots + γ (x_{r}, y_{r}) - (γ (x_{1}^{'}, y_{1}^{'}) + γ (x_{2}^{'}, y_{2}^{'}) + \dots + γ (x_{r}^{'}, y_{r}^{'})) \\ = l n \frac{f (x_{1}, y_{1}) \cdot f (x_{2}, y_{2}) \dots f (x_{r}, y_{r})}{f (x_{1}^{'}, y_{1}^{'}) \cdot f (x_{2}^{'}, y_{2}^{'}) \dots f (x_{r}^{'}, y_{r}^{'})} \geq l n 1 = 0 . \end{matrix}

So, the lemma is proved. □

Lemma 3.

Let

f (x, y) = {(x y)}^{α} (α > 0)

, then

f (x, y) = g (x) h (y)

, and

g {(s + 1)}^{s + 1} \cdot g {(t + 1)}^{t + 1} < g (1) \cdot g {(s + t + 1)}^{s + t + 1}

, where

s, t \geq 1

Proof.

Clearly,

f (x, y) = {(x y)}^{α} = g (x) h (y)

, where

g (x) = x^{α}

, and

h (y) = y^{α}

. In the following, we will verify that

g {(s + 1)}^{s + 1} \cdot g {(t + 1)}^{t + 1} < g (1) \cdot g {(s + t + 1)}^{s + t + 1}

Without loss of generality, assuming

s \leq t

. Note that

\begin{matrix} g {(s + t + 1)}^{s + t + 1} = {(s + t + 1)}^{α (s + t + 1)} \\ = {(t + 1)}^{α (t + 1)} \cdot {(\frac{s + t + 1}{t + 1})}^{α (t + 1)} \cdot {(s + t + 1)}^{α s} \\ = g {(t + 1)}^{t + 1} \cdot {(\frac{s + t + 1}{t + 1})}^{α (t + 1)} \cdot {(s + t + 1)}^{α s}, \end{matrix}

thus, lemma is true if the equality

g {(s + 1)}^{s + 1} = {(s + 1)}^{α (s + 1)} < {(\frac{s + t + 1}{t + 1})}^{α (t + 1)} \cdot {(s + t + 1)}^{α s}

holds, i.e.

\begin{matrix} {(\frac{s + t + 1}{t + 1})}^{t + 1} \cdot {(\frac{s + t + 1}{t + 1})}^{s + 1} > 1 + s . \end{matrix}

s = 1, 2

, then

\begin{matrix} {(\frac{s + t + 1}{t + 1})}^{(t + 1)} \cdot {(\frac{s + t + 1}{s + 1})}^{s} = \{\begin{matrix} {(\frac{3}{2})}^{2} (\frac{3}{2}) > 1 + 1 = 2, & if t = s = 1, \\ {(\frac{5}{3})}^{2} (\frac{5}{3}) > 1 + 2 = 3, & if t = s = 2 . \end{matrix} \end{matrix}

and

\begin{matrix} {(\frac{s + t + 1}{t + 1})}^{(t + 1)} \cdot {(\frac{s + t + 1}{s + 1})}^{s} > {(\frac{s + t + 1}{s + 1})}^{s} \\ = \{\begin{matrix} {(\frac{1 + 2 + 1}{2})}^{1} = 2 \geq 1 + 1 = 2, & if t > s = 1, \\ {(\frac{2 + 3 + 1}{2})}^{2} = 4 \geq 1 + 2 = 3, & if t > s = 2 . \end{matrix} \end{matrix}

s \geq 3

, and because

t \geq s

, then

\begin{matrix} {(\frac{s + t + 1}{t + 1})}^{(t + 1)} \cdot {(\frac{s + t + 1}{s + 1})}^{s} > {(\frac{s + t + 1}{s + 1})}^{s} \geq {(\frac{2 s + 1}{s + 1})}^{s} = {(1 + \frac{s}{s + 1})}^{s} \\ \geq C_{s}^{0} + C_{s}^{1} \frac{s}{s + 1} + C_{s}^{2} {(\frac{s}{s + 1})}^{2} + C_{s}^{3} {(\frac{s}{s + 1})}^{3} \\ = 1 + \frac{s^{2}}{s + 1} + \frac{s (s - 1) s^{2}}{2 {(s + 1)}^{2}} + \frac{s (s - 1) (s - 2) s^{3}}{6 {(s + 1)}^{3}} \\ \geq 1 + \frac{s^{2}}{s + 1} + \frac{s^{3}}{{(s + 1)}^{2}} + \frac{s^{3} (s - 2)}{{(s + 1)}^{3}} \\ > 1 + s [\frac{s {(s + 1)}^{2} + {(s + 1)}^{2}}{{(s + 1)}^{3}}] \\ = 1 + s . \end{matrix}

So, the lemma is proved. □

Lemma 4.

Let binary function

f (x, y) = \frac{x y}{x + y}

, where

x \geq 1

and

y \geq 1

. Then,

(1)

\frac{\partial f}{\partial x} < 0

f_{x x}^{''} f - {f_{x}^{'}}^{2} < 0

; and

(2)

f {(d, 1)}^{d - 1} \cdot f {(n - d, 1)}^{n - d - 1} \cdot f (d, n - d) > f {(n - 1, 1)}^{n - 1}

, where

2 \leq d \leq ⌊ \frac{n}{2} ⌋

Proof. (1) Since

\frac{\partial f}{\partial x} = \frac{y - x y}{{(x + y)}^{2}}

, and

x, y \geq 1

, thus

\frac{\partial f}{\partial x} < 0

. Note that

\begin{matrix} f_{x x}^{''} = {(\frac{y - x y}{{(x + y)}^{2}})}^{'} = \frac{- y^{2} + x y - 2 y}{{(x + y)}^{3}}, \end{matrix}

and therefore,

\begin{matrix} f_{x x}^{''} f - {f_{x}^{'}}^{2} = \frac{(- y^{2} + x y - 2 y) x y}{{(x + y)}^{4}} - \frac{{(y - x y)}^{2}}{{(x + y)}^{4}} = \frac{- x y^{3} - y^{2}}{{(x + y)}^{4}} < 0 . \end{matrix}

(2) Substituting

f (x, y) = \frac{x y}{x + y}

into

f {(d, 1)}^{d - 1} \cdot f {(n - d, 1)}^{n - d - 1} \cdot f (d, n - d) > f {(n - 1, 1)}^{n - 1}

yields that

\begin{matrix} {(\frac{d}{d + 1})}^{d - 1} \cdot {(\frac{n - d}{n - d + 1})}^{n - d - 1} \cdot \frac{d (n - d)}{n} > {(\frac{n - 1}{n})}^{n - 1}, \end{matrix}

i.e.,

\begin{matrix} \frac{d^{d} \cdot (n - d + 1)}{{(d + 1)}^{d - 1} \cdot n} \cdot {(\frac{n - d}{n - d + 1})}^{n - d} > {(\frac{n - 1}{n})}^{n - 1} . \end{matrix}

Therefore, to complete the proof of the lemma, it is only necessary to prove that

\begin{matrix} \frac{d^{d} \cdot (n - d + 1)}{{(d + 1)}^{d - 1} \cdot n} > 1, a n d {(\frac{n - d}{n - d + 1})}^{n - d} > {(\frac{n - 1}{n})}^{n - 1} . \end{matrix}

Let us first consider

\frac{d^{d} \cdot (n - d + 1)}{{(d + 1)}^{d - 1} \cdot n} > 1

. Note that

\begin{matrix} {(\frac{d}{d + 1})}^{d - 1} = {(1 - \frac{1}{d + 1})}^{d - 1} \\ = C_{d - 1}^{0} - C_{d - 1}^{1} \frac{1}{d + 1} + C_{d - 1}^{2} {(\frac{1}{d + 1})}^{2} - \dots + C_{d - 1}^{d - 1} {(- \frac{1}{d + 1})}^{d - 1} \\ > 1 - \frac{d - 1}{d + 1} = \frac{2}{d + 1} . \end{matrix}

And thus, we obtain

\begin{matrix} \frac{d^{d} \cdot (n - d + 1)}{{(d + 1)}^{d - 1} \cdot n} = {(\frac{d}{d + 1})}^{d - 1} \cdot \frac{d (n - d + 1)}{n} > \frac{2}{d + 1} \cdot \frac{d (n - d + 1)}{n} . \end{matrix}

In the following, we only need to prove that

\frac{2}{d + 1} \cdot \frac{d (n - d + 1)}{n} \geq 1

. Let

f (d) = 2 d (n - d + 1) - n (d + 1)

, where

2 \leq d \leq ⌊ \frac{n}{2} ⌋

. Since

f^{'} (d) = 2 (n - d + 1) - 2 d - n = n - 4 d + 2,

then

f_{m i n} = {f (2), f (\frac{n}{2})} = f (\frac{n}{2}) = 0 .

This implies that

2 d (n - d + 1) \geq n (d + 1)

, and therefore,

\begin{matrix} \frac{d^{d} \cdot (n - d + 1)}{{(d + 1)}^{d - 1} \cdot n} > \frac{2}{d + 1} \cdot \frac{d (n - d + 1)}{n} \geq 1 . \end{matrix}

Now, let us turn to prove

{(\frac{n - d}{n - d + 1})}^{n - d} > {(\frac{n - 1}{n})}^{n - 1}

. Let

y = {(\frac{n - x}{n - x + 1})}^{n - x}

, where

2 \leq x \leq ⌊ \frac{n}{2} ⌋

. Since

\begin{matrix} y^{'} = {(\frac{n - x}{n - x + 1})}^{n - x} (- l n \frac{n - x}{n - x + 1} - \frac{1}{n - x + 1}), \end{matrix}

and

\begin{matrix} g^{'} (x) = {(- l n \frac{n - x}{n - x + 1} - \frac{1}{n - x + 1})}^{'} = \frac{1}{{(n - x + 1)}^{2} (n - x)} > 0, \end{matrix}

thus, we have

\begin{matrix} g (x) \geq g (1) = l n \frac{n}{n - 1} - \frac{1}{n} \geq l n \frac{4}{3} - \frac{1}{4} > 0 . \end{matrix}

This is to say, y is an increasing function, and hence,

\begin{matrix} {(\frac{n - d}{n - d + 1})}^{n - d} > y (1) = {(\frac{n - 1}{n})}^{n - 1} . \end{matrix}

Therefore, combining the above two inequations, the lemma proof is completed. □

3. Sufficient Conditions for $P_{n}$ Being the Minimal Tree

In this section, we give sufficient conditions for the path

P_{n}

being the minimal tree of

T_{l n f}

. We present the following transformation at first.

Transformation 1. Assume

T \in T_{n}

, let x be the vertex in tree T.

T_{1}

is the graph obtained from T by adding two pendant paths,

P_{1}

and

P_{2}

attached at x, where

P_{1} = x u_{1} u_{2} \dots, u_{a}

, and

P_{2} = x v_{1} v_{2} \dots, v_{b}

a \geq b \geq 1

d_{T_{1}} (x) \geq 3

T_{2}

is the resulting graph obtained from

T_{1}

by deleting the edge

x v_{1}

and connecting an edge

u_{a} v_{1}

, i.e.,

T_{2} = T_{1} - x v_{1} + u_{a} v_{1}

T_{1}

and

T_{2}

are depicted in Figure 1. Clearly,

T_{1}, T_{2} \in T_{n}

Lemma 5.

Let

T_{1}

and

T_{2}

be the graphs in Transformation 1 (see Figure 1), where

a = b = 1

. If

f (x, y)

matches the conditions

\frac{\partial f}{\partial x} > 0

, and

f^{2} (1, x + 2) \geq f (2, x + 1) \cdot f (2, 1)

, then

T_{l n f} (T_{1}) > T_{l n f} (T_{2})

Proof.

Denote

d_{T_{1}} (x) = p + 2

p \geq 1

, and

N_{T} (x) = N_{T_{1}} (x) ∖ {u_{1}, u_{2}} = {w_{1}, w_{2}, \dots w_{p}}

. Since

a = b = 1

, then

d_{T_{1}} (u_{1}) = d_{T_{1}} (v_{1}) = 1

. And thus, we have

\begin{matrix} T_{l n f} (T_{1}) - T_{l n f} (T_{2}) \\ = 2 γ (p + 2, 1) + Σ_{i = 1}^{p} γ (p + 2, d_{T} (w_{i})) - (γ (p + 1, 2) + γ (2, 1) + Σ_{i = 1}^{p} γ (p + 1, d_{T} (w_{i}))) \\ = Σ_{i = 1}^{p} (γ (p + 2, d_{T} (w_{i})) - γ (p + 1, d_{T} (w_{i}))) + 2 γ (p + 2, 1) - γ (p + 1, 2) - γ (2, 1) . \end{matrix}

\frac{\partial f}{\partial x} > 0

, and Lemma 1, we obtain

Σ_{i = 1}^{p} (γ (p + 2, d_{T} (w_{i})) - γ (p + 1, d_{T} (w_{i}))) > 0

. Using Lemma 2, we have

T_{l n f} (T_{1}) - T_{l n f} (T_{2}) > 2 γ (p + 2, 1) - γ (p + 1, 2) - γ (2, 1) \geq 0 .

So, the lemma is proved. □

Lemma 6.

Let

T_{1}

and

T_{2}

be the graphs in Transformation 1 (see Figure 1), where

a > b = 1

. If

f (x, y)

matches the conditions

\frac{\partial f}{\partial x} > 0

, and

f (1, x + 2) \cdot f (2, x + 2) \geq f (2, x + 1) \cdot f (2, 2)

, then

T_{l n f} (T_{1}) > T_{l n f} (T_{2})

Proof.

Denote

d_{T_{1}} (x) = p + 2

p \geq 1

, and

N_{T} (x) = N_{T_{1}} (x) ∖ {u_{1}, u_{2}} = {w_{1}, w_{2}, \dots w_{p}}

. Since

a > b = 1

, then

d_{T_{1}} (u_{1}) = 2

, and

d_{T_{1}} (v_{1}) = 1

. Therefore, we have

\begin{matrix} T_{l n f} (T_{1}) - T_{l n f} (T_{2}) \\ = γ (p + 2, 1) + γ (p + 2, 2) + γ (2, 1) + Σ_{i = 1}^{p} γ (p + 2, d_{T} (w_{i})) \\ - (γ (p + 1, 2) + γ (2, 2) + γ (2, 1) + Σ_{i = 1}^{p} γ (p + 1, d_{T} (w_{i}))) \\ = Σ_{i = 1}^{p} (γ (p + 2, d_{T} (w_{i})) - γ (p + 1, d_{T} (w_{i}))) \\ + γ (p + 2, 1) + γ (p + 2, 2) - γ (p + 1, 2) - γ (2, 2) . \end{matrix}

According to

\frac{\partial f}{\partial x} > 0

, and Lemma 1,

Σ_{i = 1}^{p} (γ (p + 2, d_{T} (w_{i})) - γ (p + 1, d_{T} (w_{i}))) > 0

. This, together with Lemma 2, implies that

T_{l n f} (T_{1}) - T_{l n f} (T_{2}) > γ (p + 2, 1) + γ (p + 2, 2) - γ (p + 1, 2) - γ (2, 2) \geq 0 .

Hence, we finished the proof. □

Lemma 7.

Let

T_{1}

and

T_{2}

be the graphs in Transformation 1 (see Figure 1), where

a \geq b > 1

. If

f (x, y)

matches the conditions

\frac{\partial f}{\partial x} > 0

, and

f^{2} (2, x + 2) \cdot f (2, 1) \geq f (2, x + 1) \cdot f^{2} (2, 2)

, then

T_{l n f} (T_{1}) > T_{l n f} (T_{2})

Proof.

Denote

d_{T_{1}} (x) = p + 2

p \geq 1

, and

N_{T} (x) = N_{T_{1}} (x) ∖ {u_{1}, u_{2}} = {w_{1}, w_{2}, \dots w_{p}}

. Since

a \geq b > 1

, then

d_{T_{1}} (u_{1}) = d_{T_{1}} (v_{1}) = 2

. Hence, we have

\begin{matrix} T_{l n f} (T_{1}) - T_{l n f} (T_{2}) \\ = 2 γ (p + 2, 2) + 2 β (2, 1) + γ (2, 1) + Σ_{i = 1}^{p} γ (p + 2, d_{T} (w_{i})) \\ - (γ (p + 1, 2) + 2 γ (2, 2) + γ (2, 1) + Σ_{i = 1}^{p} γ (p + 1, d_{T} (w_{i}))) \\ = Σ_{i = 1}^{p} (γ (p + 2, d_{T} (w_{i})) - γ (p + 1, d_{T} (w_{i}))) \\ + 2 γ (p + 2, 2) + γ (2, 1) - γ (p + 1, 2) - 2 γ (2, 2) . \end{matrix}

\frac{\partial f}{\partial x} > 0

, and Lemma 1, have

Σ_{i = 1}^{p} (γ (p + 2, d_{T} (w_{i})) - γ (p + 1, d_{T} (w_{i}))) > 0

. Now, applying Lemma 2, we have

T_{l n f} (T_{1}) - T_{l n f} (T_{2}) > 2 γ (p + 2, 2) + γ (2, 1) - γ (p + 1, 2) - 2 γ (2, 2) \geq 0 .

So, the proof is done. □

With the above lemmas, we now present the following theorem.

Theorem 8.

Let

T \in T_{n}

, suppose

f (x, y)

meets the conditions:

(1) \frac{\partial f}{\partial x} > 0

(2) f^{2} (1, x + 2) \geq f (2, x + 1) \cdot f (2, 1)

(3) f (1, x + 2) \cdot f (2, x + 2) \geq f (2, x + 1) \cdot f (2, 2)

, and

(4) f^{2} (2, x + 2) \cdot f (2, 1) \geq f (2, x + 1) \cdot f^{2} (2, 2)

then

T_{l n f} (T) \geq T_{l n f} (P_{n})

, if and only if

T ≅ P_{n}

Proof.

The conditions (1)-(4) are satisfied for the results of Lemma 5, 6, and 7. If

T ≇ P_{n}

, then, using Transformation 1 repeatedly,

T^{'}

is attained from T. Moreover, according to Lemma 5, 6, and 7, we have

T_{l n f} (T) > T_{l n f} (T^{'})

. Therefore,

T_{l n f} (T) \geq T_{l n f} (P_{n})

, if and only if

T ≅ P_{n}

, the equality holds. This completes the proof. □

4. Sufficient Conditions for $S_{n}$ Being Extremal Trees

In this section, we provide sufficient conditions for the star

S_{n}

being the extremal trees of

T_{l n f}

. We introduce a transformation which is very useful to prove our results.

Transformation 2. Assume

T \in T_{n}

{x y, y z} \in E (T)

, and

d_{T} (x) \leq d_{T} (z) \leq 2

. Denote

N_{1} = N (x) ∖ {y}

N_{2} = N (y) ∖ {x, z}

, and

N_{3} = N (z) ∖ {y}

. Let

T^{'}

be a tree obtained from T by replacing the edge

x u

by a new edge

y u

for each vertex

u \in N_{1}

. T and

T^{'}

are depicted in Figure 2. Clearly,

T^{'} \in T_{n}

With the help of Transformation 2, we firstly give sufficient conditions for the star

S_{n}

being the maximal tree of

T_{l n f}

Lemma 9.

Let T and

T^{'}

be the graphs in Transformation 2 (see Fig. 2). If

f (x, y) = g (x) h (y)

is a real symmetric function with

x, y \geq 1

, and meets the condition

g {(s + 1)}^{s + 1} \cdot g {(t + 1)}^{t + 1} < g (1) \cdot g {(s + t + 1)}^{s + t + 1}

, then

T_{l n f} (T) < T_{l n f} (T^{'})

Proof.

Without loss of generality, we assume

N_{1} = {u_{1}, u_{2}, \dots, u_{s}}

and

N_{3} = {v_{1}, v_{2}, \dots, v_{t}}

, where

s \leq t

. Thus, we have

d_{T} (x) = s + 1

d_{T} (z) = t + 1

, and

\begin{matrix} T_{l n f} (T) - T_{l n f} (T^{'}) \\ = Σ_{i = 1}^{s} (γ (s + 1, d_{T} (u_{i})) - γ (s + t + 1, d_{T} (u_{i}))) + Σ_{i = 1}^{t} (γ (t + 1, d_{T} (v_{i})) - γ (s + t + 1, d_{T} (v_{i}))) \\ + γ (s + 1, d_{T} (w)) + γ (t + 1, d_{T} (w)) - γ (1, d_{T} (w)) - γ (s + t + 1, d_{T} (w)) \\ = l n \prod_{i = 1}^{s} \frac{f (s + 1, d_{T} (u_{i}))}{f (s + t + 1, d_{T} (u_{i}))} \cdot \prod_{i = 1}^{t} \frac{f (t + 1, d_{T} (v_{i}))}{f (s + t + 1, d_{T} (v_{i}))} \cdot \frac{f (s + 1, d_{T} (w)) \cdot f (t + 1, d_{T} (w))}{f (1, d_{T} (w)) \cdot f (s + t + 1, d_{T} (w))} . \end{matrix}

Since the same expressions

d_{T} (u_{i})

d_{T} (v_{i})

, and

d_{T} (w)

are included in the above equation, therefore, under the condition

f (x, y) = g (x) h (y)

, the above equation can be simplified as

\begin{matrix} T_{l n f} (T) - T_{l n f} (T^{'}) \\ = l n \prod_{i = 1}^{s} \frac{g (s + 1)}{g (s + t + 1)} \cdot \prod_{i = 1}^{t} \frac{g (t + 1)}{g (s + t + 1)} \cdot \frac{g (s + 1) \cdot g (t + 1)}{g (1) \cdot g (s + t + 1)} \\ = l n \frac{g {(s + 1)}^{s + 1} \cdot g {(t + 1)}^{t + 1}}{g (1) \cdot g {(s + t + 1)}^{s + t + 1}} . \end{matrix}

Furthermore, if

g {(s + 1)}^{s + 1} \cdot g {(t + 1)}^{t + 1} < g (1) \cdot g {(s + t + 1)}^{s + t + 1}

, we can easily obtain

T_{l n f} (T) - T_{l n f} (T^{'}) < l n 1 = 0

. Hence, the lemma is proved. □

Theorem 10.

Suppose

f (x, y) = g (x) h (y)

is a real symmetric function with

x, y \geq 1

, and meets the condition

g {(s + 1)}^{s + 1} \cdot g {(t + 1)}^{t + 1} < g (1) \cdot g {(s + t + 1)}^{s + t + 1}

, then among all trees of order n, the maximum index

T_{l n f}

is the star

S_{n}

Proof.

Let T be a tree with n vertices, and

| p (T) |

be the number of pendent vertices of T. Then

2 \leq | p (T) | \leq n - 1

. If

| p (T) | = n - 1

n - 2

, then T is the star

S_{n}

or double star

S_{d, n - d}

, where

2 \leq d \leq ⌊ \frac{n}{2} ⌋

. Thus assume

| p (T) | \leq n - 3

for the rest of the proof.

Let

T_{0}

be the graph obtained by removing all pendant vertices from T. Then

T_{0}

is a subtree of T with

n - | p (T) |

vertices, where

n - | p (T) | \geq 3

, and

d_{T} (v) \geq 2

hold for all

v \in V (T_{0})

. Take two adjacent edges in

T_{0}

, such as

u w w v

, thus

{u w, w v} \subseteq E (T)

d_{T} (v) \geq 2

, and

d_{T} (u) \geq 2

. Without loss of generality, let

d_{T} (v) \geq d_{T} (u)

. By transformation 2, we obtain a new tree

T^{'}

from the tree T, and have

| p (T^{'}) | = | p (T) | + 1

. According to Lemma 9,

T_{l n f} (T) < T_{l n f} (T^{'})

| p (T^{'}) | \neq n - 2

, then using Transformation 2 again for

T^{'}

, we can finally obtain the double star

S_{d, n - d}

. Therefore, applying Lemma 9, have

T_{l n f} (T) < T_{l n f} (T^{'})

To complete the proof of theorem, we only need to prove that

T_{l n f} (S_{d, n - d}) < T_{l n f} (S_{n})

. Note that

\begin{matrix} T_{l n f} (S_{d, n - d}) \\ = (d - 1) l n f (d, 1) + (n - d - 1) l n f (n - d, 1) + l n f (d, n - d) \\ = l n f {(d, 1)}^{d - 1} \cdot f {(n - d, 1)}^{n - d - 1} \cdot f (d, n - d) . \\ T_{l n f} (S_{n}) = (n - 1) l n f (n - 1, 1) = l n f {(n - 1, 1)}^{n - 1} . \end{matrix}

And thus,

\begin{matrix} T_{l n f} (S_{d, n - d}) - T_{l n f} (S_{n}) \\ = l n f {(d, 1)}^{d - 1} \cdot f {(n - d, 1)}^{n - d - 1} \cdot f (d, n - d) - l n f {(n - 1, 1)}^{n - 1} \\ = l n \frac{f {(d, 1)}^{d - 1} \cdot f {(n - d, 1)}^{n - d - 1} \cdot f (d, n - d)}{f {(n - 1, 1)}^{n - 1}} . \end{matrix}

By substituting the condition into above equation, we can obtain that

\begin{matrix} T_{l n f} (S_{d, n - d}) - T_{l n f} (S_{n}) \\ = l n \frac{g {(d)}^{d - 1} \cdot g {(n - d)}^{n - d - 1} \cdot g (d) \cdot g (n - d) \cdot g {(1)}^{n - 2}}{g {(n - 1)}^{n - 1} g {(1)}^{n - 1}} \\ = l n \frac{g {(d)}^{d} \cdot g {(n - d)}^{n - d}}{g {(n - 1)}^{n - 1} \cdot g (1)} \\ < l n 1 = 0 . \end{matrix}

Hence, the theorem holds, and this completes the proof. □

In the remaining of this section, by utilizing the monotonicity and concavity of functions, we will give sufficient conditions for the star

S_{n}

being the minimal tree of

T_{l n f}

Lemma 11.

Let T and

T^{'}

be the trees in Transformation 2 (see Fig. 2). If

f (x, y)

meets the conditions

\frac{\partial f}{\partial x} < 0

, and

\frac{\partial^{2} f}{\partial x^{2}} \cdot f - {(\frac{\partial f}{\partial x})}^{2} \leq 0

, then

T_{l n f} (T) > T_{l n f} (T^{'})

Proof.

Denote

N_{1} = {u_{1}, u_{2}, \dots, u_{s}}

and

N_{3} = {v_{1}, v_{2}, \dots, v_{t}}

, where

s \leq t

. Similar to Lemma 4.1, we have

d_{T} (x) = s + 1

d_{T} (z) = t + 1

, and

\begin{matrix} T_{l n f} (T) - T_{l n f} (T^{'}) \\ = Σ_{i = 1}^{s} (γ (s + 1, d_{T} (u_{i})) - γ (s + t + 1, d_{T} (u_{i}))) + Σ_{j = 1}^{t} (γ (t + 1, d_{T} (v_{j})) - γ (s + t + 1, d_{T} (v_{j}))) \\ + γ (s + 1, d_{T} (w)) + γ (t + 1, d_{T} (w)) - γ (1, d_{T} (w)) - γ (s + t + 1, d_{T} (w)) . \end{matrix}

\frac{\partial γ (x, y)}{\partial x} = {(l n f (x, y))}^{'} = \frac{f^{'} (x, y)}{f (x, y)}

, and

\frac{\partial f}{\partial x} < 0

γ (x, y)

is a decreasing function with respect to x. Then, for

i = 1, 2, \dots, s

\begin{matrix} (γ (s + 1, d_{T} (u_{i})) - γ (s + t + 1, d_{T} (u_{i}))) > 0, \end{matrix}

and for

j = 1, 2, \dots, t

\begin{matrix} (γ (t + 1, d_{T} (v_{i})) - γ (s + t + 1, d_{T} (v_{i}))) . \end{matrix}

Since

\frac{\partial^{2} γ (x, y)}{\partial x^{2}} = \frac{\partial (\frac{f^{'} (x, y)}{f (x, y)})}{\partial x} = \frac{f_{x x}^{'} f - f_{x}^{2}}{\partial f^{2}} \leq 0

, thus,

γ (x, y)

is concave down in respect to x. So,

\begin{matrix} γ (s + 1, d_{T} (w)) + γ (t + 1, d_{T} (w)) \geq γ (1, d_{T} (w)) + γ (s + t + 1, d_{T} (w)) . \end{matrix}

Combining the above two equations, the lemma holds true. □

Theorem 12.

Suppose

f (x, y)

meets the conditions

\frac{\partial f}{\partial x} < 0

f_{x x}^{''} f - {f_{x}^{'}}^{2} < 0

, and

f {(d, 1)}^{d - 1} \cdot f {(n - d, 1)}^{n - d - 1} \cdot f (d, n - d) > f {(n - 1, 1)}^{n - 1}

, then among all trees of order n, the minimum index

T_{l n f}

is the star

S_{n}

Proof.

Firstly, we prove the extremal tree with the minimum index of

T_{l n f}

S_{n}

S_{d, n - d}

. Let

| p (T) |

be the number of pendent vertices of T. Then

2 \leq | p (T) | \leq n - 1

. If

| p (T) | = n - 1

n - 2

, then T is the star

S_{n}

or double star

S_{d, n - d}

, where

2 \leq d \leq ⌊ \frac{n}{2} ⌋

. So, assume

| p (T) | \leq n - 3

for the rest of the proof.

Let

T_{0}

be the graph obtained by removing all pendant vertices from T. Then

T_{0}

is a subtree of T with

n - | p (T) |

vertices, where

n - | p (T) | \geq 3

, and

d_{T} (v) \geq 2

hold for all

v \in V (T_{0})

. Take two adjacent edges in

T_{0}

, such as

u w

and

w v

, thus

{u w, w v} \subseteq E (T)

d_{T} (v) \geq 2

, and

d_{T} (u) \geq 2

. Without loss of generality, let

d_{T} (v) \geq d_{T} (u)

. By Transformation 2, we obtain a new tree

T^{'}

from the tree T, and have

| p (T^{'}) | = | p (T) | + 1

. According to Lemma 4.3,

T_{l n f} (T) < T_{l n f} (T^{'})

| p (T^{'}) | \neq n - 2

, then using Transformation 2 again for

T^{'}

, we can finally obtain the double star

S_{d, n - d}

. Therefore, according to Lemma 4.3,

T_{l n f} (T) < T_{l n f} (T^{'})

Secondly, we will prove that

T_{l n f} (S_{n}) < T_{l n f} (S_{d, n - d})

. Note that

\begin{matrix} T_{l n f} (S_{d, n - d}) \\ = (d - 1) l n f (d, 1) + (n - d - 1) l n f (n - d, 1) + l n f (d, n - d) \\ = l n f {(d, 1)}^{d - 1} \cdot f {(n - d, 1)}^{n - d - 1} \cdot f (d, n - d) . \\ T_{l n f} (S_{n}) = (n - 1) l n f (n - 1, 1) = l n f {(n - 1, 1)}^{n - 1} . \end{matrix}

By the condition

f {(d, 1)}^{d - 1} \cdot f {(n - d, 1)}^{n - d - 1} \cdot f (d, n - d) > f {(n - 1, 1)}^{n - 1}

, we obtain

\begin{matrix} T_{l n f} (S_{d, n - d}) - T_{l n f} (S_{n}) \\ = l n f {(d, 1)}^{d - 1} \cdot f {(n - d, 1)}^{n - d - 1} \cdot f (d, n - d) - l n f {(n - 1, 1)}^{n - 1} \\ = l n \frac{f {(d, 1)}^{d - 1} \cdot f {(n - d, 1)}^{n - d - 1} \cdot f (d, n - d)}{f {(n - 1, 1)}^{n - 1}} \\ > l n 1 = 0 . \end{matrix}

Therefore, the theorem holds, and this completes the proof. □

5. Applications

In this paper, the main contribution of the current work is to investigate the minimal and maximal trees for logarithmic VDB topological indices. Sufficient conditions for

P_{n}

being the minimal tree, sufficient conditions for

S_{n}

being the minimal and maximal tree are given in section 3 and 4.

Note that

f (x, y) = \sqrt{(x y)}

{(x y)}^{α} (α \geq 1)

x^{2} + y^{2}

\sqrt{x^{2} + y^{2}}

\sqrt{{(x - 1)}^{2} + {(y - 1)}^{2}}

{(x + y)}^{α} (α \geq 1)

x + y + x y

{(x + y + x y)}^{2}

(x + y) x y

{(x + y + x y)}^{2}

, and

\sqrt{(x + y) x y}

, then, the conditions of Theorem 8 are established. So, as an application of Theorem 8, we declare that the minimal tree is

P_{n}

for the logarithmic VDB indices labeled in Table 1.

Likewise, if

f (x, y) = \sqrt{(x y)}

, or

{(x y)}^{α} (α \geq 1)

, by Lemma 3, the conditions of Theorem 10 are satisfied. Thus, according to Theorem 10, the maximal tree is

S_{n}

for the logarithmic reciprocal Randic̆ index and general second Zagreb index. Similarly, if

f (x, y) = \frac{x y}{x + y}

, then by Lemma 4, the conditions of Theorem 12 are satisfied. Thus, applying Theorem 12, the minimal tree is

S_{n}

for the logarithmic Inverse sum index. The relevant results are shown in Table 1, where

n \geq 5

in all cases.

Data Availability Statement

No underlying data were collected or produced in this study.

Conflicts of Interest

The authors declare that they have no conflicts of interest.

References

J. Devillers, A. T. Balaban (Eds.), Topological Indices and Related Descriptors in QSAR and QSPR, Gordon & Breach, Amsterdam, 1999.
R. Todeschini, V. Consonni, Handbook of Molecular Descriptors, Wiley-VCH, Weinheim, 2000.
R. Todeschini, V. Consonni, Molecular Descriptors for Chemoinformatics, Wiley-VCH, Weinheim, 2009.
B. Furtula, I. Gutman, M. Dehmer, On structure-sensitivity of degree-based topological indices, Appl. Math. Comput. 219 (2013) 8973-8978. [CrossRef]
B. Zhou, N. Trinajstič, On a novel connectivity index, J. Math. Chem. 46 (2009) 1252-1270. [CrossRef]
M. Chen, Y. Zhu, Extremal unicyclic graphs of Sombor index, Appl. Math. Comput. 463 (2024) 128374. [CrossRef]
I. Gutman, J. Tošović, Testing the quality of molecular structure descriptors. VertexCdegreeCbased topological indices, J. Serb. Chem. Soc. 78 (2013) 805-810. [CrossRef]
I. Gutman, Geometric approach to degree-based topological indices: Sombor indices, MATCH Commun. Math. Comput. Chem. 86 (2021) 11-16.
I. Gutman, B. Furtula, C. Elphick, Three new/old vertex-degree-based topological indices, MATCH Commun. Math. Comput. Chem. 72 (2014) 617-632.
K.C. Das, I. Gutman, Some properties of the second Zagreb index, MATCH Commun. Math. Comput. Chem. 52 (2004) 103-112.
J. Rada, Exponential vertex-degree-based topological indices and discrimination, MATCH Commun. Math. Comput. Chem. 82 (2019) 29-41.
R. Cruz, J. Rada, The path and the star as extremal values of vertex-degree-based topological indices among trees, MATCH Commun. Math. Comput. Chem. 82 (2019) 715-732.
W. Gao, Trees with maximum vertex-degree-based topological indices, MATCH Commun. Math. Comput. Chem. 88 (2022) 535-552. [CrossRef]
W. Gao, Chemical trees with maximal VDB topological indices, MATCH Commun. Math. Comput. Chem. 89 (2023) 699-722. [CrossRef]
W. Gao, Y. Gao, The extremal trees for exponential vertex-degree-based topological indices, Appl. Math. Comput. 472 (2024) 128634. [CrossRef]
K. C. Das, S. Elumalai, S. Balachandran, Open problems on the exponential vertex-degree-based topological indices of graphs, Discrete Appl. Math. 293 (2021) 38-49. [CrossRef]
R. Cruz, J. Monsalve, J. Rada, The balanced double star has maximum exponential second Zagreb index, J. Comb. Optim. 41 (2021) 544-552. [CrossRef]
H. Liu, L. You, Z. Tang, J. Liu, On the reduced Sombor index and its applications, MATCH Commun. Math. Comput. Chem. 86 (2021) 729-753.

Figure 1. Trees

T_{1}

and

T_{2}

in Transformation 1.

Figure 1. Trees

T_{1}

and

T_{2}

in Transformation 1.

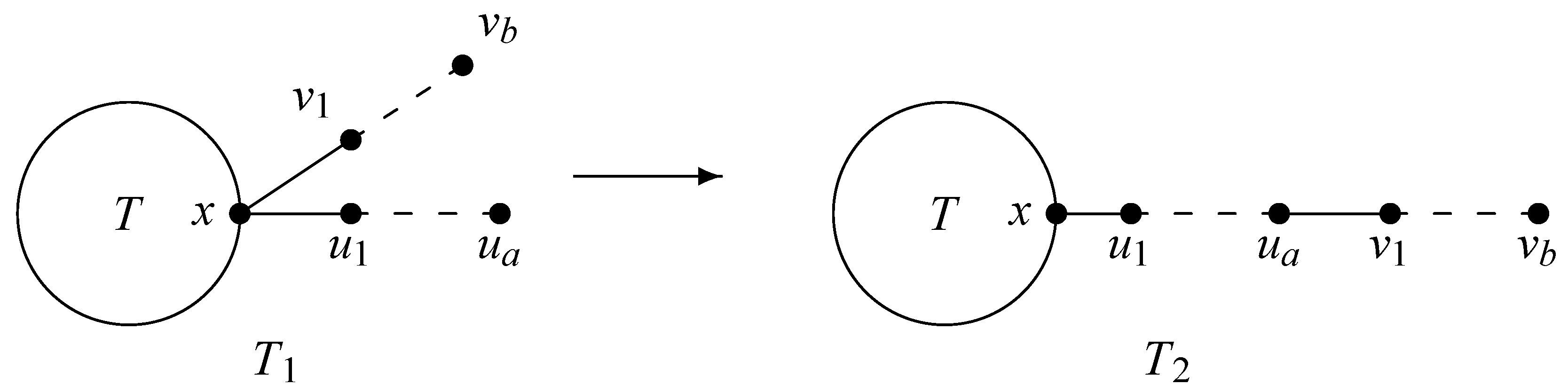
Figure 2. Trees T and

T^{'}

in Transformation 2.

Figure 2. Trees T and

T^{'}

in Transformation 2.

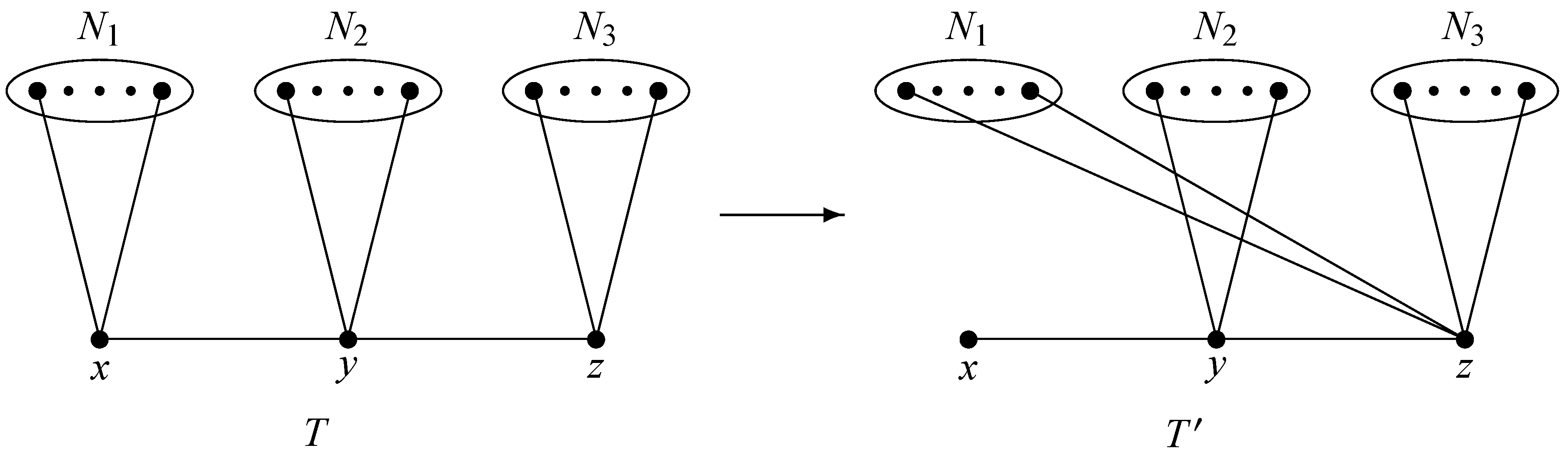
Table 1. Extremal trees of

T_{l n f}

Table 1. Extremal trees of

T_{l n f}

Indices	$f (x, y)$	Min	Max
Inverse sum index	$\frac{x y}{x + y}$	$S_{n}$
reciprocal Randic̆ index	$\sqrt{(x y)}$	$P_{n}$	$S_{n}$
general second Zagreb index	${(x y)}^{α} (α \geq 1)$	$P_{n}$	$S_{n}$
forgotten index	$x^{2} + y^{2}$	$P_{n}$
Sombor index	$\sqrt{x^{2} + y^{2}}$	$P_{n}$
reduced Sombor index	$\sqrt{{(x - 1)}^{2} + {(y - 1)}^{2}}$	$P_{n}$
general first Zagreb index	${(x + y)}^{α} (α \geq 1)$	$P_{n}$
first Gourava index	$x + y + x y$	$P_{n}$
first hyper-Gourava index	${(x + y + x y)}^{2}$	$P_{n}$
second Gourava index	$(x + y) x y$	$P_{n}$
second hyper-Gourava index	${((x + y) x y)}^{2}$	$P_{n}$
product-connectivity Gourava index	$\sqrt{(x + y) x y}$	$P_{n}$

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

The Extremal Trees for Logarithmic VDB Topological Indices

Abstract

1. Introduction

2. Preliminaries

3. Sufficient Conditions for P n Being the Minimal Tree

4. Sufficient Conditions for S n Being Extremal Trees

5. Applications

Data Availability Statement

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe

3. Sufficient Conditions for $P_{n}$ Being the Minimal Tree

4. Sufficient Conditions for $S_{n}$ Being Extremal Trees