Prerpints.org logo
Preprint
Article

Deep Learning in Finance: A Survey of Applications and Techniques

Altmetrics

Downloads

617

Views

786

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

18 August 2024

Posted:

20 August 2024

You are already at the latest version

Alerts
Abstract
Machine learning (ML) has transformed the financial industry by enabling advanced applications such as credit scoring, fraud detection, and market forecasting. At the core of this transformation is deep learning (DL), a subset of ML that is robust at processing and analyzing complex and large datasets. This paper provides a concise overview of key deep learning models, including Convolutional Neural Networks (CNNs), Long Short-Term Memory networks (LSTMs), Deep Belief Networks (DBNs), Transformers, Generative Adversarial Networks (GANs), and Deep Reinforcement Learning (Deep RL). The study examines their learning processes, mathematical foundations, and practical applications in finance. It also explores recent advances and emerging trends in the financial industry alongside critical challenges such as data quality, model interpretability, and computational complexity, offering insights into future research directions that can guide the development of more robust and explainable financial models.
Keywords: 
Subject: Computer Science and Mathematics  -   Artificial Intelligence and Machine Learning

1. Introduction

The integration of artificial intelligence (AI), particularly deep learning (DL), into financial systems has significantly transformed the finance industry. Deep learning’s ability to process and analyze vast arrays of data has led to breakthroughs in areas such as credit scoring, fraud detection, and algorithmic trading [1,2,3]. These advancements have improved accuracy and enabled the development of more sophisticated financial tools and services. Despite these advancements, the deployment of deep learning in finance is not without its challenges, such as the interpretability of DL models, their demand for large amounts of data, and the need for high computational power [4,5,6].
Recent reviews have explored various aspects of AI in finance; however, they have often focused broadly on machine learning (ML) without delving deep into the specific applications and intricacies of DL models. For example, the reviews by Ahmed et al. [7] and Goodell et al. [8] explored the applications of ML in finance, covering financial fraud, bankruptcy prediction, stock price prediction, and portfolio management. Furthermore, some studies have addressed the technical capabilities and applications of deep learning in specific financial applications. For example, Mienye and Jere [6] reviewed the application of DL architectures in credit card fraud detection, including the challenges encountered in deploying these models in real-world applications. Similarly, Gunnarsson et al. [9] reviewed deep learning with application to credit scoring, suggesting best practices to ensure optimal utilization of DL models. Other deep learning reviews include those applied to stock market prediction [10,11,12] and algorithmic trading [13].
Over the years, there have been numerous advances in deep learning architectures, such as advancements in Transformer architectures, generative adversarial networks (GANs), and deep reinforcement learning models [14,15]. These methods have played vital roles in various technological advancements and have been applied in different financial applications. For instance, Transformer models have revolutionized natural language processing tasks, which are critical in sentiment analysis and financial document analysis [16]. GANs have been effectively used in generating synthetic financial data, thereby enhancing the robustness of models trained on limited datasets [17]. Deep reinforcement learning, on the other hand, has shown promise in optimizing trading strategies and portfolio management [18]. Due to these recent advances, there is a need for an up-to-date review that consolidates these developments and critically examines their implications and potential in the financial sector.
Therefore, this paper provides a comprehensive review of deep learning and its applications in the financial industry. The study aims to critically assess the inner workings of different DL architectures and their effectiveness and explore the challenges they present in financial contexts. The goal of this review is to provide a robust analysis that highlights the current state of deep learning in finance and identifies areas where further research and development are needed. This will be beneficial to both deep learning researchers and industry professionals amining to harness these technologies for financial applications.
The remainder of this paper is organized as follows: Section 2 reviews related works, highlighting their contributions and limitations. Section 3 and 4 discuss the various deep learning models used in finance and their applications, respectively. Section 5 presents recent advances and emerging trends in deep learning. Section 6 discusses challenges limiting deep learning applications in finance. Section 7 highlights future research directions, while Section 8 concludes the study.

2. Related Works

Recently, there have been significant advancements in the application of deep learning within financial data modeling. For example, Wang et al. [19] highlighted the effectiveness of sequence-to-sequence models for predicting market movements, offering sophisticated tools for algorithmic trading. Risk management is another critical area where deep learning has made a substantial impact. Meng et al. [20] explored the application of CNNs in identifying high-risk patterns, thus aiding preemptive measures against financial instability. These models are well-suited for analyzing large volumes of unstructured data, which is common in financial datasets.
Credit scoring has also benefited from deep learning. Khandani et al. [21] demonstrated how deep learning could enhance the precision of credit scoring systems, essential for evaluating the creditworthiness of potential borrowers. Similarly, Esenegho et al. [22] employed a deep learning ensemble for credit risk and fraud detection. The study used the LSTM network as the base learner in the adaptive boosting (AdaBoost) implementation, achieving excellent performance. Mienye and Sun [23] proposed a deep ensemble learning method for credit card fraud detection using LSTM and GRU as base learners and MLP as the meta-learner, achieving classification performance that outperformed benchmark models.
Additionally, Sezer and Ozbayoglu [24] provided a comprehensive review of deep learning applications in finance, covering areas such as fraud detection, algorithmic trading, and portfolio management. Their study illustrates the adaptability of DL models and their potential to transform many aspects of the financial industry. However, their review primarily focused on established deep learning techniques like CNN, LSTM, and deep belief networks, with limited coverage of the latest advancements such as Transformer models, GANs, and Deep Reinforcement Learning, which have shown great promise in recent years. Another notable review by Lim et al. [25] focused on deep learning’s role in time series forecasting, such as financial markets. While their analysis was thorough in the context of traditional ML and DL, it did not explore recent DL architectures.
Moreover, a study by Goodell et al. [8] provided an extensive overview of AI applications in finance, including ML and DL. The study grouped all AI and ML methods together without a specific focus on the unique contributions and challenges of deep learning in finance. As a result, the review did not adequately cover the intricacies of deep learning models nor the specific advancements in architectures like GANs and Deep RL, which are crucial for understanding the current deep learning in finance.
Recent work by Mienye and Jere [6] concentrated on the challenges and applications of DL in credit card fraud detection. Although the study provided valuable insights into the practical deployment of deep learning models, it was narrowly focused on a specific application, leaving out a broader discussion of other emerging deep learning techniques and their implications for the financial industry as a whole.
Given these limitations in the existing literature, there is a gap in comprehensive reviews that not only cover traditional DL applications in finance but also explore the recent advances in DL architectures, such as Transformers, GANs, and Deep RL. These modern techniques have begun to reshape the financial industry, offering new methods for analyzing complex datasets, predicting market movements, and managing financial risk. Therefore, this paper aims to bridge this gap by providing an up-to-date review of deep learning applications in the financial industry, focusing on the latest advancements and how they can address current challenges in finance. This review is timely, given the rapid evolution of DL technologies and their increasing impact on financial systems, and it seeks to guide future research and development in this dynamic field.

3. Deep Learning Architectures

Deep learning models have significantly impacted financial data modelling, offering advanced solutions for analyzing and predicting financial variables. These DL models are discussed in this section.

3.1. Feedforward Neural Networks

Feedforward Neural Networks (FNNs), also known as Multilayer Perceptron (MLP), are the most basic type of artificial neural networks. They consist of an input layer, one or more hidden layers, and an output layer, with each node in one layer connected only to nodes in the subsequent layer [26]. This unidirectional flow of data—from the input layer to the output layer—distinguishes FNNs from other types of neural networks that may have connections cycling back to previous layers. In an FNN, each node (or neuron) in a layer computes a weighted sum of its inputs, adds a bias term, and then applies an activation function to produce its output. Mathematically, the output y of a neuron can be expressed as:
y = σ ( W x + b )
where x represents the input vector, W is the weight matrix, b is the bias vector, and σ is the activation function (commonly a ReLU or sigmoid function) [26,27]. The activation function introduces non-linearity into the model, allowing the network to learn complex patterns within the data [28]. FNNs are very useful in finance for tasks such as credit scoring, bankruptcy prediction, and customer segmentation, where the relationships between input variables and the output can be learned through straightforward mapping. Their simplicity and efficiency make them suitable for these applications, especially when the goal is to classify or predict outcomes based on historical financial data. The training process of an FNN involves adjusting the weights W and biases b to minimize a loss function, typically using a method like stochastic gradient descent (SGD). Algorithm 1 outlines the key steps in the training process of an FNN:
Algorithm 1 Training a Feedforward Neural Network
1:
Input: Training dataset { ( x ( i ) , y ( i ) ) } i = 1 N  
2:
Initialize: Weights W and biases b randomly 
3:
for each epoch do 
4:
    for each training sample ( x ( i ) , y ( i ) )  do 
5:
        Forward Pass: 
6:
        Compute the input to each neuron in the hidden layers and the output layer: a ( l ) = W ( l ) x ( l − 1 ) + b ( l )  
7:
        Apply activation function: h ( l ) = σ ( a ( l ) )  
8:
        Compute output of the network y pred = h output  
9:
        Backpropagation: 
10:
        Compute the loss L ( y pred , y ( i ) )  
11:
        Compute gradients ∇ W ( l ) and ∇ b ( l ) using backpropagation 
12:
        Update weights and biases: W ( l ) ← W ( l ) − η ∇ W ( l ) , b ( l ) ← b ( l ) − η ∇ b ( l )  
13:
    end for 
14:
end for

3.2. Simple Recurrent Neural Networks

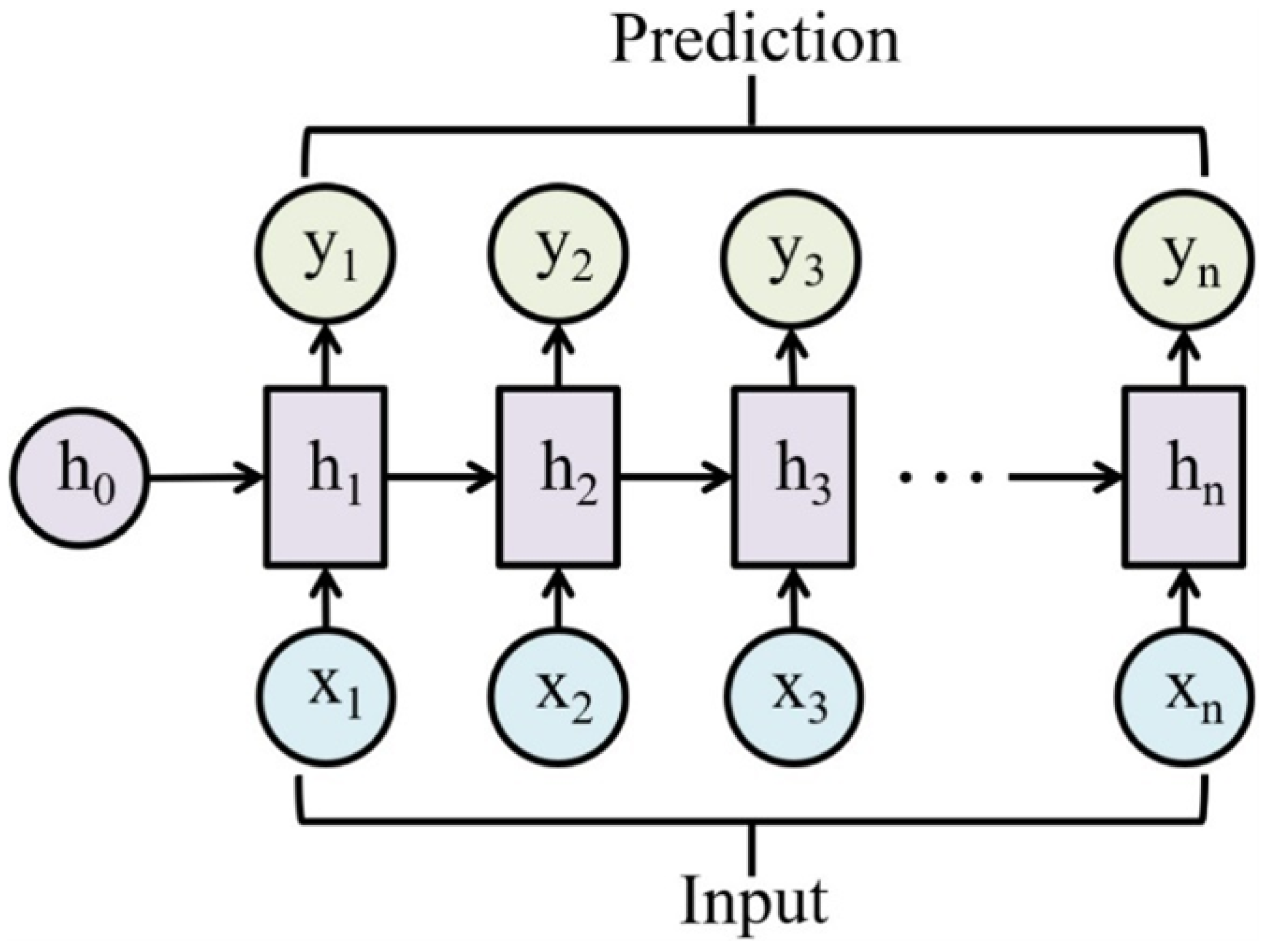
RNNs are a type of neural network designed to process sequential data by maintaining a hidden state that captures information from previous elements in the sequence [29]. Unlike feedforward neural networks, RNNs have recurrent connections that allow them to remember past inputs, making them effective for tasks involving time-dependent data such as stock price forecasting, natural language processing, and algorithmic trading [30]. The RNN architecture is shown in Figure 1. At each time step t, an RNN takes the current input x t and the hidden state from the previous time step h t − 1 to compute the current hidden state h t . The hidden state is updated using the following equation:
h t = σ ( W h x x t + W h h h t − 1 + b h )
where W h x and W h h are weight matrices, b h is the bias, and σ is a non-linear activation function, such as the hyperbolic tangent (tanh) or Rectified Linear Unit (ReLU). The hidden state h t serves as a summary of all past inputs up to time t, allowing the RNN to model temporal dependencies in the data [29,31]. This capability is crucial in financial applications where the value of an asset is influenced by its past behavior and other sequential factors. Meanwhile, despite their effectiveness, the simple RNN face a significant challenge known as the vanishing gradient problem, which arises during backpropagation. When training on long sequences, the gradients of the loss function with respect to the network parameters can diminish to near zero, hindering the model’s ability to learn long-term dependencies [32]. This limitation reduces the RNN’s effectiveness in capturing extended patterns in data, which is critical in many financial tasks. However, there are more advanced RNN architectures like Long Short-Term Memory (LSTM) networks and Gated Recurrent Units (GRUs), which are specifically designed to retain information over longer sequences.

3.3. Long Short-Term Memory Networks

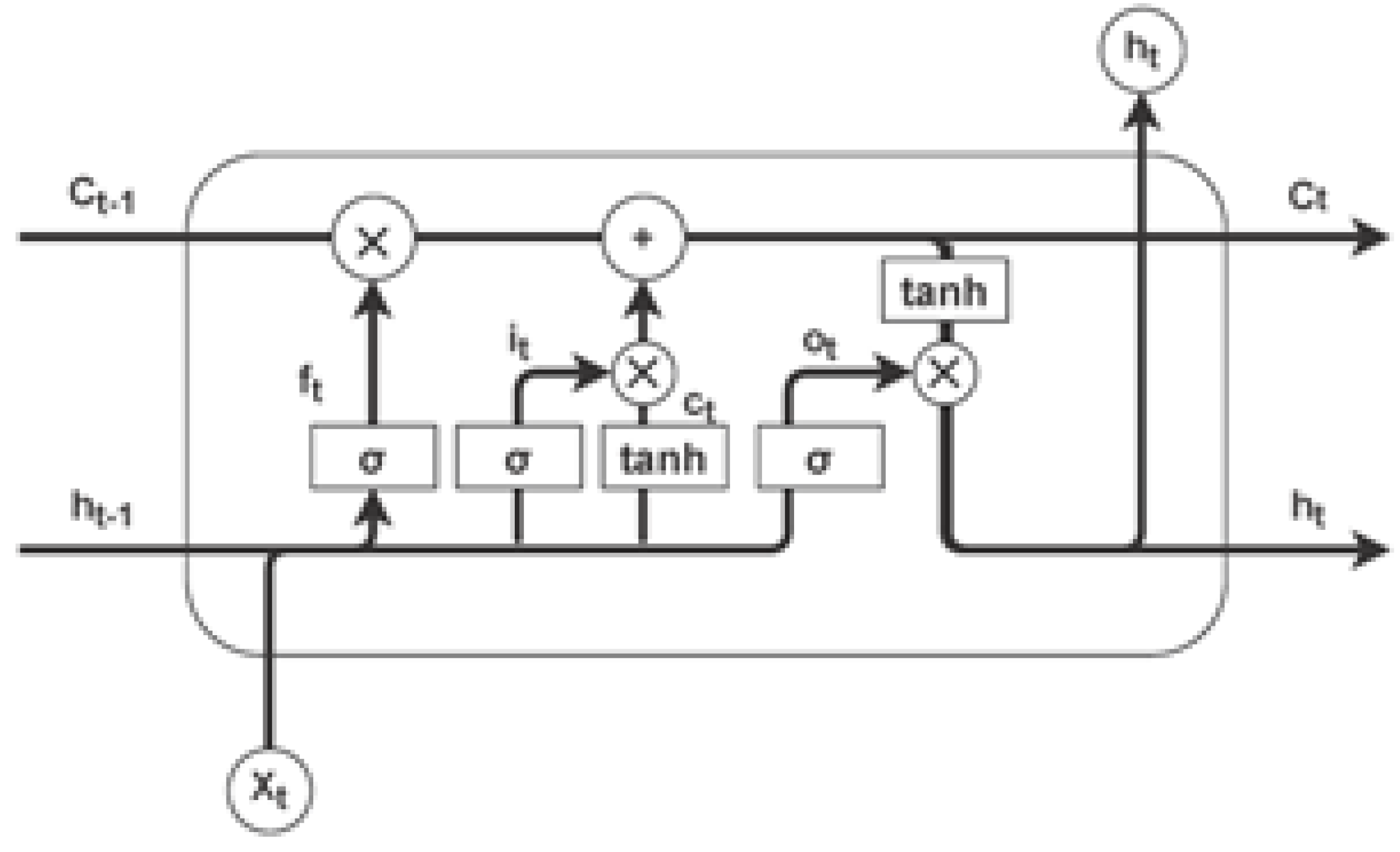
LSTMs are designed to overcome the vanishing gradient problem that can occur in traditional RNNs by incorporating gates that regulate the flow of information [33]. These gates ensure that the network can maintain long-term dependencies in the data, which is critical for applications like sequential prediction where context from far back in the sequence is important. The LSTM unit, shown in Figure 2, includes input, forget, and output gates, together with a cell state that carries information across time steps [22]. The equations governing these components are:
i t = σ ( W x i x t + W h i h t − 1 + b i ) ,
f t = σ ( W x f x t + W h f h t − 1 + b f ) ,
o t = σ ( W x o x t + W h o h t − 1 + b o ) ,
g t = tanh ( W x g x t + W h g h t − 1 + b g ) ,
c t = f t ⊙ c t − 1 + i t ⊙ g t ,
h t = o t ⊙ tanh ( c t ) ,
where i t , f t , and o t are the input, forget, and output gates, respectively, and c t represents the cell state at time t. The term σ denotes the sigmoid activation function, which squashes the input values to a range between 0 and 1, determining the extent to which information should be allowed through each gate. The cell state c t acts as the memory of the network, carrying forward relevant information across time steps. The operator ⊙ represents the element-wise (Hadamard) product, which controls how much of the past information is retained in the cell state [23]. This gating mechanism allows LSTMs to effectively manage long-term dependencies in sequential data, making them highly effective for financial time series analysis, anomaly detection in transaction data, and complex decision-making processes.

3.4. Gated Recurrent Units

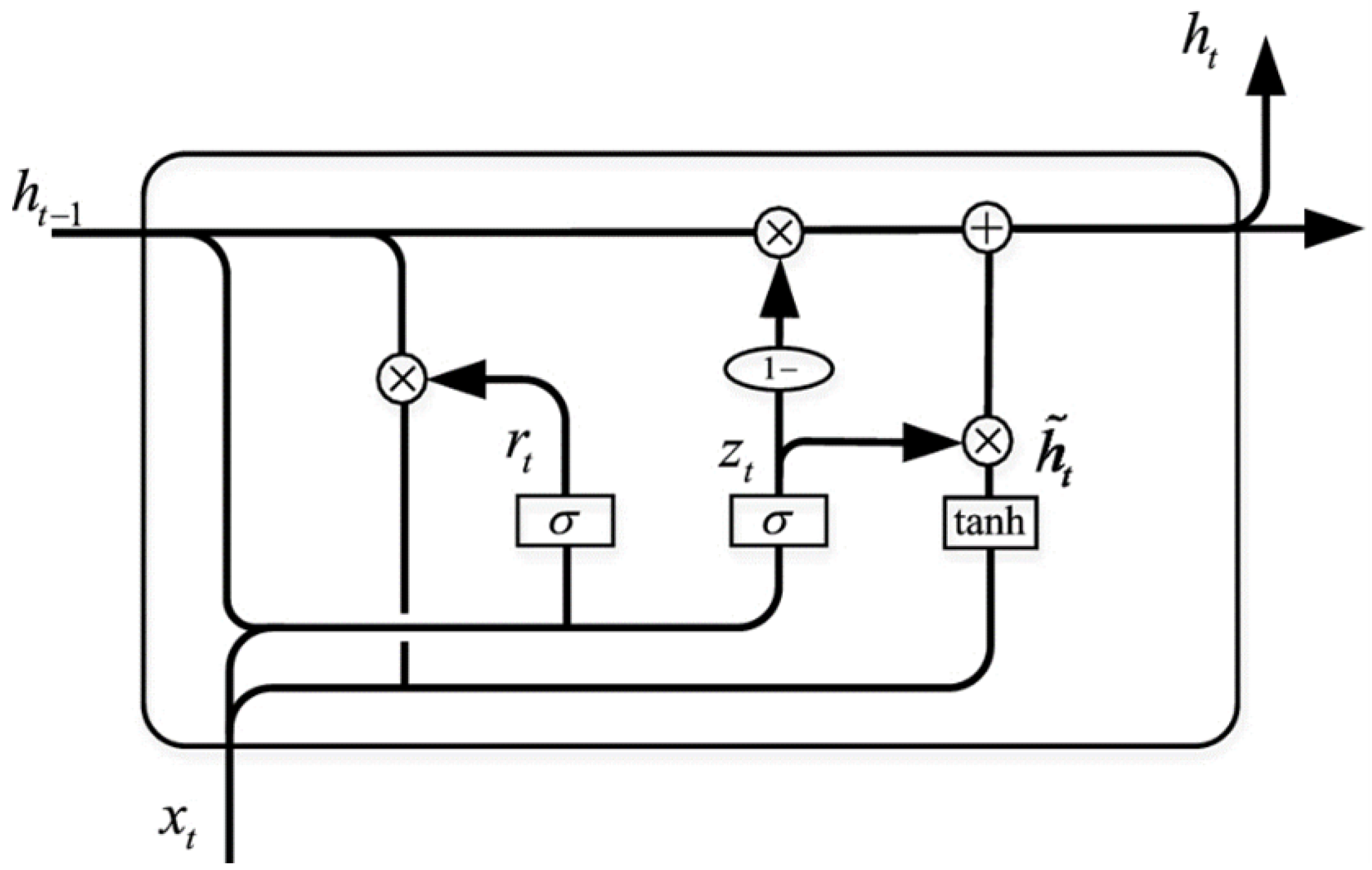
GRUs simplify the LSTM design by combining the forget and input gates into a single update gate and by merging the cell state and hidden state into one [35]. This reduction in complexity can lead to faster training times without a significant drop in performance, making GRUs a popular choice for tasks where efficiency is crucial. The architecture of a GRU is shown in Figure 3. Meanwhile, the GRU uses the following set of update equations:
z t = σ ( W x z x t + W h z h t − 1 + b z ) ,
r t = σ ( W x r x t + W h r h t − 1 + b r ) ,
h ˜ t = tanh ( W x h x t + r t ⊙ ( W h h h t − 1 + b h ) ) ,
h t = ( 1 − z t ) ⊙ h t − 1 + z t ⊙ h ˜ t ,
where z t is the update gate, determining how much of the previous hidden state h t − 1 is carried forward to the current hidden state h t . The reset gate r t controls how much of the previous hidden state contributes to the candidate hidden state h ˜ t . The term σ represents the sigmoid activation function, which outputs values between 0 and 1, controlling the influence of previous states. The candidate hidden state h ˜ t is a potential new state influenced by the reset gate and the input at time t, while the final hidden state h t is a combination of the previous hidden state and the candidate hidden state, modulated by the update gate. The operator ⊙ denotes the element-wise product [35,36].
GRUs have proven effective in various financial applications, including predictive analytics for stock prices, loan default likelihood, and identifying patterns in high-frequency trading data [37,38]. Their simplified architecture makes them suitable for scenarios where computational efficiency is crucial without compromising accuracy. For instance, in stock price prediction, GRUs can capture and model temporal dependencies within financial time series data, allowing for more accurate forecasts. The reset and update gates help the model maintain relevant historical information while discarding noise, which is valuable in volatile markets where only certain past events may be predictive of future price movements. With respect to credit risk assessment, GRUs can be used to predict loan defaults by analyzing the sequential behaviour of borrowers, such as payment histories and transaction patterns. The efficiency of GRUs allows them to be trained on large datasets, ensuring that they can process and learn from vast amounts of borrower information quickly. This capability is essential for real-time risk assessment, where decisions must be made rapidly based on the latest available data.

3.5. Convolutional Neural Networks

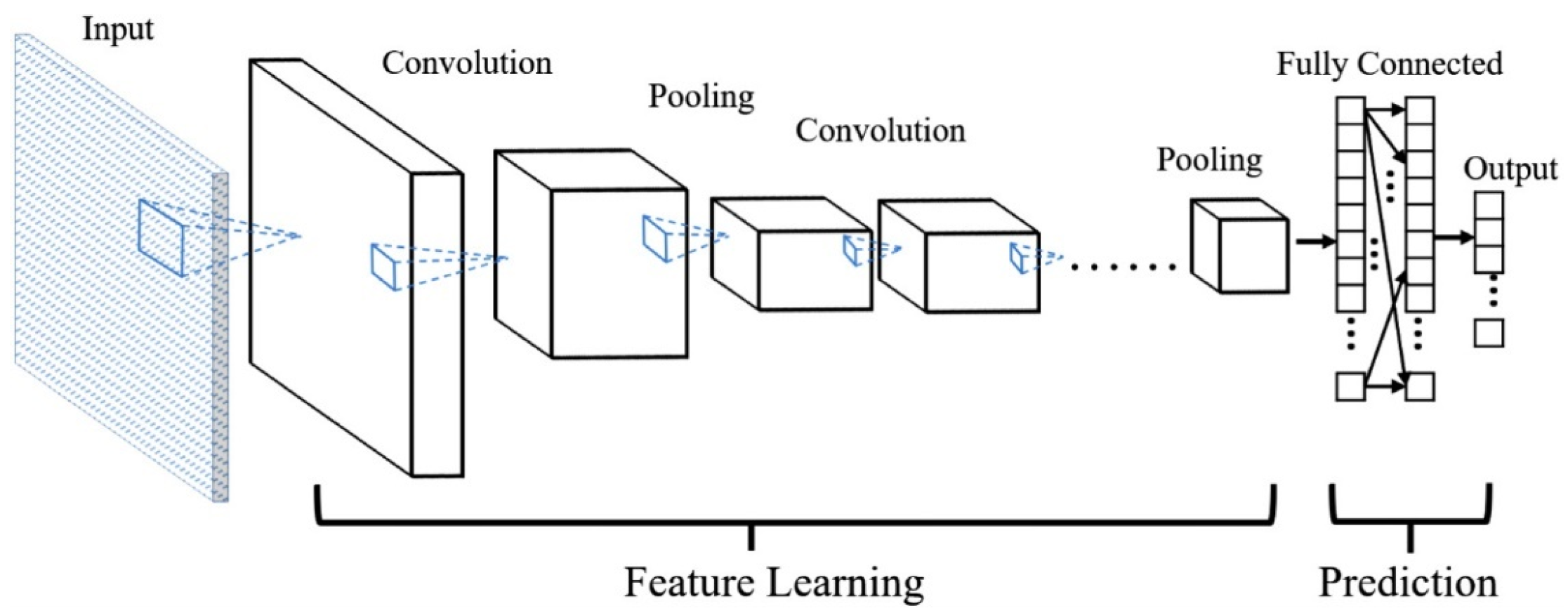
CNNs are a class of deep learning models originally designed for processing grid-like data, such as images and videos. The architecture of CNNs is particularly effective for tasks that involve identifying spatial hierarchies in data through the application of convolutional layers [39,40]. Although CNNs are most commonly associated with image processing, their powerful pattern recognition capabilities have made them highly suitable for various financial applications, especially in areas like anomaly detection, fraud detection, and financial time series analysis. The CNN architecture is shown in Figure 4. The fundamental building block of a CNN is the convolutional layer, where the convolution operation is performed. The convolution operation involves sliding a filter (also known as a kernel) across the input data to produce feature maps [41]. The mathematical operation for a convolution in one dimension is defined as:
z = σ ∑ i = 1 k W i · x i : i + n − 1 + b
where W i represents the weight of the filter, x i : i + n − 1 is the segment of the input data over which the filter is applied, b is the bias term, and σ denotes the activation function, typically a ReLU [43]. The result of the convolution operation is the feature map z, which highlights specific patterns in the input data based on the learned filter weights. Meanwhile, the pooling layers perform down-sampling operations to reduce the dimensionality of the feature maps, thereby focusing on the most critical features and reducing the computational load [44]. The pooling operation is usually defined as:
z p o o l = max ( x i : i + n − 1 )
In the case of max pooling, the operation selects the maximum value from a segment of the feature map. This helps in making the model more robust to small changes in the input, which is crucial in financial applications where noise and minor fluctuations are common in the data [45]. Furthermore, the fully connected layer is typically added after several convolutional and pooling layers. These layers integrate the features extracted by the convolutional layers to perform tasks such as classification (e.g., determining whether a transaction is fraudulent) or regression (e.g., predicting the likelihood of default). The output from the fully connected layer can be given by:
y = σ ( W f c · z f l a t t e n e d + b f c )
where W f c and b f c are the weights and biases of the fully connected layer, and z f l a t t e n e d represents the flattened output from the previous layer, which is a one-dimensional vector. The applications of CNNs in the financial domain extend beyond anomaly detection and fraud detection. CNNs have been employed in algorithmic trading to analyze market data, including order book data, where the model learns to predict price movements by identifying patterns in the order flow [46]. CNNs are also used in credit scoring systems, where they can process large volumes of borrower data to identify risk factors and make accurate predictions about creditworthiness [47].

3.6. Transformers and Attention Mechanisms

Transformers are a powerful class of DL models that have significantly impacted various domains, mostly natural language processing (NLP), due to their ability to efficiently handle large sets of time-dependent data [48,49]. The core innovation of transformers is in their use of attention mechanisms, which allow the model to dynamically weigh the importance of different parts of the input data, enabling the capture of long-range dependencies without the need for sequential processing, as required by RNNs [50]. The attention mechanism, a fundamental component of transformers, can be mathematically described as:
Attention ( Q , K , V ) = softmax Q K T d k V
where Q (queries), K (keys), and V (values) are linear projections of the input data, with Q = W q X , K = W k X , and V = W v X , where W q , W k , and W v are learned weight matrices. The dot product Q K T calculates the similarity between queries and keys, and the softmax function normalizes these into attention weights, allowing the model to focus on the most relevant parts of the input [50,51]. Algorithm 2 summarizes the key steps in the transformer model.
Algorithm 2 Training a Transformer Model
1:
Input: Sequence of data points X = { x 1 , x 2 , ⋯ , x T }  
2:
Initialize: Parameters W q , W k , W v , and other model weights 
3:
for each layer in the transformer do 
4:
    Compute queries Q = W q X , keys K = W k X , and values V = W v X  
5:
    Compute attention scores: A = softmax Q K T d k  
6:
    Compute weighted values: Z = A V  
7:
    Pass Z through feedforward network layers 
8:
end for 
9:
Output: Predicted output based on final transformer layer
Furthermore, a major advantage of this architecture is its parallelizability, making it highly scalable and efficient for processing large datasets, which is advantageous in financial applications such as market movement prediction, risk assessment, and sentiment analysis. For example, in market movement prediction, transformers can analyze sequences of historical price data, economic indicators, and textual data from news articles or social media [52]. The flexibility of transformers also extends to other financial tasks such as sentiment analysis, where they analyze textual data to gauge market sentiment [53], and portfolio optimization [54], where their ability to capture dependencies across multiple time periods ensures more informed investment strategies.

3.7. Generative Adversarial Networks

GANs are a class of DL models that consist of two neural networks: a generator and a discriminator. These networks are trained simultaneously in a competitive setting, where the generator aims to create realistic data instances while the discriminator attempts to distinguish between real data (from the actual dataset) and fake data (produced by the generator) [55,56]. The adversarial nature of this training process forces the generator to produce increasingly realistic data over time. Meanwhile, the generator takes a random noise vector z from a latent space (usually sampled from a standard normal distribution) and transforms it into a data instance G ( z ) that resembles the real data. The goal of the generator is to fool the discriminator by producing data that is indistinguishable from the real data. Whereas the discriminator receives both real data x and generated data G ( z ) . It outputs a probability D ( x ) or D ( G ( z ) ) , indicating whether the input data is real or fake [55]. The discriminator is trained to correctly classify the real data as "real" and the generated data as "fake."
The objective of the GAN is expressed as a minimax game, where the generator and discriminator are pitted against each other [57]. The generator tries to minimize the probability that the discriminator correctly classifies its outputs as fake, while the discriminator tries to maximize this probability. The overall objective function V ( D , G ) is given by:
min G max D V ( D , G ) = E x ∼ p d a t a ( x ) [ log D ( x ) ] + E z ∼ p z ( z ) [ log ( 1 − D ( G ( z ) ) ) ]
where p d a t a ( x ) is the distribution of the real data, and p z ( z ) is the distribution of the noise input to the generator. The steps in Algorithm 3 describe the training procedure of a GAN:
Algorithm 3 Training a Generative Adversarial Network (GAN)
1:
Initialize generator G and discriminator D with random weights. 
2:
while not converged do 
3:
    for each training step do 
4:
        Sample a minibatch of m noise samples { z ( 1 ) , ⋯ , z ( m ) } from the noise prior p z ( z ) . 
5:
        Sample a minibatch of m real data samples { x ( 1 ) , ⋯ , x ( m ) } from the data distribution p d a t a ( x ) . 
6:
        Compute the discriminator loss: 
L D = − 1 m ∑ i = 1 m log D ( x ( i ) ) + log ( 1 − D ( G ( z ( i ) ) ) )
7:
        Update the discriminator by performing a gradient ascent step on L D . 
8:
        Compute the generator loss: 
L G = − 1 m ∑ i = 1 m log ( D ( G ( z ( i ) ) ) )
9:
        Update the generator by performing a gradient descent step on L G . 
10:
    end for 
11:
end while
GANs have proven to be highly effective in various financial applications due to their ability to generate realistic synthetic data and model complex distributions. One prominent application is in the generation of synthetic financial datasets [58]. Financial data, especially in areas like credit scoring or market transactions, is often scarce or imbalanced. GANs can generate additional synthetic data points that resemble the original dataset, which can be used to augment training datasets, thus reducing the risk of overfitting and improving model robustness. For example, in credit risk modelling, GANs can generate synthetic borrower profiles that maintain the statistical properties of the original dataset. Similarly, in portfolio management, GANs have been used to simulate various market scenarios, helping investors to assess the robustness of different investment strategies under different market conditions [59]. GANs have also been applied to enhance algorithmic trading strategies [60].

3.8. Deep Reinforcement Learning

Deep reinforcement learning (Deep RL) combines the principles of reinforcement learning with deep learning to tackle complex decision-making problems, particularly in environments with large state or action spaces [61]. In Deep RL, DNNs are employed as function approximators to represent the policy or value functions, enabling the agent to learn optimal strategies even in high-dimensional spaces, such as those found in financial markets. Deep RL has been effective in optimizing trading strategies, portfolio management, and risk management [62]. Unlike traditional RL, where simpler function approximators like tables or linear models might be used, Deep RL leverages the representational power of DNNs to model complex relationships within data. Meanwhile, Deep RL problems are often modelled as Markov decision processes (MDPs), defined by the tuple ( S , A , P , R , γ ) , where:
  • S represents the set of possible states the agent can be in, such as different market conditions.
  • A represents the set of possible actions the agent can take, such as buying, selling, or holding assets.
  • P is the state transition probability, which defines the probability of moving from one state to another given an action.
  • R is the reward function, which assigns a reward to each state-action pair, reflecting the profitability of an action in a given state.
  • γ is the discount factor, which determines the importance of future rewards.
The agent’s goal is to learn a policy π that maximizes the expected cumulative reward, defined as:
G t = E ∑ k = 0 ∞ γ k R t + k + 1 ∣ S t = s , A t = a ,
where G t is the return at time step t, and π is the policy that maps states to actions. The policy π or value function V ( s ) is typically represented by a deep neural network, which is trained using algorithms like Deep Q-Networks (DQN), Proximal Policy Optimization (PPO), or Actor-Critic methods.

3.9. Deep Belief Networks

Deep Belief Networks (DBNs) are a class of generative DL models composed of multiple layers of stochastic, latent variables. These layers are typically Restricted Boltzmann Machines (RBMs), where each layer serves as a feature detector for the layer above it [63]. DBNs are trained in a layer-wise manner, where each RBM is trained to model the data distribution of the inputs it receives. Once trained, these layers can be stacked to form a deep network that captures complex patterns in the data. The architecture of a DBN begins with a visible layer, which directly interacts with the input data, and is followed by one or more hidden layers that learn hierarchical representations of the data [64,65]. The main advantage of DBNs is in their ability to pre-train each layer as an RBM before fine-tuning the entire network using backpropagation [66]. This pre-training assists in overcoming issues such as poor initialization and vanishing gradients, which can hinder the performance of deep neural networks. Meanwhile, an RBM is a type of Markov Random Field that consists of a visible layer v and a hidden layer h , where the joint distribution P ( v , h ) is defined as:
P ( v , h ) = 1 Z exp ( − E ( v , h ) ) ,
where E ( v , h ) is the energy function, and Z is the partition function. The energy function for an RBM is typically defined as:
E ( v , h ) = − v T W h − b T v − c T h ,
where W is the weight matrix between the visible and hidden layers, b is the bias vector for the visible layer, and c is the bias vector for the hidden layer [67]. DBNs have been successfully applied in various financial applications, particularly in tasks that require the modelling of complex, high-dimensional data distributions. For example, DBNs can be used for credit risk assessment, where they model the underlying patterns in borrower behaviour and financial histories. By learning a hierarchical representation of the data, DBNs can capture subtle patterns that traditional models might miss, leading to more accurate predictions of creditworthiness. Despite their powerful modelling capabilities, DBNs are not without challenges. One of the main difficulties is in the training process, which can be computationally expensive, especially when dealing with very deep networks. Additionally, while DBNs can model complex data distributions, they may still suffer from issues related to scalability and overfitting, particularly when applied to large financial datasets [68,69].

4. Applications of Deep Learning in Finance

Deep learning has found numerous applications in finance, providing innovative solutions across various aspects of the financial sector. This section explores some of the key applications where deep learning has made a significant impact.

4.1. Algorithmic Trading

Algorithmic trading involves the use of computer algorithms to execute trading orders based on predefined criteria [70]. Deep learning models, specifically those utilizing RNNs like LSTM and GRU, have been increasingly applied to enhance algorithmic trading strategies. These models are capable of analyzing vast amounts of historical and real-time data to identify patterns and predict market movements with greater accuracy. The ability to process and interpret sequential data allows these models to adapt to changing market conditions, offering traders a competitive edge in executing trades efficiently.
Recent studies have demonstrated the effectiveness of deep learning models in algorithmic trading. For instance, Ozbayoglu et al. [71] applied an LSTM-based model to forecast stock prices and subsequently generate trading signals. The proposed LSTM obtained a classification accuracy of 91.5%, which outperformed traditional moving average strategies. Similarly, Wang et al. [19] employed a sequence-to-sequence model, which is an extension of RNNs, to predict market trends and optimize trading algorithms. Their model achieved a prediction accuracy of 85%, leading to more profitable trades.
In addition, Sirignano and Cont [72] proposed a universal DL model using CNNs to predict price changes in limit order books. Their approach demonstrated an accuracy improvement of 5-10% over traditional methods, significantly enhancing trading strategy performance. Moreover, the model’s ability to generalize across different market conditions indicates its robustness and adaptability, making it a valuable tool in volatile trading environments.
The use of reinforcement learning (RL) in algorithmic trading has also gained traction. For instance, Huang et al. [73] developed a deep reinforcement learning model that learns optimal trading strategies by interacting with the market environment. Their model outperformed conventional strategies by achieving a higher cumulative return and a precision of 92%, which indicates the potential of RL in creating autonomous trading agents that can continuously adapt to market dynamics without the need for manual intervention.

4.2. Risk Management and Credit Scoring

Risk management and credit scoring are crucial components of the financial industry, where accurate assessment of risk is essential for maintaining financial stability. Deep learning models, including feedforward neural networks and autoencoders, have been applied to enhance the accuracy of risk assessments and credit scoring systems. These models are capable of identifying complex, non-linear relationships within financial data that traditional statistical methods may overlook. In credit scoring, deep learning has been used to analyze borrower profiles, predict default risks, and improve the overall decision-making process. For example, Khandani et al. [21] utilized a deep learning model to predict consumer credit risk, achieving a 15% improvement in predictive accuracy over logistic regression models. Their model was effective in identifying high-risk borrowers, with an AUC of 0.89, thereby enabling financial institutions to take preemptive measures to minimize losses. Furthermore, autoencoders have been used to detect anomalies in credit transactions, which often indicate potential risks [74]. The ability of these models to learn from unlabeled data makes them invaluable for identifying patterns that might otherwise go unnoticed.
Furthermore, Xiao et al. [75] proposed a deep neural network for credit scoring that outperformed traditional scoring methods such as FICO scores by up to 20% in terms of predictive accuracy, achieving an AUC of 0.92. The DNN model was able to account for non-linear interactions between variables, providing a more detailed understanding of creditworthiness. This has significant implications for improving access to credit and reducing the likelihood of defaults, especially in underserved markets. Yang et al. [76] developed a DL model that predicts market risks by analyzing historical data and market indicators. Their model achieved a lower prediction error rate compared to conventional risk assessment models, enabling better-informed decision-making regarding asset allocation and risk mitigation.

4.3. Fraud Detection

Fraud detection is another critical area where deep learning has been effectively applied. Financial institutions face significant challenges in detecting and preventing fraudulent activities, such as unauthorized transactions and money laundering. CNN and other DL architectures have been utilized to analyze transaction data, detect anomalies, and identify fraudulent patterns in real time [77]. These models can process large volumes of data, including unstructured and semi-structured data, to uncover subtle patterns that might indicate fraud.
Jurgovsky et al. [78] employed LSTM networks to detect fraudulent credit card transactions. Their model achieved an F1-score of 0.93, significantly outperforming traditional ML models such as random forests and logistic regression, which had F1-scores of 0.85. The LSTM’s ability to capture temporal dependencies in transaction sequences was crucial in identifying suspicious patterns that evolve over time. Another study by Gandhar et al. [79] used a deep learning model to detect anomalies in financial transactions. The model was able to reduce false positives, which is critical in minimizing the impact of fraud detection on legitimate transactions.
In addition to supervised learning approaches, unsupervised deep learning methods have also been explored for fraud detection. For example, Raj and Kumar [80] developed an unsupervised DL model using autoencoders to detect fraudulent patterns in banking transactions without the need for labelled data. Their model achieved a high detection rate of 95% with minimal manual intervention, making it a scalable solution for large financial institutions. Meanwhile, deep reinforcement learning has shown promise in dynamic fraud detection systems. Qayoom et al. [81] proposed a deep Q-learning model for real-time fraud detection that adapts to changing fraud patterns. The model achieved a high detection rate, demonstrating the potential of reinforcement learning in continuously evolving financial environments.

4.4. Market Forecasting

Market forecasting involves predicting future market movements and trends based on historical data. Deep learning models, such as transformers and attention mechanisms, have shown considerable promise in improving the accuracy of market forecasts. These models can analyze vast datasets, including price movements, economic indicators, and market sentiment, to generate predictions that inform investment strategies [82]. The ability of deep learning models to capture complex temporal dependencies and nonlinear relationships within the data allows for more precise and timely forecasts, which are essential for making informed investment decisions in dynamic market environments.
In recent years, transformers have been increasingly used in market forecasting. For instance, Zeng et al. [83] applied a transformer-based model to forecast stock prices, achieving a higher prediction than traditional RNN-based models. The attention mechanism inherent in transformers allowed the model to focus on the most relevant historical data points, thereby improving the quality of predictions. This approach is useful in financial markets, where certain events or periods may have a disproportionate impact on future prices. Another approach to market forecasting involves the use of ensemble deep learning methods. Li et al. [84] combined multiple DL models, including CNNs and LSTMs, to forecast market indices. The ensemble approach mitigates the weaknesses of individual models by leveraging their complementary strengths, leading to more robust and reliable market predictions.
Sentiment analysis combined with deep learning has also been explored for market forecasting. lin et al. [85] developed a hybrid model that integrates sentiment analysis from social media with LSTM networks to predict stock market movements. Their model outperformed traditional sentiment analysis methods, highlighting the value of incorporating unstructured data into financial forecasts. Additionally, the application of generative models in market forecasting has gained attention. Vuletic et al. [86] used GANs to simulate future market scenarios based on historical data. Their model provided valuable insights into potential market trends, achieving a superior performance compared to traditional forecasting models. The use of GANs in market forecasting is still in its early stages, but it shows promise as a tool for stress-testing investment strategies under various market conditions.

4.5. Portfolio Management

Portfolio management requires the optimization of asset allocation to achieve desired financial objectives, such as maximizing returns or minimizing risk [87]. Deep learning models have been applied to develop more sophisticated portfolio management strategies that account for a broader range of variables and market conditions. Techniques such as reinforcement learning and GANs have been explored to optimize portfolio allocations dynamically, considering factors such as market volatility, investor preferences, and risk tolerance. Ye et al. [88] developed a reinforcement learning-based model for portfolio management that adapts to changing market conditions by learning from historical data. The reinforcement learning approach allows the model to continuously adjust the portfolio in response to market changes, thereby providing a more dynamic and responsive investment strategy.
Another application of deep learning in portfolio management involves the use of GANs. Jiang et al. [89] applied a GAN-based model to optimize cryptocurrency portfolios, which are characterized by high volatility and non-linear market behavior. Their model outperformed traditional portfolio optimization methods. The use of GANs allows for the generation of synthetic market scenarios, enabling the model to explore a wider range of potential market conditions and optimize the portfolio accordingly. Deep learning models have also been used to personalize portfolio management strategies. Shi et al. [90] proposed a deep learning-based framework that tailors investment strategies to individual investor preferences and risk tolerance. Their model integrates reinforcement learning with DL to optimize asset allocation in real time. This approach demonstrates the potential of DL in creating more personalized and effective investment solutions.
Furthermore, DL models have been employed to enhance portfolio diversification strategies. Zhang et al. [91] utilized a deep learning model to analyze the correlation structure of assets in a portfolio, improving diversification by identifying non-obvious correlations that traditional methods might miss. Also, the integration of deep learning with traditional quantitative models has been explored to enhance portfolio management. Lin et al. [92] proposed a hybrid approach that combines deep learning with factor models to optimize asset allocation. This hybrid approach employs the strengths of both deep learning and traditional financial theories, providing a balanced and effective portfolio management strategy.

4.6. Customer Segmentation

Customer segmentation is a critical task in the financial industry, enabling personalised marketing, targeted product offerings, and improved customer service. It involves dividing a broad customer base into smaller, more manageable groups based on shared characteristics. These characteristics can include behavioural patterns, financial habits, and transaction histories. Customer segmentation has traditionally relied on clustering techniques like k-means [93], hierarchical clustering [94], and Gaussian mixture models [95], which are effective but often limited by their reliance on predefined features and linear relationships. The shift towards deep learning in recent years has addressed these limitations by leveraging the ability of neural networks to model complex, non-linear relationships and learn feature representations automatically.
Wang [96] proposed a novel unsupervised deep learning approach for customer segmentation. A Modified Social Spider Optimization algorithm is employed for feature selection, identifying relevant customer behaviours. These selected features are then used to cluster customers using a Self-Organizing Neural Network. Finally, a Deep Neural Network classifies customers based on these clusters. The proposed model achieves high segmentation accuracy (98.67%), outperforming traditional methods. Despite the recent improvement in customer segmentation, there have been challenges in understanding the reason behind the need for segmentation. This is because the task is subjective and may depend on the analyst’s perspective. To address this, Mousaeirad [97] proposes a novel customer segmentation approach using a neural embedding framework called Customer2Vec. The approach leverages feature engineering to identify important customer characteristics and combines supervised and unsupervised learning techniques to embed customers into a vector space. This allows for a better understanding of customer similarities and improves the quality of segmentation, as demonstrated in a banking sector case study.

4.7. Financial Document Analysis and Information Extraction

Financial document analysis and information extraction are vital components in the financial industry, facilitating tasks such as risk assessment, compliance monitoring, and decision-making. The process involves automatically identifying, extracting, and interpreting relevant data from vast amounts of unstructured financial documents, including invoices, contracts, reports, and transaction records. Traditionally, rule-based systems and natural language processing (NLP) techniques, such as named entity recognition (NER) [98,99,100], have been employed for these tasks. However, these methods often struggle with the complexity and variability of financial documents, especially when dealing with ambiguous language, varying formats, and domain-specific terminologies.
Recent advancements in machine learning, particularly in deep learning, have significantly enhanced the capabilities of financial document analysis. Models, such as Bidirectional Encoder Representations from Transformers (BERT) [101,102] and its domain-specific variants such as FinBERT [103,104,105] have revolutionized the extraction of information from financial texts by capturing contextual meanings and domain-specific nuances. These models excel in tasks such as sentiment analysis, entity recognition, and document classification, thereby improving the accuracy and efficiency of information extraction in financial contexts.
Melus [106] introduced an automated framework that combines a fine-tuned BERT with Optical Character Recognition (OCR) for analyzing scanned financial documents. The OCR component converts scanned images into machine-readable text, which is then processed by the BERT model to extract relevant information. This approach is particularly useful in scenarios where documents are not originally in digital format, ensuring that even legacy paper documents can be included in automated workflows. In addition, Yang et al. [104] developed FinBERT, a pre-trained language model specifically tailored for financial sentiment analysis. By fine-tuning BERT on a large corpus of financial texts, FinBERT outperforms general-purpose models in tasks such as sentiment classification and named entity recognition within financial documents, making it a powerful tool for tasks like market sentiment analysis and risk assessment. Another significant contribution by Montariol et al. [107] proposed a multi-task learning framework using BERT for financial annual report feature extraction. This model simultaneously performs multiple related tasks, such as sentiment detection, objectivity extraction, and Environmental, Social and Governance classification, by leveraging the shared representations learned by BERT. The multi-task approach not only improves the performance of individual tasks but also enhances the model’s ability to generalize across different types of feature extraction in financial report. Similarly, Moirangthem and Lee [108] explored the use of GRUs for financial text classification, utilizing a hierarchical structure to better capture the document’s contextual information. The GRUs in their model effectively processed sequential data, enabling the extraction of meaningful sentence-level and document-level representations. Through incorporating a hierarchical attention mechanism, the model could assign varying levels of importance to different sentences and words, leading to improved accuracy in classifying financial texts. This approach demonstrated the effectiveness of GRUs in handling complex financial documents, such as earnings reports and financial news articles, by emphasizing the most relevant content within the text.
Further advancements by Cheng et al. [109] introduced a GNN based approach for financial fraud detection. By representing financial transactions as graphs, where nodes represent entities and edges represent transactions, the GNN model effectively captures complex relationships and patterns indicative of fraudulent behavior. This approach is particularly effective in detecting fraudulent activities that traditional machine learning models might miss due to the intricate and often non-linear relationships within the data. Lastly, Bao et al. [110] developed a deep learning framework for predicting financial distress using LSTM networks. LSTM networks are well-suited for modeling time-series data, making them ideal for predicting financial distress based on historical financial ratios and market indicators. This model’s ability to capture temporal dependencies and long-term trends results in more accurate and timely predictions, providing valuable insights for risk management and decision-making.
While these advancements have significantly improved the state of financial document analysis, challenges remain, particularly in the areas of interpretability and the handling of noisy or incomplete data. To address these issues, recent research has focused on hybrid models that combine deep learning with rule-based approaches to balance the flexibility of machine learning with the precision of expert systems. For example, Kotios et al. [111] propose a hybrid model that integrates a rule-based system with a deep learning model for enhanced accuracy in extracting key financial metrics from complex reports. This approach not only improves the extraction accuracy but also provides better interpretability by allowing domain experts to understand and validate the extracted information.

5. Recent Advances and Emerging Trends

The field of deep learning in finance is rapidly evolving, driven by both technological advancements and the growing availability of data. This section explores recent developments and emerging trends that are shaping the future of this domain.
  • Explainable AI and Model Transparency: One of the most significant recent advances in the field has been the development of Explainable AI (XAI) techniques. These methods aim to make the decision-making processes of DL models more transparent and understandable to human users. This is important in finance, where stakeholders need to trust and comprehend the reasoning behind model predictions, especially in high-stakes environments such as credit scoring, fraud detection, and trading. Techniques such as SHapley Additive exPlanations (SHAP) and Local Interpretable Model-agnostic Explanations (LIME) are increasingly being adopted to enhance model transparency [112].
  • Transfer Learning and Pretrained Models: Transfer learning is a powerful technique in deep learning, allowing models trained on one task to be repurposed for another related task [113]. This approach is beneficial in financial applications, where labelled data is often scarce or expensive to obtain. By leveraging pre-trained models on large datasets (e.g., language models for sentiment analysis), financial institutions can achieve high performance with limited data. This trend has also led to the development of financial-specific pre-trained models, which can be fine-tuned for specific applications such as market prediction or risk assessment [113].
  • Federated Learning and Data Privacy: With increasing concerns about data privacy, federated learning has gained traction as a solution that allows for collaborative model training without the need to share raw data across institutions. In federated learning, models are trained across decentralized devices or servers, where data remains local, and only the model updates are shared. This approach is advantageous in finance since data privacy is paramount, enabling institutions to benefit from collective learning while maintaining data security and compliance with regulations like GDPR [114].
  • Reinforcement Learning in Financial Markets: Reinforcement learning has seen a surge of interest as a method for optimizing decision-making processes in financial markets. Unlike supervised learning, where models learn from labelled data, RL involves learning from the environment through trial and error, making it highly suitable for dynamic environments like trading. RL models are being used to develop autonomous trading agents, optimize portfolio management strategies, and improve algorithmic trading systems by adapting to changing market conditions [115].
  • Quantum Computing and Quantum Machine Learning: Quantum computing, though still in its infancy, is an emerging trend that holds the potential to revolutionize DL and financial modelling. Quantum ML leverages quantum computer’s ability to process information at speeds far beyond classical computers, offering the promise of solving complex optimization problems in finance more efficiently. While practical applications are still limited, ongoing research and development in quantum algorithms for financial modelling suggest that this technology could become a significant technology in the future of finance [116].
  • Ethical AI and Fairness As AI technologies become more embedded in financial systems, there is a growing emphasis on ensuring that these systems operate fairly and ethically. Recent advances have focused on developing methods to detect and mitigate biases in AI models, ensuring that financial services are accessible and equitable. This trend is driving the adoption of fairness-aware machine learning techniques and the integration of ethical considerations into the AI development lifecycle. The financial industry is increasingly prioritizing these concerns to maintain public trust and comply with evolving regulatory standards [117].

6. Challenges and Limitations

Applying deep learning in the financial sector presents several notable challenges that can hinder effectiveness and practical deployment, and they are discussed in this section.

6.1. Data Quality and Availability

One of the fundamental challenges in applying deep learning to financial data is the quality and availability of the data itself. Financial datasets often contain a high degree of noise and are subject to issues such as missing values, outliers, and inconsistencies. Moreover, the sensitive nature of financial information means that much data is not publicly available, and where it is available, it often comes with stringent usage restrictions [86]. These factors can significantly impede the training and validation of robust DL models, which require large, diverse, and representative datasets to function optimally.

6.2. Overfitting and Model Interpretability

Deep learning models, mainly those with many layers and parameters, are prone to overfitting, especially when trained on financial data that inherently exhibits high volatility and non-stationarity. Overfitting leads to models that perform well on training data but fail to generalize to unseen data. Additionally, the "black-box" nature of many deep learning models poses significant challenges in terms of interpretability [112]. Financial stakeholders typically require clear explanations for decisions made by automated systems, mostly in scenarios involving investments, lending, and risk management, where accountability is crucial.

6.3. Computational Complexity

The training of DL models often requires substantial computational resources, which can be a barrier, especially for smaller institutions or startups. The complexity and size of models necessary to capture the intricacies of financial data mean that significant investment in hardware and software is needed [118]. Furthermore, the energy consumption associated with training and maintaining these models can be considerable, adding to operational costs and environmental impact.

6.4. Ethical and Regulatory Concerns

Deep learning applications in finance must navigate a complex domain of ethical and regulatory issues. This includes ensuring that models comply with laws governing data privacy, such as the General Data Protection Regulation (GDPR) in Europe, and regulations related to financial reporting and conduct [119]. There is also a growing concern over the ethical implications of automated decision-making systems, which can exacerbate existing inequalities if not carefully managed.

6.5. Bias and Fairness

Bias in ML models is a significant issue, with the potential to lead to unfair outcomes when applied to financial services. Algorithmic biases can result from skewed training data or flawed assumptions embedded in the algorithm design [120]. In finance, this can result in discriminatory practices, such as biased credit scoring and investment advising, disproportionately affecting marginalized groups. Ensuring fairness in AI applications is essential to maintaining trust and legality in financial practices.

7. Future Research Directions

The ongoing evolution of deep learning in the financial industry presents numerous avenues for future research. One critical area is enhancing the interpretability and explainability of DL models. As these models grow in complexity, there is a pressing need to develop new techniques that can provide transparent and actionable insights, especially in financial contexts where understanding the rationale behind model predictions is crucial. While XAI has made significant strides, further research could focus on integrating domain-specific knowledge and creating more intuitive visualization tools that bridge the gap between technical complexity and practical usability, a challenge that remains largely unmet.
In addition to interpretability, improving data quality and addressing data scarcity continue to be significant challenges. Financial data often suffers from issues such as noise, missing values, and non-stationarity, which can undermine the reliability of DL models. Research into more sophisticated data preprocessing methods and techniques for augmenting scarce datasets, such as the generation of synthetic data using GANs, could greatly enhance the robustness of financial models. Furthermore, exploring federated learning as a solution to data scarcity and privacy concerns offers a promising research direction, especially in contexts where data sharing is restricted by regulatory or competitive concerns.
Addressing bias and ensuring fairness in AI systems is another critical area that requires further investigation. Bias in financial models can lead to unfair and discriminatory outcomes, which is concerning in areas such as credit scoring and lending. While some progress has been made in developing fairness-aware algorithms, there remains a substantial gap in research on how to systematically detect and mitigate bias throughout the model lifecycle, especially in the dynamic environments typical of financial markets. Future research could focus on creating comprehensive frameworks that monitor and correct biases as models are deployed in real-world scenarios, which is an essential step toward ensuring that financial AI systems operate ethically.
Reinforcement learning in financial applications, though promising, is still in its early stages and presents numerous opportunities for further research. While RL has shown potential in optimizing trading strategies and portfolio management, more work is needed to refine these approaches in order to develop risk-sensitive RL models and hybrid systems that combine RL with traditional financial techniques. This research could lead to more robust and adaptable financial decision-making systems capable of operating

8. Conclusions

Deep learning algorithms have become integral to numerous financial applications, including credit scoring, fraud detection, algorithmic trading, and market forecasting. This paper provides a concise yet comprehensive overview of key DL models, such as CNNs, LSTMs, GANs, and Deep RL. The study also addresses critical challenges associated with deploying these models in finance, including data quality, model interpretability, and computational demands. This paper is essential for researchers and practitioners looking to understand the current field of deep learning in finance and the potential future directions in this rapidly evolving field.

Author Contributions

Conceptualization, E.M., N.J., G.O., I.D.M., and K.A.; methodology, E.M., N.J., G.O., I.D.M., and K.A.; validation, I.D.M. and G.O.; investigation, E.M. and I.D.M.; writing—original draft preparation, E.M., N.J., G.O., I.D.M., and K.A.; writing—review and editing, E.M., N.J., G.O., I.D.M., and K.A.; visualization, I.D.M; supervision, N.J. and I.D.M. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Conflicts of Interest

The authors declare no conflicts of interest.

Abbreviations

The following abbreviations are used in this manuscript:
AI Artificial Intelligence
AdaBoost Adaptive Boosting
CNN Convolutional Neural Network
DNN Deep Neural Network
DL Deep Learning
FNN Feedforward Neural Network
GAN Generative Adversarial Network
GDPR General Data Protection Regulation
GRU Gated Recurrent Unit
LSTM Long Short-Term Memory
ML Machine Learning
NLP Natural Language Processing
ReLU Rectified Linear Unit
RNN Recurrent Neural Network
RL Reinforcement Learning
Tanh Hyperbolic Tangent
XAI Explainable Artificial Intelligence
XGBoost Extreme Gradient Boosting

References

  1. Talaat, F.M.; Aljadani, A.; Badawy, M.; Elhosseini, M. Toward interpretable credit scoring: integrating explainable artificial intelligence with deep learning for credit card default prediction. Neural Computing and Applications 2024, 36, 4847–4865. [Google Scholar] [CrossRef]
  2. Ganji, V.R.; Chaparala, A. Wave Hedges distance-based feature fusion and hybrid optimization-enabled deep learning for cyber credit card fraud detection. Knowledge and Information Systems 2024, 1–26. [Google Scholar] [CrossRef]
  3. Huang, Y.; Wan, X.; Zhang, L.; Lu, X. A novel deep reinforcement learning framework with BiLSTM-Attention networks for algorithmic trading. Expert Systems with Applications 2024, 240, 122581. [Google Scholar] [CrossRef]
  4. Vaca, C.; Astorgano, M.; López-Rivero, A.J.; Tejerina, F.; Sahelices, B. Interpretability of deep learning models in analysis of Spanish financial text. Neural Computing and Applications 2024, 36, 7509–7527. [Google Scholar] [CrossRef]
  5. Zhang, C.; Sjarif, N.N.A.; Ibrahim, R. Deep learning models for price forecasting of financial time series: A review of recent advancements: 2020–2022. Wiley Interdisciplinary Reviews: Data Mining and Knowledge Discovery 2024, 14, e1519. [Google Scholar] [CrossRef]
  6. Mienye, I.D.; Jere, N. Deep Learning for Credit Card Fraud Detection: A Review of Algorithms, Challenges, and Solutions. IEEE Access 2024. [Google Scholar] [CrossRef]
  7. Ahmed, S.; Alshater, M.M.; El Ammari, A.; Hammami, H. Artificial intelligence and machine learning in finance: A bibliometric review. Research in International Business and Finance 2022, 61, 101646. [Google Scholar] [CrossRef]
  8. Goodell, J.W.; Kumar, S.; Lim, W.M.; Pattnaik, D. Artificial intelligence and machine learning in finance: Identifying foundations, themes, and research clusters from bibliometric analysis. Journal of Behavioral and Experimental Finance 2021, 32, 100577. [Google Scholar] [CrossRef]
  9. Gunnarsson, B.R.; Vanden Broucke, S.; Baesens, B.; Óskarsdóttir, M.; Lemahieu, W. Deep learning for credit scoring: Do or don’t? European Journal of Operational Research 2021, 295, 292–305. [Google Scholar] [CrossRef]
  10. Jiang, W. Applications of deep learning in stock market prediction: recent progress. Expert Systems with Applications 2021, 184, 115537. [Google Scholar] [CrossRef]
  11. Li, A.W.; Bastos, G.S. Stock Market Forecasting Using Deep Learning and Technical Analysis: A Systematic Review. IEEE Access 2020, 8, 185232–185242. [Google Scholar] [CrossRef]
  12. Sonkavde, G.; Dharrao, D.S.; Bongale, A.M.; Deokate, S.T.; Doreswamy, D.; Bhat, S.K. Forecasting stock market prices using machine learning and deep learning models: A systematic review, performance analysis and discussion of implications. International Journal of Financial Studies 2023, 11, 94. [Google Scholar] [CrossRef]
  13. Pricope, T.V. Deep reinforcement learning in quantitative algorithmic trading: A review. arXiv 2021, arXiv:2106.00123. [Google Scholar]
  14. Bengesi, S.; El-Sayed, H.; Sarker, M.K.; Houkpati, Y.; Irungu, J.; Oladunni, T. Advancements in Generative AI: A Comprehensive Review of GANs, GPT, Autoencoders, Diffusion Model, and Transformers. IEEE Access 2024. [Google Scholar] [CrossRef]
  15. Dubey, S.R.; Singh, S.K. Transformer-based generative adversarial networks in computer vision: A comprehensive survey. IEEE Transactions on Artificial Intelligence 2024. [Google Scholar] [CrossRef]
  16. Khan, W.; Daud, A.; Khan, K.; Muhammad, S.; Haq, R. Exploring the frontiers of deep learning and natural language processing: A comprehensive overview of key challenges and emerging trends. Natural Language Processing Journal 2023, 100026. [Google Scholar] [CrossRef]
  17. Assefa, S.A.; Dervovic, D.; Mahfouz, M.; Tillman, R.E.; Reddy, P.; Veloso, M. Generating synthetic data in finance: opportunities, challenges and pitfalls. Proceedings of the First ACM International Conference on AI in Finance, 2020, pp. 1–8.
  18. Soleymani, F.; Paquet, E. Financial portfolio optimization with online deep reinforcement learning and restricted stacked autoencoder—DeepBreath. Expert Systems with Applications 2020, 156, 113456. [Google Scholar] [CrossRef]
  19. Wang, J.; Sun, T.; Liu, B.; Cao, Y.; Zhu, H. CLVSA: A convolutional LSTM based variational sequence-to-sequence model with attention for predicting trends of financial markets. arXiv 2021, arXiv:2104.04041. [Google Scholar]
  20. Meng, B.; Sun, J.; Shi, B. A novel URP-CNN model for bond credit risk evaluation of Chinese listed companies. Expert Systems with Applications 2024, 124861. [Google Scholar] [CrossRef]
  21. Khandani, A.E.; Kim, A.J.; Lo, A.W. Consumer credit-risk models via machine-learning algorithms. Journal of Banking & Finance 2010, 34, 2767–2787. [Google Scholar]
  22. Esenogho, E.; Mienye, I.D.; Swart, T.G.; Aruleba, K.; Obaido, G. A neural network ensemble with feature engineering for improved credit card fraud detection. IEEE Access 2022, 10, 16400–16407. [Google Scholar] [CrossRef]
  23. Mienye, I.D.; Sun, Y. A Deep Learning Ensemble With Data Resampling for Credit Card Fraud Detection. IEEE Access 2023, 11, 30628–30638. [Google Scholar] [CrossRef]
  24. Sezer, O.B.; Ozbayoglu, M. Financial time series forecasting with deep learning: A systematic literature review: 2005-2019. Applied Soft Computing 2020, 90, 106181. [Google Scholar] [CrossRef]
  25. Lim, B.; Zohren, S. Time-series forecasting with deep learning: a survey. Philosophical Transactions of the Royal Society A 2021, 379, 20200209. [Google Scholar] [CrossRef] [PubMed]
  26. Ojha, V.K.; Abraham, A.; Snášel, V. Metaheuristic design of feedforward neural networks: A review of two decades of research. Engineering Applications of Artificial Intelligence 2017, 60, 97–116. [Google Scholar] [CrossRef]
  27. Alemu, H.Z.; Wu, W.; Zhao, J. Feedforward neural networks with a hidden layer regularization method. Symmetry 2018, 10, 525. [Google Scholar] [CrossRef]
  28. Nwankpa, C.; Ijomah, W.; Gachagan, A.; Marshall, S. Activation functions: Comparison of trends in practice and research for deep learning. arXiv 2018, arXiv:1811.03378. [Google Scholar]
  29. Sherstinsky, A. Fundamentals of recurrent neural network (RNN) and long short-term memory (LSTM) network. Physica D: Nonlinear Phenomena 2020, 404, 132306. [Google Scholar] [CrossRef]
  30. Mikolov, T.; et al. . Recurrent neural network based language model. Interspeech 2010, 2, 1045–1048. [Google Scholar]
  31. Schmidt, R.M. Recurrent neural networks (rnns): A gentle introduction and overview. arXiv 2019, arXiv:1912.05911. [Google Scholar]
  32. Salehinejad, H.; Sankar, S.; Barfett, J.; Colak, E.; Valaee, S. Recent advances in recurrent neural networks. arXiv 2017, arXiv:1801.01078. [Google Scholar]
  33. Oruh, J.; Viriri, S.; Adegun, A. Long short-term memory recurrent neural network for automatic speech recognition. IEEE Access 2022, 10, 30069–30079. [Google Scholar] [CrossRef]
  34. Oliveira, P.; Fernandes, B.; Analide, C.; Novais, P. Forecasting energy consumption of wastewater treatment plants with a transfer learning approach for sustainable cities. Electronics 2021, 10, 1149. [Google Scholar] [CrossRef]
  35. Chung, J.; Gulcehre, C.; Cho, K.; Bengio, Y. Empirical evaluation of gated recurrent neural networks on sequence modeling. arXiv 2014, arXiv:1412.3555. [Google Scholar]
  36. Shen, G.; Tan, Q.; Zhang, H.; Zeng, P.; Xu, J. Deep learning with gated recurrent unit networks for financial sequence predictions. Procedia computer science 2018, 131, 895–903. [Google Scholar] [CrossRef]
  37. Dutta, A.; Kumar, S.; Basu, M. A gated recurrent unit approach to bitcoin price prediction. Journal of risk and financial management 2020, 13, 23. [Google Scholar] [CrossRef]
  38. Pirani, M.; Thakkar, P.; Jivrani, P.; Bohara, M.H.; Garg, D. A comparative analysis of ARIMA, GRU, LSTM and BiLSTM on financial time series forecasting. 2022 IEEE International Conference on Distributed Computing and Electrical Circuits and Electronics (ICDCECE). IEEE, 2022, pp. 1–6.
  39. Kattenborn, T.; Leitloff, J.; Schiefer, F.; Hinz, S. Review on Convolutional Neural Networks (CNN) in vegetation remote sensing. ISPRS journal of photogrammetry and remote sensing 2021, 173, 24–49. [Google Scholar] [CrossRef]
  40. Yamashita, R.; Nishio, M.; Do, R.K.G.; Togashi, K. Convolutional neural networks: an overview and application in radiology. Insights into imaging 2018, 9, 611–629. [Google Scholar] [CrossRef] [PubMed]
  41. Ketkar, N.; Moolayil, J.; Ketkar, N.; Moolayil, J. Convolutional neural networks. Deep learning with Python: learn best practices of deep learning models with PyTorch 2021, 197–242. [Google Scholar]
  42. González-Rodríguez, L.; Plasencia-Salgueiro, A. Uncertainty-Aware autonomous mobile robot navigation with deep reinforcement learning. Deep learning for unmanned systems 2021, 225–257. [Google Scholar]
  43. Mienye, I.D.; Ainah, P.K.; Emmanuel, I.D.; Esenogho, E. Sparse noise minimization in image classification using Genetic Algorithm and DenseNet. 2021 Conference on Information Communications Technology and Society (ICTAS). IEEE, 2021, pp. 103–108.
  44. Saeedan, F.; Weber, N.; Goesele, M.; Roth, S. Detail-preserving pooling in deep networks. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2018, pp. 9108–9116.
  45. Abou Houran, M.; Bukhari, S.M.S.; Zafar, M.H.; Mansoor, M.; Chen, W. COA-CNN-LSTM: Coati optimization algorithm-based hybrid deep learning model for PV/wind power forecasting in smart grid applications. Applied Energy 2023, 349, 121638. [Google Scholar] [CrossRef]
  46. Hilal, W.; Gadsden, S.A.; Yawney, J. Financial fraud: a review of anomaly detection techniques and recent advances. Expert systems With applications 2022, 193, 116429. [Google Scholar] [CrossRef]
  47. Zhu, B.; Yang, W.; Wang, H.; Yuan, Y. A hybrid deep learning model for consumer credit scoring. 2018 international conference on artificial intelligence and big data (ICAIBD). IEEE, 2018, pp. 205–208.
  48. Lin, T.; Wang, Y.; Liu, X.; Qiu, X. A survey of transformers. AI open 2022, 3, 111–132. [Google Scholar] [CrossRef]
  49. Chen, Z.; Ma, M.; Li, T.; Wang, H.; Li, C. Long sequence time-series forecasting with deep learning: A survey. Information Fusion 2023, 97, 101819. [Google Scholar] [CrossRef]
  50. Khan, S.; Naseer, M.; Hayat, M.; Zamir, S.W.; Khan, F.S.; Shah, M. Transformers in vision: A survey. ACM computing surveys (CSUR) 2022, 54, 1–41. [Google Scholar] [CrossRef]
  51. Wolf, T.; Debut, L.; Sanh, V.; Chaumond, J.; Delangue, C.; Moi, A.; Cistac, P.; Rault, T.; Louf, R.; Funtowicz, M. ; others. Transformers: State-of-the-art natural language processing. Proceedings of the 2020 conference on empirical methods in natural language processing: system demonstrations, 2020, pp. 38–45.
  52. Zhang, S.; et al. . Transformer-based model for financial time series forecasting. Journal of Financial Data Science 2020, 2, 98–115. [Google Scholar]
  53. Mishev, K.; Gjorgjevikj, A.; Vodenska, I.; Chitkushev, L.T.; Trajanov, D. Evaluation of sentiment analysis in finance: from lexicons to transformers. IEEE access 2020, 8, 131662–131682. [Google Scholar] [CrossRef]
  54. Kisiel, D.; Gorse, D. Portfolio transformer for attention-based asset allocation. International Conference on Artificial Intelligence and Soft Computing. Springer, 2022, pp. 61–71.
  55. Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial networks. Communications of the ACM 2020, 63, 139–144. [Google Scholar] [CrossRef]
  56. Creswell, A.; White, T.; Dumoulin, V.; Arulkumaran, K.; Sengupta, B.; Bharath, A.A. Generative adversarial networks: An overview. IEEE signal processing magazine 2018, 35, 53–65. [Google Scholar] [CrossRef]
  57. Dash, A.; Ye, J.; Wang, G. A review of generative adversarial networks (GANs) and its applications in a wide variety of disciplines: from medical to remote sensing. IEEE Access 2023. [Google Scholar] [CrossRef]
  58. Ramzan, F.; Sartori, C.; Consoli, S.; Reforgiato Recupero, D. Generative Adversarial Networks for Synthetic Data Generation in Finance: Evaluating Statistical Similarities and Quality Assessment. AI 2024, 5, 667–685. [Google Scholar] [CrossRef]
  59. Pun, C.S.; Wang, L.; Wong, H.Y. Financial thought experiment: A GAN-based approach to vast robust portfolio selection. Proceedings of the 29th International Joint Conference on Artificial Intelligence (IJCAI’20), 2020.
  60. Koshiyama, A.; Firoozye, N.; Treleaven, P. Generative adversarial networks for financial trading strategies fine-tuning and combination. Quantitative Finance 2021, 21, 797–813. [Google Scholar] [CrossRef]
  61. Nguyen, T.T.; Nguyen, N.D.; Nahavandi, S. Deep reinforcement learning for multiagent systems: A review of challenges, solutions, and applications. IEEE transactions on cybernetics 2020, 50, 3826–3839. [Google Scholar] [CrossRef]
  62. Wang, Z.; Huang, B.; Tu, S.; Zhang, K.; Xu, L. DeepTrader: a deep reinforcement learning approach for risk-return balanced portfolio management with market conditions Embedding. Proceedings of the AAAI conference on artificial intelligence, 2021, Vol. 35, pp. 643–650.
  63. Salakhutdinov, R. Learning deep generative models. Annual Review of Statistics and Its Application 2015, 2, 361–385. [Google Scholar] [CrossRef]
  64. Hu, S.; Zuo, Y.; Wang, L.; Liu, P. A review about building hidden layer methods of deep learning. Journal of Advances in Information Technology 2016, 7. [Google Scholar] [CrossRef]
  65. Lopes, N.; Ribeiro, B.; Lopes, N.; Ribeiro, B. Deep belief networks (DBNs). Machine Learning for Adaptive Many-Core Machines-A Practical Approach 2015, 155–186. [Google Scholar]
  66. Yu, D.; Deng, L.; Dahl, G. Roles of pre-training and fine-tuning in context-dependent DBN-HMMs for real-world speech recognition. Proc. NIPS Workshop on Deep Learning and Unsupervised Feature Learning. sn, 2010.
  67. Hua, Y.; Guo, J.; Zhao, H. Deep belief networks and deep learning. Proceedings of 2015 international conference on intelligent computing and internet of things. IEEE, 2015, pp. 1–4.
  68. Ramezani, S.B.; Cummins, L.; Killen, B.; Carley, R.; Amirlatifi, A.; Rahimi, S.; Seale, M.; Bian, L. Scalability, explainability and performance of data-driven algorithms in predicting the remaining useful life: A comprehensive review. Ieee Access 2023, 11, 41741–41769. [Google Scholar] [CrossRef]
  69. Ahmed, S.F.; Alam, M.S.B.; Hassan, M.; Rozbu, M.R.; Ishtiak, T.; Rafa, N.; Mofijur, M.; Shawkat Ali, A.; Gandomi, A.H. Deep learning modelling techniques: current progress, applications, advantages, and challenges. Artificial Intelligence Review 2023, 56, 13521–13617. [Google Scholar] [CrossRef]
  70. Lenglet, M. Conflicting codes and codings: How algorithmic trading is reshaping financial regulation. Theory, Culture & Society 2011, 28, 44–66. [Google Scholar]
  71. Ozbayoglu, A.M.; Gudelek, M.U.; Sezer, O.B. Deep learning for financial applications: A survey. Applied soft computing 2020, 93, 106384. [Google Scholar] [CrossRef]
  72. Sirignano, J.; Cont, R. Universal features of price formation in financial markets: Perspectives from deep learning. Quantitative Finance 2019, 19, 1449–1459. [Google Scholar] [CrossRef]
  73. Huang, Y.; Zhou, X.; et al. . Financial trading as a game: A deep reinforcement learning approach. Journal of Financial Data Science 2018, 1, 10–24. [Google Scholar]
  74. Chang, C.H. Managing credit card fraud risks by autoencoders. In Advances in Pacific Basin Business, Economics and Finance; Emerald Publishing Limited, 2021; Vol. 9, pp. 225–235.
  75. Xiao, J.; Zhong, Y.; Jia, Y.; Wang, Y.; Li, R.; Jiang, X.; Wang, S. A novel deep ensemble model for imbalanced credit scoring in internet finance. International Journal of Forecasting 2024, 40, 348–372. [Google Scholar] [CrossRef]
  76. Yang, T.; Li, A.; Xu, J.; Su, G.; Wang, J. Deep learning model-driven financial risk prediction and analysis 2024.
  77. Mienye, I.D.; Sun, Y. A machine learning method with hybrid feature selection for improved credit card fraud detection. Applied Sciences 2023, 13, 7254. [Google Scholar] [CrossRef]
  78. Jurgovsky, J.; Granitzer, M.; et al. . Sequence classification for credit-card fraud detection. Expert Systems with Applications 2018, 100, 234–245. [Google Scholar] [CrossRef]
  79. Gandhar, A.; Gupta, K.; Pandey, A.K.; Raj, D. Fraud Detection Using Machine Learning and Deep Learning. SN Computer Science 2024, 5, 1–10. [Google Scholar] [CrossRef]
  80. Rai, A.K.; Dwivedi, R.K. Fraud detection in credit card data using unsupervised machine learning based scheme. 2020 international conference on electronics and sustainable communication systems (ICESC). IEEE, 2020, pp. 421–426.
  81. Qayoom, A.; Khuhro, M.A.; Kumar, K.; Waqas, M.; Saeed, U.; ur Rehman, S.; Wu, Y.; Wang, S. A novel approach for credit card fraud transaction detection using deep reinforcement learning scheme. PeerJ Computer Science 2024, 10, e1998. [Google Scholar] [CrossRef] [PubMed]
  82. Li, A.W.; Bastos, G.S. Stock market forecasting using deep learning and technical analysis: a systematic review. IEEE access 2020, 8, 185232–185242. [Google Scholar] [CrossRef]
  83. Zeng, A.; Chen, M.; Zhang, L.; Xu, Q. Are transformers effective for time series forecasting? Proceedings of the AAAI conference on artificial intelligence, 2023, Vol. 37, pp. 11121–11128.
  84. Li, Y.; Pan, Y. A novel ensemble deep learning model for stock prediction based on stock prices and news. International Journal of Data Science and Analytics 2022, 13, 139–149. [Google Scholar] [CrossRef] [PubMed]
  85. Lin, Y.L.; Lai, C.J.; Pai, P.F. Using deep learning techniques in forecasting stock markets by hybrid data with multilingual sentiment analysis. Electronics 2022, 11, 3513. [Google Scholar] [CrossRef]
  86. Vuletić, M.; Prenzel, F.; Cucuringu, M. Fin-gan: Forecasting and classifying financial time series via generative adversarial networks. Quantitative Finance 2024, 24, 175–199. [Google Scholar] [CrossRef]
  87. Varmaz, A.; Fieberg, C.; Poddig, T. Portfolio optimization for sustainable investments. Annals of Operations Research 2024, 1–26. [Google Scholar] [CrossRef]
  88. Ye, Y.; Pei, H.; Wang, B.; Chen, P.Y.; Zhu, Y.; Xiao, J.; Li, B. Reinforcement-learning based portfolio management with augmented asset movement prediction states. Proceedings of the AAAI conference on artificial intelligence, 2020, Vol. 34, pp. 1112–1119.
  89. Jiang, Y.; et al. . Cryptocurrency portfolio management with deep reinforcement learning. Proceedings of the IEEE International Conference on Data Mining Workshops, 2017, pp. 18–25.
  90. Shi, S.; Li, J.; Li, G.; Pan, P.; Liu, K. Xpm: An explainable deep reinforcement learning framework for portfolio management. Proceedings of the 30th ACM international conference on information & knowledge management, 2021, pp. 1661–1670.
  91. Zhang, Z.; Zohren, S.; Roberts, S. Deep learning for portfolio optimization. arXiv, 2020; arXiv:2005.13665. [Google Scholar]
  92. Lin, Y.C.; Chen, C.T.; Sang, C.Y.; Huang, S.H. Multiagent-based deep reinforcement learning for risk-shifting portfolio management. Applied Soft Computing 2022, 123, 108894. [Google Scholar] [CrossRef]
  93. Kansal, T.; Bahuguna, S.; Singh, V.; Choudhury, T. Customer segmentation using K-means clustering. 2018 international conference on computational techniques, electronics and mechanical systems (CTEMS). IEEE, 2018, pp. 135–139.
  94. Abdulhafedh, A. Incorporating k-means, hierarchical clustering and pca in customer segmentation. Journal of City and Development 2021, 3, 12–30. [Google Scholar]
  95. Chang, W.; Kim, S.; Chae, H. A regularized spatial market segmentation method with Dirichlet process—Gaussian mixture prior. Spatial Statistics 2020, 35, 100402. [Google Scholar] [CrossRef]
  96. Wang, C. Efficient customer segmentation in digital marketing using deep learning with swarm intelligence approach. Information Processing & Management 2022, 59, 103085. [Google Scholar]
  97. Mousaeirad, S. Intelligent vector-based customer segmentation in the banking industry. arXiv 2020, arXiv:2012.11876. [Google Scholar]
  98. Gunter, D.; Puac-Polanco, P.; Miguel, O.; Thornhill, R.E.; Yu, A.Y.; Liu, Z.A.; Mamdani, M.; Pou-Prom, C.; Aviv, R.I. Rule-based natural language processing for automation of stroke data extraction: a validation study. Neuroradiology 2022, 64, 2357–2362. [Google Scholar] [CrossRef] [PubMed]
  99. Singh, S. Natural language processing for information extraction. arXiv, 2018; arXiv:1807.02383. [Google Scholar]
  100. Sheikh, M.; Conlon, S. A rule-based system to extract financial information. Journal of Computer Information Systems 2012, 52, 10–19. [Google Scholar]
  101. Othan, D.; Kilimci, Z.H.; Uysal, M. Financial sentiment analysis for predicting direction of stocks using bidirectional encoder representations from transformers (BERT) and deep learning models. Proc. int. conf. innov. intell. technol, 2019, Vol. 2019, pp. 30–35.
  102. Wang, W.; Liu, M.; Zhang, Y.; Xiang, J.; Mao, R. Financial numeral classification model based on BERT. NII Testbeds and Community for Information Access Research: 14th International Conference, NTCIR 2019, Tokyo, Japan, June 10–13, 2019, Revised Selected Papers 14. Springer, 2019, pp. 193–204.
  103. Araci, D. Finbert: Financial sentiment analysis with pre-trained language models. arXiv 2019, arXiv:1908.10063. [Google Scholar]
  104. Yang, Y.; Uy, M.C.S.; Huang, A. Finbert: A pretrained language model for financial communications. arXiv 2020, arXiv:2006.08097. [Google Scholar]
  105. Liu, Z.; Huang, D.; Huang, K.; Li, Z.; Zhao, J. Finbert: A pre-trained financial language representation model for financial text mining. Proceedings of the twenty-ninth international conference on international joint conferences on artificial intelligence, 2021, pp. 4513–4519.
  106. Melus, D. Enhancing Quality of Optical Character Recognition for Financial Document Processing 2023.
  107. Montariol, S.; Martinc, M.; Pelicon, A.; Pollak, S.; Koloski, B.; Lončarski, I.; Valentinčič, A.; Šuštar, K.S.; Ichev, R.; Žnidaršič, M. Multi-task Learning for Features Extraction in Financial Annual Reports. Joint European Conference on Machine Learning and Knowledge Discovery in Databases. Springer, 2022, pp. 7–24.
  108. Moirangthem, D.S.; Lee, M. Hierarchical and lateral multiple timescales gated recurrent units with pre-trained encoder for long text classification. Expert Systems with Applications 2021, 165, 113898. [Google Scholar] [CrossRef]
  109. Cheng, D.; Wang, X.; Zhang, Y.; Zhang, L. Graph neural network for fraud detection via spatial-temporal attention. IEEE Transactions on Knowledge and Data Engineering 2020, 34, 3800–3813. [Google Scholar] [CrossRef]
  110. Bao, W.; Yue, J.; Rao, Y. A deep learning framework for financial time series using stacked autoencoders and long-short term memory. PloS one 2017, 12, e0180944. [Google Scholar] [CrossRef] [PubMed]
  111. Kotios, D.; Makridis, G.; Fatouros, G.; Kyriazis, D. Deep learning enhancing banking services: a hybrid transaction classification and cash flow prediction approach. Journal of big Data 2022, 9, 100. [Google Scholar] [CrossRef]
  112. Arrieta, A.B.; Díaz-Rodríguez, N.; Del Ser, J.; Bennetot, A.; Tabik, S.; Barbado, A.; García, S.; Gil-López, S.; Molina, D.; Benjamins, R.; others. Explainable Artificial Intelligence (XAI): Concepts, taxonomies, opportunities and challenges toward responsible AI. Information Fusion 2020, 58, 82–115. [Google Scholar] [CrossRef]
  113. Pan, S.J.; Yang, Q. A survey on transfer learning. IEEE Transactions on Knowledge and Data Engineering 2010, 22, 1345–1359. [Google Scholar] [CrossRef]
  114. Yang, Q.; Liu, Y.; Chen, T.; Tong, Y. Federated machine learning: Concept and applications. ACM Transactions on Intelligent Systems and Technology (TIST) 2019, 10, 1–19. [Google Scholar] [CrossRef]
  115. Fischer, T. Reinforcement learning in financial markets—A survey. Machine Learning 2018, 108, 1683–1701. [Google Scholar]
  116. Biamonte, J.; Wittek, P.; Pancotti, N.; Rebentrost, P.; Wiebe, N.; Lloyd, S. Quantum machine learning. Nature 2017, 549, 195–202. [Google Scholar] [CrossRef] [PubMed]
  117. Barocas, S.; Selbst, A.D. Big Data’s Disparate Impact 2016.
  118. Ahmed, N.; Wahed, M. The De-democratization of AI: Deep learning and the compute divide in artificial intelligence research. arXiv 2020, arXiv:2010.15581. [Google Scholar]
  119. Politou, E.; Alepis, E.; Patsakis, C. Profiling tax and financial behaviour with Big Data under the GDPR. Computer law & security review 2019, 35, 306–329. [Google Scholar]
  120. Mehrabi, N.; Morstatter, F.; Saxena, N.; Lerman, K.; Galstyan, A. A survey on bias and fairness in machine learning. ACM computing surveys (CSUR) 2021, 54, 1–35. [Google Scholar] [CrossRef]
Preprints 115579 g001
Figure 1. RNN architecture [6].
Figure 1. RNN architecture [6].
Preprints 115579 g001
Preprints 115579 g002
Figure 2. LSTM architecture [34].
Figure 2. LSTM architecture [34].
Preprints 115579 g002
Preprints 115579 g003
Figure 3. GRU architecture [6].
Figure 3. GRU architecture [6].
Preprints 115579 g003
Preprints 115579 g004
Figure 4. CNN Architecture [42].
Figure 4. CNN Architecture [42].
Preprints 115579 g004
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated