Prerpints.org logo
Preprint
Article

Optical Angular Momentum Beam Generation Using Coherent Beam Combination

Altmetrics

Downloads

93

Views

31

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

20 August 2024

Posted:

22 August 2024

You are already at the latest version

Alerts
Abstract
(1) Background: The significant progress observed over last two decades in coherent beam combining (CBC) technology has mainly focused on its applications in high-energy physics and laser weapons. This work provides insight into the basic principles of CBC and the search for an alternative, namely optical angular momentum (OAM) generation using CBC; (2) Methods: The semi-analytical model based on the paraxial wave equation explored generating OAM-CBC beams by manipulating the tilts and phases of CBC (T&P-CBC) of hexagonal architecture; (3) Results: The specially arranged T&P-CBC shows typical properties of OAM, such as annular profiles for the zero diffraction order and 1-st order replicas in the far field and correlation coefficients of 1% between different OAM-CBC fields; (4) Conclusions: The differences between classical OAM beams and OAM-CBC are substantial due to hexagonal lattice properties. Moreover, applications in free space optical communications are feasible as T&P CBC fulfills the main conditions and requirements for OAM generation.
Keywords: 
Subject: Physical Sciences  -   Optics and Photonics

1. Introduction

Coherent beam combination (CBC) technology, including filled aperture CBC (FA-CBC) and tiled aperture CBC (TA-CBC) [1,2,3,4,5,6,7,8,9,10,11], has been developed in the last two decades, mainly for applications in laser weapons [4,12] and high energy physics [6,10]. FA-CBC offers high efficiency and robustness but it is limited by the number of emitters (not higher than 12 beams was demonstrated for high average power system [13]). In contrast, TA-CBC offers direct scalability beyond hundreds of combined beams, but has low practical efficiency [5,10,11], and difficulty scaling to high average powers. Both technologies require effective adaptive optics subsystems for outdoor applications, such as laser weapons and free-space optical communications (FSOC), over long propagation distances in horizontal directions [8,9,14,15] and/or in Earth-satellite FSOC links [16,17,18].
Since the 1990s, optical angular momentum (OAM) beams have been examined theoretically and experimentally, attracting [19,20,21,22,23] growing interest in material processing, optical tweezing and FSOC [16,18,23,24,25,26,27]. The benefits of OAM technology include propagation invariance as ‘diffraction-free’ solutions of paraxial wave equation, enhanced resilience to atmospheric turbulence, and orthogonality, enabling potential increase in FSOC channel bandwidth thanks to spatial multiplexling. However, its scalability in power and practical realization in laboratory and outdoor applications are problematic for a single aperture output.
The purpose of this study was to merge both technologies, that is, to search for the possibilities of CBC technology for generation of OAM beams (OAM-CBC). Preliminary results were presented in [28], where a segmented vortex wavefront was constructed in the near field owing to a special helix-like stepped phase shift in the hexagonal lattice. Here, we develop this approach for special type of tilted and phased CBC (T&P-CBC) concept, enabling the effective construction of segmented vortex wavefronts in the near field. Section 2 describes the semi-analytical model of CBC propagation and the OAM-CBC concept. The main results, analysis, and discussion are presented in Section 3, and conclusions are drawn in .

2. Tilted and Phased CBC for Optical Angular Momentum generation

Here, we give only a brief description of the analysis method. The full mathematical model is described in detail in [30,31]. To start, we provide the main characteristics of CBC hexagonal architecture (see Figure 1). The center and chief ray directions of each (l, n)-th emitter/beam of the CBC are defined by the geometry of hexagonal lattice; Ncr is the number of crowns; Nlat = 3Ncr (Ncr +1)+1 is the number of emitters; a is the half period of the lattice; ra is the sub aperture radius; f.f. = ra/a is the filling factor, f is the focal length. In the classical CBC configuration, each chief ray is directed to the common focal point F, with a spherical segmented wavefront of CBC lattice of radius f. Diffraction profiles of CBC in the far field are characterized by the Airy radius rAiry= 0.61λ/NAlat and Fresnel range ZFresnel=λ/NAlat2, where NAlat= (Ncr +1/2)2a/f. is the numerical aperture of lattice and λ is the wavelength.
We apply a truncated Gaussian beam as a ‘prototype’optical field. To simplify calculations, we used the once determined and calculated approximate solution of a truncated Gaussian beam, for given beam radius w1 at the aperture and truncation level εtr = exp(-2(ra/w1)2) (see [32] for details), which is valid over a wide range of propagation distances in the vicinity of focal point F. Note that the ratio of Rayleigh range of an individual beam to the caustics length defined by Fresnel range is proportional to Ncr2. Typically, for long-distance propagation, the Rayleigh range is comparable to f (‘collimation case’), whereas the Fresnel range is Nlat times shorter. We calculated the coherent sum of all input beams for specific distribution of phases and tilts for a chosen plane near focal point F.
Evidently, various T&P-CBC realizations exist in the (1+3)×Nlat dimensional space of control parameters. Exploration of this subject is far beyond the scope of this study. Here, we focus on the OAM-CBC case. We define a specific segmented vortex wavefront with a step-like helix phase and tilt vector [θx , θy ] in the near field as follows:
The OAM-CBC amplitude B m OAM with given m OAM - optical angular momentum number can be described as follows:
B m OAM = ∑ l , n A l , n exp [ i k Φ l , n ]   where   Φ l , n = r l , n 2 f + m OAM φ l , n k  
Here, l and n are the indices of the sub-aperture, Al,n is the amplitude of (l,n) sub-aperture, rl,n and ϕl,n are the radius to the lattice center and azimuth angle of each sub-aperture, f is the focal length, k is the wavenumber.
Next, we calculate vortex tilt vector [θx , θy] by gradient ∇ Φ l , n as follows:
∇ Φ l , n = [ θ x , l , n   ,   θ y , l , n ] = [ r l , n cos φ l , n f + m OAM sin φ l , n k r l , n   , r l , n sin φ l , n f − m OAM cos φ l , n k r l , n ]
Note, that for m OAM ≠ 0 the geometrical-optics caustics of OAM-CBC vortex segmented wavefront has a coiling non-linear helix shape with an inner hole (lower right part of Figure 1) corresponding to the evolving hexagonal helix of the CBC in the near field (upper left part in Figure 1). The coiling helix for mOAM =0 transforms into a distinct focal point F for classical spherical CBC case. This phenomenon is a direct geometrical-optics interpretation of vanishing irradiance at r = 0 and annular amplitude distribution in caustics for vortex OAM beam.

3. Results

We tested the proposed OAM-CBC concept for a large hexagonal lattice consisted of Ncr= 6 outer crowns (Nlat=127 emitters), assuming very dense packing (f.f.=0.99). To neglect the peculiarities of diffraction, we assumed low truncation losses εtr=0.05. Thus, an “almost” Gaussian beam is emitted by an individual emitter with a very low power content at higher diffraction orders in the caustics region. The hexagonal architecture of the CBC reflects the six-folded symmetry of 1-st diffraction orders (see Figure 2).
The basic compliance between the geometrical-optics caustics (Figure 1) and wave-optics demonstrate a dominant annular profile in the zero-order diffraction area (Figure 2, Figure 3, and Figure 4). In Figure 2 the irradiance maps for m OAM > 0 (Figure 2b-d) exhibit the expected properties of the conjunction of CBC and OAM beams. The zero-diffraction order has a nearly annular shape and 1-st diffraction orders resemble its replicas.
The typical dependencies of the far field profiles and power in bucket (PIB) curves for OAM-CBC are shown in Figure 3 and Figure 4.
With an increase in m OAM , the amplitude profiles worsen with flattening and dissipation of power density out of the low diffraction lobes (Figure 3 and Figure 4). Moreover, above m OAM >5, the 2D maps resemble the aberrated and scattered partly coherent beams with the minimum at the axis. These features are particularly highlighted for m OAM =6 (Figure 2d), for which six-fold symmetries of the vortex and hexagonal lattice overlap.
To examine the orthogonality of a set of OAM-CBC amplitude profiles in the far field and the feasibility in FSOC, we have calculated correlation coefficients γm,k defined as follows:
γ m , k = 〈 B m B k * 〉 〈 B m B m * 〉 〈 B k B k * 〉
where 〈 B m B k * 〉 denotes the discrete 2D summation of B m B k * over finite area in the far field; (15 x 15 rAiry in our case).
The results of γm,k calculations for a trail of 9 configurations with m OAM ϵ(0,8) are collected in Table 1.
Nonperfect orthogonality is caused by the characteristics of OAM-CBC concept (discrete 2D array of hexagonal symmetry), numerical errors, approximate solution of truncated Gaussian beam, and discrete summation over limited area.
The values of γm,k were in range [0.0048, 0.1]. For a narrow range of m OAM ϵ (0,5) average correlation coefficient γm,k = 0.7%, whereas for a m OAM ϵ (0,8) it increases to 1.5%. We suppose that a correlation coefficient of 1%, corresponding to the cross-channel crosstalk, is acceptable for practical applications in FSOC. Thus, we can conclude that the T&P-CBC sufficiently satisfies the main conditions and requiremnets of OAM generation.

4. Conclusions

Numerical experiments demonstrated the feasibility of merging of OAM and CBC technologies. For a densely packed CBC hexagonal array, the vortex wavefront was emulated with a step-like evolving helix of phase and tilts vectors in the near field.
i/ The irradiance maps for m OAM > 0 exhibit the expected properties of combination of CBC and OAM beams. The zero-diffraction order has a nearly annular shape and 1-st diffraction orders resemble its replicas. However, the differences between classical OAM beams and OAM-CBC are substantial owing to their hexagonal lattice properties.
ii/ The imperfect orthogonality of OAM-CBC set is attributed to the specfic characteristics of OAM-CBC concept (discrete 2D array of hexagonal symmetry), numerical errors, and discrete summation over a limited area. For the m OAM range of (0,5) the average correlation coefficient, corresponding to cross-channel crosstalk, is 0.7%, which is acceptable for practical applications in FSOC.
We conclude that the proposed here T&P-CBC concept fulfills the primary conditions and requirements for OAM generation. In further research we intend to examine the rules of OAM-CBC algebra and the impact of lattice architecture parameters and imprefections.

Author Contributions

Conceptualization, J.J. and W.Z.; methodology, L.G, W.Z. and J.J; software, P.G. and G.L.; data curation, P.G. ; writing—J.J.; writing—review and editing, P.G.. and J.J.; visualization, G.P..; supervision, J.J.

Funding

This research received no external funding.

Data Availability Statement

Dataset available on request from the authors

Acknowledgments

We would like to express our gratitude to Dr Janusz Mikołajczyk and Mr. Aluś Emo Capodilista for helpful support and discussion.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Brignon, A. Coherent Laser Beam Combining, Ed.; 2013th ed.; Wiley-VCH, Verlag GmbH & Co. KGaA , 2013; ISBN 978-3-527-65280-8.
  2. Fathi, H.; Närhi, M.; Gumenyuk, R. Towards Ultimate High-Power Scaling: Coherent Beam Combining of Fiber Lasers. Photonics 2021, 8, 566. [CrossRef]
  3. Fan, T.Y. Laser Beam Combining for High-Power, High-Radiance Sources. IEEE Journal on Selected Topics in Quantum Electronics 2005, 11, 567–577. [CrossRef]
  4. Van Zandt, N.R.; Cusumano, S.J.; Bartell, R.J.; Basu, S.; McCrae, J.E.; Fiorino, S.T. Comparison of Coherent and Incoherent Laser Beam Combination for Tactical Engagements. Optical Engineering 2012, 51, 104301. [CrossRef]
  5. Shpakovych, M.; Maulion, G.; Kermene, V.; Boju, A.; Armand, P.; Desfarges-Berthelemot, A.; Barthélemy, A. Experimental Phase Control of a 100 Laser Beam Array with Quasi-Reinforcement Learning of a Neural Network in an Error Reduction Loop. Opt Express 2021, 29, 12307. [CrossRef]
  6. Mourou, G.; Brocklesby, B.; Tajima, T.; Limpert, J. The Future Is Fibre Accelerators. Nat Photonics 2013, 7, 258–261.
  7. Leshchenko, V.E. Coherent Combining Efficiency in Tiled and Filled Aperture Approaches. Opt Express 2015, 23, 15944. [CrossRef]
  8. Jabczyński, J.K.; Gontar, P. Impact of Atmospheric Turbulence on Coherent Beam Combining for Laser Weapon Systems. Defence Technology 2021, 17, 1160–1167. [CrossRef]
  9. Weyrauch, T.; Vorontsov, M.; Mangano, J.; Ovchinnikov, V.; Bricker, D.; Polnau, E.; Rostov, A. Deep Turbulence Effects Mitigation with Coherent Combining of 21 Laser Beams over 7 Km. Opt Lett 2016, 41, 840. [CrossRef]
  10. Fsaifes, I.; Daniault, L.; Bellanger, S.; Veinhard, M.; Bourderionnet, J.; Larat, C.; Lallier, E.; Durand, E.; Brignon, A.; Chanteloup, J.-C. Coherent Beam Combining of 61 Femtosecond Fiber Amplifiers. Opt Express 2020, 28, 20152. [CrossRef]
  11. Chang, H.; Chang, Q.; Xi, J.; Hou, T.; Su, R.; Ma, P.; Wu, J.; Li, C.; Jiang, M.; Ma, Y.; et al. First Experimental Demonstration of Coherent Beam Combining of More than 100 Beams. Photonics Res 2020, 8, 1943. [CrossRef]
  12. Sprangle, P.; Ting, A.; Peñano, J.; Fischer, R.; Hafizi, B. Incoherent Combining and Atmospheric Propagation of High-Power Fiber Lasers for Directed-Energy Applications. IEEE J Quantum Electron 2009, 45, 138–148. [CrossRef]
  13. Müller, M.; Aleshire, C.; Klenke, A.; Haddad, E.; Légaré, F.; Tünnermann, A.; Limpert, J. 10.4 KW Coherently Combined Ultrafast Fiber Laser. Opt Lett 2020, 45, 3083. [CrossRef]
  14. Vorontsov, M.; Filimonov, G.; Ovchinnikov, V.; Polnau, E.; Lachinova, S.; Weyrauch, T.; Mangano, J. Comparative Efficiency Analysis of Fiber-Array and Conventional Beam Director Systems in Volume Turbulence. Appl Opt 2016, 55, 4170. [CrossRef]
  15. Weyrauch, T.; Vorontsov, M.A.; Carhart, G.W.; Beresnev, L.A.; Rostov, A.P.; Polnau, E.E.; Liu, J.J. Experimental Demonstration of Coherent Beam Combining over a 7 Km Propagation Path. Opt Lett 2011, 36, 4455-4457. [CrossRef]
  16. Meric, H. Atmospheric Turbulence Modeling and Aperture Analysis for Optimizing Receiver Design and System Performance on Free Space Optical Communication Links; PhD Thesis, 2012.
  17. Andrews, L.C.; Phillips, R.L. Laser Beam Propagation through Random Media; SPIE, 2005; ISBN 0-8194-5948-8.
  18. Stotts, L.B.; Andrews, L.C. Optical Communications in Turbulence: A Tutorial. Optical Engineering 2023, 63. [CrossRef]
  19. Allen, L.; Barnett, S.M.; Padgett, M.J. Optical Angular Momentum; CRC Press, 2016; ISBN 9781482269017.
  20. Lian, Y.; Qi, X.; Wang, Y.; Bai, Z.; Wang, Y.; Lu, Z. OAM Beam Generation in Space and Its Applications: A Review. Opt Lasers Eng 2022, 151. [CrossRef]
  21. Shiri, A.; Gbur, G. Orbital Angular Momentum Spectrum of Model Partially Coherent Beams in Turbulence. Opt Express 2024, 32, 18175. [CrossRef]
  22. Hou, T.; Zhang, Y.; Chang, Q.; Ma, P.; Su, R.; Wu, J.; Ma, Y.; Zhou, P. High-Power Vortex Beam Generation Enabled by a Phased Beam Array Fed at the Nonfocal-Plane. Opt Express 2019, 27, 4046. [CrossRef]
  23. Yu, T.; Xia, H.; Xie, W.; Peng, Y. Orbital Angular Momentum Mode Detection of the Combined Vortex Beam Generated by Coherent Combining Technology. Opt Express 2020, 28, 35795. [CrossRef]
  24. Vetter, C.; Steinkopf, R.; Bergner, K.; Ornigotti, M.; Nolte, S.; Gross, H.; Szameit, A. Realization of Free-Space Long-Distance Self-Healing Bessel Beams. Laser Photon Rev 2019, 13. [CrossRef]
  25. Rouzé, B.; Lombard, L.; Jacqmin, H.; Liméry, A.; Durécu, A.; Bourdon, P. Coherent Beam Combination of Seven 1.5 Μm Fiber Amplifiers through up to 1 Km Atmospheric Turbulence: Near- and Far-Field Experimental Analysis. Appl Opt 2021, 60, 8524. [CrossRef]
  26. Doster, T.; Watnik, A.T. Laguerre–Gauss and Bessel–Gauss Beams Propagation through Turbulence: Analysis of Channel Efficiency. Appl Opt 2016, 55, 10239. [CrossRef]
  27. Fiorino, S.T.; Bartell, R.J.; Krizo, M.J.; Caylor, G.L.; Moore, K.P.; Harris, T.R.; Cusumano, S.J. A First Principles Atmospheric Propagation & Characterization Tool: The Laser Environmental Effects Definition and Reference (LEEDR). In Proceedings of the Atmospheric Propagation of Electromagnetic Waves II; SPIE, February 7 2008; Vol. 6878, p. 68780B.
  28. Jabczynski, J.K.; Gontar, P.; Gorajek, L.; Zendzian, W. Segmented Vortex Wavefront Coherent Beam Combining. AIP Adv 2022, 12. [CrossRef]
  29. Jabczyński, J.K. Bessel-Gauss Coherently Combined Beams. Opt Express 2024, 32, 10068. [CrossRef]
  30. Jabczynski, J.K.; Gontar, P. Analysis of the Caustics of Partially Coherently Combined Truncated Gaussian Beams. Appl Opt 2020, 59, 3340. [CrossRef]
  31. Jabczyński, J.K.; Gontar, P.; Gorajek, Ł.; Żendzian, W. Simplified Sensitivity Analysis of Coherent Beam Combining in a Tiled Aperture Architecture. Appl Opt 2021, 60, 5012–5019. [CrossRef]
  32. Ding, D.; Liu, X. Approximate Description for Bessel, Bessel-Gauss, and Gaussian Beams with Finite Aperture. J. Opt Soc Am A 1999, 16, 1286–1293;. [CrossRef]
Preprints 115762 g001
Figure 1. Concept of optical angular momentum-coherent beam combining (OAM-CBC) generation via tilted &phased CBC.
Figure 1. Concept of optical angular momentum-coherent beam combining (OAM-CBC) generation via tilted &phased CBC.
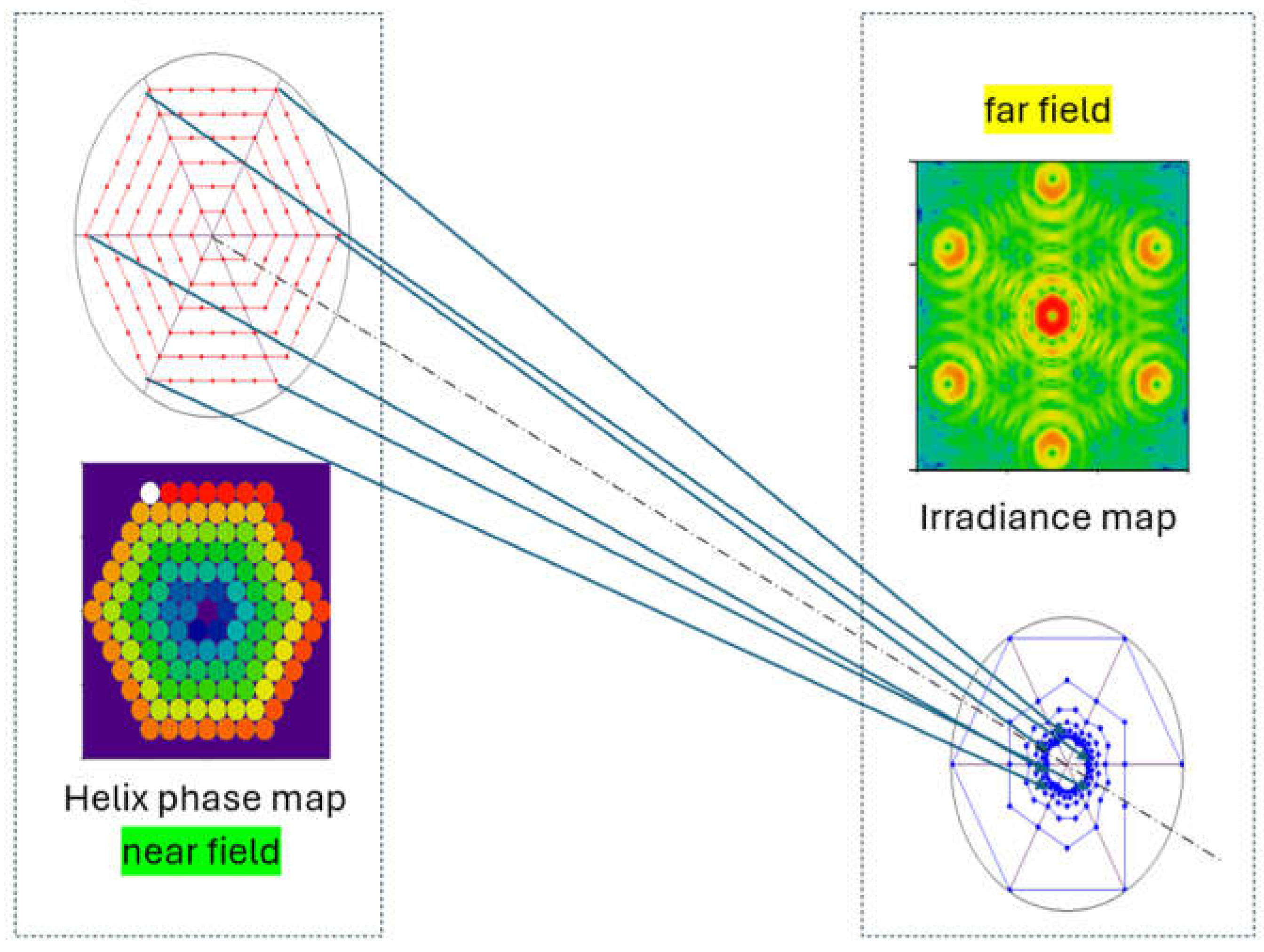
Preprints 115762 g001
Preprints 115762 g002
Figure 2. 2D maps of OAM-CBC irradiance distributions (in logarithmic scale) in the far field for optical angular momentum number; a) m OAM =0; b) 2; c) 4; d) 6; Nlat=127, f.f. =0.99, εtr=0.05.
Figure 2. 2D maps of OAM-CBC irradiance distributions (in logarithmic scale) in the far field for optical angular momentum number; a) m OAM =0; b) 2; c) 4; d) 6; Nlat=127, f.f. =0.99, εtr=0.05.
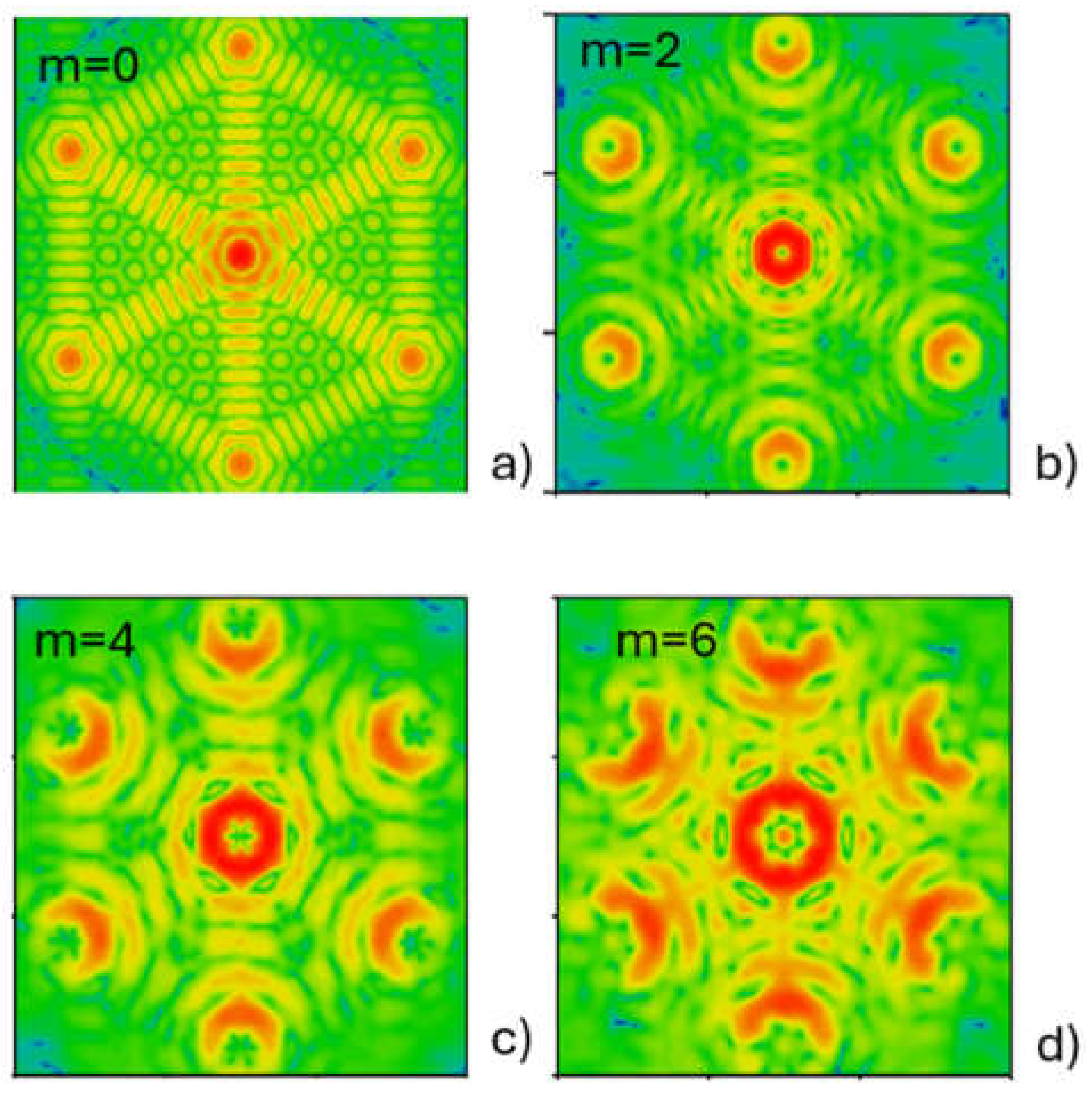
Preprints 115762 g002
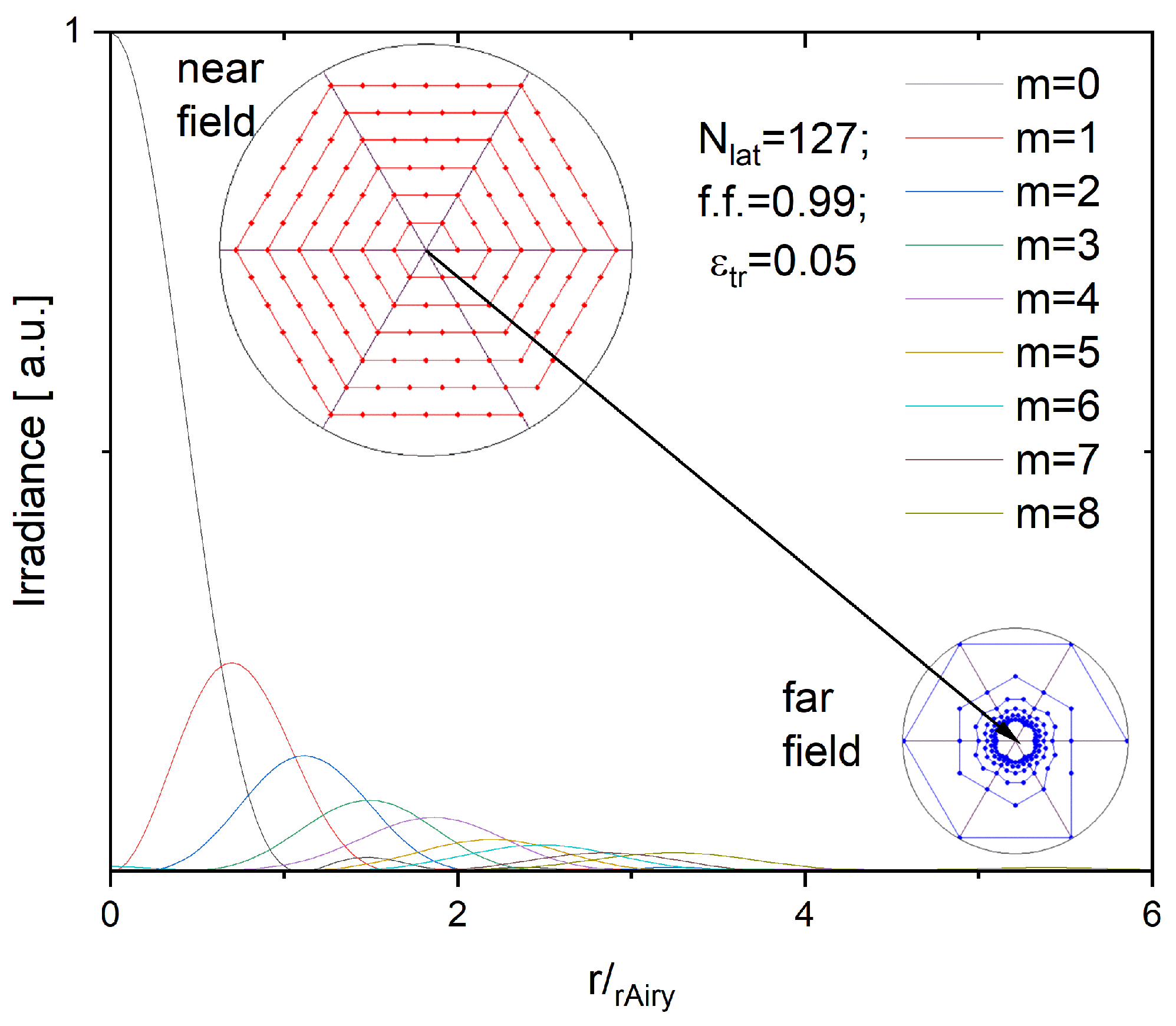
Preprints 115762 g003
Figure 3. Irradiance profiles in the far field for m OAM ϵ (0,8); f.f.=0.99 , εtr=0.05, Nlat=127.
Figure 3. Irradiance profiles in the far field for m OAM ϵ (0,8); f.f.=0.99 , εtr=0.05, Nlat=127.
Preprints 115762 g003
Preprints 115762 g004
Figure 4. Power in buckets curves for m OAM ϵ (0,8); f.f.=0.99, εtr=0.05, Nlat=127.
Figure 4. Power in buckets curves for m OAM ϵ (0,8); f.f.=0.99, εtr=0.05, Nlat=127.
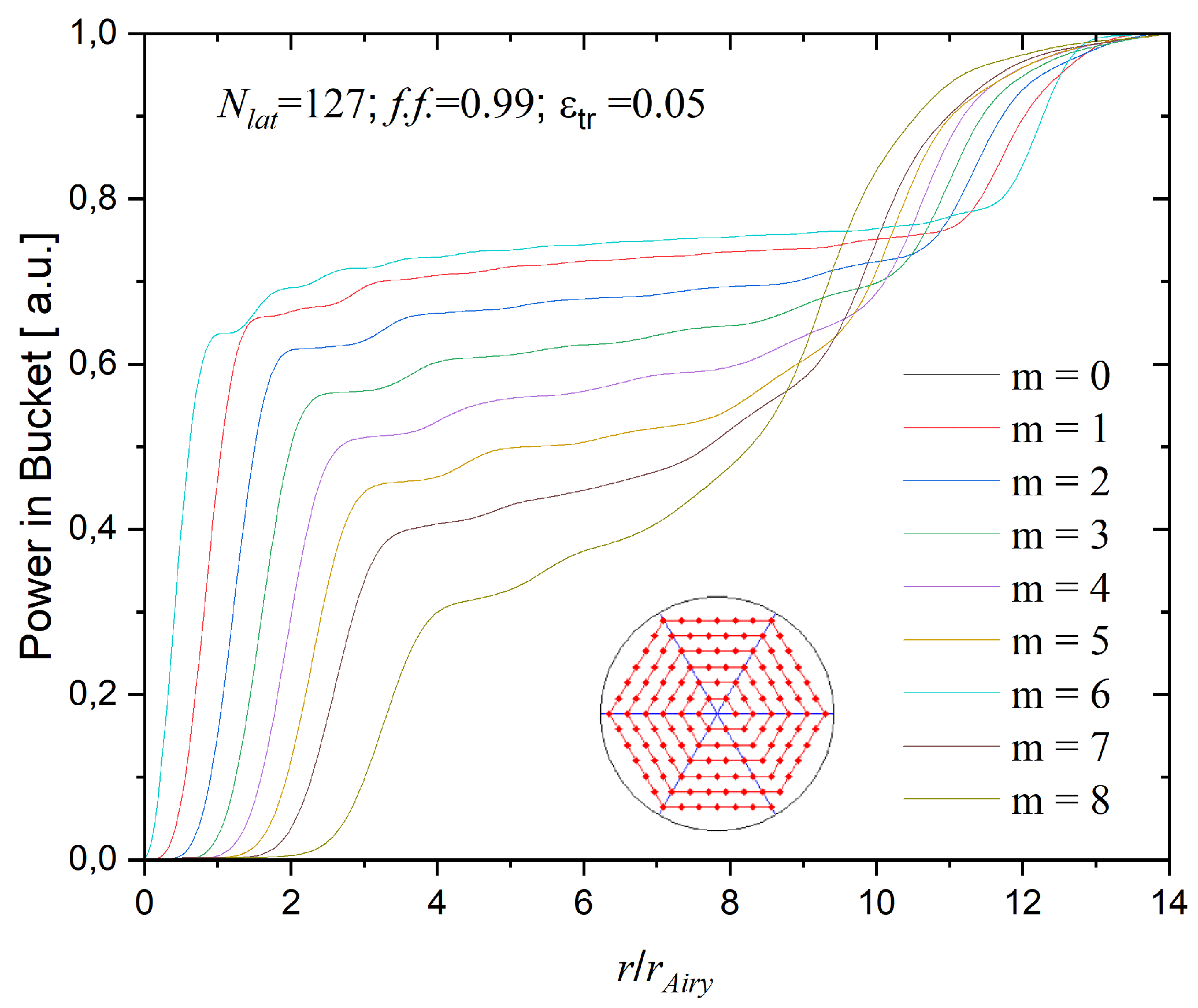
Preprints 115762 g004
Table 1. Correlation coefficients for OAM-CBC amplitude profiles in the far field; m OAM ϵ(0,8), f.f.=0.99, εtr=0.05, Nlat=127.
Table 1. Correlation coefficients for OAM-CBC amplitude profiles in the far field; m OAM ϵ(0,8), f.f.=0.99, εtr=0.05, Nlat=127.
m OAM 0 1 2 3 4 5 6 7 8
0 1.00000 0.00844 0.00875 0.00924 0.00986 0.01000 0.10100 0.01200 0.01200
1 0.00844 1.00000 0.00484 0.00507 0.00541 0.00570 0.00848 0.08800 0.00701
2 0.00875 0.00484 1.00000 0.00530 0.00562 0.00599 0.00862 0.00681 0.09500
3 0.00924 0.00507 0.00530 1.00000 0.00592 0.00621 0.00918 0.00770 0.00768
4 0.00986 0.00541 0.00562 0.00592 1.00000 0.00669 0.00958 0.00761 0.00843
5 0.01000 0.00570 0.00599 0.00621 0.00669 1.00000 0.01000 0.00846 0.00868
6 0.10100 0.00848 0.00862 0.00918 0.00958 0.01000 1.00000 0.01100 0.01200
7 0.01200 0.08800 0.00681 0.00770 0.00761 0.00846 0.01100 1.00000 0.00987
8 0.01200 0.00701 0.09500 0.00768 0.00843 0.00868 0.01200 0.00987 1.00000
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated