Prerpints.org logo
Preprint
Article

The Impact of Delayed Retirement and Adjustments to Birth Policies on the Macroeconomy

Altmetrics

Downloads

96

Views

65

Comments

0

This version is not peer-reviewed

Submitted:

20 August 2024

Posted:

21 August 2024

You are already at the latest version

Alerts
Abstract
Amidst the backdrop of continually declining total fertility rates and a population structure trending towards super-aging in China, can simple adjustments to birth policies effectively address the challenges of low fertility and aging? This study constructs a three-phase overlapping-generation model that incorporates fertility rates and delayed retirement. It investigates the economic impact of adjustments in birth policies and delayed retirement, and utilizes simulations and analyses based on real-world data from China. The research yields several key findings:1.Although theoretically, the impact of population aging on economic growth rates is uncertain, empirical data simulations indicate that the current level of population aging in China has already exerted a certain adverse impact on economic growth.2.Given the current population structure, delayed retirement can, to some extent, promote economic growth. However, due to potential vulnerabilities of older individuals who choose delayed retirement, such as reduced labor efficiency and learning abilities, the implementation of delayed retirement policies should be flexible and context-specific.3.Increasing fertility rates can mitigate the economic impact of the current demographic challenges. Thus, relaxing birth policies remains a crucial strategy that China must implement. A coordinated adjustment of delayed retirement and fertility rates is more likely to enhance economic growth.
Keywords: 
Subject: Social Sciences  -   Government

1. Introduction

In the over 70 years since the founding of the People’s Republic of China, the country has experienced robust economic and social development. As society has evolved and birth policies have been adjusted, China’s population structure has undergone significant transformations. Today, the “baby boomer” generation born in the 1960s is reaching retirement age, while the “baby bust” generations born in the 1990s and 2000s are entering the labor market. This demographic shift is resulting in a shortage of the working-age population and a rapid increase in the elderly population.
According to China’s population census data, the number of people aged 65 and above has increased from 26.32 million in 1953 to 210 million in 2022, with the proportion rising from 4.4% to 14.9%. China has entered a stage of deep aging. Additionally, China’s total fertility rate has been continuously declining, from 5.81 in the early 1970s to less than 1.1 in the seventh population census, ranking among the lowest in the world. The era of negative population growth has arrived, and the trends of aging, declining birth rates, and a rising number of people choosing not to marry are expanding.
In response to these challenges, the Chinese government has made adjustments to birth policies, but the results of the “two-child” policy have not been as expected, and concerns about the “three-child policy” are growing. Can simple adjustments to birth policies effectively address the challenges of low fertility and aging? Can other methods be introduced to cope with the profound changes in population structure and maintain economic growth?
Research on the macroeconomic impact of birth policies has delved deep, but simple adjustments to these policies are no longer sufficient to address China’s current demographic challenges. A coordinated adjustment of multiple policies is needed. Therefore, this paper builds upon existing literature, expanding upon it by incorporating aging into the overlapping generations (OLG) model, adjusting birth policies, and introducing delayed retirement policies. It discusses how the joint adjustment of delayed retirement and birth policies influences Chinese households’ decisions regarding educational investment and economic growth within the framework of a three-phase generational model that considers intergenerational transfers.

2. Literature Review

Since the latter half of the 20th century, Europe has been grappling with the phenomenon of low birth rates, and today, this issue has become widespread[1]. In fact, Asia has now emerged as the region with the lowest birth rates. Scholars from various countries have, in recent years, focused their research on low birth rates within three primary dimensions:
(1) Investigating the core factors and underlying mechanisms behind the decline in birth rates from multiple perspectives. Research from different countries consistently points to the direct causes of the current global low birth rate predicament, which stem from economic instability worldwide, resulting in income volatility, exorbitant housing prices, and the high cost of child-rearing[2,3,4,5,6,7]. Some scholars argue that the deteriorating reproductive health caused by industrialization and its association with increasing exposure to chemical substances, whether directly or indirectly derived from fossil fuels, should not be overlooked[8]. In regions heavily influenced by Confucian thought, such as East Asia, the influence of Confucian culture affects birth rates through its impact on women’s roles in the household, the effectiveness of birth policies, and the burden of parental human capital investment[9].
(2) Characterizing the intrinsic logic behind fertility desires and behaviors. Fertility expectations can be reflected through various aspects, such as the number of children, gender preferences for offspring, and the timing of pregnancies. A woman’s fertility intentions, her desired number of children, and the desired interpregnancy interval (IPI) are influenced by factors at both the micro (individual) and macro (sociocultural) levels[10]. At the individual level, factors include the desire for children, income, human capital, and the potential influence of biological and genetic traits[11]. At the macro level, these intentions are heavily influenced by national policies[12]. On the other hand, fertility intentions can be particularly unstable during uncertain times. For instance, after the outbreak of the COVID-19 pandemic in 2019, fertility intentions experienced significant fluctuations[13].
(3) Exploring the effectiveness of different fertility policies. Maternity leave policies are implemented in various countries, and while the details may differ, the implementation of such policies can enhance women’s job continuity, as well as their employment rates several years after giving birth[14,15,16]. However, extended leaves exceeding one year can have negative impacts on women’s income, employment, and career development[17]. Free maternal and child health policies have had mixed effects on increasing access to maternal health services; they should aim to improve women’s job continuity and enhance their employment rates several years after childbirth[18]. Longer leaves can adversely affect women’s income, employment, and career development[19]. The “two-child” policy in China has also shown mixed results. Based on the 2010-2018 four-wave Chinese Family Panel Studies (CFPS), the PSM-DID method was used to further identify the impact of the “universal two-child” and “selective two-child” policies on family fertility behavior. The results suggest that the “universal two-child” policy’s effectiveness is not particularly promising, and the population structure faces challenges[20].
Currently, many countries have implemented policies for delaying retirement[21,22]. Delaying retirement is an essential response to the challenges posed by an aging population and the alleviation of labor shortages[23]. Moreover, it has the potential to positively impact birth rates. There are two primary pathways for achieving this:On one hand, delaying retirement results in increased income during the senior years, allowing individuals to reduce their savings and work hours during their working-age years[24,25,26,27,28]. This, in turn, enhances their endowment for childbearing[29]. Delaying retirement has far-reaching implications for the labor market, with some studies focusing on its effects on employment opportunities, particularly for the younger generation of workers[30]. For older individuals who choose to delay retirement, their physical and cognitive functions can benefit from a few additional working years[31].Regarding the effectiveness of these policies, voluntary delayed retirement is preferable to involuntary delayed retirement, and the effectiveness of voluntary delayed retirement is further enhanced by increases in life expectancy and labor productivity[32].
In summary, Chinese scholars have conducted multidimensional research on birth policies and delayed retirement policies. However, there is a lack of studies on the macroeconomic impact of joint adjustments to birth policies and delayed retirement policies in the context of low birth rates. This paper builds upon the model developed by Yang Shuyue and Chen Zhen[33] and incorporates delayed retirement policies, capturing individuals’ behaviors of extending retirement in the model. By combining relevant data from China, this study examines the combined effects of these two policies on the macroeconomy. Finally, numerical simulations are conducted to provide quantitative support for the rational design of birth policies and delayed retirement policies in China.

3. Theoretical Model

3.1. Basic Assumptions

This paper adopts the three-period overlapping generations model and basic assumptions proposed by Yang Shuyue and Chen Zhen[33]. We assume that the economy consists of a single type of good that can be used for both consumption and investment. The representative individual’s life is divided into three periods: childhood, adulthood, and old age, each with a unit of time endowment. During childhood, there is no work, and in adulthood, all time is allocated to earning wages. In old age, only a part of the time is spent on earning wages, while the remaining time is devoted to enjoying retirement life. Therefore, at time t, there exist three generations in the population: N t y (Childhood), N t w (Adulthood), and N t o (Old age). The total population at time t is denoted as Nt= N t y + N t w + N t o . We assume that the number of children each adult chooses to have is regulated by the government’s birth policy, represented as the fertility rate   n t . Furthermore, we assume that each representative individual has a probability of surviving to adulthood and a probability of surviving from adulthood to old age p t （ p t <1）. Thus, the population relationships are as follows: N t y = n t N t w ， N t + 1 o = p t N t w . If we normalize the total population at time t to “1”, then the population structure distribution at time t is as follows:
N t y = n t − 1 n t p t − 1 + n t − 1 + n t − 1 n t N t w = n t − 1 p t − 1 + n t − 1 + n t − 1 n t N t o = p t − 1 p t − 1 + n t − 1 + n t − 1 n t

3.2. Representative Behavioral Decision of Individuals

Assuming each pair of parents needs to spend ν units of time caring for and nurturing an underage child. The support for elderly parents in China is shared among adult children, with each adult spending p t − 1 / n t − 1 of time caring for parents, leaving l t = 1 − p t − 1 / n t − 1 − v n t of working time available for each adult. Considering intergenerational transfers, representative adult agents allocate a fraction τ of their income to support their parents. In the event that the parents of an adult agent pass away before reaching old age, the savings of the deceased parents will be inherited by their children as an estate. Therefore, the lifecycle budget constraint for the representative agent is as follows:
c t w + s t + n t q t + p t − 1 τ w t l t + ξ w t l t = w t l t + ( 1 − p t − 1 ) R t s t − 1 n t − 1
c t + 1 o = R t + 1 s t + n t τ w t + 1 l t + 1 + 1 − x μ t + 1 + x ξ w t + 1
In the context provided, “ c t w   a n d   c t + 1 o ” represent the consumption of the representative individual during adulthood and old age, “ s t ” denotes savings during period “t,” “ q t ” represents the total cost of providing education for their children, “ w t l t ” stands for the total wage of the representative individual during adulthood, “ ξ ” represents the tax rate, “ R t ” is the interest rate factor, “ μ t + 1 ” indicates the retirement benefits received in period “t+1,” “ ( 1 − x ) μ t + 1 ”represents the pension received after delayed retirement. Delayed retirement is characterized by an increase in the elderly period’s working time (x) and a decrease in the retirement time (1-x). The utility function of the representative individual is given by:
U = ln ⁡ c t w + β ln ⁡ c t + 1 o + n t 1 − ε Φ ln ⁡ q t
In this context, β represents the subjective discount factor of consumption, Φ denotes the utility discount factor for parental investment in children’s education, and 1 − ε （ ε > 0 ） signifies the offspring quantity weight index factor. This factor implies that the weight of children in the parental utility function decreases as the number of offspring increases.

3.3. Enterprises

Within a closed economic system, all enterprises produce homogeneous products. These enterprises aim to maximize profits and operate in a market environment characterized by perfect competition, utilizing capital and labor for production. The production function of enterprises is formulated as follows: [Please provide the specific mathematical or functional representation of the production function you want to be translated：
Y t = D K α L 1 − α （ 0 < α < 1 ）
In the context of delayed retirement, K t and L t represent the capital and labor used in period t, respectively, while D represents the material capital production technology parameter. With delayed retirement in place, the total amount of labor is given by L t = l t N t w + x p t − 1 N t − 1 w , where c represents the current labor force and d represents those who choose to delay retirement. The output per unit of effective labor and the capital stock are denoted as y t = Y t / L t ， k t = K t / L t , respectively. Assuming that capital experiences full depreciation within the same period, the condition for maximizing corporate profits is as follows:
R t = D α k t α − 1       w t = D ( 1 − α ) k t α

3.4. Market Clearing

When the economy reaches equilibrium, total output equals the sum of total labor income and total capital income, that is, Y t = R t K t + w t L t . The capital income is obtained by the living elderly and the deceased parents’ offspring, namely：
R t K t = N t o R t s t − 1 + ( 1 − p t − 1 ) R t s t − 1 n t − 1 N t w = p t − 1 N t − 1 w R t s t − 1 + ( 1 − p t − 1 ) R t s t − 1 n t − 1 N t w Because it exists N t w = n t − 1 N t − 1 w , therefore:
R t s t − 1 = R t K t N t − 1 w = R t ( l t n t − 1 + x p t − 1 )
In a market-clearing scenario, the capital market and the labor market each reach their respective equilibriums：
k t + 1 = s t n t + x p t
L t = l t N t w + x p t − 1 N t − 1 w

3.5. Government Sector

Drawing on the setup proposed by Zhang Shiwei and Wang Jie[34] in their work in 2023, we adopt a pay-as-you-go pension system with a current revenue and expenditure approach. Under this system, the government collects pension contributions from both currently employed adult individuals and elderly individuals who are still in the workforce, and these contributions are used to fund the pensions of retired elderly individuals in the current period.The guiding principle of the government sector is fiscal balance, which means the government aims to ensure that its pension-related revenues match its pension-related expenses. So there will be:
N t + 1 o ( 1 − x ) μ t + 1 = ξ w t + 1 l t + 1 N t + 1 w + ξ x w t + 1 N t + 1 o
The pension that adult individuals can receive in period t+1 is:
μ t + 1 = ξ w t + 1 n t l t + 1 / p t + x 1 − x

4. Model Analysis

Solving the utility maximization problem for the representative agent yields the optimal consumption and optimal education investment at each period:
q t = n t − ε Φ c t w
c t + 1 o = p t β R t + 1 c t w
1 + n t 1 − ε Φ + p t β c t w = 1 − ξ − p t − 1 τ w t l t + 1 − p t − 1 R t s t − 1 n t − 1 + n t τ w t + 1 l t + 1 R t + 1 + ξ w t + 1 n t l t + 1 / p t + x R t + 1 c t w = Γ c , t 1 − ξ − p t − 1 τ w t l t + 1 − p t − 1 R t s t − 1 n t − 1 + n t τ w t + 1 l t + 1 R t + 1 + ξ w t + 1 n t l t + 1 / p t + x R t + 1
where Γ c , t = 1 1 + n t 1 − ε Φ + p t β represents the share of lifetime resources allocated to consumption during the adult period. Substituting the above equation into the budget constraint:
s t = Γ s , t 1 − ξ − p t − 1 τ w t l t + 1 − p t − 1 R t s t − 1 n t − 1 − 1 + n t 1 − ε Φ p t β n t τ w t + 1 l t + 1 R t + 1 + ξ w t + 1 n t l t + 1 / p t + x R t + 1
where Γ s , t = p t β 1 + n t 1 − ε Φ + p t β represents the proportion of lifetime resources allocated to elderly savings. From equation (5), we can derive R t k t = w t α / ( 1 − α ) . Combining equations (7) and (12), we obtain the dynamic equation for per capita private capital:
( n t + x p t ) k t + 1 = Γ s , t { D 1 − ξ − p t − 1 τ 1 − p t − 1 / n t − 1 − v n t + 1 − p t − 1 n t − 1 + x p t − 1 α n t − 1 1 − α 1 − α k t α − 1 + n t 1 − ε Φ p t β n t τ 1 − p t / n t − v n t + 1 + ξ n t 1 − p t / n t − v n t + 1 / p t +   ξ x 1 − α α k t + 1 }  
Combining equations (7), (9), and (11), we can obtain the dynamic equation for education investment:
q t = n t − ε Φ Γ c , t D 1 − ξ − p t − 1 τ 1 − p t − 1 / n t − 1 − v n t + 1 − p t − 1 n t + x p t α n t − 1 1 − α 1 − α k t α +   n t τ 1 − p t / n t − v n t + 1 + ξ n t 1 − p t / n t − v n t + 1 / p t +   ξ x 1 − α α k t + 1
When the economy reaches a steady state, the endogenous variables in the model converge to constant values, i.e., k t + 1 = k t = k * . Substituting this into equations (13) and (14) and rearranging, we obtain:
( k * ) α − 1   = 1 + n 1 − ε Φ + p β n + x p / 1 − α + 1 + n 1 − ε Φ [ n τ 1 − p / n − v n + ξ n 1 − p n − v n p + ξ x ] / α D p β [ 1 − ξ − p τ 1 − p / n − v n + 1 − p n + x p / n 1 − α ]
q * =   1 − α n − ε Φ { D 1 − ξ − p τ 1 − p / n − v n + 1 − p n + x p α / n 1 − α ( k * ) α + 1 + n 1 − ε Φ [ n τ 1 − p / n − v n + ξ n 1 − p n − v n p + ξ x ] k * / α } 1 + n − ε Φ + p β
Based on the above analysis, k * ， q * are functions of the birth rate p and delayed retire ment duration x . By simultaneously solving for k * ， q * , we can then obtain the total output at equilibrium Y * , per capita output y * , and equilibrium wage w * :
Y * =   D N * ( k * ) α l t + x p y * = Y t / L t = D ( k * ) α w * = D ( 1 − α ) ( k * ) α
Indeed, from the above equations, we can analyze that birth policies can influence the birth rate p and, in conjunction with delayed retirement x , affect per capita private capital k * , thereby impacting per capita output y * and total output Y * . Given the complexity resulting from numerous model parameters, conducting static analysis becomes challenging.Therefore, in the subsequent sections, this study will proceed with reasonable parameter values and employ numerical simulations to examine the effects of birth policies and delayed retirement policies on various economic variables. The numerical approach allows for a comprehensive exploration of the dynamic interactions among different policy scenarios and their implications for the economy. Through these simulations, we can gain valuable insights into the potential impacts of different policy measures and obtain a clearer understanding of their effects on the economy over time.

5. Parameter Value

Based on the above expressions, this study requires values for the parameters α , ε , Φ , n , β , v , ξ , τ , D , N * , p . Taking into account China’s specific context and referring to relevant literature, the parameters are set as follows:

5.1. Discounting Parameters

1.Subjective discount factor for consumption β : Existing literature often sets the subjective discount factor for consumption to 0.98 or 0.99. In this study, we continue to adopt the setting used by Yang Shuyue and Chen Zhen, which is 0.99. Since the model assumes a period of 30 years, β = 0.99 30 ≈ 0.74 .
2.The utility discount factor for parents’ investment in their children’s education Φ , based on Pecchenino and Pollard[35], is initially set at 0.98, considering the altruistic effect towards their children. However, influenced by traditional Chinese culture, Chinese parents tend to place greater emphasis on investment in their children’s education. Therefore, setting Φ = 1 aligns better with the actual situation in China, indicating that parents prioritize investment in their children’s education at the same level as their own consumption.
3.The index factor for the weight of the offspring’s quantity ε , The index factor for the weight of the offspring’s quantity is subject to significant variations in different literature. In this study, following the setting by Wang Wei, and considering the influence of the “family planning” policy, although the current birth policy has been relaxed, some individuals may still be dissatisfied with the number of children allowed under the current policy. Therefore, ε is set to 0.1 to reflect this factor.

5.2. Economic Parameters

1.Share of capital investment   α , The capital share in the investment is subject to variations among different researchers. For instance, Wang Xiaolu and Fan Gang[36] estimated a capital share of 0.5, while Guo Han and Ren Baoping[37] empirically found a capital share of about 0.4. Taking into account China’s specific context, where the capital-output elasticity is not expected to remain at a high level in the long term, this study sets   α = 0.4 .
2.Tax rate ξ , According to the information released by the National Bureau of Statistics, ξ = Total Tax Revenue / Total Income = 0.15.
3.Material capital production technology parameter D, Following the approach of Zhang et al.[38], when we set D=42.7, the economic growth rate becomes (0.093×30 = 2.79), which aligns with the actual situation in China over the past 30 years (annual economic growth rate of 9.3%).
4.The income ratio for supporting parents τ , According to the research by Liu Yongping and Lu Ming[39], this study sets τ = 0.3 .
5.The time factor for taking care of children v , Each child requires the mother’s care for 9 months after birth, and the period is 30 years. Therefore, v = 0.75 / 30 ≈ 0.03 .

5.3. Population Parameters

1.Fertility rate n , based on the latest results from the seventh national population census in China in 2020, was 1.3 for the total fertility rate of women of childbearing age. However, the current fertility rate in China is even lower, so we take it as 1.1.
2.The survival probability into the elderly period p , According to the “2021 Statistical Bulletin on the Development of Health and Health Care in China” by the National Health Commission, the current life expectancy is 78.2 years. Referring to the method of elderly survival rate proposed by Qu Dehua[40], this study sets p = 0.87 .
3.The number of adult individuals N * , The number of adult individuals can be adjusted to change the scale of economic variables without affecting the research mechanism and conclusions in this study. In theory, it can take any positive value. For the sake of convenience in the study, we set   N * = 10 .
Table 1. parameter calibration.
Table 1. parameter calibration.
parameters meaning value
β Subjective discount factor for consumption 0.74
Φ The utility discount factor for parents’ investment in their children’s education 1
ε The index factor for the weight of the offspring’s quantity 0.1
v The time factor for taking care of children 0.03
n Fertility rate 1.1
p The survival probability into the elderly period 0.87
N * The number of adult individuals 10
α Share of capital investment 0.4
ξ Tax rate 0.15
τ The income ratio for supporting parents 0.3
D Material capital production technology parameter 42.7

6. Numerical Simulation

6.1. Numerical Simulation of Delayed Retirement

The current retirement policy in China allows women to freely choose their retirement time after the age of 55, while men can do the same after reaching the age of 60. Figure 1, Figure 2 and Figure 3 show the trends of various economic variables when the average retirement age is extended from 55 to 65, assuming a life expectancy of 78.2 years per capita.
The Mechanism of the Impact of Delayed Retirement on Private Capital “k”: Delayed retirement implies an extension of the working period for laborers. While this prolongation delays the time at which laborers start receiving retirement benefits, it also grants them more time to accumulate wealth and savings. Despite the decrease in pension income compared to wages, laborers experience an overall increase in income during their later years. However, from the perspective of smoothing two-period consumption, individuals tend to balance current and future consumption. This leads to a reduction in savings during the working years to fulfill present needs, consequently resulting in a decrease in the accumulation of private capital.
.The mechanism of delayed retirement’s impact on total output: Delayed retirement means that workers extend their participation in the labor market, as they continue to work and provide labor. This increases the overall labor supply, as more workers are involved in production, leading to an increase in total output. Moreover, delayed retirement workers may continue to receive training and learn new skills, which, with accumulated experience and skills, can enhance their productivity and efficiency. Highly efficient labor Furthermore, delayed retirement can also slow down the pace of population aging. As elderly workers continue to work, the number of retirees relative to the workforce contributes to higher productivity, thus increasing total output.
Furthermore, delayed retirement can also slow down the pace of population aging. As elderly workers continue to work, the number of retirees relative to the workforce decreases, helping to mitigate the aging trend in the labor force structure and partially alleviate the negative impact of aging on total output.
The mechanism of delayed retirement’s impact on labor productivity (y): Delayed retirement extends the working time of the elderly generation, leading to an increase in labor supply. More labor supply means more people participating in production activities, thereby increasing the overall labor force and output. However, as age increases, the productivity of elderly workers may decline, especially for physically and mentally demanding tasks. Delayed retirement changes the labor structure, with a relatively smaller proportion of younger workers and a relatively larger proportion of elderly workers. Younger workers typically have higher educational qualifications and skill levels, while elderly workers may have slower skill updates. This leads to a decrease in the average skill level of the overall labor force, which, in turn, affects labor productivity and labor productivity per capita.

6.2. Numerical Simulation of Fertility Rate Variation

The most immediate change resulting from adjustments in the fertility policy is the variation in the fertility rate. Following the definition set by Yang Shuyue and Chen Zhen [2], the fertility rate “n” is defined as the number of children born to a representative couple. Therefore, when examining the impact of the fertility rate on economic variables, “n” is taken as half of the actual fertility rate. Considering the specific circumstances in China, this paper simulates the changes in relevant economic variables associated with a total fertility rate ranging from 1 to 3.
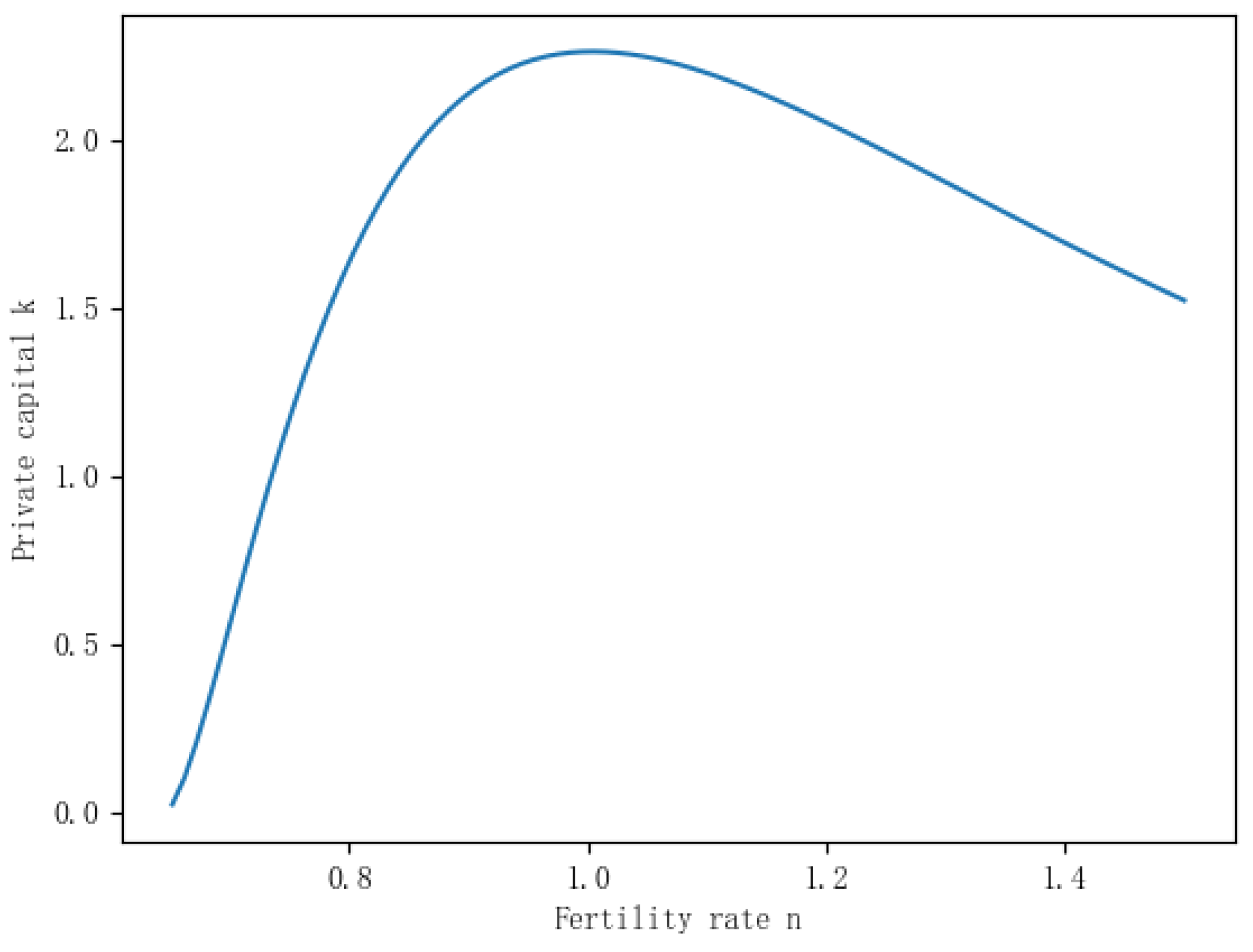
Preprints 115792 g004
Figure 4. Fertility Rate and Private Capital k
Figure 4. Fertility Rate and Private Capital k
Preprints 115792 g004
The mechanism of fertility rate’s impact on private capital (k): There is a “inverted U-shaped” relationship between fertility rate and private capital. When the fertility rate is either very low or very high, private capital tends to be relatively low. However, at a moderate fertility rate, private capital is relatively high.
Low fertility rates are often associated with an aging population structure, where there is a relatively larger proportion of elderly individuals and a smaller proportion of young labor force. Elderly individuals usually have a higher savings tendency but are less involved in production and investment activities, leading to lower private capital.
On the other hand, high fertility rates may result in an oversupply of labor in the labor market, leading to intense competition and lower returns on capital investment. This is not conducive to the accumulation of private capital.
The figure shows that private capital reaches its maximum value at around a fertility rate of 2.3. Therefore, China still needs to continue relaxing its fertility policy to maintain private capital accumulation.
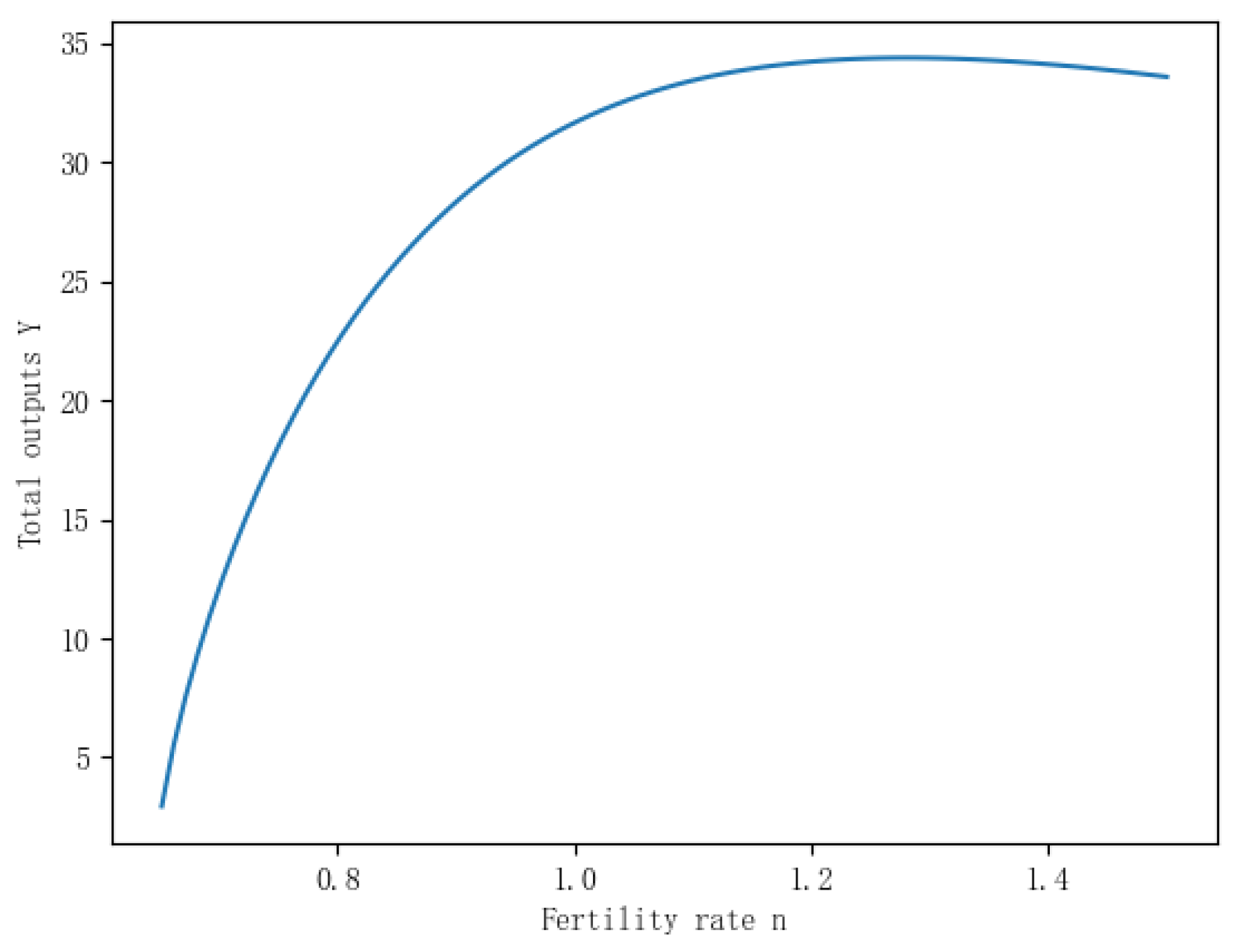
Preprints 115792 g005
Figure 5. Fertility Rate and Total Output Y
Figure 5. Fertility Rate and Total Output Y
Preprints 115792 g005
The mechanism of fertility rate’s impact on total output : High fertility rates imply an increase in the number of births, which directly leads to an increase in labor supply, thereby driving the growth of total output. At the same time, high fertility rates result in more family members, increasing household consumption demand. The increased household consumption demand promotes the demand for goods and services, thus positively affecting economic output. Moreover, high fertility rates also lead to an expansion of the market size. More population means more potential consumers and demand, which stimulates businesses to increase production and propel economic growth.
Preprints 115792 g006
Figure 6. Fertility Rate and Labor Productivity y
Figure 6. Fertility Rate and Labor Productivity y
Preprints 115792 g006
The relationship between the two also exhibits a “inverted U-shape”. On one hand, when the fertility rate is low, families are typically more inclined to invest in the education of their children because there are fewer family members, allowing for more concentrated resource allocation. This, in turn, enhances the quality and skills of the future workforce, thereby increasing labor productivity per capita. However, when the fertility rate is excessively high, family resources are spread across a greater number of children, which may lead to diminishing marginal returns on educational investments, thus affecting the quality of the workforce and labor productivity per capita.
On the other hand, when the fertility rate is low, there is a relatively scarce labor force in the labor market, and this scarcity may result in higher labor productivity per capita. However, when the fertility rate is high, there is an oversupply of labor in the market, and competition for jobs can lead to a decline in labor productivity per capita.
Preprints 115792 g007aPreprints 115792 g007b
Figure 7. The Relationship between Delayed Retirement and Fertility Rate under Different Com bina tions and Economic Variables.
Figure 7. The Relationship between Delayed Retirement and Fertility Rate under Different Com bina tions and Economic Variables.
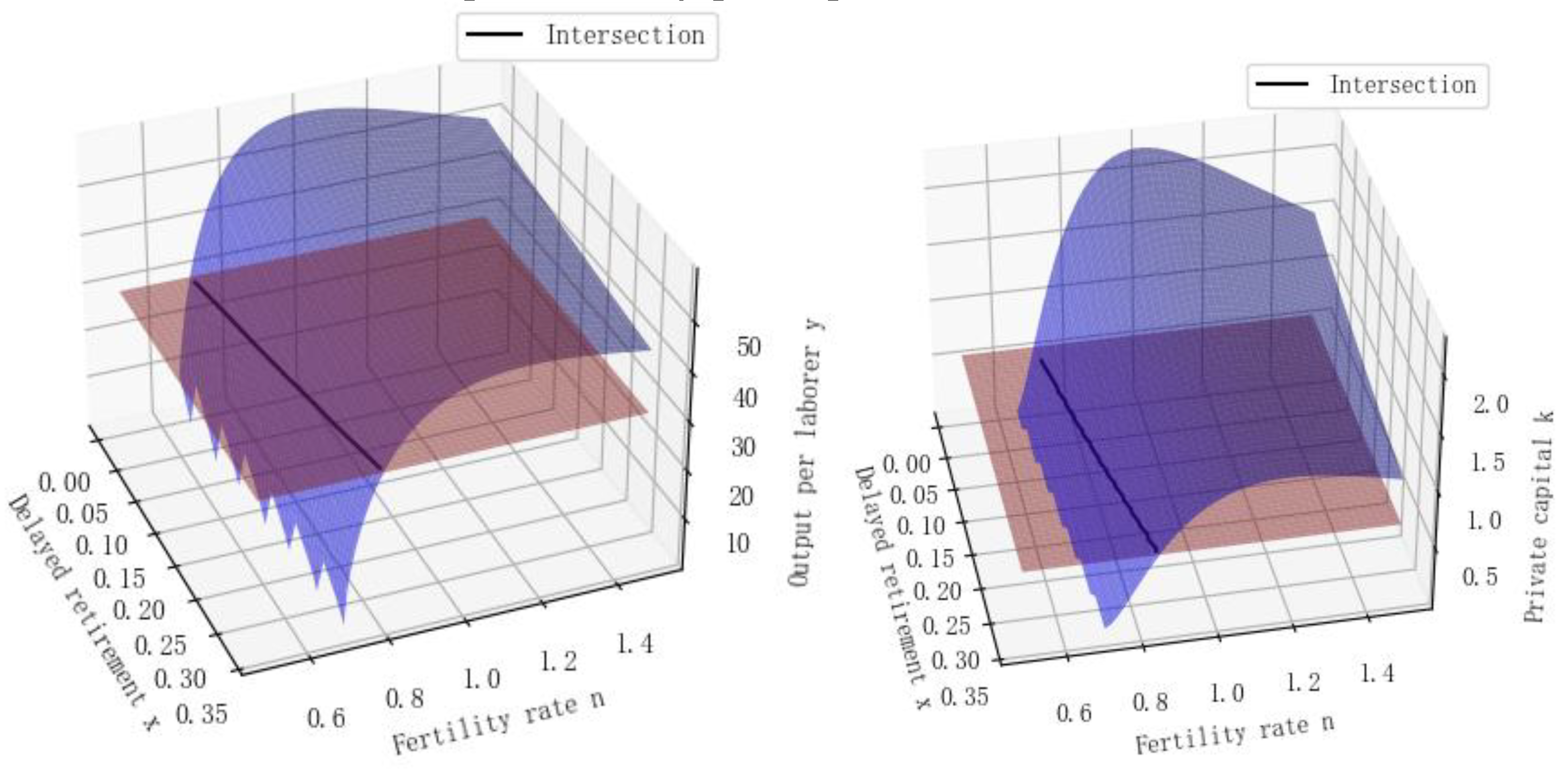
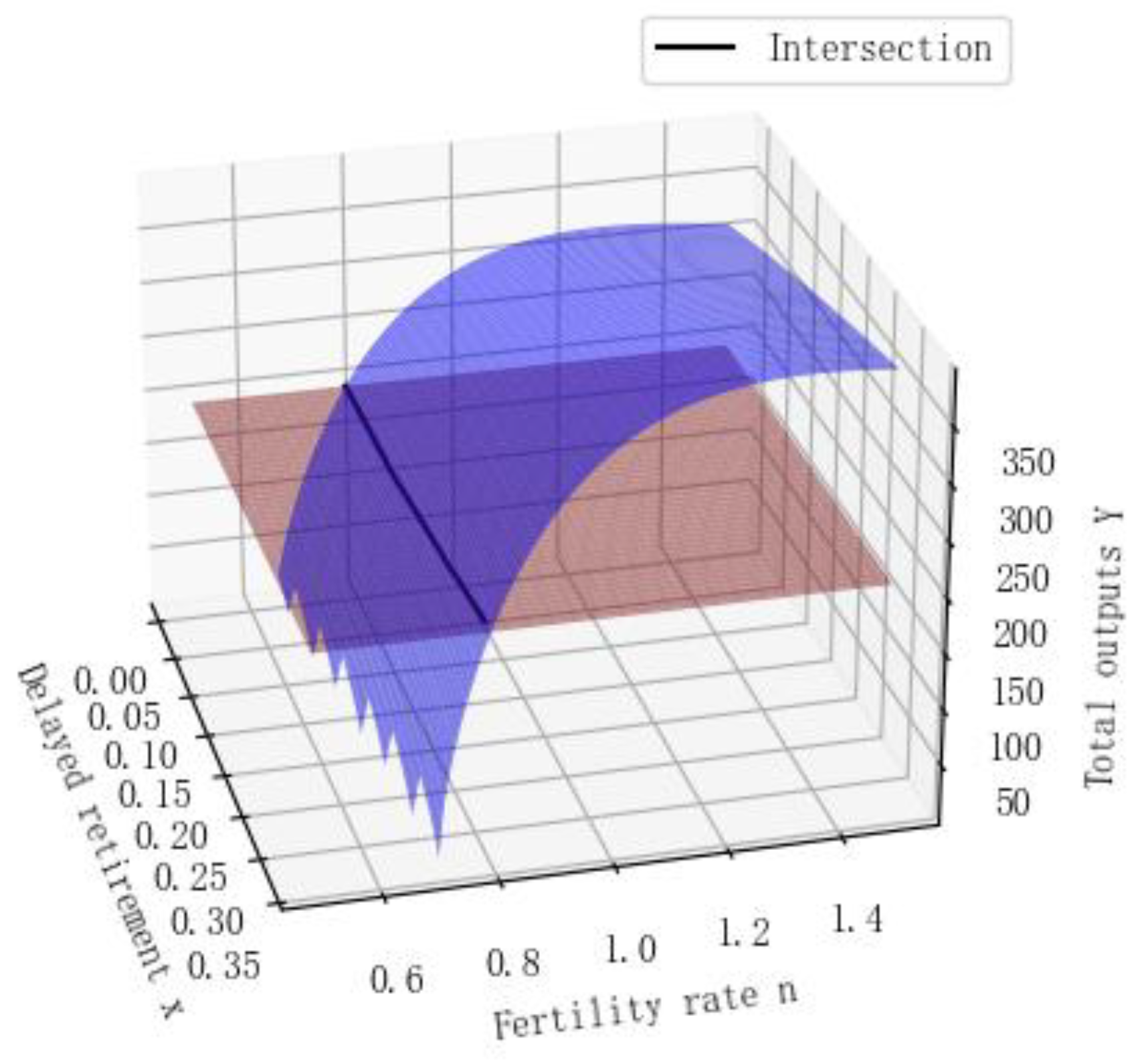
Preprints 115792 g007aPreprints 115792 g007b
The figure above describes the examination of the impact of delayed retirement or fertility rate on economic variables under the given assumptions of either delayed retirement time or fertility rate. From a practical standpoint, in the future, delayed retirement and fertility policy adjustments are likely to occur simultaneously, making it necessary to study the combined changes of both.
To investigate the relationship between fertility rate and delayed retirement, we have plotted a plane parallel to the base and intersected it with the graphical surface. The arcs formed by these intersections represent various combinations of fertility rate and delayed retirement under conditions where private capital remains constant, labor productivity per capita remains constant, and total output remains constant. Through such analysis, we can observe that delayed retirement can, to some extent, offset the negative effects of the current low fertility rate and promote population growth.

6.3. Sensitivity Analysis

In the OLG model, the representative agent’s tax rate can be an important policy variable that affects resource allocation and intergenerational equity in the economy. In real policy-making, the tax rate for the representative agent is often determined based on economic and social conditions. Policymakers typically consider multiple factors, such as the public finance needs, economic growth, and social equity, to establish an appropriate range for the tax rate. Lower tax rates can promote economic growth and individual investment but may lead to fiscal deficits. On the other hand, higher tax rates can finance public expenditures but may affect individual consumption and savings behavior.
To ensure the internal validity of the findings, this study conducts sensitivity analysis on the tax rate parameter ξ and examines its impact when varied within a reasonable range. It would include how different tax rates affect private capital, total output, labor output, and other relevant economic variables. The analysis would also consider the interactions between the tax rate and fertility rate, as well as the tax rate and delayed retirement policy. By analyzing the results, the robustness of the effects of fertility rate and delayed retirement on economic variables is tested. The analysis results are as follows:
Table 2. Sensitivity Analysis Results on Delayed Retirement.
Table 2. Sensitivity Analysis Results on Delayed Retirement.
sensitivity factors economic variables delayed retirement x,n=1.1
x=0 x=2/30 x=4/30 x=6/30 x=8/30 x=10/30
ξ=0.18 k 2.15 2.07 2 1.94 1.88 1.83
y 57.96 57.1 56.32 55.65 55 54.42
Y 102.6 134.51 165.67 194.67 224.64 254.13
ξ=0.21 k 2.07 1.99 1.92 1.86 1.8 1.75
y 57.07 56.19 55.39 54.71 54.05 53.46
Y 101.02 132.37 162.94 191.38 220.76 249.65
ξ=0.24 k 1.99 1.91 1.84 1.79 1.73 1.68
y 56.24 55.34 54.53 53.84 53.18 52.58
Y 99.55 130.37 160.42 188.34 217.18 245.53
Table 3. Sensitivity Analysis Results on Fertility Rate.
Table 3. Sensitivity Analysis Results on Fertility Rate.
sensitivity factors fertility rate n,x=0
n=1.4 n=1.6 n=1.8 n=2.0 n=2.2 n=2.4 n=2.6 n=2.8 n=3.0
ξ=0.18 k 0.5 0.83 0.95 0.97 0.94 0.9 0.85 0.8 0.75
y 52.91 89.13 101.3 103.22 100.78 96.16 90.7 85.07 79.57
Y 345.23 537.04 559.67 523.84 461.05 391.84 324.27 261.59 204.9
ξ=0.21 k 0.56 0.86 0.95 0.95 0.92 0.88 0.82 0.77 0.72
y 59.49 91.54 101.81 101.81 98.53 93.45 87.76 82.03 76.52
Y 201.22 375.06 470.05 512.21 529.42 527.77 515.14 496.38 474.45
ξ=0.24 k 0.62 0.88 0.94 0.94 0.9 0.85 0.79 0.74 0.69
y 66.14 93.6 100.85 100.21 96.12 90.61 84.71 78.91 73.41
Y 223.7 383.87 468.51 504.13 516.46 511.71 497.24 477.5 455.16
According to the results of sensitivity analysis, it is evident that within a reasonable range of variation in the tax rate parameter ξ, the impact of fertility rate and delayed retirement on economic variables remains unchanged: as the delay in retirement age increases, the equilibrium state of private capital k decreases continuously, labor productivity per capita Y decreases, and total output increases. All economic variables exhibit a “inverted U-shape” trend as the fertility rate is adjusted. This indicates that the conclusions drawn in this study are robust.
By observing the table above, it can be noted that as tax rates increase, the fertility rates at which economic variables reach their peaks gradually decrease and are notably lower than the standard replacement rate of 2.2. This suggests that excessively high tax rates can increase economic pressure, thus influencing family fertility decisions. Therefore, when designing fertility policies that encourage childbirth, appropriate adjustments to tax rates should also be considered within the scope of deliberation.

7. Conclusion and Recommendations

In the context of continuously declining total fertility rate and an aging population structure in our country, this paper has constructed a three-period overlapping generations model incorporating birth rate and delayed retirement. The study examines the effects of birth policy adjustments and delayed retirement on the economy and conducts simulations and analysis based on real data from China.
Research findings reveal the following: (1) Although the theoretical impact of population aging on economic growth rate is uncertain, empirical data simulations show that China’s current level of population aging has already exerted a certain detrimental influence on economic growth. (2) Under the current population structure, delayed retirement can to some extent promote economic growth. This indicates that delayed retirement policies can mitigate the negative effects caused by low birth rates in the context of population aging, proving that delayed retirement is a feasible policy for China at present. However, changes in labor productivity show that older workers under delayed retirement may face weaknesses in terms of labor efficiency, learning ability, etc., resulting in an increase in overall labor output but a decrease in labor output per capita. Therefore, it is essential to implement the delayed retirement policy flexibly based on specific circumstances. (3) Increasing birth rates can alleviate the impact of the current population challenges on the economy, and easing birth policies remains a necessary approach for China. However, there exists a peak in economic growth, while simultaneously lowering household utility. Synergistic adjustments to delayed retirement and birth rates will better facilitate economic growth.
In the current trend of declining birth rates and an aging population, the pressures of elder care and labor shortages continue to rise, and the demographic dividend is rapidly diminishing. To address the negative impact of population aging on the economy and society, the government has undertaken necessary adjustments to birth policies. However, merely relying on relaxing birth restrictions cannot achieve the expected outcomes. On one hand, people’s willingness to have children has generally decreased, as they are aware that the pressures on themselves would continuously increase with the number of children, potentially leading to reduced family well-being. On the other hand, solely increasing the birth rate has limited effectiveness in alleviating aging pressures and sustaining economic growth. Therefore, a singular focus on birth policies is inadequate to tackle the challenges posed by population aging. The government needs to comprehensively consider various factors and develop holistic policies to promote the accumulation of human capital in society. By doing so, it can better address the pressures of aging and achieve sustained and stable economic development. This paper proposes the following recommendations:
First and foremost, it is essential to recognize that implementing a delayed retirement policy is a rational and necessary choice for the country to address population challenges. With improvements in healthcare systems and the quality of material and spiritual life, people’s life expectancy after retirement has been increasing, leading to the waste of human resources and increasing the government’s burden for elder care. To address the negative impact of population aging and declining birth rates on the economy and society, the government must not only adjust the delayed retirement policy but also implement necessary adjustments to birth policies.
Implementing a delayed retirement policy can partially alleviate the shortage of human resources and the pressure of aging. However, relying solely on this policy will not resolve the declining birth rate issue. Therefore, the government must ensure that the public fully understands the necessity of delayed retirement and adjustments to birth policies from both an individual and national long-term development perspective. Public understanding and support are key to ensuring the smooth implementation of these policies.
Additionally, the government should consider adopting complementary policy measures to encourage childbirth and extend working years. Providing ample support, retraining opportunities, and other incentives will help individuals adapt to the changing demographic landscape and promote sustainable economic growth. Taking a comprehensive approach and combining these measures will be crucial in effectively managing population dynamics and fostering long-term economic development.
Furthermore, when implementing the delayed retirement policy, several factors should be considered comprehensively: (1) Gradual Delayed Retirement: To mitigate the pressure caused by reduced productivity among elderly workers, the delayed retirement policy should be gradually implemented rather than suddenly enforced. This approach allows elderly workers time to adapt and prepare, while also giving society and businesses the opportunity to make necessary adjustments. (2) Flexible Retirement Options: The policy can provide flexible retirement choices, allowing elderly workers to make decisions based on their individual circumstances. For instance, different retirement age options can be set, enabling elderly workers to choose the most suitable retirement time based on their health, family situation, and career characteristics. (3) Provide Training and Job Transition Opportunities: With delayed retirement, elderly workers may need to adapt to different job requirements. The policy can offer training and job transition opportunities to help them acquire new skills and adjust to new work environments, thereby enhancing their productivity and labor output. (4) Safeguard the Rights of Elderly Workers: While implementing delayed retirement, it is crucial to ensure the rights and welfare of elderly workers. The policy can provide corresponding social security and welfare measures to guarantee sufficient life security for elderly workers after retirement. (5) Guide Business Adaptation: The delayed retirement policy will also impact businesses and employers. The government can guide companies to adapt to the policy through tax incentives, subsidies, or other incentives, promoting the willingness to hire and train elderly workers. (6) Research and Evaluation: After implementing the delayed retirement policy, regular research and evaluation of its effects are necessary. This approach allows understanding the actual impact of the policy, identifying issues in a timely manner, and taking corresponding adjustment measures.
By considering these factors, the delayed retirement policy can be effectively implemented, benefiting both elderly workers and society, and contributing to a more sustainable and stable economic development amidst the challenges of an aging population and declining birth rates.
Finally, regarding adjustments to the birth policy: (1) Provide Comprehensive Birth Support: The government can consider increasing support for families, including providing birth allowances, supporting career development for women of childbearing age, and offering high-quality childcare services. These measures can reduce the financial burden of raising children for families and stimulate people’s willingness to have more children. (2) Introduce Flexible Maternity Leave Policies: It is recommended that the government introduce more flexible maternity leave policies, allowing parents to allocate maternity leave time flexibly. This approach enables more families to strike a better work-life balance and can potentially boost the birth rate. (3) Promote Pension Insurance System Reform: Optimize the pension insurance system and increase flexibility between individuals and businesses. This will instill more confidence in families to raise children by providing better social security, thus alleviating the burden of childcare. (4) Expand Investment in Education Resources: Increase investment in the education sector to enhance the quality of education. This not only improves the human resources pool but also alleviates the pressure of raising children for parents.
By implementing these measures, the government can create a more supportive environment for families and address the challenges posed by an aging population and declining birth rates. Encouraging childbirth and supporting families in raising children will contribute to sustainable economic and social development in the face of demographic changes.

Author Contributions

This work was equally contributed by all the authors.

Funding

This research was supported by the Anhui Institute of Urban-Rural Green Development and Urban Renewal (Program SN:2202001),the Anhui Province Housing and Urban-Rural Development Science and Technology Program Project: (2023-YF117), the Outstanding Youth Research Projects in Universities in Anhui Province (2022AH020023), the Commissioned Project of Anhui Provincial Department of Education for Universities (2022AH050267).

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Chen, R.; Gu, B. Childbearing intention and childbearing behavior in low fertility society: evidence from Shanghai. China Population and Development Studies 2022, 6, 115-126. [CrossRef]
  2. Kim, J.; Luke, N. Lowest-low fertility in South Korea: Policy and domestic labor supports and the transition to second birth. Social Forces 2020, 99, 700-731. [CrossRef]
  3. Innocenti, N.; Vignoli, D.; Lazzeretti, L. Economic complexity and fertility: insights from a low fertility country. Regional Studies 2021, 55, 1388-1402, doi:10.1080/00343404.2021.1896695. [CrossRef]
  4. Kim, T. The impact of working hours on pregnancy intention in childbearing-age women in Korea, the country with the world’s lowest fertility rate. PloS one 2023, 18, e0288697. [CrossRef]
  5. Lazzari, E.; Mogi, R.; Canudas-Romo, V. Educational composition and parity contribution to completed cohort fertility change in low-fertility settings. Population Studies 2021, 75, 153-167, doi:10.1080/00324728.2021.1895291. [CrossRef]
  6. Matsuda, S. Progress of low fertility in Japan and other Asian countries: a theoretical framework. Low Fertility in Advanced Asian Economies: Focusing on Families, Education, and Labor Markets 2020, 1-20. [CrossRef]
  7. Matsuda, S. Characteristics and problems of the countermeasures against low fertility in Japan: Reasons that fertility is not increasing. Low fertility in Japan, South Korea, and Singapore: Population policies and their effectiveness 2020, 1-14. [CrossRef]
  8. Skakkebaek, N.E.; Lindahl-Jacobsen, R.; Levine, H.; Andersson, A.-M.; Jørgensen, N.; Main, K.M.; Lidegaard, Ø.; Priskorn, L.; Holmboe, S.A.; Bräuner, E.V. Environmental factors in declining human fertility. Nature Reviews Endocrinology 2022, 18, 139-157. [CrossRef]
  9. Chen, S. Parental investment after the birth of a sibling: the effect of family size in low-fertility China. Demography 2020, 57, 2085-2111. [CrossRef]
  10. Preis, H.; Tovim, S.; Mor, P.; Grisaru-Granovsky, S.; Samueloff, A.; Benyamini, Y. Fertility intentions and the way they change following birth-a prospective longitudinal study. BMC pregnancy and childbirth 2020, 20, 1-11. [CrossRef]
  11. Li, M.; Xu, X. Fertility Intentions for a second child and their influencing factors in contemporary China. Frontiers in Psychology 2022, 13, 883317. [CrossRef]
  12. Jing, W.; Liu, J.; Ma, Q.; Zhang, S.; Li, Y.; Liu, M. Fertility intentions to have a second or third child under China’s three-child policy: a national cross-sectional study. Human Reproduction 2022, 37, 1907-1918. [CrossRef]
  13. Marteleto, L.J.; Dondero, M.; Kumar, S.; Mallinson, D.C. Measuring Fertility Intentions During Times of Crisis: An Example Using Survey Data Amid the Covid-19 Pandemic. Studies in Family Planning 2023, 54, 161-180. [CrossRef]
  14. Cheng, Y.-h.A. Ultra-low fertility in East Asia Confucianism and its discontents. Vienna Yearbook of Population Research 2020, 18, 83-120. [CrossRef]
  15. Fukuda, S. Marriage will (continue to) be the key to the future of fertility in Japan and East Asia. Vienna Yearbook of Population Research 2020, 18, 71-80. [CrossRef]
  16. Hwang, J. Later, fewer, none? Recent trends in cohort fertility in South Korea. Demography 2023, 60, 563-582. [CrossRef]
  17. Rossin-Slater, M. Maternity and family leave policy; National Bureau of Economic Research: 2017.
  18. Wang, S.; Zhong, S. Economic Uncertainty, Cultural and Ideational Transition, and Low Fertility. Sustainability 2022, 14, 8344. [CrossRef]
  19. Orangi, S.; Kairu, A.; Malla, L.; Ondera, J.; Mbuthia, B.; Ravishankar, N.; Barasa, E. Impact of free maternity policies in Kenya: an interrupted time-series analysis. BMJ Global Health 2021, 6, e003649. [CrossRef]
  20. Wang, W.; Ham, J.K.. Population Aging, Education Financing Patterns, and Economic Growth in China. Economic Research 2020, 55, 46-63.
  21. Bozio, A.; Garrouste, C.; Perdrix, E. Impact of later retirement on mortality: Evidence from France. Health economics 2021, 30, 1178-1199. [CrossRef]
  22. Dai, T.; Fan, H.; Liu, X.; Ma, C. Delayed retirement policy and unemployment rates. Journal of Macroeconomics 2022, 71, 103387. [CrossRef]
  23. Bratun, U.; Zurc, J. The motives of people who delay retirement: An occupational perspective. Scandinavian Journal of Occupational Therapy 2022, 29, 482-494. [CrossRef]
  24. Chen, X.; Zhong, S.; Qi, T. Delaying retirement and China’s pension payment dilemma: based on a general analysis framework. IEEE Access 2020, 8, 126559-126572. [CrossRef]
  25. Kong, W.; Ren, M.; Li, Y.; Feng, D. Predictors of delayed retirement intention in older Chinese workers. LABOUR 2022, 36, 505-524. [CrossRef]
  26. Nunes, J. The Power of Postponed Retirement. CD Howe Institute e-Brief 2020, 301. [CrossRef]
  27. Phillips, P.; Phillips, J.J. Solving the delayed retirement puzzle… and creating win-win opportunities. Strategic HR Review 2020, 19, 123-130. [CrossRef]
  28. Raihan, M.M.; Chowdhury, N.; Chowdhury, M.Z.; Turin, T.C. Involuntary delayed retirement and mental health of older adults. Aging & Mental Health 2023, 1-9. [CrossRef]
  29. Yu, Wenguang; Li, Qian; Wang, Qi. Delayed Retirement, Intergenerational Parenting and Enterprise Pension Contribution Rates. Economic Science 2021, 123-134.
  30. Naluwuge, B. Retirement saving knowledge and attitude amongst the youth. Makerere University, 2021.
  31. Li, J.; Yuan, B.; Lan, J. The influence of late retirement on health outcomes among older adults in the policy context of delayed retirement initiative: an empirical attempt of clarifying identification bias. Archives of Public Health 2021, 79, 59. [CrossRef]
  32. Wu, Y.; Xu, C.; Yi, M. The Optimal Choice of Delayed Retirement Policy in China. Sustainability 2022, 14, 12841. [CrossRef]
  33. Yang, Shu-Yue; Chen, Zhen. Macroeconomic Impacts of Synergistic Adjustment of Fertility and Education Policies in the Context of Aging. Management Review 2023, 35, 79-93+170, doi:10.14120/j.cnki.cn11-5057/f.2023.02.018. [CrossRef]
  34. Zhang, S.W.; Wang, J.. Delayed Retirement, Intergenerational Caregiving and Fertility. Journal of Central University of Finance and Economics 2023, 87-102, doi:10.19681/j.cnki.jcufe.2023.05.008. [CrossRef]
  35. Pecchenino, R.A.; Pollard, P.S. Dependent children and aged parents: funding education and social security in an aging economy. Journal of Macroeconomics 2002, 24, 145-169. [CrossRef]
  36. Wang Xiaolu. The Sustainability of China’s Economic Growth - A Cross-Century Retrospective and Prospective I. Synthesis Chapter 1 The Sustainability of China’s Economic Growth and Institutional Change. 2000; p. 66.
  37. Guo Han; Ren Baoping. Structural Change, Factor Output Elasticity and Potential Economic Growth Rate in China. Research on Quantitative and Technical Economics 2014, 31, 72-84, doi:10.13653/j.cnki.jqte.2014.12.005. [CrossRef]
  38. Zhang, J.; Zhang, J.; Lee, R. Rising longevity, education, savings, and growth. Journal of Development Economics 2003, 70, 83-101. [CrossRef]
  39. Liu, Y.P.; Lu, M.. Whether the aging Chinese economy can grow sustainably from the perspective of family old-age pension. World Economy 2008, 65-77.
  40. Zhai D. H. Indirect Estimation of National Mortality Levels in the Fifth Population Census of China. Population and Economy 2003, 65-69+31.
Preprints 115792 g001
Figure 1. Delayed Retirement and Private Capital k
Figure 1. Delayed Retirement and Private Capital k
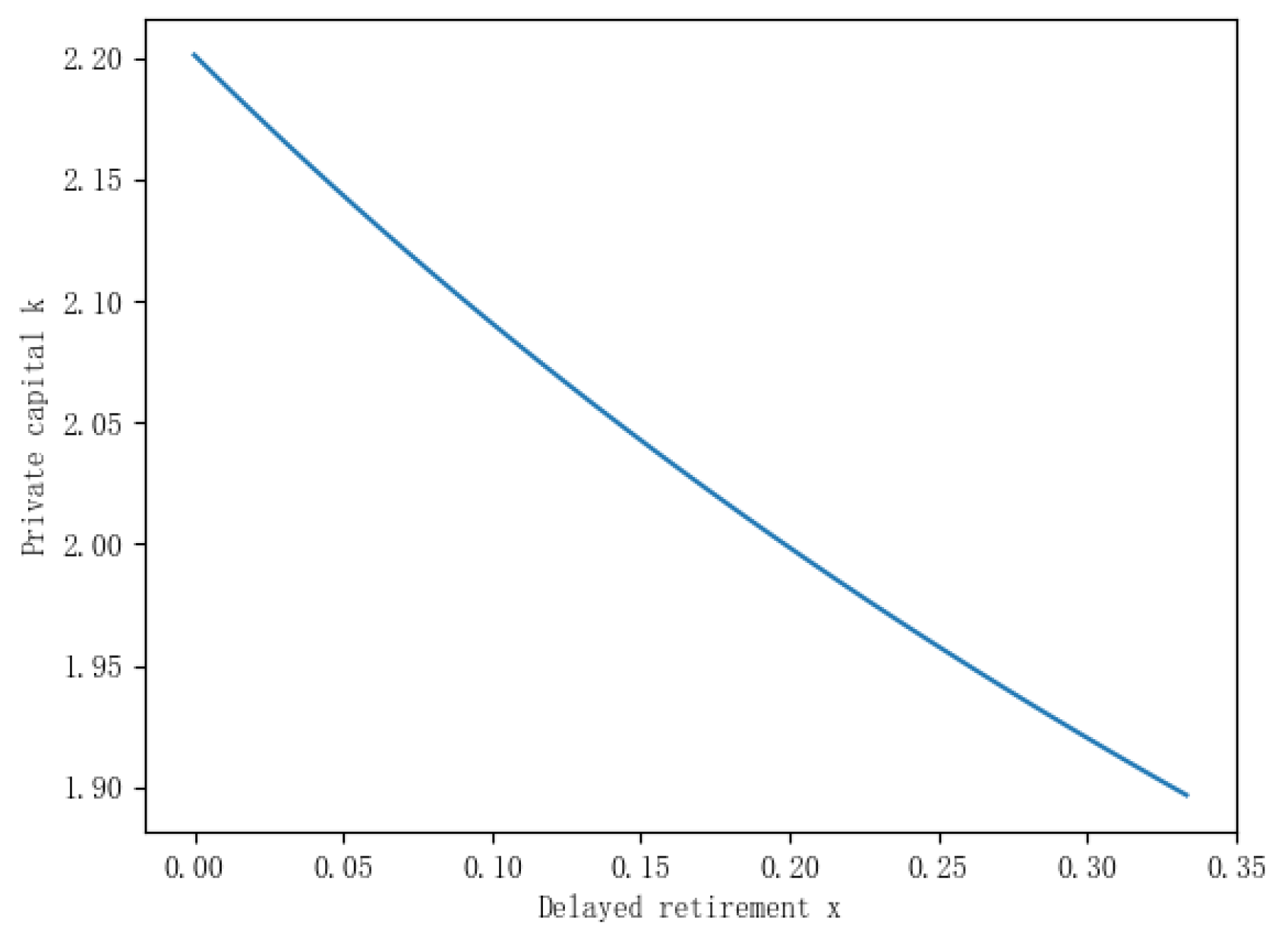
Preprints 115792 g001
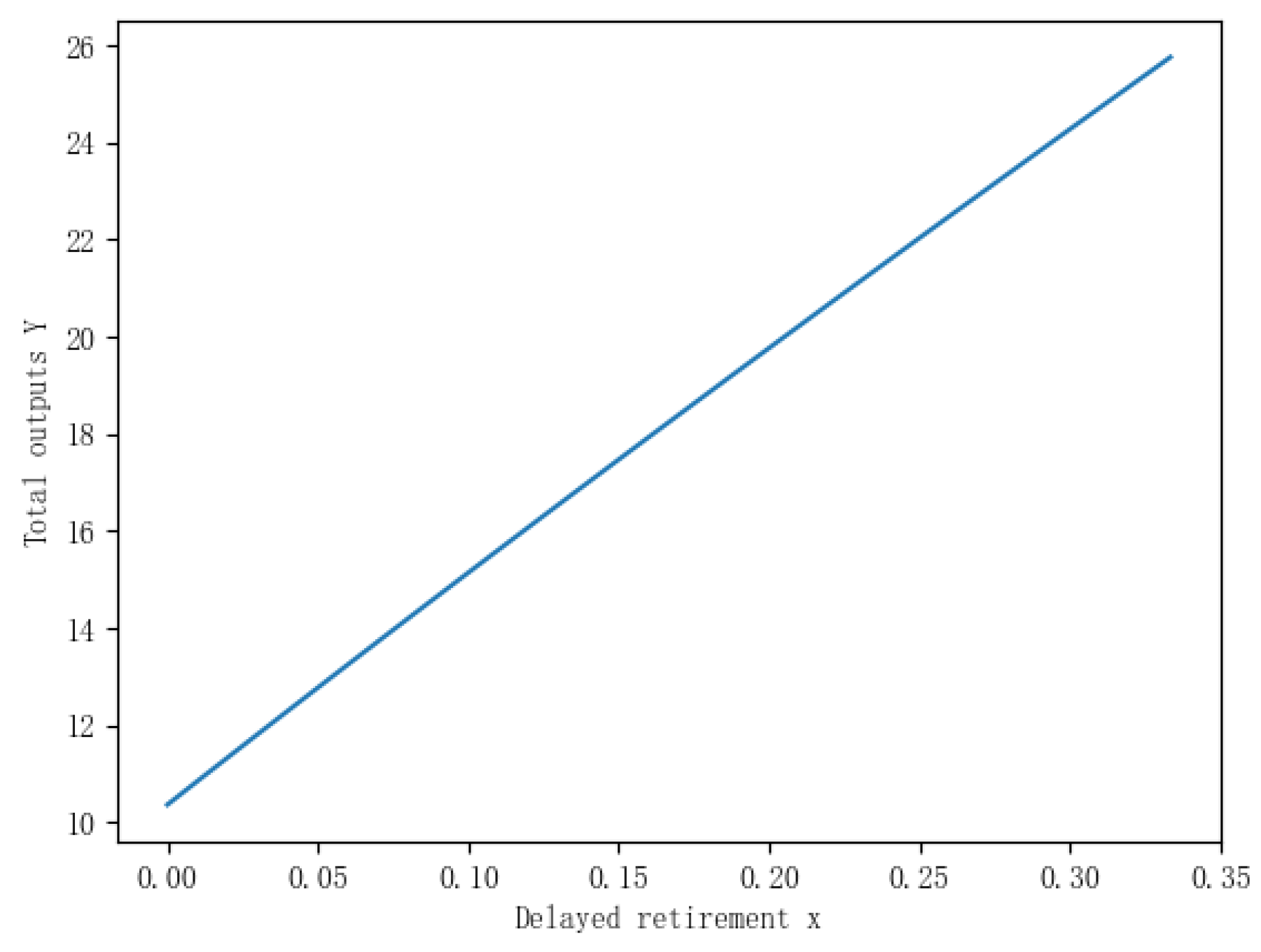
Preprints 115792 g002
Figure 2. Delayed Retirement and Total Output Y
Figure 2. Delayed Retirement and Total Output Y
Preprints 115792 g002
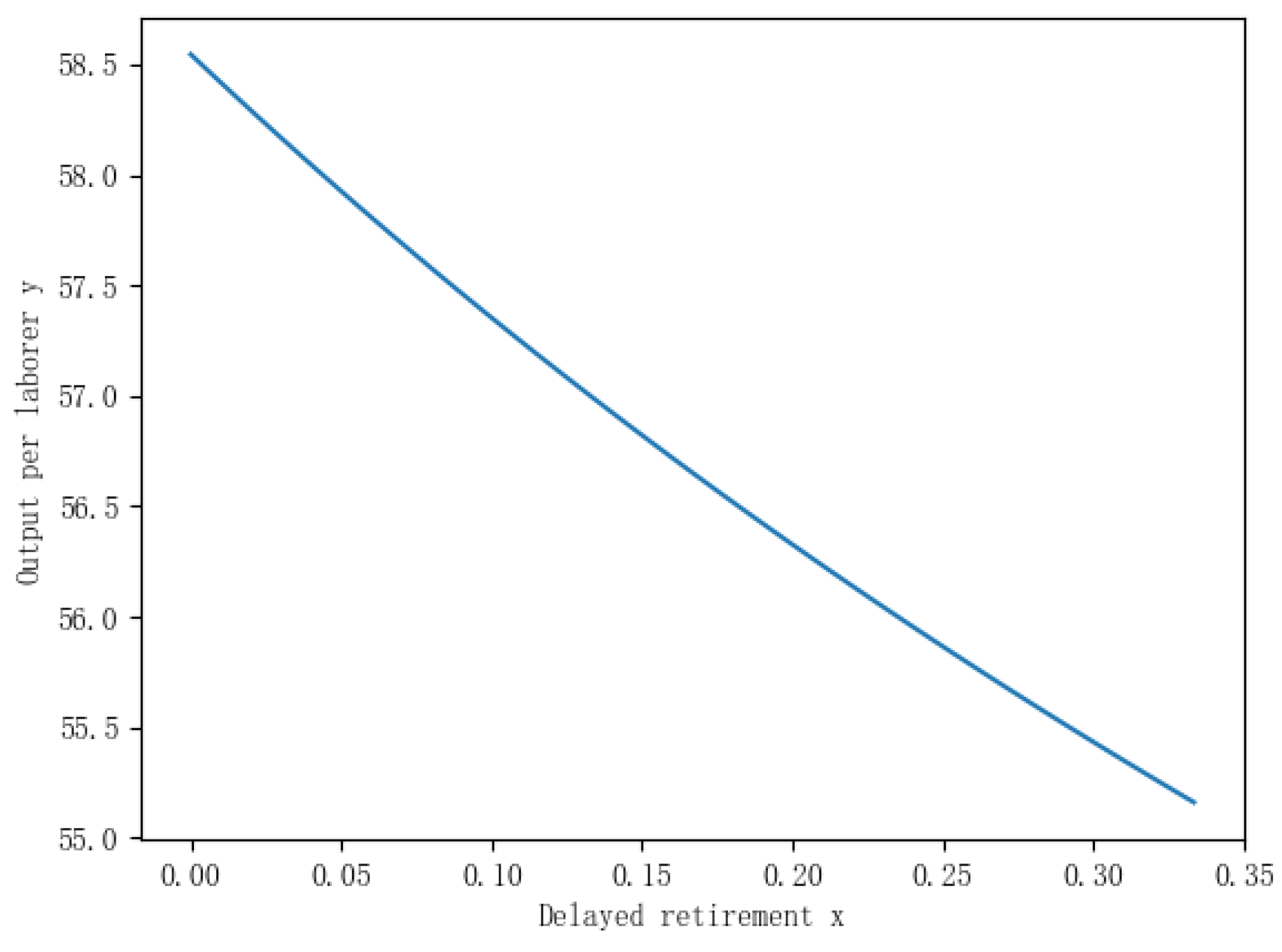
Preprints 115792 g003
Figure 3. Delayed Retirement and Labor Productivity y
Figure 3. Delayed Retirement and Labor Productivity y
Preprints 115792 g003
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated