Prerpints.org logo
Preprint
Article

The Evolution of Permeability and Sensitivity Analysis of Gas-bearing Coal Under Cyclic Dynamic Loading

Altmetrics

Downloads

74

Views

15

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

21 August 2024

Posted:

21 August 2024

You are already at the latest version

Alerts
Abstract
It is imperative to conduct experimental studies on the seepage behavior of gas-bearing coal under cyclic dynamic loading conditions. This paper focuses on the evolution of coal permeability under the combined effects of dynamic loading, static loading, and gas adsorption. The principal conclusions are as follows. (1) As the frequency and amplitude of dynamic loading increase, the development of pore and fissure structures within the coal body becomes increasingly pronounced during dynamic loading cycles, resulting in a gradual rise in permeability. Notably, as the coal approaches its yielding stage, the permeability can increase by up to 47%. (2) The permeability curve is divided into four regions: the compaction reduction zone, the oscillation zone, the gradual recovery zone, and the abrupt increase zone of failure. Ultimately, in the failure phase, the permeability surges dramatically, potentially reaching 4 to 5 times the initial permeability. (3) When the static load stage is constant, the rate of change in permeability of the coal under dynamic loading decreases with increasing adsorption amount. When the adsorption amount is constant, the rate of change in permeability of the coal under dynamic loading increases with the increase in static load stress stage, with the maximum increase reaching 75.2%. It can be concluded from the rate of change in permeability and the dynamic loading sensitivity coefficient that the permeability of the coal is highly sensitive to cyclic dynamic loading, with increased sensitivity associated with larger static load stages and decreased sensitivity with greater adsorption amounts.
Keywords: 
Subject: Engineering  -   Energy and Fuel Technology

1. Introduction

Due to the depletion of shallow coal resources, coal mining operations are progressively moving towards deeper deposits. Deep coal seams frequently experience repeated mining disturbances, resulting in cyclic dynamic loading on the coal layers. When subjected to such cyclic dynamic loading, the deformation of the coal body causes the propagation of fractures, which in turn affects the permeability of the coal, leading to abnormal gas outbursts in coal mines. In severe cases, this can result in catastrophic events such as gas explosions and coal and gas outbursts. Consequently, it is imperative to conduct experimental studies on the seepage behavior of gas-bearing coal under cyclic dynamic loading conditions.
Extensive research has been conducted by scholars both domestically and internationally on the permeability characteristics of coal rock masses[1,2,3,4,5,6,7]. Regarding the effects of coal matrix contraction and expansion on permeability, Bustin et al. [8] conducted preliminary studies on the relationship between adsorption expansion effects and permeability in coal samples under different gas purities. Wang et al. [9] investigated the relationship between coal matrix contraction and permeability under the adsorption of multiple gases. Niu et al. [10] investigated the differential effects of gas adsorption on the swelling behavior of raw coal versus structural coal. Mojgan et al. [11] conducted experiments to identify the critical point at which the effect of gas pressure on coal matrix shrinkage changes, and they noted that this pressure is approximately 1.5 MPa. Larsen [12] and Liu [13] hypothesized, based on experimental results, that the effect of gas adsorption on the permeability of coal rock is primarily due to matrix contraction and expansion. Li et al. [14] investigated the effects of effective stress, matrix expansion and contraction, temperature, and moisture on coal rock permeability, and identified the principal influencing factors. Liu et al. [15] investigated the effects of various gases on the permeability of coal rocks and analyzed the differences in adsorption of different gases concerning the contraction and expansion of the coal matrix. Zhao et al. [16] examined the mechanisms by which gas adsorption affects the permeability of coal. Zhao [17] and Hu[18] fitted the relationship between permeability and gas pressure based on experimental results.
In terms of the impact of effective stress on permeability variations, Li et al. [19] investigated the sensitivity of permeability to stress and delineated the relationship between permeability and stress fluctuations. Bai et al. [20] investigated the variations in coal-rock permeability across different stress stages. Lu [21] investigated the variations in coal rock permeability with respect to confining pressure and pore pressure, and obtained various experimental conclusions. Fan et al. [22] analyzed the variation in coal rock permeability with effective stress and delineated the characteristics of initial permeability. Mitra et al. [23] investigated the variations in coal rock permeability with changes in pore pressure and effective stress under uniaxial compression test conditions, and concluded that the rate of permeability change differs at various stages. Tang et al. [24] conducted experiments using self-developed seepage testing apparatus. Based on the experimental results, they fitted the relationship between effective stress and permeability during the testing process and highlighted the discrepancies observed between the loading and unloading phases. Zhao et al. [25] derived an equation that elucidates the correlation between coal matrix permeability and effective stress, thereby laying the groundwork for the establishment of subsequent models. Li et al. [26] investigated the sensitivity of coal rock permeability to effective stress during loading. Peng et al. [27] examined the impact of scale effects on coal rock permeability and noted that sensitivity to effective stress varies at different scales. Yin et al. [28,29] not only explored the influence of effective stress on coal rock permeability but also analyzed the effects of strain on permeability.
Regarding the influence of the Klinkenberg effect on gas permeability, Pirzada et al. [30] investigated the sensitivity of the Klinkenberg effect to confining pressure and pore pressure, and identified the inflection point of this effect; Talapatra et al. [31] conducted experimental studies on the aforementioned phenomenon, providing a quantitative analysis of the impact of the Klinkenberg effect on permeability reduction; Wang et al. [32] analyzed the discrepancies of the Klinkenberg effect between briquette coal and raw coal.
The aforementioned study primarily focuses on the gas permeability characteristics of coal under static load conditions. However, there is a paucity of research on the gas flow characteristics of coal under the combined effects of static load, dynamic load, and gas adsorption. The mechanisms of gas flow in coal under these combined influences remain to be further explored. This paper, utilizing self-developed instrumentation, investigates the impact of static load, dynamic load, and gas adsorption on the permeability of coal. The findings provide a theoretical foundation for understanding coal-rock dynamic disaster mechanisms and gas extraction processes.

2. Experimental Apparatus

A self-developed three-axis solid-gas coupling test apparatus is used to measure the permeability of the coal under cyclic dynamic and static combined loads [33]. It consists of four key units: dynamic and static loading unit, three-axis confining pressure unit, fluid injection unit, and information acquisition unit. The challenges of dynamic-static load combination, high-pressure sealing under dynamic loads, and permeability measurement during the full stress-strain process are solved.

3. Experimental Scheme

The permeability of gas-containing coal under combined static and dynamic loading is closely related to factors such as static load, dynamic load, and the amount of gas adsorption. The experimental variables chosen for this test are dynamic load impact energy, static load stress stages, and gas adsorption quantity. The dynamic impact energy is primarily achieved by adjusting the frequency and magnitude of the dynamic load. The static load stress phase is divided into the compaction stage, elastic stage, and yield stage. The gas adsorption amount is adjusted through different adsorptive gases at the same adsorption pressure. The dynamic load along the trough of the mining face is mainly caused by the excavation, and the source energy level is about 100 J. The dynamic load frequency band is mainly at 3-6 Hz, and the main deformation stage of coal and rock occurs within the first 300 cycles[34]. According to the storage conditions of the gas pressure in the coal under the actual working conditions, the gas pressure is selected as 1 MPa. At the same time, in order to create a triaxial stress environment and minimize the impact of effective stress, the confining pressure is 1.5 MPa. The ambient temperature throughout the experiment was maintained at approximately 25°C, with the adsorption time of the adsorptive gases uniformly regulated to around 48 hours. The detailed experimental plan is presented in Table 1, in which the σc is the coal compressive strength.
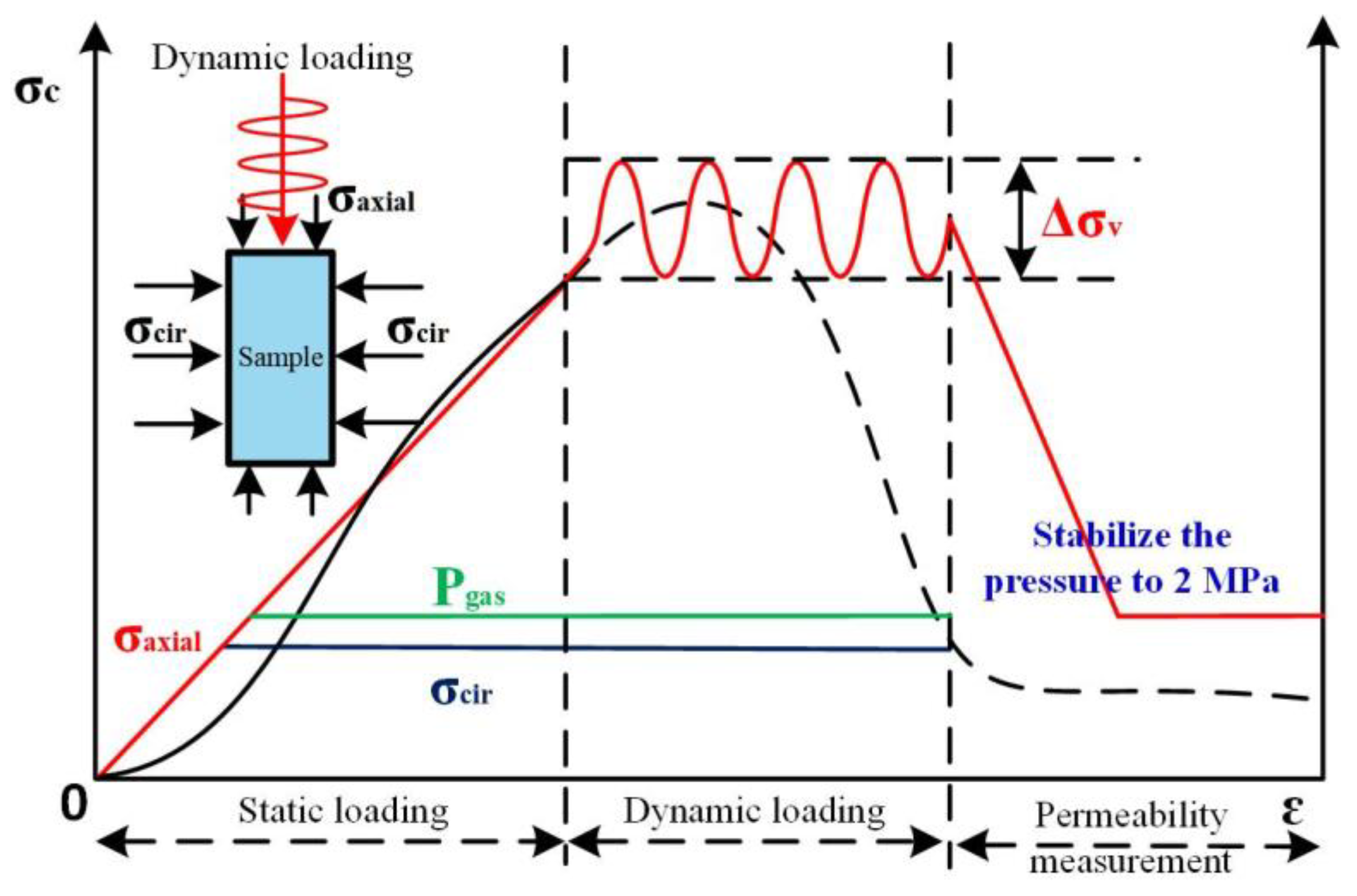
In order to ensure the comparability of experimental data, a testing loading path is designed as illustrated in Figure 1. The sample is initially subjected to a predeterminable confining pressure, after which it is infused with a predefined pressure of gas. After the gas adsorption reaches equilibrium, a static load is applied to the sample until it reaches the designated value. On this basis, a cyclic dynamic load is applied with the predetermined amplitude and frequency. After the dynamic loading disturbance concludes, return to the uniform predetermined stress state of 2 MPa and conduct the permeability test.

4. Results and Discussion

4.1. The Influence of Cyclic Loading Frequency on the Permeability

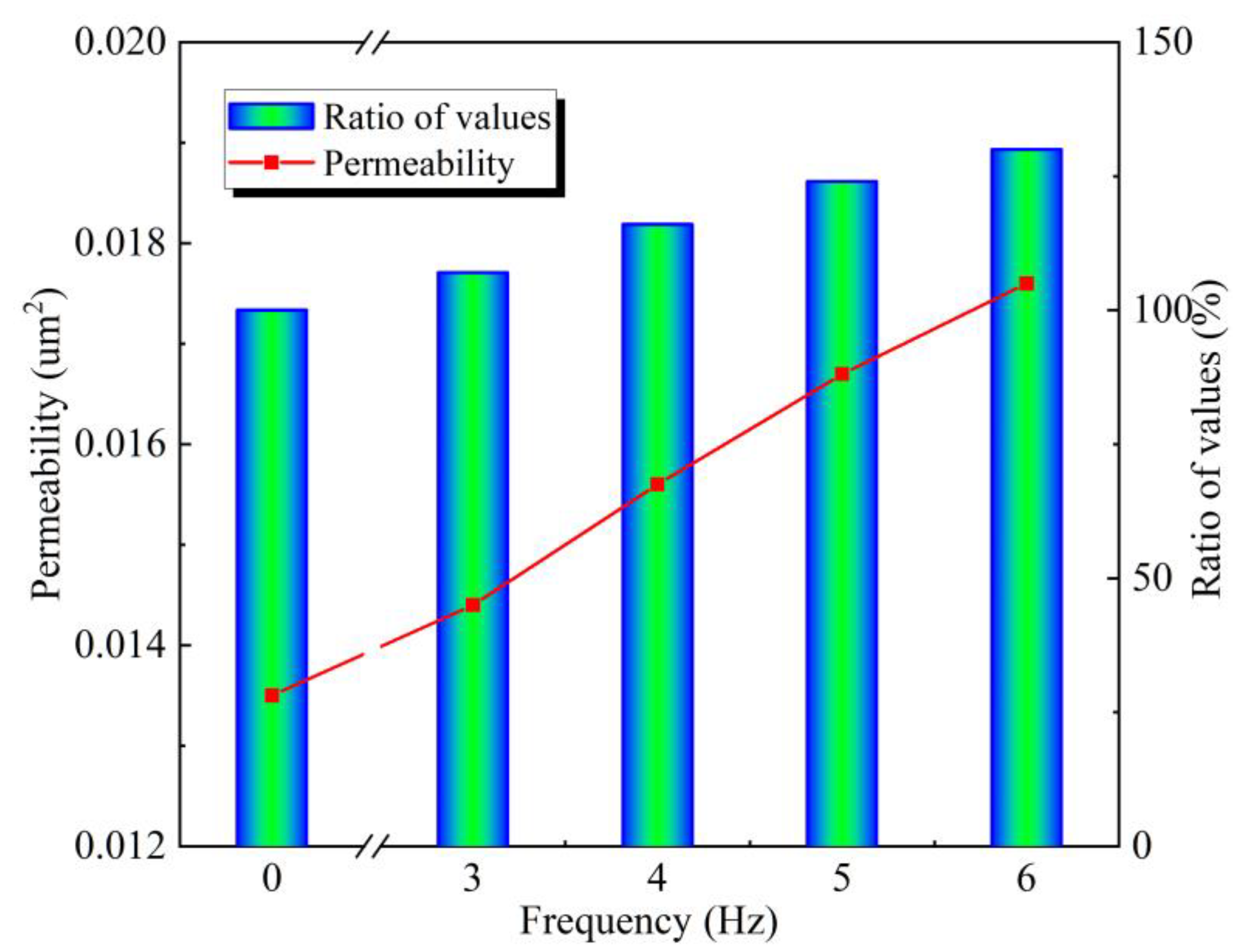
The variation of coal permeability with the frequency of cyclic dynamic loading is illustrated in Figure 2. It is evident that there is a positive correlation between the permeability of the coal body and the frequency of cyclic dynamic loading. When the coal body is undisturbed by dynamic loading, its permeability is approximately 0.0135 μm². However, after being subjected to cyclic dynamic loading with an amplitude of 2.5 MPa and a frequency of 6 Hz, the permeability increases to 0.0176 μm², reflecting an increase of approximately 30.1%. The increases in permeability at the other three dynamic loading frequencies are 7.2% (3Hz), 16.3% (4Hz), and 23.8% (5Hz), respectively. It is evident that cyclic dynamic loading has a significantly pronounced effect on increasing the permeability of coal bodies. The pores and fractures within the coal mass serve as the primary conduits for gas seepage. Under the continuous influence of cyclic loading, the primary pores and fractures further develop, resulting in an increased permeability. As the frequency of dynamic loading increases, a certain number of secondary fractures will develop, leading to a phenomenon where permeability continues to rise with the ongoing increase in dynamic loading frequency. Moreover, under the influence of cyclic dynamic loading, the gas adsorption equilibrium within the coal matrix is disrupted, further enhancing the gas adsorption and expansion effects. Thus, it is evident that the greater the external disturbance to the coal seam, the faster the gas migration within the seam, making it more prone to abnormal gas outbursts. Simultaneously, for coal seams from which gas can be extracted, external disturbances can enhance their permeability, thereby improving the efficiency of gas extraction.

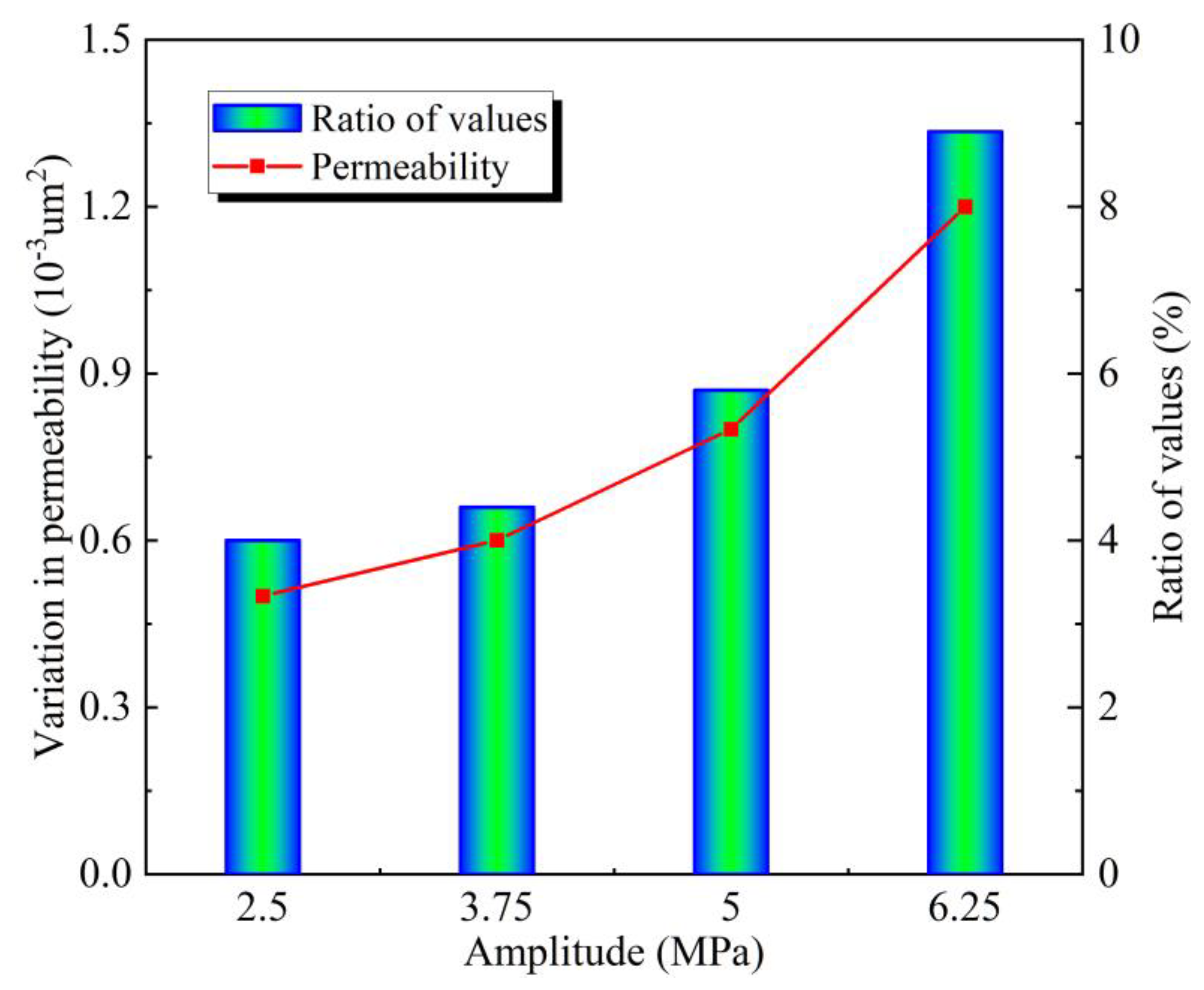
4.2. The Influence of Cyclic Loading Amplitude on the Permeability

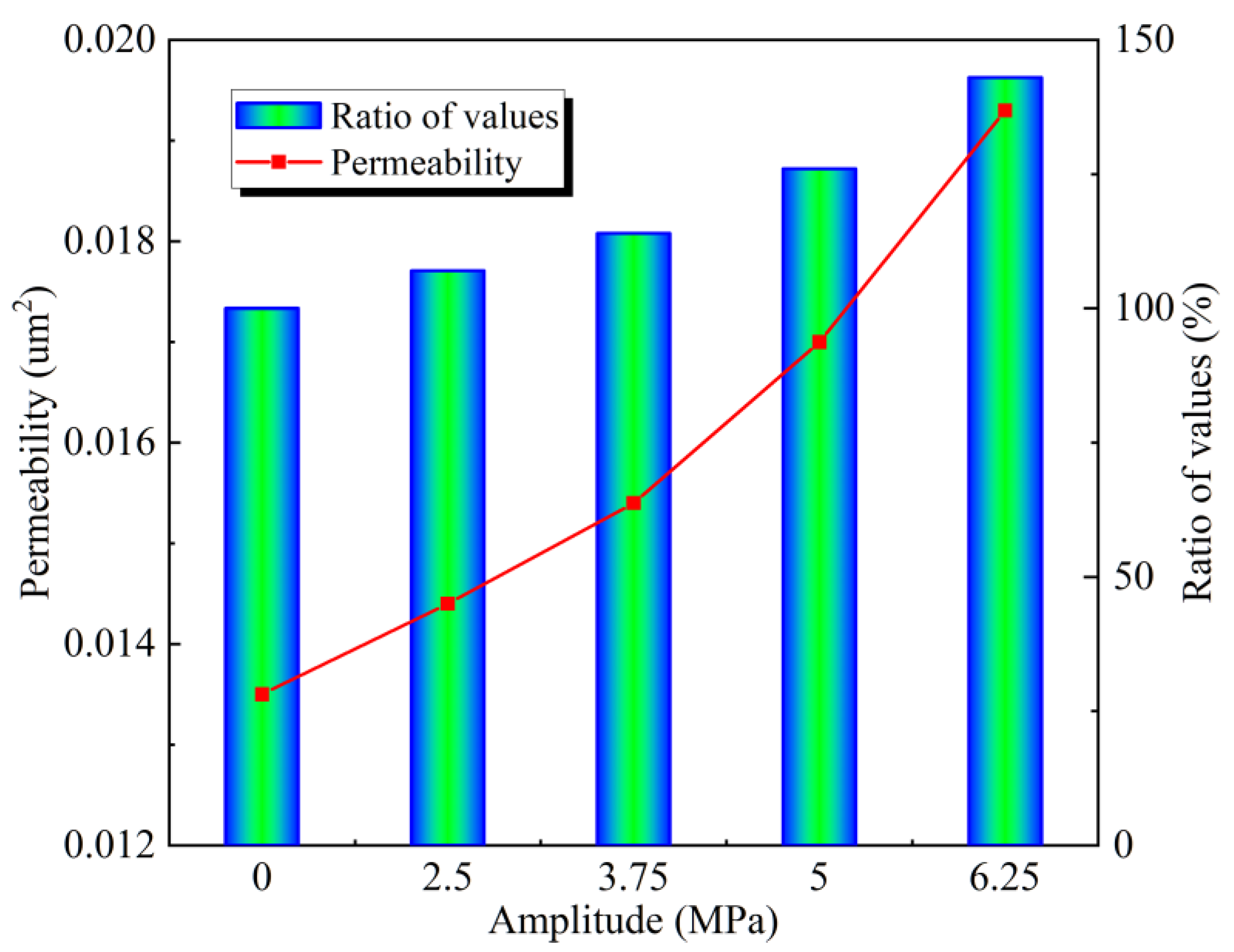
The variation in coal permeability with the amplitude of cyclic dynamic loading is illustrated in Figure 3. It is evident from the figure that the permeability of coal is positively correlated with the amplitude of cyclic dynamic loads. At amplitudes of 2.5 MPa, 3.75 MPa, 5 MPa, and 6.25 MPa, the permeabilities are recorded as 0.0144 um², 0.0154 um², 0.017 um², and 0.0193 um², respectively, with growth rates of 7.2%, 14.3%, 26.1%, and 43%. It is evident that the amplitude of dynamic loading exerts a more pronounced effect on the increase in permeability. The reasons for the increase in permeability are fundamentally consistent with that of different frequencies. The sharp 43% increase in permeability at an amplitude of 6.25 MPa is due to the fact that, at this stage, the cyclic dynamic loading is in the yield phase of the coal body stress-strain curve. Consequently, the degree of damage is greater, and the development of fractures is more pronounced.

4.3. The Influence of Static Load Stage on the Permeability

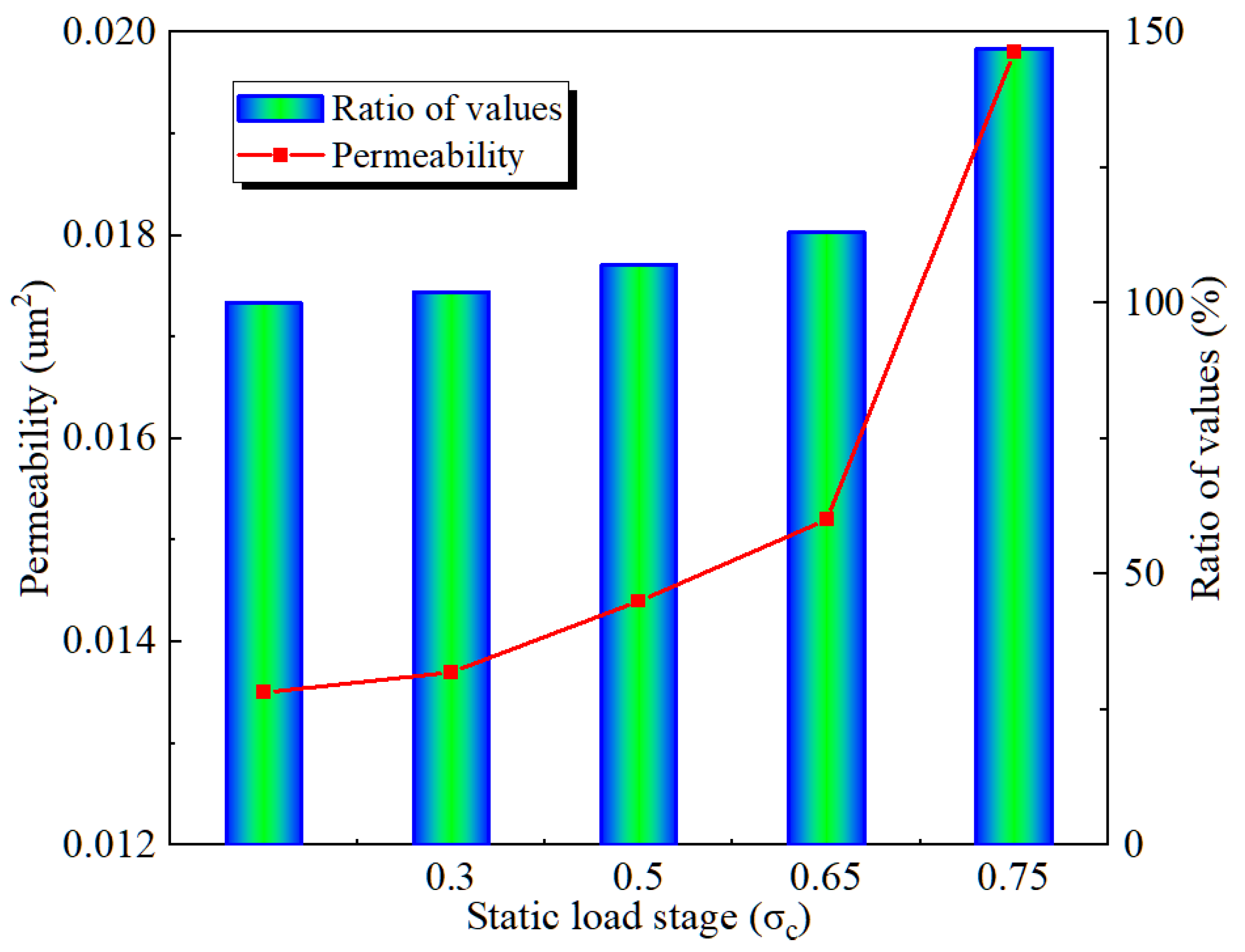
The variation in permeability with the static load stage of the cyclic dynamic load is illustrated in Figure 4. It is evident that there is a positive correlation between the permeability of the coal body and the static load stage. When the static load stages are 0.3 σc, 0.5 σc, 0.65 σc, and 0.75 σc, the permeability of the coal samples is observed to be 0.0137 μm², 0.0144 μm², 0.0152 μm², and 0.0198 μm², with corresponding growth rates of 2%, 7.1%, 13.1%, and 47.2%, respectively. During the elastic stage of coal, the impact of cyclic dynamic loading on permeability is not significant. This is because, during this phase, the internal damage to the coal body is minimal, and the resulting plastic deformations and newly-formed cracks are also relatively few. However, before and during the yield stage of the coal mass, its permeability significantly increases, with a maximum increase of up to 47.2% compared to the permeability without dynamic loading. The reason is that during this stage, the application of cyclic dynamic loads significantly exacerbates the internal damage to the coal body, leading to the expansion of primary fractures and the formation of numerous secondary fractures. It is evident that when coal seams are subjected to higher stress conditions, they are more prone to damage and abnormal gas outbursts when disturbed by external dynamic loads.

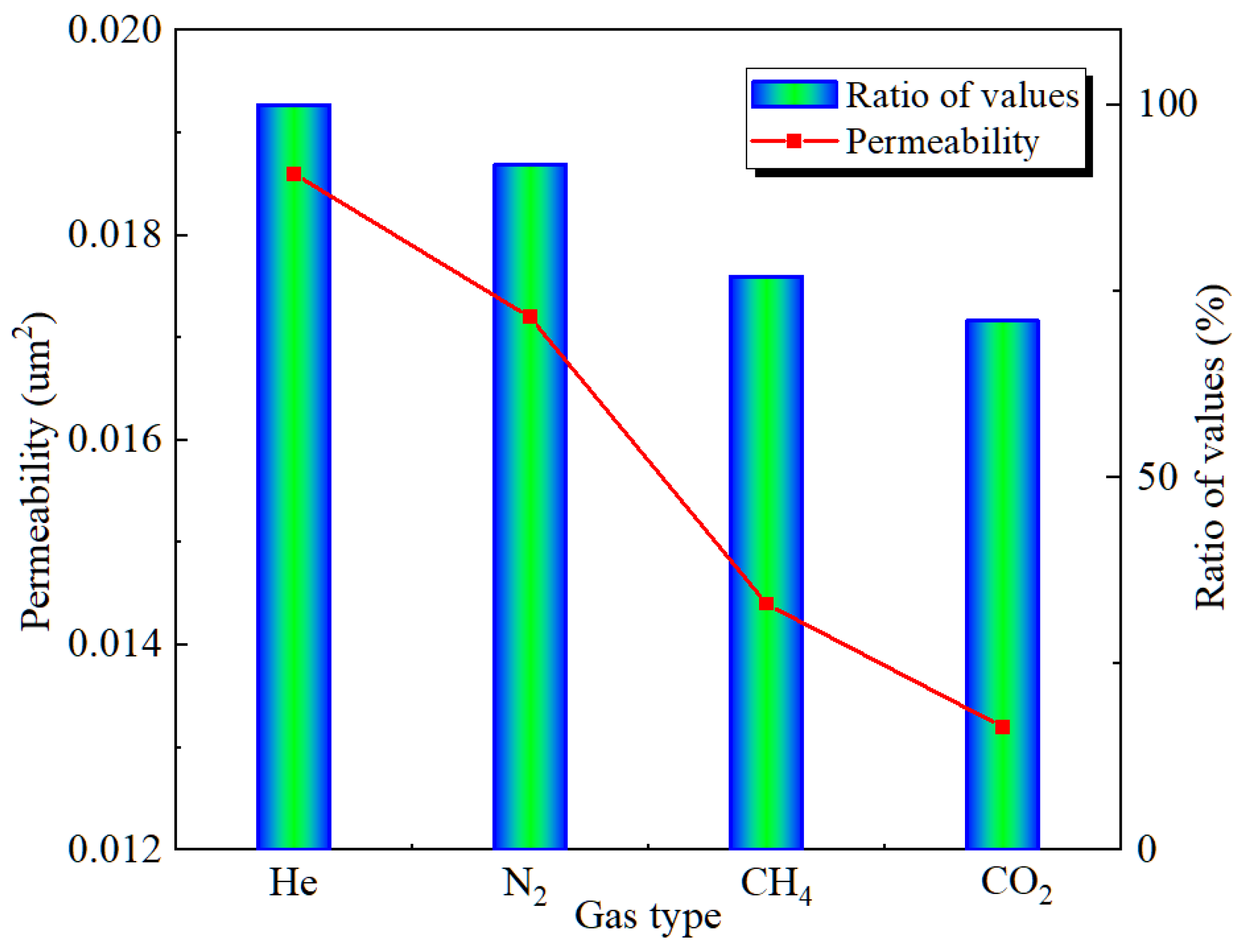
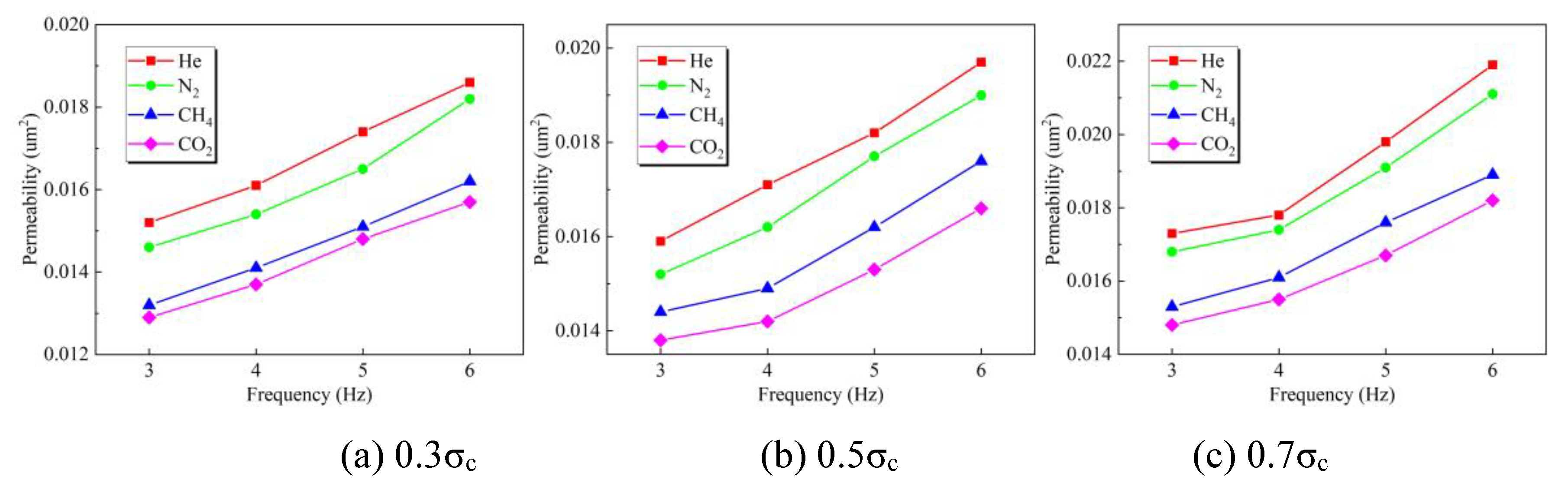
4.4. The Influence of Adsorbed Gas on the Permeability

The gas adsorption capacity is achieved through the gases at identical pressures but of different types, thereby ensuring the comparability of permeability results. The adsorption capacity of the four gases, in ascending order, are He, N2, CH4, and CO2. The variation in permeability with the capacity of gas adsorption is illustrated in Figure 5. It is evident that there is an inverse correlation between the permeability of the coal body and the gas adsorption capacity. As the capacity of gas adsorption increases, the permeability of the coal samples is 0.0186 μm², 0.0172 μm², 0.0144 μm², and 0.0132 μm², respectively. Taking the permeability of the non-adsorptive inert gas He as the baseline, the reductions in permeability for the other three gases are 8%, 23%, and 29.2%, respectively. Thus, it is evident that gas adsorption exerts an inhibitory effect on the permeability of the coal body. The reason is that after the coal body adsorbs gas, it undergoes adsorption-induced swelling and deformation. However, constrained by the confining pressure, deformation can only occur inwardly, thereby compressing the internal seepage pathways of the coal body and consequently reducing its permeability. As the amount of adsorption increases, so does the degree of adsorption-induced swelling and deformation, resulting in a more significant reduction in permeability.

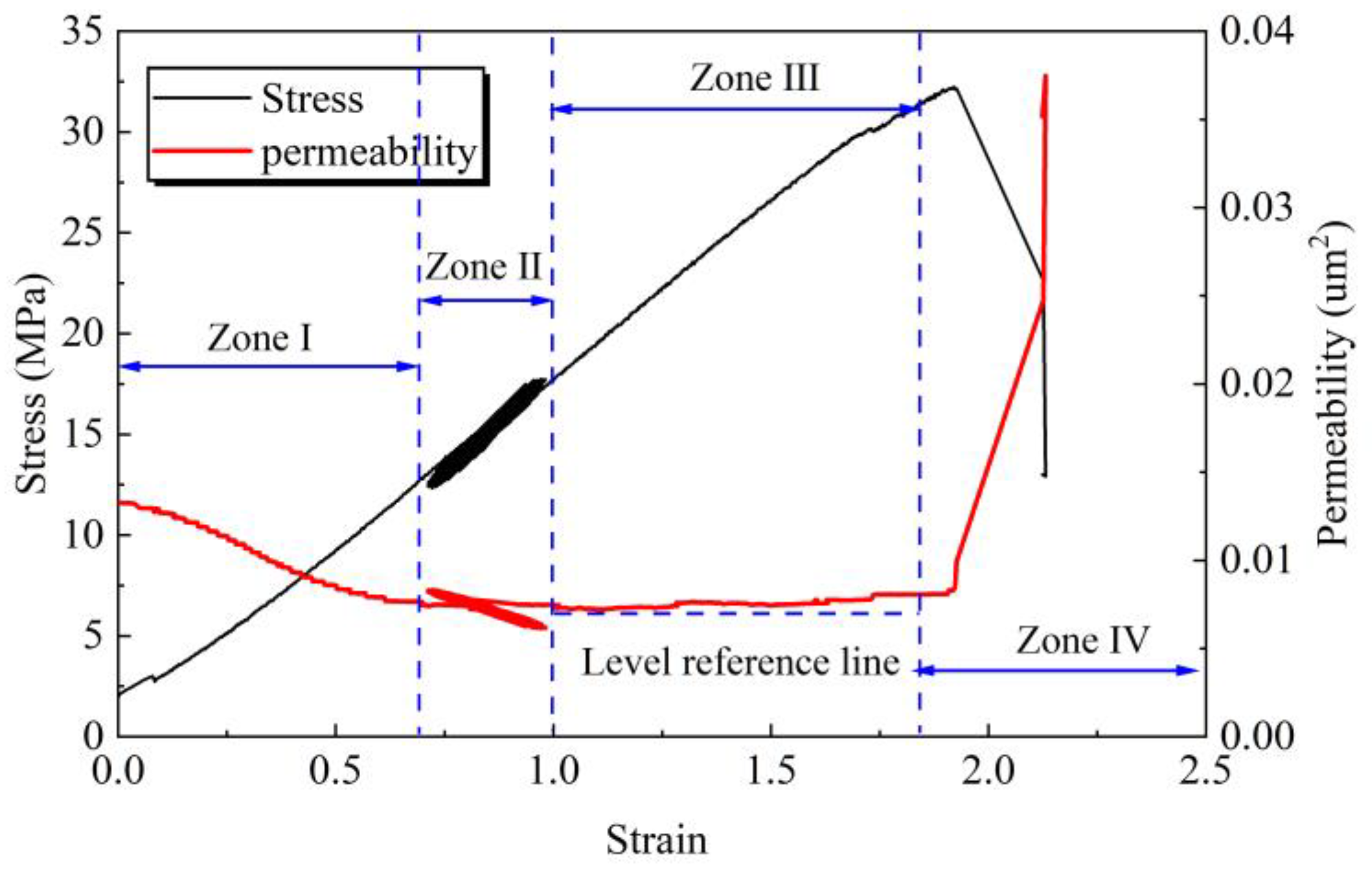
4.4. The Permeability Behavior of Coal in the Full Stress-Strain Process

To more intuitively illustrate the overall evolution of coal permeability under cyclic dynamic loading, we have also obtained the stress-strain versus permeability relationship curves of the coal body under such loading, as depicted in Figure 6. There exists a notable coupling relationship between the stress of coal samples, axial strain, and permeability. The stress-strain curve of coal can be classified into four distinct phases: the compaction stage, the elastic oscillation stage, the plastic deformation stage, and the failure stage. Correspondingly, the permeability curve is divided into four regions: the compaction reduction zone (Ⅰ), the oscillation zone (Ⅱ), the gradual recovery zone (III), and the abrupt increase zone of failure (IV).
The compaction reduction zone (Ⅰ): From the initial compression point to the lowest permeability point before the application of cyclic loading, this phase corresponds to the consolidation stage and the elastic deformation stage of the stress-strain curve. During this period, the permeability of the coal samples exhibited a non-linear decreasing trend, with the rate of decrease gradually decelerating, ultimately reducing by approximately 50% of the initial permeability. The reason is that, under the gradual application of axial load, the inherent fissures within the coal body are progressively compacted. This leads to a reduction in the connectivity of the fissures, consequently decreasing the porosity. The channels through which gas molecules flow become narrower and fewer, resulting in a noticeable decline in permeability.
The oscillation zone (Ⅱ): This zone exhibits a propensity towards coupled resonance in the permeability during the application phase of cyclic dynamic loading, which evolves in tandem with the imposition of cyclic dynamic loads. The permeability after the application of dynamic load should exceed that before the application, as cyclic dynamic loading induces irreversible plastic deformation in the coal matrix, leading to a gradual accumulation of damage and an increase in the pathways available for gas flow.
The gradual recovery zone (III): From the end of the oscillatory zone in the permeability curve to the point of sudden slope increase, this stage corresponds to the plastic deformation phase of the stress-strain curve. During this period, with the increase in axial stress, permeability also exhibited growth. Due to the external load, the coal body framework undergoes irrecoverable plastic deformation, leading to a gradual accumulation of damage and destruction. Numerous new fissures emerge, develop, and stabilize, thereby causing the permeability to progressively recover.
The abrupt increase zone of failure (IV): From the point of the sharp increase in the slope of the permeability curve until the conclusion of the test, this phase corresponds to the peak strength and post-peak phase of the stress-strain curve. During this period, the permeability curve of the coal samples exhibits an almost vertical ascent. Compared to the initial permeability, the permeability at the end of this stage has increased by approximately a factor of two.
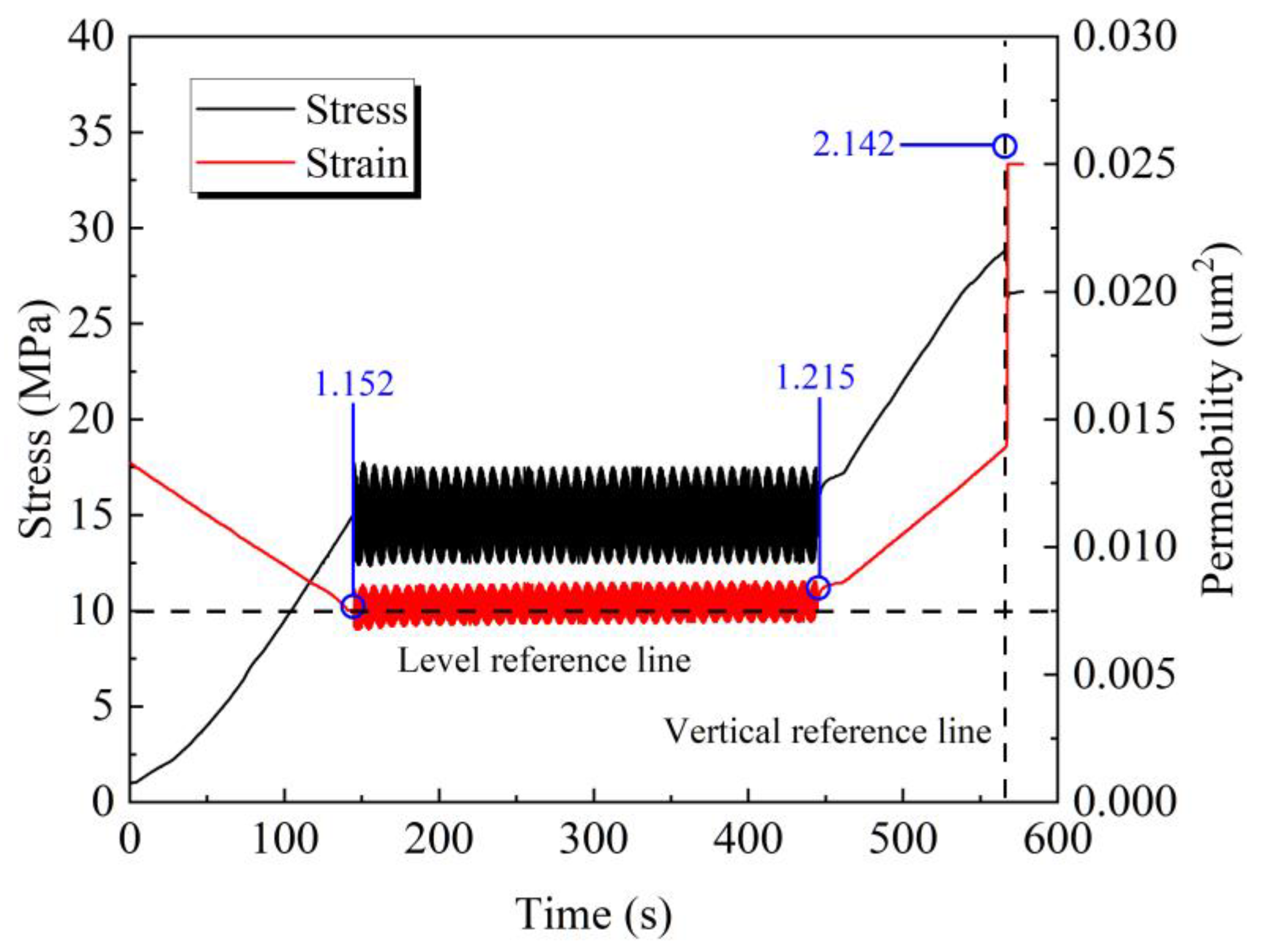
The stress-permeability temporal curve of coal under cyclic loading is illustrated in Figure 7. it is evident that the stress loading curve of the coal body and the variation in permeability exhibit a synchronous resonance pattern. When the cyclic load is applied and the stress returns to its pre-load level, the permeability fails to revert to its original state and actually increases to a certain extent. The reason lies in the fact that during the application of dynamic loading, the internal fissures within the coal body further develop, leading to the widening and proliferation of seepage pathways, which, to a certain extent, increases the permeability of the coal body.
The increase in permeability of the coal mass during different cyclic dynamic loading processes is illustrated in Figure 8. As the amplitude of the cyclic dynamic load increases, the increment in permeability of the coal mass during the application of the dynamic load also rises. This indicates that with the increase in dynamic load amplitude, the damage within the coal mass becomes more pronounced, leading to more extensive development of fractures.
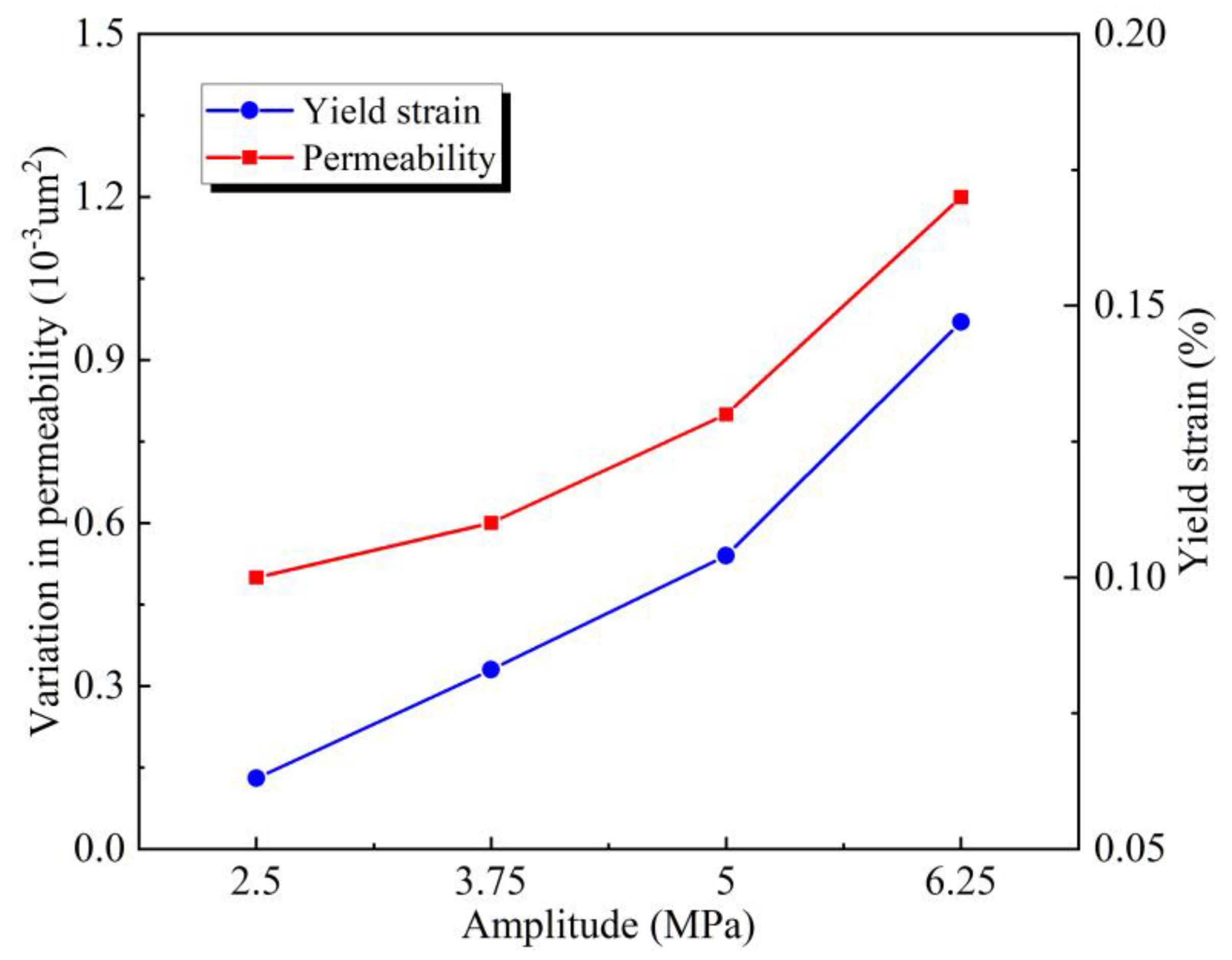
The coupling curve of permeability increase and yield strain of coal under different cyclic dynamic loading is illustrated in Figure 9. As the amplitude of dynamic loading increases, the yield strain during the dynamic loading process also becomes greater. This indicates that the coal body is subjected to further compression; however, an increase in permeability is observed. The reason for this is that, during this process, fractures radially expand further, leading to a continuous rise in permeability.
Following cyclic loading, the maximum permeability of the coal body during failure has also increased, as illustrated in Figure 10. When the cyclic loading amplitudes are 2.5 MPa, 3.25 MPa, 5 MPa, and 6.25 MPa, the maximum permeability values of the coal body are 0.0255 μm², 0.0286 μm², 0.0321 μm², and 0.0386 μm², respectively. Compared to the baseline value of 0.0135 μm², these represent increases of 88.9%, 111.9%, 137.8%, and 185.9%, respectively. It is evident that the application of dynamic loading not only enhances the current permeability of the coal body but also significantly contributes to the increase in its maximum permeability upon failure.

5. Sensitivity Analysis of Permeability to Cyclic Loading

As the depth of coal seam mining increases, the geostress (static load), gas pressure (gas adsorption), and dynamic load disturbances are continuously changing. The permeability of gas-bearing coal is not constant but rather a function of certain influencing factors. Given the numerous factors affecting coal seam permeability, this paper focuses on analyzing the impact of static and dynamic loads as well as gas adsorption. The deep coal and rock mass itself is complex in structure, surrounded by a challenging environment, and subject to rapidly changing evolutionary patterns. Ordinary control variable methods fall short in adequately describing these patterns; thus, a sensitivity coefficient for coal permeability is defined to characterize them.

5.1. Fitting of the Permeability Variation Curve

Figure 11 illustrates the variation in coal-rock permeability with respect to the frequency of cyclic dynamic loading. Under the condition of a fixed static load phase, the permeability of the coal-rock increases in an exponential manner with the rise of cyclic dynamic load. Initially, as the frequency of cyclic dynamic loading increases, the energy imparted by the load rises slowly, resulting in minimal damage and fewer fractures within the coal mass. Consequently, the rate of increase in permeability is gradual. However, as the frequency of cyclic dynamic loading continues to rise, the rate of energy increase accelerates, leading to a corresponding rapid increase in permeability.
Fitting the curve in Figure 11 reveals that when the adsorptive gas and static load phase are held constant, the permeability of the coal rock increases exponentially with the frequency v of cyclic dynamic loading:
k = a 0 e b 0 v
where, k represents the permeability of the coal body, a0 and b0 are both fitting constants. a0 signifies the magnitude of permeability, while b0 indicates the rate of change of permeability. Table 2 presents the fitting results of the permeability of the coal body for various gases across different phases of static loading, along with the R² values, illustrating that the exponential function yields a commendable fit.

5.2. Evaluation Parameters for Cyclic Load Sensitivity

The sensitivity of coal permeability to the frequency of cyclic dynamic loading is analyzed from two perspectives, primarily concerning the rate of permeability change and the permeability dynamic loading sensitivity coefficient. These two parameters respectively reflect the magnitude and the rate of change in permeability.
The rate of change in permeability described in this paper refers to the variation in permeability induced by cyclic loading frequencies during the static load phase and with a fixed type of gas.
D v = k i − k 0 k 0
Where, Dv represents the rate of change of coal permeability, indicating the magnitude of permeability variation. k0 denotes the initial permeability of the coal body, μm2. ki signifies the permeability after an increase in dynamic loading frequency, μm2.
The dynamic load sensitivity coefficient of permeability refers to the relative change in coal and rock permeability caused by an increase of 1 Hz in the frequency of cyclic dynamic loading, while the static loading phase and the type of gas are held constant. Based on the characteristics of the functions presented in this paper, the dynamic load sensitivity coefficient of permeability can be expressed using the following equation.
C v = 1 k 0 ∂ k ∂ v
Where, Cv represents the coefficient of dynamic load sensitivity, Hz−1. ∂ k signifies the variation in permeability, µm2. ∂ v denotes the change in dynamic load frequency, Hz. Higher the Cv value indicates a greater sensitivity of permeability to dynamic loads, while a lower Cv value reflects reduced sensitivity.

5.3. Sensitivity Analysis of Cyclic Load

The results of the calculation for the variation rate of coal body permeability under different cyclic dynamic loading frequencies are presented in Table 3. When the static loading stage is constant, the permeability variation rate of the coal body decreases as the adsorption amount increases, although it remains positive throughout. This indicates that cyclic dynamic loading increases the permeability of the coal body, but the extent of this increase diminishes as the adsorption amount grows. When the adsorption amount is constant, the variation rate of coal body permeability increases with the increase in the static loading stage, with the maximum increase reaching 75.2%. Hence, it is evident that coal body permeability is highly sensitive to cyclic dynamic loading, with greater sensitivity associated with larger static loading stages. Conversely, higher adsorption amounts lead to reduced sensitivity.
Substitute equation (1) into (3) to derive the relationship between the coefficient of dynamic sensitivity of permeability Cv and the dynamic loading frequency ν.
C v = a 1 e b 1 v
Where, a1 and b1 are both fitting constants. The value of a1 is related to the magnitude of the coal permeability. b1 reflects the rate of change in the dynamic loading sensitivity coefficient, with a greater value of b1 indicating a faster rate of change in the dynamic loading sensitivity factor. The relationship between the dynamic loading sensitivity coefficient and the dynamic loading frequency also follows an exponential function, with a greater dynamic loading frequency resulting in a higher sensitivity coefficient. The calculated results are presented in Table 4.
The coefficient of dynamic load sensitivity of permeability exhibits a pattern similar to that of the rate of change in permeability. The permeability of the coal body shows a pronounced sensitivity to dynamic load frequency, with this sensitivity diminishing as the adsorbed gas quantity increases, and increasing as the static load phase extends.

5. Conclusions

This paper focuses on the evolution of coal permeability under the combined effects of dynamic loading, static loading, and gas adsorption. It considers the influence of critical factors such as dynamic load frequency and amplitude, static load stage, and the types of adsorbed gases. The principal conclusions are as follows.
(1) As the frequency and amplitude of dynamic loading increase, the development of pore and fissure structures within the coal body becomes increasingly pronounced during dynamic loading cycles, resulting in a gradual rise in permeability. Notably, as the coal approaches its yielding stage, the permeability can increase by up to 47%. However, with the enhancement of gas adsorption, the permeability of the coal body gradually diminishes.
(2) The permeability curve is divided into four regions: the compaction reduction zone, the oscillation zone, the gradual recovery zone, and the abrupt increase zone of failure. It is noteworthy that the permeability and stress-strain relationship exhibit a phenomenon of resonance at the same frequency, with the permeability of the coal body gradually increasing during the dynamic load cycling. Ultimately, in the failure phase, the permeability surges dramatically, potentially reaching 4 to 5 times the initial permeability.
（3）A sensitivity analysis of permeability to dynamic and static loading and gas adsorption was conducted, defining two evaluation parameters: the rate of change in permeability and the dynamic loading sensitivity coefficient of permeability. When the static load stage is constant, the rate of change in permeability of the coal under dynamic loading decreases with increasing adsorption amount. When the adsorption amount is constant, the rate of change in permeability of the coal under dynamic loading increases with the increase in static load stress stage, with the maximum increase reaching 75.2%. It can be concluded from the rate of change in permeability and the dynamic loading sensitivity coefficient that the permeability of the coal is highly sensitive to cyclic dynamic loading, with increased sensitivity associated with larger static load stages and decreased sensitivity with greater adsorption amounts.

Author Contributions

Conceptualization, L.ZZ; methodology, L.YX; validation, W.ZH; writing-original draft preparation, H.WT; All authors have read and agreed to the published version of the manuscript.

Funding

This study was sponsored by the Basic Research Funding for Central Universities of China (Grant No. 2024KYJD1010).

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors on request.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. YANG X, CAO J, CHENG X, et al. Mechanical response characteristics and permeability evolution of coal samples under cyclic loading[J]. ENERGY SCIENCE & ENGINEERING, 2019,7(5): 1588-1604. [CrossRef]
  2. GUO J, QIN Q, ZHANG R. Evaluation of the damages of permeability and effective porosity of tectonically deformed coals[J]. ARABIAN JOURNAL OF GEOSCIENCES, 2017,10(16). [CrossRef]
  3. ZHANG G, YAO G, LI J, et al. A new experimental method for measuring the three-phase relative permeability of oil, gas, and water[J]. JOURNAL OF PETROLEUM SCIENCE AND ENGINEERING, 2018,170: 611-619. [CrossRef]
  4. XIAO F, MENG X, LI L, et al. Thermos-Solid-Gas Coupling Dynamic Model and Numerical Simulation of Coal Containing Gas[J]. GEOFLUIDS, 2020,2020. [CrossRef]
  5. DU F, WANG K, WANG G, et al. Investigation of the acoustic emission characteristics during deformation and failure of gas-bearing coal-rock combined bodies[J]. JOURNAL OF LOSS PREVENTION IN THE PROCESS INDUSTRIES, 2018,55: 253-266. [CrossRef]
  6. GUO H, CHENG Z, WANG K, et al. Coal permeability evolution characteristics: Analysis under different loading conditions[J]. GREENHOUSE GASES-SCIENCE AND TECHNOLOGY, 2020,10(2): 347-363. [CrossRef]
  7. GUO Y, WANG K, DU F, et al. Mechanical-permeability characteristics of composite coal rock under different gas pressures and damage prediction model[J]. PHYSICS OF FLUIDS, 2024,36(3). [CrossRef]
  8. R., MARC, BUSTIN, et al. Impacts of volumetric strain on CO2 sequestration in coals and enhanced CH4 recovery[J]. Aapg Bulletin, 2008. [CrossRef]
  9. WANG G X, WEI X R, WANG K, et al. Sorption-induced swelling/shrinkage and permeability of coal under stressed adsorption/desorption conditions[J]. INTERNATIONAL JOURNAL OF COAL GEOLOGY, 2010,83(1): 46-54. [CrossRef]
  10. NIU Q, CAO L, SANG S, et al. The adsorption-swelling and permeability characteristics of natural and reconstituted anthracite coals[J]. Energy, 2017,141(PT.2): 2206-2217. [CrossRef]
  11. MOSLEH M H, TURNER M, SEDIGHI M, et al. Carbon dioxide flow and interactions in a high rank coal: Permeability evolution and reversibility of reactive processes[J]. INTERNATIONAL JOURNAL OF GREENHOUSE GAS CONTROL, 2018,70: 57-67. [CrossRef]
  12. LARSEN J W. The effects of dissolved CO2 on coal structure and properties[J]. INTERNATIONAL JOURNAL OF COAL GEOLOGY, 2004,57(1): 63-70. [CrossRef]
  13. LIU C J, WANG G X, SANG S X, et al. Changes in pore structure of anthracite coal associated with CO2 sequestration process[J]. FUEL, 2010,89(10): 2665-2672. [CrossRef]
  14. LI C, DONG L, XU X, et al. Theoretical and experimental evaluation of effective stress-induced sorption capacity change and its influence on coal permeability[J]. JOURNAL OF GEOPHYSICS AND ENGINEERING, 2017,14(3). [CrossRef]
  15. LIU T, LIN B, FU X, et al. A new approach modeling permeability of mining-disturbed coal based on a conceptual model of equivalent fractured coal[J]. JOURNAL OF NATURAL GAS SCIENCE AND ENGINEERING, 2020,79. [CrossRef]
  16. ZHAO B, WEN G, SUN H, et al. Experimental Study of the Pore Structure and Permeability of Coal by Acidizing[J]. ENERGIES, 2018,11(5). [CrossRef]
  17. ZHAO Y, FENG Z, ZHAO Y, et al. Experimental investigation on thermal cracking, permeability under HTHP and application for geothermal mining of HDR[J]. ENERGY, 2017,132: 305-314. [CrossRef]
  18. MENG T, YOU Y, CHEN J, et al. Investigation on the Permeability Evolution of Gypsum Interlayer Under High Temperature and Triaxial Pressure[J]. ROCK MECHANICS AND ROCK ENGINEERING, 2017,50(8): 2059-2069. [CrossRef]
  19. LI C, DONG L, XU X, et al. Theoretical and experimental evaluation of effective stress-induced sorption capacity change and its influence on coal permeability[J]. JOURNAL OF GEOPHYSICS AND ENGINEERING, 2017,14(3). [CrossRef]
  20. BAI X, WANG Y, HE G, et al. Research on a permeability model of coal damaged under triaxial loading and unloading[J]. FUEL, 2023,354. [CrossRef]
  21. LU J, YIN G, DENG B, et al. Permeability characteristics of layered composite coal-rock under true triaxial stress conditions[J]. JOURNAL OF NATURAL GAS SCIENCE AND ENGINEERING, 2019,66: 60-76. [CrossRef]
  22. FAN C, WEN H, SUN H, et al. Experimental Investigation on the Effect of Loading and Unloading on Coal Permeability with Different Sediment Beddings[J]. LITHOSPHERE, 2022,2022. [CrossRef]
  23. MITRA A, HARPALANI S, LIU S. Laboratory measurement and modeling of coal permeability with continued methane production: Part 1-Laboratory results[J]. FUEL, 2012,94(1): 110-116. [CrossRef]
  24. TANG J, YU H, WEI Z, et al. Influence of fracture parameters on hydraulic shear seepage characteristics of granite[J]. CASE STUDIES IN THERMAL ENGINEERING, 2024,56. [CrossRef]
  25. ZHAO Y, QU F, WAN Z, et al. Experimental Investigation on Correlation Between Permeability Variation and Pore Structure During Coal Pyrolysis[J]. TRANSPORT IN POROUS MEDIA, 2010,82(2): 401-412. [CrossRef]
  26. LI Y, ZHANG C, SUN Y, et al. Experimental Study on the Influence Mechanism of Coal-Rock Fracture Differential Deformation on Composite Permeability[J]. NATURAL RESOURCES RESEARCH, 2022,31(5): 2853-2868. [CrossRef]
  27. PENG S, LOUCKS B. Permeability measurements in mudrocks using gas-expansion methods on plug and crushed-rock samples[J]. MARINE AND PETROLEUM GEOLOGY, 2016,73: 299-310. [CrossRef]
  28. YIN G, JIANG C, XU J, et al. An Experimental Study on the Effects of Water Content on Coalbed Gas Permeability in Ground Stress Fields[J]. TRANSPORT IN POROUS MEDIA, 2012,94(1): 87-99. [CrossRef]
  29. YIN G, LI M, WANG J G, et al. Mechanical behavior and permeability evolution of gas infiltrated coals during protective layer mining[J]. INTERNATIONAL JOURNAL OF ROCK MECHANICS AND MINING SCIENCES, 2015,80: 292-301. [CrossRef]
  30. PIRZADA M A, ZOORABADI M, RAMANDI H L, et al. CO2 sorption induced damage in coals in unconfined and confined stress states: A micrometer to core scale investigation[J]. INTERNATIONAL JOURNAL OF COAL GEOLOGY, 2018,198: 167-176. [CrossRef]
  31. TALAPATRA A, KARIM M M. The influence of moisture content on coal deformation and coal permeability during coalbed methane (CBM) production in wet reservoirs[J]. JOURNAL OF PETROLEUM EXPLORATION AND PRODUCTION TECHNOLOGY, 2020,10(5): 1907-1920. [CrossRef]
  32. WANG D, ZHANG P, WEI J, et al. The seepage properties and permeability enhancement mechanism in coal under temperature shocks during unloading confining pressures[J]. JOURNAL OF NATURAL GAS SCIENCE AND ENGINEERING, 2020,77. [CrossRef]
  33. LIU Z Z, WANG H P, WANG S, et al. A high-precision and user-friendly triaxial apparatus for the measurement of permeability of gassy coal[J]. MEASUREMENT, 2020,154. [CrossRef]
  34. MENG F, ZHOU H, WANG Z, et al. Experimental study on the prediction of rockburst hazards induced by dynamic structural plane shearing in deeply buried hard rock tunnels[J]. International Journal of Rock Mechanics & Mining Sciences, 2016,86: 210-223. [CrossRef]
Preprints 115878 g001
Figure 1. Experimental load path.
Figure 1. Experimental load path.
Preprints 115878 g001
Preprints 115878 g002
Figure 2. Variation law of permeability with cyclic dynamic load frequency.
Figure 2. Variation law of permeability with cyclic dynamic load frequency.
Preprints 115878 g002
Preprints 115878 g003
Figure 3. Variation of permeability with cyclic dynamic load amplitude.
Figure 3. Variation of permeability with cyclic dynamic load amplitude.
Preprints 115878 g003
Preprints 115878 g004
Figure 4. Variation law of permeability with static load stage of cyclic dynamic load.
Figure 4. Variation law of permeability with static load stage of cyclic dynamic load.
Preprints 115878 g004
Preprints 115878 g005
Figure 5. Variation of permeability with gas adsorption.
Figure 5. Variation of permeability with gas adsorption.
Preprints 115878 g005
Preprints 115878 g006
Figure 6. Stress- permeability-strain curves of coal under cyclic dynamic load.
Figure 6. Stress- permeability-strain curves of coal under cyclic dynamic load.
Preprints 115878 g006
Preprints 115878 g007
Figure 7. Stress-permeability temporal curve of coal under cyclic dynamic load.
Figure 7. Stress-permeability temporal curve of coal under cyclic dynamic load.
Preprints 115878 g007
Preprints 115878 g008
Figure 8. Increase of coal permeability under different cyclic dynamic loads.
Figure 8. Increase of coal permeability under different cyclic dynamic loads.
Preprints 115878 g008
Preprints 115878 g009
Figure 9. Permeability increase and yield strain curve of coal under different cyclic dynamic loads.
Figure 9. Permeability increase and yield strain curve of coal under different cyclic dynamic loads.
Preprints 115878 g009
Preprints 115878 g010
Figure 10. Maximum permeability curve of coal under different cyclic dynamic loads.
Figure 10. Maximum permeability curve of coal under different cyclic dynamic loads.
Preprints 115878 g010
Preprints 115878 g011
Figure 11. Variation law of coal rock permeability with cyclic dynamic load frequency.
Figure 11. Variation law of coal rock permeability with cyclic dynamic load frequency.
Preprints 115878 g011
Table 1. Experimental plan.
Table 1. Experimental plan.
Number Frequency and magnitude of dynamic load Static load stress phase Gas
1 2.50MPa、3Hz 0.5σc CH4
2 2.50MPa、4Hz 0.5σc CH4
3 2.50MPa、5Hz 0.5σc CH4
4 2.50MPa、6Hz 0.5σc CH4
5 3.75MPa、3Hz 0.5σc CH4
6 5.00MPa、3Hz 0.5σc CH4
7 6.25MPa、3Hz 0.5σc CH4
8 2.50MPa、3Hz 0.35σc CH4
9 2.50MPa、3Hz 0.65σc CH4
10 2.50MPa、3Hz 0.75σc CH4
11 2.50MPa、3Hz 0.5σc CO2
12 2.50MPa、3Hz 0.5σc N2
13 2.50MPa、3Hz 0.5σc He
Table 2. Results of fitting of permeability.
Table 2. Results of fitting of permeability.
Static load stage Gas type a0 b0 R2
0.3σc He 0.0123 0.0693 0.9973
N2 0.0116 0.0688 0.9813
CH4 0.0107 0.0683 0.9963
CO2 0.0105 0.0667 0.9972
0.5σc He 0.0129 0.0705 0.9980
N2 0.0121 0.0758 0.9967
CH4 0.0116 0.0686 0.9732
CO2 0.0113 0.0629 0.9651
0.7σc He 0.0133 0.0814 0.9584
N2 0.0131 0.0777 0.9663
CH4 0.0122 0.0723 0.9913
CO2 0.0119 0.0695 0.9842
Table 3. Calculation results of permeability change rate.
Table 3. Calculation results of permeability change rate.
Static load stage Ｄv (%)
He N2 CH4 CO2
0.3σc 48.8 45.6 29.6 25.6
0.5σc 57.6 52 40.8 32.8
0.7σc 75.2 68.8 51.2 45.6
Table 4. Calculation results of dynamic load sensitivity coefficient.
Table 4. Calculation results of dynamic load sensitivity coefficient.
Static load stage Gas type a1 b1
0.3σc He 0.0682 0.0693
N2 0.0638 0.0688
CH4 0.0585 0.0683
CO2 0.0560 0.0667
0.5σc He 0.0728 0.0705
N2 0.0734 0.0758
CH4 0.0637 0.0686
CO2 0.0569 0.0629
0.7σc He 0.0866 0.0814
N2 0.0814 0.0777
CH4 0.0706 0.0723
CO2 0.0662 0.0695
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated