Prerpints.org logo
Preprint
Review

The Zilch-Zitter Electron

Altmetrics

Downloads

119

Views

96

Comments

0

This version is not peer-reviewed

Submitted:

21 August 2024

Posted:

22 August 2024

You are already at the latest version

Alerts
Abstract
This paper contains a comparative review of existing Zitterbewegung models. It attempts to synthesize them by offering a toy model containing an extra hypothesis of electromagnetic self-oscillation at the Fermi scale (10−15m). Inspired by Bell violation experiments, Zitterbewegung models and hydrodynamic walker studies, we revisit standing waves in quantum mechanics, echoing de Broglie-Bohm pilot wave theories. Starting with the electromagnetic self-oscillation hypothesis at the Fermi scale we propose an emergent and deductive hierarchical electron structure across multiple scales. The model spans Fermi, Compton (10−13m), Bohr (10−11m) and finally de Broglie (>10−10m). At the Fermi scale, the hypothesis is one of "source-free chiral light", known as the "zilch", emerging as a self-oscillating electromagnetic field at the Schwinger limit. This self-interaction of retarded potentials due to real relativistic delays is a generic self-oscillation of Liénard-Wiechert potentials. This primary Fermi oscillation accounts for charge and mass at the Fermi scale. It generates secondary stable "auto-orbits" dynamics at the Compton scale, manifesting as observable spin and other quantum properties of the usual Dirac zitterbewegung models. These zitter models account for known electron characteristics, including mass, charge, spin and g/2 anomalous factors up to 9 digits precision. We explain the de Broglie wavelength through Doppler-shifted Compton-scale standing waves, in the tradition of de Broglie. The framework extends to electron-positron pair production at the Schwinger limit, described as a result of natural light focusing in non-homogeneous media, utilizing René Thom’s catastrophe theory. This offers a new perspective on baryogenesis and matter emergence from electromagnetic fields. We dub this toy model the "sub-standard" model of the electron.
Keywords: 
Subject: Physical Sciences  -   Quantum Science and Technology

1. QM realism is not dead

Since the advent of the 20th century and the quantum revolution, numerous scientists have endeavored to establish a realistic interpretation of quantum mechanics. A century later, a classical representation of atomic structure or quantum particles remains elusive, with quantum mechanical phenomena still shrouded in mystery. The field is replete with conceptual challenges and paradoxes. Of particular interest is the structure of the electron, which has persistently defied classical description. "Intrinsic" spin is not to be visualized. As the mantra goes for students of quantum mechanics: "Shut up and calculate!" By doing certain mathematical calculations certain results will follow, but students are most earnestly warned against attributing objective reality or philosophic validity to any of it.
As Frank Wilczek stated in [1], "To understand the electron is to understand the world," a modern echo of Albert Einstein’s famous assertion, "You know, it would really be sufficient to understand the electron." According to the standard model, the electron is a point particle, endowed with charge, mass, spin, magnetic moment, and associated matter waves. This raises the question: How can an entity without extension possess any properties?
The classical line of inquiry, originating with Bohr’s atomic model, was eventually abandoned due to some of its perceived internal contradictions. For instance, the mass of the electron cannot move at exactly the speed of light, the electron cannot have an extended charge or it would explode due to electrostatic repulsion, and the electron should radiate energy when orbiting the proton core and collapse by Bremsstrahlung. Additionally, there was the challenge of reconciling these models with the statistical "dice playing" nature of quantum mechanics.
Quantum mechanics side-stepped these issues by postulating the existence of non-radiating standing waves (the eigenstates) and a statistical framework around them (the eigenvalues). It never directly addressed these problems, but rather axiomatically circumvented them. In this essay, we propose a model that revisits the dynamic models of Bohr, unifying existing Zitterbewegung frameworks and bypassing some of these conceptual complications.

1.1. Clifford Algebras and ZitterBewegung

While we focus on a highly visual interpretation of the electron’s structure, it is crucial to acknowledge the field’s lofty mathematical origins. The concept of Zitterbewegung has a long and solid pedigree, beginning with Dirac and his eponymous equation. Dirac initially interpreted the zitter as "oscillations between positive and negative energy states". The evolution of this field has led to the modern application of Clifford algebras, known as "Space Time Algebra" (STA), as developed by Barut [2], Hestenes [3], Celani [4] and Hiley [5]. These mathematical structures have been shown to provide a geometric framework for understanding the Dirac electron, offering a more intuitive grasp of quantum mechanical spinor phenomena. Basil Hiley in particular identified the link between Clifford algebras and ’pilot-wave’ Bohmian models. We will explore the intimate link between Zitterbewegung and standing-wave "pilot-wave" models in this paper. This mathematical foundation, spanning from Dirac’s initial formulation to modern Clifford algebraic approaches, provides a robust theoretical backdrop for our visual model. It demonstrates that while our approach emphasizes intuitive understanding, it is grounded in rigorous algebraic formalism deriving from the Dirac equation.

1.2. An analog: the Hydrodynamic Quantum Analogs of Couder

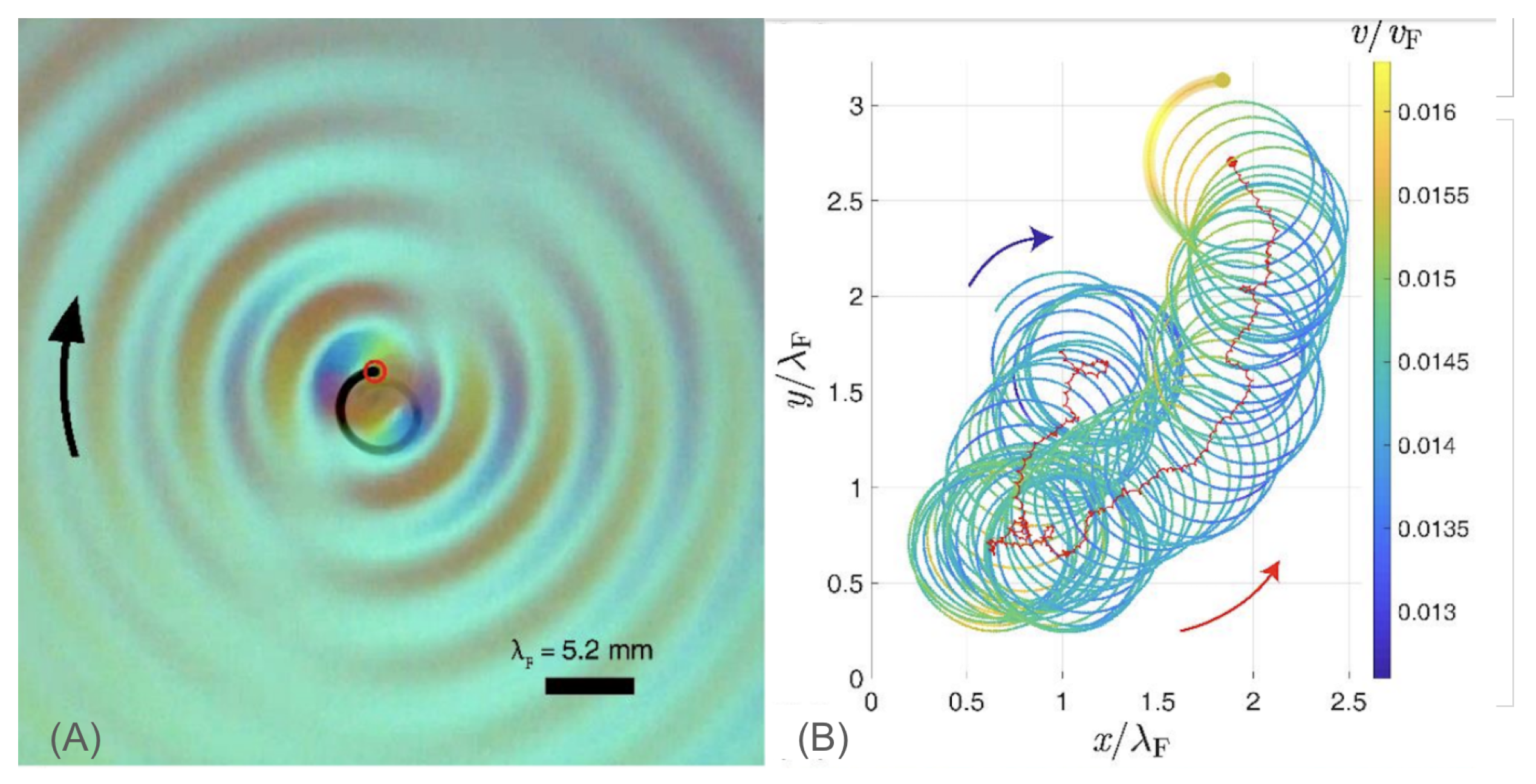
The de Broglie-Bohm approaches, so called "pilot-wave" models, have experienced a significant resurgence recently, largely due to the visualizations provided by the hydrodynamic walkers of Professor Couder [6]. We will employ these analogies throughout this paper. The droplets in Professors Couder and Fort’s experiments bounce on a silicon bath vibrating below the Faraday threshold. At each bounce, the droplets generate a Bessel standing wave. The temporal sum of these Bessel standing waves creates "the wake," see Figure 1 which functions as the "pilot wave" that guides the particle. This guiding wake is visually a field sum of the individual Bessel waves emitted at each point along the trajectory, representing a form of path memory, as Yves Couder emphasized. The walkers have provided visual analogs to numerous aspects of quantum mechanics. An exhaustive and recent survey cataloguing these quantum mechanical analogs was compiled by Professor John Bush [7]. The walkers offer a clear ontology based on a particle and the standing waves surrounding it. The non-linear dynamics resulting from this dual-interaction not only provides a clear picture of "wave-particle" duality by postulating both components but also leads to interesting chaotic dynamics, which the author has studied [8]. Deterministic chaos emerges from this coupling. The deterministic equations exhibit extreme sensitivity to initial conditions, leading, for all practical purposes, to non-determinism. This provides a natural and emergent bridge from deterministic equations to non-deterministic outcomes, addressing one of the central conceptual issues in quantum mechanics: its statistical nature. The coupling to this Bessel standing wave results in chaotic dynamics. Notably, superposition of states was naturally and elegantly recast as intermittence of a chaotic system between quantized Landau levels [9]. In the same vein, the corral of Bush, shows statistics emerging overtime, reminiscent of an electron corral [10] see Figure 2.

2. Dirac and deBroglie, Complementary Wave/Particle Views on the Electron

2.1. A Particle View: The Dirac Zitterbewegung

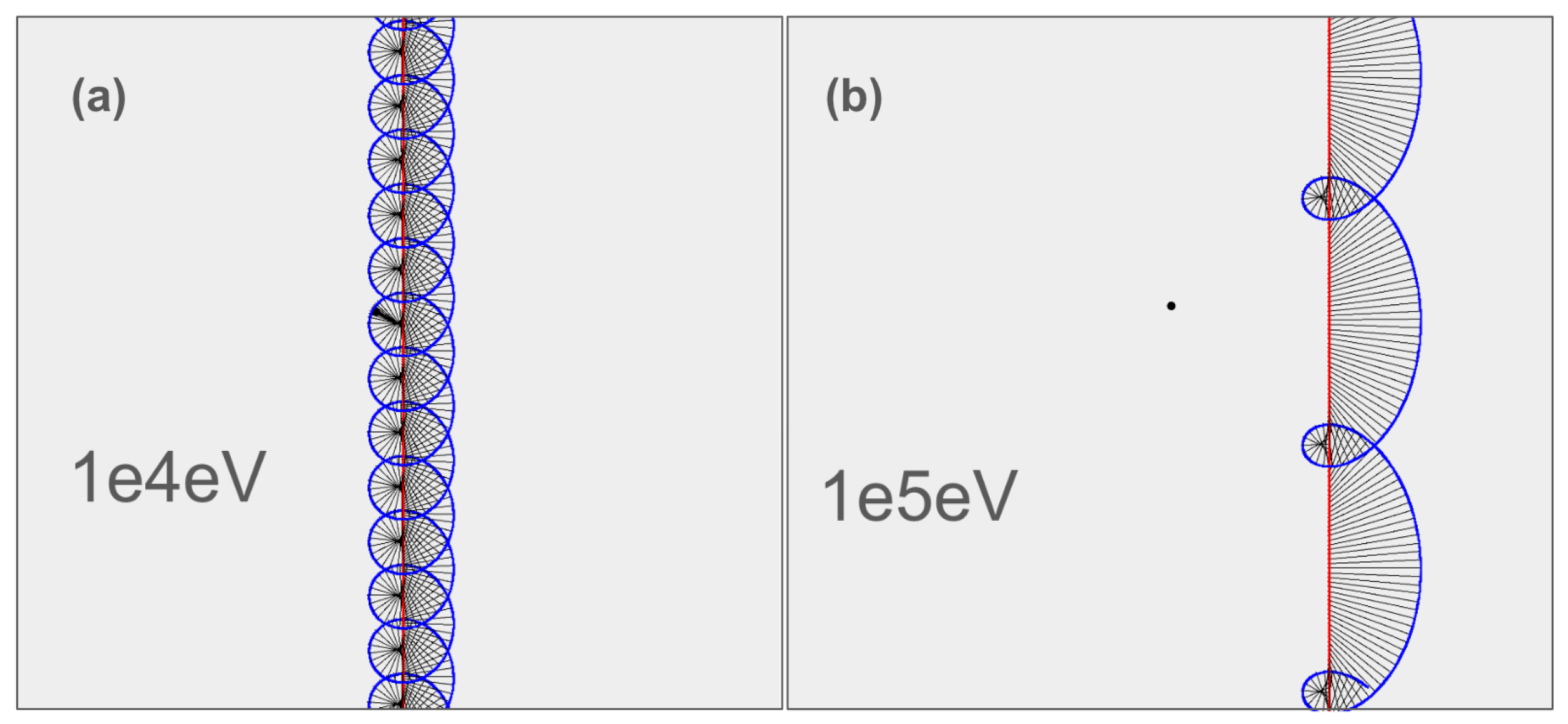
As noted, Dirac observed that the theoretical equations he discovered at the age of 26 contained an element that appeared to vibrate very rapidly, at the speed of light - the "Zitterbewegung" or "Trembling motion." Feynman would later encapsulate this jittery electron movement by postulating an interaction between the electron particle and a sea of virtual particles and photons, as represented in Feynman diagrams. While quantum field theory postulates endless combinations of field contributions resulting in a jitter, the Zitterbewegung approach postulates the jitter, it adopts the dual perspective. Zitter models typically focus on a particle view and postulate some form of physical oscillation at the Compton scale. Modern theoretical frameworks, of which there are several variants (see this review [11]), generally interpret this oscillation literally, explaining it as the real vibration of a charge moving at the speed of light around a point mass. The model we envision here is closely related to the "Helicoidal" or "Helical Solenoid" electron model as expounded by Oliver Consa in [12], with a modification regarding the nature of matter, charge, and mass at the Fermi scale, one alpha factor (of the fine structure constant) below the Compton scale. The emergence of intrinsic spin, charge, and mass can be explained by this internal helicoidal motion as we will see.

2.2. A field view: Bell inequality violations and the deBroglie standing waves

In [14], the author has conducted and published a study on experimental Bell violations under stringent isolation conditions , concluding that a standing wave, potentially associated with the electron, must be implicated. This finding has led to an investigation of the Zitterbewegung theories. In our analysis, we concluded that standing waves needed to be involved, likely the standing waves about the electron. This standing wave hypothesis led us to the Zitterbewegung studies. Therefore, as a second influence, we consider de Broglie’s standing waves as the analog of the hydrodynamic walkers’ "pilot wave." This establishes the link to de Broglie matter waves. De Broglie, in his interpretation, also identified a similar clock to Dirac’s, the "de Broglie clock." However, de Broglie introduced a second element: a standing wave dressing the particle. These matter waves would guide the particle. This concept evolved into "La double solution." Essentially, de Broglie took his wave-particle duality at face value and hypothesized a particle that generates its own wave dressing and influences its own path. In "Ondes et mouvement," [31] de Broglie emphasized the standing wave nature of matter. This perspective ushered in the "pilot wave" models. Matter was conceptualized as a point wave-dressed with standing waves which influenced the dynamics via "self-interaction" - the particle created the wave, and the wave guided the particle.

3. Brief and Non-Exhaustive Review of Existing Zitter Models

3.1. Consensus at 10 − 13 m

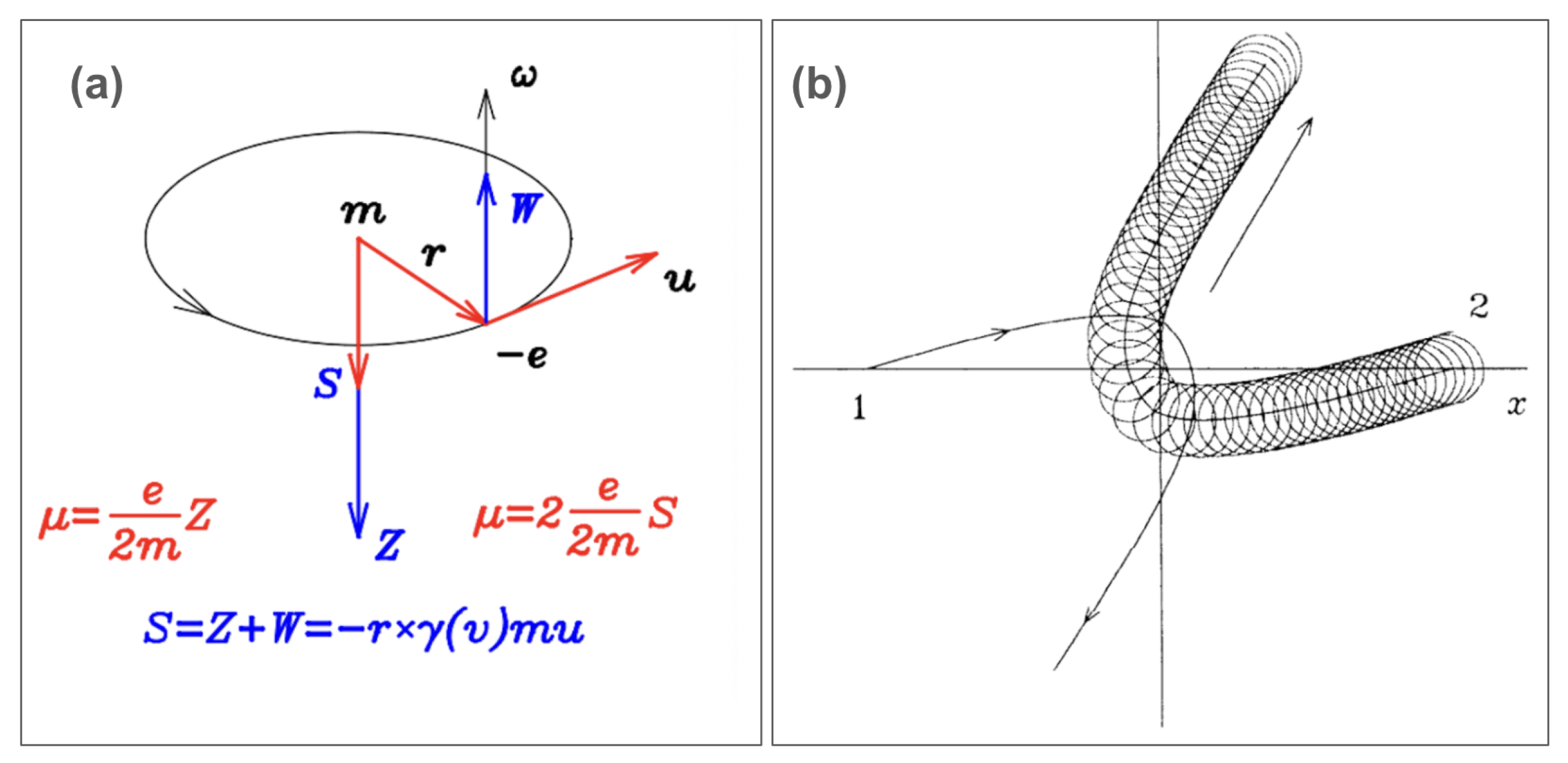
The modern Zitterbewegung models largely concur regarding the phenomena at the Compton scale of 10 − 13 m : they generally hypothesize that the electron exhibits a circular or helical movement. The reason for this high degree of alignment is that they all start from the Dirac equation. A charge is postulated to move at the speed of light and at the Compton radius. The spin, rather than being a mysterious "intrinsic" property without a classical equivalent, is understood and calculated as a charge moving at the speed of light around the Compton radius, accounting for the specific quantified magnetic moment. In most of these models, the center of charge is distinct from the center of mass. This movement is identified with the "intrinsic" spin.

3.2. No Consensus at 10 − 15 m

It is noteworthy that these studies present divergent perspectives on phenomena at the Fermi scale or "classical electron radius" length of 10 − 15 m . Each proposes distinct mechanisms operative at the classical electron radius. The subsequent analysis will delineate the variations among these models, thereby providing context on our hypothesis regarding behavior at the Fermi scale of 10 − 15 m .

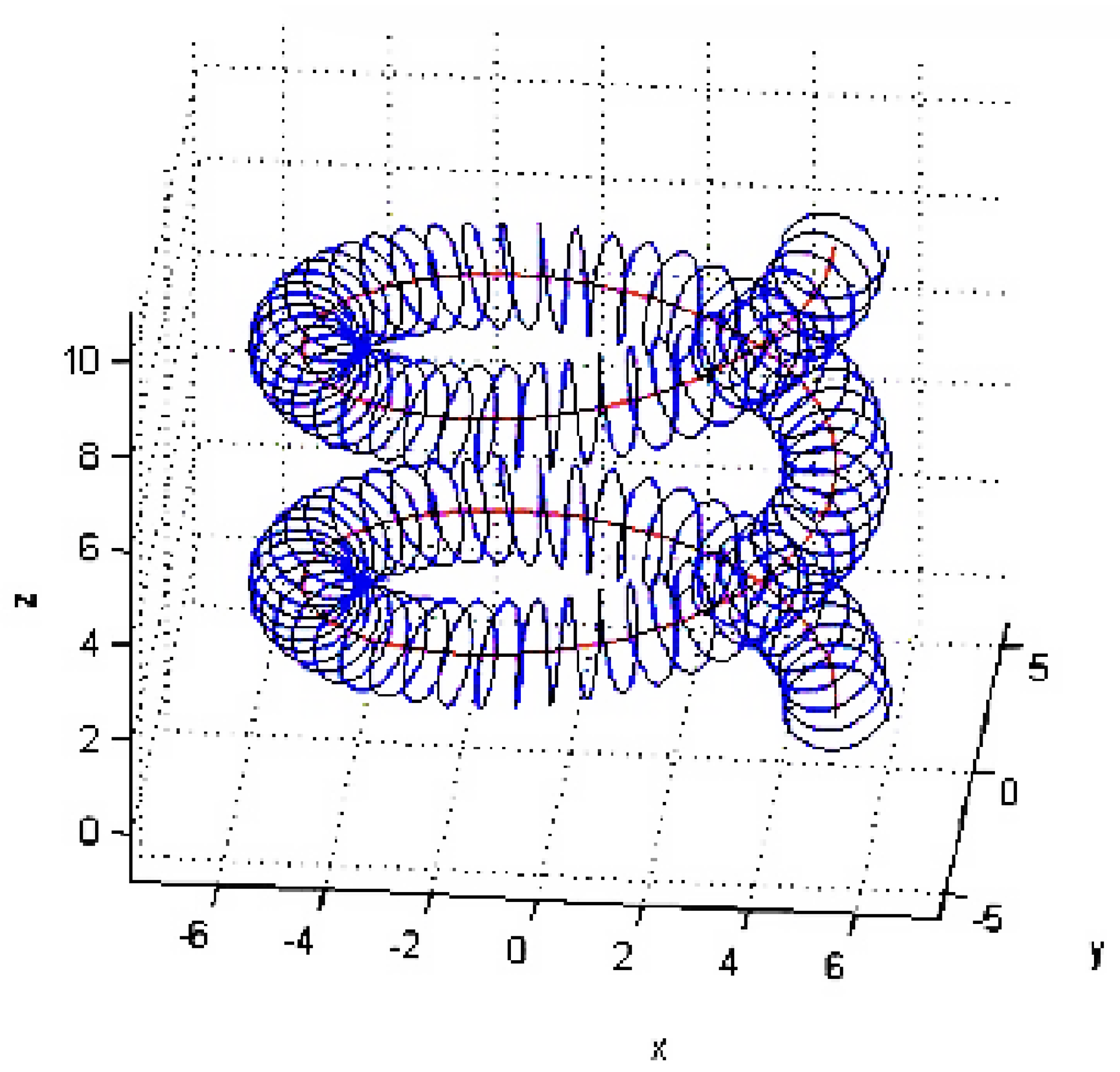
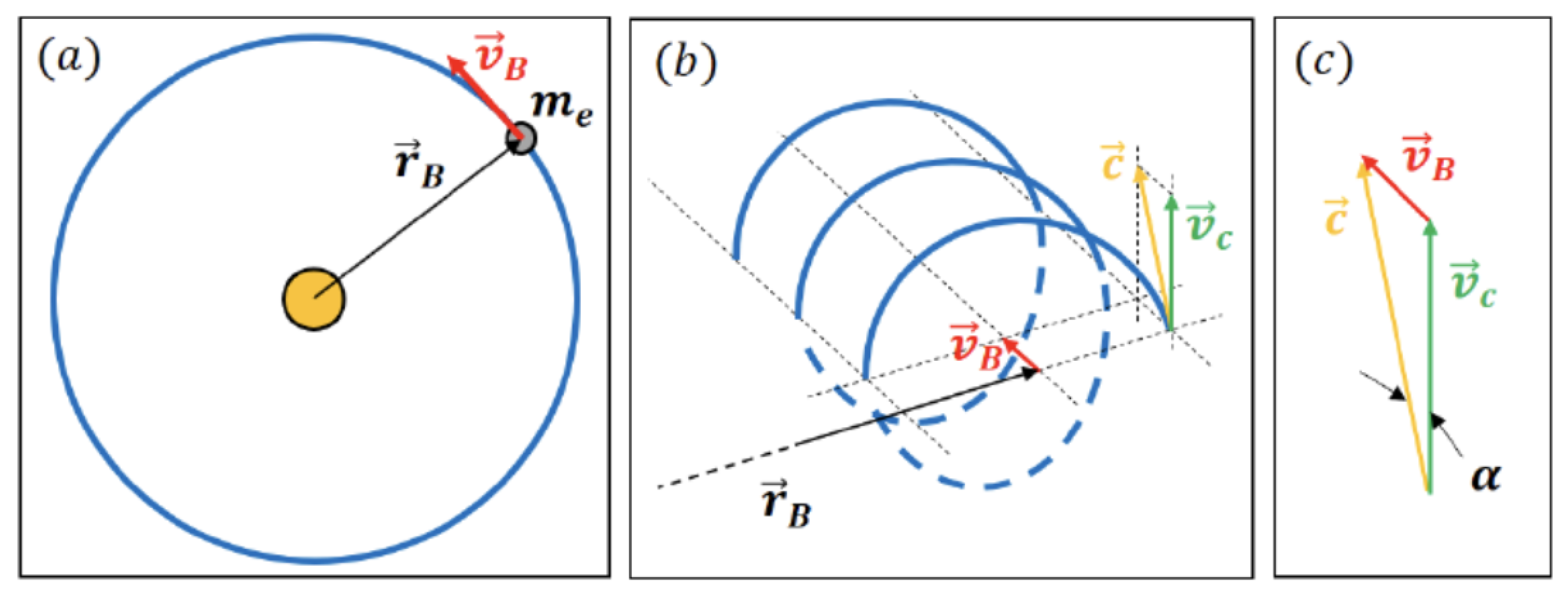
3.3. Consa’s Helicoidal Geometry

Oliver Consa proposes a model featuring a helical solenoid movement of the electron at the classical electron radius [12]. This model posits a dual motion: a circular movement at the Compton wavelength coupled with a toroidal movement about it at the classical electron radius. In this conceptualization, the electron point charge orbits at light speed around a helical solenoid geometry encompassing both the smaller 10 − 15 m radius and the larger 10 − 13 m Compton radius see Figure 3. The model stipulates that the normal to the small surface is tangential to the circular Compton radius movement, with the 10 − 15 m "spin" consistently perpendicular to the torus radius. Utilizing this geometric configuration and considering the magnetic moment of both the small tori and the larger radius, Consa derives the correct g / 2 = 1 + α / 2 π value, where α represents the fine-structure constant, see [13]. Thus, Consa’s model accounts for the gyromagnetic factor, incorporating the Schwinger correction.

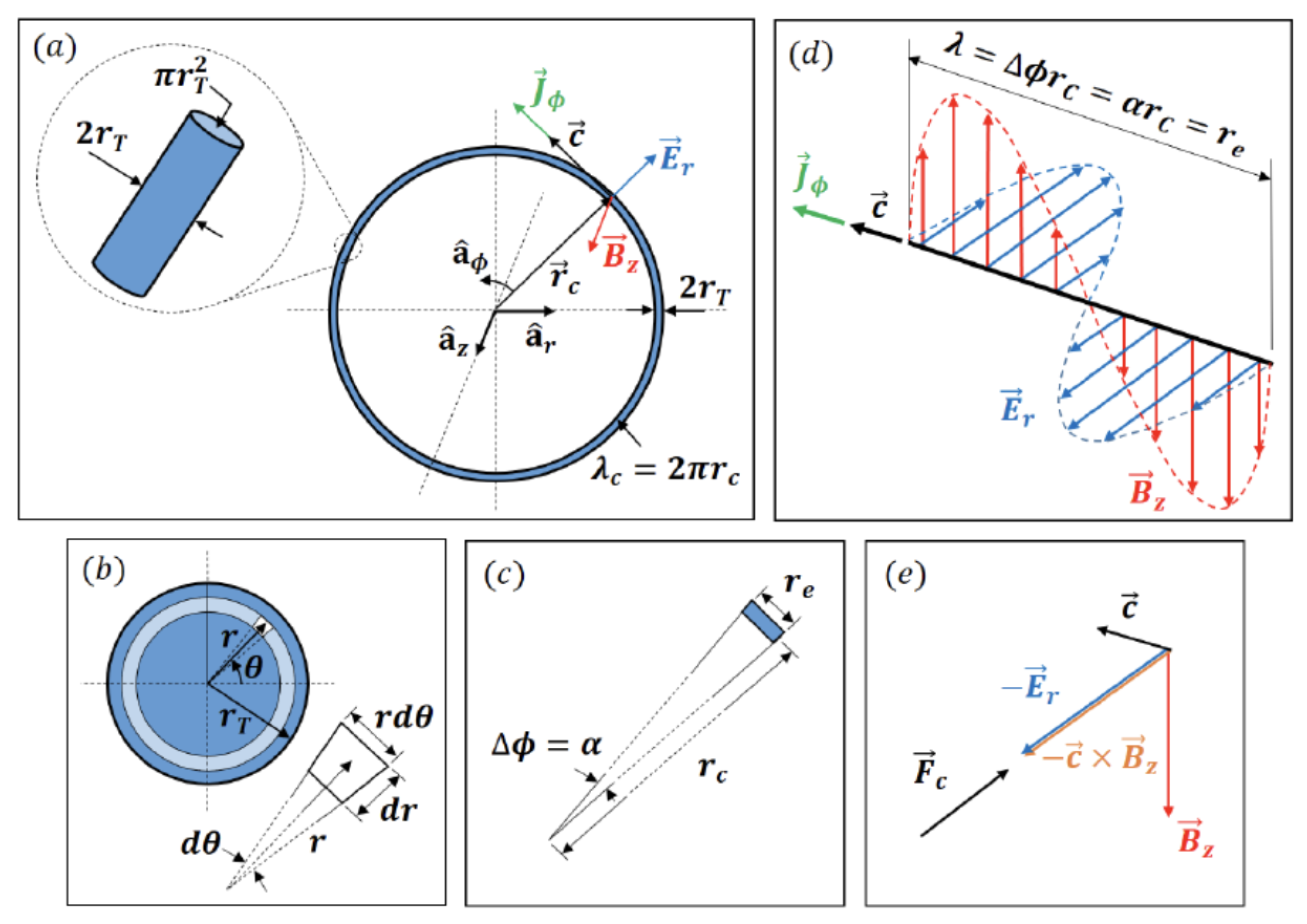
3.4. Kovacs’ Spherical Charge and Helical Geometry

Kovacs et al. in [15] present an alternative modern treatment. Their model posits the electron charge distribution on the surface of a sphere with radius equal to the classical electron radius ( 10 − 15 m ). Integration of electromagnetic energy over this geometry yields the electron’s mass-energy of 511 keV, thus fully accounting for the electron mass. This concept, previously noted by Hestenes, aligns with the definition of the classical electron radius: the radius at which electromagnetic field energy equates to the electron’s mass. This coincidence is remarkable. We observe this scale experimentally, and when we plug it in the EM energy, it gives us precisely an electromagnetic field energy measure of 511 keV. This strongly suggests the electromagnetic nature of mass, and the identification of mass with field energy. While initially counter-intuitive it finds support in relativistic mass-energy equivalence. The fact that the mass of relativistic electrons varies with the gamma Lorentz factor further suggests its electromagnetic character. The flux is quantized and rotates at Compton, by hypothesis see Figure 4. With these assumptions, in Kovacs’ model, the g / 2 factor is computed as 1 + α / 2 π for the first two terms, with a geometrical derivation. The treatment further posits that the α 2 term is identically zero, though the reasoning is not fully explicated in [15]. Numerical fitting with experimental data indicates the α 3 term as ± 8 π / 3 * α 3 , suggesting a potential spherical contribution from electron spin at the Fermi scale. It is noteworthy that the α 2 term remains undetermined in current literature. However, in recent private communication one of the first QFT practitioners to compute the Schwinger correction [16] suggests a "40 percent probability" of this term being zero [Cvitanovic Private].

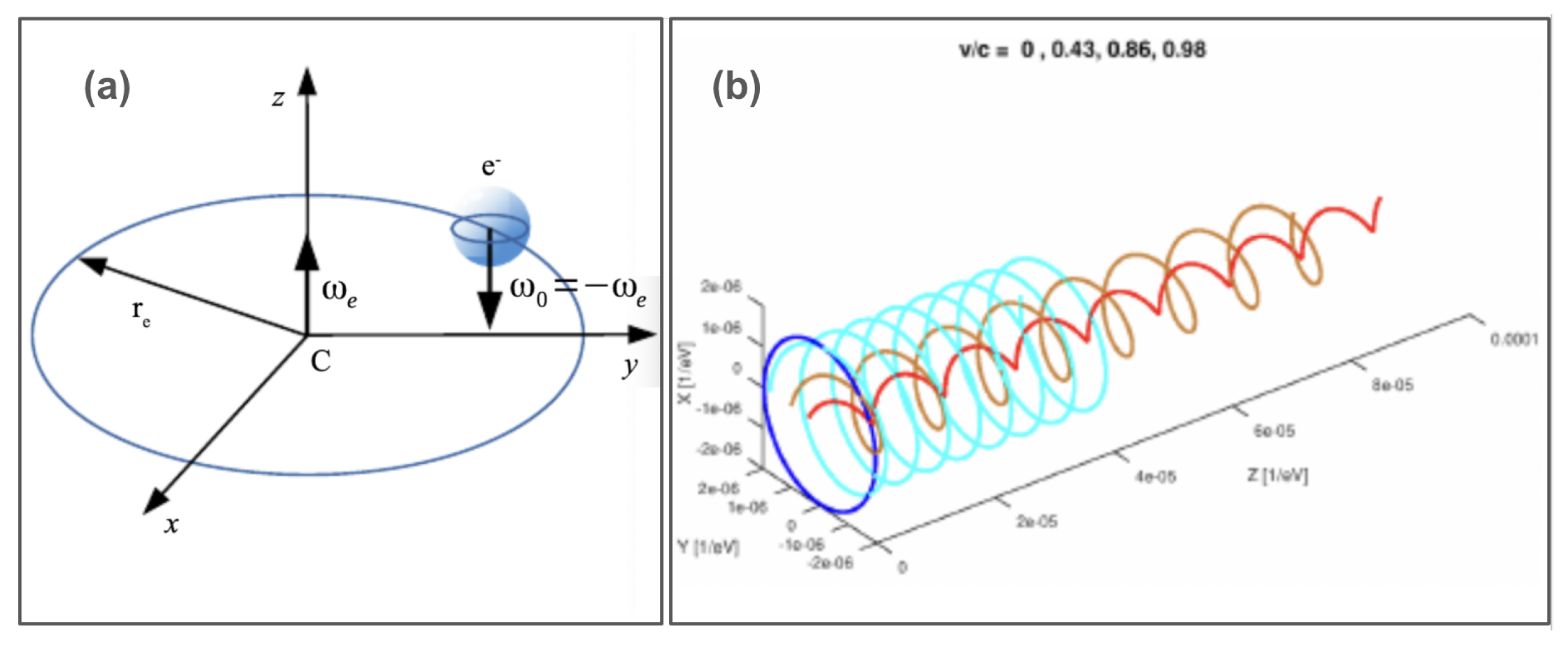
3.5. Martin Rivas Spinning Particles Model

Martin Rivas’ model, which the author has implemented in simulations, represents one of the few approaches (along with Barut’s) that provides equations of motion for the zitter electron in an electromagnetic field. Rivas postulates a separation between the center of charge and the center of mass [18]. In this model, a point charge moves at light speed around the center of mass, which itself travels at sub-relativistic velocities. See Figure 5.
Notably, Rivas’ model does not posit any structure at the 10 − 15 m scale; instead, it considers only a point. To maintain consistency with quantum mechanics, a hypothetical co-moving frame is postulated and associated with this point. This frame counter-rotates at an angular speed corresponding to the Compton scale rotation, yielding, a posteriori and by design, the correct spin value.
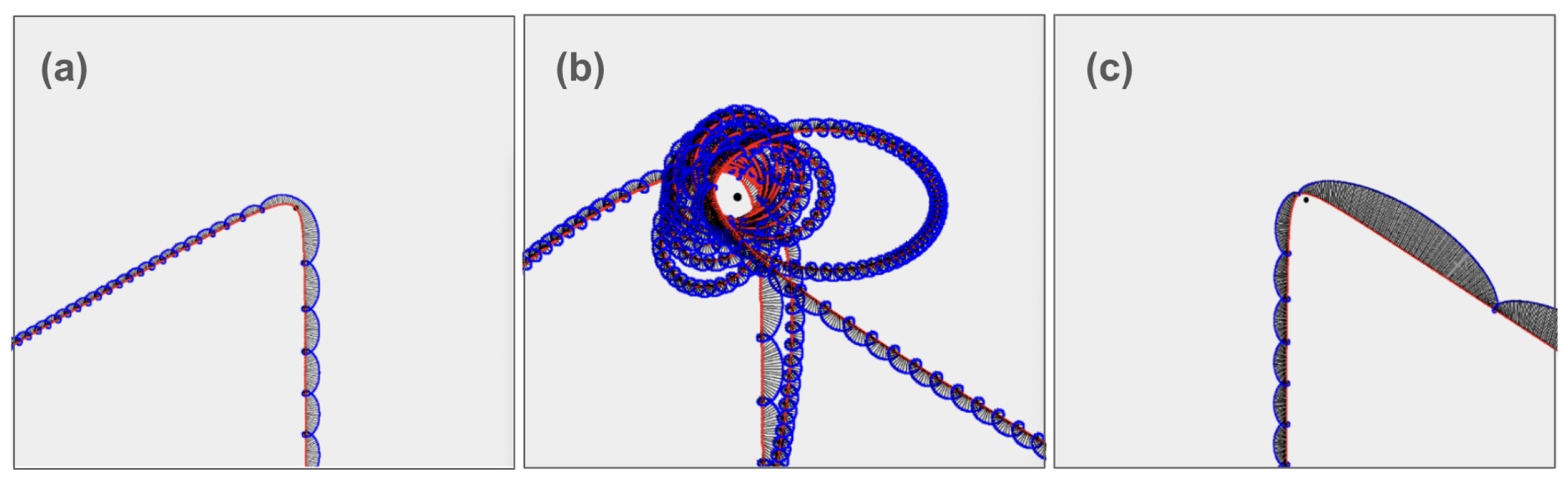
Interestingly the model contains relativistic dynamic equations. A unique feature amongst the models. The calculation of the forces is computed at the center of charge but applied to the center of mass, which is treated as a separate point. Rivas has relativistic equations that show a cycloid emergence, which the author has recreated in computation. The typical cycloid of the dynamics was recreated in 2D by the author See Figure 6.
These cycloids are enough to explain the Mott scattering effect visually. In Mott scattering 120 k e V electrons orbit a core of gold [20]. The electromagnetic attraction with the cycloid is stronger at the cusps depending on spin. If the cusp is close, the attraction is stronger, if the cusp is further from the core, the attraction is lesser. This results in a asymmetry of scattering due to the spin orientation and is experimentally observed. See Figure 7 where the cusps of the cycloid interact longer with the atomic core. Thus spin shows up in the scattering effect. Mott scattering was successfully recreated in principle with this simple cycloid model.
In simulations, the author has observed captive orbits around gold. This is a stable orbit of a chaotic dynamics. See Figure 8.
Preprints 115914 g006
Figure 6. The Cycloid of Rivas. As energy increases to relativistic speeds, here from 10 4 e V (a) on the left to 10 5 e V (b) on the right. The electron mass in red moves from bottom to top and the electron charge position in blue orbits about the center of mass. The cycloid forms depending on spin and movement of mass. Here the spin of the charge in the plane of the paper. A left zitter is shown. The distance between center of mass and center of charge changes but does not contract with velocity like in e.g. contrast with Kovacs. (Credit: author)
Figure 6. The Cycloid of Rivas. As energy increases to relativistic speeds, here from 10 4 e V (a) on the left to 10 5 e V (b) on the right. The electron mass in red moves from bottom to top and the electron charge position in blue orbits about the center of mass. The cycloid forms depending on spin and movement of mass. Here the spin of the charge in the plane of the paper. A left zitter is shown. The distance between center of mass and center of charge changes but does not contract with velocity like in e.g. contrast with Kovacs. (Credit: author)
Preprints 115914 g006
Preprints 115914 g007
Figure 7. Cycloid Mott scattering. Electrons come from the bottom up and scatter of a gold core in the center. To the left (a), a left spinning electron scattering at − 120 deg with decreased exit velocity. To the right (c), a right spinning electron scattering at + 120 deg with increased exit velocity. In the middle (b), the Egyptian eye of Ra as a semi captive orbit that ends up in Mott. Mott asymmetry means there are more in one channel depending on spin. (Credit: author).
Figure 7. Cycloid Mott scattering. Electrons come from the bottom up and scatter of a gold core in the center. To the left (a), a left spinning electron scattering at − 120 deg with decreased exit velocity. To the right (c), a right spinning electron scattering at + 120 deg with increased exit velocity. In the middle (b), the Egyptian eye of Ra as a semi captive orbit that ends up in Mott. Mott asymmetry means there are more in one channel depending on spin. (Credit: author).
Preprints 115914 g007
Preprints 115914 g008
Figure 8. Chaotic dynamics and Captive Orbits. To the left (a), a circular stable orbit of the electron. Bohr analog orbit. The "Bhorbit". To the right (b) the keplerian orbits of a relativistic Rivas electron, shadowing and then exiting to Mott detection.(Credit: author)
Figure 8. Chaotic dynamics and Captive Orbits. To the left (a), a circular stable orbit of the electron. Bohr analog orbit. The "Bhorbit". To the right (b) the keplerian orbits of a relativistic Rivas electron, shadowing and then exiting to Mott detection.(Credit: author)
Preprints 115914 g008
In Rivas’ conceptualization, the charge is treated as a point charge, with the frame, there is no Fermi structure, except to assume an intrinsic spin with its orientation, and angular velocity postulated as necessary to achieve proper "quantization", this is the ω of Figure 5. This model then successfully derives the correct gyromagnetic factor of 2, given the ad hoc values of this "intrinsic" spin. However, due to the absence of substructure below the Compton scale, Rivas’ model does not account for the Schwinger correction to the g/2 anomaly. However based on this model, Rivas achieves relevant insights into what is truly being measured in Penning traps in the most recent g/2 measures [19].

3.6. Dos Santos’ Toroidal EM field

The models previously discussed are rooted in particle ontology, positing various circular, helicoidal, or toroidal dimensions and movements of particles. In contrast, Carlos Dos Santos in [21] presents a field-based approach. This model eschews the particle concept, instead focusing on an electromagnetic wave moving at the Compton radius, confined to a torus of small radius r τ , with E and B field amplitudes approximating the Schwinger limits. Dos Santos derives a centripetal Lorentz force that establishes a stable Compton orbit, a unique feature among zitter models who mostly hypothesize both the orbit and its stability (e.g. Kovacs, Rivas). The Schwinger limits for E and B fields are given as 1 . 323 x 10 1 8 V / m and 4 . 414 x 10 9 T , respectively. The model proposes a specific ansatz for the E and B fields, incorporating phases that reflect the helicoidal geometry with azimuthal and toroidal angles. See Figure 9. This approach successfully computes the correct g/2 factor, including the Schwinger correction. However, the higher-order terms implied by this formulation do not align with the more precise analysis of Kovacs. It is noteworthy that the computation relies on the ad hoc assumption that r τ , the small toroidal radius, is precisely r τ = 1 / ( π ) * r e where r e is the classical electron radius. This fitting parameter lacks theoretical justification beyond its ability to produce correct numerical results.

3.7. Bohr Paradoxes

All of these models are subject to the Bohr paradoxes to varying extents. Dos Santos explicitly acknowledges the paradox of mass moving at light speed without offering a resolution. However, his approach benefits from an explicit computation of the Lorentz force, potentially explaining the stable zitter orbit at the Compton scale.
Kovacs’ model faces challenges primarily due to the spherical geometry of the charge distribution. The charge should theoretically explode, echoing Bohr’s original concerns. Rivas, in contrast, circumvents these issues by not specifying the Fermi-scale structure of the electron. His model treats the electron as a point particle separated from its mass, hypothesizing ad hoc intrinsic spin properties to align with known results, including the g/2 value.
Given these limitations, we will now proceed to detail a novel model that begins with a Fermi-scale hypothesis and aims to sidestep these paradoxes. This approach seeks to unify the existing models in a coherent framework at the Fermi scale.

4. Experimental Observation of Scales: A Deep Dive, > 10 − 10 m deBroglie Scale, 10 − 11 m (Bohr scale), 10 − 13 m (Dirac-Compton scale), 10 − 15 m (Fermi Scale)

This section adopts a primarily phenomenological approach, reviewing the experimental evidence regarding the electron’s structure. We focus on epistemology—what is empirically known about the electron—to inform and motivate our subsequent theoretical approach. Experimental observations have revealed four distinct scales associated with the electron:
  • The deBroglie scale: variable from 10 − 7 m to 10 − 10 depending on velocity
  • The Bohr scale: approximately 10 − 11 m
  • The Dirac-Compton scale: approximately 10 − 13 m
  • The Fermi scale: approximately 10 − 15 m
These scales represent key length dimensions at which the electron exhibits specific behaviors or properties. The deBroglie scale is not intrinsic but dependent on velocity, a point worthy of attention. The Bohr scale corresponds to the characteristic size of atomic orbitals in the hydrogen atom. The Dirac-Compton scale is associated with the electron’s Compton wavelength, the Dirac equation and the Zitterbewegung. The Fermi scale, also known as the classical electron radius, is the smallest observed scale. This empirical foundation will guide our theoretical considerations and help constrain potential models to those consistent with known observations.

4.1. deBroglie Wavelength, Matter Waves

The first observation of structure is at the deBroglie wavelength. A unique characteristic of this wavelength is that it depends on the velocity of matter. It is not a purely intrinsic property but rather depends on the velocity. This wavelength is abundantly observed. We will justify an emergence of the deBroglie wavelength and the dependency on velocity below.

4.2. Atomic Structure, 10 − 11 m Scale, Bohr Scale

The second observable electronic structure is defined by the Bohr radius, which corresponds to the radius of the first electron orbit in a hydrogen atom. This fundamental length, with a value of 0.529 Ångströms (approximately 5 . 29 × 10 − 11 m), establishes the characteristic scale for atomic phenomena. This atomic scale, on the order of 10 − 11 m , is extensively observed and verified through various experimental techniques, including spectroscopy and electron microscopy. It provides a fundamental length scale for understanding atomic structure and electron behavior in bound states.

4.3. Experimental Thomson Elastic Scattering: 10 − 13 m Scale, the Dirac-Compton scale

The third experimentally observed structure in the electron manifests at the scale of 10 − 13 m . This is known as the Dirac scale or Compton scale. The Compton wavelength is evidenced in Thomson scattering experiments. Notably, this wavelength is 137 times ( 1 / α ) smaller than the Bohr scale, where α represents the fine structure constant. The ratio between the Bohr radius and the Compton radius precisely equates to α , suggesting a purely electromagnetic relationship between these scales. While quantum mechanics posits standing waves for electron orbitals, the α signature implies an electromagnetic process underlying the emergence of stable orbits. This scale corresponds to the classical "Zitterbewegung" phenomenon. Most models concur on electron behavior at this scale, though interpretations may vary. The presence of α in this relationship strongly indicates that the ratio emerges from electromagnetic dynamic processes, aligning with α ’s role as the fundamental coupling constant for electromagnetic interactions. In subsequent sections, we will propose that this emergence results from self-oscillation of electromagnetic retarded potential, providing a mechanistic explanation for the observed Compton-scale phenomena.

4.4. Experimental Compton Inelastic Scattering: 10 − 15 m Scale, the Fermi and Classic Electron Scale

It is noteworthy that Thomson elastic scattering also reveals a geometrical cross-section associated with the 10 − 15 m scale, termed the "classical electron radius" or Fermi scale. The cross-section of 66 . 5 f m 2 represents the physical surface observed during Thomson scattering. Compton scattering further corroborates the relevance of this distance, albeit through inelastic field interactions. The Klein-Nishina formula, which explains these results, is a more complex field-theoretic derivation. Its development, requiring nearly two years of Prof. Nishina’s work [22], lacks the immediate geometric intuition of Thomson scattering. Nevertheless, this formula also incorporates the characteristic "classical electron radius" distance. Significantly, the ratio between the classical electron radius and the Compton radius is again 1 / 137 , the fine structure constant α . This recurrence of α suggests an electromagnetic phenomenon linking these two scales, which we will elucidate in subsequent sections. This relationship can be expressed as r b / r d = r d / r f = 137 , where r b , r d , and r f represent the Bohr, Dirac-Compton, and Fermi radii respectively. This electron structure at the 10 − 15 m scale is experimentally observed. However, it is important to note that the models reviewed earlier do not reach consensus on the phenomena occurring at this scale, with some not considering it at all.

4.5. No Further Electron Sub-Structure

Even more perplexing is the absence of further substructure in the electron when probed below the 10 − 15 m limit using powerful lasers. No additional "alpha-jumps" or characteristic lengths are observed. The "classical electron radius" appears to be the final observable structure, with no detectable substructure beyond this scale. Our formulas do not reveal any further cross-sections. The Klein-Nishina formula, derived from Dirac’s theory, incorporates the last known characteristic length of the electron. Experiments at CERN, probing down to the 10 − 19 m scale, have not uncovered any additional electron structure. For all practical purposes, the electron may indeed behave as a point particle in the range from 10 − 15 m down to the Planck scale.

5. The Sub-Standard Model

At this juncture in our review of existing Zitter models and considering the established phenomenology of the electron, we are positioned to propose a model that aligns with observed data. Our approach aims for generality, striving to provide a comprehensive framework that accounts for the various scales and behaviors observed in electron physics. This model will attempt to reconcile the disparate observations at the deBroglie, Bohr ( 10 − 11 m ), Compton ( 10 − 13 m ), and Fermi ( 10 − 15 m ) scales, while also addressing the apparent lack of structure below the classical electron radius. We will endeavor to explain the recurrence of the fine structure constant α in the ratios between these scales, suggesting an underlying electromagnetic nature to these relationships.

5.1. A Modern Music of the Spheres of Pythagoras, Circles within Circles within Circles

The model we present encompasses four scales:
  • The Fermi scale ( 10 − 15 m ): Hypothesized as the primary structure.
  • The Compton scale ( 10 − 13 m ): Derived as emergent.
  • The Bohr scale ( 10 − 11 m ): Also derived as emergent.
  • The deBroglie scale: also derived as emergent.
Each scale, except the last one, represents an "alpha jump" in numerics. We consider concentric circles and the standing waves these orbits create. Our study begins with the emergence of an electromagnetic self-oscillation at the classical electron radius ( 10 − 15 m ), giving rise to mass and charge. This novel self-oscillation motion will be thoroughly motivated. We then examine the emergence of a second auto-orbit at the Compton scale, corresponding to the zitterbewegung movement. Both this interaction and the initial self-oscillation are mediated by electromagnetic forces. Finally, we explore the emergence of Bohr orbits, also electromagnetically mediated. These represent stable atomic trajectories arising from the chaotic dynamics of the Compton wave-dressed zitter electron around an atomic core. Throughout, we will draw analogies from hydrodynamic walkers to illustrate these concepts.

5.2. A Toy Model

We call this model the "sub-standard" model (of retarded and catastrophic potentials). The sub-standard model is, to be sure, a toy-model. It is hypothetical and very speculative, being a derivative work of the Zitter models which are themselves rather esoteric. The fact that the Zitter models all account for the g/2 factor, and many of them for the anomaly, is intriguing. However, it is safe to bet that had the anomalous result not been known in advance, none of these inquiries would find the correct Schwinger factor. All of the studies go through rather ad-hoc and convoluted contortions to find the proper corrections. The model tries to establish points of contact with the existing zitter models so as co-opt many of their results, no need to ’re-invent the flywheel". Epistemologically, these models hold explanatory power. They are meant as aids to intuition. In short, the sub-standard model is a completely made-up analogy, in a long line of other made up analogies. We literally pull this toy-model out of thin aether. At the same time, the genericity of the edifice is worthy of notice. The model helps in providing intuitive understanding rather than claiming predictive power or empirical accuracy, 9 digits accuracy on g/2 non-withstanding.

6. The Fermi Scale, 10 − 15 m , First Self-Oscillation

6.1. Generic Dynamics of Retarded Potentials, Self Oscillation

Alvara Lopez [23] has demonstrated the emergence of quantized self-oscillation in electromagnetic fields with delays. These retarded potentials, known as Liénard-Wiechert potentials, represent sums of electromagnetic signals emitted along a path, incorporating delays due to the finite speed of light. Despite their discovery shortly after Maxwell’s equations ([24]), theoretical progress in this area has been limited due to analytical and computational challenges. Lopez’s recent work has shown that these delayed or retarded potentials give rise to generic dynamic behavior, including self-oscillation. An extended rod subjected to these potentials will self-interact and exhibit self-oscillation. Self-oscillation, distinct from resonance [25], is a purely self-interactive phenomenon. It is ubiquitous in nature, with examples ranging from the beating of the heart to various electromagnetic phenomena. In our model, we propose that the electron itself represents the first self-oscillation of a non-linear and retarded electromagnetic field at the Fermi scale.
See Figure 10 This concept of self-oscillation provides a framework for understanding the electron’s behavior at the Fermi scale ( 10 − 15 m ), offering a potential explanation for its apparent point-like nature and its fundamental properties of mass and charge as we will detail below. The model suggests that these properties emerge from the complex dynamics of self-interacting electromagnetic fields.

6.2. Hopf Bifurcation Dependent on Geometry of Charge: Tiny Strings of Light Vibrating in Space

Alvaro’s research further demonstrates that oblong geometries are necessary for dynamic oscillation to occur. A point moving at the speed of light cannot self-interact, by definition. However, an elongated rod can interact with itself, as one end can influence the other after a time delay. Lopez’s work shows that while a symmetrical sphere will not self-oscillate, a cylinder-shaped baton will. As the geometry is varied from spherical to oblong, a Hopf bifurcation emerges. This bifurcation represents a critical point where the system transitions to self-sustained oscillation. In our model, we conceptualize these structures as tiny strings of light moving at the speed of light c. The electron, in this framework, is envisioned as a tightly wound circle of light. This configuration results in a quantized charge and radius per self-oscillation of the electromagnetic field. This geometric consideration provides a potential explanation for the electron’s structure at the Fermi scale ( 10 − 15 m ). It suggests that the electron’s fundamental properties, such as its charge and apparent size, emerge from the self-interaction of these light-like structures. The quantization of charge in this model arises naturally from the discrete nature of the self-oscillation, offering a novel perspective on the origin of this fundamental property.

6.3. An Oroborous of light. Matter as trapped Light

Light, previously propagating linearly, becomes captured in a circular orbit through self-interaction beyond the Schwinger limit. This process is proposed as the mechanism for the birth of electrons and positrons. In this conceptualization, electronic matter is likened to an Ouroboros of light: an electromagnetic "snake" biting its own tail. This imagery, drawing on the mystical symbol of the Ouroboros see Figure 11, is used to signify the birth of the material universe. This ontology posits matter as essentially rotating chiral light. The transformation from linear propagation to self-interacting circular motion is seen as the fundamental process by which massless light becomes massive particles. Key points of this model include:
  • Light self-interaction beyond the Schwinger limit as the genesis of particles
  • Circular confinement of light as the essence of matter, chiral light
  • The Ouroboros as a metaphor for the self-interacting nature of fundamental particles
  • Matter and anti-matter conceived as a form of rotating and counter-rotating electromagnetic energy
This perspective offers a novel, albeit highly speculative, view on the nature of matter and its relationship to light, unifying these concepts in a single framework.
Preprints 115914 g011
Figure 11. The Egyptian symbol of the Oroborous. Birth of material universe. Creation of chiral pairs.
Figure 11. The Egyptian symbol of the Oroborous. Birth of material universe. Creation of chiral pairs.
Preprints 115914 g011

6.4. No Ontic Charge, Reversing Maxwell’s Causality

We now turn our attention to the ontology of charge, with particular consideration of the Bohr extended charge paradox. Our focus remains on electromagnetic field dynamics as described by Maxwell’s equations. A common interpretation of Maxwell’s equations narrates that "electric charges create the EM field." These equations instruct us to calculate the divergence of displacement and equate the result to a scalar charge, which is often conceptualized as a physical reality.
Consider an analogy of an elastic band pulled from both sides: The divergence of the displacement field at any point along the band computes a non-zero scalar charge. This charge appears centered on the band, even though there is no physical charge at the center. The center is purely a "geometric point charge" concept. This example emphasizes that the charge implied in Maxwell’s equations does not necessarily correspond to a physical entity. Instead, charge can be understood as the divergent signature of a given self-oscillating field. The problematic nature of extended charges, which should theoretically self-repel and thus not exist, serves as an indicator that our conventional understanding of the nature of electrical charge may be incomplete. This perspective suggests that charge and charge density might be emergent properties of field dynamics rather than fundamental, localized entities. This reinterpretation of charge aligns with our model of the electron as a self-interacting electromagnetic field, potentially resolving the paradoxes associated with point-like or extended charge distributions.

6.5. Contrast with Consa and Kovacs: From a Instantaneous Dot to Tracing a Moving Circle to Tracing a Sphere on Average

The self-oscillator emerges at the 10 − 15 m scale, manifesting as a vertex of light. This defines a mathematical point charge, determined by the divergence of the light field, oscillating in a circle at the speed of light within this tiny scale. The frequency of this oscillation exceeds that of the de Broglie clock, given that it’s a "charge" moving at c around the much smaller classical radius, rather than the Compton radius. It can be computed at 10 22 H z . This point charge traces a minuscule Fermi circle, which itself rotates into a Fermi ball. Over time, this motion averages to the surface of a sphere of charge with a radius equal to the classical electron radius. We can conceptualize this circular path as the "circle of Consa" and the averaged sphere as the "ball of Kovacs," thereby establishing links with existing models. Visualizing this process, we see the emergence of a sphere of charge, on average, over time. The virtual point charge first traces a circle, then effectively covers the surface of a sphere. This perspective unifies aspects of previous theories while emphasizing the field-based nature of the electron. The statement "matter is immaterial" underscores the abstract, field-centric nature of this concept, distancing it from traditional particle-based models.

6.6. No Ontic Mass; Electron Mass as Field Energy

The average spherical charge distribution yields an electrostatic electromagnetic field energy, precisely calculated in [15]. This calculation defines the classical electron radius: the radius at which the electromagnetic field energy of the spherical charge exactly equals the electron’s mass-energy of 511 keV. This equivalence strongly suggests the electromagnetic nature of mass. The dependency of mass in relativistic electrons on the gamma Lorentz factor further points to this identification: that mass is purely electromagnetic in nature. In this model then, and following the lead of D.Hestenes, we identify the electron’s rest mass with its electromagnetic field energy. This concept aligns with Einstein’s equivalence principle, positing that mass is purely a form of energy. In these models we can specify that it is EM energy we are talking about. The mass-energy equivalence is really mass-EM energy equivalence. The Lorentz gamma factor naturally emerges for the relativistic moving electron in this framework as seen in [15]. As the electron’s velocity increases, its electromagnetic field energy (and thus its mass) increases in accordance with special relativity. This perspective offers a unified view of mass, energy, and electromagnetic fields, potentially resolving long-standing questions about the nature of electrons and their properties. It suggests that the fundamental properties of electrons, including mass and charge, may be emergent phenomena arising from the dynamics of electromagnetic fields rather than ontic realities.

6.7. The Zilch

The phenomenon of chiral light, initially identified as "The Zilch" by Nathan Lipkin in 1964, and described as a "source free chiral field" is very similar, if not identical to what we are describing here, see [26] and Figure 10. We are talking about a Fermi scale, Schwinger limit amplitude, electromagnetic wave going in circles without an ontic charge (it is source free). Beyond the Schwinger limit, light creates counter rotating light-pools. Electrons and positrons are zilches. David Hestenes recently identified the link between Zilch and ZitterBewegung [27]. The Zilch perspective emphasizes that there are no discrete sources or particles, these are so called "source-free" fields. The word "zilch" underscores, in a rather tongue-in-cheek way, that there is literally nothing there except the field itself. We speak of spheres, planes, points, charges and sources and many other things which may or may not exist but in our mathematical formalism. The efficacy of these concepts lies in their predictive power, not necessarily in their ontological status. The Zilch-Zitter Electron may ultimately be, a tale told by an idiot, full of sound and fury, signifying nothing [28].

6.8. Solving Bohr Extended Charge Problem

This conceptualization enables us to address several paradoxes inherent in extended charge models. The conventional understanding of extended charges presents a fundamental contradiction: any such charge should theoretically repel itself, a paradox evident at the electrostatic level. While distributed charge integrations are routinely employed in electrical engineering, it is crucial to recognize that like charges invariably repel. This inconsistency suggests either a breakdown of electromagnetic formulas at microscopic scales or an inherent instability in classical electrostatics that precludes the formation of stable extended charges. In our model, the extended charge distribution is not instantaneous but rather a time-averaged concept. This approach provides a straightforward resolution to the Bohr paradox. Ironically, it is precisely this extended movement that stabilizes itself through self-oscillation. The spatiotemporal nature of the charge’s path enables self-stabilization via retarded interactions, turning the Bohr paradox on its head: it is the extended movement that stabilizes. There are no extended "statics" for they cannot exist (which stopped Bohr in his track), there are only extended "dynamics" that justify their own existence. Thus, the metaphorical "ouroboros of light" achieves a form of self-sustaining existence. This framework challenges traditional notions of extended charge distribution in electrical engineering and offers a novel perspective on the stability of fundamental particles. In this perspective, electrons are dynamically stable, they do not exist statically.

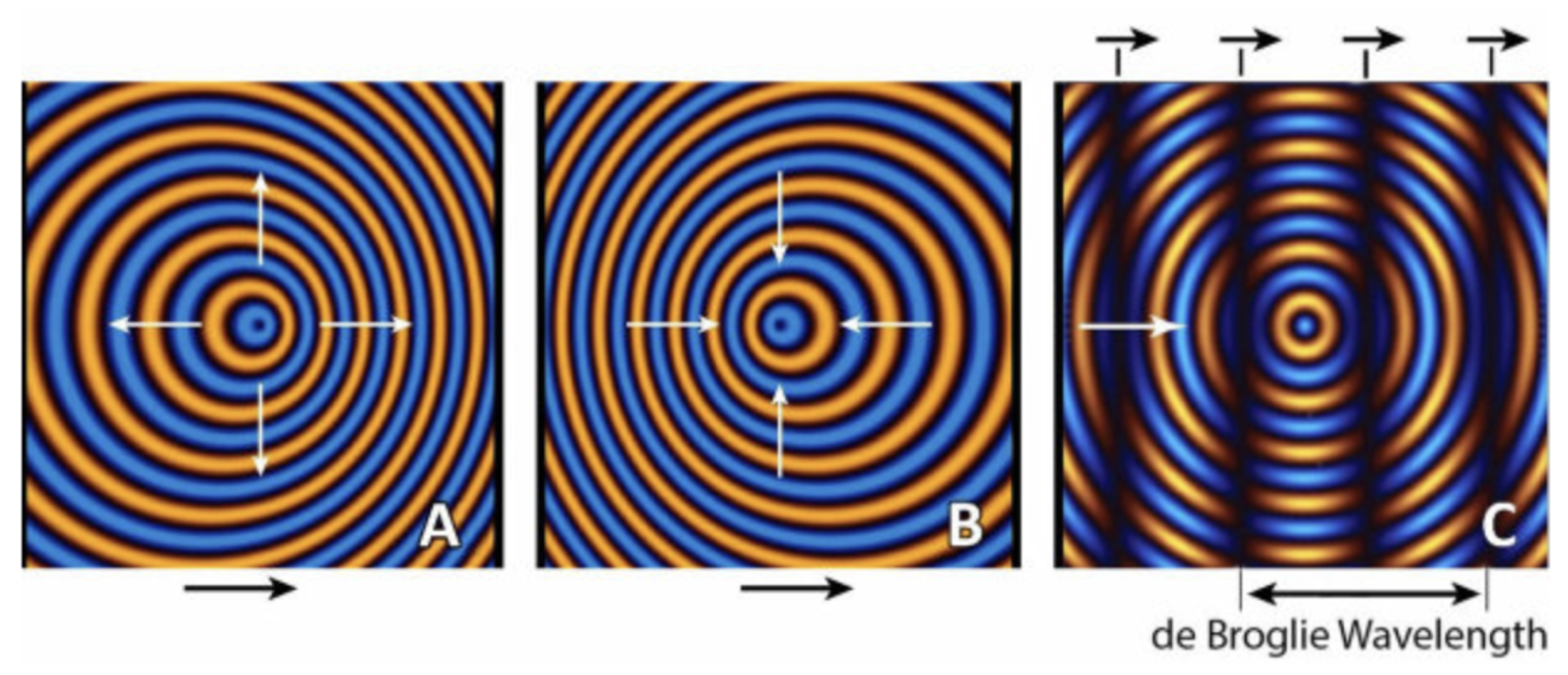
6.9. First Standing Wave at the Fermi Scale

Let us consider the emergence of a primary standing wave, in accordance with de Broglie’s hypothesis. The circular movement of charge, when analyzed through electromagnetic formulae, generates an Archimedean spiral propagating outward at light speed, [29] . Following de Broglie’s standing wave concept, we can postulate an echo image or reverse wave counter-propagating, potentially due to non-linear media effects, analogous to those observed in hydrodynamic walkers. This hypothesis aims to explain the formation of a standing wave associated with the charge’s circular motion. It is worth noting that deBroglie never fully elucidated the source of this "mirror image coming from infinity," even in the simple case of a plane wave. Extrapolating from this, we hypothesize that a propagating Archimedean spiral will result in a Bessel standing wave in its wake. See Figure 12
This framework allows us to conceptualize the emergence of an initial "matter wave" with a wavelength equivalent to the classical electron radius. It is important to acknowledge that such a Fermi scale standing wave has not been reported in the literature. The Fermi scale has been observed, but the standing wave nature of the phenomenon considered here has not. This proposition remains purely conjectural, albeit derived through logical deduction.

6.10. A Note on Chirality: Matter and Anti-Matter

Many of the zitter frameworks propose that matter and anti-matter are simply the two chiral swirls. We propose that it is the case but at the Fermi scale. A strong enough electromagnetic field creates electron and positron, the two handed chiralities of the swirls. When we talk about chirality it must be emphasized that there is no such thing as a intrinsic chirality but that chirality is always from the point of view of an observer. As one can readily visualize, the same left handed chirality is called right-handed when looked at from the other side. Individually, they are indistinguishable. However when placed in 3D space positron and electron will strongly interact, as simple magnets do, depending on their relative orientation. At the Fermi scale we are all the same, but perspective is everything.

7. The Dirac Scale: 10 − 13 m Auto-Orbits, The Zitterbewegung

Having established a Fermi scale vortex of light with the appropriate mass and charge, surrounded by a standing wave of Fermi wavelength, we now turn our attention to justifying the emergence of spin at the Compton scale. This progression from the Fermi to Compton scale is crucial in our model, as it bridges the fundamental electromagnetic nature of the electron with its quantum mechanical properties and the existing zitter models. Our analysis will focus on how the intrinsic properties and dynamics at the Fermi scale give rise to the observed spin characteristics at the larger Compton scale.

7.1. Spontaneous Emergence of Spin, a Walker Analogy

Within the context of hydrodynamic walkers, researchers have observed "auto-orbits". In this study [30], a droplet established a self-stable auto-orbit, creating another ouroboros-like shape. The stable orbit and its drift can be observed in walkers, see Figure 13. In the case of walkers, this stable orbit emerges within the standing wave field, which plays a crucial role in its formation. Notably, the radius associated with the auto-orbit is on the order of the wavelength of the standing wave.
This phenomenon in hydrodynamic systems provides an intriguing analogy for our electron model. It suggests a mechanism by which the Fermi-scale vortex, interacting with itself via its surrounding electromagnetic field, might generate a larger-scale orbital motion. This could potentially explain the emergence of spin-like behavior at the Compton scale, with the orbit radius corresponding to the Compton wavelength, as postulated in the zitter. The presence of the α -jump between Fermi and Compton scale suggests the electromagnetic nature of the interaction.

7.2. Play It Again, Sam! But This Time in the Compton-Dirac Scale

We thus invoke a second self-oscillation with the retarded potential. This circular movement involves the first vertex as a whole, as illustrated in Consa’s image see Figure 3. To align with existing zitterbewegung frameworks, we must assume this orbit occurs at the Compton radius. The ratio of the radii, r c / r f = α , indicates that the emergence of r c from the more fundamental r f is mediated by electromagnetic interaction, justifying the presence of α as a signature of EM forces. Light, in this model, is captured by its own wake and standing wave. Initially moving "straight" at light speed, it becomes trapped at the Fermi scale. The resulting orbital drift reaches light speed and stabilizes at the Compton scale. This second-order phenomenon is what we recognize as "zitterbewegung". From the Zilch emerges the Zitter. Light now traverses Compton-scale circles. Always moving at light speed, it manifests as a second-order stable orbit at the 10 − 13 m scale. An electron, in this framework, is literally light moving at light speed in tiny circles within a 2D torus, and again close to light speed in the third dimension, but now warped into a Compton-scale orbit.

7.3. Map to ZitterBewegung

This phenomenon corresponds to the Zitterbewegung described in the literature. Our model aligns closely with the Helicoidal model of the electron [12], with one key distinction: in our framework, the Fermi-scale circular movement is not fixed but traces a Fermi ball. In Consa’s Helicoidal model, the normal to the plane of Fermi-scale toroidal rotation always remains tangential to the Compton orbit. Our model, however, allows for arbitrary orientation, defaulting to tracing a sphere. The reason we do this is to establish contact with the existing framework and co-opt their results. We introduced an additional hypothesis in order to do so: this Compton scale movement occurs at the speed of light, for that is what they all postulate. While existing Zitter models assume the charge moves exactly at c around the Compton radius, our model posits that the charge moves at light speed along the 3D helicoidal shape. The projection along the tangential direction approximates c, aligning with the existing zitter literature. This formulation provides a bridge between our light-based, field-centric model and the more established particle-based Zitter models, offering a unified perspective on electron behavior at both the Fermi and Compton scales.

7.4. Ontic Spin, Gyromagnetic Anomaly Precision

As our model demonstrates, the concepts of electron charge and mass emerge at the Fermi scale. These are average quantities linked to the first-order dynamics. Spin, however, is consistently viewed across models as the magnetic moment generated by the second-order orbit at the Compton scale. The magnetic moment calculations derived from this second-order orbit yield the correct gyromagnetic factor, including the Schwinger corrections. This alignment with experimental results concerning the g/2 anomaly provides very strong support for the physical reality of spin as an emergent property both at the Compton level (for the value 1) and Fermi level (for the α / 2 π Schwinger correction). Ironically, it is this very 12-digit precision in the g/2 anomaly measures and their alignment with the predictions of QED that is hailed as un-assailable proof. (However for more context, Consa reminded us in [32] that a lot of custom fitting has been done over the years). In a further twist of irony, in traditional quantum mechanics education, students are often instructed not to assign physical reality to intrinsic spin, while charge and mass are presented as "real" properties. Our model inverts this ontology: mass and charge are treated as abstract, field-based concepts without inherent reality, while spin emerges as a tangible, physical phenomenon arising from the underlying electromagnetic dynamics. This reversal, and it’s adherence with observed data, challenges conventional notions about the fundamental properties of electrons. It suggests that the more directly observable spin might be closer to physical reality than the more abstract concepts of point-like charge or localized mass.

7.5. Second Standing Wave of Compton: The Matter Waves of deBroglie

This second circular movement at the Compton-Dirac scale generates an Archimedean spiral of electromagnetic radiation. This dynamic motion creates, on average, a standing wave through the same mechanisms as above see Figure 14. This phenomenon motivates the emergence of a second standing wave at the Compton wavelength. This larger Compton-scale standing wave provides a framework for understanding the electron’s wave-like and quantum properties at larger scales. Importantly, we will demonstrate that Doppler shifting of these Compton waves gives rise to the de Broglie wavelength. This conceptualization offers a potential bridge between the particle-like behavior observed at smaller scales and the wave-like properties manifest at larger scales. It suggests a hierarchical structure of wave phenomena, each emerging from the dynamics of the smaller scale. The derivation of the de Broglie wavelength from Doppler-shifted Compton waves represents a key feature of this model, potentially providing a mechanistic explanation for the wave-particle duality that has long puzzled physicists.

8. Back to the Bohr Scale

8.1. Second Bohr Paradox Solved: Matter always Moves with v < c

In this approach, the reason why matter can never attain light speed becomes intuitively clear. To recapitulate, a Fermi-scale object mapping to a Fermi ball (surface of sphere) evolves into a second order Compton-scale circle, the entirety forming a toroidal/helicoidal structure very akin to Consa’s. The vertex itself moves at light speed along this second order emergent structure, the zitter, aligning with predictions from the Dirac equation. Our model posits that the Fermi structure moves at a velocity very close to, but not exactly at, the speed of light along the Compton radius, a necessity imposed by geometry. This contrasts with existing zitterbewegung models that uniformely postulate the charge moving exactly at c. In this model it moves very close to c, much like a relativistic electron moves close to c but not at c. By pure geometry of the point charge moving at c, the net movement of the entire zitter electron must be less than c. This is a straightforward application of Pythagoras’ theorem, clearly illustrated in [21], see Figure 15. Matter can never exactly reach light speed; it may approach it with tremendous energy input, but its internal constituent, being made of light, is already moving at c.
Importantly, we have now accounted for all three dimensions of charge movement (two at Fermi scale, one at Compton scale) that were "free", further displacement of the zitter electron requires additional energy input. In this ontology, the relativistic principle that matter cannot move at light speed becomes a visual Pythagorean tautology. The internal light-speed movements of the electron’s components geometrically preclude the whole from attaining c, it is a drift of an object already moving at c, providing a intuitive explanation for this fundamental principle of special relativity.

8.2. From Compton Wavelength to deBroglie Wavelength

As previously noted, a puzzling feature of the de Broglie wavelength is its dependence on the velocity of the electron (or particle) in the observing reference frame. This contrasts with the other wavelengths we’ve considered, which are expressed in terms of fundamental properties and are velocity-independent. De Broglie first observed that a standing wave at the Compton scale would undergo Doppler shifting and exhibit a beating frequency [31]. Crucially, de Broglie demonstrated that the proper wavelength—the de Broglie wavelength—would emerge if and only if the starting wavelength was at the Compton scale. This calculation, detailed in Daniel Shanahan’s work [33] is relatively straightforward. See Figure 16. Visually, this phenomenon is readily apparent: a spherical standing wave is the sum of inbound and outbound waves. Under relativistic Doppler shift, each component modulates differently—one dilates while the other compresses. The resulting sum exhibits a beating at the proper de Broglie wavelength. This coincidence is striking and provides a justification for the peculiar velocity dependence of the de Broglie wavelength. It’s noteworthy that this feature is characteristic of standing waves but does not hold true for individual traveling waves. This insight offers a mechanistic explanation for the wave-particle duality observed in quantum mechanics, grounding it in classical wave phenomena and special relativity. It suggests that the de Broglie wavelength, far from being a mysterious quantum property, may be a natural consequence of the relativistic behavior of Compton-scale standing waves associated with electrons. This connection between Compton and de Broglie wavelengths also aligns with our hierarchical model of electron structure, where larger-scale properties emerge from dynamics at smaller scales in this case from Compton to de Broglie. It reinforces the idea that the electron’s wave-like properties at various scales are intimately linked, rather than being separate, unrelated phenomena.

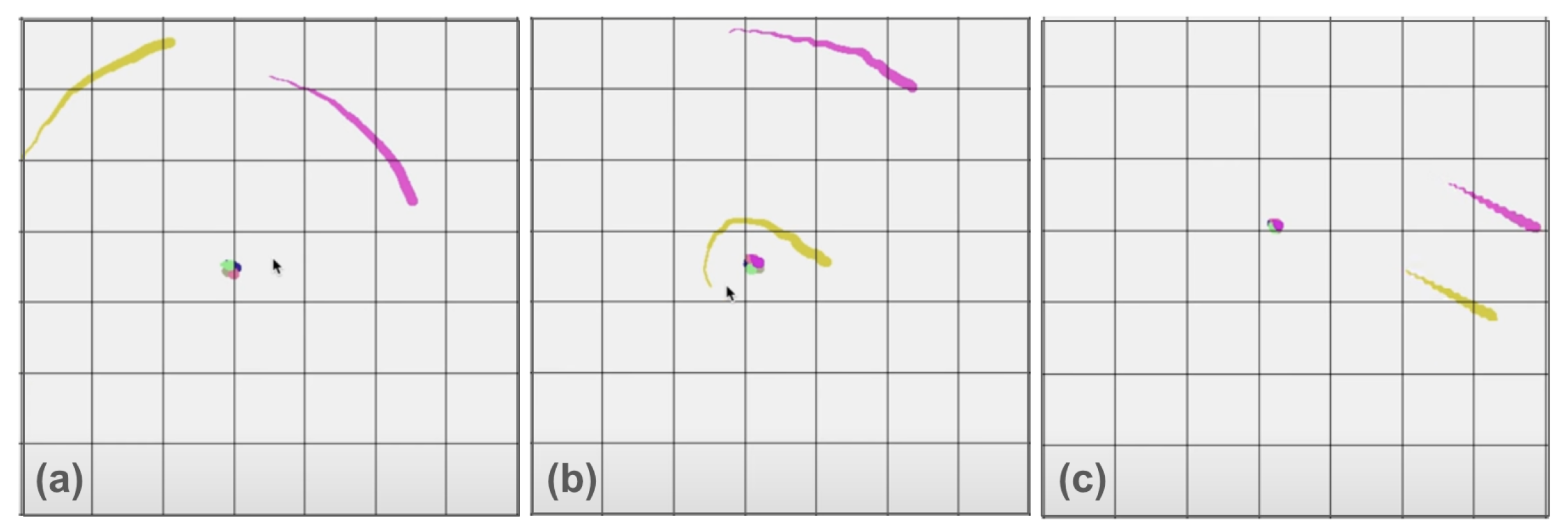
8.3. Asymptotic Freedom of Pair Formation of Walkers. Superconductivity Analog

The literature has noted that zitterbewegung may be responsible for Compton-level effects, particularly electron pair formation and superconductivity [34]. This paragraph reports on video captures of simulations of hydrodynamic walkers demonstrating similar phenomena. In the images below, see Figure 17, we observe the formation of stable clusters and orbits of walker pairs. There is continuous phase locking between walkers, resembling a form of electron entrainment. Notably, this dynamic is entirely mediated by standing waves, classifying it as a "pilot-wave" phenomenon. This behavior bears similarities to superconductivity, as the walker pairs exhibit a form of asymptotic freedom. When isolated, individual walkers are confined around clusters. However, when paired, they overcome the core’s attraction, analogous to Cooper pairs in superconductivity. In this analogy, the electron finds a form of entanglement. The pair formation allows the walkers to escape the attractive influence of the core, mirroring the behavior of electrons in superconducting materials. This effect, as noted in zitterbewegung literature, may underlie the mechanism of superconductivity. More generically a host of "Compton level effects" is reported in the literature [35]. These observations provide an intriguing macroscopic analog for quantum phenomena, potentially offering insights into the microscopic mechanisms of pair formation and superconductivity.

9. Generic Baryo-Genesis

We will now extend our model to demonstrate how natural focusing of light can reach the Schwinger limit, leading to the creation of electron-positron pairs. This extension of the model aims to bridge the gap between our understanding of light behavior and particle creation or baryo-genesis, a phenomenon typically explained through quantum field theory. The Schwinger limit represents a critical electric field strength at which the vacuum becomes unstable to electron-positron pair production. In our model, we will explore how the concentration of electromagnetic energy through natural focusing can locally exceed this limit, triggering pair creation.

9.1. Natural Focusing of Light

Light in any non-homogeneous media will focus. This generic focusing is called the "natural focusing of light". The shapes this focusing takes are those of the Catastrophe theory of Rene Thom [36]. J.F. Nye beautifully demonstrated that the natural focusing of light unfolds according to Thom’s catastrophes [37]. A simple and precise analogy is the bottom of a swimming pool on a sunny day. The moving water surface focuses light into patterns called "caustics" see Figure 18. These caustics represent the folding of light. It’s important to realize that the swimming pool caustics are a 2D slice of a 3D shape. The lines at the pool bottom represent planes in 3D, and their intersections, appearing as dots, represent lines in 3D space.
The intersection of two planes in 3D space creates a tiny string of light. While this appears as a dot on the pool bottom, the actual 3D shape is a fine light string. In catastrophe theory terminology, these shapes are "generic and structurally stable," meaning they consistently occur regardless of the medium and always take the same forms. Thom argued that these objects merit philosophical study as they represent the first order emerging from chaos. This concept of natural light focusing provides a framework for understanding how electromagnetic energy can concentrate in space, potentially reaching the intensities required for pair production.

9.2. The Schwinger Limit

If we focus (no pun intended) on the wave intensity, it becomes evident that the field intensity is discontinuously higher at the plane, and even more so ("doubly so") at the intersection of planes. This is readily observable in the lines at the pool bottom by just reading the intensities, see Figure 18. In any non-homogeneous media, the field intensity will invariably reach much higher levels at these focal points. Two intensity discontinuities occur along the tiny string: first to a plane, then to the intersection of planes. It’s reasonable to postulate that under appropriate conditions, we may well exceed the Schwinger limit in terms of intensity. Beyond the Schwinger limit, electron-positron pair creation occurs. In this model, this creation is viewed as the formation of two counter-rotating vortices, one with right helicity and the other with left helicity. This pair creation of so called "umbilical points" in focusing was reported in the work above [37]. Nye’s disciple, Michael Berry [38], mathematically described this pair creation of phase catastrophes in [39] in 1977. This scenario suggests that baryogenesis could be a generic phenomenon in chaotic media where light focuses beyond the Schwinger limit. [40]
This is effectively a natural map between the morphogenesis of Thom and the baryogenesis of QFT (or is it berry-o-genesis). The birth of shapes is also the birth of matter. The birth of matter, as understood in this framework, emerges as a "generic and structurally stable" morphogenesis process of Berry-Thom. It’s a natural consequence of light focusing behavior in any media, rather than an exceptional event. This perspective offers a novel approach to understanding particle creation.

10. Discussion

We have indeed focused exclusively on the electron, adhering to the Einstein-Wilczek mantra that understanding the electron should be sufficient to comprehend the world. This approach aligns with the fundamental role the electron plays in our understanding of matter and interactions. However, it is important to acknowledge that our model does not address the structure of the proton. This omission is significant, given the proton’s crucial role in atomic structure and nuclear physics. Interestingly, similar explorations have been conducted by Kovacs and Vassalo for the proton, utilizing a helicoidal zitterbewegung topology at the Fermi scale. These investigations, as detailed in [41] have yielded striking results that align with experimental observations in novel ways. This parallel approach to proton structure suggests that the principles we’ve applied to the electron might have broader applicability. It hints at the tantalizing possibility of a unified framework for understanding fundamental particles, based on underlying concepts of self-interacting electromagnetic fields and multi-scale wave phenomena.

11. Conclusion

Starting with experimental Bell violations and the study of hydrodynamic walkers, an intuition about the potential role of standing waves within QM has been developed. This approach is reminiscent of the classic de Broglie/Bohm pilot wave models. After a brief review of existing Zitter models was presented, a unification of these approaches was attempted by establishing a clear ontology, based on chiral zilches or "ligh-holes" at the Fermi scale. It has been demonstrated that this approach satisfies many of the observed structures of the electron at various scales: Fermi, Compton, Bohr, and de Broglie. From the hypothesis of a "light-hole" (analogous to a black hole) at the Fermi scale, most of the known structures of the electron have been deduced, mapping to existing zitter models and thus explaining the g/2 anomalous factors. The genericity and stability of the model, in the René Thom sense, have been shown. It has been argued that baryogenesis at the Schwinger limit via electron-positron pair formation should be considered the default outcome of "retarded and catastrophic potentials." This model has been termed the "sub-standard model."

Funding

The author received no external funding.

Acknowledgments

This study has encompassed many years of the author’s life. The author acknowledges many contributions over time, some as old as 10 years ago, some as recent as "yesterday" from J.F. Nye, Yves Couder, Herman Batelaan, Paul Werbos, Peter Hagelstein, Predrag Cvitanovic, Andras Kovacs, Jarek Duda, Oliver Consa, Emmanuel Fort, Carlos Dos Santos, John Bush, Tom McCarty, Samuel Bernardet and Martin Rivas.

Conflicts of Interest

The author declares no conflict of interest.

References

  1. Wilczek, F. The enigmatic electron. Nature 2013, 498, 31–32. [CrossRef]
  2. Barut, A. O.; Zanghi, N. Classical Model of the Dirac Electron. Phys. Rev. Lett. 1984, 52, 2009–2012. [CrossRef]
  3. Hestenes, D.; Sobczyk, G.; Marsh, J. Clifford Algebra to Geometric Calculus. A Unified Language for Mathematics and Physics. American Journal of Physics 1985, 53, 510–511.
  4. Celani, F.; Di Tommaso, A.; Vassallo, G. The Electron and Occam’s Razor. JCMNS 2017, 25, 76–99.
  5. Hiley, B.; Callaghan, R. The Clifford Algebra Approach to Quantum Mechanics B: The Dirac Particle and its relation to the Bohm Approach. Unpublished 2010.
  6. Couder, Y.; Protière, S.; Fort, E.; et al. Walking and orbiting droplets. Nature 2005, 437, 208. [CrossRef]
  7. Bush, J. W. M.; Oza, A. U. Walking and orbiting droplets. Rep. Prog. Phys. 2021, 84, 017001.
  8. Budanur, N. B.; Fleury, M. State space geometry of the chaotic pilot-wave hydrodynamics. Chaos: An Interdisciplinary Journal of Nonlinear Science 2019, 29, 013122.
  9. Perrard, S.; Labousse, M.; Miskin, M.; et al. Self-organization into quantized eigenstates of a classical wave-driven particle. Nat. Commun. 2014, 5, 3219. [CrossRef]
  10. Harris, D. M.; Moukhtar, J.; Fort, E.; Couder, Y.; Bush, J. W. Wavelike statistics from pilot-wave dynamics in a circular corral. Physical Review E 2013, 88, 011001. [CrossRef]
  11. Urdaneta Santos, I. The zitterbewegung electron puzzle. Physics Essays 2023, 36, 299. [CrossRef]
  12. Consa, O. Helical Solenoid Model of the Electron. Progress in Physics 2018 14(2) 80-89.
  13. Consa, O. G-Factor and the Helical Solenoid Electron Model. viXra 2017. Available online: https://api.semanticscholar.org/CorpusID:1598023.
  14. Fleury, M.J.J. Observations of Bell Inequality Violations with Causal Isolation between Source and Detectors. Entropy 2022, 24, 1230. [CrossRef]
  15. Kovacs, A.; Vassallo, G.; O’Hara, P.; Celani, F.; Di Tommaso, A. Unified Field Theory and Occam’s Razor: Simple Solutions to Deep Questions; 1st ed.; World Scientific: Singapore, 2022.
  16. Cvitanovic, P.; Kinoshita, T. Sixth-order magnetic moment of the electron. Phys. Rev. D 1974, 10, 4007–4031. [CrossRef]
  17. Cvitanovic, P.; Private Communication 2024.
  18. Rivas, M. Kinematical Theory of Spinning Particles: The Interaction Lagrangian for Two Spin 1/2 Dirac Particles; arXiv: physics/0608089, 2006.
  19. Rivas, M. Considerations about the measurement of the magnetic moment and electric dipole moment of the electron. arXiv 2024, eprint: 2406.15502. Available online: https://arxiv.org/abs/2406.15502.
  20. Gay, T. J.; Dunning, F. B. Mott Electron Polarimetry. Rev. Sci. Instrum. 1992, 63, February 1992. Copyright 1992 American Institute of Physics.
  21. dos Santos, C. A. M. The Structure of the Electron Revealed by the Schwinger Limits. Preprint available on https://www.researchgate.net/publication/371909768 (under review), 2023.
  22. Yazaki, Y. How the Klein-Nishina formula was derived: Based on the Sangokan Nishina Source Materials. Proc. Jpn. Acad. Ser. B Phys. Biol. Sci. 2017, 93, 399–421. [CrossRef]
  23. García, A. Stability analysis of the uniform motion of electrodynamic bodies. Physica Scripta 2021, 96, 015506.
  24. Liénard, A. Champ électrique et magnétique produit par une charge concentrée en un point et animée d’un mouvement quelconque. L’éclairage électrique 1898, 16.
  25. Jenkins, A. Self-oscillation. Physics Reports 2013, 525, 167.
  26. Tang, Y.; Cohen, A. Optical Chirality and Its Interaction with Matter. Physical Review Letters 2010, 104, 163901. [CrossRef]
  27. Conference presentation at the "AGACSE2024: Applied Geometric Algebras in Computer Science and Engineering 2024" conference. 2024.
  28. Shakespeare, W; Macbeth, 1623, Act 5, Scene 5, lines 17–28.
  29. Macken, J.A. Oscillating Spacetime: The Foundation of the Universe. Journal of Modern Physics 2024, 15, 1097-1143. [CrossRef]
  30. Bernard-Bernardet, S.; Fleury, M.; Fort, E. Spontaneous emergence of a spin state for an emitter in a time-varying medium. The European Physical Journal Plus 2022, 137, 1–8. [CrossRef]
  31. de Broglie, L. Ondes et Mouvements; Gauthier-Villars: Paris, France, 1926.
  32. Consa, O. Something is wrong in the state of QED. arXiv 2021, eprint: 2110.02078. Available online: https://arxiv.org/abs/2110.02078.
  33. Shanahan, D. A Case for Lorentzian Relativity. Foundations of Physics 2014, 44, 349-367. [CrossRef]
  34. Kovacs, A.; Vassallo, G. High-temperature superconductivity is the catalyzed Bose-Einstein condensation of electrons: a rigorous study of coherent electron dynamics, guiding a rational search for new superconductors.
  35. Mayer, F. J., Reitz, J. R. Electromagnetic composites at the Compton scale. International Journal of Theoretical Physics 2011, 51, 322–330.
  36. Thom, R. Structural Stability and Morphogenesis: An Outline of a General Theory of Models. Published by W. A. Benjamin: Netherlands, 1975.
  37. Nye, J. F. Natural Focusing and Fine Structure of Light: Caustics and Wave Dislocations. Published by Institute of Physics Publishing: Bristol, UK, 1999. [CrossRef]
  38. Berry, M. Obituary for John Frederick Nye. University of Bristol: 2019.
  39. Berry, M. V., Hannay, J. H. Umbilic points on Gaussian random surfaces. Journal of Physics A: Mathematical and General 1977, 10, 1809.
  40. Buchanan, M. Past the Schwinger limit. Nature Phys 2006, 2, 721. [CrossRef]
  41. Vassallo, G.; Kovacs, A. The Proton and Occam’s Razor. Journal of Physics Conference Series 2023, 2482, 012020.
Preprints 115914 g001
Figure 1. A walker and echo-location in action. The droplet creates Bessel waves that sum into a "wake" pattern. It includes echo-location of the cavity by reflection. Here the walker encounters a wall bottom right and bounces back towards the top left following the gradient of the slope. (Credit: Samuel Bernardet, http://dotwave.org)
Figure 1. A walker and echo-location in action. The droplet creates Bessel waves that sum into a "wake" pattern. It includes echo-location of the cavity by reflection. Here the walker encounters a wall bottom right and bounces back towards the top left following the gradient of the slope. (Credit: Samuel Bernardet, http://dotwave.org)
Preprints 115914 g001
Preprints 115914 g002
Figure 2. The walker and QM corrals. To the left the emergent heatmap of the walker presence in a circular cavity. (Credit: from [10]). To the right, visualization of QM electron Corral. (Credit: IBM).
Figure 2. The walker and QM corrals. To the left the emergent heatmap of the walker presence in a circular cavity. (Credit: from [10]). To the right, visualization of QM electron Corral. (Credit: IBM).
Preprints 115914 g002
Preprints 115914 g003
Figure 3. The Helicoidal solenoid electron of Oliver Consa. The small toroidal movement is on the fermi scale, the larger zitter orbit is at Compton. (Credit: Oliver Consa from [12]).
Figure 3. The Helicoidal solenoid electron of Oliver Consa. The small toroidal movement is on the fermi scale, the larger zitter orbit is at Compton. (Credit: Oliver Consa from [12]).
Preprints 115914 g003
Preprints 115914 g004
Figure 4. To the left, (a) the spherical fermi ball rotating in a Compton circle, notice intrinsic spin of ball at − ω e . The corkscrew to the right (b) is the relativistic dynamics of this electron. The "Compton" radius of the Zitter changes with v/c. Constrast this to Figure 6 and the cycloid of Rivas (Credit: Giorgio Vassallo).
Figure 4. To the left, (a) the spherical fermi ball rotating in a Compton circle, notice intrinsic spin of ball at − ω e . The corkscrew to the right (b) is the relativistic dynamics of this electron. The "Compton" radius of the Zitter changes with v/c. Constrast this to Figure 6 and the cycloid of Rivas (Credit: Giorgio Vassallo).
Preprints 115914 g004
Preprints 115914 g005
Figure 5. To the left (a), the spinning point particle model of Martin Rivas. The radius is Compton and the charge is separate from mass in center. A spin − ω is assumed to give the gyromagnetic ratio of 2. (b) The relativistic dynamics are shown to the right. Here shown the impact at Compton scale of two electrons. (Credit: Martin Rivas.).
Figure 5. To the left (a), the spinning point particle model of Martin Rivas. The radius is Compton and the charge is separate from mass in center. A spin − ω is assumed to give the gyromagnetic ratio of 2. (b) The relativistic dynamics are shown to the right. Here shown the impact at Compton scale of two electrons. (Credit: Martin Rivas.).
Preprints 115914 g005
Preprints 115914 g009
Figure 9. The EM torus of dos Santos. An electromagnetic field shown in (d) above, has a blue E and red B field. The length is the classical electron radius, the angle alpha as shown in (c) and (d). The field is confined to the torus on the figure with small radius r τ = 1 / ( π ) * r e . This is the Fermi scale. The field is circulating at the Compton radius as shown in (a). (e) shows the component of the centripetal Lorentz force stabilizing this orbit around the center. (Credit: from [21])
Figure 9. The EM torus of dos Santos. An electromagnetic field shown in (d) above, has a blue E and red B field. The length is the classical electron radius, the angle alpha as shown in (c) and (d). The field is confined to the torus on the figure with small radius r τ = 1 / ( π ) * r e . This is the Fermi scale. The field is circulating at the Compton radius as shown in (a). (e) shows the component of the centripetal Lorentz force stabilizing this orbit around the center. (Credit: from [21])
Preprints 115914 g009
Preprints 115914 g010
Figure 10. Self-oscillating electro-magnetic wave at Fermi. The chiral Zilch. The light-hole. The Oroborous of light. (Credit: from [29])
Figure 10. Self-oscillating electro-magnetic wave at Fermi. The chiral Zilch. The light-hole. The Oroborous of light. (Credit: from [29])
Preprints 115914 g010
Preprints 115914 g012
Figure 12. The archimedian spiral resulting from the zilch. One (a) outgoing the other (b) incoming. Resulting (a+b=c) standing wave about the center. Self-oscillating electro-magnetic wave at Fermi. (Credit: from [29])
Figure 12. The archimedian spiral resulting from the zilch. One (a) outgoing the other (b) incoming. Resulting (a+b=c) standing wave about the center. Self-oscillating electro-magnetic wave at Fermi. (Credit: from [29])
Preprints 115914 g012
Preprints 115914 g013
Figure 13. (a): Spontaneous emergence of Spin in hydrodynamic walker. (b): the drift over time (Credit: Samuel Bernardet from [30])
Figure 13. (a): Spontaneous emergence of Spin in hydrodynamic walker. (b): the drift over time (Credit: Samuel Bernardet from [30])
Preprints 115914 g013
Preprints 115914 g014
Figure 14. Your eyes are not deceiving you! Same mechanism, but in Compton and not in Fermi.
Figure 14. Your eyes are not deceiving you! Same mechanism, but in Compton and not in Fermi.
Preprints 115914 g014
Preprints 115914 g015
Figure 15. Back to the USS Bohr... v B < < c ! QED? (Credit: Santos y DaLuz from [21])
Figure 15. Back to the USS Bohr... v B < < c ! QED? (Credit: Santos y DaLuz from [21])
Preprints 115914 g015
Preprints 115914 g016
Figure 16. A standing wave at Compton, beats at the de Broglie matter wave under Doppler. The A and B panels are Doppler distorted spherical waves. A is going outward and B is going inward. C is a superposition of A and B, A+B=C. C beating is at the de Broglie wavelength if and only if A and B are at Compton. (credit: from [29])
Figure 16. A standing wave at Compton, beats at the de Broglie matter wave under Doppler. The A and B panels are Doppler distorted spherical waves. A is going outward and B is going inward. C is a superposition of A and B, A+B=C. C beating is at the de Broglie wavelength if and only if A and B are at Compton. (credit: from [29])
Preprints 115914 g016
Preprints 115914 g017
Figure 17. From left to right, (a) a pair of walkers finds captive orbits about the center. (b) The pair finds each other. (c) The pair finds freedom (zoom out, notice smaller tail).
Figure 17. From left to right, (a) a pair of walkers finds captive orbits about the center. (b) The pair finds each other. (c) The pair finds freedom (zoom out, notice smaller tail).
Preprints 115914 g017
Preprints 115914 g018
Figure 18. The caustic of the pool on a sunny day. The lines are planes in 3D and the dots are lines in 3D. Notice the increase of intensity on the lines and again the double increase on the dots which are bright white.
Figure 18. The caustic of the pool on a sunny day. The lines are planes in 3D and the dots are lines in 3D. Notice the increase of intensity on the lines and again the double increase on the dots which are bright white.
Preprints 115914 g018
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated