External Moderation of Reactor Core Neutrons for Optimized Production of Ultra-Cold Neutrons

Preprint

Article

External Moderation of Reactor Core Neutrons for Optimized Production of Ultra-Cold Neutrons

Altmetrics

Downloads

138

Views

Comments

A peer-reviewed article of this preprint also exists.

Submitted:

11 October 2024

Posted:

14 October 2024

You are already at the latest version

Alerts

Abstract

The Ultra-Cold Neutron (UCN) source being commissioned at North Carolina State Universityâs PULSTAR reactor is uniquely optimized for UCN production in the former graphite-filled thermal column outside of the reactor pool. The source utilizes a remote moderation design which is particularly well suited to the PULSTAR reactor on account of its large thermal and epithermal neutron leakage from the core face. This large non-equilibrium flux from the core is efficiently transported to the UCN source through the specially designed beam port in order to optimize UCN production at any given reactor power. The increased distance to the source from the core also greatly limits the heat load on the cryogenic system. A MCNP model of this system was developed and is in good agreement with gold foil activation measurements using a mock-up setup as well as with the real UCN source heavy water moderator. These results established a firm baseline for estimates of the cold neutron flux available for UCN production and prove that remote moderation in a thermal column port is a valuable option for future designs of cryogenic UCN sources.

Keywords:

Subject: Physical Sciences - Nuclear and High Energy Physics

1. Introduction

Research reactors and neutron spallation sources are normally equipped with moderation facilities to deliver neutrons in a narrow energy range around 25 meV. Beams of “cold neutrons” with energies around 10 meV are also common. Recently, even much lower energy neutrons (Ultra-Cold Neutrons, UCN, with energies below about 500 neV) became of interest to the neutron community. UCN are distinct in that they can be trapped in material, gravitational, and/or magnetic traps to facilitate studies of the neutron which require long observation times [1,2,3]. The set of UCN sources that have been commissioned around the world so far have primarily been used to perform fundamental particle physics experiments related to studies of free neutrons, but increases in available UCN flux would allow for new applications [4,5,6].

Ultra-cold neutrons are present in every reactor core at the low energy edge of the neutron spectrum with a relative amount of about

10^{- 12}

of the total thermal flux [7]. Nevertheless, direct extraction is not effective due to high losses in the beam port windows because of the

1 / v

(v being neutron velocity) dependence of the loss cross section. Therefore, the first generation of UCN sources were based on cold neutron sources since those are easier to extract via guides. These sources used gravitational [8] and mechanical [9] deceleration to shift the thermal equilibrium cold spectrum to UCN range [4]. These deceleration mechanisms must conserve phase space density (via Liouville’s theorem [10]); therefore, the maximum UCN yield is restricted by the available neutron flux of the cold source which is not easy to increase significantly.

Modern UCN source designs are based on a non-equilibrium principle, i.e. "superthermal" source design, where the UCN phase space density is not restricted by Liouville’s theorem to be the same as in the cold source [11]. Such designs use a thermal and/or cold neutron moderator coupled with a UCN “converter”, i.e. a cryogenic material which inelastically downscatters cold neutrons directly to the UCN energy range. This conversion primarily involves a single collision in contrast with the multiple collisions typically involved in the moderation process to thermal or cold neutrons. Common converter materials are solid deuterium at 5 K and liquid helium below 1.8 K. Low temperatures are needed to depopulate low energy excitation in the converter material to avoid UCN losses from scattering back to higher energies.

To obtain high UCN densities, the converter material has to be placed in a high neutron flux. However, locations near the reactor core with the highest flux will also have the largest heat load from neutrons and gamma radiation posing a challenge to the cooling equipment. Since low cryogenic temperatures are required for operating UCN converters, there is a need to increase the distance from the core to the source and to add gamma shielding.

A common design of UCN facilities at reactors is to place both the cold moderator and the UCN converter in existing beam ports, either direct [12,13] or tangential [14,15,16]. In this design, fast neutrons are moderated to the thermal range by the reactor pool, and the increased distance reduces nuclear heating because the thermal neutron flux decreases as the incident solid angle decreases. Using a larger size thermal column port improves the situation as was realized in the prototype source at PNPI, which also demonstrated an increased UCN yield from solid versus liquid deuterium [17,18]. However, this prototype source was still using thermal neutrons moderated by the reactor pool.

The UCN source at North Carolina State University’s (NCSU) PULSTAR reactor is unique in that it supplements the thermal neutron flux leaking from the core by directly moderating non-equilibrium neutrons in a heavy water tank within the thermal column port. Additionally, since the UCN converter is situated inside of the heavy water moderator tank, the effective solid angle scattering into the converter is increased to almost a full

4 π

coverage. The performance of the PULSTAR UCN source depends crucially on the transport properties of the specially designed beam port assembly, which delivers neutrons through the reactor pool to the entrance of the thermal column. In this publication we present results of the efficiency characterization of this neutron delivery system in comparison with the original thermal column flux and simulations completed with release 2 of the Los Alamos MCNP6 Monte Carlo neutron transport code [19].

2. Transport of Non-Equilibrium Neutrons from Reactor Core to the UCN Source Moderator

2.1. UCN Source at NC State University PULSTAR Reactor

The NCSU PULSTAR is a heterogeneous pool-type university research reactor that has been in operation since 1972. It operates in steady-state at power levels up to 1 MW thermal. Recently its cooling system was upgraded, and licensing is ongoing to operate up to 2 MW . The reactor has several research instruments in operation and in commissioning [20], including the UCN source. The intentionally under-moderated core design has a high leakage of fast and thermal neutrons from the core face. This feature, along with the UCN source design and efficient transport of neutrons from the core, optimizes UCN production per the available reactor power. The concept, design, and construction of the PULSTAR UCN source has been described in detail elsewhere [21,22,23]. Briefly, the UCN source utilizes a three-stage neutron deceleration process: it couples a heavy water thermal moderator with a solid methane cold moderator and with a solid deuterium converter at 5 K. The temperature of the cold methane can be adjusted from 35 K to 70 K to optimize coupling with the solid deuterium phonon spectrum in order to maximize UCN yield in the converter [24,25,26]. The cryostat containing solid deuterium and methane is immersed in the heavy water tank. The assembly is cantilevered on the thermal column door and can be easily rolled in and out.

2.2. Description of UCN Source Beam Port Components

The Thermal Column (TC) wall separating it from the reactor water pool is located 85 cm away from the core. Originally, the TC consisted of a 122 cm square column of graphite running 152 cm through the reactor biological shield from the outside of the pool liner. A 2.54 cm thick aluminum plate and a 5.08 cm deep grid of aluminum bars strengthen the pool liner inside of the thermal column void. The chamber is lined with Boral plates, surrounded by Barytes type high density concrete, and has a large Barytes concrete door, which can be rolled out. A graphite “nosepiece” displaced the water between the pool liner and the Rotary Exposure Ports (REPs) at the reactor core. The REP’s are filled with water and, in total, there was a 14.6 cm gap between the core and the nosepiece. The nosepiece had been made of an aluminum shell filled completely with graphite and was installed on the cradle in the reactor pool. It had been designed with the goal of thermalizing neutrons delivered to the TC for sample irradiation. To accommodate the UCN source, a new beam port was designed to optimize the delivery of both fast and thermal neutrons with minimal losses. A constraint on this new design was the requirement to fit it inside the already existing cradle and structural supports near the reactor core.

To aid the new nosepiece design, MCNP simulations were completed to optimize the geometry for neutron transport. Simulations were done by adding TC components to the NCSU Nuclear Reactor Program’s detailed MCNP criticality calculation (KCODE) model of the PULSTAR reactor and by using cross-section data libraries provided by the MCNP6 package [27]. The KCODE model had already been benchmarked against gold foil activation by the well-moderated neutron flux in the original graphite-filled thermal column [28].

As a result of the MCNP design study, the beam port for the UCN source was designed to include 3 parts: two of them installed in the reactor pool (called the Shielding Box (SB) and Nose Port (NP)) and one graphite structure added on the TC side of the pool liner. The latter was installed to minimize neutron loss due to the gap at the front of the UCN source moderator tank created by the aluminum bars. The final geometry of all components can be seen in Figure 1. The NP and the internal TC structure both feature a 45 cm square central void surrounded by 20 cm of graphite. The SB replaced the REP’s and is able to displace 12.7 cm of water between the NP and the core. It contains a 2.54 cm thick lead plate to reduce heating of the source by core gammas and can be removed independent of the nose port to change the type or thickness of the shielding material. Both the NP and the SB can be either flooded with pool water or vacated when pressurized with helium gas in order to serve as a neutron shutter.

Several possible configurations were explored using MCNP but had not been adopted for practical reasons. Increasing the thickness of the graphite on the TC side of the liner does not improve transmission, but enclosing the SB in the same graphite thickness as the NP would have increased the flux by about 25%. Doubling the NP graphite thickness or enclosing the SB in 6 cm thick graphite would have added 11%. The latter is the only practical option due to the cradle design. The most dramatic increase would have come from replacing the graphite with beryllium, but beryllium was not available.

3. Foil Activation Method for Neutron Flux Characterization

Neutron foil activation analysis was utilised to characterize the neutron flux delivered to the thermal column. Measurements were initially completed with a mock-up tank approximating the heavy water moderator tank of the UCN source, and were later measured inside of the actual moderator tank and along the real UCN guide. Here, we present the basics of the foil activation method necessary to those measurements.

For our tests, two foil materials were used: gold and indium. Additionally, some gold foils were covered in cadmium filters so as to separate out the epicadmium part of the spectrum from the uncovered foils’ results.

Gold, which is readily available as isotopically pure ¹⁹⁷Au, can capture a neutron to form ¹⁹⁸Au which will then beta decay to ¹⁹⁸Hg with a half-life of

2.694

days. Upon decay, a signature

411.8

keV gamma is released

95.6

% of the time.

Indium, having a higher thermal neutron cross-section and a shorter half-life than gold, was also used for determining the flux for locations that would receive less total fluence. Indium naturally exists as a composition of

4.29

% ¹¹³In and

95.71

% ¹¹⁵In. When ¹¹⁵In captures a neutron, it has a 79% chance of entering the meta-stable state of ¹¹⁶In^m which has a complex beta decay emission tree and a half life of

54.29

minutes.

3.1. Foil Activation Theory

When performing neutron activation analysis on foils within an unknown flux field that is non-homogeneous, it is not possible to determine the exact neutron flux,

ϕ

. Instead, The flux determined from foil activation methods is typically referred to as the equivalent or 2200 m/s flux,

ϕ_{0}

which is an approximation of the true thermal neutron flux made by assuming that all thermal neutrons have the same cross section as 2200 m/s neutrons,

σ_{0}

Although the activity of the foils can be determined with high precision, converting that activity into an exact flux requires precise knowledge of the energy-spectrum dependent cross section,

σ

. However, the energy spectrum can’t be known without knowledge of the flux [29]. Cadmium filters are used to reduce some of the uncertainty in the energy spectrum by effectively blocking all but epicadmium neutrons from activating the foil, but that still leaves a non-negligible contribution of epithermal (yet subcadmium) neutrons which can shift the total cross section of the target foil. To deal with these difficulties, different simplifying assumptions have arisen and form the basis of the different conventions for foil activation flux analysis. We chose to follow the Stoughton and Halperin convention as described in the standard [30], but attempted to supplement with our correction factors as described in the discussion section.

The simplest case of foil activation analysis for determining the thermal neutron flux is when a foil is exposed to a well-thermalized incoming flux of neutrons that form a Maxwell-Boltzmann distribution with a mean value of 2200 m/s (which we will call

v_{0}

). In this case, the flux is determined from the foil’s neutron capture rate R which is assumed to be equal to

R_{0}

, the capture rate for the equivalent flux:

R = R_{0} = N_{i} σ_{0} ϕ_{0},

(1)

where

N_{i}

is the total number of target atoms available in the foil. Equation (1) for R also assumes that the target foil is sufficiently thin, but in practice, a thermal self shielding factor

G_{th}

must be included in this calculation as shown below.

While the capture rate can not be directly measured, it can be determined as a function of the time of irradiation and the activity A. Every atom that captures a neutron will follow a decay path which results in the detectable release of characteristic gamma rays at a rate consistent with the half life. During irradiation, atoms activated at a rate R will immediately start to decay and continue to decay after radiation has ended so that the activity A some time later is

A (t_{w}) = R (1 - e^{- λ t_{a}}) e^{- λ t_{w}},

(2)

where

t_{a}

is the irradiation time,

t_{w}

is the time waited after radiation, and

λ = \ln (2) / t_{1 / 2}

is the decay rate which depends on the half life

t_{1 / 2}

Placing the irradiated foils in a gamma detector such as a high-purity germanium (HPGe) detector allows one to determine the activity as some function of the measurable count rate, C. The ratio between count rate and the actual activity is the efficiency

ε

of the detector, and that must be measured with a radioactive standard of known activity for a given detection geometry. Including that, the equivalent flux is

ϕ_{0} = \frac{C e^{λ t_{w}}}{p N_{i} σ_{0} G_{th} g ε (1 - e^{- λ t_{a}})},

(3)

where p is the branching ratio or the probability of emission for a particular gamma ray,

G_{th}

is the self shielding correction factor for thermal neutrons which depends on the thickness of the foil, and g is the temperature and material dependent Westcott correction factor.

For the situation of a non-homogeneous flux where a significant number of epithermal and fast neutrons are expected, it becomes useful to separate the total capture rate R out as

R = R_{0} + R_{epithermal} + R_{Cd},

(4)

where

R_{epithermal}

is the capture rate for epithermal yet subcadmium neutrons and

R_{Cd}

is the capture rate for epicadmium neutrons. While

R_{Cd}

can be calculated by measuring the activity of the cadmium covered foils and R through the activity of the bare foils, a further assumption must be made to remove

R_{epithermal}

in order to isolate

R_{0}

. When following the Stoughton and Halperin convention, it is assumed that the epithermal spectrum has a

1 / E

shape. To do this, the following approximation is made:

R_{epithermal} + R_{Cd} \approx R_{Cd} (1 + \frac{g σ_{0} f_{1}}{G_{res} I_{0}} + \frac{σ_{0} w^{'}}{G_{res} I_{0}}) = R_{Cd} γ_{epithermal},

(5)

where

f_{1}

and

w^{'}

are temperature dependent correction factors describing the epithermal activation and the change in cross section just below the cadmium cutoff, respectively, and

I_{0}

is the resonance integral. Values for all three of these are available in [30]. The term

γ_{epithermal}

is a shorthand for the correction factor term in parenthesis within Equation (5). After making these assumptions, the equivalent flux component of a non-thermalized flux can be found as

ϕ_{0} = \frac{(C_{bare} - C_{C d} γ_{epithermal}) e^{λ t_{w}}}{p N_{i} σ_{0} g G_{th} ε (1 - e^{- λ t_{a}})} .

(6)

Although Equation (6) provides a better approximation of the equivalent flux in a non-thermalized flux field than Equation (3), it is worth restating that

ϕ_{0}

will not be equal to the true thermal flux. In general, the greater the variance of the thermal spectrum from a Maxwell-Boltzmann distribution around

v_{0}

, the worse the agreement between the equivalent flux and the true flux. To remedy this, an effective flux-weighted cross section can be recalculated from the MCNP simulated flux.

Our method for calculating the effective thermal cross section

σ_{th}

was to find the discrete flux

ϕ_{i}

per energy group i and combine that with the approximate discretized cross section

σ_{i}

at each energy group in the following equation:

Effective σ_{th} = \frac{\sum_{i} σ_{i} ϕ_{i}}{\sum_{i} ϕ_{i}} .

(7)

This sum is performed over the entire thermal spectrum up until the cadmium cutoff energy of about

0.5

eV.

In order to report results without any approximations as is necessary with the determination of the flux, we also introduce the concept of the normalized activity

A^{'}

. The normalized activity corresponds to the actual activity through the following equation

A^{'} = \frac{A}{N_{i} G_{th} (1 - e^{- λ t_{a}})} .

(8)

Representing the activity like this normalizes out any differences in foil thickness, mass, and time of irradiation.

4. Experimental Results

4.1. Description of Activation Measurements Using Test Tank

The initial set of foil activation analysis tests were completed with an aluminum test tank to benchmark the performance of the neutron transport system. The test tank, a mock-up of the source’s heavy-water tank, was built to allow easy positioning of gold foils. The tank was constructed out of aluminum alloy 6061 and consisted of a horizontal cylindrical tank which was the same diameter and approximately the same length as the source tank while having a vertical well that simulated the void of the vacuum jacket of the inner source cryostat (see Figure 2). The test tank holds 175 gallons of water, compared to the 146 gallons of the UCN source heavy water tank. The test tank could be inserted into the thermal column chamber in either direction. Orienting the tank with the well on the side most distant from the reactor core approximates the thermal column filled with heavy water to provide a good estimate of the neutron flux delivered to the TC and allows comparison with the case of the original graphite filled nosepiece. Orienting the tank with the well on the core side then demonstrates the relative effect of the cryostat vacuum void.

Three measurements were done with the test tank filled with D₂O. The first two were done with the well oriented away from the core without and with SB in place (configurations A and B in Figure 2). The last run was with the well oriented toward the core (configuration C in Figure 2). For this last run, in addition to the vertical void, the tank was only partially filled with D₂O. This was to mimic the elbow of the UCN source cryostat (see Figure 3). We estimated that the water level was between 16 to 30 cm from the top of the tank.

Only gold foils were used in the test tank activation measurements. The square shaped foils, 50

μ

m thick and

6.35

mm in side length, were placed along the length of a

1.27

x 3 cm rectangular tube running down the center-line of the tank. Typically, a first measurement would be made with bare gold foils followed by a second measurement with cadmium-shielded foils at the same positions. To limit the number of experimental runs required with the test tank, bare foils and cadmium-shielded foils were alternated down the length of the stringer with the assumption that activities could be interpolated to each position.

Bare foils and cadmium-shielded foils were alternated through the tank along an aluminum wire "stringer", with bare foils at

2.54

cm,

12.70

cm,

22.86

cm and

33.02

cm, and three shielded foils at

7.62

cm,

17.78

cm and

27.94

cm measured from the front of the tank. During all measurements, the foils were irradiated for 30 minutes at a reactor power of 100 kW and counted a few days later. During data analysis, the calculated fluxes were scaled by a factor of 10 to represent the predicted flux at the full operational power of 1 MW for the PULSTAR reactor.

4.2. Description of Activation Measurements Using the Real UCN Source Tank

More recently, foil activation measurements were performed within the UCN source apparatus in a configuration as close to the final operational configuration as possible (the inner cryostat insert and methane containers were not installed to avoid activation). These results were then compared with the previous test tank flux measurements to confirm the viability of the test measurements and to estimate the effect of a minor modification made to the NP which added an extra

1.3

cm of aluminum. Additionally, these measurements tested the radiation shielding and measured streaming of scattered thermal neutrons throughout the UCN guide to outside the TC door.

The configuration of the UCN source for this set of measurements used the real D₂O moderator tank with the actual void inside of the tank made by the vacuum jacket of the cryostat insert. Both the cryostat vacuum jacket and the vacuum jacket for the UCN guide were open to atmosphere and empty except for a long aluminum wire on which the different foils were attached at the locations shown in Figure 3. Gold foils were placed at locations #1-6, which string down the UCN guide volume, and at location #7, which was inside the methane transfer line. The foils at locations #1-3 had both bare gold foils and cadmium covered gold. Some gold foils were 51

μ

m thick, and others were 127

μ

m thick; different self shielding factors were used for the different thicknesses. A sample of crushed indium wire was inserted in two locations: the exit of the UCN guide cryostat and near the exit of the cryogenic transfer tube. These indium samples were made by crushing a wire with a vise and hammer, and therefore were not uniform. The thickness varied throughout both samples, but was measured to have an average of

330 \pm 100

μ

m. The uncertainty in this measurement was included in the uncertainty of the self shielding correction factor.

During the flux test, the reactor power was ramped in increments of 5 kW up to 25 kW over a total time of 70 minutes; the average power over the full test was

13.8

kW. During calculations, it was assumed that there was a linear ratio between reactor power and neutron flux. This was achieved by scaling the flux for each recorded time step by the percent of the current maximum reactor power (1 MW). For example, during the time the reactor was at 5 kW, the foils were assumed to be receiving

0.5 %

of the maximum flux.

4.3. Results

The activity of bare and Cd covered foils for all three configurations are summarized in Table 1. One can see that there are different proportions in epicadmium and bare foil or total activities as reflected by the Cd ratio. Configuration A is similar to the original thermal column because of the presence of 14.6 cm of water between the NP and the core as opposed to having the SB inserted. As shown in [20], the epithermal flux is an order of magnitude smaller than the thermal flux at 14.6 cm from the core, where the NP wall is located. This is also confirmed by the MCNP energy spectra shown in Figure 4c. As such, the flux through the thermal column should consist of mostly thermal neutrons: this is confirmed as configuration A has the highest initial cadmium ratio in the table.

In configuration B, the water between the NP and reactor core is displaced by the SB. According to Figure 4 in [20], the fast and thermal fluxes should be about the same at the front wall of the SB; therefore we should see an increased presence of epithermal neutrons entering the test tank. Our experimental results demonstrate this through a significantly decreased cadmium ratio at the entrance of the test tank. Additionally, we observed the activity of the foils are higher in configuration B than configuration C due to the change in orientation resulting in less moderation happening at the front of the tank for configuration C. For all configurations, the contribution of epithermal neutrons decreases farther into the tank from the front wall highlighting the relative effect of more thermal moderation. Again, this is confirmed by MCNP simulations (Figure 4b).

For configuration C with the void near the tank entrance wall, the cadmium ratio is approximately constant and similar to the cadmium ratio of the first point of configuration B. This configuration was a mock-up of the real tank and we can see from Table 1 that activation results of the real tank foil located approximately below foil number 5 are very similar.

5. Discussion

The main goal of the mock-up tank activation runs was to characterize how efficiently the non-equilibrium spectrum transport increased the thermal flux as compared to the typical flux in REPs and to the flux of the original graphite-filled thermal column. The secondary goal was to benchmark the expected thermal flux inside the UCN source cryostat, which was then tested again with the real moderator tank measurements.

All three experimental configurations with the test tank were simulated using release 2 of MCNP6. Figure 4a shows the activity converted into neutron fluxes in comparison with the MCNP results for configurations A and B. The experimentally measured fluxes are calculated using Equation (6). Configuration A’s plot shows approximately

20 %

difference between the measured and simulated data throughout the whole tank. For configuration B, the foils closer to the front of the tank show a greater deviation from MCNP than foils further into the tank, from about

30 %

down to

22 %

. Greater deviations from the MCNP correlate with the cadmium ratios: the smaller the ratio, the larger the deviation. As was mentioned in Section 3.1, Equation (6) is valid only for the case of a relatively small epithermal contribution, when the spectrum below the cadmium cut-off can be described using the Maxwell-Boltzmann distribution.

As can be seen in Figure 4c, a Maxwell-Boltzmann distribution is not the case here. The vertical line marks the large resonance peak for gold just above the cadmium cut-off, below which the spectrum still has a noticeable contribution from epithermal flux. To correct for this epithermal flux, a flux-weighted effective Au cross section was calculated with Equation (7). This was only done for configurations A and B with well defined geometry. We determined the average effective cross-section to be approximately 72 b (down from

98.7

b) at the front of the tank and 80 b at 50 cm inside the tank. Since the cadmium ratio for configuration C was approximately constant and very close to the value for the front of the tank in configuration B, we used 72 b for all three points. The resulting experimental flux estimates are shown in Figure 5. After reanalyzing the foil activation data with the corrected cross-section, the results are in much better agreement with the MCNP flux.

From [28], we know that in the original graphite filled thermal column, the flux at the TC entrance was about

4 \times 10^{10}

n/cm²/s, while in configuration A (graphite replaced with D₂O) it became

2 \times 10^{11}

n/cm²/s, a 5x increase. In configuration B for which the SB was inserted and displaced pool water, the flux increased to

1 \times 10^{12}

, i.e. 25 times larger than the original thermal column. This demonstrates that our remote moderation design is able to more efficiently transport neutrons from the core to the thermal column as compared to in-core moderation and therefore increases the thermal neutron flux within the UCN source.

In PULSTAR REP’s the maximum thermal flux is

10^{13}

[20], which is 10 times higher than our result in configuration B. Nevertheless, the lower average thermal flux in the UCN source void evidenced by configuration C and by the real tank measurement is near optimal because it limits the radiation heating that the cryogenic system can remove.

During the most recent run with the real UCN source configuration, radiation surveys were performed to determine the shielding requirements for safe operation of the source. It was found that the increase of the neutron flux in the TC due to the remote moderation results in increased gamma radiation. Another contributing factor was that two grooves had to be made in the TC door Barytes block, one for the neutron guide and another for the LHe transfer tube (Figure 3); this significantly reduced the gamma shielding factor in several spots outside the TC bioshield. The gamma shielding inside the TC was increased by adding a layer of lead bricks in line with the direct view of the reactor core. The gamma radiation survey showed that adding 1 and 2 layers of lead bricks outside the TC door would be sufficient to counteract the transfer tube and neutron guide groove’s gamma hot spots, respectively. To reduce gamma dose to an acceptable public level, additional concrete blocks will be installed.

Our first line of neutron shielding consists of Boral plates covering the back surface of the moderator tank and borated polyethylene blocks around the vacuum jacket tubes located at the back shelf of the tank. Since UCN are reflected at any incident angles, the neutron guide is made from several elbows to avoid direct view of the moderators and reduce direct streaming of higher energy neutrons. As shown in Figure 3, the neutron guide external to the cryostat consists of four segments, bent in horizontal and vertical planes. The first two segments are supported by two 2.5 cm thick borated polyethylene plates each (not shown in Figure 3). The neutron guide groove through the TC door block was filled with a mixture of borated polyethylene and steel shot. The neutron guide and other tubes were also wrapped in rubber containing boron. Figure 6 shows the thermal neutron flux suppression throughout the neutron guide. At the TC door exit, location #6, the thermal flux is below

1 \times 10^{4}

n/cm²/s and can be easily shielded.

6. Conclusions

The UCN source currently being commissioned at the PULSTAR reactor is unique in that it moderates fast neutrons outside the reactor pool at a large distance from the core. It utilizes a specially designed structure which delivers fast and thermal neutrons through the reactor pool to the former thermal column facility, where a large tank with D₂O moderator is located.

There are several advantages of using remote moderation for cryogenic UCN production. The gamma heating from the core is reduced significantly while the thermal neutron flux is largely maintained from the core. In comparison, the thermal neutron flux in configuration B is 25 times greater than that from the original thermal column. This increase shows that we were able to more efficiently transport neutrons to the UCN source by moving the D₂O moderator away from the core and into the thermal column port. The increase in thermal flux was more modest for configuration C. With its thermal flux of approximately

7 \times 10^{11}

n/cm²/s near the front of the tank, it had about an 18 times increase from the original thermal column’s flux. The reason this gain factor is lower is because the tank’s orientation resulted in less moderation volume in the front of the tank and because the tank was intentionally underfilled with D₂O. Although the maximum measured thermal neutron flux at the PULSTAR reactor is

10^{13}

n/cm²/s in the REPs, a value that is a factor of 14 higher than the flux of configuration C, the lower flux is more ideal for UCN production as it perfectly matches our cryogenic setup’s cooling power. With the flux seen in configuration C, the total cryogenic heat load on our source will be less than about 20 W [22] compared to the typical kW at cold neutron sources located adjacent to reactor cores. The large size of the thermal column enclosure also affords the ability to host all required engineering components. Finally, placing flammable deuterium and methane outside the reactor pool liner is also beneficial for the safe operation of the reactor.

The agreement between MCNP and fluxes give us good confidence in predictions of the solid methane neutronic performance, which is crucial for calculating UCN production in solid deuterium. Using an approximate UCN production rate

6 \times 10^{3}

n/cm³/s (see details in [27], pages 55-56), 25 ms life time of UCN in solid deuterium bulk, and 20% extraction efficiency [31], the estimated UCN density delivered outside the biological shield is about ∼30 UCN/cm³ per 1 MW of PULSTAR reactor power [23] compared to the ∼40 UCN/cm³ or about 1 UCN per 1 MW of reactor power at the Steyerl’s turbine [32] at the 50-MW ILL reactor of the Laue-Langevin Institute, Grenoble, France.

Author Contributions

Conceptualization, B. Wehring and E. Korobkina; methodology, B. Wehring, G. Medlin, E. Sharapov, E. Korobkina and C. Teander; validation, A. I. Hawari, R. Golub and E. Sharapov ; formal analysis, G. Medlin, B. Wehring, G. Palmquist and C. Teander; investigation, B. Wehring, G. Palmquist, E. Korobkina, C. Teander, M. Morano, T. Rao, C. Hickman; data curation, G. Medlin; writing-original draft preparation, E. Korobkina, C. Teander, E. Sharapov and G. Medlin; writing–review and editing, A. I. Hawari, R. Golub, A. Young, E. Korobkina, C. Teander, C. Hickman and P. Huffman ; visualization, G. Medlin, C. Teander; supervision, E. Korobkina, P. Huffman, A. I. Hawari and A. Young; project administration, A. I. Hawari and P. Huffman; funding acquisition, A. I. Hawari, A. R. Young and P. Huffman. All authors have read and agreed to the published version of the manuscript.

Funding

This research was supported in part through NSF Award No. PHY-314114, US DOE Award No. DE-FG02-97ER41042, and the US DOE INIE program Award No. DE-FG07-03ID14532.

Acknowledgments

The flux analysis testing and work was performed at the NC State University PULSTAR reactor. The authors wish to thank Austin Wells, Anna Deak, Kerry Kincaid and all PULSTAR reactor staff for their great technical support. Special thanks to Chris Sanford for modifications of the Nose port.

Conflicts of Interest

The authors declare no conflicts of interest.

References

Ban, G.; Chen, J.; Lefort, T.; Naviliat-Cuncic, O.; Saenz-Arevalo, W.; Chiu, P.J.; Clément, B.; Larue, P.; Pignol, G.; Roccia, S.; others. Search for neutron-to-hidden-neutron oscillations in an ultracold neutron beam. Physical Review Letters 2023, 131, 191801. [Google Scholar] [CrossRef]
Zimmer, O.; Piegsa, F.M.; Ivanov, S.N. Superthermal source of ultracold neutrons for fundamental physics experiments. Physical Review Letters 2011, 107, 134801. [Google Scholar] [CrossRef]
Golub, R.; Richardson, D.; Lamoreaux, S.K. Ultra-Cold Neutrons; CRC Press, 2017. [Google Scholar]
Steyerl, A. Ultracold Neutrons; World Scientific, 2020. [Google Scholar]
Koch, B.; Muñoz, E.; Santoni, A. Ultracold neutrons in the low curvature limit: Remarks on the post-Newtonian effects. Physical Review D 2024, 109, 064085. [Google Scholar] [CrossRef]
Michaudon, A. Use of ultracold neutrons for condensed-matter studies. 1997. [Google Scholar] [CrossRef]
Ignatovich, V.K.; Pontecorvo, G. The physics of ultracold neutrons; Oxford University Press, 1990. [Google Scholar]
Altarev, I. Universal liquid-hydrogen source of polarized cold and ultracold neutrons at the VVR-M reactor of the Leningrad Institute of Nuclear Physics. Pis’ma Zh. Eksp. Teor. Fiz. 1986, 44, 269–272. [Google Scholar]
Steyerl, A.; Nagel, H.; Schreiber, F.X.; Steinhauser, K.A.; Gähler, R.; Gläser, W.; Ageron, P.; Astruc, J.; Drexel, W.; Gervais, G.; Mampe, W. A new source of cold and ultracold neutrons. Phys. Lett. A 1986, 116, 347–352. [Google Scholar] [CrossRef]
Wikipedia contributors. Liouville’s theorem (Hamiltonian). Available online: https://en.wikipedia.org/wiki/Liouville%27s_theorem_(Hamiltonian) (accessed on 26 July 2024).
Golub, R.; Ageron, P.; Mampe, W.; McLintock, P. A ‘super-thermal’source for ultra-cold neutrons. Neutron Capture Gamma-Ray Spectroscopy 1979, 615–617. [Google Scholar]
Karch, J.; Sobolev, Y.; Beck, M.; Eberhardt, K.; Hampel, G.; Heil, W.; Kieser, R.; Reich, T.; Trautmann, N.; Ziegner, M. Performance of the solid deuterium ultra-cold neutron source at the pulsed reactor TRIGA Mainz. Eur. Phys. J. A 2014, 50, 78. [Google Scholar] [CrossRef]
Serebrov, A.P.; Fomin, A.K.; Kharitonov, A.G.; Lyamkin, V.A.; Prudnikov, D.V.; Ivanov, S.A.; Erykalov, A.N.; Onegin, M.S.; Gridnev, K.A. High-density ultracold neutron sources for the WWR-M and PIK reactors. Crystallogr. Reports 2016, 61, 144–148. [Google Scholar] [CrossRef]
Serebrov, A.; Mityukhlyaev, V.; Zakharov, A.; Kharitonov, A.; Shustov, V.; Kuz’minov, V.; Lasakov, M.; Tal’daev, R.; Aldushchenkov, A.; Varlamov, V.; Vasil’ev, A.; Sazhin, M.; Greene, G.; Bowles, T.; Hill, R.; Seestrom, S.; Geltenbort, P. Studies of a solid-deuterium source for ultra-cold neutrons. Nucl. Instr. Meth. Phys. Res. A 2000, 440, 658–665. [Google Scholar] [CrossRef]
Trinks, U.; Hartmann, F.; Paul, S.; Schott, W. Concepts of UCN sources for the FRM-II. Nucl. Instr. Meth. Phys. Res. A 2000, 440, 666–673. [Google Scholar] [CrossRef]
Frei, A.; Sobolev, Y.; Altarev, I.; Eberhardt, K.; Gschrey, A.; Gutsmiedl, E.; Hackl, R.; Hampel, G.; Hartmann, F.J.; Heil, W.; Kratz, J.V.; Lauer, T.; Liźon Aguilar, A.; Müller, a.R.; Paul, S.; Pokotilovski, Y.; Schmid, W.; Tassini, L.; Tortorella, D.; Trautmann, N.; Trinks, U.; Wiehl, N. First production of ultracold neutrons with a solid deuterium source at the pulsed reactor TRIGA Mainz. Eur. Phys. J. A 2007, 34, 119–127. [Google Scholar] [CrossRef]
Serebrov, A.P.; Mityukhlyaev, V.A. Experimental study of a solid-deuterium source of ultracold neutrons. JETP Lett. 1995, 62, 785–790. [Google Scholar]
Serebrov, A.; Lyamkin, V. Development of UCN sources at PNPI. Journal of Neutron Research 2022, 24, 145–166. [Google Scholar] [CrossRef]
Goorley, T.; James, M.; Booth, T.; Brown, F.; Bull, J.; Cox, J.; Durkee, J. Initial MCNP6 Release Overview. Nucl. Technol. 2012, 180, 298–315. [Google Scholar] [CrossRef]
Hawari, A.I. North Carolina State University PULSTAR Reactor. In Encyclopedia of Nuclear Energy; Elsevier, 2021. [Google Scholar]
Wehring, B.; Young, A. Ultracold Neutron Source at the North Carolina State Research Reactor. Trans. Am. Nucl. Soc. 2001, 83, 120. [Google Scholar]
Korobkina, E.; Wehring, B.; Hawari, A.; Young, A.; Huffman, P.; Golub, R.; Xu, Y.; Palmquist, G. An ultracold neutron source at the NC State University PULSTAR reactor. Nucl. Instr. Meth. Phys. Res. A 2007, 579, 530–533. [Google Scholar] [CrossRef]
Korobkina, E.; Medlin, G.; Wehring, B.; Hawari, a.I.; Huffman, P.R.; Young, a.R.; Beaumont, B.; Palmquist, G. Ultracold neutron source at the PULSTAR reactor: Engineering design and cryogenic testing. Nucl. Instr. Meth. Phys. Res. A 2014, 767, 169–175. [Google Scholar] [CrossRef]
Yu, Z.C.; Malik, S.S.; Golub, R. A thin film source of ultra-cold neutrons. Zeitschrift für Physik B Condensed Matter 1986, 62, 137–142. [Google Scholar] [CrossRef]
Atchison, F.; Blau, B.; Bodek, K.; Van den Brandt, B.; Bryś, T.; Daum, M.; Fierlinger, P.; Frei, A.; Geltenbort, P.; Hautle, P.; others. Cold neutron energy dependent production of ultracold neutrons in solid deuterium. Physical review letters 2007, 99, 262502. [Google Scholar] [CrossRef]
Frei, A.; Gutsmiedl, E.; Morkel, C.; Müller, A.; Paul, S.; Rols, S.; Schober, H.; Unruh, T. Understanding of ultra-cold–neutron production in solid deuterium. Europhysics Letters 2011, 92, 62001. [Google Scholar] [CrossRef]
Medlin, G. Characterization of the PULSTAR Ultracold Neutron Source. PhD thesis, North Carolina State University, 2017. [Google Scholar]
Xu, Y. Characterization of solid deuterium ultracold neutron source production and UCN transport. PhD thesis, North Carolina State University, 2006. [Google Scholar]
Westcott, C.H.; Walker, W.H.; Alexander, T.K. Effective Cross Sections and Cadmium Ratios for the Neutron Spectra of Thermal Reactors. 1959. [Google Scholar]
ASTM. Standard Test Method for Determining Thermal Neutron Reaction Rates and Thermal Neutron Fluence Rates by Radioactivation Techniques; Standard, ASTM International, 2017. [Google Scholar]
Palmquist, G. Design and Construction of the Ultracold Neutron Source at the NC State PULSTAR Research Reactor. PhD thesis, North Carolina State University, 2014. [Google Scholar]
Steyerl, A. A “neutron turbine” as an efficient source of ultracold neutrons. Nucl. Instr. Meth. 1975, 125, 461. [Google Scholar] [CrossRef]

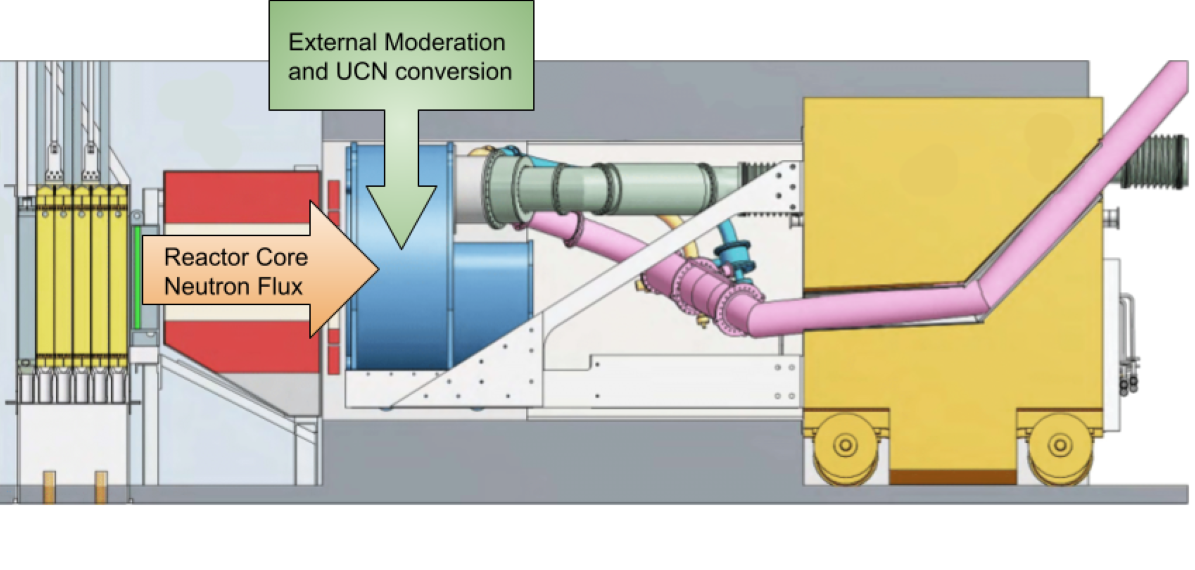
Figure 1. Components of the UCN source beam port

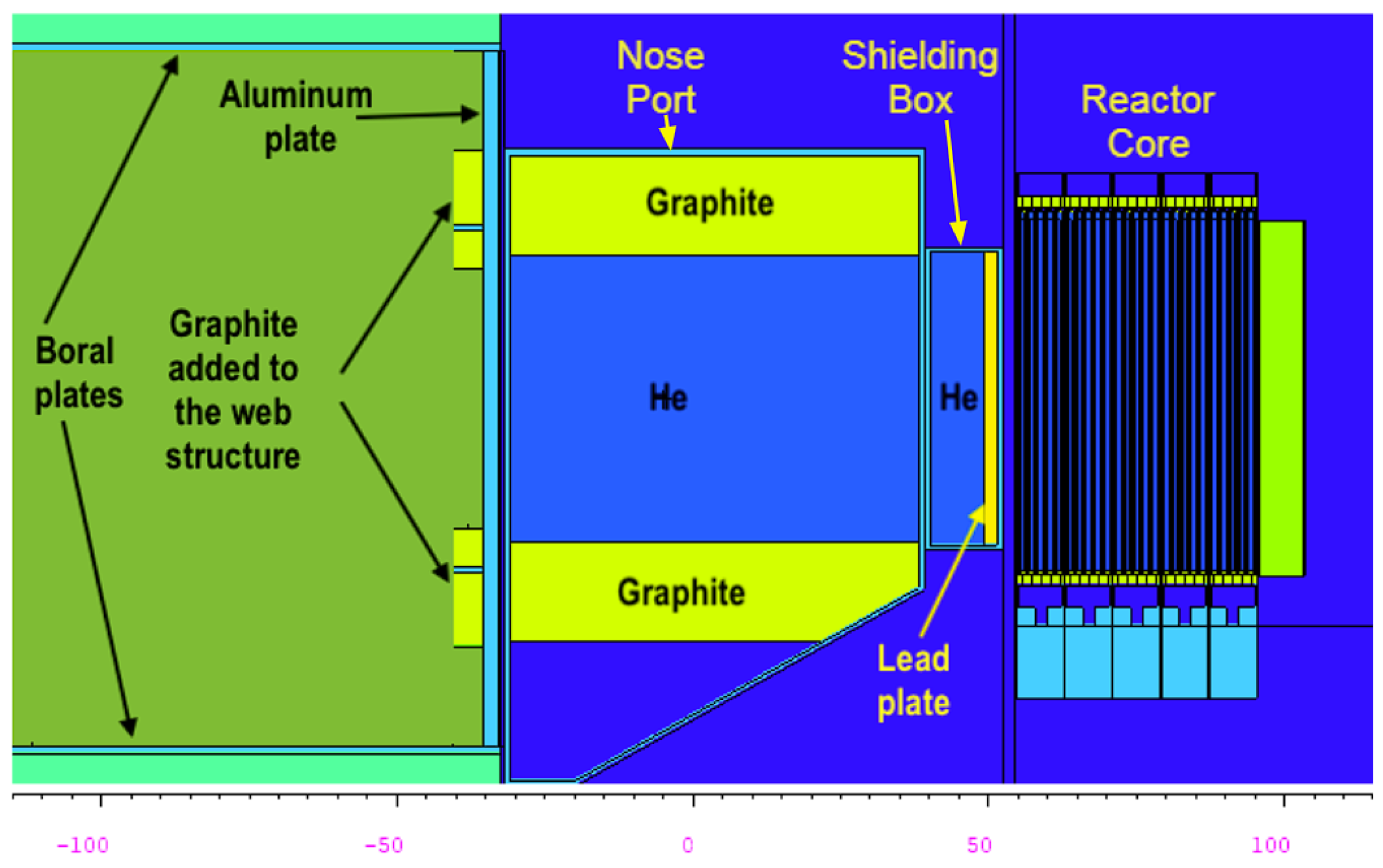
Figure 2. The MCNP geometry configurations for the foil activation using the test tank. Configuration A had the well facing away and with no shielding box. Configuration B had the well facing away with the shielding box inserted. Configuration C had the well facing towards the reactor, the shielding box inserted, acrylic blocks inside of the vertical well (as a mock-up of methane), and the test tank was not fully filled with D₂O. The horizontal top void mimicked the elbow shaped vacuum jacket of the inner cryostat and is 30 cm high on this plot. The numbers in configuration B show: (1) the reactor core, (2) the shielding box, (3) the nose port, (4) the test tank filled with D₂O, (5) the rectangular tube in which the foils were placed, and (6) the vertical well mimicking the cryostat void.

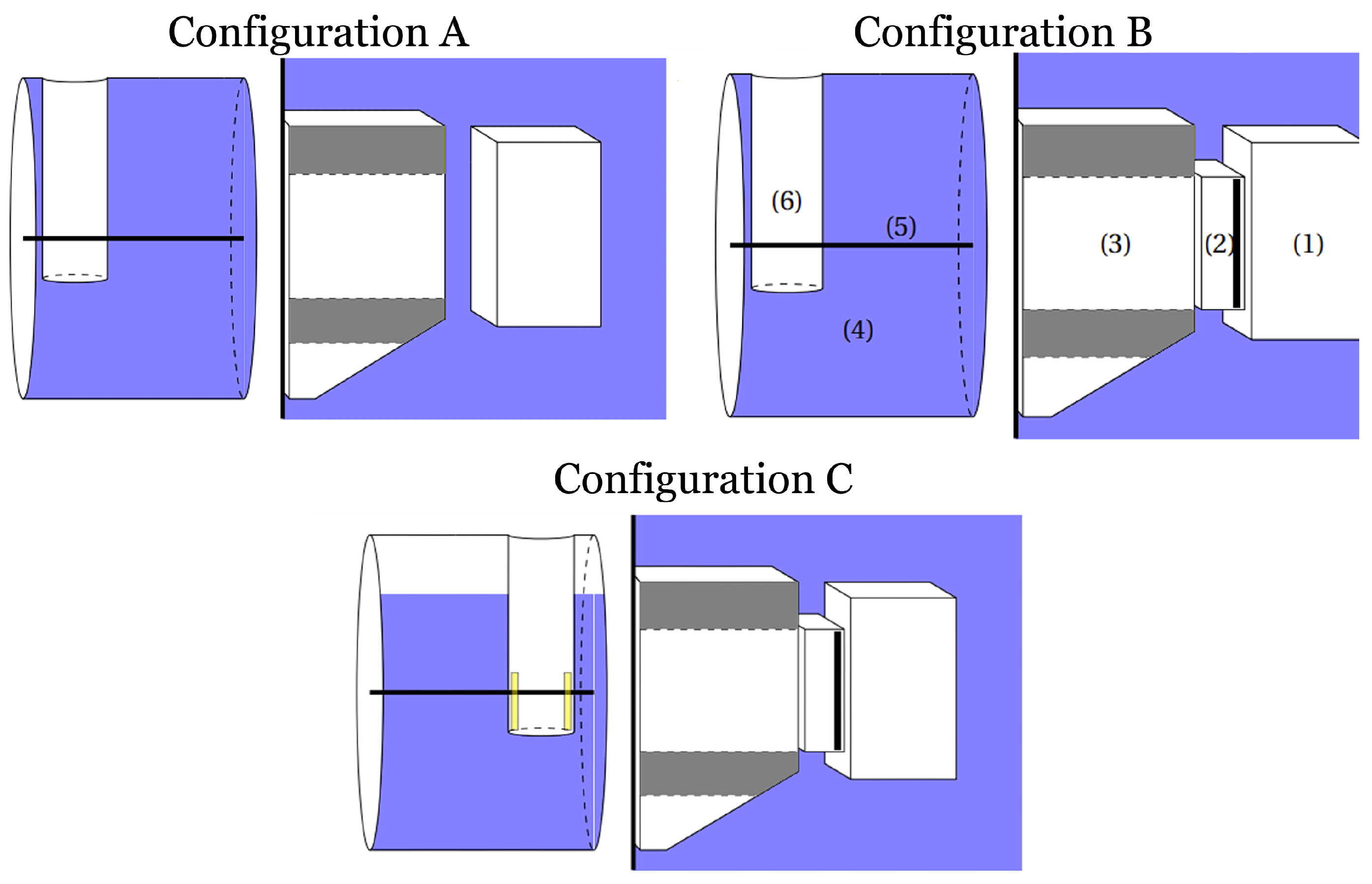
Figure 3. An engineering schematic of the UCN Source. The numbers in parenthesis correspond to: (1) - the heavy water moderator tank, (2) - solid methane container, (3) - solid deuterium and inner neutron guide container, (4) - vacuum jacket for components (2) and (3), (5) - deuterium and methane transfer lines, (6) - the external UCN guide and the surrounding vacuum jacket, (7) - thermal column door, and (8) - liquid helium transfer line. The numbers #1-7 in gold boxes represent the locations of gold foils during the foil activation test, and In1 and In2 refer to the two locations of indium samples. Note, that components (2) and (3) were not present for the gold foil activation tests.

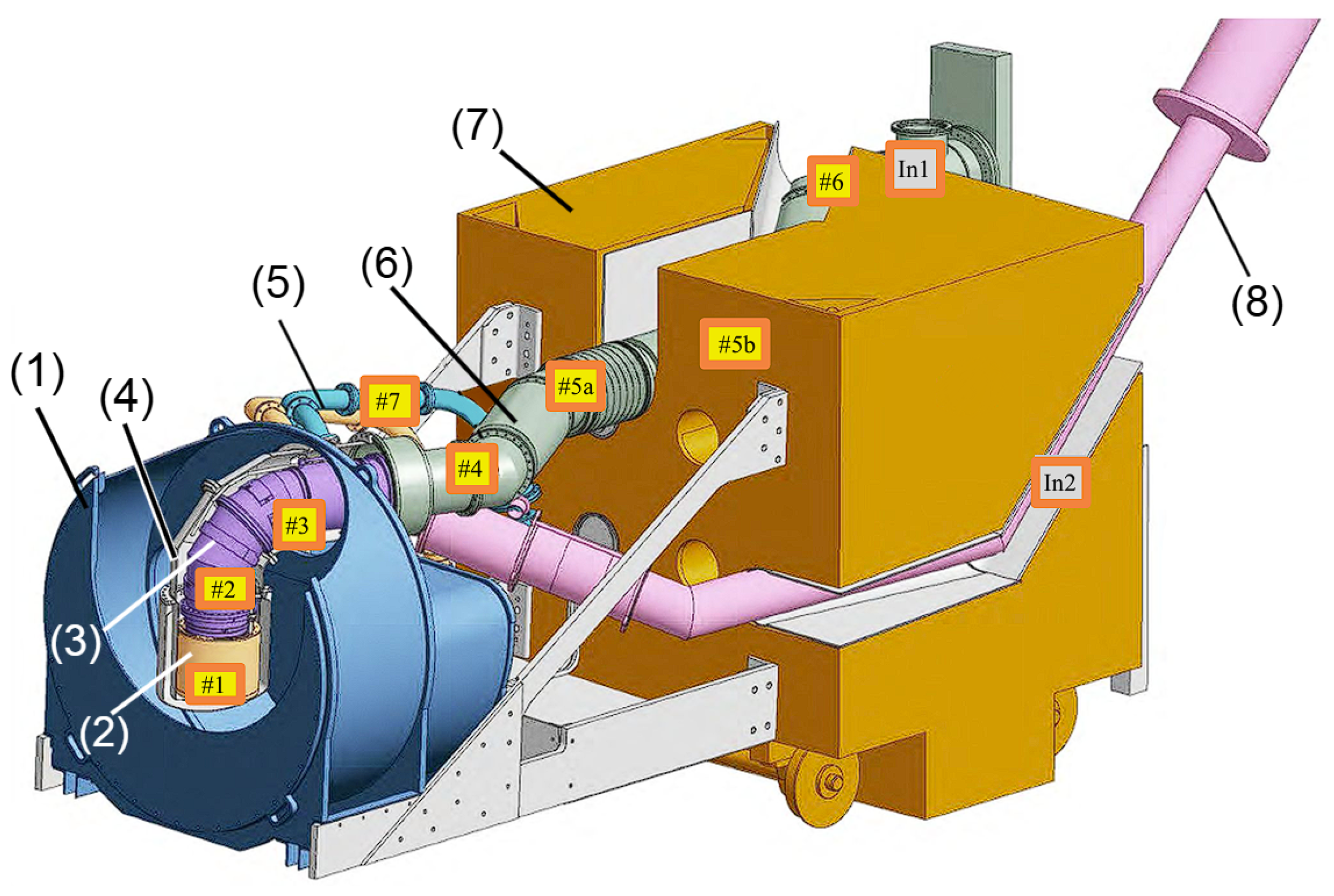
Figure 4. The top two graphs labeled (a) show the MCNP predictions for the thermal flux compared with the foil measurements for two of the different test tank configurations evaluated following the Stoughton and Halperin convention. Below those in (b) and (c) is their corresponding energy spectrum as obtained through MCNP. The more epithermal neutrons present in the system, the worse the typical foil activation analysis method for determining the thermal flux.

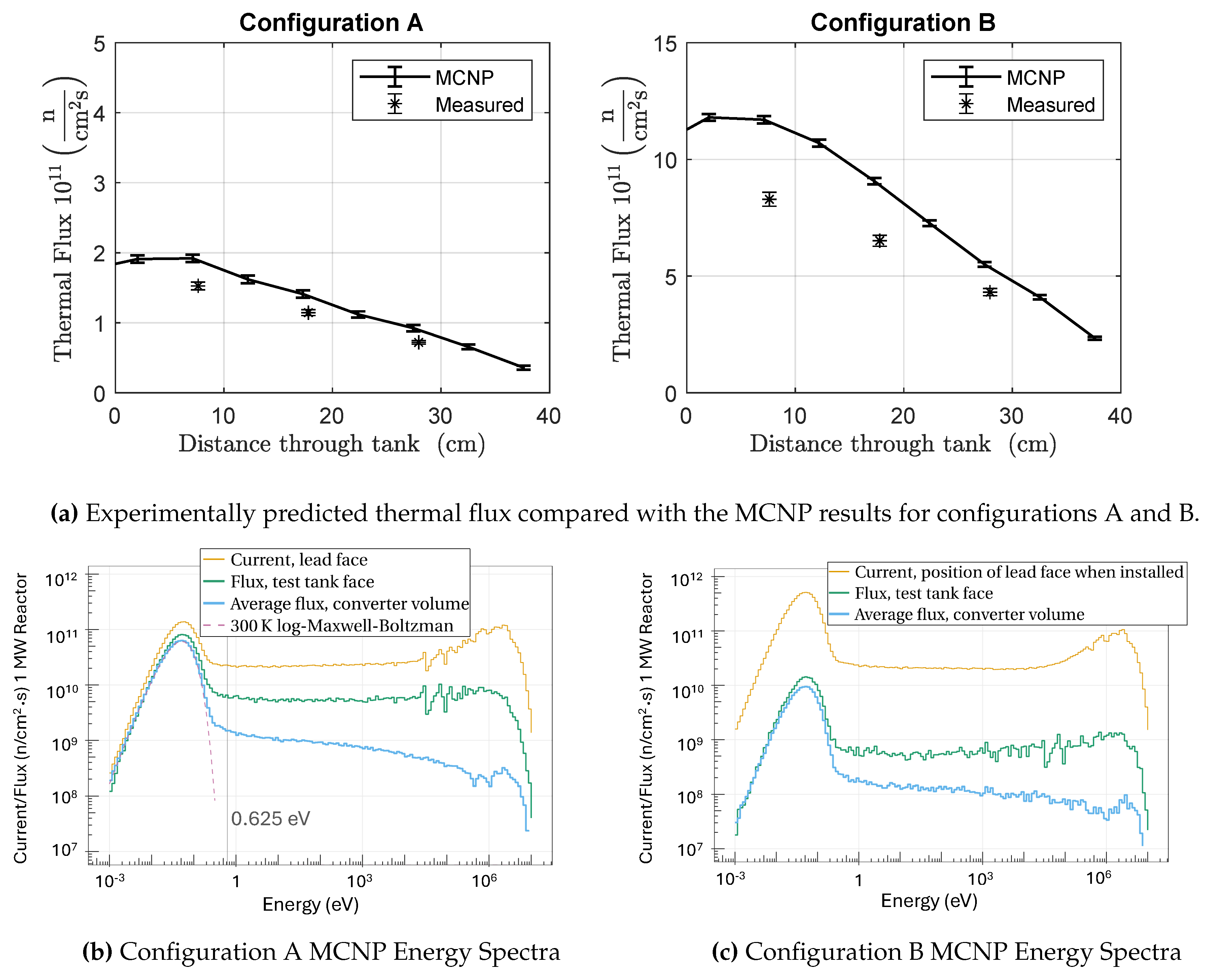
Figure 5. The results for all test tank configurations with the foil flux analysis reanalyzed using an MCNP informed flux-weighted cross section. Energy spectra simulations were completed for configurations A and B, but were not done for configuration C. The cross section used to reanalyze the data for C was a constant 72 barns which was determined by comparing experimentally measured cadmium ratios between the configurations.

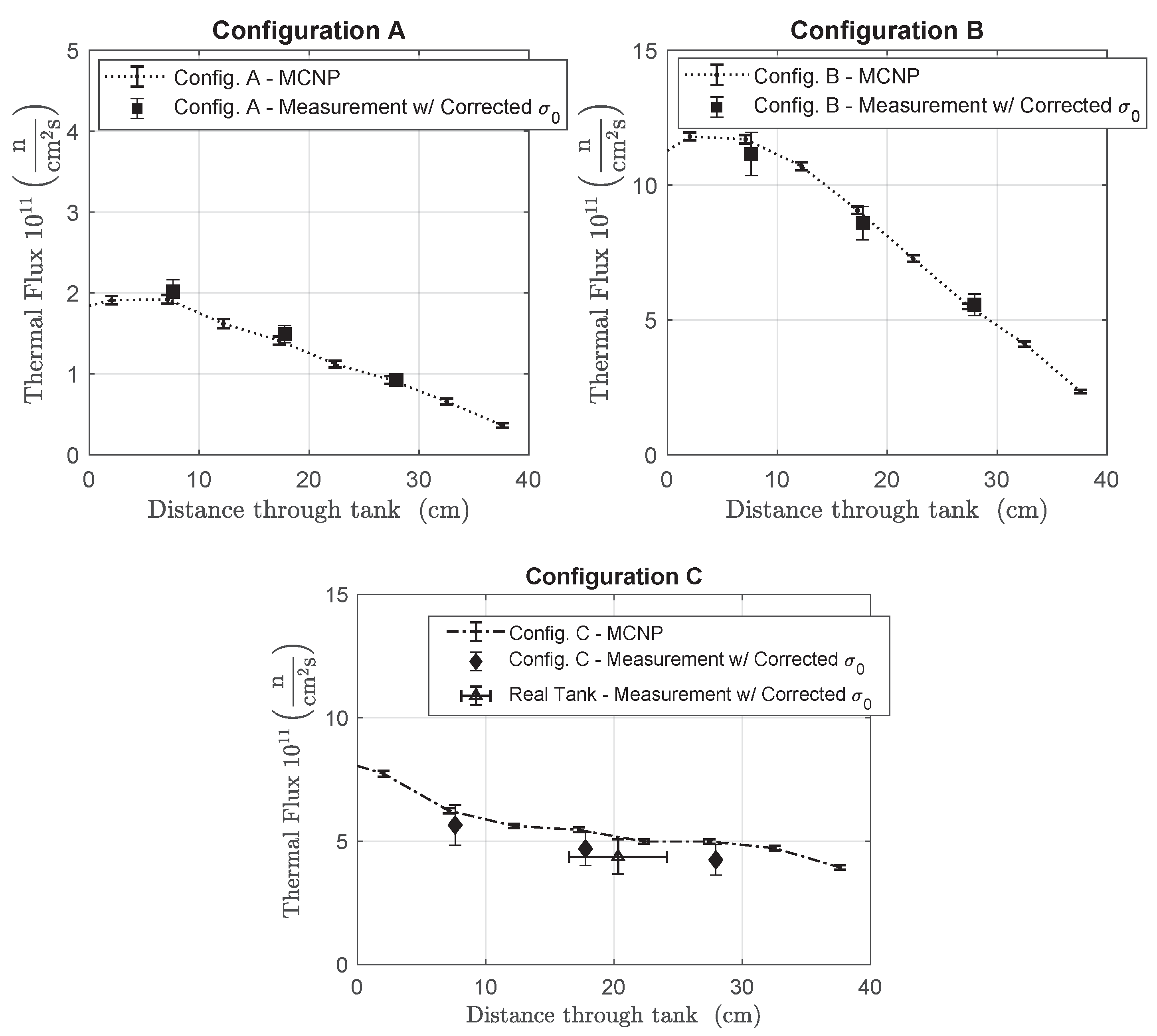
Figure 6. The thermal neutron flux at each foil location in the UCN source as shown in Figure 3. There is no data for the gold foil at location 6 as the activation of the foil was too low to measure.

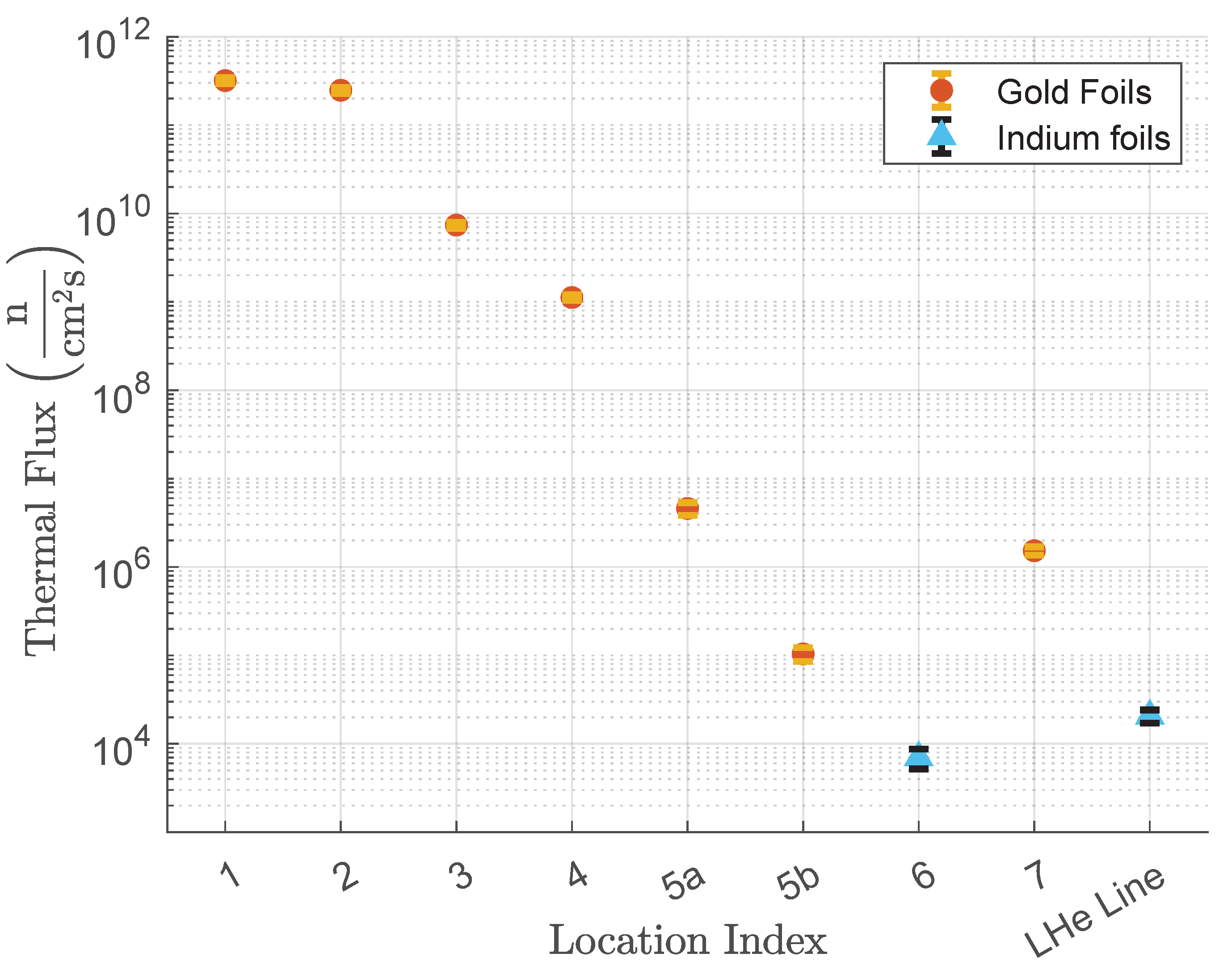
Table 1. Foil activities, cadmium ratios, and the effective cross section corrections used for the test and real tank. For configurations A,B, and C, the odd numbered bare foil activities are from the experiment, but the even numbered ones are linear interpolations from the surrounding foils. The effective cross section terms for configurations A and B were calculated from MCNP energy spectra data, but similar data did not exist for configuration C or the real tank, so a constant approximate value was used. Only one data point was included for the real tank as it was assumed that only foil location #1 (shown in Figure 3 approximately 23 cm back from the front of the tank) could be compared with the foils passing in the test tank configurations.

Configuration		1 - $2.5$ cm	2 - $7.6$ cm	3 - $12.7$ cm	4 - $17.8$ cm	5 - $22.9$ cm	6 - $28.0$ cm	7 - $33.0$ cm
Configuration A	Bare $A^{'}$	1.94 × 10⁻¹¹	1.70 × 10⁻¹¹	1.45 × 10⁻¹¹	1.21 × 10⁻¹¹	9.72 × 10⁻¹²	7.54 × 10⁻¹²	5.36 × 10⁻¹²
	Cd $A^{'}$	-	1.24 × 10⁻¹²	-	5.63 × 10⁻¹²	-	2.83 × 10⁻¹³	-
	Cd Ratio	-	13.66	-	21.54	-	26.66	-
	Eff. $σ_{0}$ (b)	-	74.69	-	75.75	-	76.82	-
Configuration B	Bare $A^{'}$	1.10 × 10⁻¹⁰	9.73 × 10⁻¹¹	8.43 × 10⁻¹¹	7.05 × 10⁻¹¹	5.67 × 10⁻¹¹	4.44 × 10⁻¹¹	3.22 × 10⁻¹¹
	Cd $A^{'}$	-	9.98 × 10⁻¹²	-	4.01 × 10⁻¹²	-	1.20 × 10⁻¹²	-
	Cd Ratio	-	9.75	-	17.58	-	37.04	-
	Eff. $σ_{0}$ (b)	-	73.35	-	74.84	-	76.55	-
Configuration C	Bare $A^{'}$	5.74 × 10⁻¹¹	5.03 × 10⁻¹¹	4.32 × 10⁻¹¹	4.01 × 10⁻¹¹	3.70 × 10⁻¹¹	3.58 × 10⁻¹¹	3.46 × 10⁻¹¹
	Cd $A^{'}$	-	6.18 × 10⁻¹²	-	4.08 × 10⁻¹²	-	3.37 × 10⁻¹²	-
	Cd Ratio	-	8.14	-	9.83	-	10.62	-
	Eff. $σ_{0}$ (b)	-	72	-	72	-	72	-
Real Tank	Bare $A^{'}$	-	-	-	-	3.88 × 10⁻¹¹	-	-
	Cd $A^{'}$	-	-	-	-	4.76 × 10⁻¹²	-	-
	Cd Ratio	-	-	-	-	8.15	-	-
	Eff. $σ_{0}$ (b)	-	-	-	-	72	-	-

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

External Moderation of Reactor Core Neutrons for Optimized Production of Ultra-Cold Neutrons

Abstract

1. Introduction

2. Transport of Non-Equilibrium Neutrons from Reactor Core to the UCN Source Moderator

2.1. UCN Source at NC State University PULSTAR Reactor

2.2. Description of UCN Source Beam Port Components

3. Foil Activation Method for Neutron Flux Characterization

3.1. Foil Activation Theory

4. Experimental Results

4.1. Description of Activation Measurements Using Test Tank

4.2. Description of Activation Measurements Using the Real UCN Source Tank

4.3. Results

5. Discussion

6. Conclusions

Author Contributions

Funding

Acknowledgments

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe