Six Dimensions for Proof of Riemann Hypothesis

Preprint

Article

Six Dimensions for Proof of Riemann Hypothesis

Altmetrics

Downloads

170

Views

Comments

seyed kazem mousavi^*

This version is not peer-reviewed

Submitted:

28 August 2024

Posted:

28 August 2024

You are already at the latest version

Alerts

Abstract

This paper presents proof of Riemann's hypothesis by utilizing the golden ratio and the ellipse's eccentricity in six dimensions. This proof extends across all scientific fields. this research introduces logical and mathematical principles for distributing, recognizing, and categorizing prime numbers. It also explores the relationship between prime numbers and the complex conjugate of five prime numbers in various dimensions. Accordingly, it delves into the classification of even numbers based on prime numbers. This study examines the proof of Riemann's hypothesis from a geometric dimension perspective. Based on this, the mathematical structure of an integrated theory is defined. properties and principles associated with prime numbers reveal connections between quantum mechanics and general relativity.

Keywords:

Subject: Computer Science and Mathematics - Mathematics

1. Introdoction

Riemann's hypothesis along with twin primes is one of Hilbert's unsolved problems. Also, this problem is one of the most important problems of the millennium [1,2]. There are many proposed methods to prove this hypothesis [2,3,4,5]. Examining the zeta function in different dimensions is a more logical approach. [6,7,8] Proving the Riemann hypothesis with six-dimensional space-time is a new approach. This research is based on this approach [9]. Examining the eccentricity of the ellipse of the zeta function determines the relationship between the variables of the Riemann function [10]. Hyper-geometry for the distribution of prime numbers is a useful step to prove the Riemann hypothesis [11].

In this article, the real Riemann function is introduced based on the eccentricity of the ellipse. The relationship between the eccentricity of the ellipse in two imaginary dimensions and the zeta function is investigated. The existence of Simple zeros for negative even numbers indicates the periodic fluctuation of the function. It has also been investigated using the golden ratio based on the doubling ratio and the 1/2 point for the real part of the zeta function. The logical connection between the eccentricity of the ellipse and the golden ratio paves the way for understanding the distribution of prime numbers. The proof of Riemann's hypothesis based on the structure of the Mobius space in six dimensions is the proof of the nature of prime numbers based on sequences such as the Fibonacci sequence.

2. Method

Ellipse eccentricity can be expressed trigonometrically. (2.1)

\sqrt{1 - \frac{x^{2}}{y^{2}}} = \sin (θ) = s i n ({c o s}^{- 1} \frac{x}{y})

(2.1)

A radian on the circumference of a circle is less than 60 degrees. (2.2) Therefore, the sum of one radian and ((π-2)/4π) is equal to 1/4 of the circumference of the circle.

60^{°} - ((\frac{1}{2 π}) 360) = {2.70422048692}^{°}

(2.2)

(\frac{1}{2 π}) + (\frac{π - 2}{4 π}) = \frac{1}{4}

The eccentricity of the ellipse can indicate changes in the circumference of the circle (density). (2.3)

{x = 1 \Rightarrow \sin}^{2} (θ) = 1 - \frac{x}{y} = 1 - y^{- 1}

(2.3)

The golden ratio uses the doubling ratio. (2.4)

\frac{1 + \sqrt{5}}{2} = φ

(2.4)

Möbius space transfers properties of higher dimensions to lower dimensions. (2.5)

w = \frac{a z + b}{c z + d} b \neq d

(2.5)

Riemann's zeta function is convergent for values greater than one. (2.6)

ζ (s) = \frac{1}{Γ (s)} \int_{0}^{\infty} \frac{x^{s - 1}}{e^{x} - 1} d x \to Γ (s) = \int_{0}^{\infty} x^{s - 1} e^{- x} d x

(2.6)

Based on the study of Leonhard Euler, the Riemann zeta function is coded based on prime numbers. (2.7)

ζ (s) = \sum_{n = 1}^{\infty} n^{- s} = \frac{1}{1^{s}} + \frac{1}{2^{s}} + \frac{1}{3^{s}} + \frac{1}{4^{s}} + \dots

(2.7)

ζ (s) = \prod_{p \in P} \frac{1}{1 - p^{- s}} = \frac{1}{1 - 2^{- s}} \cdot \frac{1}{1 - 3^{- s}} \cdot \frac{1}{1 - 5^{- s}} \cdot \frac{1}{1 - 7^{- s}} \dots

The Riemann conjecture of convergence for real points is 1/2. (2.8)

ζ (s) = ζ (\frac{1}{2} + i t) = 0

(2.8)

A one-dimensional line in the Möbius space equal to the created eccentric radius rotating a quarter in the circumference of the circle, which also applies to higher dimensions. (2.9)

{(\frac{1}{2})}^{2} 2 π r {(\frac{1}{2})}^{3} 4 π r^{2} {(\frac{1}{2})}^{4} 2 π^{2} r^{3} {(\frac{1}{2})}^{5} \frac{8}{3} π^{2} r^{4} {(\frac{1}{2})}^{6} π^{3} r^{5} {(\frac{1}{2})}^{6} π^{3} r^{5} ≅ l n (φ)

(2.9)

3. Results

Based on the Möbius function and Möbius space in 5 dimensions, we check the Riemann zeta function. (3.1)

M \{1, - 1, - 1,0, - 1,1\} \frac{1}{ζ (s)} = \sum_{n = 1}^{\infty} \frac{μ (n)}{n^{s}}

(3.1)

Ellipse eccentricity for a circle embedded on a sphere is equal to the complex conjugate product of Riemann's zeta function at the point 1/2. (3.2)

ζ ζ^{*} = {s i n}^{2} (θ) \Rightarrow s i n (\cos (\frac{1}{x^{n}})) \Rightarrow s ⟶ (\frac{1}{4} \pm 0)

(3.2)

Based on Taylor's expansion around point 0, the sine x function is expressed based on odd numbers. (3.3)

\sin (x) = x - \frac{x^{3}}{3!} + \frac{x^{5}}{5!} - \frac{x^{7}}{7!} + \dots

(3.3)

Considering the eccentricity of the ellipse from the perspective of the surface of a four-dimensional sphere, we rewrite sin^2x. (3.4)

{s i n}^{2} (θ) = 1 - x^{- 1} a_{μ ν} = [\begin{matrix} 1 & 0 & 0 \\ 0 & {s i n}^{2} θ & 0 \\ 0 & 0 & {s i n}^{2} θ {s i n}^{2} ϕ \end{matrix}] \Rightarrow

(3.4)

Considering the zeros of Riemann's zeta function for negative even numbers, we express this metric in cosine form. (3.5)

a_{μ ν} = [\begin{matrix} {c o s}^{2} θ {c o s}^{2} ϕ & 0 & 0 \\ 0 & {c o s}^{2} θ & 0 \\ 0 & 0 & 1 \end{matrix}] \Rightarrow |a_{μ ν}| = {c o s}^{2} (60) {c o s}^{2} (120) {c o s}^{2} (120) = {(\frac{1}{2})}^{6}

(3.5)

According to the Riemann hypothesis, in a real period for the Riemann function, a six-dimensional sphere is defined with five degrees of freedom and two imaginary vectors. (3.6)

g_{μ ν} = [\begin{matrix} {a^{2} c o s}^{2} θ {c o s}^{2} ϕ & 0 & 0 & 0 & 0 & 0 \\ 0 & a^{2} {c o s}^{2} θ & 0 & 0 & 0 & 0 \\ 0 & 0 & \frac{a^{2}}{r^{2}} & 0 & 0 & 0 \\ 0 & 0 & 0 & \frac{r^{2}}{a^{2}} & 0 & 0 \\ 0 & 0 & 0 & 0 & r^{2} {s i n}^{2} θ & 0 \\ 0 & 0 & 0 & 0 & 0 & r^{2} {s i n}^{2} θ {s i n}^{2} ϕ \end{matrix}]

(3.6)

According to the Möbius space, the eccentricity of the ellipse, Riemann's hypothesis, and the golden ratio, we state the equality condition. (3.7)

(3 + 6 i) (3 - 6 i) = 9 + 36 = 45 \Rightarrow \sin (45) = \cos (45) = \frac{1}{\sqrt{2}}

(3.7)

(\frac{2 \sin (60) + 1}{2 \cos (60) + 2 i}) (\frac{2 \sin (60) - 1}{2 \cos (60) - 2 i}) = \frac{2}{5} (\frac{2 \sin (30) + 1}{2 \cos (60) + 2 i}) (\frac{2 \sin (30) - 1}{2 \cos (60) - 2 i}) = 0

Based on this, the convergence of the function is natural for real numbers greater than 1. (3.8) Figure 1

\sum_{n = 0}^{\infty} \frac{{(\frac{1 + \sqrt{5}}{2})}^{n} (\frac{1}{2})}{n! e^{\frac{1 + \sqrt{5}}{2}}} (x - 0.5)

(3.8)

But it diverges at point 1/2 in an infinite period. (3.9)

Ψ (x) ~ Υ (k) = \sum_{n = 0}^{\infty} \frac{γ^{n} (k) a}{n!} {(x - a)}^{n}

f = e^{- 2 x} Ψ (x) ~ Υ (k) =

(\sum_{n = 0}^{\infty} \frac{{(\frac{1 + \sqrt{5}}{2})}^{n} (\frac{1}{2})}{n! e^{\frac{1 + \sqrt{5}}{2}}} ((\frac{1}{2 π}) - 0.5)) (\sum_{n = 0}^{\infty} \frac{{(\frac{1 + \sqrt{5}}{2})}^{n} (\frac{1}{2})}{n! e^{\frac{1 + \sqrt{5}}{2}}} (\frac{1}{2 π} + 0.5))

Based on the golden ratio and two imaginary vectors, the hypergeometric distribution is the probability distribution rate of the prime numbers in this space. (3.10)

1 + \sum_{x = 1}^{n} ((\frac{x! + 2 x!}{2})) = 1 + \frac{3}{2} H G ([1,2], [], 1) - \frac{3}{2} Γ (n + 2) H G ([1, n + 2], [], 1)

(3.10)

Therefore, by using Khayyam-Pascal's expansion, it is possible to calculate the repeatable properties of prime numbers. For example, The fifty-second number of the prime numbers. 3.11

P_{52} = 233 \Rightarrow 2 + 3 + 3 = 8 \Rightarrow (\frac{1}{2^{2}} + \frac{1}{2^{3}} + \frac{1}{2^{3}}) = 0.5 \Rightarrow {c o s}^{- 1} (0.5) = 60 \sin (60) = \sqrt{\frac{3}{2}}

According to the equality condition (3.7), the properties of prime numbers repeat periodically. Logical relationships are established for different groups of prime numbers. (3.8) Table 1.

\frac{(9^{2} \times 2^{9})}{92} = \frac{C}{23} \frac{(22^{2 + 22} \times 2^{22 + 2})}{2222} = \frac{C}{101} \frac{(8^{2} \times 2^{8})}{82} = \frac{C}{41} \Rightarrow

Due to the existence of a natural difference between one radian and a quarter of the circumference of a circle, these relationships are obtained based on the golden constant growth rate in the five dimensions of six dimensions, of the ninth prime number. (3.9)

{(\frac{1}{2 π})}^{3} {(\frac{1}{2})}^{6} π^{3} {(\frac{1}{\sqrt{2}})}^{5} = \frac{1}{2048 \sqrt{2}}

Therefore, the ninth prime number represents the end of the first period in the cycle of prime numbers. The hypergeometric distribution of this period is expressed based on the point 1/2. (3.10)

p f (X, u) = \{\begin{matrix} 0 u < 0 \\ 0 3 < u \\ (\frac{1}{6}) ((b i n o m i a l (3, u)) ((b i n o m i a l (3, 5 - u)) o t h e r \end{matrix} p f (X, 2); \frac{1}{2} \bar{X} = \frac{5}{2}

The repetition of the properties of prime numbers determines how they are distributed. (3.11)

(\sum_{x = 1}^{9} {(\frac{\ln (2)}{\ln (10)})}^{9} ≅ 60^{°} - ((\frac{1}{2 π}) 360)

(3.11)

According to Riemann's assumption about the zeros of the zeta function for the real part of 1/2, prime numbers can be categorized into two distinct groups: symmetric primes and asymmetric primes. Symmetric primes, including pairs and mirror primes, exhibit properties such as 11, 17, and 23. On the other hand, asymmetric primes, such as 23, mark the beginning of a distinct period in prime number distribution. These asymmetric primes are characterized by being a combination of an even number and ending with the digit 3. (3.12)

\frac{P_{n}}{k} = \frac{x}{2^{σ}} + \frac{y}{2^{σ}} + \frac{z}{2^{σ}} + \dots

(3.12)

The nature of prime numbers:

Every real number has a wave function. This function fluctuates in the space of complex numbers. The wave function is made up of smaller parts. Each of which represents the wavelength of the function. Y and Z axes are for one-dimensional objects on the surface of an imaginary sphere. Geometric potential difference (density) is the displacement factor. These changes are made based on the first one-digit numbers. (3.13) Different dimensions determine the geometric relationship between prime numbers based on the equality of sine, cosine, tangent, and cotangent. Figure 2 and Figure 3.

|Ψ⟩ = b_{1} |{\tilde{ψ}}_{1}⟩ + b_{2} |{\tilde{ψ}}_{2}⟩ + \dots + b_{n} |{\tilde{ψ}}_{n}⟩ |\tilde{ψ}⟩ = α_{1} |A_{1}⟩ + α_{2} |A_{2}⟩ + α_{3} |A_{3}⟩ + α_{4} |A_{4}⟩ + α_{5} |A_{5}⟩ + α_{6} |A_{6}⟩ b_{μ} = x_{μ} + t i, X_{μ} = (x_{1}, x_{2}, x_{3}, x_{4}, x_{5}, x_{6}) \Rightarrow b_{μ} {b_{μ}}^{*} = (\frac{1}{3})

(3.13)

Prime numbers are complex products of other prime numbers. (3.14)

(\sqrt{2} + 7 i) (\sqrt{2} - 7 i) = 51 (\sqrt{2} + 3 i) (\sqrt{2} - 3 i) = 11 (3 \sqrt{2} + 3 i) (3 \sqrt{2} - 3 i) = 43 (6 \sqrt{2} + 7 i) (6 \sqrt{2} - 7 i) = 121

(3.14)

Prime number:

(\sqrt{0} + 1 i) (\sqrt{0} - 1 i) = 1 (\sqrt{1} + 1 i) (\sqrt{1} - 1 i) = 2 (\sqrt{2} + 1 i) (\sqrt{2} - 1 i) = 3 (\sqrt{1} + 2 i) (\sqrt{1} - 2 i) = 5 (\sqrt{3} + 2 i) (\sqrt{3} - 2 i) = 7 (\sqrt{2} + 3 i) (\sqrt{2} - 3 i) = 11 (\sqrt{1} + 4 i) (\sqrt{1} - 4 i) = 17 (\sqrt{3} + 4 i) (\sqrt{3} - 4 i) = 19

Based on this, the nature of even, symmetrical, etc. numbers are also determined. (3.15)

(5 \sqrt{2} + 7 i) (5 \sqrt{2} - 7 i) = 99 \dots

(3.15)

Some prime numbers do not follow this rule. The reason is the geometric structure of the interaction of these numbers. (3.16) Figure 4

(\sqrt{2} + 3 i) (\sqrt{2} - 3 i) = 11 (\sqrt{2} + 1 i) (\sqrt{2} - 1 i) = 3 \Rightarrow (\sqrt{2} + ((\sqrt{2} + 1 i) (\sqrt{2} - 1 i)) i) (\sqrt{2} - ((\sqrt{2} + 1 i) (\sqrt{2} - 1 i)) i) = 11 (2 \sqrt{1} + ((\sqrt{2} + 1 i) (\sqrt{2} - 1 i)) i) (2 \sqrt{1} - ((\sqrt{2} + 1 i) (\sqrt{2} - 1 i)) i) = 13 (2 \sqrt{2} + ((\sqrt{2} + 1 i) (\sqrt{2} - 1 i)) i) (2 \sqrt{2} - ((\sqrt{2} + 1 i) (\sqrt{2} - 1 i)) i) = 17 (3 \sqrt{2} + ((\sqrt{0} + 1 i) (\sqrt{0} - 1 i)) i) (3 \sqrt{2} - ((\sqrt{0} + 1 i) (\sqrt{0} - 1 i)) i) = 19 (\sqrt{7} + 4 i) (\sqrt{7} - 4 i) = 23

(3.16)

Based on this, the table of production coefficients of prime numbers is obtained. Table 2

And finally, the numbers of the relation of production of prime numbers are obtained. (3.17)

(P_{f} \sqrt{P_{f}} + {|\tilde{ψ (a)}|}^{2} i) (P_{f} \sqrt{P_{f}} - {|\tilde{ψ (a)}|}^{2} i) = P_{n} \Rightarrow P_{f} ϵ P_{n}

(3.17)

Considering the Fibonacci sequence, and its relationship with the golden constant and two imaginary axes, we examine the order of prime numbers. (3.18)

1 2 3 5 8 13 21 34 \dots (\sqrt{1} + 2 i) (\sqrt{1} - 2 i) = 5 = x (2 \sqrt{3} + x i) (2 \sqrt{3} - x i) = 4 (3) + 5 = 17 (2 \sqrt{3} + u i) (2 \sqrt{3} - u i) = 4 (3) + 7 = 19 (2 \sqrt{5} + l i) (2 \sqrt{5} - l i) = 4 (5) + 3 = 23

(3.18)

Although there seems to be no order in this pattern. However, according to the three-dimensional golden spiral in three axes, the deep connection between prime numbers and the golden ratio is determined. Figure 5 Figure 6

4. Discussion

Based on two imaginary dimensions in the six-dimensional space, for the real part of the zeta function 1/2 and also negative even numbers, the zeta function is zero. The cause of the zeroing of the function based on the doubling of the golden ratio is quite evident. The distribution of prime numbers is also expressed based on three vectors in the complex plane. Based on the condition of equal outside from the periodic center for two imaginary vectors, the prime numbers are the areas of the unit and connected spheres that are expanding. Accordingly, at point 1/2 for a full period, the eccentricity of the ellipse is zero for two vectors. Figure 7 Figure 8

The ascending function determines the converging eccentricity of the period change points. (4.1)

\sum_{x = 1}^{n} {(\sin (\arccos (\frac{1}{x})))}^{2} ({s i n (a r c c o s (\frac{1}{n - 1}))}^{2})

(4.1)

The distribution of prime numbers follows the geometric structure of nature. Periodic periods with dimensions greater than three dimensions lead to an increase in complexity. Möbius space transfers the properties of lower dimensions to higher dimensions. And also, it regularly transfers the properties of higher dimensions to lower dimensions. In the way of distribution of prime numbers, the volume of a five-dimensional sphere should be examined. Knowing the concentrated fields of information is possible by examining Einstein's equations in six dimensions. (4.2) [12]

Ψ_{μ ν} + {(R}_{μ ν} - \frac{1}{2} R g_{μ ν} + Λ g_{μ ν}) = {(\frac{π - 2}{2})}^{6} (\frac{h e}{c}) T_{μ ν} + K_{μ ν}

(4.2)

Appreciation

I appreciate Lhm.Razzazi and all my dear professors for their education and guidance.

References

https://www.claymath.
Ely, D. R. (2024). Entangling Primes and Zeros: A Proof of the Riemann Hypothesis. David R Ely.
Shun, L.K. A Full and Detailed Proof for the Riemann Hypothesis & the Simple Inductive proof of Goldbach’s Conjecture. Int. J. Math. Stat. Stud. 2023, 11, 1–10. [Google Scholar] [CrossRef]
Lam, K.S. An Extension Proof of Riemann Hypothesis by a Logical Entails Truth Table. Int. J. Math. Stat. Stud. 2024, 12, 47–55. [Google Scholar] [CrossRef]
Wilson, J. J. (2024). Finding the proof of the Riemann hypothesis (No. yvq3p). Center for Open Science. [CrossRef]
Segun, A. O. (2024). Riemann Integration in the Euclidean Space. arXiv:2403.19703. [CrossRef]
Ivashkovich, S. Riemann surface of the Riemann zeta function. J. Math. Anal. Appl. 2022, 529. [Google Scholar] [CrossRef]
Lapidus, M. L., Radunović, G., & Žubrinić, D. (2014). Fractal zeta functions and complex dimensions: A general higher-dimensional theory. In Fractal Geometry and Stochastics V (pp. 229-257). Cham: Springer International Publishing.
https://www.researchgate.net/publication/383034464_Proof_of_Riemann's_hypothesis_based_on_the_proof_of_six-dimensional_space-time. [CrossRef]
Hemingway, X. (2023). The Generalized Riemann Hypothesis on elliptic complex fields. AIMS Mathematics, 8(11), 25772-25803.
Acedo, L. On the General Divergent Arithmetic Sums over the Primes and the Symmetries of Riemann’s Zeta Function. Symmetry 2024, 16, 970. [Google Scholar] [CrossRef]
Mousavi, S.K. General Balance in the Six-Dimensions of Space-Time. Qeios 2024. [Google Scholar] [CrossRef]

Figure 1. Zeta function based on golden ratio and Fibonacci sequence.

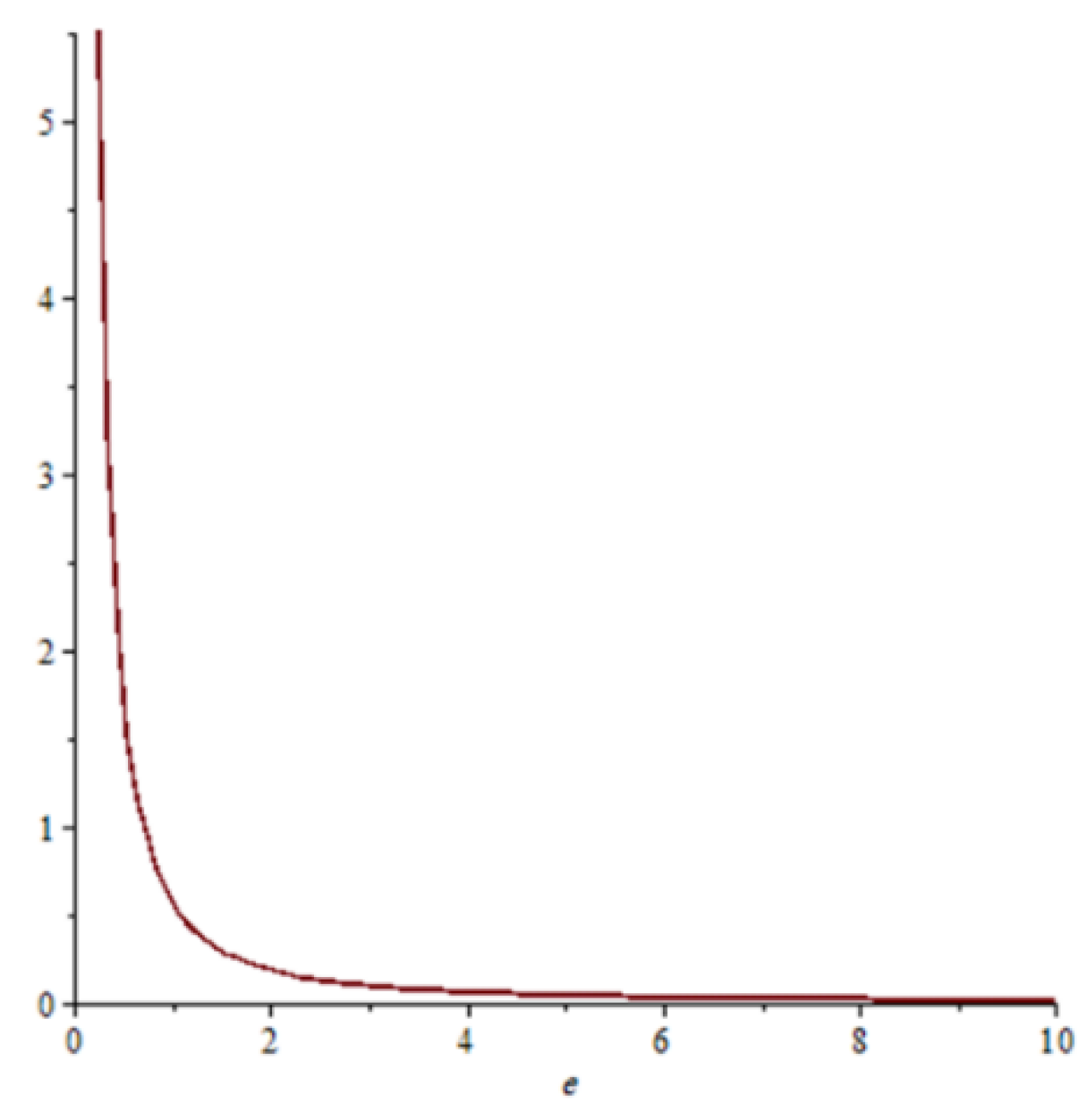
Figure 2. Rotating a dimension equivalent to one radian around the center field in higher dimensions is possible by doubling the radius of the circle.

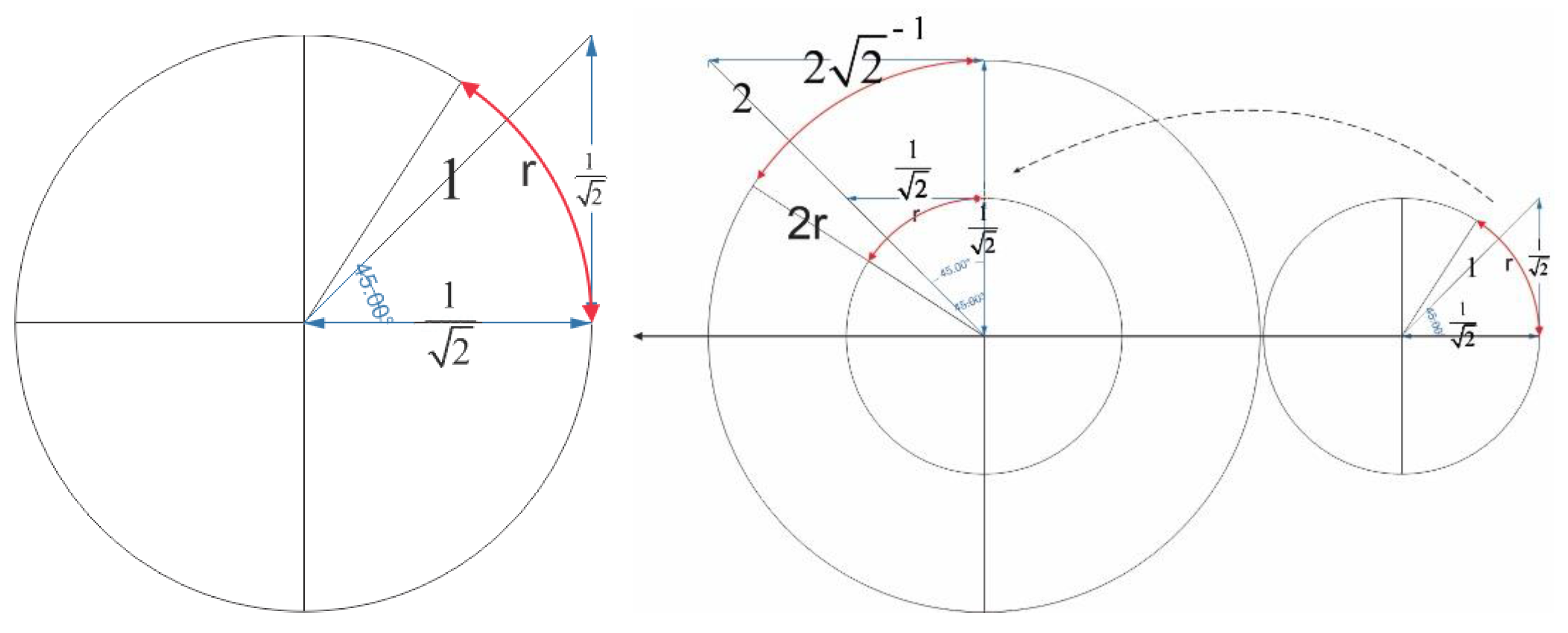
Figure 3. Rotation doubling relativity for two different spaces.

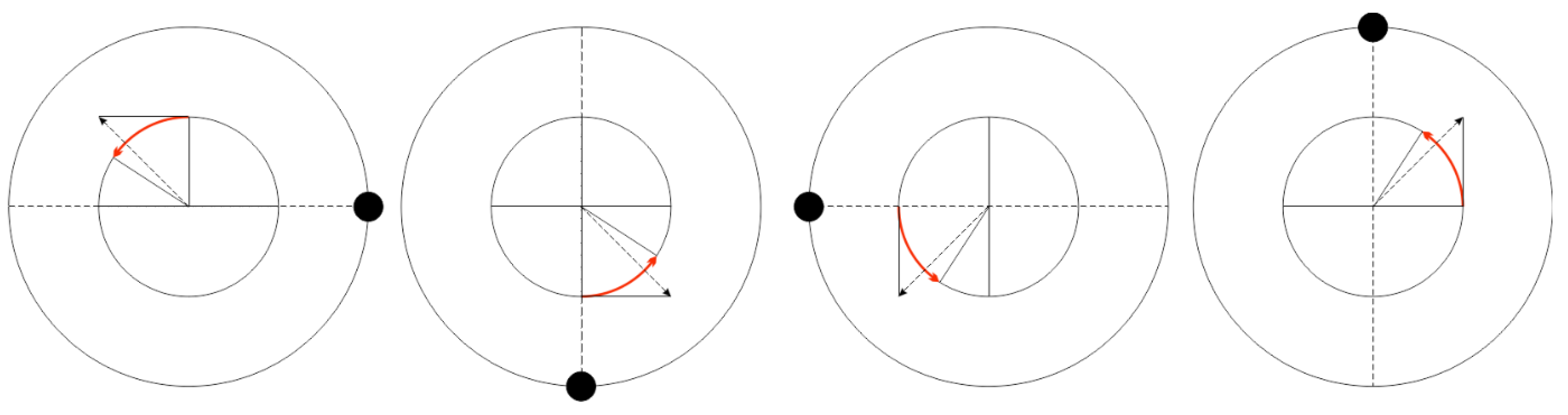
Figure 4. Each state has null parts. The geometric structure is where these parts, like the simple zeros of the Riemann function, originate.

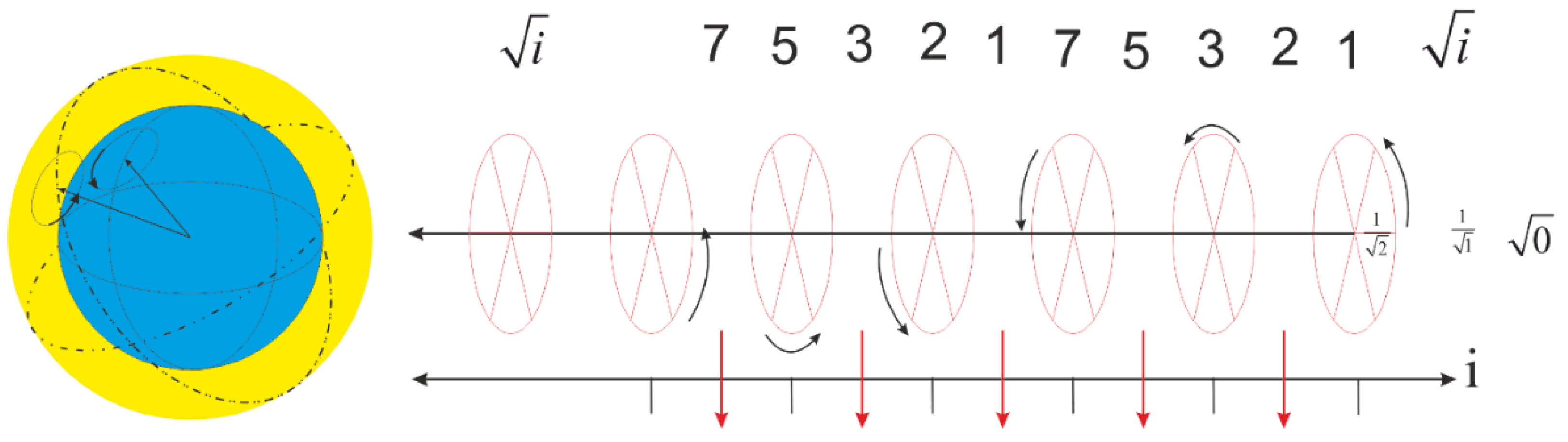
Figure 5. The imaginary part of the equation (3.18) is characterized based on the interaction of a few golden spirals with an angle of 60 degrees concerning the rail axis, and an angle of 30 degrees concerning the imaginary axis.

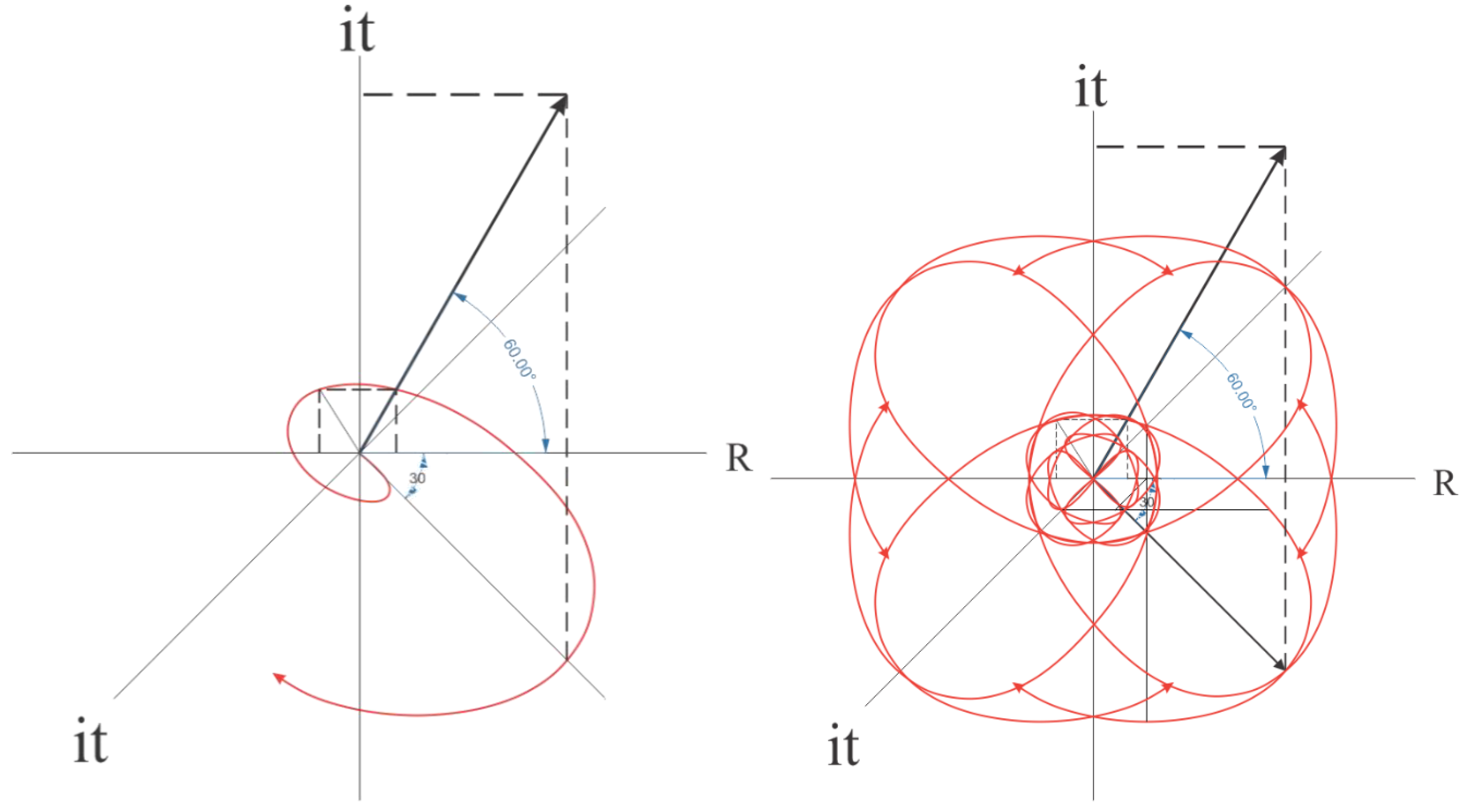
Figure 6. In the cone of natural numbers, the effect of two parallel golden spirals(2.2) has been identified for prime numbers.

Figure 7. The 1/2 point of the phase limit tends to zero.

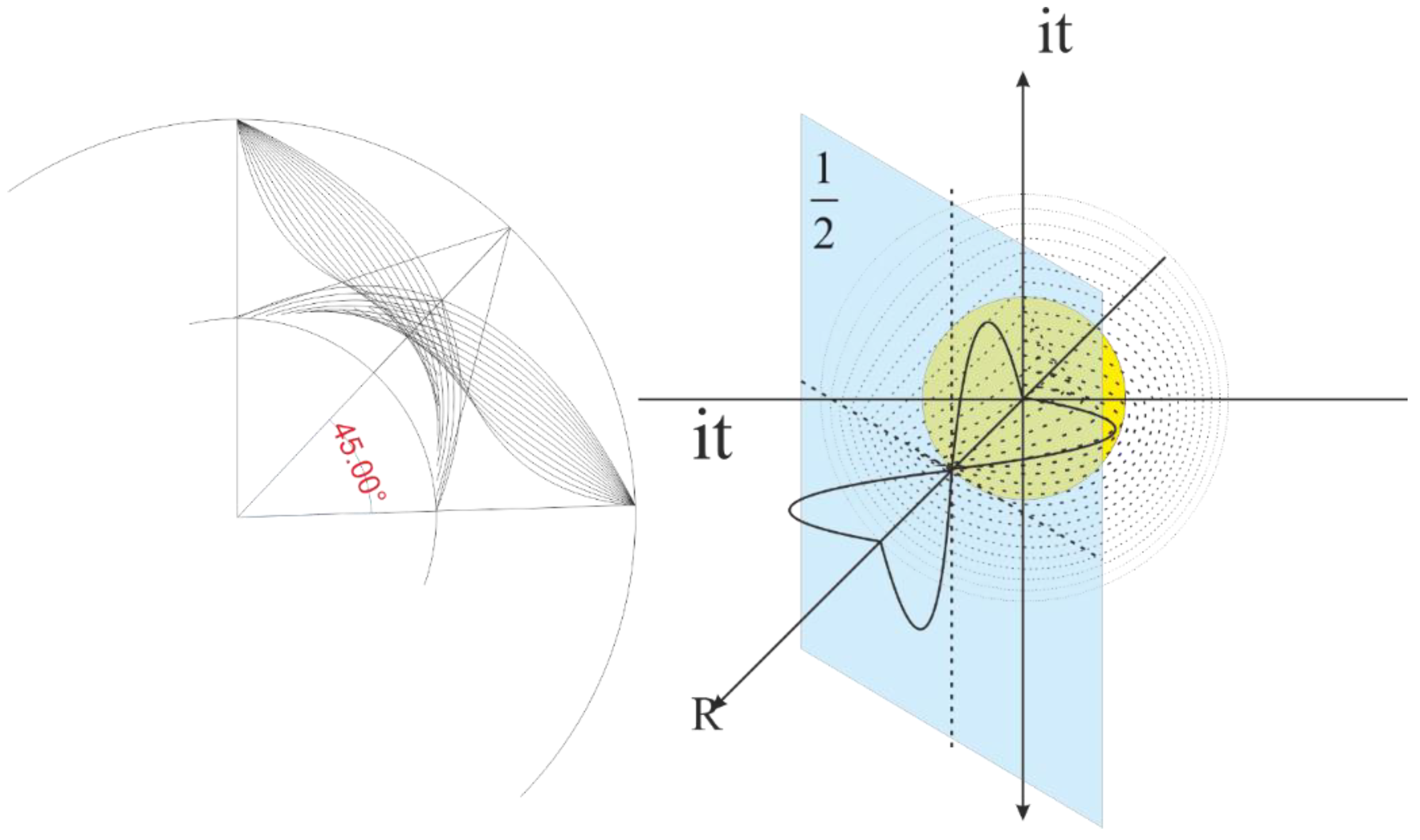
Figure 8. Sinusoidal phase shift based on ellipse eccentricity.

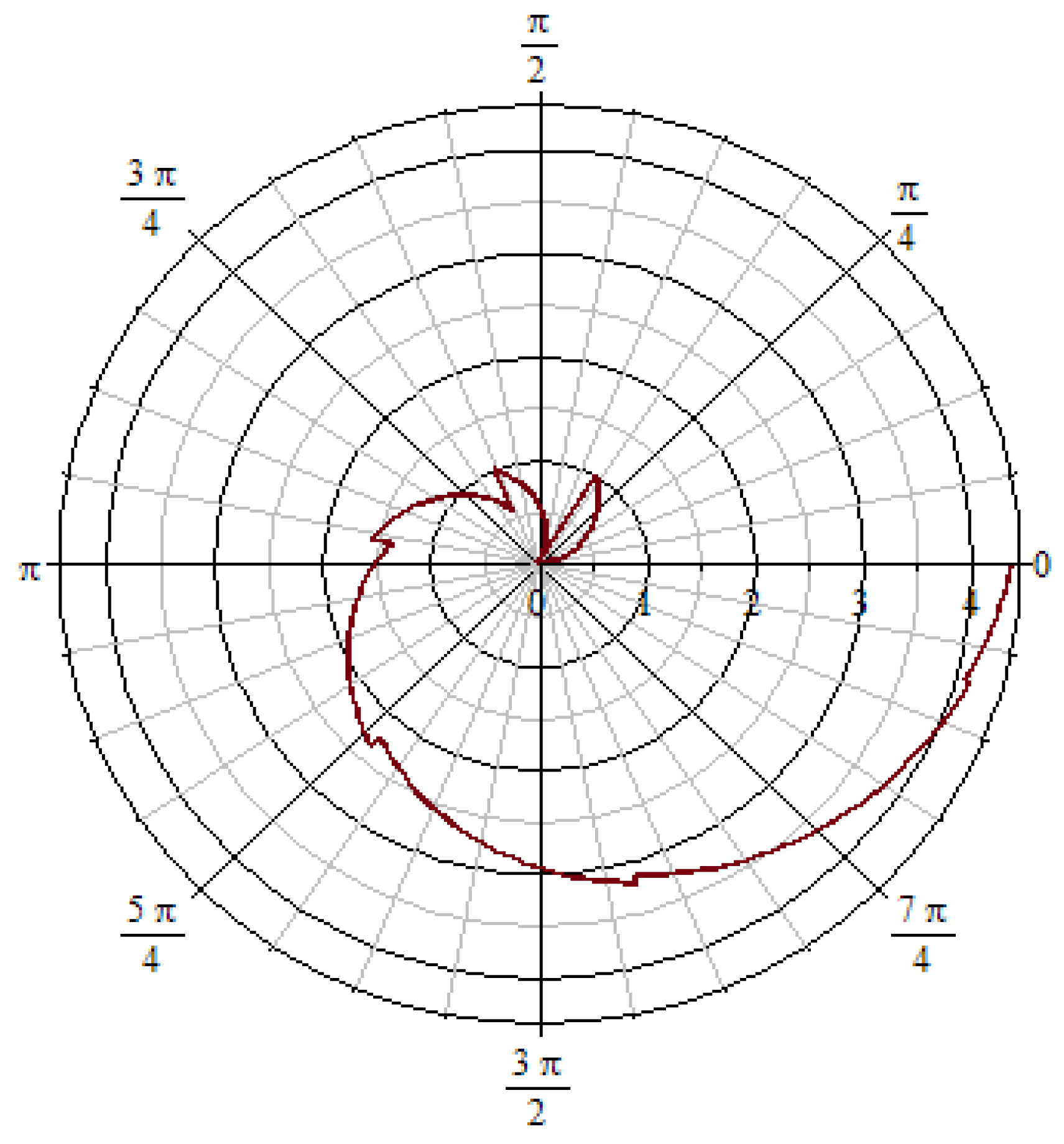
Table 1. Every prime number can be expressed based on equality conditions.

1	2	3	5	7
$\frac{1}{\sqrt{2^{1}}}$	$\frac{1}{2}$	$\frac{1}{\sqrt{{2^{2} 2}^{1}}}$	$\frac{1}{4} \frac{1}{\sqrt{2^{1}}}$	$\frac{1}{8} \frac{1}{\sqrt{2^{1}}}$
11	17	19	23	29
$\frac{1}{32} \frac{1}{\sqrt{2^{1}}}$	$\frac{1}{256} \frac{1}{\sqrt{2^{1}}}$	$\frac{1}{512} \frac{1}{\sqrt{2^{1}}}$	$\frac{1}{2048} \frac{1}{\sqrt{2^{1}}}$	$\frac{1}{16384} \frac{1}{\sqrt{2^{1}}}$
31	37	41	43	47
$\frac{1}{32768} \frac{1}{\sqrt{2^{1}}}$	$\frac{1}{262144} \frac{1}{\sqrt{2^{1}}}$	$\frac{1}{1048576} \frac{1}{\sqrt{2^{1}}}$	$\frac{1}{2097152} \frac{1}{\sqrt{2^{1}}}$	$\frac{1}{8388608} \frac{1}{\sqrt{2^{1}}}$
A	B	C	D	E
$3 + 2 + 7 + 6 + 8 = 26$ $2 + 6 = 8$	$2 + 6 + 1 + 4 + 4 = 17$ $1 + 7 = 8$	$1 + 0 + 4 + 8 + 5 + 7 + 6 = 31$ $1 + 3 = 4$	$2 + 0 + 9 + 7 + 1 + 5 + 2 = 26$ $2 + 6 = 8$	$8 + 3 + 8 + 8 + 8 + 6 + 0 + 8 = 41$ $4 + 1 = 5$
$\log_{8} (32768) = 5$	$\log_{8} (262144) = 6$	$\log_{4} (1048576) = 10$	$\log_{8} (2097152) = 7$	$\log_{5} (8388608) = 9.9 \dots$
$P_{5} = 7$	$P_{6} = 11$	$P_{10} = 29$	$P_{7} = 17$	$P_{9} = 23$

1	2	3	5	7
$\frac{1}{\sqrt{2^{1}}}$	$\frac{1}{\sqrt{2^{2}}}$	$\frac{1}{\sqrt{2^{3}}}$	$\frac{1}{\sqrt{2^{4} 2^{5}}}$	$\frac{1}{\sqrt{2^{5} 2^{2}}}$

11	17	19	23	29
$\frac{1}{\sqrt{2^{6} 2^{5}}}$	$\frac{1}{\sqrt{2^{7} 2^{9} 2^{1}}}$	$\frac{1}{\sqrt{2^{8} 2^{10} 2^{1}}}$	$\frac{1}{\sqrt{2^{9} 2^{13} 2^{1}}}$	$\frac{1}{\sqrt{2^{10} 2^{16} 2^{2} 2^{1}}}$
$\frac{1}{\sqrt{2^{6} 2^{5}}}$	$\frac{1}{\sqrt{2^{7} 2^{6} 2^{4}}}$	$\frac{1}{\sqrt{2^{8} 2^{7} 2^{4}}}$	$(23) \times 2 = 46$
			$4 + 6 = 10 = X$
			$P_{X - 1} = 9$

Table 2. These elements form the geometrical framework and resemble the simple zeros of the Riemann function. This forms the basis for Table 2, which shows the production coefficients of prime numbers.

$\sqrt{1}$	$\sqrt{2}$	$\sqrt{3}$	$\sqrt{0}$

$2 \sqrt{1}$	$2 \sqrt{2}$	$2 \sqrt{3}$	$2 \sqrt{0}$

$3 \sqrt{1}$	$3 \sqrt{2}$	$3 \sqrt{3}$	$3 \sqrt{0}$

$5 \sqrt{1}$	$5 \sqrt{2}$	$5 \sqrt{3}$	$5 \sqrt{0}$

$5 \sqrt{1}$	$5 \sqrt{2}$	$5 \sqrt{3}$	$5 \sqrt{0}$

$7 \sqrt{1}$	$7 \sqrt{2}$	$7 \sqrt{3}$	$7 \sqrt{0}$

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Six Dimensions for Proof of Riemann Hypothesis

Abstract

1. Introdoction

2. Method

3. Results

4. Discussion

Appreciation

References

MDPI Initiatives

Important Links

Subscribe