Solving NP-Complete Problems Efficiently

Preprint

Article

Solving NP-Complete Problems Efficiently

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

Frank Vega^*

This version is not peer-reviewed

Submitted:

07 September 2024

Posted:

13 September 2024

You are already at the latest version

Alerts

Abstract

The P versus NP problem is a fundamental question in computer science. It asks whether problems whose solutions can be quickly verified can also be quickly solved. Here, "quickly" refers to computational time that grows proportionally to the size of the input (polynomial time). While the problem's roots trace back to a 1955 letter from John Nash, its formalization is attributed to Stephen Cook and Leonid Levin. Despite extensive research, a definitive answer remains elusive. Closely tied to this is the concept of NP-completeness. If a single NP-complete problem could be solved efficiently, it would imply that all problems in NP can be solved efficiently, proving that P equals NP. This work posits that MONOTONE ONE-IN-THREE 3SAT, a notoriously difficult NP-complete problem, can be solved efficiently, thereby establishing the equivalence of P and NP.

Keywords:

Subject: Computer Science and Mathematics - Data Structures, Algorithms and Complexity

1. Introduction

Computer science is confronted by the formidable challenge of the P versus

N P

problem [1]. Fundamentally, this inquiry seeks to determine if the ability to swiftly verify a solution implies the capacity to swiftly compute it. Here, "swiftly" denotes algorithms with a polynomial time complexity, where computational time grows proportionally to input size. Problems solvable within polynomial time constitute the class P. Conversely,

N P

encompasses problems whose solutions can be verified efficiently given a suitable "certificate" - a piece of information enabling rapid validation [2].

The crux of the P versus

N P

question lies in whether P and

N P

are identical. A prevailing belief is that P is a strict subset of

N P

(

P \neq N P

), signifying that certain problems are inherently more difficult to solve than to verify. Resolving this enigma holds profound implications for fields such as cryptography and artificial intelligence [3,4]. The P versus

N P

problem is widely considered one of the most challenging open questions in computer science. Evidence supporting its difficulty arises from techniques like relativization and natural proofs, which have yielded inconclusive results [5,6]. Similar problems, such as the VP versus VNP problem in algebraic complexity, remain unsolved [7].

Resolving the P versus

N P

question is often described as a "holy grail" of computer science. A positive resolution would revolutionize our understanding of computation, potentially leading to groundbreaking algorithms for critical problems. Reflecting its significance, the problem is listed among the Millennium Prize Problems. While recent years have seen progress in related areas, such as finding efficient solutions to specific instances of

N P

-complete problems, the core question of P versus

N P

remains unanswered [8]. A polynomial-time algorithm for any

N P

-complete problem would directly imply P equals

N P

[9]. Our work focuses on presenting such an algorithm for a well-known

N P

-complete problem.

2. Background and Ancillary Results

N P

-complete problems are the Everest of computational challenges. Despite the ease of verifying proposed solutions with a succinct certificate [9], finding these solutions efficiently remains an elusive goal. A problem is classified as

N P

-complete if it satisfies two stringent criteria within computational complexity theory:

Efficient Verifiability: Solutions can be swiftly checked using a concise proof.
Universal Hardness: Every problem in the class $N P$ can be transformed into an instance of this problem without significant computational overhead [9].

The implications of finding an efficient algorithm for a single

N P

-complete problem are profound. Such a breakthrough would serve as a master key, unlocking efficient solutions for all problems in

N P

, with transformative consequences for fields like cryptography, artificial intelligence, and planning [3,4].

Illustrative examples of

N P

-complete problems include:

Boolean satisfiability (SAT): Given a logical expression, determine if there exists an assignment of truth values to its variables that makes the entire expression true [10].
Clique: In a given graph, identify a maximum-sized subset of vertices where every two vertices are connected by an edge [10].

The provided examples represent a small subset of the extensively studied

N P

-complete problems relevant to our current work. A chordal graph, denoted as

G = (V, E)

, is an undirected graph characterized by the existence of a chord for every cycle of length at least 4: A chord is an edge joining two nodes not adjacent in a cycle [11]. Determining whether a given graph is a chordal graph can be accomplished efficiently (in polynomial time) [11].

Definition 1.

Clique for Chordal Graph (CCG):

Given a chordal graph

G = (V, E)

and a positive integer k, the

C C G

problem asks whether there exists a subset

V^{'}

of V containing at least k vertices such that every two vertices in

V^{'}

are connected by an edge in G. This problem can be solved efficiently in polynomial time [12].

A Boolean satisfiability problem (SAT) instance is a Boolean formula constructed from:

Boolean variables: $x_{1}, x_{2}, . . ., x_{n}$ , which can take on the values true or false.
Boolean connectives: Logical operators such as AND (∧), OR (∨), NOT (¬), implication (⇒), and equivalence (⇔).
Parentheses: To specify the order of operations.

A truth assignment for a Boolean formula is a complete mapping of its variables to the values true or false. A satisfying truth assignment is one that evaluates the formula to true. If such an assignment exists, the formula is satisfiable. The

S A T

problem asks whether a given Boolean formula is satisfiable [10].

A literal is a single variable or its negation within a Boolean formula [9]. A Boolean formula is in conjunctive normal form (

C N F

) when it is expressed as a conjunction (

A N D

) of clauses, where each clause is a disjunction (

O R

) of one or more literals [9]. A 3-conjunctive normal form (

3 C N F

) formula is a specific type of

C N F

where each clause contains exactly three distinct literals [9].

For instance, the formula

(x_{1} \lor \neg x_{1} \lor x_{2}) \land (x_{1} \lor x_{2} \lor x_{3}) \land (\neg x_{1} \lor x_{2} \lor \neg x_{3})

3 C N F

. Its first clause,

(x_{1} \lor \neg x_{1} \lor x_{2})

, consists of the three literals

x_{1}

\neg x_{1}

and

x_{2}

We introduce the

MONOTONEONE - IN - THREE 3 SAT

problem:

Definition 2.

MONOTONE ONE-IN-THREE 3SAT (1-IN-3 M3SAT):

Given a Boolean formula in

3 C N F

with monotone clauses (meaning the variables are never negated), determine if there exists a truth assignment such that exactly one variable is true in each clause. This problem is a well-known

N P

-complete problem [10].

By presenting an efficient solution to

1 - IN - 3 M 3 SAT

, we would establish a proof that P equals

N P

3. Main Result

This is a key finding.

Theorem 1.

1 - IN - 3 M 3 SAT

can be solved in polynomial time.

Proof.

Let

ϕ

be a Boolean formula satisfying the specific constraints of the

1 - IN - 3 M 3 SAT

problem. A special type of graph,

G = (V, E)

, known as a chordal graph, can be constructed from the Boolean formula

ϕ

. This graph will serve as a tool to solve the formula

ϕ

Building the Graph.
- Vertex Creation: Each variable x in a clause $c_{i}$ of $ϕ$ is represented by a unique vertex in G, denoted $u_{(x, i)}$ .
- Edge Creation: For every two different clauses $c_{i}$ and $c_{j}$ in $ϕ$ , we consider the following three cases in the edge creation (This edge creation ensures chordality):
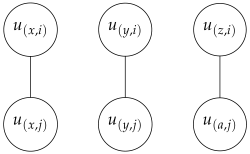
Case 1:

The clauses $c_{i} = (x \lor y \lor z)$ and $c_{j} = (a \lor b \lor c)$ do not share any variables:

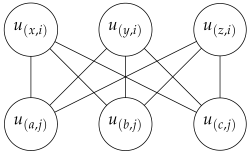
Case 2:

The clauses $c_{i} = (x \lor y \lor z)$ and $c_{j} = (x \lor a \lor b)$ both contain the variable x:

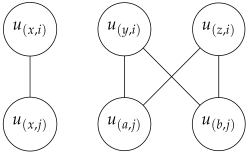
Case 3:

The clauses $c_{i} = (x \lor y \lor z)$ and $c_{j} = (x \lor y \lor a)$ both contain the variables x and y:

2.

Edge Implications. The introduced edges ensure that:

Variables are grouped: Vertices representing the same variable are always together in a clique.
Clauses are limited: At most one vertex from each clause can be in a clique.

3.

Understanding the Edges. The edges in the graph are designed to ensure the following:

Solution Mapping: A clique in the graph corresponds to a valid solution for the formula $ϕ$ .
Clause Satisfaction: A clause in $ϕ$ contains exactly one true variable if and only if at least one of its corresponding vertices is included in the clique.

4.

Mapping Between Solutions. A clique set in the graph represents a valid solution to the formula if:

Clause Coverage: It includes at least one vertex from every clause, ensuring that each clause contains exactly one true variable.
Variable Consistency: A variable consistency constraint requires that all vertices representing a specific variable are included in the same clique. This guarantees that the solution assigns the same truth value to all instances of a variable.

5.

Why it Works.

Consistency Enforcement: The graph’s structure ensures that any chosen set of vertices (clique) corresponds to a valid truth assignment for the formula’s variables.
Solution Equivalence: A truth assignment with exactly one true variable per clause in $ϕ$ is directly equivalent to a clique $V^{'}$ containing at least m vertices (where m represent the number of clauses in $ϕ$ ).

6.

Equivalence and Complexity.

Problem Equivalence: A solution to the $1 - IN - 3 M 3 SAT$ problem (a truth assignment with exactly one true variable per clause) exists if and only if a clique of size at least m exists in the corresponding chordal graph.
Polynomial Time Solvability: The $C C G$ problem, which involves finding such a clique in a chordal graph, is solvable in polynomial time. Consequently, the original $1 - IN - 3 M 3 SAT$ problem can also be solved in polynomial time. This is because determining the existence of a suitable truth assignment is equivalent to finding the clique, which is a computationally efficient task. Additionally, verifying if the constructed graph is indeed a chordal graph can be done in polynomial time [11].

In essence, this construction establishes a direct connection between solving the

C C G

problem and finding a valid solution (or certificate) for any

1 - IN - 3 M 3 SAT

instance. Since

C C G

can be solved efficiently, it follows that the original, seemingly more complex problem can also be solved efficiently. □

This is the main theorem.

Theorem 2.

P = N P

Proof.

A polynomial-time solution to any

N P

-complete problem would establish the equivalence of P and

N P

[9]. Despite extensive research on over 300 significant

N P

-complete problems, no such polynomial-time algorithm has been discovered [9]. Given that

1 - IN - 3 M 3 SAT

is a well-known

N P

-complete problem [10], a polynomial-time solution for it, as presented in Theorem 1, would directly imply P equals

N P

. □

4. Conclusion

A definitive proof that P equals

N P

would fundamentally reshape our computational landscape. The implications of such a discovery are profound and far-reaching:

Algorithmic Revolution.

−

The most immediate impact would be a dramatic acceleration of problem-solving capabilities. Complex challenges currently deemed intractable, such as protein folding, logistics optimization, and certain cryptographic problems, could become efficiently solvable [3]. This breakthrough would revolutionize fields from medicine to cybersecurity. Moreover, everyday optimization tasks, from scheduling to financial modeling, would benefit from exponentially faster algorithms, leading to improved efficiency and decision-making across industries [3].
Scientific Advancements.

−

Scientific research would undergo a paradigm shift. Complex simulations in fields like physics, chemistry, and biology could be executed at unprecedented speeds, accelerating discoveries in materials science, drug development, and climate modeling [3]. The ability to efficiently analyze massive datasets would provide unparalleled insights in social sciences, economics, and healthcare, unlocking hidden patterns and correlations [3].
Technological Transformation.

−

Artificial intelligence would be profoundly impacted. The development of more powerful AI algorithms would be significantly accelerated, leading to breakthroughs in machine learning, natural language processing, and robotics [8]. While the cryptographic landscape would face challenges, it would also present opportunities to develop new, provably secure encryption methods [8].
Economic and Societal Benefits.

−

The broader economic and societal implications are equally significant. A surge in innovation across various sectors would be fueled by the ability to efficiently solve complex problems. Resource optimization, from energy to transportation, would become more feasible, contributing to a sustainable future [3].

In conclusion, a proof of

P = N P

would usher in a new era of computational power with transformative effects on science, technology, and society. While challenges and uncertainties exist, the potential benefits are immense, making this a compelling area of continued research.

References

Cook, S.A. The P versus NP Problem, Clay Mathematics Institute. https://www.claymath.org/wp-content/uploads/2022/06/pvsnp.pdf, 2022. Accessed September 7, 2024.
Sudan, M. The P vs. NP problem. http://people.csail.mit.edu/madhu/papers/2010/pnp.pdf, 2010. Accessed September 7, 2024.
Fortnow, L. The status of the P versus NP problem. Communications of the ACM 2009, 52, 78–86. [Google Scholar] [CrossRef]
Aaronson, S. P=?NP. Open Problems in Mathematics 2016, pp. 1–122. [CrossRef]
Baker, T.; Gill, J.; Solovay, R. Relativizations of the P=?NP Question. SIAM Journal on computing 1975, 4, 431–442. [Google Scholar] [CrossRef]
Razborov, A.A.; Rudich, S. Natural Proofs. Journal of Computer and System Sciences 1997, 1, 24–35. [Google Scholar] [CrossRef]
Wigderson, A. Mathematics and Computation: A Theory Revolutionizing Technology and Science; Princeton University Press, 2019.
Fortnow, L. Fifty Years of P vs. NP and the Possibility of the Impossible. Communications of the ACM 2022, 65, 76–85. [Google Scholar] [CrossRef]
Cormen, T.H.; Leiserson, C.E.; Rivest, R.L.; Stein, C. Introduction to Algorithms, 3rd ed.; The MIT Press, 2009.
Garey, M.R.; Johnson, D.S. Computers and Intractability: A Guide to the Theory of NP-Completeness, 1st ed.; San Francisco: W. H. Freeman and Company, 1979. [Google Scholar]
Alvarez, C.; Greenlaw, R. A compendium of problems complete for symmetric logarithmic space. Computational Complexity 2000, 9, 123–145. [Google Scholar] [CrossRef]
Gavril, F. Algorithms for Minimum Coloring, Maximum Clique, Minimum Covering by Cliques, and Maximum Independent Set of a Chordal Graph. SIAM Journal on Computing 1972, 1, 180–187. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Solving NP-Complete Problems Efficiently

Abstract

1. Introduction

2. Background and Ancillary Results

3. Main Result

4. Conclusion

References

MDPI Initiatives

Important Links

Subscribe