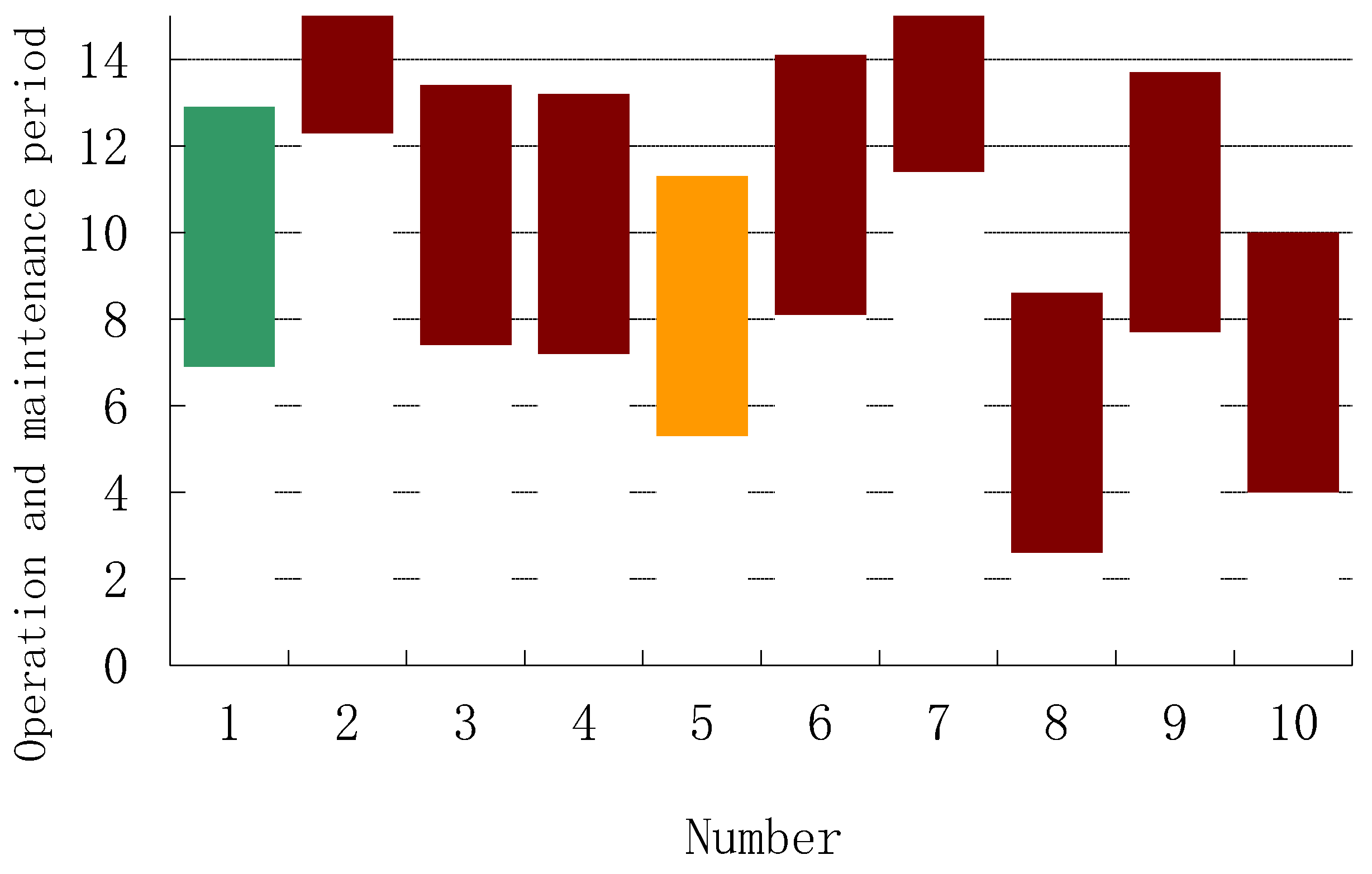Electric Vehicle DC Charging Station Based on XGboost Re-search on Condition Assessment and Operation and Mainte-nance

Preprint

Article

Electric Vehicle DC Charging Station Based on XGboost Re-search on Condition Assessment and Operation and Mainte-nance

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

Hualiang Fang^*,Jiaqi Liao,Shuo Huang,Maojie Zhang

This version is not peer-reviewed

Submitted:

22 August 2024

Posted:

25 August 2024

You are already at the latest version

Alerts

Abstract

With the rapid development of electric vehicles, the infrastructure for charging stations is also expanding quickly, and the failure rate of charging piles is increasing. To address the effective op-eration and maintenance of charging stations, a method based on the XGBoost algorithm for electric vehicle DC charging stations is proposed. An operation and maintenance system is constructed based on state analysis, considering the operation status of the charging station and users' charging habits. Factors such as driving and charging habits, road traffic, and charging station equipment are taken into account. The training sample data is established using historical data, online monitoring data, and external environmental data, and the charging station status evaluation model is trained using the XGBoost algorithm. Based on the condition assessment results, a risk assessment model is established in combination with fault parameters. Risk tracking of the charging station is conducted using the lack of power supply (ENC), evaluating the risk level of each station, and determining the operation and maintenance order. The optimal operation and maintenance model for DC charging stations, aimed at achieving both economic and reliable goals, is constructed to determine the op-eration and maintenance schedule for each station. The results of the case study demonstrate that the state evaluation and operation and maintenance strategy can significantly improve the relia-bility of the system and the overall benefits of operation and maintenance while meeting the re-quired standards.

Keywords:

Subject: Engineering - Electrical and Electronic Engineering

0. Introduction

Electric vehicles (EVs) have developed rapidly as a clean, zero-emission mode of transportation that reduces environmental pollution. Reliable charging infrastructure is a necessary condition for the large-scale adoption of electric vehicles. Compared to AC charging piles, DC charging piles have higher failure rates due to more components, larger operating power, and long-term outdoor exposure. Currently, preliminary operation and maintenance work have been carried out, but there are still issues such as rough planning, excessive dependence on experience, and unclear targets. Accurately evaluating the operation status and change trends of charging piles, taking preventive measures, reducing fault occurrences, and improving the operation efficiency of charging piles are crucial [1].

In terms of the operation and maintenance of electric vehicle DC charging stations, current research mainly focuses on the online monitoring of charging facilities. Reference [2] studied and designed a monitoring system for charging facilities through system requirements analysis and functional service requirements. The monitoring system is divided into a system platform layer, support service layer, public service layer, and application layer to facilitate the monitoring of power distribution, charging, safety protection, and measurement of charging facilities. Reference [3] established a charging station system model, equipment information model, and communication model, forming the monitoring system’s modeling scheme and monitoring the key characteristic quantities of the facilities in the charging station. In Reference [4], an online monitoring system based on a peripheral component interconnect (PCI) bus was designed to collect real-time voltage and current data from the charging facility’s co-coupling node, analyzing the equipment’s operating status and characteristics.

The above literature studies the operation and maintenance methods of charging stations from the perspective of monitoring systems. However, how to integrate the monitoring results of charging stations with the charging behavior of electric vehicles to formulate a reliable operation and maintenance strategy has not yet been studied. Risk-based maintenance (RBM) is a quantitative assessment of the consequences of equipment failure, used as the basis for formulating operation and maintenance strategies [5]. At present, RBM has been widely applied in operation and maintenance. For example, Reference [6] proposed a state model based on an improved semi-Markov chain and solved the optimal maintenance strategy with the goal of minimizing early maintenance costs and reliability loss. In Reference [7], a prediction model using Bayesian classifiers was established with historical maintenance information and fault records. Maintenance reliability and economy were taken as risk indicators, and the minimum comprehensive risk was used as the optimization goal, effectively formulating the RBM strategy for a 27.5 kV vacuum circuit breaker. Reference [8] proposed a risk assessment method for the automatic operation and maintenance of high-voltage transmission lines based on segmented pre-whitening fuzzy prediction. This method realizes risk assessment and operation and maintenance optimization through big data feature classification and fuzzy clustering processing. For distribution equipment, the average real-time failure rate can be calculated using the feeder partition method according to the health index of the equipment. A differentiated maintenance strategy is then formulated based on the risk loss cost of each piece of equipment [9].

The evaluation of the operation status and the operation and maintenance of DC charging stations (hereinafter referred to as charging stations) are important issues currently being addressed. Based on historical data, online monitoring data, and external environmental data, a training sample dataset is established, and the state evaluation model of charging stations is trained using the XGBoost algorithm. Risk tracking is employed to determine the operation and maintenance priority of each station, while road traffic and user driving models are developed to calculate relevant risk indicators. Finally, an optimization model for the charging station operation and maintenance strategy is established, focusing on operation and maintenance costs and system reliability gains. Through simulation analysis, the effectiveness and necessity of optimizing the operation and maintenance strategy are verified.

1. Operation and Maintenance System of Electric Vehicle Charging Station

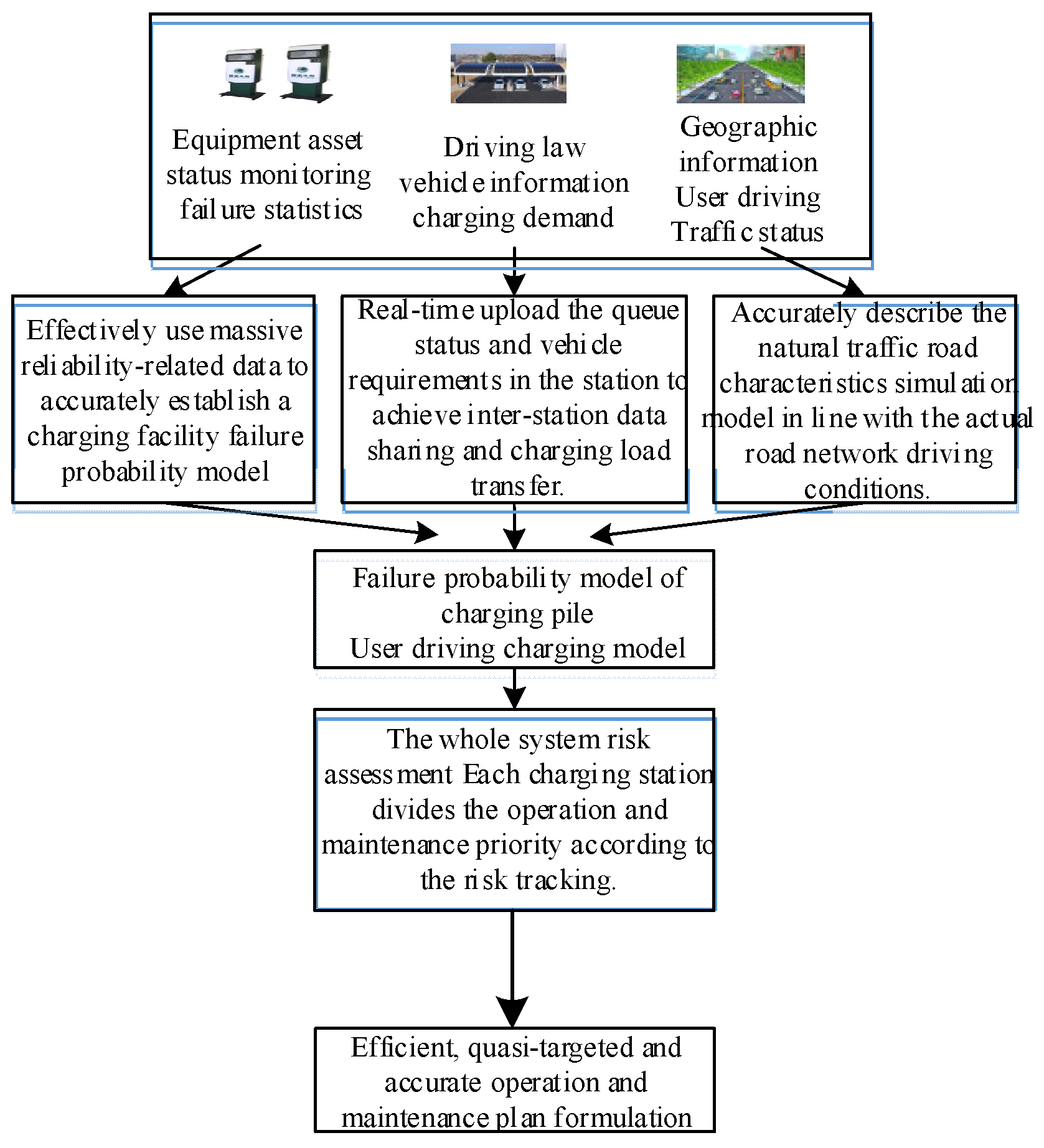
In addition to evaluating their own operations, the state assessment of charging stations should also account for their usage patterns, including user habits, the road network, external environment, climate, and other dynamic factors. By integrating real-time traffic conditions, the operational status of charging station equipment, and user travel behaviors—information gathered through crowd sensing technologies—a comprehensive operation and maintenance system can be developed. This system will consider both the equipment side and the user side, as illustrated in Figure 1.

The purpose of operation and maintenance work is to reduce the failure rate of power equipment, enhance reliability, and minimize the impact on users. The operational risk of a charging pile is determined by its inherent reliability parameters and the influence of its running state on users within the system. By conducting state evaluations, optimizing the operation and maintenance strategy can significantly improve the scientific and efficient operation of the charging pile, thereby maximizing operational and maintenance benefits.

The charging station operates in four distinct states: normal, attention, abnormal, and severe. The normal state indicates that the station’s variables are within a stable and optimal range, ensuring normal operation. The attention state signifies that the variables are close to the standard limit value, allowing continued operation but requiring enhanced monitoring. The abnormal state means that the variables slightly exceed the standard limit, necessitating continuous monitoring and appropriately scheduled maintenance outages. The severe state indicates that the variables significantly exceed the standard limit, necessitating immediate power outage maintenance.

2. XGBoost Principle

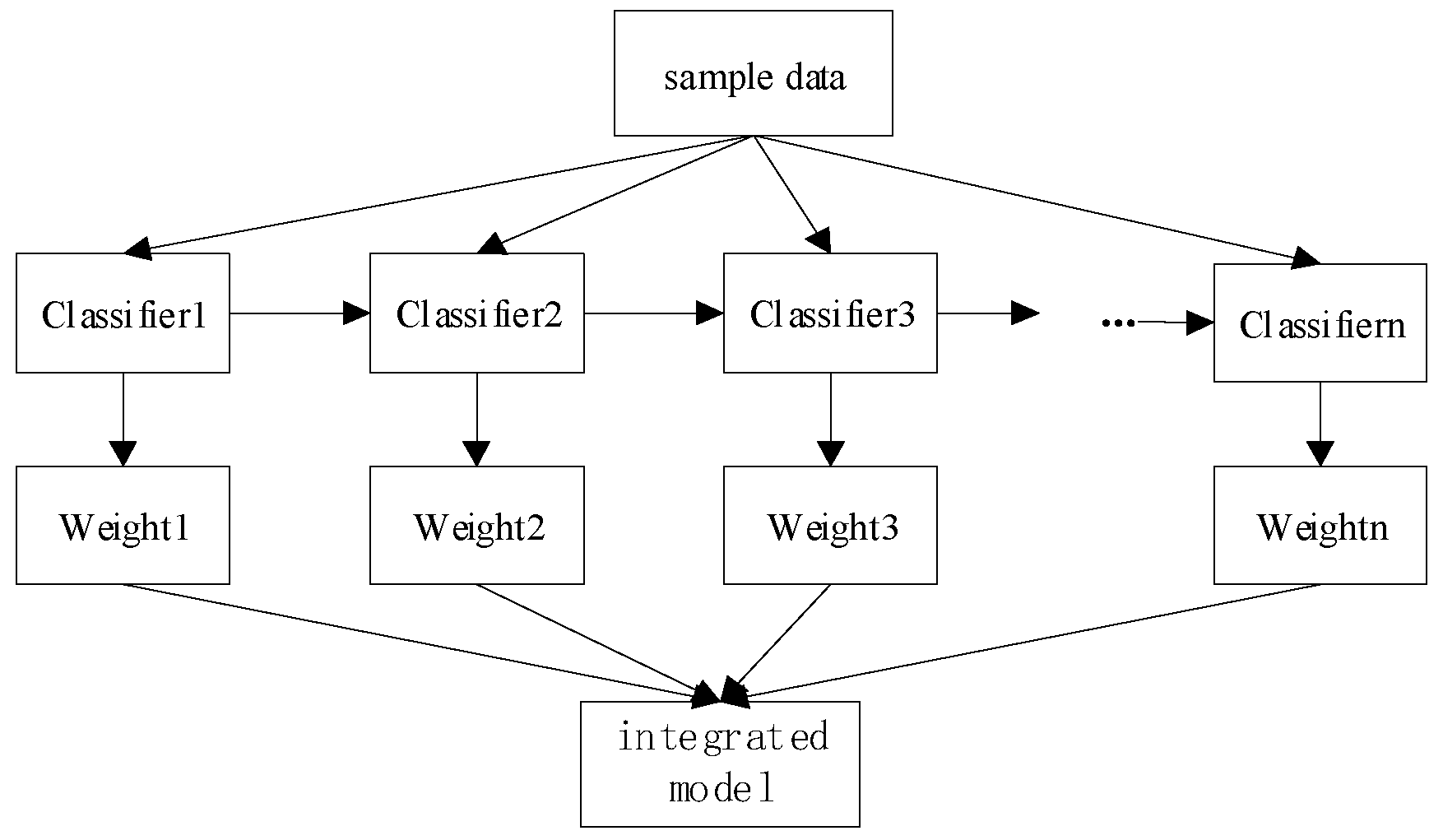
Boosting, as a classification model, is an ensemble learning technique. The fundamental idea behind boosting is to create a high-accuracy model by combining and weighting multiple low-accuracy models. This process enhances the overall performance and accuracy of the model, as illustrated in Figure 2.

XGBoost is an enhancement of the gradient boosting decision tree (GBDT) model. The main concepts underlying XGBoost are as follows [16]:

(1) Base learner: regression tree

The most fundamental component of a boosted tree is known as a regression tree, or CART (Classification and Regression Tree). CART assigns the input to each leaf node based on the input attributes, with each leaf node corresponding to a real number score.

(2) Tree complexity

Each regression tree can be divided into a structural part and a leaf weight part. The t-th tree model can be expressed as:

f_{t} (x) = w_{q (x)}, w \in R^{T}, q : R^{d} \to \{1, 2, \cdot \cdot \cdot, T\}

(1)

In the formula, w is the score of leaf nodes, q(x) represents the leaf node index number corresponding to the sample x.T is the number of leaves.

The complexity includes the number of nodes in a tree and the L2 -norm square of the output fraction on each leaf node, which is defined as follows:

Ω (f_{t}) = γ T + \frac{1}{2} λ \sum_{j = 1}^{T} w_{j}^{2}

(2)

where γ is the penalty coefficient of the number of leaf nodes, λ is the regular term coefficient.

(3) Objective function

O b j^{(t)} = \sum_{i = 1}^{n} [g_{i} f_{t} (x_{i}) + \frac{1}{2} h_{i} f_{t}^{2} (x_{i})] + Ω (f_{t})

(3)

where x_i is the i-th sample,

g_{i} = \partial_{_{\overset{\land}{y} (t - 1)}}^{2} l (y_{i}, {\overset{\land}{y}}^{(t - 1)})

h_{i} = \partial_{_{\overset{\land}{y} (t - 1)}}^{2} l (y_{i}, {\overset{\land}{y}}^{(t - 1)})

l (y_{i}, {\overset{\land}{y}}^{(t - 1)})

is the defined loss function, y_i is the true value of the i-th sample,

{\overset{\land}{y}}^{(t - 1)}

the model obtained by the previous t-1 round of training.

Defines I as the set of samples above a leaf with index j.

I_{j} = {i | q (x_{i}) = j}

, further the modified objective function is as follows:

O b j^{(t)} = \sum_{j = 1}^{T} [G_{j} w_{j} + \frac{1}{2} (H_{j} + λ) w_{j}^{2}] + γ T

(4)

where,

G_{j} = \sum_{i \in I_{j}} g_{i}

\sum H_{j} = \sum_{i \in I_{j}} h_{i}

(4) Scoring function

Suppose that the structure of the treeis known, the optimal w and the corresponding objective function value can be determined using Formula (4):

w_{j}^{*} = - \frac{G_{i}}{H_{i} + λ}

(5)

o b j = - \frac{1}{2} \sum_{j = 1}^{T} \frac{G_{i}^{2}}{H_{i} + λ} + γ T

(6)

(5) Gain

When creating a tree model, a greedy algorithm can be used to add a segmentation to the existing leaves each time. For a specific segmentation scheme, the gain obtained is:

G a i n = \frac{1}{2} [\frac{G_{L}^{2}}{H_{L} + λ} + \frac{G_{R}^{2}}{H_{R} + λ} - \frac{(G_{L}^{2} + G_{R}^{2})}{H_{L} + H_{R} + λ}] - λ

(7)

In the formula, the first term represents the fraction of the left subtree, the second term represents the fraction of the right subtree, and the third term represents the undivided fraction. This third term accounts for the complexity cost introduced by the addition of new leaf nodes.

According to this principle, XGBoost combines multiple classifiers to achieve better generalization performance compared to a single classifier. Additionally, a regularization term is added to the objective function, including the L₂ regularization term for the number of leaf nodes and the score of leaf nodes, to prevent the model from overfitting.

3. State Evaluation Model of Charging Station

In this paper, the state evaluation model of the charging station is treated as a multi-classification model. The state variables listed in Section 1.1 are used as features, and the four operating states are used as classification results. The training model’s data comprises historical fault data, maintenance data, monitoring data, and external environment data of the integrated isolation circuit breaker. This study collects and organizes 320 data points, using 280 for training and 40 for testing.

3.1. Model Building Steps

(1) Definition of loss function

The state evaluation model of the charging station is a multi-classification model, so the loss function is defined as a cross-entropy function. For a sample, the loss function is expressed as:

l (y_{k}, f_{k} (x)) = - \sum_{k = 1}^{K} y_{_{k}} \log p_{k} (x)

(8)

where y_k is the probability that the sample belongs to the category k, p_k(x) is the probability that the model predicts that the sample belongs to the category k,

p_{k} (x) = \frac{e^{f_{k} (x)}}{\sum_{k = 1}^{K} e^{f_{k} (x)}}

For all samples, the first derivative g and the second derivative h of the loss function are calculated as follows:

g_{i k} = y_{i k} - p_{k, i - 1}

(9)

h_{i k =} \{\begin{cases} p_{i, k - 1} (1 - p_{j, k - 1}), i = j \\ - p_{i, k - 1} p_{j, k - 1}, i \neq j \end{cases}

(10)

(2) Initialize the prior probability

Since the running state of the charging station is divided into four categories, determine the probability that each sample belongs to each class.

(3) Fit the first tree for the first category:

(a) Using a greedy algorithm, the tree model is established by segmenting the existing leaf nodes. According to Equations (7), (9) and (10), the gain value of each segmentation is calculated, and the segmentation scheme with the largest gain is selected to complete the establishment of each tree.

(b) For each tree established in step (a), the corresponding structure score is calculated according to Formula (6). The tree model with the smallest structure score is then selected as the first tree in the first category.

(c) According to Equation (5), the leaf score of the tree is calculated in step (b), resulting in a complete regression tree model. The probability that the model prediction sample belongs to category 1 is then updated.

(d) Fitting the first tree to the second category follows the same process as outlined in step (3), further completing the establishment of the first tree for all four categories.

(e) Repeat steps (c) through (d) until the set threshold is reached. This completes the establishment of M trees for all categories, forming the state evaluation model of the integrated isolation circuit breaker. By using historical data and calling the ECDF function in the MATLAB statistical toolbox, the empirical probability distribution of the 50 prediction boxes is estimated.

3.2. Cross Validation and Model Parameters

In this paper, the K-fold cross-validation method is used to divide the training data into K equal parts. Of these, K-1 parts are used for training, and 1 part is used for validation. The average classification error rate is used as the performance index to evaluate the model’s classification effect. The model parameters are adjusted, and the optimal parameter selection is determined based on the cross-validation results. The main parameter selections are shown in Table 1.

Except for the parameters listed in Table 2, all other parameters are set to their default values. Using the above parameter settings, the optimal charging station state evaluation model is obtained.

3.3. Appraisal Process

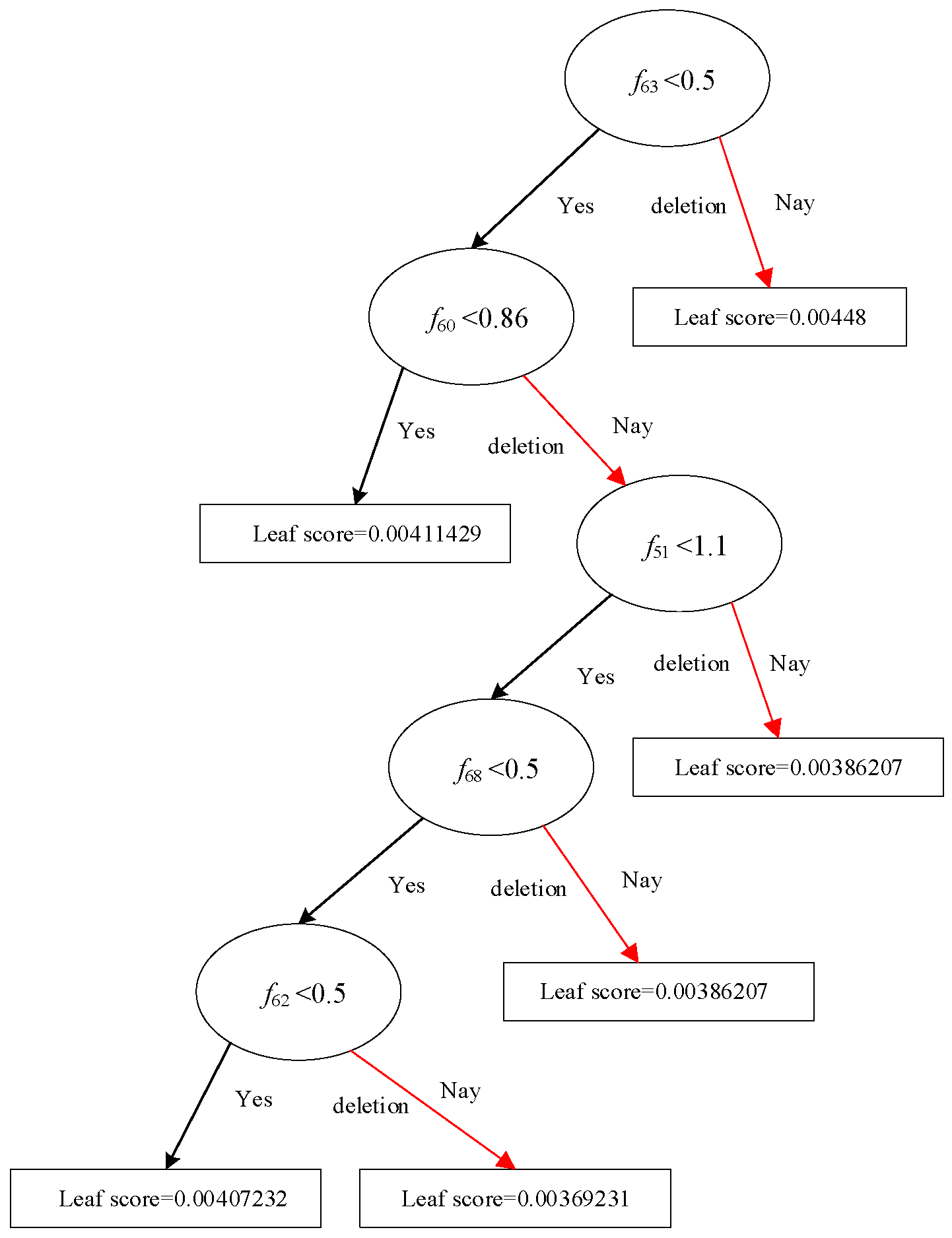
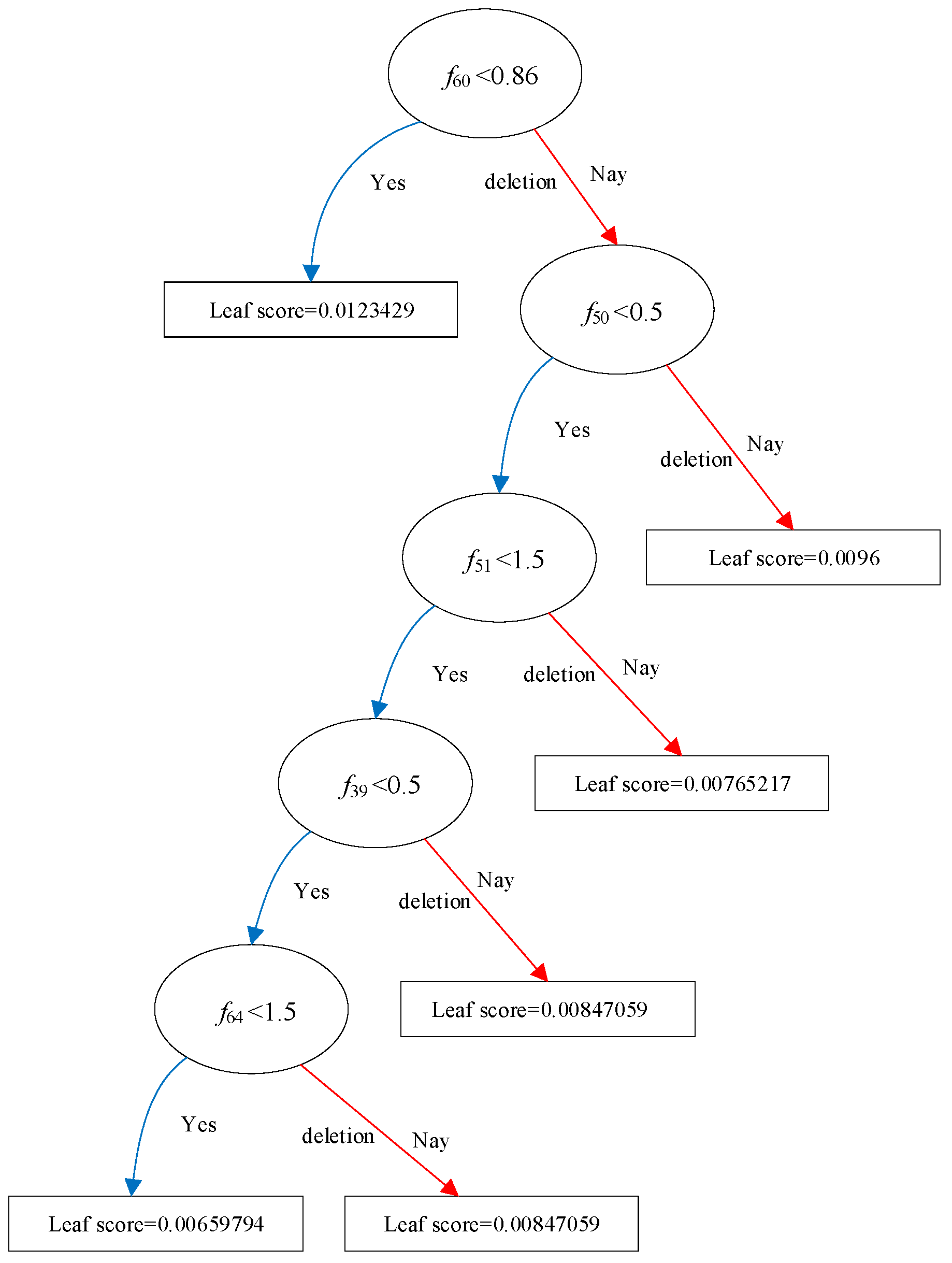
XGBoost uses the tree model as the base model to visualize the model, and the evaluation process of the operating state of the charging station can be seen. Due to the large number of trees, the first two trees of the first category are taken as examples. The tree structure is shown in Figure 3 and Figure 4.

From Figure 3 and Figure 4, it can be seen that the state quantity of each tree participates in the division with its specific division value, and the leaf nodes correspond to different scores. For a set of operating data from the charging station, the leaf nodes to which this data ultimately belongs in each tree can be determined based on the state quantity division conditions. In each category, the scores corresponding to the leaf nodes of this data set in each tree are accumulated. Assuming that in Figure 3 and Figure 4, the data of this group correspond to the leaf nodes in the lower left corner, the score is 0.003412526. The score of this group of data in each category can be expressed as[S₁, S₂, S₃, S₄]. The probability of converting the scores to the group of data corresponding to each category using the softmax function is [P₁, P₂, P₃, P₄]. The category with the highest probability is the result of this evaluation, indicating the corresponding operating state of the charging station.

4. Charging Station Optimization Operation and Maintenance

Conventional operation and maintenance of charging stations typically involves planning the work either in order of proximity or based on the years since the charging station’s investment. However, based on the state assessment of the charging station, operation and maintenance should be carried out according to the risk associated with the station’s condition. Using the risk assessment method proposed in this paper, the operation and maintenance priorities for each station are determined based on the state assessment results.

The operation and maintenance time is divided into equal-period operation and maintenance and optimized-period operation and maintenance. Equal-period operation and maintenance treats all charging stations equally, distributing the workload evenly throughout the operation and maintenance cycle. Optimized-period operation and maintenance, as proposed in this paper, considers both the operation and maintenance costs and the reliability gain. It allocates the workload for each station with the goal of minimizing the total operation and maintenance cost.

4.1. Objective Function

The objective function of the optimal operation and maintenance strategy for electric vehicle charging stations considers both the operation and maintenance costs and the reliability gain [21]:

\min F (X) = f_{c} (X) + f_{r} (X)

(11)

where F (X) is the total objective function, x_m in X is the number of m operation and maintenance periods of the m-th operation and maintenance charging station. Taking the operation and maintenance work of an electric vehicle charging station in a city as an example, the weekly working hours are 5 days, and the single-day working hours are 8:00 to 12:00 in the morning and 14:00 to 18:00 in the afternoon. Therefore, this paper considers that the operation and maintenance cycle is one week, with each operation and maintenance period lasting two hours. This period includes travel time, operation and maintenance time, information registration time, and rest time.

1) f_c (X) Indicates the economic objective function, including the cost of resources consumed during operation and maintenance:

f_{c} (X) = \sum_{m = 1}^{M} \sum_{t = 1}^{T_{s}} c_{m, t}

(12)

where T_s is the total number of time periods of operation and maintenance cycle, M is the total number of charging stations, c_m_{, t} is the operation and maintenance cost of the m-th charging station in the t-th period.

2) f_r (X) represents the expected cost of system risk. Since the purpose of operation and maintenance is to reduce the current failure rate of the equipment to improve system reliability, the system risk is calculated according to Equation (5) after each period of operation and maintenance. The time loss is then converted into economic loss.

f_{r} (X) = \sum_{t = 1}^{T_{s}} \sum_{n = 1}^{N} g \frac{L O T_{t} (n)}{N}

(13)

where N is the number of scenes, LOT_t (n) is the user ‘s loss time in the n-th scenario after the operation and maintenance t period, g is the conversion coefficient of user loss time cost per unit time [22].

According to the characteristics of the operation and maintenance work of the electric vehicle charging station, the following relevant constraints are set.

1) Each station operates and maintains at least one period of time, considering the operation and maintenance time constraints of a single charging station.

x_{m} \geq 1 (m \in C S)

(14)

2) Operation and maintenance timing constraints:

y_{m + 1} = y_{m} + x_{m} (m, m + 1 \in C S)

(15)

3) All charging stations in the system are non-simultaneous operation and maintenance, considering the total time constraint of operation and maintenance.

\sum_{m \in C S} x_{m} = T_{s}

(16)

4) Operation and maintenance resource constraints:

\sum_{x = 1}^{x_{m}} r_{m, x} \leq Y_{m, \max} (m \in C S)

(17)

where y_m denotes the start time of operation and maintenance of the m-th charging station, r_m_{, x} is the operation and maintenance resources required by the m-th charging station in the x time period, Y_m_{, max} is the maximum operation and maintenance resources that the m-th charging station can invest.

4.2. Optimistic Algorithm

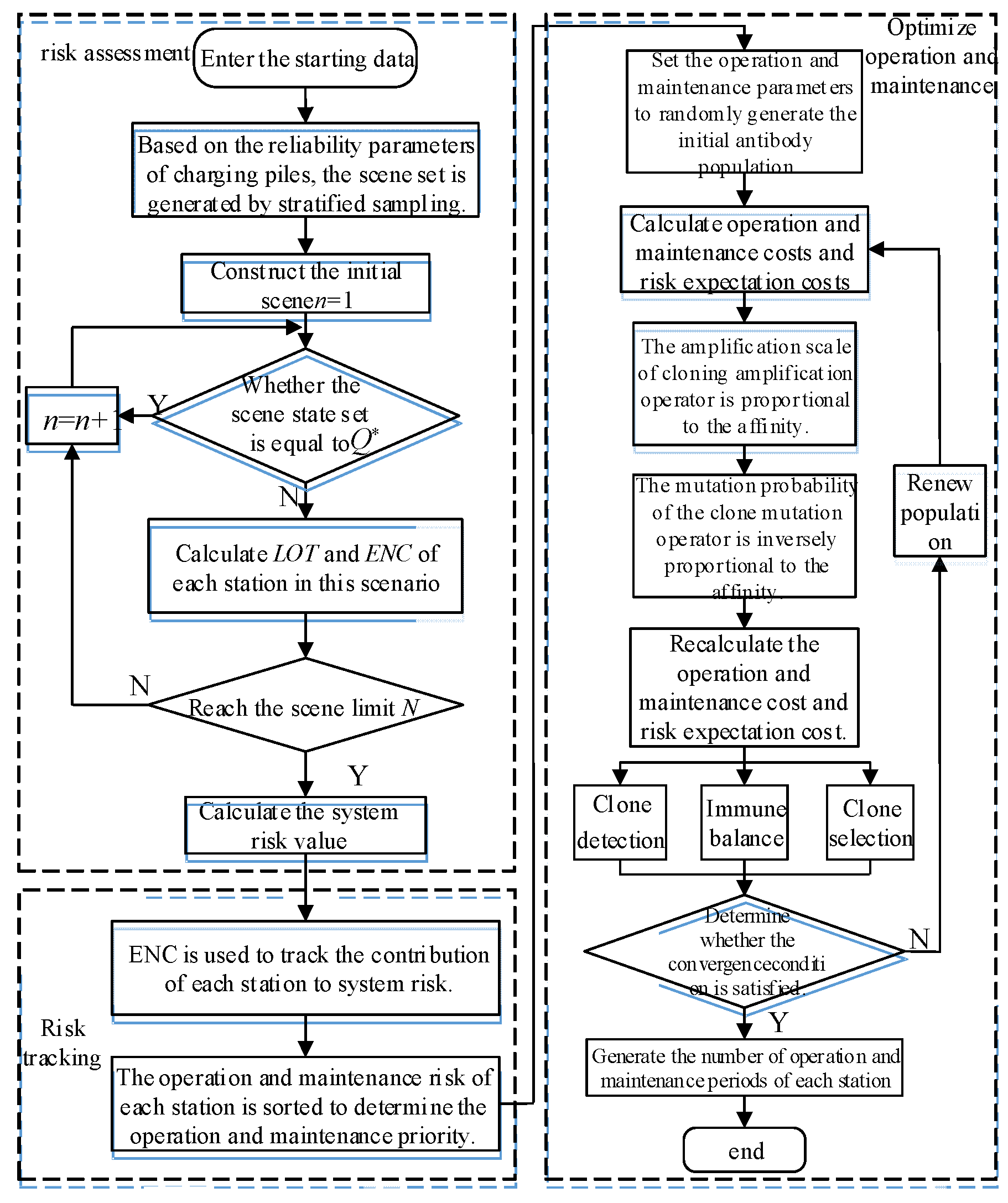
The operation and maintenance strategy optimization studied in this paper is a nonlinear integer programming problem, making it difficult to obtain results using analytical methods. Therefore, the immune clonal selection algorithm (ICSA) is used to solve the problem [23]. Compared to the traditional immune algorithm, ICSA introduces the clonal expansion operator and the clonal mutation operator, which help expand the high-quality population and eliminate the inferior population during the iterative process. This effectively improves the convergence speed of the algorithm. In ICSA, the antibody, antigen, and affinity represent the solution set, the fitness of the objective function, and the matching degree between the solution set and the objective function in the optimization problem, respectively.

The operation and maintenance strategy for charging stations proposed in this paper is mainly divided into three parts: risk assessment, risk tracking, and optimization of operation and maintenance. Firstly, the system risk value is calculated based on the charging piles and the road network. Secondly, risk tracking is used to determine the operation and maintenance priority of each station. Finally, the ICSA algorithm is employed to determine the number of operation and maintenance periods for each station, aiming to minimize the economic cost and risk expectation cost. The optimization process for the operation and maintenance strategy is illustrated in Figure 5.

5. Example Analysis

5.1. Traffic Network and Parameter Setting

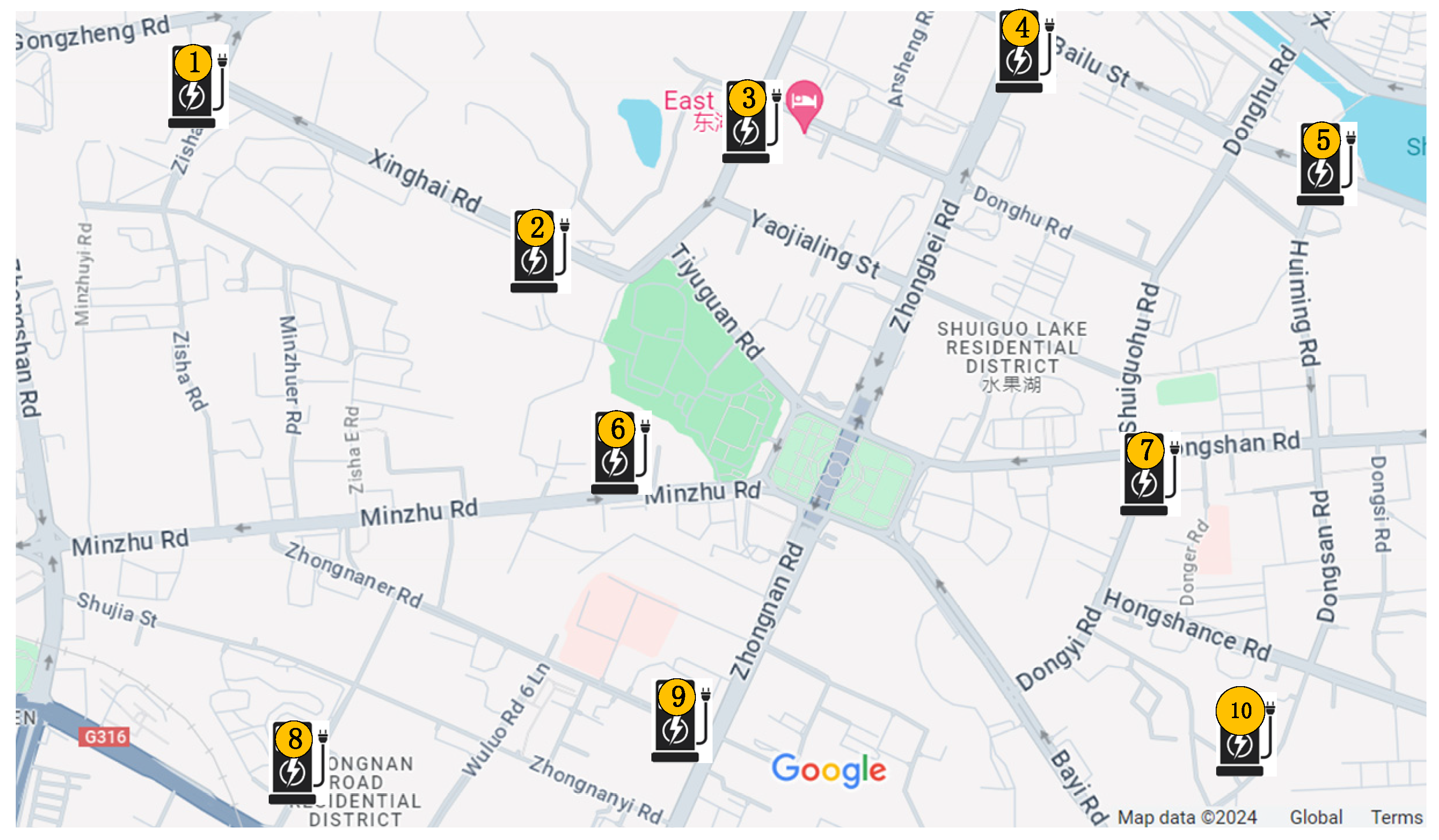
The traffic network in a specific area is analyzed as an example to illustrate the research content. The distribution of the road network and charging station sites is shown in Figure 6. Currently, some of the 10 important traffic nodes marked in the figure have been put into operation. For this study, all nodes are set as the same type of DC charging stations, each equipped with 10 charging piles, with a charging power of 30 kW. The stations are numbered according to their distance from farthest to nearest. Using failure rate, repair rate statistics, operation years, and equipment data from charging piles recently put into use, combined with a simulation model, the failure rate parameters of each charging pile are obtained. Additionally, traffic parameter attributes in the road network are valued based on the road grade.

Electric vehicles are mainly small vehicles that use DC fast charging. While private cars are numerous and primarily use fixed-site AC charging, official cars, taxis, and the currently popular personal operating vehicles primarily rely on DC charging due to their work requirements.

Therefore, the ratio of private cars to urban commuter cars is set to 1:5. To meet the dynamic and random nature of charging load distribution, this study considers 120 vehicles with charging demands driving on the road network during the peak charging period from 12:00 to 14:00 [24]. During this period, 60 vehicles are either in a waiting state or charging state at the stations, and the system reliability is evaluated. The distribution of vehicle starting positions, demand generation times, and initial SOC are referenced [25] from prior studies. The battery capacity of each vehicle is set to 25 kWh. During the simulation period, the simulation step size is set to 0.5 minutes, with the simulation time spanning from the moment the first vehicle generates a charging demand to the time the last vehicle completes charging.

5.2. Risk Calculation and Operation and Maintenance Strategy

Combining the failure probability of each charging pile in the system, stratified sampling is performed 3000 times to obtain the corresponding scenarios. The initial vehicle information is the same for all scenarios. For each scenario, road traffic simulations of the Q* state and the current sampling state are conducted to determine the time each electric vehicle takes to complete charging and the power provided by each station. The system risk value and the ENC (Expected Number of Customers) of each station are then calculated. Using Equation (8), the risk is allocated to each charging station, and the operation and maintenance order is sorted according to the risk level of each station, as shown in Table 2.

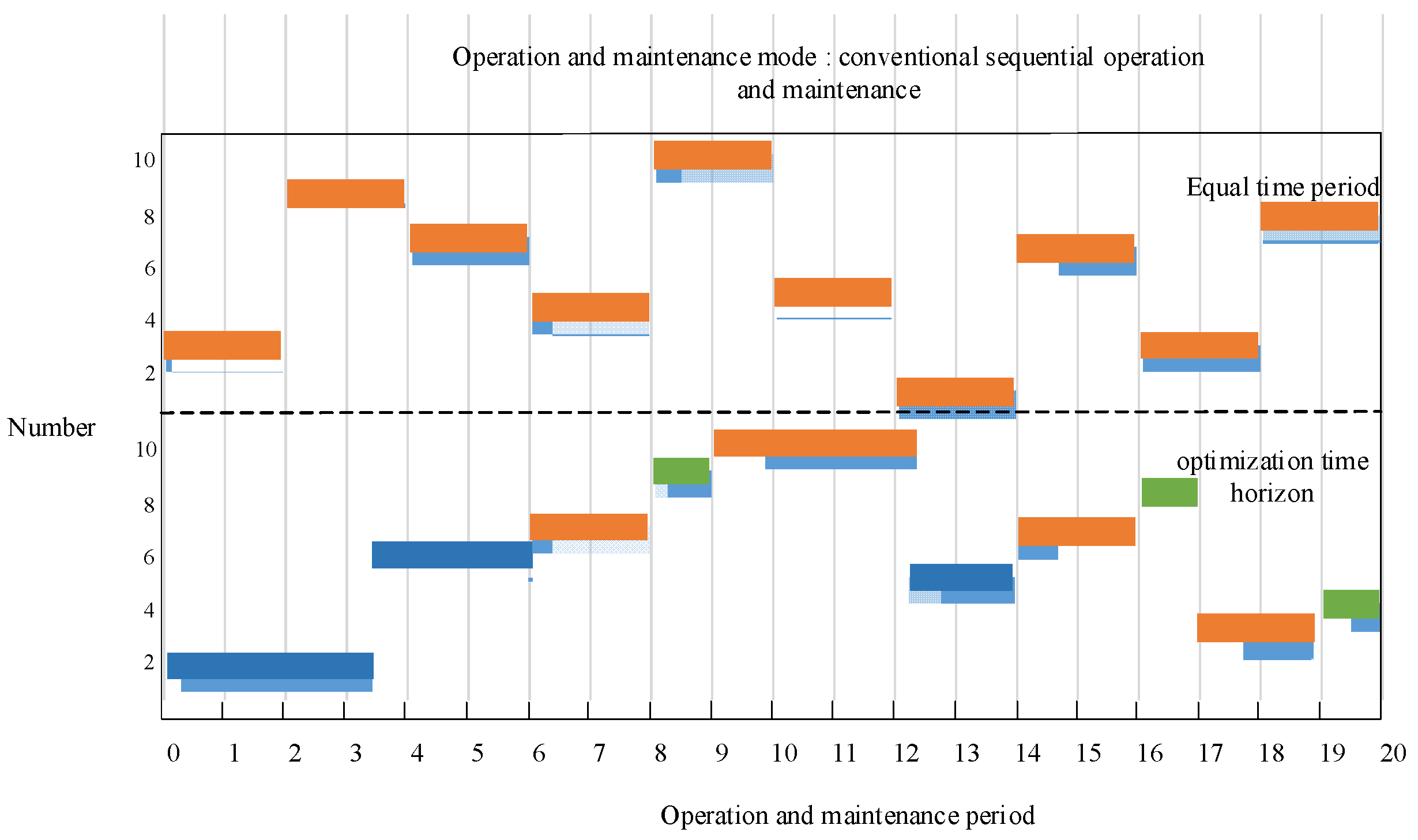
Firstly, based on the current actual operation and maintenance work, this paper optimizes the operation and maintenance periods. Secondly, the operation and maintenance methods are calculated and analyzed according to the risk order using both equal time periods and optimized time periods. The operation and maintenance information for equal time periods and optimized time periods of the conventional sequential operation and maintenance is shown in Figure 7.

It can be seen from Figure 7 that after optimizing the operation and maintenance time, Station 3 with the highest risk level increases the operation and maintenance time, while Station 2 and Station 8 with lower risk level reduce the operation and maintenance time. Additionally, to optimize the operation and maintenance costs, the operation and maintenance time for the remaining stations has been adjusted appropriately. However, due to limitations in resources and time constraints, the operation and maintenance time is only adjusted for one period. The total cost of operation and maintenance for equal time periods and optimized time periods of conventional sequential operation and maintenance is shown in Table 3.

Compared with the equal period, the operation and maintenance cost and system expected risk of the optimized period decreased by 6.63% and 18.56%, respectively, achieving better operation and maintenance benefits. The operation and maintenance information for the equal time period and the optimized time period, according to the risk order, is shown in Figure 8.

As shown in Figure 8, the operation and maintenance plan based on risk order adjusts the operation and maintenance time of certain charging stations in the optimized period to reduce the total cost, compared to the equal period. The total cost of equal-period and optimized-period operation and maintenance according to the risk order is shown in Table 4. Compared to the two operation and maintenance orders, the expected cost of system risk is reduced by 31.23% and 32.48% respectively in equal period operation and optimized period operation and maintenance according to the risk order. It can be inferred that ordering operation and maintenance by risk level can significantly improve the overall reliability of the system and reduce user losses. Compared with the current conventional sequential equal-period operation and maintenance, the risk-based optimization of time-period operation and maintenance reduces the total cost by 24.11% while maintaining the operation and maintenance cost, which effectively improves the overall operation and maintenance efficiency.

6. Conclusions

To address the shortcomings of the current operation and maintenance work of electric vehicle charging stations, this study proposes an operation and maintenance system for electric vehicle charging stations using the XGBoost integrated algorithm to evaluate the operational status of charging stations. A scientific and efficient risk-based operation and maintenance strategy is proposed.

1) The state evaluation model of charging stations is established using XGBoost. Considering factors such as driving and charging habits, road traffic, and charging station equipment, the training sample data is constructed using historical data, online monitoring data, and external environment data. The state evaluation model of charging stations is then trained based on the XGBoost algorithm.

2) Considering the operation and maintenance cost and reliability gain, an operation and maintenance strategy optimization model for electric vehicle DC charging stations is established based on the XGBoost state evaluation. According to the risk level, the operation and maintenance sequence of each charging station is determined, and the operation and maintenance time for each station within the maintenance cycle is calculated.

The operation and maintenance strategy formulated by the state evaluation and optimization model of the charging station, based on the XGBoost algorithm, overcomes the blindness and inefficiency of existing operation and maintenance methods. It significantly improves the overall efficiency of the system’s operation and maintenance and ensures the operational reliability of the charging facilities.

Funding

This research was funded by State Grid Corporation of China Headquarters Management of Science and Technology Project (5400-202128154A-0-0-00), and China Scholarship Council.

References

SU Li, LIU Ziqi, WANG Shidan, et al. Ordered charging strategy of electric vehicles based on user driving behavior characteristics. Electric Power Automation Equipment 2018, 38, 63–71.
ZHAO Mingyu, WANG Gang, WANG Yinghui, et al．Design and implementation of a supervisory and control system for charging facilities of electric vehicles. Automation of Electric Power Systems 2011, 35, 65–69.
HU Yong, GUO Zijian, LIU Qifeng, et al． Modeling scheme of supervisory control system for electric vehicle charging station based on IEC 61970 and IEC 61850. Automation of Electric Power Systems 2013, 37, 91–96.
NIE Xiaoyong, LIU Jieyi, XUAN Liang, et al． Online monitoring and integrated analysis system for EV charging station[C]//2013 IEEE PES Asia-Pacific Power and Energy Engineering Conference (APPEEC), December 8-11, 2013. Kowloon, Hong Kong, China. New York, USA: IEEE, 2013.
XU Peidong, FANG Hualiang, WANG Haiming, et al. Progressive maintenance scheduling strategy of transmission lines based on risk assessment and sensitivity clustering. Power System Technology 2018, 42, 3024–3032.
Jae-Haeng Heo, Mun-Kyeom Kim, Geun-Pyo Park, et al.．A reliability-centered approach to an optimal maintenance strategy in transmission systems using a genetic algorithm. IEEE Trans on Power Delivery 2011, 26, 2171–2179. [CrossRef]
FENG Ding, LIN Sheng, HE Zhengyou, et al.．Optimization method with prediction-based maintenance strategy for traction power supply equipment based on risk quantification. IEEE Transactions on Transportation Electrification 2018, 04, 961–970. [CrossRef]
PENG Fuxian. Research on risk assessment method for automatic operation and maintenance of high voltage transmission lines[J]. Automation and Instrumentation, 2019, 64-67.
LIANG Shuo, QIN Liwen, LI Chunhua, et al. Condition-based maintenance decision-making method for distribution equipment based on risk assessment. Proceedings of the CSU-EPSA 2019, 31, 47–52.
2017, 41, 106-113. [CrossRef]
YANG Hongming, LI Ming, WEN Fushuan, et al. Route selection and charging navigation strategy for electric vehicles employing real time traffic information perception. Automation of electric power systems 2017, 41, 106–113. [CrossRef]
Li Wenyuan. Power system risk assessment model, method and application [M]. Beijing. Science Press, 2006.
Charging pile fault code and common missing methods [S]. Beijing: National Electric Vehicle Service Co., Ltd. Technology Research and Development Center ( Technology Center ), 2018.
JIANG Cheng, WANG Shuo, WANG Baoqing, et al. Probabilistic reliability assessment of power system containing wind power based on latin hypercube sampling. Transactions of China Electrotechnical society 2016, 31, 193–206.
DENG Bin, GUO Chuangxin, WANG Yue, et al. An assessment and ranking method for component importance based on well-being analysis. Power System Technology 2013, 37, 3489–3498.
JIANG Yijing, YU Aiqing, HUANG Minli. Coordinated charging guiding strategy for electric vehicles in temporal-spatial dimension considering user satisfaction degree. Electric Power 2020, 53, 122–130.
LIU Bailiang, HUANG Xueliang, LI Jun, et al. Multi-objective planning of distribution network containing distributed generation and electric vehicle charging stations. Power System Technology 2015, 39, 450–456.
PAN Yiyong, YU Ting, MA Jianxiao. Improvement of urban road impedance function based on section impedance and node impedance. Journal of Chongqing Jiaotong University (Natural Science) 2017, 36, 76–81.
ZENG Chengbi, LIU Guang, MIAO Hong, et al. Planning of electric vehicle charging station considering urban traffic flows. Journal of electric power science and technology 2019, 34, 101–107.
XIONG Bo, SHU Zhengyu, GUO Chen, et al. Charging station optimization planning from the perspective of social benefits. Smart Power 2019, 47, 78–84.
WU Rui, ZHOU Liangsong, YAO Zhandong, et, al. Intelligent charging navigation for electric vehicles based on real-time electricity price. Electric Power 2020, 53, 131–138+146.
DONG Manling, ZHENG Hanbo, ZHANG Yiyi, et al. A novel maintenance decision making model of power transformers based on reliability and economy assessment. IEEE Access 2019, 07, 28778–28790. [CrossRef]
LI Hongzhong, QIANG Wei, GAO Yunan, et al. Charging station planning considering users’ travel characteristics and line availability of distribution network. Automation of Electric Power System 2018, 42, 48–56.
Xu Guogen. Optimization method and its MATLAB implementation [M].Beijing: Beijing University of Aeronautics and Astronautics Press, 2018.
GE Shaoyun, LI Rong, HAN Jun, et al. Charging station planning considering probability behavior characteristic of electric taxi. Automation of Electric Power System 2016, 40, 50–58.
JIANG Xin, FENG Yongtao, XIONG Hu, et al. Electric vehicle charing station planning based on travel probability matrix[J]. Transactions of China Electrotechnical Society, 2019, 1(11).

Figure 1. Maintenance system of EV charging station.

Figure 2. principle of boosting.

Figure 3. Scenario matching between generation and load.

Figure 4. The second tree of the first class.

Figure 5. Operation and maintenance strategy optimization process.

Figure 6. Road network and distribution of charging station sites.

Figure 7. Regular sequential operation and maintenance scheduling for charging station.

Figure 8. Original and optimized maintenance scheduling for charging station.

Table 1. parameters of model.

parameter	parameter value	meaning of parameters
Learning-rate	0.08	Shrinkage step size, that is, learning rate
max_depth	5	The maximum depth of the tree is 5
n_estimators	650	The number of trees per category is 650.
eval_metric	merror	Multi-classification error rate
min_child_weight	0.8	The minimum leaf node sample weight and

Table 2. Classification of charging station risk level.

Charging station number	value-at-risk	Operation and maintenance order
2	12.325	1
7	11.478	2
6	8.128	3
9	7.693	4
3	7.356	5
4	7.238	6
1	6.841	7
5	5.256	8
10	3.943	9
8	2.568	10

Table 3. Costs under different maintenance strategies.

decision-making model	Operation and maintenance cost / yuan	System risk expectation / yuan	Total cost / yuan
Equal time operation and maintenance	1098.8	1289.4	2397.2
Optimize time operation and maintenance	996.2	1023.6	2097.8

Table 4. Costs under different maintenance strategies.

decision-making model	Operation and maintenance cost / yuan	System risk expectation / yuan	Total cost / yuan
Equal time operation and maintenance	1089.6	798.6	1987.2
Optimize time operation and maintenance	997.6	703.7	1589.6

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Electric Vehicle DC Charging Station Based on XGboost Re-search on Condition Assessment and Operation and Mainte-nance

Abstract

0. Introduction

1. Operation and Maintenance System of Electric Vehicle Charging Station

2. XGBoost Principle

3. State Evaluation Model of Charging Station

3.1. Model Building Steps

3.2. Cross Validation and Model Parameters

3.3. Appraisal Process

4. Charging Station Optimization Operation and Maintenance

4.1. Objective Function

4.2. Optimistic Algorithm

5. Example Analysis

5.1. Traffic Network and Parameter Setting

5.2. Risk Calculation and Operation and Maintenance Strategy

6. Conclusions

Funding

References

MDPI Initiatives

Important Links

Subscribe