Preprint
Article
Understanding Logical Reasoning Ability of Large Language Models
Altmetrics
Downloads
171
Views
213
Comments
0
This version is not peer-reviewed
Artificial Intelligence Models, Tools and Applications
Submitted:
22 August 2024
Posted:
23 August 2024
You are already at the latest version
Alerts
Abstract
Large language models have recently made significant progress in natural language processing, and there is observation that these models exhibit reasoning abilities when they are sufficiently large. This has sparked considerable research interest since reasoning is a hallmark of human intelligence that is widely considered missed in artificial intelligence systems. Due to large size of these models, evaluation of LLMs’ reasoning ability is largely empirical. Creating datasets to evaluate the reasoning ability of LLMs is therefore an important area of LLM research. A key open question is whether LLMs reason or simply recite memorized texts they have encountered during their training phase. This work conducts simple experiments using Cheryl’s Birthday Puzzle and Cheryl’s Age Puzzle and their variants created in this work to investigate whether LLMs recite or reason and discovers that LLMs tend to recite memorized answers for well-known questions, which appear more frequently on the internet, even though such answers may not be sensible for the modified versions of the questions. When presented with less well-known questions, it is observed that LLMs answer with correct reasoning more frequently. A possible inference is that LLMs tend to reason on less well-known questions but recite memorized answers on popular questions. As a result, to accurately evaluate the reasoning ability of LLMs, it is essential to create new datasets to ensure that LLMs are elicited to truly use their reasoning ability to generate responses to the presented questions. In view of the finding, this work proposes a new dataset comprising of unseen questions requiring semantic and deductive logical reasoning skills to elicit reasoning ability from LLMs. The proposed evaluation framework is based on the intuition that some questions or puzzles can only be answered through the mastery of reasoning needed for situational awareness, and the dataset consists of 84 logical reasoning questions on room assignment subject to constraints. The proposed evaluation framework has several desirable properties, including resilience to training data contamination, ease of response verification, extensibility, usefulness and automated test case generation. This work then applies the proposed dataset to evaluate the reasoning ability of state-of-the-art LLMs, including GPT-3, GPT-4, Llama-3.1, Gemini-1.5 and Claude-3.5, and compare their performance with the performance of human intelligence on the dataset.
Keywords:
Subject: Computer Science and Mathematics - Artificial Intelligence and Machine Learning
1. Introduction
Reasoning is a fundamental aspect of human intelligence, playing a crucial role in activities such as problem solving, decision making, and critical thinking. It involves the use of evidence, arguments, and logic to arrive at conclusions or make judgments. Incorporating reasoning ability into natural language processing systems has been an active research area since the beginning of artificial intelligence (AI) [1,2].
Recently, ChatGPT and other large language models (LLMs) have made significant advancements in natural language processing. Notably, GPT-4 is highlighted as “advanced” at reasoning tasks [3]. It has been shown that these models exhibit emergent abilities, including the ability to reason, when they are large enough in terms of the number of parameters [4]. Specifically, reasoning behaviours may emerge in language models with over 100 billion parameters [4,5,6]. By providing the models with “chain of thoughts,” which are exemplars, these models have demonstrated that they can answer questions with explicit reasoning steps [5]. This has sparked considerable interest in academia since reasoning ability is a hallmark of human intelligence that is widely considered missed in AI systems [8].
Nonetheless, despite the strong performance of LLMs in certain reasoning tasks [7,8,9,10,11], it remains unclear whether LLMs are indeed reasoning when providing a correct answer to a given question, and to what extent they are capable of reasoning. For example, LLMs perform badly on common planning or reasoning tasks which pose no issues to humans [12,13,14]. This limitation is also stated by [5]: “we qualify that although chain of thought emulates the thought processes of human reasoners, this does not answer whether the neural network is actually reasoning.” Hence, a question that often crops up is whether LLMs know or understand what they are saying, or they are merely reciting texts they have encountered during their training routine, without the need for reasoning [13,15,16]. The authors of [13] even call LLMs “stochastic parrots,” meaning that LLMs, though able to generate plausible language, do not understand the meaning of the language they process.
Due to the large size of these models, despite the recent progress made in theoretical analysis of LLMs [17], it is practically impossible to understand at the algorithmic level how LLMs work to generate a response seemingly demonstrating their use of reasoning. This echoes a statement made by Alan Turing: “An important feature of a learning machine is that its teacher will often be very largely ignorant of quite what is going on inside.” As a result, evaluation of the emergent reasoning behaviours of an LLM still largely relies on empirical investigation which treats it as a black box and observes its aggregate outputs in response to different inputs at a macroscopic level. This work carries out an empirical study on the reasoning ability of LLMs.
Devising tests to evaluate the reasoning ability of LLMs [5,6,10,12,18,19,20,21,22,23,24,25,26] is an active research area. Various tasks, called datasets, and benchmarks have been created to test the arithmetic reasoning [6,20,21,22,26], common sense reasoning [10,19,23,25,26], symbolic reasoning [5], logical reasoning [12,24,28], and data understanding and causal judgement [20,24,26,28] of LLMs. Even ethics reasoning [18] is included in these datasets and benchmarks although it is generally believed that AI lacks self-awareness. However, these tests do not help answer the question on whether the LLMs are reasoning or parroting texts. Many of the tasks or questions in these tests are taken from existing public examinations. For example, the complex reasoning tasks in [26,28] are taken from the Law School Admission Test. Similarly, questions from the Chinese Civil Servant Exam are adopted as the logical reasoning tasks of [20]. We cannot completely eliminate the possibility that LLMs may have come across these tasks in their training data, and they manage to complete the given tasks correctly because of memorization of the problems and answers acquired during the training phase. That is, these datasets and benchmarks are susceptible to training data contamination, a term coined by [15]. Other tasks are relatively simple and, as [12] puts it, they require shallow reasoning. In other words, they cannot truly evaluate the cognitive limit or reasoning ability of LLMs.
To fill this gap in evaluating the reasoning ability of LLMs, this work aims to devise a novel test or dataset in the form of a set of deductive, logical reasoning puzzles. The dataset focuses on evaluating the logical reasoning ability of LLMs because only a handful of datasets exist to evaluate the logical reasoning ability of LLMs [12,24,28]. Besides, logical reasoning stands out as a quintessential form of reasoning that, unlike other types, is crucial and challenging; it epitomizes a cognitive process characterized by rigorous evidence evaluation, argument construction, and logical deduction [29]. This work is based on the intuition that some questions or puzzles can only be answered through the mastery of reasoning needed for situational awareness.
A key challenge to devising this test is to ensure that the questions have not appeared on the internet before; otherwise, the questions and their solutions could have been part of the corpus of the training texts previously used to train LLMs, and LLMs may answer them correctly without utilizing their reasoning ability. Newly crafted questions are needed. On the other hand, as noted in the observations made in the simple experiments conducted in this work, as reported in Section 3, ensuring that novel questions are presented to LLMs is also essential to elicit the reasoning behaviour of LLMs because LLMs have a strong tendency to parrot a memorized answer for questions that look very similar to a memorized question even though the memorized answer is wrong or not sensible for these questions.
In this work, an evaluation framework for LLMs is constructed to create a dataset of 84 unseen questions for LLMs, requiring them to apply semantic and deductive logical reasoning in order to solve these questions. Each question in the dataset presents a room assignment problem to LLMs requiring them to find a unique room assignment subject to the given constraints. To ensure that the questions are unseen to LLMs, the constraints are encoded in symbols with novel, proprietary definitions. Verifying a correct room assignment would require LLMs to reason on situation awareness and apply deductive logic in the thinking process. Using the dataset proposed in this work, experiments are run to fit state-of-the-art LLMs (including GPT-3, GPT-4, Gemini-1.5, Llama-3.1 and Claude-2.5) with these logical puzzles using prompting techniques to elicit and evaluate the reasoning capability of LLMs.
The contribution of this work is three-fold. First, a series of experiments are carried out to help better understand the emergent behaviour of LLMs to use their reasoning ability to respond to given tasks. Specifically, these experiments provide insights for the question of whether LLMs reason or recite memorized answers acquired during their training. While the observations made may not be conclusive, it provides valuable insights for the design criteria of testing frameworks to elicit reasoning ability of LLMs. Namely, unseen questions are required to evaluate the reasoning ability of LLMs. Second, a novel dataset is proposed to test the logical reasoning ability of LLMs. The proposed dataset has several desirable properties, including resilience to training data contamination, ease of response verification, extensibility and usefulness. In addition, the question or test case generation can possibly be automated. Finally, state-of-the-art LLMs are evaluated on the proposed dataset to serve as a new benchmark for evaluating the logical reasoning ability of LLMs.
2. Related Work
Since the discovery demonstrating that large-scale LLMs exhibit emergent abilities, advance has been made in improving the reasoning capabilities of LLMs, with a particular focus on prompting techniques [5,7,8,9,11,30]. Separately, enhancing reasoning capabilities of LLMs through fine-tuning on extensive datasets covering mathematics and reasoning tasks, such as [31], has improved LLM performance across several benchmarks. Such techniques, based on prompting or fine-tuning, have been increasingly successful in solving reasoning problems involving common sense, language inference, logical and arithmetic reasoning, demonstrating that LLMs can complete various reasoning tasks with a decent performance based on several benchmarks covering arithmetic [6,20,21,22,26], common sense [10,19,23,25,26], symbolic [5] and logical reasoning [12,24,28].
Figure 1.
Example prompts from existing benchmarks: (a) GSM8K [6], (b) SVAMP [22], (c) AQUA [32], (d) Common-SenseQA [25], (e) StrategyQA [19], (f) Tracking Shuffled Objects [24], (g) Date Understanding [24], (h) Last Letter Concatenation [5], (i) Coin Flip [5].

Despite the utility of these benchmarks, they are reportedly insufficient to make substantive claims about LLMs’ ability to reason because these existing benchmarks are limited in difficulty and do not necessarily mirror real world tasks demanding complex reasoning [12,26]. Datasets like GSM8K [6], AQUA [32] and SVAMP [22] have simple math word problems which are used for evaluating arithmetic reasoning while datasets like Common-SenseQA [25] and StrategyQA [19], which have generic multiple choice and binary yes/no questions respectively, are used for evaluating common sense reasoning. There are a few logical reasoning tasks within a comprehensive set of different types of questions in BIG-BENCH [24]. Planning or goal directed reasoning tasks on blocksworld are presented in [12] while language inference tasks are given in [26,28]. Two symbolic reasoning tasks, namely, Last Letter Concatenation and Coin Flip, are given in [5]. Most of these tasks, except [12,26], are simple in nature and do not provide insight into the reasoning capabilities of LLMs.
As LLMs have been able to perform well on such tasks, there has been a lot more triumphalism about their reasoning capabilities, which is currently being echoed in the community. Yet, there are criticisms on whether these tasks are suitable measures for the evaluation of LLM reasoning ability [12,15]. Besides simplicity of these tasks and shallow reasoning required to solve them [12], a key, valid concern is the potential leakage and memorization of similar problems by LLMs that enables them to perform well on these tasks without the use of their reasoning ability. That is, LLMs are merely reciting words acquired through the training corpus during their training phase rather than utilizing their reasoning ability to complete the tasks [15,16], and the scores achieved in these tasks therefore do not reflect or gauge the reasoning ability of LLMs. As [26] observes from the response of GPT-3.5 and GPT-4 on its datasets, “while it is difficult to quantify potential problem leakage and memorization of similar problems, some outputs suggest this might be a relevant factor” as these LLMs “appears to be memorizing the answers to some of the problems.”
In contrast, this work presents a novel dataset consisting of tasks that require multiple-step reasoning using deductive logic, as well as semantic reasoning, thus presenting sufficient difficulty to test the logical reasoning ability of LLMs. These tasks also mirror real world tasks demanding complex reasoning, namely, room assignment subject to constraints. In addition, these tasks are crafted to ensure that “unseen” questions are presented to LLMs to elicit and accurately measure their reasoning ability while guarding against that they parrot memorized answers.
3. Do LLMs Recite or Reason?
Even as users are dazzled by the virtuosity of LLMs, a question that often crops up is whether LLMs “know” or “understand” what they are saying, or — as argued by [13] — they are merely parroting text that they encountered on the internet during their extensive training routine. The rationale of those who are optimistic about LLMs’ reasoning ability is that because LLMs learned from a large amount of real-world text, they may have acquired some approximation of simple reasoning of human intelligence [4,5]. On the contrary, those who are skeptical of the reasoning ability of LLMs argue that, by design, LLMs merely selects a word probabilistically from a list of the most plausible words according to the frequency of their appearance in the training texts as the next output in response to an input. In other words, LLMs recite words that appeared in the training data according to the frequency of their appearance [13,15].
To test the capacity of LLMs to grasp what they are being asked, the authors of [16] posed GPT-4 a well-known logic puzzle known as Cheryl’s Birthday Puzzle [32,33], which has been around in various iterations since 2006 and went viral in 2015. In the puzzle, Cheryl has set her two friends Albert and Bernard the task of guessing her birthday from 10 given dates. Albert and Bernard are separately told the month and day of Cheryl’s birthday, and nothing else has been communicated to them. At first, neither Albert nor Bernard can make any further progress. But as they talked to each other, they both managed to sort out Cheryl’s birthday. Questionees are asked to find out Cheryl’s birthday through the dialogue between Albert and Bernard. Basically, one can figure it out by eliminating possible dates based on the responses of Albert and Bernard [32,33]. For details, please refer to Appendix I.
In the test of [16], GPT-4 solved the puzzle flawlessly on all the first three attempts when presented with the original wording of Cheryl’s Birthday Puzzle — the best-known version. However, it consistently failed when small incidental details — such as the names of the characters or the specific dates — were changed while keeping the original puzzle structure (i.e., the same topology of the dates). GPT-4 kept banging on about “May” and “June”, even when they were not the possible months given in the revised puzzle and started making obvious logical errors in its reasoning. The authors of [16] attribute this behaviour of GPT-4 to its “muscle memory” — reflecting the training that GPT-4 underwent — as May and June figured in the original wording of the puzzle. They therefore conclude that “it is difficult to dispel the suspicion that even when GPT-4 gets it right, it does so due to the familiarity of the wording, rather than by drawing on the necessary steps in the analysis. In this respect, the apparent mastery of the logic appears to be superficial.”
Despite the observations made by [16], it is still too early to conclude that GPT-4 lacks logical reasoning ability, even for Cheryl’s Birthday Puzzle per se. For instance, it is not possible to conclude which of the following is the cause of GPT-4’s deteriorated performance on the revised puzzle: (i) it cannot reason or lacks the required logical skill to solve the puzzle, or (ii) it does not reason on the puzzle even though it can reason.
To better understand whether GPT-4 reason or recite, this work extends the experiment of [16] with an enlarged set of questions based on the original Cheryl’s Birthday Puzzle (with an additional type of questions, namely, changing the puzzle structure) and uses its result as the baseline. Then two new experiments are performed. In the first experiment, GPT-4 is quizzed on a modified version of Cheryl’s Birthday Puzzle (which can also be found on Cheryl’s Birthday Puzzle’s Wikipedia page [33] but is less popular). The revised version presents a different dialogue between Albert and Bernard. It can be solved by the same elimination technique but would lead to a distinctly different answer. In the second experiment, GPT-4 is quizzed on a less well-known puzzle called Cheryl’s Age Puzzle [33]. The purpose of these experiments is to see whether GPT-4 behaves differently when presented with less known puzzles (i.e., with a lower likelihood that GPT-4 has encountered them in its training phase). The rationale is that if GPT-4 is presented with unseen questions, it must use its reasoning skill to get them right. Presenting a less popular question to GPT-4 may result in a lower tendency of GPT-4 to output memorized answers.
3.1. Cheryl’s Birthday Puzzle
For the original and modified versions of Cheryl’s Birthday Puzzle, GPT-4 is presented with 10 instances of each question in the experiment, with the results averaged over the instances. For each of the two puzzles, 10 variants are created by changing the names, 10 by changing the months, 10 by changing the days and 10 by changing the puzzle structures. GPT-4 is quizzed on these variants in 3 trials to take an average score. The memory is always cleared between questions. The accuracy of GPT-4 is presented in Figure 2.
When presented with the original version of Cheryl’s Birthday Puzzle in the original wordings, GPT-4 achieves 100% accuracy, which agrees with the result of [16]. However, when presented with questions with small incidental changes in names, months or days, the performance of GPT-4 is quite good, in contrast to the result of [16], which reports flawed reasoning of GPT-4 on questions with similar changes. This has been anticipated by the authors of [16], which claims that once their work “is published and is available on the internet, the flawed reasoning reported will quickly be remedied as the correct analysis will form part of the training text for LLMs.” However, the theory that LLMs parrot memorized texts does not satisfactorily explain why LLMs manage to adapt to the new questions and answer them correctly. Even if the correct analysis in [16] is memorized by GPT-4, this analysis is applicable only to the specific names, months and days used in [16]. The names, months and days in the new questions in the experiment of this work are picked randomly and distinct from those used in [16], and simply reciting texts alone should not enable LLMs to achieve the level of accuracy shown in Figure 2. If LLMs have not developed new reasoning skills since [16], they should not be able to answer these unseen questions. Purely memorizing the words in the correct analysis of [16] without fully understanding the logic embedded in the analysis of [16] should not enable LLMs to answer these new questions correctly.
Compared to [16], this work also adds 10 new questions to the original Cheryl’s Birthday Puzzle with the puzzle structure changed, and GPT-4 answer none of these questions correctly, as depicted in Figure 2. That is, GPT-4’s performance deteriorated drastically to 0% accuracy for the questions based on the original Cheryl’s Birthday Puzzle with changes in the topology of the dates. Among the flaws made by GPT-4, July 17 — the answer of the original Cheryl’s Birthday Puzzle that can be pervasively found on the internet — is frequently provided by GPT-4 although this date is not given in the questions presented to it. This behaviour resembles that of an “overfit” model when inputs very dissimilar to the training data are presented to it. Besides, this suggests that no reasoning has been applied in answering these questions. It is unclear whether LLMs’ reasoning fails or LLMs does not reason at all when answering these questions.
In the new experiment of this work wherein GPT-4 is presented with the modified version of Cheryl’s Birthday Puzzle and its variants with similar changes, GPT-4 has drastically different behaviour. This modified Cheryl’s Birthday Puzzle is less popular on the internet compared to the original Cheryl’s Birthday Puzzle. When presented with the modified Cheryl’s Birthday Puzzle in the original wordings, GPT-4 only achieves 70% accuracy, in contrast with its flawless performance on the original Cheryl’s Birthday Puzzle in the original wordings. GPT-4’s performance on the variants of the modified Cheryl’s Birthday Puzzle with the names, months, days changed is even better than its performance on the puzzle in the original wordings. When presented with questions on the modified Cheryl’s Birthday Puzzle with the puzzle structure changed, GPT-4 achieves an accuracy of 33.3%, which is considerably better than its performance on the original Cheryl’s Birthday Puzzle with the puzzle structure changed (0%). That is, changing the puzzle structure of a less popular version of Cheryl’s Birthday Puzzle seems to pose comparatively less challenge to GPT-4 than its more well-known version.
The only difference between the two setups is that the modified Cheryl’s Birthday Puzzle is far less well-known than the original Cheryl’s Birthday Puzzle, meaning that its appearance in the training texts for GPT-4 is less frequent. It should be noted that the reasoning skill required for solving the problems in the two setup is roughly similar. The disparity of GPT-4’s performance in the two setups seems to suggest that GPT-4 reasons on the less well-known version while parroting texts for the more well-known version, but this is only a conjecture or hypothesis without strong experimental evidence given the limited observations made in this work. Nevertheless, this explanation squares well with how LLMs works. By design, LLMs generate the most plausible sequence of words in response to an input based on the relative frequency of appearance of these words together in the training texts. For a well-known question, its model answer is more frequently associated with the original wordings of the question in the training data, and LLMs therefore have a high tendency to parrot the same answer that appeared frequently in association with the original wordings of the question in the training data, just like any overfit model. In contrast, when a less well-known question is presented to LLMs, its model answer may not always appear as the most likely word associated with original wordings of the question. With the question wordings as the input, the most plausible word in response to this input may not be the original model answer.
3.2. Cheryl’s Age Puzzle
To further verify this conjecture, this work carries out another experiment wherein GPT-4 is presented with a less well-known puzzle called Cheryl’s Age Puzzle, in both original wordings and modified wordings. GPT-4 is quizzed on the original version of the Cheryl’s Age Puzzle in 10 trials to take an average score. Then 10 variants of the puzzle are created by changing the product of the ages of Cheryl’s and her two brothers and adjusting other details to fit the change in the product of ages. GPT-4 is quizzed on multiple instances of these variants to take an average score. The memory is always cleared between questions. The accuracy of GPT-4 for the original and modified versions of Cheryl’s Age Puzzle is presented in Figure 3.
No significant disparity in GPT-4’s accuracy is observed for the two setups where GPT-4 is presented with the original version and modified version of Cheryl’s Age Puzzle respectively. If GPT-4 recites the model answer when presented with the original version of the puzzle, it should be able to obtain 100% accuracy. On the contrary, it performs significantly worse, inferring that it may not parrot texts in this test case. One possible explanation is that GPT-4 tends to reason sometimes rather than recite memorized answers all the time in this test case.
Although it cannot be certain due to a limited number of experiments performed and relatively few observations made in this work, it appears that GPT-4 may not always recite the model answer it has acquired during the training phase and memorizes if the question presented to it is less well-known. In other words, if we want to test the reasoning ability of GPT-4, it is necessary to craft new puzzles for it to solve in order to elicit the reasoning ability of GPT-4. That is, we need to present unseen questions to GPT-4.
4. Proposed Dataset
In view of the observations made in Section 3, this work aims to propose a new set of logical puzzles to test the reasoning capability of LLMs. The puzzles are crafted in a way to minimize the possibility that LLMs may have encountered them in its training corpus with the aim to minimize LLMs’ tendency to recite memorized answers.
4.1. Test Cases
This work proposes a new dataset to test the logical reasoning ability of LLMs. The proposed dataset consists of 84 questions, partitioned into three subsets at 3 levels of difficulty: High, Medium and Low. Each test case in the proposed dataset requires LLMs to assign a given number of rooms to a group of persons and their pets subject to certain restrictions or constraints.
Figure 4 depicts a sample question in the dataset. The question is equivalent to finding a total order [34] of a set of objects (in this case, a set of persons and pets) subject to constraints. At first, LLMs are given a common definition for use in all questions, and this definition explains the meaning of the symbolic expressions of the constraints or rules that a correct room assignment needs to satisfy. In addition, a set of common instructions are given before the questions are asked. This sets the domain knowledge required for all the questions in the dataset. The questions are designed to minimize the need to use domain knowledge or common sense to answer the questions. On one hand, this would minimize the possibility that LLMs need to look up other memorized texts and link the problem to irrelevant texts, causing them to parrot non-sensible answers. On the other hand, minimizing the domain knowledge can help focus on testing the logical reasoning ability of LLMs.
The constraints of the questions are encoded in symbolic expressions (intentionally with non-intuitive symbols), rather than in words, to serve two purposes. First, this arrangement forces LLMs to decode the expressions to understand the constraints, which would require the use of semantic reasoning ability and therefore test this ability of LLMs. Second, since the constraints in the textual form are not directly obtainable from the question itself, LLMs are less ready to recognise that it has seen the question before if, unfortunately, the question happens to be included in the LLMs’ training corpus. This indirect presentation of the constraints helps render the question as an unseen question from the perspective of LLMs and force them to apply their reasoning skill to solve it instead of reciting a memorized answer. That is, LLMs are tested at the “Apply” level, rather than the “Remember” level of the Bloom’s taxonomy [35].
Once LLMs are able to decode the symbolic constraint rules, they would need to reason about situation awareness to find the right room assignment through an educated guess. In addition, they also need to apply deductive logical reasoning to validate whether the room assignment they find is a valid assignment that meets all the given constraints. Specifically, the problem can be seen as consisting of a major premise, a minor premise and a conclusion in the following way:
| Major Premise: | Meeting all the constraints is a valid room assignment. |
| Minor Premise: | A given room assignment meets all the constraints. |
| Conclusion: | A given room assignment is a valid room assignment. |
Hence, each test case in the proposed dataset evaluates the semantic reasoning and deductive reasoning of LLMs, as well as their reasoning about situation awareness. Decoding the symbolic rules for room assignment constraints requires LLMs to apply their semantic reasoning ability, whereas, finding and validating a correct room assignment requires them to carry out deductive reasoning. As can be seen, the occurrence of the same or similar combination of words on the internet is less probable, meaning LLMs should not be able to answer a large portion of the questions correctly merely through picking the most plausible word based on the words of the question. In other words, without using some form of reasoning, getting correct answers for these questions is relatively unlikely.
4.2. Desirable Properties of the Dataset
The proposed dataset has several desirable properties, including resilience to training data contamination, ease of response verification, extensibility and usefulness.
4.2.1. Resilience to Training Data Contamination
Through symbolically expressing the room assignment constraints, it is less likely that LLMs can find a piece of memorized text in its training corpus that would resemble a question from the proposed dataset. This would prevent LLMs from parroting memorized texts to get a correct answer for a given test case or lower their tendency of reciting memorized answers. Besides, no explanation texts for the questions are available on the internet. If LLMs give a correct explanation, it is most likely generated by it. As the possibility of parroting answers is minimized, it is most probable that LLMs use their reasoning skill to answer the questions.
In addition, there are a number of safeguards which could further strengthen the resilience to training data contamination. First, it is easy to use a different set of symbols or symbolic expressions to express the room assignment constraints. Even though the current dataset is exposed to LLMs through whatever means, the symbolic expressions of its questions could possibly be modified to accommodate the undesirable exposure. Second, the person and pet names could be readily changed, and LLMs parroting texts would likely give wrong, irrelevant names in their answers.
Moreover, compared to true/false or multiple-choice questions in many of the existing datasets or benchmarks, the possibility to obtain a correct answer by random guess is significantly lower. For instance, for an assignment of 4 persons to 4 rooms, the number of possible combinations (regardless of the constraints) is 4!=24. Getting a correct answer out of 24 choices would be lower than typical multiple-choice questions.
4.2.2. Ease of Response Verification
As can be seen from Figure 4, each test case of the proposed dataset has a short answer whose correctness can be easily verified in a mechanistic manner even done manually. This would enable automated verification or lessens the burden if human verification is adopted. Besides, the explanation for each answer provided by LLMs, if any, could be easily verified based on the room assignment given in the test case. Overall, the ease of verification of the responses provided by LLMs is high even though manual verification is adopted.
4.2.3. Extensibility
The proposed dataset is extensible in the sense that new questions of varying difficulty can be easily added to the dataset. Currently, the dataset consists of 84 questions at 3 levels of difficulty. New questions of varying complexity can be easily created by adjusting the number of rooms or selecting the types of room assignment constraints. For example, if the number of rooms is increased, the number of applicable constraints could increase accordingly. The proposed dataset is easily extensible. One of the challenges faced by the community is that once a new dataset or benchmark is published on the internet, LLMs would quickly attain a perfect score [26], likely attributed to LLMs’ memorization of the questions and answers and reciting the answers. Posing reasoning questions to LLMs with meaningful difficulty is generally understood as the common goal of the community [26]. The proposed dataset in this work is designed to enable the complexity of the questions to scale up with ease, thus partially solving this issue.
4.2.4. Usefulness
Each question in the dataset requires multiple steps of reasoning to obtain a correct answer, thus posing adequate difficulty for LLMs. Besides, different types of reasoning skills are required in the process. That is, the score attained by LLMs on the dataset would constitute a meaningful measure of their reasoning ability. In addition, the tested skills in the proposed dataset correlate with generally useful human skills, namely, assignment with constraint conditions. The problem of assigning resources subject to constraints is a frequently occurring issue in our daily living. LLMs are not tested with obscurely difficult problems that even human beings do not manage to solve; testing LLMs on the proposed dataset is therefore meaningful in practical sense.
5. Experiment Setting
This work takes GPT-3 as the baseline model, and compares the performance of GPT-4, Gemini-1.5, Llama-3.1 and Claude-3.5 on the proposed dataset. These are state-of-the-art LLMs. This work uses GPT-3 and GPT-4 on Copilot, Llama-3.1 on Huggingface, and Gemini-1.5 and Claude-3.5 on Anakin to run its experiment. An instruction-prompt scheme is adopted for feeding the questions of the proposed dataset to all these LLMs. LLMs are first prompted with a header containing the symbolic constraint rule definitions and instructions which apply to all questions. Then, they are prompted with the set of questions one by one. No sample question is given to LLMs. In other words, a zero-shot prompt is used in this experiment.
The answer to each question and the respective explanation by LLMs is verified manually for correctness. Based on the answer and the restriction rules in the question, it is trivial and easy to identify any reasoning flaw made by LLMs although done manually. Two scores are tallied, one for correct answers and the other for perfectly correct explanation. An explanation is not tallied if any flaw is found in it.
For each LLM, three trials are conducted. That is, the set of 84 questions are presented to each LLM three times, and memory is cleared between trials. The correct attempts in the three trails are tallied. The accuracy of LLMs in solving the questions in the dataset is simply calculated as the total number or correct attempts in the three trails divided by 252, and no outlier answers are eliminated in the calculation. Similar calculation is performed to obtain the accuracy of LLMs’ explanations.
This work wants to establish a human intelligence baseline to compare it with the performance of LLMs. However, it is practically challenging to run through all 84 questions in the proposed dataset with human participants. Instead, this works randomly samples questions that LLMs perform badly for human participants to attempt to see whether human participants can solve the problems that LLMs find particularly difficult.
6. Empirical Results
6.1. LLM Performance Comparison
Depicted in Figure 5 is a comparison of the performance of different LLMs on the proposed dataset. As can be seen from the graph, the accuracy of getting a correct answer for a question is observably higher than the accuracy of getting the respective explanation correct (i.e., without any flaw) for all the 5 LLMs. This gap is higher for an LLM which scores comparatively poorer in terms of answer accuracy. A lower explanation accuracy relative to the answer accuracy by LLMs could lead to the inference that LLMs do not reason on the proposed questions. However, it should be noted that if one randomly guesses answers for the questions, he should not be able to achieve such a high percentage of correct answers. That means, except for Gemini-1.5, it is unlikely that LLMs achieve such a range of scores based on a random guess. However, LLMs’ behaviour in the experiment could still be explained: they may perform reasoning partially and then make an educated guess of the answer, which resembles what human beings would do sometimes. Of course, this is only a conjecture.
For questions LLMs perform poorly, they usually fail to correctly validate whether the specified constraint rules in the question are satisfied by a given assignment. In particular, when multiple rules are interlocked, LLMs seem to perform poorly in reasoning about situation awareness. Depicted in Figure 6 is a sample response generated by GPT-4. While GPT-4 rightly enumerates all possible combinations by assigning Bob to one of the two remaining rooms after the second constraint is met, it fails to verify whether an assignment meets the remaining two constraints simultaneously. After correctly assigning the first room to Bob, it rightly asserts that Charlie must be assigned to the second room to be adjacent to Bob. Then, it reasons that Alice must be assigned to the second room to be adjacent to Bob because Bob is in the second room, which is the major flaw leading to a wrong answer.
Across all the LLMs tested, Llama-3.1 has the best performance, whereas Gemini-1.5 has the worst performance, performing much poorly compared to the other 4 LLMs. The 3 LLMs in between have roughly similar performance. One of the main reasons why Gemini-1.5 performs very poorly, compared to other LLMs, is that it is unable to understand the symbolic rule definition for adjacent room assignment, which uses the equal sign. Depicted in Figure 7 is a sample response of wrong interpretation of Gemini-1.5. Gemini-1.5 always interprets X = Y as that person X and person Y stays in the same room while the correct interpretation is that X and Y have their rooms next to each other. It is unclear whether this is due to the muscle memory that the equal sign tends to refer to equality in most human texts.
While GPT-4 is frequently highlighted as advanced at reasoning tasks compared to GPT-3, GPT-4’s performance in answer accuracy is lower than that of GPT-3, though by just a small fraction. Yet, GPT-4’s explanation accuracy is higher than GPT-3’s. That could possibly evince GPT-4’s higher tendency to reason, compared to GPT-3, on the questions.
6.2. Comparison of LLMs’ Performance with Human’s
Questions that LLMs performed poorly are sampled for a number of human participants to solve. The performance of LLMs and human participants is compared in Figure 8. For LLMs, answer accuracy is averaged over all the LLMs under test in this work, including GPT-3, GPT-4, Llama-3.1, Gemini-1.5 and Claude-3.5. As can be seen, human participants have no difficulty to solve questions which are challenging for LLMs to solve. This suggests that LLMs’ logical reasoning ability, at least on the skill required to solve the proposed dataset, does not match that of human intelligence.
6.3. Salient Reasoning Characteristic of LLMs
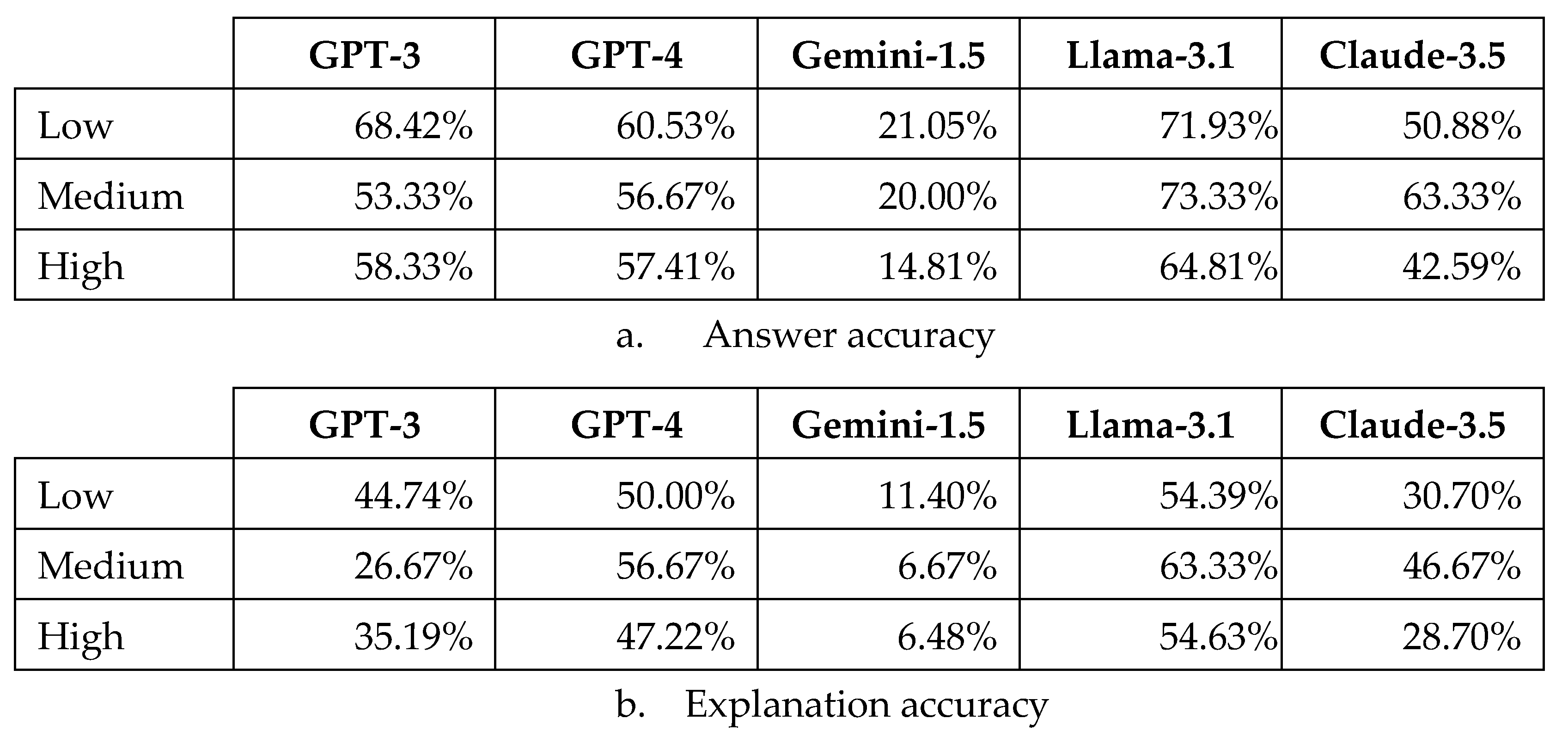
An interesting observation from this experiment is that the performance of the tested LLMs do not seem to be dependent on the complexity or difficulty of the questions. In the proposed dataset, the questions are arranged in an order of increasing complexity or difficulty. That is, later questions are more difficult than earlier ones. No observable deterioration in LLMs’ performance, in terms of both answer and explanation accuracy, is noted for the more difficult questions. This behaviour of LLMs contrasts with human behaviour as people usually perform more poorly on difficult questions than easy questions.
As can be seen in Figure 9 and Figure 10, LLMs perform roughly similarly in terms of answer and explanation accuracy regardless of the difference in difficulty of the questions. Although difference in accuracy can be observed for the three levels of question difficulty, no noticeable trend in performance degradation can be identified for all the tested LLMs. This observation prompts an interesting question: Do LLMs have no reasoning ability, or do they reason in a manner different from human reasoning? It is difficult to tell which one is a more reasonable explanation for the reasoning characteristic or behaviour of LLMs. But we could infer that LLMs use a cognitive structure which is very different from human intelligence to carry out their reasoning.
7. Future Work
7.1. Better Human Baseline
While this work presents selected questions of the proposed dataset to human participants to compare LLMs’ performance with this human baseline, the number of questions only represent a relatively small fraction of the dataset. Besides, the human performance may be skewed due to the sampling method as only questions that LLMs perform poorly are sampled for human participants to solve. While human intelligence may find it easy to solve questions that LLMs find difficult, it remains unclear whether the questions that are solved by LLMs with ease would pose challenge to human intelligence. It is therefore planned to conduct a larger and more comprehensive experiment involving a larger group of participants to work on the whole dataset with a view to creating a more precise human intelligence baseline covering a wider range of questions.
7.2. Automated Question Generation
Currently, the questions in the proposed dataset are generated manually despite that their generation can be automated. In the future, it is planned to create routine to generate questions automatically. The idea of automated test case generation is simple. For a given number of rooms, which is the input to the question generator, a random order of that number of persons and pets, if any, is created, and this will be used as the answer to the test case to be generated. Based on this answer, assignment constraints or rules are generated randomly. For instance, for the room order rule, two persons are randomly selected, and a rule is then created based on the relative positions in the sort order. Similarly, for the neighbouring rule, a person is randomly selected, and his one of his two neighbours is randomly selected to create a rule. In case the first person has only one neighbour, the unique neighbour is selected to form the neighbouring rule. This random rule generation process is repeated until a certain exit condition is met. Depending on the type of the rule, the required number of rules to ensure a unique answer varies, but this can be predetermined easily. The effective number of generated rules can be estimated, and when it reaches the required number, the generation process is complete.
8. Conclusion
We conduct experiments, using Cheryl’s Birthday Puzzle and Chery’s Age Puzzle, to evaluate the logical reasoning ability of LLMs to obtain a better understanding of whether LLMs reason or recite when presented with questions requiring logical reasoning. It appears that LLMs do not always parrot memorised texts acquired from the training data to answer these questions but sometimes exhibit a certain level of logical reasoning ability. Based on our observations, it may be inferred that whether LLMs would recite or reason depends on the popularity of the questions presented to it although this cannot be answered definitely due to the limited number of experiments and observations made. The title of [5] rightly uses the word “elicit” to describe the reasoning behaviour of LLMs. Roughly, LLMs are more likely to use their reasoning skill if presented with unseen questions.
We therefore design a novel dataset containing open-ended questions requiring semantic and deductive logical reasoning, specifically, room assignment questions subject to constraints. This dataset exhibits several desirable properties, including resilience to training data contamination, ease of response verification, extensibility, usefulness and automated test case generation. We pose this new dataset to state-of-the-art LLMs to evaluate their reasoning ability. While these LLMs exhibit a certain level of reasoning ability, their performance does not seem to match that of human intelligence on the presented dataset. One interesting observation of this work is that LLMs do not reason in the same way as human beings do. While human accuracy would normally deteriorate with increasing difficulty of the questions, this trend is not observable for LLMs, suggesting that LLMs have a different reasoning structure than human intelligence.
Appendix I: Cheryl’s Puzzles
Cheryl’s Birthday Puzzle and its Solution
Question:
Albert and Bernard just became friends with Cheryl, and they want to know when her birthday is. Cheryl gives them a list of 10 possible dates:
May 15, May 16, May 19
June 17, June 18
July 14, July 16
August 14, August 15, August 17
Cheryl then tells Albert and Bernard separately the month and the day of her birthday respectively.
Albert: I don’t know when Cheryl’s birthday is, but I know that Bernard doesn’t know too.
Bernard: At first, I don’t know when Cheryl’s birthday is, but I know now.
Albert: Then I also know when Cheryl’s birthday is.
So, when is Cheryl’s birthday?
Solution:
The answer is July 16, and the puzzle can be solved through date elimination after presenting the 10 given dates in a grid as shown below.
| May | 15 | 16 | 19 | |||
| June | 17 | 18 | ||||
| July | 14 | 16 | ||||
| August | 14 | 15 | 17 |
Based on the first line of the dialogue, Albert knows the month is not May or June and therefore claims that Bernard doesn’t know Cheryl’s birthday. All the 5 dates in May or June can be eliminated.
Based on the second line of the dialogue, Bernard finds Cheryl’s birthday because he knows the day. If the day is 14, he wouldn’t be able to distinguish between July 14 and August 14. So, both July 14 and August 14 can be eliminated.
Based on the third line of the dialogue, Albert sorts it out based on the month given to him. If the month is August, both August 15 and August 17 are possible, and he wouldn’t know Cheryl’s birthday. So, both dates are eliminated, and Cheryl’s birthday is on July 16.
Modified Cheryl’s Birthday Puzzle and its Solution
Question:
In the modified version of Cheryl’s Birthday Puzzle, the only part changed is the dialogue, which is as follows:
Bernard: I don’t know when Cheryl’s birthday is.
Albert: I still don’t know when Cheryl’s birthday is.
Bernard: At first I didn’t know when Cheryl’s birthday is, but I know now.
Albert: Then I also know when Cheryl’s birthday is.
Solution:
Despite the same date elimination technique can be leveraged, the answer is different. It is August 17.
| May | 15 | 16 | 19 | |||
| June | 17 | 18 | ||||
| July | 14 | 16 | ||||
| August | 14 | 15 | 17 |
Based on the first line of the dialogue, if Cheryl’s birthday is on May 19 or June 18, Bernard would know it. So, it cannot be on either of these 2 dates, and they can be eliminated.
Based on the second line of the dialogue, if Cheryl’s birthday is in June, Albert would know the exact date because, after June 18 has been eliminated after the first line, there is only one date left in June (i.e., June 17). So, all dates in June are eliminated.
Based on the third line of the dialogue, if Cheryl’s birthday is on 14, 15, or 16, there are two possible dates, and Bernard shouldn’t be able to sort it out. So, it can only be August 17 because June 17 has been eliminated in the second line.
Based on the fourth line, Albert can find Cheryl’s birthday by reworking of Bernard’s thinking steps.
Variants of Cheryl’s Birthday Puzzle used in the Experiments of this Work
In the experiments carried out in this work, both the original and modified versions of Cheryl’s Birthday Puzzle are twisted in four ways: (1) names changed; (2) months changed; (3) days changed; and (4) date topology changed. Changing the first three is trivial. Below are some examples for the change of the puzzle structure of date topology used in this work.
| May | 16 | 19 | ||||
| June | 14 | 17 | 18 | |||
| July | 15 | 16 | 17 | |||
| August | 15 | 18 |
| May | 16 | 19 | ||||
| June | 14 | 17 | 19 | |||
| July | 15 | 16 | 17 | |||
| August | 15 | 18 |
| May | 15 | 19 | 23 | ||||
| June | 16 | 17 | 18 | ||||
| July | 14 | 19 | |||||
| August | 14 | 15 | 17 |
| May | 15 | 19 | 23 | ||||
| June | 16 | 23 | |||||
| July | 16 | 18 | 19 | ||||
| August | 14 | 17 |
Cheryl’s Age Puzzle
Question:
Cheryl’s Age Puzzle, also created by the same team but less popular, reads as follows:
Albert and Bernard now want to know how old Cheryl is.
Cheryl: I have two younger brothers. The product of all our ages (i.e., my age and the ages of my two brothers) is 144, assuming that we use whole numbers for our ages.
Albert: We still don’t know your age. What other hints can you give us?
Cheryl: The sum of all our ages is the bus number of this bus that we are on.
Bernard: Of course, we know the bus number, but we still don’t know your age.
Cheryl: Oh, I forgot to tell you that my brothers have the same age.
Albert and Bernard: Oh, now we know your age.
So, what is Cheryl’s age?
Solution:
The answer is 9.
144 can be decomposed into prime number factors (i.e., 144 = 24 × 32), and all possible ages for Cheryl and her two brothers examined (for example, 16, 9, 1, or 8, 6, 3, and so on). The sums of the ages can then be computed.
Because Bernard (who knows the bus number) cannot determine Cheryl’s age despite having been told this sum, it must be a sum that is not unique among the possible solutions. On examining all the possible ages, it turns out there are two pairs of sets of possible ages that produce the same sum as each other: 9, 4, 4 and 8, 6, 3, which sum to 17, and 12, 4, 3 and 9, 8, 2, which sum to 19.
Cheryl then says that her brothers are the same age, which eliminates the last three possibilities and leaves only 9, 4, 4, so we can deduce that Cheryl is 9 years old, and her brothers are 4 years old, and the bus the three of them are on has the number 17.
Modified Cheryl’s Age Puzzle used in the Experiment of this Work
To carry out experiments in this work, the product of the ages of Cheryl and her two brothers is changed to form new questions. Since it is not easy to find a product with multiple factorizations leading to the same sum, the question text is modified according to the context of the new questions.
References
- M. J. Cresswell, Logics and languages (1st ed.), Routledge, 1973.
- Lucja Iwanska, “Logical reasoning in natural language: It is all about knowledge”, in Minds and Machines, 1993.
- OpenAI, “GPT-4 is OpenAI’s most advanced system, producing safer and more useful responses”, accessible at https://openai.com/index/gpt-4/.
- J. Wei, Y. Tay, et. al., “Emergent abilities of large language models”, Transactions on Machine Learning Research, 2022.
- J. Wei, X. Wang, et. al., “Chain of thought prompting elicits reasoning in large language models”, in Advances in Neural Information Processing Systems, 2022.
- K. Cobbe, V. Kosaraju, et. al., “Training verifiers to solve math word problems”, arXiv preprint, abs/2110.14168, 2021.
- T. Kojima, S. S. Gu, et. al., “Large language models are zero-shot reasoners”, in Advances in Neural Information Processing Systems, 2022.
- J. Huang and K. C.-C. Chang, “Towards reasoning in large language models: A survey”, in the Proceedings of the 61st Annual Meeting of the Association for Computational Linguistics (ACL’23), July 2023.
- A. Patel, B. Li, et. al., “Bidirectional language models are also few-shot learners”, in the Proceedings of the International Conference on Learning Representations, 2023.
- P. Bhargava and V. Ng, “Common-sense knowledge reasoning and generation with pretrained language models: a survey”, in the Thirty-Sixth AAAI Conference on Artificial Intelligence (AAAI’22), March 2022.
- S. Qiao, Y. Ou, et. al., “Reasoning with language model prompting: A survey”, in the Proceedings of the 61st Annual Meeting of the Association for Computational Linguistics (ACL’23), July 2023.
- K. Valmeekam, A. Olmo, et. al. “Large language models still can’t plan (a benchmark for LLMs on planning and reasoning about change)”, in NeurIPS 2022 - Foundation Models for Decision Making Workshop, 2022.
- E. Bender, A. Koller, “Climbing towards NLU: On meaning, form, and understanding in the age of data”, in the Proceedings of the 58th Annual Meeting of the Association for Computational Linguistics (ACL’20), July 2020.
- J. W. Rae, S. Borgeaud, et al., “Scaling language models: Methods, analysis & insights from training gopher”, arXiv preprint abs/2112.11446, 2021.
- A. Narayan and S. Kapoor, “GPT-4 and professional benchmarks: the wrong answer to the wrong question”, 2023, accessible at https://www.aisnakeoil.com/p/gpt-4-and-professional-benchmarks.
- F. Perez-Cruz and H. S. Shin, “Testing the cognitive limits of large language models”, BIS Bulletin, 2024.
- S. Arora and A. Goyal, “A theory for emergence of complex skills in language models”, arXiv preprint, abs/2307.15936, 2023.
- D. Hendrycks, C. Burns, et. al, “Aligning AI with shared human values”, in the Proceedings of International Conference on Learning Representations, 2021.
- M. Geva, D. Khashabi, el al., “Did Aristotle use a laptop? A question answering benchmark with implicit reasoning strategies”, Transactions of the Association for Computational Linguistics, 9:346–361, 2021.
- H. Liu, R. Ning, et. al., “Evaluating the Logical Reasoning Ability of ChatGPT and GPT-4”, arXiV preprint, abs/2304.03439, 2023.
- S. Mishra, A. Mitra, et. al., “NumGLUE: A suite of fundamental yet challenging mathematical reasoning tasks”, in the Proceedings of the 60th Annual Meeting of the Association for Computational Linguistics (ACL’22), May 2022.
- A. Patel, S. Bhattamishra, and N. Goyal. “Are NLP Models really able to solve simple math word problems?”, in the Proceedings of NAACL-HLT 2021, 2021.
- K. Sakaguchi, R. Le Bras, et al., “Winogrande: An adversarial winograd schema challenge at scale”, in the Proceedings of the AAAI Conference on Artificial Intelligence, volume 34, pages 8732–8740, 2020.
- A. Srivastava, A. Rastogi, et. al., “Beyond the imitation game: Quantifying and extrapolating the capabilities of language models”, Transactions on Machine Learning Research, 2023.
- A. Talmor, J. Herzig, el al., “CommonsenseQA: A question answering challenge targeting commonsense knowledge”, arXiv preprint abs/1811.00937, 2018.
- T. Sawada, D. Paleka, et. al., “ARB: Advanced reasoning benchmark for large language models”, arXiV preprint, abs/v:2307.13692, 2023.
- T. H. Kung, M. Cheatham, et al., “Performance of ChatGPT on USMLE: Potential for AI-assisted medical education using large language models”, PLOS Digital Health, 2(2), 2023.
- S. Wang, Z. Liu, et al., “From LSAT: The progress and challenges of complex reasoning”, IEEE/ACM Transactions on Audio, Speech, and Language Processing, 2022.
- H. Markovits, and R. Vachon, “Reasoning with contrary-to-fact propositions”, Journal of Experimental Child Psychology, 47:398–412, 1989.
- X. Wang, J. Wei, et. al, “Self-consistency improves chain of thought reasoning in language models,” arXiV preprint abs/2203.11171, 2022.
- A. Lewkowycz, A. Andreassen, et. al, “Solving quantitative reasoning problems with language models”, in the Proceedings of NeurIPS 2022, 2022.
- H. van Ditmarsch, M. I. Hartley, et. al, “Cheryl’s Birthday”. Electronic Proceedings in Theoretical Computer Science. 251: 1–9, 2017.
- Wikipedia, “Cheryl’s Birthday”, accessible at https://en.wikipedia.org/wiki/Cheryl%27s_Birthday.
- Wolfram MathWorld, Totally Ordered Set. Accessible at https://mathworld.wolfram.com/TotallyOrderedSet.html.
- B. S. Bloom, Taxonomy of educational objectives: The classification of educational goals: Handbook I, Cognitive domain. New York: McKay, 1969.
Figure 2.
GPT-4 accuracy on (i) Original Cheryl’s Birthday Puzzle and its variants (with the names, months, days or puzzle structure changed); and (ii) Modified Cheryl’s Birthday Puzzle and its variants (with the names, months, days or puzzle structure changed).
Figure 2.
GPT-4 accuracy on (i) Original Cheryl’s Birthday Puzzle and its variants (with the names, months, days or puzzle structure changed); and (ii) Modified Cheryl’s Birthday Puzzle and its variants (with the names, months, days or puzzle structure changed).
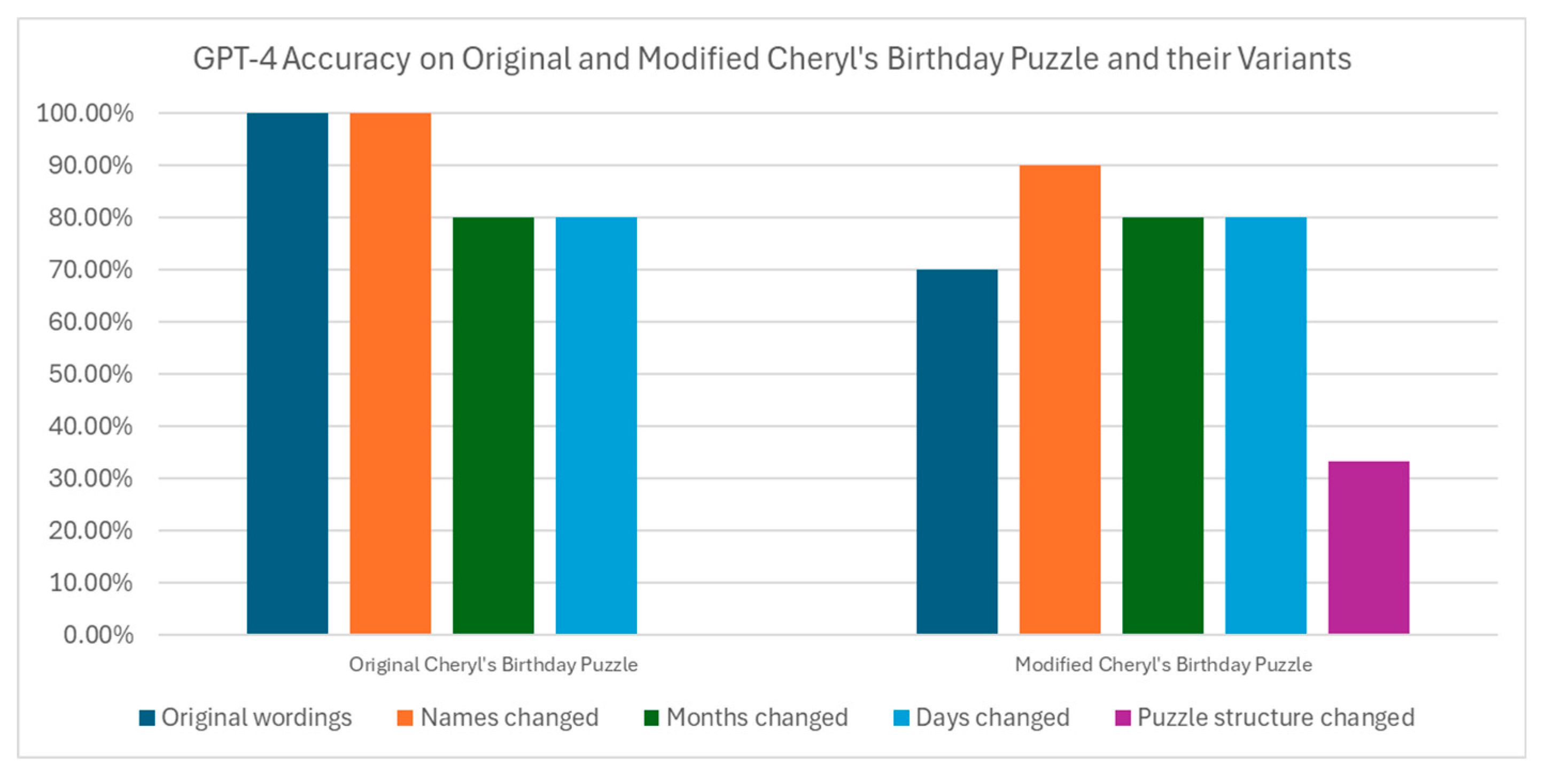
Figure 3.
GPT-4 accuracy on (i) Original Cheryl’s Age Puzzle; and (ii) Modified Cheryl’s Age Puzzle.
Figure 3.
GPT-4 accuracy on (i) Original Cheryl’s Age Puzzle; and (ii) Modified Cheryl’s Age Puzzle.
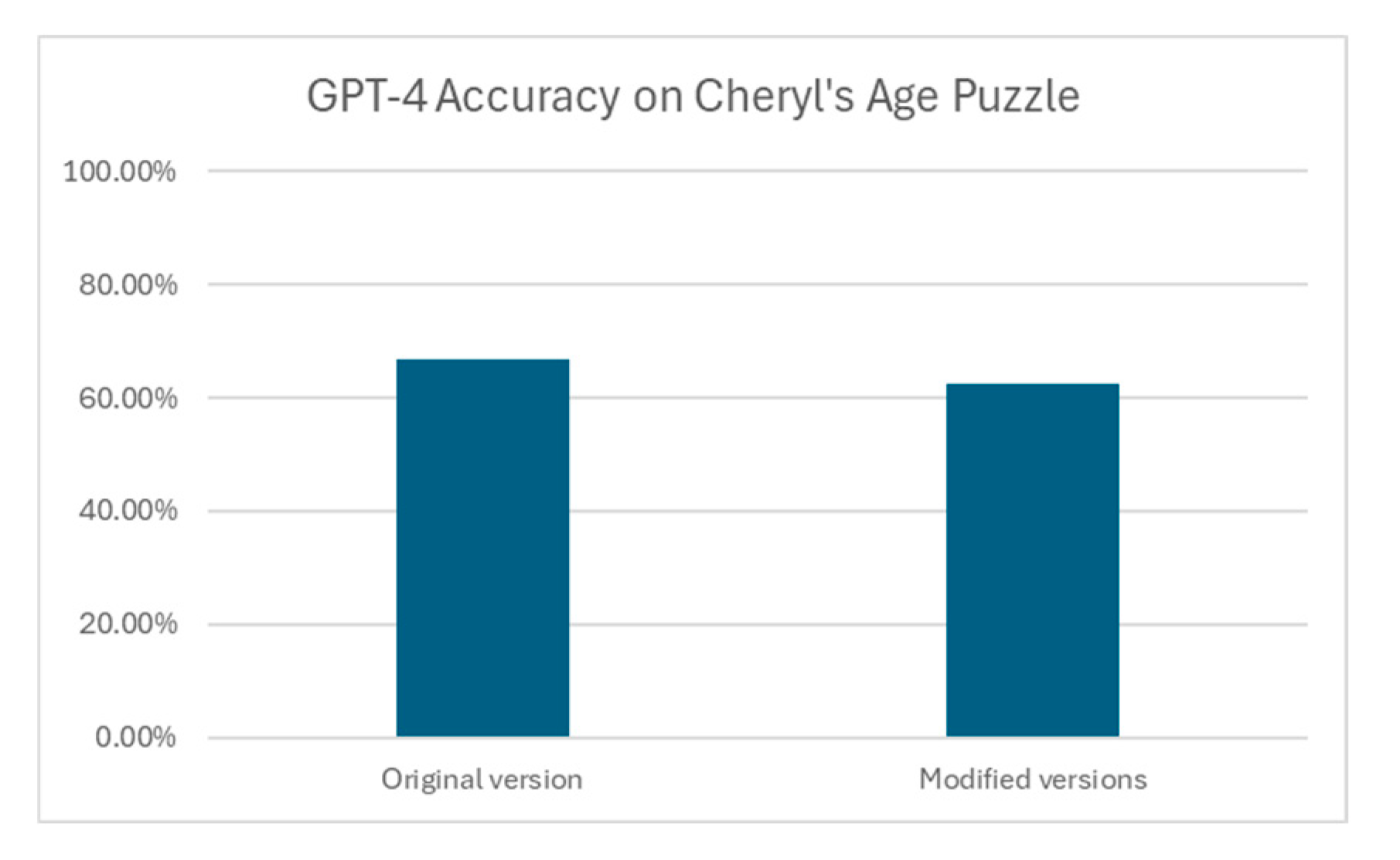
Figure 4.
A Sample Test Case to Test Logical Reasoning Ability of LLMs.

Figure 5.
Comparison of the overall performance of LLMs on the proposed logical reasoning dataset.
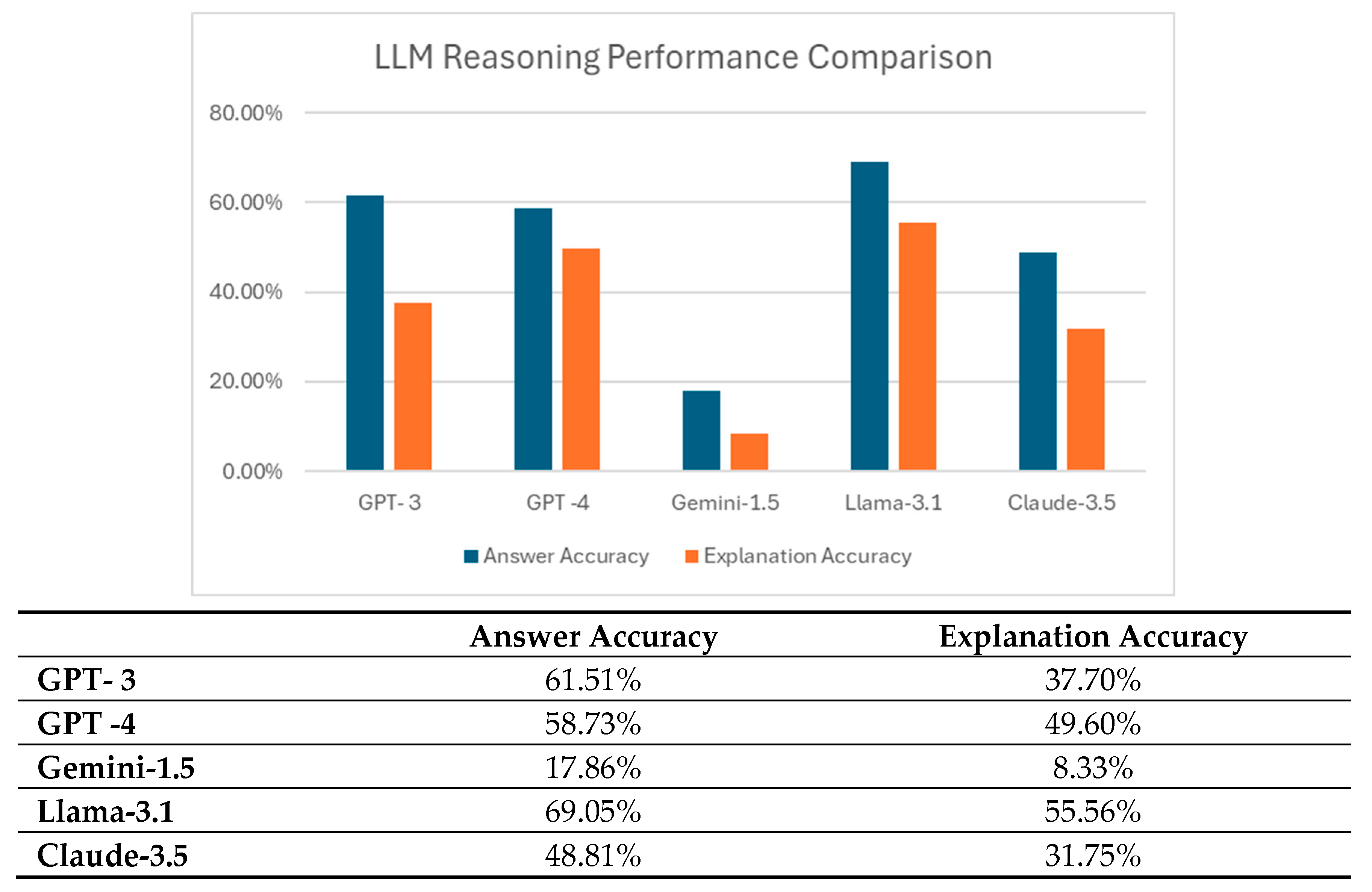
Figure 6.
A sample response showing the flawed reasoning of GPT-4 on a question of the dataset.
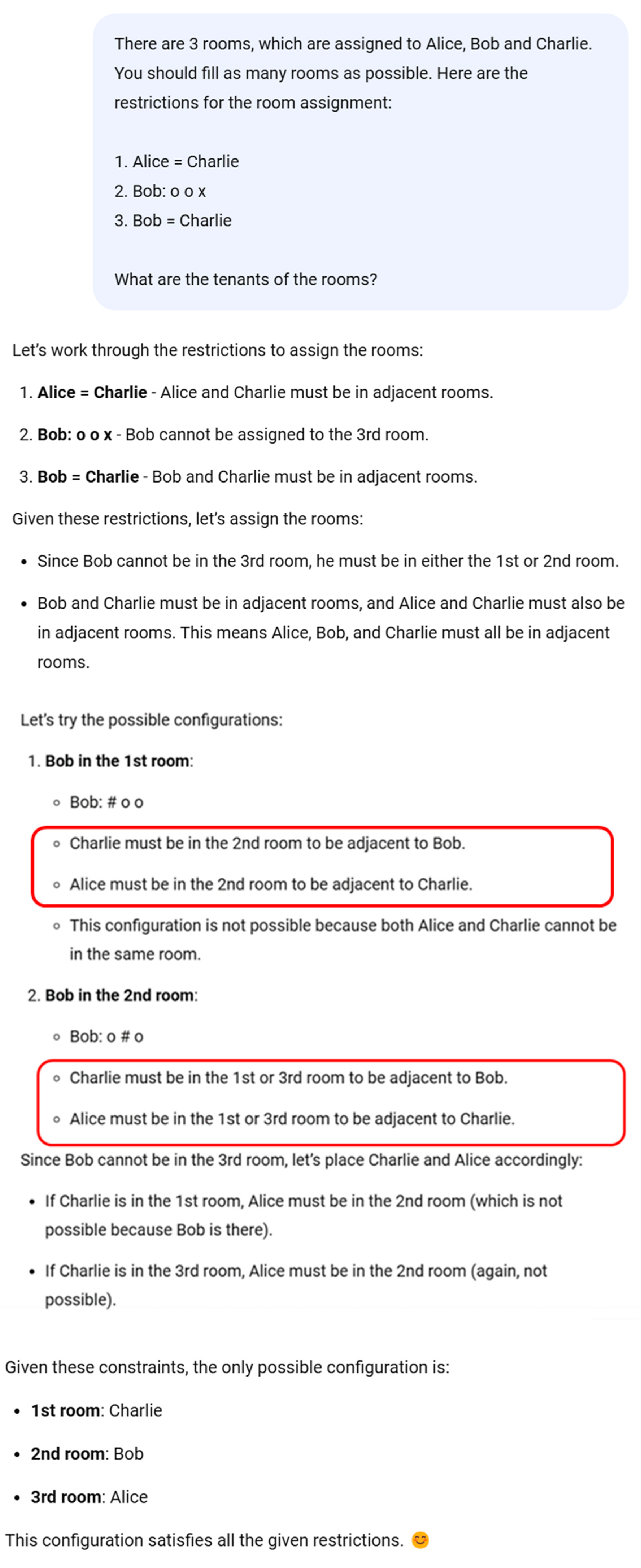
Figure 7.
A sample response showing the wrong symbol interpretation of Gemini-1.5 on a question of the dataset.
Figure 7.
A sample response showing the wrong symbol interpretation of Gemini-1.5 on a question of the dataset.

Figure 8.
Comparison of the performance (answer accuracy) of LLMs and human participants on selected questions of the proposed dataset. LLMs’ answer accuracy is an average over all the tested LLMs.
Figure 8.
Comparison of the performance (answer accuracy) of LLMs and human participants on selected questions of the proposed dataset. LLMs’ answer accuracy is an average over all the tested LLMs.
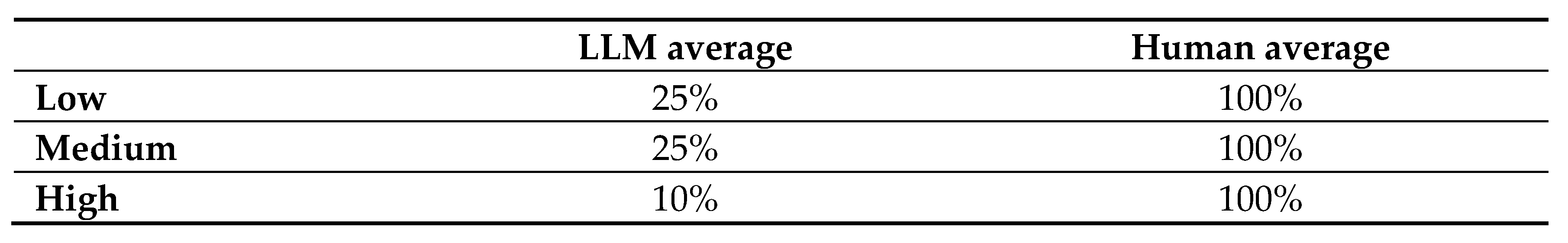
Figure 9.
Performance of LLMs on different questions in the proposed logical reasoning dataset.
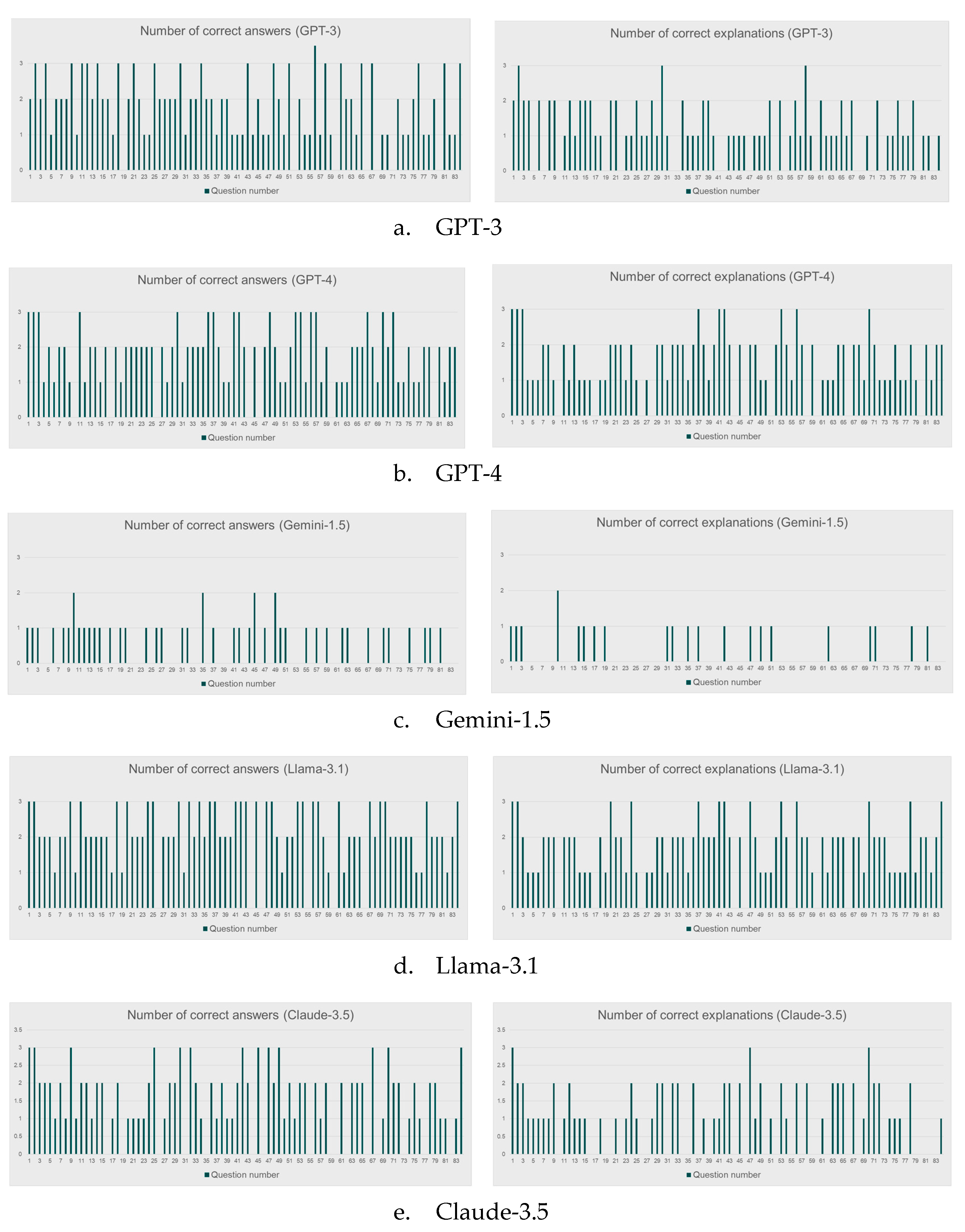
Figure 10.
Performance of LLMs with respect to different levels of question difficulty.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated




