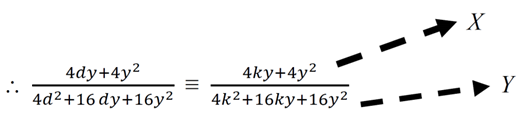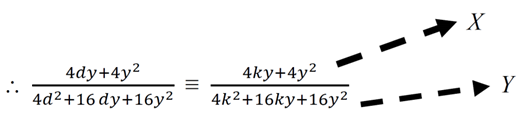Introduction

Methodology

Figure 1. Immersed circular body.

Figure 1. Immersed circular body.

3.1. Distance BETWEEN Center of Pressure & Center of Gravity

• Center of pressure, $\overline{h}$ can simply be defined as the point where pressure tends to act most.
• Similarly, center of gravity, $\overline{x }$can be defined as the point where force of gravity tends to act most (Smith et al., 2016)

Figure 2. Distance Between Center of Pressure & Center of Gravity.

Figure 2. Distance Between Center of Pressure & Center of Gravity.

From the above diagram, y = 0 ⸫ $\overline{h}$_o = ${\displaystyle \frac{5d}{8}}$ and $\overline{x}$_o = ${\displaystyle \frac{d}{2}}$ as can be seen from the derivations.

Therefore, the distance between $\overline{h}$_o and $\overline{x}$_o = ${\displaystyle \frac{5d}{8}}$ ͞ ${\displaystyle \frac{d}{2}}$

$\overline{ h}$o - $\overline{x}$o = ${\displaystyle \frac{ d }{8}}$ or d = 8 ($\overline{h}$o - $\overline{x}$o)

(6)

The distance between $\overline{h}$_o - $\overline{x}$_o can only be calculated just before the body starts to sink. In other words, when the immersed depth, y = 0

3.1. Change as an Influence of Immersion Depth on Center of Pressure Position

• Real change of CoP

${\displaystyle \frac{\Delta \overline{h}}{\mathsf{\Delta }\mathrm{y}}}$ = ${\displaystyle \frac{\overline{h}2-\overline{h}1 }{\mathrm{y}2-\mathrm{y}1}}$ = k1

(7)

k₁ signifies the constant that expresses the real change of CoP of the immersed body.

b.

Ideal Change in CoP

$\overline{ h}$ = ƒ (y)

(8)

where $\overline{h}$ is the dependent variable and y is the independent variable. From equation 7 we can differentiate the center of pressure, $\overline{h}$ with respect to the immersion depth, y by applying the quotient rule (Chen, 2012)

${\displaystyle \frac{d\varnothing }{d\beta }}$ = ${\displaystyle \frac{vdu-udv}{v^2}}$ where $\varnothing (u, v)$	(9)
⸫ ${\displaystyle \frac{\mathsf{\Delta }\overline{h}}{\mathsf{\Delta }y}}$ = ${\displaystyle \frac{\left(8d+16y\right)\left(16d+32y\right)-(5d^2+16dy+16y^2)\left(16\right) }{{\left(8d+16y\right)}^2}}$	(10)

where;

$\mathrm{v}=8(d+2y)$, $\mathrm{d}\mathrm{v}=16$ and $\mathrm{u}=5{\mathrm{d}}^2+16\mathrm{d}\mathrm{y}+16{\mathrm{y}}^2$, $\mathrm{d}\mathrm{u}=16\mathrm{d}+32\mathrm{y}$

NB: Differentiating a constant = 0 and since the diameter is a constant (it doesn’t change)

⸫ ƒ' (d) = 0

Let $\mathsf{\Delta }\overline{\mathrm{h}}$ and Δy be used as the differential since dy has been used as the product of diameter and vertical distance. By applying quotient rule and simplifying the expression, we can see that the center of pressure changes with respect to the vertical distance as given below:

From equation 9, we can conclude that the:

Ideal Change in CoP$={\displaystyle \frac{\mathsf{\Delta }\overline{h}}{\mathsf{\Delta }y}}$ $={\displaystyle \frac{3d^2+16dy+16y^2 }{4d^2+16dy+16y^2}}$ $=$ k2

(11)

where k₂ signifies the constant that expresses the ideal change of CoP of the immersed body.

However, we can simplify equation 10 even further by applying long-division method since the numerator and denominator have the same degree of terms (Nor Arzemi et al., 2010).

Long Division method $=\mathrm{Q}\left(\mathrm{x}\right)+$ ${\displaystyle \frac{R \left(x\right)}{D \left(x\right)}}$

(12)

where;

$\mathrm{Q}\left(\mathrm{x}\right)={\displaystyle \frac{3}{4}}$
$R \left(x\right)=4\mathrm{d}\mathrm{y}+4{\mathrm{y}}^2$
$D \left(x\right)=4{\mathrm{d}}^2+16\mathrm{d}\mathrm{y}+16{\mathrm{y}}^2$
${\displaystyle \frac{\mathsf{\Delta }\overline{h}}{\mathsf{\Delta }y}}$ = ${\displaystyle \frac{3}{4}}$ + ${\displaystyle \frac{4dy+4y^2}{4d^2+16dy+16y^2}}$	(13)

i.

Let X = 0

⸫ $4ky+4{\mathrm{y}}^2$ = 0

$y=-d$ or 0 (where d is the diameter of the body, see the first and last balls below)

ii.

Let Y = 0

⸪ $4{\mathrm{k}}^2+16\mathrm{k}\mathrm{y}+16{\mathrm{y}}^2=0$

(14)

y = $-{\displaystyle \frac{d}{2}}$ (this explains the movement of the middle ball)

3.1.1. Derivation of Complex Center of Pressure (iCoP) Equation

The new model for CoP has a numerator and denominator with y and d terms in both linear and quadratic manner as shown below:

$\overline{h}$ = ${\displaystyle \frac{5d^2+16dy+16y^2}{8\left(d+2y\right)}}$

• STEP ONE: Solution of the Quadratic Equation (Numerator)

To solve the equation, we first focus on the quadratic expression in the numerator:

$5d^2+16dy+16y^2$= 0

$ay$² + $by$+ $c$ = 0

Where a = $16$ b = $16d$ c = $5d$²

The general solution for a quadratic equation is given by the quadratic formula (López et al., 2015):

y = ${\displaystyle \frac{-b\pm \sqrt{b^2-4ac}}{2a}}$

Substituting the values for a, b and c:

y = ${\displaystyle \frac{-16d\pm \sqrt{{\left(16d\right)}^2-4(16 x 5d^2)}}{2x 16}}$

Simplifying the expression:

y = $-0.5d \pm 0.25di$

(15)

Therefore, y₁ = $-0.5d+0.25di$

y2 = $-0.5d-0.25di$

• b. STEP TWO: Substitution of y₁ and y₂ into the Original Equation

$\overline{h}$ = ${\displaystyle \frac{5d^2+16dy+16y^2}{8\left(d+2y\right)}}$

Case 1: Substituting y₁ = $-0.5d+0.25di$Numerator Calculation:

$16d\left(-0.5d+0.25di\right)=-8d^2+4d^{2}i$
($-0.5d+0.25di$)2 = $0.25d^2-0.25d^{2}i-0.0625d^2$
$5\left(0.25d^2-0.25d^{2}i-0.0625d^2\right)=0.9375d^2-1.25d^{2}i$
$5d^{2 }-8d^2+4d^{2}i$ + $0.9375d^2-1.25d^{2}i$ = $-2.0625d^2+2.75d^{2}i$

Denominator Calculation:

$$8\left(d+2(-0.5d+0.25di\right))=-4di$$

Substitute into the CoP equation (equation 9):

$\overline{h}$ = ${\displaystyle \frac{-2.0625d^2+2.75d^{2}i}{-4di}}$
$\overline{h}$ = ${\displaystyle \frac{-2.0625d^2}{-4di}}+{\displaystyle \frac{2.75d^{2}i}{-4di}}$

Evaluating the imaginary part:

${\displaystyle \frac{-2.0625d^2}{-4di}}={\displaystyle \frac{2.0625d^2}{4di}}$ $=$ ${\displaystyle \frac{2.0625d^2}{4di}} x {\displaystyle \frac{-i}{-i}}$ $=$ ${\displaystyle \frac{-2.0625di}{-4(-1)}}$ $=$ $-0.515625di$

Evaluating the real part:

${\displaystyle \frac{2.75d^{2}i}{-4di}}$ $=$ ${\displaystyle \frac{2.75d^{2}i}{-4di}}$ $=$ $-0.6875d$
⸫ $\overline{h}$ = $-0.6875d$ $-0.515625di$

Case 2: Substituting y₂ = $-0.5d-0.25di$

Numerator Calculation:

$16d\left(-0.5d-0.25di\right)=-8d^2-4d^{2}i$
($-0.5d-0.25di$)2 = $0.25d^2+0.25d^{2}i-0.0625d^2$
$5\left(0.25d^2+0.25d^{2}i-0.0625d^2\right)=0.9375d^2+1.25d^{2}i$
$5d^{2 }-8d^2-4d^{2}i$ + $0.9375d^2+1.25d^{2}i$ = $-2.0625d^2-2.75d^{2}i$

Denominator Calculation:

$$8\left(d+2(-0.5d-0.25di\right))=-4di$$

Substitute into the CoP equation (equation 9):

$\overline{h}$ = ${\displaystyle \frac{-2.0625d^2-2.75d^{2}i}{-4di}}$
$\overline{h}$ = ${\displaystyle \frac{-2.0625d^2}{-4di}}+{\displaystyle \frac{-2.75d^{2}i}{-4di}}$

Evaluating the imaginary part:

${\displaystyle \frac{-2.0625{\mathrm{d}}^2}{-4\mathrm{d}\mathrm{i}}}={\displaystyle \frac{2.0625{\mathrm{d}}^2}{4\mathrm{d}\mathrm{i}}}$ $=$ ${\displaystyle \frac{2.0625{\mathrm{d}}^2}{4\mathrm{d}\mathrm{i}}}\mathrm{x}{\displaystyle \frac{-\mathrm{i}}{-\mathrm{i}}}$ $=$ ${\displaystyle \frac{-2.0625\mathrm{d}\mathrm{i}}{-4(-1)}}$ $=$ $-0.515625\mathrm{d}\mathrm{i}$

Evaluating the real part:

${\displaystyle \frac{-2.75{\mathrm{d}}^2\mathrm{i}}{-4\mathrm{d}\mathrm{i}}}$ $=$ ${\displaystyle \frac{-2.75{\mathrm{d}}^2\mathrm{i}}{-4\mathrm{d}\mathrm{i}}}$ $=$ $0.6875\mathrm{d}$
⸫ $\overline{h}$ = $0.6875d$ $-0.515625di$

⸫ The i-center of pressure (iCoP) which is a function of the diameter of the body is given as

$\overline{\mathit{h}}$ =$\pm 0.6875\mathit{d}$ $-0.515625\mathit{d}\mathit{i}$

(16)

3. Results and Discussion

3.1. Change as an Influence of Immersion Depth on Center of Pressure Position

It’s obvious that the center of pressure is directly proportional to the vertical distance, so when the immersion depth changes, the center of pressure, CoP changes as well (Zemlyak et al., 2022)

Real change of CoP$={\displaystyle \frac{\Delta \overline{h}}{\mathsf{\Delta }\mathrm{y}}}$ = ${\displaystyle \frac{\overline{h}2-\overline{h}1 }{\mathrm{y}2-\mathrm{y}1}}$ = k1. k1 signifies the constant that expresses the real change of CoP of the immersed body. From the above equations, since the center of pressure changes when the immersion depth changes, then the center of pressure is a function of the immersion depth (Maleki et al., 2022; Jasim et al., 2020).

Ideal Change in CoP$={\displaystyle \frac{\mathsf{\Delta }\overline{h}}{\mathsf{\Delta }y}}$ $={\displaystyle \frac{3d^2+16dy+16y^2}{4d^2+16dy+16y^2}}$ $=$ k2

We observe that k₁ > k₂ (this may be due to the effect of temperature, pressure, viscosity, density, or impurities)

The deviation of the real change, k₁ from the ideal change, k₂ is given as:

$\gamma$ = k1 – k2

From the analysis, it is evident that the centre of pressure (CoP) for an immersed body varies with immersion depth (Podryabinkin et al., 2014). From the equations 7 and 11 respectively, ${\displaystyle \frac{\Delta \overline{h}}{\mathsf{\Delta }\mathrm{y}}}=k$​₁ and ${\displaystyle \frac{\mathsf{\Delta }\overline{h}}{\mathsf{\Delta }y}}=k$₂, we observe that CoP is indeed a function of the immersion depth. Here, $k$​₁​ represents the real change, which is influenced by factors like temperature, pressure, viscosity, density, and impurities. On the other hand, $k$₂ signifies the ideal change, assuming these external factors are not present. The distinction between $k$₁ and $k$₂, quantified as $\gamma =k\mathrm{}1-k$₂ highlights the deviation caused by real-world conditions. This difference is critical for applications where precise control of pressure distribution is necessary, such as in ocean engineering and submarine design. By applying the quotient rule to differentiate the CoP with respect to immersion depth, we obtain a non-linear two-sided quadratic relationship that captures how immersion depth affects the centre of pressure.

The derived equation ${\displaystyle \frac{\mathsf{\Delta }\overline{h}}{\mathsf{\Delta }y}}$ $={\displaystyle \frac{3d^2+16dy+16y^2 }{4d^2+16dy+16y^2}}$​ demonstrates that the ideal change of CoP which is represented by $k$₂, while $k$₁ reflects the real change. The real change, $k$₁, is greater than the ideal change, $k$₂, due to the influence of external factors. This insight enriches our understanding of the CoP dynamics and provides valuable information for designing systems that require accurate pressure control.

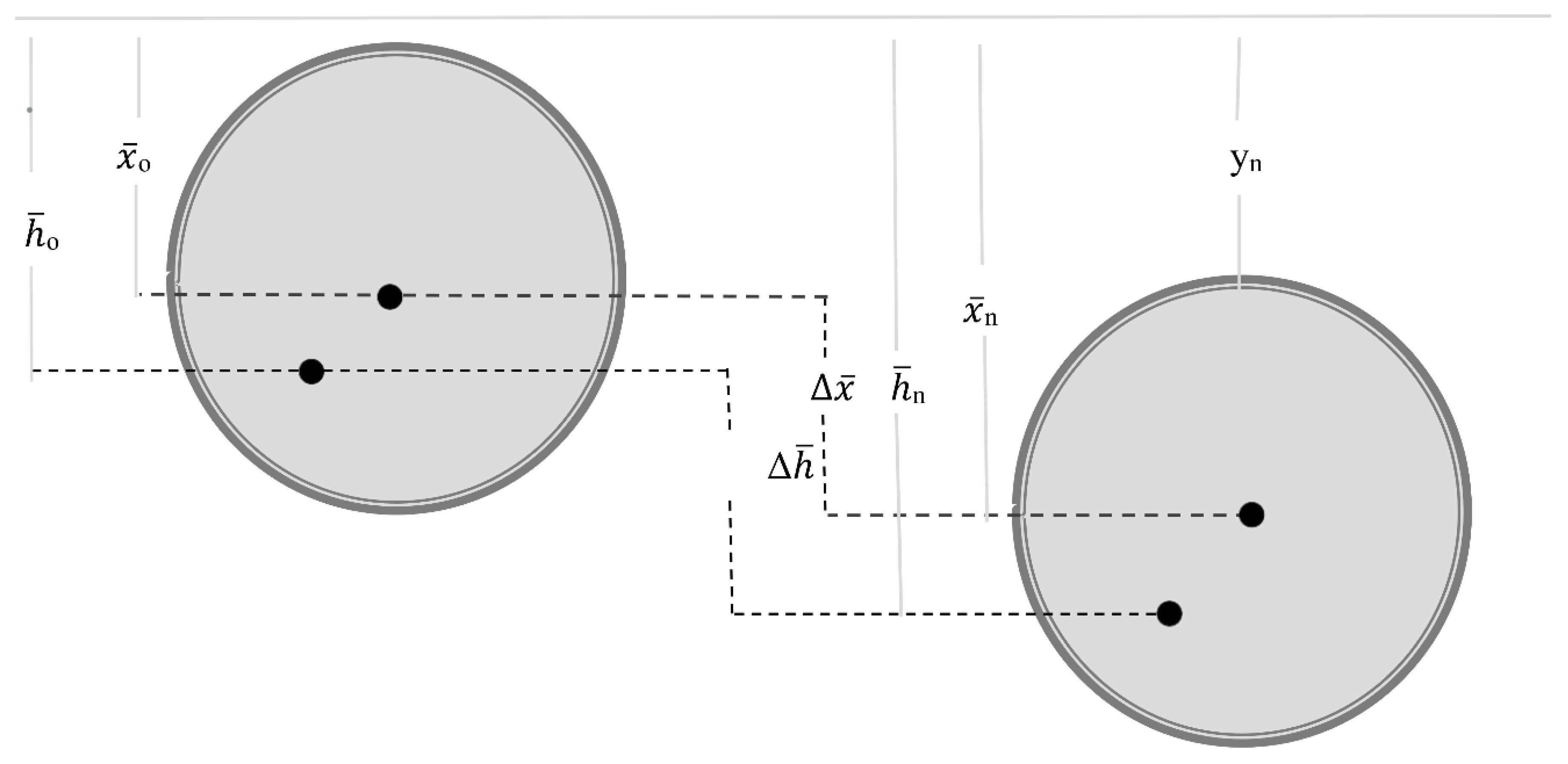
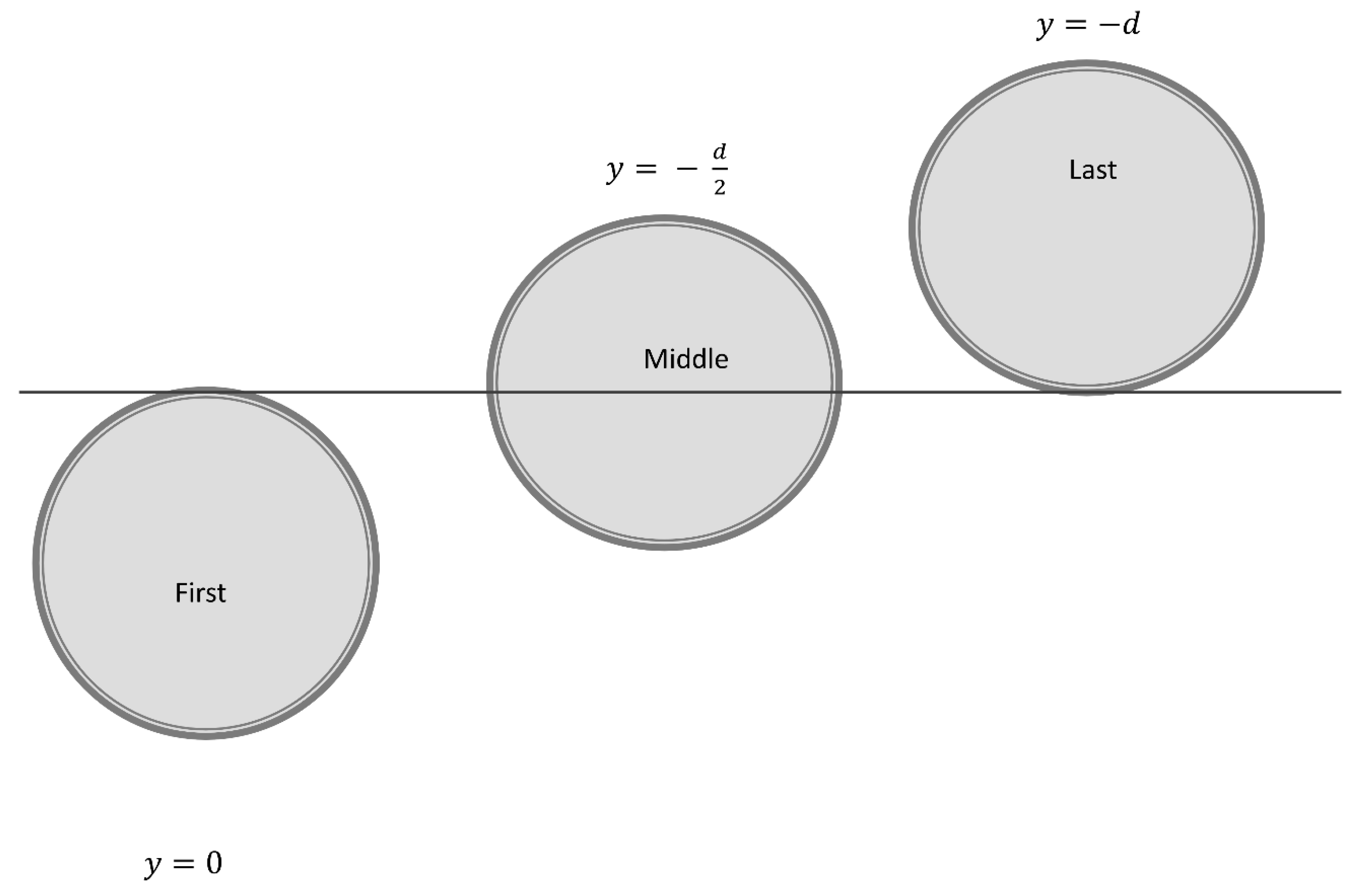
Immersion Depth Convention (From Figure 3)

In this model, the water surface is the reference axis for measuring vertical distances. The convention is as follows (Molland, 2008):

• Positive vertical distances indicate the body is submerged below the water surface.
• Negative vertical distances indicate the body has emerged above the water surface.
• When floating, the vertical distance is negative, indicating an upward direction.
• When sinking, the vertical distance is positive, indicating a downward direction.

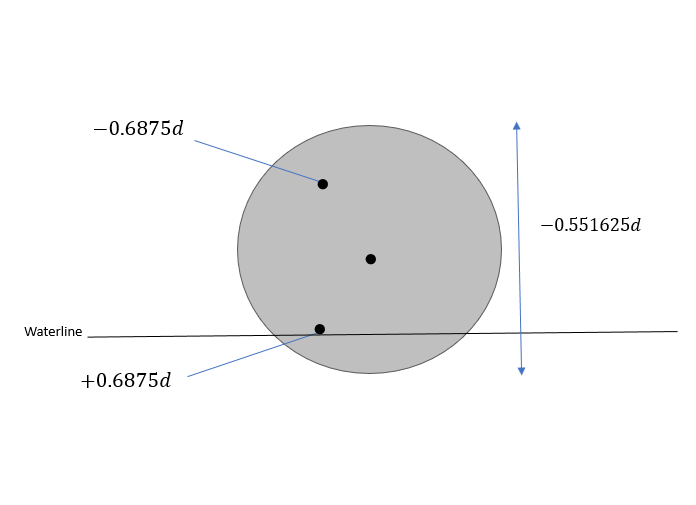
Figure 3. Different positions of the ball in the water medium.

Figure 3. Different positions of the ball in the water medium.

Section 1: Center of Pressure at Initial Contact (First Ball)

At the initial contact point (first ball) where the immersion depth $y=0$, indicates that the body is touching the water surface without any displacement. By substitution of the value of y into equation 11 and further simplification, we obtained the center of pressure ($\overline{h}$) to be $0.625\mathrm{d}$, where d is the diameter of the ball.

Section 2: Center of Pressure at Half-Immersion (Middle Ball)

Similarly, when the body is immersed halfway (second ball), the immersion depth becomes $-0.5d$. At this point, the CoP which is a theoretical singularity becomes indeterminate (infinity value, ∞) due to the symmetry of the pressure distribution about the waterline which makes it impossible to define a unique point as the center of pressure ($\overline{h}$ ). This means that the pressure acting on the body is evenly distributed on either side of the waterline.

Section 3: Center of Pressure at Full Emergence (Last Ball)

In the third scenario, the ball is entirely above the water surface, with a contact point on the surface. The vertical distance (y) is - d, indicating a complete transition from half to full diameter in the upward manner. Calculations for CoP(h) at this point is $-0.625\mathrm{d}$, identical to the first ball, but with a negative sign indicating the body's position above the water surface.

From X and Y, we can deduce (y + d) (y + 0) and (2y + d) respectively.

3.1. The Complex Center of Pressure (iCoP)

As a novel concept that we derived from in-depth studies and observations, we defined Complex Center of Pressure (iCoP) as a dynamic point that represents the oscillating or varying location of the center of pressure on a circular body. In other words, it’s the dynamic nature of the center of pressure in response to changes in the fluid flow or geometry. Let us consider the novel-derived model for CoP and how it is related to the Complex

Center of Pressure (iCoP).

$\overline{h}$ = ${\displaystyle \frac{5d^2+16dy+16y^2}{8\left(d+2y\right)}}$

• The expression is asymmetric with respect to y, indicating that the relationship between $\overline{h}$ and y is not symmetric about the midpoint, $y=-{\displaystyle \frac{d}{2}}$. At this point, CoP equals ∞.
• The presence of both quadratic and linear terms in d and y suggests a complex flow behavior, and nonlinear relationship between the body and the fluid. In addition, this suggests a possible connection to boundary layer theory, where the flow near the surface ($\mathrm{y}=0$) is different from the bulk flow.
• The quadratic terms in the equation consolidate the nonlinear pressure distribution found in advanced fluid dynamics, particularly in the study of hydrostatic forces and fluid flow around objects.

$\overline{\mathit{h}}$ =$\pm 0.6875\mathit{d}$ $-0.515625\mathit{d}\mathit{i}$

This point represents the oscillating behavior of the immersed body in response to changes in the fluid flow or geometry which in turn generates waves and vortices. In conclusion, the solutions for $\overline{h}$ are complex conjugates:

• $\overline{h}$ = $-0.6875d$ $-0.515625di$
• $\overline{h}$ = $0.6875d$ $-0.515625di$

This implies that the behaviour of $\overline{h}$depends on the specific value of the diameter, d, with the results being purely imaginary and opposite in sign.

As a new concept in fluid dynamics, Complex or Imaginary Center of Pressure (iCoP) plays a vital role in flow-body systems and how it relates to the formation of phase change, and oscillating phenomenon like waves and vortex when a body is immersed in fluid.

Figure 4. Graphical Summary of Center of Pressure.

Figure 4. Graphical Summary of Center of Pressure.

3. Conclusions

References

1. Rajput, R. K. (1998). A textbook of fluid mechanics and hydraulic machines (1st ed., pp. 98-101). S. Chand & Company Ltd.
2. Smith, A. C., Roberts, J. R., Kong, P. W., & Forrester, S. E. (2017). Comparison of centre of gravity and centre of pressure patterns in the golf swing. European Journal of Sport Science, 17(2), 168-178. [CrossRef]
3. Zemlyak, V., Pogorelova, A., & Kozin, V. (2022). Motion of a submerged body in a near-surface water environment. International Journal of Naval Architecture and Ocean Engineering, 14, 100433. [CrossRef]
4. Maleki, S., & Fiorotto, V. (2022). Immersed body motion: Near-bottom added mass effects. Journal of Fluid Mechanics, 939, A18. [CrossRef]
5. Chen, Z. (2012). Product and quotient rules from logarithmic differentiation. Teaching Mathematics and Its Applications: An International Journal of the IMA, 31(2), 118–120. [CrossRef]
6. Podryabinkin, E., Ahmed, R., Tarasevich, V., & May, R. (2014). Evaluation of pressure change while steady-state tripping. In Proceedings of the ASME 2014 33rd International Conference on Ocean, Offshore and Arctic Engineering. Volume 5: Materials Technology; Petroleum Technology (V005T11A011). San Francisco, California, USA. ASME. [CrossRef]
7. Jasim, N. A., Shamkhi, M. S., & Stojanovic, B. (2020). The design of the center of pressure apparatus with demonstration. Cogent Engineering, 7(1). [CrossRef]
8. Nor Arzemi, N. S., & Sivasubramaniam, P. (2010). Long division and the double division method. Procedia - Social and Behavioral Sciences, 8, 85-92. [CrossRef]
9. Molland, A. F. (Ed.). (2008). Chapter 3: Flotation and stability. In The maritime engineering reference book (pp. 75-115). Butterworth-Heinemann. [CrossRef]
10. López, J., Robles, I., & Martínez-Planell, R. (2015). Students’ understanding of quadratic equations. International Journal of Mathematical Education in Science and Technology, 47(4), 552–572. [CrossRef]
11. Kim, W., & Choi, H. (2019). Immersed boundary methods for fluid-structure interaction: A review. International Journal of Heat and Fluid Flow, 75, 301-309. [CrossRef]
12. Nicolaou, L., Jung, S. Y., & Zaki, T. A. (2015). A robust direct-forcing immersed boundary method with enhanced stability for moving body problems in curvilinear coordinates. Computers & Fluids, 119, 101-114. [CrossRef]