Prerpints.org logo
Preprint
Article

Coupling Fault Diagnosis of Bearings Based on Hypergraph Neural Network

Altmetrics

Downloads

60

Views

20

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

25 August 2024

Posted:

26 August 2024

You are already at the latest version

Alerts
Abstract
Coupling faults that occur simultaneously widely exist in the operation of mechanical equipment, and coupling fault features are formed by nonlinear coupling of multiple base fault features. In this paper, hypergraph neural network is used to obtain the characteristics of coupling faults, and two coupling fault diagnosis frameworks based on hypergraph are provided. 1. Coupling fault diagnosis framework based on feature generation: The hypergraph neural network is used as a generator to provide negative samples for discriminator training. The generator outputs hyperedge vectors as fake samples, and each hyperedge connects a base fault containing a fault type. 2. Coupling fault diagnosis framework based on feature extraction: Each node is regarded as a fault type, and the fault characteristics of each type of fault are extracted through the aggregation operation of hypergraph. The attention mechanism is introduced to realize the dynamic adjustment of the hyperedge, and the dynamic vertex is used to classify the unknown faults. The results show that the diagnostic accuracy of coupling faults under the two frameworks reaches 88.6% and 86.76%, respectively.
Keywords: 
Subject: Engineering  -   Safety, Risk, Reliability and Quality

1. Introduction

Coupling faults exist widely in mechanical equipment. which are formed by coupling of multiple types of base faults. Coupling faults are not linear superposition of base faults, and complex fault characteristics show emergence in the coupling process [1]. Therefore, simple linear decoupling cannot achieve accurate diagnosis of coupling faults, and a more accurate nonlinear model needs to be established to describe the fault coupling process [2]. In this paper, two kinds of data-driven methods are used to obtain the fault characteristics of multi-fault coupling, reveal the fault coupling process, and classify the coupling faults based on the obtained coupling fault characteristics.
The fault characteristics of rotating machinery can be obtained by spectral analysis [3]. Scholars mostly used traditional frequency domain feature extraction methods [4]. Ma et al. [5] proposed adaptive demodulation analysis to extract bearing early fault features. Jiang et al. [6] used short-time Fourier transform to obtain bearing amplitude, and used adaptive weights to extract characteristic frequency weighted. Zhu et al. [7] determined the hyperparameters of the SAM model by taking the maximum harmonic significance as an index, and divided the frequency band and reconstructed the signal to suppress the noise component in the fault characteristics. Frequency domain features analyze all frequency bands in the spectrum, and the energy of fault features is not concentrated. A large number of scholars use time-frequency domain feature extraction methods to extract fault features of energy-concentrated frequency bands [8]. Tang et al. [9] use time-frequency domain convolutional neural network to extract fault features of multiple energy concentrations, and introduce attention module to extract representative features weighted. Jia et al. [10] proposed Gramian based noise reduction strategy for noise suppression and feature extraction. The above method extracts the features of a single fault from the spectrum, but there is no effective solution to extract the features of the coupled fault. Based on the prior feature information of the fault, the method of extracting feature is used to estimate the fault classification, which belongs to the category of Bayesian school.
The data-driven fault feature generation method can avoid the difficulty of spectrum extraction caused by the lack of working condition information [11]. Zhang et al. [12] generated fault features adaptively through convolutional neural networks and used SVM classifiers to classify fault types. Yang et al. [13] reconstructed fault features through IMFs extracted from VMD and used SVM for fault classification in view of the unbalanced and strong noise characteristics of bearing signals. Huo et al. [14] carry out adaptive extraction of time-frequency domain features, and combine harmonic detection with noise signals to continue to reconstruct the features. Zhao et al. [15] reduce the dimensionality of features by means of depth-separable convolutional blocks, and use the global feature awareness module to perform adaptive weighting processing similar to attention mechanism for the feature signal channels to obtain fault features. Yang et al. [16] reconstructed the coupling fault features through the autoencoder to achieve feature dimension reduction and non-equilibrium data strengthening. Most of the above generative methods reconstruct the original data, but the reconstructed data lacks interpretability. The generative feature acquisition method reconstructs the critical fault information from the existing fault information and estimates the overall probability by observing a large number of samples, which belongs to the frequency school.
Both extraction and generative methods obtain the fault characteristics of bearing independent faults [17]. For complex coupling faults widely existing in bearings, non-Euclidean data-oriented fault diagnosis methods should be used [18,19]. The graph neural network constructs the topological structure of the data through the nodes and the edges connecting the nodes, which can realize the correlation description of non-Euclidean data. Traditional graph neural network describes the relationship between pairs of nodes [20]. Some scholars use graph neural network to extract fault features and perform fault diagnosis. Li et al. [21] established GCN with multiple receptive fields to conduct adaptive correlation analysis on vibration data after FFT, and took data with different receptive fields as fault characteristics. Wang et al. [22] added dynamic vertices to the graph neural network, and realized coupling fault diagnosis by establishing a pair relationship topology between faults and dynamic vertices.
It is difficult for graph neural networks to achieve high-level expression of relationships between objects [23]. To solve this problem, Feng et al. [24] proposed a hypergraph neural network method. Bai et al. [25] introduced convolution and attention mechanisms into hypergraph neural networks, further improving the ability of representation learning in hypergraph networks. At present, hypergraph neural network is mainly used in recommendation system and multi-modal data feature extraction, and has been widely used in image processing. Shi et al. [26] built unlabeled data into hypergraphs, mined higher-order information of the data, and combined the autoencoder to realize representation learning and fault classification. In this method, the hypergraph structure is taken as a layer of autoencoder, and the fault features are generated from the data-driven perspective, which is lack of interpretability. Su et al. [27] extracted the higher-order relationship between the same type of faults and different types of faults through the hypergraph structure. The above methods are applied to independent fault diagnosis. In the field of coupled fault diagnosis, the high order relation representation ability of hypergraph neural network meets the requirement of complex coupled fault feature acquisition. In this paper, two fault diagnosis architectures based on hypergraph neural network are proposed, the coupled fault diagnosis architecture based on feature generation and the coupled fault diagnosis architecture based on feature extraction, and the method is verified by coupling fault injection experimental data.
The main insights and contributions of this study are summarized as follows:
(a)
The rotary mechanical coupling fault injection test is designed. The fault injection and data acquisition of 8 kinds of independent faults and coupled faults are realized.
(b)
A coupled fault diagnosis architecture based on feature extraction is proposed. By applying hypergraph theory to GAN model, the hypergraph generative adversarial network (HGGAN) is established, vibration data generation and coupling fault diagnosis are realized.
(c)
A coupled fault diagnosis architecture based on feature generation is proposed. The coupling fault characteristics are extracted by multi-head inner product hypergraph attention network (IPHGAT), and the coupling fault diagnosis and analysis are realized.
The rest of this paper is organized as follows. Section 2 introduces the preliminary knowledge including the graph attention network, the hypergraph attention network and the generative adversarial network. Section 3 introduces two fault diagnosis frameworks based on hypergraph attention network. The coupled fault injection experiment and data preprocessing methods are introduced in Section 4. In Section 5, two frameworks of coupled fault diagnosis are conducted. Finally, conclusions are drawn in Section 6.

2. Preliminary knowledge

2.1. Graph Attention Network

In graph G = ( V , E ) , E = e i j | x i , x j ∈ V is the set of edges and V = { x 1 , x 2 , … , x N } is the set of nodes. In the graph convolutional network, interlayer information transmission based on aggregation is as follows [28]:
X l + 1 = σ D ˜ − 1 2 A D ˜ − 1 2 X l W l
where A is the adjacency matrix, D ˜ is the degree matrix added to the self-loop, and W is the linear transformation weight matrix. The graph attention network introduces the attention mechanism into the graph convolutional network, and uses the dynamic adjacency matrix to perform adaptive values of the edge vector according to the node data characteristics. The calculation method is as follows [29]:
A i j = exp   LeakyReLU   a T h i W | | h j W Σ k ∈ N i exp L e a k y R e L U a T h i W | | h k W  
Multi-head graph attention network (GAT) extracts multi- kernel features from a single node in the graph structure, which realizes the dynamic update of the relationship to adapt to the inference task, and also concentrates the feature energy. However, GAT only solves the adaptive problem of the relationship weights of binary nodes. For the multiple interactions existing in coupling faults, higher-order representation methods are needed for modeling processing.

2.2. Hypergraph Attention Network

Hypergraph neural network connects multiple nodes through hyperedges, which extract higher-order relationships of nodes. The inter-layer information transmission mode is as follows:
X l + 1 = D v   − 1 / 2 A H D e   − 1 A T D v   − 1 / 2 X l W l
where A is the adjacency matrix, D v is the node degree matrix, D e is the hyperedge degree matrix, H is the weight diagonal matrix of the hyperedge, and W is the linear transformation weight matrix. However, in hypergraph convolutional attention networks, adjacency matrix A ∈ { 0 , 1 } N × M is composed of 0 and 1, and only the correlation between two nodes is qualitatively described. The hypergraph attention network computes the values in the adjacency matrix A , realizes the quantitative description of the correlation between nodes, and enhances the information content of features through the attention-based multi-kernel convolution computation. The computation of the attention mechanism in the hypergraph structure is defined as follows:
A i j = exp LeakyReLU ( a T [ x i W | | e j W ] ) ∑ k ∈ N i exp LeakyReLU ( a T [ x i W | | e k W ] )
where N i is the neighborhood set of x i , [ , ∥ , ] is the concatenation operation, a is the weight vector, and the similarity of the two vectors can be acquired after concatenation calculation. The main difference between GAT and HGAT in the calculation of attention coefficient is that the attention score in GAT describes the correlation between a pair of nodes, while the attention score in HGAT is the correlation between nodes and hyperedges, and the neighborhood N i is the higher-order neighborhood of the hypergraph where x i is located. Therefore, the application of attention mechanism in hypergraphs requires nodes and hyperedges to be in the same homogeneous domain.

2.3. Generative Adversarial Network

The adversarial generation network realizes the modeling of data probability distribution through the game between generator and discriminator model [30]. The generator G ( z ) fools the discriminator by generating “fake” data that is sufficiently similar to the probability distribution of the real data, and the discriminator D ( x ) determines whether the input data is “true” by the probability distribution of the input data. The input of the generator is a random vector z , and the cross entropy loss function of the generator model is as follows:
L o s s G = 1 M f a k e ∑ i = 1 M f a k e log ( 1 − D ( G ( z ( i ) ) ) )
where M f a k e is the number of fake data samples. The input of the discriminator is x and the setting of loss function reflects the game between the generator and the discriminator:
L o s s D = − 1 S ∑ i = 1 M r e a l y r e a l i log ( D ( x i ) ) − 1 S ∑ i = 1 M f a k e ( 1 − y f a k e i ) log ( 1 − D ( G ( z i ) ) )
where S = M r e a l + M f a k e is the total number of false samples and true samples, M r e a l is the number of true samples, and the loss function of the discriminator consists of two cross-entropy loss functions. The first half requires the discriminator to be true to the real data, and the second half requires the discriminator to be false to the false data.

3. Algorithm Flow

Coupling faults are formed by coupling of multiple types of base faults [31], and the base faults interact with each other. Therefore, the fault characteristics of coupling faults are not simple linear superposition of base faults, but nonlinear complex coupling. In this paper, the vibration characteristics of coupled faults are not decomposed from the complex physical mechanism, but the advantages of hypergraph neural network in processing higher-order relationships are used to model the coupling faults.

3.1. Coupling Fault Diagnosis Based on Feature Generation

From the perspective of holism, the coupling faults of mechanical equipment are composed of many kinds of faults, which show unified fault characteristics. Assuming that the fault signals of coupled faults are generated by implicit nonlinear coupling between the fault signals of the base faults, this paper uses hypergraph neural network to model the nonlinear generation process and form the HGGAN coupled fault diagnosis architecture.
In this model, the graph nodes V are composed of base faults, i.e., V = M . Each fault including base faults and coupling faults constitute the hyperedge E = N , and M ≤ N , which is reduced to equality if and only if all nodes are base faults.
Based on the ability of generative adversarial network to generate probability distribution of data, a coupled fault diagnosis architecture based on feature generation is designed in this paper. The generator uses hypergraph neural network and the discriminator uses multi-layer perceptron network. The algorithm flow is shown in Figure 1:
In the HGGAN model proposed in this paper, the generator’s loss function is rewritten:
L o s s G = 1 S ∑ i = 1 S ∑ j = 1 M log ( 1 − D ( G ( x j i ) ) )
where S is the total number of samples. Compared with traditional GAN, the input of the generator changes from random vector z to the fault feature x of the base fault in the graph data. Both true samples and false samples come from the same graph data sample, so the number of true samples and false samples is the same.
Where S is the total number of samples. Compared with traditional GAN, the input of the generator changes from random vector z to the fault feature x of the base fault in graph data x j , j ∈ 1 , ⋯ , M . Both true samples and false samples come from the same graph data sample, so the number of true samples and false samples is the same.
The loss function of the discriminator is rewritten as follows:
L o s s D = − 1 S ∑ i = 1 S y M + 1 i log ( D ( x M + 1 i ) ) − 1 S ∑ i = 1 S ∑ j = 1 M ( 1 − y j i ) log ( 1 − D ( G ( x j i ) ) )
The rewritten discriminator loss function is still composed of two parts. In the first part, the input x M + 1 of the discriminator is the dynamic vertex in the graph data, that is, the fault feature of the coupling fault to be diagnosed, and its label y M + 1 is the fault type corresponding to the coupling fault x M + 1 . In the second part, the input of the discriminator is the fault characteristics of all the faults involved in this paper generated by the generator based on the base faults, which improves the stability of the model compared with random data z [32].
The HGGAN network established in this paper generates coupling fault features from the perspective of data generation. Hypergraph convolution network is used to select the generator, which avoids the uncertainty caused by random vectors in traditional GAN, provides interpretability for the network structure, and uses a data-driven approach to model the coupling fault mechanism.

3.2. Coupling Fault Diagnosis Based on Feature Extraction

From the perspective of reductionism, coupling faults of mechanical equipment are composed of multiple base faults, and the signals of coupling faults can be decomposed into those belonging to the base faults. In this framework, a coupling fault diagnosis model based on IPHGAT is established. All the fault modes, including base fault and coupling fault, are taken as graph node V = M , hyperedge E = N is the fault characteristics of all fault modes after aggregation, and M = N . Therefore, this paper applies the attention mechanism to further analyze and process the fault information.
The correlation between each base fault and each type of fault is obtained through the attention mechanism by feeding it into the network as node data and hyperedge values. In the multi-head attention mechanism, the number of heads is defined as the number of independent failures, and the network structure is shown in Figure 2.
Step1: Input the constructed hypergraph data X = [ X ( 0 ) , X ( 1 ) ] ∈ R ( M + 1 ) × Q and label Y = [ Y ( 0 ) , Y ( 1 ) ] ∈ R M into the network, where Q is the data feature dimension, and X includes M base fault node data X ( 0 ) ∈ R M × Q and the fault X ( 1 ) ∈ R Q to be predicted located at a dynamic vertex. The corresponding labels are Y ( 0 ) = [ 1 , ⋯ , M ] , Y ( 1 ) ∈ R . The X ( 0 ) passes through the first layer of m − h e a d attention hypergraph neural network, generates m features for each hyperedge, splice m features of each hyperedge into a whole as the features of the hypergraph and perform feature standardization to obtain X 1 ( 0 ) .
Step2: Input X 1 ( 0 ) into the second layer of m − h e a d attention hypergraph neural network and standardize it to obtain X 2 ( 0 ) , then input X 2 ( 0 ) into the fully connected network and Softmax layer to obtain the fault feature Y ^ ( 0 ) ∈ R m × m corresponding to each hyperedge. Calculate the cross entropy of Y ^ ( 0 ) and Y ( 0 ) as the loss function L o s s 1 .
Step3: Input X ( 1 ) into the three-layer MLP to obtain the fault feature Y ^ ( 1 ) ∈ R m of the node to be predicted. Calculate the cross entropy of Y ^ ( 1 ) and Y ( 1 ) as a loss function L o s s 2 .
Step4: Calculate the inner product between the vector Y ^ ( 1 ) and Y ^ ( 0 ) corresponding to each hyperedge as C = [ c 1 , ⋯ , c M ] , take the label Y ^ of the hyperedge corresponding to the vector with the largest inner product value, and obtain the accuracy rate of the model by judging whether Y ^ and Y ^ ( 1 ) are equal.
The loss function of the model consists of two parts, L o s s = L o s s 1 + L o s s 2 where L o s s 1 = C r o s s E n t r o p y ( Y ( 0 ) , Y ^ ( 0 ) ) and L o s s 2 = C r o s s E n t r o p y ( Y ( 1 ) , Y ^ ( 1 ) ) . Through the process of model training, the value of X ( 0 ) and X ( 1 ) corresponding to the corresponding fault mode’s hyperedge vector tends to increase, thus driving the inner product of the corresponding fault mode to increase.

4. Data Acquisition and Preprocessing

In this paper, the UCPH205 bearing is selected for fault injection experiment. The test bench is shown in Figure 3. The test bench supports real-time monitoring of three-axis vibration signals and can realize stepless adjustment of speed. Fault injection was carried out for 8 types of faults. The test included 1 normal bearing, 4 outer race fault bearings, 4 inner race fault bearings, 4 ball faulty bearings, 1 outer race + inner race fault bearing, 1 outer race + ball faulty bearing, 1 inner race + ball fault bearing, 1 outer race + inner race + ball fault bearing, and 1 outer race + inner race + ball fault bearing. The fault injection experiment was carried out at 2400rpm for each bearing. In this paper, the sample rate of 20kHz was used to collect the experimental data, and the fault size of the outer race, the inner race and the ball was 0.3mm.
Each bearing runs for 60 seconds at different speeds, and the data for each second is taken as a sample, containing a total of 1020 samples. In this paper, the X-axis vibration signal is selected for fault diagnosis and analysis. Firstly, Fourier transform is performed on the data to obtain the spectrum of the vibration data. Because the rotation speed of the outer race, inner race and ball is different, different faults produce different spectrum characteristics in the bearing rotation process. The fault spectrum of the base fault is shown in Figure 5.
Among them, the red dashed line is the fundamental frequency and its frequency double of the fault characteristic frequency value calculated theoretically based on the bearing size, in which the fundamental frequency of the outer race fault is 142.93Hz, the fundamental frequency of the inner race fault is 217.07Hz, and the fundamental frequency of the ball fault is 186.27Hz. It can be seen from the figure that the fault frequency of the bearing injected fault has a high consistency with its theoretical value.
The spectrum of coupled fault data is shown in Figure 6. The vibration spectrum of coupled fault is not a linear superposition of the base fault spectrum, but contains complex coupling relations, which requires a higher-order relationship model to obtain coupling fault features.

5. Coupling Fault Diagnosis

5.1. Coupling Fault Diagnosis Based on Feature Generation

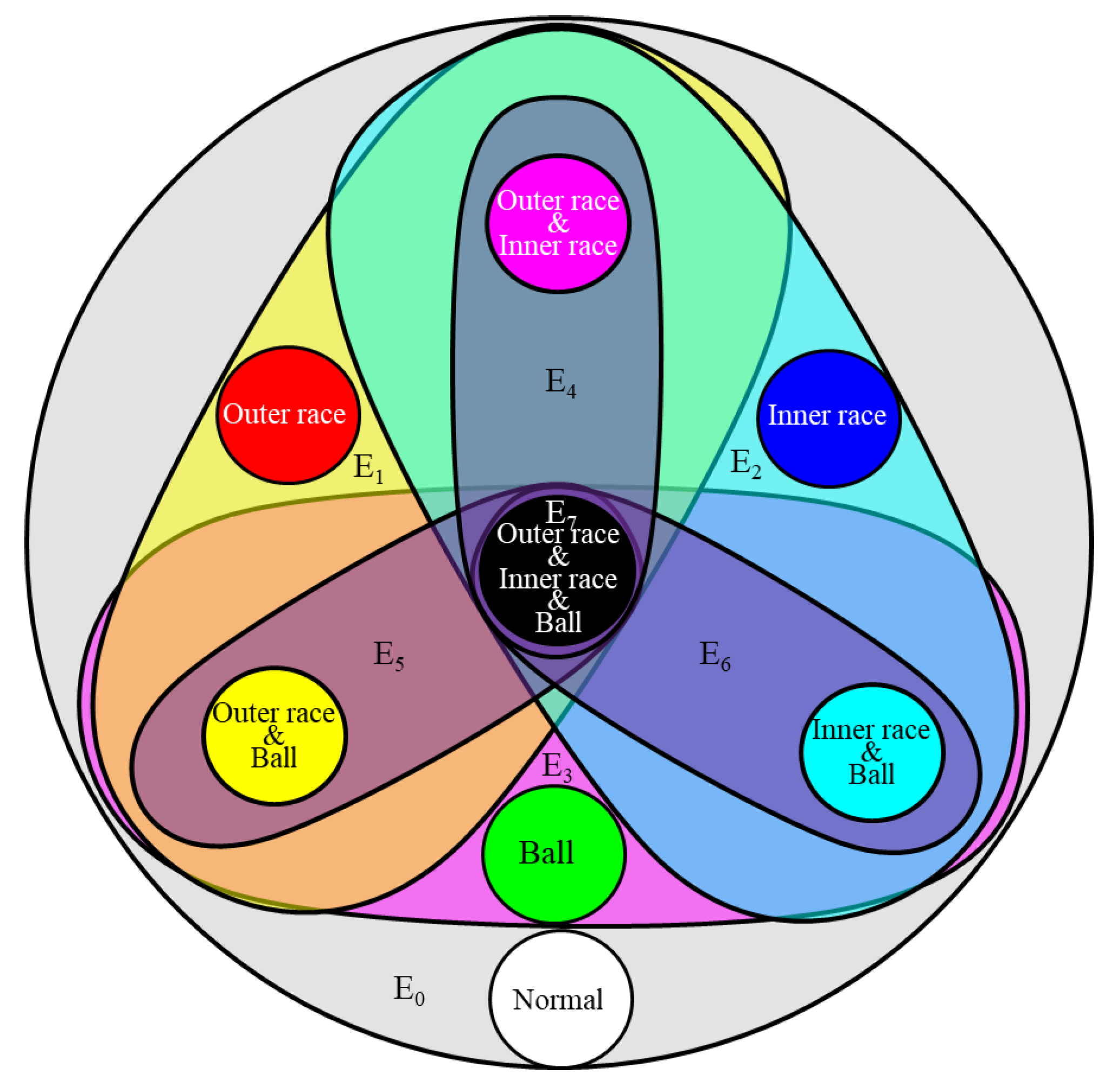
In the HGGAN architecture, the 4 base faults are defined as 4 graph nodes, and the 8 super edges represent 8 types of coupling faults respectively. As shown in Figure 7, the normal state constitutes an independent hyperedge, the inner ring, the outer ring and the ball fault constitute an independent hyperedge with three primary colors respectively, the pairy-pair coupling constitutes three hyperedges respectively, and the three fault coupling constitutes hyperedge E 7 , a total of 8 hyperedges.
Table 1. Incidence matrix of HGGAN.
Table 1. Incidence matrix of HGGAN.
Fault Types E 0 E 1 E 2 E 3 E 4 E 5 E 6 E 7
Normal 1 0 0 0 0 0 0 0
Outer race 0 1 0 0 1 1 0 1
Inner race 0 0 1 0 1 0 1 1
Ball 0 0 0 1 0 1 1 1
The data set is constructed based on the hypergraph topology, in which the training set contains 816 hypergraph samples and the test set contains 204 hypergraph samples. SGD optimizer was used for model training, SGD momentum was set to 0.9, step dynamic learning rate was adopted, the initial learning rate was 0.01, and the decay rate was 0.1. Input the sample data into the network for training, and the training results are shown in Figure 8:
The accuracy of discriminator and generator was 88.6% and 87.5% respectively. The discriminator and generator played games with each other in the training process to jointly optimize the accuracy of the model. The accuracy of the discriminator was slightly ahead of the generator in the training process. Finally, the discriminator and generator models reached similar and strong fault diagnosis capabilities respectively at the 18th iteration.
The generator aggregates the two types of base faults through the hypergraph network to obtain a total of 2 3 = 8 types of faults. The real data and the data generated by the generator are respectively reduced to 2-dimensional by TSNE, and their distribution is shown in Figure 9. Although there is a clear dividing line between the data generated by the generator and the original data, similar faults are roughly located in the same area in the 2-dimensional plane, as shown in Figure 9 (b). The reason is that the generator loss function is the cross entropy of the network output and the real label, which only has requirements on the size relationship of the output value, and has low requirements on the consistency of data values, so that the model has good generalization. Therefore, the data generated by the generator can realize more accurate fault diagnosis.
The discriminator obtained by the HGGAN model was compared with the MLP without adding a generator and the MLP-GAN model in which both the generator and discriminator is MLP. The diagnostic accuracy was shown in Table 2. HGGAN has advantages over other models in terms of accuracy.
Compared with MLP, HGGAN’s discriminator has the same structure as MLP. By adding generator HGCN to generate negative samples and optimize MLP model parameters, HGGAN’s loss function is optimized, so its fault diagnosis accuracy is improved to a certain extent. Compared with MLP-GAN, HGGAN uses HGCN as a generator to extract higher-order relationships more effectively and generate more accurate fault feature data.

5.2. Coupling Fault Diagnosis Based on Feature Extraction

Under the IPHGAT architecture, this paper takes 4 base faults: normal, outer race fault, inner race fault, ball fault and 4 coupled faults: outer race + inner ring fault, outer race + ball fault, inner race + ball fault, outer race + inner race + ball fault as graph nodes, and establishes 8 hyperedges corresponding to all fault types. The topology of the hypergraph is shown in Figure. 10:
Preprints 116220 g010
Figure 10. Coupled fault topology in IPHGAT.
Figure 10. Coupled fault topology in IPHGAT.
Preprints 116220 g010
According to the fault coupling relationship, the correlation matrix of the hypergraph topology is obtained, as shown in Table 3:
The hypergraph data X = [ X ( 0 ) , X ( 1 ) ] ∈ R 9 × 3000 was input into the network for training. SGD optimizer was used for model training, SGD momentum was set to 0.9, and step dynamic learning rate was adopted, the initial learning rate was 0.01 and the attenuation rate was 0.1. Since the number of base faults involved in this paper was 4, the number of heads in multi-head IPHGAT was set to 4, which corresponded to the fault characteristics of each base fault. In the training process, the classification accuracy A c c ( 0 ) of the base fault X ( 0 ) , the classification accuracy A c c ( 1 ) of the dynamic vertex fault X ( 1 ) to be predicted and the correlation accuracy A c c of the inner product are calculated respectively. As shown in Figure 11, A c c ( 0 ) and A c c ( 1 ) reach 99.88% and 88.60% respectively, and the internal product correlation accuracy rate A c c reaches 86.76%, so IPHGAT can effectively classify coupling faults.
The inner product correlation between dynamic vertex faults and 8 types of fault data is C = [ c 1 , ⋯ , c 8 ] ∈ R 8 . Input the test set data into the trained IPHGAT model, and take out the inner product correlation c 1 , c 2 , c 3 , c 4 of coupled fault and base fault characteristics for analysis. As shown in Figure. 12, the vertical axis is the coupling fault to be predicted, and the horizontal axis is the base fault that makes up the coupling fault. In addition, the accuracy of base fault components of coupled faults is more than 91.67%, and the coupling analysis is basically consistent with the fault injection model.
The IPHGAT model based on the reductionist feature extraction framework extracts the fault component representing the base fault from the coupling fault, and analyzes the fault mode based on the correlation of the fault component, which enhances the interpretability of the model, and is of great significance for the coupling fault diagnosis of rotating machinery in industrial production environment.

5. Discussion and Conclusions

In this paper, based on the research of coupling fault diagnosis of rotating machinery, a coupling fault diagnosis method HGGAN based on fault feature generation framework and a coupling fault diagnosis method IPHGAT based on fault feature extraction framework are proposed respectively from the perspectives of holism and reduction theory by utilizing the advantages of hypergraph neural network for analyzing higher-order relations. HGGAN uses MLP as a discriminator, and proposes to utilize HGCN as a generator to generate coupling fault data. The generated data and the real data have a unified data space, and the diagnosis accuracy of HGGAN coupling fault reaches 88.6%. IPHGAT used multi-head hypergraph neural network to extract the fault features of coupling faults, and used MLP to extract dimensionality reduction features of predictive data, and calculated the internal product correlation between the fault features and coupling faults in dynamic vertex, and realized the fault diagnosis of coupling faults. The diagnosis accuracy rate reached 86.76%.

Author Contributions

Conceptualization, S.W. and B.J.; Methodology, S.W.; Validation, S.P., Y.H., and X.M.; Investigation, J.P. and X.J.; Writing—original draft preparation, S.W.; Writing—review and editing, S.W.; Supervision, B.J. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the “14th Five-Year Plan” equipment pre-research common technology (grant number 50902060401).

Data Availability Statement

Data is unavailable due to privacy.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Xue, S.; Wang, C.S.; Howard, I.; Lian, P.Y.; Chen, G.G.; Wang, Y.; Yan, Y.F.; Xu, Q.; Shi, Y.; Jia, Y.; et al. The diagnostic analysis of the fault coupling effects in planet bearing. Engineering Failure Analysis 2020, 108, 23. [Google Scholar] [CrossRef]
  2. Lu, K.; Cheng, H.; Zhang, W.T.; Zhang, H.P.; Zhang, K.F.; Fu, C. Nonlinear dynamic behavior of a dual-rotor bearing system with coupling misalignment and rubbing faults. Measurement Science and Technology 2023, 34. [Google Scholar] [CrossRef]
  3. Ying, W.M.; Zheng, J.D.; Huang, W.; Tong, J.Y.; Pan, H.Y.; Li, Y.B. Order-frequency Holo-Hilbert spectral analysis for machinery fault diagnosis under time-varying operating conditions. Isa Transactions 2024, 146, 472–483. [Google Scholar] [CrossRef] [PubMed]
  4. Li, Y.; Cheng, G.; Ma, S.C.; Li, X. Bearing fault diagnosis method based on complete center frequency distribution feature. Structural Health Monitoring-an International Journal 2023, 22, 4100–4116. [Google Scholar] [CrossRef]
  5. Ma, J.P.; Chen, G.D.; Li, C.W.; Zhan, L.W.; Zhang, G.Z. Rolling Bearing Feature Extraction Method Based on Improved Intrinsic Time-Scale Decomposition and Mathematical Morphological Analysis. Applied Sciences-Basel 2021, 11, 26. [Google Scholar] [CrossRef]
  6. Jiang, Z.H.; Zhang, K.; Xiang, L.; Yu, G.; Xu, Y.G. A time-frequency spectral amplitude modulation method and its applications in rolling bearing fault diagnosis. Mechanical Systems and Signal Processing 2023, 185, 21. [Google Scholar] [CrossRef]
  7. Zhu, D.C.; Yin, B.L.; Teng, C.X. An improved spectral amplitude modulation method for rolling element bearing fault diagnosis. Journal of the Brazilian Society of Mechanical Sciences and Engineering 2023, 45, 16. [Google Scholar] [CrossRef]
  8. Yang, H.; Zhang, K.; Jiang, Z.H.; Zhang, X.F.; Xu, Y.G. An adaptive time-frequency demodulation method and its applications in rolling bearing fault diagnosis. Measurement Science and Technology 2023, 34, 15. [Google Scholar] [CrossRef]
  9. Tang, J.H.; Wu, J.M.; Hu, B.B.; Qing, J.J. Towards a Fault Diagnosis Method for Rolling Bearings with Time-Frequency Region-Based Convolutional Neural Network. Machines 2022, 10, 19. [Google Scholar] [CrossRef]
  10. Jia, L.S.; Chow, T.W.S.; Yuan, Y.X. GTFE-Net: A Gramian Time Frequency Enhancement CNN for bearing fault diagnosis. Engineering Applications of Artificial Intelligence 2023, 119, 13. [Google Scholar] [CrossRef]
  11. Lin, K.Y.; Jamrus, T. Industrial data-driven modeling for imbalanced fault diagnosis. Ind. Manage. Data Syst. 2024, 30. [Google Scholar] [CrossRef]
  12. Zhang, X.; Han, P.; Xu, L.; Zhang, F.; Wang, Y.; Gao, L. Research on Bearing Fault Diagnosis of Wind Turbine Gearbox Based on 1DCNN-PSO-SVM. Ieee Access 2020, 8, 192248–192258. [Google Scholar] [CrossRef]
  13. Yang, Y.; Liu, H.; Han, L.J.; Gao, P. A Feature Extraction Method Using VMD and Improved Envelope Spectrum Entropy for Rolling Bearing Fault Diagnosis. Ieee Sensors Journal 2023, 23, 3848–3858. [Google Scholar] [CrossRef]
  14. Huo, J.Y.; Yang, J.W.; Yao, D.C.; Sun, R.T.; Hu, Z.S.; Chen, Z.H.; Gao, C. Bearing fault diagnosis under variable speed conditions on adaptive time frequency extraction mode decomposition. Measurement Science and Technology 2024, 35, 15. [Google Scholar] [CrossRef]
  15. Zhao, X.Q.; Guo, H.K. Rolling bearing fault diagnosis model based on DSCB-NFAM. Measurement Science and Technology 2024, 35, 15. [Google Scholar] [CrossRef]
  16. Yang, J.; Chen, J.W.; Zhan, X.A.; Liu, C.S.; Yang, C. A feature reconstruction and SAE model based diagnosis method for multiple mixed faults. Measurement Science and Technology 2024, 35, 14. [Google Scholar] [CrossRef]
  17. Luczak, D. Data-Driven Machine Fault Diagnosis of Multisensor Vibration Data Using Synchrosqueezed Transform and Time-Frequency Image Recognition with Convolutional Neural Network. Electronics 2024, 13, 32. [Google Scholar] [CrossRef]
  18. Li, T.; Zhou, Z.; Li, S.; Sun, C.; Yan, R.; Chen, X. The emerging graph neural networks for intelligent fault diagnostics and prognostics: A guideline and a benchmark study. Mechanical Systems and Signal Processing 2022, 168. [Google Scholar] [CrossRef]
  19. Ning, S.H.; Ren, Y.L.; Wu, Y.K. Intelligent fault diagnosis of rolling bearings based on the visibility algorithm and graph neural networks. Journal of the Brazilian Society of Mechanical Sciences and Engineering 2023, 45, 14. [Google Scholar] [CrossRef]
  20. Luo, L.H.; Fang, Y.X.; Lu, M.L.; Cao, X.; Zhang, X.F.; Zhang, W.J. GSim: A Graph Neural Network Based Relevance Measure for Heterogeneous Graphs. IEEE Trans. Knowl. Data Eng. 2023, 35, 12693–12707. [Google Scholar] [CrossRef]
  21. Li, T.F.; Zhao, Z.B.; Sun, C.; Yan, R.Q.; Chen, X.F. Multireceptive Field Graph Convolutional Networks for Machine Fault Diagnosis. IEEE Trans. Ind. Electron. 2021, 68, 12739–12749. [Google Scholar] [CrossRef]
  22. Wang, S.; Jing, B.; Pan, J.; Meng, X.; Huang, Y.; Jiao, X. Coupling Fault Diagnosis Based on Dynamic Vertex Interpretable Graph Neural Network. Sensors 2024, 24, 4356. [Google Scholar] [CrossRef] [PubMed]
  23. Yan, X.S.; Liu, Y.; Zhang, C.A. Multiresolution Hypergraph Neural Network for Intelligent Fault Diagnosis. Ieee Transactions on Instrumentation and Measurement 2022, 71, 10. [Google Scholar] [CrossRef]
  24. Feng, Y.; You, H.; Zhang, Z.; Ji, R.; Gao, Y. Hypergraph neural networks. In Proceedings of the Proceedings of the Thirty-Third AAAI Conference on Artificial Intelligence and Thirty-First Innovative Applications of Artificial Intelligence Conference and Ninth AAAI Symposium on Educational Advances in Artificial Intelligence, Honolulu, Hawaii, USA, 2019; p. Article 437.
  25. Bai, S.; Zhang, F.H.; Torr, P.H.S. Hypergraph convolution and hypergraph attention. Pattern Recognit. 2021, 110, 8. [Google Scholar] [CrossRef]
  26. Shi, M.K.; Ding, C.C.; Wang, R.; Song, Q.Y.; Shen, C.Q.; Huang, W.G.; Zhu, Z.K. Deep hypergraph autoencoder embedding: An efficient intelligent approach for rotating machinery fault diagnosis. Knowledge-Based Systems 2023, 260, 16. [Google Scholar] [CrossRef]
  27. Su, S.Z.; Zhang, Z.P.; Zhu, Y.M.; Hou, Y.K. Fault diagnosis of rotating machinery via multi-structure fusion discriminative projection. Measurement Science and Technology 2023, 34, 20. [Google Scholar] [CrossRef]
  28. Yuan, Z.H.; Ma, Z.Q.; Li, X.; Li, J.J. A Multichannel MN-GCN for Wheelset-Bearing System Fault Diagnosis. Ieee Sensors Journal 2023, 23, 2481–2494. [Google Scholar] [CrossRef]
  29. Wang, Y.P.; Zhang, S.; Cao, R.F.; Xu, D.; Fan, Y.Q. A Rolling Bearing Fault Diagnosis Method Based on the WOA-VMD and the GAT. Entropy 2023, 25, 30. [Google Scholar] [CrossRef]
  30. Luo, W.; Yang, W.; He, J.L.; Huang, H.; Chi, H.D.; Wu, J.L.; Shen, Y. Fault Diagnosis Method Based on Two-Stage GAN for Data Imbalance. Ieee Sensors Journal 2022, 22, 21961–21973. [Google Scholar] [CrossRef]
  31. Liu, S.H.; Zhang, J.H.; Huang, W.D.; Lyu, F.; Wang, D.D.; Xu, B. Temporal-Spatial Attention Network: A Novel Axial Piston Pump Coupled Fault Diagnosis Method. Ieee Transactions on Instrumentation and Measurement 2024, 73, 15. [Google Scholar] [CrossRef]
  32. Hao, C.; Du, J.; Liang, H. Imbalanced Fault Diagnosis of Rolling Bearing Using Data Synthesis Based on Multi-Resolution Fusion Generative Adversarial Networks. Machines 2022, 10. [Google Scholar] [CrossRef]
Preprints 116220 g001
Figure 1. HGGAN network structure.
Figure 1. HGGAN network structure.
Preprints 116220 g001
Preprints 116220 g002
Figure 2. IPHGAT network structure.
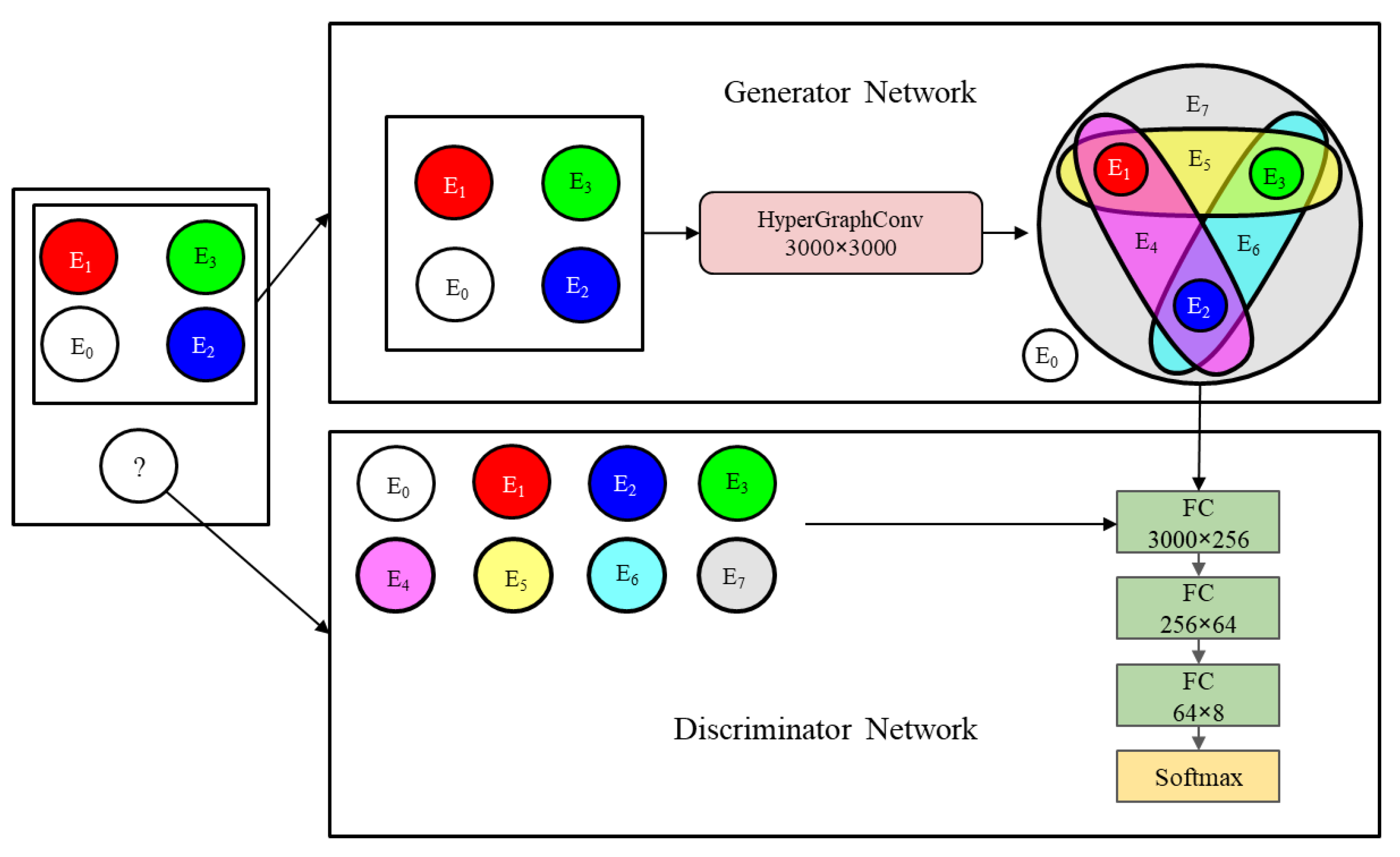
Figure 2. IPHGAT network structure.
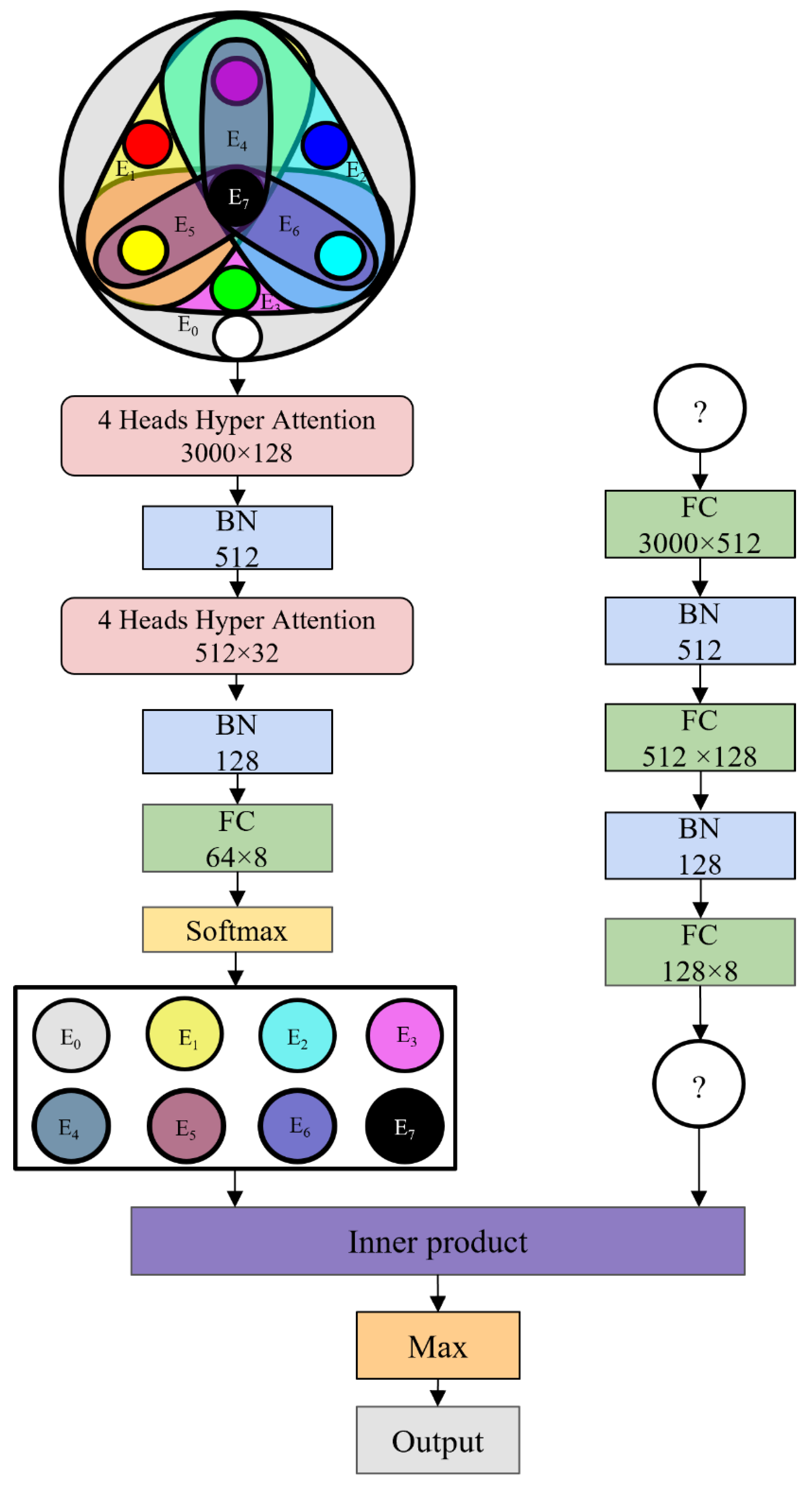
Preprints 116220 g002
Preprints 116220 g003
Figure 3. Coupling fault test bench.
Figure 3. Coupling fault test bench.
Preprints 116220 g003
Preprints 116220 g004aPreprints 116220 g004b
Figure 4. Coupling fault injection bearing.
Figure 4. Coupling fault injection bearing.
Preprints 116220 g004aPreprints 116220 g004b
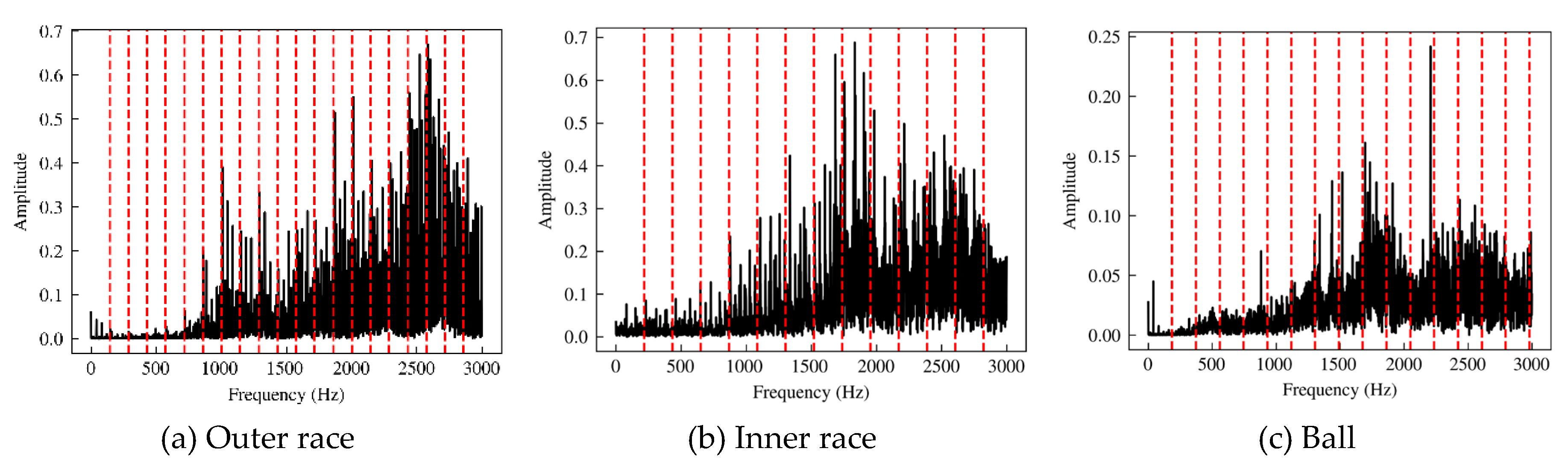
Preprints 116220 g005
Figure 5. Spectrum of the base fault bearings.
Figure 5. Spectrum of the base fault bearings.
Preprints 116220 g005
Preprints 116220 g006aPreprints 116220 g006b
Figure 6. Spectrum of the coupling fault bearings.
Figure 6. Spectrum of the coupling fault bearings.
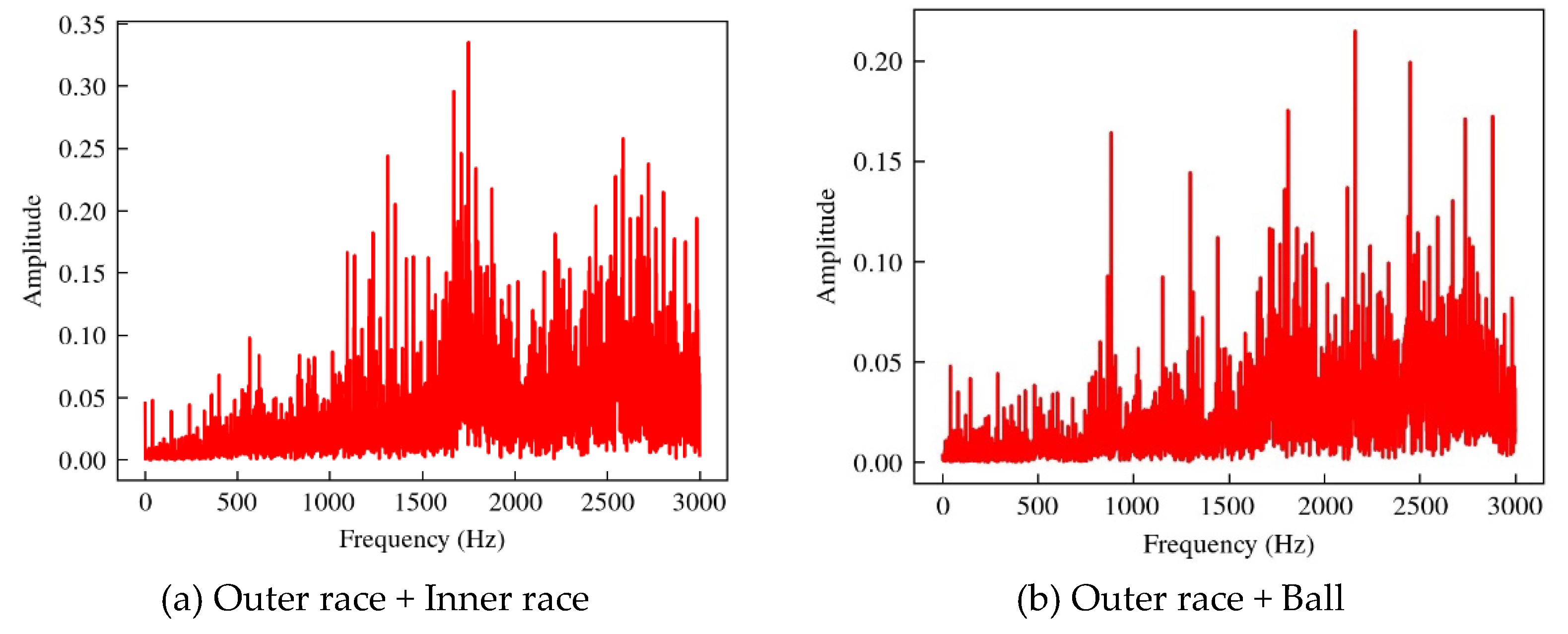
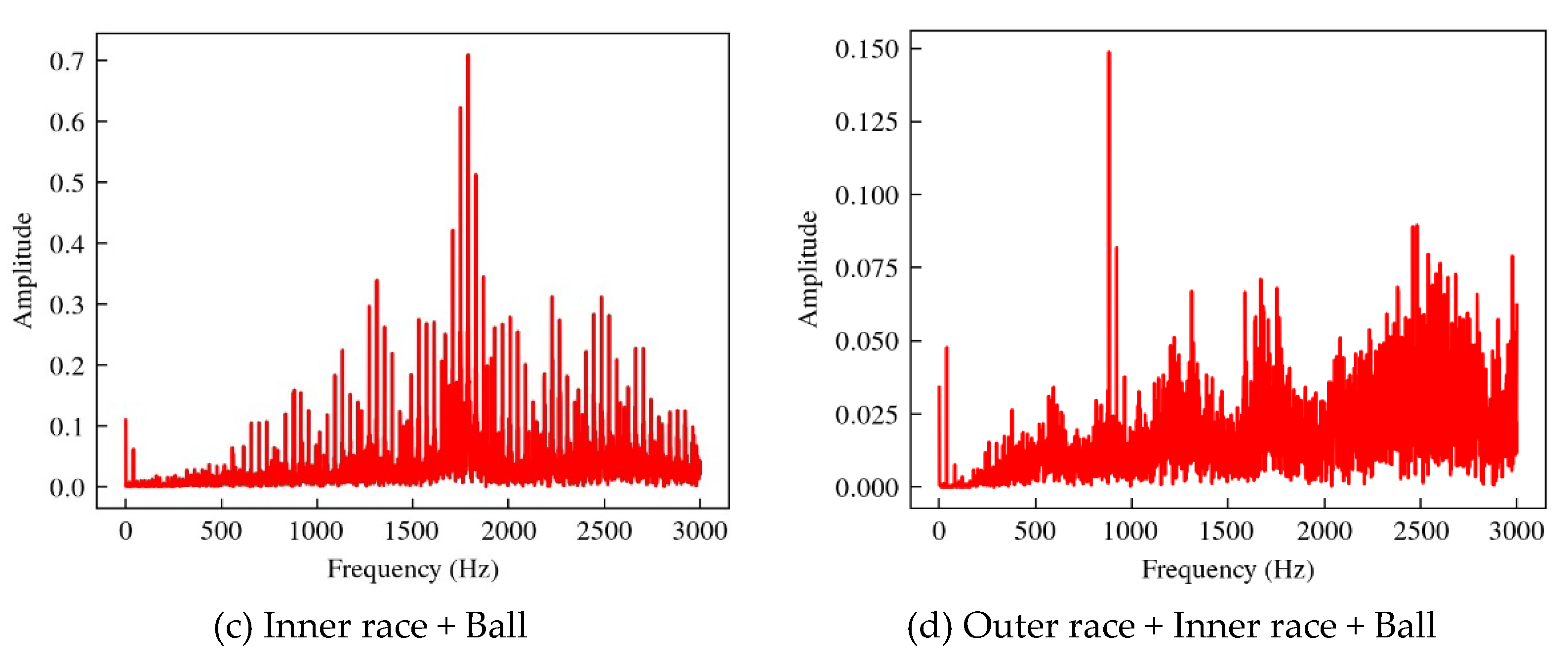
Preprints 116220 g006aPreprints 116220 g006b
Preprints 116220 g007
Figure 7. Coupled fault topology in HGGAN.
Figure 7. Coupled fault topology in HGGAN.
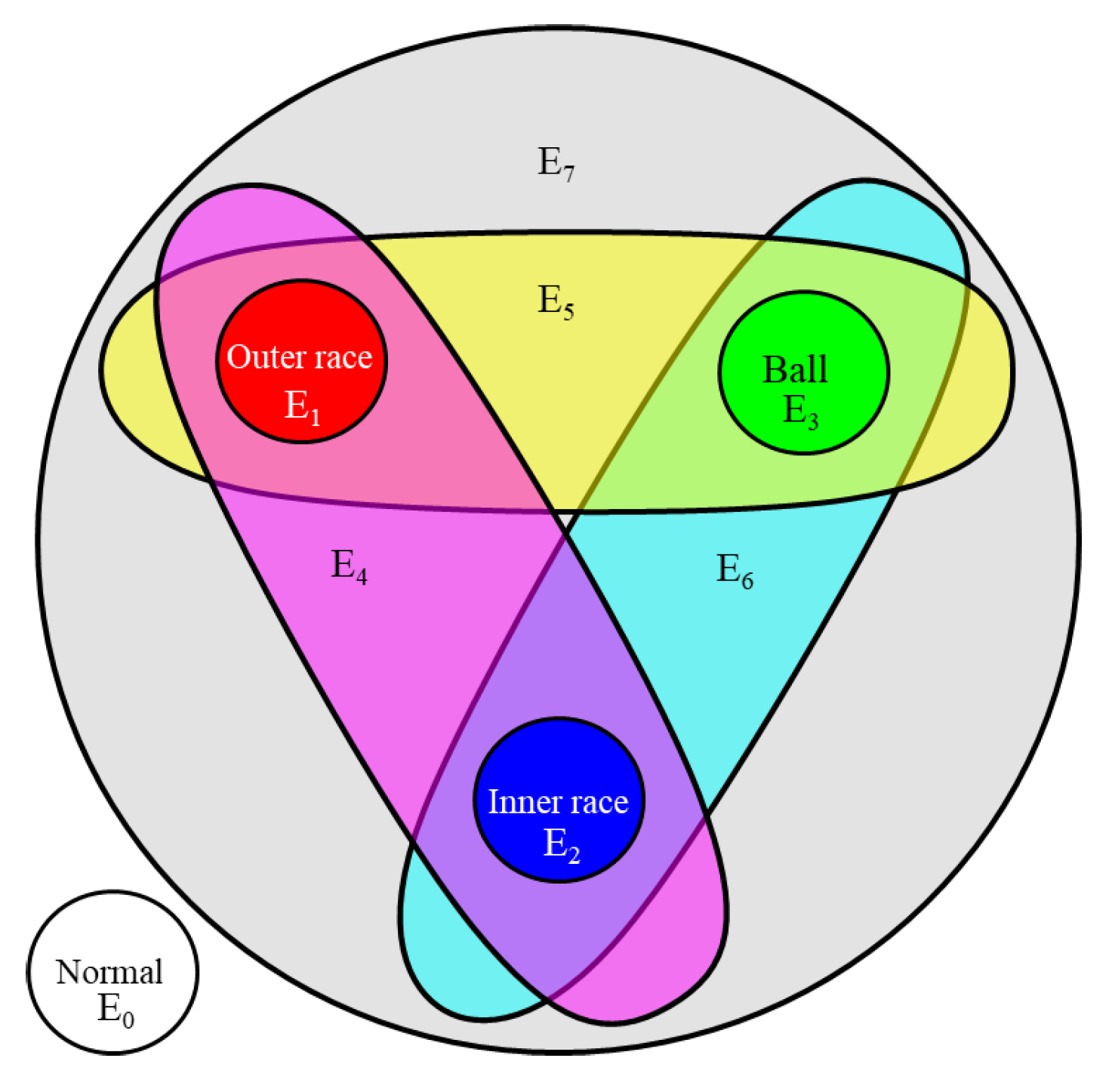
Preprints 116220 g007
Preprints 116220 g008
Figure 8. The accuracy of discriminator and generator during training process of HGGAN.
Figure 8. The accuracy of discriminator and generator during training process of HGGAN.
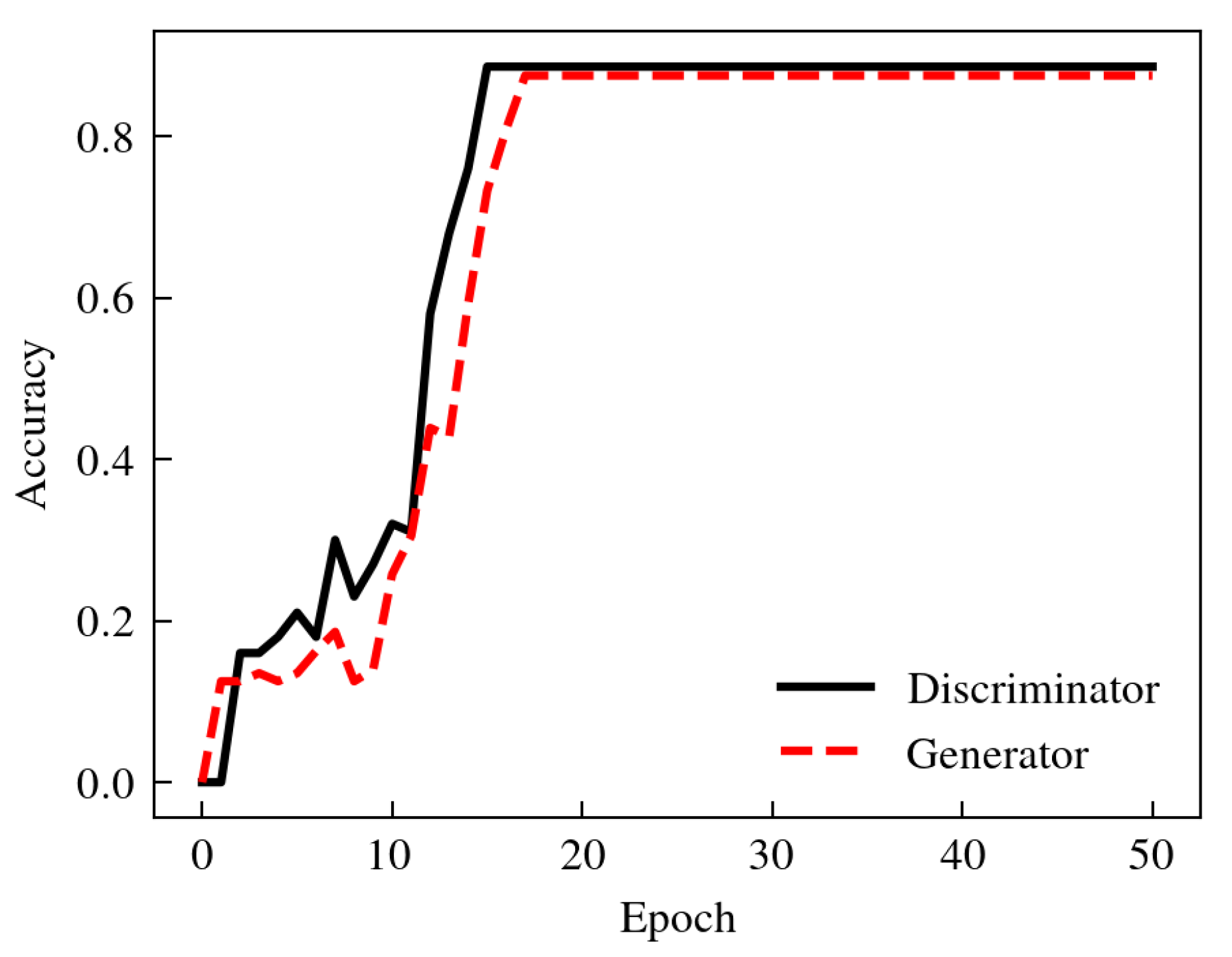
Preprints 116220 g008
Preprints 116220 g009
Figure 9. Visualization of the data from experiment and the data generated by the generator.
Figure 9. Visualization of the data from experiment and the data generated by the generator.
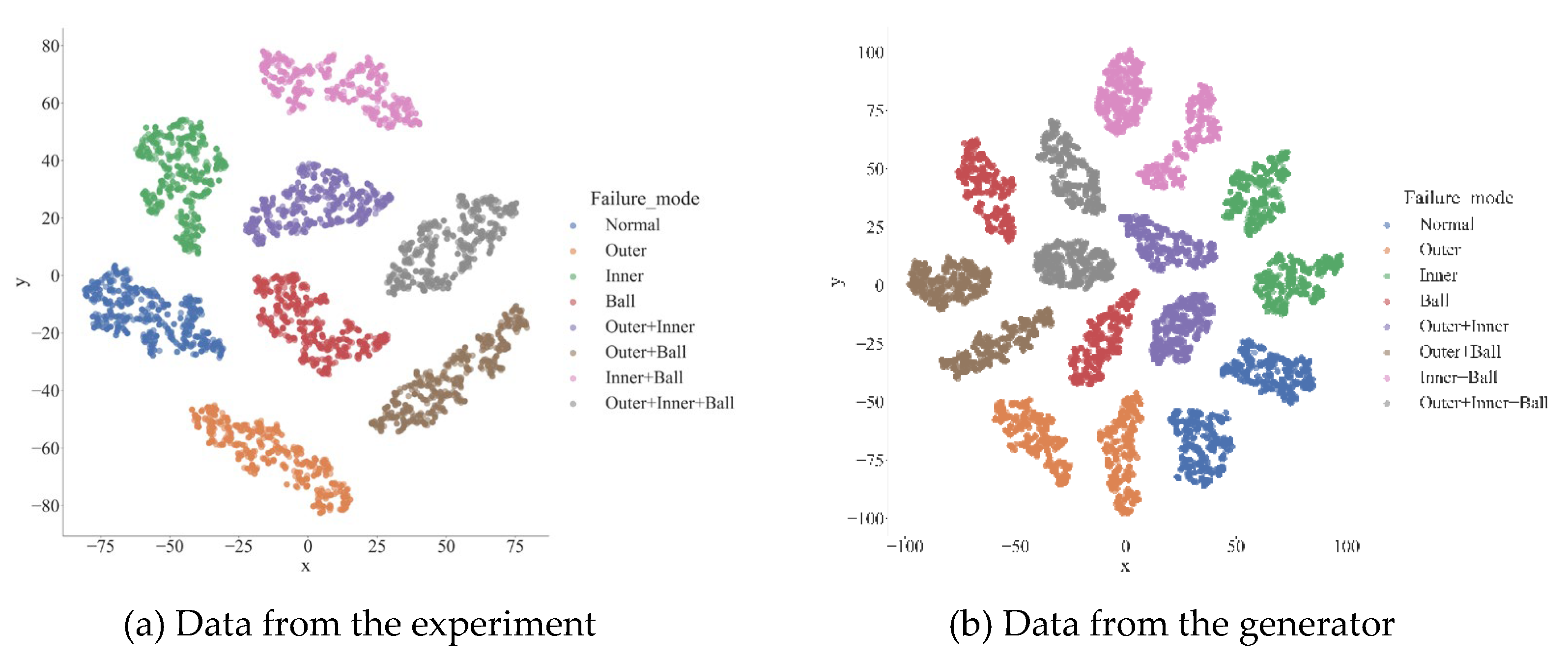
Preprints 116220 g009
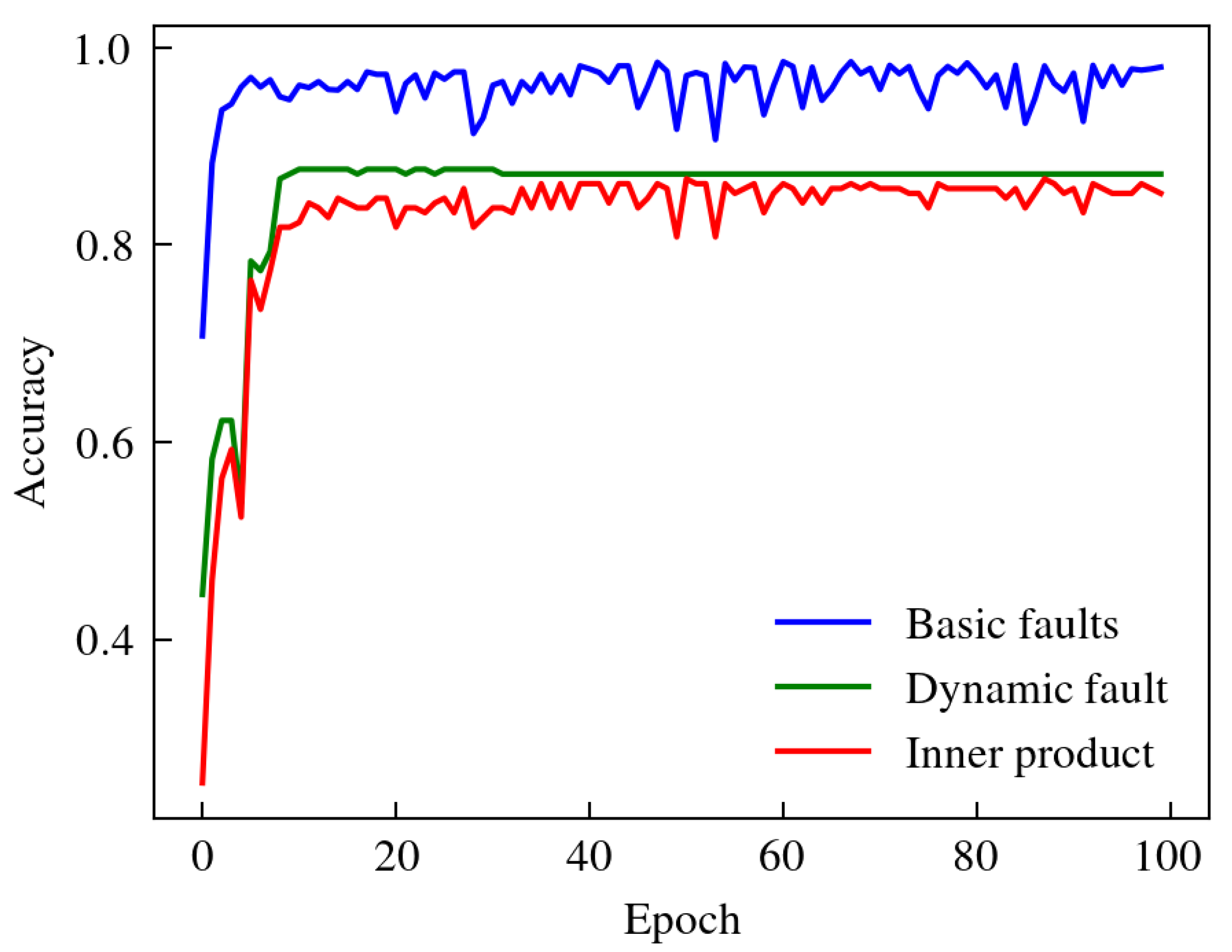
Preprints 116220 g011
Figure 11. The diagnosis accuracy of base faults, fault in dynamic vertex and the inner product accuracy during training process of IPGAT.
Figure 11. The diagnosis accuracy of base faults, fault in dynamic vertex and the inner product accuracy during training process of IPGAT.
Preprints 116220 g011
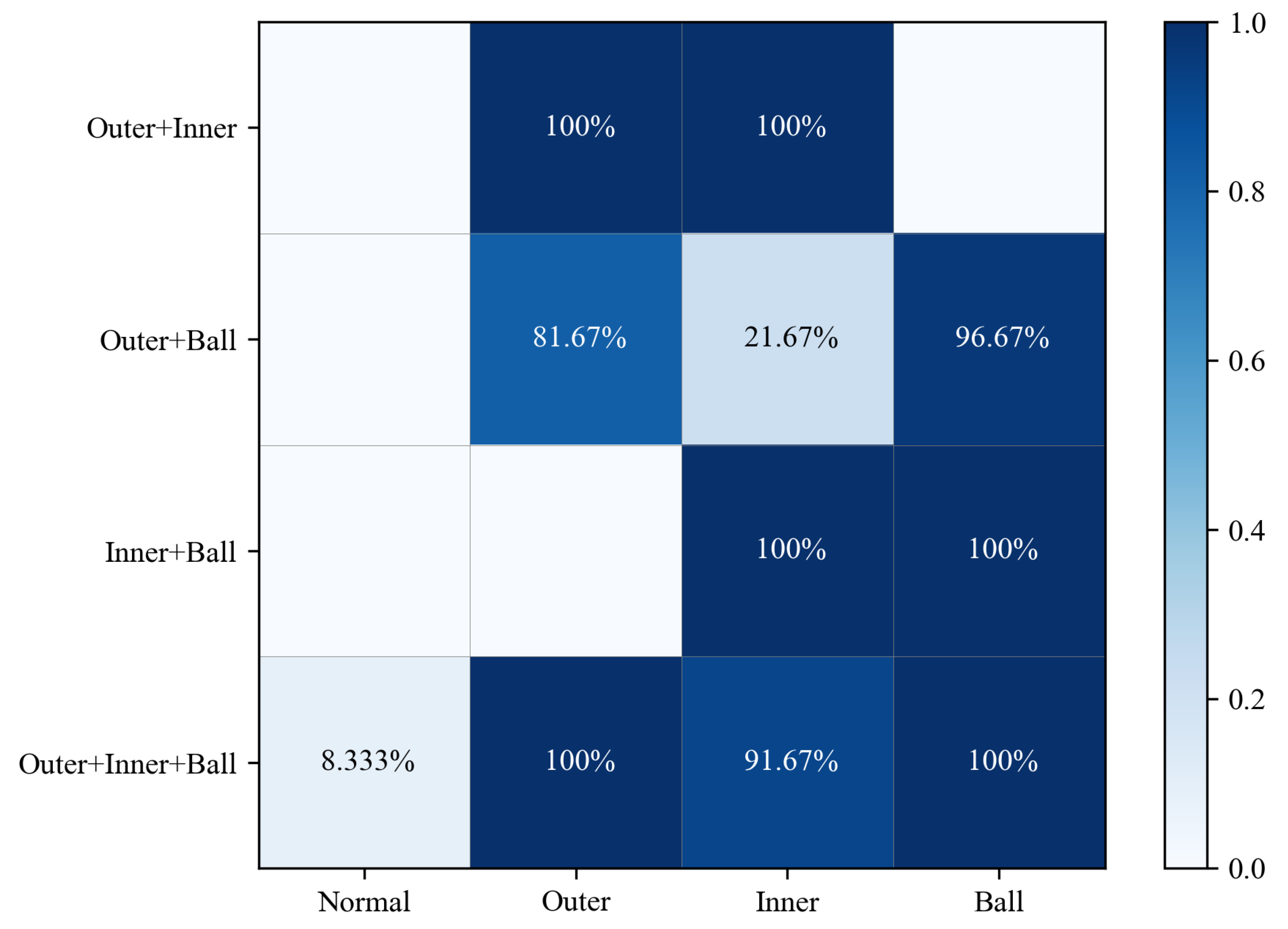
Preprints 116220 g012
Figure 12. Coupling fault classification accuracy.
Figure 12. Coupling fault classification accuracy.
Preprints 116220 g012
Table 2. Comparison of diagnostic accuracy of coupling faults.
Table 2. Comparison of diagnostic accuracy of coupling faults.
Models Accuracy of Generator Accuracy of Discriminator
MLP / 86.27%
MLP-GAN 75% 86.27%
HGGAN 87.5% 88.6%
Table 3. Comparison of diagnostic accuracy of coupling faults.
Table 3. Comparison of diagnostic accuracy of coupling faults.
Fault Types E 0 E 1 E 2 E 3 E 4 E 5 E 6 E 7
Normal 1 0 0 0 0 0 0 0
Outer race 1 1 0 0 0 0 0 0
Inner race 1 0 1 0 0 0 0 0
Ball 1 0 0 1 0 0 0 0
Outer race + Inner race 1 1 1 0 1 0 0 0
Outer race +Ball 1 1 0 1 0 1 0 0
Inner race +Ball 1 0 1 1 0 0 1 0
Outer race + Inner race +Ball 1 1 1 1 1 1 1 1
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated