Preprint
Article
Measurement and Modeling of SDC Memristors: Extensive Study
Altmetrics
Downloads
69
Views
47
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
24 August 2024
Posted:
27 August 2024
You are already at the latest version
Alerts
Abstract
This study systematically addresses the challenge of accurately modeling memristors, focusing on four distinct types doped with tungsten, tin, chromium, and carbon, fabricated by Known Inc. A comprehensive characterization was performed by subjecting the devices to sinusoidal excitations with varying frequencies and amplitudes, followed by data averaging and high-frequency filtering. The resulting measurements were fitted using three prominent memristor models: VTEAM, MMS, and Yakopcic, with additional bespoke modifications assessed. These models, typically formulated as coupled algebraic-differential equations integrating electrical quantities (voltage and current) with internal state variables governing device dynamics, were optimized using two robust approaches: (1) interior-point optimization with gradient-based search, and (2) Nelder-Mead gradient-free optimization, both with box constraints applied. A thorough comparison and discussion of the optimized model parameters ensued, accompanied by an examination of sensitivity to diverse frequency and amplitude ranges. The findings inform conclusions and provide a foundation for future refinements, underscoring the importance of multi-model evaluation and advanced optimization strategies in precise memristor modeling. The presented methodology offers a valuable framework for elucidating optimal modeling paradigms tailored to specific memristor architectures and operating regimes, ultimately enhancing their integration in emerging neuromorphic and computational applications.
Keywords:
Subject: Engineering - Electrical and Electronic Engineering
1. Introduction
Over the past decade, there has been an intense debate surrounding the issue of Moore’s Law reaching its limits. This law postulates that the number of transistors in an integrated circuit doubles at nearly regular intervals. With the development of nanometer-scale technology, standard CMOS technology has reached its scalability limits. Consequently, there is a need to find solutions that would increase both the performance of modern computers and the amount of available memory. One such idea is to shift from the classic von Neumann architecture, where the processor and memory are separated by a data bus, to an integrated architecture known as in-memory computing. Another idea is to replace the bi-stable transistor with a multi-stable element. With the emergence of actual memristive devices, both of these ideas seem feasible.
Following Professor Leon Chua’s postulation of the memristor in 1971 [1], it took another 37 years for the physical implementation of this element to be achieved. In 2008, the HP Labs team led by R. Stanley Williams published their work on creating a memristor based on titanium dioxide () [2]. Since then, numerous other memristor designs have emerged, differing in their structure, materials, and operating principles e.g. polymers memristors [3,4], ferroelectric memristors [5], spintronic memristors [6,7,8]. One of the most intriguing types of memristors are the Self Directed Channel (SDC) memristors produced by Knowm Inc. They have been described in numerous publications [9,10,11].
Realizing the multitude of memristor designs available today, in the design of each prototype circuit, a crucial aspect is simulating the behavior of the circuit under various stimuli. Therefore, it is essential to faithfully replicate the dynamics of memristive elements using their model. This paper will analyze which model best reproduces the behavior of SDC memristors and develop an algorithm to optimize model parameters based on real measurement data. Optimized parameters can be successfully applied in simulation environments such as SPICE or Simulink.
The paper discusses the optimization of parameters for various models based on real measurement data of SDC memristors with different dopings, namely tungsten, tin, chromium, and carbon, using two algorithms: SQP and Nelder-Mead. Box constraints were imposed on individual parameters during optimization. Since in the paper [12], Strukov, Assymetric Strukov and VTEAM models were compared, it was decided to compare other models with the most accurate model from this work, namely the VTEAM model.
2. Materials and Methods
The SDC memristors with tungsten W, carbon C, tin Sn and chromium Cr doping were subjected to research and measurements.
To measure the current of the memristor and limit it below the nominal value, i.e., 1 mA for memristors doped with and 50 for doping with [10], the memristor was connected in series with a linear resistor . In the case of doping with , the resistance , while for doping with , . The voltage measured across the resistor which is a high-quality resistor utilized for accurately determining the memristor’s current, according to Ohm’s law, is directly proportional to the current and its known resistance, allowing the current of the memristor to be obtained by multiplying the voltage across the resistor by the reciprocal of its resistance. The schematic diagram of the measuring circuit is presented in Figure 1a. Using myDAQ University Kit device from National Instruments containing a measurement card and function generator, the supply voltage was generated and signals and were collected [13]. The current and voltage of the memristor were calculated using Ohm’s law and Kirchhoff’s second law. The data acquisition and preliminary data processing process was written and implemented in the graphical programming environment LabVIEW [14,15]. The utilized code is provided in the attached appendices. The circuit connection diagram to the measurement device is shown in Figure 1b.
The voltage across the memristor were calculated using formula and the memristor current were calculated as .
Before starting measurements, it is necessary for the memristor to be formed. Forming is done by gradually increasing the voltage to create the necessary conductive paths inside the memristor. However, this voltage should not exceed the nominal operating voltage [10,12]. After forming the memristor, the circuit shown in Figure 1 is powered by a sinusoidal alternating voltage with amplitudes and different frequencies, where . Therefore, 18 tests were performed for one memristor, where each test consists of 100 periods and 1000 points for each period.
3. Memristor Models under Consideration
In the work [12], a comparison was made between the accuracy of various models and actual SDC memristors measurements, focusing on well-known memristor models in the literature, such as the Strukov, Asymmetric Strukov, and VTEAM models. The VTEAM model proved to be the most optimal, while the others demonstrated poor representation of real memristors, likely due to their simplicity. However, this study did not include more advanced models like the MMS model or the Yakopcic model. Therefore, it was decided to compare a slightly modified VTEAM model with these more complex models. Each of considered models are described in detail in this section.
3.1. MMS Model
To model SDC memristors, a generalized model of metastable memristor proposed by M. Nugent and T. Molter [16] is used. This model is semi-empirical. Each ion cluster is represented as a metastable switch, which probabilistically switches between two states under the influence of voltage and temperature. The switching probability between the and states is denoted as , while the transition from the to the state is denoted as . The mathematical dependencies are presented below [16,17]:
Where is the temperature parameter, represents the threshold voltage for the HRS state, denotes the threshold voltage for the LRS state, q stands for the elementary charge ( [C]), k is the Boltzmann constant ( [J/K]), T represents the absolute temperature in K, is the dimensionless time parameter, represents the time constant in s. The dynamics of the elements is described as the change of the state variable x and is expressed as:
By combining Equations (1)–(4), we obtain a comprehensive differential equation describing the state variable x as:
The variable conductance of the memristor is then the function of the memristor’s state and is expressed as [16,17]:
Where is the resistance in the state, is the resistance in the state.
3.2. Yakopcic Model
Due to the significant diversity in types of memristive devices, Yakopcic proposed a new model that introduces multiple parameters, enabling its utilization for accurate circuit simulations and power analyses across a wide range of memristive devices. The relationship between current and voltage depends on the state variable , which governs resistance changes based on physical dynamics. In the described model, the internal variable [18]. The relationship is presented in Equation (7).
Where are parameters used for adjustment for various memristive devices.
Where is the positive threshold voltage, is the negative threshold voltage, are regulatory quantities of exponential expressions.
The second function was proposed to model the behavior of the internal variable. It operates based on the assumption that the change of state in the memristive device becomes more difficult at the boundaries of the variable x limitation interval. The algorithm for calculating is presented below:
If :
Otherwise:
Where, represent the boundaries of the state variable interval x. Similarly, characterize the rate of exponent growth, and denote window functions. Each window function has the following forms:
Due to the fact that the modeled state variable should correspond to memristors of various constructions, the equation describing its derivative with respect to time significantly differs from the dependence in the Strukov-Williams model (which was introduced to model memristors) and looks as follows [2,18].
3.3. VTEAM Model
The VTEAM (Voltage Threshold Adaptive Memristor) model is based on the derivative equation of the internal state variable x of the memristor. The VTEAM model combines advantages such as accuracy and generality, but it faces difficulties in optimizing the model due to parameters that belong to integers. It takes into account the threshold voltages of the memristor at which no change in the state variable occurs. The derivative of the internal variable is expressed by the following relation [12,19]:
Where and , similarly to the previous models described, represent negative and positive threshold voltages, are real parameters and , represent integer parameters, are window functions. The current-voltage relationship and conductance are not naturally defined by the VTEAM model. A linear current-voltage relationship can be represented by the following formula:
Where represent range in which the internal state variable x can occur, are minimum and maximum resistances of the memristor.
4. Optimization Procedure
In this section, the optimization procedure will be described, aimed at finding the optimal parameters for the models described in Section 3.
The discussed optimization involves minimizing a certain objective function F, which is tasked with comparing the waveform of the model function with the actual waveform of the memristor. The requirement is for the function to decrease as the similarity between the resulting model and the estimated actual element waveform increases. The objective function used in this work is a modified coefficient of determination and is defined as [20]:
Where represents the model function, and denote the memristor voltage and current accordingly, a is a dimension vector of the real valued model parameters (), b is a dimension vector of integer valued model parameters (), RSS denotes the residual sum of squares, and TSS is the total sum of squares. The functions RSS and TSS take the following form:
The parameters are: , which represents the actual value of the i-th sample, , denoting the value predicted by the model, n, representing the number of samples in the period, and , which is the average value of the samples in the period. The reference values of the memristor current and voltage come from the determined averaged periods of the signal.
During optimization, appropriate values of parameters collected in vectors a and b need to be found so that the objective function reaches its minimum. These parameters can be defined as real or natural numbers, depending on the specific model. For parameters that should be natural numbers, the optimization process is performed using the brute force method, i.e., for each combination within a specified range, and then the ones for which the objective function is the lowest are selected. This algorithm significantly prolongs the optimization time. Parameters that should be natural numbers are the parameters and in the VTEAM model. Floating-point parameters are also subject to certain constraints, mainly due to the nature of the model. Because the input signal to the system is a continuous sinusoidal function, it is necessary to ensure that the response signal is also a continuous and periodic function. This is ensured when the internal variable of the memristor x is also a continuous and periodic function, so , where T is the period, indicating that the system is in a steady state. This condition requires optimizing an additional parameter, , which is a constant of integration when integrating the internal variable function and represents the value of the internal variable at the time of measurement. To ensure the continuity condition, an algorithm is proposed consisting of preliminary optimization of the objective function described by equation (14), followed by optimization of a new objective function, which rewards for the continuity and periodicity of the internal variable function, as proposed (17):
Parameters w, , and are elements of the optimization algorithm. Parameter w is a weight chosen according to the continuity of the function. Parameters and are, respectively, the first and last elements of the internal variable function. If the condition is met, the algorithm terminates its operation; otherwise, the optimization process of function (17) is repeated for until the condition is satisfied. To increase the number of reference points and reduce the integration step, the interpolation method called Akima Spline [21] is utilized, which performs local fitting of the function, and the number of points is increased tenfold. The optimization process for the mentioned models differs slightly. It should be noted that the obtained minima of the objective function may be only local minima, and there may be parameters for which the objective function can be even lower. Optimization methods are listed in the subsequent subsections.
4.1. MMS Model
Optimization was performed based on six degrees of freedom represented by real valued parameters only: and . Two algorithms were utilized in the optimization process. The first one is the SQP algorithm implemented in the fmincon function of MATLAB [22,23,24]. The SQP method solves a sequence of sub-problems optimizing the quadratic objective model subject to linearized constraints. It ensures box constraints in all iterations and is resilient to objective function results such as Nan and Inf. It has many advantages, including low memory consumption and the ability to quickly solve problems. However, the solution may be inaccurate due to the barrier function maintaining parameters away from the box constraints [23,24] and when the algorithm stacks in the local minima. The second algorithm is the Nelder-Mead algorithm, also known as the simplex downhill method. This algorithm does not use the gradient of the objective function [25,26]. It was implemented in the fminsearch function of MATLAB; however, the optimization process utilized the minimize function, which is available in the MATLAB external repository [27]. Unlike the fminsearch function, it allows for the introduction of box constraints within which parameters can change.
The optimization process involves initially minimizing the objective function (14) using both algorithms, selecting parameters with the lowest value of this function, then minimizing the function (17) using both algorithms, with parameters obtained in the first stage of minimization, and finally selecting parameters for which the objective function value is the smallest, while simultaneously checking whether the internal variable of the function remains continuous and periodic. A simplified block diagram of the optimization algorithm is shown in Figure 2. Box constraints for individual parameters are presented in Table 1.
For the simulation and integration of the MMS model, the Runge-Kutta method called ,,RK4” was implemented independently in MATLAB [17,28]. To ensure that the model represents the parameters of a memristor, and not a memristor-linear resistor circuit, the first step is to calculate the value of the internal variable. Subsequently, using the fact that the relationship is a linear, the memristor conductance can be calculated, as in equation (6). The voltage is then calculated using a voltage divider where represent resistance of the series resistor. Subsequently, the memristor current is the product of the voltage and the conductance .
4.2. VTEAM Model
The optimization was conducted based on nine degrees of freedom, which are: , and . All these parameters are floating-point numbers, except for and , which should be natural numbers. The optimization process occurs just as for the MMS model described in subsection 4.1, except that the optimization process takes place for each combination of the integer pair and , and then parameters are chosen for the smallest objective function. To limit the dimension of the integer space of the possible solutions the parameters and are chosen to be less then 10. Therefore, for a single test, for each amplitude of the driving signal and for each frequency, it was necessary to perform as many as 81 iterations. Additionally, the model employs the Biolek’s window function [29] with parameter p: for , i.e., for the range , and for , i.e., [19]. In the model, and is set so that the internal variable x could change within a relative range from 0 to 1. The constraints for the optimization parameters are presented in the Table 2.
4.3. Yakopcic Model
The optimization was performed based on twelve degrees of freedom. All the parameters are real. The optimization process is similar to that for the MMS and VTEAM models described in subsection 4.1. However, the system modeled is as ,,memristor-linear resistor” due to the nonlinear relationship between the memristor current and its voltage , as shown in equation (7). In this equation, it is challenging to directly obtain conductance or resistance since the voltage is an argument of the function. The box constrains for each variable used in the optimization are provided in Table 3.
5. Optimization Results
In this section, the results of the optimization process for each model have been presented, discussed, and compared with each other. Due to the high nonlinearity of the objective functions (14) and (17), the calculated minima are likely local, with global minima posing a significant challenge. The optimization process mainly depends on the specified initial points, which must be manually set based on examples from the literature and one’s own estimates. In the tests discussed, these were determined experimentally by conducting several optimization trials until a low objective function value was achieved [12].
5.1. MMS Model
Table 4 presents the optimisation results. It can be observed that the values of the objective function are quite low, with the majority being lower than . Figure 3 illustrates a comparison of the current and voltage trajectories of the memristor obtained during measurements with those of the MMS model obtained after optimization, for the lowest value of the objective function. The parameters corresponding to the most favorable case are provided in Table 5. Figure 4a shows the trajectories of the memristor’s internal state variable x as a function of the memristor voltage . Meanwhile, Figure 4b presents the trajectory of the internal variable and a comparison of the model’s resistance with the measured memristor resistance over time, featuring a logarithmic Y-axis.
In Table 6, the averaged objective function values over all combinations of the excitation signals for each doping materials are presented. As can be observed, the highest average objective function value is obtained for tungsten doping, however, all these values are close to each other.
5.2. VTEAM Model
In Table 7, the values of the objective functions are collected. In Figure 5, a comparison of the current and voltage waveforms of the memristor obtained during measurements with the waveforms of the optimized VTEAM model for the minimum value of the objective function is shown. Table 8 provides the parameters corresponding to the most favorable case. In Figure 6a, the variations of the internal state memristor variable x as a function of the memristor voltage are presented. Meanwhile, in Figure 6b, the variation of the internal variable and a comparison of the model resistance with the measured memristor resistance as a function of time are shown. A logarithmic scale is applied to the vertical axis. In Table 9, the averaged objective function values for each doping are presented. As can be observed, the highest average objective function value is obtained for carbon doping, while the lowest is for chromium doping. There is some variation in the values between the memristors doped with chromium and carbon, where the average values differ almost tenfold.
5.3. Yakopcic Model
As can be observed in Table 10, the objective function values are quite low, with the majority of them being lower than . In Figure 7, a comparison of the current and voltage waveforms of the memristor obtained during measurements with the waveforms of the Yakopcic model obtained after optimization for the minimum value of the objective function is shown. Table 11 provides the parameters corresponding to the most favorable case. Figure 8a presents the variations of the internal memristor variable x as a function of the memristor voltage , while Figure 8 shows the variation of the internal variable and the memristor resistance as a function of time.
In Table 12, the averaged objective function values for each doping are presented. The average objective function values do not significantly differ from each other and are lower than .
6. Comparative Analysis of Optimization Results
6.1. Statistical analysis of the optimization results obtained
To facilitate a comparative analysis of the optimized models, several comparative graphs have been generated. Figure 9 illustrates the average objective function values for each model as a function of the supply voltage amplitude applied to the memristor-resistor system. It is readily apparent that the VTEAM model exhibits the highest objective function values, accompanied by a significant dispersion, as indicated by the error bars associated with each data point. The error bars represent confidence intervals, which are intrinsically linked to the probability distribution of the measured values [30]. Notably, the MMS and Yakopcic models demonstrate a reduced dispersion of results. The objective function value for the MMS model increases with increasing supply signal, in contrast to the Yakopcic model.
Figure 10 depicts the average objective function values for each model as a function of the frequency of the supply voltage applied to the memristor-resistor system. It is immediately evident that the VTEAM model exhibits the highest objective function values, accompanied by a significant dispersion as indicated by the error bars. In contrast, the MMS and Yakopcic models demonstrate a reduced dispersion of results and considerably lower average objective function values. Notably, the Yakopcic and MMS models exhibit lower objective function values within the lower frequency range.
Figure 11 presents the average objective function values for each model as a function of the doping material used. It is evident that for the MMS model, the lowest average objective function values are observed for tin and carbon doping, while the highest value corresponds to chromium doping. Similarly, the Yakopcic model exhibits the lowest objective function values for carbon and tin doping, with the highest value associated with tungsten doping. In the VTEAM model, the highest values are obtained for carbon doping, and the lowest for chromium doping.
Figure 12 presents a box plot [31] illustrating the distribution of the obtained objective function values. It is evident that the median objective function value is lowest for the MMS model and highest for the VTEAM model. Furthermore, the VTEAM model exhibits the greatest dispersion of values. The objective function value axis is presented on a logarithmic scale to enhance data clarity.
Table 13 displays the average objective function values for each model. The Yakopcic model exhibits the lowest average objective function value, which is marginally lower than that of the MMS model, at . The VTEAM model presents the highest objective function value. Table 14 presents the standard deviation () of the objective function values for each model. Notably, the Yakopcic model demonstrates the lowest standard deviation at , while the VTEAM model exhibits the highest at .
6.2. Analysis of Results in the Context of Parameter Generalization
A critical factor essential for the simulation of electric circuits is that the parameters of the models remain invariant with respect to changes in the operational conditions under which these models function, such as the form of the excitation, its amplitude, and frequency. In this subsection, the examination how the optimal parameters of models, determined through optimization, vary with the frequency and amplitude of the input signal is presented. Additionally, the exploration how the optimal parameters for different types of excitation influence the objective function’s value for other excitation parameters is carried out.
In Figure 13, an exemplary heatmap is presented, displaying the objective function values for the evaluation of model parameters obtained through optimization for different excitation parameters. As can be observed, the lowest values of the objective function are located along the diagonal of the matrix. This is because these are the objective function values for the parameters for which the optimization was performed. The values in the upper right corners of the matrix are the highest. These are the regions where the objective function values are evaluated for the most divergent excitation parameters from those used during the optimization process. From the presented graph, it can be concluded that the parameters of the MMS models do not generalize the dynamics of memristors for all operational conditions. An interesting aspect is the significantly higher accuracy of the model when it is optimized at higher excitation frequencies and evaluated at lower frequencies, rather than the other way around.
In Figure 14, a matrix of plots is presented, showing the variation in MMS model parameter values (Y-axis) with linear trend lines, depending on the doping of memristors and excitation parameters (X-axis). As can be observed, the optimized parameters of the MMS model change quite drastically depending on the excitation signal parameters (in this case, the parameters of the alternating supply voltage). This necessitates adjusting the model parameters during simulation according to the intended signal.
7. Conclusions
From the conducted optimizations, it can be concluded that they were successful, and the obtained objective functions achieved relatively low values. It can also be inferred that the best models for modeling SDC memristors are the MMS and Yakopcic models. They have similar low average values of the objective function, and the dispersion of these values is not large depending on the amplitude of the supply voltage, frequency, or type of doping. Definitely, compared to the models mentioned earlier, the worst model for optimization is the VTEAM model. It has the highest average values of the objective function and the largest dispersion. Taking into account the specifics of the model, especially the fact that natural parameters are required, the optimization of this model is quite tedious due to iterating over all possible combinations of integer parameters in the interval and selecting the best solution. This means that the time needed to minimize the objective function is several dozen times longer than the time needed for the MMS model. An additional problem is the undefined values by the objective function, which the minimizing algorithm must be resistant to. Taking into account also the specifics of individual models, it can be reflected that the MMS model is best suited for modeling SDC memristors due to its simplicity (only 6 degrees of freedom), linear dependence of current on voltage, and the fact that it does not have threshold ranges, so the function of the internal variable is monotonically continuous. The MMS model also has a physical interpretation in real memristors. The Yakopcic model was created to fit every type of memristor, and in the discussed case, quite good fits and low objective functions were obtained. However, it is quite complicated and does not have a linear dependence of current on voltage. Additionally, it is a mathematical concept and does not have a physical interpretation.
From the optimization results, it can also be concluded that the lowest objective functions are obtained for quite rounded waveforms where there is no sudden switching between states, which is called soft-switching [17]. It occurs when the function of the internal variable x does not reach the upper value of the range in which it is contained. This is especially visible when powered by signals with high frequency and low amplitude, as the energy and charge in each half-period are low and do not allow reaching the limit ranges of the internal variable. During the measurements the influence of the memristor’s temperature change has been noticed. In the future Authors consider to involve in the project of creating the optimal memristor model with temperature as additional parameter involved. The first idea seems to extend the MMS memristor model of this additional feature.
Author Contributions
Conceptualization, B.G.; methodology, B.G. and K.B.; software, K.B.; validation, K.B and B.G.; resources, B.G. and K.B.; data curation, K.B.; writing—original draft preparation, K.B. and B.G.; writing—review and editing, K.B. and B.G.; visualization, K.B.; supervision, B.G. All authors have read and agreed to the published version of the manuscript.
Funding
The research presented in the article was financed by the Polish Ministry of Science and Higher Education as part of a subsidy for AGH University of Krakow.
Data Availability Statement
The data acquired during measurements and programming algorithms have been publicly shared on the GitHub platform at the following link: https://github.com/mancorz98/MemristorModelOptimization (accessed on 16 August 2024).
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Chua, L. Memristor-The missing circuit element. IEEE Transactions on Circuit Theory 1971, 18, 507–519. [Google Scholar] [CrossRef]
- Strukov, D.; Snider, G.; Stewart, D.; Williams, S. The Missing Memristor Found. Nature 2008, 453, 80–3. [Google Scholar] [CrossRef]
- Mladenov, V. Advanced Memristor Modeling. [CrossRef]
- Chen, Y.; Liu, G.; Wang, C.; Zhang, W.; Li, R.W.; Wang, L. Polymer memristor for information storage and neuromorphic applications. Mater. Horiz. 2014, 1, 489–506. [Google Scholar] [CrossRef]
- Hu, Z.; Li, Q.; Li, M.; Wang, Q.; Zhu, Y.; Liu, X.; Zhao, X.; Liu, Y.; Dong, S. Ferroelectric memristor based on Pt/BiFeO3/Nb-doped SrTiO3 heterostructure. Applied Physics Letters 2013, 102. [Google Scholar] [CrossRef]
- Wang, L.; Yang, C.; Wen, J.; Gai, S.; Peng, Y. Overview of emerging memristor families from resistive memristor to spintronic memristor. Journal of Materials Science: Materials in Electronics 2015, 26, 4618–4628. [Google Scholar] [CrossRef]
- Wang, X.; Chen, Y. Spintronic memristor devices and application 2010. pp. 667–672. [CrossRef]
- Nafea, S.F.; Dessouki, A.A.; El-Rabaie, S.; Elnaghi, B.E.; Ismail, Y.; Mostafa, H. An accurate model of domain-wall-based spintronic memristor. Integration 2019, 65, 149–162. [Google Scholar] [CrossRef]
- Garda, B.; Bednarz, K. Comprehensive Study of SDC Memristors for Resistive RAM Applications. Energies 2024, 17. [Google Scholar] [CrossRef]
- KNOWM, Santa Fe NM. Self Directed Channel Memristors, rev. 3.2 ed., 2019.
- Campbell, K.A. Self-directed channel memristor for high temperature operation. Microelectronics Journal 2017, 59, 10–14. [Google Scholar] [CrossRef]
- Garda, B. Modeling of Memristors under Periodic Signals of Different Parameters. Energies 2021, 14. [Google Scholar] [CrossRef]
- National Instruments, 11500 N Mopac Expwy. USER GUIDE NI myDAQ, 2023.
- Elliott, C.; Vijayakumar, V.; Zink, W.; Hansen, R. National Instruments LabVIEW: A Programming Environment for Laboratory Automation and Measurement. Journal of The Association for Laboratory Automation 2007, 12, 17–24. [Google Scholar] [CrossRef]
- Ponikvar, D. Programming examples for sampling and generating of analog signals Programming skeleton for on-line signal processing 2013.
- Ostrovskii, V.; Fedoseev, P.; Bobrova, Y.; Butusov, D. Structural and Parametric Identification of Knowm Memristors. Nanomaterials 2022, 12. [Google Scholar] [CrossRef] [PubMed]
- Ma, G.; Man, M.; Zhang, Y.; Liu, S. Electromagnetic Interference Effects of Continuous Waves on Memristors: A Simulation Study. Sensors 2022, 22. [Google Scholar] [CrossRef]
- Yakopcic, C.; Taha, T.M.; Subramanyam, G.; Pino, R.E.; Rogers, S. A Memristor Device Model. IEEE Electron Device Letters 2011, 32, 1436–1438. [Google Scholar] [CrossRef]
- Kvatinsky, S.; Ramadan, M.; Friedman, E.G.; Kolodny, A. VTEAM: A General Model for Voltage-Controlled Memristors. IEEE Transactions on Circuits and Systems II: Express Briefs 2015, 62, 786–790. [Google Scholar] [CrossRef]
- Renaud, O.; Victoria-Feser, M.P. A robust coefficient of determination for regression. Journal of Statistical Planning and Inference 2010, 140, 1852–1862. [Google Scholar] [CrossRef]
- Akima, H. A new method of interpolation and smooth curve fitting based on local procedures. Journal of the ACM (JACM) 1970, 17, 589–602. [Google Scholar] [CrossRef]
- Fliege, J.; Vaz, A.I.F. A Method for Constrained Multiobjective Optimization Based on SQP Techniques. SIAM Journal on Optimization 2016, 26, 2091–2119. [Google Scholar] [CrossRef]
- López, C.P. MATLAB Optimization Techniques; 2014. [CrossRef]
- Choosing the Algorithm - MATLAB & Simulink. https://www.mathworks.com/help/optim/ug/choosing-the-algorithm.html#btr9d6u, accessed on 2023-03-25.
- fminsearch Algorithm - MATLAB & Simulink. https://www.mathworks.com/help/optim/ug/fminsearch-algorithm.html, accessed on 2023-03-25.
- Luersen, M.A.; Le Riche, R. Globalized Nelder–Mead method for engineering optimization. Computers & Structures 2004, 82, 2251–2260. Computational Structures Technology. [CrossRef]
- Oldenhuis, R. FEX-minimize. https://github.com/rodyo/FEX-minimize, accessed on 2023-03-25.
- Burden, R.L.; Faires, J.D.; Company, B.P.; (Firm, C.L. Numerical analysis; Brooks/Cole, Cengage Learning, 2011.
- Mladenov, V.; Kirilov, S. A Nonlinear Drift Memristor Model with a Modified Biolek Window Function and Activation Threshold. Electronics 2017, 6. [Google Scholar] [CrossRef]
- Poole, C. Beyond the confidence interval. American Journal of Public Health 1987, 77, 195–199. [Google Scholar] [CrossRef] [PubMed]
- Williamson, D.; Parker, R.; Kendrick, J. The box plot: A simple visual method to interpret data. Annals of internal medicine 1989, 110, 916–21. [Google Scholar] [CrossRef] [PubMed]
Figure 1.
The schematics of the measurement setup: (a) schematic diagram of the measurement circuit, (b) a simplified connection diagram of the measurement device to the circuit
Figure 1.
The schematics of the measurement setup: (a) schematic diagram of the measurement circuit, (b) a simplified connection diagram of the measurement device to the circuit
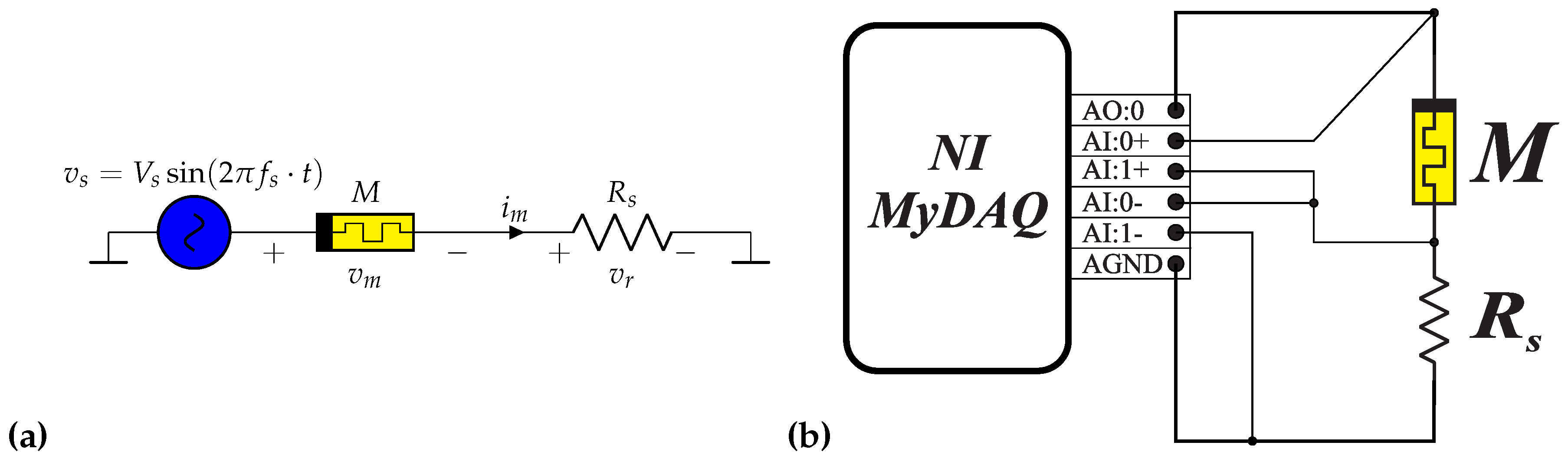
Figure 2.
Simplified block diagram of the optimization algorithm
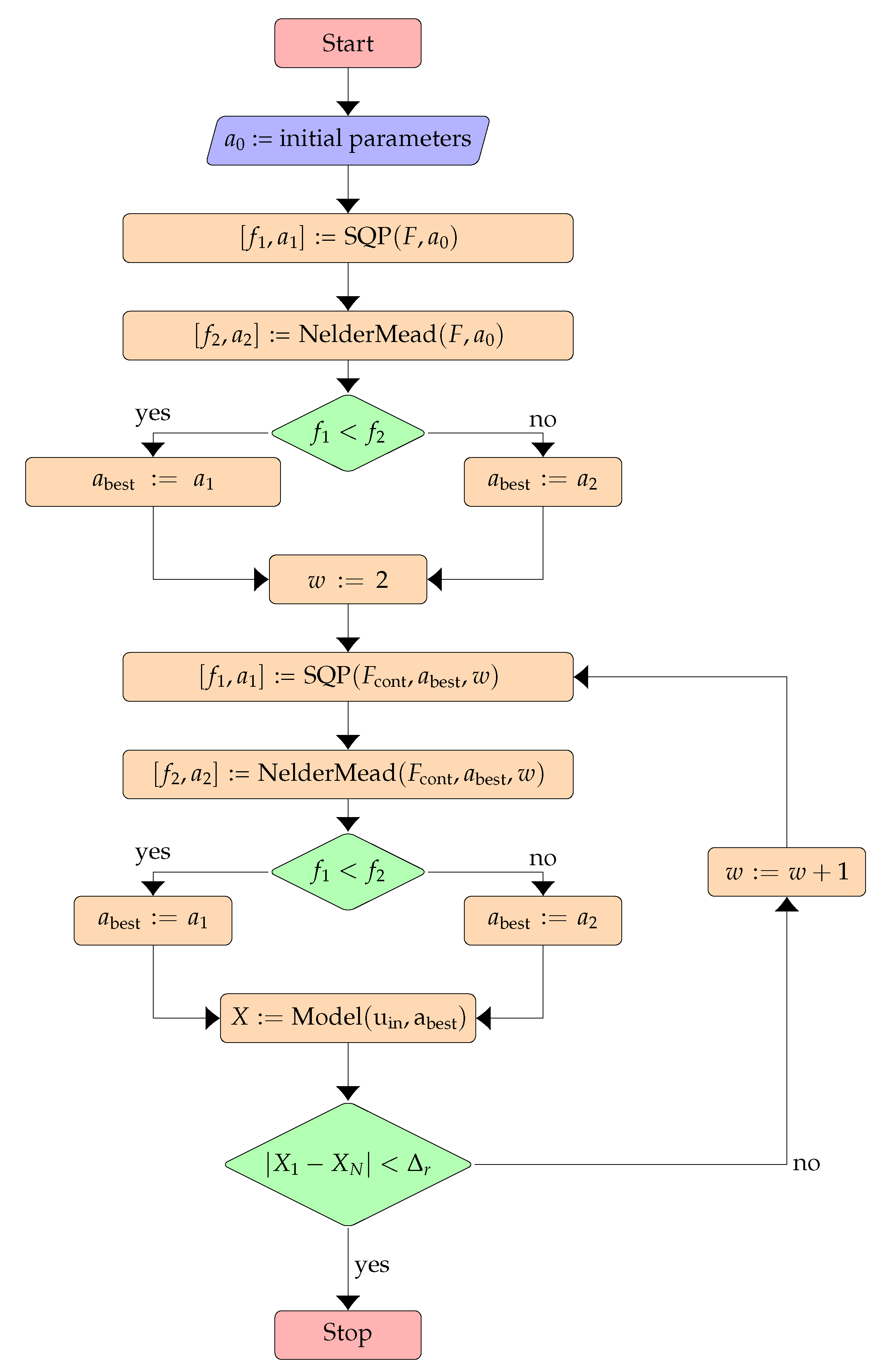
Figure 3.
The optimization results obtained for the MMS model with carbon doping, with a supply amplitude of and frequency , yield an objective function value for this case of . (a) Comparison of the hysteresis curves of the memristor , both the reference and the ones obtained during optimization. (b) Comparison of the currents and voltages of the memristor with those obtained as a result of model optimization.
Figure 3.
The optimization results obtained for the MMS model with carbon doping, with a supply amplitude of and frequency , yield an objective function value for this case of . (a) Comparison of the hysteresis curves of the memristor , both the reference and the ones obtained during optimization. (b) Comparison of the currents and voltages of the memristor with those obtained as a result of model optimization.
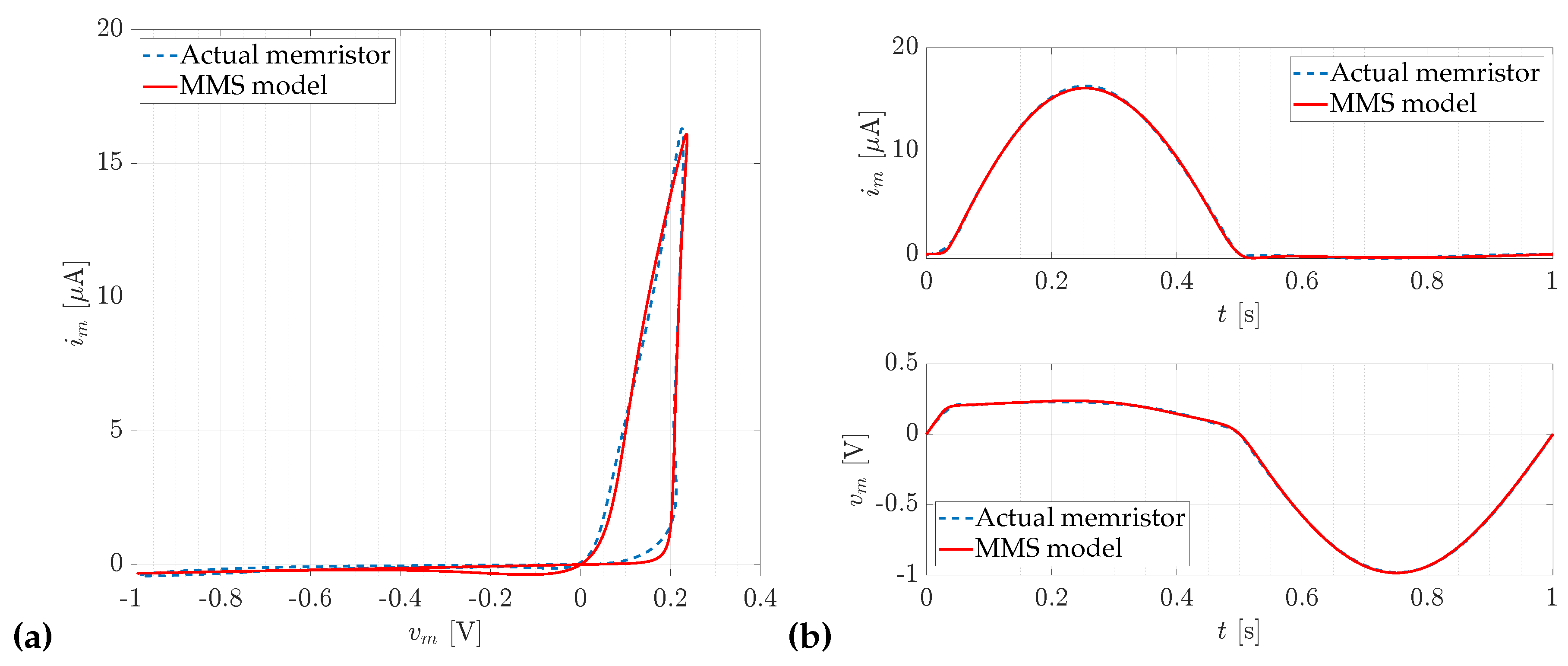
Figure 4.
The profiles of the internal variable and resistance obtained for the MMS model with carbon doping, with a supply amplitude of and frequency , yield an objective function value for this case of . (a) The variation of the internal state variable x as a function of the memristor voltage .(b) The variation of the internal variable x and the memristor resistance over time.
Figure 4.
The profiles of the internal variable and resistance obtained for the MMS model with carbon doping, with a supply amplitude of and frequency , yield an objective function value for this case of . (a) The variation of the internal state variable x as a function of the memristor voltage .(b) The variation of the internal variable x and the memristor resistance over time.
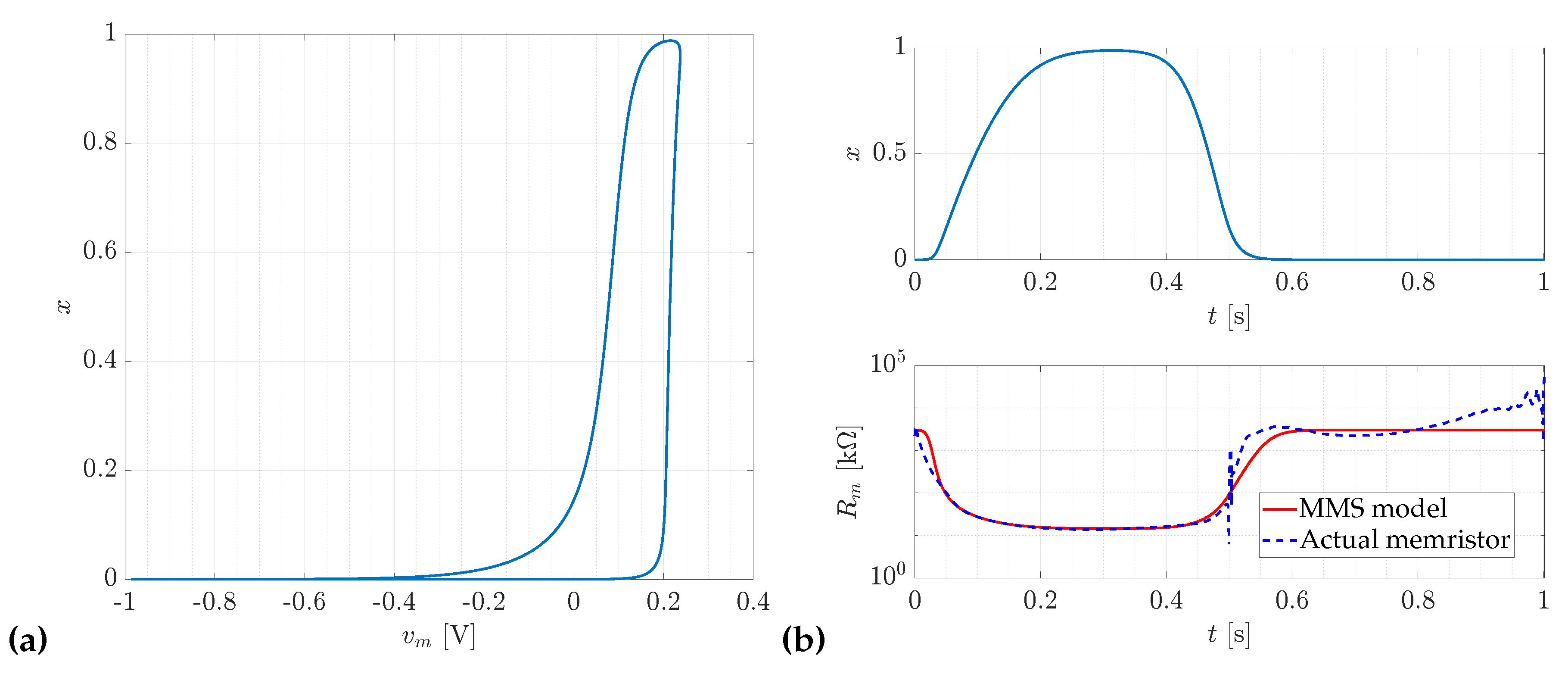
Figure 5.
The optimization results obtained for the VTEAM model with chromium doping, with a supply amplitude of and frequency , yield an objective function value for this case of . (a) Comparison of the hysteresis curves of the memristor , both the reference and the ones obtained during optimization. (b) Comparison of the currents and voltages of the memristor with those obtained as a result of model optimization.
Figure 5.
The optimization results obtained for the VTEAM model with chromium doping, with a supply amplitude of and frequency , yield an objective function value for this case of . (a) Comparison of the hysteresis curves of the memristor , both the reference and the ones obtained during optimization. (b) Comparison of the currents and voltages of the memristor with those obtained as a result of model optimization.
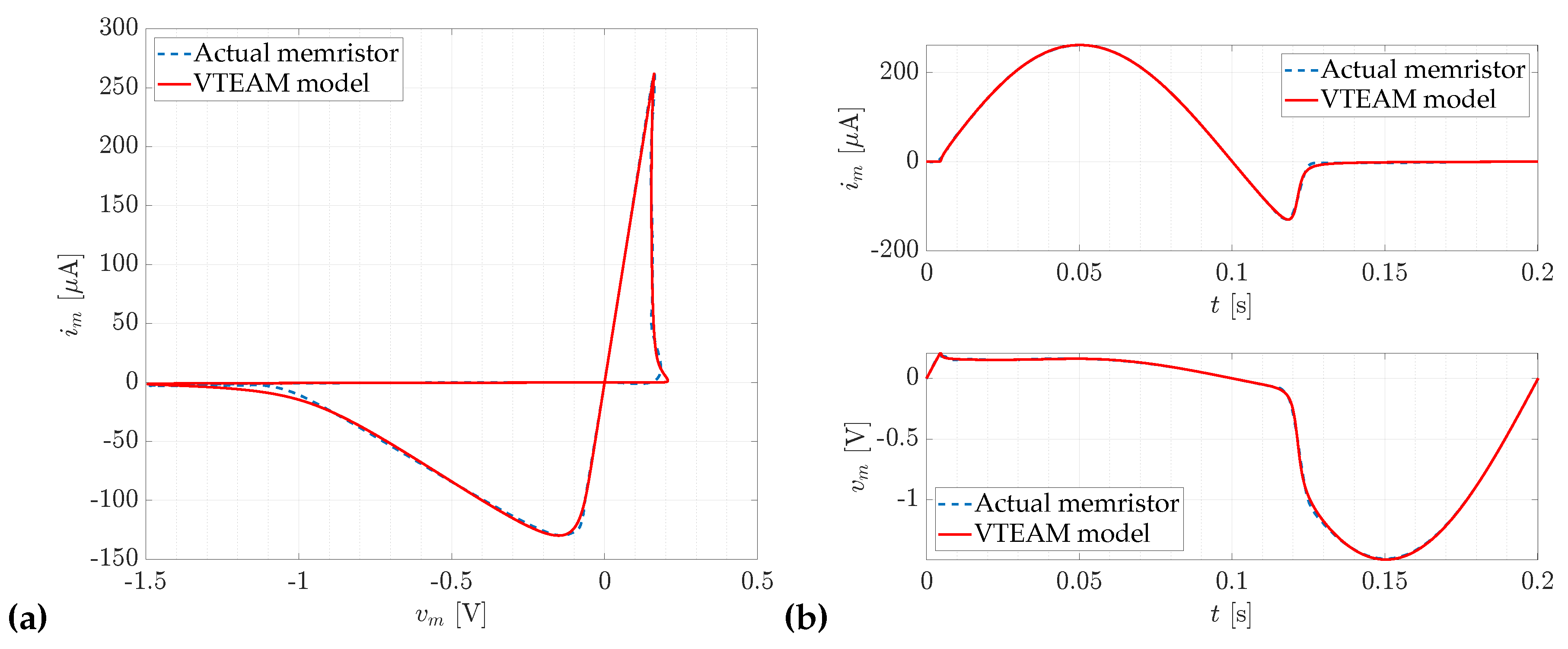
Figure 6.
The optimization results obtained for the VTEAM model with chromium doping, with a supply amplitude of and frequency , yield an objective function value for this case of . (a) The variation of the internal state variable x as a function of the memristor voltage . (b) The variation of the internal variable x and the memristor resistance over time.
Figure 6.
The optimization results obtained for the VTEAM model with chromium doping, with a supply amplitude of and frequency , yield an objective function value for this case of . (a) The variation of the internal state variable x as a function of the memristor voltage . (b) The variation of the internal variable x and the memristor resistance over time.
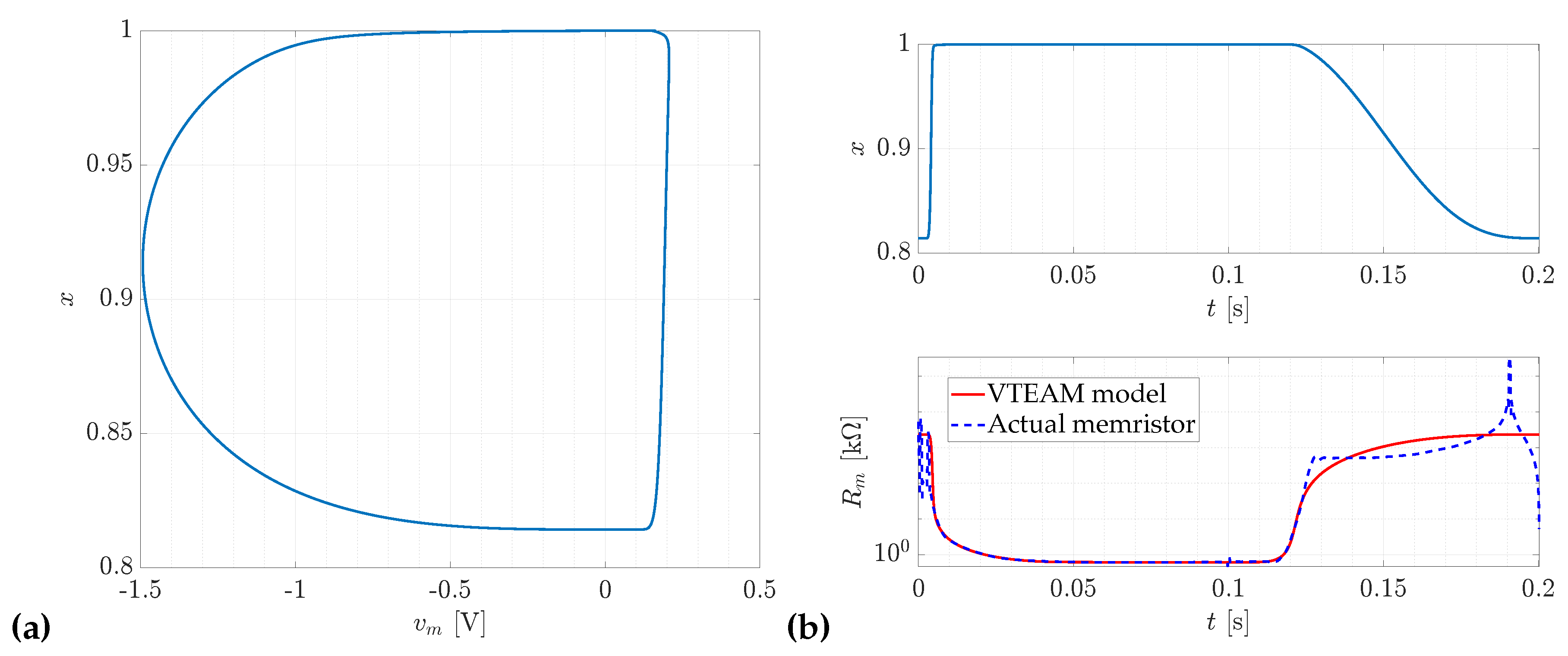
Figure 7.
The optimization results obtained for the Yakopcic model with carbon doping, at a supply amplitude of and frequency , yield an objective function value of for this particular case. (a) Comparison of the hysteresis curves of the memristor , both the reference and the ones obtained during optimization. (b) Comparison of the currents and voltages of the memristor with those obtained as a result of model optimization.
Figure 7.
The optimization results obtained for the Yakopcic model with carbon doping, at a supply amplitude of and frequency , yield an objective function value of for this particular case. (a) Comparison of the hysteresis curves of the memristor , both the reference and the ones obtained during optimization. (b) Comparison of the currents and voltages of the memristor with those obtained as a result of model optimization.
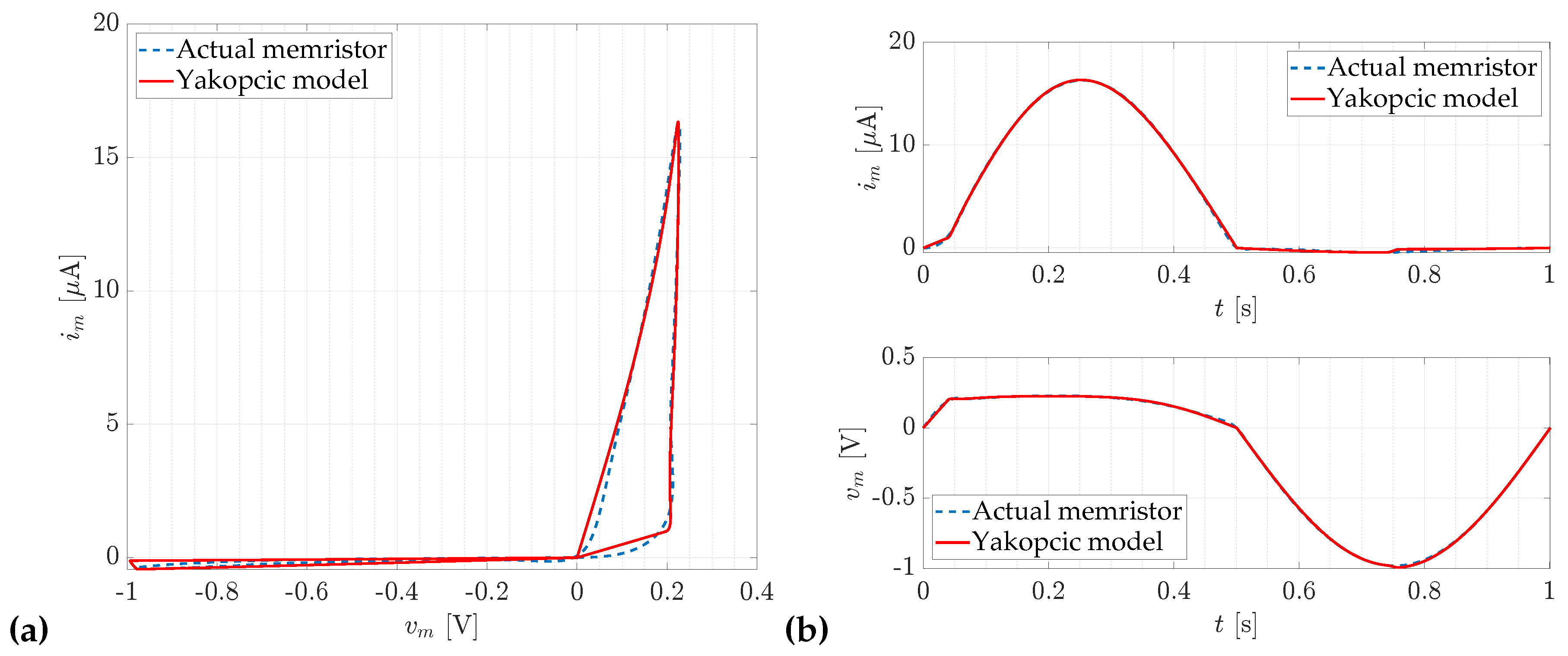
Figure 8.
The trajectories of the internal state variable and resistance obtained for the Yakopcic model with carbon doping, at a supply amplitude of and frequency , yield an objective function value of for this particular case. (a) The variation of the internal state variable x as a function of the memristor voltage . (b) The variation of the internal variable x and the memristor resistance over time.
Figure 8.
The trajectories of the internal state variable and resistance obtained for the Yakopcic model with carbon doping, at a supply amplitude of and frequency , yield an objective function value of for this particular case. (a) The variation of the internal state variable x as a function of the memristor voltage . (b) The variation of the internal variable x and the memristor resistance over time.
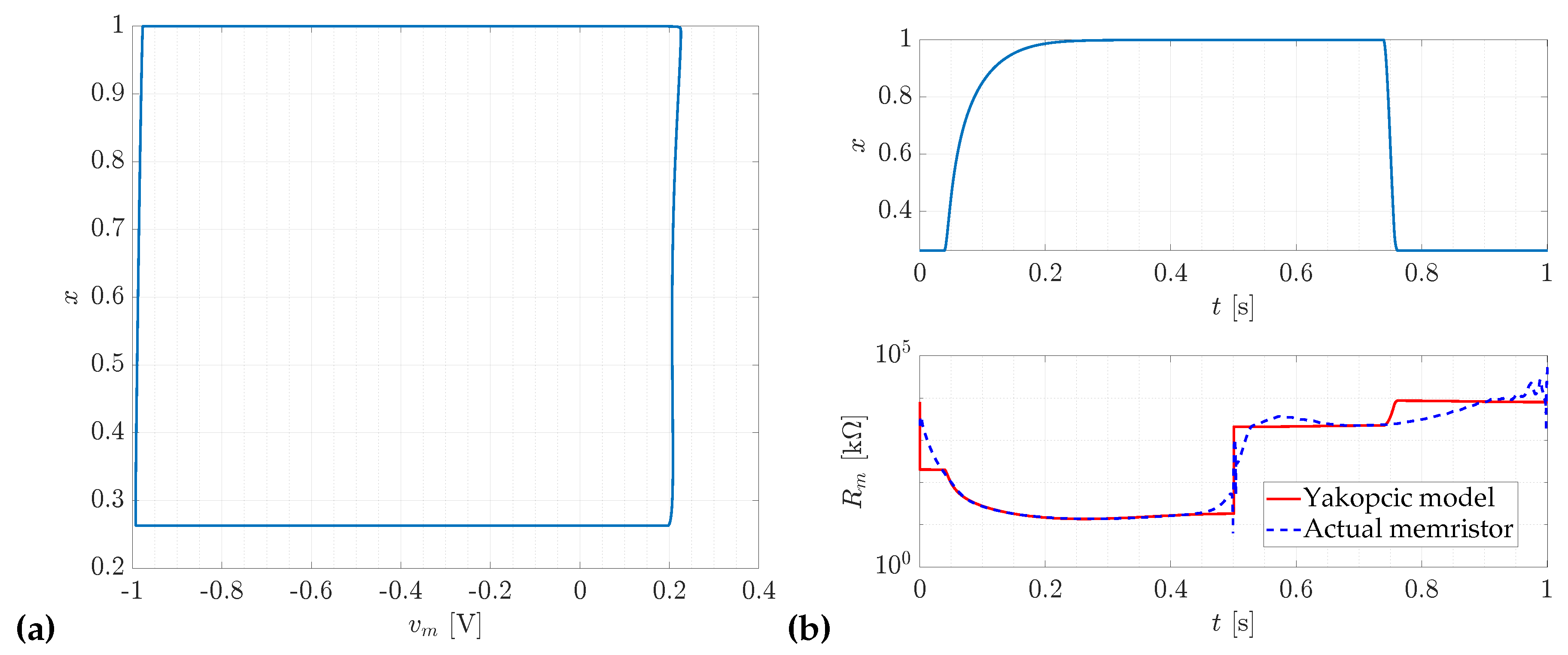
Figure 9.
The average objective function values for each model as a function of the supply voltage amplitude applied to the memristor-resistor system. The y-axis is presented on a logarithmic scale.
Figure 9.
The average objective function values for each model as a function of the supply voltage amplitude applied to the memristor-resistor system. The y-axis is presented on a logarithmic scale.
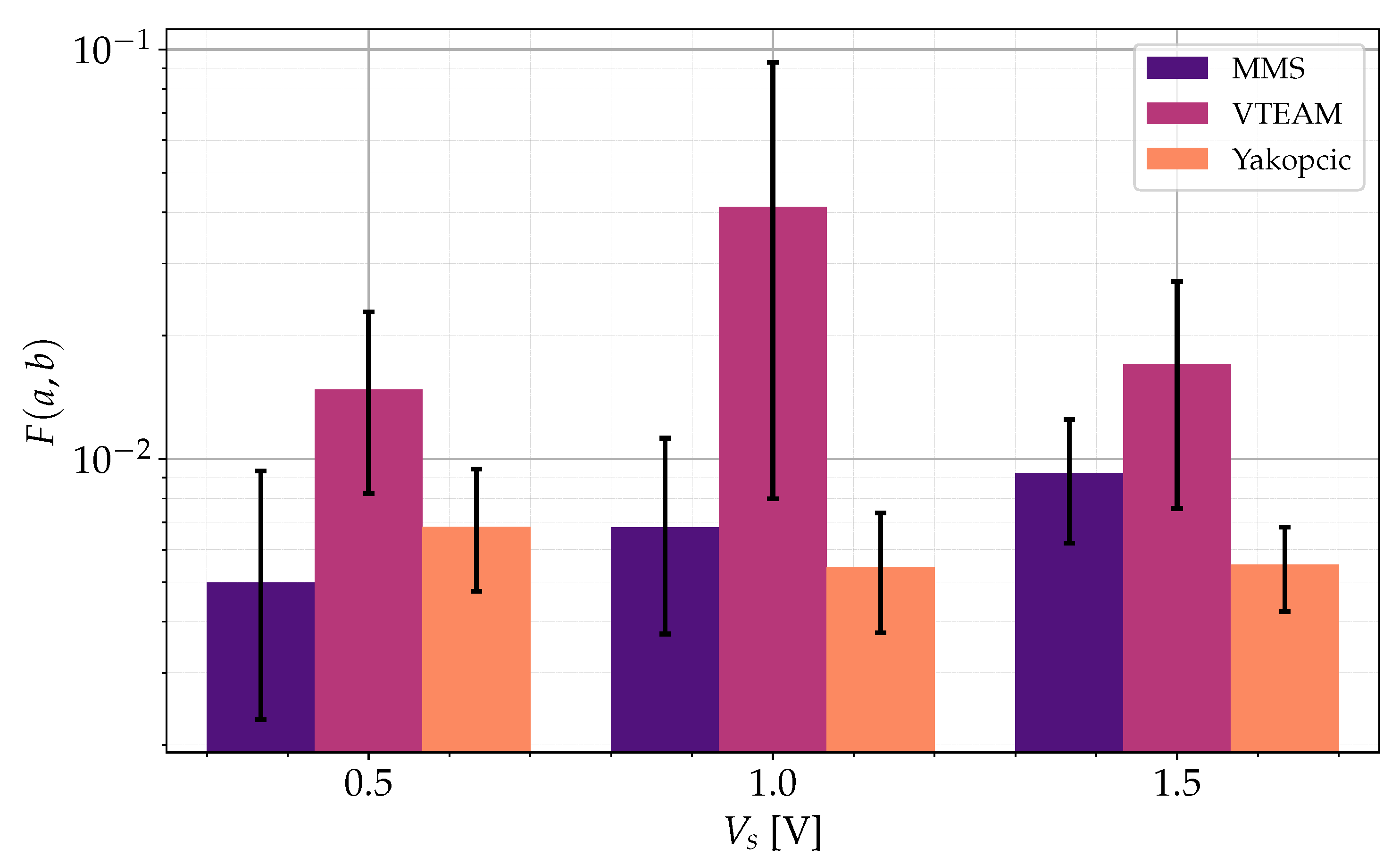
Figure 10.
The average objective function values for each model as a function of the frequency of the supply voltage applied to the memristor-resistor system. The y-axis is presented on a logarithmic scale.
Figure 10.
The average objective function values for each model as a function of the frequency of the supply voltage applied to the memristor-resistor system. The y-axis is presented on a logarithmic scale.
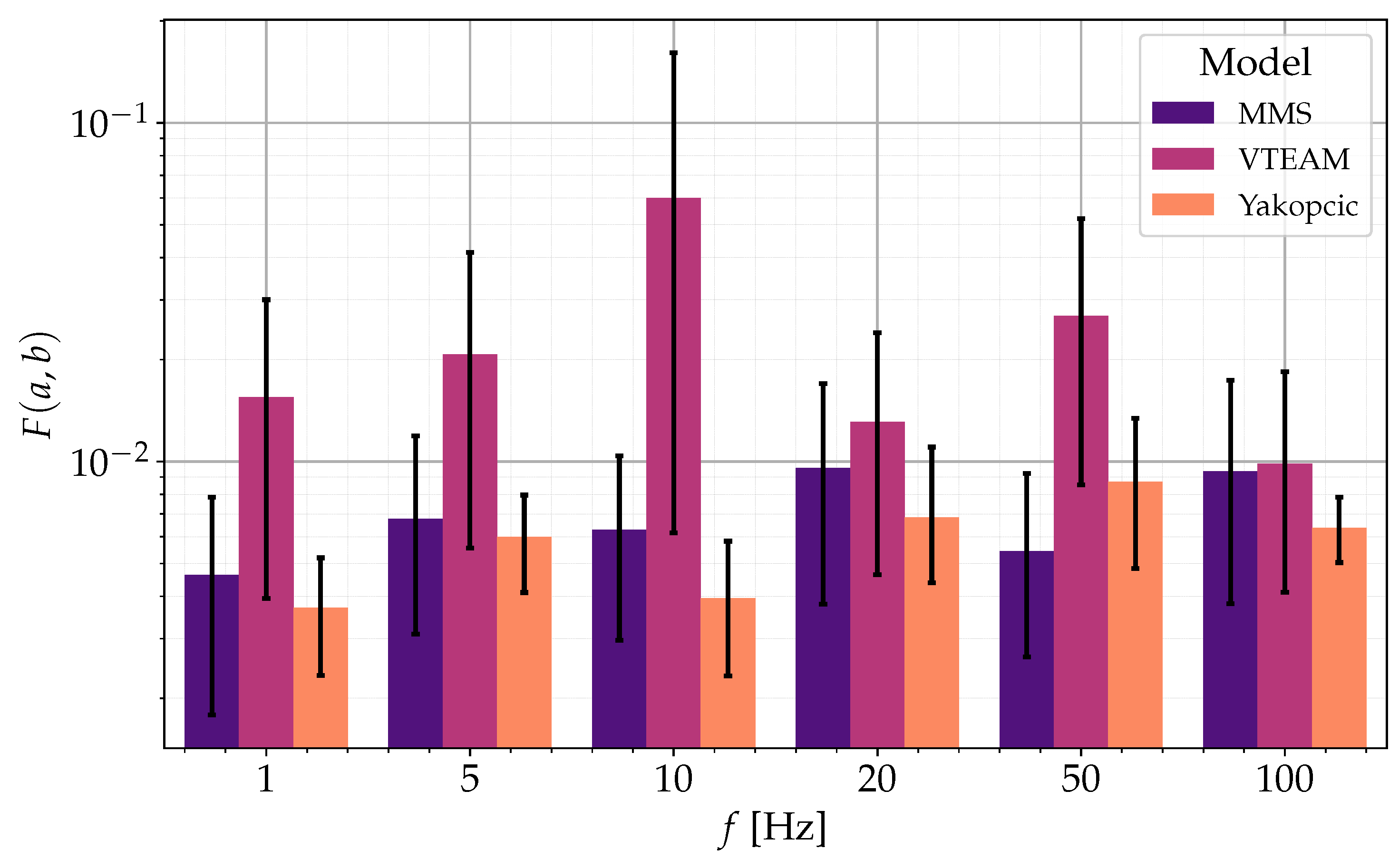
Figure 11.
The average objective function values for each model as a function of the memristor doping material. The y-axis is presented on a logarithmic scale.
Figure 11.
The average objective function values for each model as a function of the memristor doping material. The y-axis is presented on a logarithmic scale.
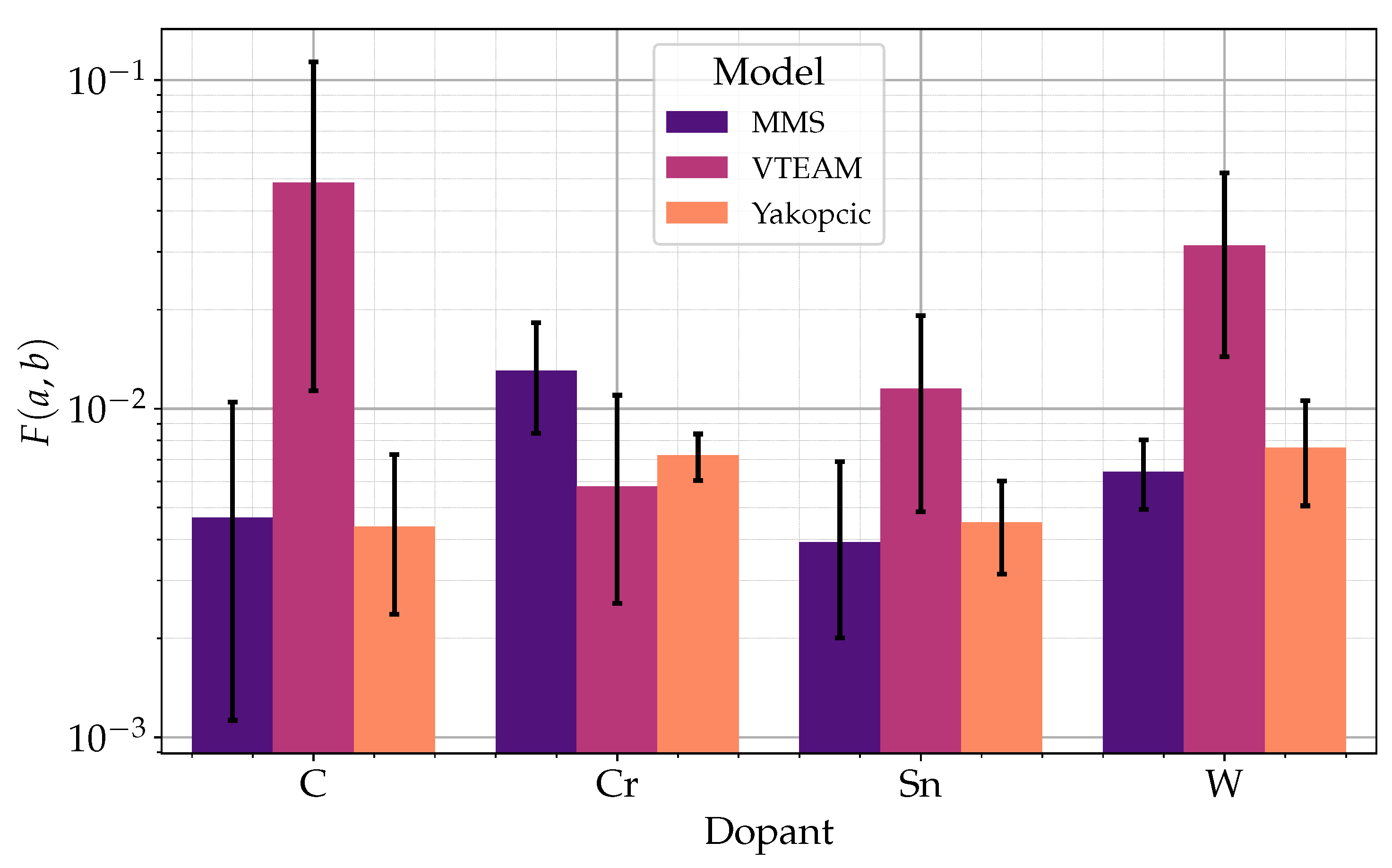
Figure 12.
Box plot of the objective function values for each model.
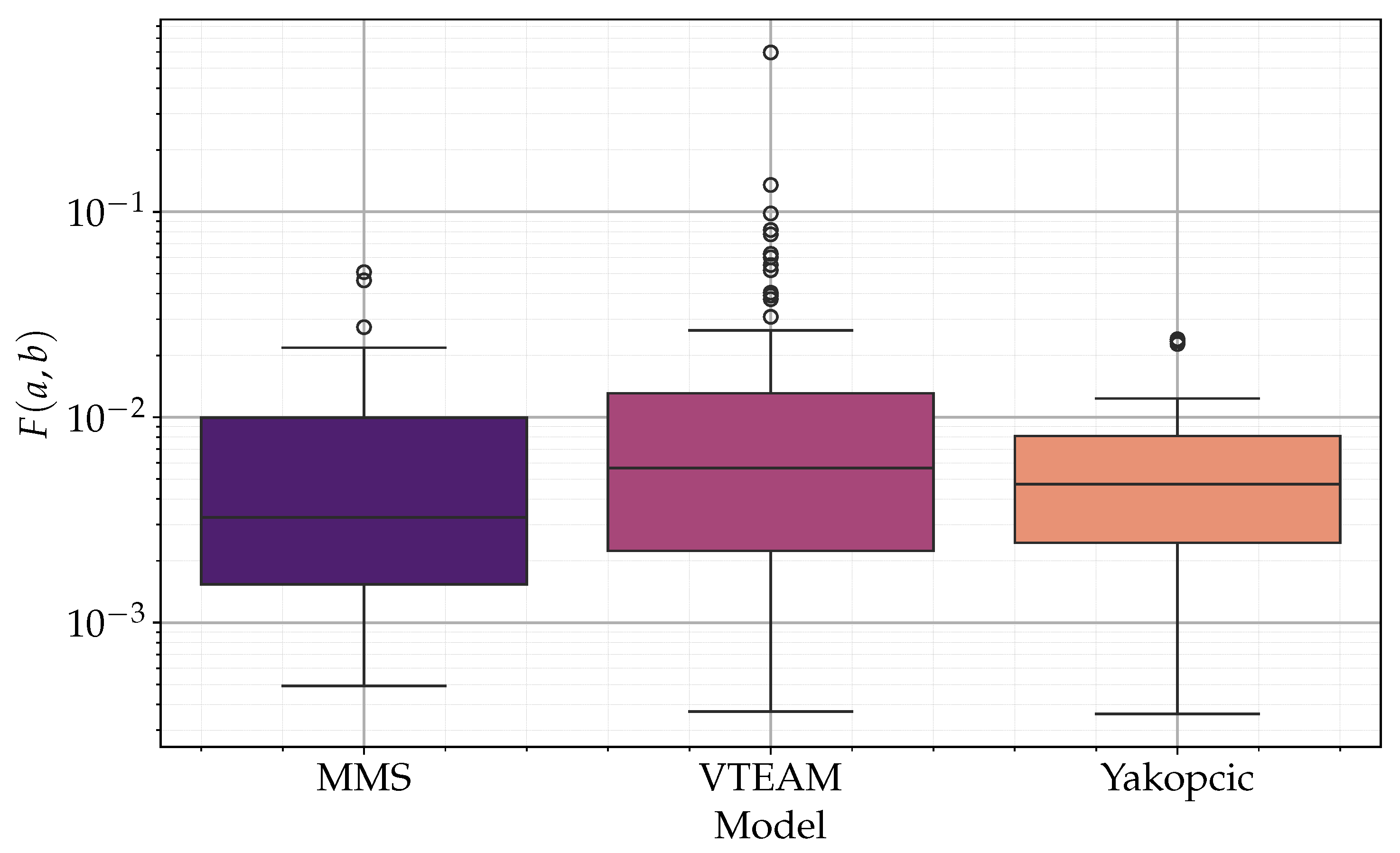
Figure 13.
An exemplary matrix in the form of a heatmap, where both color and annotation depict the value of the averaged objective function, is presented. On the left side of the graph are the excitation parameters for which the model was optimized, while along the bottom are the excitation parameters for which the model was evaluated. The graph contains data from the MMS model. For enhanced visibility, the color scale has been logarithmically adjusted.
Figure 13.
An exemplary matrix in the form of a heatmap, where both color and annotation depict the value of the averaged objective function, is presented. On the left side of the graph are the excitation parameters for which the model was optimized, while along the bottom are the excitation parameters for which the model was evaluated. The graph contains data from the MMS model. For enhanced visibility, the color scale has been logarithmically adjusted.
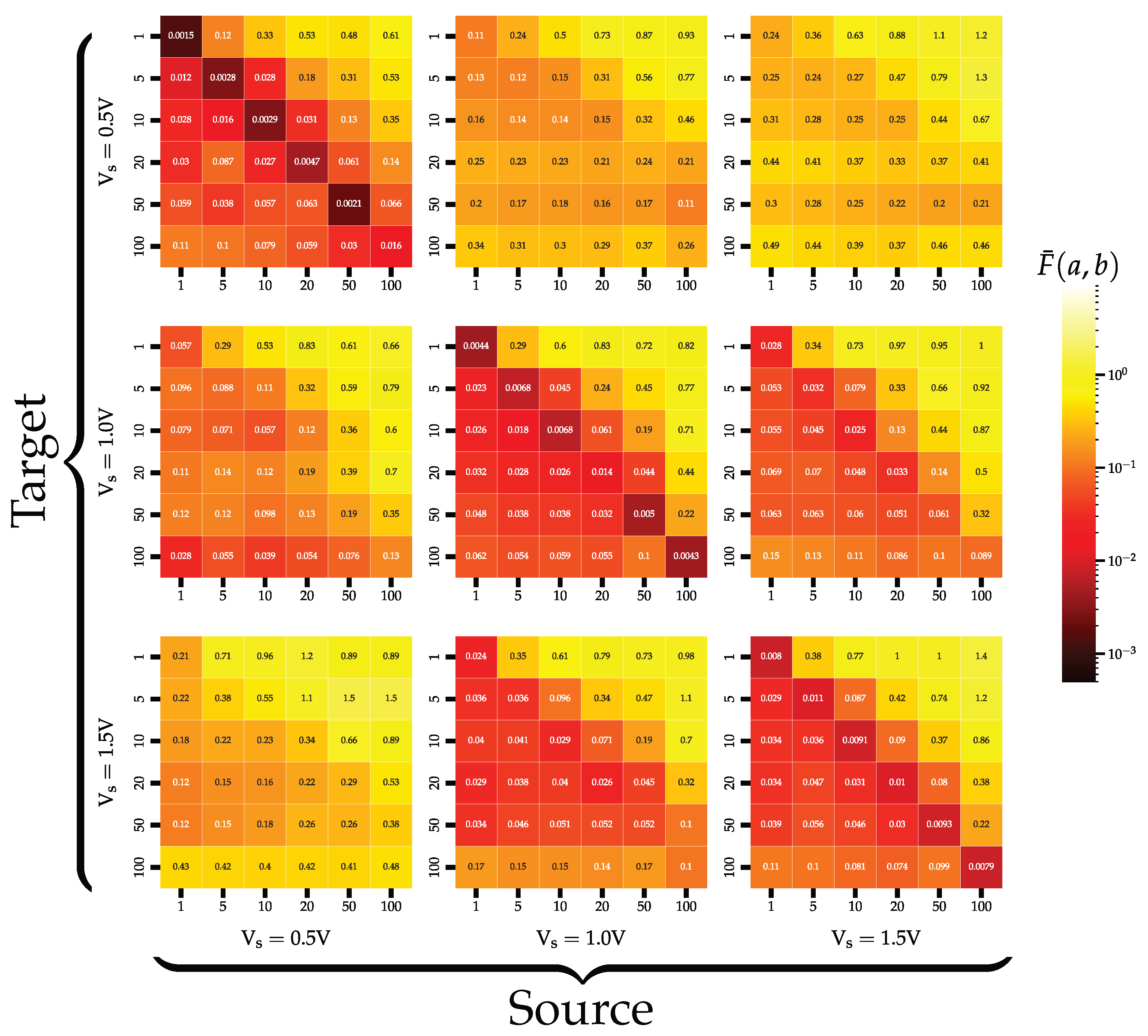
Figure 14.
A matrix of plots illustrating the variation in MMS model parameter values (y-axis) with linear trend lines, depending on the doping of memristors and excitation parameters (x-axis), is presented.
Figure 14.
A matrix of plots illustrating the variation in MMS model parameter values (y-axis) with linear trend lines, depending on the doping of memristors and excitation parameters (x-axis), is presented.
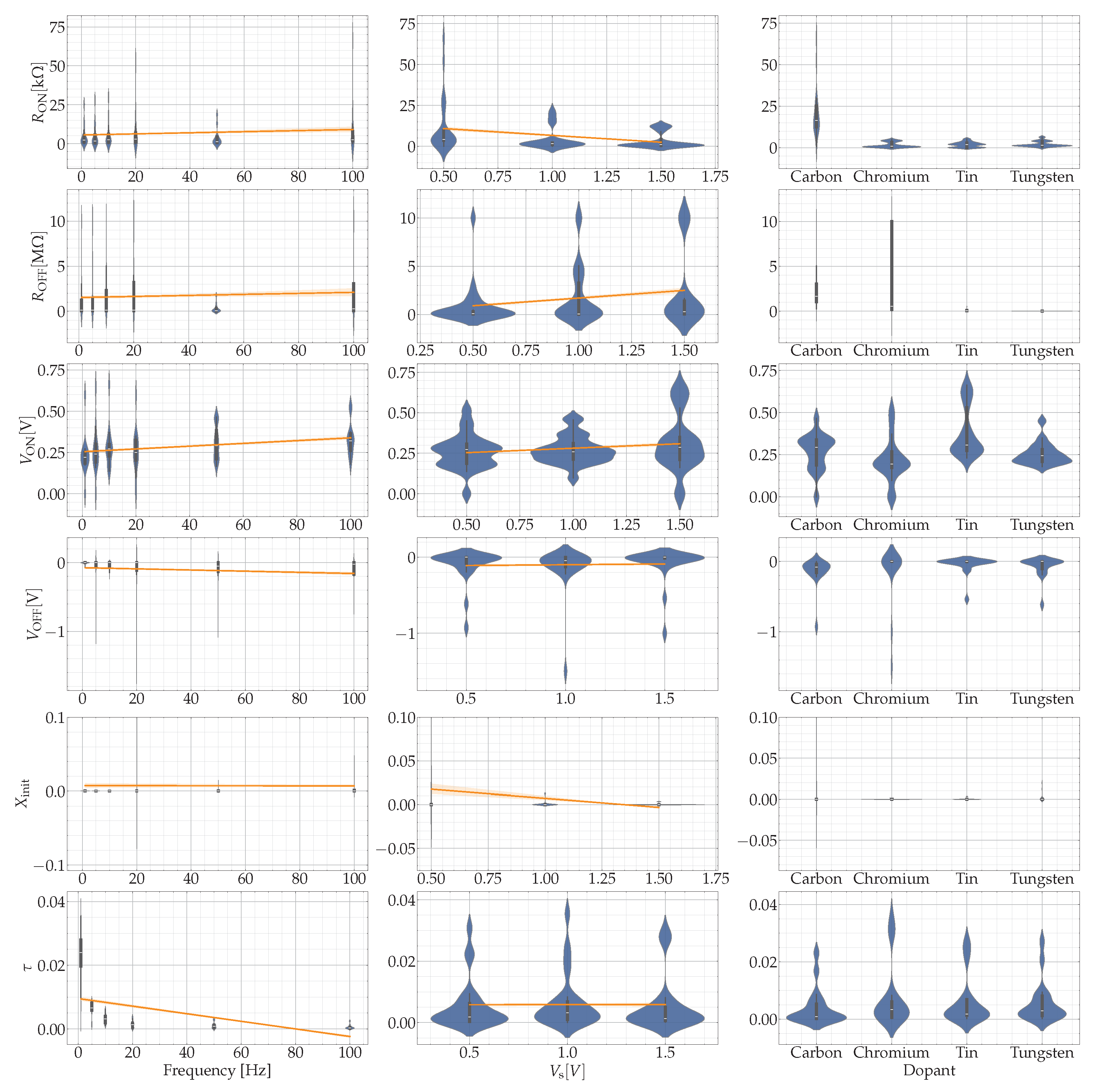
Table 1.
Box constraints on individual parameters during optimization for the MMS model.
| Parameter | Range | Parameter | Range |
Table 2.
Box constraints on individual parameters during optimization for the VTEAM model.
| Parameter | Range | Parameter | Range |
Table 3.
Box constraints on individual parameters during optimization for the Yakopcic model.
| Parameter | Range | Parameter | Range |
| b |
Table 4.
The objective function values for optimizing the MMS model when supplying the system with sinusoidal voltage of various parameters. The minimum value of the objective function is marked in green, while the maximum is marked in red.
Table 4.
The objective function values for optimizing the MMS model when supplying the system with sinusoidal voltage of various parameters. The minimum value of the objective function is marked in green, while the maximum is marked in red.
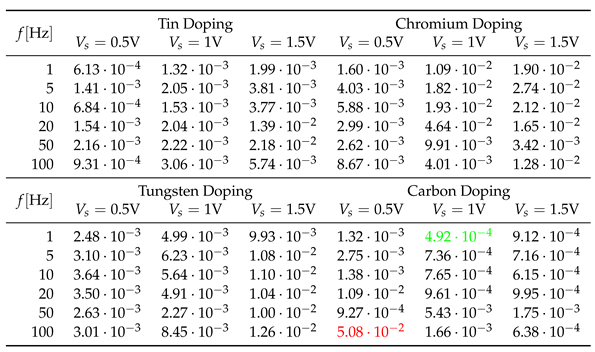 |
Table 5.
The example of the achieved parameters values for the MMS model for which the lowest objective function value was obtained(). The memristor and excitation signal parameters can be found in the Table 4.
Table 5.
The example of the achieved parameters values for the MMS model for which the lowest objective function value was obtained(). The memristor and excitation signal parameters can be found in the Table 4.
| Parameter | Value | Parameter | Value |
Table 6.
The averaged objective function values for each type of memristor doping with after optimizing MMS model.
Table 6.
The averaged objective function values for each type of memristor doping with after optimizing MMS model.
| Doping | Chromium | Tin | Tungsten | Carbon |
Table 7.
The objective function values for optimizing the VTEAM model when supplying the system with sinusoidal voltage of various parameters. The minimum value of the objective function is marked in green, while the maximum is marked in red.
Table 7.
The objective function values for optimizing the VTEAM model when supplying the system with sinusoidal voltage of various parameters. The minimum value of the objective function is marked in green, while the maximum is marked in red.
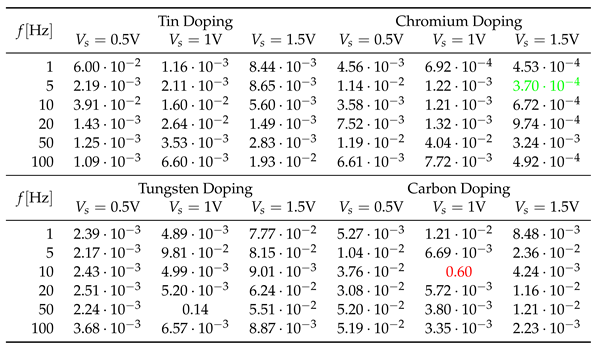 |
Table 8.
The achieved parameters values of the VTEAM model for which the lowest objective function value was obtained ().
Table 8.
The achieved parameters values of the VTEAM model for which the lowest objective function value was obtained ().
| Parameter | Value | Parameter | Value |
| 6 | 2 | ||
Table 9.
The averaged objective function values for each type of memristor doping with after optimizing VTEAM model.
Table 9.
The averaged objective function values for each type of memristor doping with after optimizing VTEAM model.
| Doping | Chromium | Tin | Tungsten | Carbon |
Table 10.
The objective function values for optimizing the Yakopcic model when supplying the system with sinusoidal voltage of various parameters. The minimum value of the objective function is marked in green, while the maximum is marked in red.
Table 10.
The objective function values for optimizing the Yakopcic model when supplying the system with sinusoidal voltage of various parameters. The minimum value of the objective function is marked in green, while the maximum is marked in red.
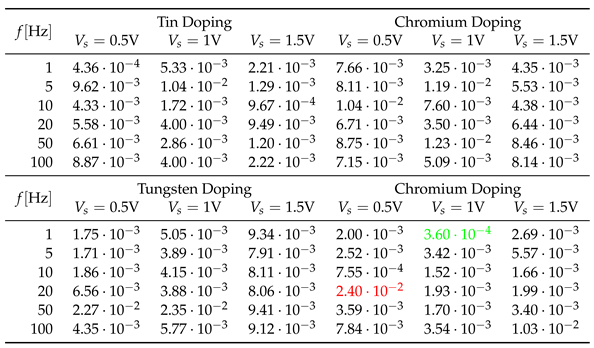 |
Table 11.
The parameters obtained for the Yakopcic model for the lowest objective function value ().
Table 11.
The parameters obtained for the Yakopcic model for the lowest objective function value ().
| Parameter | Value | Parameter | Value |
| b |
Table 12.
The averaged objective function values for each type of memristor doping after optimizing Yakopcic model.
Table 12.
The averaged objective function values for each type of memristor doping after optimizing Yakopcic model.
| Doping | Chromium | Tin | Tungsten | Carbon |
Table 13.
Mean values of the objective function for each of the models. The highest objective function is marked in red, while the lowest is marked in green
Table 13.
Mean values of the objective function for each of the models. The highest objective function is marked in red, while the lowest is marked in green
 |
Table 14.
Mean values of the objective function for each of the models. The highest objective function is indicated in red, and the lowest in green.
Table 14.
Mean values of the objective function for each of the models. The highest objective function is indicated in red, and the lowest in green.
 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated






