Dynamic Computation of an Innovative Device for Reducing the Reaction Torque

As well known, the torque produced by a rotating motor generates an opposite and equal reaction torque in the machine casing that must be transmitted to the base. In many applications, especially when the reaction moment has high values, it is necessary to apply some constructive solutions, which in certain cases are difficult to implement. In this context, the need to reduce the reaction moment from drive motors is a challenging topic, which has not been completely exhausted. In this paper, the authors present an original concept of a device which uses the centrifugal force generated by some equidistantly placed weights on a chain drive, for reducing the reaction torque of the motor used for driving a rotating tool. The proposed system is capable to produce a supplementary torque which can be added to driving moment. Due to this fact, by using this system, the power of the driving motor can be decreased, with the consequence of reducing the reaction moment, that must be absorbed by the base.

Keywords:

Subject: Engineering - Mechanical Engineering

1. Introduction

According to Newton's third law, there is an equal and opposite reaction to every action. This equation is most commonly applied to linear forces, but it also is valid for angular, or rotating, systems [1]. In this case, the torque is the angular equivalent of force. A torque can cause a mass to accelerate angularly in the same manner that a linear force can accelerate a mass linearly. Thus, a torque reaction is the equal and opposite response to a torque. Managing this reaction torque is fundamental in many technical applications, such as helicopter blade drives, motorcycle rear wheels, rotating tools operating under variable machining conditions, powered hand tools for fastening joints and so on.

A helicopter creates lift by rotating a series of blades that deflect air downward. The upward force acting on the helicopter is the equal and opposite of this downward force acting on the air. There is also an equal and opposite reaction caused by the rotating blades. The remainder of the helicopter tends to spin in the opposite direction as the engine rotates the blades in one direction. Therefore, a tail rotor, consisting of a smaller set of blades oriented to blow air horizontally, is used to counter the torque reaction caused by the engine trying to spin the main blades. Thus, a stabile flight of a helicopter can be achieved [2,3,4,5].

The torque reaction problem is solved in a different way by the Boeing CH-47 Chinook helicopters [6]. They use two sets of blades, called tandem rotors, which spin in opposite directions. By spinning, each rotor produces a torque reaction of its own, the two reactions canceling each other out. This principle is also in involved on other helicopters that are used to lift heavy loads [7,8,9,10].

Torque reaction is an important issue for terrestrial vehicles as well [11,12]. So, a motorcycle is operated by applying a torque to spin the rear wheel. If applying a low acceleration, the torque reaction is insufficient to counteract the motorcycle's front weight. However, if the rider provides enough throttle, the reaction can cause the front of the motorcycle to lift off the ground or do a wheelie. Even without contact with the ground, the rest of a motorcycle would tend to spin in the opposite direction of an accelerating rear wheel.

In case of powered hand tools involved in manufacturing and assembly jobs, such as tightening of screws, at the beginning of the fastening process, the operator holds and supports the tool. When the fastener joint begins to compress, the tool starts to build up torque and the corresponding torque reaction is transferred to the operator. When the tool torque overcomes the operator, the hand and arm exert a force to stabilize the tool in a direction opposite to the tool rotation. This may produce upper extremity musculoskeletal disorders [13,14].

In this study the authors propose an original concept of involving a special device for reducing the reaction torque of the motor used for driving a rotating tool. Similar devices have captivated the enthusiasm of many practicians, as well as of many serious researchers of high academic background, including persons coming from aerospace industry or academia who have granted an important number of patents [15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35].

The interest of the researchers on innovative driving systems is various. Some of them claimed to have discovered a means of subverting the rules of physics to accomplish action without reaction and thereby boost machine efficiency. Others have discovered a different method that saves energy by using vibrations instead of physical lifting to move big objects [36,37,38,39,40,41,42,43].

The present paper is structured as follows: in the next section we present the principle of the proposed device and we describe the main components. Further, in Section 3 we write the equations for the dynamic computation and in section 4 we present and discus the calculus outcomes for a certain application. Conclusions will be given in Section 5.

2. Device Design and Principle of Operation

The principle of the device proposed by the authors for reducing the reaction torque of a rotating tool is shown in Figure 1. It consists of following parts:

support frame;
chain wheel RC₁;
chain wheel RC₂;
chain;
mass weights;
drive motor;
tool clamping chuck;
tool;
belt wheel RB₁;
belt wheel RB₂;
synchronous belt;
fixing pin;
shaft.

In principle, we have a main transmission consisting of the electric motor (6), chuck (7) and tool (8). A second transmission is consisting of the synchronous belt (11) and the two identical belt wheels RB₁ (9) and RB₂ (10). The transmission ratio of the belt is i_B= 1.

The third transmission is the one that includes the chain (4) and the chain wheels RC₁ (2) and RC₂ (3). The diameters of the chain wheels are chosen in such a way that the transmission ratio is i_c= 8 and the chain wraps on the wheel RC₁, at an angle of 90° (π/2 radians) and on the wheel RC₂ at an angle of 270° (3π/2 radians).

The chain wheel RC₁ (2) is mounted on a shaft (13), which also supports the belt pulley RB₂ (10). The second chain wheel RC₂ (3) is rotating on the pin (12). Both, the pin (12) and the shaft (13) are fixed in the support frame (1). The support frame is connected to the tool (8) and rotates simultaneously with it.

The wheels that are part of the synchronous belt transmission are assembled in such a way that the belt pulley RB₂ (10) is mounted on the same shaft (13) as the chain wheel RC₁ (2) and the belt pulley RB₁ (9) is fixed on the driving shaft of the motor (6).

Same as in our previous research [44], on the chain (4) are mounted equidistant mass weights (5).

In operation, the drive motor (6) rotates the tool (8), the support frame (1), the belt transmission through the belt pulley RB₁ (9) and the chain transmission through the chain wheel RC₁ (2), all having the same direction of movement.

As a technical solution, for the system to be functional with the chain in any plane, guide discs profiled according to the shape of the chain with weights, mounted on the chain wheels, can be used.

When there appears a moment of resistance in the tool (8), it is transmitted through the driving system to the motor (6). As a result, the drive motor together with the whole system tends to reduce its speed. Consequently, in the chain transmission there is a moment of inertia amplified by the mass weights (5) placed on the chain (4) and which tends to mitigate the shock produced in the system. In this case, the masses have the role of reducing the moment of reaction of the chain transmission. This decrease is achieved by the fact that by rotating the chain around the tool axis, it produces an increase in the moment that appears at the tool. From here we can deduce the fact that by resetting the moment that appears at the tool, in the initial phase, implicitly, we have a reduction of the reaction moment.

Due to the rotation around the motor axis, respectively the tool, on the mass weights (5) are acting centrifugal forces which can be calculated, starting from the general equation of the centrifugal force F_c acting on a rotating mass:

F_{c} = M \cdot ω^{2} \cdot r_{c}^{O}

(1)

where:

: M-mass of the rotating body;
: ω- angular speed of the mass;
: $r_{c}^{O}$ -trajectory radius of the body’s center of gravity relative to the center of rotation O.

Next, the calculation of the centrifugal forces acting on the mass weights (5), respectively of the induced reaction torques, are presented.

3. Analytical Computation of System Dynamics

The calculation of the centrifugal forces acting on the mass weights (5) starts from the principle scheme shown in Figure 2, where with O₁ and O₂ are denoted the centers of the chain wheels RC₁ and RC₂, while O is the center around which the support frame (1) rotates with the angular speed ω.

The radius of the of the small chain wheel RC₁ was denoted with r and, consequently, the radius of the big chain wheel RC₂ will be 8r. Further, the chain was divided in 6 sections AB, BC, CD, DE, EF and FA, of which, two are linear and four are circular (in the form of an arc).

Point O was chosen at the intersection of the line defined by the straight chain section AB and a parallel line to the other straight chain section CD, which passes through the point F.

The mass of each section M_xy is calculated, starting from a specific linear mass, assumed to be

\bar{m}

and the length of the section L_xy:

M_{x y} = \bar{m} \cdot L_{x y}

(2)

where

x, y \in \{A, B, C, D, E, F\}

Based on the notation from Figure 2, we have following lengths of the sections:

L_{A B} = L_{C D} = 7 r

(3)

\hat{L_{B C}} = \frac{π \cdot r}{2}

(4)

\hat{L_{D E}} = \hat{L_{E F}} = \hat{L_{F A}} = 4 \cdot π \cdot r

(5)

Thus, based on Eq’s (1) and (2), the centrifugal forces acting on each of the upper mentioned sections become:

F_{c x y} = \bar{m} \cdot {L_{x y} \cdot ω}^{2} \cdot r_{c x y}^{O}

(6)

For the circular sections, the radii of the gravity centers are computed using the general relationship:

r_{c}^{O} = r \cdot \frac{s i n α}{α}

(7)

Based on the notation from Figure 3, the gravity center radius for the circular section BC may be calculated as follows:

r_{c B C}^{O_{1}} = r \cdot \frac{s i n \frac{π}{4}}{\frac{π}{4}}

(8)

In a similar manner, we have for the other three circular sections:

r_{c D E}^{O_{2}} = r_{c E F}^{O_{2}} = r_{c F A}^{O_{2}} = 8 r \cdot \frac{s i n \frac{π}{4}}{\frac{π}{4}}

(9)

Since the entire chain transmission rotates with angular velocity ω around point O, we will have to calculate the gravity radii centers relative to O. Using the annotation from Figure 4, following vector relations may be written:

{\vec{r}}_{c A B}^{O} = \{\begin{matrix} 0 \\ O A + \frac{A B}{2} \end{matrix}\} = \{\begin{matrix} 0 \\ 8 \cdot r + \frac{7 \cdot r}{2} \end{matrix}\} = \{\begin{matrix} 0 \\ 11,5 \cdot r \end{matrix}\}

(10)

{\vec{r}}_{c B C}^{O} = \vec{O O_{1}} + {\vec{r}}_{c B C}^{O_{1}} = \{\begin{matrix} O_{1} B \\ 0 B \end{matrix}\} + \{\begin{matrix} {- r}_{c B C}^{O_{1}} \cdot c o s \frac{π}{4} \\ r_{c B C}^{O_{1}} \cdot s i n \frac{π}{4} \end{matrix}\} = \{\begin{matrix} r - r \cdot \frac{s i n \frac{π}{4} \cdot c o s \frac{π}{4}}{\frac{π}{4}} \\ 15 \cdot r + r \cdot \frac{{s i n}^{2} \frac{π}{4}}{\frac{π}{4}} \end{matrix}\} = = \{\begin{matrix} 0.363 \cdot r \\ 15.363 \cdot r \end{matrix}\}

(11)

{\vec{r}}_{c C D}^{O} = \{\begin{matrix} O_{1} B + \frac{D C}{2} \\ 16 \cdot r \end{matrix}\} = \{\begin{matrix} r + \frac{7 \cdot r}{2} \\ 16 \cdot r \end{matrix}\} = \{\begin{matrix} 4.5 \cdot r \\ 16 \cdot r \end{matrix}\}

(12)

{\vec{r}}_{c D E}^{O} = \vec{O O_{2}} + {\vec{r}}_{c D E}^{O_{2}} = \{\begin{matrix} O F \\ O A \end{matrix}\} + \{\begin{matrix} r_{c D E}^{O_{2}} \cdot c o s \frac{π}{4} \\ r_{c B C}^{O_{2}} \cdot s i n \frac{π}{4} \end{matrix}\} = \{\begin{matrix} 8 \cdot r + 8 \cdot r \cdot \frac{s i n \frac{π}{4} \cdot c o s \frac{π}{4}}{\frac{π}{4}} \\ 8 \cdot r + 8 \cdot r \cdot \frac{{s i n}^{2} \frac{π}{4}}{\frac{π}{4}} \end{matrix}\} = = \{\begin{matrix} 13.093 \cdot r \\ 13.093 \cdot r \end{matrix}\}

(13)

{\vec{r}}_{c E F}^{O} = \vec{O O_{2}} + {\vec{r}}_{c E F}^{O_{2}} = \{\begin{matrix} O F \\ O A \end{matrix}\} + \{\begin{matrix} r_{c E F}^{O_{2}} \cdot c o s \frac{π}{4} \\ {- r}_{c E F}^{O_{2}} \cdot s i n \frac{π}{4} \end{matrix}\} = \{\begin{matrix} 8 \cdot r + 8 \cdot r \cdot \frac{s i n \frac{π}{4} \cdot c o s \frac{π}{4}}{\frac{π}{4}} \\ 8 \cdot r - 8 \cdot r \cdot \frac{{s i n}^{2} \frac{π}{4}}{\frac{π}{4}} \end{matrix}\} = = \{\begin{matrix} 13.093 \cdot r \\ 2.907 \cdot r \end{matrix}\}

(14)

{\vec{r}}_{c F A}^{O} = \vec{O O_{2}} + {\vec{r}}_{c F A}^{O_{2}} = \{\begin{matrix} O F \\ O A \end{matrix}\} + \{\begin{matrix} - r_{c F A}^{O_{2}} \cdot c o s \frac{π}{4} \\ {- r}_{c F A}^{O_{2}} \cdot s i n \frac{π}{4} \end{matrix}\} = \{\begin{matrix} 8 \cdot r - 8 \cdot r \cdot \frac{s i n \frac{π}{4} \cdot c o s \frac{π}{4}}{\frac{π}{4}} \\ 8 \cdot r - 8 \cdot r \cdot \frac{{s i n}^{2} \frac{π}{4}}{\frac{π}{4}} \end{matrix}\} = = \{\begin{matrix} 2.907 \cdot r \\ 2.907 \cdot r \end{matrix}\}

(15)

The modulus of the vectors (their length) expressed by Eq.’s (10)-(15) are:

r_{c A B}^{O} = 11.5 \cdot r

(16)

r_{c B C}^{O} = 15.367 \cdot r

(17)

r_{c C D}^{O} = 16.621 \cdot r

(18)

r_{c D E}^{O} = 18.516 \cdot r

(19)

r_{c E F}^{O} = 13.412 \cdot r

(20)

r_{c F A}^{O} = 4.111 \cdot r

(21)

Next, using Eq. (6,) the section lengths computed with Eq.’s (3)-(5) and the radii of the gravity centers deduced with Eq’s (16)-(21), we obtain following centrifugal forces acting on the six sections of the chain:

{F_{c}}_{A B} = \bar{m} \cdot 7 \cdot r \cdot ω^{2} \cdot 11.5 \cdot r

(22)

Using the notation:

\bar{m} \cdot ω^{2} \cdot r^{2} = K

(23)

Eq. (3) can be written as:

{F_{c}}_{A B} = 80.5 \cdot K

(24)

In the same way, the centrifugal forces acting on the other 5 sections are:

{F_{c}}_{B C} = 24.139 \cdot K

(25)

{F_{c}}_{C D} = 116.347 \cdot K

(26)

{F_{c}}_{D E} = 232.679 \cdot K

(27)

{F_{c}}_{E F} = 168.540 \cdot K

(28)

{F_{c}}_{F A} = 51.660 \cdot K

(29)

Figure 5 shows the arrangement of the centrifugal forces calculated above. These forces, applied on the six sections of the chain, produce additional torques at the rotation points O₁ and O₂ of the chain wheels (RC₁ and RC₂), according to the centralization presented in Table 1.

It must be mentioned that there is a torque only around the rotation point, at which the centrifugal force "pulls" the chain. Furthermore, for the section CD, the centrifugal force can be decomposed along the x and y directions. Only the component along the x-axis produces a torque, as the y-component tends to bend the chain segment. Obviously, on the sections where the direction of the centrifugal force passes through the point of rotation, there is no torque, since the distance from the force to the center of rotation is zero.

The computation of torques produced by centrifugal forces starts from the well-known relationship:

M_{{x y}_{O_{1 (2)}}} = F_{c x y} \cdot d ({O_{1 (2)}, F}_{c x y})

(30)

where:

x, y \in \{A, B, C, D, E, F\}

are the characteristic points of the chain sections;

O₁₍₂₎- rotation points of the chain wheels;

F_cxy- centrifugal forces acting on the six sections of the chain;

d ({O_{1 (2)}, F}_{c x y})

- distance from the centrifugal force to the rotation points O₁₍₂₎ of the chain wheels.

If for centrifugal forces

{F_{c}}_{A B}

and

{F_{c}}_{C D_{x}}

the distances to the points of rotation are easy to deduce (

d ({O_{2}, F}_{c A B}) = 8 \cdot r

and

d ({O_{1}, F}_{c {C D}_{x}}) = r

), for the forces

{F_{c}}_{B C}

and

{F_{c}}_{E F}

the following general relationship applies:

d (M, L) = \frac{|a \cdot x_{M} + b \cdot y_{M} + c|}{\sqrt{a^{2} + b^{2}}}

(31)

where:

d(M, L)- distance of the point M to the straight line L;

x_M, y_M- coordinates of point M;

a·x+b·y+ c= 0- equation of line L.

In the case of a straight line passing through two points P(

x_{M P}

y_{P}

) and R(

x_{R}

y_{R}

), its equation has the form:

\frac{x - x_{P}}{x_{R} - x_{P}} = \frac{y - y_{P}}{y_{R} - y_{P}}

(32)

Consequently, based on the Eq.’s (11) and (14), the support lines of the forces

{F_{c}}_{B C}

and

{F_{c}}_{E F}

will have the equations:

L ({F_{c}}_{B C}) : \frac{x - x_{O}}{0.363 \cdot r - x_{0}} = \frac{y - y_{O}}{15.363 \cdot r - y_{0}}

(33)

and:

L ({F_{c}}_{E F}) : \frac{x - x_{O}}{13.093 \cdot r - x_{0}} = \frac{y - y_{O}}{2.907 \cdot r - y_{0}}

(34)

That is:

L ({F_{c}}_{B C}) : 15.363 \cdot r \cdot x - 0.363 \cdot r \cdot y = 0

(35)

and:

L ({F_{c}}_{E F}) : 2.907 \cdot r \cdot x - 13.093 \cdot r \cdot y = 0

(36)

Accordingly, knowing the coordinates O₁(r, 15·r), respectively O₂(8·r, 8·r), together with applying the Eq.’s (31), (35) and (36), we will have following distances:

d ({O_{1}, F}_{c}_{B C}) = \frac{|15.363 \cdot r \cdot r - 0.363 \cdot r \cdot 7 \cdot r|}{\sqrt{{(15.363 \cdot r)}^{2} + {(0.363 \cdot r)}^{2}}} = 0,834 \cdot r

(37)

d ({O_{2}, F}_{c}_{E F}) = \frac{|2.907 \cdot r \cdot 8 \cdot r - 13.093 \cdot r \cdot 8 \cdot r|}{\sqrt{{(2.907 \cdot r)}^{2} + {(13.093 \cdot r)}^{2}}} = 6,076 \cdot r

(38)

Asa result, the torques produced by the centrifugal forces are:

M_{{A B}_{O_{2}}} = {- F}_{c}_{A B} \cdot d ({O_{2}, F}_{c A B}) = - 80.5 \cdot K \cdot 8 \cdot r = - 644 \cdot K \cdot r

(39)

M_{{B C}_{O_{1}}} = {- F}_{c}_{B C} \cdot d ({O_{1}, F}_{c B C}) = - 24.139 \cdot K \cdot 0,834 \cdot r = - 20,132 \cdot K \cdot r

(40)

M_{{C D}_{O_{1}}} = {- F}_{c}_{{C D}_{x}} \cdot d ({O_{1}, F}_{c D C_{x}}) = {- F}_{c}_{C D} \cdot \sin [a r c t a n (\frac{4,5 \cdot r}{16 \cdot r})] \cdot r = = 31.5 \cdot K \cdot r

(41)

M_{{D E}_{O_{2}}} = 0

(42)

M_{{E F}_{O_{2}}} {= F}_{c}_{E F} \cdot d ({O_{2}, F}_{c E F}) = 168.54 \cdot K \cdot 6.076 \cdot r = 1024.049 \cdot K \cdot r

(43)

M_{{F A}_{O_{2}}} = 0

(44)

The “+” or “-“ sign of the torques was established according to the right hand rule.

Considering the transmission ratio of the chain drive, the above computed torques can be reduced at the center of rotation O₁ as follows:

M_{{r e d}_{O_{1}}} = \sum M_{O_{1}} + \frac{\sum M_{O_{2}}}{i_{c}} = M_{{B C}_{O_{1}}} + M_{{C D}_{O_{1}}} + \frac{M_{{A B}_{O_{2}}} + M_{{E F}_{O_{2}}}}{8} = = - 20,132 \cdot K \cdot r + 31.5 \cdot K \cdot r + \frac{- 644 \cdot K \cdot r + 1024.049 \cdot K \cdot r}{8} = 58.874 \cdot K \cdot r

(45)

This supplementary torque is transmitted through the belt transmission (with ratio i_B= 1) to the tool (8).

In addition to the effect of generating torques in the chain wheel rotation centers, these centrifugal forces (which occur in the six portions of the transmission) are also inducing parallel loads at the rotation centers O₁ and O₂. These forces, denoted with

R_{x y}^{O_{1 (2)}}

, are shown in Figure 6 with red, being equal and having the same sense as the centrifugal forces by which they were generated.

In the case of the horizontal chain segment CD, because the centrifugal force acts in the middle of the segment, its vertical component (

{F_{c}}_{C D_{y}}

) generates forces, in both centers of rotation (O₁ and O₂), equal to half of this component. The situation of the load generated by the horizontal component (

{F_{c}}_{C D_{x}}

) is completely different. The induced force is acting only at the point O₁, because, in the direction of the point O₂, the chain is "pushed", without achieving a load at this point.

Taking these into account and considering Eq.’s (24)-(29) we have:

R_{A B}^{O_{2}} = F_{c_{A B}} = 80.5 \cdot K

(46)

R_{B C}^{O_{1}} = {F_{c}}_{B C} = 24.139 \cdot K

(47)

R_{C D_{x}}^{O_{1}} = {F_{c}}_{C D_{x}} = {F_{c}}_{C D} \cdot \sin [a r c t a n (\frac{4,5 \cdot r}{16 \cdot r})] = 31.5 \cdot K

(48)

R_{C D_{y}}^{O_{1}} = {0.5 \cdot F}_{c}_{C D_{y}} = 0.5 \cdot {F_{c}}_{C D} \cdot \cos [a r c t a n (\frac{4,5 \cdot r}{16 \cdot r})] = 56.001 \cdot K

(49)

R_{C D_{y}}^{O_{2}} = {0.5 \cdot F}_{c}_{C D_{y}} = 0.5 \cdot {F_{c}}_{C D} \cdot \cos [a r c t a n (\frac{4,5 \cdot r}{16 \cdot r})] = 56.001 \cdot K

(50)

R_{D E}^{O_{2}} = {F_{c}}_{D E} = 232.679 \cdot K

(51)

{R_{E F}^{O_{2}} = F}_{c}_{E F} = 168.540 \cdot K

(52)

{R_{F A}^{O_{2}} = F}_{c}_{F A} = 51.660 \cdot K

(53)

These forces, acting in the rotation centers of the two chain wheels, are generating in the rotational point O torques, which can be computed as:

M_{{x y}_{O}} = R_{x y}^{O_{1 (2)}} \cdot d (O, R_{x y}^{O_{1 (2)}})

(54)

where:

x, y \in \{A, B, C, D, E, F\}

are the characteristic points of the chain sections;

O- rotation point of the tool;

R_{x y}^{O_{1 (2)}}

- loads induced at the rotation centers O₁ and/ or O₂ by the centrifugal forces acting on the six sections of the chain;

d (O, R_{x y}^{O_{1 (2)}})

- distance from the force

R_{x y}^{O_{1 (2)}}

to the rotation point O.

The distances

d (O, R_{x y}^{O_{1 (2)}})

are:

d (O, R_{A B}^{O_{2}}) = O_{2} A = 8 \cdot r

(55)

d (O, R_{B C}^{O_{1}}) = d ({O_{1}, F}_{c}_{B C}) = 0,834 \cdot r

(56)

d ({O, R}_{C D_{x}}^{O_{1}}) = O B = 7 \cdot r

(57)

d ({O, R}_{C D_{y}}^{O_{1}}) = O_{1} B = r

(58)

d ({O, R}_{C D_{y}}^{O_{2}}) = O_{2} A = 8 \cdot r

(59)

d (O, R_{D E}^{O_{2}}) = 0

(60)

d ({O, R}_{E F}^{O_{2}}) = d ({O_{2}, F}_{c}_{E F}) = 6,076 \cdot r

(61)

d (O, R_{F A}^{O_{2}}) = 0

(62)

Thus, the torques defined by Eq. (54) are:

M_{{A B}_{O}} = R_{A B}^{O_{2}} \cdot d (O, R_{A B}^{O_{2}}) = 80.5 \cdot K \cdot 8 \cdot r = 644 \cdot K \cdot r

(63)

M_{{B C}_{O}} = R_{B C}^{O_{1}} \cdot d (O, R_{B C}^{O_{1}}) = 24.139 \cdot K \cdot 0,834 \cdot r = 20,132 \cdot K \cdot r

(64)

M_{{C D}_{O}} = {- R}_{C D_{x}}^{O_{1}} \cdot d ({O, R}_{C D_{x}}^{O_{1}}) + R_{C D_{y}}^{O_{1}} \cdot d ({O, R}_{C D_{y}}^{O_{1}}) + R_{C D_{y}}^{O_{2}} \cdot d ({O, R}_{C D_{y}}^{O_{2}}) = = - 31.5 \cdot K \cdot 7 \cdot r + 56.001 \cdot K \cdot r + 56.001 \cdot K \cdot 8 \cdot r = 283,509 \cdot K \cdot r

(65)

M_{{D E}_{O}} = R_{D E}^{O_{2}} \cdot d (O, R_{D E}^{O_{2}}) = 0

(66)

M_{{E F}_{O}} = - R_{E F}^{O_{2}} \cdot d (O, R_{E F}^{O_{2}}) = - 168.540 \cdot K \cdot 6,076 \cdot r = - 1024,049 \cdot K \cdot r

(67)

M_{{F A}_{O}} = R_{F A}^{O_{2}} \cdot d (O, R_{F A}^{O_{2}}) = 0

(68)

and their sum is:

\sum M_{{x y}_{O}} = M_{{A B}_{O}} + M_{{B C}_{O}} + M_{{C D}_{O}} + M_{{D E}_{O}} + M_{{E F}_{O}} + M_{{F A}_{O}} = - 76,409 \cdot K \cdot r

(69)

The total torque produced by the device in point O is:

M_{{t o t}_{O}} = \sum M_{{x y}_{O}} + M_{{r e d}_{O}} = - 76.409 \cdot K \cdot r + 58.874 \cdot K \cdot r = - 17.535 \cdot K \cdot r

(70)

The negative sign from Eq. (70) indicates that the produced torque is in a counterclockwise sense and coincides with the tool rotation sense, denoted by ω in Figure 2, Figure 4 and Figure 5. Thus, the supplementary torque generated by the system, through the centrifugal forces acting on the masses added to the chain is accumulated to the working torque of the tool.

4. Numerical Example and Discussion

Let us further consider a device such as the one described in Chapter 2, which has the technical data given in Table 2.

\bar{m} = 0.5 [k g / m]

For the above indicated technical data, we have a driving torque:

M_{O} = 9.55 \cdot \frac{P}{n} = 7.958 [N \cdot m],

(71)

an angular velocity:

ω = \frac{π \cdot n}{30} = 62.83 [r a d / s],

(72)

a device specific force, calculated according to Eq. (23):

K = 0.5 \cdot {62.83}^{2} \cdot {0.05}^{2} = 4.93 [N],

(73)

and a total torque produced by the device in point O, computed with Eq. (70):

M_{{t o t}_{O}} = 17.535 \cdot K \cdot r = 17.535 \cdot 4.93 \cdot 0.05 = 4.32 [N \cdot m] .

(74)

Thus, it follows that the torque produced by the system is for this specific example 54.3% from the nominal driving torque of the motor. This means that the specific power absorbed from the supply network of the electric motor can be reduced by implementing such a device. In addition, if the torque required to drive the tool increases suddenly, the reaction torque that occurs at the motor is mitigated by this device, making the handling of the entire system easier.

As the additional torque produced by the system is independent of the drive power, the system is even more efficient the lower the motor power. However, there is a limitation that considers the moment necessary to overcome the inertia of the system during the starting.

It should also be mentioned that, for reasons related to the complexity of the dynamic model, the losses due to friction and transmissions efficiency were not taken into consideration. Normally, for the proposed system, these losses do not exceed 10%.

Nevertheless, as one can observe, the torque produced by the system can be raised by increasing the masses which are added to the chain, by increasing the radii of the chain wheels and by increasing the driving speed. While the increase in the specific mass

\bar{m}

produces a directly proportional raise of the torque, by doubling the radii of the chain wheels or by doubling the drive speed, a multiplication by four times of the moment produced by the system is obtained.

The main disadvantage of the proposed system lies in the relatively large size and the need to take special protective measures, because the support frame (1) and the other associated elements are rotating together with the tool (8). Furthermore, the system is working proper only in one direction of rotation In case of a change in the direction of rotation, the centrifugal forces acting on the masses attached to the chain are lowering the driving torque of the tool.

5. Conclusions

The present study proposes a novel device capable to produce, by means of centrifugal forces generated by some masses placed on a chain drive, a supplementary torque for driving a rotating tool. In addition, the paper details the dynamics of the system and exemplifies its benefits for a concrete example.

The main conclusions which can be drawn are as follows:

The torque developed by the device is constant, if the polygonal effect of the chain is neglected.
For the exemplified technical data, the device can generate a supplementation of the nominal torque with 54,3%.
The additional torque generated by the device is independent of the drive power, the system showing a higher efficiency as the nominal motor power decreases.
The torque produced by the system can be increased by raising the masses which are added to the chain, by increasing the radii of the chain wheels and by raising the driving speed.
If during the operation, appears suddenly an increase of the resisting torque at the working tool, the reaction moment that occurs at the motor is mitigated by this device, making the handling of the entire system easier.

As future research directions, the authors propose to:

Optimize the design so as to minimize the size of the device;
Build a prototype of the device and carry out tests trials;
Investigate how the additional moment, generated by the masses attached to the chain, is influenced, if the transmission ratio of the synchronous belt is different from 1

Author Contributions

Conceptualization, Z.I.K. and A.G.; methodology, F.B.; software, A.K; validation, Z.I.K. and A.G; formal analysis, S.T..; investigation, F.B.; resources, Z.I.K; data curation, A.K.; writing—original draft preparation, S.T.; writing—review and editing, Z.I.K.; visualization, A.K.; supervision, A.G.; project administration, Z.I.K. All authors have read and agreed to the published version of the manuscript.

Conflicts of Interest

The authors declare no conflicts of interest.

References

Halliday, D.; Resnick, R.; Walker, J. Fundamental of physics, 12th ed.; Wiley: New York, USA, 2021; pp. 101-131.
Colli, A.; Zanotti, A.; Giuseppe, G. Wind-tunnel experimental investigation on rotor-rotor aerodynamic interaction in compound helicopter configuration. Aerosp. Sci. Technol. 2024, 109420.
Gunaltili, E.; Ekici, S.; Kalkan, A.; Gocmen, F.E.; Kale, U.; Yilmazoglu, Z.; Karakoc, T.H. Conceptual design and optimization of a sustainable and environmentally friendly archetypal helicopter within the selection criteria and limitations, Heliyon 2023, 9(6).
Balli, O. Exergetic, sustainability and environmental assessments of a turboshaft engine used on helicopter, Energy 2023, 127593.
Castillo-Rivera, S.; Tomas-Rodriguez, M. Helicopter modelling and study of the accelerated rotor, Adv. Eng. Softw. 2018, 115, 52-65.
Surette, J. 5 reasons why the Boeing CH-47 'Chinook' helicopter is still going strong after six decades. Published Sep 26, 2023. Available online: https://simpleflying.com/boeing-ch-47-chinook-longevity-aspects-list/ (accessed on 28 July 2024).
Duan, D.; Leng, G.; Gao, J.; Feng, X.; Li, J. Load distribution strategy for multi-lift system with helicopters based on power consumption and robust adaptive game control. Chinese. J. Aeronaut. 2023, 36(4), 268-285.
Geng, J.Y.; Langelaan, J.W. Cooperative transport of a slung load using load-leading control. J. Guid. Control Dyn. 2020, 43,1313–1331.
Chopra, O; Ghose, D. Distributed control for multiple UAV transport of slung loads. In Proceedings of AIAA SCITECH 2022 Forum, San Diego, USA, 3-7 January 2022.
Mokhtar, T.; Soltan, T.; Abdelrahman, M.M. Helicopter performance enhancement by alleviating retreating blade stall using active flow control, Sci. Afr. 2023, 21, e01888.
Yu, D.; Che, T.; Zhang, H.; Li, C.; Wang,C.; Wang, Z. Optimizing terrestrial locomotion of undulating-fin amphibious robots: Asynchronous control and phase-difference optimization. Ocean Eng. 2024, 303, 117755.
Wu, J.; Yao, Y. Design and analysis of a novel walking vehicle based on leg mechanism with variable topologies. J. Mechanism and Machine Theory 2018, 128, 663–681.
Scales, J.; Coleman, D.; Brown, M. Multiday load carriage decreases ability to mitigate ground reaction force through reduction of ankle torque production, Appl. Ergon 2022, 101, 103717.
Chan, V.C.H.; Ross G.B.; Clouthier, A.L.; Fischer, S.L.; Graham, R.B. The role of machine learning in the primary prevention of work-related musculoskeletal disorders: A scoping review, Appl. Ergon 2022, 98, 103574.
Coulombe, M. Differential Displacement Device under Simultaneous and Repetitive Electromagnetic Repulsive Forces. US Patent No. 7909669, 10 May 2010.
Benjamin, P.M. Centrifugal Thrust Motor. US Patent No. 3750484, 7 August 1973.
Booden, J.D. Electromagnetically Actuated Thrust Generator. US Patent No. 5782134, 21 July 1998.
Cuff, C.I. Device for Converting Rotary Motion into Unidirectional Motio. US Patent No. 4095460, 20 June 1978.
Dobos. E. M. Propulsion Apparatus. US Patent No. 4579011, 1 April 1986.
Farrall, A.W. Inertial Propulsion Device. US Patent No. 3266233, 16 August 1966.
Fulop, C. Flywheel. US Patent No. 4788882, 6 December 1988.
Haller, P. Propulsion Apparatus. US Patent No. 3177660, 13 April 1965.
Kellogg, H.D. Gyroscopic Inertial Space Drive. US Patent No. 3203644,31 August 1965.
Mendez Llamozas, J.D. Direct Push Propulsion Unit. US Patent No. 2636340, 28 April 1953.
North, H. Apparatus for Producing a Force. US Patent No. 4712439, 15 December 1987.
Oades, R.A. Apparatus for Generating a Propulsion Force. US Patent No. 5890400, 6 April 1999.
Shimshi, E. Apparatus for Energy Transformation and Conservation. US Patent No. 5673872, 7 October 1997.
Schnur, N.J. Method and Apparatus for Propelling an Object by an Unbalanced Centrifugal Force with Continuous Motion. US Patent No. 3979961, 14 September 1976.
Deschamplain, D. Motion Imparting System. US Patent No. 6259177B1, 10 July 2001.
Marsh, R.O. Centrifugal Drive Machine. US Patent No. 5388470, 14 February 1995.
Murray, L.D. Mechanical Force Generator. US Patent No. 6290622B1, 18 September 2001.
Kunz, W.T. Centrifugal Propulsion System. US Patent No. 5937698, 17 August 1999.
Woltermg, H.M. Rotating Eccentric Weights Vibrator System. US Patent No. 5388469, 14 February 1995.
Dean, N.L. System for Converting Rotary Motion into Unidirectional Motion. US Patent No. 2886976, 19 May 1959.
Thornson, B.R. Apparatus for Developing Propulsion Force. US Patent No. 4631971, 30 December 1986.
Goncharevich, I.F. Dynamics of vibrational transportation. Nauka, Moscow, 1972; p. 244 [in Russian].
Gerocs, A.; Gillich, G.R.; Nedelcu, D.; Korka, Z.I. A Multibody Inertial Propulsion Drive with Symmetrically Placed Balls Rotating on Eccentric Trajectories. Symmetry 2020, 12, 1422.
Blekhman I.I., “Vibrational Mechanics: Nonlinear dynamic effects, General approach, Applications”, World Scientific, Singapore, 2000, p.15 and p.19.
Gerocs, A.; Korka, Z.I.; Biro, I.; Cojocaru, V. Analytical investigation of an inertial propulsion system using rotating masses. J. Phys.: Conf. Ser. 2020, 1426 012031.
Kononenko, V. O., Vibrating Systems with a Limited Power Supply. Iliffe Books Ltd: London, 1969, p.24 (in English). Translated from Russian: V. O. Kononenko, Oscillatory Systems with Limited Excitation. Moscow, Nauka, 1964.
Blekhman, I.I. Synchronization in Science and Technology. ASME Press: New York, 1988 (in English, translated from Russian).
Timofte, S.; Miclosina, C.O.; Cojocaru, V.; Gerocs, A.; Korka, Z.I. Inertial Propulsion of a Mobile Platform Driven by Two Eccentric Bodies. Appl. Sci. 2023, 13, 9511.
Majewski. T. Vibratory Forces and Synchronization in Physical Systems. Ingeniería Mecánica Tecnología y Desarrollo 2013, 4(4), 119 – 128.
Timofte, S.; Korka, Z.I.; Gerocs, A.; Wisznovszky, S.; Sfetcu, C.R. Kinematic and Dynamic Investigation of a Novel Inertial Propulsion Drive. Analecta Technica Szegedinensia 2022, 16(1), 27-32.

Figure 1. Construction of the proposed device.

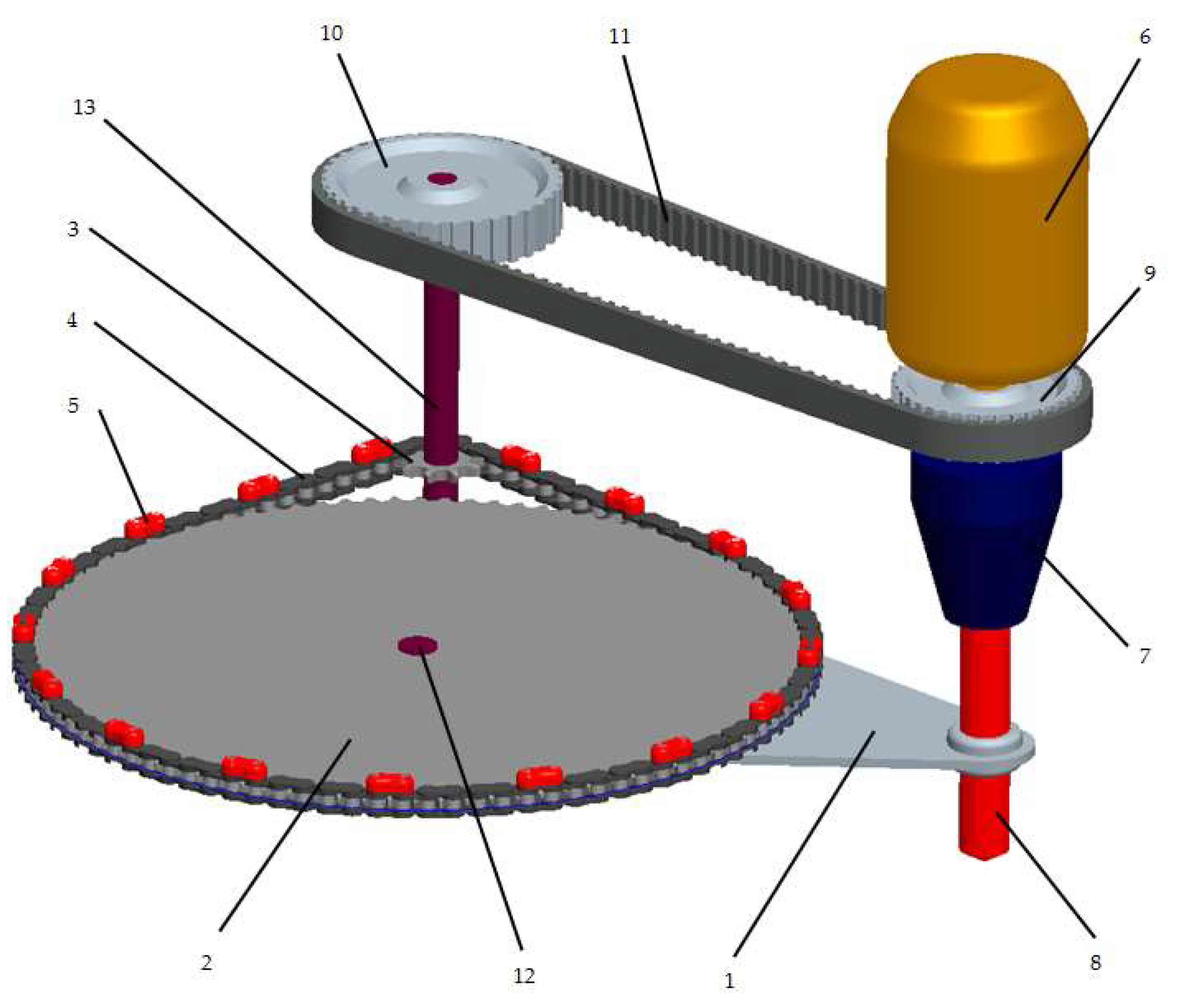
Figure 2. Simplified representation of the chain drive.

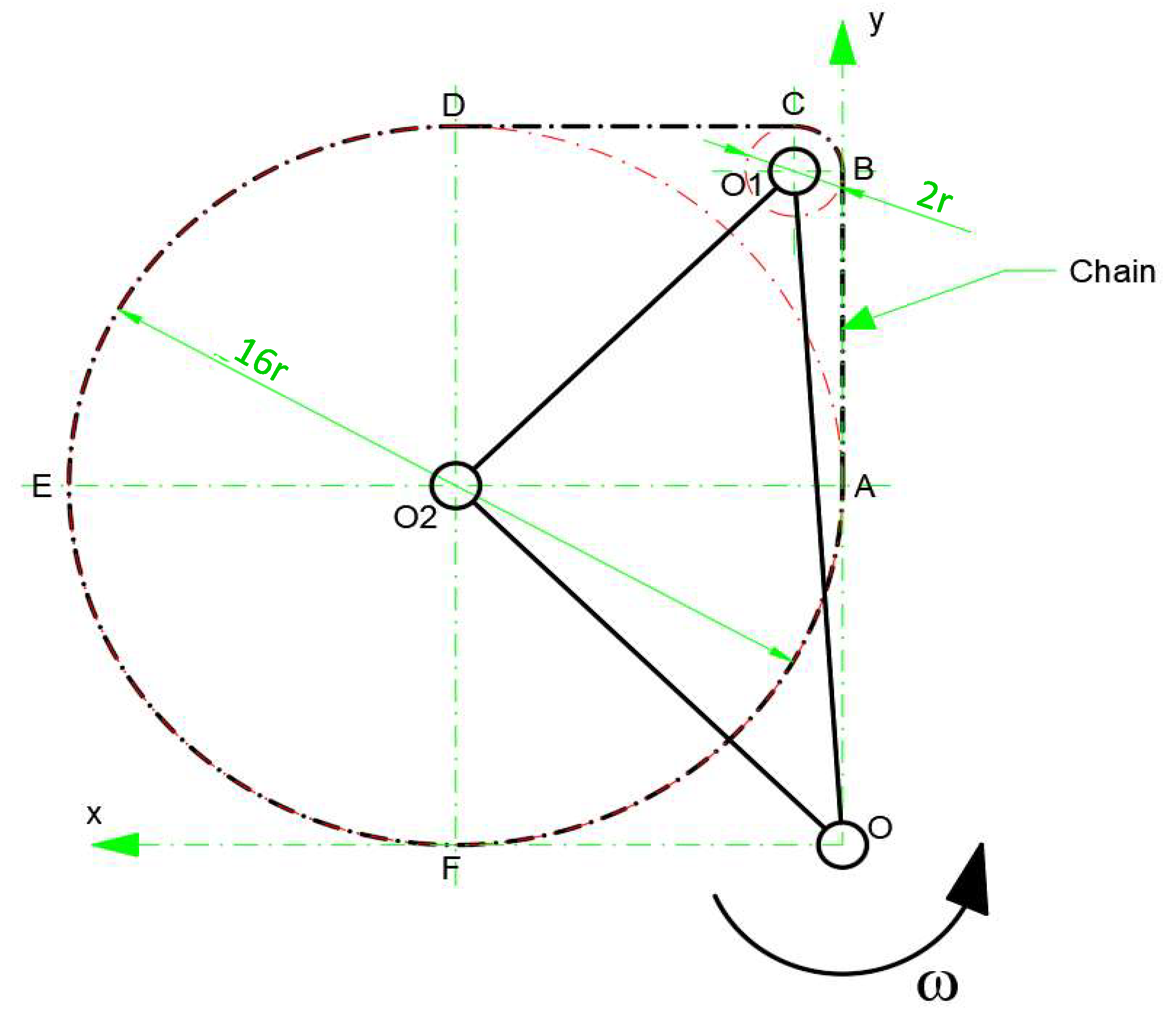
Figure 3. Calculation scheme of the gravity center radius for the circular section BC.

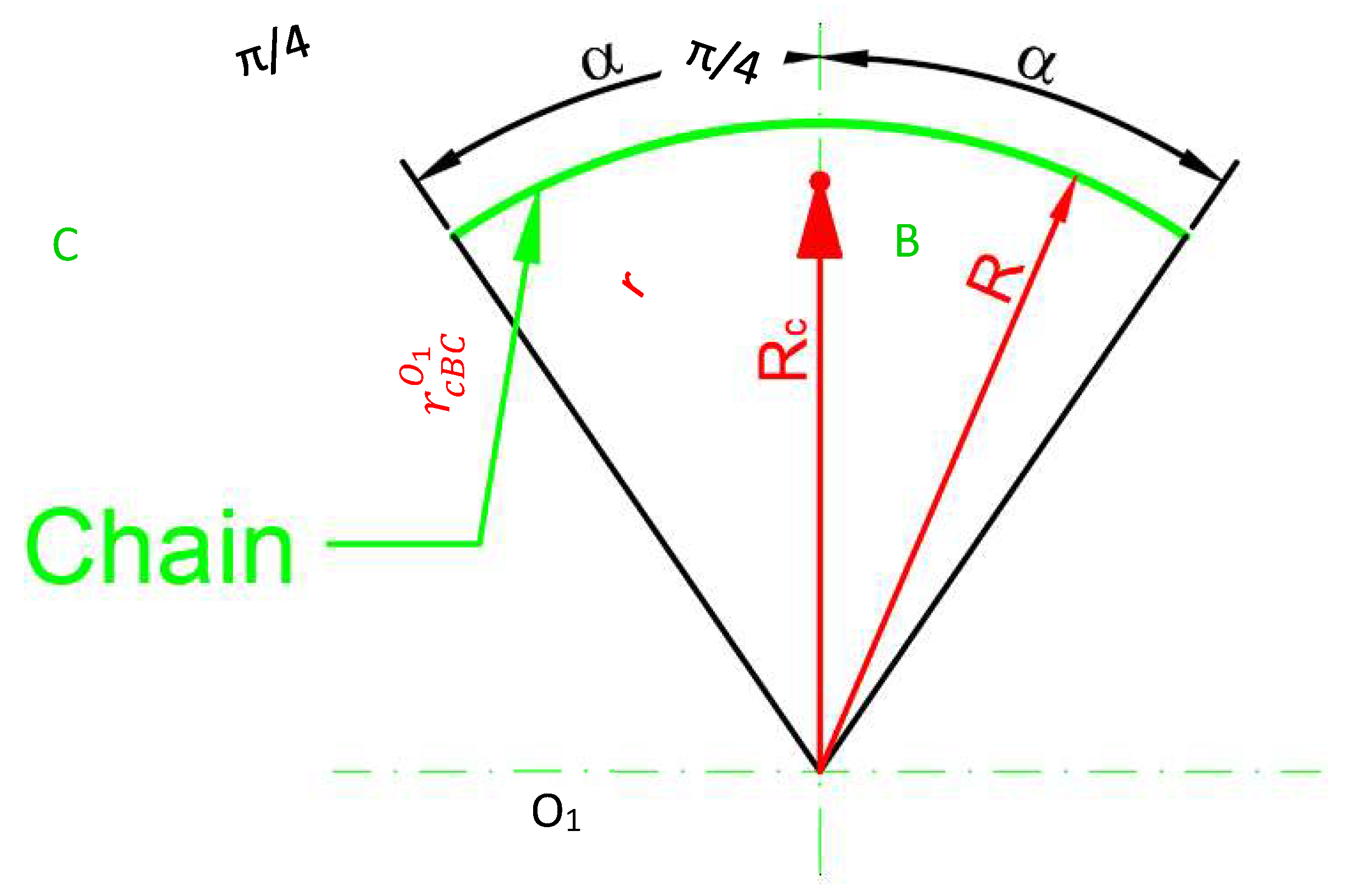
Figure 4. Location of the gravity centers for the different chain segments.

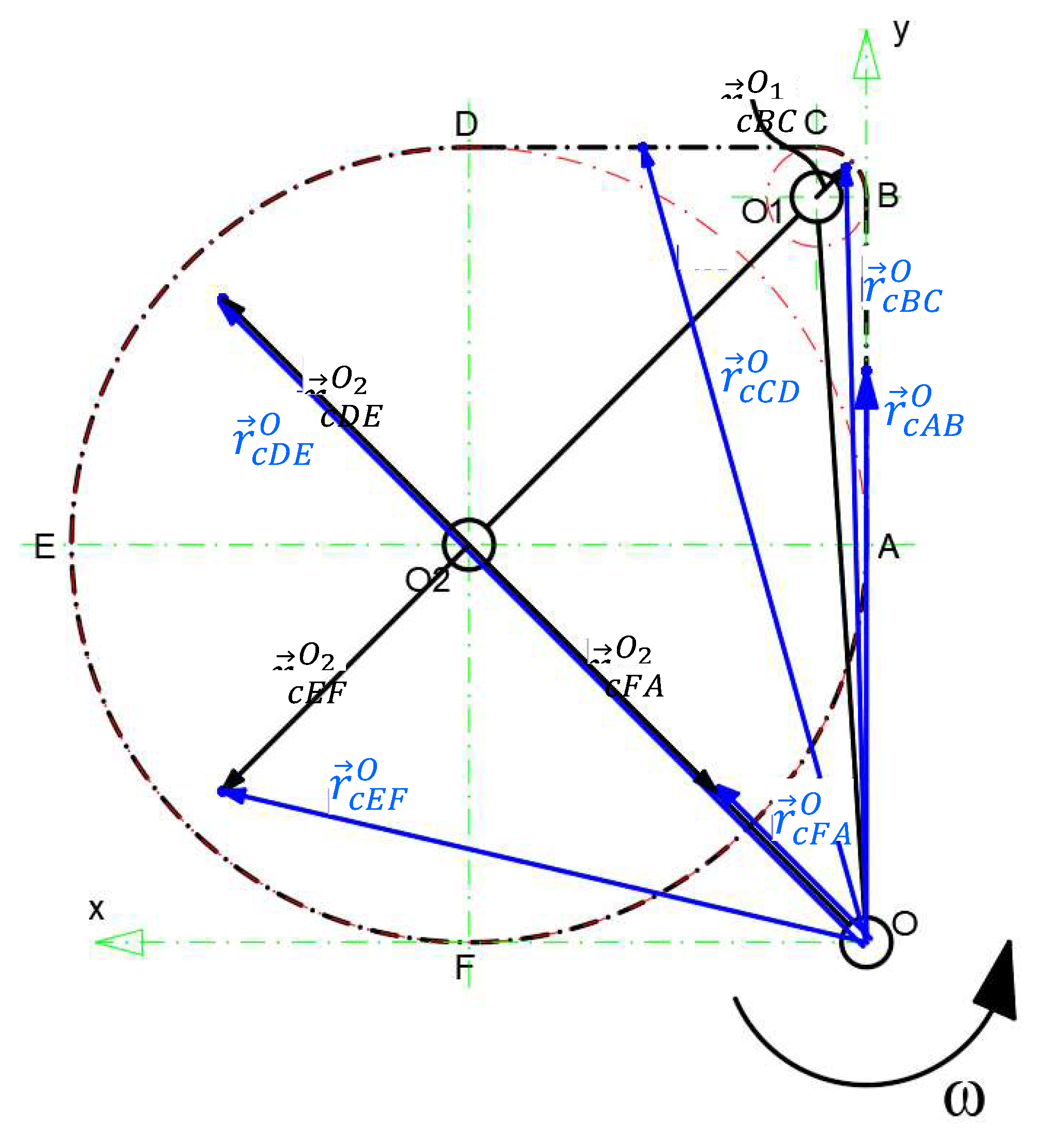
Figure 5. Centrifugal forces acting on the different chain segments.

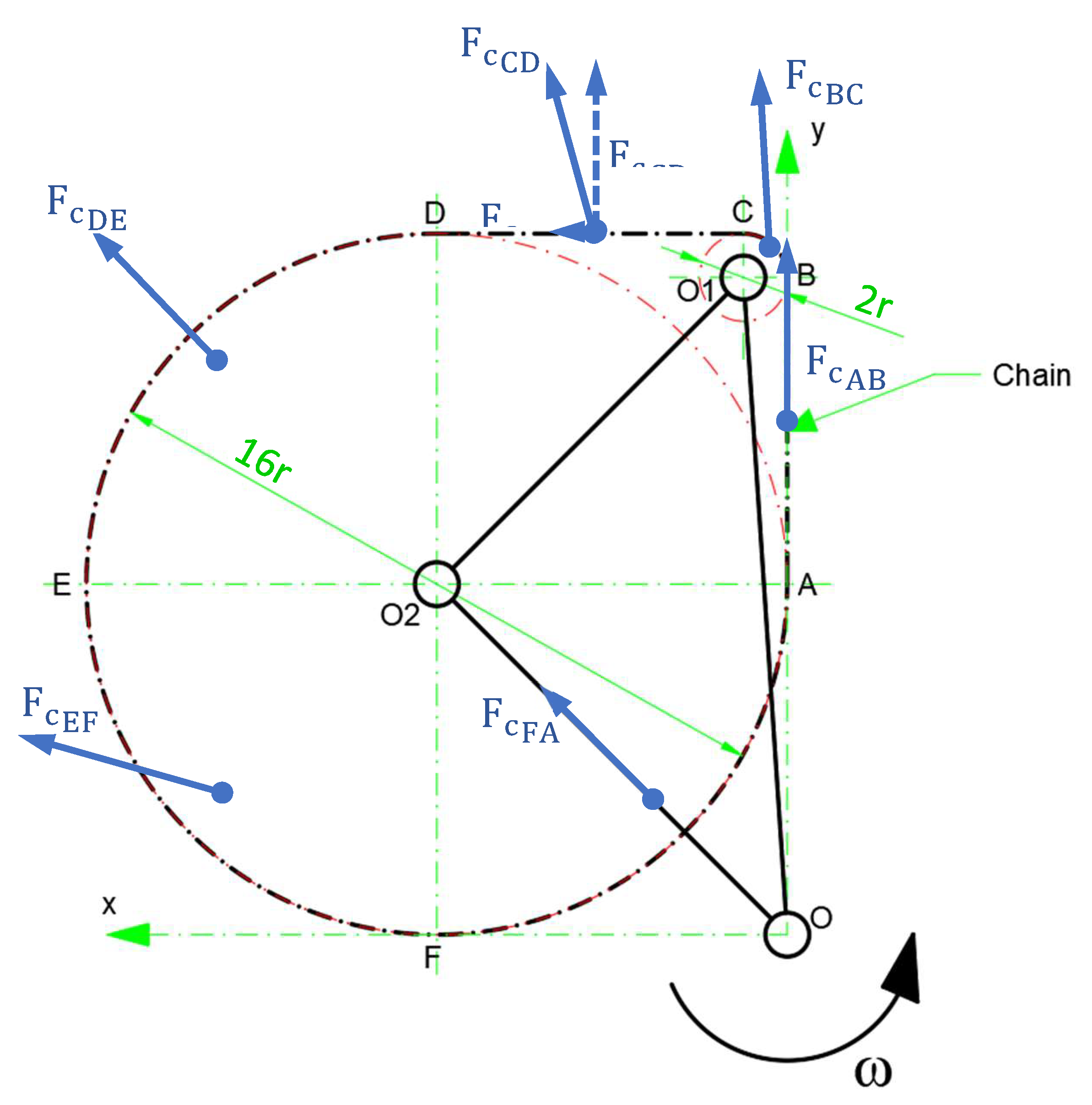
Figure 6. Forces induced in the rotation centers O₁ and O₂.

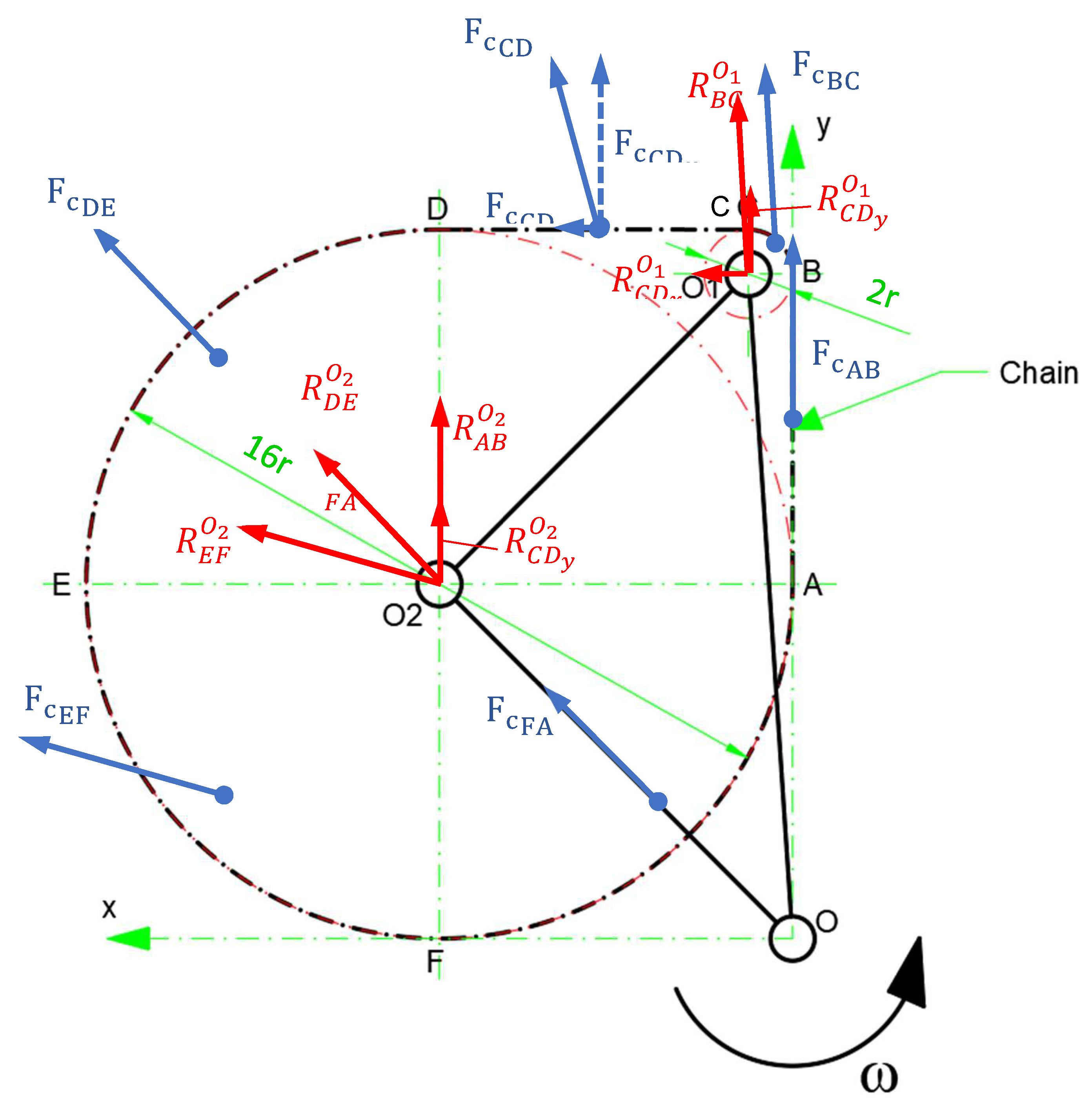
Table 1. Additional torques produced by the centrifugal forces.

Centrifugal force	Produced torque at the rotation point
Centrifugal force	O₁	O₂
${F_{c}}_{A B}$	0	${M_{A B}}_{O_{2}}$
${F_{c}}_{B C}$	${M_{B C}}_{O_{1}}$	0
${F_{c}}_{C D_{x}}$	${M_{C D}}_{O_{1}}$	0
${F_{c}}_{D E}$	0	0
${F_{c}}_{E F}$	0	${M_{E F}}_{O_{2}}$
${F_{c}}_{F A}$	0	0

Table 2. Technical data of the proposed device.

Technical data
Toll driving power	P= 500 [W]
Driving speed	n= 600 [min^-1]
Specific mass of the weights	$\bar{m} = 0.5 [k g / m]$
Radius of the small chain wheel	r= 0.05 [m]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Dynamic Computation of an Innovative Device for Reducing the Reaction Torque

Abstract

1. Introduction

2. Device Design and Principle of Operation

3. Analytical Computation of System Dynamics

4. Numerical Example and Discussion

5. Conclusions

Author Contributions

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe