A Decentralized Multi-authority Attribute-Based Encryption in eHealthcare

With the large-scale application of Internet of Things (IoT) in the medical field, eHealthcare has attracted wide attention. With the help of IoT devices, eHealthcare allows doctors to monitor patients’ health conditions and make recommendations accordingly. The addition of cloud computing greatly saves Healthcare Center’s (HC) computing resources. In order to provide privacy and fine-grained access control, Attribute-b ased encryption (ABE) is widely favored. HC usually operates multiple medical institutions in different regions, and each medical institution can be regarded as a attribute authority. Therefor, multi-authority (MA) ABE is usually concerned to encrypt the patient data. However for existing MA-ABE algorithms, the ciphertext is long and the efficiency of encryption and decryption is low. These problems will greatly increase the computing burden of patients and seriously affect the efficiency of data transmission. Hence we propose a decentralized key-policy MA-ABE in eHealthcare. The proposed algorithm can achieve decentralization, that is, it does not need central authority. Meanwhile, compared with existing MA-ABE algorithms, the length of ciphertext generated by our algorithm is shorter, and the efficiency of encryption and decryption is significantly improved. With the help of Java Pairing Based Cryptography, we carried out the experiments which show that our algorithm can effectively reduce the time required for encryption and decryption.

Keywords:

Subject: Computer Science and Mathematics - Computer Science

1. Introduction

Recent years, eHealthcare has attracted wide attention with the development of Internet of Things (IoT) technology. In eHealthcare applications, hospitals and other medical centers collect patients’ body temperature, blood pressure and other information through IoT devices, which are then transmitted to doctors. According to the transmitted information, doctors can determine the patient’s health status in time and give corresponding solutions. EHealthcare can monitor the patient’s physical condition in time, effectively ensuring people’s physical health. Especially in recent years, with the global epidemic of COVID-19, people are paying more attention to their own health. Thus the need for eHealthcare is more urgent.

Because of the large number of patients, healthcare center (HC) can not afford such a huge amount of data and calculation, so cloud servers are usually used in eHealthcare. Although the use of third-party cloud servers can effectively reduce the burden of computing and storing data, it also brings data security issues. Since cloud servers are provided by untrusted or semi-trusted third parties, these third parties can steal data during data transmission, which leads to the disclosure of patients’ privacy. Patients’ physical data and doctors’ diagnoses are important private data. Therefore, data must be encrypted to prevent third-party servers from obtaining data. At the same time, patients’ data should only be available to the patient’s attending physician and doctors in the corresponding department. Thus the encryption algorithm is supposed to implement fine-grained access control. Compared with traditional encryption algorithms, Attribute-based encryption (ABE) can encrypt data and realize fine-grained access control with less computing and storage resources, which has attracted extensive attention.

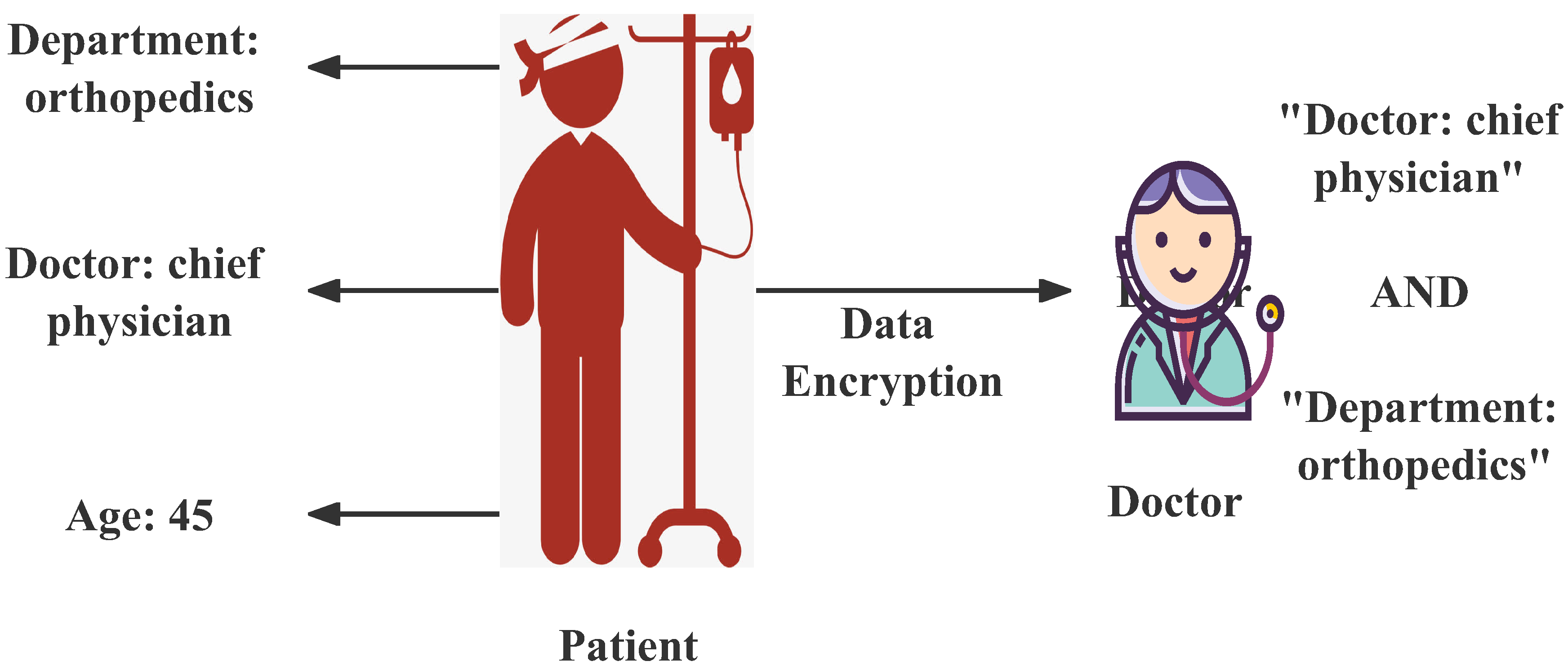
ABE is an algorithm developed from identity-based encryption (IBE)[1]. There are two kinds of ABE algorithms: Key-Policy Attribute-Based Encryption (KP-ABE)[2] and Ciphertext-Policy Attribute-Based Encryption (CP-ABE)[3]. In KP-ABE, attributes are embedded in ciphertext, and access policies are embedded in keys and sent to the user. In CP-ABE, on the contrary, attributes are embedded in keys, and access policies are embedded in ciphertext. In the eHealthcare scenario, if a patient wants to access eHealthcare’s services, he needs to obtain various physical data such as blood pressure and pulse through IoT devices. The patient needs to encrypt and send these data on time every day, just like updating logs, so that HC can judge patient’s health status in time. This data involves privacy, and the patient only wants legitimate users, such as his primary care doctor, to be able to decrypt the data. In order to properly arrange the authority of doctors, HC needs to assign the corresponding access authority, namely decryption key, to doctors equally according to their positions and departments. As long as the attributes of the patient data satisfy the doctor’s access rights, the doctor can decrypt the patient data and return a diagnosis. Obviously, KP-ABE fits perfectly into this encryption scenario.

Figure 1. KP-ABE in eHealthcare

In order to provide services to more patients, HC can open several medical facilities in different places. Patients may need to be diagnosed by a doctor in another area in order to receive better service. For unified management of patient attributes and physician permissions, each medical institution can be considered as an attribute authority responsible for assigning attributes and permissions to the region. Therefore, multiple attribute authorities are needed in ABE algorithm, that is, multi-authority ABE. Therefore, in eHealthcare applications, a multi-authority key-policy ABE (MA-KP-ABE) algorithm is necessary. In order to timely and accurately judge the patient’s physical condition, the patient needs to transmit the physical health data regularly. Due to the large amount of data transmitted and the limited computing resources of patients, MA-KP-ABE algorithm used in eHealthcare is supposed to reduce ciphertext size as much as possible and improve encryption efficiency. However, in recent years, MA-ABE algorithms mainly pay attention to improve the security of ABE algorithm and extend the function (e.g. revocable ABE and verifiable ABE). Existing algorithms do not meet the requirements of the eHealthcare scenario. Hence, an efficient and security MA-KP-ABE algorithm is very necessary.

1.1. Related Work

ABE is developed on the basis of IBE. In 2005, Sahai et al.[4] proposed fuzzy identities-based encryption, and their scheme allowed for a certain amount of error in identity in order to use biometrics as a user’s identity. Moreover, they first proposed the concept of ABE. In 2006, on the basis of fuzzy identiity-based encryption, the first practical KP-ABE was proposed by Goyal et al.[2]. At the same time, the concept of CP-ABE is also proposed in this article. In KP-ABE, attributes are embedded in ciphertext, and access policies are embedded in keys and sent to the user. Compared with the previous ABE algorithm, Goyal et al. introduced an access tree structure for access control. Based on the same access structure, Bethencour et al.[3] proposed the first CP-ABE algorithm in 2007, but their scheme was not security enough. It was considered unsafe in practical application. On this basis, Waters et al.[5] designed an efficient CP-ABE using LSSS access structure. Their scheme was proved to be selectively security without random oracles. In recent years, there are still many researches on ABE scheme[6,7,8,9,10].

When Sahai et al. proposed fuzzy identities-based encryption, they raised the open problem of whether the MA-ABE scheme could be constructed. Chase[11] solved this problem for the first time by implementing the construction of a MA-ABE scheme using the global identity and a central authority. Their scheme prevented collusion and tolerated corrupt authorities. But the addition of central authority actually violates the original intention of the MA-ABE scheme design. To avoid using central authority, Huang Lin et al.[12] realized a threshold MA-ABE scheme. But their algorithm can only resist the collusion of m (a pre-set parameter) users. When m is large, the system will be very inefficient. Chase et al.[13] further proposed a MA-ABE scheme. There is no need for central authority in their scheme. The security was higher than that of Huang Lin et al, but their algorithm required that authorities can communicate and transmit information with each other. Lewko et al.[14] proposed the decentralized MA-CP-ABE algorithm in 2011. Their algorithm did not require central authority and could resist the collusive attack of users. However, to achieve decentralization and better security, there are many deficiencies in ciphertext size and encryption and decryption efficiency. Li et al. proposed two different decentralized KP-ABE schemes in 2013[15] and 2015[16]. But all of their algorithms uses prime order bilinear group, can only achieve selective security. In the last few years, there are still a lot of studies on the multi-authority ABE scheme[17,18,19,20]. However, there is no security and decentralized efficient MA-KP-ABE scheme.

1.2. Motivation

Obviously, a MA-KP-ABE algorithm is suitable and necessary to protect data privacy for patients in eHealthcare. However, there is still no secure and efficient decentralized MA-KP-ABE algorithm. To meet the encryption and transmission requirements of large amounts of patients’ data in the preceding eHealthcare application scenarios, the MA-KP-ABE algorithm in eHealthcare is supposed to:

1.: not require any form of central authority. Because apparently there is no credible central authority for HC and patients in the cloud.
2.: achieve adaptive security. Because the data transferred in eHealthcare is the most significant privacy data, the security of the encryption algorithm is extremely important.
3.: achieve encryption and decryption efficiently. In order to improve transmission efficiency, reduce transmission and storage consumption. The algorithm is supposed to improve the efficiency of encryption and decryption.

1.3. Contribution

We propose a secure and effcient decentralized MA-KP-ABE algorithm.

1.: First, We propose a MA-KP-ABE algorithm suitable for eHealthcare. The algorithm does not require a central authority, so it can adapt to more complex scenarios
2.: Second, our proposed algorithm can resist collusive attacks and can achieve adaptive security.
3.: Finally, compared with existing algorithms, our MA-KP-ABE algorithm greatly reduces ciphertext size and improves the efficiency of encryption and decryption.

1.4. Organization

We introduce preliminaries in section 2. System model is introduced in the next section. According to our system model, we also give corresponding security assumptions. In Section 4, we describe construction of our MA-KP-ABE and prove the correct of the algorithm. Then we give security proof of the algorithm in detail according to the assumptions and definitions. In Section 6, we make a theoretical analysis and comparison between our and the existing algorithms. Then we conducted the experiment and presented the results in detail. We made a summary in Section 7.

2. Preliminaries

We introduce the mathematics and cryptography preliminaries required for algorithm in this section.

2.1. Composite Order Bilinear Groups

In order to achieve higher security, we choose to use bilinear map in composite order bilinear groups as the foundation to construct our algorithm. The definitions can be described as follows.

1.: $G_{1}$ and $G_{3}$ are composite order bilinear groups of order N where $N = p_{1} p_{2} p_{3}$ . $p_{1}$ , $p_{2}$ and $p_{3}$ are three distinct primes.
2.: e is a bilinear map defined in $G_{1} \times G_{1} \to G_{3}$ . e satisfies the basic property of bilinear maps. That is, for $\forall x, y \in G_{1}$ and $\forall u, v \in Z_{N}$ , we have $e (x^{u}, y^{v}) = e {(x, y)}^{u v}$ .
3.: Let g is a generator of $G_{1}$ . Then we have $e (g, g)$ is also a generator of $G_{3}$ .

If e,

G_{1}

and

G_{3}

satisfy the above conditions, then we have composite order bilinear groups

G_{1}

and

G_{3}

and bilinear map e. Similarly, if the order N of the multiplication cycle group G and

G_{T}

satisfies the above conditions, we can also prove that the bilinear map e is computable. In the following paper, we use

G = (G_{1}, G_{T}, p_{1}, p_{2}, p_{3}, N = p_{1} p_{2} p_{3}, e)

to represent bilinear groups and map generated by randomly selected parameters as defined above.

Then we introduce the properties and assumptions required in algorithm design and security proof. First we introduce definition of the notation which we need to use in the description of the properties and assumptions. In this paper,

G_{p_{1}}

G_{p_{2}}

G_{p_{3}}

respectively denote subgroups of order

p_{1}

p_{2}

p_{3}

G_{1}

. Similarly, we let

G_{p_{1} p_{2}}

G_{p_{2} p_{3}}

G_{p_{1} p_{3}}

donate subgroups of order

p_{1} p_{2}

p_{2} p_{3}

p_{1} p_{3}

in G. It should be noted that for a composite bilinear group

G_{1}

, the subgroups satisfy the orthogonal property. That is,

\forall x_{i} \in G_{p_{i}}, y_{j} \in G_{p_{i}}, i = 1, 2, 3

, we have

e (x_{i}, y_{j}) = 1 .

In assumptions, we use

g_{i} \overset{R}{\leftarrow} G_{p_{i}}

to represent choosing a random generator

g_{i}

G_{p_{i}}

in which

i = 1, 2, 3

and

T \overset{R}{\leftarrow} G_{1}

to represent choosing a random generator T of

G_{1}

. Our algorithm is based on composite order bilinear groups, and the security proof of the algorithm is based on some complexity assumptions. Lewko et al.[21] uses these assumptions to implement comp safe IBE and HIBE algorithms, while Lewko[14] uses these assumptions to implement a decentralized MA-ABE. These assumptions have been proven to be safe, and we can directly use these assumptions to prove our MA-KP-ABE. We give detail description of the assumption below.

Assumption 1. For

G = (G_{1}, G_{3}, p_{1}, p_{2}, p_{3}, N = p_{1} p_{2} p_{3}, e)

, we define elements as follows:

G = (N = p_{1} p_{2} p_{3}, G_{1}, G_{3}, e),

g \overset{R}{\leftarrow} G_{p_{1}}, X_{3} \overset{R}{\leftarrow} G_{p_{3}}

U = (G, g, X_{3}),

T_{1} \overset{R}{\leftarrow} G_{p_{1} p_{2}}, T_{2} \overset{R}{\leftarrow} G_{p_{1}}

. Assume there is an algorithm

S

. We define

A d v 1_{G, S} (λ) : = | P r [S (U, T_{1}) = 1] - P r [S (U, T_{2}) = 1] |

Definition 1.For any polynomial-time algorithm

S

, if

A d v 1_{G, S} (λ)

is negligible. Then we can say that

G

satisfies Assumption 1.

Assumption 2. For

G = (G_{1}, G_{3}, p_{1}, p_{2}, p_{3}, N = p_{1} p_{2} p_{3}, e)

, we define elements as follows:

G = (N = p_{1} p_{2} p_{3}, G_{1}, G_{3}, e),

g, X_{1} \overset{R}{\leftarrow} G_{p_{1}}, X_{2}, Y_{2} \overset{R}{\leftarrow} G_{p_{2}}, X_{3}, Y_{3} \overset{R}{\leftarrow} G_{p_{3}},

U = (G, g, X_{1} X_{2}, X_{3}, Y_{2} Y_{3}),

T_{1} \overset{R}{\leftarrow} G_{1}, T_{2} \overset{R}{\leftarrow} G_{p_{1} p_{3}} .

Assume there is an algorithm

S

. We define

A d v 2_{G, S} (λ) : = | P r [S (U, T_{1}) = 1] - P r [S (U, T_{2}) = 1] |

Definition 2.For any polynomial-time algorithm

S

, if

A d v 2_{G, S} (λ)

is negligible. Then we can say that

G

satisfies Assumption 2.

Assumption 3. For

G = (G_{1}, G_{3}, p_{1}, p_{2}, p_{3}, N = p_{1} p_{2} p_{3}, e)

, we define elements as follows:

G = (N = p_{1} p_{2} p_{3}, G_{1}, G_{3}, e),

α, s \overset{R}{\leftarrow} Z_{n}, g \overset{R}{\leftarrow} G_{p_{1}}, X_{2}, Y_{2}, Z_{2} \overset{R}{\leftarrow} G_{p_{2}}, X_{3} \overset{R}{\leftarrow} G_{p_{3}},

U = (G, g, g^{α} X_{2}, X_{3}, g^{s} Y_{2}, Z_{2}),

T_{1} \overset{R}{\leftarrow} e {(g, g)}^{α s}, T_{2} \overset{R}{\leftarrow} G_{3} .

Assume there is an algorithm

S

. We define

A d v 3_{G, S} (λ) : = | P r [S (U, T_{1}) = 1] - P r [S (U, T_{2}) = 1] |

Definition 3.For any polynomial-time algorithm

S

, if

A d v 3_{G, S} (λ)

is negligible. Then we can say that

G

satisfies Assumption 3.

2.2. Access Structure

Generally speaking, the access structure used in ABE includes tree, threshold and LSSS. In this paper, we choose

(t, n)

threshold as access structure. Let

{X_{1}, X_{2}, \dots, X_{n}}

be the set of attributes and

1 \leq t \leq n

. If an attribute set

A^{u}

of a user satisfies a

(t, n)

threshold, that is to say

t \leq | A^{u} \cap {X_{1}, X_{2}, \dots, X_{n}} | \leq n

2.3. MA-KP-ABE

A MA-KP-ABE includes the following five algorithms. In addition, we use K to represent the amount of attribute authorities. Each attribute is monitored by one of K attribute authorities which means there are K disjoint attribute sets. But we note that an additional attribute authorities can be added to the scheme at any time which is similarly with Chase’s scheme in 2007.

System setup $(λ) \to G P$ . Setup stage should be run by a trusted part which random chooses $λ$ and computes the public parameters $G P$ .
Attribute authority setup $(G P) \to P K_{A}, S K_{A}$ . Each attribute authority k takes $G P$ as input and generates $P K_{A}$ and $S K_{A}$ .
Key generation $(G P, G I D, {d_{k}}, {i}, S K_{A}) \to D_{k, i}$ . For an attribute authority k, define $A_{k}$ as the attribute set of all attributes handled by k. $d_{k}$ is a threshold which satisfies $1 \leq d_{k} \leq | A_{k} |$ . k runs the algorithm which takes public parameters $G P$ , a user’s $G I D$ , $d_{k}$ , attribute i belong to k and secret key $S K_{A}$ of k as input. Key generation step eventually generates a unique secret key for each user.
Encryption $(M, G P, {A_{k}^{c}}, P K_{A}) \to C$ . Define $A_{k}^{c}$ as the attribute set of ciphertext attributes handled by k. The sender takes the message M, $G P$ , attribute set $A_{k}^{c}$ and public key $P K_{A}$ of k as input. After the Encryption phase, the plaintext to be transmitted is encrypted into ciphertext C.
Decryption $(C, {d_{k}}, {D_{k, i}}, {A_{k}^{c}}, {A_{k}^{u}}, G P) \to M$ . Like $A_{k}^{c}$ , we also define $A_{k}^{u}$ in the same way where u represent a user. For every attribute authority k, if $| A_{k}^{u} \cap A_{k}^{c} | \geq d_{k}$ , the user (receiver) takes the ciphertext C as input and decrypt the corresponding M.

2.4. Security Definition

The security definition of a MA-KP-ABE can be described as a game between an adversary

A

and a challenge.

Setup. The adversary $A$ sends the corrupted attribute authorities list and good attribute authorities list respectively to the challenger. Let $A A^{'}$ be set of the corrupted authorities and $A A$ be set of good authorities. Let $A^{C}$ be the attributes set of all $A A^{'}$ and $A A$ .

The challenger generates $G P$ , $P K_{A}$ , and $S K_{A}$ . Then the challenger sends $G P$ , $P K_{A}$ of $A A$ , $P K_{A}$ of the corrupted attribute authorities $A A^{'}$ and $S K_{A}$ of the corrupted attribute authorities $A A^{'}$ to $A$ .
Phase 1. $A$ makes queries for the secret key. For a $G I D$ , the challenger generate corresponding secret key and send them to $A$ . There are two limits in the query process. First, $A$ can not get enough key to decrypt the challenge ciphertext. Second, $A$ can not query an attribute authority twice for the same $G I D$ .
Challenge. $A$ selects two message $M_{0}$ and $M_{1}$ and send to the challenger. The challenger random chooses one of the messages $M_{b}$ and encrypt $M_{b}$ for attribute sets $A^{C}$ . Then the challenger sends the ciphertext to $A$ .
Phase 2. $A$ makes more queries as query phase 1.
Guess After receive the ciphertext, $A$ guess which message has been encrypted and outputs a $b^{'}$ . We define the advantage of the adversary as $P r [b = b^{'}] - \frac{1}{2}$ .

Definition 5.A MA-KP-ABE scheme is selective secure if there exists a polynomial time function has a negligible advantage in this security game.

3. System Model

According to the application scenario we proposed, we propose the system model in eHealthcare in our system. Furthermore, we give the security assumptions of the system.

3.1. System Model

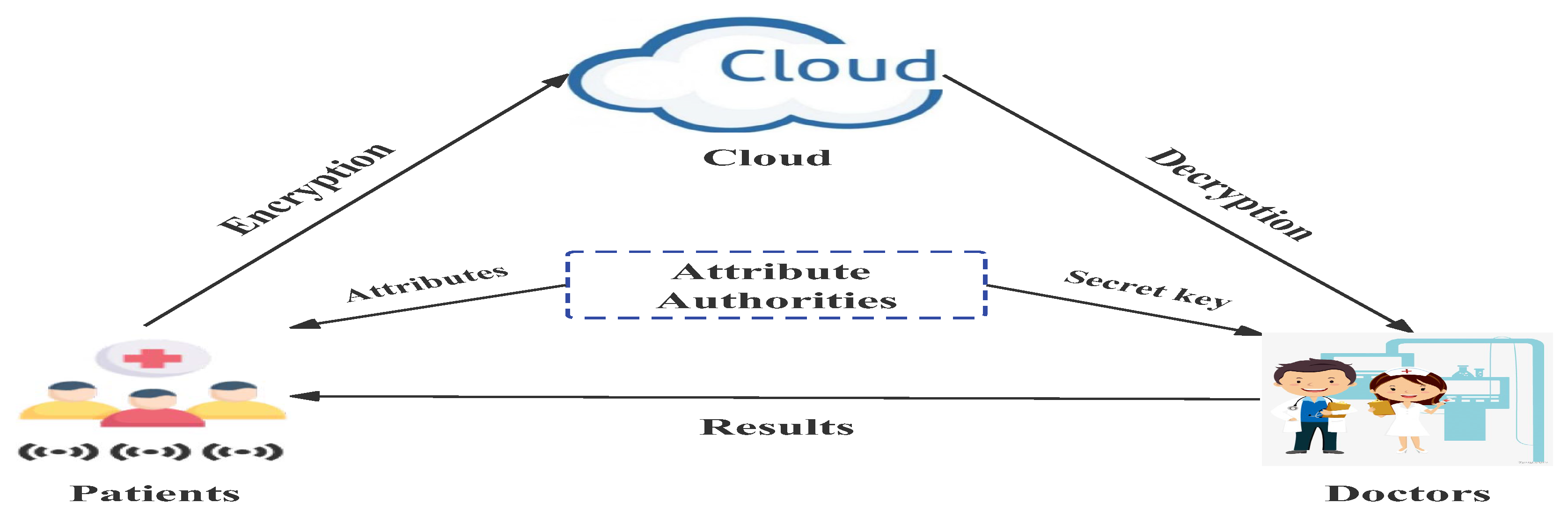
The overall structure of the system is shown in Fig.2, which includes Patients, Attribute Authorities, Cloud, and Doctors.

Figure 2. eHealthcare system model

1.: Patients: In our system, patients use IoT devices to collect their physical data (like temperature, blood pressure and so on). Patient send the encrypted data to Cloud for storage. Due to the need for timely and accurate judgment of patients’ physical conditions, data need to be uploaded at regular intervals. Hence, the amount of data that needs to be passed is quite a large number. In addition, we consider that patients are completely credible.
2.: Attribute Authorities: Attribute authorities are the most critical part of our system, responsible for managing the attributes of each patient and generating keys for each doctor. As patients and doctors belong to multiple department management, there are multiple system authorities in our system. All system authorities are responsible for managing their own attributes and there is no central attribute authority.
3.: Cloud: In our system, the cloud is responsible for receiving the data transmitted by the patient and sending it to the doctor. And the cloud stores the data for a certain amount of time so that it can be checked later. Because cloud services are provided by third parties, the cloud is not fully trusted.
4.: Doctors: In our system, doctors are data users. Doctors receive encrypted patients’ data from the Cloud. Doctors have different access rights and corresponding private keys depending on their position and department. Doctors can decrypt data using their secret keys.

3.2. Security Assumptions

In order to more accurately represent the security of our system model and the proposed algorithm, we put forward some security assumptions and give corresponding explanations.

1.: Patients are fully completely credible, while Attribute Authorities are also trusted entities. We assume that attribute authorities are independent of each other and cannot communicate with each other. This allows our system to be used in more demanding scenarios.
2.: Because Cloud are provided by third-party cloud providers, it is considered semi-credible in most research work. In this paper, we use the same assumption. That is, Cloud will try to decrypt and steal patients’ data while delivering patients’ data. Therefore, encryption algorithms need to prevent the cloud from decrypting patient data
3.: We make the worst assumptions about Doctors. That is, Doctors only diagnose patients and return results. A doctor can try, alone or in collusion with other doctors, to gain access to patients’ data that their own keys cannot decrypt. This assumption requires that encryption algorithms be resistant to collusion attack.

4. Construction

We introduce our MA-KP-ABE based on bilinear groups and give correctness proof of our algorithm in this section.

4.1. Construction of Proposed Scheme

System setup $(λ) \to G P$ . We use groups $G_{1}$ and $G_{3}$ and bilinear map e defined in Section 2. Fix generator $g_{1} \in G_{p_{1}}$ and $g_{3} \in G_{p_{3}}$ . System also chooses a hash function $H : {0, 1}^{*} \to G_{p_{3}}$ , so the hash function H maps the global ID $G I D$ of users to the elements of $G_{p_{3}}$ . Set the global parameters:

$G P = (e, N, g_{1}, g_{3}, H) .$
Attribute authority setup $(G P) \to P K_{A}, S K_{A}$ .For an attribute authority k, define $A_{k}$ as the attribute set of all attributes handled by k. Fix a random exponent $y_{k} \in Z_{N}$ and choose random $t_{k, i}, r_{k, i} \in Z_{N}$ for $\forall i \in A_{k}$ . Then calculate $Y_{k} = e {(g_{1}, g_{1})}^{y_{k}}$ , $T_{k, i} = g_{1}^{t_{k, i}}$ and $R_{k, i} = g_{3}^{r_{k, i}}$ . Set the secret key of k as:

$S K_{A} = (y_{k}, t_{k, i}, r_{k, i} \forall i \in A_{k}) .$

Set the public key of k as:

$P K_{A} = (Y_{k}, T_{k, i}, R_{k, i} \forall i \in A_{k}) .$
Key generation $(G P, G I D, {d_{k}}, {i}, S K_{A}) \to D_{k, i}$ . For each k, $A_{k}$ is the attribute set of attributes handled by k and $d_{k}$ is a threshold which satisfies $1 \leq d_{k} \leq | A_{k} |$ . For attribute i of user u belonging to k, k random choose a $d_{k} - 1$ degree polynomial p which $p_{k} (0) = y_{k}$ . The secret key of u for attribute i which belongs to attribute authority k is set as:

$D_{k, i} = g_{1}^{\frac{p_{k} (i)}{t_{k, i}}} H {(G I D_{u})}^{\frac{1}{r_{k, i}}} .$
Encryption $(M, G P, {A_{k}^{c}}, P K_{A}) \to C$ . Define $A_{k}^{c}$ as the attribute set of all attributes handled by k in the ciphertext. Choose random $s \in Z_{N}$ . For a message M, the patient computes

$E = M • \prod_{k = 1}^{K} Y_{k}^{s} = M e {(g_{1}, g_{1})}^{s \sum_{k = 1}^{K} y_{k}}$

Random choose K polynomials $q_{1}, q_{2}, \dots, q_{K}$ whose degree are respectively $d_{1}, d_{2}, \dots, d_{K}$ and let $q = q_{1} + q_{2} + \dots + q_{K}$ where $q (0) = q_{1} (0) + q_{2} (0) + \dots + q_{K} (0) = 0$ . For $\forall k$ and $\forall i \in A_{k}^{c}$ , compute

$E_{k, i} = T_{k, i}^{s} R_{k, i}^{q (i)} .$

So the ciphertext of M is:

$C = (E, E_{k, i} \forall i \in A_{k}^{c}, \forall k)$
Decryption $(C, {d_{k}}, {D_{k, i}}, G P) \to M$ . Define $A_{k}^{u}$ as the attribute set of all the properties of u that are handled by k. For every k, if $| A_{k}^{u} \cap A_{k}^{c} | \geq d_{k}$ , compute:

$e (D_{k, i}, E_{k, i}), i \in A_{k}^{u} \cap A_{k}^{c}$

Then according to Lagrange interpolation polynomial, user u gets $Y = e {(g_{1}, g_{1})}^{s \sum_{k = 1}^{K} y_{k}} = \prod_{k = 1}^{K} Y_{k}^{s}$ . Then u computes:

$M = \frac{E}{Y} .$

4.2. Proof of Correctness

If attribute sets of user u satisfies the access policy, that is to say, for every attribute authority k, let

| A_{k}^{u} \cap A_{k}^{c} | \geq d_{k}

. We assume that

H (G I D_{u}) = g_{3}^{i d}

\begin{matrix} e (D_{k, i}, E_{k, i}) & = e (g_{1}^{\frac{p_{k} (i)}{t_{k, i}}} H {(G I D_{u})}^{\frac{1}{r_{k, i}}}, T_{k, i}^{s} R_{k, i}^{q_{k} (i)}) \\ = e (g_{1}^{\frac{p_{k} (i)}{t_{k, i}}}, T_{k, i}^{s} R_{k, i}^{q_{k} (i)}) e (H {(G I D_{u})}^{\frac{1}{r_{k, i}}}, T_{k, i}^{s} R_{k, i}^{q_{k} (i)}) \end{matrix}

As we introduced in preliminaries,

g_{1}

g_{3}

are generator of

G_{p_{1}}

and

G_{p_{3}}

, so

e (g_{1}, g_{3}) = e (g_{3}, g_{1}) = 1

. Then we have

\begin{matrix} e (g_{1}^{\frac{p_{k} (i)}{t_{k, i}}}, T_{k, i}^{s} R_{k, i}^{q_{k} (i)}) & = e (g_{1}^{\frac{p_{k} (i)}{t_{k, i}}}, g_{1}^{s t_{k, i}}) e (g_{1}^{\frac{p_{k} (i)}{t_{k, i}}}, g_{3}^{q_{k} (i) r_{k, i}}) \\ = e {(g_{1}, g_{1})}^{\frac{p_{k} (i)}{t_{k, i}} s t_{k, i}} \\ = e {(g_{1}, g_{1})}^{p_{k} (i) s} \end{matrix}

and

\begin{matrix} e (H {(G I D_{u})}^{\frac{1}{r_{k, i}}}, T_{k, i}^{s} R_{k, i}^{q_{k} (i)}) & = e (g_{3}^{\frac{i d}{r_{k, i}}}, g_{1}^{s t_{k, i}}) e (g_{3}^{\frac{i d}{r_{k, i}}}, g_{3}^{q_{k} (i) r_{k, i}}) \\ = e {(g_{3}, g_{3})}^{\frac{i d}{r_{k, i}} q_{k} (i) r_{k, i}} \\ = e {(g_{3}, g_{3})}^{q_{k} (i) i d} \end{matrix}

Finally, we can get

e (D_{k, i}, E_{k, i}) = e {(g_{1}, g_{1})}^{p_{k} (i) s} e {(g_{3}, g_{3})}^{q_{k} (i) i d} .

Because

| A_{k}^{u} \cap A_{k}^{c} | \geq d_{k}

, according to Lagrange interpolation polynomial, we can interpolate to find

e {(g_{1}, g_{1})}^{p (0) s}

for every attribute authority k and

e {(g_{3}, g_{3})}^{q (0) i d}

\begin{matrix} \prod_{k = 1}^{K} \prod_{i \in A_{k}^{u} \cap A_{k}^{c}} {(e (D_{k, i}, E_{k, i}))}^{▵_{k, i} (0)} \\ = & \prod_{k = 1}^{K} \prod_{i \in A_{k}^{u} \cap A_{k}^{c}} {(e {(g_{1}, g_{1})}^{p_{k} (i) s} e {(g_{3}, g_{3})}^{q_{k} (i) i d})}^{▵_{k, i} (0)} \\ = & \prod_{k = 1}^{K} \prod_{i \in A_{k}^{u} \cap A_{k}^{c}} (e {(g_{1}, g_{1})}^{▵_{k, i} (0) p_{k} (i) s} e {(g_{3}, g_{3})}^{▵_{k, i} (0) q_{k} (i) i d}) \\ = & \prod_{k = 1}^{K} e {(g_{1}, g_{1})}^{p_{k} (0) s} \prod_{k = 1}^{K} e {(g_{3}, g_{3})}^{q_{k} (0) i d} \\ = & \prod_{k = 1}^{K} e {(g_{1}, g_{1})}^{y_{k} s} \prod_{k = 1}^{K} e {(g_{3}, g_{3})}^{q_{k} (0) i d} \\ = & e {(g_{1}, g_{1})}^{s \sum_{k = 1}^{K} y_{k}} e {(g_{3}, g_{3})}^{i d \sum_{k = 1}^{K} q_{k} (0)} \\ = & e {(g_{1}, g_{1})}^{s \sum_{k = 1}^{K} y_{k}} e {(g_{3}, g_{3})}^{q (0) i d} \\ = & e {(g_{1}, g_{1})}^{s \sum_{k = 1}^{K} y_{k}} \\ = & \prod_{k = 1}^{K} Y_{k}^{s} \end{matrix}

According to above equations, we prove the correctness of our MA-KP-ABE.

5. Proof of Security

We prove our MA-KP-ABE algorithm by employing the technique in [14]. In the dual system encryption technique, there are two additional structures we need define before beginning our proof. These two additional structures will not be used in real ABE encryption, but they will help with our proof of security.

Semi-functional Ciphertext. Let $g_{2}$ be the generator of $G_{p_{2}}$ . Assume that $C = (E, E_{k, i} \forall i \in A_{k}^{c}, \forall k)$ is a normal ciphertext, where $E_{k, i} = T_{k, i}^{s} R_{k, i}^{q (i)}$ . Choose random $α_{i} \in Z_{N}$ , then we set semi-functional ciphertexts as:

$C^{'} = (E^{'} = E, E_{k, i}^{'} = E_{k, i} g_{2}^{α_{i}}) .$
Semi-functional Key. Let $g_{2}$ be the generator of $G_{p_{2}}$ . Assume that $D_{k, i} = g_{1}^{\frac{p (i)}{t_{k, i}}} H {(G I D_{u})}^{\frac{1}{r_{k, i}}} .$ is a normal key for user u. Choose random $β_{i} \in Z_{N}$ , then we set semi-functional keys as :

$D_{k, i}^{'} = D_{k, i} g_{2}^{β_{i}}$

Now we have normal key $D_{k, i}$ , normal ciphertext C, semi-functional key $D_{k, i}^{'}$ and semi-functional ciphertext $C^{'}$ . It is obviously that $D_{k, i}^{'}$ can decrypt C for

\begin{matrix} e (D_{k, i}^{'}, c) & = e (D_{k, i} g_{2}^{β_{i}}, E_{i}) \\ = e (D_{k, i}, E_{i}) e (g_{2}^{β_{i}}, E_{i}) \\ = e (D_{k, i}, E_{i}) \end{matrix}

and

D_{k, i}

can decrypt

C^{'}

for

\begin{matrix} e (D_{k, i}, E_{i}^{'}) & = e (D_{k, i}, E_{i} g_{2}^{α_{i}}) \\ = e (D_{k, i}, E_{i}) e (D_{k, i}, g_{2}^{α_{i}}) \\ = e (D_{k, i}, E_{i}) . \end{matrix}

but

D_{k, i}^{'}

can not decrypt

C^{'}

. In the process of proof, we need to ensure that simulator should not distinguish

D_{k, i}

and

D_{k, i}^{'}

by decrypting semi-functional ciphertexts. We define the nominally semi-functional key: the key is a semi-functional key but can decrypt semi-functional ciphertexts successfully. In our scheme, when

\forall α_{i}, α_{i} = 0

, we have

\begin{matrix} e (D_{k, i}^{'}, E_{i}^{'}) & = e (D_{k, i} g_{2}^{β_{i}}, E_{i} g_{2}^{α_{i}}) \\ = e (D_{k, i}, E_{i}) e (D_{k, i}, g_{2}^{α_{i}}) e (g_{2}^{β_{i}}, E_{i}) e {(g_{2}, g_{2})}^{α_{i} β_{i}} \\ = e (D_{k, i}, E_{i}) . \end{matrix}

We will define a sequence of games in the following. Using the hybrid argument combined by the sequence of games defined below and assumptions in Section 2, we can prove the security of our scheme.

G a m e_{r e a l}

is a real game defined as Section 2.

G a m e_{0}

is a real game except that all ciphertexts given by simulator of

G a m e_{0}

are semi-functional.

G a m e_{K}

is a real game except that the first K keys of

G a m e_{K}

are semi-functional and all ciphertexts given by simulator of

G a m e_{K}

are semi-functional. We assume that q is the number of requests the attack makes, then

G a m e_{q}

is a real game except that all keys and all ciphertexts given by simulator of

G a m e_{0}

are semi-functional. It is obviously that

G a m e_{0}

and

G a m e_{q}

are two special cases of

G a m e_{K}

G a m e_{f i n a l}

is like

G a m e_{q}

except that the ciphertext is a semi-functional encryption of a random message.

Lemma 1. Suppose there exists a polynomial algorithm

A

such that

G a m e_{r e a l} A d v_{A} - G a m e_{0} A d v_{A} = ϵ

. Then we can build a polynomial algorithm

B

with advantage

ϵ

in breaking Assumption 1.

Proof.

B

first receive g, T,

X_{3}

. According to the value of T,

B

will simulate

G a m e_{r e a l}

G a m e_{0}

with

A

Setup $B$ first sets up the system. It sets $g_{1} = g, g_{3} = X_{3}$ and choose $H : {0, 1}^{*} \to G_{p_{3}}$ . $B$ has

$G P = (e, N, g, X_{3}, H) .$

$B$ sends $G P$ to $A$ . Then $B$ sets attribute authority. Random choose exponent $y_{k} \in Z_{N}$ and $t_{k, i}, r_{k, i} \in Z_{N}$ for $\forall i \in A_{k}$ . Then calculate $Y_{k} = e {(g, g)}^{y_{k}}$ , $T_{k, i} = g^{t_{k, i}}$ and $R_{k, i} = X_{3}^{r_{k, i}}$ . $B$ computes secret key

$S K_{A} = (y_{k}, t_{k, i}, r_{k, i} \forall i \in A_{k})$

and public key

$P K_{A} = (Y_{k}, T_{k, i}, R_{k, i} \forall i \in A_{k}) .$

We let k denote the good attribute authorities and $\bar{k}$ denote the corrupted attribute authorities. $B$ sends $A$ $P K_{A}$ for all $k \in K$ and $P K_{A}, S K_{A}$ for all $\bar{k} \in K$ .
Phase 1 For a user u with $G I D^{u}$ the adversary $A$ queries, $B$ generates corresponding secret key. As we introduced in Section 3, $B$ choose a random $d_{k} - 1$ degree polynomial p for attribute i of u belonging to k, and sets the secret key as:

$D_{k, i}^{u} = g^{\frac{p_{k} (i)}{t_{k, i}}} X_{3}^{\frac{i d}{r_{k, i}}} .$
Challenge $A$ sends two message $M_{0}$ and $M_{1}$ to $B$ . $B$ random chooses one of the messages $M_{b}$ and encrypt $M_{b}$ for attribute sets $A^{C}$ . To form the ciphertext, $B$ first sets:

$E = M_{b} e {(g, T)}^{\sum_{k = 1}^{K} y_{k}} .$

Then for good attribute authority k, $B$ sets:

$E_{k, i} = T^{t_{k, i}} X_{3}^{r_{k, i} q (i)}$

and for corrupted attribute authority $\bar{k}$ , $B$ sets:

$E_{k, i} = g^{s t_{k, i}} X_{3}^{r_{k, i} q (i)}$

. So the ciphertext is

$C = (E, E_{k, i} \forall i \in A_{k}^{c}, \forall k) .$

Two cases can be discussed next. First, if $T \in G_{p_{1} p_{2}}$ , then C is a semi-functional ciphertext with $r_{k, i} = α_{i}$ . $r_{k, i} mod p_{2}$ is not correlated with $α_{i} mod p_{1}$ , so this is properly distributed. If $T \in G_{p_{1}}$ , C is a normal ciphertext. So Lemma 1 holds.

Lemma 2. Suppose there exists a polynomial algorithm

A

such that

G a m e_{K - 1} A d v_{A} - G a m e_{K} A d v_{A} = ϵ

. Then we can build a polynomial algorithm

B

with advantage

ϵ

in breaking Assumption 2.

Proof.

B

first receive

g, X_{1} X_{2}, X_{3}, Y_{2} Y_{3}, T

. According to the value of T,

B

will simulate

G a m e_{K - 1}

G a m e_{K}

with

A

Setup $B$ first sets up the system. It sets $g_{1} = g, g_{3} = X_{3}$ and choose $H : {0, 1}^{*} \to G_{p_{3}}$ . $B$ has

$G P = (e, N, g, X_{3}, H) .$

$B$ sends $G P$ to $A$ . Then $B$ sets attribute authority. Random choose exponent $y_{k} \in Z_{N}$ and $t_{k, i}, r_{k, i} \in Z_{N}$ for $\forall i \in A_{k}$ . Then calculate $Y_{k} = e {(g, g)}^{y_{k}}$ , $T_{k, i} = g^{t_{k, i}}$ and $R_{k, i} = X_{3}^{r_{k, i}}$ . $B$ computes secret key

$S K_{A} = (y_{k}, t_{k, i}, r_{k, i} \forall i \in A_{k})$

and public key

$P K_{A} = (Y_{k}, T_{k, i}, R_{k, i} \forall i \in A_{k}) .$

We let k denote the good attribute authorities and $\bar{k}$ denote the corrupted attribute authorities. $B$ sends $A$ $P K_{A}$ for all $k \in K$ and $P K_{A}, S K_{A}$ for all $\bar{k} \in K$ .
Phase 1 For a user u with $G I D^{u}$ the adversary $A$ queries, $B$ generates corresponding secret key. For first $K - 1$ keys $A$ queries, $B$ generates and sends semi-functional keys. Hence, $B$ choose a random $d_{k} - 1$ degree polynomial p for attribute i of u belonging to k, and sets the secret key as:

$D_{k, i}^{u} = g^{\frac{p_{k} (i)}{t_{k, i}}} {(Y_{2} Y_{3})}^{\frac{i d}{r_{k, i}}} .$

It is obviously that $i d$ and $r_{k, i} mod p_{2}$ and $r_{k, i} mod p_{3}$ are uncorrelated. So this is a properly distributed semi-functional key with $g_{2}^{β_{i}} = Y_{2}^{\frac{i d}{r_{k, i}}}$ . For the $K^{t h}$ key $A$ queries, $B$ choose random m which $g^{m}$ is equal to the $G_{p_{1}}$ part of T and generates secret key as:

$D_{k, i}^{u} = g^{{\frac{p_{k} (i)}{g}}^{- m \frac{i d}{r_{k, i}}} t_{k, i}} T^{\frac{i d}{r_{k, i}}} .$

For last key $A$ queries, $B$ generates secret key as:

$D_{k, i}^{u} = g^{\frac{p_{k} (i)}{t_{k, i}}} X_{3}^{\frac{i d}{r_{k, i}}} .$
Challenge $A$ sends two message $M_{0}$ and $M_{1}$ to $B$ . $B$ random chooses one of the messages $M_{b}$ and encrypt $M_{b}$ for attribute sets $A^{C}$ . To form the ciphertext, $B$ first sets:

$E = M_{b} e {(g, T)}^{\sum_{k = 1}^{K} y_{k}} .$

Then for good attribute authority k, $B$ sets:

$E_{k, i} = T^{t_{k, i}} X_{3}^{r_{k, i} q (i)}$

and for corrupted attribute authority $\bar{k}$ , $B$ sets:

$E_{k, i} = g^{s t_{k, i}} X_{3}^{r_{k, i} q (i)}$

. So the ciphertext is

$C = (E, E_{k, i} \forall i \in A_{k}^{c}, \forall k) .$

If $T \in G_{1}$ , then $B$ has properly simulated $G a m e_{k - 1}$ . If $T \in G_{p_{1} p_{3}}$ , then $B$ has properly simulated $G a m e_{k}$ . Hence, Lemma 2 holds.

Lemma 3. Suppose there exists a polynomial algorithm

A

such that

G a m e_{q} A d v_{A} - G a m e_{f i n a l} A d v_{A} = ϵ

. Then we can build a polynomial algorithm

B

with advantage

ϵ

in breaking Assumption 3.

Proof.

B

first receive

g, g^{α} X_{2}, X_{3}, g^{s} Y_{2}, Z_{2}, T

. According to the value of T,

B

will simulate

G a m e_{q}

G a m e_{f i n a l}

with

A

Setup $B$ first sets up the system. It sets $g_{1} = g, g_{3} = X_{3}$ and choose $H : {0, 1}^{*} \to G_{p_{3}}$ . $B$ has

$G P = (e, N, g, X_{3}, H) .$

$B$ sends $G P$ to $A$ . Then $B$ sets attribute authority. Random choose exponent $y_{k} \in Z_{N}$ and $t_{k, i}, r_{k, i} \in Z_{N}$ for $\forall i \in A_{k}$ . Then calculate $Y_{k} = e {(g, g)}^{y_{k}}$ , $T_{k, i} = g^{t_{k, i}}$ and $R_{k, i} = X_{3}^{r_{k, i}}$ . $B$ computes secret key

$S K_{A} = (y_{k}, t_{k, i}, r_{k, i} \forall i \in A_{k})$

and public key

$P K_{A} = (Y_{k}, T_{k, i}, R_{k, i} \forall i \in A_{k}) .$

We let k denote the good attribute authorities and $\bar{k}$ denote the corrupted attribute authorities. $B$ sends $A$ $P K_{A}$ for all $k \in K$ and $P K_{A}, S K_{A}$ for all $\bar{k} \in K$ .
Phase 1 For a user u with $G I D^{u}$ the adversary $A$ queries, $B$ generates corresponding semi-functional secret key. $B$ choose a random $d_{k} - 1$ degree polynomial p for attribute i of u belonging to k, and random $c_{i} \in Z_{N}$ , then sets the semi-functional secret key as:

$D_{k, i}^{u} = g^{\frac{p_{k} (i)}{t_{k, i}}} Z_{2}^{c_{i}} X_{3}^{\frac{i d}{r_{k, i}}} .$
Challenge $A$ sends two message $M_{0}$ and $M_{1}$ to $B$ . $B$ random chooses one of the messages $M_{b}$ and encrypt $M_{b}$ for attribute sets $A^{C}$ . To form the ciphertext, $B$ first sets:

$E = M_{b} e {(g, T)}^{\sum_{k = 1}^{K} y_{k}} .$

Then for good attribute authority k, $B$ sets:

$E_{k, i} = T^{t_{k, i}} X_{3}^{r_{k, i} q (i)}$

and for corrupted attribute authority $\bar{k}$ , $B$ sets:

$E_{k, i} = g^{s t_{k, i}} X_{3}^{r_{k, i} q (i)}$

. So the ciphertext is

$C = (E, E_{k, i} \forall i \in A_{k}^{c}, \forall k) .$

It is obviously that

$\prod_{k = 1}^{K} Y_{k}^{s} = \prod_{k = 1}^{K} e {(g, g)}^{s y_{k}} = \prod_{k = 1}^{K} e {(g^{α} X_{2}, g)}^{s y_{k}^{'}}$

$= \prod_{k = 1}^{K} e {(g, g)}^{s α y_{k}^{'}} = e {(g, g)}^{α s} .$

This implicitly sets $r_{k, i} = α_{i}$ . $r_{k, i} mod p_{2}$ is not correlated with $α_{i} mod p_{1}$ , so this is properly distributed. If $T = e {(g, g)}^{α s}$ , C is a normal ciphertext. If T is a random element of $G_{3}$ , then C is a semi-functional ciphertext with a random message. Hence, Lemma 3 holds.

Theorem 1. If Assumptions 1, 2, and 3 hold, then our ABE scheme is secure.

6. Efficiency

In this section, we demonstrate the efficiency of our algorithm in detail from two aspects of theoretical analysis and experimental verification.

We first make a theoretical analysis of our algorithm and existing algorithms. Table 1. shows whether the scheme is decentralized, what access structure the scheme uses, the ciphertext size, encryption cost and decryption cost. In Table 1, we use

n_{1}

n_{2}

, and

n_{3}

to represent the number of encryption attributes, decryption attributes, and attribute authorities. In addition, we use L to represent the size of group

G_{1}

and

G_{3}

, E to represent modular exponents in the group

G_{1}

and

G_{3}

, and P to represent bilinear pairs.

In Table 1, compared with the first MA-ABE [11], the encryption and decryption efficiency of our algorithm is lower than [11]. But our scheme is decentralized and doesn’t require any trusted central authority. In eHealthcare, decentralization is essential because there is no trusted third party. Moreover, our scheme can achieve adaptive security. Compared with other multi-authority ABE algorithms, our proposed algorithm has the smallest ciphertext and the lowest encryption and decryption consumption. The ciphertext size of our algorithm is

(n_{1} + 1) L

, which is basically the same as the ciphertext size of the algorithm proposed by Rahulamathavan et al.[17], and smaller than that of algorithm [14,16,20]. In the encryption cost column, the encryption cost of our algorithm is only

(2 n_{1} + n_{3}) E

. That means our algorithm doesn’t require bilinear pair operation P which is the most computationally intensive operation. Therefore, compared with other algorithms, our algorithm has the highest encryption efficiency at present. Because encryption is done by patients with limited computing resources, efficient encryption makes our algorithm more suitable for eHealthcare application scenarios. In addition, the decryption efficiency of our algorithm is also the highest among the algorithms in the table, which can also effectively reduce the computational burden of HC. algorithm

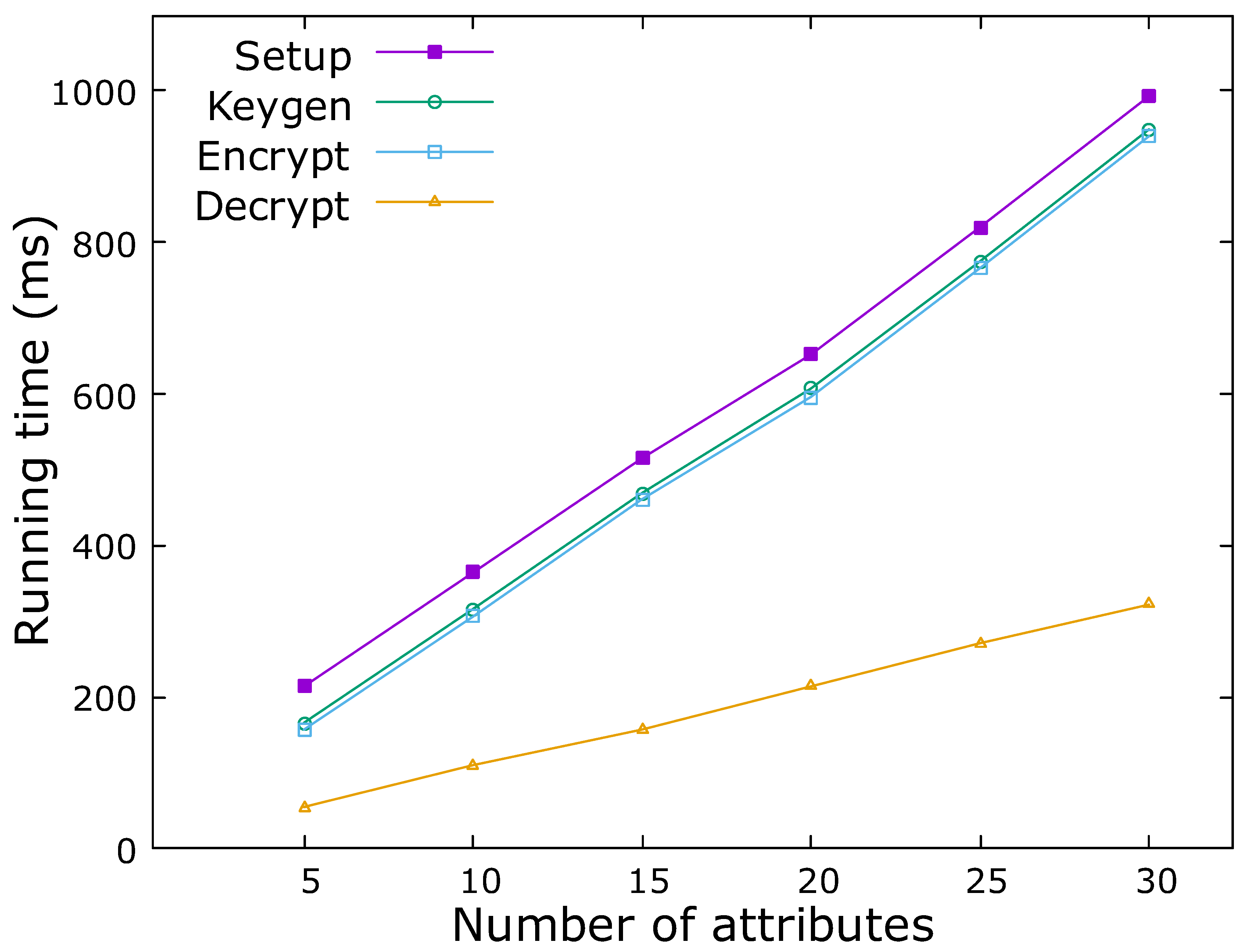
Figure 3. Our proposed MA-KP-ABE

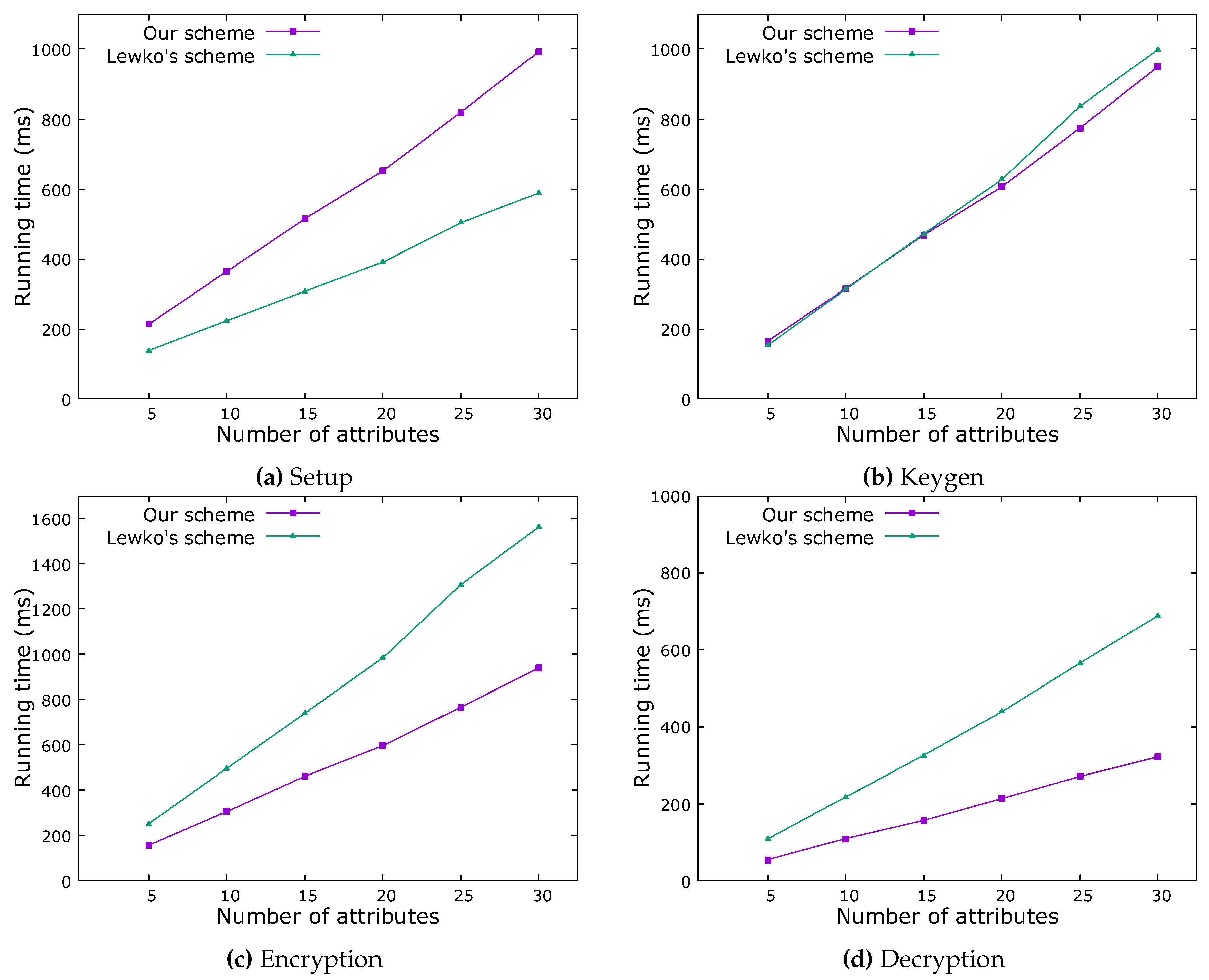
Figure 4. Comparison between our MA-KP-ABE and Lewko’ scheme

In order to show the superiority of our algorithm more intuitively, we implement Lewko’ scheme and our scheme. Both algorithms can realize adaptive security and are decentralized multi-authority ABE algorithms. The experiments are executed on Intel(R) Core(TM) i5-12500H, 2.50 GHz. With the help of Java Pairing Based Cryptography (JPBC) library, we implement our algorithm. We choose type A1 curves of JPBC library with 3 160-bit primes. Each experiment is repeated 1000 times, and the data presented is the average of the 1000 experiments.

We put the running time of each part in the same diagram to show the efficiency of each part more clearly in Fig. 3. Among the four parts, the Setup stage takes the most time, but the Setup stage only needs one time. The eHealthcare system only needs to generate public parameters at the beginning and send them to all attribute authorities. The calculations required to transfer data include only encryption and decryption operations. Therefore, the Setup stage has little effect on the efficiency of the whole algorithm.

The remaining four figures show comparison of each stage between our MA-KP-ABE and Lewko’s scheme. We use the scheme we proposed as the basis, implementing Lewko’s scheme to achieve encryption and decryption under the same access strategy and the same plaintext. Fig. 4 shows that our algorithm is slightly less efficient than Lewko’s in the Setup stage. In the Keygen stage, our algorithm runs in almost the same time as Lewko’s algorithm. But as we explained above, the calculations required to transfer data include only encryption and decryption operations. As shown in Fig. 6 and Fig. 7, the encryption and decryption running time of our algorithm is much lower than Lewko’s algorithm. This greatly improves data transfer efficiency, which is critical in eHealthcare scenarios where large amounts of data are transferred.

7. Conclusions

EHealthcare is an application field that has received wide attention at present. To protect the security of patients’ data in eHealthcare, we propose a MA-KP-ABE algorithm in this paper. Our algorithm is decentralized and can achieve adaptive security. Compared with related multi-authority ABE algorithms, our proposed algorithm greatly reduces ciphertext size, improves the efficiency of encryption and decryption, and reduces the storage space needed for ciphertext. Experiments show that our algorithm is the most efficient decentralized MA-KP-ABE algorithm at present. Therefore, in the eHealthcare, our algorithm significantly improves the data transmission efficiency between the patient, HC and cloud server, while providing patients’ data protection and fine-grained access.

Author Contributions

Conceptualization, Zhe liu. and Jian Wang; methodology, Jian Wang; software, Shenqing Wang; validation, Shenqing Wang; formal analysis, Chunpeng Ge; investigation, Shenqing Wang; resources, Shenqing Wang; data curation, Shenqing Wang; writing—original draft preparation, Shenqing Wang; writing—review and editing, Chunpeng Ge; visualization, Shenqing Wang; supervision, Shenqing Wang; project administration, Chunpeng Ge; funding acquisition, Chunpeng Ge.

Funding

This work was supported by the National Key R&D Program of China (2020YFB1005902), the National Natural Science Foundation of China (62076125, 62032025, U20B2049, U20B2050, U21A20467, 61702236, 6207020639), the Key R& D Program of Guangdong Province (2020B0101090002), the Natural Science Foundation of Jiangsu Province (BK20200418, BE2020106), the Guangdong Basic and Applied Basic Research Foundation (2021A1515012650), and the Shenzhen Science and Technology Program (JCYJ20210324134810028, JCYJ20210324134408023).

Conflicts of Interest

The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.

References

Boneh, D.; Franklin, M. Identity-based encryption from the Weil pairing. Annual international cryptology conference. Springer, 2001, pp. 213–229.
Goyal, V.; Pandey, O.; Sahai, A.; Waters, B. Attribute-based encryption for fine-grained access control of encrypted data. Proceedings of the 13th ACM conference on Computer and communications security, 2006, pp. 89–98.
Bethencourt, J.; Sahai, A.; Waters, B. Ciphertext-policy attribute-based encryption. 2007 IEEE symposium on security and privacy (SP’07). IEEE, 2007, pp. 321–334.
Sahai, A.; Waters, B. Fuzzy identity-based encryption. Annual international conference on the theory and applications of cryptographic techniques. Springer, 2005, pp. 457–473.
Waters, B. Ciphertext-policy attribute-based encryption: An expressive, efficient, and provably secure realization. International Workshop on Public Key Cryptography. Springer, 2011, pp. 53–70.
Zhang, Y.; Chen, X.; Li, J.; Wong, D.S.; Li, H. Anonymous attribute-based encryption supporting efficient decryption test. Proceedings of the 8th ACM SIGSAC symposium on Information, computer and communications security, 2013, pp. 511–516.
Hohenberger, S.; Waters, B. Attribute-based encryption with fast decryption. International workshop on public key cryptography. Springer, 2013, pp. 162–179.
Kapadia, A.; Tsang, P.P.; Smith, S.W. Attribute-Based Publishing with Hidden Credentials and Hidden Policies. NDSS, 2007, Vol. 7, pp. 179–192.
Nishide, T.; Yoneyama, K.; Ohta, K. Attribute-based encryption with partially hidden encryptor-specified access structures. International conference on applied cryptography and network security. Springer, 2008, pp. 111–129.
Rouselakis, Y.; Waters, B. Practical constructions and new proof methods for large universe attribute-based encryption. Proceedings of the 2013 ACM SIGSAC conference on Computer & communications security, 2013, pp. 463–474.
Chase, M. Multi-authority attribute based encryption. Theory of cryptography conference. Springer, 2007, pp. 515–534.
Lin, H.; Cao, Z.; Liang, X.; Shao, J. Secure threshold multi authority attribute based encryption without a central authority. International Conference on Cryptology in India. Springer, 2008, pp. 426–436.
Chase, M.; Chow, S.S. Improving privacy and security in multi-authority attribute-based encryption. Proceedings of the 16th ACM conference on Computer and communications security, 2009, pp. 121–130.
Lewko, A.; Waters, B. Decentralizing attribute-based encryption. Annual international conference on the theory and applications of cryptographic techniques. Springer, 2011, pp. 568–588.
Li, Q.; Xiong, H.; Zhang, F.; Zeng, S.; others. An expressive decentralizing kp-abe scheme with constant-size ciphertext. Int. J. Netw. Secur. 2013, 15, 161–170.
Li, Q.; Ma, J.; Li, R.; Xiong, J.; Liu, X. Large universe decentralized key-policy attribute-based encryption. Security and communication Networks 2015, 8, 501–509. [CrossRef]
Rahulamathavan, Y.; Veluru, S.; Han, J.; Li, F.; Rajarajan, M.; Lu, R. User collusion avoidance scheme for privacy-preserving decentralized key-policy attribute-based encryption. IEEE Transactions on Computers 2015, 65, 2939–2946. [CrossRef]
Yang, Y.; Chen, X.; Chen, H.; Du, X. Improving privacy and security in decentralizing multi-authority attribute-based encryption in cloud computing. IEEE Access 2018, 6, 18009–18021. [CrossRef]
Susilo, W.; Yang, G.; Guo, F.; Huang, Q. Constant-size ciphertexts in threshold attribute-based encryption without dummy attributes. Information Sciences 2018, 429, 349–360.
Yan, X.; Ni, H.; Liu, Y.; Han, D. Privacy-preserving multi-authority attribute-based encryption with dynamic policy updating in PHR. Computer Science and Information Systems 2019, 16, 831–847. [CrossRef]
Lewko, A.; Okamoto, T.; Sahai, A.; Takashima, K.; Waters, B. Fully secure functional encryption: Attribute-based encryption and (hierarchical) inner product encryption. Annual International Conference on the Theory and Applications of Cryptographic Techniques. Springer, 2010, pp. 62–91.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

A Decentralized Multi-authority Attribute-Based Encryption in eHealthcare

Abstract

1. Introduction

1.1. Related Work

1.2. Motivation

1.3. Contribution

1.4. Organization

2. Preliminaries

2.1. Composite Order Bilinear Groups

2.2. Access Structure

2.3. MA-KP-ABE

2.4. Security Definition

3. System Model

3.1. System Model

3.2. Security Assumptions

4. Construction

4.1. Construction of Proposed Scheme

4.2. Proof of Correctness

5. Proof of Security

6. Efficiency

7. Conclusions

Author Contributions

Funding

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe