Prerpints.org logo
Preprint
Article

drGAT: Attention-Guided Gene Assessment of Drug Response Utilizing a Drug-Cell-Gene Heterogeneous Network

Altmetrics

Downloads

81

Views

32

Comments

0

Submitted:

24 August 2024

Posted:

27 August 2024

You are already at the latest version

Alerts
Abstract
Drug development is a lengthy process with a high failure rate. Increasingly, machine learning is utilized to facilitate the drug development processes. These models aim to enhance our understanding of drug characteristics, including their activity in biological contexts. However, a major challenge in drug response (DR) prediction is model interpretability as it aids in the validation of findings. This is important in biomedicine, where models need to be understandable in comparison with established knowledge of drug interactions with proteins. drGAT, a graph deep learning model, leverages a heterogeneous graph composed of relationships between proteins, cell lines, and drugs. drGAT is designed with two objectives: DR prediction as a binary sensitivity prediction and elucidation of drug mechanism from attention coefficients. drGAT has demonstrated superior performance over existing models, achieving 78\% accuracy (and precision), and 76\% F1 score for 269 DNA-damaging compounds of the NCI60 drug response dataset. To assess the model's interpretability, we conducted a review of drug-gene co-occurrences in Pubmed abstracts in comparison to the top 5 genes with the highest attention coefficients for each drug. We also examined whether known relationships were retained in the model by inspecting the neighborhoods of topoisomerase-related drugs. For example, our model retained TOP1 as a highly weighted predictive feature for irinotecan and topotecan, in addition to other genes that could potentially be regulators of the drugs. Our method can be used to accurately predict sensitivity to drugs and may be useful in the identification of biomarkers relating to the treatment of cancer patients.
Keywords: 
Subject: Computer Science and Mathematics  -   Mathematical and Computational Biology

1. Introduction

Drug discovery is an expensive and lengthy process with many obstacles [1,2]. The difficulty of this process arises from the efforts needed to ensure a compound is both safe and effective. Sensitivity to a drug involves the mechanism of the drug compound and a complex interplay of various factors internal and external to a cell. These factors include the cellular context (or state) that is determined by the repertoire of transcripts and proteins, alterations to this repertoire due to disease, and the interactions between these components [3,4]. Biomarkers are crucial in drug development to understand the best use of a compound and aid our understanding of the disease biology [5,6,7]. Machine learning (ML) has emerged as an approach to understanding the role of particular genes in drug response. This makes a huge impact on the efficiency and success rates of developing new drugs [8]. The utilization of ML in this domain leverages large amounts of biological and chemical data, helping to identify drug candidates and predict their efficacy efficiently. When it comes to understanding biological phenomena, ML algorithms, especially deep learning (DL) models, have demonstrated their capability to predict the complex patterns and relationships within biological data [9,10].
However, despite the advances in using machine learning for drug discovery, a critical difficulty remains; which is the “black box” nature of the methods. While DL models have made huge strides in identifying patterns and predicting outcomes within several areas, their internal decision-making process is unclear, leading to concerns about their trustworthiness and reliability.
Interpretability in machine learning has received significant recent consideration [11,12,13] including in the area of drug discovery [14,15]. The attention mechanism, introduced in the Transformer architecture [16], is being widely used due to its capacity to include “attention coefficients” as trainable parameters to optimize how much attention the model assigns to individual components, such as a word in a sentence (i.e., a linear sequence of data); these attention parameters can be used to interpret the model’s output. While words in a sentence express a single coherent idea, regulatory networks biology are more dependent on interconnections between components; this makes graph data structures a useful representation in biology. Graph Neural Networks (GNNs) have been developed for handling this type of data. GNNs aggregate node-level features in local graph neighborhoods, thereby forming features that also incorporate node relations. GNNs that make use of the attention mechanism are known as Graph Attention Network (GAT) [17]. Thus, GAT leverages the attention mechanism to generate attention weights, which weigh the influence of feature representations from neighboring nodes when deriving node-level features. By utilizing GAT, we can offer insights into the importance of genes and enhance the interpretability of drug response models by analyzing neighborhood relationships.
We propose a novel interpretable deep learning method called “drGAT”, which leverages GAT to process a large-scale heterogeneous network. Our model processes a heterogeneous graph composed of drug compounds, cell lines, and genes. This heterogeneous graph has been constructed using integrated drug screening and molecular profiling data from the NCI60 cell line pharmacogenomics dataset (drug screening data collected on 60 cancer cell lines) taken from CellMinerCDB [18] via rcellminer [19]. The GAT layer is employed to learn embedding representations from the interconnected structure within this heterogeneous network. This approach gives us knowledge of the relative significance of individual components [20,21] and their contributions to the overall model.
We utilize drGAT for two tasks: i) drug-cell line association prediction and ii) interpretability of the individual gene importance to prediction. We make use of multi-task learning, whereby multiple learning tasks are solved simultaneously to benefit from the shared patterns and distinctions among these tasks. Towards this aim, this study focuses on drug compounds with a DNA-damaging mechanism of action (269 drugs) available in the NCI60 of which there are more than in other comparable datasets. Regarding drug response prediction, drGAT has demonstrated superior performance over existing models. Additionally, this model also shows high prediction accuracy on data not present in NCI60 but found within the GDSC dataset.
In addition, the attention coefficients from drGAT are utilized for interpreting the predictor (e.g., gene) importance and relation among components of the heterogeneous network nodes (i.e., drugs, cell lines, and genes). We present an analysis of attention coefficients for the subset of nodes that correspond to genes that propose explanations for the response mechanisms of particular drugs. Moreover, relevant biological processes for analyzed compounds are also described using the attention coefficients and an over-representation analysis.
In summary, our model shows high accuracy for drug response prediction, allowing us to determine the predictor importance using attention coefficients. This interpretability allows users to explore the relationship among drug structures, cell lines, and genes, providing insights for further drug development investigation.
The main contributions include:
  • We create a heterogeneous graph involving DNA-targeting drugs that includes three entity types: genes (i.e., gene expression), cell lines (i.e., drug responses), and drugs (i.e., structures) using the NCI60 [22].
  • We evaluate the drug-gene associations suggested by attention coefficients and systematically compare these to existing scientific publication text. We examine the abstracts of journal papers for co-mentions of drug-target relationships from our results.
  • Our results propose drug-cell line sensitivity associations based on the attention coefficients derived from the GAT. These associations were then validated through comparison with independent experimental data.

2. Results

2.1. Model Performance

In Table 1, we present the results of the drug response prediction. A comparison is made between four baseline methods and our model with several GNN layers. We train and fit the model 5 times and values show the average and standard deviation. Notably, GATv2 achieved an accuracy of 0.779, a precision of 0.775, a recall of 0.741, and an F1 score of 0.757, outperforming other methods in terms of accuracy and F1 score, two of the most important metrics in binary classification. We utilize GATv2 as the GNN layer in our model for further investigation. Furthermore, our model can provide interpretations based on attention coefficients that existing models cannot achieve.

2.1.1. Analysis of GNN Architectures and Their Impact on Performance

Three key differences exist among GNN architectures: convolution, attention, and long-range dependencies. These differences significantly impact each model’s performance and capabilities.
The MPNN (Message Passing Neural Network) updates node features by receiving messages from neighborhood nodes, capturing complex relationships within the graph. However, its computational intensity and risk of over-smoothing with increased layers limit its performance, with an accuracy of 0.620 ± 0.126.
GCN (Graph Convolutional Network) uses graph convolution operations to update node features, ensuring low computational cost. However, GCN averages neighboring nodes’ information, which can result in losing important features. This limits GCN’s performance to an accuracy of 0.678 ± 0.036.
GAT (Graph Attention Network) uses attention mechanisms to weigh the importance of neighboring nodes, focusing on relevant features. This enhances GAT’s interpretability and performance, with an accuracy of 0.763 ± 0.018, though it increases computational cost.
GATv2 is an enhanced version of GAT, with improved attention mechanisms for more accurate feature learning and better scalability. Despite sharing GAT’s higher computational cost, it achieves the highest performance among the models, with an accuracy of 0.779 ± 0.002.
The Graph Transformer applies the transformer model to graph data, capturing long-range dependencies and handling complex graph structures. However, its high computational cost limits its performance to an accuracy of 0.764 ± 0.01, not surpassing the efficiency and effectiveness of GATv2.

2.2. Interpretation

To interpret the results further, we extracted the attention coefficients from two GAT layers. Each layer includes 5 attention heads. For ease of use, we simplified the shape of the attention matrices from (n, n, 5) to (n, n) by averaging them. We then added these matrices together and used the resulting matrix in subsequent steps.

2.2.1. Evaluation of Drug-Gene Associations in Scientific Literature

We conducted an analysis of our drug-gene co-occurrences in PubMed abstracts using, for each drug, the top 5 genes by attention coefficient magnitude. We utilized the NCBI ESearch tool to retrieve abstracts that mention both the drug and gene of each relationship [23]. Queries used the following format: https://eutils.ncbi.nlm.nih.gov/entrez/eutils/esearch.fcgi?db=pubmed&term="DRUG"&term="GENE".
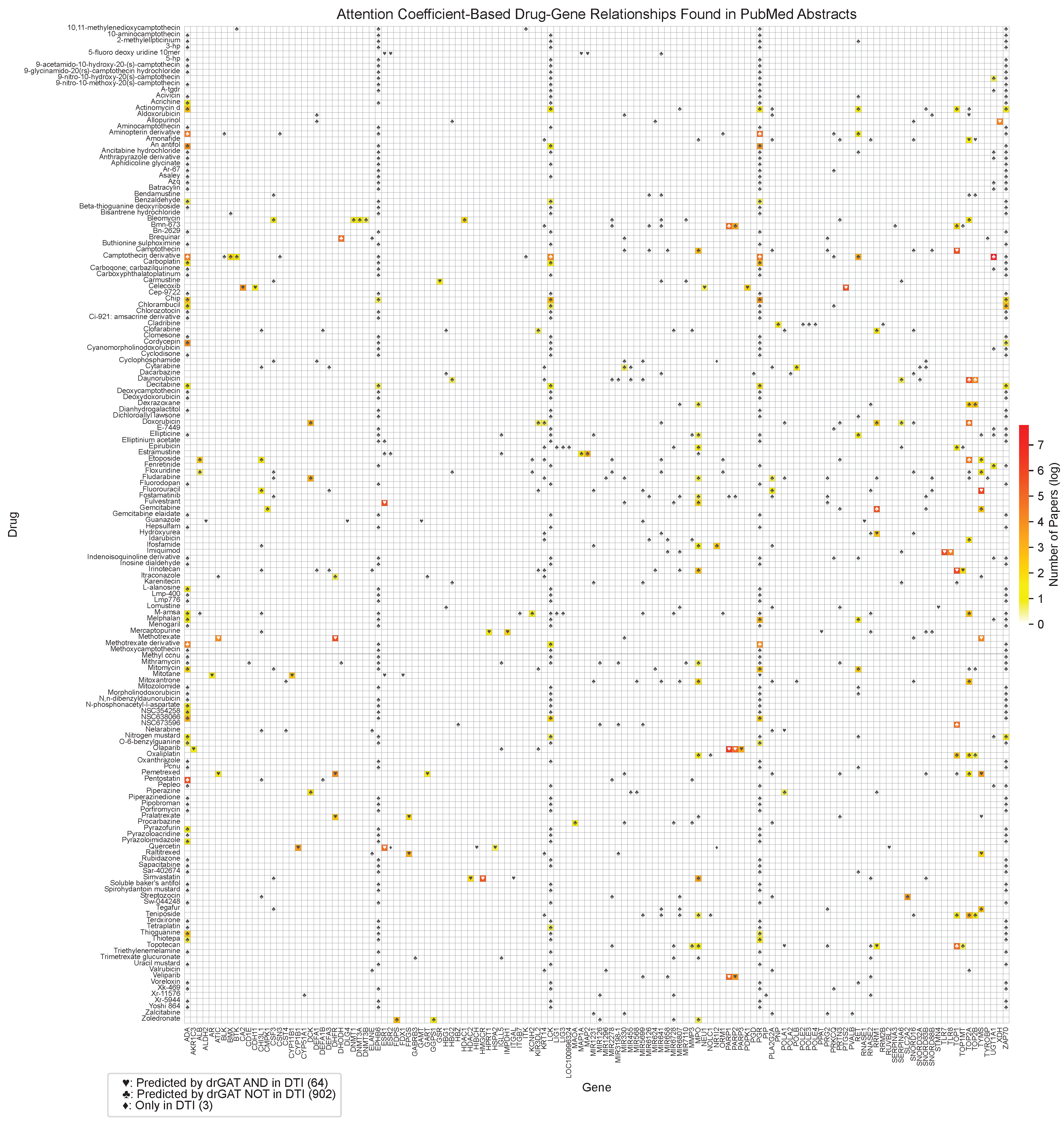
Figure 2 displays a heatmap illustrating the drug-gene co-occurrences based on PubMed abstracts. Out of 1,345 drug-gene attention-based relationships, 370 of the drug-gene co-occurrences were found in the abstracts from 10,100 articles. The color corresponds to the number of related publications by log scale. The symbols in Figure 2 indicate different relationship types. The ♡ symbol represents relationships predicted by drGAT and present in the DTI dataset (53 instances). The ♣ symbol indicates relationships predicted by drGAT but not present in the DTI dataset (495 instances). The ♢ symbol denotes relationships only present in the DTI dataset (2 instances). Our model identified 53 co-occurrences in 55 (96.4 %), demonstrating high coverage of known DTIs in the dataset. Regarding predicted-only DTIs (♣), 156 out of 495 total predictions (31.5 %) have at least one PubMed abstract. This indicates our model’s potential to suggest new drug-gene relationships.
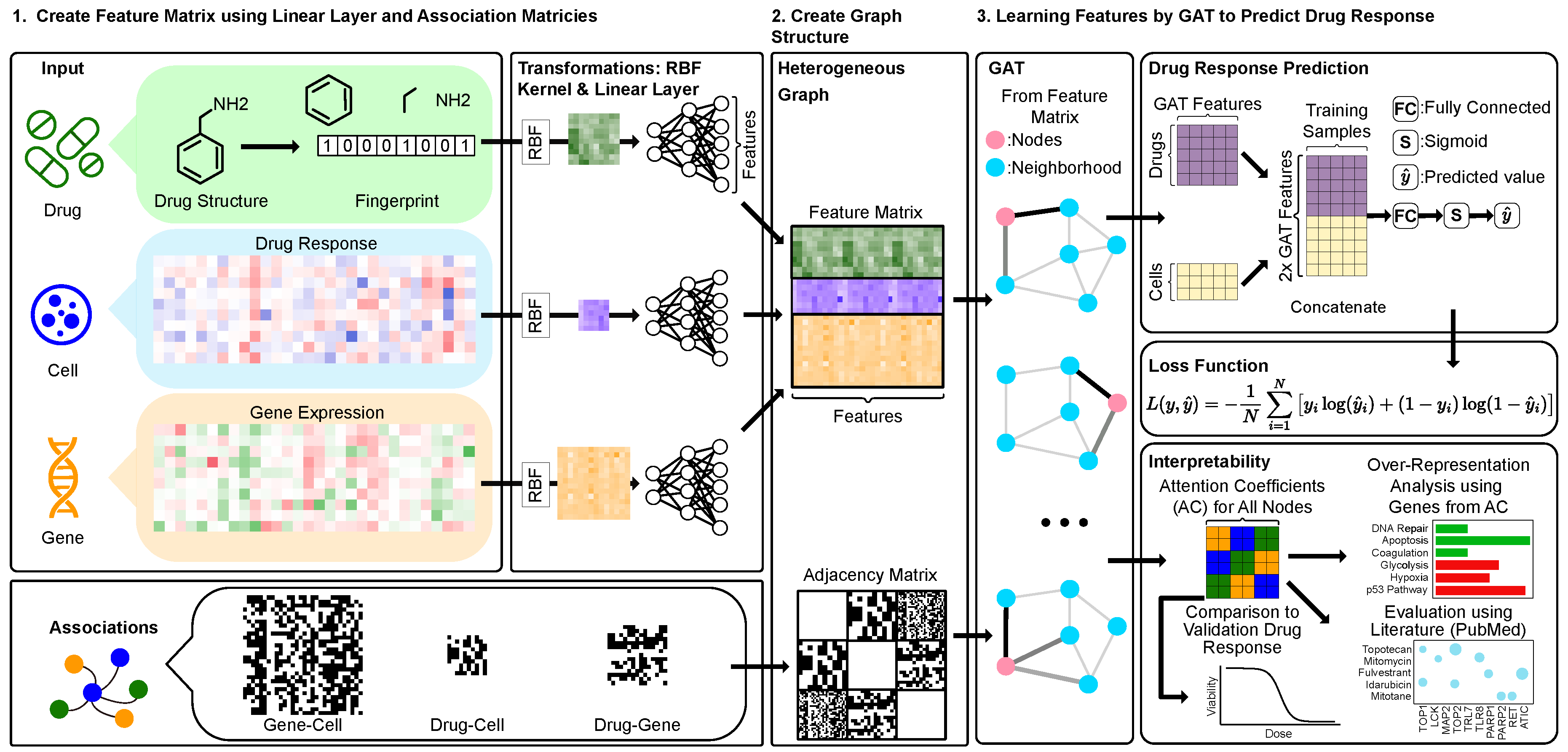
Preprints 116157 g001
Figure 1. drGAT Overview. A heterogeneous graph is constructed using drug structures, drug response, gene expression data. Each input type is transformed using RBF kernel followed by three linear layers to standardize their feature sizes, making them compatible for integration. These transformed inputs are then combined into a unified feature matrix, which is used as input to a GAT layer with an adjacency matrix. For prediction, the GAT layer output is concatenated to align with the drug response data. Following a fully connected layer, a sigmoid function generates predicted values y ^ , which are then inputs for the binary cross-entropy loss. To assess interpretability, attention coefficients are used with over-representation analysis and predicting untested sensitivities.
Figure 1. drGAT Overview. A heterogeneous graph is constructed using drug structures, drug response, gene expression data. Each input type is transformed using RBF kernel followed by three linear layers to standardize their feature sizes, making them compatible for integration. These transformed inputs are then combined into a unified feature matrix, which is used as input to a GAT layer with an adjacency matrix. For prediction, the GAT layer output is concatenated to align with the drug response data. Following a fully connected layer, a sigmoid function generates predicted values y ^ , which are then inputs for the binary cross-entropy loss. To assess interpretability, attention coefficients are used with over-representation analysis and predicting untested sensitivities.
Preprints 116157 g001

2.2.2. Evaluation of Predicted Drug-Cell Line Response by Comparison with GDSC

We systematically evaluated our results by comparing them with the Genomics of Drug Sensitivity in Cancer (GDSC) dataset [24]. The GDSC dataset is an extensive collection of drug response screening, which includes 978 cell lines and 542 drug compounds. The NCI60 subset we use here and GDSC overlap with 55 cell lines and 201 drugs. For evaluation, we use 44 overlapping drugs that have GDSC but no NCI60 response data.
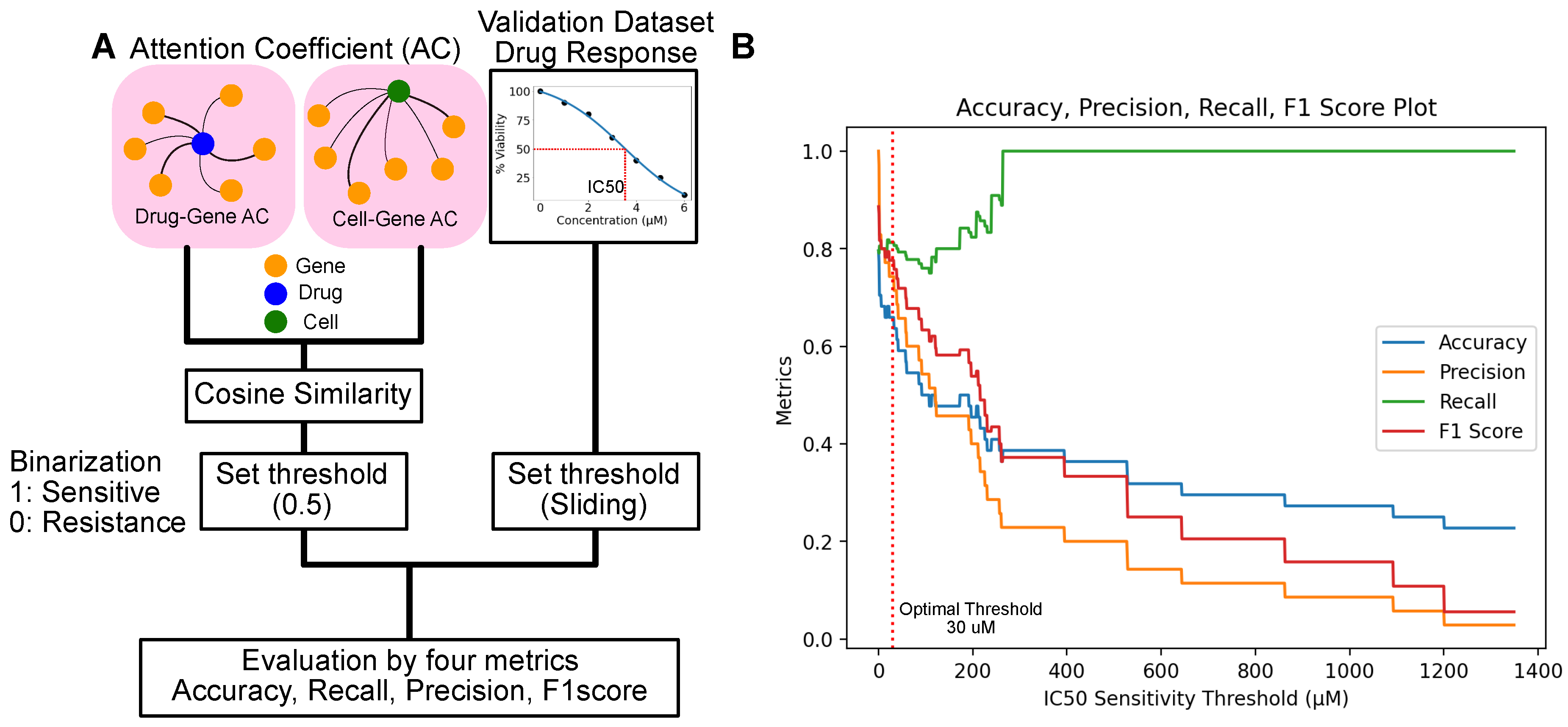
To assess these drug-cell line responses, we focused on their attention coefficients using our attention model, ensuring an accurate interpretation of their relationships. Our evaluation involved defining drug-cell sensitivity associations based on the attention coefficients of genes. We computed the cosine similarity between the attention directed towards genes from drugs and cell lines, selecting the cosine similarity due to its effectiveness in comparing sparse vectors. A cosine similarity value exceeding 0.5 was classified as positive (indicating sensitivity), whereas values below this threshold were deemed negative (resistant) (Figure 3A).
The GDSC dataset provides IC50 in micromolar ( μ M ) units. IC50 is described as the "half-maximal inhibitory concentration," referring to the concentration of a substance (such as a drug or inhibitor) required to inhibit viability or a specific biological function by 50%. This enables us to determine drug sensitivity based on dosage. We calculated four key metrics: accuracy, precision, recall, and the F1 score, across various dose thresholds ranging from 1 to 1400 μ M (Figure 3B). Figure 3B illustrates the impact of varying the sensitivity threshold value on the performance metrics of a classification model: accuracy, precision, recall, and F1 score. When the threshold is set low, the model achieves high accuracy and precision, identifying positive cases and minimizing false positives. However, a low threshold also leads to higher false negatives, as indicated by the lower recall. This scenario suggests that the model is conservative in predicting positive outcomes, leading to many positives being classified as negatives.
Conversely, setting a higher threshold improves recall, meaning the model is better at identifying all positive cases, including those that are harder to classify correctly. This comes at the expense of accuracy and precision as the model becomes more lenient, increasing the likelihood of false positives.
The balance between these metrics—accuracy, precision, and recall—highlights the trade-off in setting the threshold. While each drug may be effective at different concentrations, lower IC50 concentrations tend to be more clinically relevant. The threshold where each metric (accuracy, precision, recall, and F1 score) achieves a balance for this analysis is around 30 μ M . (Figure 3B). At this threshold, the metrics are as follows: Accuracy: 0.62, Precision: 0.70, Recall: 0.8, and F1 Score: 0.75. This optimal threshold is one that balances performance across all four metrics, managing the trade-offs between identifying positive cases, minimizing false positives, and accurately classifying negative cases. Lower IC50 values can reflect the clinical relevance for compounds utilized in the analysis. The average IC50 value from the GDSC dataset is 100 μ M . The discrepancy between the average IC50 value and the IC50 threshold used for analysis may arise because of the binarization to distinguish between positive and negative cases.
Such insights are crucial for tuning classification models to achieve the desired balance between sensitivity (recall) and specificity (accuracy and precision), especially in applications where the cost of false positives and false negatives varies significantly.

2.2.3. Drug-Target Interactions Assessment from Attention Coefficients

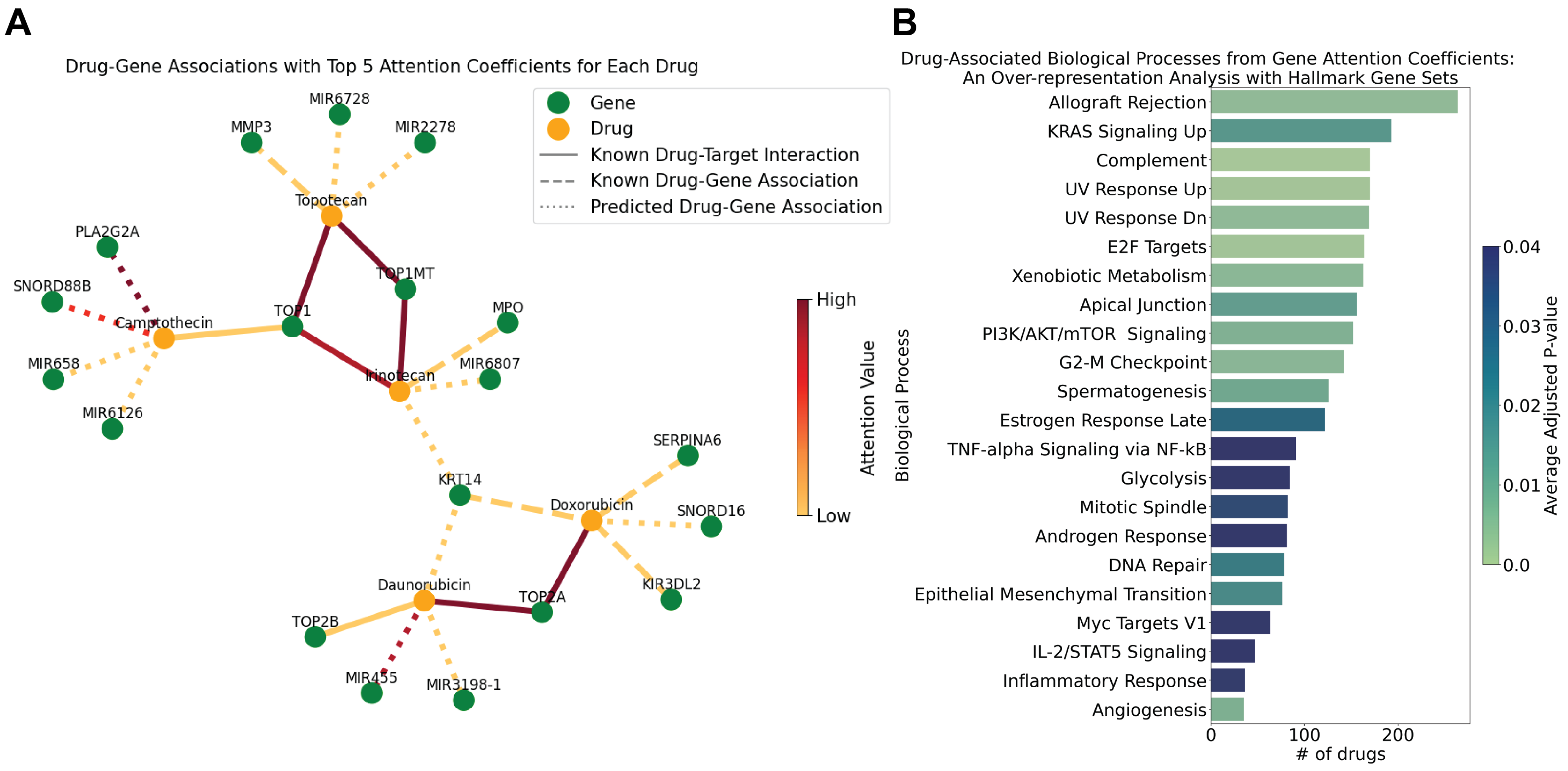
The intricate network of drug-target interactions and quantifying their relationships from the model results through attention coefficients can aid our understanding of mechanisms of action. Figure 4 (A) presents a visualization of these drug-gene relationships, employing the drGAT model to highlight the interplay between chemotherapeutic drugs and their genetic targets.
Doxorubicin (NSC-759155 and NSC-123127) and daunorubicin (NSC-756717) are both anthracycline chemotherapeutic agents and are known as TOP2 inhibitors [25,26]. Results from drGAT retain this known drug-target association; TOP2A has the highest attention coefficient for both drugs. Doxorubicin and daunorubicin share an association with KRT14; KRT14 is a gene that is a member of the keratin 1 family. There is evidence that keratin expression is altered in response to doxorubicin treatment [27] and are altered in doxorubicin-resistant cells (including specifically, KRT14) [28]. Additionally, there is interest in targeting keratins through peptide-drug conjugate featuring doxorubicin [29]. Separately, SERPINA6, returned as a top 5 attention coefficient gene for doxorubicin, has been utilized as a resistance marker gene for doxorubicin [30].
Topotecan (NSC-759263), Camptothecin (NSC-94600), and Irinotecan (NSC-759878) are topoisomerase inhibitors, specifically targeting the TOP1 cleavage complex [7,31,32], and the TOP1 drug-gene association appears in the drGAT results. MMP3 was returned as a drug-gene association for topotecan by drGAT. MMP3, and other matrix metalloproteinases (MMPs), have been analyzed as a part of a Phase I dosing study of intraventricular topotecan on children with neoplastic meningitis due to reports of correlation with leptomeningeal disease [33].
While not a comprehensive analysis, the above results show that our model retains high attention coefficients of known drug-target interactions fed as training data, and also, predicts several known drug-gene relationships that are of research interest. This suggests that our predicted drug-gene associations can be indicative of potential targets or drug-gene relationships appropriate for further study.

2.2.4. Over-Representation Analysis with Attention Coefficients

We worked to elucidate the functional roles of genes associated with the various drugs, leveraging the results provided by the attention coefficients derived from our model. We conducted an over-representation analysis (ORA) using the attention coefficients attributed to the genes associated with the drugs. Specifically, genes possessing attention values greater than 0 for each drug were taken as input for ORA. We conducted the ORA analysis using gseapy [34] and the MSigDB Hallmark 2020 [35] collection of 50 gene sets accessed via gseapy. We highlight the biological processes with p-values adjusted by Benjamini-Hochberg less than 0.05 in Figure 4B, which depicts associations with different hallmark biological processes, with the cumulative count of drugs linked to each function.
Our study focused on drugs related to DNA damage. Consequently, our analysis reproduced processes represented in the Hallmark gene sets commonly associated with these drugs such as response to ultraviolet (UV) radiation, E2F targets (i.e., cell cycle-related targets of E2F transcription factors), xenobiotic metabolism, and DNA repair. The E2F targets are crucial in cell cycle regulation and may represent how these drugs impact proliferation [36]. Similarly, the involvement of xenobiotic metabolism pathways highlights how these drugs are processed. Related, ABCB1 was a recurrent overalapping gene in the "KRAS Signaling Up" gene set; this drug efflux protein is responsible for reducing concentrations of toxic compounds, such as cancer medications, and it has been shown to be associated with the resistance to topoisomerase inhibition [37,38,39]. The gene set "Allograft Rejection" was identified with the largest number of compounds. While not obvious from the name "Allograft Rejection" (i.e., transplant reject), this gene set contains many key cancer-related genes, including various kinases (e.g., EGFR, ITK, MAP4K1, LCK). Of these genes, one recurrent overlapping gene was EGFR for 80 of topoisomerase inhibitors (both TOP1 and TOP2; 130 topoisomerase inhibitors total); the various modes of interactions between topoisomerases and EGFR have been previously reported [40]. These results corroborate our expectations of the molecular mechanisms affecting response to these drugs.

3. Methods

3.1. Building Input Matrix

In this section, we explain the construction of the heterogeneous graph. The resulting graph incorporates drug structures, cell line drug response, gene expression data, and their known drug-target interactions and similarities.

3.1.1. Preprocessing

First, we selected a subset of data from NCI60 [22] via rcellminer [19]. This dataset comprises gene expression, drug response, and drug structure data.
The complete drug response matrix contained 23,191 drugs for 60 cells. From this, we selected 269 drugs with a mechanism of action related to DNA damage [41]. Specifically, the drug response matrix forms X D R ∈ R n × m , where n is the number of drugs and m is the number of cells (i.e., n = 269 , m = 60 ).
The full NCI60 gene expression data includes 23,826 gene transcripts, where we selected 2,383 genes (the top 10% of genes with the greatest standard deviations). The selection of this highly variable gene set should allow better discrimination between different observations in the dataset. We also merged another group of genes (281 genes) that are involved in drug-target interactions. This combination resulted in a unique set of 2,718 genes. The gene expression data is part of matrix X G E ∈ R m × l , where m ( = 60 ) and l ( = 2 , 718 ) denote the number of cell lines and genes, respectively.
Subsequently, we collected the drug-target interaction data from DrugBank [42]. This dataset has 19,017 drug-target interactions (DTI) with 7,756 unique drugs and 4,755 genes. We selected 100 unique National Service Center (NSC) numbers (NSCs represent batches of screening with a particular drug structure) and 403 genes, with drugs and genes overlapping with the NCI60 pharmacogenomic data. To be the same size as other data, the matrix X D T I is filled by 0 for the unknown DTI. Therefore, X D T I ∈ R n × l (i.e., n = 269 , l = 2 , 718 ).
In addition, we also created the drug fingerprints representation matrix. SMILES structures are converted to the Morgan fingerprints [43] using RDKit [44]. We create a vector of 2048 length for each drug and concatenate to make a matrix, denoted as X M F ∈ R n × o , wherein o represents the number of drug features (i.e., n = 269 , o = 2 , 048 ).

3.1.2. Feature Matrix

To make a feature matrix, we utilize similarity matrices as inputs created from X D R , X G E , and X M F . Preceding the construction of the heterogeneous graph, similarity matrices were individually constructed for cell lines ( S c ), genes ( S g ), and drugs ( S d ). These matrices capture the element-wise similarity to homogenous entities such as gene-gene, cell-cell, and drug-drug similarity relationships.
The RBF Kernel [45] was employed to create a similarity matrix, defined as follows.
S i j = exp − γ | | X i − X j | | 2 ,
where S is a similarity matrix, γ denotes a hyperparameter (we utilize 1 length ( X i ) ), i and j are indexes, and X is an input matrix.
From Equation (1) with X D R , we obtained the cell similarity matrix S c , and the gene similarity matrix S g was built using Equation (1) based on the gene expression data X G E . Then, Equation (1) was applied to obtain the similarity matrix to the X M F to create a drug similarity matrix S d .
As a result, three similarity matrices were obtained: S c ∈ R m × m for cell lines, S d ∈ R n × n for drugs, and S g ∈ R l × l for genes. These matrices have different dimensions. To address this, we utilize three linear layers to transform them to the same size of hidden units. The unified feature matrix X is defined as follows:
X = Linear d ( S d ) 0 0 0 Linear c ( S c ) 0 0 0 Linear g ( S g ) ,
where each linear layer has a different input size and the same output size. The output size is a hyperparameter.

3.1.3. Adjacency Matrix

For the input matrix, we also create the adjacency matrix from X D R , X G E , and X D T I . The drug-cell association matrix A d c is derived from the drug response matrix, X D R ∈ R n × m . Values in this matrix have already been normalized to z-scores with an average value of 0 and a standard deviation of 1. Then, we applied the following procedures to make it a graph structure. If the z-score in the drug response data for the NCI60 is greater than 0, we consider that the cell line is sensitive to the drug, and the value is 1. Otherwise, the cell line is resistant, and the value is set to 0.
Subsequently, we establish a cell-gene association matrix, A c g , derived from the gene expression dataset X G E ∈ R m × l . Our initial step includes standardizing the data across columns (cell lines). After this, the cell-gene association matrix A c g is generated from X G E , with processing similar to drug response matrix X D R .
Lastly, we create the association matrix between drugs and genes from the drug-target interaction matrices X D T I . To make a matrix with binary values, datasets with numerical values are binarized with values greater than 0 set to 1; otherwise, they are set to 0. Then, all datasets are merged as the drug-gene association matrix A d g ∈ R n × l whereby if an interaction is present in any of the datasets, it will be retained in the final merged association matrix.
Based on the three matrices, a unified adjacency matrix A is created as the following Equation (3).
A = 0 A d c A d g A d c ⊺ 0 A c g A d g ⊺ A c g ⊺ 0 .
A ∈ R ( n + m + l ) × ( n + m + l ) represents the combined drug, cell, and gene components, where the dimension of F is (4430, 4430). In this process, the adjacency matrix A with non-zero values is represented as 1; otherwise, 0. From these processes, the input matrix X and the adjacency matrix A are utilized for the input of the GNN model.

3.1.4. Preventing Data Leakage via Masking

For evaluation, the drug response matrix X D R is partitioned into distinct subsets: training, validation, and test data (for precise specifications, refer to Appendix B.1). The test dataset is a subset of the drug-cell association matrix A d c . This overlap raises concerns about potential data leakage. To counteract this issue, we mask the association values linked with the test data. Specifically, we set the values of test data combinations to 0 in the A d c matrix. This masking process affects 20 % of total combinations, which corresponds to 3,228 drug-cell line pairs. We implement this masking utilizing the following equation:
( A d c ) i j = 0 , if ( i , j ) is a test data index , ( A d c ) i j , otherwise ,
where i is the index of a drug, and j is the index of the cell for test data.

3.2. drGAT Model

This model consists of two GAT layers and a single fully connected layer. For the implementation of our drGAT model, we utilized Graph Attention Network v2 (GATv2) [46] as the core graph neural network layer. GATv2 was chosen due to its improved attention mechanisms, which allow for more expressive feature transformations compared to the original GAT. This choice was made to enhance the model’s ability to capture complex relationships within our heterogeneous graph structure.
Equation (5) illustrates the first block of the GAT layer with feature matrix X and adjacency matrix A. The subsequent steps involve adapting the model’s output to predict drug sensitivity in a binary manner.
Z 1 = Dropout ReLU GraphNorm GAT ( X , A ) ,
where Dropout denotes the dropout layer, ReLU is a ReLU activation function, GraphNorm is a graph normalization layer [47], and GAT is a Graph Attention Layer.
Here, we utilized Graph Attention Layer (GAT) [17] defined as follows:
GAT ( x i ) = α i i W s x i + ∑ j ∈ N ( i ) α i j W t x j ,
where x i is an input, α is the attention coefficient matrix, W s and W t are weight matrices, and N ( i ) is some neighborhood of node i in the graph. Here, the attention coefficients α i j are computed as
α i j = exp LReLU a s ⊺ W s x i + a t ⊺ W t x j ∑ k ∈ N ( i ) exp LReLU a s ⊺ W s x i + a t ⊺ W t x k ,
where a s and a t are weight vectors, and LReLU describes LeakyReLU. This attention coefficient matrix α is utilized for further interpretability assessment.
From Z 1 , we utilize the same structure and obtain Z 2 as follows.
Z 2 = Dropout ReLU GraphNorm GAT ( Z 1 , A ) .
Drug-cell line associations are predicted by concatenating their respective embeddings (from Z 2 ), and passing this input through a fully connected (FC) layer followed by a sigmoid activation. Equation (9) details the entire computational procedure. Then, the predicted value, y ^ is obtained by taking the sigmoid function to the output of an FC layer as follows:
y ^ = sigmoid ( FC ( Z 2 d ∥ Z 2 c ) ) ,
where the Z 2 d and Z 2 c are referred to as the drug’s and cell’s embedding from the Z 2 , respectively, and ∥ describes concatenation. Then the output y and ground truth y ^ are fed into the binary cross entropy loss L as below:
L ( y , y ^ ) = − 1 N ∑ i = 1 N y i log y ^ i + 1 − y i log 1 − y ^ i ,
where N is the number of data. Note that this network utilized Adam [48] for optimization.

3.3. Model Configuration and Training

Our drGAT model was implemented using PyTorch 0.13.1 [49] and PyTorch Geometric 2.2.0 [50]. We utilized Optuna [51], a library that employs Bayesian Optimization, for hyperparameter tuning. Detailed hyperparameter settings can be found in Appendix B.5.

4. Discussion

In this study, we successfully developed the drGAT model, utilizing Graph Attention Networks to derive attention coefficients for each node, including genes, drugs, and cell lines. This approach is capable of binary drug response prediction, as well as, facilitating model interpretation. Our model demonstrated superior performance in terms of accuracy, recall, and F1 score, outperforming competing models in drug response prediction. Additionally, the drGAT model is capable of predicting drug sensitivity in untested drug-cell line combinations based on attention coefficients, achieving over 80% accuracy. This capability is valuable for suggesting drug efficacy to untested samples (evaluated with untested samples in from the training data).
A key highlight of our research is the ability of our drGAT model to predict drug-gene relationships beyond those included in the training data as drug-target interactions (DTI). For drug-gene relationships that are not DTIs, our analysis found many relationships that have been previously studied using the attention coefficient-based approach. This capability allows our model to not only produce accurate response predictions that utilize known drug-target interaction information but also identify potential drug-gene relationships. These relationships could be of further interest in understanding drug mechanisms. Additionally, as part of this work, we analyzed the attention coefficients to understand the biological processes relevant to each drug. Our analysis returned several key processes related to cancer, as well as, processes with genes relevant to cancer and drug response.
One challenge in this study was the modest volume of high-confidence drug-target interaction data available. Although the NCI60 dataset includes 269 DNA damage-related compounds, only 100 of the drug compounds had DrugBank drug-target interaction (for these drugs we included 571 interactions from DrugBank). This highlights the need for further collection of drug-gene relationships. Ongoing efforts by one of the present study’s authors and other colleagues are aimed at expanding such datasets. This expansion is actively utilizing advancements in information extraction from natural language processing as well as crowd-sourced curation efforts [6,52,53,54,55].
Overall, this work highlights how results from advanced machine-learning techniques can be paired with bioinformatic analyses to understand mechanisms of cellular response to treatment. We expect future work to broaden the approach while providing more granularity to its interpretability. Currently, our model leverages drug response data to generate cell line similarity. Future work could incorporate additional multi-omics data, including gene expression, methylation, copy number variation, and mutation data as has been done by others [56]. We believe this enhancement will boost both model performance and interpretability.
Code Availability: The implementation of the drGAT model, including the scripts used for training, validation, and evaluation, is available on GitHub https://github.com/inoue0426/drGAT. This repository contains all necessary dependencies, installation instructions, and guidelines for running the model.

Author Contributions

Y.I. and H.L. contributed to the conception and design of the study. Y.I. and H.L. developed the drGAT model and performed the experiments. Y.I. was responsible for data preprocessing and integration. A.L. supervised the study and provided critical revisions of the manuscript. All authors discussed the results and contributed to the final manuscript. The corresponding authors are Y.I. and A.L.

Funding

The authors received funding from the Google Summer of Code program, funding from the National Resource for Network Biology (NRNB) from the National Institute of General Medical Sciences (NIGMS P41 GM103504), and support from the Intramural Research Program of the National Library of Medicine (NLM), National Institutes of Health (NIH). The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.

Data Availability Statement

The datasets used in this study, including the NCI60 dataset, are publicly available. The NCI60 dataset, which includes gene expression data, drug response data, and drug structure data, was obtained through rcellminer [19]. Specific details on data preprocessing, selection of DNA damage-related drugs, and integration with DrugBank for drug-target interactions are provided within the Methods section. The processed data used in the drGAT model can be accessed at: https://github.com/inoue0426/drGAT.

Acknowledgments

We would like to acknowledge helpful conversations with Vinodh N. Rajapakse.

Appendix A. Related Works

Drug response prediction remains a challenging research area due to the biological factors involved. A central goal of the work is to identify novel drug-cell line sensitivity associations where a cell line’s sensitivity to a drug compound can be reliably predicted. Machine learning-based approaches have become widely used for this task [57]. These methods often use several data types, such as gene expression data [58] and alteration data [59,60,61], clinical trial data [62,63,64], as well as, chemical structures of drug compounds [65,66,67].
Of such methods, Similarity-Regularized Matrix Factorization (SRMF) [68], a Heterogeneous Network-based Method for Drug Response Prediction (HNMDRP) [69], and a Multi-Omics Data Fusion and Graph Convolution Network (MOFGCN) [56] all leverage the similarity of drugs and cells. This common approach of utilizing both drug and cell similarities is also a key feature of our method.
SRMF [68] employs matrix factorization [70] to reconstruct the drug-cell line response matrix using drug-to-drug and cell line-to-cell line similarities. This reconstruction considers the input of similarity metrics encapsulating the relationship between cell lines and drugs. Specifically, SRMF calculates the extent of similarity amongst various drugs, considering their distinct chemical structures, in tandem with assessing the similarity between cell lines and their respective gene expressions. Using these similarities, SRMF undertakes matrix factorization for drugs and cell lines separately. From both matrices, SRMF reconstructs an association matrix.
HNMDRP [69] combines gene expression, drug structures, and protein-protein interaction (PPI) networks to predict drug-cell line sensitivity associations. The proposed methodology integrates various data types, including gene expression data for cell line similarity determination, chemical structures for drug similarity establishment, and PPI information for calculating the similarity of drug target genes. The associations between drugs and cell lines are predicted using this network.
MOFGCN [56] utilizes Graph Convolutional Networks (GCNs) [71] to predict drug response from the drug and cell line similarity. The cell line similarity matrix is constructed from gene expression, somatic mutation, and copy number variation data, while the drug similarity matrix is derived using structure fingerprints taken from the PubChem database [72]. Subsequently, an association matrix was created from both matrices and utilized for an input of GCNs to predict drug-cell binary sensitivity associations.
Here, SRMF, HNMDRP, and MOFGCN make predictions using similarity. However, the methods use embeddings utilizing gene expression data, resulting in a potential loss of interpretability. In contrast, our method drGAT integrates gene expression into similarity and association matrices, enabling the measurement of the influence of genes on each drug effect.

Appendix B. Experiment

Appendix B.1. Validation

The drug response matrix X D R is utilized as the input to the prediction model, using a split of 60% for training, 20% for validation, and 20% for testing. The drug response matrix contains z-score values that are transformed into a binary association matrix as follows: if the value in the drug response data for the NCI60 is positive, we consider that the cell line is sensitive to the drug and set the value to 1; otherwise, the cell line is resistant and set the value to 0.

Appendix B.2. Baseline Methods

For comparison, we have selected four recent studies as benchmark models. As discussed in subsection A, our work is related to MOFGCN, a current state-of-the-art method that uses a heterogeneous graph from drug response and gene expression. Consequently, MOFGCN is our primary benchmark model for GNN-based methods. Furthermore, we include a deep learning method to predict the drug sensitivity of cancer cell lines, called DeepDSC [73] for the DNN-based methods. DeepDSC employs a pipeline comprising six layers of Auto Encoder to reconstruct gene expression data. The hidden layer is extracted and subjected to convolution with the parameters of the Morgan fingerprint of the compounds. This convolved information is input for a DNN with four linear layers, predicting drug responses. The parameter settings for MOFGCN and DeepDSC were utilized from the original papers. We also include a DNN-based AutoML utilizing AutoKeras [74]. In addition, we utilize tree-based methods: LightGBM and Random Forest, tuning by FLAML [75].

Appendix B.3. Comparative GNN Architecture

Our study evaluates different Graph Neural Network (GNN) layers to determine their effectiveness. The layers compared are Message Passing Neural Networks (MPNN) [76], Graph Convolutional Networks (GCN) [71], Graph Attention Network (GAT) [17], Graph Attention Network V2 (GATv2) [46], and Graph Transformer (GT) [77]. GAT introduces an attention mechanism into graph neural networks. It allows nodes to assign varying levels of importance to their neighbors dynamically. GATv2 is an advancement over GAT. It features a more expressive attention mechanism that recalculates attention coefficients in every forward pass of the model. The GT layer extends the Transformer [16] architecture to graph-structured data. It leverages self-attention mechanisms specifically tailored for graphs.

Appendix B.4. Evaluation Metrics of Prediction Performance

To evaluate the prediction performance of our drGAT model, we employed four criteria: accuracy, precision, recall, and F1 scores. In binary classification, there are four kinds of test data points based on their ground truth and the model’s prediction,
  • positive sample and is correctly predicted as positive, also known as True Positive (TP);
  • negative samples and is wrongly predicted as positive samples, also known as False Positive (FP);
  • negative samples and is correctly predicted as negative samples, also known as True Negative (TN);
  • positive samples and is wrongly predicted as negative samples, also known as False Negative (FN).
These metrics are defined as
Accuracy = TP + TN TP + TN + FP + FN , Recall = TP TP + FN , Precision = TP TP + FP , F 1 Score = 2 × Precision × Recall Precision + Recall ,
where TP , FP , TN , and FN correspondingly denote True Positive, False Positive, True Negative, and False Negative counts, respectively.

Appendix B.5. Hyperparameter Tuning

We utilized Optuna [51], a library that employs Bayesian Optimization to tune hyperparameters. Specifically, the number of epochs is 1500, the number of attention heads is 5, the number of hidden units is configured with 256 units for the first linear layer, 32 units for the second GNN layer, 128 units for the final GNN layer, the dropout ratio is 0.1, and the learning rate is 0.001. The total of parameters is 1,074,401.
Our experiments were conducted on an Ubuntu server equipped with an NVIDIA A40 GPU with 48 GB of memory. This hardware configuration allowed for efficient training and evaluation of our model, particularly beneficial for processing the large-scale heterogeneous graph data used in our study.

Appendix C. Full Drug-Gene Relationship Table

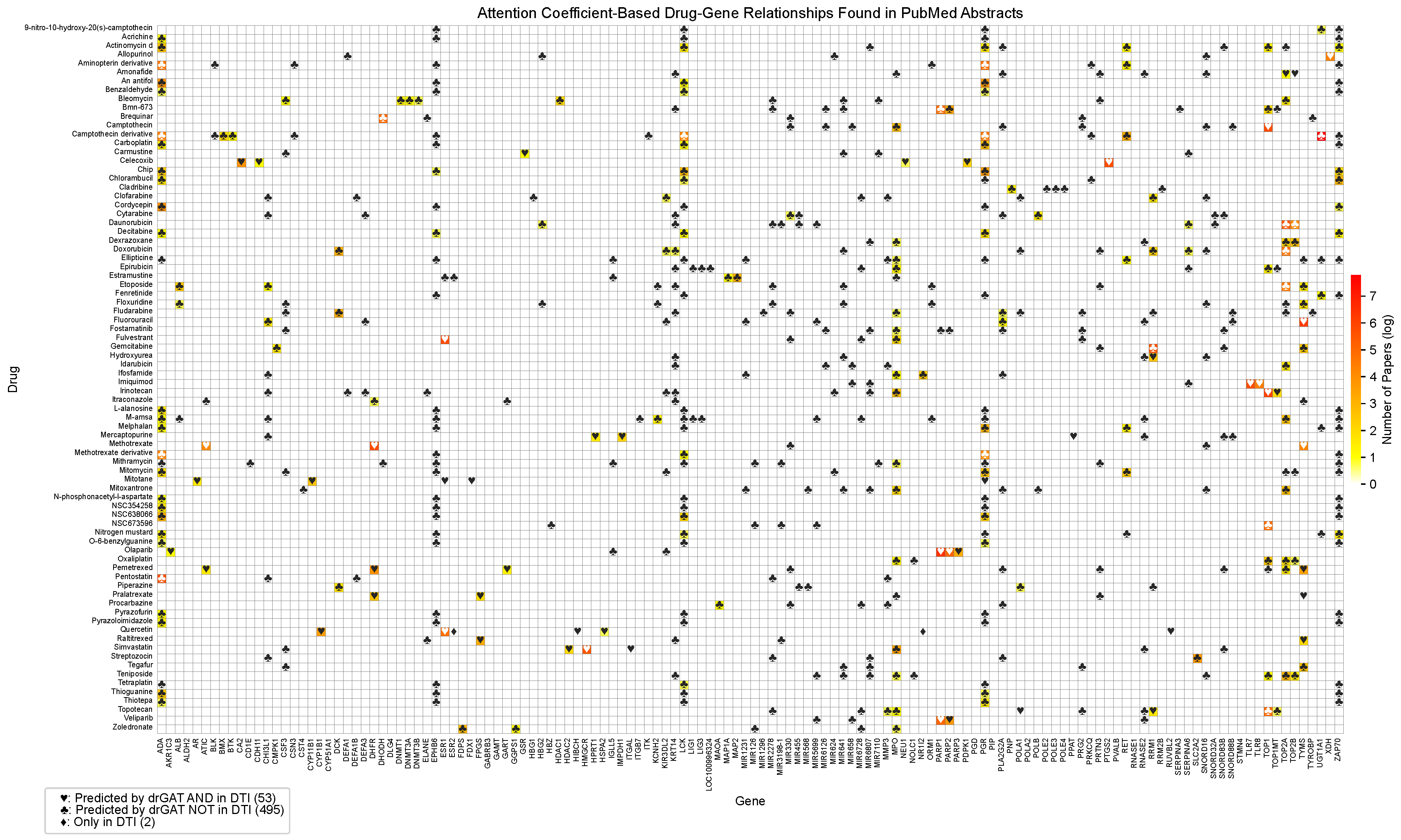
Figure A1 shows the complete drug-gene relationship matrix, including all drugs and genes analyzed in this study. This comprehensive visualization provides a more detailed view of the relationships predicted by drGAT and those present in the DTI dataset.
Preprints 116157 g0a1
Figure A1. Full drug-gene relationships and co-occurrences based on PubMed abstracts and predictions. The color represents the number of abstracts associated with a specific drug and gene pair by natural log scale. Symbols indicate the following: ♡ represents relationships predicted by drGAT and present in the DTI dataset (64 instances); ♣ represents relationships predicted by drGAT but not present in the DTI dataset (902 instances); ♢ represents relationships only present in the DTI dataset (3 instances).
Figure A1. Full drug-gene relationships and co-occurrences based on PubMed abstracts and predictions. The color represents the number of abstracts associated with a specific drug and gene pair by natural log scale. Symbols indicate the following: ♡ represents relationships predicted by drGAT and present in the DTI dataset (64 instances); ♣ represents relationships predicted by drGAT but not present in the DTI dataset (902 instances); ♢ represents relationships only present in the DTI dataset (3 instances).
Preprints 116157 g0a1
This comprehensive table provides a complete overview of all drug-gene relationships identified in our study, offering a more detailed perspective than the selected subset presented in the main text.

References

  1. Azuaje, F. Computational models for predicting drug responses in cancer research. Briefings in bioinformatics 2017, 18, 820–829. [Google Scholar] [CrossRef]
  2. Kuenzi, B.M.; Park, J.; Fong, S.H.; Sanchez, K.S.; Lee, J.; Kreisberg, J.F.; Ma, J.; Ideker, T. Predicting drug response and synergy using a deep learning model of human cancer cells. Cancer cell 2020, 38, 672–684. [Google Scholar] [CrossRef]
  3. Chang, Y.T.; Hoffman, E.P.; Yu, G.; Herrington, D.M.; Clarke, R.; Wu, C.T.; Chen, L.; Wang, Y. Integrated identification of disease specific pathways using multi-omics data. bioRxiv 2019, 666065. [Google Scholar]
  4. Xu, Y.; Liu, X.; Kong, Z.; Wu, Y.; Wang, Y.; Lu, Y.; Gao, H.; Wu, J.; Xu, H. MambaCapsule: Towards Transparent Cardiac Disease Diagnosis with Electrocardiography Using Mamba Capsule Network. arXiv preprint arXiv:2407.20893, arXiv:2407.20893 2024.
  5. Garnett, M.J.; Edelman, E.J.; Heidorn, S.J.; Greenman, C.D.; Dastur, A.; Lau, K.W.; Greninger, P.; Thompson, I.R.; Luo, X.; Soares, J.; others. Systematic identification of genomic markers of drug sensitivity in cancer cells. Nature 2012, 483, 570–575. [Google Scholar] [CrossRef] [PubMed]
  6. Wu, C.T.; Parker, S.J.; Cheng, Z.; Saylor, G.; Van Eyk, J.E.; Yu, G.; Clarke, R.; Herrington, D.M.; Wang, Y. COT: an efficient and accurate method for detecting marker genes among many subtypes. Bioinformatics Advances 2022, 2, vbac037. [Google Scholar]
  7. Chen, L.; Wu, C.T.; Clarke, R.; Yu, G.; Van Eyk, J.E.; Herrington, D.M.; Wang, Y. Data-driven detection of subtype-specific differentially expressed genes. Scientific reports 2021, 11, 332. [Google Scholar] [CrossRef] [PubMed]
  8. Leung, M.K.; Delong, A.; Alipanahi, B.; Frey, B.J. Machine learning in genomic medicine: a review of computational problems and data sets. Proceedings of the IEEE 2015, 104, 176–197. [Google Scholar] [CrossRef]
  9. Cao, C.; Liu, F.; Tan, H.; Song, D.; Shu, W.; Li, W.; Zhou, Y.; Bo, X.; Xie, Z. Deep Learning and Its Applications in Biomedicine. Genomics, Proteomics, Bioinformatics 2018, 16, 17–32. [Google Scholar] [CrossRef]
  10. Mahmud, M.; Kaiser, M.; Mcginnity, T.; Hussain, A. Deep Learning in Mining Biological Data. Cognitive Computation 2020, 13, 1–33. [Google Scholar] [CrossRef]
  11. Lipton, Z.C. The mythos of model interpretability: In machine learning, the concept of interpretability is both important and slippery. Queue 2018, 16, 31–57. [Google Scholar] [CrossRef]
  12. Gilpin, L.H.; Bau, D.; Yuan, B.Z.; Bajwa, A.; Specter, M.; Kagal, L. Explaining explanations: An overview of interpretability of machine learning. 2018 IEEE 5th International Conference on data science and advanced analytics (DSAA). IEEE, 2018, pp. 80–89.
  13. Kengkanna, A.; Ohue, M. Enhancing Model Learning and Interpretation Using Multiple Molecular Graph Representations for Compound Property and Activity Prediction. 2023 IEEE Conference on Computational Intelligence in Bioinformatics and Computational Biology (CIBCB). IEEE, 2023, pp. 1–8.
  14. Fu, T.; Huang, K.; Xiao, C.; Glass, L.M.; Sun, J. Hint: Hierarchical interaction network for clinical-trial-outcome predictions. Patterns 2022, 3. [Google Scholar] [CrossRef]
  15. Fu, T.; Gao, W.; Xiao, C.; Yasonik, J.; Coley, C.W.; Sun, J. Differentiable Scaffolding Tree for Molecular Optimization. International Conference on Learning Representations 2022. [Google Scholar]
  16. Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. Advances in neural information processing systems 2017, 30. [Google Scholar]
  17. Veličković, P.; Cucurull, G.; Casanova, A.; Romero, A.; Lio, P.; Bengio, Y. Graph attention networks. arXiv preprint arXiv:1710.10903 2017. [Google Scholar]
  18. Luna, A.; Elloumi, F.; Varma, S.; Wang, Y.; Rajapakse, V.N.; Aladjem, M.I.; Robert, J.; Sander, C.; Pommier, Y.; Reinhold, W.C. CellMiner Cross-Database (CellMinerCDB) version 1.2: Exploration of patient-derived cancer cell line pharmacogenomics. Nucleic acids research 2021, 49, D1083–D1093. [Google Scholar] [CrossRef]
  19. Luna, A.; Rajapakse, V.N.; Sousa, F.G.; Gao, J.; Schultz, N.; Varma, S.; Reinhold, W.; Sander, C.; Pommier, Y. rcellminer: exploring molecular profiles and drug response of the NCI-60 cell lines in R. Bioinformatics 2016, 32, 1272–1274. [Google Scholar] [CrossRef]
  20. Yuan, H.; Yu, H.; Wang, J.; Li, K.; Ji, S. On explainability of graph neural networks via subgraph explorations. International Conference on Machine Learning. PMLR, 2021, pp. 12241–12252.
  21. Yuan, H.; Yu, H.; Gui, S.; Ji, S. Explainability in graph neural networks: A taxonomic survey. IEEE Transactions on Pattern Analysis and Machine Intelligence 2022. [Google Scholar] [CrossRef] [PubMed]
  22. Shoemaker, R.H. The NCI60 human tumour cell line anticancer drug screen. Nature Reviews Cancer 2006, 6, 813–823. [Google Scholar] [CrossRef]
  23. Coordinators, N.R. Database resources of the national center for biotechnology information. Nucleic acids research 2012, 41, D8–D20. [Google Scholar] [CrossRef]
  24. Yang, W.; Soares, J.; Greninger, P.; Edelman, E.J.; Lightfoot, H.; Forbes, S.; Bindal, N.; Beare, D.; Smith, J.A.; Thompson, I.R.; others. Genomics of Drug Sensitivity in Cancer (GDSC): a resource for therapeutic biomarker discovery in cancer cells. Nucleic acids research 2012, 41, D955–D961. [Google Scholar] [CrossRef]
  25. Chen, T.; Sun, Y.; Ji, P.; Kopetz, S.; Zhang, W. Topoisomerase IIα in chromosome instability and personalized cancer therapy. Oncogene 2015, 34, 4019–4031. [Google Scholar] [CrossRef]
  26. Wu, C.T.; Shen, M.; Du, D.; Cheng, Z.; Parker, S.J.; Van Eyk, J.E.; Yu, G.; Clarke, R.; Herrington, D.M.; others. Cosbin: cosine score-based iterative normalization of biologically diverse samples. Bioinformatics Advances 2022, 2, vbac076. [Google Scholar] [CrossRef] [PubMed]
  27. Liao, C.; Xie, G.; Zhu, L.; Chen, X.; Li, X.; Lu, H.; Xu, B.; Ramot, Y.; Paus, R.; Yue, Z. p53 is a direct transcriptional repressor of keratin 17: lessons from a rat model of radiation dermatitis. Journal of Investigative Dermatology 2016, 136, 680–689. [Google Scholar] [CrossRef] [PubMed]
  28. Greife, A.; Tukova, J.; Steinhoff, C.; Scott, S.D.; Schulz, W.A.; Hatina, J. Establishment and characterization of a bladder cancer cell line with enhanced doxorubicin resistance by mevalonate pathway activation. Tumor Biology 2015, 36, 3293–3300. [Google Scholar] [CrossRef] [PubMed]
  29. Saghaeidehkordi, A.; Chen, S.; Yang, S.; Kaur, K. Evaluation of a keratin 1 targeting peptide-doxorubicin conjugate in a mouse model of triple-negative breast cancer. Pharmaceutics 2021, 13, 661. [Google Scholar] [CrossRef]
  30. De Ronde, J.J.; Lips, E.H.; Mulder, L.; Vincent, A.D.; Wesseling, J.; Nieuwland, M.; Kerkhoven, R.; Vrancken Peeters, M.J.T.; Sonke, G.S.; Rodenhuis, S.; others. SERPINA6, BEX1, AGTR1, SLC26A3, and LAPTM4B are markers of resistance to neoadjuvant chemotherapy in HER2-negative breast cancer. Breast cancer research and treatment 2013, 137, 213–223. [Google Scholar] [CrossRef]
  31. Han, S.; Lim, K.S.; Blackburn, B.J.; Yun, J.; Putnam, C.W.; Bull, D.A.; Won, Y.W. The Potential of Topoisomerase Inhibitor-Based Antibody–Drug Conjugates. Pharmaceutics 2022, 14, 1707. [Google Scholar] [CrossRef]
  32. Lu, Y.; Sato, K.; Wang, J. Deep Learning based Multi-Label Image Classification of Protest Activities. arXiv preprint arXiv:2301.04212 2023. [Google Scholar]
  33. Blaney, S.M.; Tagen, M.; Onar-Thomas, A.; Berg, S.L.; Gururangan, S.; Scorsone, K.; Su, J.; Goldman, S.; Kieran, M.W.; Kun, L.; others. A phase-1 pharmacokinetic optimal dosing study of intraventricular topotecan for children with neoplastic meningitis: A pediatric brain tumor consortium study. Pediatric blood & cancer 2013, 60, 627–632. [Google Scholar]
  34. Fang, Z.; Liu, X.; Peltz, G. GSEApy: a comprehensive package for performing gene set enrichment analysis in Python. Bioinformatics 2023, 39, btac757. [Google Scholar] [CrossRef]
  35. Liberzon, A.; Birger, C.; Thorvaldsdóttir, H.; Ghandi, M.; Mesirov, J.P.; Tamayo, P. The molecular signatures database hallmark gene set collection. Cell systems 2015, 1, 417–425. [Google Scholar] [CrossRef]
  36. Hamidi, M.; Eriz, A.; Mitxelena, J.; Fernandez-Ares, L.; Aurrekoetxea, I.; Aspichueta, P.; Iglesias-Ara, A.; Zubiaga, A.M. Targeting E2F Sensitizes Prostate Cancer Cells to Drug-Induced Replication Stress by Promoting Unscheduled CDK1 Activity. Cancers 2022, 14, 4952. [Google Scholar] [CrossRef]
  37. Pohl, P.C.; Klafke, G.M.; Carvalho, D.D.; Martins, J.R.; Daffre, S.; da Silva Vaz, I., Jr.; Masuda, A. ABC transporter efflux pumps: a defense mechanism against ivermectin in Rhipicephalus (Boophilus) microplus. International journal for parasitology 2011, 41, 1323–1333. [Google Scholar] [CrossRef] [PubMed]
  38. Omori, M.; Noro, R.; Seike, M.; Matsuda, K.; Hirao, M.; Fukuizumi, A.; Takano, N.; Miyanaga, A.; Gemma, A. Inhibitors of ABCB1 and ABCG2 overcame resistance to topoisomerase inhibitors in small cell lung cancer. Thoracic Cancer 2022, 13, 2142–2151. [Google Scholar] [CrossRef]
  39. Chang, Y.T.; Hoffman, E.P.; Yu, G.; Herrington, D.M.; Clarke, R.; Wu, C.T.; Chen, L.; Wang, Y. Integrated identification of disease specific pathways using multi-omics data. bioRxiv 2019, 666065. [Google Scholar]
  40. Chauhan, M.; Sharma, G.; Joshi, G.; Kumar, R. Epidermal growth factor receptor (EGFR) and its cross-talks with topoisomerases: challenges and opportunities for multi-target anticancer drugs. Current Pharmaceutical Design 2016, 22, 3226–3236. [Google Scholar] [CrossRef] [PubMed]
  41. Weber, G.F.; Weber, G.F. DNA damaging drugs. Molecular therapies of cancer 2015, 9–112. [Google Scholar]
  42. Wishart, D.S.; Feunang, Y.D.; Guo, A.C.; Lo, E.J.; Marcu, A.; Grant, J.R.; Sajed, T.; Johnson, D.; Li, C.; Sayeeda, Z.; others. DrugBank 5.0: a major update to the DrugBank database for 2018. Nucleic acids research 2018, 46, D1074–D1082. [Google Scholar] [CrossRef]
  43. Morgan, H.L. The generation of a unique machine description for chemical structures-a technique developed at chemical abstracts service. Journal of chemical documentation 1965, 5, 107–113. [Google Scholar] [CrossRef]
  44. Landrum, G.; others. Rdkit: Open-source cheminformatics software 2016.
  45. Burbidge, R.; Trotter, M.; Buxton, B.; Holden, S. Drug design by machine learning: support vector machines for pharmaceutical data analysis. Computers & chemistry 2001, 26, 5–14. [Google Scholar]
  46. Brody, S.; Alon, U.; Yahav, E. How attentive are graph attention networks? arXiv preprint arXiv:2105.14491 2021. [Google Scholar]
  47. Cai, T.; Luo, S.; Xu, K.; He, D.; Liu, T.y.; Wang, L. Graphnorm: A principled approach to accelerating graph neural network training. International Conference on Machine Learning. PMLR, 2021, pp. 1204–1215.
  48. Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv preprint arXiv:1412.6980 2014. [Google Scholar]
  49. Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; others. Pytorch: An imperative style, high-performance deep learning library. Advances in neural information processing systems 2019, 32. [Google Scholar]
  50. Fey, M.; Lenssen, J.E. Fast graph representation learning with PyTorch Geometric. arXiv preprint arXiv:1903.02428 2019. [Google Scholar]
  51. Akiba, T.; Sano, S.; Yanase, T.; Ohta, T.; Koyama, M. Optuna: A next-generation hyperparameter optimization framework. Proceedings of the 25th ACM SIGKDD international conference on knowledge discovery & data mining, 2019, pp. 2623–2631.
  52. Wong, J.V.; Franz, M.; Siper, M.C.; Fong, D.; Durupinar, F.; Dallago, C.; Luna, A.; Giorgi, J.; Rodchenkov, I.; Babur, Ö.; others. Science Forum: Author-sourced capture of pathway knowledge in computable form using Biofactoid. Elife 2021, 10, e68292. [Google Scholar] [CrossRef]
  53. Bachman, J.A.; Gyori, B.M.; Sorger, P.K. Automated assembly of molecular mechanisms at scale from text mining and curated databases. Molecular Systems Biology 2023, 19, e11325. [Google Scholar] [CrossRef]
  54. Rodchenkov, I.; Babur, O.; Luna, A.; Aksoy, B.A.; Wong, J.V.; Fong, D.; Franz, M.; Siper, M.C.; Cheung, M.; Wrana, M.; others. Pathway Commons 2019 Update: integration, analysis and exploration of pathway data. Nucleic acids research 2020, 48, D489–D497. [Google Scholar] [CrossRef]
  55. Lu, Y.; Wu, C.T.; Parker, S.J.; Chen, L.; Saylor, G.; Van Eyk, J.E.; Herrington, D.M.; Wang, Y. COT: an efficient Python tool for detecting marker genes among many subtypes. bioRxiv 2021, 2021-01. [Google Scholar]
  56. Peng, W.; Chen, T.; Dai, W. Predicting drug response based on multi-omics fusion and graph convolution. IEEE Journal of Biomedical and Health Informatics 2021, 26, 1384–1393. [Google Scholar] [CrossRef]
  57. Lu, Y.; Wang, H.; Wei, W. Machine Learning for Synthetic Data Generation: a Review. arXiv preprint arXiv:2302.04062 2023. [Google Scholar]
  58. Du, D.; Bhardwaj, S.; Parker, S.J.; Cheng, Z.; Zhang, Z.; Van Eyk, J.E.; Yu, G.; Clarke, R.; Herrington, D.M.; others. ABDS: tool suite for analyzing biologically diverse samples. bioRxiv 2023. [Google Scholar]
  59. Lu, Y. Multi-omics Data Integration for Identifying Disease Specific Biological Pathways. PhD thesis, Virginia Tech, 2018.
  60. Zhang, B.; Fu, Y.; Zhang, Z.; Clarke, R.; Van Eyk, J.E.; Herrington, D.M.; Wang, Y. DDN2. 0: R and Python packages for differential dependency network analysis of biological systems. bioRxiv 2021, 2021-04. [Google Scholar]
  61. Fu, Y.; Lu, Y.; Wang, Y.; Zhang, B.; Zhang, Z.; Yu, G.; Liu, C.; Clarke, R.; Herrington, D.M.; Wang, Y. DDN3. 0: Determining significant rewiring of biological network structure with differential dependency networks. Bioinformatics 2024, btae376. [Google Scholar] [CrossRef]
  62. Lu, Y.; Chen, T.; Hao, N.; Rechem, C.V.; Chen, J.; Fu, T. Uncertainty quantification and interpretability for clinical trial approval prediction. Health Data Science 2024. [Google Scholar] [CrossRef] [PubMed]
  63. Chen, T.; Hao, N.; Lu, Y.; Van Rechem, C. Uncertainty Quantification on Clinical Trial Outcome Prediction. arXiv preprint arXiv:2401.03482 2024. [Google Scholar]
  64. Chen, J.; Hu, Y.; Wang, Y.; Lu, Y.; Cao, X.; Lin, M.; Xu, H.; Wu, J.; Xiao, C.; Sun, J.; others. Trialbench: Multi-modal artificial intelligence-ready clinical trial datasets. arXiv preprint arXiv:2407.00631 2024. [Google Scholar]
  65. An, X.; Chen, X.; Yi, D.; Li, H.; Guan, Y. Representation of molecules for drug response prediction. Briefings in Bioinformatics 2022, 23, bbab393. [Google Scholar] [CrossRef]
  66. Lu, Y.; Hu, Y.; Li, C. DrugCLIP: Contrastive Drug-Disease Interaction For Drug Repurposing. arXiv preprint arXiv:2407.02265 2024. [Google Scholar]
  67. Xu, B.; Lu, Y.; Li, C.; Yue, L.; Wang, X.; Hao, N.; Fu, T.; Chen, J. SMILES-Mamba: Chemical Mamba Foundation Models for Drug ADMET Prediction. arXiv preprint arXiv:2408.05696 2024. [Google Scholar]
  68. Wang, L.; Li, X.; Zhang, L.; Gao, Q. Improved anticancer drug response prediction in cell lines using matrix factorization with similarity regularization. BMC cancer 2017, 17, 1–12. [Google Scholar] [CrossRef]
  69. Zhang, F.; Wang, M.; Xi, J.; Yang, J.; Li, A. A novel heterogeneous network-based method for drug response prediction in cancer cell lines. Scientific reports 2018, 8, 1–9. [Google Scholar] [CrossRef]
  70. Koren, Y.; Bell, R.; Volinsky, C. Matrix factorization techniques for recommender systems. Computer 2009, 42, 30–37. [Google Scholar] [CrossRef]
  71. Kipf, T.N.; Welling, M. Semi-supervised classification with graph convolutional networks. The International Conference on Learning Representations (ICLR) 2016. [Google Scholar]
  72. Bolton, E.E.; Wang, Y.; Thiessen, P.A.; Bryant, S.H. PubChem: integrated platform of small molecules and biological activities. In Annual reports in computational chemistry; Elsevier, 2008; Vol. 4, pp. 217–241.
  73. Li, M.; Wang, Y.; Zheng, R.; Shi, X.; Li, Y.; Wu, F.X.; Wang, J. DeepDSC: a deep learning method to predict drug sensitivity of cancer cell lines. IEEE/ACM transactions on computational biology and bioinformatics 2019, 18, 575–582. [Google Scholar] [CrossRef]
  74. Jin, H.; Song, Q.; Hu, X. Auto-keras: An efficient neural architecture search system. Proceedings of the 25th ACM SIGKDD international conference on knowledge discovery & data mining, 2019, pp. 1946–1956.
  75. Wang, C.; Wu, Q.; Weimer, M.; Zhu, E. Flaml: A fast and lightweight automl library. Proceedings of Machine Learning and Systems 2021, 3, 434–447. [Google Scholar]
  76. Gilmer, J.; Schoenholz, S.S.; Riley, P.F.; Vinyals, O.; Dahl, G.E. Neural message passing for quantum chemistry. International conference on machine learning. PMLR, 2017, pp. 1263–1272.
  77. Shi, Y.; Huang, Z.; Feng, S.; Zhong, H.; Wang, W.; Sun, Y. Masked label prediction: Unified message passing model for semi-supervised classification. arXiv preprint arXiv:2009.03509 2020. [Google Scholar]
Preprints 116157 g002
Figure 2. Selected drug-gene co-occurrences based on PubMed abstracts. The color represents the number of abstracts associated with a specific drug and gene pair by natural log scale. Symbols indicate the following: ♡ represents relationships predicted by drGAT and present in the Drug-Target Interaction (DTI) dataset (53 instances); ♣ represents relationships predicted by drGAT but not present in the DTI dataset (495 instances); ♢ represents relationships only present in the DTI dataset (2 instances). Several drugs have 5 or more co-occurrences due to multiple NSCs. This figure shows a subset of the data for clarity; the full table is available in Appendix C.
Figure 2. Selected drug-gene co-occurrences based on PubMed abstracts. The color represents the number of abstracts associated with a specific drug and gene pair by natural log scale. Symbols indicate the following: ♡ represents relationships predicted by drGAT and present in the Drug-Target Interaction (DTI) dataset (53 instances); ♣ represents relationships predicted by drGAT but not present in the DTI dataset (495 instances); ♢ represents relationships only present in the DTI dataset (2 instances). Several drugs have 5 or more co-occurrences due to multiple NSCs. This figure shows a subset of the data for clarity; the full table is available in Appendix C.
Preprints 116157 g002
Preprints 116157 g003
Figure 3. Evaluation using GDSC data. (A) Overview of calculation of 4 metrics. First, we obtained the attention coefficients between drug-gene and cell-gene. Then, calculate the cosine similarity. Next, we set the threshold to 0.5 to make it binary, 1 is sensitive and 0 is resistance. The GDSC observed drug response is given as IC50, and set some thresholds to make it binary (e.g., an IC50 > 20 μ M is resistant). Then, calculate the 4 metrics: accuracy, recall, precision, and F1 score using the binary results. (B) Performance metrics relative to different IC50 thresholds.
Figure 3. Evaluation using GDSC data. (A) Overview of calculation of 4 metrics. First, we obtained the attention coefficients between drug-gene and cell-gene. Then, calculate the cosine similarity. Next, we set the threshold to 0.5 to make it binary, 1 is sensitive and 0 is resistance. The GDSC observed drug response is given as IC50, and set some thresholds to make it binary (e.g., an IC50 > 20 μ M is resistant). Then, calculate the 4 metrics: accuracy, recall, precision, and F1 score using the binary results. (B) Performance metrics relative to different IC50 thresholds.
Preprints 116157 g003
Preprints 116157 g004
Figure 4. Drug-Gene Association Assessment. (A) Drug-gene association network based on attention coefficients. The network depicts relationships between drugs (orange nodes) and genes (green nodes) based on the top 5 attention coefficients from drGAT. For cases involving multiple NSCs, we only use data from a single NSC. Edges connecting drugs and genes are colored according to the attention coefficient value. Lines: known drug-target interactions (i.e., input training data; solid); known drug-gene association (relationships described in abstracts, but not included as model input, dashed); predicted drug-gene associations (dotted). (B) Drug-associated biological processes from gene attention coefficients. A bar chart representing the number of drugs linked to various biological processes, determined by gene attention scores and over-representation analysis of hallmark gene sets. The X-axis signifies the biological processes, while the Y-axis shows the count of drugs. The color coding of these bars corresponds to the average adjusted p-values.
Figure 4. Drug-Gene Association Assessment. (A) Drug-gene association network based on attention coefficients. The network depicts relationships between drugs (orange nodes) and genes (green nodes) based on the top 5 attention coefficients from drGAT. For cases involving multiple NSCs, we only use data from a single NSC. Edges connecting drugs and genes are colored according to the attention coefficient value. Lines: known drug-target interactions (i.e., input training data; solid); known drug-gene association (relationships described in abstracts, but not included as model input, dashed); predicted drug-gene associations (dotted). (B) Drug-associated biological processes from gene attention coefficients. A bar chart representing the number of drugs linked to various biological processes, determined by gene attention scores and over-representation analysis of hallmark gene sets. The X-axis signifies the biological processes, while the Y-axis shows the count of drugs. The color coding of these bars corresponds to the average adjusted p-values.
Preprints 116157 g004
Table 1. Classification Performance. Model run 5 times with average performance metrics presented (standard deviation indicated by ±). The best values are in bold. GNNs: Graph Neural Networks. AE: Autoencoder. Tree: Decision Tree. DNN: Deep Neural Networks. DCG: Drug-Cell-Gene Network. DF: Drug fingerprint. GE: Gene Expression. MT: Mutation. CNV: Copy Number Variation.
Table 1. Classification Performance. Model run 5 times with average performance metrics presented (standard deviation indicated by ±). The best values are in bold. GNNs: Graph Neural Networks. AE: Autoencoder. Tree: Decision Tree. DNN: Deep Neural Networks. DCG: Drug-Cell-Gene Network. DF: Drug fingerprint. GE: Gene Expression. MT: Mutation. CNV: Copy Number Variation.
Method Description Data Structure Interpretability Accuracy Precision Recall F1 score
Baseline Deep DSC AE DF, GE - 0.548 ± 0.000 0.516 ± 0.000 0.481 ± 0.000 0.498 ± 0.000
MOFGCN GNNs DF, GE, MT, CNV - 0.499 ± 0.001 0.487 ± 0.001 0.478 ± 0.002 0.482 ± 0.001
Random Forest Tree DF, GE Feature Importance 0.743 ± 0.003 0.720 ± 0.003 0.734 ± 0.006 0.727 ± 0.004
LightGBM Tree DF, GE Feature Importance 0.766 ± 0.000 0.791± 0.000 0.676 ± 0.000 0.729 ± 0.000
AutoKeras DNN PCA+DF,
PCA+GE		 - 0.733 ± 0.007 0.709 ± 0.011 0.724 ± 0.015 0.716 ± 0.007
drGAT MPNN GNNs DCG - 0.620 ± 0.126 0.623 ± 0.129 0.791± 0.182 0.664 ± 0.036
GCN GNNs DCG - 0.678 ± 0.036 0.720 ± 0.022 0.506 ± 0.119 0.587 ± 0.082
GAT GNNs DCG Attention 0.763 ± 0.018 0.730 ± 0.040 0.790 ± 0.045 0.756 ± 0.009
GATv2 GNNs DCG Attention 0.779± 0.002 0.775 ± 0.013 0.741 ± 0.023 0.757± 0.006
Graph Transformer GNNs DCG Attention 0.764 ± 0.01 0.739 ± 0.024 0.766 ± 0.025 0.752 ± 0.008
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated