Quantum-Machine-Assisted Drug Discovery: Survey and Perspective

Drug discovery and development is a highly complex and costly endeavor, typically requiring over a decade and substantial financial investment to bring a new drug to market. Traditional computer-aided drug design (CADD) has made significant progress in accelerating this process, but the development of quantum computing offers potential due to its unique capabilities. This paper discusses the integration of quantum computing into drug discovery and development, focusing on how quantum technologies might accelerate and enhance various stages of the drug development cycle. Specifically, we explore the application of quantum computing in addressing challenges related to drug discovery, such as molecular simulation and the prediction of drug-target interactions, as well as the optimization of clinical trial outcomes. By leveraging the inherent capabilities of quantum computing, we might be able to reduce the time and cost associated with bringing new drugs to market, ultimately benefiting public health.

Keywords:

Subject: Physical Sciences - Quantum Science and Technology

1. Introduction

Novel types of safe and effective drugs are needed to meet the medical needs of billions worldwide and improve the quality of human life [1,2]. The process of discovering a new drug candidate and developing it into an approved drug for clinical use is known as drug discovery and development. Two distinct stages in the process are: (1) Drug discovery focuses on identifying novel drug molecules with desirable pharmaceutical properties (Figure 1); (2) Drug development aims to test the drug’s safety and efficacy in human bodies via clinical trials (Figure 2) [3,4]. After the clinical trials, the results are reviewed by the US Food and Drug Administration (FDA) or equivalent government bodies from other countries. Upon approval, the new drug will be available for clinical use.

However, the drug discovery and development process is notorious for its protracted timeline, demanding labor requirements, and exorbitant costs. Presently, bringing a new drug to market demands a staggering 13-15 years and incurs an average expenditure of 2-3 billion [5,6,7]. The inefficiencies and high costs associated with traditional drug discovery methods have become particularly glaring in light of global health crises, such as the COVID-19 pandemic, which underscored the urgent need for accelerated and safer drug development strategies [8,9].

Quantum Computing (QC) is emerging as a revolutionary technology aiming to enhance computational processes through principles derived from quantum mechanics. The potential of Quantum Computing has significantly expanded since the early 2010s due to breakthroughs in quantum theory, improved quantum device fabrication, and the creation of more sophisticated algorithms for quantum processors [10,11]. The advancement of QC relies heavily on the development of quantum hardware capable of handling complex computations (e.g., quantum bits or qubits), scalable and reliable quantum systems, and the maturation of quantum programming frameworks such as Qiskit and Cirq [12,13,14]. These elements collectively enable the exploration of computational tasks that classical computers find challenging, opening new avenues in cryptography, optimization, and simulation.

QC could help drug discovery, offering opportunities for enhanced computational power and precision. It might potentially accelerate the identification of novel drug candidates, optimize molecular design, and streamline the drug development pipeline [15,16]. By leveraging quantum algorithms to simulate chemical reactions, model protein-ligand interactions, and perform large-scale data analysis, QC may significantly reduce the time and cost associated with traditional drug discovery methods[17,18]. Moreover, it could enhance the safety profile of new drugs by enabling more accurate predictions of pharmacological effects and toxicities. As QC continues to advance, it is anticipated to play a pivotal role in shaping the future of drug discovery and development, ultimately contributing to the acceleration of medical innovation and the improvement of patient care worldwide.

However, the integration of drug discovery and quantum computing still faces several challenges. First, large-scale, fault-tolerant, and universal quantum computers are still under development. Although existing devices have shown remarkable progress in the noisy intermediate-scale quantum (NISQ) era [19], they are still limited by quantum noise, especially when quantum circuits become deep. This limitation restricts the current capabilities for experimental explorations and demonstrations of quantum computing in drug discovery. Secondly, it remains unclear which specific problems are best suited for quantum computers at the algorithm and software levels. Even if we had a sufficiently advanced quantum computer, it is still uncertain which quantum algorithms might provide quantum advantages and outperform classical counterparts in drug discovery applications. Both hardware and software challenges are active areas of investigation.

In this perspective, we review and discuss the potential research opportunities and challenges in utilizing quantum computing techniques to accelerate drug discovery and development. In Section 2, we provide a comprehensive list of well-defined problems in drug discovery and development, including Protein Folding, Small-molecule ADMET Property Prediction, Drug-Target Interaction, Drug Design, De Novo Protein Design, Epitope Prediction, Clinical Trial Outcome Prediction, Clinical Trial Recruitment and Trial-Patient Matching, and Clinical Trial Site Selection and Ranking. In Section 3, we primarily discuss quantum computing approaches that might be beneficial for drug discovery and development. The toolbox consists of three parts: quantum simulation, quantum machine learning (QML), and security enhancement. We will also briefly comment on how these methods can be useful for solving specific drug discovery and development problems. We present the big picture in Figure 3.

We have witnessed significant progress in addressing complex computational challenges, including optimization, materials simulation, and quantum chemistry. Similarly, there are numerous exciting applications of quantum computing in drug discovery, including enhancing protein 3D structure prediction (protein folding), accelerating small-molecule ADMET property prediction, innovating de novo drug design, optimizing retrosynthesis planning, improving graph-based protein design, and advancing drug repurposing efforts, among others. Next, we briefly introduce some specific drug discovery applications facilitated by quantum computing. For each task, we describe the background, how to formulate it into a machine learning problem, and its broad impact. Figure 4 illustrates the whole drug discovery and development.

2. Drug Discovery and Development Problems

2.1. Protein Folding

Background. The key challenge in protein folding is the astronomical number of potential ways a protein could fold. In 1969, Dr. Cyrus Leventhal highlighted this conundrum, noting that brute-force calculation of all possible configurations of a typical protein would take longer than the universe’s age, despite proteins in nature folding in milliseconds—a phenomenon known as Leventhal’s paradox [20]. This paradox implies nature follows predictable folding pathways rather than random combinations. For years, scientists worldwide have been using advanced computing simulations to model this folding pathway, approximating the physical interactions underpinning the folding process [21,22]. Despite this substantial effort, the accuracy of physical-based simulations was not sufficiently practical until the advent of deep learning. Protein structure prediction (also known as protein folding problem) is a grand challenge in biology [23,24].

Broad Impact. Protein folding is crucial for understanding the three-dimensional structure of proteins, which helps in identifying potential drug targets. Knowing the folded structure of a protein can reveal pockets or sites that are amenable to binding by small molecules or antibodies.

Formulation. Protein folding takes the amino acid sequence as the input feature and predicts its 3D structure.

Technical Solutions. In 2018, AlphaFold 1.0 [25] emerged as the victor in the CASP13 competition, a biennial global competition known as the Critical Assessment of Protein Structure Prediction, which challenges research groups to predict 3D structures from amino acid sequences. Participated in by over 100 research groups worldwide, this competition witnessed a significant leap in accuracy with AlphaFold 1.0 and its successor, AlphaFold 2.0 [26], which dominated the CASP14 competition in 2020. AlphaFold 2.0 achieved nearly a 90 Global Distance Test (GDT) score, roughly equivalent to the accuracy of X-ray crystallography, marking a substantial advance in the field. In subsequent sections, we delve into the specifics of AlphaFold 1.0 and 2.0. Protein folding can also be seen as a molecule simulation problem, where the initial state can be randomly selected, and the final stable state is the target structure of interest. Thus, quantum simulation (Section 3.1) has the potential to revolutionize the process.

2.2. Small-molecule ADMET Property Prediction

Background. Small-molecule drugs, which are typically consumed orally, must travel from the site of administration to the site of action (e.g., tissue, organ) to take effect. There are five pharmaceutical properties to characterize the efficacy and safety of the drug, including absorption, distribution, metabolism, excretion, and toxicity (ADMET) properties [27]. A poor ADMET profile is the major reason for failure in pre-clinical and early clinical trial phases. Early and accurate ADMET characterization is a necessary condition for the successful development of small-molecule drug candidates during the drug discovery stage [3].

Broad Impact. Predicting molecular properties with machine learning models can help us prioritize potentially desirable molecules without wet lab experiments, which would save a large number of resources.

Formulation. This task aims at predicting drug ADMET property based on its molecular structure. It can be either a regression or a classification task.

Technical Solutions. Drug property prediction is essentially a representation learning task, multiple neural architectures are successfully applied [5,28], including convolutional neural network (CNN), recurrent neural network, transformer [29], and graph neural network (GNN) [30]. Despite initial success in accuracy, there are some challenges. For example, the drug’s molecular structure is protected by a patent and has commercial value to pharmaceutical companies. The ML property predictor may have privacy issues and leak the drug’s molecular structure. The security protection nature of QML can naturally circumvent the issue. Additionally, quantum-classical hybrid models (Section 3.2) have shown enhanced accuracy in predicting the absorption, distribution, metabolism, excretion, and toxicity (ADMET) properties of drug candidates [31]. Also, Quantum Principal Component Analysis can be employed to analyze and pinpoint key features of molecular structures and reduce the computational burden for further analysis [32]. Quantum Support Vector Machine allows for better classification of molecular properties such as toxicity, efficacy, and binding affinity [33].

2.3. Drug-Target Interaction

Background. The disease is usually related to the target protein. For example, the protein with PDB ID “7l11” is the main protease of SARS-COV-2 (2019-NCOV); the protein with PDB id “3eml” is a human A2A Adenosine receptor [34]. Drug-target interaction refers to the process by which a drug molecule binds to a specific biological target, such as a protein, enzyme, or receptor, to produce a therapeutic effect [5,35]. This binding can either activate or inhibit the target’s function, leading to the desired therapeutic outcome [36]. Understanding these interactions is crucial for optimizing a drug’s efficacy and safety by improving its binding affinity and selectivity. Existing methods are mostly based on deep representation learning to characterize the molecule structure of both drugs and targets.

Broad impact. The ability to accurately predict the binding affinity between a drug molecule and a target protein has far-reaching implications in drug discovery. By leveraging advanced drug-target interaction models, we can systematically screen all available drug molecules to identify those with high predicted affinity scores. This capability can significantly streamline the drug discovery process, reducing the time and cost associated with traditional experimental methods.

Formulation. Drug-target interaction predicts the binding affinity between drug and target based on drug molecular structure (e.g., SMILES string or molecular graph) and target information (e.g., amino acid sequence).

Technical Solutions. There are two research lines to estimate the drug-target binding affinity. First, traditional molecule dynamics can be used to simulate the drug-target binding trajectories [37]. Quantum simulation algorithms such as Quantum Phase Estimation (QPE) for Density Functional Theory (DFT) [38,39,40] and Quantum Amplitude Estimation(QAE) show remarkable promise in this area, as detailed in Section 3.1. Second, machine learning methods can be used to predict the binding affinity directly based on the drug and target’s molecular information. Considering the express ability, QML has great potential to enhance its performance [35,41].

2.4. De Novo Drug Design

Background. Traditional drug discovery approaches, such as high-throughput screening, exhaustively search the known molecule libraries to identify drug molecules with desirable pharmaceutical properties. However, the known drug molecules only take up a tiny fraction of the entire drug-like molecule space. Concretely, the size of all the chemically valid drug-like molecules is estimated to reach

10^{60}

[1]. In contrast, all the collected drug-like molecule datasets are no larger than

10^{10}

[5]. To explore the unknown molecule space, we resort to de novo drug design, whose goal is to explore the chemical space and create novel and diverse molecule structures with desirable pharmaceutical properties.

Broad impact. De novo drug design enables the creation of molecules that specifically target a particular protein or receptor, leading to more precise and effective treatments with fewer side effects. The ability to design entirely new compounds with tailored properties can lead to the discovery of first-in-class drugs that address unmet medical needs. Also, de novo design can be used to optimize the pharmacokinetic properties of a drug, such as solubility, stability, and bioavailability, which are critical for its efficacy and safety.

Formulation. It is formulated as a generation task, where computational methods can directly design novel and diverse drug molecular structures with desirable pharmaceutical properties.

Technical Solutions. The challenge is to identify desirable drug molecule structures from huge chemical space (

10^{60}

). Drug design methods can be categorized into two classes. (1) Combinatorial optimization approaches manipulate the discrete molecular space directly to identify the desirable drug molecules, including genetic algorithm (GA) [42,43,44], Monte Carlo Tree Search (MCTS) [42,45], reinforcement learning (RL) [46,47,48], etc. (2) Continuous optimization approaches learn a continuous data distribution to fit the discrete molecular structure and sample the novel molecular structure of the learned distribution, which includes most of the deep generative models, variational autoencoder (VAE) [49,50,51], generative adversarial network (GAN) [52,53,54], energy-based model [55,56], diffusion model [57], etc. QML has achieved initial success in this area thanks to its strong expressive ability. For example, quantum GAN outperforms vanilla GAN in molecule generation [58,59].

2.5. Epitope Prediction

Background. An epitope, also known as an antigenic determinant, is the region of a pathogen that can be recognized by antibodies and cause an adaptive immune response [60,61]. Identifying epitopes helps scientists determine the binding site and is a crucial problem in early target identification for biologics.

Broad impact. Accurate identification of the epitope helps pharmaceutical experts identify the region that binds to the antibody and better understand the mechanism of the antigen.

Formulation. Epitope prediction can be decomposed into multiple binary classification problems. Specifically, given an amino acid sequence, we need to predict the binary label for each amino acid (whether it belongs to epitope).

Technical Solutions. The key challenge is to represent the amino acid sequence and 3D structure simultaneously. Various neural architectures are designed to solve this problem, such as three-dimensional convolutional neural networks, and geometric deep neural networks [62].

2.6. Clinical Trial Outcome Prediction

Background. The clinical trial is an indispensable step toward developing a new drug. In it, human participants are tested to see how they respond to a treatment (e.g., a drug or drug combinations) for treating target diseases. The costs of conducting clinical trials are extremely expensive (up to hundreds of millions of dollars [63]), and the time to run a trial is very long (7-11 years on average) with low success probability [64,65]. The clinical trial outcome can be abstracted into binary labels, e.g., whether the tested drug passed a particular clinical trial phase.

Broad impact. If we can predict the clinical trial outcome before the trial starts, we can avoid running high-risk trials and save money and resources.

Formulation. Clinical trial outcome prediction is formulated as a binary classification task, where the input feature includes drug molecule, disease code, and eligibility criteria, the groundtruth is whether the trial succeeds.

Technical Solutions. The main challenge is to make the trial outcome prediction based on multimodal heterogeneous data features (e.g., drug molecule, disease, eligibility criteria, geographical location, etc). To represent multimodal data features, [66] designed a hierarchical interaction network (HINT) to capture the interaction between drug molecules, disease codes, and trial protocol (e.g., eligibility criteria). [3,4] design an interpretable and uncertainty-aware deep learning method to produce a more trustworthy estimation of the trial approval rate. However, there is a significant data privacy challenge. For instance, a drug’s molecular structure is typically protected by patents and holds substantial commercial value for pharmaceutical companies. There is a concern that a machine learning (ML) property predictor might inadvertently leak this sensitive information. The inherent security features of QML naturally mitigate this issue, offering a solution to protect such proprietary data. For example, QML algorithms, such as Quantum Support Vector Machines (QSVMs) and Quantum Neural Networks (QNNs), can analyze diverse datasets (e.g., electronic health records, genomics, and imaging data) to identify the most appropriate patient groups [67].

2.7. Clinical Trial Recruitment and Trial-Patient Matching

Background. Patient recruitment is a key step in running clinical trials. Given the trial’s eligibility criteria, matching the appropriate patients based on their electronic health records is time- and labor-intensive [2].

Broad Impact. Using AI for trial-patient matching significantly accelerates clinical trial enrollment by identifying eligible patients more quickly and accurately, thereby speeding up the development of new treatments. This approach also enhances patient access to innovative therapies and improves the overall efficiency and success rates of clinical research.

Formulation. We formulate patient-trial matching as a machine learning task (binary classification) to automate the process that selects appropriate patients for the target trial and alleviate the burden of patient recruitment. Specifically, for each data point, the input feature is one patient’s electronic health record and the trial eligibility criteria, the output is a binary variable indicating whether the patient matches the trial.

Technical Solutions. The main challenge of trial-patient matching is to capture the interaction between longitudinal patient health records and semantic information from clinical trial eligibility requirements. To address this issue, [68] propose a recurrent neural network, and BERT-pre-trained transformer to learn a homogeneous representation from the patient records and eligibility criteria, respectively. [69] further enhances it by incorporating finer-grained text features such as disease code and numeric values in patient health records.

2.8. Clinical Trial Site Selection and Ranking

Background. The trial site is the physical location where a clinical trial recruits and interacts with volunteer participants. Selecting the right trial site is crucial to the success of the trial, as it directly influences participant recruitment, data quality, compliance, and overall study efficiency. Traditionally, site selection is a complex and time-consuming process involving multiple criteria, such as the availability of eligible participants, site infrastructure, staff expertise, and historical performance data. This process often relies on manual assessment and expert judgment, which can be prone to biases and inefficiencies. Machine learning has great potential for automating and optimizing the site selection process. By leveraging large datasets and advanced algorithms, machine learning can analyze a multitude of factors simultaneously, providing a more objective and data-driven approach to site selection [70].

Broad Impact. More efficient site selection can accelerate the start-up phase of clinical trials, reducing delays and enabling earlier access to investigational treatments. Improved site selection can lead to more effective recruitment strategies, ensuring that trials are adequately powered and completed within timelines.

Formulation. It can be formulated as a ranking problem or a subset selection problem. Given a pool of all trial sites and their features (e.g., geographical location, therapy expertise), we need to select a subset of these sites. Note that there is also an association between the selected sites. We hope to make the recruited patients more diverse and cover patients from all races.

Technical Solutions. Quantum optimization algorithms like the Quantum Approximate Optimization Algorithm (QAOA) [71,72,73] and Variational Quantum Eigensolver (VQE) [74] can efficiently navigate high-dimensional parameter spaces to determine the optimal trial sites. Existing ML algorithms encounter security concerns. For instance, a drug’s molecular structure is typically protected by patents and holds substantial commercial value for pharmaceutical companies. There is a concern that a ML property predictor might inadvertently leak this sensitive information. The inherent security features of QML naturally mitigate this issue, offering a solution to protect such proprietary data.

3. Toolkit from Quantum Computing

Quantum computing leverages the fundamental principles of quantum mechanics, such as superposition and entanglement, to solve complex problems that classical computers struggle to address. Unlike classical computers, which process information in binary bits (0 or 1), quantum computers use quantum bits, or qubits, which can exist in multiple states simultaneously. This allows quantum computers to explore a vast number of possibilities at once, offering a significant advantage in solving certain types of computationally intensive problems.

This difference in structure makes quantum computers especially powerful when tackling questions involving quantum mechanical phenomena, such as simulating molecular interactions or optimizing complex systems. Classical computers are often limited by the sheer scale of these tasks, particularly when many interacting particles or highly complex optimization problems are involved. In contrast, quantum computers can process and simulate these intricate systems more efficiently, making them particularly valuable in areas like drug discovery, where understanding molecular behavior is key to identifying and developing new treatments.

While still in an early phase, quantum computing is poised to complement classical methods, offering new capabilities that could reduce the time and cost associated with solving some of the most challenging problems in fields such as pharmaceuticals and materials science. Its potential to provide faster and more accurate solutions marks it as a powerful tool for future innovations.

As quantum hardware and research progress, several key quantum algorithms have emerged as especially promising in addressing specific computational challenges. The following section delves into these algorithms and how they are being applied to accelerate advancements in drug discovery and other fields.

3.1. Quantum Simulation

3.1.1. Fault-Tolerant Quantum Algorithms for Drug Design Simulations

Quantum computing, with its transformative capabilities, is emerging as a powerful technique to enhance the accuracy and efficiency of developing potential drug candidates. Particularly, the deployment of fault-tolerant algorithms such as QPE for DFT [38,39,40] shows remarkable promise in addressing complex challenges in drug design. Here, we explore how QPE and other fault-tolerant quantum algorithms can be leveraged to resolve problems in drug design, supported by recent research findings and practical examples.

Figure 5. Quantum-Enhanced Drug Design Process. Classical data, including molecular structures and biological information, is used to construct initial models. This data undergoes preprocessing and quantum encoding before being fed into quantum algorithms for model estimation. Fault-tolerant algorithms and NISQ algorithms are utilized to model drug mechanisms of action, enhancing the precision and efficiency of drug discovery and development.

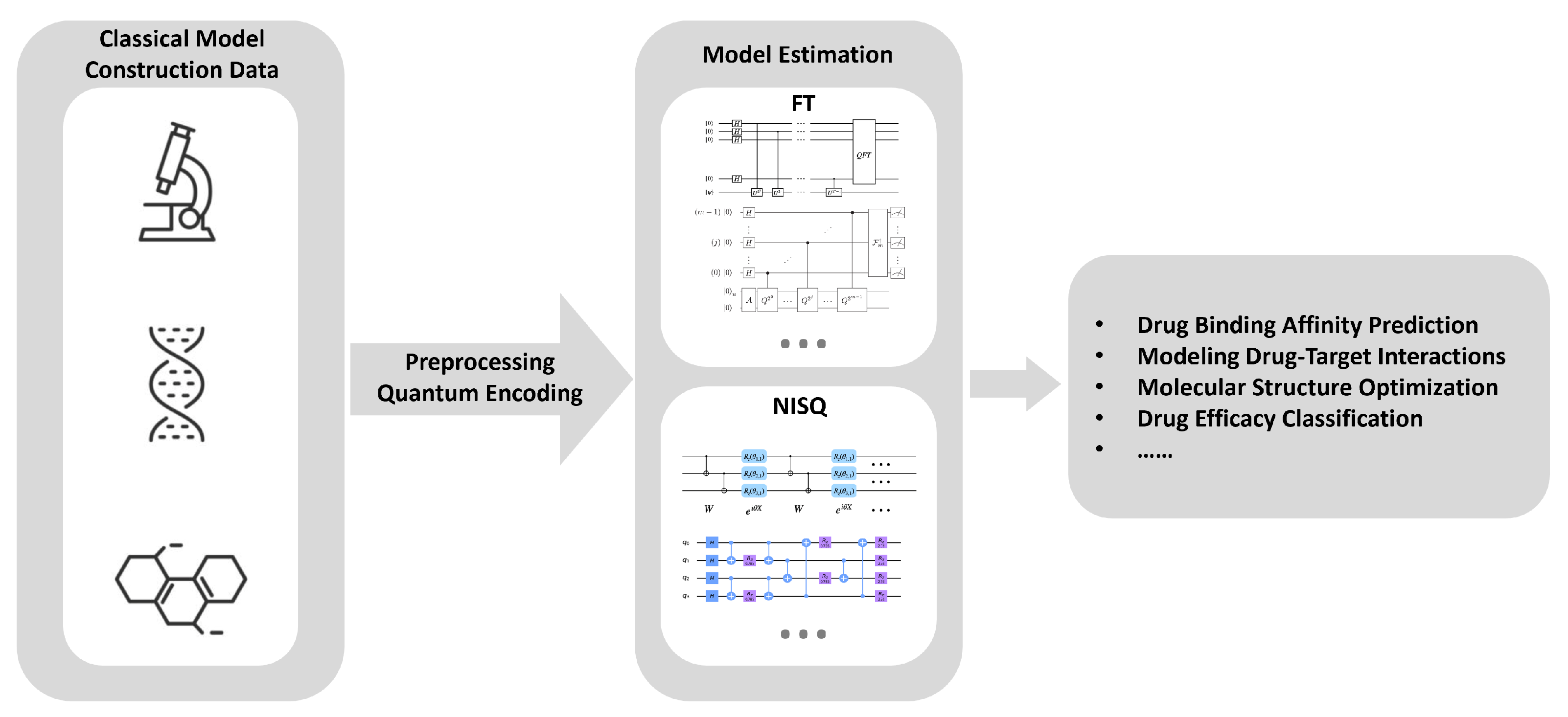
Quantum Phase Estimation

The QPE algorithm is used to determine the phase (or eigenvalue) associated with an eigenstate of a quantum operator. The algorithm begins by preparing a superposition of quantum states, followed by applying a series of controlled unitary operations that encode the phase information onto the qubits. The key step is applying the Quantum Fourier Transform (QFT) to shift the information from the phase into the probability amplitudes of the qubits as shown in Figure 6. When the qubits are measured, the output is a binary representation of the phase, which appears as a high-probability state in the measurement outcomes. This allows QPE to estimate phases efficiently—something classical computers cannot do easily in complex quantum mechanical systems, such as those found in chemistry and materials science.

The process of drug discovery involves predicting how candidate drugs interact with their targets, typically proteins, within the human body. Accurate predictions require solving the electronic structure problem, which is inherently complex and computationally intensive. Classical methods often fall short due to their inability to efficiently handle the quantum mechanical nature of these systems, particularly when strong electron correlations are present [75]. This is where QPE, a fault-tolerant quantum algorithm, comes into play.

QPE is designed to find the eigenvalues of a Hamiltonian with high precision [40,76,77]. By leveraging QPE, researchers can achieve more accurate calculations, which are crucial for predicting the binding affinities and other pharmacological properties of drug molecules [78,79]. The workflow for employing QPE in electronic structure calculations involves initial classical preprocessing to refine the molecular geometry and identify a good starting state, followed by quantum computations to determine the ground-state energy and other relevant properties [80].

The practical implementation of QPE in drug design involves several stages. Initially, a classical computer is used to optimize the molecular structure and prepare the initial state. This state is then fed into a quantum computer, where QPE is applied to determine the ground-state energy [80]. This hybrid approach capitalizes on the strengths of both classical and quantum computing, providing a more efficient and accurate solution to the electronic structure problem. The primary benefits of using QPE in drug design include increased precision, scalability, and efficiency. QPE provides high-precision estimates of eigenvalues, which enhance the accuracy of molecular simulations. This is critical for predicting binding affinities and understanding drug-target interactions. Fault-tolerant quantum algorithms have the potential to handle the exponential complexity of large molecular systems, offering a scalable solution that classical methods struggle to achieve. By leveraging quantum mechanics, QPE can perform computations more efficiently, reducing the time and computational resources required for electronic structure calculations.

Despite its potential, the application of QPE in drug design faces significant challenges. One of the main obstacles is the current state of quantum hardware, which requires substantial advancements to perform fault-tolerant computations at scale. Quantum error correction is essential for fault-tolerant algorithms but necessitates a large number of physical qubits, which presents a considerable overhead [81,82,83]. Additionally, the efficiency of QPE depends on the overlap between the initial state and the target eigenstate. Preparing an initial state with a high overlap is challenging, especially as the system size increases [84,85,86,87]. Ongoing research is focused on improving quantum algorithms and hardware to address these challenges and make QPE more practical for drug design applications.

QPE has demonstrated possible quantum advantage over classical algorithms in several applications, particularly in the realm of quantum chemistry. For instance, QPE has been successfully applied to accurately determine the ground state energies of small molecules like hydrogen and lithium hydride, outperforming classical methods in terms of precision and computational efficiency [88,89]. These applications illustrate QPE’s potential in drug design, where accurate energy calculations are crucial for predicting molecular interactions.

In drug design, QPE can be used to predict the binding affinities of drug candidates with their targets [90]. This involves solving the electronic structure problem of the drug-target complex to determine how strongly the drug binds to its target. The high precision of QPE in determining eigenvalues can lead to more accurate predictions of binding affinities, thereby identifying more effective drug candidates. For example, studies have shown that QPE can achieve high accuracy in simulating the electronic structure of complex biomolecules [91], which is essential for understanding drug interactions at a molecular level.

While direct applications of QPE in drug design are still emerging, its success in related fields such as materials science and chemical reactions underscores its potential. In materials science, QPE has been used to simulate and predict the properties of novel materials, suggesting that similar techniques can be applied to drug molecules. Additionally, QPE’s efficiency in handling large and complex quantum systems positions it as a valuable tool for exploring vast chemical spaces in drug discovery.

In conclusion, QPE might offer significant advantages in drug design by providing high-precision and scalable solutions to the electronic structure problem. Its demonstrated success in related fields further supports its potential application in drug discovery, making QPE a promising tool for developing new and effective drug candidates. As quantum computing technology continues to advance, the integration of QPE into drug design workflows is expected to accelerate, leading to more accurate predictions and faster discovery of new drugs.

Quantum Algorithms for Probability Amplification and System Simulation

QAE, amplitude amplification, and Hamiltonian simulation are interconnected quantum algorithms with significant potential in drug design. While QAE and amplitude amplification focus on enhancing the probability of desired outcomes, Hamiltonian simulation forms the backbone of many quantum chemistry applications.

QAE is one algorithm that can improve the efficiency of probabilistic simulations and Monte Carlo methods [92], which are often used in drug discovery for tasks such as calculating reaction rates and binding affinities. QAE enhances these simulations by providing quadratic speedups over classical counterparts, and this feature is also discussed in the financial realm, which is relevant to drug discovery simulations [93].

Amplitude amplification, a generalization of Grover’s search algorithm, can be used to enhance the probability of finding correct solutions in various quantum algorithms [94,95]. This technique is particularly useful in scenarios where the solution space is vast [96,97], such as identifying potential drug candidates from a large database of molecules.

Hamiltonian simulation is particularly crucial due to its broad applicability across multiple domains. In quantum chemistry, it enables the precise modeling of molecular dynamics and electronic structure [98], which is fundamental to understanding drug-target interactions. The quantum enhancement of Hamiltonian simulation lies in its ability to efficiently simulate quantum systems that are intractable for classical computers, especially as the system size increases [99,100].

For instance, in the field of materials science, quantum Hamiltonian simulation has shown promise in predicting novel materials with desired properties [101]. This capability could be extended to drug design, allowing for the prediction of molecular behavior and drug-protein interactions with unprecedented accuracy. Furthermore, recent advancements in fault-tolerant quantum error correction have paved the way for more robust and scalable Hamiltonian simulations [102], which could significantly impact drug discovery processes.

While direct applications of fault-tolerant Hamiltonian simulation in drug design are still emerging, its success in related fields suggests strong potential. For example, researchers have used quantum algorithms to simulate chemical reactions relevant to catalysis [103], a process with parallels to drug-target interactions. These advancements indicate that fault-tolerant Hamiltonian simulation could revolutionize our ability to model complex biochemical processes in drug design.

Quadratic Unconstrained Binary Optimization and Dequantization Approaches

Quadratic Unconstrained Binary Optimization (QUBO) is indeed often associated with NISQ algorithms, particularly in the context of quantum annealing [104]. However, QUBO formulations have also been explored in the context of fault-tolerant algorithms and their classical equivalents [105,106].

Recent work has investigated the use of QUBO formulations in dequantization efforts, aiming to find efficient classical algorithms that can match or approximate the performance of quantum algorithms [107,108]. For instance, researchers have explored QUBO-based approaches for solving combinatorial optimization problems that are typically targeted by quantum algorithms.

While not directly related to fault-tolerant algorithm dequantization, these efforts contribute to our understanding of the quantum-classical boundary and help benchmark the potential advantages of quantum algorithms in various domains, including drug design.

The integration of fault-tolerant algorithms, such as QPE into DFT calculations, represents a significant advancement in drug design. By enhancing the precision and efficiency of molecular simulations, QPE can accelerate the discovery and optimization of new drug candidates. In addition to QPE, exploring various advanced fault-tolerant algorithms, including QAE, Hamiltonian simulation, and amplitude amplification, offers new opportunities to further improve the accuracy and efficiency of quantum chemistry calculations. Moreover, advanced techniques such as ground state preparation and quantum linear solvers, though not directly part of these algorithms, play a crucial role in optimizing quantum computing applications. While significant challenges remain, ongoing research and technological advancements are paving the way for practical applications of quantum computing in the pharmaceutical industry.

3.1.2. NISQ Algorithms in Drug Design and Development

While fault-tolerant quantum algorithms promise significant advancements in drug design, the current state of quantum hardware necessitates the exploration of NISQ algorithms. These algorithms are designed to operate on quantum devices with a limited number of qubits and are prone to noise and errors. However, they can still provide valuable insights and speed-ups for complex computational chemistry problems [109,110]. Among the most notable NISQ algorithms are variational quantum algorithms, including QML, the QAOA [111], and the VQE [74,112,113,114].

Variational Quantum Eigensolver

VQE is a hybrid quantum-classical algorithm designed to find the ground state energy of a given Hamiltonian. It operates by preparing a quantum state using a parametrized quantum circuit, which is then measured to estimate its energy. A classical optimizer updates the parameters to minimize the energy iteratively(Figure 7).

In the context of drug design, VQE can be applied to molecular structure optimization, binding affinity predictions, and electronic structure calculations [109,115,116]. The VQE algorithm operates by preparing a trial state on a quantum computer, measuring the expectation value of the Hamiltonian, and then using a classical optimizer to adjust the parameters of the quantum circuit. This process is repeated iteratively to minimize the energy, approximating the ground state.

Recent studies have demonstrated VQE’s potential in drug discovery. Researchers have used VQE to optimize the geometry of small molecules relevant to drug design, showing comparable or better performance than classical methods for certain systems [109]. VQE has also been applied to estimate binding energies between drug candidates and target proteins, potentially accelerating the screening process in early-stage drug discovery [115]. Extensions of VQE, such as the quantum subspace expansion technique, allow for the calculation of excited states, which is crucial for understanding molecular reactivity and spectroscopic properties of potential drugs [116]. While these applications are still in the early stages, they highlight VQE’s potential to address computational challenges in drug design that are intractable for classical methods, especially as quantum hardware improves.

Quantum Coupled-Cluster (QCC) methods represent a specific application of VQE, adapting the classical Coupled-Cluster (CC) approach, which is widely regarded as the gold standard for molecular electronic structure calculations. QCC algorithms have been proposed and are actively being researched, with some early implementations demonstrating potential quantum advantages [116,117,118].

The key difference between QCC and classical CC lies in how electron correlations are treated. While classical CC methods use a truncated expansion of the wave function, QCC can potentially capture a more complete set of electron correlations, leading to higher accuracy in molecular property predictions. This feature becomes particularly significant for larger molecules where classical CC methods become computationally intractable.

Recent studies have shown promising results for QCC in calculating ground state energies of small molecules [119,120]. While direct applications in drug design are still in the early stages, the potential for QCC to handle larger molecular systems with high accuracy makes it a promising candidate for future drug discovery applications. As QCC is a specialized form of VQE, it serves as an excellent example of the power and versatility of VQE in solving complex quantum chemistry problems relevant to drug design.

Quantum Approximate Optimization Algorithm

QAOA is another hybrid quantum-classical algorithm, primarily designed for combinatorial optimization problems by preparing an initial quantum state and applying a series of alternating quantum gates controlled by variational parameters(Figure 8). These parameters are adjusted iteratively by a classical optimizer to maximize or minimize a given cost function. QAOA exemplifies quantum computing’s ability to explore vast solution spaces through quantum superposition, offering potential advantages over classical algorithms for solving combinatorial optimization problems in fields like logistics and machine learning.

In drug discovery, QAOA can be applied to various optimization tasks. It has been used to optimize molecular structures by encoding desired properties into a cost function and searching for optimal configurations [101]. Researchers have applied QAOA to predict drug-target interactions by formulating the problem as a graph-matching task [109]. QAOA can also assist in finding low-energy conformations of molecules, which is crucial for understanding drug-receptor interactions [121]. The capability of QAOA lies in its ability to potentially find near-optimal solutions to NP-hard problems more efficiently than classical algorithms, especially for medium-sized instances relevant to drug discovery.

Variational Algorithms in Partially and Early Fault-Tolerant Machines

As we transition from the NISQ era to fault-tolerant quantum computing, variational algorithms such as the VQE and the QAOA remain pivotal. These algorithms, characterized by their adaptability and robustness, are well-suited to leverage the advancements in early fault-tolerant machines, which offer limited error correction capabilities. Variational algorithms are inherently flexible, allowing them to incorporate advanced error mitigation techniques as hardware improves [109,122]. Early fault-tolerant machines, benefiting from reduced error rates and increased coherence times, can exploit these techniques to enhance algorithmic performance beyond what current NISQ devices achieve [123]. For instance, VQE can integrate error mitigation strategies such as zero-noise extrapolation and probabilistic error cancellation, enabling more accurate molecular simulations [124]. This adaptability ensures that variational algorithms can continue to provide substantial benefits even as quantum hardware evolves.

The transition from NISQ to fully fault-tolerant quantum computing is incremental, with gradual improvements in qubit quality and error rates [125]. Variational algorithms are well-positioned to take advantage of these enhancements without necessitating a complete overhaul of computational approaches. For example, VQE, with its iterative nature, can progressively utilize better qubits and lower error rates to refine the precision of electronic structure calculations [126,127]. Additionally, variational algorithms are typically less resource-intensive than fully fault-tolerant algorithms like QPE, requiring fewer qubits and shorter coherence times, making them practical for early fault-tolerant devices [128,129].

VQE has demonstrated significant success in molecular structure optimization and electronic structure calculations. For instance, in early fault-tolerant machines, VQE has been used to calculate the ground state energies of complex molecules such as lithium hydride (

L i H

) and beryllium hydride (

B e H_{2}

)[128]. These studies utilized partial error correction methods to achieve results that surpassed those obtained from purely classical simulations, highlighting VQE’s potential in leveraging improved hardware capabilities. Similarly, QAOA has been effectively applied to combinatorial optimization problems, showcasing its potential in early fault-tolerant regimes [71,111]. For example, QAOA has been used to solve instances of the Max-Cut problem, where it outperformed classical algorithms in specific cases due to enhanced hardware capabilities. This application underscores QAOA’s ability to exploit incremental hardware improvements, providing near-term quantum enhancements in optimization tasks.

The future of variational algorithms in early fault-tolerant quantum computing holds significant promise. As quantum hardware continues to improve, ongoing research aims to optimize these algorithms to harness the capabilities of early fault-tolerant machines fully. For instance, advancements in adaptive ansatz design and dynamic circuit reconfiguration are expected further to enhance the efficiency and accuracy of VQE and QAOA. Additionally, the development of hybrid quantum-classical workflows that integrate machine learning techniques with variational algorithms can lead to more robust and scalable solutions for complex problems in drug design, materials science, and beyond. In conclusion, variational algorithms such as VQE and QAOA play a critical role in bridging the gap between NISQ and fully fault-tolerant quantum computing. Their inherent adaptability, coupled with the ability to incorporate incremental hardware improvements and advanced error mitigation techniques, ensures their continued relevance and effectiveness. As quantum computing technology progresses, these algorithms are poised to deliver substantial benefits, driving significant advancements in various scientific and industrial domains.

Other NISQ Algorithms

As the field of quantum computing advances, various NISQ algorithms are being explored for their potential to revolutionize drug design and development. These algorithms offer promising approaches to solving complex problems that are currently challenging for classical methods. By leveraging quantum parallelism and other unique properties of quantum mechanics, NISQ algorithms might provide benefits in terms of efficiency, accuracy, and scalability. This section delves into several key NISQ algorithms, highlighting their applications in drug design, and their potential to help pharmaceutical research.

Quantum Semi-Definite Programming (QSDP) Solvers can address optimization problems involving semi-definite matrices, which are prevalent in quantum chemistry and drug design. By leveraging quantum parallelism, QSDP solvers can potentially solve these problems more efficiently than their classical counterparts [130,131]. Applications in finance and logistics have demonstrated the effectiveness of QSDP solvers, suggesting their potential for optimizing drug discovery processes.

Quantum Hamiltonian Descent (QHD) is an optimization technique that uses Hamiltonian dynamics to find optimal solutions. QHD has been applied to solve machine learning problems, such as training neural networks and clustering data, with promising results [37,132]. In drug design, QHD can optimize molecular conformations and reaction pathways, enhancing the accuracy of simulations and predictions.

Quantum Annealing is a metaheuristic optimization technique used to find the global minimum of an objective function. It has applications in drug design for optimizing molecular structures and predicting protein-ligand binding affinities. Quantum annealing has shown promise in solving complex optimization problems more efficiently than classical annealing methods, potentially accelerating the drug discovery process [133,134]. The potential benefits of such algorithms include the ability to explore vast solution spaces and identify optimal configurations more efficiently.

Quantum Simulated Annealing (QSA) combines classical simulated annealing with quantum mechanics to solve optimization problems. In drug discovery, QSA can be applied to optimize molecular conformations, docking poses, and other key properties of drug candidates. The benefit of QSA is its ability to leverage quantum tunneling to escape local minima, potentially finding better solutions than classical simulated annealing. This makes QSA particularly useful for solving the complex optimization problems encountered in drug design. Researchers have demonstrated the effectiveness of QSA in optimizing molecular structures, showing its potential to improve the efficiency and accuracy of the drug discovery process [135,136].

The application of NISQ algorithms in drug design is an active area of research, with several promising directions. QML models trained on NISQ devices have shown the potential to improve the accuracy of virtual screening, potentially reducing the number of false positives in early-stage drug discovery [137]. NISQ algorithms have been used to generate novel molecular structures with desired properties, potentially accelerating the discovery of new lead compounds [33]. Quantum-classical hybrid models have demonstrated improved accuracy in predicting the absorption, distribution, metabolism, excretion, and toxicity (ADMET) properties of drug candidates [31].

While many of these applications are still in the early stages, they demonstrate the potential of NISQ algorithms to offer possible enhancements over classical methods in certain scenarios. For example, a recent study showed that a quantum-inspired algorithm outperformed traditional machine learning methods in predicting protein-ligand binding affinities for a set of challenging targets [132]. NISQ algorithms, particularly VQE and QAOA, offer promising approaches to address computational challenges in drug design and development. While still in the early stages, these algorithms have demonstrated potential enhancements in molecular structure optimization, binding affinity prediction, and virtual screening. As quantum hardware continues to improve and algorithm development progresses, we can expect NISQ approaches to play an increasingly important role in pharmaceutical research, complementing both classical methods and future fault-tolerant quantum algorithms.

3.2. Data-driven Quantum Machine Learning

Rapid advances in quantum computing technology offer an exciting opportunity to utilize data-driven approaches for QML. By combining the strengths of big data and quantum algorithms, data-driven QML can improve both drug development and clinical trial processes [138,139]. This section explores potential applications of data-driven QML and how it can transform these areas by improving predictive accuracy, optimizing complex processes, and enabling personalized medicine.

3.2.1. Supervised and Unsupervised QML

QML plays a critical role in advancing drug design by leveraging the capabilities of quantum computing. These approaches can be broadly categorized into two types: supervised and unsupervised QML. Supervised QML algorithms are designed to classify data and predict outcomes based on labeled training data, while unsupervised QML algorithms aim to identify patterns and generate new data structures without labeled training data.

Within this framework, we concentrate on the unique enhancements both supervised and unsupervised QML algorithms bring to drug design and development. These algorithms are well-suited for the complexities of drug discovery and development due to their ability to process vast amounts of data and uncover intricate patterns that classical algorithms may miss.

Given the broad applications of QML, we will now focus on specific supervised algorithms like QSVM and QNN, as well as unsupervised algorithms like Quantum Boltzmann Machines (QBM) and Quantum Generative Adversarial Networks (QGANs). These algorithms harness the power of quantum computing to enhance predictive accuracy, optimize complex processes, and accelerate the discovery of new therapeutic agents.

The advent of quantum computing has brought forth powerful QML algorithms extending classical methods’ capabilities. These QML algorithms, which operate on quantum principles, offer possible enhancements in handling complex and high-dimensional data, making them highly suitable for drug discovery. By leveraging quantum parallelism and entanglement, these algorithms can uncover intricate patterns and relationships within molecular data that classical algorithms may miss. This section explores several key supervised and unsupervised QML algorithms and their applications in drug discovery.

3.2.2. Supervised QML Algorithms

Supervised QML algorithms are designed to classify data and predict outcomes based on labeled training data, making them highly effective for various tasks in drug discovery.

Quantum Neural Networks

QNNs are the quantum counterparts of classical neural networks, designed to perform complex classification and regression tasks by exploiting quantum superposition and entanglement [140]. QNNs can predict molecular activity, classify chemical compounds, and optimize drug design processes. Their ability to handle high-dimensional data spaces and uncover complex patterns makes them particularly useful in virtual screening and predicting drug-target interactions [138]. QNNs have demonstrated superior performance in tasks such as molecular property prediction and drug efficacy classification, making them a valuable tool in the pharmaceutical industry.

Quantum Kernel Methods

Quantum Kernel Methods extend classical kernel methods to the quantum domain, providing powerful tools for machine-learning tasks such as classification, regression, and clustering [141]. By mapping data into a high-dimensional quantum feature space, quantum kernel methods can exploit quantum parallelism to reveal patterns and correlations beyond the reach of classical methods [142,143,144]. In drug discovery, these methods can be used to classify molecular properties, predict drug-target interactions (Section 2.3), and optimize drug design processes, enhancing the accuracy and efficiency of pharmaceutical research.

Quantum Support Vector Machines

QSVM extends classical support vector machines to the quantum realm, providing powerful tools for classification tasks in drug discovery [145,146]. QSVMs can handle high-dimensional data spaces more efficiently, allowing for better classification of molecular properties such as toxicity, efficacy, and binding affinity [33]. By mapping classical data to a higher-dimensional quantum feature space, QSVMs can exploit quantum parallelism to uncover complex patterns that classical SVMs might miss. This capability makes QSVMs particularly attractive in screening large compound libraries and rapidly identifying promising drug candidates with desired characteristics. Researchers have demonstrated the application of QSVMs in predicting molecular activity and classifying chemical compounds, showing that QSVMs can achieve higher accuracy and faster processing times compared to classical approaches.

3.2.3. Unsupervised QML Algorithms

Unsupervised QML algorithms are used to model complex probability distributions and generate new data structures without requiring labeled training data, making them suitable for discovering new patterns and insights in drug discovery.

Quantum Boltzmann Machines

QBMs are a quantum extension of classical Boltzmann machines used to model complex probability distributions. In drug discovery, QBMs can model the distribution of molecular properties and interactions, aiding in the prediction of drug efficacy and safety. The quantum nature of QBMs allows them to capture intricate dependencies and correlations within the data, which are often missed by classical methods. This capability is particularly useful for understanding the probabilistic behavior of molecular systems and predicting how different compounds will interact with their targets. QBMs have been shown to provide more accurate models of molecular interactions, making them a valuable tool in the early stages of drug design [147,148].

Quantum Generative Adversarial Networks

QGANs extend classical GANs to the quantum domain [149,150], providing a powerful tool for generating new molecular structures. In drug discovery, QGANs can learn from existing chemical datasets to generate novel drug-like molecules with desired properties [58,59]. The possible benefits of QGANs lie in their ability to explore a vast chemical space more efficiently than classical generative models, thanks to quantum parallelism. This capability allows QGANs to propose innovative molecular structures that might not be discovered using traditional methods. Researchers have used QGANs to generate potential drug candidates, demonstrating their ability to create diverse and promising compounds for further investigation.

Quantum Principal Component Analysis

QPCA leverages quantum computing to perform PCA more efficiently than classical methods [151,152]. PCA is a widely used technique in data analysis for reducing the dimensionality of datasets while preserving their variance. In drug discovery, QPCA can be used to analyze complex biological data, identify key features of molecular structures, and reduce the computational load for subsequent analysis. This is particularly useful in handling large datasets generated from high-throughput screening and omics technologies, enabling more efficient data processing and insightful analysis [32].

Quantum Reinforcement Learning

QRL applies the principles of reinforcement learning to quantum systems. In drug discovery, QRL can be used to optimize drug development pipelines by learning from previous experiments and adjusting strategies to maximize outcomes [153,154]. This approach is beneficial for tasks such as optimizing synthetic routes for drug production, enhancing the efficiency of clinical trial designs, and dynamically adjusting treatment protocols based on patient responses. QRL’s ability to process and learn from large amounts of data in real-time makes it a powerful tool for adaptive and personalized drug development strategies.

Quantum Topological Data Analysis

QTDA leverages quantum computing to perform topological data analysis more efficiently [155,156,157,158,159,160,161,162]. QTDA can identify topological features of data, such as holes and connected components, which are useful for understanding the shape and structure of complex datasets. In drug discovery, QTDA can be used to analyze the topological features of molecular structures, identify novel drug candidates, and understand the relationships between different compounds. This approach can provide new insights into the molecular landscape, aiding in identifying and optimizing potential drugs.

3.2.4. QML in Drug Design and Clinical Trials

QML combines the power of machine learning with the unique capabilities of quantum computing to revolutionize drug design and clinical trials. By leveraging quantum algorithms, QML enhances the accuracy and efficiency of these processes through advanced classification and optimization tasks(Figure 9). In drug design, QML can classify drug efficacy, predict toxicity, assess the feasibility of clinical trial sites, and forecast patient responses. For clinical trials, QML optimizes drug binding affinities, selects the best clinical trial sites, matches patients to trials, and optimizes molecular structures. These advancements significantly improve the efficiency and accuracy of pharmaceutical research and development.

QML for Drug Design

QML holds the potential to transform drug design by tackling the inherent complexities of molecular interactions and optimizing various stages of the drug discovery process. One of the primary applications of QML is in predicting binding affinities, which is crucial for determining how well a drug candidate will interact with its target. QNNs, trained on extensive datasets of molecular structures and biological activities, offer unprecedented accuracy in these predictions. This capability allows for more efficient screening of vast chemical spaces, significantly accelerating the identification of promising drug candidates [138].

In addition to improving predictions, QML facilitates the generation of novel molecular structures. QGANs can learn from existing chemical datasets to create new drug-like molecules with desired properties. This approach not only speeds up the drug discovery process but also broadens the exploration of chemical spaces, enabling the discovery of unique compounds that may have been overlooked by traditional methods. QGANs can produce a diverse range of molecular structures that meet specific design criteria, providing a valuable tool for expanding the pool of potential drug candidates [139].

Understanding the intricate interactions between drug molecules and their targets is another critical aspect of drug design where QML excels. QBMs are particularly effective in modeling these complex interactions, offering deeper insights into the dynamics of drug-target relationships. By capturing the nuanced dependencies and correlations within molecular data, QBMs enhance the ability to design drugs with higher efficacy and reduced side effects. This advanced modeling capability is essential for developing drugs that precisely target specific molecular pathways [67].

Finally, QML plays a significant role in optimizing molecular conformations, a process critical to ensuring a drug’s effectiveness. Quantum Annealing is an optimization technique that can identify the global minimum of a cost function, thereby finding the most stable and effective molecular conformations. This optimization is crucial for drug efficacy, as the spatial arrangement of atoms within a molecule determines its interaction with biological targets. Similarly, QSA integrates the principles of classical simulated annealing with quantum mechanics, further enhancing the optimization process. These techniques collectively contribute to the discovery of stable and efficacious drug candidates, driving innovation in drug design [163].

QML for Clinical Trial

QML has the potential to significantly impact the field of clinical and drug development. Traditional computational methods often struggle with the complexity of designing and optimizing clinical trials, but quantum computers can process vast amounts of data simultaneously through superposition and entanglement. Applications of QML in clinical trials include enhancing clinical trial simulations, optimizing site and cohort selection, and improving patient stratification strategies.

In clinical trial simulations, QML can improve the prediction of drug efficacy and safety by accurately modeling drug interactions within the human body [163]. Quantum differential equation solvers and quantum-enhanced PBPK (Physiologically Based Pharmacokinetic) models can simulate these interactions more precisely, leading to better-informed trial protocols. For site selection, quantum optimization algorithms such as the QAOA and VQE can efficiently explore high-dimensional parameter spaces to identify the optimal trial sites. These algorithms can handle the non-convex optimization landscapes often encountered in site selection, thus ensuring a more effective and efficient trial setup.

Cohort identification is another area where QML can provide significant enhancements. QML algorithms, including QSVMs and QNNs, can analyze heterogeneous datasets (e.g., electronic health records, genomics, and imaging data) to identify the most suitable patient groups [67]. By uncovering complex correlations in the data, QML can improve the accuracy and relevance of cohort selection, thereby enhancing trial outcomes.

In summary, the integration of QML into clinical and drug development processes promises to overcome many current challenges, from improving trial simulations and optimizing site selection to enhancing cohort identification. As quantum hardware and algorithms continue to advance, QML will play an increasingly crucial role in transforming the landscape of clinical trials and drug development.

3.3. Security Enhancement in Quantum Machine Learning

Among the toolkits poised to revolutionize drug discovery, machine learning stands out as one of the most promising techniques for enhancing the accuracy and efficiency of developing potential drug candidates. To fuel the learning machine, it is crucial to collect high-quality biological data or clinical data for the training procedure. However, the private data, e.g., patients’ clinical data owned by a hospital, might be too sensitive to be shared [164]. Federated learning addresses this problem by proposing a framework where multiple parties, as edge devices, can collaboratively train a shared model without directly sharing the private data [165]. Instead, each party trains its models locally, after which the updated model parameters will be sent to a shared center and aggregated. During this process, the private data can be further protected by employing differential privacy, which adds noise to the updated parameters before uploading them [166].

With the advent of QML, quantum learning models hold the promise of efficiently solving sophisticated problems across various fields, ranging from quantum chemistry to generative modeling [167]. In the scenario where a quantum learner is efficient and the sensitive data is held separately by different parties, quantum federated learning has been proposed as a candidate for ensuring data privacy from being violated [168,169]. As indicated by the name, quantum federated learning leverages quantum computing into the federated learning framework. The benefit of this interdisciplinary approach is multi-fold: 1) The quantum paradigm may provide computational enhancements to boost learning efficiency; 2) As edge devices, various quantum learners can train a shared model without leaking private data [170,171,172]; 3) The privacy can be further enhanced, stemming from the intrinsic randomness of quantum mechanics.

Figure 10. Schematic illustration of quantum federated learning. Multiple clients hold private data that can not be leaked to or shared with the outside, while the quantum federated learning scheme enables the training of a public model without uploading their private data.

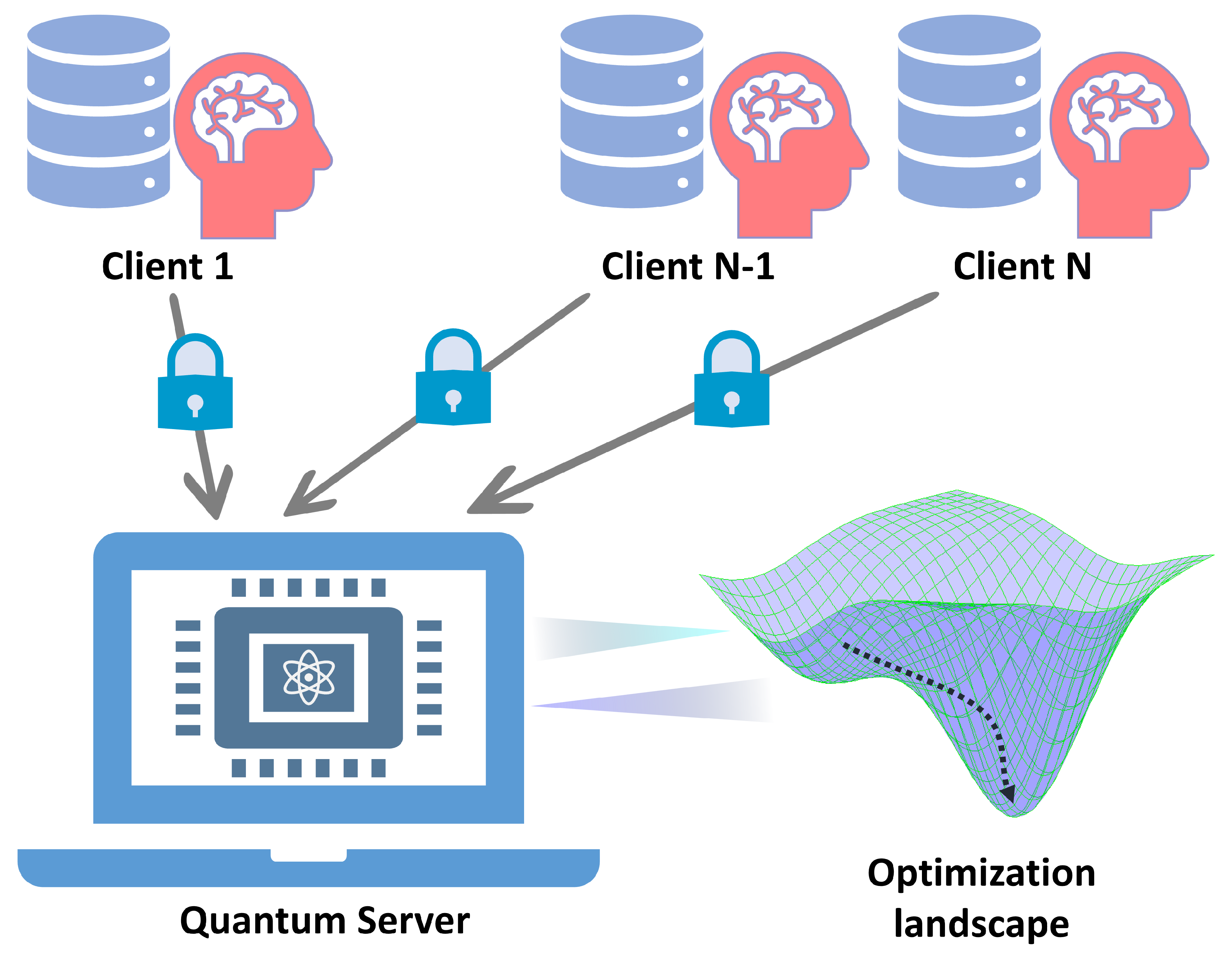
Traditional federated learning may struggle with the complexity and high dimensionality of data, such as accurate modeling of molecular interactions, leading to prohibitive computational costs on edge devices. By leveraging quantum resources, quantum learners are able to achieve possible learning advantages over their classical counterparts [173,174]. For instance, assuming the widely accepted hardness of discrete logarithm problems, quantum kernel methods provide rigorous exponential speedups for a specific supervised learning task [175]. Quantum nonlocality and contextuality also enable quantum-classical learning separations in both classifications [176] and generative models [177]. In addition, quantum learning models may potentially improve accuracy by exploring larger solution spaces, leading to more precise predictions and better generalization from training data to unseen scenarios [178]. Under the quantum federated learning framework, edge quantum devices can fully utilize the learning efficiency to handle their private data. After the local optimization, the updated model parameters from all the parties are sent to a shared center. These parameters are aggregated into global parameters for the updated shared model, which are then sent back to these parties for the next training step. During this procedure, local private data is not required to be shared. At the same time, the distributed edge quantum devices can fully exploit their quantum learning capability and enhance the collaborative training performance.

Quantum federated learning takes a further step in leveraging computational power and privacy protection. A general federated scheme utilizes differential privacy safeguards data by introducing controlled noise to the updated model parameters, making it intricate for adversaries to extract sensitive information from the aggregated data. When equipped with quantum learners, the inherent randomness stemming from the principle of quantum mechanics provides a natural source of noise, which can be adapted into differential privacy to provide an information-theoretic guarantee of privacy protection. Furthermore, the combination of federated learning and blind quantum computing allows quantum computations to be delegated on a remote quantum server and the quantum learning is executed on encrypted data without revealing the underlying information [171,179]. In this setup, data holders can send encrypted data to a quantum server, which performs computations without ever accessing the raw data, ensuring that sensitive information remains confidential throughout the process. This method, as a subroutine to implement the local training, not only maintains stringent privacy as standard federated learning, but also lightens the load on the local computing devices. In certain scenarios, there is a need to protect the transmission of parameters between edge devices and the share center from third-party adversaries. For such cases, (quantum) federated learning can be fortified with post-quantum cryptography to ensure security against intermediate quantum attacks. Post-quantum cryptographic techniques are designed to be resistant to the advanced capabilities of quantum computers [180]. By integrating these cryptographic methods, federated learning systems can safeguard against the potential threats posed by quantum computing, providing robust protection for data transmission and model updates even as computational technologies evolve.

4. Discussion

This paper has examined the integration of classical machine-aided drug discovery methods with emerging quantum computing techniques. While both approaches offer significant advancements, there remains a gap in how effectively they are combined. This section addresses that gap by outlining the costs, time constraints, and limitations inherent to classical methods, and demonstrating how quantum computing can, both theoretically and practically, serve as a complementary tool in overcoming these challenges.

Despite significant advances, quantum computing still faces several challenges before fully integrating it into drug discovery and development. Currently, we are in the NISQ era, where noise, error rates, and qubit count limit quantum devices. While NISQ algorithms have demonstrated early promise in specific drug discovery applications, particularly involving quantum simulations and optimization problems, their practical use remains constrained by hardware limitations.

One of the key challenges in integrating quantum computing into drug discovery lies in bridging the gap between classical machine-aided methods and emerging quantum algorithms. Classical computational methods—such as molecular dynamics simulations, machine learning, and structure-based drug design—have provided invaluable tools for accelerating the drug discovery pipeline. However, they often encounter computational cost, time, and precision limitations when addressing complex molecular systems. The vast search space for molecular structures and interactions can quickly become intractable for classical systems, even with advanced algorithms.

NISQ Era: Quantum as a Collaborative Tool

In the NISQ era, quantum computers are still constrained by noise, limited qubit numbers, and the lack of full error correction. Nevertheless, they are showing promise as powerful collaborators to classical systems in specific drug discovery applications. NISQ devices have demonstrated early potential in quantum simulations of molecular structures, predictions of binding affinities, and optimizations of molecular geometries—tasks that are critical to the early stages of drug design. By leveraging hybrid quantum-classical workflows, quantum computers handle the computationally intensive quantum simulations, while classical systems process broader tasks, such as initial geometry optimization and large-scale data management.

NISQ devices are not yet capable of tackling the most complex molecular systems, but they can provide speedups in smaller-scale simulations and optimization problems. These benefits, however, are limited by the noise and instability inherent in NISQ devices. Quantum error mitigation techniques and algorithmic improvements are crucial to extending the usefulness of NISQ systems in real-world applications.

Another key area where NISQ algorithms are beginning to show a tangible advantage is in optimization. Quantum algorithms, even in their noisy intermediate state, have demonstrated early success in solving complex optimization problems faster and more accurately than classical methods. This has significant implications for clinical trials, where optimization tasks—such as determining patient cohorts, dosage levels, and trial protocols—are both time-sensitive and resource-intensive. In the near future, as NISQ devices mature, they could help streamline the optimization pipeline in clinical trials, potentially reducing the reliance on classical machine learning models. By optimizing these complex variables more efficiently, quantum computing could shorten the length of trials and improve the accuracy of outcomes, leading to faster and more successful drug development processes.

Current estimations suggest that NISQ devices will continue to evolve over the next 5-10 years, with gradual improvements in qubit coherence and error mitigation techniques. During this period, NISQ systems will likely find their place as valuable tools in hybrid quantum-classical workflows, particularly for early-stage drug discovery tasks such as small molecule simulations and basic optimization processes. However, for more complex and large-scale applications, such as full protein-ligand binding simulations or multi-target drug design, NISQ systems will remain limited. As NISQ devices mature, researchers may develop more efficient quantum optimization pipelines for clinical trials, potentially reducing the role of classical machine learning in this area.

While NISQ devices offer incremental advancements, their long-term impact on drug discovery and clinical trials will depend on how effectively they can be integrated into classical workflows and whether future algorithmic developments can mitigate the noise and instability that currently limit their broader application. Nevertheless, in a hybrid context, NISQ computers are expected to support classical systems in solving specific, computationally expensive sub-problems in drug discovery and clinical trial optimization, helping to bridge the gap until fault-tolerant quantum computers become widely available.

The Future of Fault-Tolerant Quantum Algorithms

Looking ahead, the transition to fault-tolerant quantum computing (FTQC) holds significant promise for transforming drug discovery by providing the precision and scalability necessary to address some of the most complex molecular systems. Currently, quantum algorithms, such as those used in electronic-structure calculations, show potential in simulating strongly correlated systems. For instance, FTQC could help researchers better understand the physics of enzymes like cytochrome P450, which plays a critical role in drug metabolism. However, the full impact of FTQC will be realized when we move beyond single-point energy calculations to more comprehensive simulations that predict thermodynamic properties, such as binding affinities and reaction rates—properties that are essential for drug design.

While substantial progress has been made in both quantum hardware and algorithm development over the last few decades, more work is still required to make quantum computing practical for large-scale drug discovery applications. Early fault-tolerant quantum computers may not be able to run complex, useful calculations unless further improvements are made in algorithmic efficiency and error correction. Current estimates suggest that fully operational fault-tolerant quantum computers, capable of handling larger, more intricate molecules with the necessary precision, are likely to be at least 10-20 years away.

Quantum error correction, which is critical for maintaining the stability of quantum computations, presents one of the main challenges in scaling up quantum devices. Each logical qubit requires thousands of physical qubits for error correction, meaning that millions of qubits will be necessary to simulate larger molecular systems accurately. Developing more efficient algorithms and improving hardware with lower error rates and increased qubit connectivity are essential steps in reducing the overhead associated with error correction. For example, new quantum error correction codes and topological techniques, such as surface codes, are being explored to reduce the computational cost of fault-tolerant quantum calculations.

As quantum technology progresses, algorithms like Quantum Phase Estimation (QPE) could provide quadratic speedups for calculating ground-state energies, paving the way for highly accurate simulations of quantum mechanical systems. These advancements would allow researchers to solve quantum chemistry problems that are currently inaccessible to classical computers, particularly for large proteins and other complex biological structures. However, the path to realizing these benefits remains long, and ongoing research is required to refine quantum algorithms and improve their efficiency.

In an ideal scenario, fully fault-tolerant quantum computers could become more widely accessible in the next 15-20 years. Once operational, they will offer groundbreaking accuracy and efficiency in predicting molecular behavior, which will have far-reaching implications for drug discovery. This technology could significantly reduce the time and cost associated with bringing new drugs to market by enabling more accurate simulations of drug-target interactions, optimizing molecular designs, and predicting pharmacokinetic properties with greater precision than current classical methods.

The road to practical, fault-tolerant quantum computing in drug discovery is long and challenging, but the potential rewards are vast. Continued advancements in both hardware and algorithms, alongside a strong focus on quantum error correction and efficient computation, will be critical in ensuring that quantum computing becomes an essential tool in pharmaceutical research and development.

Benchmarking Quantum Algorithms: Maximizing Impact in Drug Discovery

Drug discovery often involves computationally intensive tasks, such as molecular docking, virtual screening, and structure-based design. However, classical methods struggle with the complexity and scale of these problems, creating a need for more advanced tools like quantum algorithms. Quantum algorithms have the potential to address these limitations by offering more efficient simulations, optimization, and predictive modeling, particularly in areas where classical approaches reach their limits.

As NISQ devices advance, benchmarking studies have already shown how quantum algorithms can offer concrete benefits in certain areas of drug discovery. For example, NISQ algorithms have demonstrated the potential to optimize clinical trial processes by improving cohort selection, dosage calculations, and protocol adjustments—tasks that traditionally rely on classical machine learning models. These early successes illustrate the immediate practical applications of NISQ devices in enhancing the efficiency and precision of clinical trials. Looking ahead, as FTQC becomes more accessible, their algorithms are expected to significantly accelerate larger-scale tasks, such as comprehensive molecular optimization, multi-target drug design, and the precise modeling of pharmacokinetics. Benchmarking these algorithms will be essential to understanding how quantum computing can further revolutionize drug development by speeding up processes that currently hinder the swift creation of new, effective treatments.

By continuing to evaluate the performance and limitations of both NISQ and fault-tolerant quantum algorithms, the field will gain a clearer understanding of how these tools can be effectively applied in real-world drug discovery scenarios. Benchmarking will also help pinpoint the specific areas where quantum computing can provide the greatest impact, guiding future research and highlighting where further algorithmic or hardware improvements are most needed.

In summary, while quantum computing remains in its infancy, it shows enormous potential to complement classical methods in drug discovery and development. Continued advancements in both NISQ and fault-tolerant quantum devices, along with benchmarking efforts, will determine how quickly these technologies can be fully integrated into the pharmaceutical industry. Although challenges remain, the potential benefits of quantum computing are vast, offering the prospect of faster, more accurate drug discovery processes and, ultimately, the development of more effective therapies.

5. Conclusions

In this paper, we have discussed the potential of quantum computing for drug discovery and development. We have explored how quantum technologies can accelerate and enhance various stages of the drug development cycle, focusing on the application of quantum computing in addressing challenges related to drug discovery, such as molecular simulation and the prediction of drug-target interactions, as well as the optimization of clinical trial outcomes.

We have highlighted the significant advancements in quantum computing, particularly in the areas of quantum simulation and QML, and how they can be applied to drug discovery. QCC methods, for instance, offer the potential to capture a more complete set of electron correlations, leading to higher accuracy in molecular property predictions. This feature becomes particularly significant for larger molecules where classical methods become computationally intractable.

Furthermore, we have examined how the integration of advanced, fault-tolerant quantum algorithms into established computational frameworks, such as DFT, marks a significant leap forward in drug design. This integration enhances the accuracy and efficiency of molecular simulations, potentially accelerating the identification and refinement of promising drug candidates. Beyond this, we explored various fault-tolerant quantum algorithms, such as QPE, that can significantly improve the precision of quantum chemistry calculations. Other techniques, like QAE and quantum optimization algorithms, further expand the toolkit available for tackling the intricate problems of drug discovery, offering new paths to achieve higher accuracy and efficiency in the development of novel therapeutics.

Finally, we discuss how security could be enhanced in the context of quantum federated learning. Considering the security and data privacy in quantum-computing enhanced drug discovery, we discussed the potential enhancement under the framework of quantum federated learning. Compared with the classical scenario, the intrinsic randomness of quantum mechanics and nonlocal quantum correlations can be well utilized as resources to provide an information-theoretic or unconditional security guarantee in delegated learning tasks on a quantum server, which further extends to multipartite federated learning. With QML algorithms deployed on various clients’ nodes connected by quantum and classical networks, a shared model can be trained without leaking each client’s private data. For future developments, it is appealing to develop photon-based quantum channels for clients’ side for efficient communication and link them to quantum servers of superconducting, ion-trap [181], and atomic systems for handling complex problems in drug discovery.

Despite the significant challenges that remain, ongoing research and technological advancements are paving the way for practical quantum computing applications in the pharmaceutical industry. As quantum hardware continues to evolve, the potential for quantum computing to significantly reduce the time and cost associated with bringing new drugs to market might become increasingly realistic. Ultimately, the integration of quantum computing into drug discovery and development might hold the promise of benefiting public health by accelerating the discovery of novel and effective drugs.

References

Bohacek, R.S.; McMartin, C.; Guida, W.C. The art and practice of structure-based drug design: a molecular modeling perspective. Medicinal Research Reviews 1996, 16, 3–50. [Google Scholar] [CrossRef]
Chen, J.; Hu, Y.; Wang, Y.; Cao, X.; Lin, M.; Xu, H.; Wu, J.; Xiao, C.; Sun, J.; others. TrialBench: Multi-Modal Artificial Intelligence-Ready Clinical Trial Datasets. arXiv:2407.00631 2024.
Lu, Y.; Chen, T.; Hao, N.; Van Rechem, C.; Chen, J.; Fu, T. Uncertainty quantification and interpretability for clinical trial approval prediction. Health Data Science 2024, 4, 0126. [Google Scholar] [CrossRef] [PubMed]
Chen, T.; Hao, N.; Van Rechem, C. Uncertainty Quantification on Clinical Trial Outcome Prediction, 2024, [2401.03482].
Huang, K.; Fu, T.; Gao, W.; Zhao, Y.; Roohani, Y.; Leskovec, J.; Coley, C.W.; Xiao, C.; Sun, J.; Zitnik, M. Artificial intelligence foundation for therapeutic science. Nature Chemical Biology 2022, 18, 1033. [Google Scholar] [CrossRef] [PubMed]
Wang, H.; Fu, T.; Du, Y.; Gao, W.; Huang, K.; Liu, Z.; others. Scientific discovery in the age of artificial intelligence. Nature 2023, 620, 47–60. [CrossRef]
Zhang, X.; Wang, L.; Helwig, J.; Luo, Y.; Fu, C.; Xie, Y.; Liu, M.; Lin, Y.; Xu, Z.; Yan, K.; others. Artificial intelligence for science in quantum, atomistic, and continuum systems. arXiv:2307.08423 2023.
Lu, Y.; Hu, Y.; Li, C. DrugCLIP: Contrastive Drug-Disease Interaction For Drug Repurposing. arXiv preprint arXiv:2407.02265 2024.
Yi, S.; Lu, M.; Yee, A.; Harmon, J.; Meng, F.; Hinduja, S. Enhance wound healing monitoring through a thermal imaging based smartphone app. Medical imaging 2018: Imaging informatics for healthcare, research, and applications. SPIE, 2018, Vol. 10579, pp. 438–441.
De Leon, N.P.; Itoh, K.M.; Kim, D.; Mehta, K.K.; Northup, T.E.; Paik, H.; Palmer, B.; Samarth, N.; Sangtawesin, S.; Steuerman, D.W. Materials challenges and opportunities for quantum computing hardware. Science 2021, 372, eabb2823. [Google Scholar] [CrossRef]
Bravyi, S.; Dial, O.; Gambetta, J.M.; Gil, D.; Nazario, Z. The future of quantum computing with superconducting qubits. Journal of Applied Physics 2022, 132. [Google Scholar] [CrossRef]
Wintersperger, K.; Dommert, F.; Ehmer, T.; Hoursanov, A.; Klepsch, J.; Mauerer, W.; Reuber, G.; Strohm, T.; Yin, M.; Luber, S. Neutral atom quantum computing hardware: performance and end-user perspective. EPJ Quantum Technology 2023, 10, 32. [Google Scholar] [CrossRef]
Wu, Y.; Kolkowitz, S.; Puri, S.; Thompson, J.D. Erasure conversion for fault-tolerant quantum computing in alkaline earth Rydberg atom arrays. Nature communications 2022, 13, 4657. [Google Scholar] [CrossRef]
Bandic, M.; Feld, S.; Almudever, C.G. Full-stack quantum computing systems in the NISQ era: algorithm-driven and hardware-aware compilation techniques. 2022 Design, Automation & Test in Europe Conference & Exhibition (DATE). IEEE, 2022, pp. 1–6.
Crespo, A.; Rodriguez-Granillo, A.; Lim, V.T. Quantum-mechanics methodologies in drug discovery: applications of docking and scoring in lead optimization. Current Topics in Medicinal Chemistry 2017, 17, 2663–2680. [Google Scholar] [CrossRef]
Raghavan, B.; Paulikat, M.; Ahmad, K.; Callea, L.; Rizzi, A.; Ippoliti, E.; Mandelli, D.; Bonati, L.; De Vivo, M.; Carloni, P. Drug design in the exascale era: a perspective from massively parallel QM/MM simulations. Journal of chemical information and modeling 2023, 63, 3647–3658. [Google Scholar] [CrossRef] [PubMed]
Geoffrey AS, B.; Madaj, R.; Valluri, P.P. QPoweredCompound2DeNovoDrugPropMax–a novel programmatic tool incorporating deep learning and in silico methods for automated in silico bio-activity discovery for any compound of interest. Journal of Biomolecular Structure and Dynamics 2023, 41, 1790–1797. [Google Scholar] [CrossRef] [PubMed]
Pradhan, A.K.; Shyam, A.; Mondal, P. Quantum chemical investigations on the hydrolysis of gold (III)-based anticancer drugs and their interaction with amino acid residues. ACS omega 2021, 6, 28084–28097. [Google Scholar] [CrossRef] [PubMed]
Preskill, J. Quantum computing in the NISQ era and beyond. Quantum 2018, 2, 79. [Google Scholar] [CrossRef]
Sears, D. Protein Structure Prediction: Concepts and Applications, 2007.
Scheraga, H.A.; Khalili, M.; Liwo, A. Protein-Folding Dynamics: Overview of Molecular Simulation Techniques. Annual Review of Physical Chemistry 2007, 58, 57–83. [Google Scholar] [CrossRef] [PubMed]
Lane, T.J.; Shukla, D.; Beauchamp, K.A.; Pande, V.S. To milliseconds and beyond: challenges in the simulation of protein folding. Current Opinion in Structural Biology 2013, 23, 58–65. [Google Scholar] [CrossRef]
Kuntz, I. Protein folding. Journal of the American Chemical Society 1972, 94, 4009–4012. [Google Scholar] [CrossRef]
Al-Janabi, A. Has DeepMind’s AlphaFold Solved the Protein Folding Problem? BioTechniques 2022. [Google Scholar] [CrossRef] [PubMed]
Senior, A.W.; Evans, R.; Jumper, J.; Kirkpatrick, J.; Sifre, L.; others. Improved protein structure prediction using potentials from deep learning. Nature 2020, 577, 706–710. [CrossRef]
Jumper, J.; Evans, R.; Pritzel, A.; Green, T.; Figurnov, M.; others. Highly accurate protein structure prediction with AlphaFold. Nature 2021, 596, 583–589. [CrossRef] [PubMed]
Ferreira, L.L.; Andricopulo, A.D. ADMET modeling approaches in drug discovery. Drug Discovery Today 2019, 24, 1157–1165. [Google Scholar] [CrossRef] [PubMed]
Xu, B.; Lu, Y.; Li, C.; Yue, L.; Wang, X.; Hao, N.; Fu, T.; Chen, J. SMILES-Mamba: Chemical Mamba Foundation Models for Drug ADMET Prediction. arXiv preprint arXiv:2408.05696 2024.
Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; ukasz Kaiser, Ł.; Polosukhin, I. Attention Is All You Need. Advances in Neural Information Processing Systems. Curran Associates, Inc., 2017, Vol. 30.
Kipf, T.N.; Welling, M. Semi-supervised classification with graph convolutional networks. The International Conference on Learning Representations (ICLR) 2016. [Google Scholar]
Hogg, T.; Mochon, C.; Polak, W.; Rieffel, E. Tools for quantum algorithms. International journal of modern physics C 1999, 10, 1347–1361. [Google Scholar] [CrossRef]
He, C.; Li, J.; Liu, W.; Peng, J.; Wang, Z.J. A low-complexity quantum principal component analysis algorithm. IEEE transactions on quantum engineering 2022, 3, 1–13. [Google Scholar] [CrossRef]
Cleve, R.; Ekert, A.; Henderson, L.; Macchiavello, C.; Mosca, M. On quantum algorithms. arXiv preprint quant-ph/9903061 1999.
Zhang, B.; Fu, Y.; Lu, Y.; Zhang, Z.; Clarke, R.; Van Eyk, J.E.; Herrington, D.M.; Wang, Y. DDN2.0: R and Python packages for differential dependency network analysis of biological systems. bioRxiv 2021, pp. 2021–04.
Huang, K.; Fu, T.; Glass, L.M.; Zitnik, M.; Xiao, C.; Sun, J. DeepPurpose: a deep learning library for drug–target interaction prediction. Bioinformatics 2020, 36, 5545–5547. [Google Scholar] [CrossRef] [PubMed]
Chen, L.; Lu, Y.; Wu, C.T.; Clarke, R.; Yu, G.; Van Eyk, J.E.; Herrington, D.M.; Wang, Y. Data-driven detection of subtype-specific differentially expressed genes. Scientific reports 2021, 11, 332. [Google Scholar] [CrossRef] [PubMed]
Radtke, T.; Fritzsche, S. Simulation of n-qubit quantum systems. III. Quantum operations. Computer physics communications 2007, 176, 617–633. [Google Scholar] [CrossRef]
Baker, T.E.; Poulin, D. Density functionals and Kohn-Sham potentials with minimal wavefunction preparations on a quantum computer. Physical Review Research 2020, 2, 043238. [Google Scholar] [CrossRef]
Yang, J.; Brown, J.; Whitfield, J.D. A comparison of three ways to measure time-dependent densities with quantum simulators. Frontiers in Physics 2021, 9, 546538. [Google Scholar] [CrossRef]
Brown, J. Calculating potential energy surfaces with quantum computers by measuring only the density along adiabatic transitions. Journal of Chemical Theory and Computation 2024, 20, 3096–3108. [Google Scholar] [CrossRef]
Lu, Y.; Wu, C.T.; Parker, S.J.; Cheng, Z.; Saylor, G.; Van Eyk, J.E.; Yu, G.; Clarke, R.; Herrington, D.M.; Wang, Y. COT: an efficient and accurate method for detecting marker genes among many subtypes. Bioinformatics Advances 2022, 2, vbac037. [Google Scholar] [CrossRef]
Jensen, J.H. A graph-based genetic algorithm and generative model/Monte Carlo tree search for the exploration of chemical space. Chemical Science 2019, 10, 3567–3572. [Google Scholar] [CrossRef]
Durrant, J.D.; Lindert, S.; McCammon, J.A. AutoGrow 3.0: an improved algorithm for chemically tractable, semi-automated protein inhibitor design. Journal of Molecular Graphics and Modelling 2013, 44, 104–112. [Google Scholar] [CrossRef] [PubMed]
Fu, T.; Gao, W.; Coley, C.W.; Sun, J. Reinforced Genetic Algorithm for Structure-based Drug Design. Annual Conference on Neural Information Processing Systems (NeurIPS), 2022.
Fu, T.; Xiao, C.; Li, X.; Glass, L.M.; Sun, J. MIMOSA: Multi-constraint Molecule Sampling for Molecule Optimization. Proceedings of the AAAI Conference on Artificial Intelligence, 2021, Vol. 35, pp. 125–133.
Olivecrona, M.; Blaschke, T.; Engkvist, O.; Chen, H. Molecular de-novo design through deep reinforcement learning. Journal of Cheminformatics 2017, 9, 48. [Google Scholar] [CrossRef] [PubMed]
Fu, T.; Xiao, C.; Qian, C.; Glass, L.M.; Sun, J. Probabilistic and dynamic molecule-disease interaction modeling for drug discovery. Proceedings of the 27th ACM SIGKDD Conference on Knowledge Discovery & Data Mining, 2021, pp. 404–414.
Fu, T.; Sun, J. SIPF: Sampling Method for Inverse Protein Folding. Proceedings of the 28th ACM SIGKDD Conference on Knowledge Discovery and Data Mining, 2022, pp. 378–388.
Gómez-Bombarelli, R.; Wei, J.N.; Duvenaud, D.; Hernández-Lobato, J.M.; Sánchez-Lengeling, B.; Sheberla, D.; Aguilera-Iparraguirre, J.; Hirzel, T.D.; Adams, R.P.; Aspuru-Guzik, A. Automatic chemical design using a data-driven continuous representation of molecules. ACS Central Science 2018, 4, 268–276. [Google Scholar] [CrossRef] [PubMed]
Jin, W.; Barzilay, R.; Jaakkola, T.S. Junction tree variational autoencoder for molecular graph generation. International Conference on Machine Learning (ICML), 2018.
Fu, T.; Xiao, C.; Sun, J. Core: Automatic molecule optimization using copy & refine strategy. AAAI, 2020.
Cao, N.D.; Kipf, T. MolGAN: An implicit generative model for small molecular graphs, 2018, [1805.11973].
Lu, Y.; Sato, K.; Wang, J. Deep Learning based Multi-Label Image Classification of Protest Activities. arXiv preprint arXiv:2301.04212 2023.
Fu, T.; Xiao, C.; Glass, L.M.; Sun, J. MOLER: Incorporate molecule-level reward to enhance deep generative model for molecule optimization. IEEE transactions on knowledge and data engineering 2021, 34, 5459–5471. [Google Scholar] [CrossRef] [PubMed]
Fu, T.; Sun, J. Antibody Complementarity Determining Regions (CDRs) design using Constrained Energy Model. Proceedings of the 28th ACM SIGKDD Conference on Knowledge Discovery and Data Mining, 2022, pp. 389–399.
Fu, T.; Gao, W.; Xiao, C.; Yasonik, J.; Coley, C.W.; Sun, J. Differentiable Scaffolding Tree for Molecular Optimization. International Conference on Learning Representations 2022. [Google Scholar]
Xu, M.; Yu, L.; Song, Y.; Shi, C.; Ermon, S.; Tang, J. GeoDiff: A Geometric Diffusion Model for Molecular Conformation Generation. International Conference on Learning Representations, 2021.
Braun, D.; Müller, R. Stochastic emulation of quantum algorithms. New Journal of Physics 2022, 24, 023028. [Google Scholar] [CrossRef]
Tulsi, A. Universal Quantum Algorithm. arXiv:1611.03472 2016.
Wu, C.T.; Shen, M.; Du, D.; Cheng, Z.; Parker, S.J.; Van Eyk, J.E.; Yu, G.; Clarke, R.; Herrington, D.M.; others. Cosbin: cosine score-based iterative normalization of biologically diverse samples. Bioinformatics Advances 2022, 2, vbac076.
Chang, Y.T.; Hoffman, E.P.; Yu, G.; Herrington, D.M.; Clarke, R.; Wu, C.T.; Chen, L.; Wang, Y. Integrated identification of disease specific pathways using multi-omics data. bioRxiv 2019, p. 666065.
Satorras, V.G.; Hoogeboom, E.; Welling, M. E(n) equivariant graph neural networks. International Conference on Machine Learning 2021. [Google Scholar]
Martin, L.; Hutchens, M.; Hawkins, C.; Radnov, A. How much do clinical trials cost. Nature Reviews Drug Discovery 2017, 16, 381–382. [Google Scholar] [CrossRef] [PubMed]
Peto, R. Clinical trial methodology. Nature 1978, 272, 15–16. [Google Scholar] [CrossRef]
Ledford, H. 4 Ways to fix the clinical trial: clinical trials are crumbling under modern economic and scientific pressures. Nature looks at ways they might be saved. Nature 2011, 477, 526–529. [Google Scholar] [CrossRef] [PubMed]
Fu, T.; Huang, K.; Xiao, C.; Glass, L.M.; Sun, J. HINT: Hierarchical interaction network for clinical-trial-outcome predictions. Patterns 2022, 3, 100445. [Google Scholar] [CrossRef] [PubMed]
Zinner, M.; Dahlhausen, F.; Boehme, P.; Ehlers, J.; Bieske, L.; Fehring, L. Quantum computing’s potential for drug discovery: Early stage industry dynamics. Drug Discovery Today 2021, 26, 1680–1688. [Google Scholar] [CrossRef]
Zhang, X.; Xiao, C.; Glass, L.M.; Sun, J. Deepenroll: Patient-trial matching with deep embedding and entailment prediction. Proceedings of The Web Conference 2020, 2020, pp. 1029–1037.
Gao, J.; Xiao, C.; Glass, L.M.; Sun, J. COMPOSE: Cross-Modal Pseudo-Siamese Network for Patient Trial Matching. Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, 2020, pp. 803–812.
Wang, Y.; Fu, T.; Xu, Y.; Ma, Z.; Xu, H.; Du, B.; Gao, H.; Wu, J.; Chen, J. TWIN-GPT: Digital Twins for Clinical Trials via Large Language Model. ACM Transactions on Multimedia Computing, Communications and Applications 2024.
Farhi, E.; Goldstone, J.; Gutmann, S. A quantum approximate optimization algorithm. arXiv:1411.4028 2014.
Ebadi, S.; Keesling, A.; Cain, M.; Wang, T.T.; Levine, H.; Bluvstein, D.; Semeghini, G.; Omran, A.; Liu, J.G.; Samajdar, R.; others. Quantum Optimization of Maximum Independent Set Using Rydberg Atom Arrays. Science 2022, 376, 1209–1215. [CrossRef]
Liang, Z.; Song, Z.; Cheng, J.; He, Z.; Liu, J.; Wang, H.; Qin, R.; Wang, Y.; Han, S.; Qian, X.; others. Hybrid gate-pulse model for variational quantum algorithms. 2023 60th ACM/IEEE Design Automation Conference (DAC). IEEE, 2023, pp. 1–6.
Tilly, J.; Chen, H.; Cao, S.; Picozzi, D.; Setia, K.; Li, Y.; Grant, E.; Wossnig, L.; Rungger, I.; Booth, G.H.; others. The Variational Quantum Eigensolver: A Review of Methods and Best Practices. Physics Reports 2022, 986, 1–128. [CrossRef]
Benavides-Riveros, C.L.; Wasak, T.; Recati, A. Extracting many-body quantum resources within one-body reduced density matrix functional theory. Physical Review Research 2024, 6, L012052. [Google Scholar] [CrossRef]
Ge, Y.; Tura, J.; Cirac, J.I. Faster ground state preparation and high-precision ground energy estimation with fewer qubits. Journal of Mathematical Physics 2019, 60. [Google Scholar] [CrossRef]
Lin, L.; Tong, Y. Near-optimal ground state preparation. Quantum 2020, 4, 372. [Google Scholar] [CrossRef]
Uzzaman, M.; Mahmud, T. Structural modification of aspirin to design a new potential cyclooxygenase (COX-2) inhibitors. In Silico Pharmacology 2020, 8, 1–14. [Google Scholar] [CrossRef]
Kawsar, S.M.; Hosen, M.A.; El Bakri, Y.; Ahmad, S.; Affi, S.T.; Goumri-Said, S. In silico approach for potential antimicrobial agents through antiviral, molecular docking, molecular dynamics, pharmacokinetic and bioactivity predictions of galactopyranoside derivatives. Arab Journal of Basic and Applied Sciences 2022, 29, 99–112. [Google Scholar] [CrossRef]
Santagati, R.; Aspuru-Guzik, A.; Babbush, R.; Degroote, M.; Gonzalez, L.; Kyoseva, E.; Moll, N.; Oppel, M.; Parrish, R.M.; Rubin, N.C.; others. Drug design on quantum computers. Nature Physics 2024, 20, 549–557.
Lee, S.; Lee, J.; Zhai, H.; Tong, Y.; Dalzell, A.M.; Kumar, A.; Helms, P.; Gray, J.; Cui, Z.H.; Liu, W.; others. Evaluating the evidence for exponential quantum advantage in ground-state quantum chemistry. Nature Communications 2023, 14, 1952. [CrossRef] [PubMed]
Blunt, N.S.; Gehér, G.P.; Moylett, A.E. Compiling a Simple Chemistry Application to Quantum Error Correction Primitives. 2023 IEEE International Conference on Quantum Computing and Engineering (QCE). IEEE, 2023, Vol. 2, pp. 290–291.
Otten, M.; Kang, B.; Fedorov, D.; Lee, J.H.; Benali, A.; Habib, S.; Gray, S.K.; Alexeev, Y. QREChem: quantum resource estimation software for chemistry applications. Frontiers in Quantum Science and Technology 2023, 2, 1232624. [Google Scholar] [CrossRef]
Li, H.; Ni, H.; Ying, L. Adaptive low-depth quantum algorithms for robust multiple-phase estimation. Physical Review A 2023, 108, 062408. [Google Scholar] [CrossRef]
Ollitrault, P.J.; Cortes, C.L.; Gonthier, J.F.; Parrish, R.M.; Rocca, D.; Anselmetti, G.L.; Degroote, M.; Moll, N.; Santagati, R.; Streif, M. Enhancing initial state overlap through orbital optimization for faster molecular electronic ground-state energy estimation. arXiv:2404.08565 2024.
Cao, C.; Sun, J.; Yuan, X.; Hu, H.S.; Pham, H.Q.; Lv, D. Ab initio quantum simulation of strongly correlated materials with quantum embedding. npj Computational Materials 2023, 9, 78. [Google Scholar] [CrossRef]
Choi, S.; Loaiza, I.; Lang, R.A.; Martínez-Martínez, L.A.; Izmaylov, A.F. Probing Quantum Efficiency: Exploring System Hardness in Electronic Ground State Energy Estimation. Journal of Chemical Theory and Computation 2024. [Google Scholar] [CrossRef] [PubMed]
Mucs, D.; Bryce, R.A. The application of quantum mechanics in structure-based drug design. Expert Opinion on Drug Discovery 2013, 8, 263–276. [Google Scholar] [CrossRef]
Zhou, L. Full Electronic Structure Calculation of Quantum Mechanics in Binding Site of Protease 6LU7. Authorea Preprints 2020. [Google Scholar]
Rathore, R.; Sumakanth, M.; Reddy, M.S.; Reddanna, P.; Rao, A.A.; Erion, M.D.; Reddy, M. Advances in binding free energies calculations: QM/MM-based free energy perturbation method for drug design. Current Pharmaceutical Design 2013, 19, 4674–4686. [Google Scholar] [CrossRef] [PubMed]
Prezhdo, O.V. A Modern Quantum Chemistry Sampler: From Algorithms for the Schrodinger Equation, to Medium Effects, to Large-Scale In Silico Molecule Design, 2011.
Maronese, M.; Incudini, M.; Asproni, L.; Prati, E. The maximum-likelihood quantum amplitude estimation algorithm provides the best tradeoff between accuracy and circuit depth among quantum solutions for integral estimation. 2023 IEEE International Conference on Quantum Computing and Engineering (QCE). IEEE, 2023, Vol. 1, pp. 554–559.
Miyamoto, K. Bermudan option pricing by quantum amplitude estimation and Chebyshev interpolation. EPJ Quantum Technology 2022, 9, 1–27. [Google Scholar] [CrossRef]
Wiedemann, S.; Hein, D.; Udluft, S.; Mendl, C. Quantum Policy Iteration via Amplitude Estimation and Grover Search–Towards Quantum Advantage for Reinforcement Learning. arXiv:2206.04741 2022.
Kwon, H.; Bae, J. Quantum amplitude-amplification operators. Physical Review A 2021, 104, 062438. [Google Scholar] [CrossRef]
Sanchez-Rivero, J.; Talaván, D.; Garcia-Alonso, J.; Ruiz-Cortés, A.; Murillo, J.M. Automatic generation of an efficient less-than oracle for quantum amplitude amplification. 2023 IEEE/ACM 4th International Workshop on Quantum Software Engineering (Q-SE). IEEE, 2023, pp. 26–33.
Benchasattabuse, N.; Satoh, T.; Hajdušek, M.; Van Meter, R. Amplitude amplification for optimization via subdivided phase oracle. 2022 IEEE International Conference on Quantum Computing and Engineering (QCE). IEEE, 2022, pp. 22–30.
Tolunay, M.; Liepuoniute, I.; Vyushkova, M.; Jones, B.A. Hamiltonian simulation of quantum beats in radical pairs undergoing thermal relaxation on near-term quantum computers. Physical Chemistry Chemical Physics 2023, 25, 15115–15134. [Google Scholar] [CrossRef] [PubMed]
Low, G.H.; Wiebe, N. Hamiltonian simulation in the interaction picture. arXiv:1805.00675 2018.
Schmitz, A.T.; Sawaya, N.P.; Johri, S.; Matsuura, A. Graph optimization perspective for low-depth Trotter-Suzuki decomposition. Physical Review A 2024, 109, 042418. [Google Scholar] [CrossRef]
Barkoutsos, P.K.; Gkritsis, F.; Ollitrault, P.J.; Sokolov, I.O.; Woerner, S.; Tavernelli, I. Quantum algorithm for alchemical optimization in material design. Chemical Science 2021, 12, 4345–4352. [Google Scholar] [CrossRef] [PubMed]
Noh, K.; Chamberland, C. Fault-tolerant bosonic quantum error correction with the surface–Gottesman-Kitaev-Preskill code. Physical Review A 2020, 101, 012316. [Google Scholar] [CrossRef]
Eisert, J.; Plenio, M.B. Focus on quantum information and many-body theory. New Journal of Physics 2010, 12, 025001. [Google Scholar] [CrossRef]
Alom, M.Z.; Van Essen, B.; Moody, A.T.; Widemann, D.P.; Taha, T.M. Quadratic unconstrained binary optimization (QUBO) on neuromorphic computing system. 2017 International Joint Conference on Neural Networks (IJCNN). IEEE, 2017, pp. 3922–3929.
Noh, K.; Chamberland, C.; Brandão, F.G. Low-overhead fault-tolerant quantum error correction with the surface-GKP code. PRX Quantum 2022, 3, 010315. [Google Scholar] [CrossRef]
Guerreschi, G.G. Solving quadratic unconstrained binary optimization with divide-and-conquer and quantum algorithms. arXiv:2101.07813 2021.
Yurtsever, A.; Birdal, T.; Golyanik, V. Q-FW: A hybrid classical-quantum Frank-Wolfe for quadratic binary optimization. European Conference on Computer Vision. Springer, 2022, pp. 352–369.
Jiang, J.R.; Chu, C.W. Classifying and Benchmarking Quantum Annealing Algorithms Based on Quadratic Unconstrained Binary Optimization for Solving NP-Hard Problems. IEEE Access 2023. [Google Scholar] [CrossRef]
Mustafa, H.; Morapakula, S.N.; Jain, P.; Ganguly, S. Variational quantum algorithms for chemical simulation and drug discovery. 2022 International Conference on Trends in Quantum Computing and Emerging Business Technologies (TQCEBT). IEEE, 2022, pp. 1–8.
Hubregtsen, T.; Wilde, F.; Qasim, S.; Eisert, J. Single-component gradient rules for variational quantum algorithms. Quantum Science and Technology 2022, 7, 035008. [Google Scholar] [CrossRef]
Zhou, L.; Wang, S.T.; Choi, S.; Pichler, H.; Lukin, M.D. Quantum approximate optimization algorithm: Performance, mechanism, and implementation on near-term devices. Physical Review X 2020, 10, 021067. [Google Scholar] [CrossRef]
Kandala, A.; Mezzacapo, A.; Temme, K.; Takita, M.; Brink, M.; Chow, J.M.; Gambetta, J.M. Hardware-Efficient Variational Quantum Eigensolver for Small Molecules and Quantum Magnets. Nature 2017, 549, 242–246. [Google Scholar] [CrossRef] [PubMed]
Peruzzo, A.; McClean, J.; Shadbolt, P.; Yung, M.H.; Zhou, X.Q.; Love, P.J.; Aspuru-Guzik, A.; O’Brien, J.L. A Variational Eigenvalue Solver on a Photonic Quantum Processor. Nature Communications 2014, 5, 4213. [Google Scholar] [CrossRef]
Liang, Z.; Cheng, J.; Ren, H.; Wang, H.; Hua, F.; Song, Z.; Ding, Y.; Chong, F.T.; Han, S.; Qian, X.; others. NAPA: intermediate-level variational native-pulse ansatz for variational quantum algorithms. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems 2024.
Haidar, M.; Rančić, M.J.; Ayral, T.; Maday, Y.; Piquemal, J.P. Open source variational quantum eigensolver extension of the quantum learning machine for quantum chemistry. Wiley Interdisciplinary Reviews: Computational Molecular Science 2023, 13, e1664. [Google Scholar] [CrossRef]
Kumar, A.; Asthana, A.; Masteran, C.; Valeev, E.F.; Zhang, Y.; Cincio, L.; Tretiak, S.; Dub, P.A. Quantum simulation of molecular electronic states with a transcorrelated Hamiltonian: higher accuracy with fewer qubits. Journal of Chemical Theory and Computation 2022, 18, 5312–5324. [Google Scholar] [CrossRef] [PubMed]
Sokolov, I.O.; Barkoutsos, P.K.; Ollitrault, P.J.; Greenberg, D.; Rice, J.; Pistoia, M.; Tavernelli, I. Quantum orbital-optimized unitary coupled cluster methods in the strongly correlated regime: Can quantum algorithms outperform their classical equivalents? The Journal of Chemical Physics 2020, 152. [Google Scholar] [CrossRef]
Ryabinkin, I.G.; Izmaylov, A.F.; Genin, S.N. A posteriori corrections to the iterative qubit coupled cluster method to minimize the use of quantum resources in large-scale calculations. Quantum Science and Technology 2021, 6, 024012. [Google Scholar] [CrossRef]
Zhang, J.H.; Iyengar, S.S. Graph-QC, a Graph-Based Quantum/Classical Algorithm for Efficient Electronic Structure on Hybrid Quantum/Classical Hardware Systems: Improved Quantum Circuit Depth Performance. Journal of Chemical Theory and Computation 2022, 18, 2885–2899. [Google Scholar] [CrossRef]
Sugisaki, K.; Kato, T.; Minato, Y.; Okuwaki, K.; Mochizuki, Y. Variational quantum eigensolver simulations with the multireference unitary coupled cluster ansatz: a case study of the C 2v quasi-reaction pathway of beryllium insertion into a H 2 molecule. Physical Chemistry Chemical Physics 2022, 24, 8439–8452. [Google Scholar] [CrossRef]
Ding, Q.M.; Huang, Y.M.; Yuan, X. Molecular docking via quantum approximate optimization algorithm. Physical Review Applied 2024, 21, 034036. [Google Scholar] [CrossRef]
Miháliková, I.; Pivoluska, M.; Plesch, M.; Friák, M.; Nagaj, D.; Šob, M. The cost of improving the precision of the variational quantum eigensolver for quantum chemistry. Nanomaterials 2022, 12, 243. [Google Scholar] [CrossRef] [PubMed]
Huo, M.; Li, Y. Error-resilient Monte Carlo quantum simulation of imaginary time. Quantum 2023, 7, 916. [Google Scholar] [CrossRef]
Buonaiuto, G.; Gargiulo, F.; De Pietro, G.; Esposito, M.; Pota, M. Best practices for portfolio optimization by quantum computing, experimented on real quantum devices. Scientific Reports 2023, 13, 19434. [Google Scholar] [CrossRef] [PubMed]
Vallury, H.J.; Jones, M.A.; White, G.A.; Creevey, F.M.; Hill, C.D.; Hollenberg, L.C. Noise-robust ground state energy estimates from deep quantum circuits. Quantum 2023, 7, 1109. [Google Scholar] [CrossRef]
McClean, J.R.; Romero, J.; Babbush, R.; Aspuru-Guzik, A. The theory of variational hybrid quantum-classical algorithms. New Journal of Physics 2016, 18, 023023. [Google Scholar] [CrossRef]
Hempel, C.; Maier, C.; Romero, J.; McClean, J.; Monz, T.; Shen, H.; Jurcevic, P.; Lanyon, B.P.; Love, P.; Babbush, R.; others. Quantum chemistry calculations on a trapped-ion quantum simulator. Physical Review X 2018, 8, 031022.
Kandala, A.; Mezzacapo, A.; Temme, K.; Takita, M.; Brink, M.; Chow, J.M.; Gambetta, J.M. Hardware-efficient variational quantum eigensolver for small molecules and quantum magnets. Nature 2017, 549, 242–246. [Google Scholar] [CrossRef] [PubMed]
Liang, Z.; Wang, H.; Cheng, J.; Ding, Y.; Ren, H.; Gao, Z.; Hu, Z.; Boning, D.S.; Qian, X.; Han, S.; others. Variational quantum pulse learning. 2022 IEEE International Conference on Quantum Computing and Engineering (QCE). IEEE, 2022, pp. 556–565.
Martyn, J.M.; Rossi, Z.M.; Tan, A.K.; Chuang, I.L. Grand unification of quantum algorithms. PRX quantum 2021, 2, 040203. [Google Scholar] [CrossRef]
Cleve, R.; Ekert, A.; Macchiavello, C.; Mosca, M. Quantum algorithms revisited. Proceedings of the Royal Society of London. Series A: Mathematical, Physical and Engineering Sciences 1998, 454, 339–354. [Google Scholar] [CrossRef]
Blais, A. Quantum network optimization. Physical Review A 2001, 64, 022312. [Google Scholar] [CrossRef]
Gao, M.; Ji, Z.; Li, T.; Wang, Q. Logarithmic-regret quantum learning algorithms for zero-sum games. Advances in Neural Information Processing Systems 2024, 36. [Google Scholar]
Freedman, M.; Kitaev, A.; Larsen, M.; Wang, Z. Topological quantum computation. Bulletin of the American Mathematical Society 2003, 40, 31–38. [Google Scholar] [CrossRef]
Chen, W.; Ye, Z.; Li, L. Characterization of exact one-query quantum algorithms. Physical Review A 2020, 101, 022325. [Google Scholar] [CrossRef]
Garnerone, S.; Marzuoli, A.; Rasetti, M. Quantum geometry and quantum algorithms. Journal of Physics A: Mathematical and Theoretical 2007, 40, 3047. [Google Scholar] [CrossRef]
Wichert, A. Principles of quantum artificial intelligence: quantum problem solving and machine learning; World Scientific, 2020.
Batra, K.; Zorn, K.M.; Foil, D.H.; Minerali, E.; Gawriljuk, V.O.; Lane, T.R.; Ekins, S. Quantum machine learning algorithms for drug discovery applications. Journal of chemical information and modeling 2021, 61, 2641–2647. [Google Scholar] [CrossRef]
Cao, Y.; Romero, J.; Aspuru-Guzik, A. Potential of quantum computing for drug discovery. IBM Journal of Research and Development 2018, 62, 6–1. [Google Scholar] [CrossRef]
Li, W.; Lu, Z.d.; Deng, D.L. Quantum Neural Network Classifiers: A Tutorial. SciPost Phys. Lect. Notes 2022, p. 61. [CrossRef]
Chang, D.T. Parameterized Quantum Circuits with Quantum Kernels for Machine Learning: A Hybrid Quantum-Classical Approach. arXiv:2209.14449 2022.
Havlíček, V.; Córcoles, A.D.; Temme, K.; Harrow, A.W.; Kandala, A.; Chow, J.M.; Gambetta, J.M. Supervised Learning with Quantum-Enhanced Feature Spaces. Nature 2019, 567, 209–212. [Google Scholar] [CrossRef]
Schuld, M.; Killoran, N. Quantum Machine Learning in Feature Hilbert Spaces. Physical Review Letters 2019, 122, 040504. [Google Scholar] [CrossRef]
Dehdashti, S.; Tiwari, P.; Safty, K.H.E.; Bruza, P.; Notzel, J. Enhancing Quantum Machine Learning: The Power of Non-Linear Optical Reproducing Kernels. arXiv:2407.13809 2024.
Rebentrost, P.; Mohseni, M.; Lloyd, S. Quantum Support Vector Machine for Big Data Classification. Phys. Rev. Lett. 2014, 113, 130503. [Google Scholar] [CrossRef]
Li, Z.; Liu, X.; Xu, N.; Du, J. Experimental Realization of a Quantum Support Vector Machine. Physical Review Letters 2015, 114, 140504. [Google Scholar] [CrossRef]
Colucci, G.; Giacosa, F. Quantum algorithmic differentiation. arXiv:2006.13370 2020.
Bang, J.; Ryu, J.; Lee, C.W.; Yee, K.H.; Lee, J.; Son, W. Quantifiable simulation of quantum computation beyond stochastic ensemble computation. Advanced Quantum Technologies 2018, 1, 1800037. [Google Scholar] [CrossRef]
Lloyd, S.; Weedbrook, C. Quantum Generative Adversarial Learning. Phys. Rev. Lett. 2018, 121, 040502. [Google Scholar] [CrossRef]
Dallaire-Demers, P.L.; Killoran, N. Quantum Generative Adversarial Networks. Phys. Rev. A 2018, 98, 012324. [Google Scholar] [CrossRef]
Lloyd, S.; Mohseni, M.; Rebentrost, P. Quantum Principal Component Analysis. Nat. Phys. 2014, 10, 631–633. [Google Scholar] [CrossRef]
Xin, T.; Che, L.; Xi, C.; Singh, A.; Nie, X.; Li, J.; Dong, Y.; Lu, D. Experimental Quantum Principal Component Analysis via Parametrized Quantum Circuits. Physical Review Letters 2021, 126, 110502. [Google Scholar] [CrossRef] [PubMed]
Lockwood, O.; Si, M. Reinforcement learning with quantum variational circuit. Proceedings of the AAAI conference on artificial intelligence and interactive digital entertainment, 2020, Vol. 16, pp. 245–251.
Chen, S.Y.C.; Yang, C.H.H.; Qi, J.; Chen, P.Y.; Ma, X.; Goan, H.S. Variational Quantum Circuits for Deep Reinforcement Learning. IEEE Access 2020, 8, 141007–141024. [Google Scholar] [CrossRef]
Ubaru, S.; Akhalwaya, I.Y.; Squillante, M.S.; Clarkson, K.L.; Horesh, L. Quantum Topological Data Analysis with Linear Depth and Exponential Speedup, [2108.02811].
McArdle, S.; Gilyén, A.; Berta, M. A Streamlined Quantum Algorithm for Topological Data Analysis with Exponentially Fewer Qubits, [2209.12887].
Akhalwaya, I.Y.; Ubaru, S.; Clarkson, K.L.; Squillante, M.S.; Jejjala, V.; He, Y.H.; Naidoo, K.; Kalantzis, V.; Horesh, L. Topological Data Analysis on Noisy Quantum Computers. The Twelfth International Conference on Learning Representations, 2023.
Gyurik, C.; Cade, C.; Dunjko, V. Towards Quantum Advantage via Topological Data Analysis. Quantum 2022, 6, 855. [Google Scholar] [CrossRef]
Scali, S.; Umeano, C.; Kyriienko, O. The Topology of Data Hides in Quantum Thermal States, [2402.15633].
Cade, C.; Crichigno, P.M. Complexity of Supersymmetric Systems and the Cohomology Problem. Quantum 2024, 8, 1325. [Google Scholar] [CrossRef]
Berry, D.W.; Su, Y.; Gyurik, C.; King, R.; Basso, J.; Barba, A.D.T.; Rajput, A.; Wiebe, N.; Dunjko, V.; Babbush, R. Quantifying Quantum Advantage in Topological Data Analysis, [2209.13581].
Schmidhuber, A.; Lloyd, S. Complexity-Theoretic Limitations on Quantum Algorithms for Topological Data Analysis. PRX Quantum 2023, 4, 040349. [Google Scholar] [CrossRef]
Zhang, P.; Brusic, V. Mathematical modeling for novel cancer drug discovery and development. Expert Opinion on Drug Discovery 2014, 9, 899–921. [Google Scholar] [CrossRef] [PubMed]
Goddard, M. The EU General Data Protection Regulation (GDPR): European Regulation That Has a Global Impact. International Journal of Market Research 2017, 59, 703–705. [Google Scholar] [CrossRef]
Li, L.; Fan, Y.; Tse, M.; Lin, K.Y. A Review of Applications in Federated Learning. Computers & Industrial Engineering 2020, 149, 106854. [Google Scholar] [CrossRef]
Abadi, M.; Chu, A.; Goodfellow, I.; McMahan, H.B.; Mironov, I.; Talwar, K.; Zhang, L. Deep Learning with Differential Privacy. Proceedings of the 2016 ACM SIGSAC Conference on Computer and Communications Security; Association for Computing Machinery: New York, NY, USA, 2016; CCS ’16, pp. 308–318. [CrossRef]
Biamonte, J.; Wittek, P.; Pancotti, N.; Rebentrost, P.; Wiebe, N.; Lloyd, S. Quantum Machine Learning. Nature 2017, 549, 195–202. [Google Scholar] [CrossRef]
Ren, C.; others. Towards Quantum Federated Learning, [2306.09912]. doi:10.48550/arXiv.2306.09912. [CrossRef]
Chehimi, M.; others. Foundations of Quantum Federated Learning Over Classical and Quantum Networks. IEEE Network 2024, 38, 124–130. [CrossRef]
Chen, S.Y.C.; Yoo, S. Federated Quantum Machine Learning. Entropy 2021, 23, 460. [Google Scholar] [CrossRef] [PubMed]
Li, W.; Lu, S.; Deng, D.L. Quantum Federated Learning through Blind Quantum Computing. Sci. China Phys. Mech. Astron. 2021, 64, 100312. [Google Scholar] [CrossRef]
Chehimi, M.; Saad, W. Quantum Federated Learning with Quantum Data. IEEE International Conference on Acoustics, Speech and Signal Processing, 2022, pp. 8617–8621. [CrossRef]
Zheng, H.; Li, Z.; Liu, J.; Strelchuk, S.; Kondor, R. Speeding Up Learning Quantum States Through Group Equivariant Convolutional Quantum Ansätze. PRX Quantum 2023, 4, 020327. [Google Scholar] [CrossRef]
Molteni, R.; Gyurik, C.; Dunjko, V. Exponential Quantum Advantages in Learning Quantum Observables from Classical Data, [2405.02027].
Liu, Y.; Arunachalam, S.; Temme, K. A Rigorous and Robust Quantum Speed-up in Supervised Machine Learning. Nat. Phys. 2021, 17, 1013–1017. [Google Scholar] [CrossRef]
Zhang, Z.; Gong, W.; Li, W.; Deng, D.L. Quantum-Classical Separations in Shallow-Circuit-Based Learning with and without Noises, [2405. 0 0770.
Gao, X.; Anschuetz, E.R.; Wang, S.T.; Cirac, J.I.; Lukin, M.D. Enhancing Generative Models via Quantum Correlations. Phys. Rev. X 2022, 12, 021037. [Google Scholar] [CrossRef]
Caro, M.C.; Huang, H.Y.; Cerezo, M.; Sharma, K.; Sornborger, A.; Cincio, L.; Coles, P.J. Generalization in Quantum Machine Learning from Few Training Data. Nat. Commun. 2022, 13, 4919. [Google Scholar] [CrossRef] [PubMed]
Broadbent, A.; Fitzsimons, J.; Kashefi, E. Universal Blind Quantum Computation. 50th Annual IEEE Symposium on Foundations of Computer Science 2009, pp. 517–526. [CrossRef]
Bernstein, D.J.; Lange, T. Post-Quantum Cryptography. Nature 2017, 549, 188–194. [Google Scholar] [CrossRef] [PubMed]
Drmota, P.; others. Verifiable Blind Quantum Computing with Trapped Ions and Single Photons. Physical Review Letters 2024, 132, 150604. [CrossRef] [PubMed]

Figure 1. The goal of drug discovery is to identify drug molecules with desirable pharmaceutical properties. The whole chemical space is around

10^{60}

. Traditional high-throughput screening methods exhaustively search the known molecule database and cannot explore the whole chemical space. To address this issue, de novo drug design navigates the whole molecule space. The challenge is to identify desirable drug molecule structures from huge chemical space (

10^{60}

Figure 1. The goal of drug discovery is to identify drug molecules with desirable pharmaceutical properties. The whole chemical space is around

10^{60}

10^{60}

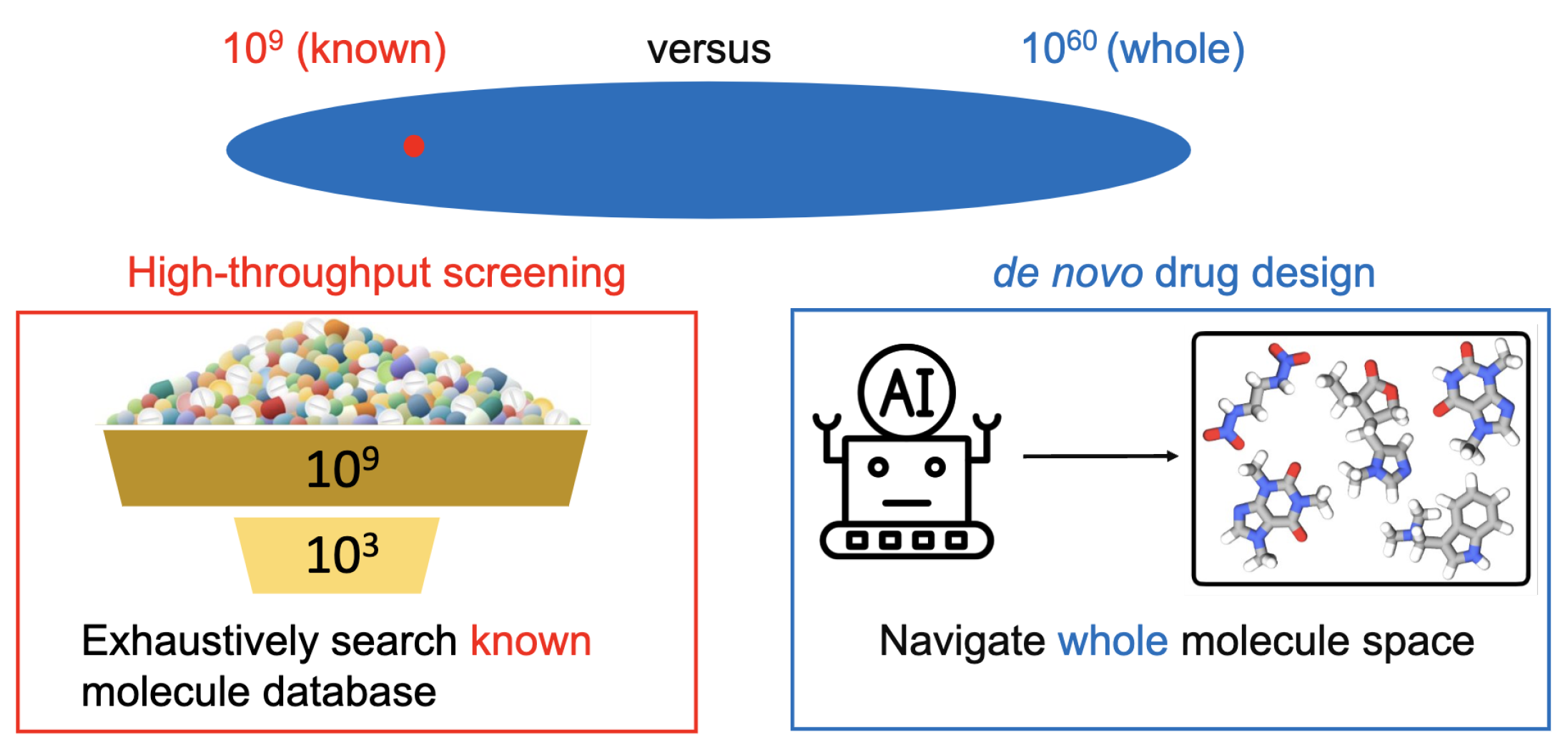
Figure 2. Drug development mainly involves clinical trials that evaluate the effectiveness and safety of the drug on patients with disease. The Challenge of drug development is to make the trial outcome prediction based on multimodal heterogeneous data features (e.g., drug molecule, disease, eligibility criteria, geographical location, etc).

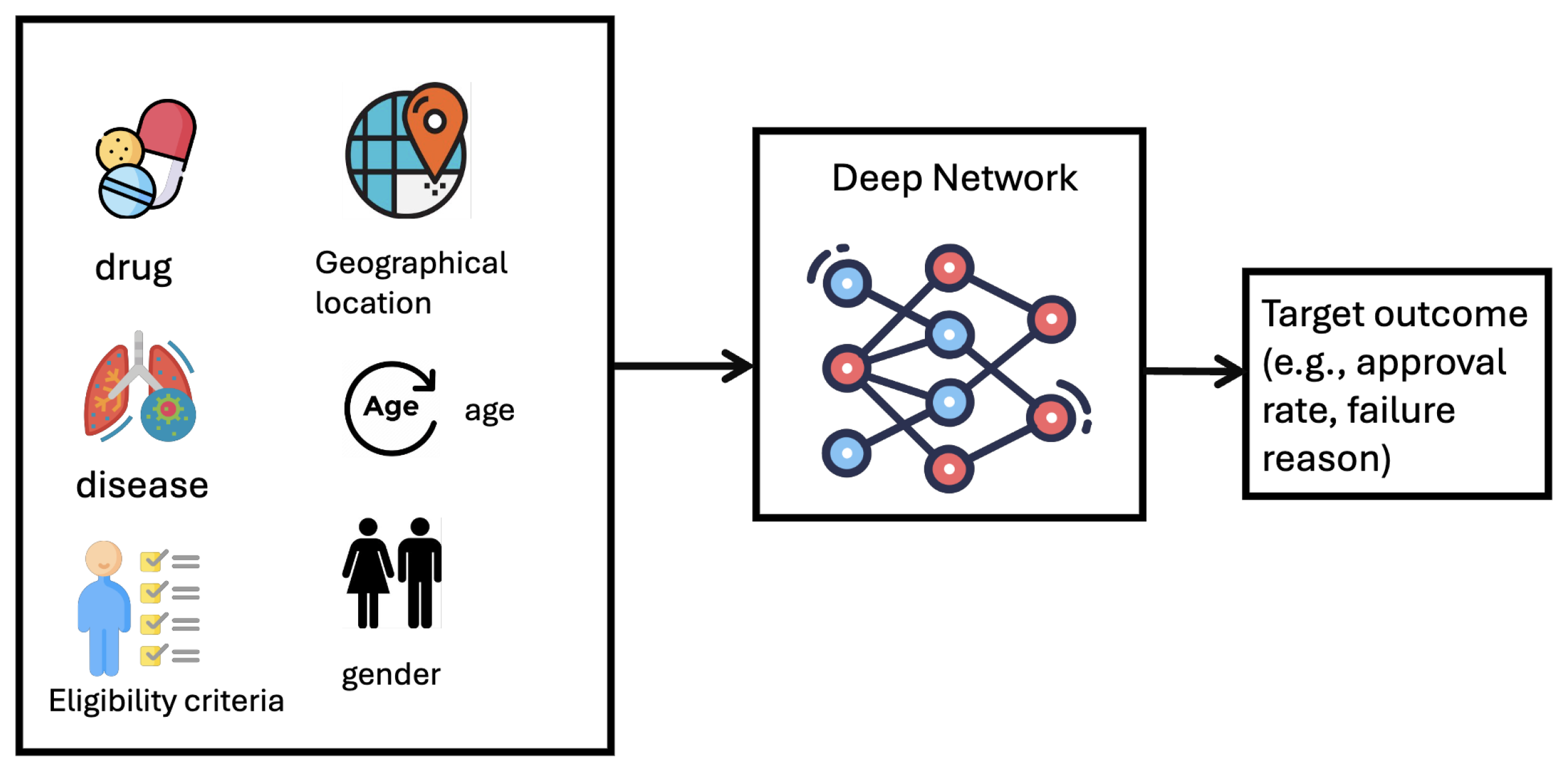
Figure 3. The process includes target identification, lead discovery, lead optimization, preclinical testing, clinical trials, and approval. Quantum Simulation and QML enhance this process by providing accurate chemical properties, navigating molecular space, and optimizing clinical trials through advanced quantum algorithms. Quantum federated learning ensures secure data handling across multiple clients.

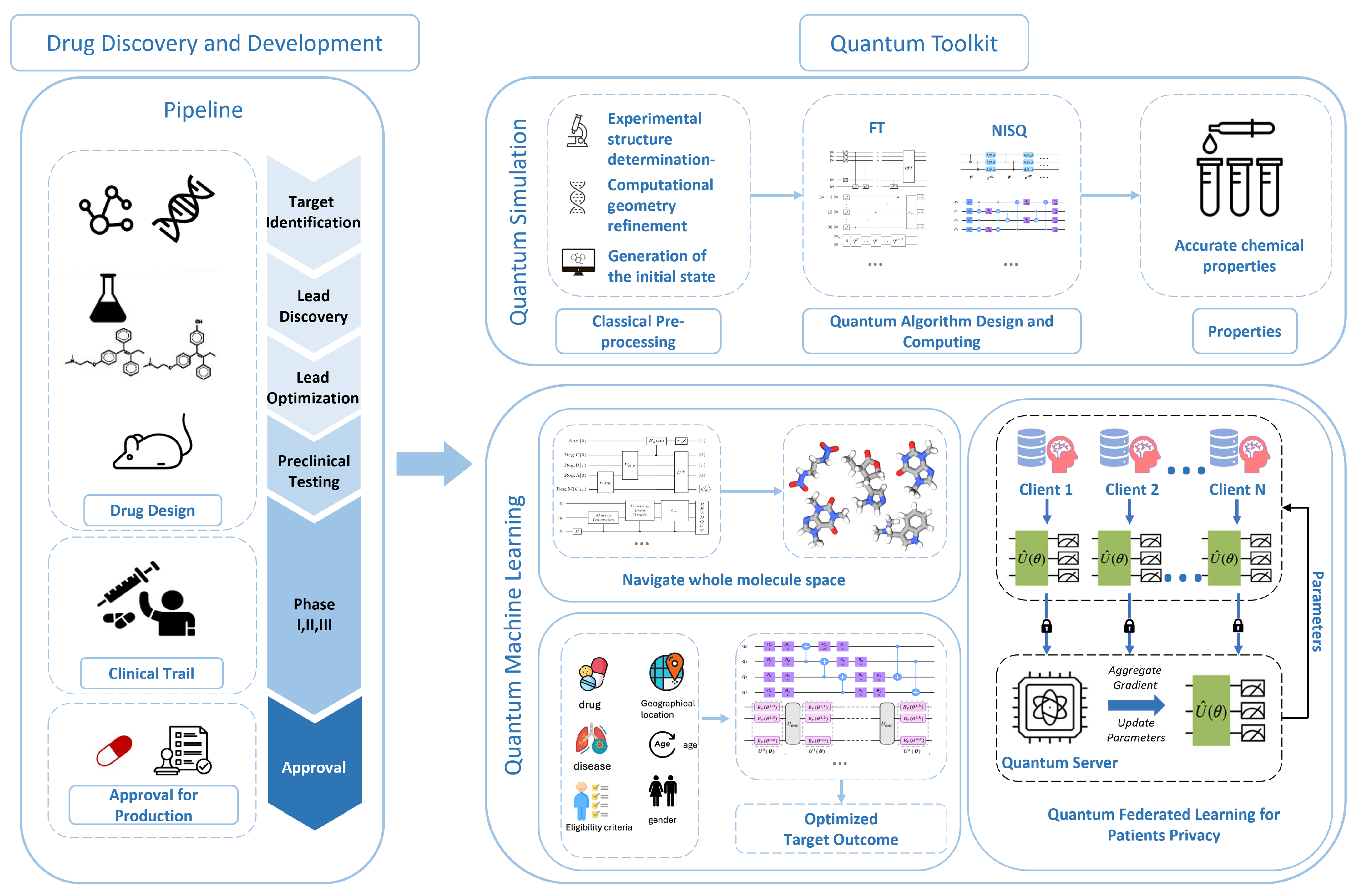
Figure 4. Pipeline of drug discovery and development. Drug discovery is the early stage and aims at identifying a handful of novel drug molecule structures with desirable pharmaceutical properties. Then, pre-clinical drug development (also known as animal model) assesses the drug molecules in animal bodies. After that, clinical drug development (also known as clinical trial) evaluates the safety and effectiveness of the drug molecules on human bodies recruiting patients).

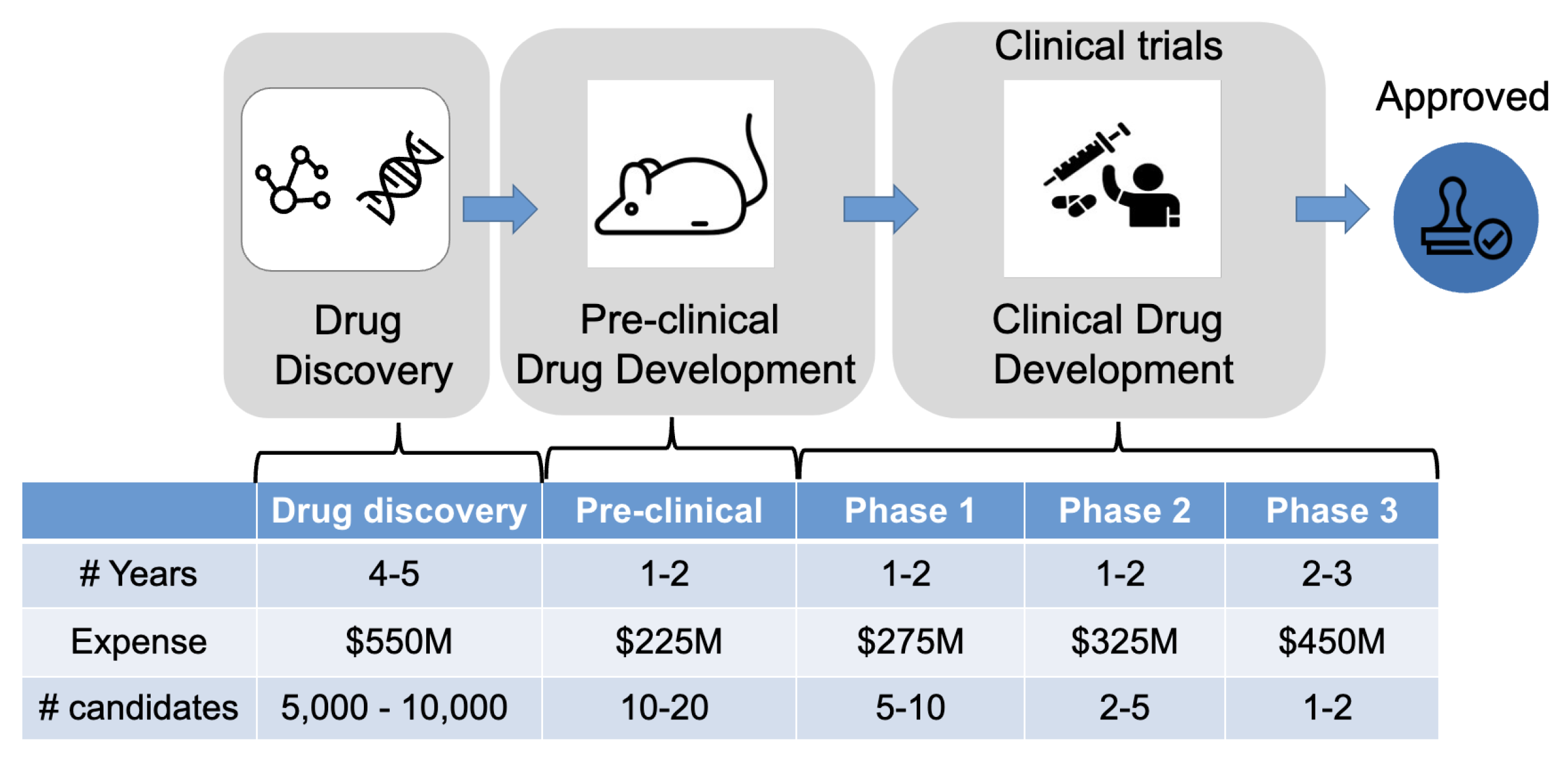
Figure 6. Quantum Circuit for Quantum Phase Estimation

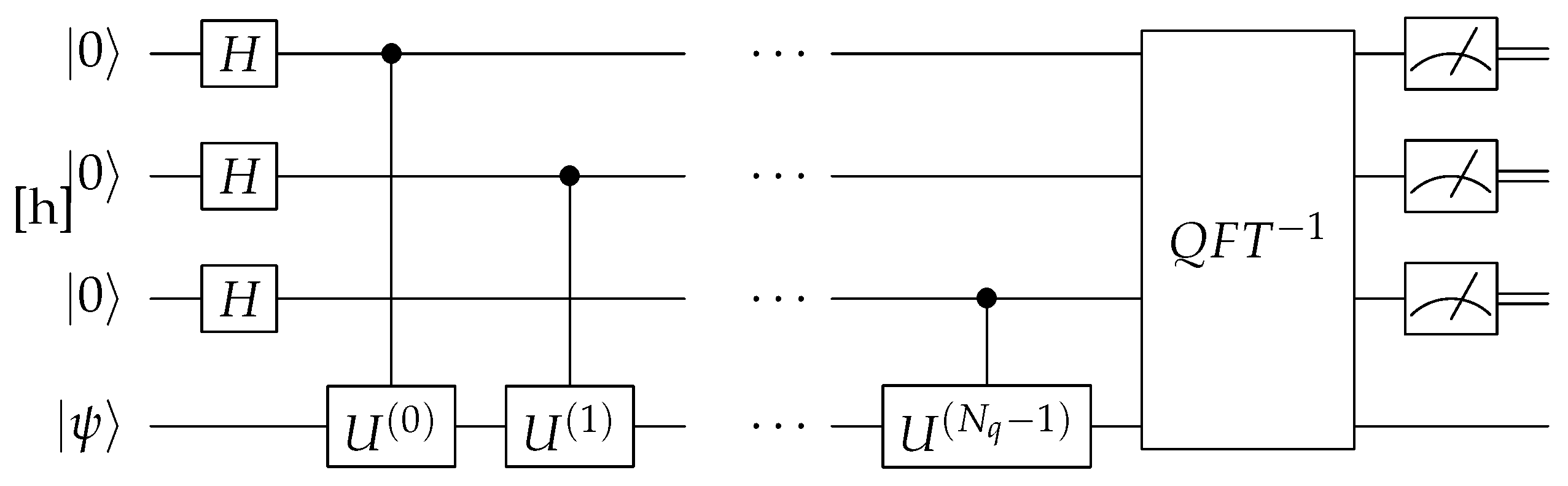
Figure 7. Schematic of the Variational Quantum Eigensolver (VQE) algorithm, which minimizes the energy of a Hamiltonian H by adjusting variational parameters

θ

. The procedure starts with a classical optimizer providing initial parameters

θ_{0}

, which are used to configure a parametrized quantum circuit for state preparation. Measurements are taken in the expectation estimation step to compute the energy

E (θ) = 〈 ψ_{θ} | H | ψ_{θ} 〉

. The classical optimizer then updates the parameters based on the energy measurements, repeating this process until convergence to the lowest energy is achieved.

Figure 7. Schematic of the Variational Quantum Eigensolver (VQE) algorithm, which minimizes the energy of a Hamiltonian H by adjusting variational parameters

θ

. The procedure starts with a classical optimizer providing initial parameters

θ_{0}

, which are used to configure a parametrized quantum circuit for state preparation. Measurements are taken in the expectation estimation step to compute the energy

E (θ) = 〈 ψ_{θ} | H | ψ_{θ} 〉

. The classical optimizer then updates the parameters based on the energy measurements, repeating this process until convergence to the lowest energy is achieved.

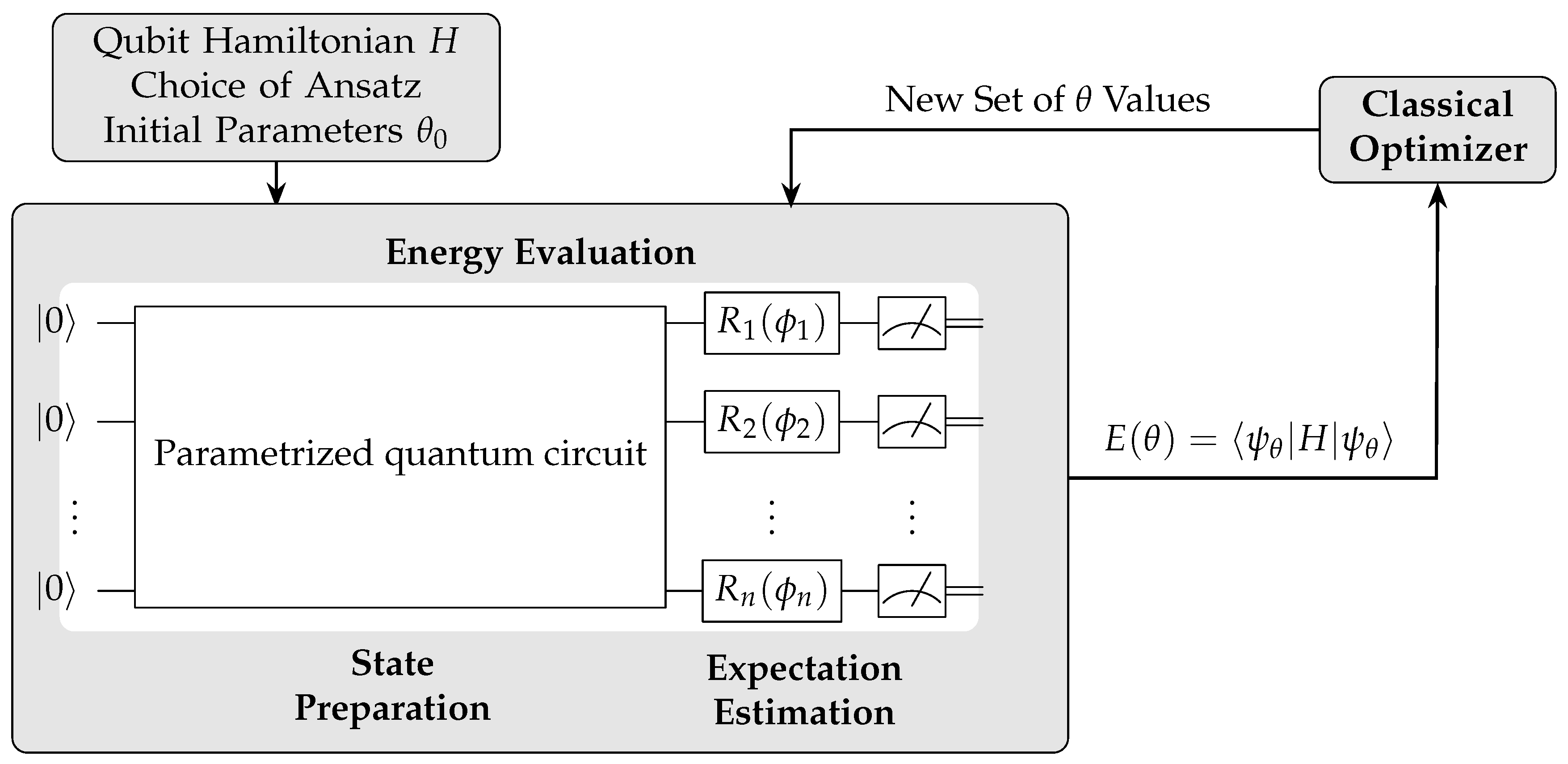
Figure 8. Illustration of the Quantum Approximate Optimization Algorithm (QAOA) process. The quantum circuit consists of alternating layers of unitary gates

U_{P} (γ)

and

U_{M} (β)

, applied to n qubits. The parameters

γ

and

β

are iteratively updated by a classical optimizer, which aims to maximize or minimize the expectation value of the Hamiltonian

〈 H_{P} 〉

. The variational parameters

(γ, β)

are adjusted based on feedback from the quantum circuit, with measurements performed at the end of each iteration. This hybrid quantum-classical algorithm continues until convergence is reached.

Figure 8. Illustration of the Quantum Approximate Optimization Algorithm (QAOA) process. The quantum circuit consists of alternating layers of unitary gates

U_{P} (γ)

and

U_{M} (β)

, applied to n qubits. The parameters

γ

and

β

are iteratively updated by a classical optimizer, which aims to maximize or minimize the expectation value of the Hamiltonian

〈 H_{P} 〉

. The variational parameters

(γ, β)

are adjusted based on feedback from the quantum circuit, with measurements performed at the end of each iteration. This hybrid quantum-classical algorithm continues until convergence is reached.

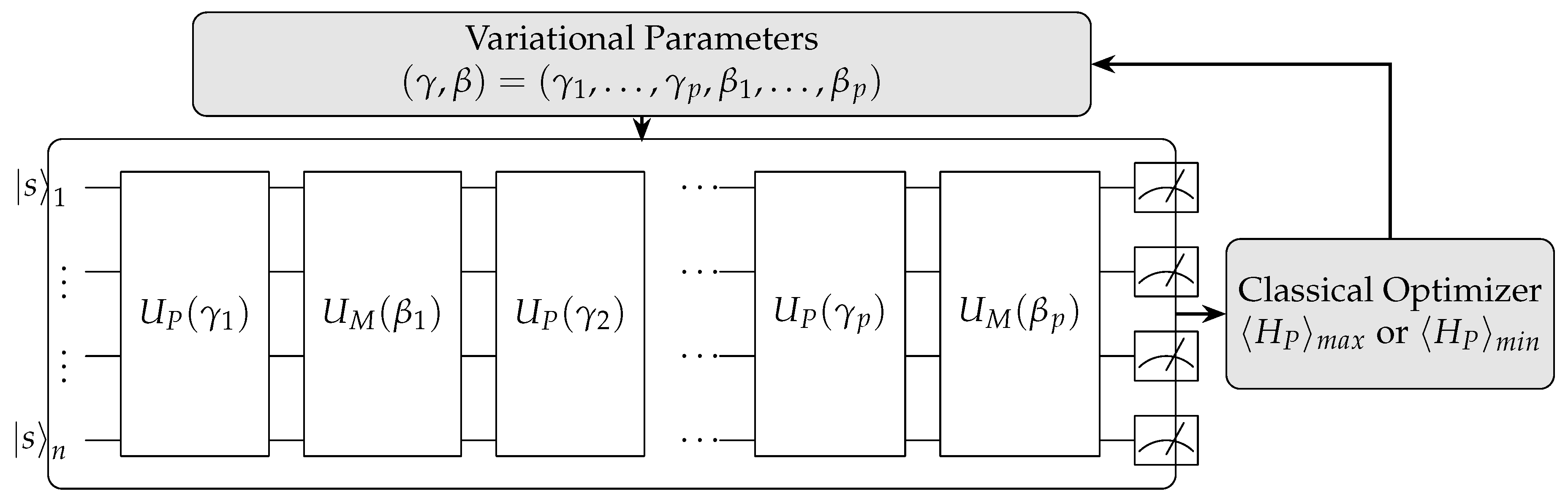
Figure 9. Machine learning and quantum computing are combined to enhance drug design and clinical trial processes. QML acts as a classifier for drug efficacy and trial site feasibility. Hybrid QML approaches optimize molecular structures, drug binding affinities, and patient-trial matching, significantly improving the efficiency and accuracy of pharmaceutical research and development.

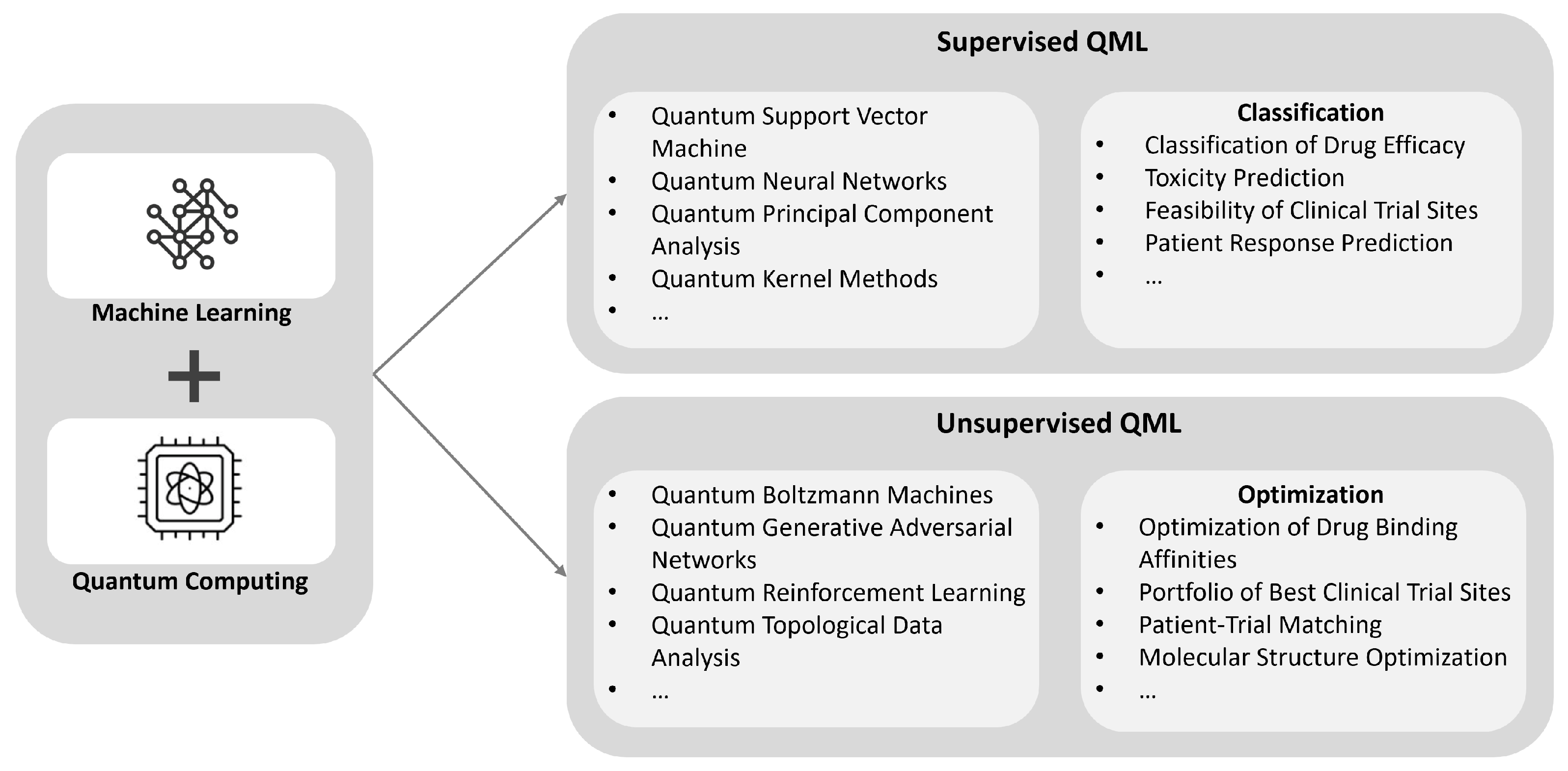
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Quantum-Machine-Assisted Drug Discovery: Survey and Perspective

Abstract

1. Introduction

2. Drug Discovery and Development Problems

2.1. Protein Folding

2.2. Small-molecule ADMET Property Prediction

2.3. Drug-Target Interaction

2.4. De Novo Drug Design

2.5. Epitope Prediction

2.6. Clinical Trial Outcome Prediction

2.7. Clinical Trial Recruitment and Trial-Patient Matching

2.8. Clinical Trial Site Selection and Ranking

3. Toolkit from Quantum Computing

3.1. Quantum Simulation

3.1.1. Fault-Tolerant Quantum Algorithms for Drug Design Simulations

Quantum Phase Estimation

Quantum Algorithms for Probability Amplification and System Simulation

Quadratic Unconstrained Binary Optimization and Dequantization Approaches

3.1.2. NISQ Algorithms in Drug Design and Development

Variational Quantum Eigensolver

Quantum Approximate Optimization Algorithm

Variational Algorithms in Partially and Early Fault-Tolerant Machines

Other NISQ Algorithms

3.2. Data-driven Quantum Machine Learning

3.2.1. Supervised and Unsupervised QML

3.2.2. Supervised QML Algorithms

Quantum Neural Networks

Quantum Kernel Methods

Quantum Support Vector Machines

3.2.3. Unsupervised QML Algorithms

Quantum Boltzmann Machines

Quantum Generative Adversarial Networks

Quantum Principal Component Analysis

Quantum Reinforcement Learning

Quantum Topological Data Analysis

3.2.4. QML in Drug Design and Clinical Trials

QML for Drug Design

QML for Clinical Trial

3.3. Security Enhancement in Quantum Machine Learning

4. Discussion

NISQ Era: Quantum as a Collaborative Tool

The Future of Fault-Tolerant Quantum Algorithms

Benchmarking Quantum Algorithms: Maximizing Impact in Drug Discovery

5. Conclusions

References

MDPI Initiatives

Important Links

Subscribe