Preprint
Article
Induced Scratches and Fatigue in Aircraft-Grade Aluminium Alloys. A Statistical Analysis on the UTS and Elongation at Break
Altmetrics
Downloads
92
Views
38
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
27 August 2024
Posted:
27 August 2024
You are already at the latest version
Alerts
Abstract
The present study analyses the influence of scratches and fatigue on the mechanical characteristics of aluminium alloys commonly used in the aviation industry: 2024-T4, 6061-T4, 6061-T4 uncoated, 6061-T6 uncoated, 7075-T0, and 7076-T6. 120 specimens were used for the study. Out of these, 60 samples were scratched, and the other 60 samples were also scratched under the same circumstances and then subjected to low-cycle fatigue (LCF) before undergoing the tensile test. Based on the statistical examination of the measured data, mathematical prediction models have been established. Compared to their unscratched counterparts, the results indicate a significant decrease in the mechanical properties of both scratched and scratched-fatigued sample sets. The LCF pre-treatment contributes to the negative impacts of scratches, resulting in a reduced value for the ultimate tensile strength and elongation at break. The results conclude that surface integrity plays an essential role in preserving aircraft components' structural strength.
Keywords:
Subject: Engineering - Mechanical Engineering
1. Introduction
Exploring the effects of different factors on aircraft materials is a significant area of study. Researchers are currently investigating how scratches, impacts, and cyclic loading affect the durability and fatigue life of various aluminium alloys commonly used in aircraft construction. Understanding this information is essential to accurately forecasting component lifespans and maintaining aircraft safety.
Gaining insights into the behaviour of aluminium alloys when subjected to intense deformation conditions is of utmost importance in enhancing the longevity and efficiency of components across diverse industries. Through the integration of numerical simulations and experimental scratch tests, researchers can acquire valuable data on the underlying wear mechanisms occurring on the surface of these alloys. This knowledge can then be utilized to enhance material design and processing strategies, resulting in more efficient outcomes. Experts are currently exploring novel approaches to improve the maintenance and safety of aircraft.
The field of aircraft inspection is rapidly advancing thanks to technological advancements such as the "Kiropter" climbing robot and the "Air-Cobot" collaborative robot. These robots capture high-resolution images of aircraft surfaces, analysing them to identify defects and stains. Researchers are also working on automated dent scanning and flaw detection algorithms to improve efficiency and precision. To test how well the model worked, real pictures of aircraft surfaces were used. These photos were taken by the remote-controlled robot of both a large Boeing 737 and a smaller plane [1].
Another study, using particle filter (PF)-based prediction algorithms, predicts crack propagation in aircraft construction using historical non-destructive testing data from an Airbus A310 aircraft. This method improves the precision of the proposed estimation, but existing simulation methods lack the necessary precision [2]. An automated vision-based inspection system was developed for identifying and analysing defects on aircraft surfaces, using local surface properties to identify undesired defects like dents, protrusions, or scratches. The Moving Least Squares (MLS) algorithm reduces noise and improves data quality. The system, which was tested on real aircraft data from an Airbus A320, has the potential for practical use in various industries [3].
In 2022, Avdelidis N.P. et al. presented a novel method for automating the recognition and classification of defects from visual images using an unmanned aerial vehicle (UAV) equipped with an image sensor. In the initial phase, the DenseNet201 CNN architecture achieved an impressive accuracy rate of 81.82%, and the proposed approach can achieve a perfect accuracy rate of 100% for the classification of missing or damaged exterior paint and primer, as well as dents [4].
In 2020, Xia R. et. al. published their work, in which they present a 3D defect detection method for monitoring riveting and seam quality in high-value aircraft using fringe projection, automated identification, localisation, and augmented reality visualization. Current methods include rivet detection algorithms, non-destructive testing devices, hand-held systems, and innovative systems like structured light scanning and industrial close-range photogrammetry [5]. Maintenance, repair, and overhaul (MRO) companies are increasingly interested in the automation of aircraft inspections, which pose significant risks, require significant time and manpower, and are prone to mistakes. Automation holds great promise for enhanced safety, increased productivity, minimised aircraft downtime, and consistent output. UAVs can utilize pattern recognition, a prominent inspection technology that offers benefits like simplicity, compatibility with standard hardware, and effectiveness in detecting scratches and lightning damage. Experts have suggested thermal imaging as a potential method for detecting delamination and corrosion [6].
In 2022, Yang S. conducted research on the impact of scratches on the fatigue of ZL114A aluminium, a widely used alloy in aerospace and machinery. Both scratched smooth specimens and scratched hole plates underwent examination during the fatigue testing. The results indicate that scratches with depths of 0.15, 0.25, and 0.35 mm had a significant impact on the average fatigue life of the specimens. These scratches led to a reduction of approximately 35%, 50%, and 61% in the average fatigue life when compared to unscratched specimens. A fatigue damage model was developed using continuum damage mechanics (CDM) to evaluate the fatigue performance of actual components with surface imperfections [7]. Due to their thermoplastic nature, high strength-to-weight ratio, and corrosion resistance, aluminium alloys play a crucial role as load-bearing components in aerospace aircraft. Often subjected to cyclic loading in service, these alloys require excellent fatigue and damage tolerance properties. For material safety and security, fatigue crack propagation is critical. Recent research has concentrated on the impact of course second-phase particles on fatigue properties. In the high-cyclic stress (HCS) regime, cracks start where the Al7Cu2Fe second-phase particles meet the matrix. Previous fatigue strength modelling and life prediction based on HCS fracture characteristics are typically expressed in terms of the crack source's effective area. However, previous studies have primarily concentrated on the size, type, and location of the fatigue sources, leaving quantitative studies on the number of fatigue sources limited [8].
Another approach proposes a new multiaxial fatigue life prediction model for aircraft aluminium alloys, specifically for thin-walled tubular and notched specimens. The model defines a new characteristic plane (subcritical plane) to describe the particularity of additional cyclic hardening under non-proportional loading conditions. A corresponding damage parameter is built on this subcritical plane, analysing the dynamic path of the stress spindle, material property, and loading environment. Multiaxial fatigue refers to the fatigue-failure behaviour of materials under multiaxial loads, which can be either proportional or non-proportional [9]. In the aerospace industry, fatigue crack propagation poses a significant problem, prompting the use of machine learning algorithms to identify the fatigue crack growth (FCG) rate. It can affect the design of aircraft structures, leading to safety issues and financial losses. However, these models have some flaws, such as not considering non-linearities and other factors like load ratio and fracture toughness. By 2022, researchers have proposed new research methodologies that combine numerical techniques with machine learning algorithms, like Bui's knowledge-based neural network (KBNN) and Bhattacharya's extended finite element method (XFEM) [10].
Li L. et al. proposed a different approach in 2024, examining the post-impact fatigue damage of the aluminium-lithium alloy, the material used in the C919 aircraft fuselage. It uses a residual stress-strain field from a quasi-static simulation to detect initial impact damage, as well as a continuum damage mechanics approach to forecast fatigue life. The study highlights the importance of post-impact fatigue life studies for the proper maintenance of aircraft structures. The study also emphasizes the influence of impact energy, impact pit dimension, and insert shape on residual fatigue life, as well as the impact of U-shaped inserts on fatigue life, highlighting the need for more research on fatigue properties. The continuum damage mechanics method is used for structural fatigue analysis, with impact tests and numerical simulations. [11].
One of the least researched topics is the investigation of the vibration fatigue behaviour of aircraft aluminium alloys. In 2022, Teng Y. et. al. researched aluminium alloy 7050, a material that holds significant importance in the aerospace industry. Researchers established the experimental criteria for concluding the vibration fatigue experiment based on the reduction in acceleration and frequency values. Researchers have put forth different approaches to investigate the vibration fatigue behaviour of structures, such as conducting fatigue tests using MZGS-100PL and NI CRIO-9074 controllers [12].
In 2018, Rayno T. et al. developed a 3D scanning method to accurately assess surface damage on aircraft structural panels. The method showed 95% accuracy in dent depth measurements compared to a Starrett 643J dial depth gauge in 54 flat panel dents and 95% in 74 curved panel dents. Dent depth quantification involved comparing a point cloud rendering of the damaged surface with a surface fit that approximated the original, undamaged surface. Convergence studies evaluated the efficiency and reliability of the technique. Image processing techniques were used to measure dent length and area, demonstrating their potential for prompt extraction of surface dent measurements during on-site aircraft inspections [13].
D. Garcia et al. investigated crack propagation analysis using linear elastic fracture mechanics, considering computer simulations. The study focuses on cruciform specimens subjected to biaxial fatigue stresses and an initial 45°-angled crack, with a loading phase angle of 90° and 180°. This study was conducted using the extended finite element technique (XFEM) to investigate crack propagation, phase angles, and orientation criteria under nonproportional loading conditions centred around engineering structures found in the automotive and aerospace industries, which frequently encounter multiaxial stresses that can lead to structural failures. Crack propagation can manifest either in a co-planar fashion or at a specific deviation angle, depending on the material's characteristics and the type of stress applied. It focuses on analysing and comparing different nonproportional loading criteria, while also assessing the influence of displacement ratio and phase angle on crack orientation [14]. A similar computer simulation approach examines fracture courses in three-wing spar designs and their impact on fatigue life calculation. It compared the efficiency of differential wing spars to two optimised integral spars using the extended finite element method (XFEM) and Morfeo/Crack software. The results showed significant strain-rate dependence for AA1050, while it was negligible for AA7075. A visco-plastic constitutive model based on Johnson-Cook was used to incorporate strain behaviour into the numerical simulations during high-velocity scratching [15].
Varga M. et al. developed a simulation framework in 2021 that targets meshless methods, which have the inherent capability to handle significant deformations and material removal that often arise in various processes. The Material Point Method (MPM) is used to accurately calculate strain rates and stresses. The study presents a potential work scheme to address the challenge of obtaining near-surface material properties at high strain rates using experimental tools and contribute to the development of a reliable and effective methodology in this field. The results indicate a significant strain-rate dependence for AA1050, while it is negligible for AA7075 [16].
Considering the research conducted in this field, the authors considered it necessary to conduct a study using six different types of aircraft-grade aluminium alloys, with scratches orientated in different directions and having different lengths and depths. We conducted this study with a focus on the previously analysed scientific documentation, emphasising the importance of maintaining integrity and predicting the fatigue phenomenon, especially in the case of scratched fuselage parts. We concluded it would be valuable to examine this data for relevance; therefore, we performed so by using the response surface methodology (RMS) approach and an ANOVA for significance.
2. Aluminium Alloys and Methodology
The experimental study's methodology includes testing 120 samples of six aluminium aircraft-grade alloys with a thickness between 1 and 2 mm: 2024-T3 (Kaiser Aluminum, Lake Forest, California, USA), 6061-T4 (AMAG, Braunau-Ranshofen, Austria), 6061-T4 uncoated (AMAG, Braunau-Ranshofen, Austria), 6061-T6 uncoated (Kaiser Aluminum, Lake Forest, California, USA), 7075-T0 (Aleris Rolled Products Germany GmbH, Koblenz, Germany), 7075-T6 (Kaiser Aluminum, Lake Forest, California, USA) for their mechanical properties using the tensile test; before the test, the samples were scratched at various angles, lengths, and depths; 60 scratched samples underwent a fatigue stress procedure. We used an ANOVA analysis to evaluate the collected data, focusing primarily on the ultimate tensile strength (UTS) and elongation at break.
2.1. Aircraft-Grad Aluminium Alloys
A variety of technical fields extensively use aluminium alloys due to their superior corrosion resistance and attractive weight-to-strength ratio. Because of their unique mechanical characteristics and application-specific applicability, the alloys in the 2024, 6061, and 7075 series have attracted a lot of interest among the many available alloys.
The high-strength aluminium alloy 2024-T3 is well known for having an exceptional strength-to-weight ratio. Through artificial age and solution heat treatment, the T3 temper imparts exceptional strength. Because of its exceptional mechanical qualities, it is a top choice for structural parts used in the aerospace sector, including aircraft landing gear, wings, and fuselages.
Two alloys that provide an excellent blend of strength, ductility, and weldability are 6061-T4 and 6061-T6. The T4 temper achieves moderate strength through natural ageing and solution heat treatment. On the other hand, the T6 temper experiences an extra artificial ageing process that increases its hardness and strength. Many different sectors, including maritime, construction, and transportation, find applications for both tempers. The mechanical qualities of uncoated 6061-T4 and 6061-T6 are comparable to those of coated, but their corrosion resistance and surface features may differ.
Of the alloys under consideration, 7075-T0 has the maximum strength when it is in the annealed (O) form. It is vulnerable to stress, corrosion, and cracking, however. The 7075-T6 temper uses artificial ageing and solution heat treatment to greatly increase strength and hardness. High-stress applications like sports goods, military gear, and aircraft components, where weight reduction is essential, mostly employ this alloy.
Tensile testing on an INSTRON 8801 servohydraulic fatigue testing system (INSTRON, Norwood, USA) with a 100 kN loading cell and a 2630-107 axial clip-on extensometer (INSTRON, Norwood, USA) determined the mechanical properties given in Table 1. For each alloy, we used five samples, orienting the load in the rolling direction. For each set of results, the arithmetic mean of the obtained values was considered.
The samples were cut into shape using an Oreelaser PH3015 CNC laser machine (Oreelaser, Shandong, China), following the specific configuration shown in Figure 1. At this stage, ensuring the accuracy of the 12.5 mm part's width (W) was important because it directly affected the calculation of the cross-sectional area (CSA). This measurement is critical for determining internal stress; therefore, it was measured before testing, with a tolerance of ± 0.1 mm.
2.2. Experimental Plan
The experimental plan was designed using the DesignExpert software (Stat-Ease, Minneapolis, USA, 2024, v. 12.0.3). The study used a Response Surface design with a Randomized subtype and a D-optimal design, suggesting 60 samples. Alloys were classified as nominal categorical components, and numerical discrete factors were also assigned to the plan, as indicated in Table 2.
Initially, we devised an experimental strategy that considered the six alloys, their varying thicknesses, and the direction, length, and depth of the scratch. Due to the integration of a significant number of samples, this experimental design proved to be advantageous in facilitating the systematic and efficient execution of the scratch creation process. After the scratching procedure, we modified the experimental plan to utilize the cross-sectional area (CSA). As the applied force is reported to the cross-section area (Figure 2), the increase in stress will occur at the point where the surface is scratched, as in this section there is a smaller cross-sectional area. Therefore, the final form in which the data was analysed is that of Table 2, which considers the 6 types of aircraft-grad aluminium alloys (2024-T3, 6061-T4, 6061-T4 uncoated, 6061-T6 uncoated, 7075-T0, 7075-T6), 6 material thicknesses (1, 1.2, 1.27, 1.6, 1.8, 2 mm), 3 scratch orientation directions (0°-rolling direction, 45°-rolling direction, 90°-perpendicular to rolling direction; the applied load direction was aligned to the rolling direction), and resulting cross-sectional area (calculated for each specimen). As for the responses, 4 sets of data were analysed regarding the ultimate tensile strength and elongation at break of the scratched (UTSs, εs) and the scratched and fatigued samples (UTSsf, εsf).
2.3. Sample Scratching Methodology
To get accurate control over the previously mentioned indicators, all the scratches were made using a Knuth Rapimill 700 CNC milling machine (Knuth, Wasbek, Germany) and a tool with a tip angle of 60° (Figure 3a and 3b). Based on the specified dimensions of the scratch and to ensure precise execution and reputability, a dedicated program was written in CNC machine code, setting a rotation speed of 1500 rpm and a feed of 5 mm/sec. The tool used for executing the scratches was manufactured on a lathe, resulting in a maximum measured radial runout of 0.07 mm. The tip angle of 60° was measured using a Mitutoyo PH-3515 profile measuring projector (Mitutoyo, Kawasaki, Japan).
The centre point of each scratch is in the centre of each specimen; at this point, the scratches could be executed as previously described:
- 3 orientation directions (Figure 4a): along the path of force application (0°), perpendicular to this direction (90°), and at an intermediate angle (45°).
- 3 scratch lengths, as a percentage of the available length, based on the angle of orientation, are as follows (Figure 4b): the whole length (100%), half of the length (50%), and one-fourth of the length (25%).
- 3 scratch depths (Figure 4c), which are expressed as percentages of the specimen thickness: 50%, 25%, and 12.5%.
For considering the cross-section area (CSA), it is necessary to calculate it based on the direction of the force exerted during the tensile test, specifically a plane that is perpendicular to the force's direction and, in normal conditions, has a cross-section area as indicated in Figure 5a (CSA = W x T).
Examining this plane, as shown in Figure 5b, 5c, and 5d, requires subtracting the area of the scratch, which varies depending on the direction of the scratch, its width (SW), its depth (SD), and its length (SL). Equations 1 through 5 present the equations used to calculate the remaining cross-section area.
CSASS = W x T
CSA0°stratch = CSASS – SD2 x tan(30°)
CSA45°stratch = CSASS – SW2 x SD x sin(45°), where SW = SW’ x sin(45°)
CSA90°stratch = CSASS – [SD2 x tan(30°) + (SD x SL)] – used for 12.5% and 50% of the scratch length
CSA90°stratch = W x (T – SD) – used for 100% of the scratch length
Therefore, based on the previously presented methodology, the lengths and depths of the scratches, as well as the minimum cross-section area, were calculated for each alloy, considering the scratch directions and the thickness of each specimen. The complete data is available in Table 3.
2.4. Fatigue Setup and Tensile Test
The fatigue and tensile tests were conducted using an Instron 8801 servohydraulic fatigue testing system with a 100 kN loading cell and a 2630-107 axial clip-on extensometer. WaveMatrix3 Dynamic Testing Software (INSTRON, Norwood, USA, 2023, version 3) is used for low cycle fatigue (LCF), and Bluehill Universal Software (INSTRON, Norwood, USA, 2023, version 4.42) is used for axial static testing.
60 specimens were fatigued by stretch-compression bending. The fatigue setup consists of a fixed and mobile component (Figure 6a). An S500 steel fixture serves as the fixed component, while two PLA 3D-printed 75 mm-radius dome-shaped geometries serve as specimen supports (Figure 6b). The upper part has four threaded holes on each corner, while M4 screws go through the lower part, fixing it around the specimen. For the mobile component of the setup, a custom modular fixture support was manufactured out of S500 steel alloy. The gripping jaws are knurled and tightened at a torque of 15 Nm using an Unior 266 dynamometric wrench.
Testing different combinations of process parameters led to the premature failure of specimens with 50% scratch depth. At this stage, the goal was to fatigue the scratched parts without breaking them. Therefore, as shown in Figure 6b and 6c, we used a symmetrical alternating cycle with a maximum amplitude of 6 mm and a 1 Hz cycle for 200 cycles.
3. Results and Statistical Analysis
Due to their favourable mechanical characteristics, aluminium alloys find widespread use in a range of technical applications. Surface defects, such as scratches, can, on the other hand, significantly undermine a structure's structural integrity, necessitating a thorough understanding of their impact on mechanical properties. This study investigates how scratching and subsequent fatigue affect the tensile properties of aluminium alloys.
This paper focuses on how the direction of scratching and the cross-sectional area impact the ultimate tensile strength (UTS) and elongation at break across multiple aluminium alloys (2xxx, 6xxx, and 7xxx series). This study aims to better understand the basic causes of mechanical property decrease by examining the failure processes of scratched and scratched-fatigued samples.
The experimental approach consisted of intentionally causing controlled scratches on tensile test specimens. The obtained data, which include ultimate tensile strength and elongation at break, provide important insights into the material's behaviour concerning surface scratches and fatigue. This data helps predict the service life and reliability of aluminium components exposed to intricate loading situations.
Controlled scratches were induced by using a milling machine to create transverse scratches of different depths and orientations on the specimen surfaces. To generate fatigue damage before conducting tensile testing, the specimens were exposed to cyclic loading under controlled circumstances during the fatigue testing process.
The experimental data, which includes the ultimate tensile strength (UTS) and elongation at break, were subjected to statistical analysis to detect patterns and relationships. The analysis uses regression analysis to create mathematical models that establish the relationship between UTS, elongation at break, and factors such as scratch direction and cross-sectional area. The model fit statistics were assessed to evaluate the predictive capabilities of the models.
Figure 8, which displays several of the samples, reveals the failure mechanism. The image representation shows that the fracture originated and propagated from the original scratch.
Figure 8.
The failure mechanism of scratched or scratched and fatigued samples; some examples of crack propagation for different scratching parameters resulting in sample failure: (a) 2024-T3; (b) 6061-T4; (c) 6061-T4 uncoated; (d) 6061-T6 uncoated; (e) 7071-T0; (f) 7071-T6.
Figure 8.
The failure mechanism of scratched or scratched and fatigued samples; some examples of crack propagation for different scratching parameters resulting in sample failure: (a) 2024-T3; (b) 6061-T4; (c) 6061-T4 uncoated; (d) 6061-T6 uncoated; (e) 7071-T0; (f) 7071-T6.

For aluminium alloy 2024-T3, a total of 30 samples were processed. The samples are categorised into two groups: the scratch-tensile test and the stretch-fatigued-tensile test. Each group consists of 15 samples. Within each group, there are 6 samples with the scratch orientated at 0°, 4 samples at 45°, and 5 samples at 90°. The results are shown in Table 4.
The data obtained for UTS and elongation at break were subjected to statistical analysis and separated into four distinct sets, as shown in Table 2. The resultant models are quadratic (the highest power of the independent variable is 2) or 2FI (two-fixed-one-random effect), which allow for the assessment of the impact of each element and the interaction between them on the outcome. The ANOVA analysis indicated that these models are statistically significant. The data presented in Table 5 indicate a p-value of less than 0.001 (the p-value is a statistical measure used to assess the significance of experimental results). The UTSsf data indicated the need for an inverse square transformation, which was subsequently done. The generated mathematical equations also emphasised this transformation.
Fit statistics play an important role in evaluating the degree to which a statistical model accurately matches a given collection of observable data. They help evaluate the model's fidelity by reflecting the fundamental patterns within the given data. The values shown in Table 6 represent the goodness-of-fit metrics and indicate a significant level of confidence. R² and Adjusted R² measure the model's fit to the existing data, while Predicted R² analyses its ability to predict outcomes on fresh data. Adequate precision assesses the model's dependability in predicting responses. Furthermore, the Model F-value and Lack of Fit F-value were calculated (the Model F-value indicates the presence of a correlation between the variables, while the Lack of Fit F-value tells if the chosen model form is correct).
- UTSs - a model F-value of 860.15 indicates that the model is statistically significant. The probability of an F-value of this magnitude occurring solely due to noise is just 0.01%; p-values below 0.0500 imply that the model terms are statistically significant. In this case, the relevant model terms are SD, CSA, material, and SD². The F-value of 4.56 for the Lack of Fit indicates that the Lack of Fit is statistically significant. The probability of a Lack of Fit F-value of this magnitude occurring solely due to noise is just 3.21%. The Predicted R² value of 0.9277 shows a strong correlation with the Adjusted R² value of 0.9266, indicating a high level of agreement between the two, the difference between these values being less than 0.2.
- εs – a model F-value of 120.93 indicates that the model is statistically significant; the p-values are below 0.0500 and imply that the model terms are statistically significant (in this scenario, the model terms SD, CSA, material, and the interaction between material and SD have major importance). A F-value of 33.44 for the Lack of Fit indicates that the Lack of Fit is statistically significant. The Predicted R² value of 0.9115 shows a strong correlation with the Adjusted R² value of 0. 8934.
- UTSsf – a model F-value of 175.70 indicates that the model is statistically significant; the p-values are below 0.0500 and indicate that the model terms are statistically significant, the relevant model terms being SD, CSA, material, and SD². The F-value of 3.80 for the Lack of Fit indicates that the Lack of Fit is statistically significant. The probability of a Lack of Fit F-value of this magnitude occurring solely due to noise is just 4.98%. The Predicted R² value of 0.8990 is quite consistent with the Adjusted R² value of 0. 8734, indicating a discrepancy of less than 0.2.
- εsf – with a model F-value of 97.40 the model is statistically significant. The probability of an F-value of this magnitude occurring solely due to noise is just 0.01%.; a p-value below 0.0500 implies that the model terms are statistically significant; SD, CSA, material, and the interaction between material and SD have major significance. A Lack of Fit F-value of 12.26 indicates that the Lack of Fit is statistically significant. The probability of a Lack of Fit F-value of this magnitude occurring solely due to noise is just 0.23%. The Predicted R² value of 0.8804 shows a strong correlation with the Adjusted R² value of 0. 8703.
3.1. UTS
3.1.1. Aluminium Alloy 2024-T3
The average UTSs of samples scratched at 0° is 444.683 MPa, whereas the UTSsf of scratched-fatigued samples is 376.959 MPa, resulting in a difference of 17.966%. The percentage decreases to 29.854% for samples scratched at 45°, from an average of 424.351 to 326.791 MPa. Scratching samples at 90° results in a significant loss in UTS, dropping from an average of 414.581 to 319.939 MPa, a decrease of 29.581%. Compared to the data from Table 1, the overall average UTSs dropped by 5.172% and the UTSsf by 31.876%.
The ANOVA analysis generated two mathematical models, represented by equations 6 and 7, which correspond to the 2024-T3 alloy UTSs and UTSsf. The estimate of UTS reveals both the individual significance of scratch direction (SDir) and CSA, as well as their combined effect. The first case established a polynomial relationship, while equation 7 underwent the inverse square transformation as mentioned in Table 4. The model from Equation 6 includes a quadratic relationship between UTSs_2024-T3, SDir, and CSA. This means that these parameters don't have a straight-line effect on the strength of the material. The negative coefficient for the SDir term indicates that increasing scratch direction generally decreases UTS. Conversely, the positive coefficient for the CSA term suggests that increasing cross-sectional area enhances UTS. The interaction term (SDir x CSA) and the quadratic terms for SDir and CSA further refine the model's predictive capabilities. Equation 7, upon analysis, models the inverse of UTSsf_2024-T3 as a linear combination of SDir, CSA, and their interaction terms, indicating a distinct functional relationship from the first model. Similar to the previous model, the negative coefficient for the SDir term indicates that scratch direction has a detrimental effect on UTS. However, the positive coefficient for the CSA term implies a less pronounced cross-sectional area influence on UTS compared to the scratched samples. The inclusion of quadratic terms for SDir and CSA suggests a complex relationship.
UTSs_2024-T3 = 413.48289 – 0.431968xSDir + 1.6023xCSA – 0.00573xSDir x CSA + 0.002552xSDir2+0.002475xCSA2
Figure 9a and 9b visually represent equations 6 and 7. The graphs are constructed depending on the orientation of the scratch and the remaining cross-sectional area following the scratch. Green represents lower UTS values, whereas yellow represents higher values. The highlighted estimations are derived from both the input data range and extrapolated beyond it, using the predictions generated by these equations. Their comparison reveals that fatigue significantly influenced the results, outweighing the impact of simply scratching the samples. Therefore, instead of 280–380 MPa, the UTS falls within the range of 400 to 450 MPa. An inverse relationship was established between the UTS and both the scratch angle and the cross-sectional area. As mentioned earlier, in Figure 2, the limit stress point is the point where the cross-sectional area is at its smallest, with the force acting perpendicular to the direction of the scratch.
It is clear from comparing the two plots that fatigue significantly affects the mechanical properties of the aluminium alloy 2024-T3. The UTS values in Figure 9b are much lower. In addition, the cross-sectional effect plays a more significant role in the case of scratched and fatigued samples.
The statistics given emphasise the significance of considering both the direction of scratching and the cross-sectional area when assessing the mechanical properties of aluminium alloy 2024-T3, especially in the context of fatigue. The results suggest that these parameters are essential for understanding the material's performance in applications that experience cyclic stress and surface deterioration.
3.1.2. Aluminium Alloy 6061-T4, 6061-T4 and -T6 Uncoated
The UTS of the 6061-T4 alloy decreases as follows: from 255 MPa to an average of 227.822 MPa (11.929%) for the scratched specimens, and then further to 189.417 MPa (34.624%) for the fatigued specimens. Examining UTSs and UTSsf at various scratch directions reveals a decrease of 21.291% for scratches made at 0°, 22.727% for 45°, and 16.568% for 90°.
Equations 8 and 9 highlight the mathematical models. Following prior indications from the 2024-T3 alloy, strong correlations have been identified between the scratch direction, cross-sectional area, and UTS. The models consider both the individual impact of each factor and their combined effect.
UTSs_6061-T4 = 211.41408 – 0.628555xSDir + 2.35351xCSA – 0.00573xSDir x CSA + 0.002552xSDir2+0.002475xCSA2
In the case of scratched samples, the predictability of UTSs values follows a linear pattern (Figure 10a), increasing as the CSA and SDir increase. However, for the UTSsf (Figure 10b), increasing the scratch angle beyond 67.5° and decreasing the CSA below 10 mm2 results in a sharp drop of 10 MPa in ultimate tensile strength.
The measurement results for the uncoated 6061-T4 alloy show an overall decrease of 6.576% in UTSs and a reduction of 41.6% in UTSsf. It is important to note that this case represents the greatest percentage difference among all the alloys examined. By increasing the scratch angle, the ultimate tensile strength decreases by 15 units, while the UTSsf decreases by 12 units. For the samples that underwent fatigue testing, the average ultimate tensile strength decreased by 32.886%, from 231.76 MPa to 174.432 MPa.
Previous observations indicate a consistent pattern in the mathematical models (Equations 10 and 11), highlighting the correlation between the direction of the scratch and the cross-sectional area. An important observation arises from the analysis of Figure 11b, constructed using equation 11. It is noticeable that in contrast to the graph in Figure 10b, there are no sudden shifts. Instead, we observe lower values of UTSsf at 0° and 90°, with the highest values observed around 45°. Regarding the UTSs, as shown in Figure 11a, a minimum value is found at 0°, followed by increases up to 67.5°, and then a decrease up to 90°. The increase in the cross-sectional area results in a corresponding increase in UTSs of up to 20 units.
UTSs_6061-T4_uncoated = 211.00629 – 0.222059xSDir + 1.13329xCSA – 0.00573xSDir x CSA
+ 0.002552xSDir2 + 0.002475xCSA2
+ 0.002552xSDir2 + 0.002475xCSA2
The uncoated 6061-T6 alloy's behaviour shows an average decrease of 298.061 MPa (7.244%) for the scratched samples and as low as 242.136 MPa (28.027%) for the scratched and fatigued samples. In this instance, the occurrence of fatigue after 200 cycles results in a decrease of 20.784% in UTS. Increasing the scratch angle concerning the load direction causes the influence on the scratched samples to decrease, from 306.074 MPa to 293.669 MPa to 267.44 MPa. In this situation, fatigue leads to a decrease in values ranging from 237.872 to 247.839 MPa, with an average reduction of 19.355%.
Equations 12 and 13 display mathematical models similar to the previous ones, which Figure 12a and 12b graphically illustrate. Peak values of UTSs fall between 45–67.5°, while scratches oriented at 0° exhibit lower values. The cross-sectional area is reduced from 22.5 to 7.5 mm2, resulting in a 40-unit drop in UTSs. Regarding the UTSsf, there is a noticeable pattern with respect to the 45°. It experiences a gradual decrease from 0° to 45°, with an increment of 10 units. Subsequently, there is a minor further increase of 10 units from 45° to 90°. Therefore, it can be deduced that the critical scratches are orientated at 45°. This, combined with a cross-sectional size of 5–6 mm2, results in the lowest UTSsf values.
UTSs_6061-T6_uncoated = 239.80017 – 0.235858xSDir + 3.28308xCSA – 0.00573xSDir x CSA + 0.002552xSDir2+0.002475xCSA2
3.1.3. Aluminium alloy 7075-T0 and 7075-T6
It is shown that the UTSsf for the 7075-T0 alloy drops by 23.445% (from 255.091 to 206.644 MPa) when scratched at 0°, 23.646% (from 233.523 to 188.872 MPa) when scratched at 45°, and 10.944% (from 215.3 to 194.063 MPa) when scratched at 90°. In this case, fatigue has a significant impact, resulting in a reduction in UTS by as much as 21.49% when comparing the scratched samples to the scratched and fatigued samples. The results indicate a significant average decrease of 32,298% in comparison to the baseline UTS.
The ANOVA analysis revealed a significant correlation between SDir and CSA in terms of outcome. Equations 14 and 15 express the mathematical models derived in this instance, and Figure 13a and 13b show their graphical representation. The orientation of the scratch in this instance, at a right angle to the load, is not optimal. It results in a maximum UTSs value ranging from 200 to 230 MPa, corresponding to a CSA between 5 and 25 mm2. For UTSsf, there is a tendency for the values to decrease as SDir changes towards the end of the analysed interval.
UTSs_7075-T0 = 213.53762 – 0.401177xSDir + 2.06010xCSA – 0.00573xSDir x CSA + 0.002552xSDir2+0.002475xCSA2
(14)
For scratched samples, the models from Equations 16 and 17 directly predict UTS, whereas the model for scratched and fatigued samples uses an inverse square relationship. This suggests fundamentally different relationships between the variables and the UTS under the two conditions.
Both models include quadratic terms for SDir and CSA, indicating non-linear relationships between the UTS (or 1/UTS) and these parameters. However, the specific coefficients and interactions between these terms likely differ, suggesting varying degrees of curvature in the relationships. In both models, the coefficients for the linear, interaction, and quadratic terms are different. This means that UTS is sensitive to scratch direction and cross-sectional area in different ways. The differences between the models indicate that whether the sample has undergone fatigue significantly influences the relationship between UTS, scratch direction, and cross-sectional area. The inclusion of quadratic terms and the use of an inverse relationship in the fatigued case highlight the complexity of the degradation mechanisms under these conditions.
UTSs_7075-T6 = 496.1882 – 0.412119 + 1.48717xCSA – 0.00573xSDir x CSA + 0.002552xSDir2+0.002475xCSA2
The plot from Figure 14a of scratched samples indicates the correlation between ultimate tensile strength and the direction of the scratch. As the scratch angle increases, there is a consistent pattern of decreasing UTS. This implies that the direction of the scratch has an important impact on the material's strength. The influence of cross-sectional area on ultimate tensile strength (UTS) seems to be less significant since there is only a slight increase in UTS for higher cross-sectional areas. Figure 14b highlights the results for the scratched and fatigued samples, indicating an intricate correlation between the variables. While the effect of scratch direction on ultimate tensile strength (UTS) remains noticeable, it appears to be less significant compared to the scratched samples. A noticeable correlation is observed between the cross-sectional area and the ultimate tensile strength (UTS), where an increase in the cross-sectional area leads to a significant decrease in UTS. The downward slope of the colour bands illustrates this relationship. The results suggest that fatigue significantly reduces the strength of the material, and the impact of the cross-sectional area becomes more important in determining the ultimate tensile strength (UTS) under such circumstances.
Upon comparing the two graphs, it is noticeable that fatigue has a substantial negative impact on the mechanical characteristics of the aluminium alloy 7075-T6, as the UTS values in Figure 14b are much lower. In addition, the impact of scratch direction and cross-sectional area varies between the two factors, with the cross-sectional area having a more significant effect in the case of scratched and fatigued samples.
3.2. Elongation at Break
3.2.1. Aluminium Alloy 2024-T3
The elongation at break of the scratched (εs) and scratched-fatigued (εsf) samples decreased by 16.941% for the samples scratched at 0°, by 31.356% for those scratched at 45°, and by 20.22% for those scratched at 90°. The εs decrease by up to 152.155% compared to the values in Table 1, whereas the εsf decreases by 210.631%.
Both models from Equations 18 and 19 aim to predict the elongation at break of aluminium alloy 2024-T3 samples by considering the scratch direction and cross-sectional area. Nevertheless, they contain distinct variables and indicate diverse levels of complexity. Both models show linear effects for SDir and CSA, indicating that these factors have a direct impact on elongation at break. The models have an interaction factor (SDir x CSA) that considers how the direction of the scratch and the cross-sectional area affect the length at break. The εsf_2024-T3 model has a lower intercept value (6.64024) in contrast to the εs_2024-T3 model (7.95718), indicating a typically reduced elongation at break for samples that are scratched and fatigued. The SDir coefficient for both models is negative, showing that an increase in scratch direction often leads to a reduction in elongation at break. However, it is much more important in the εsf_2024-T3 model, which means that the direction of the scratch has a bigger impact on the lengthening of scratched-fatigued samples. Both models have a positive CSA coefficient, indicating that increasing the cross-sectional area typically leads to an increase in elongation at break. In the εsf_2024-T3 model, the coefficient is slightly greater, indicating a stronger effect of cross-sectional area on elongation for scratched and fatigued samples. In both models, the interaction term has opposite signs. In the εs_2024-T3 model, the result is negative, indicating a decreasing impact of the combined SDir and CSA on elongation. The εsf_2024-T3 model has a positive correlation, indicating an increasing impact. The εsf_2024-T3 model has quadratic factors for SDir and CSA, suggesting a non-linear correlation between these variables and elongation at break. This implies a more complex behaviour for scratched-fatigued samples. For aluminium alloy 2024-T3, the variations in the models indicate that fatigue has a major impact on the correlation between scratch direction, cross-sectional area, and elongation at break.
εs_2024-T3 = 7.95718 – 0.079094xSDir + 0.096159xCSA – 0.00015xSDir x CSA
εsf_2024-T3 = 6.64024 – 0.08116xSDir + 0.099137xCSA + 0.000227xSDir x CSA + 0.00012xSDir2 – 0.000647xCSA2
Both plots use a colour gradient to display the elongation at break values, where warmer colours (red and orange) indicate greater elongations and cooler colours (blue and green) reflect lower elongations. The x-axis denotes the angle of the scratch direction in degrees, while the y-axis shows the cross-sectional area of the scratched sample in square millimetres.
The contour plot from Figure 15a indicates a consistent pattern of decreasing elongation at break as the scratch direction increases. This indicates that the direction of the scratch has a major impact on the material's ability to deform without breaking. Furthermore, as the cross-sectional area increases, this impact is less significant than the effects of scratch direction.
Figure 15b's contour plot for scratched and fatigued samples shows a more complex pattern than the scratched samples. The impact of the direction of scratching on elongation remains apparent since lower scratch angles are associated with larger elongations. Nevertheless, the impact of the cross-sectional area tends to be more prominent since the contour lines are more densely packed in the vertical direction. These results indicate that the simultaneous occurrence of scratching and fatigue greatly diminishes the material's ability to stretch, and the size of the cross-sectional area becomes a more important factor when determining the extent of elongation at the fracture point.
Upon comparing the two graphs, it is noticeable that fatigue significantly reduces the elongation at break of the aluminium alloy 2024-T3. Moreover, the impact of cross-sectional area becomes significantly greater when fatigue is present, indicating that the material becomes more responsive to changes in shape under these circumstances.
3.2.2. Aluminium Alloys 6061-T4, 6061-T4 and -T6 Uncoated
The analysis of the results for the 6061-T4 alloy indicates an average elongation at break of 6.084% for the scratched samples, compared to 5.148% for the scratched-fatigued ones. The percentage difference between the scratched and scratched-fatigued samples in the 0° and 90° scratch directions ranges from 16.7 to 17%, with a significant difference of 20.793% for the 45° orientation. The initial material properties from Table 1 show a decrease in elongation results of 310.942% for the scratched samples and 385.641% for the scratched-fatigued samples.
In both Equations 20 and 21, there is an interaction term (SDir x CSA) that considers how the direction of the scratch and the cross-sectional area affect the length at break. The εsf_6061-T4 model has a lower intercept value (5.48139) compared to the εs_6061-T4 model (6.1297), suggesting a generally reduced elongation at break for samples that are scraped and exhausted. Both models have a negative SDir coefficient, indicating that an increase in scratch direction results in a decrease in elongation at break. However, the rate of elongation is almost the same in all models, suggesting that the influence of scratch direction on elongation is comparable for both scratched and scratched-fatigued samples. Both models have positive CSA coefficients, indicating that an increase in cross-sectional area leads to an increase in elongation at break. Even so, the coefficient in the εs_6061-T4 model has a slightly greater value, suggesting an increased impact of the cross-sectional area on elongation for scratched samples. The sign of the interaction term varies between the two models. The εs_6061-T4 model's outcome is negative, indicating that the combined effect of SDir and CSA has a lesser influence on elongation. The εsf_6061-T4 model results in a favourable result, indicating a minor but perceptible increase in impact. It also exhibits quadratic components for SDir and CSA, indicating a non-linear relationship between these variables and elongation at break. This implies that the behaviour of scratched and fatigued samples is complex.
For aluminium alloy 6061-T4, the variations in the models suggest that fatigue significantly impacts the relationship between scratch direction, cross-sectional area, and elongation at break.
εs_6061-T4 = 6.1297 – 0.083523xSDir + 0.215888xCSA – 0.00015xSDir x CSA
εsf_6061-T4 = 5.48139 – 0.083667xSDir + 0.183291xCSA + 0.000227xSDir x CSA + 0.00012xSDir2 – 0.000647xCSA2
Figure 16a's contour map of scratched samples highlights the relationship between elongation at break and the direction of the scratch. As the scratch's angle increases, there is a consistent reduction in elongation. In this case, the cross-sectional area has a less significant influence on elongation.
Figure 16b is the contour map of the scratched and fatigued samples, indicating the complexity and correlation between the variables. Despite the noticeable effect of scratch direction on elongation, its influence appears to be less significant compared to the scratched samples. A stronger tendency is observed for the cross-sectional area, with a noticeable decrease in elongation as the cross-sectional area increases, as indicated by the downward slope. The results indicate that fatigue significantly reduces the material's capacity to elongate, and the impact of the cross-sectional area becomes even more important when considering the extent to which the material may stretch before breaking in these circumstances.
Upon comparing the two graphs, it is understood that fatigue has a substantial negative impact on the mechanical characteristics of the aluminium alloy 6061-T4. The plot in Figure 16a has significantly lower overall elongation values, as evidenced by the colour scale shifting toward cooler hues. In addition, the impact of scratch direction and cross-sectional area varies between the two conditions, with the cross-sectional area having a more significant effect in the case of scratched and fatigued samples.
On average, the elongation at break of the fatigued samples of 6061-T4 uncoated aluminium alloy decreases by up to 56.057% compared to the scratched samples. The results indicate a decrease of 237.406% (scratched samples) and 344.524% (scratched-fatigued) compared to the initial values. It can be noted that for this alloy, low values for elongation at break were measured at 0.532% to 90°, with a cross-sectional area of 12.5 mm, scratched-fatigued.
In the case of 6061-T4 uncoated aluminium alloy, the εsf_6061-T4_uncoated model from Equation 23 has an increased intercept value (5.79566) in contrast to εs_6061-T4_uncoated (5.34183), indicating a generally higher baseline elongation for scratched and fatigued samples.
Both models' SDir coefficients (Equations 22 and 23) are negative, indicating that increasing the scratch direction angle correlates to a decrease in elongation at break. However, the effect is much stronger in the εsf_6061-T4_uncoated model, showing a stronger link between the direction of the scratch and the lengthening of samples that have been scratched and fatigued
In both models, the CSA coefficient is positive, suggesting that an increase in cross-sectional area typically leads to an increase in elongation at break. Even so, the coefficient in εs_6061-T4_uncoated is higher, which means that cross-sectional area has an increased impact on elongation for scratched samples.
The interaction term's sign varies between the two models. The results of the εs_6061-T4_uncoated model led to a negative relationship, indicating that the combined action of SDir and CSA results in decreasing the elongation at break. εsf_6061-T4_uncoated leads to a favourable result, indicating a minor but noticeable increased impact.
The εsf_6061-T4_uncoated model has quadratic factors for SDir and CSA, suggesting a non-linear correlation between these parameters and elongation at break.
εs_6061-T4_uncoated = 5.34183 – 0.077772xSDir + 0.19612xCSA – 0.00015xSDir x CSA
εsf_6061-T4_uncoated = 5.79566 – 0.088381xSDir + 0.119279xCSA + 0.000227xSDir x CSA + 0.00012xSDir2 – 0.000647xCSA2
The contour map of scratched aluminium alloy 6061-T4 uncoated (Figure 17a) indicates that as the scratch angle increases, there is a gradual decrease in elongation, as seen by the transition from warmer to cooler hues. This indicates that the direction of the scratch has a major effect on the material's ability to withstand plastic deformation without breaking. The influence of cross-sectional area on elongation tends to be less significant; however, for larger cross-sectional areas. The scratched and fatigued aluminium alloy 6061-T4 uncoated contour map (Figure 17b) reveals a more complex relationship among the variables, which aligns with the mathematical model from Equation 23. While the impact of the scratch direction on elongation remains noticeable, it seems to be less significant compared to the scratched samples. A distinct pattern is seen in the cross-sectional area, where elongation decreases noticeably as the cross-sectional area increases. The downward slope of the colour bands illustrates this. Under these circumstances, fatigue significantly reduces the material's ability to stretch, and the impact of the cross-sectional area becomes more important in determining the extent of elongation at the point of fracture.
When comparing the two plots, fatigue has a significant negative impact on the mechanical characteristics of the uncoated aluminium alloy 6061-T4. The elongation values in Figure 17b are much lower. Also, the direction of the scratch and the cross-sectional area have different effects on the two factors, with the cross-sectional area having a bigger effect on scratched and fatigued samples.
The statistics given emphasise the significance of considering both the direction of scratches and the cross-sectional area when assessing the mechanical properties of uncoated aluminium alloy 6061-T4, particularly in the context of fatigue.
Scratched and fatigued samples, in the case of aluminium alloy 6061-T6 uncoated, are 57.664% likely to fail compared to scratched specimens and 251.917% when compared to the initial properties for the elongation. A 16.65% average percentage difference was measured between the scratched and scratched fatigue samples.
The intercept of Equation 25 for εsf_6061-T6_uncoated is 4.55938, which is less than the intercept for the εs_6061-T6_uncoated model, which is 6.84834. This implies that scratched-fatigued samples typically exhibit a lower elongation at break.
The SDir coefficient for both models is negative, showing that a decrease in scratch direction can result in an increase in elongation at break. Still, the magnitude is significantly greater in the εs_6061-T6_uncoated model, indicating a more significant effect of scratch direction on elongation for the scratched samples.
In both models, the CSA coefficient is positive, indicating that an increase in cross-sectional area usually leads to an increase in elongation at break. However, the coefficient in the εsf_6061-T6_uncoated model is higher, indicating that cross-sectional area has a greater impact on elongation for scratched and fatigued samples.
The interaction term's sign varies between the two models. In the εs_6061-T6_uncoated model, the coefficient is negative, indicating the decreasing impact of the combined SDir and CSA on elongation. The εsf_6061-T6_uncoated model provides an improved outcome, indicating a minor upward impact. The εsf_6061-T6_uncoated model has quadratic factors for SDir and CSA, which means that these parameters don't have a straight-line relationship with elongation at break. This implies complex behaviour in scratched and fatigued samples. The differences between the models for uncoated aluminium alloy 6061-T6 show that fatigue has a big impact on the relationship between scratch direction, cross-sectional area, and elongation at break.
εs_6061-T6_uncoated = 6.84834 – 0.074378xSDir + 0.046334xCSA – 0.00015xSDir x CSA
εsf_6061-T6_uncoated = 4.55938 – 0.067235xSDir + 0.106653xCSA + 0.000227xSDir x CSA + 0.00012xSDir2 – 0.000647xCSA2
The angle of the scratch affects the elongation at break for scratched samples of the uncoated aluminium alloy 6061-T6 (Figure 18a), as shown for all alloys, as the angle of the scratch increases, the elongation decreases. The effect of cross-sectional area on elongation tends to be less significant; however, there is a minor increase in elongation for larger cross-sectional areas, as expected.
In Figure 18b, the scratched and fatigued samples highlight a complex correlation between the variables. Despite the noticeable effect of scratch direction on elongation, the results show less significance compared to the scratched samples.
The comparison of both plots leads to the conclusion that fatigue significantly impairs the mechanical characteristics of the uncoated aluminium alloy 6061-T6.
The mathematical models depict the correlation between elongation at break and scratch direction (SDir), as well as the cross-sectional area (CSA). In all models, the key predictors of elongation at break are a linear combination of SDir, CSA, and their interactions. Each alloy's sf mode exhibits quadratic factors for both SDir and CSA, suggesting a more complex relationship between these variables and elongation at break in both scratched and fatigued samples. The intercept values show substantial variation, suggesting that there are intrinsic variances in ductility across the alloys. Also, the SDir, CSA, and interaction terms show different values, showing complicated responses to scratch direction and cross-sectional area for each alloy.
Among the many types of alloys, the models for scratched and fatigued samples exhibit significant differences. Scratched and fatigued samples have an overall tendency to decrease elongation, given a lower intercept. The coefficients for SDir and CSA show variation, indicating that fatigue has modified sensitivity to these parameters. Using quadratic factors in the models for scratched and fatigued samples also shows that the direction of the scratch and the area of the scratch do not have a straight-line effect on the lengthening when the material is fatigued.
3.2.3. Aluminium Alloy 7075-T0 and 7075-T6
The result of the aluminium alloy 7075-T0 indicates that on average, samples scratched at 0° fail at 9.586% elongation, compared to 7.861% when subjected to fatigue, meaning a decrease of 21.952%. This tendency is also noted when analysing the samples scratched at 45° (from 5.869% to 4.945%, resulting in a decrease of 18.7%) and 90° (from 1.81% to 1.545%, resulting in a decrease of 17.137%).
When looking at the aluminium alloy 7075-T0 εsf_7075-T0 model from Equation 27, it has a lower intercept value (5.74385) than the εs_7075-T0 model (6.06584) from Equation 26. This means that samples that are scratched and worn out have a lower elongation at break. The SDir coefficient for both models is negative, suggesting that an increase in scratch direction results in reduced values for the elongation at break. The value is somewhat greater in the εsf_7075-T0 model, indicating a more significant effect of scratch direction on elongation for scratched and fatigued samples.
Both models have positive CSA coefficients, indicating that an increase in the cross-sectional area leads to an increase in elongation at break. Nevertheless, the coefficient in the εs_7075-T0 model is higher, showing a greater influence of cross-sectional area on elongation for scratched samples.
The interaction term's sign varies between the two models. In the εs_7075-T0 model, the coefficient is negative, indicating the decreasing impact of the combined SDir and CSA on elongation. The εsf_7075-T0 model provides a favourable result, indicating a minor but noticeable increase. The εsf_7075-T0 model has quadratic factors for SDir and CSA, suggesting a non-linear correlation between these parameters and elongation at break.
εs_7075-T0 = 6.06584 – 0.070452xSDir + 0.17151xCSA – 0.00015xSDir x CSA
εsf_7075-T0 = 5.74385 – 0.073863xSDir + 0.1238097xCSA + 0.000227xSDir x CSA + 0.00012xSDir2 – 0.000647xCSA2
The same tendency can be noted, from Figure 19a, in the case of scratched aluminium alloy 7075-T0 samples: as the angle of the scratch increases and the cross-section area decreases, there is a consistent pattern of decreasing elongation, affecting the alloy's ductility. For scratched and fatigued samples, Figure 19b indicates the correlation between the variables, as seen in the previous cases. Although the effect of scratch direction on elongation remains noticeable, it seems to be less significant compared to the scratched samples. The same correlation can be observed between the cross-sectional area and elongation, with a decrease in elongation as the cross-sectional area decreases. Comparing the two plots reveals a substantial negative impact of fatigue on the mechanical properties of the aluminium alloy 7075-T0, with the cross-sectional area having a more significant effect in the case of scratched and fatigued samples.
In the case of aluminium alloy 7075-T6, it can be noted that, on average, scratched samples fail at 4.422%, while scratched-fatigued ones at 3.551%; this leads to a decrease of 24.54% in elongation at break. Scratched samples show an average decrease of 216.574% compared to the initial elongation value; applying fatigue bending reduces these values to 294.261%.
For the aluminium alloy 7075-T6, the εsf_7075-T6 model has a lower intercept value (3.29608) in contrast to εs_7075-T6 (4.34604), indicating a reduced elongation at break for scratched and fatigued samples.
Both models have negative SDir coefficients, suggesting that an increase in scratch direction results in a decrease in elongation at break. The effect is somewhat greater in the εsf_7075-T6 model, indicating a more significant impact of scratch direction on elongation for scratched and fatigued samples. Positive CSA coefficients indicate that an increase in cross-sectional area leads to an increase in elongation at break. In the εsf_7075-T6 model, the coefficient has a slightly larger scale, indicating an increased effect of cross-sectional area on elongation for scratched and fatigued samples. The sign of the interaction term differs between the two models. The εs_7075-T6 model has a negative relationship, indicating that the combined SDir and CSA have a decreasing impact on elongation. The εsf_7075-T6 model provides a favourable result, indicating a minor but notable improvement.
The εsf_7075-T6 model also has quadratic factors for SDir and CSA, indicating a non-linear correlation between these variables and elongation at break. As anticipated, this implies a more complex behaviour in scratched and fatigued samples.
εs_7075-T6 = 4.34604 – 0.046605xSDir + 0.112898xCSA – 0.00015xSDir x CSA
εsf_7075-T6 = 3.29608 – 0.049071xSDir + 0.116246xCSA + 0.000227xSDir x CSA + 0.00012xSDir2 – 0.000647xCSA2
The contour map from Figure 20a of scratched 7071-T6 samples highlights the relationship between elongation at break and the direction of the scratch. As the scratch angle increases, there is a consistent pattern of decreasing elongation. Lower values of the cross-section area led to low elongation at break values. In Figure 20b, the data for scratched and fatigued 7075-T6 samples shows a more complex correlation between the variables. Despite being noticeable, the influence of the scratch direction on elongation appears to be less significant compared to the scratched samples. A noticeable pattern is seen in the cross-sectional area, where elongation reduces noticeably as the cross-sectional area decreases. As previously concluded, fatigue significantly reduces the material's ductility, and the impact of the cross-sectional area becomes more important in determining the extent of elongation at the fracture point under these circumstances.
Fatigue has a substantial negative impact on the mechanical properties of the aluminium alloy 7075-T6. Figure 20b's plot shows significantly reduced overall elongation values. In addition, the cross-sectional area results have a relevant effect on scratched and fatigued samples. The results indicate that these parameters are important in reducing the material's performance in applications that experience repeated stress and surface deterioration.
4. Discussion
The interpretation of the results can be summarized in the data presented in Table 7, where the initial values for UTS and elongation at break are presented, together with the average values obtained for the scratched, scratched, and fatigued samples; the percentage difference (% diff.) between these and the initial values is also presented.
When analysing the UTSs_avg, aluminium alloys 2024-T3 and 7075-T6 withstand scratches much better, with a decrease of 5.17% and 4.151%, respectively. On the other side are the 7075-T0 and 6061-T4 alloys, which decreased by 10.8% and 11.92%, respectively. Inducing fatigue in the process alters this order, with the 6061-T6 uncoated alloy achieving superior results (28.05%), while the 6061-T4 uncoated alloy falls at the opposite end (41.6%). Thus, the data indicates a decrease between 20.78% and 30.26% in the UTS when fatigue is applied to a scratched sample.
The data indicates that 7075-T6 exhibits the highest initial UTS, followed by 2024-T3, 6061-T4, and the uncoated alloys. This suggests that alloy composition and heat treatment significantly influence the material's strength. Both scratching and fatigue lead to a substantial reduction in UTS for all alloys. The percentage decrease in UTS varies among alloys, with 6061-T4 uncoated experiencing the most significant drop.
Table 7 also notes significant variations in elongation behaviour among the investigated aluminium alloys, with 6061-T4 exhibiting the highest initial elongation (25%), followed by 2024-T3 (16%), 7075-T0 (15%), and 6061-T6 and 7075-T6 uncoated at 12.8% and 14%, respectively. The percentage difference provides quantitative insights into the percentage reduction in elongation due to scratching and fatigue. 6061-T4 experiences a 310.94% reduction in elongation due to scratching, while the reduction due to fatigue is 385.64%. After scratching, the elongation decrease of the 2024-T3 alloy is 154.15%, and after fatigue, it is 210.63%, indicating that it possesses a highly desirable behaviour.
The results explicitly indicate that scratching and subsequent fatigue have a negative impact on the ultimate tensile strength. The UTS values for both scratched and scratched and fatigued conditions consistently show considerable decreases relative to the initial UTS values for all alloys examined.
Uncoated alloy 6061-T4 exhibits a major decrease in UTS when subjected to both scratching and fatigue, suggesting an increased susceptibility to strength loss in comparison to other alloys.
The data suggests a potential correlation between the initial UTS and the extent of UTS decrease due to scratching and fatigue. Alloys that have greater initial UTS values, such as 7075-T6, show less significant decreases compared to alloys with lower initial UTS values, such as 6061-T4 uncoated. This suggests that alloys with higher initial strength may exhibit greater resistance to deterioration caused by scratching and fatigue.
The provided data reveals significant variations in elongation behaviour among the different aluminium alloys investigated. The initial elongation exhibits a clear dependence on alloy composition, with 6061-T4 demonstrating the highest ductility, followed by 7075-T0 and 2024-T3.
Both scratching and fatigue conditions lead to a substantial reduction in elongation compared to the initial values for all aluminium alloys. This indicates that these factors have a negative impact on the material's ductility. The percentage difference in elongation between the initial state and the scratched or fatigued conditions varies across different alloys. While all alloys experience a decrease in elongation, the magnitude of this reduction is not uniform.
According to the provided data, alloy 7075-T6 exhibits superior results in UTS and elongation. 7075-T6 has the highest initial UTS (530 MPa), followed by 6061-T6 (310 MPa), 2024-T3 (450 MPa), and 6061-T4 (255 MPa and 247 MPa). While all alloys experience a reduction in UTS due to scratching and fatigue, 7075-T6 maintains the highest UTS even under these adverse conditions. 6061-T4 shows the highest initial elongation (25% and 22%), indicating superior ductility compared to other alloys. However, for 6061-T4, the percentage reduction in elongation due to scratching and fatigue is also significant. 7075-T6, despite having a lower initial elongation, shows superior resistance to elongation loss under scratching and fatigue conditions. While 6061-T4 exhibits higher initial ductility, 7075-T6 offers a superior balance of strength and ductility, especially when considering the effects of scratching and fatigue. Its ability to maintain relatively high UTS and elongation under adverse conditions makes it a more suitable choice for applications demanding both strength and toughness.
Although it outperforms other alloys in terms of both UTS and elongation, the aluminium alloy 2024-T3 shows a balanced combination of strength and ductility. While it exhibits a reasonable initial UTS, its susceptibility to strength degradation under scratching and fatigue conditions is notable. The UTS of 2024-T3 situates itself between the higher strength of 7075-T6 and the lower strength of 6061-T4 alloys, while the elongation values fall between the higher ductility of 6061-T4 and the lower ductility of 7075-T6.
While 2024-T3 offers a reasonable balance of strength and ductility, its susceptibility to degradation under adverse conditions limits its suitability for applications demanding high levels of resistance to scratching and fatigue. For applications requiring optimal strength, 7075-T6 might be a more suitable choice, whereas for applications prioritising ductility, 6061-T4 could be considered.
5. Conclusions
This research study aimed to investigate the effects of induced scratches on the UTS and elongation at break for aircraft-grade aluminium alloys subjected to low-cycle fatigue bending, as well as to establish an overview of the factors that contribute to material failure and consequent loss of structural integrity.
An analysis of variance (ANOVA) was used on the data to establish mathematical models that characterize the relationship between UTS, elongation at break, and other characteristics such as scratch direction and cross-sectional area. Quadratic or 2FI interference models were used to examine the data. Each model yielded a p-value below 0.001, indicating the statistical significance of the results. A non-linear relationship between the direction of the scratch and the cross-sectional area was identified; this correlation was shown to affect the strength and elongation of the alloys. Fatigue has a significant impact on the mechanical characteristics of the aluminium alloy, resulting in a decrease in the ultimate tensile strength and elongation at break. The values continue to drop as the scratch direction and cross-sectional area decrease.
To determine the baseline mechanical characteristics and the degree of deterioration that occurs because of scratching and fatigue, the composition of the alloy is an extremely important factor. The 7075-T6 has the highest initial UTS, but it also has a slight decrease in both UTS and elongation. In contrast, the 6061-T4 alloy has a greater initial elongation but experiences a more severe decrease in both its UTS and its elongation when subjected to these circumstances.
To choose the appropriate aluminium alloy for a particular application, it is essential to consider the predicted loading conditions as well as the possibility of surface damage.
Of course, to fully understand the phenomenon, we must take into account the following aspects and explore potential future research directions: analysis of the microstructure (changes in microstructure that occur during scratching and fatigue), initiation and propagation of cracks (examine the impact of scratch shape and position on the way fatigue cracks develop, or the correlation between multiple scratches of different orientations and sizes), apply finite element analysis (FEA) to model the distribution of stress and strain around scratches and forecast the beginning and propagation of cracks or examine the effects of multi-axial loading, such as tension-torsion and bending-torsion, on the mechanical properties of aluminium alloys that have been scratched and fatigued.
Supplementary Materials
Not applicable.
Author Contributions
Conceptualization, V.Z., V.A.C. and G.C.C.; methodology, V.Z., V.A.C. and G.C.C.; software, G.C.C.; validation, V.Z. and V.A.C; formal analysis, V.A.C. and G.C.C.; investigation, V.A.C. and G.C.C.; resources, V.Z.; data curation, V.Z. and V.A.C.; writing—original draft preparation, V.A.C. and G.C.C.; writing—review and editing, V.Z., V.A.C. and G.C.C.; visualization, G.C.C.; supervision, V.Z.; project administration, V.Z. and G.C.C.; funding acquisition, V.Z. All authors have read and agreed to the published version of the manuscript.
Funding
Not applicable.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors would like to acknowledge the support of AEROSTAR S.A., Bacău, Romania, an aviation company that specializes in ground defence system integration, manufacturing, modernization, and maintenance; supplier of parts, aerostructures, subassemblies, and equipment for civil aviation; and provider of maintenance and conversion services for civil aviation. They supplied the aluminium alloys and the mounting system for the fatigue process.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Ramalingam, B.; Manuel, V.-H.; Elara, M.R.; Vengadesh, A.; Lakshmanan, A.K.; Ilyas, M.; James, T.J.Y. Visual Inspection of the Aircraft Surface Using a Teleoperated Reconfigurable Climbing Robot and Enhanced Deep Learning Technique. International Journal of Aerospace Engineering 2019, 2019, 5137139. [CrossRef]
- Hassan, M. ul; Danish, F.; Yousuf, W. Bin; Khan, T.M.R. Comparison of Different Life Distribution Schemes for Prediction of Crack Propagation in an Aircraft Wing. Eng Fail Anal 2019, 96, 241–254. [CrossRef]
- Jovančević, I.; Pham, H.-H.; Orteu, J.-J.; Gilblas, R.; Harvent, J.; Maurice, X.; Brèthes, L. 3D Point Cloud Analysis for Detection and Characterization of Defects on Airplane Exterior Surface. J Nondestr Eval 2017, 36, 74. [CrossRef]
- Avdelidis, N.P.; Tsourdos, A.; Lafiosca, P.; Plaster, R.; Plaster, A.; Droznika, M. Defects Recognition Algorithm Development from Visual UAV Inspections. Sensors 2022, 22. [CrossRef]
- Xia, R.; Zhao, J.; Zhang, T.; Su, R.; Chen, Y.; Fu, S. Detection Method of Manufacturing Defects on Aircraft Surface Based on Fringe Projection. Optik (Stuttg) 2020, 208, 164332. [CrossRef]
- Lafiosca, P.; Fan, I.-S.; Avdelidis, N.P. Automated Aircraft Dent Inspection via a Modified Fourier Transform Profilometry Algorithm. Sensors 2022, 22. [CrossRef]
- Yang, S.; Hu, W.; Zhan, Z.; Li, J.; Bai, C.; Yang, Q.; Meng, Q. Fatigue Tests and a Damage Mechanics-Based Fatigue Model on a Cast Al-Si-Mg Aluminum Alloy with Scratches. Int J Fatigue 2022, 165, 107198. [CrossRef]
- Shen, Z.; Su, Y.; Deng, J.; Huang, Z. Investigation of High-Cycle Fatigue Property and Fatigue Crack Propagation Behavior of a Die-Forged 2014 Aluminum Alloy Aircraft Wheel. Int J Fatigue 2024, 184, 108309. [CrossRef]
- Zhao, B.; Xie, L.; Wang, L.; Hu, Z.; Zhou, S.; Bai, X. A New Multiaxial Fatigue Life Prediction Model for Aircraft Aluminum Alloy. Int J Fatigue 2021, 143, 105993. [CrossRef]
- Younis, H. Bin; Kamal, K.; Sheikh, M.F.; Hamza, A. Prediction of Fatigue Crack Growth Rate in Aircraft Aluminum Alloys Using Optimized Neural Networks. Theoretical and Applied Fracture Mechanics 2022, 117, 103196. [CrossRef]
- Li, L.; Li, X.; Zhan, Z.; Hu, W.; Meng, Q. Fatigue Life Prediction for 2060 Aluminium–Lithium Alloy with Impact Damage. Aerospace 2024, 11. [CrossRef]
- Teng, Y.; Xie, L.; Zhang, H. Experimental Study on Vibration Fatigue Behavior of Aircraft Aluminum Alloy 7050. Materials 2022, 15. [CrossRef]
- Reyno, T.; Marsden, C.; Wowk, D. Surface Damage Evaluation of Honeycomb Sandwich Aircraft Panels Using 3D Scanning Technology. NDT & E International 2018, 97, 11–19. [CrossRef]
- Infante-García, D.; Qian, G.; Miguélez, H.; Giner, E. Analysis of the Effect of Out-of-Phase Biaxial Fatigue Loads on Crack Paths in Cruciform Specimens Using XFEM. Int J Fatigue 2019, 123, 87–95. [CrossRef]
- Grbović, A.; Kastratović, G.; Sedmak, A.; Balać, I.; Popović, M.D. Fatigue Crack Paths in Light Aircraft Wing Spars. Int J Fatigue 2019, 123, 96–104. [CrossRef]
- Varga, M.; Leroch, S.; Gross, T.; Rojacz, H.; Eder, S.J.; Grillenberger, M.; Rodríguez Ripoll, M. Scratching Aluminium Alloys – Modelling and Experimental Assessment of Damage as Function of the Strain Rate. Wear 2021, 476, 203670. [CrossRef]
Figure 1.
Aluminium alloy sample dimensions, indicating the gripping areas.

Figure 2.
Schematic representation of the tensile test, indicating the gripping area, fixture, applied force direction (F), cross-section area (CSA), and internal stress (σ).
Figure 2.
Schematic representation of the tensile test, indicating the gripping area, fixture, applied force direction (F), cross-section area (CSA), and internal stress (σ).

Figure 3.
Scratching process of the tensile test specimens: (a) Sample mounted on the milling machine for scratching; (b) Close-up view of the scratching tool with the corresponding parameters.
Figure 3.
Scratching process of the tensile test specimens: (a) Sample mounted on the milling machine for scratching; (b) Close-up view of the scratching tool with the corresponding parameters.

Figure 4.
Schematic representation of sample geometry, scratch area, and scratch dimensions: (a) scratch orientation (0°, 45°, 90°); (b) scratch length, as % of maximum available length, depending on the scratch angle; (c) scratch depth, as % of sample thickness; (d) 0° scratches, with lengths of 18.75, 35, and 75 mm; (e) 45° scratches, with lengths of 4.419, 8.839, and 17.678 mm; (f) 90° scratches, with lengths of 3.125, 6.25, and 12.5 mm.
Figure 4.
Schematic representation of sample geometry, scratch area, and scratch dimensions: (a) scratch orientation (0°, 45°, 90°); (b) scratch length, as % of maximum available length, depending on the scratch angle; (c) scratch depth, as % of sample thickness; (d) 0° scratches, with lengths of 18.75, 35, and 75 mm; (e) 45° scratches, with lengths of 4.419, 8.839, and 17.678 mm; (f) 90° scratches, with lengths of 3.125, 6.25, and 12.5 mm.
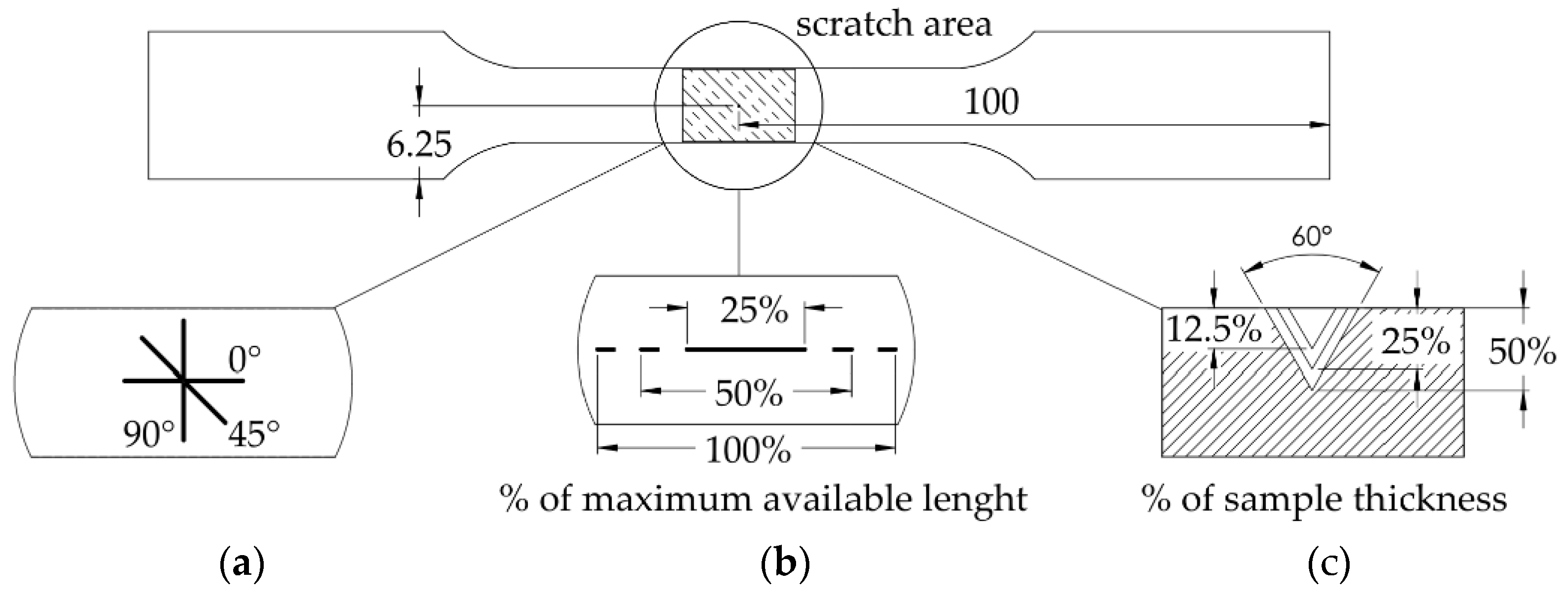
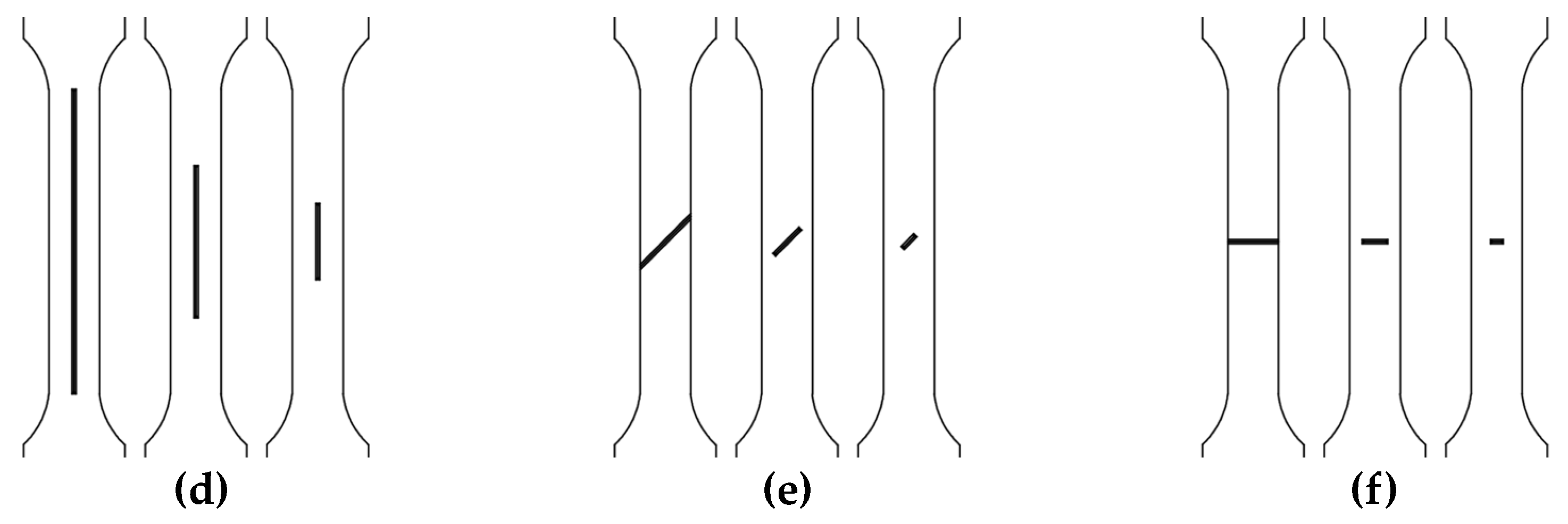
Figure 5.
Transversal section view illustrating the cross-sectional dimensions of the aluminium samples. (a) standard sample (W - sample width and T – sample thickness); (b) sample with 0° scratch (SW –scratch width and SD – scratch depth); (c) sample with 45° scratch (SW –scratch width, SD – scratch depth, and SW’ – transversal projection of SW); (d) sample with 90° scratch (SL – scratch length and SD – scratch depth).
Figure 5.
Transversal section view illustrating the cross-sectional dimensions of the aluminium samples. (a) standard sample (W - sample width and T – sample thickness); (b) sample with 0° scratch (SW –scratch width and SD – scratch depth); (c) sample with 45° scratch (SW –scratch width, SD – scratch depth, and SW’ – transversal projection of SW); (d) sample with 90° scratch (SL – scratch length and SD – scratch depth).
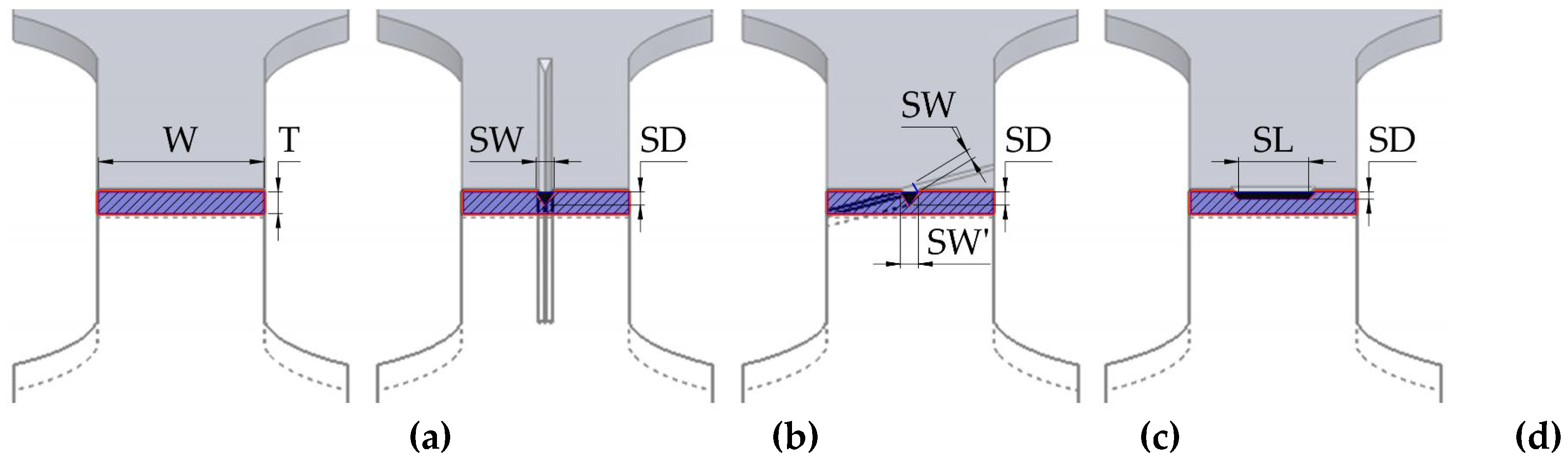
Figure 6.
Fatigue bending experimental setup and process parameters: (a) fatigue equipment with fixture system and 3D printed support; (b) schematic representation of the fatigue cycle process; (c) fatigue cycle parameters plot.
Figure 6.
Fatigue bending experimental setup and process parameters: (a) fatigue equipment with fixture system and 3D printed support; (b) schematic representation of the fatigue cycle process; (c) fatigue cycle parameters plot.
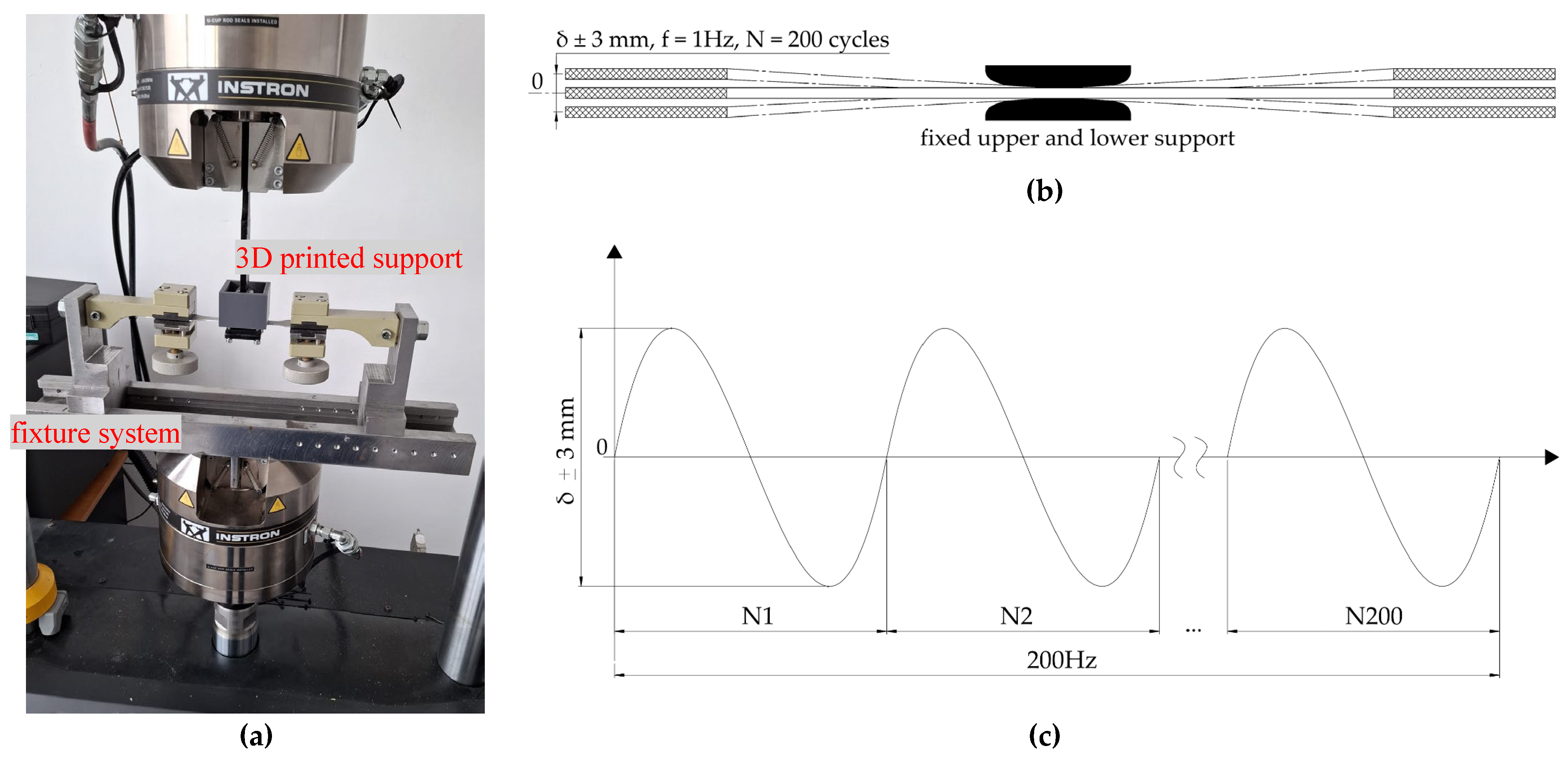
Figure 7.
Tensile test experimental setup indicating: (a) start of the process; (b) moments before crack formation; (c) crack propagation resulting in sample failure, end of the tensile test.
Figure 7.
Tensile test experimental setup indicating: (a) start of the process; (b) moments before crack formation; (c) crack propagation resulting in sample failure, end of the tensile test.

Figure 9.
Contour plots indicating the effect of SDir and CSA on the UTS for aluminium alloy 2024-T3, with warmer colours representing higher UTS values: (a) Data visualization for scratched samples; (b) Data visualization for scratched-fatigued samples.
Figure 9.
Contour plots indicating the effect of SDir and CSA on the UTS for aluminium alloy 2024-T3, with warmer colours representing higher UTS values: (a) Data visualization for scratched samples; (b) Data visualization for scratched-fatigued samples.
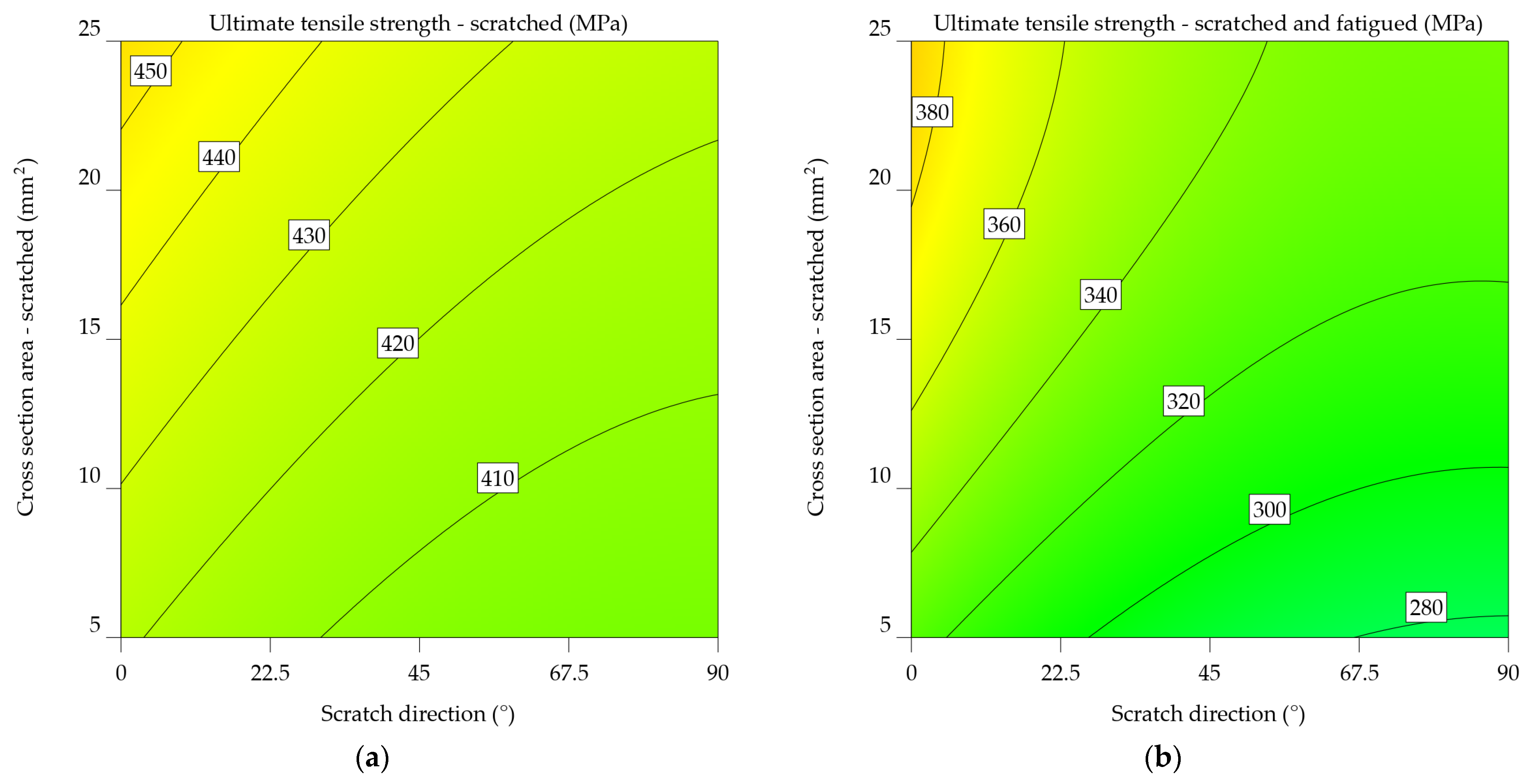
Figure 10.
Contour plots indicating the effect of SDir and CSA on the UTS for aluminium alloy 6061-T4, with warmer colours representing higher UTS values: (a) Data visualization for scratched samples; (b) Data visualization for scratched-fatigued samples.
Figure 10.
Contour plots indicating the effect of SDir and CSA on the UTS for aluminium alloy 6061-T4, with warmer colours representing higher UTS values: (a) Data visualization for scratched samples; (b) Data visualization for scratched-fatigued samples.
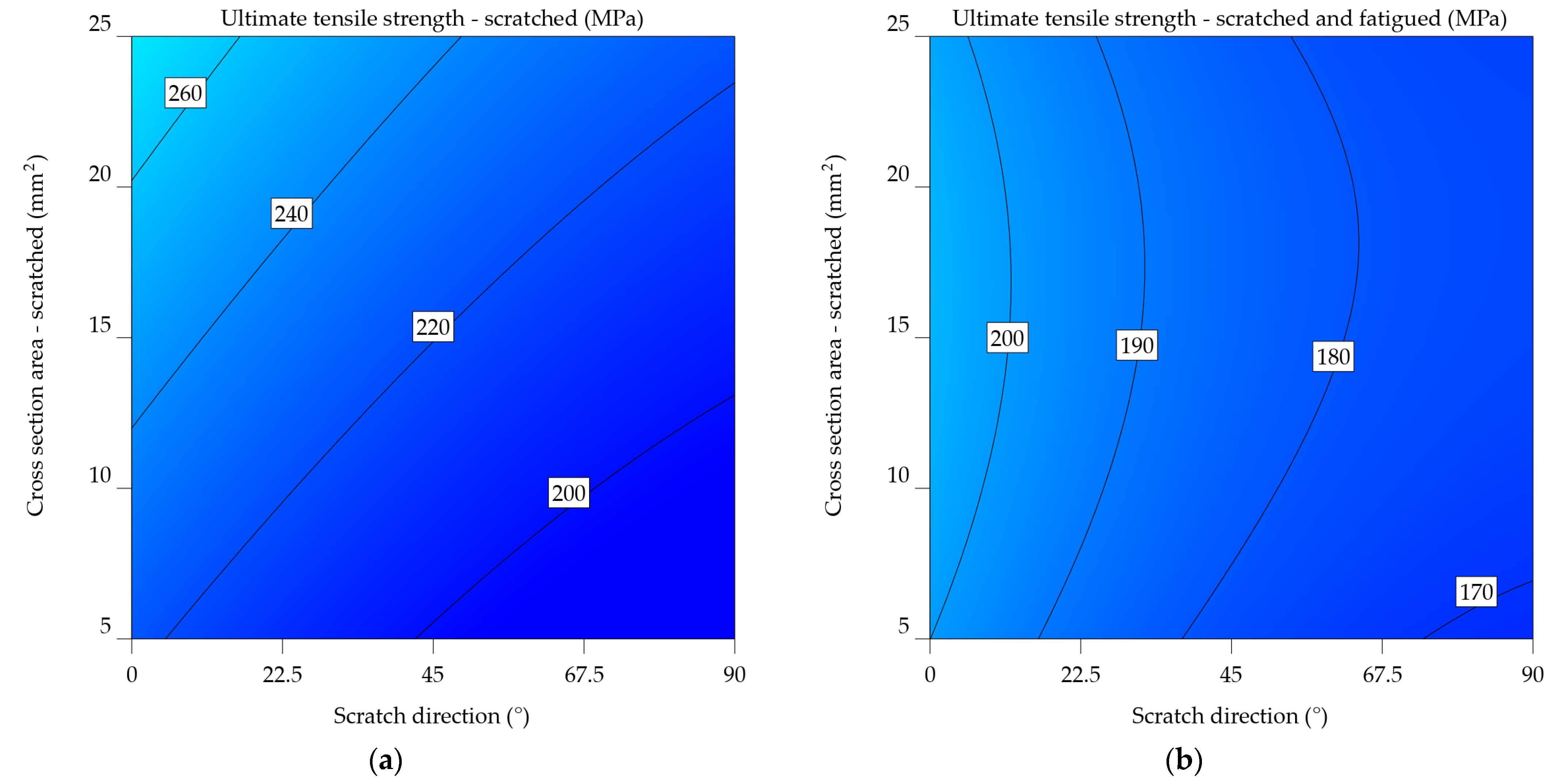
Figure 11.
Contour plots indicating the effect of SDir and CSA on the UTS for aluminium alloy 6061-T4 uncoated, with warmer colours representing higher UTS values: (a) Data visualization for scratched samples; (b) Data visualization for scratched-fatigued samples.
Figure 11.
Contour plots indicating the effect of SDir and CSA on the UTS for aluminium alloy 6061-T4 uncoated, with warmer colours representing higher UTS values: (a) Data visualization for scratched samples; (b) Data visualization for scratched-fatigued samples.
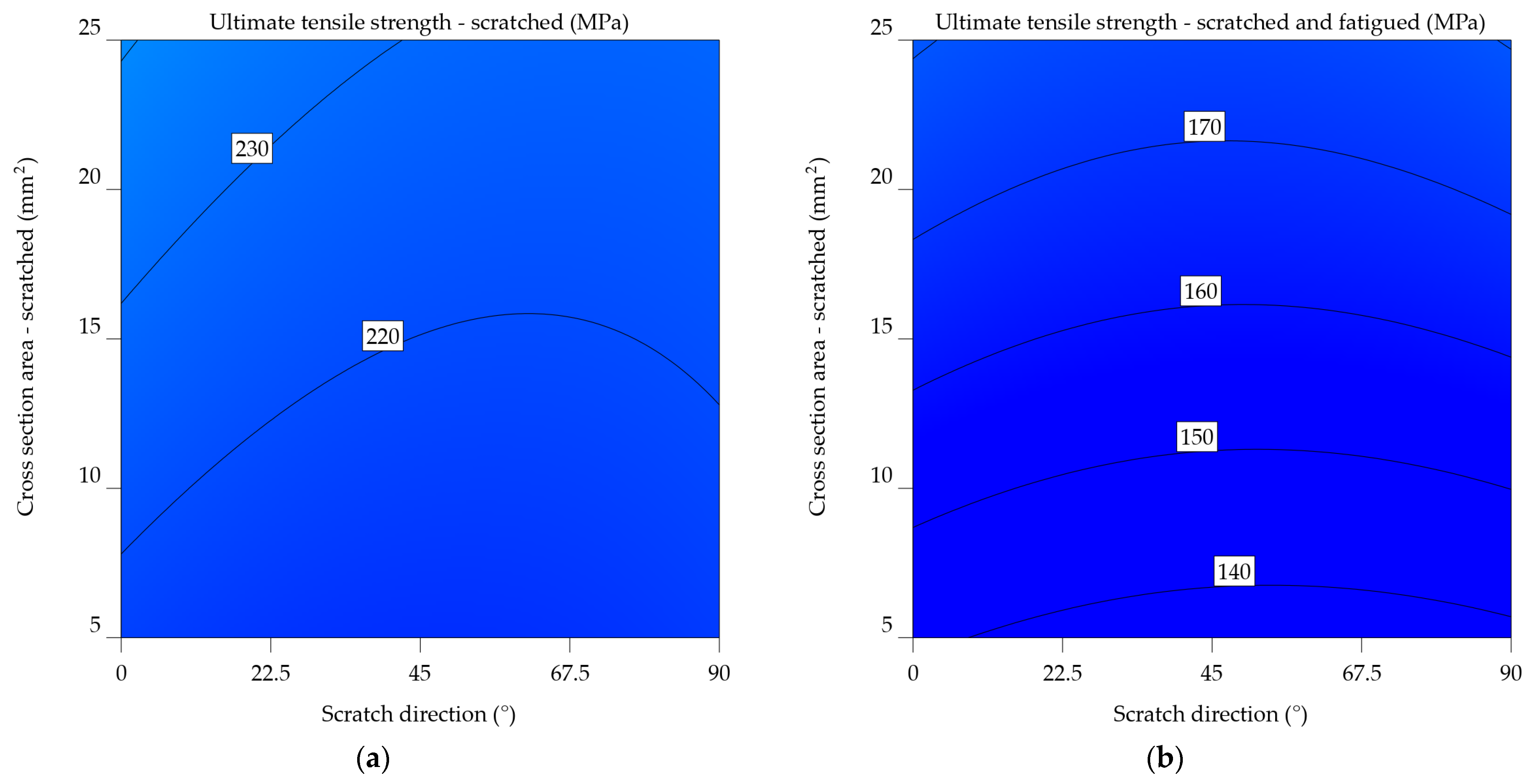
Figure 12.
Contour plots indicating the effect of SDir and CSA on the UTS for aluminium alloy 6061-T6 uncoated, with warmer colours representing higher UTS values: (a) Data visualization for scratched samples; (b) Data visualization for scratched-fatigued samples.
Figure 12.
Contour plots indicating the effect of SDir and CSA on the UTS for aluminium alloy 6061-T6 uncoated, with warmer colours representing higher UTS values: (a) Data visualization for scratched samples; (b) Data visualization for scratched-fatigued samples.
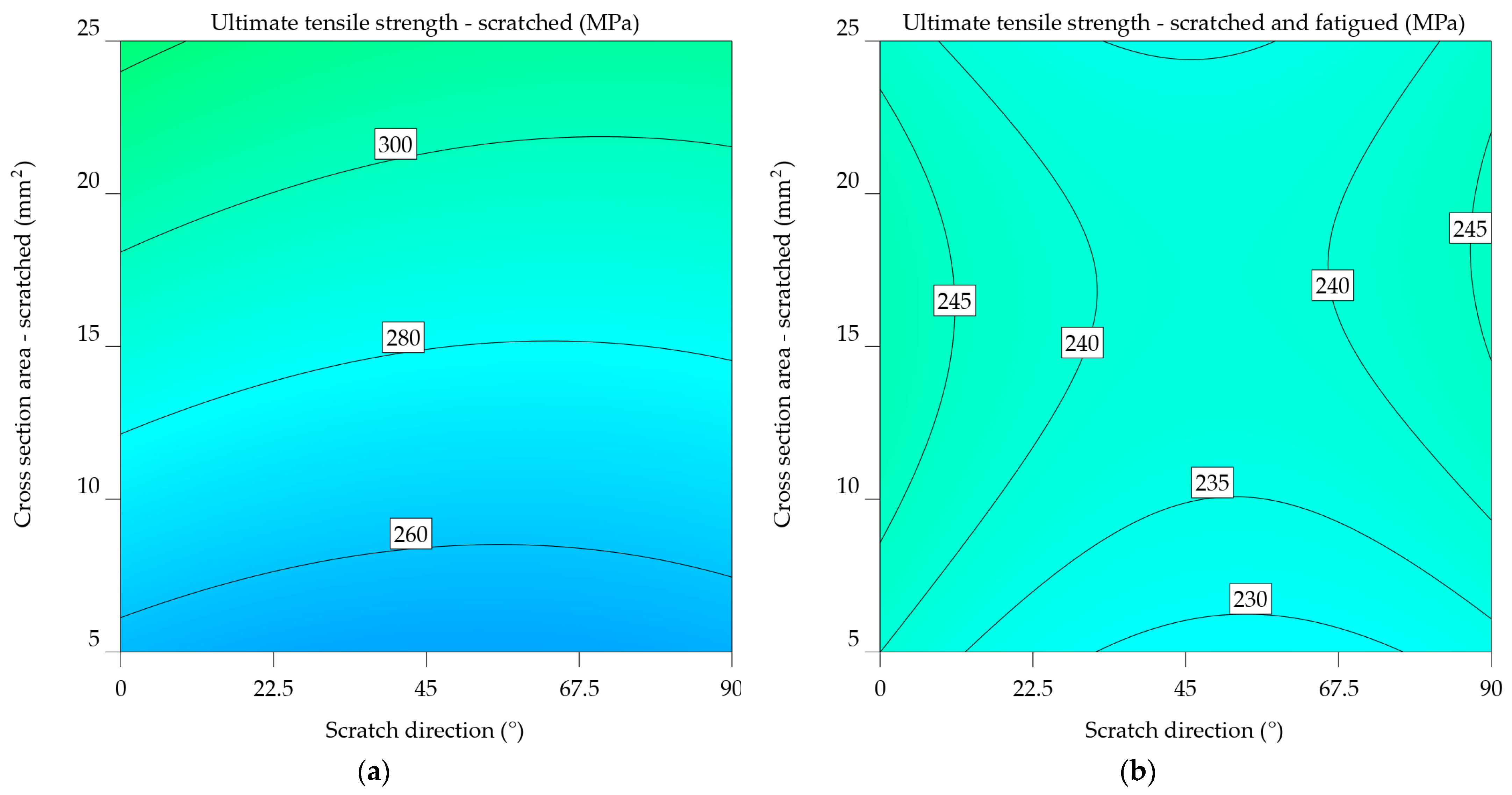
Figure 13.
Contour plots indicating the effect of SDir and CSA on the UTS for aluminium alloy 7075-T0 uncoated, with warmer colours representing higher UTS values: (a) Data visualization for scratched samples; (b) Data visualization for scratched-fatigued samples.
Figure 13.
Contour plots indicating the effect of SDir and CSA on the UTS for aluminium alloy 7075-T0 uncoated, with warmer colours representing higher UTS values: (a) Data visualization for scratched samples; (b) Data visualization for scratched-fatigued samples.
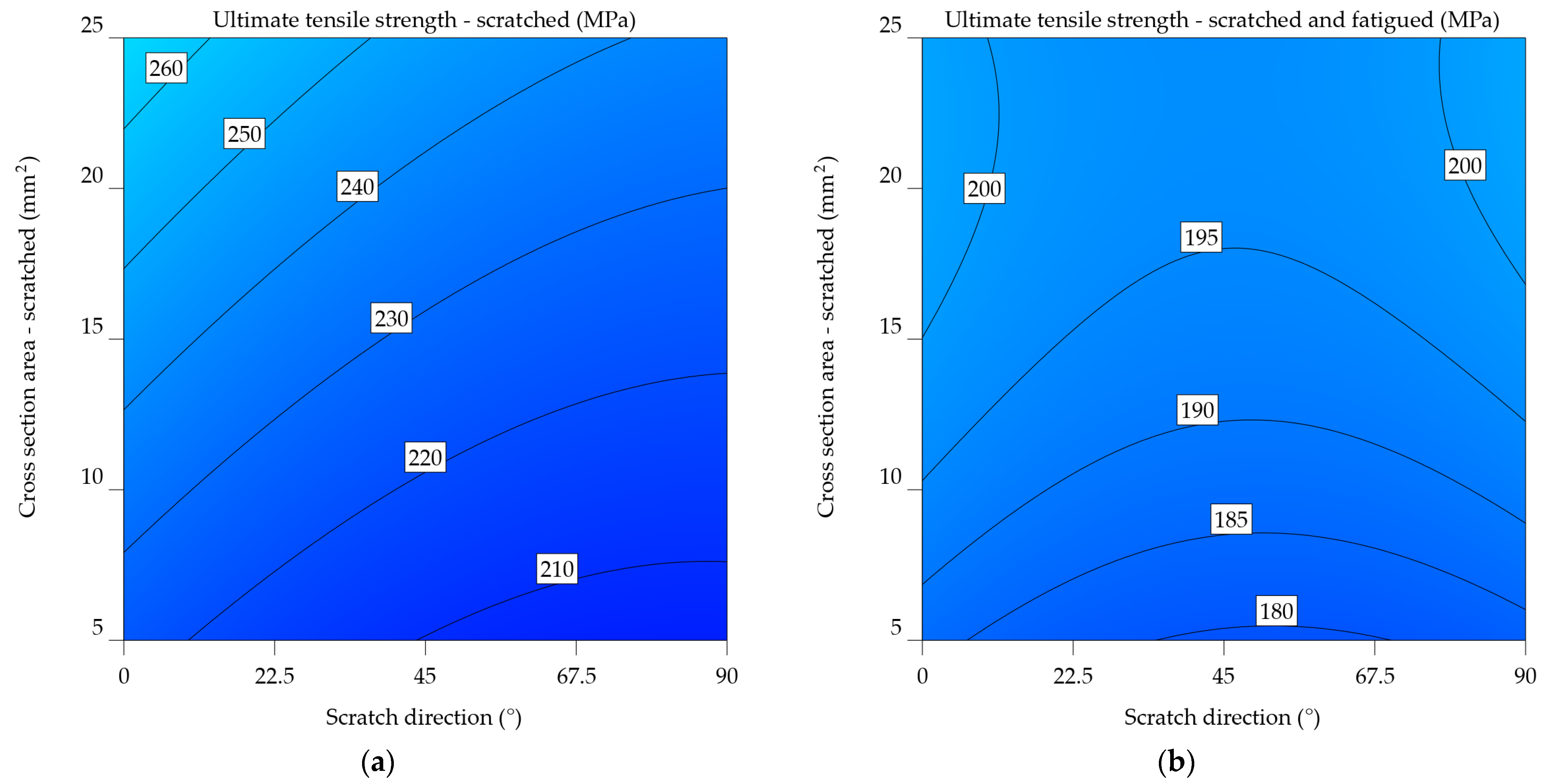
Figure 14.
Contour plots indicating the effect of SDir and CSA on the UTS for aluminium alloy 7075-T6 uncoated, with warmer colours representing higher UTS values: (a) Data visualization for scratched samples; (b) Data visualization for scratched-fatigued samples.
Figure 14.
Contour plots indicating the effect of SDir and CSA on the UTS for aluminium alloy 7075-T6 uncoated, with warmer colours representing higher UTS values: (a) Data visualization for scratched samples; (b) Data visualization for scratched-fatigued samples.
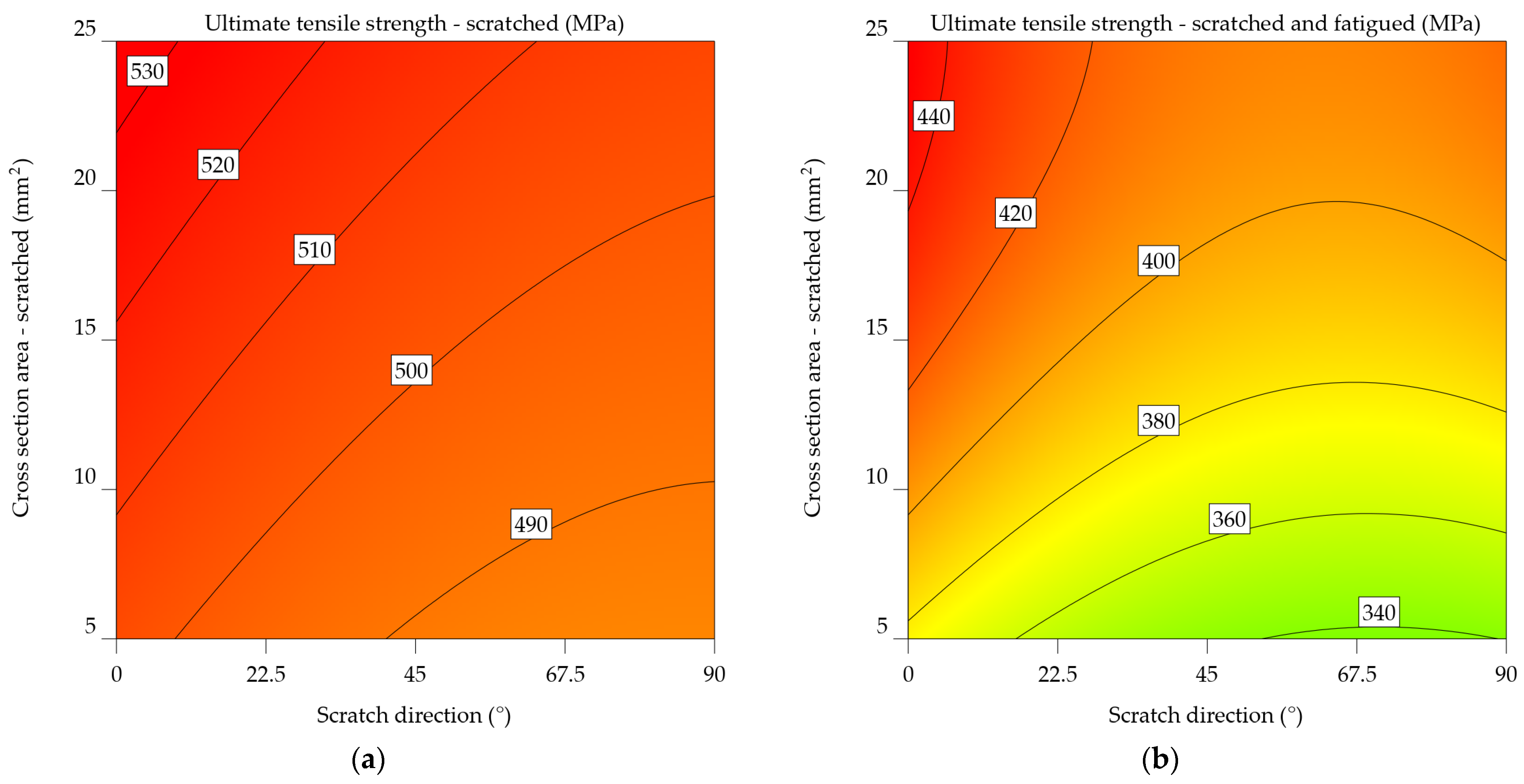
Figure 15.
Contour plots indicating the effect of SDir and CSA on the elongation at break for aluminium alloy 2024-T3, with warmer colours representing higher elongation values: (a) Data visualization for scratched samples; (b) Data visualization for scratched-fatigued samples.
Figure 15.
Contour plots indicating the effect of SDir and CSA on the elongation at break for aluminium alloy 2024-T3, with warmer colours representing higher elongation values: (a) Data visualization for scratched samples; (b) Data visualization for scratched-fatigued samples.
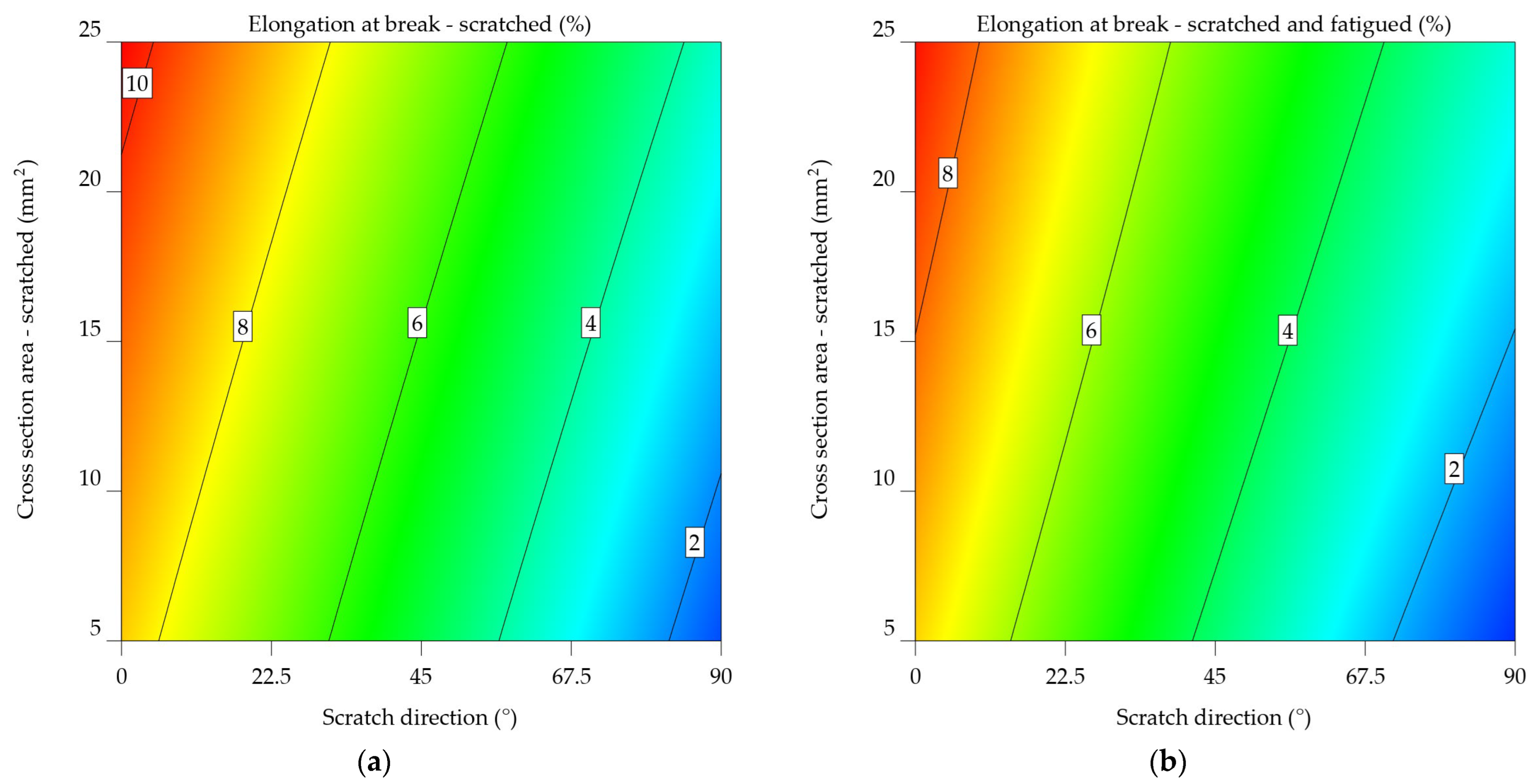
Figure 16.
Contour plots indicating the effect of SDir and CSA on the elongation at break for aluminium alloy 6061-T4, with warmer colours representing higher elongation values: (a) Data visualization for scratched samples; (b) Data visualization for scratched-fatigued samples.
Figure 16.
Contour plots indicating the effect of SDir and CSA on the elongation at break for aluminium alloy 6061-T4, with warmer colours representing higher elongation values: (a) Data visualization for scratched samples; (b) Data visualization for scratched-fatigued samples.
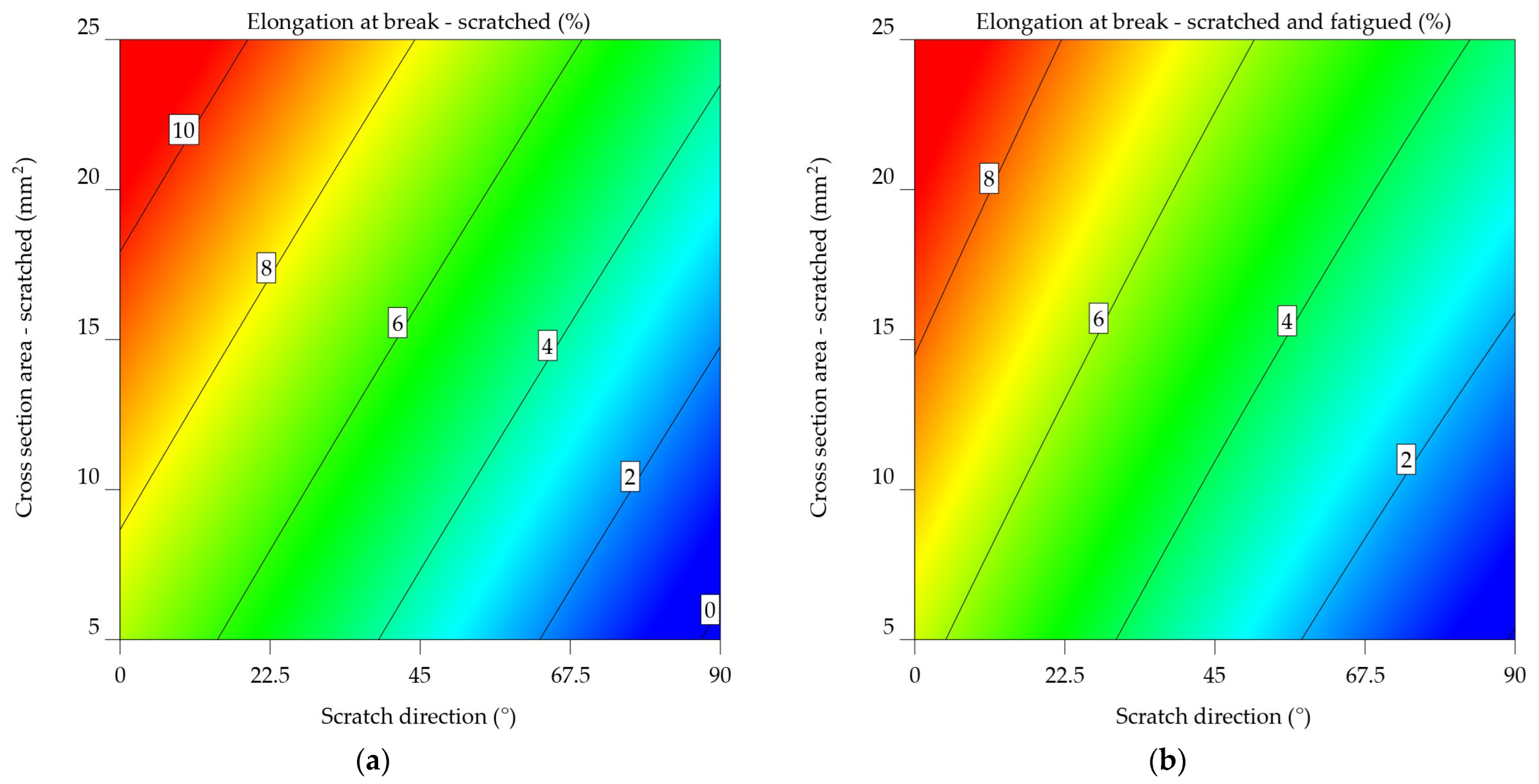
Figure 17.
Contour plots indicating the effect of SDir and CSA on the elongation at break for aluminium alloy 6061-T4 uncoated, with warmer colours representing higher elongation values: (a) Data visualization for scratched samples; (b) Data visualization for scratched-fatigued samples.
Figure 17.
Contour plots indicating the effect of SDir and CSA on the elongation at break for aluminium alloy 6061-T4 uncoated, with warmer colours representing higher elongation values: (a) Data visualization for scratched samples; (b) Data visualization for scratched-fatigued samples.
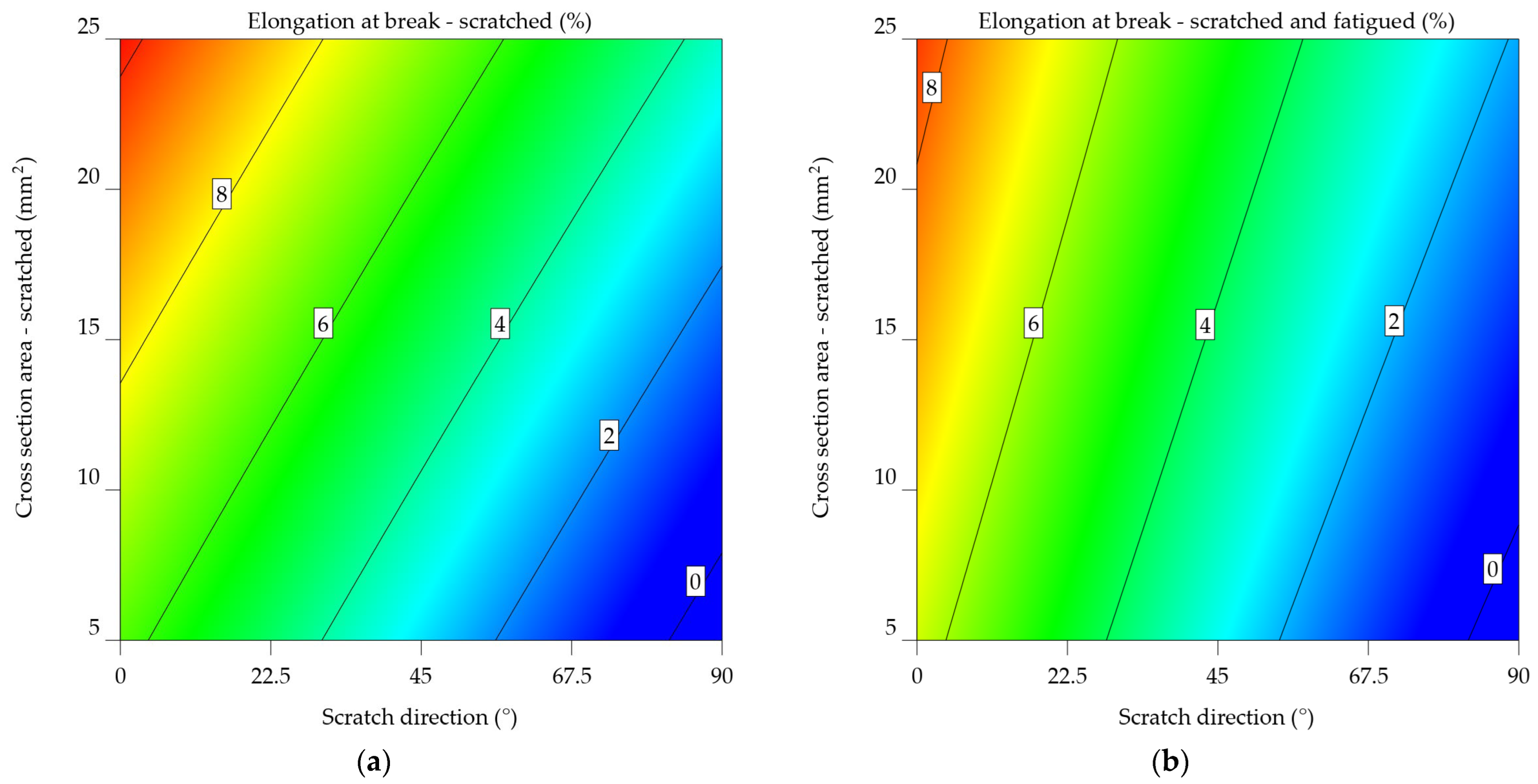
Figure 18.
Contour plots indicating the effect of SDir and CSA on the elongation at break for aluminium alloy 6061-T6 uncoated, with warmer colours representing higher elongation values: (a) Data visualization for scratched samples; (b) Data visualization for scratched-fatigued samples.
Figure 18.
Contour plots indicating the effect of SDir and CSA on the elongation at break for aluminium alloy 6061-T6 uncoated, with warmer colours representing higher elongation values: (a) Data visualization for scratched samples; (b) Data visualization for scratched-fatigued samples.
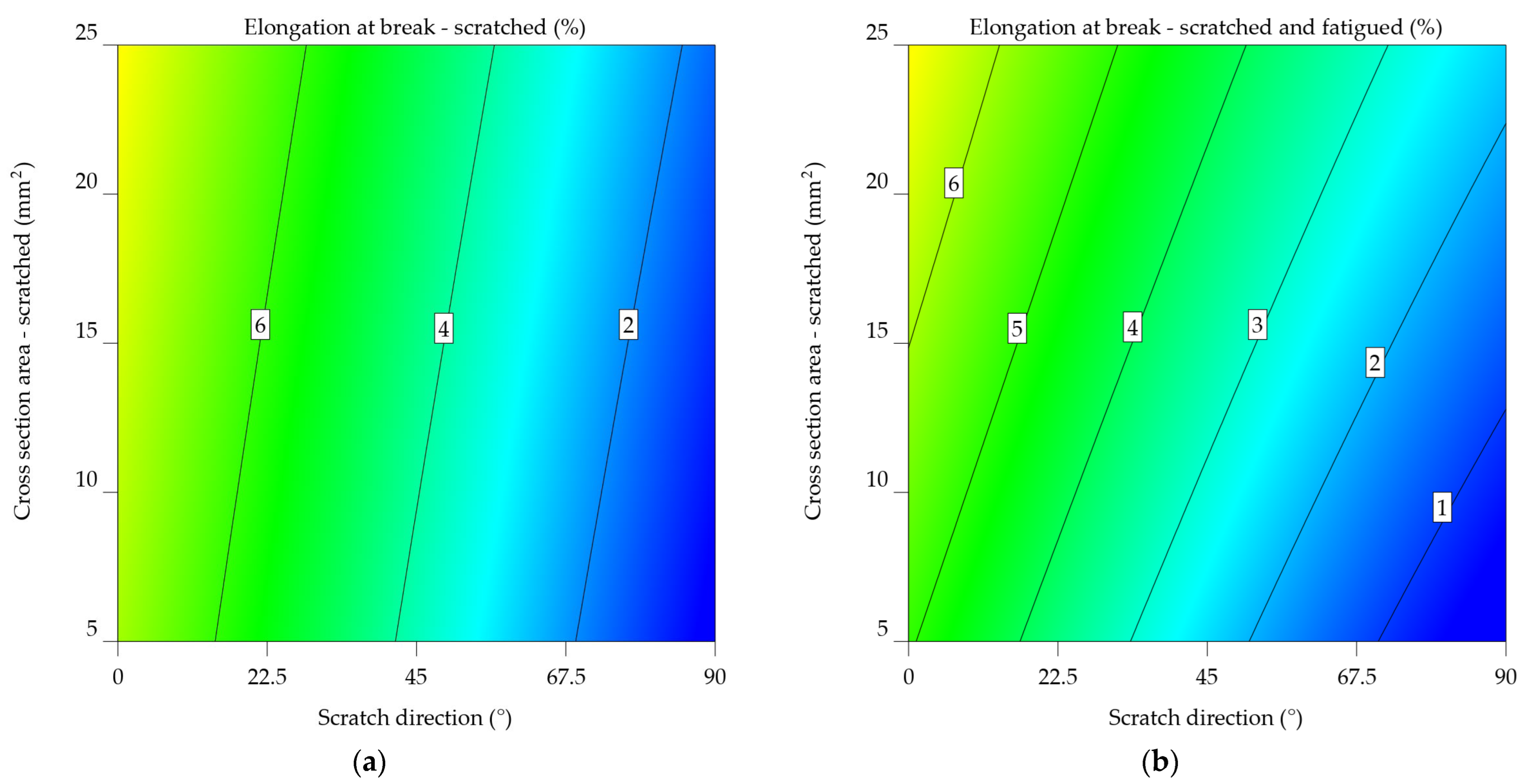
Figure 19.
Contour plots indicating the effect of SDir and CSA on the elongation at break for aluminium alloy 7075-T0 uncoated, with warmer colours representing higher elongation values: (a) Data visualization for scratched samples; (b) Data visualization for scratched-fatigued samples.
Figure 19.
Contour plots indicating the effect of SDir and CSA on the elongation at break for aluminium alloy 7075-T0 uncoated, with warmer colours representing higher elongation values: (a) Data visualization for scratched samples; (b) Data visualization for scratched-fatigued samples.
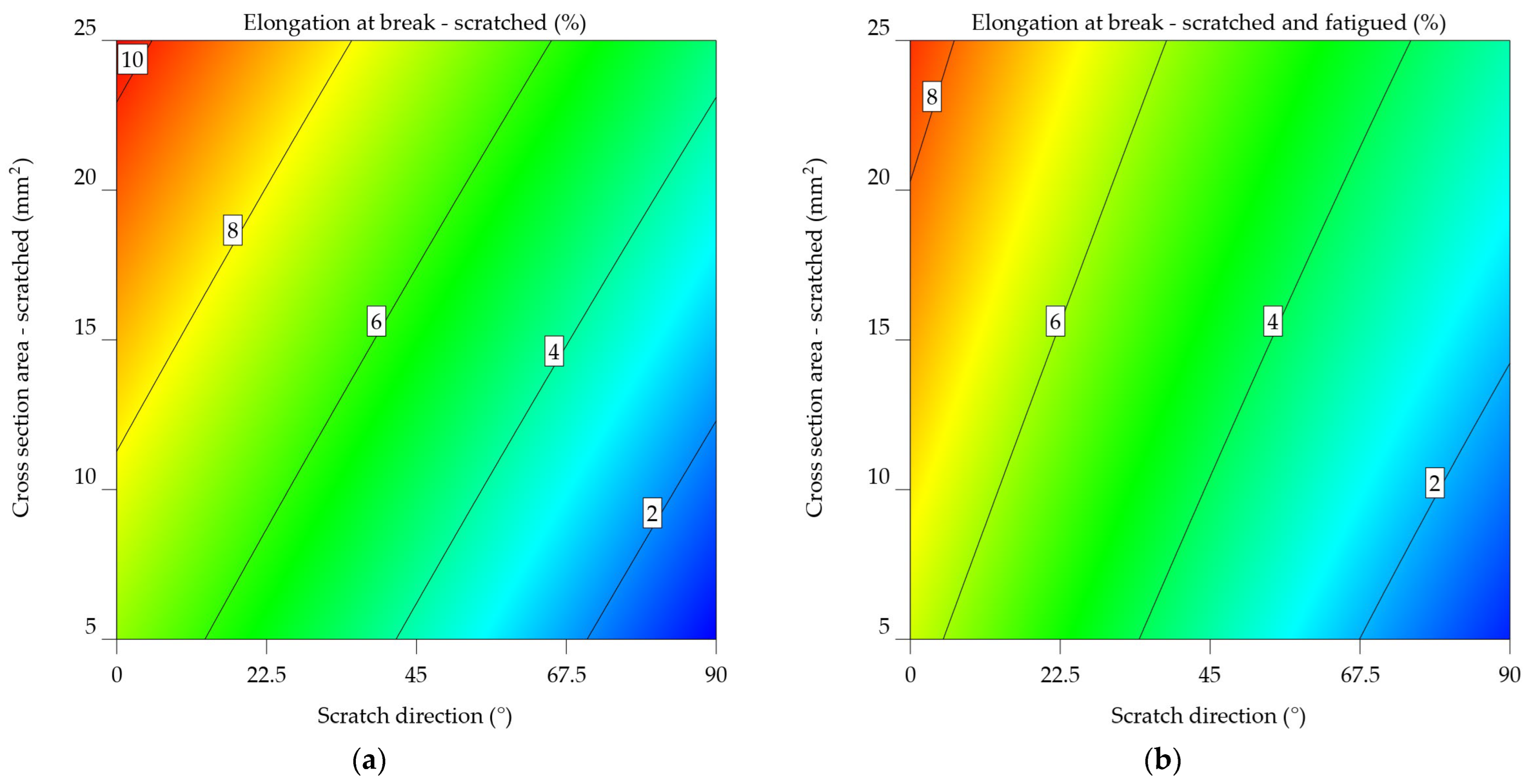
Figure 20.
Contour plots indicating the effect of SDir and CSA on the elongation at break for aluminium alloy 7075-T6, with warmer colours representing higher elongation values: (a) Data visualization for scratched samples; (b) Data visualization for scratched-fatigued samples.
Figure 20.
Contour plots indicating the effect of SDir and CSA on the elongation at break for aluminium alloy 7075-T6, with warmer colours representing higher elongation values: (a) Data visualization for scratched samples; (b) Data visualization for scratched-fatigued samples.
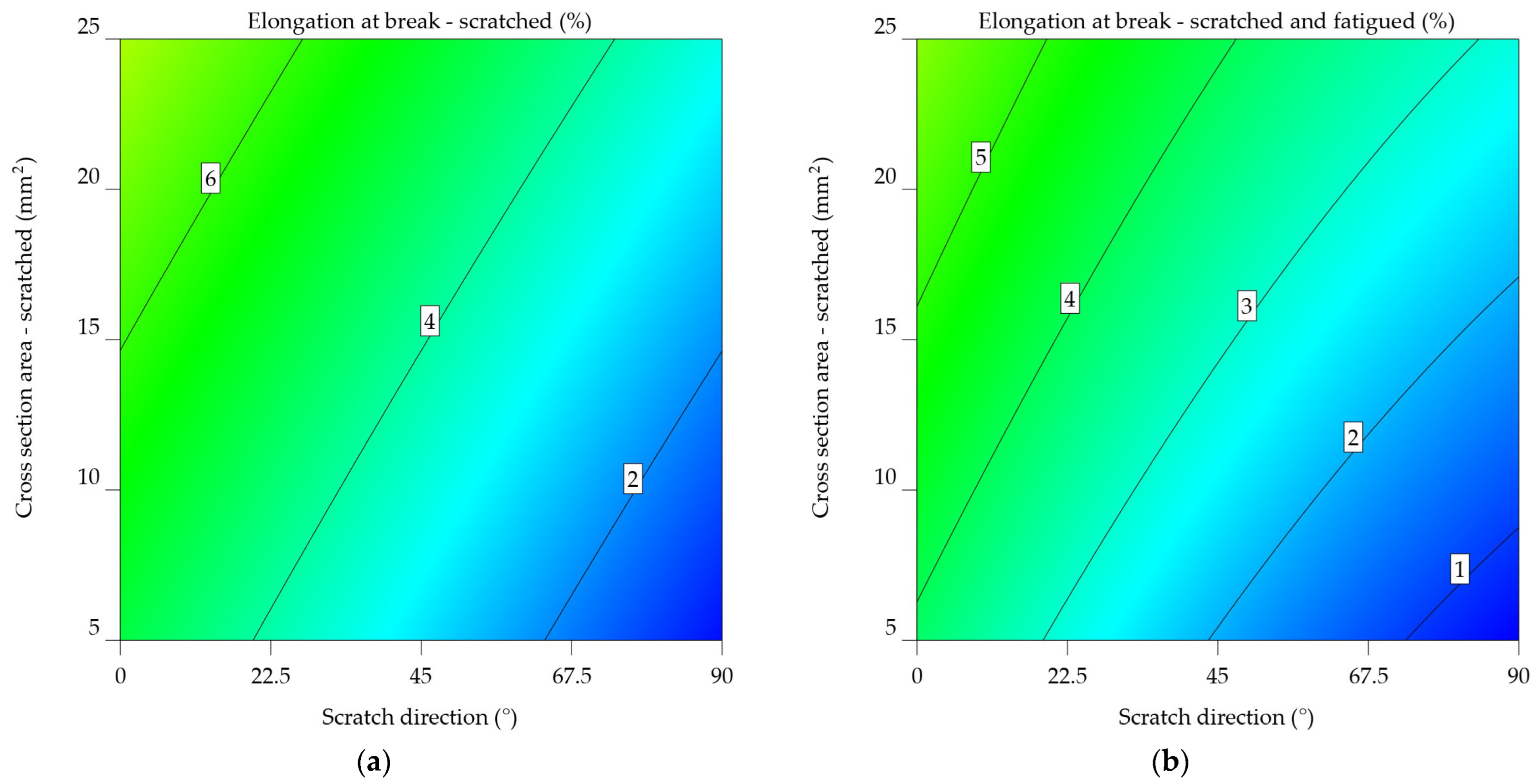
Table 1.
Aluminium alloys tensile test mechanical properties.
| Aluminium alloy | Youngs modulus (GPa) |
Yield strength (Rm 0.2%) (MPa) |
Ultimate tensile strength (MPa) | Elongation at break (%) |
|---|---|---|---|---|
| 2024-T3 | 73.1 | 291 | 450 | 16 |
| 6061-T4 | 68.9 | 165 | 255 | 25 |
| 6061-T4 uncoated | 68.9 | 138 | 247 | 22 |
| 6061-T6 uncoated | 68.9 | 281 | 310 | 12.8 |
| 7075-T0 | 71.7 | 131 | 260 | 15 |
| 7075-T6 | 70 | 487 | 530 | 14 |
Table 2.
Experimental plan data, factor type, factor description, and levels used in the study.
| Data type | Factor type | Factor description | Levels |
|---|---|---|---|
| Input | Numeric, discrete factor |
Specimen thickness T (mm) | 1, 1.2, 1.27, 1.6, 1.8, 2 |
| Scratch direction (°) | 0, 45, 90 | ||
| Cross section area CSA (mm2) | complete description in Table 3 | ||
| Categoric, nominal factor |
Specimen material | 2024-T3, 6061-T4, 6061-T4 uncoated, 6061-T6 uncoated, 7075-T0, 7075-T6 |
|
| Output | Response, analysed as polynomial |
UTSs (MPa), UTSsf (MPa) | - |
| εs (%), εsf (%) | - |
Table 3.
Scratch orientations, dimensions, and minimum cross-section area for each alloy.
| Aluminium alloy |
Scratch direction ° |
Specimen thickness mm |
Scratch length in mm as 100, 50 and 25 % of maximum available length |
Scratch depth in mm as 50, 25, 12.5 % of specimen thickness |
Minimum cross-section area mm2 |
||
|---|---|---|---|---|---|---|---|
| 2024-T3 | 0 | 1.0 | 25% | 18.75 | 12.5% | 0.125 | 12.491 |
| 50% | 37.5 | 50% | 0.5 | 12.356 | |||
| 1.6 | 50% | 37.5 | 12.5% | 0.2 | 19.977 | ||
| 100% | 75 | 12.5% | 0.2 | 19.977 | |||
| 1.8 | 100% | 75 | 50% | 0.9 | 22.032 | ||
| 2.0 | 100% | 75 | 12.5% | 0.25 | 24.964 | ||
| 45 | 1.0 | 100% | 17.678 | 12.5% | 0.125 | 12.487 | |
| 1.2 | 100% | 17.678 | 25% | 0.3 | 14.927 | ||
| 2.0 | 25% | 4.419 | 50% | 1.0 | 24.184 | ||
| 100% | 17.678 | 50% | 1.0 | 24.184 | |||
| 90 | 1.2 | 12.5 | 12.5 | 12.5% | 0.15 | 13.125 | |
| 3.125 | 3.125 | 25% | 0.30 | 14.011 | |||
| 1.6 | 6.25 | 6.25 | 25% | 0.40 | 17.408 | ||
| 1.8 | 3.125 | 3.125 | 12.5% | 0.225 | 21.768 | ||
| 12.5 | 12.5 | 25% | 0.45 | 16.875 | |||
| 6061-T4 | 0 | 1.27 | 25% | 18.75 | 12.5% | 0.159 | 15.860 |
| 100% | 75 | 12.5% | 0.159 | 15.860 | |||
| 100% | 75 | 50% | 0.635 | 15.642 | |||
| 1.6 | 25% | 18.75 | 50% | 0.8 | 19.630 | ||
| 45 | 1.27 | 12.5% | 4.419 | 50% | 0.635 | 15.546 | |
| 1.6 | 12.5% | 4.419 | 12.5% | 0.2 | 19.967 | ||
| 50% | 8.839 | 25% | 0.4 | 19.869 | |||
| 100% | 17.678 | 50% | 0.8 | 19.477 | |||
| 90 | 1.27 | 100% | 12.5 | 50% | 0.635 | 7.938 | |
| 1.6 | 25% | 3.125 | 25% | 0.4 | 18.658 | ||
| 6061-T4 uncoated |
0 | 2 | 25% | 18.75 | 12.5% | 0.25 | 24.964 |
| 45 | 2 | 100% | 17.678 | 50% | 1.0 | 24.184 | |
| 90 | 2 | 50% | 6.25 | 12.5% | 0.25 | 23.401 | |
| 2 | 50% | 6.25 | 25% | 0.5 | 21.731 | ||
| 2 | 100% | 12.5 | 50% | 1.0 | 12.5 | ||
| 6061-T6 uncoated |
0 | 1.6 | 50% | 37.5 | 12.5% | 0.2 | 19.977 |
| 1.6 | 50% | 37.5 | 50% | 0.8 | 19.630 | ||
| 1.6 | 100% | 75 | 12.5% | 0.2 | 19.977 | ||
| 45 | 1.6 | 100% | 17.678 | 50% | 0.8 | 19.477 | |
| 90 | 1.6 | 100% | 12.5 | 50% | 0.8 | 10 | |
| 7075-T0 | 0 | 1.6 | 25% | 18.75 | 12.5% | 0.2 | 19.977 |
| 1.6 | 50% | 37.5 | 25% | 0.4 | 19.908 | ||
| 45 | 1 | 100% | 17.678 | 25% | 0.25 | 12.449 | |
| 1.6 | 100% | 17.678 | 12.5% | 0.2 | 19.967 | ||
| 12.5% | 4.419 | 25% | 0.4 | 19.869 | |||
| 90 | 1 1 1 1 |
50% | 6.25 | 12.5% | 0.125 | 11.710 | |
| 100% | 12.5 | 25% | 0.25 | 9.375 | |||
| 25% | 3.125 | 50% | 0.5 | 10.793 | |||
| 100% | 12.5 | 50% | 0.5 | 6.250 | |||
| 1.6 | 25% | 3.125 | 50% | 0.8 | 17.131 | ||
| 7075-T6 | 0 | 1.27 | 100% | 75 | 50% | 0.635 | 15.642 |
| 1.8 | 25% | 18.75 | 25% | 0.45 | 22.383 | ||
| 2 | 25% | 18.75 | 12.5% | 0.25 | 24.946 | ||
| 45 | 1 | 50% | 8.839 | 12.5% | 0.125 | 12.487 | |
| 100% | 17.678 | 12.5% | 0.125 | 12.487 | |||
| 1.27 | 25% | 4.419 | 12.5% | 0.159 | 15.854 | ||
| 1.6 | 25% | 4.419 | 12.5% | 0.2 | 19.967 | ||
| 1.8 | 25% | 4.419 | 25% | 0.45 | 22.335 | ||
| 100% | 17.678 | 25% | 0.45 | 22.335 | |||
| 2 | 25% | 4.419 | 50% | 1 | 24.184 | ||
| 90 | 1 | 100% | 12.5 | 12.5% | 0.125 | 10.938 | |
| 1.27 | 100% | 12.5 | 12.5% | 4.419 | 13.888 | ||
| 1.6 | 25% | 3.125 | 50% | 0.8 | 17.131 | ||
| 100% | 12.5 | 50% | 0.8 | 10 | |||
| 2 | 100% | 12.5 | 12.5% | 0.25 | 21.875 | ||
Table 4.
Measured ultimate tensile strength (UTSs - scratched and UTSfs - scratched-fatigued) and elongation at break (εs - scratched and εfs - scratched-fatigued), along with the corresponding CSA and scratch direction for each aluminium alloy.
Table 4.
Measured ultimate tensile strength (UTSs - scratched and UTSfs - scratched-fatigued) and elongation at break (εs - scratched and εfs - scratched-fatigued), along with the corresponding CSA and scratch direction for each aluminium alloy.
| Aluminium alloy |
Scratch direction (°) |
Minimum cross section area (mm2) |
UTSs (MPa) |
εs (%) |
UTSsf (MPa) |
εsf (%) |
|---|---|---|---|---|---|---|
| 2024-T3 | 0 | 12.491 | 435.504 | 9.144 | 358.888 | 7.812 |
| 12.356 | 426.162 | 8.917 | 355.023 | 7.736 | ||
| 24.964 | 459.733 | 10.31 | 400.994 | 8.836 | ||
| 19.977 | 443.721 | 9.545 | 374.977 | 8.131 | ||
| 19.977 | 448.029 | 9.682 | 379.463 | 8.136 | ||
| 22.032 | 454.946 | 9.951 | 392.407 | 8.561 | ||
| 45 | 12.487 | 418.661 | 6.21 | 318.422 | 4.651 | |
| 14.927 | 424.708 | 6.794 | 316.755 | 4.979 | ||
| 24.184 | 426.517 | 7.013 | 325.623 | 5.40 | ||
| 24.184 | 427.517 | 7.263 | 346.363 | 5.738 | ||
| 90 | 14.011 | 411.949 | 2.14 | 322.515 | 1.883 | |
| 13.125 | 406.891 | 1.805 | 299.926 | 1.488 | ||
| 21.768 | 422.479 | 3.105 | 321.084 | 2.453 | ||
| 16.875 | 412.132 | 2.505 | 323.827 | 2.129 | ||
| 17.408 | 419.453 | 2.818 | 332.341 | 2.339 | ||
| 6061-T4 | 0 | 19.63 | 269.121 | 10.38 | 212.606 | 8.615 |
| 15.642 | 244.435 | 9.939 | 202.881 | 8.647 | ||
| 15.86 | 248.724 | 9.945 | 206.441 | 8.652 | ||
| 15.86 | 256.158 | 9.934 | 217.734 | 8.444 | ||
| 45 | 19.967 | 232.874 | 6.977 | 188.628 | 5.791 | |
| 19.869 | 227.831 | 6.604 | 184.543 | 5.481 | ||
| 19.477 | 224.98 | 6.342 | 184.484 | 5.137 | ||
| 15.546 | 203.262 | 3.796 | 166.675 | 3.227 | ||
| 90 | 18.658 | 217.627 | 3.87 | 178.454 | 3.251 | |
| 7.938 | 195.613 | 0.673 | 176.052 | 0.639 | ||
| 6061-T4 uncoated |
0 | 24.964 | 239.175 | 9.93 | 181.773 | 7.745 |
| 45 | 24.184 | 232.131 | 7.364 | 171.777 | 6.065 | |
| 90 | 23.401 | 228.432 | 3.162 | 181.324 | 1.498 | |
| 21.731 | 223.217 | 2.636 | 171.877 | 1.082 | ||
| 12.5 | 220.27 | 1.003 | 156.04 | 0.532 | ||
| 6061-T6 uncoated |
0 | 19.977 | 305.882 | 7.846 | 250.823 | 6.434 |
| 19.63 | 298.124 | 7.494 | 244.462 | 6.22 | ||
| 19.977 | 314.216 | 7.976 | 248.231 | 6.62 | ||
| 45 | 19.477 | 293.669 | 4.515 | 237.872 | 3.793 | |
| 90 | 10 | 267.44 | 0.763 | 240.696 | 0.694 | |
| 7075-T0 | 0 | 19.977 | 257.11 | 9.806 | 210.83 | 8.041 |
| 19.908 | 253.071 | 9.366 | 202.457 | 7.68 | ||
| 45 | 19.869 | 234.464 | 6.189 | 192.882 | 5.137 | |
| 19.967 | 244.867 | 6.658 | 193.445 | 5.46 | ||
| 12.449 | 221.266 | 4.761 | 180.289 | 4.237 | ||
| 90 | 17.131 | 221.074 | 2.789 | 199.913 | 1.997 | |
| 10.793 | 215.792 | 1.944 | 196.371 | 1.769 | ||
| 11.71 | 219.067 | 1.868 | 194.97 | 1.663 | ||
| 6.25 | 208.568 | 0.887 | 186.14 | 0.86 | ||
| 9.375 | 211.999 | 1.562 | 192.919 | 1.437 | ||
| 7075-T6 | 0 | 22.383 | 526.022 | 7.533 | 401.777 | 5.697 |
| 24.964 | 528.117 | 7.055 | 399.369 | 5.889 | ||
| 15.642 | 519.017 | 5.833 | 446.355 | 4.958 | ||
| 45 | 15.854 | 508.771 | 4.212 | 422.28 | 3.58 | |
| 19.967 | 510.76 | 4.376 | 422.393 | 3.588 | ||
| 22.335 | 513.81 | 4.654 | 434.496 | 3.677 | ||
| 22.335 | 514.908 | 4.703 | 435.777 | 3.762 | ||
| 12.487 | 502.155 | 3.788 | 381.853 | 2.447 | ||
| 24.184 | 516.234 | 5.133 | 445.338 | 3.952 | ||
| 12.487 | 503.662 | 3.846 | 378.259 | 2.623 | ||
| 90 | 10 | 481.875 | 1.111 | 362.869 | 1.011 | |
| 17.131 | 478.49 | 2.999 | 387.577 | 2.489 | ||
| 10.938 | 485.877 | 1.307 | 350.572 | 1.176 | ||
| 21.875 | 508.056 | 2.654 | 386.123 | 2.097 | ||
| 13.888 | 506.737 | 2.292 | 381.929 | 2.04 |
Table 5.
Model fit statistics and transformation parameters for each studied parameter.
| Fit Statistics | UTSs | εs | UTSsf | εsf |
|---|---|---|---|---|
| Model | Quadratic | 2FI | Quadratic | Quadratic |
| Model p-value | < 0.001 | < 0.001 | < 0.001 | < 0.001 |
| Box-Cox transformation | λ = 1, none | λ = 1, none | λ = -0.5, inverse sqrt | λ = 1, none |
Table 6.
Goodness-of-fit metrics; model fit statistics for predicting UTSs, UTSsf, εs, and εsf.
| Fit Statistics | UTSs | εs | UTSsf | εsf |
|---|---|---|---|---|
| R2 | 0.9277 | 0.9115 | 0.8990 | 0.8804 |
| Adjusted R2 | 0.9266 | 0.8934 | 0.8734 | 0.8703 |
| Predicted R2 | 0.8743 | 0.8108 | 0.8966 | 0.8904 |
| Adequate Precision | 82.8293 | 85.3889 | 142.2185 | 91.4676 |
Table 7.
Outline the experimental data, including the average values compared to the initial values and the percentage decrease for each alloy.
Table 7.
Outline the experimental data, including the average values compared to the initial values and the percentage decrease for each alloy.
| Aluminium alloy | UTSinitial (MPa) |
UTSs_avg | UTSsf_avg | εinitial (%) |
εs_svg | εsf_avg | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| MPa | % diff. | MPa | % diff. | % | % diff. | % | % diff. | |||
| 2024-T3 | 450 | 427.87 | 5.17 | 341.23 | 31.87 | 16 | 6.295 | 154.15 | 5.15 | 210.63 |
| 6061-T4 | 255 | 227.82 | 11.92 | 189.41 | 34.62 | 25 | 6.084 | 310.94 | 5.14 | 385.64 |
| 6061-T4 uncoated |
247 | 231.76 | 6.57 | 174.43 | 41.60 | 22 | 6.52 | 237.40 | 4.95 | 344.52 |
| 6061-T6 uncoated |
310 | 289.06 | 7.24 | 242.13 | 28.02 | 12.8 | 4.35 | 194.25 | 3.63 | 251.91 |
| 7075-T0 | 260 | 234.64 | 10.80 | 196.52 | 32.29 | 15 | 5.755 | 160.68 | 4.78 | 213.58 |
| 7075-T6 | 530 | 508.87 | 4.151 | 402.28 | 31.74 | 14 | 4.422 | 216.57 | 3.55 | 294.26 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated








